【南方新课堂】2019年高考数学理科总复习作业及测试 阶段检测卷六 含解析

专题六 立体几何 第1课时1．(2015年新课标Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如图Z6­1，则截去部分体积与剩余部分体积的比值为( )图Z6­1A.18B.17C.16D.152．如图Z6­2，方格纸上正方形小格的边长为1，图中粗实线画出的是由一个正方体截得的一个几何体的三视图，则该几何体的体积为( )图Z6­2A.163 B.323 C.643D ．32 3．某几何体的三视图如图Z6­3，则该几何体的体积为( )图Z6­3A.23B.43C.83D.163 4．(2016年河北“五校联盟”质量监测)某四面体的三视图如图Z6­4，则其四个面中最大的面积是( )图Z6­4A ．2B ．2 2 C. 3 D ．2 35．已知一个几何体的三视图如图Z6­5，则该几何体的体积为( )图Z6­5A ．8 B.223 C.233D ．76．点A ，B ，C ，D 均在同一球面上，且AB ，AC ，AD 两两垂直，且AB ＝1，AC ＝2，AD ＝3，则该球的表面积为( )A ．7π B．14π C.72π D.714π37．(2013年新课标Ⅰ)如图Z6­6，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器厚度，则球的体积为( )图Z6­6A.500π3 cm 3 B.866π3 cm 3C.1372π3 cm 3D.2048π3cm 38．(2016年北京)某四棱柱的三视图如图Z6­7，则该四棱柱的体积为________．图Z6­79．球O 半径为R ＝13，球面上有三点A ，B ，C ，AB ＝12 3，AC ＝BC ＝12，则四面体OABC 的体积是( )A ．60 3B ．50 3C ．60 6D ．50 610．如图Z 6­8，已知正三角形ABC 三个顶点都在半径为2的球面上，球心O 到平面ABC 的距离为1，点E 是线段AB 的中点，过点E 作球O 的截面，则截面面积的最小值是( )图Z6­8A.7π4 B ．2π C.9π4D ．3π 11．(2017年广东茂名一模)过球O 表面上一点A 引三条长度相等的弦AB ，AC ，AD ，且两两夹角都为60°，若球半径为R ，则△BCD 的面积为____________．12．已知三棱柱ABC ­A 1B 1C 1的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为3，AB ＝2，AC ＝1，∠BAC ＝60°，则此球的表面积等于________．第2课时1．在直三棱柱ABC ­A 1B 1C 1中，若∠BAC ＝90°，AB ＝AC ＝AA 1，则异面直线BA 1与AC 1所成的角等于( )A ．30° B．45° C．60° D．90° 2．(2016年天津模拟)如图Z6­9，以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕，把△ABD 和△ACD 折成互相垂直的两个平面后，某学生得出下列四个结论：图Z6­9①BD ⊥AC ；②△BAC 是等边三角形；③三棱锥D ­ABC 是正三棱锥； ④平面ADC ⊥平面ABC . 其中正确的是( )A ．①②④B ．①②③C ．②③④D ．①③④3．三棱锥的三组相对的棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等，且长各为2，m ，n ，其中m 2＋n 2＝6，则三棱锥体积的最大值为( )A.33B.12C.8 327D.234．(2016年辽宁葫芦岛统测)已知四棱锥P ­ABCD 的五个顶点都在球O 的球面上，底面ABCD 是矩形，平面PAD 垂直于平面ABCD ，在△PAD 中，PA ＝PD ＝2，∠APD ＝120°，AB ＝2，则球O 的外接球的表面积等于( )A ．16π B．20π C．24π D．36π5．在矩形ABCD 中，AD ＝2，AB ＝4，E ，F 分别为边AB ，AD 的中点，将△ADE 沿DE 折起，点A ，F 折起后分别为点A ′，F ′，得到四棱锥A ′­BCDE .给出下列几个结论：①A ′，B ，C ，F ′四点共面； ②EF ′∥平面A ′BC ；③若平面A ′DE ⊥平面BCDE ，则CE ⊥A ′D ； ④四棱锥A ′­BCDE 体积的最大值为2，其中正确的是________(填上所有正确的序号)．6．(2017年广东梅州一模)如图Z6­10所示的多面体是由一个直平行六面体被平面AEFG 所截后得到的，其中∠BAE ＝∠GAD ＝45°，AB ＝2AD ＝2，∠BAD ＝60°.(1)求证：BD ⊥平面ADG ；(2)求平面AEFG 与平面ABCD 所成锐二面角的余弦值．图Z6­107．(2017年广东广州二模)如图Z6­11，ABCD是边长为a的菱形，∠BAD＝60°，EB ⊥平面ABCD，FD⊥平面ABCD，EB＝2FD＝3a.(1)求证：EF⊥AC；(2)求直线CE与平面ABF所成角的正弦值．图Z6­118．(2017年广东揭阳一模)如图Z6­12，在直三棱柱ABC­A1B1C1中，AB＝BC＝BB1，AB1∩A1B ＝E，D为AC上的点，B1C∥平面A1BD；(1)求证：BD⊥平面A1ACC1；(2)若AB＝1，且AC·AD＝1，求二面角B­A1D­B1的余弦值．图Z6­12专题六 立体几何 第1课时1．D 解析：由三视图，得在正方体ABCD ­A 1B 1C 1D 1中，截去四面体A ­A 1B 1D 1，如图D164，图D164设正方体棱长为a ，则111-A A B D V ＝13×12a 3＝16a 3.则剩余几何体体积为a 3－16a 3＝56a 3.所以截去部分体积与剩余部分体积的比值为15.故选D.2．B 解析：几何体为如图D165所示的正方体中的三棱锥E ­BB 1C (E 为AA 1的中点)，它的体积为13×12×4×4×4＝323.故选B.图D165 图D1663．B 解析：由三视图知对应的几何体为如图D166所示的正方体中的三棱锥P ­ABC ，其中PC ⊥平面PAB ，PA ＝AB ，PC ＝PB ＝2，A 到PB 的距离为2，故该几何体的体积为13×12×2×2×2＝43.故选B.4．D 解析：如图D167，在正方体ABCD ­A 1B 1C 1D 1中还原出三视图的直观图，其是一个三个顶点在正方体的右侧面、一个顶点在左侧面的三棱锥，即D 1­BCB 1，其四个面的面积分别为2,2 2，2 2，2 3.故选D.图D1675．D 解析：由三视图可知该几何体是一个由棱长为2的正方体截去两个三棱锥A ­A 1PQ 和D ­PC 1D 1后剩余的部分，如图D168，其中Q 是棱A 1B 1的中点，P 是A 1D 1的中点，所以该几何体的体积为V ＝8－13×12×1×1×2－13×12×1×2×2＝7.故选D.图D1686．B 解析：三棱锥A ­BCD 的三条侧棱两两互相垂直，所以把它扩展为长方体，它也外接于球，长方体的对角线长为其外接球的直径，所以长方体的对角线长是12＋22＋32＝14，它的外接球半径是142，外接球的表面积是4π×⎝ ⎛⎭⎪⎫1422＝14π.故选B.7．A 解析：如图D169，作出球的一个截面，则MC ＝8－6＝2(cm)，BM ＝12AB ＝12×8＝4(cm)．设球的半径为R cm ，则R 2＝OM 2＋MB 2＝(R －2)2＋42，∴R ＝5.∴V 球＝43π×53＝500π3(cm 3)．图D1698.32解析：由已知的三视图，得该几何体上部是一个以俯视图为底面的四棱柱，其高为1，故该四棱柱的体积V ＝Sh ＝12×(1＋2)×1×1＝32.9．A 解析：设△ABC 外接圆半径为r ，由AB ＝12 3，AB ＝BC ＝12，得A ＝B ＝30°，C ＝120°.所以2r ＝12 3sin 120°＝24.解得r ＝12.则O 到平面ABC 的距离d ＝R 2－r 2＝132－122＝5.又S △ABC ＝12×12×12×sin 120°＝36 3，所以V O ­ABC ＝13×36 3×5＝603.故选A.10．C 解析：根据球的截面圆性质、正三角形的性质与勾股定理，知经过点E 的球O 的截面与OE 垂直时截面圆的半径最小，相应的截面圆的面积有最小值，由此算出截面圆半径的最小值，从而可得截面面积的最小值．设正三角形ABC 的中心为O 1，连接O 1A ，连接O 1O ，O 1C ，OC ，∵O 1是正三角形ABC 的中心，A ，B ，C 三点都在球面上，∴O 1O ⊥平面ABC .结合O 1C ⊂平面ABC ，可得O 1O ⊥O 1C .∵球的半径R ＝2，球心O 到平面ABC 的距离为1，∴O 1O ＝1.∴Rt △O 1OC 中，O 1C ＝R 2－O 1O 2＝ 3.又∵E 为AB 的中点，△ABC 是等边三角形．∴O 1E ＝AO 1sin 30°＝32.∴OE ＝OO 21＋O 1E 2＝72.过E 作球O 的截面，当截面与OE 垂直时，截面圆的半径最小，此时截面圆的半径r ＝R 2－OE 2＝32.可得截面面积为S ＝πr 2＝94π.故选C.11.2 33R 2 解析：方法一，由条件知A ­BCD 是正四面体，△BCD 是正三角形，A ，B ，C ，D 为球上四点，将正三棱锥A ­BCD 补充成一个正方体AGBH ­FDEC ，如图D170.则正三棱锥A ­BCD 和正方体AGBH ­FDEC 有共同的外接球，△BCD 的边长就是正方体面的对角线，设正方体AGBH ­FDEC 的棱长为a ，则正方体外接球半径R 满足：a 2＋a 2＋a 2＝(2R )2，解得a2＝43R 2.所以BC 2＝a 2＋a 2＝83R 2.所以△BCD 的面积S ＝12BC ×BD sin 60°＝12×83R 2×32＝2 33R 2.图D170 图D171方法二，由条件A ­BCD 是正四面体，△BCD 是正三角形，A ，B ，C ，D 为球上四点，球心O 在正四面体中心，如图D171.设BC ＝a ，CD 的中点为E ，O 1为过点B ，C ，D 截面圆的圆心，则截面圆半径r ＝O 1B ＝23BE ＝23×32a ＝33a .正四面体A ­BCD 的高AO 1＝a 2－⎝⎛⎭⎪⎫33a 2＝63a . ∴截面BCD 与球心的距离d ＝OO 1＝63a －R . 在Rt△BOO 1中，⎝⎛⎭⎪⎫33a 2＝R 2－⎝ ⎛⎭⎪⎫63a －R 2，解得a ＝2 63R . ∴△BCD 的面积为S ＝12BC ×BC sin 60°＝12×⎝ ⎛⎭⎪⎫2 63R 2×32＝2 33R 2. 12．8π 解析：∵三棱柱ABC ­A 1B 1C 1的侧棱垂直于底面，棱柱的体积为3，AC ＝1，AB ＝2，∠BAC ＝60°，∴12×1×2×sin 60°×AA 1＝ 3.∴AA 1＝2.∵BC 2＝AB 2＋AC 2－2AB ·AC cos 60°＝4＋1－2＝3，∴BC ＝ 3.设△ABC 外接圆的半径为R ，则BCsin 60°＝2R .∴R ＝1.故外接球的半径为12＋12＝2，外接球的表面积等于4π×(2)2＝8π.第2课时1．C 解析：延长CA 到D ，使得AD ＝AC ，则ADA 1C 1为平行四边形，∠DA 1B 就是异面直线BA 1与AC 1所成的角．又△A 1DB 为等边三角形．∴∠DA 1B ＝60°.2．B 解析：由题意知，BD ⊥平面ADC ，故BD ⊥AC ，①正确；AD 为等腰直角三角形斜边BC 上的高，平面ABD ⊥平面ACD ，所以AB ＝AC ＝BC ，△BAC 是等边三角形，②正确；易知DA ＝DB ＝DC ，又由②知③正确；由①知④错．3．D 解析：直接求三棱锥的体积很困难，因为不知三棱锥的形状，也没有数据，将该三棱锥放进长方体模型，如图D172，三棱锥A ­CB 1D 1符合题意，设AA 1＝x ，A 1D 1＝y ，A 1B 1＝z ，有⎩⎪⎨⎪⎧x 2＋y 2＝2，x 2＋z 2＝m 2，y 2＋z 2＝n 2，x 2＋y 2＋2z 2＝m 2＋n 2＝6,2z 2＝4，z ＝2，x 2＋y 2＝2≥2xy ，∴xy ≤1.三棱锥体积V ＝13V 长方体＝13xyz ＝23xy ≤23.所以三棱锥体积的最大值为23.故选D.图D1724．B 解析：取AD 的中点为E ，连接PE ，则由平面PAD 垂直于平面ABCD 可得，PE ⊥平面ABCD ，于是以点E 为原点，以ED ，EP 分别为x ，z 轴建立空间直角坐标系，其中AC 与BD 相交于F 点．于是可得E (0,0,0)，D (3，0,0)，A (－3，0,0)，P (0,0,1)，C (3，2,0)，B (－3，2,0)，F (0,1,0)，设球O 的球心的坐标为O (0，1，z 0)，则OP →＝(0，－1,1－z 0)，OB →＝(－3，1，－z 0)，由|OP →|＝|OB →|，得－2＋－z 02＝3＋1＋z 20.解之，得z 0＝－1.所以球心O (0,1，－1)．于是其半径为|OP →|＝5，由球的表面积公式知，S ＝4πr 2＝4π×(5)2＝20π.故选B.5．②③6．(1)证明：在△BAD 中，∵AB ＝2AD ＝2，∠BAD ＝60°， ∴由余弦定理，可得BD ＝ 3.∵AB 2＝AD 2＋BD 2，∴AD ⊥BD .又在直平行六面体中，GD ⊥平面ABCD ，BD ⊂平面ABCD ，∴GD ⊥BD . 又AD ∩GD ＝D ，∴BD ⊥平面ADG .(2)解：以D 为坐标原点，建立如图D173所示的空间直角坐标系D ­xyz .图D173∵∠BAE ＝∠GAD ＝45°，AB ＝2AD ＝2，∴A (1,0,0)，B (0，3，0)，G (0,0,1)，E (0，3，2)，C (－1，3，0)． ∴AE →＝(－1，3，2)，AG →＝(－1,0,1)． 设平面AEFG 的法向量为n ＝(x ，y ，z )， 故有⎩⎪⎨⎪⎧n ·AE →＝－x ＋3y ＋2z ＝0，n ·AG →＝－x ＋z ＝0.令x ＝1，得y ＝－33，z ＝1.n ＝(1，－33，1)． 而平面ABCD 的一个法向量为DG →＝(0,0,1)，∴cos 〈DG →，n 〉＝DG →·n |DG →|·|n |＝217.故平面AEFG 与平面ABCD 所成锐二面角的余弦值为217. 7．解：(1)证明：连接BD ，如图D174. 因为ABCD 是菱形，所以AC ⊥BD .因为FD ⊥平面ABCD ，AC ⊂平面ABCD ， 所以AC ⊥FD .因为BD ∩FD ＝D ，所以AC ⊥平面BDF . 因为EB ⊥平面ABCD ，FD ⊥平面ABCD ， 所以EB ∥FD .所以B ，D ，F ，E 四点共面．因为EF ⊂平面BDFE ，所以EF ⊥AC .图D174 图D175(2)如图D175，以D 为坐标原点，分别以DC →，DF →的方向为y 轴，z 轴的正方向，建立空间直角坐标系D ­xyz .可以求得A ⎝ ⎛⎭⎪⎫32a ，－12a ，0，B ⎝ ⎛⎭⎪⎫32a ，12a ，0，F ⎝ ⎛⎭⎪⎫0，0，32a ，C (0，a,0)，E ⎝ ⎛⎭⎪⎫32a ，12a ，3a .所以AB →＝(0，a,0)，AF →＝⎝ ⎛⎭⎪⎫－32a ，12a ，32a .设平面ABF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·AB →＝0，n ·AF →＝0，即⎩⎪⎨⎪⎧ ay ＝0，－32ax ＋12ay ＋32az ＝0.取x ＝1，则平面ABF 的一个法向量为n ＝(1,0,1)．因为CE →＝⎝ ⎛⎭⎪⎫32a ，－12a ，3a ，所以||cos 〈n ，CE →〉＝||n ·CE→||n ||CE →＝3 68. 所以直线CE 与平面ABF 所成角的正弦值为3 68.8．(1)证明：如图D176，连接ED ，∵平面AB 1C ∩平面A 1BD ＝ED ，B 1C ∥平面A 1BD ，∴B 1C ∥ED .∵E 为AB 1的中点，∴D 为AC 的中点．∵AB ＝BC ，∴BD ⊥AC .①方法一，由A 1A ⊥平面ABC ，BD ⊂平面ABC ，得A 1A ⊥BD ，②由①②及A 1A ，AC 是平面A 1ACC 1内的两条相交直线，∴BD ⊥平面A 1ACC 1.方法二，∵A 1A ⊥平面ABC ，A 1A ⊂平面A 1ACC 1，∴平面A 1ACC 1⊥平面ABC .又平面A 1ACC 1∩平面ABC ＝AC ， ∴BD ⊥平面A 1ACC 1.图D176 图D177(2)由AB ＝1，得BC ＝BB 1＝1.由(1)知DA ＝12AC ，由AC ·DA ＝1，得AC 2＝2.∵AC 2＝2＝AB 2＋BC 2，∴AB ⊥BC .以B 为原点，建立空间直角坐标系B ­xyz 如图D177， 则A 1(1,0,1)，B 1(0,0,1)，D ⎝ ⎛⎭⎪⎫12，12，0.所以B 1A 1→＝(1,0,0)，B 1D →＝⎝ ⎛⎭⎪⎫12，12，－1.设m ＝(x ，y ，z )是平面A 1B 1D 的一个法向量， 则⎩⎪⎨⎪⎧ m ⊥B 1A 1→，m ⊥B 1D →，得⎩⎨⎧m ·B 1A 1→＝x ＝0，m ·B 1D →＝12x ＋12y －z ＝0. 令z ＝1，得m ＝(0,2,1)．设n ＝(a ，b ，c )为平面A 1BD 的一个法向量， 则⎩⎪⎨⎪⎧ n ⊥BD →，n ⊥BA 1→，得⎩⎨⎧ n ·BD →＝a 2＋b 2＝0，n ·BA 1→＝a ＋c ＝0.令c ＝1，得n ＝(－1,1,1)．依题意知二面角B ­A 1D ­B 1为锐二面角，设其大小为θ，则cos θ＝|cos 〈n ，m 〉|＝|n ·m ||n |·|m |＝35×3＝155.即二面角B ­A 1D ­B 1的余弦值为155.。

2019年高考数学(理科)模拟试卷(二)(本试卷分第Ⅰ卷和第Ⅱ卷两部分．满分150分，考试时间120分钟)第Ⅰ卷(选择题 满分60分)一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2017年广东广州一模)若集合M ＝{x ||x |≤1}，N ＝{y |y ＝x 2，|x |≤1}，则( ) A ．M ＝N B ．M ⊆N C ．N ⊆M D ．M ∩N ＝∅2．“1<x <π2”是“(x －1)tan x >0”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．(2017年山东)已知a ∈R ，i 是虚数单位，若z ＝a ＋3i ，z ·z ＝4，则a ＝( ) A ．1或－1 B.7或－7 C ．－ 3 D. 34．已知平面向量a ＝(1,2)，b ＝(－2，k )，若a 与b 共线，则||3a ＋b ＝( ) A ．3 B ．4 C. 5 D ．55．函数y ＝12x 2－ln x 的单调递减区间为( )A ．(－1,1]B ．(0,1]C ．[1，＋∞) D．(0，＋∞)6．(2017年河南洛阳三模)利用如图M2­1所示的算法在平面直角坐标系上打印一系列点，则打印的点在圆x 2＋y 2＝25内的个数为( )图M2­1A ．2个B ．3个C ．4个D ．5个 7．(2017年广东惠州三模)某个几何体的三视图如图M2­2，若该几何体的所有顶点都在一个球面上，则该球面的表面积是( )图M2­2A ．4π B.28π3 C.44π3D ．20π8．已知F 1，F 2分别为双曲线E ：x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，离心率为53，过原点的直线l 交双曲线左、右两支分别于A ，B ，若|BF 1|－|AF 1|＝6，则该双曲线的标准方程为( )A.x 29－y 216＝1B.x 218－y 232＝1C.x 29－y 225＝1 D.x 236－y 264＝1 9．若函数f (x )＝⎩⎪⎨⎪⎧x －a 2x ≤0 ，x ＋1x＋a x >0 的最小值为f (0)，则实数a 的取值范围是( )A ．[－1,2]B ．[－1,0]C ．[1,2]D ．[0,2] 10．(2017年广东惠州三模)已知函数f (x )＝sin(ωx ＋φ)(ω>0，－π<φ<0)的最小正周期是π，将f (x )的图象向左平移π3个单位长度后所得的函数图象过点P (0，1)，则f (x )＝sin(ωx ＋φ)( )A ．在区间⎣⎢⎡⎦⎥⎤－π6，π3上单调递减B ．在区间⎣⎢⎡⎦⎥⎤－π6，π3上单调递增C ．在区间⎣⎢⎡⎦⎥⎤－π3，π6上单调递减D ．在区间⎣⎢⎡⎦⎥⎤－π3，π6上单调递增 11．已知A (2,1)，B (1，－2)，C ⎝ ⎛⎭⎪⎫35，－15，O 为坐标原点，动点P (a ，b )满足0≤OP →·OA→≤2，且0≤OP →·OB →≤2，则动点P 到点C 的距离大于14的概率为( )A ．1－5π64 B.5π64C ．1－π16 D.π1612．(2017年天津)已知函数f (x )＝⎩⎪⎨⎪⎧x 2－x ＋3，x ≤1，x ＋2x，x >1.设a ∈R ，若关于x 的不等式f (x )≥⎪⎪⎪⎪⎪⎪x2＋a 在R 上恒成立，则a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤－4716，2B.⎣⎢⎡⎦⎥⎤－4716，3916 C ．[－2 3，2] D.⎣⎢⎡⎦⎥⎤－2 3，3916 第Ⅱ卷(非选择题 满分90分)本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生必须作答．第22～23题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分，共20分．13．已知椭圆Γ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，焦距为2c ，若直线y ＝3(x ＋c )与椭圆Γ的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于__________．14．(2017年山东)已知(1＋3x )n 的展开式中含有x 2项的系数是54，则n ＝____________.15．已知正方体ABCD ­A 1B 1C 1D 1中，E ，F 分别为BB 1，CC 1的中点，那么异面直线AE 与D 1F 所成角的余弦值为________．16．(2017年广东惠州三模)已知在△ABC 中，AC ＝2，BC ＝6，∠ACB ＝π6，若线段BA 的延长线上存在点D ，使∠BDC ＝π4，则CD ＝________.三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．17．(本小题满分12分)(2017年广东惠州三模)已知等差数列{a n }满足(a 1＋a 2)＋(a 2＋a 3)＋…＋(a n ＋a n ＋1)＝2n (n ＋1)(n ∈N *)．(1)求数列{a n }的通项公式；(2)求数列⎩⎨⎧⎭⎬⎫a n 2n －1的前n 项和S n .18．(本小题满分12分)(2017年天津)从甲地到乙地要经过3个十字路口，设各路口信号灯工作相互独立，且在各路口遇到红灯的概率分别为12，13，14.(1)设X 表示一辆车从甲地到乙地遇到红灯的个数，求随机变量X 的分布列和数学期望；(2)若有2辆车独立地从甲地到乙地，求这2辆车共遇到1个红灯的概率． 19．(本小题满分12分)(2017年广东湛江二模)如图M2­3，在直三棱柱ABC ­A 1B 1C 1中，二面角A ­A 1B ­C 是直二面角，AB ＝BC ＝2，点M 是棱CC 1的中点，三棱锥M ­BCA 1的体积为1.(1)证明：BC ⊥平面ABA 1；(2)求直线MB 与平面BCA 1所成角的正弦值．图M2­320．(本小题满分12分)(2017年广东汕头一模)已知O 为坐标原点，圆M ：(x ＋1)2＋y 2＝16，定点F (1,0)，点N 是圆M 上一动点，线段NF 的垂直平分线交圆M 的半径MN 于点Q ，点Q 的轨迹为E .(1)求曲线E 的方程；(2)已知点P 是曲线E 上但不在坐标轴上的任意一点，曲线E 与y 轴的交点分别为B 1，B 2，直线B 1P 和B 2P 分别与x 轴相交于C ，D 两点，请问线段长之积|OC |·|OD |是否为定值？如果是请求出定值，如果不是请说明理由；(3)在(2)的条件下，若点C 坐标为(－1,0)，设过点C 的直线l 与E 相交于A ，B 两点，求△ABD 面积的最大值．21．(本小题满分12分)(2017年广东深圳一模)已知函数f (x )＝x ln x ，e 为自然对数的底数．(1)求曲线y ＝f (x )在x ＝e －2处的切线方程；(2)关于x 的不等式f (x )≥λ(x －1)在(0，＋∞)上恒成立，求实数λ的值；(3)关于x 的方程f (x )＝a 有两个实根x 1，x 2，求证：|x 1－x 2|<2a ＋1＋e －2.请考生在第22～23两题中任选一题作答．注意：只能作答在所选定的题目上．如果多做，则按所做的第一个题目计分．22．(本小题满分10分)选修4­4：坐标系与参数方程(2017年广东广州一模)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3－t ，y ＝1＋t(t 为参数)．在以坐标原点为极点， x 轴正半轴为极轴的极坐标系中， 曲线C ：ρ＝2 2cos ⎝⎛⎭⎪⎫θ－π4. (1)求直线l 的普通方程和曲线C 的直角坐标方程； (2)求曲线C 上的点到直线l 的距离的最大值． 23．(本小题满分10分)选修4­5：不等式选讲(2017年广东茂名一模)已知函数f (x )＝|2x －a |＋|2x ＋3|，g (x )＝|x －1|＋2. (1)若a ＝1，解不等式f (x )<6；(2)若对任意x 1∈R ，都有x 2∈R ，使得f (x 1)＝g (x 2)成立，求实数a 的取值范围．2019年高考数学(理科) 模拟试卷(二)1.C 解析：集合M ＝{x |－1≤x ≤1}，N ＝{y |0≤y ≤1}，故有N ⊆M .2．A 解析：因为1<x <π2，所以x －1>0，tan x >0，即(x －1)tan x >0，反之不成立．故选A.3．A 解析：由z ＝a ＋3i ，z ·z ＝4，得a 2＋3＝4，所以a ＝±1.故选A. 4．C 5.B6．C 解析：由程序框图知，i ＝6时，打印第一个点(－3,6)，在圆x 2＋y 2＝25外， i ＝5时，打印第二个点(－2,5)，在圆x 2＋y 2＝25外， i ＝4时，打印第三个点(－1,4)，在圆x 2＋y 2＝25内， i ＝3时，打印第四个点(0,3)，在圆x 2＋y 2＝25内， i ＝2时，打印第五个点(1,2)，在圆x 2＋y 2＝25内， i ＝1时，打印第六个点(2,1)，在圆x 2＋y 2＝25内，∴打印的点在圆x 2＋y 2＝25内的有4个． 故选C.7．B 解析：由三视图可知该几何体为棱长均为2的正三棱柱．设球心为O ，小圆的圆心为O 1，球的半径为R ，小圆的半径为r ，则R 2＝r 2＋O 1O 2.即R 2＝⎝ ⎛⎭⎪⎫23 32＋1＝73.∴S ＝28π3.故选B. 8．A 9.D10．B 解析：ω＝2, f (x )＝sin(2x ＋φ)向左平移π3个单位长度后得到的函数是y＝sin ⎝ ⎛⎭⎪⎫2x ＋φ＋2π3，其图象过(0,1)，∴sin ⎝ ⎛⎭⎪⎫φ＋2π3＝1.∵－π<φ<0，∴φ＝－π6，f (x )＝sin ⎝⎛⎭⎪⎫2x －π6.故选B. 11．A 解析：依题意有⎩⎪⎨⎪⎧0≤2a ＋b ≤2，0≤a －2b ≤2，画出可行域(图略)可知点P 的运动区域为以C ⎝ ⎛⎭⎪⎫35，－15为中心且边长为2 55的正方形，而点P 到点C 的距离小于或等于14的区域是以C ⎝ ⎛⎭⎪⎫35，－15为圆心，14为半径的圆以及圆的内部，则所求概率为45－π1645＝1－5π64.12．A 解析：不等式f (x )≥⎪⎪⎪⎪⎪⎪x 2＋a 可转化为－f (x )≤x2＋a ≤f (x )，(*)当x ≤1时，(*)式即为－x 2＋x －3≤x 2＋a ≤x 2－x ＋3，－x 2＋x 2－3≤a ≤x 2－32x ＋3，又－x 2＋x 2－3＝－⎝ ⎛⎭⎪⎫x －142－4716≤－4716，当x ＝14时取等号；x 2－32x ＋3＝⎝ ⎛⎭⎪⎫x －342＋3916≥3916，当x ＝34时取等号，所以－4716≤a ≤3916.当x >1时，(*)式为－x －2x ≤x 2＋a ≤x ＋2x ，－32x －2x ≤a ≤x 2＋2x，又－32x －2x ＝－⎝ ⎛⎭⎪⎫32x ＋2x ≤－2 3，当x ＝2 33时取等号； x 2＋2x≥2 x 2×2x＝2，当x ＝2时取等号， 所以－2 3≤a ≤2.综上所述，a 的取值范围是－4716≤a ≤2.故选A.13.3－1 解析：由直线方程y ＝3(x ＋c )⇒直线与x 轴的夹角∠MF 1F 2＝π3，且过点F 1(－c,0)，∵∠MF 1F 2＝2∠MF 2F 1＝π3，∴∠MF 2F 1＝π6.∴∠F 1MF 2＝π2.即F 1M ⊥F 2M .∴在Rt △F 1MF 2中，|F 1F 2|＝2c ，|F 1M |＝c ，|F 2M |＝3c .∴由椭圆的第一定义可得2a ＝c ＋3c ，∴c a ＝21＋3＝3－1. 14．4 解析：由二项式定理的通项公式T r ＋1＝C r n (3x )r ＝C r n 3r x r ，令r ＝2，得C 2n 32＝54.解得n ＝4.15.3516. 3 解析：因为线段BA 的延长线上存在点D ，使∠BDC ＝π4，∠ACB ＝π6，所以AB 2＝AC 2＋BC 2－2×AC ×BC ×cos π6＝2，即AB ＝ 2.所以AB ＝AC .所以∠B ＝∠ACB ＝π6.在△BCD 中，根据正弦定理BCsin ∠D ＝CDsin ∠B⇔622＝CD12⇒CD ＝ 3. 17．解：(1)设等差数列{a n }的公差为d ，由已知，得⎩⎪⎨⎪⎧a 1＋a 2＝4，a 1＋a 2 ＋ a 2＋a 3 ＝12，即⎩⎪⎨⎪⎧a 1＋a 2＝4，a 2＋a 3＝8.所以⎩⎪⎨⎪⎧ a 1＋ a 1＋d ＝4， a 1＋d ＋ a 1＋2d ＝8.解得⎩⎪⎨⎪⎧a 1＝1，d ＝2.所以a n ＝2n －1.(2)由(1)，得a n 2n －1＝2n －12n －1.所以S n ＝1＋321＋522＋…＋2n －32n －2＋2n －12n －1， ①12S n ＝12＋322＋523＋…＋2n －32n －1＋2n －12n . ② ①－②，得12S n ＝1＋1＋12＋122＋…＋12n －2－2n －12n ＝3－2n ＋32n .所以S n ＝6－4n ＋62n .18．(1)解：随机变量X 的所有可能取值为0,1,2,3.P (X ＝0)＝⎝⎛⎭⎪⎫1－12×⎝ ⎛⎭⎪⎫1－13×⎝ ⎛⎭⎪⎫1－14＝14，P (X ＝1)＝12×⎝ ⎛⎭⎪⎫1－13×⎝ ⎛⎭⎪⎫1－14＋⎝⎛⎭⎪⎫1－12×13×⎝ ⎛⎭⎪⎫1－14＋⎝ ⎛⎭⎪⎫1－12×⎝ ⎛⎭⎪⎫1－13×14＝1124，P (X ＝2)＝⎝ ⎛⎭⎪⎫1－12×13×14＋12×⎝ ⎛⎭⎪⎫1－13×14＋12×13×⎝ ⎛⎭⎪⎫1－14＝14，P (X ＝3)＝12×13×14＝124.所以随机变量X随机变量X 的数学期望E (X )＝0×4＋1×24＋2×4＋3×24＝1312.(2)设Y 表示第1辆车遇到红灯的个数，Z 表示第2辆车遇到红灯的个数，则所求事件的概率为P (X ＋Z ＝1)＝P (Y ＝0，Z ＝1)＋P (Y ＝1，Z ＝0)＝P (Y ＝0)×P (Z ＝1)＋P (Y ＝1)×P (Z ＝0)＝14×1124＋1124×14＝1148.所以这2辆车共遇到1个红灯的概率为1148.19．(1)证明：过A 在平面ABA 1内作AH ⊥A 1B ，垂足为H ，如图D207. 由题可知平面ABA 1⊥平面BCA 1，且平面ABA 1∩平面BCA 1＝BA 1， ∴AH ⊥平面BCA 1.又BC ⊂平面BCA 1，∴AH ⊥BC .由题直三棱的性质可知AA 1⊥BC ，AA 1∩AH ＝A . ∴BC ⊥平面ABA 1.图D207(2)解：设AA 1＝a ，而1-A MBC V ＝1-M BCA V ＝1.由(1)知AB ⊥BC ，结合直棱柱的性质知AB ⊥平面BCM . ∵AA 1∥平面BCM ，∴A 1到平面BCM 的距离等于AB ＝2，得1-A MBC V ＝13·AB ·S △BCM ＝23×⎝ ⎛⎭⎪⎫12×2×a 2＝a 3＝1⇔a ＝3.以B 为原点，BC ，BA ，BB 1分别作为x ，y ，z 轴，建立如图所示的空间直角坐标系．则M ⎝⎛⎭⎪⎫2，0，32，C (2,0,0)，A 1(0,2,3)． 则BM →＝⎝⎛⎭⎪⎫2，0，32，BC →＝(2,0,0)，BA 1→＝(0,2,3)．设平面BCA 1的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧2x ＝0，2y ＋3z ＝0，令y ＝3，得一个法向量n ＝(0，－3,2)．∴cos 〈BM →，n 〉＝BM →·n |BM →||n |＝322＋⎝ ⎛⎭⎪⎫322× －3 2＋22＝61365.故直线MB 与平面BCA 1所成角的正弦值为61365.20．解：(1)依题意，可得圆M 的圆心坐标为M (－1,0)，半径为r ＝4，|QN |＝|QF |， 则|QN |＋|QM |＝|QF |＋|QM |＝r ＝4>|MF | .根据椭圆定义，曲线E 是以M (－1,0)，F (1,0)为焦点，长轴长为4的椭圆．设其方程为x 2a 2＋y 2b2＝1(a >b >0)，∴2a ＝4,2c ＝2，即a ＝2，c ＝1.∴b ＝a 2－c 2＝ 3.∴曲线E 的方程为x 24＋y 23＝1.(2)设点P (x 0，y 0)，直线B 1P 方程为 y ＝y 0＋3x 0x －3，令y ＝0，得x C ＝3x 03＋y 0，同理可得x D ＝3x 03－y 0.∴|OC |·|OD |＝|x C |·|x D |＝⎪⎪⎪⎪⎪⎪3x 0 3＋y 0·⎪⎪⎪⎪⎪⎪3x 0 3－y 0＝⎪⎪⎪⎪⎪⎪3x 203－y 20.∵点P 是点E 上且不在坐标轴上的任意一点，∴x 204＋y 203＝1.∴3x 20＝12－4y 20＝4(3－y 20)．∴|OC |·|OD |＝⎪⎪⎪⎪⎪⎪3x 203－y 20＝⎪⎪⎪⎪⎪⎪4 3－y 20 3－y 20＝4. ∴|OC |·|OD |的定值为4.(3)当点C 的坐标为(－1,0)时，点D (－4,0)，|CD |＝3. 设直线l 的方程为x ＝my －1，A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧x ＝my －1，x 24＋y23＝1消去x 并整理，得(3m 2＋4)y 2－6my －9＝0.解得y 1＝3m －6m 2＋13m 2＋4，y 2＝3m ＋6m 2＋13m 2＋4. ∴|y 1－y 2|＝12m 2＋13m 2＋4. ∴S △ABD ＝12|CD |·|y 1－y 2|＝32×12m 2＋13m 2＋4＝18m 2＋13m 2＋4＝183m 2＋1＋1m 2＋1.∵m 2≥0，∴m 2＋1≥1.又y ＝3x ＋1x在[1，＋∞)上为增函数．∴3m 2＋1＋1m 2＋1≥3×1＋11＝4.∴S ≤184＝92.∴当m ＝0，即直线AB 的方程为x ＝－1时，△ABD 的面积最大，最大值是92.21．(1)解：对函数f (x )求导得f ′(x )＝ln x ＋x ·1x＝ln x ＋1，∴f ′(e －2)＝ln e －2＋1＝－1.又f (e －2)＝e －2ln e －2＝－2e －2，∴曲线y ＝f (x )在x ＝e －2处的切线方程为y －(－2e －2)＝－(x －e －2)，即y ＝－x －e－2.(2)解：记g (x )＝f (x )－λ(x －1)＝x ln x －λ(x －1)，其中x >0， 由题意知g (x )≥0在(0，＋∞)上恒成立，即g (x )min ≥0. 对g (x )求导得g ′(x )＝ln x ＋1－λ.令g ′(x )＝0，得x ＝e λ－1.当x∴g (x )min 极小值∴λ－e λ－1≥0.记G (λ)＝λ－e λ－1，则G ′(λ)＝1－e λ－1. 令G ′(λ)＝0，得λ＝1.当λ∴G (λ)max 极大值故λ－e λ－1≤0，当且仅当λ＝1时取等号．又λ－e λ－1≥0，从而得到λ＝1.(3)证明：先证f (x )≥－x －e －2，记h (x )＝f (x )－(－x －e －2)＝x ln x ＋x ＋e －2， 则h ′(x )＝ln x ＋2.令h ′(x )＝0，得x ＝e －2.当x∴h (x )min 极小值∴h (x )≥0恒成立，即f (x )≥－x －e －2.记直线y ＝－x －e －2，y ＝x －1分别与y ＝a 交于点(x 1′，a )，(x 2′，a )，不妨设x 1<x 2，则a ＝－x 1′－e －2＝f (x 1)≥－x 1－e －2.从而x 1′<x 1，当且仅当a ＝－2e －2时取等号．由(2)知，f (x )≥x －1，则a ＝x 2′－1＝f (x 2)≥x 2－1. 从而x 2≤x 2′，当且仅当a ＝0时取等号．故|x 1－x 2|＝x 2－x 1≤x 2′－x 1′＝(a ＋1)－(－a －e －2)＝2a ＋1＋e －2. 因等号成立的条件不能同时满足，故|x 1－x 2|<2a ＋1＋e －2.22．解：(1)由⎩⎪⎨⎪⎧x ＝3－t ，y ＝1＋t 消去t ，得x ＋y －4＝0.所以直线l 的普通方程为x ＋y －4＝0.由ρ＝2 2cos ⎝ ⎛⎭⎪⎫θ－π4＝2 2⎝⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2cos θ＋2sin θ，得ρ2＝2ρcos θ＋2ρsin θ.将ρ2＝x 2＋y 2，ρcos θ＝x ，ρsin θ＝y 代入上式，得曲线C 的直角坐标方程为x 2＋y 2＝2x ＋2y, 即(x －1)2＋(y －1)2＝2.(2)方法一，设曲线C 上的点为P (1＋2cos α，1＋2sin α)，则点P 到直线l 的距离为d ＝|1＋2cos α＋1＋2sin α－4|2＝|2 sin α＋cos α －2|2＝⎪⎪⎪⎪⎪⎪2sin ⎝ ⎛⎭⎪⎫α＋π4－22.当sin ⎝ ⎛⎭⎪⎫α＋π4＝－1时， d max ＝2 2. 所以曲线C 上的点到直线l 的距离的最大值为2 2.方法二，设与直线l 平行的直线为l ′：x ＋y ＋b ＝0.当直线l ′与圆C 相切时， 得|1＋1＋b |2＝2，解得b ＝0或b ＝－4(舍去)． 所以直线l ′的方程为x ＋y ＝0.所以直线l 与直线l ′的距离为d ＝|0＋4|2＝2 2.所以曲线C 上的点到直线l 的距离的最大值为2 2. 23．解：(1)当a ＝1时，f (x )<6， 即|2x －1|＋|2x ＋3|<6， 即⎩⎪⎨⎪⎧x ≤－32，1－2x －2x －3<6，或⎩⎪⎨⎪⎧－32<x <12，2x ＋3＋1－2x <6，或⎩⎪⎨⎪⎧x ≥12，2x －1＋2x ＋3<6.∴－2<x ≤－32或－32<x <12或12≤x <1.∴－2<x <1.∴不等式f (x )<6的解集为{ x |－2<x < }1.(2)对任意x 1∈R ，都有x 2∈R ，使得f (x 1)＝g (x 2)成立，则有{y |y ＝f (x )}⊆{y |y ＝g (x )}．又f (x )＝|2x －a |＋|2x ＋3|≥|(2x －a )－(2x ＋3)|＝|a ＋3|，g (x )＝|x －1|＋2≥2， 从而|a ＋3|≥2，解得a ≤－5或a ≥－1.故实数a 的取值范围为(－∞，－5]∪[－1，＋∞)．。

第六章 不等式第1讲 不等式的概念与性质1．(2017年河北承德实验中学统测)若a ，b ，c ∈R ，且a ＞b ，则下列不等式正确的个数是( )①1a <1b ；②a 2>b 2；③ac 4>bc 4；④a c 2＋1>b c 2＋1. A ．1 B ．2 C ．3 D ．42．(2016年北京)已知x ，y ∈R ，且x >y >0，则( ) A.1x －1y>0 B ．sin x －sin y >0 C.⎝⎛⎭⎫12x －⎝⎛⎭⎫12y <0 D ．ln x ＋ln y >03．已知下列不等式：①x 2＋3>2x ；②a 3＋b 3≥a 2b ＋ab 2(a ，b ∈R ＋)；③a 2＋b 2≥2(a －b －1)．其中正确的个数是( )A ．0B ．1C ．2D ．34．(2015年湖北)将离心率为e 1的双曲线C 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度，得到离心率为e 2的双曲线C 2，则( )A ．对任意的a ，b ，e 1<e 2B ．当a >b 时，e 1<e 2；当a <b 时，e 1>e 2C ．对任意的a ，b ，e 1>e 2D ．当a >b 时，e 1>e 2；当a <b 时，e 1<e 25．(2015年上海)记方程①：x 2＋a 1x ＋1＝0，方程②：x 2＋a 2x ＋2＝0，方程③：x 2＋a 3x ＋4＝0，其中a 1，a 2，a 3是正实数．当a 1，a 2，a 3成等比数列时，下列选项中，能推出方程③无实根的是( )A ．方程①有实根，且②有实根B ．方程①有实根，且②无实根C ．方程①无实根，且②有实根D ．方程①无实根，且②无实根6．已知函数f (x )＝ax 2＋bx ＋c 满足f (1)＝0，且a >b >c ，则ca的取值范围为__________．7．(2016年山东滨州模拟)A 杯中有浓度为a 的盐水x g ，B 杯中有浓度为b 的盐水y g ，其中A 杯中的盐水更咸一些．若将A ，B 两杯盐水混合在一起，其浓度可用不等式表示为______________．8．用若干辆载重为8吨的汽车运一批货物，若每辆汽车只装4吨，则剩下20吨货物；若每辆汽车装8吨，则最后一辆汽车不满也不空．则有汽车________辆．9．设a ，b 为正实数．现有下列命题： ①若a 2－b 2＝1，则a －b ＜1；②若1b －1a＝1，则a －b ＜1；③若|a －b |＝1，则|a －b |＜1； ④若|a 3－b |＝1，则|a －b |＜1.其中的真命题有__________．(写出所有真命题的编号)10．(2016年湖南怀化模拟)某单位组织职工去某地参观学习需包车前往．甲车队说：“如领队买全票一张，其余人可享受7.5折优惠”，乙车队说：“你们属团体票，按原价的8折优惠”．这两车队的原价、车型都是一样的，试根据单位的人数，比较两车队的收费哪家更优惠．11．已知a ＞0，b ＞0，求证：⎝⎛⎭⎫a 2b 12＋⎝⎛⎭⎫b 2a 12≥a 12＋b 12.12．已知α∈(0，π)，比较2sin 2α与sin α1－cos α的大小．第2讲 一元二次不等式及其解法1．(2016年湖北模拟)若关于x 的不等式ax －b >0的解集是(－∞，1)，则关于x 的不等式(ax ＋b )(x －3)>0的解集是( )A ．(－∞，－1)∪(3，＋∞)B ．(－1,3)C ．(1,3)D ．(－∞，1)∪(3，＋∞)2．如果kx 2＋2kx －(k ＋2)<0恒成立，那么实数k 的取值范围是( ) A ．－1≤k ≤0 B ．－1≤k <0 C ．－1<k ≤0 D ．－1<k <03．已知函数f (x )＝⎩⎪⎨⎪⎧x ＋2，x ≤0，－x ＋2，x ＞0，则不等式f (x )≥x 2的解集是( )A ．[－1,1]B ．[－2,2]C ．[－2,1]D ．[－1,2]4．(2016年江西九江一模)若关于x 的不等式x 2－4x －2－a >0在区间(1,4)内有解，则实数a 的取值范围是( )A ．(－∞，－2)B ．(－2，＋∞)C ．(－6，＋∞)D ．(－∞，－6)5．已知不等式x 2－2x －3＜0的解集为A ，不等式x 2＋x －6＜0的解集为B ，不等式x 2＋ax ＋b ＜0的解集是A ∩B ，则a ＋b ＝( )A ．－3B ．1C ．－1D ．36．已知f (x )是定义域为R 的偶函数，当x ≤0时，f (x )＝x 2＋2x ，则不等式f (x ＋2)<3的解集是_________．7．已知a ∈Z ，关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数，则所有符合条件的a 的值之和是________．8．不等式ax 2＋bx ＋c ＞0的解集为⎝⎛⎭⎫－13，2，对于系数a ，b ，c ，有如下结论：①a <0；②b ＞0；③c ＞0；④a ＋b ＋c ＞0；⑤a －b ＋c ＞0.其中正确的结论的序号是________．9．(2016年北京朝阳统一考试)已知函数f (x )＝x 2－2ax －1＋a ，a ∈R .(1)若a ＝2，试求函数y ＝f (x )x(x >0)的最小值；(2)对于任意的x ∈[0,2]，不等式f (x )≤a 成立，试求a 的取值范围．10．设f (x )＝ax 2＋bx ＋c ，若f (1)＝72，问是否存在a ，b ，c ∈R ，使得不等式x 2＋12≤f (x )≤2x 2＋2x ＋32对一切实数x 都成立？证明你的结论．第3讲 算术平均数与几何平均数1．下列命题正确的是( )A ．函数y ＝x ＋1x 的最小值为2B ．函数y ＝x 2＋3x 2＋2的最小值为2C ．函数y ＝2－3x －4x (x ＞0)的最小值为2－4 3D ．函数y ＝2－3x －4x (x ＞0)的最大值为2－4 32．若函数f (x )＝x ＋1x －2(x >2)在x ＝a 处取得最小值，则a ＝( )A ．1＋ 2B ．1＋ 3C ．3D ．43．设正实数x ，y ，z 满足x 2－3xy ＋4y 2－z ＝0，则当zxy取得最小值时，x ＋2y －z 的最大值为( )A ．0 B.98 C ．2 D.944．若log 4(3a ＋4b )＝log 2ab ，则a ＋b 的最小值是( ) A ．6＋2 3 B ．7＋2 3 C ．6＋4 3 D ．7＋4 35．(2015年湖南)若实数a ，b 满足1a ＋2b＝ab ，则ab 的最小值为( )A. 2 B ．2 C ．2 2 D ．46．(2015年陕西)设f (x )＝ln x,0＜a ＜b ，若p ＝f (ab )，q ＝f ⎝⎛⎭⎫a ＋b 2，r ＝12[f (a )＋f (b )]，则下列关系式正确的是( )A ．q ＝r ＜pB ．q ＝r ＞pC ．p ＝r ＜qD ．p ＝r ＞q7．已知正数x ，y 满足x ＋2y －xy ＝0，则x ＋2y 的最小值为( ) A ．8 B ．4 C ．2 D ．08．(2017年河南郑州第二次质量预测)已知正数x ，y 满足x 2＋2xy －3＝0，则2x ＋y 的最小值是__________．9．(1)设x ＞－1，则函数y ＝(x ＋5)(x ＋2)x ＋1的最小值为________．(2)已知x ＜54，则f (x )＝4x －2＋14x －5的最大值为________；10．(1)(2016年湖北七市联考)已知a >0，b >0，且2a ＋b ＝1，若不等式2a ＋1b≥m 恒成立，则m 的最大值等于( )A ．10B ．9C ．8D ．7(2)已知x >0，y >0，x ＋3y ＋xy ＝9，则x ＋3y 的最小值为________．第4讲 简单的线性规划1．(2017年北京)若x ，y 满足⎩⎪⎨⎪⎧x ≤3，x ＋y ≥2y ≤x ，，则x ＋2y 的最大值为( )A ．1B ．3C ．5D ．92．(2017年新课标Ⅲ)设x ，y 满足约束条件⎩⎪⎨⎪⎧3x ＋2y －6≤0，x ≥0，y ≥0，则z ＝x －y 的取值范围是( )A ．[－3,0]B ．[－3,2]C ．[0,2]D ．[0,3]3．已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧0≤x ≤3，2x －3y ≤6，3x ＋4y ≤12，则z ＝x ＋y －2x ＋1的取值范围是( )A.⎣⎡⎦⎤－4，716 B ．[－4,1] C.⎣⎡⎦⎤14，716 D.⎣⎡⎦⎤14，1 4．(2014年新课标Ⅰ)设x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y ≥a ，x －y ≤－1，且z ＝x ＋ay 的最小值为7，则a ＝( )A ．－5B ．3C ．－5或3D ．5或－35．设二元一次不等式组⎩⎪⎨⎪⎧2x ＋y －19≥0，x －y －8≤0，x ＋2y －14≤0所表示的平面区域为M ，则使函数y ＝log a x (a >0，a ≠1)的图象过区域M 的a 的取值范围是( )A ．[1,3]B ．[2，10]C ．[2,9]D ．[10，9]6．x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y －2≤0，x －2y －2≤0，2x －y ＋2≥0.若z ＝y －ax 取得最大值的最优解不唯一，则实数a 的值为( )A.12或－1 B ．2或12 C ．2或1 D ．2或－17．在平面直角坐标系中，不等式组⎩⎪⎨⎪⎧x ≥1，x ＋y ≤0，x －y －4≤0表示的平面区域的面积是________．8．(2016年江苏) 已知实数x ，y 满足⎩⎪⎨⎪⎧x －2y ＋4≥0，2x ＋y －2≥0，3x －y －3≤0，则x 2＋y 2的取值范围是________．9．变量x ，y 满足⎩⎪⎨⎪⎧x －4y ＋3≤0，3x ＋5y －25≤0，x ≥1.(1)设z ＝yx，求z 的最小值；(2)设z ＝x 2＋y 2，求z 的取值范围；(3)设z ＝x 2＋y 2＋6x －4y ＋13，求z 的取值范围．10．已知函数g (x )＝x 2＋(a ＋1)x ＋a ＋b ＋1，两个零点可分别作为一个椭圆和一个双曲线的离心率．求ba的取值范围．第5讲 不等式的应用1．某汽车运输公司购买了一批豪华大客车投入营运，据市场分析：每辆客车营运的总利润y (单位：10万元)与营运年数x 的函数关系为y ＝－(x －6)2＋11(x ∈N *)，要使每辆客车运营的年平均利润最大，则每辆客车营运的最佳年数为( )A ．3年B ．4年C ．5年D ．6年2．(2017年广东惠州三模)设z ＝4x ·2y ，变量x ，y 满足条件⎩⎪⎨⎪⎧x －4y ≤－3，3x ＋5y ≤25，x ≥1，则z 的最小值为( )A ．2B ．4C ．8D ．163．某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房．经测算，若将楼房建为x (x ≥10)层，则每平方米的平均建筑费用为560＋48x (单位：元)．为了使楼房每平方米的平均综合费用最少，则楼房应建为( )A ．10层B ．15层C ．20层D ．30层4．(2016年山东烟台诊断)已知在等比数列{a n }中，a 2＝1，则其前3项的和S 3的取值范围是( )A ．(－∞，－1]B ．(－∞，－1)∪(1，＋∞)C ．[3，＋∞)D ．(－∞，－1]∪[3，＋∞)5．某农户计划种植黄瓜和韭菜，种植面积不超过50亩(1亩≈666.7平方米)，投入资金不超过54植面积(单位：亩)分别为( )A ．50,0B ．30,20C ．20,30D ．0,506．某旅行社租用A ，B 两种型号的客车安排900名客人旅行，A ，B 两种车辆的载客量分别为36人和60人，租金分别为1600元/辆和2400元/辆，旅行社要求租车总数不超过21辆，且B 型车不多于A 型车7辆，则租金最少为( )A ．31 200元B ．36 000元C ．36 800元D ．38 400元7．(2017年江苏)某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年的总存储费用为4x 万元，要使一年的总运费与总存储之和最小，则x 的值是__________．8．某项研究表明，在考虑行车安全的情况下，某路段车流量F (单位时间内测量点的车辆数，单位：辆/时)与车流速度v (假设车辆以相同速度v 行驶，单位：米/秒)，平均车长l (单位：米)的值有关，其关系式为F ＝76 000vv 2＋18v ＋20l.(1)如果不限定车型，l ＝6.05，那么最大车流量为______辆/时；(2)如果限定车型，l ＝5，那么最大车流量比(1)中的最大车流量增加______辆/时．9．(2017年湖北孝感一模)经测算，某型号汽车在匀速行驶过程中每小时耗油量y (单位：升)与速度x (单位：千米/时)(50≤x ≤120)的关系可近似表示为：y ＝⎩⎨⎧175(x 2－130x ＋4900)，x ∈[50，80)，12－x60，x ∈[80，120].(1)该型号汽车速度为多少时，可使得每小时耗油量最低？(2)已知A，B两地相距120千米，假定该型号汽车匀速从A地驶向B地，则汽车速度为多少时总耗油量最少？10．(2017年天津)电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告．已不少于30分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的2倍．分别用x，y表示每周计划播出的甲、乙两套连续剧的次数．(1)用x，y列出满足题目条件的数学关系式，并画出相应的平面区域；(2)问电视台每周播出甲、乙两套连续剧各多少次，才能使收视人次最多？第六章 不等式第1讲 不等式的概念与性质1．A 解析：①a ＝1，b ＝－1，1a ＜1b不成立；②a ＝1，b ＝－1，a 2＞b 2不成立； ③c ＝0，ac 4＞bc 4 不成立；④因为c 2＋1＞0，a ＞b ，所以a c 2＋1＞bc 2＋1成立．2．C 解析：由x >y >0，得1x <1y ，即1x －1y<0，A 不正确；由x >y >0及函数y ＝sin x 的单调性，可知sin x －sin y >0不一定正确，B 不正确；由0<12<1，x >y >0，得⎝⎛⎭⎫12x <⎝⎛⎭⎫12y ，即⎝⎛⎭⎫12x－⎝⎛⎭⎫12y <0，C 正确；由x >y >0，得xy >0，但不一定大于1，故ln x ＋ln y ＝ln xy >0不一定成立，D 不正确．3．D 解析：∵x 2－2x ＋3＝(x －1)2＋2>0，∴x 2＋3>2x .∵a 3＋b 3－a 2b －ab 2＝(a －b )(a 2－b 2)＝(a ＋b )(a －b )2≥0，∴a 3＋b 3≥a 2b ＋ab 2.∵a 2＋b 2－2(a －b －1)＝(a －1)2＋(b ＋1)2≥0，∴a 2＋b 2≥2(a －b －1)．4．B 解析：e 1＝1＋b 2a 2，e 2＝1＋(b ＋m )2(a ＋m )2.不妨令e 1<e 2，化简，得b a <b ＋ma ＋m (m >0)，得bm <am ，得b <a .所以当b >a 时，有b a >b ＋m a ＋m ，即e 1>e 2；当b <a 时，有b a <b ＋ma ＋m，即e 1<e 2.故选B.5．B 解析：当方程①有实根，且②无实根时，a 21≥4，a 22<8，从而a 3＝a 22a 1<82＝4，∴a 23<16，即方程③：x 2＋a 3x ＋4＝0无实根．故选B.而A ，D 由于不等式方向不一致，不可推；C 推出③有实根．6.⎝⎛⎭⎫－2，－12 解析：因为f (1)＝0，所以a ＋b ＋c ＝0.所以b ＝－(a ＋c )． 又a >b >c ，所以a >－(a ＋c )>c ，且a >0，c <0.所以1>－a ＋c a >c a ，即1>－1－c a >ca .所以⎩⎨⎧2ca <－1，ca>－2，解得－2<c a <－12.7．b <ax ＋by x ＋y <a 解析：依题意，知a >b ，将A ，B 两杯盐水混合后，盐水的浓度变为ax ＋by x ＋y .则有ax ＋by x ＋y >bx ＋by x ＋y ＝b ，ax ＋by x ＋y <ax ＋ay x ＋y ＝a .故有b <ax ＋by x ＋y <a .8．6 解析：设有x 辆汽车，则货物重为(4x ＋20)吨．由题意，得⎩⎪⎨⎪⎧8(x －1)＜4x ＋20，8x ＞4x ＋20，x ∈N *.解得5＜x ＜7，且x ∈N *.故只有x ＝6才满足要求．9．①④ 解析：①中，∵a 2－b 2＝1，∴a －b ＝1a ＋b.∵a ＞0，b ＞0，又a 2＝b 2＋1＞1，∴a ＞1.从而1a ＋b＜1，即a －b ＜1.∴①正确．②中，取a ＝5，b ＝56，验证知②错误．③中，取a ＝4，b ＝1，验证知③错误． ④∵a ，b 是正实数，不妨设a ＞b >0， ∴a 3－b 3＝(a －b )(a 2＋b 2＋ab )．∴a －b ＝a 3－b 3a 2＋ab ＋b 2＝1a 2＋ab ＋b 2. ∵a 3＝1＋b 3＞1，∴a 2＞1.∴a 2＋ab ＋b 2＞1.∴0＜1a 2＋ab ＋b 2＜1.∴0<a －b ＝1a 2＋ab ＋b 2＜1.即|a －b |＜1.同理，设0<a ＜b ，也能得到|a －b |＜1的结论．故④正确． 10．解：设该单位职工有n 人(n ∈N *)，全票价为x 元， 坐甲车需花y 1元，坐乙车需花y 2元．则y 1＝x ＋34x ·(n －1)＝14x ＋34nx ，y 2＝45nx .因为y 1－y 2＝14x ＋34nx －45nx＝14x －120nx ＝14x ⎝⎛⎭⎫1－n 5. 当n ＝5时，y 1＝y 2； 当n >5时，y 1<y 2； 当n <5时，y 1>y 2.因此当单位去的人数为5人时，两车队收费相同；多于5人时，选甲车更优惠；少于5人时，选乙车队更优惠．11．证明：方法一，左边－右边＝(a )3＋(b )3ab－(a ＋b )＝(a ＋b )(a －ab ＋b )－ab (a ＋b )ab＝(a ＋b )(a －2 ab ＋b )ab ＝(a ＋b )(a －b )2ab≥0.∴原不等式成立．方法二，左边>0，右边>0. 左边右边＝(a ＋b )(a －ab ＋b )ab (a ＋b ) ＝a －ab ＋b ab ≥2 ab －ab ab＝1.∴原不等式成立．12．解：2sin 2α－sin α1－cos α＝4sin αcos α(1－cos α)－sin α1－cos α＝sin α1－cos α(－4cos 2α＋4cos α－1)＝－sin α1－cos α(2cos α－1)2.∵α∈(0，π)，∴sin α＞0,1－cos α＞0，(2cos α－1)2≥0.∴－sin α1－cos α(2cos α－1)2≤0，即2sin 2α－sin α1－cos α≤0.∴2sin 2α≤sin α1－cos α，当且仅当α＝π3时取等号．第2讲 一元二次不等式及其解法1．B 解析：由题意关于x 的不等式ax －b >0的解集是(－∞，1)，可得ba＝1，且a <0.则(ax ＋b )(x －3)>0可变形为(x －3)⎝⎛⎭⎫x ＋ba <0，即得(x －3)(x ＋1)<0.所以－1<x <3.所以不等式的解集是(－1,3)．故选B.2．C 解析：当k ＝0时，原不等式等价于－2＜0，显然恒成立，∴k ＝0符合题意．当k ≠0时，由题意，得⎩⎪⎨⎪⎧k <0，(2k )2－4k ·[－(k ＋2)]＜0.解得－1<k <0.∴－1＜k ≤0. 3．A 解析：依题意，得⎩⎪⎨⎪⎧ x ≤0，x ＋2≥x 2或⎩⎪⎨⎪⎧x ＞0，－x ＋2≥x 2⇒－1≤x ≤0或0＜x ≤1⇒－1≤x ≤1. 4．A 解析：不等式x 2－4x －2－a >0在区间(1,4)内有解等价于a <(x 2－4x －2)max .令g (x )＝x 2－4x －2，x ∈(1,4)，∴g (x )<g (4)＝－2.∴a <－2.5．A 解析：由题意，得A ＝{x |－1＜x ＜3}，B ＝{x |－3＜x ＜2}．A ∩B ＝{x |－1＜x ＜2}，由根与系数的关系可知，a ＝－1，b ＝－2.∴a ＋b ＝－3.6．{x |－5<x <1} 解析：设x ≥0，因为f (x )是定义域为R 的偶函数，所以f (x )＝f (－x )＝x 2－2x .又f (x ＋2)＝f (|x ＋2|)，所以f (x ＋2)<3⇔f (|x ＋2|)＝(|x ＋2|)2－2|x ＋2|<3.所以(|x ＋2|－3)(|x ＋2|＋1)<0.所以0≤|x ＋2|<3，解得－5<x <1.所以原不等式的解集为{x |－5<x <1}．7．21 解析：设f (x )＝x 2－6x ＋a ，其图象是开口向上，对称轴是x ＝3的抛物线，图象如图D115.图D115关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数，则⎩⎪⎨⎪⎧f (2)≤0，f (1)＞0即⎩⎪⎨⎪⎧f (2)＝4－12＋a ≤0，f (1)＝1－6＋a ＞0， 解得5<a ≤8.又a ∈Z ，所以a ＝6,7,8，则所有符合条件的a 的值之和是6＋7＋8＝21.8．①②③④ 解析：∵不等式ax 2＋bx ＋c ＞0的解集为⎝⎛⎭⎫－13，2，∴a <0；－13，2是方程ax 2＋bx ＋c ＝0的两根，－13＋2＝－ba>0，∴b >0；f (0)＝c >0，f (1)＝a ＋b ＋c >0，f (－1)＝a－b ＋c <0.故正确结论的序号为①②③④.9．解：(1)依题意，得y ＝f (x )x ＝x 2－4x ＋1x ＝x ＋1x－4.因为x >0，所以x ＋1x ≥2，当且仅当x ＝1x，即x ＝1时，等号成立，所以y ≥－2.所以当x ＝1时，y ＝f (x )x 的最小值为－2.(2)因为f (x )－a ＝x 2－2ax －1，所以要使得“∀x ∈[0,2]，不等式f (x )≤a 成立”只要“x 2－2ax －1≤0在[0,2]上恒成立”．不妨设g (x )＝x 2－2ax －1，则只要g (x )≤0在[0,2]上恒成立即可．所以⎩⎪⎨⎪⎧ g (0)≤0，g (2)≤0.即⎩⎪⎨⎪⎧0－0－1≤0，4－4a －1≤0. 解得a ≥34.故a 的取值范围为⎣⎡⎭⎫34，＋∞. 10．解：由f (1)＝72，得a ＋b ＋c ＝72.令x 2＋12＝2x 2＋2x ＋32⇒x ＝－1.由f (x )≤2x 2＋2x ＋32推得f (－1)≤32.由f (x )≥x 2＋12推得f (－1)≥32.∴f (－1)＝32.∴a －b ＋c ＝32.故a ＋c ＝52，且b ＝1.∴f (x )＝ax 2＋x ＋52－a .依题意ax 2＋x ＋52－a ≥x 2＋12对一切x ∈R 都成立，∴a ≠1，且Δ＝1－4(a －1)(2－a )≤0.由a －1>0，得a ＝32.∴f (x )＝32x 2＋x ＋1.证明如下： ∵32x 2＋x ＋1－2x 2－2x －32 ＝－12x 2－x －12＝－12(x ＋1)2≤0.∴32x 2＋x ＋1≤2x 2＋2x ＋32对x ∈R 都成立． ∴存在实数a ＝32，b ＝1，c ＝1，使得不等式x 2＋12≤f (x )≤2x 2＋2x ＋32对一切x ∈R 都成立．第3讲 算术平均数与几何平均数1．D 解析：y ＝x ＋1x的定义域为{x |x ≠0}，当x ＞0时，有最小值2，当x ＜0时，有最大值－2.故A 项不正确；y ＝x 2＋3x 2＋2＝x 2＋2＋1x 2＋2≥2，∵x 2＋2≥2，∴取不到“＝”．故B 项不正确；∵当x ＞0时，3x ＋4x ≥2·3x ·4x ＝4 3，当且仅当3x ＝4x ，即x ＝2 33时取“＝”．∴y ＝2－⎝⎛⎭⎫3x ＋4x 有最大值2－4 3.故C 项不正确，D 项正确． 2．C 解析：∵x ＞2，∴f (x )＝x ＋1x －2＝(x －2)＋1x －2＋2≥2 (x －2)·1x －2＋2＝4，当且仅当x －2＝1x －2，即x ＝3时取等号．3．C 解析：z ＝x 2－3xy ＋4y 2，z xy ＝x 2－3xy ＋4y 2xy ≥2x ·2y －3xy xy ＝xy xy＝1. 当且仅当x ＝2y 时，zxy取最小值，此时z ＝2y 2.x ＋2y －z ＝4y －2y 2＝－2(y 2－2y )＝－2(y －1)2＋2，最大值为2.故选C.4．D 解析：由题意知，ab >0，且3a ＋4b >0，所以a >0，b >0.又log 4(3a ＋4b )＝log 2ab ，所以3a ＋4b ＝ab .所以4a ＋3b ＝1.所以a ＋b ＝(a ＋b )·⎝⎛⎭⎫4a ＋3b ＝7＋4b a ＋3a b ≥7＋2 4b a ·3a b ＝7＋4 3.当且仅当4b a ＝3ab，即a ＝4＋2 3，b ＝3＋2 3时，等号成立．故选D.5．C 解析：∵1a ＋2b ＝ab ，∴a ＞0，b ＞0.∵ab ＝1a ＋2b ≥2 1a ·2b ＝2 2ab，∴ab ≥22(当且仅当b ＝2a 时取等号)，∴ab 的最小值为2 2.故选C.6．C 解析：p ＝f (ab )＝ln ab ＝12ln(ab )，q ＝f ⎝⎛⎭⎫a ＋b 2＝ln a ＋b 2，r ＝12[f (a )＋f (b )]＝12ln(ab )．因为a ＋b 2＞ab ，由f (x )＝ln x 在区间(0，＋∞)内是增函数，可知f ⎝⎛⎭⎫a ＋b 2＞f (ab )，所以q ＞p ＝r .故选C.7．A 解析：方法一，由x ＋2y －xy ＝0，得2x ＋1y＝1，且x >0，y >0.∴x ＋2y ＝(x ＋2y )·⎝⎛⎭⎫2x ＋1y ＝4y x ＋xy＋4≥4＋4＝8(当且仅当x ＝4，y ＝2等号成立)． 方法二，由x ＋2y ＝xy ＝12x ·2y ≤12⎝⎛⎭⎫x ＋2y 22＝()x ＋2y 28，∴x ＋2y ≥8(当且仅当x ＝2y 时取等号)．8．3 解析：由x 2＋2xy －3＝0，得y ＝3－x 22x ＝32x －12x .则2x ＋y ＝2x ＋32x －12x ＝3x 2＋32x ≥2 3x 2·32x＝3，当且仅当x ＝1时，等号成立．所以(2x＋y )min ＝3.9．(1)9 (2)1解析：(1)因为x ＞－1，所以x ＋1＞0，所以y ＝(x ＋5)(x ＋2)x ＋1＝x 2＋7x ＋10x ＋1＝(x ＋1)2＋5(x ＋1)＋4x ＋1＝(x ＋1)＋4x ＋1＋5≥2 (x ＋1)·4x ＋1＋5＝9.当且仅当x ＋1＝4x ＋1，即x ＝1时等号成立．故函数y ＝(x ＋5)(x ＋2)x ＋1的最小值为9.(2)因为x ＜54，所以5－4x ＞0.则f (x )＝4x －2＋14x －5＝－⎝⎛⎭⎫5－4x ＋15－4x ＋3≤－2＋3＝1.当且仅当5－4x ＝15－4x ，即x ＝1时，等号成立．故f (x )＝4x －2＋14x －5的最大值为1.10．(1)B (2)6解析：2a ＋1b ＝2(2a ＋b )a ＋2a ＋b b ＝4＋2b a ＋2a b ＋1＝5＋2⎝⎛⎭⎫b a ＋a b ≥5＋2×2 b a ·a b＝9. 当且仅当a ＝b ＝13时取等号．∵2a ＋1b ≥m ，∴m ≤9，即m 的最大值等于9.故选B.(2)由已知，得x ＝9－3y1＋y.方法一，(消元法)∵x >0，y >0，∴0<y <3.∴x ＋3y ＝9－3y 1＋y ＋3y ＝121＋y ＋(3y ＋3)－6≥2 121＋y ·(3y ＋3)－6＝6.当且仅当121＋y＝3y ＋3，即y ＝1，x ＝3时，取等号，故(x ＋3y )min ＝6.方法二，∵x >0，y >0，9－(x ＋3y )＝xy ＝13x ·(3y )≤13·⎝⎛⎭⎫x ＋3y 22，当且仅当x ＝3y 时等号成立．设x ＋3y ＝t >0，则t 2＋12t －108≥0. ∴(t －6)(t ＋18)≥0. 又t >0，∴t ≥6.故当x ＝3，y ＝1时，(x ＋3y )min ＝6.第4讲 简单的线性规划1．D 解析：如图D116，画出可行域．图D116z ＝x ＋2y 表示斜率为－12的一组平行线，当过点C (3，3)时，目标函数取得最大值z max＝3＋2×3＝9.2．B 解析：将点(0,0)，(2,0)，(0,3)代入z ＝x －y 解得0,2，－3.所以z ＝x －y 的取值范围是[－3,2]．故选B.3．B 解析：作出不等式组表示的平面区域(如图D117)，因为z ＝x ＋y －2x ＋1＝y －3x ＋1＋1表示平面区域内的点与点(－1，3)之间连线的斜率k 与1的和．由图知，当x ＝0，y ＝－2时，k 取得最小值k min ＝－2－30＋1＝－5；当x ＝0，y ＝3时，k 取得最大值k max ＝3－30＋1＝0.所以z ∈[－4，1]．故选B.图D1174．B 解析：根据题中约束条件可画出可行域如图D118.两直线交点坐标为A ⎝⎛⎭⎫a －12，a ＋12.又由z ＝x ＋ay 知，当a ＝0时，A ⎝⎛⎭⎫－12，12，z 的最小值为－12，不合题意；当a ≥1时，y ＝－1a x ＋za 过点A 时，z 有最小值，即z ＝a －12＋a ×a ＋12＝a 2＋2a －12＝7，解得a ＝3或a ＝－5(舍去)；当a <1时，z 无最小值．故选B.图D1185．C 解析：区域M 是一个三角形区域，三个顶点的坐标分别是(8,3)，(10,2)，(9,1)，结合图形检验，可知：当a ∈[2,9]时，符合题目要求．6．D 解析：如图D119，由y ＝ax ＋z 知z 的几何意义是直线在y 轴上的截距，故当a >0时，要使z ＝y －ax 取得最大值的最优解不唯一，则a ＝2；当a <0时，要使z ＝y －ax 取得最大值的最优解不唯一，则a ＝－1.图D1197．1 解析：不等式组表示的区域如图D120所示的阴影部分，图D120由x ＝1，x ＋y ＝0，得A (1，－1)； 由x ＝1，x －y －4＝0，得B (1，－3)； 由x ＋y ＝0，x －y －4＝0，得C (2，－2)．∴|AB |＝2.∴S △ABC ＝12×2×1＝1.8.⎣⎡⎦⎤45，13 解析：由图D121知，原点到直线2x ＋y －2＝0的距离平方为x 2＋y 2的最小值，为⎝⎛⎭⎫ 252＝45；原点到点(2,3)距离平方为x 2＋y 2的最大值，为13.因此x 2＋y 2的取值范围为⎣⎡⎦⎤45，13.图D1219．解：由约束条件⎩⎪⎨⎪⎧x －4y ＋3≤0，3x ＋5y －25≤0，x ≥1，作出(x ，y )的可行域如图D122所示的阴影部分．图D122由⎩⎪⎨⎪⎧ x ＝1，3x ＋5y －25＝0，解得A ⎝⎛⎭⎫1，225. 由⎩⎪⎨⎪⎧x ＝1，x －4y ＋3＝0，解得C (1,1)． 由⎩⎪⎨⎪⎧x －4y ＋3＝0，3x ＋5y －25＝0，解得B (5,2)． (1)∵z ＝y x ＝y －0x －0，∴z 的值即是可行域中的点与原点O 连线的斜率．观察图形可知z min＝k OB ＝25.(2)z ＝x 2＋y 2的几何意义是可行域上的点到原点O 的距离的平方． 结合图形可知，可行域上的点到原点的距离中， d min ＝|OC |＝2，d max ＝|OB |＝29. 故z 的取值范围是[2,29]．(3)z ＝x 2＋y 2＋6x －4y ＋13＝(x ＋3)2＋(y －2)2的几何意义是可行域上的点到点(－3,2)的距离的平方．结合图形可知，可行域上的点到(－3,2)的距离中， d min ＝1－(－3)＝4，d max ＝(－3－5)2＋(2－2)2＝8. 故z 的取值范围是[16,64]．10．解：g (x )＝x 2＋(a ＋1)x ＋a ＋b ＋1，两个零点为方程x 2＋(a ＋1)x ＋a ＋b ＋1＝0的两根，且一根大于1，另一根大于0且小于1，由根的分布画图，得⎩⎪⎨⎪⎧ g (0)>0，g (1)<0，即⎩⎪⎨⎪⎧a ＋b ＋1>0，2a ＋b ＋3<0.作出可行域如图D123.图D123而b a ＝b －0a －0表示可行域中的点(a ，b )与原点连线的斜率k ，直线OA 的斜率k 1＝－12，直线2a ＋b ＋3＝0的斜率k 2＝－2.所以k ∈⎝⎛⎭⎫－2，－12，即ba ∈⎝⎛⎭⎫－2，－12. 第5讲 不等式的应用1．C 解析：yx＝－⎝⎛⎭⎫x ＋25x ＋12≤－2 x ×25x ＋12，当且仅当x ＝25x，即x ＝5时取等号．2．C 解析：作出不等式组对应的平面区域，由⎩⎪⎨⎪⎧ x －4y ＝－3，x ＝1解得⎩⎪⎨⎪⎧x ＝1，y ＝1，设A (1,1)，由图可知，直线2x ＋y ＝m 经过点A 时，m 取最小值，同时z ＝4x ·2y ＝22x ＋y 取得最小值．所以z min ＝22×1＋1＝23＝8.故选C.3．B 解析：设楼房每平方米的平均综合费用为f (x )元，则f (x )＝(560＋48x )＋2160×10 0002000x＝560＋48x ＋10 800x＝560＋48⎝⎛⎭⎫x ＋225x ≥560＋48×2 x ·225x＝2000(x ≥10，x ∈N *)．当且仅当x ＝225x，即x ＝15时，f (x )取得最小值为f (15)＝2000.4．D 解析：设公比为q .因为a 2＝1＝a 1q ，所以S 3＝a 1＋1＋a 1q 2＝1q＋q ＋1.当q >0时，1q ＋q ≥2；当q <0时，1q＋q ≤－2.所以S 3≥3或S 3≤－1.故选D. 5．B 解析：设黄瓜和韭菜的种植面积分别为x ，y 亩，种植总利润为z 万元，则目标函数z ＝(0.55×4x －1.2x )＋(0.3×6y －0.9y )＝x ＋0.9y .作出约束条件如图D124所示的阴影部分．易求得点A (0,50)，B (30,20)，C (45,0)．平移直线x ＋0.9y ＝0，当直线x ＋0.9y ＝0经过点B (30,20)时，z 取得最大值为48.故选B.图D124 图D1256．C 解析：设旅行社租用A 型客车x 辆，B 型客车y 辆，租金为z 元，则线性约束条件为⎩⎪⎨⎪⎧x ＋y ≤21，y －x ≤7，36x ＋60y ≥900，x ，y ∈N ，目标函数为z ＝1600x ＋2400y .画出可行域：如图D125所示的阴影部分，可知当目标函数过点(5,12)时，有最小值z min ＝36 800(元)．7．30 解析：总费用4x ＋600x ×6＝4⎝⎛⎭⎫x ＋900x ≥4×2900＝240.当且仅当x ＝900x，即x ＝30时等号成立．8．(1)1900 (2)100解析：(1)当l ＝6.05时，F ＝76 000v v 2＋18v ＋20l ＝76 000v ＋121v ＋18≤76 0002 v ·121v ＋18＝76 00022＋18＝1900，当且仅当v ＝121v ，即v ＝11时，等号成立．(2)当l ＝5时，F ＝76 000v v 2＋18v ＋20l ＝76 000v ＋100v ＋18≤76 0002 v ·100v ＋18＝76 00020＋18＝2000，当且仅当v ＝100v ，即v ＝10时，等号成立．此时车流量比(1)中的最大车流量增加100辆/时． 9．解：(1)①当x ∈[50,80)时，y ＝175(x 2－130x ＋4900)＝175[(x －65)2＋675] 当x ＝65时，y 有最小值175×675＝9.②当x ∈[80,120]时，函数单调递减，故当x ＝120时，y 有最小值10. 因为9<10，故当x ＝65时每小时耗油量最低．(2)设总耗油量为l ，由题意，可知l ＝y ·120x .①当x ∈[50,80)时，l ＝y ·120x ＝85⎝⎛⎭⎫x ＋4900x －130≥85⎝⎛⎭⎫2 x ×4900x －130＝16. 当且仅当x ＝4900x ，即x ＝70时，l 取得最小值16.②当x ∈⎣⎢⎡⎦⎥⎤80120时，l ＝y ·120x ＝1440x －2为减函数，当x ＝120时，l 取得最小值10.因为10<16，所以当速度为120时，总耗油量最少．10．解：(1)由已知，x ，y满足的数学关系式为⎩⎪⎨⎪⎧70x ＋60y ≤600，5x ＋5y ≥30，x ≤2y ，x ≥0，y ≥0，即⎩⎪⎨⎪⎧7x ＋6y ≤60，x ＋y ≥6，x －2y ≤0，x ≥0，y ≥0，该二元一次不等式组所表示的平面区域为如图D126中的阴影部分．图D126 图D127 (2)设总收视人次为z 万， 则目标函数为z ＝60x ＋25y .考虑z ＝60x ＋25y ，将它变形为y ＝－125x ＋z 25，这是斜率为－125，随z 变化的一族平行直线.z 25为直线在y 轴上的截距，当z25取得最大值时，z 的值最大．又因为x ，y 满足约束条件，所以由图D127可知，当直线z ＝60x ＋25y 经过可行域上的点M 时，截距z25最大，即z最大．解方程组⎩⎪⎨⎪⎧7x ＋6y ＝60，x －2y ＝0得点M 的坐标为(6,3)．所以，电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多。

阶段检测卷(一)(函数与导数)时间：50分钟 满分：100分一、选择题：本大题共8小题，每小题6分，共48分，有且只有一个正确答案，请将正确选项填入题后的括号中．1．(2017年广东深圳二模)已知集合A ＝{x |x 2－2x <0}，B ＝{x ||x |<2}，则( ) A ．A ∩B ＝∅ B ．A ∩B ＝A C ．A ∪B ＝A D ．A ∪B ＝R2．已知方程x 2＋y 2a＝1(a 是常数)，则下列结论正确的是( )A ．对任意实数a ，方程表示椭圆B ．存在实数a ，使方程表示椭圆C ．对任意实数a ，方程表示双曲线D ．存在实数a ，使方程表示抛物线3．定义在R 上的奇函数f (x )满足f (x －2)＝－f (x )，且在[0,1]上是增函数，则有( )A ．f ⎝⎛⎭⎫14<f ⎝⎛⎭⎫－14<f ⎝⎛⎭⎫32B ．f ⎝⎛⎭⎫－14<f ⎝⎛⎭⎫14<f ⎝⎛⎭⎫32C ．f ⎝⎛⎭⎫14<f ⎝⎛⎭⎫32<f ⎝⎛⎭⎫－14D ．f ⎝⎛⎭⎫－14<f ⎝⎛⎭⎫32<f ⎝⎛⎭⎫14 4．(2017年广东深圳一模) 函数f (x )＝2x ＋12x －1·cos x 的图象大致是()A B C D 5．若关于x 的不等式x 3－3x 2－9x ＋2≥m 对任意x ∈[－2,2]恒成立，则m 的取值范围是( )A ．(－∞，7]B ．(－∞，－20]C ．(－∞，0]D ．[－12,7]6．已知函数f (x )＝log a (ax －1)在[2,3]上单调递减，则a 的取值范围是( )A ．(1，＋∞) B.⎝⎛⎭⎫0， 12 C.⎝⎛⎭⎫0，13 D.⎝⎛⎭⎫12，1 7．(2016年新课标Ⅱ)已知函数f (x )(x ∈R )满足f (x )＝f (2－x )，若函数y ＝|x 2－2x －3| 与y ＝f (x )图象的交点为(x 1，y 1)，(x 2，y 2)，…，(x m ，y m )，则1mi i x =∑＝( )A ．0B ．mC ．2mD ．4m8．若函数f(x)在R 上可导，且满足f (x )<xf ′(x )，则( ) A ．2f (1)<f (2) B ．2f (1)>f (2) C ．2f (1)＝f (2) D ．f (1)＝f (2)二、填空题：本大题共3小题，每小题6分，共18分，把答案填在题中横线上． 9．(2015年新课标Ⅱ)已知曲线y ＝x ＋ln x 在点(1,1)处的切线与曲线y ＝ax 2＋(a ＋2)x ＋1相切，则a ＝______________.10．若函数f (x )＝⎩⎪⎨⎪⎧x ＋1，x ≤0，log 2x ，x ＞0，则函数y ＝f [f (x )]＋1的所有零点所构成的集合为______________．11．(2017年山东)若函数e x f (x )(e ＝2.718 28…是自然对数的底数)在f (x )的定义域上单调递增，则称函数f (x )具有M 性质．下列函数中所有具有M 性质的函数的序号为________．①f (x )＝2－x ；②f (x )＝3－x ； ③f (x )＝x 3； ④f (x )＝x 2＋2.三、解答题：本大题共2小题，共34分，解答须写出文字说明、证明过程或推演步骤．12．(14分)(2017年湖北襄阳一模)已知函数f (x )＝4ln x －x ，g (x )＝ax 2＋ax ＋1(a ∈R )． (1)求函数f (x )的单调区间；(2)若af (x )>g (x )对任意x ∈(0，＋∞)恒成立，求实数a 的取值范围． 13．(20分)(2017年广东调研)已知函数f (x )＝a 2ln x －x 2＋ax (a ≠0)，g (x )＝(m －1)x 2＋2mx －1.(1)求函数f (x )的单调区间；(2)若a ＝1，关于x 的不等式f (x )≤g (x )恒成立，求整数m 的最小值．阶段检测卷(一)1．B 解析：因为集合A ＝{x |x 2－2x <0}＝{x |0<x <2}，B ＝{x ||x |<2}＝{x |－2<x <2}，所以A ∩B ＝{x |0<x <2}＝A .故选B.2．B 解析：显然当a >1时，该方程表示椭圆．故选B.3．B 解析：因为f (x －2)＝－f (x )，所以T ＝4，且关于x ＝－1对称，由奇函数和单调性得到f ⎝⎛⎭⎫－14<f ⎝⎛⎭⎫14<f ⎝⎛⎭⎫32.故选B. 4．C 解析：f (－x )＝2－x ＋12－x －1cos(－x )＝－2x ＋12x －1cos x ＝－f (x )，则函数f (x )为奇函数，图象关于原点对称，排除A ，B ；当x ∈⎝⎛⎭⎫0，π2时，f (x )＞0，所以排除D.故选C. 5．B 解析：令f (x )＝x 3－3x 2－9x ＋2， 则f ′(x )＝3x 2－6x －9.令f ′(x )＝0，得x ＝－1或x ＝3(舍去)．∵f (－1)＝7，f (－2)＝0，f (2)＝－20，∴f (x )的最小值为f (2)＝－20.故m ≤－20.6．D 解析：由于a ＞0，且a ≠1，∴u ＝ax －1为增函数，∴若函数f (x )为减函数，则f (x )＝log a u 必为减函数，因此0<a <1.又y ＝ax －1在[2,3]上恒为正，∴2a －1＞0，即a ＞12.故选D.7．B 解析：因为y ＝f (x )，y ＝|x 2－2x －3|都关于x ＝1对称，所以它们交点也关于x ＝1对称，当m 为偶数时，其和为2×m2＝m ；当m 为奇数时，其和为2×m －12＋1＝m .故选B.8．A 解析：由于f (x )<xf ′(x )，所以⎝⎛⎭⎫f (x )x ′＝f ′(x )x －f (x )x 2>0恒成立，因此f (x )x 在R 上是单调递增函数．∴f (2)2>f (1)1，即f (2)>2f (1)．故选A.9．8 解析：由y ＝x ＋ln x ，得y ′＝1＋1x，得曲线在点(1,1)的切线的斜率为k ＝y ′|x ＝1＝2.所以切线方程为y －1＝2(x －1)，即y ＝2x －1.此切线与曲线y ＝ax 2＋(a ＋2)x ＋1相切，消去y 得ax 2＋ax ＋2＝0，得a ≠0，且Δ＝a 2－8a ＝0，解得a ＝8.10.⎩⎨⎧⎭⎬⎫－3，－12，14，2 解析：本题即求方程f [f (x )]＝－1的所有根的集合，先解方程f (t )＝－1，即⎩⎪⎨⎪⎧ t ≤0，t ＋1＝－1，或⎩⎪⎨⎪⎧t ＞0，log 2t ＝－1，得t ＝－2，或t ＝12.再解方程f (x )＝－2，f (x )＝12，即⎩⎪⎨⎪⎧ x ≤0，x ＋1＝－2，或⎩⎪⎨⎪⎧x ＞0，log 2x ＝－2，或⎩⎪⎨⎪⎧x ≤0，x ＋1＝12，或⎩⎪⎨⎪⎧x ＞0，log 2x ＝12，得x ＝－3，或x ＝14，或x ＝－12，或x ＝ 2.11．①④ 解析：①e x f (x )＝e x ·2－x ＝⎝⎛⎭⎫e 2x ，在R 上单调递增，故f (x )＝2－x具有M 性质； ②e x f (x )＝e x ·3－x ＝⎝⎛⎭⎫e 3x ，在R 上单调递减，故f (x )＝3－x不具有M 性质； ③e x f (x )＝e x ·x 3，令g (x )＝e x ·x 3，则g ′(x )＝e x ·x 3＋e x ·3x 2＝x 2e x (x ＋3)，∴当x >－3时，g ′(x )>0，当x <－3时，g ′(x )<0.∴e x f (x )在(－∞，－3)上单调递减，在(－3，＋∞)上单调递增．故f (x )＝x 3不具有M 性质；④e x f (x )＝e x (x 2＋2)，令g (x )＝e x (x 2＋2)，则g ′(x )＝e x (x 2＋2)＋e x ·2x ＝e x [(x ＋1)2＋1]>0，∴e x f (x )＝e x (x 2＋2)在R 上单调递增，故f (x )＝x 2＋2具有M 性质．12．解：(1)∵f ′(x )＝4x －1＝4－x x，∴函数f (x )的单调递增区间是(0,4]，单调递减区间是[4，＋∞)． (2)不等式af (x )>g (x )等价于4a ln x －ax 2－2ax －1>0. ① 当a ＝0时，①不成立；当a > 0时，①化为1a <4ln x －x 2－2x ； ②当a < 0时，①化为1a>4ln x －x 2－2x . ③令h (x )＝4ln x －x 2－2x (x > 0)，则h ′(x )＝4x －2x －2＝－2x 2＋2x －4x ＝－2(x －1)(x ＋2)x.∴当x ∈(0,1)时，h ′(x )>0；当x ∈(1，＋∞)时，h ′(x )<0. ∴h (x )在(0,1)上是增函数，在(1，＋∞)上是减函数． ∴h max (x )＝h (1)＝－3. 因此②不成立．要③成立，只要1a >－3，解得a <－13.∴所求实数a 的取值范围是⎝⎛⎭⎫－∞，－13. 13．解：(1)f ′(x )＝a2x －2x ＋a ＝－2x 2－ax －a 2x ＝－(2x ＋a )(x －a )x(x >0)．①当a >0时，由f ′(x )>0，得0<x <a ，由f ′(x )<0，得x >a .所以f (x )的单调递增区间为(0，a )，单调递减区间为(a ，＋∞)．②当a <0时，由f ′(x )>0，得0<x <－a2，由f ′(x )<0，得x >－a2.所以f (x )的单调递增区间为⎝⎛⎭⎫0，－a 2，单调递减区间为⎝⎛⎭⎫－a2，＋∞. (2)令F (x )＝f (x )－g (x )＝ln x －mx 2＋(1－2m )x ＋1(x >0)，F ′(x )＝1x －2mx ＋1－2m ＝－2mx 2＋(1－2m )x ＋1x ＝－(2mx －1)(x ＋1)x.当m ≤0时，F ′(x )>0，所以函数F (x )在(0，＋∞)上单调递增．而F (1)＝ln 1－m ×12＋(1－2m )＋1＝－3m ＋2>0，所以关于x 的不等式f (x )≤g (x )不恒成立．故m ≤0时不满足题意．当m >0时，当0<x <12m 时，F ′(x )>0；当x >12m 时，F ′(x )<0，所以函数F (x )在⎝⎛⎭⎫0，12m 上单调递增，在⎝⎛⎭⎫12m ，＋∞上单调递减． 所以F (x )max ＝F ⎝⎛⎭⎫12m ＝ln 12m －m ⎝⎛⎭⎫12m 2＋(1－2m )×12m ＋1＝14m－ln(2m )． 令h (m )＝14m －ln(2m )，因为h ⎝⎛⎭⎫12＝12，h (1)＝14－ln 2<0， 又h (m )在(0，＋∞)上是减函数，所以当m ≥1时，h (m )<0.故整数m 的最小值为1.。

阶段检测卷(二)(三角函数、平面向量与解三角形)时间：50分钟 满分：100分一、选择题：本大题共8小题，每小题6分，共48分，有且只有一个正确答案，请将正确选项填入题后的括号中．1．下列函数中，既是偶函数又在区间(0，π)上单调递减的是( )A ．y ＝sin xB ．y ＝cos xC ．y ＝sin 2xD ．y ＝cos 2x2．已知倾斜角为θ的直线与直线x －3y ＋1＝0垂直，则23sin 2θ－cos 2θ＝( ) A.103 B ．－103C.1013 D ．－10133．已知O ，A ，B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC→＝( )A ．2OA →－OB → B ．－OA →＋2OB →C.23OA →－13OB → D ．－13OA →＋23OB → 4．如图N2-1，点P 是函数y ＝2sin(ωx ＋φ)(x ∈R ，ω>0)的图象的最高点，M ，N 是图象与x 轴的交点，若PM →·PN →＝0，则ω＝( )图N2-1A ．8 B.π8 C.π4 D.π2 5．设函数f (x )＝sin ⎝⎛⎭⎫2x －π3的图象为C ，下面结论中正确的是( ) A ．函数f (x )的最小正周期是2πB ．图象C 关于点⎝⎛⎭⎫π6，0对称C ．图象C 可由函数g (x )＝sin 2x 的图象向右平移π3个单位得到 D ．函数f (x )在区间⎝⎛⎭⎫－π12，π2上是增函数 6．如图N2-2，某船在海上航行中遇险发出呼救信号，海上救生艇在A 处获悉后，立即测出该船在方位角45°方向，相距10海里的C 处，还测得该船正沿方位角105°的方向以9海里/时的速度行驶．若救生艇立即以21海里/时的速度前往营救，则救生艇与呼救船在B 处相遇所需的最短时间为( )图N2-2A.15小时B.13小时 C.25小时 D.23小时 7．函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫其中A >0，|φ|<π2的图象如图N2-3，为了得到g (x )＝cos ⎝⎛⎭⎫2x －π2的图象，只需将f (x )的图象( )图N2-3 A ．向左平移π3个长度单位 B ．向右平移π3个长度单位 C ．向左平移π6个长度单位 D ．向右平移π6个长度单位 8．(2017年新课标Ⅱ)已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则P A →·(PB →＋PC →)的最小值是( )A ．－2B ．－32C ．－43D ．－1 二、填空题：本大题共3小题，每小题6分，共18分，把答案填在题中横线上． 9.sin 47°－sin 17°cos 30°cos 17°＝________. 10．在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知△ABC 的面积为315，b －c ＝2，cos A ＝－14，则a 的值为____________． 11．已知在△ABC 中，BC 边上的高与BC 边长相等，则AC AB ＋AB AC ＋BC 2AB ·AC的最大值是________．三、解答题：本大题共2小题，共34分，解答须写出文字说明、证明过程或演算步骤．12．(14分)(2017年广东肇庆一模)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a (sin A －sin B )＝(c －b )(sin C ＋sin B )．(1)求角C ；(2)若c ＝7，△ABC 的面积为3 32，求△ABC 的周长．13．(20分)(2017年广东调研)已知在△ABC中，角A，B，C所对的边分别为a，b，c，且2a cos2C＋2c cos A cos C＋b＝0.(1)求角C的大小；(2)若b＝4sin B，求△ABC面积的最大值．阶段检测卷(二)1．B 解析：A ，C 均为奇函数；y ＝cos 2x 在⎝⎛⎭⎫0，π2上单调递减，在⎝⎛⎭⎫π2，π上单调递增．故选B.2．C 解析：直线x －3y ＋1＝0的斜率为13，因此与此直线垂直的直线的斜率k ＝－3.∴tan θ＝－3.∴23sin 2θ－cos 2θ＝2(sin 2θ＋cos 2θ)3sin 2θ－cos 2θ＝2(tan 2θ＋1)3tan 2θ－1.把tan θ＝－3代入，得原式＝2×[(－3)2＋1]3×(－3)2－1＝1013. 3．A 解析：由2AC →＋CB →＝0，得2OC →－2OA →＋OB →－OC →＝0.故OC →＝2OA →－OB →.4．C 解析：由题意，可得点P 到MN 的距离为2，PM ⊥PN ，所以△PMN 为等腰直角三角形．所以MN ＝2×2＝4.所以函数的周期为8，即ω＝π4.故选C. 5．B 解析：f (x )的最小正周期T ＝2π2＝π.故A 错；∵f ⎝⎛⎭⎫π6＝0，∴图象C 关于点⎝⎛⎭⎫π6，0对称．故B 对；∴图象C 可由函数g (x )＝sin 2x 的图象向右平移π6个单位得到．故C 错；函数f (x )的单调递增区间是⎣⎡⎦⎤－π12＋k π，5π12＋k π(k ∈Z )，当k ＝0时，x ∈⎣⎡⎦⎤－π12，5π12⎣⎡⎦⎤－π12，π2，∴函数f (x )在区间⎝⎛⎭⎫－π12，π2上是先增后减．故D 错． 6．D 解析：设在点B 处相遇，所需时间为t 小时．在△ABC 中，∠ACB ＝120°，AC＝10，AB ＝21t ，BC ＝9t .由余弦定理，得(21t )2＝102＋(9t )2－2×10×9t ×cos 120°.整理，得36t 2－9t －10＝0.解得t ＝23或－512(舍去)．故救生艇与呼救船在B 处相遇所需的最短时间为23小时．7．D 解析：由图象知A ＝1，T 4＝7π12－π3⇒T ＝π，2πω＝π⇒ω＝2，f ⎝⎛⎭⎫7π12＝－1 ⇒2×7π12＋φ＝3π2＋2k π，|φ|<π2，得φ＝π3.∴f (x )＝sin ⎝⎛⎭⎫2x ＋π3.为了得到g (x )＝cos ⎝⎛⎭⎫2x －π2＝sin 2x 的图象，所以只需将f (x )的图象向右平移π6个长度单位即可．故选D. 8．B 解析：以BC 的中点D 为原点，BC 所在直线为x 轴，BC 的垂直平分线AD 为y 轴，建立平面直角坐标系如图D189，图D189则A (0，3)，B (－1,0)，C (1,0)．设P (x ，y )．所以P A →＝(－x ，3－y )，PB →＝(－1－x ，－y )，PC →＝(1－x ，－y )，则P A →·(PB →＋PC →)＝2x 2－2y (3－y )＝2x 2＋2⎝⎛⎭⎫y －322－32≥－32. 当点P ⎝⎛⎭⎫0，32时，所求最小值为－32.故选B. 9.12 解析：sin 47°－sin 17°cos 30°cos 17°＝sin (30°＋17°)－sin 17°cos 30°cos 17°＝sin 30°cos 17°＋cos 30°sin 17°－sin 17°cos 30°cos 17°＝sin 30°cos 17°cos 17°＝12. 10．8 解析：因为0<A <π，所以sin A ＝1－cos 2A ＝154.又S △ABC ＝12bc sin A ＝158bc ＝315，∴bc ＝24.解方程组⎩⎪⎨⎪⎧ b －c ＝2，bc ＝24得⎩⎪⎨⎪⎧b ＝6，c ＝4.由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝62＋42－2×6×4×⎝⎛⎭⎫－14＝64.所以a ＝8. 11．2 2 解析：BC 边上的高与BC 边长相等，根据面积公式， 得12BC 2＝12AB ·AC ·sin A ， 即BC 2＝AB ·AC ·sin A .AC AB ＋AB AC ＋BC 2AB ·AC ＝AC 2＋AB 2＋BC 2AB ·AC＝BC 2＋2AB ·AC ·cos A ＋BC 2AB ·AC＝2AB ·AC ·sin A ＋2AB ·AC ·cos A AB ·AC＝2sin A ＋2cos A ＝2 2sin ⎝⎛⎭⎫A ＋π4≤2 2. 12．解：(1)由已知以及正弦定理，得a (a －b )＝(c －b )(c ＋b )，即a 2＋b 2－c 2＝ab .所以cos C ＝a 2＋b 2－c 22ab ＝12. 又C ∈(0，π)，所以C ＝π3. (2)由(1)知a 2＋b 2－c 2＝ab ，所以(a ＋b )2－3ab ＝c 2＝7.又S ＝12ab ·sin C ＝34ab ＝3 32，所以ab ＝6. 所以(a ＋b )2＝7＋3ab ＝25.即a ＋b ＝5.所以△ABC 周长为a ＋b ＋c ＝5＋7.13．解：(1)∵2a cos 2C ＋2c cos A cos C ＋b ＝0，∴2sin A cos 2C ＋2sin C cos A cos C ＋sin B ＝0.∴2cos C sin(A ＋C )＋sin B ＝0.∴2cos C sin B ＋sin B ＝0.∵0°<B <180°，∴sin B ≠0.∴cos C ＝－12.∴C ＝120°.(2)根据(1)并由正弦定理，得c ＝b sin C sin B＝2 3. 由余弦定理，得(2 3)2＝a 2＋b 2－2ab cos 120°＝a 2＋b 2＋ab ≥3ab .∴ab ≤4.∴S △ABC ＝12ab sin C ≤ 3. ∴△ABC 面积的最大值为 3.。

阶段检测卷 (二)(三角函数、平面向量与解三角形)时间： 50 分钟 满分： 100 分一、选择题：本大题共 8 小题，每题 6 分，共 48 分，有且只有一个正确答案，请将正确选项填入题后的括号中．1．以下函数中，既是偶函数又在区间 (0， π)上单一递减的是 ()A ． y ＝ sin xB ．y ＝ cos xC ．y ＝ sin 2xD ． y ＝ cos 2x2．已知倾斜角为 θ的直线与直线 x － 3y ＋ 1＝ 0 垂直，则2＝ ()2 23sin θ－ cos θ 10 10A.3 B ．－31010C.13 D ．－ 133．已知 O ，A ，B 是平面上的三个点，直线 → → →AB 上有一点 C ，知足 2AC ＋ CB ＝ 0，则 OC＝()→ →→ → A ．2OA － OB B ．－ OA ＋ 2OB 2 → 1 → D ．－ 1 → 2 →C. OA － OB 3 OA ＋ OB3 3 34．如图 N2- 1，点 P 是函数 y ＝ 2sin(ωx＋ φ)(x ∈ R ，ω>0)的图象的最高点， M ，N 是图象→ →与 x 轴的交点，若 PM ·PN ＝ 0，则 ω＝ ( )图 N2-1πππA ．8 B.8C.4D.25．设函数 f( x)＝ sin 2x － π的图象为 C ，下边结论中正确的选项是 ()3A ．函数 f(x) 的最小正周期是 2ππ 对称 B ．图象 C 对于点 ， 06π C ．图象 C 可由函数 g(x)＝sin 2x 的图象向右平移 个单位获得3D ．函数 f(x) 在区间 －π， π上是增函数 12 26．如图 N2- 2，某船在海上航行中遇险发出呼救信号，海上救生艇在 A 处获悉后，立刻 测出该船在方向角 45°方向，相距 10 海里的 C 处，还测得该船正沿方向角 105°的方向以 9 海里 /时的速度行驶．若救生艇立刻以 21 海里 /时的速度前去救援，则救生艇与呼救船在B 处相遇所需的最短时间为 ()图 N2-2A. 1小时 B.1小时5 3C. 2小时D.2小时537．函数 f(x) ＝Asin(ωx＋φ) 此中 A>0， |φ|<π的图象如图 N2-3，为了获得 g(x)＝ cos 2x － π22 的图象，只要将 f(x)的图象 ( )图 N2-3πA ．向左平移 3个长度单位π B ．向右平移 3个长度单位π C ．向左平移 6个长度单位πD ．向右平移 6个长度单位8． (2017 年新课标Ⅱ )已知△ ABC 是边长为 2 的等边三角形， P 为平面 ABC 内一点，则→ → → ) PA ·(PB ＋PC)的最小值是 (3A ．－ 2B ．－ 24C ．－ 3D ．－ 13 小题，每题 6 分，共 18 分，把答案填在题中横线上．二、填空题：本大题共 sin 47 －°sin 17 cos ° 30 ° 9. cos 17 ° ＝ ________.10．在△ ABC 中，内角 A ，B ，C 所对的边分别为 a ，b ，c ，已知△ ABC 的面积为 315，1，则 a 的值为 ____________ ．b －c ＝ 2， cos A ＝－ 4ACAB BC 211．已知在△ ABC 中， BC 边上的高与 BC 边长相等，则 AB ＋AC ＋AB ·AC 的最大值是________． 2 小题，共 34 分，解答须写出文字说明、证明过程或演算步骤．三、解答题：本大题共12． (14 分 )(2017 年广东肇庆一模 )△ ABC 的内角 A， B，C 的对边分别为 a， b， c，已知a(sin A－ sin B)＝ (c－ b)(sin C＋ sin B)．(1)求角 C；(2)若 c＝ 7，△ ABC 的面积为 33，求△ ABC 的周长．213． (20 分)(2017 年广东调研 )已知在△ ABC 中，角 A， B， C 所对的边分别为a， b， c，且 2acos2C＋ 2ccos Acos C＋ b＝ 0.(1)求角 C 的大小；(2)若 b＝ 4sin B，求△ ABC 面积的最大值．阶段检测卷 (二)1．B 分析：A ，C 均为奇函数； y ＝cos 2x 在 0， π 上单一递减， 在 π2 ，π上单一递加． 故2选 B.2． C 分析： 直线 x －3y ＋ 1＝ 0 的斜率为 1，所以与此直线垂直的直线的斜率 k ＝－ 3.∴3 tan θ＝－ 3.∴ 2 22 sin 2θ＋ cos 2θ 2 tan 2θ＋ 12 ＝2 2 ＝2.把 tan θ＝－ 3 代入，得原式＝ 3sin θ－ cos θ 3sin θ－ cos θ 3tan θ－ 122×[ －3 ＋1]103． A→ → → → → → → → →分析： 由 2AC ＋ CB ＝ 0，得 2OC －2OA ＋ OB － OC ＝ 0.故OC ＝ 2OA － OB.4． C 分析： 由题意，可得点 P 到 MN 的距离为2， PM ⊥PN ，所以△PMN 为等腰直角π三角形．所以 MN ＝2× 2＝ 4.所以函数的周期为8，即 ω＝ 4.应选 C.2πππ5．B分析： f(x)的最小正周期 T ＝ 2＝ π.故 A 错；∵f 6 ＝0，∴图象 C 对于点 6，0 对称．故 B 对；∴图象 C 可由函数 g(x)＝ sin2x 的图象向右平移 π C6个单位获得．故 错；函数π 5ππ 5π π π f(x)的单一递加区间是－ 12＋ k π，12＋ k π(k ∈Z )，当 k ＝ 0 时， x ∈－ 12，12 － 12，2 ，∴函数 f( x)在区间 － π，π上是先增后减．故 D 错．12 26． D 分析： 设在点 B 处相遇，所需时间为 t 小时．在△ ABC 中，∠ACB ＝ 120 °， AC ＝10，AB ＝ 21t ，BC ＝ 9t.由余弦定理， 得(21t)2＝ 102＋ (9t)2 －2× 10× 9t × cos 120 .°整理， 得 36t 22 52 －9t －10＝ 0.解得 t ＝ 3或－ 12(舍去 )．故救生艇与呼救船在 B 处相遇所需的最短时间为 3小时．T 7π π T ＝π， 2π 7π7π 7．D 分析： 由图象知 A ＝ 1，4＝? ω＝ π? ω＝ 2，f 12 ＝－ 1 ? 2×12＋ 12－3 3π π π π πφ＝ 2 ＋ 2k π，|φ|<2，得 φ＝ 3.∴f(x)＝sin 2x ＋3 .为了获得 g(x)＝ cos 2x － 2 ＝sin 2x 的图象，所以只要将 f(x)的图象向右平移 π D. 6个长度单位即可．应选8．B 分析： 以 BC 的中点 D 为原点， BC 所在直线为 x 轴， BC 的垂直均分线 AD 为 y轴，成立平面直角坐标系如图D189 ，图 D189则 A(0， 3)，B(－ 1,0)， C(1,0)．设 P(x ， y)．→ → →所以 PA ＝ (－ x ， 3－ y)，PB ＝ (－1－ x ，－ y)，PC ＝(1 －x ，－ y)，→ → → 2 23 2 3 3 则 PA ·(PB ＋ PC)＝ 2x － 2y( 3－ y)＝ 2x ＋ 2 y － 2 －2≥ － 2.3 3 当点P0，2 时，所求最小值为－ 2.应选 B.1 分析： sin 47 －°sin 17 cos ° 30 °9.2 cos 17 °＝ sin 30°＋ 17°－ sin 17 cos ° 30 °cos 17 °＝ sin 30 cos ° 17 ＋°cos 30 sin ° 17 －°sin 17 cos ° 30 °cos 17 °sin 30 cos ° 17 °1 ＝cos 17 ° ＝ 2.215 △＝ 1 1510． 8 分析： 由于 0<A<π，所以 sin A ＝ 1－ cos A ＝ 4 .又 S ABC 2bcsin A ＝ 8 bcb －c ＝2， b ＝ 6，＝3 15，∴bc ＝ 24.解方程组 得由余弦定理， 得 a 2＝ b 2＋ c 2－ 2bccos A bc ＝ 24 c ＝ 4.＝ 62＋ 42－ 2× 6×4× －14 ＝ 64.所以 a ＝ 8.11． 2 2 分析： BC 边上的高与 BC 边长相等，依据面积公式，2 1得 2BC ＝ 2AB ·AC ·sin A ，1即 BC 2＝ AB ·AC ·sin A.222 2AC ＋AB ＋BCAC ＋ AB ＋ BC＝AB ·ACAB AC AB ·ACBC 2＋ 2AB ·AC ·cos A ＋ BC 2＝AB ·AC2AB ·AC ·sin A ＋2AB ·AC ·cos A＝AB ·ACπ≤2 2. ＝ 2sin A ＋2cos A ＝ 2 2sin A ＋4 12． 解： (1) 由已知以及正弦定理，得 a(a － b)＝ (c － b)(c ＋ b)， 即 a 2＋ b 2－ c 2＝ ab.所以 cos C ＝a 2＋b 2－c 2 12ab＝2.π又 C ∈(0， π)，所以 C ＝3. (2)由 (1) 知 a 2＋ b 2－ c 2＝ ab ， 所以 (a ＋ b)2－ 3ab ＝ c 2＝ 7.13 3 3又 S ＝ 2ab ·sin C ＝ 4 ab ＝ 2 ，所以 ab ＝ 6.2所以 (a ＋ b) ＝ 7＋ 3ab ＝ 25.即 a ＋ b ＝ 5.13．解： (1) ∵2acos2C＋ 2ccos Acos C＋b＝ 0，∴2sin Acos2C＋2sin Ccos Acos C＋ sin B＝0.∴2cos Csin(A＋C)＋ sin B＝0.∴2cos Csin B＋ sin B＝ 0.∵0°<B<180°，∴sin B≠ 0.∴cos C＝－12.∴C＝ 120 °. bsin C＝2 3.(2)依据 (1) 并由正弦定理，得c＝sin B由余弦定理，得(23)2＝ a2＋ b2－ 2abcos 120 ＝° a2＋ b2＋ ab≥3ab.1∴ab≤ 4.∴S△ABC＝2absin C≤3.∴△ABC 面积的最大值为 3.。

阶段检测卷(四)(不等式)时间：50分钟 满分：100分一、选择题：本大题共6小题，每小题6分，共36分，有且只有一个正确答案，请将正确选项填入题后的括号中．1．(2017年新课标Ⅰ)设x ，y 满足约束条件⎩⎪⎨⎪⎧ x ＋3y ≤3，x －y ≥1，y ≥0，则z ＝x ＋y 的最大值为( ) A ．0 B ．1 C ．2 D ．32．(2017年新课标Ⅱ)设x ，y 满足约束条件⎩⎪⎨⎪⎧ 2x ＋3y －3≤0，2x －3y ＋3≥0，y ＋3≥0，则z ＝2x ＋y 的最小值是( )A ．－15B ．－9C ．1D ．93．当x >1时，不等式x ＋1x －1≥a 恒成立，则实数a 的取值范围是( ) A ．(－∞，2] B ．[2，＋∞)C ．[3，＋∞)D ．(－∞，3]4．某辆汽车购买时的费用是15万元，每年使用的保险费、路桥费、汽油费等约为1.5万元．年维修保养费用第一年3000元，以后逐年递增3000元，则这辆汽车报废的最佳年限(即使用多少年的年平均费用最少)是( )A ．8年B ．10年C ．12年D ．15年5．若平面区域⎩⎪⎨⎪⎧ x ＋y －3≥0，2x －y －3≤0，x －2y ＋3≥0夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是( ) A.3 55B. 2C.3 22D. 5 6．(2017年山东)若a >b >0，且ab ＝1，则下列不等式成立的是( )A ．a ＋1b <b 2a <log 2(a ＋b ) B.b 2a <log 2(a ＋b )<a ＋1bC ．a ＋1b <log 2(a ＋b )<b 2aD ．log 2(a ＋b )<a ＋1b <b 2a 二、填空题：本大题共4小题，每小题6分，共24分，把答案填在题中横线上．7．(2013年大纲)记不等式组⎩⎪⎨⎪⎧ x ≥0，x ＋3y ≥4，3x ＋y ≤4所表示的平面区域为D ，若直线y ＝a (x ＋1)与D 有公共点，则a 的取值范围是________．8．定义运算“⊗”：x ⊗y ＝x 2－y 2xy(x ，y ∈R ，xy ≠0)．当x >0，y >0时，x ⊗y ＋(2y )⊗x 的最小值是________．9．已知x ，y ∈R 且满足x 2＋2xy ＋4y 2＝6，则z ＝x 2＋4y 2的取值范围为________．10．已知S n 是数列⎩⎨⎧⎭⎬⎫n 2n －1的前n 项和，若不等式|λ＋1|<S n ＋n 2n －1对一切n ∈N *恒成立，则λ的取值范围是__________．三、解答题：本大题共3小题，共40分，解答须写出文字说明、证明过程或推演步骤．11．(12分)桑基鱼塘是某地一种独具地方特色的农业生产形式，某研究单位打算开发一个桑基鱼塘项目，该项目准备购置一块1800平方米的矩形地块，中间挖出三个矩形池塘养鱼，挖出的泥土堆在池塘四周形成基围(阴影部分X6-5-2)种植桑树，池塘周围的基围宽均为2米，如图，设池塘所占的总面积为S 平方米．(1)试用x 表示S ；(2)当x 取何值时，才能使得S 最大？并求出S 的最大值．图X6-5-212．(12分)某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个，生产一个卫兵需5分钟，生产一个骑兵需7分钟，生产一个伞兵需4分钟，已知总生产时间不超过10小时．若生产一个卫兵可获利润5元，生产一个骑兵可获利润6元，生产一个伞兵可获利润3元．(1)试用每天生产的卫兵个数x 与骑兵个数y 表示每天的利润ω(单位：元)；(2)怎样分配生产任务才能使每天的利润最大，最大利润是多少？13．(14分)已知函数f (x )＝mx x 2＋n(m ，n ∈R )在x ＝1处取到极值2. (1)求f (x )的解析式；(2)设函数g (x )＝ln x ＋a x .若对任意的x 1∈R ，总存在x 2∈[1，e]，使得g (x 2)≤f (x 1)＋72，求实数a 的取值范围．阶段检测卷(四)1．D 解析：可行域如图D190，目标函数z ＝x ＋y 经过A (3，0)时最大，故z max ＝3＋0＝3.故选D.图D1902．A 解析：绘制不等式组表示的可行域(如图D191)，目标函数即y ＝－2x ＋z ，其中z 表示斜率为k ＝－2的直线系与可行域有交点时直线的截距，数形结合可得目标函数在点B (－6，－3)处取得最小值z ＝－12－3＝－15.故选A.图D1913．D 4．B 解析：汽车使用n 年平均费用为15＋1.5n ＋0.3n ＋n (n －1)2×0.3n ＝15n ＋3n 20＋1.65≥2 15n ×3n 20＋1.65＝4.65(万元)，当且仅当15n ＝3n 20，3n 2＝300，n 2＝100，n ＝10，即n ＝10时“＝”成立，故这辆汽车报废的最佳年限为10年．5．B 解析：画出不等式的平面区域如图D192，则⎩⎪⎨⎪⎧x －2y ＋3＝0，x ＋y －3＝0.得A (1,2)．则⎩⎪⎨⎪⎧2x －y －3＝0，x ＋y －3＝0.得B (2,1)． 由题意可知，当斜率为1的两条直线分别过点A 和点B 时，两直线的距离最小，即|AB |＝(1－2)2＋(2－1)2＝ 2.故选B.图D1926．B 解析：方法一，因为a >b >0，且ab ＝1，所以a >1，0<b <1.则b 2a <1，log 2(a ＋b )>log 22ab ＝1,2a ＋1b >a ＋1b >a ＋b ⇒a ＋1b>log 2(a ＋b )．故选B. 方法二，取a ＝2，b ＝12，b 2a ＝18，log 2(a ＋b )＝log 252∈(1,2)，a ＋1b＝4.故选B. 7.⎣⎡⎦⎤12，4 解析：如图D193，将点A (0,4)，C (1,1)分别与点B (－1,0)求斜率，得最小值为12，最大值为4.图D193 8.2 解析：由新定义运算知，x ⊗y ＝x 2－y 2xy ，(2y )⊗x ＝(2y )2－x 22yx ＝4y 2－x 22xy. 因为x >0，y >0，所以x ⊗y ＋(2y )⊗x ＝x 2－y 2xy ＋4y 2－x 22xy ＝x 2＋2y 22xy ≥2 x 2·2y 22xy ＝2 2xy 2xy＝ 2. 当且仅当x ＝2y 时取等号．所以x ⊗y ＋(2y )⊗x 的最小值是 2.9．[4,12] 解析：∵2xy ＝6－(x 2＋4y 2)，而2xy ≤x 2＋4y 22，∴6－(x 2＋4y 2)≤x 2＋4y 22.∴x 2＋4y 2≥4(当且仅当x ＝2y 时取等号)．又∵(x ＋2y )2＝6＋2xy ≥0，即2xy ≥－6.∴z ＝x 2＋4y 2＝6－2xy ≤12.综上所述，4≤x 2＋4y 2≤12.10．－3<λ<1 解析：由S n ＝1＋2×12＋3×122＋…＋(n －1)·12n －2＋n ·12n －1，12S n ＝1×12＋2×122＋…＋(n －1)·12n －1＋n ·12n ，两式相减，得12S n ＝1＋12＋122＋…＋12n －1－n ·12n ＝2－n ＋22n .所以S n ＝4－n ＋22n －1.于是由不等式|λ＋1|<4－22n －1对一切n ∈N *恒成立，得|λ＋1|<2.解得－3<λ<1. 11．解：(1)由题图知，3a ＋6＝x ，∴a ＝x －63. 则总面积S ＝⎝⎛⎭⎫1800x －4·a ＋2a ⎝⎛⎭⎫1800x －6 ＝a ⎝⎛⎭⎫5400x －16＝x －63⎝⎛⎭⎫5400x－16 ＝1832－⎝⎛⎭⎫10 800x ＋16x 3，即S ＝1832－⎝⎛⎭⎫10 800x ＋16x 3(x ＞0)．(2)由S ＝1832－⎝⎛⎭⎫10 800x ＋16x 3，得S ≤1832－2 10 800x ·16x 3＝1832－2×240＝1352. 当且仅当10 800x ＝16x 3，此时，x ＝45. 即当x 为45米时，S 最大，且S 最大值为1352平方米．12．解：(1)依题意每天生产的伞兵个数为100－x －y ，所以利润ω＝5x ＋6y ＋3(100－x －y )＝2x ＋3y ＋300(x ，y ∈N )．(2)约束条件为⎩⎪⎨⎪⎧ 5x ＋7y ＋4(100－x －y )≤600，100－x －y ≥0，x ≥0，y ≥0，x ，y ∈N ，整理，得⎩⎪⎨⎪⎧ x ＋3y ≤200，x ＋y ≤100，x ≥0，y ≥0，x ，y ∈N .目标函数为ω＝2x ＋3y ＋300，作出可行域如图D194，图D194作初始直线l 0：2x ＋3y ＝0，平移l 0，当l 0经过点A 时，ω有最大值，由⎩⎪⎨⎪⎧ x ＋3y ＝200，x ＋y ＝100得⎩⎪⎨⎪⎧x ＝50，y ＝50. 所以最优解为A (50,50)，此时ωmax ＝550元．故每天生产卫兵50个，骑兵50个，伞兵0个时利润最大，且最大利润为550元．13．解：(1)f ′(x )＝m (x 2＋n )－2mx 2(x 2＋n )2＝－mx 2＋mn (x 2＋n )2. 由f (x )在x ＝1处取到极值2，得f ′(1)＝0，f (1)＝2. 即⎩⎪⎨⎪⎧ mn －m (1＋n )2＝0，m 1＋n ＝2，解得⎩⎪⎨⎪⎧m ＝4，n ＝1. 经检验，当m ＝4，n ＝1时，f (x )在x ＝1处取得极值．故f (x )＝4x x 2＋1. (2)由(1)知，f (x )的定义域为R ，且f (－x )＝－f (x )．故f (x )为奇函数，且f (0)＝0.当x ＞0时，f (x )＞0,0<f (x )＝4x ＋1x≤2， 当且仅当x ＝1时取“＝”；当x <0时，－2≤f (x )＝－4(－x )＋1(－x )<0， 当且仅当x ＝－1时，取“＝”．故f (x )的值域为[－2,2]．从而f (x 1)＋72≥32. 依题意有g (x )最小值≤32. 函数g (x )＝ln x ＋a x的定义域为(0，＋∞)， g ′(x )＝1x －a x 2＝x －a x 2.①当a ≤1时，g ′(x )＞0，函数g (x )在[1，e]上单调递增，其最小值为g (1)＝a ≤1<32，符合题意；②当1<a <e 时，函数g (x )在[1，a )上有g ′(x )<0，单调递减，在(a ，e]上有g ′(x )>0，单调递增，所以函数g (x )的最小值为g (a )＝ln a ＋1.由ln a ＋1≤32，得0<a ≤ e.从而知1<a ≤e 符合题意；③当a ≥e 时，显然函数g (x )在[1，e]上单调递减，其最小值为g (e)＝1＋a e ≥2>32，不符合题意．综上所述，实数a 的取值范围为a ≤ e.。

第三章　三角函数与解三角形第1讲　弧度制与任意角的三角函数1．设集合M ＝Error!，N ＝Error!，则( )A ．M ＝NB ．M ⊆NC ．N ⊆MD ．M ∩N ＝∅2．(2017年青海西宁复习检测)若cos θ＞0，且sin 2θ＜0，则角θ的终边所在象限为( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．若角α是第一象限角，则是( )α2A ．第一象限角 B ．第二象限角C ．第一或第三象限角D ．第二或第四象限角4．(2016年四川成都模拟)若α是第三象限角，则下列各式中不成立的是( )A ．sin α＋cos α<0B ．tan α－sin α<0C ．cos α－tan α<0D ．tan αsin α<05．若角α的终边经过点P (1，m )，且tan α＝－2，则sin α＝( )A. B ．－ C. D ．－5555 2 55 2 556．(2014年新课标Ⅰ)若tan α>0，则( )A ．sin α>0B ．cos α>0C ．sin 2α>0D ．cos 2α>07．设α是第二象限角，点P (x,4)为其终边上的一点，且cos α＝x ，则tan α＝( )15A. B. C ．－ D ．－433434438．(2016年河北衡水二中模拟)已知角φ的终边经过点P (－4,3)，函数f (x )＝sin(ωx ＋φ)(ω＞0)图象的相邻两条对称轴之间的距离等于，则f 的值为( )π2(π4)A. B. C ．－ D ．－354535459．(2017年广东深圳二模)以角θ的顶点为坐标原点，始边为x 轴的非负半轴，建立平面直角坐标系，角θ的终边过点P (1,2)，则tan ＝________.(θ＋π4)10．在如图X3­1­1的算法中，令a ＝tan θ，b ＝sin θ，c ＝cos θ，若在集合Error!中任取θ的一个值，输出的结果是sin θ的概率是( )图X3­1­1A. B. C. D.1312233411．判断下列各式的符号：(1)tan 125°·sin 278°； (2).cos 7π12tan 23π12sin 11π1212．(1)已知扇形的周长为10，面积为4，求扇形圆心角的弧度数；(2)已知扇形的周长为40，当它的半径和圆心角取何值时，才能使扇形的面积最大？最大面积是多少？第2讲　同角三角函数的基本关系式与诱导公式1．sin 2013°的值属于区间( )A. B.(－12，0)(－1，－12)C. D.(12，1)(0，12)2．下列关系式中，正确的是( )A ．sin 11°<cos 10°<sin 168°B ．sin 168°<sin 11°<cos 10°C ．sin 11°<sin 168°<cos 10°D ．sin 168°<cos 10°<sin 11°3．已知sin α－cos α＝，α∈(0，π)，则tan α＝( )2A ．－1 B ．－ C. D ．122224．(2014年大纲)设a ＝sin 33°，b ＝cos 55°，c ＝tan 35°，则( )A ．a ＞b ＞cB ．b ＞c ＞aC ．c ＞b ＞aD ．c ＞a ＞b 5．(2011年新课标)已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝( )A ．－B ．－ C. D.453535456．下列不等式成立的是( )A ．tan >tan (9π8)(π6)B ．sin >sin (－3π10)(－π5)C ．sin >sin π18π10D ．cos >cos (－7π4)(－23π5)7．(2012年大纲)已知α为第二象限角，sin α＋cos α＝，则cos 2α＝( )33A ．－ B ．－ C. D.535959538．(2017年浙江绍兴二模)已知sin α＋cos α＝，α∈(0，π)，则tan α＝( )15A ．－ B ．－ C. D.433443349．(2013年新课标Ⅱ)设θ为第二象限角，若tan ＝，则sin θ＋cos θ＝________.(θ＋π4)1210．(2016年广东惠州三调)已知sin θ＋cos θ＝(0<θ<)，则sin θ－cos θ的值为( )43π4A. B ．－ C. D ．－2323131311．已知函数f (x )＝.1－2sin (2x －π4)cos x (1)求函数f (x )的定义域；(2)设α是第四象限角，且tan α＝－，求f (α)的值．4312．已知tan α＝2.(1)求tan 的值；(α＋π4)(2)求的值．sin 2αsin2α＋sin αcos α－cos 2α－1第3讲　三角函数的图象与性质1．下列四个函数中，最小正周期为π，且图象关于直线x ＝对称的是( )π12A ．y ＝sin B ．y ＝sin(x 2＋π3)(x 2－π3)C ．y ＝sinD ．y ＝sin (2x ＋π3)(2x －π3)2．(2017年重庆适应性测试)若函数f (x )＝sin－cos ωx (ω＞0)的图象相邻两个对(ωx ＋π6)称中心之间的距离为，则f (x )的一个单调递增区间为( )π2A. B.(－π6，π3)(－π3，π6)C. D.(π6，2π3)(π3，5π6)3．(2016年新课标Ⅱ)函数y ＝A sin(ωx ＋φ)的部分图象如图X3­3­1，则( )图X3­3­1A ．y ＝2sinB ．y ＝2sin (2x －π6)(2x －π3)C ．y ＝2sinD ．y ＝2sin (2x ＋π6)(2x ＋π3)4．(2017年广东茂名一模)已知函数f (x )＝3cos(ω>0)和g (x )＝2sin(2x ＋φ)＋1的(ωx ＋π3)图象的对称轴完全相同，若x ∈，则f (x )的取值范围是( )[0，π3]A ．[－3,3] B.[－32，3]C.D.[－3，3 32][－3，32]5．(2013年大纲)若函数y ＝sin(ωx ＋φ)(ω＞0)的部分图象如图X3­3­2，则ω＝( )图X3­3­2A ．5B ．4C ．3D ．26．函数y ＝|tan x |cos x 的图象是( )(0≤x <3π2，且x ≠π2) A B C D7．(2017年新课标Ⅲ)设函数f (x )＝cos，则下列结论错误的是( )(x ＋π3)A ．f (x )的一个周期为－2πB ．y ＝f (x )的图象关于直线x ＝对称8π3C ．f (x ＋π)的一个零点为x ＝π6D ．f (x )在上单调递减(π2，π)8．(2016年江苏)定义在区间[0,3π]上的函数y ＝sin 2x 的图象与函数y ＝cos x 的图象的交点个数是______．9．(2017年浙江温州中学统测)已知函数f (x )＝sin ωx －cos ωx (ω>0)的图象与x 轴的两3个相邻交点的距离等于，若将函数y ＝f (x )的图象向左平移个单位长度得到函数y ＝g (x )的π2π6图象，则y ＝g (x )是减函数的区间为( )A. B.(π4，π3)(－π4，π4)C. D.(0，π3)(－π3，0)10．(2012年新课标)已知ω＞0，函数f (x )＝sin 在上单调递减，则ω的取(ωx ＋π4)(π2，π)值范围是( )A. B.[12，54][12，34]C. D ．(0,2](0，12)11．已知函数f (x )＝(sin x ＋cos x )2＋cos 2x .(1)求f (x )的最小正周期；(2)求f (x )在区间上的最大值和最小值．[0，π2]12．是否存在实数a ，使得函数y ＝sin 2x ＋a cos x ＋a －在闭区间上的最大值是5832[0，π2]1？若存在，求出对应的a 值；若不存在，请说明理由．第4讲 函数y ＝A sin(ωx ＋φ)的图象1．函数y ＝sin(ωx ＋φ)(x ∈R ，ω>0,0≤φ<2π)的部分图象如图X3­4­1，则( )图X3­4­1A ．ω＝，φ＝B ．ω＝，φ＝π2π4π3π6C ．ω＝，φ＝D ．ω＝，φ＝π4π4π45π42．为了得到函数y ＝sin 3x ＋cos 3x 的图象，可以将函数y ＝cos 3x 的图象( )2A ．向右平移个单位长度 B ．向右平移个单位长度π12π4C ．向左平移个单位长度 D ．向左平移个单位长度π12π43．(2017年四川眉山中学统测)将函数f (x )＝3sin (2x ＋π3)的图象向右平移个单位长度，所得图象对应的函数( )π2A ．其一条对称轴方程为x ＝－π6B ．在区间上单调递增[π12，7π12]C ．当x ＝＋k π(k ∈Z )时取得最大值π12D ．在区间上单调递增[－π6，π3]4．(2015年湖南)将函数f (x )＝sin 2x 的图象向右平移φ个单位长度后得到函(0＜φ＜π2)数g (x )的图象，若对满足|f (x 1)－g (x 2)|＝2的x 1，x 2，有|x 1－x 2|min ＝，则φ＝( )π3A. B. C. D.5π12π3π4π65．(2017年湖北咸宁模拟)已知函数f (x )＝sin(ωx ＋φ)的最小正周期(ω>0，－π2<φ<π2)为π，将该函数的图象向左平移个单位长度后，得到的图象对应的函数为奇函数，则f (x )π6的图象( )A ．关于点对称B ．关于直线x ＝对称(π12，0)5π12C ．关于点对称 D ．关于直线x ＝对称(5π12，0)π126．设f (x )＝sin 3x ＋cos 3x ，若对任意实数x 都有|f (x )|≤a ，则实数a 的取值范围是3________．7．已知函数f (x )＝sin，其中x ∈.当a ＝时，f (x )的值域是__________；(2x ＋π6)[－π6，a ]π3若f (x )的值域是，则a 的取值范围是__________．[－12，1]8．(2015年湖南)已知ω＞0，在函数y ＝2sin ωx 与y ＝2cos ωx 的图象的交点中，距离最短的两个交点的距离为2 ，则ω＝________.39．(2015年天津)已知函数f (x )＝sin ωx ＋cos ωx (ω＞0)，x ∈R ，若函数f (x )在区间(－ω，ω)内单调递增，且函数f (x )的图象关于直线x ＝ω对称，则ω的值为____________．10．(2014年北京)函数f (x )＝3sin 的部分图象如图X3­4­2.(2x ＋π6)(1)写出f (x )的最小正周期及图中x 0，y 0的值；(2)求f (x )在区间上的最大值和最小值．[－π2，－π12]图X3­4­211．(2017年山东)设函数f (x )＝sin＋sin ，其中0<ω<3，已知f ＝0.(ωx －π6)(ωx －π2)(π6)(1)求ω；(2)将函数y ＝f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图象向左平移个单位，得到函数y ＝g (x )的图象，求g (x )在上的最小值．π4[－π4，3π4]第5讲　两角和与差及二倍角的三角函数公式1．(2016年新课标Ⅱ)若cos ＝，则sin 2α＝( )(π4－α)35A. B.72515C ．－ D ．－157252．4cos 50°－tan 40°＝( ) A. B.22＋32C. D ．2 －1323．(2017年上海师大附中统测)函数y ＝2cos 2－1是( )(x －π4)A ．最小正周期为π的奇函数B ．最小正周期为π的偶函数C ．最小正周期为的奇函数π2D ．最小正周期为的偶函数π24．(2015年上海)已知点A 的坐标为(4，1)，将OA 绕坐标原点O 逆时针旋转至3π3OB ，则点B 的纵坐标为( )A. B. C. D.3 32 5 321121325．(2017年江苏)若tan＝， 则tan α＝________.(α－π4)166．(2017年北京)在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称．若sin α＝，cos(α－β)＝________.137．(2016年新课标Ⅲ)函数y ＝sin x －cos x 的图象可由函数y ＝2sin x 的图象至少向3右平移______个单位长度得到．8．(2016年上海)若函数f (x )＝4sin x ＋a cos x 的最大值为5，则常数a ＝________.9．(2016年上海)方程3sin x ＝1＋cos 2x 在区间[0,2π]上的解为__________．10．(2015年浙江)函数f (x )＝sin 2x ＋sin x cos x ＋1的最小正周期是________，最小值是________，单调递减区间是____________________．11．(2014年江苏)已知α∈，sin α＝.(π2，π)55(1)求sin 的值；(π4＋α)(2)求cos 的值．(5π6－2α)12．(2017年北京)已知函数f (x )＝cos－2sin x cos x .3(2x －π3)(1)求f (x )的最小正周期；(2)求证：当x ∈时，f (x )≥－.[－π4，π4]12第6讲　简单的三角恒等变换1．若sin ＝，则cos α＝( )α233A ．－ B ．－ C. D.231313232．(2016年山东)函数f (x )＝(sin x ＋cos x )(cos x －sin x )的最小正周期是( )33A. B ．π C. D ．2ππ23π23．(2017年广东广州一模)已知函数f (x )＝sin(ωx ＋φ)＋cos(ωx ＋φ)(ω>0,0<φ<π)是奇函数，直线y ＝与函数f (x )的图象的两个相邻交点的横坐标之差的绝对值为，则( )2π2A ．f (x )在上单调递减(0，π4)B ．f (x )在上单调递减(π8，3π8)C ．f (x )在上单调递增(0，π4)D ．f (x )在上单调递增(π8，3π8)4．(2017年河北石家庄一模)函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0)的部分图象如图X3­6­1，则f 的值为( )(11π24)图X3­6­1A ．－B ．－C ．－D ．－16232225．若将函数y ＝tan(ω>0)的图象向右平移个单位长度后，与函数y ＝tan (ωx ＋π4)π6的图象重合，则ω的最小值为( )(ωx ＋π6)A. B. C. D.161413126．(2016年山西四校联考)已知函数f (x )＝cos 的部分图象如(ωx ＋φ－π2)(ω>0，|φ|<π2)图X3­6­2，则y ＝f 取得最小值时x 的取值集合为( )(x ＋π6)图X3­6­2A.{x |x ＝k π－π6，k ∈Z }B.{x |x ＝k π－π3，k ∈Z }C.{x |x ＝2k π－π6，k ∈Z }D.{x |x ＝2k π－π3，k ∈Z }7．已知α∈R ，sin α＋2cos α＝，则tan 2α＝( )102A. B. C ．－ D ．－433434438．(2012年大纲)当函数y ＝sin x －cos x (0≤x <2π)取最大值时，x ＝________.39．(2016年江西九江模拟)化简＝________.sin235°－12cos10°cos80°10．若函数y ＝cos 2x ＋sin 2x ＋a 在上有两个不同的零点，则实数a的取值范3[0，π2]围为____________．11．(2014年四川)已知函数f (x )＝sin.(3x ＋π4)(1)求f (x )的单调递增区间；(2)若α是第二象限角，f ＝cos cos 2α，求cos α－sin α的值．(α3)45(α＋π4)12．(2017年浙江)已知函数f (x )＝sin 2x －cos 2x －2 sin x cos x (x ∈R )．3(1)求f 的值；(2π3)(2)求f (x )的最小正周期及单调递增区间．第7讲　正弦定理和余弦定理1．设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若2sin A cos B ＝sin C ，则△ABC 一定是( )A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形2．(2017年山东)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .若△ABC 为锐角三角形，且满足sin B (1＋2cos C )＝2sin A cos C ＋cos A sin C ，则下列等式成立的是( )A ．a ＝2bB ．b ＝2aC ．A ＝2BD ．B ＝2A3．(2016年新课标Ⅲ)在△ABC 中，B ＝，BC 边上的高等于BC ，则sin A ＝( )π413A. B.3101010C. D.55310104．(2017年河南郑州模拟)已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，且 (b －c )(sin B ＋sin C )＝(a －c )sin A ，则角B 的大小为( )3A ．30° B ．45° C ．60° D ．120°5．(2013年新课标Ⅰ)已知锐角三角形ABC 的内角A ，B ，C 的对边分别为a ，b ，c ,23cos 2A ＋cos 2A ＝0，a ＝7，c ＝6，则b ＝( )A ．10B ．9C ．8D ．56．(2016年山东德州模拟)在△ABC 中，AB ＝，AC ＝1，B ＝，则△ABC 的面积是( )3π6A. B. C.或 D.或323432343237．(2017年湖北孝感一模)在锐角三角形ABC 中，已知AB ＝2 ，BC ＝3，其面积S △3ABC ＝3 ，则AC ＝________.28．(2015年重庆)在△ABC 中，B ＝120°，AB ＝，角A 的平分线AD ＝，则23AC ＝________.9．(2017年北京)在△ABC 中，∠A ＝60°，c ＝a .37(1)求sin C 的值；(2)若a ＝7，求△ABC 的面积．10．(2017年新课标Ⅱ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin(A ＋C )＝8sin 2.B 2(1)求cos B ；(2)若a ＋c ＝6，△ABC 的面积为2，求b .第8讲　解三角形应用举例1．某人向正东方向走x km 后，顺时针转150°，然后朝新方向走3 km ，结果他离出发点恰好 km ，则x ＝( )3A. B ．2 33C ．2 或D ．3332．两座灯塔A 和B 与海洋观察站C 的距离都等于a km ，灯塔A 在观察站C 的北偏东20°的方向，灯塔B 在观察站C 的南偏东40°的方向，则灯塔A 与灯塔B 的距离为( )A ．a km B.a km C ．2a km D.a km233．如图X3­8­1，一艘海轮从A 处出发，以40海里/时的速度沿南偏东40°方向直线航行，30分钟后到达B 处．在C 处有一座灯塔，海轮在A 处观察灯塔，其方向是南偏东70°，在B 处观察灯塔，其方向是北偏东65°，那么B ，C 两点间的距离是( )图X3­8­1A ．10 海里B ．10 海里C ．20 海里D ．20 海里23234．(2014年四川)如图X3­8­2，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为67°，30°，此时气球的高是46 m ，则河流的宽度BC 约等于________m ．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.80，≈1.73)3图X3­8­25．(2016年河南信阳模拟)某舰艇在A 处测得遇险渔船在北偏东45°距离为10海里的C 处，该渔船沿北偏东105°方向，以每小时9海里的速度向一小岛靠近，舰艇时速21海里，则舰艇到达渔船的最短时间是________分钟．6．(2017年浙江)已知△ABC ，AB ＝AC ＝4，BC ＝2.点D 为AB 延长线上一点，BD ＝2，连接CD ，则△BDC 的面积是________，cos ∠BDC ＝________.7．(2016年上海)已知△ABC 的三边长分别为3,5,7，则该三角形的外接圆半径等于________．8．(2017年广东揭阳一模)如图X3­8­3，在△ABC 中，∠B ＝，AC ＝1，点D 在边AB π6上，且DA ＝DC ，BD ＝1，则∠DCA ＝________.图X3­8­39．(2017年新课标Ⅲ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知sin A ＋cos 3A ＝0，a ＝2 ，b ＝2.7(1)求c ；(2)设D 为BC 边上一点，且AD ⊥AC ，求△ABD 的面积．10．(2017年广东广州一模)如图X3­8­4，在△ABC 中，点P 在BC 边上，∠PAC ＝60°，PC ＝2，AP ＋AC ＝4.(1)求∠ACP ；(2)若△APB 的面积是， 求sin ∠BAP .3 32图X3­8­4第三章　三角函数与解三角形第1讲　弧度制与任意角的三角函数1．B 解析：方法一，由于M ＝Error!＝{…，－45°，45°，135°，225°，…}，N ＝Error!＝{…，－45°，0°，45°，90°，135°，180°，225°，…}，显然有M ⊆N .故选B.方法二，在M 中，x ＝·180°＋45°＝k ·90°＋45°＝(2k ＋1)·45°，2k ＋1是奇数；在N 中，k 2x ＝·180°＋45°＝k ·45°＋45°＝(k ＋1)·45°，k ＋1是整数，因此必有M ⊆N .故选B.k 42．D 解析：由cos θ>0，sin 2θ＝2sin θcos θ＜0，得sin θ＜0，则角θ的终边在第四象限．故选D.3．C 解析：∵α是第一象限角，∴2k π＜α＜＋2k π，k ∈Z ，∴k π＜＜＋k π，k ∈Z .π2α2π4当k 为偶数时，是第一象限角；当k 为奇数时，是第三象限角．α2α24．B 解析：在第三象限，sin α<0，cos α<0，tan α>0，则tan α－sin α>0，故B 错误．故选B.5．D 解析：由三角函数的定义，得tan α＝m ＝－2.∴r ＝，sin α＝＝－.故5－25 2 55选D.6．C 解析：tan α＝>0，而sin 2α＝2sin αcos α>0.故选C.sin αcos α7．D 解析：∵α是第二象限角，∴cos α＝x ＜0，即x ＜0.又cos α＝x ＝，1515xx 2＋16解得x ＝－3.∴tan α＝＝－.4x 438．D 解析：由于角φ的终边经过点P (－4,3)，所以cosφ＝－.再根据函数f (x )45＝sin(ωx ＋φ)(ω＞0)图象的相邻两条对称轴之间的距离等于，可得＝2×，所以ω＝2.π22πωπ2所以f (x )＝sin(2x ＋φ)．所以f ＝sin ＝cos φ＝－.故选D.(π4)(π2＋φ)459．－3　解析：由题意知tan θ＝＝2，所以tan＝＝＝－3.21(θ＋π4)tan θ＋tan π41－tan θtan π42＋11－2×110．A 解析：该程序框图的功能是比较a ，b ，c 的大小并输出最大值，因此要使输出的结果是sin θ，需sin θ＞tan θ，且sin θ＞cos θ.∵当θ∈时，总有tan θ＞sin θ；当(0，π2)θ∈时，总有sin θ＞0，tan θ＜0，cos θ＜0；当θ∈时，tan θ＞0，sin θ＜0.故当(π2，π)(π，3π2)输出的结果是sin θ时，θ的取值范围是.结合几何概型公式，得输出sin θ的概率为(π2，π)＝.故选A.π－π232π－01311．解：(1)∵125°，278°角分别为第二、四象限角，∴tan 125°＜0，sin 278°＜0.因此tan 125°·sin 278°＞0.(2)∵＜＜π，<<2π，<<π，π27π123π223π12π211π12∴cos ＜0，tan ＜0，sin ＞0.7π1223π1211π12因此>0.cos 7π12tan 23π12sin 11π1212．解：设扇形半径为R ，圆心角为θ，θ所对的弧长为l .(1)依题意，得Error!∴2θ2－17θ＋8＝0.解得θ＝8或.12∵8>2π(舍去)，∴θ＝ rad.12(2)扇形的周长为40，即θR ＋2R ＝40，S ＝lR ＝θR 2＝θR ·2R ≤2＝100.12121414(θR ＋2R 2)当且仅当θR ＝2R ，即R ＝10，θ＝2时，扇形面积取得最大值，最大值为100.第2讲　同角三角函数的基本关系式与诱导公式1．B 解析：sin 2013°＝sin(5×360°＋213°)＝sin 213°＝sin(180°＋33°)＝－sin 33°<－.故12选B.2．C 解析：∵sin 168°＝sin(180°－12°)＝sin 12°，cos 10°＝cos(90°－80°)＝sin 80°.由于正弦函数y ＝sin x 在区间[0°，90°]上为递增函数，因此sin 11°<sin 12°<sin 80°，即sin 11°<sin 168°<cos 10°.3．A 解析：由Error!消去sin α，得2cos 2α＋2cos α＋1＝0，即(cos α＋1)222＝0.∴cos α＝－.又α∈(0，π)，∴α＝.∴tan α＝tan ＝－1.223π43π44．C 解析：c ＝tan 35°＞b ＝cos 55°＝sin 35°＞a ＝sin 33°.故选C.5．B 解析：由题知，tan θ＝2，cos 2θ＝＝＝－.故选B.cos2 θ－sin2 θcos2 θ＋sin2 θ1－tan2 θ1＋tan2 θ356．D 解析：cos ＝cos >0，cos ＝cos <0.故选D.(－7π4)π4(－23π5)3π57．A 解析：sin α＋cos α＝，两边平方可得1＋sin 2α＝⇒sin 2α＝－.∵α是第二331323象限角，因此sin α>0，cos α<0.所以cos α－sinα＝－＝－＝－.∴cos 2α＝cos 2 α－sin 2 α＝(cos α＋sin α)(cos α－sin (cos α－sin α)21＋23153α)＝－.538．A 解析：由题设知(sin α＋cos α)2＝，则2sin αcos α＝－，故(sin α－cos α)12524252＝1＋＝.所以sin α－cos α＝，与sin α＋cos α＝联立解之可得sin α＝，cos24254925751545α＝－，故tan α＝－.故选A.35439．－　解析：tan＝，＝，tan θ＝－，＝－，cos θ＝－3sin 105(θ＋π4)12tan θ＋11－tan θ1213sin θcos θ13θ，代入sin 2θ＋cos 2θ＝1，得Error!sin θ＋cos θ＝－.10510．B 解析：　因为sin θ＋cos θ＝(0<θ<)，两边平方可得1＋2sin θ·cos θ＝，即43π41692sin θ·cos θ＝，所以(sin θ－cos θ)2＝1－2sin θcos θ＝1－＝.又因为0<θ<，所以sin797929π4θ<cos θ.所以sin θ－cos θ<0.所以sin θ－cos θ＝－.故选B.2311．解：(1)函数f (x )要有意义，需满足cos x ≠0，解得x ≠＋k π，k ∈Z ，即函数f (x )的π2定义域为Error!.(2)f (x )＝1－2sin (2x －π4)cos x ＝＝1－2(22sin 2x －22cos 2x)cos x1＋cos 2x －sin 2xcos x＝2cos2x －2sin x cos xcos x ＝2(cos x －sin x )．由tan α＝－，得sin α＝－cos α.4343又sin 2α＋cos 2α＝1，∴cos 2α＝.925∵α是第四象限的角，∴cos α＝，sin α＝－.3545∴f (α)＝2(cos α－sin α)＝.14512．解：(1)tan ＝＝(α＋π4)tan α＋tan π41－tan αtan π4tan α＋11－tan α＝＝－3.2＋11－2(2)sin 2αsin2α＋sin αcos α－cos 2α－1＝2sin αcos αsin2α＋sin αcos α－(2cos2α－1)－1＝2sin αcos αsin2α＋sin αcos α－2cos2α＝2tan αtan2α＋tan α－2＝2×222＋2－2＝1.第3讲　三角函数的图象与性质1．C 解析：将x ＝代入选项A ，B ，C ，D 中，只有选项C 取得最大值y ＝sin π12＝sin ＝1，所以关于直线x ＝对称，且T ＝＝π.(2×π12＋π3)π2π122π22．A 解析：依题意，得f (x )＝sin ωx －cos ωx ＝sin的图象相邻两个对称中3212(ωx －π6)心之间的距离为，于是有T ＝＝2×＝π，ω＝2，f (x )＝sin.当π22πωπ2(2x －π6)2k π－≤2x －≤2k π＋，即k π－≤x ≤k π＋，k ∈Z 时，f (x )＝sin单调递增．结合π2π6π2π6π3(2x －π6)各选项知f (x )＝sin的一个单调递增区间为.故选A.(2x －π6)(－π6，π3)3．A 解析：由图知，A ＝2，周期T ＝2＝π，所以ω＝＝2.所以[π3－(－π6)]2ππy ＝2sin(2x ＋φ)．因为图象过点，所以2＝2sin .所以sin ＝1.所以(π3，2)(2×π3＋φ)(2π3＋φ)＋φ＝2k π＋(k ∈Z )．令k ＝0，得φ＝－.所以y ＝2sin .故选A.2π3π2π6(2x －π6)4．D 解析：因为函数f (x )和g (x )的图象的对称轴完全相同，故f (x )和g (x )的周期相同，所以ω ＝2，f (x )＝3cos .由x ∈，得2x ＋∈.根据余弦函数的单调性，当(2x ＋π3)[0，π3]π3[π3，π]2x ＋＝π，即x ＝时，f (x )min ＝－3；当2x ＋＝，即x ＝0时，f (x )max ＝.所以f (x )的取值π3π3π3π332范围是.故选D.[－3，32]5．B 解析：设函数的最小正周期为T ，由题图可知＝－x 0＝，所以T ＝.又T2(x 0＋π4)π4π2因为T ＝，可解得ω＝4.2πω6．C 解析：方法一，y ＝|sin x |·，分类讨论．cos x|cos x |方法二，y ＝|tan x |cos x 的符号与cos x 相同．故选C.7．D 解析：函数的最小正周期为T ＝＝2π，则周期为2k π.所以f (x )的一个周2π1(k ∈Z )期为－2π.故选项A 正确；将x ＝代入f (x )＝cos ，得f ＝cos 3π＝－1为最小8π3(x ＋π3)(8π3)值．因此直线x ＝为对称轴．故选项B 正确；将x ＝代入f (x ＋π)，得cos ＝0.故选项8π3π63π2C 正确；由x ∈，得x ＋∈.函数在该区间显然不单调．故选项D 错误．故选(π2，π)π3(5π6，4π3)D.8．7　解析：由sin 2x ＝cos x ⇒cos x ＝0或sin x ＝.因为x ∈[0,3π]，所以x ＝，，，12π23π25π2，，，，共7个．π65π613π617π69．A 解析：因为f (x )＝2sin，＝，所以T ＝＝π.则ω＝2.故f (x )＝2sin (ωx －π3)T 2π22πω.故g (x )＝2sin ＝2sin 2x ，故其单调递减区间为(2x －π3)[2(x ＋π6)－π3]2k π＋≤2x ≤2k π＋(k ∈Z )，即k π＋≤x ≤k π＋(k ∈Z )，当k ＝0时，区间为函数π23π2π43π4[π4，3π4]g (x )的一个单调递减区间，又⊆.故选A.(π4，π3)[π4，3π4]10．A 解析：方法一，ω＝2⇒∈不合题意，排除(ωx ＋π4)[5π4，9π4]D ；ω＝1⇒∈合题意，排除B ，C.故选A.(ωx ＋π4)[3π4，5π4]方法二，由＜x ＜π，得ω＋＜ωx ＋＜πω＋.π2π2π4π4π4由题意知，⊆.(π2ω＋π4，πω＋π4)[π2，3π2]∴Error!∴≤ω≤.故选A.125411．解：(1)因为f (x )＝sin 2x ＋cos 2x ＋2sin x cos x ＋cos 2x＝1＋sin 2x ＋cos 2x ＝sin＋1，2(2x ＋π4)所以函数f (x )的最小正周期为T ＝＝π.2π2(2)由(1)知，f (x )＝sin＋1.2(2x ＋π4)当x ∈时，2x ＋∈.[0，π2]π4[π4，5π4]由正弦函数y ＝sin x 在上的图象知，[π4，5π4]当2x ＋＝，即x ＝时，f (x )取最大值＋1；π4π2π82当2x ＋＝，即x ＝时，f (x )取最小值0.π45π4π2综上所述，f (x )在区间上的最大值为＋1，最小值为0.[0，π2]212．解：y ＝－2＋＋a －，(cos x －12a)a 245812当0≤x ≤时，0≤cos x ≤1.π2令t ＝cos x ，则0≤t ≤1.∴y ＝－2＋＋a －，0≤t ≤1.(t －12a)a 245812当0≤≤1，即0≤a ≤2时，则当t ＝，即cos x ＝时．a 2a2a2y max ＝＋a －＝1，解得a ＝或a ＝－4(舍去)．a 24581232当＜0，即a ＜0时，则当t ＝0，即cos x ＝0时，a 2y max ＝a －＝1，解得a ＝(舍去)．5812125当＞1，即a ＞2时，则当t ＝1，即cos x ＝1时，a2y max ＝a ＋a －＝1，解得a ＝(舍去)．58322013综上所述，存在a ＝符合题意．32第4讲　函数y ＝A sin (ωx ＋φ)的图象1．C 解析：∵＝3－1＝2，∴T ＝8，∴ω＝＝.令×1＋φ＝，得φ＝.故选C.T42πT π4π4π2π42．A 解析：由于y ＝sin 3x ＋cos 3x ＝sin，y ＝cos 3x ＝sin ，因此2(3x ＋π4)22(3x ＋π2)只需将y ＝cos 3x 的图象向右平移个单位长度，即可得到y ＝sin＝ sin 2π122[3(x －π12)＋π2]的图象．(3x ＋π4)3．B 解析：f (x )＝3sin的图象向右平移个单位长度所得图象对应的函数为f (x )(2x ＋π3)π2＝3sin＝－3sin ，其对称轴方程为2x ＋＝＋k π(k ∈Z )，即[2(x －π2)＋π3](2x ＋π3)π3π2x ＝＋(k ∈Z )，排除A.当x ＝＋k π(k ∈Z )，得－3sin ＝－3.故C 错误．由π12k π2π12(2k π＋π2)＋2k π≤2x ＋≤＋2k π(k ∈Z )，得＋k π≤x ≤＋k π(k ∈Z )，即f (x )的增区间为π2π33π2π127π12(k ∈Z )．故选B.[π12＋k π，7π12＋k π]4．D 解析：向右平移φ个单位长度后，得到g (x )＝sin(2x －2φ)，∵|f (x 1)－g (x 2)|＝2，∴不妨令2x 1＝＋2k π(k ∈Z )，2x 2－2φ＝－＋2m π(m ∈Z )．∴x 1－x 2＝－φ＋(k －m )π.又π2π2π2∵|x 1－x 2|min ＝，∴－φ＝⇒φ＝.故选D.π3π2π3π65．B 解析：由已知，得ω＝2，则f (x )＝sin(2x ＋φ)．设平移后的函数为g (x )，则g (x )＝sin，且为奇函数，所以φ＝－，f (x )＝sin .令2x －＝k π＋(2x ＋π3＋φ)(－π2<φ<π2)π3(2x －π3)π3(k ∈Z )，易得f (x )的图象关于直线x ＝对称．故选B.π25π126．[2，＋∞)　解析：f (x )＝sin 3x ＋cos 3x ＝2sin，|f (x )|max ＝2，∴a ≥2.3(3x ＋π6)7. 解析：当a ＝时，x ∈，2x ＋∈，f (x )的值域是[－12，1][π6，π2]π3[－π6，π3]π6[－π6，5π6]；若f (x )的值域是，≤2a ＋≤，解得≤a ≤.[－12，1][－12，1]π2π67π6π6π28.　解析：根据三角函数图象与性质可得交点坐标为，π2(1ω(2k 1π＋π4)，2)，k 1，k 2∈Z ＋，距离最短的两个交点一定在同一个周期内，∴2＝(1ω(2k 2π＋5π4)，－2)(2 3)2＋(－－)2.∴ω＝.1ω2(5π4－π4)22π29.　解析：由f (x )在区间(－ω，ω)内单调递增，且f (x )的图象关于直线x ＝ω对称，π2可得2ω≤，且f (ω)＝sin ω2＋cos ω2＝⇒sin＝1，所以ω2＋＝⇒ω＝.πω2(ω2＋π4)π4π2π210．解：(1)f (x )的最小正周期为π，x 0＝，y 0＝3.7π6(2)因为x ∈，[－π2，－π12]所以2x ＋∈.π6[－5π6，0]于是，当2x ＋＝0，即x ＝－时，f (x )取得最大值0；π6π12当2x ＋＝－，即x ＝－时，f (x )取得最小值－3.π6π2π311．解：(1)因为f (x )＝sin＋sin，(ωx －π6)(ωx －π2)所以f (x )＝sin ωx －cos ωx －cos ωx3212＝sin ωx －cos ωx3232＝3(12sin ωx －32cos ωx )＝sin.3(ωx －π3)由题设知，f ＝0，所以－＝k π，k ∈Z .(π6)ωπ6π3故ω＝6k ＋2，k ∈Z .又0<ω<3，所以ω＝2.(2)由(1)，得f (x )＝sin.3(2x －π3)所以g (x )＝sin＝sin .3(x ＋π4－π3)3(x －π12)根据x ∈得到x －∈，[－π4，3π4]π12[－π3，2π3]当x －＝－，即x ＝－时，g (x )取得最小值－.π12π3π432第5讲　两角和与差及二倍角的三角函数公式1．D 解析：cos ＝2cos 2－1＝2×2－1＝－，且cos ＝cos[2(π4－α)](π4－α)(35)725[2(π4－α)]＝sin 2α.故选D.(π2－2α)2．C 解析：原式＝4sin 40°－sin 40°cos 40°＝4cos 40°sin 40°－sin 40°cos 40°＝2sin 80°－sin 40°cos 40°＝2sin (120°－40°)－sin 40°cos 40°＝3cos 40°＋sin 40°－sin 40°cos 40°＝＝.故选C.3cos 40°cos 40°33．A 解析：由y ＝2cos 2－1＝cos ＝sin2x ，∴T ＝π，且y ＝sin 2x 是奇函(x －π4)(2x －π2)数，即函数y ＝2cos 2－1是奇函数．故选A.(x －π4)4．D 解析：设直线OA 的倾斜角为α，B (m ，n )(m ＞0，n ＞0)，则直线OB 的倾斜角为＋α.因为A (4 ，1)，所以tan α＝，tan ＝，＝＝，即m 2＝π3314 3(π3＋α)n m nm 3＋14 31－3·14 3133 3n 2.因为m 2＋n 2＝(4 )2＋12＝49，所以n 2＋n 2＝49.所以n ＝或n ＝－(舍去)．所27169327169132132以点B 的纵坐标为.1325. 解析：tan α＝tan＝＝＝.75[(α－π4)＋π4]tan (α－π4)＋tanπ41－tan (α－π4)tan π416＋11－16756．－　解析：因为角α与角β它们的终边关于y 轴对称，所以79α＋β＝2k π＋π，sin α＝sin β＝，cos α＝－cos β，cos(α－β)＝cos αcos β＋sin αsin(k ∈Z )13β＝－cos 2α＋sin 2α＝2sin 2α－1＝－.797.　解析：因为y ＝sin x －cos x ＝2sin，所以函数y ＝sin x －cos x 的图象可π33(x －π3)3由函数y ＝2sin x 的图象至少向右平移个单位长度得到．π38．±3　解析：f (x )＝sin(x ＋φ)，其中tan φ＝，故函数f (x )的最大值为，16＋a 2a416＋a 2由已知，得＝5，解得a ＝±3.16＋a 29.或　解析：3sin x ＝1＋cos 2x ，即3sin x ＝2－2sin 2x ，所以2sin 2x ＋3sin x －2＝0.解π65π6得sin x ＝或sin x ＝－2(舍)．所以方程在区间[0,2π]上的解为或.12π65π610．π ，k ∈Z3－22[3π8＋k π，7π8＋k π]解析：f (x )＝sin 2x ＋sin x cos x ＋1＝sin 2x ＋＋1＝sin 2x －cos 2x ＋＝·sin 121－cos 2x 212123222＋，所以T ＝＝π，f (x )min ＝－.单调递减区间为，k ∈Z .(2x －π4)322π23222[3π8＋k π，7π8＋k π]11．解：(1)因为α∈，sin α＝，(π2，π)55所以cos α＝－＝－.1－sin2α 2 55故sin ＝sin cos α＋cos sin α(π4＋α)π4π4＝×＋×＝－.22(－2 55)22551010(2)由(1)，得sin 2α＝2sin αcos α＝－，cos 2α＝2cos 2α－1＝.4535所以cos ＝cos cos 2α＋sin sin 2α(5π6－2α)5π65π6＝－×＋×＝－.323512(－45)3 3＋41012．(1)解：f (x )＝cos 2x ＋sin 2x －sin 2x3232＝sin 2x ＋cos 2x ＝sin .1232(2x ＋π3)所以f (x )的最小正周期T ＝＝π.2π2(2)证明：因为－≤x ≤，π4π4所以－≤2x ＋≤.π6π35π6所以sin≥sin ＝－.(2x ＋π3)(－π6)12所以当x ∈时，f (x )≥－.[－π4，π4]12第6讲　简单的三角恒等变换1．C2．B 解析：f (x )＝2sin ×2cos ＝2sin ，故最小正周期T ＝＝π.故选(x ＋π6)(x ＋π6)(2x ＋π3)2π2B.3．D 解析：f (x )＝sin ，因为函数为奇函数且0<φ<π，所以φ＋＝π，即2(ωx ＋φ＋π4)π4φ＝.所以f (x )＝－sin ωx .又＝，所以ω＝4，f (x )＝－sin 4x ，其一个单调递增区间3π422πωπ22为.(π8，3π8)4．D 解析：由题图可得A ＝，最小正周期T ＝4＝π，则ω＝＝2.又2(7π12－π3)2πT f ＝sin ＝－，解得φ＝－＋2k π(k ∈Z )．即k ＝1，φ＝.则f (x )＝sin(7π12)2(7π6＋φ)25π3π32.则f ＝sin ＝sin ＝－1.故选D.(2x ＋π3)(11π24)2(11π12＋π3)25π45．D 解析：函数y ＝tan的图象向右平移个单位后得到函数y ＝tan (ωx ＋π4)π6＝tan 的图象．又因为y ＝tan ，依题意可得[ω(x －π6)＋π4](ωx －ωπ6＋π4)(ωx ＋π6)－＋＝＋k π，k ∈Z ，∴ω＝－6k ，.由ω>0，得ω的最小值为.ωπ6π4π612(k ∈Z )126．B 解析：依题意，得T ＝＝4＝π，ω＝2，f ＝cos＝1.又|φ|<，因2πω(7π12－π3)(π3)(φ＋π6)π2此φ＝－.所以f (x )＝cos .当f ＝cos 取得最小值时，π6(2x －2π3)(x ＋π6)(2x －π3)2x －＝2k π－π，k ∈Z ，即x ＝k π－，k ∈Z .故选B.π3π37．C 解析：∵sin α＋2cos α＝，102∴sin 2α＋4sin αcos α＋4cos 2α＝.52化简，得4sin 2α＝－3cos 2α.∴tan 2α＝＝－.故选C.sin 2αcos 2α348.　解析：y ＝sin x －cos x ＝2sin，由0≤x <2π⇔－≤x －<，可知5π63(x －π3)π3π35π3－2≤2sin≤2.当且仅当x －＝，即x ＝时，函数取得最大值．(x －π3)π3π25π69．－1　解析：＝＝＝－1.sin235°－12cos10°cos80°1－cos70°2－12cos10°sin10°－12cos70°12sin20°10．(－2，－1]　解析：由题意可知，y ＝2sin＋a ，该函数在上有两个不(2x ＋π6)[0，π2]同的零点，即y ＝－a ，y ＝2sin的图象在上有两个不同的交点．结合函数的图(2x＋π6)[0，π2]象D104可知1≤－a ＜2，所以－2＜a ≤－1.图D10411．解：(1)－＋2k π≤3x ＋≤＋2k π⇒－＋k π≤x ≤＋k π(k ∈Z )．π2π4π2π423π1223(2)由已知，有sin ＝cos cos 2α，(α＋π4)45(α＋π4)即sin α＋cos α＝(cos α－sin α)(cos α－sin α)(sin α＋cos α)．45若sin α＋cos α＝0，则cos α－sin α＝－.2若sin α＋cos α≠0，则1＝(cos α－sin α)2⇒cos α－sin α＝－.4552综上所述，cos α－sin α的值为－或－.25212．解：(1)f ＝2－2－2 ××＝2.(2π3)(32)(－12)332(－12)(2)由cos 2x ＝cos 2x －sin 2x 与sin 2x ＝2sin x cos x ，得f (x )＝－cos 2x －sin 2x ＝－2sin.3(2x ＋π6)所以f (x )的最小正周期是π.由正弦函数的性质，得＋2k π≤2x ＋≤＋2k π，k ∈Z .π2π63π2解得＋k π≤x ≤＋k π，k ∈Z .π62π3所以f (x )的单调递增区间是，k ∈Z .[π6＋k π，2π3＋k π]第7讲　正弦定理和余弦定理1．B 解析：方法一，由已知，得2sin A cos B ＝sin C ＝sin(A ＋B )＝sin A cos B ＋cosA sinB ，即sin(A －B )＝0.因为－π＜A －B ＜π，所以A ＝B .方法二，由正弦定理，得2a cos B ＝c ，再由余弦定理，得2a ·＝c ⇒a 2＝b 2⇒a ＝b .a 2＋c 2－b 22ac 2．A 解析：sin(A ＋C )＋2sin B cos C ＝2sin A cos C ＋cos A sin C ，所以2sin B cos C ＝sin A cos C ⇒2sin B ＝sin A ⇒2b ＝a .故选A.3．D 解析：设BC 边上的高线为AD ，则BC ＝3AD ，DC ＝2AD .所以AC ＝＝AD .由正弦定理知，＝，即＝.解得sin A ＝.故选D.AD 2＋DC 25ACsin B BCsin A 5AD223ADsin A 310104．A 解析：由正弦定理＝＝及(b －c )·(sin B ＋sin C )＝(a －c )sin A ，a sin Ab sin Bc sin C 3得(b －c )(b ＋c )＝(a －c )a ，即b 2－c 2＝a 2－ac .∴a 2＋c 2－b 2＝ac .∵cos333B ＝，∴cos B ＝.∴B ＝30°.a 2＋c 2－b 22ac325．D 解析：23cos 2A ＋cos 2A ＝25cos 2A －1＝0，cosA ＝或cosA ＝－(舍)，1515a 2＝b 2＋c 2－2bc cosA,49＝b 2＋36－12b ×，5b 2－12b －65＝0，(5b ＋13)(b －5)＝0，且15b >0，所以b ＝5.6．C 解析：由正弦定理，得＝.解得sin C ＝.由题意知C 有两解．当C ＝ABsin C ACsin B 32时，A ＝，此时S △ABC ＝AB ·AC ·sin A ＝；当C ＝时，A ＝，此时S △π3π212322π3π6ABC ＝AB ·AC ·sin A ＝.故选C.12347．3　解析：依题意有S △ABC ＝AB ×BC ×sin B ＝×2 ×3sin B ＝3 ，sin B ＝.12123263又角B 为锐角，所以cosB ＝.所以AC ＝＝33AB 2＋BC 2－2AB ×BC ×cos B＝3.12＋9－2×2 3×3×338.　解析：由正弦定理，得＝，即＝.解得sin6ABsin ∠ADB ADsin B 2sin ∠ADB 3sin 120°∠ADB ＝，∠ADB ＝45°.从而∠BAD ＝15°＝∠DAC .所以C ＝180°－120°－30°＝30°，22AC ＝2AB cos 30°＝.69．解：(1)在△ABC 中，∠A ＝60°，c ＝a .37sin C ＝＝.c sin A a 3 314(2)因为a ＝7，c ＝a ＝3，37由余弦定理，得a 2＝b 2＋c 2－2bc cos A ，即72＝b 2＋32－2×b ×3×.12解得b ＝8或b ＝－5(舍)．所以S △ABC ＝bc sin A ＝×8×3×＝6 .121232310．解：(1)由A ＋C ＝π－B ，sin(A ＋C )＝sin B ＝8sin 2＝4(1－cos B )，B2两边平方，整理得17cos 2B －32cos B ＋15＝0.解得cos B ＝1(舍)或cos B ＝.1517(2)由cos B ＝，得sin B ＝.1517817故S △ABC ＝ac sin B ＝ac ＝2.∴ac ＝.12417172由余弦定理，得b 2＝a 2＋c 2－2ac cosB ＝(a ＋c )2－2ac (1＋cosB )＝36－2××＝4.172(1＋1517)所以b ＝2.第8讲　解三角形应用举例1．C 解析：如图D105，在△ABC 中，AC ＝，BC ＝3，∠ABC ＝30°.由余弦定理，3得AC 2＝AB 2＋BC 2－2AB ·BC ·cos ∠ABC .∴3＝x 2＋9－6x ·cos 30°，解得x ＝或2 .33图D105　　图D1062．D 解析：如图D106，依题意，得∠ACB ＝120°.由余弦定理，得AB 2＝AC 2＋BC 2－2AC ·BC cos 120°＝a 2＋a 2－2a 2·＝3a 2，∴AB ＝a km.故选D.(－12)33．A 解析：在△ABC 中，∠BAC ＝50°－20°＝30°，∠ABC ＝40°＋65°＝105°，AB ＝40×0.5＝20(海里)，则∠ACB ＝45°.由正弦定理，得＝.解得BC ＝10BC sin 30°20sin 45°(海里)．故选A.24．60　解析：根据已知的图形可得AB ＝.在△ABC 中，∠BCA ＝30°，46sin 67°∠BAC ＝37°，由正弦定理，得＝.所以BC ≈2××0.60＝60(m)．AB sin 30°BC sin 37°460.925．40　解析：设两船在B 处碰头，设舰艇到达渔船的最短时间是x 小时，则AC ＝10，AB ＝21x ，BC ＝9x ，∠ACB ＝120°，由余弦定理，知(21x )2＝100＋(9x )2－2×10×9x ×cos 120°，整理，得36x 2－9x －10＝0.解得x ＝或x ＝－(舍)．故舰艇到达23512渔船的最短时间是40分钟．6. 解析：取BC 中点E ，DC 中点F ，连接AE ，BF .由题意知152104AE ⊥BC ，BF ⊥CD .在△ABE 中，cos ∠ABC ＝＝，∴cos ∠DBC ＝－，sin ∠DBC ＝BE AB 1414＝.∴S△1－116154BDC ＝×BD ×BC ×sin ∠DBC ＝.∴cos ∠DBC ＝1－2sin 2∠DBF ＝－.∴sin ∠DBF ＝. 1215214104∴cos ∠BDC ＝sin ∠DBF ＝.综上所述，△BDC 的面积为，cos ∠BDC ＝.1041521047.　解析：利用余弦定理可求得最大边7所对应角的余弦值为＝－，7 3332＋52－722×3×512所以此角的正弦值为.设外接圆半径为R ，则2R ＝.所以R ＝.327327 338.或　解析：方法一，设∠A ＝∠ACD ＝θ，0<θ<，则∠ADC ＝π－2θ，又AC ＝1，π3π9π2由正弦定理，得＝⇒CD ＝.在△BDC 中，由正弦定理，得AC sin 2θCD sin θ12cos θ＝⇒＝⇒cos θ＝sin ⇒sin ＝sin ，由CDsin B BDsin ∠BCD 12cos θsin π61sin (5π6－2θ)(5π6－2θ)(π2－θ)(5π6－2θ)0<θ<⇒0<－θ<，－<－2θ<，得－θ＝－2θ或－θ＋－2θ＝π⇒θ＝或.π2π2π2π65π65π6π25π6π25π6π3π9Error!Error!方法二，过点C 作CE ⊥AB 于点E ，设∠A ＝∠ACD ＝θ，则∠CDB ＝2θ.在Rt △AEC 中，CE ＝sin θ.。

阶段检测卷(六)(立体几何)时间：分钟满分：分一、选择题：本大题共小题，每小题分，共分，有且只有一个正确答案，请将正确选项填入题后的括号中．．已知，，是三条不同的直线，命题“∥且⊥⇒⊥”是正确的，如果把，，中的两个或三个换成平面，在所得的命题中，真命题有( )．个．个．个．个．如图-，在四面体-中，截面是正方形，则在下列命题中，错误的是( )图-．⊥．∥截面．＝．异面直线与所成的角为°．如图-，在正方体-′′′′中，与′成°角的面对角线条数是( )图-．条．条．条．条．在如图-所示的空间直角坐标系-中，一个四面体的顶点坐标分别是()，()，()，()，给出编号①②③④的四个图，则该四面体的正视图和俯视图分别为( )图-．①和②．③和①．④和③．④和②．如图-，在四边形中，∥，＝，∠＝°，∠＝°，将△沿折起，使平面⊥平面，构成三棱锥-，则在三棱锥-中，下列命题正确的是( )图-．平面⊥平面．平面⊥平面．平面⊥平面．平面⊥平面．如图-，四棱锥-的底面为正方形，⊥底面，则下列结论中不正确的是( )图-．⊥．∥平面．与平面所成的角等于与平面所成的角．与所成的角等于与所成的角．(年广东深圳二模)一个长方体被一平面截去一部分后，所剩几何体的三视图如图-，则该几何体的体积为()图-．．．．．(年贵州贵阳二模)如图-，在正方形中，，分别是，的中点，沿，，把正方形折成一个四面体，使，，三点重合，重合后的点记为，点在△内的射影为，则下列说法正确的是( )图-．是△的垂心．是△的内心．是△的外心．是△的重心二、填空题：本大题共小题，每小题分，共分，把答案填在题中横线上．．圆柱形容器内部盛有高度为的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图-)，则球的半径是 .。

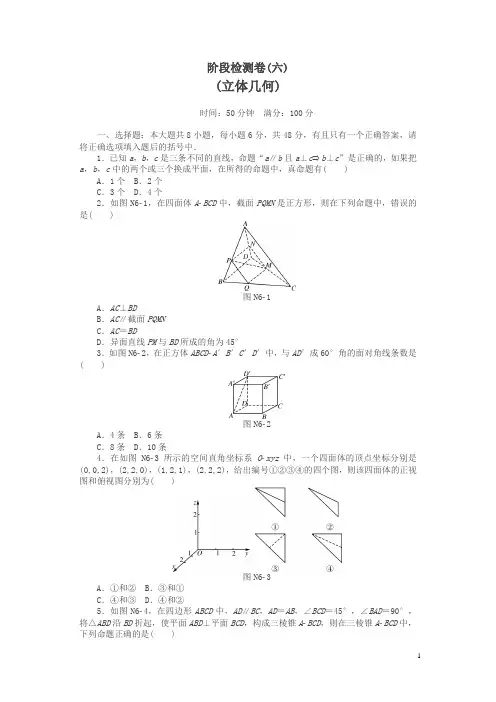
阶段检测卷(六)(立体几何)时间：50分钟满分：100分一、选择题：本大题共8小题，每小题6分，共48分，有且只有一个正确答案，请将正确选项填入题后的括号中．1．已知a，b，c是三条不同的直线，命题“a∥b且a⊥c⇒b⊥c”是正确的，如果把a，b，c中的两个或三个换成平面，在所得的命题中，真命题有( ) A．1个 B．2个C．3个 D．4个2．如图N6­1，在四面体A­BCD中，截面PQMN是正方形，则在下列命题中，错误的是( )图N6­1A．AC⊥BDB．AC∥截面PQMNC．AC＝BDD．异面直线PM与BD所成的角为45°3．如图N6­2，在正方体ABCD­A′B′C′D′中，与AD′成60°角的面对角线条数是( )图N6­2A．4条 B．6条C．8条 D．10条4．在如图N6­3所示的空间直角坐标系O­xyz中，一个四面体的顶点坐标分别是(0,0,2)，(2,2,0)，(1,2,1)，(2,2,2)，给出编号①②③④的四个图，则该四面体的正视图和俯视图分别为( )图N6­3A．①和② B．③和①C．④和③ D．④和②5．如图N6­4，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A­BCD，则在三棱锥A­BCD中，下列命题正确的是( )图N6­4A．平面ABD⊥平面ABC B．平面ADC⊥平面BDCC．平面ABC⊥平面BDC D．平面ADC⊥平面ABC6．如图N6­5，四棱锥S­ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是( )图N6­5A．AC⊥SBB．AB∥平面SCDC．SA与平面SBD所成的角等于SC与平面SBD所成的角D．AB与SC所成的角等于DC与SA所成的角7．(2017年广东深圳二模)一个长方体被一平面截去一部分后，所剩几何体的三视图如图N6­6，则该几何体的体积为( )图N6­6A．24 B．48C．72 D．968．(2017年贵州贵阳二模)如图N6­7，在正方形ABCD中，E，F分别是BC，CD的中点，沿AE，AF，EF把正方形折成一个四面体，使B，C，D三点重合，重合后的点记为P，P点在△AEF内的射影为O，则下列说法正确的是( )图N6­7A．O是△AEF的垂心B．O是△AEF的内心C．O是△AEF的外心D．O是△AEF的重心二、填空题：本大题共3小题，每小题6分，共18分，把答案填在题中横线上．9．圆柱形容器内部盛有高度为8 cm的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图N6­8)，则球的半径是________ cm.图N6­810．直三棱柱ABC­A1B1C1中，∠BCA＝90°，M，N分别是A1B1，A1C1的中点，BC＝CA ＝CC1，则BM与AN所成角的余弦值为________．11．(2016年浙江)某几何体的三视图如图N6­9(单位：cm)，则该几何体的表面积是________cm2，体积是________cm3.图N6­9三、解答题：本大题共2小题，共34分，解答须写出文字说明、证明过程或演算步骤．12．(14分)(2017年新课标Ⅲ)如图N6­10，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD＝∠CBD，AB＝BD.(1)证明：平面ACD⊥平面ABC；(2)过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D­AE­C的余弦值．图N6­1013．(20分)(2017年浙江)如图N6­11，已知四棱锥P­ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC＝AD＝2DC＝2CB，E为PD的中点．(1)证明：CE∥平面PAB；(2)求直线CE与平面PBC所成角的正弦值．图N6­11阶段检测卷(六)1．C 解析：若a ，b ，c 换成平面α，β，γ，则“α∥β且α⊥γ⇒β⊥γ”是真命题；若a ，b 换成平面α，β，则“α∥β且c ⊥α⇒c ⊥β”是真命题； 若b ，c 换成平面β，γ，则“a ∥β且a ⊥γ⇒β⊥γ”是真命题； 若a ，c 换成平面α，γ，则“b ∥α且α⊥γ⇒b ⊥γ”是假命题．2．C 解析：由PQ ∥AC ，QM ∥BD ，PQ ⊥QM ，可得AC ⊥BD ，故A 正确；由PQ ∥AC ，可得AC ∥截面PQMN ，故B 正确；异面直线PM 与BD 所成的角等于PM 与PN 所成的角，故D 正确；综上所述，C 是错误的．故选C.3．C4．D 解析：如图D196，在空间直角坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的正视图为④，俯视图为②.图D1965．D 解析：在平面图形中CD ⊥BD ，折起后仍有CD ⊥BD ，由于平面ABD ⊥平面BCD ，故CD ⊥平面ABD ，CD ⊥AB .又AB ⊥AD ，故AB ⊥平面ADC .所以平面ABC ⊥平面ADC .6．D7．B 解析：还原出空间几何体，如图D197.该平面将长方体刚好平分，所以该几何体的体积V ＝12V 长方体＝12×4×4×6＝48.故选B.图D1978．A 解析：如图D198，由题意可知PA ，PE ，PF 两两垂直， 所以PA ⊥平面PEF ，从而PA ⊥EF . 而PO ⊥平面AEF ，则PO ⊥EF .因为PO ∩PA ＝P ，所以EF ⊥平面PAO . 所以EF ⊥AO .同理可知AE ⊥FO ，AF ⊥EO . 所以O 为△AEF 的垂心．图D1989．4 解析：设球的半径为r cm ，放入3个球后，圆柱液面高度变为6r cm.则有πr 2·6r＝8πr 2＋3·43πr 3.即2r ＝8.∴r ＝4.10.3010解析：方法一，如图D199，取BC 的中点Q ，连接QN ，AQ ，易知BM ∥QN ，则∠ANQ 即为所求．设BC ＝CA ＝CC 1＝2，则AQ ＝5，AN ＝5，QN ＝ 6.∴cos ∠ANQ ＝AN 2＋NQ 2－AQ 22AN ·NQ＝5＋6－52 5×6＝6230＝3010.图D199 图D200方法二，以C 1为坐标原点，建立如图D200所示的空间直角坐标系，设BC ＝CA ＝CC 1＝2，则A (2,0,2)，N (1，0,0)，M (1,1,0)，B (0,2,2)．∴A N →＝(－1,0，－2)，BM →＝(1，－1，－2)．∴cos 〈A N →，BM →〉＝A N →·BM →|A N →||BM →|＝－1＋45×6＝330＝3010.11．72 32 解析：几何体为两个相同长方体组合而成，长方体的长、宽、高分别为4,2,2，所以体积为2×(2×2×4)＝32，由于两个长方体重叠部分为一个边长为2的正方形，所以表面积为2×(2×2×2＋2×4×4)－2(2×2)＝72.12．(1)证明：由题设可得，△ABD ≌△CBD ， 从而AD ＝DC .又△ACD 是直角三角形，所以∠ADC ＝90°. 取AC 的中点O ，连接DO ，BO ， 则DO ⊥AC ，DO ＝AO .又由于△ABC 是正三角形，故BO ⊥AC . 所以∠DOB 为二面角D ­AC ­B 的平面角．在Rt △AOB 中，BO 2＋AO 2＝AB 2. 又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2， 故∠DOB ＝90°.所以平面ACD ⊥平面ABC .图D201(2)解：由题设及(1)知，OA ，OB ，OD 两两垂直，以O 为坐标原点，OA →的方向为x 轴正方向，|OA →|为单位长，建立如图D201所示的空间直角坐标系O ­xyz .则A (1,0,0)，B (0，3，0)，C (－1,0,0)，D (0,0,1)．由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得E ⎝⎛⎭⎪⎫0，32，12.故AD →＝(－1,0,1)，AC →＝(－2,0,0)，AE →＝⎝⎛⎭⎪⎫－1，32，12.设n ＝(x ，y ，z )是平面DAE 的法向量，则⎩⎪⎨⎪⎧n ·AD →＝0，n ·AE →＝0即⎩⎪⎨⎪⎧－x ＋z ＝0，－x ＋32y ＋12z ＝0.可取n ＝⎝ ⎛⎭⎪⎫1，33，1. 设m 是平面AEC 的法向量，则⎩⎪⎨⎪⎧m ·AC →，m ·AE →＝0.同理可取m ＝(0，－1，3)． 则cos 〈n ，m 〉＝n·m |n||m|＝n·m |n||m|＝77.所以二面角D ­AE ­C 的余弦值为77. 13．(1)证明：如图D202，设PA 中点为F ，连接EF ，FB . 因为E ，F 分别为PD ，PA 中点，所以EF ∥AD ，且EF ＝12AD .又因为BC ∥AD ，BC ＝12AD ，所以EF ∥BC ，且EF ＝BC .即四边形BCEF 为平行四边形，所以CE ∥BF . 所以CE ∥平面PAB .图D202(2)如图，分别取BC ，AD 的中点为M ，N .连接PN 交EF 于点Q ，连接MQ . 因为E ，F ，N 分别是PD ，PA ，AD 的中点， 所以Q 为EF 中点．在平行四边形BCEF 中，MQ ∥CE .由△PAD 为等腰直角三角形，得PN ⊥AD . 由DC ⊥AD ，N 是AD 的中点，得BN ⊥AD . 所以AD ⊥平面PBN .由BC ∥AD ，得BC ⊥平面PBN ， 那么平面PBC ⊥平面PBN .过点Q 作PB 的垂线，垂足为H ，连接MH . MH 是MQ 在平面PBC 上的射影，所以∠QMH 是直线CE 与平面PBC 所成的角． 设CD ＝1.在△PCD 中，由PC ＝2，CD ＝1，PD ＝2，得CE ＝2，在△PBN 中，由PN ＝BN ＝1，PB ＝3，得QH ＝14，在Rt△MQH 中，QH ＝14，MQ ＝ 2.所以sin∠QMH ＝28. 所以直线CE 与平面PBC 所成角的正弦值是28.。

阶段检测卷(四)(不等式)时间：50分钟 满分：100分一、选择题：本大题共6小题，每小题6分，共36分，有且只有一个正确答案，请将正确选项填入题后的括号中．1．(2017年新课标Ⅰ)设x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋3y ≤3，x －y ≥1，y ≥0，则z ＝x ＋y 的最大值为( )A ．0B ．1C ．2D ．32．(2017年新课标Ⅱ)设x ，y 满足约束条件⎩⎪⎨⎪⎧2x ＋3y －3≤0，2x －3y ＋3≥0，y ＋3≥0，则z ＝2x ＋y 的最小值是( )A ．－15B ．－9C ．1D ．93．当x >1时，不等式x ＋1x －1≥a 恒成立，则实数a 的取值范围是( )A ．(－∞，2]B ．[2，＋∞)C ．[3，＋∞) D．(－∞，3]4．某辆汽车购买时的费用是15万元，每年使用的保险费、路桥费、汽油费等约为1.5万元．年维修保养费用第一年3000元，以后逐年递增3000元，则这辆汽车报废的最佳年限(即使用多少年的年平均费用最少)是( )A ．8年B ．10年C ．12年D ．15年5．若平面区域⎩⎪⎨⎪⎧x ＋y －3≥0，2x －y －3≤0，x －2y ＋3≥0夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是( )A.3 55B. 2C.3 22D. 5 6．(2017年山东)若a >b >0，且ab ＝1，则下列不等式成立的是( )A ．a ＋1b <b2a <log 2(a ＋b )B.b 2a <log 2(a ＋b )<a ＋1bC ．a ＋1b <log 2(a ＋b )<b 2aD ．log 2(a ＋b )<a ＋1b <b2a二、填空题：本大题共4小题，每小题6分，共24分，把答案填在题中横线上．7．(2013年大纲)记不等式组⎩⎪⎨⎪⎧x ≥0，x ＋3y ≥4，3x ＋y ≤4所表示的平面区域为D ，若直线y ＝a (x ＋1)与D 有公共点，则a 的取值范围是________． 8．定义运算“⊗”：x ⊗y ＝x 2－y 2xy(x ，y ∈R ，xy ≠0)．当x >0，y >0时，x ⊗y ＋(2y )⊗x的最小值是________．9．已知x ，y ∈R 且满足x 2＋2xy ＋4y 2＝6，则z ＝x 2＋4y 2的取值范围为________．10．已知S n 是数列⎩⎨⎧⎭⎬⎫n 2n －1的前n 项和，若不等式|λ＋1|<S n ＋n 2n －1对一切n ∈N *恒成立，则λ的取值范围是__________．三、解答题：本大题共3小题，共40分，解答须写出文字说明、证明过程或推演步骤．11．(12分)桑基鱼塘是某地一种独具地方特色的农业生产形式，某研究单位打算开发一个桑基鱼塘项目，该项目准备购置一块1800平方米的矩形地块，中间挖出三个矩形池塘养鱼，挖出的泥土堆在池塘四周形成基围(阴影部分X6­5­2)种植桑树，池塘周围的基围宽均为2米，如图，设池塘所占的总面积为S 平方米．(1)试用x 表示S ；(2)当x 取何值时，才能使得S 最大？并求出S 的最大值．图X6­5­212．(12分)某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个，生产一个卫兵需5分钟，生产一个骑兵需7分钟，生产一个伞兵需4分钟，已知总生产时间不超过10小时．若生产一个卫兵可获利润5元，生产一个骑兵可获利润6元，生产一个伞兵可获利润3元．(1)试用每天生产的卫兵个数x 与骑兵个数y 表示每天的利润ω(单位：元)； (2)怎样分配生产任务才能使每天的利润最大，最大利润是多少？13．(14分)已知函数f (x )＝mxx 2＋n(m ，n ∈R )在x ＝1处取到极值2.(1)求f (x )的解析式；(2)设函数g (x )＝ln x ＋a x.若对任意的x 1∈R ，总存在x 2∈[1，e]，使得g (x 2)≤f (x 1)＋72，求实数a 的取值范围．阶段检测卷(四)1．D 解析：可行域如图D190，目标函数z ＝x ＋y 经过A (3，0)时最大，故z max ＝3＋0＝3.故选D.图D1902．A 解析：绘制不等式组表示的可行域(如图D191)，目标函数即y ＝－2x ＋z ，其中z 表示斜率为k ＝－2的直线系与可行域有交点时直线的截距，数形结合可得目标函数在点B (－6，－3)处取得最小值z ＝－12－3＝－15.故选A.图D1913．D4．B 解析：汽车使用n 年平均费用为15＋1.5n ＋0.3n ＋n n －2×0.3n＝15n ＋3n20＋1.65≥215n ×3n 20＋1.65＝4.65(万元)，当且仅当15n ＝3n 20，3n 2＝300，n 2＝100，n ＝10，即n ＝10时“＝”成立，故这辆汽车报废的最佳年限为10年．5．B 解析：画出不等式的平面区域如图D192，则⎩⎪⎨⎪⎧x －2y ＋3＝0，x ＋y －3＝0.得A (1,2)．则⎩⎪⎨⎪⎧2x －y －3＝0，x ＋y －3＝0.得B (2,1)．由题意可知，当斜率为1的两条直线分别过点A 和点B 时，两直线的距离最小，即|AB |＝－2＋－2＝ 2.故选B.图D1926．B 解析：方法一，因为a >b >0，且ab ＝1，所以a >1，0<b <1.则b2a <1，log 2(a ＋b )>log 22ab ＝1,2a ＋1b >a ＋1b >a ＋b ⇒a ＋1b>log 2(a ＋b )．故选B.方法二，取a ＝2，b ＝12，b 2a ＝18，log 2(a ＋b )＝log 252∈(1,2)，a ＋1b＝4.故选B.7.⎣⎢⎡⎦⎥⎤12，4 解析：如图D193，将点A (0,4)，C (1,1)分别与点B (－1,0)求斜率，得最小值为12，最大值为4.图D193 8. 2 解析：由新定义运算知，x ⊗y ＝x 2－y 2xy ，(2y )⊗x ＝y2－x22yx＝4y 2－x22xy.因为x >0，y >0，所以x ⊗y ＋(2y )⊗x ＝x 2－y 2xy ＋4y 2－x 22xy ＝x 2＋2y 22xy ≥2 x 2·2y 22xy ＝2 2xy2xy＝ 2.当且仅当x ＝2y 时取等号．所以x ⊗y ＋(2y )⊗x 的最小值是 2.9．[4,12] 解析：∵2xy ＝6－(x 2＋4y 2)，而2xy ≤x 2＋4y 22，∴6－(x 2＋4y 2)≤x 2＋4y 22.∴x 2＋4y 2≥4(当且仅当x ＝2y 时取等号)．又∵(x ＋2y )2＝6＋2xy ≥0，即2xy ≥－6.∴z ＝x 2＋4y 2＝6－2xy ≤12.综上所述，4≤x 2＋4y 2≤12.10．－3<λ<1 解析：由S n ＝1＋2×12＋3×122＋…＋(n －1)·12n －2＋n ·12n －1，12S n ＝1×12＋2×122＋…＋(n －1)·12n －1＋n ·12n ，两式相减，得12S n ＝1＋12＋122＋…＋12n －1－n ·12n ＝2－n ＋22n .所以S n ＝4－n ＋22n －1.于是由不等式|λ＋1|<4－22n －1对一切n ∈N *恒成立，得|λ＋1|<2.解得－3<λ<1.11．解：(1)由题图知，3a ＋6＝x ，∴a ＝x －63.则总面积S ＝⎝ ⎛⎭⎪⎫1800x －4·a ＋2a ⎝ ⎛⎭⎪⎫1800x －6＝a ⎝ ⎛⎭⎪⎫5400x －16＝x －63⎝ ⎛⎭⎪⎫5400x －16 ＝1832－⎝ ⎛⎭⎪⎫10 800x ＋16x 3，即S ＝1832－⎝ ⎛⎭⎪⎫10 800x ＋16x 3(x ＞0)．(2)由S ＝1832－⎝ ⎛⎭⎪⎫10 800x ＋16x 3，得S ≤1832－210 800x ·16x3＝1832－2×240＝1352.当且仅当10 800x ＝16x3，此时，x ＝45.即当x 为45米时，S 最大，且S 最大值为1352平方米． 12．解：(1)依题意每天生产的伞兵个数为100－x －y ，所以利润ω＝5x ＋6y ＋3(100－x －y )＝2x ＋3y ＋300(x ，y ∈N )． (2)约束条件为⎩⎪⎨⎪⎧5x ＋7y ＋－x －y ，100－x －y ≥0，x ≥0，y ≥0，x ，y ∈N ，整理，得⎩⎪⎨⎪⎧x ＋3y ≤200，x ＋y ≤100，x ≥0，y ≥0，x ，y ∈N .目标函数为ω＝2x ＋3y ＋300，作出可行域如图D194，图D194作初始直线l 0：2x ＋3y ＝0，平移l 0，当l 0经过点A 时，ω有最大值， 由⎩⎪⎨⎪⎧ x ＋3y ＝200，x ＋y ＝100得⎩⎪⎨⎪⎧x ＝50，y ＝50. 所以最优解为A (50,50)，此时ωmax ＝550元．故每天生产卫兵50个，骑兵50个，伞兵0个时利润最大，且最大利润为550元．13．解：(1)f ′(x )＝m x 2＋n －2mx 2x 2＋n 2＝－mx 2＋mnx 2＋n 2.由f (x )在x ＝1处取到极值2，得f ′(1)＝0，f (1)＝2.即⎩⎪⎨⎪⎧mn －m ＋n 2＝0，m 1＋n ＝2，解得⎩⎪⎨⎪⎧m ＝4，n ＝1.经检验，当m ＝4，n ＝1时，f (x )在x ＝1处取得极值．故f (x )＝4xx 2＋1.(2)由(1)知，f (x )的定义域为R ，且f (－x )＝－f (x )． 故f (x )为奇函数，且f (0)＝0.当x ＞0时，f (x )＞0,0<f (x )＝4x ＋1x≤2，当且仅当x ＝1时取“＝”； 当x <0时，－2≤f (x )＝－4－x ＋1－x<0， 当且仅当x ＝－1时，取“＝”．故f (x )的值域为[－2,2]．从而f (x 1)＋72≥32.依题意有g (x )最小值≤32.函数g (x )＝ln x ＋a x的定义域为(0，＋∞)， g ′(x )＝1x －a x 2＝x －ax2.①当a ≤1时，g ′(x )＞0，函数g (x )在[1，e]上单调递增，其最小值为g (1)＝a ≤1<32，符合题意；②当1<a <e 时，函数g (x )在[1，a )上有g ′(x )<0，单调递减，在(a ，e]上有g ′(x )>0，单调递增，所以函数g (x )的最小值为g (a )＝ln a ＋1.由ln a ＋1≤32，得0<a ≤ e.从而知1<a ≤e 符合题意；③当a ≥e 时，显然函数g (x )在[1，e]上单调递减，其最小值为g (e)＝1＋a e ≥2>32，不符合题意．综上所述，实数a 的取值范围为a ≤ e.。

专题一函数与导数第课时．(年新课标Ⅲ)已知函数()＝＋＋(＋).()讨论()的单调性；()当<时，证明()≤－－.．(年新课标Ⅱ)已知函数()＝(＋)－(－)．()当＝时，求曲线＝()在(，())处的切线方程；()若当∈(，＋∞)时，()＞，求实数的取值范围．．(年湖北八校联考)设函数()＝－(>，且≠)，()＝′()[其中′()为()的导函数]．()当＝时，求()的极大值点；()讨论()的零点个数．．(年广东深圳二模)设函数()＝－(∈，为常数)，为自然对数的底数．()当()>时，求实数的取值范围；()当＝时，求使得()＋>成立的最小正整数.第课时．已知函数()的定义域是，()＝，对任意的∈，()＋′()>，则不等式·()>＋的解集是( )．{>} ．{<}．<－，或> ．{<－，或<<}．(年江西五校联考)已知函数＝()对任意的∈满足′()＋() >[其中′()是函数()的导函数]，则下列不等式成立的是( )< <．()> ．()>．(年四川雅安诊断)设函数()的导函数为′()，对任意∈，都有′()<()成立，则( )．()>()．()＝()．()<()．()与()大小不确定．(年新课标)设函数()＝＋)的最大值为，最小值为，则＋＝.．(年河北石家庄质检二)设′()是奇函数()(∈)的导函数，(－)＝，当＞时，′()－()＞，则使得()＞成立的的取值范围是．．(年湖北)π为圆周率，＝…为自然对数的底数．()求函数()＝)的单调区间；()求，，π，π，π，π这个数中的最大数与最小数．。

阶段检测卷(三)(数列)时间：50分钟　满分：100分一、选择题：本大题共8小题，每小题6分，共48分，有且只有一个正确答案，请将正确选项填入题后的括号中．1．数列，，，，…的一个通项公式为( )1318115124A ．a n ＝B ．a n ＝12n ＋11n ＋2C ．a n ＝ D ．a n ＝1n (n ＋2)12n －12．若数列{a n }满足：a 1＝19，a n ＋1＝a n －3(n ∈N *)，而数列{a n }的前n 项和数值最大时，n 的值为( )A ．6B ．7C ．8D ．93．(2017年江西南昌二模)《九章算术》卷第六《均输》中，有问题“今有竹九节，下三节容量四升，上四节容量三升．问中间二节欲均容，各多少？”其中“欲均容”的意思是：使容量变化均匀，即由下往上均匀变细．在这个问题中的中间两节容量和是( )A ．1升B ．2升C ．2升D ．3升61663224．(2017年湖北孝感一模)一个样本容量为8的样本数据，它们按一定顺序排列可以构成一个公差不为0的等差数列{a n }，若a 3＝5，且a 1，a 2，a 5成等比数列，则此样本数据的中位数是( )A ．6B ．7C ．8D ．95．设a ，b ，c 均为正实数，则三个数a ＋，b ＋，c ＋( )1b 1c 1a A ．都大于2B ．都小于2C ．至少有一个不大于2D ．至少有一个不小于26．在等差数列{a n }中，a n >0，且a 1＋a 2＋…＋a 10＝30，则a 5a 6的最大值是( )A ．3B ．6C ．9D ．367.＋＋＋…＋的值为( )122－1132－1142－11(n ＋1)2－1A.B.－n ＋12n ＋234n ＋12n ＋2C.－ D.－＋3412(1n ＋1＋1n ＋2)321n ＋11n ＋28．设n 为正整数，f (n )＝1＋＋＋…＋，经计算得f (2)＝，f (4)>2，f (8)>，f (16)>12131n 32523，f (32)>，观察上述结果，可推测出一般结论( )72A ．f (2n )>B ．f (n 2)≥2n ＋12n ＋22C ．f (2n )≥D ．以上都不对n ＋22二、填空题：本大题共3小题，每小题6分，共18分，把答案填在题中横线上．9．对于数列{a n }，定义数列{a n ＋1－a n }为数列{a n }的“差数列”，若a 1＝2，{a n }的“差数列”的通项公式为2n ，则数列{a n }的前n 项和S n ＝________.10．(2014年新课标Ⅰ)甲、乙、丙三位同学被问到是否去过A ，B ，C 三个城市时，甲说：我去过的城市比乙多，但没去过B 城市；乙说：我没去过C 城市；丙说：我们三人去过同一城市；由此可判断乙去过的城市为________．11．已知在等差数列{a n }中，前n 项的和为S n ，S 6>S 7>S 5，则：①数列的公差d <0；②S 11>0；③S 12<0；④S 13<0；⑤S 8>S 6；⑥S 8>S 3.其中正确的是______________．(只填序号)三、解答题：本大题共2小题，共34分，解答须写出文字说明、证明过程或推演步骤．12．(14分)(2017年广东广州二模)设等比数列{a n }的前n 项和为S n ，已知a 1a 2a 3＝8，S 2n ＝3(a 1＋a 3＋a 5＋…＋a 2n －1)(n ∈N *)．(1)求数列{a n }的通项公式；(2)设b n ＝nS n ，求数列的前n 项和T n .{bn }13．(20分)设数列{a n }的前n 项和为S n ，且方程x 2－a n x －a n ＝0有一根为S n －1(n ∈N *)．(1)求a 1，a 2；(2)猜想数列{S n }的通项公式，并给出证明．阶段检测卷(三)1．C 解析：观察知a n ＝＝.1(n ＋1)2－11n (n ＋2)2．B 解析：∵a n ＋1－a n ＝－3，∴数列{a n }是以19为首项，－3为公差的等差数列．∴a n ＝19＋(n －1)×(－3)＝22－3n .∵a 7＝22－21＝1>0，a 8＝22－24＝－2<0，∴当n ＝7时，数列{a n }的前n 项和最大．3．C 解析：设竹九节由上往下的容量分别为a 1，a 2，a 3，a 4，a 5，a 6，a 7，a 8，a 9，由题意可知：Error!⇒Error!所以问题中的中间两节容量和为a 5＋a 6＝2a 1＋9d ＝＝2.故选C.47223224．C 解析：因为a 1，a 2，a 5成等比数列，所以a ＝a 1a 5.设公差为d ，因为a 3＝5，2所以(5－d )2＝(5－2d )(5＋2d )．解得d ＝2或d ＝0(舍)．∴a 4＝5＋2＝7，a 5＝5＋4＝9.样本容量为8时，中位数为＝8.故选C.a 4＋a 525．D 解析：∵a ＞0，b ＞0，c ＞0，∴＋＋＝＋＋(a ＋1b )(b ＋1c )(c ＋1a )(a ＋1a )(b ＋1b )≥6，当且仅当a ＝b ＝c ＝1时，“＝”成立，故三者不能都小于2，即至少有一个不(c ＋1c )小于2.6．C 解析：a 1＋a 2＋a 3＋…＋a 10＝＝30，∴a 5＋a 6＝a 1＋a 10＝6.∴(a 1＋a 10)×102≤＝3，a 5a 6≤9.a 5a 6a 5＋a 627．C 解析：∵＝1(n ＋1)2－11n 2＋2n＝＝，1n (n ＋2)12(1n －1n ＋2)∴＋＋＋…＋122－1132－1142－11(n ＋1)2－1＝12(1－13＋12－14＋13－15＋…＋1n －1n ＋2)＝12(32－1n ＋1－1n ＋2)＝－.故选C.3412(1n ＋1＋1n ＋2)8．C 解析：f (2)＝，f (4)＝f (22)>，322＋22f (8)＝f (23)>，f (16)＝f (24)>，3＋224＋22f (32)＝f (25)>，5＋22由此可推知f (2n )≥.故选C.n ＋229．2n ＋1－2　解析：∵a n ＋1－a n ＝2n ，∴a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝2n －1＋2n －2＋…＋22＋2＋2＝＋2＝2n －2＋2＝2n .∴S n ＝＝2n ＋1－2.2－2n 1－22－2n ＋11－210．A 解析：根据题意可将三人可能去过哪些城市的情况列表如下：学生A 城市B 城市C 城市甲去过没去去过乙去过没去没去丙去过可能可能可以得出结论乙去过的城市为A.11．①②④⑥　解析：S 6>S 7>S 5⇒a 6>0，a 7<0，a 6＋a 7>0，则a 7－a 6＝d <0，①正确；S 11＝＝11a 6>0，②正确；S 12＝＝>0，③错误；S 13＝11(a 1＋a 11)212(a 1＋a 12)212(a 6＋a 7)2＝13a 7<0，④正确；S 8－S 6＝a 7＋a 8<0，⑤错误；13(a 1＋a 13)2S 8－S 3＝a 4＋a 5＋a 6＋a 7＋a 8＝5a 6>0，⑥正确．12．解：(1)因为数列{a n }是等比数列，所以a 1a 3＝a .2因为a 1a 2a 3＝8，所以a ＝8.解得a 2＝2.32因为S 2n ＝3(a 1＋a 3＋a 5＋…＋a 2n －1)，所以S 2＝3a 1，即a 1＋a 2＝3a 1.因为a 2＝2，所以a 1＝1.因为等比数列{a n }的公比为q ＝＝2，a 2a 1所以数列{a n }的通项公式为a n ＝2n －1.(2)因为等比数列{a n }的首项为a 1＝1，公比q ＝2，所以S n ＝＝＝2n －1.a 1(1－qn )1－q 1－2n1－2因为b n ＝nS n ，所以b n ＝n (2n －1)＝n ·2n －n .所以T n ＝b 1＋b 2＋b 3＋…＋b n －1＋b n＝(1×2＋2×22＋3×23＋…＋n ×2n )－(1＋2＋3＋…＋n )．设P n ＝1×2＋2×22＋3×23＋…＋n ×2n .则2P n ＝1×22＋2×23＋3×24＋…＋n ×2n ＋1.所以P n ＝n ×2n ＋1－(2＋22＋23＋24＋…＋2n )＝(n －1)2n ＋1＋2.因为1＋2＋3＋…＋n ＝，n (n ＋1)2所以T n ＝(n －1)2n ＋1＋2－.n (n ＋1)213．解：(1)当n ＝1时，方程x 2－a 1x －a 1＝0有一根为S 1－1＝a 1－1，∴(a 1－1)2－a 1(a 1－1)－a 1＝0.解得a 1＝.12当n ＝2时，方程x 2－a 2x －a 2＝0有一根为S 2－1＝a 1＋a 2－1＝a 2－，12∴2－a 2－a 2＝0.解得a 2＝.(a 2－12)(a 2－12)16(2)由题意知，(S n －1)2－a n (S n －1)－a n ＝0，当n ≥2时，a n ＝S n －S n －1，代入上式整理，得S n S n －1－2S n ＋1＝0.解得S n ＝.12－Sn －1由(1)得，S 1＝a 1＝，S 2＝a 1＋a 2＝＋＝.12121623猜想S n ＝(n ∈N *)．nn ＋1下面用数学归纳法证明这个结论．①当n ＝1时，结论成立．②假设n ＝k (k ∈N *，k ≥1)时结论成立，即S k ＝，当n ＝k ＋1时，S k ＋1＝＝kk ＋112－Sk ＝＝.即当n ＝k ＋1时结论成立．12－k k ＋1k ＋1k ＋2k ＋1(k ＋1)＋1由①②知，S n ＝对任意的正整数n 都成立．nn ＋1。

2019年高考数学(理科)模拟试卷(二)(本试卷分第Ⅰ卷和第Ⅱ卷两部分．满分150分，考试时间120分钟)第Ⅰ卷(选择题 满分60分)一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2017年广东广州一模)若集合M ＝{x ||x |≤1}，N ＝{y |y ＝x 2，|x |≤1}，则( ) A ．M ＝N B ．M ⊆N C ．N ⊆M D ．M ∩N ＝∅2．“1<x <π2”是“(x －1)tan x >0”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．(2017年山东)已知a ∈R ，i 是虚数单位，若z ＝a ＋3i ，z ·z ＝4，则a ＝( ) A ．1或－1 B.7或－7 C ．－ 3 D. 34．已知平面向量a ＝(1,2)，b ＝(－2，k )，若a 与b 共线，则||3a ＋b ＝( ) A ．3 B ．4 C. 5 D ．55．函数y ＝12x 2－ln x 的单调递减区间为( )A ．(－1,1]B ．(0,1]C ．[1，＋∞) D．(0，＋∞)6．(2017年河南洛阳三模)利用如图M2­1所示的算法在平面直角坐标系上打印一系列点，则打印的点在圆x 2＋y 2＝25内的个数为( )图M2­1A ．2个B ．3个C ．4个D ．5个 7．(2017年广东惠州三模)某个几何体的三视图如图M2­2，若该几何体的所有顶点都在一个球面上，则该球面的表面积是( )图M2­2A ．4π B.28π3 C.44π3D ．20π8．已知F 1，F 2分别为双曲线E ：x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，离心率为53，过原点的直线l 交双曲线左、右两支分别于A ，B ，若|BF 1|－|AF 1|＝6，则该双曲线的标准方程为( )A.x 29－y 216＝1B.x 218－y 232＝1C.x 29－y 225＝1 D.x 236－y 264＝1 9．若函数f (x )＝⎩⎪⎨⎪⎧x －a 2x ，x ＋1x＋a x 的最小值为f (0)，则实数a 的取值范围是( )A ．[－1,2]B ．[－1,0]C ．[1,2]D ．[0,2] 10．(2017年广东惠州三模)已知函数f (x )＝sin(ωx ＋φ)(ω>0，－π<φ<0)的最小正周期是π，将f (x )的图象向左平移π3个单位长度后所得的函数图象过点P (0，1)，则f (x )＝sin(ωx ＋φ)( )A ．在区间⎣⎢⎡⎦⎥⎤－π6，π3上单调递减B ．在区间⎣⎢⎡⎦⎥⎤－π6，π3上单调递增C ．在区间⎣⎢⎡⎦⎥⎤－π3，π6上单调递减D ．在区间⎣⎢⎡⎦⎥⎤－π3，π6上单调递增 11．已知A (2,1)，B (1，－2)，C ⎝ ⎛⎭⎪⎫35，－15，O 为坐标原点，动点P (a ，b )满足0≤OP →·OA→≤2，且0≤OP →·OB →≤2，则动点P 到点C 的距离大于14的概率为( )A ．1－5π64 B.5π64C ．1－π16 D.π1612．(2017年天津)已知函数f (x )＝⎩⎪⎨⎪⎧x 2－x ＋3，x ≤1，x ＋2x，x >1.设a ∈R ，若关于x 的不等式f (x )≥⎪⎪⎪⎪⎪⎪x2＋a 在R 上恒成立，则a 的取值范围是( ) A.⎣⎢⎡⎦⎥⎤－4716，2 B.⎣⎢⎡⎦⎥⎤－4716，3916 C ．[－2 3，2] D.⎣⎢⎡⎦⎥⎤－2 3，3916 第Ⅱ卷(非选择题 满分90分)本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生必须作答．第22～23题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分，共20分．13．已知椭圆Γ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，焦距为2c ，若直线y ＝3(x ＋c )与椭圆Γ的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于__________．14．(2017年山东)已知(1＋3x )n 的展开式中含有x 2项的系数是54，则n ＝____________.15．已知正方体ABCD ­A 1B 1C 1D 1中，E ，F 分别为BB 1，CC 1的中点，那么异面直线AE 与D 1F 所成角的余弦值为________．16．(2017年广东惠州三模)已知在△ABC 中，AC ＝2，BC ＝6，∠ACB ＝π6，若线段BA 的延长线上存在点D ，使∠BDC ＝π4，则CD ＝________.三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．17．(本小题满分12分)(2017年广东惠州三模)已知等差数列{a n }满足(a 1＋a 2)＋(a 2＋a 3)＋…＋(a n ＋a n ＋1)＝2n (n ＋1)(n ∈N *)．(1)求数列{a n }的通项公式；(2)求数列⎩⎨⎧⎭⎬⎫a n 2n －1的前n 项和S n .18．(本小题满分12分)(2017年天津)从甲地到乙地要经过3个十字路口，设各路口信号灯工作相互独立，且在各路口遇到红灯的概率分别为12，13，14.(1)设X 表示一辆车从甲地到乙地遇到红灯的个数，求随机变量X 的分布列和数学期望；(2)若有2辆车独立地从甲地到乙地，求这2辆车共遇到1个红灯的概率． 19．(本小题满分12分)(2017年广东湛江二模)如图M2­3，在直三棱柱ABC ­A 1B 1C 1中，二面角A ­A 1B ­C 是直二面角，AB ＝BC ＝2，点M 是棱CC 1的中点，三棱锥M ­BCA 1的体积为1.(1)证明：BC ⊥平面ABA 1；(2)求直线MB 与平面BCA 1所成角的正弦值．图M2­320．(本小题满分12分)(2017年广东汕头一模)已知O 为坐标原点，圆M ：(x ＋1)2＋y 2＝16，定点F (1,0)，点N 是圆M 上一动点，线段NF 的垂直平分线交圆M 的半径MN 于点Q ，点Q 的轨迹为E .(1)求曲线E 的方程；(2)已知点P 是曲线E 上但不在坐标轴上的任意一点，曲线E 与y 轴的交点分别为B 1，B 2，直线B 1P 和B 2P 分别与x 轴相交于C ，D 两点，请问线段长之积|OC |·|OD |是否为定值？如果是请求出定值，如果不是请说明理由；(3)在(2)的条件下，若点C 坐标为(－1,0)，设过点C 的直线l 与E 相交于A ，B 两点，求△ABD 面积的最大值．21．(本小题满分12分)(2017年广东深圳一模)已知函数f (x )＝x ln x ，e 为自然对数的底数．(1)求曲线y ＝f (x )在x ＝e －2处的切线方程；(2)关于x 的不等式f (x )≥λ(x －1)在(0，＋∞)上恒成立，求实数λ的值；(3)关于x 的方程f (x )＝a 有两个实根x 1，x 2，求证：|x 1－x 2|<2a ＋1＋e －2.请考生在第22～23两题中任选一题作答．注意：只能作答在所选定的题目上．如果多做，则按所做的第一个题目计分．22．(本小题满分10分)选修4­4：坐标系与参数方程(2017年广东广州一模)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝3－t ，y ＝1＋t(t 为参数)．在以坐标原点为极点， x 轴正半轴为极轴的极坐标系中， 曲线C ：ρ＝2 2cos ⎝⎛⎭⎪⎫θ－π4. (1)求直线l 的普通方程和曲线C 的直角坐标方程； (2)求曲线C 上的点到直线l 的距离的最大值． 23．(本小题满分10分)选修4­5：不等式选讲(2017年广东茂名一模)已知函数f (x )＝|2x －a |＋|2x ＋3|，g (x )＝|x －1|＋2. (1)若a ＝1，解不等式f (x )<6；(2)若对任意x 1∈R ，都有x 2∈R ，使得f (x 1)＝g (x 2)成立，求实数a 的取值范围．2019年高考数学(理科) 模拟试卷(二)1.C 解析：集合M ＝{x |－1≤x ≤1}，N ＝{y |0≤y ≤1}，故有N ⊆M .2．A 解析：因为1<x <π2，所以x －1>0，tan x >0，即(x －1)tan x >0，反之不成立．故选A.3．A 解析：由z ＝a ＋3i ，z ·z ＝4，得a 2＋3＝4，所以a ＝±1.故选A. 4．C 5.B6．C 解析：由程序框图知，i ＝6时，打印第一个点(－3,6)，在圆x 2＋y 2＝25外， i ＝5时，打印第二个点(－2,5)，在圆x 2＋y 2＝25外， i ＝4时，打印第三个点(－1,4)，在圆x 2＋y 2＝25内， i ＝3时，打印第四个点(0,3)，在圆x 2＋y 2＝25内， i ＝2时，打印第五个点(1,2)，在圆x 2＋y 2＝25内， i ＝1时，打印第六个点(2,1)，在圆x 2＋y 2＝25内，∴打印的点在圆x 2＋y 2＝25内的有4个． 故选C.7．B 解析：由三视图可知该几何体为棱长均为2的正三棱柱．设球心为O ，小圆的圆心为O 1，球的半径为R ，小圆的半径为r ，则R 2＝r 2＋O 1O 2.即R 2＝⎝ ⎛⎭⎪⎫23 32＋1＝73.∴S ＝28π3.故选B. 8．A 9.D10．B 解析：ω＝2, f (x )＝sin(2x ＋φ)向左平移π3个单位长度后得到的函数是y＝sin ⎝ ⎛⎭⎪⎫2x ＋φ＋2π3，其图象过(0,1)，∴sin ⎝ ⎛⎭⎪⎫φ＋2π3＝1.∵－π<φ<0，∴φ＝－π6，f (x )＝sin ⎝⎛⎭⎪⎫2x －π6.故选B. 11．A 解析：依题意有⎩⎪⎨⎪⎧0≤2a ＋b ≤2，0≤a －2b ≤2，画出可行域(图略)可知点P 的运动区域为以C ⎝ ⎛⎭⎪⎫35，－15为中心且边长为2 55的正方形，而点P 到点C 的距离小于或等于14的区域是以C ⎝ ⎛⎭⎪⎫35，－15为圆心，14为半径的圆以及圆的内部，则所求概率为45－π1645＝1－5π64.12．A 解析：不等式f (x )≥⎪⎪⎪⎪⎪⎪x 2＋a 可转化为－f (x )≤x2＋a ≤f (x )，(*)当x ≤1时，(*)式即为－x 2＋x －3≤x 2＋a ≤x 2－x ＋3，－x 2＋x 2－3≤a ≤x 2－32x ＋3，又－x 2＋x 2－3＝－⎝ ⎛⎭⎪⎫x －142－4716≤－4716，当x ＝14时取等号；x 2－32x ＋3＝⎝ ⎛⎭⎪⎫x －342＋3916≥3916，当x ＝34时取等号，所以－4716≤a ≤3916.当x >1时，(*)式为－x －2x ≤x 2＋a ≤x ＋2x ，－32x －2x ≤a ≤x 2＋2x，又－32x －2x ＝－⎝ ⎛⎭⎪⎫32x ＋2x ≤－2 3，当x ＝2 33时取等号； x 2＋2x≥2 x 2×2x＝2，当x ＝2时取等号， 所以－2 3≤a ≤2.综上所述，a 的取值范围是－4716≤a ≤2.故选A.13.3－1 解析：由直线方程y ＝3(x ＋c )⇒直线与x 轴的夹角∠MF 1F 2＝π3，且过点F 1(－c,0)，∵∠MF 1F 2＝2∠MF 2F 1＝π3，∴∠MF 2F 1＝π6.∴∠F 1MF 2＝π2.即F 1M ⊥F 2M .∴在Rt △F 1MF 2中，|F 1F 2|＝2c ，|F 1M |＝c ，|F 2M |＝3c .∴由椭圆的第一定义可得2a ＝c ＋3c ，∴c a ＝21＋3＝3－1. 14．4 解析：由二项式定理的通项公式T r ＋1＝C r n (3x )r ＝C r n 3r x r ，令r ＝2，得C 2n 32＝54.解得n ＝4.15.3516. 3 解析：因为线段BA 的延长线上存在点D ，使∠BDC ＝π4，∠ACB ＝π6，所以AB 2＝AC 2＋BC 2－2×AC ×BC ×cos π6＝2，即AB ＝ 2.所以AB ＝AC .所以∠B ＝∠ACB ＝π6.在△BCD 中，根据正弦定理BCsin ∠D ＝CDsin ∠B⇔622＝CD12⇒CD ＝ 3. 17．解：(1)设等差数列{a n }的公差为d ，由已知，得⎩⎪⎨⎪⎧a 1＋a 2＝4，a 1＋a 2＋a 2＋a 3＝12，即⎩⎪⎨⎪⎧a 1＋a 2＝4，a 2＋a 3＝8.所以⎩⎪⎨⎪⎧a 1＋a 1＋d ＝4，a 1＋d ＋a 1＋2d ＝8.解得⎩⎪⎨⎪⎧a 1＝1，d ＝2.所以a n ＝2n －1.(2)由(1)，得a n 2n －1＝2n －12n －1.所以S n ＝1＋321＋522＋…＋2n －32n －2＋2n －12n －1， ①12S n ＝12＋322＋523＋…＋2n －32n －1＋2n －12n . ② ①－②，得12S n ＝1＋1＋12＋122＋…＋12n －2－2n －12n ＝3－2n ＋32n .所以S n ＝6－4n ＋62n .18．(1)解：随机变量X 的所有可能取值为0,1,2,3.P (X ＝0)＝⎝⎛⎭⎪⎫1－12×⎝ ⎛⎭⎪⎫1－13×⎝ ⎛⎭⎪⎫1－14＝14，P (X ＝1)＝12×⎝ ⎛⎭⎪⎫1－13×⎝ ⎛⎭⎪⎫1－14＋⎝⎛⎭⎪⎫1－12×13×⎝ ⎛⎭⎪⎫1－14＋⎝ ⎛⎭⎪⎫1－12×⎝ ⎛⎭⎪⎫1－13×14＝1124，P (X ＝2)＝⎝ ⎛⎭⎪⎫1－12×13×14＋12×⎝ ⎛⎭⎪⎫1－13×14＋12×13×⎝ ⎛⎭⎪⎫1－14＝14，P (X ＝3)＝12×13×14＝124.所以随机变量X X 01 2 3 P 141124 14 124 随机变量X 的数学期望E (X )＝0×4＋1×24＋2×4＋3×24＝1312.(2)设Y 表示第1辆车遇到红灯的个数，Z 表示第2辆车遇到红灯的个数，则所求事件的概率为P (X ＋Z ＝1)＝P (Y ＝0，Z ＝1)＋P (Y ＝1，Z ＝0)＝P (Y ＝0)×P (Z ＝1)＋P (Y ＝1)×P (Z ＝0)＝14×1124＋1124×14＝1148.所以这2辆车共遇到1个红灯的概率为1148.19．(1)证明：过A 在平面ABA 1内作AH ⊥A 1B ，垂足为H ，如图D207. 由题可知平面ABA 1⊥平面BCA 1，且平面ABA 1∩平面BCA 1＝BA 1， ∴AH ⊥平面BCA 1.又BC ⊂平面BCA 1，∴AH ⊥BC .由题直三棱的性质可知AA 1⊥BC ，AA 1∩AH ＝A . ∴BC ⊥平面ABA 1.图D207(2)解：设AA 1＝a ，而1-A MBC V ＝1-M BCA V ＝1.由(1)知AB ⊥BC ，结合直棱柱的性质知AB ⊥平面BCM . ∵AA 1∥平面BCM ，∴A 1到平面BCM 的距离等于AB ＝2，得1-A MBC V ＝13·AB ·S △BCM ＝23×⎝ ⎛⎭⎪⎫12×2×a 2＝a 3＝1⇔a ＝3.以B 为原点，BC ，BA ，BB 1分别作为x ，y ，z 轴，建立如图所示的空间直角坐标系．则M ⎝⎛⎭⎪⎫2，0，32，C (2,0,0)，A 1(0,2,3)． 则BM →＝⎝⎛⎭⎪⎫2，0，32，BC →＝(2,0,0)，BA 1→＝(0,2,3)．设平面BCA 1的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧2x ＝0，2y ＋3z ＝0，令y ＝3，得一个法向量n ＝(0，－3,2)．∴cos 〈BM →，n 〉＝BM →·n |BM →||n |＝322＋⎝ ⎛⎭⎪⎫322×－2＋22＝61365. 故直线MB 与平面BCA 1所成角的正弦值为61365.20．解：(1)依题意，可得圆M 的圆心坐标为M (－1,0)，半径为r ＝4，|QN |＝|QF |， 则|QN |＋|QM |＝|QF |＋|QM |＝r ＝4>|MF | .根据椭圆定义，曲线E 是以M (－1,0)，F (1,0)为焦点，长轴长为4的椭圆．设其方程为x 2a 2＋y 2b2＝1(a >b >0)，∴2a ＝4,2c ＝2，即a ＝2，c ＝1.∴b ＝a 2－c 2＝ 3.∴曲线E 的方程为x 24＋y 23＝1.(2)设点P (x 0，y 0)，直线B 1P 方程为 y ＝y 0＋3x 0x －3，令y ＝0，得x C ＝3x 03＋y 0，同理可得x D ＝3x 03－y 0.∴|OC |·|OD |＝|x C |·|x D |＝⎪⎪⎪⎪⎪⎪3x 0 3＋y 0·⎪⎪⎪⎪⎪⎪3x 0 3－y 0＝⎪⎪⎪⎪⎪⎪3x 203－y 20.∵点P 是点E 上且不在坐标轴上的任意一点，∴x 204＋y 203＝1.∴3x 20＝12－4y 20＝4(3－y 20)．∴|OC |·|OD |＝⎪⎪⎪⎪⎪⎪3x 203－y 20＝⎪⎪⎪⎪⎪⎪－y 203－y 20＝4. ∴|OC |·|OD |的定值为4.(3)当点C 的坐标为(－1,0)时，点D (－4,0)，|CD |＝3. 设直线l 的方程为x ＝my －1，A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧x ＝my －1，x 24＋y23＝1消去x 并整理，得(3m 2＋4)y 2－6my －9＝0.解得y 1＝3m －6m 2＋13m 2＋4，y 2＝3m ＋6m 2＋13m 2＋4. ∴|y 1－y 2|＝12m 2＋13m 2＋4. ∴S △ABD ＝12|CD |·|y 1－y 2|＝32×12m 2＋13m 2＋4＝18m 2＋13m 2＋4＝183m 2＋1＋1m 2＋1.∵m 2≥0，∴m 2＋1≥1.又y ＝3x ＋1x在[1，＋∞)上为增函数．∴3m 2＋1＋1m 2＋1≥3×1＋11＝4.∴S ≤184＝92.∴当m ＝0，即直线AB 的方程为x ＝－1时，△ABD 的面积最大，最大值是92.21．(1)解：对函数f (x )求导得f ′(x )＝ln x ＋x ·1x＝ln x ＋1，∴f ′(e －2)＝ln e －2＋1＝－1.又f (e －2)＝e －2ln e －2＝－2e －2，∴曲线y ＝f (x )在x ＝e －2处的切线方程为y －(－2e －2)＝－(x －e －2)，即y ＝－x －e－2.(2)解：记g (x )＝f (x )－λ(x －1)＝x ln x －λ(x －1)，其中x >0， 由题意知g (x )≥0在(0，＋∞)上恒成立，即g (x )min ≥0. 对g (x )求导得g ′(x )＝ln x ＋1－λ.令g ′(x )＝0，得x ＝e λ－1.当x∴g (x )min 极小值∴λ－e λ－1≥0.记G (λ)＝λ－e λ－1，则G ′(λ)＝1－e λ－1. 令G ′(λ)＝0，得λ＝1.当λ∴G (λ)max 极大值故λ－e λ－1≤0，当且仅当λ＝1时取等号．又λ－e λ－1≥0，从而得到λ＝1.(3)证明：先证f (x )≥－x －e －2，记h (x )＝f (x )－(－x －e －2)＝x ln x ＋x ＋e －2， 则h ′(x )＝ln x ＋2.令h ′(x )＝0，得x ＝e －2.当x∴h (x )min 极小值∴h (x )≥0恒成立，即f (x )≥－x －e －2.记直线y ＝－x －e －2，y ＝x －1分别与y ＝a 交于点(x 1′，a )，(x 2′，a )，不妨设x 1<x 2，则a ＝－x 1′－e －2＝f (x 1)≥－x 1－e －2.从而x 1′<x 1，当且仅当a ＝－2e －2时取等号．由(2)知，f (x )≥x －1，则a ＝x 2′－1＝f (x 2)≥x 2－1. 从而x 2≤x 2′，当且仅当a ＝0时取等号．故|x 1－x 2|＝x 2－x 1≤x 2′－x 1′＝(a ＋1)－(－a －e －2)＝2a ＋1＋e －2. 因等号成立的条件不能同时满足，故|x 1－x 2|<2a ＋1＋e －2.22．解：(1)由⎩⎪⎨⎪⎧x ＝3－t ，y ＝1＋t 消去t ，得x ＋y －4＝0.所以直线l 的普通方程为x ＋y －4＝0.由ρ＝2 2cos ⎝ ⎛⎭⎪⎫θ－π4＝2 2⎝⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2cos θ＋2sin θ，得ρ2＝2ρcos θ＋2ρsin θ.将ρ2＝x 2＋y 2，ρcos θ＝x ，ρsin θ＝y 代入上式，得曲线C 的直角坐标方程为x 2＋y 2＝2x ＋2y, 即(x －1)2＋(y －1)2＝2.(2)方法一，设曲线C 上的点为P (1＋2cos α，1＋2sin α)，则点P 到直线l 的距离为d ＝|1＋2cos α＋1＋2sin α－4|2＝|2α＋cos α－2|2＝⎪⎪⎪⎪⎪⎪2sin ⎝⎛⎭⎪⎫α＋π4－22.当sin ⎝⎛⎭⎪⎫α＋π4＝－1时， d max ＝2 2. 所以曲线C 上的点到直线l 的距离的最大值为2 2.方法二，设与直线l 平行的直线为l ′：x ＋y ＋b ＝0.当直线l ′与圆C 相切时， 得|1＋1＋b |2＝2，解得b ＝0或b ＝－4(舍去)． 所以直线l ′的方程为x ＋y ＝0.所以直线l 与直线l ′的距离为d ＝|0＋4|2＝2 2.所以曲线C 上的点到直线l 的距离的最大值为2 2. 23．解：(1)当a ＝1时，f (x )<6， 即|2x －1|＋|2x ＋3|<6， 即⎩⎪⎨⎪⎧x ≤－32，1－2x －2x －3<6，或⎩⎪⎨⎪⎧－32<x <12，2x ＋3＋1－2x <6，或⎩⎪⎨⎪⎧x ≥12，2x －1＋2x ＋3<6.∴－2<x ≤－32或－32<x <12或12≤x <1.∴－2<x <1.∴不等式f (x )<6的解集为{ x |－2<x < }1.(2)对任意x 1∈R ，都有x 2∈R ，使得f (x 1)＝g (x 2)成立，则有{y |y ＝f (x )}⊆{y |y ＝g (x )}．又f (x )＝|2x －a |＋|2x ＋3|≥|(2x －a )－(2x ＋3)|＝|a ＋3|，g (x )＝|x －1|＋2≥2， 从而|a ＋3|≥2，解得a ≤－5或a ≥－1.故实数a 的取值范围为(－∞，－5]∪[－1，＋∞)．。

第三章 三角函数与解三角形第1讲 弧度制与任意角的三角函数1．设集合M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ x ＝k 2·180°＋45°，k ∈Z ，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k 4·180°＋45°，k ∈Z ，则( ) A ．M ＝N B ．M ⊆N C ．N ⊆M D ．M ∩N ＝∅2．(2017年青海西宁复习检测)若cos θ＞0，且sin 2θ＜0，则角θ的终边所在象限为( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．若角α是第一象限角，则α2是( )A ．第一象限角B ．第二象限角C ．第一或第三象限角D ．第二或第四象限角4．(2016年四川成都模拟)若α是第三象限角，则下列各式中不成立的是( ) A ．sin α＋cos α<0 B ．tan α－sin α<0 C ．cos α－tan α<0 D ．tan αsin α<05．若角α的终边经过点P (1，m )，且tan α＝－2，则sin α＝( )A.55 B ．－55 C.2 55 D ．－2 55 6．(2014年新课标Ⅰ)若tan α>0，则( ) A ．sin α>0 B ．cos α>0 C ．sin 2α>0 D ．cos 2α>07．设α是第二象限角，点P (x,4)为其终边上的一点，且cos α＝15x ，则tan α＝( )A.43B.34 C ．－34 D ．－43 8．(2016年河北衡水二中模拟)已知角φ的终边经过点P (－4,3)，函数f (x )＝sin(ωx ＋φ)(ω＞0)图象的相邻两条对称轴之间的距离等于π2，则f ⎝⎛⎭⎫π4的值为( ) A.35 B.45 C ．－35 D ．－45 9．(2017年广东深圳二模)以角θ的顶点为坐标原点，始边为x 轴的非负半轴，建立平面直角坐标系，角θ的终边过点P (1,2)，则tan ⎝⎛⎭⎫θ＋π4＝________.10．在如图X3-1-1的算法中，令a ＝tan θ，b ＝sin θ，c ＝cos θ，若在集合⎩⎨⎧⎭⎬⎫θ⎪⎪0<θ＜3π2中任取θ的一个值，输出的结果是sin θ的概率是( )图X3-1-1A.13B.12C.23D.3411．判断下列各式的符号：(1)tan 125°·sin 278°； (2)cos 7π12tan23π12sin11π12.12．(1)已知扇形的周长为10，面积为4，求扇形圆心角的弧度数；(2)已知扇形的周长为40，当它的半径和圆心角取何值时，才能使扇形的面积最大？最大面积是多少？第2讲 同角三角函数的基本关系式与诱导公式1．sin 2013°的值属于区间( )A.⎝⎛⎭⎫－12，0B.⎝⎛⎭⎫－1，－12C.⎝⎛⎭⎫12，1D.⎝⎛⎭⎫0，12 2．下列关系式中，正确的是( ) A ．sin 11°<cos 10°<sin 168° B ．sin 168°<sin 11°<cos 10° C ．sin 11°<sin 168°<cos 10° D ．sin 168°<cos 10°<sin 11°3．已知sin α－cos α＝2，α∈(0，π)，则tan α＝( )A ．－1B ．－22 C.22D ．14．(2014年大纲)设a ＝sin 33°，b ＝cos 55°，c ＝tan 35°，则( )A ．a ＞b ＞cB ．b ＞c ＞aC ．c ＞b ＞aD ．c ＞a ＞b5．(2011年新课标)已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝( )A ．－45B ．－35 C.35 D.456．下列不等式成立的是( )A ．tan ⎝⎛⎭⎫9π8>tan ⎝⎛⎭⎫π6B ．sin ⎝⎛⎭⎫－3π10>sin ⎝⎛⎭⎫－π5C ．sin π18>sin π10D ．cos ⎝⎛⎭⎫－7π4>cos ⎝⎛⎭⎫－23π5 7．(2012年大纲)已知α为第二象限角，sin α＋cos α＝33，则cos 2α＝( )A ．－53B ．－59 C.59 D.538．(2017年浙江绍兴二模)已知sin α＋cos α＝15，α∈(0，π)，则tan α＝( )A ．－43B ．－34 C.43 D.349．(2013年新课标Ⅱ)设θ为第二象限角，若tan ⎝⎛⎭⎫θ＋π4＝12，则sin θ＋cos θ＝________. 10．(2016年广东惠州三调)已知sin θ＋cos θ＝43(0<θ<π4)，则sin θ－cos θ的值为( )A.23 B ．－23 C.13 D ．－1311．已知函数f (x )＝1－2sin ⎝⎛⎭⎫2x －π4cos x.(1)求函数f (x )的定义域；(2)设α是第四象限角，且tan α＝－43，求f (α)的值．12．已知tan α＝2.(1)求tan ⎝⎛⎭⎫α＋π4的值； (2)求sin 2αsin 2α＋sin αcos α－cos 2α－1的值．第3讲 三角函数的图象与性质1．下列四个函数中，最小正周期为π，且图象关于直线x ＝π12对称的是( )A ．y ＝sin ⎝⎛⎭⎫x 2＋π3B ．y ＝sin ⎝⎛⎭⎫x 2－π3C ．y ＝sin ⎝⎛⎭⎫2x ＋π3D ．y ＝sin ⎝⎛⎭⎫2x －π3 2．(2017年重庆适应性测试)若函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π6－cos ωx (ω＞0)的图象相邻两个对称中心之间的距离为π2，则f (x )的一个单调递增区间为( )A.⎝⎛⎭⎫－π6，π3B.⎝⎛⎭⎫－π3，π6C.⎝⎛⎭⎫π6，2π3D.⎝⎛⎭⎫π3，5π6 3．(2016年新课标Ⅱ)函数y ＝A sin(ωx ＋φ)的部分图象如图X3-3-1，则( )图X3-3-1A ．y ＝2sin ⎝⎛⎭⎫2x －π6B ．y ＝2sin ⎝⎛⎭⎫2x －π3 C ．y ＝2sin ⎝⎛⎭⎫2x ＋π6 D ．y ＝2sin ⎝⎛⎭⎫2x ＋π3 4．(2017年广东茂名一模)已知函数f (x )＝3cos ⎝⎛⎭⎫ωx ＋π3(ω>0)和g (x )＝2sin(2x ＋φ)＋1的图象的对称轴完全相同，若x ∈⎣⎡⎦⎤0，π3，则f (x )的取值范围是( ) A ．[－3,3] B.⎣⎡⎦⎤－32，3 C.⎣⎡⎦⎤－3，3 32 D.⎣⎡⎦⎤－3，32 5．(2013年大纲)若函数y ＝sin(ωx ＋φ)(ω＞0)的部分图象如图X3-3-2，则ω＝( )图X3-3-2A ．5B ．4C ．3D ．26．函数y ＝|tan x |cos x ⎝⎛⎭⎫0≤x <3π2，且x ≠π2的图象是( )A BC D7．(2017年新课标Ⅲ)设函数f (x )＝cos ⎝⎛⎭⎫x ＋π3，则下列结论错误的是( ) A ．f (x )的一个周期为－2πB ．y ＝f (x )的图象关于直线x ＝8π3对称C ．f (x ＋π)的一个零点为x ＝π6D ．f (x )在⎝⎛⎭⎫π2，π上单调递减8．(2016年江苏)定义在区间[0,3π]上的函数y ＝sin 2x 的图象与函数y ＝cos x 的图象的交点个数是______．9．(2017年浙江温州中学统测)已知函数f (x )＝sin ωx －3cos ωx (ω>0)的图象与x 轴的两个相邻交点的距离等于π2，若将函数y ＝f (x )的图象向左平移π6个单位长度得到函数y ＝g (x )的图象，则y ＝g (x )是减函数的区间为( )A.⎝⎛⎭⎫π4，π3B.⎝⎛⎭⎫－π4，π4C.⎝⎛⎭⎫0，π3D.⎝⎛⎭⎫－π3，010．(2012年新课标)已知ω＞0，函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4在⎝⎛⎭⎫π2，π上单调递减，则ω的取值范围是( )A.⎣⎡⎦⎤12，54B.⎣⎡⎦⎤12，34C.⎝⎛⎭⎫0，12 D ．(0,2] 11．已知函数f (x )＝(sin x ＋cos x )2＋cos 2x . (1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤0，π2上的最大值和最小值．12．是否存在实数a ，使得函数y ＝sin 2x ＋a cos x ＋58a －32在闭区间⎣⎡⎦⎤0，π2上的最大值是1？若存在，求出对应的a 值；若不存在，请说明理由．第4讲 函数y ＝A sin(ωx ＋φ)的图象1．函数y ＝sin(ωx ＋φ)(x ∈R ，ω>0,0≤φ<2π)的部分图象如图X3-4-1，则( )图X3-4-1A ．ω＝π2，φ＝π4B ．ω＝π3，φ＝π6C ．ω＝π4，φ＝π4D ．ω＝π4，φ＝5π42．为了得到函数y ＝sin 3x ＋cos 3x 的图象，可以将函数y ＝2cos 3x 的图象( )A ．向右平移π12个单位长度B ．向右平移π4个单位长度C ．向左平移π12个单位长度D ．向左平移π4个单位长度3．(2017年四川眉山中学统测)将函数f (x )＝3sin ⎝⎛⎭⎫2x ＋π3 的图象向右平移π2个单位长度，所得图象对应的函数( )A ．其一条对称轴方程为x ＝－π6B ．在区间⎣⎡⎦⎤π12，7π12上单调递增C ．当x ＝π12＋k π(k ∈Z )时取得最大值D ．在区间⎣⎡⎦⎤－π6，π3上单调递增 4．(2015年湖南)将函数f (x )＝sin 2x 的图象向右平移φ⎝⎛⎭⎫0＜φ＜π2个单位长度后得到函数g (x )的图象，若对满足|f (x 1)－g (x 2)|＝2的x 1，x 2，有|x 1－x 2|min ＝π3，则φ＝( )A.5π12B.π3C.π4D.π65．(2017年湖北咸宁模拟)已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，－π2<φ<π2的最小正周期为π，将该函数的图象向左平移π6个单位长度后，得到的图象对应的函数为奇函数，则f (x )的图象( )A ．关于点⎝⎛⎭⎫π12，0对称B ．关于直线x ＝5π12对称 C ．关于点⎝⎛⎭⎫5π12，0对称 D ．关于直线x ＝π12对称 6．设f (x )＝3sin 3x ＋cos 3x ，若对任意实数x 都有|f (x )|≤a ，则实数a 的取值范围是________．7．已知函数f (x )＝sin ⎝⎛⎭⎫2x ＋π6，其中x ∈⎣⎡⎦⎤－π6，a .当a ＝π3时，f (x )的值域是__________；若f (x )的值域是⎣⎡⎦⎤－12，1，则a 的取值范围是__________． 8．(2015年湖南)已知ω＞0，在函数y ＝2sin ωx 与y ＝2cos ωx 的图象的交点中，距离最短的两个交点的距离为2 3，则ω＝________.9．(2015年天津)已知函数f (x )＝sin ωx ＋cos ωx (ω＞0)，x ∈R ，若函数f (x )在区间(－ω，ω)内单调递增，且函数f (x )的图象关于直线x ＝ω对称，则ω的值为____________．10．(2014年北京)函数f (x )＝3sin ⎝⎛⎭⎫2x ＋π6的部分图象如图X3-4-2. (1)写出f (x )的最小正周期及图中x 0，y 0的值；(2)求f (x )在区间⎣⎡⎦⎤－π2，－π12上的最大值和最小值．图X3-4-211．(2017年山东)设函数f (x )＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2，其中0<ω<3，已知f ⎝⎛⎭⎫π6＝0. (1)求ω；(2)将函数y ＝f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图象向左平移π4个单位，得到函数y ＝g (x )的图象，求g (x )在⎣⎡⎦⎤－π4，3π4上的最小值．第5讲 两角和与差及二倍角的三角函数公式1．(2016年新课标Ⅱ)若cos ⎝⎛⎭⎫π4－α＝35，则sin 2α＝( ) A.725 B.15C ．－15D ．－7252．4cos 50°－tan 40°＝( )A. 2B.2＋32C. 3 D ．2 2－13．(2017年上海师大附中统测)函数y ＝2cos 2⎝⎛⎭⎫x －π4－1是( ) A ．最小正周期为π的奇函数 B ．最小正周期为π的偶函数C ．最小正周期为π2的奇函数D ．最小正周期为π2的偶函数4．(2015年上海)已知点A 的坐标为(4 3，1)，将OA 绕坐标原点O 逆时针旋转π3至OB ，则点B 的纵坐标为( )A.3 32B.5 32C.112D.1325．(2017年江苏)若tan ⎝⎛⎭⎫α－π4＝16， 则tan α＝________. 6．(2017年北京)在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称．若sin α＝13，cos(α－β)＝________.7．(2016年新课标Ⅲ)函数y ＝sin x －3cos x 的图象可由函数y ＝2sin x 的图象至少向右平移______个单位长度得到．8．(2016年上海)若函数f (x )＝4sin x ＋a cos x 的最大值为5，则常数a ＝________. 9．(2016年上海)方程3sin x ＝1＋cos 2x 在区间[0,2π]上的解为__________．10．(2015年浙江)函数f (x )＝sin 2x ＋sin x cos x ＋1的最小正周期是________，最小值是________，单调递减区间是____________________．11．(2014年江苏)已知α∈⎝⎛⎭⎫π2，π，sin α＝55. (1)求sin ⎝⎛⎭⎫π4＋α的值；(2)求cos ⎝⎛⎭⎫5π6－2α的值．12．(2017年北京)已知函数f (x )＝3cos ⎝⎛⎭⎫2x －π3－2sin x cos x . (1)求f (x )的最小正周期；(2)求证：当x ∈⎣⎡⎦⎤－π4，π4时，f (x )≥－12.第6讲 简单的三角恒等变换1．若sin α2＝33，则cos α＝( )A ．－23B ．－13 C.13 D.232．(2016年山东)函数f (x )＝(3sin x ＋cos x )(3cos x －sin x )的最小正周期是( ) A.π2 B ．π C.3π2 D ．2π 3．(2017年广东广州一模)已知函数f (x )＝sin(ωx ＋φ)＋cos(ωx ＋φ)(ω>0,0<φ<π)是奇函数，直线y ＝2与函数f (x )的图象的两个相邻交点的横坐标之差的绝对值为π2，则( )A ．f (x )在⎝⎛⎭⎫0，π4上单调递减 B ．f (x )在⎝⎛⎭⎫π8，3π8上单调递减C ．f (x )在⎝⎛⎭⎫0，π4上单调递增 D ．f (x )在⎝⎛⎭⎫π8，3π8上单调递增 4．(2017年河北石家庄一模)函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0)的部分图象如图X3-6-1，则f ⎝⎛⎭⎫11π24的值为( )图X3-6-1A ．－62 B ．－32 C ．－22D ．－1 5．若将函数y ＝tan ⎝⎛⎭⎫ωx ＋π4(ω>0)的图象向右平移π6个单位长度后，与函数y ＝tan ⎝⎛⎭⎫ωx ＋π6的图象重合，则ω的最小值为( )A.16B.14C.13D.126．(2016年山西四校联考)已知函数f (x )＝cos ⎝⎛⎭⎫ωx ＋φ－π2⎝⎛⎭⎫ω>0，|φ|<π2的部分图象如图X3-6-2，则y ＝f ⎝⎛⎭⎫x ＋π6取得最小值时x 的取值集合为( )图X3-6-2A.⎩⎨⎧⎭⎬⎫x |x ＝k π－π6，k ∈ZB.⎩⎨⎧⎭⎬⎫x |x ＝k π－π3，k ∈Z C.⎩⎨⎧⎭⎬⎫x |x ＝2k π－π6，k ∈Z D.⎩⎨⎧⎭⎬⎫x |x ＝2k π－π3，k ∈Z 7．已知α∈R ，sin α＋2cos α＝102，则tan 2α＝( ) A.43 B.34 C ．－34 D ．－438．(2012年大纲)当函数y ＝sin x －3cos x (0≤x <2π)取最大值时，x ＝________.9．(2016年江西九江模拟)化简sin 235°－12cos10°cos80°＝________.10．若函数y ＝cos 2x ＋3sin 2x ＋a 在⎣⎡⎦⎤0，π2上有两个不同的零点，则实数a 的取值范围为____________．11．(2014年四川)已知函数f (x )＝sin ⎝⎛⎭⎫3x ＋π4. (1)求f (x )的单调递增区间；(2)若α是第二象限角，f ⎝⎛⎭⎫α3＝45cos ⎝⎛⎭⎫α＋π4cos 2α，求cos α－sin α的值．12．(2017年浙江)已知函数f (x )＝sin 2x －cos 2x －2 3 sin x cos x (x ∈R )．(1)求f ⎝⎛⎭⎫2π3的值；(2)求f (x )的最小正周期及单调递增区间．第7讲 正弦定理和余弦定理1．设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若2sin A cos B ＝sin C ，则△ABC 一定是( )A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形 2．(2017年山东)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .若△ABC 为锐角三角形，且满足sin B (1＋2cos C )＝2sin A cos C ＋cos A sin C ，则下列等式成立的是( )A ．a ＝2bB ．b ＝2aC ．A ＝2BD ．B ＝2A3．(2016年新课标Ⅲ)在△ABC 中，B ＝π4，BC 边上的高等于13BC ，则sin A ＝( )A.310B.1010C.55D.310104．(2017年河南郑州模拟)已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，且 (b －c )(sin B ＋sin C )＝(a －3c )sin A ，则角B 的大小为( ) A ．30° B ．45° C ．60° D ．120°5．(2013年新课标Ⅰ)已知锐角三角形ABC 的内角A ，B ，C 的对边分别为a ，b ，c ,23cos 2A ＋cos 2A ＝0，a ＝7，c ＝6，则b ＝( )A ．10B ．9C ．8D ．56．(2016年山东德州模拟)在△ABC 中，AB ＝3，AC ＝1，B ＝π6，则△ABC 的面积是( )A.32B.34C.32或34D.32或 3 7．(2017年湖北孝感一模)在锐角三角形ABC 中，已知AB ＝2 3，BC ＝3，其面积S △ABC ＝32，则AC ＝________.8．(2015年重庆)在△ABC 中，B ＝120°，AB ＝2，角A 的平分线AD ＝3，则AC ＝________.9．(2017年北京)在△ABC 中，∠A ＝60°，c ＝37a .(1)求sin C 的值；(2)若a ＝7，求△ABC 的面积．10．(2017年新课标Ⅱ)△ABC的内角A，B，C的对边分别为a，b，c，已知sin(A＋C)＝8sin2B 2.(1)求cos B；(2)若a＋c＝6，△ABC的面积为2，求b.第8讲解三角形应用举例1．某人向正东方向走x km后，顺时针转150°，然后朝新方向走3 km，结果他离出发点恰好 3 km，则x＝()A. 3 B．2 3C．2 3或 3 D．32．两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°的方向，灯塔B在观察站C的南偏东40°的方向，则灯塔A与灯塔B的距离为() A．a km B.2a km C．2a km D.3a km3．如图X3-8-1，一艘海轮从A处出发，以40海里/时的速度沿南偏东40°方向直线航行，30分钟后到达B处．在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是()图X3-8-1A．10 2海里B．10 3海里C．20 2海里D．20 3海里4．(2014年四川)如图X3-8-2，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46 m，则河流的宽度BC约等于________m．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.80，3≈1.73)图X3-8-25．(2016年河南信阳模拟)某舰艇在A 处测得遇险渔船在北偏东45°距离为10海里的C 处，该渔船沿北偏东105°方向，以每小时9海里的速度向一小岛靠近，舰艇时速21海里，则舰艇到达渔船的最短时间是________分钟．6．(2017年浙江)已知△ABC ，AB ＝AC ＝4，BC ＝2.点D 为AB 延长线上一点，BD ＝2，连接CD ，则△BDC 的面积是________，cos ∠BDC ＝________.7．(2016年上海)已知△ABC 的三边长分别为3,5,7，则该三角形的外接圆半径等于________．8．(2017年广东揭阳一模)如图X3-8-3，在△ABC 中，∠B ＝π6，AC ＝1，点D 在边AB上，且DA ＝DC ，BD ＝1，则∠DCA ＝________.图X3-8-39．(2017年新课标Ⅲ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知sin A ＋3cos A ＝0，a ＝2 7，b ＝2.(1)求c ；(2)设D 为BC 边上一点，且AD ⊥AC ，求△ABD 的面积． 10．(2017年广东广州一模)如图X3-8-4，在△ABC 中， 点P 在BC 边上， ∠P AC ＝60°，PC ＝2，AP ＋AC ＝4.(1)求∠ACP ；(2)若△APB 的面积是3 32， 求sin ∠BAP .图X3-8-4第三章 三角函数与解三角形 第1讲 弧度制与任意角的三角函数1．B 解析：方法一，由于M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k 2·180°＋45°，k ∈Z ＝{…，－45°，45°，135°，225°，…}，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k4·180°＋45°，k ∈Z ＝{…，－45°，0°，45°，90°，135°，180°，225°，…}，显然有M ⊆N .故选B.方法二，在M 中，x ＝k2·180°＋45°＝k ·90°＋45°＝(2k ＋1)·45°，2k ＋1是奇数；在N 中，x ＝k 4·180°＋45°＝k ·45°＋45°＝(k ＋1)·45°，k ＋1是整数，因此必有M ⊆N .故选B. 2．D 解析：由cos θ>0，sin 2θ＝2sin θcos θ＜0，得sin θ＜0，则角θ的终边在第四象限．故选D.3．C 解析：∵α是第一象限角，∴2k π＜α＜π2＋2k π，k ∈Z ，∴k π＜α2＜π4＋k π，k ∈Z .当k 为偶数时，α2是第一象限角；当k 为奇数时，α2是第三象限角．4．B 解析：在第三象限，sin α<0，cos α<0，tan α>0，则tan α－sin α>0，故B 错误．故选B.5．D 解析：由三角函数的定义，得tan α＝m ＝－2.∴r ＝5，sin α＝－25＝－2 55.故选D.6．C 解析：tan α＝sin αcos α>0，而sin 2α＝2sin αcos α>0.故选C.7．D 解析：∵α是第二象限角，∴cos α＝15x ＜0，即x ＜0.又cos α＝15x ＝xx 2＋16，解得x ＝－3.∴tan α＝4x ＝－43.8．D 解析：由于角φ的终边经过点P (－4,3)，所以cos φ＝－45.再根据函数f (x )＝sin(ωx＋φ)(ω＞0)图象的相邻两条对称轴之间的距离等于π2，可得2πω＝2×π2，所以ω＝2.所以f (x )＝sin(2x ＋φ)．所以f ⎝⎛⎭⎫π4＝sin ⎝⎛⎭⎫π2＋φ＝cos φ＝－45.故选D. 9．－3 解析：由题意知tan θ＝21＝2，所以tan ⎝⎛⎭⎫θ＋π4＝tan θ＋tan π41－tan θtanπ4＝2＋11－2×1＝－3.10．A 解析：该程序框图的功能是比较a ，b ，c 的大小并输出最大值，因此要使输出的结果是sin θ，需sin θ＞tan θ，且sin θ＞cos θ.∵当θ∈⎝⎛⎭⎫0，π2时，总有tan θ＞sin θ；当θ∈⎝⎛⎭⎫π2，π时，总有sin θ＞0，tan θ＜0，cos θ＜0；当θ∈⎝⎛⎭⎫π，3π2时，tan θ＞0，sin θ＜0.故当输出的结果是sin θ时，θ的取值范围是⎝⎛⎭⎫π2，π.结合几何概型公式，得输出sin θ的概率为π－π232π－0＝13.故选A. 11．解：(1)∵125°，278°角分别为第二、四象限角， ∴tan 125°＜0，sin 278°＜0.因此tan 125°·sin 278°＞0.(2)∵π2＜7π12＜π，3π2<23π12<2π，π2<11π12<π，∴cos 7π12＜0，tan 23π12＜0，sin 11π12＞0.因此cos 7π12tan23π12sin11π12>0.12．解：设扇形半径为R ，圆心角为θ，θ所对的弧长为l . (1)依题意，得⎩⎪⎨⎪⎧12θR 2＝4，θR ＋2R ＝10.∴2θ2－17θ＋8＝0.解得θ＝8或12.∵8>2π(舍去)，∴θ＝12 rad.(2)扇形的周长为40，即θR ＋2R ＝40， S ＝12lR ＝12θR 2＝14θR ·2R ≤14⎝ ⎛⎭⎪⎫θR ＋2R 22＝100. 当且仅当θR ＝2R ，即R ＝10，θ＝2时，扇形面积取得最大值，最大值为100.第2讲 同角三角函数的基本关系式与诱导公式1．B 解析：sin 2013°＝sin(5×360°＋213°)＝sin 213°＝sin(180°＋33°)＝－sin 33°<－12.故选B.2．C 解析：∵sin 168°＝sin(180°－12°)＝sin 12°，cos 10°＝cos(90°－80°)＝sin 80°.由于正弦函数y ＝sin x 在区间[0°，90°]上为递增函数，因此sin 11°<sin 12°<sin 80°，即sin 11°<sin 168°<cos 10°.3．A 解析：由⎩⎪⎨⎪⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，消去sin α，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0.∴cos α＝－22.又α∈(0，π)，∴α＝3π4.∴tan α＝tan 3π4＝－1. 4．C 解析：c ＝tan 35°＞b ＝cos 55°＝sin 35°＞a ＝sin 33°.故选C.5．B 解析：由题知，tan θ＝2，cos 2θ＝cos 2 θ－sin 2 θcos 2 θ＋sin 2 θ＝1－tan 2 θ1＋tan 2 θ＝－35.故选B.6．D 解析：cos ⎝⎛⎭⎫－7π4＝cos π4>0，cos ⎝⎛⎭⎫－23π5＝cos 3π5<0.故选D. 7．A 解析：sin α＋cos α＝33，两边平方可得1＋sin 2α＝13⇒sin 2α＝－23.∵α是第二象限角，因此sin α>0，cos α<0.所以cos α－sin α＝－(cos α－sin α)2＝－1＋23＝－153.∴cos 2α＝cos 2 α－sin 2 α＝(cos α＋sin α)(cos α－sin α)＝－53.8．A 解析：由题设知(sin α＋cos α)2＝125，则2sin αcos α＝－2425，故(sin α－cos α)2＝1＋2425＝4925.所以sin α－cos α＝75，与sin α＋cos α＝15联立解之可得sin α＝45，cos α＝－35，故tan α＝－43.故选A.9．－105 解析：tan ⎝⎛⎭⎫θ＋π4＝12，tan θ＋11－tan θ＝12，tan θ＝－13，sin θcos θ＝－13，cos θ＝－3sin θ，代入sin 2θ＋cos 2θ＝1，得⎩⎨⎧sin θ＝1010，cos θ＝－31010.sin θ＋cos θ＝－105. 10．B 解析： 因为sin θ＋cos θ＝43(0<θ<π4)，两边平方可得1＋2sin θ·cos θ＝169，即2sin θ·cos θ＝79，所以(sin θ－cos θ)2＝1－2sin θcos θ＝1－79＝29.又因为0<θ<π4，所以sin θ<cosθ.所以sin θ－cos θ<0.所以sin θ－cos θ＝－23.故选B.11．解：(1)函数f (x )要有意义，需满足cos x ≠0，解得x ≠π2＋k π，k ∈Z ，即函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠π2＋k π，k ∈Z . (2)f (x )＝1－2sin ⎝⎛⎭⎫2x －π4cos x＝1－2⎝⎛⎭⎫22sin 2x －22cos 2x cos x ＝1＋cos 2x －sin 2xcos x＝2cos 2x －2sin x cos x cos x＝2(cos x －sin x )．由tan α＝－43，得sin α＝－43cos α.又sin 2α＋cos 2α＝1，∴cos 2α＝925.∵α是第四象限的角，∴cos α＝35，sin α＝－45.∴f (α)＝2(cos α－sin α)＝145.12．解：(1)tan ⎝⎛⎭⎫α＋π4＝tan α＋tanπ41－tan αtanπ4＝tan α＋11－tan α＝2＋11－2＝－3. (2)sin 2αsin 2α＋sin αcos α－cos 2α－1＝2sin αcos αsin 2α＋sin αcos α－(2cos 2α－1)－1＝2sin αcos αsin 2α＋sin αcos α－2cos 2α＝2tan αtan 2α＋tan α－2 ＝2×222＋2－2＝1.第3讲 三角函数的图象与性质1．C 解析：将x ＝π12代入选项A ，B ，C ，D 中，只有选项C 取得最大值y ＝sin ⎝⎛⎭⎫2×π12＋π3＝sin π2＝1，所以关于直线x ＝π12对称，且T ＝2π2＝π.2．A 解析：依题意，得f (x )＝32sin ωx －12cos ωx ＝sin ⎝⎛⎭⎫ωx －π6的图象相邻两个对称中心之间的距离为π2，于是有T ＝2πω＝2×π2＝π，ω＝2，f (x )＝sin ⎝⎛⎭⎫2x －π6.当2k π－π2≤2x －π6≤2k π＋π2，即k π－π6≤x ≤k π＋π3，k ∈Z 时，f (x )＝sin ⎝⎛⎭⎫2x －π6单调递增．结合各选项知f (x )＝sin ⎝⎛⎭⎫2x －π6的一个单调递增区间为⎝⎛⎭⎫－π6，π3.故选A. 3．A 解析：由图知，A ＝2，周期T ＝2⎣⎡⎦⎤π3－⎝⎛⎭⎫－π6＝π，所以ω＝2ππ＝2.所以y ＝2sin(2x ＋φ)．因为图象过点⎝⎛⎭⎫π3，2，所以2＝2sin ⎝⎛⎭⎫2×π3＋φ.所以sin ⎝⎛⎭⎫2π3＋φ＝1.所以2π3＋φ＝2k π＋π2(k ∈Z )．令k ＝0，得φ＝－π6.所以y ＝2sin ⎝⎛⎭⎫2x －π6.故选A. 4．D 解析：因为函数f (x )和g (x )的图象的对称轴完全相同，故f (x )和g (x )的周期相同，所以ω ＝2，f (x )＝3cos ⎝⎛⎭⎫2x ＋π3.由x ∈⎣⎡⎦⎤0，π3，得2x ＋π3∈⎣⎡⎦⎤π3，π.根据余弦函数的单调性，当2x ＋π3＝π，即x ＝π3时，f (x )min ＝－3；当2x ＋π3＝π3，即x ＝0时，f (x )max ＝32.所以f (x )的取值范围是⎣⎡⎦⎤－3，32.故选D. 5．B 解析：设函数的最小正周期为T ，由题图可知T 2＝⎝⎛⎭⎫x 0＋π4－x 0＝π4，所以T ＝π2.又因为T ＝2πω，可解得ω＝4.6．C 解析：方法一，y ＝|sin x |·cos x|cos x |，分类讨论．方法二，y ＝|tan x |cos x 的符号与cos x 相同．故选C.7．D 解析：函数的最小正周期为T ＝2π1＝2π，则周期为2k π()k ∈Z .所以f (x )的一个周期为－2π.故选项A 正确；将x ＝8π3代入f (x )＝cos ⎝⎛⎭⎫x ＋π3，得f ⎝⎛⎭⎫8π3＝cos 3π＝－1为最小值．因此直线x ＝8π3为对称轴．故选项B 正确；将x ＝π6代入f (x ＋π)，得cos 3π2＝0.故选项C 正确；由x ∈⎝⎛⎭⎫π2，π，得x ＋π3∈⎝⎛⎭⎫5π6，4π3.函数在该区间显然不单调．故选项D 错误．故选D. 8．7 解析：由sin 2x ＝cos x ⇒cos x ＝0或sin x ＝12.因为x ∈[0,3π]，所以x ＝π2，3π2，5π2，π6，5π6，13π6，17π6，共7个． 9．A 解析：因为f (x )＝2sin ⎝⎛⎭⎫ωx －π3，T 2＝π2，所以T ＝2πω＝π.则ω＝2.故f (x )＝2sin ⎝⎛⎭⎫2x －π3.故g (x )＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6－π3＝2sin 2x ，故其单调递减区间为2k π＋π2≤2x ≤2k π＋3π2(k ∈Z )，即k π＋π4≤x ≤k π＋3π4(k ∈Z )，当k ＝0时，区间⎣⎡⎦⎤π4，3π4为函数g (x )的一个单调递减区间，又⎝⎛⎭⎫π4，π3⊆⎣⎡⎦⎤π4，3π4.故选A.10．A 解析：方法一，ω＝2⇒⎝⎛⎭⎫ωx ＋π4∈⎣⎡⎦⎤5π4，9π4不合题意，排除D ；ω＝1⇒⎝⎛⎭⎫ωx ＋π4∈⎣⎡⎦⎤3π4，5π4合题意，排除B ，C.故选A.方法二，由π2＜x ＜π，得π2ω＋π4＜ωx ＋π4＜πω＋π4.由题意知，⎝⎛⎭⎫π2ω＋π4，πω＋π4⊆⎣⎡⎦⎤π2，3π2. ∴⎩⎨⎧π2ω＋π4≥π2，πω＋π4≤3π2.∴12≤ω≤54.故选A.11．解：(1)因为f (x )＝sin 2x ＋cos 2x ＋2sin x cos x ＋cos 2x＝1＋sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π4＋1， 所以函数f (x )的最小正周期为T ＝2π2＝π.(2)由(1)知，f (x )＝2sin ⎝⎛⎭⎫2x ＋π4＋1. 当x ∈⎣⎡⎦⎤0，π2时，2x ＋π4∈⎣⎡⎦⎤π4，5π4. 由正弦函数y ＝sin x 在⎣⎡⎦⎤π4，5π4上的图象知，当2x ＋π4＝π2，即x ＝π8时，f (x )取最大值2＋1；当2x ＋π4＝5π4，即x ＝π2时，f (x )取最小值0.综上所述，f (x )在区间⎣⎡⎦⎤0，π2上的最大值为2＋1，最小值为0. 12．解：y ＝－⎝⎛⎭⎫cos x －12a 2＋a 24＋58a －12，当0≤x ≤π2时，0≤cos x ≤1.令t ＝cos x ，则0≤t ≤1.∴y ＝－⎝⎛⎭⎫t －12a 2＋a 24＋58a －12，0≤t ≤1.当0≤a 2≤1，即0≤a ≤2时，则当t ＝a 2，即cos x ＝a2时．y max ＝a 24＋58a －12＝1，解得a ＝32或a ＝－4(舍去)．当a2＜0，即a ＜0时，则当t ＝0，即cos x ＝0时， y max ＝58a －12＝1，解得a ＝125(舍去)．当a2＞1，即a ＞2时，则当t ＝1，即cos x ＝1时， y max ＝a ＋58a －32＝1，解得a ＝2013(舍去)．综上所述，存在a ＝32符合题意．第4讲 函数y ＝A sin (ωx ＋φ)的图象1．C 解析：∵T 4＝3－1＝2，∴T ＝8，∴ω＝2πT ＝π4.令π4×1＋φ＝π2，得φ＝π4.故选C.2．A 解析：由于y ＝sin 3x ＋cos 3x ＝2sin ⎝⎛⎭⎫3x ＋π4，y ＝2cos 3x ＝2sin ⎝⎛⎭⎫3x ＋π2，因此只需将y ＝2cos 3x 的图象向右平移π12个单位长度，即可得到y ＝2sin ⎣⎡⎦⎤3⎝⎛⎭⎫x －π12＋π2＝ sin ⎝⎛⎭⎫3x ＋π4的图象． 3．B 解析：f (x )＝3sin ⎝⎛⎭⎫2x ＋π3的图象向右平移π2个单位长度所得图象对应的函数为f (x )＝3sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π2＋π3＝－3sin ⎝⎛⎭⎫2x ＋π3，其对称轴方程为2x ＋π3＝π2＋k π(k ∈Z )，即x ＝π12＋k π2(k ∈Z )，排除A.当x ＝π12＋k π(k ∈Z )，得－3sin ⎝⎛⎭⎫2k π＋π2＝－3.故C 错误．由π2＋2k π≤2x ＋π3≤3π2＋2k π(k ∈Z )，得π12＋k π≤x ≤7π12＋k π(k ∈Z )，即f (x )的增区间为⎣⎡⎦⎤π12＋k π，7π12＋k π(k ∈Z )．故选B.4．D 解析：向右平移φ个单位长度后，得到g (x )＝sin(2x －2φ)，∵|f (x 1)－g (x 2)|＝2，∴不妨令2x 1＝π2＋2k π(k ∈Z )，2x 2－2φ＝－π2＋2m π(m ∈Z )．∴x 1－x 2＝π2－φ＋(k －m )π.又∵|x 1－x 2|min ＝π3，∴π2－φ＝π3⇒φ＝π6.故选D.5．B 解析：由已知，得ω＝2，则f (x )＝sin(2x ＋φ)．设平移后的函数为g (x )，则g (x )＝sin ⎝⎛⎭⎫2x ＋π3＋φ ⎝⎛⎭⎫－π2<φ<π2，且为奇函数，所以φ＝－π3，f (x )＝sin ⎝⎛⎭⎫2x －π3.令2x －π3＝k π＋π2(k ∈Z )，易得f (x )的图象关于直线x ＝5π12对称．故选B.6．[2，＋∞) 解析：f (x )＝3sin 3x ＋cos 3x ＝2sin ⎝⎛⎭⎫3x ＋π6，|f (x )|max ＝2，∴a ≥2. 7.⎣⎡⎦⎤－12，1 ⎣⎡⎦⎤π6，π2 解析：当a ＝π3时，x ∈⎣⎡⎦⎤－π6，π3，2x ＋π6∈⎣⎡⎦⎤－π6，5π6，f (x )的值域是⎣⎡⎦⎤－12，1；若f (x )的值域是⎣⎡⎦⎤－12，1，π2≤2a ＋π6≤7π6，解得π6≤a ≤π2. 8.π2 解析：根据三角函数图象与性质可得交点坐标为⎝⎛⎭⎫1ω⎝⎛⎭⎫2k 1π＋π4，2，⎝⎛⎭⎫1ω⎝⎛⎭⎫2k 2π＋5π4，－2，k 1，k 2∈Z ＋，距离最短的两个交点一定在同一个周期内，∴()2 32＝1ω2⎝⎛⎭⎫5π4－π42＋(－2－2)2.∴ω＝π2. 9.π2解析：由f (x )在区间(－ω，ω)内单调递增，且f (x )的图象关于直线x ＝ω对称，可得2ω≤πω，且f (ω)＝sin ω2＋cos ω2＝2⇒sin ⎝⎛⎭⎫ω2＋π4＝1，所以ω2＋π4＝π2⇒ω＝π2. 10．解：(1)f (x )的最小正周期为π，x 0＝7π6，y 0＝3.(2)因为x ∈⎣⎡⎦⎤－π2，－π12， 所以2x ＋π6∈⎣⎡⎦⎤－5π6，0. 于是，当2x ＋π6＝0，即x ＝－π12时，f (x )取得最大值0；当2x ＋π6＝－π2，即x ＝－π3时，f (x )取得最小值－3.11．解：(1)因为f (x )＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2， 所以f (x )＝32sin ωx －12cos ωx －cos ωx＝32sin ωx －32cos ωx ＝3⎝⎛⎭⎫12sin ωx －32cos ωx＝3sin ⎝⎛⎭⎫ωx －π3. 由题设知，f ⎝⎛⎭⎫π6＝0，所以ωπ6－π3＝k π，k ∈Z . 故ω＝6k ＋2，k ∈Z .又0<ω<3，所以ω＝2.(2)由(1)，得f (x )＝3sin ⎝⎛⎭⎫2x －π3. 所以g (x )＝3sin ⎝⎛⎭⎫x ＋π4－π3＝3sin ⎝⎛⎭⎫x －π12. 根据x ∈⎣⎡⎦⎤－π4，3π4得到x －π12∈⎣⎡⎦⎤－π3，2π3， 当x －π12＝－π3，即x ＝－π4时，g (x )取得最小值－32.第5讲 两角和与差及二倍角的三角函数公式1．D 解析：cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4－α＝2cos 2⎝⎛⎭⎫π4－α－1＝2×⎝⎛⎭⎫352－1＝－725，且cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4－α＝cos ⎝⎛⎭⎫π2－2α＝sin 2α.故选D. 2．C 解析：原式＝4sin 40°－sin 40°cos 40°＝4cos 40°sin 40°－sin 40°cos 40°＝2sin 80°－sin 40°cos 40°＝2sin (120°－40°)－sin 40°cos 40°＝3cos 40°＋sin 40°－sin 40°cos 40°＝3cos 40°cos 40°＝ 3.故选C.3．A 解析：由y ＝2cos 2⎝⎛⎭⎫x －π4－1＝cos ⎝⎛⎭⎫2x －π2＝sin2x ，∴T ＝π，且y ＝sin 2x 是奇函数，即函数y ＝2cos 2⎝⎛⎭⎫x －π4－1是奇函数．故选A. 4．D 解析：设直线OA 的倾斜角为α，B (m ，n )(m ＞0，n ＞0)，则直线OB 的倾斜角为π3＋α.因为A (4 3，1)，所以tan α＝14 3，tan ⎝⎛⎭⎫π3＋α＝n m ，n m ＝3＋14 31－3·14 3＝133 3，即m 2＝27169n 2.因为m 2＋n 2＝(4 3)2＋12＝49，所以n 2＋27169n 2＝49.所以n ＝132或n ＝－132(舍去)．所以点B 的纵坐标为132.5.75 解析：tan α＝tan ⎣⎡⎦⎤⎝⎛⎭⎫α－π4＋π4＝tan ⎝⎛⎭⎫α－π4＋tan π41－tan ⎝⎛⎭⎫α－π4tan π4＝16＋11－16＝75.6．－79解析：因为角α与角β它们的终边关于y 轴对称，所以α＋β＝2k π＋π()k ∈Z ，sin α＝sin β＝13，cos α＝－cos β，cos(α－β)＝cos αcos β＋sin αsin β＝－cos 2α＋sin 2α＝2sin 2α－1＝－79.7.π3解析：因为y ＝sin x －3cos x ＝2sin ⎝⎛⎭⎫x －π3，所以函数y ＝sin x －3cos x 的图象可由函数y ＝2sin x 的图象至少向右平移π3个单位长度得到．8．±3 解析：f (x )＝16＋a 2sin(x ＋φ)，其中tan φ＝a4，故函数f (x )的最大值为16＋a 2，由已知，得16＋a 2＝5，解得a ＝±3.9.π6或5π6 解析：3sin x ＝1＋cos 2x ，即3sin x ＝2－2sin 2x ，所以2sin 2x ＋3sin x －2＝0.解得sin x ＝12或sin x ＝－2(舍)．所以方程在区间[0,2π]上的解为π6或5π6.10．π 3－22 ⎣⎡⎦⎤3π8＋k π，7π8＋k π，k ∈Z 解析：f (x )＝sin 2x ＋sin x cos x ＋1＝12sin 2x ＋1－cos 2x 2＋1＝12sin 2x －12cos 2x ＋32＝22·sin ⎝⎛⎭⎫2x －π4＋32，所以T ＝2π2＝π，f (x )min ＝32－22.单调递减区间为⎣⎡⎦⎤3π8＋k π，7π8＋k π，k ∈Z .11．解：(1)因为α∈⎝⎛⎭⎫π2，π，sin α＝55， 所以cos α＝－1－sin 2α＝－2 55.故sin ⎝⎛⎭⎫π4＋α＝sin π4cos α＋cos π4sin α ＝22×⎝⎛⎭⎫－2 55＋22×55＝－1010. (2)由(1)，得sin 2α＝2sin αcos α＝－45，cos 2α＝2cos 2α－1＝35.所以cos ⎝⎛⎭⎫5π6－2α＝cos 5π6cos 2α＋sin 5π6sin 2α ＝－32×35＋12×⎝⎛⎭⎫－45＝－3 3＋410. 12．(1)解：f (x )＝32cos 2x ＋32sin 2x －sin 2x＝12sin 2x ＋32cos 2x ＝sin ⎝⎛⎭⎫2x ＋π3. 所以f (x )的最小正周期T ＝2π2＝π.(2)证明：因为－π4≤x ≤π4，所以－π6≤2x ＋π3≤5π6.所以sin ⎝⎛⎭⎫2x ＋π3≥sin ⎝⎛⎭⎫－π6＝－12. 所以当x ∈⎣⎡⎦⎤－π4，π4时，f (x )≥－12. 第6讲 简单的三角恒等变换1．C2．B 解析：f (x )＝2sin ⎝⎛⎭⎫x ＋π6×2cos ⎝⎛⎭⎫x ＋π6＝2sin ⎝⎛⎭⎫2x ＋π3，故最小正周期T ＝2π2＝π.故选B.3．D 解析：f (x )＝2sin ⎝⎛⎭⎫ωx ＋φ＋π4，因为函数为奇函数且0<φ<π，所以φ＋π4＝π，即φ＝3π4.所以f (x )＝－2sin ωx .又2πω＝π2，所以ω＝4，f (x )＝－2sin 4x ，其一个单调递增区间为⎝⎛⎭⎫π8，3π8.4．D 解析：由题图可得A ＝2，最小正周期T ＝4⎝⎛⎭⎫7π12－π3＝π，则ω＝2πT＝2.又f ⎝⎛⎭⎫7π12＝2sin ⎝⎛⎭⎫7π6＋φ＝－2，解得φ＝－5π3＋2k π(k ∈Z )．即k ＝1，φ＝π3.则f (x )＝2sin ⎝⎛⎭⎫2x ＋π3.则f ⎝⎛⎭⎫11π24＝2sin ⎝⎛⎭⎫11π12＋π3＝2sin 5π4＝－1.故选D. 5．D 解析：函数y ＝tan ⎝⎛⎭⎫ωx ＋π4的图象向右平移π6个单位后得到函数y ＝tan ⎣⎡⎦⎤ω⎝⎛⎭⎫x －π6＋π4＝tan ⎝⎛⎭⎫ωx －ωπ6＋π4的图象．又因为y ＝tan ⎝⎛⎭⎫ωx ＋π6，依题意可得－ωπ6＋π4＝π6＋k π，k ∈Z ，∴ω＝12－6k ，()k ∈Z .由ω>0，得ω的最小值为12.6．B 解析：依题意，得T ＝2πω＝4⎝⎛⎭⎫7π12－π3＝π，ω＝2，f ⎝⎛⎭⎫π3＝cos ⎝⎛⎭⎫φ＋π6＝1.又|φ|<π2，因此φ＝－π6.所以f (x )＝cos ⎝⎛⎭⎫2x －2π3.当f ⎝⎛⎭⎫x ＋π6＝cos ⎝⎛⎭⎫2x －π3取得最小值时，2x －π3＝2k π－π，k ∈Z ，即x ＝k π－π3，k ∈Z .故选B.7．C 解析：∵sin α＋2cos α＝102，∴sin 2α＋4sin αcos α＋4cos 2α＝52.化简，得4sin 2α＝－3cos 2α.∴tan 2α＝sin 2αcos 2α＝－34.故选C.8.5π6 解析：y ＝sin x －3cos x ＝2sin ⎝⎛⎭⎫x －π3，由0≤x <2π⇔－π3≤x －π3<5π3，可知－2≤2sin ⎝⎛⎭⎫x －π3≤2.当且仅当x －π3＝π2，即x ＝5π6时，函数取得最大值． 9．－1 解析：sin 235°－12cos10°cos80°＝1－cos70°2－12cos10°sin10°＝－12cos70°12sin20°＝－1.10．(－2，－1] 解析：由题意可知，y ＝2sin ⎝⎛⎭⎫2x ＋π6＋a ，该函数在⎣⎡⎦⎤0，π2上有两个不同的零点，即y ＝－a ，y ＝2sin ⎝⎛⎭⎫2x ＋π6的图象在⎣⎡⎦⎤0，π2上有两个不同的交点．结合函数的图象D104可知1≤－a ＜2，所以－2＜a≤－1.图D10411．解：(1)－π2＋2k π≤3x ＋π4≤π2＋2k π⇒－π4＋23k π≤x ≤π12＋23k π(k ∈Z )．(2)由已知，有sin ⎝⎛⎭⎫α＋π4＝45cos ⎝⎛⎭⎫α＋π4cos 2α， 即sin α＋cos α＝45(cos α－sin α)(cos α－sin α)(sin α＋cos α)．若sin α＋cos α＝0，则cos α－sin α＝－ 2.若sin α＋cos α≠0，则1＝45(cos α－sin α)2⇒cos α－sin α＝－52.综上所述，cos α－sin α的值为－2或－52.12．解：(1)f ⎝⎛⎭⎫2π3＝⎝⎛⎭⎫322－⎝⎛⎭⎫－122－2 3×32×⎝⎛⎭⎫－12＝2. (2)由cos 2x ＝cos 2x －sin 2x 与sin 2x ＝2sin x cos x ，得f (x )＝－cos 2x －3sin 2x ＝－2sin ⎝⎛⎭⎫2x ＋π6.所以f (x )的最小正周期是π.由正弦函数的性质，得π2＋2k π≤2x ＋π6≤3π2＋2k π，k ∈Z .解得π6＋k π≤x ≤2π3＋k π，k ∈Z .所以f (x )的单调递增区间是⎣⎡⎦⎤π6＋k π，2π3＋k π，k ∈Z . 第7讲 正弦定理和余弦定理1．B 解析：方法一，由已知，得2sin A cos B ＝sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ，即sin(A －B )＝0.因为－π＜A －B ＜π，所以A ＝B .方法二，由正弦定理，得2a cos B ＝c ，再由余弦定理，得2a ·a 2＋c 2－b 22ac ＝c ⇒a 2＝b 2⇒a＝b .2．A 解析：sin(A ＋C )＋2sin B cos C ＝2sin A cos C ＋cos A sin C ，所以2sin B cos C ＝sin A cos C ⇒2sin B ＝sin A ⇒2b ＝a .故选A.3．D 解析：设BC 边上的高线为AD ，则BC ＝3AD ，DC ＝2AD .所以AC ＝AD 2＋DC 2＝5AD .由正弦定理知，AC sin B ＝BC sin A ，即5AD 22＝3AD sin A .解得sin A ＝31010.故选D.4．A 解析：由正弦定理a sin A ＝b sin B ＝csin C及(b －c )·(sin B ＋sin C )＝(a －3c )sin A ，得(b －c )(b ＋c )＝(a －3c )a ，即b 2－c 2＝a 2－3ac .∴a 2＋c 2－b 2＝3ac .∵cos B ＝a 2＋c 2－b22ac，∴cos B ＝32.∴B ＝30°.5．D 解析：23cos 2A ＋cos 2A ＝25cos 2A －1＝0，cos A ＝15或cos A ＝－15(舍)，a 2＝b 2＋c 2－2bc cos A,49＝b 2＋36－12b ×15，5b 2－12b －65＝0，(5b ＋13)(b －5)＝0，且b >0，所以b＝5.6．C 解析：由正弦定理，得AB sin C ＝AC sin B .解得sin C ＝32.由题意知C 有两解．当C ＝π3时，A ＝π2，此时S △ABC ＝12AB ·AC ·sin A ＝32；当C ＝2π3时，A ＝π6，此时S △ABC ＝12AB ·AC ·sin A＝34.故选C. 7．3 解析：依题意有S △ABC ＝12AB ×BC ×sin B ＝12×2 3×3sin B ＝3 2，sin B ＝63.又角B 为锐角，所以cos B ＝33.所以AC ＝AB 2＋BC 2－2AB ×BC ×cos B ＝12＋9－2×2 3×3×33＝3. 8.6 解析：由正弦定理，得AB sin ∠ADB ＝AD sin B ，即2sin ∠ADB ＝3sin 120°.解得sin ∠ADB＝22，∠ADB ＝45°.从而∠BAD ＝15°＝∠DAC .所以C ＝180°－120°－30°＝30°，AC ＝2AB cos 30°＝ 6.9．解：(1)在△ABC 中，∠A ＝60°，c ＝37a .sin C ＝c sin A a ＝3 314.(2)因为a ＝7，c ＝37a ＝3，由余弦定理，得a 2＝b 2＋c 2－2bc cos A ，即72＝b 2＋32－2×b ×3×12.解得b ＝8或b ＝－5(舍)．所以S △ABC ＝12bc sin A ＝12×8×3×32＝6 3.10．解：(1)由A ＋C ＝π－B ，sin(A ＋C )＝sin B ＝8sin 2B2＝4(1－cos B )，两边平方，整理得17cos 2B －32cos B ＋15＝0.解得cos B ＝1(舍)或cos B ＝1517.(2)由cos B ＝1517，得sin B ＝817.故S △ABC ＝12ac sin B ＝417ac ＝2.∴ac ＝172.由余弦定理，得b 2＝a 2＋c 2－2ac cos B ＝(a ＋c )2－2ac (1＋cos B )＝36－2×172×⎝⎛⎭⎫1＋1517＝4.所以b ＝2.第8讲 解三角形应用举例1．C 解析：如图D105，在△ABC 中，AC ＝3，BC ＝3，∠ABC ＝30°.由余弦定理，得AC 2＝AB 2＋BC 2－2AB ·BC ·cos ∠ABC .∴3＝x 2＋9－6x ·cos 30°，解得x ＝3或2 3.图D105 图D1062．D 解析：如图D106，依题意，得∠ACB ＝120°.由余弦定理，得AB 2＝AC 2＋BC 2－2AC ·BC cos 120°＝a 2＋a 2－2a 2·⎝⎛⎭⎫－12＝3a 2，∴AB ＝3a km.故选D. 3．A 解析：在△ABC 中，∠BAC ＝50°－20°＝30°，∠ABC ＝40°＋65°＝105°，AB ＝40×0.5＝20(海里)，则∠ACB ＝45°.由正弦定理，得BC sin 30°＝20sin 45°.解得BC ＝10 2(海里)．故选A.4．60 解析：根据已知的图形可得AB ＝46sin 67°.在△ABC 中，∠BCA ＝30°，∠BAC ＝37°，由正弦定理，得AB sin 30°＝BC sin 37°.所以BC ≈2×460.92×0.60＝60(m)．5．40 解析：设两船在B 处碰头，设舰艇到达渔船的最短时间是x 小时，则AC ＝10，AB ＝21x ，BC ＝9x ，∠ACB ＝120°，由余弦定理，知(21x )2＝100＋(9x )2－2×10×9x ×cos 120°，整理，得36x 2－9x －10＝0.解得x ＝23或x ＝－512(舍)．故舰艇到达渔船的最短时间是40分钟．6.152 104解析：取BC 中点E ，DC 中点F ，连接AE ，BF .由题意知AE ⊥BC ，BF ⊥CD .在△ABE 中，cos ∠ABC ＝BE AB ＝14，∴cos ∠DBC ＝－14，sin ∠DBC ＝1－116＝154.∴S △BDC＝12×BD ×BC ×sin ∠DBC ＝152.∴cos ∠DBC ＝1－2sin 2∠DBF ＝－14.∴sin ∠DBF ＝104. ∴cos ∠BDC ＝sin ∠DBF ＝104.综上所述，△BDC 的面积为152，cos ∠BDC ＝104.7.7 33 解析：利用余弦定理可求得最大边7所对应角的余弦值为32＋52－722×3×5＝－12，所以此角的正弦值为32.设外接圆半径为R ，则2R ＝732.所以R ＝7 33.8.π3或π9 解析：方法一，设∠A ＝∠ACD ＝θ，0<θ<π2，则∠ADC ＝π－2θ，又AC ＝1，由正弦定理，得AC sin 2θ＝CD sin θ⇒CD ＝12cos θ.在△BDC 中，由正弦定理，得CD sin B ＝BDsin ∠BCD ⇒12cos θsin π6＝1sin ⎝⎛⎭⎫5π6－2θ⇒cos θ＝sin ⎝⎛⎭⎫5π6－2θ⇒sin ⎝⎛⎭⎫π2－θ＝sin ⎝⎛⎭⎫5π6－2θ，由0<θ<π2⇒0<π2－θ<π2，－π6<5π6－2θ<5π6，得π2－θ＝5π6－2θ或π2－θ＋5π6－2θ＝π⇒θ＝π3或π9.⎣⎡或cos θ＝sin ⎝⎛⎭⎫5π6－2θ⇒cos θ＝cos ⎝⎛⎭⎫2θ－π3⇒2θ－⎦⎤π3＝±θ⇒θ＝π3或π9 方法二，过点C 作CE ⊥AB 于点E ，设∠A ＝∠ACD ＝θ，则∠CDB ＝2θ.在Rt △AEC 中，CE ＝sin θ.在Rt △CED 中，DE ＝－CE tan 2θ＝－sin θtan 2θ.在Rt △CEB 中，BE ＝CEtan π6＝3sin θ.由BD ＝1，得sin θtan 2θ＋3sin θ＝1⇒sin θcos 2θ＋3sin θ·sin 2θ＝sin 2θ⇒cos 2θ＋3sin 2θ＝2cos θ⇒cos θ＝cos ⎝⎛⎭⎫2θ－π3⇒2θ－π3＝±θ⇒θ＝π3或π9. 9．解：(1)由sin A ＋3cos A ＝0，得tan A ＝－ 3.所以A ＝2π3.。