阴影部分的面积
- 格式:doc
- 大小:3.61 MB
- 文档页数:7
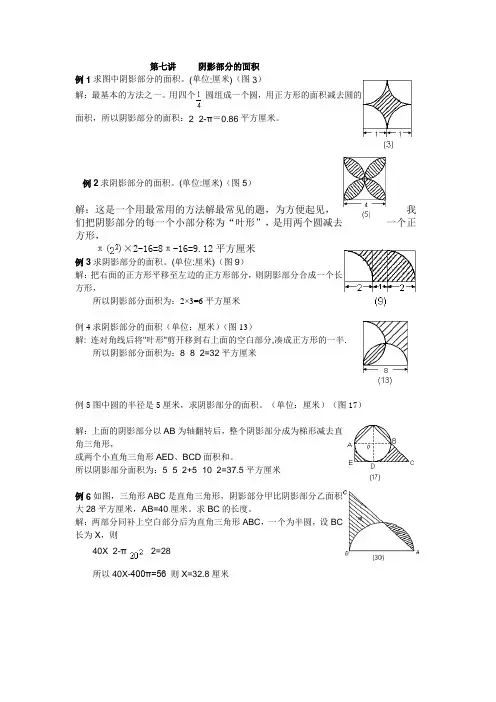
第七讲阴影部分的面积例1求图中阴影部分的面积。
(单位:厘米)(图3)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例2求阴影部分的面积。
(单位:厘米)(图5)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米例3求阴影部分的面积。
(单位:厘米)(图9)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例4求阴影部分的面积(单位:厘米)(图13)解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为:8×8÷2=32平方厘米例5图中圆的半径是5厘米,求阴影部分的面积。
(单位:厘米)(图17)解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和。
所以阴影部分面积为:5×5÷2+5×10÷2=37.5平方厘米例6如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米巩固练习:1求阴影部分的面积。
(单位:厘米)(图7)2.大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影部分的面积。
(图32)3. 求阴影部分的面积。

小学数学图形求阴影部分面积十大方法总结(附例题)_2023.9小学阶段的学生通常在学习上存在着总结归纳能力欠缺等问题,为了很好地帮助孩子系统地掌握小学阶段的数学知识,老师把小学求图形面积的十大方法给大家做了总结,各位家长,快给孩子收藏起来吧!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。
如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例题分析例1、如下图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2、如下图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF 的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米。
解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3、两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决求面积十大方法01相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积02相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差. 例如:下图,求阴影部分的面积。
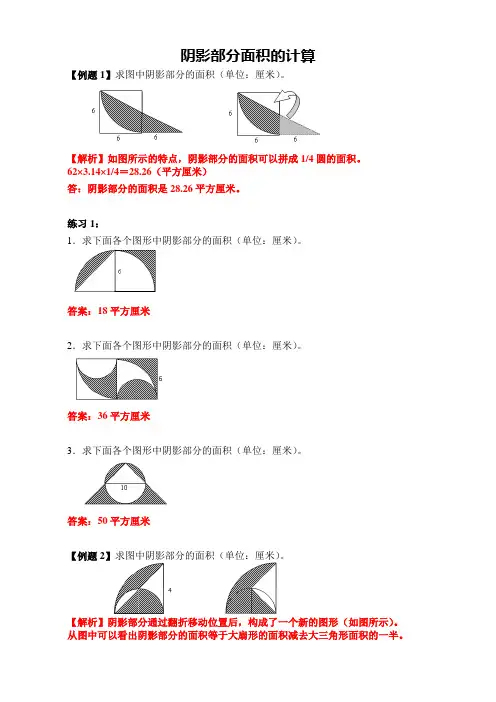
阴影部分面积的计算【例题1】求图中阴影部分的面积(单位:厘米)。
【解析】如图所示的特点,阴影部分的面积可以拼成1/4圆的面积。
62×3.14×1/4=28.26(平方厘米)答:阴影部分的面积是28.26平方厘米。
练习1:1.求下面各个图形中阴影部分的面积(单位:厘米)。
答案:18平方厘米2.求下面各个图形中阴影部分的面积(单位:厘米)。
答案:36平方厘米3.求下面各个图形中阴影部分的面积(单位:厘米)。
答案:50平方厘米【例题2】求图中阴影部分的面积(单位:厘米)。
【解析】阴影部分通过翻折移动位置后,构成了一个新的图形(如图所示)。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×4×4×1/4-4×4÷2÷2=8.56(平方厘米)答:阴影部分的面积是8.56平方厘米。
练习2:1.计算下面图形中阴影部分的面积(单位:厘米)。
答案:8平方厘米2.计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答案:8平方厘米3.计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答案:4.56平方厘米【例题3】如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO1O的面积。
【解析】因为两圆的半径相等,所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半(如图19-10右图所示)。
所以3.14×12×1/4×2=1.57(平方厘米)答:长方形长方形ABO1O的面积是1.57平方厘米。
练习3:1.如图所示,圆的周长为12.56厘米,AC两点把圆分成相等的两段弧,阴影部分(1)的面积与阴影部分(2)的面积相等,求平行四边形ABCD的面积。
答案:12.56平方厘米2.如图所示,直径BC=8厘米,AB=AC,D为AC的中点,求阴影部分的面积。

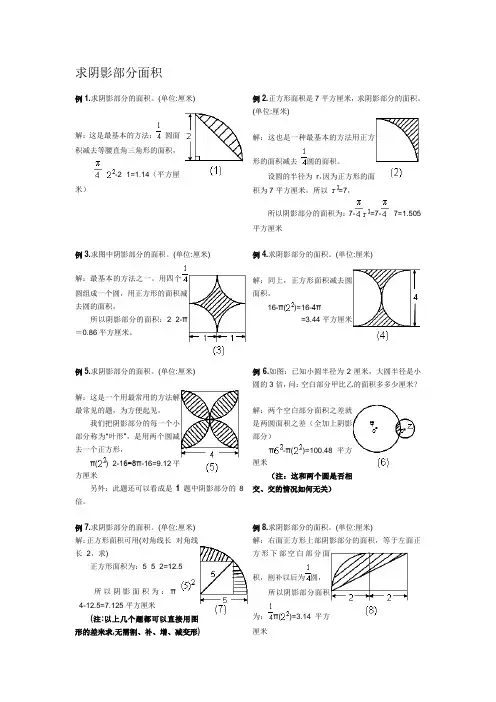
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
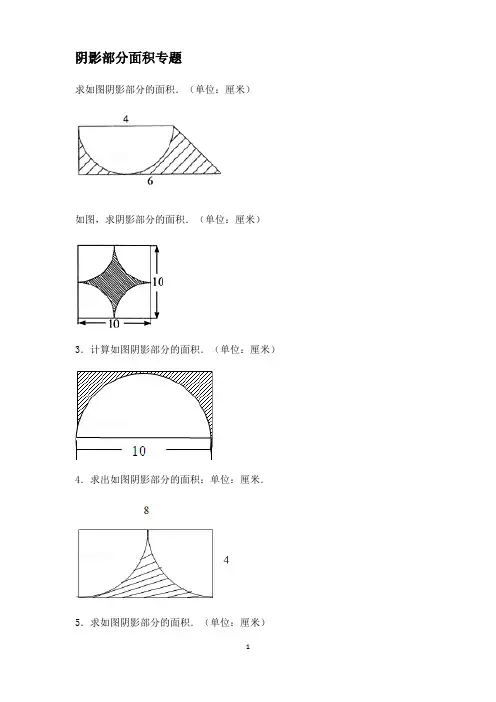
阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012•长泰县)求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。

五年级数学上册必考题求图形阴影部分的面积方法一:直接求法。
根据已知条件直接求出阴影面积。
方法二:相减法。
用整体图形的面积减去非阴影部分面积既得阴影部分面积。
方法三:辅助线法。
将复杂的图形通过做辅助线的方法简单化,形成可一直接求面积的图形,如三角形、平行四边形、梯形等。
方法四:割补法。
将不规则的图形通过割补法变为规则图形从而进行计算。
方法五:等积变换法。
通过平面图形间的等积变换,化繁为易,计算阴影面积。
1、求梯形中阴影部分的面积。
(单位:厘米)(32+18)×15÷2-32×15÷2=375-240=135(平方厘米)答:阴影部分的面积是135平方厘米。
2、求图中阴影部分的面积。
(单位:厘米)已知平行四边形面积是24平方厘米。
24-(5+6)×4÷2=2(平方厘米)答:阴影部分的面积是2平方厘米。
3、求图中阴影部分的面积。
(单位:厘米)6×6+4×4-6×6÷2-4×10÷2=14(平方厘米)答:阴影部分的面积是14平方厘米。
4、下图是平行四边形,面积是36平方米,求阴影部分的面积。
(单位:米)36÷6=6(米)6-1.5=4.5(米)4.5×6÷2=13.5(平方米)答:阴影部分的面积是13.5平方米。
5、如图,一个梯形的上、下底分别是6厘米、10厘米,已知阴影部分的面积是24平方厘米,这个梯形的面积是?三角形的高:24×2÷10=4.8(厘米),梯形面积:(6+10)×4.8÷2=38.4(平方厘米)答:这个梯形的面积是38.4平方厘米。

中考求阴影部分面积【知识概述】计算平面图形的面积问题是常见题型,求平面阴影部分的面积是这类问题的难点。
不规则阴影面积常常由三角形、四边形、弓形、扇形和圆、圆弧等基本图形组合而成的,在解此类问题时,要注意观察和分析图形,会分解和组合图形。
现介绍几种常用的方法。
一、转化法此法就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积相等的规则图形,再利用规则图形的面积公式,计算出所求的不规则图形的面积。
例1. 如图1,点C 、D 是以AB 为直径的半圆O 上的三等分点,AB=12,则图中由弦AC 、AD 和C D ⌒围成的阴影部分图形的面积为_________。
分析:连结CD 、OC 、OD ,如图2。
易证AB//CD ,则∆∆A C D O C D和的面积相等,所以图中阴影部分的面积就等于扇形OCD 的面积。
易得∠=︒C O D 60,故S S O C D阴影扇形==⋅=60636062ππ。
例2、 如图,A 是半径为1的⊙O 外的一点,OA=2,AB 是⊙O 的切线,B 是切点,弦BC ∥OA ,连结AC ,则阴影部分的面积等于_______.分析:一个图形的面积不易或难以求出时,可改求与其面积相等的图形面积,便可以使原来不规则的图形转化为规则图形。
解:连结OB 、OC .∵BC ∥OA ,∴S △ABC=S △OBC ,∴S 阴影=S 扇形OBC . ∵AB 是⊙O 的切线,∴∠BOA=90°, ∵OB=1,OA=2,∴∠OBC=∠BOA=60°,∴∠BOC= , ∴扇形OBC 是圆的 .∴S 阴影=S 扇形OBC=二、和差法有一些图形结构复杂,通过观察,分析出不规则图形的面积是由哪些规则图形组合而成的,再利用这些规则图形的面积的和或差来求,从而达到化繁为简的目的。
例3. 如图3是一个商标的设计图案,AB=2BC=8,A D E ⌒为14圆,求阴影部分面积。
分析:经观察图3可以分解出以下规则图形:矩形ABCD 、扇形ADE 、R t E B C∆。

圆阴影部分面积(含答案)求一个图形的阴影部分面积是一个基本的几何问题。
下面给出一些例子:例1:求一个圆形和一个等腰直角三角形组成的阴影部分的面积。
首先计算圆的面积,假设半径为r,则圆面积为πr²。
然后计算三角形的面积,假设直角边长为a,则三角形面积为a²/2.最终阴影部分的面积为πr²-a²/2.例2:求一个正方形中的阴影部分面积。
假设正方形面积为7平方厘米,则阴影部分可以用正方形的面积减去圆的面积来计算。
如果圆的半径为r,则圆的面积为πr²,阴影部分面积为7-πr²。
例3:求一个由四个圆和一个正方形组成的阴影部分的面积。
首先将四个圆组成一个大圆,然后用正方形的面积减去这个大圆的面积。
假设正方形边长为2,则大圆的半径为1,面积为π,阴影部分面积为2²-π=0.86平方厘米。
例4:求一个正方形中的阴影部分面积。
同样可以用正方形的面积减去圆的面积来计算。
假设正方形面积为16平方厘米,则阴影部分面积为16-πr²=3.44平方厘米。
例5:求一个由两个圆和一个正方形组成的阴影部分的面积。
将阴影部分分成两个“叶形”,每个“叶形”由两个圆和一个正方形组成。
假设圆的半径为r,则每个“叶形”的面积为2πr²-4,阴影部分的面积为2(2πr²-4)=4πr²-8.例6:已知一个小圆的半径为2厘米,大圆的半径是小圆的3倍,求空白部分甲比乙的面积多多少厘米?两个空白部分面积之差就是两圆面积之差。
假设小圆的半径为2,则小圆面积为4π,大圆面积为36π,空白部分的面积为32π-4π=28π=100.48平方厘米。
例7:求一个正方形中的阴影部分面积。
首先计算正方形的面积,假设对角线长为5,则正方形面积为25/2.然后计算圆的面积,假设圆的半径为r,则圆的面积为πr²,阴影部分的面积为πr²/4-25/2=7.125平方厘米。

【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:1、从整体图形中减去局部;2、割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
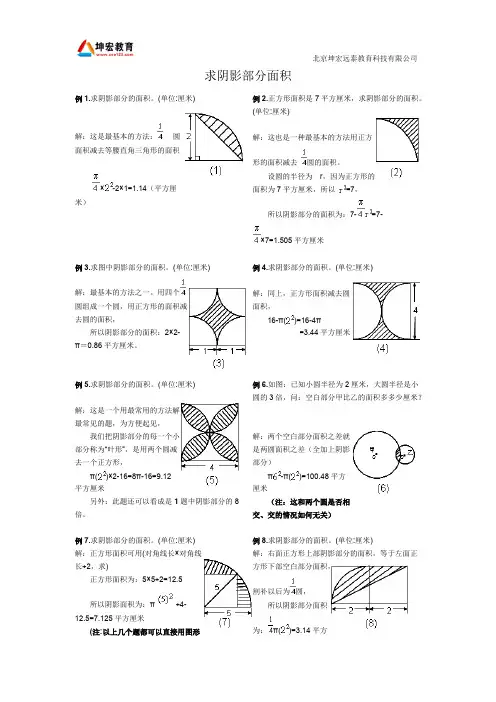
例 1.求阴影部分的面积。
例 2.正方形面积是 7 平方厘米,求阴影部分的面积。
(单位:厘米)(单位:厘米)例 4.求阴影部分的面积。
(单位:厘米)例 3.求图中阴影部分的面积。
(单位:厘米)例 5.求阴影部分的面积。
(单位:厘米) 例 6.如图:已知小圆半径为 2 厘米,大圆半径是小圆的 3 倍,问:空白部分甲比乙的面积多多少厘米?例 7.求阴影部分的面积。
(单位:厘米) 例 8.求阴影部分的面积。
(单位:厘米)例 9.求阴影部分的面积。
(单位:厘米) 例 10.求阴影部分的面积。
(单位:厘米)例 11.求阴影部分的面积。
(单位:厘米) 例 12.求阴影部分的面积。
(单位:厘米)例 13.求阴影部分的面积。
(单位:厘米) 例 14.求阴影部分的面积。
(单位:厘米)例 16.求阴影部分的面积。
(单位:厘米) 例 15.已知直角三角形面积是 12 平方厘米,求阴影部分的面积。
例 17.图中圆的半径为 5 厘米,求阴影部分的面积。
(单位:厘米) 例 18.如图,在边长为 6 厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例 19.正方形边长为 2 厘米,求阴影部分的面积。
例 20.如图,正方形 ABCD 的面积是 36 平方厘米,求阴影部分的面积。
例 21.图中四个圆的半径都是 1 厘米,求阴影部分的面积。
例 22. 如图,正方形边长为 8 厘米,求阴影部分的面积。
例 25.如图,四个扇形的半径相等,求阴影部分的面积。
小升初阴影部分面积专题姓名:1.求如图阴影部分的面积.单位:厘米2.如图,求阴影部分的面积.3.计算如图阴影部分的面积.单位:厘米4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.单位:厘米6.求如图阴影部分面积.单位:cm7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.单位:厘米10.求阴影部分的面积.单位:厘米11.求下图阴影部分的面积.单位:厘米12.求阴影部分图形的面积.单位:厘米13.计算阴影部分面积单位:厘米.14.求阴影部分的面积.单位:厘米15.求下图阴影部分的面积:单位:厘米16.求阴影部分面积单位:厘米.17.2012•长泰县求阴影部分的面积.单位:厘米参考答案与试题解析1.求如图阴影部分的面积.单位:厘米考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:4+6×4÷2÷2﹣×÷2,=10﹣×4÷2,=10﹣,=平方厘米;答:阴影部分的面积是平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.单位:厘米考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于10×10100平方厘米,4个扇形的面积等于半径为10÷25厘米的圆的面积,即:×5×5=平方厘米.解答解:扇形的半径是:10÷2,=5厘米;10×10﹣×5×5,100﹣,=平方厘米;答:阴影部分的面积为平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.单位:厘米考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5厘米,长方形的面积=长×宽=10×5=50平方厘米,半圆的面积=πr2÷2=×52÷2=平方厘米,阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣,=平方厘米;答:阴影部分的面积是.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣×42÷2,=32﹣,=平方厘米;答:阴影部分的面积是平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.单位:厘米考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=×4÷22=平方厘米;阴影部分的面积=2个圆的面积,=2×,=平方厘米;答:阴影部分的面积是平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.单位:厘米考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6平方厘米;图二中阴影部分的面积=8+15×48÷8÷2﹣48=21平方厘米;答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12厘米;阴影部分的面积:××122,=××144,=×144,=平方厘米;答:阴影部分的面积是平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析1圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;2阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:1阴影部分面积:×﹣×,=﹣,=平方厘米;2阴影部分的面积:×32﹣×3+3×3,=﹣9,=平方厘米;答:圆环的面积是平方厘米,阴影部分面积是平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.单位:厘米考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:×10+3,=×13,=厘米;面积:××10+3÷22﹣××10÷22﹣××3÷22,=××﹣25﹣,=××15,=平方厘米;答:阴影部分的周长是厘米,面积是平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.单位:厘米考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=﹣,=平方厘米;答:阴影部分的面积是平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.单位:厘米考点组合图形的面积.分析先求出半圆的面积×10÷22÷2=平方厘米,再求出空白三角形的面积10×10÷2÷2=25平方厘米,相减即可求解.解答解:×10÷22÷2﹣10×10÷2÷2=﹣25=平方厘米.答:阴影部分的面积为平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.单位:厘米考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:4+10×4÷2﹣×42÷4,=28﹣,=平方厘米;答:阴影部分的面积是平方厘米.点评解答此题的方法是用阴影部分所在的图形梯形面积减去空白图形扇形的面积,即可列式解答.13.计算阴影部分面积单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和15﹣7厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×15﹣7÷2,=150﹣40,=110平方厘米;答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.单位:厘米考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:6+10×6÷2,=16×6÷2,=96÷2,=48平方厘米;答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:单位:厘米考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3平方厘米.答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:4+9×4÷2﹣×42×,=13×4÷2﹣×4,=26﹣,=平方厘米;答:阴影部分的面积是平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.2012•长泰县求阴影部分的面积.单位:厘米考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=a+bh,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×6+8×6÷2﹣××6÷22=×14×3﹣××9,=21﹣,=平方厘米;答:阴影部分的面积为平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
六年级上册数学求阴影面积的七种类型归纳
以下是六年级上册数学求阴影面积的七种类型归纳:
1.直接计算法:当阴影部分是一个规则图形时,可以直接使用相应图形的面积公式进行计算。
2.相减法:当阴影部分是由两个或多个规则图形组成时,可以将阴影部分的面积看作是这些规则图形面积的差。
3.割补法:将阴影部分通过切割、平移、旋转等方式,拼成一个规则图形,然后计算其面积。
4.等积变形法:根据等积原理,将阴影部分与一个已知面积的规则图形进行等积变换,然后计算阴影部分的面积。
5.比例法:当阴影部分与某个规则图形之间存在比例关系时,可以利用比例关系求出阴影部分的面积。
6.方程法:通过建立方程来求解阴影部分的面积。
7.实际问题法:将阴影部分的面积问题与实际生活中的问题相结合,通过分析实际问题来求解阴影部分的面积。
需要注意的是,在解决具体问题时,需要根据具体情况选择合适的方法。
同时,要注意单位的统一和计算的准确性。
求阴影部份面积之答禄夫天创作时间:二O二一年七月二十九日例1.求阴影部份的面积.(单元:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部份的面积.(单元:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积.设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部份的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部份的面积.(单元:厘米) 解:最基本的方法之一.用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部份的面积:2×2-π=0.86平方厘米. 例4.求阴影部份的面积.(单元:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部份的面积.(单元:厘米)解:这是一个用最经常使用的方法解最罕见的题,为方便起见,我们把阴影部份的每一个小部份称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部份的8倍. 例6.如图:已知小圆半径为2厘米,年夜圆半径是小圆的3倍,问:空白部份甲比乙的面积多几多厘米?解:两个空白部份面积之差就是两圆面积之差(全加上阴影部份)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部份的面积.(单元:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π例8.求阴影部份的面积.(单元:厘米) 解:右面正方形上部阴影部份的面积,即是左面正方形下部空白部份面积,割补÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)以后为圆,所以阴影部份面积为:π()=3.14平方厘米例9.求阴影部份的面积.(单元:厘米)解:把右面的正方形平移至左边的正方形部份,则阴影部份合成一个长方形,所以阴影部份面积为:2×3=6平方厘米例10.求阴影部份的面积.(单元:厘米)解:同上,平移左右两部份至中间部份,则合成一个长方形,所以阴影部份面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部份的面积.(单元:厘米)解:这种图形称为环形,可以用两个同心圆的面积差或差的一部份来求.(π-π)×=×3.14=3.66平方厘米例12.求阴影部份的面积.(单元:厘米)解:三个部份拼成一个半圆面积.π()÷2=14.13平方厘米例13.求阴影部份的面积.(单元:厘米)解: 连对角线后将"叶形"剪开移到右上面的空白部份,凑成正方形的一半.所以阴影部份面积为:8×8÷2=32平方厘米例14.求阴影部份的面积.(单元:厘米)解:梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米.例15.已知直角三角形面积是12平方厘米,求阴影部份的面积.分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,例16.求阴影部份的面积.(单元:厘米)=6圆面积为:π÷2=3π.圆内三角形的面积为12÷2=6,阴影部份面积为:(3π-6)×=5.13平方厘米解:[π+π-π]=π(116-36)=40π=125.6平方厘米例17.图中圆的半径为5厘米,求阴影部份的面积.(单元:厘米)解:上面的阴影部份以AB为轴翻转后,整个阴影部份成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和.所以阴影部份面积为:5×5÷2+5×10÷2=37.5平方厘米例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部份的周长.解:阴影部份的周长为三个扇形弧,拼在一起为一个半圆弧,所以圆弧周长为:2×3.14×3÷2=9.42厘米例19.正方形边长为2厘米,求阴影部份的面积.解:右半部份上面部份逆时针,下面部份顺时针旋转到左半部份,组成一个矩形.所以面积为:1×2=2平方厘米例20.如图,正方形ABCD的面积是36平方厘米,求阴影部份的面积.解:设小圆半径为r,4=36,r=3,年夜圆半径为R,=2=18,将阴影部份通过转动移在一起构成半个圆环,所以面积为:π(-)÷2=4.5π=14.13平方厘米例21.图中四个圆的半径都是1厘米,求阴影部份的面积.解:把中间部份分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为:2×2=4平方厘米例22. 如图,正方形边长为8厘米,求阴影部份的面积.解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部份为一个三角形和一个半圆面积之和.π()÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部份面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16所以阴影部份的面积为:π()-8π+16=41.12平方厘米例23.图中的4个圆的圆心是正方形的4个极点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部份的面积是几多?解:面积为4个圆减去8个叶形,叶形面积为:π-1×1=π-1所以阴影部份的面积为:4π-8(π-1)=8平方厘米例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部份连成一个花瓣图形,图中的黑点是这些圆的圆心.如果圆周π率取3.1416,那么花瓣图形的的面积是几多平方厘米?分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部份正好合成3个整圆,而正方形中的空白部份合成两个小圆.解:阴影部份为年夜正方形面积与一个小圆面积之和.为:4×4+π=19.1416平方厘米例25.如图,四个扇形的半径相等,求阴影部份的面积.(单元:厘米)分析:四个空白部份可以拼成一个以2为半径的圆.所以阴影部份的面积为梯形面积减去圆的面积,4×(4+7)÷2-π=22-4π=9.44平方厘米例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部份的面积.解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部份成为三角形ACB 面积减去个小圆面积,为: 5×5÷2-π÷4=12.25-3.14=9.36平方厘米例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部份,求阴影部份的面积.解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14平方厘米例28.求阴影部份的面积.(单元:厘米)解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:[π÷2-5×5]÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米解法二:右上面空白部份为小正方形面积减去小圆面积,其值为:5×5-π=25-π阴影面积为三角形ADC减去空白部份面积,为:10×5÷2-(25-π)=π=19.625平方厘米例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD=,问:阴影部份甲比乙面积小几多?解: 甲、乙两个部份同补上空白部份的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部份差即为:π×-×4×6=5π-12=3.7平方厘米例30.如图,三角形ABC是直角三角形,阴影部份甲比阴影部份乙面积年夜28平方厘米,AB=40厘米.求BC的长度.解:两部份同补上空白部份后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部份的面积.解:连PD、PC转换为两个三角形和两个弓形,两三角形面积为:△APD面积+△QPC面积=(5×10+5×5)=37.5两弓形PC、PD 面积为:π-5×5所以阴影部份的面积为:37.5+π-25=51.75平方厘米例32.如图,年夜正方形的边长为6厘米,小正方形的边长为4厘米.求阴影部份的面积.解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积即是三角形EBF面积,阴影部份可补成圆ABE的面积,其面积为:π÷4=9π=28.26平方厘米例33.求阴影部份的面积.(单元:厘米)解:用年夜圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6=×13π-6=4.205平方厘米例34.求阴影部份的面积.(单元:厘米)解:两个弓形面积为:π-3×4÷2=π-6阴影部份为两个半圆面积减去两个弓形面积,结果为π+π-(π-6)=π(4+-)+6=6平方厘米例35.如图,三角形OAB是等腰三角形,OBC 是扇形,OB=5厘米,求阴影部份的面积.解:将两个同样的图形拼在一起成为圆减等腰直角三角形[π÷4-×5×5]÷2=(π-)÷2=3.5625平方厘米时间:二O二一年七月二十九日。
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
1/7
培养成功素质 助力国家未来
学生姓名 李同学 年级 授课时间 教师姓名 刘老师 总课时 第 次课
学生情况
分析
阴影部分的面积是小升初数学考试的必考点,掌握阴影部分面积的方法是非常重要。
教学目标 掌握阴影部分面积的求法
重点难点 掌握阴影部分面积的求法
教学用具
一、知识回顾
有关圆的面积与周长的计算,我们可以运用“化直为曲”的思想,圆的周长转化为线段的长,圆的
面积转化为长方形的面积。
二、知识检验
1、右图中正方形的面积是30平方厘米,求阴影部分的面积。
2、如右图,一个半圆的周长是41.12分米,求它的面积。
3、已知右图中正方形的面积是40平方厘米,求阴影部分的面积。
2/7
培养成功素质 助力国家未来
4、现有4跟同样长的圆木,它们的横截面的周长是9.42分米,如果将它们捆成一捆,至少要多长的铁丝?(接
头不计)
5、求右图阴影部分的面积。(单位:分米)
三、知识新授
计算组合图形的面积,常用的方法是“割补法”。
例:计算右图阴影部分的面积。(单位:厘米)
练一练:计算右图阴影部分的面积。(单位:厘米)
例:右图中阴影甲的面积比阴影乙的面积大33平方厘米,AB=60厘米,CB垂直于AB,求BC的长。
3/7
培养成功素质 助力国家未来
练一练:右图中三角形ABC是等腰直角三角形,面积是10平方分米,AB是圆的直径,求阴影①的面积与阴影
②的面积相差多少平方分米?
例:计算右图阴影部分的面积。(单位:分米)
练一练:计算右图阴影部分的面积。(单位:厘米)
例:计算右图阴影部分的面积。(单位:分米)
4/7
培养成功素质 助力国家未来
练一练:计算右图阴影部分的面积。(单位:厘米)
例:如右图所示,扇形圆心角为90°,AO=8厘米,四边形DEOF为正方形,求阴影部分的面积。
练一练:如右图所示,等腰直角三角形AOB的斜边AB长8厘米,求阴影部分的面积。
例:如右图所示,等腰直角三角形AOB的斜边AB长10厘米,求阴影的部分的面积。
5/7
培养成功素质 助力国家未来
练一练:如右图是一个圆心为O,半径是8厘米的圆。以C为圆心,AC为半径画一圆弧,且∠ACB=90°,求
阴影部分的面积。
例:求阴影部分的面积。(单位:厘米)
练一练:求阴影部分的面积。(单位:厘米)
例:右图中三个圆的面积是200平方分米,求阴影部分的面积。
6/7
培养成功素质 助力国家未来
练一练:右图中每个圆的半径都是6分米,求阴影部分的面积。
例:图中两圆半径都是1厘米,且图中两个阴影部分面积相等,求长方形ABO1O的面积。
练一练:图中长方形的长为6厘米,宽为4厘米,甲三角形的面积比乙三角形的面积大6平方厘米,求阴影部分
的面积。
例:一块正方形草地,边长是10米,一组相对的两个角顶点上各系有一只羊,绳子长10米,这两只羊都能吃到
的草的面积是多少?
7/7
培养成功素质 助力国家未来
练一练:有一块正方形草地,边长是10米,四边的中点上各系有一只羊,绳子都是5米,只能被一只羊吃到的
草地面积总共是多少平方米?
教学反思
本周作业 上周作业完成情况
学科负责人 签字日期/时间