截交线与相贯线习题答案

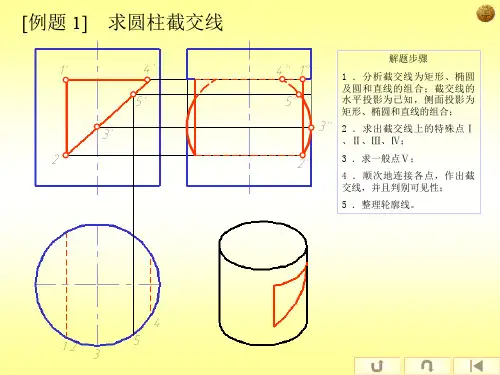
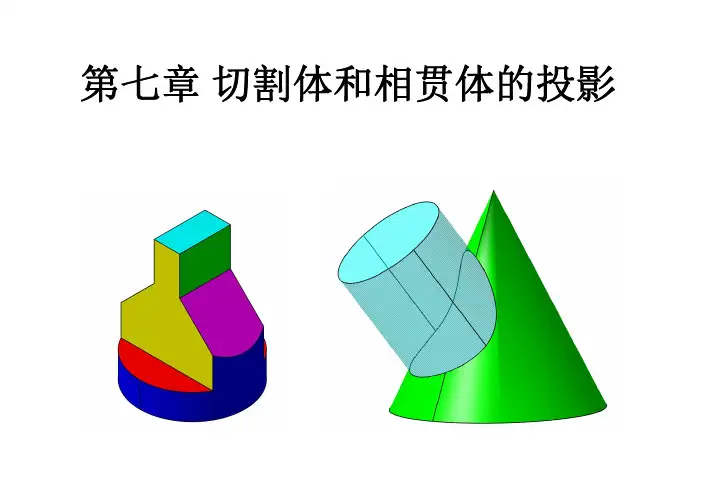
第五节截交线与相贯线截交线和相贯线是立体表面常见的两种表面交线，立体被平面截切，表面就会产生截交线，两立体相交，表面就产生相贯线，二者有共同点，也有不同点。

一、截交线的特性及画法【考纲要求】1、掌握特殊位置平面截断棱柱和棱锥的截交线画法；2、掌握特殊位置平面截断圆柱、圆锥、圆球的截交线画法；3、掌握简单的同轴回转体的截交线画法；【要点精讲】（一）截交线的定义：由平面截断基本体所形成的表面交线称为截交线。

（二）截交线的特性：1、任何基本体的截交线都是一个封闭的平面图形（平面体是平面多边形，曲面体是平面曲线或由平面曲线与直线共同组成的图形）；2、截交线是截平面与基本体表面的共有线，截交线上的每一点都是截平面与基本体表面的共有点（共有点的集合）。

（三）求截交线的方法：①积聚性求点法；②辅助（素）线法；③辅助平面法。

（四）求截交线的步骤：1、确定被截断的基本体的几何形状；2、判断截平面的截断基本体的位置（回转体判别截平面与轴线的相对位置3、想象截交线的空间形状；4、分析截平面与投影面的相对位置，弄清截交线的投影特性；5、判别截交线的可见性，确定求截交线的方法；6、将求得的各点连接，画出其三面投影。

（五）平面体的特殊截交线及画法：1、特性：平面体的截交线都是由直线所组成的封闭的平面多边形。

多边形的各个顶点是棱线与截平面的交点，多边形的每一条边是棱面与截平面的交线。

2、画法：求平面体截交线的方法主要是用积聚性求点法和辅助线法。

画平面体的截交线就是求出截平面与平面体上各被截棱线的交点（即平面多边形的各个顶点），然后依次连接即得截交线。

根据截交线是截平面与基本体表面的共有线，截交线上的点也是截平面与基本体表面的共有点，我们所要求掌握的是特殊位置平面截切平面立体的截交线，我们可以利用积聚性求点法或辅助平面法，求出截平面与平面立体的各棱线的交点，然后依次连接，也就求出了截交线。

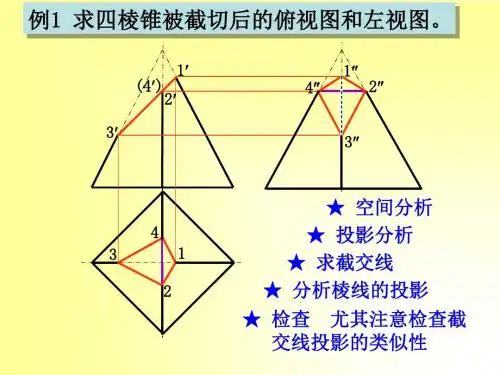
例如图5-1所示，先根据截交线具有积聚性投影的正面投影和具有收缩性的水平投影确定出截平面与六棱柱棱线的六个交点（截交线平面多边形的六个顶点），再利用积聚性求点法求出其侧面投影。

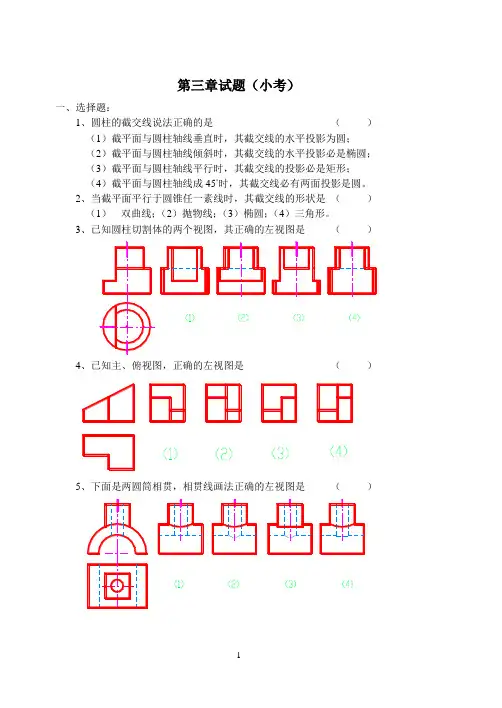
第三章试题（小考）一、选择题：1、圆柱的截交线说法正确的是（）（1）截平面与圆柱轴线垂直时，其截交线的水平投影为圆；（2）截平面与圆柱轴线倾斜时，其截交线的水平投影必是椭圆；（3）截平面与圆柱轴线平行时，其截交线的投影必是矩形；（4）截平面与圆柱轴线成45˚时，其截交线必有两面投影是圆。

2、当截平面平行于圆锥任一素线时，其截交线的形状是（）（1）双曲线；（2）抛物线；（3）椭圆；（4）三角形。

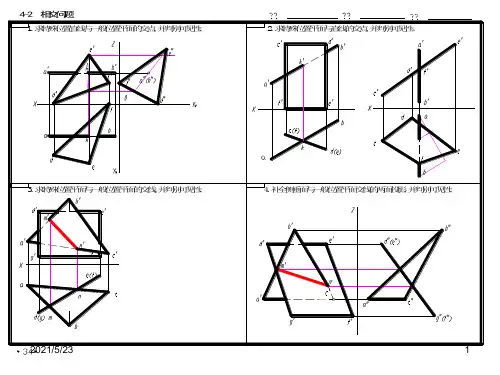
3、已知圆柱切割体的两个视图，其正确的左视图是（）4、已知主、俯视图，正确的左视图是（）5、下面是两圆筒相贯，相贯线画法正确的左视图是（）6、已知两物体相贯，左视图画法正确的是（）78、已知俯、左视图，正确的主视图是（）9、左视图正确的是（）10、下面相贯体的左视图画法正确的是（）二、下面五组视图中，左视图均相同，但主、俯视图位置排错，请用直线把对应的主、俯视图连起来：三、据轴测图补全左视图中的缺线，并判别直线或平面的位置：1、直线T是______线，2、平面P是______面，3、平面S是______面。

四、补画视图中的遗漏的图线：1、2、3、4、5、6、五、根据两视图补画第三视图：1、 2、3、 4、5、 6、六、根据立体图画出三视图[参考答案]一、选择题：1、（4）；2、（2）；3、（2）；4、（3）；5、（3）；6、（3）；7、（2）；8、（1）；9、（4）；10、（3）。

二、下面五组视图中，左视图均相同，但主、俯视图位置排错，请用直把对应的主、俯视图连起来：三、据轴测图补全左视图中的缺线，并判别直线或平面的位置：1、直线T是一般位置线，2、平面P是正垂面，3、平面S是铅垂面。

四、补画视图中的遗漏的图线：3、4、5、6、五、根据两视图补画第三视图：1、2、3、4、5、6、。

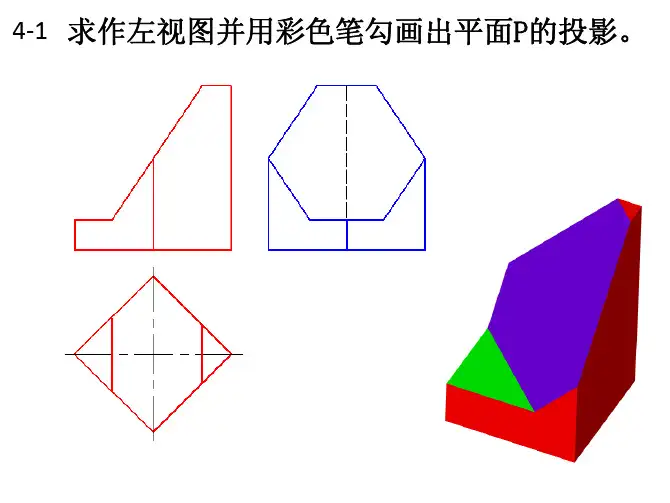
项目4组合体的投影4.1看图填空并补画图中所缺的图线(1)请将左图中满足条件的图号填在相应的横线上：左图中属于叠加型组合体的有2、3、1,属于切割型组合体的有5、6,属于综合型组合体的有L表面连接关系为相切的有2、3、6,表面连接关系为相交的有2、3、5,表面连接关系为共面有1、L表面不共面的有1、5。

(2)仔细分析图中组合体的组合型式并补面图中所缺的图线。

A.平行B.垂直C.倾斜D.相交4.当截平面与圆柱体平行时，截交线为（A ）oA.矩形B.椭圆C.圆D.正方形5.当截平面与圆柱体（B ）时，截交线为圆。

A.平行B.垂直C.倾斜D.相交。

6.当截平面与圆球体相交时，截交线为（C ）oA.矩形B.椭圆C.圆D.正方形7.当截平面通过正圆锥体轴线时，截交线为（D ）0A.矩形B.椭圆C.双曲线加直线D.等腰三角形8.当截平面垂直于正圆锥体轴线时，截交线为（B ）。

A.矩形B.圆C.椭圆D.等腰三角形9.平面切割圆球时，截交线为（C ）oA.矩形B.椭圆C.圆D.正方形10.两圆柱体垂直相交产生一条封闭的（B ）曲线。

A.平面B.空间C.平行D.相交11.当正交两圆柱的相对位置不变，而相对大小发生变化时，相贯线的（CA,形状和位置将没有变化 B.形状变化，位置不变C.位置变化，形状不变D.形状和位置将随之变化4.2按要求完成下列各题一、截交线和相贯线基础知识填空题1.平面截割立体而产生的表面交线称为截交线。

2.截交线具有以下两个基本特性：截交线为一封闭—的平面图形；截交线是截平面与立体表面的共有线。

3.平面截割圆柱体时，当截平面与圆柱轴线平行，截交线为矩形；当截平面与圆柱轴线垂直，截交线为一趴形；当截平面与圆柱轴线倾斜，截交线为椭圆形。

4.两圆柱体相交，其交线称为相贯线。

5.两圆柱体的相贯线，实际上是两圆柱体表面上一系列一亚二点的连接。

一般情况下为一封胆的空间曲线。

6.两个同轴回转体相交时，它们的相贯线一定是垂直于轴线的」a7.平面切割圆球时，其交线均为圆。

【练习1】求作主视图。

【练习2】求作主视图。

【练习3】完成相贯线的投影。

【练习4】完成相贯线的投影。

【练习5】完成立体的正面投影。

【练习6】求作左视图。

【练习7】求作俯视图。

【练习8】求立体的相贯线，完成正面投影。

【练习10】求作俯视图。

【练习11】求作俯视图。

（1）
（2）
【练习13】求作主视图。

【练习14】完成相贯线的投影。

【练习15】完成相贯线的投影。

【练习16】完成相贯线的投影。

【练习17】求作左视图。

【练习18】求作左视图。

【练习19】求作左视图。

【练习20】求作俯视图。

【练习21】求作主视图。

【练习22】求作左视图。

（1）
（2）
【练习23】求作左视图。

【练习24】求作左视图。

【练习25】求作左视图。

【练习26】完成立体的投影。

【*练习27】完成立体的投影。

【*练习28】完成立体的投影。

5-1 平面与立体表面的交线——截交线，参照轴测图完成切割体的投影1、2、
3、4、
5-2 平面与立体表面的交线——截交线，参照轴测图完成切割体的投影
2、3、4、
5-4 两回转体表面的交线——相贯线，用表面取点法，画相贯线
1、
2、3、4、
5-5 两回转体表面的交线——相贯线，补画第三视图，用表面取点法，画相贯线
1、2、
3、§2-2（3）平面与立体表面的交线——截交线
1、完成同轴的圆锥和圆柱的截交线
5-6 两回转体表面的交线——相贯线，选择正确的左视图。

1、2、3、4、
5-7 两回转体表面的交线——相贯线，补画第三视图，画相贯线
1、2、3、4、
5-8 两回转体表面的交线——相贯线
1、作四棱柱与圆锥相贯后的W、V面的投影
2、作圆柱与圆锥相贯后的H、V面的投影
5-9 两回转体表面的交线——相贯线.分析立体表面交线，补全或补画相关投影
1、作圆柱与圆锥相贯后的H、V面的投影
2、作圆柱孔与圆锥相贯后的H、V面的投影
5-10 两回转体表面的交线——相贯线.分析立体表面交线，补全正面和侧面投影
1、作圆柱孔与圆相贯后的W、V面的投影
2、作棱柱与圆相贯后的H、V面的投影。