河南省驻马店市2020届高三线上模拟测试(二)+数学(文)+Word版含答案

驻马店市高三年级线上模拟测试(二)英语第一部分听力(共两节，满分30分)做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节(共5小题；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. ￡19.15.B. ￡9.18.C.￡9.15.答案是C。

1. What can we learn about the man from the conversation?A. He won't help others.B. He is a stranger in the place.C. He will go to the London bridge.2. Where will the woman go?A. To the hospital.B. To the school.C. To the airport.3. What's the probable relationship between the speakers?A. Colleagues.B. Close friends.C. Strangers.4. Why does the man make the call?A. To repair his freezer.B. To buy a freezer.C. To sell his freezer.5. What will the man take to the zoo?A. A bus.B. A car.C. A boat.第二节(共15小题；每小题1.5分，满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项。

2020届河南省驻马店市高三第二次模拟测试数学（理科）试题一、单选题(★) 1 . 若为纯虚数，则 z＝（）A．B．6i C．D．20(★) 2 . 已知集合 A＝{ x∈ N| x 2＜8 x}， B＝{2，3，6}， C＝{2，3，7}，则＝（）A．{2，3，4，5}B．{2，3，4，5，6}C．{1，2，3，4，5，6}D．{1，3，4，5，6，7}(★) 3 . 已知向量，满足| |＝1，| |＝2，且与的夹角为120°，则＝（）A．B．C．D．(★) 4 . 若双曲线：的一条渐近线方程为，则（）A．B．C．D．(★★) 5 . 已知底面是等腰直角三角形的三棱锥 P- ABC的三视图如图所示，俯视图中的两个小三角形全等，则（）A．PA，PB，PC两两垂直B．三棱锥P-ABC的体积为C．D．三棱锥P-ABC的侧面积为(★) 6 . 山东烟台苹果因“果形端正、色泽艳丽、果肉甜脆、香气浓郁”享誉国内外.据统计，烟台苹果（把苹果近似看成球体）的直径（单位：）服从正态分布，则直径在内的概率为（）附：若，则，.A．0.6826B．0.8413C．0.8185D．0.9544(★)7 . 已知函数，，且，则（）A．3B．3或7C．5D．5或8(★★) 8 . 函数的图象大致为（）A．B．C．D．(★) 9 . 设不等式组表示的平面区域为，若从圆：的内部随机选取一点，则取自的概率为（）A．B．C．D．(★★) 10 . 已知函数，则函数的零点所在区间为（）A．B．C．D．(★) 11 . 已知直线 y＝ k（ x﹣1）与抛物线 C： y 2＝4 x交于 A， B两点，直线 y＝2 k（ x﹣2）与抛物线 D： y 2＝8 x交于 M， N两点，设λ＝| AB|﹣2| MN|，则（）A．λ＜﹣16B．λ＝﹣16C．﹣12＜λ＜0D．λ＝﹣12(★★★★)12 . “中国剩余定理”又称“孙子定理”，最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”，原文如下：今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二.问物几何？现有这样一个相关的问题：将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列，构成一个数列，则该数列各项之和为（）A．56383B．57171C．59189D．61242二、填空题(★) 13 . 展开式的第5项的系数为_____.(★) 14 . 函数的值域为_____.(★★) 15 . 在数列中，，，曲线在点处的切线经过点，下列四个结论：① ；② ；③ ；④数列是等比数列；其中所有正确结论的编号是______.(★★) 16 . 在矩形中，，为的中点，将和分别沿，翻折，使点与重合于点.若，则三棱锥的外接球的表面积为_____ .三、解答题(★) 17 . a， b， c分别为△ ABC内角 A， B， C的对边.已知 a＝3，，且 B＝60°.（1）求△ ABC的面积；（2）若 D， E是 BC边上的三等分点，求 .(★) 18 . 如图，四棱锥 E﹣ ABCD的侧棱 DE与四棱锥 F﹣ ABCD的侧棱 BF都与底面 ABCD垂直，，// ，.（1）证明： //平面 BC （2）设平面 ABF 与平面 CDF 所成的二面角为 θ，求 .A ．(★★) 19 . 追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量，某城市环保局随机抽取了一年内100天的空气质量指数（ ）的检测数据，结果统计如下：空气质量 优良轻度污染中度污染重度污染严重污染天数61418272520（1）从空气质量指数属于 ， 的天数中任取3天，求这3天中空气质量至少有2天为优的概率.（2）已知某企业每天因空气质量造成的经济损失 （单位：元）与空气质量指数 的关系式为 假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为 ， ， ， ， , ,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.（i ）记该企业9月每天因空气质量造成的经济损失为 元，求的分布列；（ii ）试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元？说明你的理由.(★★★★) 20 . 已知椭圆 ：过点 ，过坐标原点 作两条互相垂直的射线与椭圆 分别交于 ，两点.（1）证明：当取得最小值时，椭圆 的离心率为 .（2）若椭圆 的焦距为2，是否存在定圆与直线 总相切？若存在，求定圆的方程；若不存在，请说明理由.(★★★★) 21 . 已知函数，函数（）.（1）讨论的单调性；（2）证明：当时，.（3）证明：当时，.(★★) 22 . 在直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴，建立极坐标系.已知点的直角坐标为，过的直线与曲线相交于，两点.（1）若的斜率为2，求的极坐标方程和曲线的普通方程；（2）求的值.(★★) 23 . 已知函数，记不等式的解集为.（1）求；（2）设，证明：.。

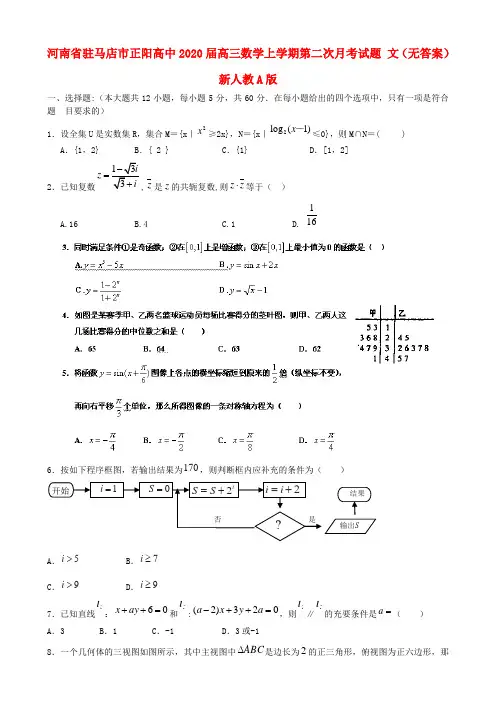
河南省驻马店市正阳高中2020届高三数学上学期第二次月考试题 文（无答案）新人教A 版一、选择题:（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题 目要求的）1．设全集U 是实数集R ，集合M ＝{x ｜2x ≥2x}，N ＝{x ｜2log (1)x －≤0}，则M∩N＝( )A ．{1，2}B ．{ 2 }C ．{1}D ．[1，2]2．已知复数133iz i -=+,z 是z 的共轭复数,则z z ⋅等于（ ）A.16B.4C.1D. 1166．按如下程序框图，若输出结果为170，则判断框内应补充的条件为（ ）A ．5i >B ．7i ≥C ．9i >D ．9i ≥7．已知直线：06=++ay x 和:023)2(=++-a y x a ，则∥的充要条件是=a （ ）A ．3B ．1C ．-1D ．3或-18．一个几何体的三视图如图所示，其中主视图中ABC ∆是边长为2的正三角形，俯视图为正六边形，那开始1=i 0=S iS S 2+=2+=i i ?否S输出结果是1l 2l1l2lXYO么该几何体的左视图的面积为（ ）A ．23B ．43C ．1D ．539．数列{}n a 的首项为3，{}n b 为等差数列且)(*1N n a a b n n n ∈-=+ .若则23-=b ，1210=b ，则=3a ( )A -3B 3C 8D -7 10．函数y ＝lg|x|x的图像大致是 ( )11．已知()y f x =为R 上的可导函数，当0x ≠时，()()'0f x f x x +>，则关于x 的函数()()1g x f x x =+ 的零点个数为 （ ）A.1B.2C.0D.0或 212．定义在R 上的函数)(x f 满足1)4(=f ，)('x f 为)(x f 的导函数，已知)('x f y =的图像如图所示，若两个正数a 、b 满足1)2(<+b a f ，则11++a b 的取值范围是 ( )A ．)31,51( B ．),5()31,(+∞⋃-∞ C ．)5,31(D ．)3,(-∞二．填空题（每小题5分，共20分）13．=+20lg 5lg 2114．设△ABC 的内角A 、B 、C 所对的边分别为c b a ,,，若c a A C B 53,sin 2sin sin ==+，则角B=15．过点（－1,1）与曲线32()21f x x x x =--+相切的直线有 条（以数字作答）.主视图俯视图左视图CAB16．已知|||lg |,0()2,0x x x f x x >⎧=⎨≤⎩，则函数22()3()1y f x f x =-+的零点的个数为_______个.三.解答题：(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17．（本小题满分10分）已知函数||)(a x x f -=。

高考文数预测密卷新课标II 卷本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分考试时间120分钟第Ⅰ卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

） 1.已知复数z 满足(1)i z i =-，其中i 为虚数单位，则复数z 所对应的点在（ ） A ．第一象限 B.第二象限 C.第三象限 D.第四象限2. 已知集合A={1，2}，B={x|ax ﹣1=0}，若A B B =I ，则实数a 的取值个数为（ ） A ．0 B.1 C.2 D.33. 已知等差数列{}n a 满足2810a a +=, 且1a ,2a ,4a 成等比数列，则2016a =( )A.2014B.2015C.2016D.2017 4.下列命题中正确的是（ ）A.命题“x R ∃∈使得210x x ++<”的否定是“x R ∀∈均有210x x ++<”.B.若p 为真命题，q 为假命题，则（¬p）∨q 为真命题.C.为了了解高考前高三学生每天的学习时间，现要用系统抽样的方法从某班50个学生中抽取一个容量为10的样本，已知50个学生的编号为1,2,3…50，若8号被选出，则18号也会被选出.D.已知m 、n 是两条不同直线，α、β是两个不同平面，α∩β=m，则“n α⊂，n⊥m”是“α⊥β”的充分条件.5. 设P 是△ABC 所在平面内的一点，且4AB AC AP +=u u u r u u u r u u u r,则△PBC 与△ABC 的面积之比是( )A.13 B.12 C.23 D.346.一个几何体的三视图如图所示，其中主（正）视图是边长为2的正三角形，俯视图是正方形，那么该几何体的侧面积是( )A ．434+ B.43 C ．8 D ．127. 已知不等式组表示的平面区域为D ，若直线2y x a =-+与区域D 有公共点，则a 的取值情况是（ ）A ．有最大值2，无最小值B ．有最小值2，无最大值C ．有最小值，最大值2D ．既无最小值，也无最大值8．已知2log (1),2()(1),2x x f x f x x +>⎧=⎨+≤⎩，执行如图所示的程序框图，若输入A的值为(1)f ，则输出的P 值为（ ） A ．2B ．3C ．4D ．59. 已知函数()2sin cos()3f x x x ωωπ=+（0ω>）的图像的相邻两条对称轴之间的距离等于2π，要得到函数3cos(2)32y x π=+-的图象，只需将函数()y f x =的图象（ ） A ．向右平移2π个单位 B ．向左平移2π个单位C ．向右平移4π个单位 D ．向左平移个单位10. 已知圆22:(3)(5)5C x y -+-=，过圆心C 的直线l 交圆C 于,A B 两点，交y 轴于点P . 若14PA AB =u u u r u u u r，则直线l 的方程为( )A. 270x y -+=B. 2130x y +-=或270x y -+= C ．2130x y +-= D. 270x y ++=11．已知()f x 为偶函数，且满足()(2)f x f x =-+，方程()0f x =在[0，1]内有且只有一个根12016，则方程()0f x =在区间[-2016，2016]内的根的个数为( ) A ．4032 B.4036 C ．2016 D.201812.已知双曲线C ：22221(0)1x y a a a-=>-的左右焦点分别为12,F F ，若存在k ，使直线(1)y k x =-与双曲线的右支交于P,Q 两点，且1PFQ ∆的周长为8，则双曲线的斜率为正的渐近线的倾斜角的取值范围是（ ） A. (,)32ππB. (,)62ππC. (0,)6πD. (0,)3π第Ⅱ卷（13-21为必做题，22-24为选做题）二、填空题（本大题共4个小题，每小题5分，共20分。

2020年河南省驻马店市高考数学模拟试卷(理科)(二)一、单项选择题（本大题共12小题，共60.0分）1.设z·i=2i+1，则z=()A. 2+iB. 2−iC. −2+iD. −2−i2.集合A={x∈Z||x|≤2}，B={−1,0，2}，C={−1,0，1，3}，则(∁A B)∪C=()A. {−1,0，1，3}B. {−1,0，1，2，3}C. {−2,−1,0，1，3}D. {−2,−1,0，1，2，3}3.已知向量a⃗⊥b⃗ ，|b⃗ |=1，则|a⃗|a⃗ |+b⃗ |=()A. √2B. √3C. √5D. √74.若双曲线x2m−y2=1的一条渐近线为x−2y=0，则实数m=()A. 2B. 4C. 6D. 85.已知某几何体的三视图是三个全等的等腰直角三角形，如图所示，则该几何体的体积为()A. 1B. 13C. 16D. 1126.已知随机变量X服从正态分布N(μ,σ2)，且P(μ−2σ<X≤μ+2σ)=0.9544，P(μ−σ<X≤μ+σ)=0.6826，若μ=4，σ=1，则P(5<X<6)=()A. 0.1358B. 0.1359C. 0.2716D. 0.27187.设函数f(x)=√2sin(ωx+φ+π4)(ω>0,|φ|<π2)的最小正周期为π，且f(−x)=f(x)，则()A. f(x)在(0,π2)单调递减 B. f(x)在(π4,3π4)单调递减C. f(x)在(0,π2)单调递增 D. f(x)在(π4,3π4)单调递增8.函数f(x)=2+ln|x|x2的图象大致为()A.B.C.D.9. 已知平面区域Ω：{(x +2y −1)(x −2y +3)≥0|x −1|≤3，则Ω的面积为( )A. 11B. 13C. 15D. 1710. 函数f(x)=x +3x 的零点所在的区间为( )A. (−2,−1)B. (−1,0)C. (0,1)D. (1,2)11. 已知抛物线C ：y 2=4x 的焦点为F ，直线l ：y =k(x −1)与抛物线C 交于A 、B 两点，若AF⃗⃗⃗⃗⃗ =3FB ⃗⃗⃗⃗⃗ ，则|AB|=( )A. 163B. 4C. 3D. 16912. “中国剩余定理”又称“孙子定理”，讲的是一个关于整除的问题，现有这样一个整除问题：已知x ∈[150,300]且x 是整数，则满足能被3除余1且被5除余3的所有x 的取值的和为( )．A. 2020B. 2305C. 4610D. 4675二、填空题（本大题共4小题，共20.0分）13. 二项式(2x 2√x )5的展开式中的第______项为常数项． 14. 函数f(x)=√x −1+2x 的值域为______ ．15. 已知等比数列{a n }中，a 1=8，a 4=1，记b n =a 1a 2a 3⋅⋅⋅a n ，当b n 达到最大值时，n 的值为________．16. 在平行四边形ABCD 中，∠ABD =90°，且AB =1，BD =√2，若将其沿BD 折起使平面ABD ⊥平面BCD ，则三棱锥A −BDC 的外接球的表面积为______． 三、解答题（本大题共7小题，共82.0分）17. 已知△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且bsin2A =asinB ．(1)求A ；(2)求cos(B+π6)+sin(C+π3)的最大值．18.如图，四棱锥P−ABCD中，PD⊥底面ABCD，AB//CD，∠BAD=π3，AB=2，CD=3，M为PC上一点，PM=2MC．(Ⅰ)证明：BM//平面PAD；(Ⅱ)若AD=2，PD=3，求二面角D−MB−C的正弦值．19.根据空气质量指数AQI(为整数)的不同，可将空气质量分级如下表：AQI(数值)0～5051～100101～150151～200201～300>300空气质量级别一级二级三级四级五级六级空气质量类别优良轻度污染中度污染重度污染严重污染空气质量类别颜色绿色黄色橙色红色紫色褐红色某市2014年11月1日−11月30日，对空气质量指数AQI进行监测，获得数据后得到如下条形图：(1)市教育局规定在空气质量类别达到中度污染及以上时学生不宜进行户外跑步活动，估计该城市本月(按30天计)学生可以进行户外跑步活动的概率；(2)在上述30个监测数据中任取2个，设ξ为空气质量类别颜色为绿色的天数，求ξ的分布列与数学期望．20.已知椭圆C：x2a2+y23=1(a>√3)的离心率为12，点P(4,0)，过右焦点F作与y轴不垂直的直线l交椭圆C于A，B两点．(Ⅰ)求椭圆C的方程；(Ⅱ)求证：以坐标原点O为圆心与PA相切的圆，必与直线PB相切．21.已知函数f(x)=(ax−1)e x，(a∈R)．(Ⅰ)讨论f(x)的单调性；(Ⅱ)当m>n>0时，证明：me n+n<ne m+m．22.在平面直角坐标系xOy中，曲线C的参数方程为{x=−1+2cosφy=2sinφ(其中φ为参数)，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l1的极坐标方程为ρ=√2sin (θ+π4)，设l1与C相交于A，B两点，AB的中点为M，过点M作l1的垂线l2交C于P，Q两点．(1)写出曲线C的普通方程与直线l1的直角坐标方程；(2)求|PQ||MP|⋅|MQ|的值．23.已知函数f(x)=|x|+|x+1|．(Ⅰ)解关于x的不等式f(x)≥2；(Ⅱ)若a，b，c∈R+，函数f(x)的最小值为m，若a+b+c=m，求证：ab+bc+ac≤1．3【答案与解析】1.答案：B解析：本题考查复数的四则运算，属于基础题.根据复数运算法则解答即可，解：因为z·i=2i+1，所以z=2i+1i=2−i故选B．2.答案：C解析：本题考查集合的综合运算，属于基础题．先化简A，再求∁A B，最后求并集即可．解：因为A={x∈Z||x|≤2}={−2,−1,0，1，2}，B={−1,0，2}，所以∁A B={−2,1}，又C={−1,0，1，3}，所以(∁A B)∪C={−2,−1,0,1,3}．故选C．3.答案：A解析：利用向量的模的运算法则，通过向量的数量积求解即可．本题考查向量的数量积的应用，是基本知识的考查．解：向量a⃗⊥b⃗ ，|b⃗ |=1，则|a⃗|a⃗ |+b⃗ |=√(a⃗|a⃗ |)2+2a⃗ ⋅b⃗|a⃗ |+b⃗ 2=√1+1=√2．故选：A．4.答案：B解析：本题考查双曲线的简单性质的应用，属于基础题．利用双曲线的渐近线方程，转化求解m即可．解：若双曲线x2m−y2=1的一条渐近线为x−2y=0，可得1√m =12，解得m=4，故选：B．5.答案：C解析：由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥，利用三视图的数据求解几何体的体积，可得答案．本题考查的知识点是由三视图，求体积，根据已知的三视图，判断几何体的形状是解答的关键．解：由题意可知几何体的直观图如图：是正方体的一部分，D−ABC，几何体的体积为：13×12×1×1×1=16．故选C．6.答案：B解析：解：∵随机变量X服从正态分布N(μ,σ2)，P(μ−2σ<X≤μ+2σ)=0.9544，P(μ−σ<X≤μ+σ)=0.6826，μ=4，σ=1，∴P(2<X≤6)=0.9544，P(3<X≤5)=0.6826，∴P(2<X≤6)−P(3<X≤5)=0.9544−0.6826=0.2718，∴P(5<X<6)=12×0.2718=0.1359．故选：B．根据变量符合正态分布，和所给的μ和σ的值，根据3σ原则，得到P(2<X≤6)=0.9544，P(3<X≤5)=0.6826，两个式子相减，根据对称性得到结果．本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量μ和σ的应用，考查曲线的对称性，本题是一个基础题．7.答案：A解析：本题主要考查正弦函数的周期性，正弦函数、余弦函数的奇偶性，属于基础题．由条件利用正弦函数的周期性求得ω的值，再根据正弦函数、余弦函数的奇偶性，求得φ的值，可得函数的解析式，从而得到它的单调性．解：函数f(x)=√2sin(ωx+φ+π4)(ω>0,|φ|<π2)的最小正周期为π，则2πω=π，求得ω=2，函数f(x)=√2sin(2x+φ+π4).再根据f(−x)=f(x)，可得f(x)为偶函数，故φ+π4=kπ+π2，k∈Z，即φ=kπ+π4，k∈Z，|φ|<π2，故取φ=π4，函数f(x)=√2sin(2x+π4+π4)=√2cos2x．故f(x)在(0,π2)单调递减，故选：A．8.答案：B解析：分析函数的奇偶性和零点，利用排除法可得答案．本题考查的知识点是函数的图象，函数的奇偶性和函数的零点，难度中档．解：函数f(x)=2+ln|x|x2满足f(−x)=f(x)，即函数为偶函数，图象关于y轴对称，故排除D；又f(1)=2≠0，故排除A、C，故选：B ．9.答案：B解析：解：作出不等式组对应的平面区域如图：由{x +2y −1=0x −2y +3=0，解得{x =−1y =1，即C(−1,1)， 当{x =−2x +2y −1=0，解得{x =−2y =32，即A(−2,32)， 由{x =−2x −2y +3=0，解得{x =−2y =12，即B(−2,12)， 由{x =4x +2y −1=0，解得{x =4y =−32，即E(4,−32)， 由{x =4x −2y +3=0，解得{x =4y =72，即D(4,72)， 则△ABC 的面积为12×(32−12)×[−1−(−2)]=12， 则△CDE 的面积为12×[72−(−32)]×[4−(−1)]=252，则阴影部分的面积之和为12+252=13，故选B ．作出不等式组对应的平面区域，根据对应的图象即可求出对应的面积．本题主要考查阴影部分的面积的计算，根据条件作出对应的平面区域是解决本题的关键．10.答案：B解析：解：由函数的解析式可得f(−1)=−1+13=−23<0，f(0)=0+1=1>0， ∴f(−1)f(0)<0，根据函数零点的判定定理可得函数f(x)=x +3x 的零点所在的区间为(−1,0)， 故选：B ．由函数的解析式可得f(−1)f(0)<0，根据函数零点的判定定理可得函数f(x)=x +3x 的零点所在的区间．本题主要考查求函数的值，函数零点的判定定理，属于基础题．11.答案：A解析：本题考查了抛物线的标准方程、简单几何性质和直线与圆锥曲线的位置关系等知识，属于中档题． 根据题意，可得抛物线焦点为F(1,0)，由直线l 方程为y =k(x −1)，与抛物线方程联解消去y ，得k 2x 2−(2k 2+4)x +k 2=0.再设A(x 1,y 1)，B(x 2,y 2)，由根与系数的关系和|AF|=3|BF|，建立关于x 1、x 2和k 的方程组，解之可得k 2值，再根据|AB|=x 1+x 2+p 即可求出． 解：∵抛物线C 方程为y 2=4x ，可得它的焦点为F(1,0)，由{y =k(x −1)y 2=4x 消去y 可得k 2x 2−(2k 2+4)x +k 2=0． 设A(x 1,y 1)，B(x 2,y 2)，可得x 1+x 2=2+4k 2，x 1x 2=1，(∗) ∵AF ⃗⃗⃗⃗⃗ =3FB ⃗⃗⃗⃗⃗ ，∴(1−x 1,−y 1)=3(x 2−1,y 2)∴1−x 1=3(x 2−1)， ∴x 1=−3x 2+4，代入(∗)得−2x 2+4=2+4k 2，且(−3x 2+4)x 2=1， 消去x 2得k 2=3，∴|AB|=x 1+x 2+p =2+43+2=163，故选：A ．12.答案：B解析：【试题解析】本题考查等差数列的通项公式与前n项和，属于中档题．满足能被3除余1且被5除余3正整数构成首项为13，公差3×5=15的等差数列，求其通项公式，由x∈[150,300]且x是整数求得n值，再由等差数列的前n项和求解．解：满足能被3除余1且被5除余3正整数构成首项为13，公差3×5=15的等差数列，记数列{a n}.则a n=13+15(n−1)=15n−2，∵x∈[150,300]，∴150≤15n−2≤300，解得15215≤n≤30215．故n从11开始，到20结束，∴a11=163，a20=298′∴该数列各项之和为10(a11+a20)2=10(163+298)2=2305，故选：B．13.答案：5解析：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．先求出二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得展开式中的常数项．解：二项式(2x2x )5的展开式的通项公式为Tr+1=C5r⋅(−1)r⋅25−r⋅x10−5r2，令10−5r2=0，求得r=4，故展开式中的第5项为常数项，故答案为5．14.答案：[2,+∞)解析：解：由x −1≥0，得x ≥1，又y =√x −1为[1,+∞)上的增函数，y =2x 在[1,+∞)上也是增函数， ∴f(x)=√x −1+2x 是[1,+∞)上的增函数，则f(x)min =2，∴函数f(x)=√x −1+2x 的值域为[2,+∞)． 故答案为：[2,+∞)．由根式内部的代数式大于等于0求出函数的定义域，再由函数的单调性求得答案． 本题考查函数的值域，训练了利用函数的单调性求函数的值域，是基础题．15.答案：3或4解析：本题考查满足的等比数列的项数的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．首先根据已知条件求出a n ，然后根据b n =a 1a 2a 3⋅⋅⋅a n 求出b n ，再根据复合函数的单调性分析最值． 解：∵等比数列{a n }的首项a 1=8，a 4=1，设公比为q ，则q 3=a 4a 1=18，q =12，∴ a n =8×(12)n−1=24−n ．∵ b n =a 1a 2a 3…a n =(12)(n−7)n 2，∴当(n−7)n 2取最小时，b n 取最大，此时n 的值为3或4，∴ b n 达到最大值时，n 的值为3或4． 故答案为3或4．16.答案：4π解析：解：由已知：平面ABD ⊥平面BCD ， CD//AB ，∠ABD =90°得：CD ⊥BD ， 故CD ⊥平面ABD ，由AB =1，BD =√2，得：三棱锥A −BDC 是一个以CD =1为高，以平面ABD 为底面的棱锥，故球心到底面的距离d =12CD =12，底面外接圆半径r =12AD =√32，故三棱锥A−BDC的外接球的表面积S=4π(d2+r2)=4π，故答案为：4π由已知可得三棱锥A−BDC是一个以CD=1为高，以平面ABD为底面的棱锥，求出球心到底面的距离及底面外接圆半径，代入外接球的表面积公式S=4π(d2+r2)，可得答案．本题考查的知识点是球的体积与表面积，根据已知求出球心到底面的距离及底面外接圆半径，是解答的关键．17.答案：解：(1)∵bsin2A=asinB，∴2bsinAcosA=asinB，∴由正弦定理，得，∵，∴，又∵三角形内角A，∴A=；(2)由(1)A=，又A+B+C=，得C=，B，cos(B+)+sin(C+)∵B，∴，∴当，即时，取最大值1，∴cos(B+)+sin(C+)的最大值为1．解析：本题考查正余弦定理在解三角形中的应用，属中档题． (1)∵bsin2A =asinB ，∴2bsinAcosA =asinB ，利用正弦定理，得，求得A ．(2)化简cos(B +)+sin(C +)求得最值．18.答案：证明：(Ⅰ)在DC 上取点E ，使DE =2，则DE//AB ，DE =AB ， 则四边形ABED 是平行四边形， 则EB//AD ，∵PMMC =DEEC =2，∴PD//ME ， 则平面PAD//平面MBE ，∵BM ⊂平面MBE ，BM ⊄平面PAD ， ∴BM//平面PAD(Ⅱ)△ABD 是正三角形，建立以D 为坐标原点的空间直角坐标系如图：则B(√3,1，0)，P(0,0，3)，C(0,3，0)，M(0,2，1)， DB ⃗⃗⃗⃗⃗⃗ =(√3,1，0)，DM ⃗⃗⃗⃗⃗⃗⃗ =(0,2，1)， 设平面DBM 的法向量为m⃗⃗⃗ =(x,y ，z)， 则由m ⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =√3x +y =0，m ⃗⃗⃗ ⋅DM⃗⃗⃗⃗⃗⃗⃗ =2y +z =0，得{y =−√3x z =−2y ， 令x =1，则y =−√3，z =2√3则m ⃗⃗⃗ =(1,−√3,2√3)，设平面MBC 的法向量为n ⃗ =(x,y ，z)，BC ⃗⃗⃗⃗⃗ =(−√3,2，0)，MC ⃗⃗⃗⃗⃗⃗ =(0,1，−1)， 则n ⃗ ⋅BC ⃗⃗⃗⃗⃗ =−√3x +2y =0，n ⃗ ⋅MC ⃗⃗⃗⃗⃗⃗ =y −z =0，令x =2，则y =√3，z =√3， 即n ⃗ =(2,√3,√3)， 则cos <m ⃗⃗⃗ ，n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗|m ⃗⃗⃗ |⋅|n ⃗⃗ |=4×√10=4√10=√108， 则二面角D −MB −C 的正弦值sinα=√1−(√108)2=3√68．解析：(Ⅰ)根据线面平行的判定定理即可证明BM//平面PAD ；(Ⅱ)若AD =2，PD =3，建立空间直角坐标系求出平面的法向量，利用向量法即可求二面角D −MB −C 的正弦值本题主要考查空间直线和平面位置关系的判断以及二面角的求解，建立坐标系，求出平面的法向量，利用向量法是解二面角的常用方法．19.答案：解：(1)由条形统计图知：空气质量类别达到中度污染及以上的天数为： 6+4+2=12天，∴该城市本月学生可以进行户外跑步活动的概率P =1−1230=35． (2)由已知得ξ的可能值为0，1，2， P(ξ=0)=C 262C 302=6587，P(ξ=1)=C 41C 261C 302=104435，P(ξ=2)=C 42C 202=2145，∴ξ的分布列为：∴Eξ=0×6587+1×104435+2×2145=116435．解析：(1)由条形统计图知空气质量类别达到中度污染及以上的天数为12天，由此利用对立事件概率计算公式能求出该城市本月学生可以进行户外跑步活动的概率．(2)由已知得ξ的可能值为0，1，2，分别求出相应的概率，由此能求出ξ的分布列与数学期望． 本题考查概率的求法，是中档题，解题时要认真审题，注意排列组合知识的合理运用．20.答案：解：(Ⅰ)由椭圆离心率为12得：√a 2−3a =12，解得a 2=4， 所以椭圆C 的方程为x 24+y 23=1;证明：(Ⅱ)由c =1，则焦点F(1,0)，当直线l 的斜率不存在时，直线l 的方程x =1， A ，B 两点关于x 轴对称，点P(4,0)在x 轴上， ∴直线PA 与直线PB 关于x 轴对称，∴点O 到直线PA 的距离与到PB 的距离相等，∴以坐标原点O 为圆心与PA 相切的圆，必与直线PB 相切，当直线l 的斜率存在时，设直线l ：y =k(x −1)，A(x 1,y 1)，B(x 2,y 2)， 由{y =k(x −1)3x 2+4y 2−12=0，整理得：(3+4k 2)x 2−8k 2x +4k 2−12=0， Δ>0，由韦达定理可知：x 1+x 2=8k 23+4k 2，x 1x 2=4k 2−123+4k 2，由k PA =y 1x1−4=k(x 1−1)x 1−4，k PB =y 2x2−4=k(x 2−1)x 2−4，则k PA +k PB =k(x 1−1)x 1−4+k(x 2−1)x 2−4=k[2x 1x 2−5(x 1+x 2)+8](x 1−4)(x 2−4)=k(8k 2−243+4k 2−40k 23+4k 2+8)(x 1−4)(x 2−4)=0，∴∠APO =∠BPO ，则点O 到直线PA 和直线PB 的距离相等， ∴以坐标原点O 为圆心与PA 相切的圆，必与直线PB 相切．解析：本题考查椭圆的标准方程及简单几何性质，直线与椭圆的位置关系，考查韦达定理，直线的斜率公式，属于中档题．(Ⅰ)由椭圆的离心率和椭圆方程，求得a 的值，即可求得；(Ⅱ)对直线斜率是否存在分类讨论，当直线斜率存在时，设直线方程，利用韦达定理及直线的斜率公式可知k PA +k PB =0，即可证明以坐标原点O 为圆心与PA 相切的圆，必与直线PB 相切．21.答案：解：(Ⅰ)f(x)的定义域为R ，且f′(x)=(ax +a −1)e x ．当a =0时，f′(x)=−e x <0，此时f(x)的单调递减区间为(−∞,+∞)； 当a >0时，由f′(x)>0，得x >−a−1a，由f′(x)<0，得x <−a−1a．此时f(x)的单调减区间为(−∞,−a−1a)，单调增区间为(−a−1a,+∞)；当a <0时，由f′(x)>0，得x <−a−1a，由f′(x)<0，得x >−a−1a．此时f(x)的单调减区间为(−a−1a,+∞)，单调增区间为(−∞,−a−1a).(Ⅱ)证明：要证me n +n <ne m +m ，即证me n −m <ne m −n ， 也就是证m(e n −1)<n(e m −1)． 也就是证e n −1n<e m −1m，令g(x)=e x −1x，x >0，g′(x)=xe x −e x +1x 2，再令ℎ(x)=xe x −e x +1，ℎ′(x)=e x +xe x −e x =xe x >0， 可得ℎ(x)在x >0递增，即有ℎ(x)>ℎ(0)=0， 则g′(x)>0，g(x)在(0,+∞)递增， 由m >n >0，可得e n −1n<e m −1m，故原不等式成立．解析：本题考查函数的单调性、导数及其应用、不等式的证明等基础知识，考查推理论证能力、运算求解能力及抽象概括能力，考查函数与方程思想、分类与整合思想，属难题．(Ⅰ)求出f(x)的定义域，以及导数，讨论a =0，a >0，a <0，判断导数符号，解不等式即可得到所求单调区间；(Ⅱ)运用分析法证明．要证me n +n <ne m +m ，即证me n −m <ne m −n ，也就是证e n −1n<e m −1m，令g(x)=e x −1x，x >0，求出导数，再令ℎ(x)=xe x −e x +1，求出导数，判断单调性，即可得证．22.答案：解：(1)由曲线C 的参数方程{x =−1+2cosφy =2sinφ，消去参数φ，得曲线C 的普通方程为(x +1)2+y 2=4．由曲线l 1的极坐标方程ρ=√2sin (θ+π4)，得ρsin θ+ρcos θ=1，将x =ρcos θ，y =ρsin θ代入，得l 1的直角坐标方程为x +y −1=0；(2)由l 1⊥l 2，得直线l 2的斜率k l 2=−1k l 1=1，所以l 2的倾斜角为π4，又l 2过圆心(−1,0)，所以l 2的方程为y =x +1，与x +y −1=0联立，得AB 的中点M(0,1)， 故l 2的参数方程为{x =tcos π4y =1+tsin π4,(t 为参数)，即{x =√22t y =1+√22t ,(t 为参数)，代入(x +1)2+y 2=4中，化简、整理得t 2+2√2t −2=0， 设P ，Q 对应的参数分别为t 1，t 2，则由韦达定理得t 1·t 2=−2， 又线段PQ 为圆的直径，所以|PQ|=4， 所以|PQ||MP|⋅|MQ|=4|−2|=2．解析：本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，一元二次方程根和系数关系式的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题型． (1)直接利用转换关系，把参数方程极坐标方程和直角坐标方程之间进行转换． (2)利用一元二次方程根和系数关系式的应用求出结果．23.答案：解：(Ⅰ)f(x)≥2即|x|+|x +1|≥2，可得{x ≥0x +x +1≥2或{−1<x <0−x +x +1≥2或{x <−1−x −x −1≥2，解得x ≥12或x ∈⌀或x ≤−32，则原不等式的解集为{x|x ≥12或x ≤−32}；(Ⅱ)证明：f(x)=|x|+|x +1|≥|x −x −1|=1， 当且仅当x(x +1)≤0，即−1≤x ≤0时，上式取得等号， 可得函数f(x)的最小值为1， 则a +b +c =1，且a ，b ，c ∈R +，由(a +b +c)2=a 2+b 2+c 2+2ab +2bc +2ca ≥ab +bc +ca +2ab +2bc +2ca =3(ab +bc +ca)，可得3(ab +bc +ca)≤1，当且仅当a =b =c =13取得等号， 即ab +bc +ac ≤13．解析：(Ⅰ)由绝对值的意义去绝对值，解不等式，求并集可得所求解集；(Ⅱ)运用绝对值不等式的性质可得f(x)的最小值m ，再由三个数的完全平方公式和基本不等式，结合不等式的性质即可得证．本题考查绝对值不等式的解法和绝对值不等式的性质的运用，考查不等式的证明，注意运用均值不等式和不等式的性质，考查化简运算能力、推理能力，属于中档题．。

2020年河南省六市高三第二次联合调研检测数学（理科）本试卷分第Ⅰ卷（选择题）和第II 卷（非选择题）两部分，满分150分，考试用时120分钟．其中第I1卷22题，23题为选考题，其它题为必考题。

考试结束后，将答题卡交回.注意事项:1．答题前，考生必须将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内.2．选择题必须用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚.3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．4．保持卡面清洁，不要折叠、不要弄破、不准使用涂改液、刮纸刀．第I 卷 选择题（共60分）一、选择题：本题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设全集U=R ，集合{}0)1)(4(≥+-=x x x A ，则A C U = A ．（1-，4] B ．[1-，4） C ．（1-，4） D ．[1-，4]2．复数z 1在复平面内对应的点为（2，3）．i z +-=22（i 为虚数单位），则复数21z z 的虚部为 A ．58 B ．58- C ．i 58 D ．i 58- 3．在△ABC 中b AC c AB ==，，若点D 满足DC BD 21=，则AD = A ．c b 3231+ B ．c b 3132+ C ．c b 3134- D ．c b 2121+ 4．南北朝时代的伟大科学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”．其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等，如图，夹在两个平行平面之间的两个几何体的体积分别为V 1，V 2，被平行于这两个平面的任意平面截得的两个截面面积分别为S 1、S 2，则“S 1、S 2不总相等”是“V 1，V 2不相等”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5．青班锁起源于中国古代建筑中首创的榫卯结构，相传由春秋时代鲁国工匠鲁班所作，下图1是经典的六柱鲁班锁及六个构件的图片，下图2是其中一个构件的三视图（图中单位mm ），则此构件的体积为A ．34000 mm 3B ．33000 mm 3C ．32000 mm 3D ．30000 mm 36．在正项等比数列{}n a 中，4651242292900a a a a a a =-=+，，则2020a 的个位数字是A ．1B ．7C ．3D ．97．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰试验．受其启发，我们也可以通过设计下面的试验来估计π的值，试验步骤如下：①先请高三年级1000名同学每人在小卡片上随机写下一个实数对（x ，y ）（0＜x ＜1，0＜y ＜1）；②若卡片上的x ，y 能与1构成锐角三角形，则将此卡片上交；③统计上交的卡片数，记为m ；④根据统计数m 估计π的值．假如本次试验的统计结果是m=218，那么可以估计π的值约为A ．124389B ．124391C ．125389D ．125391 8．已知双曲线12222=-by a x （a ＞0，b ＞0）的一条渐近线过点（3-，2），且双曲线的一个焦点在抛物线x y 742=的准线上，则双曲线的方程为A ．1282122=-y xB ．1212822=-y x C ．14322=-y x D ．13422=-y x 9．已知三棱锥A —BCD 的四个顶点都在球O 的表面上，且AB ⊥BC ，AB ⊥CD ，∠BCD=32π，若BC=CD=2，AB=32，则球O 的表面积为A ．20πB ．24πC ．28πD ．32π10．将函数)0)(3sin(4>-=ωπωx y 的图像分别向左、向右各平移6π个单位长度后，所得的两个图象对称轴重合，则的最小值为 A ．3 B ．2 C ．4 D ．611．已知函数y=f （x ）满足f （x+1）=f （x-1），当x ∈[-1，1]时f （x ）=x 2，则方程x x f lg )(=实根共有A ．10个B ．9个C ．18个D ．20个12．已知椭圆C 1：12222=+b y a x （a ＞b ＞0）与圆C 2：43222b y x =+，若在椭圆C 1上不存在点P ，使得由点P 所作的圆C 2的两条切线互相垂直，则椭圆C 1的离心率的取值范围是A ．)33,0(B ．)22,0(C ．)122[，D ．)133[， 第Ⅱ卷 非选择题（共90分）二、填空题：本题共4个小题，每小题5分，共20分．13．已知函数3()1f x ax x =++的图像在点（1，(1)f ）处的切线过点（2，11），则a= ． 14．若实数x ，y 满足约束条件工1330y x x y x y ≤⎧⎪+≥⎨⎪-+≥⎩，则z=5x +y 的最小值为 ．15．设函数22()4x x f x e e x -=--，则不等式2()(56)f x f x +--＜0的解集是 ．（用区间表示）16．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ，且BC，则c b b c +的最大值是 ． 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知数列{a n }满足：212231n a a a n n n ++⋅⋅⋅+=++（n ∈N +）． （Ⅰ）求{a n }的通项公式； （Ⅱ）设1n n b a =，若数列{b n }的前n 项和为n S ，求满足1940n S ＞的最小正整数n ．18．（本小题满分12分）在直角梯形ABCD中（如图1），AB∥DC，∠BAD =90°，AB=5，AD =2，CD=3，点E在CD上，且DE=2，将△ADE沿AE折起，使得平面ADE⊥平面ABCE（如图2），G为AE中点．（Ⅰ）求四棱锥D—ABCE的体积；（Ⅱ）在线段BD上是否存在点P，使得CP∥平面ADE？若存在，求BPBD的值；若不存在，请说明理由．19．（本小题满分12分）某快递公司招聘快递骑手，该公司提供了两种日工资方案：方案（1）规定每日底新50元，快递骑手每完成一单业务提成3元：方案（2）规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元．该快递公司记录了每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为[25，35），[35，45），[45，55），[55，65），[65，75），[75，85），[85，95] 七组，整理得到如图所示的频率分布直方图．（Ⅰ）随机选取一天，估计这一天该快递公司的骑手的人均日快递业务量不少于65单的概率；（Ⅱ）若骑手甲、乙、丙选择了日工资方案（1），丁、戊选择了日工资方案（2）．现从上述5名骑手中随机选取2人，求至少有1名骑手选择方案（2）的概率；（Ⅲ）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由（同组中的每个数据用该组区间的中点值代替）20．（本小题满分12分）设函数2()ln f x x ax x =-+．（Ⅰ）若当x=1时()f x 取得极值，求a 的值及()f x 的单调区间；（Ⅱ）若()f x 存在两个极值点1x ，2x ，证明：2121()()42f x f x a x x a ---＞．21．（本小题满分12分）已知圆F ：4)2(22=+-y x ，动点Q )(y x ，（x≥0），线段QF 与圆F 相交于点P ，线段PQ 的长度与点Q 到y 轴的距离相等．（Ⅰ）求动点Q 的轨迹W 的方程；（Ⅱ）过点A （2，4）作两条互相垂直的直线与W 的交点分别是M 和N （M 在N 的上方，A ，M ，N 为不同的三点），求向量NM 在y 轴正方向上的投影的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分．22．（本小题满分10分）在直角坐标系xOy 中，曲线C 1的参数方程为⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 213231（t 为参数），以原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为θρ22sin 213+=． （Ⅰ）求曲线C 1的极坐标方程与曲线C 2的直角坐标方程；（Ⅱ）设A ．B 为曲线C 2上位于第一，二象限的两个动点，且∠AOB=2π，射线OA ，OB 交曲线C 1分别于点D ，C ．求△AOB 面积的最小值，并求此时四边形ABCD 的面积。

驻马店市高三年级线上模拟测试(二)生物第I卷(选择题共126分)一、选择题：本题共13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.下列关于高等动物体内的一些有机物的叙述，正确的是A.脱氧核糖核酸与核糖核酸的彻底水解产物完全不同B.凋亡细胞特有的凋亡基因实质上是有遗传效应的DNA片段C.由垂体释放出的抗利尿激素，可通过血液运输到肾小管和集合管D.肝糖原的彻底水解产物转运至组织细胞的线粒体中氧化分解供能2.树突状细胞是功能强大的免疫细胞，能摄取、处理及传递抗原，并启动T细胞增殖分化(如图)。

下列有关叙述错误的是A.据图推测树突状细胞内溶酶体酶的活性较低B.树突状细胞具有一定的防卫、监控和清除功能C.树突状细胞受损对体液免疫和细胞免疫都有影响D.树突状细胞和T细胞都起源于骨髓中的造血干细胞3.兴奋在反射弧上的单向传递与神经递质有关。

下列有关神经递质的叙述，正确的是A.突触前神经元能释放神经递质，突触后神经元不能释放神经递质B.神经递质以胞吐方式从突触前膜释放时所需的ATP都来自线粒体C.神经递质与突触后膜上的受体结合后，突触后膜膜外电位一定变为负D.神经递质的受体并不都分布在突触后神经元的细胞膜上4.某地推行“退耕还草”工程，多年后农田生态系统演替为草原生态系统，下图表示生活在该地草原上的部分生物间的食物链。

下列相关叙述正确的是A.该地生物群落中植物的优势种一定是一年生草本植物B.“退耕还草”属于次生演替，可提高物种丰富度C.图中草与虫之间的能量传递效率为10%～20%D.图中蛇获取能量效率最高的食物链是草→虫→蛙→蛇5.某基因发生了一个碱基对的替换。

下列有关该突变的叙述，正确的是A.该基因的氢键总数一定发生改变B.该基因表达的蛋白质一定发生改变C.若氢键总数减少了1个，则可能是A/T替换成了G/CD.若氢键总数减少了1个，则可能导致翻译过程提前终止6.油菜的株高由等位基因G和g决定，B基因是另一种植物的高秆基因，B基因与G基因在油菜的株高上有相同的效应，且数量越多植株越高。