机械原理 王德伦 课后答案[1-24-12章].khda

习题解答第一章绪论1-1 答：1 ）机构是实现传递机械运动和动力的构件组合体。

如齿轮机构、连杆机构、凸轮机构、螺旋机构等。

2 ）机器是在组成它的实物间进行确定的相对运动时，完成能量转换或做功的多件实物的组合体。

如电动机、内燃机、起重机、汽车等。

3 ）机械是机器和机构的总称。

4 ）a. 同一台机器可由一个或多个机构组成。

b. 同一个机构可以派生出多种性能、用途、外型完全不同的机器。

c. 机构可以独立存在并加以应用。

1-2 答：机构和机器，二者都是人为的实物组合体，各实物之间都具有确定的相对运动。

但后者可以实现能量的转换而前者不具备此作用。

1-3 答：1 ）机构的分析：包括结构分析、运动分析、动力学分析。

2 ）机构的综合：包括常用机构设计、传动系统设计。

1-4 略习题解答第二章平面机构的机构分析2－1 ～2－5 （答案略）2-6(a) 自由度F＝1 (b) 自由度F＝1(c) 自由度F＝12-7题2 －7 图F ＝3 × 7 －2 × 9 －2 ＝12 -8a) n ＝7 ＝10 ＝0 F ＝3×7－2×10 ＝1b) B 局部自由度n ＝3 ＝3 ＝2 F＝3×3 －2×3－2＝1c) B 、D 局部自由度n ＝3 ＝3 ＝2 F＝3×3 －2×3－2 ＝1d) D( 或C) 处为虚约束n ＝3 ＝4 F＝3×3 －2×4＝1e) n ＝5 ＝7 F＝3×5－2×7＝1f) A 、B 、C 、E 复合铰链n ＝7 ＝10 F ＝3×7－2×10 ＝1g) A 处为复合铰链n ＝10 ＝14 F ＝3×10 －2×14＝2h) B 局部自由度n ＝8 ＝11 ＝1 F ＝3×8－2×11－1 ＝1i) B 、J 虚约束C 处局部自由度n ＝6 ＝8 ＝1 F ＝3×6 －2×8－1＝1j) BB' 处虚约束A 、C 、D 复合铰链n ＝7 ＝10 F ＝3×7－2×10＝1 k) C 、D 处复合铰链n＝5 ＝6 ＝2F ＝3×5－2×6－2 ＝1l) n ＝8 ＝11 F ＝3×8－2×11 ＝2m) B 局部自由度I 虚约束4 杆和DG 虚约束n ＝6 ＝8 ＝1 F ＝3×6－2×8－1 ＝12-9a) n ＝3 ＝4 ＝1 F ＝3 × 3 －2 × 8 －1 ＝0 不能动。

机械原理课后习题答案1. 两个质量分别为m1和m2的物体，它们分别靠在光滑水平面上的两个弹簧上，两个弹簧的弹性系数分别为k1和k2。

求当两个物体分别受到的外力分别为F1和F2时，两个物体的加速度分别是多少？答，根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。

根据这个公式，可以得出两个物体的加速度分别为a1=F1/m1，a2=F2/m2。

2. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，物体的加速度是多少？答，同样根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。

根据这个公式，可以得出物体的加速度为a=F/m。

3. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，弹簧的位移是多少？答，根据胡克定律，弹簧的位移与受到的外力成正比，即F=kx，其中x为弹簧的位移。

解出x=F/k，即弹簧的位移与外力成反比。

4. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，弹簧的振动周期是多少？答，根据弹簧的振动周期公式T=2π√(m/k)，可以得出弹簧的振动周期与物体的质量和弹簧的弹性系数有关，与受到的外力无关。

5. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，弹簧的振幅是多少？答，根据弹簧振动的公式x=Acos(ωt+φ)，可以得出弹簧的振幅与受到的外力无关，只与弹簧的弹性系数和物体的质量有关。

求当物体受到外力F时，弹簧的振动频率是多少？答，根据弹簧振动的公式f=1/2π√(k/m)，可以得出弹簧的振动频率与受到的外力无关，只与弹簧的弹性系数和物体的质量有关。

7. 一个半径为r的圆盘，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当圆盘受到外力F时，圆盘的加速度是多少？答，根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。

第四章课后习题4—12图示为一曲柄滑块机构的三个位置，F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆，试决定在此三个位置时作用在连杆AB上的作用力的真实方向（构件重量及惯性力略去不计）。

解：上图中构件2受压力。

因在转动副A处2、1之间的夹角∠OAB在逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故FR12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA在逐渐增大，相对角速度ω23也沿顺时针方向，故FR32应切于摩擦圆的上方。

R32解：上图构件2依然受压力。

因在转动副A处2、1之间的夹角∠OAB逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故F R12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿逆时针方向，F R32应切于摩擦圆的下方。

解：上图构件2受拉力。

因在转动副A处2、1之间的夹角∠OAB在逐渐增大，故相对角速度ω21沿顺时针方向，又因2受拉力，故FR12应切于摩擦圆的上方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿顺时针方向，FR32应切于摩擦圆的下方。

4-13 图示为一摆动推杆盘形凸轮机构，凸轮1沿逆时针方向回转，F为作用在推杆2上的外载荷，试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位（不考虑构件的重量及惯性力，解：经受力分析，FR12的方向如上图所示。

在FR12的作用下，2相对于3顺时针转动，故FR32应切于摩擦圆的左侧。

补充题1 如图所示，楔块机构中，已知γ＝β＝60°，Q ＝1000N 格接触面摩擦系数f ＝0.15，如Q 为有效阻力，试求所需的驱动力F 。

解:对机构进行受力分析,并作出力三角形如图。

对楔块1，R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=））o o ① 对楔块2，同理有R12R320Q F F ++=sin(90sin(602ϕϕ+-=））o o ②sin(602sin(602F Q ϕϕ+=⋅-））o o且有2112R R F F = ，8.53arctgf ϕ＝＝o ③联立以上三式，求解得F ＝1430.65N2 如图示斜面机构，已知：f （滑块1、2与导槽3相互之间摩擦系数）、λ（滑块1的倾斜角）、Q （工作阻力，沿水平方向），设不计两滑块质量，试确定该机构等速运动时所需的铅重方向的驱动力F 。

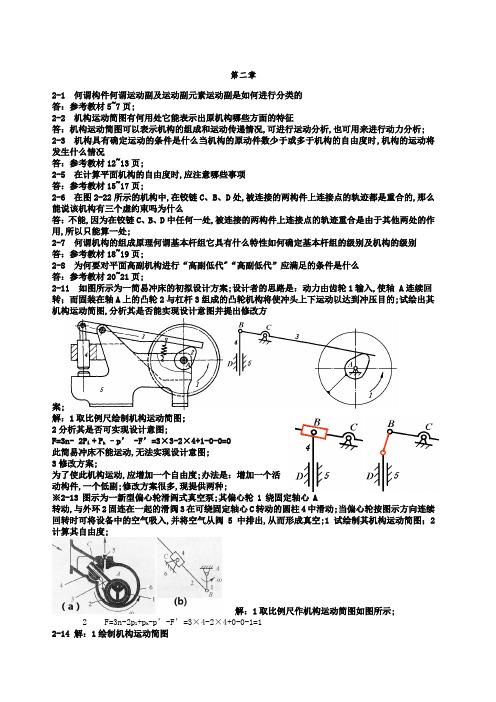
第二章2-1 何谓构件何谓运动副及运动副元素运动副是如何进行分类的答：参考教材5~7页;2-2 机构运动简图有何用处它能表示出原机构哪些方面的特征答：机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析;2-3 机构具有确定运动的条件是什么当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况答：参考教材12~13页;2-5 在计算平面机构的自由度时,应注意哪些事项答：参考教材15~17页;2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗为什么答：不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处;2-7 何谓机构的组成原理何谓基本杆组它具有什么特性如何确定基本杆组的级别及机构的级别答：参考教材18~19页;2-8 为何要对平面高副机构进行“高副低代"“高副低代”应满足的条件是什么答：参考教材20~21页;2-11 如图所示为一简易冲床的初拟设计方案;设计者的思路是：动力由齿轮1输入,使轴 A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的;试绘出其机构运动简图,分析其是否能实现设计意图并提出修改方案;解：1取比例尺绘制机构运动简图;2分析其是否可实现设计意图;F=3n- 2P l +P h –p’ -F’=3×3-2×4+1-0-0=0此简易冲床不能运动,无法实现设计意图;3修改方案;为了使此机构运动,应增加一个自由度;办法是：增加一个活动构件,一个低副;修改方案很多,现提供两种;※2-13图示为一新型偏心轮滑阎式真空泵;其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动;当偏心轮按图示方向连续回转时可将设备中的空气吸入,并将空气从阀5中排出,从而形成真空;1试绘制其机构运动简图；2计算其自由度;解：1取比例尺作机构运动简图如图所示;2 F=3n-2p1+p h-p’-F’=3×4-2×4+0-0-1=12-14 解：1绘制机构运动简图1）绘制机构运动简图F=3n-2P l +P h –p’-F’=3×5-2×7+0-0-0=12）弯曲90o 时的机构运动简图※2-15试绘制所示仿人手型机械手的食指机构的机构运动简图以手掌8作为相对固定的机架,井计算自由度;解：1取比倒尺肌作机构运动简图；2计算自由度1⨯=-F210⨯73=2-17 计算如图所示各机构的自由度;aF=3n- 2P l +P h–p’-F’=3×4-2×5+1 -0-0=1A处为复合铰链bF=3n-2P l +P h–p’-F’=3×7-2×8+2-0-2=12、4处存在局部自由度cp’= 2P l ’+P h ’-3n’=2×10+0-3×6=2,F=3n-2P l +P h–p’-F’=3×11-2×17+0-2-0=1C、F、K 处存在复合铰链,重复部分引入虚约束※2-21图示为一收放式折叠支架机构;该支架中的件1和5分别用木螺钉连接于固定台板1’和括动台板5’上．两者在D处铰接,使活动台板能相对于固定台极转动;又通过件1,2,3,4组成的铰链四杆机构及连杆3上E点处的销子与件5上的连杆曲线槽组成的销槽连接使活动台板实现收放动作;在图示位置时,虽在活动台板上放有较重的重物．活动台板也不会自动收起,必须沿箭头方向推动件2,使铰链B,D重合时．活动台板才可收起如图中双点划线所示;现已知机构尺寸l AB=l AD=90 mm；l BC=l CD=25 mm,其余尺寸见图;试绘制该机构的运动简图,并计算其自由度;解：F=3n-2p1+p b-p’-F’=3×5-2×6+1-0-1=12-23 图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组;有如在该机构中改选EG为原动件,试问组成此机构的基本杆组是否与前有所不同;解：1计算自由度F=3n-2P l +P h–p’-F’=3×7-2×10+0-0-0=12拆组3EG 为原动件,拆组2-24 试计算如图所示平面高副机构的自由度,并在高副低代后分析组成该机构的基本杆组;1、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×5-2×6+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图2所示 3高副低代如图3所示 4拆组如图4所示 2、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×-2×9+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图b 所示 3高副低代如图c 所示 4拆组如图d 所示第三章3—1 何谓速度瞬心相对瞬心与绝对瞬心有何异同点 答：参考教材30~31页;3—2 何谓三心定理何种情况下的瞬心需用三心定理来确定 答：参考教材31页;※3-3机构中,设已知构件的尺寸及点B 的速度v B 即速度矢量pb,试作出各机构在图示位置时的速度多边形;※3-4 试判断在图示的两机构中．B 点足否都存在哥氏加速度又在何位置哥氏加速度为零怍出相应的III 级组II 级组II 级组II 级组机构位置图;并思考下列问题;1什么条件下存在氏加速度2根椐上一条．请检查一下所有哥氏加速度为零的位置是否已全部找出;3图 a 中,a kB2B3=2ω2v B2B3对吗为什么;解：1图 a 存在哥氏加速度,图 b 不存在;2由于a kB2B3==2ω2v B2B3故ω3,v B2B3中只要有一项为零,则哥氏加速度为零;图 a 中B 点到达最高和最低点时构件1,3．4重合,此时v B2B3=0,当构件1与构件3相互垂直．即_f=；点到达最左及最右位置时ω2=ω3=0．故在此四个位置无哥氏加速度;图 b 中无论在什么位置都有ω2=ω3=0,故该机构在任何位置哥矢加速度都为零; 3对;因为ω3≡ω2;3-5 在图示的曲柄滑块机构中,已知mm l mm l mm l mm l DE BD A AB 40,50,100,30C ====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=451ϕ位置时,点D 、E 的速度和加速度以及构件2的角速度和角加速度;解：1以选定的比例尺l μ作机构运动简图（2）速度分析AB)(m/s 3.01⊥==AB B l v ωBCBCv v v v v C C C B C B C //32322⊥∨∨+=+=？方向：？0？大小：？根据速度影像原理,作BC BD bc bd //2=求得点d,连接pd;根据速度影像原理,作BDE bde ∆≈∆求得点e,连接pe,由图可知)(/r 2/m/s,175.0m/s,173.0,m/s 23.0223232顺时针s ad l bc c c v pe v pd v BC v v C C v E v D ========μωμμμ （3）加速度分析A)(B m/s 3221→==AB B l a ω根据速度影像原理作BC BD c b d b /''/''2=求得点'd ,连接''d p ;根据速度影像原理,作BDE e d b ∆≈'''∆求得点e ',连接e p '',由图可知)(/36.8//,m/s 8.2'',m/s 64.2''2'2'22222顺时针s rad l c n l a e p a d p a BC a BC B C a E a D =======μαμμτ 3-6 在图示机构中,设已知各构件的尺寸,原动件1以等角速度1ω顺时针方向转动,试用图解法求机构在图示位置时构件3上C 点速度和加速度比例尺任选;abc3-7 在图示机构中,已知mm l mm l mm l mm l mm l BC CD EF A AE 50,75,35,40,70B =====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=501ϕ位置时,C 点的速度c v 和加速度c a ; 解：1以选定的比例尺l μ作机构运动简图;速度分析m/s 72.0m/s,4.01111====AF F AB B l v l v ωω AFAF EFv v v v F F F F F //15145⊥⊥∨+==方向：大小：v d 用速度影响法求2速度分析CD ED v v v CDD C ⊥⊥∨+=方向：大小： BC AB v v v CBB C ⊥⊥∨+=方向：大小：3加速度分析)(m/s 2.7A),(B m/s 42211221A F l a l a AF F AB B →==→==ωω AFA F v a a a a a F F rF F k F F F F F ///21511515145→→∨++==方向：大小：ω EFEF l a a a a a EFEF n E F E F F ⊥→++==方向：大小：2444450ωτa d 用加速度影像法求CD D C l a a a a CDCDnCD D C ⊥→∨∨++=方向：大小：23ωτ CBB C l a a a a CB CBnCB B C ⊥→∨∨++=方向：大小：22ωτ 2m/s 3''=⋅=a C c p a μ3-8 在图示凸轮机构中,已知凸轮1以等角速度s rad /101=ω转动,凸轮为一偏心圆,其半径︒====90,50,15,251B ϕmm l mm l mm R AD A ;试用图解法求构件2的角速度2ω和角加速度2α; 解：1以选定的比例尺l μ作机构运动简图;2速度分析：将机构进行高副低代,其替代机构如图b 所示;m/s 15.0141===AB B B l v v ωCDAB BD v v v B B B B //4242⊥⊥∨+=方向：大小：？？)(/3.2//222逆时针s rad l pb l v BD v BD B ===μω3加速度分析A)m/s(B 5.12141→===AB B B l a a ω其中,）（顺时针222222222242242rad/s 9.143/''/,m/s 286.0,m/s 746.02=======BD a BD D B BD n D B B B k B B l b n l a l a v a μαωωτ 3-11 试求图示机构在图示位置时的全部瞬心; 解：a 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上 对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 d 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上 对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上※3-12 标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3; 解：1瞬新的数目：K=NN-1/2=66-1/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置,3)ω1/ω3= P 36P 13/P 16P 13=DK/AK,由构件1、3在K 点的速度方向相同,可知ω3与ω1同向;3-13 在图示四杆机构中,s rad mm l mm l CD AB /10,90,602===ω,试用瞬心法求：1当︒=165ϕ时点C 的速度C v ；当︒=165ϕ时构件3的BC 线上或其延长线上速度最小的一点E 的位置及其速度大小；3当0=C v 时ϕ角之值有两解;解：1以选定的比例尺l μ作机构运动简图（2）因P 24为构件2、4的顺心,则m/s 4.0rad/s 5.4424242242424=⋅==⋅=⋅=CD C D P A P l v DP AP l l ωωωω，对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上（3）因构件3的BC 线上速度最小的点到绝对瞬心P 13的距离最近,故从P 13作BC 线的垂线交于E 点; 对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上,故m/s 357.0131321313133313=⋅⋅=⋅⋅⋅=⋅⋅=⋅=E P B P l E P u B P v E P l v ABl l B l E P E ωμμωω（4）若0=C v ,则04=ω,DP AP l l DP A P 24242242424⋅=⋅=ωωω若024=A P ,则P 24与P 12重合,对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 若024=A P ,则A 、B 、C 三点共线;︒=⋅-++︒=︒=⋅-+=6.226)2arccos(1804.26)2arccos(22222221212211ADAC D C AD AC AD AC D C AD AC ϕϕ， ※3-15 在图示的牛头刨机构中,l AB =200 mnl,l CD =960 mm,l DE =160 mm, h=800mm,h 1=360mm,h 2=120mm;设曲柄以等角速度ω1=5 rad ／s ．逆时针方向回转．试以图解法求机构在φ1=135o 位置时．刨头点的速度v C ;sm AP v v P P P l p c l /24.1,,)2(151********===μωμ出瞬心利用顺心多边形依次定所示作机构运动简图，如图（1）以:解。

机械原理习题册答案机械原理习题册答案机械原理是工程学中的重要基础课程，它涉及到物体的平衡、运动和力学性质等方面。

在学习过程中，习题是非常重要的辅助工具，通过解答习题可以巩固所学的理论知识，提高解决问题的能力。

本文将为大家提供一些机械原理习题册的答案，希望能对大家的学习有所帮助。

第一章：力的平衡1. 如图所示，一个质量为10kg的物体受到一个斜面上的力F1，斜面与水平面的夹角为30度。

已知物体在斜面上不发生滑动，求力F1的大小。

解答：根据力的平衡条件，物体在斜面上的重力与斜面对物体的支持力之和等于零。

设物体的重力为G，支持力为N，则有：G = mg = 10kg * 9.8m/s^2 = 98NN = G * cosθ = 98N * cos30° ≈ 84.85N由此可得，力F1的大小为84.85N。

2. 如图所示，一个质量为5kg的物体受到一个斜面上的力F2，斜面与水平面的夹角为45度。

已知物体在斜面上发生滑动，滑动摩擦系数为0.2，求力F2的大小。

解答：根据力的平衡条件，物体在斜面上的重力与斜面对物体的支持力之和等于物体受到的力F2。

设物体的重力为G，支持力为N，则有：G = mg = 5kg * 9.8m/s^2 = 49NN = G * cosθ = 49N * cos45° ≈ 34.65N摩擦力f = μN = 0.2 * 34.65N = 6.93N由此可得，力F2的大小为49N + 6.93N = 55.93N。

第二章：力的作用效果1. 如图所示，一个质量为2kg的物体受到一个力F3，使其沿水平方向匀速运动。

已知物体受到的摩擦力为4N，求力F3的大小。

解答：根据力的作用效果，物体受到的合外力等于物体的质量乘以加速度。

设物体的质量为m，加速度为a，则有：F3 - 4N = ma由于物体沿水平方向匀速运动，加速度a为零。

因此，有：F3 - 4N = 0F3 = 4N由此可得，力F3的大小为4N。

《机械原理》课后习题答案第2章（P27）2-2 计算下列机构的自由度，如遇有复合铰链、局部自由度、虚约束等加以说明。

（a）n=3，p l=3 F=3*3-2*3=3（b）n=3，p l=3，p h=2 F=3*3-2*3-2=1 （B处有局部自由度）（c）n=7，p l=10 F=3*7-2*10=1（d）n=4，p l=4，p h=2 F=3*4-2*4-2=2 （A处有复合铰链）（e）n=3，p l=4 F=3*3-2*4=1 （A或D处有虚约束）（f）n=3，p l=4 F=3*3-2*4=1 （构件4和转动副E、F引入虚约束）（g）n=3，p l=5 F=(3-1)*3-(2-1)*5=1 （有公共约束）（h）n=9，p l=12，p h=2 F=3*9-2*12-2=1 （M处有复合铰链，C处有局部自由度）2-3 计算下列机构的自由度，拆杆组并确定机构的级别。

（a）n=5，p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组，故此机构为Ⅱ级机构。

（b）n=5，p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。

（c）n=5，p l=7 F=3*5-2*7=1拆分时只须将主动件拆下，其它构件组成一个Ⅲ级杆组，故此机构为Ⅲ级机构。

2-4 验算下列运动链的运动是否确定，并提出具有确定运动的修改方案。

（a）n=3，p l=4，p h=1 F=3*3-2*4-1=0 该运动链不能运动。

修改方案如下图所示：（b）n=4，p l=6 F=3*4-2*6=0 该运动链不能运动。

修改方案如下图所示：或第3章（P42）3-2 下列机构中，已知机构尺寸，求在图示位置时的所有瞬心。

（a）（b）（c）(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中，三个圆互作纯滚，试利用相对瞬心P13来讨论轮1与轮3的传动比i13。

第5章（P80）5-2 一铰接四杆机构（2）机构的两极限位置如下图：（3）传动角最大和最小位置如下图：5-3题略解：若使其成为曲柄摇杆机构，则最短杆必为连架杆，即a 为最短杆。

《机械原理》课后习题答案第2章（P27）2-2 计算下列机构的自由度，如遇有复合铰链、局部自由度、虚约束等加以说明。

（a）n=3，p l=3 F=3*3-2*3=3（b）n=3，p l=3，p h=2 F=3*3-2*3-2=1 （B处有局部自由度）（c）n=7，p l=10 F=3*7-2*10=1（d）n=4，p l=4，p h=2 F=3*4-2*4-2=2 （A处有复合铰链）（e）n=3，p l=4 F=3*3-2*4=1 （A或D处有虚约束）（f）n=3，p l=4 F=3*3-2*4=1 （构件4和转动副E、F引入虚约束）（g）n=3，p l=5 F=(3-1)*3-(2-1)*5=1 （有公共约束）（h）n=9，p l=12，p h=2 F=3*9-2*12-2=1 （M处有复合铰链，C处有局部自由度）2-3 计算下列机构的自由度，拆杆组并确定机构的级别。

（a）n=5，p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组，故此机构为Ⅱ级机构。

（b）n=5，p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。

（c）n=5，p l=7 F=3*5-2*7=1拆分时只须将主动件拆下，其它构件组成一个Ⅲ级杆组，故此机构为Ⅲ级机构。

2-4 验算下列运动链的运动是否确定，并提出具有确定运动的修改方案。

（a）n=3，p l=4，p h=1 F=3*3-2*4-1=0 该运动链不能运动。

修改方案如下图所示：（b）n=4，p l=6 F=3*4-2*6=0 该运动链不能运动。

修改方案如下图所示：12或第3章（P 42）3-2 下列机构中，已知机构尺寸，求在图示位置时的所有瞬心。

（a ） （b ） （c ） (a) v 3=v P13=ω1P 14P 13μl3-6 在图示齿轮连杆机构中，三个圆互作纯滚，试利用相对瞬心P 13来讨论轮1与轮3的传动比i 13。

第5章 （P 80）5-2 一铰接四杆机构（2）机构的两极限位置如下图：35-3题略解：若使其成为曲柄摇杆机构，则最短杆必为连架杆，即a 为最短杆。

机械原理课后全部习题答案目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征？机器通常由哪三部分组成？各部分的功能是什么？2）、机器与机构有什么异同点？3）、什么叫构件？什么叫零件？什么叫通用零件和专用零件？试各举二个实例。

4）、设计机器时应满足哪些基本要求？试选取一台机器，分析设计时应满足的基本要求。

2、填空题1)、机器或机构，都是由组合而成的。

2）、机器或机构的之间，具有确定的相对运动。

3）、机器可以用来人的劳动，完成有用的。

4）、组成机构、并且相互间能作的物体，叫做构件。

5）、从运动的角度看，机构的主要功用在于运动或运动的形式。

6）、构件是机器的单元。

零件是机器的单元。

7）、机器的工作部分须完成机器的动作，且处于整个传动的。

8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。

9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。

3、判断题1)、构件都是可动的。

（）2）、机器的传动部分都是机构。

（）3）、互相之间能作相对运动的物件是构件。

（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。

（）5）、机构的作用，只是传递或转换运动的形式。

（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。

（）7）、机构中的主动件和被动件，都是构件。

（）2 填空题答案1）、构件2）、构件3）、代替机械功4）、相对运动5）、传递转换6）、运动制造7）、预定终端8）、中间环节9）、确定有用构件3判断题答案1）、√2）、√3）、√4）、√5）、×6）、√7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。

机械原理课后习题答案机械原理课后习题答案机械原理是一门重要的工程学科，它研究物体在力的作用下的运动和平衡问题。

在学习机械原理的过程中，课后习题是巩固和应用所学知识的重要环节。

本文将为大家提供一些机械原理课后习题的答案，希望能对大家的学习有所帮助。

1. 一个物体质量为10kg，受到一个30N的力作用，求物体的加速度。

解答：根据牛顿第二定律，F = ma，其中F为物体所受的力，m为物体的质量，a为物体的加速度。

将已知数据代入公式，可得a = F/m = 30N/10kg = 3m/s²。

2. 一个物体受到一个10N的力作用，加速度为2m/s²，求物体的质量。

解答：同样根据牛顿第二定律，F = ma，将已知数据代入公式，可得m = F/a= 10N/2m/s² = 5kg。

3. 一个物体质量为5kg，受到一个20N的力作用，求物体的加速度。

解答：同样应用牛顿第二定律，F = ma，将已知数据代入公式，可得a = F/m= 20N/5kg = 4m/s²。

4. 一个物体受到一个8N的力作用，质量为4kg，求物体的加速度。

解答：应用牛顿第二定律，F = ma，将已知数据代入公式，可得a = F/m =8N/4kg = 2m/s²。

通过以上几道题目的解答，我们可以看到，牛顿第二定律是解决物体运动问题的基本定律，通过它我们可以计算物体的加速度和质量。

5. 一个物体质量为5kg，受到一个力的作用使其加速度为4m/s²，求作用在物体上的力。

解答：同样应用牛顿第二定律，F = ma，将已知数据代入公式，可得F = ma =5kg × 4m/s² = 20N。

6. 一个物体受到一个力的作用使其加速度为6m/s²，质量为3kg，求作用在物体上的力。

解答：应用牛顿第二定律，F = ma，将已知数据代入公式，可得F = ma = 3kg × 6m/s² = 18N。

机械原理习题集答案第一章：机械运动学1. 问题：简述平面运动的基本概念。

答案：平面运动是指物体在平面内的运动，其轨迹可以是直线或曲线。

在平面运动中，物体的每一个点都在同一平面内移动。

2. 问题：什么是四杆机构的运动规律？答案：四杆机构是最基本的机械机构之一，其运动规律取决于杆的长度和连接方式。

常见的四杆机构有双曲柄机构、曲柄滑块机构等。

第二章：机械动力学1. 问题：牛顿运动定律在机械设计中的应用是什么？答案：牛顿运动定律是描述物体运动的基本定律，包括惯性定律、力的作用与反作用定律和作用力与加速度的关系。

在机械设计中，这些定律用于预测和计算机械系统的运动状态和受力情况。

2. 问题：简述达朗贝尔原理。

答案：达朗贝尔原理是动力学中的一个基本原理，它指出在没有外力作用的系统中，系统内各部分的动量守恒。

在机械设计中，这一原理常用于分析和计算机械系统的动态平衡。

第三章：机构设计与分析1. 问题：什么是机构的自由度？答案：机构的自由度是指在没有约束的情况下，机构能够独立进行的运动的数量。

自由度的计算公式为：\( F = 3n - 2j - h \)，其中\( n \)是机构中杆件的数量，\( j \)是铰链的数量，\( h \)是高副的数量。

2. 问题：如何确定一个机构的运动类型？答案：确定机构的运动类型需要分析机构的几何形状和连接方式。

例如，如果机构中存在曲柄和滑块，它可能是一个曲柄滑块机构，其运动类型为往复直线运动。

第四章：机械结构设计1. 问题：机械结构设计中需要考虑哪些因素？答案：在机械结构设计中，需要考虑的因素包括材料的选择、强度和刚度的计算、尺寸的确定、成本控制、维护的便利性等。

2. 问题：什么是疲劳强度？答案：疲劳强度是指材料在反复加载和卸载过程中抵抗断裂的能力。

在机械结构设计中，需要考虑疲劳强度以确保结构的可靠性和耐久性。

第五章：机械传动1. 问题：什么是齿轮传动？答案：齿轮传动是一种利用齿轮啮合来传递运动和动力的机械传动方式。

第12章其他常用机构12-1棘轮机构除常用来实现间歇运动的功能外，还常用来实现什么功能？答：棘轮机构除了常用的间歇运动功能外，还能实现制动、进给、转位、分度、趙越运动等功能。

12-2某牛头刨床送进丝杠的导程为6mm,要求设计一棘轮机构，使每次送进呈可在0.2〜之间作有 级调整(共6级)。

设棘轮机构的棘爪由一曲柄摇杆机构的摇杆来推动，试绘出机构运动简图，并作必姜的计算 和说明。

解：牛头刨床送进机构的运动简图如图12-1所示，牛头刨床的横向进给是通过齿轮1、2,曲衲摇杆机构2、 3、4,練轮机构4、5、7来使与棘轮固连的丝杠6作间歇转动，从而使牛头刨床工作台实现横向间接进给。

通过 改变曲柄长度刃的大小可以改变进给的大小。

当棘爪7处于图示状态时，棘轮5沿逆时针方向作间歇进给运 动。

若将棘爪7拔出绕自身轴线转180°后再放下•由于棘爪工作面的改变.棘轮将改为沿顺时针方向间接进给。

G=^X360° = 12°O棘轮的齿数为360° 360° “0 12°设牛头刨床横向进给的初始位置如图12-1 (a)所示，则曲柄摇杆机构0。

2皿的极限位置为初始位置左右 转0/2,其中0为摇杆的摆角，极限位置如图12-1 (b)所示。

半-次进给量为0.2mm 时，帀为虽短，即得棘轮最小转角.2久 2穴 rac0 =〒仏二石".2 = 72。

每次送进量的调整方法：① 采用隐蔽棘轮罩来实现送进駅的调格：② 通过改变棘爪摆角來实现送进就的调整。

当一次进给虽为\.2tnm 时 即得棘轮最人转角当进给最为0.2/n/n 时，棘轮每次转过的角度为=—x0.2 = 6图(a)中所示，三个楝爪尖在練轮齿圈上的位置相互磅个齿風图(b)中所示，三个棘爪尖在練轮齿圈上的位買相互差I个齿距。

(a) (b)图12-212-4当电钟电压不足时，为什么步进式电钟的秒针只在原地震荡，而不能作整周回转？答：如图12-3所示为用于电钟的棘轮机构。

机械原理课后题答案1. 列举并解释一下机械原理中的三大支配因素。

- 动力：指施加在机构元件上的力或力矩，用来驱动机构执行运动或产生工作效果。

- 运动：指机构元件相对运动的方式、路径和速度。

- 连结：指机构元件之间的连接方式，包括直接和间接连接两种形式。

2. 解释一下机械原理中的三大运动副类型。

- 滑动副：两个机构元件之间只能沿着一条确定的直线运动，如推拉杆、滑块等。

- 旋转副：两个机构元件之间只能绕一条确定的轴线旋转运动，如轴承、齿轮等。

- 滚动副：两个机构元件之间存在滚动运动，如滚子轴承、滚珠丝杠等。

3. 什么是机械原理中的受力分析方法？受力分析方法是指通过分析机构元件之间的力和力矩关系，找出各个元件的受力情况，以解决机构设计和运动性能分析的方法。

常用的受力分析方法包括力平衡法、力矩平衡法、虚功原理等。

4. 什么是力平衡法？力平衡法是一种受力分析方法，通过分析机构元件之间的力平衡关系，得到各个元件所受力的大小和方向。

它基于牛顿第一定律，即所有物体受力之和为零，可用来解决机构中受力平衡问题，确定力的大小和方向。

5. 解释一下力矩平衡法。

力矩平衡法是一种受力分析方法，通过分析机构元件之间的力矩平衡关系，得到各个元件所受力的大小和方向。

在机械原理中，力矩平衡法常被用于解决转动副运动问题，根据力矩平衡条件，求解未知力矩和力矩的方向。

6. 什么是虚功原理？虚功原理是一种受力分析方法，通过分析机构元件之间的虚功平衡关系，得到各个元件所受力的大小和方向。

虚功原理是基于功率平衡的原理，即虚功平衡原理，在机械原理中常用于分析运动副的受力情况和功率传递效率。

7. 介绍一下机械原理中的摩擦现象。

摩擦是指两个物体相对运动时由接触面之间的相互作用力导致的阻碍运动的力。

在机械运动中，正常情况下不可避免地存在摩擦力，摩擦力会导致机械能的损失、能量的消耗和部件的磨损。

因此在机械原理中需要对摩擦进行充分的考虑和分析。

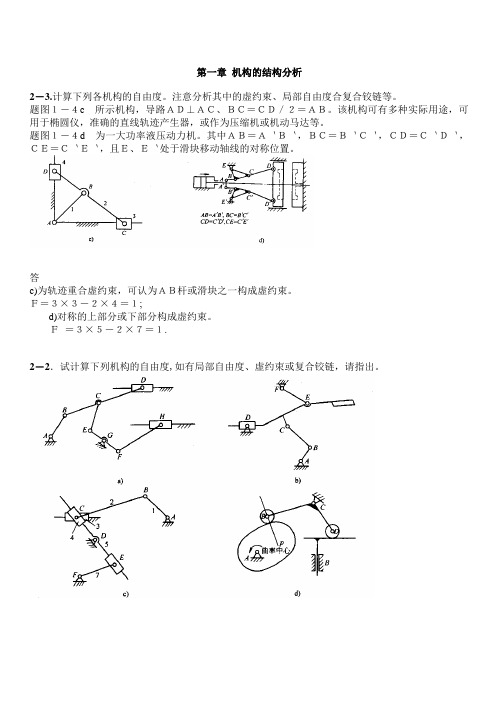
第一章机构的结构分析2－3.计算下列各机构的自由度。

注意分析其中的虚约束、局部自由度合复合铰链等。

题图１－４c所示机构，导路ＡＤ⊥ＡＣ、ＢＣ＝ＣＤ／２＝ＡＢ。

该机构可有多种实际用途，可用于椭圆仪，准确的直线轨迹产生器，或作为压缩机或机动马达等。

题图１－４d为一大功率液压动力机。

其中ＡＢ＝Ａ｀Ｂ｀，ＢＣ＝Ｂ｀Ｃ｀，ＣＤ＝Ｃ｀Ｄ｀，ＣＥ＝Ｃ｀Ｅ｀，且Ｅ、Ｅ｀处于滑块移动轴线的对称位置。

答c)为轨迹重合虚约束，可认为ＡＢ杆或滑块之一构成虚约束。

Ｆ＝３×３－２×４＝１;d)对称的上部分或下部分构成虚约束。

Ｆ＝３×５－２×７＝１.2－2．试计算下列机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。

e）答案：a)Ｆ＝３×７－２×１０＝１．注意其中的Ｃ、Ｇ、Ｄ、Ｈ点并不是复合铰链。

b)Ｆ＝３×５－２×７＝１C）Ｆ＝３×７－２×１０＝１其中Ｃ点为复合铰链，分别由2、３、４构件在Ｃ点构成复合铰。

d)Ｆ＝３×３－２×３－２＝１或者Ｆ＝３×５－２×５－２－２＝１其中Ｂ、Ｄ处的滚子具有局部自由度。

(e) F=3×9－2×12－1－1=1或者：F=3×8－2×11－1=1（注意：BCD组成的三角形为一个构件）其中B点为局部自由度2-3试计算如图所示各平面高副机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。

答：C点为局部自由度，E、F其中一点为虚约束。

F= 3×5－2×6－1－1=1或者：F=3×4－2×5－1=1第三章平面连杆机构及其分析与设计3－1．试求题图所示各机构在图示位置时全部瞬心的位置．答案：瞬心P 12在A 点 瞬心P 23、 P 24均在B 点 瞬心P 34在C 点 P 14、 P 13均在垂直导路的无 瞬心P 23、 P 13均在B 点 穷远处 瞬心P 14、 P 24均在D 点3-5在图示的齿轮-连杆组合机构中，试用瞬心法求齿轮1与齿轮3的传动比31/ωω。

机械设计王德伦第二版课后题答案1、60．从太阳发出的带电粒子流在地球两极，与地磁场相互作用，使高层大气分子或原子激发就会形成绚丽多彩的极光现象。

则引起极光现象的微粒中一定不会是（）[单选题] *A．a粒子（氦的原子核）B．质子C．中子(正确答案)D．电子2、3．一个力F和它的两个分力都是物体实际受到的力．[判断题] *对错(正确答案)3、21．关于声现象，下列说法正确的是（）[单选题] *A．人听到声音是否响亮只跟发声体发声时的振幅有关B．人们可以用声学仪器接收到超声波判断地震的方位和强度C．倒车雷达是利用回声定位探测车后的障碍物(正确答案)D．用大小不同的力敲击同一音叉是为了探究音调与频率的关系4、15．学习科学知识的价值之一，是主动将所学知识创造性地服务于社会。

如“声音的传播需要介质”就有许多实际应用。

下列发明成果应用了这一知识的是（）[单选题] *A．验钞机B．望远镜C．真空玻璃(正确答案)D．体温计5、3．对匀减速直线运动，公式v2－v02＝2ax中的a必须取负值．[判断题] *对错(正确答案)6、81．如图是A、B、C三种物质的质量m与体积V的关系图线，由图可知，A、B、C三种物质的密度ρA、ρB、ρC和水的密度ρ水之间的关系是（）[单选题] *A.ρA≥ρB＞ρC且pA＜ρ水B．ρA＜ρB＜ρC且ρC＞ρ水C．ρA＜ρB＜ρC且ρA＞ρ水D．ρA＞ρB＞ρC且ρB＝ρ水(正确答案)7、68．如图甲所示，上方装有电子阀门的圆柱形容器放在水平桌面上。

控制阀门，使容器中相同时间内流入液体的质量相等，注入液体直至图乙状态。

图丙所呈现的物理量之间的函数关系图像可能是（）[单选题] *A．液面上升速度v和时间t的关系B．液体密度ρ和液体体积V的关系C．液体质量m和液体密度ρ的关系D．液面上升高度h和时间t的关系(正确答案)8、31．在生产和生活中，人们常以密度作为选择材料的主要因素。

下面属于主要从密度的角度考虑选材的是（）[单选题] *A．用铁制作炒锅B．用塑料泡沫做表演场景中的“落石”(正确答案)C．用水银做温度计内的液体D．用软木做暖壶瓶塞9、5．合力的作用可以替代原来那几个力的作用，它与那几个力是等效替代关系．[判断题] *对(正确答案)错10、37．用同种金属制成的体积相等的甲、乙两种金属球，其中有一种是实心的，有一种是空心的。

8-3 推证渐开线齿轮法向齿距n p 、基圆齿距b p 和分度圆齿距p 之间的关系为式为απαcos cos m p p p b n ===。

证明：根据渐开线的性质：即渐开线的发生线沿基圆滚过的长度，等于基圆上被滚过的圆弧长度有b n p p =设齿轮的齿数为z ，模数为m ，基圆半径为b r ，分度圆半径为r ，压力角为α因为 b b r zp π2=，r zp π2= 又因为 αcos r r b = 所以 αcos p p b = 因为 m p π=所以 απαcos cos m p p p b n === 证毕。

8-4 用范成法加工渐开线直齿圆柱齿轮，刀具为标准齿条型刀具，其基本参数为：mm m 2=， 20=α，正常齿制。

（1）齿坯的角速度s rad5.221=ω时，欲切制齿数90=z 的标准齿轮，确定齿坯中心与刀具分度线之间的距离a 和刀具移动的线速度v ； （2）在保持上面的a 和v 不变的情况下，将齿坯的角速度改为s rad231=ω。

这样所切制出来的齿轮的齿数z 和变位系数x 各是多少？齿轮是正变位齿轮还是负变位齿轮？（3）同样，保持a 和v 不变的情况下，将齿坯的角速度改为s rad1.221=ω，所切制出来的齿轮的齿数z 和变位系数x 各是多少？最后加工的结果如何？ 解：（1）、由于是加工标准齿轮，齿坯中心与刀具分度线之间的距离为mm mz a 9029022=⨯==刀具移动的线速度为O解题8-3图s mm mz v 45.22129022=⋅⨯=⋅=ω （2）、齿轮的齿数z 为922312422=⨯⨯==ωm v z变位系数x 为122922902-=⨯-=-=m mz a x 因为变位系数小于零，所以齿轮是负变位齿轮。

（3）、齿轮的齿数z 为4.881.2212422=⨯⨯==ωm v z 变位系数x 为8.0224.882902=⨯-=-=m mz a x 因为变位系数为正，所以齿轮是正变位齿轮。