卫生AB_第四讲(3)_2009年版

2009版传染病诊断标准汇编.作：卫生监督中心标准处卫生监督中心标准处2009年10月出版16开精装全一卷光盘：0定价：298元优惠：180元..详细：.......................................... ...................................................... ............为了使读者查阅方便，卫生部卫生监督中心按国家法定传染病分类进行了汇编，分别为：甲类传染病、乙类传染病、丙类传染病，三部分组成。

可作为卫生防疫人员的培训资料，也可作为社会工作者防治活动中使用。

本书收录了2009年5月中旬以来发布传染国家标准和行业标准40余项。

（一）甲类传染病诊断标准1.WS279-2008鼠疫诊断标准2.WS289-2008霍乱诊断标准（二）乙类传染病诊断标准1.WS286-2008传染性非典型肺炎诊断标准2.WS293-2008艾滋病和艾滋病病毒感染诊断标准3.GB17010-1997甲型病毒性肝炎诊断标准4.GB15990-1995乙型病毒性肝炎诊断标准5.WS213-2008丙型病毒性肝炎诊断标准6.GB15999-1995丁型病毒性肝炎诊断标准7.GB17011-1997戊型病毒性肝炎诊断标准8.GB16394-1996脊髓灰质炎诊断标准9.WS284-2008人感染高致病性禽流感诊断准10.GB15983-1995麻疹诊断标准11.WS278-2008流行性出血热诊断标准12.WS281-2008狂犬病诊断标准13.WS216-2008登革热诊断标准14.WS283-2008炭疽诊断标准15.WS287-2008细菌性和阿米巴性痢疾诊断标准16.WS288-2008肺结核诊断标准17.WS280-2008伤寒和副伤寒诊断标准18.GB16884-1997流行性脑脊髓膜炎诊断标准19.WS214-2008流行性乙型脑炎诊断标准20.GB15998-1995百日咳诊断标准（三）丙类传染病诊断标准1.WS285-2008流行性感冒诊断标准2.WS270-2007流行性腮腺炎诊断标准3.WS276-2007地方性甲状腺肿诊断标准4.GB17009-1997风疹诊断标准5.WS217-2008急性出血性结膜炎诊断标准2009版传染病诊断标准汇编为了使读者查阅方便，卫生部卫生监督中心按国家法定传染病分类进行了汇编，分别为：甲类传染病、乙类传染病、丙类传染病，三部分组成。

数的开方与二次根式知识点：平方根、立方根、算术平方根、二次根式、二次根式性质、最简二次根式、 同类二次根式、二次根式运算、分母有理化教学目标：1.理解平方根、立方根、算术平方根的概念，会用根号表示数的平方根、立方根和算术平方根；会求实数的平方根、算术平方根和立方根；2.了解二次根式、最简二次根式、同类二次根式的概念，会辨别最简二次根式和同类二次根式；掌握二次根式的性质，会化简简单的二次根式，能根据指定字母的取值范围将二次根式化简；3.掌握二次根式的运算法则，能进行二次根式的加减乘除四则运算，会进行简单的分母有理化。

教学重难点：1.平方根、算术平方根、立方根的概念（有关试题在试题中出现的频率很高，习题类型多为选择题或填空题）；2.最简二次根式、同类二次根式概念（有关习题经常出现在选择题中）；3.二次根式的计算或化简求值（有关问题在中考题中出现的频率非常高，在选择题和中档解答题中出现的较多）。

教学过程：1、知识要点：考点1 平方根、算术平方根与立方根：若)0(2≥=a a x ，则x 叫做a 的平方根，记作a ±；正数a 的正的平方根叫做a 的算术平方根，0的算术平方根是0。

当0≥a 时，a 的算术平方根记作a 。

注意：1、非负数是指正数或0，常见的非负数有：(1）绝对值：0≥a ；(2)实数的平方：02≥a ；(3) 算术平方根：)0(0≥≥a a 。

2、如果a 、b 、 c 是实数，且满足02=++c b a ， 则有0=a，0=b ，0=c考点2 二次根式的有关概念：1、二次根式：式子)0(≥a a 叫做二次根式（注意被开方数只能是正数或0）； 二次根式a 定义中的“a ≥0”是定义的一个重要组成部分，不可以省略，因为负数没有平方根，所以当a<0时，没有意义．在具体问题中，一旦出现了二次根式a ，就意味着a ≥0，这通常作为一个重要的隐含条件来应用；被开方数a 既可以是具体的数，也可以是单项式或多项式，如：3、ab (ab ≥0)、3+x (x ≥－3)都是二次根式．2、最简二次根式：被开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式，叫做最简二次根式；最简二次根式，满足两个条件：①被开方数不含分母；②被开方数中不含开得尽方的因数或因式．3、同类二次根式：①化成最简二次根式后，被开方数相同的二次根式，叫做同类二次根式； ②二次根式的性质： )0()(2≥=a a a ⎩⎨⎧<-≥==)0()0(||2a a a a a a )0;0(≥≥⋅=b a b a ab )0;0(>≥=b a ba b a 考点3 二次根式的运算：1、二次根式的加减：二次根式相加减，先把各个二次根式化成最简二次根式，再把同类二次根式分别合并；2、二次根式的乘法： 二次根式相乘，等于各个因式的被开方数的积的算术平方根，即 ).0,0(≥≥=⋅b a ab b a（二次根式的和相乘，可参照多项式的乘法进行；两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，那么这两个二次根式互为有理化因式）；3、二次根式的除法：二次根式相除，通常先写成分式的形式，然后分子、分母都乘以分母的有理化因式，把分母的根号化去(或分子、分母约分)；把分母的根号化去，叫做分母有理化。

绝对值函数和绝对值不等式11nn ii i i z z .【方法概论】遇到绝对值的问题时，方法主要以下几种：分类讨论：即去掉绝对值；这种方法是解决绝对值问题的根本方法。

典型例题：22cos ,||1,21,||1,x x xx f (x )+f (x +l )－2|+|f (x )－.【过关习题4】1.【2018年学考选考十校联盟，☆☆】a ，b 是实数，如此“|a |≤1且|b |≤1〞是“|a +b |+|a －b |≤2〞的.A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.【2018年某某高三适应性考试，，☆☆】a >0，函数f (x )=|x 2+|x －a |－3|在区间[－1，1]上的最大值是2，如此a =.3.【2018年某某二模，17，，☆☆☆】f (x )=x 2－ax ，|f (f (x ))|≤1在[1，2]上恒成立，如此实数a 的最大值为.4.【2017年某某某某二模，，☆☆☆☆】函数f (x )=|x 2+ax +b |在区间[0，c ]内的最大值为M (a ，b ∈R ，c >0为常数)且存在实数a ，b ，使得M 取最小值2，如此a +b +c =.5.【☆☆】设正实数x ，y ，如此|x －y |+1x+y 2的最小值为.6.【2017年某某二模，10，☆☆】设函数f (x )=x 2+ax +b (a 、b ∈R)的两个零点为x 1、x 2，假如|x 1|+|x 2|≤2，如此.A .|a |≥1B .|b |≤1C .|a +2b |≥2D .|a +2b |≤27.【2017年某某4月份学考，☆☆】a ，b ∈R ，a ≠1，如此|a +b |+⎪⎪⎪⎪⎪⎪1a +1－b 的最小值为.8.【2017年某某某某市柯桥中学5月质检，8，☆☆】x ，y ∈R ，如此.A .假如|x 2+y |+|x －y 2|≤1，如此⎝ ⎛⎭⎪⎫x +122+⎝ ⎛⎭⎪⎫y －122≤32B .假如|x 2－y |+|x －y 2|≤1，如此⎝⎛⎭⎪⎫x －122+⎝⎛⎭⎪⎫y －122≤32C .假如|x +y 2|+|x 2－y |≤1，如此⎝ ⎛⎭⎪⎫x +122+⎝ ⎛⎭⎪⎫y +122≤32D .假如|x +y 2|+|x 2+y |≤1，如此⎝⎛⎭⎪⎫x －122+⎝⎛⎭⎪⎫y +122≤329.【2016年某某高考，8，☆☆☆】实数a 、b 、c ，下面四个选项中正确的答案是.A .假如|a 2+b +c |+|a +b 2+c |≤1，如此a 2+b 2+c 2<100B .假如|a 2+b +c |+|a 2+b －c |≤1，如此a 2+b 2+c 2<100C .假如|a +b +c 2|+|a +b －c 2|≤1，如此a 2+b 2+c 2<100D .假如|a 2+b +c |+|a +b 2－c |≤1，如此a 2+b 2+c 2<10010.【2017年某某高级中学最后一模，17，☆☆】设实数x ，y ，z 满足⎩⎨⎧|x +2y －3z |≤6，|x －2y +3z |≤6，|x －2y －3z |≤6，|x +2y +3z |≤6，如此|x |+|y |+|z |的最大值为.11.【2017年某某名校协作体，7，☆】设f (x )=|2x －1|，假如f (x )≥|a +1|－|2a －1||a |对任意的a ≠0恒成立，如此x 的取值X 围为.12.【2016年某某样卷，☆】f (x )=ax 2+bx +c ，a 、b 、c ∈R ，且a ≠0，记M (a ，b ，c )为|f (x )|在[0，1]上的最大值，如此a +b +2cM (a ，b ，c )的最大值是.13.【☆☆】设函数f (x )=|x 2+ax +b |，假如对任意的实数a 、b ，总存在x 0∈[0，4]使得f (x 0)≥m 成立，如此实数m 的取值X 围是.14.【2017年某某某某、富阳、长兴联考，☆☆☆】函数f (x )=－x 3－3x 2+x ，记M (a ，b )为函数g (x )=|ax +b －f (x )|(a >0，b ∈R)在[－2，0]上的最大值，如此M (a ，b )的最小值为. 15.【2017年某某一模，9，☆☆☆】设函数f (x )=x 2+ax +b ，记M 为函数y =|f (x )|在[－1，1]上的最大值，N 为|a |+|b |的最大值，如此.A .假如M =13，如此N =3 B .假如M =12，如此N =3 C .假如M =2，如此N =3 D .假如M =3，如此N =316.【2017年某某，☆☆☆】设函数f (x )=|ax +2x +b |，假如对任意的x ∈[0，4]，函数f (x )≤12恒成立，如此a +2b =.17.【某某省某某市2017届高三二模，17，☆☆☆】对任意实数x 都有|a cos 2x +b sin x +c |≤1恒成立，如此|a sin x +b |的最大值为.18.【某某省某某市2016届高三教学质量测试(二)，14，☆☆】 设max{a ，b }=⎩⎨⎧a (a ≥b )b (a <b )，x ，y ∈R ，m +n =6，如此F =max {}|x 2－4y +m |，|y 2－2x +n |的最小值为．19.【☆☆】f (x )=ax 2+bx +c (a ≠0)，假如对任意的|x |≤1，都有|f (x )|≤1，如此|a |+|b |+|c |的最大值为.20.【2014年某某高考，☆☆】在直角平面坐标系xOy 中，O 为原点，A (－1，0)，B (0，3)，C (3，0)，动点D 满足|CD →|=1，如此|OA →+OB →+OD →|的最大值为.21.【某某省2017年预赛，10，☆☆☆】f (x )=⎩⎨⎧－2x ， x <0，x 2－1，x ≥0，假如方程f (x )+21－x 2+|f(x )－21－x 2|－2ax －4=0有三个不等的实数根x 1，x 2，x 3，且x 1<x 2<x 3，假如x 3－x 2=2(x 2－x 1)，如此a =.22.【2006年某某，☆】函数f (x )=12(sin x +cos x )－12|sin x －cos x |，如此f (x )的值域为.23.【2008年某某，☆】函数y =tan x +sin x －|tan x －sin x |在区间⎝ ⎛⎭⎪⎫π2，3π2内的图像是.ABCD24.【某某省某某市2015年高三教学质量调测，15，☆☆☆】当且仅当x ∈(a ，b )∪(c ，d )(b ≤c )时，函数f (x )=2x 2+x +2的图像在函数g (x )=|2x +1|+|x －t |的下方，如此b －a+d －c 的取值X 围为.25.【2016高考某某文数，☆☆】平面向量a ，b ，|a |=1，|b |=2，a ·b =1．假如e 为平面单位向量，如此|a ·e |+|b ·e |的最大值是______．26.【2014年某某预赛，9，☆☆】a 、b 为实数，对任何满足0≤x ≤1的实数x ，都有|ax +b |≤1成立，如此|20a +14b |+|20a －14b |的最大值是.27.【2014年某某预赛，14，☆☆】f (x )=⎩⎨⎧－x 2+x ，x ≤1，log 12x ， x >1，g (x )=|x －k |+|x －1|，假如对任意的x 1，x 2∈R ，都有f (x 1)≤g (x 2)成立，如此实数k 的取值X 围为.28.【2014年全国联赛，3，☆☆】假如函数f (x )=x 2+a |x －1|在[0，+∞)上单调递增，如此实数a 的取值X 围是.29.【2015年某某预赛，1，☆☆】假如对任意实数x ，|x +a |+|x +1|≤2a 恒成立，如此实数a 的最小值为.30.【2016年某某预赛，1，☆☆☆】方程x =|x －|x －6||的解为.31.【2016年某某预赛，12，☆☆】设x ∈R ，如此函数f (x )=|2x －1|+|3x －2|+|4x －3|+|5x －4|的最小值为.32.【2016年某某预赛，11，☆☆☆】设a ∈R ，方程||x －a |－a |=2恰有三个不同的实数根，如此a =.33. 【1982年全国，4，☆☆】由曲线|x －1|+|y －1|=1确定的曲线所围成的图形的面积是.A .1B .2C .πD .434.【2017年某某预赛，5，，☆☆】定义区间[x 1，x 2]的长度为x 2－x 1.假如函数y =|log 2x |的定义域为[a ，b ]，值域为[0，2]，如此区间[a ，b ]的长度的最大值和最小值的差为. 35.【2018年某某预赛，8，☆】设f (x )=|x +1|+|x |－|x －2|，如此f (f (x ))+1=0有个不同的解.36.【2015年全国，6，☆☆】在平面直角坐标系xOy 中，点集K ={(x ，y )|(|x |+3|y |－6)(3|x |+|y |－6)≤0}所对应的平面区域的面积为.37.【2008年某某预赛，9，☆☆☆】在平行直角坐标系中，定义点P (x 1，y 1)，Q (x 2，y 2)之间的“直角距离〞为d (P ，Q )=|x 1－x 2|+|y 1－y 2|.假如C (x ，y )到点A (1，3)、B (6，9)的“直角距离〞相等，其中实数x 、y 满足0≤x ≤10，0≤y ≤10，如此所有满足条件点C 的轨迹的长度之和为.38.【2014年某某预赛，4，☆☆】在直角坐标系中，曲线|x －1|+|x+1|+|y |=3围成的图形的面积是.39.【2017年某某十校期末调研考试，9，☆☆】设x 、y ∈R ，如下不等式成立的是.A .1+|x +y |+|xy |≥|x |+|y |B .1+2|x +y |≥|x |+|y |C .1+2|xy |≥|x |+|y |D .|x +y |+2|xy |≥|x |+|y |40.【2017年某某市高三教学质量调测，9，☆☆☆】记min{x ，y }=⎩⎨⎧y ，x ≥y ，x ，x <y ，设f (x )=min{x 2，x 3}，如此.A .存在t >0，|f (t )+f (－t )|>f (t )－f (－t )B .存在t >0，|f (t )－f (－t )|≥f (t )－f (－t )C .存在t >0，|f (1+t )+f (1－t )|>f (1+t )+f (1－t )D .存在t >0，|f (1+t )－f (1－t )|>f (1+t )－f (1－t )41.【某某省2016届高三下学期第二次五校联考(理)，18，☆☆☆】函数f (x )=ax 2+bx +c ，g (x )=c |x |+bx +a ，对任意x ∈[－1，1]，|f (x )|≤12.(I)求|f (2)|的取值X 围；(II)证明：对任意的x ∈[－1，1]，都有|g (x )|≤142.【某某省某某市2016届高三期末考试，20，☆☆☆】函数f (x )=－x 2+2bx +c ，，设函数g (x )=|f (x )|在区间[－1，1]上的最大值为M ．(I)假如b =2，试求出M ；(II)假如M ≥k 对任意的b ，c 恒成立，试求出k 的最大值．43.【2016某某预赛，16，☆☆☆☆】a为实数，函数f(x)=|x2－ax|－ln x，请讨论函数f (x)的单调性.。

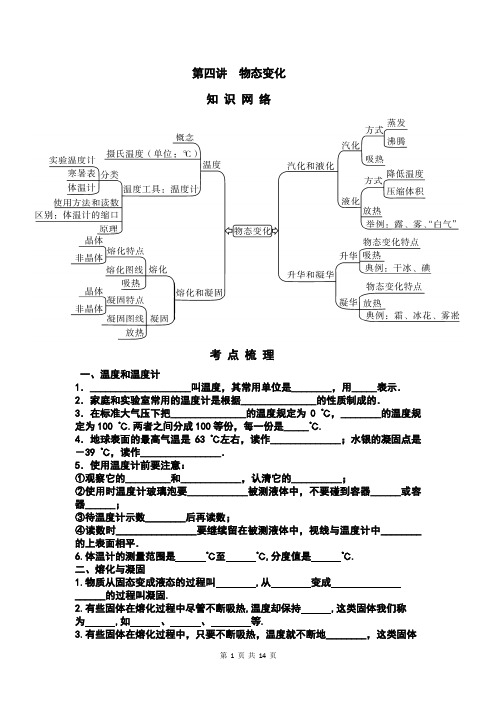
第四讲物态变化知识网络考点梳理一、温度和温度计1．____________________叫温度，其常用单位是________，用_____表示．2．家庭和实验室常用的温度计是根据_______________的性质制成的．3．在标准大气压下把_______________的温度规定为0 ℃，________的温度规定为100 ℃.两者之间分成100等份，每一份是_____℃.4．地球表面的最高气温是63 ℃左右，读作______________；水银的凝固点是－39 ℃，读作________________．5．使用温度计前要注意：①观察它的_________和____________，认清它的__________；②使用时温度计玻璃泡要____________被测液体中，不要碰到容器______或容器______；③待温度计示数________后再读数；④读数时________________要继续留在被测液体中，视线与温度计中________的上表面相平．6.体温计的测量范围是℃至℃,分度值是℃.二、熔化与凝固1.物质从固态变成液态的过程叫,从变成______的过程叫凝固.2.有些固体在熔化过程中尽管不断吸热,温度却保持,这类固体我们称为,如、、等.3.有些固体在熔化过程中，只要不断吸热，温度就不断地________，这类固体我们称为________，如________、________、________等．4.___________________叫熔点，________________________叫凝固点；同一种晶体的熔点和凝固点________．三、汽化和液化1．汽化：物质从________变为________的过程叫汽化，汽化的方式有________和________，都要________热．2．蒸发：是在________温度下，只在液体________发生的________的汽化现象．蒸发时要从周围吸收热量，使自身及周围的温度都________，故有________作用．3．沸腾：是在________温度下，在液体________和________同时发生的________的汽化现象．液体沸腾时要__________，但__________保持不变，这个温度叫________．4．影响液体蒸发快慢的因素：(1)液体______________；(2)液体______________；(3)液面__________________快慢．5．液化：物质从________变成________的过程叫液化，液化要______热．使气体液化的方法有______________和________．四、升华和凝华1．物质从固态直接变成气态的现象叫________，从______________________的现象叫凝华．2．衣柜里防虫用的樟脑球，过一段时间就变小甚至消失，这是一种________现象．3．北方秋、冬两季早晨出现霜，窗玻璃上出现冰花等现象，这些是________现象．4．升华是一个______热过程，有________作用，而凝华是一个______热过程．五、物态变化相互关系六、三个制冷作用1．蒸发吸热有制冷作用．例如：夏天在室内洒水可以降温．2．升华吸热有制冷作用．例如：用干冰人工降雨．3．熔化吸热制冷．例如：超市中用冰熔化吸热保鲜荔枝和海虾等．回归教材紧扣教材，复习教材，预习好帮手，回练教材变式题，精准高效备考！1．[人教版八上P47插图(沪粤版八上P82图4－2)改编]上课时，老师给同学们演示了一个实验，小明同学回家后，也动手做了一下这个实验．先把两手同时放入热水和冷水中，过了一段时间后，再将两手同时拿出并放入温水中，如图所示，这时两手的感觉________(选填“相同”或“不相同”)．这个事实说明__________________________．2．(人教版八上P58图 3.3－1改编)如图所示，在透明塑料袋中滴入几滴酒精，将袋挤瘪排尽袋中空气后把口扎紧，然后放入80 ℃以上的热水中，过一会儿，塑料袋鼓起，这是因为塑料袋里的酒精发生________(填物态变化名称)的缘故，此过程要______热．3．(人教版八上P60想想做做改编)纸的着火点约183 ℃，酒精灯火焰温度约500 ℃，吹风机吹出的热风温度约60 ℃.如图所示，用纸锅装些水．若用吹风机吹出的热风给纸锅加热，水________(选填“会”或“不会”)沸腾；若将纸锅放到酒精灯上加热，在水沸腾时，纸锅________(选填“会”或“不会”)燃烧．4．(人教版八上P61图3.3－5改编)如图所示，人游泳之后刚从水中出来，感觉特别冷；天热时，狗常把舌头伸出来．它们的共同之处在于水在________(选填“蒸发”或“沸腾”)过程中________(选填“吸热”或“放热”)，致使液体及与液体接触的物体温度下降．5．(人教版八上P62科学·技术·社会改编)如图是冰箱制冷剂循环路线示意图，制冷剂在冷冻室的管子里发生的物态变化名称是________，此过程________(选填“吸热”或“放热”)；夏天，打开冰箱时，可以看到从冰箱里冲出的“白气”，这是由水蒸气经过________(填物态变化的名称)产生的．6．(人教版八上P63动手动脑学物理1.改编)如图所示，盛一盆水，在盆里放两块高出水面的砖头，砖头上搁一只比盆小一点的篮子．篮子里有剩饭、剩菜，再把一个纱布袋罩在篮子上，并使布袋口的边缘浸入水中，就做成了一个简易冰箱．纱布袋口的边缘要浸入水里，这是利用水在________时________来降低温度；把这个简易冰箱放在通风的地方，里面的饭菜可以保持更长的时间不变质，这是因为_______________________________________．7．(人教版八上P66动手动脑学物理4.改编)小亮和同学做了一个小实验，如图所示，将冰块放于易拉罐中并加入适量的盐，用筷子搅拌大约半分钟，用温度计测量罐中冰与盐水混合物的温度，可以看到混合物的温度低于0 ℃.这时观察到易拉罐的下部和底部出现了白霜，这是空气中的水蒸气________(填物态变化名称)产生的．考点突破考点1:温度和温度计(高频考点)在本考点中温度计的读数是考查重点．复习时应注意：(1)普通温度计的工作原理是液体的热胀冷缩．(2)使用温度计测量液体温度时，先要弄清楚温度计的量程和分度值．(3)使用时玻璃泡要与被测物体充分接触，测量液体温度时要注意玻璃泡不能碰到杯底或者杯壁．(4)读数时普通温度计不能脱离被测物体，且视线与温度计中液柱的上表面相平，并注意区分温度是零上还是零下．(5)如果是体温计，使用前要甩一甩，让液体都回到玻璃泡中才能开始测量，如果没有做这一步，体温计不能测量比原示数低的温度；体温计的玻璃泡上方有一个弯曲的细管，使温度计能离开被测量物体进行读数．【课标重点例题指引】例1.观察生活中常见的温度计，了解它们的使用方法和测温范围．【对点训练】常用温度计是根据液体______________的规律制成的．图中________(选填“甲”或“乙”)是体温计，测量体温时，体温计________(选填“可以”或“不可以”)离开人体读数．1.常用的温度计是根据液体的______________原理制成的，如图所示是温度计的一段截面图，读数是________℃.2．据图回答下列问题：实验室里常用的液体温度计是根据________________的规律制成的，如图所示，液体温度计测量液体温度时，操作正确的是________图．拓展:若图中是测正在用酒精灯加热的液体的温度，测得的数值比液体实际温度高的图是________，测得的数值比液体实际温度低的图是______．3．如图所示为体温计和寒暑表的一部分，其中体温计的读数是_______℃.拓展：另一温度计的读数是______℃.考点2:熔化与凝固(高频考点)技巧点拨:(1)熔化和凝固的图象是考查的重点.①熔化图象,包括晶体熔化图象和非晶体熔化图象.两者的区别在于:晶体熔化过程是先升温达到熔点后,开始熔化温度保持不变,熔化完后继续升温;非晶体是边升温边熔化,没有温度保持不变的过程.(如下图所示)②凝固图象,是熔化图象的相反过程.晶体凝固时先降温达到凝固点,凝固放热,温度不变,凝固完后继续降温;非晶体边凝固边降温,没有温度保持不变的过程.(如上图所示)各图象中,平行于时间坐标的线段对应的是熔化或凝固过程,线段对应的温度是熔点或凝固点;同一晶体物质的熔点和凝固点相同,晶体物质在熔点温度时可能是固态、液态或固液共存状态.(2)常见的晶体和非晶体:晶体:冰、海波、食盐、水晶、明矾、各种金属;非晶体:松香、玻璃、蜂蜡、沥青.1.晶体在熔化的过程中需要不断从外界________，温度________；钨的熔点是3 410 ℃，它的凝固点是________℃.2.下列对如图所示图象的说法正确的是( )A．可能是海波凝固时的温度变化曲线B．可能是松香熔化时的温度变化曲线C．可能是萘熔化时的温度变化曲线D．可能是沥青熔化时的温度变化曲线3.如图所示是某物质的熔化图象，由此判断该物质是________(选填“晶体”或“非晶体”)．拓展：该晶体的熔点为________℃.4.如图所示，加热－10 ℃的冰，下列说法正确的是( )A．BC段表示当前物体的状态仍是固体B．冰的熔化过程温度不变，说明熔化不需要吸热C．水的沸腾过程温度不变，说明它的内能不变D．由图可判断，加热时间相同时冰升温比水快，说明冰的比热容比水小拓展:(1)AB段物体处于________，BC段物体处于______________，CD段物体处于________(均选填“固态”“液态”或“固液共存态”)．(2)晶体在熔化时，温度________(选填“升高”“降低”或“不变”)，需要________(选填“吸热”或“放热”)，内能________(选填“增大”“减少”或“不变”)．考点3:汽化与液化(高频考点)技巧点拨:(1)汽化与液化现象的判断是考查重点也是热点,要求了解生活中常见的汽化和液化现象.(2)汽化的两种方式:蒸发和沸腾.(3)影响液体蒸发快慢的因素:①液体表面积的大小;②液体温度的高低;③液面空气流动的快慢.将物体摊开(液体表面积变大),晒在向阳处(液体温度较高)、通风(液面空气流动快)的地方,物体更易干;若需减慢液体的蒸发则反之,如:将蔬菜装进保鲜袋,扎紧袋口,放进冰箱中,可减慢水分蒸发,使蔬菜保持新鲜.【课标重点例题指引】例3.运用物态变化的知识，说明冰熔化、水沸腾等现象．【对点训练】请解释以下生活中的热现象：皮肤涂上酒精后觉得凉快是因为酒精________(填物态变化名称)时从人体吸热；夏天吃冰棒时看见冰棒冒“白气”是冰棒周围空气中的________遇冷液化形成的小水珠所致，在海拔高的地方烧开水时水温不到100 ℃就开始沸腾，原因是水的沸点随________减小而降低．1．在探究蒸发快慢与哪些因素有关的实验中，如图主要用来探究( )A ．蒸发的快慢与液体的温度的关系B ．蒸发的快慢与气压的关系C ．蒸发的快慢与液体表面积的关系D ．蒸发的快慢与空气流动的关系2.将装有水的试管放入装有水的烧杯中，用酒精灯对烧杯进行加热，如图所示，一段时间后，观察到烧杯中的水沸腾，而试管汽化方式 蒸发 沸腾 不同点发生部位 只在液体表面发生 在液体表面和内部同时发生 温度条件任何温度下 都可能发生 在一定温度(沸点)下 才会发生 剧烈程度缓慢 剧烈 温度变化降温制冷 吸收热量，温度保持不变 (等于沸点) 相同点 都属于汽化现象，都要吸热中的水________(选填“会”或“不会”)沸腾，原因是_________________________，同时还观察到烧杯口周围出现大量的“白气”，这是由烧杯中的水蒸气在杯口周围遇冷________(填物态变化名称)形成的．3.夏日炎炎，小东从开着空调的屋内刚走到室外时，眼镜的镜片变模糊是由空气中的水蒸气______所致；他在游泳池游泳后走上岸感觉到有点冷，是由身上的水__________吸热所致；他买了冰棒含在嘴里，过了一会儿感觉到凉快，是由冰棒_______吸热所致．(均填物态变化名称)考点4:升华与凝华(高频考点)技巧点拨:(1)本考点考查的重点是生活中常见的升华和凝华现象.(2)自然界中的云、雨、雪、雾、霜等现象,都是水的物态变化形成的,是学习的难点.①冰是水凝固形成的.②露是在天气较热的时候,空气中的水蒸气于清晨前遇到温度较低的树叶、花草等,液化成小水珠附着在它们的表面上,这是一种液化现象.③雾是水蒸气在空气中遇冷液化成为小水珠,这些小水珠悬浮在地面附近的空气中,因此雾是水蒸气的液化现象.④云是水蒸气升到高空遇到冷气流液化成为小水珠或凝华成小冰晶,悬浮在空气中,因此云包括水蒸气的液化和凝华现象.⑤霜和雪都是水蒸气的凝华现象.霜是地表面的水蒸气在零摄氏度以下的温度条件下直接凝华为固体;雪是天气较冷的时候,空气的温度低于零摄氏度,水蒸气在空中凝华成固态,为六角形的冰晶(或叫雪花),在飘降时相互结合形成雪片或雪团.⑥雹是冰球,它的形成较复杂,云中的水珠被上升气流带到气温低于0 ℃的高空,凝结为小冰珠,小冰珠在下落时,其外层受热熔化成水,并彼此相结合,使冰珠越来越大,如果上升气流很强就会再升入高空,在其表面凝结一层冰壳.经过多次上下翻腾,能结合成较大的冰珠,当上升气流托不住它时,冰珠就落到地面上,形成冰雹.⑦雾凇和霜都是由水蒸气遇冷直接凝华成的小冰晶.类似的还有寒冷的冬天,我国北方一些地区,在窗玻璃上常常出现的冰花.1．一提到“雾凇”，许多人总会联想到东北地区，其实甘肃省的一些地区也会遇到这个现象．如图为天水出现的“雾凇”，下列说法正确的是( )A．雾凇是由空气中的水蒸气遇冷液化形成的B．雾凇和冰的形成过程一样C．雾凇是由空气中的水蒸气遇冷凝华形成的D．雾凇形成的过程中需要吸收热量2．四季分明的临沂有许多美丽的自然现象．下列现象由于凝华形成的是( ) 3．下列物态变化中，吸热的是( )4．人工降雨的方式之一是将干冰投撒到云层中，干冰________(选填“升华”“熔化”或“凝华”)时从周围吸收大量的热，使空气中的水蒸气液化成小水滴形成雨．我国大型客机C919，飞机上装有3D打印的钛合金零件，3D打印技术就是在高能激光的作用下，钛合金粉末会________(填物态变化名称)成液态，然后成型．考点5:综合能力拓展阅读短文,回答问题.防冻冷却液汽车行驶时,发动机的温度会升得很高,利用防冻冷却液在散热器管道内循环流动,将发动机多余内能带走,使发动机能以正常工作温度运转.防冻冷却液主要由水和不易汽化、密度比水小的某种防冻剂(简称原液)混合而成,原液含量(防冻剂占防冻冷却液体积的比例)越高,防冻冷却液的比热容越小,防冻冷却液的凝固点和沸点与原液含量的关系图象如图2和图3所示.选用时,防冻冷却液的凝固点应低于环境最低温度10 ℃以下,而沸点一般要高于发动机最高工作温度5 ℃以上.(1)若用水代替防冻冷却液，在北方寒冷的冬天，停车时间比较长，会因水结冰容易导致散热器管道胀裂，为什么？因为当水结冰时，____________，所以会把散热器管道胀裂．(2)设某品牌汽车的发动机工作温度为90～101 ℃，所在地区最低温度为－17 ℃，应选用何种较合适比例的防冻冷却液：______(选填“35%”“45%”“55%”或“65%”)，简述选用理由：____________________________________________________________________ (3)现有原液含量为75%的防冻冷却液长时间使用后，由于汽化会减少，与原来相比，防冻冷却液的哪些物理量发生了什么变化，如何变化？(示例：体积变小) ①___________，②_____________，③___________，④_____________，⑤___________．实验一探究固体熔化时温度的变化规律【实验设计】(1)测量的物理量：温度和加热时间．(2)器材和装置：将铁架台、酒精灯、石棉网、烧杯、水、试管、温度计和药品，按如图所示安装．特别容易遗漏的器材是停表．(3)实验中要将药品(如冰块)尽可能弄碎，这样药品受热更均匀．【实验分析】(4)利用“水浴法”加热，不但能使试管受热更均匀，而且物质的温度上升速度较慢，便于及时记录各个时刻的温度．(5)在晶体熔化过程中，试管中的药品是固液混合的状态．【实验结论】(6)晶体熔化时有一定的温度，即熔点，而非晶体没有熔点．晶体熔化时要持续吸热，但温度保持不变；非晶体熔化时要吸热，物质先变软再变稠，然后再变稀，温度一直升高．1.如图甲是“探究海波熔化时温度的变化规律”的实验装置．(1)如图乙温度计的示数为________℃.(2)如图丙是根据实验数据描绘出的海波温度随时间变化的图象．海波熔化过程重点实验突破对应图线中的________段(选填“AB”或“BC”)，其熔点为________℃.熔化过程中海波吸收的热量________放出的热量(选填“大于”“小于”或“等于”)．(3)用质量为m1的海波做实验，绘制的海波温度随时间变化的图线如图丁中的a 所示．若用质量为m2(m2＞m1)的海波重复实验，得到的图线可能是图丁中的_____(选填“b”“c”或“d”)．拓展：(1)安装器材时，要按___________(选填“从上到下”或“从下到上”)的顺序安装．(2)实验中的固体海波颗粒要______(选填“大”或“小”)一些，这样做的目的是：____________________.2.学习小组的同学用如图甲所示的装置探究某种晶体熔化时温度变化的规律．(1)图甲中的器材组装有一不当之处是_________________________________．实验中使晶体受热均匀的措施是_____________(写出一条即可)．(2)待温度升高到40 ℃开始，每隔1min记录一次温度计的示数，根据记录的数据得到如图乙的图象，则该晶体的熔点是______℃，熔化经历了_____min，该物质在固态时的比热容________(选填“大于”“小于”或“等于”)液态时的比热容．(3)另一小组的同学发现，在晶体熔化过程中撤去酒精灯，晶体还会继续熔化，原因是晶体可以继续________(选填“吸收”或“放出”)热量．实验二探究水沸腾时温度变化的特点【实验设计】(1)测量的物理量：温度和加热时间．(2)器材和装置：将铁架台、酒精灯、石棉网、烧杯、适量的水、温度计，按如图所示安装．特别容易遗漏的器材是停表．(3)实验中为了缩短实验时间可以采取的措施有：在烧杯口加盖、提高水的初始温度和减少水的质量．其中“适量的水”通常指水恰能浸没温度计的玻璃泡，且温度计的玻璃泡没有碰到烧杯底．(4)在刚撤去酒精灯时，水并没有立即停止沸腾，并不是因为水不需要吸热也可以沸腾，而是此时铁圈、石棉网等的温度仍高于水的沸点，水可以从中吸热沸腾．(5)水沸腾时虽不断吸热，但温度却保持不变，水沸腾时的温度就是水的沸点．在一个标准大气压下，水的沸点为100 ℃，气压越高，沸点越高；气压越低，沸点越低．在高山上煮鸡蛋煮不熟，就是因为海拔越高，气压越低，沸点就越低；压力锅利用增大气压从而提高沸点的原理工作．【实验分析】(6)水的沸点的判断：水的温度升高到一定程度后，温度保持不变，水中有大量气泡产生，此时水的温度就是水的沸点．【实验结论】(7)水在沸腾过程中不断吸热，但温度保持不变1.在“探究水的沸腾”实验中，如图甲所示．(1)此实验加热过程是通过____________(选填“做功”或“热传递”)的方式来增大烧杯中水的内能的．(2)下表是加热过程中不同时刻水的温度记录，其中有一个记录错误的实验数据，请指出该错误的数据是______，这样判断的理论依据是______________________________________.时间/min 0 1 2 3 4 5 6 7 8温度/℃90 92 94 96 98 98 95 98 98要原因是当地的大气压_____________________．(4)请根据表格的正确数据在图乙中画出水加热直至沸腾时温度随时间变化的图象．拓展：(1)为了节省时间，常常在烧杯上方加盖____________(选填“一张纸板”或“密封盖子”)．(2)在水沸腾后，将酒精灯撤掉时，会观察到水继续沸腾一会儿，原因是：_________________________________________.2．图甲是探究“水的沸腾”的实验装置．(1)安装实验器材时，应按照___________(选填“自下而上”或“自上而下”)的顺序进行．(2)A、B、C三种读数方法正确的是______(选填字母)．(3)由图乙可知，水的沸点是______℃.水沸腾过程中不断吸热，温度__________(选填“升高”“降低”或“保持不变”)．(4)实验器材中纸板的作用：____________________________、____________________________________________________________．(5)实验结束后，移开酒精灯，发现烧杯内的水没有立即停止沸腾，可能的原因是______________________________________________．重难点突破1．温度计和体温计读数．方法点拨：温度计的分度值是1 ℃，体温计的分度值是0.1 ℃；温度计读数前要弄清测量温度是0 ℃以上还是0 ℃以下．【例1】读出下列温度计或体温计的读数．图1：________ ；图2：________ ；图3：________．2．物态变化及吸、放热情况判断方法点拨:沿固态→液态→气态方向变化的物态变化要吸热;沿气态→液态→固态方向变化的物态变化要放热.【例2】下列物态变化都需要吸热的是( )A．凝固、液化、凝华 B．熔化、液化、凝华C．液化、汽化、升华 D．熔化、汽化、升华【例3】下列现象需要放热的物态变化是( )A．衣柜里的樟脑丸变小了B．冰雪消融C．夏天洒在地板上的水很快干了D．秋天雾的形成3．关于“白气”的形成分析方法点拨：冷的物体周围产生的“白气”或附着的小水珠，是空气中的水蒸气液化而成的；热的物体产生的“白气”，是热的物体中的水分先汽化产生水蒸气，这些水蒸气上升到空气中遇冷液化而成的．【例4】雪糕是大家都喜爱吃的冷饮,雪糕冒出的“白气”符合实际的是如图中,这些“白气”是而形成的;在家里水烧开时,会看见壶嘴冒出“白气”,这些“白气”是而形成的.。

定义新运算之速算与巧算定义新运算：是指用一个符号和已知运算表达式来表示一种新的运算。

例如：如规定：a⊗b=ab+a-b2⊗4=2⨯4+2-4=64⊗2=4⨯2+4-2=10定义新运算一般分为两种：⑴根据题目给的新的运算法则，进行运算，即从前往后推；⑵已知运算结果和运算法则，推出前面的数，即从后往前推。

实质：定义新运算这类题目是在考验我们的适应能力，我们大家都习惯四则运算，定义新运算就打破了运算规则，要求我们要严格按照题目的规定做题。

新定义的运算符号：常见的如△、◎、※等等，这些特殊的运算符号，表示特定的意义，是人为设定的。

解题关键：理解新定义，严格按照新定义的式子代入数值，把定义的新运算转化成我们所熟悉的四则运算。

【例1】设a△b=a⨯a-2⨯b，那么，5△6=_______，(5△2)△3=_______。

【拓展】设m、n是两个数，规定：m* n=4⨯n-(m+n)÷2，这里“⨯，+，-，÷”是通常的四则运算符号，括号的作用也是通常的含义，“ * ”是新的运算符号。

计算：3 * (4 * 6)=_______。

【例2】如果a□=a⨯(a+1)，a□□=a□⨯(a□+1)，…，那么1□□□=_________。

【拓展】P、Q表示数，P * Q表示(P+Q)÷2，求3 * (6 * 8)。

【例3】小明来到红毛族探险，看到下面几个红毛族的算式：8⨯8=8，9⨯9⨯9=5，9⨯3=3，(93+8)⨯7=837。

老师告诉他，红毛族算术中所用的符号“+、-、⨯、÷、( )、=”与我们算术中的意义相同，进位也是十进制，只是每个数字虽然与我们写法相同，但代表的数却不同。

请你按红毛族的算术规则，完成下面算式：89⨯57=___________。

【拓展】一个特殊的计算器上面有个“X *”键，当计算器上显示的数是a 时，按一下“X *”键后，计算器上的a 立刻消失并显示一个新数2a +1。

科组长签名：教师姓名 学生姓名 填写时间2013.8.1 年级 初一 学科 数学 上课时间2013-08-108:00-10:00 阶段 基础（ ） 提高（√）强化（ ） 课时计划第（ ）次课共（ ）次课教学目标1、掌握绝对值大于10的有理数的科学记数法。

2、掌握有理数混合运算法则，并能熟练地进行有理数加、减、乘、除、乘方的混合运算，能合理运用运算律简化运算。

重难点1、能正确使用科学记数法。

2、理解并掌握有理数的混合运算律，能进行熟练运算。

课后作业： 完成课后作业教师评语及建议：有理数（三）知识点梳理1．有理数混合运算法则：（1）先算 ，再算 ，最后算 ； （2）同级运算，按照 的顺序进行；（3）如果有括号，就先算 里的，再算 里的，最后算 里的。

2．在有理数计算中要学会灵活运用运算律（包括加法 、加法 、乘法 、乘法 、乘法 ），进行简便运算。

3．科学记数法：把一个大于10的数记成a ×10n的形式；其中a 是整数数位只有____位的数，即a 的取 值范围为 。

经典例题例1、计算：()[]⎪⎭⎫⎝⎛-÷+-⨯-⨯--328533835232解：原式＝变式练习1：计算：222192411124⎛⎫-+-----÷ ⎪⎝⎭解：原式＝例2、计算：()714139-⨯，看谁算得又对又快，一名同学给出的解法如下： ()21692139714139-=-=-⨯= 另一名同学给出的解法如下： ()()()21697141379714139-=-⨯+-⨯=-⨯⎪⎭⎫ ⎝⎛+= 此题还有其它解法吗？如果有，用另外的方法把它解出来？变式练习2：计算： （1）⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-+-241413221； （2） ()()()778161592-÷---⨯⎪⎭⎫ ⎝⎛-例题3：用科学记数法表示：（1）12340000＝ ，123.4＝ ，-12340000＝ ； （2）2.653×107的原数是 。

卫生部办公厅关于抗菌药物临床应用管理有关问题的通知卫办医政发〔2009〕38号各省、自治区、直辖市卫生厅局,新疆生产建设兵团卫生局:《卫生部办公厅关于进一步加强抗菌药物临床应用管理的通知》(卫办医发〔2008〕48号)下发以来,各级卫生行政部门和医疗机构认真组织学习、贯彻落实,取得了一定的成效,部分地区医疗机构抗菌药物应用比例有所下降,围手术期抗菌药物预防应用进一步规范。

为继续推进抗菌药物临床合理应用,根据2008年度全国抗菌药物临床应用监测与细菌耐药监测结果,现就抗菌药物临床应用管理有关问题通知如下:一、以严格控制Ⅰ类切口手术预防用药为重点,进一步加强围手术期抗菌药物预防性应用的管理医疗机构要严格按照《抗菌药物临床应用指导原则》中围手术期抗菌药物预防性应用的有关规定,加强围手术期抗菌药物预防性应用的管理,改变过度依赖抗菌药物预防手术感染的状况。

对具有预防使用抗菌药物指征的,参照《常见手术预防用抗菌药物表》(见附件)选用抗菌药物。

也可以根据临床实际需要,合理使用其他抗菌药物。

医疗机构要重点加强Ⅰ类切口手术预防使用抗菌药物的管理和控制。

I类切口手术一般不预防使用抗菌药物,确需使用时,要严格掌握适应证、药物选择、用药起始与持续时间。

给药方法要按照《抗菌药物临床应用指导原则》有关规定,术前0.5-2小时内,或麻醉开始时首次给药;手术时间超过3小时或失血量大于1500ml,术中可给予第二剂;总预防用药时间一般不超过24小时,个别情况可延长至48小时。

二、严格控制氟喹诺酮类药物临床应用医疗机构要进一步加强氟喹诺酮类药物临床应用管理,严格掌握临床应用指征,控制临床应用品种数量。

氟喹诺酮类药物的经验性治疗可用于肠道感染、社区获得性呼吸道感染和社区获得性泌尿系统感染,其他感染性疾病治疗要在病情和条件许可的情况下,逐步实现参照致病菌药敏试验结果或本地区细菌耐药监测结果选用该类药物。

应严格控制氟喹诺酮类药物作为外科围手术期预防用药。

第四讲三种力第一模块：力的的概念及常见的三种力一．力的定义及性质⑴物质性：力是不能脱离物体而独立存在的，任意一个力必然与两个物体密切相关，一个是其施力物体，另一个是其受力物体。

⑵矢量性：力不仅有大小，而且有方向。

⑶瞬时性：是力与其作用效果是在同一瞬间产生的。

⑷独立性：指的是某个力的作用效果与其它力是否存在毫无关系，只由该力的三要素来决定。

⑸相互性：物体在施力的同时，也是受力物体。

总成对出现（作用力与反作用力）总是“等值、反向、共线、同生、同灭、同性”。

①按性质分类：重力、弹力、摩擦力、分子力、电磁力、核力、安培力等②按效果分类：拉力、压力、支持力、动力、阻力、向心力、浮力、回复力等【说明】：性质不同的力可能有相同的效果，效果不同的力也可能是性质相同的。

动状态．A、瞬时效应：使物体产生加速度F=maB、时间积累效应：产生冲量I=Ft，使物体的动量发生变化Ft=△pC、空间积累效应：做功W=Fs，使物体的动能发生变化W=△E k(使质量为1千克的物体产生1米／秒2加速度力的大小为1牛顿)二．重力重力是由于地球的吸引而使物体受到的力。

【说明】：重力是由于地球的吸引而产生的力，但它并不就等于地球时物体的引力．重力是地球对物体的万有引力的一个分力，另一个分力提供物体随地球旋转所需的向心力。

由于物体随地球自转所需向心力很小，所以计算时一般可近似地认为物体重力的大小等于地球对物体的引力。

在地球表面近似有：mg，①在地球表面Nkgg/8.9≈②随着纬度升高，g值增大，赤道上g值最小。

③随高度升高，g 值减小，g r GM '=2。

（说明：不可说成“指向地心”）为了研究问题简单，我们认为一个物体的重力集中作用在物体的一点上，这一点称为物体的重心．【说明】⑴实际上物体的各个部分都受到重力。

⑵“认为”重力集中在一点，是一种等效模型。

⑶重心可以不在物体上，如木工尺。

⑷质量分布均匀且形状规则物体的重心才会在物体的几何中心．否则用“悬挂法”确定位置。

第四讲 四点共圆问题“四点共圆”问题在数学竞赛中经常出现，这类问题一般有两种形式：一是以“四点共圆”作为证题的目的，二是以“四点共圆”作为解题的手段，为解决其他问题铺平道路.判定“四点共圆”的方法，用得最多的是统编教材《几何》二册所介绍的两种（即P 89定理和P 93例3），由这两种基本方法推导出来的其他判别方法也可相机采用. 1 “四点共圆”作为证题目的例1．给出锐角△ABC ，以AB 为直径的圆与AB 边的高CC ′及其延长线交于M ，N .以AC 为直径的圆与AC 边的高BB ′及其延长线将于P ，Q .求证：M ，N ，P ，Q 四点共圆.(第19届美国数学奥林匹克)分析：设PQ ，MN 交于K 点，连接AP ，AM .欲证M ，N ，P ，Q 四点共圆，须证 MK ·KN ＝PK ·KQ ，即证(MC ′-KC ′)(MC ′+KC ′) ＝(PB ′-KB ′)·(PB ′+KB ′)或MC ′2-KC ′2=PB ′2-KB ′2 . ①不难证明 AP =AM ，从而有 AB ′2+PB ′2=AC ′2+MC ′2. 故 MC ′2-PB ′2=AB ′2-AC ′2ABCK M NPQ B ′C ′=(AK 2-KB ′2)-(AK 2-KC ′2)=KC ′2-KB ′2. ②由②即得①，命题得证.例2．A 、B 、C 三点共线，O 点在直线外，O 1，O 2，O 3分别为△OAB ，△OBC ， △OCA 的外心.求证：O ，O 1，O 2， O 3四点共圆.(第27届莫斯科数学奥林匹克)分析：作出图中各辅助线.易证O 1O 2垂直平分OB ，O 1O 3垂直平分OA .观察△OBC 及其外接圆，立得∠OO 2O 1=21∠OO 2B =∠OCB .观察△OCA 及其外接圆，立得∠OO 3O 1=21∠OO 3A =∠OCA .由∠OO 2O 1=∠OO 3O 1 O ，O 1，O 2，O 3共圆.利用对角互补，也可证明O ，O 1，O 2，O 3四点共圆，请同学自证.2 以“四点共圆”作为解题手段这种情况不仅题目多，而且结论变幻莫测，可大体上归纳为如下几个方面. (1)证角相等例3．在梯形ABCD 中，AB ∥DC ，AB ＞CD ，K ，M 分别在AD ，BC 上，∠DAM ＝∠CBK .A BCOO O O 123？？求证：∠DMA ＝∠CKB .（第二届袓冲之杯初中竞赛）分析：易知A ，B ，M ，K 四点共圆.连接KM ，有∠DAB ＝∠CMK .∵∠DAB +∠ADC ＝180°，∴∠CMK +∠KDC ＝180°.故C ，D ，K ，M 四点共圆 ∠CMD ＝∠DKC . 但已证∠AMB ＝∠BKA ， ∴∠DMA ＝∠CKB .(2)证线垂直例4．⊙O 过△ABC 顶点A ，C ，且与AB ， BC 交于K ，N (K 与N 不同).△ABC 外接圆和△BKN 外接圆相交于B 和 M .求证：∠BMO =90°. (第26届IMO 第五题)分析：这道国际数学竞赛题，曾使许多选手望而却步.其实，只要把握已知条件和图形特点，借助“四点共圆”，问题是不难解决的. 连接OC ，OK ，MC ，MK ，延长BM 到G .易得∠GMC =∠BAC =∠BNK =∠BMK .而∠COK =2·∠BAC =∠GMC +A BC D K M ··ABO K N CMG∠BMK =180°-∠CMK ，∴∠COK +∠CMK =180°⇒C ，O ，K ，M 四点共圆. 在这个圆中，由OC =OK ⇒ OC =OK ⇒∠OMC =∠OMK . 但∠GMC =∠BMK ， 故∠BMO =90°. (3)判断图形形状例5．四边形ABCD 内接于圆，△BCD ，△ACD ，△ABD ，△ABC的内心依次记为I A ，I B ，I C ，I D .试证：I A I B I C I D 是矩形.(第一届数学奥林匹克国家集训选拔试题) 分析：连接AI C ，AI D ，BI C ，BI D 和DI B .易得∠AI C B =90°+21∠ADB =90°+21 ∠ACB =∠AI D B ⇒A ，B ，I D ，I C 四点 共圆.同理，A ，D ，I B ，I C 四点共圆.此时 ∠AI C I D =180°-∠ABI D =180°-21∠ABC ， ∠AI C I B =180°-∠ADI B =180°-21∠ADC ， ABCDI C I DAI I B∴∠AI C I D +∠AI C I B =360°-21(∠ABC +∠ADC ) =360°-21×180°=270°. 故∠I B I C I D =90°.同样可证I A I B I C I D 其它三个内角皆为90°.该四边形必为矩形. (4)计算例6．正方形ABCD 的中心为O ，面积为1989㎝2.P 为正方形内一点，且∠OPB =45°，P A :PB =5:14.则PB =__________ (1989，全国初中联赛)分析：答案是PB =42㎝.怎样得到的呢？连接OA ，OB .易知O ，P ，A ，B四点共圆，有∠APB =∠AOB =90°. 故P A 2+PB 2=AB 2=1989. 由于P A :PB =5:14，可求PB . (5)其他例7．设有边长为1的正方形，试在这个正方形的内接正三角形中找出面积最大的和一个面积最小的，并求出这两个面积(须证明你的论断).··P OA BCD(1978，全国高中联赛)分析：设△EFG 为正方形ABCD 的一个内接正三角形，由于正三角形的三个顶点至少必落在正方形的三条边上，所以不妨令F ，G 两点在正方形的一组对边上. 作正△EFG 的高EK ，易知E ，K ，G ，D 四点共圆⇒∠KDE =∠KGE =60°.同 理，∠KAE =60°.故△KAD 也是一个正 三角形，K 必为一个定点.又正三角形面积取决于它的边长，当KF 丄AB 时，边长为1，这时边长最小，而面积S =43也最小.当KF 通过B 点时，边长为2·32-，这时边长最大，面积S =23-3也最大. 例8．NS 是⊙O 的直径，弦AB 丄NS 于M ，P 为ANB 上异于N 的任一点，PS 交AB 于R ，PM 的延长线交⊙O 于Q .求证：RS ＞MQ .(1991，江苏省初中竞赛)分析：连接NP ，NQ ，NR ，NR 的延长线交⊙O 于Q ′.连接MQ ′，SQ ′.易证N ，M ，R ，P 四点共圆，从而，∠SNQ ′=∠MNR =∠MPR =∠SPQ =∠SNQ .根据圆的轴对称性质可知Q 与Q ′关于NS 成轴对称⇒MQ ′=MQ .A BCDEF KG ······又易证M，S，Q′，R四点共圆，且RS是这个圆的直径(∠RMS=90°)，MQ′是一条弦(∠MSQ′＜90°)，故RS ＞MQ′.但MQ=MQ′，所以，RS＞MQ.练习题1.⊙O1交⊙O2于A，B两点，射线O1A交⊙O2于C点，射线O2A交⊙O1于D点.求证：点A是△BCD的内心.(提示：设法证明C，D，O1，B四点共圆，再证C，D，B，O2四点共圆，从而知C，D，O1，B，O2五点共圆.)2.△ABC为不等边三角形.∠A及其外角平分线分别交对边中垂线于A1，A2；同样得到B1，B2，C1，C2.求证：A1A2=B1B2=C1C2.(提示：设法证∠ABA1与∠ACA1互补造成A，B，A1，C四点共圆；再证A，A2，B，C四点共圆，从而知A1，A2都是△ABC的外接圆上，并注意∠A1AA2=90°.)3.设点M在正三角形三条高线上的射影分别是M1，M2，M3(互不重合).求证：△M1M2M3也是正三角形.4.在Rt△ABC中，AD为斜边BC上的高，P是AB上的点，过A 点作PC的垂线交过B所作AB的垂线于Q点.求证：PD丄QD.(提示：证B，Q，E，P和B，D，E，P分别共圆)5.AD，BE，CF是锐角△ABC的三条高.从A引EF的垂线l1，从B引FD的垂线l2，从C引DE的垂线l3.求证：l1，l2，l3三线共点.(提示：过B作AB的垂线交l1于K，证：A，B，K，C四点共圆)。

中华人民共和国卫生部公告(2009年第3号)
佚名
【期刊名称】《中华人民共和国卫生部公报》
【年(卷),期】2009(000)005
【总页数】2页(P21-22)
【正文语种】中文
【中图分类】R155.5
【相关文献】
1.中华人民共和国卫生部公告2009年第11号 [J],
2.中华人民共和国卫生部公告(2009年第10号) [J],
3.国家体育总局,中华人民共和国商务部,中华人民共和国卫生部,中华人民共和国海关总署,国家食品药品监督管理局公告第9号2009年兴奋剂目录公告 [J], ;;;;;
4.中华人民共和国卫生部公告2009年第14号 [J],
5.中华人民共和国卫生部公告2009年第19号 [J],
因版权原因，仅展示原文概要，查看原文内容请购买。

国家基本公共卫生服务规范（2009年版）2009年10月目录前言 (1)城乡居民健康档案管理服务规范 (2)健康教育服务规范 (23)0～36个月儿童健康管理服务规范 (27)孕产妇健康管理服务规范 (43)老年人健康管理服务规范 (52)预防接种服务规范 (54)传染病报告和处理服务规范 (59)高血压患者健康管理服务规范 (61)2型糖尿病患者健康管理服务规范 (66)重性精神疾病患者管理服务规范 (71)前言为贯彻落实卫生部、财政部、人口计生委联合印发的《关于促进基本公共卫生服务逐步均等化的意见》（卫妇社发…2009‟70号），规范国家基本公共卫生服务项目管理，卫生部在总结各地实施基本公共卫生服务项目经验的基础上，组织制定了《国家基本公共卫生服务规范（2009年版）》（以下简称《规范》）。

本《规范》分为10个类别，即：城乡居民健康档案管理、健康教育、0～36个月儿童健康管理、孕产妇健康管理、老年人健康管理、预防接种、传染病报告和处理、高血压患者健康管理、2型糖尿病患者健康管理、重性精神疾病患者管理。

在各项规范中，分别对国家基本公共卫生服务项目的服务对象、内容、流程、要求、考核指标及服务记录表单等作出了规定。

《规范》所列服务内容免费向城乡居民提供，其中部分检查项目鼓励有条件的地区开展，考核指标标准由各地根据本地实际情况自行确定。

各项公共卫生服务项目服务记录表单应纳入居民健康档案统一管理。

《规范》主要作为乡镇卫生院、村卫生室和社区卫生服务中心（站）等城乡基层医疗卫生机构为居民免费提供基本公共卫生服务项目的参考依据，其他医疗卫生机构提供国家基本公共卫生服务可参照执行。

《规范》所列公共卫生服务项目主要由乡镇卫生院和社区卫生服务中心负责组织实施，村卫生室、社区卫生服务站应分别接受乡镇卫生院、社区卫生服务中心的业务管理并合理承担公共卫生服务任务。

城乡基层医疗卫生机构开展国家基本公共卫生服务应接受各专业公共卫生机构的业务指导。