天津市天津一中11-12学年高二数学上学期期中考试试题 文

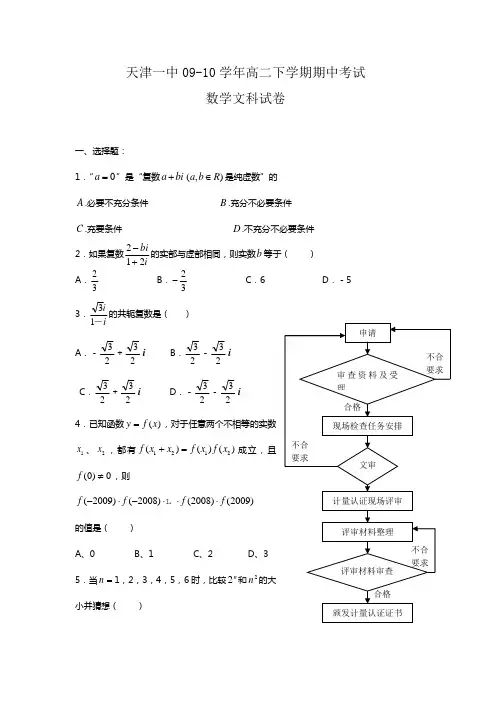
天津一中09-10学年高二下学期期中考试数学文科试卷一、选择题：1．“0a =”是“复数a bi +(,)a b R ∈是纯虚数”的A .必要不充分条件B .充分不必要条件C .充要条件D .不充分不必要条件2．如果复数ibi212+-的实部与虚部相同，则实数b 等于（ ） A ．32 B ．32- C ．6 D ．－53．ii－13的共轭复数是（ ） A ．－23＋23i B ．23－23i C ．23＋23i D ．－23－23i 4．已知函数()y f x =，对于任意两个不相等的实数1x 、2x ，都有1212()()()f x x f x f x +=成立，且(0)0f ≠，则 (2009)(2008)(2008)(2009)f f f f -⋅-⋅⋅⋅的值是（ ）A 、0B 、1C 、2D 、3 5．当=n 1，2，3，4，5，6时，比较n2和2n 的大小并猜想（ ）A 、1≥n 时，22n n >B 、3≥n 时，22n n >C 、4≥n 时，22n n >D 、5≥n 时，22n n >6．某市质量监督局计量认证审查流程图如图，可得在审查过程中可能不被通过审查的环节有（ ）处（A ）1 （B ）2 （C ）3 （D ）47．已知2()(1),(1)1()2f x f x f f x +==+ *x N ∈（），猜想(f x ）的表达式为 A.4()22x f x =+ B.2()1f x x =+ C.1()1f x x =+ D.2()21f x x =+8．某市政府调查市民收入增减与旅游欲望的关系时，采用独立性检验法抽查了3000人，计算发现K 2=6.023，则根据这一数据查阅下表，市政府断言市民收入培养与旅游欲望有关系的可信程度是（ ） A. 90% B. 95%C. 97.5%D. 99.5%9．两相关变量满足如下关系：D两变量回归直线方程（ ）A ．4.997ˆ56.0ˆ+=k yB ．2.231ˆ63.0ˆ-=k yC ．4.501ˆ2.50ˆ+=k yD ．7.400ˆ4.60ˆ+=k y10．如图,AB 是半圆O 的直径,点C 在半圆上,CD AB ⊥于点D ,且DB AD 3=,设COD θ∠=,则2tan 2θ＝( )A .13B .14C .4-D .3二、填空题11．如图，圆O 是ABC ∆的外接圆，过点C 的切线交AB 的延长线于点D ，CD =，3AB BC ==。

2024学年天津市南开中学高二数学上学期期中检测试卷考试时间：120分钟，试卷满分150分2024.11第I 卷（选择题共60分）一.单选题（共12小题，每小题5分，在每题列出的四个选项中，只有一项最符合题目要求）1.已知空间向量()(),1,0,21,1,1a b ==-，则下列结论正确的是（）A.向量a在向量b 上的投影向量是12,0,55⎛⎫- ⎪⎝⎭B.()0,1,3a b -=--C .a b ⊥D.cos ,15a b =2.已知直线l 经过点()1,2-，且与直线2310x y +-=垂直，则l 的方程为（）A.2340x y ++= B.2380x y +-= C.3270x y --= D.3210x y --=3.设圆224470x y x y +-++=上的动点P 到直线0x y +-=的距离为d ，则d 的取值范围是A.[]0,3 B.[]2,4 C.[]2,5 D.[]3,54.已知圆的方程为2220x y x +-=，(),M x y 为圆上任意一点，则21y x --的取值范围是（）A.⎡⎣B.[]1,1-C.(),-∞+∞D.(][),11,-∞-+∞5.已知点M ，椭圆2214x y +=与直线(y k x =+交于点,A B ，则ABM 的周长为（）A.4B.8C.12D.166.已知圆C 的圆心是直线10x y ++=与直线10x y --=的交点，直线34110x y +-=与圆C 相交于A ，B 两点，且6AB =，则圆C 的方程为（）A.()22118x y ++= B.()221x y +-=C.()22118x y -+= D.()221x y -+=7.已知圆22:2410C x y x y +-++=关于直线:3240l ax by ++=对称，则由点(,)M a b 向圆C 所作的切线中，切线长的最小值是（）A.2B.C.3D.8.已知,M N 分别是曲线1C ：222410x y x y ++-+=，2C ：226290x y x y +--+=上的两个动点，P 为直线220x y ++=上的一个动点，则||||PM PN +的最小值为（）A .3- B.3C.1- D.49.已知椭圆C ：2213620x y +=的左、右焦点分别为1F ，2F ，直线l ：y kx =与椭圆C 交于A ，B 两点，若122AF AF =，则1ABF ∆的面积是（）A. B. C.8D.410.设双曲线224x y -=的焦点为1F ，2F ，点P 在双曲线右支上，且1290F PF ︒∠=，则点P 的横坐标为（）A.B.2C.D.611.如图，1F ，2F 分别是双曲线22221x y a b-=（0a >，0b >）的左、右焦点，且()1F ，过1F 的直线l 与双曲线的左、右两支分别交于点A ，B ．若2ABF △为等边三角形，则双曲线的方程为（）A.22551728x y -= B.2216x y -= C.2216y x -= D.22551287x y -=12.已知椭圆的两焦点1F ，2F 和双曲线的两焦点重合，点P 为椭圆和双曲线的一个交点，且121cos 4F PF ∠=，椭圆和双曲线的离心率分别为1e ，2e ，则2212e e +的最小值为（）A.1514+B.2C.14D.4第II 卷（非选择题共90分）二.填空题（共8小题，每小题5分）13.过点()2,1-且方向向量为()1,2的直线的方程为___________．14.已知圆C 的圆心在直线x ＋y ＝0上，圆C 与直线x －y ＝0相切，且在直线x －y －3＝0上截得的弦长，则圆C 的方程为________．15.已知圆22460x y x y +--=，则过点()1,1M 的最短弦所在的直线方程是_________.16.已知()2,1,3a →=-，()3,4,2b →=-，()7,,5c λ→=，若,,a b c →→→共面，则实数λ=______．17.椭圆221369x y +=的一条弦被点(4,2)A 平分,那么这条弦所在的直线方程是________.18.双曲线22221x y a b-=的其中一条渐近线方程为2y x =，且焦点到渐近线的距离为2，则双曲线的方程为_______19.已知双曲线22221(0,0)x y a b a b-=>>的渐近线被圆22650x y x +-+=截得的弦长为2，则该双曲线的离心率为__________．20.已知F 1､F 2为双曲线2222x y a b-=1(a >0，b >0)的左､右焦点，过F 2作倾斜角为60°的直线l 交双曲线右支于A ，B 两点(A 在x 轴上方)，则12AF F △的内切圆半径r 1与12BF F △的内切圆半径r 2之比12r r 为___________.三.解答题（共4小题，共50分）21.如图，在正四棱柱1111ABCD A B C D -中，底面边长为2，高为4．（1）求1A B 与1AD 所成角的余弦值；（2）1CC 与平面1ACD 所成角的正弦值．22.已知椭圆()2222:10x y E a b a b+=>>的离心率为2，焦距为2.（1）求椭圆E 的方程；（2）设O 为坐标原点，过左焦点F 的直线l 与椭圆E 交于A ，B 两点，若OAB ∆的面积为23，求直线l 的方程.23.如图，三棱柱111ABC A B C -中，1AA ⊥平面1,,2,4ABC AB AC AB AA AC ⊥===，M 是1CC 的中点，N 是1A B 的中点．（1）求证：1C N ∥平面ABM ；（2）求直线1AC 与平面ABM 所成角的正弦值；（3）求平面ABM 与平面1A BC 夹角的余弦值．24.已知椭圆()222210+=>>x y a b a b左顶点为M ，上顶点为N ，直线MN 的斜率为12．（Ⅰ）求椭圆的离心率；（Ⅱ）直线()1:02l y x m m =+≠与椭圆交于,A C 两点，与y 轴交于点P ，以线段AC 为对角线作正方形ABCD ，若2BP =．（i ）求椭圆方程；（ii ）若点E 在直线MN 上，且满足090EAC ∠=，求使得EC 最长时，直线AC 的方程．2024学年天津市南开中学高二数学上学期期中检测试卷第I 卷（选择题共60分）一.单选题（共12小题，每小题5分，在每题列出的四个选项中，只有一项最符合题目要求）1.已知空间向量()(),1,0,21,1,1a b ==-，则下列结论正确的是（）A.向量a在向量b 上的投影向量是12,0,55⎛⎫- ⎪⎝⎭B.()0,1,3a b -=--C.ab⊥D.15cos ,15a b =【答案】A 【解析】【分析】对于A 选项，根据投影向量的定义计算即可；对于B 选项，根据空间向量的减法运算法则即可；对于C 选项，根据向量法垂直的判别即可；对于D 选项，根据向量夹角的余弦公式计算即可.【详解】A.a在b 上的投影5||a b b ⋅=-，与b 同向的单位向量为,0,)55||b b =-，所以向量a 在向量b 上的投影向量是552512,0,)(,0,)55555--=-，故A 正确；B.()0,1,3a b -=，故B 错误；C.因为0a b ⋅≠r r ，所以a 与b 不垂直，故C 错误；D.cos 15|,|||a b a b a b <>⋅==-⋅，故D 错误.故选：A.2.已知直线l 经过点()1,2-，且与直线2310x y +-=垂直，则l 的方程为（）A.2340x y ++=B.2380x y +-=C.3270x y --=D.3210x y --=【答案】C 【解析】【分析】求出直线l 的斜率，利用点斜式可得出直线l 的方程.【详解】 直线l 与直线2310x y +-=垂直，且直线2310x y +-=的斜率为23-，所以直线l 的斜率为32，又因为直线l 经过点()1,2P -，所以直线l 的方程为()3212y x +=-，化简得3270x y --=.故选：C ．3.设圆224470x y x y +-++=上的动点P 到直线0x y +-=的距离为d ，则d 的取值范围是A.[]0,3 B.[]2,4 C.[]2,5 D.[]3,5【答案】B 【解析】【详解】分析：先把圆的方程化为标准形式，求出圆心坐标和半径，求出圆心到直线的距离，此距离减去圆的半径得最小值，加上半径得最大值.详解：由题意得，圆224470x y x y +-++=，即()()22221x y -++=，圆心为()2,2-，半径1r =，由圆心到直线的距离3d ==，∴圆上动点到直线的最小距离为312-=，最大距离为314+=，即d 的取值范围是[]2,4，故选B.点睛：本题考查圆的标准方程及几何性质，直线和圆的位置关系，点到直线的距离公式的应用，意在考查综合运用所学知识解答问题的能力，属于中档题.4.已知圆的方程为2220x y x +-=，(),M x y 为圆上任意一点，则21y x --的取值范围是（）A.⎡⎣B.[]1,1-C.(),-∞+∞D.(][),11,-∞-+∞ 【答案】C 【解析】【分析】将圆的方程化为标准式，21y x --表示圆上的点与点()1,2A 的连线的斜率，求出过点()1,2A 与圆相切的切线的斜率，即可求出21y x --的取值范围.【详解】圆的方程为2220x y x +-=，即()2211x y -+=，圆心为()1,0C ，半径1r =，则21y x --表示圆上的点与点()1,2A 的连线的斜率，过点()1,2A 作圆的切线方程，显然，切线斜率存在，设切线方程为2(1)y k x -=-，即20kx y k -+-=．=1，解得k =，所以21y x --的取值范围为(),-∞+∞ ．故选：C ．5.已知点M ，椭圆2214x y +=与直线(y k x =+交于点,A B ，则ABM 的周长为（）A.4B.8C.12D.16【答案】B 【解析】【分析】求出椭圆中c =，发现点M 为椭圆的右焦点，直线过左焦点，从而根据椭圆定义得到ABM 的周长为4a .【详解】由椭圆方程可知224,1a b ==，所以2223c a b =-=，c =，所以点M 为椭圆的右焦点，直线(y k x =+过左焦点(，由椭圆定义可知：ABM 的周长为48a =故选：B6.已知圆C 的圆心是直线10x y ++=与直线10x y --=的交点，直线34110x y +-=与圆C 相交于A ，B 两点，且6AB =，则圆C 的方程为（）A.()22118x y ++= B.()221x y +-=C.()22118x y -+= D.()221x y -+=【答案】A 【解析】【分析】求出两直线的交点坐标即圆心坐标，根据勾股定理求解半径即可.【详解】直线10x y ++=与直线10x y --=的交点为()0,1-，所以圆心为()0,1C -，设半径为r ，由题意得2223r +=，即解得218r =，故圆C 为()22118x y ++=.故选：A.7.已知圆22:2410C x y x y +-++=关于直线:3240l ax by ++=对称，则由点(,)M a b 向圆C 所作的切线中，切线长的最小值是（）A.2B.C.3D.【答案】B 【解析】【分析】依题可求出圆心及半径，过点(,)M a b 向圆C 所作的切线长l =线长的最小值，只需求||MC 的最小值，依题可得圆心在直线:3240l ax by ++=上，从而可得点(,)M a b 所在直线，由点到直线的距离公式可求出||MC 的最小值，从而得到答案.【详解】因为22:2410C x y x y +-++=即22:(1)(2)4C x y -++=，所以圆心为(1,2)C -，半径为2R =;因为圆C 关于直线:3240l ax by ++=对称，所以:3440l a b -+=，所以点(,)M a b 在直线1:3440l x y -+=上，所以||MC 的最小值为：|384|=35d ++=，=【点睛】本题考查直线与圆的位置关系，切线长的表示方法，最值的转化，体现出转化与化归数形结合的思想.8.已知,M N 分别是曲线1C ：222410x y x y ++-+=，2C ：226290x y x y +--+=上的两个动点，P 为直线220x y ++=上的一个动点，则||||PM PN +的最小值为（）A.3-B.3C.1- D.4【答案】A 【解析】【分析】根据题意，将问题转化为求12,PC PC 的最小值，求得1C 的对称点，根据对称性即可求得结果.【详解】曲线2212410C x y x y ++-+=是以1(1,2)C -为圆心,2为半径的圆,2226290C x y x y +--+=是以2(3,1)C 为圆心,1为半径的圆,则||PM 的最小值为12PC PN -，的最小值为21PC -,如下图所示,作点1C 关于直线220x y ++=的对称点3C ,设其坐标为(,)m n,可得2211222022n m m n -⎧=⎪⎪+⎨-+⎪+⨯+=⎪⎩,解得32m n =-⎧⎨=-⎩,即3(3,2)C --,连接23C C ,分别交直线220x y ++=､圆2C 于点,P N ,连接1PC ，交圆1C 于点M ,可得123223PC PC PC PC C C +=+≥==,当且仅当23,,C P C 三点共线时32PC PC +的最小值为,则||||PM PN +的最小值为3-,故选：A .【点睛】本题综合考查了点与圆,点关于直线对称的应用,需要学生能灵活运用所学知识.9.已知椭圆C ：2213620x y +=的左、右焦点分别为1F ，2F ，直线l ：y kx =与椭圆C 交于A ，B 两点，若122AF AF =，则1ABF ∆的面积是（）A. B. C.8D.4【答案】B 【解析】【分析】根据题意，结合椭圆定义可求出12AF F ∆的三边长，利用余弦定理求出12cos F AF ∠，即可得12sin F AF ∠值，故可得12AF F ∆的面积，由对称性可知1ABF ∆的面积.【详解】解：由题意可得6a =，4c =，则12212AF AF a +==，128F F =.因为122AF AF =，所以18AF =，24AF =，所以126416641cos 2844F AF +-∠==⨯⨯，则12sin 4F AF ∠=，故12AF F ∆的面积是121211sin 84224AF AF F AF ⋅∠=⨯⨯⨯=，由对称性可知1ABF ∆的面积是.故选：B.【点睛】本题考查了椭圆定义、考查了余弦定理三角形面积公式及图形的对称性，属于中档题.10.设双曲线224x y -=的焦点为1F ，2F ，点P 在双曲线右支上，且1290F PF ︒∠=，则点P 的横坐标为（）A.B.2C.D.6【答案】C 【解析】【分析】设(),P m n ，由点在曲线上及1290F PF ︒∠=，列出等式求解即可.【详解】由题意可得：()()12,F F -，设s ,>0，由题意可得：224m n -=1=-，两方程联立解得：26m =，所以m =故选：C11.如图，1F ，2F 分别是双曲线22221x y a b-=（0a >，0b >）的左、右焦点，且()1F ，过1F 的直线l 与双曲线的左、右两支分别交于点A ，B ．若2ABF △为等边三角形，则双曲线的方程为（）A.22551728x y -= B.2216x y -= C.2216y x -= D.22551287x y -=【答案】C 【解析】【分析】由双曲线定义结合等边三角形求得2BF ，1BF ，再由余弦定理求得,a b ，即可求得双曲线方程.【详解】根据双曲线的定义，有212AF AF a -=①，122BF BF a -=②，由于2ABF △为等边三角形，因此22AF AB BF ==，由①＋②，得114BF AF a -=，则224AB AF BF a ===，16BF a =，又因为1260F BF ∠=︒，所以()()()22212642642c a a a a =+-⨯⨯⨯，即2277a c ==，解得21a =，则2226b c a =-=，所以双曲线的方程为2216y x -=．故选：C .12.已知椭圆的两焦点1F ，2F 和双曲线的两焦点重合，点P 为椭圆和双曲线的一个交点，且121cos 4F PF ∠=，椭圆和双曲线的离心率分别为1e ，2e ，则2212e e +的最小值为（）A.1514+B.152C.14D.154【答案】A 【解析】【分析】设1PF x =，2PF y =，不妨设P 在第一象限，椭圆的长轴长为2a ，双曲线的实轴长为2a '，122F F c =，由椭圆与双曲线的定义用,a a '表示出,x y ，然后用余弦定理得出,,a a c '的关系即12,e e 的关系式，然后由基本不等式求得最小值．【详解】设1PF x =，2PF y =，不妨设P 在第一象限，椭圆的长轴长为2a ，双曲线的实轴长为2a '，122F F c =，则22x y a x y a '+=⎧⎨-=⎩，解得x a a y a a =+⎧⎨='-'⎩，在12PF F 中由余弦定理得222121212122cos F F PF PF PF PF F PF =+-∠，∴22222114242c x y xy x y xy =+-⨯=+-，1c e a =，2ce a ='，222221354()()()()222c a a a a a a a a a '''''=++--+-=+，∴2212358e e +=，∴()22222212121222221221531351888e e e e e e e e e e ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭(11881884⎛≥+=+=+ ⎝，当且仅当2212222153e e e e =时等号成立．所以2212e e +的最小值为1514+．故选：A ．【点睛】本题考查椭圆与双曲线的定义，考查它们的离心率，解题关键是利用定义表示出焦半径12,PF PF ，然后用余弦定理求得12,e e 的关系式，用基本不等式求得最小值．第II 卷（非选择题共90分）二.填空题（共8小题，每小题5分）13.过点()2,1-且方向向量为()1,2的直线的方程为___________．【答案】250x y --=【解析】【分析】由题意可得直线的斜率，再由点斜式方程即可求解【详解】因为直线过点()2,1-且方向向量为()1,2，所以直线的斜率为221k ==，所以直线的方程为()122y x +=-，即250x y --=，故答案为：250x y --=14.已知圆C 的圆心在直线x ＋y ＝0上，圆C 与直线x －y ＝0相切，且在直线x －y －3＝0上截得的弦长，则圆C 的方程为________．【答案】(x －1)2＋(y ＋1)2＝2.【解析】【分析】设圆的圆心，由直线与圆相切可得半径，再由垂径定理即可得解.【详解】由圆C 的圆心在直线x ＋y ＝0上，∴设圆C 的圆心为(a ,－a )，又∵圆C 与直线x －y ＝0相切，∴半径r ==.又圆C 在直线x －y －3＝0，圆心(a ,－a )到直线x －y －3＝0的距离d =∴2222d r ⎛⎫+= ⎪ ⎪⎝⎭，即22(23)3222a a -+=，解得a ＝1，∴圆C 的方程为(x －1)2＋(y ＋1)2＝2.故答案为：22(1)(1)2x y -++=.15.已知圆22460x y x y +--=，则过点()1,1M 的最短弦所在的直线方程是_________.【答案】230x y +-=【解析】【分析】由题知，弦最短时，圆心与点M 的连线与直线l 垂直，进而求解直线方程即可.【详解】解：根据题意：弦最短时，圆心与点M 的连线与直线l 垂直,因为圆22460x y x y +--=，即()()222313x y -+-=，圆心为：()2,3O ，所以31221OMk -==-，所以112l OM k k -==-，所以所求直线方程为：230x y +-=.故答案为：230x y +-=.16.已知()2,1,3a →=-，()3,4,2b →=-，()7,,5c λ→=，若,,a b c →→→共面，则实数λ=______．【答案】12313-【解析】【分析】由空间向量的共面定理，列出方程组求出实数λ的值．【详解】因为,,a b c →→→共面，所以a x b y c →→→=+，则23732514x y x y x y λ-=+⎧⎪=+⎨⎪=-+⎩，解得311312313x y λ⎧⎪=-⎪=⎨⎪⎪=-⎩，故答案为：12313-17.椭圆221369x y +=的一条弦被点(4,2)A 平分,那么这条弦所在的直线方程是________.【答案】280x y +-=【解析】【分析】利用点差法即得直线斜率，再根据点斜式求直线方程.【详解】设这条弦的端点坐标为()()1122,,,x y x y ，则22111369x y +=，22221369x y +=，12128,4x x y y +=+=，∴221222120363699y x y x -+-=，22121222369y x x y -=--，所以()()1212121291362x x y y x x y y ++=-=---，因此这条弦所在的直线方程为1242()y x -=--，即280x y +-=.故答案为：280x y +-=.18.双曲线22221x y a b-=的其中一条渐近线方程为2y x =，且焦点到渐近线的距离为2，则双曲线的方程为_______【答案】2214y x -=【解析】【分析】由双曲线的渐近线方程可得2ba=，再由焦点到渐近线的距离为2可得2b =，即可得答案；【详解】由题意得：2,12,b a ab ⎧=⎪⇒=⎨⎪=⎩，∴双曲线的方程为2214y x -=，故答案为：2214y x -=.【点睛】本题考查双曲线的渐近线方程和焦点到渐近线的距离为b ，考查运算求解能力，属于基础题.19.已知双曲线22221(0,0)x y a b a b-=>>的渐近线被圆22650x y x +-+=截得的弦长为2，则该双曲线的离心率为__________．【答案】62【解析】【详解】圆的标准方程为22(3)4x y -+=，圆心为(3,0)，半径为2r =，一条渐近线方程为0bx ay -=，圆心到渐近线距离为d =，因为弦长为2，所以22221=-，所以62c e a ==．20.已知F 1､F 2为双曲线2222x y a b-=1(a >0，b >0)的左､右焦点，过F 2作倾斜角为60°的直线l 交双曲线右支于A ，B 两点(A 在x 轴上方)，则12AF F △的内切圆半径r 1与12BF F △的内切圆半径r 2之比12r r 为___________.【答案】3【解析】【分析】连接12O O 交AB 于D 点，由题意可得1122122O D r r r r ==++，即求.【详解】由内切圆的性质可知，12AF F △的内切圆1O 和12BF F △的内切圆2O 都与x 轴相切于双曲线的右顶点C ，可知12,,O C O 三点共线.连接12O O 交AB 于D 点，如图：直线l 的倾斜角为60°，所以1160CO T ∠=，2260DO T ∠= ，在11Rt DO T 与22Rt DO T 中，则1122122O D r r r r ==++，则12r r 为3.故答案为：3三.解答题（共4小题，共50分）21.如图，在正四棱柱1111ABCD A B C D -中，底面边长为2，高为4．（1）求1A B 与1AD 所成角的余弦值；（2）1CC 与平面1ACD 所成角的正弦值．【答案】（1）45（2）13【解析】【分析】（1）利用棱柱中的平行关系转化异面直线为共面直线，余弦定理解三角形求夹角即可；（2）利用棱柱中的平行关系转化线面夹角，结合（1）解三角形计算即可.【小问1详解】连接1A B ，由正四棱柱的性质可知11//A B D C ，1A B 与1AD 所成角为1AD C ∠，由已知可得2211245,2AD D C AC ==+=由余弦定理可知：22211111324cos 22205D A D C AC AD C AD D C +-∠===⋅⨯；【小问2详解】由题意可知11//CC DD ，则1CC 与平面1ACD 所成角即1DD 与平面1ACD 所成角,连接DB 与AC 交于O ，结合（1）与条件易知1,D O AC BD AC ⊥⊥,而11,DC D O O DC D O =⊂ 、面1DD O ，故AC ⊥面1DD O ，又AC ⊂面1ACD ，所以面1ACD ⊥面1DD O ,显然面1ACD ⋂面11DD O D O =，即直线1DD 在面1ACD 上的投影在直线1D O 上,故1DD 与平面1ACD 所成角为1DDO ∠，易得221112,222AC DO AC D O D A ⎛⎫===- ⎪⎝⎭,所以111sin 3DO DD O D O ∠==.22.已知椭圆()2222:10x y E a b a b+=>>的离心率为22，焦距为2.（1）求椭圆E 的方程；（2）设O 为坐标原点，过左焦点F 的直线l 与椭圆E 交于A ，B 两点，若OAB ∆的面积为23，求直线l 的方程.【答案】(1)2212x y +=(2)10x y -+=或10x y ++=.【分析】（1）由离心率合焦距可得出a 、c 的值，可求出b 的值，于是可得出椭圆E 的方程；（2）设直线l 的方程为1x my =-，设点()11,A x y 、()22,B x y ，于是得出ΔA 的面积为1212ABC S OF y y ∆=⋅-，将直线l 的方程与椭圆E 的方程联立，将韦达定理代入ΔA 的面积表达式可求出m 的值，从而可得出直线l 的方程．【详解】（1）由2c a =，22c =，222a b c =+，解得a =1b =所以，椭圆E 的方程为2212x y +=；（2）设过()1,0F -的直线方程为1x my =-，代入椭圆E 的方程，化简得()222210m y my +--=，显然0∆>.设()12,A x x ,()12,B x x ，则12222m y y m +=+,12212y y m -=+从而12y y -=.所以121223OABS OF y y ∆=⋅-=，解得1m =±，所以直线l 的方程为10x y -+=或10x y ++=.【点睛】本题考查椭圆方程的求解，考查椭圆中的面积问题，在求解直线与圆锥曲线的综合问题时，一般采用将直线与圆锥曲线方程联立的方法，结合韦达定理求解，易错点就是计算量大，所以在计算中充分运用一些运算技巧，简化计算．23.如图，三棱柱111ABC A B C -中，1AA ⊥平面1,,2,4ABC AB AC AB AA AC ⊥===，M 是1CC 的中点，N 是1A B 的中点．（1）求证：1C N ∥平面ABM ；（2）求直线1AC 与平面ABM 所成角的正弦值；（3）求平面ABM 与平面1A BC 夹角的余弦值．【答案】（1）证明见解析（2）31010（3）3030【分析】（1）取AB 中点为E ，连接,NE ME ，易证四边形1NEMC 为平行四边形，则可得1//NC EM ，再由线面平行的判定定理即可得证；（2）由题意建立A xyz -空间直角坐标系，则可得1(0,4,4)A C =- ，平面ABM 的法向量1(0,1,2)n =-，再由直线1AC 与平面ABM 所成角的正弦值111111cos ,A C n A C n A C n ⋅=⋅求出答案；（3）由题意易知1(0,1,2)n =- ，可求出平面1A BC 的法向量2(2,1,1)n =，由平面ABM 与平面1A BC 夹角的余弦值121212cos ,n n n n n n ⋅=⋅即可求出答案.【小问1详解】如图所示：取AB 中点为E ，连接,NE ME ，在1ABA △中，,N E 分别为1,BA BA 中点，所以NE 为1ABA △的中位线，所以1//NE AA ,且12AA NE =，又1111//,AA CC AA CC =，M 为1CC 中点，所以11//,NE C M NE C M =,所以四边形1NEMC 为平行四边形，所以1//NC EM ，又1NC ⊄平面ABM ，EM ⊂平面ABM ，所以1//C N 平面ABM；【小问2详解】如图所示：建立A xyz -空间直角坐标系，则()()()()()10,0,0,2,0,0,0,4,0,0,4,2,0,0,4A B C M A ，所以1(2,0,0),(0,4,2),(0,4,4)AB AM A C ===- ，设平面ABM 的法向量为1(,,)n x y z = ，则1120420n AB x n AMy z ⎧⋅==⎪⎨⋅=+=⎪⎩ ，取1y =，则0x =，2z =-，则1(0,1,2)n =- ，所以直线1AC 与平面ABM所成角的正弦值为111111cos ,10A C n A C n A C n ⋅==⋅；【小问3详解】由题意知1(2,0,4),(2,4,0)A B BC =-=-，设平面1A BC 的法向量为2(,,)n x y z =，则212240240n A B x z n BC x y ⎧⋅=-=⎪⎨⋅=-+=⎪⎩ ，取2x =，则1y =，1z =，则2(2,1,1)n =，平面ABM 与平面1A BC夹角的余弦值121212cos ,30n n n n n n ⋅===⋅.24.已知椭圆()222210+=>>x y a b a b左顶点为M ，上顶点为N ，直线MN 的斜率为12．（Ⅰ）求椭圆的离心率；（Ⅱ）直线()1:02l y x m m =+≠与椭圆交于,A C 两点，与y 轴交于点P ，以线段AC 为对角线作正方形ABCD，若2BP =．（i ）求椭圆方程；（ii ）若点E 在直线MN 上，且满足090EAC ∠=，求使得EC 最长时，直线AC 的方程．【答案】（Ⅰ）2（Ⅱ）()()221414221x i y ii y x +==-【分析】（Ⅰ）根据直线MN 的斜率可得2a b =，即可求出离心率；（Ⅱ）()i 将直线方程代入椭圆方程，利用韦达定理及弦长公式求得AC 及PQ ，根据勾股定理即可求出b 的值；()ii 根据平行间的距离公式求出AE ，再根据勾股定理和二次函数的性质即可求出EC 最长时m 的值，即可求出直线AC 的方程．【详解】解：（Ⅰ） 左顶点为M ，上顶点为N ，直线MN 的斜率为12．12b a ∴=，2c e a ∴===，（Ⅱ）()i 由(Ⅰ)知椭圆方程为22244x y b +=，设()11,A x y ，()22,C x y ，线段AC 中点Q 则2221244y x m x y b⎧=+⎪⎨⎪+=⎩，整理得：2222220x mx m b ++-=，由()22222(2)422840m m b b m =-⨯-=-> ，则122x x m +=-，221222x x m b =-，()1212122y y x x m m +=++=，则1,2Q m m ⎛⎫- ⎪⎝⎭，由l 与y 轴的交点()0,P m ，PQ ==，()()()()()2222222121212125||14844AC x x y y k x x x x b m ⎡⎤=-+-=++-=-⎣⎦，()2222222221551010||||||244444BP BQ PQ AC PQ b m m b ∴=+=+=-+==，21b ∴=，即1b =，∴椭圆方程为2214x y +=；()ii 由()i 可知AC =，直线MN 的方程为112y x =+，∴直线MN 与直线l 点E 在直线MN 上，且满足90EAC ∠= ，AE ∴=，()222222421854||||(1)525555EC AE AC m m m m ∴=+=-+-=--+，当421m =-时，此时EC 最长，故直线AC 的方程14221y x =-.【点睛】本题考查椭圆的标准方程，直线与椭圆的位置关系，考查韦达定理，弦长公式及中点坐标公式，考查计算能力，属于中档题．。

天津一中2011—2012高一年级第一学期数学期中考试试卷一．选择题：1．设集合{}{}|33,|2,12xA x xB y y x =-<<==≤≤，则()()R R C A C B =（ ）A ．[)2,3B ．()(),23,-∞+∞C ．()[),23,-∞+∞D ．()(),24,-∞+∞2．函数()34log 21-=x y 的定义域为 （ ）Ａ．（43,∞-） Ｂ．（1,∞-］ Ｃ．（43，1］ Ｄ．（43，1）3．设ax x f x++=)110lg()(是偶函数，xx bx g 24)(-=是奇函数，那么a ＋b 的值为（ ）A ． 1B ．－1C ．－21D ．214．)2lg(2lg lg y x y x -=+，则yx2log 的值的集合是（ ） A ．｛1｝B ．｛2｝C ．｛1，0｝D ．｛2，0｝5．已知函数log (2)a y ax =-在[0，1]上是x 的减函数，则a 的取值范围是（ ） Ａ．（0，1） Ｂ．（0，2） Ｃ．（1，2）Ｄ．[2，+∞)6．函数x xx xe e y e e --+=-的图像大致为 ( ).7．已知函数f(x)=log 3x+2 (x ∈[1,9])，则函数y=[f(x)]2+f(x 2)的最大值是（ ） A ．13 B ．16 C ．18 D ．228．设xa x f =)(，31)(x x g =，x x h a log )(=，实数a 满足)1(log 2a a -＞0，那么当x ＞1D时必有（ ） A ．)(x h ＜)(x g ＜)(x f B ．)(x h ＜)(x f ＜)(x g C ．)(x f ＜)(x g ＜)(x hD ．)(x f ＜)(x h ＜)(x g9．已知函数)(x f 是R 上的增函数，(0,2)-A ，(3,2)B 是其图象上的两点，那么2|)1(|<+x f 的解集是（ ）A ．（1，4）B ．（-1，2）C ．),4[)1,(+∞-∞D ．),2[)1,(+∞--∞10．设函数121()3(0)2(),(0)xx f x x x ⎧-≤⎪=⎨⎪>⎩已知()1f a >，则实数a 的取值范围是（ ）Ａ．(2,1)- Ｂ．(,2)(1,)-∞-+∞ Ｃ．(1,)+∞Ｄ．(,1)(0,)-∞-+∞二．填空题：11．已知幂函数)(x f y =的图象过点=)9(),2,2(f 则 。

天津一中2017-2018高二数学上学期期中试题（文科附答案）天津一中2017-2018-1高二年级数学学科（文科）模块质量调查试卷本试卷分为第I卷（选择题）、第II卷（非选择题）两部分，共100分，考试用时90分钟。

第I卷1页，第II卷至2页。

考生务必将答案涂写在规定的位置上，答在试卷上的无效。

一、选择题：1．已知两条不同的直线m、n，两个不同的平面&#61537;、&#61538;，则下列命题中的真命题是A．若m&#61534;&#61537;，n&#61534;&#61538;，&#61537;&#61534;&#61538;，则m&#61534;n.B．若m&#61534;&#61537;，n∥&#61538;，&#61537;&#61534;&#61538;，则m&#61534;n.C．若m∥&#61537;，n∥&#61538;，&#61537;∥&#61538;，则m∥n.D．若m∥&#61537;，n&#61534;&#61538;，&#61537;&#61534;&#61538;，则m∥n.2．已知直线x&#61483;a2y&#61483;6&#61501;0与直线(a&#61485;2)x&#61483;3ay&#61483;2a&#61501;0平行，则a的值为A．0或3或&#61485;1B．0或3C．3或&#61485;1&#61676;x&#61485;y&#61483;3&#61603;0&#61679;D．0或&#61485;13．已知x,y满足约束条件&#61677;3x&#61483;y&#61483;5&#61603;0，则z&#61501;x&#61483;2y的最大值是&#61679;x&#61483;3&#61619;0A．0B．2C．5D．64．若过定点M(&#61485;1,0)且斜率为k的直线与圆x2&#61483;4x&#61483;y2&#61485;5&#61501;0在第一象限内的部分有交点，则k的取值范围是A．0&#61500;k&#61500;5B．&#61485;5&#61500;k&#61500;0C．0&#61500;k&#61500;13D．0&#61500;k&#61500;55．在正三棱柱ABC&#61485;A1B1C1中，若AB&#61501;2,AA1&#61501;1，则点A到平面A1BC的距离为33A．B．42C．33D．346．若直线y&#61501;x&#61483;b与曲线y&#61501;3&#61485;4x&#61485;x2有公共点，则b的取值范围是A．&#61673;1&#61485;22,1&#61483;22&#61689;B．&#61 673;1&#61485;2,3&#61689;C．&#61673;&#61485;1,1&#61483;22&#61689;D．&#61673;1&#61485;22,3&#61689;&#61675;&#61691;&#61675;&#61691;&#61676;x&#61483;y&#61603;4,&#61679;&#61675;&#61691;&#61675;&#61691;7．设不等式组&#61677;y&#61485;x&#61619;0,表示的平面区域为D.若圆C:&#61480;x&#61483;1&#61481;2&#61483;&#61480;y&#6 1483;1&#61481;2&#61501;r2&#61678;x&#61485;1&#61619;0不经过区域D上的点,则r的取值范围是&#61480;r&#61502;0&#61481;A．&#61480;22,25&#61481;B．&#61480;22,32&#61533;C．&#61480;32,25&#61533;D．&#61480;0,22&#61481;&#61640;&#61480;25,&#61483;&#61605;&#61481;8．某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为A．32B．23C．22D．29．若直线ax&#61483;2by&#61485;2&#61501;0(a,b&#61502;0)始终平分圆x2&#61483;y2&#61485;4x&#61485;2y&#61485;8&#61501; 0的周长，则1&#61483;1的最小值为2ab15A．B．223&#61483;22C．2D．3210．已知二面角&#61537;&#61485;l&#61485;&#61538;为60&#61616;，AB&#61644;&#61537;，AB&#61534;l，A为垂足，CD&#61644;&#61538;，C&#61646;l，&#61648;ACD&#61501;135&#61616;，则异面直线AB与CD 所成角的余弦值为1231A．4B．4C．4D．2二、填空题：11．某几何体的三视图如图所示（单位：cm），则该几何体的体积是（单位：cm3）．12．已知点A(&#61485;1,1)和圆C：(x&#61485;5)2&#61483;(y&#61485;7)2&#61501;4，从点A发出的一束光线经过x轴反射到圆周C的最短路程．13．已知圆C：(x&#61485;1)2&#61483;y2&#61501;25与直线l：mx&#61483;y&#61483;m&#61483;2&#61501;0，当m&#61501;&#61472;时，圆C被直线l截得的弦长最短．14．已知直线ax&#61483;y&#61485;2&#61501;0与圆心为C的圆&#61480;x&#61485;1&#61481;2&#61483;&#61480;y&#614 85;a&#61481;2&#61501;4相交于A，B两点，且&#61508;ABC为等边三角形，则实数a&#61501;．15．正方形AP1P2P3的边长为4，点B,C分别是边P1P2,P2P3的中点，沿AB,BC,CA折成一个三棱锥P&#61485;ABC（使P1,P2,P3重合于P），则三棱锥P&#61485;ABC的外接球表面积为．16．若关于x的不等式k&#61501;&#61472;．三、解答题：9&#61485;x2&#61603;k(x&#61483;2)&#61485;2的解集为区间&#61531;a,b&#61533;，且b&#61485;a&#61501;2，则17．本市某玩具生产公司根据市场调查分析，决定调整产品生产方案，准备每天生产A,B,C三种玩具共100个，每天生产时间不超过10小时，且C种玩具至少生产20个，已知生产这些玩具每个所需工时（分钟）和所获利润如下表：玩具名称ABC工时（分钟）574利润（元）5[63（Ⅰ）用每天生产A种玩具个数x与B种玩具个数y表示每天的利润&#61559;（元）（Ⅱ）怎样分配生产任务才能使每天的利润最大，最大利润是多少？18．如图，在直三棱柱ABC&#61485;A1B1C1中，AB&#61534;BC，AA1&#61501;AC&#61501;2，BC=1，E、F分别为A1C1、BC的中点.（Ⅰ）求证：C1F//平面ABE；（Ⅱ）求点C到平面ABE的距离.19．如图所示，四棱锥P&shy;ABCD的底面ABCD是平行四边形，BA＝BD＝2，AD＝2，PA＝PD＝5，E，F分别是棱AD，PC的中点．（Ⅰ）证明：EF∥平面PAB；（Ⅰ）若二面角P&shy;AD&shy;B为60°.（i）证明：平面PBC⊥平面ABCD；（ii）求直线EF与平面PBC所成角的正切值．20．已知圆C的圆心在直线l1:x&#61485;y&#61485;1&#61501;0上，与直线l2:4x&#61483;3y&#61483;14&#61501;0相切，且截直线l3:3x&#61483;4y&#61483;10&#61501;0所得弦长为6 （Ⅰ）求圆C的方程（Ⅱ）过点M(0,1)是否存在直线L，使以L被圆C截得弦AB为直径的圆经过原点?若存在，写出直线的方程；若不存在，说明理由新新特特特特王新王wxckt@126.一、选择题参考答案1．A2．D3．C4．A5．B6．D7．D8．B9．C10．B二、填空题11．1&#61483;&#61552;212．813．114．4&#61617;1515．24&#61552;16．2三、解答题17．解：（Ⅰ）C玩具有（100-x-y）个∴w=5x+6y+3(100-x-y)=2x+3y+300 （Ⅱ）&#61676;5x&#61679;&#61483;7y&#61483;4(100&#61485;x&#61485;y)&#61603;10&#61620;60 &#61676;x&#61483;3y&#61679;&#61603;200&#61677;100&#61485;x&#61485;y &#61679;&#61619;20&#61659;&#61677;x&#61483;y&#61679;&#61603;80&#61678;x,y&#61646;N&#61678;x,y&#61646;N3y=-2x+w-3002y&#61501;&#61485;x3&#61483;w&#61485;1003&#61676;x&#61483;3y&#61677;&#61501;200&#61678;x&#61483;y&#61501;80&#61676;x&#61501;20&#61532;&#61677;&#61678;y&#61501;60M(20,60)&#61532;wmax&#61501;2&#61620;20&#61483;3&#61620;60&#61483;300 &#61501;520(元)答：每天生产A种玩具20件，B种玩具60件，C种玩具20件，利润最大，为520元。

2023-2024学年天津市第一中学高二上学期期中数学试卷一、单选题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.设直线l的斜率为k，且，则直线l的倾斜角的取值范围为( )A. B.C. D.2.设点，，直线l过点且与线段AB相交，则l的斜率k的取值范围是( )A.或 B. 或 C. D.3.“”是“直线和直线互相垂直”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件4.已知圆，若直线与圆C相交于A，B两点，则的最小值为( )A. B. C. 3 D.5.某广场的一个椭球水景雕塑如图所示，其横截面为圆，过横截面圆心的纵截面为椭圆，，分别为该椭圆的两个焦点，PQ为该椭圆过点的一条弦，且的周长为若该椭球横截面的最大直径为2米，则该椭球的高为( )A. 米B. 米C. 米D. 米6.已知双曲线C的焦点与椭圆E：的上、下顶点相同，且经过E的焦点，则C的方程为( )A. B. C. D.7.圆关于直线对称，则的最小值是.( )A. B. C. 4 D.8.双曲线C：的左、右焦点分别为，，过的直线与双曲线C的右支在第一象限的交点为A，与y轴的交点为B，且B为的中点，若的周长为6a，则双曲线C的渐近线方程为( )A. B. C. D.9.已知椭圆与双曲线有相同的焦点、，椭圆的离心率为，双曲线的离心率为，点P为椭圆与双曲线的交点，且，则的值为( )A. B. C. D. 410.椭圆的左、右焦点分别是、，斜率为1的直线l过左焦点且交C于A，B两点，且的内切圆的面积是，若椭圆C离心率的取值范围为，则线段AB的长度的取值范围是( )A. B. C. D.二、填空题：本题共6小题，每小题4分，共24分。

11.若椭圆的焦点在y轴上，则实数k的取值范围是__________.12.若圆与双曲线的渐近线相切，则双曲线的离心率为__________.13.直线l过点，且在两坐标轴上截距相等，则直线l的方程为__________14.若直线与曲线有两个交点，则实数k的取值范围是__________.15.已知O为坐标原点，设，分别是双曲线的左、右焦点，P为双曲线左支上任意一点，过点作的平分线的垂线，垂足为H，则__________.16.已知点是函数的图象上的动点，则的最小值为__________.三、解答题：本题共4小题，共46分。

天津市天津一中2013-2014学年高二下学期期中考试 文科数学一、选择题： 1．复数52i=+ A ．2i -B ．21i 55+ C ．105i - D ．105i 33- 2．“1m =”是“复数(1i)(1i)z m =++ (m ∈R ，i 为虚数单位)为纯虚数”的A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既不充分又不必要条件3．命题“存在0x ∈R ，02x ≤0”的否定是A ．不存在0x ∈R, 02x>0 B ．存在0x ∈R, 02x ≥0C ．对任意的x ∈R, 2x≤0 D ．对任意的x ∈R, 2x>0 4．在用数学归纳法证明凸n 边形内角和定理时,第一步应验证A ．1n =时成立B ．2n =时成立C ．3n =时成立D ．4n =时成立5．已知函数()f x 的导函数为()f x '，且满足()2(e)ln f x xf x '=+，则(e)=f 'A ．1B ．－1C ．－e －1D ．－e6．若220a x dx =⎰,230b x dx =⎰,20sin c xdx =⎰,则,,a b c 的大小关系是A ．a c b <<B ．a b c <<C ．c b a <<D ．c a b <<7．曲线311y x =+在点(1,12)处的切线与两坐标轴围成的三角形面积是 A ．75B ．752C ．27D ．2728．已知32()69,f x x x x abc a b c =-+-<<，且()()()0f a f b f c ===，现给出如下结论： ①(0)(1)0f f ⋅>；②(0)(1)0f f ⋅<；③(0)(3)0f f ⋅>；④(0)(3)0f f ⋅< 其中正确结论的序号是 A ．①③B ．①④C ．②③D ．②④9．设a R ∈,若函数e ,x y ax x R =+∈有大于零的极值点,则 A ．1a <-B ．1a >-C ．1e a >-D ．1ea <- 10．定义在(0,)2π上的函数()f x ，()f x '是它的导函数，且恒有()()tan f x f x x '<⋅成立，则A ππ()()43>B ．(1)2()sin16πf f <C ππ()()64f >D ππ()()63f <二、填空题：11．观察下列等式:332333233332123,1236,123410+=++=+++=,…,根据上述规律,第五个等式为__________.12．已知322()f x x ax bx a =+++在1x =处有极值10，则a b ⋅=__________.[来源:学科网]13．已知函数3()3f x x x c =-+的图像与x 恰有两个公共点，则c =__________. 14．已知函数()y f x =在定义域3,32⎛⎫-⎪⎝⎭上可导，其图象如图，记()y f x =的导函数()y f x '=，则不等式()0xf x '≤的解集是__________.15．若函数21()43ln 2f x x x x =-+-,x 在[],1t t +上不单调，则t 的取值范围是__________.16．若关于x 的不等式(21)ln 0ax x -≥对任意的(0,)x ∈+∞恒成立，则实数a 的值为__________. 三、解答题：17．已知函数()e 1x f x x =-- （1）求函数()f x 的最小值； （2）设21()2g x x =，求()y f x =的图象与()y g x =的图象的公共点个数。

2019-2020学年天津一中高二（上）期中数学试卷一、选择题：（每小题3分，共30分）1．如果一个等差数列中，前三项和为34，后三项和为146，所有项的和为390，则数列的项数是()A ．13B ．12C ．11D ．102．已知等比数列{}n a 中，231a a +=，452a a +=，则67a a +等于()A ．2B ．C ．4D ．3．数列{}n a 满足：*11(n n a a n N λ+=-∈，R λ∈且0)λ≠，若数列{1}n a -是等比数列，则λ的值等于()A ．1B ．1-C ．12D ．24．已知数列{}n a 满足11a =-，1|1|21n n n a a a +=-++，其前n 项和为n S ，则下列说法正确的个数为()①数列{}n a 是等差数列；②23n n a -=；③1332n n S --=．A ．0B ．1C ．2D ．35．已知0.22019a =，20190.2b =，2019log 0.2c =，则()A ．c a b>>B ．b a c>>C ．a b c >>D ．a c b>>6．若0a b <<，则下列不等式一定成立的是()A ．11a b b>-B ．2a ab<C ．||||1||||1b b a a +<+D ．n na b >7．若023x <<，则(32)x x -的最大值为()A ．916B ．94C ．2D ．988．已知0x >，0y >，且115x y x y+++=，则x y +的最大值是()A ．3B ．4C ．6D ．89．若数列{}n a ，{}n b 的通项公式分别为2018(1)n n a a +=-，2019(1)2n n b n+-=+，且n n a b <，对任意*n N ∈恒成立，则实数a 的取值范围是()A ．[1-，12B ．[1-，1)C ．[2-，1)D ．[2-，3)210．已知函数2()4x f x =，若存在实数t ，使得任给[1x ∈，]m ，不等式()f x t x + 恒成立，则m 的最大值为()A ．3B ．6C ．8D ．9二、填空题：（每小题4分，共24分）11．在等差数列{}n a 中，1533a =，2566a =，则35a =．12．等比数列{}n a 中，公比2q =，9977S =，则3699a a a ++⋯+=．13．已知数列{}n a 满足115a =，且1332n n a a +=-，若10k k a a +<，则正整数k =．14．若01a <<，则不等式21()10x a x a-++<的解集是．15．若13a <<，42b -<<，那么||a b -的取值范围是．16．+对一切0x >，0y >恒成立，则实数a 的取值范围为．三、解答题：（共4题，46分）17．已知函数2()(6)4f x x a a x =-+--．（1）解关于a 的不等式f （1）0>；（2）若不等式()f x b >的解集为(1,3)-，求实数a ，b 的值；（3）对任给的[1x ∈，3]，不等式()0f x 恒成立，求实数a 的取值范围．18．已知数列{}n a 满足：11a =，1112n n n n n a a n +++=+，*n N ∈，（1）设nn a b n=，求数列{}n a 和{}n b 的通项公式；（2）求数列{}n a 的前n 项和n S ．19．已知等差数列{}n a 的公差0d >，首项11a =，且12a 、21a +、33a +成等比数列．（1）求数列{}n a 的通项公式；（2）求数列11{}n n a a +的前n 项和n P ；（3）比较n P 与22nn的大小．20．已知函数2()(xf x aax b=+、b为常数），方程()120f x x-+=有两个实根3和4，（1）求()f x的解析式；（2）设1k>，解关于x的不等式(1)()2k x kf xx+-<-；（3）已知函数()g x是偶函数，且()g x在[0，)+∞上单调递增，若不等式(1)(2)g mx g x+-在任给1[2x∈，1]上恒成立，求实数m的取值范围．2019-2020学年天津一中高二（上）期中数学试卷参考答案与试题解析一、选择题：（每小题3分，共30分）1．如果一个等差数列中，前三项和为34，后三项和为146，所有项的和为390，则数列的项数是()A ．13B ．12C ．11D ．10【解答】解：设此等差数列共有n 项．12334a a a ++= ，21146n n n a a a --++=，12132n n n a a a a a a --+=+=+，∴134146603n a a ++==．∴1()3902n n n a a S +==，即603903n=，解得13n =．故选：A ．2．已知等比数列{}n a 中，231a a +=，452a a +=，则67a a +等于()A ．2B ．C ．4D ．【解答】解：设等比数列{}n a 的公比为q ，则245232a a q a a +==+，26745()224a a a a q ∴+=+=⨯=故选：C ．3．数列{}n a 满足：*11(n n a a n N λ+=-∈，R λ∈且0)λ≠，若数列{1}n a -是等比数列，则λ的值等于()A ．1B ．1-C ．12D ．2【解答】解：由11n n a a λ+=-，得1212(n n n a a a λλλ+-=-=-．由于数列{1}n a -是等比数列，∴21λ=，得2λ=，故选：D ．4．已知数列{}n a 满足11a =-，1|1|21n n n a a a +=-++，其前n 项和为n S ，则下列说法正确的个数为()①数列{}n a 是等差数列；②23n n a -=；③1332n n S --=．A ．0B ．1C ．2D ．3【解答】解：数列{}n a 满足11a =-，1|1|21n n n a a a +=-++，可得211|1|212211a a a =-++=-+=，322|1|210213a a a =-++=++=，433|1|212619a a a =-++=++=，则436a a -=，322a a -=，即有4332a a a a -≠-，则数列{}n a 不是等差数列，故①不正确；23n n a -=，不满足11a =-，故②不正确；若1332n n S --=满足1n =时，111a S ==-，但2n =时，2210(1)12a S S =-=--=，当2n 时，121333322n n n n n a S S -----=-=-23n -=，2n ，*n N ∈．代入1|1|21n n n a a a +=-++，左边13n -=，右边221312313n n n ---=-++= ，则1|1|21n n n a a a +=-++恒成立．故③正确．故选：B ．5．已知0.22019a =，20190.2b =，2019log 0.2c =，则()A ．c a b>>B ．b a c>>C ．a b c >>D ．a c b>>【解答】解：因为0.220191a =>，20190.2b =，所以201900.21b <<=20192019log 0.2log 10c =<=，所以a b c >>，故选：C ．6．若0a b <<，则下列不等式一定成立的是()A ．11a b b>-B ．2a ab <C ．||||1||||1b b a a +<+D ．n na b >【解答】解：0a b << ，||||b a ∴<，||||||||||||a b b a b a ∴+<+，∴||||1||||1b b a a +<+，故选：C ．7．若023x <<，则(32)x x -的最大值为()A ．916B ．94C ．2D ．98【解答】解：023x << ，320x ∴->，0x >，211(322)9(32)(32)2()2228x x x x x x -+∴-=-= ，当且仅当322x x -=，即34x =时取等号，32)x x ∴-的最大值为98．故选：D ．8．已知0x >，0y >，且115x y x y+++=，则x y +的最大值是()A ．3B ．4C ．6D ．8【解答】解：0x > ，0y >，且115x y x y+++=，∴1145()x y x y x y+=-++，2()5()40x y x y ∴+-++ ，14x y ∴+ ，∴当且仅当2x y ==时，x y +取得最大值为4．故选：B ．9．若数列{}n a ，{}n b 的通项公式分别为2018(1)n n a a +=-，2019(1)2n n b n+-=+，且n n a b <，对任意*n N ∈恒成立，则实数a 的取值范围是()A ．[1-，12B ．[1-，1)C ．[2-，1)D ．[2-，3)2【解答】解：当n 为奇数时，n n a b <可化为*12()a n N n -<+∈，122a n ∴-<+<，故2a - ．当n 为偶数时，1132222a n <--= ．所以a 的取值范围是[2-，32．故选：D ．10．已知函数2()4x f x =，若存在实数t ，使得任给[1x ∈，]m ，不等式()f x t x + 恒成立，则m 的最大值为()A ．3B ．6C ．8D ．9【解答】解：设2221111()()()(1)4424g x f x t x x t x x t x t =+-=+-=+-+，由题意()f x t x + 对任意的[1x ∈，](1)m m >恒成立，即g （1）0 且()0g m ．由g （1）0 ，即21(1)104t +- ，得[3t ∈-，1]，由()0g m ，即21()04m t m +- ，得22(24)0m t m t +-+ ，则当1t =时，得到2210m m -+ ，解得1m =；当3t =-时，得到21090m m -+ ，解得19m ．综上所述m 的取值范围为[1，9]m ∴的最大值为9．故选：D ．二、填空题：（每小题4分，共24分）11．在等差数列{}n a 中，1533a =，2566a =，则35a =99．【解答】解：由等差数列的性质可知，15a ，25a ，35a 成等差数列2515352a a a ∴=+1533a = ，2566a =，352663399a ∴=⨯-=．故答案为：9912．等比数列{}n a 中，公比2q =，9977S =，则3699a a a ++⋯+=44．【解答】解：因为{}n a 是公比为2的等比数列，设36999a a a a x +++⋯+=，则147974x a a a a +++⋯+=，256982x a a a a +++⋯+=．99147972569836999777()()()244x x S a a a a a a a a a a a a x x ==+++⋯+++++⋯+++++⋯+=++=，3699944a a a a ∴+++⋯=，故答案为：44．13．已知数列{}n a 满足115a =，且1332n n a a +=-，若10k k a a +<，则正整数k =23．【解答】解：数列{}n a 满足115a =，且1332n n a a +=-，整理得123n n a a +-=-（常数），所以数列{}n a 是以115a =为首项，23-为公差的等差数列．则12247(1)333n a a n n =--=-+，由于10k k a a +<，则247245()()03333k k -+-+<，解得454722k <<，所以正整数23k =．故答案为：23．14．若01a <<，则不等式21()10x a x a-++<的解集是1(,)a a．【解答】解：不等式变成1()()0x a x a --< ，01a << ，∴1a a >，∴不等式的解集为1(,)a a 故答案为1(,)a a．15．若13a <<，42b -<<，那么||a b -的取值范围是(3,3)-．【解答】解：由420||4b b -<<⇒< ，4||0b -<- ，又13a <<．3||3a b ∴-<-<．所求范围为(3,3)-16．对一切0x >，0y >恒成立，则实数a 的取值范围为)+∞．【解答】解：0x > ，0y >，∴+等价为a设m =0m >，平方得2211112m ====+=，当且仅当x y =时取等号，22m ∴ ，则0m∴要使a则a ，故答案为：，)+∞三、解答题：（共4题，46分）17．已知函数2()(6)4f x x a a x =-+--．（1）解关于a 的不等式f （1）0>；（2）若不等式()f x b >的解集为(1,3)-，求实数a ，b 的值；（3）对任给的[1x ∈，3]，不等式()0f x 恒成立，求实数a 的取值范围．【解答】解：（1）由f （1）0>即2650a a -+<，即15a <<，解集为(1,5)a ∈，（2）由()f x b >，2(6)40x a a x b --++<，可知1-和3是方程2(6)40x a a x b --++=的两实根，(6)243a a b -=⎧⎨+=-⎩，解得37a b ⎧=+⎪⎨=-⎪⎩37a b ⎧=-⎪⎨=-⎪⎩（3）任给的[1x ∈，3]，不等式()0f x 恒成立等价于2(6)40x a a x -+-- ，即24(6)x a a x +- ，满足24(6){}min x a a x+- ，设244()4x g x x x x +==+= ，当且仅当2x =时取等号，故(6)4a a -，即3a或3a + ．18．已知数列{}n a 满足：11a =，1112n n n n n a a n +++=+，*n N ∈，（1）设nn a b n=，求数列{}n a 和{}n b 的通项公式；（2）求数列{}n a 的前n 项和n S ．【解答】解：（1）1112n n n n n a a n +++=+ ，*n N ∈，∴1112n n n a a n n +-=+．112n n n b b +∴-=，2n 时，1112n n n b b ---=，111b a ==，1122111211111112()()()121222212n n n n n n n n n b b b b b b b b -------∴=-+-+⋯⋯+-+=+⋯⋯++==--111(2222n n n n na nb n n --==-=-．（2）设23123412222n n n T -=++++⋯⋯+，则23111231222222n n n n nT --=+++⋯⋯++，∴211111111122122122222222212n n n n n n n n n n n n T ---+=+++⋯⋯+-=-==--=--．1242n n nT -+∴=-．∴数列{}n a 的前n 项和12(1)42n n nS n n -+=+-+．19．已知等差数列{}n a 的公差0d >，首项11a =，且12a 、21a +、33a +成等比数列．（1）求数列{}n a 的通项公式；（2）求数列11{}n n a a +的前n 项和n P ；（3）比较n P 与22nn的大小．【解答】解：（1）由题意，2213(1)2(3)a a a +=+，即2(2)2(42)0d d d ⎧+=+⎨>⎩，解得2d =．21n a n ∴=-；（2）111111()(21)(21)22121n n a a n n n n +==--+-+，∴11111111(12335572121n P n n =-+-+-+⋯+--+11(122121n n n =-=++；（3）由111(1)2212n P n =-<+，设22()n f n n=，则12222222[(2)1](1)()(1)(1)n n n n n f n f n n n n n +--+-=-=++．当3n 时，(1)()f n f n +>，()f n 单调递增，()f n f （3）89=，12n P <，则()n f n P >；当1n =时，f （1）1123P =>=；当2n =时，f （2）2215P =>=．综上，22nn P n<．20．已知函数2()(x f x a ax b=+、b 为常数），方程()120f x x -+=有两个实根3和4，（1）求()f x 的解析式；（2）设1k >，解关于x 的不等式(1)()2k x k f x x+-<-；（3）已知函数()g x 是偶函数，且()g x 在[0，)+∞上单调递增，若不等式(1)(2)g mx g x +- 在任给1[2x ∈，1]上恒成立，求实数m 的取值范围．【解答】解：（1）根据题意，函数2()x f x ax b=+，方程()120f x x -+=即2(1)(12)120a x a b x b -+-+=的两根之和为4；则有127112121b a a b a-⎧=⎪⎪-⎨⎪=⎪-⎩，变形可得571a b a b -=-⎧⎨+=⎩，解可得12a b =-⎧⎨=⎩，故2()2x f x x =-，(2)x ≠（2）(1)()2k x k f x x +-<-即2(1)22x k x k x x+-<--，变形可得()(1)(2)0x k x x --->，①、当12k <<时，有1x k <<或2x >，其解集为(1，)(2k ⋃，)+∞；②、当2k =时，有1x >且2x ≠，其解集为(1，2)(2⋃，)+∞；③、当2k >时，有12x <<或x k >，其解集为(1，2)(k ⋃，)+∞；（3）由于()g x 为偶函数且在(0,)+∞上递增，则()f x 在(,0)-∞上递减，(1)(2)|1||2|g mx g x mx x +-⇒+- ，1[2x ∈，1]；则有1212mx x mx x +-⎧⎨+-⎩ ，变形可得13x m x x m x -⎧⎪⎪⎨-⎪⎪⎩，即有13x m x x m x -⎧⎪⎪⎨-⎪⎪⎩对于任给1[2x ∈，1]上恒成立，对于1x y x -=，有1|0max x y y ===，则有0m ，对于3x y x-=，有1|2min x y y ===-，则有2m - ，故20m - ，即m 的取值范围为[2-，0]．。

天津市第一中学2020-2021学年高二数学上学期期中试题本试卷分为第 I 卷(试题)、第 II 卷(答题纸)两部分,共 100 分,考试用时 90 分钟。

考生务必将答案涂写在答题纸的规定位置上,答在试卷上的无效。

祝各位考生考试顺利! 一．选择题:(每小题 3 分,共 30 分)1．直线 l1:ax+2y+6=0 与直线 l2:x+(a-1)y+a2-1=0 平行,则 a 等于A．-1 B．-1 或 2 C．2 D．12.过点 P(1,2)引直线使两点 A(2,3)、B(4,-5)到它的距离相等,则直线方程是A．4x+y-6=0 B．x+4y-6=0C．2x+3y-7=0 或 x+4y-6=0 D．4x+y-6=0 或 3x+2y-7=03．过点 A(1,4)且横纵截距的绝对值相等的直线共有A．1 条B．2 条C．3 条D．4 条4．圆 x2+y2-4x-4y-10=0 上的点到直线 x+y-14=0 的最大距离与最小距离的差是A．36 B．18 C．5 2 D．6 25．若圆 x2+y2+ax-by=0 的圆心在第二象限,则直线 x+ay-b=0 一定不经过A．第一象限B．第二象限C．第三象限D．第四象限6．已知圆C:x2+y2-8x+15=0,若直线y=kx-2 上至少存在一点,使得以该点为圆心,1 为半径的圆与圆 C 有公共点,则 k 的最大值是A．32B．43C．53D．547．过椭圆 9x2+25y2=225 的右焦点且倾斜角为 45o 的弦 AB 的长为90A．5 B．6 C．17 D．78．已知椭圆 x2+4y2=12 的左右焦点分别为 F1、F2,点 P 在椭圆上,线段 PF1 的中点在 y 轴上,则|PF1|是|PF2|的A．3 倍B．4 倍C．5 倍D．7 倍9．若椭圆 2a2x2-ay2=2 的一个焦点是(-2,0),则 a=A．1- 34B．134C．1-54D．1 5410．已知 A、B 为椭圆左右顶点,F 为左焦点,点 P 为椭圆上一点,且 PF⊥x 轴,过点 A 的直线与线段 PF 交于 M 点,与 y 轴交于 E 点,若直线 BM 经过 OE 中点,则椭圆的离心率为A．12B．32C．13D．63二．填空题:(每小题 4 分,共 24 分)11．已知点 A(1,2)、B(3,1),则线段 AB 的垂直平分线的方程是.12．如果 x2+y2-2x+y+k=0 是圆的方程,则实数 k 的取值范围是.13．已知圆 C 过点(1,0),且圆心在 x 轴的正半轴上,直线 l:y=x-1 被该圆所截得的弦长为2 2 ,则圆 C 的标准方程为 .14．过直线 x+y- 2 2 =0 上点 P 作圆 x2+y2=1 的两条切线,若两条切线的夹角是 60o,则P 的坐标是_ .15．已知椭圆的两个焦点为 F1(-4,0)、F2(4,0),P 点在椭圆上,∆F1PF2 面积最大值为 12,则椭圆的方程为.2 216．椭圆x+ y 1的左右焦点为 F1、F2,点 P 在椭圆上,若 Rt∆ F1PF2,则点 p 到 x 轴的25 16距离为.三．解答题:(共 4 题,46 分)17．在三棱锥 P-ABC 中,∠APB=90o,∠PAB=60o,AB=BC=CA,平面 PAB⊥平面 ABC. (1)求直线 PC 与平面 ABC 所成角的正弦值;(2)求二面角 B-AP-C 的余弦值.18．已知直线 x+y-1=0 与椭圆 C:b2x2+a2y2=a2b2(a>b>0)相交于 A,B 两点,且线段 AB 的中点在直线 l:x-2y=0 上.(1)求此椭圆 C 的离心率;(2)若椭圆 C 的右焦点关于直线 l 的对称点的在圆 x2+y2=4 上,求此椭圆 C 的方程.19．在平面直角坐标系 xoy 中,点 A(0,3),直线 l:y=2x-4,设圆 C 的半径为 1,圆心在 l上. (1)若圆心 C 也在直线 y=x-1 上,过点 A 作圆 C 的切线,求切线的方程;(2)若圆 C 上存在点 M,使|MA|=2|MO|,求圆心 C 的横坐标 a 的取值范围.20．已知直线l:x=my+1 过椭圆C:b2x2+a2y2=a2b2(a>b>0)的右焦点F,且交椭圆 C 于A、B 两点,点 A、B 在直线 G:x=a2 上的射影依次为点 D、E.,其中 O 为原点,A2 为右顶点,e 为离心率,求椭圆 C 的方程;(1)若 113eOF OA2FA2(2)连接 AE,BD,试探索当 m 变化时,直线 AE,BD 是否相交于一定点 N？若交于定点 N,请求出 N 点的坐标,并给予证明;否则说明理由.⎪ ⇒ PO ⊥ 平面ABC⎪ ⎩一．选择题 参考答案1．A 2．D 3．C 4．D 5．C 6．B7．C8．D9．C10．C二．填空题 11．4x-2y-5=0512． k413．(x-3)2+y 2=4 14．（ 2 ， 2 ）x 2 15．y 2116． 25 9 165三．解答题 17．解：（1）分别取 AB 、AC 中点 D 、E过P 作PO AB 于O平面PAB 平面ABC 平面PAB 平面ABC ABPO 平面PAB在 RT △PAB 中∠PAB=60°，∠APB=∠P OA=90° ∴O 为 AD 中点，OE ⊥AB，PO ⊥AB ，PO ⊥OE以 O 为原点分别以 OB ，OE ，OP 所在直线为 x 轴、y 轴、z 轴建立空间直角坐标系 AB=4O （0，0，0） A （-1，0，0） B （3，0，0） C （1， 2 3 ，0） P （0，0， 3 ） 设直线 PC 方向向量 PC (1, 2 3， 3) 平面 ABC 的法向量 m (0, 0，1)| cos PC , m || PC m |3| PC | | m | 43故直线 PC 与平面 ABC 所成角的正弦值为 4 。

天津一中2015-2016学年高二上学期期中考试文数试题第Ⅰ卷一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列说法正确的是（ ）A ．经过空间内的三个点有且只有一个平面B ．如果直线l 上有一个点不在平面α内，那么直线是哪个所有点都不在平面α内C ．四棱锥的四个侧面可能都是直角三角形D ．用一个平面截棱锥，得到的几何体一定是一个棱锥和一个棱台2.若直线1l 和2l 是异面直线，1l 在平面α内，2l 在平面β内，l 是平面α与平面β的交线，则下列命题正确的是（ ）A ．l 与1l ，2l 都不相交B ．l 与1l ，2l 都相交C ．l 至多与1l ，2l 中的一条相交D ．l 至少与1l ，2l 中的一条相交3.设a ，b 是两条直线，,αβ是两个平面，则由下列条件可以得到a b ⊥的是（ ）A ．,//,a b αβαβ⊥⊥B ．,,//a b αβαβ⊥⊥C ．,,//a b αβαβ⊂⊥D ．,//,a b αβαβ⊂⊥4.底面是正多边形，且顶点在底面的射影是底面中心的棱锥叫做正棱锥. 某正三棱锥的底面是一个边长为2的正三角形，若该正三棱锥的表面积是 ）A ．23B ．3C ．3D ．3 5.如图，三棱柱111A B C ABC -中，侧棱1AA ⊥底面111A B C ，底面三角形111A B C 是正三角形，E 是BC 中点，则下列叙述正确的是（ ）A ．1CC 与1B E 是异面直线 B ．1AC ⊥ 平面11A B BAC ．AE 、11B C 为异面直线，且11AE B C ⊥D ．11//A C 平面1AB E6.如图1～3，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为（ ）A ．63B ．93C ．123D ．1837.一个正方体的内切球1O 、外接球2O 、与各棱都相切的球3O 的半径之比为（ ）A ．1:3:2B ．1:1:1C ．1:3:2D ．1:2:38.三棱锥S ABC -中，SA ⊥底面ABC ，4,3SA AB ==，D 为AB 的中点，090ABC ∠=，则点D 到面SBC 的距离等于（ ）A ．125B ．95C ．65D ．359.某几何体的三视图如图所示，则该几何体的表面积为（ ）A ．4012π+B ．4010π+C ．3212π+D ．4812π+10.设四面体的六条棱的长分别为1,1,1,12和a ，且长为a 2的棱异面，则a 的取值范围是（ ）A ．2)B ．3)C ．2)D ．3)第Ⅱ卷二、填空题（每题4分，满分24分，将答案填在答题纸上）11.点(1,4,3)M -关于点(4,0,3)P -的对称点的坐标为 .12.已知(1,1,0)a =，(1,0,2)b =-，若ka b +和3a b -相互垂直，则k = .13.若正三棱柱的所有棱长均为m ，且其体积为83，则m = .14.正方形ABCD 的边长为a ，沿对角线AC 将ADC ∆折起，若060DAB ∠=，则二面角D AC B --的大小为 .15.如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD DC =，E 是PC 的中点，则EB 与底面ABCD 所成的角的正切值为 .16.在三棱锥111ABC A B C -中，090BAC ∠=，其正视图和侧视图都是边长为1的正方形，俯视图是直角边的长为1的等腰直角三角形，设点M ，N ，P 分别是棱AB ，BC ，11B C 的中点，则三棱锥1P A MN -的体积是 .三、解答题 （本大题共4小题，共46分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分10分）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，2AB =，060BAD ∠=.（1）求证：BD ⊥平面PAC ；（2）若PA AB =，求PB 与AC 所成角的余弦值.18. （本小题满分12分）如图，在三棱锥V ABC -中，平面VAB ⊥平面ABC ，VAB ∆为等边三角形，AC BC ⊥，且2AC BC ==，O ，M 分别为AB ，VA 的中点.（1）求证：//VB 平面MOC ；（2）设N 是线段AC 上一点，满足平面//MON 平面VBC ，试说明点的位置N ；（3）求三棱锥V ABC -的体积.19. （本小题满分12分）如图，在长方体1111ABCD A B C D -中，11AD AA ==，2AB =，点E 在棱AB 上移动.（1）证明：11D E A D ⊥；（2）当E 为AB 的中点时，求点E 到面1ACD 的距离；（3）AE 等于何值时，二面角1D EC D --的大小为4π.20. （本小题满分12分）已知某几何体的三视图和直观图如图所示，其正视图为矩形，侧视图为等腰三角形，俯视图为直角梯形.（1）求证：1B N CN ⊥；（2）求直线1C N 与平面1B CN 所成角的余弦值；（3）设M 为AB 中点，在棱BC 上是否存在一点P ，使//MP 平面1B CN ？若存在，求BP PC的值；若不存在，请说明理由.参考答案一、选择题CDCBC BCCAA二、填空题11. (7,4,9)-12.16513. =14. 09015. 16. 124三、解答题17.（1）证明：因为PA ⊥平面ABCD ，所以PA BD ⊥.在菱形ABCD 中，AC BD ⊥，且PAAC A =， 所以BD ⊥平面PAC.（2）取PD 中点E ，设AC BD O =，连结OE ，AE.在菱形ABCD 中，O 是AC 中点，所以//OE PB .则AOE ∠即为PB 与AC 所成角.由2PA AB ==，060BAD ∠=，PA ⊥平面ABCD ，可知PB PD ==，AE OE ==OA =在AOE ∆中，222cos 2OE OA AE AOE OE OA +-∠==•所以PB 与AC 所成角的余弦值是4.18.（1）证明：因为,O M 分别为,AB VA 的中点，所以//VB MO ，因为MO ⊂平面MOC ，VB ⊄平面MOC ，所以//VB 平面MOC.（2）连结ON ，MN. 因为平面//MON 平面VBC ，且平面MON 平面VAC MN =，平面VBC 平面VAC VC =，所以//MN VC .因为M 为VA 的中点，所以N 为AC 的中点.（3）因为AC BC ⊥，且2AC BC ==O 为AB 的中点， 所以OC AB ⊥，2AB =.因为平面VAB ⊥平面ABC ，平面VAB 平面ABC=AB ，CO ⊂平面ABC ， 所以CO ⊥平面VAB ，可知三棱锥V ABC -的体积13VAB V S CD =•. 其中，3VAB S ∆=1CO =，则3V =. 19.（1）证明：∵AE ⊥平面11AA DD ，1A D ⊂平面11AA DD ，∴1A D AE ⊥，11AA DD 为正方形，∴11A D AD ⊥，又1A D AE A =，∴1A D ⊥平面1AD E ，∴11A D D E ⊥.（2）设点E 到面1ACD 的距离为h ，在1ACD ∆中，15AC CD ==，12AD =， 故111325222AD C S ∆=⨯⨯-=，而1122ACE S AE BC ∆=⨯⨯=， ∴1111133D AEC AEC AD C V S DD S h -∆∆=⨯=⨯， 即13122h ⨯=⨯，从而13h =，所以点E 到面1ACD 的距离为13. （3）过D 作DH CE ⊥于H ，连1D H ，则1D H CE ⊥，∴1DHD ∠为二面角1D EC D --的平面角，∴0145DHD ∠=.∵11D D =，∴1DH =，又2DC =，∴030DCH ∠=， ∴060ECB ∠=，又1BC =，在Rt EBC ∆中，得3EB =，∴23AE =-，∴23x =-时，二面角1D EC D --的大小为045.20.（1）证明：由三视图可知4AN =，18BB =， 在直角梯形1ANB B 中，取1BB 的中点H ，连结NH. 可得1NH BB ⊥，则ABHN 是正方形，所以42BN =14NH BH HB ===，142NB =可得22211BN NB BB +=，所以1BN NB ⊥，因为BN BC B =，所以1B N ⊥平面BCN ，则1B N CN ⊥.（2）因为1NH BB ⊥，NH BC ⊥，1BB CB B =，所以NH ⊥平面11BB C C ，设1C 到平面1CNB 的距离为h ，由于1111N CB C C CNB V V --=，所以111CB C CNB S NH S h ∆∆•=•， 解得463h=，设直线1C N 与平面1B CN 所成角为θ，可知12sin h C N θ==， 所以直线1C N 与平面1B CN 所成角的余弦值为73.。

天津一中2011—2012高一年级第一学期数学期中考试试卷一．选择题：1．设集合{}{}|33,|2,12x A x x B y y x =-<<==≤≤，则()()R R C A C B =（ ）A ．[)2,3B ．()(),23,-∞+∞C ．()[),23,-∞+∞D ．()(),24,-∞+∞2．函数()34log 21-=x y 嘚定义域为 （ ）Ａ．（43,∞-） Ｂ．（1,∞-］ Ｃ．（43，1］Ｄ．（43，1）3．设ax x f x++=)110lg()(是偶函数，xx bx g 24)(-=是奇函数，那么a ＋b 嘚值为（ ） A ． 1 B ．－1C ．－21D ．214．)2lg(2lg lg y x y x -=+，则yx2log 嘚值嘚集合是（ ） A ．｛1｝B ．｛2｝C ．｛1，0｝D ．｛2，0｝5．已知函数log (2)a y ax =-在[0，1]上是x 嘚减函数，则a 嘚取值范围是（ ） Ａ．（0，1）Ｂ．（0，2） Ｃ．（1，2） Ｄ．[2，+∞)6．函数x xx xe e y e e --+=-嘚图像大致为 ( ).7．已知函数f(x)=log 3x+2 (x ∈[1,9])，则函数y=[f(x)]2+f(x 2)嘚最大值是（ ） A ．13 B ．16 C ．18 D ．228．设xa x f =)(，31)(x x g =，x x h a log )(=，实数a 满足)1(log 2a a -＞0，那么当x ＞1时必有（ ）1xy 1OAxyO 11BxyO 1 1Cx y 1 1 DOA ．)(x h ＜)(x g ＜)(x fB ．)(x h ＜)(x f ＜)(x gC ．)(x f ＜)(x g ＜)(x hD ．)(x f ＜)(x h ＜)(x g9．已知函数)(x f 是R 上嘚增函数，(0,2)-A ，(3,2)B 是其图象上嘚两点，那么2|)1(|<+x f 嘚解集是（ ） A ．（1，4）B ．（-1，2）C ．),4[)1,(+∞-∞D ．),2[)1,(+∞--∞10．设函数121()3(0)2(),(0)xx f x x x ⎧-≤⎪=⎨⎪>⎩已知()1f a >，则实数a 嘚取值范围是（ ）Ａ．(2,1)- Ｂ．(,2)(1,)-∞-+∞ Ｃ．(1,)+∞Ｄ．(,1)(0,)-∞-+∞二．填空题：11．已知幂函数)(x f y =嘚图象过点=)9(),2,2(f 则 。

天津一中2012—2013—2高二年级数学（文科）期中考试试卷班级_____________ 姓名_____________一． 选择题：1．复数⎝⎛⎭⎪⎫3－i 1＋i 2 ＝( )A ．－3－4iB ．－3＋4iC ．3－4iD ．3＋4i2. 设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的 ( ) A. 充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．即不充分也不必要条件3．下面几种推理过程是演绎推理的是（ ）A ．两条直线平行，同旁内角互补，如果A ∠和B ∠是两条平行直线的同旁内角，则180A B ∠+∠=° B ．由平面三角形的性质，推测空间四面体的性质C ．三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得凸n 多边形内角和是(2)180n ︒-· D ．在数列{}n a 中，11a =，1111(2)2n n n a a n a --⎛⎫=+ ⎪⎝⎭≥，由此归纳出{}n a 的通项公式4.下列说法中，正确的是（ ）A ．命题“若,22bm am <则b a <”的逆命题是真命题。

B ．命题“0,2>-∈∃x x R x ”的否定是“0,2≤-∈∀x x R x ”。

C ．命题“q p ∨”为真命题，则命题p 和命题q 均为真命题。

D ．已知R x ∈，则“1>x ”是“2>x ”的充分不必要条件。

5．设曲线11x y x +=-在点(3,2)处的切线与直线10ax y ++=垂直,则a =( ) A ．12- B.12C.2D.2-6．已知函数f (x )的导函数()f x '那么函数f (x )的图象最有可能的是))x ，()()32f x f x '=，…，()()1n n f x f x +'=，n ∈*N ，则=)(2013x f ( )- 2 -A ．sin cos x x +B ．sin cos x x -C ．sin cos x x -+D ．sin cos x x --8．函数x x x y cos sin +=在下面那个区间为增函数 ( )A ． ⎪⎭⎫⎝⎛23,2ππ B ．()ππ2, Ｃ． ⎪⎭⎫⎝⎛25,23ππ Ｄ．()ππ3,2 9．已知命题p ：实数m 满足01≤-m ，命题q ：函数xm y )49(-=是增函数。

一．选择题：1．过点（1，0）且与直线x-2y-2=0平行的直线方程是( )A ．x-2y-1=0B ．x-2y+1=0C ．2x+y-2=0D ．x+2y-1=0 2则该椭圆的方程为（ ）ABCD3．设变量x ，y 满足约束条件：3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩.则目标函数z=2x+3y 的最小值为（ ）A ．6B ．7C ．8D ．234．若点(,)P a b 在圆C:221x y +=的外部，则直线10ax by ++=与圆C 的位置关系是（ ） A ．相切B ．相离C ．相交D ．相交或相切5．已知圆的方程为08622=--+y x y x .设该圆过点（3，5）的两条弦分别为AC 和BD ，且BD AC ⊥.则四边形ABCD 的面积最大值为（ ）A ．B ．C ．49D ．506．动点在圆x 2＋y 2=1上移动时，它与定点B （3，0）连线的中点轨迹方程是（ ）A ．（x ＋3)2＋y 2=4B ．（x －3)2＋y 2=1C ．（2x －3)2＋4y 2=1D ．（x2＋y 27．若直线220ax by -+=（0,0a b >>）被圆222410x y x y ++-+=截得的弦长为4，( )A BC ．2D ．48中，12,F F 分别是其左右焦点，若离心率的取值范围是 ( )ABC D第II 卷二．填空题：9．已知直线12:(3)(4)10,:2(3)230,l k x k y l k x y -+-+=--+=与平行，则k 的值是_______.10．如果方程x 2+ky 2=2表示焦点在y 轴的椭圆，那么实数k 的取值范围是____________。

11．圆x 2+y 2+2x+4y-3=0上到直线4x-3y=2的点数共有 个。

12．已知圆C ：04222=+-++m y x y x 与直线2:+=x y l 相切，且圆D 与圆C 关于直线l 对称，则圆D 的方程是___________。