截一个几何体(用)
- 格式:ppt
- 大小:789.00 KB
- 文档页数:29


初中级数学分层作业设计举例--截一个几何体单元名称丰富的图形世界课题截一个几何体节次第1课时作业类型作业内容设计意图和题目来源基础性作业(必做)1.如图所示几何体的截面是()A.四边形 B.五边形 C.六边形 D.五棱柱意图:通过巩固具体几何体的截面形状,培养直观想象素养..来源:新编答案:B2.用平面去截一个几何体,如果截面是圆形,则原几何体可能是()A.正方体、球 B.圆锥、棱柱C.球、长方 D.圆柱、圆锥、球意图:通过由截面形状判断几何体的形状,培养直观想象素养.来源:新编答案:D3.用一个平面去截一个如图所示的正方体,截面形状不可能为()A.B.C.D.意图:巩固正方体的截面特征,培养直观想象素养.来源:新编答案:C4.经过圆锥顶点的截面的形状可能是()A.B.C.D.意图:巩固圆锥的截面形状,培养直观想象素养.来源:新编答案:B5.如图所示的三个几何体的截面分别是:(1)______;(2)_____ ;(3)______.意图:巩固常见几何体的截面形状,培养直观想象素养.来源:新编答案:长方形、圆、三角形6.用一个平面去截:①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是()A.①②④B.①②③C.②③④D.①③④意图:巩固常见几何体的截面形状,培养直观想象素养.来源:新编答案:B7.用平面去截一个几何体,如果所得截面的形状是三角形,则该几何体不可能是()A.圆柱B.棱柱C.圆锥D.正方体意图:通过截面形状判断几何体的形状,培养直观想象素养.来源:新编答案:A8.如图所示,截去正方体一角变成一个多面体,这个多面体有个面,有条棱,有个顶点.意图:通过截一个多面体,想象、分析截后多面体的特点,培养直观想象素养.来源:新编答案:7、12、7.拓展性作业(选做)1.用一个平面去截n棱柱,边数最多的截面是____边形.意图:巩固棱柱的截面特点,培养直观想象素养.来源:新编答案:n2.用一个平面截一个几何体,所截出的面如图所示,共有四种形状,试猜想,该几何体可能是.意图:通过一个几何体所有可能截面的形状判断该几何体的形状,培养直观想象素养.来源:新编答案:圆柱3.如图,用一个平面去截正方体,截掉了正方形的一个角,且截面经过原正方体三条棱的中点,则剩下几何体的展开图应该是()A.B.C.D.意图:通过截一个多面体,探索切截后多面体的平面展开图,培养直观想象、逻辑推理素养.来源:新编答案:B4.一个圆柱的底面半径是10cm,高是18cm,把这个圆柱放在水平桌面上,如图所示.(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?(3)怎样截时所得的截面是长方形且长方形的面积最大,请你画出这个截面并求出这个截面面积.意图:巩固圆柱的截面形状,并应用来解决问题,培养直观想象、数学抽象素养.来源:新编答案:(1)圆;(2)长方形;(3)360.单元名称丰富的图形世界课题从三个方面看物体的形状节次第1课时作业类型作业内容设计意图和题目来源1.如图所示的几何体,从左面看它的形状图是()A.B.C.D.2.下面几个几何体,从正面看到的图形是圆的是()A.B.C.D.3.如图所示的几何体为圆台,从上面看到的图形正确的是()A.B. C. D.4.下列四个几何体中,从正面、左面看到的图形都相同的有()A.1个B.2个 C.3个D.4个5.将如图所示的直角三角形ABC绕直角边AB所在直线旋转一周,所得几何体从正面看到的形状图为()A. B. C. D.6.如图是由6个相同的小正方体搭成的几何体,从上面看这个几何体的形状图是()A.B.C. D.7.如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体()A.从正面看改变,从左面看改变B.从上面看不变,从左面看不变C.从上面看改变,从左面看改变D.从上面看改变,从左面看不变8.如图是一个由多个相同小正方体搭成的几何体从上面看到的形状图,图中所标数字为该位置小正方体的个数,则这个几何体从正面看到的形状图是()A.B.C.D.9.从正面、左面、上面观察一个几何体得到的形状图如图所示,则这个几何体是()A.圆锥 B.圆柱 C.长方体 D.四棱柱10.如图,是由6个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.(1)直接写出这个几何体的表面积(包括底部):____;(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.意图:通过计算组合几何体的表面积及画组合几何体的三视图,培养直观想象、数学运算素养.来源:新编答案:(1)26cm2(2)1.学校小卖部货架上摆放着某品牌方便面,从正面、左面、上面看到的形状如图,则货架上的方便面至少有()A.7盒B.8盒 C.9盒D.10盒答案:7 3.根据如图所示(单位:mm),求该物体的体积.从正面看从上面看意图:通过由视图计算几何体体积,培养直观想象、数学运算素养.来源:新编答案:1088πmm3单元名称丰富的图形世界课题回顾与思考节次第1课时作业类型作业内容设计意图和题目来源基础性作业(必做)1.下列图形中,不属于立体图形的是()A.B.C.D.意图:通过对立体图形识别,巩固几何体的概念,培养直观想象素养.来源:新编答案:A2.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是()A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥意图:通过根据语言描述确定几何体的形状,培养直观想象素养.来源:新编答案:D3.下面现象说明“线动成面”的是()A.旋转一扇门,门在空中运动的痕迹B.扔一块小石子,石子在空中飞行的路线C.天空划过一道流星D.汽车雨刷在挡风玻璃上面画出的痕迹意图:通过具体实例巩固点、线、面、体,之间的关系,培养直观想象素养.来源:新编答案:D4.如图:CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是()A.绕着AC旋转B.绕着AB旋转C.绕着CD旋转D.绕着BC旋转意图:巩固点、线、面、体,之间的关系,巩固“面动成体”,培养直观想象素养.来源:新编答案:B5.如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是()A.正方体、圆柱、三棱锥B.正方体、三棱锥、圆柱C.正方体、圆柱、三棱柱D.三棱锥、圆锥、正方体意图:巩固常见的立体图形的表面展开图,培养直观想象素养.来源:新编答案:C6.如图的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是()意图:巩固正方体展开图的特征,由几何体各面之间的位置关系想象其展开图对应的面的位置关系,培养直观想象素养.来源:新编答案:DA .B .C.D.7.如图所示,用一个平面去截一个圆柱,则截得的形状应为()A. B.C. D.意图:巩固圆柱体的截面形状,培养直观想象素养.来源:新编答案:B8.用一个平面去截一个几何体,得到的截面形状是长方形,那么这个几何体可能是()A.正方体、长方体、圆锥B.圆柱、球、长方体C.正方体、长方体、圆柱D.正方体、圆柱、球意图:通过由截面形状判断几何体的形状,培养直观想象素养.来源:新编答案:C9.如图所示是从三个方向看一个几何体所得到的形状图,则这个几何体是()A.B.C.D.意图:巩固由从不同方向看到的图形想象几何体的形状,培养直观想象素养.来源:新编答案:A10.用小立方块搭成的几何体,从左面看和从上面看如下,设这样的几何体最多要用x个小立方块,最少要用y 个小立方块,则x+y等于()A.12 B.13C.14 D.15 意图:巩固从不同方向看到的图形想象组合几何体形状,培养直观想象、逻辑推理素养.来源:新编答案:A11.一个几何体由一些大小相同的小正方块儿搭建,如图是从上面意图:通过由俯视图及数据想象几何体,再画出其主、左视图,培养直观想象素养.来源:新编答案:看到的这个几何体的形状如图,小正方形的数字表示在该位置的小正方块儿的个数,请在网格中画出从正面和左面看到的几何体的形状图.拓展性作业(选做)1.棱长是1cm的小立方体组成如图所示的几何体,那么这个组合几何体的表面积为___________ 意图:通过根据简单组合体的三视图来求几何体的表面积,培养直观想象素养.来源:新编答案:36cm22.如图所示,木工师傅把一个长为1.6米的长方体木料锯成3段后,表面积比原来增加了80cm2,那么这根木料本来的体积是多少?意图:通过截一个长方体,识别截后长方体的特征,培养直观想象、数学运算素养.来源:新编答案:3200cm33.图①是正方体的平面展开图,六个面的点数分别为1点、2点、3点、4点、5点、6点,将点数朝外折叠成一枚正方体骰子,并放置于水平桌面上,如图②所示.(1)在图②所示的正方体骰子中,1点对面是___点;2点的对面是___点(直接填空);(2)若骰子初始位置为图②所示的状态,将骰子向右翻滚90°,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连线完成2次翻转后,骰子朝下一面的点数是____点;连续完成2016次翻转后,骰子朝下一面的点数是______点(直接填空).意图:通过操作活动巩固正方体展开图的特征,培养直观想象、逻辑推理素养.来源:新编答案:(1)6,5(2)3,4单元名称有理数及其运算课题有理数节次第一课时作业类型作业内容设计意图和题目来源基础性作业(必做)1.下列各数中,是负数的为()A.﹣1 B.0 C.0.2 D.21意图:通过对数据的识别巩固负数的定义,培养数学抽象素养.来源:新编答案:A2.陆地上最高处是珠穆朗玛峰顶,高出海平面8848m,记为+8848m;陆地上最低处是地处亚洲西部的死海,低于海平面约415m,记为()A.+415m B.﹣415mC.±415m D.﹣8848m意图:通过实际问题中相反意义的量巩固正负数的概念,培养数学抽象素养.来源:新编答案:B3.下列对有理数的理解错误的是()A.有理数分为正数和负数意图:通过命题的判断巩固有理数的分类,培养数学抽象素且行走方向顺序为先左右再上下.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,请根据如图完成如下问题:(1)A→C(,),B→D(,),C→D(+1,);(2)若快递员的行走路线为A→B→C→D,请计算该快递员走过的路程;(3)若快递员从A处去某P处的行走路线依次为(+2,+2),(+1,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置.意义,培养数学抽象、数学运算、直观想象素养.来源:新编答案:(1)+3,+4;+3,﹣2;﹣2;(2)10(3)P在第1列第4行.。



1.3截一个几何体新知概览:知识要点课标要求中考考点用平面去截几何体所得截面的形状探索并理解几何体的截面形状。
截面的定义(掌握)几种常见几何体的截面掌握几种常见几何体的截面。
判断一个几何体的截面(应用)本节重、难点1.重点:截面的定义和形状.2.难点:利用截面解决实际问题.知识全解知识点1截面(1)截面的概念:用一个平面去截几何体,截出的面叫做截面.(2)正方体的截面:根据面与面相交可以得到线可知用一个平面去截正方体的三个面,得到的截面是三角形.如果用一个平面去截正方体的四个面,就能得到四边形,除能得到正方形、长方形这样的四边形外,还能得到其他的四边形,如梯形、平行四边形等.知识警示:(1)正方体总共有六个面,用一个平面去截最多只能得到六条交线,从而截面的边数最多只能是六,还可以得到五,但不可能截得七边形.(2)一般地,截面与几何体的几个面相交就得到几条交线,截面就是几边形.因此,若一个几何体有n个面,则截面最多的边数是n.知识拓展正方体的截面主要有三角形、四边形、五边形和六边形,如图1-3-1所示.【试练例题1 】如图1-3-2所示的一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是()思路导引:首先根据两组对边平行,可确定为平行四边形;又有一角为直角,故截面图形是长方形.答案:B.长方体的截面,经过长方体四个侧面,长方体中,对边平行,故可确定为平行四边形,交点垂直于底边,故为长方形.知识方法:截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.知识点2几种常见几何体的截面(1)如图1-3-3所示,用平面截圆柱体,可能出现以下的几种情况.(2)如图1-3-4所示,用平面去截一个圆锥,能截出圆和三角形两种截面.图1-3-1A图1-3-2B C D(3)如图1-3-5所示,用平面去截球体,只能出现一种形状的截面---圆.知识警示: (1) 用一个平面去截一个圆柱所得到的截面有圆、长方形、椭圆、拱形形状和梯形.(2) 用一个平面去截圆锥,可得到圆、三角形、拱形形状和椭圆.【试练例题2】如图1-3-6中几何体的斜截面形状是( )思路导引:几何体是一个圆柱体,用一个平面斜截它,得到的截面应该是类似拱形的图形.答案C 用一个平面去截一个圆柱体,过平行于上下底面的面去截可得到圆;圆柱体的轴截面是矩形;过侧面且不平行于上下底面的面去截可得到椭圆;过一底面不平行于另一底面的面去截可得到类似拱形的截面.方法:平面与平面相交得直线,平面与曲面相交可能得到直线,也可能得到曲线.图1-3-5图1-3-4 图1-3-6。

截一个几何体
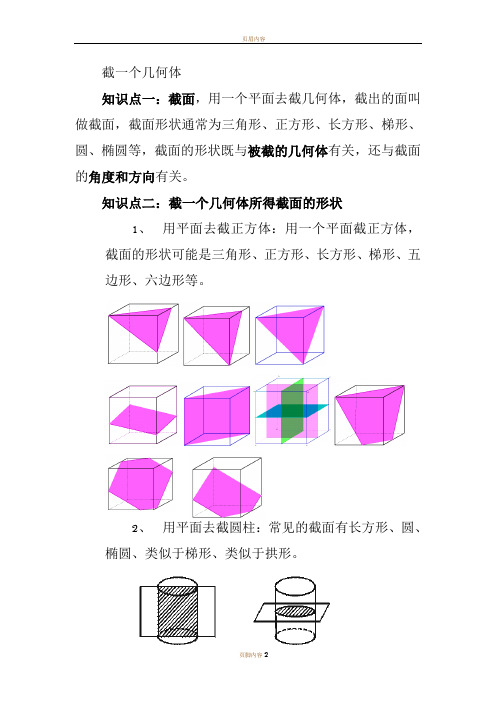
知识点一:截面,用一个平面去截几何体,截出的面叫做截面,截面形状通常为三角形、正方形、长方形、梯形、圆、椭圆等,截面的形状既与被截的几何体有关,还与截面的角度和方向有关。
知识点二:截一个几何体所得截面的形状
1、用平面去截正方体:用一个平面截正方体,
截面的形状可能是三角形、正方形、长方形、梯形、五
边形、六边形等。
2、用平面去截圆柱:常见的截面有长方形、圆、
椭圆、类似于梯形、类似于拱形。
3、用平面去截圆锥:截面的形状可能是三角形、圆、椭圆、类似于拱形。
4、用平面去截球:截面的形状都是圆。




《截一个几何体》说课稿重点:让学生经历用一个平面截正方体的活动,体会截面和几何体的关系,初步发展空间观念。
难点:发现截面产生的规律,并会运用规律解决问题。
材料准备:教师准备五个棱长为6厘米的正方体土豆块,彩色颜料;学生准备若干个正方体土豆块,小刀。
一、情境导入演示现实生活中的物体的截面。
师:引导学生观察这是何种物体的截面。
生:被画面所吸引,纷纷回答出是椰子、陨石等的截面。
师:很自然的引出截面的定义(用一个平面截一个几何体,截出的面即为截面)。
这样设计有利于激发学生的学习兴趣,体现了数学知识来源于生活。
二、新课讲授师:提出问题:用一个平面截一个正方体,截面可能是什么形状呢?让学生大胆猜想,学生凭直觉可能猜出截面是三角形、正方形、长方形,也可能会产生争论:有的认为截面可以是平行四边形、梯形,有的认为不能。
设计猜想这个环节系即能激发学生的探求欲望,又能使接下来的切截活动目的性更强。
由于七年级学生年龄小,活动经验少,动手能力不强,所以我把切截活动分为三个小活动,活动一:切三角形的截面;活动二:切四边形的截面;活动三:切五边形、六边形的截面。
先进行活动一:切三角形的截面。
提醒学生注意安全,学生可能会切掉一个小角,得到一般三角形或等腰三角形的截面;也可能经过正方体的三个顶点切掉一个大角,得到等边三角形的截面。
切完后,小组内交流切截情况。
请小组代表总结三角形的截面有一般三角形、等腰三角形、等边三角形这三种。
活动二:切四边形的截面。
相对于三角形的截面来说,四边形的截面形状多样,每一种四边形的切法也不唯一,难度较大。
所以把活动二分三步进行:第一步:学生独立切截,鼓励学生切出多种不同的四边形,切完后,总结自己切得的形状和切截的方法;第二步:带着自己的结果参与到小组的交流活动中,小组汇总共切得几种四边形及每一种四边形的不同切法;每个小组应该都能切得正方形、长方形,而平行四边形和梯形可能有困难。
这时请切得好的学生,用我准备的大土豆块,上台切出平行四边形和梯形,并把截面染成彩色,让全班同学一目了然。

12.把一个正方体用刀切去一块,能否还得到正方体?长方体、三棱柱、三棱锥、四棱柱、五棱柱呢?考点:截一个几何体。
专题:应用题。
分析:当截面的角度和方向不同时,圆柱体的截面不相同.解答:解:不能得到正方体,当截面平行正方体一面截取正方形时可以截得长方体,把正方体按面对角线垂直截取正方体可以得到三棱柱,经过正方体三个相邻的顶点截取可以得到三棱锥,经过两个相对面棱上中点截取可以得到四棱柱,经过上下两面棱的中截取可以得到五棱柱.点评:截面的形状既与被截的几何体有关,还与截面的角度和方向有关.13.今有正方形蛋糕,切两刀把蛋糕分成形状相同的4块,请设计三种不同的方法.考点:截一个几何体。
专题:作图题。
分析:可沿正方形的两条对角线切;沿过正方形的对边中点的两条线切;由此推出只要经过正方形的对角线的交点且互相垂直的两条直线均可且成形状相同的4部分.解答:解:点评:用到的知识点为:经过正方形的中心且互相垂直的两条直线把正方形分成形状相同的4块.14.如图是一个三棱柱,把它一刀切去一部分,剩下的部分会是一个什么图形?先动手做做实验,然后得出结论.考点:截一个几何体。
专题:操作型。
分析:沿垂直于轴截面剪去,可得三棱柱;沿经过上底面的一个顶点及下底面相对的顶点的对边的面剪去,可得到三棱锥;沿平行于三棱柱的一个侧面面剪去,可得到的一个四棱柱.解答:解:可以切成三棱柱、三棱锥、四棱柱.点评:用到的知识点为:棱柱的侧面是四边形;棱锥的侧面是三角形;注意根据截面经过的不同位置得到相应的几何体的形状.15.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.如A(1、5、6);则B();C();D();E().考点:截一个几何体。
分析:分别分析其余四种图形的所有的截面情况,再写出答案.解答:解:B三棱锥,截面有可能是三角形,正方形,梯形C正方体,截面有可能是三角形,四边形(矩形,正方形,梯形),五边形,六边形D球体,截面只可能是圆E圆柱体,截面有可能是椭圆,圆,矩形,梯形因此应该写B(1、3、4);C(1、2、3、4);D(5);E(3、5、6).点评:截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.16.附加题:(1)解方程:.(2)按图示切割正方体就可以切割出正六边形(正六边形的各顶点恰是其棱的中点),请你任意画出此正方体的两种平面展开图,并在展开图上画出所有的切割线.考点:截一个几何体;解一元一次方程。

截一个几何体教材分析:“截一个几何体〞是七年级?数学?〔上〕中继“生活中的立体图形〞和“展开与折叠〞之后的一个学习内容。
在本章教材的编排顺序中起着承上启下的作用,截一个几何体是让学生经历切截几何体的活动过程,探索几何体在切截过程中会有怎样的变化,体验以运动的眼光观察事物的过程,丰富几何直觉和数学活动经验,增强动手实践能力和空间想象能力。
教学目标:通过经历对几何体切截的实践过程,让学生体验面与体之间的转换,探索截面形状与切截方向之间的联系,从而丰富学生的几何直觉和数学活动经验,开展学生的空间观念和创造性思维能力,在下载学习工具的过程中学感受学习信息技术的重要性,同时培养学生的数学语言表达能力。
初步形成主动与他人合作交流的意识。
教学重点:经过切截正方体的活动过程,体会正方体截面的变化。
教学难点:正确判断用一个平面去截一个正方体得到的截面形状。
学生分析:七年级学生好奇心强,喜欢探索、解剖身边的事物,通过在网上下载,利用教学软件在运行平台上对正方体进行截割,加工的热情势必较高,如果创设一系列合理的问题情景,组织学生进行一些生动有趣的数学活动,本节课会极大地调动学生参与的积极性。
课前准备:1.在“Z+Z〞教育平台网站上下载“立体几何〞运行程序,并装在“网络教室〞的学生机及教师机上。
2.在“Z+Z〞教育平台网站上下载教学资源:1-3正方体的截面、1-3正方体的截面〔1〕、1-3正方体的截面〔2〕,共三个内容,并放在学校网站上。
3.用PowerPoint把下载的flash课件链接起来,贯穿全部教学内容。
课后反思:本堂课的教学模式设计理念较为先进,整个教学推进涉及三个维度,〔见以以下图〕彼此环环相扣,由浅入深,学生通过自己的实验操作感受并获取知识,圆满地完成了教学任务。
但在具体的操作过程中,耗时较多,这主要是学生的信息素养差,对下载和安装不熟悉,再就是运用鼠标的能力差,在托动中完不成自己的设想,故今后要加强学生的信息素养的培养。