6.5 自感
- 格式：ppt
- 大小：298.50 KB
- 文档页数：8
下载文档原格式
合集下载
高中物理电学考点总结归纳
高中物理电学考点总结归纳1. 电荷与电场1.1 电荷的性质1.2 电场的概念1.3 电场强度的计算方法1.4 电荷分布与电场1.5 电势与电势能2. 静电场2.1 静电场的性质2.2 静电力与库仑定律2.3 静电场的叠加原理2.4 高斯定律及应用2.5 电场的能量密度3. 电流与电路3.1 电流的概念与电流强度3.2 电流的连续性方程3.3 电阻与电阻率3.4 欧姆定律与电功率3.5 简单电路中的串联和并联4. 电阻、电功与电功率4.1 电阻的性质和分类4.2 线性电阻的IV特性4.3 电功的计算方法4.4 电功率的计算方法5. 电路分析5.1 罗尔定律5.2 基尔霍夫定律5.3 电路中的等效电阻5.4 电路中的戴维南定理5.5 电路中的诺顿定理6. 电磁感应6.1 磁场的概念与性质6.2 电磁感应定律6.3 法拉第电磁感应实验6.4 感应电动势的计算方法6.5 自感与互感7. 电磁场中的电荷运动7.1 洛伦兹力与洛伦兹定律7.2 质点在磁场中的运动7.3 导体中的电流7.4 长直导线产生的磁场7.5 磁场中感生电动势8. 交流电路8.1 交流电的概念与表示方法8.2 交流电的平均值与有效值8.3 电阻、电感和电容在交流电路中的作用 8.4 交流电路中的功率计算8.5 交流电路中的谐振现象9. 光学9.1 光的反射与折射9.2 光的干涉与衍射9.3 光的偏振与双折射9.4 光的反射与折射定律的应用9.5 光的波粒性与光量子的能量10. 声学10.1 声波的特性10.2 声音的传播10.3 声源和听者的特性10.4 声音的强度与声级10.5 声音的干涉与谐振以上是高中物理电学的考点总结归纳，包括电荷与电场、静电场、电流与电路、电阻、电功与电功率、电路分析、电磁感应、电磁场中的电荷运动、交流电路、光学和声学等内容。
掌握这些考点并理解其相关性质和计算方法，将有助于对高中物理电学的学习和考试备考。
几个常用的自感系数计算公式的应用
几个常用的自感系数计算公式的应用自感系数是电磁学中常用的参数之一，用于描述电流元或线圈产生的磁场与其自身的关系。
在不同的电磁学问题中，可以利用不同的公式来计算自感系数。
接下来将介绍几个常用的自感系数计算公式及其应用。
1.直线电流元的自感系数：对于一段长度为L、电流为I的直线电流元，其自感系数可以通过以下公式计算：L=μ0*I^2/(4π)其中，μ0是真空中的磁导率，其数值为4π×10^-7H/m。
应用：这个公式可以用于计算直线电流元的自感系数，例如在计算由长导线产生的磁场时，可以通过该公式计算导线的自感系数。
2.环形线圈的自感系数：对于一个半径为R、N匝的环形线圈，其自感系数可以通过以下公式计算：L=μ0*N^2*A/(2π)其中，A是线圈的面积，μ0是真空中的磁导率。
应用：这个公式可以用于计算环形线圈的自感系数，例如在计算由环形线圈产生的磁场时，可以通过该公式计算线圈的自感系数。
3.双曲线形线圈的自感系数：对于一个双曲线形线圈，其自感系数可以通过以下公式计算：L = μ0 * (N^2 * ln(8R/d) - N^2)其中，R是线圈的半径，d是双曲线形线圈的内径，N是线圈的匝数，μ0是真空中的磁导率。
应用：这个公式可以用于计算双曲线形线圈的自感系数，例如在设计电感器或传感器时，可以通过该公式计算线圈的自感系数。
4.均匀薄线圈的自感系数：对于一个半径为R、匝数为N、宽度为w的均匀薄线圈，其自感系数可以通过以下公式计算：L = μ0 * N^2 * (ln(8R/w) - 2)其中，w是线圈的宽度，μ0是真空中的磁导率。
应用：这个公式可以用于计算均匀薄线圈的自感系数，例如在设计电感器或电感元件时，可以通过该公式计算线圈的自感系数。
总结：自感系数是电磁学中重要的参数之一，用于描述电流元或线圈产生的磁场与其自身的关系。
通过不同的公式可以计算不同形状的线元或线圈的自感系数，这些公式在电磁学的理论研究和实际应用中都有广泛的应用。
第五节自感现象课件
的应用， 如日光灯、变压器等。通过实验演示 和探究，有助于学生深入理解自感现 象的本质和应用，提高对电路的分析 和设计能力。
04
自感现象的实际应用
电磁炉的工作原理
电磁炉利用自感现象产生高频交变磁 场，通过磁力线切割锅具产生大量涡 流，使锅具自身快速发热，从而实现 烹饪食物的目的。
动态自感与静态自感
总结词
动态自感和静态自感是根据自感现象中磁场变化的形式不同而划分的两种类型。
详细描述
动态自感是指磁场随时间变化而产生的自感现象，其特点是自感电动势与磁场的 变化率成正比。静态自感则是当磁场在空间位置上发生变化时产生的自感现象， 其特点是自感电动势与磁通量的变化率成正比。
自感的决定因素
次级线圈中感应出电压。
变压器在电力系统中发挥着重要 的作用，用于调节电压和传输电
能。
继电器的工作原理
继电器利用自感现象实现电流 的控制和保护功能。
当电流通过继电器线圈时，会 产生磁场，使衔铁吸合，进而 带动触点组动作，实现电路的 通断控制。
继电器广泛应用于自动化控制 、电力保护、电机控制等领域 。
理论模型不完善
目前对自感现象的理论模 型仍不完善，缺乏对自感 现象的深入理解和解释。
应用领域有限
目前自感现象的应用主要 集中在某些特定领域，尚 未得到广泛应用和推广。
未来研究的方向和展望
探索新的实验方法
未来研究需要探索新的实验方法 ，提高实验验证的精度和可靠性
。
完善理论模型
加强对自感现象的理论研究，完善 理论模型，为应用提供更可靠的依 据。
详细描述
电磁感应定律指出，当磁场发生变化时，会在导体中产生电动势，从而产生电 流。这个电流会产生自己的磁场，对原磁场的变化产生阻碍作用，这就是自感 现象。
04
自感现象的实际应用
电磁炉的工作原理
电磁炉利用自感现象产生高频交变磁 场，通过磁力线切割锅具产生大量涡 流，使锅具自身快速发热，从而实现 烹饪食物的目的。
动态自感与静态自感
总结词
动态自感和静态自感是根据自感现象中磁场变化的形式不同而划分的两种类型。
详细描述
动态自感是指磁场随时间变化而产生的自感现象，其特点是自感电动势与磁场的 变化率成正比。静态自感则是当磁场在空间位置上发生变化时产生的自感现象， 其特点是自感电动势与磁通量的变化率成正比。
自感的决定因素
次级线圈中感应出电压。
变压器在电力系统中发挥着重要 的作用，用于调节电压和传输电
能。
继电器的工作原理
继电器利用自感现象实现电流 的控制和保护功能。
当电流通过继电器线圈时，会 产生磁场，使衔铁吸合，进而 带动触点组动作，实现电路的 通断控制。
继电器广泛应用于自动化控制 、电力保护、电机控制等领域 。
理论模型不完善
目前对自感现象的理论模 型仍不完善，缺乏对自感 现象的深入理解和解释。
应用领域有限
目前自感现象的应用主要 集中在某些特定领域，尚 未得到广泛应用和推广。
未来研究的方向和展望
探索新的实验方法
未来研究需要探索新的实验方法 ，提高实验验证的精度和可靠性
。
完善理论模型
加强对自感现象的理论研究，完善 理论模型，为应用提供更可靠的依 据。
详细描述
电磁感应定律指出，当磁场发生变化时，会在导体中产生电动势，从而产生电 流。这个电流会产生自己的磁场，对原磁场的变化产生阻碍作用，这就是自感 现象。
第六章-自感式传感器
L0
L10
L20
m
0W
2
mr
rc
l2 c
l2
k1
k2
m0W 2mr rc2
l2
综上所述，螺管式自感传感器的特点： ①结构简单，制造装配容易； ②由于空气间隙大，磁路的磁阻高，因此灵敏度低 ，但线性范围大； ③由于磁路大部分为空气，易受外部磁场干扰； ④由于磁阻高，为了达到某一自感量，需要的线圈 匝数多，因而线圈分布电容大； ⑤要求线圈框架尺寸和形状必须稳定，否则影响其 线性和稳定性。
2
3
（2）单线圈是忽略
0
以上高次项，差动式是忽略
0
以上偶次项，
因此差动式自感式传感器线性度得到明显改善。
*另一种形式： Π型
6 自感式传感器
6.1 工作原理 6.2 变气隙式自感传感器 6.3 变面积式自感传感器 6.4 螺线管式自感传感器 6.5 自感式传感器测量电路 6.6 自感式传感器应用举例
第6章 电感式传感器
电感式传感器是建立在电磁感应基础上，利用 线圈自感或互感的改变来实现测量的一种装置。它 可对直线位移和角位移进行直接测量，也可通过一 定的敏感元件把振动、压力、应变、流量等转换成 位移量而进行测量。通常可由下列方法使线圈的电 感变化：
(1)改变几何形状； (2)改变磁路的磁阻； (3)改变磁芯材料的导磁率； (4)改变一组线圈的两部分或几部分间的耦合度。
1. 交流电桥 2. 变压器电桥 3. 自感传感器的灵敏度
（一）交流电桥式测量电路
分析：
• 衔铁在初始位置时，电桥平衡
L1
L2
L0
W 2m0S 20
• 若衔铁上移，则：
1 0 ,2 0
165自感现象6日光灯原理
L
A
a
b
L
a
b
再看一遍
返回题目
L
a
b
返回题目
例题1
B 如图所示，L为一个纯电感线圈（直流电阻为零），A为一个灯泡，下列说
法正确的是：（ ） A．开关S接通瞬间无电流通过灯泡 B．开关S接通后，电路稳定时，无电流通过灯泡 C．开关S断开瞬间无电流通过灯泡 D．开关S接通瞬间及接通稳定后，灯泡有由a到b的电流， 而在开关S断开瞬间，灯泡中有从b到a的电流
由于这个电压低于启辉器的电离电压，所以并联在两
端的启辉器也就不再起作用了。
关于日光灯的工作原理，下列说法正确的 （ BC ）
A. 镇流器的作用是将交流电变为直流电
B. 在日光灯的启动阶段，镇流器能提供一个瞬 时高压，使灯管开始工作
C.日光灯正常发光时，启动器的两个触片是分 离的
D.日光灯发出柔和的白光是由汞原子受到激发 后直接辐射的
两极间电压为零，辉光放电消失，管内温度降低；双
金属片自动复位，两极断开。在两极断开的瞬间，电
路电流突然切断，镇流器产生很大的自感电动势，与
电源电压叠加后作用于管两端。灯丝受热时发射出来
的大量电子，在灯管两端高电压作用下，以极大的速
度由低电势端向高电势端运动。在加速运动的过程中，
碰撞管内氩气分子，使之迅速电离。氩气电离生热，
i1 i
i2
t
O -i2
t1
-i1
B
i i1
i2
O -i2
t1ห้องสมุดไป่ตู้
t
-i1
C
i1 i
i2
O -i2
t1
-i1
D
i2
A
自感系数的计算方法
自感系数的计算方法
自感系数的计算方法是用来测量电路中电感元件对自身电流变化的敏感程度的
参数。
它表示了电感元件在电流变化时，会引起电感自感电压的变化程度。
计算自感系数的方法通常基于法拉第定律，即电感的自感电动势等于电流对时
间的导数乘以一个常数L，其中L为电感的自感系数。
一种常用的方法是利用恒定电流源和开关来测量电感的自感系数。
首先，将电
感元件与一个电流源和一个开关连接，并使电流流过电感。
然后，突然打开或关闭开关，记录电感两端的电压随时间的变化。
利用电流对时间的导数定义自感系数。
当开关关闭时，电感的自感电动势为零；当开关打开时，自感电动势随电流的变化而发生变化。
通过测量自感电动势的变化和电流对时间的导数，可以计算出电感的自感系数。
另一种常见的方法是使用电压源和电容来测量自感系数。
通过将电感元件与电
容器和电源连接，并将电容器的电压与电感元件的电流进行比较，可以计算出电感的自感系数。
总之，计算自感系数可以通过测量电感两端的电压随时间的变化或者通过比较
电容器的电压与电感元件的电流来实现。
这些方法可以帮助我们了解电感元件对电流变化的敏感程度，并在电路设计和分析中起到重要的作用。
高二物理自感现象及自感电动势
高二物理自感现象及自感电动势自感现象是指当电流通过一条线圈时，它会产生磁场，而这个磁场会影响到这条线圈本身。
这种现象被称为自感现象。
同时，根据法拉第电磁感应定律，当磁通量发生变化时，线圈两端会产生感应电动势，这个电动势即为自感电动势。
在高二物理学习中，自感现象及自感电动势是我们需要深入了解和掌握的内容。
一、自感现象自感现象指的是电流通过一条线圈时，线圈内会产生磁场，而这个磁场会影响到线圈本身，使其电流发生变化。
自感现象与电流的变化形式和大小有关，常见的自感现象包括自感电动势和电感现象。
自感电动势是指当电流在一条线圈内发生变化时，线圈两端会产生感应电动势。
自感电动势的大小与电流变化的速率有关，即自感电动势的大小正比于电流的变化速率。
当电流变化缓慢时，自感电动势的大小较小；而当电流变化快速时，自感电动势的大小较大。
电感是指线圈对通过它的电流变化产生的自感电动势的阻碍作用。
电感的大小与线圈的匝数、线圈形状、线圈材料以及磁场的强度有关。
在电路中，电感常用于滤除高频噪音、稳定电流等方面。
二、自感电动势的产生原理自感电动势的产生原理可以通过法拉第电磁感应定律来解释。
根据法拉第电磁感应定律，当磁通量发生变化时，会在电路中产生感应电动势。
在自感电动势的情况下，磁通量的变化是由电流的变化引起的。
当电流在线圈内发生变化时，该线圈会在周围产生磁场。
磁场的变化导致了磁通量的变化，从而在线圈中产生了自感电动势。
这个自感电动势的大小正比于电流的变化速率，即自感电动势的大小与电流的变化呈正比关系。
三、自感电动势的应用自感电动势在实际应用中有着广泛的用途。
以下是自感电动势的几个常见应用：1. 电感耦合：自感电动势可用于不同线圈之间的电感耦合，以实现信号的传输、电压的升降等功能。
2. 感应加热：通过在线圈中加入交变电流，产生的自感电动势在工作体上产生涡流，从而实现加热效果。
3. 电感传感器：自感电动势可以用于制作电感传感器，用于检测金属物体、测量距离、测量电流等。
6_5自感
6 - 5 自感
二 自感 穿过闭合电流回路的磁通量
第六章 电磁感应与暂态过程
Φ = LI
若线圈有 N 匝， 磁通匝链数 自感
ψ自 = NΦ = LI
ψ自
I
v B
NΦ L= = I I
无铁磁质时, 自感仅与线圈形状、大小、 无铁磁质时 自感仅与线圈形状、大小、 有关. 磁介质及 N 有关
注意
6 - 5 自感
讨论
“-”号的意义 号的意义
式中的负号是楞次定律的数学表示， 式中的负号是楞次定律的数学表示，指出自感电 负号是楞次定律的数学表示 动势反抗的是回路中电流的变化。（而不是电流本 反抗的是回路中电流的变化。（ 动势反抗的是回路中电流的变化。（而不是电流本 身）即当回路中电流增加时，自感电动势与原电流 即当回路中电流增加时 增加 反向；当电流减小时 自感电动势与原电流同向。 反向；当电流减小时，自感电动势与原电流同向。 减小 同向 越大，自感电动势反抗作用越大 反抗作用越大， 自感系数 L 越大，自感电动势反抗作用越大，自 越小，自感电动势反抗作用越小 反抗作用越小。 感系数 L 越小，自感电动势反抗作用越小。“L” 具 有电磁惯性。 有电磁惯性。
6 - 5 自感
第六章 电磁感应与暂态过程
根据自感电动势的表达式， 根据自感电动势的表达式，自感还可以表示为 自感
L = −ε自
dI dt
意义：某回路的自感， 意义：某回路的自感，在数值上等于回路中的电 流随时间的变化率为一个单位时， 流随时间的变化率为一个单位时，在回路中所引 起的自感电动势的绝对值。 起的自感电动势的绝对值。 单位： 单位：1 亨利 （ H ）= 1 韦伯 / 安培 （1 Wb / A） ）
1mH = 10 H , 1µ H = 10 H
自感与互感的概念及计算
自感与互感的概念及计算自感（Self-inductance）和互感（Mutual inductance）是电磁学中重要的概念，它们描述了电流和磁场之间的相互作用关系。
本文将对自感和互感的概念进行详细解析，并讨论其计算方法。
1. 自感的概念自感是指通过一根导线中的电流激发出的磁场引起的自身感应电动势。
当电流通过导线时，其周围会形成一个磁场，而这个磁场又会影响导线中的电流。
自感的大小取决于导线的几何形状和电流的变化速率。
自感可以用以下公式来表示：L = (μ0 * N^2 * A) / l其中，L代表自感的系数，单位为亨利（H）；μ0是真空中的磁导率，约等于4π×10^(-7) H/m；N表示导线的匝数；A是导线截面积；l是导线的长度。
2. 互感的概念互感是指两根导线之间的电流激发出的磁场引起的互相感应电动势。
当两根导线靠近并且电流变化时，它们之间会产生互感现象。
互感的大小取决于导线之间的几何关系、电流的变化速率以及它们之间的距离。
互感可以用以下公式来表示：M = k * sqrt(L1 * L2)其中，M代表互感的系数，单位为亨利（H）；k是一个比例常数，0 < k ≤ 1，表示两根导线之间的耦合系数；L1和L2分别代表两根导线的自感系数。
3. 计算示例假设有两根平行的长直导线，它们之间的距离为d，导线1的电流为I1，导线2的电流为I2。
现在我们来计算它们之间的互感系数M。
首先，我们需要计算导线1和导线2的自感系数L1和L2：L1 = (μ0 * N1^2 * A1) / l1L2 = (μ0 * N2^2 * A2) / l2其中，N1和N2分别代表两根导线的匝数，A1和A2分别代表导线1和导线2的截面积，l1和l2分别代表导线1和导线2的长度。
然后，根据互感的计算公式：M = k * sqrt(L1 * L2)通过以上计算，我们可以得到两根导线之间的互感系数M。
互感系数的大小反映了导线之间的电磁相互作用的强度。
第五节自感现象课件
自感现象在其他物理领域的应用
要点一
总结词
要点二
详细描述
自感现象不仅在电磁学中有应用，在其他物理领域也有广 泛的应用。
在电路学中，自感现象可以用来解释线圈中的电流变化和 感应电动势的产生；在电磁场理论中，自感现象是研究磁 场和电场相互转化和作用的重要方面；在物理学实验中， 自感现象的应用也十分常见，例如测量线圈的自感系数等。
线圈的自感系数
总结词
自感系数是衡量线圈自感能力的一个 物理量，它与线圈的匝数、线圈的直 径、线圈的材料等因素有关。
详细描述
自感系数是描述线圈自感能力的物理 量，它与线圈的匝数、线圈的直径、 线圈的材料等因素有关。自感系数越 大，表示线圈的自感能力越强。
线圈的互感系数
总结词
互感系数是衡量两个线圈之间互感能力的物理量，它与两个 线圈的相对位置、线圈的匝数、线圈的材料等因素有关。
01
1. 将电源、电感线圈、开关、电阻、电流 表、电压表按照电路图连接。
03
02
实验步骤
04
2. 闭合开关，观察电流表和电压表的读数， 记录下来。
3. 迅速断开开关，观察电流表和电压表的 读数，记录下来。
05
06
4. 重复实验多次，取平均值。
实验结果分析和结论
实验结果分析
在迅速断开开关时，电流表读数突然变小，而电压表读数突然升高，这说明在开关断开瞬间，线圈中 产生了感应电动势，阻碍了电流的变化。
电磁炉的工作原理
电磁炉利用自感现象产生高频交变磁 场，当有导磁性锅具放在炉面上时， 锅具中会产生涡流，实现烹饪加热。
电磁炉的效率高、热损失小，是现代 厨房中的常见设备之一。
其他自感现象的应用实例
感应式开关
8-4,5,6自感和互感
r < R1 ,
H =0
µ µ
R2
I R1 < r < R2 , H = 2π r
r > R2 , H = 0
R1 < r < R2
则
1 1 I 2 2 ) wm = µH = µ ( 2 2π r 2
8-5
磁场的能量
1 I 2 µI 2 R1 < r < R2 wm = µ ( ) = 2 2 2 2πr 8π r 2 µI Wm = ∫ wmdV = ∫ dV 2 2 V V 8π r
自感电动势总是反抗回路中电流的变化.当 自感电动势总是反抗回路中电流的变化 当 电流增大时,自感电动势与原电流的方向相反 自感电动势与原电流的方向相反. 电流增大时 自感电动势与原电流的方向相反 自感
−3
L = −ε L
单位： 单位：1 亨利 （ H ）= 1 韦伯 / 安培 （1 Wb / A） ）
I
b
d
o x dx
l
x
2π x v v µI dΦ = B ⋅ ds = ld x 2π x d +b µ I Φ=∫ ld x d 2π x
B=
µI
8-3
自感和互感
I
b
Φ= ∫
d +b
µI
2π x
d
ldx
d
o x dx
l
x
b+d = ln( ) 2π d Φ µl b+d M = = ln( ) I 2π d
磁场能量
2
Wm =
∫
V
wm d V =
∫
V
B dV 2µ
2
8-5
磁场的能量
自感的原理及应用
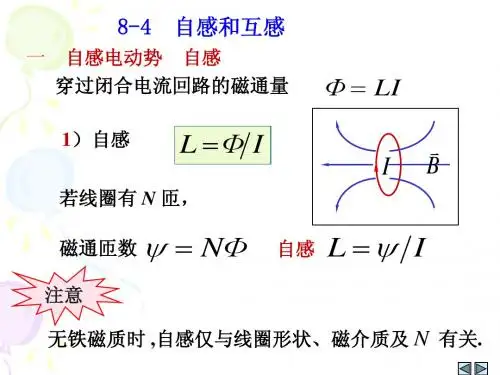
自感的原理及应用自感是一种电磁现象，当电流通过一个线圈时，产生的磁场会导致自感。
自感的原理是根据法拉第电磁感应定律，即根据电磁场的变化，产生感应电动势。
自感是由线圈的感应现象导致的，当电流通过线圈时，线圈内外都会产生磁场，磁场的变化会导致线圈内部产生感应电势。
具体来说，当电流通过线圈时，电流的流动会产生一个磁场。
磁场的强度与电流的大小成正比，与线圈的匝数成正比，与线圈的形状有关。
当电流改变时，磁场也会随之改变。
根据法拉第电磁感应定律，磁场的变化会导致线圈内部产生感应电势。
这种感应电势的方向与电流改变的方向相反，即阻碍电流改变的方向。
这就是自感的原理。
自感的应用非常广泛。
以下是一些常见的应用：1. 电感器：自感可以用于制造电感器。
电感器是一种用于储存和释放电能的元件。
当外部电流通过电感器时，电流会在电感器中产生一个磁场，随着时间的推移，电感器中的磁场储存了一定的电能。
当外部电流断开时，磁场会逐渐消失，释放储存的电能。
电感器广泛用于电子电路中，例如滤波器、振荡器等。
2. 高压变压器：自感也被广泛应用于高压变压器中。
高压变压器是一种用于改变电压的装置。
它是由一个输入线圈和一个输出线圈组成的。
当输入线圈中的电流改变时，由于自感的作用，会产生感应电势。
这个感应电势会在输出线圈中产生一个与输入线圈不同的电压。
通过调整输入输出线圈的匝数比，可以实现不同程度的电压变换。
3. 发电机和变压器：自感也是发电机和变压器中的重要组成部分。
发电机是将机械能转化为电能的装置，而变压器则是用于改变电压的装置。
在发电机和变压器中，线圈中的自感起到了重要的作用。
当电流通过线圈时，产生的磁场会导致感应电势，从而输出电能。
4. 电磁炉：自感也被广泛应用于电磁炉中。
电磁炉是一种利用电磁感应加热的设备。
通过通过变化的电流产生的变化磁场，感应炉内的金属锅具中的电流。
锅具中的电流会产生热量，从而加热食物。
电磁炉具有高效、精确控温等优点，广泛应用于家庭和商业厨房。
6.自感
系数一定较大；
C、对于同一线圈，当电流变化越大时，线 圈中产生的自感电动势也越大；
D、自感电动势总是阻碍原来电流变化的。
2、 如图示电路，合上S时，发现电流表A1向左 偏，则当断开S的瞬间，电流表A1 、 A2指针的 偏转情况是：（ B ）
A. A1向左，A2向右 B. A1向右，A2向左
S R1
为什么会出现这个现象呢?
原因分析：
当断开K的闭合，但灯A与线圈L立刻形成自右向左的 电流，由于L的电流突然增大，L产生自感现象，产生了 与原电流相反的I自，这个I自流过灯泡，电路稳定后I自消 失，所以灯泡在开关闭合瞬间的电流大于正常的电流， 灯泡闪亮。 当断开K的瞬间，灯A中原来的从右到左的电流IA立即 消失。但灯A与线圈L组成一闭合回路，由于L的自感作 用，其中的电流IL不会立即消失，而是在回路中逐渐减 弱维持短暂的时间，这个时间内灯A中有从左到右的IL 通过，IL>IA，故灯泡闪亮。
结论2：
当导体中原来的电流减小时，自感 电动势阻碍其减小．
2、自感电动势的方向： 阻碍导体中原来电流的变化。
（1）、导体中原电流增大时，自感电动势产 生的自感电流方向与原电流方向相反。 （2）、导体中原电流减小时，自感电动势产 生的自感电流方向与原电流方向相同。
3、自感电动势的大小： 自感电动势的大小跟其它感应电动势的大
R2
A1
C. A1 、A2都向右 D. A1 、A2都向左
A2
L
解：合上S后稳定时，R2和L中电流方向向右，指针左偏
断开S的瞬间， L中电流不能突变， A2向左偏， 通过闭合回路中的电流为逆时针方向， A1中电流方 向与原来相反，指针右偏。
所以 A1向右，A2向左
3、同上题的电路中，L是一带铁芯的线圈，R为电阻。两
C、对于同一线圈，当电流变化越大时，线 圈中产生的自感电动势也越大；
D、自感电动势总是阻碍原来电流变化的。
2、 如图示电路，合上S时，发现电流表A1向左 偏，则当断开S的瞬间，电流表A1 、 A2指针的 偏转情况是：（ B ）
A. A1向左，A2向右 B. A1向右，A2向左
S R1
为什么会出现这个现象呢?
原因分析：
当断开K的闭合，但灯A与线圈L立刻形成自右向左的 电流，由于L的电流突然增大，L产生自感现象，产生了 与原电流相反的I自，这个I自流过灯泡，电路稳定后I自消 失，所以灯泡在开关闭合瞬间的电流大于正常的电流， 灯泡闪亮。 当断开K的瞬间，灯A中原来的从右到左的电流IA立即 消失。但灯A与线圈L组成一闭合回路，由于L的自感作 用，其中的电流IL不会立即消失，而是在回路中逐渐减 弱维持短暂的时间，这个时间内灯A中有从左到右的IL 通过，IL>IA，故灯泡闪亮。
结论2：
当导体中原来的电流减小时，自感 电动势阻碍其减小．
2、自感电动势的方向： 阻碍导体中原来电流的变化。
（1）、导体中原电流增大时，自感电动势产 生的自感电流方向与原电流方向相反。 （2）、导体中原电流减小时，自感电动势产 生的自感电流方向与原电流方向相同。
3、自感电动势的大小： 自感电动势的大小跟其它感应电动势的大
R2
A1
C. A1 、A2都向右 D. A1 、A2都向左
A2
L
解：合上S后稳定时，R2和L中电流方向向右，指针左偏
断开S的瞬间， L中电流不能突变， A2向左偏， 通过闭合回路中的电流为逆时针方向， A1中电流方 向与原来相反，指针右偏。
所以 A1向右，A2向左
3、同上题的电路中，L是一带铁芯的线圈，R为电阻。两
自感互感磁能
自感危害：电路断开时，产生自感电弧。 自感危害：电路断开时，产生自感电弧。
第六章 电磁感应
3
§6.6 互感
互感现象： 互感现象：一个线圈中电流发生变 化会在周围空间会产生变化的磁场， 化会在周围空间会产生变化的磁场， 使处于此空间的另一个线圈中会产 B1 生感应电动势。 生感应电动势。所产生的感应电动 势称为互感电动势。 势称为互感电动势。 1 2
第六章 电磁感应 6
§6.7 磁能
自感线圈磁能
Wm
1 = LI 2
2
互感线圈系统总磁能
1 1 2 2 Wm = L1 I1 + L2 I 2 + MI 1 I 2 2 2
总磁能
1、2的自感磁能
第六章 电磁感应
互感磁能
7
dΦ12 d ε2 = − = − ( M12 I1) dt dt
在线圈的形状、大小和相对位置保持不变， 在线圈的形状、大小和相对位置保持不变，且周围不存在铁 为常量， 磁质的情况下， 磁质的情况下，互感M12为常量，上式化为
dI1 ε2 = −M12 dt
在线圈1 同样通有电流I2的线圈2在空间产生磁场B2，B2在线圈1中产生 的线圈2 的磁通量为Φ21，并且Φ21正比于I2，Φ21 = M21I2 , M12是线圈 1对线圈2的互感系数。 对线圈2的互感系数。 变化，线圈1 电流I2变化，线圈1中产生感应电动势
Φ=LI ,L为自感系数，简称自感。 为自感系数，简称自感。 I1
自感单位： 亨利) 自感单位：H (亨利)。 自感系数与线圈的大小、形状、磁介质、线圈密度有关， 自感系数与线圈的大小、形状、磁介质、线圈密度有关， 而与线圈中电流无关。 而与线圈中电流无关。
第六章 电磁感应 1
怎样计算电感的自感值
怎样计算电感的自感值电感自感值是指电感器件本身所具有的感应自感现象的量度。
电感自感值直接影响电感器件的性能和使用效果，因此对于电感自感值的准确计算与评估具有重要意义。
下面将介绍如何计算电感的自感值。
首先，我们需要了解电感的基本概念和原理。
电感是指导线圈中所具有的储存磁能的能力。
当电流通过导线圈时，会在导线周围产生磁场，而磁场的强弱取决于导线圈的结构和电流的大小。
而自感则是指导线圈中磁通量随电流变化而产生的感应电动势。
为了计算电感的自感值，我们可以采用多种方法。
下面将介绍几种常用的计算方法。
方法一：通过电感和电流的关系来计算自感值。
根据电感的定义，自感系数L可以表示为磁通量Φ和电流I的比值，即L = Φ/I。
而磁通量Φ又可以表示为磁感应强度B乘以导线圈的截面积S，即Φ = B × S。
因此，可以将自感系数L表示为L = B × S/I。
在实际计算中，可以通过测量导线圈的磁感应强度B、电流I和导线圈的截面积S，来计算电感的自感值。
这需要使用一些专业的测量设备和公式，确保测量结果的准确性。
方法二：通过导线圈的自感电动势来计算自感值。
根据电磁感应定律，导线圈中的自感电动势E与导线圈的自感系数L和电流I的变化率有关，即E = -L × (dI/dt)。
其中，dI/dt表示电流变化的速率。
为了计算自感值，我们需要测量导线圈中的自感电动势E和电流变化的速率dI/dt。
这个方法适用于测量频率较高或电流变化较快的情况。
方法三：通过频率和电容值来计算自感值。
对于简单的RL电路，自感值L可以通过电容值C和电路振荡频率f来计算。
具体计算公式为L = 1 / (4π^2f^2C)。
这个方法适用于一些特定的电路，比如谐振电路等。
综上所述，计算电感的自感值可以采用多种方法，具体选择哪种方法取决于实际需求和具体电路的特性。
在运用上述计算方法时，需要注意测量的准确性和使用适当的单位，以确保计算结果的准确性和可靠性。
高中物理《自感》科普教案分享
高中物理是一门立体化、抽象化和复杂化的学科。
自感作为其中的一个重要概念，是必须掌握的知识点之一。
本文将从什么是自感、自感的表现形式、自感的应用以及自感的公式等方面进行科普教，以期为广大中学生对该知识点的深刻理解做出一份微薄的贡献。
一、什么是自感自感是指由于在一个导体中产生电流时，由于磁场的存在而产生的电极间的电磁感应现象。
简单来说，自感是由于磁场改变时，在导体中产生的电流产生的磁场的反应。
自感的大小与导体中电流的大小、导体的形状和磁感应强度有关。
二、自感的表现形式1、自感的磁通量表现为自感系数L自感的磁通量可以用自感系数L来代表。
自感系数L用亨利（H）作单位。
单位亨利表达的大小是1VAmp^-1（1V每安珀尔）。
当一个电路的电流改变，电路中的磁通量也改变，因此产生了自感电动势，其大小由自感系数L、电流di/dt和自感回路中的自感磁通量ΦL决定。
2、自感的电势表现为自感电势自感电势产生于自感元件内部。
当一个电路中的电流改变，因为该电流对电磁场有影响，电路本身也会受到被动影响，因此会在电路的某一点产生电势差（电势差简称电势），即自感电势。
自感电势的大小与电路中电流的变化率成正比，自感电势的符号在自感的正负和电流的变化方向中。
三、自感的应用自感在电子学和通信技术中是非常重要的，自感是电子元器件中常用的组成部分，例如电感、放大器和温度计等。
自感器件会在电线传输数据时起到信号滤波、信号放大或定时噪声压制的作用。
应用自感组成的传感器可以检测气体、液体、磁场、电场大小等等。
四、自感的公式自感系数L可以用下列公式计算：L = ΦL/i其中，ΦL是自感的磁通量，i是电流的变化率。
自感电势E可以用下列公式计算：E = L*dI/dt其中，L是自感系数，dI/dt是电流的变化率。
整个路线对自感的表达可以使用以下公式：V=V0 + LdI/dt其中，V0是初始电势，dI/dt是电流的变化率，L是自感系数。
总结：在日常生活中，我们常常会接触到一些电子设备和电器用品，而高中的物理课程中自感的知识对于我们理解它们的电路原理和工作原理非常重要。
6.自感
2：当电流稳定时，阻碍作用还有吗？没有了，感应电流消失
3：电流稳定时为什么会变小？线圈有电阻
4：可以认为当电路接通瞬间，线圈L相当于什么？电路稳定后，
线圈L又相当于什么？接通瞬间：大电阻（瞬间断路） 电路稳定：导线或直流电阻
通电自感
现象：D1立即正常发光，而D2逐渐变亮，最后都 正常发光。 思考：用刚才所学知识解释以上现象
断电自感
现象：S断开时，D灯突然 闪亮一下才熄灭
1、在什么条件下，电键s断开时灯突然闪亮一 下才熄灭。 RL<RA
2、在什么条件下，电键s断开时灯一直变暗而
熄灭。
RL≥RA
一、自感定义
1、由于导体本身的电流发生变化而产生的阻 碍自身电流变化的电磁感应现象，叫自感现象 2、自感现象中产生的电动势叫自感电动势。
断电自感 A
A
断电自感
I2
A I1
断开S的瞬间， 线圈L相当于什
么呢？
I1
电源
小组讨论交流
1：断开S的瞬间，哪个电流会突然消失？ 2：I1的会如何变化呢？为什么？ 3：I1的电流要不要流过电阻R呢？与之前流过电阻的电流 I2的方向同吗？ 4：为什么反向电流会比之前的小呢？
I1小于I2，线圈的电阻比定值电阻大
1、当流过线圈L的电流突然增大瞬间，我 们可以把L看成一个阻值很大的电阻。（暂时断
路）
2、当流经线圈L的电流恒定不变时，我们 可以把L看作一个纯电阻或导线。
3、当流经线圈L的电流突然减小瞬间，我 们可以把L看作一个电源，它提供一个跟原电
流同向的电流
思考以下问题：
AB
1：当A的电流发生变化时，B能否产生感应电流呢？ 2：将B撤去，当A的电流发生变化时，A线圈能否产生感 应电流呢？
3：电流稳定时为什么会变小？线圈有电阻
4：可以认为当电路接通瞬间，线圈L相当于什么？电路稳定后，
线圈L又相当于什么？接通瞬间：大电阻（瞬间断路） 电路稳定：导线或直流电阻
通电自感
现象：D1立即正常发光，而D2逐渐变亮，最后都 正常发光。 思考：用刚才所学知识解释以上现象
断电自感
现象：S断开时，D灯突然 闪亮一下才熄灭
1、在什么条件下，电键s断开时灯突然闪亮一 下才熄灭。 RL<RA
2、在什么条件下，电键s断开时灯一直变暗而
熄灭。
RL≥RA
一、自感定义
1、由于导体本身的电流发生变化而产生的阻 碍自身电流变化的电磁感应现象，叫自感现象 2、自感现象中产生的电动势叫自感电动势。
断电自感 A
A
断电自感
I2
A I1
断开S的瞬间， 线圈L相当于什
么呢？
I1
电源
小组讨论交流
1：断开S的瞬间，哪个电流会突然消失？ 2：I1的会如何变化呢？为什么？ 3：I1的电流要不要流过电阻R呢？与之前流过电阻的电流 I2的方向同吗？ 4：为什么反向电流会比之前的小呢？
I1小于I2，线圈的电阻比定值电阻大
1、当流过线圈L的电流突然增大瞬间，我 们可以把L看成一个阻值很大的电阻。（暂时断
路）
2、当流经线圈L的电流恒定不变时，我们 可以把L看作一个纯电阻或导线。
3、当流经线圈L的电流突然减小瞬间，我 们可以把L看作一个电源，它提供一个跟原电
流同向的电流
思考以下问题：
AB
1：当A的电流发生变化时，B能否产生感应电流呢？ 2：将B撤去，当A的电流发生变化时，A线圈能否产生感 应电流呢？
自感现象及应用
小为
I EL L t
式中L是线圈的自感系数，即自感磁链与电流的比值
L L
I
线圈的自感是由线圈本身的特性决定的，与线圈中有无 电流及电流的大小无关。
L N N 2S
I
l
2．电感线圈和电容器一样，都是储能元件，磁场能量可 用下式计算
WL
1 2
LI 2
WL
1 2
LI 2
当线圈中通有电流时，线圈中就要储存磁场能量，通过线 圈的电流越大，储存的能量就越多。在通有相同电流的线圈中， 电感越大的线圈，储存的能量越多，因此线圈的电感也反映了 它储存磁场能量的能力。
与电场能量相比，磁场能量和电场能量有许多相同的特点：
(1) 磁场能量和电场能量在电路中的转化都是可逆的。例 如，随着电流的增大，线圈的磁场增强，储入的磁场能量增多； 随着电流的减小，线圈的磁场减弱，磁场能量通过电磁感应的 作用又转化为电能。因此，线圈和电容器一样是储能元件，而 不是电阻类的耗能元件。
3．产生电磁感应现象的条件是：穿过电路的磁通发生变化。 当电路闭合时，回路中有感应电流，当电路不闭合时，电路中 没有感应电流，但仍有感应电动势。
4．电路中感应电流的方向可用右手定则和楞次定律来判断。 楞次定律是判断感应电流方向的普遍规律。感应电动势的方向 与感应电流的方向相同，也用右手定则和楞次定律判断。
(2) 其他近似环形的线圈，在铁心没有饱和的条件下，也 可用上式近似计算线圈的电感，此时l是铁心的平均长度。若线 圈不闭合，不能用上式计算。
(3) 由于磁导率 不是常数，随电流而变，因此有铁心的
线圈其电感也不是一个定值，这种电感称为非线性电感。
四、自感电动势
由电磁感应定律可得，自感电动势
物理教案-自感
物理教案－自感物理教案-自感一、教学目标通过本节课的学习，学生应该能够：1. 理解什么是自感；2. 认识自感的特点和应用；3. 学会计算自感的大小和方向。
二、教学重点1. 自感的概念和特点；2. 自感的计算方法；3. 自感的应用。
三、教学难点1. 自感和磁场的关系；2. 自感和电路的关系；3. 计算自感大小和方向的方法。
四、教学过程1. 自感的概念和特点自感是指一根导体中，当电流发生变化时，导体内部会发生电磁感应现象；同时，导体里的电场也会发生变化，导致电磁波的产生。
自感是磁通量的一种，单位是亨利（H）。
自感经常用在磁性材料和线圈中，实现电子设备的设计和制造。
2. 自感的计算方法自感的计算方法是根据法拉第电磁感应定律来计算的。
法拉第电磁感应定律指出，当导体内部发生磁通量的变化时，会产生感应电动势，导体内部的电场随之变化，从而产生电磁波。
计算自感的公式为：L = Φ / I其中，L是自感值，Φ是导体中穿过的磁通量，I是电流的大小。
3. 自感的应用自感的应用非常广泛。
在电子设备中，自感常被用来制造电感和变压器。
在通信设备中，自感被用来制作天线，以便接收和发射电磁波。
在电流测量中，自感被用来制作电流传感器，可以简单地通过电路测量电流大小。
五、教学总结本节课主要介绍了自感的概念、特点、计算方法和应用。
自感是磁通量的一种，被广泛应用于电子设备、通信设备、测量设备等领域。
学生们需要掌握自感的基本概念、计算方法和应用，进一步了解电子设备的设计和制造过程。
自感系数
自感系数
物理学名词
01 系数定义
03 计算式
目录
02 决定因素 04 单位介绍
自感系数表示线圈产生自感能力的物理量，常用L来表示。简称自感或电感。自感系数的单位是亨利，简称亨， 符号是H。
系数定义
1.在单位电流变化率ΔI/Δt下，某个自感线圈产生的自感电动势E的大小。（比值法定义）
自感2.L=Ψ/i（当线圈为多匝时，通过各匝线圈的磁通量之和称为磁通匝链数Ψ，若通过每匝线圈的磁通量 Φ都相同，则Ψ=NΦ，N为线圈匝数）
决定因素
决定因素线圈的自感系数跟线圈的形状、长短、匝数以及是否有铁芯等因素有关。线圈越长，单位长度上匝 数越多，截面积越大，他的自感系数就越大。另外，有铁芯的线圈的自感系数，比没有铁芯时要大得多，对于一 个现成的线圈来说，自感系数是一定的。
计算式
线圈面积越大、线圈越长、单位长度匝数越密，它的自感系数就越大。另外，有铁芯的线圈的自感系数比没 有铁芯时大的多。计算公式为L=（uSN^2)/l，各字母含义：u代表线圈中的介质磁导率，S代表线圈面积，N代表 线圈匝数，l代表线圈长度。
自感系数的计算比较复杂，常用实验方法测定，简单情形则可由毕-萨-拉定律和Ψ=LI计算。 推导 设i为电流大小，μ为线圈中的介质磁导率，n为线圈匝数密度，N为线圈总匝数（N=nl），S为线圈面积，l 为线圈长度，V为线圈体积（V=Sl）。 根据自感系数的定义L=Ψ/i=NΦ/i=nlBS/i 根据毕奥-萨伐尔定律，计算出无限长直螺线管内部的磁感应强度B=μni。 则L=μn^2lSi/i=μn^2Sl=μn^2V① 若将n=N/l代入L=μn^2Sl即得L=μN^2Sl/l^2=μN^2S/l改变1安时产生的自感电动势是1伏，这个线圈的自感系数就是1亨。所以：1 亨=1伏·秒/安。
物理学名词
01 系数定义
03 计算式
目录
02 决定因素 04 单位介绍
自感系数表示线圈产生自感能力的物理量，常用L来表示。简称自感或电感。自感系数的单位是亨利，简称亨， 符号是H。
系数定义
1.在单位电流变化率ΔI/Δt下，某个自感线圈产生的自感电动势E的大小。（比值法定义）
自感2.L=Ψ/i（当线圈为多匝时，通过各匝线圈的磁通量之和称为磁通匝链数Ψ，若通过每匝线圈的磁通量 Φ都相同，则Ψ=NΦ，N为线圈匝数）
决定因素
决定因素线圈的自感系数跟线圈的形状、长短、匝数以及是否有铁芯等因素有关。线圈越长，单位长度上匝 数越多，截面积越大，他的自感系数就越大。另外，有铁芯的线圈的自感系数，比没有铁芯时要大得多，对于一 个现成的线圈来说，自感系数是一定的。
计算式
线圈面积越大、线圈越长、单位长度匝数越密，它的自感系数就越大。另外，有铁芯的线圈的自感系数比没 有铁芯时大的多。计算公式为L=（uSN^2)/l，各字母含义：u代表线圈中的介质磁导率，S代表线圈面积，N代表 线圈匝数，l代表线圈长度。
自感系数的计算比较复杂，常用实验方法测定，简单情形则可由毕-萨-拉定律和Ψ=LI计算。 推导 设i为电流大小，μ为线圈中的介质磁导率，n为线圈匝数密度，N为线圈总匝数（N=nl），S为线圈面积，l 为线圈长度，V为线圈体积（V=Sl）。 根据自感系数的定义L=Ψ/i=NΦ/i=nlBS/i 根据毕奥-萨伐尔定律，计算出无限长直螺线管内部的磁感应强度B=μni。 则L=μn^2lSi/i=μn^2Sl=μn^2V① 若将n=N/l代入L=μn^2Sl即得L=μN^2Sl/l^2=μN^2S/l改变1安时产生的自感电动势是1伏，这个线圈的自感系数就是1亨。所以：1 亨=1伏·秒/安。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
也不论回路周围有没有铁磁性介质都能适用。当L不 变时，定义式④与②一致。
（2） 自 、 自 、I均有正方向的约定：
（3）也称L为“电磁惯性”
自 L
dI dt
自
ε自I
dI dt
大， 自 大，而其方向又是相反的，所以
dI dt 。
自 力图阻碍原磁通的变化，即 自 阻碍
L越大，线圈阻碍电流变化的作用越大。类似于 力学中，物体质量m越大，阻碍m运动的惯性越大， 故称L为电磁惯性。
2
ln
R2 R1
R1
单位长度电缆的自感系数为：
L
0
2
ln
R2 R1
由电缆本身性质决定
习题：6.5.2
R1 R2
2 r
考虑长为 l 的部分电缆：在 两圆筒之间找一面积 ABCD， 在其中取一面积元，通过面积 元 ldr 的磁通量为：
d Bldr
A
B dr D l C
0I
2
l
dr r
两圆筒之间（ l 长的一段）的总磁通量为：
d
lI
R2
0 Il dr
2 r
0 Il
§6.5
一 自感现象
自感
定义：由于线圈自身电流不稳定，从而在自身线 圈中产生感生电动势的现象叫做自感现象。这种感 生电动势叫做自感电动势，线圈中相应的电流叫做 自感电流。 自感现象的演示实验： P243—244。
R L B1 B
B2ห้องสมุดไป่ตู้S RL=R
L S RL<<R灯
电流减少
不同线 圈产生 自感现 象的能 力不同
L
螺线管的自感：
自
I
0n V
2
例2（补充）：有一电缆，由两个“无限长”的圆
筒状导体组成，电缆中沿内圆筒和外圆筒流过的电流 I大小相等，方向相反。设内外圆筒的半径为R1、R2， 求电缆单位长度的自感系数。 P246最下面一段。 解：在内外两圆筒之间，离 I 开轴线距离为r处有 I
B
0I
L
自
dI dt
④
回路中的自感系数，在量值上等于回路中的电流 每单位时间改变1单位时，在自身回路中产生的自感 电动势。这是自感L的另一种定义。 2、说明 （1）方程④是定义L的普遍关系式，这个L值是 在dt时间内，当电流从I改变到I+dI时（即与电流值I 相应的）的自感值。这个关系式不论回路是否密绕，
电流增大
二
自感(系数) 1、自感(系数)
设导体回路由N匝密绕线圈串联而成，回路中的 电流为I，认为电流I在各匝线圈中产生的磁通量基本 相同。当电流变化时，自感电动势为：
自 N
d 自 dt d 自 dt
①
自 是穿过每一匝线圈的磁通量， 自 N 自 是 电流I在自身线圈中引起的磁通匝链数。
（4）L一般由实验测定，只有少数几种特殊情况 可由定义计算。下面举例说明L的求解方法。
计算公式： L
自
I
例1：细长螺线管体积为V，单位长度的匝数为n，
求自感系数。 P245
自
解：每匝磁通
B S 0 n IS
ε自
2
I
2
自感磁链：
自 N nl 0 n lSI 0 n IV
注意：若回路的几何形状可变，而且回路附近有
铁磁性介质时，相应于每一个电流值I，也有相应的 值，但 和I之间不是简单的线性关系。 将②代入①式得回路中的自感电动势为
自
d 自 dt L dI dt ( L 不变， dL dt 0)
③
自感电动势与电流变化率成正比。对于相同的电 流变化率，L越大的线圈，产生的自感电动势越大。 L从一个侧面反映了线圈产生自感现象的能力。 把③式改写成：
在无铁芯的情况下： B I 即 I 写成等式：
自 LI
②
L叫做线圈的自感系数，简称自感或电感。L在数 值上等于单位电流在自身线圈中产生（引起）的磁通 匝链数。 实验表明：在L内无铁磁性介质存在时，L只依赖 于线圈的几何形状、大小、匝数和磁介质的特性以及 填充情况，与电流无关（铁磁质除外）。即L是描述 线圈自身性质的物理量。