空间向量共面充要条件的应用

空间向量共面充要条件的应用共面向量定理涉及三个向量→p 、→a 、→b 共面问题，它们之间的充要条件关系为：如果两个向量→a 、→b 不共线，那么向量→p 与向量→a 、→b 共面的充要条件是：存在有序实数组(x,y)，使得→p ＝x →a ＋y →b .共面向量定理在立体几何中证明中有关有着广泛的运用，如在点线共面、线面平行等问题中，都有很好的体现.由于向量本身具有的位置不定性，使得共面向量可理解为能够平移到同一平面内的向量，或者理解为平行于同一平面的向量.下面就空间向量共面充要条件的应用分类解析，体会应用的方法与技巧.一、判断点与平面的关系例1 已知A 、B 、C 三点不共线，对平面ABC 外一点O ，若→OM ＝2→OA －→OB －→OC ，判断点M 是否在平面ABC 内.分析：点M 与A 、B 、C 不共面，即点M 不在平面ABC 内，即不存在x ，y 使→AM ＝x →AB ＋y →AC ，可用反证法证明判断.解：假设M 在平面ABC 内，则存在实数x,y ，使→AM ＝x →AB ＋y →AC ，于是对空间任意一点O ，O 在平面ABC 外，→OM ＝(1－x －y)→OA ＋x →OB ＋y →OC ，比较原式可得⎩⎪⎨⎪⎧ 1－x －y ＝2x ＝－1y ＝－1，此方程组无解，与假设不成立， ∴不存在实数x,y ，使→AM ＝x →AB＋y →AC ，∴M 与A 、B 、C 不共面. 点评：本题采用反证法来证明点M 不在平面ABC 内，因为反证法就是从正面进行解答比较困难，从对立面进行证明的一种思想方法.二、用于证明四点共面例2 如图所示，长方体ABCD －A 1B 1C 1D 1中，M 为DD 1的中点，N 在AC 上，且AN ﹕NC ＝2﹕1，求证：A 1、B 、N 、M 四点共面.分析：利用空间向量共面的充要条件，通过证明向量→A 1N 、→A 1B 、→A 1M 共面，即可证明存在唯一实数λ、μ，使→A 1N ＝λ→A 1B ＋μ→A 1M 成立.证明：如图，→AA 1＝→a ，→AB ＝→b ，→AD ＝→c ，则→A 1B ＝→AB －→AA 1＝→b －→a ，∵M 为DD 1的中点，→A 1M ＝→AD －12→AA 1＝→c －12→a ， ∵AN ﹕NC ＝2﹕1，∴→AN ＝23→AC ＝23(→AB ＋→AD)＝23(→b ＋→c )， ∴→A 1N ＝→AN －→AA 1＝23(→b ＋→c )－→a ＝23(→b －→a )＋23(→c －12→a ) ＝23→A 1B ＋23→A 1M， ∴A 1、B 、N 、M 四点共面.点评：本题根据空间向量基本定理，充分利用三角法则与平行四边形法则，通过不同的途径分别用向量→EF ﹑→EH 表示→MQ 或用向量→EG 表示→MQ ，从而建立向量→EG与向量→EF ﹑→EH 的线性关系，进而使问题得证.这是不用向量坐标形式证明几何问题的常用方法.三、证明三线平行同一平面例3 如图所示，E 、F 分别为空间四边形ABCD 中AB 、CD 的中点，证明AD 、EF 、BC 平行于同一平面.分析：证明AD 、EF 、BC 平行于同一平面，即证明向量→EF 、→AD 、→BC 共面，进而证明→EF 、→AD、→BC 之间存在线段关系. 证明：→EF ＝→EA ＋→AD ＋→DF ，且→EF＝→EB ＋→BC ＋→CF ， 又→EA ＝－→EB ，→DF ＝－→CF ，所以→EF＋→EF ＝→AD ＋→BC 即→EF ＋→EF ＝12(→AD ＋→BC)＝12→AD ＋12→BC ， 可知，→EF 、→AD 、→BC 共面，所以EF 与AD 、BC 平行于同一平面.点评：本题在证明过程中，通过利用两种不同的途径得到向量→EF的两种不同的表达式，然后两式相加就可以得到所需要证明的表达式，当然其过程要用到三角形法则或平行四边形法则，这是利用加减法处理向量线性线性关系常用的方法.四、证明线面平行例4 正方体ABCD －A 1B 1C 1D 1中，点N 在BD 上，点M 在B 1C 上，且CM ＝DN ，求证：MN ∥平面CC 1D 1D.分析：由于DC 与DD 1在同一平面上，因此可以先考虑利用空间向量共面的充要条件证明向量→NM 与→DC 、→DD 1共面，然后只须说明点M 、N 不在CC 1D 1D 内就可证明MN ∥平面CC 1D 1D.证明：设CM ＝DN ＝λDB ＝λCB 1，则→DN ＝λ→DB ＝λ(→DA ＋→DC)，→CM ＝λ→CB 1＝λ(→CB ＋→CC 1)，∴→NM ＝→ND ＋→DC ＋→CM ＝－λ(→DA ＋→DC)＋→DC ＋λ(→CB ＋→CC 1) ＝(1－λ)→DC ＋λ(→DA ＋→CB ＋→CC 1)＝(1－λ)→DC ＋λ(－→DA ＋→DA ＋→CC 1) ＝(1－λ)→DC ＋λ→DD 1∴→NM 与→DC 、→DD 1共面，又M 、N 不在面DCC 1D 1内，∴MN ∥平面CC 1D 1D.点评：利用空间证明立体几何问题，减少了利用传统法证明的繁琐的思维量，将考查难度要求较高的空间想象力与抽象的逻辑推理能力转化为考查难度要求稍微较低的运算能力.。

共面向量定理怎么证（原创实用版）目录一、共面向量定理的概念及背景二、共面向量定理的证明方法三、共面向量定理的应用举例四、总结正文一、共面向量定理的概念及背景共面向量定理是平面向量基本定理的一个重要结论。

共面向量定理描述了三个向量共面的充分必要条件，它是解决空间向量共面问题的关键定理。

在数学、物理等科学领域中，共面向量定理被广泛应用。

二、共面向量定理的证明方法共面向量定理的证明方法有多种，这里我们介绍一种较为简洁的证明方法。

证明：设向量 a、b、c 共面，那么存在实数 x、y 使得 a=xb+yc。

假设 d 是与 a、b、c 不共面的向量，那么 d 与 a、b、c 确定一个平面α。

由于 a=xb+yc，所以 d 也在平面α内。

但这与 d 与 a、b、c 不共面矛盾，所以假设不成立，即 a、b、c 共面。

三、共面向量定理的应用举例1.证明四点共面：在空间四边形 ABCD 中，M、N 分别是 AD、BC 的中点，求证：BMNADC 共面。

解：由于 M、N 分别是 AD、BC 的中点，所以 AM=MB、BN=NC。

那么向量 AM=MB=x(AB)+y(AC)，向量 BN=NC=z(AB)+w(AC)。

由于 x+z=1，y+w=1，所以 BMNADC 共面。

2.求解共面向量定理中的参数：已知向量 a、b、c 共面，且存在实数 x、y 使得 a=xb+yc，求参数 x、y 的值。

解：由于 a、b、c 共面，那么它们对应端点构成的向量也共面。

设对应端点为 A、B、C，那么向量 AB=xAC+yBC。

根据平面向量基本定理，存在实数 u、v 使得 AB=uAC+vBC。

所以 x=u，y=v。

四、总结共面向量定理是平面向量基本定理的一个重要结论，它描述了三个向量共面的充分必要条件。

空间四点共面充要条件的应用与探究平面上的三点共线与空间的四点共面，是平面向量与空间向量问题中的一类重要题型。

在高中数学人教A 版选修教材2-1《空间向量与立体几何》一章中，给出了四点共面的一个判定方法，在配套的教参中更明确为充要条件。

因此有些老师在教学中就给出了如下的空间P 、A 、B 、C 、四点共面的充要条件：对于空间任意一点O ，存在实数x 、y 、z ，使得OC OB OA x OP z y ++=且x+y+z=1。

这个结论对于解决空间四点共面问题提供了很便捷的方法，例如：● 问题1：对于空间任一点O 和不共线的三点A 、B 、C ，有OC OB OA OP 326++=，则 （ ）(A)O 、A 、B 、C 四点共面 (B) P 、A 、B 、C 四点共面(C) O 、P 、B 、C 四点共面 (D) O 、P 、A 、B 、C 五点共面 分析：由条件可以得到OC OB OA OP 213161++=，而1213161=++，则P 、A 、B 、C 四点共面。

●问题2：已知点M 在平面ABC 内，并且对空间任意一点O ，OC OB OA x OM 3121++=，则x= 。

分析：由上面的充要条件很容易得到6131211x =--=。

● 问题3：在平行六面体ABCD-A 1B 1C 1D 1中，P 、M 、N 分别是AA 1、AB 、AD 上一点，且132AA AP =,AB AM 21=,AD AN 41=，对角线AC 1与平面PMN 交与点H ，求H 点分AC 1的比。

分析：因为P 、M 、N 、H 四点共面，则可设为AN z AM y AP AH ++=x ，且x+y+z=1 由已知，132AA AP =,AB AM 21=,AD AN 41=， 则AD z AB y AA AH 4232x 1++= 又A 、H 、C 1三点共线，则1AC AH λ= 而AD AB AA AC ++=11 所以，AD z AB y AA AH 4232x 1++=AD AB AA λλλ++=1 因为向量AD AB AA ，，1不共面， 则有：λ===4232z y x ， 所以λ23=x ，λ2=y ，λ4=z 又因为x+y+z=1， 所以λ23+λ2+λ4=1， 解得152=λ 所以，1152AC AH = 即：H 点分AC 1的比为2:13.AM C 1以上三个问题的解决都用到了课本中提到的四点共面的充要条件，思路新颖，解法简洁，确实为学生们解决空间四点共面问题提供了一条重要的解题思路。

空间向量共面充要条件的应用共面向量定理涉及三个向量→p 、→a 、→b 共面问题，它们之间的充要条件关系为：如果两个向量→a 、→b 不共线，那么向量→p 与向量→a 、→b 共面的充要条件是：存在有序实数组(x,y)，使得→p ＝x →a ＋y →b .共面向量定理在立体几何中证明中有关有着广泛的运用，如在点线共面、线面平行等问题中，都有很好的体现.由于向量本身具有的位置不定性，使得共面向量可理解为能够平移到同一平面内的向量，或者理解为平行于同一平面的向量.下面就空间向量共面充要条件的应用分类解析，体会应用的方法与技巧.一、判断点与平面的关系例1 已知A 、B 、C 三点不共线，对平面ABC 外一点O ，若→OM ＝2→OA －→OB －→OC ，判断点M 是否在平面ABC 内.分析：点M 与A 、B 、C 不共面，即点M 不在平面ABC 内，即不存在x ，y 使→AM ＝x →AB ＋y →AC ，可用反证法证明判断.解：假设M 在平面ABC 内，则存在实数x,y ，使→AM ＝x →AB ＋y →AC ，于是对空间任意一点O ，O 在平面ABC 外，→OM ＝(1－x －y)→OA ＋x →OB ＋y →OC ，比较原式可得⎩⎪⎨⎪⎧ 1－x －y ＝2x ＝－1y ＝－1，此方程组无解，与假设不成立， ∴不存在实数x,y ，使→AM ＝x →AB＋y →AC ，∴M 与A 、B 、C 不共面. 点评：本题采用反证法来证明点M 不在平面ABC 内，因为反证法就是从正面进行解答比较困难，从对立面进行证明的一种思想方法.二、用于证明四点共面例2 如图所示，长方体ABCD －A 1B 1C 1D 1中，M 为DD 1的中点，N 在AC 上，且AN ﹕NC ＝2﹕1，求证：A 1、B 、N 、M 四点共面.分析：利用空间向量共面的充要条件，通过证明向量→A 1N 、→A 1B 、→A 1M 共面，即可证明存在唯一实数λ、μ，使→A 1N ＝λ→A 1B ＋μ→A 1M 成立.证明：如图，→AA 1＝→a ，→AB ＝→b ，→AD ＝→c ，则→A 1B ＝→AB －→AA 1＝→b －→a ，∵M 为DD 1的中点，→A 1M ＝→AD －12→AA 1＝→c －12→a ， ∵AN ﹕NC ＝2﹕1，∴→AN ＝23→AC ＝23(→AB ＋→AD)＝23(→b ＋→c )， ∴→A 1N ＝→AN －→AA 1＝23(→b ＋→c )－→a ＝23(→b －→a )＋23(→c －12→a ) ＝23→A 1B ＋23→A 1M， ∴A 1、B 、N 、M 四点共面.点评：本题根据空间向量基本定理，充分利用三角法则与平行四边形法则，通过不同的途径分别用向量→EF ﹑→EH 表示→MQ 或用向量→EG 表示→MQ ，从而建立向量→EG与向量→EF ﹑→EH 的线性关系，进而使问题得证.这是不用向量坐标形式证明几何问题的常用方法.三、证明三线平行同一平面例3 如图所示，E 、F 分别为空间四边形ABCD 中AB 、CD 的中点，证明AD 、EF 、BC 平行于同一平面.分析：证明AD 、EF 、BC 平行于同一平面，即证明向量→EF 、→AD 、→BC 共面，进而证明→EF 、→AD、→BC 之间存在线段关系.证明：→EF ＝→EA ＋→AD ＋→DF ，且→EF＝→EB ＋→BC ＋→CF ， 又→EA ＝－→EB ，→DF ＝－→CF ，所以→EF＋→EF ＝→AD ＋→BC 即→EF ＋→EF ＝12(→AD ＋→BC)＝12→AD ＋12→BC ， 可知，→EF 、→AD 、→BC 共面，所以EF 与AD 、BC 平行于同一平面.点评：本题在证明过程中，通过利用两种不同的途径得到向量→EF的两种不同的表达式，然后两式相加就可以得到所需要证明的表达式，当然其过程要用到三角形法则或平行四边形法则，这是利用加减法处理向量线性线性关系常用的方法.四、证明线面平行例4 正方体ABCD －A 1B 1C 1D 1中，点N 在BD 上，点M 在B 1C 上，且CM ＝DN ，求证：MN ∥平面CC 1D 1D.分析：由于DC 与DD 1在同一平面上，因此可以先考虑利用空间向量共面的充要条件证明向量→NM 与→DC 、→DD 1共面，然后只须说明点M 、N 不在CC 1D 1D 内就可证明MN ∥平面CC 1D 1D.证明：设CM ＝DN ＝λDB ＝λCB1，则→DN ＝λ→DB ＝λ(→DA ＋→DC)，→CM ＝λ→CB 1＝λ(→CB ＋→CC 1)，∴→NM ＝→ND ＋→DC ＋→CM ＝－λ(→DA ＋→DC)＋→DC ＋λ(→CB ＋→CC 1) ＝(1－λ)→DC ＋λ(→DA ＋→CB ＋→CC 1)＝(1－λ)→DC ＋λ(－→DA ＋→DA ＋→CC 1) ＝(1－λ)→DC ＋λ→DD 1∴→NM 与→DC 、→DD 1共面，又M 、N 不在面DCC 1D 1内，∴MN ∥平面CC 1D 1D.点评：利用空间证明立体几何问题，减少了利用传统法证明的繁琐的思维量，将考查难度要求较高的空间想象力与抽象的逻辑推理能力转化为考查难度要求稍微较低的运算能力.。

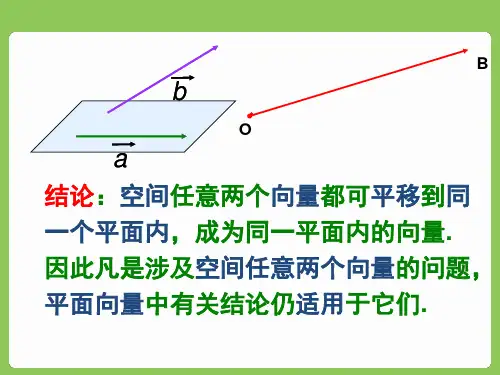
数学复习：共线向量与共面向量学习目标1.理解向量共线、向量共面的定义.2.掌握向量共线的充要条件和向量共面的充要条件，会证明空间三点共线、四点共面．导语我们知道向量是有大小、有方向的量，它可以平行移动，平面内两个向量若方向相同或相反，就说它们是共线的，那么在空间内向量共线又是怎么回事呢？今天我们就来探究一下．一、空间向量共线的充要条件问题1平面向量共线的充要条件是什么？它适用于空间向量吗？提示对任意两个平面向量a ，b (b ≠0)，a ∥b 的充要条件是存在实数λ，使a ＝λb ，由于空间向量共线的定义与平面向量相同，因此也适用于空间向量．知识梳理1．对任意两个空间向量a ，b (b ≠0)，a ∥b 的充要条件是存在实数λ，使a ＝λb .2．如图，O 是直线l 上一点，在直线l 上取非零向量a ，则对于直线l 上任意一点P ，由数乘向量的定义及向量共线的充要条件可知，存在实数λ，使得OP →＝λa ，把与向量a 平行的非零向量称为直线l 的方向向量，直线l 上任意一点都可以由直线l 上的一点和它的方向向量表示．注意点：(1)直线可以由其上一点和它的方向向量确定．(2)向量a ，b 共线时，表示向量a ，b 的两条有向线段不一定在同一条直线上．例1如图，四边形ABCD 和ABEF 都是平行四边形，且不共面，M ，N 分别是AC ，BF 的中点，则CE →与MN →是否共线？解方法一∵M ，N 分别是AC ，BF 的中点，且四边形ABCD 和ABEF 都是平行四边形，∴MN →＝MA →＋AF →＋FN →＝12CA →＋AF →＋12FB →.①又∵MN →＝MC →＋CE →＋EB →＋BN→＝－12CA →＋CE →－AF →－12FB →，②①＋②得2MN →＝CE →，∴CE →∥MN →，即CE →与MN →共线．方法二∵M ，N 分别是AC ，BF 的中点，且四边形ABCD 和ABEF 都是平行四边形，∴MN →＝AN →－AM →＝12(AB →＋AF →)－12AC→＝12(AB →＋AF →)－12(AB →＋AD →)＝12(AF →－AD →)＝12(BE →－BC →)＝12CE →.∴MN →∥CE →，即MN →与CE →共线．反思感悟向量共线的判定及应用(1)判断或证明两向量a ，b (b ≠0)共线，就是寻找实数λ，使a ＝λb 成立，为此常结合题目图形，运用空间向量的线性运算法则将目标向量化简或用同一组向量表达．(2)判断或证明空间中的三点(如P ，A ，B )共线的方法：是否存在实数λ，使PA →＝λPB →.跟踪训练1(1)已知A ，B ，C 三点共线，O 为直线外空间任意一点，若OC →＝mOA →＋nOB →，则m ＋n ＝________.答案1解析由于A ，B ，C 三点共线，所以存在实数λ，使得AC →＝λAB →，即OC →－OA →＝λ(OB →－OA →)，所以OC →＝(1－λ)OA →＋λOB →，所以m ＝1－λ，n ＝λ，所以m ＋n ＝1.(2)如图所示，已知四边形ABCD 是空间四边形，E ，H 分别是边AB ，AD 的中点，F ，G 分别是边CB ，CD 上的点，且CF →＝23CB →，CG →＝23CD →.求证：四边形EFGH 是梯形．证明∵E ，H 分别是AB ，AD 的中点，∴AE →＝12AB →，AH →＝12AD →，则EH →＝AH →－AE →＝12AD →－12AB →＝12BD→＝12(CD →－CB →)－32CF ＝34(CG →－CF →)＝34FG →，∴EH →∥FG →且|EH →|＝34|FG →|≠|FG →|.又F 不在直线EH上，∴四边形EFGH 是梯形．二、空间向量共面的充要条件问题2空间任意两个向量是共面向量，则空间任意三个向量是否共面？提示不一定，如图所示，空间中的三个向量不共面．问题3对两个不共线的空间向量a ，b ，如果p ＝x a ＋y b ，那么向量p 与向量a ，b 有什么位置关系？反过来，向量p 与向量a ，b 有什么位置关系时，p ＝x a ＋y b ?提示向量p 与不共线向量a ，b 共面的充要条件是存在唯一的有序实数对(x ，y )，使p ＝x a＋y b .知识梳理1．向量与平面平行：如果表示向量a 的有向线段OA →所在的直线OA 平行于平面α或在平面α内，那么称向量a 平行于平面α.2．共面向量定义平行于同一个平面的向量三个向量共面的充要条件向量p 与不共线向量a ，b 共面的充要条件是存在唯一的有序实数对(x ，y )使p ＝x a ＋y b问题4对于不共线的三点A ，B ，C 和平面ABC 外的一点O ，空间一点P 满足关系式OP →＝xOA →＋yOB →＋zOC →，则点P 在平面ABC 内的充要条件是什么？提示x ＋y ＋z ＝1.证明如下：(1)充分性∵OP →＝xOA →＋yOB →＋zOC→可变形为OP →＝(1－y －z )OA →＋yOB →＋zOC →，∴OP →－OA →＝y (OB →－OA →)＋z (OC →－OA →)，∴AP →＝yAB →＋zAC →，∴点P 与A ，B ，C 共面．(2)必要性∵点P 在平面ABC 内，不共线的三点A ，B ，C ，∴存在有序实数对(m ，n )使AP →＝mAB →＋nAC →，OP →－OA →＝m (OB →－OA →)＋n (OC →－OA →)，∴OP →＝(1－m －n )OA →＋mOB →＋nOC →，∵OP →＝xOA →＋yOB →＋zOC →，又∵点O 在平面ABC 外，∴OA →，OB →，OC →不共面，∴x ＝1－m －n ，y ＝m ，z ＝n ，∴x ＋y ＋z ＝1.例2(1)(多选)对空间任一点O 和不共线的三点A ，B ，C ，能得到P ，A ，B ，C 四点共面的是()A ．OP →＝OA →＋OB →＋OC →B ．OP →＝13OA →＋13OB →＋13OC→C ．OP →＝34OA →＋18OB →＋18OC→D ．OP →＝2OA →－OB →－OC →答案BC 解析方法一A 选项，OP →＝OA →＋OB →＋OC →，不能转化成AP →＝xPB →＋y PC →的形式，∴A 不正确；B 选项，∵OP →＝13OA →＋13OB →＋13OC →，∴3OP →＝OA →＋OB →＋OC →，∴OP →－OA →＝(OB →－OP →)＋(OC →－OP →)，∴AP →＝PB →＋PC →，∴PA →＝－PB →－PC →，∴P ，A ，B ，C 共面，故B 正确；C 选项，OP →＝34OA →＋18OB →＋18OC →＝34OA →＋18(OA →＋AB →)＋18(OA →＋AC →)＝OA →＋18AB →＋18AC →.∴OP →－OA →＝18AB →＋18AC →，∴AP →＝18AB →＋18AC →，由共面的充要条件知P ，A ，B ，C 四点共面，故C 选项正确；D 选项，OP →＝2OA →－OB →－OC →，无法转化成AP →＝xPB →＋y PC →的形式，D 项不正确．方法二当点P 与A ，B ，C 共面时，对空间任意一点O ，都有OP →＝xOA →＋yOB →＋zOC →，且x＋y ＋z ＝1，可判断出只有选项B ，C 符合要求．(2)(链接教材P5例1)如图所示，在长方体ABCD －A 1B 1C 1D 1中，M 为DD 1的中点，N ∈AC ，且AN ∶NC ＝2，求证：A 1，B ，N ，M 四点共面．证明设AA 1—→＝a ，AB →＝b ，AD →＝c ，则A 1B —→＝b －a ，∵M 为线段DD 1的中点，∴A 1M —→＝c －12a ，又∵AN ∶NC ＝2，∴AN →＝23AC →＝23(b ＋c )，∴A 1N —→＝AN →－AA 1—→＝23(b ＋c )－a＝23(b －a )－12a ＝23A 1B —→＋23A 1M —→，∴A 1N —→，A 1B —→，A 1M —→为共面向量．又∵三向量有相同的起点A 1，∴A 1，B ，N ，M 四点共面．反思感悟向量共面的判定及应用(1)证明三个向量共面(或四点共面)时，可以通过以下几个条件进行证明．①MP →＝xMA →＋yMB →；②对于空间任意一点O ，OP →＝OM →＋xMA →＋yMB →；③对于空间任意一点O ，OP →＝xOM →＋yOA →＋zOB →(x ＋y ＋z ＝1)；④PM →∥AB →(或PA →∥MB →或PB →∥AM →)．(2)若已知点P 在平面ABC 内，则有AP →＝xAB →＋y AC →或OP →＝xOA →＋yOB →＋zOC →(x ＋y ＋z ＝1)，然后利用指定向量表示出已知向量，用待定系数法求出参数．跟踪训练2已知E ，F ，G ，H 分别是空间四边形ABCD 的边AB ，BC ，CD ，DA 的中点，求证：E ，F ，G ，H 四点共面．证明如图，连接EG ，BG .因为EG →＝EB →＋BG →＝EB →＋12(BC →＋BD →)＝EB →＋BF →＋EH →＝EF →＋EH →，由向量共面的充要条件知向量EG →，EF →，EH →共面，即E ，F ，G ，H 四点共面．1．知识清单：(1)空间向量共线的充要条件，直线的方向向量．(2)空间向量共面的充要条件．(3)三点共线、四点共面的证明方法．2．方法归纳：转化化归、类比．3．常见误区：混淆向量共线与线段共线、点共线．1．对于空间的任意三个向量a ，b ,2a －b ，它们一定是()A ．共面向量B ．共线向量C ．不共面向量D ．既不共线也不共面的向量答案A解析由向量共面定理可知，三个向量a ，b ,2a －b 为共面向量．2．(多选)下列条件中，使M 与A ，B ，C 一定共面的是()A ．OM →＝3OA →－OB →－OC →B ．OM →＝15OA →＋13OB →＋12OC→C ．MA →＋MB →＋MC →＝0D ．OM →＋OA →＋OB →＋OC →＝0答案AC解析A 选项中，3－1－1＝1，四点共面，C 选项中，MA →＝－MB →－MC →，∴点M ，A ，B ，C 共面．3．已知点M 在平面ABC 内，并且对空间任意一点O ，有OM →＝xOA →＋13OB →＋13OC →，则x 的值为()A ．1B ．0C ．3D ．13答案D解析∵OM →＝xOA →＋13OB →＋13OC →，且M ，A ，B ，C 四点共面，∴x ＋13＋13＝1，∴x ＝13.4．设a ，b 是空间中两个不共线的向量，已知AB →＝9a ＋m b ，BC →＝－2a －b ，DC →＝a －2b ，且A ，B ，D 三点共线，则实数m ＝________.答案－3解析因为BC →＝－2a －b ，DC →＝a －2b .所以BD →＝BC →＋CD→＝BC →－DC →＝－2a －b －(a －2b )＝－3a ＋b ，因为A ，B ，D 三点共线，所以存在实数λ，使得AB →＝λBD →，即9a ＋m b ＝λ(－3a ＋b )．＝－3λ，＝λ，解得m ＝λ＝－3.练习1．下列命题中正确的是()A ．若a 与b 共线，b 与c 共线，则a 与c 共线B ．向量a ，b ，c 共面，即它们所在的直线共面C ．若两个非零空间向量AB →与CD →满足AB →＋CD →＝0，则AB →∥CD →D ．若a ∥b ，则存在唯一的实数λ，使a ＝λb答案C解析A 中，若b ＝0，则a 与c 不一定共线，故A 错误；B 中，共面向量的定义是平行于同一平面的向量，表示这些向量的有向线段所在的直线不一定共面，故B 错误；C 中，∵AB →＋CD →＝0，∴AB →＝－CD →，∴AB →与CD →共线，故AB →∥CD →，故C 正确；D 中，若b ＝0，a ≠0，则不存在λ，使a ＝λb ，故D 错误．2．已知非零向量a ，b ，且AB →＝a ＋2b ，BC →＝－5a ＋6b ，CD →＝7a －2b ，则一定共线的三点是()A ．A ，B ，D B ．A ，B ，C C ．B ，C ，D D ．A ，C ，D答案A解析∵BD →＝BC →＋CD →＝2a ＋4b ＝2AB →，∴A ，B ，D 三点共线．3．若空间中任意四点O ，A ，B ，P 满足OP →＝mOA →＋nOB →，其中m ＋n ＝1，则()A ．P ∈直线AB B ．P ∉直线ABC ．点P 可能在直线AB 上，也可能不在直线AB 上D ．以上都不对答案A解析因为m ＋n ＝1，所以m ＝1－n ，所以OP →＝(1－n )·OA →＋nOB →，即OP →－OA →＝n (OB →－OA →)，即AP →＝nAB →，所以AP →与AB →共线．又AP →，AB →有公共起点A ，所以P ，A ，B 三点在同一直线上，即P ∈直线AB .4．对于空间任意一点O 和不共线的三点A ，B ，C ，有如下关系：6OP →＝OA →＋2OB →＋3OC →，则()A ．O ，A ，B ，C 四点必共面B ．P ，A ，B ，C 四点必共面C ．O ，P ，B ，C 四点必共面D ．O ，P ，A ，B ，C 五点必共面答案B解析由6OP →＝OA →＋2OB →＋3OC →，得OA →－OP →＝2(OP →－OB →)＋3(OP →－OC →)，即PA →＝2BP →＋3CP →.由共面向量定理，知P ，A ，B ，C 四点共面．5．(多选)在以下命题中，不正确的命题是()A ．已知A ，B ，C ，D 是空间任意四点，则AB →＋BC →＋CD →＋DA →＝0B ．|a |－|b |＝|a ＋b |是a ，b 共线的充要条件C ．若a 与b 共线，则a 与b 所在的直线平行D ．对空间任意一点O 和不共线的三点A ，B ，C ，若OP →＝xOA →＋yOB →＋zOC →(其中x ，y ，z ∈R )，则P ，A ，B ，C 四点共面答案BCD解析对于A ，AB →＋BC →＋CD →＋DA →＝AC →＋CD →＋DA →＝AD →＋DA →＝0，A 正确；对于B ，若a ，b 同向共线，则|a |－|b |<|a ＋b |，故B 不正确；对于C ，由向量平行知C 不正确；对于D ，只有x ＋y ＋z ＝1时，才有P ，A ，B ，C 四点共面，故D 不正确．6．已知P 为空间中任意一点，A ，B ，C ，D 四点满足任意三点均不共线，但四点共面，且PA →＝43PB →－xPC →＋16DB →，则实数x 的值为()A ．13B ．－13C ．12D ．－12答案A解析PA →＝43PB →－xPC →＋16DB →＝43PB →－xPC →＋16(PB →－PD →)＝32PB →－xPC →－16PD →.又∵P 是空间任意一点，A ，B ，C ，D 四点满足任意三点均不共线，但四点共面，∴32－x －16＝1，解得x ＝13.7．设e 1，e 2是空间两个不共线的向量，已知AB →＝2e 1＋k e 2，CB →＝e 1＋3e 2，CD →＝2e 1－e 2，且A ，B ，D 三点共线，则k ＝________.答案－8解析由已知得BD →＝CD →－CB →＝(2e 1－e 2)－(e 1＋3e 2)＝e 1－4e 2，∵A ，B ，D 三点共线，∴AB →与BD →共线，即存在λ∈R ，使得AB →＝λBD →.∴2e 1＋k e 2＝λ(e 1－4e 2)＝λe 1－4λe 2，∵e 1，e 2不共线，＝2，＝－4λ，∴k ＝－8.8．在空间四边形ABCD 中，E ，F 分别是AB ，CD 的中点，则EF →和AD →＋BC →的关系是________．(填“平行”“相等”或“相反”)答案平行解析设G 是AC 的中点，连接EG ，FG (图略)，则EF →＝EG →＋GF →＝12BC →＋12AD →＝12(AD →＋BC →)，所以2EF →＝AD →＋BC →，从而EF →∥(AD →＋BC →)．9．已知A ，B ，C 三点不共线，平面ABC 外一点M 满足OM →＝13OA →＋13OB →＋13OC →.(1)判断MA →，MB →，MC →三个向量是否共面；(2)判断M 是否在平面ABC 内．解(1)∵OA →＋OB →＋OC →＝3OM →，∴OA →－OM →＝(OM →－OB →)＋(OM →－OC →)，∴MA →＝BM →＋CM →＝－MB →－MC →，∴向量MA →，MB →，MC →共面．(2)由(1)知，向量MA →，MB →，MC →共面，而它们有共同的起点M ，且A ，B ，C 三点不共线，∴M ，A ，B ，C 四点共面，即M 在平面ABC 内．10．如图所示，已知矩形ABCD 和矩形ADEF 所在的平面互相垂直，点M ，N 分别在对角线BD ，AE 上，且BM ＝13BD ，AN ＝13AE .求证：向量MN →，CD →，DE →共面．证明因为M 在BD 上，且BM ＝13BD ，所以MB →＝13DB →＝13DA →＋13AB →.同理AN →＝13AD →＋13DE →.所以MN →＝MB →＋BA →＋AN→＋13AB BA →＋13DE ＝23BA →＋13DE →＝23CD →＋13DE →.又CD →与DE →不共线，根据向量共面的充要条件可知MN →，CD →，DE →共面．11．若P ，A ，B ，C 为空间四点，且有PA →＝αPB →＋βPC →，则α＋β＝1是A ，B ，C 三点共线的()A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案C 解析若α＋β＝1，则PA →－PB →＝β(PC →－PB →)，即BA →＝βBC →，显然，A ，B ，C 三点共线；若A ，B ，C 三点共线，则有AB →＝λBC →，故PB →－PA →＝λ(PC →－PB →)，整理得PA →＝(1＋λ)PB →－λPC →，令α＝1＋λ，β＝－λ，则α＋β＝1.12．平面α内有五点A ，B ，C ，D ，E ，其中无三点共线，O 为空间一点，满足OA →＝12OB →＋xOC →＋yOD →，OB →＝2xOC →＋13OD →＋yOE →，则x ＋3y 等于()A ．56B ．76C ．53D ．73答案B解析由点A ，B ，C ，D 共面得x ＋y ＝12，①又由点B ，C ，D ，E 共面得2x ＋y ＝23，②联立①②，解得x ＝16，y ＝13，所以x ＋3y ＝76.13．已知正方体ABCD －A 1B 1C 1D 1中，P ，M 为空间任意两点，如果有PM →＝PB 1—→＋7BA →＋6AA 1—→－4A 1D 1——→，那么M 必()A ．在平面BAD 1内B ．在平面BA 1D 内C ．在平面BA 1D 1内D ．在平面AB 1C 1内答案C 解析PM →＝PB 1—→＋7BA →＋6AA 1—→－4A 1D 1——→＝PB 1—→＋BA →＋6BA 1—→－4A 1D 1——→＝PB 1—→＋B 1A 1——→＋6BA 1—→－4A 1D 1——→＝PA 1—→＋6(PA 1—→－PB →)－4(PD 1—→－PA 1—→)＝11PA 1—→－6PB →－4PD 1—→，又11－6－4＝1，于是M ，B ，A 1，D 1四点共面．14．已知a ＝3m －2n －4p (a ≠0)，b ＝(x ＋1)m ＋8n ＋2y p ，且m ，n ，p 不共面，若a ∥b ，则x ＋y ＝________.答案－5解析∵a ∥b 且a ≠0，∴b ＝λa ，即(x ＋1)m ＋8n ＋2y p ＝3λm －2λn －4λp ，又m ，n ，p 不共面，∴x ＋13＝8－2＝2y －4，则x ＝－13，y ＝8，x ＋y ＝－5.15．已知A ，B ，C 三点共线，则对空间任一点O ，存在三个不同为0的实数λ，m ，n ，使λOA→＋mOB →＋nOC →＝0，那么λ＋m ＋n 的值为________．答案0解析∵A ，B ，C 三点共线，∴存在实数k ，使得AB →＝kBC →，∵AB →＝OB →－OA →，BC →＝OC →－OB →，∴OB →－OA →＝k (OC →－OB →)，化简整理得OA →－(k ＋1)OB →＋kOC →＝0，∵λOA →＋mOB →＋nOC →＝0，∴①当k ＝－1时，比较系数得m ＝0且λ＝－n ，∴λ＋m ＋n ＝0；②当k ≠－1时，可得λ1＝m －k －1＝n k，得m ＝(－k －1)λ，n ＝kλ；由此可得λ＋m ＋n ＝λ＋(－k －1)λ＋kλ＝0，综上所述，λ＋m ＋n ＝0.16．如图所示，若P 为平行四边形ABCD 所在平面外一点，点H 为PC 上的点，且PH HC ＝12，点G 在AH 上，且AG AH ＝m ，若G ，B ，P ，D 四点共面，求m 的值．解如图，连接BG .因为AB →＝PB →－PA →，AB →＝DC →，所以DC →＝PB →－PA →.因为PC →＝PD →＋DC →，所以PC →＝PD →＋PB →－PA→＝－PA →＋PB →＋PD →.因为PH HC ＝12，所以PH →＝13PC →，所以PH →＝13(－PA →＋PB →＋PD →)＝－13PA →＋13PB →＋13PD →.又因为AH →＝PH →－PA →，所以AH →＝－43PA →＋13PB →＋13PD →.因为AGAH ＝m ，所以AG →＝mAH →＝－4m 3PA →＋m 3PB →＋m 3PD →.因为BG →＝－AB →＋AG →＝PA →－PB →＋AG →，所以BG →＋m 3PD →.又因为G ，B ，P ，D 四点共面，所以1－4m 3＝0，m ＝34，即m 的值是34.。

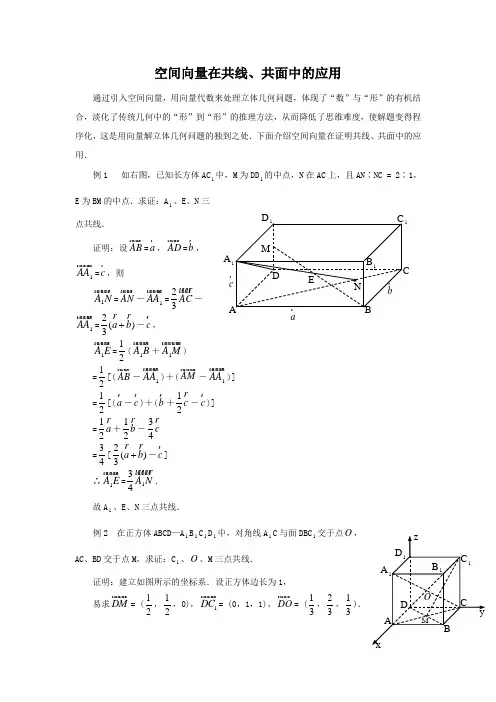
空间向量在共线、共面中的应用通过引入空间向量，用向量代数来处理立体几何问题，体现了“数”与“形”的有机结合，淡化了传统几何中的“形”到“形”的推理方法，从而降低了思维难度，使解题变得程序化，这是用向量解立体几何问题的独到之处．下面介绍空间向量在证明共线、共面中的应用．例1 如右图，已知长方体AC 1中，M 为DD 1的中点，N 在AC 上，且AN ∶NC = 2∶1，E 为BM 的中点．求证：A 1、E 、N 三点共线．证明：设AB =a ，AD =b，1AA =c，则1A N =AN －1AA =23AC －1AA =2()3a b +－c ，1A E =12(1A B ＋1A M )=12[(AB－1AA )＋(AM －1AA )] =12[(a －c)＋(b ＋12c －c )] =12a ＋12b －34c =34[2()3a b +－c ] ∴1A E =134A N ．故A 1、E 、N 三点共线．例2 在正方体ABCD —A 1B 1C 1D 1中，对角线A 1C 与面DBC 1交于点O ，AC 、BD 交于点M ，求证：C 1、O 、M 三点共线．证明：建立如图所示的坐标系．设正方体边长为1，易求DM = (12，12，0)，1DC = (0，1，1)，DO = (13，23，13)．A BCDC 1D 1 B 1A 1E· NabcM设DM = x 1DC ＋y DO = (3y ，x ＋23y ，x ＋3y)，又DM = (12，12，0)，所以有1,3221,320.3y y x y x ⎧=⎪⎪⎪+=⎨⎪⎪+=⎪⎩⇒1,23.2x y ⎧=-⎪⎪⎨⎪=⎪⎩∵x ＋y = 1，∴C 1、O 、M 三点共线．评析：利用共线向量定理中的条件“x ＋y = 1”是寻求点共线的关键． 例1 在正方体ABCD —A 1B 1C 1D 1中，点E 、F 分别是AA 1、CC 1的中点．求证：点D 1、E 、F 、B 共面．解：建立如图所示的空间直角坐标系，设正方体的边长位，于是有D 1(0，0，2)，F(0，2，1)，E(2，0，1)，B(2，2，0)，从而1D F = (0，2，－1)，EB = (0，2，－1)，所以1D F =EB，又因EB 与D 1F 无交点，所以D 1F ∥EB ， 故点D 1、E 、F 、B 共面．例2 已知P 是平行四边形ABCD 所在平面外一点，连结PA 、PB 、PC 、PD ，点E 、F 、G 、H 分别为△PAB 、△PBC 、△PCD 、△PDA 的重心。

共面向量定理证明摘要：一、共面向量定理的概念及意义二、共面向量定理的证明方法1.向量共线定理的证明2.向量共面定理的证明3.存在唯一的证明三、共面向量定理的应用举例四、总结与拓展正文：一、共面向量定理的概念及意义共面向量定理是向量空间中的一个重要定理，它描述了向量空间的一些基本性质。

共面向量定理指出，如果三个非零向量共面，那么它们就共面。

这个定理在向量空间的许多应用中都起着关键作用，如向量运算、线性方程组求解等。

二、共面向量定理的证明方法共面向量定理的证明主要分为三个部分：向量共线定理的证明、向量共面定理的证明和存在唯一的证明。

1.向量共线定理的证明向量共线定理是指，如果两个向量共线，那么它们就共面。

这个定理的证明主要通过向量的数乘运算来完成。

假设有两个共线的向量a 和b，那么可以找到一个实数k，使得a=k*b。

由此可知，向量a 与向量b 共面。

2.向量共面定理的证明向量共面定理是指，如果三个向量共面，那么它们就共面。

这个定理的证明主要通过向量的线性组合来完成。

假设有三个共面的向量a、b 和c，那么可以找到一组实数x、y 和z，使得a=x*b+y*c。

由此可知，向量a 与向量b、c 共面。

3.存在唯一的证明存在唯一的证明是指，对于任意三个非零向量，它们一定共面，且共面的向量只有一个。

这个证明主要采用反证法来完成。

假设存在三个非零向量a、b 和c，它们不共面。

那么，根据向量共面定理，我们可以找到一个实数k，使得a=k*b+c。

但这与假设矛盾，因为假设中a、b 和c 不共面，而根据向量共面定理，它们共面。

所以，假设不成立，原命题成立。

三、共面向量定理的应用举例共面向量定理在向量空间的应用非常广泛，如求解线性方程组、判断向量是否共面等。

例如，给定四个向量a、b、c 和d，如果a 与b 共线，b 与c 共线，c 与d 共线，那么根据共面向量定理，a、b、c 和d 四个向量共面。

四、总结与拓展共面向量定理是向量空间中的一个基本定理，它描述了向量空间的一些基本性质。

空间共面向量定理的推论及应用空间共面向量定理，听起来有点高大上，但其实它就像生活中的一块拼图，只有把所有的部分拼在一起，才能看出完整的图案。

想象一下，四个小朋友在操场上玩耍，他们手牵手站成一圈。

这四个小朋友，就是我们的向量，而他们共同形成的这个圈，就代表了共面。

可别小看这些小朋友，虽然每个人都有自己的性格和方向，但他们一旦手牵手，就能创造出一种特殊的和谐，简直就像是一首美妙的乐曲。

大家都知道，向量的性质和它们之间的关系就像人际关系一样，有时候很简单，有时候却复杂得让人抓狂。

说到应用，空间共面向量定理在生活中可真是无处不在。

想象一下，工程师们在设计一座大桥的时候，必须考虑到每根钢梁的方向和角度。

它们得共面，才能稳稳当当地支撑起整个桥梁。

哎呀，若是有一根钢梁不听话，跑偏了，那可就麻烦大了。

这个定理就像一个忠实的导航仪，指引着他们走向正确的方向。

说不定，正是因为这些向量的配合，才能让车水马龙的城市多了一条安全的通道，真是别有一番风味。

再说说运动员们的训练，篮球场上那些飞奔的身影，看似随意，实则背后可藏着不少讲究。

那些投篮、传球的动作，都是建立在向量之间的协调和配合上的。

篮球从手中飞出，划出一道美丽的弧线，正是因为球员们懂得如何运用空间共面向量的原理，才让每一次投篮都充满了力量与美感。

你想啊，要是球员之间不能配合，那场比赛就像无头苍蝇一样，乱成一团，绝对让人哭笑不得。

生活中的许多场景，都能找到空间共面向量的身影。

比如说，一群朋友聚会，大家围成一圈，分享故事和欢笑。

虽然每个人都有自己的观点和方向，但当他们都坐在一起时，形成的共面关系就让每个人都能听到彼此的声音。

这样的聚会就像是一个温暖的大家庭，让人觉得格外亲切。

想象一下，如果有一个朋友坐得太远，跟大家说话就是传声筒，结果也只能听到模糊的声音，那气氛可就没法调动起来了。

在教育中，老师和学生的关系也可以用这个定理来形容。

老师讲课，学生认真听，双方共同构建出一个知识的空间。

龙源期刊网 空间四点共面充要条件的应用与探究作者：姚洪琪来源：《中国校外教育·高教》2011年第04期[摘要] 平面上的三点共线与空间的四点共面，是平面向量与空间向量问题中的一类重要题型。

在高中数学人教A版选修教材2-1《空间向量与立体几何》一章中，给出了四点共面的一个判定方法，在配套的教参中更明确为充要条件。

因此有些老师在教学中就给出了如下的空间P、A、B、C、四点共面的充要条件：对于空间任意一点O，存在实数x、y、z，使得且x+y+z=1。

这个结论对于解决空间四点共面问题提供了很便捷的方法，[关键词] 立体几何充要条件高中数学平面上的三点共线与空间的四点共面，是平面向量与空间向量问题中的一类重要题型。

在高中数学人教A版选修教材2-1《空间向量与立体几何》一章中，给出了四点共面的一个判定方法，在配套的教参中更明确为充要条件。

因此有些老师在教学中就给出了如下的空间P、A、B、C、四点共面的充要条件：对于空间任意一点O，存在实数x、y、z，使得且x+y+z=1。

这个结论对于解决空间四点共面问题提供了很便捷的方法，例如：以上三个问题的解决都用到了课本中提到的四点共面的充要条件，思路新颖，解法简洁，确实为学生们解决空间四点共面问题提供了一条重要的解题思路。

但是，学生们在解决2005年全国高考数学试题时，却出现了困惑和迷茫。

甚至对该方法提出了质疑。

究竟哪一个答案是正确的？在查阅05年高考试题答案后知道，正确答案应该为1，而对于老师给出的结论也是深信不疑的，因为在平面向量中就曾经得出过类似的问题：平面内三点A、B、C共线的充要条件是：对于平面内任意一点O，存在实数λ、μ，使得 ,且λ+μ=1.课本中的结论其实就是平面向量问题的一个推广。

那么第一种解法究竟错在哪里？这个充要条件正确吗？注：本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文。

空间中三个向量共面的充要条件《空间中三个向量共面的充要条件》小朋友们，今天我们来一起探索一个神奇的数学知识——空间中三个向量共面的充要条件。

比如说，我们把向量想象成小飞机飞行的路线。

有三架小飞机，它们飞的路线如果在同一个平面上，那就叫共面。

那怎么才能知道它们是不是共面呢？这就有个小秘密啦。

假如有三个向量，a 向量、b 向量和 c 向量，如果能找到两个数 m 和 n，让 c 向量等于 m 乘以 a 向量加上 n 乘以 b 向量，那这三个向量就是共面的。

就好像三个小朋友跑步，一个小朋友跑的路程可以用另外两个小朋友跑的路程组合出来，那他们就在一个平面上跑啦。

小朋友们，你们明白了吗？《空间中三个向量共面的充要条件》亲爱的小朋友们，今天咱们来聊聊有趣的向量知识。

想象一下，空间里有三个向量，就像三个小箭头。

要是这三个小箭头能在一个大平面上，那可太棒啦！比如说，有个小三角形，三个边就是三个向量。

如果这三个边能平平地放在一起，那这三个向量就是共面的。

那怎么知道它们能不能共面呢？很简单哦，如果其中一个向量可以用另外两个向量加加减减变出来，那它们肯定就在一个平面上啦。

就像搭积木一样，一块积木可以用另外两块拼出来，它们就都在一个地方啦。

小朋友们，是不是很有趣呀？《空间中三个向量共面的充要条件》小朋友们，今天我们要一起走进数学的奇妙世界，来看看空间中三个向量共面的充要条件。

假设我们有三个小伙伴，分别沿着三条不同的路线跑。

这三条路线就像是三个向量。

如果这三个小伙伴跑的路线能在一张大大的纸上画出来，那这三个向量就是共面的。

那怎么判断呢？比如说，我们把其中一个小伙伴跑的路线长度，用另外两个小伙伴跑的路线长度通过一些计算组合起来，如果能正好对上，那这三个向量就共面啦。

就好像做蛋糕，一种口味的蛋糕分量可以用另外两种口味的蛋糕分量算出来，它们就都在一个盘子里啦。

小朋友们，懂了吗？《空间中三个向量共面的充要条件》小朋友们，今天来了解一个好玩的数学概念——空间中三个向量共面的充要条件。

三个向量共面的充要条件向量（vector）是一种非常重要的数学概念，它可以用来表示一个线性变换中的运动方向。

它们在很多领域都有广泛的应用，例如物理，工程，统计学，控制理论，信号处理，传动学等等。

其中，最为常见的应用就是三维空间中的向量与向量的共面性。

在空间中，三个向量共面的充要条件是什么呢？首先，我们需要知道三个向量的定义，即三个向量指向同一个平面上的三个不同的点。

即：三个向量的终点坐标分别为（x1, y1, z1），（x2, y2, z2）和（x3, y3, z3），这三个点定义三个向量：A = (x2-x1, y2-y1, z2-z1)，B = (x3-x1, y3-y1, z3-z1)，C = (x3-x2, y3-y2, z3-z2)。

对于三个向量共面，我们需要明确两个条件：（1）三个向量都是平行的；（2）三个向量和平面法向量夹角为零度。

我们先来看条件（1），也就是三个向量平行的充要条件。

令a = (x2-x1, y2-y1, z2-z1)，b = (x3-x1, y3-y1, z3-z1)，c = (x3-x2, y3-y2, z3-z2)，那么a、b、c三个向量平行的条件为：a×b=0和b×c=0，其中“×”表示叉乘运算，叉乘运算可以求出三个向量所在平面的法向量。

然后我们看条件（2），也就是三个向量和平面法向量夹角为零度的充要条件。

令法向量为n=(xn,yn,zn)，那么a、b、c三个向量和n 的夹角为零的条件为：an=0，bn=0，cn=0，其中“”表示点乘运算，点乘运算可以求出三个向量和平面法向量的夹角。

因此，我们可以得出三个向量共面的充要条件，即：a×b=0，b×c=0，an=0，bn=0，cn=0，其中a、b、c分别表示三个向量定义，n 表示平面法向量。

以上就是三个向量共面的充要条件。

它们在实际应用中也是非常重要的，它们可以用来判断两个平面是否相交，也可以用来计算三个向量构成的平面的法向量。

文档标题：一探究竟：空间向量共面定理是啥玩意儿？正文：大家好，今儿咱们就来聊聊一个听起来挺高大上的数学概念——空间向量的共面定理。

别一听“定理”俩字就头大，咱们就用大白话给它解释清楚，保证让你一听就明白。

首先，啥是空间向量？简单来说，空间向量就是那些在三维空间里能指个方向、有个大小的东西。

想象一下，你手里拿着一根箭头，这箭头指向不同的方向，长短也不一样，这就是空间向量。

那共面又是啥意思呢？共面，就是说这些向量都待在同一个平面里。

想象一张纸，你可以在上面画几个箭头，这些箭头都在这张纸上，这就叫共面。

好了，现在咱们来说说共面定理。

这个定理其实就是在告诉我们一个道理：在三维空间里，如果咱们有三个向量，只要这三个向量不是完全“散开”的，那么它们就能找到一个共同的平面，让这三个向量都在这个平面上。

具体咋说呢？咱们来打个比方。

想象你手里有三个可以伸缩的箭头，你可以把它们拉长缩短，也可以改变它们的方向。

只要你不是故意让这三个箭头互相垂直而且还不在同一个平面上，你总能找到一个方法，让这三个箭头都在同一张纸上。

这就是共面定理的核心意思。

咱们再来细说一下这个定理的三个关键点：1. 三个向量：就像咱们刚才说的，你手里得有三个箭头，才能玩这个共面的游戏。

2. 不完全“散开”：这就是说，这三个向量不能互相之间都垂直，而且不在同一个平面上。

如果真是那样，它们就找不到一个共同的平面了。

3. 找到共同平面：只要这三个向量不是完全“散开”的，那么总有一个办法，让它们都在同一个平面上。

这个定理有啥用呢？其实在咱们生活中，共面定理的应用可多了。

比如说，你盖房子的时候，要确保三面墙都在同一个平面上，这就用到了共面定理。

再比如，你在电脑上做三维设计，也得用到这个定理，确保你设计的各个部分能在一个平面上。

总之，空间向量的共面定理，其实就是告诉我们，三维空间里的向量，只要不是互相“散开”的，就能找到一块“公共地盘”，让它们和平共处。

这个定理虽然听起来挺抽象，但用在生活里，还是挺实用的。

向量四点共面定理等于1（实用版）目录1.引言2.向量四点共面定理的概念3.向量四点共面定理的证明4.向量四点共面定理的应用5.结论正文1.引言向量四点共面定理是线性代数中的一个基本定理，它描述了四个向量共面的充分必要条件。

在数学、物理等科学领域中，向量四点共面定理有着广泛的应用，例如在解决空间几何问题、分析力学系统等。

本篇文章将从向量四点共面定理的概念、证明和应用三个方面进行介绍。

2.向量四点共面定理的概念向量四点共面定理是指：如果四个向量满足一定的条件，那么这四个向量就共面。

具体来说，设 A、B、C、D 是空间中的四个向量，如果满足以下条件：AB·(CD) = AC·(BD) = AD·(BC) = 0其中，“·”表示向量的数量积，那么向量 AB、CD、AC、BD、AD、BC 就共面。

3.向量四点共面定理的证明向量四点共面定理的证明可以通过向量的线性组合来完成。

假设 AB、CD、AC、BD、AD、BC 共面，那么存在不全为零的实数 k1、k2、k3、k4，使得：AB = k1*CD + k2*AC + k3*AD + k4*BC由于 AB、CD、AC、BD、AD、BC 共面，所以它们的线性组合也共面。

将上式代入，得到：k1*CD + k2*AC + k3*AD + k4*BC = 0即：k1*(CD·BC) + k2*(AC·BD) + k3*(AD·CD) + k4*(AB·DC) = 0根据向量的数量积的性质，上式可以化简为：k1*(CD·BC) + k2*(AC·BD) + k3*(AD·CD) + k4*(AB·DC) = 0因为 k1、k2、k3、k4 不全为零，所以 CD·BC、AC·BD、AD·CD、AB·DC 不全为零。

空间向量四点共面的条件空间向量是空间中的有向线段，具有大小和方向。

在空间中，有时候我们会遇到四个点，我们想要判断它们是否共面。

共面的意思是四个点都在同一个平面上，也就是说它们可以用同一个平面来覆盖。

我们需要明确的是，空间中的平面由三个非共线的点确定。

也就是说，如果四个点共面，那么它们中的任意三个点都可以确定一个平面。

所以，我们可以假设四个点中的任意三个点分别为A、B、C，然后我们来看第四个点D。

如果D点在由A、B、C三个点确定的平面上，那么四个点就是共面的。

为了判断D点是否在这个平面上，我们可以通过计算向量来进行判断。

我们需要计算向量AB、AC和AD。

我们可以使用向量的减法来计算，即AD = D - A，AB = B - A，AC = C - A。

接下来，我们需要计算向量AB和AC的叉乘，得到一个新的向量n。

这个向量n垂直于平面ABC，它的方向与平面的法向量相同。

我们可以使用向量的叉乘公式来计算，即n = AB × AC。

我们需要计算向量AD与向量n的点积。

如果点积结果为0，那么向量AD与向量n是垂直的，也就是说D点在平面ABC上。

如果点积结果不为0，那么向量AD与向量n不垂直，也就是说D点不在平面ABC上。

空间向量四点共面的条件是：对于四个点A、B、C、D，如果向量AD与向量n的点积为0，则四个点共面；如果点积不为0，则四个点不共面。

需要注意的是，这个条件是严格的，如果点积结果为一个非零的数值，那么四个点不仅不共面，还可能不在同一个平面上。

通过以上的分析，我们可以得出判断空间向量四点共面的条件，并且可以应用到实际问题中。

判断四个点是否共面在几何学、物理学以及计算机图形学等领域都有广泛的应用。

对于我们来说，理解这个条件可以帮助我们更好地理解空间中的几何关系，提高我们的空间思维能力。

空间向量四点共面的条件是向量AD与向量n的点积为0。

这个条件可以通过计算向量的减法、叉乘和点积来判断。

通过理解这个条件，我们可以更好地理解空间中的几何关系，并且应用到实际问题中。