递归函数与非递归的转化

《算法分析与设计》作业参考答案作业一一、名词解释：1.递归算法：直接或间接地调用自身的算法称为递归算法。

2.程序：程序是算法用某种程序设计语言的具体实现。

二、简答题：1.算法需要满足哪些性质？简述之。

答：算法是若干指令的有穷序列，满足性质：（1）输入：有零个或多个外部量作为算法的输入。

（2）输出：算法产生至少一个量作为输出。

（3）确定性：组成算法的每条指令清晰、无歧义。

（4）有限性：算法中每条指令的执行次数有限，执行每条指令的时间也有限。

2.简要分析分治法能解决的问题具有的特征。

答：分析分治法能解决的问题主要具有如下特征：（1）该问题的规模缩小到一定的程度就可以容易地解决；（2）该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质； （3）利用该问题分解出的子问题的解可以合并为该问题的解；（4）该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

3.简要分析在递归算法中消除递归调用，将递归算法转化为非递归算法的方法。

答：将递归算法转化为非递归算法的方法主要有：（1）采用一个用户定义的栈来模拟系统的递归调用工作栈。

该方法通用性强，但本质上还是递归，只不过人工做了本来由编译器做的事情，优化效果不明显。

（2）用递推来实现递归函数。

（3）通过Cooper 变换、反演变换能将一些递归转化为尾递归，从而迭代求出结果。

后两种方法在时空复杂度上均有较大改善，但其适用范围有限。

三、算法编写及算法应用分析题： 1.冒泡排序算法的基本运算如下：for i ←1 to n-1 do for j ←1 to n-i do if a[j]<a[j+1] then 交换a[j]、a[j+1]； 分析该算法的时间复杂性。

答：排序算法的基本运算步为元素比较，冒泡排序算法的时间复杂性就是求比较次数与n 的关系。

（1）设比较一次花时间1；（2）内循环次数为：n-i 次,（i=1,…n ），花时间为：∑-=-=in j i n 1)(1（3）外循环次数为：n-1，花时间为：2.设计一个分治算法计算一棵二叉树的高度。

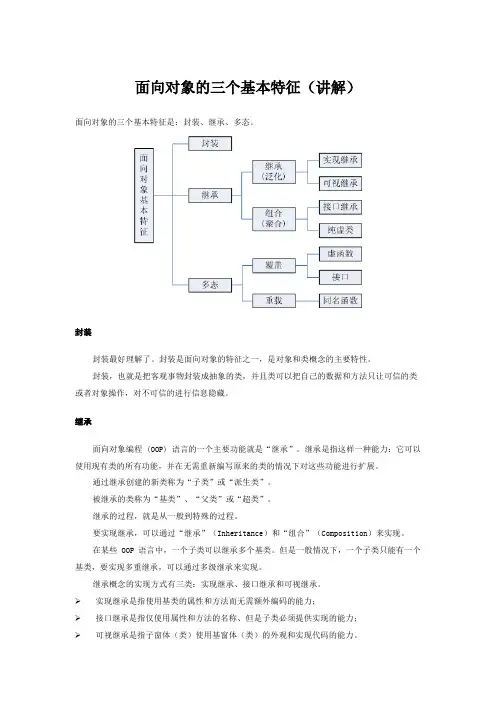
面向对象的三个基本特征（讲解）面向对象的三个基本特征是：封装、继承、多态。

封装封装最好理解了。

封装是面向对象的特征之一，是对象和类概念的主要特性。

封装，也就是把客观事物封装成抽象的类，并且类可以把自己的数据和方法只让可信的类或者对象操作，对不可信的进行信息隐藏。

继承面向对象编程 (OOP) 语言的一个主要功能就是“继承”。

继承是指这样一种能力：它可以使用现有类的所有功能，并在无需重新编写原来的类的情况下对这些功能进行扩展。

通过继承创建的新类称为“子类”或“派生类”。

被继承的类称为“基类”、“父类”或“超类”。

继承的过程，就是从一般到特殊的过程。

要实现继承，可以通过“继承”（Inheritance）和“组合”（Composition）来实现。

在某些 OOP 语言中，一个子类可以继承多个基类。

但是一般情况下，一个子类只能有一个基类，要实现多重继承，可以通过多级继承来实现。

继承概念的实现方式有三类：实现继承、接口继承和可视继承。

实现继承是指使用基类的属性和方法而无需额外编码的能力；接口继承是指仅使用属性和方法的名称、但是子类必须提供实现的能力；可视继承是指子窗体（类）使用基窗体（类）的外观和实现代码的能力。

在考虑使用继承时，有一点需要注意，那就是两个类之间的关系应该是“属于”关系。

例如，Employee 是一个人，Manager 也是一个人，因此这两个类都可以继承 Person 类。

但是 Leg 类却不能继承 Person 类，因为腿并不是一个人。

抽象类仅定义将由子类创建的一般属性和方法，创建抽象类时，请使用关键字 Interface 而不是 Class。

OO开发范式大致为：划分对象→抽象类→将类组织成为层次化结构(继承和合成) →用类与实例进行设计和实现几个阶段。

多态多态性（polymorphisn）是允许你将父对象设置成为和一个或更多的他的子对象相等的技术，赋值之后，父对象就可以根据当前赋值给它的子对象的特性以不同的方式运作。

函数的递归调用1.递归基本概念所谓递归，简而言之就是应用程序自身调用自身，以实现层次数据结构的查询和访问。

递归的使用可以使代码更简洁清晰，可读性更好。

但由于递归需要系统堆栈，所以空间消耗要比非递归代码要大很多，而且，如果递归深度太大，可能系统资源会不够用。

从理论上说，所有的递归函数都可以转换为迭代函数，反之亦然，然而代价通常都是比较高的。

但从算法结构来说，递归声明的结构并不总能够转换为迭代结构，原因在于结构的引申本身属于递归的概念，用迭代的方法在设计初期根本无法实现，这就像动多态的东西并不总是可以用静多态的方法实现一样。

这也是为什么在结构设计时，通常采用递归的方式而不是采用迭代的方式的原因，一个极典型的例子类似于链表，使用递归定义及其简单，但对于内存定义(数组方式)其定义及调用处理说明就变得很晦涩，尤其是在遇到环链、图、网格等问题时，使用迭代方式从描述到实现上都变得不现实。

因而可以从实际上说，所有的迭代可以转换为递归，但递归不一定可以转换为迭代。

2.C语言中的函数可以递归调用可以直接（简单递归）或间接（间接递归）地自己调自己。

这里我们只简单的谈谈直接递归。

采用递归方法来解决问题，必须符合以下三个条件：（1）可以把要解决的问题转化为一个新问题，而这个新的问题的解决方法仍与原来的解决方法相同，只是所处理的对象有规律地递增或递减。

说明：解决问题的方法相同，调用函数的参数每次不同（有规律的递增或递减），如果没有规律也就不能适用递归调用。

（2）可以应用这个转化过程使问题得到解决。

说明：使用其他的办法比较麻烦或很难解决，而使用递归的方法可以很好地解决问题。

（3）必定要有一个明确的结束递归的条件。

说明：一定要能够在适当的地方结束递归调用。

不然可能导致系统崩溃。

3.递归实例下面用一个实例来说明递归调用。

使用递归的方法求n!当n>1时，求n!的问题可以转化为n*(n-1)!的新问题。

比如n=5：第一部分：5*4*3*2*1 n*(n-1)!第二部分：4*3*2*1 (n-1)*(n-2)!第三部分：3*2*1 (n-2)(n-3)!第四部分：2*1 (n-3)(n-4)!第五部分：1 （n-5）! 5-5=0，得到值1，结束递归。

《算法分析与设计》课程复习资料一、名词解释：1.算法2.程序3.递归函数4.子问题的重叠性质5.队列式分支限界法6.多机调度问题7.最小生成树 二、简答题：1.备忘录方法和动态规划算法相比有何异同？简述之。

2.简述回溯法解题的主要步骤。

3.简述动态规划算法求解的基本要素。

4.简述回溯法的基本思想。

5.简要分析在递归算法中消除递归调用，将递归算法转化为非递归算法的方法。

6.简要分析分支限界法与回溯法的异同。

7.简述算法复杂性的概念，算法复杂性度量主要指哪两个方面？ 8.贪心算法求解的问题主要具有哪些性质？简述之。

9.分治法的基本思想是什么？合并排序的基本思想是什么？请分别简述之。

10.简述分析贪心算法与动态规划算法的异同。

三、算法编写及算法应用分析题：1.已知有3个物品：(w1,w2,w3)=(12,10,6),(p1,p2,p3)=(15,13,10),背包的容积M=20，根据0-1背包动态规划的递推式求出最优解。

2.按要求完成以下关于排序和查找的问题。

①对数组A={15，29，135，18，32，1，27，25，5}，用快速排序方法将其排成递减序。

②请描述递减数组进行二分搜索的基本思想，并给出非递归算法。

③给出上述算法的递归算法。

④使用上述算法对①所得到的结果搜索如下元素，并给出搜索过程：18，31，135。

3.已知1()*()i i k k ij r r A a +=，k =1，2，3，4，5，6，r 1=5，r 2=10，r 3=3，r 4=12，r 5=5，r 6=50，r 7=6，求矩阵链积A 1×A 2×A 3×A 4×A 5×A 6的最佳求积顺序（要求给出计算步骤）。

4.根据分枝限界算法基本过程,求解0-1背包问题。

已知n=3,M=20，(w1,w2,w3)=(12,10,6),(p1,p2,p3)=(15,13,10)。

递归算法修改为非递归算法1.引言1.1 概述递归算法是一种常见的计算方法，它通过将大问题拆分成一个或多个相似的子问题来解决。

递归算法通常通过不断调用自身来处理这些子问题，直到达到基本情况时停止递归。

递归算法的设计具有简洁、优雅的特点，并在某些情况下能够提供高效的解决方案。

然而，递归算法也存在一些局限性。

首先，递归调用会带来额外的函数调用开销，可能会导致程序运行速度较慢。

其次，递归算法对于大规模问题的解决可能会导致堆栈溢出的问题，因为每一次递归调用都需要在内存中保存一些信息。

为了克服递归算法的局限性，我们可以将其修改为非递归算法。

非递归算法使用迭代的方式来解决问题，通过使用循环结构来代替递归调用，从而降低了函数调用的开销。

此外，非递归算法更加直观易懂，可以减少程序的复杂性。

本文将探讨递归算法修改为非递归算法的必要性和优势，并通过具体的例子和算法讲解，详细介绍如何将递归算法转化为非递归算法的思路和方法。

通过对比和分析，我们将展示非递归算法在某些情况下的效率和可行性，以及它在解决问题时的优势和不足。

在接下来的章节中，我们将首先介绍递归算法的特点，包括递归调用和基本情况的判断。

然后，我们将讨论非递归算法的优势，包括降低函数调用开销和提高程序运行效率的能力。

最后，我们将总结递归算法的局限性，强调修改为非递归算法的必要性。

1.2 文章结构本文分为引言、正文和结论三个部分。

在引言部分，我们将概述本文的主题和目的，并介绍文章的结构。

在正文部分，我们将首先探讨递归算法的特点，包括递归算法的定义、实现方式和应用场景等。

然后我们将分析非递归算法的优势，包括非递归算法相对于递归算法的效率、可读性和内存消耗等方面的优势。

接下来，在结论部分，我们将讨论递归算法的局限性，包括递归算法在处理大规模数据时存在的问题和栈溢出的风险等。

最后，我们将强调修改为非递归算法的必要性，以解决递归算法的局限性，并总结本文的主要观点和结论。

通过以上结构，我们将全面而系统地探讨递归算法修改为非递归算法的背景、原因和优势，以及非递归算法在解决问题中的应用价值。

【关键字】分析《算法分析与设计》作业参考答案作业一一、名词解释：1.递归算法：直接或间接地调用自身的算法称为递归算法。

2.程序：程序是算法用某种程序设计语言的具体实现。

2、简答题：1.算法需要满足哪些性质？简述之。

算法是若干指令的有穷序列，满足性质：1）输入：有零个或多个外部量作为算法的输入。

2）输出：算法产生至少一个量作为输出。

3）确定性：组成算法的每条指令清晰、无歧义。

4）有限性：算法中每条指令的执行次数有限，执行每条指令的时间也有限。

2.简要分析分治法能解决的问题具有的特征。

分析分治法能解决的问题主要具有如下特征：1）该问题的规模缩小到一定的程度就可以容易地解决；2）该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；3）利用该问题分解出的子问题的解可以合并为该问题的解；4）该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

3.简要分析在递归算法中消除递归调用，将递归算法转化为非递归算法的方法。

将递归算法转化为非递归算法的方法主要有：1）采用一个用户定义的栈来模拟系统的递归调用工作栈。

该方法通用性强，但本质上还是递归，只不过人工做了本来由编译器做的事情，优化效果不明显。

2）用递推来实现递归函数。

3）通过Cooper变换、反演变换能将一些递归转化为尾递归，从而迭代求出结果。

后两种方法在时空复杂度上均有较大改善，但其适用范围有限。

三、算法编写及算法应用分析题：1.冒泡排序算法的基本运算如下：for i ←1 to n-1 dofor j ←1 to n-i doif a[j]<a[j+1] then交换a[j]、a[j+1]；分析该算法的时间复杂性。

解答：排序算法的基本运算步为元素比较，冒泡排序算法的时间复杂性就是求比较次数与n的关系。

1）设比较一次花时间1；2）内循环次数为：n-i次,（i=1,…n），花时间为：3）外循环次数为：n-1，花时间为：2.设计一个分治算法计算一棵二叉树的高度。

递归算法转换为非递归算法想象一下，递归就像是你的好朋友，老是在你耳边叨叨，告诉你：“再来一次，再来一次。

”而非递归就像是那个实在的家伙，给你一份清晰的计划，告诉你该干嘛。

用非递归的方式，咱们就能更好地控制进度，不会再像在黑暗中摸索，而是一步步地稳稳前进。

说到这里，有的人可能会问：“非递归的难度是不是太高了？”其实呢，非递归并没有想象中那么复杂，特别是如果你能掌握一些基本的技巧，就像玩拼图一样，轻松上手。

举个例子，大家都知道计算斐波那契数列吧。

那种用递归的方式计算，简直像在爬一座高山，一级一级上去，最后发现自己爬了个寂寞，特别是数字一多，简直就是给自己挖坑。

非递归的方法其实就是把这个过程变得更直白，像是在教你怎么把山坡变成一条平坦的大路。

我们可以用一个简单的循环来实现，拿着一张小纸条，把每一步都写下来。

随着每一轮的循环，数据就一点点填满，直到达成目标。

就像煮面一样，慢慢煮，耐心等待，最后面条总会熟透的。

再说个有趣的事儿，遍历树结构的时候，递归的方法就像你在给小朋友讲故事，每讲完一层就得回到上一层，像是在玩捉迷藏，兜兜转转。

可是，非递归就不一样了，咱们可以用一个栈，把要访问的节点先都存起来，等到该去的时候，再一层层取出来，就像用一根绳子把它们串起来，拉出来的时候，结果就乖乖地在眼前了。

想象一下，树上的苹果，一个一个摘下来，效率简直高得惊人，没那么多折腾。

非递归的方式往往能让代码变得更加清晰，特别是当你给别人分享你的代码时，大家都能看得明白，不会一脸懵逼。

这样的好处简直就像是给大家开了一扇窗，阳光照进来，温暖了整个房间。

哎，真的是好得不得了。

说到大家不妨试试把自己的递归代码转换成非递归，可能会觉得自己像获得了一种新技能。

学会这一招，编程之路就更加宽广了，就像是打开了一扇新天地，眼前的风景愈加美丽。

不论是递归还是非递归，各有千秋，关键是看你自己怎么用。

编程的乐趣在于探索，敢于尝试，保持好奇心，那才是最重要的！好啦，今天的分享就到这里，祝大家编程愉快，玩得开心！。

迭代与递归和还原的关系
迭代、递归和还原在计算机科学和数学中都有其特定的应用和关系，以下是它们之间的一些关系：
1. 递归与迭代：
递归是一种编程技巧，程序调用自身以解决问题。

递归将问题分解为更小的子问题，并逐个解决这些子问题，直到达到基本情况。

迭代则是通过重复执行一系列操作来解决问题，这些操作会根据某些条件进行修改，直到满足某个结束条件。

在理论上，递归和迭代的时间复杂度可能是相同的，但在实际应用中，由于函数调用和函数调用堆栈的开销，递归的效率通常较低。

理论上，递归和迭代可以相互转换。

例如，n的阶乘问题可以通过递归或迭代方法解决。

2. 迭代与还原：
还原通常指的是将一个复杂的问题或系统简化为一个或多个更简单的问题或子系统。

当使用迭代方法解决问题时，通常会将问题分解为一系列的步骤或操作，每一步都试图解决一部分问题，直到达到最终解决方案。

这种分步骤、分阶段解决问题的过程可以看作是一种还原的过程。

迭代方法通过将问题分解为更小的部分来解决问题，从而将一个复杂的问题还原为其基本的组成部分。

综上所述，递归、迭代和还原在解决问题的方法上有所不同，但它们在某些情况下可以相互关联或转换。

还原的概念可以看作是迭代方法的一个方面，因为迭代方法通过逐步解决较小的问题来还原问题的解决方案。

6.4 补考练习题及参考答案6.4.1 单项选择题1. 递归函数()(1)(1)f n f n n n =-+>的递归出口是_______。

A. (1)f =1B. (1)f =0C. (0)f =0D. ()f n n =答：当n=0时，(1)0f =。

本题答案为B 。

2. 递归函数()(1)(1)f n f n n n =-+>的递归体是________。

A. (1)1f =B. (0)0f =C. ()(1)f n f n n =-+D. ()f n n =答：递归体反映递归过程。

本题答案为C 。

3. 121()...1223(1)f n n n =+++⨯⨯⨯+，递归模型为_____。

A. 121()...1223(1)f n n n =+++⨯⨯⨯- B. 121()...(1)1223(1)f n f n n n=++++-⨯⨯-⨯ C. 1(1)2f = 1()(1)(1)f n f n n n =-+⨯- D. 1()(1)(1)f n f n n n =-+⨯- 答：递归模型由两部分组成，一是递归出口，另一是递归体，上述选项中只有C 符合条件。

本答案为C 。

4.将递归算法转换成对应的非递归算法时，通常需要使用________保存中间结果。

A.队列B.栈C.链表D.树答：递归计算过程是：先进行递归分解，知道递归出口为止，然后根据递归出口的结果反过来求值。

这样通常需要后面的递推式先计算出结果，这正好满足栈的特点。

所以本题答案为B 。

6.4.2填空题1.将转化成递归函数，其递归出口是___①____,递归体是___②___答：①(1)0f = ②()(1)f n f n =-+2.有如下递归过程：void print(int w){int i;if (w!=1){ print(w-1);for(i=1;i<=w;i++)printf(“%3d”,w);printf(“\n”);}}调用语句print(4)的结果是________。

python 自然数分割数量递归-概述说明以及解释1.引言1.1 概述在数学领域中，自然数分割是一个重要且具有挑战性的问题。

自然数分割的概念是指将一个自然数表示成一系列自然数的和，且这些自然数的顺序是无关紧要的。

例如，对于数值5，可以有不同的分割方式，比如4+1, 3+2, 3+1+1等等。

本文将探讨如何利用Python编程语言来解决自然数分割的问题，并重点讨论递归在解决自然数分割中的应用。

通过本文的学习，读者将了解到如何利用递归技术来实现自然数分割的计算，并掌握计算自然数分割数量的方法。

同时，本文还将总结递归在自然数分割中的意义，并展望未来在这一领域的研究方向。

希望通过本文的阐述，读者能够对Python自然数分割及递归有一个更深入的理解，从而为相关领域的研究和应用提供更多的思路和方法。

1.2 文章结构文章结构部分的内容可以包括以下内容：1. 本文主要介绍Python自然数分割数量问题以及递归在其中的应用。

2. 首先介绍了文章的引言部分，包括概述、文章结构和目的。

3. 接着详细介绍了Python自然数分割的概念，以及递归在这一概念中的具体应用。

4. 随后解释了Python自然数分割数量的计算方法，以及递归在其中的作用。

5. 最后总结了本文的主要观点和结论，并展望了递归在自然数分割中的意义。

"1.3 目的":本文的主要目的是介绍Python中自然数分割的概念和递归的应用，并探讨如何计算自然数的分割数量。

通过对自然数分割的原理和方法进行深入的讨论和分析，旨在帮助读者更好地理解Python编程中的递归思想和应用，并为相关学习和研究提供详细的指导和参考。

同时，本文还旨在强调递归在自然数分割中的重要性，以及展望递归在编程中的更广泛应用前景。

通过阅读本文，读者将能够深入了解Python中自然数分割的计算方法，并对递归的概念和应用有更为全面和深入的认识。

2.正文2.1 Python自然数分割的概念Python自然数分割是指将一个正整数拆分成若干个正整数的和的不同方式。

递归算法转换为⾮递归算法的技巧递归函数具有很好的可读性和可维护性，但是⼤部分情况下程序效率不如⾮递归函数，所以在程序设计中⼀般喜欢先⽤递归解决问题，在保证⽅法正确的前提下再转换为⾮递归函数以提⾼效率。

函数调⽤时，需要在栈中分配新的帧，将返回地址，调⽤参数和局部变量⼊栈。

所以递归调⽤越深，占⽤的栈空间越多。

如果层数过深，肯定会导致栈溢出，这也是消除递归的必要性之⼀。

递归函数⼜可以分为尾递归和⾮尾递归函数，前者往往具有很好的优化效率，下⾯我们分别加以讨论。

尾递归函数尾递归函数是指函数的最后⼀个动作是调⽤函数本⾝的递归函数，是递归的⼀种特殊情形。

尾递归具有两个主要的特征：1. 调⽤⾃⾝函数(Self-called)；2. 计算仅占⽤常量栈空间(Stack Space)。

为什么尾递归可以做到常量栈空间，我们⽤著名的fibonacci数列作为例⼦来说明。

fibonacci数列实现⽅法⼀般是这样的，int FibonacciRecur(int n) {if (0==n) return 0;if (1==n) return 1;return FibonacciRecur(n-1)+FibonacciRecur(n-2);}不过需要注意的是这种实现⽅法并不是尾递归，因为尾递归的最后⼀个动作必须是调⽤⾃⾝，这⾥最后的动作是加法运算，所以我们要修改⼀下，int FibonacciTailRecur(int n, int acc1, int acc2) {if (0==n) return acc1;return FibonacciTailRecur(n-1, acc2, acc1+acc2);}好了，现在符合尾递归的定义了，⽤gcc分别加-O和-O2选项编译，下⾯是部分汇编代码，-O2汇编代码FibonacciTailRecur:.LFB12:testl %edi, %edimovl %esi, %eaxmovl %edx, %esije .L4.p2align 4,,7.L7:leal (%rax,%rsi), %edxdecl %edimovl %esi, %eaxtestl %edi, %edimovl %edx, %esijne .L7 // use jne.L4:rep ; ret-O汇编代码FibonacciTailRecur:.LFB2:pushq %rbp.LCFI0:movq %rsp, %rbp.LCFI1:subq $16, %rsp.LCFI2:movl %edi, -4(%rbp)movl %esi, -8(%rbp)movl %edx, -12(%rbp)cmpl $0, -4(%rbp)jne .L2movl -8(%rbp), %eaxmovl %eax, -16(%rbp)jmp .L1.L2:movl -12(%rbp), %eaxmovl -8(%rbp), %edxaddl %eax, %edxmovl -12(%rbp), %esimovl -4(%rbp), %edidecl %edicall FibonacciTailRecur //use callmovl %eax, -16(%rbp)movl -16(%rbp), %eaxleaveret可以看到-O2时⽤了jne命令，每次调⽤下层递归并没有申请新的栈空间，⽽是更新当前帧的局部数据，重复使⽤当前帧，所以不管有多少层尾递归调⽤都不会栈溢出，这也是使⽤尾递归的意义所在。

递归算法向非递归算法转换递归算法向非递归算法转换递归算法实际上是一种分而治之的方法，它把复杂问题分解为简单问题来求解。

对于某些复杂问题(例如hanio塔问题)，递归算法是一种自然且合乎逻辑的解决问题的方式，但是递归算法的执行效率通常比较差。

因此，在求解某些问题时，常采用递归算法来分析问题，用非递归算法来求解问题；另外，有些程序设计语言不支持递归，这就需要把递归算法转换为非递归算法。

将递归算法转换为非递归算法有两种方法，一种是直接求值，不需要回溯；另一种是不能直接求值，需要回溯。

前者使用一些变量保存中间结果，称为直接转换法；后者使用栈保存中间结果，称为间接转换法，下面分别讨论这两种方法。

1. 直接转换法直接转换法通常用来消除尾递归和单向递归，将递归结构用循环结构来替代。

尾递归是指在递归算法中，递归调用语句只有一个，而且是处在算法的最后。

例如求阶乘的递归算法：long fact(int n){if (n==0) return 1;else return n*fact(n-1);}当递归调用返回时，是返回到上一层递归调用的下一条语句，而这个返回位置正好是算法的结束处，所以，不必利用栈来保存返回信息。

对于尾递归形式的递归算法，可以利用循环结构来替代。

例如求阶乘的递归算法可以写成如下循环结构的非递归算法：long fact(int n){int s=0;for (int i=1; i<=n;i++)s=s*i; //用s保存中间结果return s;}单向递归是指递归算法中虽然有多处递归调用语句，但各递归调用语句的参数之间没有关系，并且这些递归调用语句都处在递归算法的最后。

显然，尾递归是单向递归的特例。

例如求斐波那契数列的递归算法如下：int f(int n){if (n= =1 | | n= =0) return 1;else return f(n-1)+f(n-2);}对于单向递归，可以设置一些变量保存中间结构，将递归结构用循环结构来替代。

母⽜问题（递归实现、⾮递归）实现两种以及斐波那契数列的实现【题⽬】假设农场中成熟的母⽜每年只会⽣1头⼩母⽜，并且永远不会死。

第⼀年农场有1只成熟的母⽜，从第⼆年开始，母⽜开始⽣⼩母⽜。

每只⼩母⽜3年之后成熟⼜可以⽣⼩母⽜。

给定整数N，求出N年后⽜的数量。

【举例】N=6，第1年1头成熟母⽜记为a；第2年a⽣了新的⼩母⽜，记为b，总⽜数为2；第3年a⽣了新的⼩母⽜，记为c，总数为3；第4年a⽣了新⽜d，总数4；第5年b成熟了，ab分别⽣了⼀只，总数为6；第6年c也成熟了，abc分别⽣了⼀只，总数为9，故返回9.斐波那契数列的递归和⾮递归实现斐波那契数列：public static void main(String[] args) { Scanner scanner = new Scanner(System.in); System.out.println("请输⼊第⼏年？"); int n = scanner.nextInt(); int sum = dg(n);//递归⽅式// int sum = fdg(n);//⾮递归⽅式 System.out.println("第" + n + "年总共有" + sum + "头⽜");}//递归实现 public static int dg(int n) {if (n < 1) { return 0; }if (n == 1 || n == 2 || n == 3 || n == 4) { return n; }return dg(n - 1) + dg(n - 3);}//⾮递归实现 public static int fdg(int n) {int a = 1; //初始化第⼀项 int b = 2;//初始化第⼆项 int res = 3;//初始化第三项 int t = 0;//res 的原来值if (n == 1 || n == 2 || n == 3) { return n; }for (int i = 4; i <= n; i++) { t = res; res = b + a; a = b; b = t; } return res; }递归的原理：每⼀级的函数调⽤都有⾃⼰的变量。

递归与非递归转换的基础知识是能够正确理解三种树的遍历方法：前序，中序和后序，第一篇就是关于这三种遍历方法的递归和非递归算法。

一、为什么要学习递归与非递归的转换的实现方法?1>并不是每一门语言都支持递归的。

2>有助于理解递归的本质。

3>有助于理解栈，树等数据结构。

二、三种遍历树的递归和非递归算法递归与非递归的转换基于以下的原理：所有的递归程序都可以用树结构表示出来。

需要说明的是，这个”原理”并没有经过严格的数学证明，只是我的一个猜想，不过在至少在我遇到的例子中是适用的。

学习过树结构的人都知道，有三种方法可以遍历树：前序，中序，后序。

理解这三种遍历方式的递归和非递归的表达方式是能够正确实现转换的关键之处，所以我们先来谈谈这个。

需要说明的是，这里以特殊的二叉树来说明，不过大多数情况下二叉树已经够用，而且理解了二叉树的遍历，其它的树遍历方式就不难了。

1>前序遍历a>递归方式：void preorder_recursive(Bitree T> /* 先序遍历二叉树的递归算法 */{if (T> {visit(T>。

/* 访问当前结点 */preorder_recursive(T->lchild>。

/* 访问左子树 */preorder_recursive(T->rchild>。

/* 访问右子树 */}}b>非递归方式void preorder_nonrecursive(Bitree T> /* 先序遍历二叉树的非递归算法 */initstack(S>。

push(S,T>。

/* 根指针进栈 */while(!stackempty(S>> {while(gettop(S,p>&&p> { /* 向左走到尽头 */visit(p>。

/* 每向前走一步都访问当前结点 */push(S,p->lchild>。