《信号与系统引论》(第二版)郑君里_课后题答案_客观题(附答案)

1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？第L f (t)N0 ■(a) t只取1, 2, 3, 4值4321(b)iL f (t) 只取1, 2, 3值3, ! H I2I h I i10 1 2 3 4 5 6 7 8 t(C)1 I只取0,P11值___________________ k.0 12345678 n"1L f (t)h■-0 1 2 3 4 5 6 7 8 t(d)X (n)只取-1, 1值14 5 6 8 ■0 1 2 3 7 n r -1 4 JI-(f)申X(n)图1-2解信号分类如下:（a ） 连续信号（模拟信号）； （b ） 连续（量化）信号； （C ）离散信号，数字信号； （d ） 离散信号；（e ） 离散信号，数字信号； （f ） 离散信号，数字信号。

1-2分别判断下列各函数式属于何种信号？（重复 1-1题所示问） （1） e at Sin （ t ）； （2） e nτ ； （3） cos （n ）；（4） Sin （n 。

）（。

为任意值）； （5） I 2。

2解由1-1题的分析可知： （1） 连续信号； （2） 离散信号；（3） 离散信号，数字信号； （4） 离散信号； （5） 离散信号。

1-3分别求下列各周期信号的周期T ： （1） COs （Iot ） cos （30t ）； （2） e j10t ； （3） [5sin （8t ）]2 ；（4） （ 1）n u （t nT ） u （t nT T ）（ n 为整数）。

n 0解判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察 各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数； 若不存在，信号离散模拟：幅值、时间均连 量化：幅值离散，时间 续（例见图1 2（ a ））抽样 数字 时间离散，幅值 幅值、时间均离 连续（例见图1 连续（例见图1囂）图1-1所示信号分别为 散（例见图1 2（ d ））则该复合信号为非周期信号。

《信号与系统》复习参考练习题一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（）A ．400rad ／sB 。

200 rad ／sC 。

100 rad ／sD 。

50 rad ／sf如下图（a）所示，其反转右移的信号f1(t) 是（）15、已知信号)(tf如下图所示，其表达式是（）16、已知信号)(1tA、ε（t）＋2ε(t－2)－ε(t－3)B、ε(t－1)＋ε(t－2)－2ε(t－3)C、ε(t)＋ε(t－2)－ε(t－3)D、ε(t－1)＋ε(t－2)－ε(t－3)17、如图所示：f（t）为原始信号，f1(t)为变换信号，则f1(t)的表达式是（）A、f(－t+1)B、f(t+1)C、f(－2t+1)D、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++=A 、因果不稳定系统B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差 2A 、1-eB 、3eC 、3-eD 、127.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+，则其2个特征根为() A 。

3-1 解题过程：（1）三角形式的傅立叶级数（Fourier Series ，以下简称 FS ）f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π，n 为正整数，T 1 为信号周期T 11 t +T（a ）直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T（b ）余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T（c ）正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t（2）指数形式的傅立叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn =其中复数频谱F n= F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e − jn ω1t dt T 1 t 0F n =1( a n − jb n ) F − n = 1 ( a n + jb n ) 2 2由图 3-1 可知， f ( t ) 为奇函数，因而a 0 = a n = 04 Tb n = T ∫02= 2Eπ n4TE−2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 − cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以，三角形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5T指数形式的 FS 的系数为1n = 0, ±2, ±4,F n = − jb n jE=2 n = 0,−± 1, ±3,n π1所以，指数形式的 FS 为f ( t ) = − jE π ej ω1t+ πjE e − j ω1t − 3jE π e j 3ω1t + 3jEπ e − j 3ω1t +3-15 分析：半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅立叶变换有如下两种方法。

1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？第L f (t)N0 ■(a) t只取1, 2, 3, 4值4321(b)iL f (t) 只取1, 2, 3值3, ! H I2I h I i10 1 2 3 4 5 6 7 8 t(C)1 I只取0,P11值___________________ k.0 12345678 n"1L f (t)h■-0 1 2 3 4 5 6 7 8 t(d)X (n)只取-1, 1值14 5 6 8 ■0 1 2 3 7 n r -1 4 JI-(f)申X(n)图1-2解信号分类如下:（a ） 连续信号（模拟信号）； （b ） 连续（量化）信号； （C ）离散信号，数字信号； （d ） 离散信号；（e ） 离散信号，数字信号； （f ） 离散信号，数字信号。

1-2分别判断下列各函数式属于何种信号？（重复 1-1题所示问） （1） e at Sin （ t ）； （2） e nτ ； （3） cos （n ）；（4） Sin （n 。

）（。

为任意值）； （5） I 2。

2解由1-1题的分析可知： （1） 连续信号； （2） 离散信号；（3） 离散信号，数字信号； （4） 离散信号； （5） 离散信号。

1-3分别求下列各周期信号的周期T ： （1） COs （Iot ） cos （30t ）； （2） e j10t ； （3） [5sin （8t ）]2 ；（4） （ 1）n u （t nT ） u （t nT T ）（ n 为整数）。

n 0解判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察 各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数； 若不存在，信号离散模拟：幅值、时间均连 量化：幅值离散，时间 续（例见图1 2（ a ））抽样 数字 时间离散，幅值 幅值、时间均离 连续（例见图1 连续（例见图1囂）图1-1所示信号分别为 散（例见图1 2（ d ））则该复合信号为非周期信号。

《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。

1.2 已知信号[])2()1()1()(--++=t u t u t t f ，画出)32(+-t f 的波形。

1.3已知信号[])2()1()1()(--++=t u t u t t f ，试求它的直流分量。

答案：01.4 已知信号[])2()1()1()(--++=t u t u t t f ，试求它的奇分量和偶分量。

答案：偶分量：[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量：[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(tt f≥<t t 是否是奇异信号。

答案：二阶以上导数不连续，是奇异信号。

1.6 已知)(t f 是有界信号，且当∞→t 时0)(→t f ，试问)(t f 是否是能量有限信号。

答案：不一定。

1.7 对一连续三角信号进行抽样，每周期抽样8点，求抽样所得离散三角序列的离散角频率。

答案：4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样，写出抽样所得离散序列的表达式，画出它们的波形。

比较和说明两波形的差别，为什么？ （1） t t f 4cos)(1π= （2）t t f 415cos)(2π= 答案：两个离散序列是相同的。

1.9 判断下列信号是否是周期信号。

如果是周期信号，试确定其周期。

（1） t C t B t A t f 9cos 7cos 4sin )(++= 答案：是周期函数，周期π2=T 。

（2） n j d n f 8e)(π-= 答案：是周期信号，周期16=N1.10 求下列表达式的函数值（1） ⎰∞∞--dt t t t f )()(0δ； 答案：)(0t f - （2） ⎰∞∞--dt t t t f )()(0δ； 答案：)(0t f（3） ⎰∞∞---dt t t u t t )2()(00δ； 答案：当00>t 时为1；当00<t 时为0 （4） ⎰∞∞---dt t t u t t )2()(00δ； 答案：当00<t 时为1；当00>t 时为0 （5） ⎰∞∞--++dt t t e t )2()(δ； 答案：2e 2- （6） ⎰∞∞--+dt t t t )6()sin (πδ； 答案：2/16/+π（7）[]⎰∞∞----dt t t t e t j )()2(0δδω； 答案：0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果（1） tt e t r d )(d )(=； 答案：线性，时不变，因果 （2） )()()(t u t e t r =； 答案：线性，时变，因果（3） [])()(sin )(t u t e t r =； 答案：非线性，时变，因果 （4） )1()(t e t r -=； 答案：线性，时变，非因果 （5） )2()(t e t r =； 答案：线性，时变，非因果 （6） )()(2t e r r =； 答案：非线性，时不变，因果1.12 试证明：)()0(')(')0()(')(t f t f t t f δδδ-=。

信号与系统课后答案：郑君里第7章简介本文是《信号与系统》课程的第7章课后答案，该章节由著名作者郑君里所撰写。

本章主要介绍了信号与系统的离散傅里叶变换（DFT）和离散时间傅里叶变换（DTFT）。

信号处理是一门研究如何用数学方法描述和处理各种信号的科学。

信号是信息的载体，而系统是对信号进行处理的载体。

离散傅里叶变换和离散时间傅里叶变换是信号与系统理论中最基本的工具之一，它们具有广泛的应用。

理解离散傅里叶变换和离散时间傅里叶变换的原理和性质对于理解信号与系统的基本原理和实际应用非常重要。

第7章课后题答案第1题根据定义，离散傅里叶变换（DFT）的计算公式如下：$$ X(k) = \\sum_{n=0}^{N-1} x(n) \\cdot e^{-j\\frac{2\\pi}{N} nk} $$其中，N表示信号的长度，N(N)表示输入信号的离散采样值，N(N)表示变换结果中的频谱系数。

根据公式，我们可以计算出给定信号的DFT变换。

第2题离散傅里叶变换的逆变换公式如下：$$ x(n) = \\frac{1}{N}\\sum_{k=0}^{N-1} X(k) \\cdot e^{j \\frac{2\\pi}{N} nk} $$逆变换可以将频域表示的信号转换回时域表示。

第3题离散时间傅里叶变换（DTFT）的计算公式如下：$$ X(e^{j\\omega}) = \\sum_{n=-\\infty}^{\\infty} x(n)\\cdot e^{-j\\omega n} $$DTFT是连续的频域表示，它不仅适用于周期信号，也适用于非周期信号。

第4题DTFT的逆变换公式如下：$$ x(n) = \\frac{1}{2\\pi} \\int_{-\\pi}^{\\pi}X(e^{j\\omega}) \\cdot e^{j\\omega n} d\\omega $$逆变换可以将频域表示的信号转换回时域表示。

第5题离散时间傅里叶变换的频谱无法在计算机中实现，因为DTFT变换结果是连续的函数。

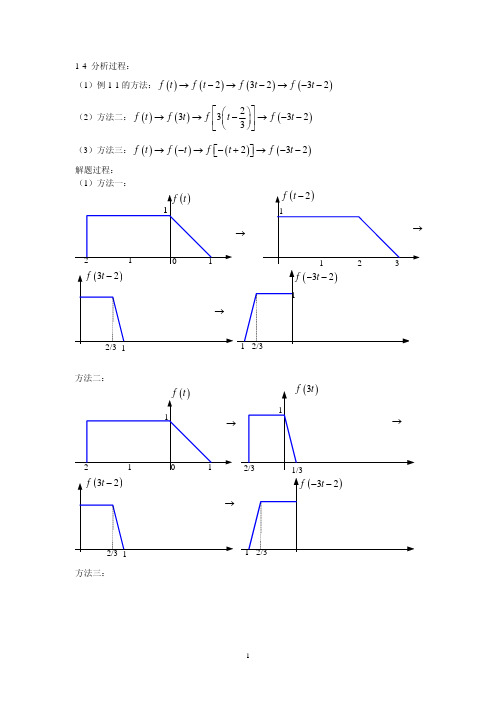
1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。

注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 解题过程： （1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。

6-1 解题过程：图6-5所示的矩形波如解图所示，它表示为()()()1012πππ+<<⎧⎪=⎨−<<⎪⎩t f t t在[]0,2π内()()()()()()()20020cos cos cos 11sin sin 01,2,3ππππππ=+−⎡⎤⎣⎦=−==∫∫∫"f t nt dt nt dt nt dtnt nt n n n故有()f t 与信号()()cos ,cos 2,cos "t t nt ,正交（n 为整数）。

6-2 解题过程： 在区间()02π，内，有()()()21212120cos cos π≠∫n t n t dt n n n n ，且均为不为零的整数()()()()2121202212121212001cos cos 21111sin sin 220πππ=++−⎡⎤⎣⎦=⋅++⋅−+−=∫n n t n n t dt n n t n n t n n n n ()()()222220001cos 2cos 21222nt nt cos nt dt dt dt dt πππππ+==+=∫∫∫∫满足正交函数集的条件，故()()cos ,cos 2,cos "t t nt ,正交（n 为整数）是区间()02π，中的正交函数集。

6-3 解题过程： 在区间02π⎛⎞⎜⎟⎝⎠，内()()()21212120cos cos π≠∫n t n t dt n n n n ，且均为不为零的整数()()()()()()212120221212121200121212121cos cos 21111sin sin 221111sin sin 2222πππππ=++−⎡⎤⎣⎦=⋅++⋅−+−+−⎡⎤⎡⎤=⋅+⋅⎢⎥⎢⎥+−⎣⎦⎣⎦∫n n t n n t dt n n t n n t n n n n n n n n n n n n只有当()12+n n 和()12−n n 均为偶数时上式为零，因此不满足函数之间的正交性条件，()()cos ,cos 2,cos "t t nt ,正交（n 为整数）不是区间02π⎛⎞⎜⎟⎝⎠，中的正交函数集。

第一章1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解 信号分类如下：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 （a ）连续信号（模拟信号）； （b ）连续（量化）信号； （c ）离散信号，数字信号； （d ）离散信号；（e ）离散信号，数字信号； （f ）离散信号，数字信号。

1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问） （1）)sin(t e at ω-；（2）nT e -； （3）)cos(πn ；（4）为任意值）（00)sin(ωωn ；（5）221⎪⎭⎫⎝⎛。

解由1-1题的分析可知： （1）连续信号； （2）离散信号；（3）离散信号，数字信号； （4）离散信号； （5）离散信号。

1-3 分别求下列各周期信号的周期T ： （1）)30t (cos )10t (cos -； （2）j10t e ；（3）2)]8t (5sin [；（4）[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----。

解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。

（1）对于分量cos (10t )其周期5T 1π=；对于分量cos (30t )，其周期15T 2π=。

由于5π为21T T 、的最小公倍数，所以此信号的周期5T π=。

（2）由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。

《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。

1.2 已知信号[])2()1()1()(--++=t u t u t t f ，画出)32(+-t f 的波形。

1.3已知信号[])2()1()1()(--++=t u t u t t f ，试求它的直流分量。

答案：01.4 已知信号[])2()1()1()(--++=t u t u t t f ，试求它的奇分量和偶分量。

答案：偶分量：[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量：[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(tt f≥<t t 是否是奇异信号。

答案：二阶以上导数不连续，是奇异信号。

1.6 已知)(t f 是有界信号，且当∞→t 时0)(→t f ，试问)(t f 是否是能量有限信号。

答案：不一定。

1.7 对一连续三角信号进行抽样，每周期抽样8点，求抽样所得离散三角序列的离散角频率。

答案：4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样，写出抽样所得离散序列的表达式，画出它们的波形。

比较和说明两波形的差别，为什么？ （1） t t f 4cos)(1π= （2）t t f 415cos)(2π= 答案：两个离散序列是相同的。

1.9 判断下列信号是否是周期信号。

如果是周期信号，试确定其周期。

（1） t C t B t A t f 9cos 7cos 4sin )(++= 答案：是周期函数，周期π2=T 。

（2） n j d n f 8e)(π-= 答案：是周期信号，周期16=N1.10 求下列表达式的函数值（1） ⎰∞∞--dt t t t f )()(0δ； 答案：)(0t f - （2） ⎰∞∞--dt t t t f )()(0δ； 答案：)(0t f（3） ⎰∞∞---dt t t u t t )2()(00δ； 答案：当00>t 时为1；当00<t 时为0 （4） ⎰∞∞---dt t t u t t )2()(00δ； 答案：当00<t 时为1；当00>t 时为0 （5） ⎰∞∞--++dt t t e t )2()(δ； 答案：2e 2- （6） ⎰∞∞--+dt t t t )6()sin (πδ； 答案：2/16/+π（7）[]⎰∞∞----dt t t t e t j )()2(0δδω； 答案：0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果（1） tt e t r d )(d )(=； 答案：线性，时不变，因果 （2） )()()(t u t e t r =； 答案：线性，时变，因果（3） [])()(sin )(t u t e t r =； 答案：非线性，时变，因果 （4） )1()(t e t r -=； 答案：线性，时变，非因果 （5） )2()(t e t r =； 答案：线性，时变，非因果 （6） )()(2t e r r =； 答案：非线性，时不变，因果 1.12 试证明：)()0(')(')0()(')(t f t f t t f δδδ-=。