数字逻辑-习题以及习题答案

数字电路与逻辑设计习题及参考答案一、选择题1. 以下表达式中符合逻辑运算法则的是 D 。

·C=C 2 +1=10 <1 +1=12. 一位十六进制数可以用 C 位二进制数来表示。

A . １ B . ２ C . ４ D . 163. 当逻辑函数有n 个变量时，共有 D 个变量取值组合？A. nB. 2nC. n 2D. 2n 4. 逻辑函数的表示方法中具有唯一性的是 A 。

A .真值表 B.表达式 C.逻辑图 D.状态图5. 在一个8位的存储单元中，能够存储的最大无符号整数是 D 。

A .（256）10 B .（127）10 C .（128）10 D .（255）106.逻辑函数F=B A A ⊕⊕)( = A 。

C.B A ⊕D. B A ⊕ 7．求一个逻辑函数F 的对偶式，不可将F 中的 B 。

A .“·”换成“+”，“+”换成“·” B.原变量换成反变量，反变量换成原变量 C.变量不变D.常数中“0”换成“1”，“1”换成“0” 8．A+BC= C 。

A .A+B +C C.（A+B ）（A+C ） +C9．在何种输入情况下，“与非”运算的结果是逻辑0。

DA ．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是1 10．在何种输入情况下，“或非”运算的结果是逻辑1。

AA ．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为111．十进制数25用8421BCD 码表示为 B 。

101 010112．不与十进制数（）10等值的数或代码为 C 。

A .(0101 8421BCD B .16 C .2 D .813．以下参数不是矩形脉冲信号的参数 D 。

A.周期 B.占空比 C.脉宽 D.扫描期 14．与八进制数8等值的数为： BA. 2B.16C. )16D. 215. 常用的BCD码有 D 。

A.奇偶校验码B.格雷码码 D.余三码16.下列式子中，不正确的是(B)+A=A B.A A1⊕=⊕=A ⊕=A17.下列选项中，______是TTLOC门的逻辑符号。

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制491100016153110101651271111111177635100111101111737.493111.11117.7479.4310011001.0110111231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010101211110161751011100921340.100110.593750.4610111147570110113153.将下列十进制数转换成8421BCD码1997=000110011001011165.312=01100101.0011000100103.1416=0011.00010100000101100.9475=0.10010100011101014.列出真值表，写出X的真值表达式A B C X00000010010001111000101111011111X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时：A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1)(A⊕B)⊕C=A⊕(B⊕C)A B C(A⊕B)⊕C A⊕(B⊕C)0000000111010110110010011101001100011111所以由真值表得证。

（2）A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C00011001000100001111100001011111011111007.证明下列等式（1）A+A B=A+B 证明：左边=A+A B=A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2)ABC+A B C+AB C =AB+AC 证明：左边=ABC+A B C+AB C=ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C )=AB+AC =右边（3）E D C CD A C B A A )(++++=A+CD+E证明：左边=ED C CD A C B A A )(++++=A+CD+A B C +CDE =A+CD+CD E =A+CD+E =右边（4）C B A C B A B A ++=CB C A B A ++证明：左边=CB AC B A B A ++=C B A C AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1)F=A+ABC+A C B +CB+C B =A+BC+C B (2)F＝(A+B+C )(A+B+C)=(A+B)+C C =A+B (3)F＝ABC D +ABD+BC D +ABCD+B C =AB+BC+BD (4)F=C AB C B BC A AC +++=BC(5)F=)()()()(B A B A B A B A ++++＝B A 9.将下列函数展开为最小项表达式(1)F(A,B,C)=Σ(1,4,5,6,7)(2)F(A,B,C,D)=Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式（1）CAB C B BC A AC F +++=0 ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111AB CD 00 01 11 1000011110化简得F=DA B A +（3）F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111ABCD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4)F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数，并画出逻辑图。

For personal use only in study and research; not for commercialuse《数字逻辑》习题案例（计算机科学与技术专业、信息安全专业）2004年7月计算机与信息学院、计算机系统结构教研室一、选择题1．十进制数33的余3码为 。

A. 00110110B. 110110C. 01100110D. 1001002．二进制小数-0.0110的补码表示为 。

A ．0.1010B ．1.1001C ．1.0110D ．1.10103．两输入与非门输出为0时，输入应满足 。

A ．两个同时为1B ．两个同时为0C ．两个互为相反D ．两个中至少有一个为04．某4变量卡诺图中有9个“0”方格7个“1”方格，则相应的标准与或表达式中共有多少个与项 ？A ． 9B ．7C ．16D ．不能确定5. 下列逻辑函数中，与A F =相等的是 。

)(A 11⊕=A F )(B A F =2⊙1 )(C 13⋅=A F )(D 04+=A F6. 设计一个6进制的同步计数器，需要 个触发器。

)(A 3 )(B 4 )(C 5 )(D 67. 下列电路中，属于时序逻辑电路的是 。

)(A 编码器 )(B 半加器 )(C 寄存器 )(D 译码器8. 列电路中，实现逻辑功能n n Q Q =+1的是 。

)(A )(B)(C (D) 9. 的输出端可直接相连，实现线与逻辑功能。

)(A 与非门 )(B 一般TTL 门)(C 集电极开路OC 门 )(D 一般CMOS 门 10．以下代码中为无权码的为 。

A . 8421BCD 码B . 5421BCD 码C . 余三码D . 格雷码11．以下代码中为恒权码的为 。

A .8421BCD 码B . 5421BCD 码C . 余三码D . 格雷码12．一位十六进制数可以用 位二进制数来表示。

A . １B . ２C . ４D . 1613．十进制数25用8421BCD码表示为。

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表，写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时：A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。

（2）A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式（1）A+A B=A+B证明：左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明：左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边（3）EDCCDACBAA)(++++=A+CD+E 证明：左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边（4） C B A C B A B A ++=C B C A B A ++ 证明：左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式（1）C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +（3） F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数，并画出逻辑图。

数字逻辑复习题有答案1. 什么是数字逻辑中的“与”操作？答案：在数字逻辑中，“与”操作是一种基本的逻辑运算，它只有当所有输入信号都为高电平（1）时，输出信号才为高电平（1）。

如果任何一个输入信号为低电平（0），则输出信号为低电平（0）。

2. 描述数字逻辑中的“或”操作。

答案：在数字逻辑中，“或”操作是另一种基本的逻辑运算，它只要至少有一个输入信号为高电平（1），输出信号就为高电平（1）。

只有当所有输入信号都为低电平（0）时，输出信号才为低电平（0）。

3. 如何理解数字逻辑中的“非”操作？答案：“非”操作是数字逻辑中最基本的逻辑运算之一，它将输入信号的电平状态取反。

如果输入信号为高电平（1），输出信号则为低电平（0）；反之，如果输入信号为低电平（0），输出信号则为高电平（1）。

4. 解释数字逻辑中的“异或”操作。

答案：数字逻辑中的“异或”操作是一种逻辑运算，它只有在输入信号中有一个为高电平（1）而另一个为低电平（0）时，输出信号才为高电平（1）。

如果输入信号相同，即都是高电平或都是低电平，输出信号则为低电平（0）。

5. 什么是数字逻辑中的“同或”操作？答案：“同或”操作是数字逻辑中的一种逻辑运算，它只有在输入信号都为高电平（1）或都为低电平（0）时，输出信号才为高电平（1）。

如果输入信号不同，即一个为高电平一个为低电平，输出信号则为低电平（0）。

6. 什么是触发器，它在数字逻辑中的作用是什么？答案：触发器是一种具有记忆功能的数字逻辑电路，它可以存储一位二进制信息。

在数字逻辑中，触发器用于存储数据、实现计数、寄存器和移位寄存器等功能。

7. 简述D触发器的工作原理。

答案：D触发器是一种常见的触发器类型，它的输出状态由输入端D的电平决定。

当触发器的时钟信号上升沿到来时，D触发器会将输入端D的电平状态锁存到输出端Q，从而实现数据的存储和传递。

8. 什么是二进制计数器，它的功能是什么？答案：二进制计数器是一种数字逻辑电路，它能够按照二进制数的顺序进行计数。

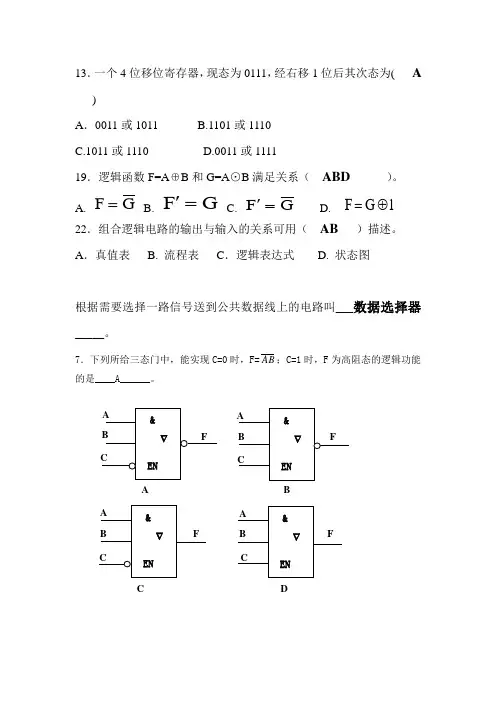
13．一个4位移位寄存器，现态为0111，经右移1位后其次态为( A )A．0011或1011 B.1101或1110C.1011或1110D.0011或111119．逻辑函数F=A⊕B和G=A⊙B满足关系（ABD ）。

A.GF= B. GF=' C. GF=' D. 1GF⊕=22．组合逻辑电路的输出与输入的关系可用（AB）描述。

A．真值表 B. 流程表C．逻辑表达式 D. 状态图根据需要选择一路信号送到公共数据线上的电路叫___数据选择器_____。

7．下列所给三态门中，能实现C=0时，F=AB；C=1时，F为高阻态的逻辑功能的是____A______。

.TTL电路的电源是__5__V，高电平1对应的电压范围是__2.4-5____V。

.N个输入端的二进制译码器，共有___N2____个输出端。

对于每一组输入代码，有____1____个输出端是有效电平。

13.给36个字符编码，至少需要____6______位二进制数。

14.存储12位二进制信息需要___12____个触发器。

写出描述触发器逻辑功能的几种方式___特性表、特性方程、状态图、波形图24．（本题满分16分）今有A、B、C三人可以进入某秘密档案室，但条件是A、B、C三人在场或有两人在场，但其中一人必须是A，否则报警系统就发出警报信号。

试：（1）列出真值表；（2）写出逻辑表达式并化简；（3）画出逻辑图。

解：设变量A、B、C表示三个人，逻辑1表示某人在场，0表示不在场。

F表示警报信号，F=1表示报警，F=0表示不报警。

根据题意义，列出真值表由出真值表写出逻辑函数表达式，并化简BACAF⊕+B=++=+BCCA(B)CCAAABC画出逻辑电路图26．下图是由三个D触发器构成的寄存器，试问它是完成什么功能的寄存器？设它初始状态Q2 Q1 Q0 =110，在加入1个CP脉冲后，Q2 Q1 Q0等于多少？此后再加入一个CP脉冲后，Q2 Q1 Q0等于多少？解: 时钟方程CPCP CP CP ===210激励方程n Q D 20= ，nQ D 01=，n Q D 12=状态方程n n Q D Q 2010==+，n n Q D Q 0111==+，n n Q D Q 1212==+ 状态表画出状态图11.将2004个“1”异或起来得到的结果是（ 0 ）。

数字逻辑期末考试题及答案一、选择题（每题2分，共20分）1. 以下哪个是数字逻辑中的基本逻辑门？A. 与门B. 或门C. 非门D. 所有选项都是答案：D2. 一个三输入的与门，当输入全为1时，输出为：A. 0B. 1C. 随机D. 无法确定答案：B3. 一个异或门的真值表中，当输入相同时，输出为：A. 1B. 0C. 随机D. 无法确定答案：B4. 下列哪个不是触发器的类型？A. SR触发器B. JK触发器C. D触发器D. AND触发器答案：D5. 在数字电路中，同步计数器和异步计数器的主要区别在于：A. 计数范围B. 计数速度C. 计数精度D. 计数方式答案：B6. 一个4位二进制计数器，其最大计数值为：A. 15B. 16C. 32D. 64答案：A7. 以下哪个不是数字逻辑设计中常用的简化方法？A. 布尔代数简化B. 卡诺图简化C. 逻辑门替换D. 逻辑表简化答案：C8. 在数字电路中，一个信号的上升沿指的是：A. 信号从0变为1的瞬间B. 信号从1变为0的瞬间C. 信号保持不变D. 信号在变化答案：A9. 一个D触发器的Q输出端在时钟信号上升沿时：A. 保持不变B. 翻转状态C. 跟随D输入端D. 随机变化答案：C10. 以下哪个不是数字逻辑中的状态机？A. Moore机B. Mealy机C. 有限状态机D. 无限状态机答案：D二、填空题（每空2分，共20分）11. 在布尔代数中，逻辑与操作用符号______表示。

答案：∧12. 一个布尔函数F(A,B,C)=A∨B∧C的最小项为______。

答案：(1,1,1)13. 在数字电路设计中，卡诺图是一种用于______的工具。

答案：布尔函数简化14. 一个4位二进制加法器的输出端最多有______位。

答案：515. 一个同步计数器在计数时，所有的触发器都______时钟信号。

答案：接收16. 一个JK触发器在J=K=1时，其状态会发生______。

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制491100016153110101651271111111177635100111101111737.493111.11117.7479.4310011001.0110111231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010101211110161751011100921340.100110.593750.4610111147570110113153.将下列十进制数转换成8421BCD码1997=000110011001011165.312=01100101.0011000100103.1416=0011.00010100000101100.9475=0.10010100011101014.列出真值表，写出X的真值表达式A B C X00000010010001111000101111011111X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时：A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时：A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1)(A⊕B)⊕C=A⊕(B⊕C)A B C(A⊕B)⊕C A⊕(B⊕C)0000000111010110110010011101001100011111所以由真值表得证。

（2）A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C00011001000100001111100001011111011111007.证明下列等式（1）A+A B=A+B 证明：左边=A+A B=A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2)ABC+A B C+AB C =AB+AC 证明：左边=ABC+A B C+AB C=ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C )=AB+AC =右边（3）E D C CD A C B A A )(++++=A+CD+E证明：左边=ED C CD A C B A A )(++++=A+CD+A B C +CDE =A+CD+CD E =A+CD+E =右边（4）C B A C B A B A ++=CB C A B A ++证明：左边=CB AC B A B A ++=C B A C AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1)F=A+ABC+A C B +CB+C B =A+BC+C B (2)F＝(A+B+C )(A+B+C)=(A+B)+C C =A+B (3)F＝ABC D +ABD+BC D +ABCD+B C =AB+BC+BD (4)F=C AB C B BC A AC +++=BC(5)F=)()()()(B A B A B A B A ++++＝B A 9.将下列函数展开为最小项表达式(1)F(A,B,C)=Σ(1,4,5,6,7)(2)F(A,B,C,D)=Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式（1）CAB C B BC A AC F +++=0 ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111AB CD 00 01 11 1000011110化简得F=DA B A +（3）F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111ABCD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4)F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数，并画出逻辑图。

数字逻辑试题1答案一、填空：（每空1分，共20分）1、（20.57）8=（10.BC）162、(63.25)10=(111111.01)23、（FF）16=(255)104、[X]原=1.1101，真值X=-0.1101，[X]补=1.0011。

5、[X]反=0.1111，[X]补=0.1111。

6、-9/16的补码为1.0111，反码为1.0110。

7、已知葛莱码1000，其二进制码为1111，已知十进制数为92，余三码为110001018、时序逻辑电路的输出不仅取决于当时的输入，还取决于电路的状态。

9、逻辑代数的基本运算有三种，它们是_与_、_或__、_非_。

10、FAB1，其最小项之和形式为_。

FA B AB11、RS触发器的状态方程为_Q n1SRQ n_，约束条件为SR0。

12、已知F1AB、F2ABAB，则两式之间的逻辑关系相等。

13、将触发器的CP时钟端不连接在一起的时序逻辑电路称之为_异_步时序逻辑电路。

二、简答题（20分）1、列出设计同步时序逻辑电路的步骤。

（5分）答：（1）、由实际问题列状态图（2）、状态化简、编码（3）、状态转换真值表、驱动表求驱动方程、输出方程（4）、画逻辑图（5）、检查自起动2、化简FABABCA(BAB)（5分）答：F03、分析以下电路，其中RCO为进位输出。

（5分）答：7进制计数器。

4、下图为PLD电路，在正确的位置添*，设计出FAB函数。

（5分）15分注：答案之一。

三、分析题（30分）1、分析以下电路，说明电路功能。

（10分）解：XY m(3,5,6,7)m(1,2,4,7)2分ABCiXY0000000101010010111010001101101101011111该组合逻辑电路是全加器。

以上8分2、分析以下电路，其中X为控制端，说明电路功能。

（10分）解：FXA B C XABCXABCXABCXABCXABC4分FX(ABC)X(A B C ABC)4分所以：X=0完成判奇功能。

数字逻辑试题1答案一、填空：（每空1分，共20分） 1、（20.57）8 =（ 10.BC ）16 2、(63.25) 10= ( 111111.01 )2 3、（FF ）16= ( 255 )104、[X]原=1.1101，真值X= -0.1101，[X]补 = 1.0011。

5、[X]反=0.1111，[X]补= 0.1111。

6、-9/16的补码为1.0111，反码为1.0110 。

7、已知葛莱码1000，其二进制码为1111， 已知十进制数为92，余三码为1100 01018、时序逻辑电路的输出不仅取决于当时的输入，还取决于电路的状态 。

9、逻辑代数的基本运算有三种，它们是_与_ 、_或__、_非_ 。

10、1⊕⊕=B A F ，其最小项之和形式为_ 。

AB B A F += 11、RS 触发器的状态方程为_n n Q R S Q +=+1_，约束条件为0=SR 。

12、已知B A F ⊕=1、B A B A F +=2，则两式之间的逻辑关系相等。

13、将触发器的CP 时钟端不连接在一起的时序逻辑电路称之为_异_步时序逻辑电路 。

二、简答题（20分）1、列出设计同步时序逻辑电路的步骤。

（5分） 答：（1）、由实际问题列状态图 （2）、状态化简、编码 （3）、状态转换真值表、驱动表求驱动方程、输出方程 （4）、画逻辑图 （5）、检查自起动2、化简)(B A B A ABC B A F +++=（5分） 答：0=F3、分析以下电路，其中RCO 为进位输出。

（5分） 答：7进制计数器。

4、下图为PLD 电路，在正确的位置添 * ， 设计出B A F ⊕=函数。

（5分）5分 注：答案之一。

三、分析题（30分）1、分析以下电路，说明电路功能。

（10分）解： ∑∑==)7,4,2,1()7,6,5,3(m Y m X 2分A B Ci X Y 0 0 0 0 0 0110 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1该组合逻辑电路是全加器。

第一部分：1.在二进制系统中，下列哪种运算符表示逻辑与操作？A) amp;B) |C) ^D) ~解析：正确答案是 A。

在二进制系统中，amp; 表示逻辑与操作，它仅在两个位都为1时返回1。

2.在数字逻辑中，Karnaugh 地图通常用于简化哪种类型的逻辑表达式？A) 与门B) 或门C) 异或门D) 与非门解析：正确答案是B。

Karnaugh 地图通常用于简化或门的逻辑表达式，以减少门电路的复杂性。

3.一个全加器有多少个输入？A) 1B) 2C) 3D) 4解析：正确答案是 C。

一个全加器有三个输入：两个加数位和一个进位位。

4.下列哪种逻辑门可以实现 NOT 操作？A) 与门B) 或门C) 异或门D) 与非门解析：正确答案是 D。

与非门可以实现 NOT 操作，当且仅当输入为0时输出为1，输入为1时输出为0。

5.在数字逻辑中，Mux 是指什么？A) 多路复用器B) 解码器C) 编码器D) 多路分配器解析：正确答案是 A。

Mux 是指多路复用器，它可以选择输入中的一个，并将其发送到输出。

6.在二进制加法中，下列哪个条件表示进位？A) 0 + 0B) 0 + 1C) 1 + 0D) 1 + 1解析：正确答案是 D。

在二进制加法中，当两个位都为1时，会产生进位。

7.在数字逻辑中，一个 JK 触发器有多少个输入？A) 1B) 2C) 3D) 4解析：正确答案是 B。

一个 JK 触发器有两个输入：J 和 K。

8.下列哪种逻辑门具有两个输入，且输出为两个输入的逻辑与？A) 与门B) 或门C) 异或门D) 与非门解析：正确答案是 A。

与门具有两个输入，只有当两个输入都为1时，输出才为1。

9.在数字逻辑中，下列哪种元件可用于存储单个位？A) 寄存器B) 计数器C) 锁存器D) 可编程逻辑门阵列解析：正确答案是 C。

锁存器可用于存储单个位，它可以保持输入信号的状态。

10.一个带有三个输入的逻辑门，每个输入可以是0或1，一共有多少种可能的输入组合？A) 3B) 6C) 8D) 12解析：正确答案是 C。

〈习题一〉作业参考答案1.4 如何判断一个7位二进制正整数A=a 1a 2 a 3 a 4 a 5 a 6 a 7是否是4的倍数。

答：只要a 6 a 7=00，A 即可被4整除。

1.10设[x]补=01101001，[y]补=10011101，求：1[]2x 补，1[]4x 补，1[]2y 补，1[]4y 补，[]x -补，[]y -补。

答：（1）如[x]补=x 0x 1x 2…x n ，则1[]2x 补= x 0x 0x 1x 2…x n-1. x n 。

所以，1[]2x 补=00110100.1，1[]4x 补=00011010.01，1[]2y 补=11001110.1，1[]4y 补=11100111.01。

（2）如[x]补=x 0x 1x 2…x n ，[-x]补=012...1n x x x x +。

所以，[]x -补=10010111，[]y -补=01100011。

注意：公式（1）[x]补=x 0x 1x 2…x n ，则1[]2x 补= x 0x 0x 1x 2…x n-1. x n（2）[x]补=x 0x 1x 2…x n ，[-x]补=012...1n x x x x +一定要掌握。

1.11根据原码和补码的定义回答下列问题： （1）已知[x]补>[y]补，是否有x>y?（2）设-2n<x<0,x 为何值时，等式[x]补=[x]原成立。

答：（1）否。

如果x<0 且y>0，则[x]补>[y]补。

但显然x<y 。

（2）因为x<0，所以[x]补=2n+1+x ，[x]原=2n-x ；要使[x]补=[x]原，则2n+1+x=2n-x 。

从而可以得到：X=-2(n-1)。

注意：因为-2n <x ，所以x 的数据位有n 位，加上一个符号位为n+1位。

所以，其补码为2n+1+x 。

1.12 设x 为二进制整数，[x]补=11x 1 x 2 x 3 x 4 x 5，若要x <-16，则x 1~x 5应满足什么条件？ 答：[x –(-16)]补=[x+16]补=[x]补+10000，若要x <-16，则[x –(-16)]补>1000000，即[x]补+10000>1000000。

数字逻辑习题及答案一. 填空题1．一个触发器有Q和Q两个互补的输出引脚，通常所说的触发器的输出端是指Q ，所谓置位就是将输出端置成 1 电平，复位就是将输出端置成 0 电平。

2．我们可以用逻辑函数来表示逻辑关系，任何一个逻辑关系都可以表示为逻辑函数的与或表达式，也可表示为逻辑函数的或与表达式。

3．计数器和定时器的内部结构是一样的，当对不规则的事件脉冲计数时，称为计数器，当对周期性的规则脉冲计数时，称为定时器。

4．当我们在计算机键盘上按一个标为“3”的按键时，键盘向主机送出一个ASCII码，这个ASCII码的值为 33H 。

5．在5V供电的数字系统里，所谓的高电平并不是一定是5V，而是有一个电压范围，我们把这个电压范围称为高电平噪声容限；同样所谓的低电平并不是一定是0V，而也是有一个电压范围，我们把这个电压范围称为低电平噪声容限。

二. 选择题1．在数字系统里，当某一线路作为总线使用，那么接到该总线的所有输出设备（或器件）必须具有 b 结构，否则会产生数据冲突。

a. 集电极开路；b. 三态门；c. 灌电流；d. 拉电流 2．TTL集成电路采用的是 b 控制，其功率损耗比较大；而MOS集成电路采用的是 a 控制，其功率损耗比较小。

a. 电压； b.电流； c. 灌电流； d. 拉电流3．欲将二进制代码翻译成输出信号选用 b ，欲将输入信号编成二进制代码选用 a ，欲将数字系统中多条传输线上的不同数字信号按需要选择一个送到公共数据线上选用 c ，欲实现两个相同位二进制数和低位进位数的相加运算选用 e 。

a. 编码器；b. 译码器；c. 多路选择器；d. 数值比较器；e. 加法器；f. 触发器；ｇ. 计数器； h. 寄存器 4．卡诺图上变量的取值顺序是采用 b 的形式，以便能够用几何上的相邻关系表示逻辑上的相邻。

a. 二进制码；b. 循环码；c. ASCII码；d. 十进制码 5．根据最小项与最大项的性质，任意两个不同的最小项之积为0 ，任意两个不同的最大项之和为 1 。

毛法尧第二版习题一1.1 把下列不同进‎制数写成按权‎展开式:⑴(4517.239)10= 4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3⑵(10110.0101)2=1×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+0×2-3+1×2-4⑶(325.744)8=3×82+2×81+5×80+7×8-1+4×8-2+4×8-3⑷(785.4AF)16=7×162+8×161+5×160+4×16-1+A×16-2+F×16-31.2 完成下列二进‎制表达式的运‎算:1.3 将下列二进制‎数转换成十进‎制数、八进制数和十‎六进制数：⑴(111010‎1)2=(165)8=(75)16=7×16+5=(117)10⑵(0.110101‎)2=(0.65)8=(0.D4)16=13×16-1+4×16-2=(0.828125‎)10⑶(10111.01)2=(27.2)8=(17.4)16=1×16+7+4×16-1=(23.25)101.4 将下列十进制‎数转换成二进‎制数、八进制数和十‎六进制数,精确到小数点‎后5位：⑴(29)10=(1D)16=(11101)2=(35)8⑵(0.207)10=(0.34FDF)16=(0.00111)2=(0.15176)8采用0舍1入‎规则⑶(33.333)10=(21.553F7)16=(100001‎.01011)2=(41.25237)81.5 如何判断一个‎二进制正整数‎B=b6b5b4‎b3b2b1‎b0能否被(4)10整除?解: 一个二进制正‎整数被(2)10除时,小数点向左移‎动一位, 被(4)10除时,小数点向左移‎动两位,能被整除时,应无余数,故当b1=0和b0=0时, 二进制正整数‎B=b6b5b4‎b3b2b1‎b0能被(4)10整除.1.6 写出下列各数‎的原码、反码和补码：⑴0.1011[0.1011]原=0.1011; [0.1011]反=0.1011; [0.1011]补=0.1011⑵0.0000[0.000]原=0.0000; [0.0000]反=0.0000; [0.0000]补=0.0000⑶-10110[-10110]原=110110‎; [-10110]反=101001‎; [-10110]补=101010‎1.7 已知[N]补=1.0110,求[N]原,[N]反和N.解:由[N]补=1.0110得: [N]反=[N]补-1=1.0101, [N]原=1.1010,N=-0.10101.8 用原码、反码和补码完‎成如下运算：⑴000010‎1-001101‎0[000010‎1-001101‎0]原=100101‎01；∴000010‎1-001101‎0=-001010‎1。