第八章分式小结与思考[下学期]--苏科版.

8.3小结与思考（1）班级 姓名 成绩1：计算：（1）23x x x ⋅⋅ （2）23)()(x x x -⋅⋅-（3）)()()(102a b b a b a -⋅-⋅- （4）4523122---⋅-⋅+⋅n n n y y y y y ya) 计算：（1）31)(-m a （2）54])[(y x +（3）325)21(b a - （4）7233323)5()3()(2x x x x x ⋅+-⋅3、 典型例题：例1、下面的计算，对不对，如不对，请改正？(1)22)(a a -=- (2) 44)()(x y y x -=-(3) 22)()(a b b a --=- (4) 332)2(x x =-例2、已知m 10＝4，n 10＝5，求n m 2310+的值．解：例3、若x ＝m 2+1，y ＝3+ m 4，则用x 的代数式表示y ．解：例4、比较332、223和114的大小解：例5、一个正方体的棱长为mm 2103⨯．求这个正方体的表面积和体积解：4、随堂练习（1）123-⋅m m a a (m 是正整数) （2）842a a a ⋅⋅（3）4235)2(a a a +⋅ （4）23)()()2(a a a ⋅---（5）若107a a a m =⋅,则=m ______（6）若n x =3, n y =7,则n xy )(的值是多少? n y x )(32呢?归纳总结：在运用幂的运算性质,首先应确定运算顺序和运算步骤；其次正确地运用性质、法则进行计算，在计算时，应注意符号和指数的变化。

【课后作业】1．填空题(1) 52y y ⋅-=______; (2) 322])2([a ---=______;(3) 200820074)25.0(⨯-=______.2．选择题(1)计算31)](2[---n x 等于 [ ]A ．332--n xB ．16--nC ．338-n xD ．338--n x(2)下述各式中计算正确的是 [ ]A ．824)(ab ab =B ．1052632y y y =⋅C ．642)()(x x x -=-⋅-D ．322233)()(b a b a =(3)计算)23()1()2(221999223y x y x -⋅-⋅--的结果应该等于 [ ] A ．10103y x B ．10103y x - C ．10109y x D ．10109y x -(4) 7x 等于 [ ]A ．52)()(x x -⋅-B ．)()(52x x ⋅-C ．)()(43x x -⋅-D ．5)()(x x ⋅-(5)在下面各式中的括号内填入3a 的是 [ ]A ．12a =( 2)B ．12a ＝( 5)C ．12a ＝( 4)D ．12a ＝( 6)(6)下列计算结果正确的是 [ ]A ．15356)2(x x =B ．734)(x x -=-C ．6232)2(x x =D ．1234])[(x x =-(7)计算323)4()5.2(a a -⋅-的结果应等于 [ ]A ．9400a -B ．9400aC ．940a -D ．940a(8)计算22)(x x -⋅-等于 [ ]A ．4422)()(x x x =-=-+B ．42222x x x x -=-=⋅-+C ．42222)(x x x x -=-=-⋅-+D ．42222x x x x -=-=⋅-⨯3．计算题(1) 999100100)1(5.02-⨯⨯-； (2) ])[(2)(2)(333323232a a a a a a a ⋅---+⋅；(3) ）（）（x y y x y x y x x y --+-+--232)(2)()(．4、比较22221111与11112222大小5、已知32=m ，52=n ，求n m 24+的值。

初中数学《苏科版》目录-孙德平七年级上册：第一章我们与数学同行⑴生活数学（61⑵活动思考（81第二章有理数⑴比0小的数（122⑵数轴（162⑶绝对值与相反数（203⑷有理数的加法与减法（264⑸有理数的乘法与除法（363⑹有理数的乘方（452⑺有理数的加减混合运算（502数学活动算“24”（541小结与思考（542复习题（55第三章用字母表示数⑴字母表示什么数（621⑵代数式（661⑶代数式的值（702⑷合并同类项（752⑸去括号（792数学活动正方体涂色（841小结与思考（842复习题（85第四章一元一次方程⑴从问题到方程（922⑵解一元一次方程（954⑶用方程解决问题（1026数学活动一元一次方程应用的调查（1111小结与思考（1112复习题（112第五章走进图形世界⑴丰富的图形世界（1182⑵图形的变化（1232⑶展开与折叠（1282⑷从三个方向看（1342数学活动设计包装纸箱（1391小结与思考（1391复习题（140第六章平面图形认识（一⑴线段、射线、直线（1482⑵角（1522⑶余角、补角、对顶角（1582⑷平等（1631⑸垂直（1671数学活动测量距离（1711小结与思考（1712复习题（172课题学习制作无盖长方体的长方体纸盒（1751数学活动评价表（176七年级下册：第七章平面图形的认识（二⑴探索直线平行的条件（62⑵探索平行线的性质（111⑶图形的平移（142⑷认识三角形（202⑸三角形的内角和（254数学活动（321小结与思考（332复习题（34第八章幂的运算⑴同底数幂的乘法（401⑵幂的乘方与积的乘方（432⑶同底数幂的除法（473数学活动（521小结与思考（522复习题（52第九章从面积到乘法公式⑴单项式乘单项式（561⑵单项式乘多项式（581⑶多项式乘多项式（611⑷乘法公式（643⑸单项式乘多项式法则的再认识―― 因式分解（一（701⑹乘法公式的再认识一一因式分解（二（723数学活动（771小结与思考（782复习题（79第十章二元一次方程组⑴二元一次方程（841⑵二元一次方程组（862⑶解二元一次方程组（892⑷用方程组解决问题（933数学活动（991小结与思考（992复习题（100第十一章图形的全等⑴全等图形（1041⑵全等三角形（1081⑶探索三角形全等的条件（1115数学活动（1251小结与思考（1252复习题（126第十二章数据在我们周围⑴普查与抽样调查（1321⑵统计图的选用（1333⑶频数分布表和频数分布直方图（1452数学活动（1521小结与思考（1521复习题（153第十三章感受概率⑴确定与不确定（1601⑵可能性（1622数学活动（1691小结与思考（1691复习题（170课题学习丢弃了多少塑料袋（1721数学活动评价表（173八年级上册：第一章轴对称图形⑴轴对称与轴对称图形（61⑵轴对称的性质（101⑶设计轴对称图案（151⑷线段、角的轴对称性（182⑸等腰三角形的轴对称性（233⑹等腰梯形的轴对称性（312数学活动剪纸（351小结与思考（362复习题（37第二章勾股定理与平方根⑴勾股定理（441⑵神秘的数组（481⑶平方根（512⑷立方根（551⑸实数（572⑹近似数与有效数字（621⑺勾股定理的应用（652数学活动关于勾股定理的研究（691小结与思考（692复习题（69第三章中心对称图形（一⑴图形的旋转（741⑵中心对称与中心对称图形（772⑶设计中心对称图案（821⑷平行四边形（853⑸矩形、菱形、正方形（925⑹三角形、梯形中位线（1022数学活动平面图形的镶嵌（1051小结与思考（1062复习题（107第四章数量、位置的变化⑴数量的变化（1142⑵位置的变化（1201⑶平面直角坐标系（1233数学活动确定藏宝地（1321小结与思考（1322复习题（133第五章一次函数⑴函数（1402⑵一次函数（1472⑶一次函数的图象（1512⑶一次函数的应用（1572⑷二元一次方程组的图象解法（161 1数学活动温度计上的一次函数（1631小结与思考（1642复习题（165第六章数据的集中程度⑴平均数（1702⑵中位数与众数（1742⑶用计算器求平均数（1791 数学活动你是“普通”学生吗？（1821小结与思考（1832复习题（183课题学习利用对称图形设计徽标（186 1数学活动评价表（187 第七章一元一次不等式⑴生活中的不等式（61 ⑵不等式的解集（91 ⑶不等式的性质（121 ⑷解一元一次不等式（152⑸用一元一次不等式解决问题（191 ⑹一元一次不等式组（212⑺一元一次不等式与一元一次方程、一次函数（261数学活动（281 小结与思考（282 复习题（29第八章分式⑴分式（341⑵分式的基本性质（373⑶分式的加减法（431⑷分式的乘除法（462⑸分式方程（513数学活动（571小结与思考（572复习题（58第九章反比例函数⑴反比例函数（621⑵反比例函数的图象与性质（653⑶反比例函数的应用（731数学活动（761小结与思考（772复习题（77第十章图形的相似⑴图上距离与实际距离（822⑵黄金分割（851⑶相似图形（892⑷探索三角形相似的条件（944⑸相似三角形性质（1052⑹图形的位似（1101⑺相似三角形的应用（1133数学活动（1201小结与思考（1202复习题（120第十一章图形与证明（一⑴你的判断对吗（1261⑵说理（1292⑶证明（1343⑷互逆命题（1422数学活动（1461小结与思考（1472复习题（148第十二章认识概率⑴等可能性（1541⑵等可能条件下的概率（一（1572⑶等可能条件下的概率（二（1651数学活动（1681小结与思考（1691复习题（170课题学习游戏公平吗?（1731数学活动评价表（174第一章图形与证明（二⑴等腰三角形的性质与判定（61⑵直角三角形全等的判定（92⑶平行四边形、矩形、菱形、正方形的性质与判定（138⑷等腰梯形的性质与判定（281⑸中位线（302数学活动折纸与证明（341小结与思考（362复习题（37第二章数据的离散程度⑴极差（421⑵方差与标准差（451⑶用计算器求标准差和方差（491数学活动估计时间（531小结与思考（531复习题（54第三章二次根式⑴二次根式（582⑵二次根式的乘除法（614⑶二次根式的加减法（692数学活动画画•算算（741小结与思考（741复习题（75第四章一元二次方程⑴一元二次方程（801⑵一元二次方程的解法（836⑶用一元二次方程解决问题（944 数学活动矩形绿地中的花圃设计（1001小结与思考（1012复习题（101第五章中心对称图形（二⑴圆（1062⑵圆的对称性（1112⑶圆周角（1172⑷确定圆的条件（1241⑸直线和圆的位置关系（1274⑹圆和圆的位置关系（1381⑺正多边形与圆（1421⑻弧长及扇形的面积（1451⑼圆锥的侧面积和全面积（1482数学活动制作冰淇淋纸筒（1511小结与思考（1512复习题（152课题学习制作“动画片”（1561数学活动评价表（158九年级下册：第六章二次函数第八章统计的简单应用⑴二次函数（6）1⑵二次函数的图象和性质（9）4⑶二次函数与一元二次方程（21）2⑷二次函数的应用（25）3数学活动（32）1小结与思考考（32）2复习题（33）⑴货比三家（66）1 ⑵中学生的视力情况调查（70）3数学活动（77）1小结与思考（78）1复习题（79）第九章概率的简单应用⑴抽签方法合理吗（84）1第七章锐角三角函数⑵ 概率帮你做估计（86）1⑶保险公司怎样才能不亏本（88）1数学活动（90）1小结与思考（91）1复习题（91）⑴正切（38）1⑵正弦、余弦（41）2⑶特殊角的三角函数（46）1⑷由三角函数值求锐角（49）1⑸解直角三角形（51）1⑹锐角三角函数的简单应用（54）2数学活动（60）1小结与思考（60）2复习题（61）课题学习探究等周长图形的最大面积（94）1数学活动评价表（95）6。

分式小结与思考（一）目标：1、掌握分式章节的知识结构和各知识点间的内在联系。

2、巩固分式章节的知识点并能熟练运用知识点解决问题。

3、培养学生学会归纳总结的方法并提高学生自主学习的能力。

重点：巩固知识点并能熟练运用知识点解决问题。

难点：掌握各知识点间的内在联系并能灵活运用知识点解决问题。

教学内容：本章知识结构图：一、分式的基本性质： （1）分式的定义：。

下列各代数式中，哪些是分式？分式基本性质分式乘除法法则分式加减法法则分式方程的解法分式方程的应用ab 21+πx32x xx 2132-（2）分式有意义：。

分式无意义：。

分式值为零：。

当x 取什么值时，分式322--x x ①分式值有意义？②分式无意义？③分式值为零？④分式值为1?⑤分式值为负数？(3 )分式的基本性质：。

分式的符号法则： 。

1.不改变分式的值，使下列分式的分子与分母中各项系数都化为整数。

（1）31.05.02.0-+x yx （2）mm 25.015.031--3.若将分式abba + (a 、b 均为正数）中的字母a 、b 的值分别扩大为原来的2倍，则分式的值为（ ）c b a +-2.下列各式中不正确的变形是( )(A) = (B) = (C) = (D) = c ab -cba --c ab --c ba -+cb a +-c ba --cb a -+A ．扩大为原来的2倍B ．缩小为原来的21 C ．不变 D ．缩小为原来的41 （4）约分：。

最简分式：。

① 约分b a b a 23246=公因式（ ）。

② 约分2222444ba b ab a -+-= 公因式（）。

（5）通分： 。

①通分29a2b ，7c12ab3=最简公分母是。

②通分1x2+x ,-1x2+2x+1=最简公分母是。

二、分式的乘、除法法则。

（1）分式的乘法法则：。

（2）分式的除法法则：。

①（a cb 32-）·2229bc a ②14322-+x x x ·312+-x x ③32+-x x ÷9342+-x x三、分式的加、减法法则： （1）同分母分式相加减：。

复习要点1. 分式的概念是中考考点之一，分式的性质是分式进行恒等变形的理论基础，通分、约分是分式性质的一种运用。

2. 分式运算是本章的重点内容之一，也是中考的考点之一，它必须在熟练运用法则的前提下，按正确的运算顺序进行运算。

3. 解分式方程的思想是将分式方程转化为整式方程，验根是解分式方程必不可少的步骤。

分式方程又是解决实际问题的工具之一。

一.选择题1. 当x 为任意实数时，下列分式中一定有意义的是 （ ） A.||1x x - B.1||1-+x x C.1||1+-x x D.21+-x x 2. 要使x x --442与xx --54的值互为倒数，则x 的值是 （ ） A ．0 B ．1 C ．-1 D ．21 3. 如果3553=-+-mA m ，那么A=（ ） A 8-mB m -2C m 318-D 123-m4. 在下列各式中正确的是 （ ） A.22a b a b = B.b a ba b a +=++22 C.y x y y x y +=+22 D.xy y x xy y x 23613121-=- 5. 如果32=b a 且2≠a ，那么51-++-b a b a 等于 （ ） A.0 B.51 C.51- D.没有意义 6. 计算11--+a a a 的结果是（ ） A 、11-a B 、11--a C 、112---a a a D 、1-a 7. y x x y m -=，yx x y n +=，那么22n m -等于 （ ）A.4B.-4C.0D.222xy 8. 第二十届电视剧飞天奖今年有a 部作品参赛，比去年增加了40%还多2部，设去年参赛作品有b 部，则b 的值是 （ ） A.%4012++a B.()2%401++a C.%4012+-a D.()2%401-+a 9. 甲、乙两班学生参加植树造林，已知甲班每天比乙班多植树5棵，甲班植80棵树所用的天数与乙班植70棵树所用天数相等，若设甲班每天植树x 棵，则根据题意列出的方程是 （ ） A.x x 70580=- B.57080+=x x C.x x 70580=+ D.57080-=x x 二.填空题10. 当x 时，分式44--x x 的值为零；11. 若当x=2时，分式 m x x 22- 没有意义，则当 x=3时，分式mx mx +的值= ； 12. 若把分式22yx y x -+中的字母x 和y 同时变为原来的3倍，分式的值 ； 13. 若分式1232-a a 的值为负，则a 的取值范围为__________； 14. 已知分式方程xk x --=+-22321有增根，则______=k ； 15. 当________=a 时，关于x 的方程4532=-+x a ax 的根是2； 16.若52=+x x ，则________422=+x x ； 17. 已知：()()5252223--+=-+-x b x a x x x ，则_______=+b a ； 18、已知2-=x 时，分式ax b x +-无意义，4=x 时，分式的值为零，则____=+b a 。

长安中学 第八章 分式 单元复习（1）导学稿 班级 姓名 年级：初二 学科：数学 时间：2017、4、12 课型：复习 主备：吴军 审核：初二数学组一、教学目标：巩固分式概念、分式的性质、分式的运算，形成完整的知识结构与体系.一、相关概念：1.什么是分式在①x 2 ；②4x x ；③b 2a ；④y-84 ；⑤x 6 －1y ；⑥15 x+y ；⑦3x-12π ；⑧2x 2+2x+1；⑨错误!中分式有哪些二、 典型例题： 1、当x_______时，分式 有意义值为零 2、若分式 表示一个整数，则整数m 可取的值 共有 个。

三、 1、.分式的基本性质:分式的分子和分母都乘以（或除以）同一个不等于0的整式，分式的值不变. (其中M 是不等于0的整式)2.什么是分式的约分3.什么是最简分式1、下列式子 （1） （2）（3） （4）中约分正确的是 （ ）A 、0个B 、1 个C 、 2 个D 、 3 个22-x x 14+m ,A A M A A M B B M B B M ⋅÷==⋅÷y x y x y x -=--1221-=--b a a b y x y x y x y x +-=-+-222)(a c b a a c c a a b --=---43)())((四、分式的通分：分式的加减法则：1、的最简公分母是 . 2、计算4、6.化简,求值： ，请你自取一个x 的值代入求值ac z b a y c b x 2,10,522-232,3x xy y y y x +-222222(1)2a b a b a b ab ab -+÷+-423)23()23()2.(5ay x y x x y -÷-⋅-x x x x x x x x 44412222-÷⎪⎭⎫ ⎝⎛+----+。

初中数学《苏科版》目录七年级上册：第一章我们与数学同行⑴生活数学（6）1⑵活动思考（8）1第二章有理数⑴比0小的数（12）2⑵数轴（16）2⑶绝对值与相反数（20）3⑷有理数的加法与减法（26）4⑸有理数的乘法与除法（36）3⑹有理数的乘方（45）2⑺有理数的加减混合运算（50）2数学活动算“24”（54）1小结与思考（54）2复习题（55）第三章用字母表示数⑴字母表示什么数（62）1⑵代数式（66）1⑶代数式的值（70）2⑷合并同类项（75）2⑸去括号（79）2数学活动正方体涂色（84）1小结与思考（84）2复习题（85）第四章一元一次方程⑴从问题到方程（92）2⑵解一元一次方程（95）4⑶用方程解决问题（102）6数学活动一元一次方程应用的调查（111）1小结与思考（111）2复习题（112）第五章走进图形世界⑴丰富的图形世界（118）2⑵图形的变化（123）2⑶展开与折叠（128）2⑷从三个方向看（134）2数学活动设计包装纸箱（139）1小结与思考（139）1复习题（140）第六章平面图形认识（一）⑴线段、射线、直线（148）2⑵角（152）2⑶余角、补角、对顶角（158）2⑷平等（163）1⑸垂直（167）1数学活动测量距离（171）1小结与思考（171）2复习题（172）课题学习制作无盖长方体的长方体纸盒（175）1数学活动评价表（176）七年级下册：第七章平面图形的认识（二）⑴探索直线平行的条件（6）2⑵探索平行线的性质（11）1⑶图形的平移（14）2⑷认识三角形（20）2⑸三角形的内角和（25）4数学活动（32）1小结与思考（33）2复习题（34）第八章幂的运算⑴同底数幂的乘法（40）1⑵幂的乘方与积的乘方（43）2⑶同底数幂的除法（47）3数学活动（52）1小结与思考（52）2复习题（52）第九章从面积到乘法公式⑴单项式乘单项式（56）1⑵单项式乘多项式（58）1⑶多项式乘多项式（61）1⑷乘法公式（64）3⑸单项式乘多项式法则的再认识――因式分解（一）（70）1⑹乘法公式的再认识――因式分解（二）（72）3数学活动（77）1小结与思考（78）2复习题（79）第十章二元一次方程组⑴二元一次方程（84）1⑵二元一次方程组（86）2⑶解二元一次方程组（89）2⑷用方程组解决问题（93）3数学活动（99）1小结与思考（99）2复习题（100）第十一章图形的全等⑴全等图形（104）1⑵全等三角形（108）1⑶探索三角形全等的条件（111）5数学活动（125）1小结与思考（125）2复习题（126）第十二章数据在我们周围⑴普查与抽样调查（132）1⑵统计图的选用（133）3⑶频数分布表和频数分布直方图（145）2数学活动（152）1小结与思考（152）1复习题（153）第十三章感受概率⑴确定与不确定（160）1⑵可能性（162）2数学活动（169）1小结与思考（169）1复习题（170）课题学习丢弃了多少塑料袋（172）1数学活动评价表（173）八年级上册：第一章轴对称图形⑴轴对称与轴对称图形（6）1⑵轴对称的性质（10）1⑶设计轴对称图案（15）1⑷线段、角的轴对称性（18）2⑸等腰三角形的轴对称性（23）3⑹等腰梯形的轴对称性（31）2数学活动剪纸（35）1小结与思考（36）2复习题（37）第二章勾股定理与平方根⑴勾股定理（44）1⑵神秘的数组（48）1⑶平方根（51）2⑷立方根（55）1⑸实数（57）2⑹近似数与有效数字（62）1⑺勾股定理的应用（65）2数学活动关于勾股定理的研究（69）1小结与思考（69）2复习题（69）第三章中心对称图形（一）⑴图形的旋转（74）1⑵中心对称与中心对称图形（77）2⑶设计中心对称图案（82）1⑷平行四边形（85）3⑸矩形、菱形、正方形（92）5⑹三角形、梯形中位线（102）2数学活动平面图形的镶嵌（105）1小结与思考（106）2复习题（107）第四章数量、位置的变化⑴数量的变化（114）2⑵位置的变化（120）1⑶平面直角坐标系（123）3数学活动确定藏宝地（132）1小结与思考（132）2复习题（133）第五章一次函数⑴函数（140）2⑵一次函数（147）2⑶一次函数的图象（151）2⑶一次函数的应用（157）2⑷二元一次方程组的图象解法（161）1数学活动温度计上的一次函数（163）1小结与思考（164）2复习题（165）第六章数据的集中程度⑴平均数（170）2⑵中位数与众数（174）2⑶用计算器求平均数（179）1数学活动你是“普通”学生吗？（182）1小结与思考（183）2复习题（183）课题学习利用对称图形设计徽标（186）1数学活动评价表（187）第七章一元一次不等式⑴生活中的不等式（6）⑵不等式的解集（9）⑶不等式的性质（12）⑷解一元一次不等式（15）⑸用一元一次不等式解决问题（19）⑹一元一次不等式组（21）⑺一元一次不等式与一元一次方程、一次函数（26）数学活动（28）小结与思考（28）复习题（29）第八章分式⑴分式（34）⑵分式的基本性质（37）⑶分式的加减法（43）⑷分式的乘除法（46）⑸分式方程（54）数学活动（57）小结与思考（57）复习题（58）第九章反比例函数⑴反比例函数（62）⑵反比例函数的图象与性质（65）⑶反比例函数的应用（73）数学活动（76）小结与思考（77）复习题（77）第十章图形的相似⑴图上距离与实际距离（82）⑵黄金分割（85）⑶相似图形（89）⑷探索三角形相似的条件（94）⑸相似三角形性质（105）⑹图形的位似（110）⑺相似三角形的应用（113）数学活动（120）小结与思考（120）复习题（120）第十一章图形与证明（一）⑴你的判断对吗（126）⑵说理（129）⑶证明（134）⑷互逆命题（142）数学活动（146）小结与思考（147）复习题（148）第十二章认识概率⑴等可能性（154）⑵等可能条件下的概率（一）（157）⑶等可能条件下的概率（二）（165）数学活动（168）小结与思考（169）复习题（170）课题学习游戏公平吗？（173）1数学活动评价表（174）第一章图形与证明（二）⑴等腰三角形的性质与判定（6）1⑵直角三角形全等的判定（9）2⑶平行四边形、矩形、菱形、正方形的性质与判定（13）8⑷等腰梯形的性质与判定（28）1⑸中位线（30）2数学活动折纸与证明（34）1小结与思考（36）2复习题（37）第二章数据的离散程度⑴极差（42）1⑵方差与标准差（45）1⑶用计算器求标准差和方差（49）1数学活动估计时间（53）1小结与思考（53）1复习题（54）第三章二次根式⑴二次根式（58）2⑵二次根式的乘除法（61）4⑶二次根式的加减法（69）2数学活动画画·算算（74）1小结与思考（74）1复习题（75）第四章一元二次方程⑴一元二次方程（80）1⑵一元二次方程的解法（83）6⑶用一元二次方程解决问题（94）4数学活动矩形绿地中的花圃设计（100）1小结与思考（101）2复习题（101）第五章中心对称图形（二）⑴圆（106）2⑵圆的对称性（111）2⑶圆周角（117）2⑷确定圆的条件（124）1⑸直线和圆的位置关系（127）4⑹圆和圆的位置关系（138）1⑺正多边形与圆（142）1⑻弧长及扇形的面积（145）1⑼圆锥的侧面积和全面积（148）2数学活动制作冰淇淋纸筒（151）1小结与思考（151）2复习题（152）课题学习制作“动画片”（156）1数学活动评价表（158）九年级下册：第六章二次函数⑴二次函数（6）1⑵二次函数的图象和性质（9）4⑶二次函数与一元二次方程（21）2⑷二次函数的应用（25）3数学活动（32）1小结与思考考（32）2复习题（33）第七章锐角三角函数⑴正切（38）1⑵正弦、余弦（41）2⑶特殊角的三角函数（46）1⑷由三角函数值求锐角（49）1⑸解直角三角形（51）1⑹锐角三角函数的简单应用（54）2数学活动（60）1小结与思考（60）2复习题（61）第八章统计的简单应用⑴货比三家（66）1⑵中学生的视力情况调查（70）3数学活动（77）1小结与思考（78）1复习题（79）第九章概率的简单应用⑴抽签方法合理吗（84）1⑵概率帮你做估计（86）1⑶保险公司怎样才能不亏本（88）1数学活动（90）1小结与思考（91）1复习题（91）课题学习探究等周长图形的最大面积（94）数学活动评价表（95）。

?分式?章节复习总结、复习目标与要求1 .本章主要学习了分式的根本概念和性质,分式的加减法和乘除法、含有字母系数的一元一次方程和分式方程的解法以及可化为一元一次方程的分式方程及其应用.2 .应当注意理解分式、有理式的概念,会求分式有意义的条件.应注意掌握分式的根本性质,能用它将分式变形,并能熟练进行通分和约分,掌握分式加减、乘除的运算法那么,进行分式的运算.3 .掌握含有字母系数的一元一次方程的解法,会进行简单的公式变形,深入理解分式方程的概念,掌握可化为一元一次方程的分式方程的解法,并能判定分式方程的增根,掌握可化为一元一次方程的分式方程的应用题的解法.4 .在进行分式加减运算时要注意通分,在进行分式的乘除运算中,注意对结果的约分化简.5 .在解含有字母系数的一元一次方程时,用含有字母的式子去乘或除方程的两边时,这个式子的 值不能为零,如果无法判断是否为零,那么应当进行讨论.定义；含字母系数的一元一衩方程 可化为一元一次方程的分式方程的解法 列方式方程就应用题1 .分式及分式的根本性质2 .分式的运算(1)约分：①约分的概念：把一个分式的分子与分母的公因式约去,叫做分式的约分.②分式约分的依据：分式的根本性质. ③分式约分的方法：把分式的分子与分母分解因式,然后约去分子与分母的6.解分式方程时,由于可能会产生增根,因而一定要进行检验.分式定义 二、知识结构梳理概念有关耦念 ,有理式 最荷分式 最简公分母分式分式的根本性僦A JxM ¥ = BxM 4 =学皆M 是不等于零的整式) ,oB TM加演法分式的运直 除法中4ab d be分式方程三、重点知识梳理乘方乘.一了就公因式.④约分的结果：最简分式(分子与分母没有公因式的分式,叫做最简分式)(2)分式的乘法：乘法法测：-£ =变.b d bd(3)分式的除法：除法法那么：-^- = - .9=史b d bc bc(4)分式的乘方：求n个相同分式的积的运算就是分式的乘方,用式子表示就是(自)：■,bn...... ............. ................. ............................... a a分式的乘方,是把分子、分母各自乘方.用式子表不为：(一)n=F(n为正整数)b b n3.分式方程及其应用(1)分式方程的概念分母中含有未知数的方程叫分式方程注意：它和整式方程的区别就在于分母中是否含未知数(2)分式方程的解法①方程两边都乘以最简公分母,去分母,化为整式方程；②解这个整式方程；③验根(3)分式方程的应用列分式方程解应用题的一般步骤：①审：审清题意；②设：设未知数；③找：找出相等关系；④列：列出分式方程；⑤解：解这个分式方程；⑥验：检验,既要验证根是否是原分式方程的根,又要验是否符合题意；⑦答：写出答案四、易混、易错,问题辨析1.符号错误a b例1.不改变分式的值,使分式 a b的分子、分母第一项的符号为正.一a 一b诊断：约分的根据是分式的根本性质,将分子、分母的公因式约去,假设分子、分母是多项式,须先分解因式,再约去公因式.错解:一a b a b -a -ba -b诊断：此题错误的原因是把分子、分母首项的符号当成了分子、分母的符号.正解:-a b -(a -b) a -b -a -b - (a b) a b2 .运算顺序错误2a - 4 a - 2 例 2.计算：22a 4 a-^ .(a 3)a 4a 3 a 3 错解：原式=2(a -2)+ (a -2) = i-2 ---------------------------- .a 4a 3 a 4a 3诊断：分式的乘除混合运算是同一级运算,运算顺序应从左至右.正解: 原式2a -4 a 3 2(a ： ~2 ------------ ■ ------- .(a 3)= -------------- a 4a 3 a-2 a-13 .错用分式根本性质3.2a - 一 b 例3.不改变分式的值,把分式 ——2一的分子、分母各项系数都化为整数.-a b3(2a --b) 2错解：原式=22------(2 a b) 3 34a -3b2a 3b诊断：应用分式的根本性质时, 分式的分子、分母必须同乘以同一个不为 0的整式,分式的值不变,而此题分子乘以2,分母乘以3,分式的值改变了.(2a --b) 6 正解：原式= ------------- 2 ---------(2a b) 6 312a -9b4a 6b4 .约分中的错误例4.约分:a 2 ab ~22a 2ab b 错解：原式1 1 12 b 23 b 2诊断：此题错误在于添加分数线时,忽略了分数线的括号作用.丘gqx 3 x 2 x 1x 3(x - 1)(x 2 x 1)x 3 x 3 -1 1正解：原式=—— ------- ----------- =—— -(----------- ------------ ) = —————x -11 x -1x -1x - 1 x - 1 x - 1五、典型问题梳理例1.判断以下各代数式中,哪些是分式?a(a b)正斛：原式= ----------- 2(a b)5 .结果不是最简分式例5.计算：力 x -yx 2y 2x - 3y ~22 + ―2 2 ,x 7 x 「y错解:原式=(x 3y )-(x 2y ) (2x -3y ) 2x -2y诊断：分式运算的结果必须化为最简分式,而上面所得结果中分子、分母还有公因式,必须进一步约分化简.正解：原式(x 3y) -(x 2y) (2x -3y) 2x -2y 2(x- y) 222二—2 2 二 IT 二x -yx —y (x y)(x-y) x y6 .误用分配律…、— m 2m 2 例 6.计算： ------------- 〒(m + 2 -------- ).2m -4 m - 21 J 3 -m 2(m -2)2 - 2(m -2)- m 2错解：原式=m --(m - 2) 2(m -2)2(m -2) m -2 诊断：乘法对加法有分配律,而除法对加法没有分配律.正解：原式_2___,m 2 , m -m -6 m 2 m -2 1--------- ~ -------------- = --------- - ----------------- - ------------2(m -2) m -22(m -2) (m 2)(m -3) 2(m -3)7 .忽略分数线的括号作用3例 7.计算：——— x 2 -x -1 .x -1x 3 (x -1)(x 2 - x -1)x -1 x -12x 2 -1 x -1错解:2x - x -11(1) 1+- (2) x (3) x —3x a5解：如果式子分母中含有字母,那么叫做分式,因此(1) (2)是分式,(3)不是分式.例2.使分式(x +7)(x -2)有意义的条件是什么?使分式的值为零的条件是什么？ |x|-7解：使分式有意义的条件是分母的值为零,所以当 |x|—7W0,即XW 土时,分式有意义；使分式值为零的条件是分式分子的值不能为零,分母的值不等于零,所以当 x+7=0或x — 2=0且xw±j 即x=2时,分式的值为零.2m -3m- 29 -m2〃 m -3m m(m -3) m解： -------- 厂二 --- --------------- 二 -- ------9 -m (m 3)(m -3) m 3说明：①当分式的分子、分母为多项式时,先要进行因式分解,才能够依据分式的根本性质进行约 分.②注意对分子、分母符号的处理. 一 x x 4x例5.先化简,再求值：( --------------------- )+——,其中x=2005x -2 x 2 x -2j -r V 14例6.斛方程 --------- --2 ------- =1 .y -1 y -1解：两边同乘以(y+1)(y —1),去分母,得(y+1)2-4=y 2- 1, y 2+2y+1 — 4=y 2—1, y=1检验：把y=1代入最简公分母：(y+1)(y —1)=(1+1)(1 — 1)=0,,y=1是增根.所以,原方程无解...、一一2x 3 -m例7.关于x 的万程 ----------- + ------- =3有增根,求 m 的值.x 122r x解：方程两边都乘以(x-2),得2x-(3-m)=3(x- 2),把x=2代入上面得到的整式方程,得 4-3+m=0.所以 m= — 1.说明：假设分式方程有增根,那么增根一定是使最简公分母等于零的未知数的值 ；反过来,使最简公分母 等于零的未知数的值不一定是方程的增根.例8.某自来水公司水费计算方法如下：假设每户每月用水不超过5 m 3,那么每立方米收费1.5元；假设每户每月用水超过5 m 3,那么超出局部每立方米收取较高的定额费用 .1月份,张家用水量是李家用水量的 3 , 张家当月水费是17.5元,李家当例4.解：原式=x 2 2x -x 2 2x (x 2)(x -2)x -2 1 14x - x 2 - 2007月水费是27.5元.超出5 m3的局部每立方米收费多少元？解：设超出5 m3局部的水,每立方米收费设为x元,根据等量关系,得17.5 -1.5 5 27.5 —1.5 5 2 加、人士加 /曰n------------------ +5= ( ----------------------- +5) X-.解这个万程,得x=2.经检验x=2是所列方程的根.答：超出 5 m3局部的水,每立方米收费2元.六、链接中考x —2 4x 1例9.有一道题先化简,再求值：( ----- 十^——)得———,其中x = -J3. 小玲做题时把x 2 x —4 x —4'x = -J3〞错抄成了‘x =百〞,但她的计算结果也是正确的,请你解释这是怎么回事？2x -八5 / x.2 4x 、 1 x .4x 4 4x , 2 ,、 2解：先化间：( ----------- 十二----- )〒二----- = --------- 2 ---------- ^(x — 4) = x +4, 由于x = J3 或x 2 x -4 x -4 x -4x=-石,x2的值均为3,原式的计算结果都是7,所以把‘x = -J3〞错抄成‘x = J3〞,计算结果也是正确的.例9.如图,小明家、王老师家、学校在同一条路上.小明家到王老师家路程为 3 km,王老师家到学校的路程为0.5 km,由于小明父母战斗在抗非典〞第一线,为了使他能按时到校,王老师每天骑自行车接小明上学.王老师骑自行车的速度是步行速度的3倍,每天比平时步行上班多用了20分钟,问王老师的步行速度及骑自行车的速度各是多少？// •学校解：分析题目中的等量关系：王老师骑车速度=王老师步行速度M；厂.王老师家王老师从家出发骑车接小明所用的时间=平时步行上学所用时间+20分钟. /设王老师步彳T速度为x km/h,那么骑自行车的速度为3xkm/h.依题意,得2父3+0.5 ="+型,解得x=5,经检验x=5是原方程的根,•小明家3x x 60这日3 3x=15.答：王老师步行速度为 5 km/h,骑自行车的速度为15 km/ h..例11我市受14号台风云娜〞的影响后,局部街道路面积水比拟严重.为了改善这一状况,市政公司决定将一总长为1200m的排水工程承包给甲、乙两工程队来施工.假设甲、乙两队合做需12天完成此项工程；假设甲队先做了8天后,剩下的由乙队单独做还需18天才能完工.问甲、乙两队单独完成此项工程各需多少天？又甲队每施工一天需要费用2万元,乙队每施工一天需要费用1万元,要使完成该工程所需费用不超过35万元,那么乙工程队至少要施工多少天？解：设甲、乙两队单独完成此项工程分别需要x天,y天.1 1 1——+ —=---- 『依题意得I工y12 解之得「二20,8 18 i y = 30.—+——=1・1「1 y经检验知它们适合方程组和题意.那么甲队每天施工1200及0=60m,乙队每天施工1200 T0=40m.设甲、乙两队实际完成此项工程分别需要a天,b天.依题意得J 解之得b>35[2a+i<35.答：甲、乙两队单独完成此项工程分别需要20天,30天；要使完成该工程所需费用不超过35万元, 那么乙工程队至少要施工15天.。

新苏科版八年级数学下册第八章《小结与思考》学案【学习目标】：1.进一步掌握分式的基本概念.能熟练的进行分式的运算.2.能进一步熟练掌握解分式方程的一般步骤.理解增根产生的原因及检验.3.分式方程的应用.【重点难点】熟练的进行分式的运算，能熟练的解分式方程【教学过程】：一、知识梳理：1分式的意义及分式的基本性质，用分式的基本性质进行约分和通分；2加、减、乘、除运算；3可化为一元一次方程的分式方程的解法及应用。

二、基础知识练习：1.下列各式：π8,11,5,21,7,322x x y x b a a -++中，分式有 （ ） A 、1个 B 、2个 C 、3个 D 、4个2.若分式112+-x x 的值为0，则x 的取值为 （ ） A 、1=x B 、1-=x C 、1±=x D 、无法确定3.如果把分式yx x +2中的x 和y 都扩大3倍，那么分式的值 （ ） A 、扩大3倍 B 、缩小3倍 C 、缩小6倍 D 、不变4.如果解分式方程14132=+--+x x x 出现了增根，那么增根可能是 （ ） A 、-2 B 、3 C 、3或-4 D 、-4 5.当x 时，分式31-+x x 有意义，当x 时，分式32-x x 无意义。

6. xyzx y xy 61,4,13-的最简公分母是 。

7.一件工作，甲单独做a 小时完成，乙单独做b 小时完成，则甲、乙合作 小时完成。

8.若分式方程21=++ax x 的一个解是1=x ，则=a 。

三、典型例题分析：1.计算：（1）y x axy 26512÷ （2）x y x y 2211-+-（3）212293m m --- （4）22424422x x x x x x x ⎛⎫---÷ ⎪-++-⎝⎭2.解下列方程：（1）512552x x x +=-- （2）253+=x x3.若方程233x k x x -=--会产生增根，试求k 的值4.A 、B 两地相距48千米，一艘轮船从A 地顺流航行至B 地，又立即从B 地逆流返回A 地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x 千米/时，则可列方程 （ ）A 、9448448=-++x x B 、9448448=-++xx C 、9448=+x D 、9496496=-++x x。

第八章《分式》（小结与复习）教案（苏科版初二下）
[教学目标]
1．能把本章基础知识条理化、系统化，熟练把握本章有关运算技能．
2．归纳小结用分式方程解决实际咨询题的差不多方法和体会，进展分析咨询题和解决咨询题能力．
3．回忆〝类比〞和〝转化〞的思想方法在探究本章基础知识、差不多方法中的作用，深化对这两种数学思想的认识．
[教学过程]
1．情境创设
可将学生在数学活动中显现的错误作为咨询题情境，展开复习小结．也能够直截了当设计咨询题串，让学生举例，展开复习．例如：
(1)本章学习了哪些知识?指导全章探究活动的要紧思想方法是什么?
(2)什么是分式?分式与分数有什么区不与联系?你能举例讲明吗?
(3)分式与分数的差不多性质相同吗?你能举例讲明吗?
(4)举例讲明分式的约分、通分与分数的约分、通分有什么相同和不同之处?
(5)能举例讲明解分式方程的差不多步骤吗?
2．探究活动
情境设计和探究活动，能够从两方面表达〝咨询题是数学的心脏〞这一推动数学发生、进展的重要理念：
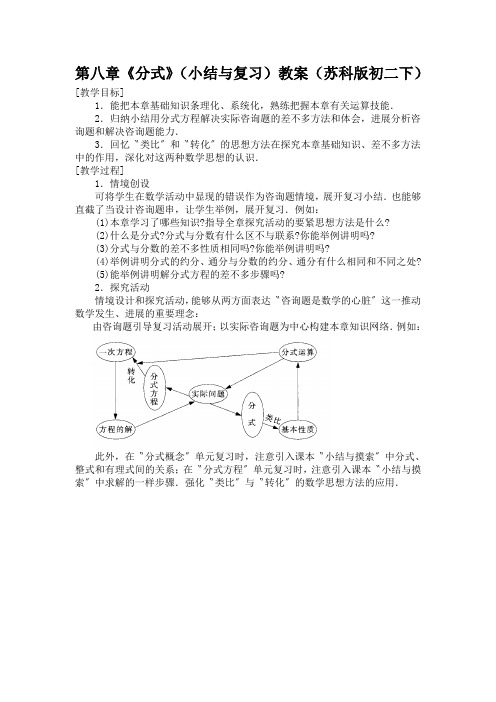
由咨询题引导复习活动展开；以实际咨询题为中心构建本章知识网络．例如：
此外，在〝分式概念〞单元复习时，注意引入课本〝小结与摸索〞中分式、整式和有理式间的关系；在〝分式方程〞单元复习时，注意引入课本〝小结与摸索〞中求解的一样步骤．强化〝类比〞与〝转化〞的数学思想方法的应用．。