2011届高考数学椭圆1

高考数学一轮复习考点知识专题讲解椭圆及其性质考点要求1.理解椭圆的定义、几何图形、标准方程.2.掌握椭圆的简单几何性质(范围、对称性、顶点、离心率).3.掌握椭圆的简单应用．知识梳理1．椭圆的定义把平面内与两个定点F1，F2的距离的和等于常数(大于|F 1F2|)的点的轨迹叫做椭圆．两个定点F1，F2叫做椭圆的焦点，两焦点间的距离|F1F2|叫做椭圆的焦距．2．椭圆的简单几何性质焦点的位置焦点在x轴上焦点在y轴上图形标准方程x2a2＋y2b2＝1(a>b>0)y2a2＋x2b2＝1(a>b>0)范围－a≤x≤a且－b≤y≤b －b≤x≤b且－a≤y≤a顶点A1(－a,0)，A2(a,0)B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)B1(－b,0)，B2(b,0)轴长 短轴长为2b ，长轴长为2a焦点 F 1(－c ,0)，F 2(c ,0) F 1(0，－c )，F 2(0，c )焦距 |F 1F 2|＝2c对称性 对称轴：x 轴和y 轴，对称中心：原点离心率e ＝ca (0<e <1)a ，b ，c 的关系a 2＝b 2＋c 2常用结论 椭圆的焦点三角形椭圆上的点P (x 0，y 0)与两焦点构成的△PF 1F 2叫做焦点三角形．如图所示，设∠F 1PF 2＝θ.(1)当P 为短轴端点时，θ最大，12F PF S △最大． (2)12F PF S △＝12|PF 1||PF 2|sin θ＝b 2tan θ2＝c |y 0|. (3)|PF 1|max ＝a ＋c ，|PF 1|min ＝a －c . (4)|PF 1|·|PF 2|≤⎝⎛⎭⎪⎫|PF 1|＋|PF 2|22＝a 2. (5)4c 2＝|PF 1|2＋|PF 2|2－2|PF 1||PF 2|cos θ. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内与两个定点F 1，F 2的距离之和等于常数的点的轨迹是椭圆．(×)(2)椭圆是轴对称图形，也是中心对称图形．(√)(3)y 2m 2＋x 2n 2＝1(m ≠n )表示焦点在y 轴上的椭圆．(×) (4)x 2a 2＋y 2b 2＝1(a >b >0)与y 2a 2＋x 2b 2＝1(a >b >0)的焦距相等．(√) 教材改编题 1．设P 是椭圆x 225＋y 216＝1上的点，若F 1，F 2是椭圆的两个焦点，则|PF 1|＋|PF 2|等于()A ．4B ．5C ．8D ．10 答案D解析依椭圆的定义知， |PF 1|＋|PF 2|＝2×5＝10.2．若椭圆C ：x 24＋y 23＝1，则该椭圆上的点到焦点距离的最大值为()A ．3B ．2＋ 3C ．2 D.3＋1 答案A解析由题意知a ＝2，b ＝3，所以c ＝1，距离的最大值为a ＋c ＝3.3．(2022·深圳模拟)已知椭圆C 的焦点在x 轴上，且离心率为12，则C 的方程可以为________．答案x 24＋y 23＝1(答案不唯一)解析因为焦点在x 轴上，所以设椭圆的方程为x 2a 2＋y 2b 2＝1，a >b >0，因为离心率为12，所以c a ＝12，所以c 2a 2＝a 2－b 2a 2＝14，则b 2a 2＝34.题型一 椭圆的定义及其应用例1(1)已知圆(x ＋2)2＋y 2＝36的圆心为M ，设A 是圆上任意一点，N (2,0)，线段AN 的垂直平分线交MA 于点P ，则动点P 的轨迹是()A ．圆B ．椭圆C ．双曲线D ．抛物线 答案B解析点P 在线段AN 的垂直平分线上，故|PA |＝|PN |.又AM 是圆的半径，所以|PM |＋|PN |＝|PM |＋|PA |＝|AM |＝6>|MN |.由椭圆的定义知，P 的轨迹是椭圆．(2)设点P 为椭圆C ：x 2a 2＋y 24＝1(a >2)上一点，F 1，F 2分别为C 的左、右焦点，且∠F 1PF 2＝60°，则△PF 1F 2的面积为________． 答案433解析由题意知，c ＝a 2－4.又∠F 1PF 2＝60°，|F 1P |＋|PF 2|＝2a ， |F 1F 2|＝2a 2－4，∴|F 1F 2|2＝(|F 1P |＋|PF 2|)2－2|F 1P ||PF 2|－2|F 1P |·|PF 2|cos60° ＝4a 2－3|F 1P |·|PF 2|＝4a 2－16，∴|F 1P |·|PF 2|＝163， ∴12PF F S △＝12|F 1P |·|PF 2|sin60°＝12×163×32 ＝433. 延伸探究 若将本例(2)中“∠F 1PF 2＝60°”改成“PF 1⊥PF 2”，求△PF 1F 2的面积． 解∵PF 1⊥PF 2，∴|PF 1|2＋|PF 2|2＝|F 1F 2|2＝4(a 2－4) ＝4a 2－16，又|PF 1|＋|PF 2|＝2a ， ∴|PF 1|·|PF 2|＝8， ∴12PF F S △＝4. 教师备选1．△ABC 的两个顶点为A (－3,0)，B (3,0)，△ABC 周长为16，则顶点C 的轨迹方程为() A.x 225＋y 216＝1(y ≠0) B.y 225＋x 216＝1(y ≠0) C.x 216＋y 29＝1(y ≠0) D.y 216＋x 29＝1(y ≠0)答案A解析由题知点C 到A ，B 两点的距离之和为10，故C 的轨迹为以A (－3,0)，B (3,0)为焦点，长轴长为10的椭圆，故2a ＝10，c ＝3，b 2＝a 2－c 2＝16.所以方程为x 225＋y 216＝1.又A ，B ，C 三点不能共线，所以x 225＋y 216＝1(y ≠0)．2．若F 1，F 2是椭圆x 29＋y 27＝1的两个焦点，A 为椭圆上一点，且∠AF 1F 2＝45°，则△AF 1F 2的面积为()A ．7 B.74 C.72 D.752答案C解析由题意得a ＝3，b ＝7，c ＝2， ∴|F 1F 2|＝22，|AF 1|＋|AF 2|＝6.∵|AF 2|2＝|AF 1|2＋|F 1F 2|2－2|AF 1|·|F 1F 2|cos45° ＝|AF 1|2＋8－4|AF 1|，∴(6－|AF 1|)2＝|AF 1|2＋8－4|AF 1|， 解得|AF 1|＝72.∴△AF 1F 2的面积S ＝12×22×72×22＝72. 思维升华 椭圆定义的应用技巧(1)椭圆定义的应用主要有：求椭圆的标准方程、求焦点三角形的周长、面积及求弦长、最值和离心率等．(2)通常将定义和余弦定理结合使用求解关于焦点三角形的周长和面积问题．跟踪训练1(1)已知两圆C 1：(x －4)2＋y 2＝169，C 2：(x ＋4)2＋y 2＝9.动圆M 在圆C 1内部且和圆C 1相内切，和圆C 2相外切，则动圆圆心M 的轨迹方程是()A.x264－y248＝1 B.x248＋y264＝1C.x248－y264＝1 D.x264＋y248＝1答案D解析设动圆的圆心M(x，y)，半径为r，圆M与圆C1：(x－4)2＋y2＝169内切，与圆C2：(x＋4)2＋y2＝9外切．所以|MC1|＝13－r，|MC2|＝3＋r.|MC1|＋|MC2|＝16>|C1C2|＝8，由椭圆的定义，M的轨迹是以C1，C2为焦点，长轴长为16的椭圆．则a＝8，c＝4，所以b2＝82－42＝48，动圆的圆心M的轨迹方程为x264＋y248＝1.(2)(2022·武汉调研)设椭圆x24＋y23＝1的一个焦点为F，则对于椭圆上两动点A，B，△ABF周长的最大值为()A．4＋ 5 B．6 C．25＋2 D．8答案D解析设F1为椭圆的另外一个焦点，则由椭圆的定义可得|AF|＋|BF|＋|AB|＝2a－|AF1|＋2a－|BF1|＋|AB|＝4a＋|AB|－|BF1|－|AF1|＝8＋|AB|－|BF1|－|AF1|，当A，B，F1三点共线时，|AB|－|BF1|－|AF1|＝0，当A，B，F1三点不共线时，|AB|－|BF1|－|AF1|<0，所以当A，B，F1三点共线时，△ABF的周长取得最大值8.题型二椭圆的标准方程命题点1定义法例2已知椭圆C的焦点为F1(－1,0)，F2(1,0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为()A.x22＋y2＝1B.x23＋y22＝1C.x24＋y23＝1D.x25＋y24＝1答案B解析设椭圆的标准方程为x2a2＋y2b2＝1(a>b>0)，由椭圆定义可得|AF1|＋|AB|＋|BF1|＝4a. ∵|AB|＝|BF1|，∴|AF1|＋2|AB|＝4a.又|AF2|＝2|F2B|，∴|AB|＝32|AF2|，∴|AF1|＋3|AF2|＝4a.又|AF1|＋|AF2|＝2a，∴|AF2|＝a，∴A为椭圆的短轴端点．如图，不妨设A(0，b)，又F 2(1,0)，AF 2—→＝2F 2B —→， ∴B ⎝ ⎛⎭⎪⎫32，－b 2.将B 点坐标代入椭圆方程x 2a 2＋y 2b 2＝1，得94a 2＋b 24b2＝1， ∴a 2＝3，b 2＝a 2－c 2＝2. ∴椭圆C 的方程为x 23＋y 22＝1.命题点2待定系数法例3已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点P 1(6，1)，P 2(－3，－2)，则该椭圆的方程为________． 答案x 29＋y 23＝1解析设椭圆的方程为mx 2＋ny 2＝1(m >0，n >0，且m ≠n )． 因为椭圆经过P 1，P 2两点， 所以点P 1，P 2的坐标满足椭圆方程，则⎩⎨⎧6m ＋n ＝1，3m ＋2n ＝1，解得⎩⎪⎨⎪⎧m ＝19，n ＝13.所以所求椭圆的方程为x 29＋y 23＝1.教师备选1．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，离心率为12，过F 2的直线与椭圆C 交于A ，B 两点，若△F 1AB 的周长为8，则椭圆方程为() A.x 24＋y 23＝1 B.x 216＋y 212＝1C.x 22＋y 2＝1 D.x 24＋y 22＝1 答案A 解析如图，由椭圆的定义可知，△F 1AB 的周长为4a ， 所以4a ＝8，a ＝2， 又离心率为12，所以c ＝1，b 2＝3， 所以椭圆方程为x 24＋y 23＝1.2．设椭圆x 2m 2＋y 2n 2＝1(m >0，n >0)的右焦点为(2,0)，离心率为22，则此椭圆的方程为________．答案x 28＋y 24＝1解析椭圆的右焦点为(2,0)， 所以m 2－n 2＝4，e ＝22＝2m，所以m ＝22，代入m 2－n 2＝4，得n 2＝4， 所以椭圆方程为x 28＋y 24＝1.思维升华 根据条件求椭圆方程的主要方法(1)定义法：根据题目所给条件确定动点的轨迹满足椭圆的定义．(2)待定系数法：根据题目所给的条件确定椭圆中的a ，b .当不知焦点在哪一个坐标轴上时，一般可设所求椭圆的方程为mx 2＋ny 2＝1(m >0，n >0，m ≠n )，不必考虑焦点位置，用待定系数法求出m ，n 的值即可．跟踪训练2(1)已知椭圆的两个焦点为F 1(－5，0)，F 2(5，0)，M 是椭圆上一点，若MF 1⊥MF 2，|MF 1|·|MF 2|＝8，则该椭圆的方程是() A.x 27＋y 22＝1 B.x 22＋y 27＝1 C.x 29＋y 24＝1 D.x 24＋y 29＝1 答案C解析设|MF 1|＝m ，|MF 2|＝n ， 因为MF 1⊥MF 2，|MF 1|·|MF 2|＝8， |F 1F 2|＝25，所以m 2＋n 2＝20，mn ＝8， 所以(m ＋n )2＝36，所以m ＋n ＝2a ＝6，所以a ＝3. 因为c ＝5， 所以b ＝a 2－c 2＝2. 所以椭圆的方程是x 29＋y 24＝1.(2)已知F 1(－1,0)，F 2(1,0)是椭圆C 的两个焦点，过F 2且垂直于x 轴的直线交C 于A ，B 两点，且|AB |＝3，则C 的方程为() A.x 22＋y 2＝1 B.x 23＋y 22＝1 C.x 24＋y 23＝1 D.x 25＋y 24＝1 答案C解析如图，|AF 2|＝12|AB |＝32，|F 1F 2|＝2，由椭圆定义， 得|AF 1|＝2a －32.①在Rt△AF 1F 2中，|AF 1|2＝|AF 2|2＋|F 1F 2|2＝⎝ ⎛⎭⎪⎫322＋22.②由①②得a ＝2，∴b 2＝a 2－c 2＝3. ∴椭圆C 的方程为x 24＋y 23＝1.题型三 椭圆的几何性质 命题点1离心率例4(1)(2022·湛江模拟)已知F 是椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的右焦点，过椭圆C 的下顶点且斜率为34的直线与以点F 为圆心、半焦距为半径的圆相切，则椭圆C 的离心率为()A.55 B.12 C.33 D.22答案A解析过椭圆C 的下顶点(0，－b )且斜率为34的直线方程为y ＝34x －b ，即34x －y －b ＝0，F (c ,0)，由点到直线距离公式， 得c ＝⎪⎪⎪⎪⎪⎪34c －b ⎝ ⎛⎭⎪⎫342＋1，即c 2＝－32bc ＋b 2，即(2c －b )(c ＋2b )＝0，则2c －b ＝0，b ＝2c .又a 2＝b 2＋c 2，即a 2＝(2c )2＋c 2＝5c 2， 解得c a ＝55. (2)已知F 1，F 2分别是椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，若椭圆上存在点P ，使∠F 1PF 2＝90°，则椭圆的离心率e 的取值范围为()A.⎝ ⎛⎦⎥⎤0，22 B.⎣⎢⎡⎭⎪⎫22，1C.⎝ ⎛⎦⎥⎤0，32 D.⎣⎢⎡⎭⎪⎫32，1答案B解析若椭圆上存在点P ，使得PF 1⊥PF 2，则以原点为圆心，F 1F 2为直径的圆与椭圆必有交点，如图，可得c ≥b ，即c 2≥b 2， 所以2c 2≥a 2，即e 2≥12，又e <1，所以e ∈⎣⎢⎡⎭⎪⎫22，1.思维升华 求椭圆离心率或其范围的方法 (1)直接求出a ，c ，利用离心率公式e ＝ca求解．(2)由a 与b 的关系求离心率，利用变形公式e ＝1－b 2a2求解． (3)构造a ，c 的齐次式．可以不求出a ，c 的具体值，而是得出a 与c 的关系，从而求得e .命题点2与椭圆有关的范围(最值)例5(1)以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1，则椭圆长轴长的最小值为()A ．1 B. 2 C ．2 D ．2 2 答案D解析设a ，b ，c 分别为椭圆的长半轴长、短半轴长、半焦距，依题意知，当三角形的高为b 时，以椭圆上一点和两个焦点为顶点的三角形的面积最大，所以12×2cb ＝1，故bc＝1，故2a ＝2b 2＋c 2≥22bc ＝22(当且仅当b ＝c ＝1时取等号)．(2)如图，焦点在x 轴上的椭圆x 24＋y 2b 2＝1(b >0)的离心率e ＝12，F ，A 分别是椭圆的左焦点和右顶点，P 是椭圆上任意一点，则PF →·PA →的最大值为________．答案4解析由题意知a ＝2，因为e ＝c a ＝12，所以c ＝1， 所以b 2＝a 2－c 2＝3， 故椭圆的方程为x 24＋y 23＝1.设P 点的坐标为(x 0，y 0)， 所以－2≤x 0≤2，－3≤y 0≤ 3. 因为F (－1,0)，A (2,0)， 所以PF →＝(－1－x 0，－y 0)， PA →＝(2－x 0，－y 0)，所以PF →·PA →＝x 20－x 0－2＋y 20＝14x 20－x 0＋1＝14(x 0－2)2，所以当x0＝－2时，PF→·PA→取得最大值4.教师备选1．嫦娥四号在绕月飞行时是以月球球心为一个焦点的椭圆形轨道，如图中轨道③所示，其近月点与月球表面距离为100公里，远月点与月球表面距离为400公里，已知月球的直径约为3476公里，则下列选项中正确的是()A．焦距长约为400公里 B．长轴长约为3988公里C．两焦点坐标约为(±150,0) D．离心率约为75 994答案D解析设该椭圆的长半轴长为a，半焦距长为c.依题意可得月球半径约为12×3476＝1738，a－c＝100＋1738＝1838，a＋c＝400＋1738＝2138，所以2a＝1838＋2138＝3976，a＝1988，c＝2138－1988＝150,2c＝300，椭圆的离心率约为e＝ca＝1501988＝75994，可得D正确，A，B错误；因为没有给坐标系，焦点坐标不确定，所以C错误．2．(2022·太原模拟)若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP →的最大值为()A ．2B ．3C ．6D ．8 答案C解析由椭圆x 24＋y 23＝1可得F (－1,0)，点O (0,0)．设P (x ，y )(－2≤x ≤2)．则OP →·FP →＝x 2＋x ＋y 2＝x 2＋x ＋3⎝ ⎛⎭⎪⎫1－x 24＝14x 2＋x ＋3＝14(x ＋2)2＋2，－2≤x ≤2， 当且仅当x ＝2时，OP →·FP →取得最大值6.思维升华 与椭圆有关的最值或范围问题的求解方法 (1)利用数形结合、几何意义，尤其是椭圆的性质； (2)利用函数，尤其是二次函数； (3)利用不等式，尤其是基本不等式．跟踪训练3(1)(2022·济南质检)设椭圆E 的两焦点分别为F 1，F 2，以F 1为圆心，|F 1F 2|为半径的圆与E 交于P ，Q 两点．若△PF 1F 2为直角三角形，则E 的离心率为() A.2－1 B.5－12 C.22D.2＋1 答案A解析不妨设椭圆E 的方程为x 2a 2＋y 2b2＝1(a >b >0)，如图所示，∵△PF 1F 2为直角三角形， ∴PF 1⊥F 1F 2，又|PF 1|＝|F 1F 2|＝2c ， ∴|PF 2|＝22c ，∴|PF 1|＋|PF 2|＝2c ＋22c ＝2a ， ∴椭圆E 的离心率e ＝c a＝2－1.(2)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)，点A ，B 是长轴的两个端点，若椭圆上存在点P ，使得∠APB ＝120°，则该椭圆的离心率的取值范围是() A.⎣⎢⎡⎭⎪⎫63，1 B.⎣⎢⎡⎭⎪⎫32，1 C.⎝ ⎛⎦⎥⎤0，22 D.⎝ ⎛⎦⎥⎤0，34答案A 解析如图，当P 在上顶点时，∠APB 最大， 此时∠APB ≥120°，则∠APO ≥60°，所以tan∠APO ≥tan60°＝3， 即a b≥3，a 2≥3b 2，a 2≥3(a 2－c 2)， 所以2a 2≤3c 2，则c a ≥63， 所以椭圆的离心率的取值范围是⎣⎢⎡⎭⎪⎫63，1.课时精练1．已知动点M 到两个定点A (－2,0)，B (2,0)的距离之和为6，则动点M 的轨迹方程为() A.x 29＋y 2＝1 B.y 29＋x 25＝1C.y 29＋x 2＝1D.x 29＋y 25＝1 答案D解析由题意有6>2＋2＝4，故点M 的轨迹为焦点在x 轴上的椭圆， 则2a ＝6，c ＝2，故a 2＝9， 所以b 2＝a 2－c 2＝5， 故椭圆的方程为x 29＋y 25＝1.2．若椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的短轴长等于焦距，则椭圆的离心率为()A.12B.33C.22D.24 答案C解析依题意可知，c ＝b ， 又a ＝b 2＋c 2＝2c ， ∴椭圆的离心率e ＝ca ＝22. 3．椭圆x 22＋y 2＝1的两个焦点分别是F 1，F 2，点P 是椭圆上任意一点，则PF 1—→·PF 2—→的取值范围是()A ．[－1,1]B ．[－1,0]C ．[0,1]D ．[－1,2] 答案C解析设F 1为左焦点，则由椭圆方程得F 1(－1,0)，F 2(1,0)， 设P (x ，y )，－2≤x ≤2，∴PF 1—→＝(－1－x ，－y )，PF 2—→＝(1－x ，－y )， 则PF 1—→·PF 2—→＝x 2＋y 2－1＝x 22∈[0,1]．4．设e 是椭圆x 24＋y 2k ＝1的离心率，且e ∈⎝ ⎛⎭⎪⎫12，1，则实数k 的取值范围是()A ．(0,3) B.⎝ ⎛⎭⎪⎫3，163C ．(0,3)∪⎝ ⎛⎭⎪⎫163，＋∞ D ．(0,2)答案C解析当k >4时，c ＝k －4， 由条件知14<k －4k <1，解得k >163； 当0<k <4时，c ＝4－k ， 由条件知14<4－k4<1，解得0<k <3.5．已知F 1，F 2分别是椭圆的左、右焦点，现以F 2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M ，N ，若过F 1的直线MF 1是圆F 2的切线，则椭圆的离心率为() A.3－1 B ．2－ 3 C.22 D.32答案A解析∵过F 1的直线MF 1是圆F 2的切线， ∴∠F 1MF 2＝90°，|MF 2|＝c ， ∵|F 1F 2|＝2c ， ∴|MF 1|＝3c ， 由椭圆定义可得|MF 1|＋|MF 2|＝c ＋3c ＝2a ， ∴椭圆的离心率e ＝21＋3＝3－1.6．(2022·济南模拟)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，且|F 1F 2|＝2，点P (1,1)在椭圆内部，点Q 在椭圆上，则以下说法不正确的是()A ．|QF 1|＋|QP |的最小值为2a －1B ．椭圆C 的短轴长可能为2C ．椭圆C 的离心率的取值范围为⎝ ⎛⎭⎪⎫0，5－12 D ．若PF 1—→＝F 1Q —→，则椭圆C 的长轴长为5＋17 答案B解析由题意可知2c ＝2，则c ＝1，因为点Q 在椭圆上， 所以|QF 1|＋|QF 2|＝2a ，|QF 1|＋|QP |＝2a －|QF 2|＋|QP |， 又－1≤－|QF 2|＋|QP |≤1，所以A 正确； 因为点P (1,1)在椭圆内部，所以b >1,2b >2， 所以B 错误；因为点P (1,1)在椭圆内部，所以1a 2＋1b2<1，即b 2＋a 2－a 2b 2<0，又c ＝1，b 2＝a 2－c 2， 所以(a 2－1)＋a 2－a 2(a 2－1)<0， 化简可得a 4－3a 2＋1>0(a >1)， 解得a 2>3＋52或a 2<3－52(舍去)， 则椭圆C 的离心率e ＝ca<13＋52＝15＋12＝5－12，又0<e <1，所以椭圆C 的离心率的取值范围为⎝ ⎛⎭⎪⎫0，5－12， 所以C 正确；由PF 1—→＝F 1Q —→可得，F 1为PQ 的中点， 而P (1,1)，F 1(－1,0)， 所以Q (－3，－1)， |QF 1|＋|QF 2|＝(－3＋1)2＋(－1－0)2＋(－3－1)2＋(－1－0)2 ＝5＋17＝2a ， 所以D 正确．7.如图是篮球在太阳光照射下的影子，已知篮球的直径为22cm ，现太阳光与地面的夹角为60°，则此椭圆形影子的离心率为________．答案12解析由图可得，椭圆的短轴长2b ＝22⇒b ＝11，2a ＝22sin60°＝2232⇒a ＝223，∴e ＝c a＝1－⎝ ⎛⎭⎪⎫b a 2＝1－34＝12. 8．(2021·全国甲卷)已知F 1，F 2为椭圆C ：x 216＋y 24＝1的两个焦点，P ，Q 为C 上关于坐标原点对称的两点，且|PQ |＝|F 1F 2|，则四边形PF 1QF 2的面积为________． 答案8解析根据椭圆的对称性及|PQ |＝|F 1F 2|可以得到四边形PF 1QF 2为对角线相等的平行四边形，所以四边形PF 1QF 2为矩形．设|PF 1|＝m ，则|PF 2|＝2a －|PF 1|＝8－m ，则|PF 1|2＋|PF 2|2＝m 2＋(8－m )2＝2m 2＋64－16m ＝|F 1F 2|2＝4c 2＝4(a 2－b 2)＝48，得m (8－m )＝8，所以四边形PF 1QF 2的面积为|PF 1|×|PF 2|＝m (8－m )＝8. 9．已知椭圆的长轴长为10，两焦点F 1，F 2的坐标分别为(3,0)和(－3,0)． (1)求椭圆的标准方程；(2)若P 为短轴的一个端点，求△F 1PF 2的面积． 解(1)设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)， 依题意得⎩⎨⎧2a ＝10，c ＝3，因此a ＝5，b ＝4，所以椭圆的标准方程为x 225＋y 216＝1.(2)易知|y P |＝4，又c ＝3，所以12F PF S △＝12|y P |×2c ＝12×4×6＝12.10．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)，焦点F 1(－c ,0)，F 2(c ,0)，左顶点为A ，点E 的坐标为(0，c )，A 到直线EF 2的距离为62b .(1)求椭圆C 的离心率；(2)若P 为椭圆C 上的一点，∠F 1PF 2＝60°，△PF 1F 2的面积为3，求椭圆C 的方程． 解(1)由题意得，A (－a ,0)，EF 2：x ＋y ＝c ， 因为A 到直线EF 2的距离为62b ， 即|－a －c |12＋12＝62b ，所以a ＋c ＝3b ，即(a ＋c )2＝3b 2，又b 2＝a 2－c 2， 所以(a ＋c )2＝3(a 2－c 2)， 所以2c 2＋ac －a 2＝0， 因为离心率e ＝c a， 所以2e 2＋e －1＝0， 解得e ＝12或e ＝－1(舍)，所以椭圆C 的离心率为12.(2)由(1)知离心率e ＝c a ＝12，即a ＝2c ，①因为∠F 1PF 2＝60°，△PF 1F 2的面积为3， 则12|PF 1||PF 2|sin60°＝3， 所以|PF 1||PF 2|＝4，又⎩⎨⎧|PF 1|＋|PF 2|＝2a ，|PF 1|2＋|PF 2|2－2|PF 1||PF 2|cos60°＝(2c )2，所以a 2－c 2＝3，②联立①②得a ＝2，c ＝1，所以b 2＝a 2－c 2＝3， 所以椭圆C 的标准方程为x 24＋y 23＝1.11．(2022·大连模拟)已知椭圆C ：x 216＋y 29＝1的左、右焦点分别是F 1，F 2，左、右顶点分别是A 1，A 2，点P 是椭圆C 上异于A 1，A 2的任意一点，则下列说法正确的是() A ．|PF 1|＋|PF 2|＝4B ．存在点P 满足∠F 1PF 2＝90°C ．直线PA 1与直线PA 2的斜率之积为－916D ．若△F 1PF 2的面积为27，则点P 的横坐标为453答案C解析由椭圆方程知a ＝4，b ＝3，c ＝7， |PF 1|＋|PF 2|＝2a ＝8，A 错误； 当P 在椭圆上、下顶点时， cos∠F 1PF 2＝2a 2－4c 22a 2＝18>0，即∠F 1PF 2最大值小于π2，B 错误； 若P (x ′，y ′)，则1PA k ＝y ′x ′＋4，2PA k ＝y ′x ′－4，有1PA k ·2PA k ＝y ′2x ′2－16，而x ′216＋y ′29＝1，所以－16y ′2＝9(x ′2－16)， 即有1PA k ·2PA k ＝－916，C 正确；若P (x ′，y ′)，△F 1PF 2的面积为27， 即2c ·|y ′|2＝27， 故y ′＝±2，代入椭圆方程得x ′＝±453，D 错误． 12．2021年10月16日，神舟十三号发射圆满成功，人民日报微博发了一条“跨越时空的同一天”，致敬每一代人的拼搏！已知飞船在以地球为焦点的椭圆轨道上绕地球运行时，其运行速度是变化的，速度的变化服从面积守恒规律，即飞船的向径(卫星与地球的连线)在相同的时间内扫过的面积相等．设椭圆的长轴长、焦距分别为2a ,2c ，下列结论不正确的是()A ．飞船向径的取值范围是[a －c ，a ＋c ]B ．飞船在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间C ．飞船向径的最小值与最大值的比值越大，椭圆轨道越扁D ．飞船运行速度在近地点时最大，在远地点时最小答案C解析根据椭圆定义知飞船向径的取值范围是[a －c ，a ＋c ]，A 正确；当飞船在左半椭圆弧上运行时，对应的面积更大，根据面积守恒规律，知在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间，B 正确；a －c a ＋c ＝1－e 1＋e ＝21＋e－1，比值越大，则e 越小，椭圆轨道越圆，C 错误； 根据面积守恒规律，飞船在近地点时向径最小，故速度最大，在远地点时向径最大，故速度最小，D 正确．13．设F 1，F 2分别是椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，若在直线x ＝a 2c 上存在点P ，使线段PF 1的中垂线过点F 2，则椭圆离心率的取值范围是() A.⎝ ⎛⎦⎥⎤0，22 B.⎝ ⎛⎦⎥⎤0，33C.⎣⎢⎡⎭⎪⎫22，1D.⎣⎢⎡⎭⎪⎫33，1 答案D解析设P ⎝ ⎛⎭⎪⎫a 2c ，m ，F 1(－c ,0)，F 2(c ,0)，由线段PF 1的中垂线过点F 2得 |PF 2|＝|F 1F 2|， 即⎝ ⎛⎭⎪⎫a 2c －c 2＋m 2＝2c ， 得m 2＝4c 2－⎝⎛⎭⎪⎫a 2c －c 2＝－a 4c 2＋2a 2＋3c 2≥0， 即3c 4＋2a 2c 2－a 4≥0，得3e 4＋2e 2－1≥0，解得e 2≥13，又0<e <1，故33≤e <1. 14．(2021·浙江)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)，焦点F 1(－c ，0)，F 2(c ,0)(c >0)．若过F 1的直线和圆⎝ ⎛⎭⎪⎫x －12c 2＋y 2＝c 2相切，与椭圆的第一象限交于点P ，且PF 2⊥x 轴，则该直线的斜率是________，椭圆的离心率是________． 答案25555解析设过F 1的直线与圆的切点为M ，圆心A ⎝ ⎛⎭⎪⎫12c ，0，则|AM |＝c ，|AF 1|＝32c ，所以|MF 1|＝52c ， 所以该直线的斜率k ＝|AM ||MF 1|＝c 52c ＝255. 因为PF 2⊥x 轴，所以|PF 2|＝b 2a ，又|F 1F 2|＝2c ，所以k ＝255＝b 2a 2c ＝a 2－c 22ac ＝1－e 22e (0<e <1)，得e ＝55.15．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的短轴长为2，上顶点为A ，左顶点为B ，左、右焦点分别为F 1，F 2，且△F 1AB 的面积为2－32，若点P 为椭圆上的任意一点，则1|PF 1|＋1|PF 2|的取值范围是________． 答案[1,4]解析由已知得2b ＝2，故b ＝1. ∵△F 1AB 的面积为2－32，∴12(a －c )b ＝2－32， ∴a －c ＝2－3，又a 2－c 2＝(a －c )(a ＋c )＝b 2＝1， ∴a ＝2，c ＝3， ∴1|PF 1|＋1|PF 2|＝|PF 1|＋|PF 2||PF 1||PF 2|＝2a|PF 1|(2a －|PF 1|)＝4－|PF 1|2＋4|PF 1|.又2－3≤|PF 1|≤2＋3， ∴1≤－|PF 1|2＋4|PF 1|≤4，∴1≤1|PF 1|＋1|PF 2|≤4， 即1|PF 1|＋1|PF 2|的取值范围为[1,4]．16．已知F 1，F 2是椭圆的两个焦点，P 为椭圆上一点，∠F 1PF 2＝60°.(1)求椭圆的离心率的取值范围；(2)求证：△F 1PF 2的面积只与椭圆的短轴长有关．(1)解不妨设椭圆的方程为x 2a 2＋y 2b 2＝1(a >b >0)，焦距为2c . 在△F 1PF 2中，由余弦定理得，cos60°＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1|·|PF 2|＝(|PF 1|＋|PF 2|)2－2|PF 1|·|PF 2|－|F 1F 2|22|PF 1|·|PF 2|， 即4a 2－2|PF 1|·|PF 2|－4c 22|PF 1|·|PF 2|＝12， 所以|PF 1|·|PF 2|＝4a 2－2|PF 1|·|PF 2|－4c 2，所以3|PF 1|·|PF 2|＝4b 2，所以|PF 1|·|PF 2|＝4b 23. 又因为|PF 1|·|PF 2|≤⎝ ⎛⎭⎪⎫|PF 1|＋|PF 2|22＝a 2， 当且仅当|PF 1|＝|PF 2|时等号成立，所以3a 2≥4(a 2－c 2)， 所以c a ≥12，所以e ≥12. 又因为0<e <1，所以所求椭圆的离心率的取值范围是⎣⎢⎡⎭⎪⎫12，1. (2)证明由(1)可知|PF 1|·|PF 2|＝43b 2， 所12F PF S △＝12|PF 1|·|PF 2|sin 60° ＝12×43b 2×32＝33b 2， 所以△F 1PF 2的面积只与椭圆的短轴长有关．。

加油！有志者事竟成
答卷时应注意事项
１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；
３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；
４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；
５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；
６、卷面要清洁，字迹要清工整，非常重要；
７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好! 经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！。

高考数学椭圆大题技巧一、设点或直线做题一般都需要设点的坐标或直线方程，其中点或直线的设法有很多种。

其中点可以设为等，如果是在椭圆上的点，还可以设为。

一般来说，如果题目中只涉及到唯一一个椭圆上的的动点，这个点可以设为。

还要注意的是，很多点的坐标都是设而不求的。

对于一条直线，如果过定点并且不与y轴平行，可以设点斜式,如果不与x轴平行，可以设，如果只是过定点，可以设参数方程，其中α是直线的倾斜角。

一般题目中涉及到唯一动直线时可以设直线的参数方程。

二、转化条件有的时候题目给的条件是不能直接用或直接用起来不方便的，这时候就需要将这些条件转化一下。

对于一道题来说这是至关重要的一步，如果转化得巧，可以极大地降低运算量。

比如点在圆上可以转化为向量点乘得零，三点共线可以转化成两个向量平行，某个角的角平分线是一条水平或竖直直线则这个角的两条边斜率和是零。

有的题目可能不需要转化直接带入条件解题即可，有的题目给的条件可能有多种转化方式，这时候最好先别急着做题，多想几种转化方法，估计一下哪种方法更简单。

三、代数运算转化完条件就剩算数了。

很多题目都要将直线与椭圆联立以便使用一元二次方程的韦达定理，但要注意并不是所有题目都是这样。

有的题目可能需要算弦长，可以用弦长公式，设参数方程时，弦长公式可以简化为解析几何中有时要求面积，如果O是坐标原点，椭圆上两点A、B坐标分别为和，AB与x轴交于D，则d是点O到AB的距离;第三个公式是我自己推的，教材上没有，解答题慎用。

解析几何中很多题都有动点或动直线。

如果题目只涉及到一个动点时，可以考虑用参数设点。

若是只涉及一个过定点的动直线，题目中又涉及到求长度面积之类的东西，这时设直线的参数方程会简单一些。

在解析几何中还有一种方法叫点差法，设椭圆上两个点的坐标，将两点在椭圆上的方程相减，整理即可得到这两点的中点的横纵坐标与这两点连线的斜率的关系式。

四、能力要求做解析几何题，首先对人的耐心与信心是一种考验。

5.（江苏18）如图，在平面直角坐标系xOy 中，M 、N 分别是椭圆12422=+yx的顶点，过坐标原点的直线交椭圆于P 、A 两点，其中P 在第一象限，过P 作x 轴的垂线，垂足为C ，连接AC ，并延长交椭圆于点B ，设直线PA 的斜率为k（1）当直线PA 平分线段MN ，求k 的值； （2）当k=2时，求点P 到直线AB 的距离d ； （3）对任意k>0，求证：PA ⊥PB解：（1）由题设知，),2,0(),0,2(,2,2--==N M b a 故所以线段MN 中点的坐标为)22,1(--，由于直线PA 平分线段MN ，故直线PA 过线段MN 的中点，又直线PA 过坐标原点，所以.22122=--=k（2）直线PA 的方程2221,42xyy x =+=代入椭圆方程得解得).34,32(),34,32(,32--±=A P x 因此于是),0,32(C 直线AC 的斜率为.032,13232340=--=++y x AB 的方程为故直线.32211|323432|,21=+--=d 因此（3）解法一：将直线PA 的方程kxy =代入2222221,,,421212xyx kkμ+==±++解得记则)0,(),,(),,(μμμμμC k A k P 于是--故直线AB 的斜率为,20kk=++μμμ其方程为,0)23(2)2(),(222222=+--+-=kx k x k x k y μμμ代入椭圆方程得解得223222(32)(32)(,)222k k kx x B kkkμμμμ++==-+++或因此.于是直线PB 的斜率.1)2(23)2(2)23(2222322231kk kk k k kk kkkk -=+-++-=++-+=μμμ因此.,11PB PA k k ⊥-=所以 解法二：设)0,(),,(,,0,0),,(),,(11121212211x C y x A x x x x y x B y x P --≠>>则.设直线PB ，AB 的斜率分别为21,k k 因为C 在直线AB 上，所以.22)()(0111112k x y x x y k ==---=从而1)()(212112121212211+----⋅--⋅=+=+x x y y x x y y k k k k.044)2(12221222122222221222122=--=-+=+--=xx xx y x xx y y因此.,11PB PA k k ⊥-=所以 6.（北京理19）已知椭圆22:14xG y +=.过点（m,0）作圆221x y +=的切线I 交椭圆G 于A ，B 两点.（I ）求椭圆G 的焦点坐标和离心率；（II ）将AB表示为m 的函数，并求AB的最大值.解：（Ⅰ）由已知得,1,2==b a所以.322--=ba c所以椭圆G 的焦点坐标为)0,3(),0,3(-离心率为.23==a c e（Ⅱ）由题意知，1||≥m .当1=m 时，切线l 的方程1=x ，点A 、B 的坐标分别为),23,1(),23,1(-此时3||=AB当m=－1时，同理可得3||=AB当1||>m 时，设切线l 的方程为),(m x k y -=由0448)41(.14),(2222222=-+-+⎪⎩⎪⎨⎧=+-=m k mx k x k y x m x k y 得设A 、B 两点的坐标分别为),)(,(2211y x y x ，则2222122214144,418km k x x km k x x +-=+=+又由l 与圆.1,11||,1222222+==+=+kkm kkm y x 即得相切所以212212)()(||y y x x AB -+-=]41)44(4)41(64)[1(2222242km k k mk k +--++=2.3||342+=m m由于当3±=m 时，,3||=AB所以),1[]1,(,3||34||2+∞--∞∈+=m m m AB .因为,2||3||343||34||2≤+=+=m m m m AB且当3±=m 时，|AB|=2，所以|AB|的最大值为2.7.（辽宁理20）如图，已知椭圆C1的中心在原点O ，长轴左、右端点M ，N 在x 轴上，椭圆C2的短轴为MN ，且C1，C2的离心率都为e ，直线l ⊥MN ，l 与C1交于两点，与C2交于两点，这四点按纵坐标从大到小依次为A ，B ，C ，D ．（I ）设12e =，求BC 与AD 的比值；（II ）当e 变化时，是否存在直线l ，使得BO ∥AN ，并说明理由． 解：（I ）因为C1，C2的离心率相同，故依题意可设 22222122242:1,:1,(0)x y b y x C C a b abaa+=+=>>设直线:(||)l x tt a =<，分别与C1，C2的方程联立，求得2222(,),(,).a b A t a t B t a t ba-- ………………4分当13,,,22A Be b a y y ==时分别用表示A ，B 的纵坐标，可知222||3||:||.2||4B A y b BC AD y a===………………6分（II ）t=0时的l 不符合题意.0t ≠时，BO//AN 当且仅当BO 的斜率kBO 与AN 的斜率kAN 相等，即2222,b a a t a t abtt a--=-解得222221.abe t a a be-=-=---因为2212||,01,1, 1.2e t a e e e-<<<<<<又所以解得所以当202e <≤时，不存在直线l ，使得BO//AN ；当212e <<时，存在直线l 使得BO//AN. ………………12分8.（全国大纲理21） 已知O 为坐标原点，F 为椭圆22:12yC x +=在y 轴正半轴上的焦点，过F 且斜率为-2的直线l 与C 交于A 、B 两点，点P 满足0.OA OB OP ++=（Ⅰ）证明：点P 在C 上；（Ⅱ）设点P 关于点O 的对称点为Q ，证明：A 、P 、B 、Q 四点在同一圆上． 解：（I ）F （0，1），l 的方程为21y x =-+，代入2212yx +=并化简得242210.x x --=…………2分 设112233(,),(,),(,),A x yB x y P x y则122626,,44x x -+==1212122,2()21,2x x y y x x +=+=-++=由题意得3123122(),() 1.2x x x y y y =-+=-=-+=-所以点P 的坐标为2(,1).2--经验证，点P 的坐标为2(,1)2--满足方程221,2yx +=故点P 在椭圆C 上。

椭圆与双曲线性质--（重要结论）清华附中高三数学备课组椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角，则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b +=上，则过0P 的椭圆的切线方程是00221x x y y a b +=.6. 若000(,)P x y 在椭圆22221x y a b+=外 ，则过Po 作椭圆的两条切线切点为P 1、P 2，则切点弦P 1P 2的直线方程是00221x x y y a b +=. 7. 椭圆22221x y a b+= (a ＞b ＞0)的左右焦点分别为F 1，F 2，点P 为椭圆上任意一点12F PF γ∠=，则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8. 椭圆22221x y a b+=（a ＞b ＞0）的焦半径公式：10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点，A 为椭圆长轴上一个顶点，连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点，则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点，A 1P 和A 2Q 交于点M ，A 2P和A 1Q 交于点N ，则MF ⊥NF.11. AB 是椭圆22221x y a b +=的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则22OM AB b k k a ⋅=-，即0202y a x b K AB -=。

12. 若000(,)P x y 在椭圆22221x y a b +=内，则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+.13. 若000(,)P x y 在椭圆22221x y a b +=内，则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角，则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.（内切：P 在右支；外切：P 在左支）5. 若000(,)P x y 在双曲线22221x y a b -=（a ＞0,b ＞0）上，则过0P 的双曲线的切线方程是00221x x y ya b -=.6. 若000(,)P x y 在双曲线22221x y a b-=（a ＞0,b ＞0）外 ，则过Po 作双曲线的两条切线切点为P 1、P 2，则切点弦P 1P 2的直线方程是00221x x y ya b-=.7. 双曲线22221x y a b-=（a ＞0,b ＞o ）的左右焦点分别为F 1，F 2，点P 为双曲线上任意一点12F PF γ∠=，则双曲线的焦点角形的面积为122t2F PF S b co γ∆=.8. 双曲线22221x y a b-=（a ＞0,b ＞o ）的焦半径公式：(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时，10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时，10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点，A 为双曲线长轴上一个顶点，连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点，则MF ⊥NF.10. 过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点，A 1P 和A 2Q 交于点M ，A 2P 和A 1Q 交于点N ，则MF ⊥NF.11. AB 是双曲线22221x y a b -=（a ＞0,b ＞0）的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则0202y a x b K K AB OM =⋅，即0202y a x b K AB =。

椭圆题组一椭圆的定义和标准方程1.(2009·陕西高考)“22y 轴上的椭圆”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件解析：把椭圆方程化成x 21m ＋y 21n ＝1.若m ＞n ＞0，则1n ＞1m ＞0.所以椭圆的焦点在y 轴上．反之， 若椭圆的焦点在y 轴上，则1n ＞1m ＞0即有m ＞n ＞0.故为充要条件．答案：C2．(2009·广东高考)已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为________________． 解析：由题意得2a ＝12，c a ＝32，所以a ＝6，c ＝33，b ＝3.故椭圆方程为x 236＋y 29＝1.答案：x 236＋y 29＝13．(2009·北京高考)椭圆x 29＋y 22＝1的焦点为F 1、F 2，点P 在椭圆上．若|PF 1|＝4，则|PF 2|＝________；∠F 1PF 2的大小为________． 解析：依题知a ＝3，b ＝2，c ＝7. 由椭圆定义得|PF 1|＋|PF 2|＝6， ∵|PF 1|＝4，∴|PF 2|＝2.又|PF 1|＝4，|PF 2|＝2，|F 1F 2|＝27.在△F 1PF 2中由余弦定理可得cos ∠F 1PF 2＝－12，∴∠F 1PF 2＝120°. 答案：2 120°题组二椭圆的几何性质4.(2010·郑州模拟)如图，A 、B 、C 分别为椭圆x a 2＋y b 2＝1(a >b >0)的顶点与焦点，若∠ABC ＝90°，则该椭圆的离心率为 ( )A.－1＋52B ．1－22 C.2－1 D.22解析：∵∠ABC ＝90°，∴|BC |2＋|AB |2＝|AC |2， ∴c 2＋b 2＋a 2＋b 2＝(a ＋c )2，又b 2＝a 2－c 2， ∴e 2＋e －1＝0，e ＝5－12. 答案：A5．如图，有公共左顶点和公共左焦点F 的椭圆Ⅰ与Ⅱ的长半轴 的长分别为a 1和a 2，半焦距分别为c 1和c 2，且椭圆Ⅱ的右顶 点为椭圆Ⅰ的中心．则下列结论不．正确的是 ( ) A ．a 1＋c 1>a 2＋c 2 B ．a 1－c 1＝a 2－c 2 C ．a 1c 2<a 2c 1 D ．a 1c 2>a 2c 1 解析：由题意知，a 1＝2a 2，c 1>2c 2，∴a 1c 2<a 2c 1. ∴不正确的为D. 答案：D6．(2009·浙江高考)已知椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF ⊥x 轴，直线AB 交y 轴于点P .若AP ＝2PB ，则椭圆的离心率是( )A.32 B.22 C.13 D.12解析：由题意知：F (－c,0)，A (a,0)，B (－c ，±b 2a )．∵BF ⊥x 轴，∴AP PB ＝ac.又∵AP ＝2PB ，∴a c ＝2即e ＝c a ＝12.答案：D7．(2009·重庆高考)已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1(－c,0)、F 2(c,0)．若椭圆上存在点P 使a sin ∠PF 1F 2＝csin ∠PF 2F 1，则该椭圆的离心率的取值范围为________．解析：在△PF 1F 2中，由正弦定理知sin ∠PF 1F 2sin ∠PF 2F 1＝|PF 2||PF 1|，∵a sin ∠PF 1F 2＝csin ∠PF 2F 1，∴|PF 2||PF 1|＝a c ＝1e，即|PF 1|＝e |PF 2|. ① 又∵P 在椭圆上，∴|PF 1|＋|PF 2|＝2a ， 将①代入得|PF 2|＝2ae ＋1∈(a －c ，a ＋c )， 同除以a 得，1－e ＜2e ＋1＜1＋e ，得2－1＜e ＜1.答案：(2－1,1)8.过椭圆x 26＋y 25＝1内的一点P (2，－1)的弦，恰好被P 点平分，则这条弦所在的直线方程是( )A ．5x －3y －13＝0B ．5x ＋3y －13＝0C ．5x －3y ＋13＝0D ．5x ＋3y ＋13＝0解析：设过点P 的弦与椭圆交于A 1(x 1，y 1)，A 2(x 2，y 2)两点，则22112222165165x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩，且x 1＋x 2＝4，y 1＋y 2＝－2， ∴23(x 1－x 2)－25(y 1－y 2)＝0， ∴kA 1A 2＝y 1－y 2x 1－x 2＝53.∴弦所在直线方程为y ＋1＝53(x －2)，即5x －3y －13＝0. 答案：A9．过点M (－2,0)的直线m 与椭圆x 22＋y 2＝1交于P 1，P 2两点，线段P 1P 2的中点为P ，设直线m 的斜率为k 1(k 1≠0)，直线OP 的斜率为k 2，则k 1k 2的值为 ( ) A ．2 B ．－2 C.12 D ．－12解析：设直线m 的方程为y ＝k 1(x ＋2)，代入椭圆方程， 得(1＋221k )x 2＋821k x ＋821k －2＝0， 设P 1(x 1，y 1)，P 2(x 2，y 2)，则x 1＋x 2＝－2121812k k +， ∴y 1＋y 2＝k 1(x 1＋x 2＋4)＝22x ，∴P (－2121412k k +，121212k k +)，∴k 2＝－12k 1，∴k 1k 2＝－12. 答案：D10.(2010·广州调研)设椭圆C ：x a 2＋y b 2＝1(a >b >0)的离心率为e ＝22，点A 是椭圆上的一点，且点A 到椭圆C 两焦点的距离之和为4. (1)求椭圆C 的方程；(2)椭圆C 上一动点P (x 0，y 0)关于直线y ＝2x 的对称点为P 1(x 1，y 1)，求3x 1－4y 1的取值范围．解：(1)依题意知，2a ＝4，∴a ＝2. ∵e ＝c a ＝22，∴c ＝2，b ＝a 2－c 2＝ 2.∴所求椭圆C 的方程为x 24＋y 22＝1.(2)∵点P (x 0，y 0)关于直线y ＝2x 的对称点为P 1(x 1，y 1)， ∴⎩⎪⎨⎪⎧y 0－y 1x 0－x 1×2＝－1，y 0＋y 12＝2×x 0＋x 12.解得：x 1＝4y 0－3x 05，y 1＝3y 0＋4x 05.∴3x 1－4y 1＝－5x 0.∵点P (x 0，y 0)在椭圆C ：x 24＋y 22＝1上，∴－2≤x 0≤2，则－10≤－5x 0≤10. ∴3x 1－4y 1的取值范围为．11．已知中心在原点的椭圆C 的一个焦点F (4,0)，长轴端点到较近焦点的距离为1，A (x 1，y 1)，B (x 2，y 2)(x 1≠x 2)为椭圆上不同的两点． (1)求椭圆的方程；(2)若x 1＋x 2＝8，在x 轴上是否存在一点D ，使|DA |＝|DB |？若存在，求出D 点的坐标；若不存在，说明理由．解：(1)由题设知c ＝4，a －c ＝1，∴a ＝5，b ＝3. ∴所求方程为x 225＋y 29＝1.(2)假设存在点D (x 0,0)，由|DA |＝|DB |， 则点D 在线段AB 的中垂线上，又线段AB 的中点为⎝ ⎛⎭⎪⎫4，y 1＋y 22，∴线段AB 的中垂线方程为：y －y 1＋y 22＝－x 1－x 2y 1－y 2(x －4)． ①又2125x ＋219y ＝1，2225x ＋229y ＝1， ∴22221212259x x y y --+＝0. ∴x 1－x 2y 1－y 2＝－259·y 1＋y 28.在①中令y ＝0，∴－y 1＋y 22＝25(y 1＋y 2)72(x 0－4)．∴x 0＝6425，∴存在点D 为⎝⎛⎭⎫6425，0. 12．(理)(2009·山东高考)设椭圆E ：x 2a 2＋y 2b 2＝1(a ，b ＞0)过M (2，2)，N (6，1)两点，O 为坐标原点． (1)求椭圆E 的方程；(2)是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E 恒有两个交点A ，B ，且OA ⊥OB ？若存在，写出该圆的方程，并求|AB |的取值范围；若不存在，说明理由．解：(1)将M 、N 的坐标代入椭圆E 的方程得⎩⎨⎧4a 2＋2b 2＝1，6a 2＋1b 2＝1，解得a 2＝8，b 2＝4，所以椭圆E 的方程为x 28＋y 24＝1.(2)证明：假设满足题意的圆存在，其方程为 x 2＋y 2＝R 2，其中0＜R ＜2.设该圆的任意一条切线AB 和椭圆E 交于A (x 1，y 1)、B (x 2，y 2)两点， 当直线AB 的斜率存在时， 令直线AB 的方程为y ＝kx ＋m ，①将其代入椭圆E 的方程并整理得 (2k 2＋1)x 2＋4kmx ＋2m 2－8＝0. 由根与系数的关系得x 1＋x 2＝－4km2k 2＋1，x 1x 2＝2m 2－82k 2＋1.②因为OA ⊥OB ，所以x 1x 2＋y 1y 2＝0.③把①代入③并整理得(1＋k 2)x 1x 2＋km (x 1＋x 2)＋m 2＝0. 联立②得m 2＝83(1＋k 2)．④因为直线AB 和圆相切，因此R ＝|m |1＋k 2，由④得R ＝263，所以存在圆x 2＋y 2＝83满足题意．当切线AB 的斜率不存在时，易得21x ＝22x ＝83，由椭圆E 的方程得21y ＝22y ＝83，显然OA ⊥OB .综上所述，存在圆x 2＋y 2＝83满足题意．法一：当切线AB 的斜率存在时，由①②④得 |AB |＝(x 1－x 2)2＋(y 1－y 2)2＝1＋k 2(x 1－x 2)2＝1＋k 2(x 1＋x 2)2－4x 1x 2＝1＋k 2(－4km 2k 2＋1)2－4×2m 2－82k 2＋1 ＝4 2k 2＋12k 2＋11－23×k 2＋12k 2＋1. 令t ＝k 2＋12k 2＋1，则12＜t ≤1，因此|AB |2＝32t (1－23t )＝－643(t －34)2＋12.所以323≤|AB |2≤12，即463≤|AB |≤2 3. 当切线AB 的斜率不存在时，易得|AB |＝463，所以463≤|AB |≤2 3.综上所述，存在圆心在原点的圆x 2＋y 2＝83满足题意，且463≤|AB |≤2 3.法二：过原点O 作OD ⊥AB ，垂足为D ，则D 为切点， 设∠OAB ＝θ，则θ为锐角， 且|AD |＝263tan θ，|BD |＝263tan θ.所以|AB |＝263(tan θ＋1tan θ)． 因为2≤|OA |≤22，所以22≤tan θ≤ 2. 令x ＝tan θ，易证：当x ∈[22，1]时， |AB |＝263(x ＋1x)单调递减． 当x ∈时，|AB |＝263(x ＋1x)单调递增． 所以463≤|AB |≤2 3.。

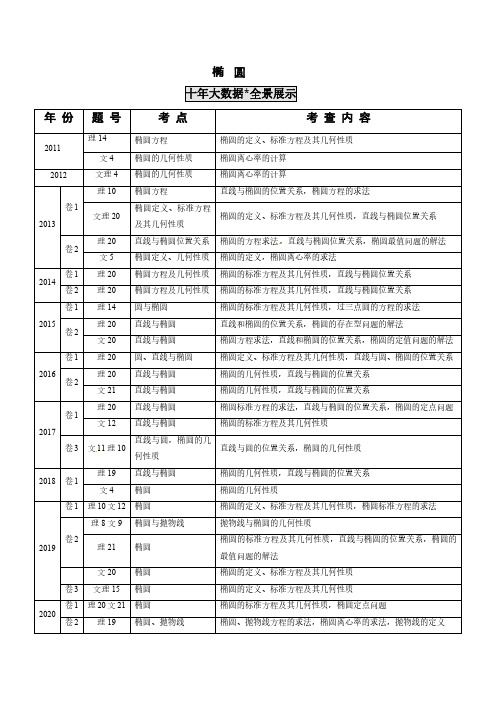
椭圆年份题号考点考查内容2011理14椭圆方程椭圆的定义、标准方程及其几何性质文4椭圆的几何性质椭圆离心率的计算2012文理4椭圆的几何性质椭圆离心率的计算2013卷1理10椭圆方程直线与椭圆的位置关系，椭圆方程的求法文理20椭圆定义、标准方程及其几何性质椭圆的定义、标准方程及其几何性质，直线与椭圆位置关系卷2理20直线与椭圆位置关系椭圆的方程求法，直线与椭圆位置关系，椭圆最值问题的解法文5椭圆定义、几何性质椭圆的定义，椭圆离心率的求法2014卷1理20椭圆方程及几何性质椭圆的标准方程及其几何性质，直线与椭圆位置关系卷2理20椭圆方程及几何性质椭圆的标准方程及其几何性质，直线与椭圆位置关系2015卷1理14圆与椭圆椭圆的标准方程及其几何性质，过三点圆的方程的求法卷2理20直线与椭圆直线和椭圆的位置关系，椭圆的存在型问题的解法文20直线与椭圆椭圆方程求法，直线和椭圆的位置关系，椭圆的定值问题的解法2016卷1理20圆、直线与椭圆椭圆定义、标准方程及其几何性质，直线与圆、椭圆的位置关系卷2理20直线与椭圆椭圆的几何性质，直线与椭圆的位置关系文21直线与椭圆椭圆的几何性质，直线与椭圆的位置关系2017卷1理20直线与椭圆椭圆标准方程的求法，直线与椭圆的位置关系，椭圆的定点问题文12直线与椭圆椭圆的标准方程及其几何性质卷3文11理10直线与圆，椭圆的几何性质直线与圆的位置关系，椭圆的几何性质2018卷1理19直线与椭圆椭圆的几何性质，直线与椭圆的位置关系文4椭圆椭圆的几何性质2019卷1理10文12椭圆椭圆的定义、标准方程及其几何性质，椭圆标准方程的求法卷2理8文9椭圆与抛物线抛物线与椭圆的几何性质理21椭圆椭圆的标准方程及其几何性质，直线与椭圆的位置关系，椭圆的最值问题的解法文20椭圆椭圆的定义、标准方程及其几何性质卷3文理15椭圆椭圆的定义、标准方程及其几何性质2020卷1理20文21椭圆椭圆的标准方程及其几何性质，椭圆定点问题卷2理19椭圆、抛物线椭圆、抛物线方程的求法，椭圆离心率的求法，抛物线的定义考点89椭圆的定义及标准方程1．(2019全国Ⅰ文12)已知椭圆C 的焦点为121,01,0F F -()，()，过F 2的直线与C 交于A ，B 两点．若22||2||AF F B =，1||||AB BF =，则C 的方程为A ．2212x y +=B ．22132x y +=C ．22143x y +=D ．22154x y +=【答案】B【解析】法一：如图，由已知可设2F B n =，则212,3AF n BF AB n ===，由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=．在1AF B △中，由余弦定理推论得22214991cos 2233n n n FAB n n +-∠==⋅⋅．在12AF F △中，由余弦定理得2214422243n n n n +-⋅⋅⋅=，解得32n =．22224,,312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=，故选B ．法二：由已知可设2F B n =，则212,3AF n BF AB n ===，由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=．在12AF F △和12BF F △中，由余弦定理得2221222144222cos 4422cos 9n n AF F n n n BF F n ⎧+-⋅⋅⋅∠=⎨+-⋅⋅⋅∠=⎩，又2121,AF F BF F ∠∠互补，2121cos cos 0AF F BF F ∴∠+∠=，两式消去2121cos cos AF F BF F ∠∠,，得223611n n +=，解得32n =．222243,3,312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=，故选B ．2．(2018高考上海13)设P 是椭圆 ²5x + ²3y =1上的动点，则P 到该椭圆的两个焦点的距离之和为()A ．22B ．23C ．25D ．42【答案】C【解析】由椭圆的定义可知椭圆上任意点P 到两个焦点的距离之和为25a =，故选C ．【考点分析】椭圆的定义，考查考生的识记及基本运算能力．3．(2013广东文)已知中心在原点的椭圆C 的右焦点为(1,0)F ，离心率等于21，则C 的方程是A ．14322=+y x B ．13422=+y x C ．12422=+y x D ．13422=+y x 【答案】D 【解析】∵1,2,3c a b ===D ．4．(2015新课标1理)一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 的正半轴上，则该圆的标准方程为_________．【答案】22325()24-+=x y 【解析】由题意圆过(4,0),(0,2),(0,2)-三个点，设圆心为(,0)a ，其中0a >，由4-=a ，解得32a =，所以圆的方程为22325()24-+=x y ．5．【2019年高考江苏卷】如图，在平面直角坐标系xOy 中，椭圆C ：22221(0)x y a b a b+=>>的焦点为F 1(–1、0)，F 2(1，0)．过F 2作x 轴的垂线l ，在x 轴的上方，l 与圆F 2：222(1)4x y a -+=交于点A ，与椭圆C 交于点D ．连结AF 1并延长交圆F 2于点B ，连结BF 2交椭圆C 于点E ，连结DF 1．已知DF 1=52．(1)求椭圆C 的标准方程；(2)求点E 的坐标．【答案】(1)22143x y +=；(2)3(1,)2E --．【解析】(1)设椭圆C 的焦距为2c ．因为F 1(−1，0)，F 2(1，0)，所以F 1F 2=2，c=1．又因为DF 1=52，AF 2⊥x 轴，所以DF 232==，因此2a=DF 1+DF 2=4，从而a=2．由b 2=a 2−c 2，得b 2=3．因此，椭圆C 的标准方程为22143x y +=．(2)解法一：由(1)知，椭圆C ：22143x y +=，a=2，因为AF 2⊥x 轴，所以点A 的横坐标为1．将x=1代入圆F 2的方程(x−1)2+y 2=16，解得y=±4．因为点A 在x 轴上方，所以A(1，4)．又F 1(−1，0)，所以直线AF 1：y=2x+2．由22()22116y x x y =+-+=⎧⎨⎩，得256110x x +-=，解得1x =或115x =-．将115x =-代入22y x =+，得125y =-，因此1112(,55B --．又F 2(1，0)，所以直线BF 2：3(1)4y x =-．由221433(1)4x y x y ⎧⎪⎪⎨⎪+=-⎩=⎪，得276130x x --=，解得1x =-或137x =．又因为E 是线段BF 2与椭圆的交点，所以1x =-．将1x =-代入3(1)4y x =-，得32y =-．因此3(1,2E --．解法二：由(1)知，椭圆C ：22143x y +=．如图，连结E F 1．因为BF 2=2a ，EF 1+EF 2=2a ，所以EF 1=EB ，从而∠BF 1E=∠B ．因为F 2A=F 2B ，所以∠A=∠B ，所以∠A=∠BF 1E ，从而EF 1∥F 2A ．因为AF 2⊥x 轴，所以EF 1⊥x 轴．因为F 1(−1，0)，由221431x x y ⎧⎪⎨+==-⎪⎩，得32y =±．又因为E 是线段BF 2与椭圆的交点，所以32y =-．因此3(1,2E --．【名师点睛】本小题主要考查直线方程、圆的方程、椭圆方程、椭圆的几何性质、直线与圆及椭圆的位置关系等基础知识，考查推理论证能力、分析问题能力和运算求解能力．考点90椭圆的几何性质6．【2019年高考全国Ⅰ理】已知椭圆C 的焦点为121,01,0F F -()，()，过F 2的直线与C 交于A ，B 两点．若22||2||AF F B =，1||||AB BF =，则C 的方程为A ．2212x y +=B ．22132x y +=C ．22143x y +=D ．22154x y +=【答案】B【解析】法一：如图，由已知可设2F B n =，则212,3AF n BF AB n ===，由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=．在1AF B △中，由余弦定理推论得22214991cos 2233n n n F AB n n +-∠==⋅⋅．在12AF F △中，由余弦定理得2214422243n n n n +-⋅⋅⋅=，解得2n =．22224,,312,a n ab a c∴==∴=∴=-=-=∴所求椭圆方程为22132x y+=，故选B．法二：由已知可设2F B n=，则212,3AF n BF AB n===，由椭圆的定义有121224,22a BF BF n AF a AF n=+=∴=-=．在12AF F△和12BF F△中，由余弦定理得2221222144222cos4422cos9n n AF F nn n BF F n⎧+-⋅⋅⋅∠=⎨+-⋅⋅⋅∠=⎩，又2121,AF F BF F∠∠互补，2121cos cos0AF F BF F∴∠+∠=，两式消去2121cos cosAF F BF F∠∠,，得223611n n+=，解得32n=．22224,,312,a n ab a c∴==∴=∴=-=-=∴所求椭圆方程为22132x y+=，故选B．7．【2019年高考北京理】已知椭圆22221x ya b+=(a＞b＞0)的离心率为12，则A．a2=2b2B．3a2=4b2C．a=2b D．3a=4b【答案】B【解析】椭圆的离心率2221,2ce c a ba===-，化简得2234a b=，故选B．8．【2018·全国Ⅰ文】已知椭圆C：22214x ya+=的一个焦点为(20)，，则C的离心率为A．13B．12C ．22D ．223【答案】C【解析】由题可得2c =，因为24b =，所以2228a b c =+=，即a =，所以椭圆C 的离心率22e ==，故选C ．9．【2018·全国Ⅱ文】已知1F ，2F 是椭圆C 的两个焦点，P 是C 上的一点，若12PF PF ⊥，且2160PF F ∠=︒，则C 的离心率为A ．12-B ．2-C ．312-D 1-【答案】D【解析】在12F PF △中，122190,60F PF PF F ∠=∠=︒，设2PF m =，则12122,c F F m PF ===，又由椭圆定义可知1221)a PF PF m =+=+，则212c c e a a ====，故选D ．10．(2018上海理)设P 是椭圆22153x y +=上的动点，则P 到该椭圆的两个焦点的距离之和为()A ．B ．C ．D ．【答案】C 【解析】由题意25=a ，=a ．由椭圆的定义可知，P 到该椭圆的两个焦点的距离之和为2=aC ．11．【2017·全国Ⅰ文】设A ，B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足∠AMB=120°，则m 的取值范围是A ．(0,1][9,)+∞B ．[9,)+∞C ．(0,1][4,)+∞ D ．[4,)+∞【答案】A【解析】当03m <<时，焦点在x 轴上，要使C 上存在点M 满足120AMB ∠= ，则tan 60ab≥= ，≥，得01m <≤；当3m >时，焦点在y 轴上，要使C 上存在点M 满足120AMB ∠= ，则tan 60ab ≥= ≥，得9m ≥，故m 的取值范围为(0,1][9,)+∞ ，故选A ．12．【2017·浙江卷】椭圆22194x y +=的离心率是()A ．133B ．53C ．23D ．59【答案】B【解析】椭圆22194x y +=的离心率94533e ==，故选B ．13．(2015新课标1文)已知椭圆E 的中心为坐标原点，离心率为12，E 的右焦点与抛物线C ：28y x =的焦点重合，A B 、是C 的准线与E 的两个交点，则AB =A ．3B ．6C ．9D ．12【答案】B 【解析】∵抛物线C ：28y x =的焦点坐标为(2,0)，准线l 的方程为2x =-①，设椭圆E 的方程为22221(0)x y a b a b +=>>，所以椭圆E 的半焦距2c =，又椭圆的离心率为12，所以4,a b ==，椭圆E 的方程为2211612x y +=②，联立①②，解得(2,3),(2,3)A B ---或(2,3),(2,3)A B ---，所以||6AB =，故选B ．14．(2015广东文)已知椭圆222125x y m+=(0m >)的左焦点为()14,0F -，则m =A ．2B ．3C ．4D ．9【答案】B 【解析】由题意得：222549m =-=，因为0m >，所以3m =，故选C ．15．(2014福建文理)设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点，则Q P ,两点间的最大距离是A ．25B ．246+C ．27+D ．26【答案】D 【解析】由题意可设10,sin )Q αα，圆的圆心坐标为(0,6)C ，圆心到Q 的距离为2222||(10cos )(sin 6)509(sin )50523CQ ααα=+-=-+=，当且仅当2sin 3α=-时取等号，所以max max ||||52262PQ CQ r +==≤，所以Q P ,两点间的最大距离是62．16．(2012新课标文理)设1F 、2F 是椭圆E ：)0(12222>>=+b a b y a x 的左、右焦点，P 为直线23a x =上一点，12PF F ∆是底角为o30的等腰三角形，则E 的离心率为A ．21B ．32C ．43D ．54【答案】C 【解析】∆21F PF 是底角为30的等腰三角形221332()224c PF F F a c c e a ⇒==-=⇔==，故选C ．17．【2019·全国Ⅲ文】设12F F ，为椭圆C ：22+13620x y =的两个焦点，M 为C 上一点且在第一象限．若12MF F △为等腰三角形，则M 的坐标为___________．【答案】(15【解析】由已知可得2222236,20,16,4a b c a b c ==∴=-=∴=，11228MF F F c ∴===，∴24MF =．设点M 的坐标为()()0000,0,0x y x y >>，则121200142MF F S F F y y =⋅⋅=△，又122201482415,4152MF F S y =⨯-=∴=△，解得015y =，2201513620x ∴+=，解得03x =(03x =-舍去)，M \的坐标为(15．18．【2019·浙江卷】已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是___________．【解析】方法1：如图，设F 1为椭圆右焦点．由题意可知||=|2OF OM |=c =，由中位线定理可得12||4PF OM ==，设(,)P x y ，可得22(2)16x y -+=，与方程22195x y +=联立，可解得321,22x x =-=(舍)，又点P 在椭圆上且在x 轴的上方，求得315,22P ⎛⎫- ⎪ ⎪⎝⎭，所以15212PFk ==．方法2：(焦半径公式应用)由题意可知|2OF |=|OM |=c =，由中位线定理可得12||4PF OM ==，即342p p a ex x -=⇒=-，从而可求得3,22P ⎛⎫- ⎪ ⎪⎝⎭，所以212PF k ==19．(2012江西文理)椭圆22221(0)x y a b a b+=>>的左、右顶点分别是,A B ，左、右焦点分别是12,F F ．若1121||,||,||AF F F F B 成等比数列，则此椭圆的离心率为_________．【答案】55【解析】由椭圆的性质可知：1AF a c =-，122F F c =，1F B a c =+．又已知1AF ，12F F ，1F B 成等比数列，故2()()(2)a c a c c -+=，即2224a c c -=，则225a c =．故55c e a ==．即椭圆的离心率为55．20．(2011浙江文理)设12,F F 分别为椭圆2213x y +=的左、右焦点，点,A B 在椭圆上，若125F A F B = ；则点A 的坐标是．【答案】(0,1)±【解析】设点A 的坐标为(,)m n ，B 点的坐标为(,)c d．12(F F，可得1()F A m n =+，2()F B c d =，∵125F A F B = ，∴62,55m n c d +==，又点,A B 在椭圆上，∴2213m n +=，2262(5()135m n ++=，解得0,1m n ==±，∴点A 的坐标是(0,1)±．21．【2019年高考全国Ⅱ文】已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点，P 为C 上一点，O为坐标原点．(1)若2POF △为等边三角形，求C 的离心率；(2)如果存在点P ，使得12PF PF ⊥，且12F PF △的面积等于16，求b 的值和a 的取值范围．【答案】(1)1-；(2)4b =，a的取值范围为)+∞．【解析】(1)连结1PF ，由2POF △为等边三角形可知在12F PF △中，1290F PF ∠=︒，2PF c =，1PF =，于是1221)a PF PF c =+=，故C的离心率是1ce a==-．(2)由题意可知，满足条件的点(,)P x y 存在．当且仅当1||2162y c ⋅=，1y y x c x c ⋅=-+-，22221x y a b+=，即||16c y =，①222x y c +=，②22221x y a b+=，③由②③及222a b c =+得422b y c =，又由①知22216y c=，故4b =．由②③得()22222a x c b c=-，所以22c b ≥，从而2222232,a b c b =+≥=故a ≥．当4b =，a ≥P ，所以4b =，a的取值范围为)+∞．22．(2015安徽理)设椭圆E 的方程为()222210x y a b a b+=>>，点O 为坐标原点，点A 的坐标为()0a ，，点B 的坐标为()0b ，，点M 在线段AB 上，满足2BM MA =，直线OM 的斜率为510．(Ⅰ)求E 的离心率e ；(Ⅱ)设点C 的坐标为()0b -，，N 为线段AC 的中点，点N 关于直线AB 的对称点的纵坐标为72，求E 的方程．【解析】(1)由题设条件知，点M 的坐标为21(,)33a b，又10OM k =，从而210b a =，进而得,2a c b ==，故255c e a ==．(2)由题设条件和(I)的计算结果可得，直线AB1y b +=，点N 的坐标为51(,)22b b -，设点N 关于直线AB 的对称点S 的坐标为17(,)2x ，则线段NS 的中点T 的坐标为1517(,4244x b b +-+．又点T 在直线AB 上，且1NS ABk k ⋅=-，从而有151742441712252x b b b b ⎧+-+⎪+=⎨+⎪=⎪⎪⎪⎩，解得3b =，所以b =故椭圆E 的方程为221459x y +=．23．(2013安徽文理)如图，21,F F 分别是椭圆C ：22a x +22by =1(0>>b a )的左、右焦点，A 是椭圆C 的顶点，B 是直线2AF 与椭圆C 的另一个交点，1F ∠A 2F =60°．(Ⅰ)求椭圆C 的离心率；(Ⅱ)已知△A B F 1的面积为403，求a ，b 的值．【解析】(Ⅰ)1216022c F AF a c e a ο∠=⇔=⇔==(Ⅱ)设2BF m =；则12BF a m =-，在12BF F ∆中，22212122122cos120BF BF F F BF F F ο=+-⨯⨯2223(2)5a m m a am m a ⇔-=++⇔=，1AF B ∆面积211133sin 60()10,5,2252S F F AB a a a a c b ο=⨯⨯⨯⇔⨯⨯+⨯=⇔===考点91直线与椭圆的位置关系24．【2018高考全国2理12】已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的左、右焦点，A 是C 的左顶点，点P 在过A 的直线上，12PF F △等腰三角形，12120F F P ∠= ，则C 的离心率为()A ．23B ．12C ．13D ．14【答案】D【解析】试题分析：先根据条件得22PF c =，再利用正弦定理得,a c 关系，即得离心率．试题解析：因为12PF F △为等腰三角形，12212120,2F F P PF F F c ∠=︒==，由AP 斜率为36得，222tan ,sin ,cos PAF PAF PAF ∠=∴∠=∴∠=，由正弦定理得22222sin 221,,4,sin 54sin 3PF PAF c a c e AF APF a c PAF ∠=∴==∴=∴=∠+-∠ ⎪⎝⎭，故选D ．25．(2017新课标Ⅲ文理)已知椭圆C ：22221(0)x y a b a b+=>>的左、右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为()A ．63B ．33C ．23D ．13【答案】A 【解析】以线段12A A 为直径的圆是222x y a +=，直线20bx ay ab -+=与圆相切，所以圆心到直线的距离d a ==，整理为223a b =，即()22222323a a c a c =-⇒=，即2223c a =，63c e a ==，故选A ．26．【2016·新课标1文数】直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为()(A)13(B)12(C)23(D)34【答案】B【解析】如图，在椭圆中，11,,242OF c OB b OD b b ===⨯=，在Rt OFB △中，||||||||OF OB BF OD ⨯=⨯，且222a b c =+，代入解得224a c =，所以椭圆的离心率为12e =，故选B ．27．(2016年全国III 文理)已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点．P 为C 上一点，且PF ⊥x 轴．过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E ．若直线BM 经过OE 的中点，则C 的离心率为A ．13B ．12C ．23D ．34【答案】A【解析】由题意设直线l 的方程为()y k x a =+，分别令x c =-与0x =得||||()FM k a c =-，||||OE k a =，设OE 的中点为H ，由OBH FBM △∽△，得1||||2||||OE OB FM BF =，即||2||()k a a k a c a c=-+，整理得13c a =，所以椭圆离心率为13e =，故选A ．28．(2016江苏理)如图，在平面直角坐标系xOy 中，F 是椭圆()222210x y a b a b +=>>的右焦点，直线2by =与椭圆交于,B C 两点，且90BFC ∠=︒，则该椭圆的离心率是．【答案】3【解析】由题意得(),0F c ，直线2by =与椭圆方程联立可得2b B ⎛⎫ ⎪ ⎪⎝⎭，2b C ⎫⎪⎪⎝⎭，由90BFC ∠=︒可得0BF CF ⋅=，,22b BF c ⎛⎫=+- ⎪ ⎪⎝⎭，,22b CF c ⎛⎫=-- ⎪ ⎪⎝⎭ ，则22231044c a b -+=，由222b a c =-可得223142c a =，则3ce a ===．29．(2015福建文)已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ．短轴的一个端点为M ，直线:340l x y -=交椭圆E 于,A B 两点．若4AF BF +=，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是A．(0,2B ．3(0,]4C．,1)2D ．3[,1)4【答案】A 【解析】设椭圆的左焦点为1F ，半焦距为c ，连结1AF ，1BF ，则四边形1AF BF 为平行四边形，所以11||||||||4AF BF AF BF +=+=，根据椭圆定义，有11||||||||4AF AF BF BF a +++=，所以84a =，解得2a =．因为点M 到直线l ：340x y +=的距离不小于45，即44,155b b ≥≥，所以21b ≥，所以2221,41a c c --≥≥，解得0c <所以02c a <≤，所以椭圆的离心率的取值范围为(0,2．30．(2013新课标1文理)已知椭圆22221(0)x y a b a b+=>>的右焦点为F(3，0)，过点F 的直线交椭圆于A ．B两点．若AB 的中点坐标为(1，－1)，则E 的方程为A ．x 245＋y 236＝1B ．x 236＋y 227＝1C ．x 227＋y 218＝1D ．x 218＋y 29＝1【答案】D 【解析】设1122(,),(,)A x y B x y ，则12x x +=2，12y y +=－2，2211221x y a b +=①2222221x y a b +=②①－②得1212121222()()()()0x x x x y y y y a b +-+-+=，∴AB k =1212y y x x --=212212()()b x x a y y +-+=22b a，又AB k =0131+-=12，∴22b a =12，又9=2c =22a b -，解得2b =9，2a =18，∴椭圆方程为221189x y +=，故选D ．31．【2020年高考上海卷10】已知椭圆22:143x y C +=，直线l 经过椭圆右焦点F ，交椭圆C 于,P Q 两点(点P 在第二象限)，若Q 关于x 轴对称的点为'Q ，且满足'PQ FQ ⊥，则直线l 的方程为．【答案】1y x =-+【解析】由条件可知FQQ ' 是等腰直角三角形，所以直线l 的倾斜角是135 ，所以直线l 的斜率是tan1351=- ，且过点()1,0F ，得到直线l 的方程为()1y x =--，即1y x =-+．故答案为：1y x =-+．32．(2018浙江理)已知点(0,1)P ，椭圆224x y m +=(1m >)上两点A ，B 满足2AP PB = ，则当m =___时，点B 横坐标的绝对值最大．【答案】5【解析】设11(,)A x y ，22(,)B x y ，由2AP PB =得122x x -=，1212(1)y y -=-，所以1223y y -=-，因为A ，B 在椭圆上，所以22114x y m +=，22224x y m +=，所以22224(23)4x y m +-=，所以224x +22324(m y -=，与22224x y m +=对应相减得234m y +=，2221(109)44x m m =--+≤，当且仅当5m =时取最大值．33．(2018浙江文)已知点(0,1)P ，椭圆224x y m +=(1m >)上两点A ，B 满足2AP PB = ，则当m =___时，点B 横坐标的绝对值最大．【答案】5【解析】设11(,)A x y ，22(,)B x y ，由2AP PB = ，得1212212(1)x x y y -=⎧⎨-=-⎩，即122x x =-，1232y y =-．因为点A ，B 在椭圆上，所以222222224(3)44x x m x y m⎧+-=⎪⎪⎨⎪+=⎪⎩，得21344y m =+，所以2222221591(32)(5)444244x m y m m m =--=-+-=--+≤，所以当5m =时，点B 横坐标的绝对值最大，最大值为2．34．(2015浙江文)椭圆22221x y a b +=(0a b >>)的右焦点(),0F c 关于直线by x c=的对称点Q 在椭圆上，则椭圆的离心率是．【答案】22【解析】设左焦点为1F ，由F 关于直线by x c=的对称点Q 在椭圆上，得||||OQ OF =，又1||||OF OF =，所以1F Q QF ⊥，不妨设1||QF ck =，则||QF bk =，1||F F ak =，因此2c ak =，又2a ck bk =+，由以上二式可得22c a k a b c ==+，即c a a b c=+，即22a c bc =+，所以bc =，22e =．35．(2014江西文理)过点(1,1)M 作斜率为12-的直线与椭圆C ：22221(0)x y a b a b+=>>相交于,A B 两点，若M 是线段AB 的中点，则椭圆C 的离心率等于．【答案】22【解析】设11(,)A x y ，22(,)B x y ，分别代入椭圆方程相减得1212121222()()()()0x x x x y y y y a b-+-++=，根据题意有12122,2x x y y +=+=，且121212y y x x -=--，所以22221(02a b +⨯-=，得222a b =，整理222a c =，所以22e =．36．(2014辽宁文)已知椭圆C ：22194x y +=，点M 与C 的焦点不重合，若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则||||AN BN +=．【答案】12【解析】设MN 交椭圆于点P ，连接1F P 和2F P ，利用中位线定理可得AN BN +=122222412F P F P a a +=⨯==．37．(2014江西文)设椭圆()01:2222>>=+b a by a x C 的左右焦点为21F F ，，作2F 作x 轴的垂线与C 交于B A ，两点，B F 1与y 轴相交于点D ，若B F AD 1⊥，则椭圆C 的离心率等于________．【答案】33【解析】由题意可得2(,b A c a ，2(,)b B c a -，由题意可知点D 为1F B 的中点，所以点D 的坐标为2(0,2b a -，由B F AD 1⊥，所以11AD F B k k ⋅=-232b ac =，解得33e =．38．(2014安徽文)设21,F F 分别是椭圆)10(1:222<<=+b by x E 的左、右焦点，过点1F 的直线交椭圆E 于B A ,两点，若x AF BF AF ⊥=211,3轴，则椭圆E 的方程为____．【答案】22312x y +=【解析】由题意得通径22AF b =，∴点B 坐标为251(,)33c B b --将点B 坐标带入椭圆方程得22221()53()13b c b--+=，又221b c =-，解得222313b c ⎧=⎪⎪⎨⎪=⎪⎩，∴椭圆方程为22312x y +=．39．(2013福建文)椭圆)0(1:2222>>=+Γb a by a x 的左、右焦点分别为21,F F ，焦距为c 2．若直线)y x c =+与椭圆Γ的一个交点M 满足12212F MF F MF ∠=∠，则该椭圆的离心率等于．【答案】13-【解析】由题意可知，21F MF ∆中，︒=∠︒=∠︒=∠90,30,60211221MF F F MF F MF ，所以有⎪⎩⎪⎨⎧==+==+12212221222132)2(MF MF a MF MF c F F MF MF ，整理得13-==ac e ，故答案为13-．40．【2020年高考全国Ⅲ文21理数20】已知椭圆()222:10525x y C m m +=<<的离心率为4，,A B 分别为C 的左、右顶点．(1)求C 的方程；(2)若点P 在C 上，点Q 在直线6x =上，且,BP BQ BP BQ =⊥，求△APQ 的面积．【解析】解法一：(1)由c e a =，得2221b e a =-，即21511625m =-，∴22516m =，故C 的方程为221612525x y +=．(2)设点P 的坐标为(,)s t ，点Q 的坐标为(6,)n ，根据对称性，只需考虑0n >的情形，此时55s -<<，504t < ．∵||||BP BQ =，∴有222(5)1s t n -+=+①．又∵BP BQ ⊥，∴50s nt -+=②．又221612525s t +=③．联立①、②、③，可得，312s t n =⎧⎪=⎨⎪=⎩或318s t n =-⎧⎪=⎨⎪=⎩．当312s t n =⎧⎪=⎨⎪=⎩时，(8,1)AP = ，(11,2)AQ =，∴15|82111|22APQ S ==⨯-⨯=△．同理可得，当318s t n =-⎧⎪=⎨⎪=⎩时，52APQ S =△．综上所述，可得APQ △的面积为52．解法二：(1) 222:1(05)25x y C m m +=<<，∴5a =，b m =，根据离心率4c e a ====，解得54m =或54m =-(舍)，∴C 的方程为：22214255x y ⎛⎫ ⎪⎝⎭+=，即221612525x y +=．(2) 点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，过点P 作x 轴垂线，交点为M ，设6x =与x 轴交点为N，根据题意画出图形，如图，||||BP BQ =，BP BQ ⊥，90PMB QNB ∠=∠=︒，又 90PBM QBN ∠+∠=︒，90BQN QBN ∠+∠=︒，∴PBM BQN ∠=∠，根据三角形全等条件“AAS ”，可得：PMB BNQ ≅△△，221612525x y +=，∴(5,0)B ，∴651PM BN ==-=．设P 点为(,)P P x y ，可得P 点纵坐标为1P y =，将其代入221612525x y +=，可得：21612525P x +=，解得：3P x =或3P x =-，∴P 点为(3,1)或(3,1)-，①当P 点为(3,1)时，故532MB =-=， PMB BNQ ≅△△，∴||||2MB NQ ==，可得：Q 点为(6,2)，画出图象，如图，(5,0)A -，(6,2)Q ，可求得直线AQ 的直线方程为：211100x y -+=，根据点到直线距离公式可得P 到直线AQ 的距离为：222311110555125211d ⨯-⨯+===+，根据两点间距离公式可得：()()22652055AQ =++-=，∴APQ 面积为：15555252⨯=．②当P 点为(3,1)-时，故5+38MB ==， PMB BNQ ≅△△，∴||||8MB NQ==，可得：Q 点为(6,8)，画出图象，如图，(5,0)A -，(6,8)Q ，可求得直线AQ 的直线方程为：811400x y -+=，根据点到直线距离公式可得P到直线AQ 的距离为：()22831114055185185811d ⨯--⨯+===+，根据两点间距离公式可得：()()226580185AQ =++-=∴APQ 面积为：1518522185=．综上所述，APQ 面积为：52．41．【2020年高考天津卷18】已知椭圆22221(0)x y a b a b +=>>的一个顶点为(0,3)A -，右焦点为F ，且||||OA OF =，其中O 为原点．(Ⅰ)求椭圆的方程；(Ⅱ)已知点C 满足3OC OF =，点B 在椭圆上(B 异于椭圆的顶点)，直线AB 与以C 为圆心的圆相切于点P ，且P 为线段AB 的中点．求直线AB 的方程．【解析】(Ⅰ) 椭圆()222210x y a b a b+=>>的一个顶点为()0,3A -，∴3b =，由OA OF =，得3c b ==，又由222a b c =+，得2228313a =+=，所以椭圆的方程为221189x y +=．(Ⅱ) 直线AB 与以C 为圆心的圆相切于点P ，所以CP AB ⊥，根据题意可知，直线AB 和直线CP 的斜率均存在，设直线AB 的斜率为k ，则直线AB 的方程为3y kx +=，即3y kx =-，2231189y kx x y =-⎧⎪⎨+=⎪⎩，消去y ，可得()2221120k x kx +-=，解得0x =或21221k x k =+．将21221k x k =+代入3y kx =-，得222126321213k y k k k k =⋅--=++，所以点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭，因为P 为线段AB 的中点，点A 的坐标为()0,3-，所以点P 的坐标为2263,2121kk k -⎛⎫ ⎪++⎝⎭，由3OC OF = ，得点C 的坐标为()1,0，所以直线CP 的斜率为222303216261121CP k kk k k k --+=-+-+=，又因为CP AB ⊥，所以231261k k k ⋅=--+，整理得22310k k -+=，解得12k =或1k =．所以，直线AB 的方程为132y x =-或3y x =-．42．【2019年高考天津理】设椭圆22221(0)x y a b a b+=>>的左焦点为F ，上顶点为B ．已知椭圆的短轴长为4，离心率为55．(1)求椭圆的方程；(2)设点P 在椭圆上，且异于椭圆的上、下顶点，点M 为直线PB 与x 轴的交点，点N 在y 轴的负半轴上．若||||ON OF =(O 为原点)，且OP MN ⊥，求直线PB 的斜率．【解析】(1)设椭圆的半焦距为c ，依题意，524,5c b a ==，又222a b c =+，可得a =，2,b =1c =．所以，椭圆的方程为22154x y +=．(2)由题意，设()()()0,,0P P p M P x y x M x ≠，．设直线PB 的斜率为()0k k ≠，又()0,2B ，则直线PB 的方程为2y kx =+，与椭圆方程联立222,1,54y kx x y =+⎧⎪⎨+=⎪⎩整理得()2245200k x kx ++=，可得22045P kx k =-+，代入2y kx =+得2281045P k y k -=+，进而直线OP 的斜率24510P p y k x k-=-．在2y kx =+中，令0y =，得2M x k=-．由题意得()0,1N -，所以直线MN 的斜率为2k -．由OP MN ⊥，得2451102k k k-⎛⎫⋅-=- ⎪-⎝⎭，化简得2245k =，从而2305k =±．所以，直线PB 的斜率为2305或2305-．43．【2019年高考天津文】设椭圆22221(0)x y a b a b +=>>的左焦点为F ，左顶点为A ，上顶点为B．已知|2||OA OB =(O 为原点)．(1)求椭圆的离心率；(2)设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ，圆C 同时与x 轴和直线l 相切，圆心C 在直线x=4上，且OC AP ∥，求椭圆的方程．【解析】(1)设椭圆的半焦距为c，由已知有2b =，又由222a b c =+，消去b 得22232a a c ⎛⎫=+ ⎪ ⎪⎝⎭，解得12c a =，所以椭圆的离心率为12．(2)由(1)知，2,a c b ==，故椭圆方程为2222143x y c c+=．由题意，(, 0)F c -，则直线l 的方程为3()4y x c =+，点P 的坐标满足22221,433(),4x y c c y x c ⎧+=⎪⎪⎨⎪=+⎪⎩消去y 并化简，得到2276130x cx c +-=，解得1213,7c x c x ==-．代入到l 的方程，解得1239,214y c y c ==-．因为点P 在x 轴上方，所以3,2P c c ⎛⎫ ⎪⎝⎭．由圆心C 在直线4x =上，可设(4, )C t ．因为OC AP ∥，且由(1)知(2 , 0)A c -，故3242ct c c=+，解得2t =．因为圆C 与x 轴相切，所以圆的半径长为2，又由圆C 与l相切，得2=，可得=2c ．所以，椭圆的方程为2211612x y +=．44．【2018高考全国III 文20】(12分)已知斜率为k 的直线l 与椭圆22:143x y C +=交于,A B 两点，线段AB 的中点为()()1,0M m m >．(1)证明：12k <-；(2)设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++=0 ．证明：2FP FA FB =+．【答案】(1)证明见解析；(2)证明见解析．【解析】试题分析：(1)设而不求，利用点差法进行证明；(2)解出m ，进而求出点P 的坐标，得到FP，再由两点间距离公式表示出,FA FB，得到直l 的方程，联立直线与椭圆方程由韦达定理进行求解．试题解析：(1)设11()A x y ，，22()B x y ，，则2211143x y +=，2222143x y +=．两式相减，并由1212=y y k x x --得1212043x x y y k +++⋅=．由题设知1212x x +=，122y y m +=，于是34k m =-．由题设得302m <<，故12k <-．(2)由题意得F(1，0)．设33()P x y ，，则331122(1)(1)(1)(00)x y x y x y -+-+-=，，，，．由(1)及题设得3123()1x x x =-+=，312()20y y y m =-+=-<．又点P 在C 上，所以34m =，从而3(1)2P -，，3||=2FP uur ．于是1||22x FA ==-uur ．同理2||=22x FB -uur ．所以1214()32FA FB x x +=-+=uur uur ，故2FA FB FP +=uur uur uur ．45．【2018高考天津文19】(本小题满分14分)设椭圆22221(0)x y a b a b +=>>的右顶点为A ，上顶点为B．已知椭圆的离心率为3，AB =．(I)求椭圆的方程；(II)设直线():0l y kx k =<与椭圆交于,P Q 两点，l 与直线AB 交于点M ，且点,P M 均在第四象限．若BPM △的面积是BPQ △面积的2倍，求k 的值．【解析】试题分析：(I)由题意结合几何关系可求得3,2a b ==．则椭圆的方程为22194x y +=．(I I)设点P 的坐标为()11,x y ，点M 的坐标为()22,x y ，由题意可得215x x =．易知直线AB 的方程为236x y +=，由方程组236,,x y y kx +=⎧⎨=⎩可得2632x k =+．由方程组221,94,x y y kx ⎧+=⎪⎨⎪=⎩可得1x =215x x =，可得89k =-，或12k =-．经检验 的值为12-．试题解析：(I)设椭圆的焦距为2c ，由已知得2259c a =，又由222a b c =+，可得23a b =．由AB ==3,2a b ==．所以，椭圆的方程为22194x y +=．(II)设点P 的坐标为()11,x y ，点M 的坐标为()22,x y ，由题意，210x x >>，点 的坐标为()11,x y --．由BPM △的面积是BPQ △面积的2倍，可得2PM PQ =，从而()21112x x x x -=--⎡⎤⎣⎦，即215x x =．易知直线AB 的方程为236x y +=，由方程组236,,x y y kx +=⎧⎨=⎩消去y ，可得2632x k =+．由方程组221,94,x y y kx ⎧+=⎪⎨⎪=⎩消去y，可得1x =．由215x x =，可得()532k =+，两边平方，整理得2182580k k ++=，解得89k =-，或12k =-．当89k =-时，290x =-<，不合题意，舍去；当12k =-时，211212,5x x ==，符合题意．所以，k 的值为12-．46．【2018高考江苏18】如图，在平面直角坐标系xOy 中，椭圆C过点12⎫⎪⎭，焦点())12,0,0F F ，圆O 的直径为12F F ．(1)求椭圆C 及圆O 的方程；(2)设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标；②直线l 与椭圆C 交于,A B 两点．若OAB △的面积为l的方程．【解析】试题分析：(1)根据条件易得圆的半径，即得圆的标准方程，再根据点在椭圆上，解方程组可得,a b ，即得椭圆方程；(2)第一问先根据直线与圆相切得一方程，再根据直线与椭圆相切得另一方程，解方程组可得切点坐标．第二问先根据三角形面积得三角形底边边长，再结合①中方程组，利用求根公式以及两点间距离公式，列方程，解得切点坐标，即得直线方程．试题解析：(1)因为椭圆C的焦点为12(),F F -，可设椭圆C 的方程为22221(0)x y a b a b+=>>．又点12在椭圆C 上，2222311,43,a ba b ⎧+=⎪∴⎨⎪-=⎩，解得224,1,a b ⎧=⎪⎨=⎪⎩因此，椭圆C 的方程为2214x y +=．因为圆O 的直径为12F F ，所以其方程为223x y +=．(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>，则22003x y +=，所以直线l 的方程为0000()x y x x y y =--+，即0003x y x y y =-+．由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩，消去y ，得222200004243640()x y x x x y +-+-=．(*) 直线l 与椭圆C 有且只有一个公共点，222222000000()()() 24443640(482)x x y y y x ∴∆=--+-=-=．0000,0,,1x y x y >∴== ．因此，点P的坐标为),1．②OAB △，所以1 2AB OP ⋅=，从而427AB =．设1122,,()(),A x y B x y ，由(*)得001,2x =2221212()()AB y x x y ∴=-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+．22003x y += ，22022016(2)32(1)49x AB x -∴==+，即42002451000x x -+=，解得22005(202x x ==舍去)，则2012y =，因此P的坐标为(22．综上，直线l的方程为y =+．47．【2018高考全国1理19】(本小题满分12分)设椭圆22:12x C y +=的右焦点为F ，过F 的直线l 与C 交于,A B 两点，点M 的坐标为()2,0．(1)当l 与x 轴垂直时，求直线AM 的方程；(2)设O 为坐标原点，证明：OMA OMB ∠=∠．【解析】试题分析：(1)首先根据l 与x 轴垂直，且过点()1,0F ，求得直线l 的方程为1x =，代入椭圆方程求得点A 的坐标为21,2⎛⎫ ⎪ ⎪⎝⎭或21,2⎛⎫- ⎪ ⎪⎝⎭，利用两点式求得直线AM 的方程；(2)分直线l 与x 轴重合、l 与x 轴垂直、l 与x 轴不重合也不垂直三种情况证明，特殊情况比较简单，也比较直观，对于一般情况将角相等通过直线的斜率的关系来体现，从而证得结果．试题解析：(1)由已知得()1,0F ，l 的方程为1x =．由已知可得，点A 的坐标为21,2⎛⎫ ⎪ ⎪⎝⎭或21,2⎛⎫- ⎪ ⎪⎝⎭．所以AM 的方程为222y x =-+222y x =．(2)当l 与x 轴重合时，0OMA OMB ∠=∠=︒．当l 与x 轴垂直时，OM 为AB 的垂直平分线，OMA OMB ∴∠=∠．当l 与x 轴不重合也不垂直时，设l 的方程为(1)(0)y k x k =-≠，1221(,),(,)A y x y x B ，则122,2x x <<，直线MA MB ,的斜率之和为212122MA MB x x y yk k +=+--．由1122,y k k x y k x k =-=-得121212(23()42)(2)MA MB x x x x k k x x kk k -+++=--．将(1)y k x =-代入2212x y +=得2222(21)4220k x k x k +-+-=．2212121333221222422441284,,23()40212121k k k k k k kk x x x x x x k k k k x x k ---+++==∴-++=∴=+++．从而0MA MB k k +=，故MA MB ,的倾斜角互补，OMA OMB ∴∠=∠．综上，OMA OMB ∠=∠．48．【2018高考全国3理20】(12分)已知斜率为k 的直线l 与椭圆22:143x y C +=交于,A B 两点，线段AB 的中点为()()1,0M m m >．(1)证明：12k <-；(2)设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++= 0．证明：,,FA FP FB成等差数列，并求该数列的公差．【解析】试题分析：(1)设而不求，利用点差法进行证明；(2)解出m ，进而求出点P 的坐标，得到FP，再由两点间距离公式表示出,FA FB，得到直l 的方程，联立直线与椭圆方程由韦达定理进行求解．试题解析：(1)设()()1122,,,A x y B x y ，则222211221,14343x y x y +=+=．两式相减，并由1212y y k x x -=-得1212043x x y y k +++⋅=．由题设知12121,22x x y y m ++==，于是34k m=-．①由题设得302m <<，故12k <-．(2)由题意得()1,0F ，设()33,P x y ，则()()()()3311221,1,1,0,0x y x y x y -+-+-=．由(1)及题设得()()31231231,20x x x y y y m =-+==-+=-<．又点P 在C 上，34m ∴=，从而331,,22P FP ⎛⎫-= ⎪⎝⎭ ．于是122xFA ==-= ．同理222x FB =- ，()121432FA FB x x +=-+=∴ ．2FP FA FB =+∴ ，即,,FA FP FB成等差数列．设该数列的公差为d ，则12122d FB FA x x =-=-=②将34m =代入①得1k =-，l ∴的方程为74y x =-+，代入C 的方程，并整理得2171404x x -+=．故121212,28x x x x +==，代入②解得28d=49．【2018高考天津理19】(本小题满分14分)设椭圆22221x x a b +=(a>b>0)的左焦点为F ，上顶点为B ．已知椭圆的离心率为53，点A 的坐标为(,0)b ，且FB AB ⋅=．(I)求椭圆的方程；(II)设直线l ：(0)y kx k =>与椭圆在第一象限的交点为P ，且l 与直线AB 交于点Q ．若4AQ AOQ PQ=∠(O 为原点)，求k 的值．【解析】试题分析：(Ⅰ)由题意结合椭圆的性质可得,32a b ==．则椭圆的方程为22194x y +=．(Ⅱ)设点P 的坐标为()11,x y ，点Q 的坐标为()22,x y ．由题意可得1259y y =．由方程组22{ 194y kx x y =+=，，可得1y =．由方程组{20y kx x y =+-=，，可得221ky k =+．据此得到关于k 的方程，解方程可得k 的值为12或1128试题解析：(Ⅰ)设椭圆的焦距为2c ，由已知有2259c a =，又由222a b c =+，可得23a b =．由已知可得，FB a =，AB =，由FB AB ⋅=，可得6ab =，从而,32a b ==，∴椭圆的方程为22194x y +=．(Ⅱ)设点P 的坐标为()11,x y ，点Q 的坐标为()22,x y ．由已知有120y y >>，故12PQ sin AOQ y y ∠=-．又2y AQ sin OAB =∠ ，而∠OAB=π4，故2AQ =．由sin 4AQ AOQ PQ =∠，可得1259y y =．由方程组22,194y kx x y =⎧⎪⎨+=⎪⎩消去x，可得1y =易知直线AB 的方程为20x y +-=，由方程组{20y kx x y =+-=，，消去x ，可得221ky k =+．由1259y y =，可得()15k +=，两边平方，整理得25650110k k -+=，解得12k =，或1128k =，k ∴的值为12或1128．50．(2017天津文)已知椭圆22221(0)x y a b a b+=>>的左焦点为,()0F c -，右顶点为A ，点E 的坐标为(0,)c ，EFA △的面积为22b ．(Ⅰ)求椭圆的离心率；(Ⅱ)设点Q 在线段AE 上，3||2FQ c =，延长线段FQ 与椭圆交于点P ，点M ，N 在x 轴上，PM QN ∥，且直线PM 与直线QN 间的距离为c ，四边形PQNM 的面积为3c ．(i)求直线FP 的斜率；(ii)求椭圆的方程．【解析】(Ⅰ)设椭圆的离心率为e ．由已知，可得21()22b c a c +=．又由222b ac =-，可得2220c ac a +-=，即2210e e +-=．又因为01e <<，解得12e =．所以，椭圆的离心率为12．(Ⅱ)(ⅰ)依题意，设直线FP 的方程为(0)x my c m =->，则直线FP 的斜率为1m．由(Ⅰ)知2a c =，可得直线AE 的方程为12x yc c+=，即220x y c +-=，与直线FP 的方程联立，可解得(22)3,22m c c x y m m -==++，即点Q 的坐标为(22)3(,)22m c cm m -++．。

2011年普通高等学校招生全国统一考试理科数学第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)复数212ii+-的共轭复数是（ ） （A ）35i - （B ）35i （C ）i - （D ）i（2）下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（ ）（A ）3y x = (B) 1y x =+ （C ）21y x =-+ (D) 2x y -= （3）执行右面的程序框图，如果输入的N 是6，那么输出的p 是（ ） （A ）120 （B ）720 （C ）1440 （D ）5040（4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（ ）（A ）13 （B ）12 （C ）23 （D ）34（5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=（ ）（A ）45- （B ）35- （C ）35 （D ）45（6）在一个几何体的三视图中，正视图和俯视图如右图所示， 则相应的侧视图可以为（ ）（7）设直线L 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，L 与C 交于A ,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（ ）（A ） （B （C ）2 （D ）3（8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为（ ）（A ）-40 （B ）-20 （C ）20 （D ）40（9）由曲线y =，直线2y x =-及y 轴所围成的图形的面积为 （ ）（A ）103 （B ）4 （C ）163（D ）6 （10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题 （ ）12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是 （ ） （A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P （11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（ ） （A ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 （B ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 （C ）()f x 在0,2π⎛⎫⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 (12)函数11-y x=的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于（ ） （A ）2 (B) 4 (C) 6 (D)8第Ⅱ卷本卷包括必考题和选考题两部分。

高考椭圆的知识点高考数学中关于椭圆的知识点主要包括以下几个方面：1、椭圆的定义：椭圆是平面内到两个固定点（焦点）的距离之和为定值（大于两焦点间距离）的所有点的轨迹。

2、椭圆的标准方程：当焦点在x轴上时，标准方程为：(x-h)^2/a^2 + (y-k)^2/b^2 = 1，其中(a > b > 0)，(h, k)是椭圆中心的坐标。

当焦点在y轴上时，标准方程为：(y-k)^2/a^2 + (x-h)^2/b^2 = 1，同样a>b>0，(h, k)为椭圆中心坐标。

3、参数形式：椭圆还可以用参数方程表示，例如：x = a * cosθ + h，y = b * sinθ + k。

4、基本性质：长半轴a和短半轴b决定了椭圆的形状和大小，离心率e = c/a（c为焦距的一半），范围在0 < e < 1。

椭圆的面积公式S = πab。

焦点与长轴、短轴的关系：焦距|F1F2| = 2c，长轴长2a，短轴长2b，有关系式a^2 = b^2 + c^2。

5、几何性质：焦点弦性质、通径（过焦点垂直于长轴的弦）、共轭直径等。

与圆锥曲线相关的光学性质，如反射定律等。

6、解题方法：利用定义求解有关焦点、焦半径等问题。

根据给定条件确定椭圆的标准方程，通常采用待定系数法。

计算椭圆上的点与焦点或准线的距离，以及运用离心率解决相关问题。

7、离心率的应用：离心率常作为约束条件出现在题目中，用来求解椭圆方程或者判断椭圆形状。

8、交点问题：椭圆与其他图形（直线、圆、抛物线等）相交时求交点坐标及相关长度、面积计算。

高考中的椭圆题目类型多样，包括但不限于以上知识点，要求考生能够灵活运用椭圆的基本概念、性质及方程来解答不同难度的问题。

一、选择题（每题5分，共50分）1. 设椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（$a>b>0$），若点$P(m,n)$在椭圆上，则下列说法正确的是（）A. $m^2+n^2=a^2-b^2$B. $m^2+n^2=a^2+b^2$C. $m^2+n^2=a^2$D. $m^2+n^2=b^2$2. 已知椭圆的离心率为$\frac{1}{2}$，且经过点$(2,3)$，则椭圆的方程为（）A. $\frac{x^2}{16}+\frac{y^2}{12}=1$B. $\frac{x^2}{9}+\frac{y^2}{4}=1$C. $\frac{x^2}{4}+\frac{y^2}{9}=1$D. $\frac{x^2}{12}+\frac{y^2}{16}=1$3. 已知椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$，则椭圆的焦距为（）A. 2B. 2$\sqrt{2}$C. 2$\sqrt{3}$D. 44. 椭圆$\frac{x^2}{4}+\frac{y^2}{9}=1$的左、右焦点分别为$F_1$、$F_2$，点$P$在椭圆上，且$\angle F_1PF_2=60^\circ$，则$|PF_1|$的取值范围是（）A. $[1,2]$B. $[2,3]$C. $[3,4]$D. $[4,5]$5. 椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的右顶点为$A$，左焦点为$F$，则直线$AF$的斜率为（）A. $\frac{3}{2}$B. $\frac{2}{3}$C. $\frac{1}{2}$D. $\frac{1}{3}$二、填空题（每题5分，共50分）1. 已知椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（$a>b>0$），若椭圆的离心率为$\frac{1}{2}$，则$\frac{b^2}{a^2}$的值为______。

椭圆的定义及标准方程主标题：椭圆的定义及标准方程副标题：•为学生详细的分析椭圆的定义及标准方程的高考考点、命题方向以及规律总结。

关键词：椭圆，椭圆的定义，椭圆标准方程难度：2重要程度：5考点剖析：1.理解椭圆的定义；2.掌握椭圆的标准方程及其儿何性质，命题方向：1. 从考查内容看，椭闘的定义、标准方程和几何性质是高考的重点，其中直线与椭闘位置关 系的问题更是高考考杏的热点•2. 从考查形式看，对定义、标准方程和儿何性质的考查常以选择题、填空题的形式出现， 属中档题；•直线・圆锥曲线位置关系的问题以及与向量、不等式、方程结合的问题常以解 答题的形式出现，具有•一定的综合性和难度.规律总结：椭関的定义及标准方程规律总结：—•条规律：椭圆焦点位置与#,戸系数间的关系：给出椭圆方程一+—=1时，椭圆的焦点在x 轴上o m>n>0；椭I 员I 的焦点在y 轴上0刀〉刃〉0. in n两种方法：求椭圆方程的两种方法：(1)定义法一：根据椭圆定义，确定必，方2的值，再结合焦点位置, 直接写出椭圆方程；(2)待定系数法：根据椭圆焦点是在才轴还是y 轴上，设出相应形式的标准方程，然后根据 条件确定关于日，b, c 的方程组,解出2,方2,从而写出椭圆的标准方程.知识梳理1. 椭圆的概念在平面内到两定点竹、仇的距离的和等于常数(大于冶纫)的点的轨迹(或集合)叫蟲 圆.这两定点叫做椭圆的焦点.，两焦点间的距离叫做焦距 .集合 P={^\MF i \ + \MF 2\=2a\9 |^/^|=2c,其中 a>0, c>0,且日,c 为常数：⑴若2d>2c ,则集合户为椭圆； (2) 若2d = 2c ,则集合戶为线段； (3) 若 莎<2c,则集合P 为空集. 2. 椭圆的标准方程和儿何性质 标准方程2X 2 a=1 （日>方>0）高效能学习的十大学习方法方法一：目标激励法成就天才的必备素质就是远大恵向，明确目标，勤奋刻苦，持Z以恒，百折不挠。

1、答案：B解析：从31.5到43.5共有22，所以221663P ==。

2、答案：A解析：12i i i i i-+=--=-3、答案：B解析：A 答案还有异面或者相交，C 、D 不一定 4、答案D解析：BA CD EF BA AF EF BF EF CE EF CF ++=++=+=+=5、答案：B解析：连续必定有定义，有定义不一定连续。

6.答案：C 解析：由题意正弦定理22222222211c o s23b c a a b c bc b c a bc A A bc π+-≤+-⇒+-≥⇒≥⇒≥⇒<≤ 7．答案：A解析：由反函数的性质原函数的值域为反函数的定义域，原函数的定义域为反函数的值域。

当10,0()1,122xx y ><<⇒<<，故选A 8.B 解析：由已知知128,28,n n n b n a a n +=--=-由叠加法21328781()()()642024603a a a a a a a a -+-++-=-+-+-++++=⇒==9.答案：C解析：由题意设派甲，乙,x y 辆，则利润450350z x y =+，得约束条件08071210672219x y x y x y x y ≤≤⎧⎪≤≤⎪⎪+≤⎨⎪+≥⎪+≤⎪⎩画出可行域在12219x y x y +≤⎧⎨+≤⎩的点75x y =⎧⎨=⎩代入目标函数4900z =10.答案：A解析：由已知的割线的坐标(4,114),(2,21),2a a K a ---=-,设直线方程为(2)y a x b =-+，则223651(2)b a =+-又2564(2,9)(2)y x ax b a y a x b⎧=+-⇒=-⇒=⇒--⎨=-+⎩11.答案：D 解析：由题意1(2)()3f x f x +=,在[22,2]n n -上，2111()111331,()1,2,(),3,()()()lim 1333213nn n n nn f x n f x n f x a S S --=======⇒=⇒=-12.答案：D基本事件：26(2,1),(2,3),(2,5),(4,1),(4,5),(4,3),3515n C ==⨯=由其中面积为1的平行四边形的个数(2,3)(4,5);(2,1)(4,3);(2,1)(4,1)其中面积为2的平行四边形的个数为(2,3)(2,5);(2,1)(2,3)其中面积为3的平行四边形的个数(2,3)(4,3);(2,1)(4,5)其中面积为4的平行四边形的个数(2,1)(2,5);(4,1)(4,3);(4,3)(4,5)其中面积为5的平行四边形的个数(2,3),(4,1);(2,5)(4,5)；其中面积为7的平行四边形的个数(2,5),(4,3)其8的平行四边形的个数(4,1)(4,5)其中面积为9的平行四边形的个数(2,5),(4,1) 二、填空题：本大题共4小题，每小题4分，共16分. 13.答案：20-解析：12111(lg lg 25)100lg20410010--÷=÷=- 14.答案：565解析：8,6,10a b c ===，点P 显然在双曲线右支上，点P 到左焦点的距离为14，所以1455645c d d a ==⇒=15.答案：22R π 解析：22222max 224()S r R rrR r Sππ=⋅-=-⇒侧侧时，22222222R r R r r r R =-⇒=⇒=，则222422R R R πππ-=16.答案：②③④解析 ：①错，12x x =± ，②③④正确。

1. 已知椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（$a>b>0$），若C关于x轴对称，则下列哪个选项是正确的？A. $a>b$B. $a<b$C. $a=b$D. 无法确定答案：A解析：由于椭圆C关于x轴对称，所以其方程中$x^2$的系数大于$y^2$的系数，即$a>b$。

2. 椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（$a>b>0$），若点P （x0，y0）在椭圆C上，则下列哪个选项是正确的？A. $x_0^2+y_0^2=a^2$B. $x_0^2+y_0^2=b^2$C. $\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$D. $\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}=1$答案：C解析：点P在椭圆C上，所以满足椭圆的方程，即$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$。

3. 椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（$a>b>0$），若直线l的方程为$y=kx+b$，且l与椭圆C相切，则下列哪个选项是正确的？A. $k^2=\frac{a^2}{b^2}$B. $k^2=\frac{b^2}{a^2}$C. $k^2=\frac{a^2+b^2}{a^2b^2}$D. $k^2=\frac{a^2-b^2}{a^2b^2}$答案：A解析：由于直线l与椭圆C相切，所以它们只有一个交点，即判别式$\Delta=0$。

根据直线与椭圆的位置关系，可得$\Delta=\frac{b^2k^2-a^2b^2}{a^2}=0$，解得$k^2=\frac{a^2}{b^2}$。

4. 椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（$a>b>0$），若椭圆C的离心率e满足$e^2=\frac{c^2}{a^2}$，则下列哪个选项是正确的？A. $e^2=\frac{a^2-b^2}{a^2}$B. $e^2=\frac{a^2+b^2}{a^2}$C. $e^2=\frac{b^2}{a^2}$D. $e^2=\frac{a^2}{b^2}$答案：A解析：椭圆的离心率e定义为$\frac{c}{a}$，其中c是焦点到中心的距离。

高考椭圆的知识点椭圆是高中数学中常见的一个几何图形，也是高考数学中的重点内容之一。

下面将详细介绍高考椭圆的知识点。

一、椭圆的定义椭圆可以定义为平面上到两个定点的距离之和等于常数的点的轨迹。

这两个定点称为焦点，两个焦点之间的距离称为焦距。

椭圆的形状由焦距和常数决定。

二、椭圆的基本要素1. 焦点和直径：椭圆有两个焦点，焦点的位置决定了椭圆的形状和大小。

椭圆的长轴是通过两个焦点的直线，它的长度称为椭圆的长径；椭圆的短轴是垂直于长轴的直线，它的长度称为椭圆的短径。

2. 中心：椭圆的中心是长轴和短轴的交点，也是椭圆的对称中心。

3. 长径和短径：椭圆的中心到椭圆上任意一点的距离称为椭圆半径，椭圆的长径是指长轴的一半，短径是指短轴的一半。

4. 离心率：椭圆的离心率是一个0到1之间的实数，它表示椭圆的扁平程度。

离心率为0时，椭圆退化为一个点；离心率为1时，椭圆变为一条直线。

三、椭圆的方程1. 标准方程：椭圆的标准方程可以表示为（x-h）^2/a^2 + （y-k）^2/b^2 = 1，其中(h, k)是椭圆的中心坐标，a是长轴的一半，b是短轴的一半。

2. 参数方程：椭圆的参数方程可以表示为x = h + a*cosθ，y = k + b*sinθ，其中(h, k)是椭圆的中心坐标，a是长轴的一半，b是短轴的一半，θ是参数。

四、椭圆的性质1. 对称性：椭圆具有两个对称轴，分别是长轴和短轴，以中心为对称中心。

2. 焦点性质：椭圆上任意一点到两个焦点的距离之和等于常数（焦距）。

3. 切线性质：椭圆上任意一点的切线和从该点出发指向焦点的直线的夹角等于切线斜率的相反数。

4. 弦长性质：椭圆上任意一条弦的长度等于焦点到弦中点的距离与焦距之和。

5. 面积性质：椭圆的面积可以用公式S = πab表示，其中a是长轴的一半，b是短轴的一半。

五、椭圆在高考中的应用1. 椭圆的参数方程可以用来描述物体在椭圆轨道上的运动。

2. 椭圆的性质可以应用于建筑结构中的设计和力学分析。