应用基本不等式求最值)

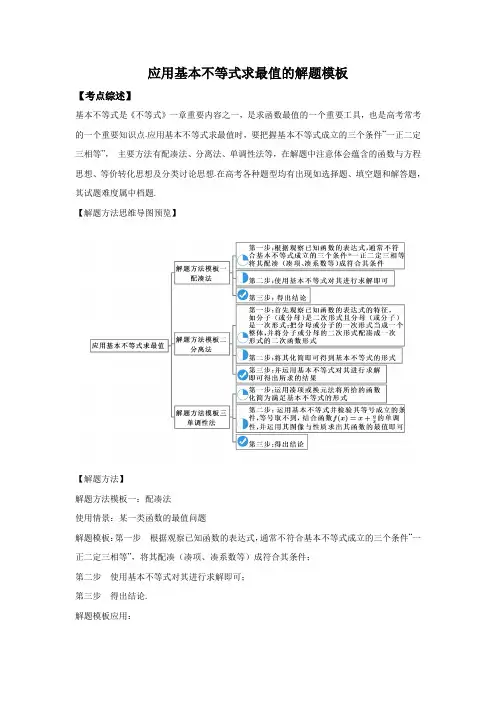
利用基本不等式求最值的技巧基本不等式是解决最值问题的一个重要工具。

它可以将一个复杂的问题简化为一个简单的不等式，从而帮助我们找到最值。

在本篇文章中，我将分享一些利用基本不等式求最值的技巧。

首先，我们回顾一下基本不等式的定义。

对于任意的正实数a和b，有以下两个基本不等式：1. 算术平均数与几何平均数不等式（AM-GM不等式）：对于任意的正实数a和b，有a+b/2≥√(ab)。

这个不等式可以表示为(a+b)/2≥√(ab)。

当且仅当a=b时，等号成立。

2.平方平均数与算术平均数不等式（QM-AM不等式）：对于任意的正实数a和b，有√(a²+b²)/2≥(a+b)/2、这个不等式可以简化为√(a²+b²)≥(a+b)/2、当且仅当a=b时，等号成立。

现在，让我们来看一些具体的例子，以说明如何利用基本不等式求最值。

例子1：求证x³+y³+z³≥3xyz，其中x、y和z是正实数。

解：根据AM-GM不等式，我们有x³/3+y³/3+z³/3≥√(x³y³z³)。

将等式两边乘以3，得到x³+y³+z³≥3√(x³y³z³)。

由于x、y和z是正实数，所以xyz>0，可以得到√(x³y³z³)≥xyz。

因此，我们有x³+y³+z³≥3xyz。

例子2：已知x+y+z=1，求证xy+yz+zx≤1/3解：根据AM-GM不等式，我们有x+y/2≥√(xy)和y+z/2≥√(yz)。

将这两个不等式相加，得到x+y/2+y+z/2≥√(xy)+√(yz)。

根据算术平均数与几何平均数不等式，有(x+y/2+y+z/2)/2≥(√(xy)+√(yz))/2根据已知条件x+y+z=1，对等式两边进行化简，可以得到(x+y/2+y+z/2)/2=(x+y+z)/2=1/2因此，我们有1/2≥(√(xy)+√(yz))/2将不等式两边乘以2，得到1≥√(xy)+√(yz)。

用基本不等式求最值时满足的条件
1 基本不等式
基本不等式是数学中一种重要的凸优化方法，它可以用来寻找满足特定条件的最优值。

它的原理是，当一组约束条件下的函数具有一个有限的唯一最小值时，可以用基本不等式求得这个最小值。

2 满足条件
要用基本不等式求最值，必须满足以下条件：首先，目标函数要是一个有界凸函数，即无论怎么变化，函数的值都不会大于给定的上限值。

其次，这个函数可用一些等式或不等式约束，以便将不合理的解从解集中排除。

最后，通过不断迭代，使函数达到最小值。

3 不等式约束
基本不等式的约束也分为两类：弱不等式约束和强不等式约束。

弱不等式约束要求函数值不能越界，但是可以接近越界；而强不等式约束要求函数值不可以接近越界。

此外，还有自变量约束，让计算机知道自变变量必须在一定的范围内，以便做出正确的计算决策。

4 迭代求最小值
根据基本不等式的原理，只要函数满足相关约束条件，就可以使用迭代法不断地求取最小值。

迭代的思路是，每次计算某点的函数值后，就会将这个点的解替换成较小的函数值，试图找到更小的解。

由
此可见，使用基本不等式求最值，必须要有正确的函数和约束条件，才能得到合理的最优值。

一、 在用基本不等式求函数的最值时，应具备三个条件：一正二定三取等。

① 一正：函数的解析式中，各项均为正数；② 二定：函数的解析式中，含变数的各项的和或积必须有一个为定值；③ 三取等：函数的解析式中，含变数的各项均相等，取得最值。

二、，且，为定值，则，等号当且仅当时成立.，且，为定值，则，等号当且仅当时成立.练习题：1. 已知a ，b 都是正数，则 a ＋b 2、a 2＋b 22的大小关系是 。

3.若,求的最大值.4 设1->x ，则函数461y x x =+++的最小值是 。

5.已知正数x y 、满足3xy x y =++，则xy 的范围是 。

6. 给出下列命题：①a,b 都为正数时,不等式a+b ≥才成立。

②y=x+1x的最小值为2。

③y=sinx+2sin x(02x π<≤)的最小值为.④当x>0时，y=x 2+16x ≥,当x 2＝16x 时，即x=16,y 取最小值512。

其中错误的命题是 。

7.已知正数y x ,满足12=+y x ,求yx11+的最小值有如下解法：解：∵12=+y x 且0,0>>y x . ∴242212)2)(11(11=⋅≥++=+xy xyy x yxy x∴24)11(min =+yx.判断以上解法是否正确？说明理由；若不正确，请给出正确解法． 8.已知141ab+=，且a>0，b>0,求a+b 最小值。

9.已知x ＞0，函数y ＝2－3x －4x 有 值是 .10．已知：226x y +=， 则2x y+的最大值是＿＿＿11.函数xx y4+=的值域是 。

12．某单位决定投资3 200元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米长造价40元，两侧墙砌砖，每米造价45元，屋顶每平方米造价20元，试计算： （1）仓库面积S 的最大允许值是多少？（2）为使S 达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？13、若实数x ，y 满足224x y +=，求xy 的最大值14、若x>0,求9()4f x x x=+的最小值; 15、若0x <，求1y x x=+的最大值16、若x<0,求9()4f x x x=+的最大值 17、求9()45f x x x =+-(x>5)的最小值.18、若x ，y R +∈，x+y=5，求xy 的最值 19、若x ，y R +∈，2x+y=5，求xy 的最值20、已知直角三角形的面积为4平方厘米，求该三角形周长的最小值 21、求1 (3)3y x x x =+>-的最小值.22、求(5) (05)y x x x =-<<的最大值. 23、求1(14)(0)4y x x x =-<<的最大值。

利用基本不等式求最值的类型及方法基本不等式是利用数学推理和不等式性质来求解最值问题的一种方法。

在解决最值问题时，运用基本不等式能够有效地简化计算过程，并找到最优解。

下面将介绍几种常见的类型和方法。

1.求函数最值：假设已知一个函数f(x)，要求其在一些区间[a,b]上的最大值或最小值。

可以利用基本不等式结合导数来求解。

首先，对函数f(x)求导得到极值点，即f'(x)=0的解，然后利用基本不等式推论得到最值。

2. 求二次函数最值：对于一个二次函数f(x) = ax² + bx + c(a≠0)，可以通过求解二次函数的顶点来确定其最值。

二次函数的最大值或最小值在顶点处取得。

通过计算出二次函数的顶点坐标，可以得到函数的最值。

3.求几何问题最值：在几何问题中，常常需要求解最长距离、最短路径等最值问题。

对于空间几何问题，可以利用三角不等式和柯西-施瓦茨不等式等基本不等式进行推导，找到满足条件的最优解。

4.求代数问题最值：在代数问题中，常常需要求解最大值或最小值。

例如，求解多项式函数的最值、线性规划等问题。

可以利用基本不等式来对多项式进行分解和化简，从而找到最大值或最小值。

5.求概率问题最值：在概率问题中，需要求解满足一定概率条件的最值问题。

例如，已知一些事件发生的概率，求解最大化或最小化概率的问题。

通过利用基本不等式可以对概率进行推导和计算，找到满足条件的最值。

在使用基本不等式求解最值问题时，需要注意以下几个基本方法：1.将问题抽象化：将具体的问题转化为符号运算和数学模型，将需要求解的最值问题用数学语言表达出来。

2.应用基本不等式：根据不同的问题类型，运用相应的基本不等式进行推导和计算。

常用的基本不等式有柯西-施瓦茨不等式、均值不等式、三角不等式等。

3.约束条件转化：将约束条件转化为等式或不等式，以便进行运算。

4.求解极值点：通过对函数求导，找到函数的极值点。

利用基本不等式结合导数求解最值问题。

重难点第一讲利用基本不等式求最值8大题型【命题趋势】基本不等式是高考热点问题，是常考常新的内容，是高中数学中一个重要的知识点，在解决数学问题中有着广泛的应用，尤其是在函数最值问题中。

题型通常为选择题与填空题，但它的应用范围几乎涉及高中数学的所有章节，它在高考中常用于大小判断、求最值、求最值范围等。

在高考中经常考察运用基本不等式求函数或代数式的最值，具有灵活多变、应用广泛、技巧性强等特点。

在复习中切忌生搬硬套，在应用时一定要紧扣“一正二定三相等”这三个条件灵活运用。

第1天认真研究满分技巧及思考热点题型【满分技巧】利用基本不等式求最值的方法1、直接法：条件和问题间存在基本不等式的关系2、配凑法：凑出“和为定值”或“积为定值”，直接使用基本不等式。

3、代换法：代换法适用于条件最值中，出现分式的情况类型1：分母为单项式，利用“1”的代换运算，也称乘“1”法；类型2：分母为多项式时方法1：观察法适合与简单型，可以让两个分母相加看是否与给的分子型成倍数关系；方法2：待定系数法，适用于所有的形式，如分母为34+a b 与3+a b ，分子为2+a b ，设()()()()2343343+=+++=+++a b a b a b a bλμλμλμ∴31432+=⎧⎨+=⎩λμλμ，解得：1525⎧=⎪⎪⎨⎪=⎪⎩λμ4、消元法：当题目中的变元比较多的时候，可以考虑削减变元，转化为双变量或者单变量问题。

5、构造不等式法：寻找条件和问题之间的关系，通过重新分配，使用基本不等式得到含有问题代数式的不等式，通过解不等式得出范围，从而求得最值。

【热点题型】第2天掌握直接法及配凑法求最值模型【题型1直接法求最值】例1（辽宁锦州·高三校考阶段练习）已知0,0x y >>，且12x y +=，则xy 的最大值为（）A．16B．25C．36D．49【答案】C【解析】因为0,0x y >>，12x y +=≥36xy ≤，当且仅当6x y ==时取到等号，故xy 的最大值为36.故选：C【变式1-1】（四川广安·广安二中校考模拟预测）已知3918x y +=，当2x y +取最大值时，则xy 的值为（）B．2C．3D．4【答案】B【解析】由已知3918x y +=可得23318x y +=，则21833x y =+≥+2381x y ≤，所以+24x y ≤，当且仅当=22x y =时取等号，即=2x ，=1y ，此时2xy =.故选：B．【变式1-2】（2023·河南郑州·高三校联考阶段练习）已知正数,a b 满足2221a b +=,则2ab 的最大值是（）A．13C．9D．19【答案】C【解析】解:由题知2222212a b a b b =+=++≥13≤,当且仅当3a b ==时取等号，所以239ab ．故选:C．【变式1-3】（2022·上海·高三统考学业考试）已知x >1，y >1且lg x ＋lg y ＝4，那么lg x ·lg y 的最大值是（）A．2B．12C．14D．4【答案】D【解析】∵x >1，y >1，∴lg x >0，lg y >0，∴22lg lg 4lg lg 422x y x y +⎛⎫⎛⎫⋅≤== ⎪ ⎪⎝⎭⎝⎭，当且仅当lg x ＝lg y ＝2，即x ＝y ＝100时等号成立．故选：D.【变式1-4】（2022春·云南·高三校联考阶段练习）已知正数,a b 满足()()5236a b a b ++=，则2+a b 的最小值为（）A．16B．12C．8D．4【答案】D【解析】因为()()()()252522a b a b a b a b ⎡⎤+++++≤⎢⎥⎣⎦，所以29(2)364a b +≥.又0,0a b >>.所以24a b +≥，当且仅当,3382a b ==时，等号成立.故选：D 【题型2配凑法求最值】【例2】（2022·全国·高三专题练习）已知30x -<<，则()f x =值为________．【答案】92-【解析】因为30x -<<，所以()229922x x f x -+==≥-=-，当且仅当229x x -=，即322x =-时取等，所以()f x =92-.【变式2-1】（2022春·上海静安·高三上海市市西中学校考期中）函数9()(1)1=+>-f x x x x 的值域为______.【答案】[)7,+∞【解析】由题知，1x >，所以10x ->，所以()9()11171f x x x =-++≥=-，当且仅当911x x -=-，即4x =时取等号，所以函数9()(1)1=+>-f x x x x 的值域为[)7,+∞.【变式2-2】（2022春·湖南长沙·高三雅礼中学校考阶段练习）已知0,0x y >>，且7x y +=，则()()12x y ++的最大值为（）A．36B．25C．16D．9【答案】B【解析】由7x y +=，得()()1210x y +++=，则()()()()21212252x y x y ⎡⎤+++++≤=⎢⎥⎣⎦，当且仅当12x y +=+，即4,3x y ==时，取等号，所以()()12x y ++的最大值为25.故选：B.【变式2-3】（2022春·山东济宁·高三统考期中）已知向量()()5,1,1,1m a n b =-=+，若0,0a b >>，且m n ⊥，则113223a b a b+++的最小值为（）A．15B．110C．115D．120【答案】A【解析】根据题意，510m n a b ⋅=-++=，即4a b +=，则()()322320a b a b +++=，又0,0a b >>，故113223a b a b +++()()1113223203223a b a b a b a b ⎛⎫⎡⎤=++++ ⎪⎣⎦++⎝⎭123321122203223205a b a b a b a b ⎛⎫++⎛⎫=++≥⨯+= ⎪ ⎪ ⎪++⎝⎭⎝⎭，当且仅当23323223a b a b a b a b++=++，且4a b +=，即2a b ==时取得等号.故选：A.第3天掌握消元法及代换法求最值模型【题型3消元法求最值】【例3】（2022春·湖南永州·高三校考阶段练习）设220,0,12y x y x ≥≥+=，则的最大值为（）A．122C．324【答案】C【解析】因为2212y x +=，所以22022y x =-≥，解得：[]0,1x ∈，故22232224x x +-===≤⨯=，当且仅当22232x x =-，即x 的最大值为4.【变式3-1】（2023春·江西鹰潭·高三贵溪市实验中学校考阶段练习）已知正数,a b 满足2240a ab -+=，则4a b -的最小值为（）A．1C．2D．【答案】B【解析】,0a b > ,2240a ab -+=，则有22a b a=+，224244a a a a b a a ∴-=+-=+ 24a a =，即a =时b =【变式3-2】（2022春·广东广州·高三执信中学校考阶段练习）设正实数x 、y 、z 满足22430x xy y z -+-=，则xyz的最大值为（）A．0B．2C．1D．3【答案】C【解析】因为正实数x 、y 、z 满足22430x xy y z -+-=，则2243z x xy y =-+，则22114433xy xy x y z x xy y y x ==-++-，当且仅当20y x =>时取等号.故xyz的最大值为1.故选：C.【变式3-3】（2023·全国·高三专题练习）设正实数x ，y ，z 满足22340x xy y z -+-=，则当xyz取得最大值时，212x y z +-的最大值为（）A．0B．3C．94D．1【答案】D【解析】由正实数x ，y ，z 满足22340x xy y z -+-=，2234z x xy y ∴=-+．∴22114343xy xy x y z x xy y y x ==-++- ，当且仅当20x y =>时取等号，此时22z y =．∴222122121(1)1122x y z y y y y+-=+-=--+ ，当且仅当1y =时取等号，即212x y z +-的最大值是1．故选：D【变式3-4】（2022春·湖南长沙·高三湖南师大附中校考阶段练习）（多选）已知a ，b ，c 均为正实数，2ab ac +=，则118ab c a b c+++++的取值不可能是（）A．1B．2C．3D．4【答案】ABC【解析】a ，b ，c 均为正实数，由2ab ac +=得：()2a b c +=，即2b c a+=，所以2211818282222a a aa b c a b c a a a a a+++=++=++++++，由基本不等式得：2211828422a a a b c a b c a a +++=+≥++++，当且仅当222822a a a a +=+，即2a =±【变式3-5】（2022春·云南昆明·高三云南师大附中校考阶段练习）若22221122124,4,2x y x y x y +=+=⋅=-，则21x y ⋅的最大值为___________．【答案】2【解析】()()()()222222121112211444444204x y y x x x x x ⎛⎫⎛⎫=--=--=-+ ⎪ ⎪⎝⎭⋅⎝⎭，由212y x -=，所以211222y x x -==≤，所以112x ≤≤，所以()222112142042044x y x x ⎛⎫=-+≤-⨯⎪⎝⎭⋅= ，当且仅当1||x 时，等号成立，所以21x y ⋅2≤，当且仅当21x y ==21x y ==时取等号，所以21x y ⋅的最大值为2．【题型4代换法求最值】【例4】（2022春·上海崇明·高三上海市崇明中学校考阶段练习）已知0,0x y >>，且41x y +=，则19x y+的最小值是_____．【答案】25【解析】因为0,0x y >>，且41x y +=，所以()1919346913254x y x y x y y x y x +=⎛⎫+=+ ⎪⎝+++⎭+≥=，当且仅当36x y y x =，即13,105x y ==时，等号成立.【变式4-1】（2022春·江西·高三九江一中校联考阶段练习）已知0a >，0b >，2a b +=，则4ba b +的最小值为_______.【答案】2【解析】因为0a >，0b >，且2a b +=，所以4422222b b a b b a a b a b a b +⎛⎫+=+=++≥= ⎪⎝⎭，当且仅当222b a =时取等号故4b a b +的最小值为2【变式4-2】（2022春·江西抚州·高三金溪一中校考阶段练习）若正实数x ，y 满足2x y xy +=，则2x y +的最小值为______．【答案】9【解析】由2x y xy +=得211y x+=，又因为0x >，0y >，所以()212222559x y x y x y y x yx ⎛⎫+=++=++≥= ⎪⎝⎭，当且仅当3x y ==时等号成立，故2x y +的最小值为9．【变式4-3】（2022春·黑龙江鹤岗·高三鹤岗一中校考阶段练习）已知2x >-，0y >，23x y +=，则2272x y x y++++的最小值为（）A．4B．6C．8D．10【答案】B【解析】因为2x >-，0y >，23x y +=，所以()227x y ++=，20x +>，()()22722222222222x y x y y x y x x y x y x y +++++=+++=++++++26≥+，当且仅当2x y +=，即13x =，73y =时等号成立，即2272x y x y++++的最小值为6，故选：B.【变式4-4】（2022·广西·统考一模）如图，在△ABC 中，M 为线段BC 的中点，G 为线段AM 上一点且2AG GM =，过点G 的直线分别交直线AB 、AC 于P 、Q 两点，(0)AB x AP x => ，(0AC y AQ y => ），则111x y ++的最小值为（）A．34B．1C．43D．4【答案】B【解析】由于M 为线段BC 的中点，则1122AM AB AC =+ ；又2AG GM =，所以32AM AG = ，又(0)AB x AP x => ，(0AC y AQ y => ）；所以3222x y AG AP AQ =+，则33x y AG AP AQ =+ ；因为,,G P Q 三点共线，则133x y+=，化得()14x y ++=；由()111111111221141414x y x y x y x y y x ⎛⎫⎛⎫⎛⎫++=+++=++≥+=⎡⎤ ⎪ ⎪ ⎪⎣⎦ ⎪+++⎝⎭⎝⎭⎝⎭；当且仅当11x y y x+=+时，即2,1x y ==时，等号成立，111x y ++的最小值为1故选：B第4天掌握双换元法及齐次化求最值模型【题型5双换元法求最值】【例5】（2022春·天津河西·高三天津市新华中学校考阶段练习）设1,2x y >->-，且4x y +=，则2212x y x y +++的最小值是__________.【答案】167【解析】令1(0)x a a +=>，2(0)y b b +=>，则1x a =-，2y b =-，因为4x y +=，则有7a b +=，所以2222(1)(2)142412x y a b a b x y a b a b--+=++-++-++14724(a b =--++1141()()7a b a b =+++141(147b a a b =++++1161(577≥+⨯+=；当且仅当2b a =，即714,33a b ==时取等号，则,x y 分别等于48,33时，2212x yx y +++的最小值是167.【变式5-1】（2022春·江西南昌·高三南昌二中校考阶段练习）已知正数x ，y满足()()381232x y y x y x +=++，则xy 的最小值是（）A．54B．83C．43D．52【答案】D【解析】()()3838232232x y xy xy x y y x y x x y x y ⎡⎤=+=+⎢⎥++++⎣⎦，令2x y m +=，32x y n +=，则2n m x -=，34m n y -=，38367752322222x y n m xy x y x y m n =+=+-≥-=++，当且仅当362n m m n =且()()381232x y y x y x +=++，即x =y =所以52xy ≥，故xy 有最小值52.故选：D.【变式5-2】（2022·全国·高三专题练习）设正实数, x y 满足1,12x y >>，不等式224121x y m y x +≥--恒成立，则m 的最大值为（）A．8B．16C．D．【答案】A【解析】设1,21y b x a -=-=，则()()()110,102y b b x a a =+>=+>所以()()2222114121a b x y y x b a ++++++++=+≥=--()222228⎛=≥=⋅+= ⎝；当且仅当1a b ==即2,1x y ==时取等号；所以224121x y y x +--的最小值是8，则m 的最大值为8.故选A【变式5-3】（2022春·浙江·高三浙江省新昌中学校联考期中）已知0,0x y >>，若1x y +=，则313213x y y+++的最小值是___________.【答案】85【解析】设()()3213x y k x y y λμ++=+++，由对应系数相等得13123k λλμμ=⎧⎪=+⎨⎪=⎩，得1319k λμ⎧=⎪⎪⎨⎪==⎪⎩；所以()()1113213939x y x y y ++=+++；整理得()()31132131010x y y =+++即()()()11961310x y y =+++；所以()()()3113196133213103213x y y x y y x y y⎛⎫+=++++ ⎪++++⎝⎭()313196811032135y x y x y y ⎛⎫++=+ ⎪++⎝⎭ .经验证当12x y ==时，等号可取到.【题型6齐次化求最值】【例6】（2020春·浙江金华·高三浙江金华第一中学校考阶段练习）已知,a b 都是负实数，则2a ba b a b+++的最小值是____________.【答案】2-【解析】222222232a b a ab b a b a b a ab b +++=++++22132ab a ab b =-++1123a b b a=-++，因为,a b 都是负实数，所以20,0a b ba >>，所以2a b b a +≥2a b b a =时等号成立）.所以233a b b a++≥，所以123a b b a≤++，所以1323a b b a -≥=++，所以1113223a b b a-≥+=++.即2a b a b a b+++的最小值是2.【变式6-1】（2021春·重庆沙坪坝·高三重庆一中校考阶段练习）已知对任意正实数x ，y ，恒有()2222x y a x xy y +-+≤，则实数a 的最小值是___________.【答案】2【解析】因为0,0x y >>，则()2220x xy y x y xy -+=-+>，则()2222x y a x xy y +-+≤，即2222x y a x xy y+-+≤，又22222211x y xy x xy y x y +=-+-+，因为222x y xy +≥，所以22112xy x y -≥+，所以22121xy x y≤-+，即22222x y x xy y +≤-+，当且仅当x y =时，取等号，所以2222max2x y x xy y ⎛⎫+= ⎪-+⎝⎭，所以2a ≥，即实数a 的最小值是2.【变式6-2】（2022·全国·高三专题练习）已知0x >，0y >，则2223x y xy y ++的最小值为____．【答案】2【解析】∵x ，y ＞0，则2223x y xy y ++＝2231x y x y++，设x y ＝t ，t ＞0，则()()2222212143311t t x y t xy y t t +-++++==+++＝（t +1）+41t +当且仅当t +1＝41t +，即t ＝1时取等号，此时x ＝y ，故2223x y xy y ++的最小值为2.第5天掌握构造不等式法及多次使用不等式求最值模型【题型7构造不等式法求最值】【例7】（2013春·浙江嘉兴·高三阶段练习）已知正实数a ，b 满足212ab a b =++，则ab 的最小值是___________.【答案】9【解析】由212ab a b =++得，212ab ≥，化简得)320≥，解得9ab ≥，所以ab 的最小值是9.【变式7-1】已知0x >，0y >，24xy x y =++，则x y +的最小值为______．【答案】4【解析】由题知0,0,x y >>由基本不等式得22x y xy +⎛⎫≤ ⎪⎝⎭，即2422x y x y +⎛⎫++≤⨯ ⎪⎝⎭，令t x y =+，0t >，则有2422t t ⎛⎫+≤⨯ ⎪⎝⎭，整理得2280t t --≥，解得2t ≤-(舍去)或4t ≥，即4x y +≥，当且仅当2x y ==时等号成立，所以x y +的最小值为4.【变式7-2】（2022·全国·高三专题练习）若2241x y xy ++=，则2x y +的最大值是___________．【解析】∵2241x y xy ++=，∴2222325(2)31(2)(2)228x y x y xy x y x y +⎛⎫+-=≥+-=+ ⎪⎝⎭，当且仅当2x y =时，等号成立，此时28(2)5x y +≤，所以2x y +≤2x y +的最大值是5.【变式7-3】（2020春·天津河北·高三天津外国语大学附属外国语学校校考阶段练习）若0x >，0y >，1425y x x y+++=，则2x y +的最小值为___________.【答案】8【解析】因为0x >，0y >，所以20x y +>；由1425y x x y+++=两边同时乘xy ，得22425y y x x xy +++=，即2244254x y xy x y xy xy ++++=+，则()()2229x y x y xy +++=，因为()2222224x y x y xy ++⎛⎫≤= ⎪⎝⎭，所以()()2229999222248x y xy xy x y +=⨯≤⨯=+，故()()()2292228x y x y x y +++≤+，整理得()()22820x y x y +-+≥，即()()2280x y x y ++-≥，所以28x y +≥或20x y +≤（舍去），故2x y +的最小值为8.【题型8多次使用不等式求最值】【例8】（2022春·重庆沙坪坝·高三重庆八中校考阶段练习）已知0,0a b >>，则242ba ba ++的最小值为（）A．B．C．1D．1【答案】B【解析】因为0,0a b >>，所以24422224b a a a b a a ++≥=+≥，当且仅当24b ba =且42a a =，即ab ==即242ba b a ++的最小值为故选：B.【变式8-1】（2022春·江苏淮安·高三校联考期中）当02,x a <<不等式()221112x a x +≥-恒成立，则实数a 的取值范围是（）A．)+∞B．(0C．(]0,2D．[)2,+∞【答案】B【解析】()221112x a x +≥-恒成立，即()22min 1112x a x ⎡⎤+≥⎢⎥-⎢⎥⎣⎦；02,20x a a x <<∴-> ，又222211222(2)(2)(22)x a x x a x x a x a +≥=≥=+---，上述两个不等式中，等号均在2x a x =-时取到，()m 222in1122x a a x ⎡⎤∴+=⎢⎥-⎢⎥⎣⎦，212a ∴≥，解得a ≤0a ≠，又0a >，实数a的取值范围是(0.故选：B.【变式8-2】（2022·全国·模拟预测）已知0a >，0b >，1c >，22a b +=，则1221c a b c ⎛⎫++⎪-⎝⎭的最小值为（）A．92B．2C．6D．212【答案】D【解析】()()121121221925542222baa b a b a b a b ⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭⎝⎭，当且仅当23a b ==时等号成立，（应用基本不等式时注意等号成立的条件）所以()12292911212c c a b c c ⎛⎫++≥-++≥ ⎪--⎝⎭92122=，当且仅当()91221c c -=-，即53c =且23a b ==时，等号成立，故最小值为212，故选：D【变式8-3】（2022春·安徽·高三校联考阶段练习）已知,,a b c +∈R ，,22ππθ⎡⎤∈-⎢⎥⎣⎦，不等式()2222cos 4b a c a b cθ+++ 恒成立，则θ的取值范围是（）A．,22ππ⎛⎫- ⎪⎝⎭B．,33ππ⎡⎤-⎢⎥⎣⎦C．,44ππ⎡⎤-⎢⎥⎣⎦D．,66ππ⎡⎤-⎢⎥⎣⎦【答案】C【解析】因为,,,,22a b c ππθ+⎡⎤∈∈-⎢⎥⎣⎦R ，不等式()2222cos 4b a ca b c θ+++ 恒成立，所以()222max2cos 4b a c a b c θ⎡⎤+⎢⎥++⎣⎦ ，因为,,a b c +∈R，所以)))2222222ab aa b ⎤=≤+=+⎥⎦，当且仅当a =时等号成立；)))2222222bc cc c b ⎤=++⎥⎦，当且仅当c 时等号成立.所以()2222222222244b a c ab bc a b c a b c ++=≤++++=，当且仅当a c ==时等号成立，所以()22224b a c a bc +++，所以cos 2θ≥，又因为,22ππθ⎡⎤∈-⎢⎥⎣⎦，所以,44ππθ⎡⎤∈-⎢⎥⎣⎦.故选：C.【变式8-4】（2023·全国·高三专题练习）若a ，b ，c 均为正实数，则2222ab bca b c +++的最大值为（）A．12B．14C．22【答案】A【解析】因为a ，b均为正实数，则2222222ab bc a c a c a b c b b ++=++++12==≤=，当且仅当222a c b b+=，且a c =，即a b c ==时取等号，则2222ab bc a b c +++的最大值为12．故选：A．第6天融会贯通限时练习（1）1．（2022春·江苏徐州·高三学业考试）若正实数x ，y 满足121x y+=，则x +2y 的最小值为（）A．7B．8C．9D．10【答案】C【解析】因为x ，y 是正数，所以有()12222559y x x y x y x y ⎛⎫++=++≥+= ⎪⎝⎭，当且仅当22y xx y=时取等号，即当且仅当3x y ==时取等号，故选：C 2．（2022春·广东湛江·高三校考阶段练习）已知12,2x y x x >=+-，则y 的最小值为（）A．2B．1C．4D．3【答案】C【解析】因为2x >，所以120,02x x ->>-，由基本不等式得11222422y x x x x =+=-++≥=--，当且仅当122x x -=-，即3x =时，等号成立，则y 的最小值为4.故选：C3．（2022春·河南·高三安阳一中校联考阶段练习）已知1a >，1b >，且ln 4ln 2a b +=，则4log lo e e g a b +的最小值为（）A．9lg2B．212C．252D．12【答案】C 【解析】n e 1log l a a =，44l l e og n b b=，因为1a >，1b >，故ln 0a >，ln 0b >，()414114log log ln 4ln ln ln 2ln ln e e a b a b a b a b ⎛⎫+=+=⨯++ ⎪⎝⎭14ln 4ln 12517172ln ln 22b a a b ⎛⎛⎫=⨯++≥⨯+= ⎪ ⎝⎭⎝，当且仅当ln ln a b =时，即25e a b ==时等号成立．所以4log lo e e g a b +的最小值为252．故选：C 4．（2022春·吉林四平·高三四平市第一高级中学校考阶段练习）已知正数,a b 满足494a b +=，则ab 的最大值为（）A．19B．16C．13D．12【答案】A【解析】正数,a b 满足494a b +=，由基本不等式得：494a b +=≥19ab ≤，当且仅当49a b =，即12,29a b ==时，等号成立，ab 的最大值为19.故选：A5．（2022春·黑龙江牡丹江·高三牡丹江一中校考期末）已知0a >，0b >，9是3a与27b的等比中项，则22231a b a b+++的最小值为（）A．9+C．7【答案】B【解析】由等比中项定义知：3232739a b a b +⋅==，34a b ∴+=，()2223121121163434544a b b a a b a b a b a b a b a b ++⎛⎫⎛⎫∴+=+++=+++=+++ ⎪⎪⎝⎭⎝⎭1521454444⎛++≥++=+= ⎝（当且仅当6b a a b =，即8a =，(433b =时取等号），即22231a b a b +++6．（2022春·河南南阳·高三校考阶段练习）在ABC 中，过重心E 任作一直线分别交AB ，AC 于M ，N 两点，设AM xAB =u u u r u u u r ，AN yAC =u u ur u u u r ，（0x >，0y >），则4x y +的最小值是（）A．43B．103C．3D．2【答案】C【解析】在ABC 中，E 为重心，所以21()32AE AB AC =⋅+ 1()3AB AC =+，设AM xAB =u u u r u u u r ，AN yAC =u u ur u u u r ，（0x >，0y >）所以1AB AM x = ，1AC AN y = ，所以111133AE AM AN x y =⋅+⋅ .因为M 、E 、N 三点共线，所以11133x y+=，所以11(4)33x y x y ⎛⎫++⎪⎝⎭4143333y x x y =+++533≥+=（当且仅当433y x x y =，即12x =，1y =时取等号）．故4x y +的最小值是3．故选：C．7．（2022春·四川德阳·高三阶段练习）已知实数0a b >、，且函数()f x =的定义域为R ，则22a b a+的最小值是（）A．4B．6C．D．2【答案】A【解析】∵()f x =定义域为R，∴22()2()10x a b x a b -+++-≥在R 上恒成立，∴2[2()]4[2()1]0a b a b ∆=-+-⨯+-≤，即：2()2()10a b a b +-++≤∴2(1)0a b +-≤，解得：1a b +=又∵0,0a b >>∴2121212222a b b a b a b a -+=+=+-1212=()()224222a b a b b a b a ++-=++≥=当且仅当22a bb a=，即21,33a b ==时取等号.故选：A.8．（2022春·江西宜春·高三校考阶段练习）设x y z >>，且11()nn x y y z x z +≥∈---N 恒成立，则n 的最大值为（）A．2B．3C．4D．5【答案】C【解析】因为x y z >>，所以0x y ->，0y z ->，0x z ->，所以不等式11n x y y z x z +≥---恒成立等价于11()n x z x y y z ⎛⎫≤-+ --⎝⎭恒成立.因为()()x z x y y z -=-+-≥，11x y y z +≥--所以11()44x z x y y z ⎛⎫-⋅+≥ ⎪--⎝⎭（当且仅当x y y z -=-时等号成立），则要使11()n x z x yy z ⎛⎫≤-⋅+⎪--⎝⎭恒成立，只需使4()n n ≤∈N ，故n 的最大值为4.故选：C第7天融会贯通限时练习（2）1．（2022春·重庆沙坪坝·高三重庆南开中学校考阶段练习）（多选）已知实数a ，b 满足2241a ab b -+=，以下说法正确的是（）A．15a ≤B．1a b +<C．2244453a b ≤+≤D．25a b -≤【答案】ACD【解析】由2241a ab b -+=，可得22410b ab a -+-=，关于b 的方程有解，所以()()224410a a ∆=---≥，所以2415a ≤，即a ≤A 正确；取0,1a b ==，2241a ab b -+=，则1a b +=，故B 错误；由2241a ab b -+=，可得22141122a b ab ab +=+=+⋅，又222244222a b a b ab ++-≤≤，令224t a b =+，则()2122t t t -≤-≤，所以4453t ≤≤，即2244453a b ≤+≤，故C 正确；由2241a ab b -+=，可得()2231a b ab -+=，所以()()23213122a b ab a b -=-=+⋅⋅-，令2u a b =-，由()2222a b a b -⎛⎫⋅-≤ ⎪⎝⎭，可得22318u u ≤+，所以285u ≤，即2a b -≤故D 正确.故选：ACD.2．（2022·浙江·模拟预测）（多选）已知a ，b 为正数，且220a b +-=，则（）A．2168a a +>B．219ab+≥5≥D．35422a b a +-<<-【答案】ACD【解析】对于A 选项，()2216840a a a +-=-≥，当且仅当4a =时等号成立，当4a =时，由于220a b +-=，得22286b a =-=-=-，与b 为正数矛盾，故4a ≠，即得2168a a +>，故A 选项正确；对于B 选项，220a b +-= ，12ba ∴+=.又0,0a b >> 212115922222b b a a a b a b a b ⎛⎫⎛⎫∴+=++=+++≥+ ⎪⎪⎝⎭⎝⎭，当且仅当b aa b =，即23a b ==时等号成立；故B 选项不正确；对于C 选项，220a b +-= ，22b a ∴=-，()0,1a ∈.()2222224422584555a b a a a a a ⎛⎫+=+-=-+=-+ ⎪⎝⎭ ，2245a b ∴+≥，当且仅当45a =时等号成立，≥C 选项正确；对于D 选项，220a b +-= ，22b a ∴=-，()0,1a ∈.()()2552253510122222a ab a a a a a a a a a ---+-+----∴====--<<-----，当01a <<时，221a -<-<-，55522a ∴-<<--，得351422a <--<-，即35422a b a +-<<-，故D 选项正确.故选：ACD3．（2022春·山西·高三校联考阶段练习）（多选）若1a b >>，且35a b +=，则（）A．141a b b +--的最小值为24B．141a b b +--的最小值为25C．2ab b a b --+的最大值为14D．2ab b a b --+的最大值为116【答案】BD【解析】由1a b >>，可知0a b ->，10b ->，()()4134541a b b a b -+-=+-=-=，()()()()441411411a b b a b b a b b a b b -+-⎡⎤-+-⎣⎦+=+--()()414171b a b a b b --=++--17≥+25=；当且仅当115a b b -=-=时，等号成立，141a b b +--的最小值为25．又()()141a b b =-+-=≥()1412a b b -=-=时，等号成立，所以()()21116ab b a b a b b --+=-⋅-≤，故2ab b a b --+的最大值为116．故选：BD .4．（2022春·山东·高三利津县高级中学校联考阶段练习）（多选）在下列函数中，最小值是4的是（）A．4y xx=+B．0)y x =>C．4sin sin y x x =+，0,2x π⎛⎤∈ ⎥⎝⎦D．144xx y -=+【答案】BD【解析】对于A，当0x >时，44y x x =+≥=，当且仅当4x x=，即2x =时取等号；当0x <时，44[()]4y x x xx=+=--+-≤-=-，当且仅当4x x-=-，即2x =-时取等号，所以(,4][4,)y ∈-∞-+∞ ，A 错误；对于B，y =，因为0x >1>，4=3x =时取等号，所以0)y x =>的最小值为4，B 正确；对于C，因为0,2x π⎛⎤∈ ⎥⎝⎦，所以sin (0,1]x ∈，由对勾函数性质可知：4sin [5,)sin y x x=+∈+∞，C 错误；对于D，40x >，1444444x x x x y -=++=≥，当且仅当444x x =，即12x =时取等号，所以144x x y -=+的最小值为4，D 正确.故选：BD5．（2022春·山东·高三利津县高级中学校联考阶段练习）已知正实数x ，y 满足474x y +=，则2132x y x y+++的最小值为______.【答案】94【解析】因为474x y +=，所以()()2112123232432x y x y x y x y x y x y ⎛⎫⎡⎤+=++++ ⎣⎦++++⎝⎭，所以()()22211413242233x y x y x y x y x y x y ⎡⎤++=+++⎢⎥++⎣+++⎦，因为,x y 为正实数，所以()()220,02233x y y y x y x x +++>>+，所以()()4222233x y x y x y x y ++++≥=+，当且仅当32474x y x y x y +=+⎧⎨+=⎩时等号成立，即84,1515x y ==时等号成立，所以()21194413244x y x y +≥++=++，当且仅当84,1515x y ==时等号成立，所以2132x y x y +++的最小值为94.6．（2022春·天津静海·高三静海一中校考阶段练习）若,a b ∈R ，且221b a -=，则22a b a b+-的最大值为___________.【解析】由题知，,a b ∈R ，且221b a -=，即221b a =+，所以221a b a a b b+-+=，当0a =时，21b =，即1b =±，此时11a b +=±，所以22a b a b+-的最大值为1，当0a ≠时，22221212211212a a a a ab b a a ⎛+⎫++==+≤+= ⎪+⎝⎭，当且仅当1=a 时取等号，此时1ab+≤；所以22a ab b+-.综上，22a ab b+-的最大值.7．（2022春·天津和平·高三耀华中学校考阶段练习）已知正数,x y 满足22831322x xy xy y +=++，则xy 的最小值是_________．【答案】52【解析】根据题意，由22831322x xy xy y +=++可得22228(2)3(32)1(32)(2)xy y x xy x xy xy y +++=++，即322223221)6914384384y x xy x x y xy yx xy y y x ++=+++=+；所以222222221691416914383844y y y x xy x x y y y x xy x xxy ++=+=+++++；又因为,x y 均是正数，令()0,y t x =∈+∞，则221614983()4xy f t t t t t =++++=；所以，22221831()4444316149348388183t t t t t t t t t f t t +++++==-=++++-+令2384)183(g t t t t ++=+，则16162112110101899()292718396183272727g t t t t t ⎛⎫=++=+++≥= ⎪++⎝⎭当且仅当1621996183t t ⎛⎫+= ⎪+⎝⎭，即12t =时，等号成立；所以2181455()44184182718332f t t t t +=+=-≥-=+；所以()f t 的最小值为min 5()2f t =;即当1,22y t x y x ====时，即x y ==时，等号成立.8．（2022春·陕西商洛·高三校联考阶段练习）已知正实数,,a b c 满足222120a ab b c ++-=，则当a bc+取得最大值时，2a b c -+的最大值为______.【答案】916【解析】由222120a ab b c ++-=，可得()()()2222231224a b c a b ab a b a b +⎛⎫=+-≥+-=+ ⎪⎝⎭，即4a b c +≤，当且仅当a b =时，等号成立，所以当a bc+取得最大值时，a b =，42a b a c +==，所以2223392416a b c a a a ⎛⎫-+=-=--+ ⎪⎝⎭，故当333,,448a b c ===时，2a b c -+取最大值916.。

一.基本不等式注：（1）当两个正数的积为定植时，可以求它们的和的最小值，当两个正数的和为定植时，可以求它们的 积的最小值，正所谓“积定和最小，和定积最大” . （2） 求最值的条件“一正，二定，三取等”（3） 均值定理在求最值、应用一：求最值 例1 :求下列函数的值域基本不等式应用1解：(1) y = 3x 2 + 21^ 1X = - 2例1 ：已知x 4，求函数y4x 2 —1—的最大值。

4x 5解：因4x 5 0 ,所以首先要 “调整”符号，又（4x 」不是常数，所以对4x 2要进行拆、凑项, Qx 544x 0, y4x 21---- 54x 52)g4x 54x 32 3 15 4x11一，即x 1时， 5 4x评注：本题需要调整项的符号，又要配凑项的系数，使其积为定值。

技巧二：凑系数当且仅当5 4x上式等号成立, 故当x 1时，y max 1。

1. (1)若 a,b R ，则 a 1 2b 2 *2ab (2)若a,bR ，则 ab 2. (1)若 a,b R *，则2Jab ⑵若a,b R ，则 a b2 .2a —L （当且仅当a22J OE （当且仅当ab 时取“二”） b 时取“=”)⑶若a,b R ,则ab（当且仅当a b 时取“=”)3.若x 0，则x— 2 （当且仅当x 1时取“=”x若x 0，则 x 1 1 1 2 即 X — 2 或 X - -2 (x x X 3.若 ab 0，则 a b .2 （当且仅当a b 时取b a1时取“=”)若ab 0,则- b-2（当且仅当a b 时取“=”）4.若 a,b2 .2a—L (当且仅当 2b 时取“=”)比较大小、求变量的取值范围、证明不等式、解决实际问题方面有广泛的应用.(1) y = 3x 2+ 女1(2) y = x + x“=”)当且仅当a b 时取“=”）2例1.当Dux 4时，求y x(8 2x)的最大值。

解析：由0 < J <4知，S- 2工> 0|,利用基本不等式求最值，必须和为定值或积为定值，此题为两个式子 积的形式，但其和不是定值。

基本不等式是求解最值问题的重要工具.运用基本不等式:ab ≤a +b2求最值需要把握三个前提条件:一正二定三相等.一正是a 、b 两个数都为正数;二定是指如果积ab 是定值p ，那么当且仅当a =b 时，和a +b 有最小值2p ，如果和a +b 是定值p ，那么当且仅当a =b时，积ab 有最大值p 24；三相等是当且仅当a =b 时不等式取等号.在运用基本不等式求最值时，要首先确定两个式子是否为正数；然后配凑出两式的和或积，使两式的和或积为定值；最后检验当且仅当两式相等时不等式是否能取等号.而运用基本不等式求最值的关键是，配凑出两式的和或积，使两式的和或积为定值.配凑出两式的和或积的常用方法有添加项、分离整式、减元、常数代换、构建目标不等式，下面举例说明.例1.当x >1时，求x +1x -1的最小值.解:∵x >1,∴x -1>0,∴x +1x -1=x -1+1x -1+1≥+1=3，，当且仅当x -1=1x -1，即x =2时取等号，∴y min =3.该目标式含有整式和分式，为了使它们的积为定值，需添加一项-1，构造出分式的分母，以便利用基本不等式来求得目标式的最小值.例2.求y =x 2+7x +10x +1(x >-1)的最小值.解：y =x 2+7x +10x +1=(x +1)2+5(x +1)+4x +1=(x +1)+4x +1+5，当x >-1,即x +1>0时,y ≥+5=9，且仅当x =1时取“=”号，所以y min 该目标式看似无法运用基本不等式，但将分式、整式分离，便创造出运用基本不等式的条件.例3.已知正数a ,b 满足1a +1b=3，求a +b 的最小值.解：由1a +1b =3得a +b =3ab ，所以b =a 3a -1，由于a >0,b >0，可得a >13，于是a +b =a +a 3a -1=a -13+19(a -13)+23≥+23=43，当a -13=19(a -13)，即a =23时取等号，所以a +b 的最小值43.在解答含有多个变元的最值问题时，可以通过减少变元的方式，把问题转化为只含一个变元的问题，然后通过添加项配凑出两式的和或者积，再利用基本不等式求最值.例4.已知x >0,y >0，且1x +9y =1，求x +y 的最小值.解：∵x >0,y >0,1x +9y=1，∴x +y =()x +y æèçöø÷1x +9y =yx +9x y +10≥16,当且仅当y x =9xy时，等号成立，又1x +9y =1，则x =4,y =12，此时()x +y min =16.这里，我们利用“1”的代换来构造出运用基本不等式的条件.通过常数代换，可把所求的目标化为可以使用基本不等式求解的式子，以达到解题的目的.例5.已知a ，b 为正实数，2b +ab +a =30，求函数y =1ab的最小值.解：由题意得30-ab =a +2b ，∵a +2b ≥22ab ，∴30-ab ≥22ab ，令u =ab ，则u 2+22u -30≤0，解得-52≤u ≤32，∴ab ≤32，ab ≤18，∴y ≥118，即当a =b =32时，y min =118.我们由已知不等式出发求出ab 的范围，进而求得目标式的最值.解答本题的关键是利用基本不等式建立a +b 与ab 之间的关系.构建目标不等式是创造应用基本不等式条件的常用方法.很多问题往往所给的条件是非“标准”的，无法直接利用基本不等式来解题，因而在解题时，我们需要将不等式进行适当的变形，通过添加项、分离整式、减元、常数代换、构建目标不等式等方法，对“原始”的条件进行整合、转化，构造出“一正二定三相等”的三个条件，以保证可以用基本不等式求最值.黎华高46。

重难点1-1 利用基本不等式求最值8大题型基本不等式是高考热点问题，是常考常新的内容，是高中数学中一个重要的知识点，在解决数学问题中有着广泛的应用，尤其是在函数最值问题中。

题型通常为选择题与填空题，但它的应用范围几乎涉及高中数学的所有章节，它在高考中常用于大小判断、求最值、求最值范围等。

在高考中经常考察运用基本不等式求函数或代数式的最值，具有灵活多变、应用广泛、技巧性强等特点。

在复习中切忌生搬硬套，在应用时一定要紧扣“一正二定三相等”这三个条件灵活运用。

利用基本不等式求最值的方法1、直接法：条件和问题间存在基本不等式的关系2、配凑法：凑出“和为定值”或“积为定值”，直接使用基本不等式。

3、代换法：代换法适用于条件最值中，出现分式的情况类型1：分母为单项式，利用“1”的代换运算，也称乘“1”法； 类型2：分母为多项式时方法1：观察法 适合与简单型，可以让两个分母相加看是否与给的分子型成倍数关系；方法2：待定系数法，适用于所有的形式，如分母为34+a b 与3+a b ，分子为2+a b ，设()()()()2343343+=+++=+++a b a b a b a b λμλμλμ∴31432+=⎧⎨+=⎩λμλμ，解得：1525⎧=⎪⎪⎨⎪=⎪⎩λμ4、消元法：当题目中的变元比较多的时候，可以考虑削减变元，转化为双变量或者单变量问题。

5、构造不等式法：寻找条件和问题之间的关系，通过重新分配，使用基本不等式得到含有问题代数式的不等式，通过解不等式得出范围，从而求得最值。

【题型1 直接法求最值】【例1】（2022春·辽宁锦州·高三校考阶段练习）已知0,0x y >>，且12x y +=，则xy 的最大值为（ ）A ．16B ．25C ．36D ．49【变式1-1】（2022·四川广安·广安二中校考模拟预测）已知3918x y +=，当2x y +取最大值时，则xy 的值为（ ）A 2B ．2C ．3D ．4【变式1-2】（2023·河南郑州·高三校联考阶段练习）已知正数,a b 满足2221a b +=,则2ab 的最大值是（ ） A ．13B 3C 3D ．19【变式1-3】（2022·上海·高三统考学业考试）已知x >1，y >1且lg x ＋lg y ＝4，那么lg x ·lg y 的最大值是（ ） A ．2 B ．12 C ． 14D ．4【变式1-4】（2022春·云南·高三校联考阶段练习）已知正数,a b 满足()()5236a b a b ++=，则2+a b 的最小值为（ ）A ．16B ．12C ．8D ．4【题型2 配凑法求最值】【例2】（2022·全国·高三专题练习）已知30x -<<，则()f x =________．【变式2-1】（2022春·上海静安·高三上海市市西中学校考期中）函数9()(1)1=+>-f x x x x 的值域为______.【变式2-2】（2022春·湖南长沙·高三雅礼中学校考阶段练习）已知0,0x y >>，且7x y +=，则()()12x y ++的最大值为（ ） A ．36 B ．25 C ．16 D ．9【变式2-3】（2022春·山东济宁·高三统考期中）已知向量()()5,1,1,1m a n b =-=+，若0,0a b >>，且m n ⊥，则113223a b a b+++的最小值为（ ） A ．15 B ．110 C ．115D ．120【题型3 消元法求最值】【例3】（2022春·湖南永州·高三校考阶段练习）设220,0,12y x y x ≥≥+=，则的最大值为（ ）A．1 B ．2C D【变式3-1】（2023春·江西鹰潭·高三贵溪市实验中学校考阶段练习）已知正数,a b 满足2240a ab -+=，则4ab -的最小值为（ ） A．1 B C ．2 D ．【变式3-2】（2022春·广东广州·高三执信中学校考阶段练习）设正实数x 、y 、z满足22430x xy y z -+-=，则xyz的最大值为（ ） A ．0 B ．2 C ．1 D ．3【变式3-3】（2023·全国·高三专题练习）设正实数x ，y ，z 满足22340x xy y z -+-=，则当xyz取得最大值时，212x y z +-的最大值为（ ）A ．0B ．3C ．94D ．1【变式3-4】（2022春·湖南长沙·高三湖南师大附中校考阶段练习）（多选）已知a ，b ，c 均为正实数，2ab ac +=，则118ab c a b c+++++的取值不可能是（ ） A ．1 B ．2 C ．3 D ．4【变式3-5】（2022春·云南昆明·高三云南师大附中校考阶段练习）若22221122124,4,2x y x y x y +=+=⋅=-，则21x y ⋅的最大值为___________．【题型4 代换法求最值】【例4】（2022春·上海崇明·高三上海市崇明中学校考阶段练习）已知0,0x y >>，且41x y +=，则19x y+的最小值是_____．【变式4-1】（2022春·江西·高三九江一中校联考阶段练习）已知0a >，0b >，2a b +=，则4ba b +的最小值为_______.【变式4-2】（2022春·江西抚州·高三金溪一中校考阶段练习）若正实数x ，y 满足2x y xy +=，则2x y +的最小值为______．【变式4-3】（2022春·黑龙江鹤岗·高三鹤岗一中校考阶段练习）已知2x >-，0y >，23x y +=，则2272x y x y++++的最小值为（ ） A ．4 B ．6 C ．8 D ．10【变式4-4】（2022·广西·统考一模）如图，在△ABC 中，M 为线段BC 的中点，G 为线段AM 上一点且2AG GM =，过点G 的直线分别交直线AB 、AC 于P 、Q 两点，(0)AB x AP x =>，(0AC y AQ y =>），则111x y ++的最小值为（ ）A ．34B ．1C ．43D ．4【题型5 双换元法求最值】【例5】（2022春·天津河西·高三天津市新华中学校考阶段练习）设1,2x y >->-，且4x y +=，则2212x y x y +++的最小值是__________.【变式5-1】（2022春·江西南昌·高三南昌二中校考阶段练习）已知正数x ，y 满足()()381232x y y x y x +=++，则xy 的最小值是（ ）A ．54B ．83C ．43D ．52【变式5-2】（2022·全国·高三专题练习）设正实数, x y 满足1,12x y >>，不等式224121x y m y x +≥--恒成立，则m 的最大值为（ ） A．8 B ．16 C ． D ．【变式5-3】（2022春·浙江·高三浙江省新昌中学校联考期中）已知0,0x y >>，若1x y +=，则313213x y y +++的最小值是___________.【题型6 齐次化求最值】【例6】（2020春·浙江金华·高三浙江金华第一中学校考阶段练习）已知,a b 都是负实数，则2a ba b a b+++的最小值是____________ .【变式6-1】（2021春·重庆沙坪坝·高三重庆一中校考阶段练习）已知对任意正实数x ，y ，恒有()2222x y a x xy y +-+≤，则实数a 的最小值是___________.【变式6-2】（2022·全国·高三专题练习）已知0x >，0y >，则2223x y xy y ++的最小值为____．【题型7 构造不等式法求最值】【例7】（2013春·浙江嘉兴·高三阶段练习）已知正实数a ，b 满足212ab a b =++，则ab 的最小值是___________.【变式7-1】已知0x >，0y >，24xy x y =++，则x y +的最小值为______．【变式7-2】（2022·全国·高三专题练习）若2241x y xy ++=，则2x y +的最大值是___________．【变式7-3】（2020春·天津河北·高三天津外国语大学附属外国语学校校考阶段练习）若0x >，0y >，1425y x x y+++=，则2x y +的最小值为___________.【题型8 多次使用不等式求最值】【例8】（2022春·重庆沙坪坝·高三重庆八中校考阶段练习）已知0,0a b >>，则242ba b a ++的最小值为（ ） A． B ． C ．1 D ．1【变式8-1】（2022春·江苏淮安·高三校联考期中）当02,x a <<不等式()221112x a x +≥-恒成立，则实数a 的取值范围是（ ）A ．)+∞B ．(0C ．(]0,2D ．[)2,+∞【变式8-2】（2022·全国·模拟预测）已知0a >，0b >，1c >，22a b +=，则1221c a b c ⎛⎫++ ⎪-⎝⎭的最小值为（ ） A ．92 B ．2 C ．6 D ．212【变式8-3】（2022春·安徽·高三校联考阶段练习）已知,,a b c +∈R ，,22ππθ⎡⎤∈-⎢⎥⎣⎦，不等式()2222cos 4b a c a b c θ+++恒成立，则θ的取值范围是（ ）A ．,22ππ⎛⎫- ⎪⎝⎭ B ．,33ππ⎡⎤-⎢⎥⎣⎦C ．,44ππ⎡⎤-⎢⎥⎣⎦ D ．,66ππ⎡⎤-⎢⎥⎣⎦【变式8-4】（2023·全国·高三专题练习）若a ，b ，c 均为正实数，则2222ab bca b c +++的最大值为（ ）A ．12 B ．14C ．22 D ．32（建议用时：60分钟）1．（2022春·江苏徐州·高三学业考试）若正实数x ，y 满足121x y +=，则x +2y 的最小值为（ ）A ．7B ．8C ．9D ．10 2．（2022春·广东湛江·高三校考阶段练习）已知12,2x y x x >=+-，则y 的最小值为（ ）A ．2B ．1C ．4D ．33．（2022春·河南·高三安阳一中校联考阶段练习）已知1a >，1b >，且ln 4ln 2a b +=，则4log lo e e g a b +的最小值为（ ）A ．9lg 2B ．212 C ．252D ．12 4．（2022春·吉林四平·高三四平市第一高级中学校考阶段练习）已知正数,a b 满足494a b +=，则ab 的最大值为（ ）A ．19 B ．16 C ．13D ．125．（2022春·黑龙江牡丹江·高三牡丹江一中校考期末）已知0a >，0b >，9是3a 与27b的等比中项，则22231a b a b+++的最小值为（ ）A ．9+BC ．7 D6．（2022春·河南南阳·高三校考阶段练习）在ABC 中，过重心E 任作一直线分别交AB ，AC 于M ，N 两点，设AM xAB =，AN yAC =，（0x >，0y >），则4x y +的最小值是（ ） A ．43B ．103C ．3D ．2 7．（2022春·四川德阳·高三阶段练习）已知实数0a b >、，且函数()f x R ，则22a b a+的最小值是（ ） A．4 B ．6 C ． D ．28．（2022春·江西宜春·高三校考阶段练习）设x y z >>，且11()nn x y y z x z +≥∈---N 恒成立，则n 的最大值为（ ）A ．2B ．3C ．4D ．59．（2022春·重庆沙坪坝·高三重庆南开中学校考阶段练习）（多选）已知实数a ，b 满足2241a ab b -+=，以下说法正确的是（ ）A ．a ≤B ．1a b +<C ．2244453a b ≤+≤D ．2a b -≤10．（2022·浙江·模拟预测）（多选）已知a ，b 为正数，且220a b +-=，则（ ）A ．2168a a +>B ．219ab+≥ CD ．35422a b a +-<<- 11．（2022春·山西·高三校联考阶段练习）（多选）若1a b >>，且35a b +=，则（ ） A ．141a b b +--的最小值为24 B ．141a b b +--的最小值为25 C ．2ab b a b --+的最大值为14D ．2ab b a b --+的最大值为11612．（2022春·山东·高三利津县高级中学校联考阶段练习）（多选）在下列函数中，最小值是4的是（ ）A ．4y xx=+ B ．0)y x >C ．4sin sin y x x =+，0,2x π⎛⎤∈ ⎥⎝⎦D ．144xx y -=+ 13．（2022春·山东·高三利津县高级中学校联考阶段练习）已知正实数x ，y 满足474x y +=，则2132x y x y+++的最小值为______. 14．（2022春·天津静海·高三静海一中校考阶段练习）若,a b ∈R ，且221b a -=，则22a b a b+-的最大值为___________.15．（2022春·天津和平·高三耀华中学校考阶段练习）已知正数,x y 满足22831322x xy xy y +=++，则xy 的最小值是_________．16．（2022春·陕西商洛·高三校联考阶段练习）已知正实数,,a b c 满足222120a ab b c ++-=，则当a bc+取得最大值时，2a b c -+的最大值为______.。