2020届湖北省大冶市第一中学高三10月月考数学(文)试题Word版含答案

湖北省大冶市一中2010年高三年级模拟考试数学（文）试题本试卷分第I 卷（选择题）和第n 卷（非选择题）两部分，共 4页，满分150分，考试时间120分钟•考试结束后，将本试卷和答题卡一并交回. 注意事项：1 •答题前，考生务必用 0• 5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类 填写在答题卡和试卷规定的位置上，并将准考证号条形码粘贴在答题卡上指定位置. 2•第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上. 3•第H 卷必须用0.5毫米黑色签字笔在答题卡各题的答题区域内作答；不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸，修正 带，不按以上要求作答的答案无效.4•填空题请直接填写答案，解答题应写出文字说明，证明过程或演算步骤. 参考公式：1锥体的体积公式：V=—Sh ,其中S 是锥体的底面积，h 是锥体的高.3如果事件 A, B 互斥，那么P （A B ） P （A ） P （B ）第I 卷（选择题共60 分）一项是符合题目要求的. D ・第四象限2.给出下列四个命题：① 若集合A,B 满足A B 代则A B ；② 给定命题p,q ,若“ p q ”为真，则“ p q ”为真;2 2③ 设 a, b, m R,若 a b,则 am bm ；如果事件A, B 相互独立，那么P(AgB) P(A)gP(B)、选择题：本大题共 12小题，每小题 5分，共60分.在每小题给出的四个选项中，只有 2i,则z 对应的点位于B .第二象限1 •若复数z 满足——1 iA •第一象限 C .第三象限④若直线l1 : ax y 1 0与直线l2: x y 1 0垂直，则a 1 .其中正确命题的个数是A . 13.设平面向量a(1,2),b(2, y),若a//b,则| 3a b |等于C. 174.已知cos(才)1,则sin 2 43132313278785•阅读如图的程序框图•若输入4,n 则输出的a,i分别等于12,12,24, 24, (第5题图)C.D .6.某校高三年级共1200名学生，状况调查，若抽到男生比女生多A . 700现采用分层抽样方法抽取一个容量为10人，B . 660则该校男生共有200的样本进行健康( )C. 630D. 6107.XA . ( , 1]U[4,) C . [1,2]B . [ 1,4] D . (,1]U[2,)10 .已知函数 f (x) log 2 x (x0）的反函数为 b 0，则1 4 的最小值为a bA . 9B .C .3D . g(x)，且有 g(a)g(b) 8，若 a 0且( )6 22y 1相交于A 、B 两点（其中a,b 是实数），且 AOB 是AB . . 2C .2 1 D . .2 112 .已知关于 x 的方程2x (1 a)x 1 a b0(a,b R ）的两根分别为 洛、X 2，且0 x 1 1 X 2，则 -的取值范围是( )a1 ,1c 1 c 1 A1,B .1, 一C .2,-D . 2,-222 2&一个体积为12^3的正三棱柱的三视图如图所示， 则这个三棱柱的侧视图的面积为 （） A . 6.3 B. 8 C. 8.3 D. 129.不等式X侧视图（第 8题图） x 1 a 23a 对任意实数x 恒成立，则实数a 的取值范围为直角三角形O 是坐标原点），则点P （a,b ）与点（0,1）之间距离的最小值为11 .直线■. 2ax by 1 与圆 x 2第H 卷（非选择题共90 分）二、填空题：本大题共 4小题，每小题4分，共16分.（注意：在试题卷上作答无效）解集是2 216.过双曲线M 古1的一个焦点F 作一条渐近线的垂线,点）的垂直平分线上，则双曲线的离心率为三、解答题：本大题共 6小题，共74分.（注意：在试题卷上作答无效） 17.（本小题满分12分）ir已知msin xir cos x,、3 cosrr x , n cosx sin x,2sin x ，其中0,若函数f 『x m n ，且函数f x的图象与直线y2相邻两公共点间的距离为.([)求 的值；(□)在ABC 中, a 、b 、c 分别是角 A 、B 、C 、的对边,且 a V 3, b c 3 f A 1,求ABC 的面积.13 .已知实数x, y 满足2x yx 2y 3x y0,0,则 x 2 0,的最大值为14•数列｛3n ｝满足a n 115.设奇函数f （X ）在（0, 2a n ,2a n + 8)1, a n3n上为增函数，且 ，若316，则32010的值为f(1) 0 ,则不等式f （x ）f （x ） 0的若垂足恰在线段 OF （ O 为原18.（本小题满分12分）某社区举办2010年上海世博会知识宣传活动，进行现场抽奖.现有“世博会会徽”、“海宝”（世博会吉祥物）图案和普通卡片三种卡片共24张.1 （I）若已知“世博会会徽”共3张，若从中任取出1张卡片，取到“海宝”的概率是-•问6 普通卡片的张数是多少？（n）现将1张“世博会会徽” 、2张“海宝”、3张普通卡片放置抽奖盒中，抽奖规则是：抽奖者每次抽取两张卡片，若抽到两张“海宝”卡获一等奖，抽到“世博会会徽”获二等奖•求抽奖者获奖的概率.19.（本小题满分12分）如图，在直三棱柱ABC A1B1C1中，ACB 90O, AA1 BC 2AC 2 ,D为AA中点.（I）求证：CD B1C1；（n）求证：平面B1CD 平面B1C1D ;（川）求三棱锥G BQD的体积.A1DAB（第19题图）(n)设 b n，求数列b n 的前n 项和T n .21.(本小题满分12分)已知直线I 与函数f (x) In x 的图象相切于点(1,0)，且I 与函数g(x)lx 2 mx - (m 0)的图象也相切. 2 2(I)求直线I 的方程及m 的值； 7 卄(n)设 h(x) ag x f(x) 2ax -a 右 h(x)2 ，丄恒成立，求实数2a 的取值范围.22.(本小题满分14分)2 2 _ 如图，已知直线I : x my 1过椭圆C : —2 %1的右焦点F ，抛物线：x 2 4-、3y a b的焦点为椭圆C 的上顶点，且直线I 交椭圆C 于A 、B 两点，点A 、F 、B 在直线g:x 4上的射影依次为点 D 、K 、E .(I)求椭圆C 的方程；20. (本小题满分12分)已知二次函数f x x 2 ax a a 0,x R 有且只有一个零点，数列a n 的前n 项 和 S n f n n N(I)求数列 a n 的通项公式;6uur UHT UJIT uuu(n)若直线l 交y 轴于点M ，且MA 1AF,MB 2BF ,探求 1 2的值是否为定值？若是，求出 1 2的值，否则，说明 理由;参考答案、选择题2sin 2 x当m 变化时, （川）连接AE 、 BD ，试证明当m 变化时，直线1 — 5: BBADD 6—10: C AABC 11 —12: CD二、填空题：本大题共 第n 卷（非选择题共90 分）4小题，每小题4分，共16分.（注意：在试题卷上作答无效）13. 14.13 3 715. (1,0)U(0,1)16.三、解答题：本大题共 17.（本小题满分12分）6小题，共74分.（注意：在试题卷上作答无效）解：（I ） f Xir rm n sin x cos x, 3cos x cos x sin x,2sin x2CO S .2sinx 2 ^ 3 sin xcos x cos2 x 3 sin 2 x2Q 函数f x 的图象与直线y 2相邻两公共点间的距离为12sin 2A 一1 sin 2A 一66 22 2b c be 3 又 b c 3b 2b 1八联立解得或................................... 10分c 1c 21 73S ABCbc cos A .............................................................. 12 分2 2（或用配方法Qb 2c 2bc2b c 3bc 3, b c 3bc 2S ABC^bccos A3)2218.（本小题满分12 分）x 1解：（「设“海宝”卡片有x张，依题意246，解得x 4“海宝”卡片有4张 ................................................. 3分 普通卡片有：24 3 4 17张.............................. 4分13 Q0 A-2A -6 662A —5A …663,2 2 2b c aQ 0 函数f x 的周期T 由（I ） 可知x 2sin 2x —6由余弦定理知cos A2bc（n）解法1:从1张“世博会会徽”、2张“海宝”、3张普通卡片中任取2张，包括5 种情况：取1张“世博会会徽”、1张“海宝”卡，有2种取法；取1张“世博会会徽”、1张普通卡，有3种取法；取1张“海宝”、1张普通卡，有6种取法；取2张“海宝” 卡，有1种取法；取2张普通卡，有3种取法；共计15种取法。

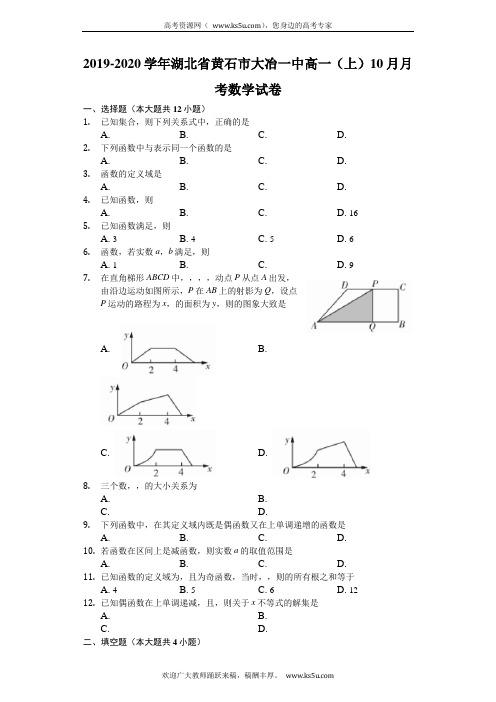
2019-2020学年湖北省黄石市大冶一中高一（上）10月月考数学试卷一、选择题（本大题共12小题）1.已知集合，则下列关系式中，正确的是A. B. C. D.2.下列函数中与表示同一个函数的是A. B. C. D.3.函数的定义域是A. B. C. D.4.已知函数，则A. B. C. D. 165.已知函数满足，则A. 3B. 4C. 5D. 66.函数，若实数a，b满足，则A. 1B.C.D. 97.在直角梯形ABCD中，，，，动点P从点A出发，由沿边运动如图所示，P在AB上的射影为Q，设点P运动的路程为x，的面积为y，则的图象大致是A. B.C. D.8.三个数，，的大小关系为A. B.C. D.9.下列函数中，在其定义域内既是偶函数又在上单调递增的函数是A. B. C. D.10.若函数在区间上是减函数，则实数a的取值范围是A. B. C. D.11.已知函数的定义域为，且为奇函数，当时，，则的所有根之和等于A. 4B. 5C. 6D. 1212.已知偶函数在上单调递减，且，则关于x不等式的解集是A. B.C. D.二、填空题（本大题共4小题）13.某班共35人，其中21人喜爱篮球运动，15人喜爱乒乓球运动，10人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为______．14.已知函数，若，求______．15.已知函数b是常数，且，在区间上有，则常数a的值等于______．16.下列结论：是指数函数函数既是偶函数又是奇函数函数的单调递减区间是在增函数与减函数的定义中，可以把任意两个自变量”改为“存在两个自变量与表示同一个集合所有的单调函数都有最值其中正确命题的序号是______．三、解答题（本大题共6小题）17.计算下列各式的值：．．18.全集，集合，求：Ⅰ；Ⅱ．19.定义在上的奇函数，已知当时，．求在上的解析式；若时，不等式恒成立，求实数m的取值范围．20.信息科技的进步和互联网商业模式的兴起，全方位地改变了大家金融消费的习惯和金融交易模式，现在银行的大部分业务都可以通过智能终端设备完成，多家银行职员人数在悄然减少．某银行现有职员320人，平均每人每年可创利20万元．据评估，在经营条件不变的前提下，每裁员1人，则留下岗位职员每人每年多创利万元．但银行需付下岗职员每人每年6万元的生活费，并且该银行正常运转所需人数不得小于现有职员的，为了使裁员后获得的经济效益最大，该银行应裁员多少人？此时银行获得的最大经济效益是多少万元？21.已知函数．求函数的单调递增区间；若对于任意的，都有成立，求实数a的范围．22.已知定义域为R，对任意x，都有，且当时，．试判断的单调性，并证明；若．求的值；求实数m的取值范围，使得方程有负实数根．。

大冶市高中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 已知函数()x e f x x=，关于x 的方程2()2()10f x af x a -+-=（a R Î）有3个相异的实数根，则a 的取值范围是（ ）A ．21(,)21e e -+?-B ．21(,)21e e --?-C ．21(0,)21e e --D ．2121e e 禳-镲睚-镲铪【命题意图】本题考查函数和方程、导数的应用等基础知识，意在考查数形结合思想、综合分析问题解决问题的能力．2． 设集合A ＝{x |x ＝2n －1，n ∈Z }，B ＝{x |（x ＋2）（x －3）＜0}，则A ∩B ＝（ ） A ．{－1，0，1，2} B ．{－1，1} C ．{1}D ．{1，3}3． 已知曲线2:4C y x =的焦点为F ，过点F 的直线与曲线C 交于,P Q 两点，且20FP FQ +=，则OP Q ∆的面积等于（ ）A ．B ．CD 4． 如图甲所示， 三棱锥P ABC - 的高8,3,30PO AC BC ACB ===∠= ，,M N 分别在BC 和PO 上，且(),203CM x PN x x ==∈（，，图乙的四个图象大致描绘了三棱锥N AMC -的体积y 与的变化关系，其中正确的是（ ）A ．B ． C. D ．1111]5． 已知，则tan2α=（ ）A ．B ．C ．D ．6． 已知集合A={x|x ＜2}，B={y|y=5x }，则A ∩B=（ ） A ．{x|x ＜2} B ．{x|x ＞2} C ．{x|o ≤x ＜2}D ．{x|0＜x ＜2}7． 设曲线y=ax ﹣ln （x+1）在点（0，0）处的切线方程为y=2x ，则a=（ ）A ．0B ．1C ．2D ．3 8． 已知f （x ）=x 3﹣3x+m ，在区间[0，2]上任取三个数a ，b ，c ，均存在以f （a ），f （b ），f （c ）为边长的三角形，则m 的取值范围是（ ）A ．m ＞2B ．m ＞4C ．m ＞6D ．m ＞89． 为了解决低收入家庭的住房问题，某城市修建了首批108套住房，已知C B A ,,三个社区分别有低收入家 庭360户，270户，180户，现采用分层抽样的方法决定各社区所分配首批经济住房的户数，则应从C 社 区抽取低收入家庭的户数为（ ）A ．48B ．36C ．24D ．18【命题意图】本题考查分层抽样的概念及其应用，在抽样考查中突出在实际中的应用，属于容易题． 10．已知向量=（1，2），=（x ，﹣4），若∥，则x=（ ） A ． 4 B ． ﹣4 C ． 2 D ． ﹣211．已知m ，n 为不同的直线，α，β为不同的平面，则下列说法正确的是（ ） A ．m ⊂α，n ∥m ⇒n ∥αB ．m ⊂α，n ⊥m ⇒n ⊥αC ．m ⊂α，n ⊂β，m ∥n ⇒α∥βD ．n ⊂β，n ⊥α⇒α⊥β12．已知函数，则=（ ）A． B． C． D．二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13()23k x =-+有两个不等实根，则的取值范围是 ．14．图中的三个直角三角形是一个体积为20的几何体的三视图，则h =__________.15．命题“∃x ∈R ，2x 2﹣3ax+9＜0”为假命题，则实数a 的取值范围为 ．16．设变量y x ,满足约束条件22022010x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩，则22(1)3(1)z a x a y =+-+的最小值是20-，则实数a =______．【命题意图】本题考查线性规划问题，意在考查作图与识图能力、逻辑思维能力、运算求解能力．三、解答题（本大共6小题，共70分。

2019-2020年高三10月月考数学（文）试题Word含解析本试卷是高三文科试卷，以基础知识和基本技能为为主导，在注重考查运算能力和分析问题解决问题的能力，知识考查注重基础、注重常规、注重主干知识，兼顾覆盖面.试题重点考查：不等式、复数、导数、圆锥曲线、数列、函数的性质及图象、三角函数的性质、三角恒等变换与解三角形、等；考查学生解决实际问题的综合能力，是份较好的试卷.【题文】一.选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个备选项中，只有一项是符合题目要求的．【题文】1．已知，为两个集合，若命题，都有，则A.，使得B.，使得C.，使得D.，使得【知识点】命题及其关系A2【答案解析】C 若命题，都有,则，使得，故选C。

【思路点拨】根据命题的关系确定非P。

【题文】2. 已知向量，，则与A.垂直B.不垂直也不平行C．平行且同向D．平行且反向【知识点】平面向量的数量积及应用F3【答案解析】A 因为=（-5）6+65=0，所以，故选A。

【思路点拨】根据向量的数量积为0，所以。

【题文】3.设集合,,则集合A. B. C. D.【知识点】集合及其运算A1【答案解析】C 由题意得M={x},N={x}则=M,所以故选C.【思路点拨】先求出M ,N再求再求出结果。

【题文】4.设一直正项等比数列中，为前项和，且，A. B. C. D.【知识点】等比数列及等比数列前n 项和D3【思路点拨】先根据等比中项的性质可知a 3=a 2a 4求得a 3，进而根据S 3=a 1+a 2+a 3求得q ，根据等比数列通项公式求得a n ，进而求得a 1，最后利用等比数列的求和公式求得答案．【题文】5.对于平面、、和直线、、、，下列命题中真命题是A.若//，，则//B.若//，，则//C.若,,,,a m a n m n αα⊥⊥⊂⊂则D.若，则 【知识点】空间中的平行关系空间中的垂直关系G4 G5【答案解析】若α∥β，α∩γ=α，β∩γ=b ，则由面面平行的性质定理可得：a ∥b ，故A 正确； 若a ∥b ，b ⊂α，则a ∥α或a ⊂α，故B 错误；若a ⊥m ，a ⊥n ，m ⊂α，n ⊂α，则m ，n 相交时a ⊥α，否则a ⊥α不一定成立，故C 错误； 若α⊥β，a ⊂α，则a 与β可能平行，可能垂直，也可能线在面内，故D 错误；故选：A【思路点拨】由面面平行的性质定理可判断A ；由线面平行的判定定理可判断B ；由线面垂直的判定定理可判断C ；由面面垂直的性质定理可判断D ．【题文】6.若实数、满足约束条件23502500x y x y x +-≤⎧⎪--≤⎨⎪≥⎩，则目标函数是最小值是A.0B.4C.D.【知识点】简单的线性规划问题E5 【答案解析】A 作出23502500x y x y x +-≤⎧⎪--≤⎨⎪≥⎩可行域如图，由，可得A (，0)，由，可得B （0, ），由，可得C （0，-5）．A 、B ．C 坐标代入z=|x+y+1|，分别为：；，4，又z=|x+y+1|≥0，当x=0，y=-1时，z 取得最小值0．z=|x+y+1|取可行域内的红线段MN 时x+y+1=0．z 都取得最小值0．故选A ．【思路点拨】先根据约束条件画出可行域，再利用几何意义求最值，只需求出直线x+y+1=0时，z 最小值即可．【题文】7.某几何体的三视图如图所示，其中俯视图为扇形，则改几何体的体积为A. B. C. D.【知识点】空间几何体的三视图和直观图G2【答案解析】C 由三视图知几何体是圆锥的一部分，由正视图可得：底面扇形的圆心角为120°，又由侧视图知几何体的高为4，底面圆的半径为2，∴几何体的体积V=××π×22×4=π．故答案为：C【思路点拨】根据三视图判断几何体是圆锥的一部分，再根据俯视图与左视图的数据可求得底面扇形的圆心角为120°，又由侧视图知几何体的高为4，底面圆的半径为2，把数据代入圆锥的体积公式计算．【题文】8.将函数的的图像向右平移个单位，再将图象上每一点横坐标伸长为原的2倍后得到图像，若在上关于的方程有两个不等的实根，则的值为A.或B.或C.或D.或【知识点】三角函数的图象与性质C3 【答案解析】D 将函数f （x ）=sin （2x+ ）的图象向右平移个单位，可得函数y=sin[2（x- ）+]=sin （2x+）的图象；再将图象上横坐标伸长为原的2倍后得到y=g （x ）=sin （x+）图象．由x+=kπ+，k ∈z ，求得g （x ）的图象的对称轴方程为 x=kπ+．若x ∈[0，2π），则g （x ）的对称轴方程为x=，或x=．关于x 的方程g （x ）=m 在[0，2π）上有两个不等的实根x 1，x 2，则x 1+x 2 =2×，或x 1+x 2 =2×，故选：D ．【思路点拨】由条件根据函数y=Asin （ωx+φ）的图象变换规律，可得g （x ）的图象的对称轴方程，从而求得x 1+x 2 的值．【题文】9.已知函数是定义在上的奇函数，且（其中是的导函数）恒成立。

湖北省大冶市第一中学2020届高三地理10月月考试题试卷满分：100分本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分100分，时间90分钟。

第Ⅰ卷(选择题共50分)一、选择题(共25小题，每小题2分，共50分，在每小题给出的四个选项中，只有一个选项符合题目要求。

)如图为全球经纬线图，甲至辛是经纬线坐标上的八个地点。

读图回答1～2题。

1．图中各点之间若以最短距离来比较，下列两点间在地球表面上实际距离最远的是A．己辛 B．丙庚 C．乙己 D．甲戊2．亚特兰蒂斯是个传说中的古文明大陆，后人曾透过柏拉图提出的地球六分说，也就是把地球360度切成六等份，来推论亚特兰蒂斯的地点。

其推论依据是沿着同一条纬线出发时，亚特兰蒂斯往东60度为古埃及文明之处，往西60度则为玛雅文明北方的美国南部沿海地区。

依此推论，亚特兰蒂斯的位置最可能位于图中A．庚 B．己 C．丙 D．乙读我国某河流上游部分河段年平均气温分布示意图，完成3～4题。

3．该河流的流向大致为A．自东南向西北 B．自西北向东南 C．自西南向东北 D．自东北向西南4．水能资源最丰富的河段是A．甲乙河段 B．乙丙河段 C．丙丁河段 D．丁戊河段右图中EF、MN两线相交于O点，O点为北极点，∠NOF等于60°。

读图回答5～6题。

5．若图中OF为晨线，太阳直射35°W，则ON的经度为A．175°E B．90°EC．65°W D．5°W6．若图中MOE表示地球上旧的一天的范围，则此时北京时间为A．20时 B．16时C．8时 D．4时“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称。

丝绸之路经济带，东边牵着亚太经济圈，西边系着欧洲经济圈，被认为是世界上最长、最具发展潜力的经济大走廊。

下图为“一带一路”示意图，依据图文材料，回答7～8题。

7．古代中国的商船航行于海上丝绸之路时，下列描述正确的是A．中国的商船一般选择夏季从中国南方沿海地区出发，冬季从非洲东部沿海地区返回B．夏季航行到索马里附近海域时发现此处水温较低，且海面上有大量捕鱼的渔船C．当他们顺风由中国泉州南下到新加坡时发现当地正午日影位于南方D．返航时途经加尔各答可以大量购置棉花，带回国内8．建设陆上丝绸之路——铁路过程中可能遇到的不利自然条件有①气候寒冷，冻土广布②生态环境脆弱，环境保护困难③多高原山地，多地质灾害④沙漠广布，气候恶劣A．①②④ B．①②③ C．②③④ D．①③④某年3月P地(位置见下图)发生强烈地震，引发大规模海啸，导致附近某核电站核物质泄漏。

2019-2020学年高三数学10月月考试题注意事项：1.答题前，考生务必用黑色碳素笔将自己的考号、姓名、考场、座位号、班级在答题卡上填写清楚。

2.每小题选出答案后，用2B 铅笔把答题卡上对应的题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

在试卷上作答无效。

第Ⅰ卷（选择题，共60分）一．选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的．1.=0330cos （ ） A.23B. 23-C.21D.21-2.已知复数z 满足i zi +-=1，则z 在平面直角坐标系中对应的点是（ ） A.()1,1- B.()1,1- C.()1,1 D.()1,1--3.已知集合{}11|≤≤-=x x A ，{}02|2>-=x x x B ，则()=B C A U （ ） A.[-1，0] B.[1，2] C.[0，1] D.（-∞，1]∪[2，+∞） 4.已知向量()2,1=，()m ,4-=，若b a +2与a 垂直，则m =（ ） A.-3 B.3 C.-8 D.85.正项等比数列{}n a 中，23=a ，6464=⋅a a ，则2165a a a a ++的值是（ ）A.4B.8C.16D.646.已知双曲线C ：()0,012222>>=-b a by a x 的渐近线方程为x y 43±=，且其左焦点为（-5,0），则双曲线C 的方程为（ ）A ．116922=-y x B ．191622=-y x C ．14322=-y x D ．13422=-y x 7．已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是（ ） A ．34000cm 3B ．38000cm 3C ．32000cmD ．34000cm8.右图程序框图输出S 的值为（ ） A.2 B.6 C.14 D.309.将函数()()ϕ+=x x f 2sin 的图象向左平移8π个单位，所得到的函数是偶函数，则ϕ的一个可能取值为（ ） A ．43π B ．4πC ．0D ．4π-10.下列三个数：2323ln-=a ，ππ-=ln b ，33ln -=c ，大小顺序是（ ） A ．b c a << B ．c b a >> C ．c a b >> D ．b c a >>11.若直线2-=kx y 与抛物线x y 82=交于A ，B 两个不同的点，且AB 的中点的横坐标为2，则=k （ ）A.-1B.2C.2或-1D.1±512.定义在R 上的奇函数()x f 和定义在{}0|≠x x 上的偶函数()x g 分别满足()⎪⎩⎪⎨⎧≥<≤-=)1(1)10(12x x x x f x ，()()0log 2>=x x x g ，若存在实数a 使得()()b g a f =成立，则实数b 的取值范围是（ ）A ．[]2,2-B ．⎥⎦⎤⎝⎛⎪⎭⎫⎢⎣⎡-21,00,21 C ．(][)+∞-∞-,22, D ．⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--2,2121,2第Ⅱ卷（非选择题，共90分）本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答． 二、填空题：本大题共4小题，每小题5分．13.若x ，y 满足约束条件⎪⎩⎪⎨⎧≤+≥+≥32320y x y x x ,则y x z -=的最小值是 ．14.若()51-ax 的展开式中3x 的系数是80，则实数a 的值是 ．15.已知四棱锥ABCD P -的顶点都在半径为2的球面上，底面ABCD 是正方形，且底面经过球心O ，E 是AB 的中点，⊥PE 底面ABCD ，则该四棱锥ABCD P -的体积于 ．16.在数列{}n a 中，已知7,221==a a ，2+n a 等于1+⋅n n a a ()+∈N n 的个位数，则=2015a ．三、解答题：解答时写出文字说明，证明过程和演算步骤． 17.（本题满分12分）已知向量()x x cos ,22sin 3+=，()x cos 2,1=，设函数()x f ⋅= （1）求()x f 的最小正周期；（2）在△ABC 中，c b a ,,分别是角A ，B ，C 的对边，若3=a ，f （A ）=4，求△ABC 的面积的最大值．18.（本题满分12分）如图，正方形ADEF 与梯形ABCD 所在的平面互相垂直，AD CD ⊥，CD AB //，4,2===CD AD AB ,M 为CE 的中点．（1）求证：BM ∥平面ADEF ；（2）求平面BEC 与平面ADEF 所成锐二面角的余弦值.19.（本题满分12分）某公司对员工进行身体素质综合测试，测试成绩分为优秀、良好、合格三个等级，测试结果如下表：（单位：人）按优秀、良好、合格三个等级分层，从中抽到50人，其中成绩为优秀的有30人. （1）求a 的值；（2）若用分层抽样的方法，在合格的员工中按男女抽取一个容量为5的样本，从中任选3人，记X 为抽取女员工的人数，求X 的分布列及数学期望.20.（本题满分12分）已知椭圆L ：()012222>>=+b a b y a x 的一个焦点与抛物线y 2=8x 的焦点重合，点()2,2在L 上． （1）求L 的方程；（2）直线l 不过原点O 且不平行于坐标轴，l 与L 有两个交点A ，B ，线段AB 的中点为M ，证明：OM 的斜率与直线l 的斜率的乘积为定值．21.（本题满分12分）已知函数()R a xax x x f ∈+-=,21ln （1）当2=a 时，求曲线()x f y =在1=x 处的切线方程； （2）当1>x 时，()0<x f 恒成立，求a 的取值范围请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分。

2019-2020中学高三上学期10月月考数学试题一、单选题A.{1,2,3,4} B.{1,2,3} C.{4,5} D .{1,4}【答案】A【解析】将阴影部分对应的集合的运算表示出来，然后根据集合AB 表示元素的范 围计算结果. 【详解】因为阴影部分是：A （C R B ）；又因为x （4—x ）<0,所以x>4或x<0,所以B = {x|x ）4或x<0},所以 C R B = {X |0<X <4},又因为 A = {1,2,3,4,51，所以 A （QB ）= {1,2,3,4}, 故选：A. 【点睛】本题考查根据已知集合计算伽"图所表示的集合，难度较易.对于图中的阴影部 分首先要将其翻译成集合间运算，然后再去求解相应值.3.设a, b 是非零向量，是“a//b”的（）4 3 . A. 1B. —1C.—I —I5 5【答案】D 【解析】【详解】由题意可得：忖=（¥ +3? = 5,且：乞=4一3几z 4-3/4 3 .据此有：旧-丁十一尹 本题选择D 选项.D.-3. —I52.若集合A = {1,2,3,4,5}傑合B = {x|x （4-x ）<0}侧图中阴影部分表示（）ZA.充分而不必要条件 C.充分必要条件【答案】A 【解析1 a-b =|a|-|Z?|cos^,Z?^ ,由已知得cos(a,b 〉= l,即仏巧=0,加/方.而当 a 〃Q 时,仏方)还可能是兀，此时a-b =-|®|j^|,故“a"=问”| ”是“a//b ”的充分 而不必要条件，故选A. 【考点】充分必要条件、向量共线.4. 设 a = log 4S,b = log 0A 8, c = 204,!S!l ()A.b<c<aB.c<b<aC.c<a<bD.b< a<c【答案】A【解析】根据指数函数、对数函数单调性比较数值大小. 【详解】因为 a = log 4 8 = ^-log 2 2 =扌’b = log 04 8 < log 041 = 0, c = 20'4< 20'5 = A /2 < 扌, 所以b<c<a , 故选：A. 【点睛】本题考查利用指、对数函数的单调性比较数值大小，难度一般•利用指、对数函数单调 性比较大小时，注意利用中间量比较大小，常用的中间量有：0,1.5. 若直线 lax-by + 2 = 0(a > 0,b > 0)被圆 x 2 + y 2+2x-4_y+ 1 = 0 截得弦长为 4,4 1一则—：的最小值是()a b1 1 A. 9B. 4C.-D.-24【答案】A 【解析】圆x2+ y 2 + 2x-4y + l = 0的标准方程为：(x+1) 2+ (y - 2) 2 =4,它表示以(-1, 2)为圆心、半径等于2的圆； 设弦心距为d,由题意可得22+d 2=4,求得d=0,可得直线经过圆心，故有-2a - 2b+2=0, 即a+b=l,再由a>0, b>0,可得B.必要而不充分条件 D.既不充分也不必要条件4 14 1I =(Ia ba b4Z? a4 ]当且仅当一=—时取等号，•••一 + 〒的最小值是9. a b a b故选：A.点睛：本题主要考查基本不等式，其难点主要在于利用三角形的一边及这条边上的高表 示内接正方形的边长.在用基本不等式求最值时，应具备三个条件：一正二定三相等.① 一正：关系式中，各项均为正数；②二定：关系式中，含变量的各项的和或积必须有一 个为定值；③三相等：含变量的各项均相等，取得最值.6.函数/(%) = x 2-cos%在-彳冷 的图像大致是()【解析】先判断奇偶性，然后通过计算导函数在特殊点的导函数值正负来判断相应结果. 【详解】因为/ (兀)定义域关于原点对称且=- cos (-%) = X 2 - cos % = /(%),所以/(X )是偶函数，排除A 、C ；又因为/,(x) = x (2cosx-xsinx),所以【点睛】 本题考查函数图象的辨别，难度一般•辨别函数图象一般可通过奇偶性、单调性、特殊 点位置、导数值正负对应的切线斜率变化等来判断.7.如图,长方体 ABCD-A.B^D, ^,AA l =AB^2,AD = l,^E,F,G 分别是 D0, AB, CC,的中点，则异面直线与GF 所成角的余弦值是71所以“护对应的切线斜率大于零，所以排除D,)(a+b) =5+ —+ ->5+2 a b=9故选：B.【答案】D 【解析】以DA,DC,DD ［所在直线为x,y,z 轴，建立空间直角坐标系，可得4疋和GF 的坐标，进而可得cos^EGF,从而可得结论. 【详解】以DA, DC, DD,所在直线为X, % z 轴，建立空间直角坐标系, 则可得 4（l,0,2）,E （0,0,l ）,G （0,2,l ）,F （l,l,0）,设异面直线4E 与GF 所成的角为0,【点睛】本题主要考查异面直线所成的角，属于中档题.求异面直线所成的角主要方法有两种： 一是向量法，根据几何体的特殊性质建立空间直角坐标系后，分别求出两直线的方向向 量，再利用空间向量夹角的余弦公式求解；二是传统法，利用平行四边形、三角形中位 线等方法找出两直线成的角，再利用平面几何性质求解.& 在AABC 中，ZA, ZB, ZC 的对边分别为 a, b, c, cos 2— =,贝U ABC2 2c的形状一定是（）A.正三角形B.直角三角形C.等腰三角形D.等腰直角三角形【答案】Byk h + C【解析】在△ ABC 中，利用二倍角的余弦与正弦定理可将已知cos?—=——，转化为2 2c cosA=^-,整理即可判断△ ABC 的形状.sinC【详解】 亠亠 c A b + c在AABC 中，Vcos2—=-------- , 2 2cD.O则 cos 0 = |cos 4E, GF | =-lxl + 0 + （-l ）x （-l ）72x^2=0, 故选D..l + cosA = sinB + sinC=j_ sinB+j_2 2sinC 2 sinC 2sinB an sinB・°・ 1+cosA = 1,艮卩cosA = ----- ,sinC sinCcosAsinC = sinB = sin (A+C) = sinAcosC+cosAsinC,:.sinAcosC=0, *.* sin A#),cosC=0,・・・c为直角.故选：B.【点睛】本题考查三角形的形状判断，着重考查二倍角的余弦与正弦定理，诱导公式的综合运用, 属于中档题.9.若函数f(x) = ^x2-2x + alnx有两个不同的极值点，则实数。

大冶市一中2018-2019学年上学期高三数学10月月考试题班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 已知函数，则（ ）(5)2()e22()2xf x x f x x f x x +>⎧⎪=-≤≤⎨⎪-<-⎩(2016)f -=A ．B ．C ．1D ．2e e 1e【命题意图】本题考查分段函数的求值，意在考查分类讨论思想与计算能力．2． 已知直线x+y+a=0与圆x 2+y 2=1交于不同的两点A 、B ，O 是坐标原点，且，那么实数a 的取值范围是（ ）A ．B．C ．D ．3． 下列说法正确的是（）A.圆锥的侧面展开图是一个等腰三角形；B.棱柱即是两个底面全等且其余各面都是矩形的多面体；C.任何一个棱台都可以补一个棱锥使他们组成一个新的棱锥；D.通过圆台侧面上的一点，有无数条母线.4． 已知函数满足，且，分别是上的偶函数和奇函数，()xF x e =()()()F x g x h x =+()g x ()h x R 若使得不等式恒成立，则实数的取值范围是（ ）(0,2]x ∀∈(2)()0g x ah x -≥A ． B ．C ．D．(,-∞(,-∞(0,)+∞5． 设曲线y=ax ﹣ln （x+1）在点（0，0）处的切线方程为y=2x ，则a=（）A ．0B ．1C ．2D ．36． 奇函数()f x 满足()10f =，且()f x 在()0+∞，上是单调递减，则()()210x f x f x -<--的解集为（）A ．()11-，B ．()()11-∞-+∞ ，，C ．()1-∞-，D ．()1+∞，7． 设集合,集合,若 ,则的取值范围3|01x A x x -⎧⎫=<⎨⎬+⎩⎭(){}2|220B x x a x a =+++>A B ⊆（）A ．B ． C. D ．1a ≥12a ≤≤a 2≥12a ≤<8． 在复平面内，复数所对应的点为，是虚数单位，则（ ）1zi+(2,1)-i z =A ．B ．C ．D ．3i--3i -+3i -3i +9． 已知角的终边经过点，则的值为（ ）α(sin15,cos15)-2cos αA ．B ． C. D ．012+123410．年月“两会”期间，有代表提出适当下调“五险一金”的缴存比例，现拟从某工厂职工中抽取20163名代表调查对这一提案的态度，已知该厂青年，中年，老年职工人数分别为，，，按分20350500150层抽样的方法，应从青年职工中抽取的人数为（ ）A. B. C. D.56710【命题意图】本题主要考查分层抽样的方法的运用，属容易题.11．已知角的终边经过点()3P x ，()0x <且cos θ=，则等于（ ）A ．1-B ．13-C ．3-D ．12．已知集合，则下列式子表示正确的有（ ）{}2|10A x x =-=①；②；③；④．1A ∈{}1A -∈A ∅⊆{}1,1A -⊆A ．1个B ．2个C ．3个D ．4个二、填空题13．已知数列中，，函数在处取得极值，则{}n a 11a =3212()3432n n a f x x x a x -=-+-+1x =_________.n a =14．已知,则函数的解析式为_________.()212811f x x x -=-+()f x 15．等比数列{a n }的公比q=﹣，a 6=1，则S 6= ．16．要使关于的不等式恰好只有一个解，则_________.x 2064x ax ≤++≤a =【命题意图】本题考查一元二次不等式等基础知识，意在考查运算求解能力.17．命题“若1x ≥，则2421x x -+≥-”的否命题为．三、解答题18．已知函数f （x ）=alnx ﹣x （a ＞0）．（Ⅰ）求函数f （x ）的最大值；（Ⅱ）若x ∈（0，a ），证明：f （a+x ）＞f （a ﹣x ）；（Ⅲ）若α，β∈（0，+∞），f （α）=f （β），且α＜β，证明：α+β＞2α19．已知椭圆的左、右焦点分别为F 1（﹣c ，0），F 2（c ，0），P 是椭圆C 上任意一点，且椭圆的离心率为．（1）求椭圆C 的方程；（2）直线l 1，l 2是椭圆的任意两条切线，且l 1∥l 2，试探究在x 轴上是否存在定点B ，点B 到l 1，l 2的距离之积恒为1？若存在，求出点B 的坐标；若不存在，请说明理由．　20．（本小题满分12分）已知函数，设，131)(23+-=ax x x h x a x h x f ln 2)(')(-=，其中，.222ln )(a x x g +=0>x R a ∈（1）若函数在区间上单调递增，求实数的取值范围； )(x f ),2(+∞（2）记，求证：.)()()(x g x f x F +=21)(≥x F21．已知△ABC的顶点A（3，2），∠C的平分线CD所在直线方程为y﹣1=0，AC边上的高BH所在直线方程为4x+2y﹣9=0．（1）求顶点C的坐标；（2）求△ABC的面积．22．某校从高一年级学生中随机抽取40名学生作为样本，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），[90，100）后得到如图的频率分布直方图．（Ⅰ）求图中实数a的值；（Ⅱ）根据频率分布直方图，试估计该校高一年级学生其中考试数学成绩的平均数；（Ⅲ）若从样本中数学成绩在[40，50）与[90，100]两个分数段内的学生中随机选取2名学生，试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率．23．如图，在四棱锥O ﹣ABCD 中，底面ABCD 四边长为1的菱形，∠ABC=，OA ⊥底面ABCD ，OA=2，M 为OA 的中点，N 为BC 的中点．（Ⅰ）证明：直线MN ∥平面OCD ；（Ⅱ）求异面直线AB 与MD 所成角的大小；（Ⅲ）求点B 到平面OCD的距离．24．（本小题满分10分）选修4—4：坐标系与参数方程以坐标原点为极点，以轴的非负半轴为极轴建立极坐标系，已知曲线的参数方程为（x C ⎪⎩⎪⎨⎧==θθsin 2cos 2y x θ为参数，），直线的参数方程为（为参数）．],0[πθ∈l 2cos 2sin x t y t ì=+ïí=+ïîaa t （I ）点在曲线上，且曲线在点处的切线与直线垂直，求点的极坐标；D C C D +2=0x y +D （II ）设直线与曲线有两个不同的交点，求直线的斜率的取值范围．l C l 【命题意图】本题考查圆的参数方程、直线参数方程、直线和圆位置关系等基础知识，意在考查数形结合思想、转化思想和基本运算能力．大冶市一中2018-2019学年上学期高三数学10月月考试题（参考答案）一、选择题1． 【答案】B【解析】，故选B ．(2016)(2016)(54031)(1)f f f f e -==⨯+==2． 【答案】A【解析】解：设AB 的中点为C ，则因为，所以|OC|≥|AC|，因为|OC|=，|AC|2=1﹣|OC|2，所以2（）2≥1，所以a ≤﹣1或a ≥1，因为＜1，所以﹣＜a ＜，所以实数a 的取值范围是，故选：A ．【点评】本题考查直线与圆的位置关系，考查点到直线的距离公式，考查学生的计算能力，属于中档题．　3． 【答案】C 【解析】考点：几何体的结构特征.4． 【答案】B 【解析】试题分析：因为函数满足,且分别是上的偶函数和奇函数,()xF x e =()()()F x g x h x =+()(),g x h x R 使得不等式()()()()()()(],,,,0,222x x x xxxe e e e e g x h x eg x h x g x h x x ---+-∴=+=-∴==∀∈ 恒成立, 即恒成立, ()()20g x ah x -≥22022xxx xe ee e a --+--≥A()2222x x x xx xx xe e e ea e e e e -----++∴≤=--, 设，则函数在上单调递增,, 此时不等()2x x x xe e e e--=-++x x t e e -=-x x t e e -=-(]0,2220t e e -∴<≤-式当且仅当,即时, 取等号,,故选B. 2t t +≥2t t=t =a ∴≤考点：1、函数奇偶性的性质；2、不等式恒成立问题及函数的最值.【方法点晴】本题主要考查函数奇偶性的性质、不等式恒成立问题及函数的最值，属于难题．不等式恒成立问题常见方法：①分离参数()a f x ≤恒成立（min ()a f x ≤即可）或()a f x ≥恒成立（max ()a f x ≥即可）；②数形结合；③讨论最值min ()0f x ≥或max ()0f x ≤恒成立；④讨论参数 .本题是利用方法①求得的最大值的.5． 【答案】D 【解析】解：，∴y ′（0）=a ﹣1=2，∴a=3．故答案选D ．【点评】本题是基础题，考查的是导数的几何意义，这个知识点在高考中是经常考查的内容，一般只要求导正确，就能够求解该题．在高考中，导数作为一个非常好的研究工具，经常会被考查到，特别是用导数研究最值，证明不等式，研究零点问题等等经常以大题的形式出现，学生在复习时要引起重视．　6． 【答案】B 【解析】试题分析：由()()()()()212102102x x x f x f x f x f x --<⇒⇒-<--，即整式21x -的值与函数()f x 的值符号相反，当0x >时，210x ->；当0x <时，210x -<，结合图象即得()()11-∞-+∞ ，，．考点：1、函数的单调性；2、函数的奇偶性；3、不等式.7． 【答案】A 【解析】考点：集合的包含关系的判断与应用.【方法点晴】本题主要考查了集合的包含关系的判定与应用，其中解答中涉及到分式不等式的求解，一元二次不等式的解法，集合的子集的相关的运算等知识点的综合考查，着重考查了转化与化归思想、分类讨论思想的应用，以及学生的推理与运算能力，属于中档试题，本题的解答中正确求解每个不等式的解集是解答的关键.8． 【答案】D【解析】解析：本题考查复数的点的表示与复数的乘法运算，，，选D ．21zi i=-+(1)(2)3z i i i =+-=+9． 【答案】B 【解析】考点：1、同角三角函数基本关系的运用；2、两角和的正弦函数；3、任意角的三角函数的定义.10．【答案】C11．【答案】A 【解析】考点：三角函数的定义.12．【答案】C 【解析】试题分析：，所以①③④正确.故选C.{}1,1A =-考点：元素与集合关系，集合与集合关系．二、填空题13．【答案】1231n --A【解析】考点：1、利用导数求函数极值；2、根据数列的递推公式求通项公式.【方法点晴】本题主要考查等比数列的定义以及已知数列的递推公式求通项，属于中档题.由数列的递推公式求通项常用的方法有：累加法、累乘法、构造法，形如的递推数列求通项往往用1(0,1)n n a qa p p q -=+≠≠构造法，利用待定系数法构造成的形式，再根据等比数例求出的通项，进而得1()n n a m q a m -+=+{}n a m +出的通项公式.{}n a 14．【答案】()2245f x x x =-+【解析】试题分析：由题意得，令，则，则，所以函数1t x =-1x t =+()222(1)8(1)11245f t t t t t =+-++=-+()f x 的解析式为.()2245f x x x =-+考点：函数的解析式.15．【答案】　﹣21　．【解析】解：∵等比数列{a n }的公比q=﹣，a 6=1，∴a 1（﹣）5=1，解得a 1=﹣32，∴S 6==﹣21故答案为：﹣21　16．【答案】.±【解析】分析题意得，问题等价于只有一解，即只有一解，264x ax ++≤220x ax ++≤∴，故填：.280a a ∆=-=⇒=±±17．【答案】若1x <，则2421x x -+<-【解析】试题分析：若1x <，则2421x x -+<-，否命题要求条件和结论都否定．考点：否命题.三、解答题18．【答案】【解析】解：（Ⅰ）令，所以x=a．易知，x∈（0，a）时，f′（x）＞0，x∈（a，+∞）时，f′（x）＜0．故函数f（x）在（0，a）上递增，在（a，+∞）递减．故f（x）max=f（a）=alna﹣a．（Ⅱ）令g（x）=f（a﹣x）﹣f（a+x），即g（x）=aln（a﹣x）﹣aln（a+x）+2x．所以，当x∈（0，a）时，g′（x）＜0．所以g（x）＜g（0）=0，即f（a+x）＞f（a﹣x）．（Ⅲ）依题意得：a＜α＜β，从而a﹣α∈（0，a）．由（Ⅱ）知，f（2a﹣α）=f[a+（a﹣α）]＞f[a﹣（a﹣α）]=f（α）=f（β）．又2a﹣α＞a，β＞a．所以2a﹣α＜β，即α+β＞2a．【点评】本题考查了利用导数证明不等式的问题，一般是转化为函数的最值问题来解，注意导数的应用．　19．【答案】【解析】解：（1）∵椭圆的左、右焦点分别为F1（﹣c，0），F2（c，0），P是椭圆C上任意一点，且椭圆的离心率为，∴=，解得，∴椭圆C的方程为．…（2）①当l1，l2的斜率存在时，设l1：y=kx+m，l2：y=kx+n（m≠n），△=0，m2=1+2k2，同理n2=1+2k2m2=n2，m=﹣n，设存在，又m2=1+2k2，则|k2（2﹣t2）+1|=1+k2，k2（1﹣t2）=0或k2（t2﹣3）=2（不恒成立，舍去）∴t2﹣1=0，t=±1，点B（±1，0），②当l1，l2的斜率不存在时，点B（±1，0）到l1，l2的距离之积为1．综上，存在B（1，0）或（﹣1，0）．…20．【答案】（1）.（2）证明见解析.]34,(-∞【解析】试题解析：解：（1）函数，，1111]131)(23+-=ax x x h ax x x h 2)('2-=所以函数，∵函数在区间上单调递增，x a ax x x a x h x f ln 22ln 2)(')(2--=-=)(x f ),2(+∞∴在区间上恒成立，所以在上恒成0222ln 2)(')('2≥--=-=x a ax x x a x h x f ),2(+∞12+≤x x a ),2(+∞∈x 立.令，则，当时，，1)(2+=x x x M 2222)1(2)1()1(2)('++=+-+=x x x x x x x x M ),2(+∞∈x 0)('>x M ∴，∴实数的取值范围为.34)2(1)(2=>+=M x x x M ]34,(-∞（2），]2ln )ln ([22ln ln 22)(222222xx a x x a a x x a ax x x F +++-=++--=令，则111]2ln )ln ()(222x x a x x a a P +++-=.4)ln (4)ln (2ln (2ln )2ln ()2ln ()(2222222x x x x x x a x x x x x x a a P +≥+-+-=+++-+-=令，则，显然在区间上单调递减，在区间上单调递增，x x x Q ln )(-=x x x x Q 111)('-=-=)(x Q )1,0(),1[+∞则，则，故.1)1()(min ==Q x Q 41)(≥a P 21412)(=⨯≥x F 考点：利用导数研究函数的单调性；利用导数求闭区间上函数的最值．【方法点晴】本题主要考查导数在解决函数问题中的应用.考查利用导数证明不等式成立.（1）利用导数的工具()x F()x F性求解实数的取值范围；（2）先写出具体函数,通过观察的解析式的形式,能够想到解析式里可能存1在完全平方式,所以试着构造完全平方式并放缩,所以只需证明放缩后的式子大于等于即可,从而对新函数求4导判单调性求出最值证得成立.21．【答案】【解析】解：（1）由高BH所在直线方程为4x+2y﹣9=0，∴=﹣2．∵直线AC⊥BH，∴k AC k BH=﹣1．∴，直线AC的方程为，联立∴点C的坐标C（1，1）．（2），∴直线BC的方程为，联立，即．点B到直线AC：x﹣2y+1=0的距离为．又，∴．【点评】本题考查了相互垂直的直线斜率之间的关系、角平分线的性质、点到直线的距离公式、两点间的距离公式、三角形的面积计算公式，属于基础题．22．【答案】【解析】解：（Ⅰ）由频率分布直方图，得：10×（0.005+0.01+0.025+a+0.01）=1，解得a=0.03．（Ⅱ）由频率分布直方图得到平均分：=0.05×45+0.1×55+0.2×65+0.3×75+0.25×85+0.1×95=74（分）．（Ⅲ）由频率分布直方图，得数学成绩在[40，50）内的学生人数为40×0.05=2，这两人分别记为A，B，数学成绩在[90，100）内的学生人数为40×0.1=4，这4人分别记为C，D，E，F，若从数学成绩在[40，50）与[90，100）两个分数段内的学生中随机选取2名学生，则所有的基本事件有：（A，B），（A，C），（A，D），（A，E），（A，F），（B，C），（B，D），（B，E），（B，F），（C，D），（C，E），（C，F），（D，E），（D，F），（E，F），共15个，如果这两名学生的数学成绩都在[40，50）或都在[90，100）内，则这两名学生的数学成绩之差的绝对值不大于10，记“这两名学生的数学成绩之差的绝对值不大于10”为事件M，则事件M包含的基本事件有：（A，B），（C，D），（C，E），（C，F），（D，E），（D，F），（E，F），共7个，所以这两名学生的数学成绩之差的绝对值不大于10的概率P=．【点评】本题考查频率和概率的求法，二查平均分的求法，是中档题，解题时要认真审题，注意频率分布直方图和列举法的合理运用．23．【答案】【解析】解：方法一（综合法）（1）取OB中点E，连接ME，NE∵ME∥AB，AB∥CD，∴ME∥CD又∵NE∥OC，∴平面MNE∥平面OCD∴MN∥平面OCD（2）∵CD∥AB，∴∠MDC为异面直线AB与MD所成的角（或其补角）作AP⊥CD于P，连接MP∵OA⊥平面ABCD，∴CD⊥MP∵，∴，，∴所以AB与MD所成角的大小为．（3）∵AB∥平面OCD，∴点A和点B到平面OCD的距离相等，连接OP，过点A作AQ⊥OP于点Q，∵AP⊥CD，OA⊥CD，∴CD⊥平面OAP，∴AQ⊥CD．又∵AQ⊥OP，∴AQ⊥平面OCD，线段AQ的长就是点A到平面OCD的距离，∵，，∴，所以点B到平面OCD的距离为．方法二（向量法）作AP⊥CD于点P，如图，分别以AB，AP，AO所在直线为x，y，z轴建立坐标系：A（0，0，0），B（1，0，0），，，O（0，0，2），M（0，0，1），（1），，设平面OCD的法向量为n=（x，y，z），则•=0，•=0即取，解得∵•=（，，﹣1）•（0，4，）=0，∴MN∥平面OCD．（2）设AB与MD所成的角为θ，∵∴，∴，AB与MD所成角的大小为．（3）设点B到平面OCD的距离为d，则d为在向量=（0，4，）上的投影的绝对值，由，得d==所以点B 到平面OCD 的距离为．【点评】培养学生利用多种方法解决数学问题的能力，考查学生利用空间向量求直线间的夹角和距离的能力．　24．【答案】【解析】（Ⅰ）设D 点坐标为，由已知得是以为半径的上半圆，)q q C (0,0)O 因为C 在点处的切线与垂直，所以直线与直线的斜率相同，，故D 点的直角坐标D l OD +2=0x y +34πθ=为，极坐标为．(1,1)-3)4p （Ⅱ）设直线：与半圆相切时l 2)2(+-=x k y )0(222≥=+y y x 21|22|2=+-kk ，（舍去）0142=+-∴k k 32-=∴k 32+=k设点，则,)0,2(-B 2ABk =-故直线.l ]22-。

2019-2020学年湖北省黄石市大冶一中高一（上）10月月考数学试卷试题数：22.满分：1501.（单选题.5分）已知集合M={0.1}.则下列关系式中.正确的是（）A.{0}∈MB.{0}∉MC.0∈MD.0⊆M2.（单选题.5分）下列函数中与y=x表示同一个函数的是（）A. y=log22xB. y=2log2xC. y=√x2D. y=(√x)23.（单选题.5分）函数f(x)=1x−3+√2x−4的定义域是（）A.[2.+∞）B.（3.+∞）C.[2.3）∪（3.+∞）D.（2.3）∪（3.+∞）4.（单选题.5分）已知函数f(x)={log12x，x＞04x，x＜0.则f（f（4））=（）A. −116B.-16C. 116D.165.（单选题.5分）已知函数f（x）满足f(x+1)=log3x+2x+1−f(x+2) .则f（2）+f（3）=（）A.3B.4C.5D.66.（单选题.5分）函数f（x）=e x-e-x.若实数a.b满足f（2a+5）+f（4-b）=0.则2a-b=（）A.1B.-1C.-9D.97.（单选题.5分）在直角梯形ABCD中.AB⊥BC.AD=DC=2. CB=√2 .动点P从点A出发.由A→D→C→B沿边运动（如图所示）.P在AB上的射影为Q.设点P运动的路程为x.△APQ的面积为y.则y=f（x）的图象大致是（）A.B.C.D.8.（单选题.5分）三个数0.993.3.log3π.log20.8的大小关系为（）A. log3π＜0.993.3＜log20.8B. log20.8＜log3π＜0.993.3C. log20.8＜0.993.3＜log3πD.0.993.3＜log20.8 l＜log3π9.（单选题.5分）下列函数中.在其定义域内既是偶函数又在（-∞.0）上单调递增的函数是（）A.f（x）=x2B.f（x）=2|x|C.f（x）=log21|x|D.f（x）=x|x|10.（单选题.5分）若函数y=x2+（2a-1）x+1在区间（-∞.2]上是减函数.则实数a的取值范围是（）.+∞）A.[- 32]B.（-∞.- 32C.[ 3.+∞）2]D.（-∞. 3211.（单选题.5分）已知函数y=f（x）的定义域为（-∞.1）∪（1.+∞）.且f（x+1）为奇函数.的所有根之和等于（）当x＜1时.f（x）=-x2-2x.则f(x)=12A.4B.5C.6D.1212.（单选题.5分）已知偶函数f（x）在（-∞.0）上单调递减.且f（2）=0.则关于x不等式xf （x）＜0的解集是（）A.（-2.2）B.（-2.0）∪（0.2）C.（-2.0）∪（2.+∞）D.（-∞.-2）∪（0.2）13.（填空题.5分）某班共35人.其中21人喜爱篮球运动.15人喜爱乒乓球运动.10人对这两项运动都不喜爱.则喜爱篮球运动但不喜爱乒乓球运动的人数为___ ．14.（填空题.5分）已知函数f（x）=ax5-bx+|x|-1.若f（-2）=2.求f（2）=___ ．15.（填空题.5分）已知函数y=b+a x2+2x（a.b是常数.且a＞0.a≠1）在区间[−3，0]上有2.则常数a的值等于___ ．y max=3，y min=5216.（填空题.5分）下列结论：① y=x2是指数函数② 函数y=√x2−2018+√2018−x2既是偶函数又是奇函数的单调递减区间是（-∞.0）∪（0.+∞）③ 函数y=1x④ 在增函数与减函数的定义中.可以把任意两个自变量”改为“存在两个自变量⑤ {（1.2）}与{（2.1）}表示同一个集合⑥ 所有的单调函数都有最值其中正确命题的序号是___ ．17.（问答题.10分）计算下列各式的值：（1）√614−(π−1)0−(338)13+(164)−23．（2）log3√27+lg25+lg4+7log72．18.（问答题.12分）全集U=R.集合A={x|2x≤16}. B={x|x−1x−5≤0}．求：（Ⅰ）∁U B；（Ⅱ）（∁U A）∩B．19.（问答题.12分）定义在[-4.4]上的奇函数f（x）.已知当x∈[-4.0]时.f（x）= 14x + a3x（a∈R）．（1）求f（x）在[0.4]上的解析式；（2）若存在x∈[-2.-1].使得不等式f（x）≤ m2x - 13x−1成立.求实数m的取值范围．20.（问答题.12分）信息科技的进步和互联网商业模式的兴起.全方位地改变了大家金融消费的习惯和金融交易模式.现在银行的大部分业务都可以通过智能终端设备完成.多家银行职员人数在悄然减少．某银行现有职员320人.平均每人每年可创利20万元．据评估.在经营条件不变的前提下.每裁员1人.则留下岗位职员每人每年多创利0.2万元．但银行需付下岗职员每人每年6万元的生活费.并且该银行正常运转所需人数不得小于现有职员的34.为了使裁员后获得的经济效益最大.该银行应裁员多少人？此时银行获得的最大经济效益是多少万元？21.（问答题.12分）已知函数f（x）=x2+|x-2|．（1）求函数f（x）的单调递增区间；（2）若对于任意的x∈[4.6].都有f(x)x−3≤a成立.求实数a的范围．22.（问答题.12分）已知f（x）定义域为R.对任意x.y∈R都有f（x+y）=f（x）+f（y）-2.且当x＞0时.f（x）＜2．（1）试判断f（x）的单调性.并证明；（2）若f（-1）=3．① 求f（1）的值；② 求实数m的取值范围.使得方程f（mx2-3x）+f（x）=3有负实数根．2019-2020学年湖北省黄石市大冶一中高一（上）10月月考数学试卷参考答案与试题解析试题数：22.满分：1501.（单选题.5分）已知集合M={0.1}.则下列关系式中.正确的是（）A.{0}∈MB.{0}∉MC.0∈MD.0⊆M【正确答案】：C【解析】：利用元素与集合、集合与集合的关系直接求解．【解答】：解：∵集合M={0.1}.∴{0}⊊M.0∈M．故A.B.D都错误.C正确．故选：C．【点评】：本题考查命题真假的判断.考查元素与集合、集合与集合的关系等基础知识.考查运算求解能力.考查函数与方程思想.是基础题．2.（单选题.5分）下列函数中与y=x表示同一个函数的是（）A. y=log22xB. y=2log2xC. y=√x2D. y=(√x)2【正确答案】：A【解析】：根据两个函数为同一函数.其定义域和对应法则完全相同.依次验证可得答案．【解答】：解：对A.y= log22x =x.定义域为x∈R.与已知函数定义域.对应法则相同.故A正确. 对B.函数y= 2log2x的定义域为x＞0.与函数的定义域不同.∴B错误；对C.y= √x2 =|x|.与函数对应法则不同.∴C错误；对D.函数y=（√x）2.的定义域为x＞0.与函数的定义域不同.∴D错误．故选：A ．【点评】：本题考查了如何判断两个函数是否为同一函数．3.（单选题.5分）函数 f (x )=1x−3+√2x −4 的定义域是（ ）A.[2.+∞）B.（3.+∞）C.[2.3）∪（3.+∞）D.（2.3）∪（3.+∞）【正确答案】：C【解析】：由根式内部的代数式大于等于0.分式的分母不为0联立不等式组求解．【解答】：解：由 {x −3≠02x −4≥0.解得x≥2且x≠3． ∴函数 f (x )=1x−3+√2x −4 的定义域是[2.3）∪（3.+∞）．故选：C ．【点评】：本题考查函数的定义域及其求法.考查指数不等式的解法.是基础题．4.（单选题.5分）已知函数 f (x )={log 12x ，x ＞04x ，x ＜0.则f （f （4））=（ ） A. −116 B.-16C. 116D.16【正确答案】：C【解析】：推导出f （4）= log 124 =-2.从而f （f （4））=f （-2）.由此能求出结果．【解答】：解：∵函数 f (x )={log 12x ，x ＞04x ，x ＜0. ∴f （4）= log 124 =-2.∴f （f （4））=f （-2）=4-2= 116 ．故选：C ．【点评】：本题考查函数值的求法.考查函数性质等基础知识.考查运算求解能力.是基础题．5.（单选题.5分）已知函数f（x）满足f(x+1)=log3x+2x+1−f(x+2) .则f（2）+f（3）=（）A.3B.4C.5D.6【正确答案】：B【解析】：根据题意.由函数的解析式用特殊值法分析：令x=1可得：f（2）=log31+21+1-f （3）.变形可得答案．【解答】：解：根据题意. f(x+1)=log3x+2x+1−f(x+2) .令x=1可得：f（2）=log31+21+1-f（3）.变形可得f（2）+f（3）=22=4.故选：B．【点评】：本题考查函数值的计算.注意利用特殊值法分析.属于基础题．6.（单选题.5分）函数f（x）=e x-e-x.若实数a.b满足f（2a+5）+f（4-b）=0.则2a-b=（）A.1B.-1C.-9D.9【正确答案】：C【解析】：利用奇函数的性质即可直接求解．【解答】：解：∵f（x）=e x-e-x为奇函数.∵f（2a+5）+f（4-b）=0.∴f（2a+5）=f（b-4）.∴2a+5=b-4即2a-b=-9.故选：C．【点评】：本题主要考查了奇函数的性质.属于基础试题．7.（单选题.5分）在直角梯形ABCD中.AB⊥BC.AD=DC=2. CB=√2 .动点P从点A出发.由A→D→C→B沿边运动（如图所示）.P在AB上的射影为Q.设点P运动的路程为x.△APQ的面积为y.则y=f（x）的图象大致是（）A.B.C.D.【正确答案】：D【解析】：结合P点的运动轨迹以及二次函数.三角形的面积公式判断即可．【解答】：解：P点在AD上时.△APQ是等腰直角三角形.此时f（x）= 12• √22x• √22x= 14x2.（0＜x＜2）是二次函数.排除A.B.P在DC上时.PQ不变.AQ增加.是递增的一次函数.排除C.故选：D．【点评】：本题考查了数形结合思想.考查二次函数以及三角形的面积问题.是一道基础题．8.（单选题.5分）三个数0.993.3.log3π.log20.8的大小关系为（）A. log3π＜0.993.3＜log20.8B. log20.8＜log3π＜0.993.3C. log20.8＜0.993.3＜log3πD.0.993.3＜log20.8 l＜log3π【正确答案】：C【解析】：利用指数函数和对数函数的运算性质.逐一比较三个数与0和1的关系即可得到答案．【解答】：解：∵0＜0.993.3＜0.990=1.log 3π＞log 33=1.log 20.8＜log 21=0．∴ log 20.8＜0.993.3＜log 3π ．故选：C ．【点评】：本题考查了对数值的大小比较.考查了不等关系与不等式.考查了指数函数和对数函数的性质.是基础题．9.（单选题.5分）下列函数中.在其定义域内既是偶函数又在（-∞.0）上单调递增的函数是（ ）A.f （x ）=x 2B.f （x ）=2|x|C.f （x ）=log 2 1|x|D.f （x ）=x|x|【正确答案】：C【解析】：根据题意.依次分析选项中函数的奇偶性与单调性.综合即可得答案．【解答】：解：根据题意.依次分析选项：对于A.y=x 2.为二次函数.其对称轴为y 轴.在其定义域内既是偶函数但在（-∞.0）上单调递减.不符合题意；对于B.y=2|x|= {2x ，x ≥02−x ，x ＜0.在其定义域内既是偶函数但在（-∞.0）上单调递减.不符合题意； 对于C.f （x ）=log 2 1|x| =f （x ）=-log 2|x|= {−log 2x ，x ＞0log 2(−x )，x ＜0.在其定义域内既是偶函数又在（-∞.0）上单调递增.符合题意； 对于D.y=x|x|= {x 2，x ≥0−x 2，x ＜0.为奇函数.不符合题意； 故选：C ．【点评】：本题考查函数的奇偶性与单调性的判定.关键是掌握常见函数的奇偶性与单调性.属于基础题．10.（单选题.5分）若函数y=x 2+（2a-1）x+1在区间（-∞.2]上是减函数.则实数a 的取值范围是（ ）A.[- 3.+∞）2B.（-∞.- 3]2C.[ 3.+∞）2]D.（-∞. 32【正确答案】：B【解析】：由已知中函数的解析式.结合二次函数的图象和性质.可以判断出函数y=x2+（2a-1）x+1图象的形状.分析区间端点与函数图象对称轴的关系.即可得到答案．为对称轴的抛物【解答】：解：∵函数y=x2+（2a-1）x+1的图象是方向朝上.以直线x= 2a−1−2线又∵函数在区间（-∞.2]上是减函数.故2≤ 2a−1−2解得a≤- 32故选：B．【点评】：本题考查的知识点是函数单调性的性质.其中熟练掌握二次函数的图象和性质是解答本题的关键．11.（单选题.5分）已知函数y=f（x）的定义域为（-∞.1）∪（1.+∞）.且f（x+1）为奇函数.的所有根之和等于（）当x＜1时.f（x）=-x2-2x.则f(x)=12A.4B.5C.6D.12【正确答案】：A【解析】：∵f（x+1）为奇函数.∴f（x+1）关于（0.0）对称.∴f（x）关于（1.0）对称.∴f（x）+f（2-x）=0.进而求解．【解答】：解：∵f（x+1）为奇函数.∴f（x+1）关于（0.0）对称.∴f（x）关于（1.0）对称.∴f （x）+f（2-x）=0.∵当x＜1时.f（x）=-x2-2x.∴x＞1.即2-x＜1时.f（x）=-f（2-x）=-[-（2-x）2-2（2-x）]=x2-6x+8.f （x ）= 12 即 {−x 2−2x =12①x 2−6x +8=12② . 由 ① 得x 1+x 2=-2.由 ② x 3+x 4=6.∴x 1+x 2+x 3+x 4=4.故选：A ．【点评】：考查抽象函数的对称性.函数的平移.韦达定理．12.（单选题.5分）已知偶函数f （x ）在（-∞.0）上单调递减.且f （2）=0.则关于x 不等式xf （x ）＜0的解集是（ ）A.（-2.2）B.（-2.0）∪（0.2）C.（-2.0）∪（2.+∞）D.（-∞.-2）∪（0.2）【正确答案】：D【解析】：先根据函数为偶函数得到.f （x ）在（0.+∞）上单调递增.f （2）=f （-2）=0.再根据函数的单调性构造不等式组解得即可．【解答】：解：∵偶函数f （x ）在（-∞.0）上单调递减.∴f （x ）在（0.+∞）上单调递增.且f （2）=f （-2）=0.则不等式xf （x ）＜0可化为： {f (x )＞0x ＜0 .或 {f (x )＜0x ＞0. 解得：x∈（-∞.-2）∪（0.2）.故选：D ．【点评】：本题主要考查了偶函数的性质.函数的单调性.以及不等式组的解法.属于基础题13.（填空题.5分）某班共35人.其中21人喜爱篮球运动.15人喜爱乒乓球运动.10人对这两项运动都不喜爱.则喜爱篮球运动但不喜爱乒乓球运动的人数为___ ．【正确答案】：[1]10【解析】：设两项运动都喜欢的人数为x.作出维恩图.列出方程.由此能求出喜爱篮球运动但不喜爱乒乓球运动的人数．【解答】：解：某班共35人.其中21人喜爱篮球运动.15人喜爱乒乓球运动.10人对这两项运动都不喜爱.设两项运动都喜欢的人数为x.作出维恩图.如右图.则：15-x+x+21-x+10=35.解得x=11.∴喜爱篮球运动但不喜爱乒乓球运动的人数为：21-x=21-11=10．故答案为：10．【点评】：本题考查喜爱篮球运动但不喜爱乒乓球运动的人数的求法.考查维恩图的性质等基础知识.考查运算求解能力.考查函数与方程思想.是基础题．14.（填空题.5分）已知函数f（x）=ax5-bx+|x|-1.若f（-2）=2.求f（2）=___ ．【正确答案】：[1]0【解析】：利用函数的解析式.结合已知条件直接求解函数值即可．【解答】：解：函数f（x）=ax5-bx+|x|-1.若f（-2）=2.可得：-32a+2b+1=2.f（2）=32a-2b+1=-1+1=0故答案为：0.【点评】：本题考查函数的解析式以及函数的奇偶性的应用.考查计算能力．15.（填空题.5分）已知函数y=b+a x2+2x（a.b是常数.且a＞0.a≠1）在区间[−32，0]上有y max=3，y min=52.则常数a的值等于___ ．【正确答案】：[1]2或23【解析】：分类讨论a与1的关系.然后根据函数的增减性.进而求解．【解答】：解：① 0＜a＜1. y=b+a x2+2x =b+a (x+1)2−1 .x=0时.y min=b+1= 52 .即b= 32；x=-1时.y max= 32 +a1-2=3.解得a= 23；② a＞1时. y=b+a x2+2x =b+a (x+1)2−1 .x=0时.y max=b+1=3.即b=2.；x=-1时.y min=2+a-.解得a=2；1= 52故答案为：2或23【点评】：考查复合函数的综合应用.二次函数的单调性.指数函数的单调性.在特定区间的值域．16.（填空题.5分）下列结论：① y=x2是指数函数② 函数y=√x2−2018+√2018−x2既是偶函数又是奇函数的单调递减区间是（-∞.0）∪（0.+∞）③ 函数y=1x④ 在增函数与减函数的定义中.可以把任意两个自变量”改为“存在两个自变量⑤ {（1.2）}与{（2.1）}表示同一个集合⑥ 所有的单调函数都有最值其中正确命题的序号是___ ．【正确答案】：[1] ②【解析】：由函数为幂函数.可判断① ；求得函数的定义域.结合奇偶性的定义可判断② ；由单调区间的定义可判断③ ；由单调性的都有可判断④ ；由点集的概念可判断⑤ ；由最值的定义可判断⑥ ．【解答】：解：① y=x2是幂函数.不是指数函数.故① 错误；② 函数y=√x2−2018+√2018−x2的定义域为{- √2018 . √2018 }.且y=0.既是偶函数又是奇函数.故② 正确；的单调递减区间是（-∞.0）.（0.+∞）.故③ 错误；③ 函数y=1x④ 在增函数与减函数的定义中.不可以把任意两个自变量”改为“存在两个自变量.否则不单调.故④ 错误；⑤ {（1.2）}与{（2.1）}表示两个点的集合.故⑤ 错误；⑥ 所有的单调函数不都有最值.比如定义域为开区间.故⑥ 错误．故答案为：②【点评】：本题考查函数的奇偶性和单调性的判断.最值的概念.考查数集和点集的区别.属于基础题．17.（问答题.10分）计算下列各式的值：（1）√614−(π−1)0−(338)13+(164)−23．（2）log3√27+lg25+lg4+7log72．【正确答案】：【解析】：（1）根据指数的运算性质计算即可. （2）根据对数的运算性质计算即可【解答】：解：（1）原式= 52 -1- 32+16=16．（2）原式= 32 +2+2= 112．【点评】：本题考查了指数幂和对数的运算性质.属于基础题18.（问答题.12分）全集U=R.集合A={x|2x≤16}. B={x|x−1x−5≤0}．求：（Ⅰ）∁U B；（Ⅱ）（∁U A）∩B．【正确答案】：【解析】：（1）先求出集合B.再求出∁U B即可；（2）先求出集合A.再求出∁U A.再利用集合的交集运算求出（∁U A）∩B即可．【解答】：解：（Ⅰ）∵集合B={x|x−1x−5≤0}={x|1≤x＜5}.∴∁U B={x|x＜1或x≥5}；（Ⅱ）∵集合A={x|2x≤16}={x|x≤4}.集合B={x|1≤x＜5}.∴∁U A={x|x＞4}.∴（∁U A）∩B={x|4＜x＜5}．【点评】：本题主要考查了集合的基本运算.是基础题．19.（问答题.12分）定义在[-4.4]上的奇函数f（x）.已知当x∈[-4.0]时.f（x）= 14x + a3x（a∈R）．（1）求f（x）在[0.4]上的解析式；（2）若存在x∈[-2.-1].使得不等式f（x）≤ m2x - 13x−1成立.求实数m的取值范围．【正确答案】：【解析】：（1）根据奇函数的性质即可求出a.设x∈[0.4].-x∈[-4.0].易求f（-x）.根据奇函数性质可得f（x）与f（-x）的关系；（2）分离参数.构造函数.求出函数的最值问题得以解决．【解答】：解：（1）f（x）是定义在[-4.4]上的奇函数.∴f（0）=1+a=0.∴a=-1.∵ f(x)=14x −13x.设x∈[0.4]. ∴-x∈[-4.0].∴ f(x)=−f(−x)=−[14−x −13−x]=3x−4x .∴x∈[0.4]时.f（x）=3x-4x（2）∵x∈[-2.-1]. f(x)≤m2x −13x−1.即14x −13x≤m2x−13x−1即14x +23x≤m2x.x∈[-2.-1]时恒成立.∵2x＞0.∴ (12)x+2•(23)x≤m .∵ g(x)=(12)x+2•(23)x在R上单调递减.∴x∈[-2.-1]时. g(x)=(12)x+2•(23)x的最小值为g(−1)=(12)−1+2•(23)−1=5 .∴m≥5．【点评】：本题考查函数的奇偶性及其应用.不等式恒成立的问题.考查学生解决问题的能力.属于中档题．20.（问答题.12分）信息科技的进步和互联网商业模式的兴起.全方位地改变了大家金融消费的习惯和金融交易模式.现在银行的大部分业务都可以通过智能终端设备完成.多家银行职员人数在悄然减少．某银行现有职员320人.平均每人每年可创利20万元．据评估.在经营条件不变的前提下.每裁员1人.则留下岗位职员每人每年多创利0.2万元．但银行需付下岗职员每人.为了使裁员后获得每年6万元的生活费.并且该银行正常运转所需人数不得小于现有职员的34的经济效益最大.该银行应裁员多少人？此时银行获得的最大经济效益是多少万元？【正确答案】：【解析】：设银行应裁员x人.所获得的经济效益为万元.由题意列y关于x的函数关系式.然后利用二次函数的单调性求最值．【解答】：解：设银行应裁员x人.所获得的经济效益为万元.x2+38x+6400 .则y=（320-x）（20+0.2x）-6x= −15×320 .又x≥0.由题意可得：320-x ≤34∴0≤x≤80且x∈N.∵对称轴x=95＞80.x2+38x+6400在[0.80]上单调递增.∴函数y= −15∴x=80时.y max=8160．即银行应裁员80人.所获得的经济效益最大.为8160万元．【点评】：本题考查简单的数学建模思想方法.训练了一元二次函数最值的求法.是中档题．21.（问答题.12分）已知函数f（x）=x2+|x-2|．（1）求函数f（x）的单调递增区间；≤a成立.求实数a的范围．（2）若对于任意的x∈[4.6].都有f(x)x−3【正确答案】：【解析】：（1）去掉绝对值符号.得到分段函数.然后判断函数的单调性．（2）当x∈[4.6]时.化简f (x )x−3 .利用换元法.结合函数的单调性求解函数的最大值.然后推出a 的范围即可．【解答】：解：（1）因为 f (x )=x 2+|x −2|={x 2+x −2，x ≥2x 2−x +2，x ＜2 . 所以当x≥2时.f （x ）单调递增.当 2＞x ≥12 时.f （x ）单调递增当 x ＜12 时.f （x ）单调递减.因此函数f （x ）的单调递增区间为 [12，+∞) .（2）当x∈[4.6]时. f (x )x−3 =x 2+x−2x−3 =x-3+ 10x−3+ 7成立. 令x-3=t.则t∈[1.3].f (x )x−3 =t+ 10t +7为[1.3]上单调递减函数. 因此t=1时. f (x )x−3 取最大值18.从而a≥18．【点评】：本题考查了函数单调性的判断与证明.含绝对值函数的解法.考查了利用单调性求函数的最值.是中档题．22.（问答题.12分）已知f （x ）定义域为R.对任意x.y∈R 都有f （x+y ）=f （x ）+f （y ）-2.且当x ＞0时.f （x ）＜2．（1）试判断f （x ）的单调性.并证明；（2）若f （-1）=3．① 求f （1）的值；② 求实数m 的取值范围.使得方程f （mx 2-3x ）+f （x ）=3有负实数根．【正确答案】：【解析】：（1）设x1＜x2.则f（x2）-f（x1）=f（x2-x1）-2＜0.从而得出f（x）的单调性；（2）① 先计算f（0）.再计算f（1）；② 方程等价于mx2-2x=-1有负实数根.讨论m的范围列出不等式得出m的范围．【解答】：解：（1）设x1.x2为R上的任意两个数.且x1＜x2.则x2-x1＞0.∴f（x2-x1）＜2．∵f（x2）=f（x2-x1+x1）=f（x2-x1）+f（x1）-2.∴f（x2）-f（x1）=f（x2-x1）-2＜0.即f（x2）＜f（x1）.∴f（x）在R上是减函数．（2）① 令x=y=0可得f（0）=2f（0）-2.∴f（0）=2.令x=1.y=-1得：f（0）=f（1）+f（-1）-2=2.∴f（1）=4-f（-1）=1．.② 方程f（mx2-3x）+f（x）=3等价于f（mx2-2x）=f（-1）.又f（x）为单调函数.故而mx2-2x=-1.即mx2-2x+1=0．∴方程mx2-2x+1=0有负实数根．当m=0时.-2x+1=0.解得x= 12.不符合题意；当m≠0时.△=4-4m≥0.即m≤1且m≠0.若△=0.即m=1时.则方程的解为x=1.不符合题意；若△＞0.即m＜1且m≠0则方程的根为x= 1±√1−mm.∴ 1+√1−mm ＜0或1−√1−mm＜0.解得m＜0．综上.m的取值范围是（-∞.0）．【点评】：本题考查了抽象函数的单调性判断.二次函数的零点分布与系数的关系.属于中档题．。

(A):有㈤而=!丽q 京⑥而=湖北省2020届高三数学10月月考试题 理注意事项：1. 本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试卷相应的位置。

3. 全部答案在答题卡上完成，答在草稿纸上无效：考试结束，将答题卡交回。

4. 满分150分.考试时间120分钟.第I 卷（选择题共60分）一、选择题（本大题共12个小题，每小题5分，共60分，在毎小题给岀的四个选项中，只有一项是符合题目要求 的）o已知集合M ={X \-4<X <2}9 /V = {X |X 2-X -6<0}> 则=6设。

灿ABC 所在平血内一点BC = 3CD.则 1. A. (x|-4<x<3}B. (x|-4<x<-2}C. {x\-2<x<2}D. {x2<x<3}2. l + 2i商A.4 3. ———i5 5B. C.3 4. 5D.-2+ii 5 53.设命题只 /r>2\则「户为3) V K W, rr>2n(^3 ns A ；/W2” (d VneA ；2" (2?) 3 n 2 =24. /i :sina = -t 则cos2a=(A. B ・ C. D.5. 记凯为等差数列｛弓｝的前〃项和・若3S 3=S 2+S 4, 6=2,则a 产<A. -12C. 10D. 127.己知n = log:0.2,力=2°2, c = 0.2°3.则9.函数f(x)=x+cosx的大致图象为()12.意大利数学家列昂那多•多波那契以兔子繁殖为例,引入“兔子数列1丄2,3,5,8,13,21,34,55,……，即F(l) = F(2) = l.F(n) = F(//-l)+F(n-2) (H>3,KE/V)*此数列在现代物理“准晶体结构”、化学等都有着广泛的应用.若此数列被2整除后的余数构成一个新数列｛nJ,则数列｛《,｝的前2019项的和为( ) 第I 【卷(非选择题共85分)A.a<b<cB.a<c<bC.c<a<bD.b<c<aa€8.已知(0三)siMa+訓)r 件2vT-hv7 \3+2v2A. B. C. D.10.函数f(x)=4cos(心+ ©)(A>0, 3>0.—M敏〈0)的部分图象如图所示■为了得到g(*)=Xsin “¥的图象.只需将函数y=f(x)的图象()A.向左平移/个单位长度B.向左平移古个单位长度C.向右平移£个单位长度D.向右平移&个单位长度b 1Z11. 己知函数/(x) = <e* xWOInx, x>0g(x) = /(x) + x + H,若g(x)存在2 个零点,则0的取值范围是(A. [-1. 0)B. [ 0, +8)C. [-1 f +8)D. [1 ♦ +8)2A. 672B. 673C. 1346D. 2019二、填空題(本大题共4个小题，每小题5分，共20分，把正确答案填在題中横线上)13.已知向星“=(1,2), 6=(2,-2), c=(l,z).若c//(2a+h).则4= .14若函数f(x) = xln (.H- Ja + x')为偶函数，则a=14..记£为等比数列｛必的前〃项和.若《=!，£=%,则* .16.在平而四边形ABCD中，AB = 1. AC=A/5. BD1BC. BD=2BC,则AD的最小值为.三、解答题(本大题共6个小题，共65分，解答应写出文字说明，证明过程或演算步骤)17.(本题满分10分)AABC的内角4, B,。

湖北省黄石市大冶市第一中学2020-2021学年高二10月月考语文试题学校:___________姓名：___________班级：___________考号：___________一、现代文阅读真正高层次的诗歌鉴赏，应该透过对诗歌字句语词的诠释、结构美感的把握、对诗人生平遭际的了解以及诗人心性思想的深刻领悟，直至与诗人的心弦发生生命的共振才能最终完成。

而这几个方面可以用“文学本位”“知人论世”与“以意逆志”予以概括。

“文学本位”的鉴赏视角是一种深入诗歌内部语境的解读，它以语词涵义的训诂诠释、经史典故的查勘考据为基础，延伸到对诗歌字法、句法、章法的研析和审美。

但是古代很多诗评家皆深信一切“评点笺释，皆后人方隅之见”，诗之高妙者实乃“羚羊挂角，无迹可求”。

这种不求甚解只求会心的印象式的鉴赏风气直到清代才有根本性的改变。

如金圣叹对杜甫诗的评点方法显然迥别于传统的诗评家，十分注意作品文本的形式技巧。

他要“分解”唐诗，像庖丁解牛那样，“细读”这个具体文本，通过对诗歌具体语词形式的把握，达到对诗歌整体神韵的体会。

可是，如果对文本的解读太具体了，就很容易变得机械、呆板，而且中国古代诗学传统中所说的“言外之意、味外之味、象外之象”等现象也的确存在。

“知人论世”作为诗歌鉴赏的一个视角，是根据诗人的生平际遇，如家世背景、仕宦经历、婚姻爱情等推断诗歌作品中蕴涵的思想情感，进而诠释诗歌语词的深层意蕴。

后来历代诗评家大都奉此为圭臬，因此便成为了诗歌鉴赏中最普遍、最传统的一种方法。

但令人遗憾的是，人们在采取这种鉴赏视角时，常常会对历史背景材料的分析过于具体，甚至穿凿附会，使得诗歌的鉴赏失去文本应有的艺术美感。

比如宋之问的《渡汉江》中“近乡情更怯，不敢问来人”，极其生动逼真地把离家日久的游子在返乡途中惴惴不安的心情表现得淋漓尽致。

可是，当“知人论世”的考据和分析，认定这是宋之问从流放地逃亡洛阳途经汉江所作时，读者心中那份美好的情感顿时烟消云散。

大冶一中高二年级2019年10月月考数 学 试 卷一、选择题(共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个选项符合题目要求)1.已知数列{}n a 为等比数列，首项12a =，数列{}n b 满足2log n n b a =，且2349b b b ++=，则5a =（ ） A. 8 B. 16 C. 32 D. 64【答案】C 【解析】 【分析】先确定{}n b 为等差数列，由等差的性质得3b 3=，进而求得{}n b 的通项公式和{}n a 的通项公式，则5a 可求【详解】由题意知{}n b 为等差数列，因为234b b b 9++=，所以3b 3=，因为1b 1=，所以公差d 1=，则n b n =，即2n n log a =，故nn a 2=，于是55a 232==.故选：C【点睛】本题考查等差与等比的通项公式，等差与等比数列性质，熟记公式与性质，准确计算是关键，是基础题2.如图，正方体1111ABCD A B C D -中，异面直线AC 和1BC 所成角的大小为（ ）A.3π B.2π C.23π D.3π或23π 【答案】A 【解析】 【分析】连接1AD ，1CD ，根据平行关系可知所求角为1D AC ∠，易知1ACD ∆为等边三角形，从而可知13D AC π∠=，得到所求结果.【详解】连接1AD ，1CD11//BC AD Q 1D AC ∴∠即为异面直线AC 与1BC 所成角又11AD AC CD == 13D AC π∴∠=即异面直线AC 与1BC 所成角为：3π 本题正确选项：A【点睛】本题考查异面直线所成角的求解，关键是通过平移直线找到所成角，再放入三角形中进行求解.3.设,a b 表示不同的直线，,αβ表示不同的平面，给出下列命题： ①若//a α，a β⊂，则//αβ； ②若a α⊂，//αβ，则//a β；③若//a b ，a α⊥，b β⊥，则//αβ； ④若a b ⊥r r，a α⊥，b β⊥，则αβ⊥. 则以上命题正确的个数为（ ） A. 1 B. 2C. 3D. 4【答案】C 【解析】 【分析】根据直线与平面、平面与平面平行、垂直的判定和性质依次判断各个选项即可. 【详解】①//a α，a β⊂，此时α与β平行或相交，①错误； ②a α⊂，//αβ，根据面面平行性质可知//a β，②正确；③//a b ，a α⊥，则b α⊥，又b β⊥，//αβ∴，③正确； ④a b ⊥r r，a α⊥，则//b α或b α⊂；又b β⊥，αβ∴⊥，④正确. 本题正确选项：C【点睛】本题考查空间中直线与平面、平面与平面位置关系相关命题的判断，考查对于平行与垂直的判定定理、性质定理的掌握情况.4.已知过点(2,)A m -和点(,4)B m 的直线为1l ，2:210l x y +-=，3:10l x ny ++=．若12l l //，23l l ⊥，则m n +的值为（ ）A. 10-B. 2-C. 0D. 8【答案】A 【解析】 【分析】利用直线平行垂直与斜率的关系即可得出． 【详解】∵l 1∥l 2，∴k AB ＝42mm -+＝－2，解得m ＝－8． 又∵l 2⊥l 3，∴1n-×(－2)＝－1，解得n ＝－2，∴m ＋n ＝－10．故选:A ． 【点睛】本题考查了直线平行垂直与斜率的关系，考查了推理能力与计算能力，属于基础题．5.直线y x b =+与曲线x =b 的取值范围是（ ）A. b =B. 11b -<≤或b =C. 1-或1D. 以上都不对 【答案】B 【解析】 【分析】把曲线方程整理后可知其图象为半圆，进而画出图象来，要使直线与曲线有且仅有一个交点，那么很容易从图上看出其三个极端情况分别是：直线在第四象限与曲线相切，交曲线于（0，−1）和另一个点，及与曲线交于点（0，1），分别求出b ，则b 的范围可得．【详解】由21x y =-可以得到221x x y ≥⎧⎨+=⎩，所以曲线21x y =-为y 轴右侧的半圆， 因为直线y x b =+与半圆有且仅有一个公共点，如图所示：所以11b -<≤或012b b <⎧=，所以11b -<≤或2b =-B ．【点睛】本题考查直线与半圆的位置关系，注意把曲线的方程变形化简时要关注等价变形．6.圆224x y +=与圆2244120x y x y +-+-=的公共弦所在直线和两坐标轴所围成图形的面积为（ ） A. 1 B. 2C. 4D. 8【答案】B 【解析】 【分析】将两圆方程相减可得公共弦所在直线的方程．【详解】将两圆方程相减可得44124x y -+=即20x y -+= 当0x =时，2y =，当0y =时，2x =-交点()0,2与()2,0-1122222S x y ∆==⨯⨯=，故选B ． 【点睛】本题考查圆与圆的位置关系．两圆方程分别为221110x y D x E y F ++++=，222220x y D x E y F ++++=，则两方程相减得()()1212120D D x E E y F F -+-+-=，为：两圆相交时是相交弦所在直线方程，两圆相切时，是过切点的公共切线的方程．7.已知椭圆222:1(0)25x y C m m+=>的左、右焦点分别为12,F F ，点P 在C 上，且12PF F ∆的周长为16，则m 的值是 A. 2 B. 3C. 23D. 4【答案】D 【解析】 【分析】由椭圆的定义知12PF F ∆的周长为2216a c +=，可求出c 的值，再结合a 、b 、c 的关系求出b 的值，即m 的值。

湖北省大冶市第一中学2020届高三数学10月月考试题 文注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试卷相应的位置。

3. 全部答案在答题卡上完成，答在草稿纸上无效；考试结束，将答题卡交回。

4.满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)。

1．已知集合}242{60{}M x x N x x x =-<<=--<，，则M N I = A ．}{43x x -<<B ．}42{x x -<<- C ．}{22x x -<< D ．}{23x x <<2．12i12i+=-（ ） A ．43i 55-- B ．43i 55-+C ．34i 55--D ．34i 55-+3.设命题P ：∃n ∈N ，2n >2n，则⌝P 为(A )∀n ∈N ，2n >2n (B )∃n ∈N ，2n ≤2n (C )∀n ∈N ，2n ≤2n (D )∃n ∈N ，2n ＝2n4．若1sin 3α=，则cos2α=（ ）A ．89B ．79C ．79-D ．89-5．记n S 为等差数列{}n a 的前n 项和．若3243S S S =+，12a =，则3a =（ ）A ． 12-B ．10-C ．10D ．126设D 为ABC 所在平面内一点3BC CD =u u u r u u u r，则(A ) 1433AD AB AC=-+u u u r u u ur u u u r (B )1433AD AB AC=-u u u r u u u r u u u r(C )4133AD AB AC=+u u u r u u u r u u u r(D )4133AD AB AC =-u u u r u u u r u u u r7．已知0.20.32log 0.220.2a b c ===，，，则 A ．a b c <<B ．a c b <<C ．c a b <<D ．b c a <<8．函数f (x )＝x ＋cos x 的大致图象为( )9．设等边三角形ABC ∆的边长为1，平面内一点M 满足1123AM AB AC =+uuu r uu u r uuu r ，向量AM u u u u r 与AB u u u r夹角的余弦值为（ ）A 6B ．36C 19D 41910．已知函数()0ln 0x e x f x x x ⎧=⎨>⎩，≤，，()()g x f x x a =++，若()g x 存在2个零点，则a 的取值范围是（） A ．[)10-，B ．[)0+∞，C ．[)1-+∞，D ．[)1+∞，11．意大利数学家列昂那多·斐波那契以兔子繁殖为例，引入“兔子数列”：1,1,2,3,5,8,13,21,34,55,L L ，即()()()()()121,12F F F n F n F n ===-+-()3,n n N *≥∈，此数列在现代物理“准晶体结构”、化学等都有着广泛的应用．若此数列被2整除后的余数构成一个新数列{}n a ，则数列{}n a 的前2019项的和为（ ）A ．672B ．673C ．1346D ．201912．已知函数在区间上单调，且在区间内恰好取得一次最大值2，则的取值范围是A ．B ．C ．D ．第Ⅱ卷(非选择题 共85分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．已知向量()=1,2a ，()=2,2-b ，()=1,λc ．若()2∥c a +b ，则λ=________．14若函数f (x )＝xln (x 2a x +为偶函数，则a ＝_________.15．已知函数()(,)xf x ae b a b R =+∈在点(0,(0))f 处的切线方程为21y x =+，则a b -=_______．16．如图，为了测量两座山峰上P ，Q 两点之间的距离，选择山坡上一段长度为300 3 m 且和P ，Q 两点在同一平面内的路段AB 的两个端点作为观测点，现测得∠PAB ＝90°，∠PAQ ＝∠PBA ＝∠PBQ ＝60°，则P ，Q 两点间的距离为________ m.三、解答题(本大题共6个小题，共65分，解答应写出文字说明，证明过程或演算步骤) 17.（本题满分11分）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知2cos (cos cos ).C a B+b A c =（I ）求C ；（II ）若c ABC =V ，求ABC △的周长． 18、（本小题11分）己知向量a r ()sin ,cos x x ωω= ，b r ()cos ,cos x x ωω=，其中0ω>，记函数()12f x a b =⋅+v v ，且最小正周期为π；(1)求函数()f x 的表达式；(2)将函数()f x 的图象向右平移4π个单位后得到函数()y g x =的图象，求()y g x =在0,2π⎡⎤⎢⎥⎣⎦上的值域．19．（本小题满分11分）设命题:p 实数x 满足22430x ax a -+<，； 命题:q 实数x 满足302x x-≥-． （1）若1a =，p q ∧为真命题，求x 的取值范围；（2）若p ⌝是q ⌝的充分不必要条件，求实数x 的取值范围．20.提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度v （单位：千米/小时）是车流密度x （单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流密度为0千米/小时；当车流密度不超过20辆/千米时，车流密度为60千米/小时，研究表明：当20200x ≤≤时，车流速度v 是车流密度x 的一次函数． （1）当0200x ≤≤时，求函数()v x 的表达式；（2）当车流密度x 为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/每小时）()()f x xv x =可以达到最大，并求出最大值（精确到1辆/小时）．21（本小题满分11分）若正项数列的前项和为，满足．（1）求数列的通项公式；（2）若，求数列的前项和．22（本小题满分12分）设函数.(1)当时，求函数的最大值；(2)当，，方程有唯一实数解，求正数的值。

2020届湖北省黄石市大冶市第一中学高三上学期10月月考数学（文）试题一、单选题1．已知集合{}}242{60M x x N x x x =-<<=--<，，则M N ⋂=A ．}{43x x -<<B ．}{42x x -<<-C ．}{22x x -<<D ．}{23x x <<【答案】C【解析】本题考查集合的交集和一元二次不等式的解法，渗透了数学运算素养．采取数轴法，利用数形结合的思想解题． 【详解】由题意得，{}{}42,23M x x N x x =-<<=-<<，则{}22M N x x ⋂=-<<．故选C ．【点睛】不能领会交集的含义易致误，区分交集与并集的不同，交集取公共部分，并集包括二者部分． 2．12i12i+=- A ．43i 55--B ．43i 55-+C ．34i 55--D ．34i 55-+【答案】D【解析】分析：根据复数除法法则化简复数，即得结果.详解：212(12)341255i i ii ++-+==∴-选D.点睛：本题考查复数除法法则，考查学生基本运算能力. 3．设命题2:,2n P n N n ∃∈>，则P ⌝为（ ） A ．2,2n n N n ∀∈> B ．2,2n n N n ∃∈≤ C ．2,2n n N n ∀∈≤ D ．2,2n n N n ∃∈=【答案】C【解析】【详解】试题分析：根据否命题的定义，即既否定原命题的条件，又否定原命题的结论，特称命题的否定为全称命题，所以命题的否命题应该为2,2nn N n ∀∈≤，即本题的正确选项为C.4．若1sin 3α=，则cos2α= A ．89B ．79C ．79-D ．89-【答案】B 【解析】【详解】分析：由公式2cos2α12sin α=-可得结果.详解：227cos2α12199sin α=-=-= 故选B.点睛：本题主要考查二倍角公式，属于基础题.5．设n S 为等差数列{}n a 的前n 项和，若3243S S S =+，12a =，则5a = A.12- B.10-C.10D.12【答案】B【解析】分析：首先设出等差数列{}n a 的公差为d ，利用等差数列的求和公式，得到公差d 所满足的等量关系式，从而求得结果3d =-，之后应用等差数列的通项公式求得51421210a a d =+=-=-，从而求得正确结果. 详解：设该等差数列的公差为d ， 根据题中的条件可得32433(32)224222d d d ⨯⨯⨯+⋅=⨯++⨯+⋅， 整理解得3d =-，所以51421210a a d =+=-=-，故选B.点睛：该题考查的是有关等差数列的求和公式和通项公式的应用，在解题的过程中，需要利用题中的条件，结合等差数列的求和公式，得到公差d 的值，之后利用等差数列的通项公式得到5a 与1a d 和的关系，从而求得结果.6．设D 为ABC ∆所在平面内一点，若3BC CD =，则下列关系中正确的是（ ） A.1433AD AB AC =-+ B.1433AD AB AC =- C.4133AD AB AC =+ D.4133AD AB AC =- 【答案】A 【解析】【详解】 ∵3BC CD =∴AC −AB =3(AD uuu v−AC )； ∴AD uuu v =43AC −13AB . 故选：A.7．已知0.20.32log 0.2,2,0.2a b c ===，则A.a b c <<B.a c b <<C.c a b <<D.b c a <<【答案】B【解析】运用中间量0比较,a c ，运用中间量1比较,b c 【详解】22log 0.2log 10,a =<=0.20221,b =>=0.3000.20.21,<<=则01,c a c b <<<<．故选B ．【点睛】本题考查指数和对数大小的比较，渗透了直观想象和数学运算素养．采取中间变量法，利用转化与化归思想解题．8．函数cos y x x =+的大致图象是（ ）A. B.C. D.【答案】B【解析】由于()()cos ,cos f x x x f x x x =+∴-=-+，()()f x f x ∴-≠，且()()f x f x -≠-，故此函数是非奇非偶函数，排除,A C ；又当2x π=时，满足cos x x x +=，即()f x 的图象与直线y x =的交点中有一个点的横坐标为2π，排除D ， 故选B ． 【方法点晴】本题通过对多个图象的选择考查函数的图象与性质，属于中档题.这类题型也是近年高考常见的命题方向，该题型的特点是综合性较强较强、考查知识点较多，但是并不是无路可循.解答这类题型可以从多方面入手，根据函数的定义域、值域、单调性、奇偶性、特殊点以及0,0,,x x x x +-→→→+∞→-∞时函数图象的变化趋势，利用排除法，将不合题意的选项一一排除9．设等边三角形ABC ∆的边长为1，平面内一点M 满足1123AM AB AC =+uuu r uu u r uuu r，向量AM 与AB 夹角的余弦值为（ ）A ．B ．6C ．12D 【答案】D【解析】根据向量的平方等于模长的平方得到19AM =，再将1123AM AB AC=+uuu r uu u r uuu r 两边用AB 点乘，2,3AB AM ⋅=由向量点积公式得到夹角的余弦值. 【详解】22211||()()23AM AM AB AC ==+22111119()()2232336AB AC AB AC =++⨯⨯⨯⋅=，19AM =，对1123AM AB AC =+uuu r uu u r uuu r 两边用AB 点乘，2112,233AB AM AB AB AC AM ⋅=+⋅=与AB 夹角的余弦值为4AM AB AM AB ⋅=故选D. 【点睛】这个题目考查了向量的模长的求法以及向量点积的运算，题目比较简单基础；平面向量数量积公式有两种形式，一是cos a b a b θ⋅=，二是1212a b x x y y ⋅=+，主要应用以下几个方面:(1)求向量的夹角， ·cos ·a ba bθ=（此时·a b 往往用坐标形式求解）；（2）求投影，a 在b 上的投影是a bb⋅；（3）,a b 向量垂直则0a b ⋅=;(4)求向量ma nb +的模（平方后需求a b ⋅）.10．已知函数e 0()ln 0x x f x x x ⎧≤=⎨>⎩，，，，()()g x f x x a =++．若g （x ）存在2个零点，则a 的取值范围是 A ．[–1，0） B ．[0，+∞） C ．[–1，+∞） D ．[1，+∞）【答案】C【解析】分析：首先根据g （x ）存在2个零点，得到方程()0f x x a ++=有两个解，将其转化为()f x x a =--有两个解，即直线y x a =--与曲线()y f x =有两个交点，根据题中所给的函数解析式，画出函数()f x 的图像（将(0)xe x >去掉），再画出直线y x =-，并将其上下移动，从图中可以发现，当1a -≤时，满足y x a =--与曲线()y f x =有两个交点，从而求得结果.详解：画出函数()f x 的图像，xy e =在y 轴右侧的去掉，再画出直线y x =-，之后上下移动，可以发现当直线过点A 时，直线与函数图像有两个交点，并且向下可以无限移动，都可以保证直线与函数的图像有两个交点， 即方程()f x x a =--有两个解， 也就是函数()g x 有两个零点， 此时满足1a -≤，即1a ≥-，故选C.点睛：该题考查的是有关已知函数零点个数求有关参数的取值范围问题，在求解的过程中，解题的思路是将函数零点个数问题转化为方程解的个数问题，将式子移项变形，转化为两条曲线交点的问题，画出函数的图像以及相应的直线，在直线移动的过程中，利用数形结合思想，求得相应的结果.11．意大利数学家列昂那多·斐波那契以兔子繁殖为例，引入“兔子数列”：1,1,2,3,5,8,13,21,34,55,，即()()()()()121,12F F F n F n F n ===-+-()3,n n N *≥∈，此数列在现代物理“准晶体结构”、化学等都有着广泛的应用．若此数列被2整除后的余数构成一个新数列{}n a ，则数列{}n a 的前2019项的和为（ ）A ．672B ．673C ．1346D ．2019【答案】C【解析】求出已知数列除以2所得的余数，归纳可得{}n a 是周期为3的周期数列，求出一个周期中三项和，从而可得结果. 【详解】由数列1,1,2,3,5,8,13,21,34,55,...各项除以2的余数， 可得{}n a 为1,1,0,1,1,0,1,1,0,1,1,0,...， 所以{}n a 是周期为3的周期数列， 一个周期中三项和为1102++=， 因为20196733=⨯，所以数列{}n a 的前2019项的和为67321346⨯=， 故选C. 【点睛】本题主要考查归纳推理的应用，考查了递推关系求数列各项的和，属于中档题.利用递推关系求数列中的项或求数列的和：（1）项的序号较小时，逐步递推求出即可；（2）项的序数较大时，考虑证明数列是等差、等比数列，或者是周期数列.12．已知函数()sin 33f x x x ππωω⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭ ()0ω>在区间3,42ππ⎡⎤-⎢⎥⎣⎦上单调，且在区间[]0,2π内恰好取得一次最大值2，则ω的取值范围是( ) A.20,3⎛⎤ ⎥⎝⎦B.12,43⎡⎤⎢⎥⎣⎦C.30,4⎛⎤ ⎥⎝⎦D.13,44⎡⎤⎢⎥⎣⎦【答案】B【解析】由三角函数恒等变换的应用化简得f （x ）=2sinωx ()0ω>可得[﹣2πω，2πω]是函数含原点的递增区间，结合已知可得[﹣2πω，2πω]⊇[3,42ππ-]，可解得0＜ω≤23，又函数在区间[0，2π]上恰好取得一次最大值，根据正弦函数的性质可得14 ⨯2πω2π≤，得14ω≥，进而得解． 【详解】()sin 33f x x x ππωω⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭=2sinωx ()0ω>，∴[﹣2πω，2πω]是函数含原点的递增区间． 又∵函数在[3,42ππ-]上递增，∴[﹣2πω，2πω]⊇[3,42ππ-]， ∴得不等式组：﹣2πω≤34π-，且2π≤2πω，又∵ω＞0， ∴0＜ω≤23， 又函数在区间[0，2π]上恰好取得一次最大值， 根据正弦函数的性质可知14 ⨯ 2πω 2π≤且54 ⨯ 2πω2π> 可得ω∈[14，5)4．综上：ω∈12,43⎡⎤⎢⎥⎣⎦故选：B ． 【点睛】本题主要考查正弦函数的图象和性质，研究有关三角的函数时要利用整体思想，灵活应用三角函数的图象和性质解题，属于中档题．二、填空题13．已知向量()=1,2a ，()=2,2b -，()=1,c λ．若()2c a b ∥+，则λ=________． 【答案】12【解析】由两向量共线的坐标关系计算即可。