2020届六校联合体高三上学期一模联考数学试题(解析版)

广东省2020届高三六校第一次联考数学（理）试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合，，则（）A. B. C. D.2.若复数满足，则的共轭复数的虚部为（）A. B. C. D.3.记为等差数列的前项和，若，，则（）A. B. C. D.4.在区间上随机取两个实数，记向量，，则的概率为（）A. B. C. D.5.已知直线的倾斜角为，直线与双曲线的左、右两支分别交于、两点，且、都垂直于轴（其中、分别为双曲线的左、右焦点），则该双曲线的离心率为（）A. B. C. D.6.在△中，为的中点，点满足，则（）A. B.C. D.7.某几何体的三视图如图所示，数量单位为，它的体积是（）A. B. C. D.8.已知是函数的最大值，若存在实数使得对任意实数总有成立，则的最小值为（）A. B. C. D.9.定义在上的函数满足及，且在上有，则（）A. B. C. D.10.抛物线上有一动弦，中点为，且弦的长度为，则点的纵坐标的最小值为（）A. B. C. D.11.已知三棱锥中，，，，，且二面角的大小为，则三棱锥外接球的表面积为（）A. B. C. D.12.已知数列满足．设，为数列的前项和．若（常数），，则的最小值是（）A. B. C. D.二、填空题：本题共4小题，每小题5分，共20分。

13.若满足约束条件则的最大值为______________．14.若，则的展开式中常数项为______________．15.已知点及圆，一光线从点出发，经轴上一点反射后与圆相切于点，则的值为______________．16.已知函数满足，则的单调递减区间是______________．三、解答题：共70分。

解答应写出文字说明、证明过程或演算步骤。

第17～21题为必考题，每个试题考生都必须作答。

第22、23题为选考题，考生根据要求作答。

17.在△中，角，，的对边分别为，，，且．（1）求角；（2）若，，求△的面积．18.如图甲，设正方形的边长为3，点、分别在、上，且满足，．如图乙，将直角梯形沿折到的位置，使得点在平面上的射影恰好在上．（1）证明：平面；（2）求平面与平面所成二面角的余弦值．19.某市大力推广纯电动汽车，对购买用户依照车辆出厂续驶里程的行业标准，予以地方财政补贴．其补贴标准如下表：2017年底随机调査该市1000辆纯电动汽车，统计其出厂续驶里程，得到频率分布直方图如上图所示．用样本估计总体，频率估计概率，解决如下问题：（1）求该市每辆纯电动汽车2017年地方财政补贴的均值；（2）某企业统计2017年其充电站100天中各天充电车辆数，得如下的频数分布表：（同一组数据用该区间的中点值作代表）2018年2月，国家出台政策，将纯电动汽车财政补贴逐步转移到充电基础设施建设上来．该企业拟将转移补贴资金用于添置新型充电设备．现有直流、交流两种充电桩可供购置．直流充电桩5万元/台，每台每天最多可以充电30辆车，每天维护费用500元/台；交流充电桩1万元/台，每台每天最多可以充电4辆车，每天维护费用80元/台．该企业现有两种购置方案：方案一：购买100台直流充电桩和900台交流充电桩；方案二：购买200台直流充电桩和400台交流充电桩．假设车辆充电时优先使用新设备，且充电一辆车产生25元的收入，用2017年的统计数据，分别估计该企业在两种方案下新设备产生的日利润.（日利润日收入日维护费用）．20.已知圆与定点，动圆过点且与圆相切．（1）求动圆圆心的轨迹的方程；（2）若过定点的直线交轨迹于不同的两点、，求弦长的最大值．21.已知函数．（1）求函数在上的值域；（2）若，恒成立，求实数的取值范围．22.在平面直角坐标系中，将曲线向左平移2个单位，再将得到的曲线上的每一个点的横坐标保持不变，纵坐标缩短为原来的，得到曲线，以坐标原点为极点，轴的正半轴为极轴，建立极坐标系，的极坐标方程为．（1）求曲线的参数方程；（2）已知点在第一象限，四边形是曲线的内接矩形，求内接矩形周长的最大值，并求周长最大时点的坐标．23.已知，．（1）当时，求不等式的解集；（2）若，且当时，恒成立，求的取值范围．广东省2020届高三六校第一次联考数学（理）试题参考答案一、选择题：本题共12小题，每小题5分，共60分。

1272Pr int i S Whilei S S ii i EndWhileS ←←<←⨯←+南京市六校联合体2019-2020学年度第一学期期初测试 高三数学 2019．08．09Ⅰ试题注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．1．集合{}1,0,1A =-，{}|20B x x =-<<，则A B 中元素的个数是________． 2．已知复数z 满足1i 1z z-=-+，则z =________． 3．某校共有学生1600人，其中高一年级400人．为了解各年级学生的兴趣爱好情况，用分层抽样的方法从中抽取容量为80的样本，则应抽取高一学生________人．4．已知函数)0)(4cos()(>+=ωπωx x f 的最小正周期为4，则ω=________． 5．若“存在R x ∈，使042<-+a ax x ”为假命题，则实数a 的取值范围是________． 6．执行如图所示的伪代码，则输出的S 的值为________． 7．从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为________．8．已知焦点在x 轴上的双曲线的渐近线方程为340x y ±=，则双曲线离心率为________．9．已知实数,x y 满足条件⎪⎩⎪⎨⎧-≥-≤+≥+144222y x y x y x ，则函数3z x y =+的取值范围为________．10．已知圆C ：22(1)()16x y a -+-=，若直线20ax y +-=与圆C 相交于A ，B 两点，且CA CB ⊥，则实数a 的值为________．11．设n S 是数列{}n a 的前n 项和，且11a =-，11n n n a S S ++=，则n S =________． 12．已知0a >，0b >，且113a b b a+=-，则b 的最大值为________． 13．如图，在平面四边形ABCD 中，90CBA CAD ∠=∠=︒，30ACD ∠=︒，AB BC =，点E 为线段BC 的中点．若AC AD AE λμ=+(,R λμ∈)，则λμ的值为________．14．已知函数330()ln 0x mx m x f x x m x ，，，⎧--≤=⎨->⎩有三个不同的零点，则实数m 的取值范围是________．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分14分）在ABC ∆中，2sin 3A =，A π(,π)2∈． （1）求sin2A 的值；（2）若1sin 3B =，求cos C 的值．。

南京市六校联合体2020届高三年级一模联考试卷数学Ⅰ试题2019.12一、填空题（本大题共14小题，每小题5分，计70分．不需写出解答过程，请把答案写在答题纸的指定位置上）1．已知集合A ＝{1，2，3，4}，B ＝{x |x 2－4x ＜0}，则A ∩B ＝__________． 2．已知复数2i 12++=iz ，则复数z 的共轭复数为__________． 3．某校有教师300人，男学生1500人，女学生1200人，现用分层抽样的办法从全校师生中抽取200人进行某项调查，则应抽取的女学生人数为__________． 4．根据如图所示的伪代码，可知输出的结果S 为__________．5．甲、乙两人依次从标有数字1，2，3的三张卡片中各抽取一张（不放回），则两人均未抽到标有数字3的卡片的概率为__________．6．若抛物线210y x =的焦点到双曲线222116x y a -=的一条渐近线的距离是2，则该双曲线的离心率为__________．7．已知f (x )是定义在R 上的奇函数，且当x ≥0时f (x )＝x ＋a ，a 为实数，则f (－4)的值是__________．8．已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 前n 项和为n T ，若918S =-，1352S =-，且55b a =，77b a =，则42T T 的值为__________．9．已知()sin(2)3f x x π=+，若)20)((πϕϕ<<-=x f y 是偶函数，则=ϕ__________．10．已知矩形ABCD 中AB ＝4，BC ＝3，若沿对角线AC 折叠，使得平面DAC Ⅰ平面BAC ，则三棱锥D －ABC 的体积是__________．11．已知实数x ，y 满足条件xy ＋1＝4x ＋y 且x ＞1，则(x ＋1)(y ＋2)的最小值是__________． 12．若直线04:=-+a y ax l 上存在相距为2的两个动点A ，B ，圆1:22=+y x O 上存在点C ，使得ABC ∆为等腰直角三角形（C 为直角顶点），则实数a 的取值范围为__________．13．如图，在平面直角坐标系x O y 中，已知点(1,0)A -，点P 是圆O ：224x y +=上的任意一点，过点(1,0)B 作直线BT 垂直于AP ，垂足为T ，则2P A +3PT 的最小值是__________．14．已知函数4)(,)(22-+-=+-=x mx x h bx x x g ，若不等式)(01)(R x b x g ∈≤++恒成立，4)(+x h 为奇函数，函数⎩⎨⎧>≤=tx x h tx x g x f ),(),()(恰有两个零点，则实数t 的取值范围为__________．二、解答题（本大题共6小题，计90分．解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15．（本小题满分14分）已知c b a ，，分别为ABC ∆三个内角A ，B ，C 的对边，且3tan 4A =． （1）若65a =，2b =，求边c 的长；（2）若()sin 10A B -=，求tan B 的值．如图，在直三棱柱ABC －A 1B 1C 1中，AC ⅠBC ，A 1B 与AB 1交于点D ，A 1C 与AC 1交于点E ．求证：（1）DE Ⅰ平面B 1BCC 1； （2）平面A 1BC Ⅰ平面A 1ACC 1．17．（本小题满分14分）如图，在平面直角坐标系xOy 中，椭圆C ：2222+10)x y a b a b=>>（的左、右顶点分别为A B ，．已知4AB =，且点3(,5)4e 在椭圆上，其中e 是椭圆的离心率． （1）求椭圆C 的方程；（2）设P 是椭圆C 上异于 A 、B 的点，与x 轴垂直的直线l 分别交直线AP ，BP 于点M ，N ，求证：直线AN 与直线BM 的斜率之积是定值．ED B 1A 1C 1CBAB xy OPA M NlCB AD东北如图，甲、乙两观察哨所位于海岸线l （一条南北方向的直线）上的点A 、B 处，两观察哨所相距32 n mile ，在海岸线东侧有一半径为6 n mile 圆形暗礁区，该暗礁区中心点C 位于乙观察哨所北偏东53︒的方向上，与甲观察哨所相距2193，暗礁中心与乙观察哨所的距离大于2193；（1）求暗礁中心点C 到海岸线l 的距离；（2）某时刻，甲观察哨所发现在其正南方向且位于暗礁中心正西方向的点D 处有一走私船正欲逃窜，甲观察哨所立即派缉私艇进行追击．已知缉私艇的最大航速是走私船最大航速的(1)λλ>倍．假设缉私艇和走私船均按直线方向以最大航速航行．问：无论走私船沿何方向逃窜，要保证缉私艇总能在暗礁区（不包含暗礁区边界）以外的海域内拦截成功，求λ的取值范围．19．（本小题满分16分）已知函数x x x x f 23)(23+-=，R t tx x g ∈=，)(，xe x x=)(ϕ．（1）求函数)()(x x f y ϕ⋅=的单调增区间；（2）令)()()(x g x f x h -=，且函数)(x h 有三个彼此不相等的零点n m ，，0，其中n m <．Ⅰ若n m 21=，求函数)(x h 在m x =处的切线方程； Ⅰ若对][n m x ，∈∀，t x h -≤16)(恒成立，求实数t 的取值范围．等差数列{a n }公差大于零，且a 2＋a 3＝52，a 22＋a 32＝134，记{a n }的前n 项和为S n ，等比数列{b n }各项均为正数，公比为q ，记{b n }的前n 项和为T n ．（1）求S n ；（2）若q 为正整数，且存在正整数k ，使得T k ，T 3k ∈{S 2，S 5，S 6}，求数列{b n }的通项公式；（3）若将S n 中的整数项按从小到大的顺序排列构成数列{c n }，求{c n }的一个通项公式．南京市六校联合体2020届高三年级一模联考试卷数学Ⅰ试题2019.12一、填空题（本大题共14小题，每小题5分，计70分．不需写出解答过程，请把答案写在答题纸的指定位置上）1．已知集合A ＝{1，2，3，4}，B ＝{x |x 2－4x ＜0}，则A ∩B ＝__________． 解：{1A =Q ，2，3，4}，{|04}B x x =<<， {1A B ∴=I ，2，3}．故答案为：{1，2，3}． 2．已知复数2i 12++=iz ，则复数z 的共轭复数为__________． 解：22(1)221211(1)(1)i z i i i i i i i i -=+=+=-+=+++-Q ， 故z 的共轭复数是：1i -3．某校有教师300人，男学生1500人，女学生1200人，现用分层抽样的办法从全校师生中抽取200人进行某项调查，则应抽取的女学生人数为__________． 解：女学生人数所占的比例为12002300150012005=++，则应抽取的女学生人数为2200805⨯=， 故答案为：80．4．根据如图所示的伪代码，可知输出的结果S 为__________．答案：模拟演示：解：1S =，1I =；3S =，4I =；7S =，7I =；15S =，10I =此时结束循坏输出15S = 故答案为：15．5．甲、乙两人依次从标有数字1，2，3的三张卡片中各抽取一张（不放回），则两人均未抽到标有数字3的卡片的概率为__________．解：甲、乙两人依次从标有数字1，2，3的三张卡片中各抽取一张（不放回）， 基本事件总数326n =⨯=，两人均未抽到标有数字3的卡片包含的基本事件个数212m =⨯=， 则两人均未抽到标有数字3的卡片的概率为2163m p n ===． 故答案为：13．6．若抛物线210y x =的焦点到双曲线222116x y a -=的一条渐近线的距离是2，则该双曲线的离心率为__________．解：抛物线210y x =的焦点为5(,0)2，双曲线222116x y a -=的一条渐近线方程为4y x a=±，542⨯=，解得3a =，则5c =，所以双曲线的离心率53e = 故答案为：537．已知f (x )是定义在R 上的奇函数，且当x ≥0时f (x )＝x ＋a ，a 为实数，则f (－4)的值是__________．解：()f x Q 是定义在R 上的奇函数，且0x …时()f x a =， (0)0f a ∴==，0x ∴…时，()f x =，∴(4)(4)2f f -=-==-．故答案为：2-．8．已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 前n 项和为n T ，若918S =-，1352S =-，且55b a =，77b a =，则42T T 的值为__________． 解：918S =-，则5918a =-，所以52a =-，即52b =-1352S =-，则71352a =-，所以74a =-，即74b =-设等比数列{}n b 的公比为22q =4124212(1)1=13(1)1b q T q q b q T q--=+=-- 故答案为：39．已知()sin(2)3f x x π=+，若)20)((πϕϕ<<-=x f y 是偶函数，则=ϕ__________．解：函数()sin(2)3f x x π=+，所以函数()sin(22)3y f x x πϕϕ=-=-+，由于函数为偶函数， 所以2()32k k Z ππϕπ-+=+∈，解得()212k k Z ππϕ=--∈， 由于02πϕ<<，所以当1k =-时，512πϕ=． 故答案为：512π． 10．已知矩形ABCD 中AB ＝4，BC ＝3，若沿对角线AC 折叠，使得平面DAC Ⅰ平面BAC ，则三棱锥D －ABC 的体积是__________．解：过B 作BE AC ⊥于E ，4AB =Q ，3BC =，5AC ∴=，125AB BC BE AC ==g ， Q 平面DAC ⊥平面BAC ，平面DAC ⋂平面BAC AC =，BE AC ⊥，BE ⊂平面ABC ，BE ∴⊥平面DAC ，11112243433255ACD D ABC B ACD V V S BE ∆--∴==⋅=⨯⨯⨯⨯=棱锥棱锥． 故答案为245．11．已知实数x ，y 满足条件xy ＋1＝4x ＋y 且x ＞1，则(x ＋1)(y ＋2)的最小值是__________． 解：14xy x y +=+Q ，且1x >， 114y x y -∴=>-，解得，4y >， (1)(2)2212(3)x y xy x y x y ∴++=+++=++ 33912()12[7(4)]44y y y y y -=++=++-+-- 12(76)27++=…．(1)(2)x y ∴++取最小值为27．故答案为：27．12．若直线04:=-+a y ax l 上存在相距为2的两个动点A ，B ，圆1:22=+y x O 上存在点C ，使得ABC ∆为等腰直角三角形（C 为直角顶点），则实数a 的取值范围为__________．解：根据题意，若ABC ∆为等腰直角三角形，其中C 为直角顶点且||2AB =， 则C 到AB 的距离为||12AB =， 若圆22:1O x y +=上存在点C ，使得ABC ∆为等腰直角三角形， 则圆心O 到直线l 的距离2d „2，解可得：a ，即a 的取值范围[；故答案为：[．13．如图，在平面直角坐标系x O y 中，已知点(1,0)A -，点P 是圆O ：224x y +=上的任意一点，过点(1,0)B 作直线BT 垂直于AP ，垂足为T ，则2P A +3PT 的最小值是__________．解：由中线长公式可得PO =22=10PA PB + 222cos 2PA PB AB P PA PB +-=⋅，则3cos P PA PB=⋅在Rt PBT ∆中，cos PT PB P =，即3PT PA=所以9232PA PT PA PA+=+≥=（当且仅当2PA =时取等）14．已知函数4)(,)(22-+-=+-=x mx x h bx x x g ，若不等式)(01)(R x b x g ∈≤++恒成立，4)(+x h 为奇函数，函数⎩⎨⎧>≤=tx x h tx x g x f ),(),()(恰有两个零点，则实数t 的取值范围为__________．解：若不等式()10()g x b x R ++∈„恒成立， 即210x bx b ---…恒成立， 则△24(1)0b b =++„，解得：2b =-， 故2()2g x x x =--， 若()4h x +为奇函数，则224444mx x mx x ---+=--+，解得：0m =， 故()4h x x =-，画出函数()g x ，()h x 的图象，如图所示：若函数()()()()()g x x t f x h x x t ⎧=⎨>⎩…恰有两个零点，结合图象：[2t ∈-，0)[4U ，)+∞， 故答案为：[2-，0)[4U ，)+∞．二、解答题（本大题共6小题，计90分．解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15．（本小题满分14分）已知c b a ，，分别为ABC ∆三个内角A ，B ，C 的对边，且3tan 4A =． （1）若65a =，2b =，求边c 的长； （2）若()sin A B -=，求tan B 的值． 解：（1）在ABC ∆中，由3tan 4A =可知(0,)2A π∈， 由22sin 3cos 4sin cos 1A A A A ⎧=⎪⎨⎪+=⎩解得3sin 54cos 5A A ⎧=⎪⎪⎨⎪=⎪⎩， 由余弦定理得2222cos a b c bc A =+-，得2226422255c c ⎛⎫=+-⋅⋅⋅ ⎪⎝⎭，即216640525c c -+=，解得85c =． （2）由(0,)2A π∈且(0,)B π∈，得(,)2A B ππ-∈-， 又()10sin 0A B -=>，则(0,)2A B π-∈，则()cos 0A B ->， 所以()2310cos 1sin ()A B A B -=--=， 所以()sin()1tan cos()3A B A B A B --==-，所以()31tan tan()143tan tan 311tan tan()3143A AB B A A B A A B ---=--===⎡⎤⎣⎦+⋅-+⋅ 16．（本小题满分14分）如图，在直三棱柱ABC －A 1B 1C 1中，AC ⅠBC ，A 1B 与AB 1交于点D ，A 1C 与AC 1交于点E ．求证：（1）DE Ⅰ平面B 1BCC 1； （2）平面A 1BC Ⅰ平面A 1ACC 1．证明：（1）直三棱柱ABC －A 1B 1C 1中，1AA //1BB ， 所以四边形11ABB A 是平行四边形，且11A B AB DE =I ， 所以D 为1A B 中点， 同理E 为1A C 中点， 所以//DE BC ，又因为DE ⊄平面11B BCC ，BC ⊂平面11B BCC ， 所以//DE 11B BCC ．ED B 1A 1C 1CBA（2）直三棱柱ABC －A 1B 1C 1中，1C C ⊥平面ABC ， 因为BC ⊂平面ABC ，所以1C C BC ⊥，因为AC BC ⊥，1AC C C C =I ，1AC C C ⊂、平面11A ACC ， 所以BC ⊥平面11A ACC ， 又因为BC ⊂平面1A BC ， 所以平面1A BC ⊥平面11A ACC ． 17．（本小题满分14分）如图，在平面直角坐标系xOy 中，椭圆C ：2222+10)x y a b a b=>>（的左、右顶点分别为A B ，．已知4AB =，且点3(,5)4e 在椭圆上，其中e 是椭圆的离心率． （1）求椭圆C 的方程；（2）设P 是椭圆C 上异于 A 、B 的点，与x 轴垂直的直线l 分别交直线AP ，BP 于点M ，N ，求证：直线AN 与直线BM 的斜率之积是定值．解：（1）因为4AB =，所以24a =，即2a =，又点3(,5)4e 在椭圆上，故22245+116e a b =，即2245+11616c b =， 又2224b c a +==， 联立方程组，解得2=3b ，故椭圆方程为22+143x y =．（2）设P 点坐标为（,s t ），M ,N 的横坐标均为2)mm ≠±（， 则直线AP 的方程为(2)2ty x s =++， B xy O PAM NlCB AD东北故(,(2))2tM m m s ++， 故直线BM 的斜率1(2)(2)(2)t m k s m +=+-，同理可得直线AN 的斜率2(-2)(2)(+2)t m k s m =-，故2122(2)(-2)=(2)(2)(2)(+2)4t m t m t k k s m s m s +=+---，又因为P 点在椭圆上，故有22+143s t =，即223(4)4t s =--，因此有21223=44t k k s =--，故直线AN 与直线BM 的斜率之积是定值． 18．（本小题满分16分）如图，甲、乙两观察哨所位于海岸线l （一条南北方向的直线）上的点A 、B 处，两观察哨所相距32 n mile ，在海岸线东侧有一半径为6 n mile 圆形暗礁区，该暗礁区中心点C 位于乙观察哨所北偏东53︒的方向上，与甲观察哨所相距2193，暗礁中心与乙观察哨所的距离大于2193；（1）求暗礁中心点C 到海岸线l 的距离；（2）某时刻，甲观察哨所发现在其正南方向且位于暗礁中心正西方向的点D 处有一走私船正欲逃窜，甲观察哨所立即派缉私艇进行追击．已知缉私艇的最大航速是走私船最大航速的(1)λλ>倍．假设缉私艇和走私船均按直线方向以最大航速航行．问：无论走私船沿何方向逃窜，要保证缉私艇总能在暗礁区（不包含暗礁区边界）以外的海域内拦截成功，求λ的取值范围．解：（1）在三角形ABC 中，由余弦定理可得2222cos AC AB BC AB BC ABC =+-⋅⋅∠，即2223322325BC BC =+-⨯⨯⨯，整理得2519212600BC BC -+=，解得30BC =或425BC =（舍去）， 过点C 作CD 垂直于l ，垂足为D ，在直角三角形CDB 中，CD =BC 4sin 30245ABC ∠=⋅=， 故暗礁中心点C 到海岸线l 的距离为24n mile ． （2）由（1）可知14AD =,18BD =，以点C 为坐标原点，建立如图所示平面直角坐标系，则A （24-，14），D （24-，0），暗礁区域边界所在的圆的方程为2236x y +=， 假设缉私艇在点T （x ,y ）处拦截成功，则ATDTλ=，则点T λ=，化简得222221414(24)()()11x y λλλ+++=--要保证缉私艇总能在暗礁区（不包含暗礁区边界）以外的海域内拦截成功， 只需要圆222221414(24)()()11x y λλλ+++=--与圆2236x y +=外离，214()61λλ>+-，整理得1352421840λλ-->，解得43λ>或4645λ<-（舍去）． 答：（1）暗礁中心点C 到海岸线l 的距离是24n mile ； （2）当43λ>时，就能保证无论走私船沿何方向逃窜，缉私艇总能在暗礁区（不包含暗礁区边界）以外的海域内拦截成功． 19．（本小题满分16分）已知函数x x x x f 23)(23+-=，R t tx x g ∈=，)(，xe x x=)(ϕ．（1）求函数)()(x x f y ϕ⋅=的单调增区间；（2）令)()()(x g x f x h -=，且函数)(x h 有三个彼此不相等的零点n m ，，0，其中n m <．Ⅰ若n m 21=，求函数)(x h 在m x =处的切线方程； Ⅰ若对][n m x ，∈∀，t x h -≤16)(恒成立，求实数t 的取值范围． 解：（1）xe x x x xf y )23()()(2+-=⋅=ϕ， 所以xe x x y )1(2'--=，令0'>y 得到251251+>-<x x 或， 所以)()(x x f y ϕ⋅=的单调增区间是),251()251,(+∞+--∞，． （2）由方程()0h x =得,m n 是方程23(2)0x x t -+-=的两实根， 故3,2m n mn t +==-，且由判别式得14t >-， Ⅰ若n m 21=，得1,2m n ==，故22mn t =-=，得0t =， 因此'(1)1h =-，故函数()h x 在1=x 处的切线方程为1y x =-+．②若对任意的[,]x m n ∈，都有()16h x t ≤-成立，所以max ()16h x t ≤-， 因为3,m n m n +=<，所以n m n m <<<<<0230或， 当302m n <<<时，对[,]x m n ∈有max ()0h x =， 所以016t ≤-， 解得16t ≤，又因为20mn t =->，得2t <，则有124t -<<； 当0m n <<时，2'()36(2)h x x x t =-+-，则存在()h x 的极大值点1(,0)x m ∈，且211362t x x =-+， 由题意得321111()3(2)16h x x x t x t =-+-≤-， 将211362t x x =-+代入得321113370x x x -++≥，进而得到31(1)8x -≥-，得110x -≤<， 又因为211362t x x =-+，得211t <≤，综上可知t 的取值范围是124t -<<或211t <≤．20．（本小题满分16分）等差数列{a n }公差大于零，且a 2＋a 3＝52，a 22＋a 32＝134，记{a n }的前n 项和为S n ，等比数列{b n }各项均为正数，公比为q ，记{b n }的前n 项和为T n ．（1）求S n ；（2）若q 为正整数，且存在正整数k ，使得T k ，T 3k ∈{S 2，S 5，S 6}，求数列{b n }的通项公式；（3）若将S n 中的整数项按从小到大的顺序排列构成数列{c n }，求{c n }的一个通项公式． 解：（1）设{a n }公差为d ，d ＞0， 因为a 2＋a 3＝52，a 22＋a 32＝134，所以a 1＋d ＋a 1＋2d ＝52，(a 1＋d )2＋(a 1＋2d )2＝134，解得a 1＝12，d ＝12，于是S n ＝12n ＋n (n －1)2×12＝n 2＋n 4．（2）{S 2，S 5，S 6}＝{32，152，212}当q ＝1时，T k ＝kb 1，T 3k ＝3kb 1，T 3kT k＝3，舍去；当q ≠1时，T k ＝b 1(1－q k )1－q ，T 3k ＝b 1(1－q 3k )1－q ，所以T 3kT k ＝1＋q k ＋q 2k ，因为q ⅠN *且q ≠1，所以q ≥2， 因此T 3kT k ≥1＋2＋4＝7，于是T k ＝32，T 3k ＝212，因此1＋q k ＋q 2k ＝7，解得q k ＝2或－3（舍去）， 从而q ＝2，k ＝1，代入T k ＝b 1(1－q k )1－q 得b 1＝32所以b n ＝3×2n－2（3）因为S n ＝n 2＋n4为整数项，所以n ＝4k 或者4k －1，k ⅠN *当n ＝4k －1，k ⅠN *时，S n ＝k (4k －1)； 当n ＝4k ，k ⅠN *时，S n ＝k (4k ＋1)；因为S n 中的整数项按从小到大的顺序排列构成数列{c n }， 且k (4k －1)＜k (4k ＋1)＜(k ＋1)[4(k ＋1)－1]＜(k ＋1)[4(k ＋1)＋1]， 所以当n 为奇数时，c n ＝(4×n ＋12－1)×n ＋12＝2n 2＋3n ＋12；当n 为偶数时，c n ＝n2×(2n ＋1)＝2n 2＋n 2；所以c n ＝⎩⎨⎧2n 2＋3n ＋12，n 为奇数，2n 2＋n2，n 为偶数．。

安徽六校教育研究会2020届高三第一次联考数学（理科）一、选择题.1.设全集U =R ，集合{|14}M x x =-<<，{}2|log (2)1N x x =-<，则()U M C N ⋂=（ ） A. φ B. {|42}x x -<≤ C. { |4<<3}x x - D. {|12}x x -<≤【答案】D 【解析】 【分析】解对数不等式求出集合N 的取值范围，然后由集合的基本运算得到答案。

【详解】由2log (2)1x -<得20x ->且22x -<，所以24x <<， 所以{}24U C N x x x =≤≥或，则()U M C N ⋂={|12}x x -<≤ 【点睛】本题考查对数不等式的解法以及集合的基本运算，属于简单题。

2.已知复数z 满足()234i z i -=+,则z =（ ） A. 2i -- B. 2i - C. 2i -+ D. 2i +【答案】D 【解析】 【分析】把已知等式变形再由复数代数形式的乘除运算化简得答案． 【详解】由(2)z |34|5i i -=+=， 得55(2)z 22(2)(2)i i i i i +===+--+． 故选：D ．【点睛】本题考查复数代数形式的乘除运算，考查复数模的求法，是基础题． 3.已知等差数列{}n a 的前n 项和是n S ，公差d 不等于零，若236,,a a a 成等比数列，则 A. 130,0a d dS >> B. 130,0a d dS >< C. 130,0a d dSD. 130,0a d dS <<【答案】C 【解析】 【分析】由236,,a a a 成等比数列．可得2326a a a =，利用等差数列的通项公式可得（211125a d a d a d +=++）（）（） ，解出11020a d a d ＜，+= ．即可． 【详解】由236,,a a a 成等比数列．可得2326a a a =，可得（211125a d a d a d +=++）（）（），即2120a d d +=，∵公差d 不等于零，11020a d a d ∴+=＜，．23133302dS d a d d ∴=+=（）＞． 故选：C ．【点睛】本题考查了等差数列的通项公式、考查了计算能力，属于基础题．4.椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为( )1C.2【答案】A 【解析】 【分析】根据12PF PF ⊥及椭圆的定义可得12PF a c =-，利用勾股定理可构造出关于,a c 的齐次方程，得到关于e 的方程，解方程求得结果.【详解】由题意得：12PF PF ⊥，且2PF c =，又122PF PF a += 12PF a c ∴=-由勾股定理得：()222224220a c c c e e -+=⇒+-=，解得：1e =-本题正确选项：A【点睛】本题考查椭圆离心率的求解，关键是能够结合椭圆定义和勾股定理建立起关于,a c 的齐次方程. 5.过三点(1,3)A ，(4,2)B ，(1,7)C -的圆截直线20x ay ++=所得弦长的最小值等于（ ）A. B. C. D. 【答案】B 【解析】 【分析】因为圆心在弦AC 的中垂线上，所以设圆心P 坐标为（a ，-2），再利用222r AP BP =+，求得1a =，确定圆的方程.又直线过定点Q ，则可以得到弦长最短时圆心与直线的定点Q 与弦垂直，然后利用勾股定理可求得弦长.【详解】解：设圆心坐标P 为（a,-2），则r 2＝()()()()2222132422a a -++=-++，解得a=1，所以P（1，-2）.又直线过定点Q （-2，0），当直线PQ 与弦垂直时，弦长最短，根据圆内特征三角形可知弦长20x ay ++=被圆截得的弦长为故选：B ．6.某罐头加工厂库存芒果()m kg ，今年又购进()n kg 新芒果后，欲将芒果总量的三分之一用于加工为芒果罐头。

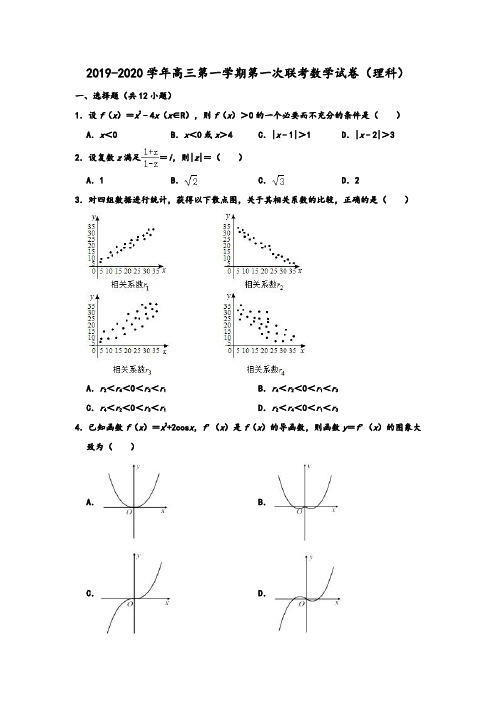
2019-2020学年高三第一学期第一次联考数学试卷（理科）一、选择题（共12小题）1．设f（x）＝x2﹣4x（x∈R），则f（x）＞0的一个必要而不充分的条件是（）A．x＜0 B．x＜0或x＞4 C．|x﹣1|＞1 D．|x﹣2|＞3 2．设复数z满足＝i，则|z|＝（）A．1 B．C．D．23．对四组数据进行统计，获得以下散点图，关于其相关系数的比较，正确的是（）A．r2＜r4＜0＜r3＜r1B．r4＜r2＜0＜r1＜r3C．r4＜r2＜0＜r3＜r1D．r2＜r4＜0＜r1＜r34．已知函数f（x）＝x2+2cos x，f'（x）是f（x）的导函数，则函数y＝f'（x）的图象大致为（）A．B．C．D．5．已知函数f（x）＝﹣x3+ax2﹣4在x＝2处取得极值，若m∈[﹣1，1]，则f（m）的最小值为（）A．﹣4 B．﹣2 C．0 D．26．正方体ABCD﹣A1B1C1D1中E为棱BB1的中点（如图），用过点A，E，C1的平面截去该正方体的上半部分，则剩余几何体的左视图为（）A．B．C．D．7．已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）A．B．C．D．8．若函数f（x）＝cos2x+a sin x在区间（，）是减函数，则a的取值范围是（）A．（2，4）B．（﹣∞，2] C．（﹣∞，4] D．[4，+∞）9．某校高三年级有男生220人，学籍编号1，2，…，220；女生380人，学籍编号221，222，…，600．为了解学生学习的心理状态，按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查（第一组采用简单随机抽样，抽到的号码为10），然后再从这10位学生中随机抽取3人座谈，则3人中既有男生又有女生的概率是（）A．B．C．D．10．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的浦丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计π的值：先请120名同学每人随机写下一个x、y都小于1的正实数对（x，y）；再统计x、y两数能与1构成钝角三角形三边的数对（x，y）的个数m；最后再根据统计数m估计π的值，假如统计结果是m＝35，那么可以估计π的值约为（）A．B．C．D．11．已知数列{a n}满足a1＝1，，则S2019等于（）A．22019﹣1 B．3×21010﹣3 C．21011﹣3 D．3×21010﹣2 12．已知函数在[﹣1，3]上的最大值为M，最小值为m，则M+m＝（）A．1 B．2 C．3 D．4二、填空题：本题共4小题，每小题5分，共20分.13．e|x|dx＝．14．已知{a n}，{b n}都是等差数列，若a1+b10＝9．a3+b8＝15，则a5+b6＝．15．抛物线y2＝2px（p＞0）的焦点为F，其准线与双曲线y2﹣x2＝1相交于A，B两点，若△ABF为等边三角形，则p＝．16．在我国南宋数学家杨辉所著的《详解》（1261年）一书中，用如图（1）的三角形，解释二项和的乘方规律．在欧洲直到1623年以后，法国数学家布莱士•帕斯卡的著作（1655年）介绍了这个三角形．近年来国外也逐渐承认这项成果属于中国，所以有些书上称这是“中国三角形”（Chinesetriangle）如图（1），17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”如图（2）．在杨辉三角中相邻两行满足关系式：∁n r+∁n r+1＝C n+1r+1，其中n是行数，r∈N．请类比上式，在莱布尼兹三角中相邻两行满足的关系式是三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17．已知△ABC的三内角A，B，C所对的边分别是a，b，c，向量＝（cos B，cos C），＝（2a+c，b），且⊥．（1）求角B的大小；（2）若b＝，求a+c的范围．18．某公司在迎新年晚会上举行抽奖活动，有甲，乙两个抽奖方案供员工选择．方案甲：员工最多有两次抽奖机会，每次抽奖的中奖率均为，第一次抽奖，若未中奖，则抽奖结束，若中奖，则通过抛一枚质地均匀的硬币，决定是否继续进行第二次抽奖，规定：若抛出硬币，反面朝上，员工则获得500元奖金，不进行第二次抽奖；若正面朝上，员工则须进行第二次抽奖，且在第二次抽奖中，若中奖，则获得1000元；若未中奖，则所获得奖金为0元．方案乙：员工连续三次抽奖，每次中奖率均为，每次中奖均可获得奖金400元．（Ⅰ）求某员工选择方案甲进行抽奖所获奖金X（元）的分布列；（Ⅱ）试比较某员工选择方案乙与选择方案甲进行抽奖，哪个方案更划算？19．如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，DC＝6，AD＝8，BC＝10，∠PAD＝45°，E为PA的中点．（1）求证：DE∥平面BPC；（2）线段AB上是否存在一点F，满足CF⊥DB？若存在，试求出二面角F﹣PC﹣D的余弦值；若不存在，请说明理由．20．已知动圆P经过点N（1，0），并且与圆M：（x+1）2+y2＝16相切．（1）求点P的轨迹C的方程；（2）设G（m，0）为轨迹C内的一个动点，过点G且斜率为k的直线l交轨迹C于A、B 两点，当k为何值时？ω＝|GA|2+|GB|2是与m无关的定值，并求出该值定值．21．设函数f（x）＝ax2lnx+b（x﹣1）（x＞0），曲线y＝f（x）过点（e，e2﹣e+1），且在点（1，0）处的切线方程为y＝0．（Ⅰ）求a，b的值；（Ⅱ）证明：当x≥1时，f（x）≥（x﹣1）2；（Ⅲ）若当x≥1时，f（x）≥m（x﹣1）2恒成立，求实数m的取值范围．（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]（本小题满分10分）22．在直角坐标系xOy中，曲线C1：，其中0≤α＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sinθ，曲线C3：ρ＝2cos θ．（1）求C2与C3交点的直角坐标；（2）若C2与C1相交于点A，C3与C1相交于点B，A、B都异于原点O，求|AB|的最大值．[选修4-5：不等式选讲]（本小题满分0分）23．已知函数f（x）＝2|x+1|+|x﹣2|．（1）求f（x）的最小值m；（2）若a，b，c均为正实数，且满足a+b+c＝m，求证：++≥3．参考答案一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设f（x）＝x2﹣4x（x∈R），则f（x）＞0的一个必要而不充分的条件是（）A．x＜0 B．x＜0或x＞4 C．|x﹣1|＞1 D．|x﹣2|＞3 【分析】利用不等式的解法、充要条件的判定方法即可得出．解：由f（x）＝x2﹣4x＞0，解得x＞4，或x＜0．由|x﹣1|＞1，解得x＜0或x＞2．由|x﹣2|＞3，解得x＜﹣1或x＞5．∴f（x）＞0的一个必要而不充分的条件是|x﹣1|＞1，故选：C．2．设复数z满足＝i，则|z|＝（）A．1 B．C．D．2【分析】先化简复数，再求模即可．解：∵复数z满足＝i，∴1+z＝i﹣zi，∴z（1+i）＝i﹣1，∴z＝＝i，∴|z|＝1，故选：A．3．对四组数据进行统计，获得以下散点图，关于其相关系数的比较，正确的是（）A．r2＜r4＜0＜r3＜r1B．r4＜r2＜0＜r1＜r3C．r4＜r2＜0＜r3＜r1D．r2＜r4＜0＜r1＜r3【分析】根据题目给出的散点图，先判断是正相关还是负相关，然后根据点的集中程度分析相关系数的大小．解：由给出的四组数据的散点图可以看出，图1和图3是正相关，相关系数大于0，图2和图4是负相关，相关系数小于0，图1和图2的点相对更加集中，所以相关性要强，所以r1接近于1，r2接近于﹣1，由此可得r2＜r4＜r3＜r1．故选：A．4．已知函数f（x）＝x2+2cos x，f'（x）是f（x）的导函数，则函数y＝f'（x）的图象大致为（）A．B．C．D．【分析】根据导数公式求出函数的导数，结合函数的奇偶性和单调性的性质判断对称性和单调性，结合排除法进行判断即可．解：函数的导数f′（x）＝2x﹣2sin x，则f′（x）为奇函数，图象关于原点对称，排除A，B，设g（x）＝f′（x）＝2x﹣2sin x，则g′（x）＝2﹣2cos x≥0，即g（x）为增函数，排除D故选：C．5．已知函数f（x）＝﹣x3+ax2﹣4在x＝2处取得极值，若m∈[﹣1，1]，则f（m）的最小值为（）A．﹣4 B．﹣2 C．0 D．2【分析】先对函数求导，结合题意可知f′（2）＝0，然后研究单调性，结合单调性可判断取得最小值的位置，即可求解．解：∵f（x）＝﹣x3+ax2﹣4，∴f′（x）＝﹣3x2+2ax，∵f（x）在x＝2处取得极值，∴f′（2）＝﹣12+4a＝0，故a＝3，f′（x）＝﹣3x2+6x，当x＜0或x＞2时，f′（x）＜0，函数f（x）单调递减，当0＜x＜2时，f′（x）＞0，函数f（x）单调递增，∵m∈[﹣1，1]，当m＝0时，f（m）的最小值为﹣4故选：A．6．正方体ABCD﹣A1B1C1D1中E为棱BB1的中点（如图），用过点A，E，C1的平面截去该正方体的上半部分，则剩余几何体的左视图为（）A．B．C．D．【分析】根据剩余几何体的直观图即可得到平面的左视图．解：过点A，E，C1的平面截去该正方体的上半部分后，剩余部分的直观图如图：则该几何体的左视图为C．故选：C．7．已知椭圆E：的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（）A．B．C．D．【分析】设A（x1，y1），B（x2，y2），代入椭圆方程得，利用“点差法”可得．利用中点坐标公式可得x1+x2＝2，y1+y2＝﹣2，利用斜率计算公式可得＝＝．于是得到，化为a2＝2b2，再利用c＝3＝，即可解得a2，b2．进而得到椭圆的方程．解：设A（x1，y1），B（x2，y2），代入椭圆方程得，相减得，∴．∵x1+x2＝2，y1+y2＝﹣2，＝＝．∴，化为a2＝2b2，又c＝3＝，解得a2＝18，b2＝9．∴椭圆E的方程为．故选：D．8．若函数f（x）＝cos2x+a sin x在区间（，）是减函数，则a的取值范围是（）A．（2，4）B．（﹣∞，2] C．（﹣∞，4] D．[4，+∞）【分析】利用二倍角的余弦公式化为正弦，然后令t＝sin x换元，根据给出的x的范围求出t的范围，结合二次函数的图象的开口方向及对称轴的位置列式求解a的范围．解：由f（x）＝cos2x+a sin x＝﹣2sin2x+a sin x+1，令t＝sin x，则原函数化为y＝﹣2t2+at+1．∵x∈（，）时f（x）为减函数，则y＝﹣2t2+at+1在t∈（，1）上为减函数，∵y＝﹣2t2+at+1的图象开口向下，且对称轴方程为t＝．∴≤，解得：a≤2．∴a的取值范围是（﹣∞，2]．故选：B．9．某校高三年级有男生220人，学籍编号1，2，…，220；女生380人，学籍编号221，222，…，600．为了解学生学习的心理状态，按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查（第一组采用简单随机抽样，抽到的号码为10），然后再从这10位学生中随机抽取3人座谈，则3人中既有男生又有女生的概率是（）A．B．C．D．【分析】由题意，得到抽到的10人中，有男生4人，女生6人，再从这10位学生中随机抽取3人座谈，基本事件总数n＝，3人中既有男生又有女生包含的基本事件个数m＝，由此能求出3人中既有男生又有女生的概率．解：由题意，得到抽到的10人中，有男生4人，女生6人，再从这10位学生中随机抽取3人座谈，基本事件总数n＝＝120，3人中既有男生又有女生包含的基本事件个数m＝＝120﹣4﹣20＝96，3人中既有男生又有女生的概率p＝＝．故选：D．10．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的浦丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计π的值：先请120名同学每人随机写下一个x、y都小于1的正实数对（x，y）；再统计x、y两数能与1构成钝角三角形三边的数对（x，y）的个数m；最后再根据统计数m估计π的值，假如统计结果是m＝35，那么可以估计π的值约为（）A．B．C．D．【分析】根据题意，由分析实数对（x，y）对应的平面区域，进而分析两数能与1构成钝角三角形三边的数对（x，y）对应的区域面积，由几何概型公式分析可得＝﹣，变形即可得答案．解：根据题意，200对都小于l的正实数对（x，y），即，对应区域为边长为1的正方形，其面积为1，若两个正实数x、y能与1构成钝角三角形三边，则有，其面积S＝；则有＝，变形可得π＝，故选：D．11．已知数列{a n}满足a1＝1，，则S2019等于（）A．22019﹣1 B．3×21010﹣3 C．21011﹣3 D．3×21010﹣2【分析】求得a2，将等式中的n换为n﹣1，相除可得数列{a n}的奇数项和偶数项均为公比为2的等比数列，由等比数列的求和公式可得所求和．解：a1＝1，，可得a2＝2，n≥2时，a n a n﹣1＝2n﹣1，又a n a n+1＝2n，相除可得＝2，可得数列{a n}的奇数项和偶数项均为公比为2的等比数列，则S2019＝（1+2+4+…+21009）+（2+4+…+21009）＝+＝21011﹣3．故选：C．12．已知函数在[﹣1，3]上的最大值为M，最小值为m，则M+m＝（）A．1 B．2 C．3 D．4【分析】利用函数的奇偶性在对称最值之和为定值即可求解．解：由f（x）＝[（x﹣1）2﹣1]sin（x﹣1）+1+令x﹣1＝t，x∈[﹣1，3]上，可得t∈[﹣2，2]；那么f（x）转化为g（t）＝t2sin t+﹣sin t+1由于h（t）＝t2sin t+﹣sin t是奇函数可得h（t），t∈[﹣2，2]的最大值与最小值之和为0，那么g（t）的最大值与最小值之和为2．故选：B．二、填空题：本题共4小题，每小题5分，共20分.13．e|x|dx＝2e﹣2 ．【分析】e|x|dx转化为e x dx+e﹣x dx，根据定积分计算法则计算即可．解：e|x|dx＝e x dx+e﹣x dx＝e x﹣e﹣x＝e﹣1﹣（1﹣e）＝2e﹣2，故答案为：2e﹣2．14．已知{a n}，{b n}都是等差数列，若a1+b10＝9．a3+b8＝15，则a5+b6＝21 ．【分析】由等差数列的性质可知a1+a5+b6+b10＝2（a3+b8）＝，代入即可求解解：∵{a n}，{b n}都是等差数列，若a1+b10＝9．a3+b8＝15，又∵a1+a5+b6+b10＝2（a3+b8）＝30a5+b6＝21故答案为：2115．抛物线y2＝2px（p＞0）的焦点为F，其准线与双曲线y2﹣x2＝1相交于A，B两点，若△ABF为等边三角形，则p＝．【分析】求出抛物线的焦点坐标，准线方程，然后求出抛物线的准线与双曲线的交点坐标，利用三角形是等边三角形求出p即可．解：抛物线的焦点坐标为（，0），准线方程为：x＝﹣，准线方程与双曲线y2﹣x2＝1联立可得：y2﹣（﹣）2＝1，解得y＝±，因为△ABF为等边三角形，所以＝2|y|，即p2＝3y2，即p2＝3（1+），解得p＝．故答案为：．16．在我国南宋数学家杨辉所著的《详解》（1261年）一书中，用如图（1）的三角形，解释二项和的乘方规律．在欧洲直到1623年以后，法国数学家布莱士•帕斯卡的著作（1655年）介绍了这个三角形．近年来国外也逐渐承认这项成果属于中国，所以有些书上称这是“中国三角形”（Chinesetriangle）如图（1），17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”如图（2）．在杨辉三角中相邻两行满足关系式：∁n r+∁n r+1＝C n+1r+1，其中n是行数，r∈N．请类比上式，在莱布尼兹三角中相邻两行满足的关系式是【分析】这是一个考查类比推理的题目，解题的关键是仔细观察图中给出的莱布尼茨三角形，并从三解数阵中，找出行与行之间数的关系，探究规律并其表示出来．解：类比观察得，将莱布尼茨三角形的每一行都能提出倍数，而相邻两项之和是上一行的两者相拱之数，所以类比式子，有．故答案为：．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17．已知△ABC的三内角A，B，C所对的边分别是a，b，c，向量＝（cos B，cos C），＝（2a+c，b），且⊥．（1）求角B的大小；（2）若b＝，求a+c的范围．【分析】（1）根据题意，由数量积的计算公式可得（2a+c）cos B+b cos C＝0，结合正弦定理可得2cos B sin A＝﹣sin（B+C）＝﹣sin A，变形可得cos B的值，即可得答案；（2）由余弦定理可得b2＝（a+c）2，分析可得（a+c）2≤4，解可得a+c≤2，由三角形的角边关系分析可得a+c的最小值，综合即可得答案．【解答】解（1）根据题意，＝（cos B，cos C），＝（2a+c，b），且⊥，则有（2a+c）cos B+b cos C＝0，即cos B（2sin A+sin C）+sin B cos C＝0，2cos B sin A+cos B sin C+sin B cos C＝0．即2cos B sin A＝﹣sin（B+C）＝﹣sin A．∵A∈（0，π），∴sin A≠0，∴cos B＝﹣．∵0＜B＜π，∴B＝．（2）由余弦定理得b2＝a2+c2﹣2ac cosπ＝a2+c2+ac＝（a+c）2﹣ac≥（a+c）2﹣（）2＝（a+c）2，当且仅当a＝c时取等号．∴（a+c）2≤4，故a+c≤2．又a+c＞b＝，∴a+c∈（，2]．即a+c的取值范围是（，2]．18．某公司在迎新年晚会上举行抽奖活动，有甲，乙两个抽奖方案供员工选择．方案甲：员工最多有两次抽奖机会，每次抽奖的中奖率均为，第一次抽奖，若未中奖，则抽奖结束，若中奖，则通过抛一枚质地均匀的硬币，决定是否继续进行第二次抽奖，规定：若抛出硬币，反面朝上，员工则获得500元奖金，不进行第二次抽奖；若正面朝上，员工则须进行第二次抽奖，且在第二次抽奖中，若中奖，则获得1000元；若未中奖，则所获得奖金为0元．方案乙：员工连续三次抽奖，每次中奖率均为，每次中奖均可获得奖金400元．（Ⅰ）求某员工选择方案甲进行抽奖所获奖金X（元）的分布列；（Ⅱ）试比较某员工选择方案乙与选择方案甲进行抽奖，哪个方案更划算？【分析】（I）利用相互独立事件的概率计算公式即可得出．（II）利用数学期望计算公式、二项分布列的性质即可得出．解：（Ⅰ），，，所以某员工选择方案甲进行抽奖所获奖金X（元）的分布列为（Ⅱ）由（Ⅰ）可知，选择方案甲进行抽奖所获得奖金X的均值，若选择方案乙进行抽奖中奖次数ξ～B，则，抽奖所获奖金X的均值E（X）＝E（400ξ）＝400E（ξ）＝480，故选择方案甲较划算．19．如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，DC＝6，AD＝8，BC＝10，∠PAD＝45°，E为PA的中点．（1）求证：DE∥平面BPC；（2）线段AB上是否存在一点F，满足CF⊥DB？若存在，试求出二面角F﹣PC﹣D的余弦值；若不存在，请说明理由．【分析】（1）取PB的中点M，连接EM和CM，过点C作CN⊥AB，垂足为点N．推导出四边形CDAN为平行四边形，从而CN＝AD＝8，DC＝AN＝6，AB＝12，推导出四边形CDEM为平行四边形，从而DE∥CM．由此能证明DE∥平面BPC．（2）由题意可得DA，DC，DP两两互相垂直，以D为原点，DA，DC，DP分别为x，y，z 轴建立空间直角坐标系D﹣xyz，利用向量法能求出二面角F﹣PC﹣D的余弦值．解：（1）证明：取PB的中点M，连接EM和CM，过点C作CN⊥AB，垂足为点N．∵CN⊥AB，DA⊥AB，∴CN∥DA，又AB∥CD，∴四边形CDAN为平行四边形，∴CN＝AD＝8，DC＝AN＝6，在Rt△BNC中，BN＝＝＝6，∴AB＝12，而E，M分别为PA，PB的中点，∴EM∥AB且EM＝6，又DC∥AB，∴EM∥CD且EM＝CD，四边形CDEM为平行四边形，∴DE∥CM．∵CM⊂平面PBC，DE⊄平面PBC，∴DE∥平面BPC．（2）解：由题意可得DA，DC，DP两两互相垂直，如图，以D为原点，DA，DC，DP分别为x，y，z轴建立空间直角坐标系D﹣xyz，则A（8，0，0），B（8，12，0），C（0，6，0），P（0，0，8）．假设AB上存在一点F使CF⊥BD，设点F坐标为（8，t，0），则＝（8，t﹣6，0），＝（8，12，0），由•＝0得t＝．又平面DPC的一个法向量为＝（1，0，0），设平面FPC的法向量＝（x，y，z），则＝（0，6，﹣8），＝（﹣8，，0），由，取y＝12，得＝（8，12，9），设二面角F﹣PC﹣D的平面角为θ，则cosθ＝＝＝．∴二面角F﹣PC﹣D的余弦值为．20．已知动圆P经过点N（1，0），并且与圆M：（x+1）2+y2＝16相切．（1）求点P的轨迹C的方程；（2）设G（m，0）为轨迹C内的一个动点，过点G且斜率为k的直线l交轨迹C于A、B 两点，当k为何值时？ω＝|GA|2+|GB|2是与m无关的定值，并求出该值定值．【分析】（1）由题意可得点P的轨迹C是以M、N为焦点的椭圆，求出半长轴及半焦距的长度，再由隐含条件求得b，则椭圆方程可求；（2）设A（x1，y1），B（x2，y2），G（m，0）（﹣2＜m＜2），直线l：y＝k（x﹣m），联立直线方程与椭圆方程，利用根与系数的关系求得A，B的横坐标与纵坐标的和与积，再由ω＝|GA|2+|GB|2是与m无关的定值求得k，进一步得到该定值．解：（1）由题设得：|PM|+|PN|＝4，∴点P的轨迹C是以M、N为焦点的椭圆，∵2a＝4，2c＝2，∴，∴椭圆方程为；（2）设A（x1，y1），B（x2，y2），G（m，0）（﹣2＜m＜2），直线l：y＝k（x﹣m），由，得（3+4k2）x2﹣8k2mx+4k2m2﹣12＝0，，∴．．∴＝．∵ω＝|GA|2+|GB|2的值与m无关，∴4k2﹣3＝0，解得．此时ω＝|GA|2+|GB|2＝7．21．设函数f（x）＝ax2lnx+b（x﹣1）（x＞0），曲线y＝f（x）过点（e，e2﹣e+1），且在点（1，0）处的切线方程为y＝0．（Ⅰ）求a，b的值；（Ⅱ）证明：当x≥1时，f（x）≥（x﹣1）2；（Ⅲ）若当x≥1时，f（x）≥m（x﹣1）2恒成立，求实数m的取值范围．【分析】（Ⅰ）求出函数的f′（x），通过f′（1）＝a+b＝0，f（e）＝e2﹣e+1，求出a，b．（Ⅱ）求出f（x）的解析式，设g（x）＝x2lnx+x﹣x2，（x≥1），求出导数，二次求导，判断g′（x）的单调性，然后证明f（x）≥（x﹣1）2．（Ⅲ）设h（x）＝x2lnx﹣x﹣m（x﹣1）2+1，求出h′（x），利用（Ⅱ）中知x2lnx≥（x﹣1）2+x﹣1＝x（x﹣1），推出h′（x）≥3（x﹣1）﹣2m（x﹣1），①当时，②当时，求解m的范围．解：（Ⅰ）函数f（x）＝ax2lnx+b（x﹣1）（x＞0），可得f′（x）＝2alnx+ax+b，∵f′（1）＝a+b＝0，f（e）＝ae2+b（e﹣1）＝a（e2﹣e+1）＝e2﹣e+1∴a＝1，b＝﹣1．…（Ⅱ）f（x）＝x2lnx﹣x+1，设g（x）＝x2lnx+x﹣x2，（x≥1），g′（x）＝2xlnx﹣x+1，（g′（x））′＝2lnx+1＞0，∴g′（x）在[0，+∞）上单调递增，∴g′（x）≥g′（1）＝0，∴g（x）在[0，+∞）上单调递增，∴g（x）≥g（1）＝0．∴f（x）≥（x﹣1）2．…（Ⅲ）设h（x）＝x2lnx﹣x﹣m（x﹣1）2+1，h′（x）＝2xlnx+x﹣2m（x﹣1）﹣1，（Ⅱ）中知x2lnx≥（x﹣1）2+x﹣1＝x（x﹣1），∴xlnx≥x﹣1，∴h′（x）≥3（x﹣1）﹣2m（x﹣1），①当3﹣2m≥0即时，h′（x）≥0，∴h（x）在[1，+∞）单调递增，∴h（x）≥h（1）＝0，成立．②当3﹣m＜0即时，h′（x）＝2xlnx﹣（1﹣2m）（x﹣1），（h′（x））′＝2lnx+3﹣2m，令（h′（x））＝0，得，当x∈[1，x0）时，h′（x）＜h′（1）＝0，∴h（x）在[1，x0）上单调递减∴h（x）＜h（1）＝0，不成立．综上，．…（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]（本小题满分10分）22．在直角坐标系xOy中，曲线C1：，其中0≤α＜π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sinθ，曲线C3：ρ＝2cosθ．（1）求C2与C3交点的直角坐标；（2）若C2与C1相交于点A，C3与C1相交于点B，A、B都异于原点O，求|AB|的最大值．【分析】（I）由曲线C2：ρ＝2sinθ，化为ρ2＝2ρsinθ，把代入可得直角坐标方程．同理由C3：ρ＝2cosθ．可得直角坐标方程，联立解出可得C2与C3交点的直角坐标．（2）由曲线C1的参数方程，消去参数t，化为普通方程：y＝x tanα，其中0≤α≤π，α≠；α＝时，为x＝0（y≠0）．其极坐标方程为：θ＝α（ρ∈R，ρ≠0），利用|AB|＝即可得出．解：（I）由曲线C2：ρ＝2sinθ，化为ρ2＝2ρsinθ，∴x2+y2＝2y．同理由C3：ρ＝2cosθ．可得直角坐标方程：，联立，解得或，∴C2与C3交点的直角坐标为（0，0），（，）．（2）曲线C1：，化为普通方程：y＝x tanα，其中0≤α≤π，α≠；当α＝时，为x＝0（y≠0），其极坐标方程为：θ＝α（ρ∈R，ρ≠0），∵A，B都在C1上，∴A（2sinα，α），B（，）．∴|AB|＝＝4||，当时，|AB|取得最大值4．[选修4-5：不等式选讲]（本小题满分0分）23．已知函数f（x）＝2|x+1|+|x﹣2|．（1）求f（x）的最小值m；（2）若a，b，c均为正实数，且满足a+b+c＝m，求证：++≥3．【分析】（1）讨论x的取值，脱去函数f（x）的绝对值，求出f（x）的最小值m；（2）根据a+b+c＝m＝3，利用基本不等式求出+++（a+b+c）的最小值，即可证明结论成立．解：（1）∵函数f（x）＝2|x+1|+|x﹣2|，当x＜﹣1时，f（x）＝﹣2（x+1）﹣（x﹣2）＝﹣3x∈（3，+∞）；当﹣1≤x＜2时，f（x）＝2（x+1）﹣（x﹣2）＝x+4∈[3，6）；当x≥2时，f（x）＝2（x+1）+（x﹣2）＝3x∈[6，+∞）；综上，f（x）的最小值为m＝3；（2）a，b，c均为正实数，且满足a+b+c＝m＝3，又因为+++（a+b+c）＝（+a）+（+b）+（+c）≥2（++）＝2（a+b+c），当且仅当a＝b＝c＝1时，取“＝”，所以，++≥a+b+c，即++≥3．。

2020届六校联高三第一次联考试题理科数学一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.1.设()()24f x x x x R =-∈，则()0f x >的一个必要而不充分的条件是( )A. 0x <B. 04x x <<或C. 11x ->D. 23x ->【答案】C 【解析】由()0f x >可得0x <或4x > ，所以，0x <是()0f x >的充分不必要条件；0x <或4x >是()0f x >的充要条件；由11x -> 得0x <或2x >，所以11x ->是()0f x >的一个必要而不充分的条件，由23x ->得，1x <-或5x >， 所以23x ->是()0f x >充分不必要条件，故选C.【方法点睛】本题通过不等式的解集主要考查充分条件与必要条件，属于中档题.判断充要条件应注意：首先弄清条件p 和结论q 分别是什么，然后直接依据定义、定理、性质尝试,p q q p ⇒⇒.对于带有否定性的命题或比较难判断的命题，除借助集合思想化抽象为直观外，还可利用原命题和逆否命题、逆命题和否命题的等价性，转化为判断它的等价命题. 2.设复数z 满足1+z1z-=i ，则|z|=( )A. 1B.C.D. 2【答案】A 【解析】试题分析：由题意得，1(1)(1)1(1)(1)i i i z i i i i ---===++-，所以1z =，故选A. 考点：复数的运算与复数的模. 【此处有视频，请去附件查看】3.某统计部门对四组数据进行统计分析后，获得如图所示的散点图，关于相关系数的比较，其中正确的是( )A. 42130r r r r <<<<B. 24130r r r r <<<<C. 24310r r r r <<<<D. 42310r r r r <<<< 【答案】C 【解析】 【分析】根据散点图的特征，数据大致呈增长趋势的是正相关，数据呈递减趋势的是负相关；数据越集中在一条线附近，说明相关性越强，进而可得出结果.【详解】根据散点图的特征，数据大致呈增长趋势的是正相关，数据呈递减趋势的是负相关；数据越集中在一条线附近，说明相关性越强，由题中数据可知：(1)(3)为正相关，(2)(4)为负相关；故1300r r >>，；2400r r <<，； 又(1)与(2)中散点图更接近于一条直线，故13r r >，24r r <， 因此，24310r r r r <<<<. 故选C【点睛】本题主要考查相关系数，根据散点图的特征进行判断即可，属于基础题型. 4.已知函数2()2cos f x x x =+，若'()f x 是()f x 的导函数，则函数'()f x 的图象大致是( )A. B.C. D.【答案】A 【解析】试题分析：函数2()2cos f x x x =+，则其导函数为.因为，即导函数为奇函数，，即在实数范围内恒有，所以在实数范围内恒为增函数，观察图像，只有选项A 满足条件，故正确选项为A. 考点：导函数以及函数的图象.【方法点睛】本题主要考察函数的性质与图像的关系，首先要求得函数的解析式，再求函数的基本性质，包括奇偶性，单调性，函数值的(正负)，以及一些特殊的点，通过这些条件结合选项，进行排除，对于较复杂的函数，经常利用导函数的性质来判断函数的单调性，本题中整式利用导函数求得函数在原点附近的单调性.5.已知函数32()4f x x ax =-+-在2x =处取得极值，若[1,1]m ∈-，则()f m 的最小值为( ) A. 4- B. 2- C. 0 D. 2【答案】A 【解析】 【分析】令导函数当2x =时为0，列出方程求出a 值，利用导数求出()f m 的极值，判断极小值且为最小值． 【详解】解：2()32f x x ax '=-+Q，函数32()4f x x ax =-+-在2x =处取得极值，1240a ∴-+=，解得3a =，2()36f x x x '∴=-+，∴当[1,1]m ∈-时，32()34f m m m =-+-，2()36f m m m '=-+，令()0f m '=得0,2m m ==(舍去)， 由于10,()0,()m f m f m '-≤<<递减，01,()0,()m f m f m '<≤>递增．所以0m =时，()f m 取极小值，也为最小值，且为−4． 故答案为：−4． 故选：A.【点睛】本题考查了利用导数求单调区间和极值，以及求闭区间上函数的最值，求函数在闭区间[,]a b 上的最大值与最小值是通过比较函数在(,)a b 内所有极值与端点函数(),()f a f b 比较而得到的，是中档题． 6.正方体ABCD ﹣A 1B 1C 1D 1中E 为棱BB 1的中点(如图)，用过点A ，E ，C 1的平面截去该正方体的上半部分，则剩余几何体的左视图为( )A. B. C. D.【答案】C 【解析】试题分析：如图补全过的平面，将上半部分切去，所以左视图如C 选项，故选C.考点：三视图7.已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为()3,0F ，过点F 的直线交椭圆E 于A 、B 两点.若AB 的中点坐标为()1,1-，则E 的方程为( )A. 2214536x y +=B. 2213627x y +=C. 2212718x y +=D. 221189x y +=【答案】D 【解析】设()()1122,,,A x y B x y ，直线AB 的斜率 101132k --==- ，2211222222221{1x y a bx y a b+=+= ，两式相减得()()()()12121212220x x x x y y y y a b +-+-+= ，即()()()()121222221212111120022y y y y a b x x x x a b +-+=⇔+⨯⨯=+-- ，即222a b = ，22229,c a b c ==+ ，解得：2218,9a b == ，方程是221189x y +=，故选D.【此处有视频，请去附件查看】8.函数()cos 2sin f x x a x =+在区间(,)62ππ上是减函数，则a 的取值范围是( ) A. (2,4) B. (],2-∞ C. (],4-∞D. [)4,+∞ 【答案】B 【解析】试题分析：∵2()cos 2sin 12sin sin f x x a x x a x =+=-+，令sin t x =，由(,)62x ππ∈得1(,1)2t ∈，依题意有2()21g t t at =-++在1(,1)2t ∈是减函数，∴142a ≤，即2a ≤，故选B ． 考点：同角三角函数的基本关系式及二次函数的单调性.9.某校高三年级有男生220人，学籍编号为1，2，…，220；女生380人，学籍编号为221，222，…，600.为了解学生学习的心理状态，按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样，抽到的号码为10)，再从这10名学生中随机抽取3人进行座谈，则这3人中既有男生又有女生的概率是( ) A.15B.310C.710D.45【答案】D 【解析】 【分析】解：由题意，得到抽到的10人中，有男生4人，女生6人，再从这10位学生中随机抽取3人座谈，可求出基本事件总数，然后求出3人中既有男生又有女生包含的基本事件个数，进而可求出3人中既有男生又有女生的概率．【详解】解：由题意，得到抽到的10人中，有男生4人，女生6人， 再从这10位学生中随机抽取3人座谈， 基本事件总数310120n C ==，3人中既有男生又有女生包含的基本事件个数333104612042096C C C --=--=，3人中既有男生又有女生的概率9641205m p n ===． 故选：D ．【点睛】本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用． 10.关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的浦丰实验和查理斯实验.受其启发，我们也可以通过设计下面的实验来估计π的值：先请120名同学每人随机写下一个x 、y 都小于1的正实数对(),x y ；再统计x 、y 两数能与1构成钝角三角形三边的数对(),x y 的个数m ；最后再根据统计数m 估计π的值，假如统计结果是35m =，那么可以估计π的值约为( ) A.227B.4715C.5116D.196【答案】D 【解析】【分析】依题意，x 、y 与1能构成钝角三角形，即221x y +<，即点(),x y 落在图中在第一象限正方形内的阴影区域，代入计算即可． 【详解】解：依题意，x 、y 与1能构成钝角三角形，即2211x y x y ⎧+<⎨+>⎩，即点(),x y 落在图中在第一象限正方形内的阴影区域，所以112042m π=-， 当35m =时，有11203542π=-， 得196π=．故选：D ．【点睛】本题考查了随机模拟法求圆周率的问题，也考查了几何概率的应用问题，是基础题．11.已知数列{}n a 满足1=1a ，*1=2()n n n a a n N +⋅∈，则2019S 等于( )A. 201921-B. 1010323⨯-C. 101123-D. 1010322⨯-【答案】C 【解析】 【分析】由1=2n n n a a +⋅得：11=2n n n a a --⋅，两式相除，可得数列{}n a 奇数项和偶数项均为等比数列，分奇数项和偶数项讨论，分别求出通项公式，进而可求2019S . 【详解】解：*1=2()nn n a a n N +⋅∈Q ，故1*1=2(2,)n n n a a n n N --⋅≥∈,两式相除得：111222nn n n a a +--==， 故数列{}n a 的奇数项和偶数项均为公比为2的等比数列，()(2019132019242018)S a a a a a a ∴=++⋯+++++L()()10101009121111a q a q qq--=+--()10091010212121212--=+-- 101010102122=-+-101123=-故选：C.【点睛】本题考查利用数列的递推式求解数列的性质，重点考查了等比数列前n 公式的运用，考查了分组求和，是中档题.12.已知函数2()(2)sin(1)1xf x x x x x =--+-在[1,3]-上的最大值为M ，最小值为m ，则M m +=( ) A. 1 B. 2C. 3D. 4【答案】B 【解析】 【分析】把已知函数变形，可得21()(1)1]sin(1)11f x x x x ⎡=---++⎣- ，令21()(1)sin(1)sin(1)1g x x x x x =----+-，结合(2)()0g x g x -+=，可得()g x 关于(1,0)中心对称，则()f x 在[1,3]-上关于(1,1)中心对称，从而求得M m +的值． 【详解】解：∵221()(2)sin(1)(1)1]sin(1)111x f x x x x x x x x ⎡=--+=---++⎣-- 令21()(1)sin(1)sin(1)1g x x x x x =----+-， 而21(2)(1)sin(1)sin(1)1g x x x x x-=----+-，∴(2)()0g x g x -+=，则()g x 关于(1,0)中心对称，则()f x 在[1,3]-上关于(1,1)中心对称．∴2M m +=． 故选：B ．【点睛】本题考查函数在闭区间上的最值，考查函数奇偶性性质的应用，考查数学转化思想方法，属中档题．二、填空题：13.1||-1x e dx ⎰值为______．【答案】22e -. 【解析】 【分析】由||x y e =是偶函数可得11||-12x x e dx e dx =⎰⎰，再用微积分基本定理求定积分即可.【详解】解：因为||x y e =是偶函数，11||1100-122|2()2(1)x x x e dx e dx e e e e ∴===-=-⎰⎰， 故答案为：22e -【点睛】本题考查定积分的计算，关键是利用被积函数是偶函数来解决问题，是基础题. 14.已知{}n a 、{}n b 都是等差数列，若110+=9a b ，38+=15a b ，则56+=a b ______． 【答案】21. 【解析】 【分析】由等差数列的性质可知()15610382a a b b a b +++=+，代入即可求解 【详解】解：∵{}n a 、{}n b 都是等差数列， 若110+=9a b ，38+=15a b ，又∵()1561038230a a b b a b +=+=++，()561103030921a b a b ∴+=-+=-=，故答案为：21.【点睛】本题主要考查了等差数列的性质的简单应用，属于基础试题15.抛物线22(0)y px p =>的焦点为F ，其准线与双曲线221y x -=相交于,A B 两点，若△ABF 为等边三角形，则p ＝ .【答案】【解析】试题分析:抛物线的准线方程为2px =-,设,A B 两点的纵坐标为,A B y y ,由双曲线方程可知22214ABp y y ==+,焦点到准线的距离为p .AB p =,p =,可得p =故答案应填考点：1.抛物线的标准方程与几何性质；2.双曲线的标准方程与几何性质.【思路点晴】本题主要考查抛物线的标准方程与几何性质,双曲性的标准方程与几何性质.本题的关键是找出关于p 的方程.将抛物线的准线与双曲线结合,又转化为直线与双曲线的位置关系的问题. (对于直线与双曲线(圆锥曲线)的位置关系.常用到设而不求的数学思想方法,即假设直线与双曲线(圆锥曲线)的交点坐标,利用韦达定理,弦长公式来构造等式).再运用数形结合,利用等边三角形的牲征得出关于p 的方程.16.在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中，用如图A 所示的三角形，解释二项和的乘方规律.在欧洲直到1623年以后，法国数学家布莱士•帕斯卡的著作(1655年)介绍了这个三角形，近年来，国外也逐渐承认这项成果属于中国，所以有些书上称这是“中国三角形”() Chinese triangle ，如图A .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”，如图B .在杨辉三角中，相邻两行满足关系式：111r r r n n n C C C ++++=，其 中n 是行数，r N ∈.请类比上式，在莱布尼茨三角形中相邻两行满足的关系式是__________．【答案】111112121111rr r n n n n n n C C C C C C ++++++=+ 【解析】分析：这是一个考查类比推理的题目，解题的关键是仔细观察图中给出的莱布尼茨三角形，并从三解数阵中，找出行与行之间数的关系，探究规律并其表示出来．详解：类比观察得，将莱布尼茨三角形的每一行都能提出倍数111n C +，而相邻两项之和是上一行的两者相拱之数，所以类比式子111r r r n n n C C C ++++=，有111112121111r r r n n n n n n C C C C C C ++++++=+． 故答案为111112121111r r r n n n n n n C C C C C C ++++++=+． 点睛：这是一道新运算类的题目，其特点一般是“新”而不“难”，处理的方法一般为：根据新运算的定义，将已知中的数据代入进行运算，易得最终结果．三、解答题：解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. (一)必考题：17.已知△ABC 的三个内角A ，B ，C 所对的边分别是a ，b ，c ，向量m u r ＝(cos B ，cos C )，n r＝(2a ＋c ，b )，且m u r ⊥n r． (1)求角B 的大小；(2)若b a ＋c 的范围．【答案】(1)23π(2)2]． 【解析】 【分析】(1)利用平面向量的数量积运算法则列出关系式，利用正弦定理化简，整理后利用两角和与差的正弦函数公式及诱导公式化简，求出cos B 的值，即可确定出B 的度数；(2)由b 及cos B 的值，利用余弦定理列出关系式，再利用基本不等式求出a +c 的最大值，最后利用三角形两边之和大于第三边求出a +c 的范围即可．【详解】(1)∵m u r ＝(cos B ，cos C )，n r ＝(2a ＋c ，b )，且m u r ⊥n r．∴(2a ＋c )cos B ＋b cos C ＝0，∴cos B (2sin A ＋sin C )＋sin B cos C ＝0，∴2cos B sin A ＋cos B sin C ＋sin B cos C ＝0．即2cos B sin A ＝－sin(B ＋C )＝－sin A ． ∵A ∈(0，π)，∴sin A ≠0，∴cos B ＝－12．∵0＜B ＜π，∴B ＝23π．(2)由余弦定理得b 2＝a 2＋c 2－2ac cos 23π＝a 2＋c 2＋ac ＝(a ＋c )2－ac ≥(a ＋c )2-22a c +⎛⎫ ⎪⎝⎭＝34 (a ＋c )2，当且仅当a ＝c 时取等号．∴(a ＋c )2≤4，故a ＋c ≤2．又a ＋c >b a ＋c ∈2]．即a ＋c 的取值范围是2]．【点睛】此题考查了正弦、余弦定理，基本不等式的运用，熟练掌握定理是解本题的关键． 18.某公司在迎新年晚会上举行抽奖活动，有甲、乙两个抽奖方案供员工选择； 方案甲：员工最多有两次抽奖机会，每次抽奖的中奖率为45.第一次抽奖，若未中奖，则抽奖结束.若中奖，则通过抛一枚质地均匀的硬币，决定是否继续进行第二次抽奖，规定：若抛出硬币，反面朝上，员工则获得500元奖金，不进行第二次抽奖；若正面朝上，员工则须进行第二次抽奖，且在第二次抽奖中，若中奖，获得奖金1000元；若未中奖，则所获奖金为0元. 方案乙：员工连续三次抽奖，每次中奖率均为25，每次中奖均可获奖金400元.(1)求某员工选择方案甲进行抽奖所获奖金X (元)的分布列；(2)某员工选择方案乙与选择方案甲进行抽奖，试比较哪个方案更划算？ 【答案】(1)详见解析；(2)选甲方案.【解析】 试题分析：(1)由题意可知X 的取值可以是0,500,1000 ，结合题意求解相应的概率即可求得分布列； (2)利用(1)中的结论结合题意求解相应的数学期望，选择期望值更大的数值即可确定选择的方案. 试题解析：(1)()141170552525P X ==+⨯⨯=， ()412500525P X ==⨯=， ()4148100052525P X ==⨯⨯=.所以某员工选择方案甲进行抽奖所获金X (元)的分布列为：(2)由(1)可知，选择方案甲进行抽奖所获得奖金X 的均值()285001000520525E X =⨯+⨯=， 若选择方案乙进行抽奖中奖次数23,5B ξ⎛⎫ ⎪⎝⎭～，则()26355E ξ=⨯=， 抽奖所获奖金X 的均值()()()400400480E X E E E ξξ===，故选择方案甲较划算.点睛：离散型随机变量的分布列指出了随机变量X 的取值范围以及取各值的概率；要理解两种特殊的概率分布——两点分布与超几何分布；并善于灵活运用两性质：一是p i ≥0(i ＝1,2，…)；二是p 1＋p 2＋…＋p n ＝1检验分布列的正误．19.如下图，在四棱锥P ABCD -中，PD ⊥面ABCD ，//AB DC ，AB AD ⊥，6DC =，8AD =，10BC =，45PAD ∠=o ，E 为PA 的中点．(1)求证：//DE 面PBC ；(2)线段AB 上是否存在一点F ，满足CF DB ⊥？若存在，试求出二面角F PC D --的余弦值；若不存在，说明理由．【答案】(1)见解析；(2)存在点F ，满足CF DB ⊥,二面角F PC D --的余弦值为817． 【解析】【详解】试题分析：(1)要证//DE 平面PBC ，只要在平面PBC 内找到一条直线与DE 平行即可，取PB的中点M ,构造平行四边形CDAN 即可证明；(2)以,,DA DC DP 分别为,,x y z 轴建立空间直角坐标系D xyz -，写出点,,,A B C D 的坐标，假设AB 上存在一点F 使CF BD ⊥，利用空间向量知识可得到在AB上存在点F 满足条件，平面DPC 的一个法向量为(1,0,0)DA =u u u r，再求出平面FPC 的法向量，即可求二面角F PC D --的余弦值．试题解析：(1)取PB 的中点M ，连EM 和CM ，过C 点作CN AB ⊥，垂足为N ∵CN AB ⊥，DA AB ⊥，∴//CN DA ，又//AB CD ∴四边形CDAN 为平行四边形，∴8,6CN AD DC AN ====，在直角三角形BNC 中，22221086BN BC CN =-=-=∴12AB =，而,E M 分别为,PA PB 的中点， ∴//EM AB 且6EM =，又//DC AB∴//EM CD 且EM CD =，四边形CDEM 为平行四边形， ∴//DE CMCM ⊂平面PBC ，DE ⊄平面PBC ，∴//DE 平面PBC ．(2)由题意可得，,,DA DC DP 两两互相垂直，如图，以,,DA DC DP 分别为,,x y z 轴建立空间直角坐标系D xyz -，则，假设AB 上存在一点F 使CF BD ⊥，设F 坐标为，则，由(1,0,0)DA =u u u r，得，又平面DPC 的一个法向量为(1,0,0)DA =u u u r设平面FPC 的法向量为(8,12,9)n =r又，，由，得，即不妨设，有则又由法向量方向知，该二面角为锐二面角， 故二面角F PC D --的余弦值为．考点：1.直线与平面平行的判定与性质；2.空间向量的应用． 20.已知动圆P 经过点()1,0N ，并且与圆()22:116.M x y ++=相切.(1)求点P 的轨迹C 的方程；(2)设(),0G m 为轨迹C 内的一个动点，过点G 且斜率为k 的直线l 交轨迹C 于A,B 两点，当k 为何值时？22||||GA GB ω=+ 是与m 无关的定值，并求出该值定值.【答案】(1)22143x y +=(2)7.【解析】 【分析】(1)由题意可得点P 的轨迹C 是以M 、N 为焦点的椭圆，求出半长轴及半焦距的长度，再由隐含条件求得b ，则椭圆方程可求；(2)设A (x 1，y 1)，B (x 2，y 2)，G (m ，0)(﹣2＜m ＜2)，直线l ：y ＝k (x ﹣m )，联立直线方程与椭圆方程，利用根与系数的关系求得A ，B 的横坐标与纵坐标的和与积，再由ω＝|GA |2+|GB |2是与m 无关的定值求得k ，进一步得到该定值．【详解】解：(1)由题设得：|PM |+|PN |＝4， ∴点P 的轨迹C 是以M 、N 为焦点的椭圆， ∵2a ＝4，2c ＝2，∴b =，∴椭圆方程为22143x y +=；(2)设A (x 1，y 1)，B (x 2，y 2)，G (m ，0)(﹣2＜m ＜2)，直线l ：y ＝k (x ﹣m )，由()22143y k x m x y ⎧=-⎪⎨+=⎪⎩，得(3+4k 2)x 2﹣8k 2mx +4k 2m 2﹣12＝0，22212122284124343mk k m x x x x k k -+=⋅=++，， ∴()()()12121226243mky y k x m k x m k x x km k +=-+-=+-=+．()()()()22222221212121223443k m y y k x m x m k x x k m x x k m k -⋅=--=-++=+．∴()22222222211221212121212||()()()222()2GA GB x m y x m y x x x x m x x m y y y y +=-++-+=+--++++-()()()()222222643243143m k k k k--++=++．∵ω＝|GA |2+|GB |2的值与m 无关，∴4k 2﹣3＝0，解得k =．此时ω＝|GA |2+|GB |2＝7． 【点睛】本题考查椭圆的简单性质，考查了直线与椭圆位置关系的应用，体现了“设而不求”的解题思想方法与待定系数法，是中档题．21.设函数2()ln (1)f x ax x b x =+-，曲线()y f x =过点2(,1)e e e -+，且在点(1,0)处的切线方程为0y =.(1)求,a b的值；(2)证明：当1x ≥时，2()(1)f x x ≥-；(3)若当1x ≥时，2()(1)f x m x ≥-恒成立，求实数m 的取值范围. 【答案】(1)1,1a b ==-；(2)详见解析；(3)32m ≤. 【解析】 【分析】(1)根据导数几何意义得()10f '=，再结合()21f e e e =-+ 联立方程组，解得,a b 的值；(2)即证明差函数()22ln g x x x x x =+-的最小值非负，先求差函数的导数，为研究导函数符号，需对导函数再次求导，得导函数最小值为零，因此差函数单调递增，也即差函数最小值为()10g =，(3)令函数()()22ln 11h x x x x m x =---+，因为()10h =，所以()min 0h x =.先求差函数导数，再求导函数的导数得()2ln 32h x x m '+'=- ，所以分33,22m m ≤>进行讨论：当32m ≤时，()()()()()01010h x h x h h x h ≥⇒≥⇒'=≥''='满足题意；当32m >时，能找到一个减区间，使得()()10h x h <=不满足题意.【详解】(1)由题意可知，()()2ln 1f x ax x b x =+-定义域为()0,,,x x o >∈∞即()2ln ,(0)f x ax x ax b x =++>'，()10f a b ='+=Q ，()()()222111f e ae b e a e e e e =+-=-+=-+1,1a b ∴==-．(2)()2ln 1f x x x x =-+，设()22ln g x x x x x =+-，()1x ≥，()2ln 1g x x x x =-+'由()()'2ln 10g x x +'=>，()g x '在[)1,+∞上单调递增，∴()()10g x g ''≥=，()g x 在[)1,+∞上单调递增，()()10g x g ≥=．∴()()21f x x ≥-．(3)设()()22ln 11h x x x x m x =---+,()1x ≥，()()2ln 211h x x x x m x =+---'，由(2)中知()()22ln 111x x x x x x ≥-+-=-，ln 1x x x ≥-，∴()()()()()3121321h x x m x m x ≥---=--'， 当320m -≥即32m ≤时，()0h x '≥， 所以()h x 在[)1,+∞单调递增，()()10h x h ∴≥=，成立． ②当320m -<即32m >时，()()()2ln 121h x x x m x +-'=- ()'()2ln 32h x x m +'=-，令()()'0h x '=，得2321m x e-=>，当[]01,x x ∈时，()h x '单调递减，则()()1h x h '<'，所以()h x 在[)01,x 上单调递减，所以()()10h x h <=，不成立． 综上，32m ≤． 【点睛】本题主要考查了导数的综合应用问题，利用导数研究函数的单调性从而得到函数的最值即可证明不等式，对于恒成立问题，一般采用变量分离的方式将参数与函数的最值比较，属于难题.(二)选考题：请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分. [选修4―4：坐标系与参数方程]22. 选修4-4：坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:{sin ,x t C y t αα==(t 为参数,且0t ≠),其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ== (Ⅰ)求2C 与3C 交点的直角坐标；(Ⅱ)若1C 与2C 相交于点A,1C 与3C 相交于点B,求AB 最大值.【答案】(Ⅰ)()330,0,,2⎛⎫⎪ ⎪⎝⎭；(Ⅱ)4.【解析】(Ⅰ)曲线2C 的直角坐标方程为2220x y y +-=，曲线3C 的直角坐标方程为22230x y x +-=．联立222220,{230,x y y x y x +-=+-=解得0,{0,x y ==或3,2{3,2x y ==所以2C 与1C 交点的直角坐标为(0,0)和33(,)22． (Ⅱ)曲线1C 的极坐标方程为(,0)R θαρρ=∈≠，其中0απ≤<．因此A 得到极坐标为(2sin ,)αα，B的极坐标为．所以2sin 23AB αα=-4()3sin πα=-，当56πα=时，AB 取得最大值，最大值为4．考点：1、极坐标方程和直角坐标方程的转化；2、三角函数的最大值． 【此处有视频，请去附件查看】[选修4―5：不等式选讲]23.已知函数()2|1||2|f x x x =++-的最小值为m . (1)求m 的值； (2)若a 、b 、c 均正实数，且满足a b c m ++=，求证：2223b c a a b c++≥.【答案】(1)3； (2)证明见解析. 【解析】【分析】(1)讨论x 的取值，去掉函数()f x 的绝对值，求出()f x 的最小值m ；(2)根据3a b c m ++==，利用基本不等式求出222()b c a a b c a b c+++++的最小值，即可证明结论成立．【详解】(1)当1x <-时，()2(1)(2)3(3,)f x x x x =-+--=-∈+∞； 当12x -<„时，()2(1)(2)4[3,6)f x x x x =+--=+∈；当2x …时，()2(1)(2)3[6,)f x x x x =++-=∈+∞． 综上，()f x 的最小值3m =.(2)证明：因为a 、b 、c 均为正实数，且满足3a b c ++=， 所以222222()b c a b c a a b c a b c a b c a b c ⎛⎫⎛⎫⎛⎫+++++=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2()a b c =++…，当且仅当1a b c ===时，取“＝”，所以222b c a a b c a b c ++++…，即2223b c a a b c++….【点睛】本题考查了求含绝对值函数的最小值问题，也考查了基本不等式的应用问题，是综合性题目，难度较大．。

2023届广东省六校高三上学期第一次联考数学试题一、单选题1．已知集合301x A xx ⎧⎫-=>⎨⎬+⎩⎭，(){}ln 3B x y x ==-，则如图中阴影部分表示的集合为（ ）A ．[]1,3-B ．()3,+∞C ．(],3-∞D ．[)1,3-【答案】D【分析】解不等式求得集合A,B ,根据已知图可知阴影部分表示的集合是()U A B ，根据集合的补集以及交集运算，可求得答案. 【详解】解301x x ->+得1x <-或3x > ，故30{|11x A xx x x ⎧⎫-=>=<-⎨⎬+⎩⎭或3}x >， (){}ln 3{|3}B x y x x x ==-=<，由图可知阴影部分表示的集合是()U A B ,而{|13}UA x x =-≤≤ ，故(){|13}U A B x x =-≤<，故选：D 2．设复数132z =，其中i 是虚数单位，z 是z 的共轭复数，下列判断中错误的是（ ） A ．1zz =B ．2z z =C ．z 是方程210x x -+=的一个根D ．满足n z ∈R 最小正整数n 为3【答案】B【分析】A 选项，得到z 的共轭复数，利用复数的乘法运算法则进行计算； B 选项，利用复数的乘方运算进行计算； C 选项，将132z =+代入方程进行验证； D 选项，由132z =，计算出23,z z ，得到结论.【详解】12z =，111312244zz ⎛⎫⎛⎫=⋅=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，A 选项说法正确； 2221131i 2442z z ⎛⎫=+=+=-≠ ⎪ ⎪⎝⎭，故B 说法错误；因为221111112222z z ⎛⎫⎛⎫-+=-+=--- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， 所以z 是方程210x x -+=的一个根，C 选项说法正确；因为12z =+，212z =-+，321131i 12244z ⎛⎫⎛⎫=-=-=- ⎪⎪ ⎪⎪⎝⎭⎝⎭， 所以满足n z ∈R 最小正整数n 为3，D 说法正确. 故选：B3．直线1y x =-过抛物线2:2(0)C y px p =>的焦点F ，且与C 交于A B 、两点，则||AB =（ ） A ．6 B ．8 C ．2 D ．4【答案】B【分析】联立直线与抛物线的方程，根据抛物线的焦点坐标，结合焦点弦长公式求解即可【详解】因为抛物线2:2(0)C y px p =>的焦点坐标为,02p F ⎛⎫⎪⎝⎭，又直线1y x =-过抛物线2:2(0)C y px p =>的焦点F ，所以2p =，抛物线C 的方程为24y x =，由214y x y x=-⎧⎨=⎩，得2610x x -+=，所以6A B x x +=，所以628A B AB x x p =++=+=．故选：B4．我们将服从二项分布的随机变量称为二项随机变量，服从正态分布的随机变量称为正态随机变量.概率论中有一个重要的结论：若随机变量(),Y B n p ~，当n 充分大时，二项随机变量Y 可以由正态随机变量X 来近似地替代，且正态随机变量X 的期望和方差与二项随机变量Y 的期望和方差相同.法国数学家棣莫弗()16671754-在1733年证明了12p =时这个结论是成立的，法国数学家､物理学家拉普拉斯()17491827-在1812年证明了这个结论对任意的实数(]0,1p ∈都成立，因此，人们把这个结论称为棣莫弗一拉普拉斯极限定理.现拋掷一枚质地均匀的硬币900次，利用正态分布估算硬币正面向上次数不少于420次的概率为（ ）(附：若()2,XN μσ，则()()0.6827,220.9545P X P X μσμσμσμσ-+≈-+≈，()330.9973)P X μσμσ-+≈A ．0.97725B ．0.84135C ．0.65865D ．0.02275【答案】A【分析】根据已知条件，结合二项分布的期望与方差公式，求出()()22450,22515E X D X μσ=====，再结合正态分布的对称性，即可求解【详解】抛掷一枚质地均匀的硬币900次，设硬币正面向上次数为X ，则()()()1111900,,900450,190012252222X B E X np D X np p ⎛⎫⎛⎫~==⨯==-=⨯⨯-= ⎪ ⎪⎝⎭⎝⎭，由题意，()2,XN μσ，且()()22450,22515E X D X μσ=====，因为()220.9545P X μσμσ-+≈，即()4502154502150.9545P X -⨯+⨯≈，所以利用正态分布估算硬币正面向上次数不少于420次的概率为()()0.95454204502150.50.977252P X P X =-⨯≈+=. 故选：A.5．已知函数π()sin()(R,0,0,)2f x A x x A ωϕωϕ=+∈>><的部分图象如图所示，则下列说法正确的是（ ）A ．直线πx =是()f x 图象的一条对称轴B ．()f x 图象的对称中心为π(π,0)12k -+，Z k ∈C ．()f x 在区间ππ,36⎡⎤-⎢⎥⎣⎦上单调递增D ．将()f x 的图象向左平移π12个单位长度后，可得到一个奇函数的图象【答案】C【分析】由已知图象求得函数解析式，将πx =代入解析式，由其结果判断A;求出函数的对称中心可判断B; 当ππ,36x ⎡⎤∈-⎢⎥⎣⎦时，πππ2[,]622x +∈-，结合正弦函数的单调性判断C;根据三角函数图象的平移变换可得平移后函数解析式，判断D. 【详解】由函数图象可知，2A =,最小正周期为5ππ4()π126T =-= ， 所以2π2πω== ， 将点π(,2)6代入函数解析式中，得：π22sin()3ϕ=+，结合π2ϕ<，所以π6ϕ<，故π()2sin(2)6f x x =+，对于A ，当πx =时，π(π)2sin(2π)16f =+=，故直线πx =不是()f x 图象的一条对称轴，A 错误;对于B ，令π()2sin(2)06f x x =+=，则πππ2π,Z,,Z 6122k x k k x k +=∈∴=-+∈， 即()f x 图象的对称中心为ππ(,0)122k -+，Z k ∈，故B 错误；对于C ，当ππ,36x ⎡⎤∈-⎢⎥⎣⎦时，πππ2[,]622x +∈-，由于正弦函数sin y x =在ππ[,]22-上递增，故()f x 在区间ππ,36⎡⎤-⎢⎥⎣⎦上单调递增，故C 正确；对于D ，将()f x 的图象向左平移π12个单位长度后，得到πππ()2sin[2()]2sin(2)1263g x x x =++=+的图象，该函数不是奇函数，故D 错误； 故选：C6．足球起源于中国古代的蹴鞠游戏.“蹴”有用脚蹴、踢的含义，“鞠”最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，如图所示.已知某“鞠”的表面上有四个点,,,P A B C ，满足1,PA PA =⊥面ABC ，AC BC ⊥，若23P ABC V -=，则该“鞠”的体积的最小值为（ ）A ．256π B ．9πC ．92πD ．98π【答案】C【分析】根据三棱锥的外接球的球心到所有顶点距离相等，且都为球半径，即可找到球心的位置，然后在直角三角形ABC 中，根据基本不等式即可求解AB 最小值，进而可得球半径的最小值.【详解】取AB 中点为D ,过D 作//OD PA ,且11==22OD PA ,因为PA ⊥平面ABC,所以OD ⊥平面ABC .由于AC BC ⊥,故DA DB DC ==,进而可知OA OB OC OP ===,所以O是球心,OA 为球的半径.由112==4323P ABC V AC CB PA AC CB -=⨯⋅⋅⇒⋅,又2222=8AB AC BC AC BC =+≥⋅,当且仅当2AC BC ==,等号成立,故此时22AB =,所以球半径()2222113+2=222R OA OD AB ⎛⎫⎛⎫==+≥ ⎪ ⎪⎝⎭⎝⎭,故min 3=2R ,体积最小值为334439πππ3322R ⎛⎫== ⎪⎝⎭ 故选:C7．设24ln 4a e -=，ln 22b =，1c e =，则（ ） A ．a c b << B ．a b c <<C ．b a c <<D ．b c a <<【答案】C【分析】结合已知要比较函数值的结构特点,可考虑构造函数()ln xf x x=,然后结合导数与单调性关系分析出e x =时,函数取得最大值()1e ef =,可得c 最大,然后结合函数单调性即可比较大小. 【详解】设()ln xf x x=,则()21ln x f x x -'=,当e x >时,()0f x '<,函数单调递减,当0e x <<时,()0f x '>,函数单调递增, 故当e x =时,函数取得最大值()1e ef =,因为()2222e ln 22ln22e e e 22af -⎛⎫=== ⎪⎝⎭,()()4ln2l e n 4e 1,24b f c f =====, 2e 42e <<,当e x >时,()0f x '<,函数单调递减,可得()()2e 4e 2f f f ⎛⎫<< ⎪⎝⎭,即b a c <<. 故选:C8．定义在R 上的函数()f x 满足()()0,()(2)f x f x f x f x -+==-；且当[0,1]x ∈时，32()f x x x x =-+．则方程7()20f x x -+=所有的根之和为（ ）A ．14B ．12C ．10D ．8【答案】A【分析】根据题中所给的函数性质可得()f x 的周期为4且关于()2,0，再画图分析()y f x =与()127y x =-的交点对数，进而根据对称性可得根之和即可. 【详解】由()()0,()(2)f x f x f x f x -+==-可得()f x 为奇函数，且关于1x =对称. 又由题意()()f x f x -=-，故()()()22f x f x f x =-=-+，所以()f x 关于()2,0对称，且()()()24f x f x f x =-+=+，故()f x 的周期为4.又当[0,1]x ∈时，32()f x x x x =-+，此时()22123213033f x x x x ⎛⎫'=-+=-+> ⎪⎝⎭，故32()f x x x x =-+在[0,1]x ∈为增函数.综上可画出()y f x =的函数部分图象.又方程7()20f x x -+=的根即()y f x =与()127y x =-的交点，易得在区间[)(]5,2,2,9-上均有3个交点，且关于()2,0对称，加上()2,0共7个交点，其根之和为322214⨯⨯+= 故选：A【点睛】本题主要考查了数形结合解决函数零点的问题，需要根据题意确定函数的性质，画出简图再根据对称性分析两函数相交的点.属于难题.二、多选题9．英国数学家贝叶斯在概率论研究方面成就显著，根据贝叶斯统计理论，随机事件A ､B 存在如下关系：()()()()P A P B A P A B P B =.某高校有甲､乙两家餐厅，王同学第一天去甲､乙两家餐厅就餐的概率分别为0.4和0.6.如果他第一天去甲餐厅，那么第二天去甲餐厅的概率为0.6；如果第一天去乙餐厅，那么第二天去甲餐厅的概率为0.5，则王同学（ ） A ．第二天去甲餐厅的概率为0.54 B ．第二天去乙餐厅的概率为0.44C ．第二天去了甲餐厅，则第一天去乙餐厅的概率为59D ．第二天去了乙餐厅，则第一天去甲餐厅的概率为49【答案】AC【分析】根据题中所给的公式进行逐一判断即可.【详解】设1A :第一天去甲餐厅，2A :第二天去甲餐厅，1B :第一天去乙餐厅，2B :第二天去乙餐厅，所以()10.4P A =，()10.6P B =，2121()0.6,()0.5P A A P A B ==， 因为212212212111()()()()()0.6,()0.5()()P A P A A P A P B A P A A P A B P A P B ====，所以212212()()0.24,()()0.3P A P A A P A P B A ==，所以有2121121()()()()()0.40.60.60.50.54P A P A P A A P b P A B =+=⨯+⨯=, 因此选项A 正确, ()()2210.46P B P A =-=，因此选项B 不正确； 因为()1220.35()9P B A P A ==，所以选项C 正确； 1211211222()()()[1()]0.4(10.6)8()()()0.4623P A P B A P A P A A P A B P B P B -⨯-====，所以选项D 不正确，故选：AC10．已知函数()sin cos f x x x =-，下列关于此函数的论述正确的是（ ） A ．π是()f x 的一个周期B ．函数()f x 的值域为⎡⎤⎣⎦C ．函数()f x 在3π4π,43⎡⎤⎢⎥⎣⎦上单调递减D ．函数()f x 在[]2π,2π-内有4个零点 【答案】BD【分析】判断A 选项，举出反例即可；判断B 、D 选项，从函数奇偶性和[0x ∈，)∞+，()(2π)f x f x =+，得到周期为2π，进而得到函数的图象性质，得到零点和值域；判断C 选项，代入检验得到函数单调性，判断C 选项．【详解】解：选项A ：因为ππ()0(π)44f f =≠+=π不是()f x 的一个周期，故A 错误；选项B 、D ：函数()f x 定义域为R ，并且()()f x f x -=，所以函数为偶函数；因为[0x ∈，)∞+，()(2π)f x f x =+，为周期函数，故仅需研究函数()f x 在区间[0，2π]上的值域及零点个数即可，因为[0x ∈，π3π][22，2π]时，π()sin cos )4f x x x x =--；当π[2x ∈，3π]2时，π()sin cos )4f x x x x =++；当[0x ∈，π3π][22，2π]时，令ππ[44x t -=∈-，π5π][44，7π]4，则y t =，π[4t ∈-，π5π][44，7π]4，可得[y ∈1]且仅一个零点；当π[2x ∈，3π]2时，令π3π[44x t +=∈，7π]4，则y t =，3π[4t ∈，7π]4，可得[y ∈1]且仅一个零点；所以函数()f x 的值域为[1]且在[2π-，2π]上有4个零点．故选项B 正确，选项D 正确．选项C ：函数()f x 在3π4π[,]43上，有π()sin cos )4f x x x x =++，所以π[π4x +∈，19π]12，则得函数()f x 在该区间上不单调．故选项C 错误． 故选：BD ．11．已知双曲线()2222:10x y C a b a b-=>>的左，右顶点分别为1A ，2A ，点P ，Q 是双曲线C 上关于原点对称的两点（异于顶点），直线1PA ，2PA ，1QA 的斜率分别为1PA k ，2PA k ，1QA k ，若1234PA PA k k ⋅=，则下列说法正确的是（ ）A ．双曲线C 的渐近线方程为34y x B ．双曲线CC ．11PA QA k k ⋅为定值D ．12tan A PA ∠的取值范围为()0,∞+【答案】BCD【分析】求得双曲线C 的渐近线方程判断选项A ；求得双曲线C 的离心率判断选项B ；化简11PA QA k k ⋅后再判断选项C ；求得12tan A PA ∠的取值范围判断选项D.【详解】设(),P x y ，则22221x y b a ⎛⎫=- ⎪⎝⎭，因为()1,0A a -，()2,0A a ，故1222222222221PA PA x b a y y y b k k x a x a x a x a a ⎛⎫- ⎪⎝⎭⋅=⋅===+---， 依题意有2234b a =，所以b a =所以双曲线C的渐近线方程为b y x a =±=，离心率e =，故选项A 错误，选项B 正确； 因为点P ，Q 关于原点对称，所以四边形12A PA Q 为平行四边形，即有12A Q A P k k =， 所以111234A P A Q A P A P k k k k ⋅=⋅=，故C 正确； 设1PA 的倾斜角为α，2PA 的倾斜角为β，由题意可得3tan tan 4αβ⋅=， 则12A PA αβ∠=-，根据对称性不妨设P 在x 轴上方，则，则12A PA βα∠=-，则()()212212tan tan 443tan tan 1tan tan 774PA PA PA PA A PA k k k k βαβααβ⎛⎫-∠=-==-=-⎪ ⎪+⋅⎝⎭， 因为P 在x轴上方，则2PA k >20PA k <<， 函数()34f x x x =-在⎛⎫ ⎪ ⎪⎝⎭和⎫+∞⎪⎪⎝⎭上单调递增， 所以()12tan 0,A PA ∠∈+∞，故D 正确. 故选：BCD.12．如图，已知正方体1111ABCD A B C D -的棱长为2，点M 为1CC 的中点，点P 为正方形1111D C B A 上的动点，则（ ）A ．满足MP //平面1BDA 的点P 2B ．满足MP AM ⊥的点P 22C ．不存在点P ，使得平面AMP 经过点BD ．存在点P 满足5PA PM += 【答案】ACD【分析】A 选项，作出辅助线得到面面平行，从而得到满足MP //平面1BDA 的点P 的轨迹长度为EF 2，A 正确；B 选项，作出辅助线得到满足MP AM ⊥的点P 的轨迹长度为线段ST 的长度， 又因为2ST =B 错误；C 选项，作出辅助线，得到平面ABM 截正方体所得的截面，根据截面与与正方形1111D C B A 没有交点，故不存在点P ，使得平面AMP 经过点B ；D 选项，作出辅助线，求出PA PM +的最小值，且存在点P 使得2255PA PM +=>，故可得到存在点P 满足5PA PM +=.【详解】如图1，取11B C 的中点F ，取11C D 的中点E ，连接EF ，FM ，EM ， 因为M 为1CC 的中点，所以//EF BD ，1//ME A B ，1//FM A D ， 因为EF ⊄平面1A BD ，BD ⊂平面1A BD ，所以//EF 平面1A BD ，同理可得：//MF 平面1A BD ， 因为,EF MF ⊂平面EFM ， 所以平面EFM //平面1A BD ， 因为点P 为正方形1111D C B A 上的动点， 所以当P 在线段EF 上时，MP //平面1BDA ，故满足MP //平面1BDA 的点P 的轨迹长度为EF 2A 正确；如图2，过点M 作MQ ⊥AM ，交11A C 于点Q ，可得：1Rt ACM Rt MC Q ~， 因为正方体1111ABCD A B C D -的棱长为2，点M 为1CC 的中点， 所以122,1AC CM C M ===，故11C MAC CM C Q=， 即12211C Q =，解得：124C Q =， 过点Q 作11//ST BD ，交11C D 于点S ，交11B C 于点T ， 则ST ⊥平面11ACC A ，因为AM ⊂平面11ACC A ， 所以ST AM ⊥，当点P 位于线段ST 上时，满足MP AM ⊥，即满足MP AM ⊥的点P 的轨迹长度为线段ST 的长度， 又因为22ST =，所以B 选项错误；如图3，连接BM ，取1DD 中点H ，连接AH ，HM ，则可知平面ABM 截正方体所得的截面为ABMH ，与正方形1111D C B A 没有交点，所以不存在点P ，使得平面AMP 经过点B 故C 正确；如图4，延长1CC 到点O ，使得11C O MC =，则点M 关于平面1111D C B A 的对称点为O ， 连接AO 交正方形1111D C B A 于点P ，则此时使得PA PM +取得最小值， 最小值为228917AO AC CO =+=+=， 当点P 与1B 重合时，此时2255PA PM +=+>， 故存在点P 满足5PA PM +=D 正确； 故选：ACD三、填空题13．若512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式的常数项为________.【答案】40【分析】由1()(2)n ax x xx+-的展开式中的各项系数的和为2，令x =1，求得1a =，写出51(2)x x-的展开式的通项，分别乘以x ，1x ，再令x 的指数为0求得r 值，则展开式中的常数项可求．【详解】解：由1()(2)n a x x xx+-的展开式中的各项系数的和为2， 令1x =，得5(1)12a +=，得1a =． ∴5111()(2)()(2)n ax x x x xxxx+-=+-，51(2)x x-的通项55521551(2)()(1)2,0,1,2,3,4,5r r r r r r r r T C x C x x r ---+=-=-⋅⋅⋅=．∴511()(2)x x x x+-的展开式中的通项有5625(1)2r r r r C x ---⋅⋅⋅和5425(1)2r r r r C x ---⋅⋅⋅．令420r -=，得2r =，则展开式中的常数项为2325(1)280C -⋅⋅=； 令620r -=，得3r =，则展开式中的常数项为3235(1)240C -⋅⋅=-， 所以该展开式的常数项为80-40=40. 故答案为：40．14．如图放置的边长为2的正方形ABCD 顶点A ，D 分别在x 轴，y 轴正半轴（含原点）上滑动，则OB OC ⋅的最大值是____________．【答案】8【分析】设(,0)A x 、(0,)D y ，易得224x y +=、(,)B x y x +、(,)C y x y +，利用向量数量积的坐标表示有222()OB OC x y ⋅≤+，即可确定最大值. 【详解】设(,0)A x ，(0,)D y ，则224x y +=， 所以(,)B x y x +，(,)C y x y +，于是2222(,)(,)22()8OB OC x y x y x y x xy y x y ⋅=+⋅+=++≤+=.当且仅当x y ==. 故答案为：8．15．已知C ：222220x y x y +---=，直线l ：220x y ++=，M 为直线l 上的动点，过点M 作C 的切线MA ，MB ，切点为A ，B ，当四边形MACB 的面积取最小值时，直线AB 的方程为 ____． 【答案】210x y ++=【分析】易知四边形MACB 的面积为S MA R =⋅=MC 最小，可得直线CM 的方程，与C 的方程联立，得到M 点坐标及CM 的值，进而得到以CM 为直径的圆的方程，与C 的方程作差可得直线AB 的方程.【详解】C ：222220x y x y +---=的标准方程为22(1)(1)4x y -+-=，则圆心()11C ，，半径2r =．因为四边形MACB 的面积2?2CAMS SCA AM AM ====要使四边形MACB 面积最小，则需CM 最小，此时CM 与直线l 垂直， 直线CM 的方程为()121y x -=-，即21y x =-，联立21220y x x y =-⎧⎨++=⎩，解得()0,1M -．则CM 则以CM 为直径的圆的方程为221524x y ⎛⎫-+= ⎪⎝⎭，与C 的方程作差可得直线AB 的方程为210x y ++=． 故答案为：210x y ++=.16．若不等式()1e 0xa x x +-<有且仅有一个正整数解，则实数a 的取值范围是______．【答案】221,3e 2e ⎡⎫⎪⎢⎣⎭【分析】()1e 0xa x x +-<→()1e x x a x +<→()()1g x a x =+，()e xxh x =，研究两个函数图像并得到点11,e A ⎛⎫ ⎪⎝⎭，222,e B ⎛⎫⎪⎝⎭→数形结合→2213e 2e a ≤<【详解】依题意不等式()1e 0xa x x +-<可化为()1ex x a x +<．令()()1g x a x =+，()e xxh x =，x ∈R ．函数()()1g x a x =+的图像恒过定点()1,0P -．函数()e x x h x =，()1e xxh x -'=， 当(),1x ∈-∞时，()0h x '>，()h x 单调递增；当()1,x ∈+∞时，()0h x '<，()h x 单调递减．所以当x ＝1时，()()max 11e h x h ==．又()222e h =，记点11,e A ⎛⎫ ⎪⎝⎭，222,e B ⎛⎫⎪⎝⎭，且()00h =，当x →+∞时，()0h x +→．作出函数()h x 大致图像，如图．若满足不等式()1e 0xa x x +-<有且仅有一个正整数解，则结合函数图像必有PB PA k a k ≤<．又因为()22202e 213e PBk-==--，()101e 112ePA k -==--，所以2213e 2e a ≤<． 【点睛】根据不等式的零点个数，求解参数的取值范围问题，通常会转化为两函数交点问题，要画出函数图象，数形结合进行求解.四、解答题17．已知在ABC 中，A ，B ，C 为三个内角，a ，b ，c 为三边，2cos c b B =，2π3C =． (1)求角B 的大小；(2)在下列两个条件中选择一个作为已知，求出BC 边上的中线的长度． ①ABC 33②ABC 的周长为43+【答案】(1)π6B = (2)答案见解析【分析】（1）由正弦定理可得sin 2sin cos C B B =，再由2π3C =和B 的范围可得答案； （2）选择（1），由（1）可得a b =，则1sin 2ABCSab C =解得a ，则由余弦定理可得BC 边上的中线的长度为：选择（2）：由（1）可得π6A =，设ABC 的外接圆半径为R ，则由正弦定理可得c ，则周长2++=a b c R 解得R ，由余弦定理可得BC 边上的中线的长度．【详解】(1)∵2cos c b B =，则由正弦定理可得sin 2sin cos C B B =，∴2πsin 2sin 3B ==，∵2π3C =，∴π0,3B ⎛⎫∈ ⎪⎝⎭，2π20,3B ⎛⎫∈ ⎪⎝⎭， ∴π23B =，解得π6B =．(2)若选择（1），由（1）可得π6A =，即a b =则211sin 22ABC S ab C a ===△，解得a = 则由余弦定理可得BC 边上的中线的长度为：． 若选择（2）：由（1）可得π6A =，设ABC 的外接圆半径为R ，则由正弦定理可得π2sin6a b R R ===，2π2sin 3c R ==，则周长24a b c R ++==+2R =，则2a =，c =由余弦定理可得BC = 18．已知数列{}n a 的前n 项和为n S ，且满足11a =，12n n S na +=，*n ∈N . （1）求{}n a 的通项公式；（2）设数列{}n b 满足11b =，12nn n b b +=，*n ∈N ，按照如下规律构造新数列{}n c ：123456,,,,,,a b a b a b ，求{}n c 的前2n 项和.【答案】（1）n a n =，*n ∈N ；（2）数列{}n c 的前2n 项和为1222++-n n .【分析】（1）由()12n n n a S S n -=-≥可得1(2)1n na a n n n+=≥+可得答案； （2）由12n n n b b +=得1122n n n b b +++=，两式相除可得数列{}n b 的偶数项构成等比数列，再由（1）可得数列{}n c 的前2n 项的和.【详解】（1）由12n n S na +=，12(1)(2)n n S n a n -=-≥， 得12(1)n n n a na n a +=--，所以1(2)1n na a n n n+=≥+. 因为122S a =，所以22a =，所以212n a a n ==，(2)n a n n =≥. 又当1n =时，11a =，适合上式. 所以n a n =，*n ∈N .（2）因为12n n n b b +=，1122n n n b b +++=，所以*22()n nb n b +=∈N ， 又122b b =，所以22b =.所以数列{}n b 的偶数项构成以22b =为首项､2为公比的等比数列. 故数列{}n c 的前2n 项的和()()21321242n n n T a a a b b b -=+++++++，()122212(121)22212nn n n n T n +-+-=+=+--所以数列{}n c 的前2n 项和为1222++-n n .【点睛】本题考查了数列的通项公式、求和，解题的关键点是利用()12n n n a S S n -=-≥求通项公式和分组转化求和，考查了学生的分析问题、解决问题和计算能力.19．如图（一）四边形ABCD 是等腰梯形，DC AB ∥，2DC =，4AB =，60ABC ∠=︒，过D 点作DE AB ⊥，垂足为E 点，将AED 沿DE 折到A ED '位置如图（二），且A C 22'=．(1)证明：平面A ED '⊥平面EBCD ；(2)已知点P 在棱A C '上，且12A P PC '=，求二面角C EP D --的余弦值． 【答案】(1)证明见解析 (2)4214【分析】（1）根据勾股定理证明A E EC '⊥，再根据线面垂直的判定证明A E '⊥面EBCD ，进而得到平面A ED '⊥平面EBCD ；（2）以E 为坐标原点，建立空间直角坐标系E xyz -，分别求得平面CEP 和平面EPD 的法向量，根据面面角的向量求法求解即可【详解】(1)证明：在等腰梯形ABCD 中，DE AB ⊥，∴DE AE ⊥，∴A E DE '⊥2DC =，4AB =，60ABC ∠=︒，∴3BE =，2BC AD ==，3DE =在EBC 中，知7EC =，∵1A E AE '==，∵A C 22'=，∴222A E EC A C ''+=A E EC '⊥，EC ，DE ⊂面EBCD ，EC DE E =，∴A E '⊥面EBCD∵A E '⊂面A ED '，∴面A ED '⊥面EBCD (2)由（1）知A E '⊥面EBCD ，ED EB ⊥∴以E 为坐标原点，建立如图所示空间直角坐标系E xyz -∴()0,0,1A '，()3,0D ，()3,0C ，()2,3,1CA '=-设∵12A P PC '=，∴23CP CA ='，∴23CP CA '=，∴23233EP EC CP ⎛⎫=+= ⎪ ⎪⎝⎭设()1111,,x n y z =是面CEP 的法向量，∴1100n EP n EC ⎧⋅=⎪⎨⋅=⎪⎩，∴11111232033230x y z x ⎧++=⎪⎨⎪=⎩，令13x∴12y =-，10z =，()13,2,0n =-设()2222,,n x y z =是面DEP 的法向量，∴2200n EP n ED ⎧⋅=⎪⎨⋅=⎪⎩，∴22222200x z ⎧+=⎪⎨=⎪⎩，∴20y =令21z =-，∴21x =，()21,0,1n =-，cos θ=由图知，二面角C EP D --20．足球是一项大众喜爱的运动.2022卡塔尔世界杯揭幕战将在2022年11月21日打响，决赛定于12月18日晚进行，全程为期28天.(1)为了解喜爱足球运动是否与性别有关，随机抽取了男性和女性各100名观众进行调查，得到2⨯2列联表如下：依据小概率值a =0.001的独立性检验，能否认为喜爱足球运动与性别有关?(2)校足球队中的甲、乙、丙、丁四名球员将进行传球训练，第1次由甲将球传出，每次传球时，传球者都等可能的将球传给另外三个人中的任何一人，如此不停地传下去，且假定每次传球都能被接到．记开始传球的人为第1次触球者，第n 次触球者是甲的概率记为n P ，即11P =．（i ）求3P （直接写出结果即可）；（ii ）证明：数列14n P ⎧⎫-⎨⎬⎩⎭为等比数列，并判断第19次与第20次触球者是甲的概率的大小．【答案】(1)喜爱足球运动与性别有关(2)（i ）313P =；（ii ）证明见解析，甲的概率大【分析】（1）计算出卡方，与10.828比较得到结论；（2）（i ）根据传球的等可能性推出313P =，（ii ）推导出()1113n n P P -=-，构造出等比数列，求出1311434n n P -⎛⎫=⨯-+ ⎪⎝⎭，得到1920,P P ，比较出大小. 【详解】(1)假设0H ：喜爱足球运动与性别独立，即喜爱足球运动与性别无关． 根据列联表数据，经计算得220.001200(60802040)10010.828100*********x χ⨯⨯-⨯==>=⨯⨯⨯根据小概率值0.001α=的独立性检验，我们推断0H 不成立， 即认为喜爱足球运动与性别有关，此推断犯错误的概率不超过0.001．(2)（i ）由题意得：第二次触球者为乙，丙，丁中的一个，第二次触球者传给包括甲的三人中的一人，故传给甲的概率为13，故313P =．（ii ）第n 次触球者是甲的概率记为n P ，则当2n ≥时，第1n -次触球者是甲的概率为1n P -， 第1n -次触球者不是甲的概率为11n P --， 则()()1111101133n n n n P P P P ---=⋅+-⋅=-， 从而1111434n n P P -⎛⎫-=-- ⎪⎝⎭， 又11344P -=，14n P ⎧⎫∴-⎨⎬⎩⎭是以34为首项，公比为13-的等比数列．则1311434n n P -⎛⎫=⨯-+ ⎪⎝⎭， ∴181931114344P ⎛⎫=⨯-+> ⎪⎝⎭，192031114344P ⎛⎫=⨯-+< ⎪⎝⎭， 1920P P >，故第19次触球者是甲的概率大21．椭圆22122:1(0)x y C a b a b +=>>经过点()1,1E 且离心率为22；直线l 与椭圆1C 交于A ，B 两点，且以AB 为直径的圆过原点.(1)求椭圆1C 的方程；(2)若过原点的直线m 与椭圆1C 交于,C D 两点，且()OC t OA OB =+，求四边形ACBD 面积的最大值.【答案】(1)222133x y +=(2)【分析】（1）根据椭圆过的点以及椭圆的离心率，可列出等式，求得a,b ，即得答案； （2）分类讨论直线AB 的斜率不存在和存在两种情况，斜率存在时，设直线AB 方程，联立椭圆方程，得到根与系数的关系式，根据条件求出参数之间的关系式，进而表示出四边形ACBD 的面积，进行化简，可求得答案.【详解】(1)椭圆22122:1(0)x y C a b a b+=>>经过点()1,1E ，22111a b +=,椭圆的离心率为2，则222a c =，即222a b =, 即221112b b +=，解得2233,2a b ==， 所以椭圆1C 的方程为222133x y +=. (2)当直线AB 斜率不存在时，设以AB 为直径的圆的圆心为(,0)t ，则222()x t y t -+= ，则不妨取(,)A t t ，故222133t t +=， 解得1t =± ，故AB 方程为1x =±，直线CD 过AB 中点，即为x 轴，得2AB =，CD =故12ACBD S AB CD =⋅= 直线AB 斜率存在时，设其方程为y kx m =+，11(,)A x y ，22(,)B x y ，联立2223x y y kx m⎧+=⎨=+⎩，可得222(21)4230k x kmx m +++-=， 则224(623)0k m ∆=-+>①，122421km x x k +=-+②， 21222321m x x k -=+③， 以AB 为直径的圆过原点即12121212()()0OA OB x x y y x x kx m kx m ⋅=+=+++=，化简可得221212(1)()0k x x km x x m ++++=，将②③两式代入，整理得2222(1)(23)(4)(21)0k m km km m k +-+-++=，即221m k =+④，将④式代入①式，得24(41)0k ∆=+>恒成立，则k ∈R ，设线段AB 中点为M ，由()2OC t OA OB tOM =+=，不妨设0t > ，得24ACBD OACB OAB S S tS==， 又∵1212OAB S m x x =-=∴4ACBD S t =， 又由()OC t OA OB =+，则C 点坐标为1212((),())t x x t y y ++， 化简可得1221224()212()21km t x x t k m t y y t k ⎧+=-⎪⎪+⎨⎪+=-⎪+⎩，代回椭圆方程可得2228321m t k =+即t =则4ACBD OAB S tS === 综上，四边形ACBD面积的最大值为【点睛】本题考查了椭圆方程的求法以及直线和椭圆相交时的四边形的面积的最大值问题，综合性强，计算量大，解答的关键是表示出四边形ACBD 的面积，并能进行正确的化简，求得最值.22．已知函数()ln(1)1,f x x =+-(1)求证：(1)3f x -≤；(2)设函数21()(1)()12=+-+g x x f x ax ，若()g x 在(0,)+∞上存在最大值，求实数a 的取值范围．【答案】(1)证明见解析(2)()0,1【分析】（1）将所证不等式转化为ln 2x ≤，再构造函数()2ln ,0x x x ϕ=->，求导分析函数的单调性，并求出最小值证明即可；（2）令()()ln(1),0h x g x x ax x ==+->'，再求导分0a ≤，1a ≥和01a <<三种情况讨论可得()g x '的单调性，结合零点存在性定理可得()g x '的零点区间，进而判断出()g x 有最大值即可.【详解】(1)要证明(1)3f x -≤，只要证明ln 2x ≤设()2ln ,0x x x ϕ=->，则1()xx ϕ'， 令()0x ϕ'<，则01x <<；令()0x ϕ'>，则1x >，所以()ϕx 在(0,1)上单调递减，在(1,)+∞单调递增，所以()(1)0x ϕϕ≥=，即2ln 0x ∴-≥，即ln 13x -≤，即(1)3f x -≤．(2)由题可得21()(1)ln(1)2=++--g x x x ax x ， 令()()ln(1),0h x g x x ax x ==+->'，则1()1h x a x '=-+， ①当0a ≤时，()0h x '>，()g x '在(0,)+∞上单调递增，所以()(0)0g x g ''>=， 所以()g x 在(0,)+∞上单调递增，无最大值，不符合题意，②当1a ≥时，1()10,()1=-<-≤+''h x a a g x x 在(0,)+∞上单调递减，所以()(0)0g x g ''<=， 所以()g x 在(0,)+∞上单调递减，无最大值，不符合题意．③当01a <<时，由1()01h x a x -+'==，可得110x a=->， ∴()10,1,0x h x a ⎛⎫'∈-> ⎪⎝⎭，()g x '在10,1a ⎛⎫- ⎪⎝⎭上单调递增，()11,,0x h x a ⎛⎫'∈-+∞< ⎪⎝⎭，()g x '在11,a ⎛⎫-+∞ ⎪⎝⎭上单调递减；由（1）知：ln 1)≤x ．所以当0x >时，()2(1)<-<+=-h x ax a x ．取241t a =-，则11t a>-，且()0h t <-=． 又11(0)0h h a ⎛⎫->= ⎪⎝⎭，所以由零点存在性定理，存在011,x t a ⎛⎫∈- ⎪⎝⎭，使得()00h x =，所以当()00,x x ∈时，()0h x >，即()0g x '>，当()0,x x ∈+∞时，()0h x <，即()0g x '<， 所以()g x 在()00,x 上单调递增，在()0,x +∞上单调递减，()g x 在(0,)+∞上存在最大值()0g x ，符合题意．综上，实数a 的取值范围为(0,1)．【点睛】本题主要考查了利用导数证明不等式的问题，同时也考查了构造函数求导分析单调性与最值的问题，在遇到极值点不能直接求出的情况，可设极值点，根据零点存在性定理确定极值点所在的区间，再根据不等式适当放缩得出极值的范围进行求解.属于难题.。