曲靖陆良七下期末模拟试题

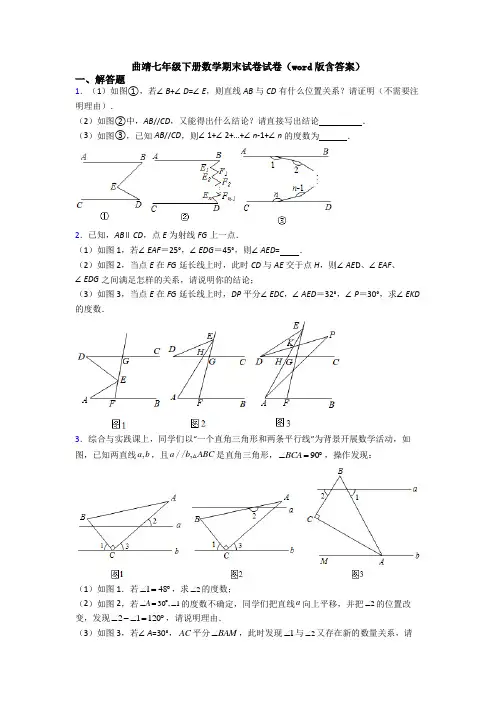
曲靖七年级下册数学期末试卷试卷（word 版含答案）一、解答题1．（1）如图①，若∠B +∠D =∠E ，则直线AB 与CD 有什么位置关系？请证明（不需要注明理由）．（2）如图②中，AB //CD ，又能得出什么结论？请直接写出结论 ． （3）如图③，已知AB //CD ，则∠1+∠2+…+∠n -1+∠n 的度数为 ．2．已知，AB ∥CD ，点E 为射线FG 上一点．（1）如图1，若∠EAF ＝25°，∠EDG ＝45°，则∠AED = ．（2）如图2，当点E 在FG 延长线上时，此时CD 与AE 交于点H ，则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系，请说明你的结论；（3）如图3，当点E 在FG 延长线上时，DP 平分∠EDC ，∠AED ＝32°，∠P ＝30°，求∠EKD 的度数．3．综合与实践课上，同学们以“一个直角三角形和两条平行线”为背景开展数学活动，如图，已知两直线,a b ，且,a b ABC //是直角三角形，90BCA ∠=︒，操作发现：（1）如图1．若148∠=︒，求2∠的度数；（2）如图2，若30,1A ∠=︒∠的度数不确定，同学们把直线a 向上平移，并把2∠的位置改变，发现21120∠-∠=︒，请说明理由．（3）如图3，若∠A =30°，AC 平分BAM ∠，此时发现1∠与2∠又存在新的数量关系，请写出1∠与2∠的数量关系并说明理由．4．如图，已知直线12//l l ，点A B 、在直线1l 上，点C D 、在直线2l 上，点C 在点D 的右侧，()80,2,ADC ABC n BE ∠=︒∠=︒平分,ABC DE ∠平分ADC ∠，直线BE DE 、交于点E ．（1）若20n =时，则BED ∠=___________；（2）试求出BED ∠的度数（用含n 的代数式表示）；（3）将线段BC 向右平行移动，其他条件不变，请画出相应图形，并直接写出BED ∠的度数．（用含n 的代数式表示）5．如图，已知//AB CD ，CN 是BCE ∠的平分线．（1）若CM 平分BCD ∠，求MCN ∠的度数；（2）若CM 在BCD ∠的内部，且CM CN ⊥于C ，求证：CM 平分BCD ∠；（3）在（2）的条件下，过点B 作BP BQ ⊥，分别交CM 、CN 于点P 、Q ，PBQ ∠绕着B 点旋转，但与CM 、CN 始终有交点，问：BPC BQC ∠+∠的值是否发生变化？若不变，求其值；若变化，求其变化范围．二、解答题6．如图1所示：点E 为BC 上一点，∠A ＝∠D ，AB ∥CD（1）直接写出∠ACB 与∠BED 的数量关系；（2）如图2，AB ∥CD ，BG 平分∠ABE ，BG 的反向延长线与∠EDF 的平分线交于H 点，若∠DEB 比∠GHD 大60°，求∠DEB 的度数；（3）保持（2）中所求的∠DEB 的度数不变，如图3，BM 平分∠EBK ，DN 平分∠CDE ，作BP ∥DN ，则∠PBM 的度数是否改变？若不发生变化，请求它的度数，若发生改变，请说明理由．（本题中的角均为大于0°且小于180°的角）．7．已知直线//AB CD ，M ，N 分别为直线AB ，CD 上的两点且70MND ∠=︒，P 为直线CD 上的一个动点．类似于平面镜成像，点N 关于镜面MP 所成的镜像为点Q ，此时,,NMP QMP NPM QPM MNP MQP ∠=∠∠=∠∠=∠．（1）当点P 在N 右侧时：①若镜像Q 点刚好落在直线AB 上（如图1），判断直线MN 与直线PQ 的位置关系，并说明理由；②若镜像Q 点落在直线AB 与CD 之间（如图2），直接写出BMQ ∠与DPQ ∠之间的数量关系；（2）若镜像PQ CD ⊥，求BMQ ∠的度数．8．综合与探究（问题情境）王老师组织同学们开展了探究三角之间数量关系的数学活动．（1）如图1，EF ∥MN ，点A 、B 分别为直线EF 、MN 上的一点，点P 为平行线间一点，请直接写出∠PAF 、∠PBN 和∠APB 之间的数量关系；（问题迁移）（2）如图2，射线OM 与射线ON 交于点O ，直线m ∥n ，直线m 分别交OM 、ON 于点A 、D ，直线n 分别交OM 、ON 于点B 、C ，点P 在射线OM 上运动．①当点P 在A 、B （不与A 、B 重合）两点之间运动时，设∠ADP ＝∠α，∠BCP ＝∠β．则∠CPD ，∠α，∠β之间有何数量关系？请说明理由；②若点P 不在线段AB 上运动时（点P 与点A 、B 、O 三点都不重合），请你画出满足条件的所有图形并直接写出∠CPD ，∠α，∠β之间的数量关系．9．如图1，//AB CD ，E 是AB 、CD 之间的一点．（1）判定BAE ∠，CDE ∠与AED ∠之间的数量关系，并证明你的结论；（2）如图2，若BAE ∠、CDE ∠的两条平分线交于点F ．直接写出AFD ∠与AED ∠之间的数量关系；（3）将图2中的射线DC 沿DE 翻折交AF 于点G 得图3，若AGD ∠的余角等于2E ∠的补角，求BAE ∠的大小．10．如图，已知AM ∥BN ，∠A ＝64°．点P 是射线AM 上一动点（与点A 不重合），BC 、BD 分别平分∠ABP 和∠PBN ，分别交射线AM 于点C ，D ．（1）①∠ABN 的度数是 ；②∵AM ∥BN ，∴∠ACB ＝∠ ；（2）求∠CBD 的度数；（3）当点P 运动时，∠APB 与∠ADB 之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律；（4）当点P 运动到使∠ACB ＝∠ABD 时，∠ABC 的度数是 ．三、解答题11．如图所示，已知射线//,//,100CB OA AB OC C OAB ︒∠=∠=.点E 、F 在射线CB 上，且满足FOB AOB ∠=∠，OE 平分COF ∠（1）求EOB ∠的度数；（2）若平行移动AB ，那么:OBC OFC ∠∠的值是否随之发生变化？如果变化，找出变化规律.若不变，求出这个比值；（3）在平行移动AB 的过程中，是否存在某种情况，使OEC OBA ∠=∠？若存在，求出其度数．若不存在，请说明理由.12．如图，已知直线a ∥b ，∠ABC ＝100°，BD 平分∠ABC 交直线a 于点D ，线段EF 在线段AB 的左侧，线段EF 沿射线AD 的方向平移，在平移的过程中BD 所在的直线与EF 所在的直线交于点P ．问∠1的度数与∠EPB 的度数又怎样的关系？（特殊化）（1）当∠1＝40°，交点P 在直线a 、直线b 之间，求∠EPB 的度数；（2）当∠1＝70°，求∠EPB 的度数；（一般化）（3）当∠1＝n°，求∠EPB 的度数（直接用含n 的代数式表示）．13．如图，在ABC 中，ABC ∠与ACB ∠的角平分线交于O 点.（1）若40A ∠=︒，则BOC ∠= ︒；（2）若A n ∠=︒，则BOC ∠= ︒；（3）若A n ∠=︒，ABC ∠与ACB ∠的角平分线交于O 点，ABO ∠的平分线与ACO ∠的平分线交于点1O ，，2016O BD ∠的平分线与2016O CE ∠的平分线交于点2017O ，则2017O ∠=︒.14．如图1，已知线段AB 、CD 相交于点O ，连接AC 、BD ，我们把形如图1的图形称之为“8字形”．如图2，∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ，并且与CD 、AB 分别相交于M 、N ．试解答下列问题：（1）仔细观察，在图2中有 个以线段AC 为边的“8字形”；（2）在图2中，若∠B=96°，∠C=100°，求∠P 的度数；（3）在图2中，若设∠C=α，∠B=β，∠CAP=13∠CAB ，∠CDP=13∠CDB ，试问∠P 与∠C 、∠B 之间存在着怎样的数量关系（用α、β表示∠P ），并说明理由；（4）如图3，则∠A+∠B+∠C+∠D+∠E+∠F 的度数为 ．15．如果三角形的两个内角α与β满足290αβ+=︒，那么我们称这样的三角形是“准互余三角形”．（1）如图1，在Rt ABC 中，90ACB ∠=︒，BD 是ABC 的角平分线，求证：ABD △是“准互余三角形”；（2）关于“准互余三角形”，有下列说法：①在ABC 中，若100A ∠=︒，70B ∠=︒，10C ∠=︒，则ABC 是“准互余三角形”； ②若ABC 是“准互余三角形”，90C ∠>︒，60A ∠=︒，则20B ∠=︒；③“准互余三角形”一定是钝角三角形．其中正确的结论是___________（填写所有正确说法的序号）；（3）如图2，B ，C 为直线l 上两点，点A 在直线l 外，且50ABC ∠=︒．若P 是直线l 上一点，且ABP △是“准互余三角形”，请直接写出APB ∠的度数．【参考答案】一、解答题1．（1）AB//CD ，证明见解析；（2）∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠Fn-1+∠D ；（3）(n-1)•180°【分析】（1）过点E 作EF//AB ，利用平行线的性质则可得出解析：（1）AB //CD ，证明见解析；（2）∠E 1+∠E 2+…∠E n =∠B +∠F 1+∠F 2+…∠F n -1+∠D ；（3）(n -1)•180°【分析】（1）过点E 作EF //AB ，利用平行线的性质则可得出∠B =∠BEF ，再由已知及平行线的判定即可得出AB ∥CD ；（2）如图，过点E 作EM ∥AB ，过点F 作FN ∥AB ，过点G 作GH ∥AB ，根据探究（1）的证明过程及方法，可推出∠E+∠G=∠B+∠F+∠D，则可由此得出规律，并得出∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D；（3）如图，过点M作EF∥AB，过点N作GH∥AB，则可由平行线的性质得出∠1+∠2+∠MNG =180°×2，依此即可得出此题结论．【详解】解：（1）过点E作EF//AB，∴∠B=∠BEF．∵∠BEF+∠FED=∠BED，∴∠B+∠FED=∠BED．∵∠B+∠D=∠E（已知），∴∠FED=∠D．∴CD//EF（内错角相等，两直线平行）．∴AB//CD．（2）过点E作EM∥AB，过点F作FN∥AB，过点G作GH∥AB，∵AB∥CD，∴AB∥EM∥FN∥GH∥CD，∴∠B=∠BEM，∠MEF=∠EFN，∠NFG=∠FGH，∠HGD=∠D，∴∠BEF+∠FGD=∠BEM+∠MEF+∠FGH+∠HGD=∠B+∠EFN+∠NFG+∠D=∠B+∠EFG+∠D，即∠E+∠G=∠B+∠F+∠D．由此可得：开口朝左的所有角度之和与开口朝右的所有角度之和相等，∴∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠F n-1+∠D．故答案为：∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D．（3）如图，过点M作EF∥AB，过点N作GH∥AB，∴∠APM+∠PME=180°，∵EF ∥AB ，GH ∥AB ，∴EF ∥GH ，∴∠EMN +∠MNG =180°，∴∠1+∠2+∠MNG =180°×2，依次类推：∠1+∠2+…+∠n -1+∠n =(n -1)•180°．故答案为：(n -1)•180°．【点睛】本题考查了平行线的性质与判定，属于基础题，关键是过E 点作AB （或CD ）的平行线，把复杂的图形化归为基本图形．2．（1）70°；（2），证明见解析；（3）122°【分析】（1）过作，根据平行线的性质得到，，即可求得；（2）过过作，根据平行线的性质得到，，即；（3）设，则，通过三角形内角和得到，由角平分线解析：（1）70°；（2）EAF AED EDG ∠=∠+∠，证明见解析；（3）122°【分析】（1）过E 作//EF AB ，根据平行线的性质得到25EAF AEH ∠=∠=︒，45EAG DEH ∠=∠=︒，即可求得AED ∠；（2）过过E 作//EM AB ，根据平行线的性质得到180EAF MEH ∠=︒-∠，180EDG AED MEH ∠+∠=︒-，即EAF AED EDG ∠=∠+∠；（3）设EAI x ∠=，则3BAE x ∠=，通过三角形内角和得到2EDK x ∠=-︒，由角平分线定义及//AB CD 得到33224x x =︒+-︒，求出x 的值再通过三角形内角和求EKD ∠．【详解】解：（1）过E 作//EF AB ，//AB CD ，//EF CD ∴，25EAF AEH ∴∠=∠=︒，45EAG DEH ∠=∠=︒，70AED AEH DEH ∴∠=∠+∠=︒，故答案为：70︒；（2）EAF AED EDG ∠=∠+∠．理由如下：过E 作//EM AB ，//AB CD ，//EM CD ∴，180EAF MEH ∴∠+∠=︒，180EDG AED MEH ∠+∠+=︒，180EAF MEH ∴∠=︒-∠，180EDG AED MEH ∠+∠=︒-，EAF AED EDG ∴∠=∠+∠；（3）:1:2EAP BAP ∠∠=，设EAP x ∠=，则3BAE x ∠=，32302AED P ∠-∠=︒-︒=︒，DKE AKP ∠=∠，又180EDK DKE DEK ∠+∠+∠=︒，180KAP KPA AKP ∠+∠+∠=︒，22EDK EAP x ∴∠=∠-︒=-︒， DP 平分EDC ∠，224CDE EDK x ∴∠=∠=-︒，//AB CD ，EHC EAF AED EDG ∴∠=∠=∠+∠，即33224x x =︒+-︒，解得28x =︒，28226EDK ∴∠=︒-︒=︒，1802632122EKD ∴∠=︒-︒-︒=︒．【点睛】本题主要考查了平行线的性质和判定，正确做出辅助线是解决问题的关键．3．（1）42°；（2）见解析；（3）∠1=∠2，理由见解析【分析】（1）由平角定义求出∠3=42°，再由平行线的性质即可得出答案；（2）过点B 作BD ∥a ．由平行线的性质得∠2+∠ABD=180°解析：（1）42°；（2）见解析；（3）∠1=∠2，理由见解析【分析】（1）由平角定义求出∠3=42°，再由平行线的性质即可得出答案；（2）过点B 作BD ∥a ．由平行线的性质得∠2+∠ABD =180°，∠1=∠DBC ，则∠ABD =∠ABC -∠DBC =60°-∠1，进而得出结论；（3）过点C 作CP ∥a ，由角平分线定义得∠CAM =∠BAC =30°，∠BAM =2∠BAC =60°，由平行线的性质得∠1=∠BAM =60°，∠PCA =∠CAM =30°，∠2=∠BCP =60°，即可得出结论．【详解】解：（1）∵∠1=48°，∠BCA =90°，∴∠3=180°-∠BCA-∠1=180°-90°-48°=42°，∵a∥b，∴∠2=∠3=42°；（2）理由如下：过点B作BD∥a．如图2所示：则∠2+∠ABD=180°，∵a∥b，∴b∥BD，∴∠1=∠DBC，∴∠ABD=∠ABC-∠DBC=60°-∠1，∴∠2+60°-∠1=180°，∴∠2-∠1=120°；（3）∠1=∠2，理由如下：过点C作CP∥a，如图3所示：∵AC平分∠BAM∴∠CAM=∠BAC=30°，∠BAM=2∠BAC=60°，又∵a∥b，∴CP∥b，∠1=∠BAM=60°，∴∠PCA=∠CAM=30°，∴∠BCP=∠BCA-∠PCA=90°-30°=60°，又∵CP∥a，∴∠2=∠BCP=60°，∴∠1=∠2．【点睛】本题是三角形综合题目，考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识；本题综合性强，熟练掌握平移的性质和平行线的性质是解题的关键．4．（1）60°；（2）n°+40°；（3）n°+40°或n°-40°或220°-n°【分析】（1）过点E作EF∥AB，然后根据两直线平行内错角相等，即可求∠BED的度数；（2）同（1）中方法求解解析：（1）60°；（2）n°+40°；（3）n°+40°或n°-40°或220°-n°【分析】（1）过点E作EF∥AB，然后根据两直线平行内错角相等，即可求∠BED的度数；（2）同（1）中方法求解即可；（3）分当点B在点A左侧和当点B在点A右侧，再分三种情况，讨论，分别过点E作EF∥AB，由角平分线的定义，平行线的性质，以及角的和差计算即可．【详解】解：（1）当n=20时，∠ABC=40°，过E作EF∥AB，则EF∥CD，∴∠BEF=∠ABE，∠DEF=∠CDE，∵BE平分∠ABC，DE平分∠ADC，∴∠BEF=∠ABE=20°，∠DEF=∠CDE=40°，∴∠BED=∠BEF+∠DEF=60°；（2）同（1）可知：∠BEF=∠ABE=n°，∠DEF=∠CDE=40°，∴∠BED=∠BEF+∠DEF=n°+40°；（3）当点B在点A左侧时，由（2）可知：∠BED=n°+40°；当点B在点A右侧时，如图所示，过点E作EF∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC=2n°，∠ADC=80°，∴∠ABE=12∠ABC=n°，∠CDG=12∠ADC=40°，∵AB∥CD∥EF，∴∠BEF=∠ABE=n°，∠CDG=∠DEF=40°，∴∠BED=∠BEF-∠DEF=n°-40°；如图所示，过点E作EF∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC=2n°，∠ADC=80°，∴∠ABE=12∠ABC=n°，∠CDG=12∠ADC=40°，∵AB∥CD∥EF，∴∠BEF=180°-∠ABE=180°-n°，∠CDE=∠DEF=40°，∴∠BED=∠BEF+∠DEF=180°-n°+40°=220°-n°；如图所示，过点E作EF∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=70°，∴∠ABG=12∠ABC=n°，∠CDE=12∠ADC=40°，∵AB∥CD∥EF，∴∠BEF=∠ABG=n°，∠CDE=∠DEF=40°，∴∠BED=∠BEF-∠DEF=n°-40°；综上所述，∠BED的度数为n°+40°或n°-40°或220°-n°．【点睛】此题考查了平行线的判定与性质，以及角平分线的定义，正确应用平行线的性质得出各角之间关系是解题关键．5．（1）90°；（2）见解析；（3）不变，180°【分析】（1）根据邻补角的定义及角平分线的定义即可得解；（2）根据垂直的定义及邻补角的定义、角平分线的定义即可得解； （3），过，分别作，，根据解析：（1）90°；（2）见解析；（3）不变，180°【分析】（1）根据邻补角的定义及角平分线的定义即可得解；（2）根据垂直的定义及邻补角的定义、角平分线的定义即可得解；（3）180BPC BQC ∠+∠=︒，过Q ，P 分别作//QG AB ，//PH AB ，根据平行线的性质及平角的定义即可得解．【详解】解（1）CN ，CM 分别平分BCE ∠和BCD ∠， 12BCN BCE ∴=∠，12BCM BCD ∠=∠， 180BCE BCD ∠+∠=︒，111()90222MCN BCN BCM BCE BCD BCE BCD ∴∠=∠+∠=∠+∠=∠+∠=︒； （2）CM CN ⊥，90MCN ∴∠=︒，即90BCN BCM ∠+∠=︒，22180BCN BCM ∴∠+∠=︒，CN 是BCE ∠的平分线，2BCE BCN ∴∠=∠，2180BCE BCM ∴∠+∠=︒，又180BCE BCD ∠+∠=︒，2BCD BCM ∴∠=∠，又CM 在BCD ∠的内部，CM ∴平分BCD ∠；（3）如图，不发生变化，180BPC BQC ∠+∠=︒，过Q ，P 分别作//QG AB ，//PH AB ，则有//////QG AB PH CD ，BQG ABQ ∴∠=∠，CQG ECQ ∠=∠，BPH FBP ∠=∠，CPH DCP ∠=∠，⊥BP BQ ，CP CQ ⊥，90PBQ PCQ ∴∠=∠=︒，180ABQ PBQ FBP ∠+∠+=︒，180ECQ PCQ DCP ∠+∠+∠=︒，180ABQ FBP ECQ DCP ∴∠+∠+∠+∠=︒，BPC BQC BPH CPH BQG CQG ∴∠+∠=∠+∠+∠+∠180ABQ FBP ECQ DCP =∠+∠+∠+∠=︒，180BPC BQC ∴∠+∠=︒不变．【点睛】此题考查了平行线的性质，熟记平行线的性质及作出合理的辅助线是解题的关键．二、解答题6．(1) ；(2) ；(3)不发生变化，理由见解析【分析】(1)如图1，延长DE 交AB 于点F ，根据平行线的性质推出；(2)如图2，过点E 作ES ∥AB ，过点H 作HT ∥AB ，根据AB ∥CD ，AB ∥E 解析：(1) +180ACB BED ∠∠=︒；(2) 100︒；(3)不发生变化，理由见解析【分析】(1)如图1，延长DE 交AB 于点F ，根据平行线的性质推出+180ACB BED ∠∠=︒；(2)如图2，过点E 作ES ∥AB ，过点H 作HT ∥AB ，根据AB ∥CD ，AB ∥ES 推出BED ABE CDE ∠=∠+∠，再根据AB ∥TH ，AB ∥CD 推出GHD THD THB ∠=∠-∠，最后根据BED ∠比BHD ∠大60︒得出BED ∠的度数；(3)如图3，过点E 作EQ ∥DN ，根据DEB CDE ABE ∠=∠+∠得出βα-的度数，根据条件再逐步求出PBM ∠的度数．【详解】(1)如答图1所示，延长DE 交AB 于点F ．AB ∥CD ，所以D EFB ∠=∠，又因为A D ∠=∠，所以A EFB ∠=∠，所以AC ∥DF ，所以ACB CED ∠=∠．因为+180CED BED ∠∠=︒，所以+180ACB BED ∠∠=︒．(2)如答图2所示，过点E 作ES ∥AB ，过点H 作HT ∥AB ．设ABG EBG α∠=∠=，FDH EDH β∠=∠=，因为AB ∥CD ，AB ∥ES ，所以ABE BES ∠=∠，SED CED ∠=∠，所以21802BED BES SED ABE CDE αβ∠=∠+∠=∠+∠=+︒-，因为AB ∥TH ，AB ∥CD ，所以ABG THB ∠=∠，FDH DHT ∠=∠，所以GHD THD THB βα∠=∠-∠=-，因为BED ∠比BHD ∠大60︒，所以2+1802()60αββα︒---=︒，所以40βα-=︒，所以40BHD ∠=︒，所以100BED ∠=︒(3)不发生变化如答图3所示，过点E 作EQ ∥DN ．设CDN EDN α∠=∠=，EBM KBM β∠=∠=，由(2)易知DEB CDE ABE ∠=∠+∠，所以2+1802100αβ︒-=︒，所以40βα-=︒， 所以180()180DEB CDE EDN EBM PBM PBM αβ∠=∠+∠+︒-∠+∠=+︒--∠， 所以80()40PBM βα∠=︒--=︒．【点睛】本题考查了平行线的性质，求角的度数，正确作出相关的辅助线，根据条件逐步求出角度的度数是解题的关键．7．（1）①，证明见解析，②，（2）或．【分析】(1) ①根据和镜像证出，即可判断直线与直线的位置关系，②过点Q 作QF ∥CD ，根据平行线的性质证即可；(2)过点Q 作QF ∥CD ，根据点P 的位置不同，解析：（1）①//MN PQ ，证明见解析，②70DPQ BMQ ∠∠+=︒，（2）160︒或20︒．【分析】(1) ①根据//AB CD 和镜像证出NMP QPM ∠=∠，即可判断直线MN 与直线PQ 的位置关系，②过点Q 作QF ∥CD ，根据平行线的性质证DPQ BM MQP Q ∠=∠∠+即可；(2)过点Q 作QF ∥CD ，根据点P 的位置不同，分类讨论，依据平行线的性质求解即可．【详解】（1）①//MN PQ ，证明：∵//AB CD ，∴NPM QMP ∠=∠，∵,NMP QMP NPM QPM ∠=∠∠=∠，∴NMP QPM ∠=∠，∴//MN PQ ；②过点Q 作QF ∥CD ，∵//AB CD ，∴////AB CD QF ，∴1BMQ ∠=∠，2QPD ∠=∠，∴DPQ BM MQP Q ∠=∠∠+，∵70MNP MQP ∠=∠=︒，∴70DPQ BMQ ∠∠+=︒；（2）如图，当点P 在N 右侧时，过点Q 作QF ∥CD ，同（1）得，////AB CD QF ，∴180NP FQP Q ∠=∠+︒，FQM BMQ ∠=∠，∵PQ CD ⊥，∴90NPQ ∠=︒，∴90FQP ∠=︒，∵70MND PQM ∠=∠=︒，∴20FQM ∠=︒，∴20BMQ ∠=︒，如图，当点P 在N 左侧时，过点Q 作QF ∥CD ，同（1）得，////AB CD QF ， 同理可得，90FQP ∠=︒，∵70MND ∠=︒，∴110MNP PQM ∠=∠=︒，∴20FQM ∠=︒，∵//AB QF ，∴180BM FQM Q ∠=∠+︒，∴160BMQ ∠=︒；综上，BMQ ∠的度数为160︒或20︒．【点睛】本题考查了平行线的性质与判定，解题关键是恰当的作辅助线，熟练利用平行线的性质推导角之间的关系．8．（1）∠PAF ＋∠PBN ＋∠APB ＝360°；（2）①，见解析；②或【分析】（1）作PC ∥EF ，如图1，由PC ∥EF ，EF ∥MN 得到PC ∥MN ，根据平行线的性质得∠PAF ＋∠APC ＝180°，∠解析：（1）∠PAF ＋∠PBN ＋∠APB ＝360°；（2）①CPD αβ∠=∠+∠，见解析；②CPD βα∠=∠-∠或CPD αβ∠=∠-∠【分析】（1）作PC ∥EF ，如图1，由PC ∥EF ，EF ∥MN 得到PC ∥MN ，根据平行线的性质得∠PAF ＋∠APC ＝180°，∠PBN ＋∠CPB ＝180°，即有∠PAF ＋∠PBN ＋∠APB ＝360°； （2）①过P 作PE ∥AD 交ON 于E ，根据平行线的性质，可得到EPD α∠=∠，CPE β∠=∠，于是CPD αβ∠=∠+∠；②分两种情况：当P 在OB 之间时；当P 在OA 的延长线上时，仿照①的方法即可解答．【详解】解：（1）∠PAF ＋∠PBN ＋∠APB ＝360°，理由如下：作PC ∥EF ，如图1，∵PC ∥EF ，EF ∥MN ，∴PC ∥MN ，∴∠PAF ＋∠APC ＝180°，∠PBN ＋∠CPB ＝180°，∴∠PAF ＋∠APC +∠PBN ＋∠CPB ＝360°,∴∠PAF ＋∠PBN ＋∠APB ＝360°；（2）①CPD αβ∠=∠+∠，理由如下：如答图，过P 作PE ∥AD 交ON 于E ，∵AD ∥BC ，∴PE ∥BC ，∴EPD α∠=∠，CPE β∠=∠，∴CPD αβ∠=∠+∠②当P 在OB 之间时，CPD αβ∠=∠-∠，理由如下：如备用图1，过P 作PE ∥AD 交ON 于E ，∵AD ∥BC ，∴PE ∥BC ，∴EPD α∠=∠，CPE β∠=∠，∴CPD αβ∠=∠-∠；当P 在OA 的延长线上时，CPD βα∠=∠-∠，理由如下：如备用图2，过P 作PE ∥AD 交ON 于E ，∵AD ∥BC ，∴PE ∥BC ，∴EPD α∠=∠，CPE β∠=∠，∴CPD βα∠=∠-∠；综上所述，∠CPD ，∠α，∠β之间的数量关系是CPD βα∠=∠-∠或CPD αβ∠=∠-∠.【点睛】本题考查了平行线的性质：两直线平行，同位角相等，内错角相等，同旁内角互补．难点是分类讨论作平行辅助线．9．（1），见解析；（2）；（3）60°【分析】（1）作EF//AB ，如图1，则EF//CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，解析：（1）BAE CDE AED ∠+∠=∠，见解析；（2）12AFD AED ∠=∠；（3）60° 【分析】（1）作EF //AB ，如图1，则EF //CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，由（1）的结论得∠AFD ＝∠BAF ＋∠CDF ，根据角平分线的定义得到∠BAF ＝12∠BAE ，∠CDF ＝12∠CDE ，则∠AFD ＝12（∠BAE ＋∠CDE ），加上（1）的结论得到∠AFD ＝12∠AED ；（3）由（1）的结论得∠AGD ＝∠BAF ＋∠CDG ，利用折叠性质得∠CDG ＝4∠CDF ，再利用等量代换得到∠AGD ＝2∠AED －32∠BAE ，加上90°－∠AGD ＝180°－2∠AED ，从而可计算出∠BAE 的度数．【详解】解：（1）BAE CDE AED ∠+∠=∠理由如下：作//EF AB ，如图1，//AB CD ，//EF CD ∴．1BAE ∴∠=∠，2CDE ∠=∠，BAE CDE AED ∴∠+∠=∠；（2）如图2，由（1）的结论得AFD BAF CDF ∠=∠+∠，BAE ∠、CDE ∠的两条平分线交于点F ，12BAF BAE ∴∠=∠，12CDF CDE ∠=∠， 1()2AFD BAE CDE ∴∠=∠+∠， BAE CDE AED ∠+∠=∠，12AFD AED ∴∠=∠； （3）由（1）的结论得AGD BAF CDG ∠=∠+∠，而射线DC 沿DE 翻折交AF 于点G ，4CDG CDF ∴∠=∠，11422()22AGD BAF CDF BAE CDE BAE AED BAE ∴∠=∠+∠=∠+∠=∠+∠-∠= 322AED BAE ∠-∠， 901802AGD AED ︒-∠=︒-∠，390218022AED BAE AED ∴︒-∠+∠=︒-∠， 60BAE ∴∠=︒．【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．10．（1）① ②；（2）；（3）不变，，理由见解析；（4）【分析】（1）①由平行线的性质，两直线平行，同旁内角互补可直接求出；②由平行线的性质，两直线平行，内错角相等可直接写出；（2）由角平分线的解析：（1）①116,︒ ②CBN ；（2）58︒；（3）不变，:2:1APB ADB ∠∠=，理由见解析；（4）29.︒【分析】（1）①由平行线的性质，两直线平行，同旁内角互补可直接求出；②由平行线的性质，两直线平行，内错角相等可直接写出；（2）由角平分线的定义可以证明∠CBD ＝12∠ABN ，即可求出结果；（3）不变，∠APB ：∠ADB ＝2：1，证∠APB ＝∠PBN ，∠PBN ＝2∠DBN ，即可推出结论； （4）可先证明∠ABC ＝∠DBN ，由（1）∠ABN ＝116°，可推出∠CBD ＝58°，所以∠ABC+∠DBN ＝58°，则可求出∠ABC 的度数．【详解】解：（1）①∵AM//BN ，∠A ＝64°，∴∠ABN ＝180°﹣∠A ＝116°，故答案为：116°；②∵AM//BN ，∴∠ACB ＝∠CBN ，故答案为：CBN ；（2）∵AM//BN ，∴∠ABN+∠A ＝180°，∴∠ABN ＝180°﹣64°＝116°，∴∠ABP+∠PBN ＝116°，∵BC 平分∠ABP ，BD 平分∠PBN ，∴∠ABP ＝2∠CBP ，∠PBN ＝2∠DBP ，∴2∠CBP+2∠DBP ＝116°，∴∠CBD ＝∠CBP+∠DBP ＝58°；（3）不变，∠APB ：∠ADB ＝2：1，∵AM//BN ，∴∠APB ＝∠PBN ，∠ADB ＝∠DBN ，∵BD 平分∠PBN ，∴∠PBN ＝2∠DBN ，∴∠APB ：∠ADB ＝2：1；（4）∵AM//BN ，∴∠ACB ＝∠CBN ，当∠ACB ＝∠ABD 时，则有∠CBN ＝∠ABD ，∴∠ABC+∠CBD ＝∠CBD+∠DBN∴∠ABC ＝∠DBN ，由（1）∠ABN ＝116°，∴∠CBD ＝58°，∴∠ABC+∠DBN ＝58°，∴∠ABC ＝29°，故答案为：29°．【点睛】本题考查了角平分线的定义，平行线的性质等，解题关键是能熟练运用平行线的性质并能灵活运用角平分线的定义等．三、解答题11．（1）40°；（2）的值不变，比值为;（3）∠OEC=∠OBA=60°.【分析】（1）根据OB 平分∠AOF ，OE 平分∠COF ，即可得出∠EOB=∠EOF+∠FOB=∠COA ，从而得出答案；（2解析：（1）40°；（2）:OBC OFC ∠∠的值不变，比值为12;（3）∠OEC=∠OBA=60°.【分析】（1）根据OB 平分∠AOF ，OE 平分∠COF ，即可得出∠EOB=∠EOF+∠FOB=12∠COA ，从而得出答案；（2）根据平行线的性质，即可得出∠OBC=∠BOA ，∠OFC=∠FOA ，再根据∠FOA=∠FOB+∠AOB=2∠AOB ，即可得出∠OBC ：∠OFC 的值为1：2．（3）设∠AOB=x ，根据两直线平行，内错角相等表示出∠CBO=∠AOB=x ，再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠OEC，然后利用三角形的内角和等于180°列式表示出∠OBA，然后列出方程求解即可．【详解】（1）∵CB∥OA∴∠C+∠COA=180°∵∠C=100°∴∠COA=180°-∠C=80°∵∠FOB=∠AOB，OE平分∠COF∴∠FOB+∠EOF=12（∠AOF+∠COF）=12∠COA=40°;∴∠EOB=40°;（2）∠OBC：∠OFC的值不发生变化∵CB∥OA∴∠OBC=∠BOA，∠OFC=∠FOA∵∠FOB=∠AOB∴∠FOA=2∠BOA∴∠OFC=2∠OBC∴∠OBC：∠OFC=1：2（3）当平行移动AB至∠OBA=60°时，∠OEC=∠OBA．设∠AOB=x，∵CB∥AO，∴∠CBO=∠AOB=x，∵CB∥OA，AB∥OC，∴∠OAB+∠ABC=180°，∠C+∠ABC=180°∴∠OAB=∠C=100°．∵∠OEC=∠CBO+∠EOB=x+40°，∠OBA=180°-∠OAB-∠AOB=180°-100°-x=80°-x，∴x+40°=80°-x，∴x=20°，∴∠OEC=∠OBA=80°-20°=60°．【点睛】本题主要考查了平行线、角平分线的性质以及三角形内角和定理，熟记各性质并准确识图理清图中各角度之间的关系是解题的关键．12．（1）∠EPB＝170°；（2）①当交点P在直线b的下方时：∠EPB＝20°，②当交点P在直线a，b之间时：∠EPB＝160°，③当交点P在直线a的上方时：∠EPB＝∠1﹣50°＝20°；（3）①当解析：（1）∠EPB＝170°；（2）①当交点P在直线b的下方时：∠EPB＝20°，②当交点P在直线a，b之间时：∠EPB＝160°，③当交点P在直线a的上方时：∠EPB＝∠1﹣50°＝20°；（3）①当交点P在直线a，b之间时：∠EPB＝180°﹣|n°﹣50°|；②当交点P在直线a上方或直线b下方时：∠EPB＝|n°﹣50°|.【分析】（1）利用外角和角平分线的性质直接可求解；（2）分三种情况讨论：①当交点P在直线b的下方时；②当交点P在直线a，b之间时；③当交点P在直线a的上方时；分别画出图形求解；（3）结合（2）的探究，分两种情况得到结论：①当交点P在直线a，b之间时；②当交点P在直线a上方或直线b下方时；【详解】解：（1）∵BD平分∠ABC，∠ABC＝50°，∴∠ABD＝∠DBC＝12∵∠EPB是△PFB的外角，∴∠EPB＝∠PFB+∠PBF＝∠1+（180°﹣50°）＝170°；（2）①当交点P在直线b的下方时：∠EPB＝∠1﹣50°＝20°；②当交点P在直线a，b之间时：∠EPB＝50°+（180°﹣∠1）＝160°；③当交点P在直线a的上方时：∠EPB＝∠1﹣50°＝20°；（3）①当交点P在直线a，b之间时：∠EPB＝180°﹣|n°﹣50°|；②当交点P在直线a上方或直线b下方时：∠EPB＝|n°﹣50°|；【点睛】考查知识点：平行线的性质；三角形外角性质．根据动点P的位置，分类画图，结合图形求解是解决本题的关键．数形结合思想的运用是解题的突破口．13．（1）110（2）（90 +n）（3）×90°+n°【分析】（1）根据角平分线的性质，结合三角形的内角和定理可得到角之间的关系，然后求解即可；（2）根据BO、CO分别是∠ABC与∠ACB的角平解析：（1）110（2）（90 +12n）（3）201712×90°+20182018212n°【分析】（1）根据角平分线的性质，结合三角形的内角和定理可得到角之间的关系，然后求解即可；（2）根据BO、CO分别是∠ABC与∠ACB的角平分线，用n°的代数式表示出∠OBC与∠OCB的和，再根据三角形的内角和定理求出∠BOC的度数；（3）根据规律直接计算即可.【详解】解：（1）∵∠A=40°，∴∠ABC+∠ACB=140°，∵点O是∠AB故答案为：110°；C与∠ACB的角平分线的交点，∴∠OBC+∠OCB=70°，∴∠BOC=110°．（2）∵∠A=n°，∴∠ABC+∠ACB=180°-n°，∵BO、CO分别是∠ABC与∠ACB的角平分线，∴∠OBC+∠OCB＝12∠ABC+12∠ACB＝12（∠ABC+∠ACB）＝12（180°﹣n°）＝90°﹣12n°，∴∠BOC＝180°﹣（∠OBC+∠OCB）＝90°+12n°．故答案为：（90+12n）；（3）由（2）得∠O＝90°+12n°，∵∠ABO的平分线与∠ACO的平分线交于点O1，∴∠O1BC＝34∠ABC，∠O1CB＝34∠ACB，∴∠O1＝180°﹣34（∠ABC+∠ACB）＝180°﹣34（180°﹣∠A）＝14×180°+34n°，同理，∠O2＝18×180°+78n°，∴∠O n ＝112n +×180°+11212n n ++- n °， ∴∠O 2017＝201812×180°+20182018212-n °， 故答案为：201712×90°+20182018212-n °． 【点睛】 本题考查了三角形内角和定理，角平分线定义的应用，注意：三角形的内角和等于180°． 14．（1）3；（2）98°；（3）∠P=（β+2α），理由见解析；（4）360°.【分析】（1）以M 为交点的“8字形”有1个，以O 为交点的“8字形”有2个； （2）根据角平分线的定义得到∠CAP=∠解析：（1）3；（2）98°；（3）∠P=（β+2α），理由见解析；（4）360°.【分析】（1）以M 为交点的“8字形”有1个，以O 为交点的“8字形”有2个；（2）根据角平分线的定义得到∠CAP=∠BAP ，∠BDP=∠CDP ，再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P ，∠BAP+∠P=∠BDP+∠B ，两等式相减得到∠C ﹣∠P=∠P ﹣∠B ，即∠P=（∠C+∠B ），然后把∠C=100°，∠B=96°代入计算即可；（3）与（2）的证明方法一样得到∠P=（2∠C+∠B ）．（4）根据三角形内角与外角的关系可得∠B+∠A=∠1，∠C+∠D=∠2，再根据四边形内角和为360°可得答案．【详解】解：（1）在图2中有3个以线段AC 为边的“8字形”，故答案为3；（2）∵∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ，∴∠CAP=∠BAP ，∠BDP=∠CDP ，∵∠CAP+∠C=∠CDP+∠P ，∠BAP+∠P=∠BDP+∠B ，∴∠C ﹣∠P=∠P ﹣∠B ，即∠P=（∠C+∠B ），∵∠C=100°，∠B=96°∴∠P=（100°+96°）=98°；（3）∠P=（β+2α）；理由：∵∠CAP=∠CAB ，∠CDP=∠CDB ，∴∠BAP=∠BAC ，∠BDP=∠BDC ，∵∠CAP+∠C=∠CDP+∠P ，∠BAP+∠P=∠BDP+∠B ，∴∠C ﹣∠P=∠BDC ﹣∠BAC ，∠P ﹣∠B=∠BDC ﹣∠BAC ，∴2（∠C ﹣∠P ）=∠P ﹣∠B ，∴∠P=（∠B+2∠C ），∵∠C=α，∠B=β，∴∠P=（β+2α）；（4）∵∠B+∠A=∠1，∠C+∠D=∠2，∴∠A+∠B+∠C+∠D=∠1+∠2，∵∠1+∠2+∠F+∠E=360°，∴∠A+∠B+∠C+∠D+∠E+∠F=360°．故答案为360°．15．（1）见解析；（2）①③；（3）∠APB 的度数是10°或20°或40°或110°【分析】（1）由和是的角平分线，证明即可；（2）根据“准互余三角形”的定义逐个判断即可；（3）根据“准互余三角解析：（1）见解析；（2）①③；（3）∠APB 的度数是10°或20°或40°或110°【分析】（1）由90ABC A ∠+∠=︒和BD 是ABC 的角平分线，证明290ABD A ∠+∠=︒即可； （2）根据“准互余三角形”的定义逐个判断即可；（3）根据“准互余三角形”的定义，分类讨论：①2∠A +∠ABC =90°；②∠A +2∠APB =90°；③2∠APB +∠ABC =90°；④2∠A +∠APB =90°，由三角形内角和定理和外角的性质结合“准互余三角形”的定义，即可求出答案．【详解】（1）证明：∵在Rt ABC 中，90ACB ∠=︒，∴90ABC A ∠+∠=︒，∵BD 是ABC ∠的角平分线，∴2ABC ABD ∠=∠，∴290ABD A ∠+∠=︒，∴ABD △是“准互余三角形”；（2）①∵70,10B C ∠=︒∠=︒，∴290B C ∠+∠=︒，∴ABC 是“准互余三角形”，故①正确；②∵60A ∠=︒， 20B ∠=︒，∴210090A B ∠+∠=︒≠︒，∴ABC 不是“准互余三角形”，故②错误；③设三角形的三个内角分别为,,αβγ，且αβγ<<，∵三角形是“准互余三角形”，∴290αβ+=︒或290αβ+=︒，∴90αβ+<︒，∴180()90γαβ=︒-+>︒，∴“准互余三角形”一定是钝角三角形，故③正确；综上所述，①③正确，故答案为：①③；（3）∠APB 的度数是10°或20°或40°或110°；如图①，当2∠A +∠ABC =90°时，△ABP 是“准直角三角形”，∵∠ABC =50°，∴∠A =20°，∴∠APB =110°；如图②，当∠A +2∠APB =90°时，△ABP 是“准直角三角形”，∵∠ABC =50°，∴∠A +∠APB =50°，∴∠APB =40°；如图③，当2∠APB +∠ABC =90°时，△ABP 是“准直角三角形”，∵∠ABC=50°，∴∠APB=20°；如图④，当2∠A+∠APB=90°时，△ABP是“准直角三角形”，∵∠ABC=50°，∴∠A+∠APB=50°，所以∠A=40°，所以∠APB=10°；综上，∠APB的度数是10°或20°或40°或110°时，ABP△是“准互余三角形”．【点睛】本题是三角形综合题，考查了三角形内角和定理，三角形的外角的性质，解题关键是理解题意，根据三角形内角和定理和三角形的外角的性质，结合新定义进行求解．。

曲靖市2023-2024学年春季学期期末考试七年级语文试题卷（全卷四个大题，共25个小题，共8页；满分100分，考试时间150分钟）注意事项：1．本卷为试题卷。

考生必须在答题卡上解题作答。

答案应书写在答题卡的相应位置上，在试题卷、草稿纸上作答无效。

2．考试结束后，将试题卷和答题卡一并交回。

一、积累与运用（1~5题，每题2分，第6题6分，共16分）阅读下面文字，按要求完成1~4题。

春回大地，万物复苏。

踏着春天的脚步，我们的生活充满了生动的色彩。

连日来，随着气温逐渐________，大家纷纷走出家门，感受春的气息。

尝美食、赏春花、踏青露营……处处春潮涌动。

明媚（mèi）春光里，各地花开成海。

樱花、梨花、海棠花、桃花、玉兰花……红的似火，白的如雪、粉的像霞，到处________出一派春意盎（àng）然、繁花盛开的景象。

立春刚过，寥廓（guò）公园、龙潭公园等地就人山人海，前来赏花的游客络绎不绝。

这几天，各大公园的海棠（táng）花开得正艳，慢步于公园中，头顶就是粉色的海棠花，触手可及，这般盛景让人陶醉。

在盛开的海棠树下，常常看见这样的场景，服装鲜艳的女士们灵活地调整着拍照姿势，在同伴“三二一”的倒数声中露出灿烂的笑容。

每年赏花季，寥廓公园都会________大量的游客，不少居民便在周边做起了小吃生意，一边做特色美食，一边卖玩具，增加收入。

赏花旅游带来人气就会有商机。

自鲜花盛开以来，公园里的生意每天都很火爆，炸洋芋、炸臭豆腐、凉米线、饮料、雪糕、烧烤……________，应有尽有，赏花季不仅带来了我们文旅的“人气”，更提升了我们的“财气”。

1．文中注音不正确的一项是（）A．媚（mèi）B．盎（àng）C．廓（guò）D．棠（táng）2．文中加点词语有错别字的一项是（）A．万物复苏B．涌动C．络绎不绝D．慢步3．文中横线上应填入的词语，最恰当的一项是（）A．回升呈现吸引琳琅满目B．回升出现引诱琳琅满目C．升高呈现引诱五花八门D．升高出现吸引五花八门4．对文中画线句子病因的分析，正确的一项是（）A．不合逻辑B．搭配不当C．成份残缺D．语序不当5．下列句子的排序，与上下文衔接最恰当的一项是（）燕子飞回来时，正是乡村的春耕春播最忙碌的时候。

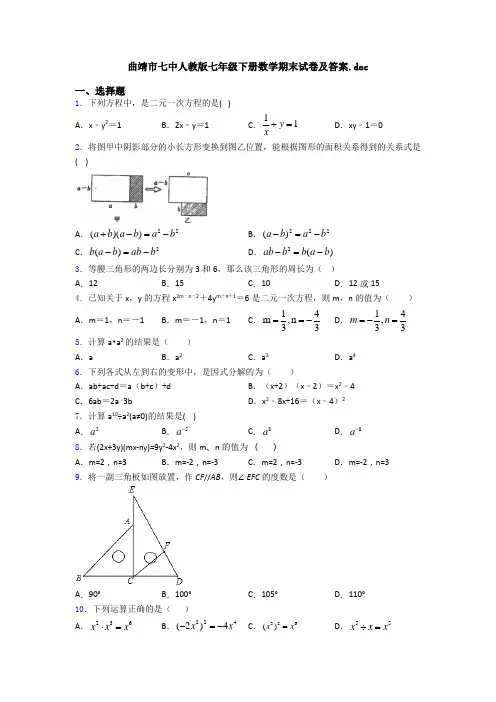
云南省曲靖市七年级（下）期末数学试卷一、选择题（本大题共8个小题每小题4分，共32分）1．将△ABC各顶点的纵坐标加“﹣3”，连接这三点所成的三角形是由△ABC （）A．向上平移3个单位得到的B．向下平移3个单位得到的C．向左平移3个单位得到的D．向右平移3个单位得到的2．下列调查中，采用了“抽样调查”方式的是（）A．为了了解某次考试试卷的质量，对全班所有学生的试卷进行分析B．调查某一品牌5万袋包装鲜奶是否符合卫生标准C．调查我国所有城市中哪些是第一批沿海开放城市D．了解全校学生100米短跑的成绩3．关于x，y的方程组的解为，则=（）A．﹣3 B．3 C．81 D．﹣814．关于无理数，有下列说法：①2个无理数之和可以是有理数②2个无理数之积可以是有理数③无理数是无限小数④有理数和数轴上的点一一对应⑤无理数一定是无限不循环小数其中正确的是（）A．①②③④B．①②③⑤C．②③④⑤D．①②④⑤5．如果点P（2x﹣6，x+4）在平面直角坐标系的第二象限内，那么x的取值范围在数轴上可表示为（）A．B．C．D．6．（4分）如图，直线∥，则∠α为（）A．140°B．130°C．120°D．110°7．有下列说法：①﹣3是的平方根；②﹣7是（﹣7）2的算术平方根；③25的平方根是±5；④﹣9的平方根是±3；⑤0没有算术平方根；⑥的平方根为；⑦平方根等于本身的数有0、1．其中，正确的有（）A．1个B．2个C．3个D．4个8．在如图所示的平面直角坐标系中，一只蚂蚁从A点出发，沿着A→B→C→D→A…循环爬行，其中A点坐标为（1，﹣1），B点坐标为（﹣1，﹣1），C点坐标为（﹣1，3），当蚂蚁爬了2017个单位时，它所处位置的坐标为（）A．（1，1）B．（1，0）C．（0，1）D．（0，﹣1）二、填空题（本大题共6个小题；每小题3分，共18分）9．把二元一次方程+x=2中的y用含x的式子表示为．10．已知点（2a，a+1）在y轴上，则该点坐标为．11．下列四个命题：①垂直平分弦的直线经过圆心；②平行弦所夹的弧能够互相重合；③平分弦所对的一条弧的直径垂直平这条弦；④经过弦中点的直径平分弦所对的弧，其中是真命题．12．若关于x，y的二元一次方程组的解满足x﹣y＞2，则a的取值范围是．13．若代数式x2﹣2x与9﹣2x的值相等，则x=．14．如图，l1∥l2，∠β=142°，∠γ=73°，则∠α=．三、解答题（本大题共9个小题；共70分．）15．（6分）已知≈1.414，≈1.732，求﹣2的近似值．16．（7分）用代入消元法解二元一次方程组：（1）（2）（3）（4）．17．（7分）解下列不等式（组），并把解集分别表示在数轴上．（1）；（2）≥（3）（4）﹣9﹣x≤4x﹣13≤2x+3．18．（6分）如图，在铺设铁轨时，两条铁轨必须是平行的，已知∠1是直角，那么再测量图中的哪个角（仅限图中已标出的角），就可以判断图中的两条铁轨AB、CD是否平行？为什么．19．（10分）某地杨梅丰收，准备将已经采摘下来的11400公斤杨梅运送杭州，现有甲、乙、丙三种车型共选择，每辆车运载能力和运费如表表示（假设每辆车均满载）车型甲乙丙汽车运载量（公斤/辆）600800900汽车运费（元/辆）500600700（1）若全部杨梅都用甲、乙两种车型来运，需运费8700元，则需甲、乙两种车型各几辆？（2）为了节省运费，现打算用甲、乙、丙三种车型都参与运送，已知它们的总辆数为15辆，你能分别求出这三种车型的辆数吗？怎样安排运费最省？20．（7分）如图，把△ABC的A（4，3）点平移到A1（﹣2，3）点，（1）画出△A1B1C1；（2）写出另外两个点B1，C1的坐标；（3）求△ABC的面积．21．（7分）根据题意结合图形填空：（1）已知：如图1，DE∥BC，∠ADE=∠EFC，将说明∠1=∠2成立的理由填写完整．解：∵DE∥BC （）∴∠ADE=（）∵∠ADE=∠EFC∴=∴DB∥EF∴∠1=∠2（2）已知：如图2，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC的平分线吗？若是，请说明理由．解：AD是∠BAC的平分线，理由如下：∵AD⊥BC，EG⊥BC（已知）∴∠4=∠5=90°∴AD∥EG∴∠1=∠E∠2=∠3∵∠E=∠3（已知）∴=∴AD是∠BAC的平分线．22．（8分）自开展“阳光体育”以来，我校学生参加课外体育活动的积极性大大增强，为了解具体情况，学校随机抽样调查了初二部分学生每周参加课外体育活动所用的时间，同时调查了参加课外体育活动的项目，并将收集到的数据绘制成如图两幅统计图，请根据图中提供的信息，解答下列问题：（1）图2是课外体育活动时间为0～2h的同学活动项目统计图，已知打篮球的同学有2人，请将两幅统计图补充完整；（2）这次调查中，抽样调查了多少名学生？（3）调查中发现，每个活动时间段参加户外跑步的同学所占的比例相类似，请估算我校初二980名学生中，参加户外跑步的有多少人？23．（12分）如图1，在正方形ABCD中，AB=4，M，N分别是AD、CD上一点．（1）若DN=1，∠AMB=90°，求AM的长；（2）若N是CD的中点，且∠NMB=∠MBC，①求tan∠ABM的值；②在图2中，请仅用无刻度的直尺作出点M的位置，并说明确定M位置的理由．（要求：写出作法，并保留作图痕迹）参考答案与试题解析一、选择题（本大题共8个小题每小题4分，共32分）1．（4分）将△ABC各顶点的纵坐标加“﹣3”，连接这三点所成的三角形是由△ABC（）A．向上平移3个单位得到的B．向下平移3个单位得到的C．向左平移3个单位得到的D．向右平移3个单位得到的【分析】根据在平面直角坐标系内，把一个图形各个点的横坐标都加上（或减去）一个整数a，相应的新图形就是把原图形向右（或向左）平移a个单位长度；如果把它各个点的纵坐标都加（或减去）一个整数a，相应的新图形就是把原图形向上（或向下）平移a个单位长度可得答案．【解答】解：△ABC各顶点的纵坐标加“﹣3”，则△ABC向下平移3个单位，故选：B．【点评】此题主要考查了坐标与图形变化，关键是掌握横坐标，右移加，左移减；纵坐标，上移加，下移减．2．（4分）下列调查中，采用了“抽样调查”方式的是（）A．为了了解某次考试试卷的质量，对全班所有学生的试卷进行分析B．调查某一品牌5万袋包装鲜奶是否符合卫生标准C．调查我国所有城市中哪些是第一批沿海开放城市D．了解全校学生100米短跑的成绩【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．【解答】解：A、为了了解某次考试试卷的质量，对全班所有学生的试卷进行分析，适合全面调查，故A错误；B、调查某一品牌5万袋包装鲜奶是否符合卫生标准，调查具有破坏性，适合抽样调查，故B正确；C、调查我国所有城市中哪些是第一批沿海开放城市，调查范围广，适合抽样调查，故C错误；D、了解全校学生100米短跑的成绩，调查范围广，适合抽样调查，故D错误；故选：B．【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．3．（4分）关于x，y的方程组的解为，则=（）A．﹣3 B．3 C．81 D．﹣81【分析】把x与y的值代入计算求出a与b的值，代入原式计算即可得到结果．【解答】解：把代入方程组得：，解得：，则原式=3，故选B【点评】此题考查了二元一次方程组的解，以及算术平方根，熟练掌握运算法则是解本题的关键．4．（4分）关于无理数，有下列说法：①2个无理数之和可以是有理数②2个无理数之积可以是有理数③无理数是无限小数④有理数和数轴上的点一一对应⑤无理数一定是无限不循环小数其中正确的是（）A．①②③④B．①②③⑤C．②③④⑤D．①②④⑤【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．两个无理数相乘或相加也可能是有理数，无限循环小数在数轴上无法表示出来，由此即可判定选择项．【解答】解：①2个无理数之和可以是有理数，如2，2，本选项正确，②2个无理数之积可以是有理数，如2，2，本选项正确，③无理数是无限小数，本选项正确，④无限循环小数在数轴上无法表示，故本选项错误，⑤无理数一定是无限不循环小数，本选项正确，故选B．【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．5．（4分）如果点P（2x﹣6，x+4）在平面直角坐标系的第二象限内，那么x 的取值范围在数轴上可表示为（）A．B．C．D．【分析】根据点P（2x﹣6，x+4）在平面直角坐标系的第二象限内得出关于x的不等式组，求出x的取值范围，并在数轴上表示出来即可．【解答】解：∵点P（2x﹣6，x+4）在平面直角坐标系的第二象限内，∴，解得﹣4＜x＜3．在数轴上表示为：．故选C．【点评】本题考查的是在数轴上表示不等式的解集，熟知“小于向左，大于向右”是解答此题的关键．6．（4分）如图，直线∥，则∠α为（）A．140°B．130°C．120°D．110°【分析】由直线∥，根据平行线的性质，可求得∠1的度数，又由对顶角相等，即可求得答案．【解答】解：∵直线∥，∴∠1=180°﹣140°=40°，∴∠α=70°+∠1=70°+40°=110°．故选D．【点评】此题考查了平行线的性质以及对顶角相等．此题比较简单，注意掌握数形结合思想的应用．7．（4分）有下列说法：①﹣3是的平方根；②﹣7是（﹣7）2的算术平方根；③25的平方根是±5；④﹣9的平方根是±3；⑤0没有算术平方根；⑥的平方根为；⑦平方根等于本身的数有0、1．其中，正确的有（）A．1个B．2个C．3个D．4个【分析】运用平方根及算术平方根的定义求解即可．【解答】解：①﹣3是的平方根；故①正确，②7是（﹣7）2的算术平方根；故②错误，③25的平方根是±5；正确④﹣9的平方根是±3；负数没有平方根，故④错误，⑤0没有算术平方根；错误，⑥的平方根为；正确，⑦平方根等于本身的数有0、1．只有0，故错误．正确的有①③⑥，故选：C．【点评】本题主要考查了平方根及算术平方根，解题的关键是熟记定义．8．（4分）在如图所示的平面直角坐标系中，一只蚂蚁从A点出发，沿着A→B→C→D→A…循环爬行，其中A点坐标为（1，﹣1），B点坐标为（﹣1，﹣1），C点坐标为（﹣1，3），当蚂蚁爬了2017个单位时，它所处位置的坐标为（）A．（1，1）B．（1，0）C．（0，1）D．（0，﹣1）【分析】由点A、B、C的坐标可得出AB、BC的长度，从而可找出爬行一圈的长度，再根据2017=168×12+1即可得出当蚂蚁爬了2017个单位时，它所处位置的坐标．【解答】解：∵A点坐标为（1，﹣1），B点坐标为（﹣1，﹣1），C点坐标为（﹣1，3），∴AB=1﹣（﹣1）=2，BC=3﹣（﹣1）=4，∴从A→B→C→D→A一圈的长度为2（AB+BC）=12．∵2017=168×12+1，∴当蚂蚁爬了2017个单位时，它所处位置在点A左边一个单位长度处，即（0，﹣1）．故选D．【点评】本题考查了规律型中点的坐标以及矩形的性质，根据蚂蚁的运动规律找出蚂蚁每运动12个单位长度是一圈．二、填空题（本大题共6个小题；每小题3分，共18分）9．（3分）把二元一次方程+x=2中的y用含x的式子表示为．【分析】要把二元一次方程+x=2中的y用含x的式子表示，首先要去分母，然后移项、合并同类项即可．【解答】解：=2﹣x，方程两边同乘3得：2y﹣5=6﹣3x，移项得：2y=11﹣3x，系数化1得：．【点评】本题考查的是方程的基本运算技能：移项、合并同类项、系数化为1等，表示谁就该把谁放到等号的一边，其他的项移到另一边，然后合并同类项、系数化1就可用含y的式子表示x的形式．10．（3分）已知点（2a，a+1）在y轴上，则该点坐标为（0，1）．【分析】根据y轴上点的横坐标为0列方程求出a，再求解即可．【解答】解：∵点（2a，a+1）在y轴上，∴2a=0，解得a=0，所以，a+1=1，所以，点的坐标为（0，1）．故答案为：（0，1）．【点评】本题考查了点的坐标，熟记y轴上点的横坐标为0是解题的关键．11．（3分）下列四个命题：①垂直平分弦的直线经过圆心；②平行弦所夹的弧能够互相重合；③平分弦所对的一条弧的直径垂直平这条弦；④经过弦中点的直径平分弦所对的弧，其中①②③是真命题．【分析】分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．【解答】解：由垂径定理知，垂直平分弦的直线经过圆的圆心；平分弦所对的一条弧的直径垂直平分这条弦；故①③正确，由圆的对称性和垂径定理知，平行弦所夹的弧能够互相重合；故②正确；当弦是直径时，经过弦的中点的直径不能平分弦所对的弧，故④错误．综上真命题有3个，它们是①②③．答案：①②③【点评】本题考查了垂径定理的相关知识．过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧五个关系式中，知二总能推导出其他三个．特别需要注意的是应用“平分弦的直径垂直于弦，平分弦所对的两弧”时，弦不能是直径．12．（3分）若关于x，y的二元一次方程组的解满足x﹣y＞2，则a 的取值范围是a＜﹣3．【分析】方程组两方程相减表示出x﹣y，代入已知不等式求出a的范围即可．【解答】解：，①﹣②得：x﹣y=﹣a﹣1，代入不等式得：﹣a﹣1＞2，解得：a＜﹣3．故答案为：a＜﹣3．【点评】此题考查了二元一次方程组的解，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．13．（3分）若代数式x2﹣2x与9﹣2x的值相等，则x=±3．【分析】根据题意先列等式，再用直接开平方法解一元二次方程即可．【解答】解：x2﹣2x=9﹣2x，整理得x2=9，开平方得，x=±3，故答案为±3．【点评】本题考查了一元二次方程的解法﹣直接开平方法．解这类问题要移项，把所含未知数的项移到等号的左边，把常数项移项等号的右边，化成x2=a（a≥0）的形式，利用数的开方直接求解．14．（3分）如图，l1∥l2，∠β=142°，∠γ=73°，则∠α=35°．【分析】过∠γ作l3∥l2，再由l1∥l2∠可知l1∥l2∥l3，故可得出∠1+∠β=180°，∠α=∠2，再由∠β=142°，∠γ=73°即可得出结论．【解答】解：过∠γ作l3∥l2，∵l1∥l2∠，∴l1∥l2∥l3，∴∠1+∠β=180°，∠α=∠2，∴∠1=180°﹣∠β=180°﹣142°=38°，∴∠2=∠γ﹣∠1=73°﹣38°=35°，∴∠α=∠2=35°．故答案为：35°．【点评】本题考查的是平行线的性质，根据题意作出平行线是解答此题的关键．三、解答题（本大题共9个小题；共70分．）15．（6分）已知≈1.414，≈1.732，求﹣2的近似值．【分析】首先化简二次根式，进而将已知代入求出即可．【解答】解：∵≈1.414，≈1.732，∴﹣2=﹣2×=≈=0.159．【点评】此题主要考查了实数运算，正确化简二次根式是解题关键．16．（7分）用代入消元法解二元一次方程组：（1）（2）（3）（4）．【分析】各方程组利用代入消元法求出解即可．【解答】解：（1）将方程组，由②得：x=1﹣2y ③，将③代入①，得：2（1﹣2y）+3y=3，解得：y=﹣1，将y=﹣1代入③，得：x=5，故方程组的解为：；（2）解方程组，由②得：a=③，将③代入②，得： +2b+4=0，解得：b=，将b=代入③，得：a=﹣，故方程组的解为：；（3）解方程组，由②得：x=3y﹣2 ③，将③代入①，得：9（3y﹣2）﹣7y﹣12=0，解得：y=，将y=代入③，得：x=，故方程组的解为：；（4）解方程组，由①得，3x=2y ③，将③代入②，得：2y+4y=18，解得：y=3，将y=3代入③，得：3x=6，解得：x=2，故方程组的解为：．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．17．（7分）解下列不等式（组），并把解集分别表示在数轴上．（1）；（2）≥（3）（4）﹣9﹣x≤4x﹣13≤2x+3．【分析】（1）（2）根据题意利用不等式的基本性质，先解不等式组的解集，再把解集画在数轴上即可，（3）（4）先求出这两个不等式的解集，再把解集画在数轴上，即可得到不等式组的解集．【解答】解：（1），x＞；把解集表示在数轴上为：（2）≥，14x ﹣7（3x ﹣8）+14≥4（10﹣x ），14x ﹣21x +56+14≥40﹣4x ，﹣3x ≥﹣30，x ≤10；把解集表示在数轴上为：（3），解①得x ＞﹣6，解②得x ＞0， 故不等式组的解集为x ＞0．把解集表示在数轴上为：（4），解①得x ≥0.8，解②得x ≤8，故不等式组的解集为0.8≤x ≤8．把解集表示在数轴上为：【点评】本题考查了一元一次不等式（组）的解法和把解集表示在数轴上，是基础知识要熟练掌握．18．（6分）如图，在铺设铁轨时，两条铁轨必须是平行的，已知∠1是直角，那么再测量图中的哪个角（仅限图中已标出的角），就可以判断图中的两条铁轨AB、CD是否平行？为什么．【分析】根据平行线的判定定理即可得出结论．【解答】解：∵∠1=90°，∴当∠5=∠1=90°时，AB∥CD（同位角相等，两直线平行）．【点评】本题考查的是平行线的判定，用到的知识点为：同位角相等，两直线平行．19．（10分）某地杨梅丰收，准备将已经采摘下来的11400公斤杨梅运送杭州，现有甲、乙、丙三种车型共选择，每辆车运载能力和运费如表表示（假设每辆车均满载）车型甲乙丙汽车运载量（公斤/辆）600800900汽车运费（元/辆）500600700（1）若全部杨梅都用甲、乙两种车型来运，需运费8700元，则需甲、乙两种车型各几辆？（2）为了节省运费，现打算用甲、乙、丙三种车型都参与运送，已知它们的总辆数为15辆，你能分别求出这三种车型的辆数吗？怎样安排运费最省？【分析】（1）设需要甲x辆，乙y辆，根据运送11400公斤和需运费8700元，可列出方程组求解．（2）因为甲的费用最少，所以尽量多用甲，然后是乙，最后是丙，列出方程，且解是整数，可列方程求解．【解答】解：（1）设需要甲x辆，乙y辆，，解得．答：甲3辆，乙12辆；（2）设需要甲x辆，乙y辆，则丙（15﹣x﹣y）辆，根据题意得．600x+800y+900（15﹣x﹣y）=11400，y=21﹣3x，x可以为7，6，5，4，3，2，1，y依次为0（舍去），3，6，9，12，15（舍去），18（舍去），21（舍去），因此方案有：甲，乙，丙的辆数分别为①6，3，6；②5，6，4；③4，9，2；④3，12，0（不合题意，舍去）．则运费分别为①6×500+3×600+6×700=9000（元），②5×500+6×600+4×700=8900（元），③4×500+9×600+2×700=8800（元），故第三种方案运费最省，为8800元．【点评】此题考查二元一次方程组与二元一次方程的实际运用，找出题目蕴含的数量关系，建立方程或方程组解决问题．20．（7分）如图，把△ABC的A（4，3）点平移到A1（﹣2，3）点，（1）画出△A1B1C1；（2）写出另外两个点B1，C1的坐标；（3）求△ABC的面积．【分析】（1）根据平移的性质，找到各点的对应点，然后顺次连接即可得出平移后的图形；（2）作出平移后的图形，然后结合直角坐标系即可得出另外两个点的坐标．（3）根据图形可得出BC、AB、AC的长，利用勾股定理的逆定理可得出△ABC 是等腰直角三角形，继而可求出面积．【解答】解：（1）所作图形如下：（2）根据（1）所作的图形可得：B1（﹣3，1），C1（﹣5，2）；（3）AB=，BC=，AC=，∴AB2+BC2=AC2，即△ABC是等腰直角三角形，∴△ABC的面积=AB×BC=2.5．【点评】此题考查了平移作图、三角形的面积、直角坐标系的知识，解答本题的关键是正确的作出图形，判断出△ABC是等腰直角三角形，难度一般．21．（7分）根据题意结合图形填空：（1）已知：如图1，DE∥BC，∠ADE=∠EFC，将说明∠1=∠2成立的理由填写完整．解：∵DE∥BC （已知）∴∠ADE=∠ABC（两直线平行，同位角相等）∵∠ADE=∠EFC（已知）∴∠ABC=∠EFC∴DB∥EF（同位角相等，两直线平行）∴∠1=∠2（两直线平行，内错角相等）（2）已知：如图2，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC的平分线吗？若是，请说明理由．解：AD是∠BAC的平分线，理由如下：∵AD⊥BC，EG⊥BC（已知）∴∠4=∠5=90°（垂直定义）∴AD∥EG（同位角相等，两直线平行）∴∠1=∠E（两直线平行，同位角相等）∠2=∠3（两直线平行，内错角相等）∵∠E=∠3（已知）∴∠1=∠2∴AD是∠BAC的平分线（角平分线定义）．【分析】（1）根据平行线的性质得出∠ADE=∠ABC，求出∠ABC=∠EFC，根据平行线的判定得出DB∥EF，根据平行线的性质得出即可；（2）根据平行线的判定得出AD∥EG，根据平行线的性质得出∠1=∠E，∠2=∠3，求出∠1=∠2，根据角平分线定义得出即可．【解答】解：（1）∵DE∥BC（已知）∴∠ADE=∠ABC（两直线平行，同位角相等），∵∠ADE=∠EFC （已知），∴∠ABC=∠EFC，∴DB∥EF（同位角相等，两直线平行），∴∠1=∠2 （两直线平行，内错角相等），故答案为：已知，∠ABC，两直线平行，同位角相等，（已知），∠ABC，∠EFC，（同位角相等，两直线平行），（两直线平行，内错角相等）；（2）解：AD是∠BAC的平分线，理由如下：∵AD⊥BC，EG⊥BC（已知），∴∠4=∠5=90°（垂直定义），∴AD∥EG （同位角相等，两直线平行），∴∠1=∠E （两直线平行，同位角相等），∠2=∠3 （两直线平行，内错角相等），∵∠E=∠3（已知）∴∠1=∠2，∴AD是∠BAC的平分线（角平分线定义），故答案为：（垂直定义），（同位角相等，两直线平行），（两直线平行，同位角相等），（两直线平行，内错角相等），∠1，∠2，（角平分线定义）．【点评】本题考查了角平分线定义和平行线的性质和判定的应用，能灵活运用定理进行推理是解此题的关键．22．（8分）自开展“阳光体育”以来，我校学生参加课外体育活动的积极性大大增强，为了解具体情况，学校随机抽样调查了初二部分学生每周参加课外体育活动所用的时间，同时调查了参加课外体育活动的项目，并将收集到的数据绘制成如图两幅统计图，请根据图中提供的信息，解答下列问题：（1）图2是课外体育活动时间为0～2h的同学活动项目统计图，已知打篮球的同学有2人，请将两幅统计图补充完整；（2）这次调查中，抽样调查了多少名学生？（3）调查中发现，每个活动时间段参加户外跑步的同学所占的比例相类似，请估算我校初二980名学生中，参加户外跑步的有多少人？【分析】（1）首先求得0﹣2小时的人中，参加篮球的人数所占的百分比，根据打篮球的人数是2即可求得0﹣2小时的人数；（2）条形统计图中每项的人数的和就是所求；（3）利用总人数980乘以对应的百分比即可．【解答】解：（1）1﹣50%﹣25%﹣12.5%=12.5%，0﹣2小时的人数是：2÷12.5%=16（人），；（2）抽样调查的学生数是：6+16+26+8+9=65（人）；（3）参加户外跑步的人数是：650×25%≈163（人）．【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题23．（12分）如图1，在正方形ABCD中，AB=4，M，N分别是AD、CD上一点．（1）若DN=1，∠AMB=90°，求AM的长；（2）若N是CD的中点，且∠NMB=∠MBC，①求tan∠ABM的值；②在图2中，请仅用无刻度的直尺作出点M的位置，并说明确定M位置的理由．（要求：写出作法，并保留作图痕迹）【分析】（1）由∠AMB+∠A+∠ABM=180°、∠AMB=90°、∠A=90°知∠ABM=0°，即点M与点A重合，可得答案；（2）①设AM=x，知DM=4﹣x，证△DMN≌△CPN得MN=NP=，根据BP=4+4﹣x=8﹣x知8﹣x=，解之可得x=4或x=，继而可得答案；②当x=4即∠ABM=45°，知AM=AB=4，即点D、M重合，连BD可得；当x=时，即点M为AD的三等分点，过点N作NP⊥AB于点P，连接AC交PD于点O，过点O作OM⊥AD于点D，证△APO∽△CDO得=，再证△DMO∽△DAP得==，即AM=AD．【解答】解：（1）∵四边形ABCD是正方形，∴∠A=90°，又∵∠AMB+∠A+∠ABM=180°，∠AMB=90°，∴∠ABM=0°，即点M与点A重合，∴AM=0；（2）①设AM=x，∵AD=4，∴DM=4﹣x，延长MN交BC于P，∵N为CD中点，∴DN=CN，在△DMN和△CPN中，∵，∴△DMN≌△CPN（ASA），∴MN=NP=，又∵BP=4+4﹣x=8﹣x，∴8﹣x=，解得：x=4或x=，∴tan==或tan∠ABM===1；②当AM=4时，即∠ABM=45°，如图2，连接BD，则AB=AD=4，此时∠ABM=45°，AM=AD=4；当AM=时，即点M为AD的三等分点，如图3，过点N作NP⊥AB于点P，连接AC交PD于点O，过点O作OM⊥AD 于点D，∵AP ∥CD ，且=，∴△APO ∽△CDO ，∴=，又∵OM ⊥AD ，∴OM ∥AP ，∴△DMO ∽△DAP ，∴==，即AM=AD ，故点M 即为所求点．【点评】本题主要考查四边形的综合，考查的知识点有全等三角形的判定与性质及相似三角形的判定与性质、解直角三角形等，熟练掌握相似三角形的判定与性质是解题的关键．。

七年级下册曲靖数学期末试卷试卷（word 版含答案）一、选择题1．下列各式中，没有平方根的是（）A ．-22B ．（-2）2C ．-（-2）D ．∣-2∣ 2．下列图中的“笑脸”，是由上面教师寄语中的图像平移得到的是（ ）A ．B ．C ．D ． 3．点()P m n ,在第二象限内，则点(),Q m m n --在第______象限．A ．一B ．二C ．三D ．四4．下列四个命题其中正确的个数是（ ）①对顶角相等；②在同一平面内，若//a b ，c 与a 相交，则b 与c 也相交；③邻补角的平分线互相垂直；④在同一平面内，垂直于同一条直线的两条直线互相垂直A ．1个B ．2个C ．3个D ．4个5．如图，已知直线AB 、CD 被直线AC 所截，//AB CD ，E 是直线AC 右边任意一点（点E 不在直线AB ，CD 上），设BAE α∠=，DCE β∠=．下列各式：①αβ+，②αβ-，③βα-，④360αβ︒--，AEC ∠的度数可能是（ ）A ．①②③B ．①②④C ．①③④D ．①②③④ 6．下列计算正确的是（ ） A ．2(3)3-=- B ．366=± C ．393= D ．382--= 7．如图，在ABC 中，//DF AB 交AC 于点E ，交BC 于点F ，连接DC ，70A ∠=︒，38D ∠=︒，则DCA ∠的度数是（ ）A ．42°B ．38°C ．40°D ．32°8．如图，长方形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙分别由点A （2，0）同时出发，沿长方形BCDE 的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2021次相遇地点的坐标是（ ）A ．（2 ，1）B ．（－1，－1）C ．（﹣2，0）D ．（2，0）二、填空题9．0.0081的算术平方根是______10．点A （－2，1）关于x 轴对称的点的坐标是____________________．11．如图，在ABC ∆中A α∠=，作ABC ∠的角平分线与ACB ∠的外角的角平分线交于点1A ；1A BC ∠的角平分线与1A CB ∠角平分线交于2A ，如此下去，则2021A ∠=__________．12．如图所示，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D ′，C ′的位置．若∠EFB ＝72°，则∠AED ′＝__．13．把一张长方形纸条按如图所示折叠后，若70AOB '∠=︒，则OGD ∠=_______；14．如图，四个实数m ，n ，p ，q 在数轴上对应的点分别为M ，N ，P ，Q ，若0n q +=，则m ，n ，p ，q 四个实数中，绝对值最大的是________．15．已知点A （0，0），|AB|=5，点B 和点A 在同一坐标轴上，那么点B 的坐标是________．16．育红中学八五班的数学社团在做如下的探究活动：在平面直角坐标系中，一个智能机器人接到如下指令：从原点O 出发，按向上、向右、向下、向右的方向依次移动，每次移动1个单位长度，其移动路线如图所示，第1次移动到点A 1，第2次移动到点A 2…第n 次移动到点A n ，则△OA 2A 2021的面积是 __________________．三、解答题17．（1）33181254++ （2）3|12|427-+-（3）2(22)3(21)+-+18．（1）已知a m ＝3，a n ＝5，求a 3m ﹣2n 的值．（2）已知x ﹣y ＝35，xy ＝1825，求下列各式的值： ①x 2y ﹣xy 2；②x 2＋y 2.19．已知如图，//BC EF ，80AOB ∠=︒，1160C ∠+∠=︒，60B ∠=︒，求证：A D ∠=∠. 完成下面的证明过程：证明：∵80AOB ∠=︒，∴80COD AOB ∠=∠=︒（______________________________）∵____________________（已知）∴1180COD ∠+∠=︒.（______________________________）∴1100∠=︒.∵1160C ∠+∠=︒，（已知）∴1601______C ∠=︒-∠=又∵60B ∠=︒，∴B C ∠=∠，∴//AB CD ，（______________________________）∴A D ∠=∠.（______________________________）20．ABC ∆与A B C '''∆在平面直角坐标系中的位置如图．（1）分别写出下列各点的坐标：A ' ； B ' ；C ' ；（2）说明A B C '''∆由ABC ∆经过怎样的平移得到？答：_______________．（3）若点(),P a b 是ABC ∆内部一点，则平移后A B C '''∆内的对应点P '的坐标为_________； （4）求ABC ∆的面积．21．阅读下面的文字，解答问题，例如：∵4＜7＜9，即2＜7＜3，∴7的整数部分为2，小数部分为（7﹣2）．请解答：（1）17的整数部分是 ，小数部分是 ．（2）已知：5﹣17小数部分是m ，6+17小数部分是n ，且（x +1）2＝m +n ，请求出满足条件的x 的值． 二十二、解答题22．（1）如图，分别把两个边长为1cm 的小正方形沿一条对角线裁成4个小三角形拼成一个大正方形，则大正方形的边长为_______cm ；（2）若一个圆的面积与一个正方形的面积都是22cm π，设圆的周长为C 圆，正方形的周长为C 正，则C 圆_____C 正（填“=”或“<”或“>”号）；（3）如图，若正方形的面积为2400cm ，李明同学想沿这块正方形边的方向裁出一块面积为2300cm 的长方形纸片，使它的长和宽之比为3:2，他能裁出吗？请说明理由？二十三、解答题23．如图1，MN ∥PQ ，点C 、B 分别在直线MN 、PQ 上，点A 在直线MN 、PQ 之间．（1）求证：∠CAB ＝∠MCA +∠PBA ；（2）如图2，CD ∥AB ，点E 在PQ 上，∠ECN ＝∠CAB ，求证：∠MCA ＝∠DCE ；（3）如图3，BF 平分∠ABP ，CG 平分∠ACN ，AF ∥CG ．若∠CAB ＝60°，求∠AFB 的度数．24．已知两条直线l 1，l 2，l 1∥l 2，点A ，B 在直线l 1上，点A 在点B 的左边，点C ，D 在直线l 2上，且满足115ADC ABC ∠=∠=o ．（1）如图①，求证：AD ∥BC ；（2）点M ，N 在线段CD 上，点M 在点N 的左边且满足MAC BAC ∠=∠，且AN 平分∠CAD ；（Ⅰ）如图②，当30ACD ∠=o 时，求∠DAM 的度数；（Ⅱ）如图③，当8CAD MAN ∠=∠时，求∠ACD 的度数．25．如图1，CE 平分ACD ∠，AE 平分BAC ∠，90EAC ACE ∠+∠=()1请判断AB 与CD 的位置关系并说明理由；()2如图2，当90E ∠=且AB 与CD 的位置关系保持不变，移动直角顶点E ，使MCE ECD ∠=∠，当直角顶点E 点移动时，问BAE ∠与MCD ∠否存在确定的数量关系？并说明理由．()3如图3，P 为线段AC 上一定点，点Q 为直线CD 上一动点且AB 与CD 的位置关系保持不变，①当点Q 在射线CD 上运动时（点C 除外），CPQ CQP ∠+∠与BAC ∠有何数量关系？猜想结论并说明理由．②当点Q 在射线CD 的反向延长线上运动时（点C 除外），CPQ CQP ∠+∠与BAC ∠有何数量关系？直接写出猜想结论，不需说明理由．26．如果三角形的两个内角α与β满足290αβ+=︒，那么我们称这样的三角形是“准互余三角形”．（1）如图1，在Rt ABC 中，90ACB ∠=︒，BD 是ABC 的角平分线，求证：ABD △是“准互余三角形”；（2）关于“准互余三角形”，有下列说法：①在ABC 中，若100A ∠=︒，70B ∠=︒，10C ∠=︒，则ABC 是“准互余三角形”； ②若ABC 是“准互余三角形”，90C ∠>︒，60A ∠=︒，则20B ∠=︒；③“准互余三角形”一定是钝角三角形．其中正确的结论是___________（填写所有正确说法的序号）；（3）如图2，B ，C 为直线l 上两点，点A 在直线l 外，且50ABC ∠=︒．若P 是直线l 上一点，且ABP △是“准互余三角形”，请直接写出APB ∠的度数．【参考答案】一、选择题1．A解析：A【分析】把各数进行化简，再根据平方根的性质即可进行求解．【详解】解：A 、-22=-4，是负数，负数没有平方根，故该选项符合题意；B 、（-2）2=4，是正数，正数有平方根，故该选项不符合题意；C 、-（-2）=2，是正数，正数有平方根，故该选项不符合题意；D 、∣-2∣=2，是正数，正数有平方根，故该选项不符合题意；故选：A ．【点睛】本题主要考查了平方根，熟练掌握平方根的性质是解本题的关键．2．D【分析】根据平移的性质，不改变图形的形状和大小，经过平移，对应点所连的线段平行且相等，对应线段平行且相等．【详解】解：A 、B 、C 都不是由平移得到的，D 是由平移得到的．故选：D ．【点睛】解析：D【分析】根据平移的性质，不改变图形的形状和大小，经过平移，对应点所连的线段平行且相等，对应线段平行且相等．【详解】解：A、B、C都不是由平移得到的，D是由平移得到的．故选：D．【点睛】本题考查平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．3．D【分析】先根据第二象限内点的横坐标是负数，纵坐标是正数判断出m、n的正负情况，再根据各象限内点的坐标特征求解．【详解】解：∵点P（m，n）在第二象限，∴m＜0，n＞0，∴-m＞0，m-n＜0，∴点Q（-m，m-n）在第四象限．故选D．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．4．D【分析】分别根据对顶角、邻补角、平行线的判定方法即可解答．【详解】①对顶角相等，正确；②在同一平面内，若//a b，c与a相交，则b与c也相交，正确；③邻补角之和为180°，所以它们平分线的夹角为180=902︒︒，即邻补角的平分线互相垂直，正确；④在同一平面内，垂直于同一条直线的两条直线互相垂直，正确．故选：D．【点睛】本题考查了平行线定理，两直线位置关系和对顶角、邻补角等知识，熟练掌握定理并灵活运用是解题关键．5．A【分析】根据点E有3种可能位置，分情况进行讨论，依据平行线的性质以及三角形外角性质进行计算求解即可．【详解】解：（1）如图，由AB∥CD，可得∠AOC=∠DCE1=β，∵∠AOC=∠BAE1+∠AE1C，∴∠AE1C=β-α．（2）如图，过E2作AB平行线，则由AB∥CD，可得∠1=∠BAE2=α，∠2=∠DCE2=β，∴∠AE2C=α+β．（3）当点E在CD的下方时，同理可得，∠AEC=α-β．综上所述，∠AEC的度数可能为β-α，α+β，α-β．即①α+β，②α-β，③β-α，都成立．故选A．【点睛】本题主要考查了平行线的性质的运用，解题时注意：两直线平行，同位角相等；两直线平行，内错角相等．6．D【分析】分别根据算术平方根的定义以及立方根的定义逐一判断即可．【详解】解：A()233-，故本选项不合题意；B 、366=，故本选项不合题意；C 、393≠，故本选项不合题意；D 、382--=，故本选项符合题意；故选：D ．【点睛】本题主要考查算术平方根及立方根，熟练掌握求一个数的算术平方根及立方根是解题的关键．7．D【分析】由//DF AB 可得到A ∠与FEC ∠的关系，利用三角形的外角与内角的关系可得结论．【详解】解：//DF AB ，70A ∠=︒，70A FEC ∴∠=∠=︒．FEC D DCA ∠=∠+∠，38D ∠=︒，DCA FEC D ∴∠=∠-∠7038=︒-︒32=︒．故选：D ．【点睛】本题考查了平行线的性质与三角形的外角性质，掌握“三角形的外角等于与它不相邻的两个内角和”是解决本题的关键．8．B【分析】根据题意得：矩形的边长为4和2，物体乙是物体甲的速度的2倍，时间相同，∴物体甲与物体乙的路程比为1：2，可得到物体甲和物体乙第一次相遇点为（-1，1）；第二次相遇点为（-1，-1）；解析：B【分析】根据题意得：矩形的边长为4和2，物体乙是物体甲的速度的2倍，时间相同， ∴物体甲与物体乙的路程比为1：2，可得到物体甲和物体乙第一次相遇点为（-1，1）；第二次相遇点为（-1，-1）；第三次相遇点为（2，0）；由此得出规律，即可求解．【详解】根据题意得：矩形的边长为4和2，物体乙是物体甲的速度的2倍，时间相同， ∴物体甲与物体乙的路程比为1：2，由题意知：第一次相遇物体甲与物体乙运动的路程和为12112⨯= ，物体甲运动的路程为11243⨯=，物体乙运动的路程为21283⨯= ，此时在BC 边相遇，即第一次相遇点为（-1，1）； 第二次相遇物体甲与物体乙运动的路程和为12224⨯= ，物体甲运动的路程为12483⨯=，物体乙运动的路程为224163⨯=，在DE 边相遇，即第二次相遇点为（-1，-1）； 第三次相遇物体甲与物体乙运动的路程和为12336⨯= ，物体甲运动的路程为136123⨯=，物体乙运动的路程为236243⨯=，在A 点相遇，即第三次相遇点为（2，0）； 此时甲乙回到原出发点，则每相遇三次，两点回到出发点，∵202136732 ， 故两个物体运动后的第2021次相遇地点的是：第二次相遇地点，即点（-1，-1）故选：B【点睛】本题主要考查了点的变化规律，以及行程问题中的相遇问题，通过计算发现规律就可以解决问题，解题的关键是找出规律每相遇三次，甲乙两物体同时回到原点． 二、填空题9．3【分析】根据算术平方根的性质解答即可．【详解】解：，0.09的算术平方根是0.3．故答案为：0.3．【点睛】本题考查了算术平方根，解题的关键是化简后再求算术平方根．解析：3【分析】根据算术平方根的性质解答即可．【详解】0.09=，0.09的算术平方根是0.3．故答案为：0.3．【点睛】本题考查了算术平方根，解题的关键是化简后再求算术平方根．10．（－2，－1）【分析】根据“关于x 轴对称的点，横坐标相同，纵坐标互为相反数”解答．【详解】解：点（-2，1）关于x 轴对称的点的坐标是（-2，-1），故答案为：（-2，-1）．【点睛】本解析：（－2，－1）【分析】根据“关于x 轴对称的点，横坐标相同，纵坐标互为相反数”解答．【详解】解：点（-2，1）关于x 轴对称的点的坐标是（-2，-1），故答案为：（-2，-1）．【点睛】本题考查了关于x 轴、y 轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x 轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y 轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．11．【分析】根据角平分线的定义以及三角形外角的性质，三角形内角和定理得出与，与的关系，找出规律即可．【详解】解：设BC 延长与点D ，∵，的角平分线与的外角的角平分线交于点，∴，同 解析：202112α【分析】根据角平分线的定义以及三角形外角的性质，三角形内角和定理得出A ∠与1A ∠，A ∠与2A ∠的关系，找出规律即可．【详解】解：设BC 延长与点D ，∵180ACD ACB ∠=︒-∠，ABC ∠的角平分线与ACD ∠的外角的角平分线交于点1A ，∴111180()A A BC ACB ACA ∠=︒-∠+∠+∠11180(180)22ABC ACB ACB =︒-∠-∠-︒-∠ 190()2ABC ACB =︒-∠+∠ 190(180)2A =︒-︒-∠ 12A =∠， 同理可得1221122A A A ∠=∠=∠， 2331122A A A ∠=∠=∠， ∴2021202112A A ∠=∠， ∵A α∠=， ∴2021202112A α∠=， 故答案为：202112α．【点睛】 本题主要考查三角形外角的性质，角平分线的定义，三角形内角和等知识点，熟知以上知识点，找出角度之间的规律是解题的关键．12．36°【分析】根据平行线的性质可知∠DEF ＝∠EFB ＝72°，由折叠的性质求出∠D′EF72°，然后可求∠AED′的值．【详解】解：∵四边形ABCD 为长方形，∴AD//BC ，∴∠DEF ＝解析：36°【分析】根据平行线的性质可知∠DEF ＝∠EFB ＝72°，由折叠的性质求出∠D ′EF 72°，然后可求∠AED ′的值．【详解】解：∵四边形ABCD 为长方形，∴AD //BC ，∴∠DEF ＝∠EFB ＝72°，又由折叠的性质可得∠D ′EF ＝∠DEF ＝72°，∴∠AED ′＝180°﹣72°﹣72°＝36°，故答案为：36°．【点睛】本题考查了平行线的性质，折叠的性质，熟练掌握折叠的性质是解答本题的关键． 13．55°【分析】直接根据补角的定义可知∠AOB′+∠BOG+∠B′OG=180°，再由图形翻折变换的性质可知∠BOG=∠B′OG ，再由平行线的性质可得出结论．【详解】解：∵∠AOB′=70°，解析：55°【分析】直接根据补角的定义可知∠AOB ′+∠BOG +∠B ′OG =180°，再由图形翻折变换的性质可知∠BOG =∠B ′OG ，再由平行线的性质可得出结论．【详解】解：∵∠AOB ′=70°，∠AOB ′+∠BOG +∠B ′OG =180°，∴∠BOG +∠B ′OG =180°-70°=110°．∵∠B ′OG 由∠BOG 翻折而成，∴∠BOG =∠B ′OG ，∴∠BOG =180702 =55°． ∵AB ∥CD ，∴∠OGD =∠BOG =55°．故答案为：55°．【点睛】本题考查的是平行线的性质，熟知图形翻折不变性的性质是解答此题的关键．14．【分析】根据可以得到的关系，从而可以判定原点的位置，从而可以得到哪个数的绝对值最大，本题得以解决．【详解】∵，∴n 和q 互为相反数，O 在线段NQ 的中点处，∴绝对值最大的是点P 表示的数．故解析：p【分析】根据0n q +=可以得到n q 、的关系，从而可以判定原点的位置，从而可以得到哪个数的绝对值最大，本题得以解决．【详解】∵0n q +=，∴n 和q 互为相反数，O 在线段NQ 的中点处，∴绝对值最大的是点P 表示的数p ．故答案为：p ．【点睛】本题考查了实数与数轴，解题的关键是明确数轴的特点，利用数形结合的思想解答． 15．（5，0）或（﹣5，0）或（0，5）或（0，﹣5）【分析】根据点A （0，0）及点B 和点A 在同一坐标轴上可知点B 在x 轴上或在y 轴上，再根据坐标轴上到一点距离相等的点有两个，可得答案．【详解】解解析：（5，0）或（﹣5，0）或（0，5）或（0，﹣5）【分析】根据点A （0，0）及点B 和点A 在同一坐标轴上可知点B 在x 轴上或在y 轴上，再根据坐标轴上到一点距离相等的点有两个，可得答案．【详解】解：∵点A （0，0），点B 和点A 在同一坐标轴上，∴点B 在x 轴上或在y 轴上，∵|AB|=5，∴当点B 在x 轴上时，点B 的坐标为（5，0）或（﹣5，0），当点B 在y 轴上时，点B 的坐标为（0，5）或（0，﹣5）；故答案为：（5，0）或（﹣5，0）或（0，5）或（0，﹣5）．【点睛】本题考查了点的坐标，解决本题的关键是要注意坐标轴上到一点距离相等的点有两个，以防遗漏．16．【分析】由题意知OA4n ＝2n ，图形运动4次一个循环，横坐标对应一个循环增加2，计算出A2A2021，由此即可解决问题．【详解】解：由题意知OA4n ＝2n （n 为正整数），图形运动4次一个循环 解析：10092【分析】由题意知OA 4n ＝2n ，图形运动4次一个循环，横坐标对应一个循环增加2，计算出A 2A 2021，由此即可解决问题．【详解】解：由题意知OA 4n ＝2n （n 为正整数），图形运动4次一个循环，横坐标对应一个循环增加2∵2021÷4＝505…1，∴A 2021与A 1是对应点，A 2020与A 0是对应点∴OA 2020＝505×2＝1010，A 1A 2021＝1010∴A 2A 2021＝1010-1=1009则△OA 2A 2019的面积是12×1×1009＝10092， 故答案为：10092． 【点睛】本题主要考查点的坐标的变化规律，解题的关键是根据图形得出下标为4的倍数时对应长度即为下标的一半，据此可得． 三、解答题17．（1）；（2）；（3）【分析】（1）先化简后计算即可；（2）先化简后计算即可；（3）首先去括号，然后再合并即可．【详解】解：（1）原式（2）原式（3）原式【点睛】此题主要考查了实解析：（1）172；（22；（3）1-【分析】（1）先化简后计算即可；（2）先化简后计算即可；（3）首先去括号，然后再合并即可．【详解】解：（1）原式1112577222=++=+=（2）原式1232=+-=（3）原式231=+=-【点睛】此题主要考查了实数运算，关键是掌握数的开方，正确化简各数．18．（1）；（2）①；②【分析】（1）逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可； （2）①利用提公因式法因式分解解答即可；②根据完全平方公式计算即可．【详解】解：（1），，解析：（1）2725；（2）①54125；②95 【分析】（1）逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可；（2）①利用提公因式法因式分解解答即可；②根据完全平方公式计算即可．【详解】解：（1）3m a =，5n a =，32m n a -∴ 32m n a a =÷32()()m n a a =÷3235=÷2725=； （2）①35x y -=，1825xy =， 22x y xy ∴-183()255xy x y =-=⨯ 54125=； ②35x y -=，1825xy =， 22x y ∴+2()2x y xy =-+23182525⎛⎫=+⨯ ⎪⎝⎭ 9362525=+ 95=． 【点睛】本题考查了完全平方公式，同底数幂的除法，提公因式法因式分解以及幂的乘方，熟记相关公式与运算法则是解答本题的关键．19．见解析【分析】根据平行线的判定和性质定理以及对顶角相等即可得到结论．【详解】解：证明：∵∠AOB=80°，∴∠COD=∠AOB=80°（对顶角相等）．∵BC ∥EF （已知），∴∠COD+解析：见解析【分析】根据平行线的判定和性质定理以及对顶角相等即可得到结论．【详解】解：证明：∵∠AOB =80°，∴∠COD =∠AOB =80°（对顶角相等）．∵BC ∥EF （已知），∴∠COD +∠1=180°（两直线平行，同旁内角互补）．∴∠1=100°．∵∠1+∠C =160°（已知），∴∠C =160°-∠1=60°．又∵∠B =60°，∴∠B =∠C ．∴AB ∥CD （内错角相等，两直线平行）．∴∠A =∠D （两直线平行，内错角相等）．【点睛】本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．也考查了对顶角的定义．20．（1）（-3，1），（-2，-2），（-1，-1）；（2）向左平移4个单位，向下平移2个单位；（3）（a-4，b-2）；（4）2【分析】（1）根据平面直角坐标系写出各点的坐标即可；（2）根据对解析：（1）（-3，1），（-2，-2），（-1，-1）；（2）向左平移4个单位，向下平移2个单位；（3）（a-4，b-2）；（4）2【分析】（1）根据平面直角坐标系写出各点的坐标即可；（2）根据对应点A、A′的变化写出平移方法即可；（3）根据平移规律逆向写出点P′的坐标；（4）利用△ABC所在的长方形的面积减去四周三个小直角三角形的面积，列式计算即可得解．【详解】解：（1）A′（-3，1）；B′（-2，-2）；C′（-1，-1）；（2）向左平移4个单位，向下平移2个单位；（3）若点P（a，b）是△ABC内部一点，则平移后△A'B'C'内的对应点P'的坐标为：（a-4，b-2）；（4）△ABC的面积=111 23131122222⨯-⨯⨯-⨯⨯-⨯⨯=2．【点睛】本题考查了利用平移变换作图，熟练掌握网格结构，根据对应点的坐标确定出平移的方法是解题的关键．21．（1）4 ，；（2）x=0或-2．【分析】（1）根据夹逼法可求的整数部分和小数部分；（2）首先估算出m，n的值，进而得出m＋n的值，可求满足条件的x的值．【详解】（1）∵4＜＜5，∴的整解析：（1）4 4；（2）x=0或-2．【分析】（1（2）首先估算出m，n的值，进而得出m＋n的值，可求满足条件的x的值．【详解】（1）∵45，∴4−4．故答案为：44；（2）∵5m，0＜51，n∴m n∴m+n =1∴（x +1）2＝1x+1=±1解得:x=0或-2．【点睛】此题主要考查了估算无理数的大小，正确得出各数的小数部分是解题关键．二十二、解答题22．（1）；（2）；（3）不能裁剪出，详见解析【分析】（1）根据所拼成的大正方形的面积为2即可求得大正方形的边长；（2）由圆和正方形的面积公式可分别求的圆的半径及正方形的边长，进而可求得圆和正方形解析：（12）<；（3）不能裁剪出，详见解析【分析】（1）根据所拼成的大正方形的面积为2即可求得大正方形的边长；（2）由圆和正方形的面积公式可分别求的圆的半径及正方形的边长，进而可求得圆和正方形的周长，利用作商法比较这两数大小即可；（3）利用方程思想求出长方形的长边，与正方形边长比较大小即可；【详解】解：（1）∵小正方形的边长为1cm ，∴小正方形的面积为1cm 2，∴两个小正方形的面积之和为2cm 2，即所拼成的大正方形的面积为2 cm 2，∴，（2）∵22r ππ=， ∴r = ∴2=2C r π=圆设正方形的边长为a∵22a π=， ∴a∴=4C a =正∴1C C =<圆正故答案为：＜；（3）解：不能裁剪出，理由如下：∵长方形纸片的长和宽之比为3:2，∴设长方形纸片的长为3x ，宽为2x ，则32300x x ⋅=，整理得：250x =，∴22(3)9950450x x ==⨯=，∵450＞400，∴22(3)20x >，∴320x >，∴长方形纸片的长大于正方形的边长，∴不能裁出这样的长方形纸片．【点睛】本题通过圆和正方形的面积考查了对算术平方根的应用，主要是对学生无理数运算及比较大小进行了考查．二十三、解答题23．（1）证明见解析；（2）证明见解析；（3）120°．【分析】（1）过点A 作AD ∥MN ，根据两直线平行，内错角相等得到∠MCA ＝∠DAC ，∠PBA ＝∠DAB ，根据角的和差等量代换即可得解；（2）解析：（1）证明见解析；（2）证明见解析；（3）120°．【分析】（1）过点A 作AD ∥MN ，根据两直线平行，内错角相等得到∠MCA ＝∠DAC ，∠PBA ＝∠DAB ，根据角的和差等量代换即可得解；（2）由两直线平行，同旁内角互补得到∴、∠CAB +∠ACD ＝180°，由邻补角定义得到∠ECM +∠ECN ＝180°，再等量代换即可得解；（3）由平行线的性质得到，∠FAB ＝120°﹣∠GCA ，再由角平分线的定义及平行线的性质得到∠GCA ﹣∠ABF ＝60°，最后根据三角形的内角和是180°即可求解．【详解】解：（1）证明：如图1，过点A 作AD ∥MN ，∵MN ∥PQ ，AD ∥MN ，∴AD ∥MN ∥PQ ，∴∠MCA ＝∠DAC ，∠PBA ＝∠DAB ，∴∠CAB ＝∠DAC +∠DAB ＝∠MCA +∠PBA ，即：∠CAB ＝∠MCA +∠PBA ；（2）如图2，∵CD ∥AB ，∴∠CAB +∠ACD ＝180°，∵∠ECM +∠ECN ＝180°，∵∠ECN ＝∠CAB∴∠ECM ＝∠ACD ，即∠MCA +∠ACE ＝∠DCE +∠ACE ，∴∠MCA ＝∠DCE ；（3）∵AF ∥CG ，∴∠GCA +∠FAC ＝180°，∵∠CAB ＝60°即∠GCA +∠CAB +∠FAB ＝180°，∴∠FAB ＝180°﹣60°﹣∠GCA ＝120°﹣∠GCA ，由（1）可知，∠CAB ＝∠MCA +∠ABP ，∵BF 平分∠ABP ，CG 平分∠ACN ，∴∠ACN ＝2∠GCA ，∠ABP ＝2∠ABF ，又∵∠MCA ＝180°﹣∠ACN ，∴∠CAB ＝180°﹣2∠GCA +2∠ABF ＝60°，∴∠GCA ﹣∠ABF ＝60°，∵∠AFB +∠ABF +∠FAB ＝180°，∴∠AFB ＝180°﹣∠FAB ﹣∠FBA＝180°﹣（120°﹣∠GCA ）﹣∠ABF＝180°﹣120°+∠GCA ﹣∠ABF＝120°．【点睛】本题主要考查了平行线的性质，线段、角、相交线与平行线，准确的推导是解决本题的关键．24．（1）证明见解析；（2）（Ⅰ）；（Ⅱ）．【分析】（1）先根据平行线的性质可得，再根据角的和差可得，然后根据平行线的判定即可得证；（2）（Ⅰ）先根据平行线的性质可得，从而可得，再根据角的和差可得 解析：（1）证明见解析；（2）（Ⅰ）5DAM ∠=︒；（Ⅱ）25ACD ∠=︒．【分析】（1）先根据平行线的性质可得65BAD ∠=︒，再根据角的和差可得180BAD ABC ∠+∠=︒，然后根据平行线的判定即可得证；（2）（Ⅰ）先根据平行线的性质可得30BAC ACD ∠=∠=︒，从而可得30MAC ∠=︒，再根据角的和差可得35DAC ∠=︒，然后根据DAM DAC MAC ∠=∠-∠即可得；（Ⅱ）设MAN x ∠=，从而可得8CAD x ∠=，先根据角平分线的定义可得142CAN CAD x ∠=∠=，再根据角的和差可得5BAC MAC x ∠=∠=，然后根据65CAD BAC BAD ∠+∠=∠=︒建立方程可求出x 的值，从而可得BAC ∠的度数，最后根据平行线的性质即可得．【详解】（1）12//,115l l ADC ∠=︒，18065BAD ADC ∴∠=︒-∠=︒，又115ABC ∠=︒，180BAD ABC ∴∠+∠=︒，//AD BC ∴；（2）（Ⅰ）12//,30l l ACD ∠=︒，30BAC ACD ∴∠=∠=︒，MAC BAC ∠=∠，30MAC ∴∠=︒，由（1）已得：65BAD ∠=︒，35DAC BAD BAC ∴∠=∠-∠=︒，35305DAM DAC MAC ∴∠=∠-∠=︒-︒=︒；（Ⅱ）设MAN x ∠=，则8CAD x ∠=， AN 平分CAD ∠，142CAN CAD x ∴∠=∠=， 5MAC CAN MAN x ∴∠=∠+∠=，MAC BAC ∠=∠，5BAC x ∴∠=，由（1）已得：65BAD ∠=︒，65CAD BAC BAD ∴∠+∠=∠=︒，即8565x x +=︒，解得5x =︒，525BAC x ∴∠==︒，又12//l l ，25ACD BAC ∴∠=∠=︒．【点睛】本题考查了平行线的判定与性质、角的和差、角平分线的定义、一元一次方程的几何应用等知识点，熟练掌握平行线的判定与性质是解题关键．25．（1）详见解析；（2）∠BAE+∠MCD=90°，理由详见解析；（3）详见解析.【详解】试题分析：（1）先根据CE 平分∠ACD ，AE 平分∠BAC 得出∠BAC=2∠EAC ，∠ACD=2∠ACE ，再解析：（1）详见解析；（2）∠BAE+12∠MCD=90°，理由详见解析；（3）详见解析.【详解】试题分析：（1）先根据CE 平分∠ACD ，AE 平分∠BAC 得出∠BAC =2∠EAC ，∠ACD =2∠ACE ，再由∠EAC +∠ACE =90°可知∠BAC +∠ACD =180，故可得出结论；（2）过E 作EF ∥AB ，根据平行线的性质可知EF ∥AB ∥CD ，∠BAE =∠AEF ，∠FEC =∠DCE ，故∠BAE +∠ECD =90°，再由∠MCE =∠ECD 即可得出结论；（3）根据AB ∥CD 可知∠BAC +∠ACD =180°，∠QPC +∠PQC +∠PCQ =180°，故∠BAC =∠PQC +∠QPC ．试题解析：证明：（1）∵CE 平分∠ACD ，AE 平分∠BAC ，∴∠BAC =2∠EAC ，∠ACD =2∠ACE ．∵∠EAC +∠ACE =90°，∴∠BAC +∠ACD =180，∴AB ∥CD ；（2）∠BAE +12∠MCD =90°．证明如下： 过E 作EF ∥AB ．∵AB ∥CD ，∴EF ∥∥AB ∥CD ，∴∠BAE =∠AEF ，∠FEC =∠DCE ． ∵∠E =90°，∴∠BAE +∠ECD =90°．∵∠MCE =∠ECD ，∴∠BAE +12∠MCD =90°； （3）①∠BAC =∠PQC +∠QPC ．理由如下：如图3：∵AB ∥CD ，∴∠BAC +∠ACD =180°．∵∠QPC +∠PQC +∠PCQ =180°，∴∠BAC =∠PQC +∠QPC ；②∠PQC +∠QPC +∠BAC =180°．理由如下：如图4：∵AB ∥CD ，∴∠BAC =∠ACQ ．∵∠PQC +∠PCQ +∠ACQ =180°，∴∠PQC +∠QPC +∠BAC =180°．点睛：本题考查了平行线的性质，根据题意作出平行线是解答此题的关键．26．（1）见解析；（2）①③；（3）∠APB 的度数是10°或20°或40°或110°【分析】 （1）由和是的角平分线，证明即可；（2）根据“准互余三角形”的定义逐个判断即可；（3）根据“准互余三角解析：（1）见解析；（2）①③；（3）∠APB 的度数是10°或20°或40°或110°【分析】（1）由90ABC A ∠+∠=︒和BD 是ABC 的角平分线，证明290ABD A ∠+∠=︒即可； （2）根据“准互余三角形”的定义逐个判断即可；（3）根据“准互余三角形”的定义，分类讨论：①2∠A +∠ABC =90°；②∠A +2∠APB =90°；③2∠APB +∠ABC =90°；④2∠A +∠APB =90°，由三角形内角和定理和外角的性质结合“准互余三角形”的定义，即可求出答案．【详解】（1）证明：∵在Rt ABC 中，90ACB ∠=︒，∴90ABC A ∠+∠=︒，∵BD 是ABC ∠的角平分线，∴2ABC ABD ∠=∠，∴290ABD A ∠+∠=︒，∴ABD △是“准互余三角形”；（2）①∵70,10B C ∠=︒∠=︒，∴290B C ∠+∠=︒，∴ABC 是“准互余三角形”，故①正确；②∵60A ∠=︒， 20B ∠=︒，∴210090A B ∠+∠=︒≠︒，∴ABC 不是“准互余三角形”，故②错误；③设三角形的三个内角分别为,,αβγ，且αβγ<<，∵三角形是“准互余三角形”，∴290αβ+=︒或290αβ+=︒，∴90αβ+<︒，∴180()90γαβ=︒-+>︒，∴“准互余三角形”一定是钝角三角形，故③正确；综上所述，①③正确，故答案为：①③；（3）∠APB 的度数是10°或20°或40°或110°；如图①，当2∠A +∠ABC =90°时，△ABP 是“准直角三角形”，∵∠ABC =50°，∴∠A =20°，∴∠APB =110°；如图②，当∠A +2∠APB =90°时，△ABP 是“准直角三角形”，∵∠ABC=50°，∴∠A+∠APB=50°，∴∠APB=40°；如图③，当2∠APB+∠ABC=90°时，△ABP是“准直角三角形”，∵∠ABC=50°，∴∠APB=20°；如图④，当2∠A+∠APB=90°时，△ABP是“准直角三角形”，∵∠ABC=50°，∴∠A+∠APB=50°，所以∠A=40°，所以∠APB=10°；综上，∠APB的度数是10°或20°或40°或110°时，ABP△是“准互余三角形”．【点睛】本题是三角形综合题，考查了三角形内角和定理，三角形的外角的性质，解题关键是理解题意，根据三角形内角和定理和三角形的外角的性质，结合新定义进行求解．。

曲靖市七中人教版七年级下册数学期末试卷及答案.doc一、选择题1．下列方程中，是二元一次方程的是( )A ．x ﹣y 2＝1B ．2x ﹣y ＝1C ．11y x +=D ．xy ﹣1＝02．将图甲中阴影部分的小长方形变换到图乙位置，能根据图形的面积关系得到的关系式是( )A ．22()()a b a b a b +-=-B ．222()a b a b -=-C ．2()b a b ab b -=-D ．2()ab b b a b -=- 3．等腰三角形的两边长分别为3和6，那么该三角形的周长为（ ） A ．12 B ．15C ．10D ．12或15 4．已知关于x ，y 的方程x 2m﹣n ﹣2＋4y m ＋n ＋1＝6是二元一次方程，则m ，n 的值为（ ） A ．m ＝1，n ＝－1 B ．m ＝－1，n ＝1 C ．14m ,n 33==- D ．14,33m n =-= 5．计算a •a 2的结果是（ ）A ．aB ．a 2C ．a 3D ．a 46．下列各式从左到右的变形中，是因式分解的为（ ）A ．ab +ac +d ＝a （b +c ）+dB ．（x +2）（x ﹣2）＝x 2﹣4C ．6ab ＝2a ⋅3bD ．x 2﹣8x +16＝（x ﹣4）27．计算a 10÷a 2(a≠0)的结果是( )A ．5aB ．5a -C ．8aD ．8a - 8．若(2x+3y)(mx-ny)=9y 2-4x 2，则m 、n 的值为 （ ）A ．m=2，n=3B ．m=-2，n=-3C ．m=2，n=-3D ．m=-2，n=3 9．将一副三角板如图放置，作CF //AB ，则∠EFC 的度数是（ ）A ．90°B ．100°C ．105°D ．110° 10．下列运算正确的是（ ） A ．236x x x ⋅= B ．224(2)4x x -=- C ．326()x x =D ．55x x x ÷=二、填空题11．直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_______．12．如图，四边形ABCD 中，E 、F 、G 、H 依次是各边中点，O 是形内一点，若四边形AEOH 、四边形BFOE 、四边形CGOF 的面积分别为6、7、8，四边形DHOG 面积为______．13．已知5x m =，4y m =，则2x y m +=______________．14．一副三角板按如图所示叠放在一起，其中点B 、D 重合，若固定三角形AOB ，改变三角板ACD 的位置（其中A 点位置始终不变），当∠BAD ＝_____时，CD ∥AB ．15．如图，AD ⊥BC 于D ，那么图中以AD 为高的三角形有______个．16．已知关于x ，y 的方程22146m n m n x y --+++=是二元一次方程，那么点(),M m n 位于平面直角坐标系中的第______象限．17．因式分解：=______．18．若2m =3，2n =5，则2m+n =______．19．甲乙两队进行篮球对抗赛，比赛规则规定每队胜一场得3分，平一场得1分，负一场得0分，两队一共比赛了10场，甲队保持不败，得分不低于24分，甲队至少胜了___________场．20．已知x 2a ＋y b ﹣1＝3是关于x 、y 的二元一次方程，则ab ＝_____． 三、解答题21．已知a+b=2，ab=-1，求下面代数式的值：（1）a 2+b 2；（2）（a-b ）2．22．（问题背景）（1）如图1的图形我们把它称为“8字形”，请说理证明∠A+∠B ＝∠C+∠D（简单应用）（2）如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC＝28°，∠ADC＝20°，求∠P的度数（可直接使用问题（1）中的结论）（问题探究）（3）如图3，直线BP平分∠ABC的外角∠FBC，DP平分∠ADC的外角∠ADE，若∠A＝30°，∠C＝18°，则∠P的度数为（拓展延伸）（4）在图4中，若设∠C＝x，∠B＝y，∠CAP＝14∠CAB，∠CDP＝14∠CDB，试问∠P与∠C、∠B之间的数量关系为（用x、y表示∠P）（5）在图5中，BP平分∠ABC，DP平分∠ADC的外角∠ADE，猜想∠P与∠A、∠C的关系，直接写出结论．23．计算(1)112(2)3π-⎛⎫---+-⎪⎝⎭；(2)52482(2)()()x x x x+-÷-．24．一个多边形的每一个内角都相等，并且每个外角都等于和它相邻的内角的一半．（1）求这个多边形是几边形；（2）求这个多边形的每一个内角的度数．25．解下列方程组（1）29321x yx y+=⎧⎨-=-⎩．（2）34332(1)11x yx y⎧+=⎪⎨⎪--=⎩．26．如图，△ABC的顶点都在方格纸的格点上，将△ABC向下平移3格，再向右平移4格.（1）请在图中画出平移后的△A′B′C′；（2）在图中画出△A′B′C′的高C′D′.27．已知1502x x +-=，求值； （1）221x x +（2）1x x- 28．已知关于x ，y 的二元一次方程组233741x y m x y m +=+⎧⎨-=+⎩它的解是正数． （1）求m 的取值范围；（2）化简：2|2|m --【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】根据二元一次方程的定义：含有两个未知数，并且含有未知数的项的次数都是1，像这样的整式方程叫做二元一次方程．据此逐一判断即可得．【详解】解：A ．x-y 2=1不是二元一次方程；B ．2x-y=1是二元一次方程；C ．1x+y ＝1不是二元一次方程； D ．xy-1=0不是二元一次方程；故选B ．【点睛】 本题考查二元一次方程的定义，解题的关键是掌握含有两个未知数，并且含有未知数的项的次数都是1，像这样的整式方程叫做二元一次方程．2．A解析：A【分析】根据长方形的面积=长⨯宽，分别表示出甲乙两个图形的面积，即可得到答案．解：()()=S a b a b +-甲，()()2222==S a a b b a b a ab ab b a b -+-=-+--乙． 所以()()a b a b +-22=a b -故选A ．【点睛】本题考查平方差公式，难度不大，通过计算两个图形的面积即可顺利解题．3．B解析：B【分析】求等腰三角形的周长，即是确定等腰三角形的腰与底的长求周长；题目给出等腰三角形有两条边长为3和6，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【详解】由题意，分以下两种情况：（1）当等腰三角形的腰为3时，三边为3，3，6此时336+=，不满足三角形的三边关系定理（2）当等腰三角形的腰为6时，三边为3，6，6此时366+>，满足三角形的三边关系定理则其周长为36615++=综上，该三角形的周长为15故选：B ．【点睛】本题考查了等腰三角形的定义、三角形的三边关系定理，依据题意，正确分两种情况讨论是解题关键．4．A解析：A【分析】根据二元一次方程的概念列出关于m 、n 的方程组，解之即可．【详解】∵关于x ，y 的方程x 2m﹣n ﹣2＋4y m ＋n ＋1＝6是二元一次方程， ∴22111m n m n --=⎧⎨++=⎩即230m n m n -=⎧⎨+=⎩， 解得：11m n =⎧⎨=-⎩ ， 故选：A ．【点睛】本题考查了二元一次方程的定义、解二元一次方程组，理解二元一次方程的定义，熟练掌握二元一次方程组的解法是解答的关键．解析：C【分析】根据同底数幂的乘法法则计算即可．【详解】解：a •a 2＝a 1＋2＝a 3．故选：C ．【点睛】本题考查了幂的运算性质，准确应用同底数幂的乘法是解题的关键．6．D解析：D【解析】【分析】根据因式分解就是把一个多项式化为几个整式的积的形式的定义判断，利用排除法求解．【详解】A 、等式右边不是整式积的形式，故不是因式分解，故本选项错误；B 、等式右边不是整式积的形式，故不是因式分解，故本选项错误；C 、等式左边是单项式，不是因式分解，故本选项错误；D 、符合因式分解的定义，故本选项正确．故选D ．【点睛】本题考查的是因式分解的意义，把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式．7．C解析：C【解析】【分析】根据同底数幂的除法法则即可得.【详解】1021028(0)a a a a a -÷==≠故选：C.【点睛】本题考查了同底数幂的除法法则：同底数幂相除，底数不变，指数相减.8．B解析：B【解析】【分析】先把等式左边利用多项式乘多项式的法则展开并整理，根据对应项系数相等列出等式，求解即可．【详解】解：将(2x+3y)(mx-ny)展开，得2mx2-2nxy+3mxy-3ny2，根据题意可得2mx2-2nxy+3mxy-3ny2=9y2-4x2，根据多项式相等，则对应项及其系数相等，可得2m=-4，-3n=9，解得m=-2，n=-3故选B．【点睛】本题是一道有关多项式乘法的题目，明确多项式的乘法法则是解题的关键．9．C解析：C【分析】根据等腰直角三角形求出∠BAC，根据平行线求出∠ACF，根据三角形内角和定理求出即可．【详解】解：∵△ACB是等腰直角三角形，∴∠BAC＝45°，∵CF//AB，∴∠ACF＝∠BAC＝45°，∵∠E＝30°，∴∠EFC＝180°﹣∠E﹣∠ACF＝105°，故选：C．【点睛】本题考查了三角形的内角和定理和平行线的性质，能求出各个角的度数是解此题的关键．10．C解析：C【解析】解：A．x2⋅x3＝x5，故A错误；B．(-2x2)2 ＝4 x4，故B错误；C．( x3 )2＝x6，正确；D．x5÷x ＝x4，故D错误．故选C．二、填空题11．30°【解析】【分析】设较小的锐角是,然后根据直角三角形两锐角互余列出方程求解即可.【详解】设较小的锐角是x，则另一个锐角是2x，由题意得，x＋2x＝90°，解得x＝30°，即此三角解析：30°【解析】【分析】设较小的锐角是x,然后根据直角三角形两锐角互余列出方程求解即可.【详解】设较小的锐角是x，则另一个锐角是2x，由题意得，x＋2x＝90°，解得x＝30°，即此三角形中最小的角是30°.故答案为：30°.【点睛】本题考查了直角三角形的性质，熟练掌握该知识点是本题解题的关键.12．7【分析】连接OC，OB，OA，OD，易证S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，S△OAE=S△OBE，从而有S四边形AEOH+S四边形CGOF=S四边形DHO解析：7【分析】连接OC，OB，OA，OD，易证S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，S△OAE=S△OBE，从而有S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，由此即可求得答案．【详解】连接OC，OB，OA，OD，∵E、F、G、H依次是各边中点，∴△AOE和△BOE等底等高，∴S△OAE=S△OBE，同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，∵S四边形AEOH=6，S四边形BFOE=7，S四边形CGOF=8，∴6+8=7+S四边形DHOG，解得：S四边形DHOG=7，故答案为：7．【点睛】本题考查了三角形的面积．解决本题的关键将各个四边形划分，充分利用给出的中点这个条件，证得三角形的面积相等，进而证得结论．13．100【分析】根据同底数幂的乘法法则、幂的乘方与积的乘方法则把所求代数式进行化简，再把，代入进行计算即可．【详解】解：，故答案为100．【点睛】本题考查同底数幂的乘法法则、幂的乘方与积解析：100【分析】根据同底数幂的乘法法则、幂的乘方与积的乘方法则把所求代数式进行化简，再把5x m =，4y m =代入进行计算即可．【详解】解：2x y m +=()()2254100xy m m ⨯=⨯=，故答案为100．【点睛】本题考查同底数幂的乘法法则、幂的乘方与积的乘方法则，先根据同底数幂的乘法法则把所求代数式进行化简是解答此题的关键． 14．150°或30°．【分析】分两种情况，再利用平行线的性质，即可求出∠BAD 的度数【详解】解：如图所示：当CD∥AB 时，∠BAD＝∠D＝30°；如图所示，当AB∥CD 时，∠C＝∠BAC＝6解析：150°或30°．【分析】分两种情况，再利用平行线的性质，即可求出∠BAD的度数【详解】解：如图所示：当CD∥AB时，∠BAD＝∠D＝30°；如图所示，当AB∥CD时，∠C＝∠BAC＝60°，∴∠BAD＝60°+90°＝150°；故答案为：150°或30°．【点睛】本题主要考查了平行线的判定，平行线的判掌握平行线的判定定理和全面思考并分类讨论是解答本题的关键.15．6【解析】试题分析：∵AD⊥BC于D，而图中有一边在直线CB上，且以A为顶点的三角形有△ABD、△ABE、△ABC、△ADE、△ADC、△AEC，共6个，∴以AD为高的三角形有6个．故答案解析：6【解析】试题分析：∵AD⊥BC于D，而图中有一边在直线CB上，且以A为顶点的三角形有△ABD、△ABE、△ABC、△ADE、△ADC、△AEC，共6个，∴以AD为高的三角形有6个．故答案为6．点睛：此题主要考查了三角形的高，三角形的高可以在三角形外，也可以在三角形内，所以确定三角形的高比较灵活．16．四【分析】根据题意得到关于m 、n 的二元一次方程组，确定点M 坐标，判断M 所在象限即可．【详解】解：由题意得，解得，∴点M 坐标为，∴点M 在第四象限．故答案为：四【点睛】本题考查了二元解析：四【分析】根据题意得到关于m 、n 的二元一次方程组，确定点M 坐标，判断M 所在象限即可．【详解】解：由题意得22111m n m n --=⎧⎨++=⎩， 解得11m n =⎧⎨=-⎩， ∴点M 坐标为()1,1-，∴点M 在第四象限．故答案为：四【点睛】本题考查了二元一次方程定义，二元一次方程组解法，点的坐标等知识，综合性较强，根据题意列出方程组是解题关键．17．2（x+3）（x ﹣3）．【解析】试题分析：先提公因式2后，再利用平方差公式分解即可，即2x2-18=2（x2-9）=2（x+3）（x-3）.考点：因式分解.解析：2（x +3）（x ﹣3）．【解析】试题分析：先提公因式2后，再利用平方差公式分解即可，即=2（x 2-9）=2（x+3）（x-3）.考点：因式分解.18．15【分析】根据同底数幂的乘法逆运算法则可得，进一步即可求出答案．【详解】解：．故答案为：15．【点睛】本题考查了同底数幂的乘法法则的逆用，属于常考题型，熟练掌握同底数幂的乘法法则是关解析：15【分析】根据同底数幂的乘法逆运算法则可得222m n m n +=⋅，进一步即可求出答案．【详解】解：2223515m n m n +=⋅=⨯=．故答案为：15．【点睛】本题考查了同底数幂的乘法法则的逆用，属于常考题型，熟练掌握同底数幂的乘法法则是关键．19．7【分析】设甲队胜了x 场，则平了（10-x ）场，根据胜一场得3分，平一场得1分，负一场得0分，比赛10场，得分24分，列出不等式，求出x 的最小整数解．【详解】设甲队胜了x 场，则平了（10-x解析：7【分析】设甲队胜了x 场，则平了（10-x ）场，根据胜一场得3分，平一场得1分，负一场得0分，比赛10场，得分24分，列出不等式，求出x 的最小整数解．【详解】设甲队胜了x 场，则平了（10-x ）场，由题意得，3x+（10-x ）≥24，解得：x≥7，即甲队至少胜了7场．故答案是：7．【点睛】考查了一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出不等关系，列出不等式求解．20．1【分析】根据题意可知该式是二元一次方程组，所以x、y的指数均为1，这样就可以分别求出a、b的值，代入计算即可．【详解】解：∵是关于x、y的二元一次方程，所以x、y的指数均为1∴2a＝1，解析：1【分析】根据题意可知该式是二元一次方程组，所以x、y的指数均为1，这样就可以分别求出a、b 的值，代入计算即可．【详解】解：∵2a b-1x+y=3是关于x、y的二元一次方程，所以x、y的指数均为1∴2a＝1，b-1＝1，解得a＝12，b＝2，则ab＝122＝1，故答案为：1．【点睛】该题考查了二元一次方程的定义，即含有两个未知量，且未知量的指数为1，将其代数式进行求解，即可求出答案．三、解答题21．（1）6；（2）8．【分析】（1）先将原式转化为（a+b）2-2ab，再将已知代入计算可得；（2）先将原式转化为（a+b）2-4ab，再将已知代入计算计算可得．【详解】解：（1）当a+b=2，ab=-1时，原式=（a+b）2-2ab=22-2×（-1）=4+2=6；（2）当a+b=2，ab=-1时，原式=（a+b）2-4ab=22-4×（-1）=4+4=8．【点睛】本题主要考查完全平方公式的变形求值问题，解题的关键是熟练掌握完全平方公式及其灵活变形．22．（1）证明见解析；（2）24°；（3）24°；（4）∠P=34x+14y；（5）∠P=180()2A C︒-∠+∠【分析】（1）根据三角形内角和为180°，对顶角相等，即可证得∠A+∠B=∠C+∠D（2）由（1）的结论得：∠BCP+∠P=∠BAP+∠ABC①，∠PAD+∠P=∠PCD+∠ADC②，将两个式子相加，已知AP、CP分别平分∠BAD、∠BCD，可得∠BAP=∠PAD，∠BCP=∠PCD，可证得∠P=12(∠ABC+∠ADC)，即可求出∠P度数．（3）已知直线BP平分∠ABC的外角∠FBC，DP平分∠ADC的外角∠ADE，可得∠1=∠2，∠3=∠4，由（1）的结论得：∠C+180°-∠3=∠P+180°-∠1，∠A+∠4=∠P+∠2，两式相加即可求出∠P的度数．（4）由（1）的结论得：14∠CAB+∠C=∠P+14∠CDB，34∠CAB+∠P=∠B+34∠CDB，第一个式子乘以3，得到的式子减去第二个式子即可得出用x、y表示∠P（5）延长AB交DP于点F，标注出∠1，∠2，∠3，∠4，由（1）的结论得：∠A+2∠1=∠C+180°-2∠3，其中根据对顶角相等，三角形内角和，以及外角的性质即可得到∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P，代入∠A+2∠1=∠C+180°-2∠3，即可得出∠P与∠A、∠C的关系．【详解】（1）如图1，∠A+∠B+∠AOB=∠C+∠D+∠COD=180°∵∠AOB=∠COD∴∠A+∠B=∠C+∠D（2）∵AP、CP分别平分∠BAD、∠BCD∴∠BAP=∠PAD，∠BCP=∠PCD，由（1）的结论得：∠BCP+∠P=∠BAP+∠ABC①，∠PAD+∠P=∠PCD+∠ADC②①+②，得2∠P+∠PAD+∠BCP=∠BAP+∠ABC +∠PCD+∠ADC∴∠P=12(∠ABC+∠ADC)∴∠ABC＝28°，∠ADC＝20°∴∠P=12(28°+20°)∴∠P=24°故答案为：24°（3）∵如图3，直线BP平分∠ABC的外角∠FBC，DP平分∠ADC的外角∠ADE，∴∠1=∠2，∠3=∠4由（1）的结论得：∠C+180°-∠3=∠P+180°-∠1①，∠A+∠4=∠P+∠2②①+②，得∠C+180°-∠3+∠A+∠4=∠P+180°-∠1+∠P+∠2∴30°+18°=2∠P∴∠P=24°故答案为：24°（4）由（1）的结论得：14∠CAB+∠C=∠P+14∠CDB①，34∠CAB+∠P=∠B+34∠CDB②①×3，得34∠CAB+3∠C=3∠P+34∠CDB③②-③，得∠P-3x=y-3∠P∴∠P=34x+14y故答案为：∠P=34x+14y（5）如图5所示，延长AB交DP于点F由（1）的结论得：∠A+2∠1=∠C+180°-2∠3∵∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P ∴∠A+360°-2∠A-2∠3-2∠P=∠C+180°-2∠3解得：∠P=180()2A C︒-∠+∠故答案为：∠P=180()2A C︒-∠+∠【点睛】本题是考查了角平分线性质及三角形内角和定理，对顶角相等，三角形任一外角等于不相邻的两个内角和等知识点，本题是典型的拓展延伸题，一般第一问得出基本结论，后面的问题将基本结论作为解题基础，进行拓展延伸．23．（1）2-；（2）103x【分析】（1）根据负整数指数幂以及零指数幂运算即可求解；（2）根据同底数幂相乘（除），底数不变，指数相加（减），即可求解．【详解】解：（1）原式=213=2---；（2）原式12252481010122101010221=24443xx x x x x x x xx x⨯+-⎛⎫⋅+⋅-=-=-=-=⎪⎝⎭．【点睛】本题目考查整数指数幂，涉及知识点有正整数指数幂、零指数幂、负整数指数幂等，难度一般，熟练掌握整数指数幂的运算法则是顺利解题的关键．24．（1）这个多边形是六边形；（2）这个多边形的每一个内角的度数是120°．【分析】（1）先设内角为x,根据题意可得:外角为12x,根据相邻内角和外角的关系可得:,x+12x=180°,从而解得:x=120°,即外角等于60°,根据外角和等于360°可得这个多边形的边数为:360 60=6,（2）先设内角为x,根据题意可得:外角为12x,根据相邻内角和外角的关系可得:,x+12x=180°,从而解得内角:x=120°,内角和=（6﹣2）×180°=720°．【详解】（1）设内角为x,则外角为12x,由题意得,x+12x =180°,解得:x=120°, 12x=60°,这个多边形的边数为:360 60=6,答:这个多边形是六边形,（2）设内角为x,则外角为12x,由题意得: x+12x =180°,解得:x=120°,答:这个多边形的每一个内角的度数是120度．内角和=（6﹣2）×180°=720°．【点睛】本题主要考查多边形内角和外角,多边形内角和以及多边形的外角和,解决本题的关键是要熟练掌握多边形内角和外角的关系以及多边形内角和.25．（1）272xy=⎧⎪⎨=⎪⎩；（2）692xy=⎧⎪⎨=⎪⎩【分析】（1）根据加减消元法，即可求解；（2）先去分母，去括号，移项，合并同类项，再通过加减消元法，即可求解．【详解】（1）29321x y x y +=⎧⎨-=-⎩①②， +①②得：48x =．解得：2x =，把2x =代入①得：229y +=，解得：72y =， ∴方程组的解为272x y =⎧⎪⎨=⎪⎩； （2）原方程可化为3436329x y x y +=⎧⎨-=⎩①②， ①-②得：627y =，解得：92y =， 把92y =代入②得：399x -=，解得：6x =， ∴方程组的解为692x y =⎧⎪⎨=⎪⎩． 【点睛】本题主要考查解二元一次方程组，掌握加减消元法，是解题的关键．26．(1)图见解析；(2)图见解析．【详解】解：（1）△A′B′C′如下图；（2）高C′D′如下图．27．（1）174；（2）32± 【分析】 （1）利用完全平方公式(a ＋b)²＝a ²＋2ab ＋b ²解答；（2）利用（1）的结果和完全平方公式(a−b)²＝a ²−2ab ＋b ²解答．【详解】解：（1）由题：152x x +=， 21254x x ⎛⎫∴+= ⎪⎝⎭ 即2212524x x ++=， 221174x x ∴+= （2）222111792244x x x x ⎛⎫-=+-=-= ⎪⎝⎭ 132x x ∴-=± 【点睛】此题是完全平方公式的应用；两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．28．（1）213m -<< （2）m -【分析】（1）先解方程组，用含m 的式子表示出x 、y ，再根据方程组的解时一对正数列出关于m 的不等式组，解之可得；（2）根据m 的取值范围判断出m-2<0、m+1>0,m-1<0，再根据绝对值性质去绝对值符号、合并同类项即可得．【详解】 解：（1）解方程组233741x y m x y m +=+⎧⎨-=+⎩， 得321x m y m =+⎧⎨=-⎩因为解为正数，则32010m m +>⎧⎨->⎩，解得213m -<<； （2）原式2(1)(1)m m m m =--+--=-.【点睛】本题考查了二元一次方程组及解法、一元一次不等式组及解法．解题的关键是根据题意列出关于m 的不等式组及绝对值的性质．。

云南省曲靖市2023-2024学年七年级下学期期末数学试卷学校：___________姓名：___________班级：___________考号：___________一、单选题1．如图,和是对顶角的是( )A. B. C.D.．的相反数是A.3 B.3．将不等式的解集表示在数轴上,正确的是( )A.B.C. D.4．在平面直角坐标系中,点位于( ).A.第一象限B.第二象限C.第三象限D.第四象限5．下列调查中,最适合采用全面调查(普查)方式的是( )A.调查某一批灯的使用寿命B.调查全国中小学生收看央视一套播出的大型公益节目《开学第一课》的收视率C.调查我国最大的航天器“天和”核心舱零件的质量情况D.调查我省居民进行垃圾分类的情况6．数学源于生活,寓于生活,用于生活.“宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学.”因而我们要学会用数学的眼光观察现实世界,学会用数学的思维思考现实世界,学会用数学的语言表达现实世界,下列各选项中能用“垂线段最短”来解释的现象是( )A.测量跳远成绩1∠2∠3-38310x x -≤-(2,3)P -LED木板上弹墨线弯曲河道改直两钉子固定木条,,3.1415926,无理数有( )A.1个B.2个C.3个D.4个8．按一定规律排列的单项式：x ,,,,,,第2024个单项式是( )A. B.C. D.9．下列方程组中,属于二元一次方程组的是( )A. B.C. D.10．为了解某市七年级20000名学生的身高,从中抽取了500名学生,对其身高进行统计分析,以下说法正确的是( )A.每个学生是个体B.20000名学生是总体C.500名学生是抽取的一个样本D.每个学生的身高是个体11．2025年第九届亚洲冬季运动会的口号是“冰雪同梦,亚洲同心(DreamofWinter,Lovea mongAsia)”,口号将“同梦”、“同心”与“中国梦”紧密联系,以亚冬会为纽带,推动亚洲各国和各地区携手合作,共同发展.如图是本届亚冬会的会徽“超越”,图案融合短道速滑运动员奋力冲刺的姿态、哈尔滨市花丁香花和亚奥理事会太阳图标等元素,将中国文化与奥林匹克元素结合,传递新时代中国加快体育强国建设,为亚洲冰雪运动作出新贡献的美好追求.将其放在如图所示平面直角坐标系中,若点C 的坐标为,则点B 的坐标为( )3923x 35x 47x 59x 20244047x 20244049x 20232023x 20252025x 13x x y =⎧⎨+=-⎩2102x y x y ⎧+=⎨+=-⎩85x y xy +=⎧⎨=-⎩51156x y x y +=⎧⎪⎨+=⎪⎩()0,2A. B. C. D.12．若是关于x 、y 的二元一次方程,则a 的值为( )A.0 B.2 C.0或2 D.1或213．下列命中,真命题是( )A.相等的两个角是对顶角B.如果两条直线被第三条直线所截,那么同位角相等C.从直线外一点到这条直线的垂线段叫做该点到直线的距离D.在同一平面内,过一点有且只有一条直线与已知直线垂直14．在曲靖人民心中,麒麟水乡就是世外桃源,也是心之归处.盛夏的麒麟水乡秀丽端庄,千亩荷花在微风中飘曳,远远望去,青山如黛,绿水生烟.此时荷花竞相开放,有的才露尖尖角,微微探出头来；有的含苞待放,一抹嫣红染透了花瓣；有的已是亭亭玉立,花辫舒展明艳清丽.勾勒出一幅美丽的夏日荷塘画卷,叫人如痴如醉、心旷神怡.为了便于游客领略“人从桥上过,如在荷中行”的美好意境,拟在如图所示的长方形荷塘上架设小桥,若长方形荷塘周长为,且桥宽忽略不计,则小桥总长为( )A. B. C. D.15．下列说法：(1)没有平方根；(2)立方根等于本身的数是0；(3)8的立方根是；(4)1的平方根是1.其中正确的个数有( )A.1个B.2个C.3个D.4个二、填空题16．“x 的2倍与3的和是非负数”用不等式表示为______.()1,2()2,1--()2,1()1,2--()1235a a xy ---=560m 260m 560m 280m 520m4-2±17．每年5月5日或6日,太阳到达黄经为“立夏”节气.我国自古习惯以立夏作为夏季开始的日子,亦称作“孟夏之月”.“斗指东南,维为立夏,万物至此皆长大,故名立夏也.”唐代诗人元稹有诗云：“欲知春与夏,仲吕启朱明.蚯蚁谁教出,王菰自合生.帘蚕呈茧样,林鸟哺雏声.渐觉云峰好,徐徐带雨行.”下图是我市某地立夏后连续10天11点时气温折线统计图,则这10天11点时气温最高是______.18．已知点,,若点A 在y 轴的正半轴上,且三角形的面积为3,则点A 的坐标为______.19．光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,会发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,,则的度数为______.三、解答题20．计算：21．如图,直线AB ,CD 相交于点O ,,垂足为O ,.求的度数.22．三角形在平面直角坐标系中的位置如图所示,将三角形向右平移3个单位长度,然后再向上平移2个单位长度,可以得到三角形.45︒C ︒()0,0O ()2,1B OAB 258∠=︒1∠(41-+-+EO AB ⊥35EOC ∠=︒BOD ∠ABC ABC 111A B C(1)画出平移后的三角形,并写出顶点的坐标；(2)求三角形的面积.23．2024年是中国航天的重要一年,也是中国航天继续迈向辉煌的一年.这一年,中国航天任务精彩纷呈！为了激发学生的航天兴趣,我市某校2000名学生举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A 组：,B 组：组：,D 组：,E 组：,并绘制了如下不完整的统计图.请结合统计图,解答下列问题：(1)本次调查一共随机抽取了_________名学生的成绩；扇形统计图中A 组所占的圆心角的度数是_________；请补全学生成绩频数分布直方图.(2)若成绩在90分及以上为优秀,该校成绩优秀的学生约有多少人？24．已知的平方根是,的立方根是2.(1)求a 和b 的值；的值.25．如图所示,于点E ,于点F ,.111A B C 1B ABC 7580x ≤<8085,C x ≤<8590x ≤<9095x ≤<95100x ≤≤21a -3±35a b +-d -AM BD ⊥GN BD ⊥12∠=∠(1)求证；(2)若,,求的度数.26．【课本再现】七年级下册教材中我们探究过《用求差法比较大小》：我们在分析解决某些数学问题时经常要比较两个数或代数式的大小.当不能直接比较大小时就要考虑进行一定的转化,其中“求差法”就是常用的方法之一.所谓“求差法”,就是通过先求差、变形,然后利用差的符号来确定它们的大小.两个数量的大小可以通过它们的差来判断.如果两个数a 和b 比较大小,那么：当时,一定有；当时,一定有；当时,一定有.反过来也对,即：当时,一定有；当时,一定有；当时,一定有.因此,我们经常把两个要比较的对象先数量化,再求它们的差,根据差的正负判断对象的大小.【类比应用】(1)用“>”或“<”填空.①若时,a ___________b ；②若时,a _________b ；③若,则_________；【解决问题】(2)如图所示,在的正方形网格中,以A 为圆心为半径画扇形,以为直径画半圆,若图中阴影部分的面积分别为,,用“求差法”比较与的大小.//AB CD 350C ∠=∠+︒480∠=︒D ∠a b >0a b ->a b =0a b -=a b <0a b -<0a b ->a b >0a b -=a b =0a b -<a b <4a b -=2a b -=-0a >5a -+24a -+44⨯AB CE 1S 2S 1S 2S27．开学前,学校要购买A、B两种消毒液,用于校园消毒,迎接同学们的到来.若购买3桶A 消毒液和2桶B消毒液,共需资金205元；若购买2桶A消毒液和3桶B消毒液,共需资金195元.(1)每桶A消毒液、每桶B消毒液的价格分别是多少元？(2)该校计划购买A、B两种消毒液共30桶,其中A消毒液的数量至少比B消毒液的数量多5桶,且不超过B消毒液的数量的2倍.请问学校共有几种购买方案,并通过计算说明,哪一种购买方案能使总费用最少？并求出最少费用.(3)开学后,李老师再次购买消毒液,回来说：“A、B两种消毒液都涨价了,两种消毒液涨价金额相同,且都是整数元.今天购买A、B两种消毒液共35桶,共需资金1505元.”请你算一算,A、B两种消毒液涨价金额可能是多少元？参考答案1．答案：B解析：如图,和是对顶角,故选：B.2．答案：D故选：D.3．答案：D解析：,移项,得,合并同类项,得,系数化为1,得,在数轴上表示为,故选：D.4．答案：B解析：点所在的象限是第二象限.故选：B.5．答案：C解析：A.调查某一批灯的使用寿命适合采用抽样调查,故不符合题意；B.调查全国中小学生收看央视一套播出的大型公益节目《开学第一课》的收视率适合采用抽样调查,故不符合题意；C.调查我国最大的航天器“天和”核心舱零件的质量情况适合采用全面调查,故符合题意；D.调查我省居民进行垃圾分类的情况适合采用抽样调查,故不符合题意；故选C.1∠2∠8310x x -≤-3810x x -≤-22x -≤-1x ≥(2,3)P -LED6．答案：A解析：A 中能用垂线段最短进行解释,符合题意；B 中能用两点确定一条直线进行解释,不符合题意；C 中能用两点之间,线段最短进行解释,不符合题意；D 中能用两点确定一条直线进行解释,不符合题意；故选：A.7．答案：C是有理数.故选C.8．答案：A解析：∵单项式：x,,,,,,∴第n 个单项式为,∴第2024个单项式是.故选：A.9．答案：A解析：A.是二元一次方程组,本选项符合题意；B.中x的最高次数为2,不是二元一次方程组,本选项不符合题意；C.中xy 的次数为2,不是二元一次方程组,本选项不符合题意；D.项不符合题意；故选：A.10．答案：D解析：A.每个学生的身高是个体,故本选项不合题意；377=23x 35x 47x 59x ()21n n x -20244047x 13x x y =⎧⎨+=-⎩2102x y x y ⎧+=⎨+=-⎩85x y xy +=⎧⎨=-⎩11x y x y +=⎧⎪⎨+=⎪⎩1y +=B.20000名学生的身高是总体,故本选项不合题意；C.500名学生的身高是抽取的一个样本,故本选项不合题意；D.每个学生的身高是个体,故本选项符合题意.故选：D.11．答案：D解析：如图,根据题意,建立平面直角坐标系,如下图：点B 的坐标为.故选：D.12．答案：A,解得,故选：A.13．答案：D解析：A 、相等的两个角不一定是对顶角,本选项说法是假命题；B 、如果两条平行线被第三条直线所截,那么同位角相等,本选项说法是假命题；C 、从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离,本选项说法是假命题；D 、在同一平面内,过一点有且只有一条直线与已知直线垂直,本选项说法是真命题；故选：D.14．答案：C解析：由平移的性质可知,小桥总长为：.故选C.()1,2--1120-=≠0a =()5602280m ÷=15．答案：A解析：(1)没有平方根,正确,符合题意；(2)立方根等于本身的数是,0,1,故不正确,不符合题意；(3)8的立方根是2,故不正确,不符合题意；(4)1的平方根是,故不正确,不符合题意.故选A.16．答案：解析：由题意可得：.故答案为：.17．答案：21解析：这10天中气温最高是,故答案为：21.18．答案：解析：设则,,∵三角形的面积为3,,,∴,∴,故答案为：.19．答案：/122度解析：如图：∵水中的两条光线平行,,∴,4-1-1±230x +≥230x +≥230x +≥21C ︒()0,3()0A m ，OA m =AOB 3B x ⋅=23⨯=3m =()0,3A ()0,3122︒258∠=︒2358∠=∠=︒∵水面和杯底互相平行,∴,∵,故答案为：.20．答案：6解析：原式.21．答案：55°解析：∵,∴,∵,∴,∴.22．答案：(1)图见解析,(2)7解析：(1)如图即为所求；顶点的坐标：；(2)的面积.23．答案：(1)400,,图见解析(2)估计该校成绩优秀的学生有1120人解析：(1)本次调查一共随机抽取的学生总人数为：(人),13180∠+∠=︒1122∠=︒122︒143=-+++33=++6=EO AB ⊥90AOE ∠=︒35EOC ∠=︒55AOC AOE EOC ∠=∠-∠=︒55BOD AOC ∠=∠=︒()16,3B 111A B C △1B 1(6,3)B ABC △111545313427222=⨯-⨯⨯-⨯⨯-⨯⨯=18︒9624%400÷=,组的人数为：(人),组的人数为：(人),补全学生成绩频数分布直方图如下：学生成绩频数直方图(2)(人),答：估计该校成绩优秀的学生有1120人.24．答案：(1),(2)2解析：(1)的平方根是,,解得：,的立方根是2,,,解得：,,.(2)∵,,,,,,∴36018︒=︒B ∴40015%60m =⨯=E 40020609614480----=14480200052241120400+⨯=⨯=5a =2b =-21a - 3±221(3)9a ∴-=±=5a =35a b +- 5a =335528b ∴⨯+-==2b =-5a ∴=2b =-469<<<<3<<c 2c ∴=459<< <<3<<d 2d ∴=-的值是2. 25．答案：(1)证明见解析(2)解析：(1),,；(2),即,,,,即,,,的度数为.26．答案：(1)①>②<③>(2)解析：(1)①∵,∴.故答案为：>；②∵,∴.故答案为：<；③,∵,∴,2)2d-=--=+=d-25︒AM BD⊥GN BD⊥90AEB GFB∴∠=∠=︒//AM GN∴2A∴∠=∠12∠=∠1A∴∠=∠//AB CD∴//AB CD180C ABC∴∠+∠=︒43180C∠+∠+∠=︒350C︒∠=∠+480∠=︒350803180∴∠+++∠=︒︒︒325∠=︒//AB CD325D∴∠=∠=︒D∴∠25︒12S S>40a b-=>a b>20a b-=-<a b<()5245241a a a a a-+--+=-++-=+a>()52410a a a-+--+=+>∴.故答案为：>；(2)设两扇形部分外的空白面积为d ,则,∴,∴.27．答案：(1)每桶A 消毒液的价格为45元,每桶B 消毒液的价格为35元(2)见解析(3)A 、B 两种消毒液涨价金额可能是2元、4元或6元解析：(1)设每桶A 消毒液的价格是x 元,每桶B 消毒液的价格是y 元,由題意可得：,解得,答：每桶A 消毒液的价格为45元,每桶B 消毒液的价格为35元；(2)设学校决定购买A 种消毒液a 桶,则购买B 种消毒液桶.由题意得：,解得,取整数,即；学校共有三种购买方案：方案1：购买A 种消毒液18桶,购买B 种消毒液12桶；方案2：购买A 种消毒液19桶,购买B 种消毒液11桶；方案3：购买A 种消毒液20桶,购买B 种消毒液10桶；方案1总费用是：元；方案2总费用是：元；方案3总费用是：元；,方案1能使总费用最少,且最少费用是1230元；524a a -+>-+2119π3π44S d d =⨯+=+221π22π2S d d =⨯+=+1291π2ππ044S S d d -=+--=>12S S >3220523195x y x y +=⎧⎨+=⎩4535x y =⎧⎨=⎩(30)a -()305230a a a a ≥-+⎧⎨≤-⎩17.520a ≤≤a 18,19,20a =∴ 451835121230⨯+⨯=451935111240⨯+⨯=452035101250⨯+⨯=123012401250∴<<∴(3)设A ,B 两种消毒液涨价金额是m 元,李老师今天购买A 种消毒液n 桶,则购买B 种消毒液桶.由题意可得：,,,,；,n 均为正整数,,,答：A 、B 两种消毒液涨价金额可能是2元、4元或6元.(35)n -(45)(35)(35)1505m n m n +++-=45122535351505n mn n m mn ++-+-=3510280m n +=1028035n m =-7282n m ∴=-m 221m n =⎧∴⎨=⎩414m n =⎧⎨=⎩67m n =⎧⎨=⎩。

曲靖市2023-2024学年春季学期期末考试七年级生物试题卷(全卷两个大题,共36个小题,共8页,满分 100分)注意事项：1.地理与生物学合场考试，考试时间共计150分钟。

同时发卷(卡)。

考试结束后，分学科交回答题卡。

2.本卷为生物试题卷。

考生解题作答必须在生物答题卡上。

答案书写在生物答题卡相应位置上，在试题卷、草稿纸上作答无效。

第Ⅰ卷 (选择题, 共60 分)一、选择题(本大题共30小题，每小题2分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的)1.现存类人猿包括猩猩、大猩猩、黑猩猩、长臂猿四种。

下列说法正确的是( )A.人类和现代类人猿有着共同的祖先森林古猿B.现代类人猿与人类的唯一区别是它没有语言C.现存类人猿是人类的祖先D.北京猿人和人类有许多相近的特征，是现代类人猿的祖先2.人体生殖系统是人类繁殖后代和分泌性激素维持第二性征的器官总称，下列结构中能产生生殖细胞的是( )A.睾丸和子宫B.输卵管和输精管C.阴道和前列腺D.睾丸和卵巢3.下图为某地男女生身高生长速度曲线图，从该图中不能得出的观点是( )A.男女生在7—8岁之间生长速度接近B.男女生身高突增的年龄不同C.男生的性器官11岁开始迅速发育D.13岁以后男女生身高增长速度都逐年下降4.下列不是构成细胞的主要原料且不为人体提供能量的营养物质是( )A. 脂肪B. 糖类C.蛋白质D. 维生素5.过桥米线是云南的一种特有小吃，属滇菜系，该菜品起源于蒙自地区，米线中含有的主要营养物质是( )A. 糖类B. 无机盐C. 蛋白质D. 脂肪6.右下图中的曲线分别表示三种营养物质在消化道内的消化情况，丙这种物质是( )A. 淀粉B. 脂肪C. 蛋白质D. 维生素7.下列营养物质中可以不经过消化就能被吸收的是( )①葡萄糖②大分子蛋白质③维生素④食用油⑤水A. ①②③B. ②③④C. ①③⑤D. ①②⑤8.食品安全指食品无毒、无害，符合应当有的营养要求，对人体健康不造成任何急性、亚急性或者慢性危害，生活中的以下做法有可能出现食品安全问题的是( )A.在冰箱放置时间超过3天的熟食，最好不要再食用B. 打开包装的盒装牛奶，应在12小时内喝完C.不购买没有检疫合格证明或者标志的肉类D.云南是野生菌王国，采回来的野生菌只要完全烹制熟透就可以食用9.某中学校运会期间，学校食堂为师生准备了丰富的食物。

云南省曲靖市七年级下学期语文期末考试试卷姓名:________ 班级:________ 成绩:________一、字词书写 (共1题；共5分)1. （5分）阅读下面的文字，完成小题。

作者对描画的物件，必须要有深入的研究，有严格的选择、充沛的感情、高度的加工。

绝不能把描写物件变成说明性的图解或地理志，使观者看了suǒ然无味、无动于zhōng，这样当然谈不上什么意境。

没有意境或意境不鲜明，绝对创作不出引人入胜的山水画。

意境的创造不是一件轻松的事情，我在画水墨山水时，感觉到自己就像进入战场，在枪林弹雨中。

因为画在宣纸上不能涂改，所以一点疏乎差错都不行。

每一笔都要解决形象问题，感情问题，远近虚实、笔墨浓淡等问题。

（1）根据拼音写汉字，给划线的字注音。

________suǒzhōng充沛________然无味无动于________（2）选文中有错别字的词语是“________”，正确写法是“________”。

（3）“引人入胜”中“胜”的意思是（）A . 胜利B . 比另一个优越C . 优美的景物或境界D . 能够承担或承受（4）把画线句改为反问句。

二、句子默写 (共1题；共5分)2. （5分）诗句默写。

（1）无丝竹之乱耳，________。

（2） ________，我言秋日胜春朝。

（3）杜甫在《望岳》一诗中，赞叹大．自然伟大神奇的诗句是：________，________。

（4）古诗词中有不少写“思乡”的句子，请写出连续的两句：________，________。

三、综合性学习 (共2题；共17分)3. （2分） (2018七上·阳江期末) 依次填入下面一段文字横线处的语句，衔接最恰当的一项是（）获得快乐，其实需要一点智慧：__________。

____________。

_________。

___________。

①站在陌生的舞台上，无论是生旦，还是净丑，尽心演好自己的角色就好②是鲤鱼，就在自己的清流里尽情遨游；是雄鹰，就在自己的蓝天里任性飞翔；是骏马，就在自己的草原上自由驰骋③减少一点欲望，减少一点苛求，不走极端，不求完美，尽力就好④因为人的能力有大小，人的水平有高低，不必拿第一来压自己，不用拿别人来逼自己，不要用名次来恼自己A . ③④①②B . ②④①③C . ③②①④D . ①④②③4. （15分）阅读下面三则关于“电子阅读与纸质阅读”的材料，完成下面的题目。

曲靖市2022-2023学年春季学期期末考试七年级生物试题卷（金卷两个大题，共36个小题，共8页，满分100分）注意事项31.地理与生物学合场考试，考试时间兴计150分钟。

同时发卷（卡〉。

考试结束后，分学科交回答题卡。

2.本卷为生物试题卷。

考生解题作答必须在生物答题卡上。

答案书写在生物答题卡相应位置上，夜，试题卷、草稿纸上作答无效。

第I卷（选择题，兴60分〉一、选择题（本大题共30小腿，每小题2分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1.“人类从哪里来？”，关于人类起源和发展的叙述不正确的是OA人类的祖先是森林古猿B.人类起源于现代类人猿c.直立行定是人与猿分界的重要标准D.距今300万年“少女露面化石”是证明人类起源和进化的证据之一2.下闺女性生�系统示意图，判断下列叙述正确的是（）②A胎儿和母体进行物质交换的结构是脐带B.女性的主要生殖器官是＠c.人的胚胎发育在③中完成。

精子和卵细胞结合的场所是①3.女性月经的形成与下列哪个结构的周期性变化有关（）A.输卵管B.子宫内膜C.子宫。

．阴道4.青春期是指由儿童阶段发展为成人阶段的过液时期，是入身心发展的重要阶段。

以下关于青春期生理特点叙述错误的是（〉A逃入青春期后男女生殖器官才开始发育B.心脏和肺等哥哥宫的功能明显增强C.大脑皮层结构和功能不断完善D.身高突然地加5.维生索和无机盐也是人类重要的营养物质，如果缺乏会引起相应疾病的产生，下列维生素或无机盐与相应缺乏疲不符合的是（〉A钙－｛句偿病B.维生素c－坏血病C维生素D－神经炎D腆－地方性甲状腺肿6.市场上某品牌碳酸饮料的营养成分与营养成分含量如下袭，中小学生如频繁大量饮用碳酸饮料，有可能影响身体健康，以下叙述不正确的是〈〉营养成分表营养成分含量（每300mL)碳酸水能量180k J糖浆蛋白质。

焦糖色萦脂肪0阿斯巴甜（甜味剂）锚类10.6咖啡因A.该饮料营养成分不够全丽B该饮料缺乏修复和！重新受损细胞的重要物质C.该饮料有可能力ni事例齿发生D.该饮料可以改善夜盲症的症状7.小肠位于腹中，上端与自相通，’f;l由与大肠相迹，是食物消化吸收的主要场所。

2022-2023学年云南省曲靖市七年级下册期末语文模拟试卷（A卷）第Ⅰ卷（选择题）一、选择题1．下面各组词语加点字的注音，完全正确的一项是（）A．累．赘（léi）驿．路（yì）颠．沛流离（diàn）B．修葺．（róng）契．约（qì）悲天悯．人（mǐng）C．迸．溅（bìng）猥．琐（wéi）忍俊不禁．（jìn）D．吞噬．（shì）俯瞰．（kàn）屏．息凝神（bǐng）2．依次填入下面句子横线处的词语，最恰当的一项是（）叶圣陶先生对普通话__________，于是不耻下问，让我帮他__________。

我出于对他的尊敬，不敢直接动笔，只提一些__________性的意见。

A．生疏修改商量B．陌生修润商量C．生疏修润商酌D．陌生修改商酌3．下面句子中有语病的一项是（）①飞行回来后我详细描述了这种难受的过程。

②经过分析研究，工作人员认为，飞船共振主要来自火箭的振动。

③随后他们改进技术工艺，解决了这个问题。

④在“神州六号”飞行时，情况有了很大提高，在后来的航天飞行中再也没出现过。

A．第①句B．第②句C．第③句D．第④句4．依次填入下面一段文字方框内的标点符号，最恰当的一项是（）英雄的力量是什么呢□郁达夫在《怀鲁迅》一文中写道：“没有伟大的人物出现的民族，是世界上最可怜的生物之群□有了伟大的人物，而不知拥护、爱戴、崇仰的国家，是没有希望的奴隶之邦□英雄，凝聚着一个民族的情感，是国家自立自强的精神内核。

因此，维护雄尊严、捍卫雄荣誉，应成为我们不变的信念。

A．，；”B．？；。

”C．？，”。

D．，，。

”5．下面对《游山西村》一诗的赏析，不恰当．．．的一项是（）游山西村陆游莫笑农家腊酒浑，丰年留客足鸡豚。

山重水复疑无路，柳暗花明又一村。

箫鼓追随春社近，衣冠简朴古风存。

从今若许闲乘月，拉杖无时夜叩门。

A．首联中“莫笑”表达了诗人对淳朴民风的赞赏，“足”字写出了农家殷勤待客的盛情。

云南省曲靖市七年级下学期数学期末模拟卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共30分)1. （3分）(2017·潮南模拟) 下列图形中，是轴对称图形，但不是中心对称图形的是（）A .B .C .D .2. （3分） (2019七下·温州期中) 一滴水重0.00005千克.用科学记数法表示这个数是（）千克.A .B .C .D .3. （3分）某型号的汽车在路面上的制动距离s=，其中变量是（）A . s，vB . s，v2C . sD . v4. （3分） (2016七上·港南期中) 下列运算正确的是（）A . 5a+7b=12abB . 3y2﹣2y2=1C . ab﹣1.5ab=0D . 3x3+5x2=5x55. （3分） (2018八上·东湖期中) 下列线段长能构成三角形的是（）A . 3、4、8B . 2、3、6C . 5、6、11D . 5、6、106. （3分）(2018·达州) 下列说法正确的是（）A . “打开电视机，正在播放《达州新闻》”是必然事件B . 天气预报“明天降水概率50%，是指明天有一半的时间会下雨”C . 甲、乙两人在相同的条件下各射击10次，他们成绩的平均数相同，方差分别是S2=0.3，S2=0.4，则甲的成绩更稳定D . 数据6，6，7，7，8的中位数与众数均为77. （3分）如图，下列能判定AB∥CD的条件有（）个（1）∠1=∠2 （2）∠3=∠4（3）∠B=∠5（4）∠B+∠BCD=180°．A . 1B . 2C . 3D . 48. （3分）下列命题中不成立的是（）A . 矩形的对角线相等B . 三边对应相等的两个三角形全等C . 两个相似三角形面积的比等于其相似比的平方D . 一组对边平行，另一组对边相等的四边形一定是平行四边形9. （3分）(2015·宁波) 如图，直线a∥b，直线c分别与a，b相交，∠1=50°，则∠2的度数为（）A . 150°B . 130°C . 100°D . 50°10. （3分）如图，C、D是线段AB上两点，分别以点A和点B为圆心，AD、BC长为半径作弧，两弧相交于点M，连接AM、BM，测量∠AMB的度数，结果为（）A . 100°B . 110°C . 120°D . 130°二、填空题 (共6题；共18分)11. （3分） (2016七下·岱岳期末) 当x= 时，（x+3）（x﹣3）﹣x（x﹣2）的值为________．12. （3分）若∠α=36°，则∠α的补角为________度．13. （3分）(2019·天门模拟) 如图，中，，，，绕顶点O逆时针旋转到处，此时线段与BO的交点E为BO的中点，则线段的长度为________.14. （3分）两个全等的转盘A、B，A盘被平均分为12份，颜色顺次为红、绿、蓝．B盘被平均分为红、绿、蓝3份．分别自由转动A盘和B盘，则A盘停止时指针指向红色的概率________B盘停止时指针指向红色的概率．（用“＞”、“＜”或“=”号填空）15. （3分） (2015八下·滦县期中) 如图，等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm，AC 与MN在同一直线上，开始时A点与M点重合，让向右运动，最后A点与N点重合，则重叠部分面积ycm2与MA长度xcm之间关系式________；自变量的取值范围是________．16. （3分） (2016九上·海淀期中) CPI指居民消费价格指数，反映居民家庭购买消费商品及服务的价格水平的变动情况．CPI的涨跌率在一定程度受到季节性因素和天气因素的影响．根据北京市2015年与2016年CPI涨跌率的统计图中的信息，请判断2015年1～8月份与2016年1～8月份，同月份比较CPI涨跌率下降最多的月份是________月；请根据图中提供的信息，预估北京市2016年第四季度CPI涨跌率变化趋势是________，你的预估理由是________．三、解答题 (共7题；共52分)17. （5分） (2017七下·南京期中) 先化简，再计算： , 其中 .18. （6分）(2018·洪泽模拟) 先化简，再求值：(x＋y)2＋(x－y)(x＋y)－2x(x－y) ，其中x＝1 ，y＝－1 ．19. （7分）如图，在△A BC中，D是BC上的一点，∠1=∠2，∠3=∠4，∠B=40°，求∠BAC的度数．20. （8分） (2017八下·邗江期中) 一只不透明的袋子中有2个红球，3个绿球和5个白球，每个球除颜色外都相同，将球搅匀，从中任意摸出一个球．（1）会有哪些可能的结果？（2）任意摸一个球是绿球的概率是多少？21. （8分）(2015·宁波模拟) 如图，AB为⊙O的直径，点C为圆上一点，AD和过点C的切线互相垂直，垂足为点D，AD交⊙O于点E．（1）求证：AC平分∠BAD；（2）若CD＝3，AC＝6，求图中阴影部分面积．22. （9分）某天早晨，王老师从家出发步行前往学校，途中在路边一饭店吃早餐，如图所示是王老师从家到学校这一过程中所走的路程S（米）与时间t(分)之间的关系.（1）学校离他家________米，从出发到学校，王老师共用了________分钟；（2）王老师吃早餐用了多少分钟？（3）王老师吃早餐以前的速度快还是吃完早餐以后的速度快？吃完早餐后的平均速度是多少？23. （9分）(2018·吉林模拟) 如图，在□ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．（1）试说明：AB=CF；（2）连接E,若AD=2AB.试说明：DE⊥AF．参考答案一、选择题 (共10题；共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共18分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共7题；共52分)17-1、18-1、19-1、20-1、20-2、21-1、21-2、22-1、22-2、22-3、23-1、23-2、。

云南省曲靖市七年级下数学期末模拟试卷（2）姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2019七下·同安期中) 在实数中，无理数的个数是（）A . 1B . 2C . 3D . 42. （2分）下列不属于抽样调查的优点是（）A . 调查范围小B . 节省时间C . 得到准确数据D . 节省人力，物力和财力3. （2分）如果- 是数a的立方根，- 是b的一个平方根，则a10×b9等于（）A . 2B . -2C . 1D . -14. （2分）已知下列命题：①若a≤0，则|a|=-a；②若ma²＞na²，则m＞n；③同位角相等，两直线平行；④对顶角相等．其中原命题与逆命题均为真命题的个数是（）A . 1 个B . 2 个C . 3 个D . 4 个5. （2分） (2018八上·江干期末) 若a＜b，则下列各式中一定成立的是（）A . a2＜b2B . a﹣1＜b﹣1C . ac＜bcD . ac2＜bc26. （2分）在平面直角坐标系中，点P（2，－m2－1）（m是实数）在（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限7. （2分）△DEF（三角形）是由△ABC平移得到的，点A（-1，-4）的对应点为D（1，-1），则点B（1，1）的对应点E，点C（-1，4）的对应点F的坐标分别为（）A . （2，2），（3，4）B . （3，4），（1，7）C . （-2，2），（1，7）D . （3，4），（2，-2）8. （2分）若关于x，y的方程组有非负整数解，则正整数m为（）A . 0，1B . 1，3，7C . 0，1，3D . 1，39. （2分）(2016·随州) 不等式组的解集表示在数轴上，正确的是（）A .B .C .D .10. （2分）超市为了制定某个时间段收银台开放方案，统计了这个时间段本超市顾客在收银台排队付款的等待时间，并绘制成如下的频数分布直方图（图中等待时间6分钟到7分钟表示＞或等于6分钟而＜7分钟，其它类同）．这个时间段内顾客等待时间不少于6分钟的人数为（）A . 5B . 7C . 16D . 3311. （2分） (2016七下·重庆期中) 某公园“6.1”期间举行特优读书游园活动，成人票和儿童票均有较大折扣．张凯、李利都随他们的家人参加了本次活动．王斌也想去，就去打听张凯、李利买门票共花了多少钱．张凯说他家去了3个大人和4个小孩，共花了38元钱；李利说他家去了4个大人和2个小孩，共花了44元钱．王斌家计划去1个大人和1个小孩，请你帮他计算一下，需准备（）元钱．A . 12B . 24C . 34D . 3612. （2分） (2016高二下·通榆期中) 如图，把一块含有45°角的直角三角板的两个顶点在放在直尺的对边上．若∠1=20°，那么∠2的度数是（）A . 30°B . 25°C . 20°D . 15°二、填空题 (共6题；共14分)13. （1分）(2017·黔东南) 在平面直角坐标系中有一点A（﹣2，1），将点A先向右平移3个单位，再向下平移2个单位，则平移后点A的坐标为________．14. （2分）﹣1的相反数是________ ．15. （1分）(2018·长宁模拟) 如果一个四边形的某个顶点到其他三个顶点的距离相等，我们把这个四边形叫做等距四边形，这个顶点叫做这个四边形的等距点．如图，已知梯形ABCD是等距四边形，AB∥CD，点B是等距点．若BC=10，cosA= ，则CD的长等于________．16. （1分） (2017七下·防城港期中) 如图，AB∥CD，BE平分∠ABD，DE平分∠BDC，且BE与DE相交于点E，求证∠E=90°证明：∵AB∥CD（________）∴∠ABD+∠BDC=180°（________）∵BE平分∠ABD（________）∴∠EBD= ________（________）又∵DE平分∠BDC∴∠BDE= ________（________）∴∠EBD+∠EDB= ∠ABD+ ∠BDC（________）= （∠ABD+∠BDC）=90°∴∠E=90°．17. （8分）(2017·曹县模拟) 某中学为了了解九年级学生的体能，从九年级学生中随机抽取部分学生进行体能测试，测试的结果分为A、B、C、D四个等级，并根据测试成绩绘制了如下两幅不完整的统计图．（1）这次抽样调查的样本容量是多少？B等级的有多少人？并补全条形统计图；（2）在扇形统计图中，C等级对应扇形的圆心角为多少度？（3）该校九年级学生有1500人，估计D等级的学生约有多少人？18. （1分）不等式3（x+2）≥4+2x的解集为________；负整数解为________．三、解答题 (共8题；共80分)19. （5分）(2016·张家界) 求不等式组的解集，并把它们的解集在数轴上表示出来．20. （5分） (2016七下·随县期末) 如图，已知AD∥BC，∠1=∠2，求证：∠3+∠4=180°．21. （10分）(2017·营口) 某中学开展“汉字听写大赛”活动，为了解学生的参与情况，在该校随机抽取了四个班级学生进行调查，将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图，请根据图中的信息，解答下列问题：（1）这四个班参与大赛的学生共________人；（2）请你补全两幅统计图；（3）求图1中甲班所对应的扇形圆心角的度数；（4）若四个班级的学生总数是160人，全校共2000人，请你估计全校的学生中参与这次活动的大约有多少人．22. （15分）(2018·大庆) 如图，A（4，3）是反比例函数y= 在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y= 的图象于点P．（1）求反比例函数y= 的表达式；（2）求点B的坐标；（3）求△OAP的面积．23. （10分）如图，已知MN∥PQ，B在MN上，C在PQ上，A在B的左侧，D在C的右侧，DE平分∠ADC，BE 平分∠ABC，直线DE，BE交于点E，∠CBN=120°．（1）若∠ADQ=110°，求∠BED的度数；（2）将线段AD沿DC方向平移，使得点D在点C的左侧，其他条件不变，若∠ADQ=n°，求∠BED的度数（用含n的代数式表示）24. （10分）(2017·罗平模拟) 解下列方程或不等式组（1）用配方法解方程：x2﹣x=3x+5（2）解不等式组：，并判断﹣1，这两个数是否为该不等式组的解．25. （10分） (2015八上·江苏开学考) 为打造阜宁老大桥西侧射阳河风光带，现有一段长为350米的河边道路整治任务由A、B两个工程队先后接力完成。

2020-2021学年云南省曲靖市七年级（下）期末数学试卷一、选择题（本大题共8小题，共24.0分） 1. 16的算术平方根是( )A. ±4B. ±8C. 4D. −42. 坐标平面内下列各点中，在x 轴上的点是( )A. (0,3)B. (−3,0)C. (−1,2)D. (−2,−3)3. 为了了解某县七年级9 800名学生的视力情况，从中抽查了100名学生的视力，就这个问题来说，下面说法正确的是( )A. 9 800名学生是总体B. 每个学生是个体C. 100名学生是所抽取的一个样本D. 样本容量是1004. 二元一次方程2x +y =5的正整数解有( )A. 1个B. 2个C. 3个D. 4个5. 若x >y ，则下列式子错误的是( )A. x −2>y −2B. −3x >−3yC. x +4>y +4D. x 3>y36. 在−2，√4，√2，3.14，√−273，227，2.010010001…(每两个1之间0的个数逐渐增加1个)，这7个数中，无理数共有( )A. 4个B. 3个C. 2个D. 1个7. 如图，点E 在AD 的延长线上，下列条件中能判断BC//AD 的是( )A. ∠3=∠4B. ∠A +∠ADC =180°C. ∠1=∠2D. ∠A =∠58. 在下列各式中，计算正确的是( )A. a 2+a 3=a 5B. √9=±3C. √(−6)2=−6D. 3√2−√2=2√2二、填空题（本大题共6小题，共18.0分） 9. 不等式x−13−3x+46>−2的解集是______ ．10. 如图，直线AB 和CD 交于点O ，EO ⊥AB ，垂足为O ，∠AOD =125°，则∠COE = ______ °.11. 将一块直角三角板的直角顶点放在长方形直尺的一边上，如∠1=43°，那么∠2的度数为______ °.12. 不等式13(x −m)>3−m 的解集为x >5，则m 的值为______． 13. 如图，已知x 2=3，那么在数轴上与实数x 对应的点可能是______．14. 下列图形都是由同样大小的圆点按照一定规律所组成的，其中第一个图形中一共有3个圆点，第二个图形中一共有8个圆点，第三个图形中一共有15个圆点，…，按此规律排列下去，第10个图形中圆点的个数为______ ．三、计算题（本大题共2小题，共9.0分）15. 计算：−22×√14−√83+√9×(−1)2021．16. 二元一次方程组{x −2y =−33x +y =5的解满足2x −ky =1，求k 的值．四、解答题（本大题共7小题，共49.0分）17. 解不等式组{2x+13−1<3x+225x ≥6x −3，并将其解集在数轴上表示出来．18. 如图，AD//BC ，AD 平分∠EAC ，你能确定∠B 与∠C 的数量关系吗？请说明理由．19. 如图，已知A(−5,5)，B(−6,1)，C(−2,2)，将三角形ABC 沿AD 方向平移，点A 平移到点D ，点B 的对应点为点E ，点C 的对应点为点F ，请完成下列问题： (1)请在图中作出三角形DEF ；点E 的坐标为______ ，点F 的坐标为______ ； (2)若连接AD 、BE ，则线段AD 与线段BE 的关系为______ ； (3)求三角形ABC 的面积．20.某市举行“展运动风采，扬工匠精神”为主题的体育活动，并开展了以下体育项目：足球，乒乓球，篮球和羽毛球，要求参加的市民只能选择一项体育项目．为了了解选择各项体育活动的人数，随机抽取了部分参加体育项目的市民进行调查，并将获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：(1)这次活动一共调查了______名市民；(2)请补全条形统计图；(3)羽毛球项目的人数在扇形统计图中所占扇形圆心角的度数是多少度？(4)若该市有2500人参加了这次主题活动，请你估计选择乒乓球项目的市民人数约是多少人？21.完成下面推理过程：如图，已知DE//BC，DF、BE分别平分∠ADE、∠ABC，可推得∠FDE=∠DEB的理由：∵DE//BC(已知)∴∠ADE=______(______)∵DF、BE分别平分∠ADE、∠ABC，∴∠ADF=1______(______)2∠ABE=1______(______)2∴∠ADF=∠ABE ∴______//______(______)∴∠FDE=∠DEB.(______ )22.一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租用这批货车的情况如表：现租用该公司4辆甲种货车和5辆乙种货车一次刚好运完这批货，如果按每吨付费30元计算，问货主应付费多少元？)为“开心点”.例如23.已知当m，n都是实数，且满足2m=8+n时，称p(m−1,n+22点A(5,3)为“开心点”．=3，得m=6，n=4，因为当A(5,3)时，m−1=5，n+22所以2m=2×6=12，8+n=8+4=12，所以2m=8+n．所以A(5,3)是“开心点”．(1)判断点B(4,10)是否为“开心点”，并说明理由；(2)若点M(a,2a−1)是“开心点”，请判断点M在第几象限？并说明理由．答案和解析1.【答案】C【解析】【分析】此题考查了算术平方根的定义．题目很简单，解题要细心．根据算术平方根的定义求解即可求得答案．【解答】解：∵42=16，∴16的算术平方根是4．故选C．2.【答案】B【解析】解：∵在x轴上的点的纵坐标是0，∴结合各选项在x轴上的点是(−3,0)．故选：B．根据点在x轴上的坐标特点解答即可．本题主要考查了点在x轴上的点的坐标特点：纵坐标为0．3.【答案】D【解析】解：A、9800名学生的视力情况是总体，故此选项错误；B、每个学生的视力情况是个体，故此选项错误；C、100名学生的视力情况是抽取的一个样本，故此选项错误；D、这组数据的样本容量是100，故此选项正确．故选：D．根据总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，即可求解．此题考查的是总体、个体、样本、样本容量．解此类题需要注意“考查对象实际应是表示事物某一特征的数据，而非考查的事物．”正确理解总体、个体、样本的概念是解决本题的关键．4.【答案】B【解析】解：方程2x+y=5，解得：y=−2x+5，当x=1时，y=3；x=2时，y=1，则方程的正整数解有2个．故选：B．方程变形后表示出y，确定出正整数解的个数即可．此题考查了解二元一次方程，解题的关键是将x看做已知数求出y．5.【答案】B【解析】解：A、在不等式x>y的两边同时减去2，不等号的方向不变，即x−2>y−2，原变形正确，故此选项不符合题意；B、在不等式x>y的两边同时乘以−3，不等号的方向改变，即−3x<−3y，原变形错误，故此选项符合题意；C、在不等式x>y的两边同时加上4，不等号的方向不变，即x+4>y+4，原变形正确，故此选项不符合题意；D、在不等式x>y的两边同时加上m2，不等号的方向不变，即x3>y3，原变形正确，故此选项不符合题意．故选：B．根据不等式的性质进行分析判断．本题考查了不等式的性质．解题的关键是掌握不等式的性质：①不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子，不等号的方向不变；②不等式的两边同时乘以(或除以)同一个正数，不等号的方向不变；③不等式的两边同时乘以(或除以)同一个负数，不等号的方向改变．6.【答案】C【解析】解：√4=2，√−273=−3，在−2，√4，√2，3.14，√−273，227，2.010010001…(每两个1之间0的个数逐渐增加1个)这七个数中，无理数有：√2，2.010010001…(每两个1之间0的个数逐渐增加1个)，共有2个． 故选：C ．根据无理数的三种形式求解．本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．7.【答案】C【解析】解：∵∠1=∠2，∴BC//AD(内错角相等，两直线平行)． 故选：C ．结合图形分析两角的位置关系，根据平行线的判定方法判断．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题是一道探索性条件开放型题目，能有效地培养“执果索因”的思维方式与能力．8.【答案】D【解析】解：A 、a 2与a 3不是同类项，不能合并计算，故此选项不符合题意； B 、√9=3，故此选项不符合题意；C 、√(−6)2=√36=6，故此选项不符合题意；D 、3√2−2√2=2，正确，故此选项符合题意； 故选：D ．利用合并同类项法则判断A ，利用算术平方根的概念判断B 和C ，利用二次根式加减法运算法则判断D ．本题考查算术平方根，二次根式的加减法，理解二次根式的性质√a 2=|a|及二次根式加减法运算法则是解题关键．9.【答案】x <6【解析】解：去分母得：2x−2−3x−4>−12，移项得：−x>−6，系数化为1得：x<6．故答案为：x<6．利用不等式的基本性质，先去分母，然后把不等号右边的x移到左边，合并同类项即可求得原不等式的解集．本题考查了解一元一次不等式，解不等式要依据不等式的基本性质：(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变；(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变；(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变．10.【答案】145【解析】解：∵EO⊥AB，∠AOD=125°，∴∠EOD=35°，∴∠DOB=55°，∴∠AOC=55°，∴∠COE=145°．故答案为：145．直接利用对顶角的定义结合垂直的定义分析得出∠AOC的度数，进而得出答案．此题主要考查了垂直的定义以及对顶角的性质，正确得出∠AOC的度数是解题关键．11.【答案】47【解析】解：如图，，∵∠1=43°，∴∠3=∠1=47°，∴∠2=90°−43°=47°．故答案为47．由两直线平行，同位角相等，可求得∠3的度数，然后求得∠2的度数．此题考查了平行线的性质．注意两直线平行，同位角相等定理的应用是解此题的关键．12.【答案】2(x−m)>3−m【解析】解：解不等式13x−m>9−3m∴x>9−2m，∵解集为x>5，∴9−2m=5，解得m=2，故答案为2．解一元一次不等式如下步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1.以上步骤中，只有①去分母和⑤化系数为1可能用到性质3，即可能变不等号方向，其他都不会改变不等号方向．本题考查了解一元一次不等式，熟练解一元一次不等式是解题的关键．13.【答案】P1或P4【解析】解：∵x2=3，∴x=±√3，∴在数轴上与实数x对应的点可能是P1或P4．故答案为P1或P4．本题需先解出x等于多少，然后根据在数轴上的表示方法即可求出答案．本题主要考查了实数与数轴，在解出得数的同时要会在数轴上表示出来．14.【答案】120【解析】解：通过观察，得到：第①个图形中的黑色圆点的个数为：12+1×2=6，第②个图形中的黑色圆点的个数为：22+2×2=8，第③个图形中的黑色圆点的个数为：32+3×2=15，第④个图形中的黑色圆点的个数为：42+4×2=24，…，所以第n 个图形中的黑色圆点的个数为：n 2+2n ，当n =1时，102+10×2=120，故答案为：120．观察图形特点，从中找出规律，根据规律求解．此题考查了规律型：图形的变化类，关键是通过归纳与总结，得到其中的规律．15.【答案】解：原式=−4×12−2+3×(−1)=−2−2−3=−7．【解析】先化简有理数的乘方，算术平方根，立方根，然后先算乘法，再算加减． 本题考查实数的混合运算，理解算术平方根和立方根的概念，掌握实数混和运算的运算顺序和计算法则是解题关键．16.【答案】解：{x −2y =−3 ①3x +y =5 ②， ①+②×2得：7x =7，即x =1，把x =1代入①得：y =2，∴方程组的解为{x =1y =2， 代入2x −ky =1中得：2−2k =1，解得：k =12．【解析】求出方程组的解，代入已知方程计算即可求出k 的值．此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．17.【答案】解：解不等式2x+13−1<3x+22，得：x >−2，解不等式5x ≥6x −3，得：x ≤3，则不等式组的解集为−2<x≤3，将不等式组的解集表示在数轴上如下：【解析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．18.【答案】解：∠B与∠C的数量关系是：∠B=∠C证明：∵AD平分∠EAC∴∠1=∠2(角平分线的定义)∵AD//BC(已知)∴∠1=∠B，∠2=∠C(两直线平行，同位角相等)∴∠B=∠C(等量代换)【解析】由角平分线的定义，平行线的性质可得∠B=∠C．本题主要考查了角平分线的定义以及两直线平行，内错角相等、同位角相等这两个性质．19.【答案】解：(1)如图，△DEF为所作；(2,−1)；(6,0)；(2)AD//BE，AD=BE；(3)三角形ABC的面积=4×4−12×4×1−12×3×3−12×4×1=152．【解析】本题主要考查了作图−平移变换：确定平移后图形的基本要素有两个：平移方向、平移距离．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．(1)利用点A(−5,5)平移到点D(3,3)得到三角形平移的规律，再利用点平移的规律写出点B的对应点E和点C的对应点F的坐标，然后描点即可得到△DEF；(2)利用平移的性质求解；(3)用一个矩形的面积分别减去三个三角形的面积可计算出△ABC的面积．20.【答案】解：(1)200；(2)选择篮球的有200−80−40−60=20(人)，补全的条形统计图如图所示；(3)360°×60200=108°，即羽毛球项目的人数在扇形统计图中所占扇形圆心角的度数是108°；(4)2500×40200=500(人)，即选择乒乓球项目的市民人数约是500人．【解析】【分析】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．(1)根据足球的人数和所占的百分比，可以求得本次调查的人数；(2)根据(1)中的结果和条形统计图中的数据，可以求得选择篮球的人数，从而可以将条形统计图补充完整；(3)根据条形统计图中的数据，可以计算出羽毛球项目的人数在扇形统计图中所占扇形圆心角的度数；(4)根据条形统计图中的数据，可以计算出择乒乓球项目的市民人数约是多少人．【解答】解：(1)这次活动一共调查了80÷40%=200名市民，故答案为200；(2)见答案；(3)见答案；(4)见答案．21.【答案】∠ABC两直线平行，同位角相等∠ADE角平分线定义∠ABC角平分线定义DF BE同位角相等，两直线平行两直线平行，内错角相等【解析】解：理由是：∵DE//BC(已知)，∴∠ADE=∠ABC(两直线平行，同位角相等)，∵DF、BE分别平分ADE、∠ABC，∠ADE(角平分线定义)，∴∠ADF=12∠ABC(角平分线定义)，∠ABE=12∴∠ADF=∠ABE，∴DF//BE(同位角相等，两直线平行)，∴∠FDE=∠DEB(两直线平行，内错角相等)，故答案为：∠ABC，两直线平行，同位角相等；∠ADE，角平分线定义；∠ABC，角平分线定义；DF，BE，同位角相等，两直线平行；两直线平行，内错角相等．∠ADE，根据平行线的性质得出∠ADE=∠ABC，根据角平分线定义得出∠ADF=12∠ABC，推出∠ADF=∠ABE，根据平行线的判定得出DF//BE即可．∠ABE=12本题考查了平行线的性质和判定的应用，能熟记平行线的性质和判定定理是解此题的关键．平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．22.【答案】解：设每辆甲种货车每次可运货x 吨，每辆乙种货车每次可运货y 吨，依题意得：{2x +4y =183x +5y =24.5， 解得：{x =4y =2.5， ∴30(4x +5y)=30×(4×4+5×2.5)=855(元)．答：货主应付费855元．【解析】设每辆甲种货车每次可运货x 吨，每辆乙种货车每次可运货y 吨，根据过去两次租用这批货车的数量及累计运货吨数，即可得出关于x ，y 的二元一次方程组，解之即可得出x ，y 的值，再将其代入30(4x +5y)中即可求出货主应付费用．本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．23.【答案】解：(1)(4,10)不是“开心点”，理由如下，当B(4,10)时，m −1=4，n+22=10， 解得m =5，n =18，则2m =10，8+18=26，所以2m ≠8+n ，所以点B(4,10)不是“开心点”；(2)点M 在第三象限，理由如下：∵点M(a,2a −1)是“开心点”，∴m −1=a ，n+22=2a −1，∴m =a +1，n =4a −4，代入2m =8+n 有2a +2=8+4a −4，∴a =−1，2a −1=−3，∴M(−1,−3)，故点M 在第三象限．【解析】(1)根据A 、B 点坐标，代入(m −1,n+22)中，求出m 和n 的值，然后代入2m =8+n检验等号是否成立即可；(2)直接利用“开心点”的定义得出a的值进而得出答案．此题主要考查了点的坐标，正确掌握“开心点”的定义是解题关键．。

一、填空题1．xy的值是____． 答案：【分析】首先根据与互为相反数，可得+=0，进而得出，然后用含的代数式表示，再代入求值即可． 【详解】解：∵与互为相反数， ∴+=0， ∴ ∴ ∴．故答案为：． 【点睛】本题主要考查了实数 解析：12【分析】，进而得出1120-+-=y x ，然后用含x 的代数式表示y ，再代入求值即可． 【详解】解：∵∴，∴1120-+-=y x ∴2y x = ∴1=22x x y x =． 故答案为：12． 【点睛】本题主要考查了实数的运算以及相反数，根据相反数的概念求得y 与x 之间的关系是解题关键．2．一副直角三角板叠放如图①，90C E ∠=∠=︒．现将含45︒角的三角板ADE 固定不动，把含30角的三角板ABC （其中30CAB ∠=︒）绕顶点A 顺时针旋转角()0180αα︒<<︒．（1）如图②，当α=______度时，边BC 和边AE 所在的直线互相垂直；（2）当旋转角α在30180α︒<<︒的旋转过程中，使得两块三角板至少有一组对应边（所在的直线）互相平行，此时符合条件的α=______．答案：60°或105°或135°【分析】（1）根据条件只需证BC⊥AE即可，α=∠DEA-∠BAC=45°-30°=15°；（2）分情况画出图形，根据平行线的性质计算即可．【详解】解：（解析：60°或105°或135°【分析】（1）根据条件只需证BC⊥AE即可，α=∠DEA-∠BAC=45°-30°=15°；（2）分情况画出图形，根据平行线的性质计算即可．【详解】解：（1）在△ABC中，AC⊥BC，AE与AC重合，则AE⊥BC，α=∠DEA-∠BAC=45°-30°=15°，∴当α=15°时，BC⊥AE．故答案为15；（2）当BC∥AD时，∠C=∠CAD=90°，∴α=∠BAD=90°-30°=60°；如图，当AC∥DE时，∠E=∠CAE=90°，则α=∠BAD=45°+60°=105°，此时∠BAE=90°-30°=60°=∠B，则AE∥BC；如图，当AB ∥DE 时， ∠E =∠BAE =90°， ∴α=∠BAD =45°+90°=135°；综上：符合条件的α为60°或105°或135°， 故答案为：（1）15；（2）60°或105°或135°． 【点睛】本题考查了平行线的性质，三角板的角度计算，正确确定△ABC 旋转的过程中可以依次出现几次平行的情况是关键．3．如图，在平面直角坐标系中，一动点从原点O 出发，按向上，向右，向下，向右的方向不断移动，每移动一个单位，得到点1(0,1)A ，()21,1A ，()31,0A ，()42,0A ，…，那么点2021A 的坐标为__________．答案：【分析】由题意可知，每隔四次移动重复一次，继续得出A5，A6，A7，A8，…，归纳出点An 的一般规律，从而可求得结果． 【详解】 ∵，，，∴根据点的平移规律，可分别得：，，，，，，，，…，，，解析：()1010,1【分析】由题意可知，每隔四次移动重复一次，继续得出A 5，A 6，A 7，A 8，…，归纳出点A n 的一般规律，从而可求得结果． 【详解】∵1(0,1)A ，()21,1A ，()31,0A ，()42,0A∴根据点的平移规律，可分别得：()52,1A ，()63,1A ，()73,0A ，()84,0A ，()94,1A ，()105,1A ，()115,0A ，()126,0A ，…，()4322,1n A n --，()4221,1n A n --，()4121,0n A n --，()42,0n A n∵2021=505×4+1∴2021A 的横坐标为2×505=1010，纵坐标为1 即2021(1010,1)A 故答案为：()1010,1 【点睛】本题考查了平面直角坐标系中点的坐标的规律问题，点平移的坐标特征，体现了由特殊到一般的数学思想，关键是由前面若干点的的坐标寻找出规律．4．如图，点A （0，1），点1A （2，0），点2A （3，2），点3A （5，1）…，按照这样的规律下去，点1000A 的坐标为 _____．答案：（1500，501）． 【分析】仔细寻找横坐标，纵坐标与点的序号之间关系，从而确定变换规律求解即可． 【详解】观察图形可得，点（2，0），点（5，1），（8，2），…，（3n ﹣1，n ﹣1）， 点解析：（1500，501）． 【分析】仔细寻找横坐标，纵坐标与点的序号之间关系，从而确定变换规律求解即可． 【详解】观察图形可得，点1A （2，0），点3A （5，1），5A （8，2），…，21n A -（3n ﹣1，n ﹣1），点2A （3，2），4A （6，3），6A （9，4），…，2n A （3n ，n +1）， ∵1000是偶数，且1000＝2n ， ∴n ＝500，∴1000A （1500，501）， 故答案为：（1500，501）． 【点睛】本题考查了图形与坐标，分类思想，通过发现特殊点的坐标与序号的关系，运用特殊与一般的思想探索规律是解题的关键．5．如图，点()11,1A ，点1A 向上平移1个单位，再向右平移2个单位，得到点2A ；点2A 向上平移2个单位，再向右平移4个单位，得到点3A ；点3A 向上平移4个单位，再向右平移8个单位，得到4A ，…，按这个规律平移得到点2021A ；则点2021A 的横坐标为________．答案：【分析】先求出点A1，A2，A3，A4的横坐标，再从特殊到一半套就出规律，然后利用规律即可解决问题． 【详解】点A1的横坐标为， 点A2的横坐标为， 点A3的横坐标为， 点A4的横坐标为， …解析：202121-【分析】先求出点A 1，A 2，A 3，A 4的横坐标，再从特殊到一半套就出规律，然后利用规律即可解决问题． 【详解】点A 1的横坐标为11=2-1， 点A 2的横坐标为23=2-1， 点A 3的横坐标为37=2-1，点A 4的横坐标为415=2-1， …，按这个规律平移得到点点A n 的横坐标为2-1n ，∴点2021A 的横坐标为20212-1，故答案为：202121-． 【点睛】本题考查坐标与图形变化-平移、规律型问题等知识，解题关键是学会套就规律的方法． 6．如图，在平面直角坐标系中，一动点沿箭头所示的方向，每次移动一个单位长度，依次得到点()10,1P ，()21,1P ，()31,0P ，()41,1P -，()52,1P-，…，则2021P 的坐标是________．答案：【分析】先根据，，即可得到，，再根据，可得，进而得到． 【详解】解：由图可得，，，…，，,,, ， ∴，即， 故答案为：． 【点睛】本题主要考查了点的坐标变化规律，解决问题的关键是根据图形的 解析：()674,1-【分析】先根据()62,0P ，()124,0P ，即可得到()62,0n P n ，()612,1n P n +，再根据()63362336,0P ⨯⨯，可得()2016672,0P ，进而得到()2021674,1P -． 【详解】解：由图可得，()62,0P ，()124,0P ，…()62,0n P n ，()612,1n P n +，()6221,1n P n ++,()6321,0n P n ++,()6421,1n P n ++-,()6522,1n P n ++- 202163365÷=⋅⋅⋅，∴()202123362,1P ⨯+-，即()2021674,1P -， 故答案为：()674,1-． 【点睛】本题主要考查了点的坐标变化规律，解决问题的关键是根据图形的变化规律得到P6n（2n，0）．7．若（a﹣1）2a2018+b2019＝_____．答案：0【分析】根据相反数的概念和非负数的性质列出方程，求出a、b的值，最后代入所求代数式计算即可．【详解】解：由题意得，（a﹣1）2+＝0，则a﹣1＝0，b+1＝0，解得，a＝1，b＝﹣1，解析：0【分析】根据相反数的概念和非负数的性质列出方程，求出a、b的值，最后代入所求代数式计算即可．【详解】解：由题意得，（a﹣1）20，则a﹣1＝0，b+1＝0，解得，a＝1，b＝﹣1，则a2018+b2019＝12018+（﹣1）2019＝1+（﹣1）＝0，故答案为：0．【点睛】本题考查了相反数的性质和算术平方根非负性的性质，正确运用算术平方根非负性的性质是解答本题的关键．8．阅读下列解题过程：计算：232425++++++122222解：设232425S=++++++①122222则232526S=+++++②222222由②-①得，26S=-21运用所学到的方法计算：2330++++⋯⋯+=______________.15555答案：.【分析】设S=，等号两边都乘以5可解决．【详解】解：设S=①则5S=②②-①得4S=，所以S=.故答案是：.【点睛】本题考查了有理数运算中的规律性问题，此题参照例子，采用类比的解析：3151 4-.【分析】设S=233015555++++⋯⋯+，等号两边都乘以5可解决．【详解】解：设S=233015555++++⋯⋯+①则5S=23303155555+++⋯⋯++②②-①得4S=311-5，所以S=3151 4-.故答案是：3151 4-.【点睛】本题考查了有理数运算中的规律性问题，此题参照例子，采用类比的方法就可以解决．9．对于这样的等式：若（x+1）5＝a0x5+a1x4+a2x3+a3x2+a4x+a5，则﹣32a0+16a1﹣8a2+4a3﹣2a4+a5的值为_____．答案：-1．【分析】根据多项式的乘法得出字母的值，进而代入解答即可．【详解】解：（x+1）5＝x5+5x4+10x3+10x2+5x+1，∵（x+1）5＝a0x5+a1x4+a2x3+a3x2+解析：-1．【分析】根据多项式的乘法得出字母的值，进而代入解答即可．【详解】解：（x+1）5＝x5+5x4+10x3+10x2+5x+1，∵（x+1）5＝a0x5+a1x4+a2x3+a3x2+a4x+a5，∴a0＝1，a1＝5，a2＝10，a3＝10，a4＝5，a5＝1，把a0＝1，a1＝5，a2＝10，a3＝10，a4＝5，a5＝1代入﹣32a0+16a1﹣8a2+4a3﹣2a4+a5中，可得：﹣32a0+16a1﹣8a2+4a3﹣2a4+a5＝﹣32+80﹣80+40﹣10+1＝﹣1，故答案为：﹣1【点睛】本题考查了代数式求值，解题的关键是根据题意求得a0，a1，a2，a3，a4，a5的值.10．某校数学课外小组利用数轴为学校门口的一条马路设计植树方案如下：第k 棵树种植在点k x 处，其中11x =，当2k ≥时，112()()55k k k k x x T T ---=+-，()T a 表示非负实数a 的整数部分，例如(26)2T .=，(02)0T .=. 按此方案，第6棵树种植点6x 为________；第2011棵树种植点2011x ________.答案：403 【解析】当k=6时，x6=T （1）+1=1+1=2， 当k=2011时,=T()+1=403. 故答案是:2,403.【点睛】本题考查了坐标确定位置，读懂题目信息，理解xk 的表达解析：403 【解析】当k=6时，x 6=T （1）+1=1+1=2， 当k=2011时,2011x =T(20105)+1=403. 故答案是:2,403.【点睛】本题考查了坐标确定位置，读懂题目信息，理解xk 的表达式并写出用T 表示出的表达式是解题的关键． 11．按下面的程序计算：若输入n=100，输出结果是501；若输入n=25，输出结果是631，若开始输入的n 值为正整数，最后输出的结果为656，则开始输入的n 值可以是________．答案：131或26或5. 【解析】试题解析：由题意得，5n+1=656， 解得n=131， 5n+1=131， 解得n=26， 5n+1=26， 解得n=5.解析：131或26或5. 【解析】试题解析：由题意得，5n+1=656， 解得n=131，5n+1=131， 解得n=26， 5n+1=26， 解得n=5. 12．已知a n ＝()211n +(n ＝1，2，3，…)，记b 1＝2(1－a 1)，b 2＝2(1－a 1)(1－a 2)，…，b n ＝2(1－a 1)(1－a 2)…(1－a n )，则通过计算推测出表达式b n ＝________ (用含n 的代数式表示)．答案：． 【详解】根据题意按规律求解：b1=2(1-a1)=，b2=2(1-a1)(1-a2)=，…，所以可得：bn=． 解：根据以上分析bn=2（1-a1）（1-a2）…（1-an ）=． “点睛”本题解析：21n n ++． 【详解】根据题意按规律求解：b 1=2(1-a 1)=131221-4211+⎛⎫⨯== ⎪+⎝⎭，b 2=2(1-a 1)(1-a 2)=314221-29321+⎛⎫⨯== ⎪+⎝⎭，…，所以可得：b n =21n n ++．解：根据以上分析b n =2（1-a 1）（1-a 2）…（1-a n ）=21n n ++． “点睛”本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．本题中表示b 值时要先算出a 的值，要注意a 中n 的取值．13．对于正整数n ，定义2,10()(),10n n F n f n n ⎧<=⎨≥⎩其中()f n 表示n 的首位数字､末位数字的平方和．例如：2(6)636F ==，2(123)(123)1F f ==2310+=．规定1()()F n F n =，()1()()k k F n F F n +=．例如：1(123)(123)10F F ==，()21(123)(123)F F F =(10)1F ==．按此定义2021(4)F =_____．答案：145 【分析】根据题意分别求出F1（4）到F8（4），通过计算发现，F1（4）=F8（4），然后根据所得的规律即可求解． 【详解】解：F1（4）=16，F2（4）=F （16）=37， F3（4解析：145【分析】根据题意分别求出F 1（4）到F 8（4），通过计算发现，F 1（4）=F 8（4），然后根据所得的规律即可求解．【详解】解：F 1（4）=16，F 2（4）=F （16）=37，F 3（4）=F （37）=58，F 4（4）=F （58）=89，F 5（4）=F （89）=145，F 6（4）=F （145）=26，F 7（4）=F （26）=40，F 8（4）=F （40）=16，……通过计算发现，F 1（4）=F 8（4），∴202172885÷=， ∴20215(4)(4)145F F ==；故答案为：145．【点睛】本题考查了有理数的乘方，新定义运算，能准确理解定义，多计算一些数字，进而确定循环规律是解题关键．14．在平面直角坐标系xOy 中，对于点P （x ，y ），我们把点P'（y －1，－x +1）叫做点P 的伴随点；已知点A 1的坐标为（3，2），点A 1的伴随点记为A 2，点A 2的伴随点记为A 3，点A 3的伴随点记为A 4，…，这样依次得到点A 1，A 2，A 3，…，A n ，…；则点A 4的坐标为_____________，点A 2020的坐标为_____________． 答案：【分析】先根据伴随点的定义依次求出点的坐标，再归纳类推出一般规律，由此即可得．【详解】，即，即，即，即归纳类推得：点的坐标是以循环变化的点的坐标与点的坐标相同，解析：(1,4)- (1,4)-【分析】先根据伴随点的定义依次求出点4235,,,A A A A 的坐标，再归纳类推出一般规律，由此即可得．【详解】1(3,2)A2(21,31)A ∴--+，即2(1,2)A -3(21,11)A ---+，即3(3,0)A -4(01,31)A -+，即4(1,4)A -5(41,11)A -+，即5(3,2)A归纳类推得：点123,,,,,n A A A A ⋯⋯的坐标是以1234,,,A A A A 循环变化的20204505=⨯∴点2020A 的坐标与点4A 的坐标相同，即为(1,4)-故答案为：(1,4)-，(1,4)-．【点睛】本题考查了点坐标的规律探索，根据点4235,,,A A A A 的坐标，正确归纳类推出一般规律是解题关键．15．在求1+3+32+33+34+35+36+37+38的值时，张红发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设：S=1+3+32+33+34+35+36+37+38①，然后在①式的两边都乘以3，得：3S=3+32+33+34+35+36+37+38+39②，②-①得，3S-S=39-1，即2S=39-1，所以S=．得出答案后，爱动脑筋的张红想：如果把“3”换成字母m （m ≠0且m ≠1），能否求出1+m +m 2+m 3+m 4+…+m 2016的值？如能求出，其正确答案是 ______ ．答案：.【解析】试题分析：设S ＝1＋m ＋m2＋m3＋m4＋…＋m2016…………………①，在①式的两边都乘以m ，得：mS ＝m ＋m2＋m3＋m4＋…＋m2016＋m2017…………………②②一①得： 解析：.【解析】试题分析：设S ＝1＋m ＋m 2＋m 3＋m 4＋…＋m 2016…………………①，在①式的两边都乘以m ，得：mS ＝m ＋m 2＋m 3＋m 4＋…＋m 2016＋m 2017…………………② ②一①得：mS―S ＝m 2017－1.∴S ＝. 考点：阅读理解题；规律探究题.16．如图，在平面直角坐标系上有个点(1,0)P ，点P 第1次向上跳动1个单位至点1(1,1)P ，紧接着第2次向右跳动2个单位至点2(1,1)P -，第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，依此规律跳动下去，4P的坐标是___________，点P 第8次跳动至8P 的坐标为__________；则点P 第256次跳动至256P 的坐标是__________．答案：【详解】由题中规律可得出如下结论：设点Pm 的横坐标的绝对值是n ，则在y 轴右侧的点的下标分别是4（n-1）和4n-3，在y 轴左侧的点的下标是：4n-2和4n-1； 结合图像解析：(2,2) (3,4) (65,128)【详解】由题中规律可得出如下结论：设点P m 的横坐标的绝对值是n ，则在y 轴右侧的点的下标分别是4（n-1）和4n-3，在y 轴左侧的点的下标是：4n-2和4n-1；结合图像可知：048(1,0)(2,2)(3,4)P P P →→→， 由此可知每经4次变化后点的横坐标增加1，纵坐标增加2，∵256464÷=，64165+=，642128⨯=，∴256P 的坐标是(65,128)．故答案为()2,2；()3,4；()65,128.点睛：此题主要考查了点的坐标，解决问题的关键是分析出题目的规律，找出题目中点的坐标的规律，总结规律时要注意观察数字之间的联系，大胆的猜想．17．若202120212a b -+=，其中a ，b 均为整数，则符合题意的有序数对(),a b 的组数是______． 答案：5【分析】由绝对值和算术平方根的非负性，求出a 、b 所有的可能值，即可得到答案．【详解】解：∵，且，均为整数，又∵，，∴可分为以下几种情况：①，，解得：，；②，，解得：或，；③，解析：5【分析】由绝对值和算术平方根的非负性，求出a 、b 所有的可能值，即可得到答案．【详解】解：∵20212a -=，且a ，b 均为整数，又∵20210a -≥0≥，∴可分为以下几种情况：①20210a -=2，解得：2021a =，2017b =-；②20211a -=1=，解得：2020a =或2022a =，2020b =-；③20212a -=0解得：2019a =或2023a =，2021b =-；∴符合题意的有序数对(),a b 共由5组；故答案为：5．【点睛】本题考查了绝对值的非负性，算术平方根的非负性，解题的关键是掌握非负的性质进行解题．18．定义运算“@”的运算法则为：2@6 =____．答案：4【分析】把x=2，y=6代入x@y=中计算即可．【详解】解：∵x@y=，∴2@6==4，故答案为4．【点睛】本题考查了有理数的运算能力，注意能由代数式转化成有理数计算的式子． 解析：4【分析】把x=2，y=6代入【详解】解：∵x@y=xy 4+，∴2@6=26416⨯+==4，故答案为4．【点睛】本题考查了有理数的运算能力，注意能由代数式转化成有理数计算的式子．19．如图1，为巡视夜间水面情况，在笔直的河岸两侧（//PQ MN ）各安置一探照灯A ，BC （A 在B 的左侧），灯A 发出的射线AC 从AM 开始以a 度/秒的速度顺时针旋转至AN 后立即回转，灯B 发出的射线BD 从BP 开始以1度/秒的速度顺时针旋转至BQ 后立即回转，两灯同时转动，经过55秒，射线AC 第一次经过点B ，此时55ABD ∠=︒，则a =________，两灯继续转动，射线AC 与射线BD 交于点E （如图2），在射线．．．BD ．．到达．．BQ ．．之前．．，当120AEB ∠=︒，MAC ∠的度数为________．答案：或．【分析】（1）由平行线的性质，得到角之间的关系，然后列出方程，解方程即可；（2）由题意，根据旋转的性质，平行线的性质，可对运动过程分成两种情况进行分析：①射线AC 没到达AN 时，；②解析：120︒或60︒．【分析】（1）由平行线的性质，得到角之间的关系，然后列出方程，解方程即可；（2）由题意，根据旋转的性质，平行线的性质，可对运动过程分成两种情况进行分析：①射线AC 没到达AN 时，120AEB ∠=︒；②射线AC 到达AN 后，返回旋转的过程中，120AEB ∠=︒；分别求出答案即可．【详解】解：（1）如图，射线AC 第一次经过点B ，∵//PQ MN，∴MAB ABP ABD DBP∠=∠=∠+∠，∴55∠=︒+∠，MAB DBP∴5555551a=︒+⨯︒，a=；解得：2故答案为：2．（2）①设射线AC的转动时间为t秒，则如图，作EF//MN//PQ，由旋转的性质，则1802∠=︒-︒，PBE tEAN t∠=︒，∵EF//MN//PQ，∴1802∠=∠=︒，∠=∠=︒-︒，FEB PBE tAEF EAN t∵120∠=∠+∠=︒，AEB AEF FEB∴1802120t t︒-︒+︒=︒，t=（秒），∴60∴260120∠=⨯=︒；MAC②设射线AC的转动时间为t秒，则如图，作EF//MN//PQ，此时AC为达到AN之后返回途中的图像；与①同理，∴3602∠=︒-︒，180MAC t∠=︒-︒，QBE t∵120∠=∠+∠=︒，AEB AEF FEB∴3602180120︒-︒+︒-︒=︒，t tt=（秒）；解得：120∴360212060∠=︒-⨯=︒；MAC∠的度数为：120︒或60︒；综合上述，MAC故答案为：120︒或60︒．【点睛】本题考查了旋转的性质，平行线的性质，解题的关键是熟练掌握所学的知识，正确的分析题意，作出辅助线，运用分类讨论的思想进行解题．20．如图，△ABC 中，∠C =90︒，AC =5cm ，CB =12cm ，AB =13cm ，将△ABC 沿直线CB 向右平移3cm 得到△DEF ，DF 交AB 于点G ，则点C 到直线DE 的距离为______cm ．答案：【分析】根据平移前后图形的大小和形状不变，添加辅助线构造梯形，利用面积相等来计算出答案．【详解】解：如图，连接AD 、CD ，作CH ⊥DE 于H ，依题意可得AD=BE=3cm ，∵梯形ACED 解析：7513【分析】根据平移前后图形的大小和形状不变，添加辅助线构造梯形，利用面积相等来计算出答案．【详解】 解：如图，连接AD 、CD ，作CH ⊥DE 于H ，依题意可得AD=BE=3cm ，∵梯形ACED 的面积()()2131235452S cm =⨯++⨯=， ∴()1153134522ADC DCE S S CH +=⨯⨯+⨯⋅=， 解得7513CH =； 故答案为：7513．【点睛】本题考查的是图形的平移和点到直线的距离，注意图形平移前后的形状和大小不变，以及平移前后对应点的连线相等．21．如图，△ABC 的边长AB =3 cm ，BC =4 cm ，AC =2 cm ，将△ABC 沿BC 方向平移a cm （a ＜4 cm ），得到△DEF ，连接AD ，则阴影部分的周长为_______cm ．答案：9【分析】根据平移的特点，可直接得出AC 、DE 、AD 的长，利用EC=BC －BE 可得出EC 的长，进而得出阴影部分周长．【详解】∵AB=3cm ，BC=4cm ，AC=2cm ，将△ABC 沿BC 方向平解析：9【分析】根据平移的特点，可直接得出AC 、DE 、AD 的长，利用EC=BC －BE 可得出EC 的长，进而得出阴影部分周长．【详解】∵AB =3cm ，BC =4cm ，AC =2cm ，将△ABC 沿BC 方向平移a cm∴DE=AB=3cm ，BE=a cm∴EC=BC －BE=(4－a )cm∴阴影部分周长=2+3+(4－a )+a =9cm故答案为：9【点睛】本题考查平移的特点，解题关键是利用平移的性质，得出EC=BC －BE ．22．如图，已知AB CD ∥，CE 、BE 的交点为E ，现作如下操作：第一次操作，分别作ABE ∠和DCE ∠的平分线，交点为1E ，第二次操作，分别作1ABE ∠和1DCE ∠的平分线，交点为2E ，第三次操作，分别作2ABE ∠和2DCE ∠的平分线，交点为3E ，…第n 次操作，分别作1n ABE -∠和1n DCE -∠的平分线，交点为n E ．若1n E ∠=度，那BEC ∠等于__________度．答案：【分析】先过E 作EF ∥AB ，根据AB ∥CD ，得出AB ∥EF ∥CD ，再根据平行线的性质，得出∠B=∠1，∠C=∠2，进而得到∠BEC=∠ABE+∠DCE ；根据∠ABE 和∠DCE 的平分线交点为E1，解析：2n【分析】先过E 作EF ∥AB ，根据AB ∥CD ，得出AB ∥EF ∥CD ，再根据平行线的性质，得出∠B =∠1，∠C =∠2，进而得到∠BEC =∠ABE +∠DCE ；根据∠ABE 和∠DCE 的平分线交点为E 1，则可得出∠CE 1B =∠ABE 1+∠DCE 112=∠ABE 12+∠DCE 12=∠BEC ；同理可得∠BE 2C =∠ABE 2+∠DCE 212=∠ABE 112+∠DCE 112=∠CE 1B 14=∠BEC ；根据∠ABE 2和∠DCE 2的平分线，交点为E 3，得出∠BE 3C 18=∠BEC ；…据此得到规律∠E n 12n =∠BEC ，最后求得∠BEC 的度数．【详解】如图1，过E 作EF ∥AB ．∵AB ∥CD ，∴AB ∥EF ∥CD ，∴∠B =∠1，∠C =∠2．∵∠BEC =∠1+∠2，∴∠BEC =∠ABE +∠DCE ；如图2．∵∠ABE 和∠DCE 的平分线交点为E 1，∴∠CE 1B =∠ABE 1+∠DCE 112=∠ABE 12+∠DCE 12=∠BEC ． ∵∠ABE 1和∠DCE 1的平分线交点为E 2，∴∠BE 2C =∠ABE 2+∠DCE 212=∠ABE 112+∠DCE 112=∠CE 1B 14=∠BEC ； ∵∠ABE 2和∠DCE 2的平分线，交点为E 3， ∴∠BE 3C =∠ABE 3+∠DCE 312=∠ABE 212+∠DCE 212=∠CE 2B 18=∠BEC ； …以此类推，∠E n 12n=∠BEC ，∴当∠E n=1度时，∠BEC等于2n度．故答案为：2n．【点睛】本题考查了角平分线的定义以及平行线性质：两直线平行，内错角相等的运用．解决问题的关键是作平行线构造内错角，解题时注意：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．23．如图,AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BFD=35°，那么∠BED的度数为_______.答案：70°【分析】此题要构造辅助线：过点E，F分别作EG∥AB，FH∥AB．然后运用平行线的性质进行推导．【详解】解：如图所示，过点E，F分别作EG∥AB，FH∥AB．∵EG∥AB，FH∥A解析：70°【分析】此题要构造辅助线：过点E，F分别作EG∥AB，FH∥AB．然后运用平行线的性质进行推导．【详解】解：如图所示，过点E，F分别作EG∥AB，FH∥AB．∵EG∥AB，FH∥AB，∴∠5=∠ABE，∠3=∠1，又∵AB∥CD，∴EG∥CD，FH∥CD，∴∠6=∠CDE，∠4=∠2，∴∠1+∠2=∠3+∠4=∠BFD=35°．∵BF平分∠ABE，DF平分∠CDE，∴∠ABE=2∠1，∠CDE=2∠2，∴∠BED=∠5+∠6=2∠1+2∠2=2（∠1+∠2）=2×35°=70°．故答案为70°．【点睛】本题主要考查了平行线的性质，根据题中的条件作出辅助线EG∥AB，FH∥AB，再灵活运用平行线的性质是解本题的关键．24．如图，Rt△AOB和Rt△COD中，∠AOB＝∠COD＝90°，∠B＝40°，∠C＝60°，点D在边OA上，将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第________秒时，边CD恰好与边AB平行．答案：10或28【分析】作出图形，分①两三角形在点O的同侧时，设CD与OB相交于点E，根据两直线平行，同位角相等可得∠CEO=∠B，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE，然解析：10或28【分析】作出图形，分①两三角形在点O的同侧时，设CD与OB相交于点E，根据两直线平行，同位角相等可得∠CEO=∠B，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE，然后求出旋转角∠AOD，再根据每秒旋转10°列式计算即可得解；②两三角形在点O的异侧时，延长BO与CD相交于点E，根据两直线平行，内错角相等可得∠CEO=∠B，再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE，然后求出旋转角度数，再根据每秒旋转10°列式计算即可得解．【详解】解：①两三角形在点O的同侧时，如图1，设CD与OB相交于点E，∵AB∥CD，∴∠CEO=∠B=40°，∵∠C=60°，∠COD=90°，∴∠D=90°-60°=30°，∴∠DOE=∠CEO-∠D=40°-30°=10°，∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°，∵每秒旋转10°，∴时间为100°÷10°=10秒；②两三角形在点O的异侧时，如图2，延长BO与CD相交于点E，∵AB∥CD，∴∠CEO=∠B=40°，∵∠C=60°，∠COD=90°，∴∠D=90°-60°=30°，∴∠DOE=∠CEO-∠D=40°-30°=10°，∴旋转角为270°+10°=280°，∵每秒旋转10°，∴时间为280°÷10°=28秒；综上所述，在第10或28秒时，边CD恰好与边AB平行．故答案为10或28．【点睛】本题考查了平行线的判定，平行线的性质，旋转变换的性质，难点在于分情况讨论，作出图形更形象直观．25．如图，a∥b，∠2＝∠3，∠1＝40°，则∠4的度数是______度．答案：40【解析】试题分析：如图，分别作a、b的平行线，然后根据a∥b，可得∠1=∠5，∠6=∠7，∠8=∠4，然后根据∠2=∠3，即∠5+∠6=∠7+∠8，然后由∠1=40°，可求得∠4=40°.解析：40【解析】试题分析：如图，分别作a、b的平行线，然后根据a∥b，可得∠1=∠5，∠6=∠7，∠8=∠4，然后根据∠2=∠3，即∠5+∠6=∠7+∠8，然后由∠1=40°，可求得∠4=40°.故答案为：40.26．如图，直线，将含有角的三角板的直角顶点放在直线上，若，则的度数为________答案：【解析】试题分析：过B作BE∥m，则根据平行公理及推论可知l∥BE，然后可证明得到∠1+∠2=∠ABC=45°，因此可求得∠2=20°.故答案为：20.解析：【解析】试题分析：过B作BE∥m，则根据平行公理及推论可知l∥BE，然后可证明得到∠1+∠2=∠ABC=45°，因此可求得∠2=20°.故答案为：20.27．如图，已知∠A＝（60﹣x）°，∠ADC＝（120+x）°，∠CDB＝∠CBD，BE平分∠CBF，若∠DBE＝59°，则∠DFB＝___．答案：【分析】根据题意可得，设，分别表示出，进而根据平行线的性质可得∠DFB．【详解】∠A＝（60﹣x）°，∠ADC＝（120+x）°，，，，，BE 平分∠CBF ，，设，∠DB解析：62︒【分析】根据题意可得//AB CD ，设EBF EBC α∠=∠=，分别表示出,ABD DBF ∠∠，进而根据平行线的性质可得∠DFB ．【详解】∠A ＝（60﹣x ）°，∠ADC ＝（120+x ）°，180A ADC ∴∠+∠=︒，//AB CD ∴，CDB ABD ∴∠=∠，CDB CBD ∠=∠，ABD CBD ∴∠=∠，BE 平分∠CBF ，EBF EBC ∴∠=∠，设EBF EBC α∠=∠=，∠DBE ＝59°，∴59DBF α∠=︒-，59ABD DBC α∴∠=∠=︒+，5959118ABF ABD DBF αα∴∠=∠+∠=︒++︒-=︒，//AB CD ，180********DFB ABF ∴∠=︒-∠=︒-︒=︒．故答案为：62︒．【点睛】本题考查了平行线的判定与性质，角平分线的定义，证明//AB CD 是解题的关键． 28．已知：如图，直线AB 、CD 相交于点O ，OA 平分∠EOC ，若∠EOC ：∠EOD ＝2：3，则∠BOD 的度数为________．答案：36°【分析】先设∠EOC ＝2x ，∠EOD ＝3x ，根据平角的定义得2x+3x ＝180°，解得x ＝36°，则∠EOC ＝2x ＝72°，根据角平分线定义得到∠AOC ∠EOC72°＝36°，然后根据对解析：36°【分析】先设∠EOC ＝2x ，∠EOD ＝3x ，根据平角的定义得2x +3x ＝180°，解得x ＝36°，则∠EOC ＝2x ＝72°，根据角平分线定义得到∠AOC 12=∠EOC 12=⨯72°＝36°，然后根据对顶角相等得到∠BOD ＝∠AOC ＝36°．【详解】解：设∠EOC ＝2x ，∠EOD ＝3x ，根据题意得2x +3x ＝180°，解得x ＝36°，∴∠EOC ＝2x ＝72°，∵OA 平分∠EOC ，∴∠AOC 12=∠EOC 12=⨯72°＝36°， ∴∠BOD ＝∠AOC ＝36°．故答案为：36°【点睛】考查了角的计算，角平分线的定义和对顶角的性质．解题的关键是明确：1直角＝90°；1平角＝180°，以及对顶角相等．29．把一张对边互相平行的纸条，折成如图所示，EF 是折痕，若32EFB ∠=︒，则下列结论：（1）'32C EF ∠=︒；（2）148AEC ∠=︒；（3）64BGE ∠=︒；（4）116BFD ∠=︒．正确的有________个．答案：3【分析】（1）根据平行线的性质即可得到答案；（2）根据平行线的性质得到：∠AEF=180°-∠EFB=180°-32°=148°，又因为∠AEF=∠AEC+∠GEF ，可得∠AEC ＜148°，解析：3【分析】（1）根据平行线的性质即可得到答案；（2）根据平行线的性质得到：∠AEF =180°-∠EFB =180°-32°=148°，又因为∠AEF =∠AEC +∠GEF ，可得∠AEC ＜148°，即可判断是否正确；（3）根据翻转的性质可得∠GEF =∠C ′EF ，又因为∠C′EG =64°，根据平行线性质即可得到∠BGE =∠C′EG =64°，即可判断是否正确；（4）根据对顶角的性质得：∠CGF =∠BGE =64°，根据平行线得性质即可得：∠BFD =180°-∠CGF即可得到结果．【详解】AE BG，∠EFB=32°，解：（1）∵//∴∠C′EF=∠EFB=32°，故本小题正确；（2）∵AE∥BG，∠EFB=32°，∴∠AEF=180°-∠EFB=180°-32°=148°，∵∠AEF=∠AEC+∠GEF，∴∠AEC＜148°，故本小题错误；（3）∵∠C′EF=32°，∴∠GEF=∠C′EF=32°，∴∠C′EG=∠C′EF+∠GEF=32°+32°=64°，∵AC′∥BD′，∴∠BGE=∠C′EG=64°，故本小题正确；（4）∵∠BGE=64°，∴∠CGF=∠BGE=64°，DF CG，∵//∴∠BFD=180°-∠CGF=180°-64°=116°，故本小题正确．故正确的为：（1）（3）（4）共3个，故答案为：3．【点睛】本题考查的是平行线的性质及翻折变换的性质，熟知图形翻折不变性的性质是解答此题的关键．30．在研究“数字黑洞”这节课中，乐乐任意写下了一个四位数（四数字完全相同的除外），重新排列各位数字，使其组成一个最大的数和一个最小的数，然后用最大的数减去最小的数，得到差:重复这个过程，……，乐乐发现最后将变成一个固定的数，则这个固定的数是__________．答案：6174【分析】任选四个不同的数字，组成个最大的数和一个最小的数，用大数减去小数，如1234，4321- 1234= 3087，8730-378= 8352 ，8532一2358= 617解析：6174【分析】任选四个不同的数字，组成个最大的数和一个最小的数，用大数减去小数，如1234，4321- 1234= 3087，8730-378= 8352 ，8532一2358= 6174，6174是符合条件的4位数中唯一会产生循环的(7641-1467= 6174) 这个在数学上被称之为卡普耶卡(Kaprekar)猜想.【详解】任选四个不同的数字，组成一个最大的数和一个最小的数，用大数减去小数，用所得的结果的四位数重复上述的过程，最多七步必得6174，如1234，4321-1234 =3087，8730 -378 = 8352，8532-2358= 6174，这一现象在数学上被称之为卡普耶卡(Kaprekar)猜想，故答案为：6174.【点睛】此题考查数字的规律运算，正确理解题意通过计算发现规律并运用解题是关键.31．历代数学家称《九章算术》为“算经之首”.书中有这样一道题的记载，译文为：今有5只雀、6只燕，分别聚集在一起称重，称得雀重，燕轻．若将一只雀、一只燕交换位置，则重量相等；将5只雀、6只燕放在一起称量，则总重量为1斤．问雀、燕每1只各重多少斤？若设雀每只重x斤，燕每只重y斤，则可列方程组为________________答案：【分析】设每只雀有x两，每只燕有y两，根据五只雀、六只燕，共重1斤（等于16两），雀重燕轻，互换其中一只，恰好一样重，列方程组即可．【详解】解：设每只雀有x两，每只燕有y两，由题意得，【解析：45561 x y y xx y+=+⎧⎨+=⎩【分析】设每只雀有x两，每只燕有y两，根据五只雀、六只燕，共重1斤（等于16两），雀重燕轻，互换其中一只，恰好一样重，列方程组即可．【详解】解：设每只雀有x两，每只燕有y两，由题意得，45561 x y y xx y+=+⎧⎨+=⎩【点睛】本题考查了有实际问题抽象出二元一次方程组，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程组．32．已知不等式组32,152,33x a xx x+<⎧⎪⎨-<+⎪⎩有解但没有整数解，则a的取值范围为________．答案：【分析】先求得不等式组的解集，根据解集没有整数解，建立起新的不等式组，解之即可【详解】∵，∴解①得，x ＜-a ，解②得，x ＞-1，∴不等式组的解集为：-1＜x ＜-a ，∵不等式组有解但没有解析：01a ≤<【分析】先求得不等式组的解集，根据解集没有整数解，建立起新的不等式组，解之即可【详解】 ∵32,152,33x a x x x +<⎧⎪⎨-<+⎪⎩①②， ∴解①得，x ＜-a ，解②得，x ＞-1，∴不等式组的解集为：-1＜x ＜-a ，∵不等式组32,152,33x a x x x +<⎧⎪⎨-<+⎪⎩有解但没有整数解， ∴01a a -≤⎧⎨-<-⎩， ∴01a ≤<，故答案为：01a ≤<．【点睛】本题考查了一元一次不等式组的解法，能根据不等式组无整数解建立新不等式组并解之是解题的关键．33．若不等式组22x a x a<⎧⎨+>⎩无解，则a 的取值范围是_________． 答案：【分析】把不等式组中每个不等式的解集求出来，然后令它们的交集为空集即可得到解答．【详解】解：解不等式组得：x<a 且x>2a-2∴要使不等式组无解，只要2a-2≥a ，即a≥2即可故答案为解析：2a ≥【分析】把不等式组中每个不等式的解集求出来，然后令它们的交集为空集即可得到解答．【详解】解：解不等式组得：x<a 且x>2a-2∴要使不等式组无解，只要2a-2≥a ，即a≥2即可故答案为a≥2．【点睛】本题考查不等式组的解集，准确求解不等式组中每个不等式的解是解题关键． 34．定义运算22a b a ab ⊗=-，下列给出了关于这种运算的几个结论：（1）2516⊗=-；（23）方程0x y ⊗=不是二元一次方程；（4）不等式组(3)10250x x -⊗+>⎧⎨⊗->⎩的解集是5134x -<<-．其中正确的是________（填序号）． 答案：（1）（3）（4）【分析】根据题中所给定义运算，依次将新定义的运算化为一般运算，再进一步分析即可．【详解】解：（1），故（1）正确；（2）是有理数，故（2）错误；（3）方程得是二元二次方解析：（1）（3）（4）【分析】根据题中所给定义运算，依次将新定义的运算化为一般运算，再进一步分析即可．【详解】解：（1）225222516⊗=-⨯⨯=-，故（1）正确；（22是有理数，故（2）错误；（3）方程0x y ⊗=得220x xy -=是二元二次方程，故（3）正确；（4）不等式组(3)10250x x -⊗+>⎧⎨⊗->⎩等价于22(3)2(3)1022250x x ⎧--⨯-+>⎨-⨯->⎩，解得 5134x -<<-，故（4）正确． 故答案为：（1）（3）（4）．【点睛】本题考查新定义的实数运算，立方根，二元一次方程的定义，解一元一次不等式组．能理解题中新的定义，并根据题中的定义将给定运算化为一般运算是解决此题的关键． 35．运行程序如图所示,规定:从“输入一个值x"”到“结果是否19≥为次程序如果程序操作进行了三次才停止，那么x 的取值范围是______________。