材料力学试题及答案
- 格式:doc
- 大小:211.50 KB
- 文档页数:9

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 导电性答案:D2. 根据胡克定律,当材料受到正应力时,其应变与应力成正比,比例系数称为:A. 杨氏模量B. 剪切模量C. 泊松比D. 屈服强度答案:A3. 在材料力学中,材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料发生弹性变形的应力D. 材料发生脆性断裂的应力答案:A4. 材料的疲劳寿命与下列哪一项无关?A. 材料的疲劳极限B. 应力循环次数C. 材料的弹性模量D. 应力循环的幅度答案:C5. 在材料力学中,下列哪一项不是材料的力学性能指标?A. 硬度B. 韧性C. 密度D. 冲击韧性答案:C二、简答题(每题5分,共10分)6. 简述材料力学中弹性模量和剪切模量的区别。
答:弹性模量,也称为杨氏模量,是描述材料在受到正应力作用时,材料的纵向应变与应力成正比的比例系数。
剪切模量,也称为刚度模量,是描述材料在受到剪切应力作用时,材料的剪切应变与剪切应力成正比的比例系数。
7. 什么是材料的疲劳寿命,它与哪些因素有关?答:材料的疲劳寿命是指材料在反复加载和卸载过程中,从开始加载到发生疲劳断裂所需的循环次数。
它与材料的疲劳极限、应力循环的幅度、材料的微观结构和环境因素等有关。
三、计算题(每题15分,共30分)8. 一根直径为20mm的圆杆,材料的杨氏模量为200GPa,当受到100N的拉力时,求圆杆的伸长量。
答:首先计算圆杆的截面积A = π * (d/2)^2 = π * (0.02/2)^2m^2 = 3.14 * 0.01 m^2。
然后根据胡克定律ΔL = F * L / (A * E),其中 L 为杆长,假设 L = 1m,代入数值得ΔL = 100 * 1 / (3.14* 0.01 * 200 * 10^9) m = 7.96 * 10^-6 m。

1第1页共28页2010— 2011材料力学试题及答案 A、单选题(每小题2分,共10小题,20 分)1、 工程构件要正常安全的工作,必须满足一定的条件。
下列除( 须满足的条件。
A 、强度条件 B 、刚度条件2、 内力和应力的关系是( ) A 、内力大于应力 C 、内力是矢量,应力是标量 C 、稳定性条件 D 、硬度条件 B 、内力等于应力的代数和 D 、应力是分布内力的集度3、 根据圆轴扭转时的平面假设,可以认为圆轴扭转时横截面( )。
)项,其他各项是必 A 、形状尺寸不变,直径线仍为直线。
B 、形状尺寸改变, 形状尺寸不变,直径线不保持直线。
D 、形状尺寸改变, 建立平面弯曲正应力公式 ,需要考虑的关系有(C 、 直径线仍为直线。
直径线不保持直线。
平衡关系,物理关系,变形几何关系;B 、变形几何关系,物理关系,静力关系;C 、变形几何关系,平衡关系,静力关系;D 、平衡关系,物理关系,静力关系; 5、利用积分法求梁的变形,不需要用到下面那类条件( )来确定积分常数。
A 、平衡条件。
B 、边界条件。
C 、连续性条件。
光滑性条件。
6、图示交变应力的循环特征r 、平均应力b m、应力幅度 6分别为()。
A -10、20、10; C 3、20、10;30、10、20; 13、10、20。
7、一点的应力状态如下图所示,则其主应力A B C D B 、3压杆临界力的大小,()。
与压杆所承受的轴向压力大小有关; 与压杆的柔度大小有关;与压杆材料无关;与压杆的柔度大小无关。
6、b 2、b 3 分别为()。
10、利用图乘法计算弹性梁或者刚架的位移, 要求结构满足三个条件。
以下那个条件不是必须的()A 、El 为常量B 、结构轴线必须为直线。
30MPa 、100 MPa 、50 MPa 50 MPa 、30MPa 、-50MPa 50 MPa 、0、-50Mpa 、 -50 MPa 、30MPa 、50MPa&对于突加载的情形,系统的动荷系数为(C 、4A 、29、A B C D I so MPa30 MPaC、M图必须是直线。

材料⼒学试题和答案解析7套材料⼒学试卷1⼀、绘制该梁的剪⼒、弯矩图。
(15分)⼆、梁的受⼒如图,截⾯为T 字型,材料的许⽤拉应⼒[σ+]=40MPa ,许⽤压应⼒[σ-]=100MPa 。
试按正应⼒强度条件校核梁的强度。
(20分)m8m 2m2M三、求图⽰单元体的主应⼒及其⽅位,画出主单元体和应⼒圆。
(15分)四、图⽰偏⼼受压柱,已知截⾯为矩形,荷载的作⽤位置在A 点,试计算截⾯上的最⼤压应⼒并标出其在截⾯上的位置,画出截⾯核⼼的形状。
(15分) 30170302002m3m1m30五、结构⽤低碳钢A 3制成,A 端固定,B 、C 为球型铰⽀,求:允许荷载[P]。
已知:E=205GPa ,σs =275MPa ,σcr=338-1.12λ,,λp =90,λs =50,强度安全系数n=2,稳定安全系数n st =3,AB 梁为N 016⼯字钢,I z =1130cm 4,W z =141cm 3,BC 杆为圆形截⾯,直径d=60mm 。
(20分)六、结构如图所⽰。
已知各杆的EI 相同,不考虑剪⼒和轴⼒的影响,试求:D 截⾯的线位移和⾓位移。
(15分)材料⼒学2⼀、回答下列各题(共4题,每题4分,共16分)1、已知低碳钢拉伸试件,标距mm l 1000=,直径mm d 10=,拉断后标距的长度变为mm l 1251=,断⼝处的直径为mm d 0.61=,试计算其延伸率和断⾯收缩率。
2、试画出图⽰截⾯弯曲中⼼的位置。
aa3、梁弯曲剪应⼒的计算公式zzQS =τ,若要计算图⽰矩形截⾯A 点的剪应⼒,试计算z S 。
4、试定性画出图⽰截⾯截⾯核⼼的形状(不⽤计算)。
4/h矩形圆形矩形截⾯中间挖掉圆形圆形截⾯中间挖掉正⽅形⼆、绘制该梁的剪⼒、弯矩图。
(15分)三、图⽰⽊梁的右端由钢拉杆⽀承。
已知梁的横截⾯为边长等于0.20m 的正⽅形,q=4OKN/m,弹性模量E 1=10GPa ;钢拉杆的横截⾯⾯积A 2=250mm 2,弹性模量E 2=210GPa 。

一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 硬度D. 韧性2. 材料在拉伸过程中,当应力达到屈服点后,材料将:A. 断裂B. 产生永久变形C. 恢复原状D. 保持不变3. 材料的弹性模量是指:A. 材料的密度B. 材料的硬度C. 材料的抗拉强度D. 材料在弹性范围内应力与应变的比值4. 根据材料力学的胡克定律,下列说法正确的是:A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成线性关系5. 材料的疲劳寿命是指:A. 材料的总寿命B. 材料在循环加载下达到破坏的周期数C. 材料的断裂寿命D. 材料的磨损寿命6. 材料的屈服强度是指:A. 材料在弹性范围内的最大应力B. 材料在塑性变形开始时的应力C. 材料的抗拉强度D. 材料的极限强度7. 材料的断裂韧性是指:A. 材料的硬度B. 材料的抗拉强度C. 材料抵抗裂纹扩展的能力D. 材料的屈服强度8. 材料力学中的泊松比是指:A. 材料的弹性模量B. 材料的屈服强度C. 材料在拉伸时横向应变与纵向应变的比值D. 材料的断裂韧性9. 在材料力学中,下列哪一项是衡量材料脆性程度的指标?A. 弹性模量B. 屈服强度C. 断裂韧性D. 泊松比10. 材料在受力过程中,当应力超过其极限强度时,将:A. 发生弹性变形B. 发生塑性变形C. 发生断裂D. 恢复原状答案1. C2. B3. D4. A5. B6. B7. C8. C9. C10. C试题二、简答题(每题10分,共30分)1. 简述材料力学中材料的三种基本力学性质。
2. 解释什么是材料的疲劳现象,并简述其对工程结构的影响。
3. 描述材料在拉伸过程中的四个主要阶段。
答案1. 材料的三种基本力学性质包括弹性、塑性和韧性。
弹性指的是材料在受到外力作用时发生变形,当外力移除后能够恢复原状的性质。
塑性是指材料在达到一定应力水平后,即使外力移除也无法完全恢复原状的性质。

材料力学的试题及答案一、选择题1. 材料力学中,下列哪个选项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案:D2. 根据材料力学的理论,下列哪个选项是正确的?A. 材料在弹性范围内,应力与应变成正比B. 材料在塑性变形后可以完全恢复原状C. 材料的屈服强度总是高于其抗拉强度D. 材料的硬度与弹性模量无关答案:A二、填空题1. 材料力学中,应力是指_______与_______的比值。
答案:单位面积上的压力;受力面积2. 在材料力学中,材料的弹性模量E与_______成正比,与_______成反比。
答案:杨氏模量;泊松比三、简答题1. 简述材料力学中材料的三种基本变形类型。
答案:材料力学中材料的三种基本变形类型包括拉伸、压缩和剪切。
2. 描述材料的弹性模量和屈服强度的区别。
答案:弹性模量是指材料在弹性范围内应力与应变的比值,反映了材料的刚性;屈服强度是指材料开始发生永久变形时的应力值,反映了材料的韧性。
四、计算题1. 已知一材料的弹性模量E=200 GPa,杨氏模量E=210 GPa,泊松比ν=0.3,试计算该材料的剪切模量G。
答案:G = E / (2(1+ν)) = 200 / (2(1+0.3)) = 200 / 2.6 ≈ 76.92 GPa2. 某材料的抗拉强度为σt=300 MPa,若该材料承受的应力为σ=200 MPa,试判断材料是否发生永久变形。
答案:由于σ < σt,材料不会发生永久变形。
五、论述题1. 论述材料力学在工程设计中的重要性。
答案:材料力学是工程设计中的基础学科,它提供了对材料在力作用下行为的深入理解。
通过材料力学的分析,工程师可以预测材料在各种载荷下的响应,设计出既安全又经济的结构。
此外,材料力学还有助于新材料的开发和现有材料性能的优化。
2. 讨论材料的疲劳寿命与其力学性能之间的关系。
答案:材料的疲劳寿命与其力学性能密切相关。
材料的疲劳寿命是指在循环载荷作用下材料能够承受的循环次数。

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,弹性模量E的单位是()。
A. N/mB. N·mC. PaD. m/N答案:C2. 材料力学中,材料的屈服强度通常用()表示。
A. σyB. σsC. σbD. E答案:A3. 根据胡克定律,当应力超过材料的弹性极限时,材料将()。
A. 保持弹性B. 发生塑性变形C. 发生断裂D. 无法预测答案:B4. 材料力学中,第一强度理论认为材料破坏的原因是()。
A. 最大正应力B. 最大剪应力C. 最大正应变D. 最大剪应变答案:A5. 下列哪种材料不属于脆性材料()。
A. 玻璃B. 铸铁C. 混凝土D. 铝答案:D6. 材料力学中,梁的弯曲应力公式为()。
A. σ = Mc/IB. σ = Mc/IbC. σ = Mc/ID. σ = Mc/Ib答案:C7. 在材料力学中,梁的剪应力公式为()。
A. τ = VQ/IB. τ = VQ/ItC. τ = VQ/ID. τ = VQ/It答案:B8. 材料力学中,梁的挠度公式为()。
A. δ = (5PL^3)/(384EI)B. δ = (5PL^3)/(384EI)C. δ = (PL^3)/(48EI)D. δ = (PL^3)/(48EI)答案:C9. 材料力学中,影响材料屈服强度的因素不包括()。
A. 材料的微观结构B. 加载速度C. 温度D. 材料的密度答案:D10. 材料力学中,影响材料疲劳强度的因素不包括()。
A. 应力集中B. 表面粗糙度C. 材料的硬度D. 材料的导热性答案:D二、填空题(每题2分,共20分)1. 材料力学中,材料在外力作用下,其形状和尺寸发生的变化称为______。
答案:变形2. 材料力学中,材料在外力作用下,其内部产生的相互作用力称为______。
答案:应力3. 材料力学中,材料在外力作用下,其内部产生的相对位移称为______。
答案:应变4. 材料力学中,材料在外力作用下,其内部产生的单位面积上的力称为______。
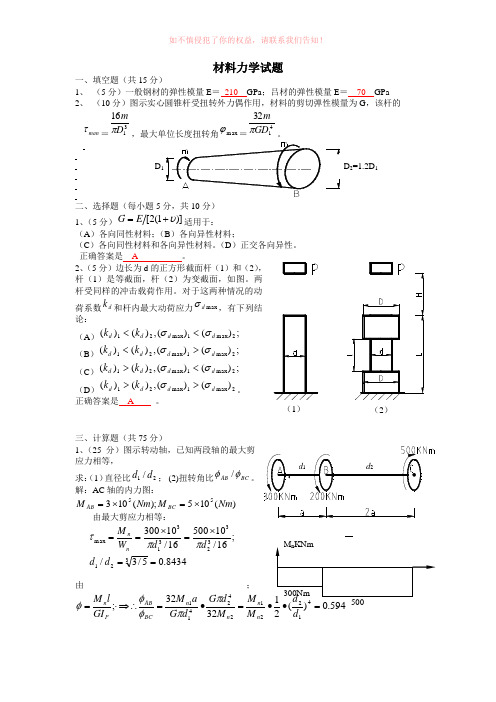
材料力学试题一、填空题(共15分)1、 (5分)一般钢材的弹性模量E = 210 GPa ;吕材的弹性模量E = 70 GPa2、 (10分)图示实心圆锥杆受扭转外力偶作用,材料的剪切弹性模量为G ,该杆的man τ1、(5(A )各向同性材料;(B )各向异性材料; (C 正确答案是 A 。
2、(5分)边长为d 杆(1)是等截面,杆(2荷系数d k 和杆内最大动荷应力d σ论:(A )()(,)()(1max 21d d d k k σ<<(B )()(,)()(1max 21d d d k k σ><(C )()(,)()(1max 21d d d k k σ<>(D )1max 21()(,)()(d d d k k σ>>正确答案是 A 。
三、计算题(共75分) 1、(25应力相等,求:(1)直径比21/d d ; (2)扭转角比AB φ解:AC 轴的内力图:(105);(10355M Nm M BC AB ⨯=⨯= 由最大剪应力相等:8434.05/3/16/1050016/10300321323313max==⨯=⨯==d d d d W M n n ππτ 由;594.0)(23232;41221242411=••=•=⇒∴⋅=d M M M d G d G a M GI l M n n n n BC AB P n ππφφφ(2)2、(3、(15分)有一厚度为6mm 的钢板在板面的两个垂直方向受拉,拉应力分别为150Mpa 和55Mpa ,材料的E=2.1×105Mpa ,υ =0.25。
求钢板厚度的减小值。
解:钢板厚度的减小值应为横向应变所产生,该板受力后的应力状态为二向应力状态,由广义胡克定律知,其Z 向应变为:0244.010)55150(101.225.0)(69-=⨯+⨯-=+-=y x z E σσνε则 mm t Z Z 146.0-=⨯=∆ε(本资料素材和资料部分来自网络,仅供参考。

材料力学试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是均匀的D. 材料是线弹性的答案:A2. 在材料力学中,下列哪个公式表示杆件的正应力?A. σ = F/AB. τ = F/AC. σ = F/LD. τ = F/L答案:A3. 当材料受到轴向拉伸时,下列哪个选项是正确的?A. 拉伸变形越大,材料的强度越高B. 拉伸变形越小,材料的强度越高C. 拉伸变形与材料的强度无关D. 拉伸变形与材料的强度成正比答案:B4. 下列哪种材料在拉伸过程中容易发生断裂?A. 钢材B. 铸铁C. 铝合金D. 塑料答案:B5. 下列哪个选项表示材料的泊松比?A. μ = E/GB. μ = G/EC. μ = σ/εD. μ = ε/σ答案:C二、填空题(每题10分,共30分)6. 材料力学研究的是材料在______作用下的力学性能。
答案:外力7. 材料的强度分为______强度和______强度。
答案:屈服强度、断裂强度8. 材料在受到轴向拉伸时,横截面上的正应力公式为______。
答案:σ = F/A三、计算题(每题25分,共50分)9. 一根直径为10mm的圆钢杆,受到轴向拉伸力F=20kN 的作用,求杆件横截面上的正应力。
解:已知:d = 10mm,F = 20kNA = π(d/2)^2 = π(10/2)^2 = 78.5mm^2σ = F/A = 20kN / 78.5mm^2 = 255.8N/mm^2答案:杆件横截面上的正应力为255.8N/mm^2。
10. 一根长度为1m的杆件,受到轴向拉伸力F=10kN的作用,已知材料的弹性模量E=200GPa,泊松比μ=0.3,求杆件的伸长量。
解:已知:L = 1m,F = 10kN,E = 200GPa,μ = 0.3ε = F/(EA) = 10kN / (200GPa × π(10mm)^2) =0.025δ = εL = 0.025 × 1000mm = 25mm答案:杆件的伸长量为25mm。

一、判断题(正确打“√",错误打“X ”,本题满分为10分) 1、拉杆伸长后,横向会缩短,这是因为杆有横向应力的存在。
( )2、圆截面杆件受扭时,横截面上的最大切应力发生在横截面离圆心最远处。
( )3、两梁的跨度、承受载荷及支承相同,但材料和横截面面积不同,因而两梁的剪力图和弯矩图不一定相同.( )4、交变应力是指构件内的应力,它随时间作周期性变化,而作用在构件上的载荷可能是动载荷,也可能是静载荷.( )5、弹性体的应变能与加载次序无关,只与载荷的最终值有关。
( )6、单元体上最大切应力作用面上必无正应力.( )7、平行移轴公式表示图形对任意两个相互平行轴的惯性矩和惯性积之间的关系。
( ) 8、动载荷作用下,构件内的动应力与材料的弹性模量有关。
( )9、构件由突加载荷所引起的应力,是由相应的静载荷所引起应力的两倍.( ) 10、包围一个点一定有一个单元体,该单元体各个面上只有正应力而无切应力.( ) 二、选择题(每个2分,本题满分16分)1.应用拉压正应力公式A FN =σ的条件是( )。
A 、应力小于比例极限;B 、外力的合力沿杆轴线;C 、应力小于弹性极限;D 、应力小于屈服极限.2.梁拟用图示两种方式搁置,则两种情况下的最大弯曲正应力之比 )(m ax )(m ax b a σσ 为( )。
A 、1/4; B 、1/16; C 、1/64; D3、关于弹性体受力后某一方向的应力与应变关系有如下论述:正确的是。
A 、有应力一定有应变,有应变不一定有应力; B 、有应力不一定有应变,有应变不一定有应力; C 、有应力不一定有应变,有应变一定有应力; D 、有应力一定有应变,有应变一定有应力。
4、火车运动时,其轮轴横截面边缘上危险点的应力有四种说法,正确的是 . A :脉动循环应力: B :非对称的循环应力; C :不变的弯曲应力;D :对称循环应力5、如图所示的铸铁制悬臂梁受集中力F 作用,其合理的截面形状应为图( )(a) (b)6、对钢制圆轴作扭转校核时,发现强度和刚度均比规定的要求低了20%,若安全因数不变,改用屈服极限提高了30%的钢材,则圆轴的( ) A 、 强度、刚度均足够;B 、强度不够,刚度足够; C 、强度足够,刚度不够;D 、强度、刚度均不够。

材料⼒学试题及答案选择题(20分)1、图⽰刚性梁AB由杆1和杆2⽀承,已知两杆的材料相同,长度不等,横截⾯积分别为A1和A2,若载荷P使刚梁平⾏下移,则其横截⾯⾯积()。
A、A1〈A2B、A1〉A2C、A1=A2D、A1、A2为任意2、建⽴圆周的扭转应⼒公式τρ=Mρρ/Iρ时需考虑下列因素中的哪⼏个答:()(1)扭矩MT 与剪应⼒τρ的关系MT=∫AτρρdA(2)变形的⼏何关系(即变形协调条件)(3)剪切虎克定律(4)极惯性矩的关系式IT =∫Aρ2dAA、(1)B、(1)(2)C、(1)(2)(3)D、全部3、⼆向应⼒状态如图所⽰,其最⼤主应⼒σ1=()A、σB、2σC、3σD、4σ4、⾼度等于宽度两倍(h=2b)的矩形截⾯梁,承受垂直⽅向的载荷,若仅将竖放截题⼀、3图题⼀、4题⼀、1图⾯改为平放截⾯,其它条件都不变,则梁的强度()A、提⾼到原来的2倍B、提⾼到原来的4倍C、降低到原来的1/2倍D、降低到原来的1/4倍5. 已知图⽰⼆梁的抗弯截⾯刚度EI相同,若⼆者⾃由端的挠度相等,则P1/P2=()A、2C、8D、16⼆、作图⽰梁的剪⼒图、弯矩图。
(15分)三、如图所⽰直径为d的圆截⾯轴,其两端承受扭转⼒偶矩m的作⽤。
设由实验测的轴表⾯上与轴线成450⽅向的正应变,试求⼒偶矩m之值、材料的弹性常数E、µ均为已知。
(15分)题⼀、5图三题图⼆题图四、电动机功率为9kW,转速为715r/min,⽪带轮直径D=250mm,主轴外伸部分长度为l=120mm,主轴直径d=40mm,〔σ〕=60MPa,⽤第三强度理论校核轴的强度。
(15分)五、重量为Q的重物⾃由下落在图⽰刚架C点,设刚架的抗弯刚度为EI,试求冲击时刚架D处的垂直位移。
(15分)六、结构如图所⽰,P=15kN,已知梁和杆为⼀种材料,E=210GPa。
梁ABC的惯性矩I=245cm4,等直圆杆BD的直径D=40mm。
规定杆BD的稳定安全系数nst求○1BD杆承受的压⼒。

材料力学试题及答案一、选择题1. 材料力学中,下列哪个参数是用来描述材料在受力时抵抗变形的能力?A. 弹性模量B. 屈服强度C. 抗拉强度D. 断裂韧性答案:A2. 以下哪种材料在受力后能够完全恢复原状?A. 弹性体B. 塑性体C. 粘弹性体D. 脆性体答案:A3. 应力集中现象主要发生在哪种情况下?A. 材料表面存在缺陷B. 材料内部存在孔洞C. 材料受到均匀分布的载荷D. 材料受到单一集中载荷答案:D4. 根据胡克定律,当应力不超过比例极限时,应力与应变之间的关系是:A. 线性的B. 非线性的C. 指数的D. 对数的答案:A5. 材料的疲劳破坏是指在何种条件下发生的?A. 单次超负荷B. 长期重复载荷C. 瞬间高温D. 腐蚀环境答案:B二、填空题1. 在简单的拉伸和压缩实验中,应力(σ)是力(F)与横截面积(A)的比值,即σ=______。
答案:F/A2. 材料的韧性是指其在断裂前能够吸收的能量,通常通过______试验来测定。
答案:冲击3. 当材料在受力时发生塑性变形,且变形量随时间增加而增加,这种现象称为______。
答案:蠕变4. 剪切应力τ是剪切力(V)与剪切面积(A)的比值,即τ=______。
答案:V/A5. 材料的泊松比是指在单轴拉伸时,横向应变与纵向应变的比值,通常用希腊字母______表示。
答案:ν三、简答题1. 请简述材料弹性模量的定义及其物理意义。
答:弹性模量,又称杨氏模量,是指材料在弹性范围内抵抗形变的能力的量度。
它定义为应力与相应应变的比值。
物理意义上,弹性模量越大,表示材料在受力时越不易发生形变,即材料越硬。
2. 描述材料的屈服现象,并解释屈服强度的重要性。
答:屈服现象是指材料在受到外力作用时,由弹性状态过渡到塑性状态的过程。
在这个过程中,材料首先经历弹性变形,当应力达到某个特定值时,即使应力不再增加,材料也会继续发生显著的塑性变形。
屈服强度是衡量材料开始屈服的应力值,它对于工程设计和材料选择具有重要意义,因为它决定了结构在载荷作用下的安全性和可靠性。

本科材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 导电性答案:D2. 根据胡克定律,当应力增加时,应变将如何变化?A. 减少B. 增加C. 不变D. 无法确定答案:B3. 在材料力学中,下列哪种情况下材料不会发生塑性变形?A. 应力超过屈服强度B. 应力超过弹性极限C. 应力低于屈服强度D. 应力低于弹性极限答案:C4. 材料力学中,哪个参数描述了材料抵抗剪切变形的能力?A. 弹性模量B. 剪切模量C. 泊松比D. 屈服强度答案:B5. 材料的疲劳寿命主要取决于哪些因素?A. 材料的弹性模量B. 材料的屈服强度C. 材料的疲劳极限D. 材料的硬度答案:C6. 根据材料力学理论,下列哪种材料的应力-应变曲线最接近理想弹性体?A. 橡胶B. 钢铁C. 玻璃D. 木材答案:C7. 材料力学中,下列哪种试验可以确定材料的弹性模量?A. 压缩试验B. 拉伸试验C. 冲击试验D. 疲劳试验答案:B8. 在材料力学中,下列哪种情况下材料的应力状态是平面应力?A. 材料厚度远小于平面尺寸B. 材料厚度远大于平面尺寸C. 材料受到均匀的三向应力D. 材料受到非均匀的三向应力答案:A9. 材料力学中,下列哪种材料的应力-应变曲线不具有明显的屈服点?A. 低碳钢B. 高碳钢C. 铝合金D. 铜合金答案:C10. 材料力学中,下列哪种材料的应力-应变曲线不具有明显的弹性阶段?A. 橡胶B. 钢铁C. 玻璃D. 木材答案:A二、填空题(每题2分,共20分)1. 材料力学中的______定律描述了在弹性范围内,应力与应变成正比的关系。
答案:胡克2. 材料的______是材料在受到外力作用下不发生永久变形的最大应力。
答案:弹性极限3. 泊松比是描述材料在______方向上的应变与______方向上的应变之比。
答案:横向;纵向4. 材料力学中,材料的______是指材料在受到重复加载时,其强度会逐渐降低直至断裂的现象。
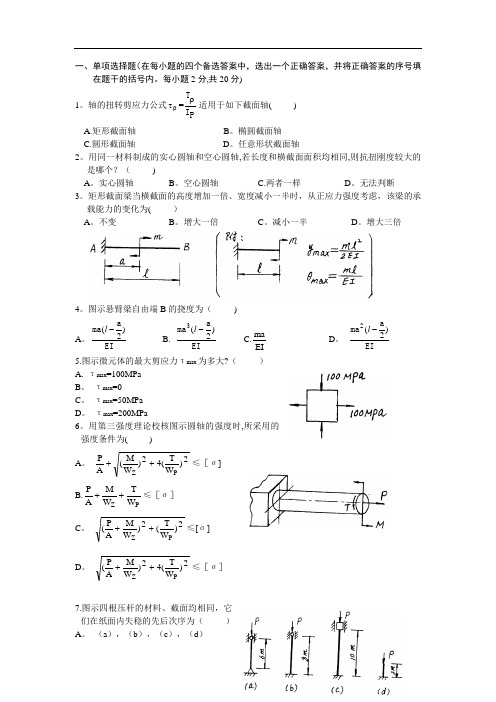
一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共20分) 1。
轴的扭转剪应力公式τρ=T I Pρ适用于如下截面轴( ) A.矩形截面轴 B 。
椭圆截面轴C.圆形截面轴 D 。
任意形状截面轴2。
用同一材料制成的实心圆轴和空心圆轴,若长度和横截面面积均相同,则抗扭刚度较大的是哪个?( )A 。
实心圆轴B 。
空心圆轴 C.两者一样 D 。
无法判断3。
矩形截面梁当横截面的高度增加一倍、宽度减小一半时,从正应力强度考虑,该梁的承载能力的变化为( )A 。
不变B 。
增大一倍C 。
减小一半D 。
增大三倍4。
图示悬臂梁自由端B 的挠度为( )A 。
ma a EI ()l -2 B. ma a EI 32()l - C.ma EID 。
ma a EI 22()l - 5.图示微元体的最大剪应力τmax 为多大?( )A. τmax =100MPaB 。
τmax =0C 。
τmax =50MPaD 。
τmax =200MPa6。
用第三强度理论校核图示圆轴的强度时,所采用的强度条件为( )A 。
P A M W T W Z P++()()242≤[σ] B.P A M W T W Z P++≤[σ] C 。
()()P A M W T W Z P++22≤[σ] D 。
()()P A M W T W Z P ++242≤[σ]7.图示四根压杆的材料、截面均相同,它们在纸面内失稳的先后次序为( )A 。
(a ),(b ),(c ),(d )B。
(d),(a),(b),(c)C。
(c),(d),(a),(b)D。
(b),(c),(d),(a)8。
图示杆件的拉压刚度为EA,在图示外力作用下其变形能U的下列表达式哪个是正确的?()A。
U=P a EA2 2B。
U=PEAP bEA 22 22l+C。
U=PEAP bEA 22 22l-D. U=PEAP bEA 22 22 a+9图示两梁抗弯刚度相同,弹簧的刚度系数也相同,则两梁中最大动应力的关系为()A. (σd)a =(σd) bB。

材料力学考试试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 硬度2. 材料在拉伸过程中,若应力超过屈服点后继续增加,材料将进入:A. 弹性阶段B. 塑性阶段C. 断裂阶段D. 疲劳阶段3. 材料的弹性模量E表示的是:A. 材料的硬度B. 材料的韧性C. 材料的弹性程度D. 材料的屈服强度4. 根据材料力学理论,下列哪一项不是材料的疲劳破坏特点?A. 疲劳破坏是局部的B. 疲劳破坏是突然的C. 疲劳破坏是可预测的D. 疲劳破坏是累积的5. 在材料力学中,下列哪一项不是材料的失效模式?A. 屈服B. 断裂C. 腐蚀D. 疲劳6. 材料的屈服强度和抗拉强度之间的关系是:A. 屈服强度总是大于抗拉强度B. 屈服强度总是小于抗拉强度C. 屈服强度等于抗拉强度D. 两者之间没有固定关系7. 材料的疲劳寿命与下列哪一项无关?A. 应力水平B. 材料的微观结构C. 环境温度D. 材料的密度8. 材料的冲击韧性通常用下列哪一项来表示?A. 抗拉强度B. 屈服强度C. 硬度D. 冲击吸收能量9. 材料的疲劳寿命与加载频率的关系是:A. 正相关B. 负相关C. 无关D. 先正相关后负相关10. 在材料力学中,下列哪一项不是材料的应力-应变曲线的特点?A. 弹性阶段B. 屈服阶段C. 塑性阶段D. 线性阶段二、简答题(每题10分,共20分)1. 请简述材料的弹性模量和屈服强度的区别和联系。
2. 材料的疲劳破坏与静载下的破坏有何不同?三、计算题(每题15分,共30分)1. 已知一材料的弹性模量E=200 GPa,泊松比ν=0.3。
若材料受到拉伸力F=10 kN,试计算材料的应变ε和应力σ。
2. 某材料的疲劳寿命S-N曲线已知,当应力水平为σ=200 MPa时,疲劳寿命N=1000次。
若应力水平降低到150 MPa,根据Basis Goodman关系,计算新的疲劳寿命。

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪个选项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 硬度2. 材料在受到外力作用时,若外力移除后材料能恢复原状,则该材料表现出的特性是:A. 塑性B. 弹性C. 脆性D. 韧性3. 材料力学中,下列哪种应力不是基本应力类型?A. 正应力B. 剪应力C. 拉应力D. 弯应力4. 材料的屈服强度是指:A. 材料开始发生永久变形的应力B. 材料发生断裂的应力C. 材料开始发生弹性变形的应力D. 材料发生塑性变形的应力5. 根据材料力学的胡克定律,当材料受到正应力作用时,其应变与应力的关系是:A. 正比B. 反比C. 无关系D. 非线性关系6. 材料力学中,下列哪种情况下材料的应力状态是平面应力?A. 材料的三个主应力中有一个为零B. 材料的三个主应力都非零C. 材料的三个主应力中有两个为零D. 材料的三个主应力都为零7. 材料力学中,下列哪个选项不是材料的疲劳破坏的特点?A. 循环加载B. 低应力水平C. 无明显征兆D. 应力水平高8. 材料在受到拉伸时,其横截面积的变化趋势是:A. 增加B. 减小C. 不变D. 先增加后减小9. 材料力学中,下列哪个选项不是材料的疲劳寿命的影响因素?A. 应力水平B. 材料的微观结构C. 材料的宏观结构D. 材料的化学成分10. 材料力学中,下列哪个选项不是材料的疲劳破坏的预防措施?A. 避免应力集中B. 提高应力水平C. 采用表面处理D. 选择适当的材料答案:1-5 DBBCA 6-10 ACCBD二、简答题(每题10分,共30分)1. 简述材料力学中材料的弹性模量和剪切模量的定义及其物理意义。
答:弹性模量,也称为杨氏模量,是材料在受到正应力作用时,其应力与应变的比值。
它反映了材料抵抗变形的能力,数值越大,表示材料越硬。
剪切模量,也称为刚度模量,是材料在受到剪应力作用时,其应力与剪应变的比值。

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学主要研究的是材料在外力作用下的______。
A. 化学变化B. 物理变化C. 力学性质D. 热学性质2. 材料力学中,应力的定义是单位面积上的______。
A. 力B. 位移C. 速度D. 加速度3. 弹性模量是描述材料______的物理量。
A. 弹性B. 塑性C. 韧性D. 硬度4. 材料力学中,材料的屈服强度是指材料在______条件下的应力。
A. 弹性变形B. 永久变形C. 断裂D. 疲劳5. 材料力学中,拉压杆件的承载能力主要取决于其______。
A. 长度B. 直径C. 材料种类D. 表面处理6. 材料力学中,剪切应力的计算公式是______。
A. τ = F/AB. τ = F/LC. τ = Fb/AD. τ = Fb/L7. 材料力学中,梁的弯曲问题主要考虑的是______。
A. 材料的弹性模量B. 梁的截面形状C. 梁的长度D. 梁的重量8. 材料力学中,疲劳破坏是指材料在______作用下发生的破坏。
A. 静载荷B. 动载荷C. 冲击载荷D. 温度变化9. 材料力学中,材料的断裂韧性是指材料在______条件下的抗断裂能力。
A. 静载荷B. 动载荷C. 冲击载荷D. 疲劳10. 材料力学中,安全系数是指实际承载能力与______的比值。
A. 设计载荷B. 最大载荷C. 极限载荷D. 疲劳载荷答案:1-5 C A A B B 6-10 C B B D C二、填空题(每空1分,共10分)1. 材料力学中的______是指材料在受到外力作用时,其形状和尺寸发生改变的能力。
2. 当材料受到的应力超过其______时,材料将发生永久变形。
3. 在材料力学中,______是指材料在受到外力作用时,其内部各点的应力状态。
4. 材料力学中,______是指材料在受到外力作用时,其内部各点的位移状态。
5. 材料力学中,______是指材料在受到外力作用时,其内部各点的应变状态。

材料力学的试题及答案一、选择题(每题2分,共20分)1. 材料力学研究的对象是什么?A. 材料的化学性质B. 材料的力学性质C. 材料的热学性质D. 材料的电学性质2. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 韧性C. 硬度D. 塑性3. 材料力学中,应力的定义是什么?A. 力与面积的比值B. 力与体积的比值C. 力与长度的比值D. 面积与力的比值4. 材料力学中,下列哪一项不是材料的基本变形形式?A. 拉伸B. 压缩C. 扭转D. 膨胀5. 材料力学中,弹性模量表示什么?A. 材料的硬度B. 材料的韧性C. 材料的弹性D. 材料的塑性二、简答题(每题10分,共30分)6. 简述材料力学中材料的三种基本力学性质。
7. 解释材料力学中的应力-应变曲线,并说明其各阶段的意义。
8. 什么是材料的屈服强度,它在工程设计中的重要性是什么?三、计算题(每题25分,共50分)9. 一根直径为20mm,长度为200mm的圆杆,在两端受到100kN的拉伸力。
如果材料的弹性模量为200GPa,求圆杆的伸长量。
10. 一个直径为50mm,长为100mm的空心圆筒,内径为40mm,受到一个扭矩为500N·m。
如果材料的剪切模量为80GPa,求圆筒的最大剪切应力。
答案一、选择题1. B. 材料的力学性质2. C. 硬度3. A. 力与面积的比值4. D. 膨胀5. C. 材料的弹性二、简答题6. 材料力学中材料的三种基本力学性质包括弹性、塑性和韧性。
弹性是指材料在受到外力作用后能恢复原状的能力;塑性是指材料在达到一定应力后,即使撤去外力也不会完全恢复原状的性质;韧性是指材料在断裂前能吸收和分散能量的能力。
7. 应力-应变曲线是描述材料在受力过程中应力与应变之间关系的曲线。
它通常包括弹性阶段、屈服阶段、强化阶段和颈缩阶段。
弹性阶段表示材料在受力后能够完全恢复原状;屈服阶段是材料开始产生永久变形的点;强化阶段是材料在屈服后继续承受更大的应力而不断裂;颈缩阶段是材料接近断裂前发生的局部变细现象。
一、判断题(正确打“√”,错误打“X ”,本题满分为10分) 1、拉杆伸长后,横向会缩短,这是因为杆有横向应力的存在。
( )2、圆截面杆件受扭时,横截面上的最大切应力发生在横截面离圆心最远处。
( )3、两梁的跨度、承受载荷及支承相同,但材料和横截面面积不同,因而两梁的剪力图和弯矩图不一定相同。
( )4、交变应力是指构件内的应力,它随时间作周期性变化,而作用在构件上的载荷可能是动载荷,也可能是静载荷。
( )5、弹性体的应变能与加载次序无关,只与载荷的最终值有关。
( )6、单元体上最大切应力作用面上必无正应力。
( )7、平行移轴公式表示图形对任意两个相互平行轴的惯性矩和惯性积之间的关系。
( ) 8、动载荷作用下,构件内的动应力与材料的弹性模量有关。
( )9、构件由突加载荷所引起的应力,是由相应的静载荷所引起应力的两倍。
( ) 10、包围一个点一定有一个单元体,该单元体各个面上只有正应力而无切应力。
( ) 二、选择题(每个2分,本题满分16分)1.应用拉压正应力公式A FN =σ的条件是( )。
A 、应力小于比例极限;B 、外力的合力沿杆轴线;C 、应力小于弹性极限;D 、应力小于屈服极限。
2.梁拟用图示两种方式搁置,则两种情况下的最大弯曲正应力之比 )(m ax )(m ax b a σσ 为( )。
A 、1/4; B 、1/16; C 、1/64; D3、关于弹性体受力后某一方向的应力与应变关系有如下论述:正确的是。
A 、有应力一定有应变,有应变不一定有应力;B 、有应力不一定有应变,有应变不一定有应力;C 、有应力不一定有应变,有应变一定有应力;D 、有应力一定有应变,有应变一定有应力。
4、火车运动时,其轮轴横截面边缘上危险点的应力有四种说法,正确的是 。
A :脉动循环应力: B :非对称的循环应力; C :不变的弯曲应力;D :对称循环应力5、如图所示的铸铁制悬臂梁受集中力F 作用,其合理的截面形状应为图( )(a)(b)6、对钢制圆轴作扭转校核时,发现强度和刚度均比规定的要求低了20%,若安全因数不变,改用屈服极限提高了30%的钢材,则圆轴的( ) A 、 强度、刚度均足够;B 、强度不够,刚度足够; C 、强度足够,刚度不够;D 、强度、刚度均不够。
7、图示拉杆的外表面上有一斜线,当拉杆变形时,斜线将 。
A :平动 ;B :转动 C :不动; D :平动加转动8、按照第三强度理论,比较图中两个应力状态的相当应力正确的是( )。
(图中应力单位为MPa )A 、两者相同;B 、(a )大; B 、C 、(b )大;D 、无法判断 一、判断:× √ × × √ × × √ √ √二、选择:B A C D B C D A 三、简要计算与回答(12分)1.标距为100mm 的标准试件,直径为10mm ,拉断后测得伸长后的标矩为123mm ,颈缩处的最小直径为,试计算该材料的延伸率和截面收缩率各为多少。
延伸率:100100100123⨯-=δ%=23%截面收缩率:1001044.6104222⨯⋅-=ππϕ)(%=% 2.如图所示圆截面轴,B 截面上有2M 0作用,C 截面有力偶M 0作用,圆截面的直径为d ,试求C 截面相对A 截面的扭转角CA和整个圆轴最大扭转剪应力max。
轴的扭矩图为:则扭转角0)(00=+-==∑pp i CA GI aM GI a M ϕϕ整个圆轴最大扭转剪应力max330m ax m ax1616d M d M W T t ππτ===3、求图示单元体指定截面上的正应力和切应力(图中单位为MPa )MPa x 30=σ MPa y 50=σ MPa x 120-=τ ︒=30αMPa 9.13860sin )120(60cos 2503025030=︒--︒-++=ασ MPa 7.6860cos )120(60sin 25030-=︒-+︒-=ατ四、(12分)绘制此梁的内力图五、(14分) 手摇绞车如图所示,轴AB 的直径d=30mm ,材料的许用应力[σ]=100Mpa ,已知P 为1000N ,试绘出危险点的内力要素,按第三强度理论校核轴的强度。
危险截面:绞车轮所在截面左边截面 危险截面上危险点的位置:最上、最下两点Nm PM 2004.02=⋅=Nm P T 18018.0=⋅=[]σπσ MPa d W T M zr 6.10132180200322223=+=+=故强度不满足。
六、(14分)图a 所示悬臂梁,自由端的挠度和转角为EIFl EI Fl w B B 2,323==θ。
图b 所示悬臂梁,已知a, b, E, I 。
重量Q 的重物自高度h 处自由下落,冲击梁上的B 点处。
试求梁在C 点处的最大冲击挠度。
C(a) (b)当Q 作为静载荷作用在B 点时,C 点的挠度为)32(623223b a EIQa EI Qa b EI Qa b w w B B C +=+=+=θ动荷因数 Bst d w hh K 211211++=∆++= 梁在C 点处的最大冲击挠度为 ⎥⎦⎤⎢⎣⎡+++==∆32611)32(6Qa hEI b a EI Qa w K C d d 七、(12分)已知AB 为刚性梁,AC 为两端铰接的钢制圆杆,横截面直径d=20mm ,σp =200Mpa ,σs =240Mpa ,E=200Gpa ,直线经验公式的系数a=304Mpa ,b=,P=4kN,稳定安全系数n st =5,试校核其稳定性。
对AB :∑=0D M 02=-Pa a F AC解得 KN P F AC 22==对杆AC ,992≈=pp E σπλ 而p d iul λλ 200410001=⨯==故杆AC 为大柔度杆,其临界压力为 4222d E F Cr πλπ= 校核其稳定性:解得 515 =ACCr F F故稳定性可以满足。
八、(10分)在受集中力F 作用的矩形截面简支梁中,测得中性层上K 点处沿45o 方向的线应变645 2.610o ε-=⨯。
已知材料弹性常数E=200Gpa , =,h=200mm , b=100mm 。
试求集中力F 。
F45o K hb2m 1m该截面上的剪力为3FF s =,中性层上K 点的切应力为bhF bh FA F s 235.123===τ0=x σ 0=yσ ττ=x︒=45ατσ-=︒45 τσ=︒1351351354511(1)()2u u Fu E E Ebhεσστ︒︒︒++=-==() 故16.25KN F =一、判断题(正确打“√”,错误打“X ”,本题满分为10分) 1、切应变是变形后构件中任意两根微线段夹角角度的变化量。
( ) 2、一点沿某一方向的正应力为零,则沿该方向的线应变也为零。
( )3、应变能等于外力所做的功,由于功有正负,因此杆的应变能也有正负。
( )4、研究杆件的应力与变形时,力可按力线平移定理进行移动。
( )5、交变应力是指构件内的应力,它随时间作周期性变化,而作用在构件上的载荷可能是动载荷,也可能是静载荷。
( )6、塑性材料制成的杆件,其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。
( )7、在单元体两个相互垂直的截面上,切应力的大小可以相等,也可以不等。
( ) 8、超静定结构的相当系统和补充方程不是唯一的,但其计算结果都是唯一的。
( ) 9、两梁的跨度、承受载荷及支承相同,但材料和横截面面积不同,因而两梁的剪力图和弯矩图不一定相同。
( )10、平行移轴公式表示图形对任意两个相互平行轴的惯性矩和惯性积之间的关系。
( ) 二、选择题(每个2分,本题满分16分)1、如图所示的铸铁制悬臂梁受集中力F 作用,其合理的截面形状应为图( )2、图示钢杆,放置在两刚性平面之间,杆内无初始应力。
当温度均匀升高Δt ℃后,杆上任一点A 处的应力σ与纵向应变ε之值的可能情形是() A 、σ≠0,ε=0 ; B 、σ=0,ε=0; C 、σ≠0,ε≠0 ;D 、σ=0,ε≠03、低碳钢拉伸经过冷作硬化后,以下四种指标得到提高的是 。
A:强度极限; B:比例极限; C:截面收缩率; D:延伸率(伸长率)4、自由落体冲击时的动荷因数,不正确答案是A 与被冲击物的刚度有关;B 与自由落体下落的高度有关;C 与被冲击物的刚度无关;D 与冲击刚发生时,自由落体下落的速度有关。
5、受轴向拉伸的等直杆,在比例极限内受力,若要减小杆的纵向变形,需要改变抗拉压刚度,即 A、减小EA B、减小EI C、增大EA D、减小EI6、两端铰支圆截面细长压杆,若在某一截面上开一小孔。
关于这一小孔对压杆稳定承载能力及强度的影响,正确的是。
A:对强度和稳定承载能力都有较大消弱;B:对强度和稳定承载能力都不会消弱;C:对强度无消弱,对稳定承载能力有较大消弱;D:对强度有较大消弱,对稳定承载能力无消弱。
7、等直杆受力如图,其横截面面积A=100mm2,则横截面mk上的正应力为()。
A、50MPa(压应力) ;B、40MPa(压应力) ;C、90MPa(压应力) ;D、90MPa(拉应力)8、矩形截面梁受弯曲变形,如果梁横截面的高度增加一倍时,则梁内的最大正应力为原来的多少倍?梁的最大挠度为原来的多少倍?()A 正应力为1/4倍,挠度为1/8倍;B正应力为1/2倍,挠度为1/4倍;;C 正应力和挠度均为1/4倍;D 无法确定三、填空题(12分)1、横截面和材料均相同的两根等长细长压杆,A为两端铰支,B为一端固定另一端自由,则前者与后者临界压力之比为。
2、已知塑性材料某点的三个主应力为30MPa、-15MPa、-45MPa,则该点的最大主应力为;第三强度理论的相当应力为。
3、受力构件的材料弹性常数为E、G、μ,该构件一点处的主应力σ1=σ2=σ3,则最大主应变为,形状改变比能为。
4、两根承受轴向拉伸的杆件均在弹性范围内,一为钢杆其弹模量为200Gpa,另一为铸铁杆其弹模量为100Gpa。
若两杆横截面上的正应力相同,则两杆纵向应变的比值为;若两杆的纵向应变相同,则两杆横截面上正应力的比值为 。
5、标距为100mm 的标准试件,直径为10 mm ,拉断后测得伸长后的标距为123 mm ,颈缩处的最小直径为 mm ,则该材料的δ= ;ψ= 。
6、从材料力学的角度来讲,为了使构件能正常的工作,必须使构件具有足够的 ; ; 。
××××√;××√××选择题B A B C C D D A1、4:12、a MP 30 ,aMP 75 3、,)21(1Eu σ-0 4、1:2,2:1 5、23%, % 6、强度、刚度、稳定性 四、绘制此梁的内力图五、如图所示结构,A ,B ,C 均为铰接,AB 杆为实心圆截面杆,其d 0=40mm ,BC 杆为空心圆管外径为D=60mm ,内径d=40mm ,已知材料的p= 200Mpa ,s =240Mpa ,E=200Gpa ,a=304Mpa ,b=,若规定稳定安全系数ηst=3,强度安全系数η=2试求结构的许可载荷[F]。