【中考复习】2018届中考数学《第19课时：线段、角、相交线》课时作业本(含答案)

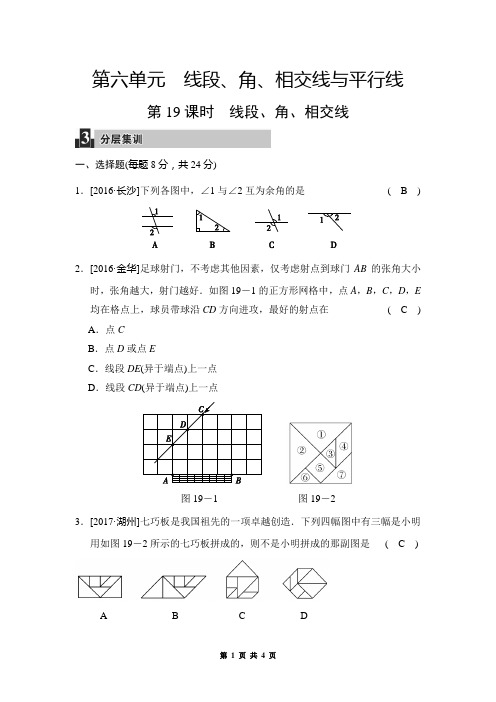
第六单元线段、角、相交线与平行线第19课时线段、角、相交线一、选择题(每题8分，共24分)1．[2016·长沙]下列各图中，∠1与∠2互为余角的是(B)2．[2016·金华]足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图19－1的正方形网格中，点A，B，C，D，E 均在格点上，球员带球沿CD方向进攻，最好的射点在(C) A．点CB．点D或点EC．线段DE(异于端点)上一点D．线段CD(异于端点)上一点图19－1图19－23．[2017·湖州]七巧板是我国祖先的一项卓越创造．下列四幅图中有三幅是小明用如图19－2所示的七巧板拼成的，则不是小明拼成的那副图是(C)A B C D【解析】 选项C 中第④块、第⑦块和原图形不符合，故不是由原图这副七巧板拼成的．二、填空题(每题8分，共32分)4．把15°30′化成度的形式，则15°30′＝____15.5__°.5．把角度化为度、分的形式，则20.5°＝20°__30__′.6．计算：50°－15°30′＝__34°30′__.7．[2016·黄石]如图19－3，一艘海轮位于灯塔P 的北偏东30°方向，距离灯塔4海里的A 处，该海轮沿南偏东30°方向航行__4__海里后，到达位于灯塔P 的正东方向的B处．(18分) 8．(8分)如图19－4，直线AB 与直线CD 相交于点O ，E 是∠AOD 内一点，已知OE ⊥AB ，∠BOD ＝45°，则∠COE 的度数是 ( B)图19－4A ．125°B ．135°C ．145°D ．155°【解析】 ∵OE ⊥AB ，∴∠AOE ＝90°，又∵∠AOC ＝∠BOD ＝45°， ∴∠COE ＝∠AOE ＋∠AOC ＝90°＋45°＝135°.故选B.9．(10分)[2017·河北]在一条不完整的数轴上从左到右有点A ，B ，C ，其中AB ＝2，BC ＝1，如图19－5所示，设点A ，B ，C 所对应数的和是p.图19－5(1)若以B 为原点，写出点A ，C 所对应的数，并计算p 的值；若以C 为原点，p 又是多少？图19－3(2)若原点O在图中数轴上点C的右边，且CO＝28，求p.解：(1)若以B为原点，则C表示1，A表示－2，∴p＝1＋0－2＝－1；若以C为原点，则A表示－3，B表示－1，∴p＝－3－1＋0＝－4；(2)若原点O在图中数轴上点C的右边，且CO＝28，则C表示－28，B表示－29，A表示－31，∴p＝－31－29－28＝－88.(26分)10．(12分)[2017·江阴期中]如图19－6，AD∥BC，∠EAD＝∠C，∠FEC＝∠BAE，∠EFC＝50°.图19－6(1)求证：AE∥CD；(2)求∠B的度数．解：(1)证明：∵AD∥BC，∴∠D＋∠C＝180°，∵∠EAD＝∠C，∴∠EAD＋∠D＝180°，∴AE∥CD；(2)∵AE∥CD，∴∠AEB＝∠C，∵∠FEC＝∠BAE，∴∠B＝∠EFC＝50°.11．(14分)如图19－7，∠AOE＝80°，OB平分∠AOC，OD平分∠COE，∠AOB ＝15°.图19－7(1)求∠COD度数；(2)若OA表示时钟时针，OD表示分针，且OA指在3点过一点儿，求此时的时刻是多少？解：(1)∵∠AOB＝15°，OB平分∠AOC，∴∠AOC＝2∠AOB＝30°，∵∠AOE＝80°，∴∠COE＝∠AOE－∠AOC＝50°，∵OD平分∠COE，∴∠COD＝12∠COE＝25°；(2)设此时的时刻为3点x分，分针每分钟转360°÷60＝6°，时针每分钟转30°÷60＝0.5°，则从3点算起，分针OD转过了(6x)°，时针OA转过了(0.5x)°，3点整时，时针与分针成90°，而∠AOD＝55°，故90－6x＋0.5x＝55，解得x＝70 11.∴此时的时刻为3点7011分．。

中考数学复习考点知识讲解与专题训练第14讲 线、角、相交线与平行线知识梳理1. 线段和直线(1) 直线公理： 经过两点有且只有一条直线.(2) 线段公理： 两点之间，线段最短．连接两点的__线段的长度__叫做这两点间的距离．(3) 直线、射线、线段的主要区别：(4) 线段的中点：若点C 是线段AB 的中点，则AB BC AC 21==；AB =2AC =2B C ．2.对顶角一个角的两边是另一个角的两边的反向延长线,则称这两个角是对顶角,对顶角相等.3.角及其平分线(1) 定义：有公共端点的两条射线组成的图形叫做角．角的分类：①角按大小可以分为周角、平角、钝角、直角、锐角．②1周角=2平角=4直角；1°=60′；1′=60″．1；∠AOB=2(2) 角的平分线：若OC平分∠AOB，则AOB∠=AOC∠∠BOC=2∠AOC=2∠BOC．4.余角、补角及性质：5. 相交线①．对顶角与邻补角：②. 垂线及性质：6. 平行线7.命题、定理5年真题命题点1 余角与补角1．（3分）（2017•广东）已知∠A＝70°，则∠A的补角为（A）A．110°B．70°C．30°D．20°命题点2平行线的性质及判定（4分）（2019•广东）如图，已知a∥b，∠1＝75°，则∠2＝105°．2．3．（3分）（2018•广东）如图，AB∥CD，则∠DEC＝100°，∠C＝40°，则∠B的大小是（B）A．30° B．40°C．50°D．60°3年模拟1．（2020•禅城区一模）如图，经过刨平的木板上的A，B两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（B）A．点动成线B．两点确定一条直线C．垂线段最短 D．两点之间，线段最短2．（2020•白云区一模）一个角是60°，则它的余角度数为（A）A．30° B．40°C．90°D．120°3．（2019•金平区一模）已知∠A与∠B的和是90°，∠C与∠B互为补角，则∠C比∠A大（C）A．180°B．135° C．90°D．45°（2020•福田区模拟）如图，下列条件中，能判定DE∥AC的是（C）4．A．∠EDC＝∠EFC B．∠AFE＝∠ACD C．∠3＝∠4 D．∠1＝∠25．（2020•英德市一模）如图，∠1＝∠2，∠D＝50°，则∠B的度数为（D）A．50° B．40°C．100° D．130°6．（2019•花都区一模）如图，直线a∥b，点A、B分别在直线a、b上，∠1＝45°，若点C在直线b上，∠BAC＝105°，且直线a和b的距离为3，则线段AC的长度为（D）A．3√2B．3√3C．3 D．67．（2020•深圳模拟）下列命题正确的是（C）A．一组对边平行，另一组对边相等的四边形是平行四边形B．对角线相等的平行四边形是正方形C．16的平方根是±4D．有两条边对应相等的两个直角三角形全等8．（2019•顺德区三模）计算：18°30′＝18.5 °．9．（2020•金平区模拟）如图，现将一块含有60°角的三角板的顶点放在直尺的一边上，若∠1＝∠2，那么∠1的度数为60°．10．（2020•靖江市一模）命题“对顶角相等”的逆命题是假命题（填“真”或“假”）．。

2018届中考数学全程演练第二部分图形与几何第六单元线段、角、相交线与平行线第20课时平行线的性质和判定编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018届中考数学全程演练第二部分图形与几何第六单元线段、角、相交线与平行线第20课时平行线的性质和判定）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018届中考数学全程演练第二部分图形与几何第六单元线段、角、相交线与平行线第20课时平行线的性质和判定的全部内容。

第20课时平行线的性质和判定(60分）一、选择题（每题6分，共24分）1．［2016·福州]下列图形中，由∠1＝∠2能得到AB∥CD的是（B）2．［2016·黔东南]如图20－1，直线a，b与直线c，d相交,已知∠1＝∠2，∠3＝110°，则∠4＝（A)A．70° B．80° C．110° D．100°图20－1 图20－23．[2016·十堰］如图20－2,AB∥CD，点E在线段BC上,若∠1＝40°，∠2＝30°，则∠3的度数是 (A)A．70°B．60°C．55°D．50°4．[2016·毕节]如图20－3,直线a∥b,直角三角形ABC的顶点B在直线a上，∠C＝90°,∠β＝55°,则∠α的度数为（C)A．15°B．25°C．35°D．55°二、填空题(每题6分，共18分）5．[2016·苏州］如图20－4，直线a∥b,∠1＝125°，则∠2的度数为__55°__。

2018年全国中考数学真题分类线段垂直平分线、角平分线、中位线（二）一、选择题1. (2018黑龙江大庆，9，3) 如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC，且∠ADC＝110°，则∠MAB的度数是( )A．30°B．35°C．45°D．60°【答案】B，【解析】过点M作MN⊥AD于N，根据角平分线上的点到角的两边的距离相等可得MC＝MN，然后求出MB＝MN，再根据到角的两边距离相等的点在角的平分线上判断出AM是∠BAD的平分线，然后求出∠AMB，再根据直角三角形两锐角互余求解即可．二、填空题1. （2018山东省东营市，15，3分）如图，在RT△ABC中，∠B=90°，以顶点C为圆心，适当长为半径画弧，分别交AC,BC于点E,F，再分别以点E,F为圆心，大于12EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D，若BD=3,AC=10，则△ACD的面积是。

15．（2018山东省东营市，15，3分）如图，在RT△ABC中，∠B=90°，以顶点C为圆心，适当长为半径画弧，分别交AC,BC于点E,F，再分别以点E,F为圆心，大于12EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D，若BD=3,AC=10，则△ACD的面积是。

【答案】15【解析】由作图语言叙述知CD是∠ACB的平分线，所以过D作AC的垂线段的长就是△ACD的高，而这个垂线段的长由角平分线的性质定理知它等于BD的长。

所以△ACD的面积12AC BD=15.【知识点】角平分线性质定理，三角形的面积公式。

2. （2018年江苏省南京市，14，2分） .如图，在ABC△中，用直尺和圆规作AB、AC的垂直平分线，分别交AB、AC于点D、E，连接DE.若10cmBC=，则DE=cm．【答案】5【解析】∵用直尺和圆规作AB、AC的垂直平分线，∴D为AB的中点，E为AC的中点，∴DE是△ABC的中位线，∴DE=BC=5cm．故答案为：5．【知识点】线段垂直平分线中位线3. （2018贵州省毕节市，17，3分）如图,在△ABC中,AC＝10,BC＝6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是________.[来源:【答案】16．第15题图第16题图【解析】∵DE 是AB 垂直平分线，∴AE ＝BE , ∴C △BCE ＝BC ＋CE ＋BE ＝BC ＋CE ＋AE ＝BC ＋AC ＝6＋10＝16．【知识点】线段垂直平分线的性质；三角形的周长公式4. （2018山西省，14题，3分） 如图，直线MN ∥PQ.直线AB 分别与MN,PQ 相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A 为圆心，以任意长为半径作弧交AN 于点C,交AB 于点D;②分别以C,D 为圆心,以大于12CD 长为半径作弧，两弧在∠NAB 内交于点E;③作射线AE 交PQ于点F.若AB=2.∠ABP =60°则线段AF 的长为 ．【答案】2√3【解析】解：过点A 作AG ⊥PQ 交PQ 与点G由作图可知，AF 平分∠NAB ∵ MN ∥PQ ；AF 平分∠NAB ；∠ABP =60°∴ ∠AFG =30°在Rt △ABG 中，∠ABP =60°，AB=2；∴ AG =√3在Rt △AFG 中，∠AFG =30°，AG =√3；∴ AF =2√3【知识点】角平分线、特殊角三角函数PP5. （2018内蒙古通辽，16，3分）如图，在△ABC 中，按以下步骤作图：①分别以点A 和点C 为圆心，以大于12AC 的长为半径作弧，两弧相交于M 、N 两点；②作直线MN 交BC 于点D ，连接A D ．若AB ＝BD ，AB ＝6，∠C ＝30°，则△ACD 的面积为 ．【答案】9 3【解析】依题意MN 是AC 的垂直平分线，所以∠C ＝∠DAC ＝30°，所以∠ADB ＝∠C ＋∠DAC ＝60°，又AB ＝BD ，所以△ABD 为等边三角形，∠BAD ＝60°，所以∠BAC ＝∠DAC ＋∠BAD ＝90°，因为AB＝6，所以AC ＝63，所以△ABC 的面积为12×6×63＝183．又BD ＝AD ＝DC ，所以S △ACD ＝12S △ABC ＝93，故应填：93．6.（2018辽宁省抚顺市，题号16，分值3）如图，ABCD 中，AB=7，BC=3，连接AC ，分别以点连接AE ，则△AED 的周长是__________.【答案】10【解析】由题可知，直线MN 是线段AC 的垂直平分线，∴AE=EC.∵在ABCD 中DE+EC=CD=AB=7,AD=BC=3，∴△AED 的周长为AD+DE+AE=BC+DE+EC=BC+CD=10.【知识点】用尺规作垂直平分线，垂直平分线的性质.三、解答题1. (2018甘肃省兰州市,20,6分)如图,在Rt△ABC中.(1)利用尺度作图,在BC边上求作一点P,使得点P到AB的距离(PD的长)等于PC的长;（2）利用尺规作图,作出(1)中的线段PD.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)【思路分析】PC⊥AC,要使P到AB的距离(PD的长)等于PC的长,即求∠A的角平分线与BC的交点.【解题过程】(1)作∠A的平分线AD,交BC于P;(2)过点P作直线AB的垂线,垂中为D｡【知识点】尺规作图2. （2018湖北省江汉油田潜江天门仙桃市，18，5分）图①、图②都是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点．点O，M，N，A，B均在格点上，请仅用无刻度直尺在网格中完成下列画图．（1）在图①中，画出∠MON的平分线OP；（2）在图②中，画一个Rt△ABC，使点C在格点上．CA B第20题图【思路分析】（1）在只能用直尺画角平分线的情况下，就设法将∠MON 放置在能画出角平分线的图形中，如菱形．（2）原图是由全等的小菱形组成的，∴要想找到直角就要从菱形的对角线方面入手考虑．设法找让三角形中的一个顶点处在两个菱形的对角线交点位置，并且在格点上．【解题过程】解：（1）如图①，将∠MON 放在菱形AOBC 中，连接对角线OC ，并取格点P ，OP 即为所求．2分 如图②所示，△ABC 或△ABC 1均可．3. （2018湖南省怀化市，19，10分）已知：如图，点A ，F ，E ，C 在同一直线上，AB//DC ，AB ＝CD ，D B ∠=∠（1）求证：∆ABE ≅∆CDF ；（2）若点E ，G 分别为线段FC ，FD 的中点，连接EG ，且EG ＝5，求AB 的长．（第18题图） 图①图② B A ONM第18题答图 PA 图①O NMBC C 1 C 图② B A【思路分析】（1）首先根据AB//DC 可得CFD AEB ∠=∠，再加上条件AB ＝CD ，D B ∠=∠可利用AAS定理证明三角形全等．（2）根据（1）中的全等，可知AB ＝CD ，再根据三角形中位线定理可知已知量EG 和未知量CD 的等量关系，即可求出CD ，继而求出AB 的长度．【解题过程】（1）证明：∵AB//DC ∴CFD AEB ∠=∠，又∵D B ∠=∠，AB ＝CD ，∴在∆ABE 和∆CDF中，⎪⎩⎪⎨⎧=∠=∠∠=∠,,,CD AB D B CFD AED ∴∆ABE ≅∆CDF(AAS)（2）∵点E ，G 分别为线段FC ，FD 的中点，∴线段EG 为CDF ∆的中位线，根据三角形中位线的性质定理，可得：CD EG 21=，又∵∆ABE ≅∆CDF ∴AB ＝CD ∴52121===AB CD EG ， ∴521=AB ，即10=AB ． 【知识点】全等三角形的判定方法 三角形中位线定理。

初三数学中考复习线段和角专题复习训练含答案1. 京广高铁全线通车，一列往复于北京和广州的火车，沿途要经过石家庄、郑州、武汉、长沙四站，铁路部门要为这趟列车预备印制车票( )A ．6种B ．12种C ．15种D ．30种2. 点A ，B ，C 在同一条数轴上，其中点A ，B 表示的数区分为－3，1，假定BC ＝2，那么AC 等于( )A ．3B ．2C ．3或5D ．2或63．线段AB ，画出它的中点C ，再画出BC 的中点D ，再画出AD 的中点E ，再画出AE 的中点F ，那么AF 等于AB 的( )A.14B.38C.18D.3164. 线段AB ＝10 cm ，点C 是直线AB 上一点，BC ＝4 cm ，假定M 是AC 的中点，N 是BC 的中点，那么线段MN 的长度是( )A ．7 cmB ．3 cmC ．5 cm 或3 cmD ．5 cm5. 如图，直线AB ，CD 交于点O ，射线OM 平分∠AOC ，假定∠AOC ＝76°，那么∠BOM 等于( )A ．38°B ．104°C ．142°D ．144°6. 学校、电影院、公园在平面图上区分用点A ，B ，C 表示，电影院在学校的正西方向，公园在学校的南偏西35°方向，那么平面图上的∠BAC 等于( )A ．115°B ．35°C ．125°D ．55°7. 一个角的补角是这个角的余角的4倍，那么这个角的大小是( )A ．60°B ．75°C ．90°D ．45°8. 如图，两块直角三角板的直角顶点O 重合在一同，且OB 恰恰平分∠COD ，那么∠AOD 的度数为( )A．20°B．150°C．135°D．105°9. 平面内两两相交的8条直线，其交点个数最少为m个，最多为n个，那么m ＋n等于( )A．16 B．18 C．29 D．2810. 如图，经过刨平的木板上的两个点，能弹出一条蜿蜒的墨线，而且只能弹出一条墨线，能解释这一实践运用的数学知识是________________________．11. 如图，从甲地到乙地有四条路途，其中最短的路途是____．12. 半夜闹钟响了，正在午睡的小明睁眼一看闹钟(如下图)，这时分针与时针所成的角的度数是______度．13. 如下图，OE平分∠AOB，OD平分∠BOC，∠AOB＝90°，∠EOD＝80°，那么∠BOC的度数为_____________．15. 如图，C，D，E将线段AB分红四局部，且AC∶CD∶DE∶EB＝2∶3∶4∶5，M，P，Q，N区分是AC，CD，DE，BE的中点，假定MN＝a，求PQ的长．16. 如图，∠AOC＝∠BOD＝100°，且∠AOB∶∠AOD＝2∶7，试求∠BOC的大小．17. 如图，直线AB和CD相交于点O，OM平分∠BOD，∠MON是直角，∠AOC ＝50°.(1)求∠AON的度数；(2)求∠DON的余角．18. 如图，数轴上点A表示的数为6，B是数轴上一点，且AB＝10.动点P从点A 动身，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t＞0)秒．(1)写出数轴上点B表示的数_______，点P表示的数_______(用含t的代数式表示)(2)动点R 从点B 动身，以每秒4个单位长度的速度沿数轴向左匀速运动，假定点P ，R 同时动身，问点P 运动多少秒时追上点R?19. 如图，∠AOB ＝m °，OC 是∠AOB 内的一条射线，OD 平分∠BOC ，OE 平分∠AOC .(1)求∠EOD 的度数；(2)假定其他条件不变，OC 在∠AOB 外部绕O 点转动，那么OD ，OE 的位置能否发作变化？(3)在(2)的条件下，∠EOD 的大小能否发作变化？假设不变，央求出其度数；假设变化，央求出其度数的范围．参考答案：1---9 DDDDC CACC10. 两点确定一条直线11. A12. 13513. 70°14. 70°15. 解：PQ ＝13a 16. 解：设∠AOB ＝2x ，那么∠AOD ＝7x ，所以∠BOD ＝∠AOD －∠AOB ＝5x ＝100°，所以x ＝20°，即∠AOB ＝∠COD ＝40°，∠AOD ＝140°，所以∠BOC ＝∠AOD －∠AOB －∠COD ＝140°－40°－40°＝60°17. 解：(1)由于∠AOC ＋∠AOD ＝∠AOD ＋∠BOD ＝180°，所以∠BOD ＝∠AOC ＝50°，由OM 平分∠BOD ，可得∠BOM ＝∠DOM ＝25°，又由∠MON ＝90°，所以∠AON ＝180°－(∠MON ＋∠BOM)＝180°－(90°＋25°)＝65°(2)由∠DON ＋∠DOM ＝∠MON ＝90°知∠DOM 为∠DON 的余角，故∠DON 的余角为25°18. (1) －4 6－6t(2) 解：设点P 运动x 秒时，在点C 处追上点R ，那么AC ＝6x ，BC ＝4x ，由于AC －BC ＝AB ，所以6x －4x ＝10，解得：x ＝5，所以点P 运动5秒时追上点R19. 解：(1)(12m)°(2)OD ，OE 的位置发作变化 (3)∠EOD 的大小坚持不变为(12m)°。

2020年七年级数学下册课后作业本《相交线》(含答案)一、选择题1.如图,CD⊥AB,垂足为D,AC⊥BC,垂足为C.图中线段的长能表示点到直线（或线段）距离线段有（）A.1条B.3条C.5条D.7条2..如图所示，下列判断正确的是( )A.图⑴中∠1和∠2是一组对顶角B.图⑵中∠1和∠2是一组对顶角C.图⑶中∠1和∠2是一对邻补角D.图⑷中∠1和∠2互为邻补角3.下列图形中，∠1与∠2是对顶角的是（）A. B. C.D.4.下面四个图形中，∠1=∠2一定成立的是（）5.下列所示的四个图形中，∠1和∠2是同位角的是（）A.②③B.①②③C.①②④D.①④6.已知∠α=35°，则∠α的补角的度数是( )A.55°B.65°C.145°D.165°7.如图，能与∠α构成同旁内角的角有（）A.1个B.2个C.5个D.4个8.如图，若两条平行线EF，MN与直线AB，CD相交，则图中共有同旁内角的对数为（）A.4B.8C.12D.16二、填空题9.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是．10.如图,与∠1构成同位角的是______,与∠2构成内错角的是______.11.如图,已知三条直线AB、CD、EF两两相交于点P、Q、R，则图中邻补角共有对，对顶角共有对（平角除外）．12.如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1与∠2的关系是．三、解答题13.如图,AB和CD交于O点,OD平分∠BOF,OE⊥CD于点O,∠AOC＝40°.求∠EOF的度数．14.直线AB、CD相交于O，OE平分∠AOC，∠EOA：∠AOD=1:4，求∠EOB的度数．15.如图,AB、CD、EF交于O点，AB⊥CD,OG平分∠AOE,∠COE=28°求∠AOG的度数.16.已知直线AB和CD相交于点O，∠AOC为锐角，过O点作直线OE、OF．若∠COE=90°，OF平分∠AOE，求∠AOF+∠COF的度数．1.C2.D3.C4.答案为：B.5.答案为：C.6.C7.C8.D9.答案为：连接直线外一点与直线上所有点的连线中，垂线段最短．10.答案为：∠B；∠BDE；11.答案为：12，612.答案为：∠1+∠2=90°13.解：∵AB，CD相交于点O，∴∠BOD＝∠AOC＝40°.∵OD平分∠BOF，∴∠DOF＝∠BOD＝40°.∵OE⊥CD，∴∠EOD＝90°.∴∠EOF＝∠EOD＋∠DOF＝130°.14.解：∵OE平分∠AOC，∴∠AOC=2x，∵∠EOA：∠AOD=1：4，∴∠AOD=4x，∵∠COA+∠AOD=180°，∴2x+4x=180°，解得x=30°，∴∠EOB=180°﹣30=150°．故∠EOB的度数是150°．15.解：∵AB⊥CD ∴∠AOC=90°∵∠COE=28°∴∠AOE=∠AOC+∠COE =90°+28°=118°∵OG平分∠AOE ∴∠AOG=∠EOG=∠AOE=59°16.解：∵OF平分∠AOE，∴∠AOF=∠EOF，∴∠AOF+∠COF=∠EOF+∠COF=∠COE=90°．。

浙江省20１8年中考数学总复习第四章基本图形(一)课后练习1７线段、角、相交线和平行线作业本编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（浙江省20１8年中考数学总复习第四章基本图形(一）课后练习17 线段、角、相交线和平行线作业本)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为浙江省2018年中考数学总复习第四章基本图形(一)课后练习17 线段、角、相交线和平行线作业本的全部内容。

课后练习17 线段、角、相交线和平行线A组１．(2015·福州)下列图形中,由∠1=∠2能得到AB∥CD的是( ）２.(2017·丽水模拟)要证明命题“若ａ〉b，则a2>b2”是假命题，下列a,ｂ的值不能作为反例的是（）Ａ．a＝１,ｂ=-2 Ｂ．a=0，b=-1C．ａ＝－1,b=-２ D.a＝２,b=-1第３题图3．(２0１5·内江）如图,在△ABC中，ＡB=AＣ，BD平分∠ＡBC交AＣ于点D,AＥ∥BＤ交CB的延长线于点Ｅ．若∠E=35°,则∠BＡＣ的度数为( ）A．40°Ｂ.45° C．60°Ｄ．７0°4．(２017·宁波)已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置(∠ABC＝30°)，其中A,B两点分别落在直线m,n上，若∠１＝20°，则∠2的度数为（ )第4题图A.２０° B．3０°Ｃ.45° D．50°5．如图所示,用直尺和三角尺作直线AＢ，ＣD,从图中可知,直线AB与直线ＣD的位置关系为。

第二部分图形与几何第六单元线段、角、相交线与平行线第19课时线段、角、相交线(60分)一、选择题(每题10分，共30分)1．[2016·济南]如图19－1，OA⊥OB，∠1＝35°，则∠2的度数是 (C)A．35° B．45° C．55° D．70°图19－1 图19－22．[2016·厦门]如图19－2，△ABC是锐角三角形，过点C作CD⊥AB，垂足为D，则点C到直线AB的距离是 (B)A．线段CA的长B．线段CD的长C．线段AD的长D．线段AB的长3．[2016·河北]已知：岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，符合条件的示意图是 (D)二、填空题(每题10分，共30分)4．把15°30′化成度的形式，则15°30′＝__15.5__°.5．把角度化为度、分的形式，则20.5°＝20°__30__′.6．[2017·湖州]计算：50°－15°30′＝__34°30′__.(20分)7．(10分)如图19－3，直线AB 与直线CD 相交于点O ，E 是∠AOD 内一点，已知OE ⊥AB ，∠BOD ＝45°，则∠COE 的度数是(B)图19－3 A ．125° B ．135° C ．145° D ．155°【解析】 ∵OE ⊥AB ，∴∠AOE ＝90°，又∵∠AOC ＝∠BOD ＝45°，∴∠COE ＝∠AOE ＋∠AOC ＝90°＋45°＝135°，选B.8．(10分)[2016·滕州模拟]直线上有n 个点，我们进行如下操作：在每相邻两点间插入2个点．经过2次这样的操作后，直线上共有__9n －8__个点．(用含n 的代数式表示)【解析】 第一次操作，共有n ＋(n －1)×2＝3n －2个点，第二次操作，共有(3n －2)＋(3n －2－1)×2＝9n －8个点．(20分)9．(20分)如图19－4，∠AOE ＝80°，OB 平分∠AOC ，OD 平分∠COE ，∠AOB ＝15°.(1)求∠COD 度数；(2)若OA 表示时钟时针，OD 表示分针，且OA 指在3点过一点，求此时的时刻是多少？图19－4解：(1)∵∠AOB ＝15°，OB 平分∠AOC ，∴∠AOC ＝2∠AOB ＝30°，∵∠AOE ＝80°，∴∠COE ＝∠AOE －∠AOC ＝50°，∵OD 平分∠COE ，∴∠COD ＝12∠COE ＝25°；(2)设此时的时刻为3点x 分，则从3点算起，分针OD 转过了6x °，时针OA 转过了0.5x °，3点时，时针与分针成90°，而∠AOD ＝55°，故90－6x ＋0.5x ＝55，解得x ＝7011. 所以此时的时刻为3点7011分．。

2019中考数学最新重点汇编-线段，角与相交线【一】选择题1、〔广东省2018初中学业水平模拟六〕假设α∠补角是α∠余角的3倍，那么α∠=、 答案：45度2、〔广东省2018初中学业水平模拟一〕如图1，AOC ∠和BOD ∠都是直角，且︒=∠30DOC ，那么=∠AOB ().A 、︒30B 、︒60C 、︒120D 、︒150答案：D3、〔广东省2018初中学业水平模拟一〕︒28的补角是().A 、︒58B 、︒72C 、︒62D 、︒152答案：C 4、〔广州海珠区2018毕业班综合调研〕如图,∠1与∠2是同位角，假设∠2=65°，那么∠1的大小是〔〕A 、25°B 、65°C 、115°D 、不能确定答案：D5、(2018湛江调研测试)∠A=20°，那么∠A 的余角为A 、20°B 、70°C 、80°D 、160°答案：B【二】填空题1、〔广州海珠区2018毕业班综合调研〕如图，AB 为⊙O 的直径，点C 在⊙O 上,假设︒=∠20C ,那么=∠BOC °、答案：40°2、(2018广西钦州市模拟)如图，点B 是线段AC 上的点，点D 是线段BC 的中点，假设AB=4cm ，AC ＝10cm ，那么 CD=▲cm 、第1题 答案：3 3、〔2018年孝感模拟〕如图,直线AB 、CD 相交于点E ，EF ⊥AB 于E ，假设∠CEF =59°，那么∠AED 的度数为.答案：︒149A O DCB图1第4题图 21第1题图 BOCAA B CD4、〔2018年孝感模拟〕在一次夏令营活动中，小明同学从营地A 出发，要到A 地的北偏东60°方向的C 处，他先沿正东方向走了200m 到达B 地，再沿北偏东30°方向走，恰能到达目的地C (如图)，那么，由此可知，B C 、两地相距m .答案：200 5、〔2018年犍为县五校联考〕某同学在纸上画了四个点，如果把这四个点彼此连接，连成一个图形，那么这个图形中会有个三角形出现。