定点小数的乘法运算及实现

计组定点数乘法
定点数乘法是指对两个定点数进行乘法运算，其中一个或两个数的小数部分占用了一定的位数。

定点数乘法可以使用如下方法进行计算：
1. 原码相乘：将两个数的小数部分补齐到相同的位数，然后进行二进制相乘。

最后将得到的结果向右移动小数点，使其对应原来的小数点位置。

2. 补码相乘：与原码相乘的方法类似，不同点在于对于负数，先要将其转化为补码表示，然后进行二进制相乘。

3. Booth算法：可以加快定点数乘法的计算速度，特别是当乘数中含有大量的1或0时。

Booth算法可以将乘数转化为只含有1和-1的序列，然后将其与被乘数进行加减运算，最后得到乘积。

4. Wallace树： Wallace树是一种用于高效计算定点数乘法的逻辑结构。

它可以将多个部分积相加，然后得到最终的乘积。

Wallace树主要是用于优化乘数位数较大的情况。

以上是一些常见的定点数乘法计算方法。

在实际应用中，选择合适的计算方法，可以有效地提高乘法计算的效率。

一、概述在计算机科学中，C语言是一种非常流行的程序设计语言，它具有高效、灵活和丰富的库函数等特点。

在C语言中实现原码一位两个定点数相乘是一个非常基础和常见的计算操作，本文将介绍如何使用C语言实现原码一位两个定点数相乘的过程。

二、原码定点数1. 定点数是计算机中用于表示实数的一种方式，它们不同于浮点数，定点数以二进制形式表示，它包含一个整数部分和一个小数部分。

2. 原码定点数中，最高位为符号位，其余位用来表示整数部分和小数部分。

当符号位为0时，表示正数，为1时表示负数。

三、原码定点数相乘1. 原码定点数相乘是指两个原码定点数相乘的操作。

2. 对于原码定点数A和B，其相乘过程可以表示为C=A×B，其中C 为相乘结果。

四、C语言实现下面是一个简单的C语言函数，实现了原码一位两个定点数相乘的功能：```c#include <stdio.h>int fix_mul(int a, int b, int n){int c;c = a * b;c = c >> n; // 将乘积右移n位，得到结果return c;}```五、代码解释1. 上述代码定义了一个名为fix_mul的函数，接受三个参数a、b、n，分别表示两个原码定点数和小数部分的位数。

2. 函数内部先将a和b相乘，然后将结果右移n位，最终得到相乘的结果，并将其返回。

六、示例下面是一个示例代码，展示了如何使用上述函数进行原码一位两个定点数相乘的操作：```c#include <stdio.h>int m本人n(){int a = 10; // 原码定点数Aint b = 20; // 原码定点数Bint n = 8; // 小数部分的位数int result = fix_mul(a, b, n);printf("The result of A * B is d\n", result);return 0;}```七、总结通过上述的介绍可以看出，使用C语言实现原码一位两个定点数相乘是一个非常简单的操作。

定点数的算术移位
在计算机科学中，定点数是表示小数的一种方式。

定点数的算术移位是指将定点数左移或右移若干位，以实现乘法或除法等运算。

本题将介绍定点数的算术移位及其在计算机中的实现。

假设我们有一个定点数x，其小数点位于第n 位之后，即x = [x_n-1, x_n,
x_n+1, ...]，其中x_n 表示小数点所在位置的数值。

算术移位包括左移和右移两种情况。

1.左移：将定点数左移k 位，相当于将该数乘以2^k。

数学模型：x << k =
x × 2^k
2.右移：将定点数右移k 位，相当于将该数除以2^k。

数学模型：x >> k =
x / 2^k
将定点数x 左移2 位后得到的数值为：493824 将定点数x 右移2 位后得到的数值为：30864
通过算术移位，我们可以方便地进行定点数的乘法和除法运算。

在实际的计算机系统中，算术移位是通过硬件或汇编语言指令来实现的。

定点数相乘定点数相乘是计算机程序设计中非常重要的概念和技术。

在电子计算机发明之前，人们只能用纸笔手工计算乘法，但随着科技的进步，程序员们可以利用计算机进行更加高效和精确的计算。

在本文中，我们将详细介绍定点数相乘的概念、用途、计算方法和注意事项。

一、定点数相乘的概念定点数是一种在计算机中表示小数的方法，它不同于浮点数，浮点数使用科学计数法表示数值，可实现更高的精度。

定点数使用固定的小数位数，常用的定点数表示方式为：Qm.n，其中m表示总位数，n表示小数位数。

例如，Q8.4表示总共8位，其中4位是小数位。

定点数相乘就是将两个定点数相乘，得到一个新的定点数。

二、定点数相乘的用途定点数相乘广泛应用于计算机程序的开发中，其中包括信号处理、图像处理、音频处理等领域。

比如，信号处理中的数字滤波器，就是利用定点数相乘的方法来实现频带滤波的操作。

在图像处理中，定点数相乘可用于对图像进行放大、缩小和旋转等操作。

在音频处理中，也需要定点数相乘来实现音频信号的滤波和变换等操作。

三、定点数相乘的计算方法在计算机中，定点数相乘通常使用乘积累加法实现，即将两个定点数转换为整数相乘，得到乘积，再将乘积右移小数位数，得到新的定点数。

这一计算方法比较高效，能够处理较大的数据量和较复杂的计算。

但值得注意的是，在计算过程中要特别关注数值溢出和舍入误差等问题。

四、定点数相乘的注意事项1.数据类型要正确在进行计算时要保证数据类型的正确，否则可能会导致计算结果错误。

2.精度要控制好定点数的精度通常由小数位数决定，过高或过低都会导致计算结果失真。

3.舍入误差要注意在计算过程中，由于位数不够，可能产生舍入误差，导致计算结果不准确。

4.数值溢出要检测定点数相乘可能会产生较大的乘积，如果计算结果超出了数值范围，就会产生溢出错误，导致程序崩溃。

综上所述，定点数相乘是计算机程序设计中重要的技术，它广泛应用于信号处理、图像处理、音频处理等领域。

在进行计算时，程序员需要注意数据类型、精度、舍入误差和数值溢出等问题，确保程序计算结果的正确性和可靠性，不断提高程序的可维护性和可扩展性。

verilog 小数乘法摘要：一、引言二、Verilog中小数乘法的实现1.定点小数乘法2.浮点小数乘法三、小数乘法的意义与计算法则1.小数乘法的意义2.小数乘法的计算法则四、Verilog中实现小数乘法的例子1.定点小数乘法例子2.浮点小数乘法例子五、总结正文：一、引言小数乘法是数学中的一种基本运算，在工程领域和科学研究中有着广泛的应用。

Verilog是一种用于描述数字电路和模拟电路的硬件描述语言，能够对小数进行精确的运算。

本文将介绍Verilog中小数乘法的实现以及其意义与计算法则。

二、Verilog中小数乘法的实现1.定点小数乘法定点小数乘法是指将两个定点小数相乘，并保留一定的小数位数。

在Verilog中，我们可以通过编写代码实现定点小数乘法。

例如，假设两个定点小数为a和b，小数点后保留n位，则可以通过以下代码实现定点小数乘法：```verilogmodule fixed_point_multiplication (input [n-1:0] a,input [n-1:0] b,output [2*n-1:0] result);wire [2*n-1:0] partial_products [1:n];genvar i;generatefor (i = 0; i < n; i++) beginpartial_products[i] = a * b[i];endendgeneratewire [n-1:0] sum [1:n];wire [n-1:0] carry;generatefor (i = 0; i < n; i++) beginsum[i] = {partial_products[i][n-1:0], carry};carry = partial_products[i][2*n-1];endendgenerateresult = sum[n-1] + carry;endmodule```2.浮点小数乘法浮点小数乘法是指将两个浮点小数相乘，并保留一定的小数位数。

定点小数二进制真值引言定点小数二进制真值是计算机科学中的一个重要概念。

在计算机中，我们通常使用二进制来表示数字，而定点小数是一种特殊的表示方式，可以表示小数部分。

了解定点小数二进制真值对于理解计算机内部运算和数值表示方式至关重要。

本文将详细探讨定点小数二进制真值的定义、表示、运算规则及其应用。

一、定点小数二进制真值的定义定点小数是一种限定了小数点位置的表示方式。

在二进制中，小数点位置是固定的，因此称之为“定点”。

定点小数二进制真值用于表示实数，使得计算机可以处理小数运算。

定点小数由两部分组成：整数部分和小数部分。

整数部分用二进制表示整数，小数部分用二进制表示小数。

二、定点小数二进制真值的表示定点小数二进制真值的表示方式很简单。

首先确定整数部分所占的位数，以确定定点的位置。

然后确定小数部分所占的位数，即小数精度。

最后，将整数部分和小数部分用二进制表示。

示例：假设我们要表示一个定点小数二进制真值，定点位置在第四位，小数精度为两位。

我们可以将其表示为：1.01，其中1是整数部分，01是小数部分。

三、定点小数二进制真值的运算规则定点小数二进制真值的运算规则与整数运算类似，但要注意定点位置和小数精度的影响。

下面是定点小数二进制真值的运算规则：1. 加法运算定点小数二进制真值的加法运算需要将定点位置对齐。

先对齐小数点，然后按位相加，最后根据定点位置重新确定小数点位置。

示例：假设有两个定点小数二进制真值：1.11和0.01。

首先将小数点对齐得到1.11和0.01，然后按位相加得到10.00。

最后确定小数点位置，得到1.00。

2. 减法运算减法运算与加法运算类似，也需要对齐定点位置。

先对齐小数点，然后按位相减，最后根据定点位置重新确定小数点位置。

示例：假设有两个定点小数二进制真值：1.11和0.01。

首先将小数点对齐得到1.11和0.01，然后按位相减得到1.10。

最后确定小数点位置，得到0.10。

3. 乘法运算定点小数二进制真值的乘法运算需要将整数部分和小数部分分开计算。

FPGA中的小数运算FPGA是一种可编程的逻辑器件，可以实现各种数字电路功能。

FPGA中的数据通常是二进制的，也就是说，只有0和1两种状态。

那么，如果我们想在FPGA中处理小数，该怎么办呢？本文将介绍一种常用的方法，即定点小数。

什么是定点小数？定点小数是一种用二进制表示小数的方式，它将一个二进制数分为整数部分和小数部分，并规定小数点的位置。

定点小数有两种类型：有符号和无符号。

有符号定点小数可以表示正负数，而无符号定点小数只能表示非负数。

有符号定点小数通常用补码来表示，即最高位为符号位，0表示正数，1表示负数。

如何进行定点小数运算？在FPGA中进行定点小数运算，需要遵循以下基本原则：加法和减法：两个操作数必须有相同的小数位数，结果也保持之和。

除法：两个操作数可以有不同的小数位数，结果的小数位数等于被除数的小数位数减去除数的小数位数。

用公式表示如下：加法和减法：q3=q1±q2，如果x3=x1±x2乘法：q3=q1×q2/2n，如果x3=x1×x2除法：q3=q1×2n/q2，如果x3=x1/x2其中，x1,x2,x3代表三个浮点数（如2.2），q1,q2,q3代表其二进制表示（如70），n代表其小以下是一些例子：加法：假设我们要计算x3=x1+x2=2.2+(−6.03125)，其中x1和x2都是8位有符号定点小数，小数位数为5，那么：q1=70=01000110q2=−193=10111111q3=q1+q2=−123=10000101将q3转换为十进制，得到：x3=−12325=−3.84375乘法：假设我们要计算x3=x1×x2=2.2×(−6.03125)，其中x1是8位无符号定点小数，小数位数为5，x2是8位有符号定点小数，小数位数为5，那么：q1=70=01000110q2=−193=10111111q3=q1×q2/210=−13465/210=−13.15625将q3转换为二进制，得到：q3=−13.15625=11000011.0010由于q3超过了8位的范围，我们需要对其进行截断或舍入，以适应FPGA的硬件资源。

定点数原码一位乘法定点数原码一位乘法是一种乘法运算的方法，它利用了二进制数的加法和移位操作来实现乘法运算。

以下是这个算法的步骤：1.将被乘数和乘数都表示为定点数，即带有符号位的纯小数。

2.将被乘数和乘数都转换为原码表示，即最高位为符号位，其余位为数值位。

3.初始化结果为0。

4.从低位到高位逐位相乘，如果该位乘积的符号与结果符号相同，则将该位乘积加到结果上，否则只做移位操作。

5.重复步骤4，直到所有位都相乘完毕。

6.对结果进行舍入或截断操作，得到最终结果。

以下是一个简单的示例：假设我们有两个定点数：被乘数为1010.101(十进制为-4.625)，乘数为1011.011(十进制为-7.25)。

按照原码一位乘法的步骤，我们可以得到以下计算过程：1.被乘数=1010.101(十进制为-4.625)2.乘数=1011.011(十进制为-7.25)3.初始化结果为0。

4.从低位到高位逐位相乘：第0位：被乘数第0位为0，乘数第0位为1，符号相同，将该位乘积加到结果上，得到0+0=0。

第1位：被乘数第1位为1，乘数第1位为1，符号相同，将该位乘积加到结果上，得到0+1*2^(-2)=0.25。

第2位：被乘数第2位为0，乘数第2位为0，符号相同，将该位乘积加到结果上，得到0.25+0=0.25。

第3位：被乘数第3位为1，乘数第3位为0，符号不同，只做移位操作，得到0.25*2=0.5。

第4位：被乘数第4位为0，乘数第4位为1，符号相同，将该位乘积加到结果上，得到0.5+0=0.5。

第5位：被乘数第5位为1，乘数第5位为1，符号相同，将该位乘积加到结果上，得到0.5+(-1)*2^(-3)=-0.25。

第6位：被乘数第6位为0，乘数第6位为0，符号相同，将该位乘积加到结果上，得到-0.25+0=-0.25。

第7位：被乘数第7位为1，乘数第7位为1，符号相同，将该位乘积加到结果上，得到-0.25+(-8)*2^(-4)=-4.875。

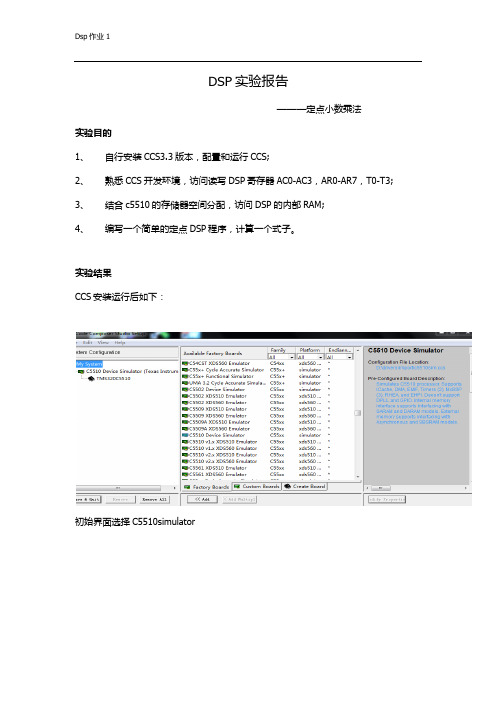
DSP实验报告———定点小数乘法实验目的1、自行安装CCS3.3版本，配置和运行CCS;2、熟悉CCS开发环境，访问读写DSP寄存器AC0-AC3，AR0-AR7，T0-T3;3、结合c5510的存储器空间分配，访问DSP的内部RAM;4、编写一个简单的定点DSP程序，计算一个式子。

实验结果CCS安装运行后如下：初始界面选择C5510simulator建立新工程；建立新汇编语言源程序文件；建立CMD文件；访问读写寄存器AC0-AC3，AR0-AR7，PC,T0-T3:计算一个简单乘加算式ASM源程序如下：.text.global startstart:MOV #0006h,AC0H;Q6MOV #0026h,AC1H;Q5MPY AC1,AC0MOV #0023h,AC1H;Q0MOV #0014h,AC2H;Q0MPY AC2,AC1MOV #03C0h,AC2H;Q6MOV #0033h,AC3H;Q5MPY AC3,AC2SFTSC AC1,#11,AC3ADD AC0,AC3ADD AC2,AC3运行后寄存器的结果如下：计算得结果应为724.12，但由于修改小数点的位置使计算结果有些偏差。

CMD文件如下：-e start-stack 500-sysstack 500MEMORY{MMR: o = 0x000000 l = 0x0000c0 /* 192B Memory Mapped Registers */ DARAM0: o = 0x0000C0 l = 0x001F40 /* 8kB Dual Access RAM 0 */DARAM1: o = 0x002000 l = 0x002000 /* 8kB Dual Access RAM 1 */DARAM2: o = 0x004000 l = 0x002000 /* 8kB Dual Access RAM 2 */DARAM3: o = 0x006000 l = 0x002000 /* 8kB Dual Access RAM 3 */DARAM4: o = 0x008000 l = 0x002000 /* 8kB Dual Access RAM 4 */DARAM5: o = 0x00A000 l = 0x002000 /* 8kB Dual Access RAM 5 */DARAM6: o = 0x00C000 l = 0x002000 /* 8kB Dual Access RAM 6 */DARAM7: o = 0x00E000 l = 0x002000 /* 8kB Dual Access RAM 7 */SARAM0: o = 0x010000 l = 0x002000 /* 8kB Single Access RAM 0 */SARAM1: o = 0x012000 l = 0x002000 /* 8kB Single Access RAM 1 */SARAM2: o = 0x014000 l = 0x002000 /* 8kB Single Access RAM 2 */SARAM3: o = 0x016000 l = 0x002000 /* 8kB Single Access RAM 3 */SARAM4: o = 0x018000 l = 0x002000 /* 8kB Single Access RAM 4 */SARAM5: o = 0x01A000 l = 0x002000 /* 8kB Single Access RAM 5 */SARAM6: o = 0x01C000 l = 0x002000 /* 8kB Single Access RAM 6 */SARAM7: o = 0x01E000 l = 0x002000 /* 8kB Single Access RAM 7 */SARAM8: o = 0x020000 l = 0x002000 /* 8kB Single Access RAM 8 */SARAM9: o = 0x022000 l = 0x002000 /* 8kB Single Access RAM 9 */SARAM10: o = 0x024000 l = 0x002000 /* 8kB Single Access RAM 10 */SARAM11: o = 0x026000 l = 0x002000 /* 8kB Single Access RAM 11 */SARAM12: o = 0x028000 l = 0x002000 /* 8kB Single Access RAM 12 */SARAM13: o = 0x02A000 l = 0x002000 /* 8kB Single Access RAM 13 */SARAM14: o = 0x02C000 l = 0x002000 /* 8kB Single Access RAM 14 */SARAM15: o = 0x02E000 l = 0x002000 /* 8kB Single Access RAM 15 */SARAM16: o = 0x030000 l = 0x002000 /* 8kB Single Access RAM 16 */SARAM17: o = 0x032000 l = 0x002000 /* 8kB Single Access RAM 17 */SARAM18: o = 0x034000 l = 0x002000 /* 8kB Single Access RAM 18 */SARAM19: o = 0x036000 l = 0x002000 /* 8kB Single Access RAM 19 */SARAM20: o = 0x038000 l = 0x002000 /* 8kB Single Access RAM 20 */SARAM21: o = 0x03A000 l = 0x002000 /* 8kB Single Access RAM 21 */SARAM22: o = 0x03C000 l = 0x002000 /* 8kB Single Access RAM 22 */SARAM23: o = 0x03E000 l = 0x002000 /* 8kB Single Access RAM 23 */CE0: o = 0x040000 l = 0x3C0000 /* 4MB CE0 external memory space */CE1: o = 0x400000 l = 0x400000 /* 4MB CE1 external memory space */CE2: o = 0x800000 l = 0x400000 /* 4MB CE2 external memory space */CE3: o = 0xC00000 l = 0x3F0000 /* 4MB CE3 external memory space */ROM: o = 0xFF0000 l = 0x00FF00 /* 64kB ROM (MPNMC=0) or CE3 (MPNMC=1) */VECS: o = 0xFFFF00 l = 0x000100 /* reset vector */}SECTIONS{vectors (NOLOAD) > VECS /* If MPNMC = 1, remove the NOLOAD directive */.cinit > DARAM0.text > DARAM1.stack > DARAM0.sysstack > DARAM0.sysmem > DARAM4.data > DARAM4.cio > DARAM0.bss > DARAM5.const > DARAM0}MAP文件：****************************************************************************** TMS320C55x Linker PC v4.2.3****************************************************************************** >> Linked Mon Apr 8 19:00:23 2016OUTPUT FILE NAME: <./Debug/test2.out>ENTRY POINT SYMBOL: "start" address: 00002000MEMORY CONFIGURATIONname origin length used unused attr fill(bytes) (bytes) (bytes) (bytes)---------------------- -------- --------- -------- -------- ---- --------MMR 00000000 000000c0 00000000 000000c0 RWIX DARAM0 000000c0 00001f40 00000000 00001f40 RWIX DARAM1 00002000 00002000 00000021 00001fdf RWIX DARAM2 00004000 00002000 00000000 00002000 RWIX DARAM3 00006000 00002000 00000000 00002000 RWIX DARAM4 00008000 00002000 00000000 00002000 RWIX DARAM5 0000a000 00002000 00000000 00002000 RWIX DARAM6 0000c000 00002000 00000000 00002000 RWIX DARAM7 0000e000 00002000 00000000 00002000 RWIX SARAM0 00010000 00002000 00000000 00002000 RWIX SARAM1 00012000 00002000 00000000 00002000 RWIX SARAM2 00014000 00002000 00000000 00002000 RWIX SARAM3 00016000 00002000 00000000 00002000 RWIX SARAM4 00018000 00002000 00000000 00002000 RWIX SARAM5 0001a000 00002000 00000000 00002000 RWIX SARAM6 0001c000 00002000 00000000 00002000 RWIX SARAM7 0001e000 00002000 00000000 00002000 RWIX SARAM8 00020000 00002000 00000000 00002000 RWIX SARAM9 00022000 00002000 00000000 00002000 RWIX SARAM10 00024000 00002000 00000000 00002000 RWIX SARAM11 00026000 00002000 00000000 00002000 RWIX SARAM12 00028000 00002000 00000000 00002000 RWIX SARAM13 0002a000 00002000 00000000 00002000 RWIX SARAM14 0002c000 00002000 00000000 00002000 RWIXSARAM15 0002e000 00002000 00000000 00002000 RWIXSARAM16 00030000 00002000 00000000 00002000 RWIXSARAM17 00032000 00002000 00000000 00002000 RWIXSARAM18 00034000 00002000 00000000 00002000 RWIXSARAM19 00036000 00002000 00000000 00002000 RWIXSARAM20 00038000 00002000 00000000 00002000 RWIXSARAM21 0003a000 00002000 00000000 00002000 RWIXSARAM22 0003c000 00002000 00000000 00002000 RWIXSARAM23 0003e000 00002000 00000000 00002000 RWIXCE0 00040000 003c0000 00000000 003c0000 RWIXCE1 00400000 00400000 00000000 00400000 RWIXCE2 00800000 00400000 00000000 00400000 RWIXCE3 00c00000 003f0000 00000000 003f0000 RWIXROM 00ff0000 0000ff00 00000000 0000ff00 RWIXVECS 00ffff00 00000100 00000000 00000100 RWIXSECTION ALLOCATION MAP(Addresses surrounded by []'s are displayed for convenience only!)output attributes/section page orgn(bytes) orgn(words) len(bytes) len(words) input sections -------- ---- ----------- ----------- ---------- ---------- --------------.cinit 0 [ 000000c0 ] 00000060 * 00000000 UNINITIALIZED.text 0 00002000 [ 00001000 ] 00000021 *00002000 [ 00001000 ] 00000020 * test2.obj (.text)00002020 [ 00001010 ] 00000001 * --HOLE-- [fill = 20].data 0 [ 00008000 ] 00004000 * 00000000 UNINITIALIZED.bss 0 [ 0000a000 ] 00005000 * 00000000 UNINITIALIZEDGLOBAL SYMBOLS: SORTED ALPHABETICALLY BY Nameabs. value/byte addr word addr name--------- --------- ----00000002 $TI_capability$C5500$CallingConvention 00000001 $TI_capability$C5500$MemoryModel 00000001 $TI_capability_requires_rev200005000 .bss00004000 .data00002000 .textffffffff ___binit__00005000 ___bss__ffffffff ___c_args__ffffffff ___cinit__00004000 ___data__00004000 ___edata__00005000 ___end__00002021 ___etext__ffffffff ___pinit__00002000 ___text__ffffffff binitffffffff cinit00004000 edata00005000 end00002021 etextffffffff pinit00002000 startGLOBAL SYMBOLS: SORTED BY Symbol Addressabs. value/byte addr word addr name--------- --------- ----00000001 $TI_capability$C5500$MemoryModel 00000001 $TI_capability_requires_rev2 00000002 $TI_capability$C5500$CallingConvention 00002000 .text00002000 ___text__00002000 start00002021 ___etext__00002021 etext00004000 .data00004000 ___data__00004000 ___edata__00004000 edata00005000 .bss00005000 ___bss__00005000 ___end__00005000 endffffffff ___binit__ffffffff ___c_args__ffffffff ___cinit__ffffffff ___pinit__ffffffff binitffffffff cinitffffffff pinit[23 symbols]。

定点数的乘法运算定点数的乘法运算是计算机科学中的一个重要概念，它在各个领域都有着广泛的应用。

本文将从概念、实现以及应用三个方面进行阐述，以便读者能够全面了解定点数的乘法运算。

一、概念定点数是一种表示数值的方式，它将小数点固定在某个位置上。

定点数的乘法运算是指对两个定点数进行相乘的操作。

在定点数的乘法运算中，需要注意保持小数点的位置不变，并对整数部分和小数部分进行相乘，最后将结果进行合并得到最终的乘积。

二、实现定点数的乘法运算可以通过数学方法来实现，也可以通过计算机程序来实现。

数学方法主要是通过手工计算来完成，而计算机程序则是利用计算机的运算能力来进行计算。

在计算机程序中，定点数的乘法运算通常使用位运算来实现。

位运算是一种对二进制数进行操作的方法，它可以高效地进行乘法运算。

计算机程序中的定点数通常使用固定的位数来表示，例如使用16位来表示定点数的整数部分和小数部分。

在进行乘法运算时，先将两个定点数的整数部分和小数部分进行相乘，然后将结果进行合并得到最终的乘积。

三、应用定点数的乘法运算在计算机科学中有着广泛的应用。

它可以用于图像处理、音频处理、视频编码等领域。

在图像处理中，定点数的乘法运算可以用于图像的缩放、旋转、平移等操作。

通过对图像的像素进行定点数的乘法运算，可以实现图像的变换和处理。

在音频处理中，定点数的乘法运算可以用于音频的滤波、均衡器等操作。

通过对音频信号进行定点数的乘法运算，可以实现音频的增强和修复。

在视频编码中，定点数的乘法运算可以用于视频的压缩和编码。

通过对视频的像素进行定点数的乘法运算，可以减少视频的数据量，从而实现视频的高效传输和存储。

总结：定点数的乘法运算是计算机科学中的一个重要概念，它在各个领域都有着广泛的应用。

本文从概念、实现以及应用三个方面进行了阐述，希望读者能够通过本文对定点数的乘法运算有更加全面的了解。

组成原理——定点原码一位乘法器设计与实现定点原码一位乘法器是一种用于进行定点数乘法运算的电路。

它是计算机系统中常用的基本算术电路，用于实现乘法操作。

在本文中，我们将讨论定点原码一位乘法器的设计原理以及其实现方法。

定点数表示法是一种用整数表示的数值表示法，其中小数点的位置是固定的。

在定点数乘法运算中，我们需要将两个输入数值进行相乘，并将结果输出。

定点原码一位乘法器的设计目标是实现高精度的乘法运算，同时保持低功耗和低延迟。

定点原码一位乘法器的设计原理基于布尔代数和逻辑电路。

其主要包括以下几个步骤：1.输入信号：定点原码一位乘法器通常有两个输入信号，分别代表两个乘数。

这些信号通常由时钟信号触发，以确保同步操作。

2.加法器和移位器：定点原码一位乘法器使用加法器和移位器来实现乘法操作。

移位器用于将乘数（或加数）进行位移操作，以便选择正确的乘积位。

加法器用于将部分乘积相加，并输出最终的乘积结果。

3.乘积位选择：乘积位选择决定了哪些部分乘积需要相加以得到最终乘积结果。

这通常通过导线连接来实现，其中每根导线对应于一个部分乘积位。

4.符号位处理：定点原码一位乘法器还需要处理符号位。

这涉及到对符号位进行逻辑与门操作，以确保最终结果的符号正确。

定点原码一位乘法器的实现通常使用逻辑门、移位寄存器、加法器等电路元件。

它的实现过程可以分为以下几个步骤：1.设计逻辑电路：根据定点原码一位乘法器的设计原理，设计逻辑电路图，其中包括逻辑门、移位寄存器和加法器等。

2.实现逻辑电路：根据设计的逻辑电路图，使用逻辑门、移位寄存器和加法器等电路元件，来实现电路的物理连接。

3.进行仿真：使用仿真工具，对设计的电路进行仿真测试，以验证电路的正确性和性能。

4.调整和优化：根据仿真结果，对电路进行调整和优化，以提高电路的性能和功耗。

5.布局和布线：根据最终设计的电路图，对电路进行布局和布线，以保证电路的可靠性和稳定性。

6.制造和测试：将电路进行制造和测试，以确保制造的电路符合设计要求，并具有良好的性能和可靠性。

小数的乘法如何进行小数的乘法运算小数的乘法是数学中基础且常见的运算，用于计算小数之间的乘积。

在进行小数的乘法运算时，我们需要遵循一定的规则和步骤来确保计算的准确性。

本文将向您介绍如何进行小数的乘法运算。

一、小数的基本概念与表示方法在开始了解小数的乘法运算之前，我们首先需要了解小数的基本概念与表示方法。

小数是指不完整的数字，由整数部分与小数部分组成。

小数点（.）用于分隔整数部分和小数部分。

例如，2.5是一个小数，其中2是整数部分，0.5是小数部分。

小数可以用分数或百分数来表示。

例如，0.5可以表示为1/2或50%。

同时，小数也可以用有限小数或无限循环小数来表示。

有限小数是指小数部分有限位数的小数，例如0.25。

无限循环小数是指小数部分有无限重复位数的小数，例如0.333...（记作0.3）。

二、小数的乘法规则在进行小数的乘法运算时，需要遵循以下规则：1. 计算整数部分的乘积：将小数去掉小数点后，只计算整数部分的乘积。

2. 计算小数部分的乘积：将小数的小数部分分别相乘，再将结果的小数点向左移动到正确的位置。

3. 将整数部分的乘积和小数部分的乘积相加得到最终结果。

三、小数的乘法运算步骤下面以一个例子来说明小数的乘法运算步骤：例：计算1.5乘以2.3的结果。

步骤1：计算整数部分的乘积。

将小数去掉小数点后，只计算整数部分的乘积。

1 ×2 = 2步骤2：计算小数部分的乘积。

将小数的小数部分分别相乘，再将结果的小数点向左移动到正确的位置。

0.5 × 0.3 = 0.15步骤3：将整数部分的乘积和小数部分的乘积相加得到最终结果。

2 + 0.15 = 2.15因此，1.5乘以2.3的结果为2.15。

四、小数乘法运算的应用举例小数的乘法运算在日常生活中有广泛的应用。

下面列举几个例子：例1：购买水果小明去超市买了0.5公斤的苹果，每公斤2.5元。

他需要计算苹果的总价格。

解：将小数转化为分数，计算得到价格：0.5 × 2.5 = 1.25（元）因此，苹果的总价格为1.25元。

小数乘法运算一致
小数乘法的运算方法与整数乘法基本相同，只是在计算时需要注意小数点的位置。

首先，将两个小数的小数点对齐，然后按照整数乘法的法则进行计算。

在计算过程中，从右往左依次用乘数的每一位去乘被乘数的每一位，乘得的积的末位要与乘数的相应位对齐。

然后，将所有的乘积相加，得到最终的结果。

在计算小数乘法时，需要特别注意小数点的位置。

如果小数位数不够，可以在前面补零。

例如，计算 0.25 × 0.4，可以将其写为 25 × 4，然后计算得到 100，再将小数点向左移动两位，得到最终结果 0.1。

此外，在计算小数乘法时，还需要注意积的小数位数。

积的小数位数等于两个乘数的小数位数之和。

例如，计算 0.3 × 0.4，两个乘数都有一位小数，因此积也有一位小数，即0.12。

总之，小数乘法的运算方法与整数乘法基本相同，只是需要注意小数点的位置和积的小数位数。

通过练习和掌握这些技巧，你可以更加熟练地进行小数乘法的运算。