【走向高考】2013年高考数学总复习 阶段性测试题九 新人教A版

1-3充分条件与必要条件基础巩固强化1.(2011·大纲全国文，5)下列四个条件中，使a>b成立的充分而不必要的条件是( )A．a>b＋1 B．a>b－1C．a2>b2D．a3>b3[答案] A[解析] ∵a>b＋1⇒a－b>1⇒a－b>0⇒a>b，∴a>b＋1是a>b的充分条件．又∵a>b⇒a－b>0⇒/ a>b＋1，∴a>b＋1不是a>b的必要条件，∴a>b＋1是a>b成立的充分而不必要条件．[点评] 如a＝2＝b，满足a>b－1，但a>b不成立；又a＝－3，b＝－2时，a2>b2，但a>b不成立；a>b⇔a3>b3.故B、C、D选项都不对．2．(2012·浙江理)设a∈R，则“a＝1”是“直线l1：ax＋2y－1＝0与直线l2：x＋(a ＋1)y＝0平行”的( )A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件[分析] 由l1∥l2的充要条件(A1B2－A2B1＝0)可求得a的值，然后进行判断．[答案] A[解析] 若两直线平行，则a(a＋1)＝2，即a2＋a－2＝0∴a＝1或－2，故a＝1是两直线平行的充分不必要条件．3．(2011·湖南湘西州联考)已知条件p：a<0，条件q：a2>a，则綈p是綈q的( ) A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件[答案] B[解析] 由a2>a得，a<0或a>1.所以q是p成立的必要不充分条件，其逆否命题綈p也是綈q的必要不充分条件4．(文)(2011·聊城模拟)“k＝1”是“直线x－y＋k＝0与圆x2＋y2＝1相交”的( ) A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件[答案] A[解析] k＝1时，圆心O(0,0)到直线距离d＝12<1，∴直线与圆相交；直线与圆相交时，圆心到直线距离d ＝|k |2<1，∴－2<k <2，故选A.(理)(2011·通化模拟)直线x －y ＋m ＝0与圆x 2＋y 2－2x －1＝0有两个不同交点的充分不必要条件是( )A ．－3<m <1B ．－4<m <2C ．0<m <1D ．m <1[答案] C[解析] 联立方程得⎩⎪⎨⎪⎧x －y ＋m ＝0x 2＋y 2－2x －1＝0，得x 2＋(x ＋m )2－2x －1＝0，即2x 2＋(2m －2)x ＋m 2－1＝0，直线与圆有两个不同交点的充要条件为Δ＝(2m －2)2－4×2(m 2－1)>0，解得－3<m <1，只有C 选项符合要求．[点评] 直线与圆有两个不同交点⇔－3<m <1，故其充分不必要条件应是(－3,1)的真子集．5．(文)(2011·太原模拟)“α≠β”是“sin α≠sin β”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件[答案] B[解析] 命题“若α≠β，则sin α≠sin β”等价于命题“若sin α＝sin β，则α＝β”，这个命题显然不正确，故条件是不充分的；命题“若sin α≠sin β，则α≠β”等价于命题“若α＝β，则sin α＝sin β”，这个命题是真命题，故条件是必要的．故选B.(理)(2011·沈阳二中月考)“θ＝2π3”是“tan θ＝2cos ⎝ ⎛⎭⎪⎫π2＋θ”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 [答案] A[解析] 解法1：∵θ＝2π3为方程tan θ＝2cos ⎝ ⎛⎭⎪⎫π2＋θ的解，∴θ＝2π3是tan θ＝2cos ⎝ ⎛⎭⎪⎫π2＋θ成立的充分条件； 又∵θ＝8π3也是方程tan θ＝2cos ⎝ ⎛⎭⎪⎫π2＋θ的解，∴θ＝2π3不是tan θ＝2cos ⎝ ⎛⎭⎪⎫π2＋θ的必要条件，故选A.解法2：∵tan θ＝2cos ⎝ ⎛⎭⎪⎫π2＋θ，∴sin θcos θ＝－2sin θ， ∴sin θ＝0或cos θ＝－12，∴方程tan θ＝2cos ⎝⎛⎭⎪⎫π2＋θ的解集为A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫θ⎪⎪⎪θ＝k π或θ＝2k π±23π，k ∈Z， 显然⎩⎨⎧⎭⎬⎫2π3 A ，故选A.6．(文)已知数列{a n }，“对任意的n ∈N *，点P n (n ，a n )都在直线y ＝3x ＋2上”是“{a n }为等差数列”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 [答案] A[解析] 点P n (n ，a n )在直线y ＝3x ＋2上，即有a n ＝3n ＋2，则能推出{a n }是等差数列；但反过来，{a n }是等差数列，a n ＝3n ＋2未必成立，所以是充分不必要条件，故选A.(理)(2011·杭州质检)设等差数列{a n }的前n 项和为S n ，则S 12>0是S 9≥S 3的( ) A ．充分但不必要条件 B ．必要但不充分条件 C ．充要条件D ．既不充分也不必要条件 [答案] A[解析] 解法1：将它们等价转化为a 1和d 的关系式．S 12>0⇒12a 1＋12×11×d 2>0⇒2a 1＋11d >0；S 9≥S 3⇒9a 1＋9×8×d 2≥3a 1＋3×2×d2⇒2a 1＋11d ≥0.故选A.解法2：S 12>0⇒12a 1＋a 122>0⇒a 1＋a 12>0.S 9≥S 3⇒a 4＋a 5＋…＋a 9≥0⇒3(a 1＋a 12)≥0.故选A.7．在平面直角坐标系xOy 中，直线x ＋(m ＋1)y ＝2－m 与直线mx ＋2y ＝－8互相垂直的充要条件是m ＝________.[答案] －23[解析] x ＋(m ＋1)y ＝2－m 与mx ＋2y ＝－8垂直⇔ 1·m ＋(m ＋1)·2＝0， 得m ＝－23.8．给出下列命题：①“m >n >0”是“方程mx 2＋ny 2＝1表示焦点在y 轴上的椭圆”的充要条件． ②对于数列{a n }，“a n ＋1>|a n |，n ＝1,2，…”是{a n }为递增数列的充分不必要条件． ③已知a ，b 为平面上两个不共线的向量，p ：|a ＋2b |＝|a －2b |；q ：a ⊥b ，则p 是q 的必要不充分条件．④“m >n ”是“(23)m <(23)n”的充分不必要条件．其中真命题的序号是________． [答案] ①②[解析] ①∵m >n >0，∴0<1m <1n ，方程mx 2＋ny 2＝1化为x 21m＋y 21n＝1，故表示焦点在y 轴上的椭圆，反之亦成立．∴①是真命题；②对任意自然数n ，a n ＋1>|a n |≥0，∴a n ＋1>a n ，∴{a n }为递增数列；当取a n ＝n －4时，则{a n }为递增数列，但a n ＋1>|a n |不一定成立，如a 2>|a 1|就不成立．∴②是真命题；③由于|a ＋2b |＝|a －2b |⇔(a ＋2b )2＝(a －2b )2⇔a ·b ＝0⇔a ⊥b ，因此p 是q 的充要条件，∴③是假命题；④∵y ＝⎝ ⎛⎭⎪⎫23x 是减函数，∴当m >n 时，⎝ ⎛⎭⎪⎫23m <⎝ ⎛⎭⎪⎫23n，反之，当(23)m <⎝ ⎛⎭⎪⎫23n 时，有m >n ，因此m >n ⇔⎝ ⎛⎭⎪⎫23m <⎝ ⎛⎭⎪⎫23n ，故④是假命题．9．(2011·济南三模)设p ：⎩⎪⎨⎪⎧4x ＋3y －12≥0，3－x ≥0，x ＋3y ≤12，q ：x 2＋y 2>r 2(x ，y ∈R ，r >0)，若p是q 的充分不必要条件，则r 的取值范围是________．[答案] (0，125][解析] 设A ＝(x ，y )⎩⎪⎨⎪⎧4x ＋3y －12≥0，3－x ≥0，x ＋3y ≤12.B ＝{(x ，y )|x 2＋y 2>r 2，x ，y ∈R ，r >0}，则集合A 表示的区域为图中阴影部分，集合B 表示以原点为圆心，以r 为半径的圆的外部，设原点到直线4x ＋3y －12＝0的距离为d ，则d ＝|4×0＋3×0－12|5＝125，∵p 是q 的充分不必要条件，∴A B ，则0<r ≤125.10．(2010·浙江温州十校联考)已知p ：|x －3|≤2，q ：(x －m ＋1)(x －m －1)≤0，若綈p 是綈q 的充分而不必要条件，求实数m 的取值范围．[解析] 由题意p ：－2≤x －3≤2，∴1≤x ≤5. ∴綈p ：x <1或x >5.q ：m －1≤x ≤m ＋1， ∴綈q ：x <m －1或x >m ＋1.又∵綈p 是綈q 的充分不必要条件， ∴⎩⎪⎨⎪⎧m －1≥1，m ＋1<5，或⎩⎪⎨⎪⎧m －1>1，m ＋1≤5.∴2≤m ≤4.能力拓展提升11.(文)(2011·湖南高考)设集合M ＝{1,2}，N ＝{a 2}，则“a ＝1”是“N ⊆M ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分又不必要条件[答案] A[解析] 显然a ＝1时一定有N ⊆M ，反之则不一定成立，如a ＝ 2.故是充分不必要条件．[点评] 若N ⊆M ，则应有a 2＝1或a 2＝2，∴a ∈{－1,1，2，－2}，由于{1} {－1,1，2，－2}，∴应选A.(理)(2011·东北三校三模)若集合A ＝{x ||x |≤3，x ∈Z }，B ＝{x |x 2－4x ＋3≤0，x ∈Z }，则( )A ．“x ∈A ”是“x ∈B ”的充分条件但不是必要条件B ．“x ∈A ”是“x ∈B ”的必要条件但不是充分条件C ．“x ∈A ”是“x ∈B ”的充要条件D ．“x ∈A ”既不是“x ∈B ”的充分条件，也不是“x ∈B ”的必要条件 [答案] B[解析] 由题可知集合A ＝{－3，－2，－1,0,1,2,3}，集合B ＝{1,2,3}，所以“x ∈A ”是“x ∈B ”的必要条件但不是充分条件，故选B.12．(文)(2011·杭州二检)已知α，β表示两个不同的平面，m 是一条直线且m ⊂α，则“α⊥β”是“m ⊥β”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件[答案] B [解析]⎭⎪⎬⎪⎫m ⊥βm ⊂α⇒α⊥β；但α⊥β时，设α∩β＝l ，当m ∥l 时，m 与β不垂直，故选B.(理)(2011·浙江五校联考)已知不重合的直线a ，b 和不重合的平面α，β，a ⊥α，b ⊥β，则“a ⊥b ”是“α⊥β”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件[答案] C[解析] ∵⎩⎪⎨⎪⎧a ⊥b b ⊥β，∴a ∥β或a ⊂β，∵a ⊥α，∴α⊥β；反之，由α⊥β也可以推出a ⊥b ，故选C.13．(文)(2011·宁夏三市联考)设x 、y 是两个实数，命题“x 、y 中至少有一个数大于1”成立的充分不必要条件是( )A ．x ＋y ＝2B ．x ＋y >2C ．x 2＋y 2>2 D ．xy >1[答案] B[解析] 命题“x 、y 中至少有一个数大于1”等价于“x >1或y >1”．若x ＋y >2，必有x >1或y >1，否则x ＋y ≤2；而当x ＝2，y ＝－1时，2－1＝1<2，所以x >1或y >1不能推出x＋y >2.对于x ＋y ＝2，当x ＝1，且y ＝1时，满足x ＋y ＝2，不能推出x >1或y >1.对于x 2＋y 2>2，当x <－1，y <－1时，满足x 2＋y 2>2，不能推出x >1或y >1.对于xy >1，当x <－1，y <－1时，满足xy >1，不能推出x >1或y >1.故选B.(理)(2012·重庆)已知f (x )是定义在R 上的偶函数，且以2为周期，则“f (x )为[0,1]上的增函数”是“f (x )为[3,4]上的减函数”的( )A ．既不充分也不必要的条件B ．充分而不必要的条件C ．必要而不充分的条件D ．充要条件 [答案] D[解析] ∵f (x )是定义在R 上的偶函数，且f (x )在[0,1]上为增函数，∴f (x )在[－1,0]上为减函数，∴当3≤x ≤4时，－1≤x －4≤0，∴当x ∈[3,4]时，f (x )是减函数，反之也成立，故选D. [点评] 本题运用数形结合的方法更容易求解．14．(2011·广州二测)已知p ：k >3；q ：方程x 23－k ＋y 2k －1＝1表示双曲线，则p 是q 的( )A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分也非必要条件[答案] A[解析] 由k >3得3－k <0，k －1>0，方程x 23－k ＋y 2k －1＝1表示双曲线，因此p 是q 的充分条件；反过来，由方程x 23－k ＋y 2k －1＝1表示双曲线不能得到k >3，如k ＝0时方程x 23－k ＋y 2k －1＝1也表示双曲线，因此p 不是q 的必要条件．综上所述，p 是q 的充分不必要条件，选A.15．(2011·日照模拟)设命题p ：实数x 满足x 2－4ax ＋3a 2<0，其中a ≠0，命题q ：实数x 满足⎩⎪⎨⎪⎧x 2－x －6≤0，x 2＋2x －8>0，(1)若a ＝1，且p ∧q 为真，求实数x 的取值范围； (2)若p 是q 的必要不充分条件，求实数a 的取值范围． [解析] (1)a ＝1时，p ：x 2－4x ＋3<0，即p ：1<x <3，q ：⎩⎪⎨⎪⎧－2≤x ≤3，x <－4或x >2，即q ：2<x ≤3，由p ∧q 为真知，2<x <3.(2)由x 2－4ax ＋3a 2<0，得(x －a )(x －3a )<0， 若a <0，则3a <x <a ，不合题意； 若a >0，则a <x <3a ，由题意知，(2,3] (a,3a )，∴⎩⎪⎨⎪⎧a ≤23a >3，∴1<a ≤2.*16.(2011·蚌埠质检)设函数f (x )＝ln x －px ＋1.(1)当p >0时，若对任意的x >0，恒有f (x )≤0，求p 的取值范围；(2)证明：当x >0时，1＋ln xx≤1.[解析] (1)显然函数定义域为(0，＋∞)． 且f ′(x )＝1x －p ＝1－px x.当p >0时，令f ′(x )＝0，∴x ＝1p∈(0，＋∞)，f ′(x )，f (x )随x 的变化情况如下表：从上表可以看出：当p >0时，有唯一的极大值点x ＝p.当p >0时在x ＝1p处取得极大值f ⎝ ⎛⎭⎪⎫1p ＝ln 1p，此极大值也是最大值，要使f (x )≤0恒成立，只需f ⎝ ⎛⎭⎪⎫1p ＝ln 1p≤0，即p ≥1.∴p 的取值范围为[1，＋∞)． (2)当p ＝1时，f (x )＝ln x －x ＋1.由(1)可知，函数f (x )在x ＝1处取最大值，即f (x )≤f (1)＝0，即ln x ≤x －1. 故当x >0时，1＋ln xx≤1.1．△ABC 中，“cos A ＝2sin B sin C ”是“△ABC 为钝角三角形”的( ) A ．必要不充分条件 B ．充分不必要条件 C ．充要条件D ．既不充分也不必要条件 [答案] B[解析] cos A ＝－cos(B ＋C )＝－cos B cos C ＋sin B sin C ＝2sin B sin C ，∴cos(B －C )＝0.∴B －C ＝π2.∴B ＝π2＋C >π2，故为钝角三角形，反之显然不成立，故选B.2．(2012·泰安质检)设集合A ＝{x |－a <x <a }，其中a >0，命题p ：1∈A ，命题q ：2∈A .若p ∨q 为真命题，p ∧q 为假命题，则a 的取值范围是( )A ．0<a <1或a >2B ．0<a <1或a ≥2C ．1<a ≤2D ．1≤a ≤2[答案] C[解析] 由1∈A 知，－a <1<a ，∴a >1；由2∈A 知，a >2.p ∨q 为真命题，只需p 与q 中至少有一个为真即可，p ∧q 为假命题，只需p 与q 中至少有一个为假即可，因此命题p 和q 只能一真一假，当p 真q 假时，可得1<a ≤2，当p 假q 真时，解集为空集．因此a 的取值范围是1<a ≤2.3．“a ＝1”是“函数f (x )＝|x －a |在区间(－∞，1]上为减函数”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件 [答案] A[解析] 当a ＝1时，f (x )＝|x －1|＝⎩⎪⎨⎪⎧x －1x ≥1，1－x x <1，所以f (x )在区间(－∞，1]上是减函数；若f (x )在区间(－∞，1]上是减函数，结合图象可得a ≥1，所以前者是后者的充分不必要条件．4．“a ＝1”是“直线x ＋y ＝0和直线x －ay ＝0互相垂直”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件[答案] C[解析] 直线x ＋y ＝0与直线x －ay ＝0垂直⇔1×1＋1×(－a )＝0⇔a ＝1. 5．“x ＝π4”是“函数y ＝sin2x 取得最大值”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 [答案] A[解析] x ＝π4时，y ＝sin2x 取最大值，但y ＝sin2x 取最大值时，2x ＝2k π＋π2，k ∈Z ，不一定有x ＝π4.6．(2012·辽宁)已知命题p ：∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≥0，则綈p 是( ) A ．∃x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≤0 B ．∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≤0 C ．∃x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)<0 D ．∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)<0 [答案] C[解析] 本题主要考查全称命题的否定．根据存在性(特称)命题与全称命题的关系求解，①量词要变化，②命题的结论要否定． [点评] 注意綈表示命题的否定，还有“∀”与“∃”的含义，要准确理解． 7．(2012·浙江省温州八校联考)已知f (x )＝2x ＋3(x ∈R )，若|f (x )－1|<a 的必要条件是|x ＋1|<b (a ，b >0)，则a 、b 之间的关系是( )A ．b ≥a 2B ．b <a 2C ．a ≤b2D ．a >b2[答案] A[解析] 由|f (x )－1|＝|2x ＋2|＝2|x ＋1|<a 得， |x ＋1|<a 2，由题意知a2≤b ，故选A.8．(2011·成都二诊)已知函数f (x )＝⎩⎪⎨⎪⎧log 2x x ≥1，x ＋c x <1，则“c ＝－1”是“函数f (x )在R 上递增”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件[答案] A[解析] 当c ＝－1时，函数f (x )＝⎩⎪⎨⎪⎧log 2x x ≥1x －1x <1，易知函数f (x )在(－∞，1)、(1，＋∞)上分别是增函数，且注意到log 21＝1－1＝0，此时函数f (x )在R 上是增函数；反过来，当函数f (x )在R 上是增函数时，不能得出c ＝－1，如c ＝－2，此时也能满足函数f (x )在R 上是增函数．综上所述，“c ＝－1”是“函数f (x )在R 上递增”的充分不必要条件，选A.9．(2012·沈阳市模拟)设a ，b 是平面α内两条不同的直线，l 是平面α外的一条直线，则“l ⊥a ，l ⊥b ”是“l ⊥α”是( )A ．充要条件B ．充分而不必要的条件C ．必要而不充分的条件D ．既不充分也不必要的条件11 [答案] C[解析] l ⊥α⇒l ⊥a ，l ⊥b ；⎭⎪⎬⎪⎫l ⊥a l ⊥b ⇒/ l ⊥α，因为a 与b 可能平行． 10．(2012·内蒙包头市模拟)有下列命题： ①设集合M ＝{x |0<x ≤3}，N ＝{x |0<x ≤2}，则“a ∈M ”是“a ∈N ”的充分而不必要条件； ②命题“若a ∈M ，则b ∉M ”的逆否命题是：若b ∈M ，则a ∉M ；③若p ∧q 是假命题，则p ，q 都是假命题；④命题p ：“∃x 0∈R ，x 20－x 0－1>0”的否定綈p ：“∀x ∈R ，x 2－x －1≤0”则上述命题中为真命题的是( )A ．①②③④B ．①③④C ．②④D ．②③④ [答案] C[解析] ∵N M ，∴a ∈M 是a ∈N 的必要不充分条件，∴①为假命题；逆否命题是将原命题的条件和结论都否定后分别作为新命题的结论与条件，a ∈M 否定后a ∉M 为结论，b ∉M 否定后b ∈M 为条件，故②为真命题；p ∧q 为假命题时，p 、q 至少有一个为假命题，不一定“p 、q 都是假命题”，故③为假命题；特称命题的否定为全称命题，>的否定为≤，故④为真命题，∴选C.。

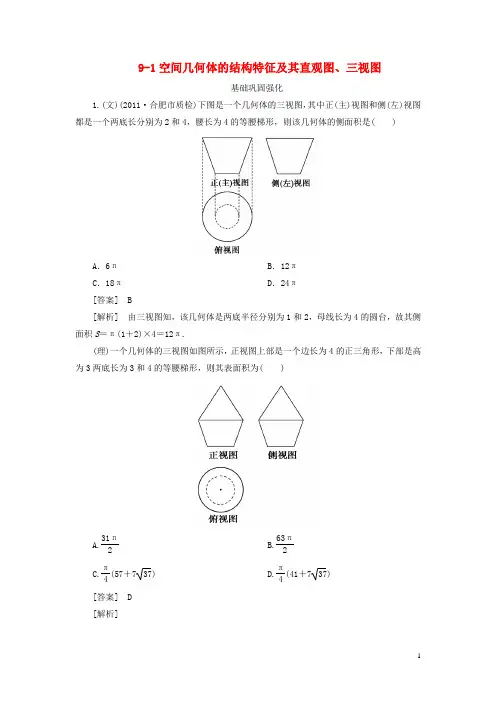
9-1空间几何体的结构特征及其直观图、三视图基础巩固强化1.(文)(2011·合肥市质检)下图是一个几何体的三视图，其中正(主)视图和侧(左)视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是( )A ．6πB ．12πC ．18πD ．24π[答案] B[解析] 由三视图知，该几何体是两底半径分别为1和2，母线长为4的圆台，故其侧面积S ＝π(1＋2)×4＝12π.(理)一个几何体的三视图如图所示，正视图上部是一个边长为4的正三角形，下部是高为3两底长为3和4的等腰梯形，则其表面积为( )A.31π2B.63π2C.π4(57＋737) D.π4(41＋737) [答案] D [解析]由三视图知，该几何体是一个组合体，上部是底半径为2，高为23的圆锥，下部是两底半径分别为2和32，高为3的圆台，其表面积S ＝π×2×4＋π(2＋32)×372＋π·(32)2＝π4(41＋737)，故选D. 2．如图所示是水平放置三角形的直观图，D 是△ABC 的BC 边中点，AB 、BC 分别与y ′轴、x ′轴平行，则三条线段AB 、AD 、AC 中( )A ．最长的是AB ，最短的是AC B ．最长的是AC ，最短的是AB C ．最长的是AB ，最短的是AD D ．最长的是AC ，最短的是AD [答案] B[解析] 由条件知，原平面图形中AB ⊥AC ，从而AB <AD <AC .3．(文)(2012·河南六市联考)如图为一个几何体的三视图，正视图和侧视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的全面积为( )A．14 3 B．6＋2 3 C．12＋2 3 D．16＋2 3 [答案] C[解析] 该几何体是一个正三棱柱，设底面正三角形边长为a，则32a＝3，∴a＝2，又其高为2，故其全面积S＝2×(34×22)＋3×(2×2)＝12＋2 3.(理)(2011·北京西城模拟)一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为：①长方形；②正方形；③圆；④椭圆．其中正确的是( )A．①②B．②③C．③④D．①④[答案] B[解析] 根据三视图画法规则“长对正，高平齐、宽相等”，俯视图应与正视图同长为3，与侧视图同宽为2，故一定不可能是圆和正方形．4．(文)(2011·广东文，9)如下图，某几何体的正视图(正视图)，侧视图(侧视图)和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为( )A ．4 3B ．4C ．2 3D ．2[答案] C[解析] 由三视图知该几何体是四棱锥，底面是菱形，其面积S ＝12×23×2＝23，高h ＝3，所以V ＝13Sh ＝13×23×3＝2 3.(理)(2012·保定市一模)一个棱锥的三视图如图(尺寸的长度单位为m)，则该棱锥的体积是(单位：m 3)．( )A ．4＋2 6B ．4＋ 6 C.23 D.43[答案] D[解析] 由侧视图和俯视图是全等的等腰三角形，及正视图为等腰直角三角形可知，该几何体可看作边长AB ＝BC ＝3，AC ＝1的△ABC 绕AC 边转动到与平面△PAC 位置(平面PAC ⊥平面ABC )所形成的几何体，故其体积V ＝13×(12×2×2)×2＝43.5．(文)(2011·广东省东莞市一模)一空间几何体的三视图如图所示，该几何体的体积为12π＋853，则正视图与侧视图中x 的值为( )A ．5B ．4C ．3D ．2 [答案] C[解析] 根据题中的三视图可知，该几何体是圆柱和正四棱锥的组合体，圆柱的底半径为2，高为x ，四棱锥的底面正方形对角线长为4，四棱锥的高h ＝32－22＝5，其体积为V ＝13×8×5＋π×22×x ＝12π＋853，解得x ＝3. (理)(2011·新课标全国理，6)在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为( )[答案] D [解析]由正视图知该几何体是锥体，由俯视图知，该几何体的底面是一个半圆和一个等腰三角形，故该几何体是一个半圆锥和一个三棱锥组成的，两锥体有公共顶点，圆锥的两条母线为棱锥的两侧棱，其直观图如图，在侧视图中，O 、A 与C 的射影重合，侧视图是一个三角形△PBD ，OB ＝OD ，PO ⊥BD ，PO 为实线，故应选D.6．(文)(2012·河北郑口中学模拟)某几何体的正视图与侧视图如图所示，若该几何体的体积为13，则该几何体的俯视图不可以是( )[答案] D[解析] 由正视图及俯视图可知该几何体的高为1，又∵其体积为13，故为锥体，∴S 底＝1，A 中为三角形，此时其底面积为12，舍去；B 为14个圆，底面积为π4，也舍去，C 为圆，其面积为π舍去，故只有D 成立．[点评] 如果不限定体积为13，则如图(1)在三棱锥P －ABC 中，AC ⊥BC ，PC ⊥平面ABC ，AC ＝BC ＝PC ＝1，则此三棱锥满足题设要求，其俯视图为等腰直角三角形A ；如图(2)，底半径为1，高为1的圆锥，被截面POA 与POB 截下一角，OA ⊥OB ，则此时几何体满足题设要求，其俯视图为B ；如图(3)，这是一个四棱锥，底面是边长为1的正方形，PA ⊥平面ABCD ，此几何体满足题设要求，其俯视图为D.(理)(2012·大同市调研)已知一个棱长为2的正方体，被一个平面截后所得几何体的三视图如图所示，则该几何体的体积是( )A ．8 B.203 C.173D.143[答案] C[解析] 由题可知，原正方体如图所示，被平面EFB 1D 1截掉的几何体为棱台AFE －A 1B 1D 1，则所求几何体的体积V ＝23－V A 1B 1D 1－AEF ＝23－13×(2＋12＋2×12)×2＝173，故选C.7．已知一个几何体的三视图如图所示(单位：cm)，其中正(主)视图是直角梯形，侧(左)视图和俯视图都是矩形，则这个几何体的体积是________cm 3.[答案] 32[解析] 依据三视图知，该几何体的上、下底面均为矩形，上底面是边长为1的正方形，下底面是长为2，宽为1的矩形，左侧面是与底面垂直的正方形，其直观图如图所示，易知该几何体是四棱柱ABCD －A 1B 1C 1D 1，其体积V ＝S 梯形ABCD ·AA 1＝1＋2×12×1＝32cm 3. 8．(2011·皖南八校联考)已知三棱锥的直观图及其俯视图与侧视图如下，俯视图是边长为2的正三角形，侧视图是有一直角边为2的直角三角形，则该三棱锥的正视图面积为________．[答案] 2[解析] 由条件知，该三棱锥底面为正三角形，边长为2，一条侧棱与底面垂直，该侧棱长为2，故正视图为一直角三角形，两直角边的长都是2，故其面积S ＝12×2×2＝2.9．(2011·安徽知名省级示范高中联考)在棱长为1的正方体ABCD －A 1B 1C 1D 1中，过对角线BD 1的一个平面交AA 1于E ，交CC 1于F ，得四边形BFD 1E ，给出下列结论：①四边形BFD 1E 有可能为梯形； ②四边形BFD 1E 有可能为菱形；③四边形BFD 1E 在底面ABCD 内的投影一定是正方形； ④四边形BFD 1E 有可能垂直于平面BB 1D 1D ； ⑤四边形BFD 1E 面积的最小值为62. 其中正确的是________．(请写出所有正确结论的序号) [答案] ②③④⑤[解析] ∵平面ADD 1A 1∥平面BCC 1B 1，平面BFD 1E ∩平面ADD 1A 1＝D 1E ，平面BFD 1E ∩平面BCC 1B 1＝BF ，∴D 1E ∥BF ；同理BE ∥FD 1，∴四边形BFD 1E 为平行四边形，①显然不成立；当E 、F 分别为AA 1、CC 1的中点时，易证BF ＝FD 1＝D 1E ＝BE ，∴EF ⊥BD 1，又EF ∥AC ，AC ⊥BD ，∴EF⊥BD ，∴EF ⊥平面BB 1D 1D ，∴平面BFD 1E ⊥平面BB 1D 1E ，∴②④成立，四边形BFD 1E 在底面的投影恒为正方形ABCD .当E 、F 分别为AA 1、CC 1的中点时，四边形BFD 1E 的面积最小，最小值为62. 10．在如图所示的几何体中，四边形 ABCD 是正方形，MA ⊥平面ABCD ，PD ∥MA ，E 、G 、F 分别为MB 、PB 、PC 的中点，且AD ＝PD ＝2MA .(1)求证：平面EFG ⊥平面PDC ；(2)求三棱锥P －MAB 与四棱锥P －ABCD 的体积之比． [解析] (1)证明：∵MA ⊥平面ABCD ，PD ∥MA ， ∴PD ⊥平面ABCD ，又BC ⊂平面ABCD ，∴PD ⊥BC ， ∵四边形ABCD 为正方形，∴BC ⊥DC . ∵PD ∩DC ＝D ，∴BC ⊥平面PDC .在△PBC 中，因为G 、F 分别为PB 、PC 的中点， ∴GF ∥BC ，∴GF ⊥平面PDC .又GF ⊂平面EFG ，∴平面EFG ⊥平面PDC .(2)不妨设MA ＝1，∵四边形ABCD 为正方形，∴PD ＝AD ＝2， 又∵PD ⊥平面ABCD ，所以V P －ABCD ＝13S 正方形ABCD ·PD ＝83.由于DA ⊥平面MAB ，且PD ∥MA ， 所以DA 即为点P 到平面MAB 的距离， 三棱锥V P －MAB ＝13×⎝ ⎛⎭⎪⎫12×1×2×2＝23.所以V P －MAB ：V P －ABCD ＝1：4.能力拓展提升11.(2011·湖南六市联考)一个几何体的三视图如下图所示，其中正视图中△ABC 是边长为2的正三角形，俯视图为正六边形，那么该几何体的侧视图的面积为( )A.32B.12 C ．1 D ．2[答案] A[解析] 由三视图知，该几何体是正六棱锥，底面正六边形的边长为1，侧棱长为2，故侧视图为一等腰三角形，底边长3，高为正六棱锥的高3，故其面积为S ＝12×3×3＝32. 12．(2011·皖南八校联考)已知三棱锥的正视图与俯视图如图所示，俯视图是边长为2的正三角形，则该三棱锥的侧视图可能为( )[答案] B [解析]由三视图间的关系，易知其侧视图是一个底边为3，高为2的直角三角形，故选B. [点评] 由题设条件及正视图、俯视图可知，此三棱锥P －ABC 的底面是正△ABC ，侧棱PB ⊥平面ABC ，AB ＝2，PB ＝2.13．(2012·内蒙包头市模拟)一个空间几何体的三视图如图所示，且这个空间几何体的所有顶点都在同一个球面上，则这个球的表面积是________．[答案] 16π[解析] 由三视图知，该几何体是一个正三棱柱，底面正三角形边长为3，高为2，故其外接球半径R 满足R 2＝(22)2＋(23×32×3)2＝4，∴R ＝2，∴S 球＝4πR 2＝16π.14．(2011·南京市调研)如图，已知正三棱柱ABC－A1B1C1的底面边长为2cm，高为5cm，则一质点自点A出发，沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为________cm.[答案] 13[解析] 如图，将三棱柱侧面A1ABB1置于桌面上，以A1A为界，滚动两周(即将侧面展开两次)，则最短线长为AA″1的长度，∴AA1＝5，AA″＝12，∴AA″1＝13.15．圆台侧面的母线长为2a，母线与轴的夹角为30°，一个底面的半径是另一个底面半径的2倍．求两底面的半径长与两底面面积的和．[解析] 如图所示，设圆台上底面半径为r，则下底面半径为2r，且∠ASO ＝30°， 在Rt △SA ′O ′中，rSA ′＝sin30°， ∴SA ′＝2r ，在Rt △SAO 中，2rSA＝sin30°，∴SA ＝4r .∵SA －SA ′＝AA ′，即4r －2r ＝2a ，r ＝a . ∴S ＝S 1＋S 2＝πr 2＋π(2r )2＝5πr 2＝5πa 2.∴圆台上底面半径为a ，下底面半径为2a ，两底面面积之和为5πa 2.16．(文)(2011·青岛质检)如下的三个图中，上面是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出(单位：cm)．(1)在正视图下面，按照画三视图的要求画出该多面体的俯视图； (2)按照给出的尺寸，求该多面体的体积． [解析] (1)如图．(2)所求多面体体积V ＝V 长方体－V 正三棱锥 ＝4×4×6－13×⎝ ⎛⎭⎪⎫12×2×2×2＝2843(cm 3)． (理)多面体PABCD 的直观图及三视图如图所示，E 、F 分别为PC 、BD 的中点．(1)求证：EF ∥平面PAD ； (2)求证：PA ⊥平面PDC .[解析] 由多面体PABCD 的三视图知，该几何体是四棱锥，四棱锥P －ABCD 的底面ABCD 是边长为2的正方形，侧面PAD 是等腰直角三角形，PA ＝PD ＝2，且平面PAD ⊥平面ABCD .(1)连接AC ，则F 是AC 的中点， 又∵E 是PC 的中点， ∴在△CPA 中，EF ∥PA ， 又PA ⊂平面PAD ，EF ⊄平面PAD ， ∴EF ∥平面PAD .(2)∵平面PAD ⊥平面ABCD ， 平面PAD ∩平面ABCD ＝AD ， 又CD ⊥AD ，∴CD ⊥平面PAD ， ∴CD ⊥PA .∵△PAD 是等腰直角三角形，且∠APD ＝π2.即PA ⊥PD .又CD ∩PD ＝D ，∴PA ⊥平面PDC .1．(2011·宁夏银川一中检测)如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h随时间t变化的可能图象是( )[答案] B[分析] 可以直接根据变化率的含义求解，也可以求出函数的解析式进行判断．[解析] 容器是一个倒置的圆锥，由于水是均匀注入的，故水面高度随时间变化的变化率逐渐减少，表现在函数图象上就是其切线的斜率逐渐减小，故选B.[点评] 本题在空间几何体三视图和函数的变化率交汇处命制，重点是对函数变化率的考查，这种在知识交汇处命制题目考查对基本概念的理解与运用的命题方式值得重视．2.(2011·惠州模拟)用若干个体积为1的正方体搭成一个几何体，其正视图、侧视图都是如图所示的图形，则这个几何体的最大体积与最小体积的差是( )A．6 B．7 C．8 D．9[答案] A3．(2011·河源模拟)如图所示，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的正视图是( )[答案] B[解析] 箭头所指正面的观察方向与底面直角三角形边长为4的边平行，故该边的射影为一点，与其垂直的直角边的长度3不变，高4不变，故选B.4.(2011·辽宁文，8)一个正三棱柱的侧棱长和底面边长相等，体积为23，它的三视图中的俯视图如右图所示，侧视图是一个矩形，则这个矩形的面积是( )A ．4B ．2 3C ．2 D. 3[答案] B[解析] 由题意可设棱柱的底面边长为a ，则其体积为34a 2·a ＝23，得a ＝2. 由俯视图易知，三棱柱的侧视图是以2为长，3为宽的矩形．∴其面积为2 3.故选B.5．(2011·天津理，10)一个几何体的三视图如下图所示(单位：m)，则该几何体的体积为________m3.[答案] π＋6[解析] 根据三视图知该几何体是一个长方体上面放一个圆锥．因而V＝V长方体＋V圆锥，又知长方体长、宽、高分别为3、2、1，圆锥的底面半径为1，高为3，从而求出体积为(π＋6)m3.6．下图是一几何体的直观图和三视图．(1)若F为PD的中点，求证：AF⊥平面PCD；(2)求几何体BEC－APD的体积．[解析] (1)证明：由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，PA＝2EB＝4.∵PA＝AD，F为PD的中点，∴PD⊥AF.又∵CD⊥DA，CD⊥PA，∴CD⊥AF.∴AF ⊥平面PCD .(2)V BEC －APD ＝V C －APEB ＋V P －ACD ＝13×12×(4＋2)×4×4＋13×12×4×4×4＝803.。

3-3导数的实际应用基础巩固强化1.(文)正三棱柱体积为V ，则其表面积最小时，底面边长为( ) A.3V B.32V C.34V D ．23V [答案] C[解析] 设正三棱柱底面边长为a ，高为h ，则体积V ＝34a 2h ，∴h ＝4V 3a2，表面积S ＝32a 2＋3ah ＝32a 2＋43V a， 由S ′＝3a －43V a2＝0，得a ＝34V ，故选C.(理)在内接于半径为R 的半圆的矩形中，周长最大的矩形的边长为( )A.R 2和32R B.55R 和455R C.45R 和75R D ．以上都不对[答案] B[解析] 设矩形垂直于半圆直径的边长为x ，则另一边长为2R 2－x 2，则l ＝2x ＋4R 2－x 2(0＜x ＜R )，l ′＝2－4xR 2－x2，令l ′＝0，解得x ＝55R . 当0＜x ＜55R 时，l ′＞0；当55R ＜x ＜R 时，l ′＜0. 所以当x ＝55R 时，l 取最大值，即周长最大的矩形的边长为55R ，455R . 2．已知某生产厂家的年利润y (单位：万元)与年产量x (单位：万件)的函数关系式为y ＝－13x 3＋81x －234，则使该生产厂家获取最大年利润的年产量为( )A ．13万件B ．11万件C ．9万件D ．7万件[答案] C[解析] ∵y ＝－13x 3＋81x －234，∴y ′＝－x 2＋81(x >0)．令y ′＝0得x ＝9，令y ′<0得x >9，令y ′>0得0<x <9，∴函数在(0,9)上单调递增，在(9，＋∞)上单调递减， ∴当x ＝9时，函数取得最大值．故选C.[点评] 利用导数求函数最值时，令y ′＝0得到x 的值，此x 的值不一定是极大(小)值时，还要判定x 值左右两边的导数的符号才能确定．3．(文)做一个圆柱形锅炉，容积为V ，两个底面的材料每单位面积的价格为a 元，侧面的材料每单位面积的价格为b 元，当造价最低时，锅炉的底面直径与高的比为( )A.a bB.a 2bC.b aD.b 2a[答案] C [解析]如图，设圆柱的底面半径为R ，高为h ，则V ＝πR 2h . 设造价为y ，则y ＝2πR 2a ＋2πRhb ＝2πaR 2＋2πRb ·V πR 2＝2πaR 2＋2bV R， ∴y ′＝4πaR －2bV R.令y ′＝0并将V ＝πR 2h 代入解得，2R h ＝b a.(理)圆柱的表面积为S ，当圆柱体积最大时，圆柱的底面半径为( ) A.S3πB.3πSC.6πS6πD ．3π·6πS[答案] C[解析] 设圆柱底面半径为r ，高为h ，∴S ＝2πr 2＋2πrh ，∴h ＝S －2πr 22πr，又V ＝πr 2h ＝rS －2πr 32，则V ′＝S －6πr 22，令V ′＝0，得S ＝6πr 2，∴h ＝2r ，r ＝6πS6π. 4．某公司生产某种产品，固定成本为20000元，每生产一单位产品，成本增加100元，已知总收益R 与产量x 的关系是R ＝⎩⎪⎨⎪⎧400x －12x 2，0≤x ≤400，80000， x ＞400.则总利润最大时，每年生产的产品是( )A ．100B ．150C ．200D ．300[答案] D[解析] 由题意，总成本为C ＝20000＋100x .所以总利润为P ＝R －C ＝⎩⎪⎨⎪⎧300x －x 22－20000，0≤x ≤400，60000－100x ，x ＞400，P ′＝⎩⎪⎨⎪⎧300－x ，0≤x ≤400，－100，x ＞400.令P ′＝0，得x ＝300，易知当x ＝300时，总利润最大． 5．(文)内接于半径为R 的球并且体积最大的圆锥的高为( ) A ．R B ．2R C.43R D.34R [答案] C[解析] 设圆锥的高为h ，底面半径为r ，则R 2＝(h －R )2＋r 2，∴r 2＝2Rh －h 2， ∴V ＝13πr 2h ＝π3h (2Rh －h 2)＝23πRh 2－π3h 3，V ′＝43πRh －πh 2，令V ′＝0得h ＝43R .(理)要制做一个圆锥形的漏斗，其母线长为20cm ，要使其体积最大，则高为( ) A.33cm B.1033cm C.1633cm D.2033cm [答案] D[解析] 设圆锥的高为x ，则底面半径为202－x 2， 其体积为V ＝13πx (400－x 2) (0＜x ＜20)，V ′＝13π(400－3x 2)，令V ′＝0，解得x ＝2033. 当0＜x ＜2033时，V ′＞0；当2033＜x ＜20时，V ′＜0，所以当x ＝2033时，V 取最大值．6．(2012·保定模拟)定义域为R 的函数f (x )满足f (1)＝1，且f (x )的导函数f ′(x )>12，则满足2f (x )<x ＋1的x 的集合为( )A ．{x |－1<x <1}B ．{x |x <1}C ．{x |x <－1或x >1}D ．{x |x >1}[答案] B[解析] 令g (x )＝2f (x )－x －1，∵f ′(x )>12，∴g ′(x )＝2f ′(x )－1>0，∴g (x )为单调增函数，∵f (1)＝1，∴g (1)＝2f (1)－1－1＝0，∴当x <1时，g (x )<0，即2f (x )<x ＋1，故选B.7．(文)用长为18m 的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2 1，该长方体的最大体积是________．[答案] 3m 3[解析] 设长方体的宽为x ，则长为2x ，高为92－3x (0<x <2)，故体积为V ＝2x 2⎝ ⎛⎭⎪⎫92－3x ＝－6x 3＋9x 2，V ′＝－18x 2＋18x ，令V ′＝0得，x ＝0或1，∵0<x <2，∴x ＝1.∴该长方体的长、宽、高各为2m 、1m 、1.5m 时，体积最大，最大体积V max ＝3m 3. (理)用总长为14.8m 的钢条制作一个长方体容器的框架，如果所制作容器的底面的一边比另一边长0.5m ，那么容器的容积最大时，容器的高为________．[答案] 1.2m[解析] 设容器的短边长为x m ， 则另一边长为(x ＋0.5)m ， 高为14.8－4x －4x ＋0.54＝3.2－2x .由3.2－2x >0和x >0，得0<x <1.6， 设容器的容积为y m 3，则有y ＝x (x ＋0.5)(3.2－2x )(0<x <1.6)， 整理得y ＝－2x 3＋2.2x 2＋1.6x ， ∴y ′＝－6x 2＋4.4x ＋1.6，令y ′＝0，有－6x 2＋4.4x ＋1.6＝0，即15x 2－11x －4＝0， 解得x 1＝1，x 2＝－415(不合题意，舍去)，∴高＝3.2－2＝1.2，容积V ＝1×1.5×1.2＝1.8.8．(文)(2011·北京模拟)若函数f (x )＝ln x －12ax 2－2x 存在单调递减区间，则实数a的取值范围是________．[答案] (－1，＋∞)[分析] 函数f (x )存在单调减区间，就是不等式f ′(x )<0有实数解，考虑到函数的定义域为(0，＋∞)，所以本题就是求f ′(x )<0在(0，＋∞)上有实数解时a 的取值范围．[解析] 解法1：f ′(x )＝1x －ax －2＝1－ax 2－2xx，由题意知f ′(x )<0有实数解，∵x >0，∴ax 2＋2x －1>0有实数解．当a ≥0时，显然满足；当a <0时，只要Δ＝4＋4a >0，∴－1<a <0，综上知a >－1.解法2：f ′(x )＝1x －ax －2＝1－ax 2－2x x，由题意可知f ′(x )<0在(0，＋∞)内有实数解． 即1－ax 2－2x <0在(0，＋∞)内有实数解． 即a >1x 2－2x在(0，＋∞)内有实数解．∵x ∈(0，＋∞)时，1x 2－2x ＝(1x－1)2－1≥－1，∴a >－1.(理)(2011～2012·黄冈市期末)对于三次函数y ＝ax 3＋bx 2＋cx ＋d (a ≠0)，给出定义：设f ′(x )是函数y ＝f (x )的导数，f ″(x )是f ′(x )的导数，若方程f ″(x )＝0有实数解x 0，则称点(x 0，f (x 0))为函数y ＝f (x )的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．若f (x )＝13x 3－12x 2＋3x －512，请你根据这一发现，求：(1)函数f (x )＝13x 3－12x 2＋3x －512的对称中心为________；(2)计算f (12014)＋f (22014)＋f (32014)＋f (42014)＋…＋f (20132014)＝________. [答案] (1)(12，1) (2)2013[解析] (1)f ′(x )＝x 2－x ＋3，f ″(x )＝2x －1，由2x －1＝0得x ＝12，f (12)＝13×(12)3－12×(12)2＋3×12－512＝1，由拐点的定义知f (x )的拐点即对称中心为(12，1)． (2)∴f (k 2014)＋f (1－k 2014)＝f (k 2014)＋f (2014－k 2014)＝2(k ＝1，2，…，1007)，∴f (12014)＋f (22014)＋…＋f (20132014)＝[f (12014)＋f (20132014)]＋[f (22014)＋f (20122014)]＋…＋[f (10062014)＋f (10082014)]＋f (10072014)＝2×1006＋1＝2013.9．有一个容积V 一定的有铝合金盖的圆柱形铁桶，已知单位面积铝合金的价格是铁的3倍，问如何设计使总造价最小？[分析] 桶的总造价要根据铁与铝合金的用量来定，由于二者单位面积的价格不同，在保持铁桶容积不变的前提下，使总造价最小．问题转化为V 一定求总造价y 的最小值，选取恰当变量(圆柱高h 或底半径r )来表示y 即变为函数极值问题．[解析] 设圆柱体高为h ，底面半径为r ，又设单位面积铁的造价为m ，桶总造价为y ，则y ＝3m πr 2＋m (πr 2＋2πrh )．由于V ＝πr 2h ，得h ＝V πr 2，所以y ＝4m πr 2＋2mV r(r >0)．所以，y ′＝8m πr －2mVr2.令y ′＝0，得r ＝⎝⎛⎭⎪⎫V 4π13，此时，h ＝V πr 2＝4⎝ ⎛⎭⎪⎫V 4π13.该函数在(0，＋∞)内连续可导，且只有一个使函数的导数为零的点，问题中总造价的最小值显然存在，当r ＝⎝⎛⎭⎪⎫V 4π13时，y 有最小值，即h r ＝4时，总造价最小．10．(文)已知球的直径为d ，求当其内接正四棱柱体积最大时，正四棱柱的高为多少？ [解析] 如右图所示，设正四棱柱的底面边长为x ，高为h ，由于x 2＋x 2＋h 2＝d 2， ∴x 2＝12(d 2－h 2)．∴球内接正四棱柱的体积为V ＝x 2·h ＝12(d 2h －h 3)，0<h <d . V ′＝12(d 2－3h 2)＝0，∴h ＝33d . 在(0，d )上，函数变化情况如下表：(理)如右图所示，扇形AOB 中，半径OA ＝1，∠AOB ＝π2，在OA 的延长线上有一动点C ，过点C 作CD 与AB 相切于点E ，且与过点B 所作的OB 的垂线交于点D ，问当点C 在什么位置时，直角梯形OCDB 的面积最小．[分析] 要求直角梯形OCDB 的面积的最小值，需先求出梯形面积，可设OC ＝x ，进而用x 表示BD ，然后利用导数的方法求最小值．[解析] 如上图所示，过D 作DF ⊥OA 于F ，可知 △OEC ≌△DFC ，所以OC ＝CD ，设OC ＝x (x ＞1)，在Rt △CDF 中，CD 2＝CF 2＋DF 2，即x 2＝(x －BD )2＋1， 所以BD ＝x －x 2－1， 所以梯形的面积为S ＝12(BD ＋OC )·OB ＝12(2x －x 2－1)， S ′＝12(2－xx 2－1)． 令S ′＝0，解得x 1＝23，x 2＝－23(舍去)．当x ＞23时，S ′＞0；当1＜x ＜23时，S ′＜0. 所以当x ＝233时，S 取最小值．即当OC ＝233时，直角梯形OCDB 的面积最小.能力拓展提升11.已知非零向量a 、b 满足：|a |＝2|b |，若函数f (x )＝13x 3＋12|a |x 2＋a ·b x 在R 上有极值，设向量a 、b 的夹角为θ，则cos θ的取值范围为( )A.⎣⎢⎡⎦⎥⎤12，1B.⎝ ⎛⎦⎥⎤12，1C.⎣⎢⎡⎦⎥⎤－1，12D.⎣⎢⎡⎭⎪⎫－1，12 [答案] D[解析] ∵函数f (x )在R 上有极值，∴f ′(x )＝x 2＋|a |x ＋a ·b ＝0有两不等实根，∴Δ＝|a |2－4|a |·|b |cos θ＝4|b |2－8|b |2cos θ>0，∴cos θ<12，∴选D.[点评] 若f (x )为三次函数，f (x )在R 上有极值，则f ′(x )＝0应有二不等实根，当f (x )有两相等实根时，不能保证f (x )有极值，这一点要特别注意，如f (x )＝13x 3，f ′(x )＝x 2＝0有实根x ＝0，但f (x )在R 上单调增，无极值．即导数为0是函数有极值的必要不充分条件．12．如图，过函数y ＝x sin x ＋cos x 图象上点(x ，y )的切线的斜率为k ，若k ＝g (x )，则函数k ＝g (x )的图象大致为( )[答案] A[解析] ∵y ′＝sin x ＋x cos x －sin x ＝x cos x ， ∴k ＝g (x )＝x cos x ，易知其图象为A.13．函数f (x )＝2x 3＋12x 2－x ＋1的图象与x 轴交点个数为________个．[答案] 1[解析] f ′(x )＝6x 2＋x －1＝(3x －1)(2x ＋1)，当x <－12时，f ′(x )>0，当－12<x <13时，f ′(x )<0，当x >13时，f ′(x )>0，∴f (x )在(－∞，－12)上单调递增，在(－12，13)上单调递减，在(13，＋∞)上单调递增，∴当x ＝－12时，f (x )取到极大值118，当x ＝13时，f (x )取到极小值4354，故f (x )的图象与x 轴只有一个交点．14．将边长为1m 的正三角形薄铁皮，沿一条平行于某边的直线剪成两块，其中一块是梯形，记s ＝梯形的周长2梯形的面积，则s 的最小值是________．[答案]3233[解析] 设DE ＝x ， 则梯形的周长为：3－x ，梯形的面积为：12(x ＋1)·32(1－x )＝34(1－x 2)，∴s ＝3－x 2341－x 2＝433·x 2－6x ＋91－x2，x ∈(0,1)， 设h (x )＝x 2－6x ＋91－x 2，h ′(x )＝－6x 2＋20x －61－x 22. 令h ′(x )＝0，得：x ＝13或x ＝3(舍)，∴h (x )最小值＝h ⎝ ⎛⎭⎪⎫13＝8， ∴s 最小值＝433×8＝3233.15．(文)甲乙两地相距400km ，汽车从甲地匀速行驶到乙地，速度不得超过100km/h ，已知该汽车每小时的运输成本P (元)关于速度v (km/h)的函数关系是P ＝119200v 4－1160v 3＋15v .(1)求全程运输成本Q (元)关于速度v 的函数关系式；(2)为使全程运输成本最少，汽车应以多大速度行驶？并求此时运输成本的最小值． [解析] (1)汽车从甲地到乙地需用400v h ，故全程运输成本为Q ＝400P v ＝v 348－5v22＋6000(0<v ≤100)．(2)Q ′＝v 216－5v ，令Q ′＝0得，v ＝80，∴当v ＝80km/h 时，全程运输成本取得最小值，最小值为20003元．(理)(2011·江苏)请你设计一个包装盒．如图所示，ABCD 是边长为60cm 的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A ，B ，C ，D 四个点重合于图中的点P ，正好形成一个正四棱柱形状的包装盒，E 、F 在AB 上，是被切去的一个等腰直角三角形斜边的两个端点，设AE ＝FB ＝x (cm)．(1)若广告商要求包装盒的侧面积S (cm 2)最大，试问x 应取何值？(2)某厂商要求包装盒容积V (cm 3)最大，试问x 应取何值？并求出此时包装盒的高与底面边长的比值．[解析] 设包装盒的高为h (cm)，底面边长为a (cm)，由已知得a ＝2x ，h ＝60－2x2＝2(30－x )，0<x <30. (1)S ＝4ah ＝8x (30－x )＝－8(x －15)2＋1800， 所以当x ＝15时，S 取得最大值．(2)V ＝a 2h ＝22(－x 3＋30x 2)，V ′＝62x (20－x )． 由V ′＝0得x ＝0(舍)或x ＝20.当x ∈(0,20)时，V ′>0；当x ∈(20,30)时，V ′<0. 所以当x ＝20时，V 取得极大值，也是最大值．此时h a ＝12.即包装盒的高与底面边长的比值为12.16．(文)用一块钢锭浇铸一个厚度均匀，且全面积为2m 2的正四棱锥形有盖容器(如右图)．设容器的高为h m ，盖子边长为a m.(1)求a 关于h 的函数解析式；(2)设容器的容积为V m 3，则当h 为何值时，V 最大？求出V 的最大值．(容器的厚度忽略不计)[解析] (1)如右图，作PO ⊥平面ABCD ，O 为垂足，作OE ⊥BC 于E ，连结PE ，则PE ⊥BC ，正四棱锥的全面积为2＝4×12×a ×h 2＋a22＋a 2.所以a ＝11＋h2(h >0)．(2)V ＝13a 2h ＝13·h 1＋h 2(h >0)，V ′＝13·1＋h 2－h 2h 1＋h 22＝1－h 231＋h 22.所以当0<h <1时，V ′>0.所以V (h )在(0,1]上为增函数． 当h >1时，V ′<0，所以V (h )在[1，＋∞)上为减函数． 故h ＝1为函数V (h )的唯一极大值点也是最大值点， ∴V max ＝16.答：当高h ＝1m 时，容积取最大值16m 3.(理)如图，有一矩形钢板ABCD 缺损了一角(如图所示)，边缘线OM 上每一点到点D 的距离都等于它到边AB 的距离．工人师傅要将缺损的一角切割下来使剩余部分成一个五边形，若AB ＝1m ，AD ＝0.5m ，问如何画切割线EF 可使剩余部分五边形ABCEF 的面积最大？[解析] 由题知，边缘线OM 是以点D 为焦点，直线AB 为准线的抛物线的一部分． 以O 点为原点，AD 所在直线为y 轴建立直角坐标系，则D (0，14)，M (12，14)．所以边缘线OM 所在抛物线的方程为y ＝x 2(0≤x ≤12)．要使如图的五边形ABCEF 面积最大，则必有EF 所在直线与抛物线相切，设切点为P (t ，t 2)．则直线EF 的方程为y ＝2t (x －t )＋t 2，即y ＝2tx －t 2， 由此可求得点E ，F 的坐标分别为E (1＋4t 28t ，14)，F (0，－t 2)．所以S △DEF ＝S (t )＝12·1＋4t 28t ·(14＋t 2)＝164·16t 4＋8t 2＋1t ，t ∈(0，12]． 所以S ′(t )＝164·48t 4＋8t 2－1t 2＝12t 2－14t 2＋164t2＝34t 2＋1t ＋36t －3616t2，显然函数S(t)在(0，36]上是减函数，在(36，12]上是增函数．所以当t＝36时，S△DEF取得最小值，相应地，五边形ABCEF的面积最大．此时点E、F的坐标分别为E(33，14)，F(0，－112)．此时沿直线EF划线可使五边形ABCEF的面积最大．1．函数f(x)的定义域为R，导函数f′(x)的图象如图所示，则函数f(x)( )A．无极大值点、有四个极小值点B．有三个极大值点、两个极小值点C．有两个极大值点、两个极小值点D．有四个极大值点、无极小值点[答案] C[解析] 设f′(x)与x轴的4个交点，从左至右依次为x1、x2、x3、x4，当x<x1时，f′(x)>0，f(x)为增函数，当x1<x<x2时，f′(x)<0，f(x)为减函数，则x＝x1为极大值点，同理，x＝x3为极大值点，x＝x2，x＝x4为极小值点．2．函数f(x)＝e x cos x的图象在点(0，f(0))处的切线的倾斜角的余弦值为( )A．－55B.55C.22D．1[答案] C[解析] f′(x)＝e x cos x－e x sin x，∴f′(0)＝1.设f (x )在点(0，f (0))处切线的倾斜角为α，则tan α＝1， ∵α∈(0，π)，∴α＝π4，∴cos α＝22.3．设函数f (x )＝sin θ3x 3＋3cos θ2x 2＋tan θ，其中θ∈⎣⎢⎡⎦⎥⎤0，5π12，则导数f ′(1)的取值范围为( )A ．[－2,2]B ．[2，3]C ．[3，2]D ．[2，2][答案] D[解析] ∵f ′(x )＝sin θ·x 2＋3cos θ·x ， ∴f ′(1)＝sin θ＋3cos θ＝2sin ⎝ ⎛⎭⎪⎫θ＋π3.∵θ∈⎣⎢⎡⎦⎥⎤0，5π12，∴θ＋π3∈⎣⎢⎡⎦⎥⎤π3，3π4.∴sin ⎝ ⎛⎭⎪⎫θ＋π3∈⎣⎢⎡⎦⎥⎤22，1，∴f ′(1)∈[2，2]，故选D. 4．某工厂要围建一个面积为128m 2的矩形堆料场，一边可以用原有的墙壁，其他三边要砌新的墙壁，要使砌墙所用的材料最省，堆料场的长、宽应分别为________．[答案] 16m 8m[解析] 设场地宽为x m ，则长为128xm ，因此新墙总长度为y ＝2x ＋128x(x ＞0)，y ′＝2－128x2，令y ′＝0，∵x >0，∴x ＝8.因为当0＜x ＜8时，y ′＜0；当x ＞8时，y ′＞0， 所以当x ＝8时，y 取最小值，此时宽为8m ，长为16m. 即当堆料场的长为16m ，宽为8m 时，可使砌墙所用材料最省． 5．(2011·陕西文)设f (x )＝ln x ，g (x )＝f (x )＋f ′(x )． (1)求g (x )的单调区间和最小值； (2)讨论g (x )与g (1x)的大小关系；(3)求a 的取值范围，使得g (a )－g (x )<1a对任意x >0成立．[解析] ∵f (x )＝ln x ，∴f ′(x )＝1x ，g (x )＝ln x ＋1x.∴g ′(x )＝x －1x 2，令g ′(x )＝0得x ＝1， 当x ∈(0,1)时，g ′(x )<0，∴(0,1)是g (x )的单调减区间； 当x ∈(1，＋∞)时，g ′(x )>0.∴(1，＋∞)是g (x )的单调增区间， 因此当x ＝1时g (x )取极小值，且x ＝1是唯一极值点，从而是最小值点． 所以g (x )最小值为g (1)＝1. (2)g (1x)＝－ln x ＋x令h (x )＝g (x )－g (1x )＝2ln x －x ＋1x，则h ′(x )＝－x －12x2，当x ＝1时，h (1)＝0，即g (x )＝g (1x)，当x ∈(0,1)∪(1，＋∞)时h ′(x )<0，h ′(1)＝0，所以h (x )在(0，＋∞)单调递减， 当x ∈(0,1)时，h (x )>h (1)＝0，即g (x )>g (1x)，当x ∈(1，＋∞)时，h (x )<h (1)＝0，即g (x )<g (1x)，综上知，当x ∈(0,1)时，g (x )>g (1x)；当x ＝1时，g (x )＝g (1x)；当x ∈(1，＋∞)时，g (x )<g (1x)．(3)由(1)可知g (x )最小值为1，所以g (a )－g (x )<1a 对任意x >0成立等价于g (a )－1<1a，即ln a <1，解得0<a <e .所以a 的取值范围是(0，e )．6．学习曲线是1936年美国康乃尔大学T.P.Wright 博士在飞机制造过程中，通过对大量有关资料、案例的观察、分析、研究，首次发现并提出来的．已知某类学习任务的学习曲线为：f (t )＝34＋a ·2－t ·100%(其中f (t )为该任务的程度，t 为学习时间)，且这类学习任务中的某项任务满足f (2)＝60%.(1)求f (t )的表达式，计算f (0)并说明f (0)的含义； (2)已知2x>x ln2对任意x >0恒成立，现定义f t t为该类学习任务在t 时刻的学习效率指数，研究表明，当学习时间t ∈(1,2)时，学习效率最佳，当学习效率最佳时，求学习效率指数相应的取值范围．[解析] (1)∵f (t )＝34＋a ·2·100%(t 为学习时间)，且f (2)＝60%，则34＋a ·2－2·100%＝60%，解得a ＝4.∴f (t )＝34＋a ·2－t ·100%＝341＋2－t·100%(t ≥0)， ∴f (0)＝341＋2－0·100%＝37.5%， f (0)表示某项学习任务在开始学习时已掌握的程度为37.5%.(2)令学习效率指数f t t＝y ， 则y ＝f t t ＝34t 1＋2－t＝34t ＋t2t (t >0)，现研究函数g (t )＝t ＋t2t 的单调性，由于g ′(t )＝1＋2t－t ·2tln22t 2＝2t－t ln2＋12t(t >0)， 又已知2x>x ln2对任意x >0恒成立，即2t－t ln2>0，则g ′(t )>0恒成立， ∴g (t )在(0，＋∞)上为增函数，且g (t )为正数． ∴y ＝f t t＝34t ＋t2(t >0)在(0，＋∞)上为减函数，而y |t ＝1＝f 11＝12，y |t ＝2＝f 22＝310， 即y ＝f t t ∈(310，12)， 故所求学习效率指数的取值范围是(310，12)．7．(2012·延边州质检)已知函数f (x )＝x 2＋ax －ln x ，a ∈R . (1)当a ＝1时，求f (x )的单调区间；(2)若函数f (x )在[1,2]上是减函数，求实数a 的取值范围；(3)令g (x )＝f (x )－x 2，是否存在实数a ，当x ∈(0，e ](e 是自然对数的底数)时，函数g (x )的最小值是3，若存在，求出a 的值；若不存在，说明理由．[解析] (1)当a ＝1时，由f ′(x )＝2x ＋1－1x ＝2x 2＋x －1x＝2x －12x ＋1x，∵函数f (x )＝x 2＋x －ln x 的定义域为(0，＋∞)，∴当x ∈(0，12]时，f ′(x )≤0，当x ∈[12，＋∞)时，f ′(x )≥0，所以函数f (x )＝x 2＋x －ln x 的单调递减区间为(0，12]单调递增区间为[12，＋∞)．(2)f ′(x )＝2x ＋a －1x ＝2x 2＋ax －1x≤0在[1,2]上恒成立，令h (x )＝2x 2＋ax －1，有⎩⎪⎨⎪⎧h 1≤0h 2≤0得⎩⎪⎨⎪⎧a ≤－1a ≤－72，得a ≤－72.(3)假设存在实数a ，使g (x )＝ax －ln x (x ∈(0，e ])有最小值3，g ′(x )＝a －1x ＝ax －1x.①当a ≤0时，g (x )在(0，e ]上单调递减，g (x )min ＝g (e )＝ae －1＝3，a ＝4e(舍去)，∴g (x )无最小值．②当0<1a <e 时，g (x )在(0，1a )上单调递减，在(1a，e ]上单调递增，∴g (x )min ＝g (1a)＝1＋ln a ＝3，a ＝e 2，满足条件．③当1a ≥e 时，g (x )在(0，e ]上单调递减，g (x )min ＝g (e )＝ae －1＝3，a ＝4e(舍去)，∴f (x )无最小值．综上，存在实数a ＝e 2，使得当x ∈(0，e ]时，f (x )有最小值3.8．(2012·山东苍山县模拟)某食品厂进行蘑菇的深加工，每公斤蘑菇的成本20元，并且每公斤蘑菇的加工费为t 元(t 为常数，且2≤t ≤5)，设该食品厂每公斤蘑菇的出厂价为x 元(25≤x ≤40)，根据市场调查，日销售量q 与e x 成反比，当每公斤蘑菇的出厂价为30元时，销售量为100kg.(每日利润＝日销售量×(每公斤出厂价－成本价－加工费))．(1)求该工厂的每日利润y 元与每公斤蘑菇的出厂价x 元的函数关系式；(2)若t ＝5，当每公斤蘑菇的出厂价x 为多少元时，该工厂的利润y 最大，并求最大值． [解析] (1)设日销售量q ＝k e x ，则k e30＝100，∴k ＝100e 30， ∴日销售量q ＝100e 30ex ，∴y ＝100e 30x －20－t e x(25≤x ≤40)．(2)当t ＝5时，y ＝100e 30x －25e x，y ′＝100e 3026－x e x.由y′≥0得x≤26，由y′≤0得x≥26，∴y在[26,25]上单调递增，在[26,40]上单调递减，∴当x＝26时，y max＝100e4.当每公斤蘑菇的出厂价为26元时，该工厂的利润最大，最大值为100e4元．。

2-3函数的奇偶性与周期性基础巩固强化1.(2012·洛阳示范高中联考)下列函数中，既是偶函数又在(0，＋∞)单调递增的函数是( )A ．y ＝x 3B ．y ＝|x |＋1C ．y ＝－x 2＋1D ．y ＝2－|x |[答案] B[解析] y ＝x 3是奇函数，y ＝－x 2＋1与y ＝2－|x |在(0，＋∞)上为减函数，故选B.2．(文)设f (x )是定义在R 上的奇函数，且当x >0时，f (x )＝2x－3，则f (－2)的值等于( )A ．－1 B.114C ．1D ．－114[答案] A[解析] f (2)＝22－3＝1，又f (x )是奇函数， ∴f (－2)＝－f (2)＝－1，故选A.(理)(2011·浙江杭州月考)已知函数f (x )为定义在R 上的奇函数，当x ≥0时，f (x )＝2x＋2x ＋m (m 为常数)，则f (－1)的值为( )A ．－3B ．－1C ．1D ．3[答案] A[解析] ∵函数f (x )是定义在R 上的奇函数， ∴f (0)＝0，即f (0)＝20＋m ＝0，解得m ＝－1.∴当x ≥0时，f (x )＝2x＋2x －1，f (1)＝21＋2×1－1＝3，f (－1)＝－f (1)＝－3.3．(文)函数f (x )(x ∈R )是周期为3的奇函数，且f (－1)＝a ，则f (2014)的值为( ) A ．a B ．－a C ．0 D ．2a[答案] B[解析] ∵f (x )周期为3， ∴f (2014)＝f (671×3＋1)＝f (1)， ∵f (x )为奇函数，f (－1)＝a ， ∴f (1)＝－a ，故选B.(理)(2012·河南商丘模拟)已知f (x )是定义在R 上的奇函数，它的最小正周期为T ，则f (－T2)的值为( )A ．－T2B ．0 C.T2 D ．T[答案] B[解析] ∵f (－T 2)＝－f (T 2)，且f (－T 2)＝f (－T 2＋T )＝f (T 2)，∴f (T 2)＝0，∴f (－T2)＝0.4．(文)(2011·北京东城一模)已知函数f (x )是定义在R 上的偶函数，且当x >0时，f (x )＝ln(x ＋1)，则函数f (x )的图象大致为( )[答案] C[解析] 函数f (x )＝ln(x ＋1)的图象由f (x )＝ln x 的图象向左平移1个单位得到，选取x >0的部分，然后作关于y 轴的对称图形即得．(理)(2011·北京西城模拟)定义在R 上的偶函数f (x )的部分图象如图所示，则在(－2,0)上，下列函数中与f (x )的单调性不同的是( )A ．y ＝x 2＋1B ．y ＝|x |＋1C ．y ＝⎩⎪⎨⎪⎧2x ＋1，x ≥0x 3＋1，x <0D ．y ＝⎩⎪⎨⎪⎧e x，x ≥0e －x，x <0[答案] C[解析] ∵f (x )为偶函数，由图象知，f (x )在(－2,0)上为减函数，而y ＝x 3＋1在(－∞，0)上为增函数．5．已知定义在R 上的函数f (x )满足f (0)＝2－3，且对任意的x 都有f (x ＋3)＝1－f x ，则f (2013)的值为( )A ．－2－ 3B ．－2＋ 3C ．2－ 3D ．－3－ 3[答案] A[解析] 由题意得f (x ＋6)＝f (x ＋3＋3)＝1－f x ＋3＝1－－1f x ＝f (x )．∴函数f (x )的周期为6.f (2013)＝f (335×6＋3)＝f (3)，而f (3)＝f (0＋3)＝－1f 0＝－12－3＝－2－ 3.6．(文)(2011·合肥模拟)设f (x )是偶函数，且当x >0时是单调函数，则满足f (2x )＝f (x ＋1x ＋4)的所有x 之和为( ) A ．－92B ．－72C ．－8D ．8[答案] C[解析] ∵f (x )是偶函数，f (2x )＝f (x ＋1x ＋4)， ∴f (|2x |)＝f (|x ＋1x ＋4|)． 又∵f (x )在(0，＋∞)上为单调函数， ∴|2x |＝|x ＋1x ＋4|，即2x ＝x ＋1x ＋4或2x ＝－x ＋1x ＋4， 整理得2x 2＋7x －1＝0或2x 2＋9x ＋1＝0，设方程2x 2＋7x －1＝0的两根为x 1，x 2，方程2x 2＋9x ＋1＝0的两根为x 3，x 4. 则(x 1＋x 2)＋(x 3＋x 4)＝－72＋(－92)＝－8.(理)已知f (x )是定义在(－∞，＋∞)上的偶函数，且在(－∞，0]上是增函数，设a ＝f (log 47)，b ＝f (log 123)，c ＝f (0.20.6)，则a 、b 、c 的大小关系是( )A ．c <b <aB ．b <c <aC ．b <a <cD ．a <b <c[答案] C[解析] 由题意知f (x )＝f (|x |)．∵log 47＝log 27>1，|log 12 3|＝log 23>log 27，0<0.20.6<1，∴|log 123|>|log 47|>|0.20.6|.又∵f (x )在(－∞，0]上是增函数，且f (x )为偶函数， ∴f (x )在[0，＋∞)上是减函数． ∴b <a <c .故选C.7．(文)若f (x )是定义在R 上的偶函数，其图象关于直线x ＝2对称，且当x ∈(－2,2)时，f (x )＝－x 2＋1.则f (－5)＝________.[答案] 0[解析] 由题意知f (－5)＝f (5)＝f (2＋3)＝f (2－3)＝f (－1)＝－(－1)2＋1＝0. (理)(2011·湖南文)已知f (x )为奇函数，g (x )＝f (x )＋9，g (－2)＝3，则f (2)＝________.[答案] 6[解析] 由g (x )＝f (x )＋9知g (－2)＝f (－2)＋9＝3， ∴f (－2)＝－6，而由于f (x )是奇函数， 所以f (2)＝－f (－2)＝－(－6)＝6.8．(文)若f (x )＝lg ⎝ ⎛⎭⎪⎫2x 1＋x ＋a (a ∈R )是奇函数，则a ＝________.[答案] －1[解析] ∵f (x )＝lg ⎝⎛⎭⎪⎫2x 1＋x ＋a 是奇函数，∴f (－x )＋f (x )＝0恒成立， 即lg ⎝⎛⎭⎪⎫2x 1＋x ＋a ＋lg ⎝ ⎛⎭⎪⎫－2x 1－x ＋a＝lg ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2x 1＋x ＋a ⎝ ⎛⎭⎪⎫2x x －1＋a ＝0. ∴⎝⎛⎭⎪⎫2x 1＋x ＋a ⎝ ⎛⎭⎪⎫2x x －1＋a ＝1，∴(a 2＋4a ＋3)x 2－(a 2－1)＝0， ∵上式对定义内的任意x 都成立，∴⎩⎪⎨⎪⎧a 2＋4a ＋3＝0，a 2－1＝0，∴a ＝－1.[点评] ①可以先将真数通分，再利用f (－x )＝－f (x )恒成立求解，运算过程稍简单些．②如果利用奇函数定义域的特点考虑，则问题变得比较简单．f (x )＝lg a ＋2x ＋a 1＋x 为奇函数，显然x ＝－1不在f (x )的定义域内，故x ＝1也不在f (x )的定义域内，令x ＝－aa ＋2＝1，得a ＝－1.故平时解题中要多思少算，培养观察、分析、捕捉信息的能力．(理)设函数f (x )＝sin(3x ＋φ)(0<φ<π)．若f (x )＋f ′(x )是奇函数，则φ＝________.[答案]2π3[解析] ∵f ′(x )＝3cos(3x ＋φ)．∴f (x )＋f ′(x )＝sin(3x ＋φ)＋3cos(3x ＋φ) ＝2sin ⎝⎛⎭⎪⎫3x ＋φ＋π3. f (x )＋f ′(x )是奇函数⇔φ＋π3＝k π(k ∈Z )，即φ＝k π－π3(k ∈Z )．又∵0<φ<π，∴k ＝1时，φ＝2π3.9．定义在R 上的偶函数f (x )在[0，＋∞)上单调递减，且f (12)＝0，则满足f (log 14 x )<0的集合为________．[答案] (0，12)∪(2，＋∞)[解析] 由题意知f (x )<0的解为x >12或x <－12，∴由f (log 14 x )<0得log 14 x >12或log 14 x <－12，∴0<x <12或x >2.10．(文)已知函数f (x )＝1－42a x＋a(a >0且a ≠1)是定义在(－∞，＋∞)上的奇函数． (1)求a 的值；(2)求函数f (x )的值域；(3)当x ∈(0,1]时，tf (x )≥2x－2恒成立，求实数t 的取值范围．[解析] (1)∵f (x )是定义在(－∞，＋∞)上的奇函数，即f (－x )＝－f (x )恒成立，∴f (0)＝0.即1－42×a 0＋a＝0，解得a ＝2. (2)∵y ＝2x－12x ＋1，∴2x＝1＋y 1－y ，由2x>0知1＋y 1－y>0，∴－1<y <1，即f (x )的值域为(－1,1)． (3)不等式tf (x )≥2x－2即为t ·2x －t2x＋1≥2x－2.即：(2x )2－(t ＋1)·2x ＋t －2≤0.设2x＝u ， ∵x ∈(0,1]，∴u ∈(1,2]．∵u ∈(1,2]时u 2－(t ＋1)·u ＋t －2≤0恒成立．∴⎩⎪⎨⎪⎧12－t ＋1×1＋t －2≤0，22－t ＋1×2＋t －2≤0，解得t ≥0.(理)(2011·烟台模拟)已知函数f (x )＝ax ＋1x2(x ≠0，常数a ∈R )．(1)讨论函数f (x )的奇偶性，并说明理由；(2)若函数f (x )在x ∈[3，＋∞)上为增函数，求a 的取值范围．[解析] (1)定义域为(－∞，0)∪(0，＋∞)，关于原点对称．当a ＝0时，f (x )＝1x，满足对定义域上任意x ，f (－x )＝f (x )，∴a ＝0时，f (x )是偶函数；当a ≠0时，f (1)＝a ＋1，f (－1)＝1－a ， 若f (x )为偶函数，则a ＋1＝1－a ，a ＝0矛盾； 若f (x )为奇函数，则1－a ＝－(a ＋1)，1＝－1矛盾， ∴当a ≠0时，f (x )是非奇非偶函数． (2)对任意x 1，x 2∈[3，＋∞)，且x 1>x 2，f (x 1)－f (x 2)＝ax 1＋1x 21－ax 2－1x 22＝a (x 1－x 2)＋x 22－x 21x 21x 22＝(x 1－x 2)(a －x 1＋x 2x 21x 22)．∵x 1－x 2>0，f (x )在[3，＋∞)上为增函数， ∴a >x 1＋x 2x 21x 22，即a >1x 1x 22＋1x 21x 2在[3，＋∞)上恒成立． ∵1x 1x 22＋1x 21x 2<227，∴a ≥227.能力拓展提升11.(文)(2011·泰安模拟)f (x )是定义在R 上的以3为周期的偶函数，且f (2)＝0，则方程f (x )＝0在区间(0,6)内解的个数至少是( )A ．1B ．4C ．3D ．2 [答案] B[解析] 由f (2)＝0，得f (5)＝0， ∴f (－2)＝0，f (－5)＝0. ∴f (－2)＝f (－2＋3)＝f (1)＝0，f (－5)＝f (－5＋9)＝f (4)＝0，故f (x )＝0在区间(0,6)内的解至少有1,2,4,5四个．(理)(2012·东北三校联考)已知f (x )是定义在R 上的偶函数，对任意x ∈R ，都有f (2＋x )＝－f (x )，且当x ∈[0,1]时有f (x )＝－x 2＋1，当x ∈(1,2]时，f (x )＝x －2，f (x )＝0在[－1,5]上有5个根x i (i ＝1,2,3,4,5)，则x 1＋x 2＋x 3＋x 4＋x 5的值为( )A ．7B ．8C ．9D ．10 [答案] D[解析] ∵f (2＋x )＝－f (x )，∴f (4＋x )＝f [2＋(2＋x )]＝－f (2＋x )＝f (x )，∴f (x )的周期为4，∵x ∈[0,1]时，f (x )＝－x 2＋1， ∴x ∈[－1,0]时，f (x )＝－x 2＋1， 即x ∈[－1,1]时，f (x )＝－x 2＋1， 又x ∈(1,2]时，f (x )＝x －2， ∴x ∈[－2，－1)时，f (x )＝－x －2，∴x ∈[2,3)时，f (x )＝f (x －4)＝－(x －4)－2＝2－x .从而可知在[－1,5]上有f (－1)＝0，f (1)＝0，f (2)＝0，f (3)＝0，f (5)＝0，∴x 1＋x 2＋x 3＋x 4＋x 5＝10，故选D.12．(2012·河南洛阳统考)设函数f (x )是定义在R 上的奇函数，若当x ∈(0，＋∞)时，f (x )＝lg x ，则满足f (x )>0的x 的取值范围是( )A ．(－1,0)B ．(－1,0)∪(1，＋∞)C ．(1，＋∞)D ．(－∞，－1)∪(1，＋∞)[答案] B[解析] ∵函数f (x )是定义在R 上的奇函数，且x ∈(0，＋∞)时，f (x )＝lg x ，∴当x∈(－∞，0)时，f (x )＝－lg(－x )，且f (0)＝0，∴f (x )>0⇔⎩⎪⎨⎪⎧x >0，lg x >0，或⎩⎪⎨⎪⎧x <0，－lg －x >0，解得x >1或－1<x <0.13．(文)(2011·山东淄博一模)设奇函数f (x )的定义域为R ，最小正周期T ＝3，若f (1)≥1，f (2)＝2a －3a ＋1，则a 的取值范围是( ) A ．a <－1或a ≥23B ．a <－1C ．－1<a ≤23D ．a ≤23[答案] C[解析] 函数f (x )为奇函数，则f (－1)＝－f (1)． 由f (1)＝－f (－1)≥1得，f (－1)≤－1； 函数的最小正周期T ＝3，则f (－1)＝f (2)，由2a －3a ＋1≤－1解得，－1<a ≤23.(理)已知定义在R 上的奇函数f (x )满足f (x －4)＝－f (x )，且在区间[0,2]上是增函数，则( )A ．f (－25)<f (11)<f (80)B ．f (80)<f (11)<f (－25)C ．f (11)<f (80)<f (－25)D ．f (－25)<f (80)<f (11) [答案] D[解析] ∵f (x －4)＝－f (x )， ∴f (x －8)＝－f (x －4)＝f (x )，∴f (x ＋8)＝f (x )，∴f (x )周期为8.∴f (80)＝f (0)， 又∵f (x )为奇函数，∴f (－25)＝f (－24－1)＝f (－1)， ∴f (11)＝f (3)＝－f (3－4)＝f (1)， 由条件知f (x )在[－2,2]上为增函数，∴f (－1)<f (0)<f (1)，∴f (－25)<f (80)<f (11)．14．若函数f (x )＝a －e x1＋aex (a 为常数)在定义域上为奇函数，则实数a 的值为________．[答案] 1或－1[解析] f (－x )＝a －e －x 1＋ae －x ＝ae x －1e x＋af (x )＋f (－x )＝a －e xa ＋e x ＋1＋ae x ae x －11＋ae x e x＋a ＝a 2－e 2x ＋a 2e 2x －11＋ae x e x＋a ＝0恒成立， 所以a ＝1或－1.15．已知函数f (x )＝e x －e －x(x ∈R 且e 为自然对数的底数)． (1)判断函数f (x )的奇偶性与单调性；(2)是否存在实数t ，使不等式f (x －t )＋f (x 2－t 2)≥0对一切x 都成立？若存在，求出t ；若不存在，请说明理由．[解析] (1)∵f (x )的定义域为R ，且f (－x )＝e －x－e x＝－f (x )，∴f (x )为奇函数； ∵f (x )＝e x －1e x ，而y ＝e x为增函数，y ＝－1ex 为增函数，∴f (x )为增函数．(2)∵f (x －t )＋f (x 2－t 2)≥0，∴f (x 2－t 2)≥－f (x －t )， ∵f (x )为奇函数，∴f (x 2－t 2)≥f (t －x )， ∵f (x )为增函数，∴x 2－t 2≥t －x ，∴t 2＋t ≤x 2＋x . 由条件知，t 2＋t ≤x 2＋x 对任意实数x 恒成立， 当x ∈R 时，x 2＋x ＝(x ＋12)2－14≥－14.∴t 2＋t ≤－14，∴(t ＋12)2≤0，∴t ＝－12.故存在t ＝－12，使不等式f (x －t )＋f (x 2－t 2)≥0对一切实数x 都成立．16．已知函数f (x )＝log a 1－mxx －1(a >0且a ≠1)是奇函数．(1)求m 的值；(2)判断f (x )在区间(1，＋∞)上的单调性并加以证明；(3)当a >1，x ∈(1，3)时，f (x )的值域是(1，＋∞)，求a 的值．[解析] (1)∵f (x )是奇函数，x ＝1不在f (x )的定义域内，∴x ＝－1也不在函数定义域内，令1－m ·(－1)＝0得m ＝－1. (也可以由f (－x )＝－f (x )恒成立求m ) (2)由(1)得f (x )＝log ax ＋1x －1(a >0且a ≠1)， 任取x 1，x 2∈(1，＋∞)，且x 1<x 2， 令t (x )＝x ＋1x －1，则t (x 1)＝x 1＋1x 1－1，t (x 2)＝x 2＋1x 2－1， ∴t (x 1)－t (x 2)＝x 1＋1x 1－1－x 2＋1x 2－1＝2x 2－x 1x 1－1x 2－1， ∵x 1>1，x 2>1，x 1<x 2， ∴x 1－1>0，x 2－1>0，x 2－x 1>0. ∴t (x 1)>t (x 2)，即x 1＋1x 1－1>x 2＋1x 2－1， ∴当a >1时，log ax 1＋1x 1－1>log a x 2＋1x 2－1， 即f (x 1)>f (x 2)； 当0<a <1时，log ax 1＋1x 1－1<log a x 2＋1x 2－1，即f (x 1)<f (x 2)， ∴当a >1时，f (x )在(1，＋∞)上是减函数，当0<a <1时，f (x )在(1，＋∞)上是增函数． (3)∵a >1，∴f (x )在(1，3)上是减函数， ∴当x ∈(1，3)时，f (x )>f (3)＝log a (2＋3)， 由条件知，log a (2＋3)＝1，∴a ＝2＋ 3.1．已知g (x )是定义在R 上的奇函数，且在(0，＋∞)内有1005个零点，则f (x )的零点共有( )A ．1005个B ．1006个C ．2009个D ．2011个[答案] D[解析] ∵奇函数的图象关于原点对称，g (x )在(0，＋∞)上与x 轴有1005个交点，故在(－∞，0)上也有1005个交点，又f (0)＝0，∴共有零点2011个．2．下列函数中既是奇函数，又在区间[－1,1]上单调递减的是( ) A ．f (x )＝sin x B ．f (x )＝－|x ＋1| C ．f (x )＝12(a x ＋a －x)D ．f (x )＝ln 2－x2＋x[答案] D[解析] y ＝sin x 与y ＝ln 2－x 2＋x 为奇函数，而y ＝12(a x ＋a －x)为偶函数，y ＝－|x ＋1|是非奇非偶函数．y ＝sin x 在[－1,1]上为增函数．故选D.3．(2012·浙江湖州第二次质检)已知图甲是函数y ＝f (x )的图象，则图乙中的图象对应的函数可能是( )A ．y ＝f (|x |)B ．y ＝|f (x )|C ．y ＝－f (－|x |)D ．y ＝f (－|x |)[答案] D[解析] 由图乙可知，该函数为偶函数，且x <0时，其函数图象与f (x )的函数图象相同，即该函数图象的解析式为y ＝⎩⎪⎨⎪⎧f x ， x <0，f －x ， x ≥0，即y ＝f (－|x |)，故应选D.4．定义两种运算：a ⊗b ＝a 2－b 2，a ⊕b ＝|a －b |，则函数f (x )＝2⊗x x ⊕2－2( )A ．是偶函数B ．是奇函数C ．既是奇函数又是偶函数D ．既不是奇函数又不是偶函数 [答案] B[解析] f(x)＝4－x2|x－2|－2，∵x2≤4，∴－2≤x≤2，又∵x≠0，∴x∈[－2,0)∪(0,2]．则f(x)＝4－x2－x，f(x)＋f(－x)＝0，故选B.5．已知函数f(x)是R上的偶函数，g(x)是R上的奇函数，且g(x)＝f(x－1)，若g(1)＝2，则f(2012)的值为( )A．2 B．0C．－2 D．±2[答案] A[解析] 由已知：g(－x)＝f(－x－1)，又g(x)、f(x)分别为R上的奇、偶函数，∴－g(x)＝f(x＋1)，∴f(x－1)＝－f(x＋1)，∴f(x)＝－f(x＋2)，∴f(x)＝f(x＋4)，即f(x)的周期T＝4，∴f(2012)＝f(0)＝g(1)＝2，故选A.。

3-4定积分与微积分基本定理(理)基础巩固强化1.(2011·宁夏银川一中月考)求曲线y ＝x 2与y ＝x 所围成图形的面积，其中正确的是( )A ．S ＝⎠⎛01(x 2－x )d xB ．S ＝⎠⎛01(x －x 2)d xC ．S ＝⎠⎛01(y 2－y )d y D ．S ＝⎠⎛01(y －y )d y[答案] B[分析] 根据定积分的几何意义，确定积分上、下限和被积函数．[解析] 两函数图象的交点坐标是(0,0)，(1,1)，故积分上限是1，下限是0，由于在[0,1]上，x ≥x 2，故函数y ＝x 2与y ＝x 所围成图形的面积S ＝⎠⎛01(x －x 2)d x .2．如图，阴影部分面积等于( )A ．2 3B ．2－ 3 C.323D.353[答案] C[解析] 图中阴影部分面积为S ＝⎠⎛-31 (3－x 2－2x )d x ＝(3x －13x 3－x 2)|1－3＝323. 3.⎠⎛024－x 2d x ＝( )A ．4πB ．2πC ．π D.π2[答案] C[解析] 令y ＝4－x 2，则x 2＋y 2＝4(y ≥0)，由定积分的几何意义知所求积分为图中阴影部分的面积，∴S ＝14×π×22＝π.4.已知甲、乙两车由同一起点同时出发，并沿同一路线(假定为直线)行驶．甲车、乙车的速度曲线分别为v 甲和v 乙(如图所示)．那么对于图中给定的t 0和t 1，下列判断中一定正确的是( )A ．在t 1时刻，甲车在乙车前面B ．在t 1时刻，甲车在乙车后面C ．在t 0时刻，两车的位置相同D ．t 0时刻后，乙车在甲车前面 [答案] A[解析] 判断甲、乙两车谁在前，谁在后的问题，实际上是判断在t 0，t 1时刻，甲、乙两车行驶路程的大小问题．根据定积分的几何意义知：车在某段时间内行驶的路程就是该时间段内速度函数的定积分，即速度函数v (t )的图象与t 轴以及时间段围成区域的面积．从图象知：在t 0时刻，v 甲的图象与t 轴和t ＝0，t ＝t 0围成区域的面积大于v 乙的图象与t 轴和t ＝0，t ＝t 0围成区域的面积，因此，在t 0时刻，甲车在乙车的前面，而且此时乙车的速度刚刚赶上甲车的速度，所以选项C ，D 错误；同样，在t 1时刻，v 甲的图象与t 轴和t ＝t 1围成区域的面积，仍然大于v 乙的图象与t 轴和t ＝t 1围成区域的面积，所以，可以断定：在t 1时刻，甲车还是在乙车的前面．所以选A.5．(2012·山东日照模拟)向平面区域Ω＝{(x ，y )|－π4≤x ≤π4，0≤y ≤1}内随机投掷一点，该点落在曲线y ＝cos2x 下方的概率是( )A.π4B.12C.π2－1 D.2π[答案] D[解析] 平面区域Ω是矩形区域，其面积是π2，在这个区6． (sin x －cos x )d x 的值是( )A ．0 B.π4 C ．2 D ．－2[答案] D[解析] (sin x －cos x )d x ＝(－cos x －sin x ) ＝－2.7．(2010·惠州模拟)⎠⎛02(2－|1－x |)d x ＝________.[答案] 3[解析] ∵y ＝⎩⎪⎨⎪⎧1＋x 0≤x ≤13－x 1<x ≤2，∴⎠⎛02(2－|1－x |)d x ＝⎠⎛01(1＋x )d x ＋⎠⎛12(3－x )d x＝(x ＋12x 2)|10＋(3x －12x 2)|21＝32＋32＝3.8．(2010·芜湖十二中)已知函数f (x )＝3x 2＋2x ＋1，若⎠⎛1－1f (x )d x ＝2f (a )成立，则a ＝________.[答案] －1或13[解析] ∵⎠⎛1－1f (x )d x ＝⎠⎛1－1(3x 2＋2x ＋1)d x ＝(x 3＋x 2＋x )|1－1＝4，⎠⎛1－1f (x )d x ＝2f (a )，∴6a 2＋4a ＋2＝4，∴a ＝－1或13.9．已知a ＝∫π20(sin x ＋cos x )d x ，则二项式(a x －1x )6的展开式中含x 2项的系数是________．[答案] －192[解析] 由已知得a ＝∫π20(sin x ＋cos x )d x ＝(－cos x ＋sin x )|π20＝(sinπ2－cos π2)－(sin0－cos0)＝2，(2x －1x)6的展开式中第r ＋1项是T r ＋1＝(－1)r ×C r 6×26－r×x3－r，令3－r ＝2得，r＝1，故其系数为(－1)1×C 16×25＝－192.10．有一条直线与抛物线y ＝x 2相交于A 、B 两点，线段AB 与抛物线所围成图形的面积恒等于43，求线段AB 的中点P 的轨迹方程．[解析] 设直线与抛物线的两个交点分别为A (a ，a 2)，B (b ，b 2)，不妨设a <b ，则直线AB 的方程为y －a 2＝b 2－a 2b －a(x －a )，即y ＝(a ＋b )x －ab .则直线AB 与抛物线围成图形的面积为S ＝⎠⎛ab [(a ＋b )x －ab －x 2]d x ＝(a ＋b2x 2－abx －x 33)|b a ＝16(b －a )3， ∴16(b －a )3＝43， 解得b －a ＝2.设线段AB 的中点坐标为P (x ，y )，其中⎩⎪⎨⎪⎧x ＝a ＋b 2，y ＝a 2＋b22.将b －a ＝2代入得⎩⎪⎨⎪⎧x ＝a ＋1，y ＝a 2＋2a ＋2.消去a 得y ＝x 2＋1.∴线段AB 的中点P 的轨迹方程为y ＝x 2＋1.能力拓展提升11.(2012·郑州二测)等比数列{a n }中，a 3＝6，前三项和S 3＝⎠⎛034x d x ，则公比q 的值为( )A ．1B ．－12C ．1或－12D ．－1或－12[答案] C[解析] 因为S 3＝⎠⎛034x d x ＝2x 2|30＝18，所以6q ＋6q2＋6＝18，化简得2q 2－q －1＝0，解得q ＝1或q ＝－12，故选C.12．(2012·太原模拟)已知(x ln x )′＝ln x ＋1，则⎠⎛1e ln x d x ＝( )A ．1B ．eC ．e －1D ．e ＋1 [答案] A[解析] 由(x ln x )′＝ln x ＋1，联想到(x ln x －x )′＝(ln x ＋1)－1＝ln x ，于是⎠⎛1e ln x d x＝(x ln x －x )|e1＝(e ln e －e )－(1×ln1－1)＝1.13．抛物线y 2＝2x 与直线y ＝4－x 围成的平面图形的面积为________． [答案] 18[解析] 由方程组⎩⎪⎨⎪⎧y 2＝2x ，y ＝4－x ，解得两交点A (2,2)、B (8，－4)，选y 作为积分变量x＝y 22、x ＝4－y ，∴S ＝⎠⎛-42[(4－y )－y 22]dy ＝(4y －y 22－y 36)|2－4＝18.14.已知函数f (x )＝e x－1，直线l 1：x ＝1，l 2：y ＝e t－1(t 为常数，且0≤t ≤1)．直线l 1，l 2与函数f (x )的图象围成的封闭图形如图中区域Ⅱ所示，其面积用S 2表示．直线l 2，y 轴与函数f (x )的图象围成的封闭图形如图中区域Ⅰ所示，其面积用S 1表示．当t 变化时，阴影部分的面积的最小值为________．[答案] (e －1)2[解析] 由题意得S 1＋S 2＝⎠⎛0t (e t－1－e x＋1)d x ＋⎠⎛t 1(e x－1－e t＋1)d x ＝⎠⎛0t (e t－e x)d x ＋⎠⎛t1(e x －e t )d x ＝(xe t －e x )|t 0＋(e x －xe t )|1t ＝(2t －3)e t ＋e ＋1，令g (t )＝(2t －3)e t ＋e ＋1(0≤t ≤1)，则g ′(t )＝2e t ＋(2t －3)e t ＝(2t －1)e t，令g ′(t )＝0，得t ＝12，∴当t ∈[0，12)时，g ′(t )<0，g (t )是减函数，当t ∈(12，1]时，g ′(t )>0，g (t )是增函数，因此g (t )的最小值为g (12)＝e ＋1－2e 12＝(e －1)2.故阴影部分的面积的最小值为(e －1)2.15．求下列定积分．(1)⎠⎛1－1|x |d x; (2)⎠⎛0πcos 2x2d x ；(3)∫e ＋121x －1d x . [解析] (1)⎠⎛1－1|x |d x ＝2⎠⎛01x d x ＝2×12x 2|10＝1.(2)⎠⎛0πcos 2x2d x ＝⎠⎛0π1＋cos x 2d x ＝12x |π0＋12sin x |π0＝π2. (3)∫e ＋121x －1d x ＝ln(x －1)|e ＋12＝1. 16．已知函数f (x )＝－x 3＋ax 2＋bx (a ，b ∈R )的图象如图所示，它与x 轴在原点处相切，且x 轴与函数图象所围区域(图中阴影部分)的面积为112，求a 的值．[解析] f ′(x )＝－3x 2＋2ax ＋b ，∵f ′(0)＝0，∴b ＝0， ∴f (x )＝－x 3＋ax 2，令f (x )＝0，得x ＝0或x ＝a (a <0)． ∴S 阴影＝⎠⎛a0[0－(－x 3＋ax 2)]d x＝(14x 4－13ax 3)|0a ＝112a 4＝112， ∵a <0，∴a ＝－1.1．(2011·龙岩质检)已知函数f (x )＝sin 5x ＋1，根据函数的性质、积分的性质和积分的几何意义，探求f (x )d x 的值，结果是( )A.16＋π2 B ．π C ．1 D ．0 [答案] B[解析]f (x )d x ＝sin 5x d x ＋1d x ，由于函数y ＝sin 5x是奇函数，所以sin 5x d x ＝0，而1d x ＝x |π2－π2＝π，故选B.2．若函数f (x )＝⎩⎪⎨⎪⎧－x －1 －1≤x <0，cos x 0≤x <π2，的图象与坐标轴所围成的封闭图形的面积为a ，则a 的值为( )A.2＋π4B.12 C ．1 D.32[答案] D[解析] 由图可知a ＝12＋⎠⎜⎛0π2cos x d x ＝12＋sin x |π20＝32.3．对任意非零实数a 、b ，若a ⊗b 的运算原理如图所示，则2⊗⎠⎛0πsin x d x ＝________.[答案]22[解析] ∵⎠⎛0πsin x d x ＝－cos x |π0＝2>2，∴2⊗⎠⎛0πsin x d x ＝2⊗2＝2－12＝22.4．设函数f (x )＝ax 2＋c (a ≠0)，若⎠⎛01f (x )d x ＝f (x 0)，0≤x 0≤1，则x 0的值为________．[答案]33[解析] ⎠⎛01f (x )d x ＝⎠⎛01(ax 2＋c )d x ＝(ax 33＋cx )|10＝a 3＋c ，故a3＋c ＝ax 20＋c ，即ax 20＝a3，又a ≠0，所以x 20＝13，又0≤x 0≤1，所以x 0＝33.故填33.5．设n ＝⎠⎛12(3x 2－2)d x ，则(x －2x)n 展开式中含x 2项的系数是________．[答案] 40[解析] ∵(x 3－2x )′＝3x 2－2， ∴n ＝⎠⎛12(3x 2－2)d x ＝(x 3－2x )|21＝(23－2×2)－(1－2)＝5. ∴(x －2x)5的通项公式为T r ＋1＝C r 5x5－r(－2x)r＝(－2)r C r5x 5－3r2，令5－3r2＝2，得r＝2，∴x2项的系数是(－2)2C25＝40.。

3-1导数的概念及运算基础巩固强化1.(文)(2011·青岛质检)设f (x )＝x ln x ，若f ′(x 0)＝2，则x 0＝( ) A ．e 2B ．e C.ln22 D ．ln2[答案] B[解析] f ′(x )＝1＋ln x ，∴f ′(x 0)＝1＋ln x 0＝2， ∴ln x 0＝1，∴x 0＝e ，故选B.(理)已知函数y ＝f (x )的图象在点(1，f (1))处的切线方程是x －2y ＋1＝0，则f (1)＋2f ′(1)的值是( )A.12 B ．1 C.32 D ．2 [答案] D[解析] 由条件知，y ＝f (x )在点(1，f (1))处切线的斜率f ′(1)＝12，又点(1，f (1))在切线x －2y ＋1＝0上，∴f (1)＝1，∴f (1)＋2f ′(1)＝1＋2×12＝2.2．(文)(2011·广东省东莞市模拟)已知曲线y ＝18x 2的一条切线的斜率为12，则切点的横坐标为( )A ．4B ．3C ．2 D.12[答案] C[解析] 由条件知，k ＝y ′＝14x ＝12，∴x ＝2.(理)(2012·乌鲁木齐地区二诊)直线y ＝12x ＋b 与曲线y ＝－12x ＋ln x 相切，则b 的值为( )A ．－2B ．－1C ．－12D ．1[答案] B[解析] 设切点(a ，－12a ＋ln a )，y ′＝－12＋1x，∴－12＋1a ＝12，a ＝1，故切点(1，－12)在直线y ＝12x ＋b 上，有－12＝12＋b ，∴b ＝－1.3．(文)(2011·皖南八校联考)直线y ＝kx ＋b 与曲线y ＝x 3＋ax ＋1相切于点(2,3)，则b 的值为( )A ．－3B ．9C ．－15D ．－7[答案] C[解析] 将点(2,3)分别代入曲线y ＝x 3＋ax ＋1和直线y ＝kx ＋b ，得a ＝－3,2k ＋b ＝3.又k ＝y ′|x ＝2＝(3x 2－3)|x ＝2＝9， ∴b ＝3－2k ＝3－18＝－15.(理)(2011·广东华南师大附中测试)曲线y ＝2x 2在点P (1，2)处的切线方程是( ) A ．4x －y －2＝0 B ．4x ＋y －2＝0 C ．4x ＋y ＋2＝0 D ．4x －y ＋2＝0[答案] A[解析] ∵k ＝y ′|x ＝1＝4x |x ＝1＝4，∴切线方程为y －2＝4(x －1)，即4x －y －2＝0.4．已知y ＝tan x ，x ∈⎝⎛⎭⎪⎫0，π2，当y ′＝2时，x 等于( )A.π3 B.23π C.π4D.π6[答案] C[解析] y ′＝(tan x )′＝⎝ ⎛⎭⎪⎫sin x cos x ′＝cos 2x ＋sin 2x cos 2x ＝1cos 2x ＝2，∴cos 2x ＝12，∴cos x ＝±22， ∵x ∈⎝⎛⎭⎪⎫0，π2，∴x ＝π4.5．(文)(2011·山东淄博一中期末)曲线y ＝13x 3＋x 在点⎝ ⎛⎭⎪⎫1，43处的切线与坐标轴围成的三角形面积为( )A ．1 B.19 C.13 D.23[答案] B[解析] ∵y ′＝x 2＋1，∴k ＝2，切线方程y －43＝2(x －1)，即6x －3y －2＝0，令x ＝0得y ＝－23，令y ＝0得x ＝13，∴S ＝12×13×23＝19.(理)(2012·烟台调研)设曲线y ＝x ＋1x －1在点(3,2)处的切线与直线ax ＋y ＋1＝0垂直，则a 等于( )A ．2B ．－2C ．－12D.12[答案] B[解析] ∵f ′(x )＝x －1－x ＋1x －12＝－2x －12，∴f ′(3)＝－12，由条件知，－12×(－a )＝－1，∴a ＝－2.6．(文)等比数列{a n }中，a 1＝2，a 8＝4，函数f (x )＝x (x －a 1)(x －a 2)…(x －a 8)，则f ′(0)＝( )A ．26B ．29C ．212D ．215[答案] C[解析] f ′(x )＝x ′·[(x －a 1)(x －a 2)…(x －a 8)]＋[(x －a 1)(x －a 2)…(x －a 8)]′·x＝(x －a 1)(x －a 2)…(x －a 8)＋[(x －a 1)(x －a 2)…(x －a 8)]′·x ，所以f ′(0)＝(0－a 1)(0－a 2)…(0－a 8)＋[(0－a 1)(0－a 2)…(0－a 8)]′·0＝a 1a 2…a 8. 因为数列{a n }为等比数列，所以a 2a 7＝a 3a 6＝a 4a 5＝a 1a 8＝8，所以f ′(0)＝84＝212. (理)(2013·辽宁大连二十四中上学期期中考试)设函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6－1(ω>0)的导函数f ′(x )的最大值为3，则f (x )图象的一条对称轴方程是( )A ．x ＝π9B ．x ＝π6C ．x ＝π3D ．x ＝π2[答案] A[解析] f ′(x )＝ωcos ⎝ ⎛⎭⎪⎫ωx ＋π6的最大值为3， 即ω＝3，∴f (x )＝sin ⎝⎛⎭⎪⎫3x ＋π6－1.由3x ＋π6＝π2＋k π得，x ＝π9＋k π3 (k ∈Z )．故A 正确．7．设θ为曲线y ＝x 3＋3x 2＋ax ＋2的切线的倾斜角，且所有θ组成的集合为[π4，π2)，则实数a 的值为________．[答案] 4[解析] 设切线的斜率为k ， 则k ＝y ′＝3x 2＋6x ＋a ， 又∵k ＝tan θ，θ∈[π4，π2)，∴k ∈[1，＋∞)． 又k ＝3(x ＋1)2＋a －3，∴当x ＝－1时，k 取最小值为a －3＝1. ∴a ＝4.8．(文)(2011·北京模拟)已知函数f (x )＝3x 3＋2x 2－1在区间(m,0)上总有f ′(x )≤0成立，则m 的取值范围为________．[答案] [－49，0)[解析] ∵f ′(x )＝9x 2＋4x ≤0在(m,0)上恒成立，且f ′(x )＝0的两根为x 1＝0，x 2＝－49，∴－49≤m <0.(理)设a ∈R ，函数f (x )＝x 3＋ax 2＋(a －3)x 的导函数是f ′(x )，若f ′(x )是偶函数，则曲线y ＝f (x )在原点处的切线方程为________．[答案] y ＝－3x[解析] f ′(x )＝3x 2＋2ax ＋(a －3)，又∵f ′(x )为偶函数，∴f ′(－x )＝f ′(x )， 即3x 2－2ax ＋(a －3)＝3x 2＋2ax ＋(a －3) 对任意x ∈R 都成立，∴a ＝0， ∴f ′(x )＝3x 2－3，f ′(0)＝－3，∴曲线y ＝f (x )在原点处的切线方程为y ＝－3x . 9．(2011·济南模拟)设曲线y ＝xn ＋1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ，令a n ＝lg x n ，则a 1＋a 2＋…＋a 99的值为________．[答案] －2[解析] 点(1,1)在曲线y ＝xn ＋1(n ∈N *)上，点(1,1)为切点，y ′＝(n ＋1)x n，故切线的斜率为k ＝n ＋1，曲线在点(1,1)处的切线方程y －1＝(n ＋1)(x －1)，令y ＝0得切点的横坐标为x n ＝nn ＋1，故a 1＋a 2＋…＋a 99＝lg(x 1x 2…x 99)＝lg(12×23×…×99100)＝lg 1100＝－2. 10．(文)设函数y ＝ax 3＋bx 2＋cx ＋d 的图象与y 轴交点为P ，且曲线在P 点处的切线方程为12x －y －4＝0. 若函数在x ＝2处取得极值0，试确定函数的解析式.[解析] ∵y ＝ax 3＋bx 2＋cx ＋d 的图象与y 轴的交点为P (0，d )，又曲线在点P 处的切线方程为y ＝12x －4，P 点坐标适合方程，从而d ＝－4； 又切线斜率k ＝12，故在x ＝0处的导数y ′|x ＝0＝12而y ′|x ＝0＝c ，从而c ＝12； 又函数在x ＝2处取得极值0，所以⎩⎪⎨⎪⎧y ′|x ＝2＝0，f 2＝0.即⎩⎪⎨⎪⎧12a ＋4b ＋12＝0，8a ＋4b ＋20＝0.解得a ＝2，b ＝－9，所以所求函数解析式为y ＝2x 3－9x 2＋12x －4. (理)已知函数f (x )＝ax 2＋b ln x 在x ＝1处有极值12.(1)求a 、b 的值；(2)判断函数y ＝f (x )的单调性并求出单调区间． [解析] (1)因为函数f (x )＝ax 2＋b ln x ， 所以f ′(x )＝2ax ＋b x. 又函数f (x )在x ＝1处有极值12，所以⎩⎪⎨⎪⎧f ′1＝0，f 1＝12，即⎩⎪⎨⎪⎧2a ＋b ＝0，a ＝12，可得a ＝12，b ＝－1.(2)由(1)可知f (x )＝12x 2－ln x ，其定义域是(0，＋∞)，且f ′(x )＝x －1x＝x ＋1x －1x.当x 变化时，f ′(x )，f (x )的变化情况如下表：所以函数y能力拓展提升11.(2013·辽宁省沈阳四校期中联考)若函数y ＝x 33－x 2＋1(0<x <2)的图象上任意点处切线的倾斜角为α，则α的最小值是( )A.π4B.π6C.5π6D.3π4[答案] D[解析] y ′＝x 2－2x ＝(x －1)2－1， ∵0<x <2，∴－1≤y ′<0， 由题意知－1≤tan α<0，∴3π4≤α<π，故选D. 12．(2011·广东省汕头市四校联考)已知函数f (x )(x ∈R )满足f (1)＝1，且f (x )的导函数f ′(x )<12，则f (x )<x 2＋12的解集为( )A ．{x |－1<x <1}B ．{x |x <－1}C ．{x |x <－1或x >1}D ．{x |x >1}[答案] D[解析] 令φ(x )＝f (x )－x 2－12，则φ′(x )＝f ′(x )－12<0，∴φ(x )在R 上是减函数，∵φ(1)＝f (1)－12－12＝1－1＝0，∴φ(x )＝f (x )－x 2－12<0的解集为{x |x >1}，选D.13．(文)二次函数y ＝f (x )的图象过原点，且它的导函数y ＝f ′(x )的图象是过第一、二、三象限的一条直线，则函数y ＝f (x )的图象的顶点在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限[答案] C[解析] 由题意可设f (x )＝ax 2＋bx ，f ′(x )＝2ax ＋b ，由于f ′(x )图象是过第一、二、三象限的一条直线，故2a >0，b >0，则f (x )＝a (x ＋b 2a )2－b 24a ，顶点(－b 2a ，－b 24a)在第三象限，故选C.(理)函数f (x )＝x cos x 的导函数f ′(x )在区间[－π，π]上的图象大致为( )[答案] A[解析] ∵f (x )＝x cos x ，∴f ′(x )＝cos x －x sin x ， ∴f ′(－x )＝f ′(x )，∴f ′(x )为偶函数，排除C ； ∵f ′(0)＝1，排除D ；由f ′⎝ ⎛⎭⎪⎫π2＝－π2<0，f ′(2π)＝1>0，排除B ，故选A. 14．(2011·朝阳区统考)若曲线f (x )＝ax 3＋ln x 存在垂直于y 轴的切线，则实数a 的取值范围是________．[答案] (－∞，0)[解析] 由题意，可知f ′(x )＝3ax 2＋1x，又因为存在垂直于y 轴的切线，所以3ax2＋1x ＝0⇒a ＝－13x3(x >0)⇒a ∈(－∞，0)． 15．(文)已知曲线y ＝13x 3＋43.(1)求曲线在点P (2,4)处的切线方程； (2)求曲线过点P (2,4)的切线方程． [解析] y ＝13x 3＋43，则y ′＝x 2.(1)由题意可知点P (2,4)为切点，y ′|x ＝2＝22＝4，所以曲线在点P (2,4)处的切线方程为y －4＝4(x －2)，即4x －y －4＝0. (2)由题意可知点P (2,4)不一定为切点，故设切点为(x 0，13x 30＋43)，y ′|x ＝x 0＝x 20，曲线过点P (2,4)的切线方程为y －(13x 30＋43)＝x 20(x －x 0)，所以4－(13x 30＋43)＝x 20(2－x 0)，x 30－3x 20＋4＝0⇔(x 30＋1)－3(x 20－1)＝0⇔(x 0＋1)(x 20－4x 0＋4)＝0.解得x 0＝－1或x 0＝2，即切点为(－1,1)或(2,4)．所以曲线过点P (2,4)的切线方程为x －y ＋2＝0和4x －y －4＝0.(理)设函数f (x )＝ax ＋b x的图象在点M (3，f (3))处的切线方程为2x －3y ＋23＝0. (1)求f (x )的解析式；(2)求函数f (x )的单调递减区间；(3)证明曲线y ＝f (x )上任一点处的切线与直线x ＝0和直线y ＝x 所围成的三角形面积为定值，并求此定值．[解析] (1)因为切点在切线上，所以将点M 坐标代入切线方程解得f (3)＝433.∵f (x )＝ax ＋b x ，∴f ′(x )＝a －b x2，根据题意，得关于a ，b 的方程组⎩⎪⎨⎪⎧a －b 3＝23，3a ＋b3＝433，解得⎩⎪⎨⎪⎧a ＝1，b ＝1.所以f (x )的解析式为f (x )＝x ＋1x.(2)由f ′(x )＝1－1x2(x ≠0)，令f ′(x )<0，解得－1<x <0或0<x <1. 所以f (x )的单调递减区间为(－1,0)，(0,1)． (3)证明：设P (x 0，y 0)为曲线上任一点，由y ′＝1－1x2知曲线在点P (x 0，y 0)处的切线方程为y －y 0＝(1－1x 20)(x －x 0)，即y －(x 0＋1x 0)＝(1－1x 20)(x －x 0)．令x ＝0，得y ＝2x 0，从而得切线与直线x ＝0的交点坐标为(0，2x 0)．令y ＝x ，得y ＝x ＝2x 0，从而得切线与直线y ＝x 的交点坐标为(2x 0,2x 0)．所以点P (x 0，y 0)处的切线与直线x ＝0，y ＝x 所围成的三角形面积为12⎪⎪⎪⎪⎪⎪2x 0|2x 0|＝2.16．(文)已知函数f (x )＝x 3－(a ＋b )x 2＋abx ，(0<a <b )．(1)若函数f (x )在点(1,0)处的切线的倾斜角为3π4，求a 、b 的值；(2)在(1)的条件下，求f (x )在区间[0,3]上的最值； (3)设f (x )在x ＝s 与x ＝t 处取得极值，其中s <t ， 求证：0<s <a <t <b .[解析] (1)f ′(x )＝3x 2－2(a ＋b )x ＋ab ，tan 3π4＝－1.由条件得⎩⎪⎨⎪⎧f 1＝0f ′1＝－1，即⎩⎪⎨⎪⎧1－a ＋b ＋ab ＝03－2a ＋b ＋ab ＝－1，解得a ＝1，b ＝2或a ＝2，b ＝1， 因为a <b ，所以a ＝1，b ＝2.(2)由(1)知f (x )＝x 3－3x 2＋2x ，f ′(x )＝3x 2－6x ＋2， 令f ′(x )＝3x 2－6x ＋2＝0，解得x 1＝1－33，x 2＝1＋33. 在区间[0,3]上，x ，f ′(x )，f (x )的变化情况如下表：(3)证明：f ′(x )＝3x 2－2(a ＋b )x ＋ab ， 依据题意知s ，t 为二次方程f ′(x )＝0的两根． ∵f ′(0)＝ab >0，f ′(a )＝a 2－ab ＝a (a －b )<0，f ′(b )＝b 2－ab ＝b (b －a )>0，∴f ′(x )＝0在区间(0，a )与(a ，b )内分别有一个根． ∵s <t ，∴0<s <a <t <b .(理)已知定义在正实数集上的函数f (x )＝12x 2＋2ax ，g (x )＝3a 2ln x ＋b ，其中a >0.设两曲线y ＝f (x )，y ＝g (x )有公共点，且在该点处的切线相同．(1)用a 表示b ，并求b 的最大值； (2)求证：f (x )≥g (x ) (x >0)．[解析] (1)设y ＝f (x )与y ＝g (x )(x >0)的公共点为(x 0，y 0)，∴x 0>0. ∵f ′(x )＝x ＋2a ，g ′(x )＝3a2x，由题意f (x 0)＝g (x 0)，且f ′(x 0)＝g ′(x 0)．∴⎩⎪⎨⎪⎧12x 2＋2ax 0＝3a 2ln x 0＋b ，x 0＋2a ＝3a2x0，由x 0＋2a ＝3a2x 0得x 0＝a 或x 0＝－3a (舍去)．则有b ＝12a 2＋2a 2－3a 2ln a ＝52a 2－3a 2ln a .令h (a )＝52a 2－3a 2ln a (a >0)，则h ′(a )＝2a (1－3ln a )． 由h ′(a )>0得，0<a <e 13，由h ′(a )<0得，a >e 13.故h (a )在(0，e 13)为增函数，在(e 13，＋∞)上为减函数， ∴h (a )在a ＝e 13 时取最大值h (e 13 )＝32e 23.即b 的最大值为32e 23.(2)设F (x )＝f (x )－g (x )＝12x 2＋2ax －3a 2ln x －b (x >0)，则F ′(x )＝x ＋2a －3a 2x＝x －a x ＋3a x(x >0)．故F (x )在(0，a )为减函数，在(a ，＋∞)为增函数，于是函数F (x )在(0，＋∞)上的最小值是F (a )＝F (x 0)＝f (x 0)－g (x 0)＝0. 故当x >0时，有f (x )－g (x )≥0， 即当x >0时，f (x )≥g (x )．1．(2011·安徽省“江南十校”高三联考)已知函数f (x )的导函数为f ′(x )，且满足f (x )＝2xf ′(1)＋x 2，则f ′(1)＝( )A ．－1B ．－2C ．1D ．2[答案] B[解析] f ′(x )＝2f ′(1)＋2x ，令x ＝1得f ′(1)＝2f ′(1)＋2，∴f ′(1)＝－2，故选B.2．(2011·茂名一模)设函数f (x )＝g (x )＋x 2，曲线y ＝g (x )在点(1，g (1))处的切线方程为y ＝2x ＋1，则曲线y ＝f (x )在点(1，f (1))处切线的斜率为( )A ．4B ．－14C ．2D ．－12[答案] A[解析] ∵f (x )＝g (x )＋x 2，∴f ′(x )＝g ′(x )＋2x ，∴f ′(1)＝g ′(1)＋2，由条件知，g ′(1)＝2，∴f ′(1)＝4，故选A. 3．曲线y ＝xx ＋2在点(－1，－1)处的切线方程为( )A ．y ＝2x ＋1B ．y ＝2x －1C ．y ＝－2x －3D ．y ＝－2x －2[答案] A [解析] ∵y ′＝x ′x ＋2－x x ＋2′x ＋22＝2x ＋22，∴k ＝y ′|x ＝－1＝2－1＋22＝2，∴切线方程为：y ＋1＝2(x ＋1)，即y ＝2x ＋1.4．(2011·湖南湘西联考)下列图象中有一个是函数f (x )＝13x 3＋ax 2＋(a 2－1)x ＋1(a ∈R ，a ≠0)的导函数f ′(x )的图象，则f (－1)＝( )A.13 B ．－13C.53 D ．－53[答案] B[解析] f ′(x )＝x 2＋2ax ＋(a 2－1)，∵a ≠0， ∴其图象为最右侧的一个． 由f ′(0)＝a 2－1＝0，得a ＝±1. 由导函数f ′(x )的图象可知，a <0， 故a ＝－1，f (－1)＝－13－1＋1＝－13.5．(2011·广东省佛山市测试)设f (x )、g (x )是R 上的可导函数，f ′(x )、g ′(x )分别为f (x )、g (x )的导函数，且满足f ′(x )g (x )＋f (x )g ′(x )<0，则当a <x <b 时，有( )A ．f (x )g (b )>f (b )g (x )B ．f (x )g (a )>f (a )g (x )C ．f (x )g (x )>f (b )g (b )D ．f (x )g (x )>f (a )g (a )[答案] C[解析] 因为f ′(x )g (x )＋f (x )g ′(x )＝[f (x )g (x )]′，所以[f (x )g (x )]′<0，所以函数y ＝f (x )g (x )在给定区间上是减函数，故选C.6．定义方程f (x )＝f ′(x )的实数根x 0叫做函数f (x )的“新驻点”，若函数g (x )＝x ，h (x )＝ln(x ＋1)，φ(x )＝x 3－1的“新驻点”分别为α，β，γ，则α，β，γ的大小关系为( )A ．α>β>γB ．β>α>γC ．γ>α>βD ．β>γ>α[答案] C[解析] 由g (x )＝g ′(x )得，x ＝1，∴α＝1，由h (x )＝h ′(x )得，ln(x ＋1)＝1x ＋1，故知1<x ＋1<2，∴0<x <1，即0<β<1，由φ(x )＝φ′(x )得，x 3－1＝3x 2，∴x 2(x －3)＝1， ∴x >3，故γ>3，∴γ>α>β. [点评] 对于ln(x ＋1)＝1x ＋1，假如0<x ＋1<1，则ln(x ＋1)<0，1x ＋1>1矛盾；假如x ＋1≥2，则1x ＋1≤12，即ln(x ＋1)≤12，∴x ＋1≤e ，∴x ≤e －1与x ≥1矛盾． 7．(2012·衡水质量检测)已知函数f (x )＝13x 3－12ax 2＋(b －1)x ＋c (a >0)，曲线y ＝f (x )在点P (0，f (0))处的切线方程为y ＝x ＋1.(1)求b 、c 的值；(2)若过点(0,3)可作曲线g (x )＝f (x )－x 的三条不同切线，求实数a 的取值范围． [解析] (1)∵f ′(x )＝x 2－ax ＋(b －1)， 又f (0)＝1，f ′(0)＝1.∴b ＝2，c ＝1.(2)设过(0,3)与曲线g (x )＝f (x )－x 相切的直线为l ，切点的坐标为(t ，g (t ))， 又g (x )＝13x 3－12ax 2＋1，g ′(x )＝x 2－ax ，则切线l 的方程为y －(13t 3－12at 2＋1)＝(t 2－at )(x －t )．又直线l 过点(0,3)，∴3－13t 3＋12at 2－1＝－t 3＋at 2，即23t 3－a 2t 2＋2＝0，又过点(0,3)可作曲线g (x )＝f (x )－x 的三条不同切线． 等价于方程23t 3－a 2t 2＋2＝0有三个相异实根．令h (t )＝23t 3－a 2t 2＋2，h ′(t )＝2t 2－at ＝t ·(2t －a )．∵a >0，∴t ，h ′(t )，h (t )的变化情况如下表：当且仅当2－a 324<0，即a >236.∴a 的取值范围是(236，＋∞)．。

2-8函数与方程、函数模型及其应用基础巩固强化1.(2011·北京东城一模)已知函数f(x)＝(12)x－x13，在下列区间中，含有函数f(x)零点的是( )A．(0，13) B．(13，12)C．(12，1) D．(1,2)[答案] B[解析] f(0)＝1>0，f(13)＝(12)13－(13)13>0，f(12)＝(12)12－(12)13<0，∵f(13)·f(12)<0，且函数f(x)的图象为连续曲线，∴函数f(x)在(13，12)内有零点．[点评] 一个简单的零点存在性判断题涵盖了幂函数、指数函数的单调性与零点存在性定理，难度不大，但有一定的综合性，要多加强这种小题训练，做题不一定多，但却能将应掌握的知识都训练到．2．(文)(2011·杭州模拟)函数f(x)＝|x－2|－ln x在定义域内零点的个数为( ) A．0 B．1 C．2 D．3[答案] C[解析] 在同一坐标系内作出函数y＝|x－2|与y＝ln x的图象，∵ln e＝1，e<3，∴由图象可见两函数图象有两个交点，∴函数f(x)有两个零点．(理)(2011·陕西)函数f (x )＝x －cos x 在[0，＋∞)内( ) A ．没有零点B ．有且仅有一个零点C ．有且仅有两个零点D ．有无穷多个零点[答案] B[解析] 在同一直角坐标系中分别作出函数y ＝x 和y ＝cos x 的图象，如图，由于x >1时，y ＝x >1，y ＝cos x ≤1，所以两图象只有一个交点，即方程x －cos x ＝0在[0，＋∞)内只有一个根，所以f (x )＝x －cos x 在[0，＋∞)内只有一个零点，所以选B.3．(文)函数f (x )＝⎝⎛⎭⎫12x －sin x 在区间[0,2π]上的零点个数为( ) A ．1 B ．2 C ．3 D ．4 [答案] B[解析] 在同一坐标系中作出函数y ＝⎝⎛⎭⎫12x 与y ＝sin x 的图象，易知两函数图象在[0,2π]内有两个交点．(理)(2011·深圳一检)已知函数f (x )＝x ＋2x ，g (x )＝x ＋ln x ，h (x )＝x －x －1的零点分别为x 1，x 2，x 3，则x 1，x 2，x 3的大小关系是( )A ．x 1<x 2<x 3B ．x 2<x 1<x 3C ．x 1<x 3<x 2D ．x 3<x 2<x 1[答案] A[解析] 令f (x )＝x ＋2x ＝0，因为2x 恒大于零，所以要使得x ＋2x＝0，x 必须小于零，即x 1小于零；令g (x )＝x ＋ln x ＝0，要使得ln x 有意义，则x 必须大于零，又x ＋ln x ＝0，所以ln x <0，解得0<x <1，即0<x 2<1；令h (x )＝x －x －1＝0，得x ＝x ＋1>1，即x 3>1，从而可知x 1<x 2<x 3.4．(2012·河南六市模拟)若定义在R 上的函数y ＝f (x )满足f (x ＋1)＝－f (x )，且当x∈[－1,1]时，f (x )＝x 2，函数g (x )＝⎩⎪⎨⎪⎧log 3x －1 x >12xx ≤1，则函数h (x )＝f (x )－g (x )在区间[－5,5]内的零点的个数为( )A ．9B ．8C ．7D ．6 [答案] B[解析] ∵f (x ＋1)＝－f (x )，∴f (x ＋2)＝f (x )，又x ∈[－1，1]时，f (x )＝x 2，∴f (x )的图象如图所示，在同一坐标系中作出函数g (x )的图象，可见y ＝f (x )(－5≤x ≤5)与y ＝2x (x ≤1)有5个交点，y ＝f (x )(－5≤x ≤5)与y ＝log 3(x －1)(x >1)的图象有3个交点，∴共有8个交点．5．(2012·新疆维吾尔自治区检测)在以下区间中，函数f (x )＝x 3－4x 2－x ＋4不存在零点的区间是( )A ．[0,1]B ．[1,2]C ．[2,3]D ．[3,4][答案] C[解析] ∵f (0)＝4，f (1)＝0，f (3)＝－8<0，f (4)＝0，f (2)＝－6，由于在区间[0,1]，[1,2]，[3,4]内都存在零点，故选C.[点评] 注意，不能由f (2)＝－6<0，f (3)＝－8<0，做出判断f (x )在区间[2,3]内无零点．6.如图，A 、B 、C 、D 是四个采矿点，图中的直线和线段均表示公路，四边形ABQP 、BCRQ 、CDSR 近似于正方形，A 、B 、C 、D 四个采矿点的采矿量之比为6 2 3 4，且运矿费用与路程和采矿量的乘积成正比．现从P 、Q 、R 、S 中选一个中转站，要使中转费用最少，则应选( )A ．P 点B ．Q 点C ．R 点D ．S 点 [答案] B[解析] 设图中每个小正方形的边长均为1，A 、B 、C 、D 四个采矿点的采矿量分别为6a,2a,3a,4a (a >0)，设s i (i ＝1,2,3,4)表示运矿费用的总和，则只需比较中转站在不同位置时s i (i ＝1,2,3,4)的大小．如果选在P 点，s 1＝6a ＋2a ×2＋3a ×3＋4a ×4＝35a ，如果选在Q 点，s 2＝6a ×2＋2a ＋3a ×2＋4a ×3＝32a ，如果选在R 处，s 3＝6a ×3＋2a ×2＋3a ＋4a ×2＝33a ，如果选在S 处，s 4＝6a ×4＋2a ×3＋3a ×2＋4a ＝40a ，显然，中转站选在Q 点时，中转费用最少．7．(2012·江苏)已知函数f (x )＝x 2＋ax ＋b (a ，b ∈R )的值域为[0，＋∞)，若关于x 的不等式f (x )<c 的解集为(m ，m ＋6)，则实数c 的值为________．[答案] 9[解析] 本题考查二次函数的值域、一元二次不等式的解法等知识．∵f (x )＝x 2＋ax ＋b ＝(x ＋a2)2＋b －a 24的最小值为b －a 24，∴b －a 24＝0，即b ＝a 24，∴f (x )＝(x ＋a2)2.∴f (x )<c ，即x 2＋ax ＋b <c ，则(x ＋a2)2<c ，∴c >0且－a 2－c <x <－a2＋c ，∴(－a 2＋c )－(－a2－c )＝6，∴2c ＝6，∴c ＝9.8．有一批材料可以建成200m 长的围墙，如果用此批材料在一边靠墙的地方围成一块矩形场地，中间用同样材料隔成三个面积相等的矩形(如图所示)，则围成场地的最大面积为________(围墙的厚度不计)．[答案] 2500m 2[解析] 设所围场地的长为x ，则宽为200－x 4，其中0<x <200，场地的面积为x ×200－x 4≤14⎝⎛x ＋200－x 22＝2500m 2，等号当且仅当x ＝100时成立． 9．某农场，可以全部种植水果、蔬菜、稻米、甘蔗等农作物，且产品全部供应距农场d (km)(d <200km)的中心城市，其产销资料如表：当距离d 达到n (km)以上时，四种农作物中以全部种植稻米的经济效益最高．(经济效益＝市场销售价值－生产成本－运输成本)，则n 的值为________.[解析] 设单位面积全部种植水果、蔬菜、稻米、甘蔗的经济效益分别为y 1、y 2、y 3、y 4，则y 1＝50－0.6d ，y 2＝15－0.3d ，y 3＝40－0.4d ，y 4＝18－0.3d ，由⎩⎪⎨⎪⎧y 3≥y 1，y 3≥y 2，y 3≥y 4，d <200.⇒50≤d <200，故n ＝50.10．当前环境问题已成为问题关注的焦点，2009年哥本哈根世界气候大会召开后，为减少汽车尾气对城市空气的污染，某市决定对出租车实行使用液化气替代汽油的改装工程，原因是液化气燃烧后不产生二氧化硫、一氧化氮等有害气体，对大气无污染，或者说非常小．请根据以下数据：①当前汽油价格为2.8元/升，市内出租车耗油情况是一升汽油大约能跑12km ；②当前液化气价格为3元/千克，一千克液化气平均可跑15～16km ；③一辆出租车日平均行程为200km.(1)从经济角度衡量一下使用液化气和使用汽油哪一种更经济(即省钱)；(2)假设出租车改装液化气设备需花费5000元，请问多长时间省出的钱等于改装设备花费的钱．[解析] (1)设出租车行驶的时间为t 天，所耗费的汽油费为W 元，耗费的液化气费为P 元，由题意可知，W ＝200t 12×2.8＝140t3(t ≥0且t ∈N )， 200t 16×3≤P ≤200t15×3 (t ≥0且t ∈N )， 即37.5t ≤P ≤40t .又140t3>40t ，即W >P ， 所以使用液化气比使用汽油省钱． (2)①设37.5t ＋5000＝140t3，解得t ≈545.5， 又t ≥0，t ∈N ，∴t ＝546. ②设40t ＋5000＝140t3，解得t ＝750. 所以，若改装液化气设备，则当行驶天数t ∈[546,750]时，省出的钱等于改装设备的钱.能力拓展提升11.(文)(2012·天津理)函数f (x )＝2x＋x 3－2在区间(0,1)内的零点个数是( ) A ．0 B ．1 C ．2 D ．3 [答案] B[解析] 本小题考查函数的零点与用导数判断函数的单调性，考查分析问题、解决问题的能力．∵f (x )＝2x＋x 3－2,0<x <1，∴f ′(x )＝2x ln2＋3x 2>0在(0,1)上恒成立，∴f (x )在(0,1)上单调递增．又f (0)＝20＋0－2＝－1<0，f (1)＝2＋1－2＝1>0，f (0)f (1)<0，则f (x )在(0,1)内至少有一个零点，又函数y ＝f (x )在(0,1)上单调递增，则函数f (x )在(0,1)内有且仅有一个零点． [点评] 有时也可以把函数零点的个数转化成两函数图象的公共点个数． (理)(2011·舟山月考)函数f (x )＝⎩⎪⎨⎪⎧ln x ＋2x －6 x >0－x x ＋1 x ≤0的零点个数是( )A ．0B ．1C ．2D ．3 [答案] D[解析] 令－x (x ＋1)＝0得x ＝0或－1，满足x ≤0； 当x >0时，∵ln x 与2x －6都是增函数， ∴f (x )＝ln x ＋2x －6(x >0)为增函数， ∵f (1)＝－4<0，f (3)＝ln3>0，∴f (x )在(0，＋∞)上有且仅有一个零点， 故f (x )共有3个零点．12．某电视新产品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y 与投放市场的月数x 之间关系的是( )A ．y ＝100xB ．y ＝50x 2－50x ＋100 C ．y ＝50×2x D ．y ＝100log 2x ＋100[答案] C[解析] 观察前四个月的数据规律，(1,100)，(2,200)，(3,400)，(4,790)，接近(4,800)，可以发现这些数据变化规律符合指数型函数模型的增长规律，故选C.[点评] 也可以将x ＝1,2,3,4，依次代入四个选项中，通过对比差异大小来作判断，但计算量比较大．13．某流程图如图所示，现输入如下四个函数，则可以输出的函数是( )A ．f (x )＝|x |xB ．f (x )＝12x－1＋12C ．f (x )＝e x －e －xe x ＋e －xD ．f (x )＝lgsin x[答案] C[解析] 根据程序框图知输出的函数为奇函数，并且此函数存在零点．经验证：f (x )＝|x |x 不存在零点；f (x )＝12x －1＋12不存在零点；f (x )＝e x －e －x e x ＋e－x 的定义域为全体实数，且f (－x )＝e －x －e x e －x ＋e x ＝－f (x )，故此函数为奇函数，且令f (x )＝e x －e －xe x ＋e－x ＝0，得x ＝0，函数f (x )存在零点；f (x )＝lgsin x 不具有奇偶性．14．(文)(2011·山东济宁一模)已知a 是函数f (x )＝2x －log 12x 的零点，若0<x 0<a ，则f (x 0)的值满足( )A ．f (x 0)＝0B ．f (x 0)<0C ．f (x 0)>0D ．f (x 0)的符号不确定[答案] B [解析]分别作出y ＝2x 与y ＝log 12x 的图象如图，当0<x 0<a 时，y ＝2x 的图象在y ＝log 12x 图象的下方，所以，f (x 0)<0.(理)已知函数f (x )＝⎩⎪⎨⎪⎧2x－1 x ≤0f x －1＋1 x >0，把函数g (x )＝f (x )－x 的零点按从小到大的顺序排列成一个数列，则该数列的通项公式为( )A ．a n ＝n n －12n ∈N *)B ．a n ＝n (n －1)(n ∈N *)C ．a n ＝n －1(n ∈N *) D ．a n ＝2n －2(n ∈N *) [答案] C[解析] 当x ≤0时，f (x )＝2x －1；当0<x ≤1时，f (x )＝f (x －1)＋1＝2x －1－1＋1＝2x－1；当1<x ≤2时，f (x )＝f (x －1)＋1＝f (x －2)＋2＝2x －2－1＋2＝2x －2＋1；… ∴当x ≤0时，g (x )的零点为x ＝0；当0<x ≤1时，g (x )的零点为x ＝1；当1<x ≤2时，g (x )的零点为x ＝2；…当n －1<x ≤n (n ∈N *)时，g (x )的零点为n ， 故a 1＝0，a 2＝1，a 3＝2，…，a n ＝n －1.15．(文)某加工厂需定期购买原材料，已知每公斤原材料的价格为1.5元，每次购买原材料需支付运费600元．每公斤原材料每天的保管费用为0.03元，该厂每天需消耗原材料400kg ，每次购买的原材料当天即开始使用(即有400kg 不需要保管)．(1)设该厂每x 天购买一次原材料，试写出每次购买的原材料在x 天内总的保管费用y 1(元)关于x 的函数关系式；(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用y (元)最少，并求出这个最小值．[解析] (1)每次购买原材料后，当天用掉的400kg 原材料不需要保管，第二天用掉的400kg 原材料需保管1天，第三天用掉的400kg 原材料需保管2天，第四天用掉的400kg 原材料需保管3天，…，第x 天(也就是下次购买原材料的前一天)用掉最后的400kg 原材料需保管x －1天．∴每次购买的原材料在x 天内的保管费用为y 1＝400×0.03[1＋2＋3＋…＋(x －1)]＝6x 2－6x .(2)由(1)可知，购买一次原材料的总的费用为6x 2－6x ＋600＋1.5×400x ＝6x 2＋594x ＋600(元)，∴购买一次原材料平均每天支付的总费用为y ＝600x＋6x ＋594≥2600x·6x ＋594＝714.当且仅当600x＝6x ，即x ＝10时，取得等号．∴该厂10天购买一次原材料可以使平均每天支付的总费用最少，最少费用为714元． (理)(2011·日照模拟)张林在李明的农场附近建了一个小型工厂，由于工厂生产须占用农场的部分资源，因此李明每年向张林索赔以弥补经济损失并获得一定的净收入．工厂在不赔付农场的情况下，工厂的年利润x (元)与年产量t (t)满足函数关系x ＝2000t ，若工厂每生产一吨产品必须赔付农场s 元(以下称s 为赔付价格)．(1)将工厂的年利润w (元)表示为年产量t (t)的函数，并求出工厂获得最大利润的年产量；(2)若农场每年受工厂生产影响的经济损失金额y ＝0.002t 2(元)，在工厂按照获得最大利润的产量进行生产的前提下，农场要在索赔中获得最大净收入，应向张林的工厂要求赔付价格s 是多少？[解析] (1)工厂的实际年利润为：w ＝2000t －st (t ≥0)． w ＝2000t －st ＝－s (t －1000s)2＋10002s，当t ＝(1000s)2时，w 取得最大值．所以工厂取得最大年利润的年产量t ＝(1000s)2(t)．(2)设农场净收入为v 元， 则v ＝st －0.002t 2.将t ＝(1000s )2代入上式， 得v ＝10002s－2×10003s 4.又v ′＝－10002s 2＋8×10003s5＝100028000－s 3s 5，令v ′＝0，得s ＝20. 当0<s <20时，v ′>0； 当s >20时，v ′<0.所以当s ＝20时，v 取得最大值．因此李明向张林要求赔付价格s 为20元/吨时，获得最大净收入． *16.已知二次函数f (x )＝ax 2＋bx ＋c .(1)若f (－1)＝0，试判断函数f (x )的零点个数；(2)若对x 1、x 2∈R ，且x 1<x 2，f (x 1)≠f (x 2)，证明方程f (x )＝12[f (x 1)＋f (x 2)]必有一个实数根属于(x 1，x 2)；(3)是否存在a 、b 、c ∈R ，使f (x )同时满足以下条件：①当x ＝－1时，函数f (x )有最小值0；②对任意实数x ，都有0≤f (x )－x ≤12(x －1)2.若存在，求出a 、b 、c 的值；若不存在，请说明理由．[解析] (1)因为f (－1)＝0， 所以a －b ＋c ＝0，故b ＝a ＋c .因为Δ＝b 2－4ac ＝(a ＋c )2－4ac ＝(a －c )2. 当a ＝c 时，Δ＝0，函数f (x )有一个零点； 当a ≠c 时，Δ>0，函数f (x )有两个零点． (2)令g (x )＝f (x )－12[f (x 1)＋f (x 2)]，则g (x 1)＝f (x 1)－12[f (x 1)＋f (x 2)]＝f x 1－f x 22，g (x 2)＝f (x 2)－12[f (x 1)＋f (x 2)]＝f x 2－f x 12，因为g (x 1)·g (x 2)＝－14[f (x 1)－f (x 2)]2<0(f (x 1)≠f (x 2))，所以g (x )＝0在(x 1，x 2)内必有一个实根．即方程f (x )＝12[f (x 1)＋f (x 2)]必有一个实数根属于(x 1，x 2)．(3)假设a 、b 、c 存在，由①得－b 2a ＝－1，4ac －b 24a＝0，即b ＝2a ，b 2＝4ac ，所以4a 2＝4ac ，故a ＝c .由②知对任意实数x ，都有0≤f (x )－x ≤12(x －1)2.令x ＝1，得0≤f (1)－1≤0，所以f (1)－1＝0，即a ＋b ＋c ＝1.由⎩⎪⎨⎪⎧a ＋b ＋c ＝1，b ＝2a ，a ＝c ，解得a ＝c ＝14b ＝12.当a ＝c ＝14，b ＝12时，f (x )＝14x 2＋12x ＋14＝14(x ＋1)2，其顶点为(－1,0)满足条件①，又f (x )－x ＝14(x －1)2，所以对任意x ∈R ，都有0≤f (x )－x ≤12(x －1)2，满足条件②.所以存在a 、b 、c ∈R ，使f (x )同时满足条件①②.1．(2012·昆明一中检测)已知函数f (x )＝|lg(x －1)|，若a ≠b ，且f (a )＝f (b )，则a ＋b 的取值范围是( )A ．[4，＋∞)B ．(4，＋∞)C ．[2，＋∞)D ．(2，＋∞)[答案] B[解析] 解法1：不妨设a <b ，∵f (x )＝|lg(x －1)|，f (a )＝f (b )，∴1<a ≤2，b >2，∴f (a )＝－lg(a －1)，f (b )＝lg(b －1)，∴－lg(a －1)＝lg(b －1)，∴(a －1)(b －1)＝1，∴a ＋b ＝(a －1)＋(b －1)＋2>2a －1b －1＋2＝4.解法2：结合f (x )的图象得－lg(b －1)＝lg(a －1)，得lg(a －1)＋lg(b －1)＝0，所以(a －1)(b －1)＝1，化简得，a ＋b ＝ab ，即1a ＋1b 1，所以a ＋b ＝(1a ＋1b )(a ＋b )＝2＋b a ＋ab＋2＝4，当a ＝b 时取“＝”，而由已知a ≠b ，故选B.2．(2011·温州十校模拟)已知函数f (x )＝2mx 2－2(4－m )x ＋1，g (x )＝mx ，若对于任一实数x ，f (x )与g (x )的值至少有一个为正数，则实数m 的取值范围是( )A ．(0,2)B ．(0,8)C ．(2,8)D ．(－∞，0)[答案] B[解析] 当m ≤0时，显然不合题意；当m >0时，f (0)＝1>0，①若对称轴4－m2m ≥0即0<m ≤4，结论显然成立；②若对称轴4－m2m <0，即m >4，只要Δ＝4(4－m )2－8m ＝4(m －8)(m －2)<0即可，即4<m <8.综上0<m <8，选B.3．(2011·江南十校联考)定义域为D 的函数f (x )同时满足条件：①常数a ，b 满足a <b ，区间[a ，b ]⊆D ，②使f (x )在[a ，b ]上的值域为[ka ，kb ](k ∈N *)，那么我们把f (x )叫做[a ，b ]上的“k 级矩形”函数．函数f (x )＝x 3是[a ，b ]上的“1级矩形”函数，则满足条件的常数对(a ，b )共有( )A ．1对B ．2对C ．3对D ．4对[答案] C[分析] 由“k 级矩形”函数的定义可知，f (x )＝x 3的定义区间为[a ，b ]时，值域为[a ，b ]，可考虑应用f (x )的单调性解决．[解析] ∵f (x )＝x 3在[a ，b ]上单调递增， ∴f (x )的值域为[a 3，b 3]．又∵f (x )＝x 3在[a ，b ]上为“1级矩形”函数，∴⎩⎪⎨⎪⎧a 3＝a b 3＝b ，解得⎩⎪⎨⎪⎧a ＝－1b ＝0或⎩⎪⎨⎪⎧a ＝0b ＝1或⎩⎪⎨⎪⎧a ＝－1b ＝1，故满足条件的常数对共有3对．[点评] 自定义题是近年来备受命题者青睐的题型，它能较好地考查学生对新知识的阅读理解能力，而这恰是学生后续学习必须具备的能力，解决这类问题的关键是先仔细审题，弄清“定义”的含义，把“定义”翻译为我们已掌握的数学知识．然后加以解决．4．(2012·龙岩质检)若偶函数f (x )满足f (x －1)＝f (x ＋1)，且在x ∈[0,1]时，f (x )＝x 2，则关于x 的方程f (x )＝(110)x 在[0，103上根的个数是( )A ．1B ．2C ．3D ．4 [答案] C[解析] 由题意知f (x )是周期为2的偶函数，故当x ∈[－1,1]时，f (x )＝x 2，画出f (x )的图象，结合y ＝(110)x 的图象可知，方程f (x )＝(110)x 在x ∈[0，103时有3个根．[点评] 要注意在x ∈(3，103]时方程无解． 5．已知函数f (x )＝a x－x －a (a >0，a ≠1)，那么函数f (x )的零点个数是( ) A ．0个 B ．1个 C ．2个 D ．至少1个[答案] D[解析] 在同一坐标系中作出函数y ＝a x 与y ＝x ＋a 的图象，a >1时，如图(1)，0<a <1时，如图(2)，故选D.[点评] 解决这类问题的有效方法是数形结合法．6．设a ∈{1,2,3,4}，b ∈{2,4,8,12}，则函数f (x )＝x 3＋ax －b 在区间[1,2]上有零点的概率为( )A.12B.58C.1116 D.34[答案] C[解析] 因为f (x )＝x 3＋ax －b ，所以f ′(x )＝3x 2＋a .因为a ∈{1,2,3,4}，因此f ′(x )>0，所以函数f (x )在区间[1,2]上为增函数．若存在零点，则⎩⎪⎨⎪⎧f 1＝1＋a －b ≤0，f 2＝8＋2a －b ≥0，解得a ＋1≤b ≤8＋2a .因此能使函数在区间[1,2]上有零点的有：a ＝1,2≤b ≤10，故b ＝2，b ＝4，b ＝8.a ＝2,3≤b ≤12，故b ＝4，b ＝8，b ＝12.a ＝3,4≤b ≤14，故b ＝4，b ＝8，b ＝12.a ＝4,5≤b ≤16，故b ＝8，b ＝12.根据古典概型可得有零点的概率为11167．(2012·河南新乡、平顶山、许昌调研)设函数f (x )＝⎩⎪⎨⎪⎧11－x ，x ∈－∞，0]，x 3－3x ＋1，x ∈0，＋∞，若方程f (x )－m ＝0有且仅有两个实数根，则实数m 的取值范围是( )A ．－1<m ≤1B ．－1<m <0或m ＝1C ．－1<m ≤0或m ＝1D ．－1<m ≤1[答案] C[解析] ∵f (x )＝⎩⎪⎨⎪⎧11－xx ∈－∞，0]，x 3－3x ＋1 x ∈0，＋∞，∴当x ≤0时，f (x )＝11－x单调递增，且0<f (x )≤1，又x >0时，f (x )＝x 3－3x ＋1，∴f ′(x )＝3x 2－3＝3(x ＋1)(x －1)，∴0<x <1时，f ′(x )<0，f (x )单调递减，x ≥1时，f ′(x )>0，f (x )单调递增，∴f (x )在x ＝1处取得极小值f (1)＝－1，∴当m ＝1时，直线y ＝m 与函数f (x )的图象有两个交点，当－1<m ≤0时，直线y ＝m 与函数y ＝f (x )的图象有两个交点，故选C.8．(2011·龙岩模拟)如图，有一直角墙角，两边的长度足够长，在P 处有一棵树与两墙的距离分别是a m(0<a ≤12)、4m ，不考虑树的粗细，现在想用16m 长的篱笆，借助墙角围成一个矩形的花园ABCD .设此矩形花园的面积为S m 2，S 的最大值为f (a )，若将这棵树围在花园内，则函数u ＝f (a )的图象大致是( )[答案] C[解析] 设BC ＝x ，则DC ＝16－x ，由⎩⎪⎨⎪⎧x ≥a ，16－x ≥4，得a ≤x ≤12，矩形面积S ＝x (16－x ) (a ≤x ≤12)，显然当a ≤8时，矩形面积最大值u ＝64，为常数，当a >8时，在x ＝a 时，矩形面积取最大值u ＝a (16－a )，在[a,12]上为减函数，故选C.9．(2012·湖南文)设定义在R 上的函数f (x )是最小正周期为2π的偶函数，f ′(x )是f (x )的导函数．当x ∈[0，π]时，0<f (x )<1；当x ∈(0，π)且x ≠π2时，(x －π2)f ′(x )>0.则函数y ＝f (x )－sin x 在[－2π，2π]上的零点个数为( )A ．2B ．4C ．5D ．8 [答案] B[解析] 本题考查函数奇偶性，利用导数研究函数单调性，图象交点个数等． 由x ∈(0，π)，x ≠π2时，(x －π2)f ′(x )>0知， 当x ∈(0，π2)时，f ′(x )<0，f (x )单调递减． 当x ∈(π2，π)时，f ′(x )>0，f (x )单调递增．当x∈(－π，0)时，f(x)∈(0,1)，且f(x)是最小正周期为2π的偶函数，则画出函数y＝f(x)示意图如下：而y＝f(x)－sin x的零点个数，即f(x)＝sin x的根，即y＝sin x与y＝f(x)图象交点个数．由图象知有4个交点．10．已知y＝x(x－1)(x＋1)的图象如图所示，今考虑f(x)＝x(x－1)(x＋1)＋0.01，则方程f(x)＝0.①有三个实根②当x<－1时，恰有一实根③当－1<x<0时，恰有一实根④当0<x<1时，恰有一实根⑤当x>1时，恰有一实根正确的有________．[答案] ①②[解析] ∵f(－2)＝－5.99<0，f(－1)＝0.01>0，即f(－2)·f(－1)<0，∴在(－2，－1)内有一个实根，结合图象知，方程在(－∞，－1)上恰有一个实根．所以②正确．又∵f (0)＝0.01>0，结合图象知f (x )＝0在(－1,0)上没有实数根，所以③不正确． 又∵f (0.5)＝0.5×(－0.5)×1.5＋0.01＝－0.365<0，f (1)>0.所以f (x )＝0在(0.5,1)上必有一实根，在(0，0.5)上也有一个实根．∴f (x )＝0在(0,1)上有两个实根．所以④不正确．由f (1)>0结合图象知，f (x )＝0在(1，＋∞)上没有实根，∴⑤不正确，由此可知①正确．11．学校请了30名木工，要制作200把椅子和100张课桌．已知制作一张课桌与制作一把椅子的工时数之比为10 7，问30名工人应当如何分组(一组制课桌，另一组制椅子)，能最快完成全部任务？[分析] 弄清题意，建立完成全部任务的时间与制课桌或椅子的人数的函数关系，转化为求函数的最值问题．[解析] 设x 名工人制课桌，(30－x )名工人制椅子，一个工人在一个单位时间里可制7张课桌或10把椅子，所以制作100张课桌所需时间为P (x )＝1007x制作200把椅子所需时间为Q (x )＝2001030－x ＝2030－x， 完成全部任务所需的时间为P (x )与Q (x )的最大值F (x )．为求得F (x )的最小值，需满足P (x )＝Q (x )，即1007x ＝2030－x，解得x ＝12.5， 考虑到x 表示人数，所以x ∈N *.∵P (12)>P (13)，Q (12)<Q (13)，故考查P (12)与Q (13)．P (12)＝10084Q (13)＝2017≈1.18. 即F (12)>F (13)．所以用13名工人制作课桌，17名工人制作椅子完成任务最快．。

2-2函数的单调性与最值基础巩固强化1.(文)(2012²陕西文)集合M ＝{x |lg x >0}，N ＝{x |x 2≤4}，则M ∩N ＝( ) A ．(1,2) B ．[1,2) C ．(1,2] D ．[1,2][答案] C[解析] 本题考查对数不等式、一元二次不等式的解法及集合的交集运算．M ＝{x |x >1}，N ＝{x |－2≤x ≤2}，所以M ∩N ＝{x |1<x ≤2}＝(1,2]．[点评] 对于对数方程或对数不等式的求解一定不要忽略要使函数有意义．应有真数>0.(理)(2011²湖北理，2)已知U ＝{y |y ＝log 2x ，x >1}，P ＝{y |y ＝1x，x >2}，则∁U P ＝( )A ．[12，＋∞)B ．(0，12)C ．(0，＋∞)D ．(－∞，0]∪[12，＋∞)[答案] A[解析] ∵U ＝{y |y ＝log 2x ，x >1}＝(0，＋∞)，P ＝{y |y ＝1x ，x >2}＝(0，12)，∴∁U P ＝[12，＋∞)．2．(文)(2011²大连模拟)下列函数在(0,1)上是减函数的是( ) A ．y ＝log 0.5(1－x ) B ．y ＝x 0.5C ．y ＝0.51－xD ．y ＝12(1－x 2)[答案] D[解析] ∵u ＝1－x 在(0,1)上为减函数，且u >0，∴y ＝log 0.5(1－x )为增函数，y ＝0.51－x为增函数；又0.5>0，∴幂函数y ＝x 0.5在(0,1)上为增函数；二次函数y ＝12(1－x 2)开口向下，对称轴x ＝0，故在(0,1)上为减函数．(理)(2011²广州模拟)下列函数f (x )中，满足“对任意x 1，x 2∈(－∞，0)，当x 1<x 2时，都有f (x 1)<f (x 2)”的函数是( )A ．f (x )＝－x ＋1B ．f (x )＝x 2－1 C ．f (x )＝2xD ．f (x )＝ln(－x )[答案] C[解析] f (x )＝－x ＋1为减函数，f (x )＝x 2－1在(－∞，1)上为减函数；f (x )＝2x为增函数，f (x )＝ln(－x )为减函数，由条件知f (x )在(－∞，0)上为增函数，故排除A 、B 、D 选C.3．(2011²上海文)下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的函数是( )A ．y ＝x －2B ．y ＝x －1C ．y ＝x 2D ．y ＝x 13[答案] A[解析] y ＝x －1是奇函数，y ＝x 2在(0，＋∞)上单调递增，y ＝x 13 是奇函数． 4．(文)(2011²江苏南通中学月考、北京东城示范校练习)设a ＝log 132，b ＝log 1213，c＝⎝ ⎛⎭⎪⎫120.3，则( ) A ．a ＜b ＜c B ．a ＜c ＜b C ．b ＜c ＜a D ．b ＜a ＜c[答案] B[解析] ∵log 132<log 131＝0，∴a <0；∵log 1213>log 1212＝1，∴b >1；∵⎝ ⎛⎭⎪⎫120.3<1，∴0<c <1，故选B. (理)(2011²天津理)已知a ＝5log 23.4，b ＝5log 43.6，c ＝(15)log 20.3，则( )A ．a >b >cB ．b >a >cC ．a >c >bD ．c >a >b[答案] C[解析] a ＝5log 23.4，b ＝5log 43.6＝5log 2 3.6，c ＝(15)log 20.3＝5log2103，由对数函数的单调性有log 23.4>log2103>log 2 3.6，由指数函数单调性，有a >c >b ，故选C.5．(2011²北京模拟)设函数f (x )＝⎩⎪⎨⎪⎧23x －1 x ≥0，1x x <0.若f (a )>a ，则实数a 的取值范围是( )A ．(－∞，－3)B ．(－∞，－1)C ．(1，＋∞)D ．(0,1)[答案] B[解析] f (a )>a 化为⎩⎪⎨⎪⎧ a ≥0，23a －1>a ，或⎩⎪⎨⎪⎧a <0，1a>a .∴a <－1.6．(文)(2011²青岛模拟)已知函数f (x )＝a x＋log a x (a >0且a ≠1)在[1,2]上的最大值与最小值之和为log a 2＋6，则a 的值为( )A.12 B.14 C ．2 D ．4[答案] C[解析] f (x )在[1,2]上是单调函数，由题意知，a ＋a 2＋log a 2＝log a 2＋6，∴a 2＋a －6＝0，∵a >0，∴a ＝2.(理)(2012²新课标全国文)当0<x ≤12时，4x<log a x ，则a 的取值范围是( )A ．(0，22) B ．(22，1) C ．(1，2) D ．(2，2)[答案] B[解析] ∵0<x ≤12时，log a x >4x >0，∴0<a <1，排除C 、D ；当x ＝12时，log a 12>412＝2＝log a a 2，∴⎩⎪⎨⎪⎧a >1，a 2<12，或⎩⎪⎨⎪⎧0<a <1，a 2>12，∴a >22，排除A ，选B. 7．(文)如果函数f (x )＝ax 2＋2x －3在区间(－∞，4)上单调递增，则实数a 的取值范围是________．[答案] [－14，0][解析] (1)当a ＝0时，f (x )＝2x －3，在定义域R 上单调递增，故在(－∞，4)上单调递增；(2)当a ≠0时，二次函数f (x )的对称轴为直线x ＝－1a，因为f (x )在(－∞，4)上单调递增，所以a <0，且－1a ≥4，解得－14≤a <0.综上所述－14≤a ≤0.(理)若函数f (x )＝－x 2＋2ax 与g (x )＝ax ＋1在区间[1,2]上都是减函数，则a 的取值范围是________．[答案] (0,1][解析] 由f (x )＝－x 2＋2ax 得函数对称轴为x ＝a ， 又在区间[1,2]上是减函数，所以a ≤1， 又g (x )＝ax ＋1在[1,2]上减函数，所以a >0，综上a 的取值范围为(0,1]．8．f (x )＝x ln x 的单调递减区间是________．[答案] ⎝⎛⎭⎪⎫0，1e[解析] f ′(x )＝ln x ＋1，令f ′(x )<0得x <1e，∴0<x <1e，∴f (x )在⎝ ⎛⎭⎪⎫0，1e 上单调递减．9．(文)函数f (x )＝log 5(2x －1)的单调增区间是________． [答案] (12，＋∞)[解析] ∵2x －1>0，∴x >12.所求单调增区间为(12，＋∞)．(理)(2011²德州月考)已知函数f (x )＝⎩⎪⎨⎪⎧12x x ≤0，log 2x ＋2 x ＞0.若f (x 0)≥2，则x 0的取值范围是____________．[答案] (－∞，－1]∪[2，＋∞)．[解析] 当x 0≤0时，f (x 0)≥2化为(12)x 0≥2，即：(12)x 0≥(12)－1，∴x 0≤－1，当x 0＞0时，f (x 0)≥2化为log 2(x 0＋2)≥2， 即log 2(x 0＋2)≥log 24，∴x 0＋2≥4，∴x 0≥2， ∴x 0的取值范围是(－∞，－1]∪[2，＋∞)． 10．(文)已知f (x )＝xx －a(x ≠a )．(1)若a ＝－2，试证f (x )在(－∞，－2)内单调递增； (2)若a >0且f (x )在(1，＋∞)内单调递减，求a 的取值范围． [解析] (1)证明：设x 1<x 2<－2， 则f (x 1)－f (x 2)＝x 1x 1＋2－x 2x 2＋2＝2x 1－x 2x 1＋2x 2＋2. ∵(x 1＋2)(x 2＋2)>0，x 1－x 2<0，∴f (x 1)<f (x 2)，∴f (x )在(－∞，－2)内单调递增． (2)解：设1<x 1<x 2，则f (x 1)－f (x 2)＝x 1x 1－a －x 2x 2－a ＝a x 2－x 1x 1－a x 2－a .∵a >0，x 2－x 1>0，∴要使f (x 1)－f (x 2)>0，只需(x 1－a )(x 2－a )>0恒成立，∴a ≤1. 综上所述知0<a ≤1.[点评] 第(2)问中，由f (x )单调递减知x 1<x 2时，f (x 1)－f (x 2)>0恒成立，从而(x 1－a )(x 2－a )>0恒成立，由于a >0，x 1>1，x 2>1，故只有当0<a ≤1时才满足．(理)(2013²唐山一中第一学期第二次月考)已知函数f (x )＝a ln x －ax －3(a ∈R )． (1)若a ＝－1，求函数f (x )的单调区间并比较f (x )与f (1)的大小关系；(2)若函数y ＝f (x )的图象在点(2，f (2))处的切线的倾斜角为45°，对于任意的t ∈[1,2]，函数g (x )＝x 3＋x 2[f ′(x )＋m2]在区间(t,3)上总不是单调函数，求m 的取值范围；(3)求证：ln22³ln33³ln44³…³ln n n <1n (n ≥2，n ∈N *)．[解析] (1)当a ＝－1时，f (x )＝－ln x ＋x －3，f ′(x )＝x －1x(x >0)， 由f ′(x )>0得x >1；由f ′(x )<0得0<x <1，所以，f (x )的单调增区间为[1，＋∞)，减区间为(0,1]， 可知f (x )min ＝f (1)，所以f (x )≥f (1)． (2)∵f ′(x )＝a 1－x x(x >0)，tan45°＝1， ∴f ′(2)＝－a2＝1，得a ＝－2，∴f (x )＝－2ln x ＋2x －3，∴g (x )＝x 3＋(m2＋2)x 2－2x ，∴g ′(x )＝3x 2＋(m ＋4)x －2.∵g (x )在区间(t,3)上总不是单调函数，且g ′(0)＝－2，∴⎩⎪⎨⎪⎧g ′t <0，g ′3>0.由题意知：对于任意的t ∈[1,2]，g ′(t )<0恒成立，所以，⎩⎪⎨⎪⎧g ′1<0，g ′2<0，g ′3>0.∴－373<m <－9.(3)证明如下：由(1)可知，当x ∈(1，＋∞)时f (x )>f (1)，即－ln x ＋x －1>0， ∴0<ln x <x －1对一切x ∈(1，＋∞)成立． ∵n ≥2，n ∈N *，则有0<ln n <n －1，∴0<ln n n <n －1n，∴ln22²ln33²ln44²…²ln n n <12²23²34²…²n －1n ＝1n(n ≥2，n ∈N *). 能力拓展提升11.(2011²山东聊城一中期末)设函数f (x )定义在实数集上，它的图象关于直线x ＝1对称，且当x ≥1时，f (x )＝3x－1，则有( )A ．f ⎝ ⎛⎭⎪⎫13<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫23B ．f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫13C ．f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫13<f ⎝ ⎛⎭⎪⎫32D ．f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫13 [答案] B[解析] ∵f (x )的图象关于直线x ＝1对称，x ≥1时，f (x )＝3x－1为增函数，故当x <1时，f (x )为减函数，且f ⎝ ⎛⎭⎪⎫32＝f ⎝ ⎛⎭⎪⎫1＋12＝f ⎝ ⎛⎭⎪⎫1－12＝f ⎝ ⎛⎭⎪⎫12，∵13<12<23，∴f ⎝ ⎛⎭⎪⎫13>f ⎝ ⎛⎭⎪⎫12>f ⎝ ⎛⎭⎪⎫23，即f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫13，故选B.12．(2011²北京)根据统计，一名工人组装第x 件某产品所用的时间(单位：min)为f (x )＝⎩⎪⎨⎪⎧c x ，x <A ，c A ，x ≥A .(A ，c 为常数)．已知工人组装第4件产品用时30min ，组装第A 件产品用时15min ，那么c 和A 的值分别是( )A ．75,25B ．75,16C ．60,25D ．60,16[答案] D[解析] 当A >4时，⎩⎪⎨⎪⎧f 4＝c2＝30，f A ＝cA ＝15，解得⎩⎪⎨⎪⎧c ＝60，A ＝16；当A ≤4时，⎩⎪⎨⎪⎧f 4＝cA＝30，f A ＝cA＝15，无解．13．(文)(2011²抚顺模拟)已知f (x )＝⎩⎪⎨⎪⎧a x x >1，4－a2x ＋2 x ≤1，是R 上的单调递增函数，则实数a 的取值范围为( )A ．(1，＋∞)B ．[4,8)C ．(4,8)D ．(1,8)[答案] B[解析] 由y ＝a x(x >1)单调增知a >1；由y ＝(4－a 2)x ＋2(x ≤1)单调增知，4－a2>0，∴a <8；又f (x )在R 上单调增，∴a ≥(4－a2)＋2，∴a ≥4，综上知，4≤a <8.[点评] 可用筛选法求解，a ＝2时，有f (1)＝5>4＝f (2)，排除A 、D.a ＝4时，f (x )＝⎩⎪⎨⎪⎧4xx >1，2x ＋2 x ≤1，在R 上单调递增，排除C ，故选B.(理)(2011²北京学普教育中心)若函数f (x )＝2x 2－ln x 在其定义域内的一个子区间(k －1，k ＋1)内不是．．单调函数，则实数k 的取值范围是( )A ．[1，＋∞)B ．[1，32)C ．[1,2)D ．[32，2)[答案] B[解析] 因为f (x )定义域为(0，＋∞)，f ′(x )＝4x －1x ，由f ′(x )＝0，得x ＝12.据题意，⎩⎪⎨⎪⎧k －1<12<k ＋1，k －1≥0，解得1≤k <32，选B.14．(2011²天津四校联考)已知函数f (x )＝x 2＋ax －1在区间[0,3]上有最小值－2，则实数a 的值为________．[答案] －2[解析] 当－a2≤0，即a ≥0时，函数f (x )在[0,3]上为增函数，此时，f (x )min ＝f (0)＝－1，不符合题意，舍去； 当－a2≥3，即a ≤－6时，函数f (x )在[0,3]上为减函数，此时，f (x )min ＝f (3)＝－2，可得a ＝－103，这与a ≤－6矛盾；当0<－a 2<3，即－6<a <0时，f (x )min ＝f (－a2)＝－2，可解得a ＝－2，符合题意．15．(文)设函数f (x )＝ax 2＋bx ＋c (a ，b ，c 为实数，且a ≠0)，F (x )＝⎩⎪⎨⎪⎧f x x >0，－f x x <0.(1)若f (－1)＝0，曲线y ＝f (x )通过点(0,2a ＋3)，且在点(－1，f (－1))处的切线垂直于y 轴，求F (x )的表达式；(2)在(1)的条件下，当x ∈[－1,1]时，g (x )＝kx －f (x )是单调函数，求实数k 的取值范围；(3)设mn <0，m ＋n >0，a >0，且f (x )为偶函数，证明F (m )＋F (n )>0. [解析] (1)因为f (x )＝ax 2＋bx ＋c ，所以f ′(x )＝2ax ＋b .又曲线y ＝f (x )在点(－1，f (－1))处的切线垂直于y 轴，故f ′(－1)＝0， 即－2a ＋b ＝0，因此b ＝2a .① 因为f (－1)＝0，所以b ＝a ＋c .② 又因为曲线y ＝f (x )通过点(0,2a ＋3)， 所以c ＝2a ＋3.③解由①，②，③组成的方程组得，a ＝－3，b ＝－6，c ＝－3.从而f (x )＝－3x 2－6x －3.所以F (x )＝⎩⎪⎨⎪⎧－3x ＋12x >0，3x ＋12x <0.(2)由(1)知f (x )＝－3x 2－6x －3， 所以g (x )＝kx －f (x )＝3x 2＋(k ＋6)x ＋3. 由g (x )在[－1,1]上是单调函数知： －k ＋66≤－1或－k ＋66≥1，得k ≤－12或k ≥0.(3)因为f (x )是偶函数，可知b ＝0. 因此f (x )＝ax 2＋c .又因为mn <0，m ＋n >0，可知m ，n 异号． 若m >0，则n <0.则F (m )＋F (n )＝f (m )－f (n )＝am 2＋c －an 2－c ＝a (m ＋n )(m －n )>0. 若m <0，则n >0. 同理可得F (m )＋F (n )>0. 综上可知F (m )＋F (n )>0.(理)已知f (x )＝ax －ln x ，x ∈(0，e ]，a ∈R . (1)若a ＝1，求f (x )的极小值；(2)是否存在实数a ，使f (x )的最小值为3.[解析] (1)∵f (x )＝x －ln x ，f ′(x )＝1－1x ＝x －1x，∴当0<x <1时，f ′(x )<0，此时f (x )单调递减； 当1<x <e 时，f ′(x )>0，此时f (x )单调递增． ∴f (x )的极小值为f (1)＝1.(2)假设存在实数a ，使f (x )＝ax －ln x ，x ∈[0，e ]有最小值3，f ′(x )＝a －1x ＝ax －1x，①当a ≤0时，f (x )在(0，e ]上单调递增，f (x )min ＝f (e )＝ae －1＝3，a ＝4e(舍去)，所以，此时f (x )最小值不为3；②当0<1a <e 时，f (x )在(0，1a)上单调递减，在⎝ ⎛⎦⎥⎤1a ，e 上单调递增，f (x )min ＝f ⎝ ⎛⎭⎪⎫1a ＝1＋ln a＝3，a ＝e 2，满足条件；③当1a ≥e 时，f (x )在(0，e ]上单调递减，f (x )min ＝f (e )＝ae －1＝3，a ＝4e(舍去)，所以，此时f (x )最小值不为3.综上，存在实数a ＝e 2，使得当x ∈(0，e ]时，f (x )有最小值为3. *16.(2011²湖南)如图所示，长方体物体E 在雨中沿面P (面积为S )的垂直方向作匀速移动，速度为v (v >0)，雨速沿E 移动方向的分速度为c (c ∈R )．E 移动时单位时间．．．．内的淋雨量包括两部分：①P 或P 的平行面(只有一个面淋雨)的淋雨量，假设其值与|v －c |³S 成正比，比例系数为110；②其他面的淋雨量之和，其值为12，记y 为E 移动过程中的总淋雨量，当移动距离d ＝100，面积S ＝32时，(1)写出y 的表达式；(2)设0<v ≤10,0<c ≤5，试根据c 的不同取值范围，确定移动速度v ，使总淋雨量y 最少．[解析] (1)由题意知，E 移动时单位时间内的淋雨量为320|v －c |＋12，故y ＝100v⎝⎛⎭⎪⎫320|v －c |＋12＝5v (3|v －c |＋10)．(2)由(1)知，当0<v ≤c 时，y ＝5v (3c －3v ＋10)＝53c ＋10v －15；当c <v ≤10时，y ＝5v(3v －3c ＋10)＝510－3c v＋15.故y ＝⎩⎪⎨⎪⎧53c ＋10v－15，0<v ≤c ，510－3c v＋15，c <v ≤10.①当0<c ≤103时，y 是关于v 的减函数．故当v ＝10时，y min ＝20－3c2.②当103<c ≤5时，在(0，c ]上，y 是关于v 的减函数；在(c,10]上，y 是关于v 的增函数，故当v ＝c 时，y min ＝50c.1．(2011²上海理，16)下列函数中，既是偶函数，又是在区间(0，＋∞)上单调递减的函数是( )A ．y ＝ln 1|x |B ．y ＝x 3C ．y ＝2|x |D ．y ＝cos x[答案] A[解析] 排除法：B 、C 在(0，＋∞)上单调递增，D 在(0，＋∞)上不单调，故选A. 2．函数f (x )＝x －3x ＋a －2在(－1，＋∞)上单调递增，则a 的取值范围是( )A ．(－∞，1)B ．(1，＋∞)C ．(－∞，3)D ．(3，＋∞)[答案] D[解析] f (x )在(－a ＋2，＋∞)上是增函数，由条件知－a ＋2<－1，且－a －1<0，∴a >3. 3．若f (x )＝x 3－6ax 的单调递减区间是(－2,2)，则a 的取值范围是( ) A ．(－∞，0] B ．[－2,2] C ．{2} D ．[2，＋∞)[答案] C[解析] f ′(x )＝3x 2－6a ，若a ≤0，则f ′(x )≥0，∴f (x )单调增，排除A ；若a >0，则由f ′(x )＝0得x ＝±2a ，当x <－2a 和x >2a 时，f ′(x )>0，f (x )单调增，当－2a <x <2a 时，f (x )单调减，∴f (x )的单调减区间为(－2a ，2a )，从而2a ＝2， ∴a ＝2.[点评] f (x )的单调递减区间是(－2,2)和f (x )在(－2，2)上单调递减是不同的，应加以区分．4．函数f (x )＝ln(x ＋1)－mx 在区间(0,1)上恒为增函数，则实数m 的取值范围是( )A ．(－∞，1)B ．(－∞，1]C ．(－∞，12]D ．(－∞，12)[答案] C[解析] ∵f (x )＝ln(x ＋1)－mx 在区间(0,1)上恒为增函数， ∴f (x )＝ln(x ＋1)－mx 在区间[0,1]上恒为增函数， ∴f ′(x )＝1x ＋1－m ≥0在[0,1]上恒成立， ∴m ≤(1x ＋1)min ＝12. 5．定义在R 上的偶函数f (x )在[0，＋∞)上是增函数，若f (13)＝0，则适合不等式f (log127x )>0的x 的取值范围是( ) A ．(3，＋∞) B ．(0，13)C ．(0，＋∞)D ．(0，13)∪(3，＋∞)[答案] D[解析] ∵定义在R 上的偶函数f (x )在[0，＋∞)上是增函数，且f (13)＝0，则由f (log 127x )>0，得|log 127x |>13，即log 127x >13或log 127x <－13.选D.6．(2011²衡水模拟)已知偶函数f (x )在区间[0，＋∞)上单调增加，则满足f (2x －1)<f (13)的x 的取值范围是( )A ．(13，23)B ．[13，23)C ．(12，23)D ．[12，23)[答案] A[解析] 当2x －1≥0，即x ≥12时，由于函数f (x )在区间[0，＋∞)上单调增加， 则由f (2x －1)<f (13)得2x －1<13，即x <23，故12≤x <23；当2x －1<0，即x <12时，由于函数f (x )是偶函数，故f (2x －1)＝f (1－2x )，此时1－2x >0， 由f (2x －1)<f (13)得1－2x <13，即x >13，故13<x <12.综上可知x 的取值范围是(13，23)．[点评] (1)由于f (x )为偶函数，∴f (2x －1)<f (13)⇔f (|2x －1|)<f (13)．(2)可借助图形分析 作出示意图可知：f (2x －1)<f ⎝ ⎛⎭⎪⎫13⇔－13<2x －1<13，即13<x <23.故选A. 7．(2011²四川一模)定义新运算⊕：当a ≥b 时，a ⊕b ＝a ；当a <b 时，a ⊕b ＝b 2，则函数f (x )＝(1⊕x )x －(2⊕x )，x ∈[－2,2]的最大值等于( )A ．－1B ．1C ．6D ．12[答案] C[解析] 由⊕的定义知1⊕x ＝⎩⎪⎨⎪⎧1， －2≤x ≤1，x 2， 1<x ≤2，2⊕x ＝2，∴f (x )＝⎩⎪⎨⎪⎧x －2， －2≤x ≤1，x 3－2， 1<x ≤2.显然f (x )在[－2,2]上为增函数， ∴f (x )max ＝f (2)＝23－2＝6.8．已知函数f (x )＝log a (x ＋1)－log a (1－x )，a >0且a ≠1. (1)求f (x )的定义域；(2)判断f (x )的奇偶性并予以证明；(3)当a >1时，求使f (x )>0的x 的取值范围．[解析] (1)要使f (x )＝log a (x ＋1)－log a (1－x )有意义，则⎩⎪⎨⎪⎧x ＋1>01－x >0，解得－1<x <1.故所求定义域为{x |－1<x <1}．(2)由(1)知f (x )的定义域为{x |－1<x <1}，且f (－x )＝log a (－x ＋1)－log a (1＋x )＝－[log a (x ＋1)－log a (1－x )]＝－f (x )，故f (x )为奇函数．(3)因为当a >1时，f (x )在定义域{x |－1<x <1}内是增函数，所以f (x )>0⇔x ＋11－x>1.解得0<x <1.所以使f (x )>0的x 的取值范围是{x |0<x <1}．。

4-4两角和与差的三角函数基础巩固强化1.(2011²银川三模)已知sin θ＝45，且sin θ－cos θ>1，则sin2θ＝( )A ．－ 2425B ．－1225C ．－45D.2425[答案] A[解析] 由题意可知cos θ＝－35，所以sin2θ＝2sin θcos θ＝－2425，故选择A.2．(文)(2011²北京东城区期末)在△ABC 中，C ＝120°，tan A ＋tan B ＝233，则tan A tan B的值为( )A.14B.13C.12D.53 [答案] B[解析] ∵C ＝120°，∴A ＋B ＝60°， ∴tan(A ＋B )＝tan A ＋tan B 1－tan A tan B ＝3，∵tan A ＋tan B ＝233，∴tan A tan B ＝13.(理)已知sin α＝35，α为第二象限角，且tan(α＋β)＝1，则tan β的值是( )A ．－7B ．7C ．－34D.34 [答案] B[解析] 由sin α＝35，α为第二象限角，得cos α＝－45，则tan α＝－34.∴tan β＝tan[(α＋β)－α]＝tan α＋β－tan α1＋tan α＋βtan α＝1＋341＋⎝ ⎛⎭⎪⎫－34＝7.3．(文)已知0<α<π2<β<π，cos α＝35，sin(α＋β)＝－35，则cos β的值为( )A ．－1B ．－1或－725C ．－2425D ．±2425[答案] C[解析] ∵0<α<π2，π2<β<π，∴π2<α＋β<3π2，∴sin α＝45，cos(α＋β)＝－45，∴cos β＝cos[(α＋β)－α]＝cos(α＋β)cos α＋sin(α＋β)sin α＝⎝ ⎛⎭⎪⎫－45²35＋⎝ ⎛⎭⎪⎫－35²45＝－2425，故选C. (理)已知sin β＝35(π2<β<π)，且sin(α＋β)＝cos α，则tan(α＋β)＝( )A ．1B ．2C ．－2 D.825[答案] C[解析] ∵sin β＝35，π2<β<π，∴cos β＝－45，∴sin(α＋β)＝cos α＝cos[(α＋β)－β] ＝cos(α＋β)cos β＋sin(α＋β)sin β ＝－45cos(α＋β)＋35sin(α＋β)，∴25sin(α＋β)＝－45cos(α＋β)，∴tan(α＋β)＝－2. 4．已知实数a ，b 均不为零，a sin2＋b cos2a cos2－b sin2＝tan β，且β－2＝π6，则ba＝( )A. 3B.33 C ．－ 3 D ．－33[答案] B[解析] tan β＝tan(2＋π6)＝tan2＋331－33tan2＝a sin2＋b cos2a cos2－b sin2＝a tan2＋b a －b tan2，所以a ＝1，b ＝33，故b a ＝33. 5．函数f (x )＝(3sin x －4cos x )²cos x 的最大值为( ) A ．5 B.92 C.12 D.52[答案] C[解析] f (x )＝(3sin x －4cos x )cos x ＝3sin x cos x －4cos 2x ＝32sin2x －2cos2x －2＝52sin(2x －θ)－2，其中tan θ＝43， 所以f (x )的最大值是52－2＝12.故选C.6．(文)(2011²合肥质检)将函数y ＝sin(2x ＋π3)的图象上各点向右平移π6个单位，再把每一点的横坐标缩短到原来的一半，纵坐标保持不变，所得函数图象的一条对称轴是( )A ．x ＝π8B ．x ＝π6C ．x ＝π3D ．x ＝π2[答案] A[解析] y ＝sin(2x ＋π3) y ＝sin2xy ＝sin4x ，其对称轴方程为4x ＝k π＋π2，k∈Z ，∴x ＝k π4＋π8，令k ＝0得x ＝π8. (理)(2013²陕西师大附中上学期一模)函数f (x )＝A sin(ωx ＋φ)(其中A >0，|φ|<π2)的图象如图所示，为了得到函数g (x )＝sin2x 的图象，则只需将f (x )的图象( )A ．向右平移π6个长度单位B ．向右平移π12个长度单位C ．向左平移π6个长度单位D ．向左平移π12个长度单位[答案] A[解析] 由图可知A ＝1，T 4＝7π12－π3＝π4，∴T ＝π，∴2πω＝π，∴ω＝2， ∴f (x )＝sin(2x ＋φ)，将(7π12，－1)代入得sin(7π6＋φ)＝－1，∴7π6＋φ＝3π2＋2k π，k ∈Z ，∴φ＝2k π＋π3，k ∈Z . ∵|φ|<π2，∴φ＝π3，∴f (x )＝sin(2x ＋π3)，将f (x )的图象向右平移π6个单位可得，sin[2(x －π6)＋π3]＝sin2x ，故选A.7．函数f (x )＝a sin x －b cos x 的图象的一条对称轴是直线x ＝π4，则直线ax －by ＋c ＝0的倾斜角的大小为________．[答案]3π4(或135°) [解析] f (x )的图象的对称轴过其最高点或最低点，∴f (π4)＝±a 2＋b 2，∴a －b 2＝±a 2＋b 2，解得a ＋b ＝0.∴直线ax －by ＋c ＝0的斜率k ＝ab＝－1， ∴直线ax －by ＋c ＝0的倾斜角为135°(或3π4)．8．下列命题：①存在α、β∈R ，使tan(α＋β)＝tan α＋tan β；②存在φ∈R ，使f (x )＝cos(3x ＋φ)为奇函数；③对任意α，β∈(0，π2)，若tan α²tan β<1，则α＋β<π2；④△ABC 中，sin A >sin B 的充要条件是A >B .其中真命题的序号是________．[答案] ①②③④[解析] ①α＝0，β＝π3时，原式成立；②φ＝π2时，f (x )为奇函数；③∵tan α²tan β<1，α，β∈⎝⎛⎭⎪⎫0，π2，∴sin α²sin βcos α²cos β<1，∴sin α²sin β<cos α²cos β，∴cos(α＋β)>0，∵α＋β∈(0，π)，∴α＋β<π2；④在△ABC 中，A >B ⇔a >b ⇔2R sin A >2R sin B ⇔sin A >sin B (其中R 为△ABC 外接圆的半径)． 9．(文)函数y ＝cos(π3－2x )＋sin(π2－2x )的最小正周期为________．[答案] π[解析] y ＝cos π3cos2x ＋sin π3sin2x ＋cos2x＝32cos2x ＋32sin2x ＝3(32cos2x ＋12sin2x ) ＝3sin(2x ＋π3)，∴T ＝π.(理)函数y ＝cos(x ＋20°)＋sin(x －10°)的最大值为________． [答案] 1[解析] y ＝cos x cos20°－sin x sin20°＋sin x cos10°－cos x sin10° ＝(cos10°－sin20°)²sin x ＋(cos20°－sin10°)cos x＝a 2＋b 2sin(x ＋φ)．这里a ＝cos10°－sin20°，b ＝cos20°－sin10°， tan φ＝co s20°－sin10°cos10°－sin20°∵a 2＋b 2＝(cos10°－sin20°)2＋(cos20°－sin10°)2＝2－2sin20°cos10°－2cos20°sin10°＝2－2sin30°＝1. ∴最大值为a 2＋b 2＝1.10．(文)设函数f (x )＝3cos 2ωx ＋sin ωx cos ωx ＋a (其中ω>0，a ∈R )，且f (x )的最小正周期是2π.(1)求ω的值；(2)如果f (x )在区间[－π3，5π6]上的最小值为3，求a 的值．[解析] (1)f (x )＝32cos2ωx ＋12sin2ωx ＋32＋a ＝sin ⎝ ⎛⎭⎪⎫2ωx ＋π3＋32＋a ， 依题意得2π2ω＝2π⇒ω＝12.(2)由(1)知，f (x )＝sin ⎝⎛⎭⎪⎫x ＋π3＋32＋a .又当x ∈[－π3，5π6]时，x ＋π3∈[0，7π6]，故－12≤sin ⎝ ⎛⎭⎪⎫x ＋π3≤1，从而f (x )在区间[－π3，5π6]上的最小值为－12＋32＋a ＝3，故a ＝3＋12.(理)(2011²日照模拟)设函数f (x )＝cos(πx 4－π3)－cos πx 4.(1)求f (x )的最小正周期；(2)设g (x )＝f (－2－x )；当x ∈[0,2]时，求函数y ＝g (x )的最大值． [解析] (1)f (x )＝cos π4x cos π3＋sin π4x sin π3－cos πx 4＝32sin π4x －12cos π4x ＝sin(π4x －π6)．故f (x )的最小正周期为T ＝2ππ4＝8. (2)由题设条件得g (x )＝f (－2－x )＝sin[π4(－2－x )－π6]＝sin[－π2－π4x －π6]＝－cos(π4x ＋π6)．当0≤x ≤2时，π6≤π4x ＋π6≤2π3，设t ＝π4x ＋π6，则y ＝－cos t ，在[π6，2π3]上是增函数，因此y ＝g (x )在区间[0,2]上的最大值为g (x )max ＝－cos 2π3＝12.能力拓展提升11.(文)(2012²河南六市联考)已知函数y ＝f (x )＝3sin(π6＋x )＋cos(π6＋x )，则函数f (x )应满足( )A ．函数y ＝f (x )在[－5π6，π6]上递增，且有一个对称中心(π6，0)B ．函数y ＝f (x )在[－3π4，π6]上递增，且有一个对称中心(－π3，0)C ．函数y ＝f (x )在[－5π6，π6]上递减，且有一个对称中心(－π3，0)D ．函数y ＝f (x )在[－3π4，π6]上递减，且有一个对称中心(π6，0)[答案] B[解析] f (x )＝3sin(π6＋x )＋cos(π6＋x )＝2sin(π6＋x ＋π6)＝2sin(x ＋π3)，故选B.(理)已知a ＝(sin α，1－4cos2α)，b ＝(1,3sin α－2)，α∈⎝⎛⎭⎪⎫0，π2，若a ∥b ，则tan ⎝⎛⎭⎪⎫α－π4＝( ) A.17 B ．－17 C.27 D ．－27 [答案] B[解析] ∵a ∥b ，∴1－4cos2α＝sin α(3sin α－2)， ∴5sin 2α＋2sin α－3＝0，∴sin α＝35或sin α＝－1，∵α∈⎝ ⎛⎭⎪⎫0，π2，∴sin α＝35，∴tan α＝34，∴tan ⎝⎛⎭⎪⎫α－π4＝tan α－11＋tan α＝－17.12．(文)设动直线x ＝a 与函数f (x )＝2sin 2(π4＋x )和g (x )＝3cos2x 的图象分别交于M ，N 两点，则|MN |的最大值为( )A. 2B. 3 C ．2 D ．3 [答案] D[解析] 易知|MN |＝|f (a )－g (a )|＝|2sin 2(π4＋a )－3cos2a |＝|1－cos(π2＋2a )－3cos2a |＝|1＋2sin(2a －π3)|≤3，即最大值是3.(理)(2012²东北三校联考)设α、β都是锐角，且cos α＝55，sin(α＋β)＝35，则cos β＝( )A.2525B.255 C.2525或255D.55或525[答案] A[解析] 依题意得sin α＝1－cos 2α＝255，cos(α＋β)＝±1－sin 2α＋β＝±45.又α、β均为锐角，因此0<α<α＋β<π，cos α>cos(α＋β)，因为45>55>－45，所以cos(α＋β)＝－45.cos β＝cos[(α＋β)－α]＝cos(α＋β)cos α＋sin(α＋β)²sin α＝－45³55＋35³255＝2525，选A.13．已知sin(2α－β)＝35，sin β＝－1213，且α∈(π2，π)，β∈(－π2，0)，则sin α＝________.[答案]3130130[解析] ∵π2<α<π，∴π<2α<2π.又－π2<β<0，∴0<－β<π2，π<2α－β<5π2，而sin(2α－β)＝35>0，∴2π<2α－β<5π2，cos(2α－β)＝45.又－π2<β<0且sin β＝－1213，∴cos β＝513，∴cos2α＝cos[(2α－β)＋β]＝cos(2α－β)cos β－sin(2α－β)sin β ＝45³513－35³(－1213)＝5665. 又cos2α＝1－2sin 2α，∴sin 2α＝9130.又α∈(π2，π)，∴sin α＝3130130.14．求值：2cos10°－sin20°cos20°＝________.[答案]3[解析] 原式＝2cos 30°－20°－sin20°cos20°＝2cos30°cos20°＋2sin30°sin20°－sin20°cos20°＝3cos20°＋sin20°－sin20°cos20°＝ 3.15．(文)(2011²珠海模拟)已知A 、B 均为钝角且sin A ＝55，sin B ＝1010，求A ＋B 的值．[解析] ∵A 、B 均为钝角且sin A ＝55，sin B ＝1010， ∴cos A ＝－1－sin 2A ＝－25＝－255，cos B ＝－1－sin 2B ＝－310＝－31010，∴cos(A ＋B )＝cos A cos B －sin A sin B ＝－255³(－31010)－55³1010＝22，又∵π2<A <π，π2<B <π，∴π<A ＋B <2π，∴A ＋B ＝7π4.(理)(2011²成都二诊)已知函数f (x )＝2sin x cos(x ＋π6)－cos2x ＋m . (1)求函数f (x )的最小正周期；(2)当x ∈[－π4，π4]时，函数f (x )的最小值为－3，求实数m 的值．[解析] (1)∵f (x )＝2sin x cos(x ＋π6)－cos2x ＋m＝2sin x (32cos x －12sin x )－cos2x ＋m ＝3sin x cos x －sin 2x －cos2x ＋m ＝32sin2x －1－cos2x 2－cos2x ＋m ＝32sin2x －12cos2x －12＋m ＝sin(2x －π6)－12＋m .∴f (x )的最小正周期T ＝2π2＝π.(2)∵－π4≤x ≤π4，∴－π2≤2x ≤π2，∴－2π3≤2x －π6≤π3，∴－1≤sin(2x －π6)≤32，∴ f (x )的最小值为－1－12＋m .由已知，有－1－12＋m ＝－3.∴m ＝－32.16．(文)(2011²晋中一模)已知sin α＋cos α＝355，α∈(0，π4)，sin(β－π4)＝35，β∈(π4，π2)．(1)求sin2α和tan2α的值； (2)求cos(α＋2β)的值．[解析] (1)由题意得(sin α＋cos α)2＝95，即1＋sin2α＝95，∴sin2α＝45.又2α∈(0，π2)，∴cos2α＝1－sin 22α＝35，∴tan2α＝sin2αcos2α＝43.(2)∵β∈(π4，π2)，β－π4∈(0，π4)，∴cos(β－π4)＝45，于是sin2(β－π4)＝2sin(β－π4)cos(β－π4)＝2425.又sin2(β－π4)＝－cos2β，∴cos2β＝－2425.又2β∈(π2，π)，∴sin2β＝725.又cos 2α＝1＋cos2α2＝45，∴cos α＝255，sin α＝55(α∈(0，π4))．∴cos(α＋2β)＝cos αcos2β－sin αsin2β ＝255³(－2425)－55³725＝－11525. (理)已知0<α<π2，π2<β<π，且tan α2＝12，sin(α＋β)＝513.(1)求cos α和cos β的值； (2)求tan α－β2的值．[解析] (1)∵tan α2＝12，∴tan α＝2tanα21－tan2α2＝43，∴sin α＝43cos α，代入sin 2α＋cos 2α＝1中消去sin α得，cos 2α＝925，∵0<α<π2，∴cos α＝35，∴sin α＝45，∵π2<α＋β<3π2，sin(α＋β)＝513>0，∴π2<α＋β<π，∴cos(α＋β)＝－1－sin 2α＋β＝－1213，∴cos β＝cos[(α＋β)－α]＝cos(α＋β)cos α＋sin(α＋β)sin α＝－1213³35＋513³45＝－1665.∴cos α和cos β的值依次为35和－1665.(2)由(1)知cos β＝－1665，又已知π2<β<π，∴sin β＝6365，∴tan β＝－6316.∴2tanβ21－tan2β2＝－6316，∵π2<β<π，∴tan β2>0，∴tan β2＝97， ∴tan α－β2＝tan α2－tan β21＋tan α2²tan β2＝12－971＋12³97＝－1123.1．方程x 2cos2012°－y 2sin2012°＝1所表示的曲线为( )A ．焦点在x 轴上的椭圆B ．焦点在y 轴上的椭圆C ．焦点在x 轴上的双曲线D ．焦点在y 轴上的双曲线 [答案] D[解析] cos2012°＝cos(5³360°＋212°)＝cos212°＝－cos32°＝－sin58°<0，而sin2012°＝sin(5³360°＋212°)＝sin212°＝－sin32°<0，所以该曲线为焦点在y 轴上的双曲线．2．已知α、β均为锐角，且tan β＝cos α－sin αcos α＋sin α，则tan(α＋β)的值为( )A ．－1B ．1 C. 3 D ．不存在 [答案] B[解析] tan β＝cos α－sin αcos α＋sin α＝1－tan α1＋tan α＝tan ⎝ ⎛⎭⎪⎫π4－α， ∵π4－α，β∈⎝ ⎛⎭⎪⎫－π2，π2且y ＝tan x 在⎝ ⎛⎭⎪⎫－π2，π2上是单调增函数，∴β＝π4－α，∴α＋β＝π4，∴tan(α＋β)＝tan π4＝1.3．已知sin α＝55，sin(α－β)＝－1010，α、β均为锐角，则β等于( )A.5π12 B.π3 C.π4 D.π6[答案] C[解析] ∵α、β均为锐角，∴－π2<α－β<π2，∴cos(α－β)＝1－sin 2α－β＝31010， ∴sin α＝55，∴cos α＝1－⎝⎛⎭⎪⎫552＝255. ∴sin β＝sin[α－(α－β)]＝sin αcos(α－β)－cos αsin(α－β)＝22. ∵0<β<π2，∴β＝π4，故选C.4．(2012²重庆文)设函数f (x )＝A sin(ωx ＋φ)(其中A ＞0，ω＞0，－π＜φ≤π)在x ＝π6处取得最大值2，其图象与x 轴的相邻两个交点的距离为π2.(1)求f (x )的解析式；(2)求函数g (x )＝6cos 4x －sin 2x －1f x ＋π6的值域．[分析] (1)由周期为π求出ω，代入点(π6，2)，由φ范围求出φ，A .(2)分子化同名，即sin 2x 用1－cos 2x 代换，分母用诱导公式和二倍角公式． [解析] (1)由题设条件知f (x )的周期T ＝π， 即2πω＝π，解得ω＝2， 因为f (x )在x ＝π6处取得最大值2，所以A ＝2，从而sin(2³π6＋φ)＝1，所以2³π6＋φ＝π2＋2k π，k ∈Z ，又由－π<φ≤π，得φ＝π6， 故f (x )的解析式为f (x )＝2sin(2x ＋π6)．(2)g (x )＝6cos 4x －sin 2x －12sin 2x ＋π2＝6cos 4x ＋cos 2x －22cos2x＝2cos 2x －13cos 2x ＋222cos 2x －1＝32cos 2x ＋1(cos 2x ≠12)． 因cos 2x ∈[0,1]，且cos 2≠12.故g (x )的值域为[1，74)∪(74，52]．[点评] 本题考查了三角函数的周期、最值、同角基本关系式、二倍角公式等．在解三角恒等变换(化简)题时的方法有：异名化同名，异角化同角，降幂化同次等．。

4-3三角函数的图象与性质基础巩固强化1.(文)(2011·大纲全国卷理)设函数f (x )＝cos ωx (ω>0)，将y ＝f (x )的图象向右平移π3个单位长度后，所得的图象与原图象重合，则ω的最小值等于( ) A.13 B ．3 C ．6 D ．9[答案] C[解析] 由题意知，π3＝2πω·k (k ∈Z )，∴ω＝6k ，令k ＝1，∴ω＝6.(理)(2012·浙江诸暨质检)函数f (x )＝sin2x ＋3cos2x 的图象可以由函数y ＝2sin2x 的图象经哪种平移得到( )A ．向左平移π12个单位B ．向左平移π6个单位C ．向右平移π12个单位D ．向右平移π6个单位[答案] B[解析] ∵f (x )＝sin2x ＋3cos2x ＝2sin(2x ＋π3＝2sin2(x ＋π6)，∴f (x )的图象可以由函数y ＝2sin2x 向左平移π6个单位得到，故应选B.2．(文)(2012·福建文，8)函数f (x )＝sin(x －π4)的图象的一条对称轴是( ) A ．x ＝π4B ．x ＝π2 C ．x ＝－π4D ．x ＝－π2[答案] C[解析] 本题考查了正弦型函数图象的对称轴问题． 函数f (x )＝sin(x －π4)的图象的对称轴是 x －π4＝k π＋π2，k ∈Z ，即x ＝k π＋3π4，k ∈Z . 当k ＝－1时，x ＝－π＋3π4＝－π4.[点评] 正弦(余弦)型函数图象的对称轴过图象的最高点或最低点． (理)(2011·海淀模拟)函数f (x )＝sin(2x ＋π3)图象的对称轴方程可以为( ) A ．x ＝π12 B ．x ＝5π12 C ．x ＝π3D ．x ＝π6[答案] A [解析] 令2x ＋π3＝k π＋π2得x ＝k π2＋π12，k ∈Z ， 令k ＝0得x ＝π12，故选A.[点评] f (x )＝sin(2x ＋π3)的图象的对称轴过最高点将选项代入检验，∵2×π12＋π3＝π2，∴选A. 3．(文)(2011·唐山模拟)函数y ＝sin(2x ＋π6)的一个递减区间为( ) A ．(π6，2π3) B ．(－π3，π6) C ．(－π2，π2) D ．(π2，3π2)[答案] A [解析] 由2k π＋π2≤2x ＋π6≤2k π＋3π2得， k π＋π6≤x ≤k π＋2π3(k ∈Z )， 令k ＝0得，π6≤x ≤2π3，故选A.(理)(2012·新课标全国理，9)已知ω>0，函数f (x )＝sin(ωx ＋π4)在(π2，π)上单调递减，则ω的取值范围是( )A ．[12，54]B ．[12，34]C ．(0，12]D ．(0,2][答案] A[解析] 本题考查了三角函数y ＝A sin(ωx ＋φ)的性质及间接法解题．ω＝2⇒ωx ＋π4∈[5π4，9π4]不合题意，排除D ，ω＝1⇒(ωx ＋π4)∈[3π4，5π4]合题意，排除B ，C.4．(2011·大连模拟)已知函数f (x )＝2sin ωx (ω>0)在区间[－π3，π4]上的最小值是－2，则ω的最小值为( )A.23 B.32 C ．2 D ．3[答案] B[解析] ∵f (x )＝2sin ωx (ω>0)在区间[－π3，π4]上的最小值为－2，∴T 4≤π3，即π2ω≤π3， ∴ω≥32，即ω的最小值为32.5．(文)(2011·吉林一中月考)函数y ＝sin(ωx ＋φ)(x ∈R ，ω>0,0≤φ<2π)的部分图象如图，则( )A ．ω＝π2，φ＝π4 B ．ω＝π3，φ＝π6 C ．ω＝π4，φ＝π4 D ．ω＝π4，φ＝5π4[答案] C[解析] ∵T 4＝3－1＝2，∴T ＝8，∴ω＝2πT ＝π4.令π4×1＋φ＝π2，得φ＝π4，∴选C. (理)函数y ＝xsin xx ∈(－π，0)∪(0，π)的图象可能是下列图象中的( )[答案] C[解析] 依题意，函数y ＝xsin x，x ∈(－π，0)∪(0，π)为偶函数，排除A ，当x ∈(0，π)时，直线y ＝x 的图象在y ＝sin x 上方，所以y ＝xsin x>1，故选C.6．(文)(2011·课标全国文)设函数f (x )＝sin(2x ＋π4)＋cos(2x ＋π4)，则( ) A ．y ＝f (x )在(0，π2)单调递增，其图象关于直线x ＝π4对称 B ．y ＝f (x )在(0，π2)单调递增，其图象关于直线x ＝π2对称 C ．y ＝f (x )在(0，π2)单调递减，其图象关于直线x ＝π4对称 D ．y ＝f (x )在(0，π2)单调递减，其图象关于直线x ＝π2对称 [答案] D[解析] f (x )＝sin ⎝⎛⎭⎫2x ＋π4＋cos ⎝⎛⎭⎫2x ＋π4＝2sin ⎝⎛⎭⎫2x ＋π2＝2cos2x . 则函数在⎝⎛⎫0，π2单调递减，其图象关于直线x ＝π2对称． (理)(2011·河南五校联考)给出下列命题：①函数y ＝cos(23x ＋π2)是奇函数；②存在实数α，使得sin α＋cos α＝32；③若α、β是第一象限角且α<β，则tan α<tan β；④x ＝π8y ＝sin(2x ＋5π4)的一条对称轴方程；⑤函数y ＝sin(2x ＋π3)的图象关于点(π12，0)成中心对称图形． 其中正确命题的序号为( ) A ．①③ B ．②④ C ．①④ D ．④⑤[答案] C[解析] ①y ＝cos(23x ＋π2)⇒y ＝－sin 23x 是奇函数；②由sin α＋cos α＝2sin(α＋π4)的最大值为2<32，所以不存在实数α，使得sin α＋cos α＝32；③α，β是第一象限角且α<β.例如：45°<30°＋360°，但tan45°>tan(30°＋360°)，即tan α<tan β不成立； ④把x ＝π8代入y ＝sin(2x ＋5π4)得y ＝sin 3π2＝－1， 所以x ＝π8是函数y ＝sin(2x ＋5π4)的一条对称轴； ⑤把x ＝π12代入y ＝sin(2x ＋π3)得y ＝sin π2＝1， 所以点(π12，0)不是函数y ＝sin(2x ＋π3)的对称中心． 综上所述，只有①④正确．[点评] 作为选择题，判断①成立后排除B 、D ，再判断③(或④)即可下结论． 7．(文)函数y ＝cos x 的定义域为[a ，b ]，值域为[－12，1]，则b －a 的最小值为________．[答案]2π3[解析] cos x ＝－12时，x ＝2k π＋2π3或x ＝2k π＋4π3，k ∈Z ，cos x ＝1时，x ＝2k π，k ∈Z .由图象观察知，b －a 的最小值为2π3.(理)(2011·江苏南通一模)函数f (x )＝sin ωx ＋3cos ωx (x ∈R )，又f (α)＝－2，f (β)＝0，且|α－β|的最小值等于π2，则正数ω的值为________．[答案] 1[解析] f (x )＝sin ωx ＋3cos ωx ＝2sin(ωx ＋π3)， 由f (α)＝－2，f (β)＝0，且|α－β|的最小值等于π2可知，T 4＝π2，T ＝2π，所以ω＝1.8．已知关于x 的方程2sin 2x －3sin2x ＋m －1＝0在x ∈(π2，π)上有两个不同的实数根，则m 的取值范围是________．[答案] －2<m <－1[解析] m ＝1－2sin 2x ＋3sin2x ＝cos2x ＋3sin2x ＝2sin(2x ＋π6)， ∵x ∈(π2，π)时，原方程有两个不同的实数根， ∴直线y ＝m 与曲线y ＝2sin(2x ＋π6)，x ∈(π2，π)有两个不同的交点，∴－2<m <－1.9．(2011·济南调研)设函数y ＝2sin(2x ＋π3)的图象关于点P (x 0,0)成中心对称，若x 0∈[－π2，0]，则x 0＝________. [答案] －π6[解析] ∵函数y ＝2sin(2x ＋π3)的对称中心是函数图象与x 轴的交点，∴2sin(2x 0＋π3)＝0， ∵x 0∈[－π2，0]∴x 0＝－π6.10．(文)(2011·北京文)已知函数f(x)＝4cos x sin(x＋π6)－1.(1)求f(x)的最小正周期；(2)求f(x)在区间[－π6，π4]上的最大值和最小值．[解析] (1)因为f(x)＝4cos x sin(x＋π6)－1＝4cos x(32sin x＋12cos x)－1＝3sin2x＋2cos2x－1＝3sin2x＋cos2x＝2sin(2x＋π6 )．所以f(x)的最小正周期为π.(2)因为－π6≤x≤π4，所以－π6≤2x＋π6≤2π3.于是，当2x＋π6＝π2，即x＝π6时，f(x)取得最大值2；当2x＋π6＝－π6，即x＝－π6时，f(x)取得最小值－1.(理)(2011·天津南开中学月考)已知a＝(sin x，－cos x)，b＝(cos x，3cos x)，函数f(x)＝a·b＋32.(1)求f(x)的最小正周期，并求其图象对称中心的坐标；(2)当0≤x≤π2时，求函数f(x)的值域．[解析] (1)f(x)＝sin x cos x－3cos2x＋3 2＝12sin2x－32(cos2x＋1)＋32＝12sin2x－32cos2x＝sin(2x－π3)，所以f(x)的最小正周期为π.令sin(2x－π3)＝0，得2x－π3＝kπ，∴x＝kπ2＋π6，k∈Z.故所求对称中心的坐标为(kπ2＋π6，0)(k∈Z)．(2)∵0≤x ≤π2，∴－π3≤2x －π3≤2π3. ∴－32x －π3)≤1，即f (x )的值域为[－32，1]. 能力拓展提升11.(文)(2011·苏州模拟)函数y ＝sin x ·|cos x sin xx <π)的图象大致是( )[答案] B[解析] y ＝sin x ·|cos xsin x|＝⎩⎪⎨⎪⎧cos x ，0<x <π20，x ＝π2－cos x ，π2<x <π.(理)(2011·辽宁文)已知函数f (x )＝A tan(ωx ＋φ)(ω>0，|φ|<π2)，y ＝f (x )的部分图象如图，则f (π24)＝( )A．2＋ 3 B. 3C.33D．2－ 3[答案] B[解析] 由图可知：T＝2×(38π－π8)＝π2，∴ω＝πT＝2，又∵图象过点(38π，0)，∴A·tan(2×38π＋φ)＝A·tan(34π＋φ)＝0，∴φ＝π4.又∵图象还过点(0,1)，∴A tan(2×0＋π4＝A＝1，∴f(x)＝tan(2x＋π4 )，∴f(π24)＝tan(2×π24＋π4)＝tan(π12＋π4)＝tanπ3＝ 3.12．(文)为了使函数y＝cosωx(ω>0)在区间[0,1]上至多出现50次最小值，则ω的最大值是( )A ．98π B.1972C ．99πD ．100π[答案] C[解析] 由题意至多出现50次最小值即至多需用4912个周期，∴992·2πω≥1，∴ω≤99π，故选C.(理)有一种波，其波形为函数y ＝sin ⎝⎛⎭⎫π2的图象，若在区间[0，t ](t >0)上至少有2个波谷(图象的最低点)，则正整数t 的最小值是( )A ．5B ．6C ．7D ．8 [答案] C[解析] ∵y ＝sin ⎝⎛⎭⎫π2x 的图象在[0，t ]上至少有2个波谷，函数y ＝sin ⎝⎛⎭⎫π2x 的周期T＝4，∴t ≥74T ＝7，故选C.13．(文)(2011·南昌调研)设函数y ＝sin(ωx ＋φ)(ω>0，φ∈(－π2，π2))的最小正周期为π，且其图象关于直线x ＝π12对称，则在下面四个结论中：①图象关于点(π4，0)对称； ②图象关于点(π3，0)对称； ③在[0，π6上是增函数； ④在[－π6，0]上是增函数中， 所有正确结论的编号为________． [答案] ②④[解析] 由最小正周期为π得，2πω＝π，∴ω＝2；再由图象关于直线x ＝π12对称，∴2×π12＋φ＝π2，∴φ＝π3， ∴f (x )＝sin(2x ＋π3)，当x ＝π4时，f (π4)＝12≠0，故①错；当x ＝π3时，f (π3)＝0，故②正确；由2k π－π2≤2x ＋π3≤2k π＋π2 (k ∈Z )得，k π－5π12≤x ≤k π＋π12，令k ＝0得，－5π12≤x ≤π12，故③错，④正确，∴正确结论为②④.(理)(2011·南京模拟)已知函数f (x )＝x sin x ，现有下列命题：①函数f (x )是偶函数；②函数f (x )的最小正周期是2π；③点(π，0)是函数f (x )的图象的一个对称中心；④函数f (x )在区间[0，π2]上单调递增，在区间[－π2，0]上单调递减．其中真命题是________(写出所有真命题的序号)． [答案] ①④[解析] ∵y ＝x 与y ＝sin x 均为奇函数，∴f (x )为偶函数，故①真；∵f (π2)＝π2，f (π2＋2π)＝π2＋2π≠π2， ∴②假；∵f (π2)＝π2，f (3π2)＝－3π2，π2＋3π2＝2π，π2＋(－3π2)≠0，∴③假；设0≤x 1<x 2≤π2，则f x 1f x 2＝x 1x 2·sin x 1sin x 2<1，∴f (x 1)<f (x 2)(f (x 2)>0)，∴f (x )在[0，π2]上为增函数，又∵f (x )为偶函数，∴f (x )在[－π2，0]上为减函数，∴④真． 14．函数f (x )＝2a cos 2x ＋b sin x cos x 满足：f (0)＝2，f (π3)＝12＋32.(1)求函数f (x )的最大值和最小值；(2)若α、β∈(0，π)，f (α)＝f (β)，且α≠β，求tan(α＋β)的值．[解析] (1)由⎩⎪⎨⎪⎧f 0＝2，f π3＝12＋32，得⎩⎪⎨⎪⎧2a ＝2，12a ＋34b ＝12＋32.解得a ＝1，b ＝2，∴f (x )＝sin2x ＋cos2x ＋1＝2sin(2x ＋π4)＋1， ∵－1≤sin(2x ＋π4)≤1， ∴f (x )max ＝2＋1，f (x )min ＝1－ 2. (2)由f (α)＝f (β)得，sin(2α＋π4＝sin(2β＋π4)．∵2α＋π4、2β＋π4∈(π4，9π4)，且α≠β， ∴2α＋π4＝π－(2β＋π4)或2α＋π4＝3π－(2β＋π4)， ∴α＋β＝π4或α＋β＝5π4，故tan(α＋β)＝1. 15．(文)(2011·长沙一中月考)已知f (x )＝sin x ＋sin(π2－x )． (1)若α∈[0，π]，且sin2α＝13，求f (α)的值；(2)若x ∈[0，π]，求f (x )的单调递增区间． [解析] (1)由题设知f (α)＝sin α＋cos α. ∵sin2α＝13＝2sin α·cos α>0，α∈[0，π]，∴α∈(0，π2)，sin α＋cos α>0. 由(sin α＋cos α)2＝1＋2sin α·cos α＝43，得sin α＋cos α＝233，∴f (α)＝233. (2)由(1)知f (x )＝2sin(x ＋π4)，又0≤x ≤π， ∴f (x )的单调递增区间为[0，π4]． (理)在△ABC 中，a 、b 、c 分别是角A 、B 、C 的对边，向量m ＝(b,2a －c )，n ＝(cos B ，cos C )，且m ∥n .(1)求角B 的大小；(2)设f (x )＝cos ⎝⎛⎭⎫ωx －B 2＋sin ωx (ω>0)，且f (x )的最小正周期为π，求f (x )在区间[0，π2]上的最大值和最小值． [解析] (1)由m ∥n 得，b cos C ＝(2a －c )cos B ， ∴b cos C ＋c cos B ＝2a cos B .由正弦定理得，sin B cos C ＋sin C cos B ＝2sin A cos B ， 即sin(B ＋C )＝2sin A cos B .又B ＋C ＝π－A ，∴sin A ＝2sin A cos B .又sin A ≠0，∴cos B ＝12.又B ∈(0，π)，∴B ＝π3.(2)由题知f (x )＝cos(ωx －π6)＋sin ωx ＝32cos ωx ＋32sin ωx ＝3sin(ωx ＋π6)， 由已知得2πω＝π，∴ω＝2，f (x )＝3sin(2x ＋π6)，当x ∈[0，π2]时，(2x ＋π6)∈[π6，7π6]， sin(2x ＋π6∈[－12，1]． 因此，当2x ＋π6＝π2，即x ＝π6时，f (x )取得最大值 3. 当2x ＋π6＝7π6，即x ＝π2时，f (x )取得最小值－32. 16．(文)(2011·福建四地六校联考)已知函数f (x )＝－1＋23sin x cos x ＋2cos 2x . (1)求f (x )的单调递减区间；(2)求f (x )图象上与原点最近的对称中心的坐标；(3)若角α，β的终边不共线，且f (α)＝f (β)，求tan(α＋β)的值． [解析] f (x )＝3sin2x ＋cos2x ＝2sin(2x ＋π6， (1)由2k π＋π2≤2x ＋π6≤2k π＋3π2k ∈Z ) 得k π＋π6≤x ≤k π＋2π3(k ∈Z )， ∴f (x )的单调减区间为[k π＋π6，k π＋2π3](k ∈Z )． (2)由sin(2x ＋π6＝0得2x ＋π6＝k π(k ∈Z )， 即x ＝k π2－π12(k ∈Z )， ∴f (x )图象上与原点最近的对称中心坐标是(－π12，0)． (3)由f (α)＝f (β)得： 2sin(2α＋π6)＝2sin(2β＋π6)， 又∵角α与β的终边不共线， ∴(2α＋π6＋(2β＋π6)＝2k π＋π(k ∈Z )，即α＋β＝k π＋π3(k ∈Z )，∴tan(α＋β)＝ 3. (理)(2011·浙江文)已知函数f (x )＝A sin(π3＋φ)，x ∈R ，A >0,0<φ<π2.y ＝f (x )的部分图象如图所示，P 、Q 分别为该图象的最高点和最低点，点P 的坐标为(1，A )．(1)求f (x )的最小正周期及φ的值；(2)若点R 的坐标为(1,0)，∠PRQ ＝2π3，求A 的值．[解析] (1)由题意得，T ＝2ππ3＝6， 因为P (1，A )在y ＝A sin(π3x ＋φ)的图象上，所以sin(π3＋φ)＝1. 又因为0<φ<π2，所以φ＝π6. (2)设点Q 的坐标为(x 0，－A )，由题意可知π3x 0＋π6＝3π2，得x 0＝4，所以Q (4，－A )．连接PQ ，在△PRQ 中，∠PRQ ＝23π，由余弦定理得，cos ∠PRQ ＝RP 2＋RQ 2－PQ 22RP ·RQ ＝A 2＋9＋A 2－9＋4A 22A ·9＋A 2＝－12，解得A 2＝3 又A >0，所以A ＝ 3.1．(2012·河北郑口中学模拟)已知函数f (x )＝A sin(x ＋φ)(A >0，－π2<φ<0)在x ＝5π6处取得最大值，则f (x )在[－π，0]上的单调增区间是( )A ．[－π，－5π6] B ．[－5π6，－π6] C ．[－π3，0] D ．[－π6，0] [答案] D[解析] ∵f (x )＝A sin(x ＋φ)在x ＝5π6处取得最大值，A >0，－π2<φ<0，∴φ＝－π3，∴f (x )＝A sin(x －π3)，由2k π－π2≤x －π3≤2k π＋π2(k ∈Z )得2k π－π6≤x ≤2k π＋5π6，令k ＝0得－π6≤x ≤0，故选D.2．(2011·长沙二模)若将函数y ＝sin ⎝⎛⎭⎫ωx ＋π4(ω>0)的图象向右平移π4个单位长度后，与函数y ＝sin ⎝⎛⎭⎫ωx ＋π3的图象重合，则ω的最小值为( ) A ．1 B ．2 C.112D.233[答案] D[解析] y ＝sin ⎝⎛⎭⎫ωx ＋π4y ＝sin ⎣⎢⎡⎦⎥⎤ω⎝⎛⎭⎫x －π4＋π4＝sin ⎝⎛⎭⎫ωx ＋π3，∴π4－π4ω＋2k π＝π3，∴ω＝8k －13(k ∈Z )，又∵ω>0，∴ωmin ＝233.3．(2011·北京大兴区模拟)已知函数f (x )＝3sinπxR图象上相邻的一个最大值点与一个最小值点恰好都在圆x 2＋y 2＝R 2上，则f (x )的最小正周期为( )A ．1B ．2C ．3D ．4 [答案] D[解析] f (x )的周期T ＝2ππR＝2R ，f (x )的最大值是3，结合图形分析知R >3，则2R >23>3，只有2R ＝4这一种可能，故选D.4．(2012·河北保定模拟)已知向量a ＝(cos θ，sin θ)与b ＝(cos θ，－sin θ)互相垂直，且θ为锐角，则函数f (x )＝sin(2x －θ)的图象的一条对称轴是直线( )A ．x ＝πB ．x ＝7π8 C ．x ＝π4D ．x ＝π2[答案] B[解析] a ·b ＝cos 2θ－sin 2θ＝cos2θ＝0， ∵θ为锐角，∴θ＝π4，∴f (x )＝sin(2x －π4)． 由2x －π4＝k π＋π2得，x ＝k π2＋3π8令k ＝1得x ＝7π8 B.5.(2011·北京西城模拟)函数y ＝sin(πx ＋φ)(φ>0)的部分图象如图所示，设P 是图象的最高点，A ，B 是图象与x 轴的交点，则tan ∠APB ＝( )A ．10B ．8 C.87 D.47[答案] B[分析] 利用正弦函数的周期、最值等性质求解．[解析] 如图，过P 作PC ⊥x 轴，垂足为C ，设∠APC ＝α，∠BPC ＝β，∴∠APB ＝α＋β，y ＝sin(πx ＋φ)，T ＝2ππ＝2，tan α＝AC PC ＝121＝12，tan β＝BC PC ＝321＝32，则tan(α＋β)＝tan α＋tan β1－tan α·tan β＝12＋321－12×32＝8，∴选B.6．对任意x 1，x 2∈⎝⎛⎭⎫0，π2，x 2>x 1，y 1＝1＋sin x 1x 1，y 2＝1＋sin x 2x 2，则( ) A ．y 1＝y 2 B ．y 1>y 2 C ．y 1<y 2D ．y 1，y 2的大小关系不能确定 [答案] B[解析] 取函数y ＝1＋sin x ，则1＋sin x 1x 1的几何意义为过原点及点(x 1,1＋sin x 1)的直线斜率，1＋sin x 2x 2的几何意义为过原点及点(x 2,1＋sin x 2)的直线斜率，由x 1<x 2，观察函数y ＝1＋sin x 的图象可得y 1>y 2.选B.7．(2011·菏泽模拟)对于函数f (x )＝⎩⎪⎨⎪⎧sin x ，sin x ≤cos xcos x ，sin x >cos x ，给出下列四个命题：①该函数是以π为最小正周期的周期函数；②当且仅当x ＝π＋k π(k ∈Z )时，该函数取得最小值是－1； ③该函数的图象关于直线x ＝5π4＋2k π(k ∈Z )对称； ④当且仅当2k π<x <π2＋2k π(k ∈Z )时，0<f (x )≤22其中正确命题的序号是________(请将所有正确命题的序号都填上) [答案] ③④[解析] 画出函数f (x )的图象，易知③④正确． 8．已知函数f (x )＝3sin(2x －π6)＋2sin 2(x －π12)(x ∈R )． (1)求函数f (x )的最小正周期；(2)求使函数f (x )取得最大值的x 的集合． [解析] (1)f (x )＝3sin(2x －π6)＋1－cos2(x －π12)＝2⎣⎢⎡⎦⎥⎤32sin ⎝⎛⎭⎫2x －π6－12cos ⎝⎛⎭⎫2x －π6＋1 ＝2sin(2x －π3)＋1. 所以最小正周期为T ＝π.(2)当f (x )取最大值时，只要sin(2x －π3＝1，得出x ＝k π＋5π12(k ∈Z )，∴x 值的集合为{x |x ＝k π＋5π12，k ∈Z }． [点评] 差异分析是解答数学问题的有效方法．诸如：化复杂为简单，异角化同角，异名化同名，高次化低次，化为一个角的同名三角函数的形式等等．。

1.(文)(2011·沈阳六校模考)设数列{(－1)n }的前n 项和为S n ，则对任意正整数n ，S n ＝( )A.n [(－1)n －1]2B.(－1)n －1＋12C.(－1)n ＋12D.(－1)n －12[答案] D[解析] 因为数列{(－1)n }是首项与公比均为－1的等比数列，所以S n ＝－1－(－1)n ×(－1)1－(－1)＝(－1)n －12，选D.[点评] 直接检验，S 1＝－1，排除B ，C ；S 3＝－1，排除A ，故选D.(理)数列{a n }的前n 项和S n ＝n 2＋2n ＋1，则{a n }的通项公式为( )A ．a n ＝2n －1B ．a n ＝2n ＋1C ．a n ＝⎩⎪⎨⎪⎧ 4 n ＝12n －1 n ≥2D ．a n ＝⎩⎪⎨⎪⎧4 n ＝12n ＋1 n ≥2[答案] D[解析] a 1＝S 1＝4，n ≥2时，a n ＝S n －S n －1＝2n ＋1，∴a n ＝⎩⎪⎨⎪⎧4 n ＝12n ＋1 n ≥2.2．(2011·许昌月考)已知数列{a n }的通项公式是a n ＝2n 3n ＋1，那么这个数列是( )A ．递增数列B ．递减数列C ．摆动数列D ．常数列 [答案] A[解析] a n ＝23－2a n ＋3，∵n ∈N *，∴a n 随n 的增大而增大，故选A.[点评] 上面解答过程利用了反比例函数y ＝－1x 的单调性，也可以直接验证a n ＋1－a n >0.3．(文)设a n ＝－2n 2＋29n ＋3，则数列{a n }中的最大项的值是( )A ．107B ．108C ．10818 D ．109[答案] B[解析] ∵a n ＝－2⎝ ⎛⎭⎪⎫n －2942＋8658，∴当n ＝7时，a n 最大．a 7＝108.(理)如果f (a ＋b )＝f (a )·f (b )(a ，b ∈R)且f (1)＝2，则f (2)f (1)＋f (4)f (3)＋f (6)f (5)＋…＋f (2012)f (2011)等于( ) A ．2007 B ．2008 C ．2010 D ．2012 [答案] D[解析] 令a ＝n ，b ＝1，f (n ＋1)＝f (n )·f (1)， ∴f (n ＋1)f (n )＝f (1)＝2，∴f(2)f(1)＋…＋f(2012)f(2011)＝2×1006＝2012.4．(文)(2011·惠州二模，天津南开中学月考)已知整数按如下规律排成一列：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，……则第60个数对是()A．(5,5) B．(5,6)C．(5,7) D．(5,8)[答案] C[解析]根据题中规律知，(1,1)为第1项，(1,2)为第2项，(1,3)为第4项，…，(1,11)为第56项，因此第60项为(5,7)．(理)将数列{3n－1}按“第n组有n个数”的规则分组如下：(1)，(3,9)，(27,81,243)，…，则第100组中的第一个数是() A．34950B．35000C．35010D．35050[答案] A[解析]由“第n组有n个数”的规则分组中，各组数的个数构成一个以1为首项，公差为1的等差数列，前99组数的个数共有(1＋99)992＝4950个，故第100组中的第1个数是34950，选A.5．(2011·太原模拟)已知正数数列{a n}对任意p，q∈N*，都有a p ＋q＝a p·a q，若a2＝4，则a9＝()A．256 B．512C．1024 D．502[答案] B[解析]依题意得a2＝a1·a1＝4，a1＝2(a1＝－2舍去)，a4＝a2·a2＝16，a8＝a4·a4＝16×16＝256，a9＝a1·a8＝2×256＝512，故选B.6．(2010·石狮石光华侨联合中学模拟)已知数列{a n}中，a1＝1，且1a n ＋1＝1a n＋3(n ∈N *)，则a 10＝( ) A ．28 B ．33 C.133 D.128 [答案] D[解析] ∵1a n ＋1－1a n＝3，∴数列⎩⎨⎧⎭⎬⎫1a n 是首项为1a 1＝1，公差为3的等差数列，∴1a n＝1＋3(n －1)＝3n －2，∴a n ＝13n －2，∴a 10＝128.7．(2011·合肥三检)已知数列{a n }中，a 1＝12，a n ＋1＝1－1a n(n ≥2)，则a 16＝________.[答案] 12[解析] 由题可知a 2＝1－1a 1＝－1，a 3＝1－1a 2＝2，a 4＝1－1a 3＝12，∴此数列是以3为周期的周期数列，a 16＝a 3×5＋1＝a 1＝12.8．(2011·吉林部分中学质量检测)已知数列{a n }的前n 项和S n ＝2n －3，则数列{a n }的通项公式为________．[答案] a n ＝⎩⎪⎨⎪⎧－1，n ＝12n －1，n ≥2[解析] 当n ≥2时，a n ＝S n －S n －1＝2n －1，当n ＝1时，a 1＝S 1＝－1，所以a n ＝⎩⎪⎨⎪⎧－1，n ＝12n －1，n ≥2.1.由1开始的奇数列，按下列方法分组：(1)，(3,5)，(7,9,11)，…，第n 组有n 个数，则第n 组的首项为( )A ．n 2－nB ．n 2－n ＋1C ．n 2＋nD ．n 2＋n ＋1 [答案] B[解析] 前n －1组共有1＋2＋…＋(n －1)＝(n －1)(n －1＋1)2＝n (n －1)2个奇数，故第n 组的首项为2×n (n －1)2＋1＝n 2－n ＋1. [点评] 可直接验证，第2组的首项为3，将n ＝2代入可知A 、C 、D 都不对，故选B.2．下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案，则按此规律第n 个图案中需用黑色瓷砖的块数为(用含n 的代数式表示)()A ．4nB ．4n ＋1C ．4n －3D ．4n ＋8 [答案] D[解析] 第(1)，(2)，(3)个图案黑色瓷砖数依次为3×5－3＝12；4×6－2×4＝16；5×7－3×5＝20，代入选项验证可得答案为D.3．(文)设数列{a n }的前n 项和为S n ，且S n ＝2(a n －1)，则a 3＝( )A ．8B ．4C ．2D ．1 [答案] A[解析] 由S 1＝2(a 1－1)得a 1＝2；由S 2＝2(a 2－1)得a 2＝4.由S 3＝2(a 3－1)得，a 3＝8.(理)(2011·三亚联考)已知数列{a n }的通项公式为a n ＝log 3nn ＋1(n∈N *)，设其前n 项和为S n ，则使S n <－4成立的最小自然数n 等于( )A ．83B ．82C ．81D ．80 [答案] C[解析] ∵a n ＝log 3nn ＋1＝log 3n －log 3(n ＋1)，∵S n ＝log 31－log 32＋log 32－log 33＋…＋log 3n －log 3(n ＋1)＝－log 3(n ＋1)<－4，解得n >34－1＝80.4．(文)在数列{a n }中，已知a n ＋1＋a n －1＝2a n (n ∈N ＋，n ≥2)，若平面上的三个不共线的向量OA →、OB →、OC →，满足OC →＝a 1005OA →＋a 1006OB →，三点A 、B 、C 共线，且直线不过O 点，则S 2010等于( )A ．1005B ．1006C ．2010D ．2011 [答案] A[解析] 由条件知{a n }成等差数列， ∵A 、B 、C 共线，∴a 1005＋a 1006＝1，∴S 2010＝2010(a 1＋a 2010)2＝1005(a 1005＋a 1006)＝1005.(理)(2011·太原模考)设数列{a n }满足a 1＋2a 2＝3，且对任意的n∈N *，点列{P n (n ，a n )}恒满足P n P n ＋1＝(1,2)，则数列{a n }的前n 项和S n 为( )A ．n (n －43)B ．n (n －34)C ．n (n －23)D ．n (n －12)[答案] A[解析] 设P n ＋1(n ＋1，a n ＋1)，则P n P n ＋1＝(1，a n ＋1－a n )＝(1,2)，即a n ＋1－a n ＝2，所以数列{a n }是以2为公差的等差数列．又a 1＋2a 2＝3，所以a 1＝－13，所以S n ＝n (n －43)，选A.5．(2010·河东区模拟)设数列{a n }的前n 项和为S n ，对于所有n∈N *，S n ＝a 1(3n－1)2，且a 4＝54，则a 1＝______.[答案] 2[解析] a 4＝S 4－S 3＝40a 1－13a 1＝27a 1＝54， ∴a 1＝2.6．已知数列{a n }的各项均为正数，S n 为其前n 项和，对于任意的n ∈N *满足关系式2S n ＝3a n －3.(1)求数列{a n }的通项公式；(2)设数列{b n }的通项公式是b n ＝1log 3a n ·log 3a n ＋1，前n 项和为T n ，求证：对于任意的正数n ，总有T n <1.[解析] (1)由已知得⎩⎪⎨⎪⎧2S n ＝3a n －32S n －1＝3a n －1－3(n ≥2)．故2(S n －S n －1)＝3a n －3a n －1，故a n ＝3a n －1(n ≥2)． 故数列{a n }为等比数列，且公比q ＝3.又当n ＝1时，2a 1＝3a 1－3，∴a 1＝3.∴a n ＝3n .(2)证明：b n ＝1n (n ＋1)＝1n －1n ＋1.∴T n ＝b 1＋b 2＋…＋b n＝⎝ ⎛⎭⎪⎫1－12＋⎝ ⎛⎭⎪⎫12－13＋…＋⎝ ⎛⎭⎪⎫1n －1n ＋1 ＝1－1n ＋1<1. 7．(文)(2010·福建文)数列{a n }中，a 1＝13.前n 项和S n 满足S n ＋1－S n ＝(13)n ＋1(n ∈N *)．(1)求数列{a n }的通项公式a n 以及前n 项和S n ；(2)若S 1，t (S 1＋S 2)，3(S 2＋S 3)成等差数列，求实数t 的值． [解析] (1)由S n ＋1－S n ＝(13)n ＋1得a n ＋1＝(13)n ＋1(n ∈N *)又a 1＝13，故a n ＝(13)n(n ∈N *)从而S n ＝13×[1－(13)n ]1－13＝12[1－(13)n](n ∈N *)(2)由(1)可得S 1＝13，S 2＝49，S 3＝1327从而由S 1，t (S 1＋S 2)，3(S 2＋S 3)成等差数列可得 13＋3×(49＋1327)＝2×(13＋49)t ，解得t ＝2. (理)(2010·吉林市质检)已知数列{a n }的前n 项和为S n ，a 1＝1，且3a n ＋1＋2S n ＝3(n 为正整数)．(1)求出数列{a n }的通项公式；(2)若对任意正整数n ，k ≤S n 恒成立，求实数k 的最大值．[解析] (1)∵3a n ＋1＋2S n ＝3① ∴当n ≥2时，3a n ＋2S n －1＝3② 由①－②得，3a n ＋1－3a n ＋2a n ＝0. ∴a n ＋1a n＝13 (n ≥2)．又∵a 1＝1,3a 2＋2a 1＝3，解得a 2＝13.∴数列{a n }是首项为1，公比q ＝13的等比数列．∴a n ＝a 1qn －1＝⎝ ⎛⎭⎪⎫13n －1(n 为正整数) (2)由(1)知，∴S n ＝32⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫13n由题意可知，对于任意的正整数n ，恒有 k ≤32⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫13n ， ∵数列⎩⎨⎧⎭⎬⎫1－⎝ ⎛⎭⎪⎫13n 单调递增，当n ＝1时，数列取最小项为23，∴必有k ≤1，即实数k 的最大值为1.1．已知数列{a n }中，a 1＝1，a n ＋1＝2a na n ＋2(n ∈N *)，则a 5等于( ) A.25 B .13 C.23 D .12 [答案] B[解析] 由a 1＝1，a n ＋1＝2a n a n ＋2得，a 2＝23，a 3＝12，a 4＝25，a 5＝13.2．已知数列{a n }的前n 项和为S n ，且有a 1＝3,4S n ＝6a n －a n －1＋4S n －1(n ≥2)，则a n ＝( )A ．3×2n －1B ．3×21－nC ．3×2nD ．3×2－n [答案] B[解析] 4(S n －S n －1)＝4a n ＝6a n －a n －1， ∴a n a n －1＝12(n ≥2)，∴a n ＝a 1⎝ ⎛⎭⎪⎫12n －1＝3×21－n .3．(2011·福州一模)把1,3,6,10,15,21这些数叫做三角形数，这是因为这些数目的点子可以排成一个正三角形(如图所示)．则第七个三角形数是( ) A ．27 B ．28 C ．29 D ．30 [答案] B[分析] 观察三角形数的增长规律，可以发现每一项与它的前一项多的点数正好是本身的序号，所以根据这个规律计算即可．[解析] 根据三角形数的增长规律可知第七个三角形数是1＋2＋3＋4＋5＋6＋7＝28.4．(2010·烟台模拟)若数列{a n }满足a n ＋1＝⎩⎪⎨⎪⎧2a n (0≤a n <12)2a n －1(12≤a n <1)，且a 1＝67，则a 2011的值为( )A.67 B .57C.37 D .17[答案] A[解析] 由a 1＝67∈[12，1)知，a 2＝2×67－1＝57；由57∈[12，1)知，a 3＝2×57－1＝37；由37∈[0，12)知，a 4＝2×37＝67；…于是可知，数列{a n }是周期为3的数列，∴a 2011＝a 1＝67.故选A. [点评] 根据数列的通项公式求数列的某些特定项，一般需要研究数列的周期性，因此求解这类问题时，首先列举数列的前若干项，发现数列的周期性，再利用周期性求解．5．如图所示的程序框图，如果输入值为2010，则输出值为________．[答案] －4[解析] 此程序框图计算数列{a n }的第n 项，并输出，其中a 1＝1，a2＝5，a n＋2＝a n＋1－a n依次计算可得数列的项为：1,5,4，－1，－5，－4,1,5,4，故该数列周期为6，又2010＝335×6，∴a2010＝a6＝－4.6．(2010·山东济宁模拟)已知数列2008,2009,1，－2008，－2009，…这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前2011项之和S2011等于________．[答案]2008[解析]由题意a n＋1＋a n－1＝a n(n≥2)，a n＋a n＋2＝a n＋1，两式相加得a n＋2＝－a n－1，∴a n＋3＝－a n，∴a n＋6＝a n，即{a n}是以6为周期的数列．∵2011＝335×6＋1，a1＋a2＋a3＋a4＋a5＋a6＝0，∴a1＋a2＋…＋a2011＝335×0＋a1＝2008.。

阶段性测试题十(算法框图与复数)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分150分。

考试时间120分钟。

第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．)1．(2011～2012·某某市质检、某某一模)设复数z 满足(1＋i)z ＝2，其中i 为虚数单位，则z ＝( )A ．1＋iB ．1－iC ．2＋2iD ．2－2i [答案] B[解析]z ＝21＋i ＝21－i 1＋i 1－i＝1－i.2．(文)(2011～2012·哈师大附中、东北师大附中、某某省实验中学模拟)复数z ＝2－i2＋i，则z 的虚部是( )A.45B ．－45 C.45i D ．－45i [答案] B[解析]z ＝2－i 2＋i ＝2－i 22＋i 2－i ＝3－4i 5，∴虚部为－45.(理)复数z 1＝3＋i ，z 2＝1－i ，则复数z 1＋1z 2的虚部为( )A ．2B ．2i C.32D.32i [答案] C[解析]z 1＋1z 2＝3＋i ＋11－i＝3＋i ＋1＋i 1－i 1＋i ＝3＋i ＋1＋i 2＝72＋32i ，∴虚部为32.3．(文)(2011～2012·某某名校联考)复数2－ii (i 为虚数单位)的共轭复数是( )A ．－1＋2iB ．－1－2iC ．1－2iD ．1＋2i [答案] A [解析]∵2－ii＝2－i ·ii2＝－1－2i ， ∴共轭复数为－1＋2i ，故选A.(理)(2011～2012·某某五校联盟模拟)已知复数z ＝a ＋b i(a 、b ∈R )，z －是z 的共轭复数，且z －＝(2＋i)(3－i)，则a 、b 的值分别为( )A ．7,1B ．6，－1C ．7，－1D ．6,1 [答案] C[解析] (2＋i)(3－i)＝7＋i ，z －＝a －b i ， ∵a －b i ＝7＋i ，a 、b ∈R ， ∴a ＝7，b ＝－1.4．(文)(2011～2012·湄潭中学第一学期期末)若复数(1＋a i)(2＋i)＝3－i ，则实数a 的值为( )A ．1B ．－1C ．±2 D．－2 [答案] B[解析]∵(1＋a i)(2＋i)＝(2－a )＋(2a ＋1)i ，∴⎩⎪⎨⎪⎧2－a ＝32a ＋1＝－1，∴a ＝－1.(理)(2011～2012·延边州质检)已知复数z 的共轭复数z －的实部为－1，虚部为－2，且z i ＝a ＋b i(a ，b ∈R )，则a ＋b ＝( )A ．－4B ．－3C ．－1D ．1 [答案] B[解析] 由条件知z －＝－1－2i ，∴z ＝－1＋2i ， ∴z i ＝－i －2，∵z i ＝a ＋b i(a 、b ∈R )， ∴a ＝－2，b ＝－1，∴a ＋b ＝－3.5．(文)(2011～2012·某某某某市一模)已知复数z ＝(a 2－1)＋(a －2)i ，(a ∈R )，则“a＝1”是“z 为纯虚数”的( )A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分也非必要条件 [答案] A[解析]a ＝1时，z ＝－i 是纯虚数；a ＝－1时，z ＝－3i 也是纯虚数，故选A. (理)(2011～2012·石景山区期末)已知复数z ＝1＋i1－i ，则复数z 的模为( )A ．2 B. 2 C ．1 D ．0 [答案] C[解析]z ＝1＋i 1－i ＝1＋i 21－i 1＋i ＝2i2＝i ，∴|z |＝1.6．如图所示，输出的n 为( )A ．10B ．11C ．12D ．13 [答案] D[解析] 程序依次运行过程为：n ＝0，S ＝0→n ＝1，S ＝S ＋12×1－13＝－111→n ＝2，S＝S ＋12×2－13＝－111－19，……∴S ＝－111－19－17－15－13－1＋1＋13＋15＋17＋19＋111＋113>0，此时输出n 的值13.7．(文)(2011～2012·某某某某中学调研)已知流程图如图所示，该程序运行后，为使输出b 的值为16，则循环体的判断框内①处应填的是( )A ．3B ．2C ．4D ．16 [答案] A[解析]a ＝1，b ＝1判断后得b ＝21＝2，a ＝1＋1＝2，再次判断后得b ＝22＝4，a ＝2＋1＝3，再次判断后得b ＝24＝16，a ＝3＋1＝4，这时经过判断满足条件，输出b 的值16，∴a >3.(理)(2011～2012·某某市一测)如图给出的是计算12＋14＋16＋…＋12012的值的一个程序框图，则判断框内应填入的条件是( )A ．i ≤1005 B．i >1005 C ．i ≤1006 D．i >1006 [答案] C[解析]i ＝1时，S ＝0＋12，i ＝2时，S ＝12＋14，……i ＝1006时，S ＝12＋14＋16＋…＋12012， 故当i ＝1007时，跳出循环，故条件为i ≤1006. 8．(文)(2011～2012·某某一中月考)在复平面内，复数2i1－i对应的点在( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 [答案] B[解析]2i 1－i ＝2i 1＋i1－i 1＋i ＝i(1＋i)＝－1＋i ，对应点(－1,1)在第二象限．(理)(2011～2012·某某市二模)已知复数a －ii－i 在复平面内对应的点在二、四象限的角平分线上，则实数a ＝( )A ．－2B ．－1C ．0D ．2 [答案] A [解析]a －ii－i ＝i a －ii2－i＝－a i －1－i ＝－1＋(－1－a )i ， 由条件知，－1＋(－1－a )＝0，∴a ＝－2.9．(2011～2012·某某师大附中模拟)若输入数据n ＝6，a 1＝－2，a 2＝－2.4，a 3＝1.6，a 4＝5.2，a 5＝－3.4，a 6＝4.6，执行下面如图所示的算法程序，则输出结果为( )A ．0.6B ．0.7C ．0.8D ．0.9 [答案] A[解析] 由程序框图知，i ＝1时，S ＝0×0＋a 11＝a 1，i ＝2时，S ＝2－1·a 1＋a 22＝a 1＋a 22，i ＝3时，S ＝3－1·a 1＋a 22＋a 33＝a 1＋a 2＋a 33，……由此可见最后输出的S 的值是输入的6个数a 1，a 2，…，a 6的平均数， ∵16(a 1＋a 2＋…＋a 6)＝16(－2－2.4＋1.6＋5.2－3.4＋4.6)＝0.6， ∴输出S 的值为0.6.10．(2011～2012·某某师大附中模拟)设i是虚数单位，则复数(3＋i1－3i)2012＝( ) A．－i B．－1C．1 D．i[答案] C[解析]∵3＋i1－3i ＝3＋i1＋3i1－3i1＋3i＝4i4＝i，∴原式＝i2012＝i4＝1.11．(2011～2012·某某市二模)执行下面的程序框图，若输入n＝6，m＝4，那么输出的值等于( )A．720 B．360C．240 D．120[答案] B[解析]程序运行过程依次为：n＝6，m＝4，k＝1，p＝1，p＝1×(6－4＋1)＝3，k<4满足→k＝2，p＝3×(6－4＋2)＝12，k<4满足→k＝3，p＝12×(6－4＋3)＝60，k<4满足→k＝4，p＝60×(6－4＋4)＝360，此时k<4不成立，输出p的值360后结束．12．(2011～2012·某某、某某、某某二调)如果执行下面的框图，输入N＝12，则输出的数等于( )A.2425B.1327C.1225D.1123[答案] B[解析] 程序运行过程依次为：N ＝12，k ＝1，S ＝0，S ＝0＋11×3，k ≤12满足→k ＝2时，S ＝11×3＋13×5，k ≤12满足→……→k ＝12时，S ＝11×3＋13×5＋…＋123×25，k ≤12满足→k ＝13时，S ＝11×3＋13×5＋…＋125×27，k ≤12不成立，此时输出S 的值应为S ＝11×3＋13×5＋…＋125×27＝12[(1－13)＋(13－15)＋…＋(125－127)]＝12×(1－127)＝1327，故选B.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题，每小题4分，共16分，把正确答案填在题中横线上．) 13．(2011～2012·某某市调研)下图是求函数值的程序框图，当输入值为2时，则输出值为________．[答案] －3[解析]∵输入值x ＝2>0，∴y ＝5－4×2＝－3，故输出y 的值为－3.14．(2011～2012·某某八市联考)已知i 是虚数单位，计算2＋i23－4i 的结果是________．[答案] －725＋2425i[解析]∵(2＋i)2＝4＋4i －1＝3＋4i ，∴原式＝3＋4i3－4i＝3＋4i 23－4i 3＋4i＝9＋24i －1625＝－725＋2425i. 15．(文)(2011～2012·某某名校联考)如图是某程序框图，则最后输出的S 的值为________．[答案]30[解析]程序运行过程为：S＝0，i＝1，S＝0＋12＝1，i＝1＋1＝2；判断i>4不满足，返回进行第二次循环，S＝1＋22＝5，i＝2＋1＝3，i>4仍不满足，再循环，S＝5＋32＝14，i＝3＋1＝4，i>4仍不满足，再循环，S＝14＋42＝30，i＝4＋1＝5，此时满足i>4输出S 的值30后结束．(理)(2011～2012·襄阳调研)阅读下图所示的程序框图，若输入的n是100，则输出的变量S的值是________．[答案]5049[解析] 第一次循环，S ＝100，n ＝99，第二次循环，S ＝100＋99，n ＝98，第三次循环，S ＝100＋99＋98，n ＝97，……，n ＝2时，不满足n <2，再进行一次循环，S ＝100＋99＋…＋2，n ＝1，此时满足n <2，输出S 的值，这时S ＝100＋99＋…＋2＝99×100＋22＝5049.16．(文)(2011～2012·某某某某市高三期末)在如图所示的算法框图中，若输入m ＝4，n ＝3，则输出a ＝________.[答案] 12[解析] 运行过程为： 开始→m ＝4，n ＝3，i ＝1a ＝4×1＝4,3不能整除4→i ＝2 a ＝4×2＝8,3不能整除8→i ＝3，a ＝4×3＝12,3能整除12→输出a 的值12后结束．(理)(2011～2012·某某某某市期末)执行如图所示的程序框图，其输出的结果是________．[答案] －54[解析] 程序运行过程为：y ＝4，x ＝4，y ＝12×4－1＝1，|y －x |＝3<1不成立→x ＝1，y ＝12×1－1＝－12，|y －x |＝32<1不成立→x ＝－12，y ＝12×(－12)－1＝－54，|y －x |＝34<1成立→此时跳出循环，输出y 的值－54后结束．三、解答题(本大题共6个小题，共74分，解答应写出文字说明，证明过程或演算步骤．)17．(本小题满分12分)已知复数z ＝a 2－4a ＋3a ＋2＋(a 3＋a 2－2a )i(a ∈R )，试某某数a 分别取何值时，(1)z 为实数；(2)z 为虚数；(3)z 为纯虚数． [解析] (1)∵z 为实数，∴a 3＋a 2－2a ＝0， ∴a ＝0，－2或1， 又a ＋2≠0，∴a ＝0或1.(2)∵z 为虚数，∴a 3＋a 2－2a ≠0， ∴a ≠0，－2,1.(3)∵z 为纯虚数，∴⎩⎪⎨⎪⎧a 2－4a ＋3a ＋2＝0a 3＋a 2－2a ≠0，∴a ＝3.18．(本小题满分12分)画程序框图(1)计算并输出1,1＋2,1＋2＋3，…，1＋2＋3＋…＋100各项的值； (2)计算1＋(1＋2)＋(1＋2＋3)＋…＋(1＋2＋3＋…＋100)的值．[分析] (1)和(2)都要依次计算1＋2,1＋2＋3,1＋2＋…＋100的值，(1)中要求每计算一个值输出一个，(2)中要求把各值计算出来后，相加，把最后结果输出，故(1)中须在循环体中加输出框，(2)只要最后加一个输出框即可．[解析] (1)(2)19．(本小题满分12分)(文)试分析方程x 2－(4－2i)x ＋3－2i ＝0是否有实根？并解方程．[解析] 设x 0是方程x 2－(4－2i)x ＋3－2i ＝0的实根，则x 20－(4－2i)x 0＋3－2i ＝0. 整理得(x 20－4x 0＋3)＋(2x 0－2)i ＝0，则⎩⎪⎨⎪⎧x 20－4x 0＋3＝02x 0－2＝0，解得x 0＝1.因此方程有实数根x ＝1，将原方程分解因式得(x －1)(x －3＋2i)＝0，∴方程的两个解为x 1＝1，x 2＝3－2i.(理)设关于x 的方程x 2－(tan θ＋i)x －(2＋i)＝0. (1)若方程有实数根，求锐角θ和实数根． (2)证明：对任意θ≠k π＋π2(k ∈Z )，方程无纯虚数根． [解析] (1)设实数根为a ，则a 2－(tan θ＋i)a －(2＋i)＝0即a 2－a tan θ－2－(a ＋1)i ＝0，∴⎩⎪⎨⎪⎧a 2－a tan θ－2＝0a ＋1＝0，∴a ＝－1，tan θ＝1，∵0<θ<π2，∴θ＝π4.(2)设方程存在纯虚数根b i(b ∈R ，b ≠0)则 (b i)2－(tan θ＋i)b i －(2＋i)＝0，∴⎩⎪⎨⎪⎧－b 2＋b －2＝0b tan θ＋1＝0此方程组无实数根，所以对任意θ≠k π＋π2(k ∈Z )，方程无纯虚数根．20．(本小题满分12分)设S 是如图所示程序框图输出的数x 为元素的集合，m ，n ∈S .(1)记“使得m ＋n ＝0成立的有序数组．．．．(m ，n )”为事件A ，试列举A 包含的基本事件，并求A 的概率．(2)(理)设ξ＝m 2，求ξ的分布列及其数学期望E (ξ)．[解析]∵x ＝－2时，x 2－x －6＝0，∴程序框图输出的数x 是不等式x 2－x －6≤0的整数解．∵x 2－x －6≤0，∴－2≤x ≤3， ∴S ＝{－2，－1,0,1,2,3}． (1)由于m ，n ∈S ，且m ＋n ＝0， 所以A 包含的基本事件为：(－2,2)，(2，－2)，(－1,1)，(1，－1)，(0,0)，m ，n ∈S 的所有基本事件(m ，n )，共有6×6＝36个，∴事件A 的概率P (A )＝536.(2)由于m 的所有不同取值为－2，－1,0,1,2,3， 所以ξ＝m 2的所有不同取值为0,1,4,9，且有P (ξ＝0)＝16，P (ξ＝1)＝26＝13，P (ξ＝4)＝26＝13，P (ξ＝9)＝16.故ξ的分布列为所以E (ξ)＝0×6＋1×3＋4×3＋9×6＝6.21．(本小题满分12分)有一个均匀的正四面体，它的四个面上分别标有数字0,1，－1,2，现随机投掷两次，记第一次向下一面上的数字为a ，第二次向下一面上的数字为b ，记z ＝a ＋b i(i 为虚数单位)．(1)求z 为纯虚数的概率．(2)求z 在复平面内的对应点在第二象限的概率． (3)若|z |＝2，称z 为“好数”，求所有好数的和与积．[解析]a 的可能取值有4个，b 的可能取值也有4个，所有(a ，b )的取法，共有4×4＝16种．(1)记“z 为纯虚数”为事件A ，z 为纯虚数时，a ＝0，b ≠0，这样的(a ，b )有(0,1)，(0，－1)，(0,2)共3个，∴所求概率P (A )＝316.(2)设“z 在复平面内的对应点在第二象限”为事件B ，则事件B 包含的基本事件有：(－1,1)，(－1,2)共2个，∴P (B )＝216＝18.(3)满足|z |＝2的复数有：1＋i,1－i ，－1＋i ，－1－i ， 它们的和为(1＋i)＋(1－i)＋(－1＋i)＋(－1－i)＝0， 它们的积为(1＋i)(1－i)(－1＋i)(－1－i)＝2×2＝4.22．(本小题满分14分)已知数列{a n }的各项全为正数，观察流程图，当k ＝2时，S ＝14；当k ＝5时，S ＝413.(1)写出k ＝4时，S 的表达式；(用a 1，a 2，a 3，a 4，…表示) (2)求{a n }的通项公式；(3)令b n ＝2na n ，求b 1＋b 2＋…＋b n . [解析] (1)当k ＝4时，S ＝1a 1a 2＋1a 2a 3＋1a 3a 4.(2)由流程图中a i ＋1＝a i ＋d 提供的信息知，{a n }是一个等差数列， 设其公差为d ，依题意d ≠0. 当k ＝2时，S ＝1a 1a 2＝14； 当k ＝5时，S ＝1a 1a 2＋1a 2a 3＋1a 3a 4＋1a 4a 5＝1d (1a 1－1a 5)＝413， 所以⎩⎪⎨⎪⎧a 1a 2＝41d a 5－a 1a 1a 5＝413，即⎩⎪⎨⎪⎧a 1a 1＋d ＝4，a 1a 1＋4d ＝13，解得a 1＝1，d ＝3，即a n ＝a 1＋(n －1)d ＝3n －2. (3)设T n ＝b 1＋b 2＋…＋b n ，则T n ＝1·21＋4·22＋7·23＋…＋(3n －2)·2n，① 2·T n ＝1·22＋4·23＋7·24＋…＋(3n －2)·2n ＋1，②①－②，得－T n ＝1·21＋3·22＋3·23＋…＋3·2n －(3n －2)·2n ＋1＝2＋121－2n －11－2－(3n －2)·2n ＋1，所以T n ＝(3n －5)·2n ＋1＋10.1．(2011～2012·某某一模)已知程序框图如图所示，若曲线E 的方程为ax 2＋by 2＝ab (a ，b ∈R )，该程序输出的结果为s ，则( ) A ．当s ＝1时，E 是椭圆 B ．当s ＝－1时，E 是双曲线 C ．当s ＝0时，E 是抛物线 D ．当s ＝0时，E 是一个点 [答案] B[解析] 当S ＝1时，c ＝ab >0，∴若a ，b 同为正且a ≠b ，则方程ax 2＋by 2＝ab 表示椭圆，否则E 不是椭圆；当S ＝－1时，c ＝ab <0，∴方程x 2b ＋y 2a ＝1表示双曲线；当S ＝0时，c ＝ab ＝0，∴a ＝0或b ＝0，无论哪种情形，E 都不是抛物线，当a ＝0，b ≠0时，方程化为by 2＝0，∴y ＝0，它表示一条直线，故A 、C 、D 都错，选B.2．(2011～2012·哈师大附中、东北师大附中、某某省实验中学联考)某程序框图如图所示，则输出的结果是________．[答案] －13[解析] 程序运行过程依次为S ＝2，n ＝1，S ＝1－21＋2＝－13，n ＝1＋1＝2，判断n ≥100不成立→S ＝1－－131＋－13＝2，n ＝2＋1＝3，判断n ≥100不成立→S ＝1－21＋2＝－13，n ＝3＋1＝4，…，可见S 的值成周期出现，周期为2，n 为奇数时，计算得到S ＝－13，n 为偶数时，计算得到S ＝2，n ＝99时n ≥100不成立，计算得S ＝－13，n ＝100，此时满足n ≥100，输出S ＝－13.。

阶段性测试题一(集合与函数)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分150分。

考试时间120分钟。

第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．)1．(文)(2011～2012·黄冈市期末)已知集合A ＝{x ||x |＝－x }，B ＝{0，－1，－2，－3}，则( )A ．AB B ．BAC ．A ∪B ＝BD ．A ∩B ＝∅ [答案] B[解析]A ＝{x ||x |＝－x }＝{x |x ≤0}，B ＝{0，－1，－2，－3}，∴B A ，故选B. (理)(2011～2012·哈师大附中、东北师大附中、某某省实验中学联考)设集合A ＝{x |－x 2－3x >0}，B ＝{x |x <－1}，则A ∩B ＝( )A ．{x |－3<x <－1}B ．{x |－3<x <0}C ．{x |x <－1}D ．{x |x >0} [答案] A[解析]∵A ＝{x |－x 2－3x >0}＝{x |－3<x <0}， ∴A ∩B ＝{x |－3<x <－1}．2．(文)(2011～2012·某某某某市期末)若f (x )＝1log 122x －1，则f (x )的定义域为( )A ．(12，1)B ．(12，1]C ．(12，＋∞) D．(1，＋∞)[答案] A[解析] 要使f (x )有意义，应有log 12 (2x －1)>0，∴0<2x －1<1，∴12<x <1，故选A.(理)(2011～2012·某某重点中学一模)函数f (x )＝3x23x ＋1＋2lg(1－x )的定义域是( )A ．(－13，＋∞) B．(－13，1)C ．(－13，13)D ．(－∞，－13)[答案] B[解析] 要使函数f (x )有意义，应有⎩⎪⎨⎪⎧3x ＋1>0，1－x >0，∴－13<x <1.故选B.3．(文)(2011～2012·黄冈市期末)设n ∈{－1，12，1,2,3}，则使得f (x )＝x n为奇函数，且在(0，＋∞)上单调递减的n 的个数为( )A ．1B ．2C ．3D ．4 [答案] A[解析]f (x )＝x n为奇函数，则n ＝－1,1或3，又f (x )在(0，＋∞)上单调递减，∴n ＝－1，故选A.(理)(2011～2012·上学期某某市质检)下列函数中既是奇函数，又在区间(－1,1)上是增函数的为( )A ．y ＝|x |B ．y ＝sin xC ．y ＝e x ＋e －xD ．y ＝－x 3[答案] B[解析]y ＝|x |是偶函数，y ＝e x＋e －x为偶函数，y ＝－x 3是减函数，故选B.4．(文)(2011～2012·某某省重点中学一模)设集合U ＝{－2，－1,0,1,2}，A ＝{1,2}，B ＝{－2，－1,2}，则A ∪(∁U B )＝( )A ．{0,1,2}B ．{1,2}C ．{2}D ．{1} [答案] A[解析]∵∁U B ＝{0,1}，∴A ∪(∁U B )＝{0,1,2}，故选A.(理)(2011～2012·石景山区期末)设集合U ＝{1,2,3,4}，A ＝{1,2}，B ＝{2,4}，则∁U (A ∪B )＝( )A ．{3}B ．{2}C ．{1,2,4}D ．{1,4} [答案] A[解析]A ∪B ＝{1,2,4}，∴∁U (A ∪B )＝{3}．5．(2011～2012·上学期某某市期末)已知f (x )＝⎩⎪⎨⎪⎧cosπxx ≤0f x －1＋1 x >0，则f (43)＋f (－43)的值为( )A.12B ．－12 C ．－1 D ．1 [答案] D[解析]∵－43<0，∴f (－43)＝cos(－4π3)＝cos(－2π＋2π3)＝cos 2π3＝－12，又∵43>0，∴f (43)＝f (43－1)＋1＝f (13)＋1＝f (13－1)＋1＋1＝f (－23)＋2＝cos(－2π3)＋2＝－12＋2＝32，∴原式＝－12＋32＝1.6．实数a ＝0.32，b ＝log20.3，c ＝(2)0.3的大小关系正确的是( )A ．a <c <bB ．a <b <cC ．b <a <cD ．b <c <a [答案] C[解析]a ＝0.32<0.30＝1，∴0<a <1，b ＝log 20.3<log21＝0，c ＝(2)0.3>(2)＝1，∴b <a <c .7．(文)(2011～2012·豫南九校联考)函数f (x )＝(13)x－x 的零点所在区间为( )A ．(0，13)B ．(13，12)C ．(12，1) D ．(1,2)[答案] B[解析]f (0)＝1>0，f (13)＝393－33>0，f (12)＝33－22<0，知f (x )的零点所在区间为(13，12)． (理)(2011～2012·某某五校联盟模拟)若方程ln x ＋x －4＝0在区间(a ，b )(a ，b ∈Z ，且b －a ＝1)上有一根，则a 的值为( )A ．1B ．2C ．3D ．4 [答案] B[解析]∵a 、b ∈Z ，b －a ＝1，∴a 、b 是相邻的两个整数，令f (x )＝ln x ＋x －4，则f (1)＝－3<0，f (2)＝ln2－2<0，f (3)＝ln3－1>0，∴f (x )在(2,3)上存在零点，即方程ln x ＋x －4＝0在(2,3)上有根，又f (x )为增函数，∴方程ln x ＋x －4＝0在(2,3)上有且仅有一根，∴a ＝2.8．(2011～2012·某某市期末)把函数y ＝cos x －3sin x 的图象向左平移m (m >0)个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是( )A.π6B.π3 C.2π3D.5π6[答案] C[解析]y ＝cos x －3sin x ＝2cos(x ＋π3)的图象向右平移π3个单位得到图象对应函数y ＝2cos x 为偶函数，故若左移m 个单位后所得图象关于y 轴对称，则m 最小值为π－π3＝2π3(注意此函数的半个周期为π)．9．(文)(2011～2012·某某省重点中学一模)设a >1，函数f (x )＝a |x |的图象大致是( )[答案] A[解析]f (x )＝a |x |＝⎩⎪⎨⎪⎧a x x ≥01axx <0，∵a >1，∴x ≥0时，f (x )＝a x单调递增，x <0时，f (x )单调递减，且f (0)＝1，故选A. (理)(2011～2012·东营市期末、某某一模)函数y ＝x 12－1的图象关于x 轴对称的图象大致是( )[答案] B[解析] 解法一：在函数y ＝x 12－1中，x ＝1时，y ＝0；x ＝0时，y ＝－1，故其关于x 轴对称的函数图象过(1,0)，(0,1)点，故选B.解法二：y ＝x 12－1可由y ＝x 的图象向下平移一个单位得到，再将其关于x 轴对称知选B.10．(文)(2011～2012·某某襄阳市调研)下列函数中，既是偶函数又在(0，＋∞)单调递增的函数是( )A ．y ＝x 3B ．y ＝|x |＋1C ．y ＝－x 2＋1 D ．y ＝2－|x |[答案] B[解析] 由函数为偶函数排除A ，由函数在(0，＋∞)上单调递增，排除C 、D ，故选B. (理)(2011～2012·某某苍山县期末)设函数f (x )，对任意的实数x 、y ，有f (x ＋y )＝f (x )＋f (y )，且当x >0时，f (x )<0，则f (x )在区间[a ，b ]上( )A ．有最大值f (a ＋b2) B ．有最小值f (a ＋b2)C ．有最大值f (a )D ．有最小值f (a ) [答案] C[解析] 令x ＝y ＝0得f (0)＝0，令y ＝－x 得f (0)＝f (x )＋f (－x )，∴f (－x )＝－f (x )，∴f (x )为奇函数，∵x >0时，f (x )<0，设a ≤x 1<x 2≤b ，则f (x 2)－f (x 1)＝f (x 2)＋f (－x 1)＝f (x 2－x 1)<0，∴f (x 1)>f (x 2)，∴f (x )在区间[a ，b ]上为减函数，故f (x )在[a ，b ]上有最大值f (a )，选C.11．(2011～2012·某某某某市质检)函数f (x )的定义域为R ，且满足f (x )是偶函数，f (x －1)是奇函数，若f (0.5)＝9，则f (8.5)等于( )A ．－9B ．9C ．－3D ．0 [答案] B[解析]∵f (x )是偶函数，∴f (－x )＝f (x )， ∵f (x －1)是奇函数，∴f (－x －1)＝－f (x －1)，∴f (x ＋1)＝－f (x －1)，在此式中以x ＋1代替x 得f (x ＋2)＝－f (x )， ∴f (x ＋4)＝－f (x ＋2)＝f (x )，∴f (x )的周期为4， ∴f (8.5)＝f (0.5)＝9.[点评] 令F (x )＝f (x －1)，∵F (x )为奇函数， ∴F (－x )＝－F (x )，∴f (－x －1)＝－f (x －1)．12．(文)若关于x 的方程log 12 x ＝m1－m 在区间(0,1)上有解，则实数m 的取值X 围是( )A ．(0,1)B ．(1,2)C ．(－∞，1)∪(2，＋∞)D ．(－∞，0)∪(1，＋∞) [答案] A[分析] 要使方程有解，只要m 1－m 在函数y ＝log 12x (0<x <1)的值域内，即m1－m>0. [解析]∵x ∈(0,1)，∴log 12 x >0，∴m1－m>0，∴0<m <1. (理)(2011～2012·某某师大附中模拟)设直线x ＝t 与函数f (x )＝x 2，g (x )＝ln x 的图象分别交于点M ，N ，则当|MN |达到最小值时t 的值为( )A ．1 B.12C.22D.52[答案] C[解析] 令F (x )＝x 2－ln x ，则F ′(x )＝2x －1x，令F ′(x )＝0，∵x >0，∴x ＝22，当x >22时，F ′(x )>0，F (x )单调递增，当0<x <22时，F ′(x )<0，F (x )单调递减，∴当x ＝22时，F (x )取到极小值，此时|MN |取到最小值，∴t ＝22. 第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题，每小题4分，共16分，把正确答案填在题中横线上．) 13．(文)已知f (x )＝log a x ，(a >0且a ≠1)满足f (9)＝2，则f (3a)＝________. [答案] 3[解析]∵f (9)＝2，∴log a 9＝2，∴a ＝3，∴f (3a )＝log 33a＝a ＝3.(理)(2011～2012·某某省苍山县期末)若幂函数f (x )的图象经过点A (2,4)，则它在A 点处的切线方程为________．[答案] 4x －y －4＝0[解析] 设f (x )＝x α，∵f (x )的图象过点A (2,4)，∴4＝2α，∴α＝2，∴f (x )＝x 2，∴f ′(x )＝2x ，故点A 处切线的斜率k ＝4，切线方程为y －4＝4(x －2)，即4x －y －4＝0.14．(2011～2012·某某市调研)已知A ，B 均为集合U ＝{2,4,6,8,10}的子集，且A ∩B ＝{4}，(∁U B )∩A ＝{10}，则A ＝________.[答案] {4,10}[解析] 设元素x 0∈A ，若x 0∈B ，则x 0∈A ∩B ，若x 0∉B ，则x 0∈∁U B ，∴x 0∈(∁U B )∩A ；∵A ∩B ＝{4}，(∁U B )∩A ＝{10}，∴A ＝{4,10}．15．(文)若偶函数f (x )满足f (x )＝2x－4(x ≥0)，则当x <0时f (x )<0的解集是________． [答案] (－2,0)[解析] 当x ≥0时，由f (x )＝2x－4<0得0≤x <2， ∵f (x )为偶函数，∴x <0时，由f (x )<0得－2<x <0.(理)(2011～2012·某某某某辅仁中学模拟)函数f (x )＝(|x |－1)(x ＋a )为奇函数，则f (x )的增区间为________．[答案] (－∞，－12]和[12，＋∞)[解析]∵f (x )是奇函数，x ∈R ，∴f (－2)＝－f (2)， ∴a ＝0，∴f (x )＝x (|x |－1)，∴f (x )＝⎩⎪⎨⎪⎧x x －1 x ≥0－x x ＋1 x <0，∴f (x )的单调增区间为(－∞，－12]和[12，＋∞)．16．(文)(2011～2012·某某实验中学四诊)已知f (x )＝1x 2＋1，则f [f (0)]＝________. [答案]12[解析]f (0)＝10＋1＝1，f [f (0)]＝f (1)＝11＋1＝12.(理)(2011～2012·黄冈市模拟)函数f (x )＝⎩⎪⎨⎪⎧1 x >00 x ＝0－1 x <0，g (x )＝x 2f (x －1)(x ∈R )，则函数g (x )的零点个数有________个．[答案] 2[解析]g (x )＝x 2f (x －1)＝⎩⎪⎨⎪⎧x 2x >10 x ＝1－x 2x <1，故零点有2个．三、解答题(本大题共6个小题，共74分，解答应写出文字说明，证明过程或演算步骤．) 17．(本小题满分12分)(文)(2011～2012·某某期末)已知集合A ＝{x |x 2－2x －3≤0}，B ＝{m －3≤x ≤m ＋3，m ∈R }．(1)若A ∩B ＝[2,3]，求m 的值； (2)若A ⊆∁R B ，求m 的取值X 围．[解析] (1)由x 2－2x －3≤0得－1≤x ≤3， ∴A ＝{x |－1≤x ≤3}， 又B ＝{x |m －3≤x ≤m ＋3}，所以由A ∩B ＝[2,3]得m －3＝2，∴m ＝5. (2)∁R B ＝{x |x <m －3或x >m ＋3}，∵A ⊆∁R B ， ∴m ＋3<－1或m －3>3，所以m <－4或m >6.(理)设A ＝{x |x 2＋4x ＝0}，B ＝{x |x 2＋2(a ＋1)x ＋a 2－1＝0}，B ⊆A ，某某数a 的取值X 围．[解析]A ＝{x |x 2＋4x ＝0}＝{0，－4}，因此A 的子集分别为∅，{0}，{－4}，{0，－4}． 又B ⊆A ，若B ＝∅，Δ＝4(a ＋1)2－4(a 2－1)<0，解得a <－1；若B ＝{0}，⎩⎪⎨⎪⎧－2a ＋1＝0，a 2－1＝0，解得a ＝－1；若B ＝{－4}，⎩⎪⎨⎪⎧－2a ＋1＝－8，a 2－1＝16，无解；若B ＝{0，－4}，⎩⎪⎨⎪⎧－2a ＋1＝－4，a 2－1＝0，解得a ＝1；综上所述，实数a 的取值X 围是a ≤－1或a ＝1.18．(本小题满分12分)(文)(2011～2012·某某市调研)经市场调查，某商品在过去100天内的销售量和价格均为时间t (天)的函数，且日销售量近似地满足g (t )＝－13t ＋1123(1≤t ≤100，t ∈N )．前40天价格为f (t )＝14t ＋22(1≤t ≤40，t ∈N )，后60天价格为f (t )＝－12t ＋52(41≤t ≤100，t ∈N )，试求该商品的日销售额S (t )的最大值和最小值．[解析] 当1≤t ≤40，t ∈N 时，S (t )＝g (t )f (t )＝(－13t ＋1123)(14t ＋22)＝－112t 2＋2t ＋112×223＝－112(t －12)2＋25003， 所以768＝S (40)≤S (t )≤S (12)＝112×223＋12＝25003.当41≤t ≤100，t ∈N 时，S (t )＝g (t )f (t )＝(－13t ＋1123)(－12t ＋52)＝16t 2－36t ＋112×523＝16(t －108)2－83， 所以8＝S (100)≤S (t )≤S (41)＝14912.所以，S (t )的最大值为25003，最小值为8.(理)(2011～2012·某某名校联考)已知一家公司生产某种商品的年固定成本为10万元，每生产1千件需另投入2.7万元．设该公司一年内共生产该商品c 千件并全部销售完，若每千件的销售收入为R (x )万元，且R (x )＝⎩⎪⎨⎪⎧10.8－130x 2， 0<x ≤10，108x －10003x 2， x >10.(1)写出年利润W (万元)关于年产量x (千件)的函数解析式；(2)年产量为多少千件时，该公司在这一商品的生产中所获得利润最大？(注：年利润＝年销售收入－年总成本)[解析] (1)当0<x ≤10时，W ＝xR (x )－(10＋2.7x )＝8.1x －x 330－10；当x >10时，W ＝xR (x )－(10＋2.7x )＝98－10003x－2.7x .∴W ＝⎩⎪⎨⎪⎧8.1x －x 330－10， 0<x ≤10，98－10003x －2.7x ， x >10.(2)①当0<x <10时，由W ′＝8.1－x 210＝0，得x ＝9，且当x ∈(0,9)时，W ′>0；当x ∈(9,10)时，W ′<0，∴当x ＝9时，W 取极大值，且W ＝8.1×9－130·93－10＝38.6.②当x >10时，W ＝98－⎝ ⎛⎭⎪⎫10003x ＋2.7x≤98－210003x·2.7x ＝38， 当且仅当10003x ＝2.7x ，即x ＝1009时，W ＝38，故当x ＝1009时，W 取极大值38.又当x ＝10时，W ＝1133.综合①②知当x ＝9时，W 取最大值38.6万元，故当年产量为9千件时，该公司在这一商品的生产中所获年利润最大．19．(本小题满分12分)(2011～2012·某某某某中学调研)设函数f (x )＝ax ＋x x －1(x >1)，若a 是从1,2,3三个数中任取的一个数，b 是从2,3,4,5四个数中任取的一个数，求f (x )>b 恒成立的概率．[解析] 若使f (x )>b 恒成立，只需使ax ＋xx －1－b >0在(1，＋∞)上恒成立． 设g (x )＝ax ＋xx －1－b ，则g ′(x )＝a －1x －12＝a x －12－1x －12，令g ′(x )＝0，则a (x －1)2－1＝0， 解得：x ＝±aa＋1， ∴x ∈(1，aa＋1)时，g ′(x )<0，x ∈(aa＋1，＋∞)时，g ′(x )>0， ∴x ＝aa＋1时，函数g (x )取得最小值为 g (aa＋1)＝2a ＋2－b ， ∴2a ＋2－b >0.∴当a ＝1时，b 的值可以是2或3， 当a ＝2时，b 的值可以是2或3或4， 当a ＝3时，b 的值可以是2或3或4或5.∴使f (x )>b 恒成立的取法共有9种，而数对(a ，b )的所有可能取法共有12种， ∴使f (x )>b 恒成立的概率为P ＝912＝34.20．(本小题满分12分)(文)(2011～2012·豫南九校联考)某商品每件成本9元，售价为30元，每星期卖出432件，如果降低价格，销售量可以增加，且每星期多卖出商品件数与商品单价的降低值x (单位：元，0≤x ≤30)的平方成正比，已知商品单价降低2元时，一星期多卖出24件．(1)将一个星期的商品销售利润表示成x 的函数f (x )； (2)如何定价才能使一个星期的商品销售利润最大？[解析] (1)设商品降价x 元，则多卖出的商品数为kx 2，在一个星期内商品的销售利润为f (x )，由题意得：24＝k ·22，∴k ＝6，所以f (x )＝(30－x －9)(432＋6x 2)＝－6x 3＋126x 2－432x ＋9072(0≤x ≤30) (2)f ′(x )＝－18(x －2)(x －12) 令f ′(x )＝0得x ＝2或x ＝12，x (0,2) 2 (2,12) 12 (12,30) f ′(x ) － 0 ＋ 0 － f (x )单调递减极小值单调递增极大值单调递减由上表可知当x ＝12时，f (x )取得极大值，而f (12)＝11664>f (0)＝9072， ∴定价为18元时利润最大．(理)设f (x )是定义在[－1,1]上的奇函数，且对任意a 、b ∈[－1,1]，当a ＋b ≠0时，都有f a ＋f ba ＋b>0.(1)若a >b ，比较f (a )与f (b )的大小；(2)解不等式f ⎝ ⎛⎭⎪⎫x －12<f ⎝ ⎛⎭⎪⎫x －14； (3)记P ＝{x |y ＝f (x －c )}，Q ＝{x |y ＝f (x －c 2)}，且P ∩Q ＝∅，求c 的取值X 围． [解析] 设－1≤x 1<x 2≤1，则x 1－x 2≠0， ∴f x 1＋f －x 2x 1＋－x 2>0.∵x 1－x 2<0，∴f (x 1)＋f (－x 2)<0. ∴f (x 1)<－f (－x 2)．又f (x )是奇函数，∴f (－x 2)＝－f (x 2)． ∴f (x 1)<f (x 2)． ∴f (x )是增函数． (1)∵a >b ，∴f (a )>f (b )．(2)由f ⎝ ⎛⎭⎪⎫x －12<f ⎝ ⎛⎭⎪⎫x －14，得 ⎩⎪⎨⎪⎧－1≤x －12≤1，－1≤x －14≤1，x －12<x －14，∴－12≤x ≤54.∴不等式的解集为{x |－12≤x ≤54}．(3)由－1≤x －c ≤1，得－1＋c ≤x ≤1＋c ， ∴P ＝{x |－1＋c ≤x ≤1＋c }．由－1≤x －c 2≤1，得－1＋c 2≤x ≤1＋c 2， ∴Q ＝{x |－1＋c 2≤x ≤1＋c 2}． ∵P ∩Q ＝∅，∴1＋c <－1＋c 2或－1＋c >1＋c 2， 解得c >2或c <－1.∴c 的取值X 围是(－∞，－1)∪(2，＋∞)．21．(本小题满分12分)(文)(2011～2012·某某省六校教育研究会联考)已知函数f (x )＝(x 2－ax )e x(x ∈R )，a 为实数．(1)当a ＝0时，求函数f (x )的单调增区间；(2)若f (x )在闭区间[－1,1]上为减函数，求a 的取值X 围． [解析] (1)当a ＝0时，f (x )＝x 2e x，f ′(x )＝2xe x ＋x 2e x ＝(x 2＋2x )e x ，由f ′(x )>0⇒x >0或x <－2，故f (x )单调增区间为(0，＋∞)和(－∞，－2)． (2)由f (x )＝(x 2－ax )e x，x ∈R 得，f ′(x )＝(2x －a )e x ＋(x 2－ax )e x＝[x 2＋(2－a )x －a ]e x， 记g (x )＝x 2＋(2－a )x －a ， 依题意可得，当x ∈[－1,1]时，g (x )≤0恒成立，结合g (x )的图象特征得⎩⎪⎨⎪⎧g1＝3－2a ≤0g －1＝－1≤0即a ≥32，∴a 的取值X 围是[32，＋∞)．(理)(2011～2012·某某省实验中学四诊)已知函数f (x )＝px －p x－2ln x ，g (x )＝2ex.(1)若p ＝2，求曲线f (x )在点(1，f (1))处的切线方程；(2)若函数f (x )在其定义域内为增函数，求正实数p 的取值X 围；(3)若p 2－p ≥0，且至少存在一点x 0∈[1，e ]，使得f (x 0)>g (x 0)成立，某某数p 的取值X 围．[解析] (1)当p ＝2时，函数f (x )＝2x －2x－2ln x ，f (1)＝2－2－2ln1＝0.f ′(x )＝2＋2x 2－2x，曲线f (x )在点(1，f (1))处的切线的斜率为f ′(1)＝2＋2－2＝2.从而曲线f (x )在点(1，f (1))处的切线方程为y －0＝2(x －1)，即y ＝2x －2.(2)f ′(x )＝p ＋p x 2－2x ＝px 2－2x ＋px 2.令h (x )＝px 2－2x ＋p ，要使f (x )在定义域(0，＋∞)内是增函数，只需h (x )≥0， 即px 2－2x ＋p ≥0⇔p ≥2xx 2＋1， ∵x >0时，2xx 2＋1≤1，∴p ≥1， ∴正实数p 的取值X 围是[1，＋∞)． (3)由p 2－p ≥0得，p ≥1或p ≤0.∵g (x )＝2ex在[1，e ]上是减函数，∴x ＝e 时，g (x )min ＝2；x ＝1时，g (x )max ＝2e ，即g (x )∈[2,2e ]，①当p ＝0时，h (x )＝－2x ，∵x ∈[1，e ]，∴h (x )<0，∴f ′(x )<0，∴f (x )在[1，e ]内是减函数；当p <0时，h (x )＝px 2－2x ＋p ，其图象为开口向下的抛物线，对称轴x ＝1p在y 轴的左侧，且h (0)<0，所以f (x )在x ∈[1，e ]内是减函数．因此，当p ≤0时，f (x )在[1，e ]内单调递减，∴f (x )≤f (1)＝0<2，故不存在x 0∈[1，e ]，使得f (x 0)>g (x 0)成立．②当p ≥1时，∵f (x )在[1，e ]上是增函数，g (x )在[1，e ]上是减函数，若存在x 0∈[1，e ]，使得f (x 0)>g (x 0)成立，则只需f (x )max >g (x )min ，x ∈[1，e ]，而f (x )max ＝f (e )＝p ⎝⎛⎭⎪⎫e －1e －2，g (x )min ＝2，即p ⎝ ⎛⎭⎪⎫e －1e －2>2，解得p >4e e 2－1，所以实数p 的取值X 围是(4ee 2－1，＋∞)． 22．(本小题满分14分)(文)(2011～2012·会昌中学月考)已知f (x )＝2x －12x 2，g (x )＝log a x (a >0且a ≠1)．(1)过P (0,2)作曲线y ＝f (x )的切线，求切线方程；(2)设h (x )＝f (x )－g (x )在定义域上为减函数，且其导函数y ＝h ′(x )存在零点，某某数a 的值．[解析] (1)∵f (0)＝0，∴P (0,2)不在曲线y ＝f (x )上，设切点为Q (x 0，y 0)，∵f ′(x )＝2－x ，∴k ＝f ′(x 0)＝2－x 0，且y 0＝f (x 0)＝2x 0－x 202，∴切线方程为y －2x 0＋x 202＝(2－x 0)(x －x 0)，即y ＝(2－x 0)x ＋x 202，∵(0,2)在切线上，代入可得x 0＝±2， ∴切线方程为y ＝2或y ＝4x ＋2.(2)h (x )＝2x －12x 2－log a x 在(0，＋∞)上单调递减，∴h ′(x )＝2－x －1x ln a≤0在(0，＋∞)上恒成立， ∵x >0，∴1ln a ≥2x －x 2在(0，＋∞)上恒成立．又2x －x 2∈(－∞，1]，∴1ln a≥1，∴0<ln a ≤1，①又∵h ′(x )＝2－x －1x ln a存在零点， 即方程ln a ·x 2－2ln a ·x ＋1＝0有正根， ∴Δ＝4ln 2a －4ln a ≥0，∴ln a ≥1或ln a <0② 由①②知ln a ＝1，∴a ＝e .当a ＝e 时，方程ln ax 2－2ln a ·x ＋1＝0有正根x ＝1. 综上知，a ＝e .(理)(2011～2012·某某某某市辅仁中学模拟)对于函数f 1(x )，f 2(x )，h (x )，如果存在实数a ，b 使得h (x )＝a ·f 1(x )＋b ·f 2(x )，那么称h (x )为f 1(x )、f 2(x )的生成函数．(1)下面给出两组函数，h (x )是否分别为f 1(x )、f 2(x )的生成函数？并说明理由； 第一组：f 1(x )＝sin x ，f 2(x )＝cos x ，h (x )＝sin(x ＋π3)；第二组：f 1(x )＝x 2－x ，f 2(x )＝x 2＋x ＋1，h (x )＝x 2－x ＋1.(2)设f 1(x )＝log 2x ，f 2(x )＝log 12 x ，a ＝2，b ＝1，生成函数h (x )．若不等式3h 2(x )＋2h (x )＋t <0在x ∈[2,4]上有解，某某数t 的取值X 围；(3)设f 1(x )＝x ，f 2(x )＝1x(1≤x ≤10)，取a ＝1，b >0，生成函数h (x )使h (x )≥b 恒成立，求b 的取值X 围．[解析] (1)①设a sin x ＋b cos x ＝sin(x ＋π3)，即a sin x ＋b cos x ＝12sin x ＋32cos x ，取a ＝12，b ＝32，所以h (x )是f 1(x )，f 2(x )的生成函数．②设a (x 2－x )＋b (x 2＋x ＋1)＝x 2－x ＋1， 即(a ＋b )x 2＋(b －a )x ＋b ＝x 2－x ＋1，则⎩⎪⎨⎪⎧a ＋b ＝1b －a ＝－1b ＝1，该方程组无解．所以h (x )不是f 1(x )，f 2(x )的生成函数．(2)h (x )＝2f 1(x )＋f 2(x )＝2log 2x ＋log 12 x ＝log 2x ，若不等式3h 2(x )＋2h (x )＋t <0在x ∈[2,4]上有解， 即t <－3h 2(x )－2h (x )＝－3log 22x －2log 2x ，x ∈[2,4]．设s ＝log 2x ，则s ∈[1,2]，y ＝－3log 22x －2log 2x ＝－3s 2－2s ＝－3(s ＋13)2＋13，∴y max ＝－5，∴t <－5.(3)由题意得，h (x )＝x ＋bx(1≤x ≤10，b >0)， 令h ′(x )＝1－b x2＝0，则x ＝b ，1°若b ∈[1,10]，则h (x )在[1，b ]上递减，在[b ，10]上递增，则h min ＝h (b )＝2b ，所以⎩⎨⎧1≤b ≤102b ≥b，得1≤b ≤4.2°若b ≤1，则h (x )在[1,10]上递增，则h min ＝h (1)＝1＋b ，所以⎩⎨⎧b ≤11＋b ≥b，得0<b ≤1.3°若b ≥10，则h (x )在[1,10]上递减，则h min ＝h (10)＝10＋b10，则⎩⎪⎨⎪⎧b ≥1010＋b 10≥b ，此时无解．综上可知，0<b ≤4.1．(2011～2012·湄潭中学上学期期末)已知集合M ＝{y |y ＝x 2－1，x ∈R }，N ＝{x |y ＝2－x 2}，则M ∩N ＝( )A ．[－1，2]B ．[－1，＋∞)C ．[2，＋∞) D．∅ [答案] A[解析]M ＝{y |y ≥－1}，由2－x 2≥0得－2≤x ≤2， ∴N ＝{x |－2≤x ≤2}， ∴M ∩N ＝{x |－1≤x ≤2}，故选A.2．(2011～2012·某某某某市一模)某程序框图如图所示，现输入如下四个函数：f (x )＝x 2，f (x )＝1x，f (x )＝e x，f (x )＝sin x ，则可以输出的函数是( )A ．f (x )＝x 2B ．f (x )＝1xC ．f (x )＝e xD ．f (x )＝sin x [答案] D[解析] 由f (x )＋f (－x )＝0知f (x )为奇函数，排除A 、C ；由f (x )存在零点排除B ，故选D.3．(2011～2012·某某名校联考)若点(a,4)在函数y ＝2x的图象上，则tan a π6的值为( )A ．0B ．1 C.3D.33[答案] C[解析] 由条件知，2a＝4，∴a ＝2，∴tana π6＝tan π3＝ 3. 4．(2011～2012·某某卫辉一中月考)下列四个函数中，在区间(0,1)上是减函数的是( )A ．y ＝log 2xB ．y ＝x 13C ．y ＝－(12)xD ．y ＝1x[答案] D[解析]y ＝log 2x ，y ＝x 13 ，y ＝－(12)x 在定义域上都是增函数，y ＝1x 在(－∞，0)上和(0，＋∞)上都是减函数，故选D.5．(2011～2012·某某一中月考)设集合U ＝R ，集合A ＝{x |(12)x ≥2}，B ＝{y |y ＝lg(x2＋1)}，则(∁U A )∩B ＝( )A ．{x |x ≤－1或x ≥0} B．{(x ，y )|x ≤－1，y ≥0} C ．{x |x ≥0} D．{x |x >－1} [答案] C[解析] 由(12)x≥2得，x ≤log 12 2＝－1，∴A ＝{x |x ≤－1}，又B ＝{y |y ≥0}，∁U A ＝{x |x >－1}， ∴(∁U A )∩B ＝{x |x ≥0}．6．(2011～2012·某某一中期末)函数f (x )在定义域R 内可导，若f (x )＝f (2－x )，且当x ∈(－∞，1)时，(x －1)f ′(x )<0，设a ＝f (0)，b ＝f (12)，c ＝f (3)，则( )A ．a <b <cB ．c <b <aC ．c <a <bD ．b <c <a [答案] C[解析] 由f (x )＝f (2－x )知f (x )的图象关于直线x ＝1对称，又x <1时，(x －1)f ′(x )<0，∴f ′(x )>0，∴f (x )在(－∞，1)上为增函数，f (3)＝f (2－3)＝f (－1)，∵－1<0<12，∴f (－1)<f (0)<f (12)，∴f (3)<f (0)<f (12)，即c <a <b .7．(2011～2012·某某某某中学调研)已知函数f (x )的定义域为[－1,5]，部分对应值如下表：f (x )的导函数y ＝f下列关于函数f (x )的命题： ①函数y ＝f (x )是周期函数； ②函数f (x )在[0,2]上是减函数；③如果当x ∈[－1，t ]时，f (x )的最大值是2，那么t 的最大值4； ④当1<a <2时，函数y ＝f (x )－a 有4个零点． 其中真命题的个数是( ) A ．4个 B ．3个 C ．2个 D ．1个 [答案] C[解析]∵f (x )定义域为[－1,5]，∴f (x )不是周期函数，故①假；当x ∈[0,2]时，f ′(x )≤0，∴f (x )为减函数，故②真；∵f (x )在(－1,0)上单调递增，在(0,2)上单调递减，在(2,4)上单调递增，在(4,5)上单调递减，极大值f (0)＝2，f (4)＝2，极小值f (2)未知，区间端点值f (－1)＝1，f (5)＝1，故在定义域[－1,5]内的最大值为2，∴当x ∈[－1，t ]时，f (x )的最大值为2，则t 的最大值应为5，故③假；由上面分析知，当1<a <2时，直线y ＝a 与函数f (x )的图象有4个交点，∴y ＝f (x )－a 有4个零点，故④真，∴真命题有2个．8．(2011～2012·黄冈市期末)某工厂生产一种产品的原材料费为每件40元，若用x 表示该厂生产这种产品的总件数，则电力与机器保养等费用为每件0.05x 元，又该厂职工工资固定支出12500元．(1)把每件产品的成本费P (x )(元)表示成产品件数x 的函数，并求每件产品的最低成本费；(2)如果该厂生产的这种产品的数量x 不超过3000件，且产品能全部销售．根据市场调查：每件产品的销售价Q (x )与产品件数x 有如下关系：Q (x )＝170－0.05x ，试问生产多少件产品时，总利润最高？(总利润＝总销售额－总的成本)[解析] (1)P (x )＝12500x＋40＋0.05x ，由基本不等式得P (x )≥212500×0.05＋40＝90，当且仅当12500x＝0.05x ，即x ＝500时，等号成立．所以P (x )＝12500x＋40＋0.05x ，成本的最小值为90元．(2)设总利润为y 元，则y ＝xQ (x )－xP (x )＝－0.1x 2＋130x －12500＝－0.1(x －650)2＋29750 当x ＝650时，y max ＝29750.所以生产650件产品时，总利润最高，最高总利润为29750元．。

阶段性测试题九(平面解析几何)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共50分)一、选择题(本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．(文)(2012·潍坊模拟)若直线x －2y ＋5＝0与直线2x ＋my －6＝0互相垂直，则实数m 的值为( )A ．1B ．－1C ．1或－1D ．－4 [答案] A[解析]∵两直线x －2y ＋5＝0与2x ＋my －6＝0互相垂直． ∴1×2＋(－2)m ＝0即m ＝1.(理)(2012·潍坊模拟)已知两直线l 1：x ＋m 2y ＋6＝0，l 2：(m －2)x ＋3my ＋2m ＝0，若l 1∥l 2，则实数m 的值为( )A ．0或3B ．－1或3C ．0或－1或3D ．0或－1 [答案] D[解析] (1)当m ＝0时，l 1：x ＋6＝0，l 2：x ＝0，l 1∥l 2； (2)当m ≠0时，l 1：y ＝－1m 2x －6m2，l 2：y ＝2－m 3m x －23， 由－1m 2＝2－m 3m 且－6m 2≠－23，∴m ＝－1.故所某某数m 的值为0或－1.2．(文)(2012·某某师大第一次模拟)过点P (1,2)的直线l 平分圆C ：x 2＋y 2＋4x ＋6y ＋1＝0的周长，则直线l 的斜率为( )A.53B ．1 C.85D.43 [答案] A[解析] 圆的方程可化为(x ＋2)2＋(y ＋3)2＝12因为l 平分圆C 的周长，所以l 过圆C的圆心(－2，－3)，又l 过P (1,2)，所以k l ＝－3－2－2－1＝53，故选A.(理)(2012·某某一模)若点P (1,1)为圆(x －3)2＋y 2＝9的弦MN 的中点，则弦MN 所在直线方程为( )A ．2x ＋y －3＝0B ．x －2y ＋1＝0C ．x ＋2y －3＝0D ．2x －y －1＝0 [答案] D[解析] 圆心C (3,0)，k CP ＝－12，由k CP ·k MN ＝－1，得k MN ＝2，所以MN 所在直线方程是2x －y －1＝0.故选D.3．(2012·某某模拟)若双曲线x 2a2－y 2＝1的一个焦点为(2,0)，则它的离心率为( )A.255B.32 C.233D ．2 [答案] C[解析] 由题意知a 2＋1＝4，∴a ＝3， ∴e ＝c a＝23＝233. 4．(2012·某某一模)已知点A (1,0)，直线l ：y ＝2x －4，点R 是直线l 上的一点，若RA →＝AP →，则点P 的轨迹方程为( )A ．y ＝－2xB ．y ＝2xC ．y ＝2x －8D ．y ＝2x ＋4 [答案] B[解析] 设点P (x ，y )，R (x 1，y 1)， ∵RA →＝AP →，∴(1－x 1，－y 1)＝(x －1，y )，∴⎩⎪⎨⎪⎧1－x 1＝x －1，－y 1＝y ，即⎩⎪⎨⎪⎧x 1＝2－x ，y 1＝－y .又点R 在直线l 上，∴－y ＝2(2－x )－4， 即2x －y ＝0为所求．5．(2012·某某调研)若椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，则双曲线x 2a 2－y 2b2＝1的离心率为( )A.54B.52C.32D.54 [答案] B[解析] 因为椭圆离心率e ＝32，即c a ＝32，也即a 2－b 2a 2＝34，所以b 2a 2＝14，则1＋b 2a 2＝54，即a 2＋b 2a 2＝54，双曲线离心率e ′＝c ′a ′＝52，故选B.6．(文)(2011·文)已知点A (0,2)，B (2,0)．若点C 在函数y ＝x 2的图像上，则使得△ABC 的面积为2的点C 的个数为( )A ．4B ．3C ．2D ．1 [答案] A[解析] 设C (t ，t 2)，由A (0,2)，B (2,0)易求得直线AB 的方程为y ＝－x ＋2. ∴点C 到直线AB 的距离d ＝|t 2＋t －2|2.又∵|AB |＝22，∴S △ABC ＝12×|AB |·d ＝|t 2＋t －2|.令|t 2＋t －2|＝2得t 2＋t －2＝±2，∴t 2＋t ＝0或t 2＋t －4＝0，符合题意的t 值有4个，故满足题意的点C 有4个．(理)(2011·某某理)若曲线C 1：x 2＋y 2－2x ＝0与曲线C 2：y (y －mx －m )＝0有四个不同的交点，则实数m 的取值X 围是( )A. (－33，33) B. (－33，0)∪(0, 33) C. [－33 ，33] D ．( －∞， －33 )∪( 33，＋∞) [答案] B[解析]C 1：(x －1)2＋y 2＝1.C 2：y ＝0或y ＝mx ＋m ＝m (x ＋1)．当m ＝0时，C 2：y ＝0，此时C 1与C 2显然只有两个交点；当m ≠0时，要满足题意，需圆(x －1)2＋y 2＝1与直线y ＝m (x ＋1)有两交点，当圆与直线相切时，m ＝±33. 即直线处于两切线之间时满足题意，则－33<m <0或0<m <33. 综上知－33<m <0或0<m <33. 7．(2012·某某模拟)已知椭圆x 216＋y 29＝1的左、右焦点分别为F 1、F 2，点P 在椭圆上．若P 、F 1、F 2是一个直角三角形的三个顶点，则点P 到x 轴的距离为( )A.95B ．3 C.977 D.94[答案] D[解析] 设椭圆短轴的一个端点为M . 由于a ＝4，b ＝3，∴c ＝7<b . ∴∠F 1MF 2<90°，∴只能∠PF 1F 2＝90°或∠PF 2F 1＝90°. 令x ＝±7，得y 2＝⎝ ⎛⎭⎪⎫1－716×9＝9216，∴|y |＝94.即P 到x 的距离为94.8．(2012·某某模拟)若椭圆x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，抛物线y2＝2bx 的焦点为F .若F 1F →＝3FF 2→，则此椭圆的离心率为( )A.12B.22C.13D.33 [答案] B[解析]∵F ⎝ ⎛⎭⎪⎫b2，0，F 1(－c,0)，F 2(c,0)， 且F 1F →＝3FF 2→，∴F 1F →＝⎝ ⎛⎭⎪⎫b 2＋c ，0，FF 2→＝⎝ ⎛⎭⎪⎫c －b 2，0，∴b 2＋c ＝3c －3b2，即b ＝c . ∴a 2＝b 2＋c 2＝2c 2， ∴c a ＝e ＝22. 9．(2012·某某一模)如下图，F 1和F 2分别是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的两个焦点，A 和B 是以O 为圆心，以|OF 1|为半径的圆与该双曲线左支的两个交点，且△F 2AB 是等边三角形，则双曲线的离心率为( )A.3B. 5C.52D ．1＋ 3 [答案] D[解析] 连接AF 1，则∠F 1AF 2＝90°，∠AF 2B ＝60°，∴|AF 1|＝12|F 1F 2|＝c ，|AF 2|＝32|F 1F 2|＝3c ， ∴3c －c ＝2a ， ∴e ＝c a＝23－1＝1＋ 3.10．(2012·某某调研)如图，过抛物线y 2＝2px (p >0)的焦点F 的直线l 交抛物线于两点A 、B ，交其准线于C ，若|BC |＝2|BF |，且|AF |＝3，则此抛物线的方程为( )A ．y 2＝9xB ．y 2＝6x C ．y 2＝3x D ．y 2＝3x [答案] C[解析] 如下图所示，分别过点A 、B 作AA 1、BB 1与准线垂直，且垂足分别为A 1、B 1，由已知条件|BC |＝2|BF |得|BC |＝2|BB 1|，∴∠BCB 1＝30°，于是可得直线AB 的倾斜角为60°. 又由|AF |＝3得|AF |＝|AA 1|＝3＝12|AC |，于是可得|CF |＝|AC |－|AF |＝6－3＝3， ∴|BF |＝13|CF |＝1.∴|AB |＝|AF |＋|BF |＝3＋1＝4.设直线AB 的方程为y ＝3(x －p2)，代入y 2＝2px 得3x 2－5px ＋34p 2＝0，∵|AB |＝|AF |＋|BF |＝|AA 1|＋|BB 1|＝x A ＋p 2＋x B ＋p 2＝x A ＋x B ＋p ＝53p ＋p ＝83p ＝4，∴p ＝32，即得抛物线方程为y 2＝3x .故选C.解法二：点F 到抛物线准线的距离为p ，又由|BC |＝2|BF |得点B 到准线的距离为|BF |，则|BF ||BC |＝12， ∴l 与准线夹角为30°，则直线l 的倾斜角为60°. 由|AF |＝3，如图作AH ⊥HC ，EF ⊥AH ，则AE ＝3－p ， 则cos60°＝3－p 3，故p ＝32.∴抛物线方程为y 2＝3x .第Ⅱ卷(非选择题 共100分)二、填空题(本大题共5个小题，每小题5分，共25分，把正确答案填在题中横线上) 11．(2012·某某模拟)设圆C 与圆x 2＋(y －3)2＝1外切，与直线y ＝0相切，则C 的圆心轨迹为________．[答案] 抛物线[解析] 设圆C 的半径为r ，则圆心C 到直线y ＝0的距离为r .由两圆外切可得，圆心C 到点(0,3)的距离为r ＋1，也就是说，圆心C 到点(0,3)的距离比到直线y ＝0的距离大1，故点C 到点(0,3)的距离和它到直线y ＝－1的距离相等，符合抛物线的特征，故点C 的轨迹为抛物线．[点评] 本题考查用定义法求点的轨迹，考查学生数形结合和转化与化归的思想方法．12．(文)(2011·文)已知双曲线x 2－y 2b2＝1(b >0)的一条渐近线的方程为y ＝2x ，则b ＝________.[答案] 2[解析] 本题主要考查双曲线的基本性质．双曲线的渐近线方程为y ＝±b ax ，因为a ＝1，又知一条渐近线方程为y ＝2x ，所以b ＝2.(理)(2011·某某文)若双曲线y 216－x 2m＝1的离心率e ＝2，则m ＝________.[答案] 48[解析] 本题主要考查双曲线的基本性质．c 2＝a 2＋b 2＝16＋m ，又∵e ＝ca，∴e ＝2＝16＋m4，∴m ＝48. 13．(2012·某某一模)设a 、b 、c 分别是△ABC 中∠A 、∠B 、∠C 所对边的边长，则直线x ·sin A ＋ay ＋c ＝0与bx －y ·sin B ＋cos C ＝0的位置关系是________．[答案] 垂直[解析] 在△ABC 中，由正弦定理得a sin A ＝bsin B ，∴a sin B －b sin A ＝0， ∴两直线垂直．14．(文)(2012·某某一模)已知点A (1,0)，B (2,0)．若动点M 满足AB →·BM →＋2|AM →|＝0，则点M 的轨迹方程为________．[答案]x 22＋y 2＝1[解析] (1)设M (x ，y )，则AB →＝(1,0)，BM →＝(x －2，y )，AM →＝(x －1，y )， 由AB →·BM →＋2|AM →|＝0得， (x －2)＋2·x －12＋y 2＝0.整理得x 22＋y 2＝1.(理)(2012·某某调研)若焦点在x 轴上的椭圆x 245＋y 2b2＝1上有一点，使它与两个焦点的连线互相垂直，则b 的取值X 围是________．[答案] －3102≤b ≤3102且b ≠0[解析] 设椭圆的两焦点为F 1(－c,0)，F 2(c,0)以F 1F 2为直径的圆与椭圆有公共点时，在椭圆上必存在点满足它与两个焦点的连线互相垂直，此时条件满足c ≥b ，从而得c 2≥b 2⇒a 2－b 2≥b 2⇒b 2≤12a 2＝452，解得－3102≤b ≤3102且b ≠0.15．(2012·某某质检)过抛物线x 2＝2py (p >0)的焦点作斜率为1的直线与该抛物线交于A ，B 两点，A ，B 在x 轴上的正射影分别为D ，C .若梯形ABCD 的面积为122，则p ＝________.[答案] 2[解析] 抛物线的焦点坐标为F (0，p 2)，则过焦点斜率为1的直线方程为y ＝x ＋p2，设A (x 1，y 1)，B (x 2，y 2)(x 2>x 1)由题意可知y 1>0，y 2>0.由⎩⎪⎨⎪⎧y ＝x ＋p 2x 2＝2py，消去y 得x 2－2px －p 2＝0.由韦达定理得：x 1＋x 2＝2p ，x 1x 2＝－p 2. 所以梯形ABCD 的面积为S ＝12(y 1＋y 2)(x 2－x 1)＝12(x 1＋x 2＋p )(x 2－x 1)＝12×3p x 1＋x 22－4x 1x 2＝12×3p 4p 2＋4p 2＝32p 2.所以32p 2＝122，又p >0.所以p ＝2.三、解答题(本大题共6个小题，共75分，解答应写出文字说明，证明过程或演算步骤) 16．(本小题满分12分)(2012·某某模拟)已知A (x 1，y 1)，B (x 2，y 2)分别在直线x ＋y －7＝0及x ＋y －5＝0上，求AB 中点M 到原点距离的最小值．[解析] 设AB 中点为(x 0，y 0)，∴⎩⎪⎨⎪⎧x 0＝x 1＋x 22，y 0＝y 1＋y22.又∵⎩⎪⎨⎪⎧x 1＋y 1－7＝0，x 2＋y 2－5＝0，∴(x 1＋x 2)＋(y 1＋y 2)＝12， ∴2x 0＋2y 0＝12， ∴x 0＋y 0＝6.∴原点到x 0＋y 0＝6距离为所求，即d ＝62＝3 2.17．(本小题满分12分)(2012·某某一模)在直角坐标系xOy 中，以O 为圆心的圆与直线x －3y ＝4相切．(1)求圆O 的方程；(2)圆O 与x 轴相交于A 、B 两点，圆内的动点P 使|PA |、|PO |、|PB |成等比数列，求PA →·PB →的取值X 围．[解析] (1)依题设，圆O 的半径r 等于原点O 到直线x －3y ＝4的距离，即r ＝41＋3＝2.得圆 O 的方程为x 2＋y 2＝4. (2)不妨设A (x 1,0)，B (x 2,0)，x 1<x 2. 由x 2＝4即得A (－2,0)，B (2,0)．设P (x ，y )，由|PA |、|PO |、|PB |成等比数列， 得x ＋22＋y 2·x －22＋y 2＝x 2＋y 2，即x 2－y 2＝2. PA →·PB →＝(－2－x ，－y )·(2－x ，－y )＝x 2－4＋y 2＝2(y 2－1)．由于点P 在圆O 内，故⎩⎪⎨⎪⎧x 2＋y 2<4，x 2－y 2＝2.由此得y 2<1.所以PA →·PB →的取值X 围为[－2,0)．18．(本小题满分12分)(2011·某某理)已知直线l ：y ＝x ＋m ，m ∈R .(1)若以点M (2,0)为圆心的圆与直线l 相切于点P ，且点P 在y 轴上，求该圆的方程； (2)若直线l 关于x 轴对称的直线为l ′，问直线l ′与抛物线C ：x 2＝4y 是否相切？说明理由．[解析]解法一：(1)依题意，点P 的坐标为(0，m )． 因为MP ⊥l ，所以0－m2－0×1＝－1，解得m ＝2，即点P 的坐标为(0,2)． 从而圆的半径r ＝|MP |＝2－02＋0－22＝22，故所求圆的方程为(x －2)2＋y 2＝8. (2)因为直线l 的方程为y ＝x ＋m ， 所以直线l ′的方程为y ＝－x －m .由⎩⎪⎨⎪⎧y ＝－x －m ，x 2＝4y 得x 2＋4x ＋4m ＝0.Δ＝42－4×4m ＝16(1－m )．①当m ＝1时，即Δ＝0时，直线l ′与抛物线C 相切； ②当m ≠1，即Δ≠0时，直线l ′与抛物线C 不相切．综上，当m ＝1时，直线l ′与抛物线C 相切；当m ≠1时，直线l ′与抛物线C 不相切． 解法二：(1)设所求圆的半径为r ，则圆的方程可设为(x －2)2＋y 2＝r 2. 依题意，所求圆与直线l ：x －y ＋m ＝0相切于点P (0，m )，则⎩⎪⎨⎪⎧4＋m 2＝r 2，|2－0＋m |2＝r ，解得⎩⎨⎧m ＝2，r ＝2 2.所以所求圆的方程为(x －2)2＋y 2＝8. (2)同解法一．19．(本小题满分12分)(文)如图，已知抛物线C 1：x 2＋by ＝b 2经过椭圆C 2：x 2a 2＋y 2b2＝1(a >b >0)的两个焦点．(1)求椭圆C 2的离心率；(2)设点Q (3，b )，又M ，N 为C 1与C 2不在y 轴上的两个交点，若△QMN 的重心在抛物线C 1上，求C 1和C 2 的方程．[解析] 本题主要考查了抛物线及椭圆的方程和性质，并涉及求离心率问题，重心坐标公式，曲线与曲线的交点等内容，注重运算变形能力的考查，综合性较强．(1)椭圆的焦点为(±a 2－b 2，0)，代入抛物线方程a 2－b 2＋b ·0＝b 2⇒b 2a 2＝12，∴e ＝1－b a2＝22. (2)由(1)问a 2＝2b 2，∴椭圆方程为x 22b 2＋y 2b2＝1，即x 2＋2y 2＝2b 2.设N (x 0，y 0)，M (－x 0，y 0)，Q (3，b )，则重心(1，2y 0＋b3)，代入抛物线方程，⎩⎪⎨⎪⎧1＋2by 0＋b 23＝b2x 20＋by 0＝b 2x 20＋2y 20＝2b2⇒⎩⎪⎨⎪⎧b 2＝1，y 0＝－b 2或y 0＝b 舍，∴抛物线C 1的方程为y ＝1－x 2， 椭圆C 2的方程为：x 22＋y 2＝1.(理)(2012·某某调研)已知点(x ，y )在曲线C 上，将此点的纵坐标变为原来的2倍，对应的横坐标不变，得到的点满足方程x 2＋y 2＝8；定点M (2,1)，平行于OM 的直线l 在y 轴上的截距为m (m ≠0)，直线l 与曲线C 交于A ，B 两个不同点．(1)求曲线C 的方程； (2)求m 的取值X 围．[解析] (1)在曲线C 上任取一个动点P (x ，y )， 则点(x,2y )在圆x 2＋y 2＝8上． 所以有x 2＋(2y )2＝8.整理得曲线C 的方程为x 28＋y 22＝1.(2)∵直线l 平行于OM ，且在y 轴上的截距为m ， 又k OM ＝12，∴直线l 的方程为y ＝12x ＋m .由⎩⎪⎨⎪⎧y ＝12x ＋m ，x 28＋y 22＝1，得x 2＋2mx ＋2m 2－4＝0.∵直线l 与椭圆交于A 、B 两个不同点， ∴Δ＝(2m )2－4(2m 2－4)>0， 解得－2<m <2且m ≠0.∴m 的取值X 围是－2<m <0或0<m <2.20．(本小题满分13分)(文)(2012·某某一模)设F 1、F 2分别是椭圆C ：x 26m 2＋y 22m2＝1(m >0)的左、右焦点．(1)当P ∈C ，且PF 1→·PF 2→＝0，|PF 1|·|PF 2|＝4时，求椭C 的左、右焦点F 1、F 2； (2)F 1、F 2是(1)中椭圆的左、右焦点，已知⊙F 2的半径为1，过动点Q 作⊙F 2的切线QM ，使得|QF 1|＝2|QM |(M 是切点)，如图所示，求动点Q 的轨迹方程．[解析] (1)∵c 2＝a 2－b 2，∴c 2＝4m 2. 又∵PF 1→·PF 2→＝0，∴PF 1⊥PF 2， ∴|PF 1→|2＋|PF 2→|2＝(2c )2＝16m 2.由椭圆定义可知|PF 1|＋|PF 2|＝2a ＝26m ， (|PF 1|＋|PF 2|)2＝16m 2＋8＝24m 2. 从而得m 2＝1，c 2＝4m 2＝4，c ＝2， ∴F 1(－2,0)，F 2(2,0)．(2)∵F 1(－2,0)，F 2(2,0)，已知|QF 1|＝2|QM |， 即|QF 1|2＝2|QM |2，∴|QF 1|2＝2(|QF 2|2－1)， 设Q (x ，y )，则(x ＋2)2＋y 2＝2[(x －2)2＋y 2－1]， 即(x －6)2＋y 2＝34(或x 2＋y 2－12x ＋2＝0)． 综上所述，所求轨迹方程为(x －6)2＋y 2＝34.[点评] 基础知识熟练即可顺利解决第(1)问，第(2)问用到了直译法求轨迹方程，运算要细心．(理)(2012·某某一模)如下图所示，等腰三角形ABC 的底边BC 的两端点是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的两焦点，且AB 的中点D 在椭圆E 上．(1)若∠ABC ＝60°，|AB |＝4，试求椭圆E 的方程； (2)设椭圆离心率为e ，求cos ∠ABC .[解析] (1)因为∠ABC ＝60°，且△ABC 为等腰三角形，所以△ABC 是正三角形． 又因为点B ，C 是椭圆的两焦点，设椭圆焦距为2c ，则2c ＝|BC |＝|AB |＝4，如图所示，连结CD ，由AB 中点D 在椭圆上，得2a ＝|BD |＋|CD |＝12|AB |＋32|AB |＝2＋23，所以a ＝1＋3，从而a 2＝4＋23，b 2＝a 2－c 2＝23， 故所求椭圆E 的方程为x 24＋23＋y 223＝1.(2)设椭圆的长半轴、短半轴、半焦距分别为a ，b ，c ，且|AD |＝|DB |＝m ，连结CD ， 则|BO |＝|OC |＝c ，|DC |＝2a －m ， 在Rt △AOB 中，cos ∠ABC ＝c2m.① 在△BCD 中，由余弦定理，得 cos ∠ABC ＝2c2＋m 2－2a －m 22×2c ×m.②由①②式得2m ＝2a 2－c2a，代入①式得cos ∠ABC ＝ac 2a 2－c 2＝e2－e2. 21．(本小题满分14分)(文)(2012·东城区模拟)已知椭圆C 的中心在原点，一个焦点为F (－2,0)，且长轴长与短轴长的比是2:3.(1)求椭圆C 的方程；(2)设点M (m,0)在椭圆C 的长轴上，点P 是椭圆上任意一点．当|MP →|最小时，点P 恰好落在椭圆的右顶点，某某数m 的取值X 围．[解析] (1)设椭圆C 的方程为x 2a 2＋y 2b2＝1(a >b >0)．由题意，得⎩⎨⎧a 2＝b 2＋c 2a :b ＝2:3，c ＝2，解得a 2＝16，b 2＝12.所以椭圆C 的方程为x 216＋y 212＝1.(2)设P (x ，y )为椭圆上的动点， 由于椭圆方程为x 216＋y 212＝1，故－4≤x ≤4.因为MP →＝(x －m ，y )， 所以|MP →|2＝(x －m )2＋y 2＝(x －m )2＋12·(1－x 216)＝14x 2－2mx ＋m 2＋12 ＝14(x －4m )2＋12－3m 2. 因为当|MP →|最小时，点P 恰好落在椭圆的右顶点，即当x ＝4时，|MP →|2取得最小值．而x ∈[－4,4]，故有4m ≥4，解得m ≥1.又点M 在椭圆的长轴上，所以－4≤m ≤4. 故实数m 的取值X 围是[1,4]．(理)(2011·某某文)已知平面内一动点P 到点F (1,0)的距离与点P 到y 轴的距离的差等于1.(1)求动点P 的轨迹C 的方程；(2)过点F 作两条斜率存在且互相垂直的直线l 1、l 2，设l 1与轨迹C 相交于点A 、B ，l 2与轨迹C 相交于点D 、E ，求AD →·EB →的最小值．[解析](1)设动点P 的坐标为(x ，y )，由题意有x －12＋y 2－|x |＝1.化简得y 2＝2x ＋2|x |.当x ≥0时，y 2＝4x ；当x <0时，y ＝0.所以，动点P 的轨迹C 的方程为y 2＝4x (x ≥0)和y ＝0(x <0)． (2)由题意知，直线l 1的斜率存在且不为0，设为k ， 则l 1的方程为y ＝k (x －1)．由⎩⎪⎨⎪⎧y ＝k x －1，y 2＝4x 得k 2x 2－(2k 2＋4)x ＋k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1，x 2是上述方程的两个实根，于是x 1＋x 2＝2＋4k2，x 1x 2＝1.因为l 1⊥l 2，所以l 2的斜率为－1k.设D (x 3，y 3)，E (x 4，y 4)，则同理可得x 3＋x 4＝2＋4k 2，x 3x 4＝1.故AD →·EB →＝(AF →＋FD →)·(EF →＋FB →) ＝AF →·EF →＋AF →·FB →＋FD →·EF →＋FD →·FB → ＝|AF →|·|FB →|＋|FD →|·|EF →| ＝(x 1＋1)(x 2＋1)＋(x 3＋1)(x 4＋1) ＝x 1x 2＋(x 1＋x 2)＋1＋x 3x 4＋(x 3＋x 4)＋1 ＝1＋(2＋4k2)＋1＋1＋(2＋4k 2)＋1＝8＋4(k 2＋1k2)≥8＋4×2k 2·1k2＝16.当且仅当k 2＝1k2，即k ＝±1时，AD →·EB →取最小值16.。

1.(2011·重庆理，6)若△ABC 的内角A 、B 、C 所对的边a 、b 、c 满足(a ＋b )2－c 2＝4，且C ＝60°，则ab 的值为( )A.43B ．8－4 3C ．1 D.23[答案] A[解析] 在△ABC 中，C ＝60°， ∴a 2＋b 2－c 2＝2ab cos C ＝ab ，∴(a ＋b )2－c 2＝a 2＋b 2－c 2＋2ab ＝3ab ＝4， ∴ab ＝43，选A.2．(文)在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，b ＝22，且三角形有两解，则角A 的取值范围是( )A.⎝ ⎛⎭⎪⎫0，π4B.⎝ ⎛⎭⎪⎫π4，π2C.⎝ ⎛⎭⎪⎫π4，3π4D.⎝ ⎛⎭⎪⎫π4，π3 [答案] A[解析] 由条件知b sin A <a ，即22sin A <2，∴sin A <22，∵a <b ，∴A <B ，∴A 为锐角，∴0<A <π4.(理)(2011·湖北八校联考)若满足条件C ＝60°，AB ＝3，BC ＝a的△ABC有两个，那么a的取值范围是()A．(1，2) B．(2，3)C．(3，2) D．(1,2)[答案] C[解析]由条件知，a sin60°<3<a，∴3<a<2.3．(2011·深圳二调)在△ABC中，已知a，b，c分别为∠A，∠B，∠C所对的边，且a＝4，b＝43，∠A＝30°，则∠B等于() A．30°B．30°或150°C．60°D．60°或120°[答案] D[解析]由正弦定理得asin A＝bsin B，所以4sin30°＝43sin B，sin B＝32.又0°<B<180°，因此有B＝60°或B＝120°，选D.4．(文)在△ABC中，角A、B、C所对的边分别为a、b、c，如果c＝3a，B＝30°，那么角C等于()A．120°B．105°C．90°D．75°[答案] A[解析]∵c＝3a，∴sin C＝3sin A＝3sin(180°－30°－C)＝3sin(30°＋C )＝3⎝ ⎛⎭⎪⎫32sin C ＋12cos C ，即sin C ＝－3cos C ，∴tan C ＝－ 3. 又C ∈(0°，180°)，∴C ＝120°.故选A.(理)(2011·郑州六校质量检测)△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若cb <cos A ，则△ABC 为( )A ．钝角三角形B ．直角三角形C ．锐角三角形D ．等边三角形 [答案] A[解析] 依题意得sin Csin B <cos A ，sin C <sin B cos A ，所以sin(A ＋B )<sin B cos A ，即sin B cos A ＋cos B sin A －sin B cos A <0，所以cos B sin A <0.又sin A >0，于是有cos B <0，B 为钝角，△ABC 是钝角三角形，选A.5．(文)(2011·福建质检)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a ＝1，c ＝42，B ＝45°，则sin C 等于( )A.441B.45 C.425 D.44141 [答案] B[解析] 依题意得b ＝a 2＋c 2－2ac cos B ＝5，又c sin C ＝b sin B ，所以sin C ＝c sin B b ＝42sin45°5＝45，选B. (理)(2010·湖南理)在ΔABC 中，角A ，B ，C 所对的边长分别为a ，b ，c .若∠C ＝120°，c ＝2a ，则( )A ．a ＞bB ．a ＜bC ．a ＝bD ．a 与b 的大小关系不能确定 [答案] A[解析] ∵∠C ＝120°，c ＝2a ，c 2＝a 2＋b 2－2ab cos C ∴a 2－b 2＝ab ，又∵a >0，b >0，∴a －b ＝ab a ＋b>0，所以a >b .6．(文)(2010·天津理)在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，若a 2－b 2＝3bc ，sin C ＝23sin B ，则A ＝( )A ．30°B ．60°C ．120°D ．150°[答案] A[解析] 由余弦定理得：cos A ＝b 2＋c 2－a 22bc ，由题知b 2－a 2＝－3bc ，c 2＝23bc ，则cos A ＝32， 又A ∈(0°，180°)，∴A ＝30°，故选A.(理)△ABC 中，a 、b 、c 分别为∠A 、∠B 、∠C 的对边，如果a 、b 、c 成等差数列，∠B ＝30°，△ABC 的面积为0.5，那么b 为( )A ．1＋ 3B ．3＋ 3 C.3＋33 D ．2＋ 3[答案] C[解析] 12ac sin B ＝12，∴ac ＝2，又2b ＝a ＋c ，∴a 2＋c 2＝4b 2－4，由余弦定理b 2＝a 2＋c 2－2ac cos B 得，b ＝3＋33.7．(文)(2010·上海模拟)在直角坐标系xOy 中，已知△ABC 的顶点A (－1,0)，C (1,0)，顶点B 在椭圆x 24＋y 23＝1上，则sin A ＋sin C sin B 的值为________．[答案] 2[解析] 由题意知△ABC 中，AC ＝2，BA ＋BC ＝4， 由正弦定理得sin A ＋sin C sin B＝BC ＋BAAC ＝2.(理)在锐角△ABC 中，边长a ＝1，b ＝2，则边长c 的取值范围是________．[答案]3<c < 5[解析] 边c 最长时：cos C ＝a 2＋b 2－c 22ab ＝1＋4－c 22×1×2>0，∴c 2<5.∴0<c < 5.边b 最长时：cos B ＝a 2＋c 2－b 22ac ＝1＋c 2－42c >0，∴c 2>3.∴c > 3. 综上，3<c < 5.8．(2011·广州一测)△ABC 的三个内角A 、B 、C 所对边的长分别为a 、b 、c ，已知c ＝3，C ＝π3，a ＝2b ，则b 的值为________．[答案]3[解析] 依题意及余弦定理得c 2＝a 2＋b 2－2ab cos C ，即9＝(2b )2＋b 2－2×2b ×b cos π3，解得b 2＝3，∴b ＝ 3.1.(文)(2011·深圳二调)已知△ABC 中，∠A ＝30°，AB ，BC 分别是3＋2，3－2的等差中项与等比中项，则△ABC 的面积等于( )A.32B.34C.32或 3D.32或34 [答案] D[解析] 依题意得AB ＝3，BC ＝1，易判断△ABC 有两解，由正弦定理得AB sin C ＝BCsin A ，3sin C ＝1sin30°，即sin C ＝32.又0°<C <180°，因此有C ＝60°或C ＝120°.当C ＝60°时，B ＝90°，△ABC 的面积为12AB ·BC＝32；当C ＝120°时，B ＝30°，△ABC 的面积为12AB ·BC ·sin B ＝12×3×1×sin30°＝34.综上所述，选D.(理)(2011·泉州质检)△ABC 的三个内角A 、B 、C 的对边分别为a 、b 、c ，且a cos C ，b cos B ，c cos A 成等差数列，则角B等于( )A ．30°B ．60°C ．90°D ．120°[答案] B[解析] 依题意得a cos C ＋c cos A ＝2b cos B ，根据正弦定理得，sin A cos C ＋sin C cos A ＝2sin B cos B ，则sin(A ＋C )＝2sin B cos B ，即sin B ＝2sin B cos B ，又0°<B <180°，所以cos B ＝12，所以B ＝60°，选B.2．(文)(2010·枣庄八中)在△ABC 中，内角A ，B ，C 对边的长度分别是a ，b ，c ，已知c ＝2，C ＝π3，△ABC 的面积等于3，则a ，b的值分别为( )A ．a ＝1，b ＝4B ．a ＝4，b ＝1C ．a ＝4，b ＝4D ．a ＝2，b ＝2 [答案] D[解析] 由余弦定理得，a 2＋b 2－ab ＝4，又因为△ABC 的面积等于3，所以12ab sin C ＝3，∴ab ＝4.联立⎩⎨⎧a 2＋b 2－ab ＝4ab ＝4，解得a ＝2，b ＝2.(理)△ABC 的周长为20，面积为103，A ＝60°，则BC 边的长是( )A ．5B ．6C ．7D ．8 [答案] C [解析] 由条件知⎩⎪⎨⎪⎧12bc sin60°＝103 (1)b ＋c ＋b 2＋c 2－2bc cos60°＝20 (2)由(1)得bc ＝40，由(2)得b ＋c ＋(b ＋c )2－3bc ＝20(3)将bc ＝40代入(3)中，解方程得b ＋c ＝13， ∴b ＝8，c ＝5或b ＝5，c ＝8， ∴a ＝b 2＋c 2－2bc cos60°＝7，故选C.3.(2011·天津理，6)如图，在△ABC 中，D 是边AC 上的点，且AB ＝AD,2AB ＝3BD ，BC ＝2BD ，则sin C 的值为( )A.33B.36 C.63 D.66[答案] D[解析] 如图，根据条件，设BD ＝2，则AB ＝3＝AD ，BC ＝4.在△ABC 中，由正弦定理：3sin C ＝4sin A在△ABD 中，由余弦定理： cos A ＝3＋3－42×3×3＝13，∴sin A ＝223∴sin C ＝3sin A 4＝3×2234＝66，故选D.4．(2010·四川双流县质检)在△ABC 中，tan A ＝12，cos B ＝31010，若最长边为1，则最短边的长为( )A.455B.355C.255D.55[答案] D[解析] 由tan A >0，cos B >0知A 、B 均为锐角， ∵tan A ＝12<1，∴0<A <π4，cos B ＝31010>32，∴0<B <π6，∴C 为最大角，由cos B ＝31010知，tan B ＝13，∴B <A ，∴b 为最短边， 由条件知，sin A ＝15，cos A ＝25，sin B ＝110， ∴sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B＝15×310＋25×110＝22，由正弦定理，b sin B ＝c sin C 知，b 110＝122，∴b ＝55.5．(文)(2011·河南质量调研)在△ABC 中，角A 、B 、C 所对应的边分别为a 、b 、c ，且满足cos A 2＝255，AB →·AC →＝3，则△ABC 的面积为________．[答案] 2[解析] 依题意得cos A ＝2cos 2A2－1＝35，∴sin A ＝1－cos 2A ＝45，∵AB →·AC →＝AB ·AC ·cos A ＝3，∴AB ·AC ＝5，∴△ABC 的面积S ＝12AB ·AC ·sin A ＝2.(理)(2011·新课标全国)在△ABC 中，B ＝60°，AC ＝3，则AB ＋2BC 的最大值为________．[答案] 27[解析] 依题意，由正弦定理得：AB ＝3sin60°·sin C ＝2sin C ，同理BC ＝2sin A .∴AB ＋2BC ＝2sin C ＋4sin A ＝2sin(120°－A )＋4sin A ＝3cos A ＋5sin A ＝27sin(A ＋φ)(其中tan φ＝35) ∴AB ＋2BC 的最大值为27.6．(文)△ABC 中内角A ，B ，C 的对边分别为a ，b ，c ，向量m＝(2sin B ，－3)，n ＝(cos2B,2cos 2B2－1)且m ∥n .(1)求锐角B 的大小；(2)如果b ＝2，求△ABC 的面积S △ABC 的最大值．[分析] (1)问利用平行向量的坐标表示将向量知识转化为三角函数，利用三角恒等变换知识解决；(2)问利用余弦定理与基本不等式结合三角形面积公式解决．[解析] (1)∵m ∥n ，∴2sin B ⎝ ⎛⎭⎪⎫2cos 2B 2－1＝－3cos2B ∴sin2B ＝－3cos2B ，即tan2B ＝－ 3 又∵B 为锐角，∴2B ∈(0，π) ∴2B ＝2π3，∴B ＝π3.(2)∵B ＝π3，b ＝2，∴由余弦定理cos B ＝a 2＋c 2－b 22ac 得，a 2＋c 2－ac －4＝0又∵a 2＋c 2≥2ac ，∴ac ≤4(当且仅当a ＝c ＝2时等号成立) S △ABC ＝12ac sin B ＝34ac ≤3(当且仅当a ＝c ＝2时等号成立)．即△ABC 面积的最大值为 3.[点评] 本题将三角函数、向量与解三角形有机的结合在一起，题目新颖精巧，难度也不大，即符合在知识“交汇点”处命题，又能加强对双基的考查，特别是向量的坐标表示及运算，大大简化了向量的关系的运算，该类问题的解题思路通常是将向量的关系用坐标运算后转化为三角函数问题，然后用三角函数基本公式结合正、余弦定理求解．(理)(2010·山东滨州)已知A 、B 、C 分别为△ABC 的三边a 、b 、c 所对的角，向量m ＝(sin A ，sin B )，n ＝(cos B ，cos A )，且m ·n ＝sin2C .(1)求角C 的大小；(2)若sin A ，sin C ，sin B 成等差数列，且CA →·(AB →－AC →)＝18，求边c 的长．[解析] (1)m ·n ＝sin A ·cos B ＋sin B ·cos A ＝sin(A ＋B )． 在△ABC 中，由于sin(A ＋B )＝sin C . ∴m ·n ＝sin C . 又∵m ·n ＝sin2C ，∴sin2C ＝sin C ，∴2sin C cos C ＝sin C .又sin C ≠0，所以cos C ＝12.而0<C <π，因此C ＝π3.(2)由sin A ，sin C ，sin B 成等差数列得， 2sin C ＝sin A ＋sin B ， 由正弦定理得，2c ＝a ＋b .∵CA →·(AB →－AC →)＝18，∴CA →·CB→＝18.即ab cos C ＝18，由(1)知，cos C ＝12，所以ab ＝36.由余弦定理得，c 2＝a 2＋b 2－2ab cos C ＝(a ＋b )2－3ab .∴c 2＝4c 2－3×36，∴c 2＝36.∴c ＝6.7．(文)(2010·安徽文)△ABC 的面积是30，内角A ，B ，C 所对边长分别为a ，b ，c ，cosA ＝1213.(1)求AB →·AC→； (2)若c －b ＝1，求a 的值．[解析] ∵0<A <π，cos A ＝1213，∴sin A ＝513.又S △ABC ＝12bc sin A ＝12bc ×513＝30.∴bc ＝156.(1)AB →·AC →＝|AB →|·|AC →|·cos A ＝b ·c ·1213＝156×1213＝144.(2)由题意知⎩⎨⎧bc ＝156c －b ＝1，∴⎩⎨⎧b ＝－13c ＝12(舍)或⎩⎨⎧b ＝12c ＝13∴⎩⎨⎧b ＝12c ＝13在△ABC 中，由余弦定理a 2＝b 2＋c 2－2bc cos A ＝132＋122－2×13×12×1213＝132－122＝(13＋12)(13－12)＝25.∴a ＝5.(理)(2010·东北师大附中、辽宁省实验中学联考)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a cos C ＋12c ＝b .(1)求角A 的大小；(2)若a ＝1，求△ABC 的周长l 的取值范围． [解析] (1)由a cos C ＋12c ＝b 得sin A cos C ＋12sin C ＝sin B又sin B ＝sin(A ＋C )＝sin A cos C ＋cos A sin C ∴12sin C ＝cos A sin C ， ∵sin C ≠0，∴cos A ＝12，又∵0<A <π，∴A ＝π3.(2)解法1：由正弦定理得：b ＝a sin B sin A ＝23sin B ，c ＝23sin Cl ＝a ＋b ＋c ＝1＋23(sin B ＋sin C )＝1＋23(sin B ＋sin(A ＋B ))＝1＋2⎝ ⎛⎭⎪⎫32sin B ＋12cos B ＝1＋2sin ⎝ ⎛⎭⎪⎫B ＋π6 ∵A ＝π3，∴B ∈⎝ ⎛⎭⎪⎫0，2π3，∴B ＋π6∈⎝ ⎛⎭⎪⎫π6，5π6，∴sin ⎝⎛⎭⎪⎫B ＋π6∈⎝⎛⎦⎥⎤12，1.故△ABC 的周长l 的取值范围是(2,3]．解法2：周长l ＝a ＋b ＋c ＝1＋b ＋c 由(1)及余弦定理a 2＝b 2＋c 2－2bc cos A ， ∴b 2＋c 2＝bc ＋1，∴(b ＋c )2＝1＋3bc ≤1＋3⎝ ⎛⎭⎪⎪⎫b ＋c 22，∴b ＋c ≤2，又b ＋c >a ＝1，∴l ＝a ＋b ＋c ∈(2,3]， 即△ABC 的周长l 的取值范围为(2,3]．1．(2010·泰安模考)在△ABC 中，若A ＝60°，BC ＝43，AC ＝42，则角B 的大小为( )A ．30°B ．45°C ．135°D ．45°或135° [答案] B[解析] ∵AC ·sin60°＝42×32＝26<42<43，故△ABC 只有一解，由正弦定理得，42sin B ＝43sin60°，∴sin B ＝22，∵42<43，∴B <A ，∴B ＝45°.2．(2010·厦门市检测)在△ABC 中，角A 、B 、C 所对应的边分别为a 、b 、c ，若角A 、B 、C 依次成等差数列，且a ＝1，b ＝3，则S △ABC 等于( )A. 2B. 3C.32D ．2 [答案] C[解析] ∵A 、B 、C 成等差数列，∴B ＝60°， ∵b sin B ＝asin A ，∴sin A ＝a sin B b ＝1×323＝12， ∴A ＝30°或A ＝150°(舍去)，∴C ＝90°， ∴S △ABC ＝12ab ＝32.3．(2011·豫南四校调研考试)若AB ＝2，AC ＝2BC ，则S △ABC的最大值为( )A ．2 2 B.32C.23 D ．3 2 [答案] A[解析] 设BC ＝x ，则AC ＝2x ，根据面积公式得S △ABC ＝12×AB ×BC sin B ＝x1－cos 2B ①，根据余弦定理得cos B ＝AB 2＋BC 2－AC 22AB ·BC ＝4＋x 2－2x 24x ＝4－x 24x ②，将②代入①得，S △ABC ＝x1－(4－x 24x)2＝128－(x 2－12)216，由三角形的三边关系得⎩⎨⎧2x ＋x >2x ＋2>2x，解得22－2<x <22＋2，故当x ＝23时，S △ABC 取得最大值22，故选A.4．(2011·金华期末)△ABC 中，若a 4＋b 4＋c 4＝2c 2(a 2＋b 2)，则角C 的度数是( )A ．60°B ．45°或135°C ．120°D ．30° [答案] B[解析] ∵a 4＋b 4＋c 4＝2c 2a 2＋2b 2c 2，∴cos 2C ＝(a 2＋b 2－c 2)2(2ab )2＝a 4＋b 4＋c 4＋2a 2b 2－2c 2a 2－2b 2c 24a 2b 2＝12⇒cos C ＝±22.∴C ＝45°或135°.5．(2010·山东济南)在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若(a 2＋c 2－b 2)tan B ＝3ac ，则角B 的值为( )A.π6B.π3C.π6或5π6D.π3或2π3 [答案] D[解析] 由(a 2＋c 2－b 2)tan B ＝3ac 得，a 2＋c 2－b2ac·tan B ＝3，再由余弦定理cos B ＝a 2＋c 2－b 22ac 得，2cos B ·tan B ＝3，即sin B ＝32，∴角B 的值为π3或2π3，故应选D.6．判断下列三角形解的情况，有且仅有一解的是________．①a ＝1，b ＝2，B ＝45°； ②a ＝5，b ＝15，A ＝30°； ③a ＝6，b ＝20，A ＝30°； ④a ＝5，B ＝60°，C ＝45°. [答案] ①④ [解析] ①由a sin B ＝22<1<2知，有一解． ②由b ·sin A ＝152<5<15知，有两解；③由b ·sin A ＝10>6知，无解．④一解，已知两角和一边，三角形唯一确定．7．(2010·海淀市模拟)在△ABC 中，角A 、B 、C 所对应的边分别为a 、b 、c ，若a ＝c sin A ，则a ＋bc 的最大值为________．[答案]2[解析] 由a ＝c sin A 及正弦定理得sin A ＝sin C ·sin A ，从而有sin C ＝1，∠C ＝90°，所以有a 2＋b 2＝c 2，a ＋b c ＝⎝ ⎛⎭⎪⎪⎫a ＋b c 2＝a 2＋b 2＋2abc 2≤a 2＋b 2＋a 2＋b 2c 2＝ 2.8．(2011·安阳月考)在△ABC 中，C ＝60°，a ，b ，c 分别为A ，B ，C 的对边，则a b ＋c ＋bc ＋a＝________. [答案] 1[解析] ∵C ＝60°，∴a 2＋b 2－c 2＝ab ，∴(a2＋ac)＋(b2＋bc)＝(b＋c)(a＋c)，∴ab＋c＋ba＋c＝1.。