博弈论的军事应用

数学与军事数学在军事战略和武器设计中的应用数学与军事：数学在军事战略和武器设计中的应用导言：数学与军事的关系是密不可分的。

在军事战略和武器设计中，数学为决策制定提供了理论基础，为军事活动的规划和执行提供了重要的支持。

本文将探讨数学在军事领域中的应用，包括战略决策、兵力运用、武器设计等方面。

一、战略决策战略决策是军事活动的核心，涉及到军队的布局、作战计划和指挥调度等。

数学在战略决策中发挥了重要的作用。

1. 战略模型战略模型是应用数学方法分析和研究军事战略问题的数学模型。

其中包括线性规划、对策论、博弈论等方法。

通过这些模型，军事指挥官可以优化资源配置、提高作战效率。

例如，线性规划可以帮助军事指挥官确定兵力部署，使得兵力分配合理，最大程度地发挥作战效能。

2. 网络优化网络优化是利用图论和最优化理论解决军事行动中的路径规划、网络流等问题。

在军事行动中，兵力的移动路径和资源的分配是关键问题。

通过网络优化方法，可以找到最优路径、减少时间和能量消耗，提高作战效果。

3. 决策支持系统决策支持系统是基于数学模型和信息技术的复杂决策问题的支持系统。

通过决策支持系统，军事指挥官可以实时获取战场情报、模拟战场环境、进行决策分析等。

决策支持系统的应用，可以提高军事指挥官的决策能力和决策效率。

二、兵力运用兵力运用是军事指挥活动中的关键环节，涉及到兵力部署、打击效果评估等问题。

数学在兵力运用中具有重要的应用价值。

1. 兵力部署数学方法可以帮助军事指挥官确定兵力部署的最佳方案。

通过模型和算法，可以考虑到地理条件、敌情分析、兵种特性等因素，制定出有效的兵力部署方案。

例如，最短路径算法可以帮助军事指挥官找到最优的兵力部署方案，使得兵力能够迅速集中、及时响应。

2. 打击效果评估数学方法可以对军事打击效果进行评估和优化。

通过模拟实验和数据分析，可以评估不同作战方案和武器装备的打击效果，为军事指挥官提供决策参考。

例如，使用数学模型和仿真技术，可以评估不同武器系统的打击精度、杀伤能力，为军事指挥官的决策提供科学依据。

运用合作博弈理论提升武警部队军事经济监督实效的必要性思考合作博弈理论是博弈论中的一个重要分支，它研究的是在博弈过程中，博弈各方之间通过合作达成共赢的方式。

在军事经济监督领域，合作博弈理论的运用能够提升武警部队的监督实效，从而更好地维护国家安全和军队稳定发展。

本文将就运用合作博弈理论提升武警部队军事经济监督实效的必要性进行思考。

合作博弈理论能够帮助武警部队建立有效的监督合作机制。

军事经济活动本身就具有复杂性和特殊性，需要各个部门之间形成紧密配合和有效协作的监督机制。

合作博弈理论提供了一种全新的思路，通过合作博弈的方式，各个部门可以在监督过程中相互协作，达成共赢。

可以建立联合监督机制，各部门之间共同制定监督方案，明确监督责任和监督标准，从而确保各方在监督过程中相互协作、相互支持，达成监督的最优结果。

合作博弈理论可以促进武警部队与其他部门之间的良性互动。

军事经济监督既涉及到武警部队内部的监督，也涉及到武警部队与其他部门之间的监督互动。

合作博弈理论可以帮助各部门之间通过合作博弈的方式，形成良性互动，共同推动军事经济监督工作的开展。

可以通过合作博弈的方式，各部门之间协商、合作，明确各自的监督责任和监督标准，建立起稳定的监督互动关系，推进军事经济监督工作的全面开展。

合作博弈理论能够有效促进监督工作的持续改进和完善。

军事经济监督工作是一个不断完善的过程，需要各方不断改进监督方法和监督手段，提升监督工作的效能和效果。

合作博弈理论可以帮助各方通过博弈的方式，不断寻求监督工作的改进和完善，形成监督工作的良性循环。

可以通过合作博弈的方式，各方之间进行讨论、协商，发现监督工作存在的问题和不足，形成共识，共同制定监督改进方案，不断完善监督工作的方法和手段，提升监督工作的效能和效果。

运用合作博弈理论提升武警部队军事经济监督实效具有重要的现实意义和必要性。

通过合作博弈理论的运用，可以建立有效的监督合作机制，建立良好的监督合作关系，促进武警部队与其他部门之间的良性互动，推动监督工作的持续改进和完善，从而更好地维护国家安全和军队稳定发展。

无人机对抗任务中的博弈论研究无人机技术的发展已经取得了飞速的进展，这些飞行器的用途越来越广泛，其中包括军事领域。

在军事应用中，无人机具有广阔的前景，尤其是在情报获取和目标攻击方面，因为无人机具有更好的隐蔽性和迅速的反应速度。

然而，无人机在军事领域的应用，也提出了许多新的技术问题。

其中一个显著的经济性问题是，如何保证无人机的任务成功率并减少无人机被敌方拦截的可能性，这需要考虑到无人机的设计和使用禁止措施，但更加关键的是开发博弈论模型。

博弈论是研究策略在竞争场合下的互动战略的一种数学分析方法。

它通常涉及多个参与者，每个参与者在毫不知情的情况下最大化自己的获利，并尽可能减少他人的收益。

博弈论的研究可以产生对策，使其获得最好的结果。

如何利用博弈论进行无人机对抗任务，是一个值得探讨的话题。

首先，我们需要探讨的是无人机的任务成功率，以及在此过程中可能面临的风险和障碍。

通过深入了解无人机的各种功能和机制，可以得出以下结论：首先，无人机具有更好的隐蔽性，在隐蔽条件下具有较高的幸存率，并且可以逃脱敌人的视线。

其次，无人机拥有更快的反应速度，在战斗中具有更好的机动性和灵活性。

然而，这些优点也带来了一些挑战，如无人机的设备容易被敌人检测，以及无人机的操作可能受制于天气等自然因素。

考虑到无人机的特点，我们可以用博弈论研究来解决一些问题。

对于无人机任务的成功率，我们可以运用博弈论的模型来优化无人机的设计和操作策略。

例如，我们可以运用最小最大（Min-Max）策略来确定无人机的路径，这可以最大限度地减少被敌人拦截的可能性。

同样，博弈论也可以帮助无人机在遇到敌军时尽可能地幸存下来。

针对这一问题，可以使用博弈论来分析无人机的运动轨迹和目标，以实现最大化的敌方威慑。

这需要博弈论分析每个参与者的收益和成本，并确定最好的策略，以支持无人机在战斗中的幸存率。

实际上，博弈论不仅适用于无人机的单一任务，也适用于无人机在群体和系统中的运营。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载浅谈博弈论在军事领域的应用地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容浅谈博弈论在军事领域的应用一营三连谢寒学号：33320111022现如今博弈论已经发展成为经济学的标准分析工具之一。

目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。

特别是其在军事战略方面的运用更是自古有之，中国古代的《孙子兵法》就不仅是一部军事著作，而且算是最早的一部博弈论著作。

博弈论研究的不是“一场战斗”的胜负，它要说明在“棋逢对手，将遇良才”时，战争如何会处于一种“胶着”状态——即实现了纳什均衡。

如果排除蜀汉的粮草问题及两人的健康问题，诸葛亮与司马懿的这场“零和博弈”（不存在纯策略均衡）的结果应该是谁也吃不掉谁，谁也不能进一步占谁的便宜。

每个人在选择自己的计策时都会考虑对手的反应，双方只会在概率的意义上实现“平手”（博弈论至少可以说明“空城计”不可能使用第二遍）。

司马懿笑诸葛亮不肯兵出子午谷，诸葛亮笑司马懿不肯马踏西城，双手打了个“平手”。

其实这正是“混合策略均衡”的表现。

博弈论的一个关键要求是，博弈树对所有参与人是“共同知识”，因此应用博弈论描述“现实情形”时，要注意这一点。

让博弈树成为共同知识也许需要一个过程（究竟博弈树是什么样子，也许过一段时间参与人才能反应过来），而博弈论描述的是这个过程实现后的情况。

谢林是美国著名学者、经济学家，也是有限战争理论的奠基人之一，还是外交事务、国家安全、核战略以及军备控制方面的研究专家。

因此，对于谢林这个名字，军事迷可能比经济学专业的学生们更加熟悉。

从上个世纪50年代开始，谢林的研究成果就已经应用于美苏冷战中。

博弈论的军事应用作者：姚实来源：《商情》2014年第45期【摘要】本文运用博弈论对古代中国经典军事案例进行分析，提出无论是合作博弈还是非合作博弈，各方掌握的信息数量作用至关重要，在战争之中一次博弈其实包含着不完全信息情况下多次博弈状况。

军事战争中各方应该通过信息及概率随时了解收益矩阵的变化并及时做出修正，才能在博弈中掌握主动。

【关键词】博弈论军事合作博弈不对称信息一、重复合作博弈（一）作壁上观的内在逻辑在战争中经常会因为实力的差别出现结盟的现象，会盟各方常会遇到合力战胜强大对手和保存自己的实力之间的选择问题，如项羽联合各路诸侯攻秦的巨鹿之战，各路诸侯作壁上观。

直至项羽破釜沉舟，身先士卒，以两万先锋搅乱了秦军的阵势，诸侯方投入战斗，秦军遂寡不敌众。

如果项羽兵败，各路诸侯要么引兵而去保存实力，要么直接卸甲投降。

简化其收益矩阵如下图。

打败秦朝是各路诸侯联盟的最初目的，争夺天下才是最终目的，所以诸侯是在保存自己的情况下才出兵灭秦，其先决条件是项羽的兵胜。

所以我们看到了联盟是多么的脆弱，一旦项羽兵败，即使各路诸侯占有军队数量的绝对优势也将难挽败局。

（二）监管的重要性巨鹿之战中各路诸侯既没有内在道德制约又不受外部势力的管控，这是一种不稳定状态。

如丘吉尔所言没有永远的朋友，只有永远的利益，但是其前提是各方势力相差无几，背叛的后果并不严重，仍有重复合作博弈的可能。

三国时期魏蜀吴三国不断的相互背叛，攻击，却仍然能在大敌当前的时候相互结盟合作。

重复合作博弈最终需要各方实力悬殊不大或者拥有强力的监管才可能真正对合作中的背叛者起到震慑作用。

如果我们将三国看做是两家垄断企业和消费者之间的价格竞争的话，两家企业想要商品价格维持高位又想扩大各自的市场占有率，而消费者的目的是在买到足够多的商品的情况下尽量压低商品的价格，那么当相互合作的两垄断企业维持高价的情况下会导致消费者不得不在高价的时候购买商品，当两方企业达到价格相同时将会达到一种暂时的稳定。

博弈论在兵法中的应用每个中国人对博弈都不会感到陌生，从经典到民谚，从战场到麻将桌，每个中国人都会使用博弈论，只是运用的恰当与否的区别罢了。

全世界都承认中国人是善良的，也是老练的。

博弈论在中国很早就流行了，并不是舶来品。

要知道什么事博弈论，首先要清楚什么事博弈。

《现代汉语词典》中对博弈一词的解释是：（1）古代指下围棋，也指赌博。

（2）比喻为谋取利益而竞争。

博弈无处不在，无时不在，无人不在博弈，无人不会博弈，但博弈有胜负，策略有高低。

因此，我们可以通过学习，通过探讨，作出更佳的抉择，让我们的生活、我们的社会变得更加美好。

既然我们如此离不开博弈，就必须学习博弈，一定要懂得博弈论。

博弈论是一种“游戏理论”。

其准确的定义是：一些个人、团体或其他组织，面对一定的环境条件，在一定的规则约束下，依靠所掌握的信息，同时或先后，一次或多次，对各自允许选择的行为或策略进行选择并加以实施，并从其中各自取得相应结果或收益的过程。

在战争中，如果我们在足够多的战场中集中足够多的兵力的话，我们将有很大可能赢得战争的胜利。

如果我们的兵力等可利用的资源有限时，我们要想在战争中取胜，就必须学会“集中优势兵力”这一战术原则，将我们的时间、精力、才能等投入最有希望获胜的战场，确保在这一领域的优势地位。

历史上有个发生过的真实例子，“田忌赛马”。

在这个故事中，齐王的上、中、下三种赛马都要比田忌的同等赛马要好，但却输掉比赛，这是因为孙膑采取了“下驷对上驷、上驷对中驷、中驷对下驷”的巧妙策略，取得了胜利。

这就是在足够多的战场中集中足够多的兵力最终取得胜利。

主动放弃在另一战场上的投入，有时并不会失败，相反，它才是赢得战争的正确思路。

由英国工程师蓝彻斯特提出的“蓝彻斯特定律”，给我们提供了一个优势兵力转化为优势战果的量化指标。

他设想了一个战斗模式，敌对双方彼此相互射击，而且双方在准确性、人员、武器等各方面都势均力敌。

因此，军队数量决定了敌对双方的攻击力：一方面增加自己的命中率，另一方面则分散对方的攻击火力。

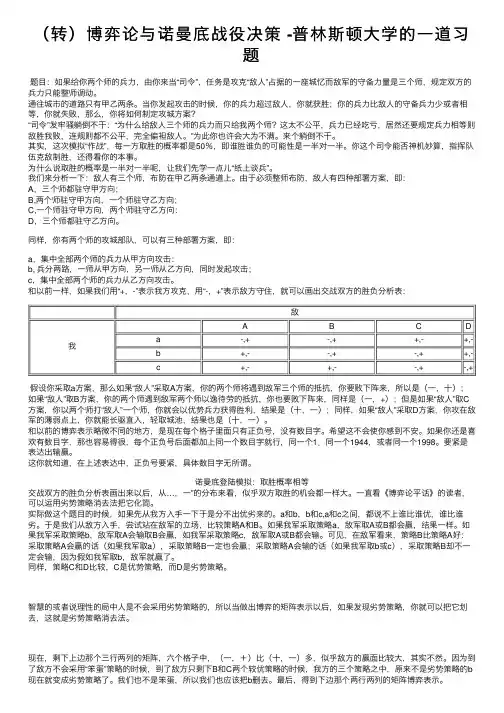
（转）博弈论与诺曼底战役决策 -普林斯顿⼤学的⼀道习题题⽬：如果给你两个师的兵⼒，由你来当“司令”，任务是攻克“敌⼈”占据的⼀座城忆⽽敌军的守备⼒量是三个师，规定双⽅的兵⼒只能整师调动。

通往城市的道路只有甲⼄两条。

当你发起攻击的时候，你的兵⼒超过敌⼈，你就获胜；你的兵⼒⽐敌⼈的守备兵⼒少或者相等，你就失败，那么，你将如何制定攻城⽅案？“司令”发牢骚躺倒不⼲：“为什么给敌⼈三个师的兵⼒⽽只给我两个师？这太不公平，兵⼒已经吃亏，居然还要规定兵⼒相等则敌胜我败，连规则都不公平，完全偏袒敌⼈。

”为此你也许会⼤为不满。

来个躺倒不⼲。

其实，这次模拟“作战”，每⼀⽅取胜的概率都是50％，即谁胜谁负的可能性是⼀半对⼀半。

你这个司令能否神机妙算，指挥队伍克敌制胜，还得看你的本事。

为什么说取胜的概率是⼀半对⼀半呢，让我们先学⼀点⼉“纸上谈兵”。

我们来分析⼀下：敌⼈有三个师，布防在甲⼄两条通道上。

由于必须整师布防，敌⼈有四种部署⽅案，即：A，三个师都驻守甲⽅向；B,两个师驻守甲⽅向，⼀个师驻守⼄⽅向；C,⼀个师驻守甲⽅向，两个师驻守⼄⽅向：D，三个师都驻守⼄⽅向。

同样，你有两个师的攻城部队，可以有三种部署⽅案，即：a，集中全部两个师的兵⼒从甲⽅向攻击：b, 兵分两路，⼀师从甲⽅向，另⼀师从⼄⽅向，同时发起攻击；c，集中全部两个师的兵⼒从⼄⽅向攻击。

和以前⼀样，如果我们⽤“+，-”表⽰我⽅攻克，⽤“-，+”表⽰敌⽅守住，就可以画出交战双⽅的胜负分析表：　敌我　A B C D a-,+-,++,-+,-b+,--,+-,++,-c+,-+,--,+-,+假设你采取a⽅案，那么如果“敌⼈”采取A⽅案，你的两个师将遇到敌军三个师的抵抗，你要败下阵来，所以是（⼀，⼗）；如果“敌⼈”取B⽅案，你的两个师遇到敌军两个师以逸待劳的抵抗，你也要败下阵来，同样是（⼀，+）；但是如果“敌⼈”取C ⽅案，你以两个师打“敌⼈”⼀个师，你就会以优势兵⼒获得胜利，结果是（⼗，⼀）；同样，如果“敌⼈”采取D⽅案，你攻在敌军的薄弱点上，你就能长驱直⼊，轻取城池，结果也是（⼗，⼀）。

博弈论的军事应用博弈论是通过模型表征决策参与者之间的相互作用，利用概率、数学和统计来分析和预测行为的综合理论之一。

自20世纪50年代以来，博弈论已经广泛应用于涉及彼此冲突且具有双赢特性的复杂决策环境中。

其中，军事应用是博弈论有效应用的一个重要领域。

军事活动对拥有强大军队的国家来说是非常重要的，面对挑战，国家需要运用博弈手段来解决冲突。

博弈论在军事上的应用主要是用于分析不同的军事行为，以帮助国家判断哪种行为更能帮助他们实现最佳战略目标。

比如，美国和俄罗斯就经常利用博弈论来评估互相的战略行动。

如果针对一个双方都有兴趣的问题，比如核不扩散、亚太地区的安全等，双方就可以共同使用博弈论来模拟各种可能的军事行动并分析不同结果。

例如，协商者可以通过分析出他们之间军事行动的收益，以帮助他们采取最佳行动，从而在现实中有效地解决冲突。

另外，博弈论也可以用于研究军事取舍。

换句话说，在一个具有双赢特性的决策中，决策者需要评估收益机会和风险，以做出最佳决策。

在这种情况下，决策者将模拟出系统中各种可能的行动，并根据这些行动产生的不同最终结果评估可能的后果和可能的收益。

除此之外，博弈论还可以用于研究军事信息，比如双方之间的谈判，或者评估国家间的安全环境。

例如，博弈论可以帮助决策者评估彼此之间相互之间安全环境的风险，以及评估协议的可行性。

总之，博弈论在军事活动中具有广泛的应用。

博弈论可以帮助分析不同的军事行为，评估双方的行动收益，并对收益和风险进行比较，有助于做出最佳决策。

而且，博弈论也可以用于评估安全问题，以及协商双方之间有关军事变动的协议。

因此，博弈论一直被认为是军事行动中有效和实用的分析工具。

博弈论的应用领域博弈论的应用领域非常广泛，包括但不限于以下领域：1.经济学：现代博弈论在经济学的各个领域都有广泛的应用，如微观经济学、宏观经济学、产业组织理论、贸易政策、经济发展、公共财政、企业理论、福利经济学等。

2.政治学：政治学领域的许多问题可以通过博弈论来分析。

例如，研究选举过程中的投票策略，分析国家之间的外交博弈，或者理解利益集团如何影响政策制定等。

3.生物学：在生物学中，博弈论被用于解释进化论中的某些现象，如合作行为的进化等。

4.计算机科学：在计算机科学中，博弈论用于设计和分析人工智能系统的交互策略。

例如，计算机安全中的网络安全问题可以通过博弈论来理解和解决。

5.国际关系：在国际关系中，博弈论被用于研究国家之间的竞争和冲突。

例如，冷战期间的军备竞赛、贸易争端和外交角力等都可以通过博弈论来理解。

6.军事战略：在军事战略中，博弈论被用于研究战争和冲突中的策略和均衡。

例如，冷战期间的美苏核武器竞争和阿富汗战争等都可以通过博弈论来分析。

7.法律和伦理学：在法律和伦理学中，博弈论被用于研究法律规则和道德规范如何影响人们的行为决策。

例如，分析如何防止腐败、制定公平的贸易规则或制定有效的法律制裁等。

8.社会学：在社会学中，博弈论被用于研究社会互动和社会现象。

例如，分析社会规范和习俗的形成、社会群体的分化和冲突等。

9.哲学：在哲学中，博弈论被用于研究和解释道德哲学、政治哲学和社会哲学等领域的问题。

例如，探讨正义的本质、探究权力与自由的关系或分析社会契约的理论基础等。

10.生物学：在生物学中，博弈论被用于解释物种之间的相互作用和进化策略。

例如，研究捕食者和猎物之间的相互作用、种群动态或合作行为的进化等。

这只是博弈论应用领域的一个概览，实际上，博弈论在许多其他领域也有广泛的应用，如心理学、地理学、化学等。

二战中的军事博弈与战术创新二战是人类历史上规模最大、影响最深远的战争之一。

在这场战争中，各国军事力量之间的博弈和战术创新发挥了至关重要的作用。

本文将探讨二战中军事博弈的一些典型案例，以及双方在战术上的创新。

一、军事博弈1.1 德国的闪电战在二战初期，德国军队以其独特的战术手段给世界各国以极大震撼。

德国采用闪电战战术，即通过迅速、突然的进攻迅速击垮敌军。

这种战术依靠快速机动、全力进攻、突至敌后等手段，打破了传统战争理念，对敌军和指挥官造成了极大困扰。

1.2 英国的信息战英国在军事博弈中也有自己的特色。

英国利用情报信息的收集和利用，进行精确打击和战略布局。

著名的英国间谍机构“国家情报局”对德国情报机构进行了有效的渗透，并提供了大量关键信息。

这些信息对于战局的发展和决策制定起到了重要作用。

1.3 美国的经济战美国在二战中采取了一系列经济手段来加大对敌军的打击。

美国通过封锁敌军的经济链条，使其无法获取战争所需的资源和物资。

同时，美国还通过经济援助和军事援助来帮助其盟国。

这种经济战对于扭转战局具有重要作用。

二、战术创新2.1 坦克战术二战中，坦克作为一种新型装备在战场上发挥了巨大作用。

各国不断创新坦克战术，以适应快速推进的战争需求。

例如，德国推出了“闪电战”坦克战术，将坦克编成装甲师，以快速机动的方式击溃敌军。

苏联则采取了人海战术，利用数量优势对德国坦克构成压力。

2.2 空中战术二战见证了空中战术的迅猛发展。

双方在空中展开了激烈的博弈。

例如，德国发展出了“突袭战术”，将轰炸机编成编队进行突袭，以获得制空权。

而英国则采取了“夜间防空战术”，在夜间利用雷达等技术对德军轰炸机进行拦截。

2.3 海战战术二战中的海战也积累了许多战术创新的案例。

例如，日本海军发起了袭击珍珠港的行动，采取了突袭战术，并配备了载飞机的航空母舰，改变了传统海战的格局。

而美国则发起了中途岛海战，利用侦查和情报优势，采取袭击敌舰编队的战术手段，从而获得了决定性的胜利。

博弈论是研究决策者之间相互影响及其行为的一门学科，它对于分析复杂的决策情境和竞争环境有着重要的应用价值。

博弈论的概念最早可以追溯到数学家冯·诺伊曼和经济学家米尔顿·弗里德曼在20世纪40年代提出的。

博弈论的应用领域非常广泛，包括经济学、政治学、生物学、军事以及社会科学等。

博弈论的核心思想是通过对决策者之间的相互作用进行建模和分析，来预测他们的最佳行为策略。

每位决策者的行为都会对其他人产生影响，而其他人的反应又会对自己产生影响，从而形成一个相互影响的网络。

博弈论的目标是找到每位决策者的最优策略，即在给定其他人的行为情况下，使得自己的收益最大化。

博弈论可以分为合作博弈和非合作博弈两种类型。

合作博弈是指决策者之间可以合作并达成共识的情况下进行决策，而非合作博弈则是指决策者之间缺少合作和共识的情况下进行决策。

非合作博弈又可以进一步分为纳什均衡和博弈树等不同形式。

在经济学中，博弈论被广泛应用于研究市场竞争、价格形成和产业结构等问题。

例如，在价格竞争中，博弈论可以帮助分析参与者的最佳定价策略，并预测市场的均衡价格。

在国际贸易中，博弈论可以研究贸易政策的制定和影响，以及国际市场的竞争策略。

在政治学中，博弈论可以分析选举、议会投票和决策过程等问题。

例如，在选举中，博弈论可以研究候选人的竞选策略和选民的投票决策。

在议会投票中，博弈论可以帮助分析议员之间的合作关系和利益博弈。

在生物学中，博弈论可以解释进化和合作的现象。

例如，在动物中的群体行为和繁殖策略等问题中，博弈论可以揭示个体之间的博弈和合作策略。

在进化生物学中，博弈论可以研究适应性演化中的策略和结果。

在军事领域，博弈论可以帮助分析战略和战术决策。

例如，在决策制定中，博弈论可以研究不同决策者的束缚和选择，以及他们之间的相互影响。

总结来说，博弈论是一门研究决策者之间相互影响及其行为的学科。

它在经济学、政治学、生物学、军事以及社会科学等领域中有重要的应用。

博弈论在动态武器目标分配问题中的应用博弈论是研究决策和策略的一门学科，它在各个领域都有广泛的应用，包括经济学、政治学、计算机科学等等。

其中，博弈论在动态武器目标分配问题中的应用也非常重要。

动态武器目标分配问题是指在一场战争中，需要分配有限的武器目标给不同的参与方，以达到最优的效果。

这是一个典型的多方博弈问题，因为参与者之间的互动关系很复杂，每个人都追求自己的最大利益，而且参与者的数量和策略层次都很多样化。

博弈论可以帮助解决动态武器目标分配问题的优化和决策过程。

它提供了一种系统的分析框架，可以用来研究不同参与者的策略选择和可能的结果，以及他们之间的相互作用和影响。

首先，博弈论提供了一些基本的概念和解决方法，如博弈形式、纳什均衡和最大最小化原则等。

这些概念和方法可以帮助我们描述和分析动态武器目标分配问题，并找到最优的决策策略。

其次，博弈论可以对不同参与者的策略进行建模和分析。

在动态武器目标分配问题中，不同参与者可以是不同的军队、组织或个体，他们的策略可以是武器的部署、目标选择、攻击顺序等。

博弈论可以帮助我们确定参与者的策略选择和影响因素，以及他们之间可能的竞争和合作关系。

此外，博弈论还可以解决动态武器目标分配问题中的合作与冲突的平衡。

在动态武器目标分配问题中，参与者之间常常存在着竞争和合作的关系。

博弈论可以帮助我们研究合作和冲突的平衡点，以及如何通过博弈的方式达成合作和解决冲突问题。

博弈论的一个重要应用是建立数学模型和算法来解决动态武器目标分配问题。

通过建立模型，我们可以对问题进行抽象和简化，以便进行定量分析和计算。

通过算法，我们可以有效地求解模型，找到最优的分配策略和结果。

例如，博弈论可以用来解决动态武器目标分配问题中的两个极端情况。

一种情况是零和博弈，即参与者之间的利益是相互矛盾的，一方的利益损失就是另一方的利益增加。

在这种情况下，我们可以通过最大化自己的利益来寻求最优的分配策略。

另一种情况是合作博弈，即参与者之间的利益是相互依存的，一方的利益增加也会带来其他方的利益增加。

博弈论及其在决策中的应用博弈论是一门研究决策策略的数学理论，旨在分析不同利益相关方之间的冲突与合作关系。

它涵盖了很多基本概念和方法，为实施最优决策提供了一套理论框架。

博弈论在各个领域的决策问题中得到了广泛的应用，如经济学、管理学、政治学等。

博弈论的基本概念有玩家、策略、收益和博弈形式。

玩家是参与博弈的个体或群体，策略是玩家选择的行动，收益是博弈结果带给玩家的效益，而博弈形式描述了玩家在不同策略下获得的收益的矩阵。

博弈论在决策中的应用主要体现在以下几个方面。

首先，博弈论可用于分析竞争性市场中的决策问题。

当多个企业在一个市场上竞争时，它们需要决定合适的定价、广告和产品策略。

通过博弈论的方法，可以预测竞争双方的最优策略，并帮助企业做出相应的决策，达到最大利益。

其次，博弈论可用于研究战略决策问题。

例如，军事战争中的战略决策，政治竞选中的策略制定等。

博弈论可以帮助参与者评估不同策略下的可能结果，并制定出最佳的决策方案。

再次，博弈论可用于分析合作博弈中的决策问题。

在合作博弈中，参与者可以通过合作来达到更好的效果。

通过博弈论的方法，可以分析合作博弈中的稳定合作策略，并帮助参与者做出合适的决策。

最后，博弈论可用于分析资源分配问题。

在资源有限的情况下，如何进行公平合理的分配是一个重要的决策问题。

博弈论可以帮助参与者评估不同资源分配策略下的可能结果，并找到最佳的分配方案。

总之，博弈论在各个领域的决策问题中有着重要的应用价值。

通过博弈论的方法，可以分析不同决策策略下的可能结果，并帮助决策者做出最优决策。

在实际应用中，需要综合考虑各个因素，如参与者的利益、目标和约束条件等，以便找到最适合的决策方案。

运用合作博弈理论提升武警部队军事经济监督实效的必要性思考合作博弈理论是博弈论中的一个重要分支，它研究博弈参与者之间通过合作协商取得最优结果的方法和方式。

在武警部队的军事经济监督中，运用合作博弈理论可以帮助提升监督实效，加强资源管理和监督，促进武警部队的可持续发展。

本文将从合作博弈理论的角度对武警部队军事经济监督进行思考，探讨其必要性和可能的效果。

合作博弈理论可以帮助武警部队建立更加完善的监督机制。

在军事经济领域，资源的分配和利用是一个复杂的问题，需要各级部队和相关部门之间建立起有效的协作关系。

合作博弈理论可以帮助各部门之间进行合作博弈，明确各自的利益和责任，协商共同的监督标准和机制，确保资源的合理配置和利用。

这样可以避免资源的浪费和滥用，提高武警部队的经济效益。

合作博弈理论可以帮助武警部队建立有效的激励机制。

在军事经济监督中，存在着一些监督者可能存在监督不力的情况，因为他们可能受到一些利益和激励因素的影响。

合作博弈理论可以帮助武警部队建立起有效的激励机制，让监督者能够根据自身的努力和贡献得到相应的回报，从而提高监督的积极性和主动性。

通过合作博弈理论，可以建立起一套完善的激励机制，激发监督者的积极性，提高监督的效率和实效。

合作博弈理论可以帮助武警部队建立信任和合作关系。

在军事经济监督中，存在着各种各样的利益冲突和矛盾问题，需要各部门之间建立起相互信任和合作的关系，共同推进监督工作。

合作博弈理论可以通过建模分析各方的利益和风险，找到双方合作的最优解，并建立共同的信任基础。

通过合作博弈理论的引导，可以使各部门之间建立起相互信任和合作的关系，共同为军事经济监督的实效努力。

合作博弈理论可以帮助武警部队建立起更加公平和公正的监督制度。

军事经济监督需要保证监督制度的公平和公正，避免出现以权谋私、搞特权的情况。

合作博弈理论可以帮助各部门之间建立起公平的博弈机制，让各方都能在博弈中得到公平的对待和机会。

通过合作博弈理论的指导，可以建立起更加公平和公正的监督制度，保证监督工作的公平性和有效性。

军事谋略的骰子——博弈论西方有个上帝，手里捏着个骰子，但这个骰子是被动过手脚的，因此世界原本就是不公平的。

在被创造的1个纳世纪里，π秒间谋略便已生根。

从创世纪到鬼谷时代、时势的纵横捭阖、奇正相克催生谋略的枝繁叶茂；从孙子兵法到西点军校，战场的草木皆兵、瞬息万变促进谋略的日益健壮。

到了1928年，冯·诺依曼证明了博弈论的基本原理，博弈论正式诞生。

等等，进程似乎有点快，暂且回到民国时期的广西，那有个富有博弈的故事。

民国时期广西三足鼎立：李宗仁一处有两万多人、陆荣廷有三万多人、沈鸿英两万多人。

有一年，陆、沈桂林鏖战，相持三日不分胜负。

此时，李宗仁忽闻陆、沈开始媾和，李认为，双方议和广西仍是三分之地，对方还要合谋他，不能错失良机，火势将，熄要趁火打劫，问题是先打陆好呢，还是先打沈好？李宗仁认为：就道义来说应该讨沈，此人反复无常，久为两粤人民所痛恨，讨伐他定可大快人心，至于陆，广西人一般并无厌恶。

白崇禧说：我认为应先打陆，理由有三：其一，陆驻守在桂林、南宁为广西政治中心，防务空虚易于进攻；其二，陆与湖南相通，湖南又得吴佩孚援助，应于其支援未至，出其不意攻其不备；其三，若先攻沈胜了，陆之势力犹存，广西仍不能统一，败了就更不能打陆。

此刻之处境如楚汉争霸之韩信，联陆则沈败，联沈则陆败，我们应当联弱攻强、避实击虚。

经过协商，“联沈倒陆、先陆后沈”的决策定出，李宗仁于是发出通电请陆荣廷下野，兵分水陆进击南宁、兵不血刃；白崇禧军亦横扫敌军，会师南宁，其后趁热打铁，一一剪除残余势力一统广西。

这场以少胜多的著名战役，除了当时有利的环境因素外，李宗仁、白崇禧对于攻击方向和先后顺序的安排，就充满了博弈论的智慧。

上述便是博弈论一例，那么何为博弈论呢？博弈论本质上是一个现代数学的分支，是研究互动决策的理论。

博弈论的目的在于巧妙的策略，在于赢得更好的结局，毕竟在博弈中，特别是多个参与者的博弈中，结果不仅取决于自己的实力与策略，还取决于其他参与者的制约和策略。

博弈论为军队政治工作管理开辟新视域［摘要］博弈论正逐渐成为社会科学研究范式中的一个核心工具，被称作“社会科学中的数学”。

博弈论在军队政治工作管理中的运用必将为管理的科学化开辟新的研究视域。

［关键词］博弈论；军队政治工作管理；科学化一、博弈论：社会科学中的数学博弈论（GａｍｅTｈｅｏｒｙ）又称为对策论，原本是运筹学的一个分支，在２０世纪４０年代才建立起来，是研究主体行为发生直接相互作用时的决策以及这种决策的均衡问题的理论，后来发展为研究多方的、对立的或非对立的策略选择。

博弈论在经济学领域的应用日益红火、非常活跃。

１９９４年诺贝尔经济学奖授给了3位博弈论专家：纳什、泽尔腾和海萨尼，以表彰他们对非合作博弈研究的贡献。

１９９６年的诺贝尔经济学奖授给了另一位博弈论专家维克瑞。

目前，博弈论正深入到经济学、政治学、社会学、法学等领域，被各门社会科学研究所应用，逐渐成为社会科学研究范式中的一个核心工具，可以说博弈论是“社会科学中的数学”，或者说是关于社会的数学。

博弈论不仅广泛深远地改变了经济学家的思维方式，而且正在或必将改变所有社会科学家的思维方式。

管理博弈论已经成为博弈论的一个分支，对其的研究正在深入地开展。

博弈论目前主要有两个研究角度：一是从博弈参与人的行动先后顺序研究，把博弈分为静态博弈和动态博弈。

所谓静态博弈是指博弈时，博弈参与人同时选择行动或虽非同时但后行动者并不知先行动者采取了什么具体行动。

所谓动态博弈是指后行动的参与人能够观察到先行动者的选择。

二是从参与人信息相互了解程度，分为完全信息博弈和不完全信息博弈。

每种博弈都存在博弈均衡问题。

这样就有4种博弈均衡。

这就是：完全信息静态博弈均衡——纳什均衡；完全信息动态博弈均衡——子博弈精炼纳什均衡；不完全信息静态博弈均衡——贝叶斯纳什均衡；不完全信息动态博弈均衡——精炼贝叶斯纳什均衡。

二、博弈论与军队政治工作管理中的博弈军队政治工作管理涉及的是部队生活中每个人和集体的利益关系，在管理过程中应贯彻以人为本的理念，着眼于官兵的全面发展，尊重人、理解人，关注每一个人的利益，构建新型的官兵个人之间、个人与集体之间、集体与集体之间的相互制约和依存关系。

军棋中的博弈论思想军棋，又名陆战棋，是一款制作精良、功能丰富的军棋游戏;下面是有，欢迎参阅。

最先是从一个同学那里听说博弈论这个词，当时他给我讲了智猪博弈的故事，我就深深的被这种思维方式吸引了，放假回家在书店很多关于博弈论的实例，所以决定选了这门课程。

最近一段时间，我喜欢上了下军旗，是军旗中的暗旗也叫翻旗玩法，在网上和不同的人下，虽然水平一般，但是在每一步的布局中，我深深体会到了博弈论思想在实际中的应用，了解对手的思想，懂得牵制和舍弃，往往才能出奇制胜，扭转败局。

而且，无论是中文的“博弈”，还是英文的“Game Theory”，都不难看出它与游戏的亲密关系，军棋其实就是一种博弈，用博弈论的思想来研究军棋，弈是理所当然的事情。

当然，我在这里要做的也只是对各种局势的简单阐述，如果要用数学表达，我觉得完全超出了我的数学水平，但这的确是很值得研究的一个领域。

军旗属于博弈论里面的动态博弈。

1.含义博弈论是有关“互动行为”interactive behavior的科学，是一些个人和组织在一定的条件下，按照一定规则同时或先后，一次或多次，进行行为或策略选择，从而获得各自结果的过程。

2.博弈结构要素博弈方：在博弈过程中独立决策，独立承担结果的个人和组织博弈策略：在一定的条件下做出的行为选择的判断和实行收益：参加博弈的博弈各方从博弈中所获得的利益博弈的过程：分静态博弈，动态博弈和重复博弈等3.博弈论的结果博弈论不只是一种技术手段，而且在一定程度上反映了社会生活的本质和规律。

根据博弈论基本观点，一种策略选择以及一种制度安排要发生效力或实现，必须是一种纳什均衡。

否则，这种策略选择或制度安排便不能成立。

首先，在博弈论中我们要假设博弈的双方都是理性人，这也是博弈理论建立的基础，同样，在军旗游戏中，我们也要知道对方都是理性人，同时保证自己也是理性人，即知道了解游戏的规则，不然肯定要闹出大笑话。

游戏字朝下摆的也叫翻棋规则如下：1、军棋的棋子各方均有25个，分别为军旗、司令、军长各一;师长、旅长、团长、营长、炸弹各二;连长、排长、工兵、地雷各三。