设计将中缀表达式转换为后缀表达式的算法
- 格式:docx
- 大小:16.04 KB
- 文档页数:5

中缀转后缀表达式算法
中缀表达式转后缀表达式(也称为逆波兰表达式)是一种将中缀表达式转换为后缀表达式的算法。
它的基本思想是将中缀表达式转换为一个后缀表达式,其中操作符位于操作数之后,而不是操作数之前。
中缀表达式转后缀表达式的算法步骤如下:
1. 从左到右扫描中缀表达式;
2. 如果读取的是操作数,则将其压入堆栈;
3. 如果读取的是运算符,则比较其与栈顶运算符的优先级:
(1)如果栈顶运算符的优先级高于或等于读取的运算符,则将栈顶运算符弹出,并将其压入输出队列;
(2)如果栈顶运算符的优先级低于读取的运算符,则将读取的运算符压入堆栈;
4. 重复步骤2和3,直到表达式末尾;
5. 将栈中所有元素依次弹出,压入输出队列,完成中缀表达式到后缀表达式的转换。
中缀表达式转后缀表达式算法的优点是它可以有效地将中缀表达式转换为后缀表达式,从而简化表达式的计算过程。
它的缺点是它需要记住操作符的优先级,并且需要使用堆栈来存储操作符,这可能会增加算法的复杂度。
总之,中缀表达式转后缀表达式算法是一种有效的算法,它可以有效地将中缀表达式转换为后缀表达式,从而简化表达式的计算过程。

中缀表达式转换为后缀表达式课程设计任务:中缀表达式转后缀表达式,并求值。
课程设计思路:把中缀表达式转换为后缀表达式算法的基本思路是从头到尾地扫描中缀表达式中的每个字符,对于不同类型的字符按不情况进行处理。
若遇到的是空格则认为是分隔符,不需要进行处理;若遇到的是数字或小数点,则直接写入到c2中;若遇到的是左括号,则应把它压入到运算符栈中,待以它开始的括号内的表达式转换完毕后再出栈;若遇到的是右括号,则表明括号内的中缀表达式已经扫描完毕,把从栈底直到保存着的对应左括号之间的运算符依次退栈并写入c2串中;若遇到的是运算符,当该运算符的优先级大于栈顶运算符的优先级(加减运算符的优先级设定为1,乘除运算符的优先级设定为2,在栈中保存的特殊运算符’(’的优先级设定为0)时,表明该运算符的后一个运算对象还没有被扫描并放入到c2串中,应把它暂存于运算符栈中,待它的后一个运算对象从c1串中读出并写入到c2串中后,再另其出栈并写入c2串中;若遇到的运算符的优先级小于等于栈顶运算符的优先级,这表明栈顶运算符的两个运算对象已经被保存到c2串中,应将栈顶运算符退栈并写入到c2串中,对于新的栈顶运算符仍继续进行比较和处理,直到被处理的运算符的优先级大于栈顶运算符的优先级为止,然后另该运算符进栈即可。
按照以上过程扫描到中缀表达式结束符时,把栈中剩余的运算符依次退栈并写入到后缀表达式中,再向c2写入表达式结束符和字符串结束符’\0’,整个转换过程就处理完毕,在c2中就得到了转换成的后缀表达式。
课程设计流程:设中缀算术表达式为:10+(18+9*3)/15-6,则转换过程如下:(1)开始时存放后缀表达式的字符串c2为空:(2)当扫描到左括号时,c2和栈中的数据变化如下:1 0((3)当扫描到数值3时,c2和栈中的数据变化为:1 0 1 8 9 3( + *(4)当扫描到右括号时,c2和栈变为:1 0 1 8 9 3 * +(5)当扫描到的数值15时,c2和栈又变为:1 0 1 8 9 3 * + 1 5/(6)当扫描到‘’字符时,c2和栈为:1 0 1 8 9 3 * + 1 5 / + 6-7)当整个处理过程结束后,栈为空,c2为:1 0 1 8 9 3 * + 1 5 / + 6 -算法基本思想:从头到尾扫描中缀表达式,对不同类型的字符按不同情况处理;1、如果是数字则直接放入后缀表达式数组;2、如果是左括号则直接入栈;3、如果是右括号,则把从栈顶直到对应左括号之间的运算符依次退栈,并清除对应的左括号;4、对于运算符,如果该运算符的优先级大于栈顶优先级,则直接入栈,若该运算符的优先级小于等于栈顶优先级,则先把栈顶运算符出栈,写入后缀表达式数组,然后再入栈;5、扫描完成后,取出栈中所有运算符,写入后缀表达式数组。

将中缀表达式转换成后缀表达式的三种方法中缀表达式是我们平常最常见的表达式形式,但在计算机的运算过程中,我们常常需要将中缀表达式转换成后缀表达式,因为后缀表达式具有易于计算的特点。
那么,接下来我们将介绍三种将中缀表达式转换成后缀表达式的方法。
一、栈的方法这种方法是最常见的一种方法,也是比较易理解的一种方法。
我们可以借助栈来完成中缀表达式转换成后缀表达式的过程。
具体的操作如下:1. 声明一个操作符的栈stack(栈中存放操作符)和一个后缀表达式的列表res(列表中存放转换后的后缀表达式)。
2. 从左到右遍历中缀表达式。
3. 若当前字符为数字,则直接将该数字添加到res中。
4. 若当前字符为左括号“(”,则将其压入stack栈中。
5. 若当前字符为右括号“)”,则依次弹出stack栈中的操作符并加入到res中,直到遇到左括号为止。
6. 若当前字符为操作符,那么则需判断当前操作符与stack栈顶操作符的优先级,若当前操作符的优先级小于等于栈顶操作符,则弹出栈顶操作符并加入到res中,重复此步骤,直到当前操作符大于栈顶操作符优先级,最后将当前操作符压入stack栈。
7. 当遍历完整个中缀表达式后,若stack栈中还有剩余操作符,则依次弹出栈顶操作符并加入到res中。
8. 最终,res中的表达式就是转换后的后缀表达式。
二、递归调用方法这种方法是使用递归的方式来完成。
具体的操作如下:1. 若当前遍历的字符为数字,则直接输出该数字。
2. 若当前遍历的字符为左括号“(”,则递归读取该括号内的表达式。
3. 若当前遍历的字符为右括号“)”,则返回。
4. 若当前遍历的字符为操作符,“x”,“/”,“+”,“-”,则递归调用该表达式右边的操作符,比如“x”,“/”,然后再递归调用左边的操作符,比如“+”,“-”,然后输出左操作数和右操作数,最后输出当前操作符。
5. 最终,输出的表达式即为转换后的后缀表达式。
三、判断法这种方法也是比较常见的一种方法。
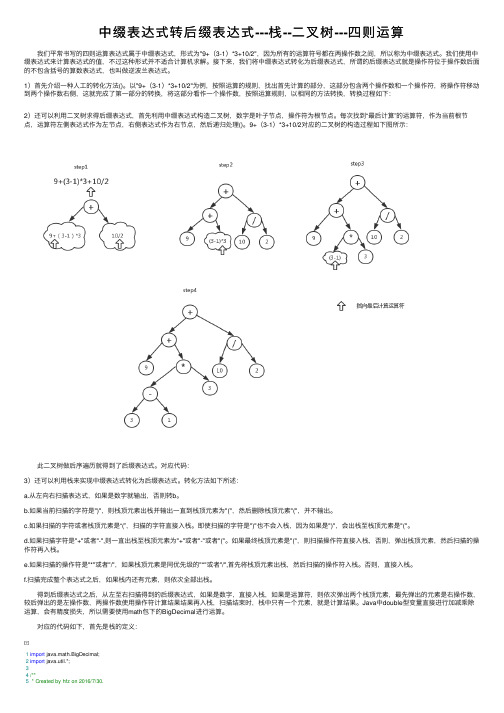
中缀表达式转后缀表达式---栈--⼆叉树---四则运算 我们平常书写的四则运算表达式属于中缀表达式,形式为"9+(3-1)*3+10/2",因为所有的运算符号都在两操作数之间,所以称为中缀表达式。
我们使⽤中缀表达式来计算表达式的值,不过这种形式并不适合计算机求解。
接下来,我们将中缀表达式转化为后缀表达式,所谓的后缀表达式就是操作符位于操作数后⾯的不包含括号的算数表达式,也叫做逆波兰表达式。
1)⾸先介绍⼀种⼈⼯的转化⽅法()。
以"9+(3-1)*3+10/2"为例,按照运算的规则,找出⾸先计算的部分,这部分包含两个操作数和⼀个操作符,将操作符移动到两个操作数右侧,这就完成了第⼀部分的转换,将这部分看作⼀个操作数,按照运算规则,以相同的⽅法转换,转换过程如下:2)还可以利⽤⼆叉树求得后缀表达式,⾸先利⽤中缀表达式构造⼆叉树,数字是叶⼦节点,操作符为根节点。
每次找到“最后计算”的运算符,作为当前根节点,运算符左侧表达式作为左节点,右侧表达式作为右节点,然后递归处理()。
9+(3-1)*3+10/2对应的⼆叉树的构造过程如下图所⽰: 此⼆叉树做后序遍历就得到了后缀表达式。
对应代码:3)还可以利⽤栈来实现中缀表达式转化为后缀表达式。
转化⽅法如下所述:a.从左向右扫描表达式,如果是数字就输出,否则转b。
b.如果当前扫描的字符是")",则栈顶元素出栈并输出⼀直到栈顶元素为"(",然后删除栈顶元素"(",并不输出。
c.如果扫描的字符或者栈顶元素是“(”,扫描的字符直接⼊栈。
即使扫描的字符是")"也不会⼊栈,因为如果是")",会出栈⾄栈顶元素是"("。
d.如果扫描字符是"+"或者"-",则⼀直出栈⾄栈顶元素为"+"或者"-"或者"("。

算术表达式(中缀表达式)转换为后缀表达式将后缀表达式exp转换为postexp的过程如下:while(从exp读取字符ch,ch!='\0'){ 若ch为数字,将后继的数字都⼀次存放到postexp中,并以字符'#'标志数值串的结束; 若ch为左括号“(”,将此括号进栈到运算符栈op中; 若ch为右括号“)”,将运算符栈op依次出栈,直到“(”,并将“(”也出栈; 若ch为运算符,优先级不⼤于运算符op的栈顶运算符(除栈顶运算符为“(”外)的优先级,则依次出栈并存⼊到postexp中,然后将ch 进栈}若中缀表达式exp扫描完毕,将运算符栈op中的所有运算符依次出栈并存放到postexp中,就得到了后缀表达式。
完整代码:#include <stdio.h>#define MAXSIZE 50typedef char elemType;//运算符栈typedef struct{elemType data[MAXSIZE];int top;}OP;OP op;//中缀表达式转为后缀表达式void trans(char exp[],char postexp[]){op.top=-1;int i=0,j=0;char ch=exp[i];while(ch!='\0'){switch(ch){case'(':{op.top++;op.data[op.top] = ch;break;}case')':{while(op.data[op.top]!='('){postexp[j++]=op.data[op.top--];}op.top--; //去除 '('break;}case'+':case'-':{while(op.top!=-1&&op.data[op.top]!='('){postexp[j++]=op.data[op.top--];}op.top++;op.data[op.top]=ch;break;}case'*':case'/':{while(op.top!=-1&&(op.data[op.top]=='*'||op.data[op.top]=='/')){postexp[j++]=op.data[op.top];op.top--;}op.top++;op.data[op.top]=ch;break;}case'':break;default :{while(ch>='0'&&ch<='9'){postexp[j++]=ch;i++;ch=exp[i];}i--; //不是数字退后⼀个,⽤switch来进⾏判断 postexp[j++]='#'; //在数字结束后添加'#'以便区分}}i++;ch=exp[i];}while(op.top!=-1){ //将运算符栈中postexp[j++]=op.data[op.top--];}postexp[j]='\0';}。

将中缀表达式转换为后缀表达式需要使用栈数据结构。
具体步骤如下:1. 读入中缀表达式,遇到数字时将其输出,遇到左括号时将其压入栈中。
2. 读入运算符,如果该运算符优先级高于栈顶运算符的优先级,则将栈顶元素弹出并输出,直到遇到优先级更高的运算符或遇到右括号为止。
3. 如果该运算符优先级等于栈顶运算符的优先级,则将该运算符压入栈中。
4. 如果该运算符优先级低于栈顶运算符的优先级,则忽略该运算符。
5. 重复上述步骤,直到读完整个中缀表达式。
6. 将栈中的元素依次弹出并输出,即为转换后的后缀表达式。
例如,对于中缀表达式a + b * c + (d * e + f) * g,其转换成后缀表达式的步骤如下:1. 读到a,直接输出。
2. 读到+,将+ 压入栈中。
3. 读到b,直接输出。
4. 读到*,将* 压入栈中。
5. 读到c,直接输出。
6. 读到+,将栈顶的* 弹出并输出,然后将+ 压入栈中。
7. 读到(,将( 压入栈中。
8. 读到d,直接输出。
9. 读到*,将* 压入栈中。
10. 读到e,直接输出。
11. 读到+,将栈顶的* 弹出并输出,然后将+ 压入栈中。
12. 读到f,直接输出。
13. 读到),将栈顶的+ 弹出并输出,直到遇到左括号为止。
此时右括号")" 的优先级最高,所以直接将其弹出并输出。
然后继续弹出并输出左括号"(" 前遇到的运算符和操作数,直到遇到右括号为止。
此时右括号")" 前已经没有运算符和操作数了,所以直接将其弹出并输出。
14. 读到*,将* 压入栈中。
15. 读到g,直接输出。
16. 中缀表达式已经读完,将栈中的元素依次弹出并输出,得到后缀表达式a b * c + d * e + f * g + 。

中缀表达式转后缀表达式 先看⼏个中缀表达式和它们对应的后缀表达式的例⼦ 可以看到操作数a, b, c 在中缀表达式中的顺序和在后缀表达式中的顺序是⼀致的,但操作符的顺序可能不⼀致,因为在中缀表达式中操作符有优先级,括号也能改变运算的优先级,这些都要在后缀表达式中体现出来,后缀表达式中没有括号。
那怎么转化呢? 1,创建⼀个变量,初始化为空的字符串,来表⽰要完成的后缀表达式,创建⼀个字符栈,⽤来存储操作符 2,从左向右依次扫描中缀表达式, 遇到操作数,直接加到后缀表达式的后⾯,因为,在中缀表达式和后缀表达式中,操作数的顺序是⼀样的, 遇到操作符,要先存起来,存到栈中,因为操作符有优先级,它要和后⾯的操作符⽐较优先级,然后才能决定把它放到什么哪个位置。
如果栈为空,直接把操作符放⼊栈中 如果栈不为空,⽐较优先级。
如果遇到的操作符⽐栈顶中的操作符优先级⾼,把遇到的操作符放⼊栈中。
如果遇到的操作符和栈顶操作符的优先级相等,这要考虑操作符的结合性,它是从左到右结合,还是从右到左结合。
从左到右接合,就是操作数属于它前⾯的操作符⽽不是它后⾯操作符。
+, - , * , / 就是从左向右结合,⽐如a-b+c中的b 是-的操作数,⽽不是+的操作数,整个表达式,也是从左向右计算的。
从右向左结合,操作数属于它前⾯的操作符⽽不是它后⾯操作符,⽐如阶乘。
a ^ b ^ c, b是第⼆个^的操作数,⽽不是第⼀个^的操作数,整个表达式也是从右向左计算,a ^ (b ^ c)。
如果从左向右接合,那就弹栈,把操作符放到后缀表达式中,如果从右向左结合,则把遇到的操作符放⼊栈中(和优先级⾼的情况⼀致) 如果遇到的操作符⽐栈顶中的操作符优先级低,那就弹栈,把操作符放到后缀表达式中 遇到(,放到字符栈,因为要等到)才能知道怎么操作。
遇到),依次从字栈中弹栈,放到后缀表达式中,直到遇到(, 遇到(, 要把它弹栈,然后舍弃掉。
3,循环完毕,如果字符栈中还有操作符,依次弹栈放到后缀表达式中,最终栈为空,得到完整的后缀表达式。

中缀转后缀并输出运算步骤从中缀表达式转换为后缀表达式的过程中,需要遵循一定的规则和算法。
下面将具体介绍中缀转后缀的步骤及其运算过程。
一、引言中缀表达式是我们日常生活中最常见的表达式形式,例如:2 + 3 * 4。
但是,对于计算机来说,中缀表达式并不方便进行计算,因此需要将其转换为后缀表达式。
后缀表达式也被称为逆波兰表达式,它的计算规则更加简单明了。
二、中缀转后缀的规则和算法1. 创建一个空的栈,用于存储运算符。
2. 从左到右遍历中缀表达式的每个元素。
3. 如果当前元素是操作数,则直接输出到后缀表达式。
4. 如果当前元素是左括号"(",则将其压入栈中。
5. 如果当前元素是右括号")",则将栈中的运算符依次弹出并输出到后缀表达式,直到遇到左括号为止。
注意:左括号不输出。
6. 如果当前元素是运算符,则判断栈顶运算符的优先级:- 若栈为空,则直接将当前运算符压入栈中。
- 若栈不为空,且当前运算符的优先级小于等于栈顶运算符的优先级,则将栈顶运算符弹出并输出到后缀表达式,直到栈为空或者栈顶运算符的优先级小于当前运算符。
- 将当前运算符压入栈中。
7. 遍历完中缀表达式后,如果栈中还有运算符,则依次弹出并输出到后缀表达式。
三、运算过程示例考虑中缀表达式:"2 + 3 * 4 - (5 + 6) / 7"1. 创建空栈和空后缀表达式。
2. 从左到右遍历中缀表达式的每个元素:- 遇到"2",为操作数,直接输出到后缀表达式。
- 遇到"+",为运算符,将其压入栈中。
- 遇到"3",为操作数,直接输出到后缀表达式。
- 遇到"*",为运算符,将其压入栈中。
- 遇到"4",为操作数,直接输出到后缀表达式。
- 遇到"-",为运算符,栈顶为"*",优先级高于"-",因此将"*"弹出并输出到后缀表达式,然后将"-"压入栈中。

中缀式和后缀式的相互转换中缀式和后缀式是数学表达式的两种常见表示方式。
中缀式是我们常见的表达式形式,例如"3 + 4 * 5",而后缀式是将运算符放在操作数后面表示,例如"3 4 5 * +"。
将中缀式转换为后缀式可以通过使用栈和优先级规则来完成。
具体步骤如下:1. 创建一个空栈和一个空字符串后缀表达式2. 从左到右扫描中缀表达式的每个元素3. 如果遇到操作数,则将其添加到后缀表达式中4. 如果遇到运算符,则将其与栈顶运算符进行比较:- 如果栈为空或栈顶是左括号"(",则将运算符入栈- 如果运算符优先级高于栈顶运算符,则将运算符入栈- 否则,将栈顶运算符弹出并添加到后缀表达式中,直到栈为空或栈顶是左括号为止,然后将当前运算符入栈5. 如果遇到左括号"(",则将其入栈6. 如果遇到右括号")",则将栈顶运算符弹出并添加到后缀表达式中,直到遇到左括号为止,然后将左括号弹出(左括号不添加到后缀表达式中)7. 扫描完整个中缀表达式后,将栈中剩余的运算符依次弹出并添加到后缀表达式中8. 后缀表达式即为转换结果例如,将中缀式"3 + 4 * 5"转换为后缀式的过程如下:中缀表达式: 3 + 4 * 5初始化:栈为空,后缀表达式为空扫描 3:后缀表达式:3扫描 +:栈为空,运算符入栈扫描 4:后缀表达式:3 4扫描 *:栈顶运算符优先级低于当前运算符,运算符入栈扫描 5:后缀表达式:3 4 5扫描完毕,将栈中剩余运算符弹出:后缀表达式:3 4 5 * +因此,中缀式"3 + 4 * 5"转化为后缀式"3 4 5 * +"。
将后缀式转换为中缀式可以通过使用栈和逆序扫描后缀表达式的方式来完成。
具体步骤如下:1. 创建一个空栈2. 从左到右逆序扫描后缀表达式的每个元素3. 如果遇到操作数,则将其入栈4. 如果遇到运算符,则从栈中弹出两个操作数,并将运算符与操作数组合成一个中缀表达式,并将该中缀表达式入栈5. 扫描完整个后缀表达式后,栈顶的中缀表达式即为转换结果例如,将后缀式"3 4 5 * +"转换为中缀式的过程如下:后缀表达式:3 4 5 * +初始化:栈为空从右到左逆序扫描:扫描 +:弹出操作数5和4,组合为中缀表达式"4 + 5",入栈扫描 *:弹出操作数4和中缀表达式"4 + 5",组合为中缀表达式"(4 + 5) * 4",入栈扫描 3:入栈扫描完毕,栈顶的中缀表达式即为转换结果:中缀表达式:"(4 + 5) * 3"因此,后缀式"3 4 5 * +"转化为中缀式"(4 + 5) * 3"。

算法笔记--中缀表达式转后缀表达式后缀表达式计算中缀表达式转后缀表达式规则中缀表达式a + b*c + (d * e + f) * g,转换成后缀表达式则为a b c * + d e * f + g * +转换过程需要⽤到栈,具体过程如下:1 如果遇到操作数,我们就直接将其输出。
2 如果遇到操作符,则我们将其放⼊到栈中,遇到左括号时我们也将其放⼊栈中。
3 如果遇到⼀个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为⽌。
注意,左括号只弹出并不输出。
4 如果遇到任何其他的操作符,如+, *, (等,从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为⽌。
弹出完这些元素后,才将遇到的操作符压⼊到栈中。
有⼀点需要注意,只有在遇到 )的情况下我们才弹出( ,其他情况我们都不会弹出( 。
即:若操作符op的优先级⾼于栈顶操作符的优先级,则压⼊操作符栈若操作符op的优先级⼩于等于栈顶操作符的优先级,则将操作栈的操作符不断弹出到后缀表达式中,直到op的优先级⾼于栈顶操作符的优先级5 如果我们读到了输⼊的末尾,则将栈中所有元素依次弹出。
实例a +b *c + (d *e + f) * g1. ⾸先读到a,直接输出。
2. 读到“+”,将其放⼊到栈中。
3. 读到b,直接输出。
此时栈和输出的情况如下:4. 读到“*”,因为栈顶元素"+"优先级⽐" * " 低,所以将" * "直接压⼊栈中。
5. 读到c,直接输出。
此时栈和输出情况如下:6. 读到" + ",因为栈顶元素" * "的优先级⽐它⾼,所以弹出" * "并输出,同理,栈中下⼀个元素" + "优先级与读到的操作符" + "⼀样,所以也要弹出并输出。
然后再将读到的" + "压⼊栈中。

中缀表达式转后缀表达式最难例题以下是一个较复杂的中缀表达式转后缀表达式的示例:中缀表达式:(3+4*2)/(1-5)^2^3后缀表达式:342*+15-23^^/首先,我们可以使用运算符优先级来决定操作符的顺序。
一般来说,乘法和除法的优先级最高,然后是加法和减法,最后是幂运算。
在同一优先级下,操作符从左到右处理。
接下来,我们使用一个栈来辅助转换。
按照从左到右的顺序扫描中缀表达式:1. 如果遇到数字,直接将其添加到后缀表达式中。
2. 如果遇到运算符,首先将栈顶的运算符与当前运算符进行优先级比较:- 如果栈为空,或者栈顶运算符为左括号"(",则将当前运算符直接入栈。
- 如果当前运算符的优先级高于栈顶运算符,则将当前运算符入栈。
- 如果当前运算符的优先级低于或等于栈顶运算符,则将栈顶运算符弹出并添加到后缀表达式中,然后继续比较当前运算符与新的栈顶运算符的优先级,直到当前运算符可以入栈。
3. 如果遇到左括号"(",直接将其入栈。
4. 如果遇到右括号")",则将栈顶运算符弹出并添加到后缀表达式中,直到遇到左括号"("。
注意,左括号"("只弹出并丢弃,不添加到后缀表达式中。
5. 最后,如果中缀表达式扫描完成,但栈中仍有运算符,则依次弹出并添加到后缀表达式中。
根据上述规则,将中缀表达式“(3+4*2)/(1-5)^2^3”转换为后缀表达式的过程如下:中缀表达式: (3+4*2)/(1-5)^2^3后缀表达式:遍历字符"(",将其入栈。
中缀表达式: 3+4*2)/(1-5)^2^3后缀表达式:遍历数字"3",将其添加到后缀表达式中。
中缀表达式: +4*2)/(1-5)^2^3后缀表达式: 3遍历字符"+",将其入栈。
中缀表达式: 4*2)/(1-5)^2^3后缀表达式: 3遍历数字"4",将其添加到后缀表达式中。

c++中缀转后缀表达式
在计算机科学中,中缀表达式和后缀表达式是两种不同的数学表达式表示方法。
中缀表达式是我们在日常生活中所使用的表达式形式,例如"2+3"。
而后缀表达式,也称为逆波兰表示法,是一种更简洁的表达式形式,例如"23+"。
下面是一个详细的步骤,说明如何将中缀表达式转换为后缀表达式:
1.创建一个空的后缀表达式列表:这个列表将用于存储转换后的后缀表达式。
2.创建一个符号栈:这个栈用于临时存储中缀表达式中的操作数和操作符。
3.遍历中缀表达式的每个字符:
如果字符是一个操作数(数字),则直接将其添加到后缀表达式列表中。
如果字符是一个操作符(如+、-、、/),则检查栈顶的两个元素。
如果栈顶的两个元素是操作数,则将操作符压入栈中。
否则,从栈中弹出操作符,并将其与栈顶的操作数结合,形成新的后缀表达式,添加到后缀表达式列表中。
然后将当前的操作数压入栈中。
4.处理中缀表达式的最后一个字符:此时,如果栈中仍有操作符,则将其与栈顶的操作数结合,形成新的后缀表达式,添加到后缀表达式列表中。
5.清空符号栈中剩余的元素:此时,栈中可能还有未使用的操作数。
将这些操作数依次添加到后缀表达式列表中。
6.返回后缀表达式列表:此时,后缀表达式列表就是转换后的后缀表达式。
这个算法的时间复杂度是O(n),其中n是中缀表达式的长度。
这是因为我们需要遍历每个字符一次,并且栈操作的时间复杂度是线性的。
空间复杂度也是O(n),因为我们需要使用一个大小与输入长度相同的栈。

中缀表达式转换为后缀表达式中缀表达式转换成后缀表达式 1、概述 可以看到,后缀表达式适合计算式进⾏运算,但是⼈却不太容易写出来,尤其是表达式很长得情况下,因此在开发中,需要将中缀表达式转成后缀表达式。
2、具体步骤1.初始化两个栈:运算符栈s1和储存中间结果的栈s2;2.从左⾄右扫描中缀表达式;3.遇到操作数时,将其压s2;4.遇到运算符时,⽐较其与s1栈顶运算符的优先级: (1)如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符⼊栈; (2)否则,若优先级⽐栈顶运算符的⾼,也将运算符压⼊s1; (3)否则,将s1栈顶的运算符弹出并压⼊到s2中,再次转到(4.1)与s1中新的栈顶运算符相⽐较;5.遇到括号时: (1)如果是左括号"(",则直接压⼊s1 (2)如果是右括号")",则依次弹出s1栈顶的运算符,并压⼊s2,直到遇到左括号为⽌,此时将这⼀对括号丢弃6.重复步骤2⾄5,直到表达式的最右边7.将s1中剩余的运算符依次弹出并压⼊s28.依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式 3、案例 将中缀表达式 "1+((2+3)*4)-5" 转换为后缀表达式的过程如下: 结果为:"1 2 3 + 4 * 5 - " 4、思路分析⽰意图 5、代码实现1import java.util.ArrayList;2import java.util.List;3import java.util.Stack;45/**6 * 把中缀表达式转成后缀表达式7 *8*/9public class ToSuffixExpression {1011public static void main(String[] args) {12// 完成⼀个中缀表达式转成后缀表达式13// 说明14// 1. 1+((2+3)*4)-5 => 转成 123 + 4 * + 5-15// 2. 因为对 str进⾏操作不⽅便,先将中缀表达式存⼊ list16// 3.将得到的中缀表达式对应的 list转成 =>后缀表达式对应的list17// 即[1,+,(,(,2,+,3,),*,4,),-,5] => [1,2,3,+,4,*,+,5,-]1819 String expression = "1+((2+3)*4)-5";20 List<String> list = toInfixExpressionList(expression);21 System.out.println("中缀表达式对应的list="+list);22 List<String> list2 = parseSuffixExpressionList(list);23 System.out.println("后缀表达式对应的list="+list2);24 }2526//⽅法:将得到的中缀表达式对应的 list转成 =>后缀表达式对应的list27public static List<String> parseSuffixExpressionList(List<String> ls) {28//定义两个栈29 Stack<String> s1 = new Stack<String>(); // 符号栈3031//说明:因为 s2这个栈,在整个转换过程中,没有pop操作,后⾯还需要逆序输出 32//所以,把 s2 这个栈换成 List<String> 即可33//Stack<String> s2 = new Stack<String>(); // 存储中间结果的栈34 List<String> s2 = new ArrayList<String>(); //存储中间结果的list3536//遍历 ls37for(String item : ls) {38//如果是⼀个栈,就加⼊到s239if(item.matches("\\d+")) {40 s2.add(item);41 } else if (item.equals("(")) {42 s1.push(item);43 } else if (item.equals(")")) {44// 如果是右括号,则依次弹出s1栈顶的运算符,并压⼊ s2,知道遇到左括号为⽌,此时将这⼀对括号丢弃4546while(!s1.peek().equals("(")) {47 s2.add(s1.pop());48 }49 s1.pop(); // 将左括号弹出,消除⼩括号50 } else {51// 当 item 的优先级⼩于或等于栈顶运算符,将s1栈顶的运算符弹出并压⼊s2中,再次转到4.1与s1中新的栈顶运算符相⽐较 52//问题:缺少⽐较优先级⾼低的⽅法53while(s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {54 s2.add(s1.pop());55 }56//还需要将 item 压⼊栈中57 s1.push(item);58 }59 }6061//将s1中剩余的运算符依次弹出加⼊s262while(s1.size()!=0) {63 s2.add(s1.pop());64 }6566return s2; //因为存放到list中,因此,按顺序输出就是对应的后缀表达式对应的 list67 }686970// ⽅法:将中缀表达式转成对应的 list71public static List<String> toInfixExpressionList(String s) {72// 定义⼀个 list,存放中缀表达式对应的内容73 List<String> ls = new ArrayList<String>();74int i = 0; // 指针,⽤于遍历中缀表达式字符串75 String str; // 做对多位数的拼接⼯作76char c; // 每遍历到⼀个字符,就放⼊到 c7778do {79// 如果c是⼀个⾮数字,就需要加⼊到 ls80if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {81 ls.add("" + c);82 i++; // i后移83 } else { // 如果是数字,考虑多位数问题84 str = ""; // 将 str置空85while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {86 str += c; // 拼接87 i++;88 }89 ls.add(str);90 }9192 } while (i < s.length());93return ls; // 返回94 }95 }9697/**98 * 可以返回⼀个运算符的对应的优先级99 *100*/101public class Operation {102private static int ADD = 1;103private static int SUB = 1;104private static int MUL = 2;105private static int DIV = 2;106107// 写⼀个⽅法,返回对应的优先级数字108public static int getValue(String operation) { 109int result = 0;110switch(operation) {111case "+":112 result = ADD;113break;114case "-":115 result = SUB;116break;117case "*":118 result = MUL;119break;120case "/":121 result = DIV;122break;123default:124 System.out.println("不存在该运算符"); 125break;126 }127return result;128 }129 }。

编写Java程序时,我们可能会碰到解释数学表达式的问题,例如,输入字符串“(5+4)*10”,求出其算术结果,对于这个问题,可以通过后缀表达式来解决。
首先,让我们看看后缀表达式的算法:1) 将中缀表达式转换为后缀表达式:•当读到数字直接送至输出队列中;•当读到运算符t时:a.将栈中所有优先级高于或等于t的运算符弹出,送到输出队列中;b.t进栈;•读到左括号时总是将它压入栈中;•读到右括号时,将靠近栈顶的第一个左括号上面的运算符全部依次弹出,送至输出队列后,再丢弃左括号;•中缀表达式全部读完后,若栈中仍有运算符,将其送到输出队列中。
2) 运用后缀表达式进行计算:•建立一个栈S;•从左到右读后缀表达式,读到数字就将它转换为数值压入栈S中,读到运算符则从栈中依次弹出两个数分别到Y和X,然后以“X 运算符Y”的形式计算机出结果,再压加栈S中;•如果后缀表达式未读完,就重复上面过程,最后输出栈顶的数值则为结束。
以下是代码实现:package wenly.util;import java.util.Stack;import java.util.regex.*;public class StringToArithmetic {private StringToArithmetic() {}/*** 给出一个算术表达式,返回结果。
例如(5+8+10)*1,返回23** @param string*/public static double stringToArithmetic(String string) { return postfixExprToArithmetic(prefixExprToPostfixExpr(string)); }/*** 中缀表达式转后缀表达式** @param String* prefix* @return String*/private static String prefixExprToPostfixExpr(String prefix) { Stack<Character> stack = new Stack<Character>();String postfix = "";int length = prefix.length();for(int i = 0; i < length; i++) {Character temp;char c = prefix.charAt(i);switch(c) {// 忽略空格case' ':break;// 碰到'(',push到栈case'(':stack.push(c);break;// 碰到'+''-',将栈中所有运算符弹出,送到输出队列中case'+':case'-':while(stack.size() != 0) {temp = stack.pop();if(temp == '(') {stack.push('(');break;}postfix += " " + temp;}stack.push(c);postfix += " ";break;// 碰到'*''/',将栈中所有乘除运算符弹出,送到输出队列中case'*':case'/':while(stack.size() != 0) {temp = stack.pop();if(temp == '(' || temp == '+' || temp == '-') {stack.push(temp);break;} else{postfix += " " + temp;}}stack.push(c);postfix += " ";break;// 碰到右括号,将靠近栈顶的第一个左括号上面的运算符全部依次弹出,送至输出队列后,再丢弃左括号case')':while(stack.size() != 0) {temp = stack.pop();if(temp == '(')break;elsepostfix += " " + temp;}postfix += " ";break;default:postfix += c;}}while(stack.size() != 0)postfix += " " + stack.pop();return postfix;}/*** 通过后缀表达式求出算术结果** @param String* postfix* @return double*/private static double postfixExprToArithmetic(String postfix) { Pattern pattern = pile("/d+||/d+/./d*"); // 匹配数字String strings[] = postfix.split(" ");for(int i = 0; i < strings.length; i++)strings[i].trim();Stack<Double> stack = new Stack<Double>();for(int i = 0; i < strings.length; i++) {if(strings[i].equals(""))continue;if((pattern.matcher(strings[i])).matches()) {stack.push(Double.parseDouble(strings[i]));} else{double y = stack.pop();double x = stack.pop();stack.push(caculate(x, y, strings[i]));}}return stack.pop();}private static double caculate(double x, double y, String simble) { if(simble.trim().equals("+"))return x + y;if(simble.trim().equals("-"))return x - y;if(simble.trim().equals("*"))return x * y;if(simble.trim().equals("/"))return x / y;return0;}}。

中缀表达式转后缀表达式详解中缀表达式和后缀表达式是两种常见的数学表达式形式。
中缀表达式是我们通常使用的表达式形式,即运算符位于操作数的中间,例如:'2 + 3'。
而后缀表达式(也称为逆波兰表达式)是一种更为简洁和易于计算机处理的表达式形式,其中运算符位于操作数的后面,例如:'2 3 +'。
将中缀表达式转换为后缀表达式的主要目的是减少表达式的复杂性,使其更容易被计算机处理。
转换过程涉及使用栈来保存运算符,并按照一定的规则重新排列表达式中的元素。
下面是将中缀表达式转换为后缀表达式的步骤:1. 创建一个空栈和一个空列表,用于保存转换后的后缀表达式。
2. 从左到右遍历中缀表达式的每个元素。
3. 如果遇到操作数(数字),将其添加到后缀表达式列表中。
4. 如果遇到左括号'(',将其推入栈中。
5. 如果遇到操作符,比较其与栈顶操作符的优先级。
a. 如果栈为空或栈顶为左括号'(',则将操作符推入栈中。
b. 如果操作符的优先级大于栈顶操作符的优先级,将其推入栈中。
c. 如果操作符的优先级小于或等于栈顶操作符的优先级,将栈顶操作符弹出并添加到后缀表达式列表中,然后将操作符推入栈中。
6. 如果遇到右括号')',将栈中的操作符弹出并添加到后缀表达式列表中,直到遇到左括号'('。
注意,左右括号不会被添加到后缀表达式中。
7. 当中缀表达式遍历完毕后,将栈中剩余的操作符依次弹出并添加到后缀表达式列表中。
8. 后缀表达式列表即为转换后的后缀表达式。
例如,将中缀表达式 '2 + 3 * 4' 转换为后缀表达式的步骤如下:中缀表达式:2 + 3 * 4后缀表达式列表(初始为空):[]遍历中缀表达式的每个元素:1. 遇到操作数2,添加到后缀表达式列表中:[2]2. 遇到操作符+,将其推入栈中:[+]3. 遇到操作数3,添加到后缀表达式列表中:[2, 3]4. 遇到操作符*,将其推入栈中:[+, *]5. 遇到操作数4,添加到后缀表达式列表中:[2, 3, 4]6. 中缀表达式遍历完毕,将栈中剩余的操作符弹出并添加到后缀表达式列表中:[2, 3, 4, *]最终转换后的后缀表达式为:'2 3 4 * +'后缀表达式的计算可以通过遍历列表中的元素来完成。

举个例子吧:对于算式1*2+(2-1)来说,这是一个中缀表达式(就是平时计算用的式子)转化为后缀表达式的过程为:先说统一的过程:1.从左到右依次读取算式的一个字符2.如果读到括号,入栈,等到遇到另外半边括号,则两括号都出栈括号3.如果读到的字符是数字,则直接输出到一个结果字符串的末尾(这个结果字符串到最后就是要的后缀表达式)4.如果读到的是运算符,则要将此运算符入栈(1) 若栈空,则直接入栈;(2) 若栈不空则要判断栈顶运算符的优先级:<1>若栈顶运算符的优先级低于要入栈的运算符,直接入栈<2>若栈顶运算符的优先级高于要入栈的运算符,要将栈顶位置的高优先级的运算符出栈,出栈的运算符输出到结果字符串的末尾.,直到栈顶运算符优先级低于要入栈的运算符为止.(实际上就是要保证栈中的运算符优先级从栈顶到栈底是依次从高到低的)5.依次按上述方式读取,直到将次中缀表达式读完.最后的结果就保存在这个结果字符串.6.最后将栈中还有的运算符出栈,加入到结果字符串中去.就得到了后缀表达式举例说明1*2+(2-1)设结果字符串String result="";//开始为空设存储运算符的栈为stack=空//开始为空,从左到右为栈底和栈顶第一个字符为1,直接加入到结果字符串result=="1";第二个字符为*,栈为空,直接入栈.stack=*第三个字符为2,加入到结果字符串result=="12";第四个字符为+.栈不空,入栈.栈顶运算符*优先级高于要入栈运算符+,故*先出栈,加入到结果字符串result=="12*";然后入栈stack=+第五个字符为(直接入栈第六个字符为2,加入结果字符串result=="12*2"第七个字符为-.栈不空,入栈,栈顶运算符+优先级高于要入栈运算符-,故+先出栈,加入到结果字符串result=="12*2+";然后入栈stack=-第七个字符为1,加入结果字符串result=="12*2+1"第八个字符为),( ) 都出栈到此为止中缀表达式读取完毕将栈里的运算符依次出栈加入结果字符串result=="12*2+1-"得到了最终的后缀表达式第二个问题:后缀表达式的计算1.将后缀表达式从左到右依次读取2.如果读到数字,直接入栈3.如果读到运算符,则将栈顶的两个数字出栈,和此运算符做运算注意: 先出栈的数为减数,后出栈的为被减数(除法类似)将此计算的结果再压入栈中4.重复上述步骤,最终的运算结果就存在栈里举例说明:上面得到的后缀表达式:12*2+1-设栈为stack第一个字符1,入栈stack=1第二个字符2,入栈stack=12第三个字符*.栈元素出栈做运算1*2得到2,再入栈stack=2的四个字符2,入栈stack=22第五个字符+,栈元素出栈做运算2+2得到4,再入栈stack=4第六个字符1,入栈stack=41第七个字符-,栈元素出栈做运算4-1得到3,再入栈stack=3到此为止,后缀表达式读取完毕,栈中就存储最终结果3你可以算算和原始的中缀表达式1*2+(2-1)结果相同吧~注意:+、-、*、/、的优先级均低于“(”但高于“)”。

标题:C++语言中的中缀表达式转后缀表达式原理与实现正文:1.中缀表达式和后缀表达式简介中缀表达式是我们日常生活中最常见的数学表达方式,例如 3 + 4 * 5。
而后缀表达式又被称为逆波兰表达式,它的运算符放在操作数的后面,例如 3 4 5 * +。
在计算机科学领域中,后缀表达式由于其计算机友好的特性,被广泛应用于编译器和计算器等领域。
2.中缀表达式转后缀表达式原理中缀表达式转后缀表达式的原理主要是利用栈来实现。
我们从左到右遍历中缀表达式的每一个字符,遇到操作数直接输出,遇到操作符,则与栈顶操作符比较优先级,如果当前操作符优先级大于等于栈顶操作符,则直接入栈;如果当前操作符优先级小于栈顶操作符,则将栈顶操作符弹出并输出,直到栈为空或者栈顶操作符优先级小于当前操作符。
遍历完整个中缀表达式后,将栈中剩余的操作符依次弹出并输出即得到后缀表达式。
3.C++语言实现中缀表达式转后缀表达式在C++语言中,我们可以通过栈来实现中缀表达式转后缀表达式的算法。
以下是一个简单的C++代码示例:```cpp#include <iostream>#include <stack>#include <string>using namespace std;int precedence(char op) {if (op == '+' || op == '-') {return 1;} else if (op == '*' || op == '/') {return 2;}return 0;}string infixToPostfix(string infix) {stack<char> s;string postfix = "";for (char &c : infix) {if (c >= '0' && c <= '9') {postfix += c;} else if (c == '(') {s.push(c);} else if (c == ')') {while (!s.empty() && s.top() != '(') {postfix += s.top();s.pop();}s.pop();} else {while (!s.empty() && precedence(s.top()) >= precedence(c)) {postfix += s.top();s.pop();}s.push(c);}}while (!s.empty()) {postfix += s.top();s.pop();}return postfix;}int main() {string infix = "3+4*5";string postfix = infixToPostfix(infix);cout << postfix << endl;return 0;}```在上面的代码中,我们定义了一个函数`infixToPostfix`,该函数接受一个中缀表达式作为输入,并返回转换得到的后缀表达式。

中缀表达式转化为后缀表达式算法首先需要分配2个栈,一个作为临时存储运算符的栈S1(含一个结束符号),一个作为输入后缀表达式的栈S2(空栈),S1栈可先放入优先级最低的运算符#,注意,中缀式应以此最低优先级的运算符结束。
可指定其他字符,不一定非#不可。
从中缀式的左端开始取字符,逐序进行如下步骤:(1)若取出的字符是数字,则分析出完整的运算数,该运算数直接送入S2栈(2)若取出的字符是运算符,则将该运算符与S1栈栈顶元素比较,如果该运算符优先级大于S1栈栈顶运算符优先级,则将该运算符进S1栈,否者,将S1栈的栈顶运算符弹出,送入S2栈中,直至S1栈栈顶运算符低于(不包括等于)该运算符优先级,则将该运算符送入S1栈。
(3)若取出的字符是“(”,则直接送入S1栈栈顶。
(4)若取出的字符是“)”,则将距离S1栈栈顶最近的“(”之间的运算符,逐个出栈,依次送入S2栈,此时抛弃“(”。
(5)重复上面的1~4步,直至处理完所有的输入字符(6)若取出的字符是“#”,则将S1栈内所有运算符(不包括“#”),逐个出栈,依次送入S2栈。
完成以上步骤,S2栈便为后缀表达式输出结果。
不过S2应做一下逆序处理。
便可以按照后缀表达式的计算方法计算了!做法如下将该字符与运算符栈顶的运算符的优先关系相比较。
如果,该字符优先关系高于此运算符栈顶的运算符,则将该运算符入栈。
倘若不是的话,则将栈顶的运算符从栈中弹出,直到栈顶运算符的优先级低于当前运算符,将该字符入栈。
(5)重复上述操作(1)-(2)直至扫描完整个简单算术表达式,确定所有字符都得到正确处理,我们便可以将中缀式表示的简单算术表达式转化为逆波兰表示的简单算术表达式。
后缀表达式的作用对于实现后缀表达式算法,难度并不大,但为什么要将看似简单的中缀表达式转换为复杂的后缀表达式?原因就在于这个简单是相对人类的思维结构来说的,对计算机而言中缀表达式是非常复杂的结构。
相对的,后缀表达式在计算机看来却是比较简单易懂的结构。

目录一、设计思想 (01)二、算法流程图 (02)三、源代码 (03)四、运行结果 (16)五、遇到的问题及解决 (17)六、心得体会 (18)一、设计思想第一种算法先把算术表达式转化成后缀表达式,在对后缀表达式进行计算。
首先建立一个符号栈,用于存放字符和字符的优先级别;然后在建立一个数栈,用于辅助后缀表达式的计算;最后在定义一个字符串数组,用于存放后缀表达式。
建立一个计算的函数,该函数用于两个数的计算,在调用这个函数的时候,传入三个参数,两个浮点型参数和一个字符型参数,根据不同的符号进行不同的计算。
定义一个判断优先级别的函数,用于判断两个操作符的优先级别,在根据优先级的不同决定不同的操作。
后缀表达式的取得,对算术表达式字符串进行挨个的扫描,如果是数字或者是小数点,则将数字或者小数点存放到字符数组中,每取完一个数字,则在后面用“|”隔开,如果是操作符,则和栈中得操作符进行比较,若扫描到的符号优先级比栈里的符号优先级低,则栈中元素出栈并存放到字符数组中。
每出一个字符到字符数组中就在后面加“|”分隔。
继续检查栈顶比较优先级,直到栈中元素优先级比扫描到的符号优先级低或者符号栈为空,则将此操作符入栈。
若是“(”则无条件入字符栈,若是“)”则从字符栈中出字符直到遇到“(”为止。
当字符数组扫描到最后的时候,计算并没有结束。
然后得进行字符栈的判断,看是否已经为空栈,若不是空栈,则出栈字符,将字符存放到数组中。
最后字符串数组中存放的就是后缀表达式。
得到后缀表达式后,要用数栈进行后缀表达式的计算,后缀表达式的计算中,对新的数组进行从道到尾的扫描,如果遇到数字,以“|”为标记取出完整的操作数,用辅助数组存放,然后转化成浮点数存放到数栈中,遇到“|”则直接将数组下标往后走。
遇到字符,则从数栈取出两个数进行计算,将计算的结果从新存放到数栈中,循环直到接到结束。
最后存放在数栈中的数就是计算的结果。
最后在主函数中调用此函数,进行结果的输出。

c++ 中缀转后缀表达式摘要:1.C++中缀转后缀表达式的概念2.中缀转后缀的转换方法3.转换过程中的数据结构和算法4.实际应用案例和注意事项正文:C++中缀转后缀表达式在C++编程语言中,表达式是程序设计中常见的概念。
表达式分为中缀表达式和后缀表达式两种形式。
中缀表达式是运算符写在运算对象的中间,而后缀表达式则是运算对象写在运算符的后面。
为了方便编程和计算,有时候需要将中缀表达式转换为后缀表达式。
下面我们来探讨一下C++中缀转后缀表达式的相关知识。
一、C++中缀转后缀表达式的概念中缀转后缀表达式是指将一个中缀表达式转换为一个后缀表达式的过程。
例如,给定中缀表达式"a + b * c",转换后的后缀表达式为"ab + c *"。
在后缀表达式中,运算符位于运算对象的后面,这样可以方便计算。
二、中缀转后缀的转换方法中缀转后缀的转换方法有多种,其中一种比较常见的方法是采用栈来实现。
具体步骤如下:1.初始化一个空栈。
2.从中缀表达式的左端开始,依次将每个运算对象和运算符入栈。
3.当遇到运算对象时,将其入栈;当遇到运算符时,进行以下操作:a.弹出栈顶的两个运算对象,记为a 和b。
b.将弹出的运算对象a 和当前运算符进行运算,得到一个新的运算对象。
c.将新运算对象入栈。
4.当栈为空时,转换完成。
此时栈中的元素就是后缀表达式的运算对象序列。
三、转换过程中的数据结构和算法在转换过程中,需要使用栈这种数据结构来存储运算对象。
栈是一种遵循后进先出(LIFO)原则的数据结构,可以用来存储序列中的运算对象。
算法方面,主要是通过栈的入栈和出栈操作来实现中缀表达式到后缀表达式的转换。
在遇到运算对象时,将其入栈;在遇到运算符时,弹出栈顶的两个运算对象进行运算,并将新的运算对象入栈。
这样,当栈为空时,就完成了中缀转后缀的转换。
四、实际应用案例和注意事项中缀转后缀表达式在实际编程中有很多应用,例如表达式求值、中缀表达式遍历等。
设计将中缀表达式转换为后缀表达式的算法整代码如下:
#include<stdio.h>
#include<stdlib.h>
#include<ctype.h>
#include"Stack.h"
#define MAX 30
int Precedence(char ch)
{
if(ch=='+'||ch=='-')return 2;
else if(ch=='*'||ch=='/')return 3;
else if(ch=='('||ch==')')return 4;
else if(ch=='@')return 1;
else return 0;
}
void Change(char *s1,char *s2)
{
Stack S=NewEmpty(MAX);
int i=0,j=0,one=0;
char ch=s1[i];
Push('@',S);
while(ch!='@')
{
if(ch==' ')
ch=s1[++i];
else if(isalnum(ch)!=0)
{
if(one==1)
{
s2[j++]=' ';
}
s2[j++]=ch;
ch=s1[++i];
one=0;
}
else if(ch=='(')
{
Push(ch,S);
ch=s1[++i];
one=1;
}
else if(ch==')')
{
while(Peek(S)!='(')
s2[j++]=Pop(S);
Pop(S);
ch=s1[++i];
one=1;
}
else if(ch=='+'||ch=='-'||ch=='*'||ch=='/')
{
while(Peek(S)!='('&&Precedence(Peek(S))>=Precedence(ch)) {
s2[j++]=Pop(S);
one=1;
}
Push(ch,S);
ch=s1[++i];
one=1;
}
}
while(StackEmpty(S)!=1)
{
s2[j++]=Pop(S);
one=1;
}
s2[j]='\0';
}
int main()
{
char s1[MAX],s2[MAX];
printf("Enter the equation:\n");
gets(s1);
Change(s1,s2);
printf("%s\n",s2);
return 0;
}
其中:Stack.h如下:
#ifndef STACK_H
#define STACK_H
#include<stdio.h>
#include<stdlib.h> typedefstructastack *Stack; typedefstructastack
{
int top;
intmaxtop;
char* data;
}Astack;
Stack NewEmpty(int size)
{
Stack S=(Stack)malloc(sizeof(Astack)); S->maxtop=size;
S->top=-1;
S->data=(char*)malloc(size*sizeof(char)); return S;
}
intStackEmpty(Stack S)
{
return S->top<0;
}
intStackFull(Stack S)
{
return S->top==S->maxtop;
}
int Peek(Stack S)
{
return S->data[S->top];
}
void Push(char x,Stack S)
{
if(StackFull(S))
{
printf("Stack is full!\n");
exit(1);
}
else
S->data[++S->top]=x;
}
int Pop(Stack S)
{
if(StackEmpty(S))
{
printf("Stack is empty!\n");
exit(1);
}
else
return S->data[S->top--];
}
Stack NewStack(int size)
{
Stack S=NewEmpty(size);
inti,x,num;
printf("Please enter the number of data:\n"); scanf("%d",&num);
for(i=0;i<num;i++)
{
printf("Please enter the %d date:\n",i+1); scanf("%c",&x);
Push(x,S);
}
return S;
}
void ShowStack(Stack S)
{
int i;
for(i=0;i<=S->top;i++) {
printf(" %c",S->data[i]); }
printf("\n");
}
#endif。