圆的认识单元能力测试与评价

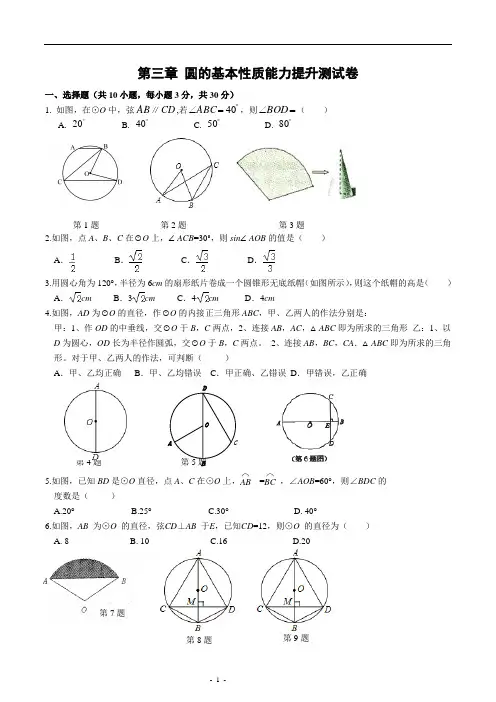
第7题第8题第三章 圆的基本性质能力提升测试卷一、选择题（共10小题，每小题3分，共30分）1. 如图，在⊙O 中，弦AB ∥CD ,若︒=∠40ABC ，则=∠BOD （ ） A. ︒20 B. ︒40 C. ︒50 D. ︒802.如图，点A 、B 、C 在⊙O 上，∠ACB =30°，则sin ∠AOB 的值是（ ） A ． B ．C ．D ．3.用圆心角为120°，半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的高是（ ） A ．cm B ．3cm C ．4cm D ．4cm4.如图，AD 为⊙O 的直径，作⊙O 的内接正三角形ABC ，甲、乙两人的作法分别是：甲：1、作OD 的中垂线，交⊙O 于B ，C 两点，2、连接AB ，AC ，△ABC 即为所求的三角形 乙：1、以D 为圆心，OD 长为半径作圆弧，交⊙O 于B ，C 两点。

2、连接AB ，BC ，CA ．△ABC 即为所求的三角形。

对于甲、乙两人的作法，可判断（ ）A ．甲、乙均正确B ．甲、乙均错误C ．甲正确、乙错误D ．甲错误，乙正确第4题 第5题 5.如图，已知BD 是⊙O 直径，点A 、C 在⊙O 上，⌒AB =⌒BC，∠AOB =60°，则∠BDC 的 度数是（ ）A.20°B.25°C.30°D. 40°6.如图，AB 为⊙O 的直径，弦CD ⊥AB 于E ，已知CD =12，则⊙O 的直径为（ ） A. 8 B. 10 C.16 D.20第1题 第2题 第3题DCB AO第9题7.如图所示，扇形AOB的圆心角为120︒，半径为2，则图中阴影部分的面积为( )334.-πA2334.-πB3234.-πC34.πD8.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（）A．CM=DM B．CB=DB C．∠ACD=∠ADC D．OM=MD9.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（）A．CM=DM B．CB=DB C．∠ACD=∠ADC D．OM=MD10.如图所示，圆O的弦AB垂直平分半径OC，则四边形OACB（）A、是正方形B、是长方形C、是菱形D、以上答案都不对二、填空题（共6小题，每小题4分，共24分）如图所示的圆面图案是用相同半径的圆与圆弧构成的．若向圆面投掷飞镖，则飞镖落在黑色区域的概率为．12．如图，AB是⊙O的弦，OC⊥AB于C．若AB=23，0C=1，则半径OB的长为________．13.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，B，A，C′三点共线，则线段BC扫过的区域面积为．14．如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成. 已知正三角形的边长为1，则凸轮的周长等于_________．15.如图所示，AB为⊙O的直径，AC为弦，OD∥BC交AC于点D，若AB=20cm，∠A=30°，则AD=cm．16.如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交AB于E，交⊙O于D．则AD=_____________．三、解答题（共7题，共66分）17、（本题8分）如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的A BCO第10题第11题第12题第13题第14题第15题第16题中点,AD ⊥BC 于点D .求证:AD =12BF .18（本题8分）.如图,⊙O 的直径AB 和弦CD 相交于点E ,∠CEA =30°, 求CD 的长.19．（本题8分）如图所示,OA 、OB 、OC都是圆O 的半径,∠AOB =2∠BOC ． 求证:∠ACB =2∠BAC .20、（本题10分）如图，弧AC 是劣弧，M 是弧AC 中点，B 为弧AC 上任意一点，自M 向BC 弦引垂线，垂足为D ，求证：AB +BD =DC 。

一．填空（20分）1．圆中心的一点叫做（），用字母（）表示，它到圆上任意一点的距离都（）。

2．（）叫做半径，用字母（）表示。

3．（）叫做直径，用字母（）表示。

4．在一个圆里，有（）条半径、有（）条直径。

5．（）确定圆的位置，（）确定圆的大小。

6．在一个直径是8分米的圆里，半径是（）厘米。

7．画圆时，圆规两脚间的距离是圆的( )。

8．在同一圆内，所有的（）都相等，所有的（）也相等。

（）的长度等于（）长度的2倍。

9．大圆半径等于小圆直径的长度，则大圆的面积是小圆面积的（）倍，小圆周长是大圆周长的（）。

10．用圆规画一个周长是25.12厘米的圆，那么圆规两脚之间的距离应为( )厘米。

二．判断题（10分）1．直径都是半径的2倍。

（）2．一端在圆里，另一端在圆上的线段是半径。

（）3．在连接圆上任意两点的线段中，直径最长。

（）4．画一个直径是4厘米的圆，圆规两脚应叉开4厘米。

（）5．通过圆心，且两端都在圆上的线段是直径。

（）6．圆的所有半径都相等，所有的直径也相等。

（）7．半径一定等于直径的21。

（）8．面积相等的两个圆，它们的半径一定相等。

（）三．选择题（24）1．一个圆和一个正方形的周长都是25.12厘米，它们的面积（）A．正方形大 B．圆大 C．一样大2．在一张长12厘米，宽8厘米的长方形纸中剪一个最大的圆，这个圆的面积是（）平方厘米。

A．113.04 B．50.24 C．963．如果大圆的周长是小圆的2倍，当小圆的直径是2分米时，大圆的直径是（）分米。

A．8 B．4 C．64．下面三种图形中，（）的对称轴最多。

A．正方形 B．圆 C．扇形5．一根铁丝可以围成一个半径是3厘米和圆，如果用它围成一个等边三角形，这个三角形的边长是（）厘米。

A．18.84 B．6.28 C．3.146.大圆的直径是6厘米，小圆的直径是3厘米，大圆的面积是小圆面积的( )倍。

A． 2 B.4 C.67.把一个长20厘米的铁丝，弯成一个半径是0.5的小圆，可以弯（）个。

人教版六年级上册《4.1 圆的认识》单元测试卷（2）一、填空（第12题每格0.5分，其余每空1分，共35.5分）．1. 从圆心到圆上任意一点的线段叫________．通过________并且________都在________的线段叫________．圆的位置由________确定，圆的大小决定于圆的________长短。

2. 在同一个圆里，所有的半径________，所有的________也都相等，直径等于半径的________．3. 圆周率表示同一圆内________和________的倍数关系，它用字母________表示，保留两位小数后的近似值是________．4. 在同一个圆内可以画________条直径；如果用圆规画一个直径是10厘米的圆，圆规的两脚尖间的距离应该是________厘米。

5. 在长6厘米，宽4厘米的长方形内剪下一个最大的圆，这个圆的周长是________，面积是________，还剩下面积________．6. 一个圆环外圆半径是6分米，内圆半径是4分米，圆环的面积是________．7. 甲圆直径长8厘米，是乙圆直径的40%．乙圆的周长是________厘米。

8. 一个圆的半径是8厘米，这个圆面积的3是________平方厘米。

49. 大圆的半径等于小圆直径，则大圆面积是小圆面积的________倍，小圆周长是大圆周长的________．10. 在一张长32厘米，宽16厘米的长方形内画半径是4厘米的圆，这样的圆最多能画________个，这些圆的面积和是________．11. 圆是________图形，它有________对称轴。

正方形有________条对称轴，长方形有________条对称轴，等腰三角形有________条对称轴，等边三角形有________条对称轴。

圆的周长是它的直径的π倍。

________．（判断对错）半径为1厘米的圆的周长是3.14厘米。

第一单元《圆》单元提优测试2022—2023北师大版六年级上册（含答案）一、选择题1. 如果圆的半径扩大到原来的3倍，那么面积就（）。

A．扩大到原来的3倍B．扩大到原来的6倍C．扩大到原来的9倍D．不变2. 圆的周长是2πr，那么半圆的周长是()．A．πr B．πr＋r C．πr＋2r D．无法确定3. 圆周率π是一个（）。

A．有限小数B．无限循环小数C．无限不循环小数D．以上都不对4. 10时整，钟面上分针与时针所成的角为（）。

A．锐角B．直角C．钝角5. ( )确定圆的位置．A．半径B．直径C．圆心D．圆规两脚间的距离二、填空题6. 锦华园有一个圆形花坛，直径是15m。

如果在花坛的边缘每隔0.3m安装一盏地灯，一共要安装( )盏。

7. 在一个长8cm，宽6cm的长方形中画一个最大的圆，这个圆的直径是( )，面积是( )。

8. 圆周率用字母( )表示，保留两位小数取近似值( )。

9. 圆上任意一点到圆心的距离都相等．．10. 圆的周长是62.8cm，圆的面积和长方形的面积相等，阴影部分周长是__________厘米。

（π＝3.14）11. 小猴子在钢丝上表演独轮车杂技，车轮的直径为40厘米，要骑过31.4米长的钢丝，车轮要转动( )圈。

12. 把一个圆等分成16份，拼成一个近似的长方形，周长增加了6cm，这个圆的面积是( )cm2。

13. 大圆的半径是小圆的2倍，小圆的周长是大圆周长的( )，小圆的面积是大圆面积的( )。

14. 长方形的长是( )dm，宽是( )dm。

15. 一个圆的周长是18.84厘米，面积是( )平方厘米。

三、判断题16. 两个圆的直径相等，则这两个圆的面积也相等。

( )17. 在同一个圆内可以画100条直径．( )18. 同圆中，所有的直径都相等，所有的半径都相等．____（判断对错）19. 圆的对称轴就是直径所在的直线．( )20. 周长相等的两个圆，面积也一定相等．_____（判断对错）四、其它计算21. 根据下列条件，求各圆的面积．(1)r＝8dm(2)d＝1.8cm(3)C＝37.68m五、图形计算22. 想一想：下面图形的周长是多少？（单位：cm）六、作图题23. 画出下面图形的所有对称轴．七、解答题24. 以A为圆心，画一个半径是1.5cm的圆，并画出圆的2条对称轴．25. 先画一直角梯形，然后在梯形内画一个最大的正方形，最后在正方形内画一个最大的圆．26. 在一块长3m、宽1m的长方形铁板上截下一块最大的半圆形铁板，半圆形铁板的面积是多少平方米？27. 海平面下有一处暗礁要实施爆破，你能画出图中的危险区域吗？信息1：危险半径为2千米。

第一单元 圆的认识学习评价一、选择题1．如图，点A 、B 、C 在⊙O 上，∠AOB ＝140o，∠ACB 的度数为（ ）（A ）140o ． （B ）110o ． （C ）70o ． （D ）120．（第1题） （第2题） （第3题）2．如图，AB 为⊙O 的弦，OC ⊥AB 于点D ，且AB ＝8cm ，OC ＝5cm ，则CD 的长为（ ） （A ）3cm ． （B ）2cm ． （C ）4cm ． （D ）5cm ．3．如图，弦AB 的长等于半径，P 为AmB 上一动点，则∠P 的度数为（ ） （A ）30o ． （B ）60o ． （C ）72o ． （D ）120o ． 4．半径为5的圆中，100o的圆心角所对的弦长为（ ）（A ）5sin50o． （B ）10sin50o． （C ）5cos50o． （D ）10cos50o． 5．半径为25cm 的⊙O 中，两条平行弦长为40cm ，14cm ，则两条平行弦间的距离为（ ） （A ）15cm ． （B ）15cm 或24cm ． （C ）39cm ． （D ）39cm 或9cm ． 6．如图，在⊙O 中，OA ∥BC ，∠ACB ＝20o ，则∠1的度数为（ ）（A ）40o ． （B ）45o ． （C ）50o ． （D ）60o ．（第6题） （第7题） （第8题）7．如图，CD 是⊙O 的直径，OC ＝13，弦MN ＝10，则点O 到直线MN 的距离等于（ ） （A ）12． （B ）6． （C ）8． （D ）3． 8．如图，AC 与BD 交于P ，AD 、BC 延长交于点E ，∠AEC ＝37o ，∠CAE ＝31o ，则∠APB 的度数为（ ）（A ）90o ． （B ）31o ． （C ）99o ． （D ）68o ． 9．若一个圆的半径是6cm ，则此圆的最长弦的长度为（ ）（A ）6cm ． （B ）8cm ． （C ）10cm ． （D ）12cm ． 二、填空题10．在半径为4cm 的圆中，垂直平分半径的弦长为____________．11．已知，⊙O 的直径为10，弦AB 的长为8，P 是弦AB 上的一个动点，那么OP 长的取值范围是___________．12．已知，点P 是半径为5的⊙O 内一定点，且OP ＝4，则过点P 的所有弦中，长度为整ACAE数的弦有___________条．13．如图，A 、B 为⊙O 上的两点，AC 与半径OA 垂直，∠B ＝70o ，则∠BAC ＝__________．（第13题）（第14题）（第15题）14．如图，⊙O 是△ABC 的外接圆，若∠ACO ＝30o ，则∠B 的度数为____________． 15．如图，⊙O 中弦AB ＝，半径为4cm ，则∠BAC 的度数为____________． 16．在半径为1的⊙O 中，弦AB 、AC ，则∠BAC ＝___________． 三、解答题17．如图，在⊙O 中，ON ＝3cm ，OA ＝5cm ，AB ＝8cm ，求OM 及CD 的长．18．如图，BC 为⊙O 的直径，弦AB ，BC ＝2，D 为 AB 上一点，求∠ADC 的度数．19．如图，AB 为半圆O 的直径，弦AD 、BC 相交于点P ，若CD ＝3，AB ＝4，求tan ∠BPD的值．20．如图，AB 、CD 是⊙O 的直径，DF 、BE 是弦，且DF ＝BE ，求证：∠D ＝∠B ．CABCFECBA21．如图，AB是半圆O的直径，E是弧BC的中点，OE交弦BC于点D，已知BC＝8，DE ＝2，求圆O的半径的长．22．在△ABC中，以AB为直径的⊙O交BC边于点D，连结AD，要使△ABD与△ACD相似，线段AB与AC应满足怎样的关系？并证明你的结论．23．在⊙O中，AB是⊙O直径，CD是弦，AB⊥CD．（1）P是 CAD上一点（不与C、D重合）时，∠CPD与∠COB有怎样的大小关系？并说明理由；（2）当点P在⊙O外时，∠CPD与∠COB有怎样的大小关系？并说明理由．24．已知：如图，BC是半圆的直径，O为圆心，D是 A C的中点，四边形ABCD的对角线AC、BD交于点E．（1）试说明△ABE∽△DBC；（2）已知BC＝52，CD＝2，求sin∠AEB的值．BBAB25．已知：如图，AB是⊙O的一条弦，点C为 AB的中点，CD是⊙O的一条直径，过C 点的直线l交AB所在直线于点E，交⊙O于点F．（1）判断∠CEB与∠FDC的数量关系，并写出结论；（2）将直线l绕C点旋转（与CD不重合），在旋转过程中，E点、F点的位置也随之变化，请你在下面两个备用图中分别画出l在不同位置时，使（1）的结论仍然成立的图形，标上相应字母，选其中一个图形给予证明．lD。

AB3.1-3.3圆的基本性质学习检测与评价姓名 得分 ________（每题3分，共42分）（ ）B .弧是半圆D .过圆心的线段是直径2. 与圆心的距离不大于半径的点的集合是 （ ）3. 两圆的圆心都是0,半径分别是r i , r 2 （ r i < r 2 ）,若r i v OP v 门、则点P 在 A .大圆外 B .小圆内 C .大圆内，小圆外4. 若。

P 的半径为13,圆心P 的坐标为（5, 12 ）, 与。

P 的位置关系是 A .在O P 内 B .在O P 上 C .在O P 夕卜5. 已知O 0的半径长6cm , P 为线段O A 的中点，若点P 在O 0上，则0A 的长是（）A .等于6cmB .等于12cmC .小于6cmD .大于12cm 6. 下列说法正确的是（）A. —个点可以确定一条直线 B .两个点可以确定两条直线 C •三个点可以确定一个圆 D .不在同一直线上的三点确定一个圆7. 下列说法不正确的是（）A.过一点可作无数个圆，那是因为圆心不确定，半径也不确定 B •过两个点可以画无数个圆，圆心在这两点连线段的中垂线上C. 过不在同一直线上的三个点只能画一个圆，圆心是这三点构成的三角形的 三内角平分线的交点，叫做内心D. 过不在同一直线上的三个点只能画一个圆，圆心是这三点构成的三角形的 三边中垂线的交点，叫做外心 A .一条B 两条C . 一条A .圆的外部B .圆的内部C .圆D .圆的内部和圆一、 精心选一选i .下列结论正确的是A .弦是直径 C .半圆是弧（ ）D .无法确定则平面直角坐标系的原点0（ ） D .无法确定 8.圆是轴对称图形，它的对称轴有（ ） D .无数条AO=5,OC=3，则弦AB 的长9. 如图，在O 0中,AB为弦,0C丄AB,垂足为C若为（）A.10B.8C.6D.410. 下列命题中，真命题是（A •相等的圆心角所对的弧相等B •相等的弦所对的弧相等C .度数相等的弧是等弧D .在同心圆中，同一圆心角所对的两条弧的度数相等11. 若一个三角形的外心在这个三角形的边上，那么这个三角形是14. 在直角三角 ABC 中，/ C=90,AC=3cm,BC=4cm,CD 是AB 边上的高，贝U D 在以A 为圆心，AC 为半径的 （ ） A 、圆内 B 、圆上C 、圆外 D 、无法确定15. 已知O o 的半径为1，OP=1.5，则点P 在O O ________ 。

青岛版九年级数学上册第三章対圆的进一步认识单元评估检测试卷一、单选题（共10题；共30分）1.一个扇形的圆心角为60°，弧长为2π厘米，则这个扇形的半径为（）A. 6厘米B. 12厘米C. 厘米D. 厘米2.（2016•宜宾）半径为6，圆心角为120°的扇形的面积是（）A. 3πB. 6πC. 9πD. 12π3.如图，四边形ABCD内接于⊙O，若∠A=62°，则∠BCE等于（）A. 28°B. 31°C. 62°D. 118°4.如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（）A. 8cmB. 5cmC. 3cmD. 2cm5.已知A为⊙O上的点，⊙O的半径为1，该平面上另有一点P，PA=，那么点P与⊙O的位置关系是（）A. 点P在⊙O内B. 点P在⊙O上C. 点P在⊙O外D. 无法确定6.下列命题中的假命题是（）A. 三点确定一个圆B. 三角形的内心到三角形各边的距离都相等C. 同圆中，同弧或等弧所对的圆周角相等D. 同圆中，相等的弧所对的弦相等7.如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则劣弧AC的长（）A. 8B. 4C. 2πD. π8.如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（）A. B. 2 C. 2 D. 89.如图，⊙O的半径为5，AB为弦，点C为的中点，若∠ABC=30°，则弦AB的长为（）A. B. 5 C. D. 510.已知：如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=130°，过D点的切线PD与直线AB交于P点，则∠ADP的度数为（）A. 45°B. 40°C. 50°D. 65°二、填空题（共10题；共30分）11.如图，已知∠BPC=50°，则∠BAC=________12.已知，如图，半径为1的⊙M经过直角坐标系的原点O，且与x轴、y轴分别交于点A、B，点A的坐标为( ，0 )，⊙M的切线OC与直线AB交于点C.则∠ACO＝________.13.已知圆锥的底面半径为3cm，其母线长为5cm，则它的侧面积为________ ．14.正八边形的中心角等于________度.15.已知AB，AC是半径为R的圆O中两条弦，AB=R，AC=R，则∠BAC的度数为 ________16.直角三角形两边长分别为3和4，这个三角形内切圆的半径为________.17.△ABC中，∠ACB=120°，AC=BC=3，点D为平面内一点，满足∠ADB=60°，若CD的长度为整数，则所有满足题意的CD的长度的可能值为 ________．18.如图，在半径为 的⊙中，弦 ，于点，则________19.如图，四边形ABCD内接于⊙O，OC∥AD，∠DAB＝60°，∠ADC＝106°，则∠OCB＝________°．20.如图，点A、B在直线l上，AB=10cm，⊙B的半径为1cm，点C在直线l上，过点C作直线CD且∠DCB=30°，直线CD从A点出发以每秒4cm的速度自左向右平行运动，与此同时，⊙B的半径也不断增大，其半径r（cm）与时间t（秒）之间的关系式为r=1+t（t≥0），当直线CD出发 ________秒直线CD恰好与⊙B相切．三、解答题（共8题；共60分）21.如图，已知AB是⊙O的直径，CD⊥AB ，垂足为点E，如果BE=OE ，AB=12，求△ACD的周长22.已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．求证：AC=BD.23.如图，在半径为13的⊙O中，OC垂直弦AB于点D，交⊙O于点C，AB=24，求CD的长．24.如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半径为2，圆心角为60°，求图中阴影部分的面积．25.如图，已知AB是半圆O的直径，∠BAC=32°，D是弧AC的中点，求∠DAC的度数．26.如图：AB是半圆的直径，O是圆心，C是半圆上一点，E是弧AC的中点，OE交弦AC于D，若AC=8cm，DE=2cm,求OD的长。

第一单元《圆》单元质量监测试题2022—2023北师大版六年级上册（含答案）一、选择题1. 在同一平面内，直线a和b分别与直线m垂直，那么直线a和b的关系是（）。

A．互相平行B．相交C．互相垂直2. 下列图形中，对称轴最少的是（）。

A．圆B．正方形C．等边三角形D．长方形3. 下列各图，没有运用“转化”方法的是（）。

A．B．C．D．4. 一个半径为5cm的半圆,周长是()．A．20.7 cm B．25.7cm C．31.4 cm5. 一个圆的周长是18.84厘米，它的面积是（）平方厘米。

A．9.42 B．18.84 C．28.26二、填空题6. 一个半圆形花坛的周长是25.7米，它的面积是( )平方米。

7. 将一个圈沿半径剪开，得到若干个小扇形，然后拼成一个近似的长方形，如果这个长方形的宽是4厘米，那么这个长方形的长是( )厘米，圆的面积是( )平方厘米。

8. 如图,直角三角形的面积是16cm2，则圆的面积是( )cm2。

9. 圆的( )和( )的比值，就是圆周率，用字母( )表示，它是一个( )小数。

10. 圆的对称轴有( )条，正方形有( )条对称轴，长方形的对称轴有( )条。

11. 如图,其中一个圆的直径是( )厘米，长方形的长是( )厘米。

12. 把一个周长是6.28分米的圆沿一条直径切成两个半圆，每个半圆的周长是( )分米，面积是( )平方分米。

13. 在一张长16cm，宽10cm的长方形纸里，最多可以画( )个半径2cm的圆。

14. 在一个直径为10米的圆形水池周围有一条宽1米的环形小路，这条小路的面积是( )平方米。

15. ( )决定圆的位置，半径决定圆的( )。

三、判断题16. 长方形、正方形、等腰三角形、扇形都是轴对称图形。

( )17. 把一个圆分成5份，每一份都是扇形．( )18. 圆的周长与它的半径的比是2π：1．___．（判断对错）19. 同一个圆中，半圆的周长就是圆周长的一半。

一定要仔细哦！《圆的认识》单元卷班：姓名：成：一、填空。

（每空 1 分，共 27 分）1、 504 平方分米 =（）平方米7 米 8 厘米 =（）厘米2、一个的半径是 5 厘米，直径是（），周是（），面是（）。

3、一个的面是28.26 平方厘米，用画，两脚之的距离是（）厘米。

个的直径是（）厘米，周是（）厘米。

4、一个半形的养池，直径 14 米，它的周是（）米，占地面是（）平方米。

5、一个形水池，直径400 米，沿池隔 4 米栽一棵，一共能栽（）棵。

6、一位老奶奶沿着街心公园的一个形花走了一圈，走了 18.84 米，花占地 ( )平方米。

7、一个的“ ” 10 厘米，一昼夜根的尖端走了（）厘米。

8、在是 4 厘米的正方形中，画一个最大的，的直径是（）厘米，面是（）平方厘米。

9、一个的半径大了 3 倍，它的周大了（）倍，面大了（）倍。

10、一形白，直径是20 厘米，把白平均分成 5 份，用去了其中的 1 份，用去部分的是白的（），是（）平方厘米。

（）11、将一个沿半径剪开，得到若干个小扇形，然后拼成一个近似的方形，个方形的是的（），是的（）。

如果个方形的是 2 厘米，那么个方形的是（）厘米，周是（）厘米，面是（）平方厘米。

如果拼成的长方形的长9.42 分米，那么原来圆的面积是（）平方分米。

12、半径是 4 厘米的半，它的周是（）厘米，面是（）平方厘米。

二、判断。

（每 1 分，共 5 分）1、直径一定比半径。

（）2、半径 2 厘米的，它的周和面相等。

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（）3、直径 5 厘米的比半径 3 厘米的的周率大一些。

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（）4、两端都在上的段中，直径最。

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（）5、周相等的两个，面也一定相等。

（）三、。

（每 1 分，共 5 分）1、一个的直径小 3 倍，它的周小（）。

A 3 倍B 6 倍C 9 倍2、周率π的（）3.14。

A 大于B 等于C 小于3、在周相等的情况下，下面的形中（）的面最大。

圆的认识一单元测试卷一、选择题（每题2分，共10分）1. 下列哪个图形是圆？A. 正方形B. 长方形C. 圆形D. 三角形2. 圆的周长公式是什么？A. C = πdB. C = 2πrC. C = πrD. C = 2d3. 圆的半径增加1倍，其面积增加多少倍？A. 1倍B. 2倍C. 3倍D. 4倍4. 圆的直径是半径的多少倍？A. 1倍B. 2倍C. 3倍D. 4倍5. 圆内最长的线段是？A. 半径B. 直径C. 弦D. 弧二、填空题（每空1分，共10分）1. 圆心是圆的______，用字母O表示。

2. 圆的半径是圆心到圆上任意一点的距离，用字母r表示。

3. 圆的直径是圆的两个点之间的距离，且这两个点都在圆上，用字母d表示。

4. 圆的周长是圆的边缘的长度，其公式为C=______。

5. 圆的面积是圆内部的平面区域，其公式为A=______。

三、判断题（每题1分，共5分）1. 所有圆的周长都是相同的。

（）2. 圆的半径是直径的一半。

（）3. 圆的面积与半径的平方成正比。

（）4. 圆的周长和直径成正比。

（）5. 圆内任意两点之间的最短距离是直径。

（）四、简答题（每题5分，共10分）1. 请简述圆的对称性。

2. 请解释圆周角和圆心角的区别。

五、计算题（每题10分，共20分）1. 已知圆的半径为5厘米，求其周长和面积。

2. 如果一个圆的周长是31.4厘米，请计算其半径。

六、作图题（每题5分，共5分）1. 根据题目要求，在给定的坐标系中画出一个半径为3厘米的圆。

七、思考题（每题5分，共5分）1. 圆的周长和面积公式在实际生活中的应用有哪些？八、结束语本单元测试卷旨在帮助学生巩固对圆的基本性质和公式的理解，以及在实际问题中的应用能力。

希望同学们通过本测试卷能够更好地掌握圆的相关知识。

【注】本测试卷仅供参考，具体题目和分值可能根据教学大纲和课程要求有所调整。

圆的认识单元测试卷（一）一、填空（第12题每格0.5分，其余每空1分，共35.5分）。

1．从圆心到圆上任意一点的线段叫( )。

通过（）并且（）都在（）的线段叫做直径。

圆的位置是由（）确定的，圆的大小决定于（）的长短。

2．在同一个圆里，所有的半径（），所有的（）也都相等，直径等于半径的（）。

3．圆周率表示同一圆内（）和（）的倍数关系，它用字母（）表示，保留两位小数后的近似值是（）。

4．在同一个圆内可以画（）条直径；如果用圆规画一个直径是10厘米的圆，圆规的两脚间的距离应该是（）厘米。

5．在长6厘米，宽4厘米的长方形内剪下一个最大的圆，这个圆的周长是（），面积是（），还剩下面积( )。

6．一个圆环，外圆半径是6分米，内圆半径4分米，圆环的面积是（）。

7．甲圆直径长8厘米，是乙圆直径的40%。

乙圆的周长是（）。

8．一个圆的半径是8厘米，这个圆面积的是（）平方厘米。

9．大圆的半径等于小圆直径，则大圆面积是小圆面积的（）倍，小圆周长是大圆周长的（）。

10．在一张长32厘米，宽16厘米的长方形内画半径是4厘米的圆，这样的圆最多能画（）个，这些圆的面积和是（）。

11．圆是（）图形，它有（）对称轴。

正方形有（）条对称轴，长方形有（）条对称轴，等边三角形有（）条对称轴。

12．填表：1．圆的周长是它的直径的π倍。

（）2．半径为1厘米的圆的周长是3.14厘米。

（）3．一个圆的周长是12.56厘米，面积是12.56平方厘米。

（）4．圆的半径由6分米增加到9分米，圆的面积增加了45平方分米。

（）5．当长方形、正方形、圆的周长相等时，圆的面积最大。

（）6．水桶是圆形的。

（）7．半个圆的周长就是圆周长的一半。

（）8．所有的直径都相等。

（）9．π＝3.14．（）三、画一画。

(共7.5分)1．以O为圆心，画一个直径是4厘米的圆。

2.在正方形中画一个最大的圆。

3，画出所有对称轴。

·O四、计算下列各圆的周长。

（6分）1．直径是6厘米 2.半径是5分米五、计算下列各圆的面积。

新人教版六年级上册《第4章圆的认识》单元测试卷一、概念1. 圆是由________围成的________图形。

2. 圆中心的一点，叫做________，用字母________表示；连接________和________的线段叫做半径，用字母________表示；通过________并且________的线段叫做直径，用字母________表示。

3. 圆是平面上的一种________对称图形，将一张圆形纸片至少对折________次可以得到这个圆的圆心。

4. 一个圆有________条半径，并且都________；有________条直径，并且都________．5. 在同一个圆内，直径是半径的________；用字母表示为：________或________．6. 圆的位置是由________决定，圆的大小是由________决定。

7. 圆内的所有线段中，________最长。

8. 画圆的步骤：(1)定________，(2)定________，(3)________．9. 时钟的分针转动一周形成的图形是________，分针转动20度形成的图形是________．10. 扇形都有________个角，角的顶点在________．11. 扇形是由________和________围成的。

12. 扇形中________的夹角叫做圆心角。

13. 扇形的大小与________和________有关。

14. 同一圆内扇形的大小由________决定；________越大，扇形就越大。

15. 扇形圆心角的度数大于________小于________．二、判断并改错．所有的半径长度都相等，所有的直径长度都相等。

________．（判断对错）．改错________．直径是半径长度的2倍。

________．（判断对错）．改错________．两个圆的直径相等，它们的半径也一定相等。

________．（判断对错）．改错________．半径是射线，直径是线段。

完整版)《圆的认识》单元测试卷(1)圆的认识》单元卷班级：__________ 姓名：__________ 成绩：__________一、填空题。

（每空1分，共27分）1、504平方分米=（）平方米，7米8厘米=（）厘米。

2、一个圆的半径是5厘米，直径是（），周长是（），面积是（）。

3、一个圆的面积是28.26平方厘米，用圆规画圆时，圆规两脚之间的距离是（）厘米。

这个圆的直径是（）厘米，周长是（）厘米。

4、一个半圆形的养鱼池，直径14米，它的周长是（）米，占地面积是（）平方米。

5、一个圆形水池，直径400米，沿池边隔4米栽一棵树，一共能栽（）棵树。

6、一位老奶奶沿着街心公园的一个圆形花坛走了一圈，走了18.84米，花坛占地（）平方米。

7、一个时钟的“时针”长10厘米，一昼夜这根时针的尖端走了（）厘米。

8、在边长是4厘米的正方形中，画一个最大的圆，圆的直径是（）厘米，面积是（）平方厘米。

9、一个圆的半径扩大了3倍，它的周长扩大了（）倍，面积扩大了（）倍。

10、一张圆形白纸，直径是20厘米，把这张白纸平均分成5份，用去了其中的1份，用去部分（）的是这张白纸的，是（）平方厘米。

11、将一个圆沿半径剪开，得到若干个小扇形，然后拼成一个近似的长方形，这个长方形的长是圆的（），宽是圆的（）。

如果这个长方形的宽是2厘米，那么这个长方形的长是（）厘米，周长是（）厘米，面积是（）平方厘米。

如果拼成的长方形的长9.42分米，那么原来圆的面积是（）平方分米。

12、半径是4厘米的半圆，它的周长是（）厘米，面积是（）平方厘米。

二、判断题。

（每题1分，共5分）1、直径一定比半径长。

（×）2、半径2厘米的圆，它的周长和面积相等。

（×）3、直径5厘米的圆比半径为3厘米的圆的圆周率大一些。

（×）4、两端都在圆上的线段中，直径最长。

（√）5、周长相等的两个圆，面积也一定相等。

（×）三、选择题。

圆的认识（二）教学目标：1、通过折纸活动，探索并发现圆是轴对称图形，理解同一个圆里半径和直径的关系。

2、进一步理解轴对称图形的特征，体会圆的对称性。

3、在折纸找圆心验证圆是轴对称图形等活动，发展空间观念。

检测题：一、基础训练题1、填空。

（1）在一个半径是2厘米的圆内，两端都在圆上的最长线段长( )厘米。

（2）在同一个圆里，直径的长度是半径的 ( )，半径的长度是直径的( )，用关系式( )或( )来表示。

（3）圆规两脚间的距离是3厘米，画出的圆的直径是( )厘米。

（4）长方形有( )条对称轴，正方形有( )条对称轴，圆有( )条对称轴，等边三角形有( )条对称轴。

2．判断（对的打“√”，错的打“×”）。

(1)半径的长度是直径的。

( )(2)一个圆的半径是5厘米，它的直径一定是10厘米。

( )(3)直径是6 cm的圆一定比半径是3 cm的圆小。

( )(4)通过圆心的线段一定是直径。

( )(5)圆的半径越大，直径就越大。

( )(6)一个圆的直径是6分米，它的半径是2分米。

( )二、运用练习题(48分)l．填表（给出图形填出对应的有几条对称轴）。

2、画一画（画出下列图形的对称轴）。

检测结果分析：检测分为基础训练和运用练习两个部分，基础练习有两个环节，填空和判断，填空部分主要以考察学生对半径和直径的、图形的对称轴为主，学生完成的较好，判断题主要考察学生对于半径、直径关系的运用，大部分学生完成的较好，小部分学生在第三、四小题出现失误。

运用练习部分主要是检测学生对于第五个活动中的巩固练习，帮助学生巩固深化，拓展延伸。

整体学生完成的较好。

圆的认识单元测试题及答案一、选择题：1. 圆的周长公式是（）。

A. C = πrB. C = 2πrC. C = πdD. C = 2πd2. 半径为2厘米的圆的面积是（）平方厘米。

A. 12.56B. 3.14C. 4D. 6.283. 圆的直径是半径的（）倍。

A. 1B. 2C. 3D. 4二、填空题：4. 圆的半径为3厘米，其周长是________厘米。

5. 一个圆的直径是8厘米，那么它的半径是________厘米。

三、判断题：6. 圆的直径是圆内最长的线段。

（）7. 圆心决定圆的位置，半径决定圆的大小。

（）四、简答题：8. 请简述圆的基本概念。

五、计算题：9. 已知一个圆的半径为5厘米，求这个圆的周长和面积。

六、应用题：10. 一个圆形花坛的直径是20米，如果绕着花坛走一圈，需要走多少米？如果花坛的面积是1256平方米，那么它的半径是多少米？答案：一、选择题：1. B2. A3. B二、填空题：4. 18.845. 4三、判断题：6. 正确7. 正确四、简答题：圆是一个平面上所有与定点（圆心）距离相等的点的集合。

这个定点称为圆心，距离称为半径。

圆的边界称为圆周。

五、计算题：9. 周长：C = 2πr = 2 × 3.14 × 5 = 31.4厘米面积：A = πr² = 3.14 × 5² = 3.14 × 25 = 78.5平方厘米六、应用题：10. 周长：C = πd = 3.14 × 20 = 62.8米半径：A = πr²，所以 r² = A / π，r = √(A / π) =√(1256 / 3.14) ≈ 20米结束语：通过本单元测试题，同学们应该能够更好地理解和掌握圆的基本性质和计算方法。

希望同学们能够通过练习，加深对圆的认识，提高解题能力。

《圆》单元学习自我检测一、选择题： 袁鋆 2009.12.211、在半径为1的⊙O 中，120°的圆心角所对的弧长是 （ ）A ．3π B ．23π C ．π D ．32π 2、下列四个命题：①直径所对的圆周角是直角；②圆既是轴对称图形，又是中心对称图形；③在同圆中，相等的圆周角所对的弦相等；④三点确定一个圆．其中正确命题的个数为（ ）A ．1B ． 2C ．3D ． 43、已知⊙O 和三点P 、Q 、R ，⊙O 的半径为3，OP=2，OQ=3，OR=4，经过这三点中的一点任意作直线总是与⊙O 相交，这个点是 ( )A ．PB ．QC ．RD ．P 或Q4、如图，AD 是△ABC 的高，AE 是△ABC 的外接圆⊙O 的直径，且AC=5，DC=3，AB=24，则⊙O 的直径AE=（ ）．A ． 25B ． 5C ． 24D ． 235、一个形式如圆锥的冰淇淋纸筒，其底面直径为cm 6，母线长为cm 5，围成这样的冰淇淋纸筒所需纸片的面积是 （ ）A ． 266cm πB ． 230cm πC ． 228cm πD ． 215cm π6、如图, ⊙O 的半径OA=6，以A 为圆心OA 为半径的弧交⊙O 于B 、 C 点， 则BC= ( )A ． 36B ． 26C ．33D ． 23二、填空题：7、两条边是6和8的直角三角形，其内切圆的半径是 ．8、如图，某传送带的一个转动轮的半径为20cm ，当物体从A 传送20cm 至B 时，这个转动8题 10题4题 6题轮转了_ 度．9、已知弦AB的长等于⊙O的半径，弦AB所对的圆周角是____ ___ 度．10、如图，A、B、C是⊙O上三点，∠BOC=150º，则∠A=_______．11、在矩形ABCD中，AB＝5，BC＝12，若分别以点A，C为圆心的两圆外切．．，点D在⊙C内，点B在⊙C外，则⊙A的半径r的取值范围是．12、已知圆锥底面半径是2，母线长是4，则圆锥的侧面展开的扇形圆心角是．13、如图，在⊙O中，弦AB=1.8cm，圆周角∠ACB =30，则⊙O的直径为__________cm.14、同圆中，内接正四边形与正六边形面积之比是．三、解答题：15、（8分）已知，AB为⊙O 的直径，点E 为弧AB 任意一点，如图，AC平分∠BAE,交⊙O于C ,过点C作CD⊥AE于D,与AB的延长线交于P．⑴求证：PC是⊙O的切线．⑵若∠BAE=60°，求线段PB与AB的数量关系．A。

《圆的认识》教案教学内容：苏教版教材五年级下册第十单元《圆》。

教学目标：1、通过欣赏生活中的圆、用圆设计的图案，发现数学美，提高学习的兴趣。

2、掌握圆规画圆的正确方法，会画规定大小的圆。

3、认识直径、半径、圆心等概念及其相互关系，掌握圆的基本特征，感受圆的特性在生活中的运用。

4、通过一系列的探索活动，培养大家科学的探究态度，发展大家的空间观念。

教学重点：1、知道圆各部分名称与关系2、学会画规定大小的圆。

学具准备：直尺圆规纸片教学过程：课前欣赏图片《美丽的圆》：大自然中的圆、建筑设计中的圆、工艺设计中的圆、标志设计中的圆、工业生产中的圆、科技中的圆。

一、直观感受-----体会生活中的圆1、谈话：今天这节课丁老师将带着大家走进圆的世界，一起来学习《圆的认识》。

2、课前同学们欣赏了一组图片《美妙的圆》，现在你能说说哪些地方看到了圆？全班交流。

指出球是立体图形，圆是平面图片，球的一个切面是一个圆形。

3、圆和我们以前学过的平面图形有什么不同？板书：圆是由曲线组成的平面图形。

曲线图形还有吗？二、动手操作----画圆中感受圆1、想办法画一个圆，在小组里交流。

说说是怎样画的。

归两类：一类借用物体的圆面描画，一类用圆规来画，你觉得哪种更好些？2、介绍体育老师在操场上画圆。

3、用钉绳画圆。

师生比赛，学生用的绳是有弹力的。

思考：要画好一个圆，关键是什么？强调：绳的长度不能改变。

那用圆规画圆呢？关键是什么？（圆规两脚间的距离不变。

）4、思考：我们用圆规画圆，用钉绳画圆，它们有什么相同的地方？强调画圆时要定点、定长。

介绍圆心（o ）、半径（ r）、直径（d ）。

指出：这固定的一点，绳子不变的长度，在数学上还有专门的名称呢。

揭示：固定的一点是圆心，用字母“o”表示。

问：用圆规画圆时圆心就是什么？出示定义：圆心：画圆时，针尖固定的一点是圆心，通常用字母O表示；指出这条绳子的长就是半径，我们可以用线段把它画下来。

用圆规画圆时半径在哪里？出示定义：半径：连接圆心和圆上任意一点的线段是半径，通常用字母r表示；你还能找一条半径吗？对吗？你是怎么判断他对不对呢？还有一个很关键的要素：直径。

第一单元《圆》单元基础知识测试2022—2023北师大版六年级上册（含答案）一、选择题1. 下图中，圆的半径是1cm，把这个圆在一把破损的直尺上向前滚动一周，此时圆中半径所在的箭头会落在（）之间，（π取3.14）A．9和10 B．10和11 C．11和12 D．13和142. 如图,线段OA和线段BC分别是圆的半径和直径，已知线段OA长5厘米，若一只蚂蚁从B点出发沿逆时方向绕着圆的边线爬行至C点，所经过的路程是多少厘米？正确的算式是（）。

A．5×2 B．5πC．1 (5) 23. 一个圆的周长和正方形的周长都是6.28分米，圆的面积（）正方形的面积。

A．大于B．小于C．等于4. 观察下图，甲、乙是两个同样大小的正方形，两图中阴影部分的周长和面积的关系是（）。

A．周长和面积都相等B．周长和面积都不相等C．周长相等，面积不相等D．周长不相等，面积相等5. 如果一个圆的直径与一个正方形的边长相等那么圆的面积与正方形的面积相比（）。

A．圆的面积稍大 B．正方形的面积稍大 C．两者相等二、填空题6. 在一块长9分米，宽5分米的长方形铁板上，最多能剪( )个直径是2分米的圆。

7. (下图）一个环形，外圆半径为12厘米，内圆半径为8厘米，这个环形的面积是( )平方厘米。

8. 用圆规画圆，圆规两脚间的距离是圆的( )决定圆的大小，( )确定圆的位置。

9. 画圆时，圆规两脚之间的距离是5厘米，那么画出的圆的直径是( )厘米，半径是( )厘米。

10. 把一个周长是6.28分米的圆沿一条直径切成两个半圆，每个半圆的周长是( )分米，面积是( )平方分米。

11. 一个圆的直径是d，连续对折2次后（不打开），周长是( )。

12. 在一个长6厘米，宽4厘米的长方形纸片内剪下半径为1厘米的圆，最多可以剪________个。

13. 在同圆或等圆中，圆的周长是直径的( )倍，直径是半径的( )倍。

周长计算公式用字母表示( )或( )，圆的面积计算公式用字母表示是( )。