结构力学_习题集(含答案)

第 1 页 共 28 页 《钢结构》课程习题集

【说明】:本课程《钢结构》（编号为06004）共有单选题，填空题1，判断改错题,计算题，简答题等多种试题类型，其中,本习题集中有［判断改错题］等试题类型未进入.

一、单选题

1. 钢结构最大的优点在于（ ）。

A。塑性和韧性好 B.接近匀质等向体

C。钢材具有可焊性 D。钢材强度高自重轻

2。 钢结构的最大缺点是（ ).

A.造价高，不经济 B。防火性能差

C.耐腐蚀性能差 D。脆性断裂

3。 在其他条件（如荷载、跨度等）相同的情况下，自重最轻的是( )。

A。木结构 B。钢筋混凝土结构

C.钢结构 D。砖石结构

4。 钢材的性能因温度而变化，在负温范围内钢材的塑性和韧性( ）。

A。不变 B。降低

C.升高 D.稍有提高，但变化不大

5。 钢结构表面长期承受某一温度下的辐射热时,需加隔热保护层。该温度是( ）。

A.150°C B。250°C

C.320°C D。600°C

6. 大跨度结构应优先选用钢材，其主要原因是（ ）.

A。钢结构具有良好的装配性

B。钢材的韧性好

C。钢材接近各项均质体，力学计算结果与实际结果最符合

D。钢材的重量与强度之比小于混凝土等其他材料

7. 钢中主要的有害元素是（ ）。

A.硫、磷、碳、锰 B。硫、磷、硅、锰

C.硫、磷、氮、氧 D。硫、磷、硅、碳

《结构力学》课程习题集

一、单项选择题

1. 弯矩图必定发生突变的截面是（ ）。

A. 有集中力作用的截面； B.剪力为零的截面；

C.荷载为零的截面； D.有集中力偶作用的截面。

2. 图示梁中 C 截面的弯矩是（ ）。

12kN . m 4kN 3kN / m

C

4m 4m 2m

A.12kN.m( 下拉 )； B.3kN.m( 上拉 )；

C.8kN.m( 下拉 )； D.11kN.m( 下拉 )。

3. 静定结构有变温时， （ ）。

A. 无变形，无位移，无内力； B.有变形，有位移，有内力；

C.有变形，有位移，无内力； D.无变形，有位移，无内力。

4. 图示桁架 a 杆的内力是（ ）。

A.2P ； B. －2P； ； D. － 3P。

P P P

d

a

3 d

5. 图示桁架，各杆 EA 为常数，除支座链杆外，零杆数为（ ）。

A. 四根； B. 二根； C.一根； D. 零根。

P P

a

P P

l = 6a

6. 图示梁 A 点的竖向位移为（向下为正） （ ）。

A. Pl 3 /( 24 EI ) ； B. Pl 3 /(16 EI ) ； C. 5Pl 3 /( 96EI ) ； D. 5Pl 3 /(48 EI ) 。

第 1 页 共 26 页

P

2 EI EI

l/ 2 A l/ 2

7. 静定结构的内力计算与（ ）。

A.EI 没关； B.EI 相对值相关；

C.EI 绝对值相关； D.E 没关， I 相关。 8. 图示桁架，零杆的数量为： （ ）。

A.5 ； ； ； D.20 。

9. 图示结构的零杆数量为（ ）。

《应用文写作》课程习题集

一、单选题

1. “缺勤三天以上者，扣发当月全勤奖”是属（ ）方面的错误。

A. 逻辑混乱 B. 语义模糊

C. 搭配不当 D. 用语不当

2. 发文字号指的是（ ）。

A. 代字 B. 文件年号

C. 同文本文件的印刷份数编号 D. 制发公文依次编排的顺序代码

3. 下级机关针对工作中出现的具体问题，对吃不准的上级方针、政策、法律、条例等，向上级机关申明情况，请求答复和下达处理意见，应该书写的是（ ）

A. 通知 B. 请示

C. 申请书 D. 意向书

4. 判定文件主送机关的依据是（ ）

A. 机关级别层次的高低 B. 是否对文件承担主办或答复的责任

C. 对文件所负主办或答复责任的大小 D. 与发文机关之间的关系

5. 将本单位法规性、会议性文件等印发给下级机关并提出执行意见及要求的通知称为（ ）

A. 规定 B. 颁发

C. 批转 D. 转发

6. 向不相隶属机关之间请求批准，用文种（ ）

A. 请示 B. 报告

C. 函 D. 申请

7. 政府机关行政公文正本上的成文日期应写为（ ）

A. 一九九九年十月二十八日 B. 1999-10-28

C. 一九九九.十.二十八 D. 1999.10.28

8. 集体或个人对一定时期内的任务预先设想、部署、安排的一种应用文体是（ ）

A. 总结 B. 请示

C. 计划 D. 申请

9. 撰写批复，开头应写明（ ）

A. 所回复请示的标题、日期、发文字号或事由

B. 国家的有关法规

C. 下级机关的有关情况

D. 上级机关的指示

10. 内容较多的章程、条例，其组成部分一般有总则、（ ）和附则。

第 1 页 共 15 页 《财政学》课程习题集

一、单选题

1. 下列属于典型公共产品的是（ ）。

A、公共汽车 B、高等教育 C、国防设施 D、高速公路

2. 社会主义市场经济体制下财政职能包括（ ）。

A、筹集资金、供给资金、调节经济

B、资源配置、调节经济、发展经济

C、资源配置、收入分配、调控经济、公平与效率

D、收入分配、稳定经济、发展经济

3. 消费者的增加不引起生产成本增加的公共产品特征是指（ ）

A、非盈利性 B、非排他性 C、不可分割性 D、非竞争性

4. 财政分配的对象主要是（ ）

A、社会产品 B、社会财富 C、剩余产品 D、国民收入

5. 财政在社会再生产中属于（ ）

A、交换环节 B、生产环节 C、消费环节 D、分配环节

6. 下列指标中，哪一个指标最能切近实际地反映财政活动规模？（ ）

A、财政收入占GDP比重 B、中央收入占GDP比重

C、地方收入占GDP比重 D、财政支出占GDP比重

7. 从经济发达国家的发展历史来看，财政支出规模的发展趋势是（ ）。

A、不断膨胀 B、日渐缩小 C、基本保持不变 D、无规律波动

8. 可以反映出国家政治经济活动的全貌和各个时期政府职能与活动范围变化情况的财政支出分类方法是（ ）

A、按支出具体用途分 B、按国家职能分

C、按最终用途分 D、按支出经济性质分

9. 在下列方法中，最适用于财政支出有关投资性项目的效益评价的是（ ）

A、企业投资财务分析法 B、“成本一效益”分析法

C、最低费用选择法 D、“公共劳务”收费法

精品文档

.

一、单选题

1. （ ）是教育发展的一个高级阶段，也是社会文化发展到较高水平的一个标志。

A．个性化教育B．制度化教育C．学校教育D．终身教育

2. 教育学史上第一次正式提出的有关教育起源的学说是（ ）

A．教育的神话起源说B．教育的生物起源说C．教育的心理起源说D．教育的劳动起源说

3. 教育的劳动起源说的直接理论依据和方法论基础是（ ）

A．达尔文的生物进化学说B．上帝造人C．天降生民D．《劳动在从猿到人的转变过程中的作用》

4. 下列关于教育的劳动起源说主要观点概括错误的是（ ）

A．人类教育起源于其劳动或劳动过程中所产生的需要

B．教育产生于劳动是以人类语言意识的发展为条件的C．教育是永恒不变的范畴

D．教育从产生之日起其职能就是传递劳动过程中形成与积淀的社会生产和生活经验

5. 人类最早的学校出现在（ ）

A．埃及B．中国C．印度D．希腊

6. （ ）的出现意味着人类正规教育制度的诞生，是人类教育文明发展的一个质的飞跃。

A．文字B．有闲者C．学校D．教师

7. 我国学校最早产生于（ ）

A．夏代B．商代C．周代D．春秋战国时期

8. 学校教育具有鲜明的等级性特点，这是（ ）

A．奴隶社会的教育B．封建社会的教育C．资本主义社会的教育D．社会主义社会的教育

9. 我国封建社会教育的主要内容有（ ）

A．四书五经B．七艺C．六艺D．骑士七技

10. 马克思在《资本论》中指出，（ ）不仅是提高社会生产的一种方法，而且是造就全面发展的人的唯一方法。

A．普及教育B．义务教育C．教育机会平等D．教育与生产劳动相结合

11. 教育学的研究对象是（ ）

A．教育现象B．教育事实C．教育规律D．教育问题

12. 在世界教育学史上被认为是“现代教育学之父”的是 （ ）

A．夸美纽斯B．康德C．赫尔巴特D．洛克

13. 被认为是第一本现代教育学著作的是 （ ）

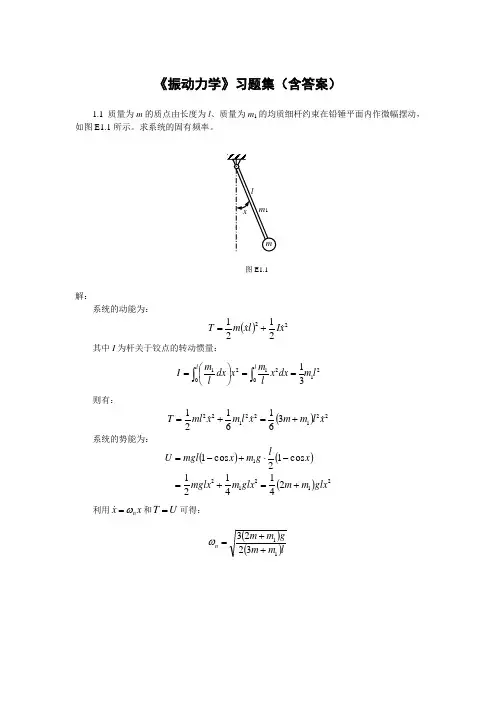
《振动力学》习题集（含答案）

1.1 质量为m的质点由长度为l、质量为m1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。求系统的固有频率。

图E1.1

解：

系统的动能为：

222121xIlxmT

其中I为杆关于铰点的转动惯量：

2102120131lmdxxlmxdxlmIll

则有：

221221223616121xlmmxlmxmlT

系统的势能为：

2121212414121 cos12cos1glxmmglxmmglxxlgmxmglU

利用xxn和UT可得：

lmmgmmn113223

m l

m1 x

1.2 质量为m、半径为R的均质柱体在水平面上作无滑动的微幅滚动，在CA=a的A点系有两根弹性刚度系数为k的水平弹簧，如图E1.2所示。求系统的固有频率。

图E1.2

解：

如图，令为柱体的转角，则系统的动能和势能分别为：

22222243212121mRmRmRITB

222212aRkaRkU

利用n和UT可得：

mkRaRmRaRkn343422

k k A

C a

R



1.3 转动惯量为J的圆盘由三段抗扭刚度分别为1k，2k和3k的轴约束，如图E1.3所示。求系统的固有频率。

图E1.3

解：

系统的动能为：

221JT

2k和3k相当于串联，则有：

332232 , kk

以上两式联立可得：

32233232 , kkkkkk

系统的势能为：

232323212332222121212121kkkkkkkkkkU

利用n和UT可得：

第 1 页 共 9 页 《施工组织》

一、单选题

1. 施工进度检查的主要方法是（ ）。

（A）对比法 （B）纠偏法 （C）调整法 （D）分析法

2. 在双代号时标网络计划中，当某项工作有紧后工作，该工作箭线上的波形线表示（ ）。

（A）该工作的总时差 （B）该工作的自由时差

（C）该工作的持续时间 （D）该工作的拖延时间

3. 当利用S形曲线进行比较时，如果检查日期实际进展点落在计划S形曲线的右侧，则该实际进展点与计划S形曲线的垂直距离表示工程项目（ ）。

（A）实际超额完成的任务量 （B）实际拖欠的任务量

（C）实际进度超前的时间 （D）实际进度拖后的时间

4. 在工程网络计划中，工作的最迟完成时间应为其所有紧后工作（ ）。

（A）最早完成时间的最大值 （B）最迟完成时间的最小值

（C）最迟开始时间的最小值 （D）最早开始时间的最大值

5. CM法的基本指导思想是（ ）。

（A）保证工程项目的建设质量 （B）减少工程项目的投资

（C）避免工程项目发生过多的索赔 （D）缩短工程项目的建设周期

6. 在双代号时标网络计划中，某工作箭线上没有波形线，则该工作（ ）。

（A）为关键工作 （B）总时差为0

（C）自由时差为0 （D）总时差等于自由时差

7. 在工程网络计划的实施过程中，监理工程师检查实际进度时只发现工作M的总时差由原计划的3变成-2天，说明工作M的实际进度（ ）。

（A）拖后3天，影响工期3天 （B）拖后5天，影响工期2天

（C）拖后2天，影响工期2天 （D）拖后5天，影响工期5天

8. 既适用于工作实际进度与计划进度之间的局部比较，又可以用来分析和预测工程项目整体进度状况的方法是（ ）。

（A）S曲线比较法 （B）横道图比较法

第 1 页 共 19 页 《民法学》课程习题集

西南科技大学成人、网络教育学院 版权所有

习题

【说明】：本课程《民法学》（编号为05008）共有单选题,多项选择题,填空题1,名词解释题,论述题,简答题,案例分析题,填空题2,填空题3等多种试题类型，其中，本习题集中有[案例分析题]等试题类型未进入。

一、单选题

1. 某甲户籍在北京，因工作需要长期派往西安，其住所应该视为（）。

A.北京 B.西安 C.北京或西安 D.北京和西安

2. （）依法引起诉讼时效的中止。

A.权利人请求义务人履行义务 B.权利人死亡而其继承人尚未确定

C.义务人同意履行义务 D.权利人提起诉讼

3. 法院宣告失踪的公告期是（）。

A.一年 B.六个月 C.三个月 D.四年

4. 民事权利能力是（）。

A.民事主体享有民事权利和承担民事义务的资格

B.民事主体行使民事权利和履行民事义务的资格

C.民事主体亲自实施民事法律行为的资格

D.民事主体在权利受侵害时请求诉讼保护的资格

5. 以确定的一人或几人为义务主体的民事权利，民法上称为（）。

A.抗辩权 B.绝对权 C.相对权 D.支配权

6. 张某有水蜜桃十余棵，果实成熟时，他生病住院。某天，气象预报将有暴风雨来临。邻居李某请人及时代为抢收，得水蜜桃300斤，运到集镇，售给小贩，得210元，支出抢收工资和运费30元。小贩卖出后400元，依照法律李某应该（）。

A.归还张某400元 B.归还张某210元 C.归还张某180元 D.不返还

7. 依据我国物权法规定，下列财产中不能适用善意取得制度所有权的是（）

A.毒品 B.运动枪支 C.房屋 D.手表

8. 诉讼时效届满后，义务人自愿履行义务的（）。

A.无法律效力，自然债务不应履行

第 2 页 共 19 页 B.债权人有权接受履行，义务人履行义务后，又以诉讼时效届满为由要求返还的，人民法院不予支持

第 1 页 共 26 页 《结构力学》课程习题集

西南科技大学成人、网络教育学院 版权所有

习题

【说明】：本课程《结构力学》（编号为06014）共有单选题,判断题,计算题1,计算题2,计算题3,计算题4,几何构造分析等多种试题类型，其中，本习题集中有[计算题4]等试题类型未进入。

一、单选题

1. 弯矩图肯定发生突变的截面是（ ）。

A.有集中力作用的截面； B.剪力为零的截面；

C.荷载为零的截面； D.有集中力偶作用的截面。

2. 图示梁中C截面的弯矩是（ ）。

4m3kNm/12kNm.2m4m4kNC

A.12kN.m(下拉)； B.3kN.m(上拉)；

C.8kN.m(下拉)； D.11kN.m(下拉)。

3. 静定结构有变温时，（ ）。

A.无变形，无位移，无内力； B.有变形，有位移，有内力；

C.有变形，有位移，无内力； D.无变形，有位移，无内力。

4. 图示桁架a杆的内力是（ ）。

A.2P； B.－2P； C.3P； D.－3P。

adPPP3d

5. 图示桁架，各杆EA为常数，除支座链杆外，零杆数为（ ）。

第 1 页 共 26 页 A.四根； B.二根； C.一根； D.零根。

Pal= aPPP6

6. 图示梁A点的竖向位移为（向下为正）（ ）。

A.)24/(3EIPl； B.)16/(3EIPl； C.)96/(53EIPl； D.)48/(53EIPl。

PEIEIAl/l/222

7. 静定结构的内力计算与（ ）。

A.EI无关； B.EI相对值有关；

C.EI绝对值有关； D.E无关，I有关。

8. 图示桁架，零杆的数目为：（ ）。

A.5； B.10； C.15； D.20。

9. 图示结构的零杆数目为（ ）。

第 1 页 共 26 页 《结构力学》课程习题集

西南科技大学成人、网络教育学院 版权所有

习题

【说明】：本课程《结构力学》（编号为06014）共有单选题,判断题,计算题1,计算题2,计算题3,计算题4,几何构造分析等多种试题类型，其中，本习题集中有[计算题4]等试题类型未进入。

一、单选题

1. 弯矩图肯定发生突变的截面是（ ）。

A.有集中力作用的截面； B.剪力为零的截面；

C.荷载为零的截面； D.有集中力偶作用的截面。

2. 图示梁中C截面的弯矩是（ ）。

4m3kNm/12kNm.2m4m4kNC

A.12kN.m(下拉)； B.3kN.m(上拉)；

C.8kN.m(下拉)； D.11kN.m(下拉)。

3. 静定结构有变温时，（ ）。

A.无变形，无位移，无内力； B.有变形，有位移，有内力；

C.有变形，有位移，无内力； D.无变形，有位移，无内力。

4. 图示桁架a杆的内力是（ ）。

A.2P； B.－2P； C.3P； D.－3P。

adPPP3d

5. 图示桁架，各杆EA为常数，除支座链杆外，零杆数为（ ）。

第 2 页 共 26 页 A.四根； B.二根； C.一根； D.零根。

Pal= aPPP6

6. 图示梁A点的竖向位移为（向下为正）（ ）。

A.)24/(3EIPl； B.)16/(3EIPl； C.)96/(53EIPl； D.)48/(53EIPl。

PEIEIAl/l/222

7. 静定结构的内力计算与（ ）。

A.EI无关； B.EI相对值有关；

C.EI绝对值有关； D.E无关，I有关。

8. 图示桁架，零杆的数目为：（ ）。

A.5； B.10； C.15； D.20。

9. 图示结构的零杆数目为（ ）。

注::作红色标记的为答案

一、选择题

模块1：

1．当时引入多道程序的目的在于（ ）。

A.有利于代码共享，减少主、辅存信息交换量 B．充分利用存储器

C.充分利用CPU，减少CPU等待时间 D．提高实时响应速度

2. 在单处理机计算机系统中，（ ）是并行操作的。

A.程序与程序

B.处理机的操作与通道的操作

C.主程序与子程序

D.用户程序与操作系统程序

3.下面哪一个不是程序在并发系统内执行的特点（ ）。

A.产生死锁的必然性 B.资源分配的动态性

C.程序执行的间断性 D.相互通信的可能性

4．进程和程序的一个本质区别是( D )。

A. 进程分时使用CPU，程序独占CPU

B．进程存储在内存，程序存储在外存

C. 进程在一个文件中，程序在多个文件中

D．进程为动态的，程序为静态的

5．在下列情况( )，系统需要进行进程调度。

A. 某一进程正访问一临界资源

B．某一进程运行时因缺乏资源进入阻塞状态

C．某一进程处于运行状态，而另一进程处于自由状态

D．某一进程正在访问打印机，而另一进程处于就绪状态

6．与设备控制器关系最密切的软件是（ ）。

A.编译程序 B.设备驱动程序 C.存储管理程序 D.处理机管理

7. 若进程P一旦被唤醒就能够投入运行，系统可能（ ）。

A.在抢占调度方式中，P的优先级高于当前运行的进程

B.进程P的优先级最高

C.就绪队列为空队列

D.在抢占调度方式中，P的优先级高于就绪队列中所有的进程

8. 在下列选项中，属于预防死锁的方法是（ ）。

A.剥夺资源法 B.资源分配图法

C.资源随意分配 D.银行家算法

9. 如果要使装入内存的程序，在内存中移动后仍能正常运行，必须要有( )的支持。

第 1 页 共 26 页 《结构力学》课程习题集

一、单选题

1. 弯矩图肯定发生突变的截面是（ ）。

A.有集中力作用的截面； B.剪力为零的截面；

C.荷载为零的截面； D.有集中力偶作用的截面。

2. 图示梁中C截面的弯矩是（ ）。

4m3kNm/12kNm.2m4m4kNC

A.12kN.m(下拉)； B.3kN.m(上拉)；

C.8kN.m(下拉)； D.11kN.m(下拉)。

3. 静定结构有变温时，（ ）。

A.无变形，无位移，无内力； B.有变形，有位移，有内力；

C.有变形，有位移，无内力； D.无变形，有位移，无内力。

4. 图示桁架a杆的内力是（ ）。

A.2P； B.－2P； C.3P； D.－3P。

adPPP3d

5. 图示桁架，各杆EA为常数，除支座链杆外，零杆数为（ ）。

A.四根； B.二根； C.一根； D.零根。

Pal= aPPP6

6. 图示梁A点的竖向位移为（向下为正）（ ）。

A.)24/(3EIPl； B.)16/(3EIPl； C.)96/(53EIPl； D.)48/(53EIPl。

第 2 页 共 26 页 PEIEIAl/l/222

7. 静定结构的内力计算与（ ）。

A.EI无关； B.EI相对值有关；

C.EI绝对值有关； D.E无关，I有关。

8. 图示桁架，零杆的数目为：（ ）。

A.5； B.10； C.15； D.20。

9. 图示结构的零杆数目为（ ）。

A.5； B.6； C.7；

D.8。

10.

图示两结构及其受力状态，它们的内力符合（ ）。

A.弯矩相同，剪力不同； B.弯矩相同，轴力不同；

C.弯矩不同，剪力相同；

第 1 页 共 24 页 《英语B1》课程习题集

西南科技大学成人、网络教育学院 版权所有

习题

【说明】：本课程《英语B1》（编号为01004）共有单选题,写作题,英语完形填空,英语阅读理解,汉译英等多种试题类型，其中，本习题集中有[汉译英,写作题]等试题类型未进入。

一、单选题

1. Can you find out _______ her pen?

A. where Alice had put B. where had Alice put

C. where Alice has put D. where has Alice put

2. The reason we’re so late is ________.

A. for the car breaks down B. due to the car breaking down

C. that the car broke down D. because the car broke down

3. Word has come _____ some guests from Canada will visit our school.

A. what B. that C. whether D. when

4. The two elements _______ water is made are oxygen and hydrogen.

A. that B. which C. of which D. with which

5. The time will come ______ man can fly ______ he likes in the universe.

A. how…where B. when…wherever C. where…where D. what…which

6. Women workers wear hats __ _ their hair gets caught in the machinery.

第 1 页 共 19 页 《投资经济学》课程习题集

西南科技大学成人、网络教育学院 版权所有

习题

【说明】：本课程《投资经济学》（编号为02030）共有单选题,多项选择题,名词解释题,论述题,简答题等多种试题类型，其中，本习题集中有[论述题]等试题类型未进入。

一、单选题

1. 根据我国的经验，在绝大多数情况下，投资增长率上升经济增长率也（ ）

A．上升 B．下降 C．不变 D．波动

2. 缩短投资回收期，全部回收，并实现投资增殖是投资回收的（ ）

A．短期任务 B．长期任务 C．紧迫任务 D．根本任务

3. 国民收入中的积累基金是形成我国固定资产投资的（ ）

A．重要来源 B．主要来源 C．补充来源 D．增加来源

4. 国际上一般认为，一国当年外债还本付息的金额以不超过当年出口创汇的（ ）为宜。

A．10％ B．20－25％ C．30－40％ D．40－50％

5. （ ）不合理是投资膨胀的一个重要因素，它可以导致投资规模膨胀。

A．投资规模 B．投资结构 C．在建投资规模 D．年度投资规模

6. 投资波动是指（ ）的上升或下降。

A．投资数量的变化 B．投资规模的变化

C．投资总量增长率 D．投资主体的变化

7. 投资的三次产业结构是指投资在第一产业、第二产业、第三产业之间的（ ）

A．分配关系 B．数量关系 C．分配及数量比例关系 D．相互关系

8. 固定资产净投资率＝国民收入积累率×（ ）

A．固定资产投资额 B．生产性投资比重

C．非生产性投资额 D．固定资产积累比重

9. 国家一定时期投资结构政策首先必须与国民经济的（ ）保持一致。

A．产业组织政策 B．产业调控政策 C．产业结构政策 D．产业人事政策

10. 工业基地按其性质可划分为专业性和（ ）基地两种。

A．重工性工业 B．轻工性工业 C．农业性工业 D．综合性工业

精品文档

精细；挑选； 《振动力学》习题集（含答案）

1.1 质量为m的质点由长度为l、质量为m1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。求系统的固有频率。

图E1.1

解：

系统的动能为：

222121xIlxmT

其中I为杆关于铰点的转动惯量：

2102120131lmdxxlmxdxlmIll

则有：

221221223616121xlmmxlmxmlT

系统的势能为：

2121212414121 cos12cos1glxmmglxmmglxxlgmxmglU

利用xxn和UT可得：

lmmgmmn113223

m l

m1 x 精品文档

精细；挑选； 1.2 质量为m、半径为R的均质柱体在水平面上作无滑动的微幅滚动，在CA=a的A点系有两根弹性刚度系数为k的水平弹簧，如图E1.2所示。求系统的固有频率。

图E1.2

解：

如图，令为柱体的转角，则系统的动能和势能分别为：

22222243212121mRmRmRITB

222212aRkaRkU

利用n和UT可得：

mkRaRmRaRkn343422

k k A

C a

R

 精品文档

精细；挑选； 1.3 转动惯量为J的圆盘由三段抗扭刚度分别为1k，2k和3k的轴约束，如图E1.3所示。求系统的固有频率。

图E1.3

解：

系统的动能为：

221JT

2k和3k相当于串联，则有：

332232 , kk

以上两式联立可得：

32233232 , kkkkkk

第 1 页 共 26 页 《结构力学》课程习题集

西南科技大学成人、网络教育学院 版权所有

习题

【说明】：本课程《结构力学》（编号为06014）共有单选题,判断题,计算题1,计算题2,计算题3,计算题4,几何构造分析等多种试题类型，其中，本习题集中有[计算题4]等试题类型未进入。

一、单选题

1. 弯矩图肯定发生突变的截面是（ ）。

A.有集中力作用的截面； B.剪力为零的截面；

C.荷载为零的截面； D.有集中力偶作用的截面。

2. 图示梁中C截面的弯矩是（ ）。

4m3kNm/12kNm.2m4m4kNC

A.12kN.m(下拉)； B.3kN.m(上拉)；

C.8kN.m(下拉)； D.11kN.m(下拉)。

3. 静定结构有变温时，（ ）。

A.无变形，无位移，无内力； B.有变形，有位移，有内力；

C.有变形，有位移，无内力； D.无变形，有位移，无内力。

4. 图示桁架a杆的内力是（ ）。

A.2P； B.－2P； C.3P； D.－3P。

adPPP3d

5. 图示桁架，各杆EA为常数，除支座链杆外，零杆数为（ ）。

第 2 页 共 26 页 A.四根； B.二根； C.一根； D.零根。

Pal= aPPP6

6. 图示梁A点的竖向位移为（向下为正）（ ）。

A.)24/(3EIPl； B.)16/(3EIPl； C.)96/(53EIPl； D.)48/(53EIPl。

PEIEIAl/l/222

7. 静定结构的内力计算与（ ）。

A.EI无关； B.EI相对值有关；

C.EI绝对值有关； D.E无关，I有关。

8. 图示桁架，零杆的数目为：（ ）。

A.5； B.10； C.15； D.20。

9. 图示结构的零杆数目为（ ）。