DH算法C语言实现

大连海事大学

人工智能基础课程实验报告

（2011-2012学年第一学期）

王浩算法

班 级：

学 号：

姓 名：

指导老师：

2011年 12月 7日

王浩算法的实现

一．实验内容

实现命题逻辑框架内的王浩算法。

1.将命题逻辑中的王浩算法推广至下述命题语言的情形之下：

(1).命题变量符号：p1,p2,p3,……

(2).逻辑连接符：﹁，︿，﹀，->，……

(3).间隔符：（，）……

2.在上述1中所定义的命题语言中实现王浩算法。

二．实验目的

熟练掌握命题逻辑中的王浩算法。

三．实验要求

1.实验题目必须由个人独立完成，允许自行参考相关文献资料，但严禁同学间相互拷贝和抄袭程序以及文档资料。实验结束后一周内上交实验报告和实验文档资料。

2.提交的文档资料包括设计文档和程序源代码。设计文档和程序源代码以书面文档方式提供（用A4纸打印），并提交电子文档备查。

四．数据结构

给定公式，例如：(p1->(q1->r1))->((p1->q1)->(p1->r1))

函数inite主要作用是负责将符号初始化成树的结构。

函数clone复制一棵完全相同的符号树。

函数restruct查找所有&，|， <->等符号，并将其拆分成新形式：！，->符号。

函数searching王浩算法的主要函数。

函数show和output:显示符号串和推理过程。

五．实验结果

公式正确

公式错误

六．实验总结

公式不是恒真的时候，不一定是恒假的，王浩算法实质上是一个反向推理过程，它把给定的公式化成合取范式，然后通过判断每个子句是否恒真的来判定给定的公式是否是恒真的。所以，王浩算法不能说明公式恒假，只能说明不是恒真的。程序中的move函数十分重要，有的时候可能出现程序不能运行的情况所以，写这个函数时候是非常谨慎小心的。

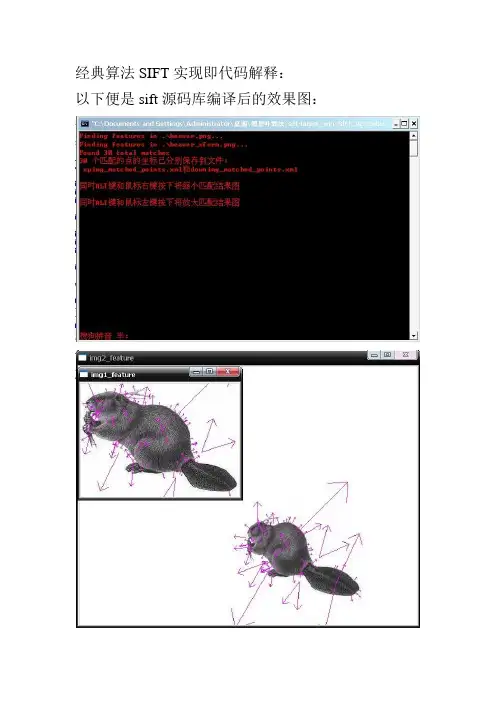
经典算法SIFT实现即代码解释：

以下便是sift源码库编译后的效果图：

为了给有兴趣实现sift算法的朋友提供个参考，特整理此文如下。要了解什么是sift算法，请参考：九、图像特征提取与匹配之SIFT算法。ok，咱们下面，就来利用Rob Hess维护的sift 库来实现sift算法：

首先，请下载Rob Hess维护的sift 库：

/hess/code/sift/

下载Rob Hess的这个压缩包后，如果直接解压缩，直接编译，那么会出现下面的错误提示：

编译提示:error C1083: Cannot open include file: 'cxcore.h': No such file or

directory，找不到这个头文件。

这个错误，是因为你还没有安装opencv，因为：cxcore.h和cv.h是开源的OPEN

CV头文件,不是VC++的默认安装文件,所以你还得下载OpenCV并进行安装。然后，可以在OpenCV文件夹下找到你所需要的头文件了。

据网友称，截止2010年4月4日，还没有在VC6.0下成功使用opencv2.0的案例。所以，如果你是VC6.0的用户请下载opencv1.0版本。vs的话，opencv2.0,1.0任意下载。

以下，咱们就以vc6.0为平台举例，下载并安装opencv1.0版本、gsl等。当然，你也可以用vs编译，同样下载opencv（具体版本不受限制）、gsl等。

请按以下步骤操作：

一、下载opencv1.0

/projects/opencvlibrary/files/opencv-win/1.0/OpenCV_1.0.exe/download

二、安装opencv1.0，配置Windows环境变量

1、安装注意：假如你是将OpenCV安装到C:/Program Files/OpenCV（如果你安装的时候选择不是安装在C盘，则下面所有对应的C盘都改为你所安装在的那个“X盘”，即可），在安装时选择"将/OpenCV/bin加入系统变量"，打上“勾”。（Add/OpenCV/bin to the systerm PATH。这一步确认选上了之后，下面的检查环境变量的步骤，便可免去）

实验五 查找的实现

一、 实验目的

1．通过实验掌握查找的基本概念；

2．掌握顺序查找算法与实现；

3．掌握折半查找算法与实现。

二、 实验要求

1． 认真阅读和掌握本实验的参考程序。

2． 保存程序的运行结果，并结合程序进行分析。

三、 实验内容

1、建立一个线性表，对表中数据元素存放的先后次序没有任何要求。输入待查数据元素的关键字进行查找。为了简化算法，数据元素只含一个整型关键字字段，数据元素的其余数据部分忽略不考虑。建议采用前哨的作用，以提高查找效率。

2、查找表的存储结构为有序表，输入待查数据元素的关键字利用折半查找方法进行查找。此程序中要求对整型量关键字数据的输入按从小到大排序输入。

一、顺序查找

顺序查找代码：

#include"stdio.h"

#include"stdlib.h"

typedef struct node{

int key;

}keynode;

typedef struct Node{

keynode r[50];

int length;

}list,*sqlist;

int Createsqlist(sqlist s)

{

int i;

printf("请输入您要输入的数据的个数:\n");

scanf("%d",&(s->length));

printf("请输入您想输入的%d个数据;\n\n",s->length);

for(i=0;ilength;i++)

scanf("%d",&(s->r[i].key));

printf("\n");

printf("您所输入的数据为:\n\n"); for(i=0;ilength;i++)

printf("%-5d",s->r[i].key);

printf("\n\n");

return 1;

}

int searchsqlist(sqlist s,int k)

{

int i=0;

#include

#include

#include

# define m 50

int no1; //进程数

int no2; //资源数

int r;

int allocation[m][m],need[m][m],available[m],max[m][m];

char name1[m],name2[m]; //定义全局变量

void main()

{

void check();

void print();

int i,j,p=0,q=0;

char c;

int request[m],allocation1[m][m],need1[m][m],available1[m];

printf("**********************************************\n");

printf("* 银行家算法的设计与实现 *\n");

printf("**********************************************\n");

printf("请输入进程总数:\n");

scanf("%d",&no1);

printf("请输入资源种类数: \n");

scanf("%d",&no2);

printf("请输入Max矩阵:\n");

for(i=0;i

for(j=0;j

scanf("%d",&max[i][j]); //输入已知进程最大资源需求量

printf("请输入Allocation矩阵:\n");

for(i=0;i

for(j=0;j

scanf("%d",&allocation[i][j]); //输入已知的进程已分配的资源数

for(i=0;i

for(j=0;j

need[i][j]=max[i][j]-allocation[i][j]; //根据输入的两个数组计

龙源期刊网

国密SM2密码算法的C语言实现

作者：邢维哲

来源：《中国新通信》2017年第18期

【摘要】 N.Koblitz和ler在1985年各自独立地提出将椭圆曲线应用于公钥密码系统。SM2椭圆曲线密码算法是国家密码管理局批准的一组算法，在电力自动化通讯中得到了广泛应用。本文介绍了SM2椭圆曲线公钥密码算法和加密解密算法中一部分过程的C语言实现。

【关键词】 椭圆曲线 SM2 密码算法 公钥 加密解密

Implementation of Public Key Cryptographic Algorithm SM2 based on C language

XINGWEIZHE （1. XINGWEIZHE COLLEGE OF ENGINEERING， PEKING UNIVERSITY，BEIJING，100871）

Abstract： Applying elliptic curves on public key cryptosystem was put forward independently

by Koblitz and ler in 1985. Public Key Cryptographic Algorithm SM2 is Public Key

Cryptographic Algorithm SM2， as the Chinese national cryptographic standard， is widely used in

communications of automation system. This paper introduces elliptic curve cryptosystem and gives an

implementation based on C language.

Key word： elliptic curve cryptosystem； Public Key Cryptographic Algorithm SM2； elliptic

SSTF算法C语言实现，已通过调试！

#include

#include

#include

void main()

{

int a[100],b[100],c[100];

int i,n,k,h,t,p,l,sum;

printf("请输入总磁道数：\n");

scanf("%d",&n);

printf("请输入磁道:\n");

for(i=0;i

scanf("%d",&a[i]);

for(i=0;i

for(k=i+1;k

if(a[i]>a[k])

{

h=a[i];

a[i]=a[k];

a[k]=h;

}

printf("排序后的数组为：\n");

for(i=0;i

printf("%d\n",a[i]);

printf("请输入当前磁道数：\n");

scanf("%d",&p);

for(i=0;i

if(a[i]<=p && a[i+1]>=p)

{

printf("在第%d个位置插入\n",i);

break;

}

t=0;//输出数组下标

l=i+1;

while(i>0 || l<=n)

{

if((p-a[i])<(a[l]-p))

{

c[t]=p-a[i];

b[t++]=a[i];

p=a[i];

i--; }

else

{

c[t]=a[l]-p;

b[t++]=a[l];

p=a[l];

l++;

}

}

i--;

if(i==0)

while(l<=n)

b[t++]=a[l++];

else

while(i>=0)

b[t++]=a[i--];

printf("SSTF磁头移动顺序和相应的移动距离为：\n");

for(k=0;k

printf("%d %d\n",b[k],c[k]);

第１１卷第４期　２Ｏｌ２年４月　软件导刊　Ｓｏｆｔｗａｒｅ　Ｇｕｉｄｅ　Ｖｏｌ　ｌ１Ｎ０．４　ＡＤｒ．２Ｏ１２　

基于Ｃ＋＋语言的Ｇ　ＲＡＰＰＡ算法实现　

黄　敏，汪　超　

（中南民族大学生物医学工程学院，湖北武汉４３００７４）　

摘　要：对并行磁共振成像图像重建算法的工程实现进行了研究，采用Ｃ　语言创建了ＧＲＡＰＰＡ算法类。用成员　

函数的形式对ＧＲＡＰＰＡ算法中的关键步骤进行了封装，完成了重建系数的求解、拟合缺失的相位编码行、傅立叶重　建等功能。调用ＧＲＡＰＰＡ类可以快速地重建出高质量的ＭＲＩ图像，在图像重建领域为国内开发具有并行成像功能　的超导ＭＲＩ扫描仪提供了参考。　关键词：并行磁共振成像；ＧＲＡＰＰＡ算法；图像重建；数据拟合　

中图分类号：ＴＰ３１２　文献标识码：Ａ　文章编号：１６７２—７８００（２Ｏ１２）００４—００５６—０３　

磁共振成像（ＭＲＩ）具有无射线危害、软组织分辨率　

高、多方位成像的优点，是当今重要的医学成像技术之一。　

提高ＭＲＩ成像速度可以克服病人由于受检时间过长带来　

的不自主运动伪影影响，并可提高ＭＲＩ扫描仪的检查效　

率，提升医院的经济效益和服务病人的能力。以前提高　

ＭＲＩ成像速度主要依赖各种快速成像序列（如ＥＰＩ，Ｓｐｉｒａｌ　

等），但快速成像序列设计复杂，对梯度切换速率等要求较　

高，在提升ＭＲＩ成像速度方面已达到瓶颈。多线圈多通　

道并行采集技术克服了这种限制，成为近年来国外ＭＲ扫　

描仪厂家提升ＭＲＩ成像速度的新途径。目前，国内高场　

ＭＲＩ扫描仪的研发刚刚起步，对并行成像等功能也有了　

相应的需求。本文介绍了ＧＲＡＰＰＡ算法的基本原理，分　

析了采用Ｃ　语言创建了ＧＲＡＰＰＡ类的关键步骤，并在　

ＶＣ环境下调用该类实现了并行ＭＲＩ的图像重建。　

１　算法原理　

ＧＲＡＰＰＡ算法，全称为广义自动校准部分并行采集　

（Ｇｅｎｅｒａｌｉｚｅｄ　Ａｕｔｏｃａｌｉｂｒａｔｉｎｇ　Ｐａｒｔｉａｌｌｙ　Ｐａｒａｌｌｅｌ　Ａｃｑｕｉｓｉ—　ｔｉｏｎｓ），是一种基于频率域的并行ＭＲＩ重建算法。主要是　

龙源期刊网

常见密码算法分析及C语言实现

作者：郭萌萌

来源：《电脑知识与技术》2014年第35期

摘要：计算机的高速发展使信息安全面临着巨大的挑战。在计算机应用中要想确保信息安全，就必须要对密码算法进行合理应用。基于此，该文对密码算法进行了分析，并将密码算法的C语言实现进行了简单介绍和说明。

关键词：密码算法；C语言；随机数

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2014）35-8371-02

密码学具有悠久的历史，但同时也是一门崭新的课程，人们从来没有停止对密码学的研究。现代密码学理论十分复杂，现代密码学的发展需要现代数学和计计算机科学的支持。进入二十一世纪后，人们已经计入到了计算机时代，如何确保计算机中的信息在存储、传输、交换中的安全性是一个值得探讨的话题。

1 计算机密码学发展历史

密码学在人类发展历史中有着不可代替的作用，从2000多年前古埃及发生战争，密码就出现在了人类中，起初的密码就是简单的记录符号。随着时代的推移，在两次世界大战中人们开始意识到密码的重要性。

密码学真正成为一门学科是在二十世纪七十年代。美国国家标准局在1977年对DES（数据加密标准）进行了公布，并批准在非商业和非机密单位中对其进行应用，从此解开了密码的神秘面纱。早在1975年“密码学的新方向”一文中就提出了适用于网络的公钥密码理念，这也是人们对公钥密码进行研究的开始。受“密码学的新方向”影响，各种公钥密码体制被提了出来，在众多体制中，RSA成为了密码学研究的一个里程碑。不夸张的说，“没有公钥密码的研究也不会有近代密码学”。现代社会是一个信息高速发展的社会，随着科技的发展，密码学也取得了巨大进步，而且也成为了许多学科发展的基础。

2 常见的密码算法

2.1 密码系统保密机理

龙源期刊网

数据拟合算法分析及Ｃ语言实现

作者：邵慧莹

来源：《硅谷》2009年第18期

[摘要]数据拟合在很多地方都有应用,主要用来处理实验或观测的原始离散数据。通过拟合可以更好的分析和解释数据。在引用前人的算法基础上,采用正交多项式最小二乘法进行曲线拟合,通过实验对算法进行了分析,并给出了C语言实现的代码。

[关键词]数据拟合 正交多项式 最小二乘法 算法分析 代码实现

中图分类号:TP301文献标识码:A文章编号:1671-7597(2009)0920093-02

在科学实验和工程实践中,会产生很多原始数据,为更好地分析和解释这些数据,通常用曲线来进行拟合。借助于数据拟合可以很好地获取数据的整体特征,但拟合的方式、次数都将影响最终的效果。一般来说,拟合效果是通过误差来判断的。下文先是介绍了拟合算法,随后根据实验数据,从误差角度进行了分析。

一、算法分析

曲线拟合是数值逼近的一种方法。它用带有参数的简单函数逼近待定函数,并根据函数在观察点的取值状况确定参数。给定一组观测值,(xi,yi)(I=0,1,…n),选取一组简单函数φk(x)(k=0,1,…n)作为基函数,通过确定拟合模型φ(x)=μkφk(x)的待定参数μk,使φ(x)与观测值(xi,yi)在总体上尽可能接近。这种确定φ(x)的方法称为离散数据的曲线拟合。

离散数据的曲线拟合需要解决两个问题:

1.合模型的选取。在线性模型中,拟合函数是一些基函数的线性组合,选取一组适当的基函数是决定拟合效果好坏的关键因素。一般来说,需要对问题进行仔细的分析,根据问题本身的性质决定基函数的形式。如果没有与问题有关的背景信息,则可以通过分析观测数据的分步规律,选择拟合模型的基函数。通常基函数可以取多项式函数、三角函数、指数函数和样条函数等。本文主要采用多项式函数。 龙源期刊网

RC4加密算法C语言实现

代码文件名

RC4.cpp Encrypt.h（代码详见后文）

备注：将以上两个文件放在相同的路径（建议不要放在中文路径下）编译执行！

编译环境

Microsoft Visual C++ 6.0

C-Free 5.0

代码解释

RC4加密算法是大名鼎鼎的RSA三人组中的头号人物Ron Rivest在1987年设计的密钥长度可变的流加密算法簇。之所以称其为簇，是由于其核心部分的S-box长度可为任意，但一般为256字节。该算法的速度可以达到DES加密的10倍左右。

RC4算法的原理很简单，包括初始化算法和伪随机子密码生成算法两大部分。假设S-box长度和密钥长度均为为n。先来看看算法的初始化部分（用类C伪代码表示）：

for (i=0; i

s=i;

j=0;

for (i=0; i

{

j=(j+s+k)%256;

swap(s, s[j]);

}

在初始化的过程中，密钥的主要功能是将S-box搅乱，i确保S-box的每个元素都得到处理，j保证S-box的搅乱是随机的。而不同的S-box在经过伪随机子密码生成算法的处理后可以得到不同的子密钥序列，并且，该序列是随机的：

i=j=0;

while (明文未结束)

{

++i%=n;

j=(j+s)%n; swap(s, s[j]);

sub_k=s((s+s[j])%n);

}

得到的子密码sub_k用以和明文进行xor运算，得到密文，解密过程也完全相同。

RC4加密算法在C++中的实现：

RC4函数（加密/解密）：其实RC4只有加密，将密文再加密一次，就是解密了。

GetKey函数：随机字符串产生器。

ByteToHex函数：把字节码转为十六进制码，一个字节两个十六进制。十六进制字符串非常适合在HTTP中传输。

HexToByte函数：把十六进制字符串，转为字节码。。

FFT的C语言算法实现

程序如下：

/************FFT***********/

#include

#include

#include

#define N 1000

typedef struct

{

double real;

double img;

}complex;

void fft(); /*快速傅里叶变换*/

void ifft(); /*快速傅里叶逆变换*/

void initW();

void change();

void add(complex ,complex ,complex *); /*复数加法*/

void mul(complex ,complex ,complex *); /*复数乘法*/

void sub(complex ,complex ,complex *); /*复数减法*/ void divi(complex ,complex ,complex *);/*复数除法*/

void output(); /*输出结果*/

complex x[N], *W;/*输出序列的值*/

int size_x=0;/*输入序列的长度，只限2的N次方*/

double PI;

int main()

{

int i,method;

system("cls");

PI=atan(1)*4;

printf("Please input the size of x:\n");

/*输入序列的长度*/

scanf("%d",&size_x);

printf("Please input the data in x[N]:(such as:5

PID算法的C语⾔实现

1.根据我控制算法类⽂章中关于PID的理论的⼀些描述，同时也根据⽹络上⼀些其他的PID⽂章，以及⾃⼰最近⼀个项⽬的实践后，总结了⼏套基于C语⾔的PID算

法，由于⽹络中很少有⼈进⾏分享完整的PID算法实现，我这⾥分享下。

（1）头⽂件，定义pid的结构体，类的概念，包含pid的属性和⽅法

#ifndef __PID_H_

#define __PID_H_

#include

typedef struct _pid

{

int16_t set_value; // 给定值，rin(k)

int16_t actual_value; // 实际值，反馈值，rout(k)

int16_t err; // 偏差值，rin(k) - rout(k)

int16_t err_last; // 上⼀次偏差值，rin(k - 1) - rout(k - 1)

int16_t err_last_last; // 上⼀次上⼀次的偏差值，rin(k - 2) - rout(k - 2)

float kp; // ⽐例系数

float ki; // 积分系数

float kd; // 微分系数

float uk; // pid公式运算结果值

float incremental_value; // 增量值

float integral_value; // 积分值

float umax; // uk的上限值，抗积分饱和⽤

float umin; // uk的下限值，抗积分饱和⽤

int16_t err_up_value; // 偏差上限值，积分分离⽤

int16_t ki_k; // 积分的再次乘机系数，积分分离⽤

float out_value; //

float(*position_type)(struct _pid *ppid); // 位置型PID算法，⽆积分分离、⽆抗积分饱和

float(*incremental_type)(struct _pid *ppid); // 增量型PID算法

/*此算法为FFT相位差算法的C语言实现，经验证可用（网上有很多此类程序无法运行）；前半部分为FFT算法的子程序，也可用作其它用途*/

#include

#include

#include

typedef struct {double real,imag;} complex;

complex cexp(complex a)

{

complex z;

z.real=exp(a.real)*cos(a.imag);

z.imag=exp(a.real)*sin(a.imag);

return(z);

}

void mcmpfft(complex x[],int n,int isign)

{

complex t,z,ce;

double pisign;

int mr,m,l,j,i,nn;

for(i=1;i<=16;i++) /*n must be power of 2 */

{

nn=(int)pow(2,i);

if(n==nn) break;

}

if(i>16)

{

printf(" N is not a power of 2 ! \n");

return;

}

z.real=0.0;

pisign=4*isign*atan(1.); /*pisign的值为+180度或-180度*/

mr=0;

for(m=1;m

{l=n;

while(mr+l>=n) l=l/2;

mr=mr%l+l;

if(mr<=m) continue;

t.real=x[m].real;t.imag=x[m].imag;

C语言实现PID算法

#include

struct _pid {

int pv; /*integer that contains the process value*/

int sp; /*integer that contains the set point*/

float integral;

float pgain;

float igain;

float dgain;

int deadband;

int last_error;

};

struct _pid warm,*pid;

int process_point, set_point,dead_band;

float p_gain, i_gain, d_gain, integral_val,new_integ;;

/*------------------------------------------------------------------------

pid_init

DESCRIPTION This function initializes the pointers in the _pid structure

to the process variable and the setpoint. *pv and *sp are

integer pointers.

------------------------------------------------------------------------*/

void pid_init(struct _pid *warm, int process_point, int set_point)

{

struct _pid *pid;

pid = warm;

Dijkstra算法 C语言实现 2008-08-26 12:07

#include

#include

#define INFINITY 1000000000 //最大距离

#define MAX_NODES 1024 //最大节点数

int n,dist[MAX_NODES][MAX_NODES]; //dist[i][j]表示从 i 到 j 的距离

void shortest_path(int s, int t, int path[])

{

struct state

{

int predecessor; //前驱节点

int length; //到起始点的距离

enum {permanent, tentative} label;

}state[MAX_NODES];

int i,k,min;

struct state * p;

for(p=&state[0]; p<&state[n]; p++)

{

p->predecessor = -1;

p->length = INFINITY;

p->label = tentative;

}

state[t].length = 0;

state[t].label = permanent;

k = t; //k 是当前工作节点

do

{

for(i=0; i

{

if(dist[k][i]!=0 && state[i].label==tentative)

龙源期刊网

DES算法的C语言实现

作者：王颖,石云峰

来源：《电脑知识与技术》2011年第10期

摘要：对称密码算法又称单钥或私钥或传统密码体制，其发方和收方使用相同的密钥，即加密密钥和解密密钥是相同的。在众多的常规密码中影响最大的是DES密码。该文介绍DES算法的C语言实现。

关键词：DES；密钥；初始置换；逆置换

中图分类号：TP311文献标识码：A文章编号：1009-3044(2011)10-2295-02

The Realization of DES Algorithm with C Language

WANG Ying, SHI Yun-feng

(College of the Information Technology, Dalian Ocean University, Dalian 116023, China)

Abstract: Symmetric key cryptography, also called single key or private key or traditional

cryptography, whose sender and receiver use the same key, in the other word, the encrypt key is just

the decipher key. DES is the representative of the symmetric key cryptography. This paper describes

DES algorithm using C language.

Key words: DES;key; initial permutation; inverse permutation