第二章波粒二象性 第五节 德布罗意波 学案

第五节 德布罗意波对应学生用书页码1．任何一个实物粒子都和一个波相对应，这种波称为德布罗意波，也称为物质波。

2．实物粒子的物质波波长与其动量之间的关系为λ＝h p。

3．电子束在晶体的晶格上会发生衍射。

电子束在单晶MnO 3上和在多晶Au 上都能产生衍射图样，且衍射图样都跟光通过小孔的衍射图样相同，说明电子与光有相似之处，都具有波粒二象性，即电子具有波动性。

4．总的来讲，波粒二象性是包括光子在内的一切微观粒子的共同特征，和光子一样，对微观粒子运动状态的最准确的描述是概率波。

5．当原子处于稳定状态时，电子会形成一个稳定的概率分布，由于历史上的原因，人们常用一些小圆点来表示这种概率分布，概率大的地方小圆点密一些，概率小的地方小圆点疏一些，这样的概率分布图称为电子云。

6．如果用Δx 表示微观粒子位置的不确定性，用Δp 表示微观粒子动量的不确定性，则两者之间的关系为Δx Δp ≥h4π，此式称为微观粒子的不确定性关系。

对应学生用书页码1.任何一个实物粒子都和一个波相对应。

2．德布罗意波假说的提出背景德布罗意认识到人们讨论光时过分地强调了波动性，忽略了粒子性，同样，在讨论实物粒子时，人们只讨论粒子性，忽略了波动性，于是把光的波粒二象性推广到了实物粒子，用类比的方法，从理论上预言了物质波的存在。

3．德布罗意波(1)定义：实物粒子所对应的波称为德布罗意波，也称为物质波。

(2)德布罗意波长与动量的关系：λ＝h p其中λ是德布罗意波长，h 是普朗克常量，p 是相应的实物粒子的动量。

4．德布罗意波的实验验证(1)实验探究思路：干涉、衍射是波特有的表现，如果实物粒子具有波动性，则在一定条件下，也应该发生衍射现象。

(2)实验验证：1927年戴维孙和G.P.汤姆生分别利用晶体进行了电子束衍射实验，从而证实了电子的波动性。

说明电子具有波粒二象性。

不仅电子，后来通过实验还陆续证实了质子、中子以及原子、分子的波动性，对于这些粒子，ν＝εh ，λ＝hp同样成立。

第五节德布罗意波[学习目标］１.知道实物粒子具有波动性.2．知道光波和物质波都是概率波．３．理解德布罗意波，会解释相关现象．(重点、难点）4。

知道电子云,了解“不确定性关系”的具体含义．一、德布罗意波假说及电子衍射1.德布罗意波：任何一个实物粒子都和一个波相对应，这种波后来被称为德布罗意波,也称为物质波．2．波长与动量关系：λ＝错误!未定义书签。

．3．电子衍射：电子束在晶体上反射可能发生衍射.二、电子云和不确定性关系1.电子云:原子中的电子在原子核的周围运动,在空间各点出现的概率是不同的,当原子处于稳定状态时，电子会形成一个稳定的概率分布．由于历史上的原因，人们常用一些小圆点来表示这种概率分布，概率大的地方小圆点密一些,概率小的地方小圆点疏一些,这样的概率分布图称为电子云.2.不确定性关系：用Δx表示微观粒子位置的不确定性，用Δp表示微观粒子动量的不确定性，则两者之间的关系为ΔｘΔp≥错误!,即不确定性关系．它意味着微观粒子的坐标和动量不可能同时完全精确地确定．1.正误判断(正确的打“√”,错误的打“×”)（1)电子衍射的发现证明了德布罗意波假说．ﻩ(√)(2）包括光子在内的一切微观粒子都具有波粒二象性，而实物粒子不具有波粒二象性．ﻩﻩ(×)（３)在讨论微观粒子的运动时,只能给出微观粒子在空间各点出现的概率分布，无法给出微观粒子运行的轨迹．(√)ﻬ（4）微观粒子运动的状态,不能像宏观物体的运动那样通过确定的轨迹来描述,而是只能通过概率波作统计性的描述. (√）(5）改进测量技术,不确定性关系可以确定,微观粒子的坐标和动量可以同时确定．ﻩ2．在历史上,最早证明了德布罗意波存在的实验是( )A．弱光衍射实验B.电子束在晶体上的衍射实验C．弱光干涉实验D．以上都不正确B[由课本知识可知，最早证明德布罗意波假说的是电子束在晶体上的衍射实验,选项B正确.］３.关于电子云,下列说法正确的是( ）A．电子云是真实存在的实体B．电子云周围的小黑圆点就是电子的真实位置C.电子云上的小黑圆点表示的是电子的概率分布D．电子云说明电子在绕原子核运动时有固定轨道C ［由电子云的定义我们知道，电子云是一种稳定的概率分布,人们常用小黑圆点表示这种概率分布,小黑圆点的密疏代表电子在这一位置出现的概率大小,故选项Ｃ正确．］1.对物质波的理解（1）任何物体,小到电子、质子,大到行星、太阳，都存在波动性，我们之所以观察不到宏观物体的波动性，是因为宏观物体对应的波长太小的缘故.(２)粒子在空间各处出现的几率受统计规律支配,不要以宏观观点中的波来理解德布罗意波．（3）德布罗意假说是光子的波粒二象性的一种推广,使之包括了所有的物质粒子，即光子与实物粒子都具有粒子性,又都具有波动性，与光子对应的波是电磁波,与实物粒子对应的波是物质波.ﻬ2．计算物质波波长的方法(1）根据已知条件,写出宏观物体或微观粒子动量的表达式p＝mｖ.(2)根据波长公式λ＝＼f(h,ｐ)求解．(3)注意区分光子和微观粒子的能量和动量的不同表达式．如光子的能量ε=hν，动量p=错误!;微观粒子的动能E k=错误!未定义书签。

第五节 德布罗意波课前预习情景导入光的波粒二象性理论告诉我们：光既是电磁波，又是光子,这表明场和实物并非泾渭分明。

那么，电子、质子、中子,甚至原子、分子、物体是否也具有波动性？图2—5—1德布罗意简答：1924年，德布罗意推想：自然在许多方面是对称的，“波粒共存的观念可以推广到所有粒子”。

既然光具有波粒二象性，则实物粒子或许也有这种二象性，在这样的推想下，德布罗意提出假设：实物粒子和光一样，也具有波粒二象性.知识预览⎪⎪⎪⎩⎪⎪⎪⎨⎧≥∆∆=πλ4::::h P x p h 不确定关系电子的衍射和电子云证实物质波的波长一种波相对应任何一个实物粒子都和物质波波意罗布德尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

学 习 目 标知 识 脉 络1.知道实物粒子具有波动性．2．知道光波和物质波都是概率波．3．理解德布罗意波，会解释相关现象．(重点、难点)4．知道电子云，了解“不确定性关系”的具体含义.德布罗意波假说及电子衍射[先填空]1．德布罗意波：任何一个实物粒子都和一个波相对应，这种波后来被称为德布罗意波，也称为物质波．2．波长与动量关系：λ＝.3．电子衍射：电子束在晶体上反射可能发生衍射．[再判断]1．电子衍射的发现证明了德布罗意波假说．(√)2．电子不仅会发生衍射，还会发生干涉．(√)3．包括光子在内的一切微观粒子都具有波粒二象性，而实物粒子不具有波粒二象性．(×)[后思考]既然德布罗意提出了物质波的概念，为什么我们生活中却体会不到？【提示】平时所见的宏观物体的质量比微观粒子的质量大得多，运动的动量很大，由λ＝可知，它们对应的物质波波长很小，因此，无法观察到它们的波动性．1．任何物体，小到电子、质子，大到行星、太阳都存在波动性，我们之所以观察不到宏观物体的波动性，是因为宏观物体对应的波长太小的缘故．2．德布罗意波是一种概率波，粒子在空间各处出现的概率受波动规律支配，不要以宏观观点中的波来理解德布罗意波．3．德布罗意假说是光子的波粒二象性的一种推广，使之包括了所有的物质粒子，即光子与实物粒子都具有粒子性，又都具有波动性，与光子对应的波是电磁波，与实物粒子对应的波是物质波．1．下列说法中正确的是( )【导学号：55272058】A．物质波属于机械波B．只有像电子、质子、中子这样的微观粒子才具有波动性C．德布罗意认为，任何一个运动着的物体，小到电子、质子，大到行星、太阳，都有一种波和它对应，这种波叫物质波D．宏观物体运动时，看不到它的衍射或干涉现象，因此宏观物体运动时不具有波动性【解析】物质波是一切运动着的物体所具有的波，与机械波性质不同，A错误；宏观物体也具有波动性，只是干涉、衍射现象不明显，看不出来，B、D错误；德布罗意认为，任何一个运动着的物体，小到电子、质子，大到行星、太阳，都有一种波和它对应，这种波叫物质波，C正确．【答案】C2．如果一个中子和一个质量为10 g的子弹都以103 m/s的速度运动，则它们的德布罗意波的波长分别是多长？(中子的质量为1.67×10－27 kg)【解析】中子的动量为p1＝m1v，子弹的动量为p2＝m2v，据λ＝知中子和子弹的德布罗意波的波长分别为λ1＝，λ2＝hp2联立以上各式解得：λ1＝，λ2＝hm2v将m1＝1.67×10－27 kg，v＝1×103 m/s，h＝6.63×10－34 J·s，m2＝1.0×10－2 kg代入上面两式可解得λ1＝4.0×10－10 m，λ2＝6.63×10－35 m.【答案】 4.0×10－10 m 6.63×10－35 m宏观物体波动性的三点提醒1．一切运动着的物体都具有波动性，宏观物体观察不到其波动性，但并不否定其波动性．2．要注意大量光子、个别光子、宏观物体、微观粒子等相关概念的区别．3．在宏观世界中，波与粒子是对立的概念；在微观世界中，波与粒子可以统一．电子云和不确定性关系[先填空]1．电子云：原子中的电子在原子核的周围运动，在空间各点出现的概率是不同的，当原子处于稳定状态时，电子会形成一个稳定的概率分布．由于历史上的原因，人们常用一些小圆点来表示这种概率分布，概率大的地方小圆点密一些，概率小的地方小圆点疏一些，这样的概率分布图称为电子云．2．不确定性关系：用Δx表示微观粒子位置的不确定性，用Δp 表示微观粒子动量的不确定性，则两者之间的关系为ΔxΔp≥，即不确定性关系．它意味着微观粒子的坐标和动量不可能同时完全精确地确定．[再判断]1．在讨论微观粒子的运动时，只能给出微观粒子在空间各点出现的概率分布，无法给出微观粒子运行的轨迹．(√)2．微观粒子运动的状态，不能像宏观物体的运动那样通过确定的轨迹来描述，而是只能通过概率波作统计性的描述．(√) 3．改进测量技术，不确定性关系可以确定，微观粒子的坐标和动量可以同时确定．(×)[后思考]对微观粒子的运动分析能不能用“轨迹”来描述？【提示】不能．微观粒子的运动遵循不确定关系，也就是说，要准确确定粒子的位置，动量(或速度)的不确定量就更大；反之，要准确确定粒子的动量(或速度)，位置的不确定量就更大，也就是说不可能同时准确地知道粒子的位置和动量．因而不可能用“轨迹”来描述微观粒子的运动．1．粒子位置的不确定性：单缝衍射现象中，入射的粒子有确定的动量，但它们可以处于挡板左侧的任何位置，也就是说，粒子在挡板左侧的位置是完全不确定的．2．粒子动量的不确定性(1)微观粒子具有波动性，会发生衍射．大部分粒子到达狭缝之前沿水平方向运动，而在经过狭缝之后，有些粒子跑到投影位置以外．这些粒子具有与其原来运动方向垂直的动量．(2)由于哪个粒子到达屏上的哪个位置是完全随机的，所以粒子在垂直方向上的动量也具有不确定性，不确定量的大小可以由中央亮条纹的宽度来衡量．3．位置和动量的不确定性关系：ΔxΔp≥h4π由ΔxΔp≥可以知道，在微观领域，要准确地确定粒子的位置，动量的不确定性就更大；反之，要准确地确定粒子的动量，那么位置的不确定性就更大．4．微观粒子的运动没有特定的轨道：由不确定关系ΔxΔp≥可知，微观粒子的位置和动量是不能同时被确定的，这也就决定了不能用“轨迹”的观点来描述粒子的运动．5．经典物理和微观物理的区别(1)在经典物理学中，可以同时用位置和动量精确地描述质点的运动，如果知道质点的加速度，还可以预言质点在以后任意时刻的位置和动量，从而描绘它的运动轨迹．(2)在微观物理学中，不可能同时准确地知道粒子的位置和动量．因而也就不可能用“轨迹”来描述粒子的运动．但是，我们可以准确地知道大量粒子运动时的统计规律．3．对不确定性关系ΔxΔp≥有以下几种理解，其中正确的是( )【导学号：55272059】A．微观粒子的动量不可能确定B．微观粒子的坐标不可能确定C．微观粒子的动量和坐标不可能同时确定D．不确定性关系仅适用于电子和光子等微观粒子，不适用于其他宏观物体【解析】不确定性关系ΔxΔp≥表示确定位置、动量的精确度互相制约，此长彼消，当粒子位置的不确定性变小时，粒子动量的不确定性变大；当粒子位置的不确定性变大时，粒子动量的不确定性变小，故不能同时准确确定粒子的动量和坐标．不确定性关系也适用于其他宏观物体，不过这些不确定量微乎其微．【答案】C4．已知＝5.3×10－35 J·s，试求下列情况中速度测定的不确定量．(1)一个球的质量m＝1.0 kg，测定其位置的不确定量为10－6 m；(2)电子的质量me＝9.0×10－31 kg，测定其位置的不确定量为10－10 m(即在原子的数量级)．【解析】(1)m＝1.0 kg，Δx1＝10－6 m，由ΔxΔp≥，Δp＝mΔv知Δv1≥h4πΔx1m＝m/s＝5.3×10－29 m/s.(2)me＝9.0×10－31 kg，Δx2＝10－10 mΔv2≥＝ m/s＝5.89×105 m/s.【答案】(1)5.3×10－29 m/s (2)5.89×105 m/s对不确定性关系的两点提醒1．不确定性关系ΔxΔp≥是自然界的普遍规律，对微观世界的影响显著，对宏观世界的影响可忽略不计．也就是说，宏观世界中的物体质量较大，位置和速度的不确定范围较小，可同时较精确测出物体的位置和动量．2．在微观世界中，粒子质量较小，不能同时精确地测出粒子的位置和动量，也就不能准确地把握粒子的运动状态了．。

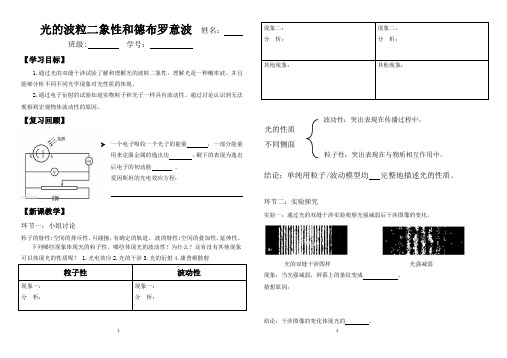
光的波粒二象性和德布罗意波姓名：班级: 学号： 1【学习目标】1.通过光的双缝干涉试验了解和理解光的波粒二象性，理解光是一种概率波。

并且能够分析不同不同光学现象对光性质的体现。

2.通过电子衍射的试验知道实物粒子和光子一样具有波动性。

通过讨论认识到无法观察到宏观物体波动性的原因。

【复习回顾】【新课教学】环节一：小组讨论粒子的特性:空间的排斥性，可碰撞，有确定的轨道。

波的特性:空间的叠加性，延伸性。

下列哪些现象体现光的粒子性，哪些体现光的波动性？为什么？还有没有其他现象可以体现光的性质呢？ 1.光电效应 2.光的干涉 3.光的衍射 4.康普顿散射粒子性波动性现象一： 分 析：现象一： 分 析：现象二：分 析：现象二： 分 析：其他现象： 其他现象：结论：单纯用粒子/波动模型均 完整地描述光的性质。

环节二：实验探究实验一：通过光的双缝干涉实验观察光强减弱后干涉图像的变化。

光的双缝干涉图样 光强减弱 现象：当光强减弱，屏幕上的条纹变成 。

猜想原因：结论：干涉图像的变化体现光的 。

➢ 一个电子吸收一个光子的能量 ，一部分能量用来克服金属的逸出功 ，剩下的表现为逸出后电子的初动能 。

爱因斯坦的光电效应方程：光的性质不同侧面波动性：突出表现在传播过程中。

粒子性：突出表现在与物质相互作用中。

实验二：将光源的强度减弱，每次只有一个光子通过狭缝，观察感光片上亮点变化。

观察随着记录时间的增加，感光屏上图像的变化。

记录时间短：记录时间长：结论：单个光子也具有。

光同时具有波动性和粒子性，即波粒二象性。

一般来说频率越高、波长越短、能量越大的光子其粒子性越显著，频率越低、波长越长、能量越小的光子其波动性越显著。

环节三：德布罗意的猜想和验证实物粒子和光一样具有波粒二象性。

这种与实物粒子相联系的波后来被称为德布罗意波或物质波。

实物粒子的德布罗意波的波长和动量满足以下关系：λ=h/p。

若以电子为例，电子的质量为9.1×10-31 kg，某电子速度大小为4.0×106m/s，请计算该电子对应的德布罗意波长。

2.5 德布罗意波课堂互动三点剖析一、德布罗意波德布罗意波也称为“物质波”或“实物波”，是对微观粒子所具有的波动性的描述，是由法国物理学家德布罗意在1924年首先提出的.他把当时已发现的关于波粒二象性这一事实加以推广，提出一切微观粒子也都具有波粒二象性的论点.他认为19世纪在对光的研究上，只重视光的波动性，忽视了光的微粒性；而在对实体的研究上则过分重视了实体的微粒性，而忽略了实体的波动性.因此他提出了微观粒子也具有波动性的假设，德布罗意把粒子和波通过下面的关系联系起来，粒子的能量E 和动量p 与平面波的频率ν和波长λ之间的关系正像光子与光波的关系一样，即ν=hE ，λ=p h 且平面波沿着粒子运动方向传播（h 为普朗克常量）.电子衍射实验完全证实了物质波的存在，它成为建立量子力学的重要基础之一.二、电子的衍射和电子云1.电子的衍射1927年美国工程师戴维孙获得了电子束在晶体上的衍射图样.同时英国物理学家汤姆生也独立地完成了这一实验，从而证明了实物粒子也具有波动性.2.电子云描写原子或分子中电子在原子核外围各区域出现的几率的状况时，为直观起见，把电子的这种几率分布状况用图象表示时，以不同的浓淡程度代表几率的大小，这种图象所显示的结果，如电子在原子核周围形成云雾，故称“电子云”.在距原子核很远的地方，电子出现的几率几乎等于零，意味着不可能在那里发现电子；有些非常靠近核的区域，其几率也是零，也是无法发现电子的区域.三、不确定性关系微观粒子既具有波动性又具有粒子性，这个事实表明运用经典概念处理微观粒子的运动问题，其有效性是有一定限度的.1927年春，海森堡在哥本哈根玻尔研究所看到云室中的电子轨迹是那么粗大，而电子本身并没有那么大，便思索如何解释云室中的电子轨迹问题.他觉得也许是电子的位置具有某种不确定性？经过分析发现，微观粒子的动量和位置坐标不能同时准确地确定，它们的不确定量的乘积，约为普朗克常量的数量级，量子力学的严格证明给出Δx·Δp x ≥h4π，式中Δx 表示粒子在x 方向上的位置的不确定范围，Δp x 表示在x 方向上动量的不确定范围，其乘积不得小于一个常数h4π，h 为普朗克常数.上式称为不确定关系或不确定原理，它是自然界的客观规律，是量子理论中的一个基本原理.各个击破【例1】以下说法正确的是（ ）A.物体都具有波动性B.抖动细绳一端，绳上的波就是物质波C.通常情况下，质子比电子的波长长D.核外电子绕核运动时，并没有确定的轨道 解析：任何物体都具有波动性，故A 项对，对宏观物体而言，其波动性难以观测，我们所看到的绳波是机械波，不是物质波，故B 项错.电子的动量往往比质子的动量小，由λ=ph 知，电子的波长长，故C 项错.核外电子绕核运动的规律是概率问题，无确定的轨道，故D 项对.答案：AD类题演练1如果一个中子和一个质量为10 g 的子弹都以103 m/s 的速度运动，则它们的德布罗意波的波长分别是多长？（中子的质量为1.67×10-27kg ）解析：中子的动量为p 1=m 1v,子弹的动量为p 2=m 2v,据λ=ph 知中子和子弹的德布罗意波长分别为λ1=1p h ,λ2=2p h . 联立以上各式解得λ1=v m h 1,λ2=vm h 2 将m 1=1.67×10-27 kg,v=1×103 m/s,h=6.63×10-34 J·s,m 2=1.0×10-2 kg代入上面两式可解得λ1=4.0×10-10 m,λ2=6.63×10-35 m.答案：4.0×10-10 m 6.63×10-35 m【例2】说一说你对“电子云”的理解.解析：电子云是一种形象化的比喻.电子在原子核外空间的某区域内出现，好像带负电荷的云笼罩在原子核的周围，人们形象地称它为电子云.电子是一种微观粒子，在原子如此小的空间（直径约10-10米）内做高速运动.核外电子的运动与宏观物体运动不同，没有确定的方向和轨迹，只能用电子云描述它在原子核外空间某处出现机会的大小.答案：见“解析”.类题演练2原子中电子运动是不是存在“轨道”？解析：设电子的动能E k =10 eV ，电子运动速度，v=mE k 2=106 m·s -1 速度的不确定度Δv=xm h m p ∆≥∆≈106 m·s -1 Δv —v 轨道概念不适用！ 答案：不存在.【例3】 人们能准确预知单个粒子的运动情况吗？解析：由Δx·Δp≥π4h 可知，我们不能准确知道单个粒子的实际运动情况，但可以知道大量粒子运动时的统计规律.当粒子数很少时，我们不能预言粒子通过挡板上的狭缝后落在屏上的什么位置，但可以准确地知道粒子落在屏上某点的概率；概率大的位置正好是某种波通过狭缝发生衍射时产生亮条纹的位置.答案：见“解析”.类题演练3质量为10 g 的子弹，以300 m/s 的速度射向靶子，试计算此子弹位置不确定性的范围.（其动量的不确定范围为0.02 %）解析：Δp x =mv×0.02%=10×10-3×300×0.02×10-2 N·m·s -1=6×10-4 N·m·s -1由Δx·Δp x ≥π4h 知，位置的不确定性的范围是 Δx≥43410614.341063.64--⨯⨯⨯⨯=∆∙p h πm=9×10-28 m . 答案：大于等于9×10-28 m。

第二章波粒二象性 第五节 德布罗意波 学案〖学习目标〗1、知道什么是德布罗意波，了解德布罗意波长与实物粒子的动量的关系；2、知道实物粒子和光子一样具有波粒二象性；3、了解不确定性关系.〖学习难点〗对德布罗意波的理解〖自主学习〗一、德布罗意波假说及实验验证1、德布罗意波任何一个实物粒子都和一个 相对应，这种与实物粒子相联系的波称为德布罗意波，也 叫做 。

2、物质波的波长、频率关系式：λ= 和v=3、实验验证：1927年带戴维孙和汤姆生分别利用晶体做了 的实验，得到了电子的 ，证实了电子的波动性。

二、不确定性关系以△x 表示微观粒子位置的 ，以△p 表示微观粒子 的不确定性，那么△x △p ≥h/4π，式中h 式普朗克常量。

【重难点阐释】一、说明：光的波粒二象性的联系（1）、E=h ν 光子说不否定波动性光具有能量动量，表明光具有粒子性。

光又具有波长、频率，表明光具有波动性。

且由E=h ν，光子说中E=h ν，ν是表示波的物理量，可见光子说不否定波动说。

（2）、光子的动量和光子能量的比较：p=λh 与ε=h ν Ｐ与ε是描述粒子性的，λ、ν是描述波动性的，h 则是连接粒子和波动的桥梁波粒二象性对光子来讲是统一的。

二、德布罗意波（物质波）德布罗意(due de Broglie, 1892-1960)提出：一切实物粒子都有具有波粒二象性。

即每一个运动的粒子都与一个对应的波相联系。

能量为E 、动量为p 的粒子与频率为v 、波长为λ的波相联系，并遵从以下关系：E=mc 2=hv p=mv=λh 其中p ：运动物体的动量 h ：普朗克常量 1、德布罗意波这种和实物粒子相联系的波称为德布罗意波(物质波或概率波),其波长λ称为德布罗意波长。

2、一切实物粒子都有波动性。

后来，大量实验都证实了：质子、中子和原子、分子等实物微观粒子都具有波动性，并都满足德布罗意关系。

一颗子弹、一个足球有没有波动性呢？【例1】试估算一个中学生在跑百米时的德布罗意波的波长。

第五节德布罗意波[学习目标］ 1.了解物质波的概念，知道实物粒子具有波粒二象性.2.了解电子衍射实验及对德布罗意波假说的证明.3。

了解什么是电子云，知道物质波也是一种概率波。

4.了解不确定性关系及对一些现象的解释．一、德布罗波假说和电子衍射［导学探究] 德布罗意认为任何运动着的物体均具有波动性,可是我们观察运动着的汽车，并未感觉到它的波动性，你如何理解该问题？答案波粒二象性是微观粒子的特殊规律,一切微观粒子都存在波动性，宏观物体（如汽车）也存在波动性，只是因为宏观物体质量大，动量大，波长短，难以观测．［知识梳理]1．粒子的波动性（1)任何运动着的物体，小到电子、质子，大到行星、太阳，都有一种波与它相对应，这种波叫物质波,又叫德布罗意波．（2)德布罗意波波长、频率的计算公式为λ＝错误!,ν＝错误!.（3)我们之所以看不到宏观物体的波动性，是因为宏观物体的动量太大，德布罗意波长太小的缘故．2．物质波的实验验证：电子衍射(1)实验探究思路：干涉、衍射是波特有的现象，如果实物粒子具有波动性，则在一定条件下，也能够发生干涉或衍射现象．（2)实验验证：1927年戴维孙和汤姆生分别利用晶体做了电子束衍射的实验，得到了电子的衍射图样,证实了电子的波动性．（3)说明①人们陆续证实了质子、中子以及原子、分子的波动性，对于这些粒子，德布罗意给出的λ＝hp关系同样正确．②物质波也是一种概率波．[即学即用］判断下列说法的正误．（1)一切宏观物体都伴随一种波，即物质波．( ×)(2）湖面上的水波就是物质波．（×)（3）电子的衍射现象证实了实物粒子具有波动性．( √）二、电子云当原子处于稳定状态时，电子会形成一个稳定的概率分布，概率大的地方小圆点密一些,概率小的地方小圆点疏一些．这样的概率分布图称为电子云．这也说明，德布罗意波是一种概率波．三、不确定性关系1．定义:在经典物理学中，可以同时用质点的位置和动量精确描述它的运动,在微观物理学中，要同时测出微观粒子的位置和动量是不太可能的，这种关系叫不确定性关系．2．表达式：ΔxΔp≥错误!.其中以Δx表示微观粒子位置的不确定性,以Δp表示微观粒子在x方向上的动量的不确定性，h是普朗克常量．3．微观粒子运动的基本特征:不再遵守牛顿运动定律，不可能同时准确地知道粒子的位置和动量，不可能用“轨迹"来描述粒子的运动，微观粒子的运动状态只能通过概率做统计性的描述．[即学即用］判断下列说法的正误．(1）在电子衍射中，电子通过狭缝后运动的轨迹是确定的．( ×)(2)宏观物体的动量和位置可准确测定．（√）(3）微观粒子的动量和位置不可同时准确测定．( √)一、对德布罗意波的理解德布罗意波也是概率波：对于电子和其他微观粒子，单个粒子的位置是不确定的，但在某点出现的概率的大小可以由波动的规律确定,而且对于大量粒子，这种概率分布导致确定的宏观结果，所以德布罗意波也是概率波．例1下列关于德布罗意波的认识，正确的解释是（)A．光波是一种物质波B．X光的衍射证实了物质波的假设是正确的C．电子的衍射证实了物质波的假设是正确的D．宏观物体运动时，看不到它的衍射或干涉现象，所以宏观物体不具有波动性答案C解析宏观物体由于动量太大,德布罗意波长太小，所以看不到它的干涉、衍射现象，但仍具有波动性，D项错；X光是波长极短的电磁波，是光子,它的衍射不能证实物质波的假设是正确的，B项错．只有C项正确．例2如果一个中子和一个质量为10 g的子弹都以103 m/s的速度运动，则它们的德布罗意波的波长分别是多大？(中子的质量为1.67×10－27 kg)答案3。

课时：2课时教学目标：1. 理解德布罗意波的概念及其意义。

2. 掌握德布罗意波波长和频率的计算方法。

3. 能够运用德布罗意波理论解释一些实际现象。

教学重点：1. 德布罗意波的概念。

2. 德布罗意波波长和频率的计算方法。

教学难点：1. 德布罗意波与经典波的区别。

2. 德布罗意波在实际现象中的应用。

教学过程：第一课时：一、导入1. 引入量子力学的基本概念，引导学生了解波粒二象性。

2. 介绍德布罗意波的概念及其意义。

二、德布罗意波的概念1. 讲解德布罗意波的定义：物质粒子也具有波动性。

2. 分析德布罗意波与经典波的区别，强调德布罗意波的特殊性。

三、德布罗意波波长和频率的计算1. 介绍德布罗意波波长和频率的计算公式。

2. 通过实例讲解如何运用公式计算德布罗意波的波长和频率。

四、课堂练习1. 给出几个实例，让学生运用德布罗意波理论进行计算。

2. 指导学生分析计算结果，总结规律。

第二课时：一、复习导入1. 回顾德布罗意波的概念和计算方法。

2. 引导学生思考德布罗意波在实际现象中的应用。

二、德布罗意波的实际应用1. 介绍德布罗意波在电子显微镜、激光技术等领域的应用。

2. 分析德布罗意波在物质结构、化学反应等方面的作用。

三、课堂讨论1. 让学生分组讨论德布罗意波在实际生活中的应用。

2. 邀请学生分享自己的观点和见解。

四、总结与拓展1. 总结德布罗意波的主要内容和意义。

2. 拓展：介绍德布罗意波与量子力学其他理论的关系。

教学评价：1. 课后作业：布置与德布罗意波相关的习题，考察学生对知识点的掌握程度。

2. 课堂表现：观察学生在课堂上的讨论、提问和回答问题的情况，评估学生的参与度和理解程度。

第五节 德布罗意波[A 级 抓基础]1．(多选)下列关于微观粒子波粒二象性的认识，正确的是( ) A ．因实物粒子具有波动性，故其轨迹是波浪线B ．由概率波的知识可知，因微观粒子落在哪个位置不能确定，所以粒子没有确定的轨迹C ．由概率波的知识可知，因微观粒子落在哪个位置不能确定，再由不确定性关系知粒子动量将完全确定D ．大量光子表现出波动性，此时光子仍具有粒子性解析：实物粒子的波动性指实物粒子是概率波，与经典的波不同，故A 错误；微观粒子落在哪个位置不能确定，与经典粒子有确定轨迹不同，故B 正确；单缝衍射中，微观粒子通过狭缝，其位置的不确定量等于缝宽，其动量也有一定的不确定量，故C 错误；波动性和粒子性是微观粒子的固有特性，无论何时二者都同时存在，故D 正确．答案：BD2．质量为m 的粒子原来的速度为v ，现将粒子的速度增大到2v ，则该粒子的物质波的波长将(粒子的质量保持不变)( )A ．变为原来波长的一半B ．保持不变C ．变为原来波长的 2D ．变为原来波长的两倍 解析：由物质波波长公式λ＝h p ＝hmv可知选项A 对． 答案：A3．(多选)根据不确定性关系Δx ·Δp ≥h4π判断下列说法正确的是( )A ．采取办法提高测量Δx 精度时，Δp 的精度下降B ．采取办法提高测量Δx 精度时，Δp 的精度上升C ．Δx 与Δp 测量精度与测量仪器及测量方法是否完备有关D ．Δx 与Δp 测量精度与测量仪器及测量方法是否完备无关解析：不确定性关系表明无论采用什么方法试图确定坐标和相应动量中的一个，必然引起另一个较大的不确定性，这样的结果与测量仪器及测量方法是否完备无关．无论怎样改善测量仪器和测量方法，都不可能逾越不确定性关系所给出的限度，故A 、D 正确．答案：AD4．一个质量为m 、电荷量为q 的带电粒子，由静止开始经加速电场加速后(加速电压为U )，该粒子的德布罗意波长为( )A. h2mqUB.h 2mqUC.h2mqU2mqU D.h mqU解析：加速后的速度为v ，根据动能定理，可得qU ＝12mv 2，所以v ＝2qU m .由德布罗意波公式可得：λ＝h p＝hm2qU m＝h2mqU2mqU .所以选项C 正确．答案：CB 级 提能力5．(多选)在单缝衍射实验中，从微观粒子运动的不确定性关系可知( ) A ．缝越窄，粒子位置的不确定性越大 B ．缝越宽，粒子位置的不确定性越大 C ．缝越窄，粒子动量的不确定性越大 D ．缝越宽，粒子动量的不确定性越大解析：由不确定性关系Δx Δp ≥h4π知缝越宽时，位置的不确定性越大，则动量的不确定性越小，反之亦然，故B 、C 正确．答案：BC6．一个德布罗意波波长为λ1的中子和另一个德布罗意波波长为λ2的氘核同向正碰后结合成一个氚核，该氚核的德布罗意波波长为( )A.λ1λ2λ1＋λ2B.λ1λ2λ1－λ2C.λ1＋λ22D.λ1－λ22解析：中子的动量p 1＝h λ1，氘核的动量p 2＝hλ2，对撞后形成的氚核的动量p 3＝p 2＋p 1，所以氚核的德布罗意波波长为λ3＝h p 3＝λ1λ2λ1＋λ2.答案：A7．已知α粒子的质量m α＝6.64×10－27kg ，速度v ＝3×107m/s ，要观察到α粒子明显的衍射现象，障碍物的尺寸约为( )A ．3.3×10－10m B ．3.3×10－12m C ．3.3×10－15 mD ．3.3×10－18m解析：λ＝h p ＝h mv ＝ 6.63×10－346.64×10－27×3×107 m ≈3.3×10－15m ．要观察到明显的衍射现象，障碍物的尺寸与波长差不多，C 正确．答案：C8．已知h4π＝5.3×10－35J ·s ，试求下列情况中速度测定的不确定量．(1)一个球的质量m ＝1.0 kg ，测定其位置的不确定量为10－6m ； (2)电子的质量m e ＝9.1×10－31kg ，测定其位置的不确定量为10－10m(即在原子直径的数量级内)．解析：(1)m ＝1.0 kg ，Δx 1＝10－6m ，由Δx Δp ≥h 4π及Δp ＝m Δv 知Δv 1＝Δp m ≥h 4πΔx 1m＝5.3×10－3510－6×1.0m/s ＝5.3×10－29m/s. (2)m e ＝9.1×10－31kg ，Δx 2＝10－10m ，同理得Δv 2≥h4πΔx 2m e ＝ 5.3×10－3510－10×9.1×10－31 m/s＝5.8×105m/s.答案：(1)大于等于5.3×10－29m/s(2)大于等于5.8×105m/s。

第五节德布罗意波1。

知道实物粒子具有波动性．2。

通过对实物波实验内容的学习，感受实验探究这一重要方法．3．初步了解不确定性关系的内容，感受数学工具在物理学发展过程中的作用．一、德布罗意波假说1．德布罗意波:任何一个实物粒子都和一个波相对应．这种波称为德布罗意波，也称为物质波．2．物质波的波长与其动量之间的关系式粒子的动量p与波长λ之间的关系为λ＝错误!．1．射击运动员射击时会因为子弹的波动性而“失准”吗？为什么？根据现实情况下子弹质量、速度大小所对应的德布罗意波长来做定性说明．提示:不会．因为宏观的子弹质量、速度大,动量大，德布罗意波长非常小．二、电子衍射1．物质波的实验验证：1927年戴维孙和汤姆生分别利用晶体做了衍射实验，得到了电子的衍射图样，证明了德布罗意波的假说．2．实物粒子的波粒二象性：波粒二象性是包括光子在内的一切微观粒子的共同特征，和光子一样，对微观粒子运动状态的最准确的描述是概率波．三、电子云当原子处于稳定状态时，电子会形成一个稳定的概率分布，人们常用一些小圆点来表示这种概率分布,概率大的地方小圆点密一些，概率小的地方小圆点疏一些，这样的概率分布图称为电子云．四、不确定性关系1．不确定性关系：用Δx表示微观粒子位置的不确定性,用Δp表示微观粒子在x方向上的动量的不确定性，那么ΔxΔp≥错误!，式中h是普朗克常量．2．意义：微观粒子的波粒二象性及不确定性关系,在本质上是一致的．它们都导致了一个共同的结果:微观粒子运动的状态，不能像宏观物体的运动那样通过确定的轨迹来描述,而是只能通过概率波作统计性的描述．2．“在微观物理学中，由于我们不可能同时准确地知道某个粒子的位置和动量，粒子出现的位置是无规律可循的．"你认为呢？提示：虽然我们不可能同时准确地知道某个粒子的位置和动量,但粒子的运动却有规律可循,那就是统计规律,比如，衍射的亮斑位置就是粒子出现概率大的位置．理解德布罗意波1．德布罗意认为：任何一个运动的物体，小的如电子、质子,大的如行星、太阳，平时所见到的行驶的火车、流动的人群等，都有一种波与之对应，称为德布罗意波，也叫物质波．物质波的动量与波长之间的关系为p＝错误!.2．德布罗意波和光波一样，也是概率波，即实物粒子在空间各处出现的概率受波动规律支配．微观粒子的运动状态不可能用“轨迹"来描述，只能通过大量粒子的运动作统计性的描述．因此电子在原子内没有确定的位置，在原子核外任何地方都有可能出现，只是概率不同．用点的疏密描绘出来就是电子云．3．根据德布罗意波假说,实物粒子也具有波粒二象性，宏观物体的动量比较大，所以德布罗意波波长很短,波动性不明显．微观粒子的德布罗意波波长较长，在一些特定环境下可以观察到他们的干涉和衍射等波的现象．电子的衍射等现象证明电子具有波动性，也为德布罗意假设提供了实验依据．电子的波动性和粒子性是统一的,并不是相互矛盾．如果一个中子和一个质量为10 g的子弹都以103 m/s的速度运动，则它们的德布罗意波的波长分别是多长?（中子的质量为1。

第二章波粒二象性 第五节 德布罗意波 学案〖学习目标〗1、知道什么是德布罗意波，了解德布罗意波长与实物粒子的动量的关系；2、知道实物粒子和光子一样具有波粒二象性；3、了解不确定性关系.〖学习难点〗对德布罗意波的理解〖自主学习〗一、德布罗意波假说及实验验证1、德布罗意波任何一个实物粒子都和一个 相对应，这种与实物粒子相联系的波称为德布罗意波，也 叫做 。

2、物质波的波长、频率关系式：λ= 和v=3、实验验证：1927年带戴维孙和汤姆生分别利用晶体做了 的实验，得到了电子的 ，证实了电子的波动性。

二、不确定性关系以△x 表示微观粒子位置的 ，以△p 表示微观粒子 的不确定性，那么△x △p ≥h/4π，式中h 式普朗克常量。

【重难点阐释】一、说明：光的波粒二象性的联系（1）、E=h ν 光子说不否定波动性光具有能量动量，表明光具有粒子性。

光又具有波长、频率，表明光具有波动性。

且由E=h ν，光子说中E=h ν，ν是表示波的物理量，可见光子说不否定波动说。

（2）、光子的动量和光子能量的比较：p=λh与ε=h νＰ与ε是描述粒子性的，λ、ν是描述波动性的，h 则是连接粒子和波动的桥梁波粒二象性对光子来讲是统一的。

二、德布罗意波（物质波）德布罗意(due de Broglie, 1892-1960)提出：一切实物粒子都有具有波粒二象性。

即每一个运动的粒子都与一个对应的波相联系。

能量为E 、动量为p 的粒子与频率为v 、波长为λ的波相联系，并遵从以下关系：E=mc 2=hv p=mv=λh其中p ：运动物体的动量 h ：普朗克常量1、德布罗意波这种和实物粒子相联系的波称为德布罗意波(物质波或概率波),其波长λ称为德布罗意波长。

2、一切实物粒子都有波动性。

后来，大量实验都证实了：质子、中子和原子、分子等实物微观粒子都具有波动性，并都满足德布罗意关系。

一颗子弹、一个足球有没有波动性呢？【例1】试估算一个中学生在跑百米时的德布罗意波的波长。

第五节 德布罗意波系”的具体含义．1．德布罗意波假说任何一个实物粒子都和一种波相对应，这种波被称为__________，也称物质波． 预习交流1射击运动员射击时会因为子弹的波动性而“失准”吗？为什么？根据现实情况下子弹质量、速度大小所对应的德布罗意波波长来做定性说明．2．电子衍射________的发现证明了德布罗意波假说，实验表明，其他______微观粒子也都具有波动性．3．电子云当原子处于稳定状态时，电子会形成一个稳定的概率分布，这种概率分布称为________． 4．不确定关系的表达式实验发现，对光子位置的测量越精确，其______的不确定性就越大，反之亦然．微观粒子的不确定性关系的表达式为____________．预习交流2“在微观物理学中，由于我们不可能同时准确地知道某个粒子的位置和动量，粒子出现的位置是无规律可循的．”你认为呢？答案：1．德布罗意波预习交流1：答案：不会．因为宏观的子弹质量和速度较大，动量较大，德布罗意波波长非常小．2．电子衍射 一切 3．电子云 4．动量 Δx Δp ≥h4π预习交流2：答案：虽然我们不可能同时准确地知道某个粒子的位置和动量，但粒子的运动却有规律可循，那就是统计规律，比如，衍射的亮斑位置就是粒子出现概率大的位置．一、理解德布罗意波1．德布罗意认为任何运动着的物体均有波动性，可是我们观察运动着的汽车，并未感觉到它的波动性，你如何理解该问题，谈谈自己的认识．2．德布罗意波波长与动量的关系是怎样的？3．描述波的物理量及波动特有的现象是什么？粒子具有哪些特征？4．宏观物体也具有波粒二象性吗？（2011·安庆高二检测）在一束电子中，电子的动能为200 eV，忽略相对论效应，求此电子的德布罗意波波长λ．德布罗意关于波粒二象性的思辨过程德布罗意之前，人们对自然界的认识，只局限于两种基本的物质类型：实物和场．但是，许多实验结果之间出现了难以解释的矛盾．物理学家们相信，这些表面上的矛盾，势必有其深刻的根源．1923年，德布罗意最早想到了这个问题，并且大胆地设想，人们对于光子建立起来的两个关系式ε＝hν，p＝mv＝hλ会不会也适用于实物粒子．如果成立的话，实物粒子也同样具有波动性．二、理解不确定性关系1．有人说：在微观物理学中，由于我们不可能同时准确地知道某个粒子的位置和动量，粒子出现的位置是无规律可循的．这种说法对吗？为什么？谈一谈你的观点．2．既然单个粒子的运动情况不可预知，为什么还要研究粒子的运动规律？3．谈谈你对位置和动量的不确定性关系ΔxΔp≥h4π的理解．一颗质量为10 g的子弹，具有200 m/s的速率，若其动量的不确定范围为其动量的0.01%（这在宏观范围是十分精确的了），则该子弹位置的不确定范围为多大？不确定性关系不是说微观粒子的坐标测不准，也不是说微观粒子的动量测不准，更不是说微观粒子的坐标和动量都测不准，而是说微观粒子的坐标和动量不能同时测准．不确定性关系是自然界的一条客观规律，不是测量技术和主观能力的问题．1．关于物质波的认识，错误的是（）．A．只要是运动着的物体，不论是宏观物体还是微观粒子，都有相应的波动性，这就是物质波B．只有运动着的微观粒子才有与之对应的物质波，对于宏观物体，不论其是否运动，都没有相对应的物质波C．由于宏观物体的德布罗意波波长太小，所以无法观察到它们的波动性D．电子束照射到金属晶体上得到了电子束的衍射图样，从而证实了德布罗意的假设是正确的2．在历史上，最早证明了德布罗意波存在的实验是（）．A．弱光衍射实验B．电子束在晶体上的衍射实验C．弱光干涉实验D．以上选项都不正确3．关于电子云，下列说法正确的是（）．A．电子云是真实存在的实体B．电子云周围的小黑点就是电子的真实位置C．电子云上的小黑点表示的是电子的概率分布D ．电子云说明电子在绕原子核运动时有固定轨道4．试估算质量为1 000 kg 的汽车，以10 m/s 运动时的德布罗意波波长． 5．电子经电势差为U ＝200 V 的电场加速，在v ≤c 的情况下， 求此电子的德布罗意波波长．答案：活动与探究1：1．答案：一切微观粒子都存在波动性，宏观物体（汽车）也存在波动性，只是因为宏观物体质量大，动量大，波长短，难以观测，而微观实物粒子如电子、质子、中子以及原子、分子的波动性为宏观物体具有波动性奠定了事实基础．2．答案：如果用动量p 来表征实物粒子的粒子性，用波长λ来表征实物粒子的波动性．那么，对光适用的关系式也适用于实物粒子，即：λ＝h p，这种与实物粒子相联系的波后来称为德布罗意波，也叫做物质波．其中λ是德布罗意波波长，h 是普朗克常量，p 是相应的实物粒子的动量．3．答案：描述波的物理量有：波长、频率和波速．波动特有的现象是：干涉、衍射等． 描述粒子的物理量有质量、能量、动量等，还具有与其他物质碰撞、入射、贯穿结合等作用特征．4．答案：电子、质子等微观粒子具有波粒二象性已是无可争议的事实，因为，人们已经通过实验观察到了它们的干涉和衍射等现象．宏观物体由于运动动量较大，根据德布罗意波波长与动量的关系λ＝h p，波长非常非常小，尽管不容易观察到它们的干涉、衍射等波的现象，但它们仍然具有波动性，有它们的波长，因此宏观物体也具有波粒二象性．迁移与应用1：答案：见解析解析：忽略相对论效应，电子的动能为：E k ＝12mv 2①电子的动量为：p ＝mv ②电子的德布罗意波波长为：λ＝h p③ 代入数据得：λ＝8.7×10－11m ．活动与探究2：1．答案：不对．由Δx Δp ≥h4π可知，虽然我们不能准确地知道单个粒子的实际运动情况，但粒子出现的位置并不是无规律可循的．我们可以根据大量粒子运动的统计规律知道粒子在某点出现的概率．2．答案：由不确定性关系可知，我们不能准确预知单个粒子的实际运动情况，但是大量粒子运动的统计规律是可以准确预知的，可以从宏观上对一个系统进行干预和控制． 3．答案：由Δx Δp ≥h4π可以知道，在微观领域，要准确地测定粒子的位置，动量的不确定性就变大；反之，要准确确定粒子的动量，那么位置的不确定性就变大．如将狭缝变成宽缝，粒子的动量能被精确测定（可认为此时不发生衍射），但粒子通过缝的位置的不确定性却增大了；反之取狭缝Δx →0，粒子的位置测定精确了，但衍射范围会随Δx 的减小而增大，这时动量的测定就更加不准确了．迁移与应用2：答案：见解析解析：子弹的动量为p ＝mv ＝0.01×200kg·m /s ＝2.0 kg·m/s 动量的不确定范围为： Δp ＝0.01%×p＝1.0×10－4×2.0 kg·m/s＝2.0×10－4kg·m/s由不确定关系式Δx Δp ≥h4π，得子弹位置的不确定范围Δx ≥h4π·Δp＝ 6.63×10－344×3.14×2.0×10－4m ＝2.6×10－31m ． 当堂检测1．B 解析：所有运动的物体都具有波动性，只是宏观物体的德布罗意波波长太短，无法观察到它们的波动性．2．B 解析：最早证明德布罗意波假说的是电子束在晶体上的衍射实验．故B 正确． 3．C 解析：由电子云的定义我们知道，电子云不是一种稳定的概率分布，在历史上，人们常用小圆点表示这种概率，小圆点的密疏代表电子在这一位置出现的概率大小，故只有C 正确．4．答案：6.63×10－38m 解析：汽车运动时的动量p ＝mv ＝1 000×10 kg·m/s＝104 kg·m/s 根据德布罗意波长计算公式有λ＝h p ＝6.63×10－34104m ＝6.63×10－38m ． 5．答案：8.7×10－2nm解析：已知12m 0v 2＝E k ＝eU ，λ＝h p ＝h 2m 0E k ＝h 2em 0U ＝h 2em 0·1U＝8.7×10－2nm ．。