数字信号处理作业答案

目录习题一 (3)习题二 (26)习题三 (40)习题四 (61)习题五 (83)习题一1.1序列)(n x 如图T1.1所示，用延迟的单位采样序列加权和表示出这个序列。

图 T1.1 习题1.1图【解答】 任一数字序列都可表达为)()()(k n k x n x k -=∑∞-∞=δ所以图T1-1信号可表达为)3(2)1(3)()3(2)(-+-+-+-=n n n n n x δδδδ1.2 分别绘出以下各序列的图形： （1）)(2)(1n u n x n =（2）)(21)(2n u n x n⎪⎭⎫⎝⎛=（3）()3()2()nx n u n =-（4）)(21)(4n u n x n⎪⎭⎫⎝⎛-=【解答】 用MATLAB 得到的各序列图形如图T1.2所示。

图T1.2习题1.2解答1.3 判断下列每个序列是否是周期性的；若是周期性的，试确定其周期。

（1）⎪⎭⎫ ⎝⎛-=873cos )(ππn A n x（2）⎪⎭⎫⎝⎛=n A n x 313sin )(π（3）⎪⎭⎫⎝⎛-=n j e n x 6)(π（4）{}{}/12/18()Re Im jn jn x n e e ππ=+（5）16()cos(/17)jnx n e n ππ=【解答】（1）因为730πω=，而31473220==ππωπ，这是一有理数。

所以)(n x 是周期的，周期为14。

（2）因为3130πω=，而136313220==ππωπ，也为有理数。

所以)(n x 是周期的，周期为6。

（3）注意此序列的10=ω，πωπ220=，是无理数，所以)(n x 是非周期的。

（4）实际上()cos(/12)sin(/18)x n n n ππ=+因此)(n x 有两个频率分量，即1201πω=，1802πω=，而 24122201==ππωπ；02223618πππω==都是有理数，所以)(n x 是两个周期信号之和，第一个周期信号的周期241=N ，第二个周期信号的周期362=N ，因此)(n x 的周期是这两个周期的最小公倍数，即72123624)36,24gcd(3624),gcd(2121=⋅=⋅=⋅=N N N N N（5）()x n 是两个周期序列的乘积，其中132N =，234N =，所以该序列的周期是121232343234544gcd(,)gcd(32,34)2N N N N N ⋅⋅⋅====1.4 已知序列)]6()()[6()(---=n u n u n n x ，画出下面序列的示意图。

1-2习题1-2图所示为一个理想采样—恢复系统，采样频率Ωs =8π,采样后经过理想低通G jΩ 还原。

解：(1)根据余弦函数傅里叶变换知：)]2()2([)]2[cos(πδπδππ-Ω++Ω=t F ，)]6()6([)]6[cos(πδπδππ-Ω++Ω=t F 。

又根据抽样后频谱公式：∑∞-∞=∧Ω-Ω=Ωk s a a jk j X T j X )(1)(，得到14T= ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]82()82([4)(1ππδππδπ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]86()86([4)(2ππδππδπ所以，)(1t x a ∧频谱如下所示)(2t x a ∧频谱如下所示（2）)(1t y a 是由)(1t x a ∧经过理想低通滤波器)(Ωj G 得到，)]2()2([)()()]([11πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a ，故)2cos()(1t t y a π=(4π) (4π) (4π)(4π)(4π) (4π) Ω-6π-10π-2π 2π0 6π10π)(1Ω∧j X a Ω10π-10π -6π-2π 0 2π6π-14π 14π(4π)(4π) (4π)(4π) (4π) (4π)(4π) (4π))(2Ω∧j X a同理，)]2()2([)()()]([22πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a 故)2cos()(2t t y a π=（3）由题（2）可知，无失真，有失真。

原因是根据采样定理，采样频率满足信号)(1t x a 的采样率，而不满足)(2t x a 的，发生了频谱混叠。

1-3判断下列序列是否为周期序列，对周期序列确定其周期。

（1）()5cos 86x n A ππ⎛⎫=+ ⎪⎝⎭（2）()8n j x n eπ⎛⎫- ⎪⎝⎭=（3）()3sin 43x n A ππ⎛⎫=+ ⎪⎝⎭解：（1）85πω=，5162=ωπ为有理数，是周期序列，.16=N （2）πωπω162,81==，为无理数，是非周期序列； （3）382,43==ωππω，为有理数，是周期序列，8=N 。

==============================绪论==============================1。

A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1。

①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用（n ） 表示y （n )=｛2，7,19，28,29，15｝2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的； 若是周期的， 确定其周期。

（1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2）)81(j e )(π-=n n x 解: （1） 因为ω=73π， 所以314π2=ω， 这是有理数， 因此是周期序列， 周期T =14。

（2） 因为ω=81, 所以ωπ2=16π， 这是无理数, 因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法 乘法序列｛2，3，2，1}与序列｛2，3，5，2，1}相加为__｛4，6，7,3，1}__，相乘为___｛4，9，10，2｝ 。

移位翻转：①已知x(n)波形，画出x(—n ）的波形图。

②尺度变换:已知x(n)波形，画出x （2n ）及x(n/2）波形图.卷积和:①h(n)*求x(n)，其他2n 0n 3，h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4，23{0,h(n)*答案：x(n)=②已知x (n )=｛1,2，4,3},h （n ）={2，3，5}， 求y （n ）=x （n ）＊h （n ）x (m ）={1，2，4,3},h （m ）=｛2,3,5｝，则h (—m ）={5，3,2｝(Step1：翻转)解得y （n )=｛2，7，19,28,29，15}③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案：x(n)=4. 如果输入信号为,求下述系统的输出信号。

数字信号处理试题及答案一、选择题1. 数字信号处理中的离散傅里叶变换（DFT）是傅里叶变换的______。

A. 连续形式B. 离散形式C. 快速算法D. 近似计算答案：B2. 在数字信号处理中，若信号是周期的，则其傅里叶变换是______。

A. 周期的B. 非周期的C. 连续的D. 离散的答案：A二、填空题1. 数字信号处理中，______是将模拟信号转换为数字信号的过程。

答案：采样2. 快速傅里叶变换（FFT）是一种高效的______算法。

答案：DFT三、简答题1. 简述数字滤波器的基本原理。

答案：数字滤波器的基本原理是根据信号的频率特性，通过数学运算对信号进行滤波处理。

它通常包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等类型，用于选择性地保留或抑制信号中的某些频率成分。

2. 解释什么是窗函数，并说明其在信号处理中的作用。

答案：窗函数是一种数学函数，用于对信号进行加权，以减少信号在离散化过程中的不连续性带来的影响。

在信号处理中，窗函数用于平滑信号的开始和结束部分，减少频谱泄露效应，提高频谱分析的准确性。

四、计算题1. 给定一个信号 x[n] = {1, 2, 3, 4}，计算其 DFT X[k]。

答案：首先，根据 DFT 的定义，计算 X[k] 的每个分量：X[0] = 1 + 2 + 3 + 4 = 10X[1] = 1 - 2 + 3 - 4 = -2X[2] = 1 + 2 - 3 - 4 = -4X[3] = 1 - 2 - 3 + 4 = 0因此，X[k] = {10, -2, -4, 0}。

2. 已知一个低通滤波器的截止频率为0.3π rad/sample，设计一个简单的理想低通滤波器。

答案：理想低通滤波器的频率响应为：H(ω) = { 1, |ω| ≤ 0.3π{ 0, |ω| > 0.3π }五、论述题1. 论述数字信号处理在现代通信系统中的应用及其重要性。

答案：数字信号处理在现代通信系统中扮演着至关重要的角色。

《数字信号处理》考试试卷（附答案）一、填空（每空 2 分 共20分）1．连续时间信号与数字信号的区别是：连续时间信号时间上是连续的，除了在若干个不连续点外，在任何时刻都有定义，数字信号的自变量不能连续取值，仅在一些离散时刻有定义，并且幅值也离散化㈠。

2．因果系统的单位冲激响应h (n )应满足的条件是：h(n)=0,当n<0时㈡。

3．线性移不变系统的输出与该系统的单位冲激响应以及该系统的输入之间存在关系式为：()()*()()()m y n x n h n x m h n m ∞=-∞==-∑，其中x(n)为系统的输入，y(n)为系统的输出，h(n)w 为系统的单位冲激响应。

㈢。

4．若离散信号x (n )和h (n )的长度分别为L 、M ，那么用圆周卷积)()()(n h n x n y N O=代替线性卷积)()(n x n y l =*h (n)的条件是：1N L M ≥+-㈣。

5．如果用采样频率f s = 1000 Hz 对模拟信号x a (t ) 进行采样，那么相应的折叠频率应为 500 Hz ㈤，奈奎斯特率（Nyquist ）为1000Hz ㈥。

6．N 点FFT 所需乘法（复数乘法）次数为2N ㈦。

7．最小相位延迟系统的逆系统一定是最小相位延迟系统㈧。

8．一般来说，傅立叶变换具有4形式㈨。

9．FIR 线性相位滤波器有4 种类型㈩。

二、叙述题（每小题 10 分 共30分） 1．简述FIR 滤波器的窗函数设计步骤。

答：（1）根据实际问题所提出的要求来确定频率响应函数()j d H e ω;（2.5分）（2）利用公式1()()2j j d d h n H e e d πωωπωπ-=⎰来求取()d h n ； （2.5分）（3）根据过渡带宽及阻带最小衰减的要求，查表选定窗的形状及N 的大小；（2.5分）（4）计算()()(),0,1,...1d h n h n w n n N ==-，便得到所要设计的FRI 滤波器。

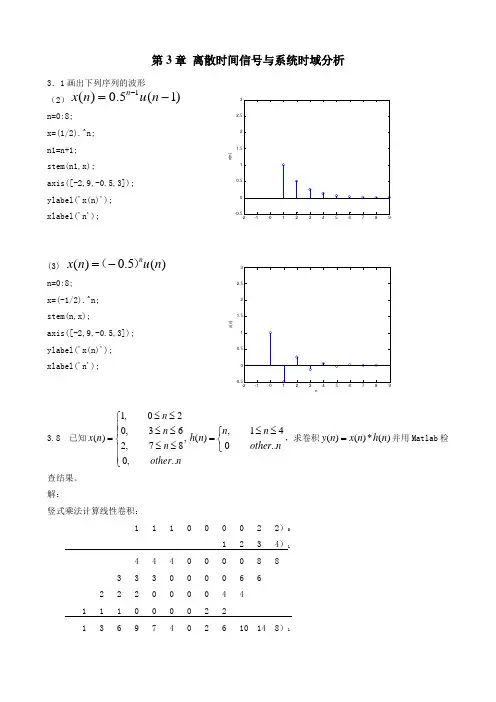
第3章 离散时间信号与系统时域分析3．1画出下列序列的波形（2）1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-（）n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩，求卷积()()*()y n x n h n =并用Matlab 检查结果。

解：竖式乘法计算线性卷积： 1 1 1 0 0 0 0 2 2）01 2 3 4）14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8）1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果：x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx （n ）=5sin(n) 解：2214337w πππ==，所以N=14 (2) 326n ππ-x （n ）=sin()-sin(n)解：22211213322212,2122612T N w T N w N ππππππ=========，所以(6) 3228n π-x （n ）=5sin()-cos(n) 解：22161116313822222()T N w T w x n ππππππ=======，为无理数，所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=，()4()nx n u n -=，(1)4y -=，(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应，并画出图形。

数字信号处理试题及答案1. 试题1.1 选择题1. 设x(n)为长度为N的实序列，其中0≤n≤N-1。

要将其进行离散傅立叶变换（DFT），DFT的结果为X(k)，其中0≤k≤N-1。

以下哪个式子为正确的傅立叶变换公式？A. X(k) = ∑[x(n) * exp(-j2πkn/N)]，0≤k≤N-1B. X(k) = ∑[x(n) * exp(-j2πnk/N)]，0≤k≤N-1C. X(k) = ∑[x(n) * exp(-jπkn/N)]，0≤k≤N-1D. X(k) = ∑[x(n) * exp(-jπnk/N)]，0≤k≤N-12. 在基于FFT算法的离散傅立叶变换中，当序列长度N为2的整数幂时，计算复杂度为：A. O(N^2)B. O(NlogN)C. O(logN)D. O(N)3. 对于一个由N个采样值组成的序列，它的z变换被定义为下式：X(z) = ∑[x(n) * z^(-n)]，其中n取0至N-1以下哪个选项正确表示该序列的z变换？A. X(z) = X(z)e^(-i2π/N)B. X(z) = X(z)e^(-iπ/N)C. X(z) = X(z^-1)e^(-i2π/N)D. X(z) = X(z^-1)e^(-iπ/N)1.2 简答题1. 请简要说明数字信号处理（DSP）的基本概念和应用领域。

2. 解释频率抽样定理（Nyquist定理）。

3. 在数字滤波器设计中，有两种常见的滤波器类型：FIR和IIR滤波器。

请解释它们的区别，并举例说明各自应用的情况。

2. 答案1.1 选择题答案1. B2. B3. D1.2 简答题答案1. 数字信号处理（DSP）是一种利用数字计算机或数字信号处理器对信号进行采样、量化、处理和重建的技术。

它可以应用于音频处理、图像处理、通信系统、雷达系统等领域。

DSP可以实现信号的滤波、变换、编码、解码、增强等功能。

2. 频率抽样定理（Nyquist定理）指出，为了正确地恢复一个连续时间信号，我们需要对其进行采样，并且采样频率要大于信号中最高频率的两倍。

1-1画出下列序列的示意图（1)（2）（3)（1）（2）(3)1-2已知序列x(n）的图形如图1.41，试画出下列序列的示意图。

图1。

41信号x(n)的波形（1）（2）(3)(4)（5)(6)(修正：n=4处的值为0，不是3） (修正：应该再向右移4个采样点）1-3判断下列序列是否满足周期性，若满足求其基本周期（1)解：非周期序列;（2)解:为周期序列，基本周期N=5；(3）解：，，取为周期序列,基本周期。

(4）解：其中，为常数，取，，取则为周期序列，基本周期N=40。

1—4判断下列系统是否为线性的？是否为移不变的？(1）非线性移不变系统（2）非线性移变系统(修正：线性移变系统)（3）非线性移不变系统（4)线性移不变系统（5）线性移不变系统（修正：线性移变系统）1—5判断下列系统是否为因果的？是否为稳定的？(1),其中因果非稳定系统(2）非因果稳定系统（3）非因果稳定系统（4)非因果非稳定系统（5)因果稳定系统1-6已知线性移不变系统的输入为x(n），系统的单位脉冲响应为h（n），试求系统的输出y(n）及其示意图(1）（2）（3）解:（1）（2）（3）1—7若采样信号m（t)的采样频率fs=1500Hz，下列信号经m（t）采样后哪些信号不失真？（1)(2）(3）解：（1)采样不失真(2）采样不失真(3)，采样失真1-8已知,采样信号的采样周期为。

（1)的截止模拟角频率是多少？(2)将进行A/D采样后，的数字角频率与的模拟角频率的关系如何?（3）若，求的数字截止角频率。

解：（1)（2)(3)1—9计算下列序列的Z变换，并标明收敛域。

（1)(2）(3）(4)（5）解：（1）(2)(3）(4)，,收敛域不存在(5）1-10利用Z变换性质求下列序列的Z变换.(1)(2）（3)（4）解：(1),（2)，(3）,（4），1—11利用Z变换性质求下列序列的卷积和。

(1)（2)(3)（4）(5）(6)解：(1），，，,（2),,，(3）, ，,（4），,（5),,，(6）,，，1—12利用的自相关序列定义为，试用的Z变换来表示的Z变换。

数字信号处理作业DFT 习题1. 如果)(~n x 是一个周期为N 的周期序列，那么它也是周期为N 2的周期序列。

把)(~n x 看作周期为N 的周期序列，令)(~1k X 表示)(~n x 的离散傅里叶级数之系数，再把)(~n x 看作周期为N 2的周期序列，再令)(~2k X 表示)(~n x 的离散傅里叶级数之系数。

当然，)(~1k X 是周期性的，周期为N ，而)(~2k X 也是周期性的，周期为N 2。

试利用)(~1k X 确定)(~2k X 。

（76-4）2. 研究两个周期序列)(~n x 和)(~n y 。

)(~n x 具有周期N ,而)(~n y 具有周期M 。

序列)(~n w 定义为)()()(~~~n y n x n w +=。

a. 证明)(~n w 是周期性的，周期为MN 。

b. 由于)(~n x 的周期为N ，其离散傅里叶级数之系数)(~k X 的周期也是N 。

类似地，由于)(~n y 的周期为M ，其离散傅里叶级数之系数)(~k Y 的周期也是M 。

)(~n w 的离散傅里叶级数之系数)(~k W 的周期为MN 。

试利用)(~k X 和)(~k Y 求)(~k W 。

（76-5）3. 计算下列各有限长度序列DFT （假设长度为N ）:a. )()(n n x δ= b ．N n n n n x <<-=000)()(δc ．10)(-≤≤=N n an x n（78-7）4. 欲作频谱分析的模拟数据以10千赫速率被取样，且计算了1024个取样的离散傅里叶变换。

试求频谱取样之间的频率间隔，并证明你的回答。

（79 -10）5. 令)(k X 表示N 点序列)(n x 的N 点离散傅里叶变换(a ） 证明如果)(n x 满足关系式：)1()(n N x n x ---=，则0)0(=X 。

(b ） 证明当N 为偶数时，如果)1()(n N x n x --=，则0)2/(=N X 。

数字信号处理习题解答（范文大全）第一篇：数字信号处理习题解答数字信号处理习题解答第1-2章：1.判断下列信号是否为周期信号，若是，确定其周期。

若不是，说明理由（1）f1(t)= sin2t + cos3t（2）f2(t)= cos2t + sinπt2、判断下列序列是否为周期信号，若是，确定其周期。

若不是，说明理由（1）f1(k)= sin(3πk/4)+ cos(0.5πk)（2）f2(k)= sin(2k)(3)若正弦序列x(n)=cos(3πn /13)是周期的, 则周期是N=3、判断下列信号是否为周期信号，若是，确定其周期;若不是，说明理由（1）f(k)= sin(πk/4)+ cos(0.5πk)（2）f2(k)= sin(3πk/4)+ cos(0.5πk)解1、解β1 = π/4 rad，β2 = 0.5π rad 由于2π/ β1 = 8 N1 =8，N2 = 4，故f(k)为周期序列，其周期为N1和N2的最小公倍数8。

（2）β1 = 3π/4 rad，β2 = 0.5π rad 由于2π/ β1 = 8/3 N1 =8，N2 = 4，故f1(k)为周期序列，其周期为N1和N2的最小公倍数8。

4、画出下列函数的波形(1).(2).解 f1(t)=tu(t-1)f2(t)=u(t)-2u(t-1)+u(t-2)5、画出下列函数的波形x(n)=3δ(n+3)+δ(n+1)-3δ(n-1)+2δ(n-2)6.离散线性时不变系统单位阶跃响应g(n)=8nu(n)，则单位响应h(n)=?h(n)=g(n)-g(n-1)=8nu(n)-8n-1u(n-1)7、已知信号为fs=（200)Hz。

πf(t)=5cos(200πt+)，则奈奎斯特取样频率38、在已知信号的最高频率为100Hz(即谱分析范围)时，为了避免频率混叠现象，采样频率最少要200 Hz：9.若信号f(t)的最高频率为20KHz，则对该信号取样，为使频谱不混叠，最低取样频率是40KHz10、连续信号：xa(t)=5sin(2π*20*t+π3)用采样频率fs=100Hz 采样，写出所得到的信号序列x(n)表达式，求出该序列x(n)的最小周期解：T=π1=0.01，x(n)=xa(nT)=5sin(0.4πn+)3fs=2π Nω0=2π=5 0.4π11、连续信号：xa(t)=Acos(80πt+π3)用采样频率fs=100Hz 采样，写出所得到的信号序列x(n)表达式，求出该序列x(n)的最小周期长度。

一、选择题1.D2.A3.B4.B5.B6.D7.C8.C9.B 10.D 11.C 12.B 13.B 14.B 15.D 16.B 17.B 18.C 19.B 20.A 21.C 2 2.B 23.B 24.B 25.B 26.B 27.D 28.A 29.B 30.C 31.D 32.A 33.C 34.D 35.C 36.A 37.C 38.D 39.D 40.D 41.D 42.B 43.B 44.C 45.D 46.B 47.A 48.C 49.B 50.D 51．C 52.B 53.C 54.B 55.A 56.D 57.C 58.A 59.B 60.B 61.D 62.D 63.B 64.B 65.A 66.A 67.B 68.C 69.C 70.D 71.D 72.C 73.B 74.C 75.A 76.D 77.D 78.A 79.C 80.C 81.D 82.D 83.A 84.B 85.A 86.D 87.B 88.C 89.C 90.D 91.D 92.C 93.D 94.A 95.A 96.D 97.B 98.D 99.B 100.C 101.C 102.B 103.D 104.B 105.B 106.D 107.D 108.C 109.C 110.D 111.C 112.A 113.A 114.D 115.D 116.B 117.D 118.C 119.B 120.B 121.B 122.B 123.C 124.B 125.B 126.D 127.D 128.C 129.A 130.D 131.B 132.B 133.C 134.C 135.B 136.C 137.C 138.B 139.D 140.C 141.B 142.B 143.B 144.B 145.D 146.B 147.B 148.A 149.C 150.C 151.B 152.A 153.C 154.B 155.D 156.B 157.A 158.D 159.D 160.A 二、判断题1. ×2. √3. ×4.×5. √6.√7. √8. √9.√ 10.× 11. √ 12. × 13. × 14.× 15. × 16. × 17. × 18. × 19. × 20. √ 21. × 22. √ 23. √ 24.× 25. √ 26. × 27. × 28. √ 29. × 30. √ 31. √ 32. × 33. √ 34. √ 35. × 36. √ 37. × 38. × 39. × 40. √ 41. × 42. × 43. √ 44. × 45. × 46. √ 47. √ 48. √ 49. √ 50. × 51. √ 52. × 53. √ 54. √ 55. × 56. √ 57. √ 58. √ 59. × 60. × 61. × 62. × 63. √ 64. × 65. × 66. × 67. × 68. × 69. × 70. √ 71. × 72. × 73. √ 74. × 75. × 76. × 77. × 78. × 79. √ 80. × 三、填空题1.22.栅栏3.圆周卷积的长度L ≥N 1+N 2-14.∑∞-∞=∞≤n n h )( 5.N π26.IIR 滤波器7.周期为N 的周期序列8.L9.21521)(--++=z z z H10.∑∞-∞=-=m m n m x n x )()()(δ11. 1 12.频谱泄漏 13. N 1+N 2-1 14.H （z ）的极点全部在单位圆内 15.单位圆 16.IIR 滤波器 137.∑∞-∞=+r rN n x )(，r 为整数 18.2N19.jw jw jw e e e H 2521)(--++= 20.)3()2()1()()(-+-+-+=n n n n n x δδδδ21. 40 22.N f s23.N 24.H （z ）收敛域包含单位圆 25.2)(∑∞-∞=n n x26.FIR 滤波器 27.720Hz 28.30720 29.∞≤<z 0 30.偶对称31. 5 32.频率混叠 33.2N-1 34.原点 35.4 36.并联型 37.21)(--++=cz bz a z H 38.10 39.32132---++z z z 40.z=-131. 14 32.蝶形 33.脉冲响应不变法 34.1±=z 35.直接型 36.按频率抽取 37.21)(--++=cz bz a z H 38.3 39.14 40.)1(zX41. 2 42.0,0)(<≡n n h 43.)2()1()(-+-=n n n h δδ 44.1=z 45.线性相位型 46.FIR 滤波器 47.按时间抽取 48.6 49.98 50.)(**z X 51.10 52.圆周卷积长度L ≥N 1＋N 2－1 53.2111-----+dz cz bz a54.jwjwjwe e e H 21)(--++= 55.直接型 56.∑∞-∞=+r rN n x )(57. 1024 58. 6 59. 30 60.)1(zX61.40 62.∑∞=-0)(m m n δ 63.N N2log 2 64. 2111-----+dz cz bz a 65.带限 66.j -1 67.主瓣宽度和旁瓣幅度 68.4 69.14 70.)(**z X 四、简答题1．信号分为连续信号和数字信号。

习题一1。

2 在过滤限带的模拟数据时，常采用数字滤波器，如图中T 表示采样周期（假设T 足够小，足以防止混迭效应），把从)()(t y t x 到的整个系统等效为一个模拟滤波器。

（a ） 如果kHz rad n h 101,8)(=π截止于，求整个系统的截止频率. （b)对于kHz T 201=，重复(a)的计算。

解 （a)因为当0)(=≥ωπωj e H rad 时，在数—模变换中)(1)(1)(Tj X T j X T e Y a a j ωω=Ω= 所以)(n h 得截止频率πω=c对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ，因此对T 8π没有影响，故整个系统的截止频率由)(ωj eH 决定,是625Hz.(b ）采用同样的方法求得kHz T 201=，整个系统的截止频率为 Hz Tf c 1250161==1。

3 一模拟信号x(t ）具有如图所示的带通型频谱，若对其进行采样,试确定最佳采样频率，并绘制采样信号的频谱.解：由已知可得：==35,25H L f kHz f kHz ,10k H L B f f Hz =-＝，为使无失真的恢复原始信号，采样频率应满足：2f 21c c s B f Bf m m+-≤≤+且220s f B kHz >=、0/12H m f B ≤≤-=⎡⎤⎣⎦ 当m=1时，2501c s f Bf kHz -==，满足： 3550s kHz f kHz ≤≤ 当m=2时,2252c s f Bf kHz -==，满足:23.325s kHz f kHz ≤≤ 故最佳采样频率为25kHz,采样信号的频谱图如下图所示 ：1。

5 判断下面的序列是否是周期的,若是周期的，确定其周期，并绘制一个周期的序列图（1）16()cos()58x n A n ππ=-，A 是常数 解：2251685N wπππ===，所以x （n ）是周期的，且最小正周期为5 1285()cos()40n x n A π-= 绘图：方法一:计算法 当n=0时,1()cos()8x n A π-==0。

数字信号处理习题及答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】==============================绪论============================== 1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统================== 1.①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用(n) 表示y (n )={2,7,19,28,29,15} 2. ①求下列周期②判断下面的序列是否是周期的; 若是周期的， 确定其周期。

（1）A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= （2）)81(j e )(π-=n n x 解： （1） 因为ω=73π, 所以314π2=ω, 这是有理数， 因此是周期序列， 周期T =14。

（2） 因为ω=81, 所以ωπ2=16π, 这是无理数， 因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法乘法序列{2，3，2，1}与序列{2，3，5，2，1}相加为__{4，6，7，3，1}__，相乘为___{4，9，10，2} 。

移位翻转：①已知x(n)波形，画出x(-n)的波形图。

②尺度变换：已知x(n)波形，画出x(2n)及x(n/2)波形图。

卷积和：①h(n)*求x(n)，其他2n 0n 3，h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5}，则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15} ③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=4. 如果输入信号为，求下述系统的输出信号。