不可能的图形

两可图1在这个图中，你看见的是一个老妇人还是一个年轻的少女？她们都存在在于插图中，但你不可能同时看见老妇人和少女。

一旦你知觉到这两种图形轮廓，看一看你是否能够在这两种图形轮廓之间来回转换。

两可图2在上图中，你看见了什么？你看见的是两个头，还是一个花瓶的轮廓？两可图3上面这幅图你看到了什么？是两个老人晚年的相聚，还是少女在倾听两个快乐的流浪歌手在弹唱？两可图3上面这幅图，你看到的是一位少女的脸还是一位萨克斯演奏家？两可图评注：根据人的不同知识背景或心理状态，同一个事物，不同的人会有不同的看法。

这和人的知觉选择性有关。

知觉选择性是指人根据当前的需要，对外来刺激有选择地作为知觉对象进行组织加工的过程。

这就是说，我们并不是对同时作用于感觉器官的所有刺激都进行反映，而是选择一个或几个刺激。

这些被选择的刺激就是知觉对象，其他没有被选择的就成了知觉背景。

知觉对象和知觉背景之间的关系是相对的。

此时的知觉对象可以成为彼时的知觉对象，而此时的知觉背景也可以成为彼时的知觉对象，它们之间是可以不断发生对换的。

当然，这种选择性会受到我们已有的知识经验、生活经历以及兴趣爱好等的影响。

"我们对世界的感知，部分依赖于对客观事物的感觉，另一部分---- 可能是更重要的的一部分，来自于我们的思维。

"---- William James 都说"耳听为虚，眼见为实"，可是我们的眼睛所见到的都是真实的吗？当你看了下面的心理错觉图片之后就会有一个比较客观的认识了。

如果大家想知道为什么会出现这些现象的话，可以看看后面的解释。

1缪勒－莱耶错觉2闪烁的格子人们在知觉两个相对立的颜色时，这两种相对立的颜色导致一种叫做侧抑制的生理机制，这个机制能使被白色环绕的区域显得更黑，相反，能使被黑色环绕的区域显得更白。

由于在看图的过程中，眼睛不停的跳动，使得侧抑制不停的产生，从而使得上图中出现了闪烁的黑点。

3深度知觉看着图形，慢慢移动你的眼睛，中间的圆形部分看起来是不是与其它的图形分离开来4咖啡墙错觉看一看，上面的这些线条是平行的吗？用尺子量一量，看看你的判断是否正确。

不可能图形的精品之作作者：
来源：《初中生世界·七年级》2013年第12期
不可能立体框架
右边几幅图画中的主体形象都是一个类似六面体的框架，但是仔细观察你就会发现，这些立体框架是不可能图形，根本无法造出来.
荷兰艺术家埃舍尔在1948年创作的名作《互绘的手》.
在一块四角被钉住的图板上，一只手被另一只手所描绘，与此同时，被描绘的手又画着另一只手. 平面的线描袖口贴在画板上，而画中的主体，两只拿着笔互绘的手则凸显在画板上，立体感十足.
瑞士艺术家普瑞特创作的不可能图形《晒台》，展示的是地坪与晒台上的工人们在协作施工的场景，感觉像在同一平面却又不在同一平面.
这是埃舍尔1960年创作的石板画《升与降》. 他在二维的画面上创造出一个不可能的三维图形，还不让你轻易地看出其中的奥秘. 两队士兵在一座城堡里走楼梯，一队士兵是一直上楼
梯，累得要死；另一队相向的士兵下楼梯，轻松自在地往下走. 如此走法，按正常道理两队人应该越走分离越远，但是图中这两队人却走成了个循环，这到底是怎么一回事？
《瀑布》是埃舍尔1961年的石版画. 楼顶水槽的水冲下来，带动底层的水轮转动. 由此推
动水向前流去，流水竟然会一直流呀流，流向楼顶水槽再冲下来，转动水轮……如此循环不止.
《相对论》是埃舍尔1953年的石版画. 也是他利用透视原理和光影效果画的一幅杰作.不
断地切换视线，你看到上楼的人、下楼的人都走得很合理，什么叫上，什么叫下，什么叫正面，什么叫背面，这些都是相对的.。

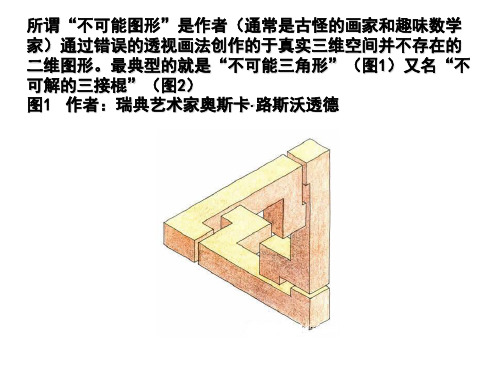
不可能图形
1958年美国的《心理学杂志》上，彭罗斯发表了他的不可解的三接棍.如图1-1.他称之为立体的矩形构造：三个直角并显示出垂直，但它是不可能存在于空间的，因为在这里三个直角似乎成了一个“三角形”，但三角形是平面而非立体的图形，三个内角和为180°，而非270°.
图1-1
20世纪50年代，罗格和彭罗斯写了论不可能图形的文章，文章描述了一种“没有尽头的楼梯”，踏着楼梯好像是一步一步地上升，然而楼梯都是停留在一个水平面上.如图1-2.
图1-2
荷兰著名画家埃舍尔被认为是20世纪公认的视错觉画大师.他
的作品以其深刻的数学、物理含义特别得到科学家的重视.如图1-3，他为第十届国际数学大会所作的会标，就是一个三维空间不可能的图形.
图1-3。

不可能立方体彭罗斯三角形彭罗斯三角形（Penrose triangle）第一次是被瑞典艺术家Oscar Reutersvärd创造出来，而后在20世纪50年代被数学家罗杰·彭罗斯（Roger Penrose）所推广。

其特点被以不可能图形为灵感来创作的艺术家埃舍尔（M. C. Escher）在其作品中很好地体现出来。

类似的图形还有彭罗斯正方形、彭罗斯五边形等。

彭罗斯三角形(2张)彭罗斯阶梯彭罗斯阶梯（Penrose Stairs），由莱昂内尔·彭罗斯（Lionel Penrose）和他的儿子罗杰·彭罗斯（Roger Penrose）创作。

是彭罗斯三角形的一个变式。

这是一个由二维图形的形式表现出来的拥有4个90°拐角的四边形楼梯。

由于它是个从不上升或下降的连续封闭循环图，所以一个人可以永进在上面走下去而不会升高。

显然这在三维空间中是不可能的。

[1]潘洛斯阶梯，又名潘罗斯阶梯、彭罗斯阶梯，由英国著名数学物理学家、牛津大学数学系名誉教授潘洛斯（Roger Penrose）提出。

潘洛斯阶梯是：四条楼梯，四角相连，但是每条楼梯都是向上的，因此可以无限延伸发展，是三维世界里需要在一定角度下才能看到的楼梯。

潘洛斯阶梯，曾出现在电影《盗梦空间》（Inception）里面的清醒梦境（lucid dream）中。

Arthur 展示给Ariadne看的奇怪阶梯，以及Arthur绕到佣兵背后的楼梯间，这是一座无限循环的阶梯。

这种不可能出现的物体来自于将三维物体描绘于二维平面时出现的错视现象。

其名称Penrose来自于英国数学物理学家罗杰·潘洛斯（Roger Penrose），他于1950年代设计了Penrose triangle，潘洛斯写了几篇文章讨论这些所谓的不可能事件，On the Cohomology of Impossible Figure这篇短文讨论了这些对象的群的上同调。

视错觉视错觉就是当人观察物体时，基于经验主义或不当的参照形成的错误的判断和感知。

我们日常生活中，所遇到的视错觉的例子有很多。

比如，法国国旗红：白：蓝三色的比例为35：33：37，而我们却感觉三种颜色面积相等。

这是因为白色给人以扩张感觉，而蓝色则有收缩的感觉，这就是视错觉。

2）比如把两个有盖的桶装上沙子，一个小桶装满了沙，另一个大桶装的沙和小桶的一样多。

当人们不知道里面的沙子有多少时，大多数人拎起两个桶时都会说小桶重得多。

他们之所以判断错误，是看见小桶较小，想来该轻一些，谁知一拎起来竟那么重，于是过高估计了它的重量。

3）比如我们在的士高厅跳舞时，在旋转耀眼的灯光中，你会觉得天旋地转，而其中的舞者跳得特别的活跃。

事实上，如果没有灯光的情况同一样的动作，你只会只是普通的扭来扭去罢了。

4）比如我们在高速公路用100公里的时速驾驭，会觉得车速很慢。

而我们在普通公路上用100公里的时速驾驭则会感到一种风驰电擎的感觉。

这就是因为我们的视觉受到了在同一条公路的其他车辆车速所影响。

从上面的几个例子我们可以得知，形成视错觉的原因有多种，它们可以是在快中见慢，在大中见小，在重中见轻，在虚中见实，在深中见浅，在矮中见高。

但他们的最终结果，都是使人或者动物形成错误的判断和感知。

所以，有效地利用视错觉，针对性地作出改善措施，有利于提高日常生活中的认识和识别能力。

如何利用视错觉1）矮中见高。

就是在居室中，其中一部分做吊灯，而另一部分不做，那么没有吊灯的部分就会显得“高”了。

2）虚中见实。

通过条形或整幅的镜面玻璃，可以在一个实在窨里制造出一个虚的空间，而虚的空间在视觉上却是实的空间。

3）冷调降温。

例如厨房大面积使用深色时，我们呆在里面，就会觉得温度下降2-3度。

4）粗中见细。

在实木地板或者玻化砖等光洁度比较高的材质会显得较高的材质边上，放置一些粗糙的材质，例如复古砖和鹅卵石，那么光洁的材质会显得更光洁，这就是对比形成的视错觉。

常见视错觉现象及其原理目录不可能三角形不可能的楼梯图形--背景错觉知觉的模糊深度错觉Ouchi错觉大小恒常性错觉左氏错觉弗雷泽螺旋缪勒--莱耶错觉达尔马提亚狗“反重力”的房屋浮箱错觉立体图像黑白视觉后像填充错觉赫尔曼栅格栅格火花错觉不可能的三角形这是怎么回事?!尽管这个不可能的三角形任何一个角看起来都是合情合理的,但是当你从整体来看,你就会发现一个自相矛盾的地方:这个三角形的三条边看起来都向后退并同时朝着你偏靠。

但是,不知何故,它们组成了一个不可能的结构!我们很难设想这些不同的部分是怎么构成一个看似非常真实的三维物体的!其实,造成“不可能图形”的并不是图形本身,而是你对图形的三维知觉系统,这一系统在你知觉图形的立体心理模型时强制作用。

在解释一幅三维图形的时候,你的视觉系统将会自动产生这一作用。

在现实生活中,我们可以构造出这个不可能三角形的物理模型,但这个模型只能从某一个角度看才是不可能的。

看一看下面的这个例子!其中,在镜子中显示的才是真实的结构!在把二维平面图形知觉为你三维立体心理图形时,执行这一过程的机制会极大地影响你的视觉系统。

正是在这一强制执行的机制的影响下,你的视觉系统对图形中的每一个点都赋予了深度。

此外,对你的视觉系统来说,当你感觉到一个荒谬的、不和常理的或者是矛盾的图形线索时,它将坚持这些强制约束机制,而不去否认这些线索。

具体来说,一幅图像的某些结构元素和你三维知觉解释系统的某些结构元素相对应。

例如,一个规则就是,二维直线应该被解释成三维直线。

同样的,二维的平行线应该被解释为三维的平行线。

连续的直线被解释为连续的直线。

在透视图像中,锐角和钝角都被解释为90°角。

外面的线段被看作是外形轮廓的分界线。

这一外形分界线在你定义整个心理图像的外形轮廓时起着及其重要的作用。

这些规则可以被总称为“一般视觉规则”,这一规则说明,在没有相反信息的影响下,你的视觉系统总是假定你在从一个主要视角观看事物。

怪图大全玛丽林门罗余象：盯着玛丽林门罗的像看三十秒或三十秒以上，不要动。

然后迅速朝一个硬的白色背景或灰色背景看。

你将发现她的嘴唇是红色的..变老的错觉：这个年轻人老了以后什么样儿?把图形倒过来就能找到答案填充物幻觉：用一只眼盯着左边暗影的中心点不要动。

几种钟后，左边暗影会消失。

用同样办法再试着看右边暗影的中心点。

这次暗影没有消失背景幻觉：你看到的是紫色的还是白色的厨房不可能的书架：这幅图形可能不可能?仔细看书架不可能发生的怪事：瑞典艺术家奥斯卡路透斯沃德创造的又一个奇思异想之物小丑还是马戏团?这里你能看到一个小丑的脸的幻觉图，但同时你也能找到马戏团吗有几个女人青涩宝贝大象有几条腿盯着左手边的格栅看三十秒或更久，保持不要动。

然后再迅速盯着右手边的格栅栏看。

你会发现右边的弯曲变形了隐藏的图像：你在这里看到了什么白色的幻觉两个灰色竖条块一样还是不一样呢不可能的叉子：你能数出几个分岔?把每个分岔的一半遮住，你将发现分岔另一半的端口都是完全成立的。

但当你把揭开盖住的另一半，你又会得到一个完全不可能的图形。

这幅图1964年开始出现于各种出版物中，没有人知道谁首先创造了这个著名的不可能图形摇动这幅图，你将看到虚幻的运动反射错觉,由麻省理工学院视力科学家泰德·安德森创作的这个图像中有两个幻觉。

左边的楼梯看起来象堆积的木块；但右边的却象台阶，这是一种不可能的建筑.第二，有一个反射幻觉：左端的木块深浅颜色的部分和右边向下的台阶的灰色条纹是一样的颜色排错的眼睛,眼睛看起来排错了吗？眼睛是排列整齐的。

圆圈对每一只眼睛是一个参照物,而你的意图是以参照物的顺序来判断秩序，既然圆圈打乱秩序，那么眼睛看起来也不齐。

这种幻觉只是面部二维代表下的一种幻觉效果。

摩托车的影子.用勺子叉子和刀子组合投射出一辆摩托车的影子克塔卡的螺旋.看起来像螺旋.但实际上是一系列的同心圆，当你盖住一半的图像，会看到什么照片A：美国魔术师杰瑞·安德鲁斯发明了一个“疯狂的板条箱”。

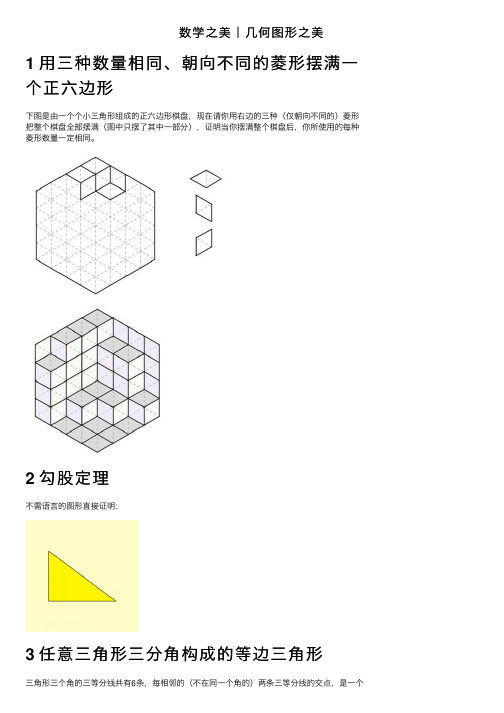
数学之美｜⼏何图形之美1 ⽤三种数量相同、朝向不同的菱形摆满⼀个正六边形下图是由⼀个个⼩三⾓形组成的正六边形棋盘，现在请你⽤右边的三种（仅朝向不同的）菱形把整个棋盘全部摆满（图中只摆了其中⼀部分），证明当你摆满整个棋盘后，你所使⽤的每种菱形数量⼀定相同。

2 勾股定理不需语⾔的图形直接证明：3 任意三⾓形三分⾓构成的等边三⾓形三⾓形三个⾓的三等分线共有6条，每相邻的（不在同⼀个⾓的）两条三等分线的交点，是⼀个等边三⾓形的顶点。

如下图①。

4 勒沃三⾓形，如上图②。

以等边三⾓形每个顶点为圆⼼，以边长为半径，在另两个顶点间作⼀段弧，三段弧围成的曲边三⾓形就是勒洛三⾓形（reuleaux triangle ），也称鲁洛三⾓形。

5 任意四边形的平形四边形任意四边形，每条边的中点的连续就是⼀平⾏四边形，如下：6 ⼏何平均值⼩于算术平均值⼏何平均数（geometric mean）是指n个观察值连乘积的n次⽅根。

是不等式中最重要和基础的等式。

7 黄⾦⽐例φ和黄⾦长⽅形把⼀条线段分割为两部分，使其中⼀部分与全长之⽐等于另⼀部分与这部分之⽐。

其⽐值是⼀个⽆理数，取其前三位数字的近似值是0.618。

由于按此⽐例设计的造型⼗分美丽，因此称为黄⾦分割，也称为中外⽐。

这是⼀个⼗分有趣的数字，我们以0.618来近似，通过简单的计算就可以发现：1/0.618=1.618(1-0.618)/0.618=0.618做⼀个RT三⾓形ABC,直边AC的长度是斜边BC的⼀半，以C为圆⼼，AC为半径，做圆交BC于D,以B为圆⼼，BD为半径做圆交AB于E，BE与EA之⽐即为黄⾦分割。

笔直可计算出，为[5^(1/2)-1]/2≈0.6188 不可能图形：彭罗斯三⾓形、彭罗斯阶梯不可能图形是由⼈类的视觉系统瞬间意识地对⼀个⼆维图形的三维投射⽽形成的光学错觉，在三维空间中它不可能存在，但研究它将会对⼈脑图像形成提供医学上的帮助。

9 透视错觉图下图中的两条红线因为透视的关系会给你⼀种错觉，认为处于右边较远透视位置的的红线要长。