最新分数乘除法易混淆易错题集中讲解

分数除法知识盘点知识点1：倒数1、意义：乘积是1的两个数互为倒数，互为倒数是两个数之间的关系，这两个数是相互依存的。

2、判断两个数是否互为倒数的唯一标准是：两数相乘的积是否为“1”。

例如：a×b=1则a 、b 互为倒数。

3、求倒数的方法： ①整数的倒数：1整数②真分数的假分数的倒数：分子、分母交换位置。

③小数与带分数的倒数：把小数和带分数化成分数，在把分子、分母交换位置。

知识点2：分数除法1、分数除以整数：除以一个不为0的整数，等于乘这个数的倒数。

2、被除数与商的变化规律：①除以大于1的数，商小于被除数：a÷b=c 当b>1时，c<a (a≠0) ②除以小于1的数，商大于被除数：a÷b=c 当b<1时，c>a (a≠0 b≠0)③除以等于1的数，商等于被除数：a÷b=c 当b=1时，c=a3、分数混合运算：①有括号的先算小括号里面的，再算中括号里面的，最后算括号外面的。

②没有括号的，先算乘除法，再算加减法。

③同级运算，从左往右依次计算。

知识点3：解决问题1、“已知一个数的几分之几是多少，求这个数”的问题的解法。

①设单位“1”的量为x ，列方程解答。

②已知量已知量占单位“1”的几分之几=单位“1”的量2、“已知比一个数多（或少）几分之几的数是多少，求这个数” 的问题的解法。

①根据数量关系“单位‘1’的量”或“单位‘1’的量单位‘1’的量” ，设单位“1”的量为x，列方程解答。

②确定单位‘1’的量，计算出已知量占单位“1”的几分之几，再根据分数除法的意义列式解答。

3、“已知两个数的和或差及这两个数的倍数关系，求这两个数” 的问题的解法。

先找出单位“1”的量并设为x，用含有x的式子表示另一个量，再根据两个数的和或差列方程解答。

4、工程问题数量关系式：工作总量=工作效率×工作时间；工作效率=工作总量÷工作时间；工作时间=工作总量÷工作效率易错集合易错点1：求一个数的倒数典例 0.5的倒数是多少？解析思路1：乘积是1的两个数互为倒数。

原题目：《分数乘法》易错题整理一、简介：本文档旨在整理《分数乘法》中易错的题目，帮助学生更好地掌握这一知识点。

共收集了多个题目，并针对每个题目进行解析和答案解释。

二、题目整理：1. 题目一：题目：1/2 × 3/4 = ？解析：在分数乘法中，我们需要将两个分数的分子相乘，分母相乘。

所以，1/2 × 3/4 = (1 × 3) / (2 × 4) = 3/8。

答案：3/82. 题目二：题目：2/3 × 1/5 = ？解析：同样地，我们将两个分数的分子相乘，分母相乘。

所以，2/3 × 1/5 = (2 × 1) / (3 × 5) = 2/15。

答案：2/153. 题目三：题目：4/5 × 1/2 = ？解析：继续将两个分数的分子相乘，分母相乘。

所以，4/5 ×1/2 = (4 × 1) / (5 × 2) = 4/10，可以约分为2/5。

答案：2/54. 题目四：题目：3/4 × 2/3 = ？解析：再次将两个分数的分子相乘，分母相乘。

所以，3/4 ×2/3 = (3 × 2) / (4 × 3) = 6/12，可以约分为1/2。

答案：1/25. 题目五：题目：5/6 × 2/5 = ？解析：继续将两个分数的分子相乘，分母相乘。

所以，5/6 ×2/5 = (5 × 2) / (6 × 5) = 10/30，可以约分为1/3。

答案：1/3三、结论：通过对以上题目的整理和解析，我们可以得出以下结论：- 在分数乘法中，将两个分数的分子相乘，分母相乘，得到乘积分数。

- 可以进一步约分乘积分数，使结果更加简化。

以上是《分数乘法》易错题整理的内容，希望对学生们的学习有所帮助。

分数乘除法应用题解题方法总结汇总在小学数学中，分数乘除法应用题是一个重点和难点。

很多同学在面对这类题目时，常常感到困惑，不知道如何下手。

其实，只要掌握了正确的解题方法和思路，这类问题就能迎刃而解。

接下来，我将为大家详细总结分数乘除法应用题的解题方法。

一、分数乘法应用题1、求一个数的几分之几是多少这是分数乘法应用题中最常见的类型。

例如：“小明有 120 元零花钱，花去了 1/3，花了多少钱？”解题思路：单位“1”的量×分率＝对应量在这个例子中，单位“1”的量是小明原有的 120 元零花钱，分率是1/3，所以用 120×1/3 ＝ 40（元），即小明花了 40 元。

2、连续求一个数的几分之几是多少例如：“果园里有苹果树 180 棵，梨树的棵数是苹果树的 2/3，桃树的棵数是梨树的 3/4，桃树有多少棵？”解题思路：先求出梨树的棵数，即 180×2/3 ＝ 120（棵），再求出桃树的棵数，120×3/4 ＝ 90（棵）。

二、分数除法应用题1、已知一个数的几分之几是多少，求这个数例如：“一本书，已经看了 1/4，正好是 50 页，这本书共有多少页？”解题思路：对应量÷分率＝单位“1”的量在这里，对应量是 50 页，分率是 1/4，所以用 50÷1/4 ＝ 200（页），即这本书共有 200 页。

2、已知比一个数多（或少）几分之几的数是多少，求这个数例如：“一件衣服，现价 120 元，比原价降低了 1/5，原价是多少元？”解题思路：如果单位“1”的量未知，设单位“1”的量为 x，根据数量关系列出方程求解。

设原价为 x 元，则（1 1/5）x ＝ 120，解得 x ＝ 150 元。

三、解题关键1、找准单位“1”单位“1”是分数乘除法应用题中的关键。

通常情况下，“是”“比”“占”后面的量就是单位“1”。

例如“男生人数是女生人数的3/4”，这里女生人数就是单位“1”。

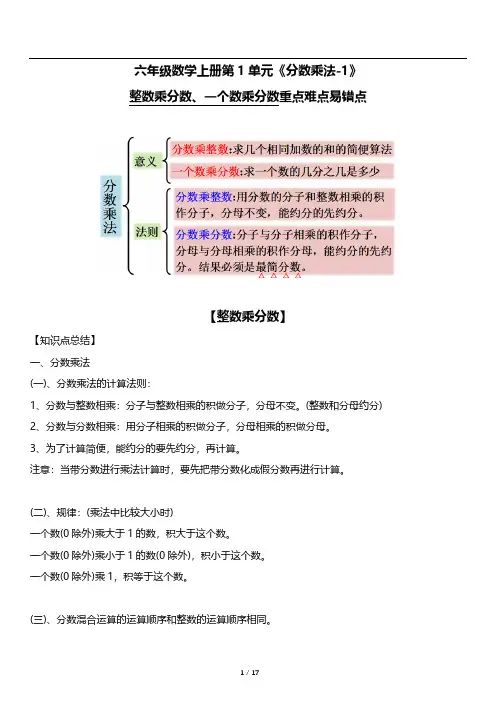
六年级数学上册第1单元《分数乘法-1》整数乘分数、一个数乘分数重点难点易错点【整数乘分数】【知识点总结】一、分数乘法(一)、分数乘法的计算法则：1、分数与整数相乘：分子与整数相乘的积做分子，分母不变。

(整数和分母约分)2、分数与分数相乘：用分子相乘的积做分子，分母相乘的积做分母。

3、为了计算简便，能约分的要先约分，再计算。

注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

(二)、规律：(乘法中比较大小时)一个数(0除外)乘大于1的数，积大于这个数。

一个数(0除外)乘小于1的数(0除外)，积小于这个数。

一个数(0除外)乘1，积等于这个数。

(三)、分数混合运算的运算顺序和整数的运算顺序相同。

(四)、整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

乘法交换律：a × b = b × a乘法结合律：( a × b )×c = a × ( b × c )乘法分配律：( a + b )×c = a c + b c a c + b c = ( a + b )×c【典例引入】看图列式【易错典例1】5个是多少？的是多少？【思路引导】要求5个是多少，用乘法计算，列式为×5；要求的是多少，同样用乘法计算，列式为×，计算即可．【完整解答】×5＝，×＝；答：5个是，的是．【易错注意点】此题考查了“一个数的几倍是多少”以及“已知一个数，求它的几分之几是多少”的应用题，用乘法计算．【易错典例2】（2019秋•洪泽区期中）在下面的长方形中画图，表示算式×．【思路引导】由分数乘法的意义可知：×表示是求的是多少，所以可把一个长方形的面积看作单位“1”，平均分成4份，取其中的3份，即表示出，再把这3份平均分成5份，取其中的2份即可．【完整解答】如图：靛青色表示的就是．【易错注意点】本题考查了分数的意义及分数乘法的意义，掌握以谁为单位“1”，平均分成几份是解决此题的关键．考点1：分数乘整数1．（2020春•新野县期末）下面说法中不能表示出kg的是（ ）A．1kg的B．5kg的C．6kg的D．5个kg【思路引导】根据求一个数的几分之几是多少，用乘法分别求出各个选项中结果，再进一步解答。

分数乘除法易错点讲义一、分数乘法意义与整数乘法的意义的区分一个数乘以一个分数的意义是求这个数的几分之几；一个数乘以整数的意义是求这个数的几倍.整数乘法的意义是表示几个相同加数和的运算。

那么分数乘法的意义和整数乘法的意义相同吗？请说出表示的意义：2×3211×3 3×211211×13得出结论：一个数乘以整数的意义与整数乘法意义相同，而一个数乘以分数的意义与整数乘法不同。

总得来讲分数乘法意义与整数乘法意义不同。

二、没有真正理解分数除法的意义分数除法的意义：已知两个因数的积与其中一个因数，求另一个因数。

很多同学无法区分题目中的积与因数，导致技术出错。

请看以下两个题目。

1、把215米长的铁丝平均分成4段，每段是全长的（），每段长（）米。

2、一辆汽车行10千米用汽油45千克，平均1千米用汽油多少千克？三、没有真正理解单位“1”，在做相关题是没有做到“一一对应”（单位“1”的分率对应相关的量）1、小明看一本故事书，第一天看了全书的14，第二天看了全书的15,第一天比第二天多看了10页，这本故事书一共有多少页？2、运送一批水泥，第一天运了这堆水泥的14，第二天运的是第一天的23,还剩84吨没有运，这堆水泥多少吨？练习题1. 李师傅加工一批零件，每天加工这批零件的,5天加工330个零件，求这批零件一共有多少个？2. 甲、乙、丙三人种树，甲种的棵树是乙丙和的，乙种的棵树是甲丙和的，已知丙种了260棵，求甲乙各种了多少棵？3. 图书馆新购进3种书，其中工具书有180本，科技树占总数的，文艺书的本数是其他两种书本数的。

购进的3种书共有多少本？。

《分数乘法》易错题整理引言分数乘法是数学中的一个重要概念，是进一步学习数学和其他科学知识的基础。

在分数乘法的学习过程中，学生需要掌握分数乘法的规则、方法和技巧，同时还需要注意一些易错点。

本文将整理常见的分数乘法易错题，并进行分析和解答，以帮助学生更好地掌握分数乘法的知识和技能。

易错点1：分子、分母颠倒在分数乘法中，分子和分母的位置是固定的，不能颠倒。

一些学生常常犯分子、分母颠倒的错误，导致计算结果错误。

例如，将的分子和分母颠倒成，就会得出错误的结果。

应对策略：正确理解分数的基本概念，始终保持分数的分子和分母位置正确。

可以在计算时，采用“分子乘分子，分母乘分母”的方法，以避免分子、分母颠倒的错误。

易错点2：忽略分数单位的转换在分数乘法中，有时会涉及到不同单位的分数之间的计算。

一些学生常常忽略分数单位的转换，导致计算结果错误。

例如，将“米”和“分米”两个单位直接相乘，得出错误的结果。

应对策略：在进行分数乘法计算时，首先要将分数转换成相同的单位，然后再进行计算。

如果分数的单位不同，需要将单位进行转换，如将“米”转换为“分米”，或将“小时”转换为“分钟”等。

转换单位的计算方法为：小单位除以大单位。

例如，“米”转换为“分米”的计算方法为：1米=10分米，因此1米/10=1分米。

易错点3：运算顺序错误在分数乘法中，运算顺序是非常重要的。

一些学生常常因为运算顺序错误而导致计算结果错误。

例如，在计算时，先将分子和分母约去，再与另一个分数相乘，就会得出错误的结果。

应对策略：在进行分数乘法计算时，要遵循运算顺序。

首先应该进行乘法运算，再进行除法运算。

正确的计算方法是：先不考虑运算顺序，直接将分子和分母约去，然后再进行乘法运算。

这样可以避免运算顺序错误导致的计算结果错误。

总结本文整理了《分数乘法》中的三个易错点：分子、分母颠倒，忽略分数单位的转换和运算顺序错误。

这些易错点是学生在学习分数乘法时容易出现的错误，也是教师需要重点关注和纠正的地方。

人教版六年级数学上册分数乘除法易错题精选分数乘除法易错题精选一、倒数的意义：乘积为1的两个数互为倒数。

1.倒数是两个数的关系，它们互相依存，不能单独存在。

必须明确谁是谁的倒数。

2.判断两个数是否互为倒数的唯一标准是：两数相乘的积是否为1.例如：a×b=1则a、b互为倒数。

举例：1.一个数加上它的倒数，结果正好是2，这个数是多少？2.最小的奇数的倒数和最小的合数的倒数的和是多少？3.互为倒数的两个数，它们的乘积比它们的和小。

4.所有自然数都有倒数。

3.求倒数的方法：交换分数的分子、分母的位置。

举例：1.375的倒数是1/375.2.10的倒数是1/10，2/5的倒数是5/2.二、分数除法的意义：分数除法是分数乘法的逆运算，已知两个数的积与其中一个因数，求另一个因数的运算。

举例：1.2/9÷5的意义是，已知2/9×5，求另一个因数。

2.1/2÷4/3的意义是，已知1/2×4/3，求另一个因数。

三、分数除法计算法则：除以一个数（除外），等于乘上这个数的倒数。

注意：除法转化成乘法时，被除数一定不能变，“÷”变成“×”，除数变成它的倒数。

被除数与商的变化规律：（比较大小时使用）1.除以大于1的数，商小于被除数：a÷b=c当b>1时，c<a。

(a≠0)2.除以小于1的数，商大于被除数：a÷b=c当ba。

(a≠0.b≠0)3.除以等于1的数，商等于被除数：a÷b=c当b=1时，c=a举例：1.如果1/5×A=5/8×B=1，那么A+B=？2.已知a、b、c都不是零，a×13/12=b×14/15=c×8/8，那么a、b、c有小到大的顺序是什么？3.一个数除以4就是把这个数缩小到原来的1/4.单位换算技巧：四、填空易错题：1.14÷3小时=（）分，25米=（）厘米，5公顷=（）m²，5/2平方分米=（）平方米。

第7讲分数除法（讲义）学校数学六班级上册易错专项练（学问梳理+易错汇总+易错精讲+易错专练）1.分数除法的意义。

分数除法的意义与整数除法的意义相同，都是已知两个因数的积与其中一个因数，求另一个因数的运算。

2.分数除法的计算方法。

除以一个不等于0的数，等于乘这个数的倒数。

3.分数四则混合运算的运算挨次。

分数四则混合运算的运算挨次和整数四则混合运算的运算挨次相同。

含有两级运算的，要先算乘、除法，再算加、减法;只含有同级运算的，要依据从左到右的挨次依次计算；算式中带有括号的，要先算括号里面的，再算括号外面的。

4.已知一个数的几分之几是多少，求这个数的问题的解法。

方法一：列方程解答，单位“1”的量（这个数）未知。

方法二：用算术法解答，已知量÷已知量占单位“1”的几分之几=单位“1”的量。

5.已知比一个数多（或少）几分之几的数是多少，求这个数的解题方法。

方法一：列方程解答，单位“1”的量（这个数）±单位“1”的量（这个数）×几分之几＝已知量；单位“１”的量（这个数）×(1±几分之几)＝已知量。

方法二：用算术法解答，已知量÷（1±几分之几）=单位“1”的量（这个数）。

6.已知一个数是另一个数的几分之几及这两个数的和（或差），求这两个数分别是多少的问题的解法。

先找出单位“1”的量并设为x，用含有x的式子表示另一个量，再依据两个数的和（或差）列方程解答。

7.被除数与商的变化规律①除以大于 1 的数，商小于被除数：a÷b=c 当 b>1 时，c<a (a≠0) ②除以小于 1 的数，商大于被除数：a÷b=c 当 b<1 时，c>a (a≠0 b≠0) ③除以等于 1 的数，商等于被除数：a÷b=c 当 b=1 时，c=a 8.工程问题。

设这项工程为一个具体数量或者“１”，依据“工作总量÷工作效率总和 ＝工作时间总和”列式解答。

新人教版小学六年级数学上册第3单元“分数除法”易错知识点解析易错点1没有理解倒数的意义【错例1】一个数的倒数是67，这个数的是34（）。

【错误答案】9 14【错因】本题错在没有正确理解倒数的意义。

错题闯关1．下面四组数，（）的两个数互为倒数。

A．3与0.3B．35与73C．213与37D．0.2与25【答案】C2．下列几组数中，互为倒数的两个数是（）A．23和13B．10和101C．67和116D．32和123【答案】C3．0.2和（）互为倒数。

A．5B．15C．12D．0.5【答案】A4．下列说法错误的是（）A．1的倒数是它本身，0没有倒数B．真分数的倒数一定比它大C．用互为倒数的两个数做长方形的长和宽，这个长方形的面积一定是1 D．因为13+23=1，所以13和23互为倒数【答案】D5．下列各组的两个数互为倒数的是（）A．35和25B．17和7C．15和54D．12和0.5【答案】B6．因为311×113=1，所以（）A．311是倒数B．113是倒数C．311和113都是倒数D．311和113互为倒数【答案】D7．一个分数的分子是互为倒数的两个数的积，分母是20以内最大的质数，这个分数是（）A．12B．119C．419D．417【答案】B8．100以内的自然数（不包含100）中，（）的倒数最大。

A．0B．1C．99【答案】B9．下列各题中，互为倒数的是（）。

A．4.1和1.4B．56和16C．0.8和1.25D．0和0【答案】C10．将互为倒数的两个数用线连起来．【答案】11．甲数是56，乙数是甲数的倒数的5倍，乙数是多少？【答案】1÷56×5=65×5＝6答：乙数是6。

易错点2不理解分数除法的意义【错例2】计算712÷14。

【错误答案】12711147121424÷=⨯=【错因】本题错在没有掌握分数除以整数的计算方法。

被除数712不应该变成它的倒数。

分数乘法的易错点总结
在分数乘法中，经常出现一些易错点，可能会导致计算错误。

为了
帮助大家更好地掌握分数乘法，下面总结了一些常见的易错点，并提
供了相应的解决方法。

首先，一些学生在进行分数乘法时容易忽略分子之间的相乘，仅仅
将分母相乘或者只将分子相乘。

这样的错误会导致计算结果不正确。

解决这个问题的方法是，在进行分数相乘时，一定要同时考虑到分子
和分母的相乘，不能忽略其中任何一个部分。

其次，有些学生在化简分数乘法的过程中，忘记了对结果进行最简
形式的约分。

这样会使得计算结果不够精确，给答案带来误差。

因此，在进行分数乘法后，一定要将结果化简至最简形式，以确保计算的准
确性。

另外，有时候学生在进行带分数的乘法时，容易将分子和分母乘错
位置，导致答案错误。

为了避免这种错误，建议在进行带分数的乘法时，先将带分数化成假分数，然后再进行相乘。

这样可以减少混淆，
降低出错率。

此外，有些学生在进行混合分数的乘法时，容易混淆整数与分数的
相乘。

这种情况下，需要先将混合分数转化成假分数，然后再进行相乘。

正确的顺序可以帮助避免混淆，确保计算结果的正确性。

总的来说，在进行分数乘法时，要注意分子和分母的相乘，化简结果，正确处理带分数和混合分数的计算，以避免常见的易错点。

通过
加强练习和理解，相信大家都能够掌握好分数乘法，提高计算准确性。

【总结完毕】。

分数乘除法易错题一、填空题。

51、把一根长9 m 的绳索均匀分红5 段，每段长（） m ，每段是全长的（）。

932、张亮步行10千米要10小时，那么步行 1 千米要（）小时， 1 小时步行（）千米。

333、A=4× B=C ÷2=D ÷2 (A ≠0)将 A 、B 、C 、D 从大到小的次序摆列为：（）。

14、养殖场有鸡 320 只，比鸭的只数多4，鸭有（）只。

63395、（）的 7 是 5 千米。

4 千克是10千克的（）。

36一个数的4是 60，这个数的5是（）。

1160 千克比（）千克少 4，比 60 千克多 5的是（ ）千克。

3甲数是乙数的 4 ，甲比乙少（），乙比甲多（）。

6、把 25 克糖放入 100 克水中，糖占糖水的（ ），糖占水的（）。

127、一个最简分数，假如分子加上1，能够约分为 3 ，假如分子减去 1，能够约分为 9 。

那么这个最简分数是（）。

8、水结成冰后体积增添了 111 ，冰化成水后，体积减少了（）。

二、选择题。

4（）1、男生人数是女生人数的 5，女生人数是男生人数的（）(1)男生是 份，女生是份。

1 1 (2)男生比女生少。

A 、4B 、511(3)女生比男生多。

A 、4B 、53（）2、泊车场里有小汽车的辆数是大汽车的4，大汽车的辆数是小汽车的（）？34 A 、4 B 、3C 、不会1（）3、小汽车比大汽车少4，大汽车比小汽车多（）?1 4 3 1 A 、4B 、3C 、4D 、3一、 看图，列式计算。

45 人7 、？人？人8 、52 人 65 人9 、比合唱队少54 人三、解决问题。

4 1、（1）某校美术班有男生20 人，是女生的5，该校美术班女生有多少人？ 4（ 2）某校美术班有男生 20 人，女生是男生的5，该校美术班女生有多少人？62、（1）小明家九月份电话费相当于八月份的7，小明家九月份电话费 42 元，八月份电话费多少元？6（2）小明家九月份电话费相当于八月份的7，小明家八月份电话费 49 元，九月份电话费多少元？33、（1）一套真皮沙发原价 2100 元，此刻比本来降低了10。

2020年人教版六年级数学上册优选易错题专项汇总第一章《分数乘法》一．选择题1．5米的和1米的相比，下面说法正确的是（）A．5米的长B．1米的长C．一样长D．无法比较【分析】首先计算出5米的和1米的分别是多少都用乘法，然后比较分数的大小．【解答】解：5×＝（米），1×＝（米），所以5米的和1米的大小相等；故选：C．2．当a是一个大于0的数时，下列各式计算结果最大的是（）A．a×B．a÷C．a÷D．不能确定大小【分析】用举例法，a是一个大于0的数，可假设a＝5，代入各选项，然后比较得解．【解答】解：设a＝5，代入得：A、a×＝5×＝4，B、a÷＝5×＝6，C、a÷＝5×＝4，6最大，故选：B．3．a是一个大于0的数，下面的算式中得数最大的是（）A．a×B．a÷C．a÷D．a【分析】a是一个大于0的数，假设a＝5，代入各选项，验证得解．【解答】解：A、a×＝5×＝3；B、a÷＝5×＝8；C、a÷＝5×＝3；D、a＝×5＝38最大，故选：B．4．如图中的阴影部分表示（）A．÷B．×C．÷D．×【分析】图中是先把长方形平均分成了3份，其中的两份就是，再把这两份平均分成了5份，给其中的4份涂色，就是这两份的，也就是的，即×．【解答】解：表示的含义是：×．故选：B．5．甲数的等于乙数的时，甲数（）乙数．A．大于B．小于C．等于【分析】根据题意列出算式，再根据比例的基本性质进行化简，由于甲数除以乙数大于1，所以可以根据此判断两数的大小．【解答】解：甲数×＝乙数×，＝，＝，所以甲数大于乙数，故选：A．二．填空题6．在横线里填上“＜、＞或＝”．÷＞＜×3×1＝÷1．【分析】根据一个数（0除外）乘等于1的数，积就等于这个数，一个数（0除外）乘大于1的数，积就比这个数大，一个数（0除外）乘小于1的数，积就比这个数小，如果算式是除法就变成乘法再判断．【解答】解：（1）÷＝，因为＞1，所以，即÷＞，（2）因为3＞1，所以，即＜×3，（1）因为×1＝1，÷1＝1，所以×1＝÷1．故答案为：＞，＜，＝．7．4＝．【分析】因为4个相加，所以+++＝×4，再根据分数乘整数的计算方法：分母不变，分子和整数相乘，求出答案．【解答】解：+++＝×4＝；故答案为：4，．8．30米增加是36米，30米增加米是30米．【分析】①把30米看作单位“1”，也就是求30米的（1），根据一个数乘分数的意义，用乘法解答．②因为米是一个具体数量，所以直接用加法解答．【解答】解：①30×（1），＝30×，＝36（米）；②30＝30（米）；故答案为：36，30．9．36千克的是24千克；36比30多20%．【分析】（1）把36千克看成单位“1”，用36乘即可求出要求的质量；（2）把要求的质量看成单位“1”，它的（1+20%）是36千克，根据分数除法的意义，用36千克除以（1+20%）即可求解．【解答】解：（1）36×＝24（千克）答：36千克的是24千克．（2）36÷（1+20%）＝36÷1.2＝30（千克）答：36比30多20%；故答案为：24，30．10．4千克的和1千克的相等．√．【分析】根据一个数乘分数的意义，分别用乘法求出4千克的和1千克的分别是多少千克，然后比较即可．【解答】解：4×＝（千克），1×＝（千克），所以4千克的和1千克的相等；故答案为：√．三．判断题11．1吨的等于3吨的．√．（判断对错）【分析】根据一个数乘分数的意义，用乘法分别求出1吨的和3吨的，然后进行比较即可．【解答】解：1×＝（吨）3×＝（吨）所以1吨的等于3吨的．故答案为：√．12．甲数比乙数多，乙数是甲数的．√．（判断对错）【分析】可以根据题意把甲数和乙数设为具体数，然后再求乙数是甲数的几分之几，据此判断即可．【解答】解：由题意知，可设甲数7，则乙数为6，正好符合甲数比乙数多，乙数是甲数的：6÷7＝，所以上面的说法是正确的．故答案为：√．13．7个米是7米．×．（判断对错）【分析】7个米是多少，用7×求出得数，然后与7米比较即可．【解答】解：7×＝1（米）；1≠7；故答案为：错误．14．两根各1米长的绳子，分别剪去和米，剩下的部分同样长．√（判断对错）【分析】第一个的单位“1”是1米长的绳子，剩下的长度就是单位“1”的1﹣，用乘法可以求出剩下的长度；第二个表示一个具体的数量，剩下的长度就用全长减去剪去的长度；分别求出两根绳子的长度，再比较．【解答】解：第一根剩下的长度：1×（1﹣）＝1×＝（米）；第二根剩下的长度：1﹣＝（米）；两部分相等．故答案为：√．四．计算题15．直接计算×12＝6×＝×＝+＝2×＝72÷＝﹣＝÷12＝÷＝÷＝××10＝÷＝÷÷＝＝【分析】根据分数乘法、分数除法、分数加法和分数减法的计算方法进行计算即可得到答案．【解答】解：×12＝6×＝×＝+＝2×＝2 72÷＝81 ﹣＝÷12＝÷＝÷＝××10＝÷＝÷÷＝＝516．直接写得数9×＝×＝×12＝×＝45×＝÷＝25÷＝÷＝÷＝÷28＝【分析】根据分数乘除法的计算方法计算即可解答．【解答】解：9×＝×＝×12＝10 ×＝45×＝27÷＝25÷＝55 ÷＝6 ÷＝÷28＝17．列式计算．①18米的是多少米？②比10的多2的数是多少？【分析】①根据一个数乘分数的意义：求这个数的几分之几是多少，用乘法解答；②先用乘法求出10的，然后加上2即可．【解答】解：①18×＝8（米）答：18米的是8米；②10×+2＝6+2＝8；答：比10的多2的数是8．18．图中的大长方形表示“1”，根据图中的斜线部分写出乘法算式．【分析】通过观察图示，把大长方形看作“1”，把整个图形平均分成3份，取其中的2份，即；图中的斜线部分表示又把这2份平均分成了5份，取其中的3份，即．因此图中的斜线部分写成乘法算式为．【解答】解：＝．五．解答题19．+++＝×4＝＝．【分析】根据分数乘整数的意义：求几个相同分数的和是多少，用乘法解答，然后根据分数乘整数的计算法则，进行解答即可．【解答】解：+++＝×4＝＝．故答案为：，4，，．20．请你列式计算．（1）9个是多少？（2）kg的是多少千克？（3）小时的是多少小时？【分析】（1）根据分数乘整数的意义：求几个相同加数的和是多少，用乘法解答；（2）、（3）根据求一个数的几分之几是多少，用乘法解答．【解答】解：（1）×9＝答：9个是；（2）×＝（千克）；答：kg的是千克；（3）×＝（小时）答：小时的是小时．21．千克的是千克，吨是吨的．【分析】根据一个数乘分数的意义：求这个数的几分之几是多少，用乘法解答；根据求一个数是另一个数的几分之几，用除法解答．【解答】解：×＝（千克）÷＝答：千克的是千克，吨是吨的；故答案为：，．22．根据算式涂一涂，画一画，再计算．×＝．【分析】根据乘法算式，把长方形看作单位“1”，平均分成4份，表示其中的3份是，再把看作单位“1”，平均分成3份，表示其中的2份，就是求的是多少用乘法计算．【解答】解：根据分数的意义可得，故答案为：．23．乙是甲的，丙是乙的，用线段图表示它们的关系．【分析】把甲看作单位“1”，平均分成3份，表示其中的2份就是乙，再把乙看作单位“1”，平均分成4份，表示其中的一份就是丙，据此解答．【解答】解：画图如下，24．计算下面各题××3×4×2×51×21．【分析】根据分数乘整数的计算法则：用分数的分子和整数相乘的积作分子，分母相乘的积作分母，能约分的先约分，然后再乘．【解答】解：××3＝×4＝×2＝×51＝24×21＝。

六年级分数乘除法易错题1、计算（1）7226123÷+÷ （2）1913352219133548÷+÷ （3）652.054⨯÷（4）⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫⎝⎛+÷131513215 （5）⎥⎦⎤⎢⎣⎡÷⎪⎭⎫ ⎝⎛-⨯735.05410 （6）⎥⎦⎤⎢⎣⎡÷⎪⎭⎫ ⎝⎛-+⨯21411671615982、解方程（1）12031=+x x （2）158272876÷=÷x （3）43194=÷x3、把一根109米长的木料锯成长度相等的几段，一共锯了5次。

平均每段长多少米？4、王阿姨到菜场买了52千克的白菜，用去53元。

每千克白菜多少元？5、一个三角形的面积是245平方分米，它的底边长是41分米，底边上的高是多少分米？6、某车间有女工30人，女工调走51后，剩下的女工人数正好是男工人数的98，这个车间男工有多少人？7、小东和小亮共有邮票420张，其中小东的邮票枚数是小亮的43，小亮和小东各有多少枚？8、一辆汽车从甲城到乙城，上午行了200千米，下午行了250千米，还剩下全程的101。

甲、乙两城之间的路程有多少千米？9、一个工程队修一条水渠，第一周修了全长的83，第二周修了全长的21，还剩下110米没修完，这条水渠共有多少米？10、小明家养了56只鸡，其中公鸡只数比母鸡少53，小明家公鸡和母鸡各多少只？11、一桶油，第一天用去它的52，第二天用去10千克，两天正好用去这桶油的一半，这桶油原有多少千克？12、一袋大米，用去31后又加入8千克，这时袋里的大米恰好是原来的54，这袋大米原来有多少千克？13、某机器制造厂生产机器，上半年完成全年计划的74，下半年完成全年计划的53，结果全年超额生产了120台机器，全年计划生产多少台机器？14、原来生产一台机床需要用钢材54吨，技术革新后，每台比以前节约钢材101吨。

分式乘除运算中应注意的问题1．分式乘以分式，用分子的积做积的分子，分母的积做积的分母；分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘。

用式子表示是bc ad c d b a d c b a bd ac d c b a =⨯=÷=⨯；，其中，a ，b ，c ，d 表示整式。

2．（1）①应用分式的乘法法则，用分子的积做积的分子，分母的积做积的分母；②把分式的分子、分母分别写成它们的公因式的积的形式；③约分，得到计算的结果。

（2）①应用分式的除法法则，把除式的分子、分母颠倒位置后，与被除式相乘；②根据分式的符号法则，把第二个分式的分母中的负号提到分式的前面，同时改变了分母与分式的符号；③把分式的分子、分母分别写成它们的公因式与另一个因式积的形式；④约分，得到计算的结果。

（3）①先把第一个分式的分子与分母、第二个分式的分母分别进行因式分解；②用分子的积做积的分子，分母的积做积的分母；③约分，并运用乘法公式，得到计算结果。

3．当分式的分子与分母都是单项式时：（1）乘法运算步骤是，①用分子的积做积的分子，分母的积做积的分母；②把分式积中的分子与分母分别写成分子与分母的公因式与另一个因式的乘积的形式，如果分子（或分母）的符号是负号，应把负号提到分式的前面；③约分，得到计算的结果。

（2）除法的运算步骤是，把除式中的分子与分母颠倒位置后，与被除式相乘。

其它与乘法运算步骤相同。

当分子与分母都是多项式时：（1）乘法的运算步骤是，①把各个分式的分子与分母分解因式；②用分子的积做积的分子，分母的积做积的分母；③约分，计算，得出结果。

（2）除法的运算步骤是，①把各个分式的分子与分母分解因式；②把除式的分子与分母颠倒位置后，与被除式相乘；③约分，得到计算结果。

4．（1）如果分式的分子、分母中有多项式，可先分解因式；如果分子与分母有公因式，先约分在计算。

（2）如果分式的分子（或分母）的符号是负号时，应把负号提到分式的前面。