1.1.2 弧度制 (1)

3.弧度制与角度制之间如何换算？ 利用：
角度制与弧度制的换算公式：
[例1]把下列各角化为弧度
（1）30°（2）-45°（3）6730
解：∵
6730
67
1 2
∴
6730
π 180
rad
67
1 2
3πrad 8
例2 角度与弧度互化
(1)22 30'
(4)
12
(2)-210
(5)- 4
3
(3)1200
You Know, The More Powerful You Will Be
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
演讲人：XXXXXX 时 间：XX年XX月XX日
2rad
A
r
Oo
AOB=1rad
AOC=2rad
1弧度：α
L r
?
我们把等于半径长的圆弧所对的圆心角
叫做1弧度的角．
完成下列填空：若圆的半径为 r；弧长为 L．
当L取下列值时写出对应的 圆心角
(1)L r
α _1_r__a__d;
(2)L 2.5r α2_._源自_r__a_d;(3)L πr α __r__a_d_;
(4)L 2πr α2___r__a_d;
思考：若角α是一个负 角；它的弧度数如何表示？
若L 4πr;α 0则：
L 4r 4
rr
|α|
L r
结论：正角的弧度数是 正数；
负角的弧度数是一个负 数；
零角的弧度数是0。
2.周角是多少度？多少弧度？平角呢？ 直角呢？

180 1 rad 57.30 57 18
1

180
rad 0.01745 rad
180 rad
精确值
近似值
180 1 rad 57.30 57 18
例1、按照下列要求,把67030'化成弧度. (1)精确值; (2)精确到0.001的近似值.
所有与角 终边相同的角，连同角 在内， 可构成一个集合
S = = +k 360 , k Z


即任一与角 终边相同的角，都可以表示成角 与整数个周角的和。
1、什么叫角度制 ？
用度作单位来度量角的单位制叫做角度 制。单位为“度”（即“ º ”）。
2、1º 的角是怎样规定的？
135 (1)因为 67 30 解： ， 2

所以
135 3 67 30 rad rad. 180 2 8
(2)由于 1 所以

180
rad 0.01745 rad ，
67 30 67.5 67.5 0.01745 rad 1.178 rad.
三、弧度与角度的换算
用角度制和弧度制来度量零角，单位不同，但 数量相同（都是0）；用角度制和弧度制来度量任一 非零角，单位不同，数量也不同。 因为周角的弧度数是 2 ，而在角度制下的度数 是 360 。所以有：
360 2 rad 180 rad 1 rad 0.01745 rad 180
例2、把3.14rad换算成角度(用度数表示,精确 到0.001).
解： 因为
180 180 1 rad 57.2956 , 3.1416 所以

圆心角α （弧度）
r r
1
2r r
2
3r r
3
2r
r
r
r
2

l r
l r
引申
若∠AOB为负角，且 l 2r ，∠AOB为多少弧度？ -2 rad l 公式 应该如何修改？ r
1.正角的弧度数 负角的弧度数 零角的弧度数
正数 负数 零
l 2. r
弧长公式：l
3.利用弧度制,使得弧长公式和扇形的面 积公式得以简化,这体现了弧度制优点.
作业：
P10 习题1.1 A组： 6，7，8，9，10.
练习 已知
则:
A B | 6 , 或0
A | 2 (2k 1) ( ) B | 6 6
1.1
任意角和弧度制 弧度制
1.1.2
问题提出 1.角是由平面内一条射线绕其端点从一个位置 旋转到另一个位置所组成的图形，其中正角、负 角、零角分别是怎样规定的？ 2.在直角坐标系内讨论角,象限角是什么概念？ 3.与角α 终边相同的角的一般表达式是什么？ S={β|β=α＋k· 360°，k∈Z} 4.长度可以用米、厘米、英尺、码等不同的单位度量, 物体的重量可以用千克、磅等不同的单位度量.不同的 单位制能给解决问题带来方便,以度为单位度量角的大 小是一种常用方法,为了进一步研究的需要,我们还需 建立一个度量角的单位制.
例2：请用弧度制表示下列角度所在区间。
锐角：{θ|0°＜θ＜90°}
直角： {θ|θ=90°} 钝角： {θ|90°＜θ＜180°} 平角： {θ|θ=180°} 0°到90°的角：{θ|0°≤θ<90°}
0,

3.利用弧度制，使得弧长公式和扇形的 面积公式得以简化，这体现了弧度制优 点.
作业
课本第10页习题1.1A组7,8,9
1 360
所对的圆心角
③不论是以“弧度”还是以“度”为单位的角 的大小都是一个与半径大小无关的定值．
思考：在弧度制下，与角α 终边相同的角如何表 示？ 终边在坐标轴上的角如何表示？
2k (k Z ) 终边x轴上： k (k Z ) 终边y轴上： k (k Z )

填写下列特殊角的度数与弧度数的对应表
60 270 0 30 45 120 135 90 360 180 150 角 度 2 3 5 3 2 弧 0 4 3 2 3 4 6 6 度 2
角的概念推广以后,在弧度制下,角的集 合与实数集 R之间建立了一一对应关系
∠AOB的 度数 180° 360°
-180° 0° 180° 360°
角有正负零角之分,它的弧度数也应该 有正负零之分,如π,-2π,0等等. 正角的弧度数是一个正数,负角的弧度 数是一个负数,零角的弧度数是0.
角的正负主要由角的旋转方向来决定.
思考:如果一个半径为r的圆的圆 心角α所对的弧长是l,那么α的弧 度数是多少? l = 角α的弧度数的绝对值是 r
知圆心角为n°的扇形的弧长公式和面积 2 公式分别是 n R n R
l
180
,S
360
n°转换为弧度
1 2 S R 2
n 180 1 S lR 2
角度制与弧度制的比较
①弧度制是以“弧度”为单位度量角的制度， 角度制是以“度”为单位度量角的制度；
②1弧度是等于半径长的圆弧所对的圆心角 的大小，而 1 是圆的 的大小；

B r o A r o A
y
弧度 角度 弧度 角度 弧度 反思： ① 1 rad 等于 度； 1° 等于 弧度. ② 角的概念推广之后， 无论用角度制还是弧度制都能在角的集合与实数的集合之间 建立一种一一对应的关系.
270° 300° 315° 330° 360° 135° 150° 180° 210° 225° 240°
教学重点、 1． 教学重点：掌握换算. 2．教学难点：理解弧度意义 难点
πr 2π r r 2r
逆时针 逆时针
1 −2 −π 0
教学过程 课堂导入 复习 1：写出写出终边在下列位置的角的集合. （1）x 轴： . . （2）y 轴： （3）第三象限： . （4）第一、三象限： . 复习 2：角度制规定，将一个圆周分成 份，每一份叫做 度， 故一周等于 度，平角等于 度，直角等于 度.
rad
l=2r
C
.
B α O A x
正角 零角 负角
正实数 零 负实数
典型例题 例 1 把 67o 30' 化成弧度.
3 变式：把 π rad 化成度. 5
小结：在具体运算时， “弧度”二字和单位符号“rad”可省略，如：3 表示 3rad ， sinπ表示πrad 角的正弦.
例 2 用弧度制表示： （1）终边在 x 轴上的角的集合； （2）终边在 y 轴上的角的集合.
2. 圆弧长度等于截其圆的内接正三角形边长，求其圆心角的弧度数，并化为度表示.
rad .
变式：终边在坐标轴上的角的集合.
作业布置： 1. 用弧度制表示终边在下列位置的角的集合： （1）直线 y=x； （2）第二象限.
※ 学习小结 1. 弧度数定义； 2. 换算公式（180°=π rad） ； 3. 弧度制与角度制互化. ※ 知识拓展 弧度制的基本思想是使圆半径与圆周长有同一度量单位， 然后用对应的弧长 与圆半径之比来度量角度，这一思想的雏型起源于印度. 印度著名数学家阿利 耶毗陀﹝476？-550？﹞定圆周长为 21600 分，相度地定圆半径为 3438 分 ﹝即取圆周率π=3.142﹞， 但阿利耶毗陀没有明确提出弧度制这个概念. 严格 的弧度概念是由瑞士数学家欧拉﹝1707-1783﹞于 1748 年引入. 欧拉与阿利 耶毗陀不同，先定半径为 1 个单位，那么半圆的弧长为π，此时的正弦值为 0， 就记为 sinπ= 0，同理，1/4 圆周的弧长为π/2，此时的正弦为 1，记为 sin(π /2)=1. 从而确立了用π、 π/2 分别表示半圆及 1/4 圆弧所对的中心角. 其它的 角也可依此类推.

3.无论是以“弧度”还是以“度”为单位, 角的大小都是一个与半径大小无关的定值.
（二）弧度制的绝对值公式
完成下列表格,你能得出哪些结论？
弧AB的长 OB旋转的方向 AOB 的弧度数 AOB 的度数
r
逆时针方向
2 r 逆时针方向
r
逆时针方向
1
2r
顺时针方向
-2
顺时针方向
未旋转
0
逆时针方向
180
逆时针方向
运用新知
根据度与弧度的换算关系，下表中各特殊角对应 的弧度数分别是多少？
注意：用弧度制表示角时，“弧度”二字或 “rad”通常略去不写，而只写该角所对应的弧 度数.如α=2表示α是2rad的角.
随堂练习： 1.根据条件完成下列度和弧度的转化；
（1）把 - 35 化成弧度；
（2）把 - 弧度化成度； 2.把下列角化成 0 到 2 的角加上 2 k 的形式；
4.在半径为r的圆中，n°的圆心角所对的圆弧长 如何计算？
l 2r n nr
360 180
5. 圆心角的大小是否与圆半径的大小有关?
探究新知
（一）弧度制的概念
讨论：角除了以度为单位，还有分和秒，他们 是六十进制的，计算不方便，角的度量是否也 能用不同的单位制？（类比长度的度量单位）
新知1：弧度制的定义
3.正角的弧度数是一个正数，负角的弧度数是一 个负数，零角的弧度数是0.
4.如果半径为R的圆的圆心角 所对弧的长为l，
那么，角的弧度数的绝对值是 l.
r
5.角度制与弧度制换算 ：180°=π rad
运用新知
例1按照下列要求，把67°30′化成弧度：
（1）精确值；
（2）精确到0.001的近似值.

1º=
π
180
rad0.01745rad
1rad = ( 1π80) º 57.3º =57º 18′
特殊角的度数与弧度数的对应表:
0º 30º 45º 60º 90º 180º 270º 0 4 3 2 32
由弧度的定义可知：
圆心角AOB的弧度数等于它所对的弧的长与半径
弧度制
弧度制的定义:用弧度做单位来度量
角的制度叫做 弧度制
1.定义：把长度等于半径长的弧所对的圆 心角叫做1弧度的角.用符号rad表示。
正角
2.正角的弧负度角数 负角的弧零度角数
零角的任弧意度角数的集合
正数
负数 正数 0 负数
实数集R 零
角度制与弧度制的换算:
360º = 2π rad, 180º = π rad

1 2
R
2;
(2)S
1lR. 2
l OS
R
小 结 1.圆心角α所对弧长与半径的比是一个
仅与角α大小有关的常数,所以作为度 量角的标准.
2.角度是一个量,弧度数表示弧长与半 径的比,是一个实数,这样在角集合与实 数集之间就建立了一个一一对应关系.
正角
正实数
零角 负角
零 负实数
定
长的比的ቤተ መጻሕፍቲ ባይዱ对值。
义
B
的 合 理
B
l=r
1弧度
l=r
1弧度
OO r r A A
的与 一半 个径 比长 值无
性
关
3.任一已知角α的弧度数的绝对值
|α| = —lr
α 其中l为以角 作为圆心角时所对圆弧的
长,r为圆的半径.
4.
l = |α| r (弧长计算公式)

3π 2 5π 3
7π 4 11π 6
2π
扇形AOB中， 例4. 扇形 中 半径是50米，求 半径是 米
π
所对的圆心角是60º， AB 所对的圆心角是 ， 的长l 的长 AB
解：因为60º= 3 ,所以 因为 所以 π l=α·r= 3×50≈52.5 . 的长约为52.5米. 答： AB 的长约为 米
弧度制与角度制的换算
零角既是0º 又是0 ① 零角既是 º角，又是 rad角 角 平角、周角的弧度数： ② 平角、周角的弧度数： 180°=π rad ° π 360°=2π rad ° π
o
1°= °
π
180
rad
180 o o 1 rad = ≈ 57.3 = 5718' π
例5. 在半径为R的圆中，240º的中心角所对的 在半径为 的圆中， º 的圆中 弧长为 中心角等于 ，面积为2R2的扇形的 面积为 弧度。 弧度。
4 ：（1） 根据l=αR，得 解：（ ）240º= π ，根据 ， 3
4 l = πR 3 1 2 1 （2）根据 ）根据S= lR= αR ，且S=2R2. 2 2
l 的弧度数的绝对值: ③角α的弧度数的绝对值 α = r
用弧度制表示弧长公式： 用弧度制表示弧长公式：
弧长公式： ① 弧长公式： l = r ⋅ α
l 由公式： 由公式：α = ⇒ l = r ⋅ α r
nπr 简单. 比公式 l = 简单 180
弧长等于弧所对的圆心角弧度的绝对值 弧长等于弧所对的圆心角弧度的绝对值 与半径的积. 与半径的积
5 合 − 36 π
已知一半径为R的扇形 的扇形， 例7. 已知一半径为 的扇形，它的周长等于 所在圆的周长， 所在圆的周长，那么扇形的中心角是多少弧 度？扇形的面积是多少？ 扇形的面积是多少？ 解：周长=2πR=2R+l，所以l=2(π－1)R. 周长=2πR=2R+l，所以l=2(π－ 所以扇形的中心角是2(π－ 所以扇形的中心角是 －1) rad. 扇形面积是 (π − 1)R 2

例4 将3.14rad换算成角度(用度数表示，精确到 0.0001) 1800 3.14rad 3.14 解: ≈179.9090
注意几点： 1．度数与弧度数的换算也可借助“计算器” 《中学数学用表》进行 2．今后在具体运算时，“弧度”二字和单位 如： 符号“rad”可以省略 , 3表示3rad. sin2表示2rad角的正弦 3．一些特殊角的度数与弧度数的对应值应 该记住(见课本P10表)
2
0 , k∈Z} ＋ k 2 · kπ 360 6
0+k· k· 360 3600 , k∈ Z } <180 < ＋ ＋ 2 kπ 0<< 2kπ (3): S={ | 900+
注意：单位不能混用！
知识迁移 例3.把－18450化成α＋2kπ(0≤α<2π, k∈Z) 的形式
解: ∵－18450 =3150＋(－6)×3600 7 12 (k=－6) 4
正角 零角 负角 任意角集合 正实数 0 负实数 实数集
5 . 终边与 角 相同的角： 2· kπ 3600 k∈Z ＋k
终边落在坐标轴上的角.
0 ＋ k· 3600
90 1800 ＋k· 3600 =π＋ 2kπ

2
y
2k
O
0＋k· 0 =2kπ 0 360 x
3600 2700＋k·
rad 0.01745rad
本节课到此结束，请同学们课后再 做好复习与作业。谢谢！ 作业：P10 习题1.1 A组：6，7，8， 《聚焦课堂》(作业手册)P64: ：1、 2、4、5
再见！
温故知新
复习回顾
正角：射线按逆时针方向旋转形成的角 1.任意角的概念 负角：射线按顺时针方向旋转形成的角 零角：射线不作旋转形成的角 2.象限角 1)置角的顶点于原点 2)始边重合于x轴的正半轴

终边在直线y=x上 {β |β =450+K∙1800，K∈Z}
例4.与角－1825º 的终边相同，且绝对值最小 的角的度数是＿＿＿，合＿＿＿弧度。 解：－1825º =－5×360º －25º ， 所以与角－1825º 的终边相同，且绝对值 最小的角是－25º .
5 合 36
例5. 扇形AOB中， AB 所对的圆心角是60º ，
0
6
4
3 2
2 3 5 3 4 6

3 2 2
2、用弧度为单位表示角的大小时， “弧度”二字通常 省略不写，但用“度”（°）为单位不能省。不能“混 和”用 3、用弧度为单位表示角时，通常写 成“多少π”的形 式。如无特别要求，不用将π化成小数。
写出一些特殊角的弧度数
角 度
弧 度
0 30 45 60 90 120 135 150180 270 360







0
6
4
2 3 5 3 2 3 4 6

3 2 2
三、例2
（1）、把67°30′化成弧度。
1 解：67 30' 67 2

1 3 67 30' rad 67 rad 180 2 8
负数
零
弧度与角度的换算
若l=2 π r，则∠AOB=
此角为周角 即为360°
l = 2π弧度 r
l=2 π r
2π弧度
360°= 2π 弧度 180°= π 弧度
O
r
（B） A
（2）弧度与角度的换算公式是怎样的？
换算公式 180º = rad
1

三）弧度数 1、在单位圆中，当圆心角为周角时，它所对的 弧长为2π，所以周角的弧度数为2π，周角是 2πrad 的角. 2、任意一个00~3600的角的弧度数必然适合不 等式 0≤x<2π. 3、任一正角的弧度数都是一个正实数； 任一负角的弧度数都是一个负实数； 零角的弧度数是0. 弧度制下的角与实数建立一一对应关系
舍去
练习1：课本P9 题1、2、3 练习2：当扇形的中心角为600，半径为10cm， 求扇形的弧长及该弧所在的弓形面积 600=π/3 L=10π/3
3 S = 50( − )cm 2 3 2
π
π表示时等于1800，表示的数是 3.141592….
小结： 1、弧度制的意义——角与实数一一对应； 2、换算公式及方法； 3、弧度制下的弧长公式、扇形面积公式及应用 作业：课本P10 7、8 补充作业：扇形的周长L为定值，问它的圆心 角θ取和值时，扇形的面积最大？最大值是多 少？ θ =2，S大=1/16·L2
3、实验结果表明：当半径不同时，同样的圆 心角所对的弧长与半径的比是常数.称这个常数 为该角的弧度数.
l α = R
1弧度=L/R(L=R) 当半径为1时，α=L. α R
L
二）弧度制定义：在单位圆（半径为1的圆）长 为1个单位长度的弧所对应的圆心角称为1弧度的 角 单位符号是 rad,读作弧度 弧度把角度单位与长度单位统一起来. 如图α=1rad α R=1 L=1
方法：用互化公式先约分
练习： 练习：填表
度 弧度 30 ° 45 ° 60 ° 90 ° 180 ° 270 ° 360 °
π
6
π
4
π
3
π
2
π
3π 2
2π

【学习目标】⒈理解1弧度的角及弧度的定义；掌握角度与弧度的换算公式；2.熟练进行角度与弧度的换算；理解角的集合与实数集R 之间的一一对应关系；【自主探究1】1、 角度制：用_____作为度量角的单位,1度的角等于周角的_______;弧度制：用弧度作为度量角的单位.1弧度的规定：长度等于_________长的弧所对的__________叫做1弧度.用符号______表示。

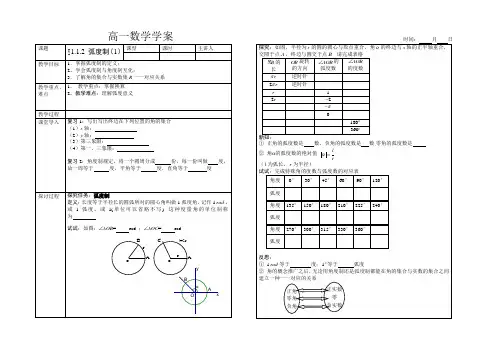
2、阅读P6“探究”，将表格填写完整：思考:如果一个半径为r 的圆的圆心角α所对的弧长是l ,那么α的弧度数是多少?角α的弧度数的绝对值是：=||α______________应确立这样的概念：角的概念推广之后，无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一 种一一对应的关系 任意角的集合 实数集R3、常用换算关系（1）︒360=______rad （2）︒180=______rad （3）︒1=________rad（4）1rad= ( ) º≈________ º=___________【自主探究2】1、把'3067 化成弧度，把rad π53化成度2、一些常用角度和弧度之间的关系：【自主训练】1、弧度和角度的互化：o 360=_________rad ；o 1=_______rad ；1rad=__________o .2、下列命题中，正确的序号是__________．(1)1弧度是长度为半径的弧(2)大圆中1弧度角比小圆中1弧度的角大(3)1弧度的角是长度等于半径长的弧所对的圆心角(4)圆心角为1弧度的扇形的弧长都相等(5)长度等于半径的弦所对的圆心角是1弧度的角3、把下列弧度化成角度: (1) 12π (4) 76π- (2) 43π-(5) 1.4 (3) 310π (6) 234、把下列角度化成弧度:(1) '2230 (4) 36(2) 1200 (5) 150-5、（1）第一象限角的集合 用度表示：______________________________________；用弧度表示：_______________________________________；（2）终边在x 轴上的角的集合 用度表示：______________________________________；用弧度表示：___________________________________________；6、把角16π3化为α＋2k π(k ∈Z,0<α<2π)的形式。

1.1.2 弧度制（1）一、课题：弧度制（1）二、三维目标：1、 知识与技能目标：理解弧度制的意义2、 过程与方法目标：能正确的应用弧度与角度之间的换算；3、 记住公式||l rα= 4、 情感态度价值目标：使学生更全面地看问题，从多角度考虑问题。

三、教学重、难点：弧度与角度之间的换算。

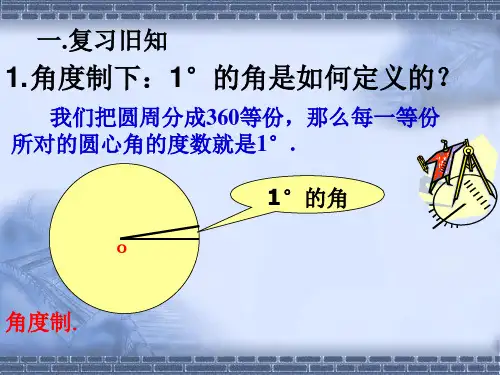
教学方法：讲述法、启发法四、教学过程：（一）复习：初中时所学的角度制，是怎么规定1 角的？ （初中时把一个周角的1360记为1 ） （二）新课讲解：1．弧度角的定义：规定：我们把长度等于半径的弧所对的圆心角叫做1弧度的角，记此角为1rad ．练习：圆的半径为r ，圆弧长为2r 、3r 、2r 的弧所对的圆心角分别为多少？说明：一个角的弧度由该角的大小来确定，与求比值时所取的圆的半径大小无关。

思考：什么π弧度角？一个周角的弧度是多少？一个平角、直角的弧度分别又是多少？2．弧度的推广及角的弧度数的计算：规定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零；角α的弧度数的绝对值是rl =||α，（其中l 是以角α作为圆心角时所对弧的长，r 是圆的半径）。

说明：我们用弧度制表示角的时候，“弧度”或rad 经常省略，即只写一实数表示角的度量。

例如：当弧长4l r π=且所对的圆心角表示负角时，这个圆心角的弧度数是：4||4l r r rπαπ-=-=-=- 3．角度与弧度的换算3602π= rad 180π= rad 1801π=︒rad 0.01745≈rad 1rad =︒)180(π5718'≈4．例题分析：例1 把'3067︒化成弧度．解：因为6730' 67.5= ，所以 3671567.51808rad ππ'=⨯= rad ． 例2 把35πrad 化成度。

取什么值时，才能使扇形的面积最大？最大面积
是多少？
答案
半径R=10㎝时，扇形的面积最大，最大值为
100㎝²。此时圆心角为2rad
题型三
自行车大链轮有48个齿，小链轮有20个齿，彼此
由链条连接，当大链轮转过一周时，小链轮转过
的角是多少度？多少弧度？（三维）
题型三
解：由于大链轮与小链轮在相同时间内转过的
式可得解。
解析(1)因为α=120°=2/3πrad, R=6
所以，AB的弧长为 l=2/3π×6=4π
(2)因为S扇形OAB=1/2lr=1/2×4π×6=12π
S
=1/2R²×sin2/3π=1/2×6²×√3/2=9√3
三角形ABO
S弓形OAB=S扇形OAB－S三角形OAB=12π－9√3
已知一扇形的周长为 ，当它的半径和圆心角
式中。
考点分析：
1、弧度制与实数的集合之间建立一种一一对
应的关系。
2、一些特殊角的度数与弧度数的对应值应
该记住。但值得注意的是，用“度”为单位度
量时，“度”不能省略。
3、今后在具体运算时，“弧度”二字和单位
符号“rad”可以省略 如：3表示3rad 。sinπ表
示πrad角的正弦。
总结提炼
（1）
式有诸多优越性，但是如果已知的角是以“度”
为单位，则必须先把它化成弧度后再计算，这
样可避免计算过程或结果出错。
要点阐释
3.与 终边相同的角的一般形式为
+ ∗ º, ∈
注意以下四点：
① k∈Z；②是任意角；
③ k·360º与之间是“+”号，如k·360º－30º,应看成
k·360º+(－30º)；

解：1rad= (
180

)
8 8 180 ( ) 5 5
288
三、特殊角的弧度 角 o 0 度 弧 度 30o 45o 60o 90o 120o
0

6
5 6

4

3

2
270
o
2 3
360
o
角 o o o 135 150 180 度
弧 度
3 4

3 2
2
用弧度来度量角，实现角的集合 与实数集R之间建立一一对应的关系：
③ 正角的弧度数是正数，负角的弧度数是 负数，零角的弧度数是0.
l ④角的弧度数的绝对值: r
（l为弧长，r为半径） 这里， 的正负由角的终边的旋转方向决定。
360°=2 rad 180°= rad
1° =

180
rad

0.01745 rad
180 57 .30 1 rad= =57°18′
正角 正实数 对应角的 弧度数
零角
负角
零
负实数
角的集合
实数集R
1.1.2
弧度制
复习引入
初中所学的角度制是怎样规定角的度量的?
1 规定把周角的 作为1度的角，用度做单位 360 来度量角的制度叫做角度制．
讲授新课
一 、 弧度制定义
把长度等于半径的弧所对的圆心角叫做1弧度的
角；用弧度来度量角的单位制叫做弧度制． 在弧度制下，1弧度记做1 rad. 思考： 一定大小的圆心角 所对应的弧长与半径的比值 是否是确定的？与圆的半径大小有关吗？
弧长 比值 半径
B O
B2

o
90
o
120
o
0

6

4

3
270
o
角 o o o 135 150 180 度 弧 度
360
o
特殊角的弧度
角 o 0 度 弧 度 30
o
45
o
60
o
90
o
120
o
0

6

4

3

2
270
o
角 o o o 135 150 180 度 弧 度
360
o
特殊角的弧度
角 o 0 度 弧 度 30
o
45
o
④负角的弧度数是一个负数．
⑤零角的弧度数是零．
l ⑥角的弧度数的绝对值||= . r
角度与弧度之间的转换
①将角度化为弧度：
角度与弧度之间的转换
①将角度化为弧度：
角度与弧度之间的转换
①将角度化为弧度：
角度与弧度之间的转换
①将角度化为弧度：
角度与弧度之间的转换
①将角度化为弧度：
n 180
o
45
o
60
o
90
o
120
o
0

6

4

3

2
270
o
2 3
360
o
角 o o o 135 150 180 度 弧 3 度 4
5 6
特殊角的弧度
角 o 0 度 弧 度 30
o
45
o
60
o
90
o
120
o
0

6

1 .这种用度 360 作为单位来度量角的单 位制, 称之角度制. 规定1度的角等于圆周角的
角度制 初中 角的度量 高中 弧度制
???
B
弧AB的长＝半径r
1 rad
·
O
A
弧长＝半径
弧度制
定义：
长度等于半径的圆弧所对的圆心角叫做1弧度 长度等于半径的圆弧所对的圆心角叫做 弧度 的角，记作1 的角，记作 rad. 用弧度为单位来度量角的制度叫做弧度制。 用弧度为单位来度量角的制度叫做弧度制。 用弧度表示角的大小时，可以省略单位。 用弧度表示角的大小时，可以省略单位。 负角的弧度数是负数， 负角的弧度数是负数， 正角的弧度数是正数， 正角的弧度数是正数， 零角的弧度数零。 零角的弧度数零。
正实数 零 负实数
3 6 0 = 2π
o
ra d ra d
rad ≈ 0.01745rad
度 ≈ 57.30
180 = π
o
1度角等于多少弧度？ 度角等于多少弧度？ 度角等于多少弧度
1 =
o
π
180
1弧度角等于多少度？ 弧度角等于多少度？ 弧度角等于多少度
1rad =
180
o
π
π 7 π 2 π 2 π 3 3 12 4
弧度制
l α= R
l | α |= R
有正有负也可能是0 用于计算
其中 : 1、l是以角α作为圆心角时所对弧的长，r是半径； 2πr 2、圆心角θ为周角时，l = 2πr，则θ = = 2π r πr 3、圆心角θ为半角时，l = πr，则θ = =π r
角度制与弧度制：一一对应：
正角 零角 负角
5π 4
弧长是500 mm, 求此弧长所对的圆心角 的弧度数。