例题图形计数进阶_尖子班(学而思)
- 格式:doc
- 大小:206.50 KB
- 文档页数:6
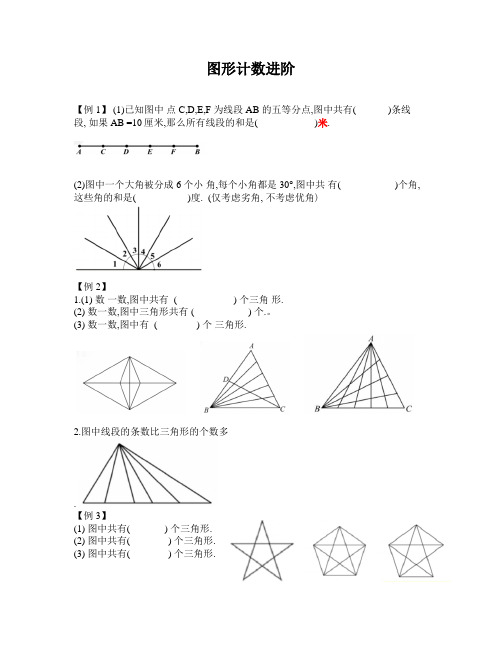
图形计数进阶【例 1】 (1)已知图中点 C,D,E,F 为线段 AB 的五等分点,图中共有( )条线段, 如果AB =10厘米,那么所有线段的和是( )米.(2)图中一个大角被分成 6 个小角,每个小角都是 30°,图中共有( )个角,这些角的和是( )度. (仅考虑劣角, 不考虑优角)【例 2】1.(1) 数一数,图中共有( ) 个三角形.(2) 数一数,图中三角形共有 ( ) 个.。
(3) 数一数,图中有( ) 个三角形.2.图中线段的条数比三角形的个数多 ____________________.【例 3】(1) 图中共有( ) 个三角形.(2) 图中共有( ) 个三角形.(3) 图中共有( ) 个三角形.【例 4】1. (1)数一数,图中有( )个长方形.(2)用16个同样大小的正方形组成如图的一个大正方形,下图中有( )个正方形.(3)如图,四条边长度都相等的四边形称为菱形.用16个同样大小的菱形组成如图的一个大菱形.数一数,图中共有( ) 个菱形.2.图中有______个正方形【例 5】下图中共有( )个长方形,这些长方形的面积和是( )【例 6】1.在图所示的线段中,包含“☆”的线段有 ( )条;包含“△”的线段有( )条; 至少包含“☆”和“△”中的一个的线段有( )条.2。
在图所示的线段中,包含“A”的线段有( )条;包含“B”的线段有( )条;至少包含“A”和“B”中的一个的线段有( )条.【例 7】 (1)下图中包含五角星的长方形一共有()个(2)下图中包含五角星的长方形一共有( )个.(3)只包含一个字母的长方形有( )个【例 8】1.由 20 个单位小正方形组成的长方形中,包含☆的正方形共有( )个.2.在下面的图中,包含苹果的正方形一共有()个.。


⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎨⎨⎩⎪⎪⎧⎪⎨⎪⎩⎪⎪⎩定义轴对称基本知识点对称点与对称轴垂直平分线性质与判定做图形的对称轴轴对称轴对称变换用坐标表示轴对称等腰三角形性质、判定等腰三角形等边三角形性质、判定【例1】 ⑴如图,把矩形纸片ABCD 纸沿对角线折叠,设重叠部分为△EBD ,那么下列说法错误的是( )A .△EBD 是等腰三角形,EB =EDB .折叠后∠ABE 和∠CBD 一定相等C .折叠后得到的图形是轴对称图形D .△EBA 和△EDC 一定是全等三角形⑵将一个矩形纸片依次按图①、图②的方式对折,然后沿图③中的虚线裁剪,最后将图④的纸再展开铺平,所得到的图案是( )典题精练思路导航题型一:轴对称7期中复习E DCA图(4)图(3)图(2)图(1)向右对折(向上对折)D.C.B.A.【例2】 如图,A 为马厩,B 为帐篷,牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,请你帮他确定这一天的最短路线.作出图形并说明理由.河草地BASSS SAS ASA AAS HL⎧⎧⎪⎨⎨⎩⎪⎩对应边相等全等三角形性质全等三角形对应角相等全等三角形判定:,,,, 思路导航题型二:全等三角形⎧⎨⎩性质、判定角平分线有关角平分线辅助线【例3】 如图,在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD =AC ,在CF 的延长线上截取CG =AB ,连接AD 、AG . 请你确定△ADG 的形状,并证明你的结论.BAC DEFG【例4】 △ABC 中,∠CAB =∠CBA =50°,O 为△ABC 内一点,∠OAB =10°,∠OBC =20°,求∠OCA 的度数.COBA【例5】 在Rt △ABC 中,∠ACB =90°,∠A =30°,BD 是△ABC 的角平分线,DE ⊥AB于点E .⑴如图1,连接EC ,求证:△EBC 是等边三角形; ⑵点M 是线段CD 上的一点(不与点C 、D 重合),以BM 为一边,在BM 的下方作∠BMG =60°,MG 交DE 延长线于点G .请你在图2中画出完整图形,并直接写出MD ,DG 与AD 之间的数量关系;⑶如图3,点N 是线段AD 上的一点,以BN 为一边,在BN 的下方作典题精练∠BNG =60°,NG 交DE 延长线于点G .试探究ND ,DG 与AD 数量之间的关系,并说明理由.GN图3图2图1AE BCDAE BCDDC BE A【例6】 已知四个实数a 、b 、c 、d ,且a ≠b ,c ≠d .满足:a 2+ac =4,b 2+bc =4,c 2+ac =8,d 2+ad =8.⑴求a +c 的值;⑵分别求a 、b 、c 、d 的值. 典题精练题型三:因式分解【例7】 设a 1=32-12,a 2=52-32,…,a n =()()222121n n +--(n 为大于0的自然数).⑴探究a n 是否为8的倍数,并用文字语言表述你所获得的结论;⑵若一个数的算术平方根是一个自然数,则称这个数是“完全平方数”.试找出a 1,a 2,…,a n ,…这一列数中从小到大排列的前4个完全平方数,并指出当n 满足什么条件时,a n 为完全平方数(不必说明理由).训练1. 阅读理解如图1,△ABC 中,沿∠BAC 的平分线AB 1折叠,剪掉重复部分;将余下部分沿∠B 1A 1C 的平分线A 1B 2折叠,剪掉重复部分;…;将余下部分沿∠B n A n C 的平分线A n B n +1折叠,点B n 与点C 重合,无论折叠多少次,只要最后一次恰好重合,∠BAC 是△ABC 的好角.小丽展示了确定∠BAC 是△ABC 的好角的两种情形.情形一:如图2,沿等腰三角形ABC 顶角∠BAC 的平分线AB 1折叠,点B 与点C 重合;情形二:如图3,沿∠BAC 的平分线AB 1折叠,剪掉重复部分;将余下部分沿∠B 1A 1C 的平分线A 1B 2折叠,此时点B 1与点C 重合. 探究发现⑴△ABC 中,∠B =2∠C ,经过两次折叠,∠BAC 是不是△ABC 的好角?(回答“是”或“不是”).⑵小丽经过三次折叠发现了∠BAC 是△ABC 的好角,请探究∠B 与∠C (不妨设∠B >∠C )之间的等量关系.根据以上内容猜想:若经过n 次折叠∠BAC 是△ABC 的好角,则∠B 与∠C (不妨设∠B >∠C )之间的等量关系为 . 应用提升⑶小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角. 请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.图3ABCA 1B 1B 2CD BA图2图1C…B n+1A 3A 2A 1B nB 2B 1BA训练2. 一节数学课后,老师布置了一道课后练习题:如图,已知在Rt △ABC 中,AB =BC ,∠ABC =90°,BO ⊥AC ,于点O ,点PD 分别在AO 和BC 上,PB =PD ,DE ⊥AC 于点E , 思维拓展训练(选讲)求证:△BPO ≌△PDE .备用图2431COBAD CE OP AB⑴理清思路,完成解答⑵本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写本题的证明过程. ⑵特殊位置,证明结论若PB 平分∠ABO ,其余条件不变.求证:AP =CD .训练3. 因式分解⑴()22223103x a b x a ab b ++-+- ⑵()()211a b ab +-+⑶()()2222483482x x x x x x ++++++ ⑷2222223a b ab a c ac abc b c bc -+--++训练4. 按下面规则扩充新数:已有a 和b 两个数,可按规则c =ab +a +b 扩充一个新数,而a ,b ,c 三个数中任取两数,按规则又可扩充一个新数,…,每扩充一个新数叫做一次操作.现有数2和3.⑴求按上述规则操作三次得到扩充的最大新数;⑵能否通过上述规则扩充得到新数5183?并说明理由.题型一 轴对称 巩固练习【练习1】 如图1,两个等边△ABD ,△CBD 的边长均为1,将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置,得到图2,则阴影部分的周长为 .图2图1CB D'DA'CDB A题型二 全等三角形 巩固练习【练习2】 在等边△ABC 中,AC =9,点O 在AC 上,且AO =3,P是AB 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD ,若使点D 恰好落在BC 上,则线段AP 的长是( )A .4B .5C .6D .8【练习3】 如图⑴,BD 、CE 分别是△ABC 的外角平分线,过点A 作AF ⊥BD ,AG ⊥CE ,垂足分别为F 、G ,连接FG ,延长AF 、AG ,与直线BC 相交于M 、N .⑴试说明:FG =12(AB +BC +AC ); ⑵①如图⑵,BD 、CE 分别是△ABC 的内角平分线;②如图⑶,BD 为△ABC 的内角平分线,CE 为△ABC 的外角平分线. 则在图⑵、图⑶两种情况下,线段FG 与△ABC 三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况说明理由. 复习巩固BP A O DC(3)GE FD A(2)AB CD E FG(1)GE DF A题型三 因式分解 巩固练习【练习4】 分解因式:()4442x y x y +++-.【练习5】 图①是一个长为2m 、宽为2n 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形. ⑴图②中的阴影部分的面积为 ;33初二秋季·第7讲·尖子班·学生版⑵观察图②请你写出三个代数式()2m n +、()2m n -、mn 之间的等量关系⑷实际上有许多代数恒等式可以用图形的面积来表示. 如图③,它表示了 .⑸试画出一个几何图形,使它的面积能表示()()22343m n m n m mn n ++=++.③②①nnm m m nm n mmmnmmnn初二秋季·第7讲·尖子班·学生版第十五种品格:创新成功往往就藏在你没注意的地方有一家电台请来了一位商业奇才做嘉宾主持。
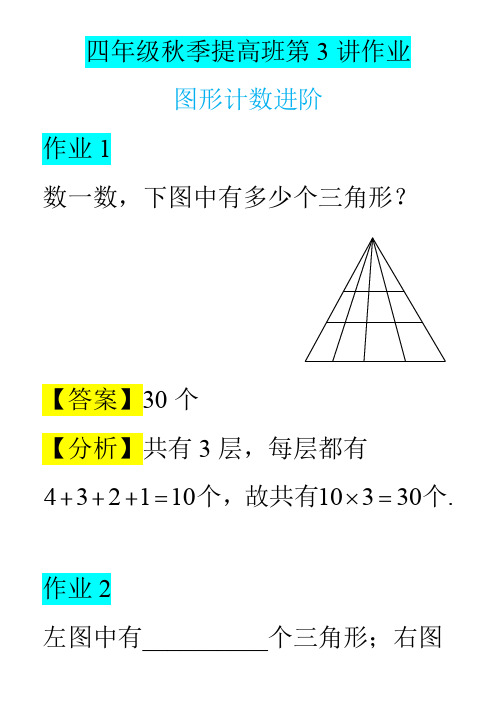
四年级秋季提高班第3讲作业图形计数进阶作业1数一数,下图中有多少个三角形?【答案】30个【分析】共有3层,每层都有432110个,故共有10330个.作业2左图中有__________个三角形;右图中有__________个三角形.【答案】35;43【分析】左:1515535;右:355343作业3下面的图形中有多少个长方形?【答案】60个【分析】长有3216种,宽是432110种,故共有61060个长方形.作业4下图中包含有“好未来”三个汉字的长方形有多少个?好未来【答案】18个【分析】3618个.作业5图中有__________个(可旋转可翻转).【答案】34个【分析】对应到中,每个小长方形内有2个,所以有21734个.复习巩固作业6观察5*255560,7*477777777778638,推知9*5的值是__________.【答案】111105【分析】原式999999999999999111105作业7某班有3个小组,赵、钱、孙三人分属不同的小组.这次语文考试成绩公布,情况如下:赵和第3小组的那位成绩不一样,孙比第1小组的那位成绩低,三人中第3小组的那位比钱分数高:若赵、钱、孙三人按语文成绩由高到低排列,正确的顺序是__________.【答案】赵、孙、钱【分析】赵不属于第3小组,钱也不属于第3小组,所以孙属于第3小组,孙比第1小组的成绩低,且比钱的分数高,所以赵是第1小组的,分数最高,钱分数最低.作业85个足球队进行比赛,每个球队都与其他球队各比一场,胜方得3分,负方得0分,平局各得1分.最后四个队分别得1分、2分、5分和7分,那么第五个队得__________分.【答案】12【分析】前4队3胜7负,所以第5个队只能4场全胜,12分.四年级秋季提高班第3讲练习册答案图形计数进阶同步练习1.35个。
左边15个,右边15个,左右结合有5个.2.22个按大小分类(边长为1、2的三角形),共有16622个三角形;方法二:“向右”的三角形有8311个,故“向左”的三角形也有11个,共有22个.3.100个,有(4321)(4321)100个平行四边形.4.30个左下可选3个点,右上可选10个点,则共有31030个.5.(1)43213434()个;(2)新增的三角形以新产生的线段为边,上半部分有639个,下半部分有4个,总共新增9413个;有341347个;(3)又新增一条一样的线段,所以边长在这条线段上三角形也有13个,边长同时在这两条新增线段上的三角形总共有4个;所以图中总共有三角形341313464个.6.36个中心正方形内有84416个,其外有8412个,“跨界”的有8个,故共有1612836个.深化练习7.38个添线法,原有10个,添上右倾的斜线增加了10414个,再添上左倾的斜线,增加了634114个,所以共10141438个.最后添左倾斜线时,为保证不重不漏,可将这条斜线以外的每个交点与斜线形成的新三角形个数标在点上,最后相加得到总数,如下图,共增加了63514个三角形. 1111060138.添线法,1520253590.9.85由2个例2(1)的图构成,新增加含4块的三角形有10个,含8块的三角形有5个,所以共35210585个.实战练习10.20个按大小分类枚举(正放:面积为1、4的正方形;斜放:面积为2、5的正方形),共有826420个正方形.阶段测试1.1*2=121=32.原式=101102103104105 (12345)1015101503.依题意,A A A A A*2224,A A A A A4*3=8+3=11,A A A A A11*4=22+4=26,得26260,10.A A4.图中共有19+11+5+1=36个正方形.5.观察图形可知,在题述图形中由实线和虚线构成的长方形各有9个,共计9+9=18个.6.个数=6×8=48(个).7.“甲已经赛了4盘”,说明甲与乙、丙、丁、小强各赛了1盘(小强与甲赛了1盘)“丁赛了1盘”,肯定丁只与甲比赛. “乙赛了3盘”,说明乙与甲、丙、小强各赛了1盘(小强与乙赛了1盘).现在已经知道,丙赛的2盘是与甲、乙各赛了1盘,所以,小强赛了2盘.8.四个人循环比赛总共比赛5×4÷2=10(场),每场无论分出胜负还是打平,两人的得分和一定是2分,因此最终四个人的得分加起来一定是10×2=20(分).9.每场平局两队共得2分,如果分出胜负则两队共得3分.6支球队共要比65215场比赛,其中有4场平局,所以有15411场分出了胜负,那么6支球队总得分为2431141分,由于有5支球队共得了31分,所以第6支球队得了413110分.10.法一:四人共赛6局,总分为6212(分),因为没有人全胜,所以得分最高的选手最多是两胜一平得5分,因此在另外的3局比赛中:如果全部是平局,则4个人的分数只能分别为5,3,2,2,就会出现分数相同的情况,如下左图(图中箭头表示有胜负,箭头指向输者,虚线表示平局)如果有2局是平局,则可以出现满足条件的情况:4人分数分别为5,4,2,1,如下右图②③②⑤D C B A ④①②⑤D C B A所以至少有3局是平局.法二:四人共赛6局,如果6局都是平局,那么四人总分相同,不合题意.如果有5局平局,那么除有胜负的两人外,另两人总分相同,不合题意.如果有4局平局,那么可分为三种情况:一个人胜两局,输的两个人总分相同;一个人输两局,胜的两个人总分相同;四个人中两人胜两人负,两个胜的人总分相同,两个负的人总分相同,都不合题意.3局平局是可能的,如下图所示,连线表示平局,箭头指向的一方为负方,图中数字为各人总分.②④①⑤四年级秋季提高班第3讲图形计数进阶例1图(1)中有__________个三角形;图(2)中有__________个三角形;图(3)中有__________个三角形;图(4)中有__________个三角形.(1)(2)(3)(4)【答案】30;20;37;50【分析】(1)151530;(2)增加一条线,线上面增加3个三角形,线下面增加2个三角形,153220个;(3)在(1)、(2)的基础上增加2个三角形,305237个;(4)在(3)的基础上增加633113个,所以共371350个.【随堂练】(1)图中有多少个三角形(2)图中有多少个三角形(3)图中有多少个三角形【答案】(1)20个(2)30个(3)27个拓展5图(1)有__________个三角形;图(2)有__________个三角形;图(3)有__________个三角形.(1)(2)(3)【答案】34;47;64【分析】(1)43213434()个;(2)新增的三角形以新产生的线段为边,上半部分有639个,下半部分有4个,总共新增9413个;有341347个;(3)又新增一条一样的线段,所以边长在这条线段上三角形也有13个,边长同时在这两条新增线段上的三角形总共有4个;所以图中总共有三角形341313464个.例2图(1)有__________个三角形;图(2)有__________个三角形.(1)(2)【答案】35;29【分析】(1)分类枚举,含1块、2块、3块、5块的分别有10、10、10、5个,共有101010535个;(2)以去掉的线为边的三角形有6个,所以剩下35629个;练一练下图中有多少个三角形?(3)【答案】47【分析】以新增的线为边的三角形左右两边各6个,所以共有356247个.拓展9数出下图中三角形的个数.【答案】85【分析】由2个例2(1)的图构成,新增加含4块的三角形有10个,含8块的三角形有5个,所以共35210585个.例3(1)图中有__________个长方形.(2)下图中含“★”的长方形有多少个?★(3)下图中含两个“★”的长方形有多少个?★★【答案】150;54;54【分析】(1)长方形邻边对应:一条水平线段和一条竖直线段可确定一个长方形.根据乘法原理可知,长方形有()()1234512341510150个.(2)长方形两点对应:只要确定对角的两个顶点就可以确定一个水平的长方形,就像在电脑桌面上拖动鼠标选中文件一样.这种对应法专门用来解决包含某个区域的长方形个数.如下图所示,★的左上角有6个点,右下角有9个点,根据乘法原理,共有6954个长方形.★(3)同(2),包含两个★的长方形有9654个.★★【随堂练】1.图中有多少个长方形【答案】10660个2.图中有多少个包含“心”的长方形【答案】4624例4在下图45的方格中:(1)有__________个;(2)有__________个(可旋转可翻转);(3)有__________个(可旋转可翻转);(4)有__________个(可旋转可翻转).【答案】(1)12;(2)48;(3)17;(4)34【分析】特殊图形的对应:可将特殊图形对应到能包含自身的最小长方形中.(1)4312个;(2)对应到中,每个田字格内有4个,所以有41248个;(3)横向的有339个,纵向的有248个,共9817个;(4)对应到中,每个小长方形内有2个,所以有21734个.【随堂练】图中有多少个【答案】66224()练一练下图中,共有__________个(可旋转可翻转).【答案】30【分析】图中有7个田字格,4728个,注意左上角与右下角还各有1个,共28230个.例5用9个钉子钉成相互间隔为1厘米的正方阵(如下图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于2平方厘米的三角形有多少个?面积等于1平方厘米的三角形有多少个?【答案】8;32【分析】(1)面积等于2平方厘米的分类统计如下:3×2=6(个)1×2=2(个)所以,面积等于2平方厘米的三角形的个数有:6+2=8(个).(2)面积等于1平方厘米的分类统计如下:3×2×4=24(个)2×4=8(个)面积等于2平方厘米的三角形有8个;面积等于1平方厘米的三角形有32个.练一练13枚钉子钉成水平和竖直间隔都为1厘米的点阵. 用一根橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等.请回答:可以构成多少个正方形?【答案】11【分析】按大小分类枚举(正放:面积为1、4的正方形;斜放:面积为2、8的正方形),共有415111个正方形.拓展1016枚钉子钉成水平和竖直间隔都为1厘米的点阵. 用一根橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等.请回答:可以构成多少个正方形?【答案】20【分析】按大小分类枚举(正放:面积为1、4的正方形;斜放:面积为2、5的正方形),共有826420个正方形.拓展练习拓1☆数一数下图中,有多少个三角形?【答案】35个【分析】左边15个,右边15个,左右结合有5个.拓2☆☆图中共有多少个三角形?【答案】22个【分析】按大小分类(边长为1、2的三角形),共有16622个三角形;方法二:“向右”的三角形有8311个,故“向左”的三角形也有11个,共有22个.拓3☆☆下面的图中共有多少个平行四边形?【答案】100个【分析】有(4321)(4321)100个平行四边形.拓4☆☆下图中有多少个同时包含2个五角星的长方形?★★【答案】30个【分析】左下可选3个点,右上可选10个点,则共有31030个.拓5☆☆☆图(1)有_________个三角形;图(2)有_________个三角形;图(3)有_________个三角形.(1)(2)(3)【答案】34;47;64【分析】(1)43213434()个;(2)新增的三角形以新产生的线段为边,上半部分有639个,下半部分有4个,总共新增9413个;有341347个;(3)又新增一条一样的线段,所以边长在这条线段上三角形也有13个,边长同时在这两条新增线段上的三角形总共有4个;所以图中总共有三角形341313464个.拓6☆☆☆下图中有多少个三角形?【答案】36个【分析】中心正方形内有84416个,其外有8412个,“跨界”的有8个,故共有1612836个.拓7☆☆☆下图中有多少个三角形?【答案】38个【分析】添线法,原有10个,添上右倾的斜线增加了10414个,再添上左倾的斜线,增加了634114个,所以共10141438个.最后添左倾斜线时,为保证不重不漏,可将这条斜线以外的每个交点与斜线形成的新三角形个数标在点上,最后相加得到总数,如下图,共增加了63514个三角形. 111106013拓8☆☆☆图中有多少个三角形?【答案】90【分析】添线法,1520253590.拓9☆☆☆数出下图中三角形的个数.【答案】85【分析】由2个例2(1)的图构成,新增加含4块的三角形有10个,含8块的三角形有5个,所以共35210585个.拓10☆☆☆16枚钉子钉成水平和竖直间隔都为1厘米的点阵. 用一根橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等.请回答:可以构成多少个正方形?【答案】20【分析】按大小分类枚举(正放:面积为1、4的正方形;斜放:面积为2、5的正方形),共有826420个正方形.。


初三寒假·第1讲·尖子班·学生版考试内容考试要求层次ABC三角形了解三角形的有关概念;了解三角形的稳定性;会按边和角对三角形进行分类;理解三角形的内角和、外角和及三边关系;会画三角形的主要线段;知道三角形的内心、外心和重心会用尺规作给定条件的三角形;掌握三角形内角和定理及推论;会按要求解决三角形的边、角的计算问题;能用三角形的内心、外心的知识解决简单问题;会证明三角形的中位线定理,并会应用三角形中位线性质解决有关问题等腰三角形和直角三角形了解等腰三角形、等边三角形、直角三角形的概念,会识别这三种图形;理解等腰三角形、等边三角形、直角三角形的性质和判定能用等腰三角形、等边三角形、直角三角形的性质和判定解决简单问题会运用等腰三角形、等边三角形、直角三角形的知识解决有关问题 全等三角形 了解全等三角形的概念,了解相似三角形与全等三角形之间的关系 掌握两个三角形全等的条件和性质;会应用全等三角形的性质与判定解决有关问题 会运用全等三角形的知识和方法解决有关问题勾股定理及其逆定理 已知直角三角形的两边长,会求第三边长会用勾股定理及其逆定理解决简单问题相似三角形了解两个三角形相似的概念会利用相似三角形的性质与判定进行简单的推理和计算;会利用三角形的相似解决一些实际问题锐角三角函数了解锐角三角函数(sin cos tan A A A ,,);知道304560︒︒︒,,角的三角函数值由某个角的一个三角函数值,会求这个角的其余两个三角函数值;会计算含有 304560︒︒︒,,角的三角函数式的值能运用三角函数解决与直角三角形有关的简单问题解直角三角形知道解直角三角形的含义会解直角三角形;能根据问题的需要添加辅助线构造直角三角形;会解由两个特殊直角三角形构成的组合图形的问题能综合运用直角三角形的性质解决有关问题本讲结构中考大纲剖析1中考第一轮复习三角形初三寒假·第1讲·尖子班·学生版一、等腰三角形二、直角三角形1.直角三角形的边角关系.①.直角三角形的两锐角互余. ②.三边满足勾股定理. ③.边角间满足锐角三角函数.知识导航初三寒假·第1讲·尖子班·学生版45°60°2.特殊直角三角形“等腰直角三角形”“含30︒和60︒的直角三角形”边的比:112∶∶边的比:132∶∶3.直角三角形中的特殊线.d cba“直角三角形斜边中线2c d =” acbh “直角三角形斜边高abh c=”三.尺规构造等腰三角形和直角三角形问题作图求点坐标 “万能法”其他方法 等腰三角形 lAB已知点A 、B 和直线l ,在l 上求点P ,使PAB △为等腰三角形lP 4P 5P 3P 2P 1BA“两圆一垂”分别表示出点A 、B 、P 的坐标,再表示出线段AB 、BP 、AP 的长度,由①AB=AP ②AB=BP③BP=AP 列方程解出坐标 作等腰三角形底边的高,用勾股或相似建立等量关系直角三角形lAB已知点A 、B 和直线l ,在l 上求点P ,使PAB △为直角三角形BA P 1P 2P 3P 4l“两垂一圆”分别表示出点A 、B 、P 的坐标,再表示出线段AB 、BP 、AP 的长度,由①222AB BP AP =+ ②222BP AB AP =+ ③222AP AB BP =+ 列方程解出坐标作垂线,用勾股或相似建立等量关系四.全等三角形全等三角形的性质:全等三角形的对应边相等,对应角相等. 全等三角形的判定:⑴SSS ;⑵SAS ;⑶ASA ;⑷AAS ;⑸HL .在证明图形的线或角关系时,通常需要将全等与图形变换(旋转、平移、轴对称等)相结合.初三寒假·第1讲·尖子班·学生版五.相似三角形相似三角形的性质:⑴ 相似三角形的对应角相等,对应边成比例,其比值称为相似比.⑵ 相似三角形对应高的比等于相似比,周长比等于相似比,面积比等于相似比的平方. 相似三角形的判定:⑴ 平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似; ⑵ 两角对应相等,两三角形相似;⑶ 两边对应成比例且夹角相等,两三角形相似; ⑷ 三边对应成比例,两三角形相似. 相似三角形的基本模型:(1)EDC BA(3)ED CBA(4)D CBADCBA(6)EDCBA(2)EDCBA(5)EDCBA(10)(9)(8)A BDEABC DEEDBA【例1】 (1)如图所示的正方形网格中,网格线的交点称为格点,已知A 、B 是两格点,如果C 也是图中的格点,且使得ABC △为等腰三角形,则点C 的个数是( ) A.6 B.7 C.8 D.9(2)在平面直角坐标系中,点A 的坐标为(4),0,点B 的坐标为(410),,点C 在y 轴上,且ABC △是直角三角形,则满足条件的C 点的坐标为 .(3)如图所示,在△ABC 中,BC =6,E ,F 分别是AB ,AC 的中点,点P在射线EF 上,BP 交CE 于D ,点Q 在CE 上且BQ 平分∠CBP ,设BP =y ,PE =x .当CQ =21CE 时,y 与x 之间的函数关系式是 ; 当CQ =n1CE (n 为不小于2的常数)时, y 与x 之间的函数关系式是 .模块一 特殊三角形夯实基础初三寒假·第1讲·尖子班·学生版(4)已知:如图,在ABC △中,B ACB ∠=∠,点D 在AB 边上,点 E 在AC 边的延长线上,且BD CE =,连接DE 交BC 于F . 求证:DF EF =.【例2】 (1)如图,正方形ABCD 的边长为2, 将长为2的线段QF 的两端放在正方形相邻的两边上同时滑动.如果点Q 从点A 出发,沿 图中所示方向按A D C B A →→→→滑动到点A 为止,同时点 F 从点B 出发,沿图中所示方向按B A D C B →→→→滑动到 点B 为止,那么在这个过程中,线段QF 的中点M 所经过的路线围 成的图形的面积为( )A. 2B. 4-πC.πD.1π-(2)如图,在△ABC 中,∠C =90°,AC =4,BC =2,点A 、C 分别在x轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动, 在 运动过程中,点B 到原点的最大距离是( )A. 222+ B .52 C .62 D . 6以下探究主题为:几何最值问题【探究1】如图,在ABC △中,∠C =90°,AC =4,BC =3,点A 、C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程 中,点B 到原点的最小距离是__________.【探究2】如图,在Rt ABC △ 中,∠C =90°,tan 12BAC ∠=,BC =6,点D在边AC 上,且23AD AC =,连结BD ,F 为BD 中点,将线段AD 绕 点A 旋转,在旋转过程中线段CF 长度的最大值为________,最小值 为_______.能力提升ACFEDB BC 第8题图QFMABC y xO CBA C BAO y x初三寒假·第1讲·尖子班·学生版【探究3】 如图,在Rt ABC △中,∠ACB =90°,∠B =30°,CB =33,点D 是平面上一点且CD =2,点P 为线段AB 上一动点,当△ ABC 绕点C 任意旋转时,在旋转过程中线段DP 长度的最大值 为_______,最小值为_______.【探究4】如图,Rt ABC △中,∠C =90°,∠ABC =30°,AB =6.点D 在AB 边上,点E 是BC 边上一点(不与点B 、C 重合), 且DA =DE ,则AD 的取值范围是___________________.【例3】 在△ABC 中,AB =AC ,∠BAC =α(︒<<︒600α),将线段BC 绕点B 逆时针旋转60°得到线段BD .图1图2A BCDEDCBA(1)如图1,直接写出∠ABD 的大小(用含α的式子表示);(2)如图2,∠BCE =150°,∠ABE =60°,判断△ABE 的形状并加以证明; (3)在(2)的条件下,连结DE ,若∠DEC =45°,求α的值.夯实基础模块二 全等三角形PDCBACDABE初三寒假·第1讲·尖子班·学生版【例4】 等边三角形ABO 的边长为2个单位长度,点P 、Q 分别从点B 、O 同时出发,以每秒1个单位长度向点O 、A 运动.(到达点O 、A 时停止运动)⑴ 如图1,连接AP 、BQ 相交于点C .证明:AP BQ =,60ACQ =︒∠. ⑵ 如图2,连接PQ ,探讨2PQ 与AB 之间的大小关系并证明你的结论.QA图1ACP QQP A图2夯实基础模块三 相似三角形能力提升初三寒假·第1讲·尖子班·学生版图3图2图12n-1B 2C 2A B CB 1C 1C 1B1C B A【例5】 (1)已知在△ABC 中,BC=a .如图1,点B 1 、C 1分别是AB 、AC 的中点,则线段B 1C 1的长是_______;如图2,点B 1 、B 2 ,C 1 、C 2分别是AB 、AC 的三等分点,则线段B 1C 1 + B 2C 2的值是__________;如图3, 点12......、、、n B B B ,12......、、、n C C C 分别是AB 、AC 的(n +1)等分点,则线段B 1C 1 + B 2C 2+……+ B n C n 的值是 ______.(2)如图,在正方形ABCD 中,AB =1,E 、F 分别是BC 、CD 边上点,① 若CE =12CB ,CF =12CD ,则图中阴影部分的面积是________;② 若CE =1n CB ,CF =1nCD ,则图中阴影部分的面积是_________.(用含n 的式子表示,n 是正整数).(3)如图,在矩形ABCD 中, AB =4,BC =6,当直角三角板MPN 的直角顶点P 在BC 边上移动时,直角边MP 始终经过点A ,设直角 三角板的另一直角边PN 与CD 相交于点Q .BP =x ,CQ=y ,那么y 与x 之间的函数图象大致是( )A能力提升【例6】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA 的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.初三寒假·第1讲·尖子班·学生版初三寒假·第1讲·尖子班·学生版【例7】 在△ABC 中,AB =4,BC =6,∠ACB =30°,将△ABC 绕点B 按逆时针方向旋转,得到△A 1BC 1. (1)如图1,当点C 1在线段CA 的延长线上时,求∠CC 1A 1的度数; (2)如图2,连接AA 1,CC 1.若△CBC 1的面积为3,求△ABA 1的面积;(3)如图3,点E 为线段AB 中点,点P 是线段AC 上的动点,在△ABC 绕点B 按逆时针方向旋转的过程中,点P 的对应点是点P 1,直接写出线段EP 1长度的最大值与最小值.C 1C BA 1A图2A 1C 1ABC图1图3A模块一 特殊三角形 课后演练【演练1】 ⑴如图,等腰ABC △中,AB AC =,20A =︒∠,线段AB 的垂直平分 线交AB 于D ,交AC 于E ,连接BE ,则CBE ∠等于( ) A .80° B . 70° C .60° D .50°实战演练图1EDBA11初三寒假·第1讲·尖子班·学生版⑵ 在等腰ABC △中,AB AC =,中线BD 将这个三角形的周长分别为15和 12两个部分,则这个等腰三角形的底边长为______________.⑶ 如图,等边三角形ABC 中,D 、E 分别为AB 、BC 边上的点,AD BE =, AE 与CD 交于点F ,AG CD ⊥于点G ,则AGAF = .【演练2】 如图,P 为边长为2的正三角形中任意一点,连接P A 、PB 、P C ,过P 点分别做三边的垂线,垂足分别为D 、E 、F ,则PD+PE+PF= ;阴影部分的面积为__________.模块二 全等三角形 课后演练 【演练3】 ⑴如图1,已知矩形ABCD 中,点E 是BC 上的一动点,过点E 作EF ⊥BD 于点F ,EG ⊥AC于点G ,CH ⊥BD 于点H ,试证明CH =EF +EG ;图3GEFL ABCDABCD EFGH图2图1H GFE DCBA⑵ 若点E 在BC 的延长线上,如图2,过点E 作EF ⊥BD 于点F ,EG ⊥AC 的延长线于点G ,CH ⊥BD 于点H , 则EF 、EG 、CH 三者之间具有怎样的数量关系,直接写出你的猜想;⑶ 如图3,BD 是正方形ABCD 的对角线,L 在BD 上,且BL =BC , 连接CL ,点E 是CL 上任一点, EF ⊥BD 于点F ,EG ⊥BC 于点G ,猜想EF 、EG 、BD 之间具有怎样的数量关系,直接写出你的猜想;⑷ 观察图1、图2、图3的特性,请你根据这一特性构造一个图形,使它仍然具有EF 、EG 、CH 这样的线段,并满足⑴或⑵的结论,写出相关题设的条件和结论.GFED CBAP F EA12初三寒假·第1讲·尖子班·学生版E 3E 2E 1D 4D 3D 2D 1CBA 【演练4】 图中是一副三角板,45︒的三角板Rt DEF △的直角顶点D 恰好在30︒的三角板Rt ABC △斜边AB 的中点处,304590A E EDF ACB ∠=︒∠=︒∠=∠=︒,,,DE 交AC 于点G ,GM AB ⊥ 于M .⑴ 如图1,当DF 经过点C 时,作CN AB ⊥于N ,求证:AM DN =.⑵ 如图2,当DF AC ∥时,DF 交BC 于H ,作HN AB ⊥于N ,⑴的结论仍然成立,请 你说明理由.图2图1EHABCD FGN NMGF ED CBA模块三 相似三角形 课后演练【演练5】 如图,已知Rt ABC △,1D 是斜边AB 的中点,过1D 作11D E AC ⊥于1E ,连接1BE 交1CD 于2D ;过2D 作22D E AC ⊥ 于2E ,连接2BE 交1CD 于3D ;过3D 作33D E AC ⊥于3E ,…, 如此继续,可以依次得到点45n D D D ,,…,,分别记11BD E △, 22BD E △,33BD E △,…,n n BD E △的面积为123S S S ,,,…n S .则n S =_________ABC S △(用含n 的代数式表示).第十八种品格:坚持品格教育—坚持有些人,做事是怕别人说失败,为不失败而坚持。



小学四年级尖子生数学辅导拔高训练
第二讲图形计数【学生版】几何图形计数问题往往没有显而易见的顺序,而且要数的对象通常是重叠交
错的,要准确计数就需要一些智慧了.实际上,图形计数问题,通常采用一种简单原始的计数方法-一枚举法.具体而言,它是指把所要计数的对象一一列举出来,以保证枚举时无一重复、.无一遗漏,然后计算其总和.正确地解答较复杂的图形个数问题,有助于培养同学们思维的有序性和良好的学习习惯.
一:简单图形计数的方法。
二:复杂图形计数的方法和找规律的方法。
例(1)数出右图中总共有多少个角
例(2 )数一数共有多少条线段?共有多少个三角形?
例(3)数一数图中长方形的个数
例(4)数一数图中有多少个正方形(其中每个小方格都是边长为1个长度单位的正方形)
.
例(5)数一数图中三角形的个数
例(6)数一数图中一共有多少个三角形?。

二年级第一讲平面图形计数进阶
姓名:________ 得分:__________
1.数一数,图(1)中有()条线段,图(2)中有( )个角?
2.数一数,下面有多少个三角形?
()个三角形
3.数一数,下面有多少个长方形?
()个长方形
答案与解析
1. 数一数,图(1)中有(6)条线段,图(2)中有( 6)个角?
[解析]数线段时,从左往右一个端点一个端点的出发,从A 点出发有3 条线段,从B点出发有2 条线段,从C 点出发有1 条线段,一共有6条线段。
数角时,从最上面的一条射线出发,从OA出发能画出3个角,从OB出发能画出2个角,从OC出发能画出1个角,一共有6个角。
2.数一数,下面有多少个三角形?
[解析]数“伞”状三角形时,可以类比数线段,底边有多少条线段就有多少个三角形。
所以可以知道底边有6+5+4+3+2+1=21条线段,所以一共有21个三角形。
3.数一数,下面有多少个长方形?
[解析]数2层的长方形,需要进行分层数,先数1层的长方形,再数2层的长方形。
上面一层有4+3+2+1=10个长方形,下面一层也有4+3+2+1=10个长方形,另外把第一层和第二层合在一起还有大的长方形,也有4+3+2+1=10个,所以一个有10+10+10=30个长方形。

第7讲 归纳与递推计数
1、一个长方形把平面分成两部分,那么四个长方形最多把平面分成部分.
2、有10 枚棋子,每次拿出2 枚或3 枚,要想将10 枚棋子全部拿完,共有多少种不同的拿法?
4、下图的两个图形(实线) 分别是用10 根和16 根单位长的小棍围成的.如果按此规律(每一层比上面一层多摆出两个小正方形)围成的某个图形共用了60 多根小棍,那么围成的图形有几层,共用了多少根小棍?
5、平面上有101 条直线,它们最多有多少个不同的交点?
3、如下图,一只蜜蜂从A 处出发,回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?
B
A 1个长方形:2
2个长方形:2+8, 第2个长方形与第1个长方形有8个交点,被分成8段,每一段把所在的平面一分为二,所以增加了8个平面。
=10
解析:因为:10=2+2+2+2+2=2+2+3+3
取5个2只有一种方法,去2个3和2个2,利用枚举法可知为6种。
一共7种。
解析:从A 开始往后依次形成斐波那契数列,1、1、2、3、5、8、13、21、34、55.所以到达B 时共有55种方法
解析:根据题意,可发现规律:后一个图形比前一个多6根小棍。
根据等差数列:60多减去10后为6的倍数。
则某层的根数为6×9+10=64(根) 层数:(64-10)÷6+1=10(层) 解析:
1条直线: 0
2条直线: 1,第2条直线被第1条直线分成2段,只有一个交点。
3条直线: 1+2,第3条直线与前两条直线相交,新产生2个交点。
…………
101条直线:1+2+3+4+5+6+……+100=5050(个)。

学而思尖子班考试试题学而思尖子班考试试题随着社会的发展,教育越来越受到家长和学生的重视。
为了提高学生的学习成绩和竞争力,许多家长选择将孩子送到学而思尖子班进行学习。
学而思尖子班以其严格的教学和考试要求而闻名,今天我们就来探讨一下学而思尖子班考试试题的特点和对学生的影响。
首先,学而思尖子班的考试试题具有一定的难度和深度。
这些试题往往涉及到高年级的知识点,要求学生具备扎实的基础知识和较强的分析能力。
试题中融入了一些实际问题,需要学生进行推理和解决,培养了学生的综合思考能力。
这种考试试题的设置,可以激发学生的学习兴趣,提高他们的学习动力和自信心。
其次,学而思尖子班的考试试题注重培养学生的创新思维和解决问题的能力。
试题中往往存在一定的难点和陷阱,需要学生通过自己的思考和探索来解决。
这种考试试题的设计,可以培养学生的创新思维和解决问题的能力,提高他们的自主学习能力和独立思考能力。
另外,学而思尖子班的考试试题注重培养学生的综合素质和团队合作能力。
试题往往涉及到多个学科的知识点,要求学生进行跨学科的综合运用。
学生需要在团队中进行合作,共同解决问题。
这种考试试题的设置,可以培养学生的综合素质和团队合作能力,提高他们的综合能力和合作意识。
然而,学而思尖子班考试试题也存在一些问题。
首先,试题的难度可能超出了学生的实际水平,给学生带来了过大的学习压力。
有些学生可能因为无法适应这种高强度的学习和考试要求而感到焦虑和沮丧。
其次,试题的设计可能过于注重知识点的考察,忽视了学生的实际应用能力。
有些学生可能只注重死记硬背,而忽视了对知识的理解和运用。
为了解决这些问题,学而思尖子班可以适当调整考试试题的难度和深度,根据学生的实际水平和能力进行设置。
同时,可以加强对学生的心理辅导和关怀,帮助他们调整好学习状态和心态。
此外,学而思尖子班可以通过增加实际应用题和开放性问题的设置,培养学生的创新思维和解决问题的能力。
总之,学而思尖子班考试试题的特点和对学生的影响是多方面的。

树妖跑了多少米
第一讲
树妖围着一个长方形的操场跑步,这个操场长28米,宽15米,这个操场的周长是多少米?
跑完步树妖累得满头大汗,凯奥斯递给它们一个手帕,这个手帕是正方形的,树妖量了量每条边的长,发现边长是2分米,这个正方形手帕的周长是多少分米?
凯奥斯用一根长30分米的黑线,刚好给大眼怪的照片镶了一圈黑边,这个长方形相框的宽是6分米,这个相框的长是多少分米?
有一个正方形的花坛,这个花坛的四周围着栏杆,栏杆共长80米,这个正方形花坛的边长是多少米?
有一个正方形的花坛,这个花坛的四周围着栏杆,栏杆共长36米,这个正方形花坛的边长是多少米?
两个大小相同的正方形,拼成一个长方形后,周长比原来两个正方形周长的和减少了4厘米,原来一个正方形的周长是多少厘米?
一个长方形的花坛被平均分成八个小正方形花坛,已知每个小正方形花坛的周长是15米,长方形花坛的周长是多少米?
(附加题)
分别求出下面图形的周长.(单位:厘米)
求下列图形的周长.(单位:厘米
)
小明将5张扑克牌如下图摆放,已知扑克牌的长是86毫米,宽56毫米,那么这个摆成后的图形的周长是多少毫米?。

二年级秋季创新拓展习题课
第3讲平面图形计数进阶
1、下面是新型材料组成的三角形,数一数,下图的三角形有多少个。
2、数一数,下图中共有()个三角形.
3、数一数,下图一共有多少个长方形?
(1)(2)
有()个长方形有()个长方形
二年级秋季创新拓展习题课4、想一想,如何快速得出下图中长方形的数量呢?(写出算式即可)
5、数一数,下图一共有()个长方形。
6、数一数,下图中包含这个绿色三角形的长方形(正方形也算)有()个。
7、下图的棋盘是由一些边长一样的小正方形组成,小正方形拼到一起可以组成一些大正方形,那么下图中一共可以数到()个正方形。
其中有的正方形内的黑、白方格数量各占一半.这样的正方形一共有()个.
8、数一数,下图中有多少个指定的图形?
(1)图中有()个“”型
(2)图中有()个“”型
1、数一数,下图一共有()个长方形。
2、为了防止小鱼偷吃零食,妈妈在冰箱外面建立了很多防护网,只有数清楚有多少正方形才能进入,你能帮帮小鱼么?
有()个
3、在下面的图中,包含苹果的三角形一共有()个.
4、数一数,下图中共有______个正方形.
5、下图包含绿色小三角形的长方形有_____个.。



春季班第一讲——我会数图形
【知识点】:
一、规则图形(肩并肩手拉手排成一排)
线段
角
1. 分类数(恰含法)。
每层个数×层数=总数
【例】数一数图中有多少个三角形?
每层个数:3+2+1=6(个) 层数:2层
总数:6×2=12(个) 一共12个。
2. 多层长方形
每层个数×层数=总数
(长边线段总数)×(宽边线段总数)=总数
【例】数一数下图中一共有多少个长方形?
总数:6×3=18(个)一共18个。
础、提高、尖子)
2. 数一数图中有多少个正方形?(提高、尖子)
3. 数一数下图中一共有多少个三角形?(基础、提高)
4. 数一数,图中共有个长方形,个三角形,条线段。
(尖子)
【学习建议】:
本讲讲的是数图形的方法,根据不同类型的图形有不同的巧妙方法,同学们要仔细辨认图形种类,像是规则图形和多层图形都是有巧妙方法的;如果是不规则图形,那么一定要注意分类,数的时候思路要清楚,这样才不会数错。

第二讲第几何计数问题进阶几何计数问题进阶第四级下几何计数问题进阶第三级下我会数图形(二年级秋季第一讲)第五级上巧求周长(三年级暑假第四讲)第三级下我会数图形本讲中重点学习数平面图形个数的方法,如数线段、数三角形、长方形、正方形等.第四级下几何计数问题进阶本讲中重点学习复杂图形的计数问题,包括数方块,简单的染色问题等.第五级上巧求周长本讲中重点学习立体图形的染色和平面图形的剪拼问题.第二讲第几何计数问题进阶(10)个正方形(16)个三角形【例题分析】低年级孩子对知识的掌握学得快,遗忘得也快,只有举一反三的练习才能达到熟能生巧的程度.因此开课的时候要引导学生复习之前所学的平面图形的计数,进一步巩固方法,掌握技巧.⑴对于线段,要注意引导学生回忆方法:如果线段中有n 个端点,那么线段的总条数就是:14321n -+++++ ().本题答案:432110+++=(条).⑵对于数长方形,我们要分层数,每层是3216++=(个),一共有6318⨯=(个).⑶按从小到大的顺序分类数:441110+++=(个).⑷分类数:只含有一个基本三角形的三角形有6个;恰含两个基本三角形的三角形有3个;恰含三个基本三角形的三角形有6个;恰含四个或五个基本三角形的三角形一个也没有;恰含六个基本三角形的三角形只有1个.图中共有三角形:636116+++=(个).总结:数平面图形时如果图形排列有规律,我们可以根据图形的规律来数,如线段、角、三角形等,如果图形的排列没有规律,我们可以分类来数,分类计数,最后算它们的总和.课前准备第二讲第几何计数问题进阶小朋友,你会数图形吗?无论是平面图形还是几何图形,在数复杂图形的个数时,只要我们认真仔细观察图形特点,有次序地去数,不遗漏不重复,就能数得又对又快.今天这节课我们也去闯一闯几何王国,让我们用我们的智慧去挑战这些图形吧!我是计数小冠军对于简单的图形,我们可以找规律按顺序数或分类来数.遇到较复杂的图形这些方法同样适用,不信就跟小精灵一起来试一试.你能根据这个侧面图算算砌好这面墙一共需要多少块砖吗?例1第二讲第几何计数问题进阶第二讲第几何计数问题进阶(9)块(10)块列式:549+=(块)列式:63110++=(块)或:639+=(块)(9)块(12)块列式:639+=(块)列式:15612++=(块)或:549+=(块)【例题分析】课前引导学生复习之前所学的数方块的方法,让学生进一步感受到在数图形的时候找规律按顺序数可以数得又对又快,为后面学习复杂图形的计数做铺垫.下面这堆木方块共有多少块?(中间画阴影的部分从上到下是空心)例2第二讲第几何计数问题进阶【例题分析】在这道题中,一定要注意引导学生观察的到中间是空心的,那么从不同的角度观察,方法也就不同,具体分析如下:方法一:因为中间是空心的,所以一层只有8块,4层一共8432⨯=(块).方法二:第一列有12个,第二列有8个,第三列有12个,一共有:1281232++=(块)方法三:不看阴影部分一共有:12336⨯=(块),中间缺的部分是4个,一共有方块:36432-=(块).下面的图形被云彩遮住了,你能数出有多少个方块吗?(中间阴影部分是空心的)想想做做第二讲第几何计数问题进阶【例题分析】虽然部分方块被遮住了,但是我们还是可以发现,如果不看中间空心的部分,每边是3个方块,共3层.方法一:第一排9个,第二排6个,第三排9个,一共:96924++=(块).方法二:一层8个,共8324⨯=(块).方法三:先看成一个整体,39324⨯-=(块).【例题分析】先从整体上考虑组成一个较大的正方体需要多少个小正方体,再数出已有的小正方体的个数,便能得出相差的个数.⑴组成较大的正方体需要的小正方体个数:33327⨯⨯=(个).已有小正方体个数:96318++=(个).还差正方体个数:27189-=(个).至少添加9个小正方体可以组成一个较大的正方体.⑵组成较大的正方体需要的小正方体个数:33327⨯⨯=(个).已有小正方体个数:96419++=(个).还差正方体个数:27198-=(个).至少添加8个小正方体可以组成一个较大的正方体.下图中至少添加多少个小正方体可以组成一个较大的正方体?⑴⑵例3第二讲第几何计数问题进阶【答案】人的脑袋露出“石头”,相当“石”字出头,即暗示为“右”.因此应向右走.下面是用小正方体堆成的图形,现在把这个图形的表面涂上黄色,想一想有多少个小正方形没有被涂色?古时候一人赴京赶考.来到三岔路口,不知该走哪条路.见一人在石头后面干活,便上前询问.不料此人竟不言语,只把头探出石头上面望着他.赶考者欲发怒,忽然想到了答案,于是选了一条路继续赶路.你知道他选的是哪条路吗?例4第二讲第几何计数问题进阶【例题分析】如果把两个小正方体堆在一起,那么两个小正方体有一个面会重合,观察这个图一共由四个小正方体堆成,把这个图形表面涂上黄色,要想知道有几个小正方形没有被染色,我们可以先来观察有多少个重合面,数一数一共有3个重合面,每个重合面有2个小正方形重合在一起,这2个小正方形没有被涂色,那么在这个图形中一共有6个面没有被涂成黄色.【例题分析】立体图形的分割可以培养学生的空间想象能力,而学生空间想象能力的形成又需要一个具体到抽象的过程,因此在处理这个题的时候老师可以先让学生去猜测,发挥自己的想象,然后通过实际操作进行验证,为后面的学习进行铺垫.正方体有6个面,6个面都是正方形,在这个题中把一个正方体切割成8个小正方体,其中每个小正方体有3个面被涂上了绿色,还有三个面没有颜色.把一个正方体木块表面涂上绿色,然后再把它切成8个小正方体,想一想每个小正方体有几个面没有颜色?想想做做例5第二讲第几何计数问题进阶【例题分析】这个题引导学生动手切一切.一共可以切成8个三棱柱,每个三棱柱有2个面没有颜色,这两个面是两个长方形,这样一共就有2816⨯=(个)面没有被涂上颜色.⑴3面涂成黄色的小正方体有()个.⑵4面涂成黄色的小正方体有()个.⑶5面涂成黄色的小正方体有()个.下图是一个正方体木块,在它的表面涂上蓝色,然后沿正方体上面直线垂直切开.切成了()个三棱柱.这些三棱柱一共有()个面没有被涂色.用10个小正方体摆成一个“工"字形(如下图),然后又将表面涂成黄色(下面也被涂色),最后又把小正方体分开,数一数:例6第【例题分析】整个图形表面涂成黄色,只有那些“黏在一起”的面没有被涂色.左、右两端中间各有1个小正方体3面涂色,中间的4个小正方体4面涂色,剩下的4个小正方体都是5面涂色.3面涂成黄色的小正方体有2个;4面涂成黄色的有4个;5面涂成黄色的有4个.拓展与提高一个大长方体的表面上都涂上红色,然后切成18个小立方体(切线如图中虚线所示).在这些切成的小立方体中,问:⑴1面涂成红色的有()个.⑵2面涂成红色的有()个.⑶3面涂成红色的有()个.第【例题分析】仔细观察图形,并发挥想象力,可知:⑴上下两层中间的2块只有一面涂色;⑵每层四边中间的1块有两面涂色,上下两层共8块;⑶每层四角的4块有三面涂色,上下两层共有8块.最后检验一下小立方体总块数:28818++=(个).在教学过程中,老师可以让学生先观察上面一层的情况,并把每个小正方体染了几个面标注出来,因为上下情况一样,所以数上面一层的个数再乘2就能得到答案.(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)附加题一个由小正方体堆成的“塔”.如果把它的外表面(包括底面)全部涂成绿色,那么当把“塔”完全拆开时,3面被涂成绿色的小正方体有多少块?【答案】最下层有3412⨯=(个),上一层有4个,这样一共有16个小正方体被3面涂色.如右上图所示.第下面两个图形能拼成一个长方体吗?【例题分析】这道题考查学生的空间想象能力,如果把第二个图打倒(如下图),就能够发现这两个图形不能拼成一个长方体,因为第一个图中的一块和第二个图中的一块在同一个位置.如图所示,数一数,需要多少块砖才能把坏了的墙补好?【例题分析】用10块砖可把墙补好,可以从下往上一层一层地数(发挥想像力):一个大正方体的表面上都涂上绿色,然后切成27个小立方体(切线如图中虚线所示).在这些切成的小立方体中,问:第⑴1面涂成绿色的有()个.⑵2面涂成绿色的有()个.⑶3面涂成绿色的有()个.⑷1个面也没有被涂成绿色的有()个.【例题分析】⑴每个面中间的1个小正方体有一面被涂上了绿色,因为有6个面,这样一面被涂成绿色的有6个小正方体.⑵每条棱上中间的这个小正方体有2个面被涂上了绿色,一共有12个小正方体有两面被涂成了绿色.⑶8个顶点处的小正方体有3面被涂成绿色.⑷一个面也没有被涂成绿色的有1个,就是第二层最中心的这个小正方体.1.数一数.(15)个三角形(17)个正方形(44)个三角形第2.下图中每个图形各由几个小正方体拼成,至少再增加几个小正方体就可以把这个图形拼成一个长方体?【答案】⑴有9个小正方体,至少增加7个小正方体就可以拼成一个长方体.⑵有10个小正方体,至少增加2个小正方体就可以拼成一个长方体.⑶有12个小正方体,至少增加6个小正方体就可以拼成一个长方体.3.如图所示砖墙是由正六边形的特型砖砌成,问需要几块正六边形的砖才能把它补好?【答案】一共需要7块正六边形的砖才能把它补好,如右图.4.这堆木方块共有多少块?(中间打阴影部分是空心)⑴⑵⑶有()个有()个有()个补()个补()个补()个第【答案】3352339⨯⨯-⨯=(块)或3336239⨯⨯+⨯=(块)或31339⨯=(块).5.如图所示为一堆砖.中央最高一摞是10块,它的左右两边各是9块,再往两边是8块、7块、6块、5块、4块、3块、2块、1块.问:这堆砖共有多少块?【答案】当中央最高一摞是10块时,这堆砖的总数是:12345678910987654321++++++++++++++++++1010=⨯100=(块)6.将8个小立方块组成“丁”字型,再将表面都涂成红色,然后再把小立方块分开.⑴3面被涂成红色的小立方块有()个.⑵4面被涂成红色的小立方块有()个.⑶5面被涂成红色的小立方块有()个.第【答案】看着图,想象涂色情况.当把整个表面都涂成红色后,只有那些“粘在一起”的面(又叫互相接触的面),没有被涂色.每个小立方体都有6个面,减去没涂色的面数,就得涂色的面数.每个小立方体涂色面数都写在了它的上面.3面涂色的小立方体共有1个;4面涂色的小立方体共有4个;5面涂色的小立方体共有3个.【答案】红球白球一样多。
图形计数进阶
【例1】(1)已知图中点C,D,E,F 为线段AB 的五等分点,图中共有( )条线段, 如果AB =10厘米,那么所有线段的和是
( )米.
(2)图中一个大角被分成 6 个小角,每个小角都是30°,图中共有( )个角,这些角的和是( )度. (仅考虑劣角, 不考虑优角)
【例2】
1.(1) 数一数,图中共有 ( ) 个三角形.
(2) 数一数,图中三角形共有( ) 个.。
(3) 数一数,图中有 ( ) 个三角形.
2.图中线段的条数比三角形的个数多____________________
.
【例3】
(1) 图中共有
( ) 个三角形.
(2) 图中共有
( ) 个三角形.
(3) 图中共有( ) 个三角形.
【例4】
1. (1)数一数,图中有( )个长方形.
(2)用16个同样大小的正方形组成如图的一个大正方形,下图中有
( )个正方形.
(3)如图,四条边长度都相等的四边形称为菱形.用16个同样大小的菱形组成如
图的一个大菱形.数一数,图中共有( ) 个菱形.
2.图中有______个正方形
【例5】下图中共有( )个长方形,这些长方形的面积和是( )
【例6】1.在图所示的线段中,包含“☆”的线段有( )
条;包含“△”的线段有( )条; 至少包含“☆”和
“△”中的一个的线段有( )条.
2。
在图所示的线段中,包含“A”的线段有( )条;包含“B”的线段有( )条;至少包含“A”和“B”中的一个的线段有( )条.
【例7】(1)下图中包含五角星的长方形一共有()个
(2)下图中包含五角星的长方形一共有( )个.
(3)只包含一个字母的长方形有( )个
【例8】
1.由20 个单位小正方形组成的长方形中,包含☆的正方形共有
( )个.
2.在下面的图中,包含苹果的正方形一共有()个.。