线面、面面平行的判定与性质
- 格式:pdf
- 大小:178.05 KB
- 文档页数:4

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平a a P'b 二.•「a// ■-面平行。
符合表示:a//b2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:a広oa//«=■ a//ba -:-b二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
n 〃b "m // aa"b = Mm □ n = N符号表示:2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
a //P ]符号表示:: =| = l//d (更加实用的性质:一个平厂L: d面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面符号表示:$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直符号表示:oA 二、:po -:2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
a _ ■ ,a---:2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面:=b, a x 上,a_b= a -:Welcome !!! 欢迎您的下载, 资料仅供参考!。

9.4 线面、面面平行的判断与性质编制人:高三数学组 负责人:__________________ 【使用说明】:1.课前认真研读课本,完成自主研读学习单设计的问题..2.课堂内限时完成合作探究学习单,书写规范.3.找出疑问和不能独立解决的问题,通过合作探究,教师指导等方式解决.4.课后认真完成反馈巩固学习单. 【大纲要求】 1..2.※自主研读学习单※知识体系一、直线与平面平行1.判定方法(1)用定义:直线与平面无公共点.(2)判定定理: (线线平行⇒线面平行) (3)其他方法: (面面平行⇒线面平行) 2、性质定理: (线面平行⇒线线平行) 二、平面与平面平行 1、判定方法(1)用定义:两个平面无公共点(2)判定定理: (线面平行⇒面面平行) (3)其他方法: (线面垂直⇒面面平行);(面面平行的传递性)(两个平面内相交的两条直线平行,那么这两个平面平行)2、性质定理: (面面平行⇒线线平行)3、两条直线被三个平行平面所截,截得的线段对应 。
基础自测1.已知直线、和平面,那么的一个必要不充分的条件是( ), ,a b αb a //()A α//a α//b ()B α⊥a α⊥b且 、与成等角2.、表示平面,、表示直线,则的一个充分条件是 ( ),且 ,且 ,且 ,且3.已知平面平面,是外一点,过点的直线与分别交于点,过点的直线与分别交于点,且,,,则的长为( )或4.空间四边形的两条对角线,,则平行于两对角线的截面四边形的周长的取值范围是 .※合作探究学习单※ 题型一:直线与平面平行的判定与性质 【例1】►(2011·天津改编)如图,在四棱锥P ABCD 中,底面ABCD 为平行四边形,O 为AC 的中点,M 为PD 的()C α⊂b α//a ()D a b ααβa b α//a ()A βα⊥β⊥a ()B b =βα b a //)(C b a //α//b ()D βα//β⊂a //αβP βα,P m βα,C A ,P n βα,D B ,6=PA 9=AC 8=PD BD ()A 16()B 24524()C 14()D 20ABCD 4=AC 6=BD中点.求证:PB∥平面ACM.例2.正方体ABCD—A1B1C1D1中.(1)求证:平面A1BD∥平面B1D1C;(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.练习:1、如图,若P A⊥平面ABCD,四边形ABCD是矩形,E、F分别是AB、PD的中点,求证:AF∥平面PCE.2.如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.求证:(1)线段MP和NQ相交且互相平分;(2)AC∥平面MNP,BD∥平面MNP.题型二平面与平面平行的判定与性质【例2】►如图,在正方体ABCDA1B1C1D1中,M、N、P分别为所在边的中点.求证:平面MNP∥平面A1C1B;练习:1、如图,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:BADC PNQM(1)B ,C ,H ,G 四点共面; (2)平面EF A 1∥平面BCHG .2、已知正四棱锥的底面边长为,侧棱长为,点分别在和上,并且,平面,求线段的长.题型三:线面平行中的探索问题 【例3】►如图所示,在三棱柱ABCA 1B 1C 1中,A 1A ⊥平面ABC ,若D 是棱CC 1的中点,问在棱AB 上是否存在一点E ,使DE ∥平面AB 1C 1?若存在,请确定点E 的位置;若不存在,请说明理由.练习:1、 如图,在四棱锥P ABCD 中,底面是平行四边形,P A ⊥平面ABCD ,点M 、N 分别为BC 、P A 的中点.在线段PD 上是否存在一点E ,使NM ∥平面ACE ?若存在,请确定点E 的位置;若不存在,请说明理由.高考真题 共3-5题1.(文)已知两条直线m 、n ,两个平面α、β.给出下面四个命题:①m ∥n ,m ⊥α⇒nABCD S -a a 2Q P ,BD SC 2:1:=PD BP //PQ SAD PQ⊥α;②α∥β,m⊂α,n⊂β⇒m∥n;③m∥n,m∥α⇒n∥α;④α∥β,m ∥n,m⊥α⇒n⊥β.其中正确命题的序号是(C)A.①③B.②④C.①④D.②③2. (理)对于任意的直线l与平面α,在平面α内必有直线m,使m与l(C)A.平行B.相交C.垂直D.互为异面直线3.(2010·浙江理)设m,l是两条不同的直线,α是一个平面,则下列命题正确的是(B) A.若l⊥m,m⊂α,则l⊥αB.若l⊥α,l∥m,则m⊥αC.若l∥α,m⊂α,则l∥mD.若l∥α,m∥α,则l∥m4.(2010·山东文,4)在空间,下列命题正确的是(D)A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行5、(2011·山东)如图,在四棱台ABCDA1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB =2AD,AD=A1B1,∠BAD=60°.(1)证明:AA1⊥BD;(2)证明:CC1∥平面A1BD.6、(2010·安徽)如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB;(3)求四面体BDEF的体积.※巩固提升学习单※共12题左右1.(文)(2011·泰安模拟)设m、n表示不同直线,α、β表示不同平面,则下列命题中正确的是( )A.若m∥α,m∥n,则n∥αB.若m⊂α,n⊂β,m∥β,n∥α,则α∥βC.若α∥β,m∥α,m∥n,则n∥βD.若α∥β,m∥α,n∥m,n⊄β,则n∥β2.(文)(2011·宁波模拟)已知直线l、m,平面α、β,则下列命题中的假命题是( ) A.若α∥β,l⊂α,则l∥βB.若α∥β,l⊥α,则l⊥βC.若l∥α,m⊂α,则l∥mD.若α⊥β,α∩β=l,m⊂α,m⊥l,则m⊥β3.(2011·北京海淀期中)已知平面α∩β=l,m是α内不同于l的直线,那么下列命题中错误..的是( )A.若m∥β,则m∥l B.若m∥l,则m∥βC.若m⊥β,则m⊥l D.若m⊥l,则m⊥β4.(文)(2011·浙江省温州市高三适应性测试)已知m,n,l为三条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )A.α∥β,m⊂α,n⊂β⇒m∥nB.l⊥β,α⊥β⇒l∥αC.m⊥α,m⊥n⇒n∥αD.α∥β,l⊥α⇒l⊥β5.(2011·广东揭阳模拟)若a不平行于平面α,且a⊄α,则下列结论成立的是( ) A.α内的所有直线与a异面B.α内与a平行的直线不存在C.α内存在唯一的直线与a平行D.α内的直线与a都相交6.(文)(2010·福建福州市)对于平面α和共面的直线m,n,下列命题是真命题的是( )A.若m,n与α所成的角相等,则m∥nB.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n7.(2011·浙江五校联考)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:①若m∥α,n∥α,m∥β,n∥β,则α∥β;②若α⊥γ,β⊥γ,α∩β=m,n⊂γ,则m⊥n;③若m⊥α,α⊥β,m∥n,则n∥β;④若n∥α,n∥β,α∩β=m,那么m∥n.其中正确命题的序号是________.8.(2011·福建文,15)如下图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于________.9.(2011·郑州一检)已知两条不重合的直线m、n,两个不重合的平面α、β,有下列命题:①若m∥n,n⊂α,则m∥α;②若n⊥α,m⊥β,且n∥m,则α∥β;③若m⊂α,n⊂α,m∥β,n∥β,则α∥β;④若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α.其中正确命题的序号是________.10.(2011·广东揭阳一模)如下图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.(1)求证:GH∥平面CDE;(2)若CD=2,DB=42,求四棱锥F-ABCD的体积.11.(2011·广东省广州市质检)如下图,正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线( ) A.不存在B.有1条C.有2条D.有无数条12.(文)(2011·北京模拟)给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.其中真命题的个数为( )13、点是所在平面外一点,分别是、、的重心,求证:(1)平面平面;(2)求.P ABC ∆C B A ''',,PBC ∆PCA ∆PAB ∆ABC //C B A '''AB B A :''。

1.线线平行判定:a用向量,方向向量平行b一条直线平行于另一个平面,则它平行于它所在平面与那个平面的交线。
C若一平面与两平行平面相交,则两交线平行。
D同时与一平面垂直的两直线平行。
E同时平行于一条直线的两直线平行。
性质:貌似没啥性质,一般是证明线面关系的时候先证明线线关系。
2.线线垂直判定:a向量,方向向量垂直b直线垂直于平面,则直线与平面中的任意直线都垂直c第一条直线与第二条直线平行,第一条垂直于第三条,则第二条也垂直于第三条d把两直线放在一个平面中,利用平面几何各种判定方法,如等腰三角形的底和高等。
E(重点)三垂线定理:平面内的一条直线,如果和过平面的一条斜线在平面内的射影垂直,那么它就和这条斜线垂直。
三垂线逆定理:在平面内的一条直线,如果和过平面的一条斜线垂直,那么它也垂直于斜线在平面内的射影。
(这个比较重要,记不住的话找一下例题,多看看图就好了)性质:貌似也没什么性质,一般也是要证明线面关系的时候用到它。
注意:第一条直线垂直于第二条直线,第一条直线垂直于第三条直线,则第二条直线与第三条直线可垂直可平行也可普通相交。
3,线面平行判定:a面外一条线与面内一条线平行。
(常用)b空间向量法,证明线一平行向量与面内一向量(x1x2-y1y2=0)(常用)c面外一直线上不同两点到面的距离相等d证明线面无交点(定义)e反证法(线与面相交,再推翻)性质:平面外一条直线与此平面平行,则过这条直线的任意平面与此平面的交线与该直线平行。
4.线面垂直判定:a一条线和平面内两条相交直线都垂直,那么这条直线和这个平面垂直b两个平面垂直,其中一个平面内的直线垂直两平面的交线,那么这条直线和这个平面垂直c直线的方向向量与平面的法向量平行性质:如果两条直线同时垂直一个平面,那么这两条直线平行。
5.面面平行判定a一个平面内的两条相交直线分别与另一个平面平行,则这两个平面平行。
(常用)b如果两平面同时垂直于一条直线,则两平面平行(大题一般不用)性质:a两个平面平行,在一个平面内的任意一条直线平行于另外一个平面b两个平面平行,和一个平面垂直的直线必垂直于另外一个平面 c 两个平行平面,分别和第三个平面相交,交线平行d平行平面所截的线段对应成比例(这个是推论,不好描述,书上或练习册上应该有类似的题)6.面面垂直判定:一个面如果过另外一个面的垂线,那么这两个面相互垂直性质:a如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。

线面平行的性质定理和判定定理
面面平行的性质定理:
一、线线平行
1、同位角成正比两直线平行:在同一平面内,两条直线被第三条直线所封盖,如果
内错角成正比,那么这两条直线平行。
2、内错角相等两直线平行:在同一平面内,两条直线被第三条直线所截,如果同旁
内角互补,那么这两条直线平行。
3、同旁内角优势互补两直线平行。
二、线面平行
1、利用定义:证明直线与平面并无公共点;
2、利用判定定理:从直线与直线平行得到直线与平面平行;
3、利用面面平行的性质:两个平面平行,则一个平面内的'直线必平行于另一个平面。
平行平面间的距离处处相等。
已知:α∥β,ab⊥α,dc⊥α,且a、d∈α,b、
c∈β求证:ab=cd证明:连接ad、bc由线面垂直的性质定理可知ab∥cd,那么ab和cd
构成了平面abcd∵平面abcd∩α=ad,平面abcd∩β=bc,且α∥β∴ad∥bc(定理2)
∴四边形abcd是平行四边形∴ab=cd。
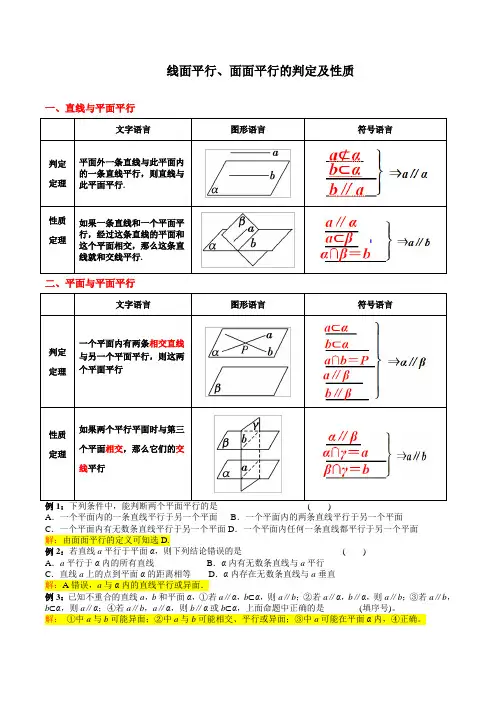
线面平行、面面平行的判定及性质一、直线与平面平行文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则直线与此平面平行.性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.二、平面与平面平行文字语言图形语言符号语言判定定理一个平面内有两条相交直线与另一个平面平行,则这两个平面平行性质定理如果两个平行平面时与第三个平面相交,那么它们的交线平行A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面解:由面面平行的定义可知选D.例2:若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直解:A错误,a与α内的直线平行或异面.例3:已知不重合的直线a,b和平面α,①若a∥α,b⊂α,则a∥b;②若a∥α,b∥α,则a∥b;③若a∥b,b⊂α,则a∥α;④若a∥b,a∥α,则b∥α或b⊂α,上面命题中正确的是________(填序号)。
解:①中a与b可能异面;②中a与b可能相交、平行或异面;③中a可能在平面α内,④正确。
例4:已知α、β是平面,m 、n 是直线,给出下列命题:①若m ⊥α,m ⊂β,则α⊥β.②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β.③如果m ⊂α,n ⊄α,m 、n 是异面直线,那么n 与α相交.④若α∩β=m ,n ∥m ,且n ⊄α,n ⊄β,则n ∥α且n ∥β其中正确命题的个数是 ( ) A .1 B .2 C .3 D .4解:对于①,由定理“如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直”得知,①正确;对于②,注意到直线m ,n 可能是两条平行直线,此时平面α,β可能是相交平面,因此②不正确;对于③,满足条件的直线n 可能平行于平面α,因此③不正确;对于④,由定理“如果平面外一条直线平行于平面内一条直线,那么这条直线平行于这个平面”得知,④正确.综上所述,其中正确的命题是①④,选B.例5:已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题:(1)⎩⎪⎨⎪⎧ m ⊥αn ⊥α⇒m ∥n ;(2)⎩⎪⎨⎪⎧ m ⊥αm ⊥n ⇒n ∥α (3)⎩⎪⎨⎪⎧m ⊥αn ∥α⇒m ⊥n 其中真命题的个数为 ( ) A .0 B .1 C .2 D .3 解:若⎩⎪⎨⎪⎧ m ⊥α,n ⊥α,则m ∥n ,即命题(1)正确;若⎩⎪⎨⎪⎧ m ⊥α,m ⊥n ,则n ∥α或n ⊂α,即命题(2)不正确;若⎩⎪⎨⎪⎧m ⊥αn ∥α,则m ⊥n ,即命题(3)正确;综上可得,真命题共有2个.选C例6:已知m 、n 、l 1、l 2表示直线,α、β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则以下条件中,能推出α∥β的是 ( )A .m ∥β且l 1∥αB .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2解:由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.例7:在下列条件中,可判断平面α与β平行的是( ).A. α、β都平行于直线lB. α内存在不共线的三点到β的距离相等C. l 、m 是α内两条直线,且l ∥β,m ∥βD. l 、m 是两条异面直线,且l ∥α,m ∥α,l ∥β,m ∥β 解:排除法,A中α、β可以是相交平面;B中三点可面平面两侧;C中两直线可以不相交.故选D,也可直接证明.例8:经过平面外的两点作该平面的平行平面可以作( ).A. 0个B. 1个C. 0个或1个D. 1个或2个解:这两点可以是在平面同侧或两侧.选C 。

2线线、线面、面面平行的判定与性质姓名: 分数:知识记忆:1.空间两条直线有 种位置关系: 、 、 .2.平行线的传递性: 。
3.空间中,如果两个角的两边分别对应平行,那么这两个角4.直线与平面的位置关系有 种:直线在平面 、直线与平面 、直线与平面 .5.线面平行判断:如果面外线平行于面内线,那么 .(线线平行 ,则 )6.线面平行性质:如果一条直线与一个平面平行,并且经过这条直线的一个平面和这个平面相交,那么这条直线与交线 。
(线面平行,则 ).7.空间两个平面就有 种位置关系: 与 .8.面面平行的判定:如果一个平面内的两条相交直线都与另一个平面平行,那么这两个平面 .(线线平行 ,则 )9.面面平行的判定:如果一个平面与两个平行平面相交,那么它们的交线平行.(面面平行,则 )一、填空题:1.长方体1111ABCD A B C D 中,直线1DD 平面11BCC B (平行、垂直),理由是 。
二、选择题1“空间四点D C B A ,,,不在同一平面内”是“直线CD AB ,异面”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件2.两个平面平行的条件是( )A .一个平面内有一条直线平行于另一个平面B .一个平面内有两条平行直线都平行于另一个平面C .一平面内有两条相交直线都平行于另一个平面D .一平面内有无数条直线都平行于另一个平面3.下列命题中正确的是( )A .分别在两个平行平面内的两条直线是异面直线 B. 分别通过两条平行直线的两个平面平行C. 分别在两个平行平面内的两条直线平行D. 分别在两个平行平面内的两条直线平行或异面三、解答题:1.已知空间四边形ABCD 中,E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点(如图).判断四边形EFGH 是否为平行四边形?2. 在如图所示的一块木料中,已知BC ∥平面1111A B C D ,BC ∥11B C ,要经过平面11A C 内的一点P 与棱BC 将木料锯开,应当怎样画线?3. 设平面α内的两条相交直线m ,n 分别平行于另一个平面β内的两条直线k ,l ,试判断平面α,β是否平行?4.如图所示,//αβ,M 在α与β同侧,过M 作直线a 与b ,a 分别与α、β相交于A 、B ,b 分别与、β相交于C 、D .⑴ 判断直线AC 与直线BD 是否平行;⑵ 如果 4M A =cm ,5AB =cm ,3MC =cm ,求MD 的长.b a第4题图βαMA CDB。

线面、面面平行的判定与性质(教师版)知识回顾1.线面平行的判定(1)直线与平面平行的定义:直线与平面无公共点. (2)直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 用符号表示为:a ⊄α,b ⊂α,且a ∥b ⇒a ∥α. 2.线面平行的性质直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行符号语言描述:⎭⎪⎬⎪⎫a ∥αa ⊂ββ∩α=b ⇒a ∥b . 3. 面面平行的判定(1)平面α与平面β平行的定义:两平面无公共点. (2)直线与平面平行的判定定理:下面的命题在“________”处缺少一个条件,补上这个条件,使其构成真命题(m ,n 为直线,α,β为平面),则此条件应为m ,n 相交.⎭⎪⎬⎪⎫m ⊂αn ⊂αm ∥βn ∥β⇒α∥β 4.面面平行的性质平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.符号表示为:⎭⎪⎬⎪⎫α∥βα∩γ=a β∩γ=b ⇒a ∥b . 题型讲解题型一 利用三角形中位线证明线面平行例1、如图,ABCD 是平行四边形,S 是平面ABCD 外一点,M 为SC 的中点.求证:SA∥平面MDB.答案:证明:连结AC交BD于N,因为ABCD是平行四边形,所以N是AC的中点.又因为M是SC的中点,所以MN∥SA.因为MN平面MDB,所以SA∥平面MDB.例2、如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,求证:MN∥平面PB1C.答案证明:如图,连结AC,则P为AC的中点,连结AB1,∵M、N分别是A1A与A1B1的中点,∴MN∥AB1.又∵平面PB1C,平面PB1C,故MN∥面PB1C.例3、如图所示,P是▱ABCD所在平面外一点,E、F分别在PA、BD上,且PE∶EA=BF∶FD.求证:EF∥平面PBC.证明连接AF延长交BC于G,连接PG.在▱ABCD中,易证△BFG∽△DFA.∴GFFA=BFFD=PEEA,∴EF∥PG.而EF⊄平面PBC,PG⊂平面PBC,∴EF∥平面PBC.练习在正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与过点A,E,C的平面的位置关系是______.答案:平行题型二利用平行四边形证明线面平行例1、如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱BC、C1D1的中点.求证:EF∥平面BDD1B1.证明:取D1B1的中点O,连接OF,OB.∵OF 12B1C1,BE12B1C1,∴OF BE.∴四边形OFEB是平行四边形,∴EF∥BO.∵EF⊄平面BDD1B1,BO⊂平面BDD1B1,∴EF∥平面BDD1B1.例2、如图所示,已知正方体ABCD-A1B1C1D1中,面对角线AB1、BC1上分别有两点E、F,且B1E=C1F.求证:EF∥平面ABCD.证明方法一过E、F分别作AB、BC的垂线,EM、FN分别交AB、BC于M、N,连接MN.∵BB1⊥平面ABCD,∴BB1⊥AB,BB1⊥BC,∴EM∥BB1,FN∥BB1,∴EM∥FN,∵AB1=BC1,B1E=C1F,∴AE=BF,又∠B1AB=∠C1BC=45°,∴Rt△AME≌Rt△BNF,∴EM=FN.∴四边形MNFE是平行四边形,∴EF∥MN.又MN⊂平面ABCD,EF⊄平面ABCD,∴EF∥平面ABCD.方法二过E作EG∥AB交BB1于G,连接GF,∴B1EB1A=B1GB1B,B1E=C1F,B1A=C1B,∴C1FC1B=B1GB1B,∴FG∥B1C1∥BC.又∵EG∩FG=G,AB∩BC=B,∴平面EFG∥平面ABCD.又EF⊂平面EFG,∴EF∥平面ABCD.题型三利用面面平行证明线面平行例. 如图,在四棱锥中,是平行四边形,,分别是,的中点.求证:平面.答案:证明:如图,取的中点,连接,,分别是,的中点,,,P ABCDABCD M N AB PCMN//PADCD E NE ME∵M N AB PCNE PD∴//ME AD//可证明平面,平面.又,平面平面,又平面,平面.题型四面面平行的证明例1、如图所示,在正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?解:当Q为CC1的中点时,平面D1BQ∥平面PAO.∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.∵P、O为DD1、DB的中点,∴D1B∥PO.又PO∩PA=P,D1B∩QB=B,D1B∥平面PAO,QB∥平面PAO,∴平面D1BQ∥平面PAO.题型五平行性质NE//PAD ME//PADNE ME E=∴MNE//PADMN⊂MNE∴MN//PAD例1、如图所示,长方体ABCD-A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是()A.平行 B.相交C.异面 D.平行和异面答案:A例2、ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.证明如图所示,连接AC交BD于O,连接MO,∵ABCD是平行四边形,∴O是AC中点,又M是PC的中点,∴AP∥OM.根据直线和平面平行的判定定理,则有PA∥平面BMD.∵平面PAHG∩平面BMD=GH,根据直线和平面平行的性质定理,∴AP∥GH.练习、如图,在三棱柱ABC-A1B1C1中,M是A1C1的中点,平面AB1M∥平面BC1N,AC∩平面BC1N=N.求证:N为AC的中点.证明 ∵平面AB 1M ∥平面BC 1N , 平面ACC 1A 1∩平面AB 1M =AM , 平面BC 1N∩平面ACC 1A 1=C 1N , ∴C 1N ∥AM ,又AC ∥A 1C 1, ∴四边形ANC 1M 为平行四边形, ∴AN 綊C 1M =12A 1C 1=12AC ,∴N 为AC 的中点.跟踪训练1.如右图所示的三棱柱ABC -A 1B 1C 1中,过A 1B 1的平面与平面ABC 交于直线DE ,则DE 与AB 的位置关系是( )A .异面B .平行C .相交D .以上均有可能 答案:B[解析] ∵A 1B 1∥AB ,AB ⊂平面ABC ,A 1B 1⊄平面ABC , ∴A 1B 1∥平面ABC.又A 1B 1⊂平面A 1B 1ED ,平面A 1B 1ED∩平面ABC =DE ,∴DE ∥A 1B 1. 又AB ∥A 1B 1,∴DE ∥AB.2.已知直线l ,m ,平面α,β,下列命题正确的是( ) A .l ∥β,l ⊂α⇒α∥βB .l ∥β,m ∥β,l ⊂α,m ⊂α⇒α∥βC .l ∥m ,l ⊂α,m ⊂β⇒α∥βD .l ∥β,m ∥β,l ⊂α,m ⊂α,l ∩m =M ⇒α∥β 答案:D3、直线a ∥平面α,α内有n 条直线交于一点,则这n 条直线中与直线a 平行的直线( )A.至少有一条 B.至多有一条C.有且只有一条 D.没有答案:B4、给出下列结论,正确的有()①平行于同一条直线的两个平面平行;②平行于同一平面的两个平面平行;③过平面外两点,不能作一个平面与已知平面平行;④若a,b为异面直线,则过a与b平行的平面只有一个.A.1个 B.2个 C.3个 D.4个答案:B5.正方体EFGH—E1F1G1H1中,下列四对截面中,彼此平行的一对截面是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G答案:A6.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为________.答案:平行四边形[解析]∵平面ABFE∥平面CDHG,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面CDHG=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH的形状是平行四边形.7. 如图所示,在三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点,求证:BC1∥平面CA1D.证明:如图所示,连接AC1交A1C于点O,连接OD,则O是AC1的中点.∵点D是AB的中点,∴OD∥BC1.又∵OD⊂平面CA1D,BC1⊄平面CA1D,∴BC1∥平面CA1D.8.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC和SC的中点.求证:平面EFG∥平面BDD 1B1.证明如图所示,连接SB,SD,∵F、G分别是DC、SC的中点,∴FG∥SD.又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1,∴直线FG∥平面BDD1B1.同理可证EG∥平面BDD1B1,又∵EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面BDD1B1.9.(本小题满分12分)在四棱锥S-ABCD中,底面ABCD是正方形, M、N分别为AB、SC的中点,SA⊥底面ABCD.求证://MN平面SAD;答案.证明(Ⅰ): E 为SD 中点,连接AE ,NE ,因为M 、N 分别为AB 、SC 的中点,所以AM//EN ,AM=EN ,即四边形AMNE 是平行四边形,所以MN//AE ,可得//MN 平面SAD ;10. 一个多面体的直观图及三视图如图所示:(其中M 、N 分别是AF 、BC 的中点).(1)求证:MN ∥平面CDEF ;(2)求多面体A -CDEF 的体积.答案 由三视图可知,该多面体是底面为直角三角形的直三棱柱ADE-BCF ,且AB =BC =BF=2,DE =CF=2,∴∠CBF =. (1)证明:取BF 的中点G ,连结MG 、NG ,由M 、N 分别为AF 、BC 的中点可得,NG ∥CF ,MG ∥EF ,∴平面MNG ∥平面CDEF ,又MN ⊂平面MNG ,∴MN ∥平面CDEF .(2)取DE 的中点H .∵AD =AE ,∴AH ⊥DE , 在直三棱柱ADE-BCF 中,平面ADE ⊥平面CDEF ,平面A DE ∩平面CDEF=DE .∴AH ⊥平面CDEF.∴多面体A-CDEF 是以AH 为高,以矩形CDE F 为底面的棱锥,在△ADE 中,AH =. S 矩形CDEF =DE ·EF =4,∴棱锥A-CDEF 的体积为2222V=·S 矩形CDEF ·AH =×4×= 解法2:13218222323A CDEF AED BFC A BFCAED V V V S AB S AB ---=-=⨯-⨯⨯=⨯⨯⨯⨯=△△BFC 11如图,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB ∥CD ,且AB =2CD ,在棱AB 上是否存在一点F ,使平面C 1CF ∥平面ADD 1A 1?若存在,求点F 的位置;若不存在,请说明理由.答案 存在这样的点F ,使平面C 1CF ∥平面ADD 1A 1,此时点F 为AB的中点,证明如下:∵AB ∥CD ,AB =2CD ,∴AF ∥CD ,∴四边形AFCD 是平行四边形,∴AD ∥CF ,又AD ⊂平面ADD 1A 1,CF ⊄平面ADD 1A 1,∴CF ∥平面ADD 1A 1.又CC 1∥DD 1,CC 1⊄平面ADD 1A 1,DD 1⊂平面ADD 1A 1,∴CC 1∥平面ADD 1A 1,又CC 1、CF ⊂平面C 1CF ,CC 1∩CF =C ,∴平面C 1CF ∥平面ADD 1A 1.12. 如图,在底面是平行四边形的四棱锥P -ABCD 中,点E 在PD 上,且PE ∶ED =2∶1,在棱PC 上是否存在一点F ,使BF ∥平面AEC ?证明你的结论.答案 存在.证明如下:取棱PC 的中点F ,线段PE 的中点M ,连接BD .设BD ∩AC =O .连接BF ,MF ,BM ,OE .13132283∵PE ∶ED =2∶1,F 为PC 的中点,M 是PE 的中点,E 是MD的中点,∴MF ∥EC ,BM ∥OE .∵MF ⊄平面AEC ,CE ⊂平面AEC ,BM ⊄平面AEC ,OE ⊂平面AEC ,∴MF ∥平面AEC ,BM ∥平面AEC .∵MF ∩BM =M ,∴平面BMF ∥平面AEC .又BF ⊂平面BMF ,∴BF ∥平面AEC .13. (北京)如图,在四面体PABC 中,PC ⊥AB ,PA ⊥BC ,点D ,E ,F ,G 分别是棱AP ,AC ,BC ,PB 的中点.(1)求证:DE ∥平面BCP ;(2)求证:四边形DEFG 为矩形;(3)是否存在点Q ,到四面体PABC 六条棱的中点的距离相等?说明理由.答案 (1)证明:因为D ,E 分别为AP ,AC 的中点,所以DE ∥PC .又因为DE ⊄平面BCP ,PC ⊂平面BCP ,所以DE ∥平面BCP .(2)证明:因为D ,E ,F ,G 分别为AP ,AC ,BC ,PB 的中点所以DE ∥PC ∥FG ,DG ∥AB ∥EF ,所以四边形DEFG 为平行四边形.又因为PC ⊥AB ,所以DE ⊥DG ,所以四边形DEFG 为矩形.(3)存在点Q 满足条件,理由如下:连接DF ,EG ,设Q 为EG 的中点.由(2)知,DF ∩EG =Q ,且QD =QE =QF =QG =12EG .分别取PC ,AB 的中点M ,N ,连接ME ,EN ,NG ,MG ,MN .与(2)同理可证四边形MENG 为矩形,其对象线交点为EG 的中点Q ,且QM =QN =12EG ,所以EG 的中点Q 是满足条件的点.。




一、知识要点线线平行⇒线面平行线面平行的判定定理:如果直线外一条直线平行于直线内一条直线,那么这条直线和平面平行。
注:当直线与平面平行时,这条直线平行于平面内的无数条直线,而不是所有的直线。
线面平行⇒线线平行线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面与这个平面相交,那么这条直线和交线平行。
面面平行的判定:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行。
注:垂直于同一条直线的两个平面平行。
三个两两相交的平面,它们的三条交线交于一点或两两平行。
二、巩固练习1.已知l 是直线,α、β是两个不同平面,下列命题中的真命题是( )A .若l ∥α,l ∥β,则α∥βB .若α⊥β,l ∥α,则l ⊥βC .若l ⊥α,l ∥β,则α⊥βD .若l ∥α,α∥β,则l ∥β2.(文)已知m 、n 是两条直线,α、β是两个平面,给出下列命题:①若n ⊥α,n ⊥β,则α∥β;②若平面α上有不共线的三点到平面β的距离相等,则α∥β;③若n 、m 为异面直线,n ⊂α,n ∥β,m ⊂β,m ∥α,则α∥β.其中正确命题的个数是( )A .3个B .2个C .1个D .0个3.一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:①AB⊥EF ②AB 与CM 成60°③EF 与MN 是异面直线④MN ∥CD 其中正确的是( )A .①②B .③④C .②③D .①③4.(2011·北京海淀期中)已知平面α∩β=l ,m 是α内不同于l 的直线,那么下列命题中错误..的是( ) A .若m ∥β,则m ∥l B .若m ∥l ,则m ∥βC .若m ⊥β,则m ⊥lD .若m ⊥l ,则m ⊥β线面、面面平行的判定与性质5.(2011·安徽省合肥市高三教学质量检测)设a、b是两条不同的直线,α、β是两个不同的平面,则下列命题错误的是()A.若a⊥α,b∥α,则a⊥b B.若a⊥α,b∥a,b⊂β,则α⊥βC.若a⊥α,b⊥β,α∥β,则a∥b D.若a∥α,a∥β,则α∥β6.对于平面α和共面的直线m、n,下列命题是真命题的是()A.若m,n与α所成的角相等,则m∥n B.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n7.(2011·河南省郑州市模拟)设α、β是两个不同的平面,a、b是两条不同的直线,给出下列四个命题,其中真命题是()A.若a∥α,b∥α,则a∥b B.若a∥α,b∥β,a∥b,则α∥βC.若a⊥α,b⊥β,a∥b,则α∥βD.若a、b在平面α内的射影互相垂直,则a⊥b 8.(2011·青岛模拟)设两个平面α、β,直线l,下列三个条件:①l⊥α;②l∥β;③α⊥β.若以其中两个作为前提,另一个作为结论,则可构成三个命题,这三个命题中正确命题的个数为() A.3B.2C.1D.09.正方体ABCD-A1B1C1D1的棱长为1cm,过AC作平行于对角线BD1的截面,则截面面积为________.8.(2012·北京东城区综合练习)在空间中,有如下命题:①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线;②若平面α∥平面β,则平面α内任意一条直线m∥平面β;③若平面α与平面β的交线为m,平面α内的直线n⊥直线m,则直线n⊥平面β;④若平面α内的三点A、B、C到平面β的距离相等,则α∥β.其中正确命题的序号为________.10.(2011·浙江五校联考)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:①若m∥α,n∥α,m∥β,n∥β,则α∥β;②若α⊥γ,β⊥γ,α∩β=m,n⊂γ,则m⊥n;③若m⊥α,α⊥β,m∥n,则n∥β;④若n∥α,n∥β,α∩β=m,那么m∥n.其中正确命题的序号是________.11.(2012·四川文,6)下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行12.(2012·东营市期末)设m、n是两条不同的直线,α、β是两个不同的平面,给出下列四个命题:①若m⊥n,m⊥α,n⊄α,则n∥α;②若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;③若m⊥β,α⊥β,则m∥α;④若m⊥n,m⊥α,n⊥β,则α⊥β.其中真命题的序号是________13.(2011·广东省广州市质检)如图,正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线()A.不存在B.有1条C.有2条D.有无数条14.(文)如图,若Ω是长方体ABCD—A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确...的是()A.EH∥FG B.四边形EFGH是矩形C.Ω是棱柱D.Ω是棱台15.(2011·苏州模拟)下列命题中,是假命题的是()A.三角形的两条边平行于一个平面,则第三边也平行于这个平面B.平面α∥平面β,a⊂α,过β内的一点B有唯一的一条直线b,使b∥aC.α∥β,γ∥δ,α、β与γ、δ的交线分别为a、b和c、d,则a∥b∥c∥dD.一条直线与两个平面成等角是这两个平面平行的充要条件16.(2012·南昌二模)若P是两条异面直线l、m外的任意一点,则下列命题中假命题的序号是________.①过点P有且仅有一条直线与l、m都平行;②过点P有且仅有一条直线与l、m都垂直;③过点P有且仅有一条直线与l、m都相交;④过点P有且仅有一条直线与l、m都异面.17.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是______(写出所有符合要求的图形序号).18.与两个相交平面的交线平行的直线和这两个平面的位置关系是()A.都平行B.相交C.在两个平面内D.至少和其中一个平行19.(文)(2011·广东揭阳一模)如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G、H分别是DF、BE的中点.(1)求证:GH∥平面CDE;(2)若CD=2,DB=42,求四棱锥F-ABCD的体积..20.如图,在四面体ABCD中,平面EFGH分别平行于棱CD、AB,E、F、G、H分别在BD、BC、AC、AD上,且CD=a,AB=b,CD⊥AB.(1)求证:四边形EFGH是矩形.(2)点E在什么位置时,四边形EFGH的面积最大?21.如图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE.22.如图,设AB、CD分别是平面α两侧的异面直线AB//α,CD//α,直线AC、AD、BC、BD 分别交α于点E、F、H、G,求证:EG与FH互相平分23.ABCD-A1B1C1D1是正方体,B1E1=D1F1=411BA,求BE1与DF1所成角的余弦值24.如图,A、B、C、D 是异面直线AB、CD上的点,线段AB=4,CD=4,M为AC的中点,N为BD 的中点,MN=3,求异面直线AB与CD所成角的余弦值.。
在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法(1)在同一平面内没有公共点的两条直线平行(定义)(2)先证在同一平面内,再用平面几何中的平行线的判定理或者相关图形的性质进行证明。
如①在同一平面内,两条直线被第三条直线所截,如果同位角或内错角相等,或同旁内角互补,则两直线平行。
②三角形、梯形中位线定理。
③平行四边形、矩形、菱形、正方形性质(对边平行)。
④在同一个平面内,同垂直于一条直线的两条直线平行(注意:此结论在空间不适合)。
(3)(线面平行的性质)如果一条直线和一个平面平行,则经过这条直线的一个平面与这个平面相交,那么这条直线和交线平行。
(4)如果两直线都平行于第三条直线,那么这两条直线互相平行(平行的传递性)。
(5)(面面平行的性质)如果两个平行平面分别和第三个平面相交,则它们的交线平行。
(6)(线面垂直的性质之一)如果两条直线垂直于同一个平面,那么这两条直线平行。
(7)用向量证明。
二、一条直线和一个平面平行的判定(1)如果一直线和一平面没有公共点,那么这条直线就和这个平面平行(定义)(2)平面外的一条直线,如果和这个平面内的一条直线平行,那么这条直线就和这个平面平行(线面平行的判定定理)。
(3)如果两个平面相互平行,那么在一个平面内的任何一条直线都平行于另一个平面.(线面平行的性质)。
(4)向量法。
三、两个平面平行的判定(1)如果两个平面没有公共点,那么这两个平面互相平行(定义)(2)如果一个平面内的两条相交直线分别和另一个平面平行,那么这两个平面平行。
(3)如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
(4)如果两个平面分别平行于第三个平面,那么这两个平面平行。
(5)如果两个平面垂直于同一条直线,那么这两个平面平行。
在空间“线线垂直、线面垂直、面面垂直”的判定方法一、 两条直线垂直的判定(1) 在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。
【线面平行】
1.判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.符号表示:ααα//,//,,a b a b a 则⊂⊄.
2.直线与平面平行的性质
性质定理:如果一条直线与一个平面平行,经过这条直线的任一平面和这个平面相交,那么这条直线和交线平行.
符号表示:b a b a a //,,,//则=⋂⊂βαβα3.直线与平面平行的证明方法
(1)利用定义:证明直线与平面无公共点.
(2)利用直线与平面平行的判定定理:即证明平面外的一条直线与平面内的一条直线平行.(3)利用平面与平面平行的的定义:两个平面平行,则一个平面内的所有直线都平行于另一个平面,
即若βαβα//,,//l l 则⊂.
【例题与变式】
例1.在长方体1111ABCD A B C D -中,1AB BC ==,12AA =,点M 是BC 的中点.点
N 是1AA 的中点.求证://MN 平面1A CD ;
F
E
D
C
A
P
变式2-1.如图,在四棱锥P ABCD -中,底面ABCD 是边长为a 的正方形,侧面PAD ⊥底面ABCD ,且2
2
PA PD AD ==
,若E 、F 分别为线段PC 、BD 的中点.求证:直线EF //平面PAD ;
变式2-2.已知,,,E F G H 为空间四边形ABCD 的边,,,AB BC CD DA 上的点,且
//EH FG .
求证://EH BD .
变式2-3.如图,在正方体ABCD D C B A 1111-中,
(1)求证:1BC ∥平面11D AB ;
(2)若E、F 分别为C D 1、BD 的中点,则EF∥平面11A ADD .
H G F
E D B
A
C
【面面平行】
2.平面与平面平行的判定:
定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.符号表示:.//,//,//,,,βαααββ则b a P b a b a =⋂⊂⊂3.平面与平面平行的性质
定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
【例题与变式】
例2.已知m、n 是两条直线,βα、是两个平面,有以下命题:①m,n 相交且都在平面βα、外,βαβαβα//,//,//,//,//则n n m m ;②若βαβα//,//,//则m m ;③若
βαβα//,//,//,//则n m n m .其中正确的命题个数是(
)
A.0
B.1
C.2
D.3
变式2-1.已知βα、是两个不重合的平面,在下列条件中,可确定βα//的是()
A.βα、都平行于直线l
B.α内有三个不共线的点到β的距离相等
C.l,m 是α内两条直线,且β
β//,//m l D.l,m 是两条异面直线,且α
αββ//,////,//m l m l ,例3.如图,在三棱锥S −ABC 中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A 作AF⊥SB,垂足为F,点E,G 分别是棱SA,SC 的中点.求证:(1)平面EFG∥平面ABC;
变式3-1.如图所示,在三棱柱1111D C B A ABCD -中,点D,E 分别是BC 与11C B 的中点.求证:平面EB A 1//平面1ADC .
1.如图,已知在正方体''''D C B A ABCD -中,对角线'AB 、'
BC 上分别有两点E、F
,且
F
C E B ''=求证:(1)
EF
∥平面
ABCD
;
(2)平面'
ACD ∥平面'
'
BC A .。