工程测试-第二章测试系统基本特性1(精)

绪论0-1 叙述我国法定计量单位的基本内容。

我国的法定计量单位是以国际单位制为基础并选用少数其他单位制的计量单位来组成的。

1. 基本单位 根据国际单位制（SI ），七个基本量的单位分别是：长度——米（m ），质量——千克（kg ），时间——秒（s ），温度——开尔文（K ）,电流——安培（A ），发光强度——坎德拉（cd ），物质的量——摩尔（mol ）。

2. 辅助单位在国际单位制中，平面角的单位——弧度(rad)和立体角的单位——球面度（sr ）未归入基本单位，称为辅助单位。

3. 导出单位在选定了基本单位和辅助单位后，按物理量之间的关系，由基本单位和辅助单位以相乘或相除的形式所构成的单位称为导出单位。

0-2 如何保证量值的准确和一致？通过对计量器具实施检定或校准，将国家基准所复现的计量单位量值经过各级计量标准传递到工作计量器具，以保证被测对象量值的准确和一致。

0-3 何谓测量误差？通常测量误差是如何分类、表示的？测量结果与被测量真值之差就是测量误差。

即测量误差=测量结果-真值通常根据误差的统计特征，可以将误差分为系统误差、随机误差、粗大误差三种 常用的误差表示方法有下列几种：(1) 绝对误差，就是用测量结果与真值之差来表示。

(2) 相对误差，相对误差=误差/真值，误差较小时，可采用相对误差≌误差÷测量结果相对误差常用百分比来表示。

(3) 引用误差，这种表示方法只用于表示计量器具特性的情况中。

工程上采用引用误差作为判断精度等级的尺度，以允许引用误差值作为精度级别的代号。

计量器具的引用误差就是计量器具的绝对误差与引用值之比。

而引用值一般是计量器具的标称范围的最高值或量程。

(4) 分贝误差，单位是db 。

分贝误差=20×lg （测量结果÷真值）0-4 请将下列诸测量结果中的绝对误差改为相对误差。

（1）1.0182544V ±7.8µV （2）(25.04894±0.00003)g（3）（5.482±0.026）g/cm 2解：（1）相对误差=%00077.010*******.18.7100182544.18.766±=⨯±=⨯±VVV V μμμμ(2)相对误差=%00012.004894.2500003.004894.2500003.0±=±=±g g(3) 相对误差=%474.0482.5026.0/482.5/026.022±=±=±cm g cm g 0-5 何谓测量不确定度？国家计量局于1980年提出的建议《实验不确定度的规定建议书INC-1(1980)》的要点是什么？不确定度表示对被测量所处量值范围的评定。

测试技术与信号处理课后答案机械工程测试技术基础习题解答教材：机械工程测试技术基础，熊诗波 黄长艺主编，机械工业出版社，2006年9月第3版第二次印刷。

第一章 信号的分类与描述1-1 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出|c n |–ω和φn –ω图，并与表1-1对比。

解答：在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取（-T/2，T/2）000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )L T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为 001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ，=0, 1, 2, 3, n ±±±L 。

(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩L ππ图1-4 周期方波21,3,,(1cos)00,2,4,6,nAnAc n nnn⎧=±±±⎪==-=⎨⎪=±±±⎩LLπππ1,3,5,2arctan1,3,5,200,2,4,6,nInnRπncπφncn⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩LLL没有偶次谐波。

其频谱图如下图所示。

1-2 求正弦信号0()sinx t xωt=的绝对均值xμ和均方根值rms x。

解答：00002200000224211()d sin d sin d cosT TT Txx x x x μx t t xωt tωt tωtT T T TωTωπ====-==⎰⎰⎰rmsx====1-3 求指数函数()(0,0)atx t Ae a t-=>≥的频谱。

《机械工程测试技术基础》课后答案章节测试题第1章 信号及其描述（一）填空题1、 测试的基本任务是获取有用的信息，而信息总是蕴涵在某些物理量之中，并依靠它们来传输的。

这些物理量就是 ，其中目前应用最广泛的是电信号。

2、 信号的时域描述，以 为独立变量；而信号的频域描述，以 为独立变量。

3、 周期信号的频谱具有三个特点： ， ， 。

4、 非周期信号包括 信号和 信号。

5、 描述随机信号的时域特征参数有 、 、 。

6、 对信号的双边谱而言，实频谱（幅频谱）总是 对称，虚频谱（相频谱）总是 对称。

（二）判断对错题（用√或×表示）1、 各态历经随机过程一定是平稳随机过程。

（ ）2、 信号的时域描述与频域描述包含相同的信息量。

（ ）3、 非周期信号的频谱一定是连续的。

（ ）4、 非周期信号幅频谱与周期信号幅值谱的量纲一样。

（ ）5、 随机信号的频域描述为功率谱。

（ ）（三）简答和计算题1、 求正弦信号t x t x ωsin )(0=的绝对均值μ|x|和均方根值x rms 。

2、 求正弦信号)sin()(0ϕω+=t x t x 的均值x μ，均方值2x ψ，和概率密度函数p(x)。

3、 求指数函数)0,0()(≥>=-t a Ae t x at 的频谱。

4、求被截断的余弦函数⎩⎨⎧≥<=T t T t t t x ||0||cos )(0ω的傅立叶变换。

5、求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x at ω的频谱。

第二章 测试装置的基本特性（一）填空题1、 某一阶系统的频率响应函数为121)(+=ωωj j H ，输入信号2sin )(t t x =，则输出信号)(t y 的频率为=ω ，幅值=y ，相位=φ 。

2、 试求传递函数分别为5.05.35.1+s 和2224.141n n n s s ωωω++的两个环节串联后组成的系统的总灵敏度。

第一章 信号及其描述（一）填空题1、 测试的基本任务是获取有用的信息，而信息总是蕴涵在某些物理量之中，并依靠它们来传输的。

这些物理量就是 信号 ，其中目前应用最广泛的是电信号。

2、 信号的时域描述，以 时间 为独立变量；而信号的频域描述，以 频率 为独立变量。

3、 周期信号的频谱具有三个特点： 离散性 ， 谐波性 ， 收敛性 。

4、 非周期信号包括 准周期 信号和 瞬变周期 信号。

5、 描述随机信号的时域特征参数有 均值 、 均方值 、 方差 。

6、 对信号的双边谱而言，实频谱（幅频谱）总是 关于Y 轴 （偶） 对称，虚频谱（相频谱）总是 关于原点（奇） 对称。

（二）判断对错题（用√或×表示）1、 各态历经随机过程一定是平稳随机过程。

（ √ ）2、 信号的时域描述与频域描述包含相同的信息量。

（ √ ）3、 非周期信号的频谱一定是连续的。

（ × ）4、 非周期信号幅频谱与周期信号幅值谱的量纲一样。

（ × ）5、 随机信号的频域描述为功率谱。

（ √ ）（三）简答和计算题1、 求正弦信号t x t x ωsin )(0=的绝对均值μ|x|和均方根值x rms 。

2、 求正弦信号)sin()(0ϕω+=t x t x 的均值x μ，均方值2x ψ，和概率密度函数p(x)。

3、 求指数函数)0,0()(≥>=-t a Ae t x at 的频谱。

4、求被截断的余弦函数⎩⎨⎧≥<=T t T t t t x ||0||cos )(0ω的傅立叶变换。

5、求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x at ω的频谱。

第二章 测试装置的基本特性（一）填空题1、 某一阶系统的频率响应函数为121)(+=ωωj j H ，输入信号2sin )(t t x =，则输出信号)(t y 的频率为=ω ，幅值=y ，相位=φ 。

2、 试求传递函数分别为5.05.35.1+s 和2224.141n n n s s ωωω++的两个环节串联后组成的系统的总灵敏度。

机械工程测试技术基础习题解答教材：机械工程测试技术基础，熊诗波 黄长艺主编，机械工业，2006年9月第3版第二次印刷。

绪 论0-1 叙述我国法定计量单位的基本容。

解答：教材P4~5，二、法定计量单位。

0-2 如何保证量值的准确和一致？ 解答：（参考教材P4~6，二、法定计量单位~五、量值的传递和计量器具检定） 1、对计量单位做出严格的定义；2、有保存、复现和传递单位的一整套制度和设备；3、必须保存有基准计量器具，包括国家基准、副基准、工作基准等。

3、必须按检定规程对计量器具实施检定或校准，将国家级准所复现的计量单位量值经过各级计算标准传递到工作计量器具。

0-3 何谓测量误差？通常测量误差是如何分类表示的？ 解答：（教材P8~10，八、测量误差）0-4 请将下列诸测量结果中的绝对误差改写为相对误差。

①1.0182544V±7.8μV ②(25.04894±0.00003)g③(5.482±0.026)g/cm 2解答： ①-667.810/1.01825447.6601682/10±⨯≈±②60.00003/25.04894 1.197655/10±≈±③0.026/5.482 4.743±≈‰0-5 何谓测量不确定度？国际计量局于1980年提出的建议《实验不确定度的规定建议书INC-1(1980)》的要点是什么？ 解答：(1)测量不确定度是表征被测量值的真值在所处量值围的一个估计，亦即由于测量误差的存在而对被测量值不能肯定的程度。

(2)要点：见教材P11。

0-6为什么选用电表时，不但要考虑它的准确度，而且要考虑它的量程？为什么是用电表时应尽可能地在电表量程上限的三分之二以上使用？用量程为150V 的0.5级电压表和量程为30V 的1.5级电压表分别测量25V 电压，请问哪一个测量准确度高？ 解答：(1)因为多数的电工仪表、热工仪表和部分无线电测量仪器是按引用误差分级的（例如，精度等级为0.2级的电表，其引用误差为0.2%），而 引用误差=绝对误差/引用值其中的引用值一般是仪表的满度值(或量程)，所以用电表测量的结果的绝对误差大小与量程有关。

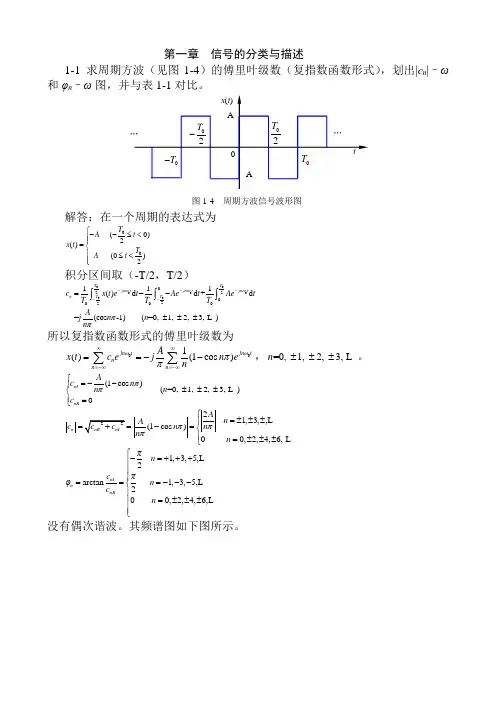
第一章 信号的分类与描述1-1 求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出|c n |–ω和φn –ω图，并与表1-1对比。

解答：在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩ 积分区间取（-T/2，T/2）000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, ) T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为 001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ，=0, 1, 2, 3, n ±±± 。

(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ ππ21,3,,(1cos )00,2,4,6, n An A c n n n n ⎧=±±±⎪==-=⎨⎪=±±±⎩πππ1,3,5,2arctan1,3,5,200,2,4,6,nI n nRπn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩没有偶次谐波。

其频谱图如下图所示。

图1-4 周期方波信号波形图1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。

解答：00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T TT ωT ωπ====-==⎰⎰⎰rmsx ==== 1-3 求指数函数()(0,0)at x t Ae a t -=>≥的频谱。

一、填空（每空1份.共20分）1.测试技术的基本任务是获取有用的信息2.从时域看.系统的输出是其输入与该系统脉冲响应函数的卷积。

3.信号的时域描述.以时间(t) 为独立变量；而信号的频域描述.以频率f或)(ω为独立变量。

4.如果一个信号的最高频率为50Hz.为了防止在时域采样过程中出现混叠现象.采样频率应该大于 100Hz。

5.在桥式测量电路中.根据其激励电压（或工作电压或桥压或电源）的性质.可将其分为直流电桥与交流电桥。

6.金属电阻应变片与半导体应变片的主要区别在于：前者利用导体机械形变引起的电阻变化.后者利用半导体电阻率的（或半导体压阻效应）变化引起的电阻变化。

7.压电式传感器是利用某些物质的压电效应而工作的。

8.带通滤波器的上下限截止频率为fc2、fc1.其带宽B =12ccff-；若其带宽为1/3倍频程则fc2= 32 fc1。

9.属于能量控制型的传感器有电阻式传感器、涡电流传感器电容式传感器、电感式传感器等。

10. 根据载波受调制的参数不同.调制可分为调幅、调频、调相。

11. 相关滤波的工作原理是同频相关不同频不相关/同频检测原理12 测试装置的动态特性可以用传递函数、频率响应函数和脉冲响应函数进行数学描述。

二、选择题（把正确答案前的字母填在空格上.每题1分.共10分）1．不能用确定的数学公式表达的信号是 D 信号。

A 复杂周期B 非周期C 瞬态D 随机2．平稳随机过程必须 B 。

A 连续 B统计特征与时间无关 C 各态历经 D 统计特征等于时间平均3．一阶系统的动态特性参数是 C 。

A 固有频率B 阻尼比C 时间常数D 灵敏度4．系统在全量程内.输入量由小到大及由大到小时.对于同一个输入量所得到的两个数值不同的输出量之间的最大差值称为 A 。

A 回程误差B 绝对误差C 相对误差D 非线性误差5．电阻应变片的输入为 B 。

A 力B 应变C 速度D 加速度6． D 用于评价系统的输出信号和输入信号之间的因果性。

(精编)机械工程测量与试验技术课后习题答案绪论0-1叙述我国法定计量单位的基本内容。

解答：教材P4~5，二、法定计量单位。

0-2如何保证量值的准确和一致？解答：（参考教材P4~6，二、法定计量单位~五、量值的传递和计量器具检定）1、对计量单位做出严格的定义；2、有保存、复现和传递单位的一整套制度和设备；3、必须保存有基准计量器具，包括国家基准、副基准、工作基准等。

3、必须按检定规程对计量器具实施检定或校准，将国家级准所复现的计量单位量值经过各级计算标准传递到工作计量器具。

0-3何谓测量误差？通常测量误差是如何分类表示的？解答：（教材P8~10，八、测量误差）0-4请将下列诸测量结果中的绝对误差改写为相对误差。

①1.0182544V±7.8μV②(25.04894±0.00003)g③(5.482±0.026)g/cm2解答：①②③0-5何谓测量不确定度？国际计量局于1980年提出的建议《实验不确定度的规定建议书INC-1(1980)》的要点是什么？解答：(1)测量不确定度是表征被测量值的真值在所处量值范围的一个估计，亦即由于测量误差的存在而对被测量值不能肯定的程度。

(2)要点：见教材P11。

0-6为什么选用电表时，不但要考虑它的准确度，而且要考虑它的量程？为什么是用电表时应尽可能地在电表量程上限的三分之二以上使用？用量程为150V 的0.5级电压表和量程为30V的1.5级电压表分别测量25V电压，请问哪一个测量准确度高？解答：(1)因为多数的电工仪表、热工仪表和部分无线电测量仪器是按引用误差分级的（例如，精度等级为0.2级的电表，其引用误差为0.2%），而引用误差=绝对误差/引用值其中的引用值一般是仪表的满度值(或量程)，所以用电表测量的结果的绝对误差大小与量程有关。

量程越大，引起的绝对误差越大，所以在选用电表时，不但要考虑它的准确度，而且要考虑它的量程。

(2)从(1)中可知，电表测量所带来的绝对误差=精度等级×量程/100，即电表所带来的绝对误差是一定的，这样，当被测量值越大，测量结果的相对误差就越小，测量准确度就越高，所以用电表时应尽可能地在电表量程上限的三分之二以上使用。

绪论0-1叙述我国法定计量单位的基本内容.我国的法定计量单位是以国际单位制为基础并选用少数其他单位制的计量单位来组成的。

1.基本单位根据国际单位制(SI）,七个基本量的单位分别是：长度—-米（m），质量——千克（kg),时间——秒(s），温度——开尔文（K),电流—-安培（A），发光强度—-坎德拉（cd），物质的量—-摩尔（mol）。

2.辅助单位在国际单位制中，平面角的单位——弧度（rad）和立体角的单位——球面度(sr）未归入基本单位，称为辅助单位.3.导出单位在选定了基本单位和辅助单位后,按物理量之间的关系，由基本单位和辅助单位以相乘或相除的形式所构成的单位称为导出单位。

0-2如何保证量值的准确和一致？通过对计量器具实施检定或校准，将国家基准所复现的计量单位量值经过各级计量标准传递到工作计量器具，以保证被测对象量值的准确和一致。

0-3何谓测量误差？通常测量误差是如何分类、表示的?测量结果与被测量真值之差就是测量误差。

即测量误差=测量结果-真值通常根据误差的统计特征,可以将误差分为系统误差、随机误差、粗大误差三种常用的误差表示方法有下列几种:(1)绝对误差，就是用测量结果与真值之差来表示.(2)相对误差,相对误差=误差/真值,误差较小时，可采用相对误差≌误差÷测量结果相对误差常用百分比来表示.(3)引用误差，这种表示方法只用于表示计量器具特性的情况中.工程上采用引用误差作为判断精度等级的尺度,以允许引用误差值作为精度级别的代号。

计量器具的引用误差就是计量器具的绝对误差与引用值之比。

而引用值一般是计量器具的标称范围的最高值或量程。

(4)分贝误差,单位是db.分贝误差=20×lg（测量结果÷真值）0-4请将下列诸测量结果中的绝对误差改为相对误差。

（1）1。

0182544V±7。

8µV（2)（25。

04894±0。

00003）g（3)（5.482±0.026）g/cm2解：（1）相对误差=（2）相对误差=(3）相对误差=0—5 何谓测量不确定度？国家计量局于1980年提出的建议《实验不确定度的规定建议书INC-1(1980）》的要点是什么?不确定度表示对被测量所处量值范围的评定.或者说,对被测量真值不能肯定的误差范围的一种评定。

第二章测试系统的基本特性第一节概述测试的目的是为了准确了解被测物理量，而研究测试系统特性的目的则是为了能使系统尽可能准确真实地反映被测物理量，且为测试系统性能的评价提出一个标准。

1.测试系统能完成对某一物理量进行测取的装置，它即可以是一个单一环节组成的装置，如传感器，又可以是一个由多个功能环节组成的系统，如应变测量中的“传感器－应变仪－记录仪”。

2.对测试系统的基本要求工程测试的基本传输关系如图示，所要寻求的是输入x(t)，输出y(t),系统传输性三者的关系，即1）由已知的系统的输入和输出量，求系统的传递特性。

2）由已知的输入量和系统的传递特性，推求系统的输出量。

3）由已知系统的传递特性和输出量，来推知系统的输入量。

为使上述三种问题能由已知方便的确定未知，为此提出，对于一个测试来说，应具有的基本特性是：单值的、确定的输入-输出关系，即对应于每一个输入量都应只有单一的输出量与之对应，能满足上述要求的系统一般是线性系统。

3.测试系统的特性的描述对测试系统特性的描述通常有静态特性、动态特性、负载特性、抗干扰特性。

4.线性系统简介二、线性系统及其主要性质当系统的输入x(t)和输出y(t)之间的关系可用常系数线性微分方程(2-1)来描述时，则称该系统为定常线性系统。

线性系统有如下性质（以x(t) y(t)表示系统的输入、输出关系）：1)叠加性表明作用于线性系统的各个输人所产生的输出互不影响，这样当分析众多输人同时加在系统上所产生的总效果时，可以先分别分析单个输入(假定其他输入不存往)的效果，然后将这些效果叠加起来以表示总的效果。

2）比例特性若 x(t)→y(t)则3）微分性质 系统对输入导数的响应等于对原输入响应的导数，即4）积分性质 系统对输入积分的响应等于对原输入响应的积分，即5）频率保持性 若输入为某一频率的间谐信号，则系统的稳态输出必是、也只是同频率的间谐信号。

由于按线性系统的比例特性，对于某一已知频率ω有又根据线性系统的微分特性，有应用叠加原理，有现令输人为某一单一频率的简谐信号，记作t j e X t x ω0)(=，那么其二阶导数应为由此，得相应的输出也应为于是输出y(ｔ)的唯一的可能解只能是线性系统的这些主要特性，特别是叠加性和频率保持性，在测试工作中具有重要的作用。

《 机械工程测试技术基础 》-第三版- 熊诗波等 著绪 论0-1 叙述我国法定计量单位的基本内容。

解答：教材P4~5，二、法定计量单位。

0-2 如何保证量值的准确和一致？解答：（参考教材P4~6，二、法定计量单位~五、量值的传递和计量器具检定） 1、对计量单位做出严格的定义；2、有保存、复现和传递单位的一整套制度和设备；3、必须保存有基准计量器具，包括国家基准、副基准、工作基准等。

3、必须按检定规程对计量器具实施检定或校准，将国家级准所复现的计量单位量值经过各级计算标准传递到工作计量器具。

0-3 何谓测量误差？通常测量误差是如何分类表示的？解答：（教材P8~10，八、测量误差）0-4 请将下列诸测量结果中的绝对误差改写为相对误差。

①1.0182544V±7.8μV ②(25.04894±0.00003)g ③(5.482±0.026)g/cm 2 解答：①-667.810/1.01825447.6601682/10±⨯≈± ②60.00003/25.04894 1.197655/10±≈± ③0.026/5.482 4.743±≈‰0-5 何谓测量不确定度？国际计量局于1980年提出的建议《实验不确定度的规定建议书INC-1(1980)》的要点是什么？解答：(1)测量不确定度是表征被测量值的真值在所处量值范围的一个估计，亦即由于测量误差的存在而对被测量值不能肯定的程度。

(2)要点：见教材P11。

0-6为什么选用电表时，不但要考虑它的准确度，而且要考虑它的量程？为什么是用电表时应尽可能地在电表量程上限的三分之二以上使用？用量程为150V 的0.5级电压表和量程为30V 的1.5级电压表分别测量25V 电压，请问哪一个测量准确度高？ 解答：(1)因为多数的电工仪表、热工仪表和部分无线电测量仪器是按引用误差分级的（例如，精度等级为0.2级的电表，其引用误差为0.2%），而引用误差=绝对误差/引用值其中的引用值一般是仪表的满度值(或量程)，所以用电表测量的结果的绝对误差大小与量程有关。

第一章 信号及其描述（一）填空题1、 测试的基本任务是获取有用的信息，而信息总是蕴涵在某些物理量之中，并依靠它们来传输的。

这些物理量就是 信号 ，其中目前应用最广泛的是电信号。

2、 信号的时域描述，以 时间 为独立变量；而信号的频域描述，以 频率 为独立变量。

3、 周期信号的频谱具有三个特点： 离散性 ， 谐波性 ， 收敛性 。

4、 非周期信号包括 准周期 信号和 瞬变周期 信号。

5、 描述随机信号的时域特征参数有 均值 、 均方值 、 方差 。

6、 对信号的双边谱而言，实频谱（幅频谱）总是 关于Y 轴 （偶） 对称，虚频谱（相频谱）总是 关于原点（奇） 对称。

（二）判断对错题（用√或×表示）1、 各态历经随机过程一定是平稳随机过程。

（ √ ）2、 信号的时域描述与频域描述包含相同的信息量。

（ √ ）3、 非周期信号的频谱一定是连续的。

（ × ）4、 非周期信号幅频谱与周期信号幅值谱的量纲一样。

（ × ）5、 随机信号的频域描述为功率谱。

（ √ ）（三）简答和计算题1、 求正弦信号t x t x ωsin )(0=的绝对均值μ|x|和均方根值x rms 。

2、 求正弦信号)sin()(0ϕω+=t x t x 的均值x μ，均方值2x ψ，和概率密度函数p(x)。

3、 求指数函数)0,0()(≥>=-t a Ae t x at 的频谱。

4、求被截断的余弦函数⎩⎨⎧≥<=T t T t t t x ||0||cos )(0ω的傅立叶变换。

5、求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x at ω的频谱。

第二章 测试装置的基本特性（一）填空题1、 某一阶系统的频率响应函数为121)(+=ωωj j H ，输入信号2sin )(t t x =，则输出信号)(t y 的频率为=ω ，幅值=y ，相位=φ 。

2、 试求传递函数分别为5.05.35.1+s 和2224.141n n n s s ωωω++的两个环节串联后组成的系统的总灵敏度。

（机械制造⾏业）机械⼯程测试技术基础课后试题及答案《机械⼯程测试技术基础》课后答案章节测试题第⼀章信号及其描述（⼀）填空题1、测试的基本任务是获取有⽤的信息，⽽信息总是蕴涵在某些物理量之中，并依靠它们来传输的。

这些物理量就是，其中⽬前应⽤最⼴泛的是电信号。

2、信号的时域描述，以为独⽴变量；⽽信号的频域描述，以为独⽴变量。

3、周期信号的频谱具有三个特点：，，。

4、⾮周期信号包括信号和信号。

5、描述随机信号的时域特征参数有、、。

6、对信号的双边谱⽽⾔，实频谱（幅频谱）总是对称，虚频谱（相频谱）总是对称。

（⼆）判断对错题（⽤√或×表⽰）1、各态历经随机过程⼀定是平稳随机过程。

（）2、信号的时域描述与频域描述包含相同的信息量。

（）3、⾮周期信号的频谱⼀定是连续的。

（）4、⾮周期信号幅频谱与周期信号幅值谱的量纲⼀样。

（）5、随机信号的频域描述为功率谱。

（）（三）简答和计算题1、求正弦信号t x t x ωsin )(0=的绝对均值µ|x|和均⽅根值x rms 。

2、求正弦信号)sin()(0?ω+=t x t x 的均值x µ，均⽅值2x ψ，和概率密度函数p(x)。

3、求指数函数)0,0()(≥>=-t a Ae t x at 的频谱。

4、求被截断的余弦函数≥<=T t T t tt x ||0||cos )(0ω的傅⽴叶变换。

5、求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x at ω的频谱。

第⼆章测试装置的基本特性（⼀）填空题1、某⼀阶系统的频率响应函数为121)(+=ωωj j H ，输⼊信号2sin )(t t x =，则输出信号)(t y 的频率为=ω，幅值=y ，相位=φ。

2、试求传递函数分别为5.05.35.1+s 和2224.141n n n s s ωωω++的两个环节串联后组成的系统的总灵敏度。

3、为了获得测试信号的频谱，常⽤的信号分析⽅法有、和。

一、填空（每空1份，共20分）1.测试技术的基本任务是获取有用的信息2.从时域看，系统的输出是其输入与该系统脉冲响应函数的卷积。

3.信号的时域描述，以时间(t) 为独立变量；而信号的频域描述，以频率f 或)(ω为独立变量。

4.如果一个信号的最高频率为50Hz，为了防止在时域采样过程中出现混叠现象，采样频率应该大于 100Hz。

5.在桥式测量电路中，根据其激励电压（或工作电压或桥压或电源）的性质，可将其分为直流电桥与交流电桥。

6.金属电阻应变片与半导体应变片的主要区别在于：前者利用导体机械形变引起的电阻变化，后者利用半导体电阻率的（或半导体压阻效应）变化引起的电阻变化。

7.压电式传感器是利用某些物质的压电效应而工作的。

8.带通滤波器的上下限截止频率为fc2、fc1，其带宽B =12ccff-；若其带宽为1/3倍频程则fc2= 32 fc1。

9.属于能量控制型的传感器有电阻式传感器、涡电流传感器电容式传感器、电感式传感器等。

10. 根据载波受调制的参数不同，调制可分为调幅、调频、调相。

11. 相关滤波的工作原理是同频相关不同频不相关/同频检测原理12 测试装置的动态特性可以用传递函数、频率响应函数和脉冲响应函数进行数学描述。

二、选择题（把正确答案前的字母填在空格上，每题1分，共10分）1．不能用确定的数学公式表达的信号是 D 信号。

A 复杂周期B 非周期C 瞬态D 随机2．平稳随机过程必须 B 。

A 连续 B统计特征与时间无关 C 各态历经 D 统计特征等于时间平均3．一阶系统的动态特性参数是 C 。

A 固有频率B 阻尼比C 时间常数D 灵敏度4．系统在全量程内，输入量由小到大及由大到小时，对于同一个输入量所得到的两个数值不同的输出量之间的最大差值称为 A 。

A 回程误差B 绝对误差C 相对误差D 非线性误差5．电阻应变片的输入为 B 。

A 力B 应变C 速度D 加速度6． D 用于评价系统的输出信号和输入信号之间的因果性。

机械工程测试技术基础习题解答第一章 信号的分类与描述1-1 求周期方波（见图1-4）的xx 级数（复指数函数形式），划出|cn|–ω和φn–ω图，并与表1-1对比。

解答：在一个周期的表达式为 .积分区间取（-T/2，T/2）000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的xx 级数为 ，。

(1cos ) (=0, 1, 2, 3, )0nInR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ图1-4 周期方波信号波形图21,3,,(1cos)00,2,4,6,nAnAc n nnn⎧=±±±⎪==-=⎨⎪=±±±⎩πππ1,3,5,2arctan1,3,5,200,2,4,6,nInnRπncπφncn⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩没有偶次谐波。

其频谱图如下图所示。

1-2 求正弦信号的绝对均值和均方根值。

解答：rmsx====1-3 求指数函数的频谱。

解答：(2)22022(2) ()()(2)2(2)a j f tj f t at j f te A A a jf X f x t e dt Ae e dt Aa j f a j f a f-+∞∞---∞-∞-=====-+++⎰⎰πππππππ幅频图相频图周期方波复指数函数形式频谱图22()(2)k X f a f π=+Im ()2()arctanarctan Re ()X f ff X f a==-πϕ1-4 求符号函数(见图1)和单位阶跃函数(见图1-25b)的频谱。