含参函数的最值与函数.ppt
- 格式:ppt
- 大小:916.57 KB
- 文档页数:11



![5.3 5.3.2 第二课时 函数的最大[小]值公开课](https://uimg.taocdn.com/0269882882c4bb4cf7ec4afe04a1b0717fd5b3b2.webp)

专题10 含参函数的极值、最值讨论考点一 含参函数的极值 【例题选讲】[例1] 设a >0,函数f (x )=12x 2-(a +1)x +a (1+ln x ).(1)若曲线y =f (x )在(2,f (2))处的切线与直线y =-x +1垂直,求切线方程. (2)求函数f (x )的极值.解析 (1)由已知,得f ′(x )=x -(a +1)+ax (x >0),又由题意可知y =f (x )在(2,f (2))处切线的斜率为1,所以f ′(2)=1,即2-(a +1)+a2=1,解得a =0,此时f (2)=2-2=0,故所求的切线方程为y =x -2.(2)f ′(x )=x -(a +1)+a x =x 2-(a +1)x +a x =(x -1)(x -a )x(x >0).①当0<a <1时,若x ∈(0,a ),则f ′(x )>0,函数f (x )单调递增;若x ∈(a ,1),则f ′(x )<0,函数f (x )单调递减;若x ∈(1,+∞),则f ′(x )>0,函数f (x )单调递增.此时x =a 是f (x )的极大值点,x =1是f (x )的极小值点,函数f (x )的极大值是f (a )=-12a 2+a ln a ,极小值是f (1)=-12.②当a =1时,f ′(x )=(x -1)2x ≥0,所以函数f (x )在定义域(0,+∞)内单调递增,此时f (x )没有极值点,故无极值.③当a >1时,若x ∈(0,1),则f ′(x )>0,函数f (x )单调递增;若x ∈(1,a ),则f ′(x )<0,函数f (x )单调递减;若x ∈(a ,+∞),则f ′(x )>0,函数f (x )单调递增. 此时x =1是f (x )的极大值点,x =a 是f (x )的极小值点, 函数f (x )的极大值是f (1)=-12,极小值是f (a )=-12a 2+a ln a .综上,当0<a <1时,f (x )的极大值是-12a 2+a ln a ,极小值是-12;当a =1时,f (x )没有极值;当a >1时f (x )的极大值是-12,极小值是-12a 2+a ln a .[例2] 已知函数f (x )=ln x -ax (a ∈R ). (1)当a =12时,求f (x )的极值;(2)讨论函数f (x )在定义域内极值点的个数.解析 (1)当a =12时,f (x )=ln x -12x ,函数的定义域为(0,+∞)且f ′(x )=1x -12=2-x2x ,令f ′(x )=0,得x =2,于是当x 变化时,f ′(x ),f (x )的变化情况如下表.x (0,2) 2 (2,+∞) f ′(x )+-f (x ) ln 2-1故f (x )在定义域上的极大值为f (x )极大值=f (2)=ln 2-1,无极小值. (2)由(1)知,函数的定义域为(0,+∞),f ′(x )=1x -a =1-ax x .当a ≤0时,f ′(x )>0在(0,+∞)上恒成立,则函数在(0,+∞)上单调递增,此时函数在定义域上无极值点; 当a >0时,若x ∈⎝⎛⎭⎫0,1a ,则f ′(x )>0, 若x ∈⎝⎛⎭⎫1a ,+∞,则f ′(x )<0,故函数在x =1a处有极大值. 综上可知,当a ≤0时,函数f (x )无极值点,当a >0时,函数y =f (x )有一个极大值点,且为x =1a .[例3] 设f (x )=x ln x -32ax 2+(3a -1)x .(1)若g (x )=f ′(x )在[1,2]上单调,求a 的取值范围; (2)已知f (x )在x =1处取得极小值,求a 的取值范围.解析 (1)由f ′(x )=ln x -3ax +3a ,即g (x )=ln x -3ax +3a ,x ∈(0,+∞),g ′(x )=1x-3a ,①g (x )在[1,2]上单调递增,∴1x -3a ≥0对x ∈[1,2]恒成立,即a ≤13x 对x ∈[1,2]恒成立,得a ≤16;②g (x )在[1,2]上单调递减,∴1x -3a ≤0对x ∈[1,2]恒成立,即a ≥13x 对x ∈[1,2]恒成立,得a ≥13,由①②可得a 的取值范围为⎝⎛⎦⎤-∞,16∪⎣⎡⎭⎫13,+∞. (2)由(1)知,①当a ≤0时,f ′(x )在(0,+∞)上单调递增,∴x ∈(0,1)时,f ′(x )<0,f (x )单调递减, x ∈(1,+∞)时,f ′(x )>0,f (x )单调递增,∴f (x )在x =1处取得极小值,符合题意;②当0<a <13时,13a >1,又f ′(x )在⎝⎛⎭⎫0,13a 上单调递增,∴x ∈(0,1)时,f ′(x )<0,x ∈⎝⎛⎭⎫1,13a 时,f ′(x )>0, ∴f (x )在(0,1)上单调递减,在⎝⎛⎭⎫1,13a 上单调递增,f (x )在x =1处取得极小值,符合题意; ③当a =13时,13a =1,f ′(x )在(0,1)上单调递增,在(1,+∞)上单调递减,∴x ∈(0,+∞)时,f ′(x )≤0,f (x )单调递减,不合题意;④当a >13时,0<13a<1,当x ∈⎝⎛⎭⎫13a ,1时,f ′(x )>0,f (x )单调递增, 当x ∈(1,+∞)时,f ′(x )<0,f (x )单调递减,∴f (x )在x =1处取得极大值,不符合题意. 综上所述,可得a 的取值范围为⎝⎛⎭⎫-∞,13. [例4] (2016·山东)设f (x )=x ln x -ax 2+(2a -1)x ,a ∈R . (1)令g (x )=f ′(x ),求g (x )的单调区间;(2)已知f (x )在x =1处取得极大值,求实数a 的取值范围.解析 (1)由f ′(x )=ln x -2ax +2a ,可得g (x )=ln x -2ax +2a ,x ∈(0,+∞).所以g ′(x )=1x -2a =1-2ax x .当a ≤0,x ∈(0,+∞)时,g ′(x )>0,函数g (x )单调递增;当a >0,x ∈⎝⎛⎭⎫0,12a 时,g ′(x )>0,函数g (x )单调递增,x ∈⎝⎛⎭⎫12a ,+∞时,g ′(x )<0,函数g (x )单调递减. 所以当a ≤0时,g (x )的单调增区间为(0,+∞);当a >0时,g (x )的单调增区间为⎝⎛⎭⎫0,12a ,单调减区间为⎝⎛⎭⎫12a ,+∞. (2)由(1)知,f ′(1)=0.①当a ≤0时,f ′(x )单调递增,所以当x ∈(0,1)时,f ′(x )<0,f (x )单调递减; 当x ∈(1,+∞)时,f ′(x )>0,f (x )单调递增.所以f (x )在x =1处取得极小值,不合题意. ②当0<a <12时,12a >1,由(1)知f ′(x )在⎝⎛⎭⎫0,12a 内单调递增, 可得当x ∈(0,1)时,f ′(x )<0,当x ∈⎝⎛⎭⎫1,12a 时,f ′(x )>0. 所以f (x )在(0,1)内单调递减,在⎝⎛⎭⎫1,12a 内单调递增,所以f (x )在x =1处取得极小值,不合题意. ③当a =12时,12a =1,f ′(x )在(0,1)内单调递增,在(1,+∞)内单调递减,所以当x ∈(0,+∞)时,f ′(x )≤0,f (x )单调递减,不合题意.④当a >12时,0<12a <1,当x ∈⎝⎛⎭⎫12a ,1时,f ′(x )>0,f (x )单调递增,当x ∈(1,+∞)时,f ′(x )<0,f (x )单调递减.所以f (x )在x =1处取极大值,符合题意. 综上可知,实数a 的取值范围为⎝⎛⎭⎫12,+∞. [例5] 已知函数f (x )=⎝⎛⎭⎫x -1-a6e x +1,其中e =2.718…为自然对数的底数,常数a >0. (1)求函数f (x )在区间(0,+∞)上的零点个数;(2)函数F (x )的导数F ′(x )=()e x -a f (x ),是否存在无数个a ∈(1,4),使得ln a 为函数F (x )的极大值点?请说明理由.解析 (1)f ′(x )=⎝⎛⎭⎫x -a 6e x ,当0<x <a 6时,f ′(x )<0,f (x )单调递减;当x >a6时,f ′(x )>0,f (x )单调递增, 所以当x ∈(0,+∞)时,f (x )min =f ⎝⎛⎭⎫a 6,因为f ⎝⎛⎭⎫a 6<f (0)=-a 6<0,f ⎝⎛⎭⎫1+a 6=1>0, 所以存在x 0∈⎝⎛⎭⎫a 6,1+a6,使f (x 0)=0,且当0<x <x 0时,f (x )<0,当x >x 0时,f (x )>0. 故函数f (x )在(0,+∞)上有1个零点,即x 0.(2)方法一 当a >1时,ln a >0.因为当x ∈()0,ln a 时,e x -a <0;当x ∈()ln a ,+∞时,e x -a >0. 由(1)知,当x ∈(0,x 0)时,f (x )<0;当x ∈(x 0,+∞)时,f (x )>0.下面证:当a ∈()1,e 时,ln a <x 0,即证f ()ln a <0.f ()ln a =⎝⎛⎭⎫ln a -1-a 6a +1=a ln a -a -a 26+1,记g (x )=x ln x -x -x26+1,x ∈(1,e), g ′(x )=ln x -x3,x ∈(1,e),令h (x )=g ′(x ),则h ′(x )=3-x 3x >0,所以g ′(x )在()1,e 上单调递增,由g ′(1)=-13<0,g ′(e)=1-e3>0,所以存在唯一零点t 0∈()1,e ,使得g ′()t 0=0,且x ∈()1,t 0时,g ′(x )<0,g (x )单调递减,x ∈()t 0,e 时,g ′(x )>0,g (x )单调递增. 所以当x ∈()1,e 时,g (x )<max {}g (1),g (e).由g (1)=-16<0,g (e)=6-e 26<0,得当x ∈()1,e 时,g (x )<0.故f ()ln a <0,0<ln a <x 0.当0<x <ln a 时,e x -a <0,f (x )<0, F ′(x )=()e x -a f (x )>0,F (x )单调递增;当ln a <x <x 0时,e x -a >0,f (x )<0,F ′(x )=()e x -a f (x )<0,F (x )单调递减.所以存在a ∈()1,e ⊆(1,4),使得ln a 为F (x )的极大值点. 方法二 因为当x ∈()0,ln a 时,e x -a <0;当x ∈()ln a ,+∞时,e x -a >0. 由(1)知,当x ∈(0,x 0)时,f (x )<0;当x ∈(x 0,+∞)时,f (x )>0. 所以存在无数个a ∈(1,4),使得ln a 为函数F (x )的极大值点, 即存在无数个a ∈(1,4),使得ln a <x 0成立,①由(1),问题①等价于存在无数个a ∈(1,4),使得f ()ln a <0成立,因为f ()ln a =⎝⎛⎭⎫ln a -1-a 6a +1=a ln a -a -a 26+1,记g (x )=x ln x -x -x26+1,x ∈(1,4), g ′(x )=ln x -x3,x ∈(1,4),设k (x )=g ′(x ),因为k ′(x )=3-x 3x,当x ∈⎝⎛⎭⎫32,2时,k ′(x )>0,所以g ′(x )在⎝⎛⎭⎫32,2上单调递增,因为g ′⎝⎛⎭⎫32=ln 32-12<0,g ′(2)=ln 2-23>0, 所以存在唯一零点t 0∈⎝⎛⎭⎫32,2,使得g ′()t 0=0,且当x ∈⎝⎛⎭⎫32,t 0时,g ′(x )<0,g (x )单调递减;当x ∈()t 0,2时,g ′(x )>0,g (x )单调递增; 所以当x ∈⎣⎡⎦⎤32,2时,g (x )min =g ()t 0=t 0ln t 0-t 0-t 26+1,② 由g ′()t 0=0,可得ln t 0=t 03,代入②式可得g (x )min =g ()t 0=t 206-t 0+1,当t 0∈⎝⎛⎭⎫32,2时,g ()t 0=t 206-t 0+1=()t 0-326-12<-18<0,所以必存在x ∈⎝⎛⎭⎫32,2,使得g (x )<0,即对任意a ∈⎝⎛⎭⎫32,2,f ()ln a <0有解, 所以对任意a ∈⎝⎛⎭⎫32,2⊆(1,4),函数F (x )存在极大值点为ln a . 【对点训练】1.已知函数f (x )=ln x -12ax 2+x ,a ∈R .(1)当a =0时,求曲线y =f (x )在(1,f (1))处的切线方程; (2)令g (x )=f (x )-(ax -1),求函数g (x )的极值.1.解析 (1)当a =0时,f (x )=ln x +x ,则f (1)=1,∴切点为(1,1),又f ′(x )=1x +1,∴切线斜率k =f ′(1)=2,故切线方程为y -1=2(x -1),即2x -y -1=0.(2)g (x )=f (x )-(ax -1)=ln x -12ax 2+(1-a )x +1,则g ′(x )=1x -ax +(1-a )=-ax 2+(1-a )x +1x ,①当a ≤0时,∵x >0,∴g ′(x )>0,∴g (x )在(0,+∞)上是增函数,函数g (x )无极值点.②当a >0时,g ′(x )=-ax 2+(1-a )x +1x =-a ⎝⎛⎭⎫x -1a (x +1)x ,令g ′(x )=0得x =1a.∴当x ∈⎝⎛⎭⎫0,1a 时,g ′(x )>0;当x ∈⎝⎛⎭⎫1a ,+∞时,g ′(x )<0. 因此g (x )在⎝⎛⎭⎫0,1a 上是增函数,在⎝⎛⎭⎫1a ,+∞上是减函数. ∴x =1a 时,g (x )取极大值g ⎝⎛⎭⎫1a =ln 1a -a 2×1a 2+(1-a )×1a +1=12a -ln a . 由①②得,当a ≤0时,函数g (x )无极值;当a >0时,函数g (x )有极大值12a -ln a ,无极小值.2.设函数f (x )=[ax 2-(4a +1)x +4a +3]e x .(1)若曲线y =f (x )在点(1,f (1))处的切线与x 轴平行,求a ; (2)若f (x )在x =2处取得极小值,求a 的取值范围.2.解析 (1)因为f (x )=[ax 2-(4a +1)x +4a +3]e x ,所以f ′(x )=[ax 2-(2a +1)x +2]e x .f ′(1)=(1-a )e . 由题设知f ′(1)=0,即(1-a )e =0,解得a =1.此时f (1)=3e≠0.所以a 的值为1. (2)f ′(x )=[ax 2-(2a +1)x +2]e x =(ax -1)(x -2)e x .若a >12,则当x ∈⎝⎛⎭⎫1a ,2时,f ′(x )<0;当x ∈(2,+∞)时,f ′(x )>0.所以f (x )在x =2处取得极小值. 若a ≤12,则当x ∈(0,2)时,x -2<0,ax -1≤12x -1<0,所以f ′(x )>0,所以2不是f (x )的极小值点.综上可知,a 的取值范围是⎝⎛⎭⎫12,+∞. 3.已知函数f (x )=x 2-3x +ax .(1)若a =4,讨论f (x )的单调性;(2)若f (x )有3个极值点,求实数a 的取值范围. 3.解析 (1)因为a =4时,f (x )=x 2-3x +4x,所以f ′(x )=2x -3-4x 2=2x 3-3x 2-4x 2=2x 3-4x 2+x 2-4x 2=(x -2)(2x 2+x +2)x 2(x ≠0),令f ′(x )>0,得x >2;令f ′(x )<0,得x <0或0<x <2.所以f (x )在(-∞,0),(0,2)上单调递减,在(2,+∞)上单调递增.(2)由题意知,f ′(x )=2x -3-a x 2=2x 3-3x 2-ax 2(x ≠0),设函数g (x )=2x 3-3x 2-a ,则原条件等价于g (x )在(-∞,0)∪(0,+∞)上有3个零点,且3个零点附近的左、右两侧的函数值异号,又g ′(x )=6x 2-6x =6x (x -1), 由g ′(x )>0,得x >1或x <0;由g ′(x )<0,得0<x <1.故g (x )在(-∞,0)上单调递增,在(0,1)上单调递减,在(1,+∞)上单调递增,故原条件等价于g (x )在(-∞,0),(0,1),(1,+∞)上各有一个零点,令g (0)=-a >0,得a <0, 当a <0时,--a <0,g (--a )=2(--a )3-3(-a )-a =2a (-a +1)<0, 故a <0时,g (x )在(-∞,0)上有唯一零点;令g (1)=-1-a <0,解得a >-1,故-1<a <0时,g (x )在(0,1)上有唯一零点; 又-1<a <0时,g (2)=4-a >0,所以g (x )在(1,+∞)上有唯一零点. 综上可知,实数a 的取值范围是(-1,0). 4.已知函数f (x )=ax -x 2-ln x (a ∈R ). (1)求函数f (x )的单调区间;(2)若函数f (x )存在极值,且这些极值的和大于5+ln2,求实数a 的取值范围.4.解析 (1)f (x )的定义域为(0,+∞).f ′(x )=a -2x -1x .∵2x +1x ≥22⎝⎛⎭⎫当且仅当x =22时等号成立,当a ≤22时,f ′(x )≤0,函数f (x )在(0,+∞)上单调递减. 当a >22时,f ′(x )=a -2x -1x =-2x 2-ax +1x.由f ′(x )=0得x 1=a -a 2-84,x 2=a +a 2-84且x 2>x 1>0.由f ′(x )>0得x 1<x <x 2,由f ′(x )<0得0<x <x 1,或x >x 2, ∴函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫a -a 2-84,a +a 2-84, 单调递减区间为⎝ ⎛⎭⎪⎫0,a -a 2-84,⎝ ⎛⎭⎪⎫a +a 2-84,+∞.综上所述,当a ≤22时,函数f (x )的单调递减区间为(0,+∞),无单调递增区间;当a >22时,函数f (x )的单调递减区间为⎝ ⎛⎭⎪⎫0,a -a 2-84,⎝ ⎛⎭⎪⎫a + a 2-84,+∞,单调递增区间为⎝ ⎛⎭⎪⎫a -a 2-84,a +a 2-84.(2)由(1)知,当f (x )存在极值时,a >22.即方程2x 2-ax +1=0有两个不相等的正根x 1,x 2, ∴⎩⎨⎧x 1+x 2=a2>0,x 1x 2=12>0.∴f (x 1)+f (x 2)=a (x 1+x 2)-(x 21+x 22)-(ln x 1+ln x 2)=a (x 1+x 2)-[](x 1+x 2)2-2x 1x 2-ln(x 1x 2)=a 22-a 24+1-ln 12=a 24+1-ln 12.依题意a 24+1-ln 12>5+ln 2,即a 2>16,∴a >4或a <-4.又a >22.∴a >4,即实数a 的取值范围是(4,+∞). 5.(2018·全国Ⅲ)已知函数f (x )=(2+x +ax 2)·ln(1+x )-2x . (1)若a =0,证明:当-1<x <0时,f (x )<0;当x >0时,f (x )>0. (2)若x =0是f (x )的极大值点,求a .5.解析 (1)证明:当a =0时,f (x )=(2+x )ln(1+x )-2x ,f ′(x )=ln(1+x )-x1+x .设函数g (x )=f ′(x )=ln (1+x )-x 1+x ,则g ′(x )=x(1+x )2.当-1<x <0时,g ′(x )<0;当x >0时,g ′(x )>0.故当x >-1时,g (x )≥g (0)=0, 且仅当x =0时,g (x )=0,从而f ′(x )≥0,且仅当x =0时,f ′(x )=0.所以f (x )在(-1,+∞)单调递增.又f (0)=0,故当-1<x <0时,f (x )<0;当x >0时,f (x )>0. (2)(ⅰ)若a ≥0,由(1)知,当x >0时,f (x )≥(2+x )·ln (1+x )-2x >0=f (0),这与x =0是f (x )的极大值点矛盾.(ⅱ)若a <0,设函数h (x )=f (x )2+x +ax 2=ln(1+x )-2x2+x +ax 2.由于当|x |<min{1,1|a |}时,2+x +ax 2>0,故h (x )与f (x )符号相同. 又h (0)=f (0)=0,故x =0是f (x )的极大值点当且仅当x =0是h (x )的极大值点. h ′(x )=11+x -2(2+x +ax 2)-2x (1+2ax )(2+x +ax 2)2=x 2(a 2x 2+4ax +6a +1)(x +1)(ax 2+x +2)2.如果6a +1>0,则当0<x <-6a +14a,且|x |<min{1,1|a |}时,h ′(x )>0,故x =0不是h (x )的极大值点. 如果6a +1<0,则a 2x 2+4ax +6a +1=0存在根x 1<0,故当x ∈(x 1,0),且|x |<min{1,1|a |}时,h ′(x )<0,所以x =0不是h (x )的极大值点. 如果6a +1=0,则h ′(x )=x 3(x -24)(x +1)(x 2-6x -12)2,则当x ∈(-1,0)时,h ′(x )>0;当x ∈(0,1)时,h ′(x )<0.所以x =0是h (x )的极大值点,从而x =0是f (x )的极大值点. 综上,a =-16.考点二 含参函数的最值 【例题选讲】[例1] 已知函数f (x )=ln x -ax (a ∈R ). (1)求函数f (x )的单调区间;(2)当a >0时,求函数f (x )在[1,2]上的最小值. 解析 (1)f ′(x )=1x-a (x >0),①当a ≤0时,f ′(x )=1x -a >0,即函数f (x )的单调递增区间为(0,+∞).②当a >0时,令f ′(x )=1x -a =0,可得x =1a,当0<x <1a 时,f ′(x )=1-ax x >0;当x >1a 时,f ′(x )=1-ax x <0,故函数f (x )的单调递增区间为⎝⎛⎭⎫0,1a ,单调递减区间为⎝⎛⎭⎫1a ,+∞. 综上可知,当a ≤0时,函数f (x )的单调递增区间为(0,+∞);当a >0时,函数f (x )的单调递增区间为⎝⎛⎭⎫0,1a ,单调递减区间为⎝⎛⎭⎫1a ,+∞. (2)①当0<1a ≤1,即a ≥1时,函数f (x )在区间[1,2]上是减函数,所以f (x )的最小值是f (2)=ln 2-2a .②当1a ≥2,即0<a ≤12时,函数f (x )在区间[1,2]上是增函数,所以f (x )的最小值是f (1)=-a .③当1<1a <2,即12<a <1时,函数f (x )在⎣⎡⎦⎤1,1a 上是增函数,在⎣⎡⎦⎤1a ,2上是减函数. 又f (2)-f (1)=ln 2-a ,所以当12<a <ln 2时,最小值是f (1)=-a ;当ln 2≤a <1时,最小值为f (2)=ln 2-2a .综上可知,当0<a <ln2时,函数f (x )的最小值是f (1)=-a ;当a ≥ln2时,函数f (x )的最小值是f (2)=ln2-2a .[例2] 已知函数f (x )=ax 2+(1-2a )x -ln x . (1)当a >0时,求函数f (x )的单调递增区间; (2)当a <0时,求函数f (x )在⎣⎡⎦⎤12,1上的最小值.解析 (1)因为f (x )=ax 2+(1-2a )x -ln x ,所以f ′(x )=2ax +1-2a -1x =(2ax +1)(x -1)x .因为a >0,x >0,所以2ax +1>0,令f ′(x )>0,得x >1,所以f (x )的单调递增区间为(1,+∞).(2)当a <0时,令f ′(x )=0,得x 1=-12a,x 2=1,当-12a >1,即-12<a <0时,f (x )在(0,1]上是减函数,所以f (x )在⎣⎡⎦⎤12,1上的最小值为f (1)=1-a . 当12≤-12a ≤1,即-1≤a ≤-12时,f (x )在⎣⎡⎦⎤12,-12a 上是减函数,在⎣⎡⎦⎤-12a ,1上是增函数, 所以f (x )在⎣⎡⎦⎤12,1上的最小值为f ⎝⎛⎭⎫-12a =1-14a+ln(-2a ). 当-12a <12,即a <-1时,f (x )在⎣⎡⎦⎤12,1上是增函数,所以f (x )在⎣⎡⎦⎤12,1上的最小值为f ⎝⎛⎭⎫12=12-34a +ln 2. 综上,函数f (x )在区间⎣⎡⎦⎤12,1上的最小值为f (x )min=⎩⎪⎨⎪⎧12-34a +ln 2,a <-1,1-14a +ln(-2a ),-1≤a ≤-12,1-a ,-12<a <0.[例3] 已知函数f (x )=ln xx -1.(1)求函数f (x )的单调区间及极值;(2)设m >0,求函数f (x )在区间[m ,2m ]上的最大值.解析 (1)因为函数f (x )的定义域为(0,+∞),且f ′(x )=1-ln xx 2,由⎩⎪⎨⎪⎧f ′(x )>0,x >0,得0<x <e ;由⎩⎪⎨⎪⎧f ′(x )<0,x >0,得x >e .所以函数f (x )的单调递增区间为(0,e),单调递减区间为(e ,+∞), 且f (x )极大值=f (e)=1e-1,无极小值.(2)①当⎩⎪⎨⎪⎧2m ≤e ,m >0,即0<m ≤e 2时,函数f (x )在区间[m ,2m ]上单调递增,所以f (x )max =f (2m )=ln 2m2m -1;②当m <e<2m ,即e2<m <e 时,函数f (x )在区间(m ,e)上单调递增,在(e ,2m )上单调递减,所以f (x )max =f (e)=ln e e -1=1e-1; ③当m ≥e 时,函数f (x )在区间[m ,2m ]上单调递减,所以f (x )max =f (m )=ln mm-1.综上所述,当0<m ≤e 2时,f (x )max =ln 2m 2m -1;当e 2<m <e 时,f (x )max =1e -1;当m ≥e 时,f (x )max =ln mm -1.[例4] 已知函数f (x )=m ln xx +n ,g (x )=x 2⎣⎡⎦⎤f (x )-1x -a 2(m ,n ,a ∈R ),且曲线y =f (x )在点(1,f (1))处的切线方程为y =x -1.(1)求实数m ,n 的值及函数f (x )的最大值;(2)当a ∈⎝⎛⎭⎫-e ,1e 时,记函数g (x )的最小值为b ,求b 的取值范围. 解析 (1)函数f (x )的定义域为(0,+∞),f ′(x )=m (1-ln x )x 2, 因为f (x )的图象在点(1,f (1))处的切线方程为y =x -1,所以⎩⎪⎨⎪⎧f ′(1)=m =1,f (1)=m ln 11+n =0,解得⎩⎪⎨⎪⎧m =1,n =0. 所以f (x )=ln xx ,f ′(x )=1-ln x x 2,令f ′(x )=0,得x =e ,当0<x <e 时,f ′(x )>0,f (x )单调递增;当x >e 时,f ′(x )<0,f (x )单调递减. 所以当x =e 时,f (x )取得最大值,最大值为f (e)=1e .(2)因为g (x )=x 2⎣⎡⎦⎤f (x )-1x -a 2=x ln x -ax 22-x ,所以g ′(x )=ln x -ax =x ⎝⎛⎭⎫ln x x -a .①当a ∈⎝⎛⎭⎫0,1e 时,x →+∞时,g (x )→-∞,g (x )无最小值. ②当a =0时,g ′(x )=ln x ,由g ′(x )>0得x >1,由g ′(x )<0得0<x <1,所以g (x )在(0,1)上单调递减,在(1,+∞)上单调递增,g (x )的最小值b =g (1)=-1. ③当a ∈(-e ,0)时,由(1)知方程ln xx-a =0有唯一实根,又f ⎝⎛⎭⎫1e =-e ,f (1)=0,f (x )在⎝⎛⎭⎫1e ,1上单调递增,所以存在t ∈⎝⎛⎭⎫1e ,1,使得g ′(t )=0,即ln t =at . 当x ∈(0,t )时,g ′(x )<0;当x ∈(t ,+∞)时,g ′(x )>0, 所以g (x )在(0,t )上单调递减,在(t ,+∞)上单调递增,g (x )的最小值b =g (t )=t ln t -a 2t 2-t =t ln t 2-t ,令h (t )=t ln t 2-t ,t ∈⎝⎛⎭⎫1e ,1, 则h ′(t )=ln t -12<0,所以h (t )在⎝⎛⎭⎫1e ,1上单调递减,从而b =h (t )∈⎝⎛⎭⎫-1,-32e . 综上所述,当a ∈(-e ,0]时,b ∈⎣⎡⎭⎫-1,-32e ;当a ∈⎝⎛⎭⎫0,1e 时,b 不存在. [例5] (2019·全国Ⅲ)已知函数f (x )=2x 3-ax 2+b . (1)讨论f (x )的单调性;(2)是否存在a ,b ,使得f (x )在区间[0,1]的最小值为-1且最大值为1?若存在,求出a ,b 的所有值;若不存在,说明理由.解析 (1)f ′(x )=6x 2-2ax =2x (3x -a ). 令f ′(x )=0,得x =0或x =a3.若a >0,则当x ∈(-∞,0)∪⎝⎛⎭⎫a3,+∞时,f ′(x )>0;当x ∈⎝⎛⎭⎫0,a 3时,f ′(x )<0.故f (x )在(-∞,0),⎝⎛⎭⎫a 3,+∞单调递增,在⎝⎛⎭⎫0,a3单调递减. 若a =0,f (x )在(-∞,+∞)单调递增.若a <0,则当x ∈⎝⎛⎭⎫-∞,a3∪(0,+∞)时,f ′(x )>0; 当x ∈⎝⎛⎭⎫a 3,0时,f ′(x )<0.故f (x )在⎝⎛⎭⎫-∞,a 3,(0,+∞)单调递增,在⎝⎛⎭⎫a3,0单调递减. (2)满足题设条件的a ,b 存在.①当a ≤0时,由(1)知,f (x )在[0,1]单调递增,所以f (x )在区间[0,1]的最小值为f (0)=b ,最大值为f (1)=2-a +b .此时a ,b 满足题设条件当且仅当b =-1,2-a +b =1,即a =0,b =-1.②当a ≥3时,由(1)知,f (x )在[0,1]单调递减,所以f (x )在区间[0,1]的最大值为f (0)=b ,最小值为f (1)=2-a +b .此时a ,b 满足题设条件当且仅当2-a +b =-1,b =1,即a =4,b =1.③当0<a <3时,由(1)知,f (x )在[0,1]的最小值为f ⎝⎛⎭⎫a 3=-a327+b ,最大值为b 或2-a +b . 若-a 327+b =-1,b =1,则a =332,与0<a <3矛盾.若-a 327+b =-1,2-a +b =1,则a =33或a =-33或a =0,与0<a <3矛盾.综上,当且仅当a =0,b =-1或a =4,b =1时,f (x )在[0,1]的最小值为-1,最大值为1. 【对点训练】1.已知函数g (x )=a ln x +x 2-(a +2)x (a ∈R ). (1)若a =1,求g (x )在区间[1,e]上的最大值; (2)求g (x )在区间[1,e]上的最小值h (a ).1.解析 (1)∵a =1,∴g (x )=ln x +x 2-3x ,∴g ′(x )=1x +2x -3=(2x -1)(x -1)x ,∵x ∈[1,e],∴g ′(x )≥0,∴g (x )在[1,e]上单调递增,∴g (x )max =g (e)=e 2-3e +1. (2)g (x )的定义域为(0,+∞),g ′(x )=ax +2x -(a +2)=2x 2-(a +2)x +a x =(2x -a )(x -1)x .①当a2≤1,即a ≤2时,g (x )在[1,e]上单调递增,h (a )=g (1)=-a -1;②当1<a2<e ,即2<a <2e 时,g (x )在⎣⎡⎭⎫1,a 2上单调递减,在⎝⎛⎦⎤a 2,e 上单调递增, h (a )=g ⎝⎛⎭⎫a 2=a ln a 2-14a 2-a ; ③当a2≥e ,即a ≥2e 时,g (x )在[1,e]上单调递减,h (a )=g (e)=(1-e)a +e 2-2e .综上,h (a )=⎩⎪⎨⎪⎧-a -1,a ≤2,a ln a 2-14a 2-a ,2<a <2e ,(1-e)a +e 2-2e ,a ≥2e.2.已知函数f (x )=(x -a )e x (a ∈R ).(1)当a =2时,求函数f (x )的图象在x =0处的切线方程; (2)求函数f (x )在区间[1,2]上的最小值. 2.解析 f ′(x )=(x +1-a )e x .(1)当a =2时,f ′(x )=(x -1)e x .∴f (0)=-2,f ′(0)=-1, ∴所求切线方程为y +2=-x ,即x +y +2=0. (2)令f ′(x )=0得x =a -1.①若a -1≤1,则a ≤2.当x ∈[1,2]时,f ′(x )≥0,则f (x )在[1,2]上单调递增.∴f (x )min =f (1)=(1-a )e ; ②若a -1≥2,则a ≥3.当x ∈[1,2]时,f ′(x )≤0,则f (x )在[1,2]上单调递减.∴f (x )min =f (2)=(2-a )e 2; ③若1<a -1<2,则2<a <3.f ′(x ),f (x )随x 的变化情况如表:x 1 (1,a -1)a -1 (a -1,2)2 f ′(x ) -0 +f (x )极小值∴f (x )的单调递减区间为(1,a -1),单调递增区间为(a -1,2),∴f (x )min =f (a -1)=-e a -1. 综上可知,当a ≤2时,f (x )min =(1-a )e ;当a ≥3时,f (x )min =(2-a )e 2;当2<a <3时,f (x )min =-e a -1. 3.已知函数f (x )=ax -ln x ,F (x )=e x +ax ,其中x >0,a <0.(1)若f (x )和F (x )在区间(0,ln 3)上具有相同的单调性,求实数a 的取值范围;(2)若a ∈⎝⎛⎦⎤-∞,-1e 2,且函数g (x )=x e ax -1-2ax +f (x )的最小值为M ,求M 的最小值. 3.解析 (1)由题意得f ′(x )=a -1x =ax -1x,F ′(x )=e x +a ,x >0,∵a <0,∴f ′(x )<0在(0,+∞)上恒成立,即f (x )在(0,+∞)上单调递减, 当-1≤a <0时,F ′(x )>0,即F (x )在(0,+∞)上单调递增,不合题意, 当a <-1时,由F ′(x )>0,得x >ln(-a ),由F ′(x )<0,得0<x <ln(-a ), ∴F (x )的单调递减区间为(0,ln(-a )),单调递增区间为(ln(-a ),+∞). ∵f (x )和F (x )在区间(0,ln 3)上具有相同的单调性,∴ln(-a )≥ln 3,解得a ≤-3, 综上,a 的取值范围是(-∞,-3].(2)g ′(x )=e ax -1+ax e ax -1-a -1x =(ax +1)⎝⎛⎭⎫e ax -1-1x ,由e ax -1-1x =0,解得a =1-ln x x , 设p (x )=1-ln x x ,则p ′(x )=ln x -2x2,当x >e 2时,p ′(x )>0,当0<x <e 2时,p ′(x )<0,从而p (x )在(0,e 2)上单调递减,在(e 2,+∞)上单调递增,p (x )min =p (e 2)=-1e 2,当a ≤-1e 2时,a ≤1-ln x x ,即e ax -1-1x≤0,当x ∈⎝⎛⎭⎫0,-1a 时,ax +1>0,g ′(x )≤0,g (x )单调递减, 当x ∈⎝⎛⎭⎫-1a ,+∞时,ax +1<0,g ′(x )≥0,g (x )单调递增,∴g (x )min =g ⎝⎛⎭⎫-1a =M , 设t =-1a ∈(0,e 2],M =h (t )=t e 2-ln t +1(0<t ≤e 2),则h ′(t )=1e 2-1t ≤0,h (t )在(0,e 2]上单调递减,∴h (t )≥h (e 2)=0,即M ≥0,∴M 的最小值为0. 4.已知函数f (x )=ax +ln x ,其中a 为常数. (1)当a =-1时,求f (x )的最大值;(2)若f (x )在区间(0,e]上的最大值为-3,求a 的值.4.解析 (1)易知f (x )的定义域为(0,+∞),当a =-1时,f (x )=-x +ln x ,f ′(x )=-1+1x =1-xx ,令f ′(x )=0,得x =1.当0<x <1时,f ′(x )>0;当x >1时,f ′(x )<0.∴f (x )在(0,1)上单调递增,在(1,+∞)上单调递减.∴f (x )max =f (1)=-1.∴当a =-1时,函数f (x )在(0,+∞)上的最大值为-1. (2)f ′(x )=a +1x ,x ∈(0,e],1x ∈⎣⎡⎭⎫1e,+∞. ①若a ≥-1e ,则f ′(x )≥0,从而f (x )在(0,e]上单调递增,∴f (x )max =f (e)=a e +1≥0,不符合题意.②若a <-1e ,令f ′(x )>0得a +1x >0,结合x ∈(0,e],解得0<x <-1a ;令f ′(x )<0得a +1x <0,结合x ∈(0,e],解得-1a <x ≤e .从而f (x )在⎝⎛⎭⎫0,-1a 上单调递增,在⎝⎛⎦⎤-1a ,e 上单调递减, ∴f (x )max =f ⎝⎛⎭⎫-1a =-1+ln ⎝⎛⎭⎫-1a .令-1+ln ⎝⎛⎭⎫-1a =-3,得ln ⎝⎛⎭⎫-1a =-2,即a =-e 2. ∵-e 2<-1e ,∴a =-e 2为所求.故实数a 的值为-e 2.5.已知函数f (x )=ax 2-(a +2)x +ln x ,其中a ∈R .(1)当a =1时,求曲线y =f (x )在点(1,f (1))处的切线方程;(2)当a >0时,若f (x )在区间[1,e]上的最小值为-2,求a 的取值范围. 5.解析 (1)当a =1时,f (x )=x 2-3x +ln x (x >0),所以f ′(x )=2x -3+1x =2x 2-3x +1x,所以f (1)=-2,f ′(1)=0.所以切线方程为y +2=0. (2)函数f (x )=ax 2-(a +2)x +ln x 的定义域为(0,+∞),当a >0时,f ′(x )=2ax -(a +2)+1x =2ax 2-(a +2)x +1x =(2x -1)(ax -1)x ,令f ′(x )=0,解得x =12或x =1a.①当0<1a ≤1,即a ≥1时,f (x )在[1,e]上单调递增.所以f (x )在[1,e]上的最小值为f (1)=-2,符合题意;②当1<1a <e ,即1e <a <1时,f (x )在⎣⎡⎦⎤1,1a 上单调递减,在⎣⎡⎦⎤1a ,e 上单调递增, 所以f (x )在[1,e]上的最小值为f ⎝⎛⎭⎫1a <f (1)=-2,不合题意; ③当1a ≥e ,即0<a ≤1e时,f (x )在[1,e]上单调递减,所以f (x )在[1,e]上的最小值为f (e)<f (1)=-2,不合题意. 综上,实数a 的取值范围是[1,+∞). 考点三 含参函数的极值与最值的综合问题 【例题选讲】[例1] 已知函数f (x )=e x 1+ax 2,其中a 为正实数,x =12是f (x )的一个极值点.(1)求a 的值;(2)当b >12时,求函数f (x )在[b ,+∞)上的最小值.解析 f ′(x )=(ax 2-2ax +1)e x(1+ax 2)2.(1)因为x =12是函数y =f (x )的一个极值点,所以f ′⎝⎛⎭⎫12=0,因此14a -a +1=0,解得a =43. 经检验,当a =43时,x =12是y =f (x )的一个极值点,故所求a 的值为43.(2)由(1)可知,f ′(x )=⎝⎛⎭⎫43x 2-83x +1e x⎝⎛⎭⎫1+43x 22,令f ′(x )=0,得x 1=12,x 2=32.f (x )与f ′(x )随x 的变化情况如下:x ⎝⎛⎭⎫-∞,1212 ⎝⎛⎭⎫12,32 32 ⎝⎛⎭⎫32,+∞ f ′(x ) + 0 -0 +f (x )3e4e e4所以f (x )的单调递增区间是⎝⎛⎭⎫-∞,12,⎝⎛⎭⎫32,+∞,单调递减区间是⎝⎛⎭⎫12,32.当12<b <32时,f (x )在[b ,32)上单调递减,在⎝⎛⎭⎫32,+∞上单调递增. 所以f (x )在[b ,+∞)上的最小值为f ⎝⎛⎭⎫32=e e4; 当b ≥32时,f (x )在[b ,+∞)上单调递增,所以f (x )在[b ,+∞)上的最小值为f (b )=e b 1+ab 2=3e b3+4b 2.[例2] 已知函数f (x )=a ln (x +b )-x . (1)若a =1,b =0,求f (x )的最大值; (2)当b >0时,讨论f (x )极值点的个数.解析 (1)当a =1,b =0时,f (x )=ln x -x ,此时,f (x )的定义域是(0,+∞), f ′(x )=1x -12x =2-x 2x,由f ′(x )>0,解得0<x <4,由f ′(x )<0,解得x >4,故f (x )在(0,4)上单调递增,在(4,+∞)上单调递减,故f (x )max =f (4)=2ln 2-2. (2)当b >0时,函数的定义域是[0,+∞),f ′(x )=a x +b -12x =-x +2a x -b 2x x +b, ①当a ≤0时,f ′(x )<0对任意x ∈(0,+∞)恒成立,故此时f (x )的极值点的个数为0; ②当a >0时,设h (x )=-x +2a x -b ,(Ⅲ)当4a 2-4b ≤0即0<a ≤ b 时,f ′(x )≤0对任意x ∈(0,+∞)恒成立,即f ′(x )在(0,+∞)上无变号零点, 故此时f (x )的极值点个数是0;(Ⅲ)当4a 2-4b >0即a >b 时,记方程h (x )=0的两根分别为x 1,x 2,由于x 1+x 2=2a >0,x 1x 2=b >0,故x 1,x 2都大于0,即f ′(x )在(0,+∞)上有2个变号零点, 故此时f (x )的极值点的个数是2.综上,a ≤b 时,f (x )极值点的个数是0;a >b 时,f (x )极值点的个数是2. [例3] 设函数f (x )=a x +e -x (a >1). (1)求证:f (x )有极值;(2)若x =x 0时f (x )取得极值,且对任意正整数a 都有x 0∈(m ,n ),其中m ,n ∈Z ,求n -m 的最小值. 解析 (1)由题意得f ′(x )=a x ln a -e -x ,令h (x )=f ′(x )=a x ln a -e -x , 则h ′(x )=a x (ln a )2+e -x >0,所以函数h (x ),即f ′(x )在R 上单调递增. 由f ′(x )=0,得a x e x ln a =1,因为a >1,所以a x e x =1ln a >0,得x =log a e 1ln a ,当x >log a e1ln a 时,f ′(x )>0;当x <log a e 1ln a时,f ′(x )<0. 所以函数f (x )在⎝⎛⎭⎫-∞,log a e 1ln a 上单调递减,在⎝⎛⎭⎫log a e 1ln a ,+∞上单调递增,因此,当x =log a e 1ln a时函数f (x )取极值.(2)由(1)知,函数f (x )的极值点x 0(即函数f ′(x )的零点)唯一.由f ′(-1)=ln a a -e ,令g (a )=ln aa ,则g ′(a )=1-ln a a 2,由g ′(a )=0,得a =e ,当a >e 时,g ′(a )<0;当0<a <e 时,g ′(a )>0.所以g (a )在(0,e)上单调递增,在(e ,+∞)上单调递减,所以g (a )≤g (e)=1e ,所以f ′(-1)=ln aa-e <0.当a 为大于1的正整数时,f ′(0)=ln a -1的值有正有负.f ′(1)=a ln a -1e ,因为a 为正整数且a >1,所以a ln a ≥2ln 2>1e ,所以f ′(1)>0.所以x 0∈(-1,1)恒成立,所以n -m 的最小值为2. [例4] 已知函数f (x )=a ln x +1x (a >0).(1)求函数f (x )的单调区间和极值;(2)是否存在实数a ,使得函数f (x )在[1,e]上的最小值为0?若存在,求出a 的值;若不存在,请说明理由.解析 由题意,知函数的定义域为{x |x >0},f ′(x )=a x -1x 2(a >0).(1)由f ′(x )>0解得x >1a ,所以函数f (x )的单调递增区间是⎝⎛⎭⎫1a ,+∞; 由f ′(x )<0解得x <1a,所以函数f (x )的单调递减区间是⎝⎛⎭⎫0,1a . 所以当x =1a 时,函数f (x )有极小值f ⎝⎛⎭⎫1a =a ln 1a +a =a -a ln a ,无极大值. (2)不存在.理由如下:由(1)可知,当x ∈⎝⎛⎭⎫0,1a 时,函数f (x )单调递减;当x ∈⎝⎛⎭⎫1a ,+∞时,函数f (x )单调递增. ①若0<1a≤1,即a ≥1时,函数f (x )在[1,e]上为增函数,故函数f (x )的最小值为f (1)=a ln 1+1=1,显然1≠0,故不满足条件.②若1<1a ≤e ,即1e ≤a <1时,函数f (x )在⎣⎡⎭⎫1,1a 上为减函数,在⎣⎡⎦⎤1a ,e 上为增函数, 故函数f (x )的最小值为f (x )的极小值f ⎝⎛⎭⎫1a =a ln 1a +a =a -a ln a =a (1-ln a )=0,即ln a =1, 解得a =e ,而1e≤a <1,故不满足条件.③若1a >e ,即0<a <1e 时,函数f (x )在[1,e]上为减函数,故函数f (x )的最小值为f (e)=a +1e=0,解得a =-1e ,而0<a <1e ,故不满足条件.综上所述,这样的a 不存在.[例5] 已知函数f (x )=(ax -1)ln x +x 22.(1)若a =2,求曲线y =f (x )在点(1,f (1))处的切线l 的方程;(2)设函数g (x )=f ′(x )有两个极值点x 1,x 2,其中x 1∈(0,e],求g (x 1)-g (x 2)的最小值. 解析 (1)当a =2时,f (x )=(2x -1)ln x +x 22,则f ′(x )=2ln x +x -1x +2,f ′(1)=2,f (1)=12,∴切线l 的方程为y -12=2(x -1),即4x -2y -3=0.(2)函数g (x )=a ln x +x -1x +a ,定义域为(0,+∞),则g ′(x )=1+a x +1x 2=x 2+ax +1x 2,令g ′(x )=0,得x 2+ax +1=0,其两根为x 1,x 2,且x 1+x 2=-a ,x 1x 2=1,故x 2=1x 1,a =-⎝⎛⎭⎫x 1+1x 1. g (x 1)-g (x 2)=g (x 1)-g ⎝⎛⎭⎫1x 1=a ln x 1+x 1-1x 1+a -⎝⎛⎭⎫a ln 1x 1+1x 1-x 1+a =2⎝⎛⎭⎫x 1-1x 1+2a ln x 1=2⎝⎛⎭⎫x 1-1x 1-2⎝⎛⎭⎫x 1+1x 1ln x 1, 令h (x )=2⎝⎛⎭⎫x -1x -2⎝⎛⎭⎫x +1x ln x .则[g (x 1)-g (x 2)]min =h (x )min , 又h ′(x )=2(1+x )(1-x )ln xx 2,当x ∈(0,1]时,h ′(x )≤0,当x ∈(1,e]时,h ′(x )<0,即当x ∈(0,e]时,h (x )单调递减,∴h (x )min =h (e)=-4e ,故[g (x 1)-g (x 2)]min =-4e .[例6] 已知函数g (x )=x 22+x +ln x .(1)若函数g ′(x )≥a 恒成立,求实数a 的取值范围;(2)函数f (x )=g (x )-mx ,若f (x )存在单调递减区间,求实数m 的取值范围; (3)设x 1,x 2(x 1<x 2)是函数f (x )的两个极值点,若m ≥72,求f (x 1)-f (x 2)的最小值.解析 (1)∵g ′(x )=x +1x +1,g ′(x )=x +1x+1≥2x ·1x+1=3,g ′(x )≥a ,∴a ≤3. (2)∴f ′(x )=x +1-m +1x =x 2+(1-m )x +1x,又∵f ′(x )<0在(0,+∞)上有解,令h (x )=x 2+(1-m )x +1,则h (0)=1>0,只需⎩⎪⎨⎪⎧m -12>0,(m -1)2-4>0,解得⎩⎪⎨⎪⎧m >1,m >0或m <-1,即m >3(3)∵f ′(x )=x 2+(1-m )x +1x,令f ′(x )=0,即x 2+(1-m )x +1=0,两根分别为x 1,x 2,则⎩⎪⎨⎪⎧x 1+x 2=m -1,x 1x 2=1,又∵f (x 1)-f (x 2)=12(x 21-x 22)+(1-m )(x 1-x 2)+ln x 1x 2=12(x 21-x 22)-(x 21-x 22)+ln x 1x 2, =ln x 1x 2-12(x 21-x 22)=ln x 1x 2-12⎝⎛⎭⎫x 1x 2-x 2x 1. 令t =x 1x 2,由于x 1<x 2,∴0<t <1.又∵m ≥72,(x 1+x 2)2=(m -1)2≥254,即(x 1+x 2)2x 1x 2=x 1x 2+2+x 2x 1,即t +2+1t ≥254,∴4t 2-17t +4≥0,解得t ≥4或t ≤14,即0<t ≤14.令h (t )=ln t -12⎝⎛⎭⎫t -1t (0<t ≤14),h ′(t )=1t -12⎝⎛⎭⎫1+1t 2=-(t -1)22t 2<0,∴h (t )在(0,14]上单调递减,h (t )min =h (14)=-2ln2+158.∴f (x 1)-f (x 2)的最小值为-2ln2+158.【对点训练】 1.已知函数f (x )=x ln x . (1)求函数f (x )的极值点;(2)设函数g (x )=f (x )-a (x -1),其中a ∈R ,求函数g (x )在区间(0,e]上的最小值(其中e 为自然对数的底数).1.解析 (1)f ′(x )=ln x +1,x >0,由f ′(x )=0,得x =1e .当x ∈⎝⎛⎭⎫0,1e 时,f ′(x )<0,当x ∈⎝⎛⎭⎫1e ,+∞时,f ′(x )>0, 所以f (x )在区间⎝⎛⎭⎫0,1e 上单调递减,在区间⎝⎛⎭⎫1e ,+∞上单调递增. 所以x =1e是函数f (x )的极小值点,极大值点不存在.(2)g (x )=x ln x -a (x -1),则g ′(x )=ln x +1-a ,由g ′(x )=0,得x =e a -1. 所以在区间(0,e a -1)上,g (x )单调递减,在区间(e a -1,+∞)上,g (x )单调递增. 当e a -1≥e ,即a ≥2时,g (x )在(0,e]上单调递减,∴g (x )min =g (e)=a +e -a e , 当e a -1<e 即a <2时,g (x )在(0,e a -1)上单调递减,在(e a -1,e]上单调递增, ∴g (x )min =g (e a -1)=a -e a -1,令g (x )的最小值为h (a ),综上有h (a )=⎩⎪⎨⎪⎧a -e a -1,a <2,a +e -a e ,a ≥2.2.已知函数f (x )=⎩⎪⎨⎪⎧-x 3+x 2,x <1,a ln x ,x ≥1.(1)求f (x )在区间(-∞,1)上的极小值和极大值; (2)求f (x )在[-1,e](e 为自然对数的底数)上的最大值. 2.解析 (1)当x <1时,f ′(x )=-3x 2+2x =-x (3x -2), 令f ′(x )=0,解得x =0或x =23.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,0) 0 ⎝⎛⎭⎫0,23 23 ⎝⎛⎭⎫23,1 f ′(x ) - 0 + 0 -f (x )极小值极大值故当x =0当x =23时,函数f (x )取到极大值,极大值为f ⎝⎛⎭⎫23=427. (2)①当-1≤x <1时,根据(1)知,函数f (x )在[-1,0)和⎝⎛⎭⎫23,1上单调递减,在⎣⎡⎦⎤0,23上单调递增. 因为f (-1)=2,f ⎝⎛⎭⎫23=427,f (0)=0,所以f (x )在[-1,1)上的最大值为2. ②当1≤x ≤e 时,f (x )=a ln x ,当a ≤0时,f (x )≤0;当a >0时,f (x )在[1,e]上单调递增.则f (x )在[1,e]上的最大值为f (e)=a . 故当a ≥2时,f (x )在[-1,e]上的最大值为a ; 当a <2时,f (x )在[-1,e]上的最大值为2. 3.已知函数f (x )=a ln x +x 2-ax (a ∈R ).(1)若x =3是f (x )的极值点,求f (x )的单调区间; (2)求g (x )=f (x )-2x 在区间[1,e]上的最小值h (a ).3.解析 (1)f (x )的定义域为(0,+∞),f ′(x )=ax +2x -a =2x 2-ax +a x ,因为x =3是f (x )的极值点,所以f ′(3)=18-3a +a3=0,解得a =9,所以f ′(x )=2x 2-9x +9x =(2x -3)(x -3)x ,所以当0<x <32或x >3时,f ′(x )>0,当32<x <3时,f ′(x )<0,即x =3是f (x )的极小值点, 所以f (x )的单调递增区间为⎝⎛⎭⎫0,32,(3,+∞),单调递减区间为⎝⎛⎭⎫32,3.(2)g ′(x )=2x 2-ax +a x -2=(2x -a )(x -1)x ,令g ′(x )=0,得x 1=a2,x 2=1.①当a2≤1,即a ≤2时,g (x )在[1,e]上为增函数,h (a )=g (1)=-a -1;②当1<a2<e ,即2<a <2e 时,g (x )在⎣⎡⎭⎫1,a 2上为减函数,在⎝⎛⎦⎤a 2,e 上为增函数, h (a )=g ⎝⎛⎭⎫a 2=a ln a 2-14a 2-a ; ③当a2≥e ,即a ≥2e 时,g (x )在[1,e]上为减函数,h (a )=g (e)=(1-e)a +e 2-2e.综上,h (a )=⎩⎪⎨⎪⎧-a -1,a ≤2,a ln a 2-14a 2-a ,2<a <2e ,1-e a +e 2-2e ,a ≥2e.4.已知常数a ≠0,f (x )=a ln x +2x . (1)当a =-4时,求f (x )的极值;(2)当f (x )的最小值不小于-a 时,求实数a 的取值范围.4.解析 (1)由已知得f (x )的定义域为(0,+∞),f ′(x )=ax +2=a +2x x .当a =-4时,f ′(x )=2x -4x. 所以当0<x <2时,f ′(x )<0,即f (x )在(0,2)上单调递减; 当x >2时,f ′(x )>0,即f (x )在(2,+∞)上单调递增.所以f (x )只有极小值,且当x =2时,f (x )取得极小值f (2)=4-4ln 2. 所以当a =-4时,f (x )只有极小值4-4ln 2,无极大值. (2)因为f ′(x )=a +2xx,所以当a >0,x ∈(0,+∞)时, f ′(x )>0,即f (x )在(0,+∞)上单调递增,没有最小值.当a <0时,由f ′(x )>0,得x >-a2,所以f (x )在⎝⎛⎭⎫-a 2,+∞上单调递增; 由f ′(x )<0,得x <-a2,所以f (x )在⎝⎛⎭⎫0,-a 2上单调递减. 所以当a <0时,f (x )的最小值为f ⎝⎛⎭⎫-a 2=a ln ⎝⎛⎭⎫-a 2+2⎝⎛⎭⎫-a 2. 根据题意,知f ⎝⎛⎭⎫-a 2=a ln ⎝⎛⎭⎫-a 2+2⎝⎛⎭⎫-a2≥-a ,即a [ln (-a )-ln 2]≥0. 因为a <0,所以ln (-a )-ln 2≤0,解得a ≥-2, 所以实数a 的取值范围是[-2,0). 5.已知函数f (x )=a sin x +sin2x ,a ∈R .(1)若f (x )在⎝⎛⎭⎫0,π2上有极值点,求a 的取值范围; (2)若a =1,x ∈⎝⎛⎭⎫0,2π3时,f (x )≥bx cos x ,求b 的最大值. 5.解析 (1)f ′(x )=a cos x +2cos 2x =4cos 2x +a cos x -2,依题意,f ′(x )在⎝⎛⎭⎫0,π2上有变号零点,令cos x =t ,则t ∈(0,1), 所以g (t )=4t 2+at -2=0在(0,1)有实根,注意到Δ>0,所以g (0)·g (1)<0,解得a >-2,即a ∈(-2,+∞).(2)a =1时,f (x )=sin x +sin 2x ,当x ∈⎣⎡⎭⎫π2,2π3时,f (x )≥0≥bx cos x ,显然成立;当x ∈⎝⎛⎭⎫0,π2时,cos x >0,所以tan x +2sin x ≥bx . 记h (x )=tan x +2sin x -bx ,则h (x )≥0恒成立,h ′(x )=1cos 2x +2cos x -b ,h ″(x )=2sin x cos 3x -2sin x =2sin x (1-cos 3x )cos 3x>0, h ′(x )在⎝⎛⎭⎫0,π2单调递增,h ′(0)=3-b , 若b >3,则h ′(0)<0,记cos θ=1b ,θ∈⎝⎛⎭⎫0,π2,则h ′(θ)=b +2b -b =2b>0, 所以存在x 0∈(0,θ),使得h ′(x 0)=0,当x ∈(0,x 0)时,h ′(x )<0,h (x )单调递减, 所以x ∈(0,x 0)时,h (x )<h (0)=0,不符题意.当b =3时,h ′(x )>h ′(0)=0,即x ∈⎝⎛⎭⎫0,π2时,h (x )单调递增,所以h (x )>h (0)=0,符合题意, 当x ∈⎝⎛⎭⎫π2,2π3时,f (x )=sin x +2sin x cos x =sin x (1+2cos x ),由2cos x +1>2cos 2π3+1=0,sin x >0,所以f (x )>0, 而b =3时,bx cos x <0,所以f (x )>bx cos x 成立,综上所述,b 的最大值为3.6.已知函数f (x )=ln x +12x 2-ax +a (a ∈R ). (1)若函数f (x )在(0,+∞)上为单调递增函数,求实数a 的取值范围;(2)若函数f (x )在x =x 1和x =x 2处取得极值,且x 2≥e x 1(e 为自然对数的底数),求f (x 2)-f (x 1)的最大值.6.解析 (1)∵f ′(x )=1x+x -a (x >0),又f (x )在(0,+∞)上单调递增,∴恒有f ′(x )≥0, 即1x +x -a ≥0恒成立,∴a ≤⎝⎛⎭⎫x +1x min ,而x +1x ≥2 x ·1x=2,当且仅当x =1时取“=”,∴a ≤2. 即函数f (x )在(0,+∞)上为单调递增函数时,a 的取值范围是(-∞,2].(2)∵f (x )在x =x 1和x =x 2处取得极值,且f ′(x )=1x +x -a =x 2-ax +1x(x >0),。


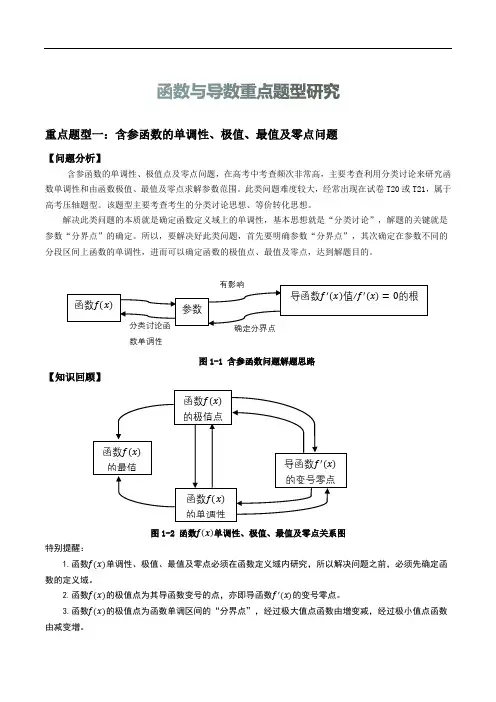
重点题型一:含参函数的单调性、极值、最值及零点问题【问题分析】含参函数的单调性、极值点及零点问题,在高考中考查频次非常高,主要考查利用分类讨论来研究函数单调性和由函数极值、最值及零点求解参数范围。
此类问题难度较大,经常出现在试卷T20或T21,属于高考压轴题型。
该题型主要考查考生的分类讨论思想、等价转化思想。
解决此类问题的本质就是确定函数定义域上的单调性,基本思想就是“分类讨论”,解题的关键就是参数“分界点”的确定。
所以,要解决好此类问题,首先要明确参数“分界点”,其次确定在参数不同的分段区间上函数的单调性,进而可以确定函数的极值点、最值及零点,达到解题目的。
图1-1 含参函数问题解题思路【知识回顾】图1-2 函数f (x )单调性、极值、最值及零点关系图特别提醒:1.函数f (x )单调性、极值、最值及零点必须在函数定义域内研究,所以解决问题之前,必须先确定函数的定义域。
2.函数f (x )的极值点为其导函数变号的点,亦即导函数f ′(x )的变号零点。
3.函数f (x )的极值点为函数单调区间的“分界点”,经过极大值点函数由增变减,经过极小值点函数由减变增。
函数f(x)的单调性函数f(x)的极值点导函数f ′(x)的变号零点函数f(x)的最值确定分界点有影响分类讨论函数单调性参数导函数f ′(x)值/f ′(x )=0的根函数f(x)4. 函数f (x )单调区间不能写成并集,也不能用“或”连接,只能用逗号“,”或“和”连接。
【“分界点”确认】参数对导函数f ′(x )的值符号有影响,就必须根据参数对导函数的影响确定参数“分界点”,然后在进行分类讨论函数的单调性。
常见的“分界点”确认方法如下: 1.观察法:解决问题的过程中,我们会发现导函数形式比较简单的情况下,我们可以通过观察直接确定参数的“分界点”,例如:当导函数f ′(x )的值与y =x 2+a 函数有关,可以直接观察得到:当a ≥0时,y ≥0;当a <0时,y =0有两个根x 1=−√−a,x 2=√−a,当x ∈(−∞,−√−a)∪(√−a,+∞)时,y >0,当x ∈(−√−a,√−a)时,y <0.所以我们可以根据常见函数的性质及其之间的不等关系,通过直接观察确定“分界点”,常见函数性质及其之间的关系如下: ①x 2≥0 (x ∈R ), 完全平方式不小于0 ②tanx >x >sinx (0<x <π2)③e x ≥x +1 (x ∈R ),仅当x =0时,等号成立e x =x +1 ④lnx ≤x −1 (x >0),仅当x =1时,等号成立lnx =x −1 ⑤lnx <x <e x (x >0) ⑥a x >0 (x ∈R )2.由二次函数引发的“分界点”当函数f (x )求导后,导函数f ′(x )值符号由一个含参的二次函数(二次三项式)决定,一般可以从两个方面进行“分界点”的确定:(1)通过二次函数(一元二次方程)的∆判别式进行“分界点”的确定. 对于一个二次函数y =ax 2+bx +c (a ≠0): ① {a >0∆≤0⟹y ≥0或{a <0∆≤0⟹y ≤0.② {a >0∆>0⟹二次函数有两个零点(或二次方程y =0有两个不同实根)x 1,x 2(x 1<x 2),x 在两根之外函数大于0,两根之内函数小于0.③ {a <0∆>0⟹二次函数有两个零点(或二次方程y =0有两个不同实根)x 1,x 2(x 1<x 2),x 在两根之外函数小于0,两根之内函数大于0. 特别提醒:当二次函数有两个零点时,需要确定两个零点是否在函数定义域之内,若不在需要舍弃. (2)由二次函数零点分布(一元二次方程实根分布)进行“分界点”确定设x 1,x 2(x 1<x 2)是二次函数y =ax 2+bx +c (a >0)的两个零点(一元二次方程ax 2+bx +c =0(a >0)的两个根),则x 1,x 2的分布情况与二次函数系数之间的关系如下(k,k 1,k 2∈R,k 1<k 2):零点分布函数图像等价条件x 1<x 2<k{∆>0f (k )>0−b 2a<kk <x 1<x 2{∆>0f (k )>0−b 2a>kx 1<k <x 2f (k )<0k 1<x 1<x 2<k 2{∆>0f (k 1)>0f (k 2)>0k 1<−b 2a<k2 x 1,x 2中仅有一个在(k 1,k 2)内\f (k 1)∙f (k 2)<0或f (k 1)=0,k 1<−b2a <k 1+k 22或f (k 2)=0,k 1+k 22<−b2a <k 2或{∆=0k 1<−b 2a<k 2当二次函数定义域受限,可以根据上表情况进行“分界点”确认,进而进行分类讨论。

初中含参二次函数的最值问题二次函数在数学中是一种比较常见的函数形式,也是我们初中阶段需要掌握的重要知识点之一。
其中,最值问题是二次函数题目中比较典型和常见的一类问题。
在这篇文章中,我将通过一些例题和解题思路的介绍,来帮助大家更好地理解含参二次函数的最值问题。
1. 带参数二次函数的最值问题下面是一个含参数的二次函数的例子:$y=ax^2+bx+c(a>0)$ 。
我们来考虑这个函数的最值问题。
(1)当$a>0$时,这个二次函数的值域为$[q,\infty)$。
其中$q$为$a,b,c$的函数,满足$a>0$时,有如下的公式:$$q=f(\frac{-b}{2a})=\frac{4ac-b^2}{4a}$$那么,这个二次函数的最小值就是$q$,也就是当$x=\frac{-b}{2a}$时,函数取得最小值。
(2)当$a<0$时,这个二次函数的值域为$(-\infty,q]$。
其最大值也是$q$,即当$x=\frac{-b}{2a}$时,函数取得最大值。
可以通过公式来求解含参二次函数的最值问题。
具体来说,找到函数的最小值或最大值所在的$x$坐标,然后代入函数中求出对应的函数值即可。
下面让我们通过一个例题来进一步了解含参二次函数的最值问题。
2. 例题分析【例题】已知函数$y=ax^2+bx+c(a>0)$,并满足:$|x-2|+|x-4|+|x-6|=k(k>0)$求函数$y$的最小值和最大值并确定此时$x$的值。
【解题思路】该题要求我们求解带有约束条件的含参二次函数的最值问题。
实际上,约束条件中的绝对值形式会让我们比较难受,不过我们可以将其转化为分段描述,从而更好地理解这个问题。
具体来说,考虑以下的情况:(1)当$x\leq 2$时,有$|x-2|=2-x$。
(2)当$2<x\leq4$时,有$|x-2|=x-2$、$|x-4|=4-x$。
(3)当$4<x\leq 6$时,有$|x-4|=x-4$、$|x-6|=6-x$。


第十一讲 含参函数策略一:“消参”化解“多参”例1.在平面直角坐标系xOy 中,已知点A (1,-1)在抛物线c bx x y ++=2(b >0)上.(1)若b -c =4,求b 、c 的值;(2)若该抛物线与y 轴交于点B ,其对称轴与x 轴交于点C ,求tan ∠OBC 的取值范围.变式:将抛物线平移,平移后的抛物线仍经过点A ,点A 的对应点A 1为(1-m ,2b -1),当m ≥23-时,求平移后抛物线的顶点所能达到的最高点的坐标.策略归纳:对于多参函数问题,可以利用题目中给出的有效信息进行转化、消参,使得多个参数最后消成一个参数.策略二:“图象”化解“抽象”例2.在平面直角坐标系xOy 中,抛物线a bx ax y 32-+=(a ≠0)经过A (-1,0).(1)求抛物线的对称轴;(2)若点B (0,4)、点C (5,4),且抛物线与线段BC 恰有一个公共点,求a 的取值范围.变式:已知在平面直角坐标系xOy 中,点A (1,0),抛物线y =ax 2+bx +3(a ≠0)经过点B (-2,3).若此抛物线与线段AB 有两个不同的交点,求a 的取值范围.策略归纳:含参函数问题一般都很抽象,借助图象,再利用函数的性质往往可以巧妙的解决含参函数问题.策略三:“动点”化为“定线”例3.已知,正方形ABCD 中,A (0,-4),B (-1,-4),C (-1,-5),D (0,-5),抛物线422-++=m mx x y (m 为常数),顶点为M .(1)抛物线经过定点坐标是 ,顶点M 的坐标是 (用含m 的代数式表示);(2)若抛物线422-++=m mx x y (m 为常数)与正方形ABCD 的边有交点,求m 的取值范围.变式:若∠ABM =45°,求m 的值.策略归纳:动点即为一条定线,所以遇到动点时,可以尝试通过求动点的解析式来解决问题.二、同类训练1.在平面直角坐标系xOy 中,已知抛物线y =x 2-2ax +b 的顶点在x 轴上,P (x 1 ,m ),Q (x 2 ,m )(x 1<x 2)是此抛物线上的两点.(1)将抛物线沿y 轴平移,使得它与x 轴的两个交点间的距离为4,试描述出这一变化过程;(2)若存在实数c ,使得x 1≤c -1,且x 2≥c +5成立,求m 的取值范围.(3)若存在实数c ,使得x 1≥c -1,且x 2≤c +5成立,求m 的取值范围.2.已知抛物线122-++=m mx mx y (m >0)与x 轴的交点为A 、B ,若抛物线在A 、B之间的部分与线段AB 所围成的区域内(包含边界)恰有8个整点(横纵坐标均为整数),求m 的取值范围.3.已知抛物线2222+-=x m mx y ,当0<x <4时,满足2222+-x m mx <2,求m 的取值范围.4.已知x =-m 和x =m -2时,多项式142+++a bx ax 的值都相等,且m ≠1,若当1<x <2时,存在x 的值,使得多项式142+++a bx ax 的值为3,求a 的取值范围.5.如图,已知点M 为二次函数14)(2++--=b b x y 图象的顶点,直线5+=mx y 分别交x 轴、y 轴于点A 、B .若点A 的坐标为(5,0),点M 在△AOB 内部,求b 的取值范围.第十二讲 含参函数策略一:“消参”化解“多参”例1.解:(1)由题意得⎩⎨⎧=--=++411c b c b 解之⎩⎨⎧-==31c b (2)∵点A 在抛物线上,∴11-=++c b ,∴b c --=2,∴b bx x y --+=22,∴B (0,-2-b )、C )0,2(b -, ∵b >0,∴OB =2+b ,OC =2b , ∴tan ∠OBC=24122+=+=bb bOB OC , ∵b >0, ∴24+b>2, ∴0<tan ∠OBC <21; 变式:由(2)得,b bx x y --+=22=b b b x ---+24)2(22, ∵A (1,-1)平移后的对应点为A 1为(1-m ,2b -1),∴抛物线向左平移m 个单位长度,向上平移2b 个单位长度,∴平移后的抛物线的解析式为b b m b x b b b m b x y +--++=+---++=24)2(224)2(2222, ∵平移后的抛物线也经过点(1,-1), ∴124)21(22-=+--++b b m b ,即22)12()21(-=++b m b , ∴1221-=++b m b 或01221=-+++b m b ,∴m =-2(舍去)或m =-b , ∴抛物线解析式为b b b x y +---=24)2(22, 设1)2(412422---=+--=b b b p , ∵m ≥23-, ∴0<23≤b , ∴由图象可知当b =23时,p 取得最大值为1617-, 顶点所能达到的最高点的坐标为(1617,43-).策略二:“图象”化解“抽象”例2.解:(1)∵A (-1,0)在抛物线上,∴03=--a b a ,∴a b 2-=, ∴对称轴为直线122=--=aa x ; (2)①当a >0时, 431025≥--a a a 解之31≥a , ②当a <0时,(Ⅰ)当抛物线顶点不在BC 上时,-3a >4解之a <34-, (Ⅱ)当抛物线顶点在BC 上时,432=--a a a解之a =-1, 综合①②得31≥a 或a <34-或a =-1. 变式:解:∵点B (-2,3)在抛物线上,∴3324=+-b a ,∴a b 2=,∴二次函数的解析式为322++=ax ax y ,∵点A (1,0),点B (-2,3),∴直线AB 的解析式为1+-=x y ,(1)当a >0时, 1322+-=++x ax ax ,02)12(2=+++x a ax ,0)2)(1(=++x ax , 解之ax x 1,221-=-=, ∵抛物线与线段AB 有两个交点,∴-2<a1-≤1, 由图象知a >21或a ≤-1, ∴a >21 (2)当a <0时,032≤++a a解之a ≤-1,综合(1)(2)得a >21或a ≤-1.策略三:“动点”化为“定线”例3.(1)(-2,0),(4168,22-+--m m m ); (2)令x =2m -,y =41682-+-m m , ∴2)2(+-=x y∵抛物线与正方形ABCD 的边有交点,∴⎩⎨⎧-≥-+--≤-5421442m m m ,解之02≤≤-m .变式:∵∠ABM =45°,∴直线BM 的解析式为3-=x y 或5--=x y ,(1)当直线BM 的解析式为3-=x y 时3)2(2-=+-x x , 解之2215,221521--=+-=x x (舍去) ∴2215+-=m , (2)当直线BM 的解析式为5--=x y 时5)2(2--=+-x x , 解之2133,213321--=+-=x x (舍去) ∴2133+-=m , 综合(1)(2)得m 的值为2215+-或2133+-.二、同类训练1.解:(1)∵抛物线y=x 2-2ax +b 的顶点在x 轴上,∴0442=-b a ,∴2a b =,∴抛物线的解析式为y =x 2-2ax +a 2,设平移后的抛物线解析式为y =x 2-2ax +a 2+d ,它与x 轴的交点横坐标为43,x x ,∴a x x 243=+,d a x x +=•243, ∵443=-x x ,∴164)(43243=-+x x x x ,∴16)(4)2(22=+-d a a ,解之d =-4,∴抛物线向下平移4个单位长度;(2)∵x 1≤c -1,且x 2≥c +5,∴61512=+-+≥-c c x x ,由(1)得y =x 2-2ax +a 2,∴x 2-2ax +a 2=m ,∴m a x x a x x -=•=+22121,2, ∴m m a a x x x x x x 44444)(222122112=+-=-+=-∴ 64≥m ,解之9≥m ;(3)∵x 1≥c -1,且x 2≤c +5,∴61512=+-+≤-c c x x ,由(1)得y =x 2-2ax +a 2,∴x 2-2ax +a 2=m ,∴m a x x a x x -=•=+22121,2,∴m m a a x x x x x x 44444)(222122112=+-=-+=-∴64≤m ,解之9≤m ;∵抛物线的顶点在x 轴上,开口向上,x 1<x 2,∴m >0,∴0<9≤m .2.解:由题意得,抛物线的顶点为(-1,-1)∵若抛物线在A 、B 之间的部分与线段AB 所围成的区域内(包含边界)恰有8个整点, ∴⎩⎨⎧-+--+-01816011025 m m m m m m ,解之91161 m . 3.解:由题意得,抛物线的对称轴为直线x =m(1)当m >0时,由对称性可知m ≥2;(2)当m <0时,符合题意,综合(1)(2)得m ≥2或m <0.4.解:令142+++=a bx ax y ,则 抛物线的对称轴为直线122-=-+-=m m x , ∴12-=-ab , ∴a b 2=, ∴1422+++=a ax ax y ,(1)当a >0时, ⎩⎨⎧++++++314443142 a a a a a a ,解之7261 m , (2) 当a <0时,⎩⎨⎧++++++314443142 a a a a a a ,无解, 综合(1)(2)得,7261 m .5.解:由题意得抛物线的顶点M 为(b ,4b +1), ∴令x =b ,y=4b +1,∴y =4x +1,∵A (5,0),∴直线AB 的解析式为5+-=x y , ∴514+-=+x x解之x=54, ∴540 b .。