计算方法第三章(插值法)解答
- 格式:ppt
- 大小:1.61 MB
- 文档页数:3

第三章 插 值 法在观察或总结某些现象时,往往会发现所关心变量之间存在着某种联系,但是这种联一般很难用解析式表达。
有时即便找出了其解析表达式,由于表达式过于复杂,使用或计算起来也可能十分困难。
于是就想到能否用形式比较简单的函数去近似原来很困难得到或应用起来不便的函数。
本章所讨论的插值法就是函数近似表达的一种方法。
这里介绍的插值方法本身也是以后介绍的方法如:数值积分,数值微分,以及微分方程的数值解的基础。
本章主要介绍插值函数的构造,误差估计及简单介绍方法的收敛性和稳定性。
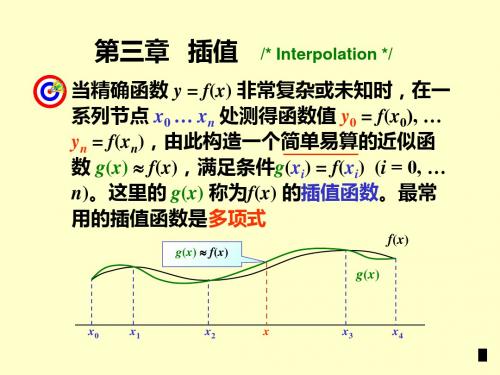
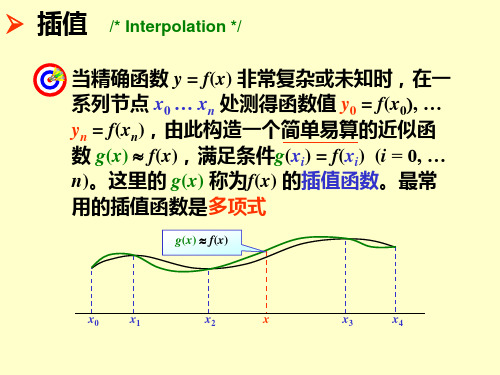
§1.插值的基本概念插值定义:设f(x)为定义在[a,b]上的函数,n 10x ,,x ,x 为[a,b ]上n+1个互不相同的点,Y为给定的某一个函数类,若Y上有函数y(x),满足:n ,,2,1,0i ),x (f )x (y i i ==(3—1)则称y(x)为f(x)关于节点n 10x ,,x ,x 在Y上的插值函数,点n 10x ,,x ,x 称为插值节点,f(x)称为被插值函数。
包含插值节点的区间[a,b]称为插值区间,条件(3—1)称为插值条件。
关于函数插值,我们要回答以下几个问题:(1)给定了被插函数(即f(x)),插值节点n 10x ,,x ,x 及插值函数类Y,那么满足插值条件的插值函数是否存在?若存在,是否唯一?即插值的存在性与唯一性问题。
(2)如若插值函数存在唯一,如何构造插值函数?即采用何种插值方法问题。
(3)y(x)作为f(x)的近似函数,存在误差R(x)=f(x)-y(x)。
如何估计其误差?当不斯地增加插值节点,那么插值函数列是否收敛被插函数。
现在首先回答第一个问题:由于我们这里介绍的插值函数类Y是多项式类。
故要求插值函数是多项式的情况下,来回答存在性与唯一性问题。
定理:设)x (M n 表示次数不超过n 次的多项式的全体,则满足插值条件(3—1)的,属于函数类Y=)x (M n 的插值多项y(x)存在且唯一。


计算方法第三章习题答案计算方法第三章习题答案计算方法是一门涵盖了数值计算和计算机编程的学科,它在现代科学和工程中扮演着重要的角色。
第三章是计算方法课程中的重要章节,主要涉及到数值计算中的误差分析和插值方法。
本文将为大家提供第三章习题的详细答案,帮助读者更好地理解和应用这些概念。
1. 误差分析误差分析是计算方法中非常重要的一部分,它帮助我们理解和评估数值计算中的误差来源。
以下是一些常见的误差类型:- 绝对误差:绝对误差是指数值计算结果与真实值之间的差异。
它可以通过计算两者之差来得到。
- 相对误差:相对误差是指绝对误差与真实值之间的比值。
通常以百分比的形式表示。
- 截断误差:截断误差是由于在计算过程中舍入或截断数字而引入的误差。
它通常是由于计算机的有限精度导致的。
- 舍入误差:舍入误差是由于将无限位数的小数截断为有限位数而引入的误差。
它通常是由于计算机的有限精度或计算方法的近似性质导致的。
2. 插值方法插值方法是一种用于通过已知数据点来估计未知数据点的技术。
以下是一些常见的插值方法:- 线性插值:线性插值是一种简单的插值方法,它假设两个已知数据点之间的未知数据点的取值在直线上。
通过已知数据点的斜率和截距,我们可以计算出未知数据点的值。
- 拉格朗日插值:拉格朗日插值是一种使用多项式来逼近已知数据点的方法。
它通过构造一个满足通过已知数据点的多项式来估计未知数据点的值。
- 牛顿插值:牛顿插值是一种使用差商来逼近已知数据点的方法。
它通过构造一个满足通过已知数据点的差商多项式来估计未知数据点的值。
3. 习题答案以下是一些第三章习题的答案,供大家参考:- 习题1:已知函数f(x)在区间[a, b]上连续,且在[a, b]上的导数存在且连续,证明存在一点c∈(a, b),使得f(b) - f(a) = (b - a)f'(c)。
这是拉格朗日中值定理的一个特例,根据定理的条件,我们可以得到上述结论。
- 习题2:已知函数f(x)在区间[a, b]上连续,且在(a, b)内可导,证明存在一点c∈(a, b),使得f'(c) = (f(b) - f(a))/(b - a)。

实验一插值方法一. 实验目的(1)熟悉数值插值方法的基本思想,解决某些实际插值问题,加深对数值插值方法的理解。
(2)熟悉Matlab 编程环境,利用Matlab 实现具体的插值算法,并进行可视化显示。
二. 实验要求用Matlab 软件实现Lagrange 插值、分段线性插值、三次Hermite 插值、Aitken 逐步插值算法,并用实例在计算机上计算和作图。
三. 实验内容1. 实验题目 (1)已知概率积分dxe y xx ⎰-=22π的数据表构造适合该数据表的一次、二次和三次Lagrange 插值公式,输出公式及其图形,并计算x =0.472时的积分值。
答:①一次插值公式:输入下面内容就可以得到一次插值结果 >> X=[0.47,0.48];Y=[0.4937452,0.5027498]; >> x=0.472;>> (x-X(2))/(X(1)-X(2))*Y(1)+(x-X(1))/(X(2)-X(1))*Y(2)ans =0.495546120000000>>②两次插值公式为:输入下面内容就可以得到两次插值结果>> X=[0.46,0.47,0.48];Y=[0.4846555,0.4937452,0.5027498]; >> x=0.472;>>(x-X(2))*(x-X(3))/((X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(1))*(x-X(3))/((X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(2))*(x-X(1))/((X(3)-X(2))*(X(3)-X(1)))*Y(3)i 0123x 0.46 047 0.48 0.49 y0.4846555 0.4937452 0.5027498 0.5116683ans =0.495552928000000>>③三次插值公式为:输入下面内容就可以得到三次插值结果>> X=[0.46,0.47,0.48,0.49];Y=[0.4846555,0.4937452,0.5027498,0.5116683];>> x=0.472;>>(x-X(2))*(x-X(3))*(x-X(4))/((X(1)-X(4))*(X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(4))*( x-X(1))*(x-X(3))/((X(2)-X(4))*(X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(4))*(x-X(2))*( x-X(1))/((X(3)-X(4))*(X(3)-X(2))*(X(3)-X(1)))*Y(3)+(x-X(3))*(x-X(2))*(x-X(1))/(( X(4)-X(1))*(X(4)-X(2))*(X(4)-X(3)))*Y(4)ans =0.495552960000000输入下面内容,绘出三点插值的图:>> X=[0.46,0.47,0.48,0.49];Y=[0.4846555,0.4937452,0.5027498,0.5116683];>> x=linspace(0.46,0.49);>>y=(x-X(2)).*(x-X(3)).*(x-X(4))/((X(1)-X(4))*(X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(4) ).*(x-X(1)).*(x-X(3))/((X(2)-X(4))*(X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(4)).*(x-X(2) ).*(x-X(1))/((X(3)-X(4))*(X(3)-X(2))*(X(3)-X(1)))*Y(3)+(x-X(3)).*(x-X(2)).*(x-X(1) )/((X(4)-X(1))*(X(4)-X(2))*(X(4)-X(3)))*Y(4);>>plot(x,y)(注意上面的“.*”不能用“*”替代);(2)将区间[-5,5]分为10等份,求作211)(x x f +=的分段线性插值函数,输出函数表达式及其图形,并计算x =3.3152时的函数值。


习 题 一3.已知函数y =4, 6.25,9x x x ===处的函数值,试通过一个二次插值函解:0120124, 6.25,9;2, 2.5,3y x x x y y y =======由题意 (1) 采用Lagrange插值多项式220()()j j j y L x l x y ==≈=∑27020112012010*********()|()()()()()()()()()()()()(7 6.25)(79)(74)(79)(74)(7 6.25)2 2.532.255 2.25 2.75 2.7552.6484848x y L x x x x x x x x x x x x x y y y x x x x x x x x x x x x ==≈------=++------------=⨯+⨯+⨯⨯-⨯⨯= 其误差为(3)25(3)25(3)2[4,9]2()(7)(74)(7 6.25)(79)3!3()83max |()|40.0117281|(7)|(4.5)(0.01172)0.008796f R f x x f x R ξ--=---==<∴<=又则(2)采用Newton插值多项式2()y N x =≈ 根据题意作差商表:224(7)2(74)()(74)(7 6.25) 2.64848489495N =+⨯-+-⨯-⨯-≈4. 设()()0,1,...,k f x x k n ==,试列出()f x 关于互异节点()0,1,...,i x i n =的Lagrange 插值多项式。
注意到:若1n +个节点()0,1,...,i x i n =互异,则对任意次数n ≤的多项式()f x ,它关于节点()0,1,...,i x i n =满足条件(),0,1,...,i i P x y i n ==的插值多项式()P x 就是它本身。
可见,当k n ≤时幂函数()(0,1,...,)kf x x k n ==关于1n +个节点()0,1,...,i x i n =的插值多项式就是它本身,故依Lagrange 公式有()00(),0,1,...,nn n k kk i j j j j j i j ii jx x x l x x x k n x x ===≠-=≡=-∑∑∏特别地,当0k =时,有()0001nn n ij j j i j ii jx x l x x x ===≠-=≡-∑∑∏而当1k =时有()000nnn ij j j j j i j ii jx x x l x x x x x ===≠⎛⎫- ⎪=≡ ⎪- ⎪⎝⎭∑∑∏ 5.依据下列函数表分别建立次数不超过3的Lagrange 插值多项式和Newton 插值多项式,并验证插值多项式的唯一性。






插值法例题计算过程
(原创实用版)
目录
1.插值法的概念与应用
2.插值法例题的解答过程
3.插值法在实际问题中的应用
4.总结
正文
一、插值法的概念与应用
插值法是一种求解未知数值的方法,它通过已知的数据点来预测或推断未知数据点的值。
在数学、工程、物理等学科中都有广泛的应用。
插值法可以分为拉格朗日插值法、牛顿插值法、三次样条插值法等。
二、插值法例题的解答过程
假设我们有一组数据:当折现率为 10% 时,净现值为 121765;当折现率为 12% 时,净现值为 116530。
现在需要求解当折现率为 i 时,净现值的值。
我们可以使用插值法来解决这个问题。
首先,我们假设净现值为120000,然后列出一个方程:
(i-12%)/(10%-12%)=(120000-116530)/(121765-116530)
解这个方程,我们可以得到 i 的值。
三、插值法在实际问题中的应用
插值法在实际问题中有广泛的应用,例如在财务管理中,我们可以使用插值法来计算债券的收益率、股票的预期收益等。
在工程领域,插值法可以用来预测工程项目的进度、成本等。
在物理学中,插值法可以用来预
测物体的运动轨迹等。
四、总结
插值法是一种强大的求解未知数值的方法,它可以通过已知的数据点来预测或推断未知数据点的值。

第三章 插值法与最小二乘法1. 已知下列表值x 10 11 12 13 lnx 2.3026 2.3979 2.4849 2.5649用线形插值与二次Lagrange 插值计算ln11.75的近似值,并估计误差。
解:(1)线形插值说明:当插值点落在被插区间之内,这种方法称为内插法,此时插值精度较好。
x ],12,11[75.11∈=故选择x 0=11,x 1=12,求线形插值函数。
11001y x l y x l x P ⨯+⨯=∴)()()(=10100101y x x x x y x x x x ⨯--+⨯--=4849.21112113979.2121112⨯--+⨯--x x=2.4849(x-11)-2.3979(x-12))1275.11(3979.2)1175.11(4849.2)75.11(75.11ln 1---=≈∴p =2.46315(2)二次拉格朗日插值选择插值结点:x 12,11,10210===x x P 2211002)()()()(y x l y x l y x l x ++= =212021012101200201021))(())(())(())(())(())((y x x x x x x x x y x x x x x x x x y x x x x x x x x ----+----+----=4849.2)1112)(1012()11)(10(3979.2)1211)(1011()12)(10(3026.2)1210)(1110()12)(11(----+----+----x x x x x x=1.1513(x-11)(x-12)-2.3979(x-10)(x-12)+1.24425(x-10)(x-11))1175.11)(1011075(24245.1)1275.11)(1075.11(3979.2)1275.11)(1175.11(1513.1)75.11(75.11ln 2--+-----=≈∴P =1.15133125.124245.14375.03979.2)1875.0(⨯+⨯+-⨯ =2.4639282. 已知下列表值求f(x)在[0,2]之间零点近似值。

第3章函数近似方法(习题及答案)§3.1插值法【3.1.1】已知sin()x 在030,45,60的值分别为1/2,分别用一次插值和二次插值求0sin(50)近似值。
【3.1.2】误差函数的数据表:x 0.460.470.480.49…f(x)0.48465550.49374520.50274980.5116683…利用二次插值计算:(1)(0.472)f ;(2)()0.5,?f x x ==【3.1.3】【3.1.4】已知列表函数x -101y-15-5-3给出二次插值函数【解】0(0)(1)1()(1)(10)(11)2x x l x x x --==-----;1(1)(1)()(1)(1)(01)(01)x x l x x x +-==--++-2(1)(0)1()(1)(11)(10)2x x l x x x +-==++-2153()(1)5(1)(1)(1)22L x x x x x x x =--+-+--【3.1.5】已知,3)9(,2)4(==f f 用线性插值计算)5(f ,并估计误差。
【解】取插值节点014, 9x x ==,两个插值基函数分别为)9(51)(1010--=--=x x x x x x l )4(51)(0101-=--=x x x x x x l 故有565)4(53)9(52)()()(11001+=-+--=+=x x x y x l y x l x L 2.25655)5()5(1=+=»L f 误差为)(2)95)(45(!2)()5(2x x f f R ¢¢-=--¢¢=【3.1.6】已知(1)2,(1)1,(2)1f f f -===,求()f x 的二次拉格郎日插值多项式【解】22(1)(2)(1)(2)(1)(1)()21(11)(12)(11)(12)(21)(21)1(38)6x x x x x x L x x x --+-+-=++----+-+-=-+【3.1.7】求经过(0,1),(1,2),(2,3)A B C 三点的二次拉格郎日插值多项式【解】22(1)(2)(0)(2)(0)(1)()123(01)(02)(10)(12)(20)(21)1(343)2x x x x x x L x x x ------=++------=-+【3.1.8】编写拉格朗日三点插值程序,绘出)cos(x y =在[p ,0]区间的插值曲线,将[p ,0]区间8等份(9个插值点),由插值函数取25个点绘出插值曲线。