探索规律练习题

小学生规律探索题（二）1．如图，摆一个△用3根小棒，摆2个△用5根小棒，摆3个△用7根小棒．照这样，摆5个△用多少根小棒？用21根小棒可以摆多少△？2．现有若干圆环，它的外直径5厘米，环宽0.5厘米，将它们（如图）扣在一起，拉紧后测其长度．（1）根据规律，则2个圆环拉紧后的长度是多少厘米？10个圆环拉紧后的长度是多少厘米？（2）若拉紧后的长度是77厘米，它由多少个环扣成的？（3）设环的个数为a，拉紧后总长为S，请你用一个关系式表示你发现的规律。

3．甲种茶叶每千克40元，乙种茶叶每千克24元，按3：2的比例混合后共80千克，求混合后的茶叶每千克至少要卖多少元？4．某省原来用电收费标准统一为每度电0.65元．但由于当前物价上涨，省物价局决定，从2012年6月1日起，全省居民实行阶梯电价收费，新收费标准如下：电量电价收费标准第一档：每月每户用电量在0﹣210度每度0.65元第二档：每月每户用电量在211﹣430度这部分每度加价0.05元第三档：每月每户用电量在431度以上这部分每度加价0.30元华家6月用电量为500度，则华家6月份的电费一共是多少元？5．“学雷锋见行动”活动中，六年级部分学生为社区服务，其中男生人数和女生人数比是2：3．后来又有3名男生参加，有3名女生有事离开，这时男生人数是女生的75%．原来参加社区服务的男、女生各有多少人？6．（2014•荔波县模拟）有A、B两个容器，如图先把A装满水，然后倒入B中，B中水的深度是多少厘米？7．一件商品打九折后，现在的价格是990元，仍可获利10%．这件商品的成本价是多少元？这件商品的原来的价格是多少元？8．一个边长为8厘米的正方体，从如图示挖掉一侧面为正方形（边长为2厘米）的长方体，求剩余部分的表面积．9．某地出租车的收费标准如下：里程收费3千米及3千米以下7.003千米以上，单程，每增加1千米 1.203千米以上，往返，每增加1千米0.80（1）、老师从学校到相距5千米的教育局取文件并立即回到学校，他应该怎样坐车比较合算？需付出租车车费多少元？（2）小文乘出租车从家到外婆家，共付费22.6元，小文家到外婆家相距多少千米？10.华中心小学为了增强学生体质打算买60个足球，现有三个超市可以选择，三个超市足球的价格都是25元，但各商店的优惠办法不同．成和商厦家庭号超市金超市买五送一每个足球优惠5元．购物每满200元，返现金30元为了节省费用，华中心小学应到哪个商店购买？（请写出计算过程）规律探索题参考答案与试题解析一．填空题（共2小题）1．如图，摆一个△用3根小棒，摆2个△用5根小棒，摆3个△用7根小棒．照这样，摆5个△用11 根小棒，用21根小棒可以摆10 △．考点：数与形结合的规律．专题：探索数的规律．分析：搭一个三角形需要3根火柴，搭两个三角形需要5根火柴，搭三个三角形需要7根火柴，则知搭n个三角形需要（2n+1）根火柴，有这个式子即可摆5个△用：2×5+1个；也可以算出21根小棒可以搭成这样三角形的个数．解答：解：由分析及规律知：搭n个三角形需要（2n+1）根火柴，n为正整数，当n=5时，即摆5个△用 11根小棒．当2n+1=21时，解得整数n=10．即用21根火柴可以搭成这样三角形的个数是10．故答案为：11；10．点评：本题考查规律型问题中的图形变化问题，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．2．现有若干圆环，它的外直径5厘米，环宽0.5厘米，将它们（如图）扣在一起，拉紧后测其长度．（1）根据规律，则2个圆环拉紧后的长度是9 厘米，10个圆环拉紧后的长度是41 厘米．（2）若拉紧后的长度是77厘米，它由19 个环扣成的．（3）设环的个数为a，拉紧后总长为S，请你用一个关系式表示你发现的规律．S=4a+1 ．考点：重叠问题．专题：传统应用题专题．分析：（1）根据题干可知：1个圆环的长度是5厘米，以后每增加一个圆环，就增加5﹣0.5×2=4厘米，由此可以求解；（2）设是有a个环扣成的，由上面得出的关系式即可得出一个一元一次方程，解这个方程即可；（3）根据上面规律，代入数据即可得出用字母a、s表示的关系式．解答：解：（1）5﹣0.5×2=5﹣1=4（厘米），5+4×（2﹣1）=5+4=9（厘米），5+4×（10﹣1）=5+36=41（厘米）．答：2个圆环拉紧后的长度是9厘米，10个圆环拉紧后的长度是41厘米．（2）设是有x个环扣成的，根据上述关系式可得：5+4（x﹣1）=774x=76x=19．答：是由19个环组成的．（3）设环的个数为a，拉紧后总长为S，则可得圆环与拉紧后的总长度的关系式是：S=5+4（a﹣1）=4a+1．答：这个关系式是：S=4a+1．故答案为：9，41；19；S=4a+1．点评：主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．二．解答题（共7小题）3．甲种茶叶每千克40元，乙种茶叶每千克24元，按3：2的比例混合后共80千克，求混合后的茶叶每千克至少要卖多少元？考点：按比例分配应用题．专题：比和比例应用题．位“1”，根据一个数乘分数的意义，用乘法分别求出甲种茶叶和乙种茶叶的重量，进而根据：单价×数量=总价，求出混合后的茶叶的成本价，继而每千克至少要卖的钱数．解答：解：3+2=5，甲种茶叶：80×=48（千克），乙种茶叶：60×=32（千克），至少卖：（48×40+32×24）÷80=（1920+768）÷80=2688÷80=33.6（元）答：混合后的茶叶每千克至少要卖33.6元．点评：求出混合后的茶叶茶叶的成本价，是解答此题的关键；用到的知识点：（1）按比例分配知识；（2）单价、数量和总价三者之间的关系．4．某省原来用电收费标准统一为每度电0.65元．但由于当前物价上涨，省物价局决定，从2012年6月1日起，全省居民实行阶梯电价收费，新收费标准如下：电量电价收费标准第一档：每月每户用电量在0﹣210度每度0.65元第二档：每月每户用电量在211﹣430度这部分每度加价0.05元第三档：每月每户用电量在431度以上这部分每度加价0.30元华家6月用电量为500度，则华家6月份的电费一共是多少元？考点：整数、小数复合应用题．专题：简单应用题和一般复合应用题．分析：根据表格可知，用电不超过210度每度0.65元，210～430之间部分每度0.7元，430度以上部分每度0.95元，用电量为500度，应分3段收费：①210度以下部分：210×0.65，②210～430之间部分：（430﹣210）×0.7，③430～500之间部分（500﹣430）×0.95，3部分相加即可．解答：解：210×0.65+（430﹣210）×0.7+（500﹣430）×0.95=136.5+220×0.7+70×0.95=136.5+154+66.5=357（元）答：华家6月份的电费一共是357元．点评：解答本题的关键是，理解阶梯电价收费的方法，即分段收费，每段对应不同的电价．5．“学雷锋见行动”活动中，六年级部分学生为社区服务，其中男生人数和女生人数比是2：3．后来又有3名男生参加，有3名女生有事离开，这时男生人数是女生的75%．原来参加社区服务的男、女生各有多少人？考点：分数和百分数应用题（多重条件）．专题：分数百分数应用专题．分析：把现在女生人数看作单位“1”，设现在有女生x人，则现在男生为75%x人，由后来又有3名男生参加得出原来男生为（75%x﹣3）人，由有3名女生有事离开得出原来的女生有（x+3）人，由等量关系式原来男生人数和女生人数比是2：3，列出方程：（75%x﹣3）：（x+3）=2：3求解．解答：解：设现在有女生x人，则现在男生为75%x人，根据题意得（75%x﹣3）：（x+3）=2：3（75%x﹣3）×3=（x+3）×275%x×3﹣3×3=2x+3×22.25x﹣9=2x+62.25x﹣9﹣2x=2x+6﹣2x0.25x﹣9=60.25x=150.25x÷0.25=15÷0.25x=60原来女生为：60+3=63（人）原来男生为：75%×60﹣3=42（人）答：原来参加社区服务的男生有42人，女生有63人．点评：本题关键是把现在女生人数看作单位“1”，设现在有女生X人，求出原来男女生的人数，找准等量关系式列出方程．6．（2014•荔波县模拟）有A、B两个容器，如图先把A装满水，然后倒入B中，B中水的深度是多少厘米？考点：关于圆锥的应用题；关于圆柱的应用题；圆柱的侧面积、表面积和体积；圆锥的体积．专题：压轴题．分析：由题意知，“水”在两个容器中只是形状变了，体积没变；所以先利用圆锥的体积公式V=sh求出水的体积，再利用圆柱的体积公式V=Sh求出B中水的深度即可．解答：解：×3.14×62×10÷（3.14×42），=×3.14×36×10÷3.14÷16，=12×10÷16，=7.5（厘米）；答：B中水的深度是7.5厘米．点评：此题是考查圆柱、圆锥的体积计算，可利用它们的体积公式解答，同时不要漏了．7．一件商品打九折后，现在的价格是990元，仍可获利10%．这件商品的成本价是多少元？这件商品的原来的价格是多少元？考点：百分数的实际应用．专题：分数百分数应用题．分析：（1）先把成本价看成单位“1”，它的（1+10%）对应的数量是990元，用除法求出成本价；（2）九折是指现价是原价的90%，把原价看成单位“1”，它的90%对应的数量是990元，由此用除法求出原价．解答：解：（1）990÷（1+10%），=990÷110%，=900（元）；（2）990÷90%=1100（元）；答：这件商品的成本价是900元，原价是1100元．点评：本题关键是分清楚两个单位“1”的不同，找出单位“1”的百分之几对应的数量，用除法就可以求出单位“1”的量．8．一个边长为8厘米的正方体，从如图示挖掉一侧面为正方形（边长为2厘米）的长方体，求剩余部分的表面积．考点：规则立体图形的表面积；长方体和正方体的表面积．专题：立体图形的认识与计算．分析：根据题干可知，挖掉这个小长方体后，剩下的部分的表面积，在原来的正方体的表面积的基础上，减少了2个2×2面的正方形的面积，同时也增加了4个8×2的长方形的面积，据此计算即可解答．解答：解：8×8×6﹣2×2×2+8×2×4，=384﹣8+64，=440（平方厘米），答：剩下的部分的表面积是440平方厘米．点评：解答此题的关键是根据切割特点，明确出剩下的部分的表面积比原来增加或减少了哪几个面的面积．里程收费3千米及3千米以下7.003千米以上，单程，每增加1千米 1.203千米以上，往返，每增加1千米0.80（1）、老师从学校到相距5千米的教育局取文件并立即回到学校，他应该怎样坐车比较合算？需付出租车车费多少元？（2）小文乘出租车从家到外婆家，共付费22.6元，小文家到外婆家相距多少千米？考点：整数、小数复合应用题；最优化问题．专题：压轴题．分析：老师因为是往返，所以增加5×2﹣3=7千米，每增加1千米，收费0.8元，可算出增加的车费为7×0.8=5.6元，再加上7元即可；小文是单程，用付费的总钱数﹣7即可得出多付的钱数，单程每增加1千米，多付费0.8元，用多付的钱数÷0.8即可得出增加的路程，再加上3千米即可得出结论．解答：解；（1）5×2﹣3=7（千米）；7×0.8+7=12.6（元）；答：王老师应该选择第3种，需要付出租车费12.6元．（2）22.6﹣7=15.6（元）；15.6÷1.2=13（千米）；13+3=16（千米）；答：小文家到外婆家相距16千米．点评：此题应弄清题意，理清思路，然后根据题中给出的条件进行分析，进而解决问题．10、华中心小学为了增强学生体质打算买60个足球，现有三个超市可以选择，三个超市足球的价格都是25元，但各商店的优惠办法不同．成和商厦家庭号超市金超市买五送一每个足球优惠5元．购物每满200元，返现金30元为了节省费用，华中心小学应到哪个商店购买？（请写出计算过程）考点：最优化问题．专题：优化问题．分析：由题意可得出，成和商厦：买50个，送50÷5=10个刚好60个，即需要买50个足球的钱即可；家庭号超市：每个足球25﹣5=20元；金超市：先算出买60个球花60×25=1500元，1500÷200=7.5，返还30×7=210元，用花的总钱数减去返还的即可．解答：解：成和商厦：50÷5=10（个），60﹣10=50（个）50×25=1250（元）家庭号超市：60×（25﹣5）=1200（元）金超市：60×25=1500（元），1500÷200=7.5（个），1500﹣30×7=1290（元）1200＜1250＜1290所以家庭号超市最划算；答：到家庭号超市购买便宜，最划算．点评：此题关键理解题意，分别列式进行解答，进而根据所得数据，进行比较，得出最佳方案．。

探索规律练习题1、我们平常用的数是十进制数，如2639=2×103+6×102+3×101+9×100，表示十进制的数要用10个数码（又叫数字）：0，1，2，3，4，5，6，7，8，9。

在电子数字计算机中用的是二进制，只要两个数码：0和1。

如二进制中101=1×22+0×21+1×20等于十进制的数5，10111=1×24+0×23＋1×22＋1×21＋1×20等于十进制中的数23，那么二进制中的1101等于十进制的数 。

2、从1开始，将连续的奇数相加，和的情况有如下规律：1=1=12；1+3=4=22；1+3+5=9=32；1+3+5+7=16=42；1+3+5+7+9=25=52；…按此规律请你猜想从1开始，将前10个奇数（即当最后一个奇数是19时），它们的和是 。

3、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：A 、618 B 、638 C 、658 D 、6784、如下左图所示，摆第一个“小屋子”要5枚棋子，摆第二个要11枚棋子，摆第三个要17枚棋子，则摆第30个“小屋子”要 枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子，观察图形的变化规律，写出第n 个小房子用了 块石子。

6、如下图是用棋子摆成的“上”字：第一个“上”字 第二个“上”字 第三个“上”字如果按照以上规律继续摆下去，那么通过观察，可以发现：（1）第四、第五个“上” 字分别需用 和枚棋子；（2）第n 个“上”字需用 枚棋子。

7、如图一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分，则这串珠子被盒子遮住的部分有_______颗. 8、用边长为1cm 的小正方形搭成如下的塔状图形，则第n 次所搭图形的周长是_______________cm （用含n 的代数式表示）。

9、用“”定义新运算：对于任意实数a ，b ，都有a .b a b 2-=例如，4,97472=-=那么53＝_____________，－1（－12）＝___________。

探索规律专项练习1、亮亮用“○”摆图形。

照这样的规律摆下去，图8有( )个O。

2、观察下图，小正方体的棱是由1米长的木条构成。

第11个图形至少需要（）米的木条。

3、用同样大小的黑色棋子按下图所示的方式摆图形，按照这样的规律摆下去，则第8个图形需棋子( )枚。

4、如图小正方体的棱长为1厘米，按这种方式摆下去，第10个长方体的表面积是（）平方厘米，第n个长方体的表面积是（）平方厘米，如果摆成的长方体表面积是364平方厘米，那么这个长方体排在第（）个。

5、如图，用若干个棱长1厘米的照这样摆下去，第10个图形的表面积是( )平方厘米。

若摆出的长方体表面积是210平方厘米，则它是由( )个摆成的。

6、观察下图，小正方体的棱长是1cm。

按照这样的规摆下去，第10个图形的表面积是（）平方厘米。

7、观察下图，回答问题。

按上图方式摆放桌子和椅子，5张桌子可坐（）人，按照上图的方式继续摆放桌子和椅子，n张桌子可坐（）人。

8、小明在超市帮妈妈买回一袋纸杯，他把纸杯整齐地叠放在一起(如图)，小明把100个纸杯整齐叠敢在一起时，它的高度约是多少?9、有5块长10厘米的未板，把它们如下图那样连接起来。

连接后，木板的总长是（）厘米。

10、下图是6个大小相同的铁环连在一起拉直的图形。

每个铁环的长度10厘米，铁环粗1厘米,这条锁链的长度是（）厘米。

10、两摞相同规格的羽毛球整齐的叠放在地面上，如图所示（单位：厘米)(1）一个羽毛球高多少厘米?(2）9个羽毛球这样摞在一起，高多少厘米?(3)40厘米的羽毛球筒最多可以装多少个这样的羽毛球?11、在同一平面内，直线与直线相交的情况如下表所示,请你把下表补充完整。

再想一想：在同一平面内，6条直线最多可以有( )个交点；8条直线最多可以有( )个交点。

11、将一个田字格的一格或几格图上黑色或不涂色，可以代表数字0~15这16个数。

请你根据下面前5个图形表示数的规律，写出后面两个图形表示的数。

2023年数学小升初一轮基础复习10：探索规律一、单选题1．如图是由同样大小的圆按一定规律排列所组成的，其中第1个图形中有4个圆，第2个图形中有8个圆，第3个图形中有14个圆，第4个图形中有22个圆……，按此规律排列下去，第20个图形中有（）个圆。

A．422B．412C．402D．3922．按如图的规律，用小三角形摆图形，摆第⑥个图形共需要小三角形（）个。

A．25B．36C．40D．493．按如图方式摆放桌子和椅子，如果用x表示桌子张数，用y表示可坐人数，下面式子能表示可坐人数与桌子张数的关系的是（）A．y＝2x（x+2）B．y＝2x+2C．y＝4x D．y＝4x+14．在一个平面上有68个点，一共可以连（）条线段。

A．68B．2278C．2346D．11905．按如图的规律摆图形，第n个图形的周长是（）cm。

（每个小正方形的边长是1cm）A．3n+4B．4n+2C．2n+4D．5n+26．用火柴棒按照如图的方法摆正方形（每条边摆1根火柴棒），照这样摆8个正方形共需要（）根火柴棒。

A．19B．22C．24D．257．下图是玲玲用小棒和纽扣摆的图案。

照这样摆下去，摆n根小棒共需要（）颗纽扣。

A．n B．6n C．2n+4D．4n+28．浩浩按照一定的规律用小棒摆出了下面的4幅图；如果按照这个规律继续摆，第五幅图要用（）根小棒。

A．23B．31C．35D．459．按下图的规律用小棒摆正六边形。

摆6个正六边形需要（）根小棒。

A．26B．28C．30D．3110．奇思发现蟋蟀每分钟叫的次数与气温有一定关系，下表是他通过实验记录的数据。

按这个规律，气温18℃时，蟋蟀每分钟叫（）次。

气温/℃12131415蟋蟀每分钟叫的次数63707784A．87B．91C．98D．105二、填空题11．如图，如果一个小三角形的边长为1厘米，那么第6个图形的周长是厘米。

12．如图所示，摆放小正方体，当摆到第4层时一共有个小正方体。

四年级数学探索规律练习题1. 请观察下列数字序列并写出下一个数字：2, 4, 6, 8, ...2. 请观察下列数字序列并写出下一个数字：10, 7, 4, 1, ...3. 请观察下列数字序列并写出下一个数字：1, 3, 6, 10, ...4. 请观察下列数字序列并写出下一个数字：9, 16, 25, 36, ...5. 请观察下列数字序列并写出下一个数字：3, 8, 13, 18, ...6. 请观察下列数字序列并写出下一个数字：100, 90, 80, 70, ...7. 请观察下列数字序列并写出下一个数字：25, 20, 15, 10, ...8. 请观察下列数字序列并写出下一个数字：6, 12, 24, 48, ...9. 请观察下列数字序列并写出下一个数字：50, 45, 40, 35, ...10. 请观察下列数字序列并写出下一个数字：4, 7, 12, 19, ...解答：1. 下一个数字是10。

每个数字都比前一个数字大2。

2. 下一个数字是-2。

每个数字都比前一个数字减去3。

3. 下一个数字是15。

每个数字都是前一个数字加上递增的数列，递增数列从2开始。

4. 下一个数字是49。

每个数字都是前一个数字加上递增的奇数数列。

5. 下一个数字是23。

每个数字都比前一个数字增加5。

6. 下一个数字是60。

每个数字都比前一个数字减去10。

7. 下一个数字是5。

每个数字都比前一个数字减去5。

8. 下一个数字是96。

每个数字都是前一个数字乘以2。

9. 下一个数字是30。

每个数字都比前一个数字减去5。

10. 下一个数字是30。

每个数字都是前一个数字加上递增的数列，递增数列从3开始。

这些练习题帮助学生思考数字序列中的规律，并通过观察和推理来找出下一个数字。

规律性是数学中一项重要的概念，通过训练学生观察、归纳、总结规律的能力，可以提高他们的逻辑思维能力和解决问题的能力。

以上题目旨在培养学生探索规律的能力，并帮助他们理解数列中数字之间的关系。

3.6《探索规律》练习题一、基础过关1．找规律，在括号里填上适当的数.（1）,65,54,43,32,21( ); （2）1，2，4，8，16，32，（ ）；（3）1，1，2，3，5，8，13，（ ）；2．观察下列各等式：（1）,41549,31439,21329,11219,1109=+⨯=+⨯=+⨯=+⨯=+⨯猜想：第n 个等式（n 为正整数）应为 .(2),32353,22242,12131222⨯+=⨯⨯+=⨯⨯+=⨯猜想：第n 个等式（n 为正整数）应为 . 3．观察下列各式，找出规律.2224161234321391232124121==++++++==++++==++利用上面规律，请计算：1+2+3+……+99+100+99+……+3+2+1= .4．联欢会上，小文按照3个红气球，2个黄气球，1个绿气球的顺序把气球串起来，装饰教室,那么第2008个气球的颜色是 ；当n 为自然数时，第6n +1个气球的颜色是 .5（（2）生长了11年的树的高度是多少？二、能力提升6．古希腊数学家把数1，3，6，10，15，21，……叫做三角形数，它有一定的规律，则第24个三角形数与第22个三角形数的差为 .7.观察下面等式，483279382457281635188132222222⨯==-⨯==-⨯==-⨯==-分析这个规律，并用字母表示第10个式子为： ；第n 个式子为： .（n 为正整数）8．小华同学在电脑中找出如下排列的若干个圆：表示实心圆，表示空心圆）若将上面一组圆按此规律继续排列得到一系列圆，那么前2008个圆中，有 个空心圆.9．观察各式， ,2562,1282,642,322,162,82,42,2287654321========，（1）你能根据上面的规律，判断20082的个位数字是多少吗？（2）若把底数2换成3，请你找出规律，并求20083的个位数字.10．阅读下面一段话，并解决问题.观察一列数：1，2，4，8，…….我们发现这一列数从第2项起，每一项与它前一项的比都等于2，一般地，如果一列数从第2项起，每一项与它前一项的比都等于同一个常数，这一列数就叫做等比数列，这个常数叫做数列的公比.（1）上述等比数列的第6项是 .（2）如果一列数 ,,,,4321a a a a 是等比数列，且公比为q ，那么根据上述的规定有： ,,,342312q a a q a a q a a === 所以3121342112312)(,)(,q a q q a q a a q a q q a q a a q a a =======，……则 =n a .（用1a 和q 的代数式表示）（3）一个等比数列的第二项是10，第三项是20，求它的第一项、第四项及第n 项.三、聚沙成塔从一加到一百七岁时高斯进了 St. Catherine小学.大约在十岁时，老师在算数课上出了一道难题：“把1到 100的整数写下来，然後把它们加起来！”每当有考试时他们有如下的习惯：第一个做完的就把石板﹝当时通行，写字用﹞面朝下地放在老师的桌子上，第二个做完的就把石板摆在第一张石板上，就这样一个一个落起来.这个难题当然难不倒学过算数级数的人，但这些孩子才刚开始学算数呢！老师心想他可以休息一下了.但他错了，因为还不到几秒钟，高斯已经把石板放在讲桌上了，同时说道：“答案在这儿！”其他的学生把数字一个个加起来，额头都出了汗水，但高斯却静静坐着，对老师投来的，轻蔑的、怀疑的眼光毫不在意.考完後，老师一张张地检查着石板.大部分都做错了，学生就吃了一顿鞭打.最後，高斯的石板被翻了过来，只见上面只有一个数字：5050（用不着说，这是正确的答案.）老师吃了一惊，高斯就解释他如何找到答案：1＋100＝101，2＋99＝101，3＋98＝101，……，49＋52＝101，50＋51＝101，一共有50对和为 101的数目，所以答案是 50×101＝5050.由此可见高斯找到了算术级数的对称性，然後就像求得一般算术级数合的过程一样，把数目一对对地凑在一起.。

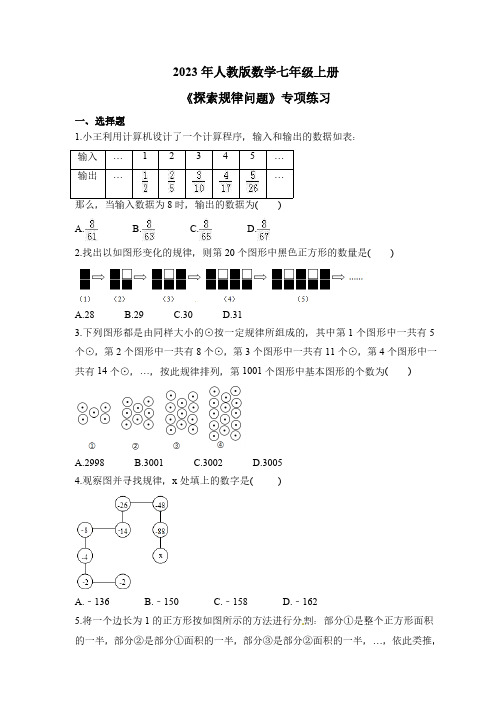
2023年人教版数学七年级上册《探索规律问题》专项练习一、选择题1.小王利用计算机设计了一个计算程序，输入和输出的数据如表：输入…12345…输出……那么，当输入数据为8时，输出的数据为( )A. B. C. D.2.找出以如图形变化的规律，则第20个图形中黑色正方形的数量是( )A.28B.29C.30D.313.下列图形都是由同样大小的⊙按一定规律所组成的，其中第1个图形中一共有5个⊙，第2个图形中一共有8个⊙，第3个图形中一共有11个⊙，第4个图形中一共有14个⊙，…，按此规律排列，第1001个图形中基本图形的个数为( )A.2998B.3001C.3002D.30054.观察图并寻找规律，x处填上的数字是( )A.﹣136B.﹣150C.﹣158D.﹣1625.将一个边长为1的正方形按如图所示的方法进行分割：部分①是整个正方形面积通过计算此图形中部分①、部分②、部分③…的面积之和，可得到式子12＋14＋18＋…的近似值为()A.0.5B.1C.2D.46.观察下列算式：21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128，28＝256，…根据上述算式中的规律，你认为22024的末位数字是( )A.2B.4C.6D.87.如图所示，图①中的多边形(边数为12)是由等边三角形“扩展”而来的，图②中的多边形是由正方形“扩展”而来的，…，依此类推，则由正n 边形“扩展”而来的多边形的边数为( )A.n(n ﹣1)B.n(n ＋1)C.(n ＋1)(n ﹣1)D.n 2＋28.观察等式：2＋22＝23－2；2＋22＋23＝24－2；2＋22＋23＋24＝25－2…已知按一定规律排列的一组数：250，251，252，…，299，2100.若250＝a ，用含a 的式子表示这组数的和是( )A.2a 2－2aB.2a 2－2a －2C.2a 2－aD.2a 2＋a9.已知一组数a 1，a 2，a 3，…，a n ，…，其中a 1＝1，对于任意的正整数n ，满足a n ＋1a n ＋a n ＋1﹣a n ＝0，通过计算a 2，a 3，a 4的值，猜想a n 可能是( )A.1n B.nC.n 2D.110.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为( )A.12B.14C.16D.18二、填空题11.用●表示实心圆，用○表示空心圆，现有若干个实心圆与空心圆，按一定的规律排列如下：●○●●○●●●○●○●●○●●●○●○●●○●●●○…，在前2029个圆中，有 个实心圆.12.下图是某同学一次旅游时在沙滩上用石子摆成的小房子．观察图形的变化规律，写出第n个小房子用了块石子．13.下面是按照一定规律画出的一列“树型”图：经观察可以发现：图(2)比图(1)多出2个“树枝”，图(3)比图(2)多出5个“树枝”，图(4)比图(3)多出10个“树枝”，照此规律，图(7)比图(6)多出 个“树枝”．14.有一串式子：﹣x，2x2，﹣3x3，4x4，…，﹣19x19，20x20，… ,写出第n个 .15.按下列图示的程序计算，若开始输入的值为x=﹣6，则最后输出的结果是 ．16.观察下列各正方形图案，每条边上有n(n≥2)个圆点，每个图案中圆点的总数是s，按此规律推断出s与n的关系为 .17.如图，将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪裁成四个小正方形，如此继续下去，…，根据以上操作方法，请你填写表：操作次数N 12345…n 正方形的个数47101316…a n则a n ＝ (用含n 的代数式表示).18.如图是用小棒按一定规律摆成的一组图案，第1个图案中有5根小棒，第2个图案中有9个小棒，…，若第n 个图案中有65根小棒，则n 的值为　.三、解答题19.寻找公式，求代数式的值：从2开始，连续的偶数相加，它们的和的情况如下表：(1)当n 个最小的连续偶数相加时，它们的和S 与n 之间有什么样的关系，用公式表示出来；(2)按此规律计算：①2＋4＋6＋…＋200值；②162＋164＋166＋…＋400值．20.下面的图形是由边长为l 的正方形按照某种规律排列而组成的.(1)观察图形，填写下表：图形①②③正方形的个数8 图形的周长18 (2)推测第n个图形中，正方形的个数为 ，周长为 (都用含n的代数式表示).(3)这些图形中，任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y ＝ .21.用火柴棒摆出下列一组图形：(1)填写下表：图形编号123图形中的火柴棒数 (2)照这样的方式摆下去，写出摆第n个图形中的火柴棒数；(用含n的代数式表示)(3)如果某一图形共有2027根火柴棒，你知道它是第几个图形吗？22.观察下列等式：13＋23＝3213＋23＋33＝6213＋23＋33＋43＝102…(1)根据观察得到规律写出：13＋23＋33＋43＋53＝ .(2)根据观察得到规律写出13＋23＋33＋43＋…＋1003＝ .(3)13＋23＋33＋43＋53＋…＋n3＝ .23.阅读材料：求1＋2＋22＋23＋24＋…＋22023的值.解：设S＝1＋2＋22＋23＋24＋…＋22022＋22023，将等式两边同时乘以2得：2S＝2＋22＋23＋24＋25＋…＋22023＋22024将下式减去上式得2S﹣S＝22024﹣1即S＝22024﹣1即1＋2＋22＋23＋24＋…＋22023＝22024﹣1请你仿照此法计算：(1)1＋2＋22＋23＋24＋…＋210(2)1＋3＋32＋33＋34＋…＋3n(其中n为正整数).答案1.C2.C.4.D．5.B．6.C.7.B.8.C9.A10.C11.答案为：1353.12.答案为：(n2＋4n).13.答案为：80.14.答案为：(﹣1)n nx n .15.答案为：120．16.答案为：S＝4(n﹣1).17.答案为：1＋3n.18.答案为：16.19.解：(1))∵1个最小的连续偶数相加时，S＝1×(1＋1)，2个最小的连续偶数相加时，S＝2×(2＋1)，3个最小的连续偶数相加时，S＝3×(3＋1)，…∴n个最小的连续偶数相加时，S＝n(n＋1)；(2)①根据(1)得：2＋4＋6＋…＋200＝100×(100＋1)＝10100；②162＋164＋166＋ (400)＝(2＋4＋6＋…＋400)﹣(2＋4＋6＋…＋160)，＝200×201﹣80×81，＝40200﹣6480，＝33720．20.解：(1)∵n＝1时，正方形有8个，即8＝5×1＋3，周长是18，即18＝10×1＋8；n＝2时，正方形有13个，即13＝5×2＋3，周长是28，即28＝10×2＋8；n＝3时，正方形有18个，即18＝5×3＋3，周长是38，即38＝10×3＋8；(2)由(1)可知，n＝n时，正方形有5n＋3个，周长是10n＋8.(3)∵y＝10n＋8，x＝5n＋3，∴y＝2x＋2.21.解：(1)第一个图形中火柴棒数＝2＋5＝7，第二个图形中火柴棒数＝2＋5＋5＝12，第三个图形中火柴棒数＝2＋5＋5＋5＝17；故答案为：7；12；17；(2)由(1)的规律可知第n个图形的火柴棒根数＝2＋5n；(3)由题意可知2027＝2＋5n，解得n＝407，∴是第402个图形.22.解：(1)依题意，得13＋23＋33＋43＋53＝(1＋2＋3＋4＋5)2＝152＝225；(2)依题意，得13＋23＋33＋…＋1003＝(1＋2＋3＋…＋100)2＝50502；(3)一般规律为：13＋23＋33＋…＋n3＝(1＋2＋3＋…＋n)2＝[]2.故答案为225；50502；[]2.23.解：(1)设S＝1＋2＋22＋23＋24＋ (210)将等式两边同时乘以2得：2S＝2＋22＋23＋24＋…＋210＋211，将下式减去上式得：2S﹣S＝211﹣1，即S＝211﹣1，则1＋2＋22＋23＋24＋…＋210＝211﹣1；(2)设S＝1＋3＋32＋33＋34＋…＋3n①，两边同时乘以3得：3S＝3＋32＋33＋34＋…＋3n＋3n＋1②，②﹣①得：3S﹣S＝3n＋1﹣1，即S＝12(3n＋1﹣1)，则1＋3＋32＋33＋34＋…＋3n＝12(3n＋1﹣1).。

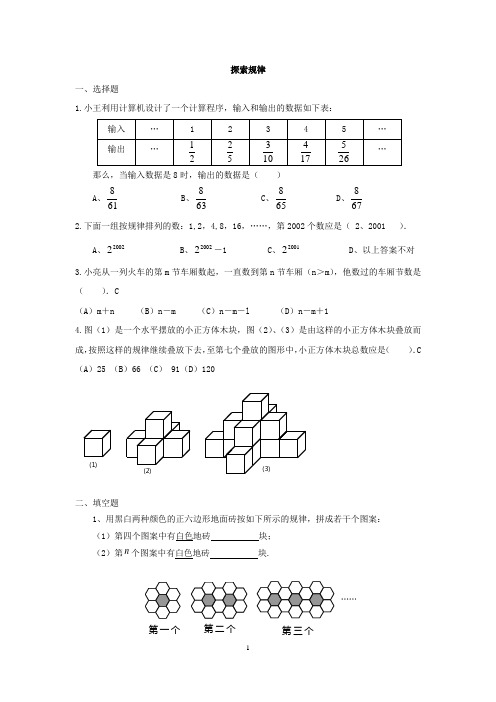
探索规律一、选择题1.小王利用计算机设计了一个计算程序，输入和输出的数据如下表：那么，当输入数据是8时，输出的数据是（ ）A 、618 B 、638 C 、658 D 、678 2.下面一组按规律排列的数：1,2，4,8，16，……，第2002个数应是（ 2、2001 ）．A 、20022B 、20022－1C 、20012D 、以上答案不对3.小亮从一列火车的第m 节车厢数起，一直数到第n 节车厢（n ＞m ），他数过的车厢节数是（ ）．C（A ）m ＋n （B ）n －m （C ）n －m －l （D ）n －m ＋14.图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（ ）．C （A ）25 （B ）66 （C ）91（D ）120二、填空题1、用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案： （1）第四个图案中有白色地砖 块；（2）第n 个图案中有白色地砖 块.……第三个第二个第一个(1)(2)(3)2、观察下列算式：221= 422= 823= 1624= 3225= 6426=12827= 25628= 通过观察，用你所发现的规律写出98的末位数是 . 23、古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为 .4、请你观察思考下列计算过程：∵211＝121，∴121＝11； 同样：∵2111＝12321，∴12321＝111；…… 由此猜想76543211234567898= 。

5、下表为杨辉三角系数表，它的作用是指导读者按规律写出形如n b a )(+（其中n 为正整数）展开式的系数，请你仔细观察下表中的规律，填出4)(b a +展开式中所缺的系数．b a b a +=+)(2222)(b ab a b a ++=+ 3223333)(b ab b a a b a +++=+44)(a b a =++ 4322346b ab b a b a +++6、观察下列各式()()1112-=+-x x x ；()()11132-=++-x x x x ；()1-x ()11423-=+++x x x x ,根据前面各式的规律可得()()=++++--111x x x x n n ．7、观察下列各式：21112⨯=+，32222⨯=+，43332⨯=+，…………请你将猜想到的规律用自然数n （n ＞l ）表示出来 ． 8、已知：3223222⨯=+，8338332⨯=+，154415442⨯=+，…若ba b a ⨯=+21010（a 、b 为正整数），则a ＋b ＝ 。

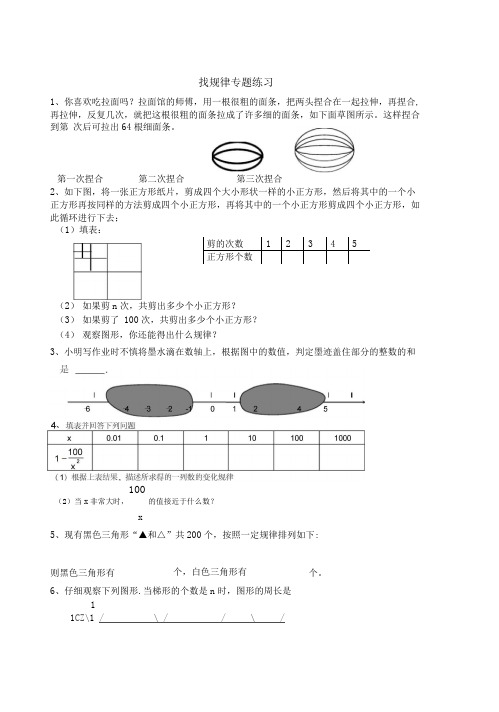
找规律专题练习1、你喜欢吃拉面吗？拉面馆的师傅，用一根很粗的面条，把两头捏合在一起拉伸，再捏合,再拉伸，反复几次，就把这根很粗的面条拉成了许多细的面条，如下面草图所示。

这样捏合 到第 次后可拉出64根细面条。

第一次捏合 第二次捏合 第三次捏合2、如下图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小 正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如 此循环进行下去； （1）填表：（2） 如果剪n 次，共剪出多少个小正方形？ （3） 如果剪了 100次，共剪出多少个小正方形？ （4） 观察图形，你还能得出什么规律？3、小明写作业时不慎将墨水滴在数轴上，根据图中的数值，判定墨迹盖住部分的整数的和（2）当x 非常大时，100的值接近于什么数？x5、现有黑色三角形“▲和△”共200个，按照一定规律排列如下:个，白色三角形有 6、仔细观察下列图形.当梯形的个数是n 时，图形的周长是1 1CZ\1/ \ / / \ /剪的次数 1 2 3 4 5 正方形个数则黑色三角形有 个。

27、用火柴棒按如下方式搭三角形：(1) 填写下表：(2) 照这样的规律搭下去，搭n 个这样的三角形需要2 2 2 210、观察下列算式：1 X 5 +4 =32 , 2x 6 +4 =42 , 3^7 + 4=52 , 4天8 + 4=62，请你在察规律之后11、一张长方形桌子可坐6人，按下列方式讲桌子拼在一起。

②一家餐厅有40张这样的长方形桌子，按照上图方式每 5张桌子拼成1张大桌子，则40张桌子可拼成8张大桌子，共可坐 。

③ 若在②中，改成每8张桌子拼成1张大桌子，则共可坐 12、用计算器计算下列各式，并将结果填写在横线上。

① ② ③ ④O OO OOO O3 OOO3 OO O O O O OC3C&把编号为1, 2, 3, 4,…的若干盆花按右图所示摆放，花盆中 的花按红、黄、蓝、紫的颜色依次循环排列，则第 8行从左边数第 6盆花的颜色为 色. 9、已知一列数：1, 下列形式：第1行 第2行 第3行 第4行 第5行—2 , 3, —4, 5, —6, 7,…将这列数排成1 -2 -4 7 113 5-8 -12-69 13—10 —1415按照上述规律排下去，那么第 10行从左边数第5个数等于并用你得到的规律填空:=502,第n 个式子呢？①张桌子拼在一起可坐______ 人。

完整)初中数学找规律专项练习题(有答案)1、观察规律：1=1；1+3=4；1+3+5=9；1+3+5+7=16；…，则2+6+10+14+…+2014的值是多少？2、用四舍五入法对取近似数，并精确到千位，用科学计数法表示为多少？3、观察下面的一列数：-1，2，-3，4，-5，6…请找出其中排列的规律，并按此规律填空。

（1）第10个数是多少？第21个数是多少？（2）-40是第几个数？26是第几个数？4、一组按规律排列的数：1，3，6，10，15…请推断第9个数是多少？5、计算：（-100）+（-101）=多少？（-2）+（-2）=多少？6、若。

则等于多少？7、大肠杆菌每过20分钟便由1个分裂成2个，经过3小时后这种大肠杆菌由1个分裂成多少个？8、猜数字游戏中，XXX写出如下一组数：1，3，5，7，9…n个数是…，XXX猜想出第六个数字是多少？根据此规律，第9、10个数字分别是多少？9、若。

与｜b+5|的值互为相反数，则等于多少？10、在计数制中，通常我们使用的是“十进位制”，即“逢十进一”.而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据.已知二进位制与十进位制的比较如下表：十进位制二进制 1 1 2 10 3 11 4 100 5 101 6 110 …… 请将二进位制xxxxxxxx（二）写成十进位制数为多少？11、为求。

值，可令S=。

则2S=。

因此所以。

仿照以上推理计算出的值是多少？二、选择题13、的值是多少？【】A．-2 B．-1 C．0 D．114、已知8.62=73.96，若x=0.7396，则x的值等于（）A.86.2B.862C.±0.862D.±86215、计算：(-2)+(-2)的值是多少？A.2B.-1C.-2D.-416、计算等于多少？A． B． C． D．17、已知a、b互为相反数，c、d互为倒数，m的绝对值为1，p是数轴到原点距离为1的数，那么的值是多少？A．3 B．2 C．1 D．018、若。

小学数学奥数训练：探索规律专项练习试卷及答案(50道解答题有详细答案解析)小学数学奥数训练：探索规律专项练试卷及答案（50道解答题有详细答案解析）1、在大于1000的整数中，找出所有被34除后商与余数相等的数，那么这些数的和是多少?2、动脑筋，探索规律。

1.2×2.1=11.2×2.11=111.2×2.111=1111.2×2.1111=.2×2.=你发现了什么规律？3、按照规律接着画出第4幅图。

第10幅图中一共有()个点。

4、用火柴棒摆出图形。

摆第1个图形要4根火柴棒。

那么摆第5个图形要多少根火柴棒?5、一张桌子坐4人，两张桌子并起来坐6人，三张桌子并起来坐8人，…照这样计算，10张桌子并成一排可坐多少人？如果一共有26人，需要并多少张桌子？6、图形三角形个数所需火柴数1234……………10n3579 (1001)(1)10个三角形需要几根洋火？摆n个呢？(2)如果有1001根火柴可以摆几个三角形？共20页，第1页7、观察：÷3=﹣3，差．÷4=﹣4，请再写出两个数，使它们的商等于它们的8、已知1+3=4=2，1+3+5=9=3，1+3+5+7=16=4，1+3+5+7+9=25=5，...(1)仿照上例，计算：1+3+5+7+ (99)(2)按照上述纪律，请你用自然数n（n≥1）表示一般纪律．22229、下列图案由边长相等的黑、白两色小正方形按一定规律拼接而成。

照如许画下去，第10个图形中分别有几何个玄色小正方形和白色小正方形？你能说明个中的道理吗？10、有一个挂钟，每小时敲一次钟，几点敲几下，钟敲6下，5秒钟敲完，钟敲12下，几秒钟敲完？11、观察点子图，找一找有什么纪律，想一想，第8个方框里有______个点，第20个方框内呢？12、图(1)是一个三角形，分别连接这个三角形三边的中点得到图(2)，再分别连接图(2)中间的小三角形三边的中点，得到图(3)．按这样的方法继续下去，第100个图形有多少个小三角形？共20页，第2页13、用三条边都是l厘米的三角形拼图形，按如下规律拼下去．想一想：用29个如许的三角形拼成的图形是什么图形？14、（2012•成都）一串分数：，，，，，，，，，…（1）是此串分数中的第多少个分数？（2）第115个分数是多少？15、（2013•长沙）有这样一串数、、、、、、、、、…（1）第407个分数是多少？（2）从开始，前407个分数的和是几何？16、（2011•海港区）判断推理．三角形个数1个2个3个4个…小棒的根数3根5根7根9根…观察图形和表格，如果要摆100个三角形，需要多少根小棒？要摆n个三角形，需要多少根小棒？17、观察下图，按规律填表。

第五节计算器探索规律
小博士提示：数学中有好多有趣的规律，你发现了吗？
教材连线：
1、用计算器计算前3题，直接写出后4题的得数
11×11= 12×11= 23×11= 35×11=
124×11= 2633×11= 3054×11=
2、先找出规律，再按规律填数。

（1），，，，，
（2），，，，。

3、用计算器计算前3题，然后仔细观察，找出规律，再把其它算式补充完整，并直接写得数。

÷9=
÷9=
÷9=
÷=
÷=
÷=
4、除法计算中有很多有趣的规律，你能试着找一找规律吗？
1÷41 （）÷（）
2÷41 （）÷（）
3÷41 （）÷（）
4÷41 （）÷（）
（）÷41 （）÷（）
（）÷41 （）÷（）
智能升级：
1、说说哪道题的商比被除数大，再用计算器计算商。

35．56÷÷
÷÷127
2、据统计，一个没有关紧的水龙头，每小时大约滴水千克。

（1）、照这样计算，一天会浪费多少千克水？
（2）、一年（按365天计算）会浪费多少千克水？
（3）、我们学校有45个水龙头，一年会浪费多少千克水？
（4）、如果一个3口之家，每月用水20吨，这些水可供他们用多少时
间？
智力：
巧算：
（2002002+）÷（8008008+。

探索规律练习专题（含答案）1、（2015•山东临沂,第11题3分）观察下列关于x的单项式，探究其规律：x，3x2，5x3，7x4，9x5，11x6，….按照上述规律，第2015个单项式是（）(A) 2015x2015. (B) 4029x2014. (C) 4029x2015. (D) 4031x2015. 【答案】C【解析】试题分析：根据这组数的系数可知它们都是连续奇数，即系数为（2n －1），而后面因式x的指数是连续自然数，因此关于x的单项式是，所以第2015个单项式的系数为2×2015－1=4029，因此这个单项式为. 故选C考点：探索规律2、（2015•四川省内江市，第16题，5分）如图是由火柴棒搭成的几何图案，则第n个图案中有根火柴棒．（用含n的代数式表示）考点：规律型：图形的变化类．. 专题：压轴题．分析：本题可分别写出n=1，2，3，…，所对应的火柴棒的根数．然后进行归纳即可得出解答：解：依题意得：n=1，根数为：4=2×1×（1+1）；n=2，根数为：12=2×2×（2+1）；n=3，根数为：24=2×3×（3+1）；…n=n时，根数为：2n（n+1）．点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．3、(2015·深圳，第15题分)观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有个太阳。

【答案】21【解析】第一行的规律是1，2，3，4，…，故第五个数是5；第二行的规律是1，2，4，8，…，故第五个数是16；故第五个图中共有21个太阳。

4、(2015·南宁，第18题3分)如图9，在数轴上，点A表示1，现将点A沿x轴做如下移动，第一次点A向左移动3 个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种移动规律移动下去，第n次移动到点A N，如果点A N与原点的距离不小于20，那么n的最小值是．考点：规律型：图形的变化类；数轴．.分析：序号为奇数的点在点A的左边，各点所表示的数依次减少3，序号为偶数的点在点A的右侧，各点所表示的数依次增加3，于是可得到A13表示的数为﹣17﹣3=﹣20，A12表示的数为16+3=19，则可判断点A n与原点的距离不小于20时，n的最小值是13．解答：解：第一次点A向左移动3个单位长度至点A1，则A1表示的数，1﹣3=﹣2﹣2；第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为﹣2+6=4；第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4﹣9=﹣5；第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为﹣5+12=7；第5次从点A4向左移动15个单位长度至点A5，则A5表示的数为7﹣15=﹣8；…；则A7表示的数为﹣8﹣3=﹣11，A9表示的数为﹣11﹣3=﹣14，A11表示的数为﹣14﹣3=﹣17，A13表示的数为﹣17﹣3=﹣20，A6表示的数为7+3=10，A8表示的数为10+3=13，A10表示的数为13+3=16，A12表示的数为16+3=19，所以点A n与原点的距离不小于20，那么n的最小值是13．故答案为：13．点评：本题考查了规律型，认真观察、仔细思考，找出点表示的数的变化规律是解决本题的关键．5、（2015·湖北省孝感市，第15题3分）观察下列等式：1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，则1+3+5+…+2015＝．考点：规律型：数字的变化类分析：根据1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，可得1+3+5+…+（2n ﹣1）=n2，据此求出1+3+5+…+2015的值是多少即可．解答：解：因为1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，所以1+3+5+…+2015=1+3+5+…+（2×1008﹣1）=10082=1016064 故答案为：1016064．点评：此题主要考查了探寻数列规律问题，注意观察总结规律，并能正确的应用规律，解答此题的关键是判断出：1+3+5+…+（2n﹣1）=n2．6、（2015·湖南省益阳市，第13题5分）如图是用长度相等的小棒按一定规律摆成的一组图案，第1个图案中有6根小棒，第2个图案中有11根小棒，…，则第n个图案中有有根小棒．考点：规律型：图形的变化类．分析： 由图可知：第1个图案中有5+1=6根小棒，第2个图案中有2×5+2﹣1=11根小棒，第3个图案中有3×5+3﹣2=16根小棒，…由此得出第n 个图案中有5n +n ﹣（n ﹣1）=5n +1根小棒．解答： 解：∵第1个图案中有5+1=6根小棒，第2个图案中有2×5+2﹣1=11根小棒， 第3个图案中有3×5+3﹣2=16根小棒， …∴第n 个图案中有5n +n ﹣（n ﹣1）=5n +1根小棒．故答案为：5n +1．点评： 此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．7、(2015·黑龙江绥化，第20题分)填在下面各正方形中的四个数之间都有一定的规律 ，按此规律得出a +b +c =__________考点：规律型：数字的变化类．分析：观察不难发现，左上角+4=左下角，左上角+3=右上角，右下角的数是左下角与右上角两个数的乘积减去1的差，根据此规律列式进行计算即可得解． 解答：解：根据左上角+4=左下角，左上角+3=右上角，右下角的数是左下角与右上角两个数的乘积减去1的差，可得6+4=a ，6+3=c ，ac +1=b ，可得：a =10，c =9，b =91，所以a +b +c =10+9+91=110，故答案为：110点评：本题是对数字变化规律的考查，仔细观察前三个图形，找出四个数之间的变化规律是解题的关键．8、（2015•广东省,第15题，4分）观察下列一组数：13，25，37，49，511，…，根据该组数的排列规律，可推出第10个数是 . 【答案】1221. 【考点】探索规律题（数字的变化类）. 【分析】观察得该组数的排列规律为：分母为奇数，分子为自然数，第n 个数为21+n n ，所以，第10个数是1012210121=⨯+。