《物理光学》郁道银版第十三章习题解答(全)汇编

第一章习题1、已知真空中的光速c＝3m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25m/s,当光在冕牌玻璃中，n=1.51时，v=1.99m/s,当光在火石玻璃中，n＝1.65时，v=1.82m/s，当光在加拿大树胶中，n=1.526时，v=1.97m/s，当光在金刚石中，n=2.417时，v=1.24m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1,n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1.5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

习题十三13-1 衍射的本质是什么？衍射和干涉有什么联系和区别 ？答：波的衍射现象是波在传播过程中经过障碍物边缘或孔隙时所发生的展衍现象• 其实质是 由被障碍物或孔隙的边缘限制的波阵面上各点发出的无数子波相互叠加而产生. 而干涉则是 由同频率、同方向及位相差恒定的两列波的叠加形成.13-2 在夫琅禾费单缝衍射实验中，如果把单缝沿透镜光轴方向平移时，衍射图样是否会 跟着移动？若把单缝沿垂直于光轴方向平移时，衍射图样是否会跟着移动 ？答：把单缝沿透镜光轴方向平移时， 衍射图样不会跟着移动. 单缝沿垂直于光轴方向平移时， 衍射图样不会跟着移动.13-3 什么叫半波带？单缝衍射中怎样划分半波带 ？对应于单缝衍射第 3级明条纹和第4级暗条纹，单缝处波面各可分成几个半波带？λ答：半波带由单缝 A 、B 首尾两点向'方向发出的衍射线的光程差用2来划分•对应于第3级明纹和第4级暗纹，单缝处波面可分成 7个和8个半波带. a Sin =(2k • 1) “ =(2 3 ■ 1) “ =7∙.∙由 22 2a Sin -4 ' - 8—213-4 在单缝衍射中，为什么衍射角 ，愈大(级数愈大)的那些明条纹的亮度愈小 ？ 答：因为衍射角「愈大则asin「值愈大，分成的半波带数愈多，每个半波带透过的光通量 就愈小，而明条纹的亮度是由一个半波带的光能量决定的，所以亮度减小.13-5 若把单缝衍射实验装置全部浸入水中时，衍射图样将发生怎样的变化？如果此时用公mλasin =(2k 1) (k =1,2,)式 2来测定光的波长，问测出的波长是光在空气中的还是在水中的波长？k ■解：当全部装置浸入水中时，由于水中波长变短，对应asin 「= k ∙ = n ,而空气中为asi n「= k ∙,∙. Si n 「=n Sin ",即「=n :,水中同级衍射角变小，条纹变密.λ如用asin(2k ■ I)2 (k=1,2,…)来测光的波长，则应是光在水中的波长.(因asin‘ 只代表光在水中的波程差)•13-6 在单缝夫琅禾费衍射中，改变下列条件，衍射条纹有何变化 ?(1)缝宽变窄；(2)入射光波长变长；(3)入射平行光由正入射变为斜入射. 解：(1)缝宽变窄，由asin ' =k'知，衍射角「变大，条纹变稀；(2) ,变大，保持a, k不变，则衍射角 「亦变大，条纹变稀； (3) 由正入射变为斜入射时， 因正入射时asin即=k ∙；斜入射时，a(Sin「-Sin^)^k-,保持a ,'不变，则应有 ^ k或k二：：k •即原来的k 级条纹现为k级.13-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似，两者是否矛盾 ？怎样说明？λ答：不矛盾•单缝衍射暗纹条件为.asin=k' =2k 2 ,是用半波带法分析(子波叠加问 题)•相邻两半波带上对应点向'方向发出的光波在屏上会聚点一一相消， 而半波带为偶数，故形成暗纹；而双缝干涉明纹条件为dsin a ,描述的是两路相干波叠加问题，其波程差为波长的整数倍，相干加强为明纹.13-8 光栅衍射与单缝衍射有何区别 ？为何光栅衍射的明条纹特别明亮而暗区很宽 ？答：光栅衍射是多光束干涉和单缝衍射的总效果. 其明条纹主要取决于多光束干涉.光强与缝数N 2成正比，所以明纹很亮；又因为在相邻明纹间有 (N -1)个暗纹，而一般很大，故 实际上在两相邻明纹间形成一片黑暗背景.13-9 试指出当衍射光栅的光栅常数为下述三种情况时，哪些级次的衍射明条纹缺级 ?(1) a+b=2a;(2)a+b=3a;(3)a+b=4a.解：由光栅明纹条件和单缝衍射暗纹条件同时满足时，出现缺级.即"(a +b)si n d =±k ?* (k =0,1,2,…) a sin W = ±k 九 (^ = 1,2∙…)a +b * k = k H可知，当 a 时明纹缺级.(1)a∙b =2a 时，k = 2,4,6,•…偶数级缺级；(2) a b =3a 时，k=3,6,9,•…级次缺级；⑶ a ∙b =4a , k=4,8,12,∙∙级次缺级.13-10 若以白光垂直入射光栅，不同波长的光将会有不同的衍射角.问 (1)零级明条纹能 否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大 ？不同波长的光分开程度与什 么因素有关？解：(1)零级明纹不会分开不同波长的光. 因为各种波长的光在零级明纹处均各自相干加强. ⑵可见光中红光的衍射角最大，因为由(a' b) sin :护=k ‘，对同一 k 值，衍射角 -'.ο13-11 一单色平行光垂直照射一单缝， 若其第三级明条纹位置正好与 6000 A的单色平行光的第二级明条纹位置重合，求前一种单色光的波长. 解：单缝衍射的明纹公式为a sin = (2 k 1)2o当人=6000 A 时 k = 2，='X 时，k = 3 重合时'角相同，所以有5 ■ X6000 =4286 o7Ao13-12 单缝宽0.10mm,透镜焦距为50Cm 用^ =5000 A 的绿光垂直照射单缝•求：(1) 位于透镜焦平面处的屏幕上中央明条纹的宽度和半角宽度各为多少 ?(2)若把此装置浸入水中(n=1.33),中央明条纹的半角宽度又为多少 ？AλL X = 2 f解：中央明纹的宽度为na-Sin —半角宽度为 na(1)空气中，n=1,所以A5000 汇 10 “J：x =2 0.5厂=5.0 100.10 汉 10ma sin 即=(22 1)-6000=(2 3 ■ 1)1015000 X 10 一 3V - Sin厂=5.0 10 一0.10x10 一rad(2)浸入水中，n=1.33 ,所以有105000 x10一3：^=2 0.50- 3.76 10 _1.33x0.10x10—mI5000 00」° 3V - Sin 3 : 3.7610 一 1.33 X 0.1 X10 一 rad13-13 用橙黄色的平行光垂直照射一宽为 a=0.60mm 的单缝，缝后凸透镜的焦距 f=40.0cm ,观察屏幕上形成的衍射条纹•若屏上离中央明条纹中心 1.40mm 处的P 点为一明条纹；求：（1）入射光的波长；（2）P 点处条纹的级数；（3）从P 点看，对该光波而言，狭缝处的波面可分成几个半波带？X 1.4 J3.5 10 tan f 4002 0.6 3.5 10 2k 1k = 4 得)-4 = 4700o若-3 = 6000 A ,则P 点是第3级明纹;o若-4 =4700 A ,贝U P 点是第4级明纹.a Sin = （2k 亠 1）-⑶由2可知，当k=3时，单缝处的波面可分成2k 1当k=4时，单缝处的波面可分成2kTo13-14用‘氛=5900A 的钠黄光垂直入射到每毫米有500条刻痕的光栅上，问最多能看到第几级明条纹？ 1 a+b = J二o解：500 mm =2.010 mm = 2.010 A由（a ' b ）sin ' = k '知，最多见到的条纹级数ka +b 2.0 汇104k max ==fc3.39∣Z-Qkmax^3所以有5900,即实际见到的最高级次为o 13-15 波长为5000A 的平行单色光垂直照射到每毫米有200条刻痕的光栅上，光栅后的透解：（1）由于P 点是明纹，故有a sin ' = (2k 1)—2 , k =1,2,3 - ■ 2a sin 2k 1X4.2 X10 °2k 1k =3，得 K =6000 mmoA=7个半波带;=9个半波带.<Pmax 对应的max镜焦距为60cm. 求：（1）屏幕上中央明条纹与第一级明条纹的间距；（2）当光线与光栅法线成30°斜入射时，中央明条纹的位移为多少？1a +b = ------ =5.0x10~6解： 200 mm 5.0 10 - m(1)由光栅衍射明纹公式X Sin Φ = tan W =— (a +b) sin 申=k k ,因k =1 ,又fX 1(a +b)所以有f这就是中央明条纹的位移值•o13-16 波长九=6000A 的单色光垂直入射到一光栅上，第二、第三级明条纹分别出现在 Sin=0∙20与Sin =0∙30处，第四级缺级.求：(1)光栅常数；(2)光栅上狭缝的宽度;⑶ 在90°> ’ > -90 °范围内，实际呈现的全部级数.解：(1)由(a b) Sin= k，式对应于Sin ：1=0∙2° 与Sin ；：2=0∙30 处满足：-Lo0.20 (a b) =2 6000 10 I. 100.30 (a b) =3 600010得 a ∙ b =6.0 10 * m(2)因第四级缺级，故此须同时满足(a ■ b) Sin = k ■a sin = k ，= 1.5 10 "βk解得取=1 ,得光栅狭缝的最小宽度为 1.5 10 m⑶由(a b) Sin = k ■k 土(a ■ b) Sin λπW =—当 2,对应 k = k m aXa +b .66.0 10 k10λ6000 10500010 210 恥 60 10 一X l5.0 10 -⑵对应中央明纹, 2= 6.0 10 一k = 0 =6 Cm正入射时, (a -b) Sin 斜入射时, (a -b)(sin=0二Sin所以 Sin=0日)=0 即Sin 申±sin 日=0Sinl : tanXCP二 30=1 60 10 2 2=3010m = 30Cm因_4 , _ 8缺级，所以在-9°：：：「：：： 9°范围内实际呈现的全部级数为k = 0, 一1, _2, _3, _5, _6, 一7, _9 共 15 条明条纹（k= 1° 在 k= 9° 处看不到）.o13-17 一双缝，两缝间距为 0.1mm ,每缝宽为0.02mm ,用波长为4800A 的平行单色光垂 直入射双缝，双缝后放一焦距为 50cm 的透镜.试求：（1）透镜焦平面上单缝衍射中央明条纹 的宽度；（2）单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹 ？ 解：（1）中央明纹宽度为 （2）由缺级条件a sin = k '■(a - b) sin = k ■0.1k " = 5k ' 0.02 k =1,2,即k=5,10,15,…缺级V -1.221 .22 5000= 30.5 10 D0.2d4f tan v : f v - 50030 .5 10 一 =1.5.∙.爱里斑半径2mm13-19已知天空中两颗星相对于一望远镜的角距离为 4.84 × 10-6rad ,它们都发出波长为o5500A 的光，试问望远镜的口径至少要多大，才能分辨出这两颗星 ？解：由最小分辨角公式J -1.22 —D5λ5.5j<10D =1.22 — =1 .22- = 13.864.84 10 Cmo13-20已知入射的X 射线束含有从0.95〜1.30A 范围内的各种波长，晶体的晶格常数为 o2.75 A ,当X 射线以45°角入射到晶体时，问对哪些波长的 X 射线能产生强反射？ 解：由布喇格公式2d Sin=k'_ 2d Sin 申λ = --------得k时满足干涉相长Qo当 k =1 时，& = m 、s in 45=3.89 A2 2.75 sin 45Λ --1.91 ok =2 时，2AI 。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=）、冕牌玻璃（n=）、火石玻璃（n=）、加拿大树胶（n=）、金刚石（n=）等介质中的光速。

解：则当光在水中，n=时，v= m/s,当光在冕牌玻璃中，n=时，v= m/s,当光在火石玻璃中，n＝时，v= m/s，当光在加拿大树胶中，n=时，v= m/s，当光在金刚石中，n=时，v= m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=，所以纸片最小直径为。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到nsinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=的玻璃球上，求其会聚点的位置。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51)、火石玻璃（n=1。

65)、加拿大树胶(n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中,n=1。

333时，v=2.25 m/s，当光在冕牌玻璃中，n=1。

51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时,v=1。

82 m/s,当光在加拿大树胶中,n=1.526时，v=1。

97 m/s,当光在金刚石中，n=2.417时，v=1.24 m/s.2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm,则像的大小变为70mm，求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x,则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃(设n=1.5）,下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x，则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：（1)其中n2=1， n1=1。

5，同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2)式可以求出纸片最小直径x=179。

385mm，所以纸片最小直径为358。

77mm.4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1，其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有:n0sinI1=n2sinI2 (1）而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播，则有:（2）由（1）式和（2）式联立得到n0 sinI1 。

工程光学第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

第13章习题答案13—7 在双缝干涉实验中，两缝的间距为mm 5.0，照亮狭缝S 的光源是汞弧灯加上绿色滤光片。

在m 5.2远处的屏幕上出现干涉条纹，测得相邻两明条纹中心的距离为mm 2。

试计算入射光的波长。

解：已知条纹间距32210-==⨯x mm m ∆，缝宽405510-==⨯d .mm m ，缝离屏的距离25=D .m=D x d∆λ∴ 43751021041025---⨯==⨯⨯=⨯dx m D .λ∆13—8用很薄的云母片（58.1=n ）覆盖在双缝实验中的一条缝上，这时屏幕上的零级明条纹移到原来的第七级明条纹的位置上，如果入射光波长为nm 550，试问此云母片的厚度为多少？解: 设云母片厚度为e ，则由云母片引起的光程差为e n e ne )1(-=-=δ 按题意 λδ7= ∴ 610106.6158.1105500717--⨯=-⨯⨯=-=n e λm 6.6=m μ13—9 用包含两种波长成分的复色光做双缝实验，其中一种波长nm 5501=λ。

已知双缝间距为mm 6.0，屏和缝的距离为m 2.1，求屏上1λ的第三级明条纹中心位置。

已知在屏上1λ的第六级明条纹和未知波长光的第五级明条纹重合，求未知光的波长。

解：屏上1λ的三级明纹中心的位置m 103.310550106.02.133933---⨯=⨯⨯⨯⨯==λdD kx依题意屏上1λ的第六级明条纹和波长为λ的第五级明条纹重合于x 处 则有 λλdD k dD k x 516== 即 λλ516k k =m 106.6105505679156--⨯=⨯⨯==λλk k13—10平板玻璃（5.1=n ）表面上的一层水（33.1=n ）薄膜被垂直入射的光束照射，光束中的光波波长可变。

当波长连续变化时，反射强度从nm 500=λ时的最小变到nm 750=λ时的同级最大，求膜的厚度。

习题13-10图解∵ 321n n n <<,故有 ,3,2,1,02)12(21112=+==k k e n λδ ① 3,2,12222222===k k e n λδ ②由上两式21312k k =+⇒当231-=n k 时满足上式 n =1,2,3,…但由于λ是连续可调的，在1λ和2λ间无其他波长消失与增强，所以取,1,121==k k 把11=k 或12=k 代入①式或②式972275010310(m )22 1.33e n λ--⨯==≈⨯⨯13—11一玻璃劈尖的末端的厚度为mm 5.0，折射率为50.1。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。

6、一直径为400mm，折射率为1.5的玻璃球中有两个小气泡，一个位于球心，另一个位于1／2半径处。

沿两气泡连线方向在球两边观察，问看到的气泡在何处？如果在水中观察，看到的气泡又在何处？解：设一个气泡在中心处，另一个在第二面和中心之间。

（1）从第一面向第二面看（2）从第二面向第一面看（3）在水中。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水〔n=1.333〕、冕牌玻璃〔n=1.51〕、火石玻璃〔n=1.65〕、加拿大树胶〔n=1.526〕、金刚石〔n=2.417〕等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，假设将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃〔设n=1.5〕，下面放一直径为1mm的金属片。

假设在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立〔1〕式和〔2〕式可以求出纸片最小直径x=，所以纸片最小直径为。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径〔即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角〕。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由〔1〕式和〔2〕式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1。

51)、火石玻璃(n=1。

65)、加拿大树胶（n=1.526）、金刚石（n=2。

417）等介质中的光速。

解：则当光在水中，n=1。

333时，v=2。

25 m/s，当光在冕牌玻璃中,n=1。

51时,v=1.99 m/s,当光在火石玻璃中，n＝1。

65时，v=1。

82 m/s,当光在加拿大树胶中，n=1.526时,v=1。

97 m/s，当光在金刚石中，n=2。

417时，v=1.24 m/s.2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃(设n=1。

5)，下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为:(1)其中n2=1， n1=1。

5，同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1)式和（2)式可以求出纸片最小直径x=179。

385mm, 所以纸片最小直径为358。

77mm。

4、光纤芯的折射率为n1、包层的折射率为n2，光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有:n0sinI1=n2sinI2 (1）而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：（2）由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1。

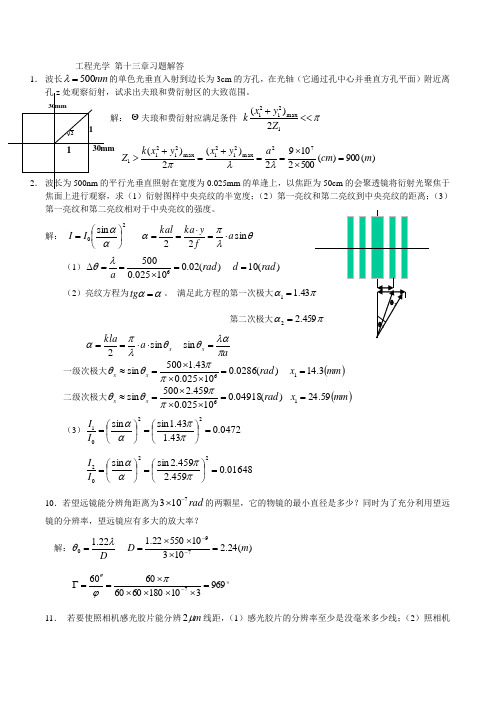
1θ2θ2mm3011mm30工程光学 第十三章习题解答1． 波长nm 500=λ的单色光垂直入射到边长为3cm 的方孔，在光轴（它通过孔中心并垂直方孔平面）附近离孔z 处观察衍射，试求出夫琅和费衍射区的大致范围。

解： 夫琅和费衍射应满足条件 π<<+1max21212)(Z y x k)(900)(50021092)(2)(72max 2121max 21211m cm a y x y x k Z =⨯⨯==+=+>λλπ2． 波长为500nm 的平行光垂直照射在宽度为0.025mm 的单逢上，以焦距为50cm 的会聚透镜将衍射光聚焦于焦面上进行观察，求（1）衍射图样中央亮纹的半宽度；（2）第一亮纹和第二亮纹到中央亮纹的距离；（3）第一亮纹和第二亮纹相对于中央亮纹的强度。

解： 20sin ⎪⎭⎫⎝⎛=ααI I θλπαs i n 22a f y ka kal ⋅=⋅== （1）)(02.010025.05006rad a=⨯==∆λθ )(10rad d = （2）亮纹方程为αα=tg 。

满足此方程的第一次极大πα43.11= 第二次极大πα459.22=x a k l a θλπαs i n 2⋅⋅==ax πλαθ=sin 一级次极大)(0286.010025.043.1500sin 6rad x x =⨯⨯⨯=≈ππθθ ()mm x 3.141= 二级次极大)(04918.010025.0459.2500sin 6rad x x =⨯⨯⨯=≈ππθθ ()mm x 59.241= （3）0472.043.143.1sin sin 2201=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=ππααI I01648.0459.2459.2s i n s i n2202=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=ππααI I 10．若望远镜能分辨角距离为rad 7103-⨯的两颗星，它的物镜的最小直径是多少？同时为了充分利用望远镜的分辨率，望远镜应有多大的放大率？解：D λθ22.10= )(24.21031055022.179m D =⨯⨯⨯=-- ⨯-=⨯⨯⨯⨯⨯=''=Γ969310180606060067πϕ11． 若要使照相机感光胶片能分辨m μ2线距，（1）感光胶片的分辨率至少是没毫米多少线；（2）照相机镜头的相对孔径fD 至少是多大？（设光波波长550nm ）解：)(50010213mm N 线=⨯=- 3355.01490=≈'Nf D 12． 一台显微镜的数值孔径为0。

物理光学知识点汇总一、 名词：（共41个）1、 全 反 射：光从光密介质入射到光疏介质，并且当入射角大于临界角时，在两个不同介质的分界面上，入射光全部返回到原介质中的现象，就叫全反射。

2、 折射定律：①折射光位于由入射光和法线所确定的平面内。

②折射光与入射光分居在法线的两侧。

③折射角与入射角满足：n n I I '='sin sin 。

3、 瑞利判据：（注：考试时答哪个都对）定义一：一个点物衍射图样的中央极大与近旁另一点物衍射图样的第一极小重合，作为光学系统的分辨极限，认为此时系统恰好可以分辨开两个点物，称此分辨标准为瑞利判据。

定义二：两个波长的亮条纹只有当它们合强度曲线中央极小值低于两边极大值的0.81时才能被分辨开。

4、 干 涉：在两个（或多个）光波叠加的区域，某些点的振动始终加强，另一些点的振动始终减弱，形成在该区域内稳定的光强强弱分布的现象。

5、 衍 射：通俗的讲，衍射就是当入射光波面受到限制后，将会背离原来的几何传播路径，并呈现光强不均匀分布的现象。

6、 倏 逝 波：沿着第二介质表面流动的波。

7、 光拍现象：光强随时间时大时小变化的现象。

8、 相干光束会聚角：对应干涉场上某一点P 的两支相干光线的夹角)(ω。

9、 干涉孔径角：对于干涉场某一点P 的两支相干光线从光源发出时的张角)(β。

10、 缺级现象：当干涉因子的某级主极大值刚好与衍射因子的某级极小值重合，这些主极大值就被调制为零，对应级次的主极大就消失了，这种现象就是缺级。

11、 坡印亭矢量（34、辐射强度矢量）：它表示单位时间内，通过垂直于传播方向的，单位面积的电磁能量的大小。

它的方向代表的是能量流动的方向，B E S⨯=μ1。

12、 相干长度：对于光谱宽度为λ∆的光源而言，能够发生干涉现象的最大光程差。

13、 发光强度：辐射强度矢量的时间平均值)(I 。

14、 全偏振现象（15、布儒斯特角）：当入射光是自然光，入射角满足o 9021=+θθ时，0=P r ，0≠s r ，即反射光中只有S 波，没有P 波，这样的现象就叫全偏振现象。

第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

第一章习题1、真空中的光速c＝3m/s，求光在水〔〕、冕牌玻璃〔〕、火石玻璃〔〕、加拿大树胶〔〕、金刚石〔〕等介质中的光速。

解：那么当光在水中，时，m/s,当光在冕牌玻璃中，时，m/s,当光在火石玻璃中，n＝时，m/s，当光在加拿大树胶中，时，m/s，当光在金刚石中，时，m/s。

2、一物体经针孔相机在屏上成一60mm大小的像，假设将屏拉远50mm，那么像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线那么方向不变，令屏到针孔的初始距离为x，那么可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃〔设〕，下面放一直径为1mm的金属片。

假设在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,那么根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：(1)其中n2=1,n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立〔1〕式和〔2〕式可以求出纸片最小直径，所以纸片最小直径为。

4、光纤芯的折射率为 n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径〔即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角〕。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律那么有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，那么有：(2)由〔1〕式和〔2〕式联立得到n0sinI1.5、一束平行细光束入射到一半径r=30mm、折射率的玻璃球上，求其会聚点的位置。

第一章1、一物体经针孔相机在 屏上成一60mm 大小的像，若将屏拉远50mm ，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x ，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm 。

2、一厚度为200mm 的平行平板玻璃（设n =1.5），下面放一直径为1mm 的金属片。

若在玻璃板上盖一圆形的纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片的最小直径应为多少？2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=3、.光纤芯的折射率为1n ，包层的折射率为2n ，光纤所在介质的折射率为0n ，求光纤的数值孔径（即10sin I n ，其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有： n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n 0 .4、一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上，求其会聚点的位置。

如果在凸面镀反射膜，其会聚点应在何处？如果在凹面镀反射膜，则反射光束在玻璃中的会聚点又在何处？反射光束经前表面折射后，会聚点又在何处？说明各会聚点的虚实。

解：该题可以应用单个折射面的高斯公式来解决，设凸面为第一面，凹面为第二面。

（1）首先考虑光束射入玻璃球第一面时的状态，使用高斯公式：会聚点位于第二面后15mm处。

（2）将第一面镀膜，就相当于凸面镜像位于第一面的右侧，只是延长线的交点，因此是虚像。