最新中考数学超好几何证明压轴题汇编

1、如图，在梯形ABCD 中，AB ∥CD ，∠BCD=90°,且AB=1，BC=2，tan ∠ADC=2.(1)求证：DC=BC;(2)E 是梯形内一点，F 是梯形外一点，且∠EDC=∠FBC ，DE=BF ，试判断△ECF 的形状，并证明你的结论；(3)在（2）的条件下，当BE ：CE=1：2，∠BEC=135°时，求sin ∠BFE 的值.2、已知：如图，在□ABCD 中，E 、F 分别为边AB 、CD 的中点，BD 是对角线，AG ∥DB 交CB 的延长线于G ．（1）求证：△ADE ≌△CBF ；（2）若四边形 BEDF 是菱形，则四边形AGBD 是什么特殊四边形？并证明你的结论．3、如图13－1，一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图13－2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 满足的数量关系，并证明你的猜想； （2）若三角尺GEF 旋转到如图13－3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由． 4、如图，已知⊙O 的直径AB 垂直于弦CD 于E ，连结AD 、BD 、OC 、OD ，且OD ＝5。

（1）若，求CD 的长； （2）若 ∠ADO ：∠EDO ＝4：1，求扇形OAC （阴影部分）的面积（结果保留）。

5、如图，已知：C 是以AB 为直径的半圆O 上一点，CH ⊥AB 于点H ，直线AC 与过B 点的切线相交于点D ，E 为CH 中点，连接AE 并延长交BD 于点F ，直线CF 交直线AB 于点G.（1）求证：点F 是BD 中点；（2）求证：CG 是⊙O 的切线；（3）若FB=FE=2，求⊙O 的半径．6、如图，已知O 为原点，点A 的坐标为（4，3），⊙A 的半径为2．过A 作直线l 平行于x 轴，点P 在直线l 上运动．（１）当点P 在⊙O 上时，请你直接写出它的坐标；（２）设点P 的横坐标为12，试判断直线OP 与⊙A 的位置关系，并说明理由.7、如图，延长⊙O 的半径OA 到B ，使OA=AB ，DE 是圆的一条切线，E 是切点，过点B 作DE 的垂线，垂足为点C .求证：∠ACB=31∠OAC . 8、如图１，一架长4米的梯子AB 斜靠在与地面OM 垂直的墙壁ON 上，梯子与地面的倾斜角α为 60． E B F C D A 图13－2 E A B D G F O M N C 图13－3A B DG E FOMNC 图13－1 A ( E ) C OD F C A BD O E⑴求AO 与BO 的长；⑵若梯子顶端A 沿NO 下滑，同时底端B 沿OM 向右滑行.①如图2，设A 点下滑到C 点，B 点向右滑行到D 点，并且AC:BD=2:3，试计算梯子顶端A 沿NO 下滑多少米；②如图３，当A 点下滑到A ’点，B 点向右滑行到B ’点时，梯子AB 的中点P 也随之运动到P ’点．若∠POP ’＝ ο15，试求AA ’的长．[解析]⑴AOB Rt ∆中,∠O=90o ,∠α=ο60∴,∠OAB=ο30，又ＡＢ＝4米，9.（重庆，10分）如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒．(1) 求直线AB 的解析式；(2) 当t 为何值时，△APQ 与△AOB 相似？(3) 当t 为何值时，△APQ 的面积为524个平方单位？10．（南充，10分）如图2－5－7，矩形ABCD 中，AB ＝8，BC ＝6，对角线AC 上有一个动点P （不包括点A 和点C ）．设AP ＝x ，四边形PBCD 的面积为y ．（1）写出y 与x 的函数关系，并确定自变量x 的范围．（2）有人提出一个判断：“关于动点P ，⊿PBC 面积与⊿PAD 面积之和为常数”．请你说明此判断是否正确，并说明理由．。

中考数学几何证明题正文第一篇：中考数学几何证明题中考几何证明题一、证明两线段相等1、真题再现18．如图3，在梯形abcd中，ad∥bc，ea⊥ad，m是ae上一点，2．如图，在△abc中，点p是边ac上的一个动点，过点p作直线mn∥bc，设mn交∠bca的平分线于点e，交∠bca的外角平分线于点f．(1)求证：pe＝pf；(2)*当点p在边ac上运动时，四边形bcfe可能是菱形吗？说明理由；ap 3(3)*若在ac边上存在点p，使四边形aecf是正方形，且．求此时∠abc2的大小．c二、证明两角相等、三角形相似及全等1、真题再现∠bae?∠mce，∠mbe?45．（1）求证：be?me．（2）若ab?7，求mc的长．bne图321、（8分）如图11，一张矩形纸片abcd，其中ad=8cm，ab=6cm，先沿对角线bd折叠，点c落在点c′的位置，bc′交ad于点g. （1）求证：ag=c′g；（2）如图12，再折叠一次，使点d与点a重合，的折痕en，en角ad于m，求em的长.2、类题演练1、如图，分别以rt△abc的直角边ac及斜边ab向外作等边△acd、等边△abe．已知∠bac=30o，ef⊥ab，垂足为f，连结df． e （1）试说明ac=ef；（2）求证：四边形adfe是平行四边形．22、（9分）ab是⊙o的直径，点e是半圆上一动点（点e与点a、b都不重合），点c是be延长线上的一点，且cd⊥ab，垂足为d，cd与ae交于点h，点h与点a不重合。

（1）（5分）求证：△ahd∽△cbd（2）（4分）连hb，若cd=ab=2，求hd+ho的值。

ao dbe 20．如图9，四边形abcd是正方形，be⊥bf，be=bf，ef与bc交于点g。

（1）求证：△abe≌△cbf；（4分）（2）若∠abe=50o，求∠egc的大小。

（4分）cb图9第20题图如图8，△aob和△cod均为等腰直角三角形，∠aob＝∠cod＝90o，d在ab上．（1）求证：△aoc≌△bod；（4分）（2）若ad＝1，bd＝2，求cd的长．（3分）o图8 2、类题演练1、(肇庆20XX) (8分)如图，已知∠acb＝90°，ac＝bc，be⊥ce于e，ad⊥ce于d，ce与ab相交于f．(1)求证：△ceb≌△adc；e (2)若ad＝9cm，de＝6cm，求be 及ef的长．acbc、cd、da上的2、（佛山20XX）已知，在平行四边形abcd中，efgh分别是ab、点，且ae=cg，bf=dh，求证：?aeh≌?cgfb fc3、（茂名20XX）如图，已知oa⊥ob，oa＝4，ob＝3，以ab为边作矩形c abcd，使ad＝a，过点d作de垂直oa的延长线交于点e．(1)证明：△oab∽△eda；bd (2)当a为何值时，△oab≌△eda？*请说明理由，并求此时点c到oe的距离．o a e 图1三、证明两直线平行1、真题再现（20XX年）22．(10分)如图10-1，在平面直角坐标系xoy中，点m在x轴的正半轴上，⊙m交x轴于a、b两点，交y轴于c、d两点，且c为ae的中点，ae 交y轴于g点，若点a的坐标为（－2，0），ae?8 (1)(3分)求点c的坐标.(2)(3分)连结mg、bc，求证：mg∥bc图10－12、类题演练1、(湛江20XX) (10分)如图，在□abcd中，点e、f是对角线bd上的两点，且be ＝df．d求证：(1)△abe≌△cdf；(2)ae∥cf．c四、证明两直线互相垂直1、真题再现18．（７分）如图7，在梯形abcd中，ad∥bc, ab?dc?ad，?adc?120．（1）（３分）求证：bd?dcbcbd （2）（４分）若ab?4，求梯形abcd的面积图7o ae 图22、类题演练1．已知：如图，在△abc中，d是ab边上一点，⊙o过d、b、c三点，?doc?2?acd?90?．（1）求证：直线ac是⊙o的切线；（2）如果?acb?75?，⊙o的半径为2，求bd的长．2、如图，以△abc的一边ab为直径作⊙o，⊙o与bc边的交点d恰好为bc的中点.过点d作⊙o的切线交ac边于点e.（1）求证：de⊥ac；（2）若∠abc=30°，求tan∠bco的值.（第2题图）3．（20XX年深圳二模）如图所示，矩形abcd中，点e在cb的延长线上，使ce＝ac，连结ae，点f是ae 的中点，连结bf、df，求证：bf⊥dfcd于f，若⊙o的半径为r求证：ae·af＝2 r2、类题演练1．在△abc中，ac＝bc，∠acb＝90°，d、e是直线ab上两点．∠dce＝45°（１）当ce⊥ab时，点d与点a重合，显然de＝ad＋be（不必证明）（２）如图，当点d不与点a重合时，求证：de＝ad＋be（３）当点d在ba的延长线上时，（２）中的结论是否成立？画出图形，说明理由．2.（本小题满分10分）如图，已知△abc，∠acb=90o，ac=bc，点e、f在ab上，∠ecf=45o，（1）求证：△acf∽△bec（5分）（2）设△abc的面积为s，求证：af·be=2s（3）3.（2）如图，ab为⊙o的直径，bc切⊙o于b，ac交⊙o于d.①求证：ab=ad·ac. a ②当点d运动到半圆ab什么位置时，△abc为等腰直角三角形，为什么？五、证明比例式或等积式1、真题再现1．已知⊙o的直径ab、cd互相垂直，弦ae交第3题图b第3（2）题图c4、（本小题满分9分）如图，ab为⊙o的直径，劣弧bc?be，bd∥ce，连接ae并延长交bd于d．求证：（1）bd是⊙o的切线；2、类题演练1、如图5，在等腰梯形abcd中，ad∥bc．求证：∠a＋∠c＝180°·ad．（2）ab?acb第4题图??5. 如图所示，⊙o中，弦ac、bd交于e，bd?2ab。

矩形24.已知:如图，在△ABC 中，AB=AC ，A D ⊥BC ，垂足为点D ，M 在BA 的延长线上AN 是∠MAC 的平分线，CE ⊥AN ，垂足为E 。

（1）试说明：四边形ADCE 为矩形；（2）当△ABC 满足什么条件时，四边形ADCE 是一个正方形？说明理由。

24．（本小题9分）已知：如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，垂足为D ，AN 是△ABC 外角∠CAM 的平分线，CE ⊥AN ，垂足为E ，连接DE 交AC 于F （1）求证：四边形ADCE 为矩形 （2）求证：DF ∥AB ，DF ＝12AB21.如图所示折叠长方形的一边AD ，点D 落在BC 边的点F 处，已知AB ＝12cm ， BC ＝13cm,求EC 的长。

5.如图8，将矩形纸片ABCD 沿对角线AC 折叠，使点B 落在点E 处，求证：EF =DF .BDECF19．如图，把一张矩形的纸ABCD 沿对角线BD 折叠，使点C 落在点E 处，BE 与AD 交于点F ．①求证：ΔABF ≌ΔEDF ；②若将折叠的图形恢复原状，点F 与BC 边上的点M 正好重合，连接DM ，试判断四边形BMDF 的形状，并说明理由．12、如图，矩形ABCD 中，O 是AC 与BD 的交点，过O 点的直线EF 与AB CD ，的延长线分别交于E F ，．（1）求证：BOE DOF △≌△； （2）当EF 与AC 满足什么关系时，以A E C F ，，，为顶点的四边形是菱形？证明你的结论．1.如图，在△ABC 中，D 是BC 边上的一点，E 是AD 的中点，过A 点作BC 的平行线交CE 的延长线于点F ，且AF =BD ，连结BF 。

（1） 求证：BD =CD ； （2） 如果AB =AC ，试判断四边形AFBD 的形状，并证明你的结论。

F D OB E AC D B A M 第22题图F EFED C B A 3.如图，四边形ABCD 是矩形，△PBC 和△QCD 都是等边三角形，且点P 在矩形上方，点Q 在矩形内． 求证：（1）∠PBA =∠PCQ =30°；（2）P A =PQ ．7、已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF=ED,EF ⊥ED. 求证:AE 平分∠BAD.8、如图，矩形ABCD 中，点E 是BC 上一点，AE ＝AD ，DF ⊥AE 于F ，连结DE ，求证：DF ＝DC ．23．（本小题6分）已知如图,在矩形ABCD 中,E 为BC 上的一点,且DE=BC,AF ⊥DE 于点F,求证:EF=BE 14、（本题8分）已知：如图，在矩形ABCD 中，AF=DE,求证：BE=CF（第23题）ACBD PQBDDC BAOE18.在矩形ABCD 中，O 是对角线AC 的中点，EF 是线段AC 的中垂线，交AD 、BC 于E 、F .求证：四边形AECF 是菱形1、如左下图，在矩形ABCD 中，AC 、BD 相交于O ，AE 平分∠BAD ，交BC 于E ，若∠CAE =15°，求∠BOE 的度数.2、如右上图ABCD ，四内角平分线相交于E 、F 、G 、H .求证：四边形EFGH 是矩形6．（2012•聊城）如图，矩形ABCD 的对角线相交于点O ，DE∥AC，CE∥BD． 求证：四边形OCED 是菱形．9．（2010四川眉山）如图，O 为矩形ABCD 对角线的交点，DE ∥AC ，CE ∥BD ．（1）试判断四边形OCED 的形状，并说明理由； （2）若AB =6，BC =8，求四边形OCED 的面积．10．（2012娄底）如图，在矩形ABCD 中，M 、N 分别是AD ．BC 的中点，P 、Q 分别是BM 、DN 的中点．（1）求证：△MBA ≌△NDC ；（2）四边形MPNQ 是什么样的特殊四边形？请说明理由．16．（2012六盘水）如图，已知E 是▱ABCD 中BC 边的中点，连接AE 并延长AE 交DC 的延长线于点F ．（1）求证：△ABE ≌△FCE ．（2）连接AC ．BF ，若∠AEC=2∠ABC ，求证：四边形ABFC 为矩形．5.两个完全相同的矩形纸片ABCD 、BFDE 如图7放置，AB BF ，求证：四边形BNDM 为菱形．19. （2012.云南省）如图，在矩形ABCD 中，对角线BD 的垂直平分线MN 与AD 相交于点M ，与BD 相交于点N ，连接BM ，DN ． （1）求证：四边形BMDN 是菱形； （2）若AB=4，AD=8，求MD 的长．8.如图，矩形ABCD 中，AC 、BD 相交于点O ，AE 平分∠BAD ，若∠EAO=15°，求∠BOE 的度数。

几何中的折叠问题一、单选题1如图，在菱形ABCD中，AD=5，tan B=2，E是AB上一点，将菱形ABCD沿DE折叠，使B、C的对应点分别是B 、C ，当∠BEB =90°时，则点C 到BC的距离是()A.5+5B.25+2C.6D.35【答案】D【分析】过C作CH⊥AD于H，C 作C F⊥AD于F，HD=5，HC=25，再由折叠证明∠BED=∠B ED=135°，∠EDC=∠EDC =45°，△CHD≌△DFC ，C F= HD=5，【C作CH⊥AD于H，C 作C F⊥AD于F，由已知AD=5，tan B=2，=2，∴CD=5，tan∠CDH=HCHD∴设HD=x，HC=2x，∴在Rt△HDC中HC2+HD2=CD2，2x2+x2=52，解得x=5，∴HD=5，HC=25，由折叠可知∠BED=∠B ED，∠EDC=∠EDC ，CD=C D∵∠BEB =90°，∴∠BED=∠B ED=135°，∵AB∥DC，∴∠EDC=180°-∠BED=45°，∴∠EDC=∠EDC =45°∴∠CDC =90°∵∠CHD =∠C AD =90°，∴∠CDH +C DF =90°，∵∠CDH +∠HCD =90°，∴∠C DF =∠HCD ，∴△CHD ≌△DFC ，∴C F =HD =5，∴点C 到BC 的距离是C F +CH =5+25=35．故选：D ．【点睛】本题考查了全等三角形的性质和判定、菱形的性质、图形的折叠以及正切定义的应用，解答关键是根据折叠的条件推出∠BED =∠B ED =135°．2如图，将△ABC 折叠，使AC 边落在AB 边上，展开后得到折痕l 与BC 交于点P ，且点P 到AB 的距离为3cm ，点Q 为AC 上任意一点，则PQ 的最小值为()A.2cmB.2.5cmC.3cmD.3.5cm【答案】C【分析】由折叠可得：PA 为∠BAC 的角平分线，根据垂线段最短即可解答．【详解】解：∵将△ABC 折叠，使AC 边落在AB 边上，∴PA 为∠BAC 的角平分线，∵点Q 为AC 上任意一点，∴PQ 的最小值等于点P 到AB 的距离3cm ．故选C ．【点睛】本题主要考查了折叠的性质、角平分线的性质定理等知识点，掌握角平分线上的点到两边距离相等是解答本题的关键．3如图，在▱ABCD 中，BC =8,AB =AC =45，点E 为BC 边上一点，BE =6，点F 是AB 边上的动点，将△BEF 沿直线EF 折叠得到△GEF ，点B 的对应点为点G ，连接DE ，有下列4个结论：①tan B =2；②DE =10；③当GE ⊥BC 时，EF =32；④若点G 恰好落在线段DE 上时，则AF BF=13．其中正确的是()A.①②③B.②③④C.①③④D.①②④【答案】D【分析】过点A 作AH ⊥BC 于点H ，利用三线和一以及正切的定义，求出tan B ，即可判断①；过点D 作DK ⊥BC 于点K ，利用勾股定理求出DE ，判断②；过点F 作FM ⊥BC 于点M ，证明△EMF 为等腰直角三角形，设EM =FM =x ，三角函数求出BM 的长，利用BE =BM +EM ，求出x 的值，进而求出EF 的长，判断③；证明△AND ∽△CNE ，推出∠ENC =∠ECN ，根据折叠的性质，推出EF ∥CA ，利用平行线分线段成比例，即可得出结论，判断④．【详解】解：①过点A 作AH ⊥BC 于点H ，∵BC =8,AB =AC =45，∴BH =12BC =4，∴AH =AB 2-BH 2=8，∴tan B =AHBH=2；故①正确；②过点D 作DK ⊥BC 于点K ，则：四边形AHKD 为矩形，∴DK =AH =8，HK =AD =BC =8，∵BE =6，∴CE =2，∵CH =12BC =4，∴CK =4，∴EK =CE +CK =6，∴DE =EK 2+DK 2=10；故②正确；③过点F 作FM ⊥BC 于点M ，∵GE ⊥BC ，∴∠BEG =90°，∵翻折，∴∠BEF =∠GEF =45°，∴∠EFM =∠BEF =45°，∴EM =FM ，设EM =FM =x ，∵tan B =FMBM =2，∴BM =12FM =12x ，∴BE =BM +EM =12x +x =6，∴x =4，∴EM =FM =4，∴EF =2EM =42；故③错误；④当点G 恰好落在线段DE 上时，如图：设AC 与DE 交于点N ，∵▱ABCD ，∴AD ∥BC ，∴△AND ∽△CNE ，∴EN DN =CE AD=28=14，∴EN DE =15，∴EN =15DE =2=CE ，∴∠ENC =∠ECN ，∴∠BEN =∠ENC +∠ECN =2∠ECN ，∵翻折，∴∠BEN =2∠BEF ，∴∠BEF =∠ECN ，∴EF ∥AC ，∴AF BF =CE BE=26=13；故④正确，综上：正确的是①②④；故选D ．【点睛】本题考查平行四边形的折叠问题，同时考查了解直角三角形，相似三角形的判定和性质，等腰三角形的判定和性质，勾股定理．本题的综合性强，难度较大，是中考常见的压轴题，熟练掌握相关性质，添加合适的辅助线，构造特殊三角形，是解题的关键．4如图，AB 是⊙O 的直径，点C 是⊙O 上一点，将劣弧BC 沿弦BC 折叠交直径AB 于点D ，连接CD ，若∠ABC =α0°<α<45° ，则下列式子正确的是()A.sin α=BCABB.sin α=CD ABC.cos α=AD BDD.cos α=CD BC【答案】B【分析】连AC ，由AB 是⊙O 的直径，可知∠ACB =90°，由折叠，AC和CD所在的圆为等圆，可推得AC =CD ，再利用正弦定义求解即可．【详解】解：连AC ，∵AB 是⊙O 的直径，∴∠ACB =90°，由折叠，AC 和CD所在的圆为等圆，又∵∠CBD =∠ABC ，∴AC和CD所对的圆周角相等，∴AC=CD，∴AC =CD ，在Rt △ACB 中，sin α=AC AB =CDAB，故选：B ．【点睛】本题考查圆周角定理和圆心角、弦、弧之间的关系以及正弦、余弦定义，解答关键是通过折叠找到公共的圆周角推出等弦．5如图，在平面直角坐标系中，OA 在x 轴正半轴上，OC 在y 轴正半轴上，以OA ，OC 为边构造矩形OABC ，点B 的坐标为8,6 ，D ，E 分别为OA ，BC 的中点，将△ABE 沿AE 折叠，点B 的对应点F 恰好落在CD 上，则点F 的坐标为()A.3213,3013B.3013,3213C.3013,2013D.2013,3013【答案】A【分析】先求得直线CD 的解析式，过点F 作FM ⊥CE 于点M ，过点F 作FN ⊥OC 于点N ，设点F m ,-32m +6 ，在Rt △EMF 中，再利用勾股定理得到关于m 的方程，解方程即可．【详解】解：∵点B 的坐标为8,6 ，四边形OABC 是矩形，D ，E 分别为OA ，BC 的中点，∴C 0,6 ，D 4,0 ，E 4,6 ，由折叠的性质可得：EF =BE =4，设直线CD 的解析式为y =kx +b ，则6=b 4k +b =0 ，解得：k =-32b =6，∴直线CD 的解析式为y =-32x +6，过点F 作FM ⊥CE 于点M ，过点F 作FN ⊥OC 于点N ，设点F m,-32m+6，则MF=CN=6--32m+6=32m，EM=4-m，在Rt△EMF中，EM2+MF2=EF2，∴4-m2+32m2=42，解得：m=3213或m=0(不合题意，舍去)，当m=3213时，y=-32×3213+6=3013，∴点F的坐标为3213,30 13，故选：A．【点睛】本题是一次函数与几何综合题，考查了求一次函数解析式，勾股定理，翻折的性质，矩形的性质，中点的性质，熟练掌握知识点并灵活运用是解题的关键．6综合与实践课上，李老师让同学们以矩形纸片的折叠为主题开展数学活动．如图，将矩形纸片ABCD对折，折痕为EF，再把点A折叠在折痕EF上，其对应点为A ，折痕为DP，连接A B，若AB=2，BC =3，则tan∠A BF的值为()A.33B.3 C.32D.12【答案】A【分析】先证明EF=AB=CD=2，CF=BF=DE=32，∠DEA=90°，∠A FB=90°，AD=A D=3，可得A E=A D2-DE2=32，AF=2-32=12，再利用正切的定义求解即可.【详解】解：∵矩形纸片ABCD对折，折痕为EF，AB=2，BC=3，∴EF=AB=CD=2，CF=BF=DE=32，∠DEA=90°，∠A FB=90°，由折叠可得：AD=A D=3，∴A E=A D2-DE2=32，∴A F=2-32=12，∴tan ∠A BF =1232=33.故选A【点睛】本题考查的是轴对称的性质,矩形的性质,勾股定理的应用,求解锐角的正切,熟记轴对称的性质是解本题的关键.7如图，矩形ABCD 中，AB =2，BC =3，P 是边BC 中点，将顶点D 折叠至线段AP 上一点D ，折痕为EF ，此时，点C 折叠至点C ．下列说法中错误的是()A.cos ∠BAP =45B.当AE =53时，D E ⊥AP C.当AE =18-65时，△AD E 是等腰三角形 D.sin ∠DAP =45【答案】C【分析】根据矩形的性质，直角三角形的性质，三角函数，勾股定理，折叠的性质计算判断即可．【详解】∵矩形ABCD 中，AB =2，BC =3，P 是边BC 中点，∴BP =12BC =32，∠B =90°，∴AP =AB 2+BP 2=22+32 2=52，∴cos ∠BAP =AB AP=252=45，故A 正确；∵矩形ABCD ，∴AD ∥BC ，∴∠DAP =∠APB ，∴sin ∠DAP =sin ∠APB =cos ∠BAP =45，故D 正确；设DE =D E =x ，根据题意，得AE =AD -DE =3-x ，sin ∠DAP =45，∵D E ⊥AP ，∴sin ∠DAP =D E AE=x 3-x =45，解得x =43，∴AE =AD -DE =3-x =53，故B 正确；当D E =AE 时，∴x =3-x ，解得x =32；此时D ,A 重合，三角形不存在，不符合题意；当D E =AD 时，过点D 作D N ⊥AD 于点N ，则AN =NE ；∵矩形ABCD ，∴AD ∥BC ，∴∠DAP =∠APB ，∴cos ∠DAP =cos ∠APB =3252=35，设DE =D E =x ，根据题意，得AE =AD -DE =3-x ，D E =AD =x ，∴AN AD=AN x =35，解得AN =35x ；∴AE =AD -DE =3-x =2AN =65x ，解得x =1511；∴AE =65×1511=1811；当AE =AD 时，过点D 作D H ⊥AD 于点H ，设DE =D E =x ，根据题意，得AE =AD =AD -DE =3-x ，∴D H =AD sin ∠DAP =453-x ，AH =AD cos ∠DAP =353-x ，∴HE =AE -AH =3-x -353-x =253-x ，根据勾股定理，得HE 2+D H 2=D E 2，∴253-x 2+453-x2=x 2解得x =65-12；∴AE =3-x =15-65；综上所述，AE =15-65或AE =1811，故C 错误，故选C ．【点睛】本题考查了矩形的性质，直角三角形的性质，三角函数，勾股定理，折叠的性质，熟练掌握三角函数，勾股定理，矩形的性质，折叠的性质是解题的关键．8如图，AB 为半圆O 的直径，点O 为圆心，点C 是弧上的一点，沿CB 为折痕折叠BC交AB 于点M ，连接CM ，若点M 为AB 的黄金分割点(BM >AM )，则sin ∠BCM 的值为()A.5-12B.5+12C.5-14D.12【答案】A【分析】过点M作MD⊥CB，垂足为D，延长MD交半⊙O于点M′，连接CM ，BM′，根据折叠的性质可得：∠CMB=∠CM′B，BC⊥MM′，从而可得∠BDM=90°，再根据黄金分割的定义可得BMAB =5-12，然后利用直径所对的圆周角是直角可得∠ACB=90°，从而证明A字模型相似三角形△DBM∽△CBA，进而利用相似三角形的性质可得DMAC=BMAB=5-12，最后根据圆内接四边形对角互补以及平角定义定义可得：∠A=∠AMC，从而可得CA=CM，再在Rt△CDM中，利用锐角三角函数的定义进行计算，即可解答．【详解】解：过点M作MD⊥CB，垂足为D，延长MD交半⊙O于点M′，连接CM ，BM′，由折叠得：∠CMB=∠CM′B，BC⊥MM′，∴∠BDM=90°，∵点M为AB的黄金分割点(BM>AM)，∴BMAB =5-12，∵AB为半圆O的直径，∴∠ACB=90°，∴∠ACB=∠MDB，∵∠DBM=∠CBA，∴△DBM∽△CBA，∴DMAC =BMAB=5-12，∵四边形ACM′B是半⊙O的内接四边形，∴∠A+∠CM′B=180°，∵∠AMC+∠CMB=180°，∠CMB=∠CM′B，∴∠A=∠AMC，∴CA=CM，在Rt△CDM中，sin∠BCM=DMCM=DMAC=5-12．故选：A．【点睛】本题考查了相似三角形的判定与性质，黄金分割，解直角三角形，翻折变换(折叠问题)，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．二、填空题9如图，将一张矩形纸片ABCD折叠，折痕为EF，折叠后，EC的对应边EH经过点A，CD的对应边HG交BA的延长线于点P．若PA=PG，AH=BE，CD=3，则BC的长为．【答案】43【分析】本题考查了矩形与折叠问题，全等三角形的判定和性质，勾股定理．连接PF ，设BC =2x ，AH =BE=a ，证明Rt △PAF ≌Rt △PGF HL ，求得FA =FG =FD =x ，由折叠的性质求得BE =12x ，在Rt △ABE中，利用勾股定理列式计算，即可求解．【详解】解：连接PF ，设BC =2x ，AH =BE =a ，由矩形的性质和折叠的性质知FG =FD ，∠G =∠FAP =90°，AB =CD =3，AD =BC ，∵PA =PG ，PF =PF ，∴Rt △PAF ≌Rt △PGF HL ，∴FA =FG =FD =12AD =12BC =x ，由矩形的性质知：AD ∥BC ∴∠AFE =∠FEC ，折叠的性质知：∠FEA =∠FEC ，∴∠FEA =∠AFE ，∴AE =FA =x ，由折叠的性质知EC =EH =AE +AH =x +a ，∴BC =BE +EC =a +x +a =2x ，∴a =12x ，即BE =12x ，在Rt △ABE 中，AB 2+BE 2=AE 2，即32+12x 2=x 2，解得x =23，∴BC =2x =43，故答案为：4310如图，在矩形ABCD 中，AB =3，AD =6，M 为AD 的中点，N 为BC 边上一动点，把矩形沿MN 折叠，点A ，B 的对应点分别为A ，B ，连接AA '并延长交射线CD 于点P ，交MN 于点O ，当N 恰好运动到BC 的三等分点处时，CP 的长为．【答案】1或5【分析】分两种情况：①当CN =2BN 时．过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形；②当BN =2CN 时，过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形，根据矩形的性质得GM =AM -AG =1.再由折叠的性质可得∠AOM =90°，然后根据相似三角形的判定与性质可得答案．【详解】解：①当CN =2BN 时．如图1，过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形，∴NG =AB =3，AG =BN =2．∵M 为AD 的中点，∴AM =3，∴GM =AM -AG =1．由折叠A 与A 对应，∴∠AOM =90°，∵∠MAO +∠APD =90°，∠MAO +∠AMO =90°，∴∠AMO =∠APD ，即∠GMN =∠APD ．又∵∠NGM =∠ADP =90°，∴△ADP ∽△NGM ，∴NG AD=GM DP =12，解得DP =2，∴CP =CD -DP =1．②当BN =2CN 时，如图2，过点N 作NG ⊥AD 于点G ，则四边形ABNG 为矩形，∴NG =AB =3，AG =BN =4．∵M 为AD 的中点，∴AM =3，∴GM =AG -AM =1．由折叠A 与A 对应，∴∠AOM =90°∠MAO +∠AMO =90°，∠MAO +∠APD =90°，∴∠AMO =∠APD ，即∠GMN =∠APD ．又∠ADP =∠NGM =90°，∴△ADP ∽△NGM ，∴NG AD=GM DP =12，解得DP =2，∴CP =CD +DP =5．综上，CP 的长为1或5．故答案为：1或5．【点睛】此题考查的是翻折变换-折叠问题、矩形的性质，正确作出辅助线是解决此题的关键．11如图，DE 平分等边△ABC 的面积，折叠△BDE 得到△FDE ,AC 分别与DF ,EF 相交于G ,H 两点．若DG =m ,EH =n ，用含m ,n 的式子表示GH 的长是．【答案】m 2+n 2【分析】先根据折叠的性质可得S △BDE =S △FDE ，∠F =∠B =60°，从而可得S △FHG =S △ADG +S △CHE ，再根据相似三角形的判定可证△ADG ∽△FHG ,△CHE ∽△FHG ，根据相似三角形的性质可得S △ADG S △FHG =DG GH2=m 2GH 2，S △CHE S △FHG =EH GH 2=n 2GH 2，然后将两个等式相加即可得．【详解】解：∵△ABC 是等边三角形，∴∠A =∠B =∠C =60°，∵折叠△BDE 得到△FDE ，∴△BDE ≌△FDE ，∴S △BDE =S △FDE ，∠F =∠B =60°=∠A =∠C ，∵DE 平分等边△ABC 的面积，∴S 梯形ACED =S △BDE =S △FDE ，∴S △FHG =S △ADG +S △CHE ，又∵∠AGD =∠FGH ,∠CHE =∠FHG ，∴△ADG ∽△FHG ,△CHE ∽△FHG ，∴S △ADG S △FHG =DG GH 2=m 2GH 2，S △CHE S △FHG =EH GH 2=n 2GH 2，∴S △ADG S △FHG +S △CHE S △FHG =m 2+n 2GH 2=S △ADG +S △CHE S △FHG =1，∴GH 2=m 2+n 2，解得GH =m 2+n 2或GH =-m 2+n 2(不符合题意，舍去)，故答案为：m 2+n 2．【点睛】本题考查了等边三角形的性质、折叠的性质、相似三角形的判定与性质等知识点，熟练掌握相似三角形的判定与性质是解题关键．12在矩形ABCD 中，点E 为AD 边上一点(不与端点重合)，连接BE ，将矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，连接并延长EF ，BF 分别交BC ，CD 于G ，H 两点.若BA =6，BC =8，FH =CH ，则AE 的长为．【答案】92【分析】连接GH ，证明Rt △FHG ≅Rt △CHG (HL )，可得FG =CG ，设FG =CG =x ，在Rt △BFG 中，有62+x 2=(8-x )2，可解得CG =FG =74，知BG =254，由矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，得∠AEB =∠FEB ，可得∠FEB =∠EBG ，EG =BG =254，故EF =EG -FG =92，从而得到AE =92．【详解】连接GH ，如图：∵四边形ABCD 是矩形，∴∠A =∠C =90°，∵将矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，∴BF =AB =6,AE =EF ,∠BFE =∠A =90°，∴∠GFH =90°=∠C ，∵GH =GH ,FH =CH ，∴Rt △FHG ≅Rt △CHG (HL )，∴FG =CG ，设FG =CG =x ，则BG =BC -CG =8-x在Rt △BFG 中，BF 2+FG 2=BG 2∴62+x 2=(8-x )2，解得：x =74，∴CG =FG =74，∴BG =8-x =25x，∵将矩形ABCD 沿BE 折叠，折叠后点A 与点F 重合，∴∠AEB =∠FEB ，∵AD ⎳BC ，∴∠AEB =∠EBG ，∴∠FEB =∠EBG ，∴EG =BG =254，∴AE =92，故答案为：92．【点睛】本题考查矩形中的翻折变换，涉及三角形全等的判定与性质，勾股定理及应用，掌握相关知识是解题的关键．13如图，在矩形ABCD 中，AD =23，CD =6，E 是AB 的中点，F 是线段BC 上的一点，连接EF ，把△BEF 沿EF 折叠，使点B 落在点G 处，连接DG ，BG 的延长线交线段CD 于点H ．给出下列判断：①∠BAC =30°；②△EBF ∽△BCH ；③当∠EGD =90°时，DG 的长度是23 ④线段DG 长度的最小值是21-3；⑤当点G 落在矩形ABCD 的对角线上，BG 的长度是3或33；其中正确的是．(写出所有正确判断的序号)【答案】①②③【分析】利用正切函数的定义即可判断①正确；利用同角的余角相等推出∠HBC =∠BEF ，可判断②正确；推出点D 、G 、F 三点共线，证明Rt △EAD ≌Rt △EGD HL ，可判断③正确；当点D 、G 、E 三点共线，线段DG 长度的最小值是21-3，由于F 是线段BC 上的一点，不存在D 、G 、E 三点共线，可判断④不正确；证明△BGE 是等边三角形，可判断⑤．【详解】解：连接AC ，∵矩形ABCD 中，AD =23，CD =6，∴tan ∠ACD =AD CD=236=33，∴∠ACD =30°，∴∠BAC =30°，故①正确；由折叠的性质知EF 是BG 的垂直平分线，∴∠HBC +∠BFE =90°=∠BEF +∠BFE ，∴∠HBC =∠BEF ，∴△EBF ∽△BCH ，故②正确；由折叠的性质知∠EGF =∠ABC =90°，∵∠EGD =90°，∴点D 、G 、F 三点共线，连接DE ，在Rt △EAD 和Rt △EGD 中，AE =BE =EG ，DE =DE ，∴Rt △EAD ≌Rt △EGD HL ，∴DG =AD =23，故③正确；∵AE =BE =EG ，∴点A 、G 、B 都在以E 为圆心，3为半径的圆上，DE =23 2+32=21，∴当点D 、G 、E 三点共线，线段DG 长度的最小值是21-3，但F 是线段BC 上的一点，∴D 、G 、E 三点不可能共线，故④不正确；当点G 落在矩形ABCD 的对角线AC 上时，由折叠的性质知BE =EG ，∵E 是AB 的中点，由①知∠BAC =30°，∴BE =EG =EA ，∠BAC =∠EGA =30°，∴∠BEG =∠BAC +∠EGA =60°，∴△BGE 是等边三角形，∴BG 的长度是3；由于F 是线段BC 上的一点，则点G 不会落在矩形ABCD 的对角线BD 上，故⑤不正确；综上，①②③说法正确，故答案为：①②③．【点睛】本题考查了矩形与折叠问题，正切函数，相似三角形的判定，勾股定理等知识，解答本题的关键是明确题意，找出所求问题需要的条件．14如图，将矩形ABCD沿BE折叠，点A与点A 重合，连接EA 并延长分别交BD、BC于点G、F，且BG=BF．(1)若∠AEB=55°，则∠GBF=；(2)若AB=3，BC=4，则ED=．【答案】40°/40度5-10/-10+5【分析】(1)先证明∠DEF=180°-2×55°=70°，∠BFG=∠DEF=70°，利用BG=BF，可得答案；(2)如图，过F作FQ⊥AD于Q，可得CF=DQ，FQ=CD=3，同理可得：∠BGF=∠BFG，∠DEG=∠BFG，而∠DGE=∠BGF，则∠DEG=∠DGE，设DE=DG=x，而BD=32+42=5，则BG=BF=5-x，CF=4-5-x=1，再求解EF=12+32=10，由折叠可得：A E=AE=4 =x-1，EQ=x-x-1-x，AF=10-4+x，利用cos∠BFA=cos∠FEQ，再建立方程求解即可．【详解】解：(1)∵∠AEB=55°，结合折叠可得：∠AEB=∠A EB=55°，∴∠DEF=180°-2×55°=70°，∵矩形ABCD，∴AD∥BC，∴∠BFG=∠DEF=70°，∵BG=BF，∴∠BGF=∠BFG=70°；∴∠GBF=180°-2×70°=40°；故答案为：40°．(2)如图，过F作FQ⊥AD于Q，∴四边形FCDQ是矩形，则CF=DQ，FQ=CD=3，同理可得：∠BGF=∠BFG，∠DEG=∠BFG，而∠DGE=∠BGF，∴∠DEG=∠DGE，∴设DE=DG=x，∵矩形ABCD，AB=3，BC=4，∴BD=32+42=5，∴BG=BF=5-x，∴CF=4-5-x=x-1，∴EQ=x-x-1=1，∴EF=12+32=10，由折叠可得：A E=AE=4-x，∴AF =10-4+x，∵∠QEF=∠BFA ，∴cos∠BFA =cos∠FEQ，∴EQEF=A FBF，∴110=10-4+x5-x，解得：x=5-10，经检验符合题意；∴DE=5-10．故答案为：5-10．【点睛】本题考查的是轴对称的性质，矩形的性质与判定，勾股定理的应用，锐角三角函数的应用，等腰三角形的判定与性质，熟练的利用以上知识解题是关键．三、解答题15综合与实践课上，老师让同学们以“正方形的折叠”为主题开展实践活动．(1)操作判断操作一：如图(1)，正方形纸片ABCD，点E是BC边上(点E不与点B，C重合)任意一点，沿AE折叠△ABE到△AFE，如图(2)所示；操作二：将图(2)沿过点F的直线折叠，使点E的对称点G落在AE上，得到折痕MN，点C的对称点记为H，如图(3)所示；操作三：将纸片展平，连接BM，如图(4)所示．根据以上操作，回答下列问题：①B，M，N三点(填“在”或“不在”)一条直线上；②AE和BN的位置关系是，数量关系是；③如图(5)，连接AN，改变点E在BC上的位置，(填“存在”或“不存在”)点E，使AN平分∠DAE．(2)迁移探究苏钰同学将正方形纸片换成矩形纸片ABCD，AB=4，BC=6，按照(1)中的方式操作，得到图(6)或图(7)．请完成下列探究：①当点N在CD上时，如图(6)，BE和CN有何数量关系？并说明理由；②当DN的长为1时，请直接写出BE的长．【答案】(1)①在，②AE⊥BN，相等；③不存在；(2)①BECN =23，理由见解析；②BE=2或165．【分析】(1)①E的对称点为E ，BF⊥EE ，MF⊥EE ，即可判断；②由①AE⊥BN，由同角的余角相等得∠BAE=∠CBN，由AAS可判定△ABE≌△BCN，由全等三角形的性质即可得证；③由AAS可判定△DAN≌△MAN，由全等三角形的性质得AM=AD，等量代换得AB=AM，与AB>AM矛盾，即可得证；(2)①由(1)中的②可判定△ABE∽△BCN，由三角形相似的性质即可求解；②当N在CD上时，△ABE∽△BCN，由三角形相似的性质即可求解；当N在AD上时，同理可判定△ABE∽△NAB，由三角形相似的性质即可求解．【详解】(1)解：①E的对称点为E ，∴BF⊥EE ，MF⊥EE ，∴B、F、M共线，故答案为：在；②由①知：B、F、M共线，N在FM上，∴AE⊥BN，∴∠AMB=90°，∴∠ABM+∠BAE=90°，∵四边形ABCD是正方形，∴∠ABC=∠BCN=90°，AB=BC，∴∠CBN+∠ABM=90°，∴∠BAE=∠CBN，在△ABE和△BCN中，∠BAE=∠CBN ∠ABC=∠BCN AB=BC，∴△ABE≌△BCN(AAS)，∴AE=BN，故答案为：相等；③不存在，理由如下：假如存在，∵AN平分∠DAE，∴∠DAN=∠MAN，∵四边形ABCD是正方形，AM⊥BN，∴∠D=∠AMN=90°，在△DAN和△MAN中，∠D=∠AMN∠DAN=∠MAN AN=ANN∴△DAN≌△MAN(AAS)，∴AM=AD，∵AD=AB，∴AB=AM，∵AB是Rt△ABM的斜边，∴AB>AM，∴AB =AM 与AB >AM 矛盾，故假设不成立，所以答案为：不存在；(2)解：①BE CN=23，理由如下：由(1)中的②得：∠BAE =∠CBN ，∠ABE =∠C =90°，∴△ABE ∽△BCN ，∴BE CN =AB BC=23；②当N 在CD 上时，CN =CD -DN =3，由①知：△ABE ∽△BCN ，∴BE CN =AB BC =23，∴BE =23CN =2，当N 在AD 上时，AN =AD -DN =5，∵∠BAE =∠CBN =∠ANB ，∠ABE =∠BAN =90°，∴△ABE ∽△NAB ，∴BE AB =AB AN ，∴BE 4=45，∴BE =165，综上所述：BE =2或165．【点睛】本题考查了折叠的性质，矩形的性质，正方形的性质，全等三角形的判定及性质，三角形相似的判定及性质，掌握相关的判定方法及性质，“十字架”典型问题的解法是解题的关键．16在矩形ABCD 中，AD =2AB =8，点P 是边CD 上的一个动点，将△BPC 沿直线BP 折叠得到△BPC ．(1)如图1，当点P 与点D 重合时，BC ′与AD 交于点E ，求BE 的长度；(2)当点P 为CD 的三等分点时，直线BC ′与直线AD 相交于点E ，求DE 的长度；(3)如图2，取AB 中点F ，连接DF ，若点C ′恰好落在DF 边上时，试判断四边形BFDP 的形状，并说明理由．【答案】(1)BE 的长度为5；(2)DE 的长度为113或83;(3)四边形BFDP 是平行四边形(理由见解析)【分析】本题利用了折叠的知识(折叠后的两个图形全等)以及矩形的性质(矩形的对边相等，对角相等)，以及平行四边形的判定有关知识．(1)利用矩形性质和折叠的性质可推出BE=DE，设BE=x,则DE=x,AE=8-x,利用勾股定理建立方程求解即可得出答案；(2)设DE=m,则AE=m+8，设BE交CD于G，可证得△AEB∽△CBG，得出CGAB =BCAE，即CG4=8m+8，求得CG=32m+8，分两种情况：当PC=13CD=43时，当PC=23CD=83时，分别添加辅助线构造相似三角形，利用相似三角形性质建立方程求解即可得出答案；(3)由中点定义可得AF=BF，过点C 作C M∥AD交AB于点M，过点F作FN⊥BC 于点N，由矩形性质和翻折的性质可得∠C BP=∠CBP=12∠C BC，可证得△FC M∽△FDA，得出FMAF=C MAD，再证得△BFN∽△BC M，进而推出FM=FN，利用角平分线的判定定理可得∠BC F=∠MC F=12∠BC M推出∠BC F=∠C BP，再由平行线的判定定理可得DF∥BP，运用平行四边形的判定定理即可证得四边形BFDP是平行四边形．【点睛】点睛片段【详解】(1)解：∵AD=2AB=8，∴AB=4，∵四边形ABCD是矩形，∴∠A=90°，AD∥BC，∴∠ADB=∠DBC，由折叠得：∠DBC=∠DBC ，∴∠ADB=∠DBC ，即∠EDB=∠EBD，∴BE=DE，设BE=x，则DE=x，AE=8-x，在Rt△ABE中，AE2+AB2=BE2，∴(8-x)2+42=x2，解得：x=5，∴BE的长度为5；(2)设DE=m，则AE=m+8，设BE交CD于G，∵四边形ABCD是矩形，∴BC=AD=8，CD=AB=4，AD∥BC，∠A=∠BCG=90°，∴∠AEB=∠CBG，∴△AEB∽△CBG，∴CG AB =BCAE，即CG4=8m+8，∴CG=32m+8，当PC=13CD=43时，BP=BC2+PC2=82+432=4373，连接CC ，过点C 作C H⊥CD于点H，如图，∵将△BPC沿直线BP折叠得到△BPC ，∴CC ⊥BP，△BPC ≌△BPC，∴S四边形BCPC =2S△BPC，∴1BP⋅CC =2×1BC⋅PC，即12×4373CC =2×12×8×43，∴CC =163737，∵∠C CH +∠BPC =90°，∠PBC +∠BPC =90°，∴∠C CH =∠PBC ，∵∠CHC =∠BCP =90°，∴△CC H ∽△BPC ，∴C H PC =CH BC =CC BP ，即CH 43=CH 8=1637374373，∴C H =1637，CH =9637，∵∠C HG =∠EDG =90°，∴C H ∥AE ，∴∠GC ′H =∠AEB ，∴△C GH ∽△EBA ，∴GH AB =C H AE ，即GH 4=1637m +8，∴GH =6437(m +8)，∵CH +GH =CG ，∴9637+6437(m +8)=32m +8，解得：m =113，经检验，m =113是该方程的解，∴DE =113；当PC =23CD =83时，BP =BC 2+PC 2=82+83 2=8103，连接CC ，过点C 作C H ⊥CD 交CD 的延长线于点H ，作C G ⊥AD 于点G ，如图，同理可得：CC =8105，同理△CC H ∽△BPC ，∴C H PC =CH BC =CC BP ，即CH 83=CH 8=81058103，∴C H =85，CH =245，∴DH =CH -CD =245-4=45，∵∠HDG =∠H =∠C GD =90°，∴四边形DGC H 是矩形，∴C G =DH =45，DG =C H =85，∵∠C GE =∠A =90°，∠C EG =∠BEA ，∴△C EG ∽△BEA ，∴EG AE =C G AB =454=15，∴AE =5EG ，∵AE +EG =AG =AD -DG =8-85=325，∴5EG +EG =325，∴EG =1615，∴DE =DG +EG =85+1615=83，综上所述，DE 的长度为113或83；(3)四边形BFDP 是平行四边形，理由如下：∵点F 是AB 的中点，∴AF =BF ，过点C 作C M ∥AD 交AB 于点M ，过点F 作FN ⊥BC 于点N ，如图，则∠FC M =∠ADF ，∵四边形ABCD 是矩形，∴AD ∥BC ,AB ∥CD ，∴C M ∥BC ，∴∠BC M =∠C BC ，由翻折得：∠C BP =∠CBP =12∠C BC ，BC =BC =8，∵C M ∥AD ，∴△FC M ∽△FDA ，∴FM AF =C M AD ，∴FM BF =C MBC ，∵∠BNF =∠BMC =90°，∠FBN =∠C BM ，∴△BFN ∼△BC M∴FN BF =C MBC ，∴FM BF =FN BF ，∴FM =FN ，又∵FM ⊥C M ，FN ⊥C B ，∴∠BC F =∠MC F =12∠BC M ，∴∠BC F =∠C BP ，∴DF ∥BP ，∴四边形BFDP 是平行四边形．17矩形ABCD 中，AB =6，AD =8，点E 为对角线AC 上一点，过点E 作EF ⊥AD 于点F ，EG ⊥AC 交边BC 于点G ，将△AEF 沿AC 折叠得△AEH ，连接HG ．(1)如图1，若点H 落在边BC 上，求证：AH =CH ；(2)如图2，若A ，H ，G 三点在同一条直线上，求HG 的长；(3)若△EHG 是以EG 为腰的等腰三角形，求EF 的长．【答案】(1)见解析(2)HG =94(3)EF =103或4【分析】(1)根据矩形的性质和翻折的性质证明∠ACH =∠HAC ，即可解决问题；(2)结合(1)的方法AG =CG ，解Rt △AEG ，Rt △HEG 分别求得EG ,HG ；(3)当△EHG 是以EG 为腰的等腰三角形时，分两种情况：①当EG =EH ，②当EG =HG ，结合(2)的方法，利用全等三角形的判定与性质和相似三角形的判定与性质即可解决问题．【详解】(1)∵四边形ABCD 是矩形，∴AD ∥BC ．∴∠DAE =∠ACH .∵△AHE 由△AFE 折叠得到，∴∠HAC =∠DAE ，∴∠HAC =∠ACH ，∴AH =CH ；(2)∵矩形ABCD 中，AB =6,AD =8．∴AC =10.当A ，H ，G 三点在同一条直线上时，∠EHG =90°．同(1)可得AG =CG ．又∵EG ⊥AC ，∴AE =12AC =5．∵∠AEH +∠HEG =90°，∠AEH +∠HAE =90°，∴∠HEG =∠HAC =∠CAD ．∵在Rt △AEG 中，tan ∠EAG =EG AE =34，∴EG =34AE =154．∵在Rt △HEG 中，sin ∠HEG =HG EG =35，∴HG =35EG =94．(3)①若EH =EG ，如图3①设EF =EH =EG =x ，∵EF ⊥AD ，∴EF ∥CD ，∴△AEF ∽△ACD ，∴AE AC =AF AD =EF CD ∴AE 10=AF 8=x 6∴AE =53x ,AF =43x ，∴AH =AF =43x ，∵∠AHE =∠CEG =90°，∠HAE =∠GCE ，EH =EH ，∴△AHE ≌△CGE AAS ，∴AH =CE ，∴43x =10-53x ，∴x =103∴EF =103．②若HG =GE ，如图3②．(图3②)过点G 作GM ⊥HE ，设EF =a ,∵EC =10-53a ，∵∠AHE =∠CEG =90°，∠HAE =∠GCE ，∴△AHE ∽△CGE ，∴EG =34EC =3410-53a =152-54a ，∵∠GME =∠EHA ，∠MGE =90°-∠MEG =∠HAE ，∴△MGE ∽△HEA ，∴ME AH =EG AE ，∵AH AE =AD AC =45，∴AH =45AE ，∴ME =45EG =45152-54a =6-a ，∴HE =2ME =12-2a =EF ，∴12-2a =a ，∴a =4，∴EF =4，综上，EF =103或4．【点睛】本题考查了矩形的性质，解直角三角形，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，等腰三角形的性质，翻折的性质，解决本题的关键是综合运用以上知识．18综合与实践【问题情境】数学活动课上，老师准备了若干张正方形纸片ABCD，组织同学们进行折纸探究活动．【初步尝试】把正方形对折，折痕为EF，然后展开，沿过点A与点E所在的直线折叠，点B落在点B 处，连接 B C，如图1，请直接写出∠AEB 与∠ECB 的数量关系．【能力提升】把正方形对折，折痕为EF，然后展开，沿过点A与BE上的点G所在的直线折叠，使点B落在EF上的点P处，连接PD，如图2，猜想∠APD的度数，并说明理由．【拓展延伸】在图2的条件下，作点A关于直线CP的对称点A ，连接PA ，BA ，AC，如图3，求∠PA B的度数．【答案】初步尝试：∠AEB =∠ECB ；能力提升：猜想：∠APD=60°，理由见解析；拓展延伸：∠PA B=15°【分析】初步尝试：连接BB ，由折叠的性质可知，BE=CE，BE=BE ，∠AEB=∠AEB ，BB ⊥AE，根据等边对等角的性质和三角形内角和定理，得出∠BB C=90°，推出AE∥CB ，即可得出答案；能力提升：根据正方形的性质和折叠的性质，易证△AFP≌△DFP SAS，从而证明△APD是等边三角形，即可得到答案；拓展延伸：连接A C、AA ，由(2)得△APD是等边三角形，进而得出∠PDC=30°，再结合等边对等角的性质和三角形内角和定理，求得∠PAC=15°，∠ACP=30°，由对称性质得：AC=A C，∠ACP=∠A CP=30°，证明△AA B≌△CA B SSS，得到∠CA B=30°，再由∠CA P=∠CAP=15°，即可求出∠PA B的度数．【详解】解：初步尝试：∠AEB =∠ECB ，理由如下：如图，连接BB ，由折叠的性质可知，BE=CE，BE=BE ，∠AEB=∠AEB ，BB ⊥AE，∴BE=CE=BE ，∴∠EBB =∠EB B，∠ECB =∠EB C，∵∠EBB +∠EB B+∠EB C+∠ECB =2∠EB B+∠EB C=180°，∴∠BB C=90°，即BB ⊥CB ，∴AE∥CB ，∴∠AEB=∠ECB ，∴∠AEB =∠ECB ；解：能力提升：猜想：∠APD=60°，理由如下：理由：∵四边形ABCD是正方形，∴AB=AD，∠ADC=90°，由折叠性质可得：AF =DF ，EF ⊥AD ，AB =AP ，在△AFP 和△DFP 中，AF =DF∠AFP =∠DFP =90°FP =FP，∴△AFP ≌△DFP SAS ，∴AP =PD ，∴AP =AD =PD ，∴△APD 是等边三角形，∴∠APD =60°；解：拓展延伸：如图，连接A C 、AA ，由(2)得△APD 是等边三角形，∴∠PAD =∠PDA =∠APD =60°，AP =DP =AD ，∵∠ADC =90°，∴∠PDC =30°，又∵PD =AD =DC ，∴∠DPC =∠DCP =12×180°-30° =75°，∠DAC =∠DCA =45°，∴∠PAC =∠PAD -∠DAC =60°-45°=15°，∠ACP =∠DCP -∠DCA =75°-45°=30°，由对称性质得：AC =A C ，∠ACP =∠A CP =30°，∴∠ACA =60°，∴△ACA 是等边三角形，在△AA B 与△CA B 中，A A =A CA B =A B AB =BC，∴△AA B ≌△CA B SSS ，∴∠AA B =∠CA B =12∠AA C =30°，又∵∠CA P =∠CAP =15°，∴∠PA B =∠CA B -∠CA P =15°．【点睛】本题考查了折叠的性质，等腰三角形的判定和性质，三角形内角和定理，正方形的性质，全等三角形的判定和性质，等边三角形的判定和性质等知识，作辅助线构造全等三角形是解题关键．19综合与实践数学活动课上，数学老师以“矩形纸片的折叠”为课题开展数学活动：将矩形纸片ABCD 对折，使得点A ，D 重合，点B ，C 重合，折痕为EF ，展开后沿过点B 的直线再次折叠纸片，点A 的对应点为点N ，折痕为BM ． (1)如图(1)若AB =BC ，则当点N 落在EF 上时，BF 和BN 的数量关系是，∠NBF 的度数为．思考探究：(2)在AB=BC的条件下进一步进行探究，将△BMN沿BN所在的直线折叠，点M的对应点为点M ．当点M 落在CD上时，如图(2)，设BN，BM 分别交EF于点J，K．若DM =4，请求出三角形BJK的面积．开放拓展：(3)如图(3)，在矩形纸片ABCD中，AB=2，AD=4，将纸片沿过点B的直线折叠，折痕为BM，点A的对应点为点N，展开后再将四边形ABNM沿BN所在的直线折叠，点A的对应点为点P，点M的对应点为点M ，连接CP，DP，若PC=PD，请直接写出AM的长．(温馨提示：12+3=2-3，12+1=2-1)【答案】(1)BF=12BN，60°(2)2+2(3)4-23【分析】(1)根据折叠的性质得：AB=BN，BF=CF=12BC，根据直角三角形的性质可得∠BNF=30°，由直角三角形的两锐角互余可得结论；(2)由折叠得：BM=BM ，证明Rt△ABM≌Rt△CBM (HL)，可知AM=CM ，∠ABM=∠CBM ，得△BFJ是等腰直角三角形，再证明四边形ABCD是正方形，分别计算BF=FJ=12BC=2+2，JK=2，由三角形面积公式可得结论；(3)如图(3)，过点P作PG⊥BC于G，PH⊥CD于H，根据等腰三角形的三线合一可得DH=CH=12CD=12AB=1，由折叠的性质和矩形的性质可得PG=CH=1，BN=BP=AB=2，∠NBP=∠ABN，设PL=x，则M L=2x，M P=3x，根据NL=233=NM +M L，列方程可解答．【详解】(1)解：由折叠得：AB=BN，BF=CF，∠BFN=90°，∵AB=BC，∴BF=12BN，∴∠BNF=30°，∴∠NBF=90°-30°=60°，故答案为：BF=12BN，60°；(2)由折叠得：BM=BM ，∵四边形ABCD是矩形，∴∠A=∠C=90°，∵AB=BC，∴Rt△ABM≌Rt△CBM (HL)，∴AM=CM ，∠ABM=∠CBM ，∴∠ABM=∠MBN=∠NBM =∠CBM ，∴∠FBJ=45°，∴△BFJ是等腰直角三角形，∵四边形ABCD是矩形，AB=BC，∴矩形ABCD是正方形，∴AD=CD，∠D=90°，∴DM=DM =4，∴MM =42，∵AM=MN=M N=CM ，∴CM =22，∴BC =CD =4+22，∴BF =FC =2+2，∵FK ∥CM ，∴BK =KM ，∴FK =12CM =2，∵△BFJ 是等腰直角三角形，∴BF =FJ =12BC =2+2，∴JK =2+2-2=2，∴S △BJK =12⋅JK ⋅BF =12×2×(2+2)=2+2；(3)如图，过点P 作PG ⊥BC 于G ，PH ⊥CD 于H ，∵PC =PD ，∴DH =CH =12CD =12AB =1，∵∠PGC =∠PHC =∠BCH =90°，∵四边形PGCH 是矩形，∴PG =CH =1，由折叠得：BN =BP =AB =2，∠NBP =∠ABN ，Rt △BPG 中，∠PBG =30°，∴∠ABN =∠NBP =90°-30°2=30°，延长NM ，BP 交于L ，Rt △BNL 中，BN =2，∠NBL =30°，∴NL =2×33=233，Rt △M PL 中，∠M LP =90°-30°=60°，∴∠PM L =30°，设PL =x ，则M L =2x ，M P =3x ，∵NL =233=NM +M L ，∴3x +2x =233，∴x =433-2，∴AM =3x =3×433-2 =4-23．【点睛】本题是四边形的综合题，考查了折叠的性质，含30°角的直角三角形的性质，矩形的性质和判定，正方形的判定和性质，三角函数等知识，掌握折叠的性质和正确作辅助线是解题的关键，题目具有一定的综合性，比较新颖．20综合与实践综合与实践课上，老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动．(1)操作判断如图1，先用对折的方式确定矩形ABCD 的边AB 的中点E ，再沿DE 折叠，点A 落在点F 处，把纸片展平，延长DF ，与BC 交点为G ．。

近6年全国各地中考数学真题压轴题训练——几何图形的证明（100题）（解析版) 1．把正方形ABCD绕着点A，按顺时针方向旋转得到正方形AEFG，边FG与BC交于点H（如图）．试问线段HG与线段HB相等吗？请先观察猜想，然后再证明你的猜想．【答案】解：．证法1：连结，四边形，都是正方形．．由题意知，又．，．证法2：连结．四边形，都是正方形，．由题意知．．．．【解析】试题分析：要证明HG与HB是否相等，可以把线段放在两个三角形中证明这两个三角形全等，或放在一个三角形中证明这个三角形是等腰三角形，而图中没有这样的三角形，因此需要作辅助线，构造三角形．试题解析：HG=HB，证法1：连接AH，∵四边形ABCD，AEFG都是正方形，∴∠B=∠G=90°，由题意知AG=AB，又AH=AH，∴Rt AGH≌Rt ABH（HL），∴HG=HB．证法2：连接GB，∵四边形ABCD，AEFG都是正方形，∴∠ABC=∠AGF=90°，由题意知AB=AG，∴∠AGB=∠ABG，∴∠HGB=∠HBG，∴HG=HB．考点;1.正方形的性质；2.全等三角形的判定.2．（13分）如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点．（1）求证：ADP≌△ECP；（2）若BP=n•PK，试求出n的值；（3）作BM丄AE于点M，作KN丄AE于点N，连结MO、NO，如图2所示，请证明MON是等腰三角形，并直接写出∠MON的度数．【答案】（1）证明见试题解析；（2）3；（3）证明见试题解析，120°．【解析】试题分析：（1）由菱形的性质得到AD∥BC，根据由平行线的性质得到∠DAP=∠CEP，∠ADP=∠ECP，根据全等三角形的判定定理证明结论；（2）作PI∥CE交DE于I，由点P是CD的中点证明CE=2PI，BE=4PI，根据相似三角形的性质证明结论；（3）作OG⊥AE于G，由平行线等分线段定理得到MG=NG，又OG⊥MN，可证明MON是等腰三角形，由直角三角形的性质和锐角三角函数求出∠MON的度数．试题解析：（1）∵四边形ABCD为菱形，∴AD∥BC，∴∠DAP=∠CEP，∠ADP=∠ECP，在ADP和ECP中，∵∠DAP=∠CEP，∠ADP=∠ECP，DP=CP，∴△ADP≌△ECP；（2）如图1，作PI∥CE交DE于I，则，又点P是CD的中点，∴，∵△ADP≌△ECP，∴AD=CE，∴，∴BP=3PK，∴n=3；（3）如图2，作OG⊥AE于G，∵BM丄AE于，KN丄AE，∴BM∥OG∥KN，∵点O是线段BK的中点，∴MG=NG，又OG⊥MN，∴OM=ON，即MON是等腰三角形，由题意得，BPC，AMB，ABP为直角三角形，设BC=2，则CP=1，由勾股定理得，BP=，则AP=，根据三角形面积公式，BM=，由（2）得，PB=3PO，∴OG=BM=，MG=MP=，tan∠MOG=，∴∠MOG=60°，∴∠MON的度数为120°．考点：1．四边形综合题；2．压轴题．3．如图，EF=BC，DF=AC，DA=EB．求证：∠F=∠C．【答案】见解析.【解析】【分析】欲证明∠F ＝∠C ，只要证明△ABC ≌△DEF(SSS)即可.【详解】证明：DA BE =，DE AB ∴=，在ABC ∆和DEF ∆中，AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩，()ABC DEF SSS ∴∆≅∆，C F ∴∠=∠．【点睛】本题主要考查全等三角形的判定与性质.4．如图，平行四边形ABCD 中，AB=3cm ，BC=5cm ，∠B=60°，G 是CD 的中点，E 是边AD 上的动点，EG 的延长线与BC 的延长线交于点F ，连接CE ，DF ．（1）求证：四边形CEDF 是平行四边形；（2）①当AE= cm 时，四边形CEDF 是矩形；②当AE= cm 时，四边形CEDF 是菱形；（直接写出答案，不需要说明理由）【答案】（1）证明见解析；（2）① 当AE ＝3．5cm 时，四边形CEDF 是矩形．② 当AE ＝2cm 时，四边形CEDF 是菱形．【解析】【详解】（1）∵ 四边形ABCD 是平行四边形， ∴ CF ∥ED ， ∴ ∠FCG ＝∠EDG ，∵ G 是CD 的中点，∴ CG ＝DG ，在 FCG和 EDG 中，{FCG EDGCG DG CGF DGE∠=∠=∠=∠，∴ FCG ≌△EDG （ASA ），∴ FG ＝EG ，∵ CG ＝DG ，∴ 四边形CEDF 是平行四边形；(2)①当AE=3.5时，平行四边形CEDF 是矩形，理由是：过A 作AM ⊥BC 于M ，∵∠B=60°，AB=3，∴BM=1.5，∵四边形ABCD 是平行四边形，∴∠CDA=∠B=60°，DC=AB=3，BC=AD=5，∵AE=3.5，∴DE=1.5=BM ，在 MBA 和 EDC 中，BM DE B CDA AB CD =⎧⎪∠=∠⎨⎪=⎩∴ MBA ≌ EDC(SAS)，∴∠CED=∠AMB=90°，∵四边形CEDF 是平行四边形，∴四边形CEDF 是矩形，故答案为：3.5；②当AE=2时，四边形CEDF 是菱形，理由是：∵AD=5,AE=2,∴DE=3，∵CD=3,∠CDE=60°，∴ CDE 是等边三角形，∴CE=DE ，∵四边形CEDF 是平行四边形，∴四边形CEDF 是菱形，故答案为： 2.考点：1．平行四边形的性质；2．全等三角形的判定与性质；3．矩形的判定；4．菱形的判定．5．在ABCD 中，BE 平分ABC ∠交AD 于点E ．（1）如图1，若30D ︒∠=，AB =，求ABE ∆的面积；（2）如图2，过点A 作AF DC ⊥，交DC 的延长线于点F ，分别交BE ，BC 于点G ，H ，且 AB AF =．求证：ED AG FC -=．【答案】（1）32；（2）证明见解析. 【解析】【分析】（1）作BO AD ⊥于O ，由平行四边形的性质得出30BAO D ︒∠=∠=，由直角三角形的性质得出12BQ AB ==，证出ABE AEB ∠=∠，得出AE AB == （2）作AQ BE ⊥交DF 的延长线于P ，垂足为Q ，连接PB 、PE ，证明ABG AFP ∆≅∆得出AG FP =，再证明BPC PED ∆≅∆得出PC ED =，即可得出结论．【详解】（1）解：作BO AD ⊥于O ，如图1所示：∵四边形ABCD 是平行四边形，∴AD BC ∥，AB CD ∥，AB CD =，30ABC D ︒∠=∠=，∴AEB CBE ∠=∠，30BAO D ︒∠=∠=，∴12BQ AB ==， ∵BE 平分ABC ∠，∴ABE CBE ∠=∠，∴ABE AEB ∠=∠，∴AE AB ==∴ABE ∆的面积1132222AE BO =⨯=⨯=；（2）证明：作AQ BE ⊥交DF 的延长线于P ，垂足为Q ，连接PB 、PE ，如图2所示：∵AB AE =，AQ BE ⊥，∴ABE AEB ∠=∠，BQ EQ =，∴PB PE =，∴PBE PEB ∠=∠，∴ABP AEP ∠=∠，∵AB CD ∥，AF CD ⊥，∴AF AB ⊥，∴90BAF ︒∠=，∵AQ BE ⊥，∴ABG FAP ∠=∠，在ABG ∆和FAP ∆中，90ABG FAP AB AF BAG AFP ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩，∴(ASA)ABG AFP ∆≅∆，∴AG FP =，∵AB CD ∥，AD BC ∥，∴180ABP BPC ︒∠+∠=，BCP D ∠=∠，∵180AEP PED ︒∠+∠=，∴BPC PED ∠=∠，在BPC ∆和PED ∆中，BCP D BPC PED PB PE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴(AAS)BPC PED ∆≅∆，∴PC ED =，∴---ED AG PC AG PC FP FC ===．【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角三角形的性质、线段垂直平分线的性质等知识；熟练掌握平行四边形的性质，证明三角形全等是解题的关键．6．如图，点A 、D 、C 、F 在同一条直线上，AD=CF ，AB=DE ，BC=EF.(1)求证：ΔABC ≌ DEF ；(2)若∠A=55°，∠B=88°，求∠F 的度数.【答案】（1）证明见解析；（2）37°【解析】分析：（1）先证明AC=DF ，再运用SSS 证明 ABC ≌△DEF ；（2）根据三角形内角和定理可求∠ACB=37°，由（1）知∠F=∠ACB ，从而可得结论.解析：（1）∵AC=AD+DC ， DF=DC+CF ，且AD=CF∴AC=DF在 ABC 和 DEF 中，AB DE BC EF AC DF =⎧⎪=⎨⎪=⎩∴ ABC ≌△DEF （SSS ）（2）由（1）可知，∠F=∠ACB∵∠A=55°，∠B=88° ∴∠ACB=180°－（∠A+∠B ）=180°－（55°+88°）=37° ∴∠F=∠ACB=37°点睛：本题考查三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．7．如图，点D 在△ABC 的AB 边上，且∠ACD=∠A．（1）作△BDC的平分线DE，交BC于点E（用尺规作图法，保留作图痕迹，不要求写作法）；（2）在（1）的条件下，判断直线DE与直线AC的位置关系（不要求证明）.【答案】（1）作图见解析；（2）DE∥AC.【解析】【分析】(1)、根据角平分线的画法画出角平分线；(2)、根据角平分线的性质和三角形外角的性质得出DE和AC平行. 【详解】解：(1)、如图所示：（2）DE∥AC∵DE平分∠BDC，∴∠BDE=12∠BDC，∵∠ACD=∠A，∠ACD+∠A=∠BDC，∴∠A=12∠BDC，∴∠A=∠BDE，∴DE∥AC．(2)、DE∥AC.考点：(1)、角平分线的画法；(2)、角平分线的性质.8．如图，分别以Rt ABC的直角边AC及斜边AB向外作等边ACD，等边ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．（1）试说明AC=EF；（2）求证：四边形ADFE是平行四边形．【答案】证明见解析．【解析】【分析】（1）一方面Rt ABC中，由∠BAC=30°可以得到AB=2BC，另一方面ABE是等边三角形，EF⊥AB，由此得到AE=2AF，并且AB=2AF，从而可证明AFE≌△BCA，再根据全等三角形的性质即可证明AC=EF．（2）根据（1）知道EF=AC，而ACD是等边三角形，所以EF=AC=AD，并且AD⊥AB，而EF⊥AB，由此得到EF∥AD，再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形．【详解】证明：（1）∵Rt ABC中，∠BAC=30°，∴AB=2BC．又∵△ABE是等边三角形，EF⊥AB，∴AB=2AF．∴AF=BC．∵在Rt AFE和Rt BCA中，AF=BC，AE=BA，∴△AFE≌△BCA（HL）．∴AC=EF．（2）∵△ACD是等边三角形，∴∠DAC=60°，AC=AD．∴∠DAB=∠DAC+∠BAC=90°．∴EF∥AD．∵AC=EF，AC=AD，∴EF=AD．∴四边形ADFE是平行四边形．考点：1．全等三角形的判定与性质；2．等边三角形的性质；3．平行四边形的判定．9．如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：ABC与DEC 全等．【答案】证明过程见解析【解析】【分析】由∠BAE=∠BCE=∠ACD=90°，可求得∠DCE=∠ACB，且∠B+∠CEA=∠CEA+∠DEC=180°，可求得∠DEC=∠ABC，再结合条件可证明△ABC≌△DEC．【详解】∵∠BAE=∠BCE=∠ACD=90°，∴∠5+∠4=∠4+∠3，∴∠5=∠3，且∠B+∠CEA=180°，又∠7+∠CEA=180°，∴∠B=∠7，在△ABC 和△DEC 中537BC CE B ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC≌△DEC（ASA ）．10．如图， ABC 中，AB=AC ，点E ，F 在边BC 上，BE=CF ，点D 在AF 的延长线上，AD=AC ，（1）求证： ABE ≌△ACF ；（2）若∠BAE=30°，则∠ADC= °．【答案】（1）证明见解析；（2）75．【解析】【分析】（1）根据等边对等角可得∠B=∠ACF ，然后利用SAS 证明 ABE ≌△ACF 即可；（2）根据 ABE ≌△ACF ，可得∠CAF=∠BAE=30°，再根据AD=AC ，利用等腰三角形的性质即可求得∠ADC 的度数.【详解】（1）∵AB=AC ，∴∠B=∠ACF ，在 ABE 和 ACF 中，AB AC B ACF BE CF =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ACF （SAS ）；（2）∵△ABE ≌△ACF ，∠BAE=30°，∴∠CAF=∠BAE=30°， ∵AD=AC ，∴∠ADC=∠ACD ，∴∠ADC=280013︒-︒=75°， 故答案为75．【点睛】本题考查了全等三角形的判定与性质、等腰三角形的性质，熟练掌握相关性质与定理是解题的关键.11．如图， ABC 中，∠ACB ＞∠ABC ．（1）用直尺和圆规在∠ACB 的内部作射线CM ，使∠ACM =∠ABC （不要求写作法，保留作图痕迹）； （2）若（1）中的射线CM 交AB 于点D ，AB =9，AC =6，求AD 的长．【答案】（1）作图见解析；（2）4．【解析】试题分析：（1）根据尺规作图的方法，以AC 为一边，在∠ACB 的内部作∠ACM =∠ABC 即可；（2）根据 ACD 与 ABC 相似，运用相似三角形的对应边成比例进行计算即可．试题解析：解：（1）如图所示，射线CM 即为所求；（2）∵∠ACD =∠ABC ，∠CAD =∠BAC ，∴△ACD ∽△ABC ，∴AD AC AC AB =，即669AD =，∴AD =4． 点睛：本题主要考查了基本作图以及相似三角形的判定与性质的运用，解题时注意：两角对应相等的两个三角形相似；相似三角形的对应边成比例．12．已知：如图，点A 、D 、C 、B 在同一条直线上，AD=BC ，AE=BF ，CE=DF ，求证：AE ∥BF ．【答案】证明见解析.【解析】分析：可证明 ACE ≌△BDF ，得出∠A=∠B ，即可得出AE ∥BF ；详证明：∵AD=BC ，∴AC=BD ，在 ACE 和 BDF 中，AC BD AE BF CE DF ⎧⎪⎨⎪⎩＝＝＝，∴△ACE ≌△BDF （SSS ）∴∠A=∠B ，∴AE ∥BF ；点睛：本题考查了全等三角形的判定及性质以及平行线的判定问题，关键是用SSS 证明 ACE ≌△BDF ． 13．如图，AD 平分∠BAC ，AD ⊥BD ，垂足为点D ，DE ∥AC ．求证：△BDE 是等腰三角形．【答案】证明见解析．【解析】试题分析：直接利用平行线的性质得出∠1=∠3，进而利用角平分线的定义结合互余的性质得出∠B=∠BDE ，即可得出答案．试题解析：∵DE ∥AC ，∴∠1=∠3，∵AD 平分∠BAC ，∴∠1=∠2，∴∠2=∠3，∵AD ⊥BD ，∴∠2+∠B=90°，∠3+∠BDE=90°，∴∠B=∠BDE ，∴△BDE 是等腰三角形．考点：等腰三角形的判定；平行线的性质．14．在Rt ABC中，∠ABC=90°，∠BAC＝30°，将ABC绕点A顺时针旋转一定的角度α得到AED，点B、C 的对应点分别是E、D.(1)如图1，当点E恰好在AC上时，求∠CDE的度数；(2)如图2，若α=60°时，点F是边AC中点，求证：四边形BFDE是平行四边形.【答案】（1）15°；（2）证明见解析.【解析】【分析】（1）如图1，利用旋转的性质得CA＝DA，∠CAD＝∠BAC＝30°，∠DEA＝∠ABC＝90°，再根据等腰三角形的性质求出∠ADC，从而计算出∠CDE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝12AC，利用含30度的直角三角形三边的关系得到BC＝12AC，则BF＝BC，再根据旋转的性质得到∠BAE＝∠CAD＝60°，AB＝AE，AC＝AD ，DE＝BC，从而得到DE＝BF，ACD和BAE为等边三角形，接着由AFD≌△CBA得到DF＝BA，然后根据平行四边形的判定方法得到结论．【详解】解：（1）如图1，∵△ABC绕点A顺时针旋转α得到AED，点E恰好在AC上，∴CA＝CD，∠CAD＝∠BAC＝30°，∠DEA＝∠ABC＝90°，∵CA＝DA，∴∠ACD＝∠ADC＝12（180°−30°）＝75°，∠ADE=90°-30°=60°，∴∠CDE＝75°−60°＝15°；（2）证明：如图2，∵点F是边AC中点，∴BF＝12 AC，∵∠BAC＝30°，∴BC＝12 AC，∴BF＝BC，∵△ABC绕点A顺时针旋转60°得到AED，∴∠BAE＝∠CAD＝60°，AB＝AE，AC＝AD，DE＝BC，∴DE＝BF，ACD和BAE为等边三角形，∴BE＝AB，∵点F为ACD的边AC的中点，∴DF⊥AC，易证得AFD≌△CBA，∴DF＝BA，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了平行四边形的判定．15．综合与实践问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM．试判断线段AM与DE的位置关系．探究展示：勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：证明：∵BE=AB，∴AE=2AB．∵AD=2AB ，∴AD=AE ．∵四边形ABCD 是矩形，∴AD ∥BC ． ∴EM EB DM AB=．（依据1） ∵BE=AB ，∴1EM DM =．∴EM=DM ． 即AM 是 ADE 的DE 边上的中线，又∵AD=AE ，∴AM ⊥DE ．（依据2）∴AM 垂直平分DE ．反思交流：（1）①上述证明过程中的“依据1”“依据2”分别是指什么？②试判断图1中的点A 是否在线段GF 的垂直平分线上，请直接回答，不必证明；（2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE ，以CE 为一边在CE 的左下方作正方形CEFG ，发现点G 在线段BC 的垂直平分线上，请你给出证明；探索发现：（3）如图3，连接CE ，以CE 为一边在CE 的右上方作正方形CEFG ，可以发现点C ，点B 都在线段AE 的垂直平分线上，除此之外，请观察矩形ABCD 和正方形CEFG 的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．【答案】（1）详见解析；（2）详见解析；（3）详见解析.【解析】【分析】（1）①直接得出结论；②借助问题情景即可得出结论；（2）先判断出∠BCE+∠BEC=90°，进而判断出∠BEC=∠BCG ，得出 GHC ≌△CBE ，判断出AD=BC ，进而判断出HC=BH ，即可得出结论；（3）先判断出四边形BENM 为矩形，进而得出∠1+∠2=90°，再判断出∠1=∠3，得出 ENF ≌△EBC ，即可得出结论．【详解】（1）①依据1：两条直线被一组平行线所截，所得的对应线段成比例（或平行线分线段成比例）．依据2：等腰三角形顶角的平分线，底边上的中线及底边上的高互相重合（或等腰三角形的“三线合一”）．②答：点A在线段GF的垂直平分线上．理由：由问题情景知，AM⊥DE，∵四边形DEFG是正方形，∴DE∥FG，∴点A在线段GF的垂直平分线上．（2）证明：过点G作GH⊥BC于点H，∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=∠GHC=90°，∴∠BCE+∠BEC=90°．∵四边形CEFG为正方形，∴CG=CE，∠GCE=90°，∴∠BCE+∠BCG=90°．∴∠2BEC=∠BCG．∴△GHC≌△CBE．∴HC=BE，∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，BE=AB，∴BC=2BE=2HC，∴HC=BH．∴GH垂直平分BC．∴点G在BC的垂直平分线上．（3）答：点F在BC边的垂直平分线上（或点F在AD边的垂直平分线上）．过点F作FM⊥BC于点M，过点E作EN⊥FM于点N．∴∠BMN=∠ENM=∠ENF=90°．∵四边形ABCD是矩形，点E在AB的延长线上，∴∠CBE=∠ABC=90°，∴四边形BENM为矩形．∴BM=EN，∠BEN=90°．∴∠1+∠2=90°．∵四边形CEFG为正方形，∴EF=EC，∠CEF=90°．∴∠2+∠3=90°．∴∠1=∠3．∵∠CBE=∠ENF=90°，∴△ENF≌△EBC．∴NE=BE．∴BM=BE．∵四边形ABCD是矩形，∴AD=BC．∵AD=2AB，AB=BE．∴BC=2BM．∴BM=MC．∴FM垂直平分BC．∴点F在BC边的垂直平分线上．【点睛】此题是四边形综合题，主要考查了正方形的性质，矩形的性质，全等三角形的判定和性质，线段垂直平分线的判定和性质，构造全等三角形是解本题的关键．16．如图，在五边形ABCDE中，∠BCD=∠EDC=90°，BC=ED，AC=AD．（1）求证：ABC≌△AED；（2）当∠B=140°时，求∠BAE的度数．【答案】（1）详见解析；（2）80°．【分析】（1）根据∠ACD=∠ADC，∠BCD=∠EDC=90°，可得∠ACB=∠ADE，进而运用SAS即可判定全等三角形；（2）根据全等三角形对应角相等，运用五边形内角和，即可得到∠BAE的度数．【解析】【分析】（1）根据∠ACD=∠ADC，∠BCD=∠EDC=90°，可得∠ACB=∠ADE，进而运用SAS即可判定全等三角形；（2）根据全等三角形对应角相等，运用五边形内角和，即可得到∠BAE的度数．【详解】证明：（1）∵AC=AD ，∴∠ACD=∠ADC ，又∵∠BCD=∠EDC=90°，∴∠ACB=∠ADE ，在 ABC 和 AED 中，BC ED ACB ADE AC AD =⎧⎪∠=∠⎨⎪=⎩，∴△ABC ≌△AED （SAS ）；解：（2）当∠B=140°时，∠E=140°，又∵∠BCD=∠EDC=90°，∴五边形ABCDE 中，∠BAE=540°﹣140°×2﹣90°×2=80°．【点睛】考点：全等三角形的判定与性质．17．如图，在▱ABCD 中，E ，F 分别是AD ，BC 上的点，且DE=BF ，AC⊥EF．求证：四边形AECF 是菱形．【答案】见解析.【解析】【分析】根据对角线互相垂直的平行四边形是菱形即可证明【详解】 证明：四边形ABCD 是平行四边形，AD BC ∴=，//AD BC ，DE BF =，AE CF ∴=，//AE CF ，∴四边形AECF 是平行四边形，AC EF ⊥，∴四边形AECF 是菱形．【点睛】本题考查平行四边形的性质、菱形的判定等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．18．如图，AC=DC，BC=EC，∠ACD=∠BCE．求证：∠A=∠D．【答案】证明见试题解析．【解析】试题分析：首先根据∠ACD=∠BCE得出∠ACB=∠DCE，结合已知条件利用SAS判定ABC和DEC全等，从而得出答案.试题解析：∵∠ACD=∠BCE ∴∠ACB=∠DCE 又∵AC=DC BC=EC ∴△ABC≌△DEC ∴∠A=∠D考点：三角形全等的证明19．如图，在∆ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.求证：∠CBE=∠BAD．【答案】见解析【解析】试题分析：根据等腰三角形的性质得出∠ADC=∠BEC=90°，再根据∠C为公共角即可得∠CBE=∠CAD．试题解析：∵AB=AC，AD是BC边上的中线，∴AD⊥BC，又∵BE⊥AC，∴∠ADC=∠BEC=90°，∴∠CBE+∠C=∠CAD+∠C=90°，∴∠CBE=∠CAD．20．如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝OC，BO＝OD，且∠AOB＝2∠OAD．(1)求证：四边形ABCD是矩形；(2)若∠AOB∶∠ODC＝4∶3，求∠ADO的度数.【答案】(1)证明见解析；(2)∠ADO==36°.【解析】【分析】(1)先判断四边形ABCD是平行四边形，继而根据已知条件推导出AC=BD，然后根据对角线相等的平行四边形是矩形即可；(2)设∠AOB=4x，∠ODC=3x，则∠OCD=∠ODC=3x.，在ODC中，利用三角形内角和定理求出x的值，继而求得∠ODC的度数，由此即可求得答案.【详解】(1)∵AO＝OC，BO＝OD，∴四边形ABCD是平行四边形，又∵∠AOB＝2∠OAD，∠AOB是AOD的外角，∴∠AOB＝∠OAD＋∠ADO.∴∠OAD＝∠ADO.∴AO＝OD.又∵AC＝AO＋OC＝2AO，BD＝BO＋OD＝2OD，∴AC＝BD.∴四边形ABCD是矩形.(2)设∠AOB=4x，∠ODC=3x，则∠ODC=∠OCD=3x，在ODC中，∠DOC+∠OCD+∠CDO=180°∴4x+3x+3x=180°，解得x=18°，∴∠ODC=3×18°=54°，∵四边形ABCD是矩形，∴∠ADC=90°，∴∠ADO=∠ADC－∠ODC=90°－54°=36°.【点睛】本题考查了矩形的判定与性质，三角形内角和定理等知识，熟练掌握和灵活运用相关知识是解题的关键.21．如图，在□ABCD中，E、F分别是AB、DC边上的点，且AE=CF，（1）求证：≌. （2）若DEB=90，求证四边形DEBF 是矩形.【答案】（1）利用SAS 证明；（2）证明见解析.【解析】试题分析：此题考查了平行四边形的判定与性质、矩形的判定以及全等三角形的判定与性质．注意有一个角是直角的平行四边形是矩形，首先证得四边形ABCD 是平行四边形是关键．（1）由在□ABCD 中，AE=CF ，可利用SAS 判定 ADE ≌△CBF ．（2）由在▱ABCD 中，且AE=CF ，利用一组对边平行且相等的四边形是平行四边形，可证得四边形DEBF 是平行四边形，又由∠DEB=90°，可证得四边形DEBF 是矩形．试题解析：（1）∵四边形ABCD 是平行四边形，∴AD=CB ，∠A=∠C ，在 ADE 和 CBF 中，，∴ ADE ≌△CBF （SAS ）．（2）∵四边形ABCD 是平行四边形，∴AB=CD ，AB ∥CD ，∵AE=CF ，∴BE=DF ，∴四边形ABCD 是平行四边形，∵∠DEB=90°，∴四边形DEBF 是矩形．故答案为（1）利用SAS 证明；（2）证明见解析.考点：平行四边形的性质；全等三角形的判定与性质；矩形的判定．22．如图，ABC ∆中，90C =∠，4AC =，8BC =．（1）用直尺和圆规作AB 的垂直平分线；（保留作图痕迹，不要求写作法）（2）若（1）中所作的垂直平分线交BC 于点D ，求BD 的长．【答案】（1）详见解析；（2）5BD =．【解析】【分析】（1）分别以A ，B 为圆心，大于12AB 为半径画弧，两弧交于点M ，N ，作直线MN 即可． （2）设AD BD x ==，在Rt ACD ∆中，利用勾股定理构建方程即可解决问题．【详解】（1）如图直线MN 即为所求．（2）∵MN 垂直平分线段AB ，∴DA DB =，设DA DB x ==，在Rt ACD ∆中，∵222AD AC CD =+，∴()22248x x =+-，解得5x =，∴5BD =．【点睛】本题考查作图﹣基本作图，线段的垂直平分线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型． 23．如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC 的三个顶点坐标分别为A （1，4），B （1，1），C （3，1）．（1）画出△ABC 关于x 轴对称的△A 1B 1C 1；（2）画出△ABC 绕点O 逆时针旋转90°后的△A 2B 2C 2；（3）在（2）的条件下，求线段BC 扫过的面积（结果保留π）．【答案】（1）作图见解析；（2）作图见解析；（3）2π.【解析】【分析】（1）利用轴对称的性质画出图形即可；（2）利用旋转变换的性质画出图形即可；（3）BC 扫过的面积=22OCC OBB S S -扇形扇形，由此计算即可；【详解】（1） ABC 关于x 轴对称的 A 1B 1C 1如图所示；（2） ABC 绕点O 逆时针旋转90°后的 A 2B 2C 2如图所示；（3）BC 扫过的面积=22OCC OBB S S -扇形扇形=2290?90?360360ππ-=2π．【点睛】本题考查了利用轴对称和旋转变换作图，扇形面积公式等知识，熟练掌握网格结构准确找出对应点的位置是解题的关键．24．如图，AC 和BD 相交于点0，OA=OC, OB=OD ．求证：DC//AB【答案】证明见解析【解析】试题分析：根据SAS 可知 AOB ≌△COD ，从而得出∠A=∠C ，根据内错角相等两直线增选2的判定可得结论.． 试题解析：∵OA=OC ，∠AOB=∠COD ，OB=OD ，∴△AOB ≌△COD （SAS ）.∴∠A=∠C.∴AB ∥CD.考点：1.全等三角形的的判定和性质；2.平行的判定．25．如图所示，AC=AE ，∠1=∠2，AB=AD ．求证：BC=DE ．【答案】证明见解析.【解析】试题分析：由1=2∠∠，可得,CAB EAD ∠=∠,,AC AE AB AD ==则可证明ABC ADE ≅，因此可得.BC DE =试题解析：1=2∠∠，12,EAB EAB ∴∠+∠=∠+∠即CAB EAD ∠=∠,在ABC 和ADE 中，{AC AECAB EAD AB AD=∠=∠=(),ABC ADE SAS ∴≅.BC DE ∴=考点：三角形全等的判定．26．如图， ABC 中，∠BAC=90°，AB=AC ，AD ⊥BC ，垂足是D ，AE 平分∠BAD ，交BC 于点E.在 ABC 外有一点F ，使FA ⊥AE ，FC ⊥BC ．（1）求证：BE=CF ；（2）在AB 上取一点M ，使BM=2DE ，连接MC ，交AD 于点N ，连接ME.求证：①ME ⊥BC ；②DE=DN.【答案】（1）证明见解析；（2）①证明见解析；②证明见解析.【解析】试题分析：（1）通过角的转换和等腰直角三角形的性质，得到∠BAE=∠CAF 和∠B=∠FCA ，从而ASA 证明 ABF ≌△ACF ，根据全等三角形对应边相等得到结论.（2）①过E 点作EG ⊥AB 于点G ，通过证明EG 是BM 的垂直平分线就易得出结论.②通过证明Rt AMC ≌Rt EMC 和 ADE ≌△CDN 来证明结论.试题解析：（1）如图，∵∠BAC=90°，FA ⊥AE ，∴∠1+∠EAC=90°，∠2+∠EAC=90°. ∴∠1=∠2.又∵AB=AC ，∴∠B=∠ACB=45°.∵FC ⊥BC ，∴∠FCA=90°-∠ACB=45°.∴∠B=∠FCA.∴△ABF ≌△ACF （ASA ）.∴BE=CF.（2）①如图，过E 点作EG ⊥AB 于点G ，∵∠B=45°，∴△CBE 是等腰直角三角形.∴BG=EG ，∠3=45°. ∵BM=2DE ，∴BM=2BG ，即点G 是BM 的中点.∴EG 是BM 的垂直平分线.∴∠4=∠3=45°.∴∠MEB=∠4+∠3=90°.∴ME ⊥BC.②∵AD ⊥BC ，∴ME ∥AD.∴∠5=∠6.∵∠1=∠5，∴∠1=∠6.∴AM=EM.∵MC=MC ，∴Rt AMC ≌Rt EMC （HL ）.∴∠7=∠8.∵∠BAC=90°，，AB=AC ，∴∠ACB=45°，∠BAD=∠CAD=45°. ∴∠5=∠7=22.5°，AD=CD.∵∠ADE=∠CDN=90°，∴△ADE ≌△CDN （ASA ）.∴DE=DN.考点：1.等腰直角三角形的判定和性质；2.全等三角形的判定和性质；3.线段垂直平分线的判定和性质.27．如图，ABC △中，点E 在BC 边上，AE AB =，将线段AC 绕点A 旋转到AF 的位置，使得CAF BAE ∠=∠，连接EF ，EF 与AC 交于点G(1)求证：EF BC =；(2)若65ABC ∠=︒，28ACB ∠=︒，求FGC ∠的度数.【答案】(1)证明见解析；(2)78°.【解析】【分析】（1）因为CAF BAE ∠=∠，所以有BAC EAF ∠=∠，又因为AE AB AC AF ==，，所以有()BAC EAF SAS △≌△，得到EF BC =；（2）利用等腰三角形ABE 内角和定理，求得∠BAE=50°，即∠FAG=50°，又因为第一问证的三角形全等，得到28F C ∠=∠=︒，从而算出∠FGC【详解】(1)CAF BAE ∠=∠BAC EAF∴∠=∠ AE AB AC AF==， ()B A C E A FS A S ∴△≌△ EF BC ∴=(2)65AB AE ABC =∠=︒，18065250BAE ∴∠=︒-︒⨯=︒ 50FAG ∴∠=︒BAC EAF△≌△ 28F C ∴∠=∠=︒502878FGC ∴∠=︒+︒=︒ 【点睛】本题主要考查全等三角形证明与性质，等腰三角形性质，旋转性质等知识点，比较简单，基础知识扎实是解题关键 28．已知：如图，AB∥CD，E 是AB 的中点，CE=DE ．求证：（1）∠AEC=∠BED；（2）AC=BD ．【答案】见解析【解析】（1）根据CE=DE 得出∠ECD=∠EDC，再利用平行线的性质进行证明即可；（2）根据SAS 证明△AEC 与△BED 全等，再利用全等三角形的性质证明即可．证明：（1）∵AB∥CD，∴∠AEC=∠ECD，∠BED=∠EDC，∵CE=DE，∴∠ECD=∠EDC，∴∠AEC=∠BED；（2）∵E是AB的中点，∴AE=BE，在△AEC和△BED中，AE=BE，∠AEC=∠BED，EC=ED，∴△AEC≌△BED（SAS），∴AC=BD．29．如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．（1）求证：ABM∽△EFA；（2）若AB=12，BM=5，求DE的长．【答案】（1）见解析；（2）4.9【解析】【详解】试题分析：（1）由正方形的性质得出AB=AD，∠B=90°，AD∥BC，得出∠AMB=∠EAF，再由∠B=∠AFE，即可得出结论；（2）由勾股定理求出AM，得出AF，由ABM∽△EFA得出比例式，求出AE，即可得出DE的长．试题解析：（1）∵四边形ABCD是正方形，∴AB=AD，∠B=90°，AD∥BC，∴∠AMB=∠EAF，又∵EF⊥AM，∴∠AFE=90°，∴∠B=∠AFE，∴△ABM∽△EFA；（2）∵∠B=90°，AB=12，BM=5，∴=13，AD=12，∵F是AM的中点，∴AF=12AM=6.5， ∵△ABM ∽△EFA ， ∴BM AM AF AE =， 即5136.5AE=， ∴AE=16.9，∴DE=AE-AD=4.9．考点：1.相似三角形的判定与性质；2.正方形的性质．30．如图，在ABC ∆中，AB AC =，AD BC ⊥于点D ．（1）若42C ︒∠=，求BAD ∠的度数；（2）若点E 在边AB 上，EF AC 交AD 的延长线于点F ．求证：AE FE =．【答案】（1）48°；（2）证明见解析.【解析】【分析】（1）根据等腰三角形的性质得到BAD CAD ∠=∠，根据三角形的内角和即可得到904248BAD CAD ︒︒︒∠=∠=-=；（2）根据等腰三角形的性质得到BAD CAD ∠=∠根据平行线的性质得到F CAD ∠=∠，等量代换得到BAD F ∠=∠，于是得到结论．【详解】解：（1）∵AB AC =，AD BC ⊥于点D ，∴BAD CAD ∠=∠，90ADC ︒∠=，又42C ︒∠=，∴904248BAD CAD ︒︒︒∠=∠=-=；（2）∵AB AC =，AD BC ⊥于点D ，∴BAD CAD ∠=∠，∵EF AC，∴F CAD∠=∠，∴BAD F∠=∠，∴AE FE=．【点睛】本题考查了等腰三角形的性质，平行线的性质，正确的识别图形是解题的关键．31．已知，在ABC中，∠A=90°，AB=AC，点D为BC的中点．（1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE=AF；（2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE=AF吗？请利用图②说明理由．【答案】（1）证明见解析；（2）BE=AF，证明见解析.【解析】分析：（1）连接AD，根据等腰三角形的性质可得出AD=BD、∠EBD=∠FAD，根据同角的余角相等可得出∠BDE=∠ADF，由此即可证出BDE≌△ADF（ASA），再根据全等三角形的性质即可证出BE=AF；（2）连接AD，根据等腰三角形的性质及等角的补角相等可得出∠EBD=∠FAD、BD=AD，根据同角的余角相等可得出∠BDE=∠ADF，由此即可证出EDB≌△FDA（ASA），再根据全等三角形的性质即可得出BE=AF．详（1）证明：连接AD，如图①所示．∵∠A=90°，AB=AC，∴△ABC为等腰直角三角形，∠EBD=45°．∵点D为BC的中点，∴AD=12BC=BD，∠FAD=45°．∵∠BDE+∠EDA=90°，∠EDA+∠ADF=90°，∴∠BDE=∠ADF．在BDE和ADF中，EBD FAD BD ADBDE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△BDE ≌△ADF （ASA ），∴BE=AF ；（2）BE=AF ，证明如下：连接AD ，如图②所示．∵∠ABD=∠BAD=45°， ∴∠EBD=∠FAD=135°． ∵∠EDB+∠BDF=90°，∠BDF+∠FDA=90°， ∴∠EDB=∠FDA ．在 EDB 和 FDA 中，EBD FAD BD ADEDB FDA ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△EDB ≌△FDA （ASA ），∴BE=AF ．点睛：本题考查了全等三角形的判定与性质、等腰直角三角形、补角及余角，解题的关键是：（1）根据全等三角形的判定定理ASA 证出 BDE ≌△ADF ；（2）根据全等三角形的判定定理ASA 证出 EDB ≌△FDA ．32．如图，D 是AB 上一点，DF 交AC 于点E ，DE=FE ，FC ∥AB ，求证：ADE CFE ∆≅【答案】见解析.【解析】【分析】利用AAS 证明：△ADE ≌CFE ．【详解】证明：∵FC ∥AB∴∠A=∠FCE ，∠ADE=∠F所以在△ADE 与△CFE 中：A FCE ADE F DE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△CFE.【点睛】本题考查了三角形全等的判定，熟练掌握是解题的关键.33．如图，已知点A 、F 、E 、C 在同一直线上，AB ∥CD ，∠ABE=∠CDF ，AF=CE ．（1）从图中任找两组全等三角形；（2）从（1）中任选一组进行证明．【答案】（1） ABE ≌△CDF ， AFD ≌△CEB(2)略【解析】试题分析：（1）根据题目所给条件可分析出 ABE ≌△CDF ， AFD ≌△CEB ；（2）根据已知条件易得∠ACD=∠CAB ，AE=FC ，再由∠ABE=∠CDF ，根据AAS 可判定 ABE ≌△CDF ．试题解析：解：（1） ABE ≌△CDF ， AFD ≌△CEB ；（2）∵AB ∥CD ，∴∠ACD=∠CAB ，∵AF=CE ，∴AF+EF=CE+EF ，即AE=FC ，在 ABE 和 CDF 中，，∴△ABE ≌△CDF （AAS ）．考点：全等三角形的判定．34．在 ABC 中，AB=AC ，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧．．作 ADE ，使AD=AE ，∠DAE =∠BAC ，连接CE ．（1）如图1，当点D 在线段BC 上，如果∠BAC=90°，则∠BCE=________度；（2）设BAC α∠=，BCE β∠=．①如图2，当点在线段BC 上移动，则α，β之间有怎样的数量关系？请说明理由；②当点在直线BC 上移动，则α，β之间有怎样的数量关系？请直接写出你的结论．【答案】90°【解析】【分析】（1）可以证明 BAD ≌△CAE ，得到∠B ＝∠ACE ，证明∠ACB ＝45°，即可解决问题；（2）①证明 BAD ≌△CAE ，得到∠B ＝∠ACE ，β＝∠B ＋∠ACB ，即可解决问题；②证明 BAD ≌△CAE ，得到∠ABD ＝∠ACE ，借助三角形外角性质即可解决问题．【详解】（1）90︒；（2）①αβ180+=︒．理由：∵BAC DAE ∠∠=，∴BAC DAC DAE DAC ∠∠∠∠-=-．即BAD CAE ∠∠=．又AB AC AD AE ==，，∴ABD ACE ≌．∴B ACE ∠∠=．∴B ACB ACE ACB ∠∠∠∠+=+．∴B ACB β∠∠+=．∵αB ACB 180∠∠++=︒，∴αβ180+=︒．②当点D 在射线BC 上时，αβ180+=︒．当点D 在射线BC 的反向延长线上时，αβ=．【点睛】该题主要考查了等腰直角三角形的性质、全等三角形的判定及其性质等几何知识点及其应用问题；应牢固掌握等腰直角三角形的性质、全等三角形的判定及其性质等几何知识点．35．已知：如图，ABC是任意一个三角形，求证：∠A+∠B+∠C=180°．【答案】证明见解析【解析】分析：过点A作EF∥BC，利用EF∥BC，可得∠1=∠B，∠2=∠C，而∠1+∠2+∠BAC=180°，利用等量代换可证∠BAC+∠B+∠C=180°．详解：如图，过点A作EF∥BC，∵EF∥BC，∴∠1=∠B，∠2=∠C，∵∠1+∠2+∠BAC=180°，∴∠BAC+∠B+∠C=180°，即∠A+∠B+∠C=180°．点睛：本题考查了三角形的内角和定理的证明，作辅助线把三角形的三个内角转化到一个平角上是解题的关键．36．如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．【答案】答案见解析【解析】【分析】由BE＝CF可得BF＝CE，再结合AB＝DC，∠B＝∠C可证得ABF≌△DCE，问题得证.【详解】。

中考数学几何压轴题及答案一、解答题（共30小题）1.观察猜想（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是，BE+BF＝；探究证明（2）在（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；拓展延伸（3）如图③，在△ABC中，AB＝AC，∠BAC＝α，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝α，连接BF，则BE+BF的值是多少？请用含有n，α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点，使∠AB′B＝∠AC′C＝∠BAC（1）如图1中∠BAC为直角，∠BAC＝∠AB′B＝∠AC′C＝90°（点B′与点C′重合），则△ABC∽△B'BA∽△C'AC，，，进而可得AB2+AC2＝；（2）如图2中当∠BAC为锐角，图3中∠BAC为钝角时（1）中的结论还成立吗？若不成立，则AB2+AC2等于什么（用含用BC和B′C′的式子表示）？并说明理由（3）若在△ABC中，AB＝5，AC＝6，BC＝9，请你先判断出△ABC的类型，再求出B′C′的长3．（1）问题发现如图1，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，点D是线段AB上一动点，连接BE填空：①的值为；②∠DBE的度数为．（2）类比探究如图2，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，点D是线段AB上一动点，连接BE．请判断的值及∠DBE的度数，并说明理由；（3）拓展延伸如图3，在（2）的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE 的中点M，连接BM、CM，若AC＝2，则当△CBM是直角三角形时，线段BE的长是多少？请直接写出答案．4.（1）问题发现：如图①，在△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，以点D为顶点作正方形DFGE，使点A、C分别在DE和DF上，连接BE、AF．则线段BE 和AF数量关系．（2）类比探究：如图②，保持△ABC固定不动，将正方形DFGE绕点D旋转α（0°＜α≤360°），则（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由．（3）解决问题：若BC＝DF＝2，在（2）的旋转过程中，连接AE，请直接写出AE的最大值．5.如图，在平行四边形ABCD中，AC与BD交于点O，以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F，且∠EOF与∠BAD互补．（1）若四边形ABCD是正方形，则线段OE与OF有何数量关系？请直接写出结论；（2）若四边形ABCD是菱形，那么（1）中的结论是否成立？若成立，请画出图形并给出证明；若不成立，请说明理由；（3）若AB：AD＝m：n，探索线段OE与OF的数量关系，并证明你的结论.6.如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F.（1）证明与推断：①求证：四边形CEGF是正方形；②推断：的值为：（2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG＝6，GH＝2，则BC＝．7.如图1，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E分别是AC、BC的中点，连接DE.定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．探索发现：图1中，的值为；的值为．（2）拓展探完若将△CDE绕点C逆时针方向旋转一周，在旋转过程中的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△CDE旋转至A，D，E三点共线时，直接写出线段BE的长．8.已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE，设OD＝m．（1）问题发现如图1，△CDE的形状是三角形．（2）探究证明如图2，当6＜m＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．（3）解决问题是否存在m的值，使△DEB是直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．9.等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD 的中点，连接MN、NF．问题提出：（1）如图1，当AD在线段AC上时，则∠MNF的度数为，线段MN 和线段NF的数量关系为；深入讨论：（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系；拓展延伸：（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为．10．四边形是我们在学习和生活中常见的图形，而对角线互相垂直的四边形也比较常见，比如筝形、菱形、图1中的四边形ABCD等．它们给我们的学习和生活带来了很多的乐趣和美感．（1）如图2，在四边形ABCD中，AB＝AD，CB＝CD，则AC与BD的位置关系是，请说明理由．（2）试探究图1中四边形ABCD的两组对边AB，CD与BC，AD之间的数量关系，请写出证明过程．（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连接CE，BG，GE，已知AC＝4，AB＝5，求GE的长．11．问题发现：如图（1）在Rt△ABC和Rt△BDE中，∠A＝∠DEB＝30°，BC＝BE＝6，Rt△BDE绕点B逆时针旋转，H为CD的中点，当点C与点E重合时，BH与AE的位置关系为，BH与AE的数量关系为；问题证明：在Rt△BDE绕点B旋转的过程中，（1）中的结论是否仍然成立？若成立，请就图（2）的情形给出证明若不成立，请说明理由；拓展应用：在Rt△BDE绕点B旋转的过程中，当DE∥BC时，请直接写出BH2的长．12．如图1，菱形ABCD与菱形GECF的顶点C重合，点G在对角线AC上，且∠BCD＝∠ECF＝60°，（1）问题发现的值为；（2）探究与证明将菱形GECF绕点C按顺时针方向旋转α角（0°＜α＜60°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：菱形GECF在旋转过程中，当点A，G，F三点在一条直线上时，如图3所示连接CG并延长，交AD于点H，若CE＝2，GH＝，则AH的长为．13．如图，在Rt△ABC中，∠ACB＝90°，＝，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．（1）探究发现：如图1，若m＝n，点E在线段AC上，则＝；（2）数学思考：①如图2，若点E在线段AC上，则＝（用含m，n的代数式表示）；②当点E在直线AC上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；（3）拓展应用：若AC＝，BC＝2，DF＝4，请直接写出CE的长．14．如图，已知点E是射线BC上的一点，以BC、CE为边作正方形ABCD和正方形CEFG，连接AF，取AF的中点M，连接DM、MG（1）如图1，判断线段DM和GM的数量关系是，位置关系是；（2）如图2，在图中的正方形CEFG绕点C逆时针旋转的过程中，其他条件不变，（1）中的结论是否成立？说明理由；（3）已知BC＝10，CE＝2，正方形CEFG绕点C旋转的过程中，当A、F、E共线时，直接写出△DMG的面积．15.在Rt△ABC中，∠ACB＝90°，AB＝，AC＝2，过点B作直线m∥AC，将△ABC绕点C顺时针旋转得到△A′B′C（点A，B的对应点分别为A'，B′），射线CA′，CB′分别交直线m于点P，Q．（1）如图1，当P与A′重合时，求∠ACA′的度数；（2）如图2，设A′B′与BC的交点为M，当M为A′B′的中点时，求线段PQ的长；（3）在旋转过程中，当点P，Q分别在CA′，CB′的延长线上时，试探究四边形P A'B′Q的面积是否存在最小值．若存在，求出四边形P A′B′Q的最小面积；若不存在，请说明理由．16.如图（1），在等边三角形ABC中，点D，E分别在边AB，AC上，AD＝AE，连接BE，CD，点M，N，P分别是BE，CD，BC的中点，连接DE，PM，PN，MN．（1）观察猜想，图（1）中△PMN是（填特殊三角形的名称）（2）探究证明，如图（2），△ADE绕点A按逆时针方向旋转，则△PMN的形状是否发生改变？并就图（2）说明理由．（3）拓展延伸，若△ADE绕点A在平面内自由旋转，AD＝2，AB＝6，请直接写出△PMN 的周长的最大值．17.已知△ABC，AB＝AC，D为直线BC上一点，E为直线AC上一点，AD＝AE，设∠BAD＝α，∠CDE＝β，（1）如图1，若点D在线段BC上，点E在线段AC上．∠ABC＝60°，∠ADE＝70°，则α＝°；β＝°.（2）如图2，若点D在线段BC上，点E在线段AC上，则α，β之间有什么关系式？说明理由．（3）是否存在不同于（2）中的α，β之间的关系式？若存在，请写出这个关系式（写出一种即可），说明理由；若不存在，请说明理由.18.问题提出：（1）如图1，在四边形ABCD中，连接AC、BD，AB＝AD，∠BAD＝∠BCD＝90°，将△ABC绕点A逆时针旋转90°，得到△ADE，点B的对应点落在点D，点C的对应点为点E，可知点C、D、E在一条直线上，则△ACE为三角形，BC、CD、AC的数量关系为；探究发现：（2）如图2，在⊙O中，AB为直径，点C为的中点，点D为圆上一个点，连接AD、CD、AC、BC、BD，且AD＜BD，请求出CD、AD、BD间的数量关系.拓展延伸：（3）如图3，在等腰直角三角形ABC中，点P为AB的中点，若AC＝13，平面内存在一点E，且AE＝10，CE＝13，当点Q为AE中点时，PQ＝.19.已知△ABC中，CA＝CB，0°＜∠ACB≤90°，点M、N分别在边CA，CB上（不与端点重合），BN＝AM，射线AG∥BC交BM延长线于点D，点E在直线AN上，EA＝ED．（1）【观察猜想】如图1，点E在射线NA上，当∠ACB＝45°时，①线段BM与AN的数量关系是；②∠BDE的度数是；（2）【探究证明】如图2点E在射线AN上，当∠ACB＝30°时，判断并证明线段BM与AN的数量关系，求∠BDE的度数；（3）【拓展延伸】如图3，点E在直线AN上，当∠ACB＝60°时，AB＝3，点N是BC 边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长．20.如图①，在正方形ABCD和正方形AB'C'D'中，AB＝2，AB'＝，连接CC’（1）问题发现：．（2）拓展探究：将正方形AB'C'D'绕点A逆时针旋转，记旋转角为θ，连接BB'，试判断：当0°≤θ＜360°时，的值有无变化？请仅就图②中的情形给出你的证明；（3）问题解决：请直接写出在旋转过程中，当C，C′，D'三点共线时BB′的长．21.如图1，在正方形ABCD中，点O是对角线BD的中点．（1）观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置，连接AC，DE，则线段AC与DE的数量关系是，直线AC与DE的位置关系是．（2）类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置，（1）中的结论是否成立？并说明理由．（3）拓展延伸将图2中的△ECF在平面内旋转，设直线AC与DE的交点为M，若AB＝4，请直接写出BM的最大值与最小值．22.如图1，点B在直线l上，过点B构建等腰直角三角形ABC，使∠BAC＝90°，且AB＝AC，过点C作CD⊥直线l于点D，连接AD．（1）小亮在研究这个图形时发现，∠BAC＝∠BDC＝90°，点A，D应该在以BC为直径的圆上，则∠ADB的度数为°，将射线AD顺时针旋转90°交直线l于点E，可求出线段AD，BD，CD的数量关系为；（2）小亮将等腰直角三角形ABC绕点B在平面内旋转，当旋转到图2位置时，线段AD，BD，CD的数量关系是否变化，请说明理由；（3）在旋转过程中，若CD长为1，当△ABD面积取得最大值时，请直接写AD的长．23．如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）观察猜想：线段EF与线段EG的数量关系是；（2）探究证明：如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）拓展延伸：如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB＝a、BC＝b，求的值．24．如图1，在Rt△ABC中，∠B＝90°，AB＝2，BC＝1，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现①当α＝0°时，＝；②当α＝180°时，＝．（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明．（3）问题解决当△EDC旋转至A、B、E三点共线时，直接写出线段BD的长．25.在△ABC中，AD为BC边上的中线，E为AD上一动点，设DE＝nEA，连接CE并延长，交AB于点F．（1）尝试探究如图（1），当∠BAC＝90°，∠B＝30°，DE＝EA时，BF，BA之间的数量关系是；（2）类比延伸如图（2），当△ABC为锐角三角形，DE＝EA时，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）拓展迁移如图（3），当△ABC为锐角三角形，DE＝nEA时，请直接写出BF，BA之间的数量关系．26.古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE ⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC．（1）求证：CD是⊙O的切线；（2）小明在研究的过程中发现是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．27．定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．（2）如图2，四边形ABCD内接于⊙O，＝，四边形ABCD的外角平分线DF交⊙O 于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．28.【性质探究】如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF＝2OG．【迁移应用】（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．【拓展延伸】（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．29．如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．30．如图1和图2，在△ABC中，AB＝AC，BC＝8，tan C＝．点K在AC边上，点M，N 分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；（3）设点P移动的路程为x，当0≤x≤3及3＜x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝，请直接写出点K被扫描到的总时长．参考答案与试题解析一．解答题（共30小题）1．【解答】解：（1）如图①中，∵∠EAF＝∠BAC＝90°，∴∠BAF＝∠CAE，∵AF＝AE，AB＝AC，∴△BAF≌△CAE，∴∠ABF＝∠C，BF＝CE，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠C＝45°，∴∠FBE＝∠ABF+∠ABC＝90°，BC＝BE+EC＝BE+BF，故答案为：BF⊥BE，BC．（2）如图②中，作DH∥AC交BC于H．∵DH∥AC，∴∠BDH＝∠A＝90°，△DBH是等腰直角三角形，由（1）可知，BF⊥BE，BF+BE＝BH，∵AB＝AC＝3，AD＝1，∴BD＝DH＝2，∴BH＝2，∴BF+BE＝BH＝2；（3）如图③中，作DH∥AC交BC的延长线于H，作DM⊥BC于M．∵AC∥DH，∴∠ACB＝∠H，∠BDH＝∠BAC＝α，∵AB＝AC，∴∠ABC＝∠ACB∴∠DBH＝∠H，∴DB＝DH，∵∠EDF＝∠BDH＝α，∴∠BDF＝∠HDE，∵DF＝DE，DB＝DH，∴△BDF≌△HDE，∴BF＝EH，∴BF+BE＝EH+BE＝BH，∵DB＝DH，DM⊥BH，∴BM＝MH，∠BDM＝∠HDM，∴BM＝MH＝BD•sin．∴BF+BE＝BH＝2n•sin．2．【解答】解：（1）如图1中，∵△ABC∽△B'BA∽△C'AC，∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC×BC＝BC2，故答案为BC2．（2）不成立．理由：如图2中当∠BAC为锐角时，BB′+CC′﹣B′C′＝BC，且△ABC∽△B'BA∽△C'AC，∴∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC2+BC•B′C′．图3中∠BAC为钝角时，BB′+CC′+B′C′＝BC．AB2+AC2＝BC（BB′+CC′）＝BC2﹣BC•B′C′．（3）当AB＝5，AC＝6，BC＝9时，则AB2+AC2＜BC2，可知△ABC为钝角三角形，由图3可知：AB2+AC2＝BC2﹣BC•B′C′，∴52+62＝92﹣9B′C′，∴B′C′＝．3．【解答】解：（1）∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，∴∠ABC＝∠CAB＝45°＝∠CDE＝∠CED，∴AC＝BC，CD＝CE，∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD，∠CAB＝∠CBE＝45°，∴∠DBE＝∠ABC+∠CBE＝90°，＝1，故答案为：1，90°（2），∠DBE＝90°理由如下：∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴∠ACD＝∠BCE，∠CED＝∠ABC＝30°∴tan∠ABC＝tan30°＝＝∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴Rt△ACB∽Rt△DCE∴∴，且∠ACD＝∠BCE∴△ACD∽△BCE∴＝，∠CBE＝∠CAD＝60°∴∠DBE＝∠ABC+∠CBE＝90°（3）若点D在线段AB上，如图，由（2）知：＝，∠ABE＝90°∴BE＝AD∵AC＝2，∠ACB＝90°，∠CAB＝90°∴AB＝4，BC＝2∵∠ECD＝∠ABE＝90°，且点M是DE中点，∴CM＝BM＝DE，∵△CBM是直角三角形∴CM2+BM2＝BC2＝（2）2，∴BM＝CM＝∴DE＝2∵DB2+BE2＝DE2，∴（4﹣AD）2+（AD）2＝24∴AD＝+1∴BE＝AD＝3+若点D在线段BA延长线上，如图同理可得：DE＝2，BE＝AD∵BD2+BE2＝DE2，∴（4+AD）2+（AD）2＝24，∴AD＝﹣1∴BE＝AD＝3﹣综上所述：BE的长为3+或3﹣4．【解答】解：（1）∵△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，∴AD＝BD＝DC，∠BDA＝90°，∵四边形DFGE是正方形，∴DE＝DF，∠EDF＝90°，∴∠BDE＝∠ADF＝90°，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF故答案为：BE＝AF；（2）成立；理由如下：当正方形DFGE在BC的上方时，如图②所示，连接AD，∵在Rt△ABC中，AB＝AC，D为斜边BC的中点，∴AD＝BD，AD⊥BC，∴∠ADE+∠EDB＝90°，∵四边形DFGE为正方形，∴DE＝DF，且∠EDF＝90°，∴∠ADE+∠ADF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；当正方形DFGE在BC的下方时，连接AD，如图③所示：∵∠BDE＝∠BDF+90°，∠ADF＝∠BDF+90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；综上所述，（1）中的结论BE＝AF成立；（3）在△ADE中，∵AE＜AD+DE，∴当点A、D、E共线时，AE取得最大值，最大值为AD+DE．如图④所示：则AD＝BC＝1，DE＝DF＝2，∴AE＝AD+DE＝3，即AE的最大值为3．5．【解答】解：（1）如图1，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是正方形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（2）（1）的结论成立；理由：如图2，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是菱形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（3）如图3，过点O作OG⊥AB于G，OH⊥AD于H，∴∠OGE＝∠OHF＝90°，∴∠BAD+∠GOH＝180°，∵∠BAD+∠EOF＝180°，∴∠GOH＝∠EOF，∴△EOG∽△FOH，∴，∵O是▱ABCD的对角线的交点，∴S△AOB＝S△AOD，∵S△AOB＝AB•OG，S△AOD＝AD•OH，∴AB•OG＝AD•OH，∴＝，∴．6．【解答】解：（1）①∵四边形ABCD是正方形，∴∠BCD＝90°，∠BCA＝45°，∵GE⊥BC、GF⊥CD，∴∠CEG＝∠CFG＝∠ECF＝90°，∴四边形CEGF是矩形，∠CGE＝∠ECG＝45°，∴EG＝EC，∴四边形CEGF是正方形；②由①知四边形CEGF是正方形，∴∠CEG＝∠B＝90°，∠ECG＝45°，∴＝，GE∥AB，∴＝＝，故答案为：；（2）连接CG，由旋转性质知∠BCE＝∠ACG＝α，在Rt△CEG和Rt△CBA中，＝cos45°＝、＝cos45°＝，∴＝＝，∴△ACG∽△BCE，∴＝＝，∴线段AG与BE之间的数量关系为AG＝BE；（3）∵∠CEF＝45°，点B、E、F三点共线，∴∠BEC＝135°，∵△ACG∽△BCE，∴∠AGC＝∠BEC＝135°，∴∠AGH＝∠CAH＝45°，∵∠CHA＝∠AHG，∴△AHG∽△CHA，∴＝＝，设BC＝CD＝AD＝a，则AC＝a，则由＝得＝，∴AH＝a，则DH＝AD﹣AH＝a，CH＝＝a，∴＝得＝，解得：a＝3，即BC＝3，故答案为：3．7．【解答】解：（1）如图1，连接AE，∵AB＝AC＝2，点E分别是BC的中点，∴AE⊥BC，∴∠BEC＝90°，∵AB＝AC＝2，∠BAC＝120°，∴∠B＝∠C＝30°，在Rt△ABE中，AE＝AB＝1，根据勾股定理得，BE＝∵点E是BC的中点，∴BC＝2BE＝2，∴＝＝，∵点D是AC的中点，∴AD＝CD＝AC＝1，∴＝＝，故答案为：，；（2）无变化，理由：由（1）知，CD＝1，CE＝BE＝，∴＝，，∴＝，由（1）知，∠ACB＝∠DCE＝30°，∴∠ACD＝∠BCE，∴△ACD∽△BCE，∴，（3）当点D在线段AE上时，如图2，过点C作CF⊥AE于F，∠CDF＝180°﹣∠CDE＝60°，∴∠DCF＝30°，∴DF＝CD＝，∴CF＝DF＝，在Rt△AFC中，AC＝2，根据勾股定理得，AF＝＝，∴AD＝AF+DF＝，由（2）知，，∴BE＝AD＝当点D在线段AE的延长线上时，如图3，过点C作CG⊥AD交AD的延长线于G，∵∠CDG＝60°，∴∠DCG＝30°，∴DG＝CD＝，∴CG＝DG＝，在Rt△ACG中，根据勾股定理得，AG＝，∴AD＝AG﹣DG＝，由（2）知，，∴BE＝AD＝即：线段BE的长为或．8．【解答】解：（1）证明：∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；故答案为：等边；（2）存在，当6＜t＜10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，由（1）知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD+4，由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝2，∴△BDE的最小周长＝CD+4＝2+4；（3）存在，①∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意，②当0≤m＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°，由（1）可知，△CDE是等边三角形，∴∠DEB＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA﹣DA＝6﹣4＝2，∴m＝2；③当6＜m＜10时，由∠DBE＝120°＞90°，∴此时不存在；④当m＞10时，由旋转的性质可知，∠DBE＝60°，又由（1）知∠CDE＝60°，∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，而∠BDC＞0°，∴∠BDE＞60°，∴只能∠BDE＝90°，从而∠BCD＝30°，∴BD＝BC＝4，∴OD＝14，∴m＝14，综上所述：当m＝2或14时，以D、E、B为顶点的三角形是直角三角形．9．【解答】解：（1）如图1中，连接DB，MF，CE，延长BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠ABD+∠ADB＝90°，∠ADB＝∠CDH，∴∠ADH+∠DCH＝90°，∴∠CHD＝90°，∴EC⊥BH，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．故答案为：45°（2）：如图2中，连接MF，EC，BD．设EC交AB于O，BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠AOC+∠ACO＝90°，∠AOC＝∠BOH，∴∠OBH+∠BOH＝90°，∴∠BHO＝90°，∴EC⊥BD，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．（3）：如图3中，如图以A为圆心AD为半径作⊙A．当直线PB与⊙A相切时，此时∠CBP的值最小，点P到BC的距离最小，即△BCP的面积最小，∵AD＝AE，AB＝AC，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE＝∠ABD，BD＝EC，∵∠ABD+∠AOB＝90°，∠AOB＝∠CPO，∴∠CPB＝90°，∵PB是⊙A的切线，∴∠ADP＝90°，∵∠DPE＝∠ADP＝∠DAE＝90°，∴四边形ADPE是矩形，∵AE＝AD，∴四边形ADPE是正方形，∴AD＝AE＝PD＝PE＝2，BD＝EC＝＝2，∴PC＝2﹣2，PB＝2+2，∴S△BCP的最小值＝×PC×PB＝（2﹣2）（2+2）＝4．10．【解答】（1）解：AC⊥BD，理由如下：连接AC、BD，如图2所示：∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，故答案为：AC⊥BD；（2）解：AD2+BC2＝AB2+CD2；理由如下：如图1，已知四边形ABCD中，AC⊥BD，设BD、AC相交于E，∵AC⊥BD，∴∠AED＝∠AEB＝∠BEC＝∠CED＝90°，由勾股定理得，AD2+BC2＝AE2+DE2+BE2+CE2，AB2+CD2＝AE2+BE2+CE2+DE2，∴AD2+BC2＝AB2+CD2；（3）解：如图3，连接CG、BE，∵四边形ACFG和四边形ABDE是正方形，∴AC＝AG，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，即CE⊥BG，由（2）得，CG2+BE2＝CB2+GE2，在Rt△ABC中，AC＝4，AB＝5，根据勾股定理得，BC2＝52﹣42＝9，∵CG和BE分别是正方形ACFG和正方形ABDG的对角线，∴CG2＝42+42＝32，BE2＝52+52＝50，∴GE2＝CG2+BE2﹣CB2＝32+50﹣9＝73，∴GE＝．11．【解答】解：问题发现：如图1中，结论：AE＝2BH，AE⊥BH．理由：在Rt△ABC中，∵BC＝6，∠A＝30°，∴AE＝2BC＝12，在Rt△CDB中，∵∠DCB＝30°，∴CD＝＝4，∵CH＝DH，∴BH＝CD＝2，∴＝＝2，∴AE＝2BH．故答案为AE⊥BH，AE＝2BH．问题证明：如图2中，（1）中结论成立．理由：延长BH到F使得HF＝BH，连接CF．设AE交BF于O．∵CH＝DH，BH＝HF，∠CHF＝∠BHD，∴△CHF≌△DHB（SAS），∴BD＝CF，∠F＝∠DBH，∴CF∥BD，∵AB＝BC，BE＝BD，∴BE＝CF，∴＝＝，∵CF∥BD，∴∠BCF+∠CBD＝180°，∵∠ABC+∠DBE＝∠ABD+∠CBD+∠CBD+∠CBE＝∠CBD+∠ABE＝180°，∴∠BCF＝∠ABE，∴△ABE∽△BCF，∴∠CBF＝∠BAE，＝＝，∴AE＝BF＝2BH，∵∠CBF+∠ABF＝90°，∴∠ABF+∠BAE＝90°，∴∠AOB＝90°，∴BH⊥AE．拓展应用：如图3﹣1中，当DE在BC的下方时，延长AB交DE于F．∵DE∥BC∴∠ABC＝∠BFD＝90°，由题意BC＝BE＝6，AB＝6，BD＝2，DE＝4，∵•BD•BE＝•DE•BF，∴BF＝＝3，∴EF＝BF＝3，∴AF＝6+3，∴AE2＝AF2+EF2＝（6+3）2+（3）2＝144+36．∵AE＝2BH，∴AE2＝12BH2，∴BH2＝12+3如图3﹣2中，当DE在BC的上方时，同法可得AF＝6﹣3，EF＝3，∴BH2＝＝（＝12﹣3．12．【解答】解：（1）如图1中，作EH⊥CG于H．∵四边形ECFG是菱形，∠ECF＝60°，∴∠ECH＝∠ECF＝30°，EC＝EG，∵EH⊥CG，∴GH＝CG，∴＝cos30°＝，∴＝2•＝，∵EG∥CD，AB∥CD，∴GE∥AB，∴＝＝．故答案为．（2）结论：AG＝BE．理由：如图2中，连接CG．∵四边形ABCD，四边形ECFG都是菱形，∠ECF＝∠DCB＝60°，∴∠ECG＝∠EGC＝∠BCA＝∠BAC＝30°，∴△ECG∽△BCE，∴＝，∵∠ECB＝∠GCA，∴△ECB∽△GCA，∴＝＝，∴AG＝BE．（3）如图3中，∵∠AGH＝∠CGF＝30°．∠AGH＝∠GAC+∠GCA，又∵∠DAC＝∠HAG+∠GAC＝30°，∴∠HAG＝∠ACH，∵∠AHG＝∠AHC，∴△HAG∽△HCA，∴HA：HC＝GH：HA，∴AH2＝HG•HC，∴FC＝2，CG＝CF，∴GC＝2，∵HG＝，∴AH2＝HG•HC＝•3＝9，∵AH＞0，∴AH＝3．故答案为3．13．【解答】解：（1）当m＝n时，即：BC＝AC，∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴＝1，∴＝1（2）①∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴②成立．如图，∵∠ACB＝90°，∴∠A+∠ABC＝90°，又∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE+∠CDE＝∠ADC+∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴．（3）由（2）有，△ADE∽△CDF，∵＝，∴＝，∴CF＝2AE，在Rt△DEF中，DE＝2，DF＝4，∴EF＝2，①当E在线段AC上时，在Rt△CEF中，CF＝2AE＝2（AC﹣CE）＝2（﹣CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（﹣CE）]2＝40∴CE＝2，或CE＝﹣（舍）而AC＝＜CE，∴此种情况不存在，②当E在AC延长线上时，在Rt△CEF中，CF＝2AE＝2（AC+CE）＝2（+CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（+CE）]2＝40，∴CE＝，或CE＝﹣2（舍），③如图1，当点E在CA延长线上时，CF＝2AE＝2（CE﹣AC）＝2（CE﹣），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（CE﹣）]2＝40，∴CE＝2，或CE＝﹣（舍）即：CE＝2或CE＝．14．【解答】解：（1）如图1，延长GM交AD于H，∵AD∥GF，∴∠GFM＝∠HAM，在△FMG和△AMH中，，∴△FMG≌△AMH（ASA），∴HM＝GM，AH＝FG，∵AD＝CD，AH＝FG＝CG，∴DH＝DG，∵∠HDG＝90°，HM＝GM，∴DM＝MG，DM⊥MG，故答案为DM＝MG，DM⊥MG．（2）结论成立：DM＝MG，DM⊥MG，理由：如图2中，延长GM使得MH＝GM，连接AH、DH、DG，延长AD交GF的延长线于N，交CD于O．∵AM＝MF，∠AMH＝∠FMG，MH＝MG，∴△AMH≌△FMG（SAS），∴AH＝GF＝CG，∠AHM＝∠FGM，∴AH∥GN，∴∠HAD＝∠N，∵∠ODN＝∠OGC＝90°，∠DON＝∠GOC，∴∠N＝∠OCG，∴∠HAD＝∠DCG，∵AH＝CG，AD＝CD，∴△HAD≌△GCD（SAS），∴DH＝DG，∠HDA＝∠CDG，∴∠HDG＝∠ADC＝90°，∴△HDG是等腰直角三角形，∵MH＝MG，∴DM⊥GH，DM＝MH＝MG，（3）①如图3﹣1中，连接AC．在Rt△ABC中，AC＝＝10，在Rt△ACE中，AE＝＝14，∴AF＝AE＝EF＝14﹣2＝12，∴FM＝AM＝AF＝6，在Rt△MGF中，MG＝＝2，∴S△DMG＝×2×2＝20，②如图3﹣2中，连接AC．同法可得AE＝14，AF＝16，FM＝8，MG＝＝2，∴S△DMG＝×2×2＝34，综上所述，满足条件的△DMG的面积为20或34．15．【解答】解：（1）由旋转可得：AC＝A'C＝2，∵∠ACB＝90°，AB＝，AC＝2，∴BC＝，∵∠ACB＝90°，m∥AC，∴∠A'BC＝90°，∴cos∠A'CB＝＝，∴∠A'CB＝30°，∴∠ACA'＝60°；（2）∵M为A'B'的中点，∴∠A'CM＝∠MA'C，由旋转可得，∠MA'C＝∠A，∴∠A＝∠A'CM，∴tan∠PCB＝tan∠A＝，∴PB＝BC＝，∵∠PCQ＝∠PBC＝90°，∴∠BQC+∠BPC＝∠BCP+∠BPC＝90°，∴∠BQC＝∠BCP＝∠A，∴tan∠BQC＝tan∠A＝，∴BQ＝BC×＝2，∴PQ＝PB+BQ＝；（3）∵S四边形P A'B′Q＝S△PCQ﹣S△A'CB'＝S△PCQ﹣，∴S四边形P A'B′Q最小，即S△PCQ最小，∴S△PCQ＝PQ×BC＝PQ，法一：（几何法）取PQ的中点G，∵∠PCQ＝90°，∴CG＝PQ，即PQ＝2CG，当CG最小时，PQ最小，∴CG⊥PQ，即CG与CB重合时，CG最小，∴CG min＝，PQ min＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣；法二（代数法）设PB＝x，BQ＝y，由射影定理得：xy＝3，∴当PQ最小时，x+y最小，∴（x+y）2＝x2+2xy+y2＝x2+6+y2≥2xy+6＝12，当x＝y＝时，“＝”成立，∴PQ＝+＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣．16．【解答】解：（1）结论：△PMN是等边三角形．理由：如图1中，∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∵AD＝AE，∴BD＝EC，∵PB＝PC，CN＝ND，BM＝EM，∴PN∥BD，PM∥EC，PN＝BD，PM＝EC，∴PM＝PN，∠NPC＝∠ABC＝60°，∠MPB＝∠ACB＝60°，∴∠MPN＝60°，∴△PMN是等边三角形，故答案为等边三角形．（2）△PMN的形状不发生改变，仍为等边三角形，理由如下：如图2中，连接BD，CE．由旋转可得∠BAD＝∠CAE，∵△ABC是等边三角形，∴AB＝AC，∠ACB＝∠ABC＝60°又∵AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE，∠ABD＝∠ACE，∵M是BE的中点，P是BC的中点，∴PM是△BCE的中位线，∴PM＝，且PM∥CE．同理可证PN＝BD且PN∥BD，∴PM＝PN，∠MPB＝∠ECB，∠NPC＝∠DBC，∴∠MPB+∠NPC＝∠ECB+∠DBC＝（∠ACB+∠ACE）+（∠ABC﹣∠ABD）＝∠ACB+∠ABC＝120°，∴∠MPN＝60°，∴△PMN是等边三角形．（3）∵PM＝EC，∴当EC最大时，等边△PMN的周长最大，∵EC≤AE+AC，∴EC≤8，∴PM≤4，∴PM的最大值为4，∴△PMN的周长的最大值为12．17．【解答】解：（1）∵AB＝AC，∠ABC＝60°，∴∠BAC＝60°，∵AD＝AE，∠ADE＝70°，∴∠DAE＝180°﹣2∠ADE＝40°，∴α＝∠BAD＝60°﹣40°＝20°，∴∠ADC＝∠BAD+∠ABD＝60°+20°＝80°，∴β＝∠CDE＝∠ADC﹣∠ADE＝10°，故答案为：20，10；（2）设∠ABC＝x，∠AED＝y，∴∠ACB＝x，∠AED＝y，在△DEC中，y＝β+x，在△ABD中，α+x＝y+β＝β+x+β，∴α＝2β；（3）①当点E在CA的延长线上，点D在线段BC上，如图1设∠ABC＝x，∠ADE＝y，∴∠ACB＝x，∠ACE＝y，在△ABD中，x+α＝β﹣y，在△DEC中，x+y+β＝180°，∴α＝2β﹣180°，②当点E在CA的延长线上，点D在CB的延长线上，如图2，同①的方法可得α＝180°﹣2β．18．【解答】解：（1）由旋转变换的性质可知，∠CAE＝90°，AC＝AE，∴△ACE为等腰直角三角形，∴CE＝AC，∵CE＝CD+DE＝CD+BC，∴BC+CD＝AC，故答案为：等腰直角；BC+CD＝AC；（2）延长CO交⊙O于E，连接AE、BE、DE，则∠CDE＝90°，∵点C为的中点，∴点E为的中点，∴EA＝EB，∵AB为⊙O的直径，∴∠ADB＝90°，由（1）得，DE＝（AD+BD），由勾股定理得，CD2＝CE2﹣DE2＝AD2+BD2﹣（AD+BD）2＝（AD﹣BD）2，∴CD＝（BD﹣AD）；（3）如图3，当点E在直线AC的左侧时，连接CQ、PC，∵CA＝CB，点P为AB的中点，∴CP⊥AB，∵CA＝CE，点Q为AE中点，∴CQ⊥AE，AQ＝QE＝AE＝5，∴由勾股定理得，CQ＝＝12，由（1）得，AQ+CQ＝PQ，。

2023年九年级数学中考专题：几何探究压轴题一、解答题1．如图，在ABC 中，4AC =，3BC =，90ACB ∠=︒，D 是边AC 上一动点（不与点A 、C 重合），CE BD ⊥，垂足为E ，交边AB 于点F ．(1)当点D 是边AC 中点时，求DE ，EC 的值；(2)设CD x =，AF y =，求y 关于x 的函数关系式，并写出定义域；(3)当EFD △与EFB △相似时，求线段CD 的长．2．【温故知新】黄金分割是一种最能引起美感的分割比例，具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值．我们知道：如图1，点C 把线段AB 分成两部分，如果BC AC AC AB=，那么称点C 为线段AB 的黄金分割点．(1)【问题发现】如图1，点C 为线段AB 的黄金分割点，且AC BC >，若2AB =，请直接写出CB 的值是__________．(2)【问题探究】如图2，在Rt ABC △中，90C ∠=︒，2AC =，1BC =，在BA 上截取BD BC =，再在AC 上截取AE AD =，则AE AC的值为__________． (3)【问题解决】如图3，用边长为6的正方形纸片进行如下操作：对折正方形ABDE 得折痕MN ，连接EN ，将AE 折叠到EN 上，点A 对应点H ，得折痕CE ，试说明：C 是AB 的黄金分割点．3．定义：若连接三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形，我们称这条线段为该三角形的智慧线，这个三角形叫做智慧三角形．(1)如图1，在智慧三角形ABC 中，AD BC ⊥，AD 为该三角形的智慧线，1CD =，则BD 长为_____，B ∠的度数为_____．(2)如图2，ABC 为等腰直角三角形，90BAC ∠︒＝，2AB =，F 是斜边BC 延长线上一点，连接AF ，以AF为直角边作等腰直角三角形AFE （点A ，F ，E 按顺时针排列），90EAF ∠=︒, CF =AE 交BC 于点D ，连接EC ，EB ．当2BDE BCE ∠=∠时，求线段ED 的长；(3)如图3，ABC 中，5AB AC ==，BC =BCD △是智慧三角形，且AC 为智慧线，求BCD △的面积．4．【问题提出】如图1，在等边三角形ABC 内部有一点P ，3PA＝，4PB ＝，5PC ＝，求APB ∠的度数．(1)【尝试解决】将APC △绕点A 逆时针旋转60︒，得到AP B '△，连接PP '，则APP '为等边三角形． ∵3P P PA '==，4PB =，5P B PC '==，∴222=P P PB P B ''+∴BPP '为三角形∴APB ∠的度数为．(2)【类比探究】如图2，在等边三角形ABC 外部有一点P ，若∠BP A ＝30°，求证222PA PB PC +=．(3)【联想拓展】如图3，在ABC 中，90BAC ∠︒＝，AB AC ＝．点P 在直线BC 上方且45APB ∠︒＝，PC BC ==求PA 的长．5．已知正方形 ABCD 和正方形 CEFG ，连接 AF 交 BC 于点 O ，点 P 是 AF 的中点，过点 P 作 PH DG ⊥ 于 H ，2CD =，1CG =．(1)如图1，点 D ，C ，G 在同一直线上，点 E 在 BC 边上，求 PH 的长；(2)把正方形 CEFG 绕着点C 逆时针旋转 ()0180αα<<．①如图2，当点E 落在AF 上时，求CO 的长；②如图3，当DG =PH 的长．6．在ABC ∆中，点E 为AC 边上一动点，以CE 为边在CE 上方作等边CEN ．(1)如图1，EN 与AB 交于点P ，连接PC ，若tan A =，1AE =，5CN =，求PC 的长： (2)如图2．当N 与B 重合时，在BC 上取一点D ，过点D 作DF AC ∥，连接BF ，EF ，过C 作CH EF ⊥交EF 于点H ，若30FBC DFE ︒∠-∠=，求证：CH BF +=；(3)如图3，若BC AB ⊥，且4AB BC ==，过点B 作BQ AC ∥，I 为射线.BQ 上一动点，取AC 中点M ，连接MI ，过点B 作BK MI ⊥交M 于点K ，连接NK ，直接写出NK 的最小值．7．问题情境：如图1，在Rt △ABC 和Rt △BEF 中，∠ACB ＝∠EFB ＝90°，AC ＝3，BC ＝4，且M ，N 分别为AE ，CF 的中点．(1)猜想证明：如图2，将Rt △BEF 绕点B 按逆时针方向旋转90°，其他条件不变．试判断54AM CN =是否成立？若成立，请写出证明过程；若不成立，请说明理由．(2)解决问题：如图3，将图2中的Rt △BEF 沿BF 所在直线折叠得到Rt BE F '，连接AE '，CF ，并分别取它们的中点P ，H ，连接CP ，FP ，PH ．①试判断CP 与FP 之间的数量关系，并说明理由．②若AB ＝2BE '，BC ＝2BF ，请直接写出PH 的长．8．【方法尝试】（1）如图1，矩形ABFC 是矩形ADGE 以点A 为旋转中心，按逆时针方向旋转90︒所得的图形，CB ED 、分别是它们的对角线．则CB 与ED 数量关系________，位置关系________．【类比迁移】（2）如图2，在Rt ABC 和Rt ADE △中，90,9,6,3,2BAC DAE AC AB AE AD ∠=∠=︒====．将DAE 绕点A 在平面内逆时针旋转，设旋转角BAE ∠为()0360αα︒<︒，连接,CE BD ．请判断线段CE 和BD 的数量关系和位置关系，并说明理由；【拓展延伸】（3）如图3，在Rt ABC 中，90,6ACB AB ∠=︒=，过点A 作AP BC ∥，在射线AP 上取一点D ，连结CD，使得3tan4ACD∠=，请求写出线段BD的最大值．9．如图①，在正方形ABCD中，点N、M分别在边BC、CD上，连接AM、AN、MN．∠MAN＝45°，将△AMD 绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而得DM＋BN＝MN．【实践探究】(1)在图①条件下，若CN＝6，CM＝8，则正方形ABCD的边长是______．(2)如图②，点M、N分别在边CD、AB上，且BN＝DM．点E、F分别在BM、DN上，∠EAF＝45°，连接EF，猜想三条线段EF、BE、DF之间满足的数量关系，并说明理由．(3)【拓展应用】如图③，在矩形ABCD中，AB＝6，AD＝8，点M、N分别在边DC、BC上，连接AM，AN，已知∠MAN＝45°，BN＝2，求DM的长．10．小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究．(1)猜测探究：在△ABC中，AB＝AC，M是平面内任意一点，将线段AM绕点A按顺时针方向旋转与∠BAC 相等的角度，得到线段AN，连接NB．①如图1，若M是线段BC上的任意一点，请直接写出∠NAB与∠MAC的数量关系是，NB与MC的数量关系是；②如图2，点E是AB延长线上点，若M是∠CBE内部射线BD上任意一点，连接MC，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由．(2)拓展应用：如图3，在△A 1B 1C 1中，A 1B 1＝8，∠A 1B 1C 1＝60°，∠B 1A 1C 1＝75°，P 是B 1C 1上的任意点，连接A 1P ，将A 1P 绕点A 1按顺时针方向旋转75°，得到线段A 1Q ，连接B 1Q ．求线段B 1Q 长度的最小值． 11．如图，在Rt ABC △中，90BAC ∠=︒，AB AC =，D 为AC 边上一点，连接BD ，作AP BD ⊥于点P ，过点C 作CE AC ⊥交AP 延长线于点E ．(1)如图1，求证：AD CE =；(2)如图2，以AD ，BD 为邻边作ADBF ，连接EF 交BC 于点G ，连接AG ，①求证：AG EF ⊥；②若点D 为AC 中点，EF 、AB 交于点H ，求BH AB的值． 12．如图1，在ABC 中，90ACB ∠=︒，D 为AC 边上的一点，过点D 作DE AB ⊥，垂足为E ，连接BD ，P 为BD 中点，连接PC ，PE ．(1)求证：PC PE =；(2)将图1中ADE 绕着点A 顺时针旋转如图2的位置，其他条件不变，（1）中的结论是否成立？若成立，请证明：若不成立，请说明理由；(3)若10AB =，6AD =，30BAC DAE ∠=∠=︒，在平面内，将Rt ADE △绕点A 旋转一周，当A ，C ，E 三点共线时，请直接写出PCE 的面积．13．如图1，在直角坐标系中，点()2,0A ，点()0,2C ，点D ，点E 分别为OA ，OC 的中点，ODE 绕原点O 顺时针旋转α角（090α︒<<︒）得11OD E ，射线1CD ，1AE 相交于点F ．(1)求证：11OCD OAE △≌△；(2)如图2，在ODE 旋转过程中，当点1D 恰好落在线段CE 上时，求AF 的长；(3)如图3，在旋转α角从090α︒≤≤︒逐渐增大ODE 旋转过程中，求点F 的运动路线长．14．已知ABC 为等边三角形，边长为4，点D 、E 分别是BC 、AC 边上一点，连接AD 、BE ．AE CD =．(1)如图1，若2AE =，求BE 的长度；(2)如图2，点F 为AD 延长线上一点，连接BF 、CF ，AD 、BE 相交于点G ，连接CG ，已知60,∠=︒=EBF CE CG ，求证：2+=BF GE CF ；(3)如图3，点P 是ABC 内部一动点，顺次连接PA PB PC 、、++的最小值．15．【问题提出】（1）如图1，在ABC 中，90C ∠=︒，BD 平分ABC ∠交AC 于点D ，设CD 的长为m ，点D 到边AB 的距离为n ，则m _______n ；（填“＞”“＜”或“＝”）【问题探究】（2）如图2，在梯形ABCD 中，90A ∠=︒，AD BC ∥，(201AB =，BD 为对角线，且45BDC ∠=︒，求BCD △面积的最小值；【问题解决】（3）某景点有一个形状为菱形ABCD 的草坪，如图3，AB ==60B ∠︒，现欲将该草坪扩建为BEF △，使得点E 、F 分别在BA 、BC 的延长线上，且边EF 经过点D ，为了节省成本，要求扩建后的草坪面积（BEF △的面积）尽可能小，问BEF △的面积是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．16．综合与实践：数学课外小组研究了两个问题，请你帮助解答．问题一：如图1，在矩形ABCD 中，6AB =，8AD =，E ，F 分别为AB ，AD 边的中点，四边形AEGF 为矩形，连接CG ．问题二：数学小组对图形的旋转进行了拓展研究，如图4，在平行四边形ABCD 中，=60B ∠︒，6AB =，8AD =，E ，F 分别为AB ，AD 边的中点，四边形AEGF 为平行四边形，连接CG ．数学小组发现DF 与CG 仍然存在着特定的数量关系．(1)请直接写出CG 的长是______．如图2，当矩形AEGF 绕点A 旋转（如顺时针旋转）至点G 落在边AB 上时，DF =______，CG =______，DF 与CG 之间的数量关系是______．(2)当矩形AEGF 绕点A 旋转至如图3的位置时，（1）中DF 与CG 之间的数量关系是否还成立？并说明理由．(3)如图5，当平行四边形ABCD 绕点A 旋转（如顺时针旋转），其它条件不变时，数学小组发现DF 与CG 仍然存在着这一特定的数量关系．请你直接写出这个特定的数量关系是______．17．如图，在四边形ABCD 中，AD ∥BC ，∠ABC ＝90°，AD ＝CD ，O 是对角线AC 的中点，连接BO 并延长交边AD 或边CD 于点E ．(1)如图1，当点E 在AD 上时，连接CE ，求证：四边形ABCE 是矩形．(2)如图2，当点E 在CD 上时，当AC ＝4，BC ＝3时，求DAC S △与OBC S的比值．(3)若DE ＝2，OE ＝3，直接写出CD 的长．18．已知在正方形ABCD 中，E 是BC 边上一动点，作点B 关于AE 的对称点F ，BF 交AE 于点G ，连结DF ．(1)如图1，求DFB ∠的度数；(2)如图2，过点D 作DM BF ⊥交BF 的延长线于点M ，连结,CM CF ．若DF CM =，试探究四边形DFCM 的形状，并说明理由；(3)如图3，连结BD ，在AG 上截取=GT GB ，点P ，Q 分别是,AD BD 上的动点．若正方形ABCD 的面积为32，直接写出PTQ 周长的最小值．。

几何难题精选解答题〔共 30 小题〕1 ．〔2021 ?河南〕如图 1，在 Rt △ABC 中，∠B=90 °，BC=2AB=8 ，点 D、E 分别是边 BC、AC 的中点，连接DE，将△EDC 绕点 C 按顺时针方向旋转，记旋转角为α．〔1〕问题发现①当α=0 °时， = ；②当α=180 °时， = ．〔2〕拓展研究试判断：当 0°≤α＜360 °时，的大小有无变化？请仅就图 2 的状况给出证明．〔3〕问题解决当△EDC 旋转至 A，D，E 三点共线时，直接写出线段 BD 的长．2．〔2021 ?济南〕如图 1 ，在△ABC 中，∠ACB=90 °，AC=BC ，∠EAC=90 °，点M 为射线 AE 上任意一点〔不与 A 重合〕，连接 CM ，将线段 CM 绕点 C 按顺时针方向旋转 90 °获取线段CN ，直线 NB 分别交直线 CM 、射线 AE 于点 F、D．〔1〕直接写出∠ NDE 的度数；〔2〕如图 2、图 3，当∠EAC 为锐角或钝角时，其他条件不变，〔 1〕中的结论可否发生变化？若是不变，采用其中一种状况加以证明；若是变化，请说明原由；〔3〕如图 4，假设∠EAC=15 °，∠ACM=60 °，直线CM 与 AB 交于 G，BD= ，其他条件不变，求线段 AM的长．3 ．〔2021 ?岳阳〕直线 m ∥n ，点 C 是直线 m 上一点，点 D 是直线 n 上一点， CD 与直线 m 、n 不垂直，点 P 为线段 CD 的中点．〔1〕操作发现：直线 l ⊥m ，l⊥n，垂足分别为 A、B，当点 A 与点 C 重合时〔如图①所示〕，连接 PB，请直接写出线段 PA 与 PB 的数量关系：．〔2〕猜想证明：在图①的状况下，把直线 l 向上平移到如图②的地址，试问〔 1〕中的 PA 与 PB 的关系式可否依旧成立？假设成立，请证明；假设不成立，请说明原由．〔3〕延伸研究：在图②的状况下，把直线 l 绕点 A 旋转，使得∠ APB=90 °〔如图③所示〕，假设两平行线 m 、n 之间的距离为 2k ．求证： PA ?PB=k ?AB．4 ．〔2021 ?重庆〕在△ABC 中，AB=AC ，∠A=60 °，点D 是线段 BC 的中点，∠EDF=120 °，DE 与线段 AB 相交于点 E．DF 与线段 AC 〔或 AC 的延伸线〕订交于点 F．〔1〕如图 1，假设 DF⊥AC，垂足为 F，AB=4 ，求 BE 的长；〔2〕如图 2，将〔1 〕中的∠EDF 绕点 D 顺时针旋转必然的角度， DF 仍与线段 AC 订交于点 F．求证：BE+CF= AB；〔3〕如图 3，将〔 2〕中的∠EDF 连续绕点 D 顺时针旋转必然的角度，使 DF 与线段 AC 的延伸线订交于点 F，作 DN ⊥AC 于点 N ，假设 DN ⊥AC 于点 N ，假设 DN=FN ，求证： BE+CF= 〔BE﹣CF〕．5 ．〔2021 ?烟台〕【问题提出】如图①，△ ABC 是等腰三角形，点 E 在线段 AB 上，点 D 在直线 BC 上，且 ED=EC ，将△BCE 绕点 C 顺时针旋转 60°至△ACF 连接 EF试证明： AB=DB+AF【类比研究】〔1〕如图②，若是点 E 在线段 AB 的延伸线上，其他条件不变，线段 AB ，DB，AF 之间又有怎样的数量关系？请说明原由〔2〕若是点 E 在线段 BA 的延伸线上，其他条件不变，请在图③的基础大将图形补充完满，并写出 AB ，DB ，AF 之间的数量关系，不用说明原由．6 ．〔2021 ?莆田〕在 Rt△ACB 和 Rt △AEF 中，∠ACB= ∠AEF=90 °，假设点P 是 BF 的中点，连接 PC，PE．特别发现：如图 1，假设点 E，F 分别落在边 AB，AC 上，那么结论： PC=PE 成立〔不要求证明〕．问题研究：把图 1 中的△AEF 绕着点 A 顺时针旋转．〔1〕如图 2，假设点 E 落在边 CA 的延伸线上，那么上述结论可否成立？假设成立，请恩赐证明；假设不成立，请说明原由；〔2〕如图 3，假设点 F 落在边 AB 上，那么上述结论可否依旧成立？假设成立，请恩赐证明；假设不成立，请说明原由；〔3〕记 =k ，当 k 为何值时，△ CPE 总是等边三角形？〔请直接写出 k 的值，不用说明原由〕7 ．〔2021 ?襄城区模拟〕如图，正方形 ABCO 的边 OA 、OC 在坐标轴上，点 B 坐标为〔3，3〕．将正方形 ABCO绕点 A 顺时针旋转角度α〔 0°＜α＜90 °〕，获取正方形 ADEF ，ED 交线段 OC 于点 G，ED 的延伸线交线段 BC于点 P，连 AP 、AG ．〔1〕求证：△AOG ≌△ADG ；〔2〕求∠PAG 的度数；并判断线段 OG 、PG、BP 之间的数量关系，说明原由；〔3〕当∠1= ∠2 时，求直线 PE 的解析式；〔4〕在〔3〕的条件下，直线 PE 上可否存在点 M ，使以 M 、A、G 为极点的三角形是等腰三角形？假设存在，请直接写出 M 点坐标；假设不存在，请说明原由．8 ．〔2021 ?重庆校级一模〕，四边形 ABCD 是正方形，点 P 在直线 BC 上，点 G 在直线 AD 上〔P、G 不与正方形极点重合，且在 CD 的同侧〕， PD=PG ，DF⊥PG 于点 H，DF 交直线 AB 于点 F，将线段 PG 绕点 P逆时针旋转 90 °获取线段P E，连接 EF．〔1〕如图 1，当点 P 与点 G 分别在线段 BC 与线段 AD 上时，假设 PC=1 ，计算出 DG 的长；〔2〕如图 1，当点 P 与点 G 分别在线段 BC 与线段 AD 上时，证明：四边形 DFEP 为菱形；〔3〕如图 2，当点 P 与点 G 分别在线段 BC 与线段 AD 的延伸线上时，〔2〕的结论：四边形 DFEP 为菱形可否依旧成立？假设成立，请给出证明；假设不成立，请说明原由．9 ．〔2021 ?房山区二模〕在△ ABC 中，AB=BC=2 ，∠ABC=90 °，BD 为斜边 AC 上的中线，将△ ABD 绕点 D 顺时针旋转α〔0°＜α＜180 °〕获取△EFD，其中点 A 的对应点为点 E，点 B 的对应点为点 F．BE 与 FC 订交于点 H．〔1〕如图 1，直接写出 BE 与 FC 的数量关系：；〔2〕如图 2，M 、N 分别为 EF、BC 的中点．求证： MN= ；〔3〕连接 BF，CE，如图 3，直接写出在此旋转过程中，线段 BF、CE 与 AC 之间的数量关系：．10 ．〔2021 ?衢州校级模拟〕图 1 是边长分别为 4 和 2 的两个等边三角形纸片 ABC 和 ODE 叠放在一起〔 C与 O 重合〕．〔1〕操作：固定△ ABC ，将△0DE 绕点 C 顺时针旋转 30 °后获取△ODE ，连接 AD 、B E，CE 的延伸线交 AB 于 F 〔图 2〕；研究：在图 2 中，线段 BE 与 AD 之间有怎样的大小关系？试证明你的结论．〔2〕在〔 1〕的条件下将的△ ODE ，在线段 CF 上沿着 CF 方向以每秒 1 个单位的速度平移，平移后的△ CDE 设为△PQR，当点 P 与点 F 重合时停止运动〔图 3〕研究：设△PQR 搬动的时间为 x 秒，△PQR 与△ABC 重叠局部的面积为 y，求 y 与 x 之间的函数解析式，并写出函数自变量 x 的取值范围．〔3〕将图 1 中△0DE 固定，把△ABC 沿着 OE 方向平移，使极点 C 落在 OE 的中点 G 处，设为△ABG ，尔后将△ABG 绕点 G 顺时针旋转，边 BG 交边 DE 于点 M ，边 AG 交边 DO 于点 N ，设∠BGE= α〔30 °＜α＜90 °〕；〔图4 〕研究：在图 4 中，线段 ON ?EM 的值可否随α的变化而变化？若是没有变化，请你求出 ON ?EM 的值，若是有变化，请你说明原由．11 ．〔2021 ?武义县模拟〕〔 1 〕将矩形 OABC 放在平面直角坐标系中，极点 O 为原点，极点 C、A 分别在 x轴和 y 轴上， OA=8 ，OC=10 ，点 E 为 OA 边上一点，连接 CE，将△EOC 沿 CE 折叠．①如图 1，当点 O 落在 AB 边上的点 D 处时，求点 E 的坐标；②如图 2，当点 O 落在矩形 OABC 内部的点 D 处时，过点 E 作 EG∥x 轴交 CD 于点 H，交 BC 于点 G，设 H〔m ，n 〕，求 m 与 n 之间的关系式；〔2〕如图 3，将矩形 OABC 变为边长为 10 的正方形，点 E 为 y 轴上一动点，将△ EOC 沿 CE 折叠．点 O 落在点 D 处，延伸 CD 交直线 AB 于点 T，假设 = ，求 AT 的长．12 ．〔2021 ?石家庄校级模拟〕如图 1，在菱形 ABCD 中，AC=6 ，BD=6 ，AC，BD 订交于点 O ．〔1〕求边 AB 的长；〔2〕如图 2，将一个足够大的直角三角板 60 °角的极点放在菱形 ABCD 的极点 A 处，绕点 A 左右旋转，其中三角板 60 °角的两边分别于边 BC，CD 订交于 E，F，连接 EF 与 AC 订交于点 G．①判断△AEF 是哪一种特别三角形，并说明原由；②旋转过程中可否存在线段 EF 最短，假设存在，求出最小值，假设不存在，请说明原由．13 ．〔2021 春 ?泰安校级期中〕如图，正方形 OEFG 绕着边长为 30 的正方形 ABCD 的对角线的交点 O 旋转，边 OE、OG 分别交边 AD 、AB 于点 M 、N ．〔1〕求证： OM=ON ；〔2〕设正方形 OEFG 的对角线 OF 与边 AB 订交于点 P，连接 PM ．假设 PM=13 ，试求 AM 的长；〔3〕连接 MN ，求△AMN 周长的最小值，并指出此时线段 MN 与线段 BD 的关系．14 ．〔2021 ?天津〕在平面直角坐标系中， O 为原点，点 A〔﹣2 ，0〕，点 B〔0，2〕，点 E，点 F 分别为 OA ，OB 的中点．假设正方形 OEDF 绕点 O 顺时针旋转，得正方形 OE ′D′F′，记旋转角为α．〔Ⅰ〕如图①，当α =90 °时，求AE′，BF′的长；〔Ⅱ〕如图②，当α =135 °时，求证AE′=BF ′，且AE′⊥BF′；〔Ⅲ〕假设直线 AE′与直线BF′订交于点P，求点 P 的纵坐标的最大值〔直接写出结果即可〕．15 ．〔2021 春 ?青山区期末〕正方形 ABCD 和正方形 EBGF 共极点 B，连 AF，H 为 AF 的中点，连 EH，正方形 EBGF 绕点 B 旋转．〔1〕如图 1，当 F 点落在 BC 上时，求证： EH= FC；〔2〕如图 2，当点 E 落在 BC 上时，连 BH ，假设 AB=5 ，BG=2 ，求 BH 的长；〔3〕当正方形 EBGF 绕点 B 旋转到如图 3 的地址时，求的值．16 ．〔2021 ?盐城〕阅读资料如图①，△ABC 与△DEF 都是等腰直角三角形，∠ACB= ∠EDF=90 °，且点 D 在 AB 边上，AB、EF的中点均为 O ，连接 BF、CD 、CO ，显然点 C、F、O 在同一条直线上，可以证明△ BOF≌△COD ，那么 BF=CD ．解决问题〔1〕将图①中的 Rt△DEF 绕点 O 旋转获取图②，猜想此时线段 BF 与 CD 的数量关系，并证明你的结论；〔2〕如图③，假设△ ABC 与△DEF 都是等边三角形， AB 、EF 的中点均为 O ，上述〔 1 〕中的结论依旧成立吗？如果成立，请说明原由；如不成立，央求出 BF 与 CD 之间的数量关系；〔3〕如图④，假设△ABC 与△DEF 都是等腰三角形， AB 、EF 的中点均为 0，且顶角∠ACB= ∠EDF= α，请直接写出的值〔用含α的式子表示出来〕17 ．〔2021 ?梅州〕用如图①，②所示的两个直角三角形〔局部边长及角的度数在图中已标出〕，完成以下两个研究问题：研究一：将以上两个三角形如图③拼接〔 BC 和 ED 重合〕，在 BC 边上有一动点 P．〔1〕当点 P 运动到∠CFB 的角均分线上时，连接 AP，求线段 AP 的长；〔2〕当点 P 在运动的过程中出现 PA=FC 时，求∠PAB 的度数．研究二：如图④，将△ DEF 的极点 D 放在△ABC 的 BC 边上的中点处，并以点 D 为旋转中心旋转△ DEF，使△DEF 的两直角边与△ ABC 的两直角边分别交于 M 、N 两点，连接 MN ．在旋转△DEF 的过程中，△ AMN 的周长可否存在有最小值？假设存在，求出它的最小值；假设不存在，请说明原由．18 ．〔2021 ?营口〕如图，点 P 是⊙O 外一点， PA 切⊙O 于点 A，AB 是⊙O 的直径，连接 OP ，过点 B 作 BC∥OP 交⊙O 于点 C，连接 AC 交 OP 于点 D ．〔1〕求证： PC 是⊙ O 的切线；〔2〕假设 PD= ，AC=8 ，求图中阴影局部的面积；〔3〕在〔 2〕的条件下，假设点 E是的中点，连接 CE，求 CE 的长．19 ．〔2021 ?永州〕问题研究：〔一〕新知学习：圆内接四边形的判判断理：若是四边形对角互补，那么这个四边形内接于圆〔即若是四边形 EFGH 的对角互补，那么四边形 EFGH 的四个极点 E、F、G、H 都在同个圆上〕．〔二〕问题解决：⊙ O 的半径为 2，AB ，CD 是⊙O 的直径． P 是上任意一点，过点 P 分别作 AB，CD 的垂线，垂足分别为 N，M ．〔1〕假设直径 AB⊥CD，关于上任意一点 P〔不与 B、C 重合〕〔如图一〕，证明四边形 PMON 内接于圆，并求此圆直径的长；〔2〕假设直径 AB⊥CD ，在点 P〔不与 B、C 重合〕从 B 运动到 C 的过程中，证明 MN 的长为定值，并求其定值；〔3〕假设直径 AB 与 CD 订交成 120 °角．①当点 P 运动到的中点 P1 时〔如图二〕，求 MN 的长；②当点 P〔不与 B、C 重合〕从 B 运动到 C 的过程中〔如图三〕，证明 MN 的长为定值．〔4〕试问当直径 AB 与 CD 订交成多少度角时， MN 的长取最大值，并写出其最大值．20 ．〔2021 ?盘锦〕如图 1，△ABC 和△AED 都是等腰直角三角形，∠ BAC= ∠EAD=90 °，点B 在线段 AE 上，点C 在线段 AD 上．〔1〕请直接写出线段 BE 与线段 CD 的关系：；〔2〕如图 2，将图 1 中的△ABC 绕点 A 顺时针旋转角α〔 0＜α＜360 °〕，①〔1〕中的结论可否成立？假设成立，请利用图 2 证明；假设不成立，请说明原由；②当 AC= ED 时，研究在△ABC 旋转的过程中，可否存在这样的角α，使以 A、B、C、D 四点为极点的四边形是平行四边形？假设存在，请直接写出角α的度数；假设不存在，请说明原由．21 ．〔2021 ?旭日〕问题：如图〔 1〕，在 Rt△ACB 中，∠ACB=90 °，AC=CB ，∠DCE=45 °，试试究AD 、DE、EB 满足的等量关系．[研究发现 ]小聪同学利用图形变换，将△ CAD 绕点 C 逆时针旋转 90°获取△CBH，连接 EH，由条件易得∠ EBH=90 °，∠ECH= ∠ECB+ ∠BCH= ∠ECB+ ∠ACD=45 °．依照“边角边〞，可证△ CEH ≌，得 EH=ED ．在 Rt△HBE 中，由定理，可得 BH 2+EB 2=EH 2，由 BH=AD ，可得 AD 、DE、EB 之间的等量关系是．[实践运用 ]〔1〕如图〔 2 〕，在正方形 ABCD 中，△AEF 的极点 E、F 分别在 BC、CD 边上，高 AG 与正方形的边长相等，求∠EAF 的度数；〔2〕在〔 1〕条件下，连接 BD ，分别交 AE、AF 于点 M 、N ，假设 BE=2 ，DF=3 ，BM=2 ，运用小聪同学探究的结论，求正方形的边长及 MN 的长．22 ．〔2021 ?自贡〕在△ABC 中，AB=AC=5 ，cos ∠ABC= ，将△ABC 绕点 C 顺时针旋转，获取△ A1B1C．〔1〕如图①，当点 B1 在线段 BA 延伸线上时．①求证： BB1∥CA 1；②求△AB1C 的面积；〔2〕如图②，点 E 是 BC 边的中点，点 F 为线段 AB 上的动点，在△ ABC 绕点 C 顺时针旋转过程中，点 F 的对应点是 F1，求线段 EF1 长度的最大值与最小值的差．23 ．〔2021 ?吉林〕两个三角板 ABC，DEF，按以以下图的地址摆放，点 B 与点 D 重合，边 AB 与边 DE 在同一条直线上〔假设图形中所有的点，线都在同一平面内〕．其中，∠C= ∠DEF=90 °，∠ABC= ∠F=30 °，AC=DE=6cm ．现固定三角板 DEF，将三角板 ABC 沿射线 DE 方向平移，当点 C 落在边 EF 上时停止运动．设三角板平移的距离为 x〔cm 〕，两个三角板重叠局部的面积为 y〔cm 2〕．〔1〕当点 C 落在边 EF 上时， x= cm ；〔2〕求 y 关于 x 的函数解析式，并写出自变量 x 的取值范围；〔3〕设边 BC 的中点为点 M ，边 DF 的中点为点 N ．直接写出在三角板平移过程中，点 M 与点 N 之间距离的最小值．24 ．〔2021 ?汕尾〕在 Rt△ABC 中，∠A=90 °，AC=AB=4 ，D，E 分别是边 AB ，AC 的中点，假设等腰 Rt△ADE绕点 A 逆时针旋转，获取等腰 Rt△AD 1E1，设旋转角为α〔 0＜α≤180 °〕，记直线 BD1 与 CE1 的交点为 P．〔1〕如图 1，当α=90 °时，线段BD 1 的长等于，线段 CE1 的长等于；〔直接填写结果〕〔2〕如图 2，当α=135 °时，求证：BD 1=CE 1，且 BD1⊥CE1；〔3〕求点 P 到 AB 所在直线的距离的最大值．〔直接写出结果〕25 ．〔2021 ?赤峰〕如图，四边形 ABCD 是边长为 2，一个锐角等于 60°的菱形纸片，小芳同学将一个三角形纸片的一个极点与该菱形极点 D 重合，按顺时针方向旋转三角形纸片，使它的两边分别交 CB、BA〔或它们的延长线〕于点 E、F，∠EDF=60 °，当CE=AF 时，如图 1 小芳同学得出的结论是 DE=DF ．〔1〕连续旋转三角形纸片，当 CE≠AF 时，如图 2 小芳的结论可否成立？假设成立，加以证明；假设不成立，请说明原由；〔2〕再次旋转三角形纸片，当点 E、F 分别在 CB、BA 的延伸线上时，如图 3 请直接写出 DE 与 DF 的数量关系；〔3〕连 EF，假设△DEF 的面积为 y ，CE=x ，求 y 与 x 的关系式，并指出当 x 为何值时， y 有最小值，最小值是多少？26 ．〔2021 ?海南〕如图，菱形 ABCD 中，点 P 是 CD 的中点，∠BCD=60 °，射线AP 交 BC 的延伸线于点 E，射线 BP 交 DE 于点 K，点 O 是线段 BK 的中点．〔1〕求证：△ADP ≌△ECP；〔2〕假设 BP=n ?PK，试求出 n 的值；〔3〕作 BM 丄 AE 于点 M ，作 KN 丄 AE 于点 N，连接 MO 、NO ，如图 2 所示，请证明△MON 是等腰三角形，并直接写出∠ MON 的度数．27 ．〔2021 ?丹东〕在正方形 ABCD 中，对角线 AC 与 BD 交于点 O；在 Rt△PMN 中，∠MPN=90 °．〔1〕如图 1，假设点 P 与点 O 重合且 PM ⊥AD 、PN ⊥AB ，分别交 AD 、AB 于点 E、F，请直接写出 PE 与 PF 的数量关系；〔2〕将图 1 中的 Rt△PMN 绕点 O 顺时针旋转角度α〔 0 °＜α＜45 °〕．①如图 2，在旋转过程中〔 1〕中的结论依旧成立吗？假设成立，请证明；假设不成立，请说明原由；②如图 2，在旋转过程中，当∠ DOM=15 °时，连接EF，假设正方形的边长为 2，请直接写出线段 EF 的长；③如图 3，旋转后，假设 Rt△PMN 的极点 P 在线段 OB 上搬动〔不与点 O 、B 重合〕，当 BD=3BP 时，猜想此时PE 与 PF 的数量关系，并给出证明；当 BD=m ?BP 时，请直接写出 PE 与 PF 的数量关系．28 ．〔2021 ?成都〕 AC ，EC 分别是四边形 ABCD 和 EFDC 的对角线，点 E 在△ABC 内，∠CAE+ ∠CBE=90 °．〔1〕如图①，当四边形 ABCD 和 EFCG 均为正方形时，连接 BF．〔i〕求证：△CAE∽△CBF；〔ii 〕假设 BE=1 ，AE=2 ，求 CE 的长；〔2〕如图②，当四边形 ABCD 和 EFCG 均为矩形，且 = =k 时，假设 BE=1 ，AE=2 ，CE=3 ，求 k 的值；〔3〕如图③，当四边形 ABCD 和 EFCG 均为菱形，且∠ DAB= ∠GEF=45 °时，设BE=m ，AE=n ，CE=p ，试试究 m ，n，p 三者之间满足的等量关系．〔直接写出结果，不用写出解答过程〕29 ．〔2021 ?锦州〕如图①，∠ QPN 的极点 P 在正方形 ABCD 两条对角线的交点处，∠ QPN= α，将∠QPN 绕点P 旋转，旋转过程中∠ QPN 的两边分别与正方形 ABCD 的边 AD 和 CD 交于点 E 和点 F〔点 F 与点 C，D 不重合〕．〔1〕如图①，当α =90 °时，DE，DF，AD 之间满足的数量关系是；〔2〕如图②，将图①中的正方形 ABCD 改为∠ADC=120 °的菱形，其他条件不变，当α =60 °时，〔1〕中的结论变为 DE+DF= AD ，请给出证明；〔3〕在〔2〕的条件下，假设旋转过程中∠ QPN 的边 PQ 与射线 AD 交于点 E，其他条件不变，研究在整个运动变化过程中， DE，DF ，AD 之间满足的数量关系，直接写出结论，不用加以证明．30 ．〔2021 ?绵阳〕如图 1，矩形 ABCD 中，AB=4 ，AD=3 ，把矩形沿直线 AC 折叠，使点 B 落在点 E 处，AE交 CD 于点 F，连接 DE．〔1〕求证：△DEC≌△EDA；〔2〕求 DF 的值；〔3〕如图 2，假设 P 为线段 EC 上一动点，过点 P 作△AEC 的内接矩形，使其极点 Q 落在线段 AE 上，定点 M 、N 落在线段 AC 上，当线段 PE 的长为何值时，矩形 PQMN 的面积最大？并求出其最大值．几何难题精选 (1) 旋转圆四边形参照答案与试题解析一．解答题〔共 30 小题〕1 ．〔2021 ?河南〕如图 1，在 Rt △ABC 中，∠B=90 °，BC=2AB=8 ，点 D、E 分别是边 BC、AC 的中点，连接DE，将△EDC 绕点 C 按顺时针方向旋转，记旋转角为α．〔1〕问题发现①当α=0 °时， = ；②当α=180 °时， = ．〔2〕拓展研究试判断：当 0°≤α＜360 °时，的大小有无变化？请仅就图 2 的状况给出证明．〔3〕问题解决当△EDC 旋转至 A，D，E 三点共线时，直接写出线段 BD 的长．【考点】几何变换综合题．【专题】压轴题．【解析】〔1〕①当α=0 °时，在Rt △ABC 中，由勾股定理，求出 AC 的值是多少；尔后依照点 D、E 分别是边BC、AC 的中点，分别求出 AE、BD 的大小，即可求出的值是多少．②α=180 °时，可得AB ∥DE，尔后依照，求出的值是多少即可．〔2〕第一判断出∠ ECA= ∠DCB ，再依照，判断出△ECA∽△DCB，即可求出的值是多少，进而判断出的大小没有变化即可．〔3〕依照题意，分两种状况：①点 A，D，E 所在的直线和 BC 平行时；②点 A ，D，E 所在的直线和 BC 订交时；尔后分类谈论，求出线段 BD 的长各是多少即可．【解答】解：〔 1〕①当α=0 °时，∵Rt △ABC 中，∠B=90 °，∴AC= ，∵点D、E 分别是边 BC、AC 的中点，∴，∴．②如图 1，，当α=180 °时，可得 AB∥DE，∵，∴ = ．故答案为：．〔2〕如图 2，，当 0°≤α＜360 °时，的大小没有变化，∵∠ECD= ∠ACB ，∴∠ECA= ∠DCB ，又∵，∴△ECA∽△DCB ，∴．〔3〕①如图 3 ，，∵AC=4 ，CD=4 ，CD ⊥AD ，∴AD= = ，∵AD=BC ，AB=DC ，∠B=90 °，∴四边形 ABCD 是矩形，∴．②如图 4，连接 BD，过点 D 作 AC 的垂线交 AC 于点 Q ，过点 B作 AC 的垂线交 AC 于点 P，，∵AC=4 ，CD=4 ，CD ⊥AD ，∴AD= = ，∵点D、E 分别是边 BC、AC 的中点，∴DE= =2 ，∴AE=AD ﹣DE=8 ﹣2=6 ，由〔2〕，可得，∴BD= = ．综上所述， BD 的长为 4 或．【谈论】〔1〕此题主要观察了几何变换综合题，观察了解析推理能力，观察了分类谈论思想的应用，观察了数形结合思想的应用，要熟练掌握．〔2〕此题还观察了相似三角形、全等三角形的判断和性质的应用，要熟练掌握．〔3〕此题还观察了线段长度的求法，以及矩形的判断和性质的应用，要熟练掌握．2．〔2021 ?济南〕如图 1 ，在△ABC 中，∠ACB=90 °，AC=BC ，∠EAC=90 °，点M 为射线 AE 上任意一点〔不与 A 重合〕，连接 CM ，将线段 CM 绕点 C 按顺时针方向旋转 90 °获取线段CN ，直线 NB 分别交直线 CM 、射线 AE 于点 F、D．〔1〕直接写出∠ NDE 的度数；〔2〕如图 2、图 3，当∠EAC 为锐角或钝角时，其他条件不变，〔 1〕中的结论可否发生变化？若是不变，采用其中一种状况加以证明；若是变化，请说明原由；〔3〕如图 4，假设∠EAC=15 °，∠ACM=60 °，直线CM 与 AB 交于 G，BD= ，其他条件不变，求线段 AM的长．【考点】几何变换综合题．【专题】压轴题．【解析】〔1〕依照题意证明△ MAC ≌△NBC 即可；〔2〕与〔 1〕的证明方法相似，证明△ MAC ≌△NBC 即可；〔3〕作 GK ⊥BC 于 K，证明 AM=AG ，依照△MAC ≌△NBC ，获取∠BDA=90 °，依照直角三角形的性质和条件求出 AG 的长，获取答案．【解答】解：〔 1〕∵∠ACB=90 °，∠MCN=90 °，∴∠ACM= ∠BCN ，在△MAC 和△NBC 中，，∴△MAC ≌△NBC ，∴∠NBC= ∠MAC=90 °，又∵∠ACB=90 °，∠EAC=90 °，∴∠NDE=90 °；〔2〕不变，在△MAC ≌△NBC 中，，∴△MAC ≌△NBC ，∴∠N= ∠AMC ，又∵∠MFD= ∠NFC，∠MDF= ∠FCN=90 °，即∠NDE=90 °；〔3〕作 GK⊥BC 于 K，∵∠EAC=15 °，∴∠BAD=30 °，∵∠ACM=60 °，∴∠GCB=30 °，∴∠AGC= ∠ABC+ ∠GCB=75 °，∠AMG=75 °，∴AM=AG ，∵△MAC ≌△NBC ，∴∠MAC= ∠NBC ，∴∠BDA= ∠BCA=90 °，∵BD= ，∴AB= + ，AC=BC= +1 ，设 BK=a ，那么 GK=a ，CK= a，∴a+ a= +1 ，∴a=1 ，∴KB=KG=1 ，BG= ，AG= ，∴AM= ．【谈论】此题观察的是矩形的判断和性质以及三角形全等的判断和性质，正确作出辅助线、利用方程的思想是解题的重点，注意旋转的性质的灵便运用．3 ．〔2021 ?岳阳〕直线 m ∥n ，点 C 是直线 m 上一点，点 D 是直线 n 上一点， CD 与直线 m 、n 不垂直，点 P 为线段 CD 的中点．〔1〕操作发现：直线 l ⊥m ，l⊥n，垂足分别为 A、B，当点 A 与点 C 重合时〔如图①所示〕，连接 PB，请直接写出线段 PA 与 PB 的数量关系： PA=PB ．〔2〕猜想证明：在图①的状况下，把直线 l 向上平移到如图②的地址，试问〔 1〕中的 PA 与 PB 的关系式可否依旧成立？假设成立，请证明；假设不成立，请说明原由．〔3〕延伸研究：在图②的状况下，把直线 l 绕点 A 旋转，使得∠ APB=90 °〔如图③所示〕，假设两平行线 m 、n 之间的距离为 2k ．求证： PA ?PB=k ?AB．【考点】几何变换综合题．【专题】压轴题．【解析】〔1〕依照三角形 CBD 是直角三角形，而且点 P 为线段 CD 的中点，应用直角三角形的性质，可得 PA=PB ，据此解答即可．〔2〕第一过 C 作 CE⊥n 于点 E，连接 P E，尔后分别判断出 PC=PE 、∠PCA= ∠PEB、AC=BE ；尔后依照全等三角形判断的方法，判断出△ PAC∽△PBE，即可判断出 PA=PB 依旧成立．〔3〕第一延伸 AP 交直线 n 于点 F，作 AE⊥BD 于点 E，尔后依照相似三角形判断的方法，判断出△AEF∽△BPF，即可判断出 AF ?BP=AE ?BF，再个 AF=2PA ，AE=2k ，BF=AB ，可得 2PA ?PB=2k ．AB，因此 PA?PB=k ?AB，据此解答即可．【解答】解：〔 1〕∵l⊥n，∴BC⊥BD，∴三角形 CBD 是直角三角形，又∵点 P 为线段 CD 的中点，∴PA=PB ．〔2〕把直线 l 向上平移到如图②的地址， PA=PB 依旧成立，原由以下：如图②，过 C 作 CE⊥n 于点 E，连接 P E，，∵三角形 CED 是直角三角形，点 P 为线段 CD 的中点，∴PD=PE ，又∵点 P 为线段 CD 的中点，∴PC=PD ，∴PC=PE ；∵PD=PE ，∴∠CDE= ∠PEB，∵直线 m ∥n ，∴∠CDE= ∠PCA ，∴∠PCA= ∠PEB，又∵直线 l⊥m ，l⊥n，CE⊥m ，CE⊥n ，∴l∥CE，∴AC=BE ，在△PAC 和△PBE 中，∴△PAC≌△PBE，∴PA=PB ．〔3〕如图③，延伸 AP 交直线 n 于点 F，作 AE⊥BD 于点 E，，∵直线 m ∥n ，∴，∴AP=PF ，∵∠APB=90 °，∴BP⊥AF，又∵AP=PF ，∴BF=AB ；在△AEF 和△BPF 中，∴△AEF∽△BPF，∴，∴AF ?BP=AE ?BF，∵AF=2PA ，AE=2k ，BF=AB ，∴2PA ?PB=2k ．AB ，∴PA?PB=k ?AB ．【谈论】〔1〕此题主要观察了几何变换综合题，观察了解析推理能力，观察了分类谈论思想的应用，观察了数形结合思想的应用，观察了从图象中获守信息，并能利用获取的信息解答相应的问题的能力．〔2〕此题还观察了直角三角形的性质和应用，要熟练掌握．〔3〕此题还观察了全等三角形的判断和性质的应用，以及相似三角形的判断和性质的应用，要熟练掌握．4 ．〔2021 ?重庆〕在△ABC 中，AB=AC ，∠A=60 °，点D 是线段 BC 的中点，∠EDF=120 °，DE 与线段 AB 相交于点 E．DF 与线段 AC 〔或 AC 的延伸线〕订交于点 F．〔1〕如图 1，假设 DF⊥AC，垂足为 F，AB=4 ，求 BE 的长；〔2〕如图 2，将〔1 〕中的∠EDF 绕点 D 顺时针旋转必然的角度， DF 仍与线段 AC 订交于点 F．求证：BE+CF= AB；〔3〕如图 3，将〔 2〕中的∠EDF 连续绕点 D 顺时针旋转必然的角度，使 DF 与线段 AC 的延伸线订交于点 F，作 DN ⊥AC 于点 N ，假设 DN ⊥AC 于点 N ，假设 DN=FN ，求证： BE+CF= 〔BE﹣CF〕．【考点】几何变换综合题；全等三角形的判断与性质；等边三角形的判断与性质；锐角三角函数的定义．【专题】压轴题．【解析】〔1〕如图 1，易求得∠B=60 °，∠BED=90 °，BD=2 ，尔后运用三角函数的定义即可求出 BE 的值；〔2〕过点 D 作 DM ⊥AB 于 M ，作 DN ⊥AC 于 N，如图 2，易证△MBD ≌△NCD ，那么有 BM=CN ，DM=DN ，进而可证到△ EMD ≌△FND ，那么有 EM=FN ，即可获取 BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60 °=BD= BC= AB；〔3〕过点 D 作 DM ⊥AB 于 M ，如图 3．同〔1〕可得：∠B= ∠ACD=60 °，同〔2〕可得： BM=CN ，DM=DN ，EM=FN ．由 DN=FN 可得 DM=DN=FN=EM ，进而可得BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM ，B E﹣CF=BM+EM ﹣CF=BM+NF ﹣CF=BM+NC=2BM ．尔后在 Rt△BMD 中，运用三角函数即可获取 DM= BM ，即 BE+CF= 〔B E﹣CF〕．【解答】解：〔 1〕如图 1，∵AB=AC ，∠A=60 °，∴△ABC 是等边三角形，∴∠B= ∠C=60 °，BC=AC=AB=4 ．∵点D 是线段 BC 的中点，∴BD=DC= BC=2 ．∵DF⊥AC，即∠AFD=90 °，∴∠AED=360 °﹣60 °﹣90 °﹣120 °=90 °，∴∠BED=90 °，∴BE=BD ×cos ∠B=2 ×cos60 °=2 × =1 ；〔2〕过点 D 作 DM ⊥AB 于 M ，作 DN ⊥AC 于 N，如图 2，那么有∠AMD= ∠BMD= ∠AND= ∠CND=90 °．∵∠A=60 °，∴∠MDN=360 °﹣60 °﹣90 °﹣90 °=120 °．∵∠EDF=120 °，∴∠MDE= ∠NDF ．在△MBD 和△NCD 中，，∴△MBD ≌△NCD ，∴BM=CN ，DM=DN ．在△EMD 和△FND 中，，∴△EMD ≌△FND ，∴EM=FN ，∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD ×cos60 °=BD= BC= AB ；〔3〕过点 D 作 DM ⊥AB 于 M ，如图 3．同〔1〕可得：∠B= ∠ACD=60 °．同〔2〕可得： BM=CN ，DM=DN ，EM=FN ．∵DN=FN ，∴DM=DN=FN=EM ，∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM ，BE﹣CF=BM+EM ﹣CF=BM+NF ﹣CF=BM+NC=2BM ．在 Rt△BMD 中，DM=BM ?tanB= BM ，∴BE+CF= 〔BE﹣CF〕．【谈论】此题主要观察了等边三角形的判断与性质、四边形的内角和定理、全等三角形的判断与性质、三角函数的定义、特别角的三角函数值等知识，经过证明三角形全等获取 BM=CN ，DM=DN ，EM=FN 是解决此题的关键．5 ．〔2021 ?烟台〕【问题提出】如图①，△ ABC 是等腰三角形，点 E 在线段 AB 上，点 D 在直线 BC 上，且 ED=EC ，将△BCE 绕点 C 顺时针旋转 60°至△ACF 连接 EF试证明： AB=DB+AF【类比研究】〔1〕如图②，若是点 E 在线段 AB 的延伸线上，其他条件不变，线段 AB ，DB，AF 之间又有怎样的数量关系？请说明原由〔2〕若是点 E 在线段 BA 的延伸线上，其他条件不变，请在图③的基础大将图形补充完满，并写出 AB ，DB ，AF 之间的数量关系，不用说明原由．【考点】几何变换综合题．【专题】压轴题．【解析】第一判断出△ CEF 是等边三角形，即可判断出 EF=EC，再依照 ED=EC ，可得 ED=EF ，∠CAF= ∠BAC=60 °，因此∠EAF= ∠BAC+ ∠CAF=120 °，∠DBE=120 °，∠EAF= ∠DBE；尔后依照全等三角形判断的方法，判断出△EDB ≌△FEA ，即可判断出 BD=AE ，AB=AE+BF ，因此 AB=DB+AF ．〔1〕第一判断出△CEF 是等边三角形，即可判断出 EF=EC，再依照 ED=EC ，可得 ED=EF ，∠CAF= ∠BAC=60 °，因此∠EFC= ∠FGC+ ∠FCG，∠BAC= ∠FGC+ ∠FEA，∠FCG= ∠FEA，再依照∠FCG= ∠EAD ，∠D= ∠EAD，可得∠D= ∠FEA；尔后依照全等三角形判断的方法，判断出△ EDB≌△FEA，即可判断出 BD=AE ，EB=AF ，进而判断出AB=BD ﹣AF 即可．〔2〕第一依照点 E 在线段 BA 的延伸线上，在图③的基础大将图形补充完满，尔后判断出△ CEF 是等边三角形，即可判断出 EF=EC ，再依照 ED=EC ，可得 ED=EF ，∠CAF= ∠BAC=60 °，再判断出∠ DBE= ∠EAF，∠BDE= ∠AEF；。

几何综合压轴问题(40题)1(2023·四川自贡·统考中考真题)如图1，一大一小两个等腰直角三角形叠放在一起，M，N分别是斜边DE，AB的中点，DE=2,AB=4．(1)将△CDE绕顶点C旋转一周，请直接写出点M，N距离的最大值和最小值；(2)将△CDE绕顶点C逆时针旋转120°(如图2)，求MN的长．2(2023·山东烟台·统考中考真题)如图，点C为线段AB上一点，分别以AC,BC为等腰三角形的底边，在AB的同侧作等腰△ACD和等腰△BCE，且∠A=∠CBE．在线段EC上取一点F，使EF=AD，连接BF,DE．(1)如图1，求证：DE=BF；(2)如图2，若AD=2，BF的延长线恰好经过DE的中点G，求BE的长．3(2023·浙江绍兴·统考中考真题)在平行四边形ABCD中(顶点A,B,C,D按逆时针方向排列)，AB= 12,AD=10,∠B为锐角，且sin B=45．(1)如图1，求AB边上的高CH的长．(2)P是边AB上的一动点，点C,D同时绕点P按逆时针方向旋转90°得点C ,D ．①如图2，当点C 落在射线CA上时，求BP的长．②当△AC D 是直角三角形时，求BP的长．4(2023·甘肃武威·统考中考真题)【模型建立】(1)如图1，△ABC和△BDE都是等边三角形，点C关于AD的对称点F在BD边上．①求证：AE=CD；②用等式写出线段AD，BD，DF的数量关系，并说明理由．【模型应用】(2)如图2，△ABC是直角三角形，AB=AC，CD⊥BD，垂足为D，点C关于AD的对称点F在BD边上．用等式写出线段AD，BD，DF的数量关系，并说明理由．【模型迁移】(3)在(2)的条件下，若AD=42，BD=3CD，求cos∠AFB的值．5(2023·江西·统考中考真题)课本再现思考我们知道，菱形的对角线互相垂直．反过来，对角线互相垂直的平行四边形是菱形吗？可以发现并证明菱形的一个判定定理；对角线互相垂直的平行四边形是菱形．(1)定理证明：为了证明该定理，小明同学画出了图形(如图1)，并写出了“已知”和“求证”，请你完成证明过程．己知：在▱ABCD中，对角线BD⊥AC，垂足为O．求证：▱ABCD是菱形．(2)知识应用：如图2，在▱ABCD中，对角线AC和BD相交于点O，AD=5，AC=8，BD=6．①求证：▱ABCD是菱形；②延长BC至点E，连接OE交CD于点F，若∠E=12∠ACD，求OFEF的值．6(2023·湖北随州·统考中考真题)1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．(1)下面是该问题的一种常见的解决方法，请补充以下推理过程：(其中①处从“直角”和“等边”中选择填空，②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，③处填写角度数，④处填写该三角形的某个顶点)当△ABC的三个内角均小于120°时，如图1，将△APC绕，点C顺时针旋转60°得到△A P C，连接PP ，由PC=P C，∠PCP =60°，可知△PCP 为三角形，故PP =PC，又P A =PA，故PA+PB+PC =PA +PB+PP ≥A B，由可知，当B，P，P ，A在同一条直线上时，PA+PB+PC取最小值，如图2，最小值为A B，此时的P点为该三角形的“费马点”，且有∠APC=∠BPC=∠APB=；已知当△ABC有一个内角大于或等于120°时，“费马点”为该三角形的某个顶点．如图3，若∠BAC≥120°，则该三角形的“费马点”为点．(2)如图4，在△ABC中，三个内角均小于120°，且AC=3，BC=4，∠ACB=30°，已知点P为△ABC的“费马点”，求PA+PB+PC的值；(3)如图5，设村庄A，B，C的连线构成一个三角形，且已知AC=4km，BC=23km，∠ACB=60°．现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a 元/km，a元/km，2a元/km，选取合适的P的位置，可以使总的铺设成本最低为元．(结果用含a的式子表示)7(2023·山东枣庄·统考中考真题)问题情境：如图1，在△ABC中，AB=AC=17，BC=30，AD是BC边上的中线．如图2，将△ABC的两个顶点B，C分别沿EF,GH折叠后均与点D重合，折痕分别交AB,AC,BC于点E，G，F，H．猜想证明：(1)如图2，试判断四边形AEDG的形状，并说明理由．问题解决；(2)如图3，将图2中左侧折叠的三角形展开后，重新沿MN折叠，使得顶点B与点H重合，折痕分别交AB, BC于点M，N，BM的对应线段交DG于点K，求四边形MKGA的面积．8(2023·湖南·统考中考真题)(1)[问题探究]如图1，在正方形ABCD中，对角线AC、BD相交于点O．在线段AO上任取一点P(端点除外)，连接PD、PB．①求证：PD=PB；②将线段DP绕点P逆时针旋转，使点D落在BA的延长线上的点Q处．当点P在线段AO上的位置发生变化时，∠DPQ的大小是否发生变化？请说明理由；③探究AQ与OP的数量关系，并说明理由．(2)[迁移探究]如图2，将正方形ABCD换成菱形ABCD，且∠ABC=60°，其他条件不变．试探究AQ与CP的数量关系，并说明理由．9(2023·湖南岳阳·统考中考真题)如图1，在△ABC中，AB=AC，点M,N分别为边AB,BC的中点，连接MN．初步尝试：(1)MN与AC的数量关系是，MN与AC的位置关系是．特例研讨：(2)如图2，若∠BAC=90°,BC=42，先将△BMN绕点B顺时针旋转α(α为锐角)，得到△BEF，当点A,E,F在同一直线上时，AE与BC相交于点D，连接CF．(1)求∠BCF的度数；(2)求CD的长．深入探究：(3)若∠BAC<90°，将△BMN绕点B顺时针旋转α，得到△BEF，连接AE，CF．当旋转角α满足0°<α<360°，点C,E,F在同一直线上时，利用所提供的备用图探究∠BAE与∠ABF的数量关系，并说明理由．10(2023·湖北黄冈·统考中考真题)【问题呈现】△CAB和△CDE都是直角三角形，∠ACB=∠DCE=90°,CB=mCA,CE=mCD，连接AD，BE，探究AD，BE的位置关系．(1)如图1，当m=1时，直接写出AD，BE的位置关系：；(2)如图2，当m≠1时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由．【拓展应用】(3)当m=3,AB=47,DE=4时，将△CDE绕点C旋转，使A,D,E三点恰好在同一直线上，求BE的长．11(2023·河北·统考中考真题)如图1和图2，平面上，四边形ABCD中，AB=8,BC=211,CD=12, DA=6,∠A=90°，点M在AD边上，且DM=2．将线段MA绕点M顺时针旋转n°(0<n≤180)到MA ,∠A MA的平分线MP所在直线交折线AB-BC于点P，设点P在该折线上运动的路径长为x(x>0)，连接A P．(1)若点P在AB上，求证：A P=AP；(2)如图2．连接BD．①求∠CBD的度数，并直接写出当n=180时，x的值；②若点P到BD的距离为2，求tan∠A MP的值；(3)当0<x≤8时，请直接写出点A 到直线AB的距离．(用含x的式子表示)．12(2023·四川达州·统考中考真题)(1)如图①，在矩形ABCD的AB边上取一点E，将△ADE沿DE翻折，使点A落在BC上A 处，若AB=6,BC=10，求AEEB的值；(2)如图②，在矩形ABCD 的BC 边上取一点E ，将四边形ABED 沿DE 翻折，使点B 落在DC 的延长线上B 处，若BC ⋅CE =24,AB =6，求BE 的值；(3)如图③，在△ABC 中，∠BAC =45°,AD ⊥BC ，垂足为点D ,AD =10,AE =6，过点E 作EF ⊥AD 交AC 于点F ，连接DF ，且满足∠DFE =2∠DAC ，直接写出BD +53EF 的值．13(2023·湖南郴州·统考中考真题)已知△ABC 是等边三角形，点D 是射线AB 上的一个动点，延长BC 至点E ，使CE =AD ，连接DE 交射线AC 于点F ．(1)如图1，当点D 在线段AB 上时，猜测线段CF 与BD 的数量关系并说明理由；(2)如图2，当点D 在线段AB 的延长线上时，①线段CF 与BD 的数量关系是否仍然成立？请说明理由；②如图3，连接AE ．设AB =4，若∠AEB =∠DEB ，求四边形BDFC 的面积．14(2023·湖北宜昌·统考中考真题)如图，在正方形ABCD 中，E ，F 分别是边AD ，AB 上的点，连接CE ，EF ，CF ．(1)若正方形ABCD 的边长为2，E 是AD 的中点．①如图1，当∠FEC =90°时，求证：△AEF ∽△DCE ；②如图2，当tan ∠FCE =23时，求AF 的长；(2)如图3，延长CF ，DA 交于点G ，当GE =DE ,sin ∠FCE =13时，求证：AE =AF ．15(2023·湖北武汉·统考中考真题)问题提出：如图(1)，E 是菱形ABCD 边BC 上一点，△AEF 是等腰三角形，AE =EF ，∠AEF =∠ABC =αa ≥90° ,AF 交CD 于点G ，探究∠GCF 与α的数量关系．问题探究：(1)先将问题特殊化，如图(2)，当α=90°时，直接写出∠GCF 的大小；(2)再探究一般情形，如图(1)，求∠GCF 与α的数量关系．问题拓展：(3)将图(1)特殊化，如图(3)，当α=120°时，若DG CG =12，求BECE的值．16(2023·山西·统考中考真题)问题情境：“综合与实践”课上，老师提出如下问题：将图1中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为△ABC 和△DFE ，其中∠ACB =∠DEF =90°,∠A =∠D ．将△ABC 和△DFE 按图2所示方式摆放，其中点B 与点F 重合(标记为点B )．当∠ABE =∠A 时，延长DE 交AC 于点G ．试判断四边形BCGE 的形状，并说明理由．(1)数学思考：谈你解答老师提出的问题；(2)深入探究：老师将图2中的△DBE 绕点B 逆时针方向旋转，使点E 落在△ABC 内部，并让同学们提出新的问题．①“善思小组”提出问题：如图3，当∠ABE =∠BAC 时，过点A 作AM ⊥BE 交BE 的延长线于点M ,BM 与AC 交于点N ．试猜想线段AM 和BE 的数量关系，并加以证明．请你解答此问题；②“智慧小组”提出问题：如图4，当∠CBE=∠BAC时，过点A作AH⊥DE于点H，若BC=9,AC=12，求AH的长．请你思考此问题，直接写出结果．17(2023·湖北十堰·统考中考真题)过正方形ABCD的顶点D作直线DP，点C关于直线DP的对称点为点E，连接AE，直线AE交直线DP于点F．(1)如图1，若∠CDP=25°，则∠DAF=°；(2)如图1，请探究线段CD，EF，AF之间的数量关系，并证明你的结论；(3)在DP绕点D转动的过程中，设AF=a，EF=b请直接用含a,b的式子表示DF的长．18(2023·辽宁大连·统考中考真题)综合与实践问题情境：数学活动课上，王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质．已知AB=AC,∠A>90°，点E为AC上一动点，将△ABE以BE为对称轴翻折．同学们经过思考后进行如下探究：独立思考：小明：“当点D落在BC上时，∠EDC=2∠ACB．”小红：“若点E为AC中点，给出AC与DC的长，就可求出BE的长．”实践探究：奋进小组的同学们经过探究后提出问题1，请你回答：问题1：在等腰△ABC中，AB=AC,∠A>90°,△BDE由△ABE翻折得到．(1)如图1，当点D落在BC上时，求证：∠EDC=2∠ACB；(2)如图2，若点E为AC中点，AC=4,CD=3，求BE的长．问题解决：小明经过探究发现：若将问题1中的等腰三角形换成∠A<90°的等腰三角形，可以将问题进一步拓展．问题2：如图3，在等腰△ABC中，∠A<90°,AB=AC=BD=4,2∠D=∠ABD．若CD=1，则求BC的长．19(2023·山东·统考中考真题)(1)如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】(2)如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE=DF，延长BC到点H，使CH=DE，连接DH．求证：∠ADF=∠H．【类比迁移】(3)如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE=DF=11，DE=8，∠AED=60°，求CF 的长．20(2023·福建·统考中考真题)如图1，在△ABC中，∠BAC=90°,AB=AC,D是AB边上不与A,B重合的一个定点．AO⊥BC于点O，交CD于点E．DF是由线段DC绕点D顺时针旋转90°得到的，FD,CA的延长线相交于点M．(1)求证：△ADE∽△FMC；(2)求∠ABF的度数；(3)若N是AF的中点，如图2．求证：ND=NO．21(2023·四川·统考中考真题)如图1，已知线段AB，AC，线段AC绕点A在直线AB上方旋转，连接BC，以BC为边在BC上方作Rt△BDC，且∠DBC=30°．(1)若∠BDC=90°，以AB为边在AB上方作Rt△BAE，且∠AEB=90°，∠EBA=30°，连接DE，用等式表示线段AC与DE的数量关系是；(2)如图2，在(1)的条件下，若DE⊥AB，AB=4，AC=2，求BC的长；(3)如图3，若∠BCD=90°，AB=4，AC=2，当AD的值最大时，求此时tan∠CBA的值．22(2023·广西·统考中考真题)【探究与证明】折纸，操作简单，富有数学趣味，我们可以通过折纸开展数学探究，探索数学奥秘．【动手操作】如图1，将矩形纸片ABCD对折，使AD与BC重合，展平纸片，得到折痕EF；折叠纸片，使点B 落在EF上，并使折痕经过点A，得到折痕AM，点B，E的对应点分别为B ，E ，展平纸片，连接AB ，BB ，BE ．请完成：(1)观察图1中∠1，∠2和∠3，试猜想这三个角的大小关系；(2)证明(1)中的猜想；【类比操作】如图2，N为矩形纸片ABCD的边AD上的一点，连接BN，在AB上取一点P，折叠纸片，使B ，P 两点重合，展平纸片，得到折痕EF ；折叠纸片，使点B ，P 分别落在EF ，BN 上，得到折痕l ，点B ，P 的对应点分别为B ，P ，展平纸片，连接，P B ．请完成：(3)证明BB 是∠NBC 的一条三等分线．23(2023·重庆·统考中考真题)在Rt △ABC 中，∠ACB =90°，∠B =60°，点D 为线段AB 上一动点，连接CD ．(1)如图1，若AC =9，BD =3，求线段AD 的长．(2)如图2，以CD 为边在CD 上方作等边△CDE ，点F 是DE 的中点，连接BF 并延长，交CD 的延长线于点G ．若∠G =∠BCE ，求证：GF =BF +BE ．(3)在CD 取得最小值的条件下，以CD 为边在CD 右侧作等边△CDE ．点M 为CD 所在直线上一点，将△BEM 沿BM 所在直线翻折至△ABC 所在平面内得到△BNM ．连接AN ，点P 为AN 的中点，连接CP ，当CP 取最大值时，连接BP ，将△BCP 沿BC 所在直线翻折至△ABC 所在平面内得到△BCQ ，请直接写出此时NQ CP的值．24(2023·湖南·统考中考真题)如图，在等边三角形ABC 中，D 为AB 上的一点，过点D 作BC 的平行线DE 交AC 于点E ，点P 是线段DE 上的动点(点P 不与D 、E 重合)．将△ABP 绕点A 逆时针方向旋转60°，得到△ACQ ，连接EQ 、PQ ,PQ 交AC 于F ．(1)证明：在点P 的运动过程中，总有∠PEQ =120°．(2)当AP DP为何值时，△AQF 是直角三角形？25(2023·黑龙江·统考中考真题)如图①，△ABC和△ADE是等边三角形，连接DC，点F，G，H分别是DE,DC和BC的中点，连接FG,FH．易证：FH=3FG．若△ABC和△ADE都是等腰直角三角形，且∠BAC=∠DAE=90°，如图②：若△ABC和△ADE都是等腰三角形，且∠BAC=∠DAE=120°，如图③：其他条件不变，判断FH和FG之间的数量关系，写出你的猜想，并利用图②或图③进行证明．26(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．(1)发现问题：如图1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：，∠BDC=°；(2)类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；(3)拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：；(4)实践应用：正方形ABCD中，AB=2，若平面内存在点P满足∠BPD=90°，PD=1，则S△ABP=．27(2023·广东深圳·统考中考真题)(1)如图，在矩形ABCD中，E为AD边上一点，连接BE，①若BE=BC，过C作CF⊥BE交BE于点F，求证：△ABE≌△FCB；=20时，则BE⋅CF=．②若S矩形ABCD(2)如图，在菱形ABCD中，cos A=13，过C作CE⊥AB交AB的延长线于点E，过E作EF⊥AD交AD =24时，求EF⋅BC的值．于点F，若S菱形ABCD(3)如图，在平行四边形ABCD中，∠A=60°，AB=6，AD=5，点E在CD上，且CE=2，点F为BC上一点，连接EF，过E作EG⊥EF交平行四边形ABCD的边于点G，若EF⋅EG=73时，请直接写出AG的长．28(2023·内蒙古·统考中考真题)如图，在菱形ABCD中，对角线AC,BD相交于点O，点P,Q分别是边BC，线段OD上的点，连接AP,QP,AP与OB相交于点E．(1)如图1，连接QA．当QA=QP时，试判断点Q是否在线段PC的垂直平分线上，并说明理由；(2)如图2，若∠APB=90°，且∠BAP=∠ADB，①求证：AE=2EP；②当OQ=OE时，设EP=a，求PQ的长(用含a的代数式表示)．29(2023·内蒙古赤峰·统考中考真题)数学兴趣小组探究了以下几何图形．如图①，把一个含有45°角的三角尺放在正方形ABCD中，使45°角的顶点始终与正方形的顶点C重合，绕点C旋转三角尺时，45°角的两边CM ，CN 始终与正方形的边AD ，AB 所在直线分别相交于点M ，N ，连接MN ，可得△CMN ．【探究一】如图②，把△CDM 绕点C 逆时针旋转90°得到△CBH ，同时得到点H 在直线AB 上．求证：∠CNM =∠CNH ；【探究二】在图②中，连接BD ，分别交CM ，CN 于点E ，F ．求证：△CEF ∽△CNM ；【探究三】把三角尺旋转到如图③所示位置，直线BD 与三角尺45°角两边CM ，CN 分别交于点E ，F ．连接AC 交BD 于点O ，求EFNM的值．30(2023·山东东营·统考中考真题)(1)用数学的眼光观察．如图，在四边形ABCD 中，AD =BC ，P 是对角线BD 的中点，M 是AB 的中点，N 是DC 的中点，求证：∠PMN =∠PNM ．(2)用数学的思维思考．如图，延长图中的线段AD 交MN 的延长线于点E ，延长线段BC 交MN 的延长线于点F ，求证：∠AEM =∠F ．(3)用数学的语言表达．如图，在△ABC 中，AC <AB ，点D 在AC 上，AD =BC ，M 是AB 的中点，N 是DC 的中点，连接MN 并延长，与BC 的延长线交于点G ，连接GD ，若∠ANM =60°，试判断△CGD 的形状，并进行证明．31(2023·甘肃兰州·统考中考真题)综合与实践【思考尝试】(1)数学活动课上，老师出示了一个问题：如图1，在矩形ABCD中，E是边AB上一点，DF⊥CE于点F，GD⊥DF，AG⊥DG，AG=CF．试猜想四边形ABCD的形状，并说明理由；【实践探究】(2)小睿受此问题启发，逆向思考并提出新的问题：如图2，在正方形ABCD中，E是边AB上一点，DF⊥CE于点F，AH⊥CE于点H，GD⊥DF交AH于点G，可以用等式表示线段FH，AH，CF的数量关系，请你思考并解答这个问题；【拓展迁移】(3)小博深入研究小睿提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD中，E是边AB上一点，AH⊥CE于点H，点M在CH上，且AH=HM，连接AM，BH，可以用等式表示线段CM，BH的数量关系，请你思考并解答这个问题．32(2023·贵州·统考中考真题)如图①，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA=CB,∠C=90°，过点B作射线BD⊥AB，垂足为B，点P在CB上．(1)【动手操作】如图②，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E，根据题意在图中画出图形，图中∠PBE的度数为度；(2)【问题探究】根据(1)所画图形，探究线段PA与PE的数量关系，并说明理由；(3)【拓展延伸】如图③，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD交于点E，探究线段BA,BP, BE之间的数量关系，并说明理由．33(2023·辽宁·统考中考真题)在RtΔABC中，∠ACB=90°，CA=CB，点O为AB的中点，点D在直线AB上(不与点A,B重合)，连接CD，线段CD绕点C逆时针旋转90°，得到线段CE，过点B作直线l⊥BC，过点E作EF⊥l，垂足为点F，直线EF交直线OC于点G．(1)如图，当点D与点O重合时，请直接写出线段AD与线段EF的数量关系；(2)如图，当点D在线段AB上时，求证：CG+BD=2BC；(3)连接DE，△CDE的面积记为S1，△ABC的面积记为S2，当EF:BC=1:3时，请直接写出S1S2的值．34(2023·四川成都·统考中考真题)探究式学习是新课程倡导的重要学习方式，某兴趣小组拟做以下探究．在Rt△ABC中，∠C=90°,AC=BC，D是AB边上一点，且ADBD=1n(n为正整数)，E是AC边上的动点，过点D作DE的垂线交直线BC于点F．【初步感知】(1)如图1，当n=1时，兴趣小组探究得出结论：AE+BF=22AB，请写出证明过程．【深入探究】(2)①如图2，当n=2，且点F在线段BC上时，试探究线段AE，BF，AB之间的数量关系，请写出结论并证明；②请通过类比、归纳、猜想，探究出线段AE，BF，AB之间数量关系的一般结论(直接写出结论，不必证明)【拓展运用】(3)如图3，连接EF，设EF的中点为M．若AB=22，求点E从点A运动到点C的过程中，点M运动的路径长(用含n的代数式表示)．35(2023·江苏徐州·统考中考真题)【阅读理解】如图1，在矩形ABCD中，若AB=a,BC=b，由勾股定理，得AC2=a2+b2，同理BD2=a2+b2，故AC2+BD2=2a2+b2．【探究发现】如图2，四边形ABCD为平行四边形，若AB=a,BC=b，则上述结论是否依然成立？请加以判断，并说明理由．【拓展提升】如图3，已知BO为△ABC的一条中线，AB=a,BC=b,AC=c．求证：BO2=a2+b22-c24．【尝试应用】如图4，在矩形ABCD中，若AB=8,BC=12，点P在边AD上，则PB2+PC2的最小值为．36(2023·四川南充·统考中考真题)如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．(1)求证：ED=EC；(2)将BE绕点E逆时针旋转，使点B的对应点B 落在AC上，连接MB′．当点M在边BC上运动时(点M 不与B，C重合)，判断△CMB′的形状，并说明理由．(3)在(2)的条件下，已知AB=1，当∠DEB′=45°时，求BM的长．37(2023·安徽·统考中考真题)在Rt△ABC中，M是斜边AB的中点，将线段MA绕点M旋转至MD 位置，点D在直线AB外，连接AD,BD．(1)如图1，求∠ADB的大小；(2)已知点D和边AC上的点E满足ME⊥AD,DE∥AB．(ⅰ)如图2，连接CD，求证：BD=CD；(ⅱ)如图3，连接BE，若AC=8,BC=6，求tan∠ABE的值．38(2023·浙江宁波·统考中考真题)定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形，相等两邻边的夹角称为邻等角．(1)如图1，在四边形ABCD中，AD∥BC,∠A=90°，对角线BD平分∠ADC．求证：四边形ABCD为邻等四边形．(2)如图2，在6×5的方格纸中，A，B，C三点均在格点上，若四边形ABCD是邻等四边形，请画出所有符合条件的格点D．(3)如图3，四边形ABCD是邻等四边形，∠DAB=∠ABC=90°，∠BCD为邻等角，连接AC，过B作BE∥AC交DA的延长线于点E．若AC=8,DE=10，求四边形EBCD的周长．39(2023·江苏扬州·统考中考真题)【问题情境】在综合实践活动课上，李老师让同桌两位同学用相同的两块含30°的三角板开展数学探究活动，两块三角板分别记作△ADB和△A D C,∠ADB=∠A D C=90°,∠B=∠C=30°，设AB=2．【操作探究】如图1，先将△ADB和△A D C的边AD、A D 重合，再将△A D C绕着点A按顺时针方向旋转，旋转角为α0°≤α≤360°，旋转过程中△ADB保持不动，连接BC．(1)当α=60°时，BC=；当BC=22时，α=°；(2)当α=90°时，画出图形，并求两块三角板重叠部分图形的面积；(3)如图2，取BC的中点F，将△A D C绕着点A旋转一周，点F的运动路径长为．40(2023·四川乐山·统考中考真题)在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：如图，将一个三角形纸板△ABC绕点A逆时针旋转θ到达△AB C 的位置，那么可以得到：AB=AB ，AC =AC ，BC=B C ；∠BAC=∠B AC ，∠ABC=∠AB C ，∠ACB=∠AC B ()刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键；故数学就是一门哲学．【问题解决】(1)上述问题情境中“( )”处应填理由：；(2)如图，小王将一个半径为4cm，圆心角为60°的扇形纸板ABC绕点O逆时针旋转90°到达扇形纸板A BC 的位置．①请在图中作出点O；②如果BB =6cm，则在旋转过程中，点B经过的路径长为；【问题拓展】小李突发奇想，将与(2)中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置，另一个在弧的中点处固定，然后放开纸板，使其摆动到竖直位置时静止，此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．。

中考平面几何压轴（三角形与四边形）训练15题（精选）1.如图，四边形ABCD 是平行四边形，且对角线AC , BD 交于点O ，点M , N 分别在AD , BC 上，且AM = CN ,点E ，F 分别是BD 与AN ，CM 的交点.(1)求证:OE = OF ;(2)连接BM 交AC 于点H ,连接HE ，HF ;(i)如图2，若HE ∥AB ,求证: FH ∥AD ;(ii)如图3,若四边形ABCD 为菱形且DM = 2AM ,∠EHF=60°，求AC BD 的值.2.(1)如图①，在矩形ABCD 的AB 边上取一点E ，将ΔADE 沿DE 翻折，使点A 落在BC 上的A′处，若AB =6，BC =10，求AEEB 的值；(2)如图②，在矩形ABCD 的BC 上取一点E ，将四边形ABED 沿DE 翻折，使点B 落在DC 的延长线上B′处，若BC ·CE =24，AB =6，求BE 的值；(3)如图③，在ΔABC 中，∠BAC =45°，AD ⊥BC ，垂足为点D ，AD =10，AE =6，过点E 作EF ⊥AD 交AC 于点F ，连接DF ，且满足∠DFE =2∠DAC ，直接写出BD+53EF 的值.3. 在正方形ABCD 中，AB =10, AC 是对角线，点O 是AC 的中点，点E 在AC 上，连接DE ，点C 关于DE 的对称点是C',连接DC' ,EC'.(1) 如图1，若DC'经过点O ,求证:OC ′CE = √22. (2) 如图2，连接CC'，BC',若∠ADC' = 2∠CBC',求CC'的长;(3) 当点B , C', E 三点共线时，直接写出CE 的长.4.如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．（1）求证：ED= EC；（2）将BE绕点E逆时针旋转，使点B的对应点B′落在AC上，连接MB′．当点M在边BC上运动时（点M不与B，C 重合），判断△CMB′的形状，并说明理由．（3）在（2）的条件下，已知AB= 1，当∠DEB′=45°时，求BM的长．5.如图，在正方形ABCD中，点M、N在直线BD上，连接AM，AN并延长交BC、CD于点E、F，连接EN.(1)如图1，若M，N都在线段BD上，且AN = NE，求∠MAN;(2)如图2.当点M在线段DB 延长线上时,AN = NE,(1)中∠MAN的度数不变，判断BM，DN，MN之间的数量关系并证明;(3)如图3,若点M在DB的延长线上,N在BD的延长线上,且∠MAN=135°(i)AB=√6,MB=√3,求DN.(ii)求证:2AM2 - MB 2= MN2 - BN2.6.如图，在RtΔABC与RtΔBDE中,∠BAC=∠BDE=90°,∠ABC=∠DBE=α.（1)如图1,当α= 60°,且点E为BC的中点时,若AB=2,连接AD.求AD的长度；（2)如图2,若α≠ 60°,且点E为BC中点时,取CE中点F,连接AF、DF。

中考28汇编1．如图，在四边ABCD 中，BC=DC ，∠BAD+∠BCD=180°，AC ⊥BC ，O 是AB 的中点 （1） 如图1，求证：∠OCD=∠OBC（2） 如图2，E 是AC 上一点，连接OE 并延长交AD 于点F ，连接BD ，分别交AC 、OC 于点M 、N ，若∠FOC=3∠CBD ，BN DM 76，试探究线段OE 和EF 之间的数量关系，并证明你的结论。

DCAO NMFEDCBA（图1）（图2）2．△ABC ，∠ACB=90°，点D 在BC 上，点E 在AD 上，∠CEB=90°，∠CED=∠CBA ，CE 的延长线交AB 于点F ，连接DF 。

（1） 如图1，求证：∠EFD=∠DBE ； （2） 如图2，若32cos =∠CAB ，DF 与BE 交于点G ，猜想GF 与DB 之间的数量关系并证明。

FEDCBAGFEDCBA（图1）（图2）3．已知，如图1，等腰直角△ABC中，AC=BC，等腰直角△CDE中，CD=DE，AD∥BC，CE与AB 相交于点F，AB与CD相交于点O，连接BE（1）求证：F为CE中点；（2）如图2，过点D作DG⊥BE于G，连接AE交DG于点H，连接HF，请探究线段HF与BC 之间的数量及位置关系，并证明你的结论。

OF EDC B A（图1）OGHFEDC BA（图2）4如图在四边形ABCD 中，连结BD 、AC 相交于F ，AB=BC ，AD=DE=DC ，∠ABC+∠EDC=180°，且AB AE AD ⋅=2。

（1） 如图1，求证：∠ADE=2∠DCA ；（2） 如图2，过点B 作BH ⊥CD 于点H ，交AC 于点G ，连结EC 交BD 于点P ，交BH 于点Q ，若31tan =∠ACD ，试探究线段PE 与PQ 之间的数量关系，并证明你的结论。

PG H QFEDCBAFEDCBA（图1）（图2）5．在Rt △ABC 中，∠ACB=90°，54sin =B ，作CH ⊥AB 于点H ，D 、K 分别为边AB 、AC 上的点，连接CD 、DK ，在射线DK 上取一点E ，使∠DCE=∠B ，且CE CD CK BC ⋅=⋅54。

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图，在矩形ABCD 中，AB =8，AD =4，点E 是矩形ABCD 内部一动点，且∠BEC =90°，点P 是AB 边上一动点，连接PD 、PE ，则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹，利用“将军饮马”模型将PE 进行转化即可求解．【详解】解：如图，设点O 为BC 的中点，由题意可知，点E 在以BC 为直径的半圆O 上运动，作半圆O 关于AB 的对称图形(半圆O ')，点E 的对称点为E 1，连接O 'E 1,则PE =PE 1，∴当点D 、P 、E 1、O '共线时，PD +PE 的值最小，最小值为DE 1的长，如图所示，在Rt △DCO '中，CD =8，CO '=6，∴DO '=82+62=10，又∵O 'E 1=2，∴DE 1=DO '-O 'E 1=8，即PD +PE 的最小值为8，故选：A ．【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理，利用“将军饮马”模型将PE 进行转化时解题的关键．2(2023·安徽黄山·校考模拟预测)如图，在平面直角坐标系中，二次函数y =32x 2-32x -3的图象与x 轴交于点A ，C 两点，与y 轴交于点B ，对称轴与x 轴交于点D ，若P 为y 轴上的一个动点，连接PD ，则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ，作PE ⊥BA 于E ，作DF ⊥BA 于F ，交y 轴于P ，可求得∠ABO =30°，从而得出PE =12PB ，进而得出PD +12PB =PD +EP ，进一步得出结果．【详解】解：如图，作射线BA ，作PE ⊥BA 于E ，作DF ⊥BA 于F ，交y 轴于P ，抛物线的对称轴为直线x =--322×32=12，∴OD =12，当x =0时，y =-3，∴OB =3，当y =0时，32x 2-32x -3=0，∴x 1=-1，x 2=2，∴A (-1,0)，∴OA =1，∵tan ∠ABO =OA OB =13=33，∴∠ABO =30°，∴PE =12PB ，∴12PB +PD =PD +PE ≥DF ，当点P 在P 时，PD +PE 最小，最大值等于DF ，在Rt △ADF 中，∠DAF =90°-∠ABO =60°，AD =OD +PA =12+1=32，∴DF =AD ⋅sin ∠DAE =32×32-334，∴12PB +PD 最小=DF =334，故选：A ．【点睛】本题以二次函数为背景，考查了二次函数与一元二次方程之间的关系，解直角三角形等知识，解决问题的关键是用三角函数构造12PB ．3(2023秋·浙江金华·九年级统考期末)如图，正方形ABCD 的边长为4，点E 是正方形ABCD 内的动点，点P 是BC 边上的动点，且∠EAB =∠EBC ．连结AE ，BE ，PD ，PE ，则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°，即可得点E 在以AB 为直径的半圆上移动，设AB 的中点为O ，作正方形ABCD 关于直线BC 对称的正方形CFGB ，则点D 的对应点是F ，连接FO 交BC 于P ，交半圆O 于E ，根据对称性有：PD =PF ，则有：PE +PD =PE +PF ，则线段EF 的长即为PE +PD 的长度最小值，问题随之得解．【详解】解：∵四边形ABCD 是正方形，∴∠ABC =90°，∴∠ABE +∠EBC =90°，∵∠EAB =∠EBC ，∴∠EAB +∠EBA =90°，∴∠AEB =90°，∴点E 在以AB 为直径的半圆上移动，如图，设AB 的中点为O ，作正方形ABCD 关于直线BC 对称的正方形CFGB ，则点D 的对应点是F ，连接FO 交BC 于P ，交半圆O 于E ，根据对称性有：PD =PF ，则有：PE +PD =PE +PF ，则线段EF 的长即为PE +PD 的长度最小值，E∵∠G =90°，FG =BG =AB =4，∴OG =6，OA =OB =OE =2，∴OF =FG 2+OG 2=213，∴EF =OF -OE =213-2，故PE +PD 的长度最小值为213-2，故选：A ．【点睛】本题考查了轴对称-最短路线问题，正方形的性质，勾股定理，正确的作出辅助线，得出点E 的运动路线是解题的关键．4(2022秋·安徽池州·九年级统考期末)如图，Rt △ABC 中，∠C =90°，AC =4，BC =3，点P 为AC 边上的动点，过点P 作PD ⊥AB 于点D ，则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ，过点B 作B D ⊥AB 于点D ，交AC 于点P ，点P 即为所求作的点，此时PB +PD 有最小值，连接AB ，根据对称性的性质，可知：BP =B P ，△ABC ≅△AB C ，根据S △ABB =S △ABC +S △AB C =2S △ABC ，即可求出PB +PD 的最小值．【详解】解：如下图，作点B 关于AC 的对称点B ，过点B 作B D ⊥AB 于点D ，交AC 于点P ，连接AB ，点P 即为所求作的点，此时PB +PD 有最小值，根据对称性的性质，可知：BP =B P ，在Rt △ABC 中，∠ACB =90°,AC =4,BC =3，∴AB =AC 2+BC 2=5，根据对称性的性质，可知：△ABC ≅△AB C ，∴S △ABB =S △ABC +S △ABC =2S △ABC ，即12×AB ⋅B D =2×12BC ⋅AC ，∴5B D =24，∴B D =245，故选：B ．【点睛】本题考查了轴对称一最短路线问题，解题的关键是掌握轴对称的性质．5(2023秋·甘肃定西·八年级校考期末)如图所示，在△ABC 中，∠ABC =68°，BD 平分∠ABC ，P 为线段BD 上一动点，Q 为 边AB 上一动点，当AP +PQ 的值最小时，∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ，连接PE ，证明△PBQ ≌△PBE SAS ，得出PE =PQ ，说明AP +PQ =AP +PE ，找出当A 、P 、E 在同一直线上，且AE ⊥BC 时，AP +PE 最小，即AP +PQ 最小，过点A 作AE ⊥BC 于点E ，交BD 于点P ，根据三角形外角的性质可得答案．【详解】解：在BC 上截取BE =BQ ，连接PE ，如图：∵BD 平分∠ABC ，∠ABC =68°，∴∠ABD =∠CBD =12∠ABC =34°，∵BP =BP ，∴△PBQ ≌△PBE SAS ，∴PE =PQ ，∴AP +PQ =AP +PE ，∴当A 、P 、E 在同一直线上，且AE ⊥BC 时，AP +PE 最小，即AP +PQ最小，过点A作AE ⊥BC 于点E ，交BD 于点P ，如图：∵∠AEB =90°，∠CBD =34°，∴∠APB =∠AEB +∠CBD =124°．故选：D ．5【点睛】本题主要考查了角平分线的定义，三角形全等的判定和性质，垂线段最短，三角形内角和定理与三角形的外角的性质，解题的关键是找出使AP +PQ 最小时点P 的位置．6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图，E 为正方形ABCD 边AD 上一点，AE =1，DE =3，P 为对角线BD 上一个动点，则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点，根据“两点之间线段最短”，可知PA +PE 的最小值即为线段EC 的长，求出EC 的长即可.【详解】连接EC ，交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”，可知PA +PE 的最小值即为线段EC 的长.∵AE =1，DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选：A【点睛】本题主要考查了正方形的性质和两点之间线段最短，这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图，正方形ABCD 的边长为4，点M 在DC 上，且DM =1，N 是AC 上一动点，则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称，连接BM 交AC 于N ′，N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可．【详解】∵四边形ABCD 是正方形，∴点B 与D 关于直线AC 对称，6连接BD ，BM 交AC 于N ′，连接DN ′，∴当B 、N 、M 共线时，DN +MN 有最小值，则BM 的长即为DN +MN 的最小值，∴AC 是线段BD 的垂直平分线，又∵CD =4，DM =1∴CM =CD -DM =4-1=3，在Rt △BCM 中，BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5．故选：D ．【点睛】本题考查的是轴对称-最短路线问题及正方形的性质，先作出D 关于直线AC 的对称点，由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键．8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图，在平面直角坐标系中，二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点，与x 轴交于点C (3,0)，若P 是x 轴上一动点，点D 的坐标为(0,-1)，连接PD ，则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ，过点D 作DH ⊥BC 于H ，根据2PD +PC =2PD +22PC =2PD +PJ ，求出DP +PJ 的最小值即可解决问题．【详解】解：连接BC ，过点P 作PJ ⊥BC 于J ，过点D 作DH ⊥BC 于H ．∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0)，∴b =2，∴二次函数的解析式为y =-x 2+2x +3，令y =0，-x 2+2x +3=0，解得x =-1或3，∴A (-1，0)，令x =0，y =3，∴B (0，3)，∴OB =OC =3，∵∠BOC =90°，∴∠OBC =∠OCB =45°，∵D(0，-1)，∴OD =1，BD =4，∵DH ⊥BC ，∴∠DHB =90°，设DH =x ，则BH =x ,∵DH 2+BH 2=BD 2，7∴x =22，∴DH =22，∵PJ ⊥CB ，∴∠PJC =90°，∴PJ =22PC ，∴2PD +PC =2PD +22PC =2PD +PJ ，∵DP +PJ ≥DH ，∴DP +PJ ≥22，∴DP +PJ 的最小值为22，∴2PD +PC 的最小值为4．故选：A ．【点睛】本题考查了二次函数的相关性质，以及等腰直角三角形的判定和性质，垂线段最短等知识，得到∠OBC =∠OCB =45°，PJ =22PC 是解题的关键．9(2022·山东泰安·统考中考真题)如图，四边形ABCD 为矩形，AB =3，BC =4．点P 是线段BC 上一动点，点M 为线段AP 上一点．∠ADM =∠BAP ，则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°，得出点M 在O 点为圆心，以AO 为半径的圆上，从而计算出答案．【详解】设AD 的中点为O ，以O 点为圆心，AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心，以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时，BM 最短∵BO 2=AB 2+AO 2，AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选：D ．【点睛】本题考查直角三角形、圆的性质，解题的关键是熟练掌握直角三角形和圆的相关知识．810(2022·河南·校联考三模)如图1，正方形ABCD 中，点E 是BC 的中点，点P 是对角线AC 上的一个动点，设AP =x ，PB +PE =y ，当点P 从A 向点C 运动时，y 与x 的函数关系如图2所示，其中点M 是函数图象的最低点，则点M 的坐标是()A.42，35B.22,35C.35,22D.35,42【答案】A【分析】根据图像，当P 与C 重合时，PB +PE =9即CB +CE =9，从而确定正方形的边长为6，根据将军饮马河原理，连接DE 交AC 于点G ，当点P 与点G 重合时，PE +PB 最小，且为DE 的长即点M 的纵坐标，利用相似三角形，计算AG 的长即为横坐标．【详解】如图，根据图像，当P 与C 重合时，PB +PE =9即CB +CE =9，∵点E 是BC 的中点，∴BC =6，连接DE 交AC 于点G ，当点P 与点G 重合时，PE +PB 最小，且为DE 的长即点M 的纵坐标，∵四边形ABCD 是正方形，AB =6，∴CE ∥AD ，AC =62+62=62，DE =62+32=35，∴△CGE ∽△AGD ，∴CG AG =CE AD =12，∴AC AG=32，∴AG =42，故点M 的坐标为(42，35)，故A 正确．故选：A ．【点睛】本题考查了正方形的性质，三角形相似的判定和性质，函数图像信息的获取，将军饮马河原理，熟练掌握正方形的性质，灵活运用三角形相似，构造将军饮马河模型求解是解题的关键．2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图，矩形ABCD ，AB =4，BC =8，E 为AB 中点，F 为直线BC 上动点，B 、G 关于EF 对称，连接AG ，点P 为平面上的动点，满足∠APB =12∠AGB ，则DP 的最小值．【答案】210-22【分析】由题意可知，∠AGB =90°，可得∠APB =12∠AGB =45°，可知点P 在以AB 为弦，圆周角∠APB =45°的9圆上，(要使DP 最小，则点P 要靠近蒂点D ，即点P 在AB 的右侧)，设圆心为O ，连接OA ，OB ，OE ，OP ，OD ，过点O 作OQ ⊥AD ，可知△AOB 为等腰直角三角形，求得OA =22AB =22=OP ，AQ =OQ =22OA =2，QD =AD -AQ =6，OD =OQ 2+QD 2=210，再由三角形三边关系可得：DP ≥OD -OP =210-22，当点P 在线段OD 上时去等号，即可求得DP 的最小值．【详解】解：∵B 、G 关于EF 对称，∴BH =GH ，且EF ⊥BG∵E 为AB 中点，则EH 为△ABG 的中位线，∴EH ∥AG ，∴∠AGB =90°，∵∠APB =12∠AGB ，即∠APB =12∠AGB =45°，∴点P 在以AB 为弦，圆周角∠APB =45°的圆上，(要使DP 最小，则点P 要靠近蒂点D ，即点P 在AB 的右侧)设圆心为O ，连接OA ，OB ，OE ，OP ，OD ，过点O 作OQ ⊥AD ，则OA =OB =OP ，∵∠APB =45°，∴∠AOB =90°，则△AOB 为等腰直角三角形，∴OA =22AB =22=OP ，又∵E 为AB 中点，∴OE ⊥AB ，OE =12AB =AE =BE ，又∵四边形ABCD 是矩形，∴∠BAD =90°，AD =BC =8，∴四边形AEOQ 是正方形，∴AQ =OQ =22OA =2，QD =AD -AQ =6，∴OD =OQ 2+QD 2=210，由三角形三边关系可得：DP ≥OD-OP =210-22，当点P 在线段OD 上时去等号，∴DP 的最小值为210-22，故答案为：210-22．【点睛】本题考查轴对称的性质，矩形的性质，隐形圆，三角形三边关系，正方形的判定及性质，等腰直角三角形的判定及性质，根据∠APB =12∠AGB =45°得知点P 在以AB 为弦，圆周角∠APB =45°的圆上是解决问题的关键．12(2023春·江苏连云港·八年级期中)如图，在边长为8的正方形ABCD 中，点G 是BC 边的中点，E 、F 分别是AD 和CD 边上的点，则四边形BEFG 周长的最小值为．【答案】2410【分析】作点G 关于CD 的对称点G ，作点B 关于AD 的对称点B ，连接B G ，根据两点之间线段最短即可解决问题．【详解】作点G 关于CD 的对称点G ，作点B 关于AD 的对称点B ，连接B G∵EB =EB ,FG =FG ，∴BE +EF +FG +BG =B E +EF +FG +BG ，∵EB +EF +FG ≥B G ，∴四边形BEFG 的周长的最小值=BG +B G ，∵正方形ABCD 的边长为8∴BG =4，BB =16，BG =12，∴B G =162+122=20，∴四边形BEFG 的周长的最小值为=4+20=24．故答案为：24．【点睛】本题考查轴对称求线段和的最短问题，正方形的性质，勾股定理，解题的关键是学会利用轴对称解决最短问题．13(2022·湖南湘潭·校考模拟预测)如图，菱形草地ABCD 中，沿对角线修建60米和80米两条道路AC <BD ，M 、N 分别是草地边BC 、CD 的中点，在线段BD 上有一个流动饮水点P ，若要使PM +PN 的距离最短，则最短距离是米．【答案】50【分析】作M 关于BD 的对称点Q ，连接NQ ，交BD 于P ，连接MP ，当P 点与P 重合时，MP +NP =MP +NP =NQ 的值最小，根据菱形的性质和勾股定理求出BC 长，即可得出答案．【详解】解：作M 关于BD 的对称点Q ，连接NQ ，交BD 于P ，连接MP ，当P 点与P 重合时，MP +NP =MP +NP =NQ 的值最小，∵四边形ABCD 是菱形，∴AC ⊥BD ，∠QBP =∠MBP ，即Q 在AB 上，∵MQ ⊥BD ，∴AC ∥MQ ，∴M 为BC 中点，∴Q 为AB 中点，∵N 为CD 中点，四边形ABCD 是菱形，∴BQ ∥CD ，BQ =CN ，∴四边形BQNC 是平行四边形，∴NQ =BC ，设AC 与BD 的交点为点O ，∵四边形ABCD 是菱形，∴AC ⊥BD，OC =12AC =30米，OB =12BD =40米，∴BC =OB 2+OC 2=50米，∴PM +PN 的最小值是50米．故答案为：50．11【点睛】本题考查了轴对称-最短路线问题，平行四边形的性质和判定，菱形的性质，勾股定理的应用，解此题的关键是能根据轴对称找出P 的位置．14(2023春·江苏·九年级校考阶段练习)如图，正方形ABCD 的边长为4，⊙B 的半径为2，P 为⊙B 上的动点，则2PC -PD 的最大值是．【答案】2【分析】解法1，如图：以PD 为斜边构造等腰直角三角形△PDM ，连接MC ，BD ，连接PM 、DM ，推得2PC -PD=2PC -22PD =2PC -PM ，因为PC -PM ≤MC ，求出MC 即可求出答案．解法2：如图：连接BD 、BP 、PC ，在BD 上做点M ，使BM BP =24，连接MP ，证明△BMP ∼△BPD ，在BC 上做点N ，使BN BP=12，连接NP ，证明△BNP ∼△BPC ，接着推导出2PC -PD =22MN ，最后证明△BMN ∼△BCD ，即可求解．【详解】解法1如图：以PD 为斜边构造等腰直角三角形△PDM ，连接MC ，BD ，∴∠PDM =45，DM =PM =22PD ，∵四边形ABCD 正方形∴∠BDC =45°，DB DC=2又∵∠PDM =∠PDB +MDB ，∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ，DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为：2．解法2如图：连接BD 、BP 、PC根据题意正方形ABCD 的边长为4，⊙B 的半径为2∴BP =2，BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ，使BM BP=24，则BM =22，连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ，BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24，则PD =22PM ∵BP BC =24=12在BC 上做点N ，使BN BP=12，则BN =1，连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ，BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12，则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ，BM BC =224=28，BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为：2．【点睛】本题考查正方形的性质，相似三角形，勾股定理等知识，难度较大，熟悉以上知识点运用是解题关键．15(2023秋·广东广州·九年级统考期末)如图，四边形ABCD 中，AB ∥CD ，AC ⊥BC ，∠DAB =60°，AD =CD =4，点M 是四边形ABCD 内的一个动点，满足∠AMD =90°，则△MBC 面积的最小值为．【答案】63-4【分析】取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于点E ，过点O 作OF ⊥BC 于F ，交CD 于G ，则OM +ME ≥OF ，通过计算得出当O ,M ,E 三点共线时，ME 有最小值，求出最小值即可．【详解】解：如图，取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于点E ，过点O 作OF ⊥BC 于F ，交CD 于G ，则13OM +ME ≥OF ，∵AB ∥CD ，∠DAB =60°，AD =CD =4，∴∠ADC =120°，∵AD =CD ，∴∠DAC =30°，∴∠CAB =30°，∵AC ⊥BC ，∴∠ACB =90°∴∠B =90°-30°=60°，∴∠B =∠DAB ，∴四边形ABCD 为等腰梯形，∴BC =AD =4，∵∠AMD =90°，AD =4，OA =OD ，∴OM =12AD =2，∴点M 在以点O 为圆心，2为半径的圆上，∵AB ∥CD ，∴∠GCF =∠B =60°，∴∠DGO =∠CGF =30°，∵OF ⊥BC ，AC ⊥BC ，∴∠DOG =∠DAC =30°=∠DGO ，∴DG =DO =2，∴OG =2OD ⋅cos30°=23，GF =3，OF =33，∴ME ≥OF -OM =33-2，∴当O ,M ,E 三点共线时，ME 有最小值33-2，∴△MBC 面积的最小值为=12×4×33-2 =63-4．【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点，点M 位置的确定是解题关键．16(2023春·全国·八年级专题练习)如图，在等边△ABC 中，BD ⊥AC 于D ，AD =3cm ．点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ，点M 为线段BD 上一动点，连接PM ,QM ，则PM +QM 的最小值为cm ．【答案】5【分析】如图所示，作点P 关于BD 的对称点P ，且点P 在BC 上，则PM +QM =P M+QM ，当P ,M ,Q 在同一条直线上时，有最小值，证明四边形PP QA 是平行四边形，P Q =AP =AB -BP ，由此即可求解．【详解】解：如图所示，作点P 关于BD 的对称点P ，∵△ABC 是等边三角形，BD ⊥AC ，∴∠ABD =∠DBC =12∠ABC =12×60°=30°，14∴点P 在BC 上，∴P M =PM ，则PM +QM =P M +QM ，当P ,M ,Q 在同一条直线上时，有最小值，∵点P 关于BD 的对称点P ，∠ABD =∠DBC =30°，∴PP ⊥BM ，BP =BP =1cm ，∴∠BP P =60°，∴△BPP 是等边三角形，即∠BP P =∠C =60°，∴PP ∥AC ，且PP =AQ =1cm ，∴四边形PP QA 是平行四边形，∴P Q =AP =AB -BP ，在Rt △ABD 中，∠ABD =30°，AD =3，∴AB =2AD =2×3=6，∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5，故答案为：5．【点睛】本题主要考查动点与等边三角形，对称-最短路径，平行四边形的判定和性质的综合，理解并掌握等边三角形得性质，对称-最短路径的计算方法，平行四边形的判定和性质是解题的关键．17(2022秋·山东菏泽·九年级校考阶段练习)如图，在周长为12的菱形ABCD 中，DE =1，DF =2，若P 为对角线AC 上一动点，则EP +FP 的最小值为．【答案】3【分析】作F 点关于BD 的对称点F ，连接EF 交BD 于点P ，则PF =PF ，由两点之间线段最短可知当E 、P 、F 在一条直线上时，EP +FP 有最小值，然后求得EF 的长度即可．【详解】解：作F 点关于BD 的对称点F ，则PF =PF ，连接EF '交BD 于点P ．∴EP +FP =EP +F P ．由两点之间线段最短可知：当E 、P 、F '在一条直线上时，EP +FP 的值最小，此时EP +FP =EP +F P =EF ．∵四边形ABCD 为菱形，周长为12，∴AB =BC =CD =DA =3，AB ∥CD ，∵AF =2，AE =1，∴DF =AE =1，∴四边形AEF D 是平行四边形，∴EF =AD =3．∴EP +FP 的最小值为3．故答案为：3．【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题，明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键．18(2023春·上海·八年级专题练习)如图，直线y =x +4与x 轴，y 轴分别交于A和B ，点C 、D 分别为线段AB 、OB 的中点，P 为OA 上一动点，当PC +PD 的值最小时，点P 的坐标为．15【答案】(-1,0)【分析】直线y =x +4与x 轴，y 轴分别交于A 和B ，可求出点A ，B 的坐标，点C 、D 分别为线段AB 、OB 的中点，可求出点C 、D 的坐标，作点C 关于x 轴的对称点C ，连接C D 与x 轴的交点就是所求点P 的坐标．【详解】解：直线y =x +4与x 轴，y 轴分别交于A 和B ，∴当y =0，x =-4，即A (-4,0)；当x =0，y =4，即B (0,4)，∵点C 、D 分别为线段AB 、OB 的中点，∴C (-2,2)，D (0,2)，如图所示，过点C 关于x 轴的对称点C，∴C (-2,-2)，∴直线C D 的解析式为：y =2x +2，当y =0，x =-1，即P (-1,0)，故答案为：(-1,0)．【点睛】本题主要考查一次函数与最短线段的综合，掌握对称中最短线段的解题方法是解题的关键．19(2023秋·黑龙江鸡西·九年级统考期末)如图，抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧)，与y 轴交于点C ，在其对称轴上有一动点M ，连接MA ,MC ,AC ，则△MAC 周长的最小值是．【答案】32+10【分析】根据“将军饮马”模型，先求出A 1,0 ,B 3,0 ,C 0,3 ，由二次函数对称性，A ,B 关于对称轴对称，从而C △MAC =CA +CM +MA =CA +CM +MB ，AC =OA 2+OC 2=10，则△MAC 周长的最小值就是CM +MB 的最小值，根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长，从而得到CB =OC 2+OB 2=32，即可得到答案．【详解】解：∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧)，与y 轴交于点C ，16∴当y =0时，0=x 2-4x +3解得x =1或x =3，即A 1,0 ,B 3,0 ；当x =0时，y =3，即C 0,3 ，由二次函数对称性，A ,B 关于对称轴对称，即MA =MB ，∴C △MAC =CA +CM +MA =CA +CM +MB ，∵AC =OA 2+OC 2=10，∴△MAC 周长的最小值就是CM +MB 的最小值，根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长，∵CB =OC 2+OB 2=32，∴△MAC 周长的最小值为CA +CB =32+10，故答案为：32+10．【点睛】本题考查动点最值问题与二次函数综合，涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识，熟练掌握动点最值的常见模型是解决问题的关键．20(2023秋·浙江温州·九年级校考期末)如图所示，∠ACB =60°，半径为2的圆O 内切于∠ACB．P 为圆O 上一动点，过点P 作PM 、PN 分别垂直于∠ACB 的两边，垂足为M 、N ，则PM +2PN 的取值范围为．【答案】6-23≤PM +2PN ≤6+23【分析】根据题意，本题属于动点最值问题-“阿氏圆”模型，首先作MH ⊥NP 于H ，作MF ⊥BC 于F ，如图所示，通过代换，将PM +2PN 转化为PN +12PM =PN +HP =NH ，得到当MP 与⊙O 相切时，MF 取得最大值和最小值，分两种情况，作出图形，数形结合解直角三角形即可得到相应最值，进而得到取值范围．【详解】解：作MH ⊥NP 于H ，作MF ⊥BC 于F ，如图所示：∵PM ⊥AC ，PN ⊥CB ，∴∠PMC =∠PNC =90°，∴∠MPN =360°-∠PMC -∠PNC -∠C =120°，∴∠MPH =180°-∠MPN =60°，∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ，∴PN +12PM =PN +HP =NH ，∵MF =NH ，∴当MP 与⊙O 相切时，MF 取得最大和最小，①连接OP ，OG ，OC ，如图1所示：可得：四边形OPMG 是正方形，∴MG =OP =2，在Rt △COG 中，CG =OG ⋅tan60°=23，∴CM =CG +GM =2+23，在Rt △CMF 中，MF =CM ⋅sin60°=3+3，∴HN =MF =3+3，即PM +2PN =212PM +PN =2HN =6+23；②连接OP ，OG ，OC ，如图2所示：可得：四边形OPMG 是正方形，17∴MG =OP =2，由上同理可知：在Rt △COG 中，CG =OG ⋅tan60°=23，∴CM =CG -GM =23-2，在Rt △CMF 中，MF =CM ⋅sin60°=3-3，∴HN =MF =3-3，即PM +2PN =212PM +PN =2HN =6-23，∴6-23≤PM +2PN ≤6+23．故答案为：6-23≤PM +2PN ≤6+23．【点睛】本题考查动点最值模型-“阿氏圆”，难度较大，掌握解决动点最值问题的方法，熟记相关几何知识，尤其是圆的相关知识是解决问题的关键．3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图，已知抛物线y =ax 2+bx +4经过A -1,0 ，B 4,0 两点，交y 轴于点C ．(1)求抛物线的解析式，连接BC ，并求出直线BC 的解析式；(2)请在抛物线的对称轴上找一点P ，使AP +PC 的值最小，此时点P 的坐标是；(3)点Q 在第一象限的抛物线上，连接CQ ，BQ ，求出△BCQ 面积的最大值．【答案】(1)y =-x 2+3x +4；y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ，B 4,0 两点，代入抛物线解析式，可得到抛物线解析式，从而得到C 0,4 ，再设直线BC 的解析式为y =kx +b k ≠0 ，把点B 、C 的坐标代入，即可求解；(2)连接BC ，PB ，根据题意可得A 、B 关于抛物线的对称轴直线x =32对称，从而得到当P 在直线AB 上三点共线时，AP +CP 的值最小，把x =32代入直线BC 的解析式，即可求解；(3)过Q 作QD ⊥x 轴，交BC 于D ，设Q d ,-d 2+3d +4 ，其中0≤d ≤4，则D d ,-d +4 ，可得QD =-d 2+4d ，从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8，即可求解；【详解】(1)解：(1)∵抛物线y =ax 2+bx +4经过A -1,0 ，B 4,0 两点，∴a -b +4=016a +4b +4=0，解得：a =-1b =3 ，18∴抛物线的解析式为y =-x 2+3x +4；∵抛物线与y 轴的交点为C ，∴C 0,4 ，设直线BC 的解析式为y =kx +b k ≠0 ，把点B 、C 的坐标代入得：4k +b =0b =4 ，解得：k =-1b =4 ，∴直线BC 的解析式为y =-x +4；(2)如图，连接BC ，PB ，∵y =-x 2+3x +4=-x -32 2+74，∴抛物线的对称轴为直线x =32，根据题意得：A 、B 关于抛物线的对称轴直线x =32对称，∴AP =BP ，∴AP +CP =BP +CP ≥BC ，即当P 在直线AB 上时，AP +CP 的值最小，∴当x =32时，y =-32+4=52，∴P 32,52 ，故答案是：32,52 ；(3)过Q 作QD ⊥x 轴，交BC 于D ，设Q d ,-d 2+3d +4 ，其中0≤d ≤4，则D d ,-d +4 ，∴QD =-d 2+3d +4 --d +4 =-d 2+4d ，∵B 4,0 ，∴OB =4，∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8，当d =2时，S ΔBCQ 取最大值，最大值为8，∴△BCQ 的最大面积为8；【点睛】本题主要考查了二次函数的图像和性质，利用数形结合思想和分类讨论思想是解题的关键．22(2023秋·江苏淮安·八年级统考期末)如图1，直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点，过点B 的直线交x 轴负半轴于点C -3,0 ．(1)请直接写出直线BC 的关系式：(2)在直线BC 上是否存在点D，使得S △ABD =S △AOD 若存在，求出点D 坐标：若不存请说明理由；(3)如图2，D 11,0 ，P 为x 轴正半轴上的一动点，以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ，连接QA ,QD ．请直接写出QB -QD 的最大值：．19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时，S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点，可求出点B 的坐标，再用待定系数法即可求解；(2)设D (a ,2a +6)，分别用含a 的式子表示出出S △AOD ,S △ABD ，由此即可求解；(3)△BPQ 是等腰直角三角形，设P (m ,0)(m >0)，可表示出QB ，再证Rt △BOP ≌Rt △PTQ (AAS )，如图所示，当点B ,R ,Q 在一条直线上时，QB -QD 的值最大，最大值为BR 的值，可求得点R 的坐标，根据勾股定理即可求解．【详解】(1)解：∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点，令x =0，则y =6，∴B (0,6)，且C -3,0 ，设直线BC 的解析式为y =kx +b ，∴b =6-3k +b =0，解得，k =2b =6 ，∴直线BC 的解析式为y =2x +6，故答案为：y =2x +6．(2)解：由(1)可知直线BC 的解析式为y =2x +6，直线AB 的解析式为y =-x +6，∴A (6,0),B (0,6),C (-3,0)，∴OA =6,BO =6,OC =3，如图所示，点D 在直线BC 上，过点D 作DE ⊥x 轴于E ，∴设D (a ,2a +6)，E (a ,0)，∴S △ABC =12AC ·OB =12×(6+3)×6=27，S △ADC =12AC ·DE =12×(6+3)×a =92a ，S △AOD =12OA ·DE =12×6×a =3a ，∴S △ABD =S △ABC -S △ADC =27-92a ，若S △ABD =S △AOD ，则27-92a =3a ，当a >0时，27-92a =3a ，解得，a =185，即D 185,665 ；当a <0时，27+92a =-3a ，解得，a =-185，即D -185,-65 ；综上所述，当D 185,665 或D -185,-65时，S △ABD =S △AOD ．(3)解：已知A (6,0),B (0,6),D (11,0)，设P (m ,0)(m >0)，∴在Rt △BOP 中，OB =6,OP =m ，∵△BPQ 是等腰直角三角形，∠BPQ =90°，∴BP =QP ；如图所示，过点Q 作QT ⊥x 轴于T ，20在Rt △BOP ,Rt △PTQ 中，∠BOP =∠PTQ =90°，∠BPO +∠QPA =∠QPA +∠PQT =90°，∴∠BPO =∠PQT ，∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP，∴Rt △BOP ≌Rt △PTQ (AAS )，∴OP =TQ =m ，OB =PT =6，∴AT =OP +PT -OA =m +6-6=m ，∴AT =QT ，且QT ⊥x 轴，∴△ATQ 是等腰直角三角形，∠QAT =45°，则点Q 的轨迹在射线AQ 上，如图所示，作点D 关于直线AQ 的对称点R，连接QR ,BR ,AR ，A (6,0)，B (0,6)，D (11,0)，∵△ATQ 是等腰直角三角形，即∠QAT =45°，根据对称性质，∴∠QAR =45°，∴RA ⊥x 轴，且△DQA ≌△RQA ，∴AR =AD =11-6=5，则R (6,5)，如图所示，当点B ,R ,Q 在一条直线上时，QB -QD 的值最大，最大值为BR 的值；∴由勾股定理得：BR =62+(6-5)2=37，故答案为：37．【点睛】本题主要考查一次函数，几何的综合，掌握待定系数法求解析式，将军饮马问题，等腰直角三角形的性质，勾股定理是解题的关键．23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中，∠B =60°．(1)如图1，若AC >BC ，CD 平分∠ACB 交AB 于点D ，且AD =3BD ．证明：∠A =30°；(2)如图2，若AC <BC ，取AC 中点E ，将CE 绕点C 逆时针旋转60°至CF ，连接BF 并延长至G ，使BF =FG ，猜想线段AB 、BC 、CG 之间存在的数量关系，并证明你的猜想；(3)如图3，若AC =BC ，P 为平面内一点，将△ABP 沿直线AB 翻折至△ABQ ，当3AQ +2BQ +13CQ 取得最小值时，直接写出BPCQ的值．【答案】(1)见解析(2)BC =AB +CG ，理由见解析(3)213+33913【分析】(1)过点D 分别作BC ，AC 的垂线，垂足为E ，F ，易得DE =DF ，由∠B =60°，可得DE =DF =32BD ，由AD =3BD ，求得sin A =DE AD=12，可证得∠A =30°；(2)延长BA ，使得BH =BC ，连接EH ，CH ，易证△BCH 为等边三角形，进而可证△BCF ≌△HCE SAS ，可得BF =HE ，∠BFC =∠HEC ，可知∠AEH =∠CFG ，易证得△AEH ≌△CFG SAS ，可得AH =CG ，由BC =BH =AB +AH =AB +CG 可得结论；(3)由题意可知△ABC 是等边三角形，如图，作CM ⊥CA ，且CM =32CA ，作CN ⊥CQ ，且CN =32CQ ，可得CM CA=CN CQ =32，QN =CQ 2+CN 2=132CQ ，可知△ACQ ∽△MCN ，可得MN =32AQ ，由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ，N 都在线段BM 上时，3AQ +2BQ+13CQ 有最小值，过点C 作CR ⊥BM ，过点M 作MT ⊥BC 交BC 延长线于T ，可得CR =CQ ⋅sin ∠CQN =313CQ ，QR =CQ ⋅cos ∠CQN =213CQ ，可证△CBR ∽△MBT ，得BR CR =BT MT ，设BC =a 由等边三角形的性质，可得CM =32a ，进而可得CT =CM ⋅cos30°=334a ，MT =CM ⋅sin30°=34a ，结合BR CR=BTMT 可得：BQ +213CQ 313CQ =a +334a 34a ，可得BQ CQ =213+33913，由翻折可知，BP =BQ ，可求得BP CQ的值．【详解】(1)证明：过点D 分别作BC ，AC 的垂线，垂足为E ，F ，∵CD 平分∠ACB ，DE ⊥BC ，DF ⊥AC ，∴DE =DF ，又∵∠B =60°，∴DE =BD ⋅sin60°=32BD ，则DE =DF =32BD ，又∵AD =3BD ，∴sin A =DE AD =32BD3BD=12，∴∠A =30°；(2)BC =AB +CG ，理由如下：延长BA ，使得BH =BC ，连接EH ，CH ，∵∠ABC =60°，BH =BC ，∴△BCH 为等边三角形，∴CB =CH ，∠BCH =60°，∵CE 绕点C 逆时针旋转60°至CF ，∴CE =CF ，∠ECF =60°，则∠BCH -∠ACB =∠ECF -∠ACB ，∴∠ECH =∠FCB ，∴△BCF ≌△HCE SAS ，∴BF =HE ，∠BFC =∠HEC ，则∠AEH =∠CFG ，∵BF =FG ，∴BF =HE =FG ，又∵E 为AC 中点，∴AE =CE =CF ，∴△AEH ≌△CFG SAS ，∴AH =CG ，∴BC =BH =AB +AH =AB +CG ；(3)∵∠ABC =60°，AC =BC ，∴△ABC 是等边三角形，如图，作CM ⊥CA ，且CM =32CA ，作CN ⊥CQ ，且CN =32CQ ，则CM CA=CN CQ =32，QN =CQ 2+CN 2=132CQ ，∴sin ∠CQN =CN QN =313，cos ∠CQN =CQ QN =213，则∠ACM =∠QCN =90°，∴∠ACM -∠ACN =∠QCN -∠ACN ，则∠ACQ =∠MCN∴△ACQ ∽△MCN ，∴MN AQ =CM CA=32，即：MN =32AQ ，∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即：点Q ，N 都在线段BM 上时，3AQ +2BQ +13CQ 有最小值，如下图，过点C 作CR ⊥BM ，过点M 作MT ⊥BC 交BC 延长线于T ，则∠BRC =∠BTM =90°，CR =CQ ⋅sin ∠CQN =313CQ ，QR =CQ ⋅cos ∠CQN =213CQ ，又∵∠CBR =∠MBT ，∴△CBR ∽△MBT ，∴BR CR=BT MT ，∵△ABC 是等边三角形，设BC =a ∴∠ACB =60°，AC =BC =a ，则CM =32a ，∵∠ACM =90°，∴∠MCT =30°，则CT =CM ⋅cos30°=334a ，MT =CM ⋅sin30°=34a ，则由BR CR=BT MT 可得：BQ +213CQ 313CQ =a +334a34a ，整理得：133BQ CQ +23=4+333，得BQ CQ=213+33913，由翻折可知，BP =BQ ，∴BP CQ =BQ CQ=213+33913．【点睛】本题属于几何综合，考查了解直角三角形，等边三角形的判定及性质，全等三角形的判定及性质，相似三角形的判定及性质，旋转的性质以及费马点问题，掌握费马点问题的解决方法，添加辅助线构造全等三角形和相似三角形是解决问题的关键．24(2023春·江苏·八年级专题练习)定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在Rt △ABC 中，∠A =90°，AB =AC ，点D 、E 分别在边AB 、AC 上，AD =AE ，连接DE 、DC ，点M 、P 、N 分别为DE 、DC 、BC 的中点，且连接PM 、PN ．(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”．(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置，连接BD ，CE ，试判断PM 与PN 是否为“等垂线段”，并说明理由．(3)拓展延伸把△ADE 绕点A 在平面内自由旋转，若DE =2，BC =4，请直接写出PM 与PN 的积的最大值．。

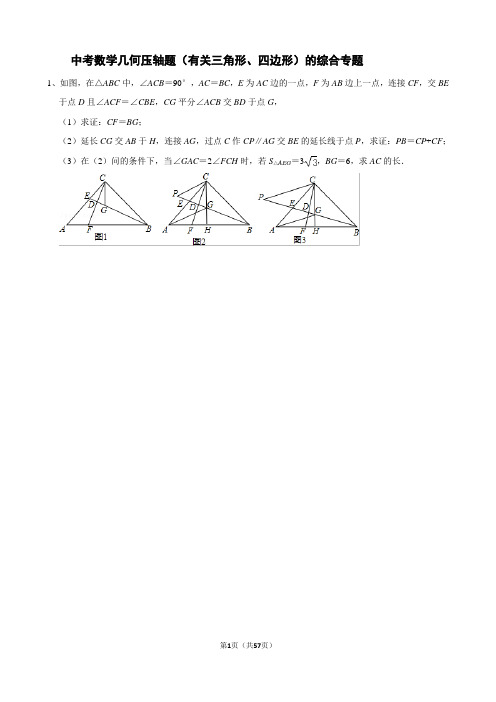
中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。

2021中考考点必杀500题专练16（几何类压轴题）（30道）1．（2021·江西九年级一模）如图1，在菱形ABCD 中，2AB =，60ABC ∠=︒，点E 为BD 上一动点，在点E 的运动过程中，始终保持//EF AB ，EF AB =，连接DF ，CF ，CF 与BD 相交于点O ．（1）如图1，求证四边形CDFE 为平行四边形；（2）当点E 运动到什么位置时，四边形CDFE 为矩形？并说明理由；（3）如图2，延长DA 到M ，使AM AD =，连接ME ，判断ME 与CF 的数量关系，并说明理由．【答案】（1）见解析；（2）BC 的垂直平分线上，理由见解析；（3）=CF ME ，理由见解析【分析】（1）菱形的性质可得AB CD =，//AB CD ，根据平移的性质可得EF AB =，//EF AB ，继而可证得四边形CDFE 为平行四边形；（2）通过证得90ECD ∠=︒，再结合四边形CDFE 为平行四边形，即可得证；（3）连接AO ，根据四边形CDFE 为平行四边形及AM AD =，可得AO 是△DEM 的中位线，继而得到2ME AO =，根据菱形的轴对称可得AO OC =，继而可得=CF ME ．【详解】解：（1）证明：由菱形的性质可得AB CD =，//AB CD ，由平移可得，EF AB =，//EF AB ；∴EF CD =，//EF CD ，∴四边形CDFE 为平行四边形；（2）当点E 运动到BC 的垂直平分线上时，四边形CDFE 为矩形．∵菱形ABCD 中，60ABC ∠=︒，∴30DBC ∠=︒，120BCD ∠=︒，∵BE CE =，∴30ECB DBC ∠=∠=︒，即90ECD ∠=︒，又∵四边形CDFE 为平行四边形，∴四边形CDFE 为矩形；（3）如图，连接AO ，由（1）得四边形CDFE 为平行四边形，∴EO DO =，又∵AM AD =，∴AO 是DEM △的中位线，∴2ME AO =，由菱形的轴对称可得AO OC =，即2CF AO =，∴=CF ME ．【点睛】本题考查平行四边形的性质、矩形的判定与性质，三角形的中位线的性质，解题的关键是掌握相关判定与性质．2．（2021·江西九年级二模）如图1，在正方形ABCD 中，点,E F 分别在边,AB AD 上，且AE AF =，延长FD 到点G ，使得DG DF =，连接,,EF GE CE ．（特例感知）（1）图1中GE 与CE 的数量关系是______________．（结论探索）（2）图2，将图1中的AEF 绕着点A 逆时针旋转()090αα︒<<︒，连接FD 并延长到点G ，使得DC DF =，连接,,GE CE BE ，此时GE 与CE 还存在（1）中的数量关系吗？判断并说明理由．（拓展应用）（3）在（2）的条件下，若5,32AB AE ==，当EFG 是以EF 为直角边的直角三角形时，请直接写出GE 的长．【答案】(1)GE 2CE ，(2)存在，证明见解析，（3）25810或16或4．【分析】(1)连接GC ，证△CDG ≌△CBE ，得出△GCE 为等腰直角三角形即可；(2)类似（1）的方法，先证△AFD ≌△AEB ，再证△CDG ≌△CBE ，得出△GCE 为等腰直角三角形即可；(3)根据E 、F 是直角顶点分类讨论，结合（2）中结论，利用勾股定理求解即可．【详解】解：(1)连接GC ，∵AE =AF ，AD =AB ，∴DF =BE ，∵DG DF =，∴DG =BE ，∵∠GDC =∠B =90°，DC =BC ，∴△CDG ≌△CBE ，∴CE =CG ，∠GCD =∠ECB ，∵∠ECB+∠DCE=90°，∴∠GCE=∠GCD+∠DCE=90°，∴GE；故答案为：GE；(2)存在，连接GC，∵AE=AF，AD=AB，∠FAE=∠DAB=90°，∴∠FAD=∠EAB，∴△FAD≌△EAB，∴FD=EB=GD，∠FDA=∠EBA，∵∠GDC+∠FDA=90°，∠EBC+∠EBA=90°，∴∠GDC=∠EBC，∵DC=BD，∴△CDG≌△CBE，与（1）同理，GE；(3)当∠FEG=90°时，如图1，因为∠FEA=∠GEC=45°，所以，A、E、C在一条直线上，∵AB=5，∴AC2,CE222,GE2EC=4；如图2，E在CA延长线上，同理可得，EC2，GE2EC=16；当∠EFG =90°时，如图3，∠AFD =∠EFG +∠AFE =135°，由（2）得，∠AFD =∠AEB =135°，DF =BE ，所以，B 、E 、F 在一条直线上，作AM ⊥EF ，垂足为M ，∵5,32AB AE ==，∴EF =6，AM =ME =MF =3，224BM AB AM =-=，BE =DF =1,FG =2，22210GE FG EF =+=如图4，同图3，BE =DF =7，FG =14，EF =6，GE==，综上，GE的长为或16或4．【点睛】本题考查了旋转的性质、全等三角形的判定与性质、勾股定理和等腰直角三角形的性质，解题关键是恰当的连接辅助线，构造全等三角形；会分类讨论，结合题目前后联系，解决问题．3．（2021·江西九年级一模）定义：在凸四边形中，我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”．（1）在正方形、矩形、菱形中，一定是“完美四边形”的是．（2）如图1，在“完美四边形”ABCD中，AB＝AD＝CD＝2，BC＝52，AC＝3，求线段BD的长．（3）如图2，⊙O内接四边形EFGH，GE为⊙O的直径．①求证：四边形EFGH为“完美四边形”．②若EF＝6，FG＝8，FH是否存在一个值使四边形EFGH的面积最大？若存在，求出FH的值；若不存在，请说明理由．【答案】（1）正方形、矩形；（2）3；（3）存在，．【分析】（1）依次判断正方形、矩形、菱形是否满足定义条件即可；（2）根据“完美四边形”的定义，得到边和对角线之间的关系式，代入数据运算即可求解；（3）①做辅助线构造出两组相似三角形，得到四边形的边和对角线之间的关系，再利用等式的性质代换即可得到所需条件，进而得以求证；②将四边形分成两部分，一部分是GEF ∆，得到它的面积为定值，另一部分为GEH ∆，它的面积随H 点位置的变化而变化，当H 点到GE 的垂线段就是半径时为最大，此时GEH ∆的面积也最大，从而整个四边形的面积就最大；再利用勾股定理和“完美四边形”的定义等进行求解即可．【详解】解：（1）正方形、矩形理由如下：①如图，设正方形边长为a ，==，所以对角线的积为)222a =，因为两组对边的积的和为222=2a a a +，∴正方形为“完美四边形”．②如图，设矩形的两邻边长分别为b 和c ，∵矩形的对角线长相等，∴矩形对角线的积为222b c =+，又∵矩形对边的积分别为2b 和2c ，则对边积的和为22b c +∴矩形为“完美四边形”．③如图，设菱形的两条对角线长的一半分别为m 和n ，，∵菱形的四条边相等，∴菱形的对边的积的和为222222m n +=+，∵菱形的对角线的积为224m n mn ⋅=，令22224m n mn +=，∴m n=∴只有当m n =时，该菱形才为“完美四边形”，当m n ≠时，则它不是“完美四边形”，∴菱形不是“完美四边形”．综上可知：只有正方形和矩形是“完美四边形”．（2）由“完美四边形”的定义可知：522232BD ⨯+⨯=，∴3BD =．（3）①如图，在GE 上取一点M ，使∠GFM=∠HFE ，∵∠FGM=∠FHE （同弧所对的圆周角相等），∴FGM ∆∽FHE∆∴FG GM FH HE=∴FG HE FH GM ⋅=⋅，∵∠GFM=∠HFE ，∴∠GFH=∠MFE ，又∵∠GHF=∠MEF ，∴GHF ∆∽MEF ∆，∴GH HF ME FE=，∴GH FE FH ME ⋅=⋅，∴()+GH FE FG HE FH ME FH GM FH ME GM FH GE⋅⋅=⋅+⋅=⋅+=⋅∴四边形EFGH 为“完美四边形”．②存在；理由：如下面图①，∵GE 是直径，∴∠EFG=90°，∴10GE ==，GEF ∆的面积为168=242⨯⨯∴要使四边形GFEH 面积最大，则只需GEH ∆面积最大，作HN ⊥GE ，垂足为N ，则HN 的值最大时，GEH ∆面积就最大，因为H 点到直径DE 的垂线段的长最大为半径，即垂足N 点在原点时最大；如下面图②，当O 点与N 点重合时，由GE 是直径，∴∠GHE=90°，∵HN 垂直平分GE ，∴HG=HE ，∵222GE GH HE =+∴HG HE ===；由它是“完美四边形”，∴1068FH =⨯+⨯∴FH =，∴存在，当FH =时，面积最大．【点睛】本题为新定义型试题，综合考查了圆、相似、勾股定理、四边形等内容，考查了学生对相关概念的理解与应用，本题属于压轴题，其中作辅助线是一个难点，对学生的综合分析与知识点运用的能力有着十分高的要求，本题蕴含了数形结合等思想．4．（2021·江西赣州市·九年级一模）定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．（2）如图2，四边形ABCD内接于⊙O， AD＝ BD，四边形ABCD的外角平分线DF交⊙O于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．【答案】（1）∠E＝12α；（2）见解析；（3）①∠AED＝45°；②259【分析】（1）由角平分线的定义可得出结论；（2）由圆内接四边形的性质得出∠FDC+∠FBC=180°，得出∠FDE=∠FBC ，证得∠ABF=∠FBC ，证出∠ACD=∠DCT ，则CE 是△ABC 的外角平分线，可得出结论；（3）①连接CF ，由条件得出∠BFC=∠BAC ，则∠BFC=2∠BEC ，得出∠BEC=∠FAD ，证明△FDE ≌△FDA （AAS ），由全等三角形的性质得出DE=DA ，则∠AED=∠DAE ，得出∠ADC=90°，则可求出答案；②过点A 作AG ⊥BE 于点G ，过点F 作FM ⊥CE 于点M ，证得△EGA ∽△ADC ，得出AE AG AC CD=，求出45AD AC =，设AD=4x ，AC=5x ，则有（4x ）2+52=（5x ）2，解得x=53，求出ED ，CE 的长，求出DM ，由等腰直角三角形的性质求出FM ，根据三角形的面积公式可得出答案．【详解】解：（1）∵BE 平分∠ABC ，CE 平分∠ACD ，∴∠E ＝∠ECD ﹣∠EBD ＝12（∠ACD ﹣∠ABC ）＝11A 22∠=α，（2）如图1，延长BC 到点T ，∵四边形FBCD 内接于⊙O ，∴∠FDC+∠FBC ＝180°，又∵∠FDE+∠FDC ＝180°，∴∠FDE ＝∠FBC ，∵DF 平分∠ADE ，∴∠ADF ＝∠FDE ，∵∠ADF ＝∠ABF ，∴∠ABF ＝∠FBC ，∴BE 是∠ABC 的平分线，∵ AD BD=，∴∠ACD ＝∠BFD ，∵∠BFD+∠BCD＝180°，∠DCT+∠BCD＝180°，∴∠DCT＝∠BFD，∴∠ACD＝∠DCT，∴CE是△ABC的外角平分线，∴∠BEC是△ABC中∠BAC的遥望角．（3）①如图2，连接CF，∵∠BEC是△ABC中∠BAC的遥望角，∴∠BAC＝2∠BEC，∵∠BFC＝∠BAC，∴∠BFC＝2∠BEC，∵∠BFC＝∠BEC+∠FCE，∴∠BEC＝∠FCE，∵∠FCE＝∠FAD，∴∠BEC＝∠FAD，又∵∠FDE＝∠FDA，FD＝FD，∴△FDE≌△FDA（AAS），∴DE＝DA，∴∠AED＝∠DAE，∵AC是⊙O的直径，∴∠ADC＝90°，∴∠AED+∠DAE＝90°，∴∠AED＝∠DAE＝45°，②如图3，过点A作AG⊥BE于点G，过点F作FM⊥CE于点M，∵AC是⊙O的直径，∴∠ABC＝90°，∵BE平分∠ABC，∴∠FAC＝∠EBC＝12∠ABC＝45°，∵∠AED＝45°，∴∠AED＝∠FAC，∵∠FED＝∠FAD，∴∠AED﹣∠FED＝∠FAC﹣∠FAD，∴∠AEG＝∠CAD，∵∠EGA＝∠ADC＝90°，∴△EGA∽△ADC，∴AE AG AC CD=，∵在Rt△ABG中，AG＝2AB2 2=，在Rt△ADE中，AE2AD，∴45 ADAC=，在Rt△ADC中，AD2+DC2＝AC2，∴设AD＝4x，AC＝5x，则有（4x）2+52＝（5x）2，∴x＝5 3，∴ED＝AD＝20 3，∴CE＝CD+DE＝35 3，∵∠BEC ＝∠FCE ，∴FC ＝FE ，∵FM ⊥CE ，∴EM ＝12CE ＝356，∴DM ＝DE ﹣EM ＝56，∵∠FDM ＝45°，∴FM ＝DM ＝56，∴S △DEF ＝12DE•FM ＝259．【点睛】本题是圆的综合题，考查了角平分线的定义，圆周角定理，圆内接四边形的性质，相似三角形的判定与性质，全等三角形的判定与性质，勾股定理，等腰直角三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．5．（2021·江西赣州市·九年级期末）（问题提出）如图1，在等边三角形ABC 内部有一点P ，3PA =，4PB =，5PC =．求APB ∠的度数．（数学思考）当图形中有一组邻边相等时，通过旋转可以将分散的条件集中起来解决问题．（尝试解决）（1）将APC △绕点A 逆时针旋转60°，得到AP B '△，连接PP '，则APP ' 为等边三角形．3P P PA '== ，4PB =，5P B PC '==，222P P PB P B ''∴+=BPP ' 为______三角形APB ∴∠的度数为______．（类比探究）（2）如图2，在等边三角形ABC 外部有一点P ，若30BPA ∠=︒，求证222PA PB PC +=．（联想拓展）（3）如图3，在ABC 中，90BAC ∠=︒，AB AC =．点P 在直线BC 上方且45APB ∠=︒，PC BC ==PA 的长．【答案】（1）直角；150°；（2）见详解；（3）PA =．【分析】（1）由旋转的性质、等边三角形的性质，以及勾股定理的逆定理，判定BPP ' 为直角三角形，即可得到答案；（2）将△APC 绕点C 顺时针旋转60°，得到如图所示A CP ''∆，再连接PP '，由等边三角形的性质和旋转的性质，得到90PBP '∠=︒，从而得到结论成立；（3）将△PAB 绕点A 顺时针旋转90°，得到如图所示P AB ''∆，由旋转的性质和等腰直角三角形的性质，以及勾股定理，即可求出答案．【详解】解：（1）将APC △绕点A 逆时针旋转60°，得到AP B '△，连接PP '，则APP ' 为等边三角形．∴60APP '∠=︒，3P P PA '== ，4PB =，5P B PC '==，222P P PB P B ''∴+=BPP ' 为直角三角形，∴90BPP '∠=︒,APB ∴∠的度数为：9060150︒+︒=︒．故答案为：直角；150°．（2）将△APC 绕点C 顺时针旋转60°，得到如图所示A CP ''∆，再连接PP '，∵△ABC 是等边三角形，则点A '与点B 重合，由旋转的性质，则CP CP '=，60PCP '∠=︒，13∠=∠∴PCP '∆是等边三角形，则PP CP '=，∴6060120CPP CP P ''∠+∠=︒+︒=︒，∵13∠=∠，1230APB ∠+∠=∠=︒，∴2330∠+∠=︒，∴451203090∠+∠=︒-︒=︒，∴90PBP '∠=︒，∴PBP '∆是直角三角形，∴222PP PB BP ''=+，∵PA P B '=，PP CP '=，∴222PA PB PC +=．（3）将△PAB 绕点A 顺时针旋转90°，得到如图所示P AB ''∆，∵AB=AC ，∠BAC=90°，则点B '与点C 重合，由旋转的性质，得AP AP '=，CP PB '⊥，90P AP '∠=︒，∴APP ∆'是等腰直角三角形，∴PC BC =，45APP APB '∠=∠=︒，则点P 、P '、B 三点共线，∵PC BC ==CP PB '⊥，∴点P '是PB 的中点，设2CP BP x '==，则12PP BP BP x ''===，由勾股定理，得=，∴2x =，∴2PP BP ''==，∵APP ∆'是等腰直角三角形，∴PA P A '==【点睛】本题考查了等边三角形的性质，旋转的性质，等腰直角三角形的判定和性质，以及勾股定理进行解题，解题的关键是掌握旋转的性质，正确作出辅助线进行分析．6．（2021·江西吉安市·）如图，在正方形ABCD 中，点E 在对角线AC 上，12AC =，过点E 的直线分别交AD ，BC 于点M ，N ．（1）当MN BC ⊥时，MN 的长为________，AEM △∽________；（2）已知2EC AE =．①若9MN =，求此时AM 的长；②当E ，F 为AC 的三等分点，点P 在正方形的边上时，是否存在满足9+=PE EF 的情况？如果存在，请通过分析指出这样的点的个数；如果不存在，说明理由．【答案】（1）；CEN ；（2）①1AM =；②存在，有8个．【分析】解：（1）由四边形ABCD 为正方形，得到△ACD 为等腰直角三角形，在Rt △ACD 中由勾股定理求得CD 的长，由MN=CD ，可以求出MN 的长，由AD ∥BC 得到△AEM ∽△CEN.（2）①过点E 作EG ⊥AD 于点G ．由AM ∥CN ，得到△AEM ∽△CEN ．得到对应边成比例，由勾股定理求出GM 的长，再由AM=AG+GM 可求出．②画出图形，过点F 作点F 关于BC 的对称点M ，连接FM 交BC 于点N ，连接EM ，根据点M 与点F 关于BC 对称，计算出PE+PF 的最小值，与PE+PF=9比较．得出BC 上存在两个点，同理在线段AB ，AD ，CD 上都存在两个点使PE+PF=9．【详解】解：（1）CEN∵四边形ABCD 为正方形∴△ACD 为等腰直角三角形，则，在Rt △ACD 中有AD=AC ，AD 2+DC 2=AC 2，∵AC=12，解得：，又∵MN ⊥BC ，CD ⊥BC∴MN ∥CD ，且MN=CD ，即，又∵AD ∥BC∴△AEM ∽△CEN.（2）①如图，过点E 作EG AD ⊥于点G ．∵//AM CN ，∴ ∽AEM CEN ．∴12==EM AE EN EC ．∵12AC =，9MN =，∴4AE =，3ME =．∵45EAG ∠=︒，∴==AG GE ．∴1===GM ．∴1=+=+AM AG GM ．②存在，这样的点有8个．如图，过点F 作点F 关于BC 的对称点M ，连接FM 交BC 于点N ，连接EM ，∵点E ，F 将对角线AC 三等分，且12AC =，∴8EC =，4FC =．∵点M 与点F 关于BC 对称，∴4==CF CM ，45ACB BCM ∠=∠=︒．∴90ACM ∠=︒．∴==EM则在线段BC 上存在点N 到点E 和点F 的距离之和最小为9<．∴在线段BC 上，点N 的左右两边各有一个点P 使9+=PE PF ．同理在线段AB ，AD ，CD 上都存在两个点使9+=PE PF ．即共有8个点P 满足9+=PE PF ．【点睛】本题考查正方形的性质，相似三角形的判定及性质、线段和的最值问题等，体现了逻辑推理、直观想象核心素养.7．（2021·江西上饶市·九年级期末）观察猜想：（1）如图1，在Rt △ABC 中，∠ACB ＝90°，∠BAC ＝30°，点D 与点C 重合，点E 在斜边AB 上，连接DE ，且DE ＝AE ，将线段DE 绕点D 顺时针旋转90°得到线段DF ，连接EF ，则EF AD ＝______，sin ∠ADE ＝________，探究证明：（2）在（1）中，如果将点D 沿CA 方向移动，使CD ＝13AC ，其余条件不变，如图2，上述结论是否保持不变？若改变，请求出具体数值：若不变，请说明理由．拓展延伸（3）如图3，在△ABC 中，∠ACB ＝90°，∠CAB ＝a ，点D 在边AC 的延长线上，E 是AB 上任意一点，连接DE ．ED ＝nAE ，将线段DE 绕着点D 顺时针旋转90°至点F ，连接EF ．求EF AD和sin ∠ADE 的值分别是多少？（请用含有n ，a 的式子表示）【答案】（1）63；12；（2）不变；（3）EF AD ；sin ∠ADE ＝sin n α．【分析】（1）由等腰三角形的性质和等边三角形的判定得到∠A ＝∠ACE ＝30°，△BEC 是等边三角形，据此求得CE 的长度，根据等腰直角三角形的性质来求EF 的长度，易得答案；（2）不变．理由：如图2，过点D 作DG ∥BC 交AB 于点G ，构造直角三角形：△ADG ，结合含30度角的直角三角形的性质和锐角三角函数的定义，结合方程求得答案；（3）如图3，过点E 作EG ⊥AD 于点G ，构造直角三角形，根据锐角三角函数的定义列出方程并解答．【详解】（1）如图1，∵在Rt △ABC 中，∠ACB ＝90°，∠BAC ＝30°，∴∠B ＝60°．又CE ＝AE ，∴∠ACE ＝∠A ＝30°，∴∠BCE ＝60°，∴△BEC 是等边三角形，∴BE ＝CE ．∴AE ＝CE ＝BE ．∴AD ＝32AB CE ．又由旋转的性质知：FC ＝EC ，∠FCE ＝90°，∴EF CE ，∴EF AD＝63．∵∠ADE ＝30°，∴sin ∠ADE ＝12．故答案是：63；12；（2）不变，理由：如图2，过点D 作DG ∥BC 交AB 于点G ，则△ADG 是直角三角形．∵∠DAG ＝30°，DE ＝AE ，设DG ＝x ，∴∠AED ＝30°，AD ＝x ，∠DEG ＝∠DGE ＝60°．∴DE ＝DF ＝x ，sin ∠ADE ＝12．∵∠EDF ＝90°，∴EF x ．∴EFAD ＝63．∵∠ADE ＝30°，∴sin ∠ADE ＝12．（3）过点E 作EG ⊥AD 于点G ，设AE ＝x ，则DE ＝nx ．∵∠CAB ＝a ，∴AG ＝cosα•x ，EG ＝sinα•x ．∴DG •x ．∴AD ＝•x ．∵∠EDF ＝90°，DE ＝DF ，∴EF DE nx ．∴EFAD ，sin ∠ADE ＝GE DE ＝sin x nx α⋅＝sin nα．【点睛】本题考查了等腰三角形的性质和等边三角形的判定，作辅助线构造直角三角形，根据锐角三角函数的定义求解．8．（2021·江西景德镇市·九年级期末）如图1将ABC 绕点A 逆时针旋转α角度后，与ADE 构成位似图形，则称ABC 与ADE 互为“旋转位似图形”．（1）知识理解：①两个重合了一个顶点且边长不相等的等边三角形________（填：是或不是）“旋转位似图形”．如图1，ABC 与ADE 互为“旋转位似图形”②若26α=︒，100B ∠=︒，29E ∠=︒，则BAE ∠的度数为________；③若6AD =，8DE =，4AB =，则BC 的长度为________；（2）知识运用：如图2，在四边形ABCD 中，90ADC ABC ∠=∠=︒，AE BD ⊥于E ，12∠=∠．求证：ACD △与ABE △互为“旋转位似图形”．（3）拓展提高：如图3，ABC 为等腰直角三角形，点G 为斜边AC 的中点，点F 是AB 上一点，D 是GF 延长上一点，点E 在线段GF 上，且ABD △与AGE 互为“旋转位似图形”，若6AC =，AD =DE 和BD 的长．【答案】（1）①是；②25︒；③163；（2）证明见解析；（2）；．【分析】（1）①根据“旋转位似图形”的定义即可得答案；②由“旋转位似图形”的定义可得△ABC ∽△ADE ，根据相似三角形的性质及三角形内角和定理可得∠C 、∠BAC 的度数，根据旋转的性质可得∠EAC=26°，利用角的和差关系即可得答案；③由“旋转位似图形”的定义可得△ABC ∽△ADE ，根据相似三角形的性质即可得答案；（2）根据直角三角形两锐角互余的性质及角的和差关系可得∠2=∠BAE ，即可得出∠1=∠BAE ，进而可证明△ACD ∽△ABE ，即可得结论；（3）作DE AE '⊥交直线AE 于点E '，根据等腰直角三角形的性质可求出AB 的长，根据相似三角形的性质可求出AE 的长，根据角的和差关系可得∠DAE=45°，根据等腰直角三角形的性质可得AE=AE′，即可证明点E 与点E′重合，可得AE ⊥DG ，可得DE=AE ，即可得出DE 的长，利用勾股定理即可求出BD 的长．【详解】（1）①如图，△ABC 和△ADE 是等边三角形，∴△ABC ∽△ADE ，∴ABC 绕点A 逆时针旋转α角度后与ADE 构成位似图形，故答案为：是②∵ABC 与ADE 互为“旋转位似图形”∴△ABC ∽△ADE ，∴∠C=∠E=29°，∴∠BAC=180°-∠B-∠C=180°-100°-29°=51°，∵△ADE 绕点A 逆时针旋转α角度后，与△ABC 构成位似图形，∴∠EAC=α=26°，∴∠BAE=∠BAC-∠EAC=51°-26°=25°，故答案为：25°③∵ABC 与ADE 互为“旋转位似图形”∴△ABC ∽△ADE ，∴AD DE AB BC =，即684BC =，解得：BC=163，故答案为：163（2）∵AE ⊥BD ，∠ABC=90°，∴∠2+∠ABD=90°，∠BAE+∠ABD=90°，∴∠BAE=∠2，∵∠1=∠2，∴∠1=∠BAE ，∵∠ADC=∠AEB=90°，∴△ACD ∽△ABE ，∵△ACD 与△ABE 有一个公共顶点A ，∴△ACD 与△ABE 互为“旋转位似图形”．（3）如图，作DE AE '⊥交直线AE 于点E '，∵△ABC 是等腰直角三角形，AC=6，∴AB=22AC= ABD 与AGE 互为“旋转位似图形”，ABD AGE ∴△∽△．AD AB AE AG∴=，DAB EAG ∠=∠23323AE =，AE =；45DAB BAE EAG BAE ∠+∠=∠+∠=︒．∴∠DAE′=45°，∴ADE '△为等腰直角三角形．AD =，AE '∴=AE AE '=，点E '和点E 重合，90AED AEG ∴∠=∠=︒．∴DE AE ==，90ADB AEG ∠=∠=︒，∴BD ==【点睛】本题考查位似图形及相似三角形的判定与性质的综合，理解“旋转位似图形”的定义并熟练掌握相似三角形的判定定理、是解题关键．9．（2021·江西）在Rt ABC 中，90,ABC AB BC ∠=︒=，点E 在射线CB 上运动．连接AE ，将线段AE 绕点E 顺时针旋转90︒得到EF ，连接CF ．（1）如图1，点E 在点B 的左侧运动．①当1BE =，BC =时，则EAB ∠=_________︒；②猜想线段,CA CF 与CE 之间的数量关系为_____________________________．（2）如图2，点E 在线段CB 上运动时，第（1）问中线段,CA CF 与CE 之间的数量关系是否仍然成立？如果成立，请说明理由；如果不成立，请求出它们之间新的数量关系．（3）点E 在射线CB 上运动，BC =，设BE x =，以A ，E ，C ，F 为顶点的四边形面积为y ，请直接写出y 与x 之间的函数关系式（不用写出x 的取值范围）．【答案】（1）①30；②CA CF +=；（2）不成立，CA CF -=；（3）点E 在点B 左侧运动时，21322y x =++；点E 在线段CB 上运动时，322y x =+．【分析】(1)①根据勾股定理，得AE=2，逆用直角三角形中，30°角的性质即可得到答案；②过点F 作FD ⊥EC ，垂足为D ，证△ABE ≌△EDF ，从而证明AB=ED=BC ，FD=DC ，可探解结论；(2)按照（1）的思路，探解，可得到不同的结论；(3)按照（1），（2）两种情形，分别表示四边形的面积即可.【详解】解：（1）①根据勾股定理,得==2，∵BE=1=12AE ，∴∠BAE=30°；②CA CF +=．理由如下：如图1，过点F 作FD ⊥EC ，垂足为D ，∵∠BAE+∠AEB=90°，∠DEF+∠AEB=90°，∴∠BAE=∠DEF ，∵AE=EF ，∠ABE=∠EDF=90°，∴△ABE ≌△EDF ，∴AB=ED=BC ，∴FD=DC ，∴CF=CD ，ED ，∴(CD+ED)=CE ；（2）不成立．如图2，过点F 作FH BC ⊥交BC 的延长线于点H ．∴90,AEF AE EF ∠=︒=，∴∠AEB+∠FEH=90°，∠AEB+∠BAE=90°，∴∠FEH=∠BAE ，∴Rt ABE Rt EHF ≌，∴,FH BE EH AB BC ===,∴CH BE FH ==,∴FHC 为等腰直角三角形，∴22CH BE FC ==．又∵2222EC BC BE AC FC =-=-,即2CA CF CE -=．（3）如图1，当点E 在点B 左侧运动时，y=12CE×(AB+FD)=1233)x x ++=21322x ++；如图2，当点E 在点B 右侧运动时，连接AF ，根据勾股定理，得=，根据旋转性质，得AE=EF ，∴EC=EH-CH=BC-BE=)x -∴y=12AE×EF+12EC×FH=12232x ++12)x x=12232x ++2122x x -=3322x +．【点睛】本题考查了等腰直角三角形的性质，旋转的性质，勾股定理，三角形的全等，线段之间关系的猜想与证明，分类思想，图形的面积，熟练掌握分类思想，学会构造直角三角形，图形面积的分割是解题的关键.10．（2021·江西宜春市·九年级期中）如图①，正方形ABCD 的边长为4，将正方形ABCD 绕点A 逆时针旋转α（0°＜α≤90°）得到正方形AEFG ，连接BE 并延长交CF 于点O ，连接AC ，AF ．（1）旋转角α与∠OBC 的数量关系是，∠OBC 与∠OEF 的数量关系是；（2）猜想：在旋转过程中，OC 与OF 的数量关系是什么？请证明你的结论；（3）如图②，当α＝45°时，求△BCH 的面积．【答案】（1）α＝2∠OBC ，∠OBC ＝∠OEF ；（2）OC ＝OF ，理由见解析；（3）﹣8【分析】（1）如图，作AK⊥BE于K，由∠ABK+∠BAK＝90°，和∠ABK+∠OBC＝90°，可得∠BAK＝∠OBC，由旋转的性质可知，AB＝AE，由AK⊥BE，∠ABE＝∠AEB，可得∠BAK＝12α，由∠AEB+∠OEF＝90°，可得∠OBC＝∠OEF；（2）OC＝OF，理由如下：如图，过点F作FM⊥BO交BO的延长线于M，过点C作CN⊥BO于N，可证△BCN≌△EFM（AAS），再证△OCN≌△OFM（AAS），可得OC＝OF；（3）当α＝45°时，AF与AD在同一条直线上，可求AF＝，DF＝﹣4，由面积公式△CDF的面积＝12×DF×CD＝﹣8，可证△BCH≌△CDF（ASA），可得△BCH的面积＝△CDF的面积＝﹣8．【详解】解：（1）如图，作AK⊥BE于K，∴∠ABK+∠BAK＝90°，∵∠ABC＝90°，∴∠ABK+∠OBC＝90°，∴∠BAK＝∠OBC，由旋转的性质可知，AB＝AE，∵AK⊥BE，∠ABE＝∠AEB，∴∠BAK＝12α，∴α＝2∠OBC，∵∠AEF＝90°，∴∠AEB+∠OEF＝90°，∴∠OBC＝∠OEF，故答案为：α＝2∠OBC，∠OBC＝∠OEF；（2）OC ＝OF ，理由如下：如图①，过点F 作FM ⊥BO 交BO 的延长线于M ，过点C 作CN ⊥BO 于N ，在△BCN 和△EFM 中，90NBC MEF BNC EMF BC EF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴△BCN ≌△EFM （AAS ），∴NC ＝FM ，在△OCN 和△OFM 中，NOC MOF ONC OMF CN MF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△OCN ≌△OFM （AAS ），∴OC ＝OF；（3）当α＝45°时，AF 与AD 在同一条直线上，∵正方形的边长为4，∴AF=，∴DF ＝4﹣4，∴△CDF 的面积＝12×DF ×CD ＝8﹣8，∵AB ＝AE ，AC ＝AF ，∠BAE ＝∠CAF ＝∠ACD ＝45°，∴∠ABE ＝∠ACF ＝67.5°，∴∠OBC ＝90°﹣∠ABE ＝22.5°，∠DCF ＝∠ACF ﹣45°＝22.5°．∴∠OBC ＝∠DCF ．在△BCH 和△CDF 中，BCH CDF BC CD CBH DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BCH ≌△CDF （ASA ），∴△BCH 的面积＝△CDF 的面积＝﹣8．【点睛】本题考查正方形性质，旋转特征，互余角关系，三角形全等判定与性质，勾股定理，三角形面积，掌握正方形性质，旋转特征，互余角关系，三角形全等判定与性质，勾股定理，三角形面积是解题关键．11．（2021·江西抚州市·九年级月考）（1）发现问题如图（1），在正方形ABCD 中，若点E ，F 分别是边BC ，CD 边上的动点（均不与端点重合），且∠EAF =45°，试判断BE ，EF ，DF 之间的数量关系．小明把△ABE 绕点A 顺时针旋转90°得到△ADG ，发现EF =BE +DF ，请你给出证明过程；（2）类比探究①如图（2），在正方形ABCD 中，若点E ，F 分别是边CB ，DC 延长线上的动点，且∠EAF =45°，则（1）中的结论还成立吗？请写出证明过程．②如图（3），在正方形ABCD 中，若点E ，F 分别是边BC ，CD 延长线上的动点，且∠EAF =45°，请直接写出EF ，BE ，DF 之间的数量关系．（不要求证明）（3）拓展应用在（1）中，若正方形ABCD 的边长为6，AE=，求EF 的长．【答案】（1）见解析；（2）①不成立，理由见解析；②BE=EF+DF；（3）5【分析】（1）证明△EAF≌△GAF，可得出EF=FG，则结论得证；（2）①将△ABE绕点A顺时针旋转90°至△ADM根据SAS可证明△EAF≌△MAF，可得EF=FM，则结论得证；②将△ADF绕点A逆时针旋转90°至△ABN，证明△AFE≌△ANE，可得出EF=EN，则结论得证；（3）求出DG=2，设DF=x，则EF=FG=x+3，CF=6-x，在Rt△EFC中，得出关于x的方程，解出x则可得解．【详解】（1）证明：把△ABE绕点A顺时针旋转90°至△ADG，如图1，∴∠BAE=∠DAG，AE=AG，∠B=∠ADG=90°，∴∠ADF+∠ADG=180°，∴F，D，G三点共线，∵∠EAF=45°，∴∠BAE+∠FAD=45°，∴∠DAG+∠FAD=45°，∴∠EAF=∠FAG，∵AF=AF，∴△EAF≌△GAF（SAS），∴EF=FG=DF+DG，∴EF=DF+BE；（2）①不成立，结论：EF=DF-BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB=∠MAD，AE=AM，∠EAM=90°，BE=DM，∴∠FAM=45°=∠EAF，∵AF=AF，∴△EAF≌△MAF（SAS），∴EF=FM=DF-DM=DF-BE；②结论为：BE=EF+DF，如图3，将△ADF绕点A逆时针旋转90°至△ABN，∴AN=AF，∠NAF=90°，∵∠EAF=45°，∴∠NAE=45°，∴∠NAE=∠FAE，∵AE=AE，∴△AFE≌△ANE（SAS），∴EF=EN，∴BE=BN+NE=DF+EF．即BE=EF+DF；（3）解：由（1）可知，∵正方形ABCD的边长为6，∴DC=BC=AD=6，==，∴DG=3∴BE=DG=3，∴CE=BC-BE=6-3=3，设DF=x，则EF=FG=x+3，CF=6-x，在Rt△EFC中，∵CF2+CE2=EF2，∴(6-x)2+32=(x+3)2，解得：x=2．∴EF=x+3=5．【点睛】本题属于四边形综合题，主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等进行推导．12．（2021·江西赣州市·九年级期末）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°．若固定△ABC，将△DEC绕点C旋转．（1）当△DEC统点C旋转到点D恰好落在AB边上时，如图2．①当∠B=∠E=30°时，此时旋转角的大小为；②当∠B=∠E=α时，此时旋转角的大小为(用含a的式子表示)．（2）当△DEC绕点C旋转到如图3所示的位置时，小杨同学猜想：△BDC的面积与△AEC的面积相等，试判断小杨同学的猜想是否正确，若正确，请你证明小杨同学的猜想．若不正确，请说明理由．【答案】（1）①60°；②2α；（2）小杨同学猜想是正确的．证明见解析．【分析】（1）①证明△ADC是等边三角形即可．②如图2中，作CH⊥AD于H．想办法证明∠ACD=2∠B即可解决问题．（2）小扬同学猜想是正确的．过B作BN⊥CD于N，过E作EM⊥AC于M，如图3，想办法证明△CBN≌△CEM （AAS）即可解决问题．【详解】解：（1）①∵∠B=30°，∠ACB=90°，∴∠CAD=90°﹣30°=60°．∵CA=CD，∴△ACD是等边三角形，∴∠ACD=60°，∴旋转角为60°．故答案为：60°．②如图2中，作CH⊥AD于H．∵CA=CD，CH⊥AD，∴∠ACH=∠DCH．∵∠ACH+∠CAB=90°，∠CAB+∠B=90°，∴∠ACH=∠B，∴∠ACD=2∠ACH=2∠B=2α，∴旋转角为2α．故答案为：2α．（2）小杨同学猜想是正确的．证明如下：过B作BN⊥CD于N，过E作EM⊥AC于M，如图3，∵∠ACB=∠DCE=90°，∴∠1+∠2=90°，∠3+∠2=90°，∴∠1=∠3．∵BN⊥CD于N，EM⊥AC于M，∴∠BNC=∠EMC=90°．∵△ACB≌△DCE，∴BC=EC，在△CBN和△CEM中，∠BNC=∠EMC，∠1=∠3，BC=EC，∴△CBN≌△CEM(AAS)，∴BN=EM．∵S△BDC12=•CD•BN，S△ACE12=•AC•EM．∵CD=AC，∴S△BDC=S△ACE．【点睛】本题考查旋转变换，全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．13．（2021·江西吉安市·九年级一模）在△ABC中，AB=BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF（1）如图1，请直接写出线段OE与OF的数量关系；（2）如图2，当∠ABC=90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由（3）若|CF﹣AE|=2，EF POF为等腰三角形时，请直接写出线段OP的长．【答案】（1）OF=OE；（2）OF⊥EK，OF=OE，理由见解析；（3）OP或23 3.【分析】（1）如图1中，延长EO交CF于K，证明△AOE≌△COK，从而可得OE=OK，再根据直角三角形斜边中线等于斜边一半即可得OF=OE；（2）如图2中，延长EO交CF于K，由已知证明△ABE≌△BCF，△AOE≌△COK，继而可证得△EFK是等腰直角三角形，由等腰直角三角形的性质即可得OF⊥EK，OF=OE；（3）分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】（1）如图1中，延长EO交CF于K，∵AE⊥BE，CF⊥BE，∴AE∥CK，∴∠EAO=∠KCO，∵OA=OC，∠AOE=∠COK，∴△AOE≌△COK，∴OE=OK，∵△EFK是直角三角形，∴OF=12EK=OE；（2）如图2中，延长EO交CF于K，∵∠ABC=∠AEB=∠CFB=90°，∴∠ABE+∠BAE=90°，∠ABE+∠CBF=90°，∴∠BAE=∠CBF，∵AB=BC，∴△ABE≌△BCF，∴BE=CF，AE=BF，∵△AOE≌△COK，∴AE=CK，OE=OK，∴FK=EF，∴△EFK是等腰直角三角形，∴OF⊥EK，OF=OE；（3）如图3中，点P在线段AO上，延长EO交CF于K，作PH⊥OF于H，∵|CF ﹣AE |=2，EF ，AE =CK ，∴FK =2，在Rt △EFK 中，tan ∠FEK =33，∴∠FEK =30°，∠EKF =60°，∴EK =2FK =4，OF =12EK =2，∵△OPF 是等腰三角形，观察图形可知，只有OF =FP =2，在Rt △PHF 中，PH =12PF =1，HF OH =2﹣，∴OP =.如图4中，点P 在线段OC 上，当PO =PF 时，∠POF =∠PFO =30°，∴∠BOP =90°，∴OP =33OE =233，综上所述：OP 的长为-233.【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等，综合性较强，正确添加辅助线是解题的关键.14．（2021·赣州市南康区教学研究室九年级一模）在Rt ABC △中，90BAC ∠=︒，AB AC =，动点D 在直线BC 上（不与点B ，C 重合），连接AD ，把AD 绕点A 逆时针旋转90°得到AE ，连接DE ，F ，G 分别是DE ，CD 的中点，连接FG ．（特例感知）（1）如图1，当点D 是BC 的中点时，FG 与BD 的数量关系是______．FG 与直线BC 的位置关系是______．（猜想论证）（2）当点D 在线段BC 上且不是BC 的中点时，（1）中的结论是否仍然成立？①请在图2中补全图形；②若成立，请给出证明；若不成立，请说明理由．（拓展应用）（3）若2AB AC ==，其他条件不变，连接BF 、CF ．当ACF 是等边三角形时，请直接写出BDF 的面积．【答案】（1）12FG BD =，FG BC ⊥；（2）①见解析；②结论仍然成立，理由见解析；（3）1132或1132+【分析】（1）由把AD 绕点A 逆时针旋转90°得到AE ，可得AD =AE ，∠DAE =90°，∠ADE =∠AED =45°由点D 为BC 中点，AB =AC ，∠BAC =90°，可得AD ⊥BC ，∠ABC =∠B CA =45°，AD =BD =CD ，可证DF ⊥AC ，AF =CF ，由FG 为△ADC 的中位线，FG ∥AD ，FG 1122AD BD ==，FG ⊥BC ；（2）①补全图形如图所示；②结论仍然成立，理由如下：如图2，CE ．连结EC ，由把AD 绕点A 逆时针旋转90°得到AE ，可得AD =AE ，∠DAE =90°，可证△BAD ≌△CAE （SAS ）∠ABD =∠ACE =45°，BD =CE ，由F ，G 分别是DE ，CD 的中点，可得FG 为△DEC 的中位线即可；（3）连接AF ，作AM BC ⊥，由2AB AC ==结合勾股定理AM 2+BM 2=AB 2，即2AM 2=2，可求AM 2=1，AM =1，当点D 在点B 的左侧时，15CAE BAD ∠=︒=∠，可得30ADM ∠=︒，DM ×tan30°=AM ，可求DM 3BDF 的面积为：1132-，当点D 在点C 的右侧时，105CAE BAD ∠=︒=∠，可得30ADM ∠=︒，可求BDF 的面积为：1132即可．【详解】解：（1）∵把AD 绕点A 逆时针旋转90°得到AE ，。

中考初三数学整合压轴题100题附答案一、中考压轴题1．用两种方法解答：已知m、n是关于x的方程x2+（p﹣2）x+1＝0两个实数根，求代数式（m2+mp+1）（n2+np+1）的值．【分析】本题主要是利用韦达定理来计算．已知m、n是关于x的方程x2+（p﹣2）x+1＝0两个实数根，有四个等式可供使用：m+n＝2﹣p①，mn＝1②，m2+（p﹣2）m+1＝0③，n2+（p﹣2）n+1＝0④．通过变形方法，合理地选择解题方法．【解答】解：∵m、n是x2+（p﹣2）x+1＝0的根，∴m+n＝2﹣p，mn＝1．方法一：m2+（p﹣2）m+1＝0，n2+（p﹣2）n+1＝0．即m2+pm+1＝2m，n2+pn+1＝2n．原式＝2m×2n＝4mn＝4．方法二：（m2+mp+1）（n2+np+1）＝（m2+mp）（n2+np）+m2+mp+n2+np+1＝m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1＝1+mp+np+p2+m2+n2+mp+np+1＝2+p2+m2+n2+2（m+n）p＝2+p2+m2+n2+2（2﹣p）p＝2+p2+m2+n2+4p﹣2p2＝2+（m+n）2﹣2mn+4p﹣2p2+p2＝2+（2﹣p）2﹣2+4p﹣2p2+p2＝4﹣4p+p2+4p﹣p2＝4．【点评】本题主要是通过根与系数的关系来求值．注意把所求的代数式转化成m+n＝2﹣p，mn＝1的形式，正确对所求式子进行变形是解题的关键．2．已知：y关于x的函数y＝（k﹣1）x2﹣2kx+k+2的图象与x轴有交点．（1）求k的取值范围；（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足（k﹣1）x12+2kx2+k+2＝4x1x2．①求k的值；②当k≤x≤k+2时，请结合函数图象确定y的最大值和最小值．【分析】（1）分两种情况讨论，当k＝1时，可求出函数为一次函数，必与x轴有一交点；当k≠1时，函数为二次函数，若与x轴有交点，则△≥0．（2）①根据（k﹣1）x12+2kx2+k+2＝4x1x2及根与系数的关系，建立关于k的方程，求出k 的值；②充分利用图象，直接得出y的最大值和最小值．【解答】解：（1）当k＝1时，函数为一次函数y＝﹣2x+3，其图象与x轴有一个交点．当k≠1时，函数为二次函数，其图象与x轴有一个或两个交点，令y＝0得（k﹣1）x2﹣2kx+k+2＝0．△＝（﹣2k）2﹣4（k﹣1）（k+2）≥0，解得k≤2．即k≤2且k≠1．综上所述，k的取值范围是k≤2．（2）①∵x1≠x2，由（1）知k＜2且k≠1，函数图象与x轴两个交点，∴k＜2，且k≠1．由题意得（k﹣1）x12+（k+2）＝2kx1①，将①代入（k﹣1）x12+2kx2+k+2＝4x1x2中得：2k（x1+x2）＝4x1x2．又∵x1+x2＝，x1x2＝，∴2k•＝4•．解得：k1＝﹣1，k2＝2（不合题意，舍去）．∴所求k值为﹣1．②如图，∵k1＝﹣1，y＝﹣2x2+2x+1＝﹣2（x﹣）2+．且﹣1≤x≤1．由图象知：当x＝﹣1时，y最小＝﹣3；当x＝时，y最大＝．∴y的最大值为，最小值为﹣3．【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值，充分利用图象是解题的关键．3．如图①，有四张编号为1、2、3、4的卡片，卡片的背面完全相同．现将它们搅匀并正面朝下放置在桌面上．（1）从中随机抽取一张，抽到的卡片是眼睛的概率是多少？（2）从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处，然后再随机抽取一张贴在大头娃娃的右眼处，用树状图或列表法求贴法正确的概率．【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【解答】解：（1）所求概率为；（2）方法①（树状图法）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3）∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为，方法②（列表法）1 2 3 4第一次抽取第二次抽取1（2，1）（3，1）（4，1）2（1，2）（3，2）（4，2）3（1，3）（2，3）（4，3）4（1，4）（2，4）（3，4）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3），∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为．【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝．4．如图，反比例函数的图象经过点A（4，b），过点A作AB⊥x轴于点B，△AOB 的面积为2．（1）求k和b的值；（2）若一次函数y＝ax﹣3的图象经过点A，求这个一次函数的解析式．【分析】（1）由△AOB的面积为2，根据反比例函数的比例系数k的几何意义，可知k的值，得出反比例函数的解析式，然后把x＝4代入，即可求出b的值；（2）把点A的坐标代入y＝ax﹣3，即可求出这个一次函数的解析式．【解答】解：（1）∵反比例函数的图象经过点A，AB⊥x轴于点B，△AOB的面积为2，A（4，b），∴OB×AB＝2，×4×b＝2，∴AB＝b＝1，∴A（4，1），∴k＝xy＝4，∴反比例函数的解析式为y＝，即k＝4，b＝1．（2）∵A（4，1）在一次函数y＝ax﹣3的图象上，∴1＝4a﹣3，∴a＝1．∴这个一次函数的解析式为y＝x﹣3．【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义．这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．5．我国年人均用纸量约为28公斤，每个初中毕业生离校时大约有10公斤废纸；用1吨废纸造出的再生好纸，所能节约的造纸木材相当于18棵大树，而平均每亩森林只有50至80棵这样的大树．（1）若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸，那么最少可使多少亩森林免遭砍伐？（2）我市从2000年初开始实施天然林保护工程，大力倡导废纸回收再生，如今成效显著，森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩．假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变，请你按全市总人口约为1000万计算：在从2005年初到2006年初这一年度内，我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的百分之几？（精确到1%）【分析】（1）因为每个初中毕业生离校时大约有10公斤废纸，用1吨废纸造出的再生好纸，所能节约的造纸木材相当于18棵大树，而平均每亩森林只有50至80棵这样的大树，所以有40000×10÷1000×18÷80，计算出即可求出答案；（2）森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩，可先求出森林面积年均增长率，进而求出2005到2006年新增加的森林面积，而因回收废纸所能保护的最大森林面积＝1000×10000×28×20%÷1000×18÷50，然后进行简单的计算即可求出答案．【解答】解：（1）4×104×10÷1000×18÷80＝90（亩）．答：若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸，那么最少可使90亩森林免遭砍伐．（2）设我市森林面积年平均增长率为x，依题意列方程得50（1+x）2＝60.5，解得x1＝10%，x2＝﹣2.1（不合题意，舍去），1000×104×28×20%÷1000×18÷50＝20160，20160÷（605000×10%）≈33%．答：在从2005年初到2006年初这一年度内，我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的33%．【点评】本题以保护环境为主题，考查了增长率问题，阅读理解题意，并从题目中提炼出平均增长率的数学模型并解答的能力；解答时需仔细分析题意，利用方程即可解决问题．6．广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．（1）求平均每次下调的百分率．（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？【分析】（1）根据题意设平均每次下调的百分率为x，列出一元二次方程，解方程即可得出答案；（2）分别计算两种方案的优惠价格，比较后发现方案①更优惠．【解答】解：（1）设平均每次下调的百分率为x，则6000（1﹣x）2＝4860，解得：x1＝0.1＝10%，x2＝1.9（舍去），故平均每次下调的百分率为10%；（2）方案①购房优惠：4860×100×（1﹣0.98）＝9720（元）；方案②可优惠：80×100＝8000（元）．故选择方案①更优惠．【点评】本题主要考查一元二次方程的实际应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解，属于中档题．7．如图，一次函数y＝﹣x﹣2的图象分别交x轴、y轴于A、B两点，P为AB的中点，PC⊥x轴于点C，延长PC交反比例函数y＝（x＜0）的图象于点Q，且tan∠AOQ＝．（1）求k的值；（2）连接OP、AQ，求证：四边形APOQ是菱形．【分析】（1）由一次函数解析式确定A点坐标，进而确定C，Q的坐标，将Q的坐标代入反比例函数关系式可求出k的值．（2）由（1）可分别确定QC＝CP，AC＝OC，且QP垂直平分AO，故可证明四边形APOQ是菱形．【解答】（1）解：∵y＝﹣x﹣2令y＝0，得x＝﹣4，即A（﹣4，0）由P为AB的中点，PC⊥x轴可知C点坐标为（﹣2，0）又∵tan∠AOQ＝可知QC＝1∴Q点坐标为（﹣2，1）将Q点坐标代入反比例函数得：1＝，∴可得k＝﹣2；（2）证明：由（1）可知QC＝PC＝1，AC＝CO＝2，且A0⊥PQ∴四边形APOQ是菱形．【点评】本题考查了待定系数法求函数解析式，又结合了几何图形进行考查，属于综合性比较强的题目，有一定难度．8．某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售；B类杨梅深加工后再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图；B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s＝12+3t，平均销售价格为9万元/吨．（1）直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式；（2）第一次，该公司收购了20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元（毛利润＝销售总收入﹣经营总成本）．①求w关于x的函数关系式；②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？（3）第二次，该公司准备投入132万元资金，请设计一种经营方案，使公司获得最大毛利润，并求出最大毛利润．【分析】（1）这是一个分段函数，分别求出其函数关系式；（2）①当2≤x＜8时及当x≥8时，分别求出w关于x的表达式．注意w＝销售总收入﹣经营总成本＝w A+w B﹣3×20；②若该公司获得了30万元毛利润，将30万元代入①中求得的表达式，求出A类杨梅的数量；（3）本问是方案设计问题，总投入为132万元，这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本．共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，分别求出当2≤x＜8时及当x≥8时w关于x的表达式，并分别求出其最大值．【解答】解：（1）①当2≤x＜8时，如图，设直线AB解析式为：y＝kx+b，将A（2，12）、B（8，6）代入得：，解得，∴y＝﹣x+14；②当x≥8时，y＝6．所以A类杨梅平均销售价格y与销售量x之间的函数关系式为：y＝；（2）设销售A类杨梅x吨，则销售B类杨梅（20﹣x）吨．①当2≤x＜8时，w A＝x（﹣x+14）﹣x＝﹣x2+13x；w B＝9（20﹣x）﹣[12+3（20﹣x）]＝108﹣6x∴w＝w A+w B﹣3×20＝（﹣x2+13x）+（108﹣6x）﹣60＝﹣x2+7x+48；当x≥8时，w A＝6x﹣x＝5x；w B＝9（20﹣x）﹣[12+3（20﹣x）]＝108﹣6x∴w＝w A+w B﹣3×20＝（5x）+（108﹣6x）﹣60＝﹣x+48．∴w关于x的函数关系式为：w＝．②当2≤x＜8时，﹣x2+7x+48＝30，解得x1＝9，x2＝﹣2，均不合题意；当x≥8时，﹣x+48＝30，解得x＝18．∴当毛利润达到30万元时，直接销售的A类杨梅有18吨．（3）设该公司用132万元共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，则购买费用为3m万元，A类杨梅加工成本为x万元，B类杨梅加工成本为[12+3（m﹣x）]万元，∴3m+x+[12+3（m﹣x）]＝132，化简得：x＝3m﹣60．①当2≤x＜8时，w A＝x（﹣x+14）﹣x＝﹣x2+13x；w B＝9（m﹣x）﹣[12+3（m﹣x）]＝6m﹣6x﹣12∴w＝w A+w B﹣3×m＝（﹣x2+13x）+（6m﹣6x﹣12）﹣3m＝﹣x2+7x+3m﹣12．将3m＝x+60代入得：w＝﹣x2+8x+48＝﹣（x﹣4）2+64∴当x＝4时，有最大毛利润64万元，此时m＝，m﹣x＝；②当x≥8时，w A＝6x﹣x＝5x；w B＝9（m﹣x）﹣[12+3（m﹣x）]＝6m﹣6x﹣12∴w＝w A+w B﹣3×m＝（5x）+（6m﹣6x﹣12）﹣3m＝﹣x+3m﹣12．将3m＝x+60代入得：w＝48∴当x＞8时，有最大毛利润48万元．综上所述，购买杨梅共吨，其中A类杨梅4吨，B类吨，公司能够获得最大毛利润，最大毛利润为64万元．【点评】本题是二次函数、一次函数的综合应用题，难度较大．解题关键是理清售价、成本、利润三者之间的关系．涉及到分段函数时，注意要分类讨论．9．经统计分析，某市跨河大桥上的车流速度v（千米/小时）是车流密度x（辆/千米）的函数，当桥上的车流密度达到220辆/千米时，造成堵塞，此时车流速度为0千米/小时；当车流密度不超过20辆/千米时，车流速度为80千米/小时，研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．（1）求大桥上车流密度为100辆/千米时的车流速度；（2）在交通高峰时段，为使大桥上的车流速度大于40千米/小时且小于60千米/小时，应控制大桥上的车流密度在什么范围内？（3）车流量（辆/小时）是单位时间内通过桥上某观测点的车辆数，即：车流量＝车流速度×车流密度．求大桥上车流量y的最大值．【分析】（1）当20≤x≤220时，设车流速度v与车流密度x的函数关系式为v＝kx+b，根据题意的数量关系建立方程组求出其解即可；（2）由（1）的解析式建立不等式组求出其解即可；（3）设车流量y与x之间的关系式为y＝vx，当x＜20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论．【解答】解：（1）设车流速度v与车流密度x的函数关系式为v＝kx+b，由题意，得，解得：，∴当20≤x≤220时，v＝﹣x+88，当x＝100时，v＝﹣×100+88＝48（千米/小时）；（2）由题意，得，解得：70＜x＜120．∴应控制大桥上的车流密度在70＜x＜120范围内；（3）设车流量y与x之间的关系式为y＝vx，当0≤x≤20时y＝80x，∴k＝80＞0，∴y随x的增大而增大，∴x＝20时，y最大＝1600；当20≤x≤220时y＝（﹣x+88）x＝﹣（x﹣110）2+4840，∴当x＝110时，y最大＝4840．∵4840＞1600，∴当车流密度是110辆/千米，车流量y取得最大值是每小时4840辆．【点评】本题考查了车流量＝车流速度×车流密度的运用，一次函数的解析式的运用，一元一次不等式组的运用，二次函数的性质的运用，解答时求出函数的解析式是关键．10．⊙O1与⊙O2相交于A、B两点，如图（1），连接O2O1并延长交⊙O1于P点，连接P A、PB并分别延长交⊙O2于C、D两点，连接CO2并延长交⊙O2于E点．已知⊙O2的半径为R，设∠CAD＝α．（1）求CD的长（用含R、α的式子表示）；（2）试判断CD与PO1的位置关系，并说明理由；（3）设点P’为⊙O1上（⊙O2外）的动点，连接P’A、P’B并分别延长交⊙O2于C’、D’，请你探究∠C’AD’是否等于α？C’D’与P’O1的位置关系如何？并说明理由．（注：图（2）与图（3）中⊙O1和⊙O2的大小及位置关系与图（1）完全相同，若你感到继续在图（1）中探究问题（3），图形太复杂，不便于观察，可以选择图（2）或图（3）中的一图说明理由）．【分析】（1）作⊙O2的直径CE，连接DE．根据圆周角定理的推论，得∠E＝∠CAD＝α，再利用解直角三角形的知识求解；（2）连接AB，延长PO1与⊙O1相交于点E，连接AE．根据圆内接四边形的性质，得∠ABP′＝∠C′，根据圆周角定理的推论，得∠ABP′＝∠E，∠EAP′＝90°，从而证明∠AP′E+∠C′＝90°，则CD与PO1的位置关系是互相垂直；（3）根据同弧所对的圆周角相等，则说明∠C’AD’等于α；根据（2）中的证明过程，则可以证明C’D’与P’O1的位置关系是互相垂直．【解答】解：（1）连接DE．根据圆周角定理的推论，得∠E＝∠CAD＝α．∵CE是直径，∴∠CDE＝90°．∴CD＝CE•sin E＝2R sinα；（2）CD与PO1的位置关系是互相垂直．理由如下：连接AB，延长PO1与⊙O1相交于点E，连接AE．∵四边形BAC′D′是圆内接四边形，∴∠ABP′＝∠C′．∵P′E是直径，∴∠EAP′＝90°，∴∠AP′E+∠E＝90°．又∠ABP′＝∠E，∴∠AP′E+∠C′＝90°，即CD与PO1的位置关系是互相垂直；（3）根据同弧所对的圆周角相等，则说明∠C’AD’等于α；根据（2）中的证明过程，则可以证明C’D’与P’O1的位置关系是互相垂直．【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质．注意：连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线．11．如图，已知直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，连接PC 并延长PC交y轴于点D（0，3）．（1）求证：△POD≌△ABO；（2）若直线l：y＝kx+b经过圆心P和D，求直线l的解析式．【分析】（1）首先连接PB，由直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，可求得∠APB＝∠DPO＝60°，∠ABO＝∠POD＝90°，即可得△P AB是等边三角形，可得AB＝OP，然后由ASA，即可判定：△POD≌△ABO；（2）易求得∠PDO＝30°，由OP＝OD•tan30°，即可求得点P的坐标，然后利用待定系数法，即可求得直线l的解析式．【解答】（1）证明：连接PB，∵直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，∴∠APB＝∠DPO＝×180°＝60°，∠ABO＝∠POD＝90°，∵P A＝PB，∴△P AB是等边三角形，∴AB＝P A，∠BAO＝60°，∴AB＝OP，∠BAO＝∠OPD，在△POD和△ABO中，∴△POD≌△ABO（ASA）；（2）解：由（1）得△POD≌△ABO，∴∠PDO＝∠AOB，∵∠AOB＝∠APB＝×60°＝30°，∴∠PDO＝30°，∴OP＝OD•tan30°＝3×＝，∴点P的坐标为：（﹣，0）∴，解得：，∴直线l的解析式为：y＝x+3．【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式．此题综合性较强，难度适中，注意准确作出辅助线，注意数形结合思想的应用．12．如图，△ABC内接于⊙O，AB＝6，AC＝4，D是AB边上一点，P是优弧BAC的中点，连接P A、PB、PC、PD．（1）当BD的长度为多少时，△P AD是以AD为底边的等腰三角形？并证明；（2）在（1）的条件下，若cos∠PCB＝，求P A的长．【分析】（1）根据等弧对等弦以及全等三角形的判定和性质进行求解；（2）过点P作PE⊥AD于E．根据锐角三角函数的知识和垂径定理进行求解．【解答】解：（1）当BD＝AC＝4时，△P AD是以AD为底边的等腰三角形．∵P是优弧BAC的中点，∴＝．∴PB＝PC．又∵∠PBD＝∠PCA（圆周角定理），∴当BD＝AC＝4，△PBD≌△PCA．∴P A＝PD，即△P AD是以AD为底边的等腰三角形．（2）过点P作PE⊥AD于E，由（1）可知，当BD＝4时，PD＝P A，AD＝AB﹣BD＝6﹣4＝2，则AE＝AD＝1．∵∠PCB＝∠P AD（在同圆或等圆中，同弧所对的圆周角相等），∴cos∠P AD＝cos∠PCB＝，∴P A＝．【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理．13．已知⊙O1与⊙O2相交于A、B两点，点O1在⊙O2上，C为⊙O2上一点（不与A，B，O1重合），直线CB与⊙O1交于另一点D．（1）如图（1），若AD是⊙O1的直径，AC是⊙O2的直径，求证：AC＝CD；（2）如图（2），若C是⊙O1外一点，求证：O1C丄AD；（3）如图（3），若C是⊙O1内的一点，判断（2）中的结论是否成立？【分析】（1）连接C01，利用直径所对圆周角等于90度，以及垂直平分线的性质得出即可；（2）根据已知得出四边形AEDB内接于⊙O1，得出∠ABC＝∠E，再利用＝，得出∠E＝∠AO1C，进而得出CO1∥ED即可求出；（3）根据已知得出∠B＝∠EO1C，又∠E＝∠B，即可得出∠EO1C＝∠E，得出CO1∥ED，即可求出．【解答】（1）证明：连接C01∵AC为⊙O2直径∴∠AO1C＝90°即CO1⊥AD，∵AO1＝DO1∴DC＝AC（垂直平分线的性质）；（2）证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵四边形AEDB内接于⊙O1，∴∠E+∠ABD＝180°，∵∠ABC+∠ABD＝180°，∴∠ABC＝∠E，又∵＝，∴∠ABC＝∠AO1C，∴∠E＝∠AO1C，∴CO1∥ED，又AE为⊙O1的直径，∴ED⊥AD，∴O1C⊥AD，（3）（2）中的结论仍然成立．证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵∠B+∠AO1C＝180°，∠EO1C+∠AO1C═180°，∴∠B＝∠EO1C，又∵∠E＝∠B，∴∠EO1C＝∠E，∴CO1∥ED，又ED⊥AD，∴CO1⊥AD．【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质，根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键．14．如图，在△ABC中，∠BAC＝30°，以AB为直径的⊙O经过点C．过点C作⊙O的切线交AB的延长线于点P．点D为圆上一点，且＝，弦AD的延长线交切线PC于点E，连接BC．（1）判断OB和BP的数量关系，并说明理由；（2）若⊙O的半径为2，求AE的长．【分析】（1）首先连接OC，由PC切⊙O于点C，可得∠OCP＝90°，又由∠BAC＝30°，即可求得∠COP＝60°，∠P＝30°，然后根据直角三角形中30°角所对的直角边等于斜边的一半，证得OB＝BP；（2）由（1）可得OB＝OP，即可求得AP的长，又由＝，即可得∠CAD＝∠BAC＝30°，继而求得∠E＝90°，继而在Rt△AEP中求得答案．【解答】解：（1）OB＝BP．理由：连接OC，∵PC切⊙O于点C，∴∠OCP＝90°，∵OA＝OC，∠OAC＝30°，∴∠OAC＝∠OCA＝30°，∴∠COP＝60°，∴∠P＝30°，在Rt△OCP中，OC＝OP＝OB＝BP；（2）由（1）得OB＝OP，∵⊙O的半径是2，∴AP＝3OB＝3×2＝6，∵＝，∴∠CAD＝∠BAC＝30°，∴∠BAD＝60°，∵∠P＝30°，∴∠E＝90°，在Rt△AEP中，AE＝AP＝×6＝3．【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理．此题难度适中，注意掌握数形结合思想的应用，注意掌握辅助线的作法．15．如图，菱形、矩形与正方形的形状有差异，我们将菱形、矩形与正方形的接近程度称为“接近度”．在研究“接近度”时，应保证相似图形的“接近度”相等．（1）设菱形相邻两个内角的度数分别为m°和n°，将菱形的“接近度”定义为|m﹣n|，于是|m﹣n|越小，菱形越接近于正方形．①若菱形的一个内角为70°，则该菱形的“接近度”等于40；②当菱形的“接近度”等于0时，菱形是正方形．（2）设矩形相邻两条边长分别是a和b（a≤b），将矩形的“接近度”定义为|a﹣b|，于是|a﹣b|越小，矩形越接近于正方形．你认为这种说法是否合理？若不合理，给出矩形的“接近度”一个合理定义．【分析】（1）根据相似图形的定义知，相似图形的形状相同，但大小不一定相同，相似图形的“接近度”相等．所以若菱形的一个内角为70°，则该菱形的“接近度”等于|m﹣n|；当菱形的“接近度”等于0时，菱形是正方形；（2）不合理，举例进行说明．【解答】解：（1）①∵内角为70°，∴与它相邻内角的度数为110°．∴菱形的“接近度”＝|m﹣n|＝|110﹣70|＝40．②当菱形的“接近度”等于0时，菱形是正方形．（2）不合理．例如，对两个相似而不全等的矩形来说，它们接近正方形的程度是相同的，但|a﹣b|却不相等．合理定义方法不唯一．如定义为，越接近1，矩形越接近于正方形；越大，矩形与正方形的形状差异越大；当时，矩形就变成了正方形，即只有矩形的越接近1，矩形才越接近正方形．【点评】正确理解“接近度”的意思，矩形的“接近度”|a﹣b|越小，矩形越接近于正方形．这是解决问题的关键．16．如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）①画出△ABC关于x轴对称的△A1B1C1；②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2；③△A1B1C1与△A2B2C2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标．【分析】（1）将三角形的各顶点，向x轴作垂线并延长相同长度得到三点的对应点，顺次连接；（2）将三角形的各顶点，绕原点O按逆时针旋转90°得到三点的对应点．顺次连接各对应点得△A2B2C2；（3）从图中可发现成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的线段，做它的垂直平分线；（4）成中心对称图形，画出两条对应点的连线，交点就是对称中心．【解答】解：如下图所示：（3）成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的线段，作它的垂直平分线，或连接A1C1，A2C2的中点的连线为对称轴．（4）成中心对称，对称中心为线段BB2的中点P，坐标是（，）．【点评】本题综合考查了图形的变换，在图形的变换中，关键是找到图形的对应点．17．图（1）是一个10×10格点正方形组成的网格．△ABC是格点三角形（顶点在网格交点处），请你完成下面的两个问题：（1）在图（1）中画出与△ABC相似的格点△A1B1C1和△A2B2C2，且△A1B1C1与△ABC的相似比是2，△A2B2C2与△ABC的相似比是；（2）在图（2）中用与△ABC，△A1B1C1，△A2B2C2全等的格点三角形（每个三角形至少使用一次），拼出一个你熟悉的图案，并为你设计的图案配一句贴切的解说词．【分析】（1）△A1B1C1与△ABC的相似比是2，则让△ABC的各边都扩大2倍就可．△A2B2C2与△ABC的相似比是；△ABC的直角边是2，所以△A2B2C2与的直角边是即一个对角线的长度．斜边为2．依此画图即可；（2）拼图有审美意义即可，答案不唯一．【解答】解：【点评】本题主要考查了相似图形的画法，做这类题时根据的是相似图形的性质，即相似比相等．对应角相等．18．如图，矩形ABCD的边AD、AB分别与⊙O相切于点E、F，（1）求的长；（2）若，直线MN分别交射线DA、DC于点M、N，∠DMN＝60°，将直线MN沿射线DA方向平移，设点D到直线的距离为d，当时1≤d≤4，请判断直线MN与⊙O的位置关系，并说明理由．【分析】（1）连接OE、OF，利用相切证明四边形AFOE是正方形，再根据弧长公式求弧长；（2）先求出直线M1N1与圆相切时d的值，结合1≤d≤4，划分d的范围，分类讨论．【解答】解：（1）连接OE、OF，∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F，∴∠A＝90°，∠OEA＝∠OF A＝90°∴四边形AFOE是正方形∴∠EOF＝90°，OE＝AE＝∴的长＝＝π．（2）如图，将直线MN沿射线DA方向平移，当其与⊙O相切时，记为M1N1，切点为R，交AD于M1，交BC于N1，连接OM1、OR，∵M1N1∥MN∴∠DM1N1＝∠DMN＝60°∴∠EM1N1＝120°∵MA、M1N1切⊙O于点E、R∴∠EM1O＝∠EM1N1＝60°在Rt△EM1O中，EM1＝＝＝1∴DM1＝AD﹣AE﹣EM1＝+5﹣﹣1＝4．过点D作DK⊥M1N1于K在Rt△DM1K中DK＝DM1×sin∠DM1K＝4×sin∠60°＝2即d＝2，∴当d＝2时，直线MN与⊙O相切，当1≤d＜2时，直线MN与⊙O相离，当直线MN平移到过圆心O时，记为M2N2，点D到M2N2的距离d＝DK+OR＝2+＝3＞4，∴当2＜d≤4时，MN直线与⊙O相交．【点评】本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定．19．如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连接ED、BE．（1）试判断DE与BD是否相等，并说明理由；（2）如果BC＝6，AB＝5，求BE的长．【分析】（1）可通过连接AD，AD就是等腰三角形ABC底边上的高，根据等腰三角形三线合一的特点，可得出∠CAD＝∠BAD，根据圆周角定理即可得出∠DEB＝∠DBE，便可证得DE＝DB．（2）本题中由于BE⊥AC，那么BE就是三角形ABC中AC边上的高，可用面积的不同表示方法得出AC•BE＝CB•AD．进而求出BE的长．【解答】解：（1）DE＝BD证明：连接AD，则AD⊥BC，在等腰三角形ABC中，AD⊥BC，∴∠CAD＝∠BAD（等腰三角形三线合一），∴＝，∴DE＝BD；（2）∵AB＝5，BD＝BC＝3，∴AD＝4，∵AB＝AC＝5，∴S△ABC＝•AC•BE＝•CB•AD，∴BE＝4.8．【点评】本题主要考查了等腰三角形的性质，圆周角定理等知识点的运用，用等腰三角形三线合一的特点得出圆周角相等是解题的关键．20．下框中是小明对一道题目的解答以及老师的批改．题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留3m的空地，其他三侧内墙各保留1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是288m2？解：设矩形蔬菜种植区域的宽为xm，则长为2xm，根据题意，得x•2x＝288．解这个方程，得x1＝﹣12（不合题意，舍去），x2＝12所以温室的长为2×12+3+1＝28（m），宽为12+1+1＝14（m）答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288m2．我的结果也正确！小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个？．结果为何正确呢？（1）请指出小明解答中存在的问题，并补充缺少的过程：变化一下会怎样…（2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB＝2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由．【分析】（1）根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由，所以应设矩形蔬菜种植区域的宽为xm，则长为2xm，然后由题意得，矩形蔬菜种植区域的长与宽之比为2：1，再利用小明的解法求解即可；（2）由使矩形A′B′C′D′∽矩形ABCD，利用相似多边形的性质，可得，即，然后利用比例的性质，即可求得答案．【解答】解：（1）小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由．在“设矩形蔬菜种植区域的宽为xm，则长为2xm．”前补充以下过程：设温室的宽为xm，则长为2xm．则矩形蔬菜种植区域的宽为（x﹣1﹣1）m，长为（2x﹣3﹣1）m．∵，∴矩形蔬菜种植区域的长与宽之比为2：1；（2）要使矩形A′B′C′D′∽矩形ABCD，就要，即，即，即2AB﹣2（b+d）＝2AB﹣（a+c），∴a+c＝2（b+d），即．【点评】此题考查了相似多边形的性质．此题属于阅读性题目，注意理解题意，读懂题目是解此题的关键．21．二次函数y＝ax2+bx+c图象的一部分如图所示，则a的取值范围是﹣1＜a＜0．。

1、如图，在梯形ABCD 中，AB ∥CD ，∠BCD=90°,且AB=1，BC=2，tan ∠ADC=2.(1) 求证：DC=BC;(2) E 是梯形内一点，F 是梯形外一点，且∠E DC=∠F BC ，DE=BF ，试判断△E CF 的形状，并证明你的结论；(3) 在（2）的条件下，当BE ：CE=1：2，∠BEC=135°时，求sin ∠BFE 的值.2、已知：如图，在□ABCD 中，E 、F 分别为边AB 、CD 的中点，BD 是对角线，AG ∥DB 交CB 的延长线于G ．（1）求证：△ADE ≌△CBF ；（2）若四边形 BEDF 是菱形，则四边形AGBD 是什么特殊四边形？并证明你的结论．3、如图13－1，一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图13－2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 满足的数量关系，并证明你的猜想；（2）若三角尺GEF 旋转到如图13－3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．E B FCDA 图13－2图13－3图13－1 A ( E )4、如图，已知⊙O的直径AB垂直于弦CD于E，连结AD、BD、OC、OD，且OD＝5。

（1）若sin∠BAD=35，求CD的长；（2）若∠ADO：∠EDO＝4：1，求扇形OAC（阴影部分）的面积（结果保留π）。

5、如图，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G.（1）求证：点F是BD中点；（2）求证：CG是⊙O的切线；（3）若FB=FE=2，求⊙O的半径．6、如图，已知O为原点，点A的坐标为（4，3），⊙A的半径为2．过A作直线l平行于x轴，点P在直线l上运动．（１）当点P在⊙O上时，请你直接写出它的坐标；（２）设点P的横坐标为12，试判断直线OP与⊙A的位置关系，并说明理由.7、如图，延长⊙O 的半径OA 到B ，使OA=AB ，DE 是圆的一条切线，E 是切点，过点B 作DE 的垂线，垂足为点C .求证：∠ACB=31∠OAC .8、如图１，一架长4米的梯子AB 斜靠在与地面OM 垂直的墙壁ON 上，梯子与地面的倾斜角α为60．⑴求AO 与BO 的长；⑵若梯子顶端A 沿NO 下滑，同时底端B 沿OM 向右滑行.①如图2，设A 点下滑到C 点，B 点向右滑行到D 点，并且AC:BD=2:3，试计算梯子顶端A 沿NO 下滑多少米；②如图３，当A 点下滑到A ’点，B 点向右滑行到B ’点时，梯子AB 的中点P 也随之运动到P ’点．若∠POP ’＝ 15，试求AA ’的长．[解析]⑴AOB Rt 中,∠O =90 ,∠α=60∴,∠OAB= 30，又ＡＢ＝4米，C A BD O E9.（重庆，10分）如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒．(1) 求直线AB 的解析式；(2) 当t 为何值时，△APQ 与△AOB 相似？(3) 当t 为何值时，△APQ 的面积为524个平方单位？10．（南充，10分）如图2－5－7，矩形ABCD 中，AB ＝8，BC ＝6，对角线AC 上有一个动点P （不包括点A 和点C ）．设AP ＝x ，四边形PBCD 的面积为y ．（1）写出y 与x 的函数关系，并确定自变量x 的范围．（2）有人提出一个判断：“关于动点P ，⊿PBC 面积与⊿PAD 面积之和为常数”．请你说明此判断是否正确，并说明理由．。

中考考点必杀500题专练14（几何压轴大题）（30道）1．（2022·浙江杭州·一模）如图，已知扇形AOB 的半径8OA =，90AOB ∠=︒，点C ，D 分别在半径OA ，OB 上（点C 不与点A 重合），连结CD ．(1)当4sin 5ODC ∠=，BD CD =时，求OC 的长． (2)点P 是弧AB 上一点，PC PD =．①当点D 与点B 重合，点P 为弧AB 的中点时，求证：PC PD ⊥．②当4OC =，90PDO ∠=︒时，求PCD OCD S S △△的值． 【答案】(1)3；(2)①证明见解析；②2；【解析】(1)解： Rt △ODC中，4sin 5ODC ∠=OC =4a ，CD =5a ，则OD3a =，sin ∠OCD =OD CD =35， 设OD =x ，则BD =CD =（8-x ），则385x x =-，解得：x =3， ∴OC 的长为3；(2)解：①如图，连接OP ，AP ，∵P 是弧AB 的中点，∴∠POB =12∠AOB =45°，PB =PA ，△OPB 中，OP =OB ，则∠OPB =∠OBP =12（180°-∠POB ）=67.5°，△OPA 中，OP =OA ，则∠OAP =∠OPA =12（180°-∠POA ）=67.5°，∴∠APB =∠OPA +∠OPB =135°，∵PB =PB =BA ，∴∠PAC =∠PCA =67.5°，△PAC 中，∠APC =180°-∠PAC -∠PCA =45°，∴∠CPB =∠APB -∠APC =90°，∴PC ⊥PD ；②如图，连接OP ，过C 作CE ⊥PD 于E ，∵∠COD =∠ODP =∠DEC =90°，∴四边形CODE 是矩形，∴DE =OC =4，CE =OD ，设PC =PD =x ，则PE =（x -4），Rt △PEC 中，222CE CP PE =-，Rt △POD 中，222OD OP PD =-，∴22CP PE -=22OP PD -，()222464x x x --=-，解得：4x =±，∵x ＞0，∴4x =-， ∵△PCD 面积=12PD CE ⋅，△OCD 面积=12OD OC ⋅，CE =OD ， ∴PCD OCD S S △△=PD OC=2； 【点睛】本题考查了解直角三角形，圆心角、弧、弦之间的关系，等腰三角形的判定和性质，矩形的判定和性质，勾股定理等知识；此题综合性强，正确作出辅助线是解题关键． 2．（2022·河北保定外国语学校一模）如图，点P 在射线AB 的上方，060PAM ︒<∠<︒、4PA =，点M 是射线AB 上的动点（点M 不与点A 重合），现将点P 绕点A 按顺时针方向旋转60︒到点Q ，将点M 绕点P 按逆时针方向旋转60︒到点N ，连接,,AQ PM PN ，作直线QN ．(1)求证：AM QN =；(2)直线QN 与以点P 为圆心，PN 的长为半径的圆是否存在相切的情况？若存在，请求出此时APN ∠和PAM ∠的关系，若不存在，请说明理由；(3)若50PAB ∠=︒，当以点P 为圆心，PN 长为半径的圆经过点Q 时，直接写出劣弧NQ 与两条半径所围成的扇形的面积．【答案】(1)见解析(2)存在，150APN PAM ∠+∠=︒ (3)329π (1)证明：如图1，连接PQ ，由点P 绕点A 按顺时针方向旋转60︒到点Q ，可得，,60AP AQ PAQ =∠=︒，∴APQ 为等边三角形，∴,60PA PQ APQ =∠=︒，由点M 绕点P 按逆时针方向旋转60︒到点N ，可得，,60PM PN MPN =∠=︒，∴APM QPN ∠=∠，则()APM QPN SAS ≌，∴AM QN =．(2)存在，如图2，由（1）中的证明可知，APM QPN ≌，∴AMP QNP ∠=∠，∵直线QN 与以点P 为圆心，PN 的长为半径的圆相切，∴90AMP QNP ∠=∠=︒，∵90,60APM PAM MPN ∠=︒-∠∠=︒，∴60APN APM MPN APM ∠=∠+∠=∠+︒．∴()6090150APN PAM APM APM ∠+∠=∠+︒+︒-∠=︒ (3)329π， 如图3，由（1）知，APQ 是等边三角形，∴,60PA PQ APQ =∠=︒，∵以点P 为圆心，PN 的长为半径的圆经过点Q ，∴PN PQ PA ==，∵PM PN =，∴PA PM =，∵50PAB ∠=︒，∴80APM ∠=︒，∴20MPQ APM APQ ∠=∠-∠=︒，∵60MPN ∠=︒，∴80QPN ∠=︒，∴劣弧NQ 与两条半径所围成的扇形的面积是扇形QPN 的面积，而此扇形的圆心角80QPN ∠=︒，半径为4PN PM PQ ===，∴劣弧NQ 与两条半径所围成的扇形的面积2804323609ππ⨯==．【点睛】此题是圆的综合题，主要考查了旋转的性质，等边三角形的判定和性质，全等三角形的判定和性质，切线的性质，扇形的面积公式，解(1) 的关键是得出PA = PQ ，解(2)的关键是得出PN ⊥QN ，解(3)的关键是得出PN = PQ = PA ，解本题的难点是画出符合题意的图形． 3．（2022·河北保定外国语学校一模）在ABC 中，10AC BC ==，4sin 5A =，点D 是线段AB 上一点，且不与点A 、点B 重合．(1)当点D 为AB 中点时，AD 的长为__________；(2)如图1，过点D 作DM AC ⊥于点M ，DN BC ⊥于点N ．DM DN +的值是否为定值．如果是请求出定值；如果不是，请说明理由；(3)将B Ð沿着过点D 的直线折叠，使点B 落作AC 边的点P 处（不与点A 、C 重合），折痕交BC 边于点E ；①如图2，当点D 是AB 的中点时，求AP 的长度；②如图3，设AD a =，若存在两次不同的折痕，使点B 落在AC 边上两个不同的位置，直接写出a 的取值范围．【答案】(1)6(2)是定值，485 (3)①365；②2063a << 【解析】(1)解：∵点D 为AB 中点又10AC BC ==∴CD ⊥AB ∵4sin 5A = ∴CD =41085⨯=∴6AD ===故答案为：6；(2)解：DM DN +的值是定值，连接CD ，过点C 作CH AB ⊥于H ．∵CA CB CH AB =⊥，，∴6AH HB ==，∵ABC ACD BCD S S S =+△△△，DM AC DN BC ⊥⊥，，由（1）得62128AB CH =⨯====，， ∴111222AB CH AC DM BC DN ⋅⋅=⋅⋅+⋅⋅， ∴1111281010222DM DN ⨯⨯=⨯⨯+⨯⨯， ∴485DM DN +=， 即DM DN +的值是定值，定值为485． (3)解：①如图2中，连接PB CD ，，∵CA CB AD DB ==，，∴CD AB ⊥，由（2）可知，8CD =，∵DP DA DB ==，∴90APB ∠=︒，即BP AC ⊥，∵1122AB CD AC BP ⋅⋅=⋅⋅， ∴485BP =，∴365AP ===．②2063a <<， 如图3中，过点C 作CH AB ⊥于H ，过点D 作DP AC ⊥于P ．∵CA CB CH AB =⊥，，∴6AH HB ==，∴8CH ===，当BD PD =时，设BD PD x ==，则12AD x =-， ∵sin CH PD A AC AD ==， ∴81012x x=-， ∴163x =， ∴203AD AB BD =-=， 观察图形可知当2063a <<时，存在两次不同的折叠，使点B 落在AC 边上两个不同的位置．【点睛】本题考查翻折问题，涉及的知识点有等腰三角形的性质，翻折的性质，勾股定理求直角三角形以及等面积法．4．（2022·四川成都·二模）已知在正方形ABCD 中，E 是BC 边上一动点，作点B 关于AE 的对称点F ，BF 交AE 于点G ，连结DF ．(1)如图1，求DFB ∠的度数；(2)如图2，过点D 作DM BF ⊥交BF 的延长线于点M ，连结,CM CF ．若DF CM =，试探究四边形DFCM 的形状，并说明理由；(3)如图3，连结BD ，在AG 上截取=GT GB ，点P ，Q 分别是,AD BD 上的动点．若正方形ABCD 的面积为32，直接写出PTQ 周长的最小值．【答案】(1)135∠=︒DFB(2)四边形DFCM 是平行四边形，理由见解析(3)【解析】(1)如图1，连结AF ，∵点B ，F 关于AE 对称，∴AF AB =．∵正方形ABCD ，∴,90AD AB DAB =∠=︒．∴AD AF AB ==．∴12,34∠=∠∠=∠．∵在四边形ABFD 中，有1234360∠+∠+∠+∠+∠=︒DAB ， ∴()1233601352︒∠︒+∠=-∠=DAB ．即135∠=︒DFB ．(2)四边形DFCM 是平行四边形，理由如下：如图2，连接DB ，∵135∠=︒DFB ，∴45∠=︒DFM ．∵DM BF ⊥，∴90DMF ∠=︒．在Rt DMF △中，45∠=∠=︒MDF DFM ，∴=DM DF ．又∵正方形,=DC ABCD BD ， ∴=DM DC DF BD． 又∵45∠=∠=︒-∠MDC FDB CDF ，∴ ∽DMC DFB ．∴135∠=∠︒=DMC DFB ．∵90DMF ∠=︒，∴45∠=︒=∠CMF DFM ，∴∥DF MC ．又∵DF MC =，∴四边形DFCM 是平行四边形．(3)PTQ周长的最小值为解：如图3，作点T 关于AD 的对称点T ''，作点T 关于BD 的对称点''T ，连结,,'''DT DT DT ，连结'''T T 交AD 于点P ，交BD 于点Q ，连结TP 、TQ ，则PQT △周长的最小值为'''T T 的长，由对称知,,,'''==∠=∠∠=∠'''DT DT DT DT ADT ADT TDB T DB ，∴,290''''''=∠=∠=︒DT DT T DT ADB ．∴''==''T T ．由⊥BG GA 且=GT GB ，有==∠=∠BT BD CBG DBT GB BC， ∴ ∽DTB CGB ．∴==DT TB CG GB ．∴DT ．∵BF AE ⊥于点G ，∴点G 在以AB 为直径的圆弧上运动．取AB 中点N ，则==NG 当C 、N 、G 三点共线时CG 最小()≥-CG CN GN ．CG 最小值为∴DT ．∴PQF △周长的最小值为．【点睛】本题考查了正方形的性质、平行四边形的判定、轴对称的性质和相似三角形的判定和性质，利用轴对称的性质得到相等的边和角，找出相似三角形是解题的关键． 5．（2022·安徽芜湖·二模）在△ABC 中．∠C =90°，点D ，E 分别在BC 边和AC 边上，AD ，BE 相交于点F ．(1)图1，若∠AEF=∠BDF，求证：CD AC CE BC=；(2)如图2．若D为BC的中点，AE=EF．求证：AC=BF；(3)如图3．若AE=CD，BD=AC．求∠AFE的度数．【答案】(1)见解析(2)见解析(3)∠AFE的度数为45°．【解析】(1)证明：连接DE，∵∠AEF=∠BDF，即∠AEB=∠BDA，∴A、E、D、B四点共圆，∴∠ABD+∠AED=180°，∵∠CED+∠AED=180°，∴∠CED=∠ABD，又∠C公共，∴△CED∽△CBA，∴CD AC CE BC=；(2)证明：延长AD到G，使DG=AD，∵D为BC的中点，∴BD=CD，又∠BDG=∠CDA，∴△BDG≌△CDA，∴∠G=∠CAD，BG= CA，∵AE=EF，∴∠AFE=∠CAD，∵∠AFE=∠BFG，∴∠G=∠BFG，∴BF=BG=AC，即AC=BF；(3)解：过点A作AM∥BC，在AM上截取点M，使AM=AC，再过点M作MN⊥BC于点N，连接出BM，ME，如图：∵AM∥BC，∠C=90°，MN⊥BC，∴四边形AMNC是矩形，又AM=AC，∴四边形AMNC是正方形，∴AM=MN=AC=CN，∵BD=AC，则BD= CN，∴BN= CD，∵AE=CD，∴AE= BN=CD，∵AM=MN=AC，∠MAE=∠MNB=∠ACD=90°，∴△MAE≌△MNB≌△ACD，∴EM=MB=AD，∠AME=∠BMN，∵∠NME+∠AME =90°，∴∠NME+∠BMN=90°，即∠BME=90°，∴△MEB是等腰直角三角形，∴∠MBE=45°，∵AM∥BD，AM=CN=BD，∴四边形AMBD是平行四边形，∴∠AFE=∠MBE=45°，∴∠AFE的度数为45°．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，全等三角形的判定和性质，正方形的判定和性质，等腰直角三角形的判定和性质，解答本题的关键是明确题意，找出所求问题需要的条件．6．（2022·安徽合肥·二模）已知，在△ABC中，∠ACB=90°，AC=BC，CD是AB边上的中线，点E为CD上一点，连接BE，作FB⊥BE，且FB=EB，连接FE和FC，FE交BC于点G．(1)如图1，若点E与点D重合，求证：点G是BC的中点；(2)如图2，求证：CF//AB；(3)如图3，若BE平分∠DBC，AB=2，求CG：BC的值．【答案】(1)见解析(2)见解析1-【解析】(1)证明： 在△ABC中，∠ACB=90°，AC=BC，∴ACB△是等腰直角三角形CD是AB边上的中线，∴=⊥，,CD BD CD BDFB⊥BE，FBD∴∠=︒，90∴CD FB∥，FB=EB，∴ 是等腰直角三角形，DBFDB BF∴=,∴=，BF CD∴四边形CDBF是平行四边形，90∠=︒，FBD∴四边形CDBF是矩形，CD BD=，∴四边形CDBF是正方形，FE交BC于点G．∴G是正方形对角线交点，∴点G是BC的中点；(2)证明：如图，过点F 作FH BD ⊥，交DB 延长线于点H ，,CD BD FH DB ⊥⊥，90EDB BHF ∴∠=∠=︒，CD EH ∥，90DEB DBE ∴∠+∠=，EB BF ⊥，90,90EBF EBD FBH ∴∠=︒∠+∠=︒，DEB HBF ∴∠=∠，EB EF = ，EDB BHF ∴ ≌，DB HF ∴=，DC DB =Q ，DC FH ∴=，又CD EH ∥，∴四边形CDHF 是平行四边形，FH DB ⊥，∴四边形CDHF 是矩形，FC DH ∴∥；(3)解：如图，CBD 是等腰直角三角形，45CBD ∴∠=︒，CB =，BE 平分∠DBC ，11222.52DBC ∴∠=∠=∠=︒， CF DB ∥ ，45FCG CBD ∴∠=∠=︒，BEF 是等腰直角三角形，45,BEF EF ∴∠=︒=，FEB FCG ∴∠=∠，又CGF EGB ∠=∠，23∴∠=∠，1322.5∴∠=∠=︒，534522.567.5BCF ∴∠=∠+∠=︒+︒=︒，4180367.5ECF ∴∠=︒-∠-∠=︒，45∴∠=∠，CE CG ∴=，13,90EDB ECF ∠=∠∠=∠=︒ ，ECF EDB ∽，EC EF ED EB ∴==EC ED∴=设,EC =则ED a =，(1DC a ∴=，(2CB a ∴==+，1CG BC ∴==. 【点睛】本题考查了等腰直角三角形的性质，勾股定理，正方形的性质与判定，矩形的性质与判定，相似三角形的性质与判定，掌握以上知识是解题的关键．7．（2022·江苏南通·一模）如图，矩形ABCD 中，12,9AB BC ==．P 是边BC 上一动点（不与点B 重合），延长CB 到Q ，使1,,2=BQ BP AP DQ 交于点E ，连接BE 并延长交AD 于点F ．(1)若6BP =，求证：ADE PQE ∆∆≌；(2)探究：当点P 运动时，点F 的位置是否发生变化？请说明理由；(3)求C ，E 两点距离的最小值．【答案】(1)见解析(2)点F 的位置不发生变化，理由见解析(3)185(1)证明：∵四边形ABCD 是矩形，12,9AB BC ==，∴9AD BC ==，AD BC ∥，∴DAE QPE ∠=∠，ADE PQE ∠=∠，∵6BP =，∴132BQ BP ==， ∴369PQ BQ BP =+=+=，∴AD PQ =，∴()ADE PQE ASA ∆∆≌．(2)解；点F 的位置不发生变化．理由为：∵12BQ BP =， ∴13BQ PQ =， ∵四边形ABCD 是矩形，∴AD BC ∥，∴DAE QPE ∠=∠，ADE PQE ∠=∠，又∵AED PEQ ∠=∠，DEF QEB ∠=∠，∴ADE PQE ∆∆∽，DEF QEB ∆∆∽， ∴DE AD EQ PQ =，DE DF EQ BQ =， ∴DF AD BQ PQ =，即13BQ DF PQ AD ==， ∵9AD BC ==， ∴133DF AD ==， ∴当点P 运动时，点F 的位置是不发生变化．(3)由（2）得，当点P 运动时，点F 的位置是不发生变化，即3DF =，∴点E 在线段BF 上随着点P 的运动，而位置发生改变，连接CE ，当CE BF ⊥时，可知C ，E 两点之间的距离最小，如图所示，∵四边形ABCD 是矩形，∴90DAB ∠=︒，∵9AD =，3DF =，12AB =，∴Rt ABF ∆中，BF === ∵AD BC ∥，∴CBE BFA ∠=∠，∵90DAB ∠=︒，CE BF ⊥，∴90DAB CEB ∠=∠=︒，∴BCE FBA ∆∆∽，∴BC CE BF AB =12CE =，解得CE =∴C ，E 两点距离的最小值是185 【点睛】本题考查了矩形的性质，全等三角形的判定和性质以及相似三角形的判定和性质，勾股定理的运用等，第（3）中能分析出点E 在什么位置时，C ，E 两点距离最小是解题的关键． 8．（2022·四川眉山·二模）如图ABC 和ADE 是有公共顶点的等腰直角三角形，90BAC DAE ∠=∠=︒．(1)如图1连结BE 、CD ，BE 的延长线交AC 于点F ，交CD 于点P ，求证：①ABE ACD △≌△；②BP CD ⊥(2)如图2把ADE 绕点A 顺时针旋转，当点D 落在AB 上时，连结BE 、CD ，CD 的延长线交BE 于点P ，若3BC AD ==，①求证：BDP CDA △∽△；②求PDE △的面积．【答案】(1)①见解析；②见解析(2)①见解析；②2710【解析】(1)①证明∵ABC 和ADE 是有公共顶点的等腰直角三角形．∴90,,BAC DAE AD AE AB AC =∠=︒==BAC EAF EAD EAF ∠-∠=∠-∠即BAE CAD ∠=∠在ABE △和ACD △中AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩()ABE ACD SAS ∴V V ≌②∵()ABE ACD SAS △≌△∴ABE ACD ∠=∠∵90ABE AFB ACD CFP ∠+∠=∠+∠=︒∴90CPF ∠=︒∴BP CD ⊥(2)①证明：在ABE △和ACD △中，AE AD EAB DAC AB AC =⎧⎪∠=∠⎨⎪=⎩∴()ABE ACD SAS △≌△∵,ABE ACD BE CD ∠=∠=∵PDB ADC ∠=∠，∴90BPD CAB ∠==︒∴BDP CDA △∽△②∵90,3EPD BC AD ∠=︒==∴6DE AB ==∴633BD =-=，CD ==∵BDP CDA △∽△，∴BD PD PB CD AD AC ==36PD PB ==，∴PD =PB∴PE BE BP =-==∴127210PDE S == 【点睛】本题考查了全等三角形的判定和性质、直角三角形的性质、相似三角形的判定和性质及勾股定理，熟练掌握知识点是解题的关键．9．（2022·吉林长春·一模）阅读理解：辅助线是几何解题中沟通条件与结论的桥梁，在众多类型的辅助线中，辅助圆作为一条曲线型辅助线，显得独特而隐蔽．例如：在图(1)中，AB AC AD ==，求证：2BAC BDC ∠=∠．(请写出证明过程)证明：方法运用：如图(1)已知AB AC AD ==，2BAC BDC ∠=∠，44BAC ∠=︒，则∠CAD 的度数为______．方法拓展：如图(2)在矩形ABCD 中，4AB =，6AD =，E 是AB 边的中点，F 是线段BC 边上的动点，将EBF △沿EF 所在直线折叠得到EB F '△，连结B D '，则B D '的最小值是______．【答案】88°；2．【解析】(1) 证明：以A 点为圆心，AB 为半径画圆，∴AB =AC =AD ，∴B 、C 、D 点都在圆A 上，∴∠DBC =12∠DAC ，∠BDC =12∠BAC ．(2)解：∵AB AC AD ==，∴B ，C ，D 三点在以A 为圆心，AB 为半径的圆上，∴∠CAD =2∠CBD ，2BAC BDC ∠=∠，∵∠CBD =2∠BDC ，∠BAC =44°，∴∠CAD =2∠BAC =88°∠CAD 的度数为88°．(3)如图，当∠BFE =∠B FE '，点B '在DE 上时，此时B D '的值最小，根据折叠的性质△EBF ≌△FB F ',∴EB '⊥B F '，∴EB '=EB ，∵E 是AB 边的中点，AB =4，∴AE =EB '=2，∵AD =6，∴DE = ∴2DB '=-．B D '的最小值是2．【点睛】本题主要考查圆周角定理、折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用，确定点B '在何位置时，B D '的值最小，注意得到B ,C ,D 在以A 为圆心，AB 为半径的圆上是解决问题的关键．10．（2022·辽宁·黑山县教师进修学校一模）阅读材料：如图①，ABC 与DEF 都是等腰直角三角形，90ACB EDF ∠=∠=︒，且点D 在AB 边上，AB 、EF 的中点均为O ，连接BF 、CD 、CO ，显然，点C 、F 、O 在同一条直线上，可以证明BOF COD V V ≌，所以BF CD =．解决问题：（1）将图①中的Rt DEF △绕点O 旋转到图②的位置，猜想此时线段BF 与CD 的数量关系，并证明你的结论．（2）如图③，若ABC 与DEF 都是等边三角形，AB 、EF 的中点均为O ，上述（1）中结论仍然成立吗？如果成立，请说明理由；如果不成立，请求出BF 与CD 之间的数量关系．（3）如图④，若ABC 与DEF 都是等腰三角形，AB 、EF 的中点均为O ，且顶角ACB EDF α∠=∠=，请直接写出BF 与CD 之间的数量关系（用含有α的式子表示出来）．【答案】（1）BF CD =；（2）不成立，BF CD =（3）tan 2BF CD α= 【解析】解：（1）猜想：BF CD =．理由如下：如答图②所示，连接OC 、OD ，∵ABC 为等腰直角三角形，点O 为斜边AB 的中点，∴OB OC =，90BOC ∠=°，∵DEF 为等腰直角三角形，点O 为斜边EF 的中点，∴OF OD =，90DOF ∠=︒，∵90BOF BOC COF COF ∠=∠+∠=︒+∠，90COD DOF COF COF ∠=∠+∠=︒+∠，∴BOF COD ∠=∠，在BOF 与COD △中，OB OC BOF COD OF OD =⎧⎪∠=∠⎨⎪=⎩，∴BOF COD V V ≌（SAS ）∴BF CD =；（2）不成立．如答图③所示，连接OC 、OD ，∵ABC 为等边三角形，点O 为边AB 的中点，∴tan 30OB OC =︒=90BOC ∠=°， ∵DEF 为等边三角形，点O 为边EF 的中点，∴tan 30OF OD =︒=90DOF ∠=︒，∴OB OF OC OD =， ∵90BOF BOC COF COF ∠=∠+∠=︒+∠，90COD DOF COF COF ∠=∠+∠=︒+∠，∴BOF COD ∠=∠，在BOF 与COD △中，∵OB OF OC OD =，BOF COD ∠=∠， ∴BOF COD V V ∽∴BF CD =；∴BF CD =；（3）tan 2BF CD α=．理由如下： 如答图④所示，连接OC 、OD ，∵ABC 为等腰三角形，点O 为底边AB 的中点， ∴tan 2OB OC α=，90BOC ∠=°， ∵DEF 为等腰三角形，点O 为底边EF 的中点， ∴tan 2OF OD α=，90DOF ∠=︒， ∴tan 2OB OF OC OD α==， ∵90BOF BOC COF COF ∠=∠+∠=︒+∠，90COD DOF COF COF ∠=∠+∠=︒+∠，∴BOF COD ∠=∠，在BOF 与COD △中， ∵tan 2OB OF OC OD α==，BOF COD ∠=∠， ∴BOF COD V V ∽ ∴tan 2BF CD α=．【点睛】本题是几何综合题，考查了旋转变换中相似三角形、全等三角形的判定与性质、等腰三角形的三线合一的性质、锐角三角函数．解题关键是：第一，善于发现几何变换中不变的逻辑关系，即BOF COD V V ≌或BOF COD V V ∽；第二，熟练运用等腰直角三角形、等边三角形、等腰三角形的相关性质．本题（1）（2）（3）问的解题思路一脉相承，体现了由特殊到一般的解题思想方法．11．（2022·浙江嘉兴·一模）转化是解决数学问题常用的思想方法之一，它可以在数与数、数与形、形与形之间灵活应用．请解答下面的问题：如图1，在AOB 中，OA OB =，90AOB ∠=︒．【基础巩固】（1）将图1中AOB 绕点B 按顺时针方向旋转60°得到DCB （如图2），连结OC ．求证：OC OB =．【思考探究】（2）将图1中AOB 绕点B 按顺时针方向旋转60°并缩小得到DCB （如图3），使12BC BO =，连结OC ，AD ． ①求证：OBC ABD △△②用等式表示AD 与AB 之间的数量关系，并说明理由．【拓展延伸】（3）将图1中AOB 绕点B 按顺时针方向旋转某个角度（小于180°）并缩小得到DCB（如图4），使12BC BO =，连结OC ，AC ，AD ．当OC OB =时，求AC AD 的值．【答案】（1）证明见解析 ；（2）① 证明见解析；②AD AB =，理由见解析；（3）． 【解析】（1）证明：由旋转的性质得60OBC ∠=︒，OB CB =，∴OBC 为等边三角形，∴OC OB =．（2）①∵AOB 和DCB 都为等腰直角三角形∴OB BC AB BD ==60OBC ABD ∠=∠=︒ ∴OBC ABD △△∽．②AD AB =，理由如下：作CF OB ⊥于点F ，∵60OBC ABD ∠=∠=︒，∴12BF BC =，CF =， ∵12BC OB =，∴CF OF =， ∴30COF ∠=︒，∴90OCB ∠=︒∵OBC ABD △△∽，∴90OCB ADB ∠==︒， ∴sin 60AD AB ︒=，∴AD AB =．（3）解：延长AC 交BD 于点E ．∵OBC ABD ∠=∠，∴OB BC AB BD == ∴OBC ABD △△∽，∵OB OC =，∴AB AD =．∵BC DC =，AC AC =，∴ABC ADC △△≌，∴135ACD ACB ∠=∠=︒∴45BCE DCE ∠=∠=︒，∴90CEB ∠=︒设2BC a =，4OB a =，则AB =，CE BE ==，AE ==∴AC AD = 【点睛】本题考查了旋转的性质，相似三角形的判定与性质，锐角三角函数的应用以及勾股定理的知识，根据题意作出适当的辅助线是解题的关键．12．（2022·山东济南·一模）图1是边长分别为a 和()b a b >的两个等边三角形纸片ABC 和CDE △叠放在一起（C 与C '重合）的图形．(1)操作：固定ABC ，将CDE △绕点C 按顺时针方向旋转20°，连结AD ，BE ，如图2，则ECA ∠=______度，并直接写出线段BE 与AD 的数量关系____．(2)操作：若将图1中的CDE △，绕点C 按顺时针方向旋转120°，使点B 、C 、D 在同一条直线上，连结AD 、BE ，如图3．①线段BE 与AD 之间是否仍存在（1）中的结论？若是，请证明；若不是，请直接写出BE 与AD 之间的数量关系；②求APB ∠的度数．(3)若将图1中的CDE △，绕点C 按逆时针方向旋转一个角()0360αα<<︒，当α等于多少度时，BCD △的面积最大？请直接写出答案．【答案】(1)40，BE ＝AD(2)①存在，理由见详解；②60°(3)当α＝150°或330°时，BCD △的面积最大【解析】(1)∵△ABC 和△CDE 是等边三角形，∴BC ＝AC ，CE ＝CD ，∠BCA =60°，∵旋转20°∴∠BCE ＝∠ACD ＝20°，∴△CBE ≌△CAD （SAS ），∴BE ＝AD （全等三角形的对应边相等），∵ECA ∠=∠BCA －∠BCE∴ECA ∠=60°-20°=40°故答案为：40，BE ＝AD(2)如图1，①（1）中结论仍然成立，理由如下：∵△ABC 和△CDE 是等边三角形，BC ＝AC ，CE ＝CD ，∵∠BCE ＝∠ACD ＝120°，∴△CBE ≌△CAD （SAS ），∴BE ＝AD ；②∵△CBE≌△CAD，∴∠CBE＝∠CAD，又∠AOP＝∠BOC，∴∠APB＝∠ACB＝60°；(3)如图2，当D运动到D1或D2，即BC⊥D1D2S△BCD最大12BC CD =⋅12=ab，此时旋转角是60°+90°＝150°，或360°﹣30°＝330°，∴当α＝150°或330°．【点睛】本题考查了等边三角形的性质，全等三角形的判定和性质以及旋转等知识，解决问题的关键是找全等的对应边和对应角，题目属于中考常考题型．13．（2022·重庆·一模）在 ABC中，点D在边AB上，AE CD⊥于F交BC于E，AE CD=，2ACD BAE∠=∠．(1)如图1，若 ACE为等边三角形，2CD=，求AB的长；(2)如图2，作EG AB ⊥，求证：AD =；(3)如图3，作EG AB ⊥，当点D 与点G 重合时，连接BF ，请直接写出BF CE 的值．【答案】(2)见解析【解析】(1)∵△ACE 为等边三角形，∴∠CAE ＝∠ACB ＝∠CEA ＝60°，∵AE CD ⊥∴∠CAE +ACD ∠＝90°，∵2ACD BAE ∠=∠，∴∠CAE +2∠BAE ＝90°，∴∠BAE ＝15°，∴∠CBA ＝∠CEA ﹣∠BAE ＝60°﹣15°＝45°，如图，过点A 作AN ⊥BC 于点N ，∴△ABN 为等腰直角三角形，在等边△ACE 中，AN ＝sin 60°•AE 2∴AB ．(2)证明：如图，过点C 作CM ⊥AB 于点M ，设∠EAB ＝α，∵∠CAE +2∠BAE ＝90°，∴∠CAE ＝90°﹣2α，∵AE ⊥CD ，∴∠ACD ＝2α，∴∠CAB ＝90°﹣2α+α＝90°﹣α，∴∠ACM ＝α，∴CM 平分∠ACD ，∴AM ＝DM ＝12AD ，AC ＝CD ＝AE ，在△ACM 和△EAG 中， EGA AMC EAG ACM AE AD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACM ≌△EAG （AAS ），∴EG ＝AM ，∴AD ＝2AM ＝2EG ，∵AC ＝AE ，∠CAE ＝90°﹣2α，∴∠CEA ＝45°+α，又∵∠CEA ＝∠B +∠EAG ，∴∠B ＝45°，∵EG ⊥AB ，∴△EBG 为等腰直角三角形，∴BEAMAD ． ∴AD．(3)如图，BF 与EC之间的数量关系为CE BF =过点F作FH⊥AB于点H，过点C作CM⊥AB于点M，设BD＝a，由（2）可知DE＝a，AD＝2a，AM＝DM＝a，∵DE∥CM，BD＝DM，∴BE＝CE，∵DE＝a，AD＝2a，∠ADE＝90°，∴AE，∵CD⊥AE，DE⊥AB，∴∠EFD＝∠ADE＝90°∴∠EDF＝∠DAE，∴△DEF∽△AED，∴DE AE EF DE=，∴a EF=∴EF a，∴AF，∴14 EFAF=，∴45 AFAE=．∵FH∥DE，∴△AFH∽△AED，∴45 FH AH AFDE AD AE===，∴FH＝48,55a AH=a，∴DH ＝2a ﹣85a ＝25a ， ∴BH ＝a +2755a =a ， ∴BF．∴BF CE == 【点睛】本题是三角形综合题，涉及特殊三角形的性质，全等三角形的性质和判定，相似三角形的性质和判定，锐角三角函数的运用，解题的关键是针对每一小问的条件构造合适的辅助线利用图形的性质和判定去证明．14．（2022·江苏·连云港市新海初级中学一模）将正方形ABCD 绕点A 逆时针旋α 到正方形AEFG ．(1)如图1，当0°＜α＜90°时，EF 与CD 相交与点H ．求证：DH ＝EH ；(2)如图2，当0°＜α＜90°，点F 、D 、B 正好共线时，①求∠AFB 度数；②若正方形ABCD 的边长为1，求CH 的长：(3)连接DE ， EC ，FC ．如图3，正方形AEFG 在旋转过程中，是否存在实数m 使AE 2＝DE 2＋mFC 2－EC 2总成立？若存在，求m 的值；若不存在，请说明理由．【答案】(1)见解析(2)②30°；1(3)存在，m =12【解析】(1)如图，连接AH ，正方形ABCD 绕点A 逆时针旋α 得到正方形AEFG ，,,AE AD D E AH AH ∴=∠=∠=，()Rt Rt HL AHE AHD ∴ ≌，HD HE ∴=，(2)①如图，连接AC ，交BD 于点O ，连接BE ，EC ，正方形ABCD 绕点A 逆时针旋α 到正方形AEFG ，AF AC ∴=，12AO AC =，AO OD ⊥， 12AF AF ∴=， 点F 、D 、B 共线，AO OF ∴⊥，1sin sin 2AO AFB AFO AF ∴∠=∠==，30AFB ∴∠=︒，②如图，过点E 作EK CD ⊥，交DC 于点K ，交AB 于点L ，则四边形ALKD 是矩形，45ADB AFD FAD ∠=︒=∠+∠ ，30AFB ∠=︒，15FAD ∴∠=︒，45FAE ∠=︒ ，30DAE ∴∠=︒，60EAB ∴∠=︒，AE AB =Q ，AEB ∴ 是等边三角形，LE AE ∴==12AL LB DK KC ====，1EK LK LE ∴=-= 由（1）可得EH HD =，设DH a =，则1,2EH a HK a ==-， Rt EKH 中，222EH HK EK =+，即222112a a ⎛⎛⎫=-+ ⎪ ⎝⎭⎝，解得2a =， ∴2DH =，(121CH DC DH =-=-=∴，(3) 存在，12m =，理由如下，如图，连接,,,,AC AF BE FC DE ，过点E 作MN BC ∥，交AB 于点N ，交CD 于M ， 正方形AEFG 是由正方形ABCD 旋转而成，,AF AC AB AE ∴==，BAE CAF ∠=∠BAE CAF ∴ ∽BE AB CF AC ∴==2212BE CF ∴= 90ENB EMC ∴∠=∠=︒∴四边形BCMN 是矩形，四边形ANMD 是矩形BN MC ∴=，AN DM =∴,NBE EMC 是直角三角形∴222BE NE NB =+222BE NE MC ∴=+222222222,,AE AN NE DE EM DM EC EM MC =+=+=+ ，DM AN =222AE EC DE ∴+-()222222AN NE EM MC EM DM =+++-+222222AN NE EM MC EM DM =+++--22NE MC =+22NE NB =+=2BE2212BE FC = 222AE EC DE ∴+-212FC =即222212AE DE FC EC =+- AE 2＝DE 2＋mFC 2－EC 2∴12m = 【点睛】本题考查了正方形的性质，旋转的性质，根据特殊角的三角函数值求角度，相似三角形的性质与判定，勾股定理，全等的性质与判定，等边三角形的性质与判定，综合运用以上知识是解题的关键．15．（2022·安徽六安·一模）如图1，在正方形ABCD 中，E 为AD 边上一点，CO ⊥BE 交AB 于F ．EF 交CB 延长线于G ．(1)当E 为AD 中点时，求证：BC ＝2BG ；(2)如图2，当BG ＝BC 时，求证：2AE AF AB =⋅；(3)在（2）的条件下，连接OD ，求tan ∠EOD 的值．【答案】(1)见解析(2)见解析【解析】(1)证明：∵四边形ABCD 为正方形，∴∠A ＝∠ABC =90°，AB =BC ，∵CF ⊥BE ，∴∠FCB +∠EBC ＝∠EBC +∠ABE =90°，∴∠FCB ＝∠ABE ，又AB ＝BC ，∠A ＝∠FBC ，∴AEB BFC △△≌（ASA ），∴BF ＝AE ，∵E 为AD 中点， ∴12AE AD =， ∴F 为AB 中点，∴AE ＝AF ，∴∠AFE ＝45°，∴∠GFB =∠AFE ＝45°，∴∠G ＝90°-45°＝45°， ∴12BF BG BC ==， 即BC ＝2BG ；(2)证明：∵BG ＝BC ，BF ⊥CG ，∴FG ＝FC ，∴∠G ＝∠FCG ，∵AE CG ∥，∴∠AEF ＝∠G ，∴∠AEF ＝∠FCG ，又∠A ＝∠ABC =90°，∴AEF BCF △△∽， ∴AF AE BF BC=， ∴AE •BF ＝AF •BC ，由（1）可知，AEB BFC △△≌，∴AE ＝BF ，AB ＝BC ，∴2AE AF AB =⋅；(3)解：如图，延长OE 、CD 交于P 点，连接CE ，∵∠PDE ＝∠POC =90°，又∠P ＝∠P ，∴PDE POC △△∽， ∴PD PE PO PC=， 又∠P ＝∠P ，∴POD PCE △△∽，∴∠EOD ＝∠ECD ，设AE ＝x ，AB ＝1，则AF ＝1-x ，由（2）可得2AE AF AB =⋅，∴()211x x =-⨯，解得1x =2x =，∴1DE AF ===，∴tan DE ECD DC ∠==即tan EOD ∠=． 【点睛】本题考查正方形的几何综合，涉及的知识点有全等三角形的判定和性质，正方形的性质，相似三角形的判定和性质，正切值的求解等知识点，综合性较强，属于压轴类题目． 16．（2022·辽宁沈阳·一模）如图1，在ABC 中，AB AC =，AO BC ⊥于点O ，5AB =，6BC =，在ABC 的外部以AB 为边作等边ABD △，点E 是线段AO 所在直线上一动点（点E 不与点A 重合），将线段BE 绕点B 顺时针方向旋转60°得到线段BF ，连接EF ．(1)求AO 的长；(2)如图2，当点E 在线段AO 上，且点F ，E ，C 三点在同一条直线上时，求BF 的长；(3)连接DF ，若BDF 的面积为3，请直接写出BF 的长．【答案】(1)4(2)或(1)AB AC = ，AO BC ⊥，6BC =13,902OB BC AOB ∴==∠=︒ 5AB =4OA ∴==(2)将线段BE 绕点B 顺时针方向旋转60°得到线段BF ,60BE BF EF EBF ∴==∠=︒BEF ∴∆是等边三角形BE EF ∴=，60F BEF ∠=∠=︒,OA BC OB OC ⊥=OA ∴是线段BC 的垂直平分线BE CE ∴=BE CE EF ∴==30ECB EBC ∴∠=∠=︒90CBF ∴∠=︒6BC =tan 6tan 306BF BC BCF ∴=⋅∠=⨯︒==(3)①当点E 在线段AO 上时，将线段BE 绕点B 顺时针方向旋转60°得到线段BF ,60BE BF EF EBF ∴==∠=︒BEF ∴∆是等边三角形,60BE BF EBF ∴=∠=︒ABD △为等边三角形,60BA BD ABD ∴=∠=︒ABE DBF ∴∠=∠()ABE DBF SAS ∴∆≅∆ABE BDF S S ∆∆∴=BDF 的面积为3132ABE S OB AE ∆∴==⋅⋅ 3OB =2AE ∴=422OE OA AE ∴=-=-=在Rt OBE ∆中，由勾股定理得BE ==BF ∴=②当点E 在线段OA 延长线上时，同①可得2AE =426OE OA AE ∴=+=+=在Rt OBE ∆中，由勾股定理得BE ===BF ∴=③当点E 在线段AO 延长线上时，同①可得2AE =，不合题意，舍去综上，BF ．【点睛】本题考查了等边三角形的判定和性质、勾股定理、等腰三角形的性质、线段垂直平分线的性质、解直角三角形等，熟练掌握并能够灵活运用知识点是解题的关键．17．（2022·安徽芜湖·二模）如图．P 是菱形ABCD 的对角线BD 上一点，E 是BC 边上一点，EAP ABD AE ∠=∠，交BD 于点F ．(1)求证： ∽ABP FBE ；(2)过点P 作PH AE ⊥于点H ，若34=AP AD ，求AH BD的值．【答案】(1)证明见解析(2)38(1)证明：∵四边形ABCD 是菱形∴ABD CBD ∠=∠∵EAP ABD ∠=∠∴EAP CBD ∠=∠∵AFP BFE ∠=∠，180EBF BFE BEF ∠+∠+∠=︒，180FAP AFP APF ∠+∠+∠=︒ ∴BEF APF ∠=∠∵PBA EBF ∠=∠，BPA BEF ∠=∠∴ ∽ABP FBE ．(2)解：如图，作AM BD ⊥∵四边形ABCD 是菱形∴AB AD =，12BM DM BD ==，90BMA ∠=︒ ∵PH AE ⊥∴90AHP BMA ∠=︒=∠∵HAP MBA ∠=∠∴APH BAM ∽ ∴AP AH AB BM = ∴34AP AH AP AB BM AD === ∴1332248AH AH BD BM ==⨯= ∴AH BD 的值为38． 【点睛】 本题考查了菱形的性质，对顶角相等，三角形内角和定理，相似三角形的判定与性质等知识．解题的关键在于熟练掌握菱形的性质，相似三角形的判定与性质．18．（2022·广东广州·一模）如图，矩形ABCD中AB=10，AD=6，点E为AB边上的动点（不与A，B重合），把△ADE沿DE翻折，点A的对应点为G，延长EG交直线DC于点F，再把△BEH沿EH翻折，使点B的对应点T落在EF上，折痕EH交直线BC于点H．(1)求证：△GDE∽△TEH；(2)若点G落在矩形ABCD的对称轴上，求AE的长；(3)是否存在点T落在DC边上？若存在，求出此时AE的长度，若不存在，请说明理由．【答案】(1)见解析(2)AE的长为；(3)不存在这样的点T落在DC边上．理由见解析【解析】(1)证明：由折叠的性质可知：∠DAE=∠DGE=90°，∠EBH=∠ETH=90°，∠AED=∠GED，∠BEH=∠TEH，∴∠DEG+∠HET=90°．又∵∠HET+∠EHT=90°，∴∠DEG=∠EHT，∴△GDE∽△TEH；(2)解：当点G落在如图的矩形ABCD的对称轴MN上时，∵直线MN是矩形ABCD的对称轴，∴点G是EF的中点，即GE=GF，在△GDE和△GDF中90DG DG DGE DGF GE GF =⎧⎪∠=∠=︒⎨⎪=⎩，∴△GDE ≌△GDF （SAS ），∴DE =DF ，∠FDG =∠EDG ，又∵△ADE ≌△GDE ，∠ADF =90°．∴∠ADE =∠EDG =∠FDG =30°，∴AE =AD当点G 落在如图的矩形ABCD 的对称轴PQ 上时，P 、Q 分别是AB 、CD 的中点，∴DQ =AP =5，DG =AD =PQ =6，∴QG=，∴PG，设AE =a ，则GE =a ，PE =5-a ，∴GE 2=PE 2+PG 2，即a 2=(5-a )2)2，解得：aAE； 综上，AE 的长为(3)解：假设存在点T 落在DC 边上，此时点T 与点F 重合，过点T 作TI ⊥AB 于点I ，如图：设AE =x ，则GE =x ，BE =TE =10-x ，TI =AD =DG =6，∴GT =10-2x ，∴DT 2= DG 2+TG 2，即DT∵∠IET =∠GTD ，∴sin ∠IET =TI DG ET DT=，即610x =-，10x =-，整理得3x 2-20x +36=0，∵()224204336b ac =-=--⨯⨯= -32<0，∴不存在这样的点T 落在DC 边上．【点睛】本题考查翻折变换、相似三角形证明、全等三角形的判定和性质、勾股定理、解直角三角形，矩形的性质等知识，解（2）题的关键是要注意分类讨论．19．（2022·上海市进才中学一模）已知：AB =5，tan ∠ABM =34，点 C 、D 、E 为动点，其中点 C 、D 在射线 BM 上（点 C 在点 D 的左侧），点 E 和点 D 分别在射线 BA 的两侧，且 AC =AD ，AB =AE ，∠CAD =∠BAE ．(1)当点 C 与点 B 重合时（如图 1），联结 ED ，求 ED 的长；(2)当 EA BM 时（如图 2），求四边形 AEBD 的面积；(3)联结 CE ，当△ACE 是等腰三角形时，求点 B 、C 间的距离．【答案】(1)485(2)15(3)3 【解析】 (1) （1)如图1中，图一延长BA 交DE 于F ，作AH ⊥BD 于H ．在Rt ΔABH 中，∵∠AHB =90°，∴sin ∠ABH =35AHAB =∴AH =3， BH=4，∵AB = AD ， AH ⊥BD ，在ΔABE 和ΔABD 中，AE ADBAE BADAB AB=⎧⎪∠=∠⎨⎪=⎩∴ΔABD ≌ΔABE ，∴BE =BD ，∵∠ABE =∠ABD ，∴BF ⊥DE ， EF =DF ，∵∠ABH = ∠DBF ，∠AHB =<BFD ，∴ΔABH ≌ΔDBF ， ∴AH ABDF BD =,∴DF =245，∴DE =2DF =485．(2)如图2中，图二作AH ⊥BD 于H ，∵AC =AD ， AB =AE ，∠CAD = ∠BAE ，∴∠AEB =∠ABE =∠ACD =∠ADC ，∵AE //BD ，∴∠AEB +∠EBD =180°，∴∠EBD +∠ADC =180°，∴EB ∥AD ，∵AE ∥BD ，∴四边形ADBE 是平行四边形，∴BD =AE =AB =5，AH =3，∴ADBE S 平行四边形=BD ·AH =15．(3)由题意AC ≠AE ，EC ≠AC ，只有EA =EC ，图三∵∠ACD =∠AEB (已证），∴A 、C 、B 、E 四点共圆，∵AE =EC =AB ，∴ EC AB =，∴ EB AC =，∴∠AEC =∠ABC ，。

中考数学几何压轴题及答案一、解答题（共30小题）1.观察猜想（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是，BE+BF＝；探究证明（2）在（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；拓展延伸（3）如图③，在△ABC中，AB＝AC，∠BAC＝α，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝α，连接BF，则BE+BF的值是多少？请用含有n，α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点，使∠AB′B＝∠AC′C＝∠BAC（1）如图1中∠BAC为直角，∠BAC＝∠AB′B＝∠AC′C＝90°（点B′与点C′重合），则△ABC∽△B'BA∽△C'AC，，，进而可得AB2+AC2＝；（2）如图2中当∠BAC为锐角，图3中∠BAC为钝角时（1）中的结论还成立吗？若不成立，则AB2+AC2等于什么（用含用BC和B′C′的式子表示）？并说明理由（3）若在△ABC中，AB＝5，AC＝6，BC＝9，请你先判断出△ABC的类型，再求出B′C′的长3．（1）问题发现如图1，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，点D是线段AB上一动点，连接BE填空：①的值为；②∠DBE的度数为．（2）类比探究如图2，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，点D是线段AB上一动点，连接BE．请判断的值及∠DBE的度数，并说明理由；（3）拓展延伸如图3，在（2）的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE 的中点M，连接BM、CM，若AC＝2，则当△CBM是直角三角形时，线段BE的长是多少？请直接写出答案．4.（1）问题发现：如图①，在△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，以点D为顶点作正方形DFGE，使点A、C分别在DE和DF上，连接BE、AF．则线段BE 和AF数量关系．（2）类比探究：如图②，保持△ABC固定不动，将正方形DFGE绕点D旋转α（0°＜α≤360°），则（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由．（3）解决问题：若BC＝DF＝2，在（2）的旋转过程中，连接AE，请直接写出AE的最大值．5.如图，在平行四边形ABCD中，AC与BD交于点O，以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F，且∠EOF与∠BAD互补．（1）若四边形ABCD是正方形，则线段OE与OF有何数量关系？请直接写出结论；（2）若四边形ABCD是菱形，那么（1）中的结论是否成立？若成立，请画出图形并给出证明；若不成立，请说明理由；（3）若AB：AD＝m：n，探索线段OE与OF的数量关系，并证明你的结论.6.如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F.（1）证明与推断：①求证：四边形CEGF是正方形；②推断：的值为：（2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG＝6，GH＝2，则BC＝．7.如图1，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E分别是AC、BC的中点，连接DE.定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．探索发现：图1中，的值为；的值为．（2）拓展探完若将△CDE绕点C逆时针方向旋转一周，在旋转过程中的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△CDE旋转至A，D，E三点共线时，直接写出线段BE的长．8.已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE，设OD＝m．（1）问题发现如图1，△CDE的形状是三角形．（2）探究证明如图2，当6＜m＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．（3）解决问题是否存在m的值，使△DEB是直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．9.等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD 的中点，连接MN、NF．问题提出：（1）如图1，当AD在线段AC上时，则∠MNF的度数为，线段MN 和线段NF的数量关系为；深入讨论：（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系；拓展延伸：（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为．10．四边形是我们在学习和生活中常见的图形，而对角线互相垂直的四边形也比较常见，比如筝形、菱形、图1中的四边形ABCD等．它们给我们的学习和生活带来了很多的乐趣和美感．（1）如图2，在四边形ABCD中，AB＝AD，CB＝CD，则AC与BD的位置关系是，请说明理由．（2）试探究图1中四边形ABCD的两组对边AB，CD与BC，AD之间的数量关系，请写出证明过程．（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连接CE，BG，GE，已知AC＝4，AB＝5，求GE的长．11．问题发现：如图（1）在Rt△ABC和Rt△BDE中，∠A＝∠DEB＝30°，BC＝BE＝6，Rt△BDE绕点B逆时针旋转，H为CD的中点，当点C与点E重合时，BH与AE的位置关系为，BH与AE的数量关系为；问题证明：在Rt△BDE绕点B旋转的过程中，（1）中的结论是否仍然成立？若成立，请就图（2）的情形给出证明若不成立，请说明理由；拓展应用：在Rt△BDE绕点B旋转的过程中，当DE∥BC时，请直接写出BH2的长．12．如图1，菱形ABCD与菱形GECF的顶点C重合，点G在对角线AC上，且∠BCD＝∠ECF＝60°，（1）问题发现的值为；（2）探究与证明将菱形GECF绕点C按顺时针方向旋转α角（0°＜α＜60°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：菱形GECF在旋转过程中，当点A，G，F三点在一条直线上时，如图3所示连接CG并延长，交AD于点H，若CE＝2，GH＝，则AH的长为．13．如图，在Rt△ABC中，∠ACB＝90°，＝，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．（1）探究发现：如图1，若m＝n，点E在线段AC上，则＝；（2）数学思考：①如图2，若点E在线段AC上，则＝（用含m，n的代数式表示）；②当点E在直线AC上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；（3）拓展应用：若AC＝，BC＝2，DF＝4，请直接写出CE的长．14．如图，已知点E是射线BC上的一点，以BC、CE为边作正方形ABCD和正方形CEFG，连接AF，取AF的中点M，连接DM、MG（1）如图1，判断线段DM和GM的数量关系是，位置关系是；（2）如图2，在图中的正方形CEFG绕点C逆时针旋转的过程中，其他条件不变，（1）中的结论是否成立？说明理由；（3）已知BC＝10，CE＝2，正方形CEFG绕点C旋转的过程中，当A、F、E共线时，直接写出△DMG的面积．15.在Rt△ABC中，∠ACB＝90°，AB＝，AC＝2，过点B作直线m∥AC，将△ABC绕点C顺时针旋转得到△A′B′C（点A，B的对应点分别为A'，B′），射线CA′，CB′分别交直线m于点P，Q．（1）如图1，当P与A′重合时，求∠ACA′的度数；（2）如图2，设A′B′与BC的交点为M，当M为A′B′的中点时，求线段PQ的长；（3）在旋转过程中，当点P，Q分别在CA′，CB′的延长线上时，试探究四边形P A'B′Q的面积是否存在最小值．若存在，求出四边形P A′B′Q的最小面积；若不存在，请说明理由．16.如图（1），在等边三角形ABC中，点D，E分别在边AB，AC上，AD＝AE，连接BE，CD，点M，N，P分别是BE，CD，BC的中点，连接DE，PM，PN，MN．（1）观察猜想，图（1）中△PMN是（填特殊三角形的名称）（2）探究证明，如图（2），△ADE绕点A按逆时针方向旋转，则△PMN的形状是否发生改变？并就图（2）说明理由．（3）拓展延伸，若△ADE绕点A在平面内自由旋转，AD＝2，AB＝6，请直接写出△PMN 的周长的最大值．17.已知△ABC，AB＝AC，D为直线BC上一点，E为直线AC上一点，AD＝AE，设∠BAD＝α，∠CDE＝β，（1）如图1，若点D在线段BC上，点E在线段AC上．∠ABC＝60°，∠ADE＝70°，则α＝°；β＝°.（2）如图2，若点D在线段BC上，点E在线段AC上，则α，β之间有什么关系式？说明理由．（3）是否存在不同于（2）中的α，β之间的关系式？若存在，请写出这个关系式（写出一种即可），说明理由；若不存在，请说明理由.18.问题提出：（1）如图1，在四边形ABCD中，连接AC、BD，AB＝AD，∠BAD＝∠BCD＝90°，将△ABC绕点A逆时针旋转90°，得到△ADE，点B的对应点落在点D，点C的对应点为点E，可知点C、D、E在一条直线上，则△ACE为三角形，BC、CD、AC的数量关系为；探究发现：（2）如图2，在⊙O中，AB为直径，点C为的中点，点D为圆上一个点，连接AD、CD、AC、BC、BD，且AD＜BD，请求出CD、AD、BD间的数量关系.拓展延伸：（3）如图3，在等腰直角三角形ABC中，点P为AB的中点，若AC＝13，平面内存在一点E，且AE＝10，CE＝13，当点Q为AE中点时，PQ＝.19.已知△ABC中，CA＝CB，0°＜∠ACB≤90°，点M、N分别在边CA，CB上（不与端点重合），BN＝AM，射线AG∥BC交BM延长线于点D，点E在直线AN上，EA＝ED．（1）【观察猜想】如图1，点E在射线NA上，当∠ACB＝45°时，①线段BM与AN的数量关系是；②∠BDE的度数是；（2）【探究证明】如图2点E在射线AN上，当∠ACB＝30°时，判断并证明线段BM与AN的数量关系，求∠BDE的度数；（3）【拓展延伸】如图3，点E在直线AN上，当∠ACB＝60°时，AB＝3，点N是BC 边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长．20.如图①，在正方形ABCD和正方形AB'C'D'中，AB＝2，AB'＝，连接CC’（1）问题发现：．（2）拓展探究：将正方形AB'C'D'绕点A逆时针旋转，记旋转角为θ，连接BB'，试判断：当0°≤θ＜360°时，的值有无变化？请仅就图②中的情形给出你的证明；（3）问题解决：请直接写出在旋转过程中，当C，C′，D'三点共线时BB′的长．21.如图1，在正方形ABCD中，点O是对角线BD的中点．（1）观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置，连接AC，DE，则线段AC与DE的数量关系是，直线AC与DE的位置关系是．（2）类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置，（1）中的结论是否成立？并说明理由．（3）拓展延伸将图2中的△ECF在平面内旋转，设直线AC与DE的交点为M，若AB＝4，请直接写出BM的最大值与最小值．22.如图1，点B在直线l上，过点B构建等腰直角三角形ABC，使∠BAC＝90°，且AB＝AC，过点C作CD⊥直线l于点D，连接AD．（1）小亮在研究这个图形时发现，∠BAC＝∠BDC＝90°，点A，D应该在以BC为直径的圆上，则∠ADB的度数为°，将射线AD顺时针旋转90°交直线l于点E，可求出线段AD，BD，CD的数量关系为；（2）小亮将等腰直角三角形ABC绕点B在平面内旋转，当旋转到图2位置时，线段AD，BD，CD的数量关系是否变化，请说明理由；（3）在旋转过程中，若CD长为1，当△ABD面积取得最大值时，请直接写AD的长．23．如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）观察猜想：线段EF与线段EG的数量关系是；（2）探究证明：如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）拓展延伸：如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB＝a、BC＝b，求的值．24．如图1，在Rt△ABC中，∠B＝90°，AB＝2，BC＝1，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现①当α＝0°时，＝；②当α＝180°时，＝．（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明．（3）问题解决当△EDC旋转至A、B、E三点共线时，直接写出线段BD的长．25.在△ABC中，AD为BC边上的中线，E为AD上一动点，设DE＝nEA，连接CE并延长，交AB于点F．（1）尝试探究如图（1），当∠BAC＝90°，∠B＝30°，DE＝EA时，BF，BA之间的数量关系是；（2）类比延伸如图（2），当△ABC为锐角三角形，DE＝EA时，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）拓展迁移如图（3），当△ABC为锐角三角形，DE＝nEA时，请直接写出BF，BA之间的数量关系．26.古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE ⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC．（1）求证：CD是⊙O的切线；（2）小明在研究的过程中发现是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．27．定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．（2）如图2，四边形ABCD内接于⊙O，＝，四边形ABCD的外角平分线DF交⊙O 于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．28.【性质探究】如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF＝2OG．【迁移应用】（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．【拓展延伸】（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．29．如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．30．如图1和图2，在△ABC中，AB＝AC，BC＝8，tan C＝．点K在AC边上，点M，N 分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；（3）设点P移动的路程为x，当0≤x≤3及3＜x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝，请直接写出点K被扫描到的总时长．参考答案与试题解析一．解答题（共30小题）1．【解答】解：（1）如图①中，∵∠EAF＝∠BAC＝90°，∴∠BAF＝∠CAE，∵AF＝AE，AB＝AC，∴△BAF≌△CAE，∴∠ABF＝∠C，BF＝CE，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠C＝45°，∴∠FBE＝∠ABF+∠ABC＝90°，BC＝BE+EC＝BE+BF，故答案为：BF⊥BE，BC．（2）如图②中，作DH∥AC交BC于H．∵DH∥AC，∴∠BDH＝∠A＝90°，△DBH是等腰直角三角形，由（1）可知，BF⊥BE，BF+BE＝BH，∵AB＝AC＝3，AD＝1，∴BD＝DH＝2，∴BH＝2，∴BF+BE＝BH＝2；（3）如图③中，作DH∥AC交BC的延长线于H，作DM⊥BC于M．∵AC∥DH，∴∠ACB＝∠H，∠BDH＝∠BAC＝α，∵AB＝AC，∴∠ABC＝∠ACB∴∠DBH＝∠H，∴DB＝DH，∵∠EDF＝∠BDH＝α，∴∠BDF＝∠HDE，∵DF＝DE，DB＝DH，∴△BDF≌△HDE，∴BF＝EH，∴BF+BE＝EH+BE＝BH，∵DB＝DH，DM⊥BH，∴BM＝MH，∠BDM＝∠HDM，∴BM＝MH＝BD•sin．∴BF+BE＝BH＝2n•sin．2．【解答】解：（1）如图1中，∵△ABC∽△B'BA∽△C'AC，∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC×BC＝BC2，故答案为BC2．（2）不成立．理由：如图2中当∠BAC为锐角时，BB′+CC′﹣B′C′＝BC，且△ABC∽△B'BA∽△C'AC，∴∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC2+BC•B′C′．图3中∠BAC为钝角时，BB′+CC′+B′C′＝BC．AB2+AC2＝BC（BB′+CC′）＝BC2﹣BC•B′C′．（3）当AB＝5，AC＝6，BC＝9时，则AB2+AC2＜BC2，可知△ABC为钝角三角形，由图3可知：AB2+AC2＝BC2﹣BC•B′C′，∴52+62＝92﹣9B′C′，∴B′C′＝．3．【解答】解：（1）∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，∴∠ABC＝∠CAB＝45°＝∠CDE＝∠CED，∴AC＝BC，CD＝CE，∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD，∠CAB＝∠CBE＝45°，∴∠DBE＝∠ABC+∠CBE＝90°，＝1，故答案为：1，90°（2），∠DBE＝90°理由如下：∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴∠ACD＝∠BCE，∠CED＝∠ABC＝30°∴tan∠ABC＝tan30°＝＝∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴Rt△ACB∽Rt△DCE∴∴，且∠ACD＝∠BCE∴△ACD∽△BCE∴＝，∠CBE＝∠CAD＝60°∴∠DBE＝∠ABC+∠CBE＝90°（3）若点D在线段AB上，如图，由（2）知：＝，∠ABE＝90°∴BE＝AD∵AC＝2，∠ACB＝90°，∠CAB＝90°∴AB＝4，BC＝2∵∠ECD＝∠ABE＝90°，且点M是DE中点，∴CM＝BM＝DE，∵△CBM是直角三角形∴CM2+BM2＝BC2＝（2）2，∴BM＝CM＝∴DE＝2∵DB2+BE2＝DE2，∴（4﹣AD）2+（AD）2＝24∴AD＝+1∴BE＝AD＝3+若点D在线段BA延长线上，如图同理可得：DE＝2，BE＝AD∵BD2+BE2＝DE2，∴（4+AD）2+（AD）2＝24，∴AD＝﹣1∴BE＝AD＝3﹣综上所述：BE的长为3+或3﹣4．【解答】解：（1）∵△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，∴AD＝BD＝DC，∠BDA＝90°，∵四边形DFGE是正方形，∴DE＝DF，∠EDF＝90°，∴∠BDE＝∠ADF＝90°，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF故答案为：BE＝AF；（2）成立；理由如下：当正方形DFGE在BC的上方时，如图②所示，连接AD，∵在Rt△ABC中，AB＝AC，D为斜边BC的中点，∴AD＝BD，AD⊥BC，∴∠ADE+∠EDB＝90°，∵四边形DFGE为正方形，∴DE＝DF，且∠EDF＝90°，∴∠ADE+∠ADF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；当正方形DFGE在BC的下方时，连接AD，如图③所示：∵∠BDE＝∠BDF+90°，∠ADF＝∠BDF+90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；综上所述，（1）中的结论BE＝AF成立；（3）在△ADE中，∵AE＜AD+DE，∴当点A、D、E共线时，AE取得最大值，最大值为AD+DE．如图④所示：则AD＝BC＝1，DE＝DF＝2，∴AE＝AD+DE＝3，即AE的最大值为3．5．【解答】解：（1）如图1，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是正方形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（2）（1）的结论成立；理由：如图2，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是菱形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（3）如图3，过点O作OG⊥AB于G，OH⊥AD于H，∴∠OGE＝∠OHF＝90°，∴∠BAD+∠GOH＝180°，∵∠BAD+∠EOF＝180°，∴∠GOH＝∠EOF，∴△EOG∽△FOH，∴，∵O是▱ABCD的对角线的交点，∴S△AOB＝S△AOD，∵S△AOB＝AB•OG，S△AOD＝AD•OH，∴AB•OG＝AD•OH，∴＝，∴．6．【解答】解：（1）①∵四边形ABCD是正方形，∴∠BCD＝90°，∠BCA＝45°，∵GE⊥BC、GF⊥CD，∴∠CEG＝∠CFG＝∠ECF＝90°，∴四边形CEGF是矩形，∠CGE＝∠ECG＝45°，∴EG＝EC，∴四边形CEGF是正方形；②由①知四边形CEGF是正方形，∴∠CEG＝∠B＝90°，∠ECG＝45°，∴＝，GE∥AB，∴＝＝，故答案为：；（2）连接CG，由旋转性质知∠BCE＝∠ACG＝α，在Rt△CEG和Rt△CBA中，＝cos45°＝、＝cos45°＝，∴＝＝，∴△ACG∽△BCE，∴＝＝，∴线段AG与BE之间的数量关系为AG＝BE；（3）∵∠CEF＝45°，点B、E、F三点共线，∴∠BEC＝135°，∵△ACG∽△BCE，∴∠AGC＝∠BEC＝135°，∴∠AGH＝∠CAH＝45°，∵∠CHA＝∠AHG，∴△AHG∽△CHA，∴＝＝，设BC＝CD＝AD＝a，则AC＝a，则由＝得＝，∴AH＝a，则DH＝AD﹣AH＝a，CH＝＝a，∴＝得＝，解得：a＝3，即BC＝3，故答案为：3．7．【解答】解：（1）如图1，连接AE，∵AB＝AC＝2，点E分别是BC的中点，∴AE⊥BC，∴∠BEC＝90°，∵AB＝AC＝2，∠BAC＝120°，∴∠B＝∠C＝30°，在Rt△ABE中，AE＝AB＝1，根据勾股定理得，BE＝∵点E是BC的中点，∴BC＝2BE＝2，∴＝＝，∵点D是AC的中点，∴AD＝CD＝AC＝1，∴＝＝，故答案为：，；（2）无变化，理由：由（1）知，CD＝1，CE＝BE＝，∴＝，，∴＝，由（1）知，∠ACB＝∠DCE＝30°，∴∠ACD＝∠BCE，∴△ACD∽△BCE，∴，（3）当点D在线段AE上时，如图2，过点C作CF⊥AE于F，∠CDF＝180°﹣∠CDE＝60°，∴∠DCF＝30°，∴DF＝CD＝，∴CF＝DF＝，在Rt△AFC中，AC＝2，根据勾股定理得，AF＝＝，∴AD＝AF+DF＝，由（2）知，，∴BE＝AD＝当点D在线段AE的延长线上时，如图3，过点C作CG⊥AD交AD的延长线于G，∵∠CDG＝60°，∴∠DCG＝30°，∴DG＝CD＝，∴CG＝DG＝，在Rt△ACG中，根据勾股定理得，AG＝，∴AD＝AG﹣DG＝，由（2）知，，∴BE＝AD＝即：线段BE的长为或．8．【解答】解：（1）证明：∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；故答案为：等边；（2）存在，当6＜t＜10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，由（1）知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD+4，由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝2，∴△BDE的最小周长＝CD+4＝2+4；（3）存在，①∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意，②当0≤m＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°，由（1）可知，△CDE是等边三角形，∴∠DEB＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA﹣DA＝6﹣4＝2，∴m＝2；③当6＜m＜10时，由∠DBE＝120°＞90°，∴此时不存在；④当m＞10时，由旋转的性质可知，∠DBE＝60°，又由（1）知∠CDE＝60°，∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，而∠BDC＞0°，∴∠BDE＞60°，∴只能∠BDE＝90°，从而∠BCD＝30°，∴BD＝BC＝4，∴OD＝14，∴m＝14，综上所述：当m＝2或14时，以D、E、B为顶点的三角形是直角三角形．9．【解答】解：（1）如图1中，连接DB，MF，CE，延长BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠ABD+∠ADB＝90°，∠ADB＝∠CDH，∴∠ADH+∠DCH＝90°，∴∠CHD＝90°，∴EC⊥BH，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．故答案为：45°（2）：如图2中，连接MF，EC，BD．设EC交AB于O，BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠AOC+∠ACO＝90°，∠AOC＝∠BOH，∴∠OBH+∠BOH＝90°，∴∠BHO＝90°，∴EC⊥BD，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．（3）：如图3中，如图以A为圆心AD为半径作⊙A．当直线PB与⊙A相切时，此时∠CBP的值最小，点P到BC的距离最小，即△BCP的面积最小，∵AD＝AE，AB＝AC，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE＝∠ABD，BD＝EC，∵∠ABD+∠AOB＝90°，∠AOB＝∠CPO，∴∠CPB＝90°，∵PB是⊙A的切线，∴∠ADP＝90°，∵∠DPE＝∠ADP＝∠DAE＝90°，∴四边形ADPE是矩形，∵AE＝AD，∴四边形ADPE是正方形，∴AD＝AE＝PD＝PE＝2，BD＝EC＝＝2，∴PC＝2﹣2，PB＝2+2，∴S△BCP的最小值＝×PC×PB＝（2﹣2）（2+2）＝4．10．【解答】（1）解：AC⊥BD，理由如下：连接AC、BD，如图2所示：∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，故答案为：AC⊥BD；（2）解：AD2+BC2＝AB2+CD2；理由如下：如图1，已知四边形ABCD中，AC⊥BD，设BD、AC相交于E，∵AC⊥BD，∴∠AED＝∠AEB＝∠BEC＝∠CED＝90°，由勾股定理得，AD2+BC2＝AE2+DE2+BE2+CE2，AB2+CD2＝AE2+BE2+CE2+DE2，∴AD2+BC2＝AB2+CD2；（3）解：如图3，连接CG、BE，∵四边形ACFG和四边形ABDE是正方形，∴AC＝AG，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，即CE⊥BG，由（2）得，CG2+BE2＝CB2+GE2，在Rt△ABC中，AC＝4，AB＝5，根据勾股定理得，BC2＝52﹣42＝9，∵CG和BE分别是正方形ACFG和正方形ABDG的对角线，∴CG2＝42+42＝32，BE2＝52+52＝50，∴GE2＝CG2+BE2﹣CB2＝32+50﹣9＝73，∴GE＝．11．【解答】解：问题发现：如图1中，结论：AE＝2BH，AE⊥BH．理由：在Rt△ABC中，∵BC＝6，∠A＝30°，∴AE＝2BC＝12，在Rt△CDB中，∵∠DCB＝30°，∴CD＝＝4，∵CH＝DH，∴BH＝CD＝2，∴＝＝2，∴AE＝2BH．故答案为AE⊥BH，AE＝2BH．问题证明：如图2中，（1）中结论成立．理由：延长BH到F使得HF＝BH，连接CF．设AE交BF于O．∵CH＝DH，BH＝HF，∠CHF＝∠BHD，∴△CHF≌△DHB（SAS），∴BD＝CF，∠F＝∠DBH，∴CF∥BD，∵AB＝BC，BE＝BD，∴BE＝CF，∴＝＝，∵CF∥BD，∴∠BCF+∠CBD＝180°，∵∠ABC+∠DBE＝∠ABD+∠CBD+∠CBD+∠CBE＝∠CBD+∠ABE＝180°，∴∠BCF＝∠ABE，∴△ABE∽△BCF，∴∠CBF＝∠BAE，＝＝，∴AE＝BF＝2BH，∵∠CBF+∠ABF＝90°，∴∠ABF+∠BAE＝90°，∴∠AOB＝90°，∴BH⊥AE．拓展应用：如图3﹣1中，当DE在BC的下方时，延长AB交DE于F．∵DE∥BC∴∠ABC＝∠BFD＝90°，由题意BC＝BE＝6，AB＝6，BD＝2，DE＝4，∵•BD•BE＝•DE•BF，∴BF＝＝3，∴EF＝BF＝3，∴AF＝6+3，∴AE2＝AF2+EF2＝（6+3）2+（3）2＝144+36．∵AE＝2BH，∴AE2＝12BH2，∴BH2＝12+3如图3﹣2中，当DE在BC的上方时，同法可得AF＝6﹣3，EF＝3，∴BH2＝＝（＝12﹣3．12．【解答】解：（1）如图1中，作EH⊥CG于H．∵四边形ECFG是菱形，∠ECF＝60°，∴∠ECH＝∠ECF＝30°，EC＝EG，∵EH⊥CG，∴GH＝CG，∴＝cos30°＝，∴＝2•＝，∵EG∥CD，AB∥CD，∴GE∥AB，∴＝＝．故答案为．（2）结论：AG＝BE．理由：如图2中，连接CG．∵四边形ABCD，四边形ECFG都是菱形，∠ECF＝∠DCB＝60°，∴∠ECG＝∠EGC＝∠BCA＝∠BAC＝30°，∴△ECG∽△BCE，∴＝，∵∠ECB＝∠GCA，∴△ECB∽△GCA，∴＝＝，∴AG＝BE．（3）如图3中，∵∠AGH＝∠CGF＝30°．∠AGH＝∠GAC+∠GCA，又∵∠DAC＝∠HAG+∠GAC＝30°，∴∠HAG＝∠ACH，∵∠AHG＝∠AHC，∴△HAG∽△HCA，∴HA：HC＝GH：HA，∴AH2＝HG•HC，∴FC＝2，CG＝CF，∴GC＝2，∵HG＝，∴AH2＝HG•HC＝•3＝9，∵AH＞0，∴AH＝3．故答案为3．13．【解答】解：（1）当m＝n时，即：BC＝AC，∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴＝1，∴＝1（2）①∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴②成立．如图，∵∠ACB＝90°，∴∠A+∠ABC＝90°，又∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE+∠CDE＝∠ADC+∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴．（3）由（2）有，△ADE∽△CDF，∵＝，∴＝，∴CF＝2AE，在Rt△DEF中，DE＝2，DF＝4，∴EF＝2，①当E在线段AC上时，在Rt△CEF中，CF＝2AE＝2（AC﹣CE）＝2（﹣CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（﹣CE）]2＝40∴CE＝2，或CE＝﹣（舍）而AC＝＜CE，∴此种情况不存在，②当E在AC延长线上时，在Rt△CEF中，CF＝2AE＝2（AC+CE）＝2（+CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（+CE）]2＝40，∴CE＝，或CE＝﹣2（舍），③如图1，当点E在CA延长线上时，CF＝2AE＝2（CE﹣AC）＝2（CE﹣），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（CE﹣）]2＝40，∴CE＝2，或CE＝﹣（舍）即：CE＝2或CE＝．14．【解答】解：（1）如图1，延长GM交AD于H，∵AD∥GF，∴∠GFM＝∠HAM，在△FMG和△AMH中，，∴△FMG≌△AMH（ASA），∴HM＝GM，AH＝FG，∵AD＝CD，AH＝FG＝CG，∴DH＝DG，∵∠HDG＝90°，HM＝GM，∴DM＝MG，DM⊥MG，故答案为DM＝MG，DM⊥MG．（2）结论成立：DM＝MG，DM⊥MG，理由：如图2中，延长GM使得MH＝GM，连接AH、DH、DG，延长AD交GF的延长线于N，交CD于O．∵AM＝MF，∠AMH＝∠FMG，MH＝MG，∴△AMH≌△FMG（SAS），∴AH＝GF＝CG，∠AHM＝∠FGM，∴AH∥GN，∴∠HAD＝∠N，∵∠ODN＝∠OGC＝90°，∠DON＝∠GOC，∴∠N＝∠OCG，∴∠HAD＝∠DCG，∵AH＝CG，AD＝CD，∴△HAD≌△GCD（SAS），∴DH＝DG，∠HDA＝∠CDG，∴∠HDG＝∠ADC＝90°，∴△HDG是等腰直角三角形，∵MH＝MG，∴DM⊥GH，DM＝MH＝MG，（3）①如图3﹣1中，连接AC．在Rt△ABC中，AC＝＝10，在Rt△ACE中，AE＝＝14，∴AF＝AE＝EF＝14﹣2＝12，∴FM＝AM＝AF＝6，在Rt△MGF中，MG＝＝2，∴S△DMG＝×2×2＝20，②如图3﹣2中，连接AC．同法可得AE＝14，AF＝16，FM＝8，MG＝＝2，∴S△DMG＝×2×2＝34，综上所述，满足条件的△DMG的面积为20或34．15．【解答】解：（1）由旋转可得：AC＝A'C＝2，∵∠ACB＝90°，AB＝，AC＝2，∴BC＝，∵∠ACB＝90°，m∥AC，∴∠A'BC＝90°，∴cos∠A'CB＝＝，∴∠A'CB＝30°，∴∠ACA'＝60°；（2）∵M为A'B'的中点，∴∠A'CM＝∠MA'C，由旋转可得，∠MA'C＝∠A，∴∠A＝∠A'CM，∴tan∠PCB＝tan∠A＝，∴PB＝BC＝，∵∠PCQ＝∠PBC＝90°，∴∠BQC+∠BPC＝∠BCP+∠BPC＝90°，∴∠BQC＝∠BCP＝∠A，∴tan∠BQC＝tan∠A＝，∴BQ＝BC×＝2，∴PQ＝PB+BQ＝；（3）∵S四边形P A'B′Q＝S△PCQ﹣S△A'CB'＝S△PCQ﹣，∴S四边形P A'B′Q最小，即S△PCQ最小，∴S△PCQ＝PQ×BC＝PQ，法一：（几何法）取PQ的中点G，∵∠PCQ＝90°，∴CG＝PQ，即PQ＝2CG，当CG最小时，PQ最小，∴CG⊥PQ，即CG与CB重合时，CG最小，∴CG min＝，PQ min＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣；法二（代数法）设PB＝x，BQ＝y，由射影定理得：xy＝3，∴当PQ最小时，x+y最小，∴（x+y）2＝x2+2xy+y2＝x2+6+y2≥2xy+6＝12，当x＝y＝时，“＝”成立，∴PQ＝+＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣．16．【解答】解：（1）结论：△PMN是等边三角形．理由：如图1中，∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∵AD＝AE，∴BD＝EC，∵PB＝PC，CN＝ND，BM＝EM，∴PN∥BD，PM∥EC，PN＝BD，PM＝EC，∴PM＝PN，∠NPC＝∠ABC＝60°，∠MPB＝∠ACB＝60°，∴∠MPN＝60°，∴△PMN是等边三角形，故答案为等边三角形．（2）△PMN的形状不发生改变，仍为等边三角形，理由如下：如图2中，连接BD，CE．由旋转可得∠BAD＝∠CAE，∵△ABC是等边三角形，∴AB＝AC，∠ACB＝∠ABC＝60°又∵AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE，∠ABD＝∠ACE，∵M是BE的中点，P是BC的中点，∴PM是△BCE的中位线，∴PM＝，且PM∥CE．同理可证PN＝BD且PN∥BD，∴PM＝PN，∠MPB＝∠ECB，∠NPC＝∠DBC，∴∠MPB+∠NPC＝∠ECB+∠DBC＝（∠ACB+∠ACE）+（∠ABC﹣∠ABD）＝∠ACB+∠ABC＝120°，∴∠MPN＝60°，∴△PMN是等边三角形．（3）∵PM＝EC，∴当EC最大时，等边△PMN的周长最大，∵EC≤AE+AC，∴EC≤8，∴PM≤4，∴PM的最大值为4，∴△PMN的周长的最大值为12．17．【解答】解：（1）∵AB＝AC，∠ABC＝60°，∴∠BAC＝60°，∵AD＝AE，∠ADE＝70°，∴∠DAE＝180°﹣2∠ADE＝40°，∴α＝∠BAD＝60°﹣40°＝20°，∴∠ADC＝∠BAD+∠ABD＝60°+20°＝80°，∴β＝∠CDE＝∠ADC﹣∠ADE＝10°，故答案为：20，10；（2）设∠ABC＝x，∠AED＝y，∴∠ACB＝x，∠AED＝y，在△DEC中，y＝β+x，在△ABD中，α+x＝y+β＝β+x+β，∴α＝2β；（3）①当点E在CA的延长线上，点D在线段BC上，如图1设∠ABC＝x，∠ADE＝y，∴∠ACB＝x，∠ACE＝y，在△ABD中，x+α＝β﹣y，在△DEC中，x+y+β＝180°，∴α＝2β﹣180°，②当点E在CA的延长线上，点D在CB的延长线上，如图2，同①的方法可得α＝180°﹣2β．18．【解答】解：（1）由旋转变换的性质可知，∠CAE＝90°，AC＝AE，∴△ACE为等腰直角三角形，∴CE＝AC，∵CE＝CD+DE＝CD+BC，∴BC+CD＝AC，故答案为：等腰直角；BC+CD＝AC；（2）延长CO交⊙O于E，连接AE、BE、DE，则∠CDE＝90°，∵点C为的中点，∴点E为的中点，∴EA＝EB，∵AB为⊙O的直径，∴∠ADB＝90°，由（1）得，DE＝（AD+BD），由勾股定理得，CD2＝CE2﹣DE2＝AD2+BD2﹣（AD+BD）2＝（AD﹣BD）2，∴CD＝（BD﹣AD）；（3）如图3，当点E在直线AC的左侧时，连接CQ、PC，∵CA＝CB，点P为AB的中点，∴CP⊥AB，∵CA＝CE，点Q为AE中点，∴CQ⊥AE，AQ＝QE＝AE＝5，∴由勾股定理得，CQ＝＝12，由（1）得，AQ+CQ＝PQ，。