成桥预拱度计算方法

桥博预拱度计算
连续刚构预拱度分为施工预拱度和成桥预拱度，设置施工预拱度主要为了消除施工过程中各种荷载对成桥线形的影响，设置成桥预拱度主要为了消除后期运营过程中后期收缩、徐变、后期预应力损失及汽车荷载对桥面线形的影响。

采用挂篮悬臂浇筑的连续刚构桥在设置施工预拱度时应考虑下表所列因素的影响：
表连续刚构桥施工预拱度的主要影响因素
采用挂篮悬臂浇筑连续刚构桥，其成桥预拱度应考虑下表所列因素的影响：。

成桥预拱度设置的正交多项式拟合法随着城市化进程的加快，城市交通拥堵问题愈加突出，因此高速公路建设越来越受到社会的关注。

在高速公路桥梁的设计和施工中，桥梁的预测弯度和预拱度的准确预测和控制非常重要，影响着整个桥梁的安全和使用寿命。

然而，传统的预测方法受到现场实际环境的影响很大，存在许多不确定因素。

本文提出了一种基于正交多项式拟合法的预测方法，能够较准确地预测桥梁的预测弯度和预拱度，可为桥梁设计和施工提供重要的科学依据。

正交多项式拟合法是利用正交多项式的性质进行函数拟合的一种方法。

其基本思想是将自变量x用正交多项式表示，并将拟合函数表示为正交多项式的线性组合。

由于正交多项式具有自身的特殊性质，因此可以较好地满足预测精度和拟合效果的要求。

在实际研究中，利用正交多项式拟合法可以有效地预测一些物理现象的变化趋势和规律。

桥梁的预拱度设置是桥梁设计中的重要环节之一，不仅决定着桥梁的结构形态，同时也影响着桥梁的受力性能。

在成桥预拱度设置中，我们可以利用正交多项式拟合法进行预测和控制。

具体实现步骤如下：1.选取适当的自变量和正交多项式：根据桥梁的结构形态和实际情况，选取合适的自变量和正交多项式。

在实际研究中，我们通常选取桥梁的跨度、跨径比、荷载等作为自变量，并采用对应的正交多项式进行拟合。

2.确定拟合函数：根据实际需要，确定需要拟合的函数形式，常见的包括多项式、指数函数等。

在成桥预拱度设置中，我们通常采用二次函数或三次函数进行拟合。

3.确定拟合系数：通过对样本数据进行拟合，计算出拟合函数的系数，这些系数可以反映出桥梁预拱度的变化规律。

4.预测预拱度：利用拟合函数和拟合系数，可以预测出不同自变量取值下桥梁的预拱度。

同时还可以根据拟合精度和实际情况对拟合函数进行调整和优化，以提高预测和控制的准确性。

三、总结正交多项式拟合法是一种较为有效的预测方法，可以适用于许多物理现象的研究和预测。

在成桥预拱度设置中，采用正交多项式拟合法能够较好地预测桥梁的预拱度变化趋势和规律，有效地控制桥梁的结构形态和受力性能。

预拱度问题一般讨论1、什么是预拱度？（或为什么要计算预拱度）为了得到成桥线形而在施工阶段预先设置的施工高差，最常见的是预抛高设置。

注意事项：模型建立时的坐标点就是成桥的目标控制线形。

预拱度是相对于成桥目标控制线形的相对高差值。

2、预拱度分类及针对的工程类型目前程序提供的预拱度计算有两种：施工预拱度和制作预拱度施工预拱度针对的是悬浇施工的混凝土梁；制作预拱度针对的是悬拼施工的混凝土梁和钢梁。

3、预拱度在程序中的计算方法施工预拱度：施工每个悬臂段时，该阶段的每个控制位置都对应一个施工预拱度（预抛高），该预拱度=从激活阶段到成桥阶段所有施工荷载引起的该点处位移的累计值，符号反号。

对应成桥阶段该点合计下的累计位移值反号。

制作预拱度：该预拱度=从激活阶段到成桥阶段所有施工荷载和初始切向位移引起的该点处位移的累计值，符号反号。

对应成桥阶段该点合计下的实际位移值反号。

要得到制作预拱度必须在施工阶段分析控制中选择考虑所有构件的初始切向位移。

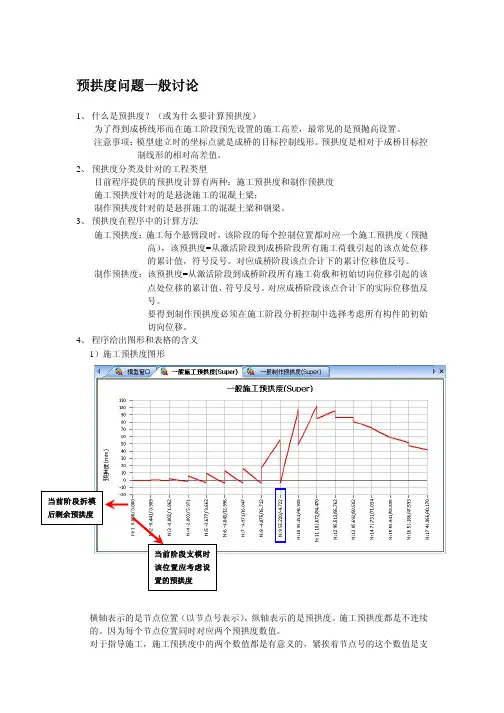
4、程序给出图形和表格的含义1）施工预拱度图形横轴表示的是节点位置（以节点号表示），纵轴表示的是预拱度。

施工预拱度都是不连续的。

因为每个节点位置同时对应两个预拱度数值。

对于指导施工，施工预拱度中的两个数值都是有意义的，紧挨着节点号的这个数值是支模时预拱度，用于控制支模标高。

紧挨图表的数字表示混凝土达到强度拆除模板时该位置的残留预拱度，这两个数值都是相对于成桥控制线形而言的相对高差。

以图示的节点9而言，支模时标高高于成桥控制线形55.22mm，当前阶段结束时，拆模该点的标高低于成桥控制线形4.722mm。

* 支模标高=成桥时（或最后一个施工阶段）该点的累加位移反号；拆模标高=（成桥时累加位移—该点激活阶段最终步骤累加位移）反号。

累加位移是施工阶段作用荷载引起的结构的纯位移，关于midas中三种位移结果的含义请查看midas的在线帮助或相关技术资料。

2）施工预拱度表格每一列对应一个节点在各个施工阶段所设的预拱度值。

5.5.1 成桥预拱度计算方法目前，由于对混凝土徐变的计算，不论是老化理论，修正老化理论还是规范规定的计算方法，都难以正确地估算混凝土徐变的影响，在施工中对这一影响不直接识别、修正，通常是用以往建成的同类跨径的下挠量来类比的，并且通过立模标高的预留来实现的。

因此，成桥预拱度合理设置尤为重要。

根据近几年来工程实践检验，后期混凝土收缩、徐变对中孔跨中挠度影响约为L/500~L/1000（L：中孔跨径），边孔最大挠度一般发生在3/4L处，约为中孔最大挠度1/4。

另外，连续刚构桥边中跨比例0.52~0.6，桥墩采用柔性墩。

在后期运营中向跨中方向产生位移，刚构墩、梁固结，由变形协调可知，转角位移使边孔上挠。

中孔跨中下挠。

因此，边跨成桥预拱度一般设置较小，在3/4L处设置fc/4预拱度（fc：中孔跨中成桥预拱度）。

根据陕西省连续刚构桥成桥预拱度计算方法：“中跨预拱度在设计预拱度的基础上，按L/1000+1/2d2(L为中跨跨径，d2为活载挠度)提高预拱度（最大挠度在跨中），边跨预拱度按中跨最大挠度1/4计算，边跨最大挠度在3/4L处。

其余各点按余弦曲线分配。

在中孔跨中fc确定后，中孔其余各点按y=fc/2(1-cos(2πx/L))进行分配。

边孔3/4L处成桥预拱度取中孔跨中成桥预拱度fc的1/4，边孔其余各点按余弦曲线分配。

原因：(1)余弦曲线在墩顶两曲线连接处切线斜率为零，满足平顺要求；(2)余弦曲线在L/4处预拱度为跨中预拱度1/2，与有限元计算吻合。

1．活载挠度计算1) 荷载等级：公路—Ⅰ；2) 车道系数：三车道，车道折减系数0.78；3) 中跨活载最大挠度： d 2＝0.029m;A 曲线：1cos()290y =-⎢⎥⎣⎦ (090x ≤≤) B 曲线：21cos()261fc x y π⎡⎤=-⎢⎥⎣⎦ (22.553x ≤≤) C 曲线：21cos()245fc x y π⎡⎤=-⎢⎥⎣⎦(022.5x ≤≤) 5.5.2 施工预拱度的计算方法不论采用什么施工方法，桥梁结构在施工过程中总要产生变形，并且结构的变形将受到诸多因素的影响，极易使桥梁结构在施工过程中的实际位置（立面标高、平面位置）状态偏离预期状态，使桥梁难以顺利合拢，或成桥线形与设计要求不符，所以必须对桥梁进行施工控制，使其在施工中的实际位置状态与预期状态之间的误差在容许范围和成桥状态符合设计要求。

三跨钢构的成桥预拱度全文共四篇示例，供读者参考第一篇示例：随着现代钢结构技术的不断发展，三跨钢构桥在桥梁工程中得到了广泛的应用。

在桥梁设计和施工过程中，成桥预拱度是一个十分重要的参数，它直接影响着桥梁的稳定性和承载能力。

本文将就三跨钢构的成桥预拱度进行探讨。

一、三跨钢构桥的概念三跨钢构桥是指桥梁结构中跨度为三的桥梁，通常由两个主跨和一个中间的辅跨组成。

这种桥梁结构设计简洁、经济，适用于跨度较大的公路和铁路桥梁。

三跨钢构桥因其较大的跨度和结构合理性，能够有效地满足不同地理环境和交通要求，得到了广泛应用。

二、成桥预拱度的定义成桥预拱度是指在桥梁施工完成后，桥梁自重和温度变化引起的桥面变形、拱度变化。

在桥梁施工过程中，桥梁结构需要经历多次施工荷载的作用，桥面、支座和梁体等部位会因此发生一定的变形。

通过对这些变形情况进行分析，就可以得到桥梁的成桥预拱度。

三、影响三跨钢构桥成桥预拱度的因素1. 桥梁结构形式：桁架式、悬索式、悬臂式等不同的桥梁结构形式会对成桥预拱度产生不同的影响。

2. 桥梁跨度：桥梁跨度越大，成桥预拱度越大，因为跨度较大的桥梁在施工过程中会受到更大的荷载作用。

3. 施工工艺：施工工艺的不同会导致桥梁结构的变形程度不同，从而影响成桥预拱度。

4. 材料弹性模量：材料的弹性模量会影响桥梁的刚度和变形能力，从而对成桥预拱度产生影响。

五、结语通过对三跨钢构桥的成桥预拱度进行分析和探讨，可以更好地理解和掌握桥梁工程中的关键参数。

合理设计桥梁结构、控制跨度、优化施工工艺和选用合适的材料，是减小成桥预拱度的有效途径。

只有在减小成桥预拱度的基础上，才能确保桥梁结构的稳定性和承载能力，从而保障桥梁的安全运行和使用。

愿本文能够为相关从业者提供一些参考和启示，推动三跨钢构桥在桥梁工程中的进一步发展和应用。

第二篇示例：三跨钢构桥是一种常见的桥梁结构形式，通常由三跨钢梁和桥面铺装构成。

在桥梁设计和施工中，预拱度是一个非常重要的参数，它直接影响着桥梁的受力性能和整体稳定性。

预拱度的设置一、基本原理1、预拱度的设置只针对桥面系，考虑的是行车时线路的平顺性。

2、预拱度的设置只考虑恒载与活载，不考虑温度及支座沉降。

其中，恒载：结构自重、预应力、二期恒载、收缩徐变（对混凝土梁）。

由于收缩徐变跟时间有关，预拱度分成桥及成桥3年后两种，一般以成桥3年后为准。

活载：按静活载考虑。

3、针对简支结构预拱度值= —（恒载挠度+0.5*静活载最大挠度）即保证不行车时结构上拱0.5*静活载最大挠度，行车最大时结构下挠0.5*静活载最大挠度。

4、针对连续结构预拱度值有两种设法，不同之处在于对活载的处理，目前没有统一。

预拱度值1 = —[恒载挠度+0.5*静活载(最大挠度+最小挠度)]预拱度值2 = —[恒载挠度+0.5*静活载最大挠度]方法1理由如下：火车过桥时，结构各点位移可上可下，直接取下值会使得预拱度过大，取两者平均值切合实际。

由于简支结构最小挠度为0，该方法针对简支结构也能说通。

方法2理由如下：火车过桥时，某处发生最小挠度时表明火车还没有到达该处，此时的挠度对火车走行没有影响，而火车到达该处时一般挠度达到最大值，因此该值才具备实际意义。

实际上火车是由一节节车厢组成，而不是一个移动的集中荷载，因此两种做法不好判别，目前公司说做的连续结构均按第一种办法。

二、施工方案对预拱度的影响针对常规的混凝土结构和钢结构，计算程序及预拱度设置均遵循小变形假定，均即结构形状的微小改变不影响结构受力及位移，程序各阶段处理结构内力及变位时均按直线计算，但是结构的总变形是各阶段的累计（计入位移及转角）。

预拱度= - [最后恒载挠度（成桥3年）+1/2静活载挠度]立模标高= 线路标高+预拱度也就是说，每个节点（梁段）第一次出现（不受力，标高即模板标高）时，按照（线路标高+预拱度）立模，施工完成后得到的就是设计线形，一次成桥如此，悬臂施工及支架施工也是如此。

三、钢梁的预拱度使得桥面节点加工（平躺时）的坐标等于预拱度值即可，方法可多种。

钢箱梁制作预拱度计算钢箱梁是一种常用的桥梁结构，由于其结构的特殊性，预拱度计算对于钢箱梁的设计和施工至关重要。

本文将详细介绍钢箱梁制作预拱度计算的方法。

钢箱梁作为一种常用的桥梁结构，在桥梁工程中得到了广泛应用。

它由上、下翼板和纵向隔板组成，具有结构稳定、承载能力强等优点。

在钢箱梁的制作过程中，预拱度计算是一个重要的环节，它能够保证钢箱梁在荷载作用下具有合适的拱度，从而确保桥梁的安全使用。

我们需要了解预拱度的概念。

预拱度是指在制作钢箱梁时，在其两端进行适当的抬高，使得钢箱梁在自身重力以及荷载作用下能够呈现出合适的拱形。

这样可以减小桥梁所受的弯矩和剪力，提高其承载能力和抗震性能。

钢箱梁的预拱度计算需要考虑多个因素，包括桥梁的跨度、荷载类型和荷载大小等。

在计算过程中，通常采用有限元方法进行模拟分析，通过求解结构的位移和应力分布来确定合适的预拱度。

具体而言，预拱度计算可以分为以下几个步骤：1. 确定桥梁的跨度。

桥梁的跨度是指两个支点之间的水平距离，是预拱度计算的基本参数之一。

2. 确定荷载类型和荷载大小。

根据桥梁所处的位置和用途，确定合适的荷载类型，如活载、恒载和附加荷载等。

同时还需要考虑荷载的大小，通常通过设计标准或者实际测量得到。

3. 建立钢箱梁的有限元模型。

通过计算机软件，将钢箱梁的几何形状、材料特性和边界条件等输入到模型中，建立起一个准确的结构模型。

4. 进行荷载分析。

在有限元模型的基础上，施加相应的荷载，进行荷载分析。

通过求解结构的位移和应力分布，得到钢箱梁在荷载作用下的变形情况。

5. 确定合适的预拱度。

根据荷载分析的结果，结合设计要求和实际情况，确定合适的预拱度。

通常可以通过试错法或者经验公式进行求解。

需要注意的是，在进行预拱度计算时，还应考虑到钢箱梁的施工工艺和材料特性等因素。

例如，钢箱梁在制作过程中可能会发生塑性变形，因此需要对预拱度进行适当的修正。

钢箱梁制作预拱度计算是桥梁工程中的关键环节。

5.5.1 成桥预拱度计算方法目前，由于对混凝土徐变的计算，不论是老化理论，修正老化理论还是规范规定的计算方法，都难以正确地估算混凝土徐变的影响，在施工中对这一影响不直接识别、修正，通常是用以往建成的同类跨径的下挠量来类比的，并且通过立模标高的预留来实现的。

因此，成桥预拱度合理设置尤为重要。

根据近几年来工程实践检验，后期混凝土收缩、徐变对中孔跨中挠度影响约为L/500~L/1000（L：中孔跨径），边孔最大挠度一般发生在3/4L处，约为中孔最大挠度1/4。

另外，连续刚构桥边中跨比例0.52~0.6，桥墩采用柔性墩。

在后期运营中向跨中方向产生位移，刚构墩、梁固结，由变形协调可知，转角位移使边孔上挠。

中孔跨中下挠。

因此，边跨成桥预拱度一般设置较小，在3/4L处设置fc/4预拱度（fc：中孔跨中成桥预拱度）。

根据陕西省连续刚构桥成桥预拱度计算方法：“中跨预拱度在设计预拱度的基础上，按L/1000+1/2d2(L为中跨跨径，d2为活载挠度)提高预拱度（最大挠度在跨中），边跨预拱度按中跨最大挠度1/4计算，边跨最大挠度在3/4L处。

其余各点按余弦曲线分配。

在中孔跨中fc确定后，中孔其余各点按y=fc/2(1-cos(2πx/L))进行分配。

边孔3/4L处成桥预拱度取中孔跨中成桥预拱度fc的1/4，边孔其余各点按余弦曲线分配。

原因：(1)余弦曲线在墩顶两曲线连接处切线斜率为零，满足平顺要求；(2)余弦曲线在L/4处预拱度为跨中预拱度1/2，与有限元计算吻合。

1．活载挠度计算1) 荷载等级：公路—Ⅰ；2) 车道系数：三车道，车道折减系数0.78；3) 中跨活载最大挠度： d 2＝0.029m; 2．中跨最大预拱度的确定 210002L d fc =+＝0.09+0.0145＝0.1045m;3．余弦曲线成桥预拱度线形示意图各曲线函数表达如下：A 曲线：21cos()290fa x y π⎡⎤=-⎢⎥⎣⎦ (090x ≤≤) B 曲线：21cos()261fc x y π⎡⎤=-⎢⎥⎣⎦ (22.553x ≤≤) C 曲线：21cos()245fc x y π⎡⎤=-⎢⎥⎣⎦(022.5x ≤≤) 5.5.2 施工预拱度的计算方法不论采用什么施工方法，桥梁结构在施工过程中总要产生变形，并且结构的变形将受到诸多因素的影响，极易使桥梁结构在施工过程中的实际位置（立面标高、平面位置）状态偏离预期状态，使桥梁难以顺利合拢，或成桥线形与设计要求不符，所以必须对桥梁进行施工控制，使其在施工中的实际位置状态与预期状态之间的误差在容许范围和成桥状态符合设计要求。

施工预拱度计算
在桥梁悬臂施工的控制中，最困难的任务之一就是施工
预拱度的计算。

箱梁预拱度计算根据现场测定的各项参数由
专业程序计算得出并结合实际测量值进行比对：
①在第N#梁段混凝土灌注前，精确测量该梁段端头测
点的标高(即为段测点处的顶板施工立模标高)Ml。

②在第N#梁段混凝土灌注硬化后，精确测量该梁段端
头测点的标高M2。

③在第N#梁段纵向预应力束张拉前，精确测量该梁段
端头测点的标高M3。

④在第N#梁段纵向预应力束张拉压浆完成后、移挂篮前，精确测量该端头测点的标高M4。

⑤计算第N#梁段混凝土灌注前后测点的标高差d1=M2—Ml，以及该段纵向预应力束张拉压浆完成前后的标高差的d2=M4—M3。

将这两个标高差与线形控制软件计算得出的结果ΔMl、ΔM3分别进行比较，如果d1与ΔM 1、d2与ΔM3相比的误差都小于设计值，则按上述步骤进行下一梁段的施工；若两个误差值中有一个或两个都大于规定值，则需要从施工现场和数据文件两个方面查找产生差别的并修改相应的数据文件、输入微机、重新计算后，对下一梁段的立模实际标高进行修正。

按上述步骤不断循环，直至悬灌梁段施工完毕。

桥梁的制作预拱度和施工预拱度1. 概要在设计斜拉桥中，一般用成桥阶段模型估算结构的截面和索的截面、索的布置以及索的张力，用施工阶段模型分析并确定各施工阶段索的张力(如何调索)以及制作预拱度(Fabrication camber)和施工预拱度。

通过施工阶段分析可以确定构件在各施工阶段的应力，用户可通过调整测试施工阶段确定较优的施工方案。

在施工过程中，当沿着前一阶段施工的桥梁段的切线方向添加新的桥梁段时，对后续的节点会产生假想位移，结构真实的位移(Real displacement)也称为总位移是由自重和荷载作用的纯位移(net displacement)和假想位移构成的。

为了决定制作预拱度(Fabrication camber)，需要输出总位移结果。

本资料将说明制作预拱度和施工预拱度的概念，并说明在MIDAS/Civil中如何查看各施工阶段的总位移以及如何输出制作预拱度和施工预拱度。

2. 制作预拱度和施工预拱度的概念使用悬臂法施工的斜拉桥最重要课题的就是控制形状(位移控制，geometry control)。

有时为了减少徐变的影响会采用提前两个月左右预制桥梁段的方法，预制时会给桥梁段一定量的预拱度，使其在组装时不至于产生较大的应力。

制作预拱度 =最终线型 – 最终位移量 + 附加预拱度施工预拱度 =制作预拱度 + 到相应阶段的总位移图1. 制作预拱度概念图示在做施工阶段分析前一定要了解整个施工顺序和各阶段的荷载，因为当按预期的制作预拱度浇筑后，如果发生了意外的荷载或其他没有考虑到的情况，重新调整会很困难，所以斜拉桥的施工必须有专业的工程技术人员(construction engineering)进行严密的分析和验算。

图2中简单说明了制作预拱度和施工预拱度的差异。

图2(a)表现的是施工各桥梁段时的位移量。

在施工第2个桥梁段后，节点1和节点2的位移量(不包含施工桥梁段1时的位移量)分别为12δ和22δ，在节点3产生假想位移32δ(不包含施工桥梁段1时的假想位移量)。

钢箱梁制作预拱度计算钢箱梁是一种常用的桥梁结构，它由多个钢板焊接而成，具有较高的强度和刚度。

在制作钢箱梁的过程中，预拱度计算是一个至关重要的步骤。

本文将介绍钢箱梁预拱度计算的方法和步骤。

我们需要了解什么是预拱度。

预拱度是指在桥梁建造过程中，在桥梁支撑前，为了抵消最终荷载引起的变形而给桥梁构件施加的逆方向曲率。

预拱度的作用是使桥梁在最终使用状态下保持平直。

钢箱梁的预拱度计算一般分为以下几个步骤：1. 确定桥梁的几何形状：首先需要确定钢箱梁的几何形状，包括梁的长度、宽度、高度等参数。

这些参数将直接影响到预拱度计算的结果。

2. 确定材料的力学性质：钢箱梁的预拱度计算需要知道材料的力学性质，包括弹性模量、屈服强度等。

这些参数可以通过材料试验或者查阅相关资料得到。

3. 计算桥梁的刚度：在计算预拱度之前，需要先计算钢箱梁的刚度。

刚度是指单位载荷作用下的变形量。

通过计算钢箱梁的刚度，可以确定在不同荷载作用下的变形量。

4. 计算预拱度：根据钢箱梁的刚度和荷载作用下的变形量，可以计算出预拱度。

预拱度的计算一般使用弹性理论或者有限元分析方法。

5. 考虑其他因素：在进行预拱度计算时，还需要考虑其他因素的影响，如温度变化、施工误差等。

这些因素可能会引起桥梁的变形，需要在预拱度计算中进行修正。

需要注意的是，钢箱梁的预拱度计算是一个复杂的过程，需要考虑多个因素的综合作用。

因此，在进行预拱度计算时，需要仔细分析各项参数，并结合实际情况进行修正。

钢箱梁的预拱度计算是桥梁建造过程中必不可少的一步。

通过合理计算和施工，可以保证钢箱梁在最终使用状态下保持平直，提高桥梁的安全性和稳定性。

在实际工程中，预拱度计算是桥梁设计和施工过程中不可或缺的一环，需要经验丰富的工程师和技术人员进行准确计算和判断。

桥梁的制作预拱度和施工预拱度1. 概要在设计斜拉桥中，一般用成桥阶段模型估算结构的截面和索的截面、索的布置以及索的张力，用施工阶段模型分析并确定各施工阶段索的张力( 如何调索) 以及制作预拱度(Fabrication camber)和施工预拱度。

通过施工阶段分析可以确定构件在各施工阶段的应力，用户可通过调整测试施工阶段确定较优的施工方案。

在施工过程中，当沿着前一阶段施工的桥梁段的切线方向添加新的桥梁段时，对后续的节点会产生假想位移，结构真实的位移(Real displacement)也称为总位移是由自重和荷载作用的纯位移(net displacem ent)和假想位移构成的。

为了决定制作预拱度(Fabrication camber)，需要输出总位移结果。

本资料将说明制作预拱度和施工预拱度的概念，并说明在MIDAS/Civil中如何查看各施工阶段的总位移以及如何输出制作预拱度和施工预拱度。

2. 制作预拱度和施工预拱度的概念使用悬臂法施工的斜拉桥最重要课题的就是控制形状(位移控制，geometry control)。

有时为了减少徐变的影响会采用提前两个月左右预制桥梁段的方法，预制时会给桥梁段一定量的预拱度，使其在组装时不至于产生较大的应力。

制作预拱度= 最终线型–最终位移量+ 附加预拱度施工预拱度= 制作预拱度+ 到相应阶段的总位移在做施工阶段分析前一定要了解整个施工顺序和各阶段的荷载，因为当按预期的制作预拱度浇筑后，如果发生了意外的荷载或其他没有考虑到的情况，重新调整会很困难，所以斜拉桥的施工必须有专业的工程技术人员(construction engineering)进行严密的分析和验算。

图2中简单说明了制作预拱度和施工预拱度的差异。

图2(a)表现的是施工各桥梁段时的位移量。

在施工第2个桥梁段后，节点1和节点2的位移量(不包含施工桥梁段1时的位移量)分别为δ12和δ22,在节点3产生假想位移δ32(不包含施工桥梁段1时的假想位移量)。

3。

5挠度、预拱度的计算一、变形（挠度）计算的目的与要求桥梁上部结构在荷载作用下将产生挠曲变形，使桥面成凹形或凸形,多孔桥梁甚至呈波浪形。

因此设计钢筋混凝土受弯构件时，应使其具有足够的刚度，以免产生过大的变形，影响结构的正常使用.过大的变形将影响车辆高速平稳的运行，并将导致桥面铺装的迅速破坏；车辆行驶时引起的颠簸和冲击，会伴随有较大的噪音和对桥梁结构加载的不利影响；构件变形过大，也会给人们带来不安全感。

变形验算是指钢筋混凝土桥梁以汽车荷载（不计冲击力）计算的上部结构最大竖向挠度，不应超过规定的允许值。

《公桥规》对最大竖向挠度的限值规定如下表：钢筋混凝土梁桥允许的挠度值注：1。

此处L为计算跨径,L1为悬臂长度;2.荷载在一个桥跨范围内移动产生正负不同的挠度时，计算挠度应为其正负挠度的最大绝对值之和。

二、刚度和挠度计算桥梁的挠度，根据产生原因可分成永久作用（结构自重力、桥面铺装、预应力、混凝土徐变和收缩作用等）产生的和可变作用（汽车、人群）产生的两种.永久作用产生的挠度是恒久存在的且与持续的时间有关，可分为短期挠度和长期挠度.可变作用产生的挠度是临时出现的，在最不利的作用位置下，挠度达到最大值,随着可变作用位置的移动，挠度逐渐减小，一旦可变作用离开桥梁，挠度随即消失。

永久作用产生的挠度并不表征结构的刚度特性，通常可以通过施工时预设的反向挠度(即预拱度）来加以抵消，使竣工后的桥梁达到理想的设计线形。

可变作用产生的挠度，使梁产生反复变形，变形的幅度越大，可能发生的冲击和振动作用也越强烈，对行车的影响也越大。

因此，在桥梁设计中，需要通过验算可变作用产生的挠度以体现结构的刚度特性。

钢筋混凝土和预应力混凝土受弯构件,在正常使用极限状态下的挠度，可根据给定的构件刚度用结构力学的方法来计算。

对于均布荷载作用下的简支梁，跨中最大挠度值为：4224553844848ql Ml Ml f EI EI b=⋅=⋅=⋅ （1）钢筋混凝土构件220()[1()]cr cr s s cr B B M M B M M B =+-0cr tk M f W γ=； 002/S W γ=(2）预应力混凝土构件1） 全预应力混凝土和A 类预应力混凝土构件 000.95B EI =2） 允许开裂的B 类预应力混凝土构件在开裂弯矩cr M 作用下： 000.95B EI =在（s cr M M -）作用下:cr cr B EI =开裂弯矩： 0()cr pc tk M f W σγ=+受弯构件在使用阶段的挠度应考虑荷载长期效应的影响（长期挠度），即按荷载短期效应计算的挠度值,乘以挠度长期增长系数0η，可按下列规定取值：当采用C40及以下混凝土时，0 1.60η=；当采用C40～C80混凝土时,0 1.45~1.35η=,中间强度等级可按直线内插取用.三、预拱度钢筋混凝土受弯构件预拱度可按下列规定设置：1） 荷载短期效应组合并考虑荷载长期效应影响产生的长期挠度不超过L/1600时，可不设预拱度;2） 不符合上述规定则应设预拱度,预拱度值应按结构自重和1/2可变荷载频遇值计算的长期挠度值之和采用。

连续刚构桥梁跨中成桥预拱度估算公式摘要：计算连续钢构桥梁中成桥预拱度是非常困难的。

因此为求解连续刚构桥梁跨中成桥预拱度设置值，将影响其运营期间跨中挠度值增大的多种主要因素给定合理量值并考虑相互耦合作用，建立多种不同跨径组合的在役刚构桥梁有限元模型，对其进行分析求解。

利用最小二乘法进行多项式拟合，最终推导出适用于主跨跨径２００ｍ以内的连续刚构桥梁跨中成桥预拱度估算公式，并与规范解、经验解、实测值进行对比，证明了该估算公式的适用性。

关键词：桥梁工程；连续刚构桥；成桥预拱度；拟合；估算公式引言为使连续刚构桥梁最终线形达到设计线形，施工立模标高要增加施工预拱度ｆ１与成桥预拱度ｆ２，如图１所示。

其中ｆ１由模型计算所得，而ｆ２的取值是根据桥梁后期运营过程中跨中下挠经验值来确定的，没有统一的标准。

我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》中引入挠度增长系数ηθ，Ｍｓ来计算结构长期挠度，反映结构由于收缩徐变及混凝土弹性模量降低而造成的挠度的增加，但其计算值与桥梁实际下挠值相差很大，起不到使结构最终线形平顺的作用为此本文建立大量的连续刚构模型，对影响跨中后期下挠的参数进行适当调整，求得结构运营３年后的跨中挠度，对大量离散数据进行拟合，得出适用于主跨小于２００ｍ的连续刚构桥梁成桥预拱度估算公式，可为后续连续刚构桥梁成桥预拱度ｆ２计算提供参考。

1确定影响因素的参数量值连续刚构属于超静定桥梁结构，运营后期跨中下挠是多种因素耦合作用下的结果，且混凝土收缩徐变是最主要的影响因素。

混凝土收缩徐变、主梁刚度变化、纵向预应力的有效性、活载、施工质量及运营管理等是跨中下挠的影响因素。

在建立有限元模型的过程中，为真实模拟结构运营后期的状态，需调整各主要影响因素的参数，确保挠度计算值更贴近实际情况。

1.1混凝土收缩徐变时间参数混凝土的收缩徐变持续６个月后结构变形可达到最终徐变变形的７０％～８０％，之后变形增长逐渐缓慢。

根据这一特点以及桥梁设计时通常考虑１０００～１５００ｄ的收缩徐变计算时间，将结构运营３年后的挠度值作为成桥预拱度估算公式的计算目标值，即按估算公式计算值设置的成桥预拱度，可在桥梁运营３年后其跨中桥面标高基本达到设计高程，且之后变化不大，可满足桥面平稳行车的要求。

预拱度相关问题一、预拱度的概念及确定因素预拱度：为抵消梁、拱、桁架等结构在荷载作用下产生的挠度，而在施工或制造时所预留的与位移方向相反的校正量。

确定因素：①脚手架承受施工荷载后引起的弹性变形；②超静定结构由于混凝土收缩及徐变而引起的挠度；③由于杆件接头的挤压和卸落设备的压缩而产生的塑性变形；④脚手架基础在受载后的塑弹性沉降；⑤梁、板、拱的底模板的预拱度设置。

二、拱桥预拱度的设置与计算2.1预拱度的设置当结构自重和汽车荷载（不计冲击力）产生的最大竖向挠度，不超过计算跨径的1/1600 时，可不设预拱度，超过就要设预拱度。

预拱度的设置值为按结构自重和 1/2 可变荷载频遇值计算的长期挠度值之和采用。

上部结构和支架的各变形值之和,即为应设置的预拱度。

支架受载后将产生弹性和非弹性变形,桥梁上部结构在自重作用下会产生挠度,为了保证桥梁竣后尺寸的准确性,在施工时支架须设置一定数量的预拱度。

钢桥预共度是通过改变螺栓间距实现的，混凝土桥是靠桥梁线形控制的，调整立模标高。

预共度值一般是恒载+1/2静活载挠度。

预拱度应根据上述各项因素产生的挠度曲线反向设置；可根据以往的实践经验按下述方法之一设置：1 按抛物线设置。

2 按推力影响线的比例设置。

3 对于不对称拱桥或坡拱桥，按拱的弹性挠度反向比例设置。

根据近几年来工程实践检验，后期混凝土收缩、徐变对中孔跨中挠度影响约为L/500~L/1000（L：中孔跨径），边孔最大挠度一般发生在3/4L处，约为中孔最大挠度1/4。

另外，连续刚构桥边中跨比例0.52~0.6，桥墩采用柔性墩。

在后期运营中向跨中方向产生位移，刚构墩、梁固结，由变形协调可知，转角位移使边孔上挠。

中孔跨中下挠。

因此，边跨成桥预拱度一般设置较小，在3/4L处设置fc/4预拱度（fc：中孔跨中成桥预拱度）。

中跨预拱度在设计预拱度的基础上，按L/1000+1/2d2(L为中跨跨径，d2为活载挠度)提高预拱度（最大挠度在跨中），边跨预拱度按中跨最大挠度1/4计算，边跨最大挠度在3/4L处。

桥梁预拱度二次抛物线的计算1. 桥梁的神秘世界说到桥梁，大家心里首先想的是什么呢？是那壮观的拱形结构，还是那些在桥上飞驰而过的小车？桥梁可不是简单的土块和木头搭起来的，它们背后藏着许多精妙的数学和工程学原理。

其中，预拱度的计算就是个有趣的话题！今天我们就来聊聊桥梁预拱度二次抛物线的那些事儿。

1.1 预拱度是什么？首先，咱们得弄明白什么是“预拱度”。

简单来说，预拱度就像是桥梁的“预设姿势”。

想象一下，如果桥梁一开始就是平的，那在重力的影响下，它可就得“趴下”了。

这就像你坐在沙发上，懒得动，时间长了肯定会陷下去。

所以，桥梁设计师们就让桥梁“翘起来”，形成一个优雅的拱形，这样就能更好地承受重力，避免“趴下”的尴尬。

1.2 二次抛物线的魅力说到这里，大家可能会问，为什么要用二次抛物线呢？这就像是选衣服，要找最合适的那一件！二次抛物线的形状恰到好处，既能分散压力，又美观大方。

就像画画一样，好的线条总能让人眼前一亮。

通过计算二次抛物线的方程，工程师们可以准确地预测出桥梁在不同负载下的表现，简直是“神通广大”！2. 预拱度的计算方法好啦，聊了这么多，咱们进入正题，来看看怎么计算这个预拱度。

别担心，这里没有复杂的公式让你抓狂，咱们就来用一种轻松的方式来理解它。

2.1 基本公式我们知道，二次抛物线的标准方程是y = ax² + bx + c。

这里的“a”、“b”、“c”就像是咱们的调味料，不同的搭配会让这道数学题的味道大不相同。

在桥梁设计中，我们主要关注“a”，它决定了曲线的陡峭程度。

更陡峭的曲线可以承受更多的压力，就像山坡越陡，滑雪的刺激感就越强！2.2 数据输入为了计算出合适的“a”，我们需要一些数据，比如桥的跨度、载荷、材料强度等等。

想象一下，就像做菜要准备好食材，少了哪一样都不好！通过这些数据，我们可以用公式来计算出合适的预拱度，然后就能放心大胆地建造桥梁，心里乐得比吃了蜜还甜！3. 实际应用与趣味现在，咱们来聊聊这些理论在实际中是怎么运用的。

成桥预拱度设置的正交多项式拟合法黄文通;李平杰【摘要】连续刚构桥预拱度可分为施工预拱度和成桥预拱度.对于成桥预拱度的设置问题,目前通常的计算方法原理不清晰,且随意性较大.为了有效地克服了通常算法的不足之处,本文提出了一种正交多项式拟合法去计算成桥预拱度,并通过一座实桥的成桥预拱度分析,验证了该法的可靠性.【期刊名称】《公路工程》【年(卷),期】2013(038)005【总页数】5页(P103-106,111)【关键词】成桥预拱度;曲线拟合;正交多项式拟合法;大跨连续刚构桥【作者】黄文通;李平杰【作者单位】华南理工大学土木与交通学院,广东广州510641;华南理工大学土木与交通学院,广东广州510641【正文语种】中文【中图分类】U445.40 引言目前，连续刚构桥一般采用悬臂浇筑法、悬臂拼装法、顶推法施工的，其过程的线形控制一般都是通过设置预拱度而实现的［1－2］。

预拱度可分为施工预拱度和成桥预拱度。

设置施工预拱度主要是为消除施工过程中恒载、挂篮变形、温度、前期混凝土收缩徐变、预应力损失等对桥梁线形的影响，由于施工监控过程可以对每一施工阶段的施工预拱度进行参数识别、分析和修正，使得施工预拱度的设置可达到比较高的精度;设置成桥预拱度主要是为了消除混凝土后期收缩徐变、活载、后期预应力损失对桥梁线形的影响，成桥预拱度的设置直接关系到桥梁运营线形的好坏。

成桥预拱度的计算多采用二次抛物线法或者余弦曲线法［3－6］，而本文采用正交多项式拟合法来拟合一座跨径为(88+2×160+88)m的连续刚构桥的成桥预拱度，拟合后的成桥预拱度曲线模型与用有限元计算得出的成桥预拱度数据的相关系数达到0.99以上，由此验证了正交多项式拟合法的可靠性。

因此，采用正交多项式拟合法计算的成桥预拱度不仅保证了桥梁成桥线形的平顺，而且保证了桥梁线形受力合理性，具有较高的推广与应用价值。

1 成桥预拱度的概述1.1 成桥预拱度及其影响因素目前，在施工过程中对成桥预拱度不直接识别、修正，而成桥预拱度线形是通过在立模标高中预留来实现的。