
P(4)置换群乘法表
第六章 置换群 一. 概念题 1.置换群 以n 个数字{}1,2,...,n 间的所有置换操作为元素构成的群,称为n 阶置换群n S 。 2.置换群的类 置换群中有相同轮换结构的元素互相共轭,他们的集合构成置换群的类。 3.置换群的产生子 任两个数字的对换(),i j 可以写成()()()()111i j i j i =,因此n S 中任一置换都可以由 ()()()()12,13,14,,1n ???这些基本对换中的一些相乘得到, 所以就称这()1n -个与符号'1'对换(){} 1i 为n S 的产生子。 4.杨图 任取一组配分数[]λ,12[][,,......]m λλλλ=,1210,m m j j n λλλλ =≥≥???≥>=∑,画n 格方格 图,分成m 行,左边对齐,第一行含1λ格,第二行含2λ格,以此类推,这样的方格图称为杨图。 5.杨算符 对于给定的杨表,所有横向置换之和称为它的横向算符P p = ∑,所有纵向置换乘其置换宇称之和称为它的纵向算符q Q q δ=∑,杨算符等于横向算符和纵向算符的乘积,E PQ =。 6.杨盘与正则杨盘 把自然数1到n 填入杨图,得到杨盘。如在杨盘中,同一行中左面数小,同一列中上面数小,则称为正则杨盘。 7.什么是关联杨图?什么是关联表示? 有些杨氏图,像[]4与41????,[]3,1与22,1????等,分别沿第一个方块的左上角到右下角的对 角线转π角后可以互相重合,称之为关联杨图,这种图对应的不可约表示称为关联表示。
8.正则杨盘的大小 自第一行开始自左至右比较两杨盘的填数,如果都相同,再比较第二行、第三行等,第一次发现填数不同时,填数大的正则杨盘大于填数小的正则杨盘。 9.置换 n 个客体排列次序的变换称为置换。 10.轮换 有一类特殊的群,如果在一个置换中,有(n-1)个客体保持不变,而余下的l 个客体顺序变换,即第1a 个位置的客体排列第2a 的位置,第2a 位置的客体排到第3a 位置,以此类推,最后第l a 位置的客体排到第1a 位置,形成一个循环。则这样的置换叫轮换。 二. 计算题 1.写出对应下列杨表的杨算符。 (1) 1 2 3 4 (2) 1 2 3 4 (1)()()()()()()()()()()() ()()()()()()() 1213231233211412132312332114214314231423143214E E E +++++-???????? =+++++------ (2)()()()()()()()()()() ()()()()()() ()()()()()()12341324123412341321343121432412434212341324132431423214E E E E E ++--???????????????? =+++--------++++ 2.试计算5S 群对应于杨图[]3,2的正则杨图有多少个,并按自小到大的 顺序写出。 杨图形式为 根据构型规则计算:
近世代数学习系列二群 近世代数的主要研究对象是具有代数运算的集合,这样的集合称为代数系。群就是具有一个代数运算的代数系,群的理论是代数学中最古老最丰富的分支之一,是近世代数的基础.现在它已发展成为一门内容丰富、应用广泛的数学分支,在物理学、力学、化学、生物学、计算机科学等方面都有越来越广泛的应用。 群是一个集合,在这集合上定义了一种二项演算,也就是说存在一个映射,给这集合的任意两个元的有序对,都对应了这集合的另一个元,作为这两个元关于这种演算的结果。这演算通常称为乘法,两个元a、b关于这乘法进行演算的结果,通常写为a?b或者就简略记为ab。乘法被要求满足下面三个条件: 1.结合律。a? ( b?c ) = ( a?b ) ?c 2.存在单位元e,对任意元a都有e?a = a?e = a 3.对任意元a,都存在a的逆元a-1,满足a?a-1 = a-1?a = e 如果这乘法还满足交换律a?b = b?a,则把这群称为加群或Abel群。这时更多地把演算写成加法。群的单位元有时写为 1,Abel群的时候则写为0。单位元是唯一的,这是因为如果d和e都是单位元,则根据定义我们有d = de = e。同样逆元也是唯一的,因为如果b和c都是a的逆元,则b = bac = c。显然 ( a-1 ) -1 = a。 在一个集合A上定义一个满足上面三个条件的演算使其做成一个群,这有时被称为“给集合A加上了群的结构”。有一种结构就有保持这种结构的映射。从群G到群H的映射f被称为同态映射,如果f满足条件:对于G中任意两个元σ、τ,总有f ( στ ) = f ( σ ) f ( τ )。这也可以说成f是和两个群中的乘法演算相容的。容易看出同态映射一定把单位元映到单位元,逆元映到逆元。如果一个同态映射是全单射,那它一定是同构,也就是说其逆映射也一定是同态映射。
高中数学1置换与置换群 试题 2019.09 1,在极坐标系中,点P 1 6sin 6 112=??? ?? -??? ??πθρπ到直线, 的距离等于________。 2,已知二项分布满足X ~B (6,32 ),则P(X=2)= ________。 3,已知点P (-3,2),若极点O '的直角坐标为(-2,1),极轴方向与x 轴 相同,两个坐标系的长度单位相同,则点P 的极坐标为_____。 4,如图所示的是2008年北京奥运会的会徽,其中的“中国印”的外围是由四个不同形状的色块构成,可以用线段在不穿越另两个色块的条件下将其中任意两个色块连接起来(如同架桥),如果用三条线段将这四个色块连接起来,不同的连接方法共有________种(用数字作答)。 5,过点A (5,-2)的直线l 交 224424360x y x y ----=于1P 、2P 两点,A 恰为线段12P P 的中点,求线段12P P 的长。 6,从数字0、1、3、5、7中取出不同的3个数作系数,可以组成多少个不 同的一元二次方程2 0ax bx c ++=?其中有实根的方程有多少个? 7,(12)n x +的展开式中第6项与第7项的系数相等 (1)求展开式中二项式系数最大的项; (2)求展开式中系数最大的项。 8,袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为1 7,现 有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取、、、、、、
取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的。 (1)求袋中所有的白球的个数; (2)用ξ表示取球终止所需要的取球次数,求随机变量ξ的概率分布列; (3)求甲取到白球的期望。 9,已知直线k x y +=2被抛物线y x 42 =截得的弦长AB 为20,O 为坐标原 点. (1)求实数k 的值; (2)问点C 位于抛物线弧AOB 上何处时,△ABC 面积最大? 10,6个人坐在一排10个座位上,问: (1)空位不相邻的坐法有多少种? (2)4个空位只有3个相邻的坐法有多少种? (3)4个空位至多有2个相邻的坐法有多少种?(答案用数字表示) 11,已知a 、b 、c 是直线,β是平面,给出下列命题:①若c a c b b a //,,则⊥⊥;②若c a c b b a ⊥⊥则,,//;③若//,,a a b βααβ??=则a ‖b ;④若a 与b 异面,且ββ与则b a ,//相交;其中真命题的序号是 .(要求写出所有真命题的序号) 12,若集合 }1 |{2 x y y M = =,{|P y y ==,那么=P M A .),0(+∞ B .),0[+∞ C .),1(+∞ D . ),1[+∞
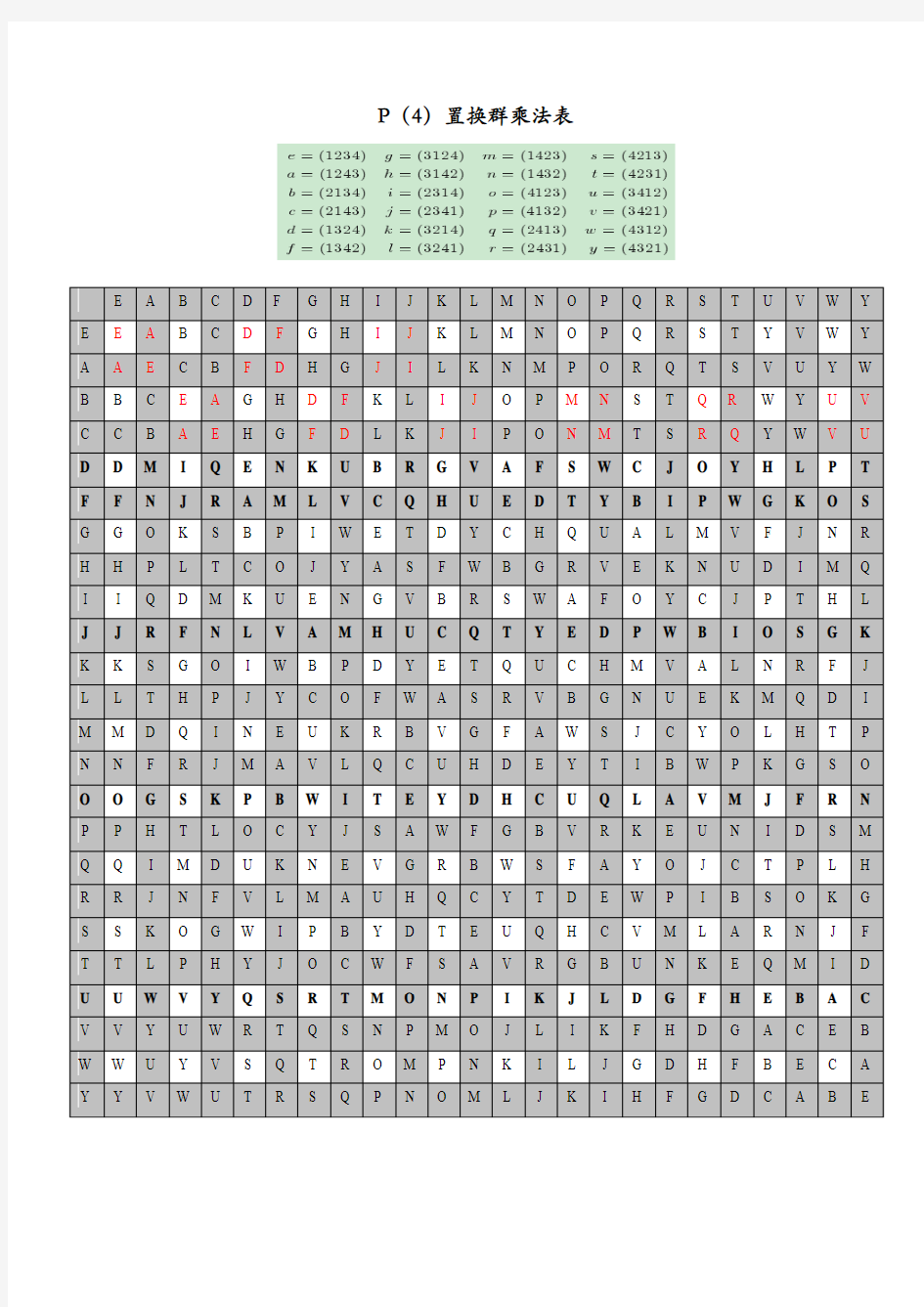
ACM 暑期集训 组合数学(5) 置换群与P ólya 定理 1 群的基本概念 b a e a b b a a a e e a a b b a c b a c b a A A b a A b a A =======∈∈?-1543)()(21,,,则)逆元:()单位元:()可交换性:()可结合性:()封闭性 (算的性质上的二元运算。二元运为,则称都有,如果对于,运算设非空集合 上的二元运算。是非空集合,代数系统A A ?? 为无限群。 为有限群。否则,称是有限集合,称如果。,下是一个群,记作群在运算则称集合存在逆元)对于()存在单位元(是可结合的)运算(是封闭的)运算(,满足下述条件:,设给定代数系统G G G G G G G a G a e G *??=*∈∈?***??-1 ,43212 置换群 {}个不同的置换。 次置换共有例如:到自身的双射 ,,,次置换:集合!1423432132 1,321321 n n s k k k k n n X n n ??? ? ??=?? ?? ??== ? ?? ? ? ??=???? ??????? ? ?=????? ? ?=???? ??=?≠?=??4312 4321 32144321142 3432 1321443 211423 4321 ))(()(t s t s s t t s i s t i t s X t s t s X 则例如律。。即置换的乘法无交换。一般地,为上的一个置换,且定义仍是,置换的乘法和上的置换设 ?? ? ? ??=? ??? ??=???? ??=-n k k k k s k k k k n s n n I n n X 32 132132132132 11 321 的逆置换为为恒等置换。 称 {},称为置换群。 乘法运算下构成一个群在置换的的置换组成的集合,是由集合设G X t t t G m ,,,21 = ?? ???????? ?????? ?????? ?????? ?????? ?????? ? ?=312321,123321,231321,213321,132321,3213213S S n X n 次对称群,记作法下构成一个上的全体置换在置换乘集合 POJ 2369 Permutations 求置换P 的秩k (order ):P k =I POJ 1026 Cipher 求置换P 的k 次幂P k 。题目大意:首先输入长度为n 的数字串构成置换P 。然后求字符序列Src 进行k 次置换后的字符序列。 POJ 1721 CARDS 已知置换P 的k 次幂P k ,求P (是k 次方根吗)
(V )循环群·变换群和置换群 一、定义及例子 1、定义:设G 是群,若存在a ∈G 使得G 中任意元素均为a 的幂,即G=(a )【=(a -1)】 2、例子: (1)Z =(1) (2)(Z 12,+)=([1])=([11]) 注:([5])=Z 12,([7]),([11])【小于12的素数都能生成Z 12】 (3)n 次单位根群Un 【Unit 】 )(),(},1|{0ω=??∈==∈≠*C C x x x U N n n n n n i ππω22 sin cos += 二、生成元,循环群 1、循环群的元素 ???∞ =∈>===-)(},|{0)(},,...,,{)(1a o Z i a m a o a a e a G i m 2、生成元 (1)1,)(±=?∞=r a a o r 是生成元 (2)1),(,)(=?=n r a n a o r 是生成元 {} x i x e n r n r r n n ix sin cos Enler 1,1),(|)(n n )(#+=≤≤==):欧拉公式(互素的。 的数中与:小于欧拉数?? 如(Z 12,+)=([1])=([5])=([7])=([11]) 三、循环群的子群 1、循环群的子群是循环群 2、循环群子群的分类 } |1|){(G ),(,0)()2(} 0|){(G ),(,)()1(n r n r a a G n a o r a a G a o r r 且的所有子群为 则设的所有子群为 则设≤≤=>=≥=∞= 变换群和置换群
·任意一个置换可以写成若干个对换的乘积。 ·(ij)=(1i)(1j)(1i) ·任意一个置换可以写成若干个形如(1i )的乘积(2≤i ≤n ) 置换的性质 ) ()...()()...(6],...,,[)()(5/ */*)...)(...()...)( (4) ...()...(3))...((2) ...()...()...(12112121212121212111121211113221r r t i i t r r r r r r r r r r r r i i i i i i r r r r o r o i i i j j j j j j i i i i i i i i i r i i i o i i i i i i i i i i σσσσσσσσσσσ====???======----、附加:则不相连)且是循环置换的表示(互、前提:无交、、、、
伽罗瓦理论:人类至今无解的五次方程用汗水和生命浇灌出来的理论之花,困扰人类300多年的高阶谜团 1832年,自知必死的伽罗瓦奋笔疾书,写出了一篇几乎半个世纪都没人看懂、只有32页纸的论文,并时不时在一旁写下“我没有时间”,第二天他毅然决然参与决斗并身亡,一个瘦弱而极富激情的天才就这样走了,最后闪现出的是绝世才华,他的生命只有21岁! 群论、数学质变的前夕 为什么数学家对五次方程如此迷恋,因为在五次方程的求解过程中,数学家们第一次凿开了隐藏在冰山下的现代科学,将数学带入了精妙绝伦的现代群论。群论的出现,直接奠定了20世纪的物理基础,从此,统治人类近200年的牛顿机械宇宙观开始迈入随机和不确定性的量子世界和广袤无垠的时空相对论。一场空前伟大的科学革命如疾风骤雨般来临。 在这次暴风雨的前夜,历史上最伟大的数学家们悉数登场,他们为五次方程的求解而苦苦思索。 在五次方程获得求解之前,一元三、四次方程在数学大神塔尔塔利亚、卡尔达诺、费拉里的努力下,顺利得到了解决,然而到了五次方程,再传统地以根用系数的代数式求解却始终行不通。在各大高手尝试失败后,它很快成了数学家心中的顶尖难题,这是属于神的命题,与人类无关。 在这条解方程的漫漫长路上,最先为五次方程求解提供了新思路的是上帝之子欧拉,他通过一个巧妙的变换把任何一个全系数的五次方程转化为具有“x+ax+b=0”的形式。出于对这一优美表达的倾心喜爱,欧拉自以为是地认为可以找出五次方程的通解表达式。 与此同时,数学天才拉格朗日也在为寻找五次方程的解而废寝忘食。很快,他便欣喜地发现了一种特别的方法,若将四次方程降阶为三次方程,就能找到一种求解四次方程的简单方法。但遗憾的是,同样的变换却将五次方程升阶为六次方程。 此后,五次方程的进展一度陷入迷局。当时五次方程的焦点主要集中在两大问题上,第一个问题是,对N次方程,至少都有一个解吗?第二个问题则更进
阿贝尔群、循环群、置换群:各种不同的群。
?什么是阿贝尔群 ?若群
知识回顾 ?生成子群 设G为群, a G, 即a的所有的幂构成的集合, 为G的子群, 称为由a生成的子群.
循环群的定义 定义8.10 设G是群,若存在a∈G使得 G={a k| k∈Z} 则称G是循环群,记作G=,称a 为G 的生成元. 循环群的分类:n 阶循环群和无限循环群. 设G=是循环群,若a是n 阶元,则 G = { a0=e, a1, a2, … , a n-1 } 那么|G| = n,称G 为n 阶循环群. 若a 是无限阶元,则 G = { a0=e, a±1, a±2, … } 称G 为无限循环群. 实例:
例10 (1) 设G={e, a, … , a11}是12阶循环群,则φ(12)=4. 小于12且与12互素的数是1, 5, 7, 11, 由定理8.13可知a, a5, a7和a11是G的生成元. (2) 设G=
近世代数小结1群理论知识体系 1、代数系统:) ,( A )( ) ( 复合运算三元间关系 集一同 变换乘法 代数运算 ↓↓?→?? 2、两个代数系统:(对等)映射对应 集合对应系统等价 系统过渡 --运算 象射-映 运算原象 算运持保 同构(映射) 单射 同态(满射) 满射同态映射 )(------ | | →→→↓ ↓↓+?→?+?→??? 3、映射与变换群: 置换群 个元子群对称群次 变换群 象 同 不元同不射单 象逆 有都射满 部 全 换变射双 应 对) 对 应依次换位(一一变换有限集 同集同集 集集循环置换置 换 变 换 映 射 元 间元 间!n )n ( )( )()( ↓? ↓↓↓??→???→??→??→??→? 4、群系统: 陪集群 商 群 相同相同, 相同相同, 不变子群子群群元逆元位单律合结代数运算集 子集 ?→=→↓ ↓↓?→???→????????????????+--? ≥ Na aN a e a e 11 5、群同态(同构)体系: (自然同态)商群群关于核 ~ 子群 子群群群 )()( 11?↓ ↓?→??→?↓ ↓?→?--a e a e G G ~ ???++?),([1])(n Z , 有限无限循环群 N G ~G N φ ) (,: //)(a a N a aN N G N G N N φ=→ψ↓??φ= 6、关于阶: ⑴n G a G a =?∈||||;||||s a n st a t ==?=,||(,) k n a k n = ; ⑵)():(||||||||定理Lagrange n H G H G G H G H ==??≤,)(|,/|):(G N N G N G = ⑶||()|a n n k n ??=<<∞?1时n k a ???使||n k a k ??=?共有|()d n T n =∑1个子群.
第九讲 §置换群(pormutation group) 本讲的教学目的和要求:置换群是一种特殊的变换群。换句话说,置换群就是有限集上的变换群。由于是定义在有限集上,故每个置换的表现形式,固有特点都是可揣测的。这一讲主要要求: 1o弄清置换与双射的等同关系。 2o掌握置换—轮换—对换之间的联系和置换的奇偶性。 3o置换的分解以及将轮换表成对换之积的基本方法要把握。 4o对称群与交错群的结构以及有限群的cayley定理需要理解。 本讲的重点与难点:对于置换以及置换群需要侧重注意的是:对称群和交错群的结构和置换的分解定理(定理2)。 注意:由有限群的cayley定理可知:如把所有置换群研究清楚了。就等于把所有有限群都研究清楚了,但经验告诉我们,研究置换群并不比研究抽象群容易。所以,一般研究抽象群用的还是直接的方法。并且也不能一下子把所有群都不得找出来。因为问题太复杂了。人们的方法是将群分成若干类(即附加一定条件);譬如有限群;无限群;变换群;非变换群等等。对每个群类进行研究以设法回答上述三个问题。可惜,人们能弄清的群当今只有少数几类(后面的循环群就是完全解决了的一类群)大多数还在等待人们去解决。 变换群是一类应用非常广泛的群,它的具有代表性的特征—置换群,是现今所研究的一切抽象群的来源,是抽象代数创始人E.Galais(1811-1832)在证明次数大于四的一元代数方程不可能用根号求解时引进的。 一.置换群的基本概念 定义 1.任一集合A到自身的映射都叫做A的一个变换,如果A是有限集且变换是一一变换(双射),那么这个变换为A的一个置换。 有限集合A的若干个置换若作成群,就叫做置换群。含有n个元素的有 限群A的全体置换作成的群,叫做n次对称群。通常记为 S. n 明示:由定义1知道,置换群就是一种特殊的变换群(即有限集合上的变换群)而n次对称群 S也就是有限集合A的完全变换群。 n
11.7 循环群与置换群 一、循环群 1. 循环群的定义 定义11.14 设G 是群,若a G ?∈使得{|}k G a k Z =∈, 则称G 是循环群,记作 G a =<> ,称a 为G 的生成元。 注意:(1) 对于任何群G ,由G 中元素a 生成的子群是循环群。 (2) 任何素数阶的群都是循环群。 设G 是循环群,若a 是n 阶元,则 012 1 {,,,,}n G a e a a a - == , 那么|G|=n ,称G 为n 阶循环群。 若a 是无限阶元,则 1 2 {,,, }G a e a a ±± == , 这时称G 为无限阶循环群。 例如 (1)G=
Pure Mathematics 理论数学, 2016, 6(1), 17-22 Published Online January 2016 in Hans. https://www.doczj.com/doc/1b12060773.html,/journal/pm https://www.doczj.com/doc/1b12060773.html,/10.12677/pm.2016.61003 On Quasiprimitive Permutation Groups of Cube-Free Degree Shiqin Peng1, Xiaofen Yu2, Jiangmin Pan1* 1College of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan 2School of Mathematics and Information Science, Neijiang Normal University, Neijiang Sichuan Received: Dec. 14th, 2015; accepted: Jan. 17th, 2016; published: Jan. 21st, 2016 Copyright ? 2016 by authors and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). https://www.doczj.com/doc/1b12060773.html,/licenses/by/4.0/ Abstract Li and Seress [The primitive permutation groups of square-free degree, BULL. London Math. Soc. 35 (2003), 635-644] classified primitive permutation groups of square-free degree. In this paper, we will characterize quasiprimitive permutation groups of cube-free degree, and give several prob-lems worth further research. Keywords Quasiprimitive Permutation Group, O’Nan-Scott Theorem, Simple Group 立方自由次拟本原置换群 彭仕芹1,余小芬2,潘江敏1* 1云南财经大学统计与数学学院,云南昆明 2内江师范学院数学与信息科学学院,四川内江 收稿日期:2015年12月14日;录用日期:2016年1月17日;发布日期:2016年1月21日 *通讯作者。
置换群快速幂运算 研究与探讨 江苏省苏州中学 潘震皓 [关键词] 置换 循环 分裂 合并 [摘要] 群是一个古老的数学分支,近几年来在程序设计中置换群得到了一定的应用。本文针对置换群的特点提出了线性时间的幂运算算法,并举例说明了优化后算法的效果。 [正文] 一、引言 置换群是一种优秀的结构,在程序设计中,它的大部分基本操作,时间和空间复杂度都是线性的,甚至有的还是常数的。所以一个问题如果能够抽象归结为一个置换群模型的话,往往能够在程序设计中轻松地解决。但是对于整幂运算来说,似乎只能通过反复做乘法来获得O(k*乘法)或是O(logk*乘法)的算法;而对于分数幂运算,则找不到较好的方法实现。 二、置换群的整幂运算 2.1 整幂运算的一个转化 在置换群中有一个定理:设e T k =,(T 为一置换,e 为单位置换(映射函数为x x f =)(的置换)),那么k 的最小正整数解是T 的拆分的所有循环长度的最小公倍数。 或者有个更一般的结论:设e T k =,(T 为一循环,e 为单位置换),那么k 的最小正整数解为T 的长度。 我们知道,单位置换就是若干个只含单个元素的循环......... 的并。也就是说,长度为l 的循环,l 次的幂,把所有元素都完全分裂了。这是为什么呢? 我们来做一个试验:(下面的置换均以循环的连接表示) 设n=6,那么3 26)(T T =。任取一T=(1 3 5 2 4 6),来做一遍乘法: ()() 3624513412656543213412651265431265436543211265436543211265436543212=??? ? ??=???? ?????? ??=???? ?????? ? ?=T 分裂成了2份!而且这2份恰好是T 的奇数项和偶数项!(注意可以写成(1 5 4)(3 2 6))