对财政支出数据的回归分析
- 格式:doc
- 大小:2.06 MB
- 文档页数:20

中文题目:中国1978-2008年财政收入数据的回归分析外文题目:Regression analysis of China 1978-2008 fiscal revenue data毕业设计(论文)共69页(其中译文及原文共19页)图纸共0张完成日期:2013年6月答辩日期:2013年6月辽宁工程技术大学本科毕业设计(论文)学生诚信承诺保证书本人郑重承诺:《回归分析及其在财政收入预测中的应用》毕业设计(论文)的内容真实、可靠,系本人在胡行华指导教师的指导下,独立完成。
如果存在弄虚作假、抄袭的情况,本人承担全部责任。
学生签名:年月日辽宁工程技术大学本科毕业设计(论文)指导教师诚信承诺保证书本人郑重承诺:我已按学校相关规定对黄均铭同学的毕业设计(论文)的选题与内容进行了指导和审核,确认由该生独立完成。
如果存在弄虚作假、抄袭的情况,本人承担指导教师相关责任。
指导教师签名:年月日摘要财政收入是衡量一个地区和国家经济实力的重要标准,控制着国民经济的命脉, 对财政收入进行定量分析并对其做出比较准确的预测可以为相关部门或者企业制定发展规则,实施相关措施提供可靠的理论预测参考.科学、合理地预测财政收入,对于克服年度预算收支确定的随意性和盲目性,正确处理财政与经济的相互关系具有十分重要的意义.本文主要介绍了一元线性回归分析,多元线性回归分析和逐步回归法.通过多元线性回归分析和逐步回归法对国家财政收入进行建模,然后利用Matlab对其分析,找到能反映财政收入与各因素之间关系的最优回归方程.并且分析模型得出结论,并提出了提高财政收入质量的政策建议.关键词:线性回归分析;逐步回归;中国财政收入预测AbstractFiscal revenue is an important standard to measure a regional and national economic strength, it controls the lifeline of national economy, the quantitative analysis of the fiscal revenue and accurate forecasts on the development rules can provide a reliable theoretical prediction reference for the relevant departments or enterprises to formulate the developing plan. The scientific, rational prediction of fiscal revenue is very important to overcome the annual budget to the randomness and blindness, correctly handle the relationship between finance and economy.This paper mainly introduces the method of linear regression analysis, multivariate linear regression analysis and stepwise regression method. Modeling the national fiscal revenue by multiple linear regression analysis and stepwise regression method, and then use the MATLAB to analysis it, find the potimal equation that can reflect the relationship between the fiscal revenue and the factors. Analysis the model to draw conclusion, and provide policy recommendations to improve the quality of fiscal revenue.Key words:linear regression analysis;stepwise regression;China's fiscal revenue forecast目录摘要 ........................................................................................................................... I Abstract ..................................................................................................................... I I 前言 .. (1)1回归分析理论基础 (5)1.1一元线性回归分析 (5)1.1.1一元线性回归的总体模型 (5)1.1.2回归参数的最小二乘估计 (8)1.1.3回归方程的显著性检验 (9)1.2多元线性回归分析 (11)1.2.1高斯—马尔科夫假定 (11)1.2.2最小二乘估计量 (12)1.2.3 F检验 (16)1.2.4回归参数的显著性检验 (17)1.3逐步回归分析 (18)1.3.1逐步回归分析的主要思路 (18)1.3.2逐步回归分析的主要计算步骤 (18)2回归分析的Matlab实现 (20)2.1线性回归的Matlab数据处理 (20)2.1.1确定回归系数的点估计值 (20)2.1.2求回归系数的点估计和区间估计、并检验回归模型 (20)2.2逐步回归的Matlab数据处理 (22)3回归分析在财政收入预测中的运用 (28)3.1数据的采集 (28)3.2数据的处理 (28)3.3结果论证 (37)4结论与展望 (39)致谢 (41)参考文献 (42)附录A译文 (43)附录B原文 (51)附录C数据采集 (62)辽宁工程技术大学毕业设计(论文)前言(1)目的和意义财政收入是衡量一个地区和国家经济实力的重要标准,控制着国民经济的命脉, 对财政收入进行定量分析并对其做出比较准确的预测可以为相关部门或者企业制定发展规则,实施相关措施提供可靠的理论预测参考.科学、合理地预测财政收入,对于克服年度预算收支确定的随意性和盲目性,正确处理财政与经济的相互关系具有十分重要的意义.回归分析模型是众多预测方法中的一种,它是通过一组自变量来预测一个或多个因变量的数据分析方法.多元回归方法具有很强的实用性及有效性,在现今社会越来越多的领域得到广泛应用.逐步回归法是目前使用较为广泛的选择最优回归方程的方法.它的计算量较小,而且一般也能得到一个较合理的“最优”回归方程[1].本文深入探讨它的性质, 用于财政收入预测.(2)回归分析的发展回归分析最早是19世纪末期高尔顿(Sir Francis Galton)所发展.高尔顿是生物统计学派的奠基人,他的表哥达尔文的巨著《物种起源》问世以后,触动他用统计方法研究智力进化问题,统计学上的“相关”和“回归”的概念也是高尔顿第一次使用的.1855年,他发表了一篇“遗传的身高向平均数方向的回归”文章,分析儿童身高与父母身高之间的关系,发现父母的身高可以预测子女的身高,当父母越高或越矮时,子女的身高会比一般儿童高或矮,他将儿子与父母身高的这种现象拟合出一种线形关系.但是有趣的是:通过观察他注意到,尽管这是一种拟合较好的线形关系,但仍然存在例外现象:矮个的人的儿子比其父要高,身材较高的父母所生子女的身高将回降到人的平均身高.换句话说,当父母身高走向极端(或者非常高,或者非常矮)的人的子女,子女的身高不会象父母身高那样极端化,其身高要比父母们的身高更接近平均身高.高尔顿选用“回归”一词,把这一现象叫做“向平均数方向的回归”(regression toward mediocrity).虽然这是一种特殊情况,与线形关系拟合的一般规则无关,但“线形回归”的术语仍被沿用下来.作为根据一种变量(父母身高)预测另一种变量(子女身高)的一般名称沿用至今,后被引用到对多种变量关系的描述[2].而关于父辈身高与子代身高的具体关系是如何的,高尔顿和他的学生K·Pearson通过观察了1078对夫妇,以每对夫妇的平均身高作为自变量,取他们的一个成年儿子的身高作为因变量,结果发现两者近乎一条直线,其回归直线方程为黄均铭:回归分析及其在财政收入预测中的应用x y516.073.33ˆ+= 这种趋势及回归方程表明父母身高每增加一个单位时,其成年儿子的身高也平均增加0.516个单位[3].在1983年,伍德(S.Wold )和阿巴诺(C.Albano)等人首次提出偏最小二乘回归理论.在伍德教授的指导下,瑞典的Umea 大学有机化学系发表了许多有关偏最小二乘回归理论与应用的博士论文.他与他的合作者们还展开了广泛深入的理论探讨,并且开发了在Windows 下面运行的SMCA-P 数据分析软件,用以支持偏最小二乘回归计算和结果解释.因此,偏最小二乘回归首先在化工领域的到广泛的运用.早在1986年,郑钟光就将多元回归分析应用在矿石体重测定中,并用实践证明了这一方法具有较大的优越性[4].苑玉风应用多元回归分析和逐步回归分析,研究某种汽车发动机用球墨铸铁活塞环球化率的影响因素,并建立了相关关系[5].李金海在多元回归数学模型基础上,提出了多元回归方法的应用步骤[6].另外这一方法也被广泛的应用于预报各种气象参数,黄祖英用多元回归分析做暴雨的长期预报,虽然误差较大,但他们同时指出有待于因子本身作进一步的改进[7].林祖享,梁舜华运用多元回归方程,绘制出赤潮生物的变化趋势图,并预报是否可能发生赤潮[8].此外,多元回归分析方法也被越来越多的应用于预报各种自然灾害,王震宇等将这一方法用于滑坡预报,并用实例证明了能在一定程度上解决滑坡的预报问题.刘昌蓉等采用多元线性回归分析方法,建立地质灾害危险级别的评价模型,按照计算结果综合反映出的地质灾害活跃程度的高低,对该区域进行有效防治,从而有利于地质灾害的减轻减少.袁宇运用多元回归分析法,建立了化学污染面积,纵身与诸条件的关系,快速估算预测出突出性化学污染危害,并提前做出防范措施.多元统计分析是统计学中内容十分丰富、应用范围极为广泛的一个分支,是一种非常重要和实用的多元数据处理方法[9].六种经典的多元统计分析方法为:多元线性回归分析、主成分分析[10]、因子分析[11]、典型相关分析[12]、聚类分析、判别分析.回归分析方法是多元统计分析的各种方法中应用最广泛的一种[13].它是处理多个变量间相互依赖关系的一种数理统计方法,变量间的相互依赖关系在实际问题中是大量存在的,回归分析是研究这种相互依赖关系的有效数学方法.温忠麟在其所编的《心理与教育统计》一书中,对回归分析定义为:“用统计的方法研究变量y 和x 的不确定的共变关系”,“描述y 的均值与x 的关系的函数通常称为回归方程”,并通过讨论线性回归模型,从一个自变量到多个自变量的情形进行介绍如何建立回归方程,如何检验、评价和解释回归方程,如何利用回归方程进行预测等,具体从直线回辽宁工程技术大学毕业设计(论文)归、可线形化的曲线回归和多元回归分析三个方面进行阐述[14].张厚粲、徐建平在他们编著的《现代心理与教育统计学》一书中提到:回归分析是通过大量的观测数据,可以发现变量之间存在的统计规律性,并用一定的数学模型表示出来,这种用一定模型来表述变量相关关系的方法[15].回归分析不但适用于实验数据,还可以分析未作实验控制的观测数据或历史资料.作者主要简单介绍了简单回归分析模型以及如何拟合这一模型.在简单回归模型中ˆ=y+abx其中参数a,b分别表示截距与斜率,yˆ叫做因变量或被测变量,x叫做自变量或预测变量.因变量的观察值与预测值之间的差异叫做残差.运用最小二乘法和平均数可以建立这一模型.回归分析的主要目的是建立一种线性模型,然后通过这种模型进行分析和预测.张敏强在其主编的《教育与心理统计学》一书中认为统计学中的回归分析是借助于数学模型对客观世界所存在的事物间的不确定关系的一种数量化描写,其目的在于为不确定现象的研究提供更为科学、精细的手段,以应用于相关随机变量的鼓励、预测和控制[16].回归分析的三大部分是:①建立回归方程,依据专业知识调查所研究现象可能涉及到的变量的种类和个数,并且进行实验或调查以获取实际数据,然后结合以往的经验,对所获得数据进行分析研究,确定回归方程的函数形式.②检验和评价所建回归方程的有效性,检验方程有无使用价值,并找到评价回归方程有效性高低的统计指标来评价所建回归方程使用价值的高低.③利用所建回归方程进行预测和控制.这正是研究回归现象、进行回归分析的根本目的所在.利用回归方程进行控制,多见于自然科学研究领域,在教育和心理科学研究中,更多的是利用所建回归方程进行估计和预测.回归分析的描述:为了表示响应y是怎样和因子x相联系的,可以用一条回归直线ˆ去拟合.斜率b和截距a可以用最小二乘的简单公式来计算.实际的观测值必须=bxy+a假定是取自某一潜在总体的样本[17].对于这个总体,我们用希腊字母β表示真实回归直线的斜率,它就是用样本斜率b来估计的那个目标.如果抽样是随机的,那么b随着样本的不同围绕着其目标β以一个特定的标准误差近似正态地波动.由b的抽样分布,可以构造β概值.根据这两个结果中的任何一个,都可以检验假设β的置信区间,或计算0=黄均铭:回归分析及其在财政收入预测中的应用β.在非线性关系中,例如抛物线关系,可以利用简单的变换化为标准的多元回归来=拟合.也可以利用现有的统计软件来寻求一条比较合理的拟合曲线.有相关关系的两个变量,如果一个为自变量,另一个为因变量,因变量随自变量的变化而作程度不同的变化,这种近似确定性质的关系可以用数学方程式来表达,从中可以由自变量的值推算或预测因变量的估计值,这个过程称为回归分析[18].书中进一步介绍如何建立回归方程式,如何计算回归系数,如何估测和估计标准误差等方面进行详细介绍.茆诗松等编著的《回归分析及其试验设计》,是我目前找到的整本都是介绍回归分析的书.书中提到:回归分析是研究随机现象中变量之间关系的一种数理统计方法,它在工农业生产和科学实验中有着广泛的应用.书中通过生产中的实际问题,较详细地介绍了回归分析中的参数估计、统计检验和预报控制等问题.然后再阐述逐步回归及多项式回归分析方法,而且还介绍了如何回归的试验设计[19].回归设计在20世纪五十年代初,为了适应生产的发展,寻求最佳工艺和配方以及建立生产过程的数学模型等的需要而产生的,根据试验目的和数据分析来选择的每一个试验点在数据获取上含有最大的信息,从而减少试验次数,并使数据的统计分析具有一些较好的性质.发展到今天,回归设计的内容已相当丰富,有回归的正交设计,回归的旋转设计,回归的D-最优设计等.在这些设计的基础上,人们还进一步研究各种“最优设计”的标准,从而可以评定各种设计的好坏,以利于探索新的设计方案.(3)主要内容本文主要介绍一元回归分析,多元回归分析,逐步回归分析理论基础.并且从中国统计年鉴中选取1978-2008年这31年间中国财政收入为因变量,自变量为8个可能影响财政收入的因素,第一产业、工业、建筑业、交通运输和邮政业、批发和零售业、住宿和餐饮业、金融业、房地产业.通过多元线性回归分析和逐步回归法对中国财政收入进行建模,通过建立的模型对2009-2011年中国财政收入预测及分析,说明模型的合理性.1回归分析理论基础计算相关系数只能说明现象间相关关系的方向和程度,关系密切与否,但不能说明一个现象发生一定量的变化,另一个现象一般也会发生多大的变化.如销售收入每增加一万元时,销售利润一般会增加多少?施肥量增加一斤,一般地会增加多少产量?研究一个随机变量与一个(或几个)可控变量之间的相关关系的统计方法称为回归分析.这是测定现象之间数量变化上的一般关系的数学方法.“回归”这个词的意思,就是指的变量之间的一般数量关系.根据现象之间相关关系的表现形式,配合一条直线或曲线,用这条直线或曲线来代表自变量和因变量相随变动的一般数量关系.也就是要建立并求解直线或曲线的数学方程式,从而求得变量间的一般关系值.回归有不同种类,按照自变量的个数分,有一元回归和多元回归.只有一个自变量的叫一元回归,有两个或两个以上自变量的叫多元回归;按照回归曲线的形态分,有线性(直线)回归和非线性(曲线)回归.实际分析时应根据客观现象的性质、特点、研究目的和任务选取回归分析的方法.可控变量称为自变量x ,而不可控变量(随机变量)称为因变量y .回归分析主要包括三方面内容:(1)提供建立有相关关系的变量之间的数学关系式(通常称为经验公式)的一般方法; (2)判别所建立的经验公式是否有效,并从影响随机变量的诸变量中判别哪些变量的影响是显著的,哪些是不显著的;(3)利用所得的经验公式进行预测和控制.1.1一元线性回归分析1.1.1一元线性回归的总体模型在回归分析与建模中,如果因变量与自变量之间的关系是线性关系,则称之为线性回归模型;否则,称之为非线性回归模型.一元线性回归模型就是描述两个变量之间相关关系的最简单的回归模型[20].对于具有线性相关关系的两个变量y 与x ,由于有随机因素干扰,两个变量的线性关系包括随机误差项ε,即:εββ++=x y 10 (1-1)在1-1式中,0β,1β为模型参数(或称回归系数).它是一元线性回归的理论模型.对它的理论讨论是研究其他更为复杂的回归模型的基础.一元线性回归分析的基本出发点是它对总体模型的假设.只有准确的理解一元线性回归的总体模型,才能真正把握它的工作原理与方法,在各种复杂的应用条件下能清晰自如的进行分析与处理.总体是指被研究对象的全体,在回归分析中提到的总体模型是指在客观世界中,被研究的数据全体所符合的真实模型.假设在总体数据中,影响因变量y 变化的系统因素完全可以由自变量x 以线性形式加以解释,也就是说,对所研究的全体数据,那个真实的总体模型可以表示成y 随x 线性变化的统计关系.如果对y 和x 分别进行n 次独立观测,得到以下n 对观测值n i x y i i ,,2,1),,( =这n 对观测值之间的关系符合模型n i x y i i i ,,2,1,10 =++=εββ (1-2)在1-2式中,i x 是自变量在第i 次观测时的取值,它是一个非随机变量,并且没有观测误差.对应于i x ,i y 是一个随机变量,它的随机性是由i ε造成的.而随机误差项i ε是一个随机变量,其均值为零,方差为2σ,对于不同的观测,当j i ≠时,i ε与j ε是互不相关的.在模型中,0β,1β被称为总体回归参数,0β是回归直线的截距,1β是回归直线的斜率.上述模型就是一元线性回归模型的总体模型.由它可以看出,当在第i 次观测中,x 的水平取i x 时,相应的i y 来自于一个概率分布,它的均值i i i i x x y 1010)()(ββεββ+=++E =E或者,可更准确的写为i i i x x y 10)(ββ+=E (1-3))(i i x y E 是i y 的条件期望值.式1-3说明了一个重要的统计概念:对于一个给定的i x ,虽然随机变量i y 的取值是未定的,i y 在其概率分布范围内都有可能取值,但是i y 的平均水平)(i i x y E 却与i x 有准确的线性关系.这就用数学的方式解释了我们在大量感性认识中所看到的所谓统计关系.i y 的随机性来自于随机误差项i ε.i y 的方差为2)Var(σ=i y这是因为210)Var()Var()Var(σεεββ==++=i i i i x y因此,无论自变量x 取何值,模型总假设y 的概率分布具有相等的方差2σ.在模型中,还假设误差项互不相关,即对不同观测j i ≠时,有0),Cov(=j i εε因此,任何一次观测的结果对其他各次观测的误差项都没有影响.因为误差项i ε与jε无不相关,所以,任意俩个观测值i y 与j y 也是互不相关的.在一个标准的一元线性回归模型中,还假设误差项i ε服从均值为零、方差为2σ的正太分布.因此,我们前面给出的i ε互不相关的假设变成了独立性的假设.随机误差项服从正态分布),0(2σN 的假设具有相当普遍的实用意义.因为误差项通常代表模型中被忽略的许多微小随机因素的影响.当这些微小因素数量众多,并且这些随机因素在一定程度上相互独立时,根据中心极限定理,代表所有这些因素的综合误差项i ε近似服从正态分布.再假设i ε服从正态分布),0(2σN 的情况下,i y 也是独立的正态随机变量,并且具有均值)(10i x ββ+和2σ方差,即),(~210σββi i x N y +图1-1给出了这个正态误差回归模型的示意图:对于任一给定的i i y x ,是一个随机变量,它服从正态分布,且方差是一个常量2σ,而条件均值)(i i x y E 与i x 呈线性关系.图1-1 正态误差回归模型示意图 Figure 1-1 normal error regression model diagram1.1.2回归参数的最小二乘估计如果在总体中y 与x 的统计关系符合一元线性的正态误差模型,即给定的i x ,有i i i x y εββ++=10如何求0β,1β呢?将估计的回归参数纪为00ˆb =β,11ˆb =β.对于给定的数据,对应于n x x ,,1 ,相应地,有n y y ,,1 .假定我们通过莫一方法,找到了0β与1β的估计值,则有线性估计方程n i x b b yi i ,,2,1,ˆ10 =+= 对于每个给定的i x ,这个估计方程有一个确定的i y ˆ与之对应.显而易见,i y ˆ往往不与实际i y 值相等,而是存在着偏差i ε,即)ˆ(i i i yy -=ε i ε有时也称为残差.一个好的回归方程应该能使估计值的偏差总的达到最小,所以,把问题归结为求估计参数10,b b ,使得min )()ˆ(12101212→--=-=∑∑∑===ni i i n i i i ni ix b b y yy ε所以,求解该最小值问题,就是对∑=ni i 12ε分别求关于10,b b 的偏导数,并令之为零,从而解出10,b b .这种方法称为最小二乘估计方法.即∑∑===---=∂∂ni i i ni i x b b y b 1100120)(2)(ε∑∑===---=∂∂ni i i i ni i x b b y x b 1101120)(2)(ε整理后,得下面的方程组⎪⎪⎩⎪⎪⎨⎧+=+=∑∑∑∑∑=====n i n i ni i i i i ni n i i i x b x by x x b nb y 1112101110由这个方程组解得估计值10,b b 为⎪⎪⎪⎩⎪⎪⎪⎨⎧-=---=∑∑==xb y b x x y y x x b ni ini i i 101211)())(( (1-4) 在1-4式中,y x ,分别是i x 与i y 的样本均值,即∑∑====ni i n i i y n y x n x 111,11.1.3回归方程的显著性检验由最小二乘法作出模型参数的估计,并非完成了回归方程的建立.容易理解,模型系数1β描述的是自变量x 每个单位量的变化对因变量y 的贡献.如果回归方程系数1ˆβ的值很小,可能是0)ˆ(11==ββE ,只是由于数据的随机性使得0ˆ1≠β,这意味着回归方程描述的因变量y 对自变量x 的依赖关系是“虚假”的[21].因此,对回归方程x y 10ββ+=的显著性检验,归结为对假设0:;0:1110≠=ββH H进行检验.假设0:10=βH 被拒绝,则回归显著,认为y 与x 存在线性关系,所求的线性回归方程有意义;否则回归不显著,y 与x 的关系不能用一元线性回归模型来描述,所得的回归方程也无意义.方程显著性可用方程的F 比值和复相关系数r 描述.复相关系数r 接近1较好,随着项数的引进多,r 会自动增加,容易形成假象.样本的预留检验,是用预留的样本值直观检验回归方程预报值的拟合精度.(1)F 检验法 当0H 成立时)2,1(~)2/(--=n F n Q UF e其中回归平方和为()∑=-=ni i y yU 12ˆ 故)2,1(1->-n F F α,拒绝0H ,否则就接受0H . (2)t 检验法 当0H 成立时)2(~ˆˆ1-=n t L T e xx σβ, 故)2(21->-n t T α,拒绝0H ,否则就接受0H ,其中∑∑==-=-=ni i n i i xx x n x x x L 12212)((3)r 检验法 记∑∑∑===----=n i ni ii ni i iy y x x y y x xr 11221)()())(( ,当α->1r r 时,拒绝0H ;否则就接受0H . 其中()()111121,2r n F n αα--=+--注意,F 检验是单侧检验,将显著水平全a 部配置在F 分布的右侧尾端,拒绝0H 的临界值偏小,对回归方程中自变量与因变量相关性的要求较低,作出“接受0H ”的结论较为慎重;t 检验室双侧检验,将显著性水平a 分别在t 分布双侧尾端各配置一半,因此自变量的引入门槛较高,作出“拒绝0H ”的结论较为慎重.1.2多元线性回归分析1.2.1高斯—马尔科夫假定在实际问题中,对于因变量y 的全面解释往往需要多个自变量的共同作用.例如,在研究某化学反应时,影响反应速度的因素不仅跟所使用的催化剂的用量有关,还与所加的温度有关.记y 为因变量,当有p 个自变量p x x x ,,,21 时,多元线性回归的理论模型为εβββ++++=p p x x y 110 (1-5)在1-5式中,ε是随机误差,它的期望值0)(=E ε.如果对y 和p x x x ,,,21 分别进行n 次独立观测,取得样本),,,(1ip i i x x y 后,可得到模型n i x x y i ip p i i ,,2,1,110 =++++=εβββ (1-6)在1-6式中ip p i ip p i i x x x x x x y βββ+++===E 11011),,(这里,p βββ,,,10 为回归参数.把这个模型写成矩阵形式,记1211)1(10)1(1221111121111⨯⨯++⨯⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n n p p p n np n p p n n x x x x x x X y y y Y εεεεββββ 则用矩阵表示的多元线性回归模型为11)1()1(1⨯⨯++⨯⨯+=n p p n n X Y εβ (1-7)在1-7式中 Y ——观测值向量; β——参数向量; X ——常数矩阵; ε——随机误差向量.在关于总体的多元线性模型中,假定ε是独立正态随机变量组成的向量,并且有期望值0)(=E ε方差——协方差矩阵)Cov()'(2εσεε∆=E I简记为).0(~2I N σε上述假定被称为高斯—马尔科夫假定.在这一假定下,随机向量Y 有条件期望值βX X Y =E )(Y 的方差—协方差矩阵为I Y 2)Cov(σ=1.2.2最小二乘估计量首先,要估计总体参数T p ),,,(10ββββ =.记β的估计量为T p b b b B ),,,(10 =,因此,Y 的估计量为XB Y=ˆ 要求估计量Yˆ与原观测向量Y 的差异最小.记 YY e ˆ-= 采用最小二乘的计算方法,因此要使得min )ˆ()ˆ(2→--=Y Y YY e T XB X B Y Y XB Y XB Y e T T T T 2)()(2-=--=对2e 求偏导0222=+-=∂∂XB X Y X Be T T从而,得到方程。

2009年各省市国内生产总值和财政支出回归分析作者:荆长春来源:《北方经济》2010年第08期摘要:本文利用空间计量经济学模型的常系数空间滞后模型、空间误差模型,在内生经济增长模型下对2009年省级地方政府财政支出对各省国内生产总值用最小二乘法(OLS)进行回归分析的结果做了比较研究。
结论是具有空间经济联系的省市之间合作协同将会使所有省市的发展受益。
一个省市国内生产总值的增加会对周边所有省市产生带动作用,而地方财政支出的增加对周边省市影响不显著。
关键词:财政支出小二乘法一、研究背景随着财政体制改革的逐步深入,特别是1994年分税制改革与1995年财政部制定实施《过渡期财政转移支付办法》后,我国中央地方多级财政结构初步完善。
地方政府拥有了相对独立的一级财政,也有了本地经济与社会方面的诸多发展目标和各自的地方利益。
但是,由于分税制设计上存在缺陷,税收收入在中央地方之间的分配不够合理,各级政府事权与财权不相匹配。
财权向中央集中,事权则不断下放。
在以投资带动为主要特征的经济增长方式下,地方政府由于追求GDP产生过度的投资冲动,往往造成收入不能弥补支出。
当前,随着国际金融危机对世界经济的严重冲击,中国经济也开始陷入比较困难的境地。
金融动荡影响美欧口等发达国家的投资、消费、就业、居民收入,由于其消费和投资下降,从中国进口相应减少。
面对现状,政府制定出台了十大措施以及两年4万亿元的刺激经济方案。
中央政府希望通过财政支出拉动经济增长,保证8%的经济年增长率,增加就业,维持社会稳定。
二、数据与研究方法(一)数据本文涉及的变量是2009年全国除港澳台以外的31个省级行政单位的国内生产总值(GDP)与地方政府财政支出(GS)。
数据主要来自历年《中国统计年鉴》。
(二)研究方法本文进行数据分析和处理所使用的软件是GeoDAO.95-i和SPSS11.0。
三、结果分析(一)最小二乘(OLS)方法回归估计由于GeoDA0.95-i软件只能进行横截面分析,把2009年数据进行回归分析。

中国财政支出乘数的测算及其政策效应分析中国财政支出乘数的测算及其政策效应分析近年来,随着中国经济的快速发展和财政支出规模的不断扩大,中国财政支出乘数的测算及其对经济的政策效应引起了广泛关注。
财政支出乘数是指财政支出对于国内生产总值(GDP)变动的影响程度,是衡量财政政策对经济增长的影响的重要指标。
首先,测算中国财政支出乘数的方法有多种,包括传统乘数模型、结构向量自回归模型等。
其中,传统的乘数模型可通过以下公式进行测算:乘数 = 1 / (1 - MPC),其中MPC(边际消费倾向)为国民收入的每一增加单位所引发的消费支出的变化。
在中国,由于消费支出在国内生产总值中所占比例较高,因此MPC较高,进而导致财政支出乘数相对较大。
其次,中国财政支出乘数对经济的政策效应也具有一定特点。
一方面,财政支出乘数的增加会刺激经济的需求,推动GDP的增长。
在经济下行压力加大时,适当增加财政支出可以通过拉动有效需求而促进经济的回升。
另一方面,财政支出的乘数效应也受到一些因素的制约,例如民众对财政支出的预期、财政支出的结构与质量等。
如果财政支出的效果不如预期,民众对未来的消费预期不佳,那么财政支出的乘数效应可能会减弱。
进一步分析表明,中国财政支出乘数的政策效应也与财政政策的调控力度有关。
通过提高财政支出规模,政府可以加大对重点领域的投资力度,推动相关行业的发展,进而形成一定的经济增长效应。
此外,适当调整财政支出的结构也能够提高财政支出的乘数效应。
例如,在发展新能源、促进创新科技等领域适量增加财政支出,可以推动相关产业的发展,同时对未来经济增长也具有一定的拉动效果。
然而,需要注意的是,中国财政支出乘数的增长也带来了一些风险和问题。
例如,财政过度支出可能导致财政赤字的增加,从而增加了财政风险。
同时,如果财政支出过度依赖债务融资,可能导致债务风险的积累,给未来经济的可持续发展带来困难。
因此,政府在制定财政政策时,需要综合考虑财政支出的规模、结构和质量等因素,以充分发挥财政支出乘数的积极效应,同时避免可能带来的负面影响。

三大民生类公共支出影响因素灰色关联及回归分析内容摘要:基于灰色关联及回归分析方法,本文运用1999-2009年我国时间序列数据对政府卫生支出、预算内教育支出及社会保障支出三大民生类公共支出与国内生产总值、财政支出、城乡恩格尔系数等8个影响因素进行分析。
结果表明,财政支出、国内生产总值、城乡居民人均年收入是影响三大民生类公共支出的前四位重要因素。
因此本文认为,提高中央政府财政转移力度、提高城乡居民收入水平、缩小收入差距、加大教育支出力度等措施是关注和重视民生的必然举措。
关键词:民生公共支出影响因素关联度回归三大民生类公共服务支出影响因素在我国“十一五”规划中,民生领域的范围主要包括义务教育、公共卫生、社会保障、社会救助、促进就业、减少贫困、防灾减灾、公共安全、公共文化、基础科学与前沿技术以及社会公益性技术研究等领域。
本文主要分析传统意义上的、与多数民众息息相关的三类民生公共支出,包括教育、公共卫生、社会保障(包含社会保险、社会救助和社会福利)三大类。
依据马斯格雷夫(Richard A.Musgrave,1973)关于公共支出三阶段理论,本文认为影响三大民生类公共支出的因素主要有以下几方面:一是社会经济发展水平,它是民生类公共支出增长的基础,随着社会经济发展水平的提高,三大民生类公共支出一般也会随之增长,一般用国内生产总值GDP来度量。
二是财政规模,其规模可以衡量政府职能的大小,制约着三大民生类公共支出的规模,一般用财政支出来度量。
三是城乡人民生活状况,随着经济社会的发展,人民生活水平越高,大众普遍关心的教育、公共卫生、社会保障等问题凸显,要求政府更多地投入民生领域以满足民众的偏好。
该类因素一般可用城乡恩格尔系数来度量。
四是城乡人民收入状况,用城乡人均年收入来度量。
五是城市化进程,随着城市化进程的加速发展,它必然促使三大民生类公共支出不断提高。
城市化进程可用城市化率来度量。
六是总人口数,由于我国人口基数较大,人口数量也是影响三大民生类公共支出的重要因素。



重庆市财政收入的回归分析摘要文章首先运用SPSS工具对2000-2010年我国GDP、财政收入与存款汇率和年份等数据进行回归分析,得出存款汇率与GDP和年份及财政收入的回归模型。
其次,分别建立逐步回归模型,得到最优回归模型结果。
关键词: GDP 财政收入经济指标回归分析逐步回归一、前言近年来,我国财政收入的增长却远远快于经济增长的速度,针对这一情况,本文通过对财政收入和中国GDP变化的计量经济分析,试追寻问题所在,并希望对改善我国财政和GDP的合理关系提供对策。
国内生产总值(GDP)是指在一定时期内(一个季度或一年),一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,常被公认为衡量国家经济状况的最佳指标。
而财政收入是政府部门的公共收入,是国民收入分配中用于保证政府行使其公共职能、实施公共政策以及提供公共服务的资金需求。
国内生产总值和财政收入是众多经济指标中的两个关键性指标,通过回归分析等研究手段,思考和研究这两个指标的相互关系,并正确把握,对于促进经济可持续健康发展,具有非常重要的意义。
国内生产总值(gross domestic product GDP)是按市场价格计算的国内生产总值的简称。
它是一个国家(地区)所有常住单位在一定时期内生产活动的最终成果。
20世纪90年代以前,资本主义世界各国主要侧重采用GNP和人均GNP。
但进入90年代后,96%的国家纷纷放弃GNP和人均GNP,而开始重点采用GDP和人均GDP来衡量经济增长快慢以及经济实力的强,一般将国民总收入GNI(Gross National Income),指一个国家或地区所有常住单位在一定时期内收入初次分配的最终结果)看作是GNP,各国(包括中国)也仅对外公布GDP与GNI数据。
美国经济学家萨缪尔森(Paul A Samuelson)认为,GDP是20世纪最伟大的发明之一。
他将GDP比做描述天气的卫星云图,能够提供经济状况的完整图像,能够帮助领导者判断经济是在萎缩还是在膨胀,是需要刺激还是需要控制,是处于严重衰退还是处于通胀威胁之中。

浅析运用多元线性回归模型分析影响税收收入的经济因素一、概述税收收入作为国家财政收入的重要组成部分,其变化情况与国家的经济状况密切相关。
为了探究影响税收收入的经济因素,本文将运用多元线性回归模型进行分析。
我们需要明确研究的问题。
影响税收变化的因素多种多样,为了找出对税收具有显著性影响的指标,我们将根据文献阅读和实际经济经验,选取国内生产总值(GDP)、财政支出、物价水平等因素作为模型的自变量,进行多因素计量分析。
近年来,我国税收的增长速度显著超过了GDP的增长速度,这一现象可能暗示着我国的经济政策体系、政府调控机制等方面存在一些问题。
对税收收入及其主要影响因素进行多元线性回归分析,有助于我们改善税收现状,并为完善税收政策和经济体制提供参考。
在建立计量经济模型时,我们将明确解释变量和被解释变量。
被解释变量为税收收入总额,而解释变量则包括国内生产总值(GDP)、财政支出、物价水平等。
通过建立模型,我们可以得出各个变量与税收收入之间的变动关系,从而为税收收入的预测和政策制定提供依据。
1. 税收收入在国家经济中的重要地位税收收入作为国家财政收入的主要来源之一,在国家经济中占据了举足轻重的地位。
它不仅关系到政府的财政状况和公共服务的提供,更是衡量一个国家经济发展水平和社会稳定程度的重要指标。
税收收入是国家实现宏观经济调控的重要工具。
政府通过调整税收政策,如改变税率、调整税目或实行税收优惠等,可以影响企业和个人的经济行为,进而调控宏观经济运行。
例如,降低企业所得税率可以激励企业增加投资,扩大生产规模,从而促进经济增长提高个人所得税起征点则可以增加居民的可支配收入,刺激消费需求,拉动内需增长。
税收收入对于保障社会公共服务和基础设施建设具有重要意义。
税收作为一种强制性的财政收入形式,能够确保政府有足够的资金用于提供公共教育、医疗、社会保障等公共服务,以及建设交通、水利、能源等基础设施。
这些服务和设施的建设和完善,不仅能够提高人民的生活质量,也是国家经济发展的重要支撑。

基于SPSS回归分析研究影响国家财政收入的因素一、本文概述随着全球经济的不断发展和国家财政管理体系的日益完善,探究影响国家财政收入的因素变得尤为重要。
财政收入作为衡量一个国家经济实力和政府治理能力的重要指标,其稳定与增长对于国家的可持续发展和社会福祉具有决定性的影响。
本文旨在通过SPSS回归分析,深入探讨影响国家财政收入的各项因素,以期为政策制定者提供科学依据,推动国家财政收入的稳步增长。
具体而言,本文将首先对相关文献进行梳理,总结前人研究成果和不足,明确研究问题和假设。
接着,通过收集各国财政收入及相关影响因素的数据,运用SPSS软件进行多元线性回归分析,探讨各因素对国家财政收入的影响程度和方向。
在分析结果的基础上,本文将进一步讨论各因素之间的相互作用及其对国家财政收入的共同影响,揭示影响国家财政收入的关键因素。
本文的研究不仅有助于丰富和发展财政收入理论,还为政策制定者提供了实践指导。
通过深入了解影响国家财政收入的因素,政府可以更加精准地制定财政政策,优化税收结构,提高财政收入的稳定性和可持续性。
本文的研究也有助于增进国际社会对国家财政收入问题的认识和理解,促进全球经济的健康发展。
二、研究方法和数据来源本研究旨在通过SPSS回归分析,深入探究影响国家财政收入的因素。
SPSS,即Statistical Package for the Social Sciences,是一款广泛应用于社会科学领域的统计分析软件,其功能强大,包括数据管理、统计分析、图表分析等多个方面。
本研究选择SPSS作为主要分析工具,正是基于其强大的数据处理能力和多样的统计分析方法。
在数据来源方面,本研究主要采用了国家统计局、财政部等官方渠道发布的国家财政收入相关数据。
这些数据具有权威性、准确性、全面性等特点,能够为本研究提供坚实的数据基础。
同时,为了更全面地分析影响国家财政收入的因素,本研究还结合了国内外相关文献,对相关影响因素进行了梳理和分类。

我国财政支出规模的变化趋势及分析判断收藏人:猫的雅舍| 来源 | 分享2014-10-03 | 阅:1 转:79一、我国财政支出规模的变化趋势及分析判断(一)我国财政支出规模的变化趋势1.我国小口径的财政支出规模的变化趋势改革开放以来,我国小口径的财政支出规模即预算内财政支出占GDP的比重呈现出先降后升的变化趋势,预算内财政支出占GDP的比重1978年为30 .96%,1995年降到最低点11.6%,以后逐渐上升,2002年上升到21.4%。
2003年估计这一比重达到21.6%,见下表一。
2.中口径的财政支出规模的变化趋势中口径的财政支出规模即预算内财政支出与预算外财政支出之和占GDP的比重的变化,必须联系国家对于预算外支出资金口径的调整来考察。
1993、1996年国务院两次调整了预算外资金支出口径,从而导致预算外资金范围的缩小,这样预算外资金1993、1997年两次大幅度下降,因此对中口径的财政支出规模变化可以按照预算外资金口径两次调整的时间来分析。
1993年国务院对1986年决定的预算外资金范围进行了调整,原来确定为预算外资金的国有企业留利和专项基金不再作为预算外资金,而此项资金占预算外资金的比重一直维持在80%左右。
这就是说按1993年调整后的预算外资金口径计算,1978—1992年间预算外资金规模只有统计年鉴公布的预算外资金规模的20%,这样对1978—1992年间的中口径财政支出规模就可以用该期间(预算内支出十统计年鉴公布的预算外资金支出的20%)占GDP的比重来计算。
1996年国务院发布《关于加强预算外资金管理的决定》,对预算外资金的概念作了明确的规定,同时将 13项数额较大的政府性基金纳入预算管理,地方财政部门掌管的预算外资金也纳入地方预算。
因此,1996年国务院只是将预算内外资金相互间进行了调整,一部分预算外资金纳入预算管理,并没有缩减预算内外资金的总规模。
这样,1993年以后中口径的财政支出规模就可以用统计年鉴公布的预算内外支出之和占 GDP的比重来衡量,不需调整,据此可以得到我国中口径的财政支出规模的变化趋势。
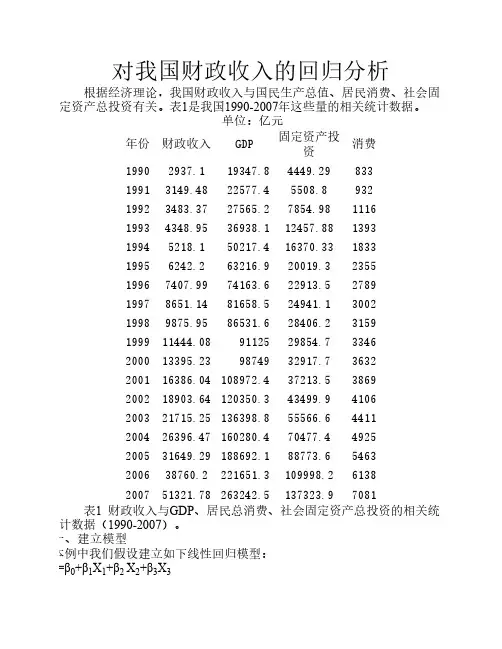
对我国财政收入的回归分析根据经济理论,我国财政收入与国民生产总值、居民消费、社会固定资产总投资有关。
表1是我国1990-2007年这些量的相关统计数据。
单位:亿元年份财政收入GDP 固定资产投资消费19902937.119347.84449.2983319913149.4822577.45508.893219923483.3727565.27854.98111619934348.9536938.112457.88139319945218.150217.416370.33183319956242.263216.920019.3235519967407.9974163.622913.5278919978651.1481658.524941.1300219989875.9586531.628406.23159199911444.0891********.73346200013395.239874932917.73632200116386.04108972.437213.53869200218903.64120350.343499.94106200321715.25136398.855566.64411200426396.47160280.470477.44925200531649.29188692.188773.65463200638760.2221651.3109998.26138200751321.78263242.5137323.97081表1 财政收入与GDP、居民总消费、社会固定资产总投资的相关统计数据(1990-2007)。
一、建立模型本例中我们假设建立如下线性回归模型:Y=β0+β1X1+β2 X2+β3X3Dependent Variable: YMethod: Least Squares Date: 10/14/10 Time: 19:30Sample: 1990 2007 Included observations: 18VariableCoefficientStd. Error t-Statistic Prob.表1给出了采用Eviews 软件对1990-2007年的财政收入与国内生产总值、国民消费、社会总投资三个因素进行回归分析的计算结果。
中国财政收入增长分析一、 案例:中国财政收入增长分析改革开放以来,中国经济的各项指标节节攀升,其中财政收入更是以持续两位数的高增长让人刮目相看,为了分析财政收入的持续增长原因,我从国家统计局网站收集了包括GDP 、居民储蓄存款余额以及房地产投资等可能影响财政收入的主要因素近十五年的数据建立模型进行分析。
二、 回归模型建立Y=α+1βX 1+2βX 2+3βX 3 其中:Y=财政收入 X 1=GDPX 2=居民储蓄存款余额 X 3=房地产投资三、 统计数据:(单位:亿元)年份 财政收入 GDP 居民储蓄存款余额 房地产投资 1995 6242 60794 29662 3149 1996 7408 71177 38521 3216 1997 8651 78973 46280 3178 1998 9876 84402 53408 3614 1999 11444 89677 59622 4103 2000 13395 99215 64332 4984 2001 16386 109655 73762 6344 2002 18904 120333 86911 7791 2003 21715 135823 103618 10154 2004 26396 159878 119555 13158 2005 31649 184937 141051 15909 2006 38760 184937 161587 19423 2007 51322 265810 161587 25289 2008 61330 314045 217885 31203 20096851834050726077236242数据来源:国家统计局网站:四、 使用EXCEL 回归结果检验结果如下:回归统计Multiple R 0.998878772R Square 0.997758802Adjusted R Square 0.997147566标准误差1079.619537观测值15方差分析df SS MS F Significance F回归分析 3 5.71E+09 1.9E+09 1632.363 7.5474E-15残差11 12821362 1165578总计14 5.72E+09Coefficients 标准误差t Stat P-value Lower 95% Upper 95% Intercept -1876.09422 1781.937 -1.05284 0.314993 -5798.111236 2045.92279 GDP 0.086579244 0.030202 2.866698 0.015332 0.020105687 0.1530528 居民储蓄存款余额0.01352142 0.025319 0.534034 0.603943 -0.042206241 0.06924908 房地产投资 1.060447108 0.290672 3.648262 0.003832 0.420682626 1.70021159五、模型的回归分析解释根据上述结果,可把模型描写为:Y= -1876+0.0866X1+0.0135 X2+1.0604 X3统计中:Multiple R: 相关系数,-11≤≤R,正为正相关,负为负相关,越接近1相关性越高。
一,数据收集从《国家统计局》获取以下数据:年份财政收入(亿元)Y 国内生产总值(亿元)X2财政支出(亿元)X3商品零售价格指数(%)X41978 519.28 3624.1 1122.09 100.7 1979 537.82 4038.2 1281.79 102 1980 571.7 4517.8 1228.83 106 1981 629.89 4862.4 1138.41 102.4 1982 700.02 5294.7 1229.98 101.9 1983 775.59 5934.5 1409.52 101.5 1984 947.35 7171 1701.02 102.8 1985 2040.79 8964.4 2004.25 108.8 1986 2090.73 10202.2 2204.91 106 1987 2140.36 11962.5 2262.18 107.3 1988 2390.47 14928.3 2491.21 118.5 1989 2727.4 16909.2 2823.78 117.8 1990 2821.86 18547.9 3083.59 102.1 1991 2990.17 21617.8 3386.62 102.9 1992 3296.91 26638.1 3742.2 105.4 1993 4255.3 34636.4 4642.3 113.2 1994 5126.88 46759.4 5792.62 121.7 1995 6038.04 58478.1 6823.72 114.8 1996 6909.82 67884.6 7937.55 106.1 1997 8234.04 74462.6 9233.56 100.8 1998 9262.8 78345.2 10798.18 97.4 1999 10682.58 82067.5 13187.67 97 2000 12581.51 89468.1 15886.5 98.5 2001 15301.38 97314.8 18902.58 99.2 2002 17636.45 104790.6 22053.15 98.7二,参数估计利用eviews软件可以得到Y关于X2的散点图:可以看出Y和X2成线性相关关系200001600012000Y80004000020000400006000080000100000X2Y关于X3的散点图:可以看出Y和X3成线性相关关系200001600012000Y800040000500010000150002000025000X3Y关于X1的散点图:200001600012000Y8000400095100105110115120125X4Dependent Variable: YMethod: Least SquaresDate: 01/09/10 Time: 13:16Sample: 1978 2002Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -2582.755 940.6119 -2.745825 0.0121X2 0.022067 0.005577 3.956633 0.0007X3 0.702104 0.033236 21.12474 0.0000X4 23.98506 8.738296 2.744821 0.0121R-squared 0.997430 Mean dependent var 4848.366 Adjusted R-squared 0.997063 S.D. dependent var 4870.971S.E. of regression 263.9591 Akaike info criterion 14.13511Sum squared resid 1463163. Schwarz criterion 14.33013Log likelihood -172.6889 F-statistic 2717.254 Durbin-Watson stat 0.948521 Prob(F-statistic) 0.000000模型估计的结果为:Y i=-2582.755+0.022067X2+0.702104X3+23.98506X4(940.6119) (0.0056) (0.0332) (8.7383)t={-2.7458} {3.9567} {21.1247} {2.7449}R2=0.997 R2=0.997 F=2717.254 df=21三,相关检验1.经济意义检验模型估计结果说明,在假定其他变量不变的情况下,当年GDP 每增长1亿元,税收收入就会增长0.02207亿元;在假定其他变量不变的情况下,当年财政支出每增长1亿元,税收收入就会增长0.7021亿元;在假定其他变量不变的情况下,当零售商品物价指数上涨一个百分点,税收收入就会增长23.985亿元。
财政收入的逐步回归分析摘要:财政收入是国民经济基础,是实现国家职能的财力保证。
本文采用SPSS19.0多元统计软件中的逐步回归分析方法,得出影响我国财政收入的显著性变量,建立国家财政收入回归模型,并将所得的模型给予合理的经济解释。
关键词:财政收入;逐步回归;显著性;SPSS1.引言财政收入是指国家财政参与社会产品分配所取得的收入,是实现国家职能的财力保证[1]。
一方面,国家可通过控制财政收入的计划和执行情况,起到宏观调控的效果;其次,在安排和预测财政一般收入的过程中,也能够了解到经济系统的变化过程,从而及时发现经济系统运行中可能存在的问题并加以纠正;此外,通过对财政一般收入中的各分项收入进行预测,能够及时地发现现行税制和政策是否适应经济发展情况,产业结构是否合理。
因此,有必要建立一套科学的国家财政收入模型使收入预算尽量适应经济形势的变化,及时反映政府的宏观经济政策和政府活动对经济的影响。
本文选取1990年-2009年20个年度的国家财政收入数据,采用线性回归中的逐步回归方法,利用SPSS多元统计软件得出影响我国财政收入的显著性变量,建立国家财政收入回归模型,并将所得的模型给予合理的经济解释。
2.提出问题2.1 提出自变量与因变量从定性分析的角度来说,财政收入会受到各种不同因素的影响,如:农业总产值、工业总产值、建筑业总产值、人口数、社会消费品零售总额、国土受灾面积等等。
本文选取财政收入y(亿元)为因变量,自变量选取如下:第一产业国内生产总值x1(亿元), 第二产业国内生产总值x2(亿元),第三产业国内生产总值x3(亿元), 人口数x4(万人),社会消费品零售总额x5(亿元),受灾面积x6(万公顷)。
由《中国统计年鉴》获取20个年份的统计数据,见表1。
表1 1990-2009年财政收入与部分项目的统计数据2.2做散点图,设定理论模型作数据散点图,并进行线性拟合,观察因变量与自变量之间关系是否有线性特点。
应用数理统计论文基于逐步回归法的国家财政收入回归分析学院:专业:姓名:学号:任课教师:基于逐步回归法的国家财政收入回归分析摘要财政收入是衡量一国政府财力的重要指标,政府在社会经济活动中提供公共物品和服务的围和数量,在很大程度上决定于财政收入的充裕状况。
对财政收入的影响因素进行分析,有助于更好的把握财政收入并做出相应的宏观调控。
本文采用逐步回归法,基于SPSS统计分析软件建立了国家财政收入的回归模型,研究了一些相关因素对国家财政收入的影响,涵盖了工业、农业、建筑业、第三产业的总产值以及社会商品零售总额、人口、受灾面积、居民消费水平八个因素,同时对回归模型进行了分析、检验和预测,验证了模型的正确性。
关键词:SPSS 财政收入逐步回归回归模型AbstractThe fiscal revenue is an important index that evaluates the financial capability of a government. The scale and amount of public facilities and services that the government offers in social and economic activities depend a lot on the condition of its fiscal revenue. The analysis on the possible factors that may influence the fiscal revenue can contribute to the proper control and arrangement of the revenue. Based on the SPSS software, the paper applies the stepwise regression method to build the regression model of the national fiscal revenue. The influence caused by some possible factors are also analyzed, which include industry, agriculture, architecture, the gross output value of tertiary industry, total volume of retail sales, population, damage area and resident consumption level. The regression model is also verified and estimated to ensure its accuracy.Key words: SPSS, fiscal revenue, stepwise regression, regression model1 引言国家财政收入对于国民经济的正常运行以及社会的蓬勃发展有着重要的影响。