六年级下册数学试题-能力提升:第10讲 特殊图形(解析版)全国通用
- 格式:docx
- 大小:1.52 MB
- 文档页数:9

小学六年级下册数学试卷一.选择题(共8题,共16分)1.今天的气温从-3℃上升了5℃,现在的温度是()℃。
A.8B.-8C.2D.-22.一艘潜水艇所处的高度是海拔-50米,一条鲨鱼在潜水艇上方30米,鲨鱼所处的位置是海拔()米。
A.80B.-80C.20D.-203.把一段铁丝截成同样长的小段,每段的长度和段数。
()A.成正比例B.成反比例C.不成比例4.下列每组中两个量不是具有相反意义的量是()。
A.收入100元与支出70元B.浪费1吨煤与节约1吨煤C.增产45吨与减产2吨D.向东与向南5.把圆柱的底面平均分成16份切开后,照图拼成近似的长方体,()发生了变化。
A.底面积B.表面积C.体积6.大于-5的整数有()。
A.5个B.10个C.无数个7.河东乡前年水稻总产量是20万千克,去年水稻总产量比前年增产一成五,去年全乡水稻总产量是()。
A.3万千克B.46万千克C.23万千克 D.32万千克8.将圆柱侧面展开得到的图形不可能是()。
A.梯形B.长方形C.正方形二.判断题(共8题,共16分)1.教室的面积一定,铺的瓷砖块数和瓷砖的面积成反比。
()2.甲量比乙量多10%,则甲、乙两量一定成正比例。
()3.一个圆柱给出了底面半径,我能求出该圆柱的侧面积。
()4.14∶21=12∶18。
()5.把一个圆柱体削成一个最大的圆锥体,圆锥体的体积是削去部分的。
()6.三角形高一定,底和面积成正比例。
()7.∶和3∶4可以组成比例。
()8.五月份比四月份节约用水15%,则四月份比五月份多用水15%。
()三.填空题(共8题,共18分)1.填上适当的数。
2.________既不是正数,也不是负数;________和________表示具有相反意义的量。
3.甲、乙两数的比值是,若甲数和乙数同时乘0.469,则新的两数的最简整数比是()。
4.某钟面时针长15厘米,分针长18厘米,一昼夜时针与分针尖端所走路程的比是()。

第十讲 计数之加乘原理与技巧1. 回顾分类枚举与排列组合; 2. 精讲计数问题的经典范例。
排列最简单的计数问题,只需一一列举就可以;复杂的计数问题则需要借助排列与组合的相关知识予以解决.一般地,从n 个不同的元素中,任取m(m≤n)个不同的元素,按照一定的顺序排成一列,叫做从n 个不同元素中任取m 个元素的一个排列.我们主要来研究满足某种条件的排列的个数.相同的排列应满足: 它们所含的元素均相同; 它们的顺序也一样.一般地,从n 个不同元素中取出m 个元素的排列的个数称为从n 个不同元素中取出m 个元素的排列数,记作:mn A (m ≤n).从n 个元素中取出m 个元素排成一排,有多少种排法,是从n 个元素中取出m 个元素的排列数.这个问题可以看成有m 个位置,从n 个元素中取m 个元素放到m 个位置中,可分m 个步骤:第①步:第1个位置有n 种选择; 第②步:第2个位置有n -1种选择; 第③步:第3个位置有n -2种选择; ……第m 步:第m 个位置有n -m+1种选择.由乘法原理:mn A = n ×(n - 1)×(n - 2)×…×(n -m+1).——乘积中共有m 项特别地,当m=n 时, ()1...21mnn n A A n n ==⨯-⨯⨯叫做n 个元素的全排列数.1×2×3×…×n 称为n 的阶乘,记作n!因此()!!mn n A n m =- (m≤n).排列数乘积形式的公式:mn A =n×(n - 1)×(n - 2)×…×(n -m+1).教学目标专题回顾本讲内容非常有趣,不过要在计数过程中达到“不重不漏”,必须掌握计数问题的原理与一些技巧才行。
在小升初的考试与其它的竞赛活动中,计数问题出现频率很高。
排列数阶乘形式的公式: ()!!mn n A n m =- (m≤n).组合有时我们只需从若干元素中取出一些就可以了,这种问题称为组合问题,组合问题与排列问题的区别就是:组合问题是将元素取出即可,不需排序,而排列问题是取出后要进行排序.一般地,从n 个不同元素中任取m(m≤n)个不同的元素并成一组,叫做从n 个不同元素中取出,n 个元素的组合.从n 个不同元素中,每次取出m 个元素的组合总数,叫做从n 个不同元素中取出m 个元素的组合数,记作mn C (m ≤n).从n 个元素中取出m 个元素的排列问题可以看成分两步完成: 第①步:从n 个元素中取出m 个元素,这时有多少种取法?实际上就是从n 个元素中取出m 个元素的组合数mn C ;第②步:对取出的m 个元素进行排列,排法数就是mm A .由乘法原理可知:mmmn nmA C A =,因此,mmn nm mA C A =. 将排列数公式代人得:()()().1...1.1...3.2.1mn n n n m C m m --+=-或 ()!!!mn n C n m m =-.分类枚举【例1】 ★★★(《小数报》数学竞赛决赛填空题第ll 题)方格纸上有一只小虫,从直线AB 上的一点O 出发,沿方格纸上的横线或竖线爬行.方格纸上每小段的长为1厘米.小虫爬过若干小段后仍然在直线AB 上,但不一定回到O 点.如果小虫一共爬过2厘米,那么小虫的爬行路线有____种;如果小虫一共爬过3厘米,那么小虫爬行的路线有___种.【解】为了方便,下面叙述省去“上、下、左、右”4个字前面的“向”. (1)小虫爬过2厘米,可有以下6种路线,分别是: 左,右;右,左; 上,下;下,上;左,左;右,右.(以上前4种路线均回到O点)(2)小虫爬过3厘米,可有20种路线,分别是:上,左,下;上,右,下;下,左,上;下,右,上;上,下,左;上,下,右;下,上,左;下,上,右.(以上8种都是先“上”或先“下”.)如果第一步为“左”或“右”,那么转化为第(1)题,各有6种路线,一共是8+6×2=20(种)答案是:(1)6;(2)20。


【小升初专题复习】北师大版六年级下册数学-第十讲立体图形综合(解析版)一、知识点1、长方体总棱长:(长十宽十高)×4C=(a+b+h)×4侧面积:底面周长×高=(长十宽)×2×高S=Ch=(a+b)×2×h表面积:(长×宽十长×高十宽×高)×2S=(ab+ah+bh)×2体积:长×宽×高V=abh2、正方体总棱长:棱长×12C=12a侧面积:底面周长×高=棱长×4×棱长S=Ch=4a²表面积:棱长×棱长×6S=6a²体积:棱长×棱长×棱长V=a³3、圆柱侧面积:底面周长×高S=2πrh侧表面积:侧面积+2个底面积=2πrh+2πr²S表体积:底面积×高V=πr²h4、圆锥体积:底面积×高÷3V=πr²h÷35、染色问题公式三面:8个二面:(长-2)×4+(宽-2)×4+(高-2)×4一面:(长-2)(宽-2)×2+(长-2)(高-2)×2+(宽-2)(高-2)×2 零面:(长-2)(宽-2)(高-2)二、学习目标1.我能够运用公式解决立体图形的计算问题。
2.我能够灵活应用排水法求物体的体积。
三、课前练习1.判断题。
(1)用9个一样大小的小正方体能拼成一个大正方体。
()(2)如果圆柱的底面半径扩大2倍,那么它的体积就扩大4倍。
()(3)如果两个正方体的棱长之比是2:3,那么它们的体积之比就是4:9。
()【答案】(1)×;(2)×;(3)×【解析】(2)圆柱的体积是由底面积和高两个条件决定的,本题没有说明高不变,因此这种说法是错误的。
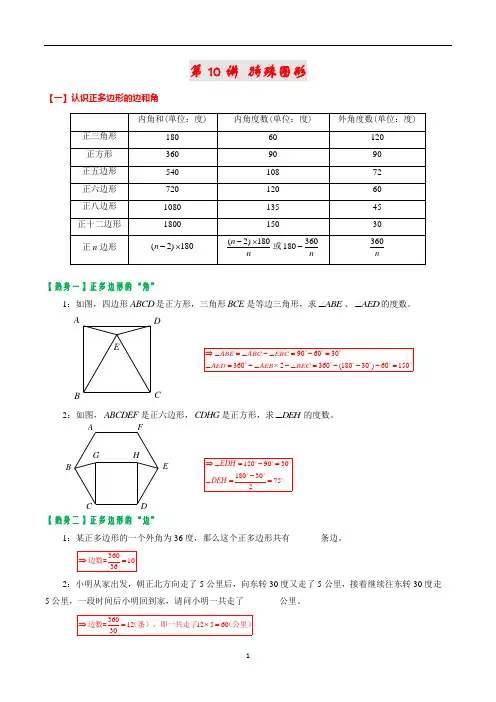
第10讲 特殊图形【一】认识正多边形的边和角【热身一】正多边形的“角”1:如图,四边形ABCD 是正方形,三角形BCE 是等边三角形,求ABE ∠、AED ∠的度数。
9060303602360(18030)60150ABE ABC EBC AED AEB BEC ⇒∠=∠-∠=-=∠=-∠⨯-∠=---=o o oo o o o o o2:如图,ABCDEF 是正六边形,CDHG 是正方形,求DEH ∠的度数。
120903018030752EDH DEH ⇒∠=-=-∠==o o o o oo【热身二】正多边形的“边”1:某正多边形的一个外角为36度,那么这个正多边形共有_______条边。
3601036⇒=边数=2:小明从家出发,朝正北方向走了5公里后,向东转30度又走了5公里,接着继续往东转30度走5公里,一段时间后小明回到家,请问小明一共走了________公里。
360121256030⇒=⨯=边数=(条),即一共走了(公里) EDCB AHGFEDC BA3:如图,B∠和D∠都是直角,13584A BC AD∠=︒==,,,求四边形ABCD的面积。
88442422ABCDS⨯⨯⇒=-=4:如图,从正方形ABCD的四个角上各切掉一个等腰直角三角形后,剩下一个八边形,已知EF=4,GH=7,而切掉的三角形IHC的面积等于2,那么切掉的三角形AEL的面积等于多少?2255512.52IHCAELS IC HCBG GH HC BF EF AE AE S∆∆⇒=→==⨯++=++→=→==++例题1练一练例题2【二】正多边形的分割【热身一】常见正多边形的“分割”正三角形常见分割方法:正方形常见分割方法:正六边形常见分割方法:DCBA1:在图中,三角形ABC 和DEF 是两个完全相同的等腰直角三角形,其中DF 长9厘米,CF 长3厘米,那么阴影部分的面积是多少平方厘米?2:正六边形ABCDEF 的面积是1平方米,将六条边分别向两端各延长一倍,交于六个点,组成如下图的图形,求这个图形的面积.{2平方米}3:如图所示的正六边形,连接每两个间隔开一个点的顶点,形成图中的阴影部分,已知阴影部分的面积是24平方厘米,请问空白部分的面积是多少?{48平方厘米}4,把三角形的三边沿两端向外延长一倍,得到了如图所示的六边形.已知原来的正三角形ABC 的面积是1,请问新六边形的面积是多少?{13}5:如右图所示,正六边形ABCDEF 的面积是120平方厘米,G 、H 、I 分别是所在边的中点,请问:GHI 的面积是多少平方厘米?{45平方厘米}6:下面的两个图中,每个小正三角形的面积为1,阴影部分的面积分别是多少?{3、13}EDCAFED CB A BC AG H I BC DEF A7:正方形ABCD与等腰直角三角形BEF叠放在一起(如图),M N、正方形边的中点,五边形ABCNM的面积是214cm,三角形BEF的面积是多少?8:如图,在两个相同的等腰三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少?9:两个正方形如图放置,图中的每个三角形都是等腰直角三角形;若其中较小正方形的边长为12厘米,那么较大的正方形的面积是多少?10:如图,大正六边形的面积是224cm,其中放了三个一样的小正六边形,阴影面积是多少?11:已知大的正六边形面积是260cm,按图中方式分割(切割均为等分点),形成的阴影部分面积是多少?NM DECBAFBA12:如图,正六边形ABCDEF 的面积为240,那么阴影部分的面积是多少?13:图中的小正六边形面积为2,求阴影部分的面积.{7}14:三个正六边形如图放置,其中各点均为对应边的中点,若阴影三角形面积为1,则正六边形ABCDEF 的面积为___________.{32}+例题4练一练【热身二】特殊正多边形的“分割(1)”正八边形常见分割方法:正八边形分成“4个长方形”和“8个直角三角形”中间的大长方形是整个正八边形的231:如图所示,正八边形的边长为8,将其进行下图的切割,切割后灰色部分面积与斜线部分面积之差为_________(大减小).{16}2:如图,正六边形的面积为120,P是其内任意一点,求三角形PBC和三角形PEF 的面积之和.{40}【热身三】特殊正多边形的“分割(2)”正十二边形常见分割方法:正十二边形分成“12个正三角形”和“6个正方形”1:东东在生日会上订了一个直径20cm的圆形披萨,他平均切成了12块,每一块的形状如图;因为外围的边不好吃,实际上每一块只吃里面的部分(三角形ABC),求每一小块披萨可吃的面积.{25平方厘米}2:如图,正十二边形和中心白色正六边形的边长均为12厘米,图中阴影部分的面积是多少平方厘米?例题5例题6+。

小学数学六年级下册期末测试卷一.选择题(共6题,共12分)1.下面的平面图形分别绕虚线旋转一周会形成圆柱的是()。
A. B. C. D.2.圆柱的侧面展开可能是()。
A.正方形B.长方形C.平行四边形D.以上三种情况都有可能3.一个圆柱与一个长6分米,宽5分米,高2分米的长方体体积相等,已知圆柱的底面积是10平方分米,它的高是()。
A.6分米B.8分米C.16分米D.3分米4.把一个圆柱的侧面展开,不可能得到下面的图形是()。
A. B. C. D.5.一辆汽车从甲站出发向东行驶30km,然后再向西行驶20km,此时汽车的位置是()。
A.甲站的东边50km处B.甲站的东边10km处C.甲站的西边10km处 D.甲站的西边50km处6.甲处海拔-100米,乙处海拔-80米,两处相比,()处比较低一点。
A.甲B.乙C.一样高D.无法确定二.判断题(共6题,共12分)1.某城市一天的气温是-5℃~7℃,最高气温和最低气温相差2℃。
()2.圆锥体的体积是8立方厘米,高是2厘米,底面积是12平方厘米。
()3.订阅《中国少年报》的份数和总钱数成正比例。
()4.零上12℃(+12℃)和零下12℃(-12℃)是两种相反意义的量。
()5.如果高于平均分5分记作+5分,那么低于平均分10分记作+10分。
()6.队员每人做好事的件数一定,做好事的总件数与做好事的少先队员人数成正比例。
()三.填空题(共8题,共15分)1.一袋化肥包装标有:净重(50±0.5)千克,表示这袋化肥最少________千克,最重是________千克。
2.通常我们规定海平面的海拔高度为0米,我国的城市拉萨,是世界上海拔最高的城市,高于海平面3658米,记作________米;死海是世界上海拔最低的海,低于海平面480米,记作________米。
3.从正面看到的图形是()形,从左面看是()形,从上面看是()形。
4.做一个圆柱形厨师帽底面圆周长为45厘米,高是底面直径的2倍,至少需要()平方厘米布料。

神奇图形一、知识要点1、组合图形主要圆、扇形、三角形、平行四边形、梯形等图形组合而成的不规则图形2、组合图形面积①整体➖空白②割补法差不变二、实例演练例1求下图阴影部分的面积。
阴影部分面积=扇形面积➖正方形面积阴影:23.14545527.125⨯÷-⨯÷=练习1下图梯形的上底为4cm,下底为8cm,高为4cm,求阴影部分的面积。
例2求右图阴影部分的面积。
阴影部分面积=扇形面积阴影:23.144412.56⨯÷=练习2求右图阴影部分的面积。
例3已知小圆半径为4厘米,大圆半径是小圆的2倍,问:空白部分甲比乙的面积多多少平方厘米?同时加上阴影部分后差不改变,两个空白部分面积之差就是两圆面积之差小圆半径:4cm大圆半径:4×2=8(cm)多:()288-44=150.72cm ππ⨯⨯⨯⨯答:空白部分甲比乙的面积多150.72平方厘米。
练习3下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积。
例题4求图中阴影部分的面积。
(单位:厘米)四个扇形组成一个半径为1的圆,阴影部分面积为:正方形的面积➖圆的面积,阴影:2×2-π×1×1=0.86(平方厘米)练习4求阴影部分的面积。
(单位:厘米)三、巩固练习参考答案练习1阴影部分面积=梯形面积➖扇形面积阴影:(4+8)×4÷2-23.1444⨯÷=24+12.56=36.56(cm 2)练习2阴影部分面积=正方形面积的一半阴影:5×5÷2=12.5练习3所求面积等于图中阴影部分的面积:2052082140-+⨯÷=()(平方厘米)练习4阴影部分为:正方形面积减去圆面积,4×4➖π×2×2=3.44(平方厘米)。
六年级下册数学试题-能力提升:第10讲 特殊图形(解析版)全国通用
【一】认识正多边形的边和角
【热身一】正多边形的“角”
1:如图,四边形ABCD 是正方形,三角形BCE 是等边三角形,求ABE ∠、AED ∠的度数。
9060303602360(18030)60150ABE ABC EBC AED AEB BEC ⇒∠=∠-∠=-=∠=-∠⨯-∠=---=o o o
o o o o o o
2:如图,ABCDEF 是正六边形,CDHG 是正方形,求DEH ∠的度数。
E
D
C
B
A
H
G
F E
D
C B
A
120903018030752
EDH DEH ⇒∠=-=-∠==o o o o o
o
【热身二】正多边形的“边”
1:某正多边形的一个外角为36度,那么这个正多边形共有_______条边。
360
1036
⇒=边数=
2:小明从家出发,朝正北方向走了5公里后,向东转30度又走了5公里,接着继续往东转30度走5公里,一段时间后小明回到家,请问小明一共走了________公里。
360
121256030
⇒=⨯=边数=
(条),即一共走了(公里) 3:如图,B ∠和D ∠都是直角,13584A BC AD ∠=︒==,,,求四边形ABCD 的面积。
8844
2422
ABCD S ⨯⨯⇒=
-=
4:如图,从正方形ABCD 的四个角上各切掉一个等腰直角三角形后,剩下一个八边形,已知EF=4,GH=7,而切掉的三角形IHC 的面积等于2,那么切掉的三角形AEL 的面积等于多少?
22
55
512.52
IHC AEL S IC HC BG GH HC BF EF AE AE S ∆∆⇒=→==⨯++=++→=→=
=
++例题1练一练例题2
D
C
B
A
【二】正多边形的分割
【热身一】常见正多边形的“分割”
正三角形常见分割方法:
正方形常见分割方法:
正六边形常见分割方法:
1:在图中,三角形ABC 和DEF 是两个完全相同的等腰直角三角形,其中DF 长9厘米,CF 长3厘米,那么阴影部分的面积是多少平方厘米
?
E
D
C
A
2:正六边形ABCDEF 的面积是1平方米,将六条边分别向两端各延长一倍,交于六个点,组成如下图的图形,求这个图形的面积.{2平方米}
3:如图所示的正六边形,连接每两个间隔开一个点的顶点,形成图中的阴影部分,已知阴影部分的面积是24平方厘米,请问空白部分的面积是多少?{48平方厘米}
4:有一个正三角形ABC ,把三角形的三边沿两端向外延长一倍,得到了如图所示的六边形.已知原来的正三角形ABC 的面积是1,请问新六边形的面积是多少?{13}
5:如右图所示,正六边形ABCDEF 的面积是120平方厘米,G 、H 、I 分别是所在边的中点,请问:GHI 的面积是多少平方厘米?{45平方厘米}
6:下面的两个图中,每个小正三角形的面积为1,阴影部分的面积分别是多少?{3、13}
F
E
D
C B A B
C A
G H I B
C D
E
F
A
7:正方形ABCD与等腰直角三角形BEF叠放在一起(如图),M N
、正方形边的中点,五边形ABCNM的面积是2
14cm,三角形BEF的面积是多少?
8:如图,在两个相同的等腰三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少?
9:两个正方形如图放置,图中的每个三角形都是等腰直角三角形;若其中较小正方形的边长为12厘米,那么较大的正方形的面积是多少?
10:如图,大正六边形的面积是2
24cm,其中放了三个一样的小正六边形,阴影面积是多少?
N
M D
E
C
B
A
F
B
A
11:已知大的正六边形面积是2
60cm,按图中方式分割(切割均为等分点),形成的阴影部分面积是多少?
12:如图,正六边形ABCDEF的面积为240,那么阴影部分的面积是多少?
13:图中的小正六边形面积为2,求阴影部分的面积.{7}
14:三个正六边形如图放置,其中各点均为对应边的中点,若阴影三角形面积为1,则正六边形ABCDEF 的面积为___________.{32}
+例题4练一练
【热身二】特殊正多边形的“分割(1)”
正八边形常见分割方法:
正八边形分成“4个长方形”和“8个直角三角形” 中间的大长方形是整个正八边形的2
3 1:如图所示,正八边形的边长为8,将其进行下图的切割,切割后灰色部分面积与斜线部分面积之差为_________(大减小).{16}
2:如图,正六边形的面积为120,P是其内任意一点,求三角形PBC和三角形PEF 的面积之和.{40}
【热身三】特殊正多边形的“分割(2)”
正十二边形常见分割方法:
正十二边形分成“12个正三角形”和“6个正方形”
1:东东在生日会上订了一个直径20cm的圆形披萨,他平均切成了12块,每一块的形状如图;因为外围的边不好吃,实际上每一块只吃里面的部分(三角形ABC),求每一小块披萨可吃的面积.{25平方厘米}
2:如图,正十二边形和中心白色正六边形的边长均为12厘米,图中阴影部分的面积是多少平方厘米?
例题5例题6
+。