第四章 物料衡算
- 格式:docx
- 大小:239.26 KB
- 文档页数:20

(四)过程的物料衡算
1、循环过程
例如在生产 中一般将未反应的原料与产品先分离,后循环返回原料进口处,与新原料一起再进入反应器反应
例如苯直接加氢转化环己烷中的循环过程:
在没有循环时,一系列单元步骤的物料衡算可按顺序依次进行,每次可取一个单元.但是,如果有循环的话,由于循环量并不知道,所以逐次计算并不能计算出循环量.
试差法:假定一个循环量估计值进行计算,将估计值与计算值比较,若不符,重新假定一个估计值,一直计算到估计值与计算值之差在一定的误差范围内.
代数解法:在循环存在时,列出物料平衡方程式,并求解一般方程式中以循环量作为未知数,应用联立方程式的方法进行求解.
苯直接加氢转化环己烷中的循环过程的衡算
解:反应为:C6H6+3H2→C6H12
基准:100kmol/h 环己烷
查苯的转化率为99%
则生产100kmol/h 环己烷需苯
100/0.99=101.01kmol/h
未反应的苯为
101.01-100=1.01kmol/h
产物中含H2,设含量为nH2
总产量=100+1.01+3.12=104.13kmol/h
其摩尔分数为
H2的进料率为 100×3+3.12=303.12kmol/h
苯的进料率为 101.01kmol/h
设H2循环量为R
R=100.92kmol/h
纯C 6H 6
20%C 6H 6 96.0126=H C x 01.066=H C x 03
.02=H x 3.001.110022=++H H n n h Kmol n H /12.32=2.012.30301.10101.101=++R。
物料衡算物料衡算的准则就是质量守恒定律,即“进入一个系统的全部物料必等于离开这个系统的全部物料,再加上过程损失量和在系统中积累量”。
依据质量守恒定律,对研究系统作物料衡算,可由下式表示[13]:∑G进=∑G出+∑G损+∑G积其中式中:∑G进——输入物料量总和;∑G出——输出物料量总和;∑G损——总的物料损失量;∑G积——系统中的积累量。
根据设计任务,苯酐生产能力为80000吨/年,产品纯度达到99.9wt%按照8000小时开工计算,每小时的生产能力:80000×1000×99.9%/8000= 9990kg/h3.1 反应器中氧化反应的物料衡算3.1.1 氧化反应过程的衡算基准本次设计以每小时生产9990kg为基准,进料量9400kg/h,转化率99.8%;生成苯酐的选择性约为0.8;空气与邻二甲苯进料比为9.5:1;主要副产品为苯酞、顺酐、苯甲酸、柠槺酐、二氧化碳、一氧化碳等。
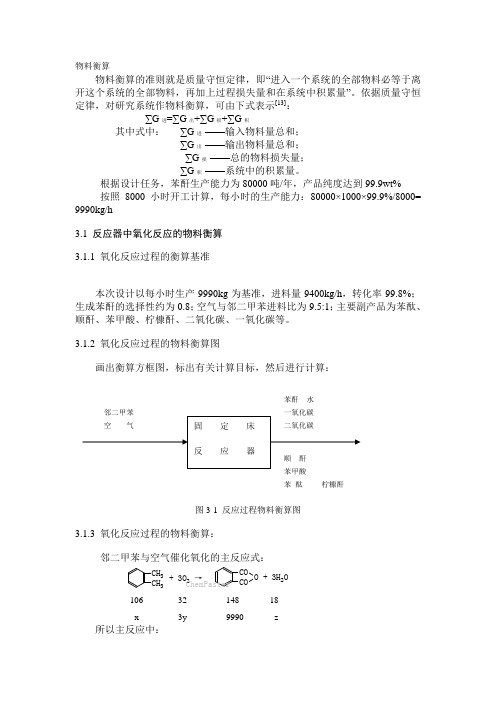
3.1.2 氧化反应过程的物料衡算图画出衡算方框图,标出有关计算目标,然后进行计算:图3-1 反应过程物料衡算图3.1.3 氧化反应过程的物料衡算:邻二甲苯与空气催化氧化的主反应式:106 32 148 18x 3y 9990 z所以主反应中:(1)邻二甲苯消耗量:9990148106=x x = 7155 kg/h 氧气消耗量:9990148y 332=⨯ y =6480 kg/h 水的生成量: 9990148z 318=⨯ z = 3645 kg/h (2) 邻二甲苯转化率为99.8%,且邻二甲苯的进气量为9400kg/h ,所以: 邻二甲苯生产苯酐的选择性为:7155/9400/99.8%=77.27%。
(3)设计进料空邻比为9.5:1,所以空气进料量计算:5.91w 9400=w 空 =89300 kg/h 空气中 O 2所占的比例为21%,所以工艺空气中氧气的进料量:w 氧 = 89300×21%= 18753kg/h 。


第四章物料衡算第四章物料衡算1.教学⽬的与要求掌握化⼯过程物料衡算的基本⽅法,包括⽆化学反应的物料衡算、有化学反应的物料衡算。
2.主要教学内容物料衡算式、物料衡算的基本⽅法、⽆化学反应的物料衡算、有化学反应的物料衡算以及物料衡算的计算机解题。
3.重点与难点:重点:⽆化学反应及有化学反应的物料衡算⽅法难点:具有循环、排放及旁路过程的物料衡算4.学时分配: 8+6S 学时物料衡算是化⼯计算中最基本、也是最重要的内容之⼀,它是能量衡算的基础。
通常,物料衡算有两种情况,⼀种是对已有的⽣产设备或装置,利⽤实际测定的数据,算出另—些不能直接测定的物料量。
⽤此计算结果,对⽣产情况进⾏分析、作出判断、提出改进措施。
另⼀种是设计⼀种新的设备或装置,根据设计任务,先作物料衡算,求出进出各设备的物料量,然后再作能量衡算,求出设备或过程的热负荷,从⽽确定设备尺⼨及整个⼯艺流程。
物料衡算的理论依据是质量守恒定律,即在—个孤⽴物系中,不论物质发⽣任何变化,它的质量始终不变(不包括核反应,团为核反应能量变⽐⾮常⼤,此定律不适⽤)。
第⼀节物料衡算式4-1 化⼯过程的类型化⼯过程根据其操作⽅式可以分成间歇操作、连续操作以及半连续操作三类。
或⾏将其分为稳定状态操作和不稳定状态操作两类。
在对某个化⼯过程作物料或能量衡算时,必须先了解⽣产过程的类型。
间歇操作过程:4-2 物料衡算式物料衡算是研究某⼀个体系内进、出物料量及组成的变化。
根据质量守恒定律,对某⼀个体系,输⼊体系的物料量应该等于输出物料量与体系内积累量之和。
所以,物料衡算的基本关系式应该表⽰为;如果体系内发⽣化学反应,则对任⼀个组分或任⼀种元素作衡算时,必须把由反应消耗或⽣成的量亦考虑在内。
所以(4—1)式成为:上式对反应物作衡算时.由反应⽽消耗的量,应取减号,对⽣成物作衡算时,由反应⽽⽣成的量,应取加号。
但是,列物料衡算式时应该注意,物料平衡是指质量平衡,不是体积或物质的量(摩尔数)平衡。



三.工艺设计计算3.1 物料横算3.1.1物料衡算的意义物料横算,是在已知产品规格和产量前提下算出所需原料量、废品量及消耗量。
同时,还可拟定出原料消耗定额,并在此基础上做能量平衡计算。
通过物料横算可算出:(1)实际动力消耗量(2)生产过程所需热量或冷量(3)为设备选型、决定规格、台数(或台时产量)提供依据(4)在拟定原料消耗定额的基础上,可进一步计算日消耗量,每小时消耗量等设备所需的基础数据。
综上所述,物料衡算是紧密配合车间生产工艺设计而进行的,因此,物料衡算是工艺设计过程的一项重要的计算内容。
3.1.2物料横算的方法塑料制品的生产过程多采用全流程、连续操作的形式。
物料衡算的步骤如下:(1)确定物料衡算范围,画出物料衡算示意图,注上与物料衡算有关的数据。
物料衡算示意图如下:(2)说明计算任务。
如:年产量、年工时数等。
(3)选定计算基准。
生产上常用的计算基准有:①单位时间产品数量或单位时间原谅投入量,如:kg/h,件/h,t/h(连续操作常采用此种基准);②加入设备的原料量(间歇操作常采用此种基准)。
(4)由已知数据,根据下列公式进行物料衡算:ΣG1=ΣG1+ΣG3式中:ΣG1——进入设备的物料量总和ΣG2——离开设备的正品量和次品量总和ΣG3——加工过程中物料损失量总和(5)收集数据资料。
一般包括以下方面:①年生产时间:连续生产300~350 d间歇生产200~250 d连续生产时,年生产的天数较多,在300d左右,其他时间将考虑全长检修,车间检修或5%~10%意外停机。
当间歇生产时,就要减去全年的休息日,目前为双休日加上法定假日全年约为110d,所以间歇生产比连续生产少110个工作日。
总之,确定了每年有效地工作时数后就能正确定出物料衡算的时间基准,算出每小时的生产任务,进而在以后的计算中选定设备的规格。
具体的选择天数要通过分析得出。
②有关定额、合格率、废品率、消耗率、回收率等。
在任何一个产品加工过程中,合格产品都不是百分之百。

第四章物料衡算❖第一节概述❖第二节物料衡算基本理论❖第三节物料衡算举例4.1 概述❖4.1.1.物料衡算的重要性❖求出各种物料的数量和组成,设计由定性转入定量。
❖设计中,物料衡算是最先进行的计算项目,其结果是后续各单项设计的依据,物料衡算结果的直接关系到整个工艺设计可靠程度。
❖4.1.2.物料衡算的依据❖工艺流程示意图以及为物料衡算收集的有关资料。
4.1.3.物料衡算的作用❖将工艺流程示意图进一步深化,可绘制出物料流程图。
❖在物料衡算的基础上,可进行能量衡算、设备的选型或工艺设计,以确定设备的容积、台数和主要工艺尺寸、确定消耗定额、进行车间布置设计和管道设计。
❖对已投产的设备、装置、车间或工厂进行物料衡算,以寻找薄弱环节,为改进生产、完善管理提供可靠的依据❖可作为判断工程项目是否达到设计要求以及检查原料利用率和三废处理完善程度的一种手段。
4.1.4.物料衡算的类型❖按物质变化分为:❖物理过程的物料衡算❖化学过程的物料衡算❖按操作方式分为:❖连续过程的物料衡算❖间歇过程的物料衡算❖按衡算目的分为:4.2 物料衡算的基本理论4.2.1物料平衡方程式❖理论基础是质量守恒定律。
❖1.物理过程❖稳态过程,物料在体系内没有累积2.化学过程❖对于稳态过程使用上述各式时要注意以下几点:4.2.2 衡算基准❖1、时间基准❖对连续稳定流动体系,以单位时间作基准。
该基准可与生产规模直接联系❖对间歇过程,以处理一批物料的生产周期作基准。
❖2、质量基准❖对于液、固系统,因其多为复杂混合物选择一定质量的原料或产品作为计算基准。
❖若原料产品为单一化合物或组成已知,取物质量(mol)作基准更方便。
3、体积基准❖对气体选用体积作基准。
通常取标况下体积Nm3(Hm3)❖在进行物料衡算或热量衡算时,均须选择相应的衡算基准。
合理地选择衡算基准,不仅可以简化计算过程,而且可以缩小计算误差基准选取中几点说明:❖(1)上面几种基准具体选哪种(有时几种共用)视具体条件而定,难以硬性规定。




第四章物料衡算与能量衡算本设计的产量为320吨/年的清爽沐浴露,工作时间250天,则每天的产量:G1=320×1000÷250=1280Kg,根据本设计的特点选用的是间歇式的批量化生产工艺,本工厂设计每天的工作时数是8小时,并分2批进行生产。
则每批产量G2=1280÷2=640Kg 每批生产所需要的时间为8÷2=4h。
在生产过程中,由于设备的问题,如加热、冷却、过滤、包装和输送等都会造成原料和成品的不同程度的损失,对总的生产来说这个损失是不可忽略的,必须把损失量算入到总的生产量中去,本工厂设计设计的产品的收率都为97%,损失量为3%。
因此,沐浴露一年的实际原料用量:G=320÷97%=329.89t每天的实际原料用量: G‵=329.89×1000÷250=1319.56Kg每批的实际原料用量:G批=1319.56Kg÷2=659.78kg根据物料衡算式可知:∑G1=∑G2+∑G3,式中的∑G1表示输入原料的总量,∑G2表示为输出后的总量,∑G3表示生产过程中损失总量。
现以每批的原料为计算的基准,得:∑G1=659.78kg ,∑G2=∑G1×97%=659.78×97%=640kg ,∑G3=∑G1×3%=659.78kg×3%=19.79kg1.输入原料的用量如下:G MAP=∑G1×38.5%=494.84×38.5%=254.02kgG月桂酸=∑G1×11%=72.57 kgG乙二醇二硬脂酸酯=∑G1×2%=13.19kgG KOH =∑G1×3.8%=25.07 kgG5-羟磺酸甜菜碱=∑G1×6%=39.59 kgG羟乙基纤维素=∑G1×0.8%=5.28 kgG珠光片=∑G1×1.5%=9.90 kgG EDTA-2Na=∑G1×0.1%=0.66 kgG凯松=∑G1×0.1%=0.66kgG香精=∑G1×0.3%=1.98 kgG柠檬酸=∑G1×0.1%=0.66kgG M550=∑G1×1.6%=10.56 kgG薄荷脑=∑G1×0.5%=3.30kgG 水=∑G1×66.3%=437.43kg2.输出原料用量如下G MAP=∑G2×38.5%=640×38.5%=246.4kg G月桂酸=∑G2×11%=70.4 kgG乙二醇二硬脂酸酯=∑G2×2%=12.8kgG KOH =∑G2×3.8%=24.32kgG5-羟磺酸甜菜碱=∑G2×6%=38.4 kgG羟乙基纤维素=∑G2×0.8%=5.12kgG珠光片=∑G2×1.5%=9.6kgG EDTA-2Na=∑G2×0.1%=0.64 kgG凯松=∑G2×0.1%=0.64kgG香精=∑G2×0.3%=1.92 kgG柠檬酸=∑G2×0.1%=0.64kgG M550=∑G2×1.6%=10.24 kgG薄荷脑=∑G2×0.5%=3.5 kgG 水=∑G2×66.3%=424.32kg3. 由以上的数据可得沐浴露生产的物料衡算表如下:能量衡算已知能量衡算式如下:∑Q入=∑Q出+∑Q设备式中∑Q入表示物料进入时带入反应釜的热量,∑Q出表示物料带出时热量,∑Q设备表示设备带出的热量。






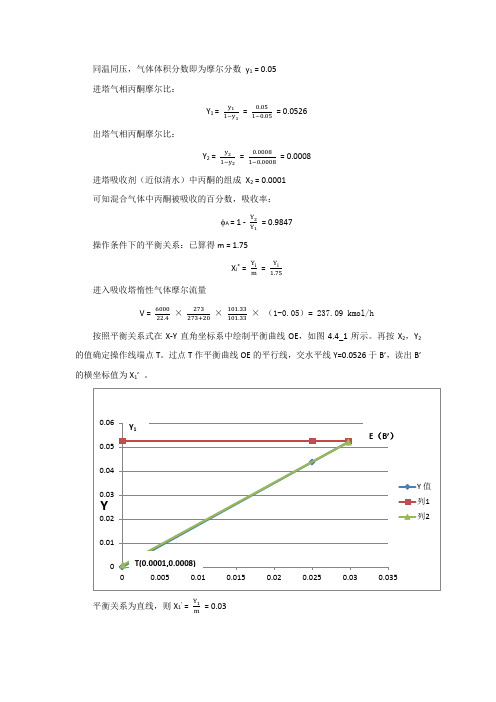
同温同压,气体体积分数即为摩尔分数y1 = 0.05 进塔气相丙酮摩尔比:Y1 = y11−y1= 0.051−0.05= 0.0526出塔气相丙酮摩尔比:Y2 = y21−y2= 0.00081−0.0008= 0.0008进塔吸收剂(近似清水)中丙酮的组成X2 = 0.0001 可知混合气体中丙酮被吸收的百分数,吸收率:A = 1 - Y2Y1= 0.9847 操作条件下的平衡关系:已算得m = 1.75X i* = Y im = Y i1.75进入吸收塔惰性气体摩尔流量V = 600022.4×273273+20×101.33101.33×(1-0.05)= 237.09 kmol/h按照平衡关系式在X-Y直角坐标系中绘制平衡曲线OE,如图4.4_1所示。
再按X2,Y2的值确定操作线端点T。
过点T作平衡曲线OE的平行线,交水平线Y=0.0526于B’,读出B’的横坐标值为X1’。
平衡关系为直线,则X1’ = Y1m= 0.03最小液气比按照下式计算(LV )min =Y 1—Y 2Y 1m−X 2 =0.0526−0.0008 0.03−0.0001= 1.729取操作液气比为:(LV)= 1.5(LV)min(LV )=1.5 × 1.729 = 2.59 L = 237 × 2.59 = 614.71 kmol/hV (Y 1 - Y 2)=L (X 1 - X 2) X 1 =237×(0.0526−0.0008)614.71= 0.020采用Eckert 通用关联式计算泛点气速。
气相质量流量w V = V V ×Vm = 6000× 1.245 = 7470 kg/h液相质量流量可近似按纯水的流量计算W L = L X M L = 263.45 X 18.02 = 4747.37 kg/hEckert 通用关联图的横坐标w L w V (ρV ρL )0.5 = 4747.377470 (1.245998.2)0.5= 0.0224气相质量流量w V = V V × ρVm = 6000 × 1.245 = 7470 kg/h液相质量流量可近似按纯水的流量计算W L = L X M L = 263.45 X 18.02 = 4747.37 kg/h泛点气速 u f 采用贝恩—霍根关联式计算lg [u F 2g (αtε3)(ρV ρL)μL 0.2] = A – K (w L w V)1/4(ρV ρL)1/8g = 9.81 m/s 2 αt = 132.5 m 2/m 3 ε = 0.91ρVm = 1.245 kg/m 3 ρL = 998.2 kg/m 3 A = 0.204 K = 1.75 μL = 1 mpa ·s W L = 11077.07 kg/h W V = 7470 kg/h代入贝恩—霍根关联式可得泛点气速u f = 1.068 m/s 对于散装填料 u = 0.6 u f = 0.6409 m/s 塔径 D = √4V s πu√4×60003600×3.14×3.655= 0.762 m圆整后 D = 800 mm泛点率校核 u =6000/36000.785×0.82 = 3.317 m/sf = uu f= 3.3174.873 x 100% = 68.08 %f 在50% - 80%之间,符合要求在此处键入公式。
第四章物料衡算1.教学目的与要求掌握化工过程物料衡算的基本方法,包括无化学反应的物料衡算、有化学反应的物料衡算。
2.主要教学内容物料衡算式、物料衡算的基本方法、无化学反应的物料衡算、有化学反应的物料衡算以及物料衡算的计算机解题。
3.重点与难点:重点:无化学反应及有化学反应的物料衡算方法难点:具有循环、排放及旁路过程的物料衡算4.学时分配: 8+6S 学时物料衡算是化工计算中最基本、也是最重要的内容之一,它是能量衡算的基础。
通常,物料衡算有两种情况,一种是对已有的生产设备或装置,利用实际测定的数据,算出另—些不能直接测定的物料量。
用此计算结果,对生产情况进行分析、作出判断、提出改进措施。
另一种是设计一种新的设备或装置,根据设计任务,先作物料衡算,求出进出各设备的物料量,然后再作能量衡算,求出设备或过程的热负荷,从而确定设备尺寸及整个工艺流程。
物料衡算的理论依据是质量守恒定律,即在—个孤立物系中,不论物质发生任何变化,它的质量始终不变(不包括核反应,团为核反应能量变比非常大,此定律不适用)。
第一节物料衡算式4-1 化工过程的类型化工过程根据其操作方式可以分成间歇操作、连续操作以及半连续操作三类。
或行将其分为稳定状态操作和不稳定状态操作两类。
在对某个化工过程作物料或能量衡算时,必须先了解生产过程的类型。
间歇操作过程:4-2 物料衡算式物料衡算是研究某一个体系内进、出物料量及组成的变化。
根据质量守恒定律,对某一个体系,输入体系的物料量应该等于输出物料量与体系内积累量之和。
所以,物料衡算的基本关系式应该表示为;如果体系内发生化学反应,则对任一个组分或任一种元素作衡算时,必须把由反应消耗或生成的量亦考虑在内。
所以(4—1)式成为:上式对反应物作衡算时.由反应而消耗的量,应取减号,对生成物作衡算时,由反应而生成的量,应取加号。
但是,列物料衡算式时应该注意,物料平衡是指质量平衡,不是体积或物质的量(摩尔数)平衡。
若体系内有化学反应,则衡算式中各项用摩尔/时为单位时,,必须考虑反应式中的化学计量系数。
出为反应前后物料中的分子数不守恒。
第二节物料衡算的基本方法进行物料衡算时,为了能顺利地解题,避免错误,必须掌握解题技巧,按正确的解题方法和步骤进行。
尤其是对复杂的物料衡算题,更应如此,这样才能获得准确的计算结果。
4-3 画物料流程简图方法求解物料衡算问题,首先应该根据给定的条件画出流程简图。
图中用简单的方框表示过程中的设备,用线条和箭头表示每个流股的途径和流向。
并标出每个流股的已知变量(如流量、组成)及单位。
对一些未知的变量,可用符号表示。
4—4 计算基准及其选择进行物料、能虽衡算时,必须选择一个计算基准。
从原则上说选择任何一种计算基准,都能得到正确的解答。
但是,计算基准选择得恰当,可以使计算简化,避免错误。
对于不同化工过程,采用什么基准适宜,需视具体情况而定,不能什硬性规定。
根据不同过程的特点,选样计算基准时,应该注意以下几点:1. 应选择已知变量数最多的流股作为计算基准。
2.对液体或固体的体系,常选取单位质量作基准。
3. 对连续流动体系,用单位时间作计算基准有时较方便。
4. 对于气体物料,如果环境条件(如温度、压力)已定,则可选取体积作基准。
4—5物料衡算的步骤1搜集计算数据。
2画出物料流程简图。
3确定衡算体系。
4写比化学反应方程式,包括主反应和副反应,标出有用的分子量,如果无化学反应,则此步可免去。
5选择合适的计算基准,并在流程图上注明所选的基准值。
6.列出物料衡算式,然后用数学方法求解。
7.将计算结果列成输入一输出物料表。
第三节无化学反应过程的物料衡算在化工过程中,—些只有物理变化不发生化学反应的单元操作,如混合、蒸馏、蒸发、干燥、吸收、结晶、萃取等,这些过程的物料衡算都可以根据物料衡算式(4—3),列出总物料和各组分的衡算式,再用代数法求解。
4-6 简单过程的物料衡算简单过程是指仅有一个设备或一个单元操作或整个过程简化成一个设备的过程。
这种过程由物料衡算比较简单,在物料流程简图中,设备边界就是体系边界。
当利用代数法求解时,列衡算式应注意下列几点:1.无化学反应体系,能列出的独立物料衡算式数目,最多等于输入和输出物料中化学组分的数目。
2.首先列出含未知量数目最少的物料衡算方程,以便于解题。
3.总体系内具有很多多组分的物料,则最好将每个流股编号.并列表表示出己知的量和组成.检查能列出的衡算方程数目是否等于未知量的数目。
4—7 有多个设备过程的物料衡算对有多个设备的过程,进行物料衡算时,可以划分多个衡算体系。
此时,必须选择恰当的衡算体系,这是很重要的步骤。
不然会使计算繁琐,甚至无法求解。
例4—7 有两个蒸馏塔的分离装置,将含50%苯、30%甲苯和20%(mol%)二甲苯的混合物分成较纯的三个馏试份,其流程图及各流股组成如下图,计算蒸馏1000mol/h原料所得各流股的量及进塔2物料组成。
有化学反应过程的物料衡算有化学反应的过程,物料中的组分比较复杂。
因为,工业上的化学反应,,各反应物的实际用量.并不等于化学反应式中的理论量。
为了使所需的反应顺利进行,或使其中较昂贵的反应物全部转化,常常使价格较低廉的一些反应物用量过量。
4—8 反应转化率、选择性及收率等概念工业化学反应过程中,当反应原料的配比不按化学计量比时,根据反应物的化学计量数大小可称其为限制反应物与过量反应物。
1.限制反应物:化学反应原料不按化学计量比配料时,其中以最小化学计量数存在的反应物称为限制反应物。
2.过量反应物:不按化学计量比配料的原料中,某种反应物的量超过限制反应物完全反应所需总的理论量,该反应物称为过量反应物。
3.过量百分数:过量反应物超过限制反应物所需理论量的部分占所需理论量的百分数。
4.转化率:5.选择性;6.收率:4—9 一般反应过程的物料衡算对有化学反应过程的物料衡算,由于各组分在过程中发生了化学反应,因此就不能简单地按(4—3)式列组分的衡算式,必须考虑化学反应中生成或消耗的量,应该根据化学反应式,按(4—4)式列衡算方程。
对一般的反应过程,可用下列几种方法求解。
一、直接求解法有些化学反应过程的物料衡算,有时只含一个未知量或组成,这类问题比较简单可根据化学反应式直接求解,不必列出衡算式,如下例。
二、元素衡算元素衡算是物料衡算的一种重要形式。
在作这类衡算时,并不需要考虑具体的化学反应,而是按照元素种类被转化及重新组合的概念表示为输入(某种元素)=输出(同种元素)对反应过程中化学反应很复杂,无法用一、两个反应式表示的物料衡算题,可以列出元素衡算式,用代数法求解。
三、用联系组分作衡算“联系组分”是指随物料输入体系,但完全不参加反应,又随物料从体系输出的组分。
在整个反应过程中,它的数量不变。
如果体系中存在联系组分,那么输入物料和输出物料之间就可以根据联系组分的含量进行关联。
例如,F、P分别为输入、输出物料,T为联系组分。
T在F中的质量分数为xfT在P中的质量分数为xPT,则F与P之间的关系为4—10 有平衡反应过程的物料衡算对有平衡反应过程的物料衡算,除了需要建立物料或元素衡算式以外,常常还需要利用反应的平衡关系来计算产物的平衡组成。
讨算方法见下例。
4—11 具有循环、排放及旁路过程的物料衡算在化工过程中,有一些具有循环、排放及旁路的过程,这类过程的物料衡算与以上介绍的方法相类似,只是需要先根据已知的条件及所求的未知量选择合适的衡算体系,列出物料衡算式再求解。
如果存在联系组分,则可以利用联系组分计算。
一、循环过程的物料衡算在化工生产中,有一些反应过程每次经反应器后的转化率不高,有的甚至很低。
如乙烯氧化制环氧乙烷的过程,乙烯的单程转化率(即原料一次通过反应器的转化率)约30%左右;由氢、氮合成氨的单程转化率一般也只有20%左右。
而乙烯直接水合制乙醇的过程,乙烯的单程转化率只有4—5%。
因此在反应器出口的产物中有大量原料未反应。
为提高原料的利用率,把这部分末反应的原料从反应产物中分离出来,然后把它循环返回反应器,与新鲜物料一起再进行反应。
此过程即为循环过程。
其流程如图4—5。
某些无化学反应过程,如蒸发.结晶过程、精馏过程等,为了提高原料利用率或为保证产品质量、改善经济指标、也有采用循环过程的。
二、具有循环及排放过程的物料衡算循环过程在稳定状态下操作时,物料的质量既不积累也不消失,各流股的组分恒定。
但是,如果原料中含有不反应的杂质或惰性物质,经长时间的循环会使其浓度逐渐增加,因此就必须把一部分循环物料不断地排放掉,以维持进料中杂质的含量不再增大。
例如,假定反应器进料A的最初流量是100kg/h,进料含10ppm的惰性物质(以I表示),单程转化率为50%。
经反应后,剩下50kg/h未反应的原料和惰性物,将其与产物分离后全部循环。
由于总量减少了一半,所以循环料中惰性杂质含量增加一倍,为20ppm。
如图4—6①。
第二次进反应器的原料变成新鲜原料50%和循环物料50%的混合料,其中含I组份15ppm(因为循环料中含20ppm的I),第二次循环料中I组分含量增加到30ppm。
第三次通过反应器的原料中I组分就变成20ppm。
这样经长时间不停地循环,将会使循环料中杂质积累.浓度增高,以至影响正常生产。
为了排除积累的杂质,就必须排放一部分循环料。
图4—7为具有循环及排放过程的物料流程图。
图中W为排放物料,即从分离器出来的分三、具有旁路过程的物料衡算具有旁路的过程,就是把一部分物料绕过一个或多个设备,直接与另一流股物料相混,其流程如图4—8。
这类过程的物料衡算与循环过程的物料衡算相类似,计算时应注意结点平衡。