2015年湖北省高考数学试卷理科-高考
- 格式:doc
- 大小:636.55 KB
- 文档页数:31
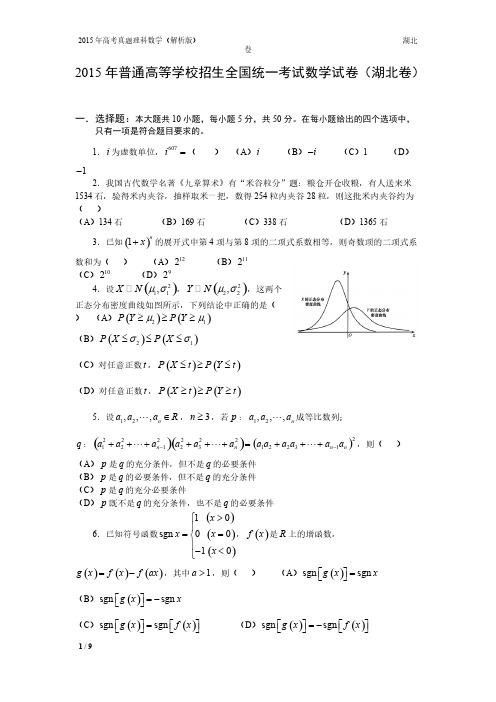
2015年普通高等学校招生全国统一考试数学试卷(湖北卷)一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.为虚数单位,( ) (A ) (B ) (C )1 (D )i 607i=i i -1-2.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )(A )134石 (B )169石 (C )338石 (D )1365石3.已知的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系()1nx +数和为( ) (A )(B )122112(C ) (D )102924.设,,这两个()211,X Nμσ:()222,Y N μσ:正态分布密度曲线如图所示,下列结论中正确的是( ) (A )()()21P Y P Y μμ≥≥≥(B )()()21P X P X σσ≤≤≤(C )对任意正数,t ()()P X t P Y t ≤≥≤(D )对任意正数,t ()()P X t P Y t ≥≥≥5.设,,若:成等比数列;12,,,n a a a R ∈ 3n ≥p 12,,,n a a a :,则( )q ()()()22222221212312231n n n n a a a a a a a a a a a a --++++++=+++ (A )是的充分条件,但不是的必要条件p q q (B )是的必要条件,但不是的充分条件p q q (C )是的充分必要条件p q (D )既不是的充分条件,也不是的必要条件p q q 6.已知符号函数,是上的增函数,()()()10sgn 0010x x x x >⎧⎪==⎨⎪-<⎩()f x R ,其中,则( ) (A )()()()g x f x f ax =-1a >()sgn sgn g x x =⎡⎤⎣⎦(B )()sgn sgn g x x =-⎡⎤⎣⎦(C )(D )()()sgn sgn g x f x =⎡⎤⎡⎤⎣⎦⎣⎦()()sgn sgn g x f x =-⎡⎤⎡⎤⎣⎦⎣⎦7.在区间上随机取两个数,记1p 为事件“”的概率,2p 为事件[]0,1,x y 12x y +≥“”的概率,3p 为事件“12xy ≤”的概率,则( )1||2x y -≤12xy ≤(A )123p p p << (B )231p p p <<(C )312p p p <<(D )321p p p <<8.将离心率为的双曲线的实半轴长和虚半轴长同时增加1e 1C a ()b a b ≠个单位长度,得到离心率为的双曲线,则( ) (A )对任意的,()0m m >2e 2C ,a b 12e e >(B )当时,;当时, (C )对任意的,a b >12e e >a b <12e e <,a b 12e e <(D )当时,;当时,12e e >a b >12e e <a b <9.设集合,(){}22,|1,,A x y xy x y Z =+≤∈,定义集合(){},|2,2,,B x y x y x y Z =≤≤∈,则中元素的个数为(()()(){}12121122,|,,,A B x x y y x y A x y B ⊕=++∈∈A B ⊕) (A )77 (B )49(C )45(D )3010.设,表示不超过x 的最大整数。


2015年普通高等学校招生全国统一考试理科数学(湖北卷)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的. 1.i 为虚数单位,607i 的共轭复数为A .iB .i -C .1D .1-2.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534 石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为 A .134石 B .169石 C .338石 D .1365石3.已知(1)n x +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数 和为A .122B .112C .102D .924.设X :211(,)N μσ,Y :222(,)N μσ,这两个正态分布密度曲线如图所示.下列结论中正确的是A .21()()P Y P Y μμ≥≥≥B .21()()P X P X σσ≤≤≤C .对任意正数t ,()()P X t P Y t ≤≥≤D .对任意正数t ,()()P X t P Y t ≥≥≥5.设1a ,2a ,L ,n a R ∈,3n ≥.若p :1a ,2a ,L ,n a 成等比数列;q :22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++L L L ,则A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件6.已知符号函数10sgn 0010x x x x >⎧⎪==⎨⎪-<⎩,()f x 是R 上的增函数,()()()g x f x f ax =-(1a >),则A .sgn[()]sgn g x x =B .sgn[()]sgn g x x =-C .sgn[()]sgn[()]g x f x =D .sgn[()]sgn[()]g x f x =-7.在区间[0,1]上随机取两个数x ,y ,记1p 为事件“12x y +≥”的概率,2p 为事件“12x y -≤”的概率,3p 为事件“12xy ≤”的概率,则A .123p p p <<B .231p p p <<C .312p p p <<D .321p p p << 8.将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长b (a b ≠)同时增加m (0m >)个单位长度,得到离心率为2e 的双曲线2C ,则A .对任意的a ,b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的a ,b ,12e e <D .当a b >时,12e e <;当a b <时,12e e > 9.已知集合22{(,)1,,}A x y x y x y Z =+≤∈,{(,)2,2,,}A x y x y x y Z =≤≤∈,定义集合12121221{(,)(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为 A .77 B .49 C .45 D .3010.设x R ∈,[]x 表示不超过x 的最大整数.若存在实数t ,使得[]1t =,2[]2t =,…,[]n t n =同时成立,则正整数n 的最大值是A .3B .4C .5D .6 二、填空题:本大题共6小题,考生需作答5小题,每小题5分,共25分. (一)必考题(11—14题)11.已知向量OA OB ⊥u u u r u u u r ,3OA =u u u r,则OA OB ⋅=u u u r u u u r . 12.函数2()4cos cos()2sin ln(1)22x f x x x x π=---+的零点个数为 . 13.如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30o 的方向上,行驶600m 后到达B 处,测得此山顶在西偏北75o 的方向上,仰角为30o ,则此山的高度CD = m .14.如图,圆C 与x 轴相切于点(1,0)T ,与y 轴正半轴交于两点,A B (B 在A 的上方),且2AB =.(1)圆C 的标准..方程为 ; (2)过点A 任作一条直线与圆22:1O x y +=相交于,M N 两点,下列三个结论: ①NA MA NBMB=; ②2NB MA NAMB-=;③NB MA NAMB+=其中正确结论的序号是 .(写出所有正确结论的序号)(二)选考题:请考生在第15、16两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑.如果全选,则按第15题作答结果计分. 15.(选修4-1:几何证明选讲)如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且3BC PB =,则ABAC= .APBCAB16.(选修4-4:坐标系与参数方程)在直角坐标系xoy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l 的极坐标方程为(sin 3cos )0ρθθ-=,曲线C 的参数方程为11x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),l 与C相交于A ,B 两点,则AB = .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分11分)某同学用“五点法”画函数()sin()f x A x ωϕ=+,0ω>,2πϕ<,在某一个周期内的(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数()f x 的解析式;(Ⅱ)将()y f x =图象上所有点向左平行移动θ(0θ>)个单位长度,得到()y g x =的图象.若()y g x =图象的一个对称中心为5(,0)12π,求θ的最小值.18.(本小题满分12分)设等差数列{}n a 的公差为d ,前n 项和为n S ,等比数列{}n b 的公比为q .已知11b a =,22b =,q d =,10100S =.(Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)当1d >时,记n n n ac b =,求数列{}n c 的前n 项和n T .19.(本小题满分12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ABCD -中,侧棱PD ⊥底面ABCD ,且PD CD =,过棱PC 的中点E ,作EF PB ⊥交PB 于点F ,连接DE ,DF ,BD ,BE .(Ⅰ)证明:PB ⊥平面DEF .试判断四面体DBEF 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(Ⅱ)若面DEF 与面ABCD 所成二面角的大小为3π,求DC BC 的值.20.(本小题满分12分)某厂用鲜牛奶在某台设备上生产A ,B 两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B 产品的产量不超过A 产品产量的2倍,设备每天生产A ,B 两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W 单位:吨)是一个随该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量. (Ⅰ)求Z 的分布列和均值;(Ⅱ)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率. 21.(本小题满分14分)一种作图工具如图1所示.O 是滑槽AB 的中点,短杆ON 可绕O 转动,长杆MN 通过N 处铰链与ON 连接,MN 上的栓子D 可沿滑槽AB 滑动,且1DN ON ==,3MN =.当栓子D 在滑槽AB 内作往复运动时,带动N 绕O 转动一周(D 不动时,N 也不动),M 处的笔尖画出的曲线记为C .以O 为原点,AB 所在的直线为x 轴建立如图2所示的平面直角坐标系. (Ⅰ)求曲线C 的方程;(Ⅱ)设动直线l 与两定直线1l :20x y -=和2l :20x y +=分别交于P ,Q 两点.若直线l 总与曲线C 有且只有一个公共点,试探究:OPQ ∆的面积是否存在最小值?若 存在,求出该最小值;若不存在,说明理由.22.(本小题满分14分)已知数列{}n a 的各项均为正数,1(1)n n n b n a n=+(n N *∈),e 为自然对数的底数.(Ⅰ)求函数()1x f x x e =+-的单调区间,并比较1(1)n n+与e 的大小; (Ⅱ)计算11b a ,1212b ba a ,123123b b b a a a ,由此推测计算1212n nb b b a a a L L 的公式,并给出证明; (Ⅲ)令112()nn n c a a a =L ,数列{}n a ,{}n c 的前n 项和分别记为n S ,n T ,证明:n n T eS <.。


2015年湖北省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•湖北)i为虚数单位,i607的共轭复数为()A.i B.﹣i C.1 D.﹣12.(5分)(2015•湖北)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石3.(5分)(2015•湖北)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A.212B.211C.210D.294.(5分)(2015•湖北)设X~N(μ1,ς12),Y~N(μ2,ς22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤ς2)≤P(X≤ς1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y≥t)5.(5分)(2015•湖北)设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件6.(5分)(2015•湖北)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnx C.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]7.(5分)(2015•湖北)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P18.(5分)(2015•湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e29.(5分)(2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.3010.(5分)(2015•湖北)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3 B.4 C.5 D.6二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)(2015•湖北)已知向量⊥,||=3,则•=.12.(5分)(2015•湖北)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为.13.(5分)(2015•湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.14.(5分)(2015•湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是.(写出所有正确结论的序号)选修4-1:几何证明选讲15.(5分)(2015•湖北)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.选修4-4:坐标系与参数方程16.(2015•湖北)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t为参数),l与C相交于A,B两点,则|AB|=.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)(2015•湖北)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.18.(12分)(2015•湖北)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.19.(12分)(2015•湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD 中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.20.(12分)(2015•湖北)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.21.(14分)(2015•湖北)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON 可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(14分)(2015•湖北)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.2015年湖北省高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•湖北)i为虚数单位,i607的共轭复数为()A.i B.﹣i C.1 D.﹣1【分析】直接利用复数的单位的幂运算求解即可.【解答】解:i607=i604+3=i3=﹣i,它的共轭复数为:i.故选:A.【点评】本题考查复数的基本运算,复式单位的幂运算以及共轭复数的知识,基本知识的考查.2.(5分)(2015•湖北)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石【分析】根据254粒内夹谷28粒,可得比例,即可得出结论.【解答】解:由题意,这批米内夹谷约为1534×≈169石,故选:B.【点评】本题考查利用数学知识解决实际问题,考查学生的计算能力,比较基础.3.(5分)(2015•湖北)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A.212B.211C.210D.29【分析】直接利用二项式定理求出n,然后利用二项式定理系数的性质求出结果即可.【解答】解:已知(1+x)n的展开式中第4项与第8项的二项式系数相等,可得,可得n=3+7=10.(1+x)10的展开式中奇数项的二项式系数和为:=29.故选:D.【点评】本题考查二项式定理的应用,组合数的形状的应用,考查基本知识的灵活运用以及计算能力.4.(5分)(2015•湖北)设X~N(μ1,ς12),Y~N(μ2,ς22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤ς2)≤P(X≤ς1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y≥t)【分析】直接利用正态分布曲线的特征,集合概率,直接判断即可.【解答】解:正态分布密度曲线图象关于x=μ对称,所以μ1<μ2,从图中容易得到P(X≤t)≥P(Y≤t).故选:C.【点评】本题考查了正态分布的图象与性质,学习正态分布,一定要紧紧抓住平均数μ和标准差ς这两个关键量,结合正态曲线的图形特征,归纳正态曲线的性质.5.(5分)(2015•湖北)设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件【分析】运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣2,讨论等号成立的条件,结合等比数列的定义和充分必要条件的定义,即可得到.1a n)【解答】解:由a1,a2,…,a n∈R,n≥3.运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,若a1,a2,…,a n成等比数列,即有==…=,则(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,即由p推得q,但由q推不到p,比如a1=a2=a3=…=a n=0,则a1,a2,…,a n不成等比数列.故p是q的充分不必要条件.故选:A.【点评】本题考查充分必要条件的判断,同时考查等比数列的定义,注意运用定义法和柯西不等式解题是关键.6.(5分)(2015•湖北)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnx C.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]【分析】直接利用特殊法,设出函数f(x),以及a的值,判断选项即可.【解答】解:由于本题是选择题,可以常用特殊法,符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),不妨令f(x)=x,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[g(x)]=﹣sgnx.所以A不正确,B正确,sgn[f(x)]=sgnx,C不正确;D正确;对于D,令f(x)=x+1,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[f(x)]=sgn(x+1)=;sgn[g(x)]=sgn(﹣x)=,﹣sgn[f(x)]=﹣sgn(x+1)=;所以D不正确;故选:B.【点评】本题考查函数表达式的比较,选取特殊值法是解决本题的关键,注意解题方法的积累,属于中档题.7.(5分)(2015•湖北)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P1【分析】作出每个事件对应的平面区域,求出对应的面积,利用几何概型的概率公式进行计算比较即可.【解答】解:分别作出事件对应的图象如图(阴影部分):P1:D(0,),F(,0),A(0,1),B(1,1),C(1,0),则阴影部分的面积S1=1×1﹣=1﹣=,S2=1×1﹣2×=1﹣=,S3=1×+dx=+lnx|=﹣ln=+ln2,∴S2<S3<S1,即P2<P3<P1,故选:B.【点评】本题主要考查几何概型的概率计算,利用数形结合是解决本题的关键.本题也可以直接通过图象比较面积的大小即可比较大小.8.(5分)(2015•湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e2【分析】分别求出双曲线的离心率,再平方作差,即可得出结论.【解答】解:由题意,双曲线C1:c2=a2+b2,e1=;双曲线C2:c′2=(a+m)2+(b+m)2,e2=,∴=﹣=,∴当a>b时,e1<e2;当a<b时,e1>e2,故选:D.【点评】本题考查双曲线的性质,考查学生的计算能力,比较基础.9.(5分)(2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.30【分析】由题意可得,A={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)},根据定义可求【解答】解:解法一:∵A={(x,y)|x2+y2≤1,x,y∈Z}={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(x,y)||x|≤2,|y|≤2,x,y∈Z}={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)}∵A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},∴A⊕B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2),(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2),(﹣2,3),(﹣2,﹣3),(0,﹣3),(2,﹣3),(﹣1,3),(﹣1,﹣3),(1,3),(2,3),(0,3),(3,﹣1),(3,0)(3,1),(3,2),(3,﹣2)(﹣3,2)(﹣3,1),(1,﹣3),(﹣3,﹣1),(﹣3,0),(﹣3,﹣2)}共45个元素;解法二:因为集合A={(x,y)|x2+y2≤1,x,y∈Z},所以集合A中有5个元素,即图中圆中的整点,B={(x,y)||x|≤2,|y|≤2,x,y∈Z},中有5×5=25个元素,即图中正方形ABCD 中的整点,A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B}的元素可看作正方形A1B1C1D1中的整点(除去四个顶点),即7×7﹣4=45个.故选:C.【点评】本题以新定义为载体,主要考查了集合的基本定义及运算,解题中需要取得重复的元素.10.(5分)(2015•湖北)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3 B.4 C.5 D.6【分析】由新定义可得t的范围,验证可得最大的正整数n为4.【解答】解:若[t]=1,则t∈[1,2),若[t2]=2,则t∈[,)(因为题目需要同时成立,则负区间舍去),若[t3]=3,则t∈[,),若[t4]=4,则t∈[,),若[t5]=5,则t∈[,),其中≈1.732,≈1.587,≈1.495,≈1.431<1.495,通过上述可以发现,当t=4时,可以找到实数t使其在区间[1,2)∩[,)∩[,)∩[,)上,但当t=5时,无法找到实数t使其在区间[1,2)∩[,)∩[,)∩[,)∩[,)上,∴正整数n的最大值4故选:B.【点评】本题考查简单的演绎推理,涉及新定义,属基础题.二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)(2015•湖北)已知向量⊥,||=3,则•=9.【分析】由已知结合平面向量是数量积运算求得答案.【解答】解:由⊥,得•=0,即•()=0,∵||=3,∴.故答案为:9.【点评】本题考查了平面向量的数量积运算,考查了向量模的求法,是基础的计算题.12.(5分)(2015•湖北)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为2.【分析】利用二倍角公式化简函数的解析式,求出函数的定义域,画出函数的图象,求出交点个数即可.【解答】解:函数f(x)的定义域为:{x|x>﹣1}.f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|=2sinx﹣|ln(x+1)|=sin2x﹣|ln(x+1)|,分别画出函数y=sin2x,y=|ln(x+1)|的图象,由函数的图象可知,交点个数为2.所以函数的零点有2个.故答案为:2.【点评】本题考查三角函数的化简,函数的零点个数的判断,考查数形结合与转化思想的应用.13.(5分)(2015•湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=100m.【分析】设此山高h(m),在△BCD中,利用仰角的正切表示出BC,进而在△ABC中利用正弦定理求得h.【解答】解:设此山高h(m),则BC=h,在△ABC中,∠BAC=30°,∠CBA=105°,∠BCA=45°,AB=600.根据正弦定理得=,解得h=100(m)故答案为:100.【点评】本题主要考查了解三角形的实际应用.关键是构造三角形,将各个已知条件向这个主三角形集中,再通过正弦、余弦定理或其他基本性质建立条件之间的联系,列方程或列式求解.14.(5分)(2015•湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为(x﹣1)2+(y﹣)2=2;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是①②③.(写出所有正确结论的序号)【分析】(1)取AB的中点E,通过圆C与x轴相切于点T,利用弦心距、半径与半弦长之间的关系,计算即可;(2)设M(cosα,sinα),N(cosβ,sinβ),计算出、、的值即可.【解答】解:(1)∵圆C与x轴相切于点T(1,0),∴圆心的横坐标x=1,取AB的中点E,∵|AB|=2,∴|BE|=1,则|BC|=,即圆的半径r=|BC|=,∴圆心C(1,),则圆的标准方程为(x﹣1)2+(y﹣)2=2,故答案为:(x﹣1)2+(y﹣)2=2.(2)∵圆心C(1,),∴E(0,),又∵|AB|=2,且E为AB中点,∴A(0,﹣1),B(0,+1),∵M、N在圆O:x2+y2=1上,∴可设M(cosα,sinα),N(cosβ,sinβ),∴|NA|=====,|NB|====,∴===,同理可得=,∴=,①成立,﹣=﹣()=2,②正确.+=+()=,③正确.故答案为:①②③.【点评】本题考查求圆的标准方程,用三角函数值表示单位圆上点的坐标是解决本题的关键,注意解题方法的积累,属于难题.选修4-1:几何证明选讲15.(5分)(2015•湖北)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.【分析】利用切割线定理推出PA=2PB,利用相似三角形求出比值即可.【解答】解:由切割线定理可知:PA2=PB•PC,又BC=3PB,可得PA=2PB,在△PAB与△PAC中,∠P=∠P,∠PAB=∠PCA(同弧上的圆周角与弦切角相等),可得△PAB∽△PAC,∴==.故答案为:.【点评】本题考查切割线定理以及相似三角形的判定与应用,考查逻辑推理能力.选修4-4:坐标系与参数方程16.(2015•湖北)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t为参数),l与C相交于A,B两点,则|AB|=.【分析】化极坐标方程化直角坐标方程,参数方程化普通方程,联立直线方程和双曲线方程后求得交点坐标,由两点间的距离公式得答案.【解答】解:由ρ(sinθ﹣3cosθ)=0,得y﹣3x=0,由C的参数方程为(t为参数),两式平方作差得:x2﹣y2=﹣4.联立,得,即.∴A(),B(),∴|AB|=.故答案为:.【点评】本题考查极坐标方程化直角坐标方程,参数方程化普通方程,考查了直线和圆锥曲线的位置关系,是基础的计算题.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)(2015•湖北)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.【分析】(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.从而可补全数据,解得函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)及函数y=Asin(ωx+φ)的图象变换规律得g(x)=5sin(2x+2θ﹣).令2x+2θ﹣=kπ,解得x=,k∈Z.令=,解得θ=,k∈Z.由θ>0可得解.【解答】解:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.数据补全如下表:且函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)知f(x)=5sin(2x﹣),得g(x)=5sin(2x+2θ﹣).因为y=sinx的对称中心为(kπ,0),k∈Z.令2x+2θ﹣=kπ,解得x=,k∈Z.由于函数y=g(x)的图象关于点(,0)成中心对称,令=,解得θ=,k∈Z.由θ>0可知,当K=1时,θ取得最小值.【点评】本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换规律的应用,属于基本知识的考查.18.(12分)(2015•湖北)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.【分析】(1)利用前10项和与首项、公差的关系,联立方程组计算即可;(2)当d>1时,由(1)知c n=,写出T n、T n的表达式,利用错位相减法及等比数列的求和公式,计算即可.【解答】解:(1)设a1=a,由题意可得,解得,或,当时,a n=2n﹣1,b n=2n﹣1;当时,a n=(2n+79),b n=9•;(2)当d>1时,由(1)知a n=2n﹣1,b n=2n﹣1,∴c n==,∴T n=1+3•+5•+7•+9•+…+(2n﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.【点评】本题考查求数列的通项及求和,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.19.(12分)(2015•湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD 中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.【分析】解法1)(1)直线与直线,直线与平面的垂直的转化证明得出PB⊥EF,DE∩FE=E,所以PB⊥平面DEF,即可判断DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,确定直角.(2)根据公理2得出DG是平面DEF与平面ACBD的交线.利用直线平面的垂直判断出DG⊥DF,DG⊥DB,根据平面角的定义得出∠BDF是面DEF与面ABCD所成二面角的平面角,转化到直角三角形求解即可.解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系,运用向量的数量积判断即可.2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.根据数量积得出夹角的余弦即可得出所求解的答案.【解答】解法1)(1)因为PD⊥底面ABCD,所以PD⊥BC,由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,所以BC⊥平面PCD.而DE⊂平面PDC,所以BC⊥DE.又因为PD=CD,点E是PC的中点,所以DE⊥PC.而PC∩CB=C,所以DE⊥平面PBC.而PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)如图1,在面BPC内,延长BC与FE交于点G,则DG是平面DEF与平面ACBD的交线.由(Ⅰ)知,PB⊥平面DEF,所以PB⊥DG.又因为PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.所以DG⊥DF,DG⊥DB故∠BDF是面DEF与面ABCD所成二面角的平面角,设PD=DC=1,BC=λ,有BD=,在Rt△PDB中,由DF⊥PB,得∠DGF=∠FDB=,则tan=tan∠DPF===,解得.所以==故当面DEF与面ABCD所成二面角的大小为时,=.(解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),=(λ1,﹣1),点E是PC的中点,所以E(0,,),=(0,,),于是=0,即PB⊥DE.又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.因=(0,1,﹣1),=0,则DE⊥PC,所以DE⊥平面PBC.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.若面DEF与面ABCD所成二面角的大小为,则运用向量的数量积求解得出cos==,解得.所以所以==故当面DEF与面ABCD所成二面角的大小为时,=.【点评】本题综合考查了空间直线平面的垂直问题,直线与直线,直线与平面的垂直的转化,空间角的求解,属于难题.20.(12分)(2015•湖北)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.【分析】(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,列出可行域,目标函数,通过当W=12时,当W=15时,当W=18时,分别求出目标函数的最大获利,然后得到Z的分布列.求出期望即可.(2)判断概率类型是二项分布,然后求解所求概率即可.【解答】(12分)解:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,则有,①如图1,目标函数为:z=1000x+1200y.当W=12时,①表示的平面区域如图1,三个顶点分别为A(0,0),B(2.4,4.8),C(6,0).将z=1000x+1200y变形为,当x=2.4,y=4.8时,直线l:在y轴上的截距最大,最大获利Z=Z max=2.4×1000+4.8×1200=8160.当W=15时,①表示的平面区域如图2,三个顶点分别为A(0,0),B(3,6),C(7.5,0)..将z=1000x+1200y变形为,当x=3,y=6时,直线l:在y轴上的截距最大,最大获利Z=Z max=3×1000+6×1200=10200.当W=18时,①表示的平面区域如图3,四个顶点分别为A(0,0),B(3,6),C(6,4),D(9,0).将z=1000x+1200y变形为:,当x=6,y=4时,直线l:y=﹣56x+z1200在y轴上的截距最大,最大获利Z=Z max=6×1000+4×1200=10800.(2)由(Ⅰ)知,一天最大获利超过10000元的概率P1=P(Z>10000)=0.5+0.2=0.7,由二项分布,3天中至少有1天最大获利超过10000元的概率为:.【点评】本题考查离散型随机变量的分布列以及期望的求法,线性规划的应用,二项分布概率的求法,考查分析问题解决问题的能力.21.(14分)(2015•湖北)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON 可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.【分析】(1)根据条件求出a,b即可求椭圆C的方程;(2)联立直线方程和椭圆方程,求出原点到直线的距离,结合三角形的面积公式进行求解即可.【解答】解:(1)设D(t,0),|t|≤2,N(x0,y0),M(x,y),由题意得=2,且||=||=1,∴(t﹣x,﹣y)=2(x0﹣t,y0),且,即,且t(t﹣2x0)=0,由于当点D不动时,点N也不动,∴t不恒等于0,于是t=2x0,故x0=,y0=﹣,代入x02+y02=1,得方程为.(2)①当直线l的斜率k不存在时,直线l为:x=4或x=﹣4,都有S△OPQ=,②直线l的斜率k存在时,直线l为:y=kx+m,(k),由消去y,可得(1+4k2)x2+8kmx+4m2﹣16=0,∵直线l总与椭圆C有且只有一个公共点,∴△=64k2m2﹣4(1+4k2)(4m2﹣16)=0,即m2=16k2+4,①,由,可得P(,),同理得Q(,),原点O到直线PQ的距离d=和|PQ|=•|x P﹣x Q|,可得S△OPQ=|PQ|d=|m||x P﹣x Q|=|m|||=||②,将①代入②得S△OPQ=||=8||,当k2>时,S△OPQ=8()=8(1+)>8,当0≤k2<时,S△OPQ=8||=﹣8()=8(﹣1+),∵0≤k2<时,∴0<1﹣4k2≤1,≥2,∴S△OPQ=8(﹣1+)≥8,当且仅当k=0时取等号,∴当k=0时,S△OPQ的最小值为8,综上可知当直线l与椭圆C在四个顶点处相切时,三角形OPQ的面积存在最小值为8.【点评】本题主要考查椭圆方程的求解,以及直线和圆锥曲线的位置关系的应用,结合三角形的面积公式是解决本题的关键.综合性较强,运算量较大.22.(14分)(2015•湖北)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.【分析】(1)求出f(x)的定义域,利用导数求其最大值,得到1+x<e x.取x=即可得到答案;(2)由b n=n(1+)n a n(n∈N+),变形求得,,,由此推测=(n+1)n.然后利用数学归纳法证明.(3)由c n的定义、=(n+1)n、算术﹣几何平均不等式、b n的定义及,利用放缩法证得T n<eS n.【解答】(1)解:f(x)的定义域为(﹣∞,+∞),f′(x)=1﹣e x.当f′(x)>0,即x<0时,f(x)单调递增;当f′(x)<0,即x>0时,f(x)单调递减.故f(x)的单调递增区间为(﹣∞,0),单调递减区间为(0,+∞).当x>0时,f(x)<f(0)=0,即1+x<e x.令,得,即.①(2)解:;=;.由此推测:=(n+1)n.②下面用数学归纳法证明②.(1)当n=1时,左边=右边=2,②成立.(2)假设当n=k时,②成立,即.当n=k+1时,,由归纳假设可得=.∴当n=k+1时,②也成立.根据(1)(2),可知②对一切正整数n都成立.(3)证明:由c n的定义,②,算术﹣几何平均不等式,b n的定义及①得T n=c1+c2+…+c n=====<ea1+ea2+…+ea n=eS n.即T n<eS n.【点评】本题主要考查导数在研究函数中的应用,考查利用归纳法证明与自然数有关的问题,考查推理论证能力、运算求解能力、创新知识,考查了利用放缩法法证明数列不等式,是压轴题.参与本试卷答题和审题的老师有:qiss;刘长柏;双曲线;maths;吕静;lincy;sxs123;cst;w3239003;sdpyqzh(排名不分先后)菁优网2016年8月29日。

2015年湖北省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)i为虚数单位,i607的共轭复数为()A.i B.﹣i C.1 D.﹣12.(5分)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石3.(5分)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A.212B.211C.210D.294.(5分)设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y ≥t)5.(5分)设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件6.(5分)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnx C.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]7.(5分)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P18.(5分)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e29.(5分)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.3010.(5分)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3 B.4 C.5 D.6二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)已知向量⊥,||=3,则•=.12.(5分)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为.13.(5分)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.14.(5分)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B (B在A的上方),且|AB|=2.(1)圆C的标准方程为;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是.(写出所有正确结论的序号)选修4-1:几何证明选讲15.(5分)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.选修4-4:坐标系与参数方程16.在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t 为参数),l与C相交于A,B两点,则|AB|=.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0π2πxAsin(ωx+φ)05﹣50(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g (x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.18.(12分)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.19.(12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.20.(12分)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W121518P0.30.50.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.21.(14分)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(14分)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.2015年湖北省高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)i为虚数单位,i607的共轭复数为()A.i B.﹣i C.1 D.﹣1【分析】直接利用复数的单位的幂运算求解即可.【解答】解:i607=i604+3=i3=﹣i,它的共轭复数为:i.故选:A.【点评】本题考查复数的基本运算,复式单位的幂运算以及共轭复数的知识,基本知识的考查.2.(5分)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石【分析】根据254粒内夹谷28粒,可得比例,即可得出结论.【解答】解:由题意,这批米内夹谷约为1534×≈169石,故选:B.【点评】本题考查利用数学知识解决实际问题,考查学生的计算能力,比较基础.3.(5分)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A.212B.211C.210D.29【分析】直接利用二项式定理求出n,然后利用二项式定理系数的性质求出结果即可.【解答】解:已知(1+x)n的展开式中第4项与第8项的二项式系数相等,可得,可得n=3+7=10.(1+x)10的展开式中奇数项的二项式系数和为:=29.故选:D.【点评】本题考查二项式定理的应用,组合数的形状的应用,考查基本知识的灵活运用以及计算能力.4.(5分)设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y ≥t)【分析】直接利用正态分布曲线的特征,集合概率,直接判断即可.【解答】解:正态分布密度曲线图象关于x=μ对称,所以μ1<μ2,从图中容易得到P(X≤t)≥P(Y≤t).故选:C.【点评】本题考查了正态分布的图象与性质,学习正态分布,一定要紧紧抓住平均数μ和标准差σ这两个关键量,结合正态曲线的图形特征,归纳正态曲线的性质.5.(5分)设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件【分析】运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,讨论等号成立的条件,结合等比数列的定义和充分必要条件的定义,即可得到.【解答】解:由a1,a2,…,a n∈R,n≥3.运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,若a1,a2,…,a n成等比数列,即有==…=,则(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,即由p推得q,但由q推不到p,比如a1=a2=a3=…=a n=0,则a1,a2,…,a n不成等比数列.故p是q的充分不必要条件.故选:A.【点评】本题考查充分必要条件的判断,同时考查等比数列的定义,注意运用定义法和柯西不等式解题是关键.6.(5分)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnx C.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]【分析】直接利用特殊法,设出函数f(x),以及a的值,判断选项即可.【解答】解:由于本题是选择题,可以采用特殊法,符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),不妨令f(x)=x,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[g(x)]=﹣sgnx.所以A不正确,B正确,sgn[f(x)]=sgnx,C不正确;D正确;对于D,令f(x)=x+1,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[f(x)]=sgn(x+1)=;sgn[g(x)]=sgn(﹣x)=,﹣sgn[f(x)]=﹣sgn(x+1)=;所以D不正确;故选:B.【点评】本题考查函数表达式的比较,选取特殊值法是解决本题的关键,注意解题方法的积累,属于中档题.7.(5分)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P1【分析】作出每个事件对应的平面区域,求出对应的面积,利用几何概型的概率公式进行计算比较即可.【解答】解:分别作出事件对应的图象如图(阴影部分):P1:D(0,),F(,0),A(0,1),B(1,1),C(1,0),则阴影部分的面积S1=1×1﹣=1﹣=,S2=1×1﹣2×=1﹣=,S3=1×+dx=+lnx|=﹣ln=+ln2,∴S2<S3<S1,即P2<P3<P1,故选:B.【点评】本题主要考查几何概型的概率计算,利用数形结合是解决本题的关键.本题也可以直接通过图象比较面积的大小即可比较大小.8.(5分)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e2【分析】分别求出双曲线的离心率,再平方作差,即可得出结论.【解答】解:由题意,双曲线C1:c2=a2+b2,e1=;双曲线C2:c′2=(a+m)2+(b+m)2,e2=,∴=﹣=,∴当a>b时,e1>e2;当a<b时,e1<e2,故选:B.【点评】本题考查双曲线的性质,考查学生的计算能力,比较基础.9.(5分)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.30【分析】由题意可得,A={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)},根据定义可求【解答】解:解法一:∵A={(x,y)|x2+y2≤1,x,y∈Z}={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(x,y)||x|≤2,|y|≤2,x,y∈Z}={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)}∵A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},∴A⊕B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2),(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2),(﹣2,3),(﹣2,﹣3),(0,﹣3),(2,﹣3),(﹣1,3),(﹣1,﹣3),(1,3),(2,3),(0,3),(3,﹣1),(3,0)(3,1),(3,2),(3,﹣2)(﹣3,2)(﹣3,1),(1,﹣3),(﹣3,﹣1),(﹣3,0),(﹣3,﹣2)}共45个元素;解法二:因为集合A={(x,y)|x2+y2≤1,x,y∈Z},所以集合A中有5个元素,即图中圆中的整点,B={(x,y)||x|≤2,|y|≤2,x,y∈Z},中有5×5=25个元素,即图中正方形ABCD中的整点,A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B}的元素可看作正方形A1B1C1D1中的整点(除去四个顶点),即7×7﹣4=45个.故选:C.【点评】本题以新定义为载体,主要考查了集合的基本定义及运算,解题中需要取得重复的元素.10.(5分)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3 B.4 C.5 D.6【分析】由新定义可得t的范围,验证可得最大的正整数n为4.【解答】解:若[t]=1,则t∈[1,2),若[t2]=2,则t∈[,)(因为题目需要同时成立,则负区间舍去),若[t3]=3,则t∈[,),若[t4]=4,则t∈[,),若[t5]=5,则t∈[,),其中≈1.732,≈1.587,≈1.495,≈1.431<1.495,通过上述可以发现,当t=4时,可以找到实数t使其在区间[1,2)∩[,)∩[,)∩[,)上,但当t=5时,无法找到实数t使其在区间[1,2)∩[,)∩[,)∩[,)∩[,)上,∴正整数n的最大值4故选:B.【点评】本题考查简单的演绎推理,涉及新定义,属基础题.二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)已知向量⊥,||=3,则•=9.【分析】由已知结合平面向量是数量积运算求得答案.【解答】解:由⊥,得•=0,即•()=0,∵||=3,∴.故答案为:9.【点评】本题考查了平面向量的数量积运算,考查了向量模的求法,是基础的计算题.12.(5分)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为2.【分析】利用二倍角公式化简函数的解析式,求出函数的定义域,画出函数的图象,求出交点个数即可.【解答】解:函数f(x)的定义域为:{x|x>﹣1}.f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|=2sinx﹣|ln(x+1)|=sin2x﹣|ln(x+1)|,分别画出函数y=sin2x,y=|ln(x+1)|的图象,由函数的图象可知,交点个数为2.所以函数的零点有2个.故答案为:2.【点评】本题考查三角函数的化简,函数的零点个数的判断,考查数形结合与转化思想的应用.13.(5分)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=100m.【分析】设此山高h(m),在△BCD中,利用仰角的正切表示出BC,进而在△ABC中利用正弦定理求得h.【解答】解:设此山高h(m),则BC=h,在△ABC中,∠BAC=30°,∠CBA=105°,∠BCA=45°,AB=600.根据正弦定理得=,解得h=100(m)故答案为:100.【点评】本题主要考查了解三角形的实际应用.关键是构造三角形,将各个已知条件向这个主三角形集中,再通过正弦、余弦定理或其他基本性质建立条件之间的联系,列方程或列式求解.14.(5分)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B (B在A的上方),且|AB|=2.(1)圆C的标准方程为(x﹣1)2+(y﹣)2=2;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是①②③.(写出所有正确结论的序号)【分析】(1)取AB的中点E,通过圆C与x轴相切于点T,利用弦心距、半径与半弦长之间的关系,计算即可;(2)设M(cosα,sinα),N(cosβ,sinβ),计算出、、的值即可.【解答】解:(1)∵圆C与x轴相切于点T(1,0),∴圆心的横坐标x=1,取AB的中点E,∵|AB|=2,∴|BE|=1,则|BC|=,即圆的半径r=|BC|=,∴圆心C(1,),则圆的标准方程为(x﹣1)2+(y﹣)2=2,故答案为:(x﹣1)2+(y﹣)2=2.(2)∵圆心C(1,),∴E(0,),又∵|AB|=2,且E为AB中点,∴A(0,﹣1),B(0,+1),∵M、N在圆O:x2+y2=1上,∴可设M(cosα,sinα),N(cosβ,sinβ),∴|NA|=====,|NB|====,∴===,同理可得=,∴=,①成立,﹣=﹣()=2,②正确.+=+()=,③正确.故答案为:①②③.【点评】本题考查求圆的标准方程,用三角函数值表示单位圆上点的坐标是解决本题的关键,注意解题方法的积累,属于难题.选修4-1:几何证明选讲15.(5分)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.【分析】利用切割线定理推出PA=2PB,利用相似三角形求出比值即可.【解答】解:由切割线定理可知:PA2=PB•PC,又BC=3PB,可得PA=2PB,在△PAB与△PAC中,∠P=∠P,∠PAB=∠PCA(同弧上的圆周角与弦切角相等),可得△PAB∽△PAC,∴==.故答案为:.【点评】本题考查切割线定理以及相似三角形的判定与应用,考查逻辑推理能力.选修4-4:坐标系与参数方程16.在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t 为参数),l与C相交于A,B两点,则|AB|=.【分析】化极坐标方程化直角坐标方程,参数方程化普通方程,联立直线方程和双曲线方程后求得交点坐标,由两点间的距离公式得答案.【解答】解:由ρ(sinθ﹣3cosθ)=0,得y﹣3x=0,由C的参数方程为(t为参数),两式平方作差得:x2﹣y2=﹣4.联立,得,即.∴A(),B(),∴|AB|=.故答案为:.【点评】本题考查极坐标方程化直角坐标方程,参数方程化普通方程,考查了直线和圆锥曲线的位置关系,是基础的计算题.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0π2πxAsin(ωx+φ)05﹣50(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g (x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.【分析】(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.从而可补全数据,解得函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)及函数y=Asin(ωx+φ)的图象变换规律得g(x)=5sin(2x+2θ﹣).令2x+2θ﹣=kπ,解得x=,k∈Z.令=,解得θ=,k∈Z.由θ>0可得解.【解答】解:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.数据补全如下表:ωx+φ0π2πxAsin(ωx+φ)050﹣50且函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)知f(x)=5sin(2x﹣),得g(x)=5sin(2x+2θ﹣).因为y=sinx的对称中心为(kπ,0),k∈Z.令2x+2θ﹣=kπ,解得x=,k∈Z.由于函数y=g(x)的图象关于点(,0)成中心对称,令=,解得θ=,k∈Z.由θ>0可知,当K=1时,θ取得最小值.【点评】本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin (ωx+φ)的图象变换规律的应用,属于基本知识的考查.18.(12分)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.【分析】(1)利用前10项和与首项、公差的关系,联立方程组计算即可;(2)当d>1时,由(1)知c n=,写出T n、T n的表达式,利用错位相减法及等比数列的求和公式,计算即可.【解答】解:(1)设a1=a,由题意可得,解得,或,当时,a n=2n﹣1,b n=2n﹣1;当时,a n=(2n+79),b n=9•;(2)当d>1时,由(1)知a n=2n﹣1,b n=2n﹣1,∴c n==,∴T n=1+3•+5•+7•+9•+…+(2n﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.【点评】本题考查求数列的通项及求和,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.19.(12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.【分析】解法1)(1)直线与直线,直线与平面的垂直的转化证明得出PB⊥EF,DE∩FE=E,所以PB⊥平面DEF,即可判断DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,确定直角.(2)根据公理2得出DG是平面DEF与平面ACBD的交线.利用直线平面的垂直判断出DG⊥DF,DG⊥DB,根据平面角的定义得出∠BDF是面DEF与面ABCD所成二面角的平面角,转化到直角三角形求解即可.解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系,运用向量的数量积判断即可.2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.根据数量积得出夹角的余弦即可得出所求解的答案.【解答】解法1)(1)因为PD⊥底面ABCD,所以PD⊥BC,由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,所以BC⊥平面PCD.而DE⊂平面PDC,所以BC⊥DE.又因为PD=CD,点E是PC的中点,所以DE⊥PC.而PC∩CB=C,所以DE⊥平面PBC.而PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)如图1,在面BPC内,延长BC与FE交于点G,则DG是平面DEF与平面ACBD的交线.由(Ⅰ)知,PB⊥平面DEF,所以PB⊥DG.又因为PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.所以DG⊥DF,DG⊥DB故∠BDF是面DEF与面ABCD所成二面角的平面角,设PD=DC=1,BC=λ,有BD=,在Rt△PDB中,由DF⊥PB,得∠DPB=∠FDB=,则tan=tan∠DPF===,解得.所以==故当面DEF与面ABCD所成二面角的大小为时,=.(解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),=(λ1,﹣1),点E是PC的中点,所以E(0,,),=(0,,),于是=0,即PB⊥DE.又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.因=(0,1,﹣1),=0,则DE⊥PC,所以DE⊥平面PBC.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.若面DEF与面ABCD所成二面角的大小为,则运用向量的数量积求解得出cos==,解得.所以所以==故当面DEF与面ABCD所成二面角的大小为时,=.【点评】本题综合考查了空间直线平面的垂直问题,直线与直线,直线与平面的垂直的转化,空间角的求解,属于难题.20.(12分)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W121518P0.30.50.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.【分析】(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,列出可行域,目标函数,通过当W=12时,当W=15时,当W=18时,分别求出目标函数的最大获利,然后得到Z的分布列.求出期望即可.(2)判断概率类型是二项分布,然后求解所求概率即可.【解答】(12分)解:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,则有,①如图1,目标函数为:z=1000x+1200y.当W=12时,①表示的平面区域如图1,三个顶点分别为A(0,0),B(2.4,4.8),C(6,0).将z=1000x+1200y变形为,当x=2.4,y=4.8时,直线l:在y轴上的截距最大,最大获利Z=Z max=2.4×1000+4.8×1200=8160.当W=15时,①表示的平面区域如图2,三个顶点分别为A(0,0),B(3,6),C(7.5,0)..将z=1000x+1200y变形为,当x=3,y=6时,直线l:在y轴上的截距最大,最大获利Z=Z max=3×1000+6×1200=10200.当W=18时,①表示的平面区域如图3,四个顶点分别为A(0,0),B(3,6),C(6,4),D(9,0).将z=1000x+1200y变形为:,当x=6,y=4时,直线l:y=﹣56x+z1200在y轴上的截距最大,最大获利Z=Z max=6×1000+4×1200=10800.故最大获利Z的分布列为:Z81601020010800P0.30.50.2因此,E(Z)=8160×0.3+10200×0.5+10800×0.2=9708(2)由(Ⅰ)知,一天最大获利超过10000元的概率P1=P(Z>10000)=0.5+0.2=0.7,由二项分布,3天中至少有1天最大获利超过10000元的概率为:.【点评】本题考查离散型随机变量的分布列以及期望的求法,线性规划的应用,二项分布概率的求法,考查分析问题解决问题的能力.21.(14分)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.【分析】(1)根据条件求出a,b即可求椭圆C的方程;(2)联立直线方程和椭圆方程,求出原点到直线的距离,结合三角形的面积公式进行求解即可.【解答】解:(1)设D(t,0),|t|≤2,N(x0,y0),M(x,y),由题意得=2,且||=||=1,∴(t﹣x,﹣y)=2(x0﹣t,y0),且,即,且t(t﹣2x0)=0,由于当点D不动时,点N也不动,∴t不恒等于0,于是t=2x0,故x0=,y0=﹣,代入x02+y02=1,得方程为.=,(2)①当直线l的斜率k不存在时,直线l为:x=4或x=﹣4,都有S△OPQ②直线l的斜率k存在时,直线l为:y=kx+m,(k),由消去y,可得(1+4k2)x2+8kmx+4m2﹣16=0,∵直线l总与椭圆C有且只有一个公共点,∴△=64k2m2﹣4(1+4k2)(4m2﹣16)=0,即m2=16k2+4,①,由,可得P(,),同理得Q(,),原点O到直线PQ的距离d=和|PQ|=•|x P﹣x Q|,=|PQ|d=|m||x P﹣x Q|=|m|||=||②,可得S△OPQ将①代入②得S=||=8||,△OPQ=8()=8(1+)>8,当k2>时,S△OPQ=8||=﹣8()=8(﹣1+),当0≤k2<时,S△OPQ∵0≤k2<时,∴0<1﹣4k2≤1,≥2,∴S=8(﹣1+)≥8,当且仅当k=0时取等号,△OPQ的最小值为8,∴当k=0时,S△OPQ综上可知当直线l与椭圆C在四个顶点处相切时,三角形OPQ的面积存在最小值为8.【点评】本题主要考查椭圆方程的求解,以及直线和圆锥曲线的位置关系的应用,结合三角形的面积公式是解决本题的关键.综合性较强,运算量较大.22.(14分)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.【分析】(1)求出f(x)的定义域,利用导数求其最大值,得到1+x<e x.取x=即可得到答案;(2)由b n=n(1+)n a n(n∈N+),变形求得,,,由此推测=(n+1)n.然后利用数学归纳法证明.(3)由c n的定义、=(n+1)n、算术﹣几何平均不等式、b n的定义及,利用放缩法证得T n<eS n.【解答】(1)解:f(x)的定义域为(﹣∞,+∞),f′(x)=1﹣e x.当f′(x)>0,即x<0时,f(x)单调递增;当f′(x)<0,即x>0时,f(x)单调递减.故f(x)的单调递增区间为(﹣∞,0),单调递减区间为(0,+∞).当x>0时,f(x)<f(0)=0,即1+x<e x.令,得,即.①(2)解:;=;.由此推测:=(n+1)n.②下面用数学归纳法证明②.(1)当n=1时,左边=右边=2,②成立.(2)假设当n=k时,②成立,即.当n=k+1时,,由归纳假设可得=.∴当n=k+1时,②也成立.根据(1)(2),可知②对一切正整数n都成立.(3)证明:由c n的定义,②,算术﹣几何平均不等式,b n的定义及①得T n=c1+c2+…+c n=====<ea1+ea2+…+ea n=eS n.即T n<eS n.【点评】本题主要考查导数在研究函数中的应用,考查利用归纳法证明与自然数有关的问题,考查推理论证能力、运算求解能力、创新知识,考查了利用放缩法证明数列不等式,是压轴题.。

数学试卷 第1页(共51页)数学试卷 第2页(共51页)数学试卷 第3页(共51页)绝密★启用前2015年普通高等学校招生全国统一考试(湖北卷)数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟. 注意事项:1.答卷前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.用2B 铅笔将答题卡上试卷类型A 后的方框涂黑. 2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑,再在答题卡上对应的答题区域内答题.写在试题卷、草稿纸和答题卡上的非答题区域均无效.5.考试结束后,请将本试题卷和答题卡一并上交.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.i 为虚数单位,607i 的共轭复数为( )A .iB .i -C .1D .1-2.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1 534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )A .134石B .169石C .338石D .1 365石3.已知(1)nx +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A .122 B .112C .102 D .924.设211(,)X N μσ~,222(,)Y N μσ~,这两个正态分布密度曲线如图所示.下列结论中正确的是 ( )A .21()()P Y P Y μμ≥≥≥B .21()()P X P X σσ≤≤≤C .对任意正数t ,()()P X t P Y t ≤≥≤D .对任意正数t ,()()P X t P Y t ≥≥≥5.设12,,,n a a a ∈R ,3n ≥.若p :12,,,n a a a 成等比数列;q :222121()n a a a -+++22(a +222312231)()n n n a a a a a a a a -++=+++,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件6.已知符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩()f x 是R 上的增函数,()()()(1)g x f x f ax a =->,则( )A .sgn[()]sgn g x x =B .sgn[()]sgn g x x =-C .sgn[()]sgn[()]g x f x =D .sgn[()]sgn[()]g x f x =-7.在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y +≥”的概率,2p 为事件“1||2x y -≤”的概率,3p 为事件“12xy ≤”的概率,则( )A .123p p p <<B .231p p p <<C .312p p p <<D .321p p p <<8.将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则( )A .对任意的,a b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的,a b ,12e e <D .当a b >时,12e e <;当a b <时,12e e >9.已知集合22{(,)|1,,}A x y x y x y =+∈Z ≤,{(,)|||2,||2,,}B x y x y x y =∈Z ≤≤,定义集合12121122{(,)(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为 ( ) A .77B .49C .45D .30 10.设x ∈R ,[]x 表示不超过x 的最大整数.若存在实数t ,使得[]1t =,2[]2t =,…,[]n t n =同时成立,则正整数n 的最大值是( )A .3B .4C .5D .6 第Ⅱ卷(非选择题 共100分)二、填空题:本大题共6小题,考生需作答5小题,每小题5分,共25分.把答案填在题中的横线上. (一)必考题(11~14题)11.已知向量OA AB ⊥,||3OA =,则OA OB =___________. 12.函数2π()4cos cos()2sin |ln(1)|22xf x x x x =---+的零点个数为___________. 13.如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30的方向上,行驶600m 后到达B 处,测得此山顶在西偏北75的方向上,仰角为30,则此山的高度CD =___________m .14.如图,圆C 与x 轴相切于点(1,0)T ,与y 轴正半轴交于两点,A B (B 在A 的上方),且2AB =.(1)圆C 的标准方程为___________;(2)过点A 任作一条直线与圆22:1O x y +=相交于M ,N 两点,下列三个结论: ①||||||||NA MA NB NB =; ②||||2||||NB MA NA MB -=;③||||||||NB MA NA MB += 其中正确结论的序号是___________(写出所有正确结论的序号). -------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共51页)数学试卷 第5页(共51页)数学试卷 第6页(共51页)(二)选考题(请考生在第15,16两题中任选一题作答,如果全选,则按第15题作答结果记分) 15.(选修4—1:几何证明选讲)如图,P A 是圆的切线,A 为切点,PBC 是圆的割线,且3BC PB =,则ABAC=___________. 16.(选修4—4:坐标系与参数方程)在直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为(sin 3cos )0ρθθ-=,曲线C 的参数方程为1,1,x t t y t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),l 与C 相交于A ,B 两点,则||AB =___________.三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分11分)某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象时,列表并填入了部分数据,如下表:(Ⅰ)请将上表数据补充完整,并直接写出函数()f x 的解析式;(Ⅱ)将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度,得到()y g x =的图象.若()y g x =图象的一个对称中心为5π(,0)12,求θ的最小值.18.(本小题满分12分)设等差数列{}n a 的公差为d ,前n 项和为n S ,等比数列{}n b 的公比为q .已知11b a =,22b =,q d =,10100S =.(Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)当1d >时,记nn na cb =,求数列{}n c 的前n 项和n T .19.(本小题满分12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 如图,在阳马P ABCD -中,侧棱PD ⊥底面ABCD , 且PD CD =,过棱PC 的中点E ,作E F P B ⊥交PB 于点F ,连接,,,DE DF BD BE . (Ⅰ)证明:PB DEF ⊥平面.试判断四面体DBEF 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(Ⅱ)若面DEF 与面ABCD 所成二面角的大小为π3,求DC BC的值.20.(本小题满分12分)某厂用鲜牛奶在某台设备上生产,A B 两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1 000元;生产1吨B 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1 200元.要求每天B 产品的产量不超过A 产品产量的2倍,设备每天生产,A B 两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W (单位:吨)是一个该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z (单位:元)是一个随机变量. (Ⅰ)求Z 的分布列和均值;(Ⅱ)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10 000元的概率. 21.(本小题满分14分)一种作图工具如图1所示.O 是滑槽AB 的中点,短杆ON 可绕O 转动,长杆MN 通过N 处铰链与ON 连接,MN 上的栓子D 可沿滑槽AB 滑动,且1DN ON ==,MN 3=.当栓子D 在滑槽AB 内作往复运动时,带动N 绕O 转动一周(D 不动时,N 也不动),M 处的笔尖画出的曲线记为C .以O 为原点,AB 所在的直线为x 轴建立如图2所示的平面直角坐标系.(Ⅰ)求曲线C 的方程;(Ⅱ)设动直线l 与两定直线1:20l x y -=和2:20l x y +=分别交于,P Q 两点.若直线l 总与曲线C 有且只有一个公共点,试探究:△OPQ 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(本小题满分14分)已知数列{}n a 的各项均为正数,*1(1)()n n n b na n n=+∈N ,e 为自然对数的底数. (Ⅰ)求函数()1e x f x x =+-的单调区间,并比较1(1)n n +与e 的大小; (Ⅱ)计算11b a ,1212b ba a ,123123b b b a a a ,由此推测计算1212nnb b b a a a 的公式,并给出证明; (Ⅲ)令112()nn n c a a a =,数列{}n a ,{}n c 的前n 项和分别记为n S ,n T ,证明:e n n T S <2015年普通高等学校招生全国统一考试(湖北卷)3 / 17数学试卷第10页(共51页)数学试卷第11页(共51页)数学试卷第12页(共51页)即77445⨯-=个.5 / 17数学试卷 第16页(共51页) 数学试卷 第17页(共51页)数学试卷 第18页(共51页)334554,2)[2,3)[3,4)[4,5)[5,6)上,334554,2)[2,3)[3,4)[4,5)[5,6)上,∴正整数n 的最的范围,验证可得最大的正整数n 为4.∠,∠,45BCACBA30,105=,解得h30sin457 / 17数学试卷 第22页(共51页) 数学试卷 第23页(共51页)数学试卷 第24页(共51页)22AC PA PB9 / 17数学试卷第28页(共51页)数学试卷第29页(共51页)数学试卷第30页(共51页)PD CD D=,所以⊥,DE PC11 / 17数学试卷 第34页(共51页) 数学试卷 第35页(共51页)数学试卷 第36页(共51页)32BC13 / 17数学试卷 第40页(共51页) 数学试卷 第41页(共51页)数学试卷 第42页(共51页)因此,.1641直线15 / 17数学试卷 第46页(共51页) 数学试卷 第47页(共51页)数学试卷 第48页(共51页)20k ≤<OPQS ∴=△17 / 17111131211212312()()()()nn n c a a a a a a a a a ++=++++113()()nb b b b b b b b bb b b b ++++L 1211112nn b b b b n n n⎛⎫++-<+++⎪+⎝⎭ 1n22(nnb n a =+22(n nb n a =+。

2015年湖北省高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•湖北)i为虚数单位,i607的共轭复数为()A.i B.﹣i C.1D.﹣12.(5分)(2015•湖北)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石3.(5分)(2015•湖北)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A.212B.211C.210D.294.(5分)(2015•湖北)设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y≥t)5.(5分)(2015•湖北)设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件6.(5分)(2015•湖北)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A sgn[g(x)]=sgnxB sgn[g(x)]=﹣sgnxC sgn[g(x)]=sgn[f(x)]D sgn[g(x)]=﹣sgn[f(x)]7.(5分)(2015•湖北)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P18.(5分)(2015•湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e29.(5分)(2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.3010.(5分)(2015•湖北)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3B.4C.5D.6二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)(2015•湖北)已知向量⊥,||=3,则•=.12.(5分)(2015•湖北)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为.13.(5分)(2015•湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.14.(5分)(2015•湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是.(写出所有正确结论的序号)选修4-1:几何证明选讲15.(5分)(2015•湖北)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.选修4-4:坐标系与参数方程16.(2015•湖北)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t为参数),l与C相交于A,B两点,则|AB|=.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)(2015•湖北)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0 π2πxAsin(ωx+φ)0 5 ﹣5 0(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.18.(12分)(2015•湖北)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.19.(12分)(2015•湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD 中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.20.(12分)(2015•湖北)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W 12 15 18P 0.3 0.5 0.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.21.(14分)(2015•湖北)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON 可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(14分)(2015•湖北)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.答案:1、解:i607=i604+3=i3=﹣i,它的共轭复数为:i.故选:A.2、解:由题意,这批米内夹谷约为1534×≈169石,故选:B.3、解:已知(1+x)n的展开式中第4项与第8项的二项式系数相等,可得,可得n=3+7=10.(1+x)10的展开式中奇数项的二项式系数和为:=29.故选:D.4、解:正态分布密度曲线图象关于x=μ对称,所以μ1<μ2,从图中容易得到P(X≤t)≥P(Y≤t).故选:C.5、解:由a1,a2,…,a n∈R,n≥3.运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,若a1,a2,…,a n成等比数列,即有==…=,则(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,即由p推得q,但由q推不到p,比如a1=a2=a3=…=a n=0,则a1,a2,…,a n不成等比数列.故p是q的充分不必要条件.故选:A.6、解:由于本题是选择题,可以常用特殊法,符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),不妨令f(x)=x,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[g(x)]=﹣sgnx.所以A不正确,B正确,sgn[f(x)]=sgnx,C不正确;D正确;对于D,令f(x)=x+1,a=2,则g(x)=f(x)﹣f(ax)=﹣x﹣1,sgn[f(x)]=sgn(x+1)=;sgn[g(x)]=sgn(﹣x﹣1)=,﹣sgn[f(x)]=﹣sgn(x+1)=;所以D不正确;故选:B.7、解:分别作出事件对应的图象如图(阴影部分):P1:D(0,),F(,0),A(0,1),B(1,1),C(1,0),则阴影部分的面积S1=1×1﹣=1﹣=,S2=1×1﹣2×=1﹣=,S3=1×+dx=+lnx|=﹣ln=+ln2,∴S2<S3<S1,即P2<P3<P1,故选:B.8、解:由题意,双曲线C1:c2=a2+b2,e1=;双曲线C2:c′2=(a+m)2+(b+m)2,e2=,∴=﹣=,∴当a>b时,e1<e2;当a<b时,e1>e2,故选:D.9、解:∵A={(x,y)|x2+y2≤1,x,y∈Z}={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(x,y)||x|≤2,|y|≤2,x,y∈Z}={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)}∵A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},∴A⊕B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2),(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2),(﹣2,3),(﹣2,﹣3),(0,﹣3),(2,﹣3),(﹣1,3),(﹣1,﹣3),(1,3),(2,3),(0,3),(3,﹣1),(3,0)(3,1),(3,2),(3,﹣2)(﹣3,2)(﹣3,1),(1,﹣3),(﹣3,﹣1),(﹣3,0),(﹣3,﹣2)}共45个元素故选:C.10、解:∵[t]=1,∴t∈[1,2),又∵[t2]=2,∴t2∈[2,3),∴t∈[,),又t2∈[2,3),∴t4∈[4,9),∴[t4]=4,∴正整数n的最大值4故选:B.11、解:由⊥,得•=0,即•()=0,∵||=3,∴.故答案为:9.12、解:函数f(x)的定义域为:{x|x>﹣1}.f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|=2sinx﹣|ln(x+1)|=sin2x﹣|ln(x+1)|,分别画出函数y=sin2x,y=|ln(x+1)|的图象,由函数的图象可知,交点个数为2.所以函数的零点有2个.故答案为:2.13、解:设此山高h(m),则BC=h,在△ABC中,∠BAC=30°,∠CBA=105°,∠BCA=45°,AB=600.根据正弦定理得=,解得h=100(m)故答案为:100.14、解:(1)∵圆C与x轴相切于点T(1,0),∴圆心的横坐标x=1,取AB的中点E,∵|AB|=2,∴|BE|=1,则|BC|=,即圆的半径r=|BC|=,∴圆心C(1,),则圆的标准方程为(x﹣1)2+(y﹣)2=2,故答案为:(x﹣1)2+(y﹣)2=2.(2)∵圆心C(1,),∴E(0,),又∵|AB|=2,且E为AB中点,∴A(0,﹣1),B(0,+1),∵M、N在圆O:x2+y2=1上,∴可设M(cosα,sinα),N(cosβ,sinβ),∴|NA|=====,|NB|====,∴===,同理可得=,∴=,①成立,﹣=﹣()=2,②正确.+=+()=,③正确.故答案为:①②③.15、解:由切割线定理可知:PA2=PB•PC,又BC=3PB,可得PA=2PB,在△PAB与△PAC中,∠P=∠P,∠PAB=∠PCA(同弧上的圆周角与弦切角相等),可得△PAB∽△PAC,∴==.故答案为:.16、解:由ρ(sinθ﹣3cosθ)=0,得y﹣3x=0,由C的参数方程为(t为参数),两式平方作差得:x2﹣y2=﹣4.联立,得,即.∴A(),B(),∴|AB|=.故答案为:.17、解:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.数据补全如下表:ωx+φ0 π2πxAsin(ωx+φ)0 5 0 ﹣5 0且函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)知f(x)=5sin(2x﹣),得g(x)=5sin(2x+2θ﹣).因为y=sinx的对称中心为(kπ,0),k∈Z.令2x+2θ﹣=kπ,解得x=,k∈Z.由于函数y=g(x)的图象关于点(,0)成中心对称,令=,解得θ=,k∈Z.由θ>0可知,当K=1时,θ取得最小值.18、解:(1)设a1=a,由题意可得,解得,或,当时,a n=2n﹣1,b n=2n﹣1;当时,a n=(2n+79),b n=9•;(2)当d>1时,由(1)知a n=2n﹣1,b n=2n﹣1,∴c n==,∴T n=1+3•+5•+7•+9•+…+(2n﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.19、解法1)(1)因为PD⊥底面ABCD,所以PD⊥BC,由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,所以BC⊥平面ABCD.而DE⊂平面PDC,所以BC⊥DE.又因为PD=CD,点E是PC的中点,所以DE⊥PC.而PC∩CB=C,所以DE⊥平面PBC.而PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)如图1,在面BPC内,延长BC与FE交于点G,则DG是平面DEF与平面ACBD的交线.由(Ⅰ)知,PB⊥平面DEF,所以PB⊥DG.又因为PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.所以DG⊥DF,DG⊥DB故∠BDF是面DEF与面ABCD所成二面角的平面角,设PD=DC=1,BC=λ,有BD=,在Rt△PDB中,由DF⊥PB,得∠DGF=∠FDB=,则tan=tan∠DPF===,解得.所以==故当面DEF与面ABCD所成二面角的大小为时,=.(解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),=(λ1,﹣1),点E是PC的中点,所以E(0,,),=(0,,),于是=0,即PB⊥DE.又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.因=(0,1,﹣1),=0,则DE⊥PC,所以DE⊥平面PBC.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个矩形,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.若面DEF与面ABCD所成二面角的大小为,则运用向量的数量积求解得出cos==,解得.所以所以==故当面DEF与面ABCD所成二面角的大小为时,=.20、(12分)解:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,则有,①如图1,目标函数为:z=1000x+1200y.当W=12时,①表示的平面区域如图1,三个顶点分别为A(0,0),B(2.4,4.8),C(6,0).将z=1000x+1200y变形为,当x=2.4,y=4.8时,直线l:在y轴上的截距最大,最大获利Z=Z max=2.4×1000+4.8×1200=8160.当W=15时,①表示的平面区域如图2,三个顶点分别为A(0,0),B(3,6),C (7.5,0)..将z=1000x+1200y变形为,当x=3,y=6时,直线l:在y轴上的截距最大,最大获利Z=Z max=3×1000+6×1200=10200.当W=18时,①表示的平面区域如图3,四个顶点分别为A(0,0),B(3,6),C(6,4),D(9,0).将z=1000x+1200y变形为:,当x=6,y=4时,直线l:y=﹣56x+z1200在y轴上的截距最大,最大获利Z=Z max=6×1000+4×1200=10800.故最大获利Z的分布列为:Z 8160 10200 10800P 0.3 0.5 0.2因此,E(Z)=8160×0.3+10200×0.5+10800×0.2=9708(2)由(Ⅰ)知,一天最大获利超过10000元的概率P1=P(Z>10000)=0.5+0.2=0.7,由二项分布,3天中至少有1天最大获利超过10000元的概率为:21、解:(1)∵|OM|≤|MN|+|NO|=3+1=4,当M,N在x轴上时,等号成立,同理|OM|≥|MN|﹣|NO|=3﹣1=2,当D,O重合,即MN⊥x轴时,等号成立.∴椭圆C的中心为原点O,长半轴长为4,短半轴长为2,其方程为.(2)①当直线l的斜率k不存在时,直线l为:x=4或x=﹣4,都有S△OPQ=,②直线l的斜率k存在时,直线l为:y=kx+m,(k),由消去y,可得(1+4k2)x2+8kmx+4m2﹣16=0,∵直线l总与椭圆C有且只有一个公共点,∴△=64k2m2﹣4(1+4k2)(4m2﹣16)=0,即m2=16k2+4,①,由,可得P(,),同理得Q(,),原点O到直线PQ的距离d=和|PQ|=•|x P﹣x Q|,可得S△OPQ=|PQ|d=|m||x P﹣x Q|=|m|||=||②,将①代入②得S△OPQ=||=8||,当k2>时,S△OPQ=8()=8(1+)>8,当0≤k2<时,S△OPQ=8||=﹣8()=8(﹣1+),∵0≤k2<时,∴0<1﹣4k2≤1,≥2,∴S△OPQ=8(﹣1+)≥8,当且仅当k=0时取等号,∴当k=0时,S△OPQ的最小值为8,综上可知当直线l与椭圆C在四个顶点处相切时,三角形OPQ的面积存在最小值为8.22、(1)解:f(x)的定义域为(﹣∞,+∞),f′(x)=1﹣e x.当f′(x)>0,即x<0时,f(x)单调递增;当f′(x)<0,即x>0时,f(x)单调递减.故f(x)的单调递增区间为(﹣∞,0),单调递减区间为(0,+∞).当x>0时,f(x)<f(0)=0,即1+x<e x.令,得,即.①(2)解:;=;.由此推测:=(n+1)n.②下面用数学归纳法证明②.(1)当n=1时,左边=右边=2,②成立.(2)假设当n=k时,②成立,即.当n=k+1时,,由归纳假设可得=.∴当n=k+1时,②也成立.根据(1)(2),可知②对一切正整数n都成立.(3)证明:由c n的定义,②,算术﹣几何平均不等式,b n的定义及①得T n=c1+c2+…+c n=====<ea1+ea2+…+ea n=eS n.即T n<eS n.。

第1页2015年普通高等学校招生全国统一考试(湖北卷)数学(理工类)本试题卷共6页,22题,其中第15、16题为选考题。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1.答卷前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑,再在答题卡上对应的答题区域内答题。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.i 为虚数单位,607i的共轭复数....为A .i B .i C .1 D .12.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534 石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为A .134石B .169石C .338石D .1365石3.已知(1)n x 的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为A .122B .112C .102D .92。

2015年普通高等学校招生全国统一考试数学试卷(湖北卷)一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.i 为虚数单位,607i=( ) (A )i (B )i - (C )1 (D )1-2.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( ) (A )134石 (B )169石 (C )338石 (D )1365石3.已知()1nx +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( ) (A )122 (B )112 (C )102 (D )924.设()211,X N μσ ,()222,Y N μσ ,这两个正态分布密度曲线如图所示,下列结论中正确的是( ) (A )()()21P Y P Y μμ≥≥≥ (B )()()21P X P X σσ≤≤≤(C )对任意正数t ,()()P X t P Y t ≤≥≤ (D )对任意正数t ,()()P X t P Y t ≥≥≥5.设12,,,n a a a R ∈ ,3n ≥,若p :12,,,n a a a 成等比数列;q :()()()22222221212312231n n n n a a a a a a a a a a a a --++++++=+++ ,则( ) (A )p 是q 的充分条件,但不是q 的必要条件 (B )p 是q 的必要条件,但不是q 的充分条件 (C )p 是q 的充分必要条件(D )p 既不是q 的充分条件,也不是q 的必要条件6.已知符号函数()()()10sgn 0010x x x x >⎧⎪==⎨⎪-<⎩,()f x 是R 上的增函数,()()()g x f x f ax =-,其中1a >,则( ) (A )()sgn sgn g x x =⎡⎤⎣⎦ (B )()sgn sgn g x x =-⎡⎤⎣⎦ (C )()()sgn sgn g x f x =⎡⎤⎡⎤⎣⎦⎣⎦ (D )()()sgn sgn g x f x =-⎡⎤⎡⎤⎣⎦⎣⎦7.在区间[]0,1上随机取两个数,x y ,记1p 为事件“12x y +≥”的概率,2p 为事件“1||2x y -≤”的概率,3p 为事件“12xy ≤12xy ≤”的概率,则( )(A )123p p p << (B )231p p p << (C )312p p p << (D )321p p p <<8.将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加()0m m >个单位长度,得到离心率为2e 的双曲线2C ,则( ) (A )对任意的,a b ,12e e > (B )当a b >时,12e e >;当a b <时,12e e < (C )对任意的,a b ,12e e < (D )当a b >时,12e e <;当a b <时,12e e > 9.设集合(){}22,|1,,A x y xy x y Z =+≤∈,(){},|2,2,,B x y x y x y Z =≤≤∈,定义集合()()(){}12121122,|,,,A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为( ) (A )77 (B )49 (C )45 (D )3010.设x R ∈,[]x 表示不超过x 的最大整数。


数学试卷 第1页(共24页)数学试卷 第2页(共24页)数学试卷 第3页(共24页)绝密★启用前2015年普通高等学校招生全国统一考试(湖北卷)数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟. 注意事项:1.答卷前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.用2B 铅笔将答题卡上试卷类型A 后的方框涂黑. 2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑,再在答题卡上对应的答题区域内答题.写在试题卷、草稿纸和答题卡上的非答题区域均无效.5.考试结束后,请将本试题卷和答题卡一并上交.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.i 为虚数单位,607i 的共轭复数为( )A .iB .i -C .1D .1-2.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1 534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )A .134石B .169石C .338石D .1 365石3.已知(1)nx +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A .122B .112C .102D .924.设211(,)X N μσ~,222(,)Y N μσ~,这两个正态分布密度曲线如图所示.下列结论中正确的是 ( )A .21()()P Y P Y μμ≥≥≥B .21()()P X P X σσ≤≤≤C .对任意正数t ,()()P X t P Y t ≤≥≤D .对任意正数t ,()()P X t P Y t ≥≥≥5.设12,,,n a a a ∈R ,3n ≥.若p :12,,,n a a a 成等比数列;q :222121()n a a a -+++22(a +222312231)()n n n a a a a a a a a -++=+++,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件6.已知符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩()f x 是R 上的增函数,()()()(1)g x f x f ax a =->,则( )A .sgn[()]sgn g x x =B .sgn[()]sgn g x x =-C .sgn[()]sgn[()]g x f x =D .sgn[()]sgn[()]g x f x =-7.在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y +≥”的概率,2p 为事件“1||2x y -≤”的概率,3p 为事件“12xy ≤”的概率,则( )A .123p p p <<B .231p p p <<C .312p p p <<D .321p p p <<8.将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则( )A .对任意的,a b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的,a b ,12e e <D .当a b >时,12e e <;当a b <时,12e e >9.已知集合22{(,)|1,,}A x y x y x y =+∈Z ≤,{(,)|||2,||2,,}B x y x y x y =∈Z ≤≤,定义集合12121122{(,)(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为 ( ) A .77B .49C .45D .30 10.设x ∈R ,[]x 表示不超过x 的最大整数.若存在实数t ,使得[]1t =,2[]2t =,…,[]n t n =同时成立,则正整数n 的最大值是( )A .3B .4C .5D .6 第Ⅱ卷(非选择题 共100分)二、填空题:本大题共6小题,考生需作答5小题,每小题5分,共25分.把答案填在题中的横线上. (一)必考题(11~14题)11.已知向量OA AB ⊥,||3OA =,则OA OB =___________. 12.函数2π()4cos cos()2sin |ln(1)|22xf x x x x =---+的零点个数为___________. 13.如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30的方向上,行驶600m 后到达B 处,测得此山顶在西偏北75的方向上,仰角为30,则此山的高度CD =___________m .14.如图,圆C 与x 轴相切于点(1,0)T ,与y 轴正半轴交于两点,A B (B 在A 的上方),且2AB =.(1)圆C 的标准方程为___________;(2)过点A 任作一条直线与圆22:1O x y +=相交于M ,N 两点,下列三个结论: ①||||||||NA MA NB NB =; ②||||2||||NB MA NA MB -=;③||||||||NB MA NA MB += 其中正确结论的序号是___________(写出所有正确结论的序号). -------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共24页)数学试卷 第5页(共24页)数学试卷 第6页(共24页)(二)选考题(请考生在第15,16两题中任选一题作答,如果全选,则按第15题作答结果记分) 15.(选修4—1:几何证明选讲)如图,P A 是圆的切线,A 为切点,PBC 是圆的割线,且3BC PB =,则ABAC=___________. 16.(选修4—4:坐标系与参数方程)在直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为(sin 3cos )0ρθθ-=,曲线C 的参数方程为1,1,x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),l与C 相交于A ,B 两点,则||AB =___________.三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分11分)某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象时,列表并填入了部分数据,如下表:(Ⅰ)请将上表数据补充完整,并直接写出函数()f x 的解析式;(Ⅱ)将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度,得到()y g x =的图象.若()y g x =图象的一个对称中心为5π(,0)12,求θ的最小值.18.(本小题满分12分)设等差数列{}n a 的公差为d ,前n 项和为n S ,等比数列{}n b 的公比为q .已知11b a =,22b =,q d =,10100S =. (Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)当1d >时,记n n nac b =,求数列{}n c 的前n 项和n T .19.(本小题满分12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 如图,在阳马P ABCD -中,侧棱PD ⊥底面ABCD , 且PD CD =,过棱PC 的中点E ,作EF PB ⊥交PB 于点F ,连接,,,DE DF BD BE . (Ⅰ)证明:PB DEF ⊥平面.试判断四面体DBEF 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由; (Ⅱ)若面DEF 与面ABCD 所成二面角的大小为π3,求DCBC的值.20.(本小题满分12分)某厂用鲜牛奶在某台设备上生产,A B 两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1 000元;生产1吨B 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1 200元.要求每天B 产品的产量不超过A 产品产量的2倍,设备每天生产,A B 两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W (单位:吨)是一个该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z (单位:元)是一个随机变量. (Ⅰ)求Z 的分布列和均值;(Ⅱ)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10 000元的概率. 21.(本小题满分14分)一种作图工具如图1所示.O 是滑槽AB 的中点,短杆ON 可绕O 转动,长杆MN 通过N 处铰链与ON 连接,MN 上的栓子D 可沿滑槽AB 滑动,且1DN ON ==,MN 3=.当栓子D 在滑槽AB 内作往复运动时,带动N 绕O 转动一周(D 不动时,N 也不动),M 处的笔尖画出的曲线记为C .以O 为原点,AB 所在的直线为x 轴建立如图2所示的平面直角坐标系.(Ⅰ)求曲线C 的方程;(Ⅱ)设动直线l 与两定直线1:20l x y -=和2:20l x y +=分别交于,P Q 两点.若直线l 总与曲线C 有且只有一个公共点,试探究:△OPQ 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(本小题满分14分)已知数列{}n a 的各项均为正数,*1(1)()n n n b n a n n=+∈N ,e 为自然对数的底数. (Ⅰ)求函数()1e x f x x =+-的单调区间,并比较1(1)n n +与e 的大小; (Ⅱ)计算11b a ,1212b ba a ,123123b b b a a a ,由此推测计算1212nnb b b a a a 的公式,并给出证明; (Ⅲ)令112()nn n c a a a =,数列{}n a ,{}n c 的前n 项和分别记为n S ,n T ,证明:e n n T S <.数学试卷 第7页(共24页)数学试卷 第8页(共24页)数学试卷 第9页(共24页)2015年普通高等学校招生全国统一考试(湖北卷)数学(理科)答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】60760433i i i i +===-,它的共轭复数为i . 【提示】直接利用复数的单位的幂运算求解即可. 【考点】虚数单位i 及其性质 2.【答案】B【解析】由题意,这批米内夹谷约为281534169254⨯≈石. 【提示】根据254粒内夹谷28粒,可得比例,即可得出结论. 【考点】随机抽样,样本估计总体的实际应用 3.【答案】D【解析】已知(1)nx +的展开式中第4项与第8项的二项式系数相等,可得37nnC C =,可得3710n =+=,10(1)x +的展开式中奇数项的二项式系数和为1091222⨯=.【提示】直接利用二项式定理求出n ,然后利用二项式定理系数的性质求出结果即可. 【考点】二项式定理,二项式系数的性质 4.【答案】C【解析】正态分布密度曲线图象关于x μ=对称,所以12μμ<,从图中容易得到()()P X t P Y t ≤≥≤.【提示】直接利用正态分布曲线的特征,集合概率,直接判断即可.【考点】正态分布曲线的特点及曲线所表示的意义 5.【答案】A【解析】由12,,,,3n a a a n ⋯∈≥R ,运用柯西不等式,可得:222222212-1231223-1()()()n n n n a a a a a a a a a a a a ++⋯+++⋯+≥++⋯+,若12,,,na a a ⋯成等比数列,即有32121n n a a a a a a -==⋯=,则22222212-1231223-1()()()nnn n a a a aaa a a a a a a ++⋯+++⋯+=++⋯+,即由p 推得q ,但由q 推不到p ,比如1230n a a a a ===⋯==,则12,,,n a a a ⋯不成等比数列,故p 是q 的充分不必要条件.【提示】运用柯西不等式,可得22222212-1231223-1()()()nn nn a a a aaa a a a a a a++⋯+++⋯+≥++⋯+,讨论等号成立的条件,结合等比数列的定义和充分必要条件的定义,即可得到. 【考点】等比数列的性质 6.【答案】B【解析】由于本题是选择题,可以常用特殊法,符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩,()f x 是R 上的增函数,()()()(1)g x f x f ax a =->,令()f x x =,2a =,则()()()g x f x f a x x=-=-,sgn[()]sgn()g x x =-,所以A 不正确,B 正确,sgn[()]sgn()f x x =,C 不正确;D 正确;对于D ,令()1f x x =+,2a =, 则()()()g x f x f ax x=-=-,1,1sgn[()]sgn(1)0,11,1x f x x x x >⎧⎪=+==-⎨⎪-<-⎩;1,0sgn[()]sgn()0,01,0x g x x x x >⎧⎪=-==⎨⎪-<⎩,1,1sgn[()]sgn(1)0,11,1x f x x x x ->-⎧⎪-=+==-⎨⎪<-⎩;所以D 不正确;故选B .【提示】直接利用特殊法,设出函数()f x ,以及a 的值,判断选项即可.【考点】函数与方程的综合运用 7.【答案】B【解析】分别作出事件对应的图象如图(阴影部分).P 1:10,2D ⎛⎫ ⎪⎝⎭,1,02F ⎛⎫⎪⎝⎭,(0,1)A ,(1,1)B ,(1,0)C ,则阴影部分的面积11111711122288S =⨯-⨯⨯=-=,211113112122243S =⨯-⨯⨯⨯=-=, 31111121ln 212222S dx x =⨯+=+⎰,231S S S ∴<<,即231p p p <<.【提示】作出每个事件对应的平面区域,求出对应的面积,利用几何概型的概率公式进行计算比较即可. 【考点】几何概型 8.【答案】D【解析】由题意,双曲线C 1:222c a b =+,1ce a =;双曲线C 2:222()()c a m b m '=+++,2e =,222222122()(2)()b b m abm bm am e e a a a m +++∴-=-+,∴当a b >时,12e e <;当a b <时,12e e >.【提示】分别求出双曲线的离心率,再平方作差,即可得出结论.【考点】双曲线的简单性质 9.【答案】C【解析】因为集合22{(,)1,,}A x y x y x y =+≤∈Z ,所以集合A 中有5个元素,即图中圆中的整点,{(,)||2,||2,,}B x y x y x y =≤≤∈Z ,中有5525⨯=个元素,即图中正方形ABCD 中的整点,12121122{(,)|(,),(,)}A B x x y y x y A x y B ⊕=++∈∈的元素可看作正方形1111A B C D 中的整点(除去四个顶点),即77445⨯-=个.数学试卷 第10页(共24页)数学试卷 第11页(共24页)数学试卷 第12页(共24页)【提示】分别求出集合A 与集合B 的解集,将其在坐标系中标出,即可求. 【考点】集合中元素个数的最值 10.【答案】B【解析】若[]1t =,则[1,2)t ∈,若2[]2t =,则t ∈(因为题目需要同时成立,则负区间舍去),若3[]3t =,则t ∈,若4[]4t =,则t ∈,若5[]5t =,则t ∈,1.732≈1.587≈1.4951.431 1.495≈<; 通过上述可以发现,当4t =时,可以找到实数t使其在区间334554[1,2)[2,3)[3,4)[4,5)[5,6)上,但当5t =时,无法找到实数t 使其在区间334554[1,2)[2,3)[3,4)[4,5)[5,6)上,∴正整数n 的最大值4.【提示】由新定义可得t 的范围,验证可得最大的正整数n 为4. 【考点】进行简单的演绎推理第Ⅱ卷二、填空题 (一)必考题 11.【答案】9【解析】由OA AB ⊥uu r uu u r ,得0O A A B =u u r u uur g ,即()0O A O B O A -=uu r uu u r uu r g ,3OA =uu rQ ,2||9OA AB OA ∴==u u r u u u r u u r g .【提示】由已知结合平面向量是数量积运算求得答案. 【考点】平面向量数量积的运算 12.【答案】2【解析】函数()f x 的定义域为{|1}x x >-.22π()4cos cos 2sin |ln(1)|2sin 2cos 1|ln(1)|sin 2|ln(1)|222x x f x x x x x x x x ⎛⎫⎛⎫=---+=--+=-+ ⎪ ⎪⎝⎭⎝⎭,分别画出函数sin 2y x =,|ln(1)|y x =+的图象,由函数的图象可知,交点个数为2,所以函数的零点有2个.【提示】利用二倍角公式化简函数的解析式,求出函数的定义域,画出函数的图象,求出交点个数即可.【考点】根的存在性及根的个数判断 13.【答案】【解析】设此山高h (m ),则BC =,在ABC △中,30BAC ∠=,105CBA ∠=,45BCA ∠=,600AB =,根据正弦定理得600sin 30sin 45=,解得h =m ). 【提示】设此山高h (m ),在BCD △中,利用仰角的正切表示出BC ,进而在ABC △中利用正弦定理求得h .【考点】解三角形的实际应用 14.【答案】(1)22(1)(2x y -+= (2)①②③【解析】解:(1)Q 圆C 与x 轴相切于点(1,0)T ,∴圆心的横坐标1x =,取AB 的中点E ,||2AB =Q ,||1BE ∴=,则||BC=,即圆的半径||rBC ==∴圆心C ,则圆的标准方程为22(1)(2x y -+=.(2)Q 圆心C,E ∴,又||2AB =Q,且E 为AB 中点,1)A ∴,1)B ,Q M 、N 在圆O :221x y +=上,∴可设(cos ,sin )M αα,(cos ,sin )N ββ, ||NA ∴=====||NB====||1||NA NB∴===, 同理可得||1||MA MB =,||||||||NA MA NB MB ∴=,①成立; ||||1)2||||NB NA NA NB-==,②正确; ||||1)||||NB MA NA MB +==,③正确.【提示】(1)取AB 的中点E ,通过圆C 与x 轴相切于点T ,利用弦心距、半径与半弦长之间的关系,计算即可;(2)设(cos ,sin )M αα,(cos ,sin )N ββ,计算出||||MA MB 、||||NA NB、||||NB NA 的值即可. 【考点】命题的真假判断与应用,圆与圆的位置关系及其判定 (二)选考题 15.【答案】12数学试卷 第13页(共24页)数学试卷 第14页(共24页)数学试卷 第15页(共24页)【解析】由切割线定理可知2PA PB PC =g ,又3BC PB =,可得2PA PB =,在PAB △与PAC △中,P P ∠=∠,PAB PCA ∠=∠(同弧上的圆周角与弦切角相等),可得PAB PCA△∽△, 122AB PB PB AC PA PB ∴===.【提示】利用切割线定理推出2PA PB =,利用相似三角形求出比值即可. 【考点】与圆有关的比例线段 16.【答案】【解析】由(sin 3cos )0ρθθ-=,得30y x -=,由C 的参数方程为11x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),两式平方作差得224x y -=-.联立2234y x x y =⎧⎨-=-⎩,得212x =,即2x =±,22A ⎛∴ ⎝⎭,,22B ⎛-- ⎝⎭,||AB ∴==.【提示】化极坐标方程化直角坐标方程,参数方程化为普通方程,联立直线方程和双曲线方程后求得交点坐标,由两点间的距离公式可得答案. 【考点】简单曲线的极坐标方程,双曲线的参数方程 三、解答题 17.【答案】(Ⅰ)π127π12 13π12π()5sin 26f x x ⎛⎫=- ⎪⎝⎭(Ⅱ)π6【解析】(Ⅰ)根据表中已知数据,解得5A =,2,ω=,π6ϕ=-,数据补全如下表:且函数表达式为()5sin 26f x x ⎛⎫=- ⎪⎝⎭.(Ⅱ)由(Ⅰ)知π()5sin 26f x x ⎛⎫=- ⎪⎝⎭,得π()5sin 226g x x θ⎛⎫=+- ⎪⎝⎭,因为sin y x =的对称中心为(π,0)k ,k ∈Z ,令π22π6x k θ+-=,解得ππ212k x θ=+-,k ∈Z , 由于函数()y g x =的图象关于点5π,012⎛⎫⎪⎝⎭成中心对称, 令ππ5π21212k θ+-=,解得ππ23k θ=-,k ∈Z . 由0θ>可知,当1k =时,θ取得最小值π6. 【提示】(Ⅰ)根据表中已知数据,解得5A =,2,ω=,π6ϕ=-,从而可补全数据,解得函数表达式为π()5sin 26f x x ⎛⎫=- ⎪⎝⎭;(Ⅱ)由(Ⅰ)及函数sin()y A x ωϕ=+的图象变换规律得π()5sin 226g x x θ⎛⎫=+- ⎪⎝⎭.令π22π6x k θ+-=,解得ππ212k x θ=+-,k ∈Z ,令ππ5π21212k θ+-=,解得ππ23k θ=-,k ∈Z ,由0θ>可得解.【考点】由sin()y A x ωϕ=+的部分图象确定其解析式,函数sin()y A x ωϕ=+的图象变换18.【答案】(Ⅰ)21n a n =-,12n n b -=或1(279)9n a n =+,1299n n b -⎛⎫= ⎪⎝⎭g (Ⅱ)12362n n n T -+=-【解析】(Ⅰ)设1a a =,由题意可得10451002a d ad +=⎧⎨=⎩,解得12a d =⎧⎨=⎩,或929a d =⎧⎪⎨=⎪⎩,当12a d =⎧⎨=⎩时,21n a n =-,12n nb -=; 当929a d =⎧⎪⎨=⎪⎩时,1(279)9n a n =+,1299n n b -⎛⎫= ⎪⎝⎭g .(Ⅱ)当1d >时,由(Ⅰ)知21n a n =-,12n n b -=,1212n n n n a n c b --∴==, 23411111113579(21)22222n n T n -∴=++++++-g g g g L g ,234111*********(23)(21)2222222n n n T n n -∴=+++++-+-g g g g L g g 23421111111232(21)322222222n n n n n T n -+=++++++--=-L g 12362n n n T -+∴=-.【提示】(Ⅰ)利用前10项和与首项、公差的关系,联立方程组计算即可;(Ⅱ)当1d >时,由(Ⅰ)知1212nn n c --=,写出n T 、12n T 的表达式,利用错位相减法及等比数列的求和公式,计算即可. 【考点】数列的求和 19.【答案】(Ⅰ)见解析(Ⅱ)DC BC =【解析】解法一:(Ⅰ)因为PD ⊥底面ABCD ,所以PD BC ⊥,由底面ABCD 为长方形,有BC CD ⊥,而PD CD D =,所以BC ⊥平面PCD , 而DE ⊂平面PDC ,所以BC DE ⊥.又因为PD CD =,点E 是PC 的中点,所以DE PC ⊥, 而PC CB C =I ,所以DE ⊥平面PBC ,而PB ⊂平面PBC ,所以PB DE ⊥.又PB EF ⊥,DE FE E =I ,所以PB ⊥平面DEF .数学试卷 第16页(共24页)数学试卷 第17页(共24页) 数学试卷 第18页(共24页)由DE ⊥平面PBC ,PB ⊥平面DEF ,可知四面体BDEF 的四个面都是直角三角形, 即四面体BDEF 是一个鳖臑,其四个面的直角分别为DEB ∠,DEF ∠,EFB ∠,DFB ∠. (Ⅱ)如图,在面BPC 内,延长BC 与FE 交于点G ,则D G 是平面DEF 与平面ACBD 的交线.由(Ⅰ)知,PB ⊥平面DEF ,所以PB DG ⊥. 又因为PD ⊥底面ABCD ,所以PD DG ⊥, 而PD PB P =I ,所以DG ⊥平面PBD , 所以DG DF ⊥,DG DB ⊥.故BDF ∠是面DEF 与面ABCD 所成二面角的平面角, 设1PD DC ==,BC λ=,有BD =在Rt PDB △中,由DF PB ⊥,得π3DPF FDB ∠=∠=,则πtan tan 3BDDPF PD=∠===解得λ=1DC BC λ=, 故当面DEF 与面ABCD 所成二面角的大小为π3时,DC BC =解法二:(Ⅰ)以D 为原点,射线DA ,DC ,DP 分别为x ,y ,z 轴的正半轴,建立空间直角坐标系.设1PD DC ==,BC λ=,则(0,0,0)D ,(0,0,1)P ,(,1,0)B λ,(0,1,0)C ,(,1,1)PB λ=-uu r,点E 是PC 的中点,所以110,,22E ⎛⎫ ⎪⎝⎭,110,,22DE ⎛⎫= ⎪⎝⎭uuur ,于是0PB DE =uu r uuu rg ,即PB DE ⊥.又已知EF PB ⊥,而ED EF E =I ,所以PB ⊥平面DEF , 因(0,1,1)PC =-uu u r ,0DE PC =uuu r uu u rg ,则DE PC ⊥,所以DE ⊥平面PBC .由DE ⊥平面PBC ,PB ⊥平面DEF ,可知四面体BDEF 的四个面都是直角三角形, 即四面体BDEF 是一个鳖臑,其四个面的直角分别为DEB ∠,DEF ∠,EFB ∠,DFB ∠.(Ⅱ)由PD ⊥底面ABCD ,所以(0,0,1)DP =uu u r是平面ACDB 的一个法向量;由(Ⅰ)知,PB ⊥平面DEF ,所以(,1,1)BP λ=--uu r是平面DEF 的一个法向量.若面DEF 与面ABCD 所成二面角的大小为π3,则运用向量的数量积求解得出π1cos 32==,解得λ=12DC BC λ==, 故当面DEF 与面ABCD 所成二面角的大小为π3时,DC BC =【提示】解法一:(Ⅰ)直线与直线,直线与平面的垂直的转化证明得出PB EF ⊥,DE FE E =I ,所以PB ⊥平面DEF ,即可判断DE ⊥平面PBC ,PB ⊥平面DEF ,可知四面体BDEF 的四个面都是直角三角形,确定直角;(Ⅱ)根据公理2得出DG 是平面DEF 与平面ACBD 的交线,利用直线平面的垂直判断出DG DF ⊥,DG DB ⊥,根据平面角的定义得出BDF ∠是面DEF 与面ABCD 所成二面角的平面角,转化到直角三角形求解即可.解法二:(Ⅰ)以D 为原点,射线DA ,DC ,DP 分别为x ,y ,z 轴的正半轴,建立空间直角坐标系,运用向量的数量积判断即可;(Ⅱ)由PD ⊥底面ABCD ,所以(0,0,1)DP =uu u r是平面ACDB 的一个法向量;由(Ⅰ)知,PB ⊥平面DEF ,所以(,1,1)BP λ=--uu r是平面DEF 的一个法向量,根据数量积得出夹角的余弦即可得出所求解的答案.【考点】用空间向量求平面间的夹角,直线与平面垂直的判定 20.【答案】(Ⅰ)见解析 (Ⅱ)0.973【解析】(Ⅰ)设每天A ,B 两种产品的生产数量分别为x ,y ,相应的获利为Z ,则有2 1.51.512200,0x y W x y x y x y +≤⎧⎪+≤⎪⎨-≥⎪⎪≥≥⎩①,如图1,目标函数为10001200Z x y =+.当12W =时,①表示的平面区域如图1,三个顶点分别为(0,0)A ,(2.4,4.8)B ,(6,0)C ,将10001200Z x y =+变形为561200Zy x =-+,当 2.4x =, 4.8y =时,直线l :561200Zy x =-+在y 轴上的截距最大,最大获利max 2.41000 4.812008160Z Z ==⨯+⨯=; 当15W =时,①表示的平面区域如图2,三个顶点分别为(0,0)A ,(3,6)B ,(7.5,0)C , 将10001200Z x y =+变形为561200Zy x =-+,当3x =,6y =时,直线l :561200Zy x =-+在y 轴上的截距最大,最大获利max 310006120010200Z Z ==⨯+⨯=; 当18W =时,①表示的平面区域如图3,四个顶点分别为(0,0)A ,(3,6)B ,(6,4)C ,(9,0)D , 将10001200Z x y =+变形为561200Zy x =-+,当6x =,4y =时,直线l :561200Zy x =-+在y 轴上的截距最大,最大获利max 610004120010800Z Z ==⨯+⨯=.因此,()81600.3102000.5108000.29708E Z =⨯+⨯+⨯=.数学试卷 第19页(共24页)数学试卷 第20页(共24页)数学试卷 第21页(共24页)(Ⅱ)由(Ⅰ)知,一天最大获利超过10000元的概率1(10000)0.50.20.7P P Z =>=+=,由二项分布,3天中至少有1天最大获利超过10000元的概率为311(1)0.973P P =--=.【提示】(Ⅰ)设每天A ,B 两种产品的生产数量分别为x ,y ,相应的获利为z ,列出可行域,目标函数,通过当12W =时,当15W =时,当18W =时,分别求出目标函数的最大获利,然后得到Z 的分布列,求出期望即可;(Ⅱ)判断概率类型是二项分布,然后求解所求概率即可. 【考点】简单线性规划的应用,离散型随机变量的期望与方差21.【答案】(Ⅰ)221164x y += (Ⅱ)见解析【解析】(Ⅰ)设(,0)(||2)D t t ≤,00(,)N x y ,(,)M x y ,由题意得2MD DN =uuu r uuu r,且||||1DN ON ==uuu r uuu r ,00(,)2(,)t x y x t y ∴--=-,且22002200()11x t y x y ⎧-+=⎪⎨+=⎪⎩,即00222t x x t y y -=-⎧⎨=-⎩,且0(2)0t t x -=, 由于当点D 不动时,点N 也不动,∴t 不恒等于0,于是02t x =,故04x x =,02yy =-, 代入2201x y +=,得方程221164x y +=.(Ⅱ)(1)当直线l 的斜率k 不存在时,直线l 为:4x =或4x =-,都有14482OPQ S =⨯⨯=△, (2)直线l 的斜率k 存在时,直线l 为:12y kx m k ⎛⎫=+≠± ⎪⎝⎭,由22416y kx m x y =+⎧⎨+=⎩消去y ,可得222(14)84160k x kmx m +++-=, 直线l 总与椭圆C 有且只有一个公共点,2222644(14)(416)0k m k m ∴∆=-+-=,即22164m k =+①. 由20y kx m x y =+⎧⎨-=⎩,可得2,1212m m P k k ⎛⎫ ⎪--⎝⎭,同理得2,1212mm Q k k -⎛⎫ ⎪++⎝⎭, 原点O 到直线PQ的距离d =和|||P Q PQ x x -, 可得22111222||||||||222121214OPQP Q m m m S PQ d m x x m k k k ==-=+=-+-△②. 将①代入②得222224181441OPQm k S k k +==--△, 当214k >时,22241288184141OPQ k S k k ⎛⎫+⎛⎫==+> ⎪ ⎪--⎝⎭⎝⎭△, 当2104k ≤<时,22222414128881414114OPQ k k S k k k ⎛⎫++⎛⎫==-=-+ ⎪ ⎪---⎝⎭⎝⎭△, 2104k ≤<时,20141k ∴<-≤,22214k ≥-, 2281814OPQS k ⎛⎫∴=-+≥ ⎪-⎝⎭△,当且仅当0k =时取等号,0k ∴=时,OPQ S △的最小值为8.综上可知当直线l 与椭圆C 在四个顶点处相切时,三角形OPQ 的面积存在最小值为8. 【提示】(Ⅰ)根据条件求出a ,b 即可求椭圆C 的方程;(Ⅱ)联立直线方程和椭圆方程,求出原点到直线的距离,结合三角形的面积公式进行求解即可.【考点】直线与圆锥曲线的关系,椭圆的标准方程22.【答案】(Ⅰ)()f x 的单调递增区间为(,0)-∞,单调递减区间为(0,)+∞11e nn ⎛⎫+< ⎪⎝⎭ (Ⅱ)见解析 (Ⅲ)见解析【解析】(Ⅰ)()f x 的定义域为(,)-∞+∞,()1e x f x '=-, 当()0f x '>,即0x <时,()f x 单调递增, 当()0f x '<,即0x >时,()f x 单调递减,故()f x 的单调递增区间为(,0)-∞,单调递减区间为(0,)+∞. 当0x >时,()(0)0f x f <=,即1e x x +<,令1x n =,得111e n n +<,即11e nn ⎛⎫+< ⎪⎝⎭①(Ⅱ)1111111121b a ⎛⎫=+=+= ⎪⎝⎭g ;222121212121221(21)32b b b b a a a a ⎛⎫==+=+= ⎪⎝⎭g g ;32331233121231231331(31)43b b b b b b a a a a a a ⎛⎫==+=+= ⎪⎝⎭g g ; 由此推测:1212(1)n nnb b b n a a a =+L L ② 下面用数学归纳法证明②,(1)当1n =时,2==左边右边,②成立.(2)假设当n k =时,②成立,即1212(1)k kk b b b k a a a =+L L , 当1n k =+时,1111(1)11k k k b k a k +++⎛⎫=++ ⎪+⎝⎭,由归纳假设可得111211211211211(1)(1)1(2)1k k k k k k k k k k k b b b b b b b b k k k a a a a a a a a k ++++++⎛⎫==+++=+ ⎪+⎝⎭L L g L L∴当1n k =+时,②也成立.根据(1)(2),可知②对一切正整数n 都成立.(Ⅲ)证明:由n c 的定义,②,算术-几何平均不等式,n b 的定义及①得数学试卷 第22页(共24页) 数学试卷 第23页(共24页) 数学试卷 第24页(共24页)111131212311212312()()()()nn n n T c c c c a a a a a a a a a =++++=++++11113121231212312112112()()()()2341122334(1)nn n b b b b b b b b bb b b b b b b b b n n n ++++++=++++≤+++++⨯⨯⨯+L L L L1211111111223(1)2334(1)(1)n b b b n n n n n n ⎡⎤⎡⎤=+++++++++⎢⎥⎢⎥⨯⨯+⨯⨯++⎣⎦⎣⎦L L L g 1212111111121112n n b b b b b b n n n n n ⎛⎫⎛⎫⎛⎫=-+-++-<+++ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭ 121212111111e e e 12nn n a a a a a a n ⎛⎫⎛⎫⎛⎫=++++++<+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L L即e n n T S <.【提示】(Ⅰ)求出()f x 的定义域,利用导数求其最大值,得到1e x x +<,取1x n=即可得到答案;(Ⅱ)由11()nn n b n a n n +⎛⎫=+∈ ⎪⎝⎭N ,变形求得11b a ,1212b b a a ,123123b b b a a a ,由此推测1212(1)n nnb b b n a a a =+,然后利用数学归纳法证明;(Ⅲ)由n c 的定义、1212(1)n n n b b b n a a a =+、算术-几何平均不等式、n b 的定义及11e nn ⎛⎫+< ⎪⎝⎭,利用放缩法证得e n n T S <. 【考点】数列与不等式的综合。

2015年湖北省高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•湖北)i为虚数单位,i607的共轭复数为()A .i B.﹣i C.1 D.﹣1考点:虚数单位i及其性质.专题:数系的扩充和复数.分析:直接利用复数的单位的幂运算求解即可.解答:解:i607=i604+3=i3=﹣i,它的共轭复数为:i.故选:A.点评:本题考查复数的基本运算,复式单位的幂运算以及共轭复数的知识,基本知识的考查.2.(5分)(2015•湖北)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A .134石B.169石C.338石D.1365石考点:随机抽样和样本估计总体的实际应用.专题:计算题;概率与统计.分析:根据254粒内夹谷28粒,可得比例,即可得出结论.解答:解:由题意,这批米内夹谷约为1534×≈169石,故选:B.点评:本题考查利用数学知识解决实际问题,考查学生的计算能力,比较基础.3.(5分)(2015•湖北)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A .212B.211C.210D.29考点:二项式定理;二项式系数的性质.专题:二项式定理.分析:直接利用二项式定理求出n,然后利用二项式定理系数的性质求出结果即可.解答:解:已知(1+x)n的展开式中第4项与第8项的二项式系数相等,可得,可得n=3+7=10.(1+x )10的展开式中奇数项的二项式系数和为:=29.故选:D .点评: 本题考查二项式定理的应用,组合数的形状的应用,考查基本知识的灵活运用以及计算能力.4.(5分)(2015•湖北)设X ~N (μ1,σ12),Y ~N (μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )A . P (Y ≥μ2)≥P (Y ≥μ1)B . P (X ≤σ2)≤P(X ≤σ1) C . 对任意正数t ,P (X ≤t )≥P (Y ≤t )D .对任意正数t ,P (X ≥t )≥P (Y ≥t )考点: 正态分布曲线的特点及曲线所表示的意义. 专题: 概率与统计.分析: 直接利用正态分布曲线的特征,集合概率,直接判断即可.解答:解:正态分布密度曲线图象关于x=μ对称,所以μ1<μ2,从图中容易得到P (X ≤t )≥P (Y ≤t ). 故选:C .点评:本题考查了正态分布的图象与性质,学习正态分布,一定要紧紧抓住平均数μ和标准差σ这两个关键量,结合正态曲线的图形特征,归纳正态曲线的性质.5.(5分)(2015•湖北)设a 1,a 2,…,a n ∈R ,n ≥3.若p :a 1,a 2,…,a n 成等比数列;q :(a 12+a 22+…+a n ﹣12)(a 22+a 32+…+a n 2)=(a 1a 2+a 2a 3+…+a n ﹣1a n )2,则( )A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件考点:等比数列的性质.专题:等差数列与等比数列;简易逻辑.分析:运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,讨论等号成立的条件,结合等比数列的定义和充分必要条件的定义,即可得到.解答:解:由a1,a2,…,a n∈R,n≥3.运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,若a1,a2,…,a n成等比数列,即有==…=,则(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,即由p推得q,但由q推不到p,比如a1=a2=a3=…=a n=0,则a1,a2,…,a n不成等比数列.故p是q的充分不必要条件.故选:A.点评:本题考查充分必要条件的判断,同时考查等比数列的定义,注意运用定义法和柯西不等式解题是关键.6.(5分)(2015•湖北)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnxC.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]函数与方程的综合运用.考点:专函数的性质及应用.题:直接利用特殊法,设出函数f(x),以及a的值,判断选项即可.分析:解答:解:由于本题是选择题,可以常用特殊法,符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),不妨令f(x)=x,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[g(x)]=﹣sgnx.所以A不正确,B正确,sgn[f(x)]=sgnx,C不正确;D正确;对于D,令f(x)=x+1,a=2,则g(x)=f(x)﹣f(ax)=﹣x﹣1,sgn[f(x)]=sgn(x+1)=;sgn[g(x)]=sgn(﹣x﹣1)=,﹣sgn[f(x)]=﹣sgn(x+1)=;所以D不正确;故选:B.点评:本题考查函数表达式的比较,选取特殊值法是解决本题的关键,注意解题方法的积累,属于中档题.7.(5分)(2015•湖北)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A .P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P1考点:几何概型.专题:概率与统计.分析:作出每个事件对应的平面区域,求出对应的面积,利用几何概型的概率公式进行计算比较即可.解答:解:分别作出事件对应的图象如图(阴影部分):P1:D(0,),F(,0),A(0,1),B(1,1),C(1,0),则阴影部分的面积S1=1×1﹣=1﹣=,S2=1×1﹣2×=1﹣=,S3=1×+dx=+lnx|=﹣ln=+ln2,∴S2<S3<S1,即P2<P3<P1,故选:B.点评:本题主要考查几何概型的概率计算,利用数形结合是解决本题的关键.本题也可以直接通过图象比较面积的大小即可比较大小.8.(5分)(2015•湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e2考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:分别求出双曲线的离心率,再平方作差,即可得出结论.解答:解:由题意,双曲线C1:c2=a2+b2,e1=;双曲线C2:c′2=(a+m)2+(b+m)2,e2=,∴=﹣=,∴当a>b时,e1<e2;当a<b时,e1>e2,故选:D.点评:本题考查双曲线的性质,考查学生的计算能力,比较基础.9.(5分)(2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A .77 B.49 C.45 D.30考点:集合中元素个数的最值.专题:新定义;开放型;集合.分析:由题意可得,A={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)},根据定义可求解答:解:∵A={(x,y)|x2+y2≤1,x,y∈Z}={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(x,y)||x|≤2,|y|≤2,x,y∈Z}={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)}∵A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},∴A⊕B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2),(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2),(﹣2,3),(﹣2,﹣3),(0,﹣3),(2,﹣3),(﹣1,3),(﹣1,﹣3),(1,3),(2,3),(0,3),(3,﹣1),(3,0)(3,1),(3,2),(3,﹣2)(﹣3,2)(﹣3,1),(1,﹣3),(﹣3,﹣1),(﹣3,0),(﹣3,﹣2)}共45个元素故选:C.点评:本题以新定义为载体,主要考查了几何的基本定义及运算,解题中需要取得重复的元素.10.(5分)(2015•湖北)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A .3 B.4 C.5 D.6考点:进行简单的演绎推理.专题:创新题型;简易逻辑.分析:由新定义可得t的范围,验证可得最大的正整数n为4解答:解:∵[t]=1,∴t∈[1,2),又∵[t2]=2,∴t2∈[2,3),∴t∈[,),又t2∈[2,3),∴t4∈[4,9),∴[t4]=4,∴正整数n的最大值4故选:B.点评:本题考查简单的演绎推理,涉及新定义,属基础题.二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)(2015•湖北)已知向量⊥,||=3,则•=9.考点:平面向量数量积的运算.专题:平面向量及应用.分析:由已知结合平面向量是数量积运算求得答案.解答:解:由⊥,得•=0,即•()=0,∵||=3,∴.故答案为:9.点评:本题考查了平面向量的数量积运算,考查了向量模的求法,是基础的计算题.12.(5分)(2015•湖北)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为2.考点:根的存在性及根的个数判断.专题:函数的性质及应用.分析:利用二倍角公式化简函数的解析式,求出函数的定义域,画出函数的图象,求出交点个数即可.解答:解:函数f(x)的定义域为:{x|x>﹣1}.f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|=2sinx﹣|ln(x+1)|=sin2x﹣|ln(x+1)|,分别画出函数y=sin2x,y=|ln(x+1)|的图象,由函数的图象可知,交点个数为2.所以函数的零点有2个.故答案为:2.点评:本题考查三角函数的化简,函数的零点个数的判断,考查数形结合与转化思想的应用.13.(5分)(2015•湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=100m.考点:解三角形的实际应用.专题:计算题;解三角形.分析:设此山高h(m),在△BCD中,利用仰角的正切表示出BC,进而在△ABC中利用正弦定理求得h.解答:解:设此山高h(m),则BC=h,在△ABC中,∠BAC=30°,∠CBA=105°,∠BCA=45°,AB=600.根据正弦定理得=,解得h=100(m)故答案为:100.点评:本题主要考查了解三角形的实际应用.关键是构造三角形,将各个已知条件向这个主三角形集中,再通过正弦、余弦定理或其他基本性质建立条件之间的联系,列方程或列式求解.14.(5分)(2015•湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为(x﹣1)2+(y﹣)2=2;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是①②③.(写出所有正确结论的序号)考点:命题的真假判断与应用;圆与圆的位置关系及其判定.专题:创新题型;简易逻辑.分析:(1)取AB的中点E,通过圆C与x轴相切于点T,利用弦心距、半径与半弦长之间的关系,计算即可;(2)设M(cosα,sinα),N(cosβ,sinβ),计算出、、的值即可.解答:解:(1)∵圆C与x轴相切于点T(1,0),∴圆心的横坐标x=1,取AB的中点E,∵|AB|=2,∴|BE|=1,则|BC|=,即圆的半径r=|BC|=,∴圆心C(1,),则圆的标准方程为(x﹣1)2+(y﹣)2=2,故答案为:(x﹣1)2+(y﹣)2=2.(2)∵圆心C(1,),∴E(0,),又∵|AB|=2,且E为AB中点,∴A(0,﹣1),B(0,+1),∵M、N在圆O:x2+y2=1上,∴可设M(cosα,sinα),N(cosβ,sinβ),∴|NA|=====,|NB|====,∴===,同理可得=,∴=,①成立,﹣=﹣()=2,②正确.+=+()=,③正确.故答案为:①②③.点评:本题考查求圆的标准方程,用三角函数值表示单位圆上点的坐标是解决本题的关键,注意解题方法的积累,属于难题.选修4-1:几何证明选讲15.(5分)(2015•湖北)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.考点:与圆有关的比例线段.专题:推理和证明.分析:利用切割线定理推出PA=2PB,利用相似三角形求出比值即可.解答:解:由切割线定理可知:PA2=PB•PC,又BC=3PB,可得PA=2PB,在△PAB与△PAC中,∠P=∠P,∠PAB=∠PCA(同弧上的圆周角与弦切角相等),可得△PAB∽△PAC,∴==.故答案为:.点评:本题考查切割线定理以及相似三角形的判定与应用,考查逻辑推理能力.选修4-4:坐标系与参数方程16.(2015•湖北)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t为参数),l与C相交于A,B两点,则|AB|=.考点:简单曲线的极坐标方程;双曲线的参数方程.专题:坐标系和参数方程.分析:化极坐标方程化直角坐标方程,参数方程化普通方程,联立直线方程和双曲线方程后求得交点坐标,由两点间的距离公式得答案.解答:解:由ρ(sinθ﹣3cosθ)=0,得y﹣3x=0,由C的参数方程为(t为参数),两式平方作差得:x2﹣y2=﹣4.联立,得,即.∴A(),B(),∴|AB|=.故答案为:.点评:本题考查极坐标方程化直角坐标方程,参数方程化普通方程,考查了直线和圆锥曲线的位置关系,是基础的计算题.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)(2015•湖北)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0 π2πxAsin(ωx+φ)0 5 ﹣5 0(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.从而可补全数据,解得函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)及函数y=Asin(ωx+φ)的图象变换规律得g(x)=5sin(2x+2θ﹣).令2x+2θ﹣=kπ,解得x=,k∈Z.令=,解得θ=,k∈Z.由θ>0可得解.解答:解:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.数据补全如下表:ωx+φ0 π2πxAsin(ωx+φ)0 5 0 ﹣5 0且函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)知f(x)=5sin(2x﹣),得g(x)=5sin(2x+2θ﹣).因为y=sinx的对称中心为(kπ,0),k∈Z.令2x+2θ﹣=kπ,解得x=,k∈Z.由于函数y=g(x)的图象关于点(,0)成中心对称,令=,解得θ=,k∈Z.由θ>0可知,当K=1时,θ取得最小值.点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换规律的应用,属于基本知识的考查.18.(12分)(2015•湖北)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.数列的求和.考点:等差数列与等比数列.专题:(1)利用前10项和与首项、公差的关系,联立方程组计算即可;分析:(2)当d>1时,由(1)知c n=,写出T n、T n的表达式,利用错位相减法及等比数列的求和公式,计算即可.解解:(1)设a1=a,由题意可得,答:解得,或,当时,a n=2n﹣1,b n=2n﹣1;当时,a n=(2n+79),b n=9•;(2)当d>1时,由(1)知a n=2n﹣1,b n=2n﹣1,∴c n==,∴T n=1+3•+5•+7•+9•+…+(2n﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.点评:本题考查求数列的通项及求和,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.19.(12分)(2015•湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD 中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.考点:用空间向量求平面间的夹角;直线与平面垂直的判定.专题:空间位置关系与距离;空间向量及应用.分析:解法1)(1)直线与直线,直线与平面的垂直的转化证明得出PB⊥EF,DE∩FE=E,所以PB⊥平面DEF,即可判断DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,确定直角.(2)根据公理2得出DG是平面DEF与平面ACBD的交线.利用直线平面的垂直判断出DG⊥DF,DG⊥DB,根据平面角的定义得出∠BDF是面DEF与面ABCD所成二面角的平面角,转化到直角三角形求解即可.解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系,运用向量的数量积判断即可.2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.根据数量积得出夹角的余弦即可得出所求解的答案.解答:解法1)(1)因为PD⊥底面ABCD,所以PD⊥BC,由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,所以BC⊥平面ABCD.而DE⊂平面PDC,所以BC⊥DE.又因为PD=CD,点E是PC的中点,所以DE⊥PC.而PC∩CB=C,所以DE⊥平面PBC.而PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)如图1,在面BPC内,延长BC与FE交于点G,则DG是平面DEF与平面ACBD的交线.由(Ⅰ)知,PB⊥平面DEF,所以PB⊥DG.又因为PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.所以DG⊥DF,DG⊥DB故∠BDF是面DEF与面ABCD所成二面角的平面角,设PD=DC=1,BC=λ,有BD=,在Rt△PDB中,由DF⊥PB,得∠DGF=∠FDB=,则tan=tan∠DPF===,解得.所以==故当面DEF与面ABCD所成二面角的大小为时,=.(解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),=(λ1,﹣1),点E是PC的中点,所以E(0,,),=(0,,),于是=0,即PB⊥DE.又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.因=(0,1,﹣1),=0,则DE⊥PC,所以DE⊥平面PBC.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.若面DEF与面ABCD所成二面角的大小为,则运用向量的数量积求解得出cos==,解得.所以所以==故当面DEF与面ABCD所成二面角的大小为时,=.点评:本题综合考查了空间直线平面的垂直问题,直线与直线,直线与平面的垂直的转化,空间角的求解,属于难题.20.(12分)(2015•湖北)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W 12 15 18P 0.3 0.5 0.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.考点:简单线性规划的应用;离散型随机变量的期望与方差.专题:不等式的解法及应用;概率与统计.分析:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,列出可行域,目标函数,通过当W=12时,当W=15时,当W=18时,分别求出目标函数的最大获利,然后得到Z的分布列.求出期望即可.(2)判断概率类型是二项分布,然后求解所求概率即可.解答:(12分)解:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,则有,①如图1,目标函数为:z=1000x+1200y.当W=12时,①表示的平面区域如图1,三个顶点分别为A(0,0),B(2.4,4.8),C(6,0).将z=1000x+1200y变形为,当x=2.4,y=4.8时,直线l:在y轴上的截距最大,最大获利Z=Z max=2.4×1000+4.8×1200=8160.当W=15时,①表示的平面区域如图2,三个顶点分别为A(0,0),B(3,6),C(7.5,0)..将z=1000x+1200y变形为,当x=3,y=6时,直线l:在y轴上的截距最大,最大获利Z=Z max=3×1000+6×1200=10200.当W=18时,①表示的平面区域如图3,四个顶点分别为A(0,0),B(3,6),C (6,4),D(9,0).将z=1000x+1200y变形为:,当x=6,y=4时,直线l:y=﹣56x+z1200在y轴上的截距最大,最大获利Z=Z max=6×1000+4×1200=10800.故最大获利Z的分布列为:Z 8160 10200 10800P 0.3 0.5 0.2因此,E(Z)=8160×0.3+10200×0.5+10800×0.2=9708(2)由(Ⅰ)知,一天最大获利超过10000元的概率P1=P(Z>10000)=0.5+0.2=0.7,由二项分布,3天中至少有1天最大获利超过10000元的概率为:.点评:本题考查离散型随机变量的分布列以及期望的求法,线性规划的应用,二项分布概率的求法,考查分析问题解决问题的能力.21.(14分)(2015•湖北)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON 可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:创新题型;开放型;圆锥曲线中的最值与范围问题.分析:(1)根据条件求出a,b即可求椭圆C的方程;(2)联立直线方程和椭圆方程,求出原点到直线的距离,结合三角形的面积公式进行求解即可.解答:解:(1)∵|OM|≤|MN|+|NO|=3+1=4,当M,N在x轴上时,等号成立,同理|OM|≥|MN|﹣|NO|=3﹣1=2,当D,O重合,即MN⊥x轴时,等号成立.∴椭圆C的中心为原点O,长半轴长为4,短半轴长为2,其方程为.(2)①当直线l的斜率k不存在时,直线l为:x=4或x=﹣4,都有S△OPQ=,②直线l的斜率k存在时,直线l为:y=kx+m,(k),由消去y,可得(1+4k2)x2+8kmx+4m2﹣16=0,∵直线l总与椭圆C有且只有一个公共点,∴△=64k2m2﹣4(1+4k2)(4m2﹣16)=0,即m2=16k2+4,①,由,可得P(,),同理得Q(,),原点O到直线PQ的距离d=和|PQ|=•|x P﹣x Q|,可得S△OPQ=|PQ|d=|m||x P﹣x Q|=|m|||=||②,将①代入②得S△OPQ=||=8||,当k2>时,S△OPQ=8()=8(1+)>8,当0≤k2<时,S△OPQ=8||=﹣8()=8(﹣1+),∵0≤k2<时,∴0<1﹣4k2≤1,≥2,∴S△OPQ=8(﹣1+)≥8,当且仅当k=0时取等号,∴当k=0时,S△OPQ的最小值为8,综上可知当直线l与椭圆C在四个顶点处相切时,三角形OPQ的面积存在最小值为8.点评:本题主要考查椭圆方程的求解,以及直线和圆锥曲线的位置关系的应用,结合三角形的面积公式是解决本题的关键.综合性较强,运算量较大.22.(14分)(2015•湖北)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.考点:数列与不等式的综合.专题:创新题型;导数的综合应用;点列、递归数列与数学归纳法;不等式的解法及应用.分析:(1)求出f(x)的定义域,利用导数求其最大值,得到1+x<e x.取x=即可得到答案;(2)由b n=n(1+)n a n(n∈N+),变形求得,,,由此推测=(n+1)n.然后利用数学归纳法证明.(3)由c n的定义、=(n+1)n、算术﹣几何平均不等式、b n的定义及,利用放缩法证得T n<eS n.解答:(1)解:f(x)的定义域为(﹣∞,+∞),f′(x)=1﹣e x.当f′(x)>0,即x<0时,f(x)单调递增;当f′(x)<0,即x>0时,f(x)单调递减.故f(x)的单调递增区间为(﹣∞,0),单调递减区间为(0,+∞).当x>0时,f(x)<f(0)=0,即1+x<e x.令,得,即.①(2)解:;=;.由此推测:=(n+1)n.②下面用数学归纳法证明②.(1)当n=1时,左边=右边=2,②成立.(2)假设当n=k时,②成立,即.当n=k+1时,,由归纳假设可得=.∴当n=k+1时,②也成立.根据(1)(2),可知②对一切正整数n都成立.(3)证明:由c n的定义,②,算术﹣几何平均不等式,b n的定义及①得T n=c1+c2+…+c n=====<ea1+ea2+…+ea n=eS n.即T n<eS n.点评:本题主要考查导数在研究函数中的应用,考查利用归纳法证明与自然数有关的问题,考查推理论证能力、运算求解能力、创新知识,考查了利用放缩法法证明数列不等式,是压轴题.2015年湖北省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•湖北)i 为虚数单位,i 607的共轭复数为( ) A . i B . ﹣i C . 1 D . ﹣1 2.(5分)(2015•湖北)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( ) A . 134石 B . 169石 C . 338石 D . 1365石3.(5分)(2015•湖北)已知(1+x )n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A . 212B . 211C . 210D . 294.(5分)(2015•湖北)设X ~N (μ1,σ12),Y ~N (μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )A . P (Y ≥μ2)≥P (Y ≥μ1)B . P(X ≤σ2)≤P (X ≤σ1) C . 对任意正数t ,P (X ≤t )≥P (Y ≤t ) D . 对任意正数t ,P(X ≥t )≥P (Y ≥t )5.(5分)(2015•湖北)设a 1,a 2,…,a n ∈R ,n ≥3.若p :a 1,a 2,…,a n 成等比数列;q :(a 12+a 22+…+a n ﹣12)(a 22+a 32+…+a n 2)=(a 1a 2+a 2a 3+…+a n ﹣1a n )2,则( ) A . p 是q 的充分条件,但不是q 的必要条件 B . p 是q 的必要条件,但不是q 的充分条件 C . p 是q 的充分必要条件 D . p 既不是q 的充分条件,也不是q 的必要条件6.(5分)(2015•湖北)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.s gn[g(x)]=sgnx B.s gn[g(x)]=﹣sgnx C.s gn[g(x)]=sgn[f(x)]D.s gn[g(x)]=﹣sgn[f(x)]7.(5分)(2015•湖北)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P18.(5分)(2015•湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e29.(5分)(2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.3010.(5分)(2015•湖北)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3B.4C.5D.6二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)(2015•湖北)已知向量⊥,||=3,则•=.12.(5分)(2015•湖北)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为.13.(5分)(2015•湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.14.(5分)(2015•湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是.(写出所有正确结论的序号)选修4-1:几何证明选讲15.(5分)(2015•湖北)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.选修4-4:坐标系与参数方程16.(2015•湖北)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t为参数),l与C相交于A,B两点,则|AB|=.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)(2015•湖北)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0 π2πxAsin(ωx+φ)0 5 ﹣5 0(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.18.(12分)(2015•湖北)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.19.(12分)(2015•湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD 中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.20.(12分)(2015•湖北)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W 12 15 18P 0.3 0.5 0.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.21.(14分)(2015•湖北)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON 可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(14分)(2015•湖北)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.。


2015年湖北省高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•湖北)i为虚数单位,i607的共轭复数为()A .i B.﹣i C.1 D.﹣1考点:虚数单位i及其性质.专题:数系的扩充和复数.分析:直接利用复数的单位的幂运算求解即可.解答:解:i607=i604+3=i3=﹣i,它的共轭复数为:i.故选:A.点评:本题考查复数的基本运算,复式单位的幂运算以及共轭复数的知识,基本知识的考查.2.(5分)(2015•湖北)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A .134石B.169石C.338石D.1365石考点:随机抽样和样本估计总体的实际应用.专题:计算题;概率与统计.分析:根据254粒内夹谷28粒,可得比例,即可得出结论.解答:解:由题意,这批米内夹谷约为1534×≈169石,故选:B.点评:本题考查利用数学知识解决实际问题,考查学生的计算能力,比较基础.3.(5分)(2015•湖北)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A .212B.211C.210D.29考点:二项式定理;二项式系数的性质.专题:二项式定理.分析:直接利用二项式定理求出n,然后利用二项式定理系数的性质求出结果即可.解答:解:已知(1+x)n的展开式中第4项与第8项的二项式系数相等,可得,可得n=3+7=10.(1+x )10的展开式中奇数项的二项式系数和为:=29.故选:D .点评: 本题考查二项式定理的应用,组合数的形状的应用,考查基本知识的灵活运用以及计算能力.4.(5分)(2015•湖北)设X ~N (μ1,ς12),Y ~N (μ2,ς22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )A . P (Y ≥μ2)≥P (Y ≥μ1)B . P (X ≤ς2)≤P(X ≤ς1) C . 对任意正数t ,P (X ≤t )≥P (Y ≤t )D .对任意正数t ,P (X ≥t )≥P (Y ≥t )考点: 正态分布曲线的特点及曲线所表示的意义. 专题: 概率与统计.分析: 直接利用正态分布曲线的特征,集合概率,直接判断即可.解答:解:正态分布密度曲线图象关于x=μ对称,所以μ1<μ2,从图中容易得到P (X ≤t )≥P (Y ≤t ). 故选:C .点评:本题考查了正态分布的图象与性质,学习正态分布,一定要紧紧抓住平均数μ和标准差ς这两个关键量,结合正态曲线的图形特征,归纳正态曲线的性质.5.(5分)(2015•湖北)设a 1,a 2,…,a n ∈R ,n ≥3.若p :a 1,a 2,…,a n 成等比数列;q :(a 12+a 22+…+a n ﹣12)(a 22+a 32+…+a n 2)=(a 1a 2+a 2a 3+…+a n ﹣1a n )2,则( )A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件考点:等比数列的性质.专题:等差数列与等比数列;简易逻辑.分析:运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,讨论等号成立的条件,结合等比数列的定义和充分必要条件的定义,即可得到.解答:解:由a1,a2,…,a n∈R,n≥3.运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,若a1,a2,…,a n成等比数列,即有==…=,则(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,即由p推得q,但由q推不到p,比如a1=a2=a3=…=a n=0,则a1,a2,…,a n不成等比数列.故p是q的充分不必要条件.故选:A.点评:本题考查充分必要条件的判断,同时考查等比数列的定义,注意运用定义法和柯西不等式解题是关键.6.(5分)(2015•湖北)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnxC.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]函数与方程的综合运用.考点:专函数的性质及应用.题:直接利用特殊法,设出函数f(x),以及a的值,判断选项即可.分析:解答:解:由于本题是选择题,可以常用特殊法,符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),不妨令f(x)=x,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[g(x)]=﹣sgnx.所以A不正确,B正确,sgn[f(x)]=sgnx,C不正确;D正确;对于D,令f(x)=x+1,a=2,则g(x)=f(x)﹣f(ax)=﹣x﹣1,sgn[f(x)]=sgn(x+1)=;sgn[g(x)]=sgn(﹣x﹣1)=,﹣sgn[f(x)]=﹣sgn(x+1)=;所以D不正确;故选:B.点评:本题考查函数表达式的比较,选取特殊值法是解决本题的关键,注意解题方法的积累,属于中档题.7.(5分)(2015•湖北)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A .P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P1考点:几何概型.专题:概率与统计.分析:作出每个事件对应的平面区域,求出对应的面积,利用几何概型的概率公式进行计算比较即可.解答:解:分别作出事件对应的图象如图(阴影部分):P1:D(0,),F(,0),A(0,1),B(1,1),C(1,0),则阴影部分的面积S1=1×1﹣=1﹣=,S2=1×1﹣2×=1﹣=,S3=1×+dx=+lnx|=﹣ln=+ln2,∴S2<S3<S1,即P2<P3<P1,故选:B.点评:本题主要考查几何概型的概率计算,利用数形结合是解决本题的关键.本题也可以直接通过图象比较面积的大小即可比较大小.8.(5分)(2015•湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e2考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:分别求出双曲线的离心率,再平方作差,即可得出结论.解答:解:由题意,双曲线C1:c2=a2+b2,e1=;双曲线C2:c′2=(a+m)2+(b+m)2,e2=,∴=﹣=,∴当a>b时,e1<e2;当a<b时,e1>e2,故选:D.点评:本题考查双曲线的性质,考查学生的计算能力,比较基础.9.(5分)(2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A .77 B.49 C.45 D.30考点:集合中元素个数的最值.专题:新定义;开放型;集合.分析:由题意可得,A={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)},根据定义可求解答:解:∵A={(x,y)|x2+y2≤1,x,y∈Z}={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(x,y)||x|≤2,|y|≤2,x,y∈Z}={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)}∵A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},∴A⊕B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2),(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2),(﹣2,3),(﹣2,﹣3),(0,﹣3),(2,﹣3),(﹣1,3),(﹣1,﹣3),(1,3),(2,3),(0,3),(3,﹣1),(3,0)(3,1),(3,2),(3,﹣2)(﹣3,2)(﹣3,1),(1,﹣3),(﹣3,﹣1),(﹣3,0),(﹣3,﹣2)}共45个元素故选:C.点评:本题以新定义为载体,主要考查了几何的基本定义及运算,解题中需要取得重复的元素.10.(5分)(2015•湖北)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A .3 B.4 C.5 D.6考点:进行简单的演绎推理.专题:创新题型;简易逻辑.分析:由新定义可得t的范围,验证可得最大的正整数n为4解答:解:∵[t]=1,∴t∈[1,2),又∵[t2]=2,∴t2∈[2,3),∴t∈[,),又t2∈[2,3),∴t4∈[4,9),∴[t4]=4,∴正整数n的最大值4故选:B.点评:本题考查简单的演绎推理,涉及新定义,属基础题.二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)(2015•湖北)已知向量⊥,||=3,则•=9.考点:平面向量数量积的运算.专题:平面向量及应用.分析:由已知结合平面向量是数量积运算求得答案.解答:解:由⊥,得•=0,即•()=0,∵||=3,∴.故答案为:9.点评:本题考查了平面向量的数量积运算,考查了向量模的求法,是基础的计算题.12.(5分)(2015•湖北)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为2.考点:根的存在性及根的个数判断.专题:函数的性质及应用.分析:利用二倍角公式化简函数的解析式,求出函数的定义域,画出函数的图象,求出交点个数即可.解答:解:函数f(x)的定义域为:{x|x>﹣1}.f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|=2sinx﹣|ln(x+1)|=sin2x﹣|ln(x+1)|,分别画出函数y=sin2x,y=|ln(x+1)|的图象,由函数的图象可知,交点个数为2.所以函数的零点有2个.故答案为:2.点评:本题考查三角函数的化简,函数的零点个数的判断,考查数形结合与转化思想的应用.13.(5分)(2015•湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=100m.考点:解三角形的实际应用.专题:计算题;解三角形.分析:设此山高h(m),在△BCD中,利用仰角的正切表示出BC,进而在△ABC中利用正弦定理求得h.解答:解:设此山高h(m),则BC=h,在△ABC中,∠BAC=30°,∠CBA=105°,∠BCA=45°,AB=600.根据正弦定理得=,解得h=100(m)故答案为:100.点评:本题主要考查了解三角形的实际应用.关键是构造三角形,将各个已知条件向这个主三角形集中,再通过正弦、余弦定理或其他基本性质建立条件之间的联系,列方程或列式求解.14.(5分)(2015•湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为(x﹣1)2+(y﹣)2=2;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是①②③.(写出所有正确结论的序号)考点:命题的真假判断与应用;圆与圆的位置关系及其判定.专题:创新题型;简易逻辑.分析:(1)取AB的中点E,通过圆C与x轴相切于点T,利用弦心距、半径与半弦长之间的关系,计算即可;(2)设M(cosα,sinα),N(cosβ,sinβ),计算出、、的值即可.解答:解:(1)∵圆C与x轴相切于点T(1,0),∴圆心的横坐标x=1,取AB的中点E,∵|AB|=2,∴|BE|=1,则|BC|=,即圆的半径r=|BC|=,∴圆心C(1,),则圆的标准方程为(x﹣1)2+(y﹣)2=2,故答案为:(x﹣1)2+(y﹣)2=2.(2)∵圆心C(1,),∴E(0,),又∵|AB|=2,且E为AB中点,∴A(0,﹣1),B(0,+1),∵M、N在圆O:x2+y2=1上,∴可设M(cosα,sinα),N(cosβ,sinβ),∴|NA|=====,|NB|====,∴===,同理可得=,∴=,①成立,﹣=﹣()=2,②正确.+=+()=,③正确.故答案为:①②③.点评:本题考查求圆的标准方程,用三角函数值表示单位圆上点的坐标是解决本题的关键,注意解题方法的积累,属于难题.选修4-1:几何证明选讲15.(5分)(2015•湖北)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.考点:与圆有关的比例线段.专题:推理和证明.分析:利用切割线定理推出PA=2PB,利用相似三角形求出比值即可.解答:解:由切割线定理可知:PA2=PB•PC,又BC=3PB,可得PA=2PB,在△PAB与△PAC中,∠P=∠P,∠PAB=∠PCA(同弧上的圆周角与弦切角相等),可得△PAB∽△PAC,∴==.故答案为:.点评:本题考查切割线定理以及相似三角形的判定与应用,考查逻辑推理能力.选修4-4:坐标系与参数方程16.(2015•湖北)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t为参数),l与C相交于A,B两点,则|AB|=.考点:简单曲线的极坐标方程;双曲线的参数方程.专题:坐标系和参数方程.分析:化极坐标方程化直角坐标方程,参数方程化普通方程,联立直线方程和双曲线方程后求得交点坐标,由两点间的距离公式得答案.解答:解:由ρ(sinθ﹣3cosθ)=0,得y﹣3x=0,由C的参数方程为(t为参数),两式平方作差得:x2﹣y2=﹣4.联立,得,即.∴A(),B(),∴|AB|=.故答案为:.点评:本题考查极坐标方程化直角坐标方程,参数方程化普通方程,考查了直线和圆锥曲线的位置关系,是基础的计算题.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)(2015•湖北)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0 π2πxAsin(ωx+φ)0 5 ﹣5 0(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.从而可补全数据,解得函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)及函数y=Asin(ωx+φ)的图象变换规律得g(x)=5sin(2x+2θ﹣).令2x+2θ﹣=kπ,解得x=,k∈Z.令=,解得θ=,k∈Z.由θ>0可得解.解答:解:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.数据补全如下表:ωx+φ0 π2πxAsin(ωx+φ)0 5 0 ﹣5 0且函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)知f(x)=5sin(2x﹣),得g(x)=5sin(2x+2θ﹣).因为y=sinx的对称中心为(kπ,0),k∈Z.令2x+2θ﹣=kπ,解得x=,k∈Z.由于函数y=g(x)的图象关于点(,0)成中心对称,令=,解得θ=,k∈Z.由θ>0可知,当K=1时,θ取得最小值.点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换规律的应用,属于基本知识的考查.18.(12分)(2015•湖北)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.数列的求和.考点:等差数列与等比数列.专题:(1)利用前10项和与首项、公差的关系,联立方程组计算即可;分析:(2)当d>1时,由(1)知c n=,写出T n、T n的表达式,利用错位相减法及等比数列的求和公式,计算即可.解解:(1)设a1=a,由题意可得,答:解得,或,当时,a n=2n﹣1,b n=2n﹣1;当时,a n=(2n+79),b n=9•;(2)当d>1时,由(1)知a n=2n﹣1,b n=2n﹣1,∴c n==,∴T n=1+3•+5•+7•+9•+…+(2n﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.点评:本题考查求数列的通项及求和,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.19.(12分)(2015•湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD 中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.考点:用空间向量求平面间的夹角;直线与平面垂直的判定.专题:空间位置关系与距离;空间向量及应用.分析:解法1)(1)直线与直线,直线与平面的垂直的转化证明得出PB⊥EF,DE∩FE=E,所以PB⊥平面DEF,即可判断DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,确定直角.(2)根据公理2得出DG是平面DEF与平面ACBD的交线.利用直线平面的垂直判断出DG⊥DF,DG⊥DB,根据平面角的定义得出∠BDF是面DEF与面ABCD所成二面角的平面角,转化到直角三角形求解即可.解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系,运用向量的数量积判断即可.2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.根据数量积得出夹角的余弦即可得出所求解的答案.解答:解法1)(1)因为PD⊥底面ABCD,所以PD⊥BC,由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,所以BC⊥平面ABCD.而DE⊂平面PDC,所以BC⊥DE.又因为PD=CD,点E是PC的中点,所以DE⊥PC.而PC∩CB=C,所以DE⊥平面PBC.而PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)如图1,在面BPC内,延长BC与FE交于点G,则DG是平面DEF与平面ACBD的交线.由(Ⅰ)知,PB⊥平面DEF,所以PB⊥DG.又因为PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.所以DG⊥DF,DG⊥DB故∠BDF是面DEF与面ABCD所成二面角的平面角,设PD=DC=1,BC=λ,有BD=,在Rt△PDB中,由DF⊥PB,得∠DGF=∠FDB=,则tan=tan∠DPF===,解得.所以==故当面DEF与面ABCD所成二面角的大小为时,=.(解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),=(λ1,﹣1),点E是PC的中点,所以E(0,,),=(0,,),于是=0,即PB⊥DE.又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.因=(0,1,﹣1),=0,则DE⊥PC,所以DE⊥平面PBC.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.若面DEF与面ABCD所成二面角的大小为,则运用向量的数量积求解得出cos==,解得.所以所以==故当面DEF与面ABCD所成二面角的大小为时,=.点评:本题综合考查了空间直线平面的垂直问题,直线与直线,直线与平面的垂直的转化,空间角的求解,属于难题.20.(12分)(2015•湖北)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W 12 15 18P 0.3 0.5 0.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.考点:简单线性规划的应用;离散型随机变量的期望与方差.专题:不等式的解法及应用;概率与统计.分析:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,列出可行域,目标函数,通过当W=12时,当W=15时,当W=18时,分别求出目标函数的最大获利,然后得到Z的分布列.求出期望即可.(2)判断概率类型是二项分布,然后求解所求概率即可.解答:(12分)解:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,则有,①如图1,目标函数为:z=1000x+1200y.当W=12时,①表示的平面区域如图1,三个顶点分别为A(0,0),B(2.4,4.8),C(6,0).将z=1000x+1200y变形为,当x=2.4,y=4.8时,直线l:在y轴上的截距最大,最大获利Z=Z max=2.4×1000+4.8×1200=8160.当W=15时,①表示的平面区域如图2,三个顶点分别为A(0,0),B(3,6),C(7.5,0)..将z=1000x+1200y变形为,当x=3,y=6时,直线l:在y轴上的截距最大,最大获利Z=Z max=3×1000+6×1200=10200.当W=18时,①表示的平面区域如图3,四个顶点分别为A(0,0),B(3,6),C (6,4),D(9,0).将z=1000x+1200y变形为:,当x=6,y=4时,直线l:y=﹣56x+z1200在y轴上的截距最大,最大获利Z=Z max=6×1000+4×1200=10800.故最大获利Z的分布列为:Z 8160 10200 10800P 0.3 0.5 0.2因此,E(Z)=8160×0.3+10200×0.5+10800×0.2=9708(2)由(Ⅰ)知,一天最大获利超过10000元的概率P1=P(Z>10000)=0.5+0.2=0.7,由二项分布,3天中至少有1天最大获利超过10000元的概率为:.点评:本题考查离散型随机变量的分布列以及期望的求法,线性规划的应用,二项分布概率的求法,考查分析问题解决问题的能力.21.(14分)(2015•湖北)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON 可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:创新题型;开放型;圆锥曲线中的最值与范围问题.分析:(1)根据条件求出a,b即可求椭圆C的方程;(2)联立直线方程和椭圆方程,求出原点到直线的距离,结合三角形的面积公式进行求解即可.解答:解:(1)∵|OM|≤|MN|+|NO|=3+1=4,当M,N在x轴上时,等号成立,同理|OM|≥|MN|﹣|NO|=3﹣1=2,当D,O重合,即MN⊥x轴时,等号成立.∴椭圆C的中心为原点O,长半轴长为4,短半轴长为2,其方程为.(2)①当直线l的斜率k不存在时,直线l为:x=4或x=﹣4,都有S△OPQ=,②直线l的斜率k存在时,直线l为:y=kx+m,(k),由消去y,可得(1+4k2)x2+8kmx+4m2﹣16=0,∵直线l总与椭圆C有且只有一个公共点,∴△=64k2m2﹣4(1+4k2)(4m2﹣16)=0,即m2=16k2+4,①,由,可得P(,),同理得Q(,),原点O到直线PQ的距离d=和|PQ|=•|x P﹣x Q|,可得S△OPQ=|PQ|d=|m||x P﹣x Q|=|m|||=||②,将①代入②得S△OPQ=||=8||,当k2>时,S△OPQ=8()=8(1+)>8,当0≤k2<时,S△OPQ=8||=﹣8()=8(﹣1+),∵0≤k2<时,∴0<1﹣4k2≤1,≥2,∴S△OPQ=8(﹣1+)≥8,当且仅当k=0时取等号,∴当k=0时,S△OPQ的最小值为8,综上可知当直线l与椭圆C在四个顶点处相切时,三角形OPQ的面积存在最小值为8.点评:本题主要考查椭圆方程的求解,以及直线和圆锥曲线的位置关系的应用,结合三角形的面积公式是解决本题的关键.综合性较强,运算量较大.22.(14分)(2015•湖北)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.考点:数列与不等式的综合.专题:创新题型;导数的综合应用;点列、递归数列与数学归纳法;不等式的解法及应用.分析:(1)求出f(x)的定义域,利用导数求其最大值,得到1+x<e x.取x=即可得到答案;(2)由b n=n(1+)n a n(n∈N+),变形求得,,,由此推测=(n+1)n.然后利用数学归纳法证明.(3)由c n的定义、=(n+1)n、算术﹣几何平均不等式、b n的定义及,利用放缩法证得T n<eS n.解答:(1)解:f(x)的定义域为(﹣∞,+∞),f′(x)=1﹣e x.当f′(x)>0,即x<0时,f(x)单调递增;当f′(x)<0,即x>0时,f(x)单调递减.故f(x)的单调递增区间为(﹣∞,0),单调递减区间为(0,+∞).当x>0时,f(x)<f(0)=0,即1+x<e x.令,得,即.①(2)解:;=;.由此推测:=(n+1)n.②下面用数学归纳法证明②.(1)当n=1时,左边=右边=2,②成立.(2)假设当n=k时,②成立,即.当n=k+1时,,由归纳假设可得=.∴当n=k+1时,②也成立.根据(1)(2),可知②对一切正整数n都成立.(3)证明:由c n的定义,②,算术﹣几何平均不等式,b n的定义及①得T n=c1+c2+…+c n=====<ea1+ea2+…+ea n=eS n.即T n<eS n.点评:本题主要考查导数在研究函数中的应用,考查利用归纳法证明与自然数有关的问题,考查推理论证能力、运算求解能力、创新知识,考查了利用放缩法法证明数列不等式,是压轴题.2015年湖北省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•湖北)i 为虚数单位,i 607的共轭复数为( ) A . i B . ﹣i C . 1 D . ﹣1 2.(5分)(2015•湖北)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( ) A . 134石 B . 169石 C . 338石 D . 1365石3.(5分)(2015•湖北)已知(1+x )n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A . 212B . 211C . 210D . 294.(5分)(2015•湖北)设X ~N (μ1,ς12),Y ~N (μ2,ς22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )A . P (Y ≥μ2)≥P (Y ≥μ1)B . P(X ≤ς2)≤P (X ≤ς1) C . 对任意正数t ,P (X ≤t )≥P (Y ≤t ) D . 对任意正数t ,P(X ≥t )≥P (Y ≥t )5.(5分)(2015•湖北)设a 1,a 2,…,a n ∈R ,n ≥3.若p :a 1,a 2,…,a n 成等比数列;q :(a 12+a 22+…+a n ﹣12)(a 22+a 32+…+a n 2)=(a 1a 2+a 2a 3+…+a n ﹣1a n )2,则( ) A . p 是q 的充分条件,但不是q 的必要条件 B . p 是q 的必要条件,但不是q 的充分条件 C . p 是q 的充分必要条件 D . p 既不是q 的充分条件,也不是q 的必要条件6.(5分)(2015•湖北)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.s gn[g(x)]=sgnx B.s gn[g(x)]=﹣sgnx C.s gn[g(x)]=sgn[f(x)]D.s gn[g(x)]=﹣sgn[f(x)]7.(5分)(2015•湖北)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P18.(5分)(2015•湖北)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e29.(5分)(2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.3010.(5分)(2015•湖北)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3B.4C.5D.6二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)(2015•湖北)已知向量⊥,||=3,则•=.12.(5分)(2015•湖北)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为.13.(5分)(2015•湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.14.(5分)(2015•湖北)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的标准方程为;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是.(写出所有正确结论的序号)选修4-1:几何证明选讲15.(5分)(2015•湖北)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.选修4-4:坐标系与参数方程16.(2015•湖北)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t为参数),l与C相交于A,B两点,则|AB|=.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)(2015•湖北)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0 π2πxAsin(ωx+φ)0 5 ﹣5 0(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.18.(12分)(2015•湖北)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.19.(12分)(2015•湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD 中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.20.(12分)(2015•湖北)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W 12 15 18P 0.3 0.5 0.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.21.(14分)(2015•湖北)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON 可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(14分)(2015•湖北)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.。
2015年湖北省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)i为虚数单位,i607的共轭复数为()A.i B.﹣i C.1 D.﹣12.(5分)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石3.(5分)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A.212B.211C.210D.294.(5分)设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y ≥t)5.(5分)设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件6.(5分)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnx C.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]7.(5分)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P18.(5分)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e29.(5分)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.3010.(5分)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3 B.4 C.5 D.6二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)已知向量⊥,||=3,则•=.12.(5分)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为.13.(5分)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.14.(5分)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B (B在A的上方),且|AB|=2.(1)圆C的标准方程为;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是.(写出所有正确结论的序号)选修4-1:几何证明选讲15.(5分)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.选修4-4:坐标系与参数方程16.在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t 为参数),l与C相交于A,B两点,则|AB|=.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0π2πxAsin(ωx+φ)05﹣50(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g (x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.18.(12分)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.19.(12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.20.(12分)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W121518P0.30.50.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.21.(14分)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.22.(14分)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.2015年湖北省高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)i为虚数单位,i607的共轭复数为()A.i B.﹣i C.1 D.﹣1【分析】直接利用复数的单位的幂运算求解即可.【解答】解:i607=i604+3=i3=﹣i,它的共轭复数为:i.故选:A.【点评】本题考查复数的基本运算,复式单位的幂运算以及共轭复数的知识,基本知识的考查.2.(5分)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为()A.134石B.169石C.338石D.1365石【分析】根据254粒内夹谷28粒,可得比例,即可得出结论.【解答】解:由题意,这批米内夹谷约为1534×≈169石,故选:B.【点评】本题考查利用数学知识解决实际问题,考查学生的计算能力,比较基础.3.(5分)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为()A.212B.211C.210D.29【分析】直接利用二项式定理求出n,然后利用二项式定理系数的性质求出结果即可.【解答】解:已知(1+x)n的展开式中第4项与第8项的二项式系数相等,可得,可得n=3+7=10.(1+x)10的展开式中奇数项的二项式系数和为:=29.故选:D.【点评】本题考查二项式定理的应用,组合数的形状的应用,考查基本知识的灵活运用以及计算能力.4.(5分)设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≤t)≥P(Y≤t)D.对任意正数t,P(X≥t)≥P(Y ≥t)【分析】直接利用正态分布曲线的特征,集合概率,直接判断即可.【解答】解:正态分布密度曲线图象关于x=μ对称,所以μ1<μ2,从图中容易得到P(X≤t)≥P(Y≤t).故选:C.【点评】本题考查了正态分布的图象与性质,学习正态分布,一定要紧紧抓住平均数μ和标准差σ这两个关键量,结合正态曲线的图形特征,归纳正态曲线的性质.5.(5分)设a1,a2,…,a n∈R,n≥3.若p:a1,a2,…,a n成等比数列;q:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件【分析】运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,讨论等号成立的条件,结合等比数列的定义和充分必要条件的定义,即可得到.【解答】解:由a1,a2,…,a n∈R,n≥3.运用柯西不等式,可得:(a12+a22+…+a n﹣12)(a22+a32+…+a n2)≥(a1a2+a2a3+…+a n﹣1a n)2,若a1,a2,…,a n成等比数列,即有==…=,则(a12+a22+…+a n﹣12)(a22+a32+…+a n2)=(a1a2+a2a3+…+a n﹣1a n)2,即由p推得q,但由q推不到p,比如a1=a2=a3=…=a n=0,则a1,a2,…,a n不成等比数列.故p是q的充分不必要条件.故选:A.【点评】本题考查充分必要条件的判断,同时考查等比数列的定义,注意运用定义法和柯西不等式解题是关键.6.(5分)已知符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则()A.sgn[g(x)]=sgnx B.sgn[g(x)]=﹣sgnx C.sgn[g(x)]=sgn[f(x)] D.sgn[g(x)]=﹣sgn[f(x)]【分析】直接利用特殊法,设出函数f(x),以及a的值,判断选项即可.【解答】解:由于本题是选择题,可以采用特殊法,符号函数sgnx=,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),不妨令f(x)=x,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[g(x)]=﹣sgnx.所以A不正确,B正确,sgn[f(x)]=sgnx,C不正确;D正确;对于D,令f(x)=x+1,a=2,则g(x)=f(x)﹣f(ax)=﹣x,sgn[f(x)]=sgn(x+1)=;sgn[g(x)]=sgn(﹣x)=,﹣sgn[f(x)]=﹣sgn(x+1)=;所以D不正确;故选:B.【点评】本题考查函数表达式的比较,选取特殊值法是解决本题的关键,注意解题方法的积累,属于中档题.7.(5分)在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥”的概率,P2为事件“|x﹣y|≤”的概率,P3为事件“xy≤”的概率,则()A.P1<P2<P3B.P2<P3<P1C.P3<P1<P2D.P3<P2<P1【分析】作出每个事件对应的平面区域,求出对应的面积,利用几何概型的概率公式进行计算比较即可.【解答】解:分别作出事件对应的图象如图(阴影部分):P1:D(0,),F(,0),A(0,1),B(1,1),C(1,0),则阴影部分的面积S1=1×1﹣=1﹣=,S2=1×1﹣2×=1﹣=,S3=1×+dx=+lnx|=﹣ln=+ln2,∴S2<S3<S1,即P2<P3<P1,故选:B.【点评】本题主要考查几何概型的概率计算,利用数形结合是解决本题的关键.本题也可以直接通过图象比较面积的大小即可比较大小.8.(5分)将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则()A.对任意的a,b,e1>e2B.当a>b时,e1>e2;当a<b时,e1<e2C.对任意的a,b,e1<e2D.当a>b时,e1<e2;当a<b时,e1>e2【分析】分别求出双曲线的离心率,再平方作差,即可得出结论.【解答】解:由题意,双曲线C1:c2=a2+b2,e1=;双曲线C2:c′2=(a+m)2+(b+m)2,e2=,∴=﹣=,∴当a>b时,e1>e2;当a<b时,e1<e2,故选:B.【点评】本题考查双曲线的性质,考查学生的计算能力,比较基础.9.(5分)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77 B.49 C.45 D.30【分析】由题意可得,A={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)},根据定义可求【解答】解:解法一:∵A={(x,y)|x2+y2≤1,x,y∈Z}={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0),B={(x,y)||x|≤2,|y|≤2,x,y∈Z}={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)}∵A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},∴A⊕B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2),(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2),(﹣2,3),(﹣2,﹣3),(0,﹣3),(2,﹣3),(﹣1,3),(﹣1,﹣3),(1,3),(2,3),(0,3),(3,﹣1),(3,0)(3,1),(3,2),(3,﹣2)(﹣3,2)(﹣3,1),(1,﹣3),(﹣3,﹣1),(﹣3,0),(﹣3,﹣2)}共45个元素;解法二:因为集合A={(x,y)|x2+y2≤1,x,y∈Z},所以集合A中有5个元素,即图中圆中的整点,B={(x,y)||x|≤2,|y|≤2,x,y∈Z},中有5×5=25个元素,即图中正方形ABCD中的整点,A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B}的元素可看作正方形A1B1C1D1中的整点(除去四个顶点),即7×7﹣4=45个.故选:C.【点评】本题以新定义为载体,主要考查了集合的基本定义及运算,解题中需要取得重复的元素.10.(5分)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[t n]=n同时成立,则正整数n的最大值是()A.3 B.4 C.5 D.6【分析】由新定义可得t的范围,验证可得最大的正整数n为4.【解答】解:若[t]=1,则t∈[1,2),若[t2]=2,则t∈[,)(因为题目需要同时成立,则负区间舍去),若[t3]=3,则t∈[,),若[t4]=4,则t∈[,),若[t5]=5,则t∈[,),其中≈1.732,≈1.587,≈1.495,≈1.431<1.495,通过上述可以发现,当t=4时,可以找到实数t使其在区间[1,2)∩[,)∩[,)∩[,)上,但当t=5时,无法找到实数t使其在区间[1,2)∩[,)∩[,)∩[,)∩[,)上,∴正整数n的最大值4故选:B.【点评】本题考查简单的演绎推理,涉及新定义,属基础题.二、填空题:本大题共4小题,考生需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)已知向量⊥,||=3,则•=9.【分析】由已知结合平面向量是数量积运算求得答案.【解答】解:由⊥,得•=0,即•()=0,∵||=3,∴.故答案为:9.【点评】本题考查了平面向量的数量积运算,考查了向量模的求法,是基础的计算题.12.(5分)函数f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|的零点个数为2.【分析】利用二倍角公式化简函数的解析式,求出函数的定义域,画出函数的图象,求出交点个数即可.【解答】解:函数f(x)的定义域为:{x|x>﹣1}.f(x)=4cos2cos(﹣x)﹣2sinx﹣|ln(x+1)|=2sinx﹣|ln(x+1)|=sin2x﹣|ln(x+1)|,分别画出函数y=sin2x,y=|ln(x+1)|的图象,由函数的图象可知,交点个数为2.所以函数的零点有2个.故答案为:2.【点评】本题考查三角函数的化简,函数的零点个数的判断,考查数形结合与转化思想的应用.13.(5分)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=100m.【分析】设此山高h(m),在△BCD中,利用仰角的正切表示出BC,进而在△ABC中利用正弦定理求得h.【解答】解:设此山高h(m),则BC=h,在△ABC中,∠BAC=30°,∠CBA=105°,∠BCA=45°,AB=600.根据正弦定理得=,解得h=100(m)故答案为:100.【点评】本题主要考查了解三角形的实际应用.关键是构造三角形,将各个已知条件向这个主三角形集中,再通过正弦、余弦定理或其他基本性质建立条件之间的联系,列方程或列式求解.14.(5分)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B (B在A的上方),且|AB|=2.(1)圆C的标准方程为(x﹣1)2+(y﹣)2=2;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②﹣=2;③+=2.其中正确结论的序号是①②③.(写出所有正确结论的序号)【分析】(1)取AB的中点E,通过圆C与x轴相切于点T,利用弦心距、半径与半弦长之间的关系,计算即可;(2)设M(cosα,sinα),N(cosβ,sinβ),计算出、、的值即可.【解答】解:(1)∵圆C与x轴相切于点T(1,0),∴圆心的横坐标x=1,取AB的中点E,∵|AB|=2,∴|BE|=1,则|BC|=,即圆的半径r=|BC|=,∴圆心C(1,),则圆的标准方程为(x﹣1)2+(y﹣)2=2,故答案为:(x﹣1)2+(y﹣)2=2.(2)∵圆心C(1,),∴E(0,),又∵|AB|=2,且E为AB中点,∴A(0,﹣1),B(0,+1),∵M、N在圆O:x2+y2=1上,∴可设M(cosα,sinα),N(cosβ,sinβ),∴|NA|=====,|NB|====,∴===,同理可得=,∴=,①成立,﹣=﹣()=2,②正确.+=+()=,③正确.故答案为:①②③.【点评】本题考查求圆的标准方程,用三角函数值表示单位圆上点的坐标是解决本题的关键,注意解题方法的积累,属于难题.选修4-1:几何证明选讲15.(5分)如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=3PB,则=.【分析】利用切割线定理推出PA=2PB,利用相似三角形求出比值即可.【解答】解:由切割线定理可知:PA2=PB•PC,又BC=3PB,可得PA=2PB,在△PAB与△PAC中,∠P=∠P,∠PAB=∠PCA(同弧上的圆周角与弦切角相等),可得△PAB∽△PAC,∴==.故答案为:.【点评】本题考查切割线定理以及相似三角形的判定与应用,考查逻辑推理能力.选修4-4:坐标系与参数方程16.在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l的极坐标方程为ρ(sinθ﹣3cosθ)=0,曲线C的参数方程为(t 为参数),l与C相交于A,B两点,则|AB|=.【分析】化极坐标方程化直角坐标方程,参数方程化普通方程,联立直线方程和双曲线方程后求得交点坐标,由两点间的距离公式得答案.【解答】解:由ρ(sinθ﹣3cosθ)=0,得y﹣3x=0,由C的参数方程为(t为参数),两式平方作差得:x2﹣y2=﹣4.联立,得,即.∴A(),B(),∴|AB|=.故答案为:.【点评】本题考查极坐标方程化直角坐标方程,参数方程化普通方程,考查了直线和圆锥曲线的位置关系,是基础的计算题.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(11分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<)在某一个周期内的图象时,列表并填入了部分数据,如表:ωx+φ0π2πxAsin(ωx+φ)05﹣50(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g (x)的图象.若y=g(x)图象的一个对称中心为(,0),求θ的最小值.【分析】(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.从而可补全数据,解得函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)及函数y=Asin(ωx+φ)的图象变换规律得g(x)=5sin(2x+2θ﹣).令2x+2θ﹣=kπ,解得x=,k∈Z.令=,解得θ=,k∈Z.由θ>0可得解.【解答】解:(1)根据表中已知数据,解得A=5,ω=2,φ=﹣.数据补全如下表:ωx+φ0π2πxAsin(ωx+φ)050﹣50且函数表达式为f(x)=5sin(2x﹣).(2)由(Ⅰ)知f(x)=5sin(2x﹣),得g(x)=5sin(2x+2θ﹣).因为y=sinx的对称中心为(kπ,0),k∈Z.令2x+2θ﹣=kπ,解得x=,k∈Z.由于函数y=g(x)的图象关于点(,0)成中心对称,令=,解得θ=,k∈Z.由θ>0可知,当K=1时,θ取得最小值.【点评】本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin (ωx+φ)的图象变换规律的应用,属于基本知识的考查.18.(12分)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.【分析】(1)利用前10项和与首项、公差的关系,联立方程组计算即可;(2)当d>1时,由(1)知c n=,写出T n、T n的表达式,利用错位相减法及等比数列的求和公式,计算即可.【解答】解:(1)设a1=a,由题意可得,解得,或,当时,a n=2n﹣1,b n=2n﹣1;当时,a n=(2n+79),b n=9•;(2)当d>1时,由(1)知a n=2n﹣1,b n=2n﹣1,∴c n==,∴T n=1+3•+5•+7•+9•+…+(2n﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.【点评】本题考查求数列的通项及求和,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.19.(12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF与面ABCD所成二面角的大小为,求的值.【分析】解法1)(1)直线与直线,直线与平面的垂直的转化证明得出PB⊥EF,DE∩FE=E,所以PB⊥平面DEF,即可判断DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,确定直角.(2)根据公理2得出DG是平面DEF与平面ACBD的交线.利用直线平面的垂直判断出DG⊥DF,DG⊥DB,根据平面角的定义得出∠BDF是面DEF与面ABCD所成二面角的平面角,转化到直角三角形求解即可.解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系,运用向量的数量积判断即可.2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.根据数量积得出夹角的余弦即可得出所求解的答案.【解答】解法1)(1)因为PD⊥底面ABCD,所以PD⊥BC,由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,所以BC⊥平面PCD.而DE⊂平面PDC,所以BC⊥DE.又因为PD=CD,点E是PC的中点,所以DE⊥PC.而PC∩CB=C,所以DE⊥平面PBC.而PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)如图1,在面BPC内,延长BC与FE交于点G,则DG是平面DEF与平面ACBD的交线.由(Ⅰ)知,PB⊥平面DEF,所以PB⊥DG.又因为PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.所以DG⊥DF,DG⊥DB故∠BDF是面DEF与面ABCD所成二面角的平面角,设PD=DC=1,BC=λ,有BD=,在Rt△PDB中,由DF⊥PB,得∠DPB=∠FDB=,则tan=tan∠DPF===,解得.所以==故当面DEF与面ABCD所成二面角的大小为时,=.(解法2)(1)以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),=(λ1,﹣1),点E是PC的中点,所以E(0,,),=(0,,),于是=0,即PB⊥DE.又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.因=(0,1,﹣1),=0,则DE⊥PC,所以DE⊥平面PBC.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)由PD⊥底面ABCD,所以=(0,0,1)是平面ACDB的一个法向量;由(Ⅰ)知,PB⊥平面DEF,所以=(﹣λ,﹣1,1)是平面DEF的一个法向量.若面DEF与面ABCD所成二面角的大小为,则运用向量的数量积求解得出cos==,解得.所以所以==故当面DEF与面ABCD所成二面角的大小为时,=.【点评】本题综合考查了空间直线平面的垂直问题,直线与直线,直线与平面的垂直的转化,空间角的求解,属于难题.20.(12分)某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为W121518P0.30.50.2该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.(1)求Z的分布列和均值;(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.【分析】(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,列出可行域,目标函数,通过当W=12时,当W=15时,当W=18时,分别求出目标函数的最大获利,然后得到Z的分布列.求出期望即可.(2)判断概率类型是二项分布,然后求解所求概率即可.【解答】(12分)解:(1)设每天A,B两种产品的生产数量分别为x,y,相应的获利为z,则有,①如图1,目标函数为:z=1000x+1200y.当W=12时,①表示的平面区域如图1,三个顶点分别为A(0,0),B(2.4,4.8),C(6,0).将z=1000x+1200y变形为,当x=2.4,y=4.8时,直线l:在y轴上的截距最大,最大获利Z=Z max=2.4×1000+4.8×1200=8160.当W=15时,①表示的平面区域如图2,三个顶点分别为A(0,0),B(3,6),C(7.5,0)..将z=1000x+1200y变形为,当x=3,y=6时,直线l:在y轴上的截距最大,最大获利Z=Z max=3×1000+6×1200=10200.当W=18时,①表示的平面区域如图3,四个顶点分别为A(0,0),B(3,6),C(6,4),D(9,0).将z=1000x+1200y变形为:,当x=6,y=4时,直线l:y=﹣56x+z1200在y轴上的截距最大,最大获利Z=Z max=6×1000+4×1200=10800.故最大获利Z的分布列为:Z81601020010800P0.30.50.2因此,E(Z)=8160×0.3+10200×0.5+10800×0.2=9708(2)由(Ⅰ)知,一天最大获利超过10000元的概率P1=P(Z>10000)=0.5+0.2=0.7,由二项分布,3天中至少有1天最大获利超过10000元的概率为:.【点评】本题考查离散型随机变量的分布列以及期望的求法,线性规划的应用,二项分布概率的求法,考查分析问题解决问题的能力.21.(14分)一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系.(1)求椭圆C的方程;(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.【分析】(1)根据条件求出a,b即可求椭圆C的方程;(2)联立直线方程和椭圆方程,求出原点到直线的距离,结合三角形的面积公式进行求解即可.【解答】解:(1)设D(t,0),|t|≤2,N(x0,y0),M(x,y),由题意得=2,且||=||=1,∴(t﹣x,﹣y)=2(x0﹣t,y0),且,即,且t(t﹣2x0)=0,由于当点D不动时,点N也不动,∴t不恒等于0,于是t=2x0,故x0=,y0=﹣,代入x02+y02=1,得方程为.=,(2)①当直线l的斜率k不存在时,直线l为:x=4或x=﹣4,都有S△OPQ②直线l的斜率k存在时,直线l为:y=kx+m,(k),由消去y,可得(1+4k2)x2+8kmx+4m2﹣16=0,∵直线l总与椭圆C有且只有一个公共点,∴△=64k2m2﹣4(1+4k2)(4m2﹣16)=0,即m2=16k2+4,①,由,可得P(,),同理得Q(,),原点O到直线PQ的距离d=和|PQ|=•|x P﹣x Q|,=|PQ|d=|m||x P﹣x Q|=|m|||=||②,可得S△OPQ将①代入②得S=||=8||,△OPQ=8()=8(1+)>8,当k2>时,S△OPQ=8||=﹣8()=8(﹣1+),当0≤k2<时,S△OPQ∵0≤k2<时,∴0<1﹣4k2≤1,≥2,∴S=8(﹣1+)≥8,当且仅当k=0时取等号,△OPQ的最小值为8,∴当k=0时,S△OPQ综上可知当直线l与椭圆C在四个顶点处相切时,三角形OPQ的面积存在最小值为8.【点评】本题主要考查椭圆方程的求解,以及直线和圆锥曲线的位置关系的应用,结合三角形的面积公式是解决本题的关键.综合性较强,运算量较大.22.(14分)已知数列{a n}的各项均为正数,b n=n(1+)n a n(n∈N+),e为自然对数的底数.(1)求函数f(x)=1+x﹣e x的单调区间,并比较(1+)n与e的大小;(2)计算,,,由此推测计算的公式,并给出证明;(3)令c n=(a1a2…a n),数列{a n},{c n}的前n项和分别记为S n,T n,证明:T n<eS n.【分析】(1)求出f(x)的定义域,利用导数求其最大值,得到1+x<e x.取x=即可得到答案;(2)由b n=n(1+)n a n(n∈N+),变形求得,,,由此推测=(n+1)n.然后利用数学归纳法证明.(3)由c n的定义、=(n+1)n、算术﹣几何平均不等式、b n的定义及,利用放缩法证得T n<eS n.【解答】(1)解:f(x)的定义域为(﹣∞,+∞),f′(x)=1﹣e x.当f′(x)>0,即x<0时,f(x)单调递增;当f′(x)<0,即x>0时,f(x)单调递减.故f(x)的单调递增区间为(﹣∞,0),单调递减区间为(0,+∞).当x>0时,f(x)<f(0)=0,即1+x<e x.令,得,即.①(2)解:;=;.由此推测:=(n+1)n.②下面用数学归纳法证明②.(1)当n=1时,左边=右边=2,②成立.(2)假设当n=k时,②成立,即.当n=k+1时,,由归纳假设可得=.∴当n=k+1时,②也成立.根据(1)(2),可知②对一切正整数n都成立.(3)证明:由c n的定义,②,算术﹣几何平均不等式,b n的定义及①得T n=c1+c2+…+c n=====<ea1+ea2+…+ea n=eS n.即T n<eS n.【点评】本题主要考查导数在研究函数中的应用,考查利用归纳法证明与自然数有关的问题,考查推理论证能力、运算求解能力、创新知识,考查了利用放缩法证明数列不等式,是压轴题.第31页(共31页)。