动量和角动量习题思考题

动量与角动量习题解答(总9页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第三章 动量与动量守恒定律习题一选择题1. 一辆洒水车正在马路上工作，要使车匀速直线行驶，则车受到的合外力：（ ）A. 必为零；B. 必不为零，合力方向与行进方向相同；C. 必不为零，合力方向与行进方向相反；D. 必不为零，合力方向是任意的。

解：答案是C 。

简要提示：根据动量定理，合力F 的冲量F d t = d p = d (m v )=md v +v d m =v d m 。

因d m <0，所以F 的方向与车行进速度v 的方向相反。

2. 两大小和质量均相同的小球，一为弹性球，另一为非弹性球，它们从同一高度落下与地面碰撞时，则有：（）A. 地面给予两球的冲量相同；B. 地面给予弹性球的冲量较大；C. 地面给予非弹性球的冲量较大； A. 无法确定反冲量谁大谁小。

解：答案是B 。

简要提示：)(12v v -=m I3. 质量为m 的铁锤竖直向下打在桩上而静止，设打击时间为∆t ，打击前锤的速率为v ，则打击时铁锤受到的合外力大小应为：（）A ．mg tm +∆vB ．mgC ．mg tm -∆vD ．tm ∆v解：答案是D 。

简要提示：v m t F =∆⋅4. 将一长木板安上轮子放在光滑平面上，两质量不同的人从板的两端以相同速率相向行走，则板的运动状况是：（）选择题4图3A. 静止不动；B. 朝质量大的人行走的方向移动；C. 朝质量小的人行走的方向移动；D.无法确定。

解：答案是B 。

简要提示：取m 1的运动方向为正方向，由动量守恒：02211='+-v v v M m m ，得：M m m /)(21v v --='如果m 1> m 2，则v ′< 0。

5. 一只猴子用绳子拉着一个和它质量相同的石头，在一水平的无摩擦的地面上运动，开始时猴子和石头都保持静止，然后猴子以相对绳子的速度u 拉绳，则石头的速率为：（） A. u B. u /2 C. u /4 D. 0解：答案是B 。

第三章 动量定理及动量守恒定律（思考题与习题解答）（一）思考题3.1试表述质量的操作型定义。

解答，kgv v m m 00 ∆∆=式中kg 1m 0=（标准物体质量） 0v∆：为m 与m0碰撞m0的速度改变 v∆：为m 与m0碰撞m 的速度改变这样定义的质量，其大小反映了质点在相互作用的过程中速度改变的难易程度，或者说，其量值反映了质量惯性的大小。

这样定义的质量为操作型定义。

3.2如何从动量守恒得出牛顿第二、第三定律，何种情况下牛顿第三定律不成立？ 解答，由动量守恒)p p (p p ,p p p p 22112121 -'-=-'+='+' ,p p 21 ∆-=∆t p t p 21∆∆-=∆∆取极限dt p d dtp d 21 -= 动量瞬时变化率是两质点间的相互作用力。

,a m )v m (dt d dt p d F 111111=== ,a m )v m (dt d dt p d F 222222 ===21F F -=对于运动电荷之间的电磁作用力，一般来说第三定律不成立。

（参见P63最后一自然段） 3.3在磅秤上称物体重量，磅秤读数给出物体的“视重”或“表现重量”。

现在电梯中测视重，何时视重小于重量（称作失重）？何时视重大于重量（称作超重）？在电梯中，视重可能等于零吗？能否指出另一种情况使视重等于零？ 解答，①电梯加速下降视重小于重量； ②电梯加速上升视重大于重量；③当电梯下降的加速度为重力加速度g 时，视重为零； ④飞行员在铅直平面内的圆形轨道飞行，飞机飞到最高点时，gR v ,0mg R v m N ,N mg R v m 22==-=+=飞行员的视重为零3.4一物体静止于固定斜面上。

（1）可将物体所受重力分解为沿斜面的下滑力和作用于斜面的正压力。

（2）因物体静止，故下滑力mg sin α与静摩擦力N 0μ相等。

α表示斜面倾角，N 为作用于斜面的正压力，0μ为静摩擦系数。

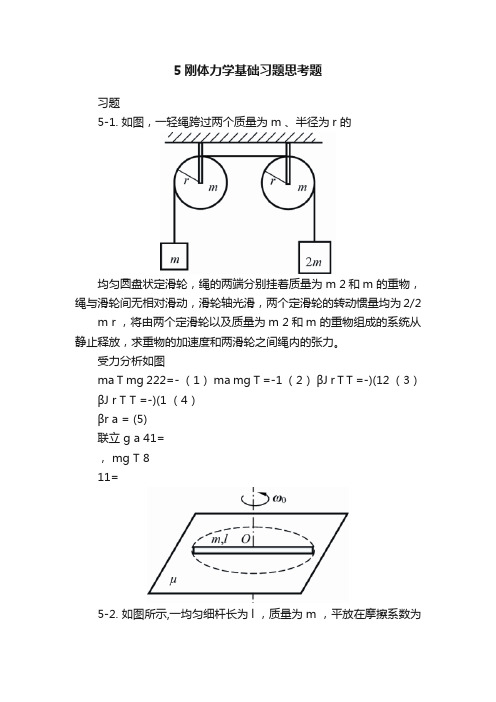
5刚体力学基础习题思考题习题5-1. 如图，一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮，绳的两端分别挂着质量为m 2和m 的重物，绳与滑轮间无相对滑动，滑轮轴光滑，两个定滑轮的转动惯量均为2/2 m r ，将由两个定滑轮以及质量为m 2和m 的重物组成的系统从静止释放，求重物的加速度和两滑轮之间绳内的张力。

受力分析如图ma T mg 222=- （1） ma mg T =-1 （2）βJ r T T =-)(12 （3）βJ r T T =-)(1 （4）βr a = (5)联立 g a 41=， mg T 811=5-2. 如图所示,一均匀细杆长为l ，质量为m ，平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过中心O 且垂直与桌面的轴转动，试求:（1）作用于杆的摩擦力矩；（2）经过多长时间杆才会停止转动。

（1）设杆的线lm=λ，在杆上取一小质元dx dm λ= gdx dmg df μλμ==gxdx dM μλ= 考虑对称mgl gxdx M l μμλ?==20412（2）根据转动定律dtd J JB M ω===-tw Jd Mdt 0ω0212141ωμml mglt -=-所以 glt μω30=5-3. 如图所示，一个质量为m 的物体与绕在定滑轮上的绳子相联，绳子的质量可以忽略，它与定滑轮之间无滑动。

假设定滑轮质量为M 、半径为R ,其转动惯量为2/2MR ，试求该物体由静止开始下落的过程中，下落速度与时间的关系。

dtdvmma T mg ==- βJ TR = βR dtdv= 整理 mg dt dv M m =+)21( gdt M m m dv t v ??+=0021 2 Mm mgtv +=5-4. 轻绳绕过一定滑轮，滑轮轴光滑，滑轮的质量为4/M ，均匀分布在其边缘上，绳子A 端有一质量为M 的人抓住了绳端，而在绳的另一端B 系了一质量为4/M 的重物，如图。

daan第1章 质点运动学和牛顿运动定律参考习题答案1-1 已知质点的运动学方程为x = R cos ωt , y = R sin ωt , z = hωt /(2π),其中R 、ω、h为常量．求：（1）质点的运动方程的矢量形式； （2）任一时刻质点的速度和加速度．解：k j ir ˆ)2/(ˆsin ˆcos πωωωt h t R t R ++= k j i r υˆ2/(ˆcos ˆsin )πωωωωωh t R t R dt d ++-==)ˆsin ˆ(cos ˆsin ˆcos 222j i j iυa t t R t R t R dt d ωωωωωωω+-=--== 1-3半径为R 的轮子沿y = 0的直线作无滑滚动时，轮边缘质点的轨迹为)sin (θθ-=R x )cos 1(θ-=R y求质点的速度；当d θ / d t = ω为常量时，求速度为0的点．解：)cos (dt d dt d R dt dx x θθθυ-==， dtd R dt dy y θθυsin == 即 ()d ˆˆ1c o s s i n d R tθθθ⎡⎤=-⎣⎦υi +j 当ωθ=dtd 为常数时，)cos 1(θωυ-==R dt dx x ， θωυsin R dt dy y ==，速度为0 即 0)c o s 1(=-==θωυR dt dx x ， 0sin ===θωυR dtdyy 故 ,2,1,0,2==k k πθ1-5一质点沿半径为R 的圆周按规律2012S t bt υ=-运动，其中0υ、b 都是常量．（1）求t 时刻质点的总加速度；（2）t 为何值时总加速度数值上等于b ？（3）当加速度达到b 时，质点已沿圆周运行了多少圈？ 解：⑴ 速率bt dt dS -==0υυ， 切向加速度的大小b dtd a -==υτ， 法向加速度的大小Rbt R a n 202)(-==υυ，加速度n n e a ea a ˆˆ+=ττ加速度的大小()240222Rbt b a a a n-+=+=υτ（2）a = bb t bυ==，，(3) a = b 时， bb b b bt t S 2200020212121υυυυυ=⎪⎭⎫ ⎝⎛-⋅=-=转动圈数 bRR Sn πυπ4220== 1-7 在图1-16所示的装置中，两物体的质量为m 1和m 2，物体之间及物体与桌面间的摩擦系数都是μ，求在力F 的作用下两物体的加速度及绳内张力，不计滑轮和绳的质量及轴承摩擦，绳不可伸长．解：根据题意，由滑轮的关系可知绳内张力T = 2F ，设m 1受到m 2的摩擦力f 1，m 2受到地面的摩擦力为f 2，m 1受到的最大静摩擦力为μg m 1，受力如图所示。

清华出版社专项练习动量与角动量一、选择题 1、（0063A15）质量为m 的质点，以不变速率v 沿图中正三角形ABC 的水平光滑轨道运动．质点越过A 角时，轨道作用于质点的冲量的大小为(A) m v ． (B) 2m v ． (C) 3m v ． (D) 2m v ． ［ ］ 2、（0067B30）两辆小车A 、B ，可在光滑平直轨道上运动．第一次实验，B 静止，A 以0.5 m/s 的速率向右与B 碰撞，其结果A以 0.1 m/s 的速率弹回，B 以0.3 m/s 的速率向右运动；第二次实验，B 仍静止，A 装上1 kg 的物体后仍以0.5 m/s的速率与B 碰撞，结果A 静止，B 以0.5 m/s 的速率向右运动，如图．则A 和B 的质量分别为(A) m A ＝2 kg , m B ＝1 kg (B) m A ＝1 kg , m B ＝2 kg (C) m A ＝3 kg , m B ＝4 kg (D) m A ＝4 kg, m B ＝3 kg ［ ］3、（0367A10）质量为20 g 的子弹沿X 轴正向以 500 m/s 的速率射入一木块后，与木块一起仍沿X 轴正向以50 m/s 的速率前进，在此过程中木块所受冲量的大小为(A) 9 N·s . (B) －9 N·s ．(C)10 N·s ． (D) －10 N·s ． ［ ］ 4、（0368A10） 质量分别为m A 和m B (m A >m B )、速度分别为A v 和B v (v A > v B )的两质点A 和B ，受到相同的冲量作用，则(A) A 的动量增量的绝对值比B 的小．(B) A 的动量增量的绝对值比B 的大．(C) A 、B 的动量增量相等．(D) A 、B 的速度增量相等． ［ ］ 5、（0384A20）质量为20 g 的子弹，以400 m/s 的速率沿图示方向射入一原来静止的质量为980 g 的摆球中，摆线长度不可伸缩．子弹射入后开始与摆球一起运动的速率为 (A) 2 m/s ． (B) 4 m/s ． (C) 7 m/s ． (D) 8 m/s ． ［ ］6、（0385B25）一质量为M 的斜面原来静止于水平光滑平面上，将一质量为m 的木块轻轻放于斜面上，如图．如果此后木块能静止于斜面上，则斜面将(A) 保持静止． (B) 向右加速运动． (C) 向右匀速运动． (D) 向左加速运动．［ ］ 7、（0386A20） A 、B 两木块质量分别为m A 和m B ，且m B ＝2m A ，两者用一轻弹簧连接后静止于光滑水平桌面上，如图所示．若用外力将两木块压近使弹簧被压缩，然后将外力撤去，则此后两木块运动动能之比E KA /E KB 为C(A) 21． (B) 2/2． (C) 2． (D) 2． ［ ］8、（0629C45）用一根细线吊一重物，重物质量为5 kg ，重物下面再系一根同样的细线，细线只能经受70 N 的拉力.现在突然向下拉一下下面的线.设力最大值为50 N ，则(A)下面的线先断． (B)上面的线先断．(C)两根线一起断． (D)两根线都不断． ［ ］ 9、（0632A10）质量为m 的小球，沿水平方向以速率v 与固定的竖直壁作弹性碰撞，设指向壁内的方向为正方向，则由于此碰撞，小球的动量增量为(A) v m ． (B) 0．(C) v m 2． (D) v m 2-． ［ ］ 10、（0633A20）机枪每分钟可射出质量为20 g 的子弹900颗，子弹射出的速率为800 m/s ，则射击时的平均反冲力大小为(A) 0.267 N ． (B) 16 N ．(C)240 N ． (D) 14400 N ． ［ ］ 11、（0659A15）一炮弹由于特殊原因在水平飞行过程中，突然炸裂成两块，其中一块作自由下落，则另一块着地点（飞行过程中阻力不计）(A) 比原来更远． (B) 比原来更近．(C) 仍和原来一样远． (D) 条件不足，不能判定． ［ ］ 12、（0702B25）如图所示，圆锥摆的摆球质量为m ，速率为v ，圆半径为当摆球在轨道上运动半周时，摆球所受重力冲量的大小为(A) 2m v ． (B) 22)/()2(v v R mg m π+(C) v /Rmg π． (D) 0．［ ］13、（0703A15）如图所示，砂子从h ＝0.8 m 高处下落到以3 m ／s 向右运动的传送带上．取重力加速度g ＝10 m ／s 2落到传送带上的砂子的作用力的方向为(A) 与水平夹角53°向下．(B) 与水平夹角53°向上． (C) 与水平夹角37°向上． (D) 与水平夹角37°向下． ［ ］14、（0706B30） 如图所示．一斜面固定在卡车上，一物块置于该斜面上．在卡车沿水平方向加速起动的过程中，物块在斜面上无相对滑动.此时斜面上摩擦力对物块的冲量的方向(A) 是水平向前的． (B) 只可能沿斜面向上． (C) 只可能沿斜面向下．(D) 沿斜面向上或向下均有可能． ［ ］15、（5260A20）动能为E K 的A 物体与静止的B 物体碰撞，设A 物体的质量为B 物体的二倍，m A ＝2m B ．若碰撞为完全非弹性的，则碰撞后两物体总动能为(A) E K (B)K E 32． (C) K E 21． (D)　K E 31． ［ ］ 16、（0405A20）人造地球卫星，绕地球作椭圆轨道运动，地球在椭圆的一个焦点上，则卫星的(A)动量不守恒，动能守恒．(B)动量守恒，动能不守恒．(C)对地心的角动量守恒，动能不守恒．(D)对地心的角动量不守恒，动能守恒． ［ ］17、（0406B30） 人造地球卫星绕地球作椭圆轨道运动，卫星轨道近地点和远地点分别为A 和B ．用L 和E K 分别表示卫星对地心的角动量及其动能的瞬时值，则应有(A) L A >L B ，E KA >E kB ． (B) L A ＝L B ，E KA <E KB ．(C) L A ＝L B ，E KA >E KB ． (D) L A <L B ，E KA <E KB ． ［ ］18、（0407C45） 体重、身高相同的甲乙两人，分别用双手握住跨过无摩擦轻滑轮的绳子各一端．他们从同一高度由初速为零向上爬，经过一定时间，甲相对绳子的速率是乙相对绳子速率的两倍，则到达顶点的情况是(A)甲先到达． (B)乙先到达．(C)同时到达． (D)谁先到达不能确定． ［ ］19、（5636A15） 一质点作匀速率圆周运动时，(A) 它的动量不变，对圆心的角动量也不变．(B) 它的动量不变，对圆心的角动量不断改变．(C) 它的动量不断改变，对圆心的角动量不变．(D) 它的动量不断改变，对圆心的角动量也不断改变． ［ ］二、填空题：1、（0055A20） 质量为m 的小球自高为y 0处沿水平方向以速率v 0抛出,与地面碰撞后跳起的最大高度为21y 0，水平速率为21v 0，则碰撞过程中 (1) 地面对小球的竖直冲量的大小为 ________________________；(2)2、（0056B40） 质量m ＝10 kg 的木箱放在地面上，在水平拉力F 的作用下由静止开始沿直线运动，其拉力随时间的变化关系如图所示．若已知木箱与地面间的摩擦系数μ＝0.2，那么在t ＝ 4 s 时，木箱的速度大小为______________；在t ＝7 s 时，木箱的速度大小为______________．(g 取10 m/s 23、（0060A10） 一质量为m 的物体，原来以速率v 向北运动，它突然受到外力打击，变为向西运动，速率仍为v ，则外力的冲量大小为________________________，方向为____________________．4、（0061A10） y 21y有两艘停在湖上的船，它们之间用一根很轻的绳子连接．设第一艘船和人的总质量为250 kg ，第二艘船的总质量为500 kg ，水的阻力不计．现在站在第一艘船上的人用F ＝50 N 的水平力来拉绳子，则 5 s 后第一艘船的速度大小为_________；第二艘船的速度大小为______．5、（0062B30） 两块并排的木块A 和B ，质量分别为m 1和m 2 ，静止地放置在光滑的水平面上，一子弹水平地穿过两木块，设子弹穿过两木块所用的时间分别为∆t 1 和∆t 2 ,木块对子弹的阻力为恒力F ，则子弹穿出后，木块A 的速度大小为_________________________________，木块B 的速度大小为______________________．6、（0066A20） 两个相互作用的物体A 和B ，无摩擦地在一条水平直线上运动．物体A 的动量是时间的函数，表达式为P A ＝P 0－bt ，式中P 0 、b 分别为正值常量，t 是时间．在下列两种情况下，写出物体B 的动量作为时间函数的表达式：(1) 开始时，若B 静止，则P B 1＝______________________；(2) 开始时，若B 的动量为－P 0，则P B 2＝_____________．7、（0068A15） 一质量为m 的小球A ，在距离地面某一高度处以速度v 水平抛出，触地后反跳．在抛出t 秒后小球A 跳回原高度，速度仍沿水平方向，速度大小也与抛出时相同，如图．则小球A 与地面碰撞过程中，地面给它的冲量的方向为________________，冲量的大小为____________________．8、（0184A15） 设作用在质量为1 kg 的物体上的力F ＝6t ＋3(SI)．如果物体在这一力的作用下，由静止开始沿直线运动，在0到 2.0 s 的时间间隔内，这个力作用在物体上的冲量大小I ＝__________________．9、（0222A20） 一物体质量M ＝2 kg ，在合外力i t F )23(+= (SI)的作用下，从静止开始运动，式中i 为方向一定的单位矢量，则当t ＝1 s 时物体的速度1v ＝__________．10、（0371A20） 一颗子弹在枪筒里前进时所受的合力大小为t F 31044005⨯-= (SI)子弹从枪口射出时的速率为300 m/s ．假设子弹离开枪口时合力刚好为零，则(1)子弹走完枪筒全长所用的时间t ＝____________，(2)子弹在枪筒中所受力的冲量I ＝________________，(3)子弹的质量m ＝__________________．11、（0372A15） 水流流过一个固定的涡轮叶片，如图所示．水流流过叶片曲面前后的速率都等于v ，每单位时间流向叶片的水的质量保持不变且等于Q ，则水作用于叶片的力大小为______________，方向为_________．12、（0374B40） 图示一圆锥摆，质量为m 的小球在水平面内以角速度ω匀速转动．在小球转动一周的过程中，(1) 小球动量增量的大小等于__________________．(2) 小球所受重力的冲量的大小等于________________．(3) 小球所受绳子拉力的冲量大小等于_______________． 13、（0387B25） 质量为1 kg 的球A 以5 m/s 的速率和另一静止的、质量也为1 kg 的球B 在光滑水平面上作弹性碰撞，碰撞后球B 以2.5 m/s 的速率，沿与A 原先运动的方向成60°v的方向运动，则球A 的速率为____________，方向为______________________.14、（0393B25） 两球质量分别为m 1＝2.0 g ，m 2＝5.0 g ，在光滑的水平桌面上运动．用直角坐标OXY 描述其运动，两者速度分别为i 101=v cm/s ，)0.50.3(2j i v += cm/s ．若碰撞后两球合为一体，则碰撞后两球速度v 的大小v ＝_________，v 与x 轴的夹角α＝__________．15、（0630A10） 一质量m ＝10 g 的子弹，以速率v 0＝500 m/s 沿水平方向射穿一物体．穿出时，子弹的速率为v ＝30 m/s ，仍是水平方向．则子弹在穿透过程中所受的冲量的大小为________，方向为_________．16、（0631A15） 一物体质量为10 kg ，受到方向不变的力F ＝30＋40t (SI)作用，在开始的两秒内，此力冲量的大小等于________________；若物体的初速度大小为10 m/s ，方向与力F 的方向相同，则在2s 末物体速度的大小等于___________________．17、（0707B25） 假设作用在一质量为10 kg 的物体上的力，在4秒内均匀地从零增加到50 N ，使物体沿力的方向由静止开始作直线运动．则物体最后的速率v ＝_______________．18、（0708B35） 一质量为1 kg 的物体，置于水平地面上，物体与地面之间的静摩擦系数μ 0＝0.20，滑动摩擦系数μ＝0.16，现对物体施一水平拉力F ＝t ＋0.96(SI)，则2秒末物体的速度大小v ＝______________．19、（0709A15） 质量为1500 kg 的一辆吉普车静止在一艘驳船上．驳船在缆绳拉力(方向不变)的作用下沿缆绳方向起动，在5秒内速率增加至5 m/s ，则该吉普车作用于驳船的水平方向的平均力大小为______________．20、（0710B30） 一吊车底板上放一质量为10 kg 的物体，若吊车底板加速上升，加速度大小为a ＝3＋5t (SI)，则2秒内吊车底板给物体的冲量大小I ＝___________；2秒内物体动量的增量大小P ∆＝__________________.21、（0711A20） 粒子B 的质量是粒子A 的质量的4倍，开始时粒子A 的速度j i 43+=0A v ,粒子B 的速度j i 72-=0B v ；在无外力作用的情况下两者发生碰撞，碰后粒子A 的速度变为j i 47-=A v ，则此时粒子B 的速度B v ＝______________．22、（0715B30）有一质量为M （含炮弹）的炮车，在一倾角为θ 的光滑斜面上下滑，当它滑到某处速率为v 0时，从炮内射出一质量为m 的炮弹沿水平方向． 欲使炮车在发射炮弹后的瞬时停止下滑，则炮弹射出时对地的速率v ＝__________．23、（0717A10） 如图所示，质量为m 的子弹以水平速度0v 射入静止的木 块并陷入木块内，设子弹入射过程中木块M 不反弹，则墙壁 对木块的冲量＝____________________.24、（0718A15） 一质量为30 kg 的物体以10 m·s －1的速率水平向东运动，另一质量为20 kg 的物体以20m·s －1的速率水平向北运动。

第3章 动量 角动量3-1一架飞机以300m/s 的速度水平飞行，与一只身长0.20m 、质量0.50kg 的飞鸟相撞，设碰撞后飞鸟的尸身与飞机具有一样的速度，而原先飞鸟关于地面的速度很小，能够忽略不计。

试估量飞鸟对飞机的冲击力(碰撞时刻可用飞鸟身长被飞机速度相除来估算)。

依照此题计算结果,谈谈高速运动的物体(如飞机、汽车)与通常情形下不足以引发危害的物体(如飞鸟、小石子)相碰撞后会产生什么后果？解 飞鸟碰撞前速度能够忽略,碰撞进程中冲量的大小为:I m Ft υ==考虑到碰撞时刻可估算为 lt υ=即得飞鸟对飞机的冲击力2250.5300 2.2510(N)0.2m F l υ⨯===⨯由此可见飞机所受冲击力是相当大的，足以致使机毁人亡，后果很严峻。

3-2 水力采煤,是用高压水枪喷出的强力水柱冲击煤层。

如图，设水柱直径30mm D =，水速56m/s υ=，水柱垂直射在煤层表面上，冲击煤层后的速度为零，求水柱对煤的平均冲力。

解 △t 时刻内射向煤层的水柱质量为21π4m V D x ρρ∆=∆=∆ 煤层对水柱的平均冲击力（如图以向右为正方向）为211x x x m m m F t t υυυ∆-∆∆==-∆∆211π4x xD t ρυ∆=-∆3322311.010π(3010)562.2210(N)4-=-⨯⨯⨯⨯⨯⨯=-⨯水柱对煤层的平均冲力为'32.2210N F F =-=⨯，方向向右。

3-3 质量10kg m =的物体沿x 轴无摩擦地运动，设0t =时，物体位于原点，速度为零。

若是物体在作使劲()34N Ft =+的作用下运动了3秒，计算3秒末物体的速度和加速度各为多少？（题中F 作用线沿着x 轴方向）解 力F 在3秒内的冲量33d (34)d 27N s I F t t t ==+=⋅⎰⎰习题3-2图依照质点的动量定理 ()30m I υ-=得()3 2.7m/s Imυ== 加速度()()223153m/s 1.5m/s 10F a m === 3-4 质量为m 的物体，开始时静止，在时刻距离T t 20≤≤内，受力()2021t T F F T ⎡⎤-=-⎢⎥⎢⎥⎣⎦作用，试证明，在2t T =时物体的速度为043F Tm。

第三章 动量定理及动量守恒定律（思考题）3.1试表述质量的操作型定义。

解答，kgv v m m 00 ∆∆=式中kg 1m 0=（标准物体质量） 0v∆：为m 与m 0碰撞m 0的速度改变 v∆：为m 与m 0碰撞m 的速度改变这样定义的质量，其大小反映了质点在相互作用的过程中速度改变的难易程度，或者说，其量值反映了质量惯性的大小。

这样定义的质量为操作型定义。

3.2如何从动量守恒得出牛顿第二、第三定律，何种情况下牛顿第三定律不成立？ 解答，由动量守恒)p p (p p ,p p p p 22112121 -'-=-'+='+' ,p p 21 ∆-=∆ t p t p 21∆∆-=∆∆ 取极限dt p d dtp d 21-= 动量瞬时变化率是两质点间的相互作用力。

,a m )v m (dt d dt p d F 111111 === ,a m )v m (dt d dt p d F 222222 === 21F F -=对于运动电荷之间的电磁作用力，一般来说第三定律不成立。

（参见P 63最后一自然段）3.3在磅秤上称物体重量，磅秤读数给出物体的“视重”或“表现重量”。

现在电梯中测视重，何时视重小于重量（称作失重）？何时视重大于重量（称作超重）？在电梯中，视重可能等于零吗？能否指出另一种情况使视重等于零？解答，①电梯加速下降视重小于重量； ②电梯加速上升视重大于重量；③当电梯下降的加速度为重力加速度g 时，视重为零；④飞行员在铅直平面内的圆形轨道飞行，飞机飞到最高点时，gR v ,0mg R v m N ,N mg R v m 22==-=+=飞行员的视重为零3.4一物体静止于固定斜面上。

（1）可将物体所受重力分解为沿斜面的下滑力和作用于斜面的正压力。

（2）因物体静止，故下滑力mg sin α与静摩擦力N 0μ相等。

α表示斜面倾角，N 为作用于斜面的正压力，0μ为静摩擦系数。

第四章 动量和角动量答案一．选择题 １．（Ｃ）２.(Ｂ)３．（Ｃ）４．（Ｃ）５．（Ｃ）６．（Ｄ）７．（Ｃ）８．（Ｃ）９．（Ａ）10．（Ｄ）11.（Ａ）12．（Ａ）13．（Ｂ） 14. （Ｂ） 15.（Ｂ） 二．填空题：１．s N ⋅7.4； 与速度方向相反． ２．mM Mv V +=．３．s N ⋅18．４．)cos sin (j t b i t a m m Pωωωωυ+-==；零．５．s rad /36．６．不一定； 动量．７．s N ⋅140； s m /24．８．s 003.0； s N ⋅6.0； g 2． ９．s m /10； 北偏东087.36．10．c x 2311．０； k ab mω． 12．s cm /14.6； 05.35． 13．０． 14．Mk l 0；Mk nmM Ml +0． 15．RGMm 32； RG M m 3-．三． 计算题：1.解：由动量定理知质点所受外力的总冲量12)(v m v m v m I -=∆=由Ａ→Ｂ1683.045cos -⋅⋅-=--=-=sm kg mvmv mvmv I AB AxBx x1283.045sin 0-⋅⋅-=-=-=sm kg mvmvI A Ayys N I I I y x ⋅=+=739.022方向：x y I I tg /1=θ，5.202=θ（与Ｘ轴正向夹角）．2.解：（１）因穿透时间极短，故可认为物体未离开平衡位置．因此，作用于子弹、物体系统上的外力均在铅直方向，故系统在水平方向动量守恒．令子弹穿出时物体的水平速度为v '，有： v M mv mv '+=0s m M v v m v /13.3/)(0=-=' N l Mv Mg T 5.26/2=+=（２）s N mv mv t f ⋅-=-=∆7.40（0v方向为正,负号表示冲量与0v方向相反）． 3.解：完全弹性碰撞，动量守恒，机械能守恒碰前：对Ａ：gl v A 21= 方向向右，对Ｂ：01=B v ；碰后：对Ａ：gh v A 22= 方向向左，对Ｂ：2B v ，方向向右． 动量守恒：221A A B B A A v m v m v m -= （１） 机械能守恒：222221212121B B A A A A v m v m v m +=（２）联立（１）、（２）两式解得： 2/321A A v v =， 2/22A B v v =而 s m gh v A /66.222==s m v A /41= s m v B /33.12= m l 8.0=；Ｂ克服阻力作的功为动能的减少，由动能定理： )(42.42/22J v m W B B f ==．．4．解：∑∑<<in exii F F ==∴∑=ni i m p 1i v恒矢量0N νe =++p p p即αθep Np νp 又因为 νe p p ⊥)(212ν2e N p p p +=∴︒==9.61arctanνe p p α122N sm kg 1036.1--⋅⋅⨯=p 代入数据计算得系统动量守恒 , 即0N νe =++p p p 122e s m kg 102.1--⋅⋅⨯=p 123sm kg 104.6--⋅⋅⨯=νp。

第三章 动量定理及动量守恒定律（思考题）3.1、力的独立作用原理为何？3.2、什么是主动力和被动力？ 主动力 重力、弹簧弹性力、静电力和洛伦磁力等有其“独立自主”的方向和大小，不受质点所受其它力的影响，处于主动地位，称主动力。

被动力物体间的挤压力、绳内张力和摩擦力常常没有自己独立自主的大小和方向，要看质点受到的主动力及运动状态而定，称为被动力。

3.3、什么是伽里略的相对性原理？任何惯性参考系在牛顿动力学规律面前都是平等的或平权的。

这称为经典力学相对性原理或伽利略相对性原理。

最后经爱因斯坦推广为全部物理学。

对于物理学规律来说，一切惯性系都是等价的。

我们说“一切惯性系都等价”，是指不同惯性系中的动力学规律（如牛顿三定律）都一样，从而都能正确地解释所看到的现象。

3.4、物体运动时，如果它的速率不变化，它所受的合力是否为零？答：如果它的速率不变化，它所受的合力可能为零，比如匀速圆周运动，速率不变化，但是合力变化。

3.5、棒球运动员在接球时为何要戴厚而软的手套？篮球运动员接急球时往往持球缩手，这是为什么？答，根据tp p t dt F t I F t t ∆-=∆=∆=⎰00，↓↑∆F t 棒球运动员在接球时戴厚而软的手套是为了延长球在手中停止的时间，从而缓冲手受到的冲力多人手的伤害。

3.6、质点系的内力之和有何特点？答；内力之合为零，内力对空间定点或定轴的力矩之合为零。

内力不改变质点系整体的运动状态，但是改变质点的运动状态。

3.7，“质心的定义是质点系质量集中的一点，它的运动即代表了质点系的运动，若掌握质点系质心的运动，质点系的运动状况就一目了然了。

”对否？ 答，不对。

质心运动情况不能说明质点系内各质点的运动情况。

3.8悬浮在空气中的气球下面吊有软梯，有一人站在上面。

最初，均处于静止，后来，人开始向上爬，问气球是否运动？答，运动。

内力不影响质心的运动，人向上爬，气球向下运动，达到质点系的质心位置不变。