电力系统分析潮流计算大作业
- 格式:doc
- 大小:566.00 KB
- 文档页数:9
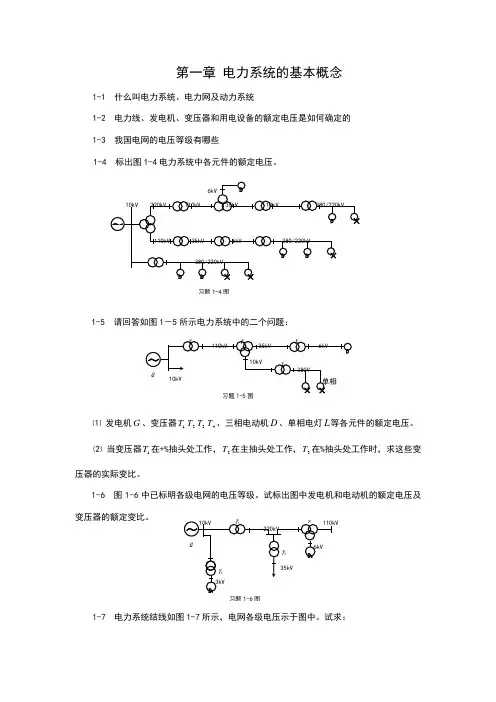
第一章 电力系统的基本概念1-1 什么叫电力系统、电力网及动力系统1-2 电力线、发电机、变压器和用电设备的额定电压是如何确定的 1-3 我国电网的电压等级有哪些1-4 标出图1-4电力系统中各元件的额定电压。
1-5 请回答如图1-5所示电力系统中的二个问题:⑴ 发电机G 、变压器1T 2T 3T 4T 、三相电动机D 、单相电灯L 等各元件的额定电压。
⑵ 当变压器1T 在+%抽头处工作,2T 在主抽头处工作,3T 在%抽头处工作时,求这些变压器的实际变比。
1-6 图1-6中已标明各级电网的电压等级。
试标出图中发电机和电动机的额定电压及变压器的额定变比。
1-7 电力系统结线如图1-7所示,电网各级电压示于图中。
试求:习题1-5图习题1-6图习题1-4图⑴发电机G 和变压器1T 、2T 、3T 高低压侧的额定电压。
⑵设变压器1T 工作于+%抽头, 2T 工作于主抽头,3T 工作于-5%抽头,求这些变压器的实际变比。
1-8 比较两种接地方式的优缺点,分析其适用范围。
1-9 什么叫三相系统中性点位移它在什么情况下发生中性点不接地系统发生单相接地时,非故障相电压为什么增加3倍1-10 若在变压器中性点经消弧线圈接地,消弧线圈的作用是什么第二章 电力系统各元件的参数及等值网络2-1 一条110kV 、80km 的单回输电线路,导线型号为LGJ —150,水平排列,其线间距离为4m ,求此输电线路在40℃时的参数,并画出等值电路。
2-2 三相双绕组变压器的型号为SSPL —63000/220,额定容量为63000kVA ,额定电压为242/,短路损耗404=k P kW ,短路电压45.14%=k U ,空载损耗93=o P kW ,空载电流41.2%=o I 。
求该变压器归算到高压侧的参数,并作出等值电路。
2-3 已知电力网如图2-3所示:各元件参数如下:变压器:1T :S =400MVA ,12%=k U , 242/ kV2T :S =400MVA ,12%=k U , 220/121 kV线路:2001=l km, /4.01Ω=x km (每回路)习题1-7图115kVT 1T 2l 1l 2习题2-3图602=l km, /4.01Ω=x km其余参数均略去不计,取基准容量S B =1000MVA ,基准电压av B U U =,试作出等值电路图,并标上各元件的标么值参数。

东北农业大学网络教育学院电力系统分析作业题参考答案作业题一参考答案一、填空题1.降压变压器高压侧的主分接头电压为220kv ,若选择+2×%的分接头,则该分接头电压为 231KV 。
2.电力系统中性点有效接地方式指的是 中性点直接接地 。
3.输电线路的电气参数包括电抗、电导、电纳和 电阻 。
4.输电线路的电压偏移是指线路始端或末端母线的实际运行电压与线路 额定电压 的数值差。
5.电力系统的潮流分布一般是用各节点的电压和 功率 表示。
6.调整发电机组输出的有功功率用来调整电力系统运行的 频率 。
7.复合故障一般是指某一时刻在电力系统 二个及以上地方 发生故障。
8.用对称分量法计算不对称故障,当三相阻抗完全对称时,则其序阻抗矩阵Zsc 的非对角元素为 零 。
9.系统中发生单相接地短路时故障点短路电流的大小是零序电流的 3 倍。
10.减小输出电元件的电抗将 提高(改善) 系统的静态稳定性。
二、单项选择题11.同步发电机的转速和系统频率之间是否有严格的关系( ② )①否 ②是 ③不一定 ④根据发电机的形式定12.三绕组变压器的结构、通常将高压绕组放在( ③ )①内层 ②中间层 ③外层 ④独立设置13.中性点以消弧线圈接地的电力系统,通常采用的补偿方式是( ③ )①全补偿 ②欠补偿 ③过补偿 ④有时全补偿,有时欠补偿14.三相导线的几何均距越大,则导线的电抗( ② )①越大 ②越小 ③不变 ④无法确定15.变压器的电导参数G T ,主要决定于哪一个实验数据( ① )①△P O ②△P K ③U K % ④I O %16.当功率的有名值为s =P +jQ 时(功率因数角为ϕ)取基准功率为S n ,则有功功率的标么值为( ③ ) ①ϕcos S P n ⋅ ②ϕsin S P n ⋅ ③n S P ④nS cos P ϕ⋅17.环网中功率的自然分布是( ④ )①与电阻成正比分布 ②与电抗成正比分布③与阻抗成正比分布 ④与阻抗成反比分布18.电力系统中PQ 节点的数量( ② )①全都是 ②大量的 ③少量的 ④必有且一般只设一个19.潮流计算中,要求某些节点之间电压的相位差应满足的约束条件是(④ )①|-j i δδ|>|-j i δδ|min ②|-j i δδ|<|-j i δδ|min③|-j i δδ|>|-j i δδ|max ④|-j i δδ|<|-j i δδ|max20.在同一时间内,电力网的电能损耗与供电量之比的百分值称为( ② )①负载率 ②网损率 ③供电率 ④厂用电率21.电力系统的频率主要决定于( ① )①有功功率的平衡 ②无功功率的平衡③电压质量 ④电流的大小22.关于顺调压电压调整方式的描述,错误的是( ② )①高峰负荷时允许中枢点电压略低②低谷负荷时允许中枢点电压略低③适用于用户对电压要求不高的场合④适用于供电线路不长的场合23.通过改变变压器变比,实质上( ③ )①改变了电压损耗的数值 ②改变了负荷变化时次级电压的变化幅度③改变了电力网的无功功率分布 ④增加了整个电力系统的无功功率容量24.三相短路时,非周期分量极小值,只能是在某种情况(① )①一相中出现 ②同时在两相中出现③三相均不出现 ④只有故障相出现其它相不出现25.同步机的各种电抗间关系为(③ )①'x "x x x d d q d >>> ②"x 'x x x d d d q >>>③ "x 'x x x d d q d >>> ④"x x 'x x d q d d >>>26.若ac 两相发生短路,则基准相选择为( ② )①a 相 ②b 相 ③c 相 ④a 相和c27.下网K 点发生两相短路接地,其复合序网为图所示( ③ )(其中,1,2,0分别为正序、负序、零序阻抗)28.越靠近电源点负序电压越( ① )①低 ②高 ③不变 ④无法确定29.作为判据0d dP E >δ主要应用于分析简单系统的( ③ ) ①暂态稳定 ②故障计算 ③静态稳定 ④调压计算30.分析简单系统的暂态稳定性可以应用( ② )①等耗量微增率准则 ②等面积定则 ③小干扰法 ④对称分量法三、简答题31.电力变压器的主要作用是什么答:电力变压器的主要作用是升高或降低电压,另外还起到将不同电压等级电网相联系的作用。


电力系统潮流计算综述学院:电气工程学院专业:电力系统及其自动化学号:s姓名:张雪摘要电力系统潮流计算是电力系统分析中最基本的一项计算。
本文对电力系统潮流计算进行了综述。
首先简单回顾了潮流计算的发展历史,对当前基于计算机的各种潮流算法的原理及其优缺点,作了简要介绍和比较,并介绍了它们采用的一些特别技术及程序设计技巧;接着简要分析了三种新型的潮流计算方法的计算原理及优缺点,它们分别是基于人工智能的潮流计算方法、基于L1范数和现代内点理论的电力系统潮流计算方法、基于符号分析的潮流计算方法等。
除此之外还介绍了配电系统潮流计算算法。
关键词:电力系统;潮流计算;综述;新型潮流计算方法;配电系统1 概述电力系统潮流计算是研究电力系统稳态运行的一项基本运算。
它根据给定系统的网络结构及运行条件来确定整个系统的运行状态:主要是各节点电压(幅值和相角),网络中功率分布及功率损耗等。
它既是对电力系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的依据,又是电力系统静态和暂态稳定计算的基础。
潮流计算经历了一个由手工,利用交、直流计算台到应用数字电子计算机的发展过程。
现在的潮流算法都以计算机的应用为前提。
1956年ward 等人编制成实用的计算机潮流计算程序,标志着电子计算机开始在电力系统潮流计算中应用。
基于导纳矩阵的高斯—塞德尔法是电力系统中最早得到应用的潮流计算方法。
因它对病态条件(所谓具有病态条件的系统是指:重负荷系统;包含有负电抗支路的系统;具有较长辐射型线路的系统;长线路与短线路接在同一节点,且其长度比值又很大的系统;或平衡节点位于网络远端的系统)特别敏感,又发展了基于阻抗阵的高斯—塞德尔法,但此法中阻抗阵是满阵占大量内存,而限制了其应用。
1961年VanNes等人提出用牛顿法求解系统潮流问题,经后人的不断改进,而得到广泛应用并出现了多种变型以满足不同的需要,如快速解耦法、直流法、保留非线性算法等。
同时,60年代初开始出现运用非线性规划的最优潮流算法。

电力系统分析综合实验一:潮流计算实验课程名称:电力系统分综合实验指导老师:成绩:实验名称:潮流分析实验实验类型:一、实验目的和要求(必填)二、实验内容和原理(必填)三、主要仪器设备(必填)四、操作方法和实验步骤五、实验数据记录和处理六、实验结果与分析(必填)七、讨论、心得一、实验目的和要求通过本实验熟悉PSCAD仿真软件,了解电力系统有功、无功的概念,掌握简单的潮流计算二、原理与说明(1)PSCAD/EMTDC是加拿大马尼托巴高压直流研究中心(ManitobaHVDCResearchCenter)推出的一款电力系统电磁暂态仿真软件。
EMTDC (ElectroMagneticTransientinDCSystem)是一种电力系统仿真分析软件,既可以研究交直流电力系统问题,又能完成电力电子仿真及其非线性控制的多功能工具。
PSCAD(PowerSystemComputerAidedDesign)是EMTDC的用户图形界面,也是EMTDC的图形用户接口,它的存在是为了更方便用户使用EMTDC。
PSCAD的开发成功,使得用户能更方便地使用EMTDC进行电力系统分析,使电力系统复杂部分可视化成为可能,而且软件可以作为实时数字仿真器的前置端。
用PSCAD进行潮流计算的时候要注意:①选取元件的时候,须辨别元件的属性,例如电源是三相还是单相;②设置元件参数时,要注意参数的物理意义③注意测量信号的方向④将多个曲线绘制在一张图表上时,须选取合适的范围,将单位标注清楚。
(2)三节点单相实验系统介绍在PSCAD界面搭建一个系统为50Hz的单相系统,如下图所示参数如下:G1:理想电压电源,100kVRMS,相角为0,频率为50HzG2:理想电压电源,100kVRMS,相角为60,频率为50HzG3:理想电压电源,100kVRMS,相角为30,频率为50HzX1:频率为50Hz的条件下,感抗为2X2:频率为50Hz的条件下,感抗为2X3:频率为50Hz的条件下,感抗为3X4:频率为50Hz的条件下,感抗为3X5:频率为50Hz的条件下,感抗为4X6:频率为50Hz的条件下,感抗为4Xline1:频率为50Hz的条件下,感抗为40Xline2:频率为50Hz的条件下,感抗为20Xline3:频率为50Hz的条件下,感抗为20仿真设置:电源:电压源输出坡至1.0p.u.的时间:0.05s仿真过程总时长:1s (确保仿真过程达到稳态)仿真步长:=50s(3)并联电容器并联电容器又称为移相电容器,是电力系统中一种重要的无功功率补偿设备,广泛地应用于改善负荷的功率因数。

电力系统分析潮流计算大作业电力系统潮流计算是电力系统分析的一项重要工作。
通过对电力系统中各个节点之间的电压、电流等参数进行计算和分析,可以有效地评估电力系统的运行状态,保证电力系统的安全稳定运行。
潮流计算主要包括节点电压、机组输出以及线路功率等参数的计算。
通过潮流计算,可以得到节点电压的大小、相位,电网各发电机的负荷分担,线路的负载情况等重要信息,为电力系统的运行和调度提供重要参考。
在进行潮流计算时,常用的方法有直流潮流计算和交流潮流计算两种。
直流潮流计算是通过假设电网中的所有元件都是直流的,然后根据节点电压平衡、功率平衡等方程进行计算。
直流潮流计算方法简单、计算速度快,但对于系统中大量的非线性元素无法准确描述,因此适用于简单的系统。
交流潮流计算是基于电力系统的非线性特性进行计算的,适用于复杂的电力系统。
交流潮流计算考虑了系统中各元件的非线性特性,并且能够考虑系统中的各种限制条件,如发电机容量限制、变压器容量限制等。
交流潮流计算的过程中,需要对电力系统的节点电压和功率进行迭代计算,直到满足系统的平衡条件为止。
在进行潮流计算时,需要准确的系统数据,包括发电机的容量、变压器的参数、线路的参数等。
同时,还需要对系统的边界条件进行定义,如负荷水平、变压器的调整范围等。
在计算的过程中,还需要考虑一些特殊情况的处理,如发电机的启停、线路的开关操作等。
电力系统潮流计算是电力系统分析的基础,对电力系统的运行和调度具有重要作用。
通过潮流计算,可以评估电力系统的运行状态,确定电力系统的运行可行性,指导电力系统的运行和调度。
同时,也可以为电力系统的规划和设计提供重要参考。
因此,电力系统潮流计算是电力系统工程中一项重要的研究内容。
总之,电力系统潮流计算是评估电力系统运行状态和指导电力系统运行调度的重要工具。
通过对节点电压、机组输出和线路功率等参数的计算,可以为电力系统的运行和调度提供重要参考。
在进行潮流计算时,需要准确的系统数据和边界条件,并考虑特殊情况的处理。

摘要潮流计算是电力系统最基本最常用的计算。
根据系统给定的运行条件,网络接线及元件参数,通过潮流计算可以确定各母线的电压,包括电压的幅值和相角,各元件流过的功率,整个系统的功率损耗等一系列数据。
牛顿—拉夫逊Newton-Raphson法是数学上解非线性方程组的有效方法,有较好的收敛性。
将N-R法用于潮流计算是以导纳矩阵为基础的,由于利用了导纳矩阵的对称性,稀疏性及节点编号顺序优划等技巧,使N-R法在收敛性,占用内存,计算速度等方面的优点都超过了阻抗法。
本文首先介绍了电力系统潮流利用PSASP仿真软件进行计算机辅助分析的基本知识及潮流计算牛顿-拉夫逊法,然后通过PSASP仿真软件输出结果得出相应结论。
由于利用了PSASP仿真软件,使得结果合理、可靠。
关键词:潮流计算,牛顿-拉夫逊法,PSASP,电力系统仿真目录1 绪论 (1)1.1 电力系统潮流分析计算的意义和目的 (1)1.2 课程设计要求 (1)2牛顿拉夫逊潮流计算简介 (4)3 PSASP软件简介 (7)4仿真结果及报表输出 (8)4.1 线路图仿真结果 (8)4.2 潮流分析报表输出结果 (9)5结论 (12)参考文献 (13)辽宁工程技术大学电力系统分析课程设计1 绪论1.1电力系统潮流分析计算的意义和目的1、在电网规划阶段,通过潮流计算,合理规划电源容量及接入点,合理规划网架,选择无功补偿方案,满足规划水平的大、小方式下潮流交换控制、调峰、调相、调压的要求。
2、在编制年运行方式时,在预计负荷增长及新设备投运基础上,选择典型方式进行潮流计算,发现电网中薄弱环节,供调度员日常调度控制参考,并对规划、基建部门提出改进网架结构,加快基建进度的建议。
3、正常检修及特殊运行方式下的潮流计算,用于日运行方式的编制,指导发电厂开机方式,有功、无功调整方案及负荷调整方案,满足线路、变压器热稳定要求及电压质量要求。
4、预想事故、设备退出运行对静态安全的影响分析及作出预想的运行方式调整方案。

电力系统分析课后作业题及练习题第一章 电力系统的基本概念1-1 什么叫电力系统、电力网及动力系统?1-2 电力线、发电机、变压器和用电设备的额定电压是如何确定的?1-3 我国电网的电压等级有哪些? 1-4 标出图1-4电力系统中各元件的额定电压。
1-5 请回答如图1-5所示电力系统中的二个问题:⑴ 发电机G 、变压器1T 2T3T 4T 、三相电动机D 、1 2 3~D×× L35kV GT 410kV110kV6kV380V10kV单相习题1-5图10kV 220kV 110kV 35kV 10kV 380/220kV6kV110kV 35kV 6kV 380/220kV380/220kV × DD×~12 3D×D1 23 ×DD习题1-4图单相电灯L 等各元件的额定电压。
⑵ 当变压器1T 在+2.5%抽头处工作,2T 在主抽头处工作,3T 在-2.5%抽头处工作时,求这些变压器的实际变比。
1-6 图1-6中已标明各级电网的电压等级。
试标出图中发电机和电动机的额定电压及变压器的额定变比。
1-7 电力系统结线如图1-7所示,电网各级电压示于图中。
试求:⑴发电机G 和变压器1T 、2T 、3T 高低压侧的额定电压。
⑵设变压器1T 工作于+2.5%抽头, 2T 工作于主抽头,3T 工作于-5%抽头,求这些变压器的实际变比。
~D 1D 2T 2 T 4 6kV10kV110kV35kV3kV GT 3习题1-6图220kV~T 3G10kV110kV35kV10kVT 1T 21-8 比较两种接地方式的优缺点,分析其适用范围。
1-9 什么叫三相系统中性点位移?它在什么情况下发生?中性点不接地系统发生单相接地时,非故障相电压为什么增加3倍? 1-10 若在变压器中性点经消弧线圈接地,消弧线圈的作用是什么?第二章 电力系统各元件的参数及等值网络2-1 一条110kV 、80km 的单回输电线路,导线型号为LGJ —150,水平排列,其线间距离为4m ,求此输电线路在40℃时的参数,并画出等值电路。

南昌大学实验报告学生姓名:学号:专业班级:实验类型:□验证□综合■设计□创新实验日期:实验成绩:电力系统潮流计算实验一、实验目的:本实验通过对电力系统潮流计算的计算机程序的编制与调试,获得对复杂电力系统进行潮流计算的计算机程序,使系统潮流计算能够由计算机自行完成,即根据已知的电力网的数学模型(节点导纳矩阵)及各节点参数,由计算程序运行完成该电力系统的潮流计算。
通过实验教学加深学生对复杂电力系统潮流计算计算方法的理解,学会运用电力系统的数学模型,掌握潮流计算的过程及其特点,熟悉各种常用应用软件,熟悉硬件设备的使用方法,加强编制调试计算机程序的能力,提高工程计算的能力,学习如何将理论知识和实际工程问题结合起来。
二、实验内容:编制调试电力系统潮流计算的计算机程序。
程序要求根据已知的电力网的数学模型(节点导纳矩阵)及各节点参数,完成该电力系统的潮流计算,要求计算出节点电压、功率等参数。
1、在各种潮流计算的算法中选择一种,按照计算方法编制程序。
2、将事先编制好的电力系统潮流计算的计算程序原代码由自备移动存储设备导入计算机。
3、在相应的编程环境下对程序进行组织调试。
4、应用计算例题验证程序的计算效果。
三、实验程序:function [e,f,p,q]=flow_out(g,b,kind,e,f)%计算潮流后efpq的终值s=flow(g,b,kind,e,f);k=0;while max(abs(s))>10^-5J=J_out(g,b,kind,e,f);J_ni=inv(J);dv=J_ni*s;l=length(dv)/2;for i=1:le(i)=e(i)-dv(2*i-1);f(i)=f(i)-dv(2*i);ends=flow(g,b,kind,e,f);endl=length(e);for i=1:ls1=0;s2=0;for j=1:ls1=s1+g(i,j)*e(j)-b(i,j)*f(j);s2=s2+g(i,j)*f(j)+b(i,j)*e(j);endp(i)=e(i)*s1+f(i)*s2;q(i)=f(i)*s1-e(i)*s2;endfunction s=flow(g,b,kind,e,f)%计算当前ef与规定的pqv的差值l=length(e);s=zeros(2*l-2,1);for i=1:(l-1)s1=0;s2=0;for j=1:ls1=s1+g(i,j)*e(j)-b(i,j)*f(j);s2=s2+g(i,j)*f(j)+b(i,j)*e(j);ends(2*i-1)=kind(2,i)-e(i)*s1-f(i)*s2;if kind(1,i)==1s(2*i)=kind(3,i)-f(i)*s1+e(i)*s2;elses(2*i)=kind(3,i)^2-f(i)^2-e(i)^2;endendfunction J=J_out(g,b,kind,e,f)%计算节点的雅克比矩阵l=length(e);J=zeros(2*l-2,2*l-2);for i=1:(l-1);if kind(1,i)==1s=PQ_out(g,b,e,f,i);for j=1:(2*l-2)J(2*i-1,j)=s(1,j);J(2*i,j)=s(2,j);endelses=PV_out(g,b,e,f,i);for j=1:(2*l-2)J(2*i-1,j)=s(1,j);J(2*i,j)=s(2,j);endendendfunction pq=PQ_out(g,b,e,f,i)%计算pq节点的雅克比矩阵l=length(e);pq=zeros(2,2*l-2);for j=1:(l-1)if j==is=0;for k=1:ls=s-(g(i,k)*e(k)-b(i,k)*f(k));endpq(1,2*i-1)=s-g(i,i)*e(i)-b(i,i)*f(i); s=0;for k=1:ls=s-(g(i,k)*f(k)+b(i,k)*e(k));endpq(1,2*i)=s+b(i,i)*e(i)-g(i,i)*f(i);s=0;for k=1:ls=s+(g(i,k)*f(k)+b(i,k)*e(k));endpq(2,2*i-1)=s+b(i,i)*e(i)-g(i,i)*f(i); s=0;for k=1:ls=s-(g(i,k)*e(k)-b(i,k)*f(k));endpq(2,2*i)=s+g(i,i)*e(i)+b(i,i)*f(i);elsepq(1,2*j-1)=-(g(i,j)*e(i)+b(i,j)*f(i)); pq(1,2*j)=b(i,j)*e(i)-g(i,j)*f(i);pq(2,2*j)=-pq(1,2*j-1);pq(2,2*j-1)=pq(1,2*j);endendfunction pv=PV_out(g,b,e,f,i)%计算pv节点的雅克比矩阵l=length(e);pv=zeros(2,2*l-2);for j=1:(l-1)if j==is=0;for k=1:ls=s-(g(i,k)*e(k)-b(i,k)*f(k));endpv(1,2*i-1)=s-g(i,i)*e(i)-b(i,i)*f(i); s=0;for k=1:ls=s-(g(i,k)*f(k)+b(i,k)*e(k));endpv(1,2*i)=s+b(i,i)*e(i)-g(i,i)*f(i);pv(2,2*i-1)=-2*e(i);pv(2,2*i)=-2*f(i);elsepv(1,2*j-1)=-(g(i,j)*e(i)+b(i,j)*f(i)); pv(1,2*j)=b(i,j)*e(i)-g(i,j)*f(i);endend%数据输入g=[1.042093 -0.588235 0 -0.453858-0.588235 1.069005 0 -0.4807690 0 0 0-0.453858 -0.480769 0 0.9344627];b=[-8.242876 2.352941 3.666667 1.8910742.352941 -4.727377 0 2.4038463.666667 0 -3.333333 01.8910742.40385 0 4.26159];e=[1 1 1.1 1.05];f=[0 0 0 0];kind=[1 1 2 0-0.3 -0.55 0.5 1.05-0.18 -0.13 1.1 0];[e,f,p,q]=flow_out(g,b,kind,e,f);ef四、例题及运行结果在上图所示的简单电力系统中,系统中节点1、2为PQ节点,节点3为PV节点,节点4为平衡节点,已给定P1s+jQ1s=-0.30-j0.18 P2s+jQ2s=-0.55-j0.13 P3s=0.5 V3s=1.10 V4s=1.05∠0°容许误差ε=10-5节点导纳矩阵:各节点电压:节点 e f v ζ1.0.984637 -0.008596 0.984675 -0.5001722.0.958690 -0.108387 0.964798 -6.4503063. 1.092415 0.128955 1.100000 6.7323474. 1.050000 0.000000 1.050000 0.000000各节点功率:节点P Q1-0.300000 -0.1800002–0.550000 -0.13000030.500000 -0.55130540.367883 0.264698结果:五、思考讨论题1.潮流计算有几种方法?简述各种算法的优缺点。

第4章复杂电力系统的潮流计算一、填空题1.用计算机进行潮流计算时,按照给定量的不同,可将电力系统节点分为节点、节点、节点三大类,其中, 节点数目最多,节点数目很少、可有可无,节点至少要有一个.二、选择题1。
若在两个节点i、j之间增加一条支路,则下列关于节点导纳矩阵的说法正确的是()A。
阶数增加1B.节点i的自导纳不变C。
节点i、j间的互导纳发生变化D。
节点j的自导纳不变2.若从节点i引出一条对地支路,则下列关于节点导纳矩阵的说法正确的是()A.阶数增加1B.节点i的自导纳发生变化C。
节点i和其余节点间的互导纳均发生变化D。
节点导纳矩阵的所有元素均不变3。
若从两个节点i、j之间切除掉一条支路,则下列关于节点导纳矩阵的说法正确的是()A.阶数减少1B.节点i、j间的互导纳一定变为0C。
节点i、j间的互导纳发生变化,但不一定变为0D.节点i、j的自导纳均不变4.若网络中增加一个节点k,且增加一条节点i与之相连的支路,则下列关于节点导纳矩阵的说法正确的是()(1)阶数增加1(2)节点k的自导纳等于题干中所述支路的导纳(3)节点i的自导纳等于题干中所述支路的导纳(4)节点i、k间的互导纳等于题干中所述支路的导纳A.(1)(2)B。
(2)(3) C.(1)(4)D。
(2)(4)三、简答题1.什么是潮流计算?潮流计算的主要作用有哪些?潮流计算,电力学名词,指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下,计算有功功率、无功功率及电压在电力网中的分布。
潮流计算是电力系统非常重要的分析计算,用以研究系统规划和运行中提出的各种问题.对规划中的电力系统,通过潮流计算可以检验所提出的电力系统规划方案能否满足各种运行方式的要求;对运行中的电力系统,通过潮流计算可以预知各种负荷变化和网络结构的改变会不会危及系统的安全,系统中所有母线的电压是否在允许的范围以内,系统中各种元件(线路、变压器等)是否会出现过负荷,以及可能出现过负荷时应事先采取哪些预防措施等。
电力系统稳态分析大作业——基于高斯赛德尔法潮流计算电力系统稳态分析姓名: 学号:学院(系):自动化学院专业: 电气工程题目: 基于Matlab的高斯和高斯—赛德尔法的潮流计算指导老师:2014年12月摘要电力系统潮流计算是电力系统稳态运行分析中最基本和最重要的计算之一,是电力系统其他分析计算的基础,也是电力网规划、运行研究分析的一种方法,在电力系统中具有举足轻重的作用。
经典算法有高斯法,高斯-赛德尔迭代法及牛顿法等,近年来学者们开始应用非线性规划法及智能算法等优化方法求解潮流问题,提高了收敛的可靠性。
高斯-赛德尔迭代法开始于上世纪50年代,是一种直接迭代求解方程的算法,既可以解线性方程组,可以解非线性方程组。
高斯法求解节点电压的特点是: 在计算节点 i第k+1次的迭代电压时,前后所用的电压都是第k次迭代的结果,整个一轮潮流迭代完成后,把所有计算出的电压新值用于下一轮电压新值的计算过程中。
该计算方法简单,占用计算机内存小,能直接利用迭代求解节点电压方程,对电压初值的选取要求不是很严格。
但它的收敛性能较差,系统规模增大时,迭代次数急剧上升。
本文首先对高斯—赛德尔算法进行了综述,然后推导了该算法的计算过程,通过MATLAB软件计算了该算法的实例。
关键字:潮流计算高斯法高斯-赛德尔法迭代AbstractPower flow calculation is the one of the most basic and the most important calculation in the steady state analysis of power system .It is the foundation of other analytical calculation of power system, a method of analysis and planning, operation of power network.So it plays a decisive role in the power system. The classical algorithm is the Gauss method, Gauss - Seidel iterative method and Newton's method, in recent years.Scholars began to applicate nonlinear programming method and intelligent algorithm optimization method for solving power flow problem, enhances the reliability of convergence.Gauss - Seidel iterative method began in the 50's of last century, is a direct iteration equation algorithm, which can solve the linear equation and nonlinear equations. Characteristics of Gauss's method to calculate the node voltage is: in the iterative calculation of node i’s K + 1-times voltage, the voltage is used the results of K-times iterative.After completing the whole round of power flow iteration, all voltage value is used to calculate the next round of new voltage value of . The method is simple and captures small memory.It also can directly use the iterative solution of the node voltage equation .the selection of initial values are not very strict. But it has poor convergence performance. The system scale increases,when the number of iterations rise.This paper gives an overview of the Gauss Seidel algorithm at the first.Then it show the calculation process of this algorithm through the MATLAB software.Keywords: Gauss Gauss - Seidel iterative method the method of power flow calculation目录1 高斯迭代法和高斯—赛德尔迭代法概述 (5)2 节点导纳矩阵 (6)2.1不定导纳矩阵 (6)2.2导纳矩阵 (6)3 高斯迭代法 (7)4 高斯-赛德尔迭代法 (8)4.1高斯-赛德尔法的原理 (8)4.2 关于高斯法和高斯-赛德尔法的讨论 (8)5实例验证 (9)5.1 案例描述 (9)5.2 模型的建立 (10)5.3 案例程序流程图 (11)5.4 案例程序 (13)5.5 程序运行步骤和结果 (17)6结果分析 (20)7总结 (21)7参考文献 (22)一高斯迭代法和高斯—赛德尔迭代法概述电力系统潮流计算是研究电力系统稳态运行情况的一种基本电气计算。
电力系统分析大作业一、设计题目本次设计题目选自课本第五章例5—8,美国西部联合电网WSCC系统的简化三机九节点系统,例题中已经给出了潮流结果,计算结果可以与之对照.取ε=0。
00001 .二、计算步骤第一步,为了方便编程,修改节点的序号,将平衡节点放在最后。
如下图:9第二步,这样得出的系统参数如下表所示:第三步,形成节点导纳矩阵。
第四步,设定初值:;,。
第五步,计算失配功率=0,=—1。
25,=—0.9,=0,=—1,=0,=1。
63,=0。
85;=0。
8614,=—0。
2590,=—0。
0420,=0。
6275,=—0.1710,=0。
7101。
显然,.第六步,形成雅克比矩阵(阶数为14×14)第七步,解修正方程,得到:-0.0371,—0.0668,—0.0628,0。
0732,0。
0191,0。
0422,0。
1726,0。
0908;0.0334,0。
0084,0。
0223,0.0372,0。
0266,0。
0400。
从而—0.0371,-0。
0668,-0。
0628,0。
0732,0。
0191,0。
0422,0.1726,0。
0908;1。
0334,1.0084,1。
0223,1。
0372,1.0266,1。
0400。
然后转入下一次迭代。
经三次迭代后。
迭代过程中节点电压变化情况如下表:迭代收敛后各节点的电压和功率:最后得出迭代收敛后各支路的功率和功率损耗:三、源程序及注释由于计算流程比较简单,所以编写程序过程中没有采用模块化的形式,直接按顺序一步步进行。
disp(’【节点数:】’);[n1]=xlsread(’input。
xls’,'A3:A3')%节点数disp('【支路数:】');[n]=xlsread('input。
xls’,’B3:B3')%支路数disp('【精度:】’);Accuracy=xlsread('input。
第4章复杂电力系统的潮流计算一、填空题1。
用计算机进行潮流计算时,按照给定量的不同,可将电力系统节点分为节点、节点、节点三大类,其中,节点数目最多,节点数目很少、可有可无,节点至少要有一个。
二、选择题1.若在两个节点i、j之间增加一条支路,则下列关于节点导纳矩阵的说法正确的是( )A。
阶数增加1B.节点i的自导纳不变C.节点i、j间的互导纳发生变化D。
节点j的自导纳不变2。
若从节点i引出一条对地支路,则下列关于节点导纳矩阵的说法正确的是( )A。
阶数增加1B.节点i的自导纳发生变化C.节点i和其余节点间的互导纳均发生变化D.节点导纳矩阵的所有元素均不变3。
若从两个节点i、j之间切除掉一条支路,则下列关于节点导纳矩阵的说法正确的是()A。
阶数减少1B。
节点i、j间的互导纳一定变为0C.节点i、j间的互导纳发生变化,但不一定变为0D。
节点i、j的自导纳均不变4。
若网络中增加一个节点k,且增加一条节点i与之相连的支路,则下列关于节点导纳矩阵的说法正确的是( )(1)阶数增加1(2)节点k的自导纳等于题干中所述支路的导纳(3)节点i的自导纳等于题干中所述支路的导纳(4)节点i、k间的互导纳等于题干中所述支路的导纳A。
(1)(2)B。
(2)(3)C。
(1)(4) D.(2)(4)三、简答题1. 什么是潮流计算?潮流计算的主要作用有哪些?潮流计算,电力学名词,指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下,计算有功功率、无功功率及电压在电力网中的分布。
潮流计算是电力系统非常重要的分析计算,用以研究系统规划和运行中提出的各种问题。
对规划中的电力系统,通过潮流计算可以检验所提出的电力系统规划方案能否满足各种运行方式的要求;对运行中的电力系统,通过潮流计算可以预知各种负荷变化和网络结构的改变会不会危及系统的安全,系统中所有母线的电压是否在允许的范围以内,系统中各种元件(线路、变压器等)是否会出现过负荷,以及可能出现过负荷时应事先采取哪些预防措施等。
电力系统的潮流计算与分析引言电力是现代社会不可或缺的能源,电力系统的稳定运行和高效管理对整个社会经济发展起着重要作用。
而电力系统的潮流计算与分析是电力系统运行和管理的重要工具。
本文将探讨电力系统潮流计算与分析的原理、方法以及应用领域,旨在增进读者对该领域的了解。
一、电力系统潮流计算的原理电力系统潮流计算是指在给定电网拓扑结构、负荷需求和发电机输出等条件下,通过数学模型计算各节点的电压幅值和相位角,以获取电网各元件的电流分布和功率流向。
潮流计算的核心是建立电力系统的节点电压和传输功率的联立方程组,并通过求解方程组得到节点电压和功率流向的数值解。
潮流计算的基本原理是基于电力系统的各节点之间存在有功功率平衡和无功功率平衡,即电力系统各节点的有功功率和无功功率之和等于节点的负荷功率和发电机输出功率之和。
通过对电力系统进行潮流计算,可以得出各节点的电压、功率因数、功率损耗等参数,为电力系统的运行和管理提供依据。
二、电力系统潮流计算的方法1. 直流潮流计算方法直流潮流计算方法是一种较为简化的计算方法,适用于较小规模的电力系统以及初步的潮流计算。
该算法假设电力系统中各节点电压的相角都为零,即所有节点电压相位角均取0°,从而简化了潮流计算的计算量。
然而,直流潮流计算方法无法考虑电网的无功功率平衡,无法准确得到节点的功率因数和无功功率分布。
2. 迭代法潮流计算方法迭代法是一种常用的潮流计算方法,其基本思路是通过反复迭代计算节点电压和功率分布,直到达到收敛条件为止。
迭代法潮流计算方法常用的算法包括高斯-赛德尔迭代法和牛顿-拉夫逊迭代法。
迭代法潮流计算方法能较好地考虑电网的无功功率平衡,可以获得较为准确的节点电压和功率分布。
3. 双切迭代法潮流计算方法双切迭代法是一种相对较新的潮流计算方法,其基本思路是通过分析电力系统的分割区域,将电力系统划分为多个小区域进行潮流计算,并通过切割和迭代的方式逐步求解整个电力系统。
第一章 电力系统的基本概念1-1 什么叫电力系统、电力网及动力系统?1-2 电力线、发电机、变压器和用电设备的额定电压是如何确定的? 1-3 我国电网的电压等级有哪些?1-4 标出图1-4电力系统中各元件的额定电压。
1-5 请回答如图1-5所示电力系统中的二个问题:⑴ 发电机G 、变压器1T 2T 3T 4T 、三相电动机D 、单相电灯L 等各元件的额定电压。
⑵ 当变压器1T 在+2.5%抽头处工作,2T 在主抽头处工作,3T 在-2.5%抽头处工作时,求这些变压器的实际变比。
1-6 图1-6中已标明各级电网的电压等级。
试标出图中发电机和电动机的额定电压及变压器的额定变比。
1-7 电力系统结线如图1-7所示,电网各级电压示于图中。
试求: ⑴发电机G 和变压器1T 、2T 、3T 高低压侧的额定电压。
习题1-4图⑵设变压器1T 工作于+2.5%抽头, 2T 工作于主抽头,3T 工作于-5%抽头,求这些变压器的实际变比。
1-8 比较两种接地方式的优缺点,分析其适用范围。
1-9 什么叫三相系统中性点位移?它在什么情况下发生?中性点不接地系统发生单相接地时,非故障相电压为什么增加3倍?1-10 若在变压器中性点经消弧线圈接地,消弧线圈的作用是什么?第二章 电力系统各元件的参数及等值网络2-1 一条110kV 、80km 的单回输电线路,导线型号为LGJ —150,水平排列,其线间距离为4m ,求此输电线路在40℃时的参数,并画出等值电路。
2-2 三相双绕组变压器的型号为SSPL —63000/220,额定容量为63000kVA ,额定电压为242/10.5kV ,短路损耗404=k P kW ,短路电压45.14%=k U ,空载损耗93=o P kW ,空载电流41.2%=o I 。
求该变压器归算到高压侧的参数,并作出等值电路。
2-3 已知电力网如图2-3所示:各元件参数如下:变压器:1T :S =400MVA ,12%=k U , 242/10.5 kV2T :S =400MVA ,12%=k U , 220/121 kV线路:2001=l km, /4.01Ω=x km (每回路)602=l km, /4.01Ω=x km10.5kV115kVT 1T 2l 1l 2习题2-3图其余参数均略去不计,取基准容量S B =1000MVA ,基准电压av B U U =,试作出等值电路图,并标上各元件的标么值参数。
电力系统分析潮流计算大作业(源程序及实验报告)
源程序如下:
采用直角坐标系的牛顿-拉夫逊迭代
function chaoliujisuan()
m=3; %m=PQ节点个数
v=1;%v=PV节点个数
P=[-0.8055 -0.18 0]; %P=PQ节点的P值
Q=[-0.5320 -0.12 0]; %Q=PQ节点的Q值
PP=[0.5];%PP=PV节点的P值
V=[1.0];%V=PV节点的U值
E=[1 1 1 1.0 1.0]'; %E=PQ,PV,Vθ节点e的初值
F=[0 0 0 0 0]'; %F=PQ,PV,Vθ节点f的初值
G=[
6.3110 -3.5587 -2.7523 0 0;
-3.5587 8.5587 -5 0 0;
-2.7523 -5 7.7523 0 0;
0 0 0 0 0;
0 0 0 0 0
];
B=[
-20.4022 11.3879 9.1743 0 0;
11.3879 -31.00937 15 4.9889 0;
9.1743 15 -28.7757 0 4.9889;
0 4.9889 0 5.2493 0;
0 0 4.9889 0 -5.2493
];
Y=G+j*B;
X=[]; %X=△X
n=m+v+1;%总的节点数
FX=ones(2*n-2,1);%F(x)矩阵
F1=zeros(n-1,n-1);%F(x)导数矩阵
a=0;%记录迭代次数
EF=zeros(n-1,n-1);%最后的节点电压矩阵
while max(FX)>=10^(-5)
for i=1:m %PQ节点
FX(i)=P(i);%△P
FX(n+i-1)=Q(i);%△Q
for w=1:n
FX(i)=
FX(i)-E(i)*G(i,w)*E(w)+E(i)*B(i,w)*F(w)-F(i)*G(i,w)*F(w)-F(i)*B(i,w)*E(w); %△P
FX(n+i-1)=FX(n+i-1)-F(i)*G(i,w)*E(w)+F(i)*B(i,w)*F(w)+E(i)*G(i,w)*F(w)+E(i)*B(i ,w)*E(w); %△Q
end
end
for i=m+1:n-1 %PV节点
FX(i)=PP(i-m);%△P
FX(n+i-1)=V(i-m)^2-E(i)^2-F(i)^2; %△Q
for w=1:n
FX(i)=
FX(i)-E(i)*G(i,w)*E(w)+E(i)*B(i,w)*F(w)-F(i)*G(i,w)*F(w)-F(i)*B(i,w)*E(w);%△P end
end
for i=1:m %PQ节点
for w=1:n-1
if i~=w
F1(i,w)=-(G(i,w)*E(i)+B(i,w)*F(i));
F1(i,n+w-1)=B(i,w)*E(i)-G(i,w)*F(i);
F1(n+i-1,w)=B(i,w)*E(i)-G(i,w)*F(i);
F1(n+i-1,n+w-1)=G(i,w)*E(i)+B(i,w)*F(i);
else
F1(i,w)=-G(i,i)*E(i)-B(i,i)*F(i);
F1(i,n+w-1)=B(i,i)*E(i)-G(i,i)*F(i);
F1(n+i-1,w)=B(i,i)*E(i)-G(i,i)*F(i);
F1(n+i-1,n+w-1)=G(i,i)*E(i)+B(i,i)*F(i);
for k=1:n
F1(i,w)=F1(i,w)-G(i,k)*E(k)+B(i,k)*F(k);
F1(i,n+w-1)= F1(i,n+w-1)-G(i,k)*F(k)-B(i,k)*E(k);
F1(n+i-1,w)=F1(n+i-1,w)+G(i,k)*F(k)+B(i,k)*E(k);
F1(n+i-1,n+w-1)=F1(n+i-1,n+w-1)-G(i,k)*E(k)+B(i,k)*F(k);
end
end
end
end
for i=m+1:n-1 %PV节点
for w=1:n-1
if i~=w
F1(i,w)=-(G(i,w)*E(i)+B(i,w)*F(i));
F1(i,n+w-1)=B(i,w)*E(i)-G(i,w)*F(i);
F1(n+i-1,w)=0;
F1(n+i-1,n+w-1)=0;
else
F1(i,w)=-G(i,i)*E(i)-B(i,i)*F(i);
F1(i,n+w-1)=B(i,i)*E(i)-G(i,i)*F(i);
F1(n+i-1,w)=-2*E(i);
F1(n+i-1,n+w-1)=-2*F(i);
for k=1:n
F1(i,w)=F1(i,w)-G(i,k)*E(k)+B(i,k)*F(k);
F1(i,n+w-1)= F1(i,n+w-1)-G(i,k)*F(k)-B(i,k)*E(k);
end
end
end
end
X=inv(F1)*(-FX) ;
for i=1:n-1
E(i)=E(i)+X(i);
F(i)=F(i)+X(n+i-1);
end
a=a+1;
fprintf('第%d次迭代后的节点电压分别为:\n',a);
disp(E+j*F);
fprintf('第%d次迭代后功率偏差△P △Q电压偏差△V的平方分别为:\n',a); disp(FX);
end
disp('收敛后的节点电压用极坐标表示为:');
EF=E+j*F;
for i=1:n-1
fprintf('%d号节点电压的幅值为:',i)
disp(abs(EF(i)));
fprintf('%d号节点电压的相角度数为',i)
disp(angle(EF(i))*180/pi);
end
PPH=0;
for i=1:n
PPH=PPH+EF(n)*conj(Y(n,i))*conj(EF(i));
end
fprintf('平衡节点的功率');
disp(PPH);
运行结果:
运行结果复制如下:
第1次迭代后的节点电压分别为:
1.0034 - 0.1306i
1.0285 - 0.1019i
1.0339 - 0.0973i
1.0000 - 0.0017i
1.0000
第1次迭代后功率偏差△P △Q电压偏差△V的平方分别为: -0.8055
-0.1800
0.5000
-0.3720
0.2474
0.3875
第2次迭代后的节点电压分别为:
0.9836 - 0.1290i
1.0126 - 0.1038i
1.0183 - 0.0995i
1.0000 - 0.0035i
1.0000
第2次迭代后功率偏差△P △Q电压偏差△V的平方分别为:
0.0512
-0.0222
-0.0403
0.0002
-0.1012
-0.0219
-0.0099
-0.0000
第3次迭代后的节点电压分别为:
0.9831 - 0.1290i
1.0122 - 0.1038i
1.0180 - 0.0996i
1.0000 - 0.0035i
1.0000
第3次迭代后功率偏差△P △Q电压偏差△V的平方分别为:
0.0008
-0.0003
-0.0005
-0.0001
-0.0021
-0.0004
-0.0003
-0.0000
第4次迭代后的节点电压分别为:
0.9831 - 0.1290i
1.0122 - 0.1038i
1.0180 - 0.0996i
1.0000 - 0.0035i
1.0000
第4次迭代后功率偏差△P △Q电压偏差△V的平方分别为: 1.0e-005 *
0.0280
-0.0083
-0.0164
-0.0121
-0.1085
-0.0199
-0.0135
-0.0005
收敛后的节点电压用极坐标表示为:
1号节点电压的幅值为: 0.9916
1号节点电压的相角度数为-7.4748 2号节点电压的幅值为: 1.0175
2号节点电压的相角度数为-5.8548 3号节点电压的幅值为: 1.0229
3号节点电压的相角度数为-5.5864 4号节点电压的幅值为: 1.0000
4号节点电压的相角度数为-0.2021 平衡节点的功率0.4968 -10.3280i。