下载文档原格式
人教版八年级数学上册14.1.4.3《多项式与多项式相乘》教学设计一. 教材分析人教版八年级数学上册14.1.4.3《多项式与多项式相乘》是整式乘法的一个重要内容。
这部分内容主要让学生掌握多项式乘多项式的法则，并能灵活运用这个法则进行计算。
在学习了单项式乘单项式和多项式乘单项式的基础上，学生能够更好地理解和掌握多项式乘多项式的概念和方法。
二. 学情分析学生在学习这个知识点时，已经掌握了单项式乘单项式和多项式乘单项式的知识，具备了一定的数学基础。
但学生在应用多项式乘多项式的法则时，可能会出现混淆和错误。
因此，在教学过程中，需要引导学生明确多项式乘多项式的法则，并通过大量的练习来巩固这个知识点。
三. 教学目标1.让学生理解多项式乘多项式的概念，掌握多项式乘多项式的法则。
2.培养学生运用多项式乘多项式的法则进行计算的能力。
3.提高学生的数学思维能力和解决问题的能力。
四. 教学重难点1.重点：掌握多项式乘多项式的法则，并能灵活运用。
2.难点：理解多项式乘多项式的法则，并在实际计算中运用。
五. 教学方法1.采用讲解法，引导学生理解多项式乘多项式的概念和法则。
2.采用练习法，让学生在实践中运用多项式乘多项式的法则。
3.采用小组合作法，让学生在小组讨论中解决问题，提高合作能力。
六. 教学准备1.准备相关的教学PPT，展示多项式乘多项式的例子。
2.准备一些练习题，用于课堂练习和课后作业。
3.准备黑板，用于板书解题过程。
七. 教学过程1.导入（5分钟）通过一个具体的例子，引导学生回顾单项式乘单项式和多项式乘单项式的知识，为新课的学习做好铺垫。
2.呈现（10分钟）展示多项式乘多项式的例子，引导学生观察和思考。
让学生尝试用自己的语言描述多项式乘多项式的过程，培养学生的数学表达能力。
3.操练（10分钟）让学生独立完成一些多项式乘多项式的练习题，教师巡回指导，及时纠正学生的错误。
这个环节可以让学生更好地理解和掌握多项式乘多项式的法则。
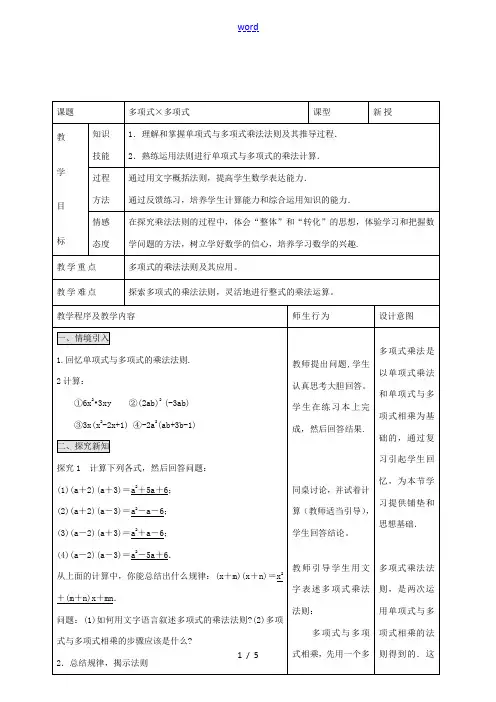
第十四章《整式的乘法与因式分解》多项式乘多项式例 1 计算：(1)(x+2y)(5a+3b)； (2)(2x-3)(x+4)；(3)(x+y)2； (4)(x+y)(x2-xy+y2)结合例题讲解，提醒学生在解题时要注意：(1)解题书写和格式的规X性；(2)注意总结不同类型题目的解题方法、步骤和结果；(3)注意各项的符号，并要注意做到不重复、不遗漏。
三、课堂训练1．先化简，再求值：(x－2y)(x＋3y)－(2x－y)(x－4y)，其中：x ＝－1，y＝2.解：∵(x－2y)(x＋3y)－(2x－y)(x－4y)＝x2＋3xy－2xy－6y2－(2x2－8xy－xy＋4y2)＝x2＋3xy－2xy－6y2－2x2＋8xy＋xy－4y2＝－x2＋10xy－10y2.当x＝－1，y＝2时，原式＝－(－1)2＋10×(－1)×2－10×22＝－1－20－40＝－61.2．计算：(1)(x－1)(x－2)；(2)(m－3)(m＋5)；(3)(x＋2)(x－2)．解：(1)(x－1)(x－2)＝x2－3x＋2；(2)(m－3)(m＋5)＝m2＋2m－15；(3)(x＋2)(x－2)＝x2－4.3．若(x＋4)(x－6)＝x2＋ax＋b，求a2＋ab的值．解：∵(x＋4)(x－6)＝x2－2x－24，又∵(x＋4)(x－6)＝x2＋ax＋b，∴a＝－2，b＝－24.∴a2＋ab＝(－2)2＋(－2)×(－24)＝4＋48＝52.点拨精讲：第2题应先将等式两边计算出来，再对比各项，得出结果．小结归纳启发引导学生归纳本节所学的内容：1．多项式的乘法法则：(a+b)(m+n)＝am+an+bm+bn2．解题(计算)步骤(略)。
3．解题(计算)应注意：(1)不重复、不遗漏；(2)符号问题。
五、作业设计2。
八年级数学上册第十四章整式的乘法与因式分解14.1 整式的乘法14.1.4 第3课时多项式与多项式相乘同步训练（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学上册第十四章整式的乘法与因式分解14.1 整式的乘法14.1.4 第3课时多项式与多项式相乘同步训练（新版）新人教版）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学上册第十四章整式的乘法与因式分解14.1 整式的乘法14.1.4 第3课时多项式与多项式相乘同步训练（新版）新人教版的全部内容。
第3课时多项式与多项式相乘［学生用书P77]1．下列各式中：①（a－2b)(3a＋b）＝3a2－5ab－2b2；②(2x＋1）（2x－1）＝4x2－x－1；③（x－y)(x＋y）＝x2－y2；④(x＋2）（3x＋6）＝3x2＋6x＋12。
其中正确的有( )A．4个B．3个C．2个D．1个2．［2015·佛山］若(x＋2）（x－1)＝x2＋mx＋n，则m＋n＝（)A．1 B．－2 C．－1 D．23．计算：(1）(x－1）(x＋1）＝_ __；(2)（x－3）（x＋2）＝_ _；（3)(3x＋y)(x－2y)＝__ __；（4）(2a－5b)(a＋5b)＝__ __．4．一幅宣传画的长为a cm，宽为b cm，把它贴在一块长方形木板上，四周刚好留出 2 cm宽的边框，则这块木板的面积是__ __cm2。
5．计算:（1）(x－1)(x＋3）;(2)(x＋1）·x·（x－1）;(3)(x－y)（x2＋xy＋y2）．6．[2016·睢宁月考］先化简，再求值:（x－1）(2x＋1)－2（x－5）（x ＋2），其中x＝－2.7．已知a＋b＝3，ab＝2，则(a－2）（b－2）＝__ __．8．[2016·天水期中］若(x2＋nx＋3)(x2－3x＋m)的展开式中不含x2和x3项,求m，n的值．9．如图14-1—5，有一张长为10 cm，宽为 6 cm 的长方形纸片，在4个角剪去4个边长为x cm的小正方形，按折痕做一个有底无盖的长方形盒子，试求盒子的体积．图14—1—510．［2015·鄄城期中］先阅读后作答：根据几何图形的面积关系可以说明整式的乘法．例如：(2a＋b）(a＋b)＝2a2＋3ab＋b2可以用图14-1—6（1)的面积关系来说明．(1) (2)图14-1—6（1）根据图14-1—6(2）写出一个等式；(2）已知（x＋p)（x＋q）＝x2＋（p＋q)x＋pq，请你画出一个相应的几何图形加以说明．参考答案【知识管理】每一项相加am＋an＋bm＋bn【归类探究】例1(1)3x2＋8x＋4 （2）－4y2＋21y－5 (3)x3＋8例2（1）m(m＋x）＝（m2＋mx） cm2(2）(3mx＋3x2） cm2例3(1）m＝－1，n＝2 (2）－9【当堂测评】1．B 2。
第2课时 多项式与多项式相乘
一、选择题（每小题2分，共20分）
1．1．化简的结果是（ ）
A ．0
B ．
C ．
D ．
2．下列计算中，正确的是（ ）
A ．
B ．
C ．
D ．
3．若的积中不含有的一次项，则的值是（ ）
A ．0
B ．5
C ．－5
D ．－5或5
4．下列各式中，从左到右的变形是因式分解的是（ ）
A ．
B ．
B ． D ．
5．如图，在矩形ABCD 中，横向阴影部分是矩形，另一阴影部分是平行四边行．依
照图中标注的数据，计算图中空白部分的面积为（ ） A ． B ． C ． D ． 6．三个连续奇数，中间一个是，则这三个数之积是（ A ． B ． C ． D ．
7．如果，，那么的值是（ ）
A ．2
B ．－8
C ．1
D ．－1
8．如果多项式能写成两数和的平方，那么的值为（ ）
A ．2
B ．±2
C ．4
D ．±4
9．已知，，，则、、的大小关系是（ ）
A ．＞＞
B ．＞＞
C ．＜＜
D ．＞＞
10．多项式的最小值为（ ）
A ．4
B ．5
C ．16
D ．25
二、填空题（每小题2分，共20分）
11．已知，则＝ ．
12．计算：＝ ．
13．计算：＝ ． 14．计算：＝ ．
15．计算：＝ ．
16． ．
17．分解因式：＝ ．
2)2()2(a a a --⋅-22a 26a -24a -ab b a 532=+33a a a =⋅a a a =-56222)(b a ab =-)5)((-+x k x x k a a a a +=+2)1(b a b a b a b a b a -+-+=-+-))((22)4)(4(422y x y x y x -+=-))((222a bc a bc c b a -+=+-2c ac ab bc ++-2c ac bc ab +--ac bc ab a -++2ab a bc b -+-22k k k 43-k k 883-k k -34k k 283-7)(2=+b a 3)(2=-b a ab 224y kxy x ++k 3181=a 4127=b 619=c a b c a b c a c b a b c b c a 251244522+++-x y xy x 23-=a 6a 3222)()3(xy y x -⋅-)13
12)(3(22+--y x y xy )32)(23(+-x x 22)2()2(+-x x +24x (2)32(9)-=+x 23123xy x -
↑
18．分解因式：＝ ．
19．已知，，则＝ ．
20．设，则＝ ．
三、解答题（本大题共60分）
21．计算：（每小题3分，共12分）
（1）；
（2）；
（3）；
（4）．
22．先化简，再求值：（第小题4分，共8分）
（1），其中．
（2），其中，
．
22242y xy x -+-3=-b a 1=ab 2)(b a +322)2()1(dx cx bx a x x +++=-+d b +)31
1(3)()2(2x xy y x -⋅+-⋅-)12(4)392(32--+-a a a a a )42)(2(22b ab a b a ++-))(())(())((a x c x c x b x b x a x --+--+--)1)(2(2)3(3)2)(1(-+++---x x x x x x 31
=x 2222)5()5()3()3(b a b a b a b a -++-++-8-=a 6-=b
23．分解因式（每小题4分，共16分）：
（1）； （2）．
（3）； （4）；
（5）； （6）．
24．（本题4分）已知，，求代数式的值．
25．（本题5分）解方程：．
26．（本题5分）已知、、满足，，求的值．
)()(22a b b b a a -+-)44(22+--y y x xy y x 4)(2+-)1(4)(2-+-+y x y x 1)3)(1(+--x x 22222222x b y a y b x a -+-4
1=-b a 25-=ab 32232ab b a b a +-)2)(13()2(2)1)(1(2+-=++-+x x x x x a b c 5=+b a 92-+=b ab c c
27．（本题5分）某公园计划砌一个形状如图1所示的喷水池．①有人建议改为
图2的形状，且外圆直径不变，只是担心原来备好的材料不够，请你比较两种方案，哪一种需要的材料多（即比较哪个周长更长）？②若将三个小圆改成个小圆，结论是否还成立？请说明．
28．（本题5分）这是一个著名定理的一种说理过程：将四个如图1所示的直角
三角形经过平移、旋转、对称等变换运动，拼成如图2所示的中空的四边形ABCD ．
（1）请说明：四边形ABCD 和EFG H 都是正方形；
（2）结合图形说明等式成立，并用适当的文字叙述这个定理的
结论．
n 222c b a =
+ a a b b G H
图1 图2
四、附加题（每小题10分，共20分）
29．已知是正整数，且是质数，求的值．
30．已知是的一个因式，求的值．
参考答案
一、选择题
1．C 2．D 3．B 4．D 5．B 6．A 7．C 8．D 9．A 10．C
二、填空题
11．4 12． 13． 14．
15．
16． 17． 18． 19．13 20．2
三、解答题
21．（1） （2） （3）
（4）
n 1001624+-n n n 522++x x b ax x ++24b a +879b a -xy y x xy 36233-+-6562-+x x 16824+-x x x 12-)2)(2(3y x y x x -+2)(2y x --xy y x 32+a a a 1335623+-338b a -ca bc ab x c b a x +++++-)(22
22．（1）， （2），40 23．（1） （2） （3）
（4） （5） （6）
24．原式＝ 25．
26．由，得，
把代入，得
∴． ∵≥0，
∴≤0．
又≥0，所以，＝0，故＝0．
27． ①设大圆的直径为，周长为，图2中三个小圆的直径分别为、、
，周长分别为、、，由
．
可见图2大圆周长与三个小圆周长之和相等，即两种方案所用材料一样多．
②结论：材料一样多，同样成立．
设大圆的直径为，周长为，个小圆的直径分别为，，，…，，周长为，，，…，，由
…
…
…．
所以大圆周长与个小圆周长和相等，所以两种方案所需材料一样多．
28．（1）在四边形ABCD 中， 因为AB ＝BC ＝CD ＝DA ＝， 所以四边形ABCD 是菱形．
又因为∠A 是直角， 所以四边形ABCD 是正方形． 在四边形EFGH 中， 因为EF ＝FG ＝GH ＝HE ＝，
所以四边形EFGH 是菱形．
因为∠AFE ＋∠AEF ＝90°，∠AFE ＝∠HED ，
所以∠HED ＋∠AEF ＝90°，即∠FEH ＝90°，
所以四边形EFGH 是正方形．
（2）因为S 正方形ABCD ＝4S △AEF ＋S 正方形EFGH ，
所以，， 整理，得．
这个定理是：直角三角形两条直角边的平方和等于斜边的平方．
210--x 3
15-22102010b ab a +-)()(2b a b a +-)2)(2(+--+y x y x 2)(y x +2)2(-+y x 2)2(-x ))()((22b a b a y x -++32
54125)(2
2-=⎪⎭⎫ ⎝⎛⨯-=-b a ab 3-=x 5=+b a b a -=5b a -=592-+=b ab c 222)3(969)5(--=--=-+-=b b b b b b c 2)3(-b 22)3(--=b c 2c 2c c d l 1d 2d 3d 1l 2l 3l 321321321)(l l l d d d d d d d l ++=++=++==πππππd l n 1d 2d 3d n d 1l 2l 3l n l +++==321(d d d d l ππ)n d ++++=321d d d πππn d π++++=321l l l n l +n b a +c 222
14)(c ab b a +⨯=+222c b a =
+a a b b G H F
四、附加题
29．，
∵是正整数，∴与的值均为正整数， 且＞1．
∵是质数，
∴必有＝1，
解得．
30．设，
展开，得
． 比较比较边的系数，得
解得，，，． 所以，．
)106)(106(100162224+-++=+-n n n n n n n 1062++n n 1062+-n n 1062++n n 1001624+-n n 1062+-n n 3=n ))(52(2224n mx x x x b ax x ++++=++n x m n x m n x m x b ax x 5)52()52()2(23424++++++++=++⎪⎪⎩⎪⎪⎨⎧==++=+=+.
5,52,052,02b n a m n m n m 2-=m 5=n 6=a 25=b 31256=+=+b a。
